«Հետաքրքրաշարժ Հանրահաշիվ»–ի խմբագրումների տարբերություն
No edit summary |
չNo edit summary |
||
| (Միևնույն մասնակցի 4 միջանկյալ տարբերակներ թաքցված է) | |||
| Տող 5. | Տող 5. | ||
|աղբյուր = [[«Հետաքրքրաշարժ Հանրահաշիվ»]] |
|աղբյուր = [[«Հետաքրքրաշարժ Հանրահաշիվ»]] |
||
}} |
}} |
||
{{Անավարտ}} |
|||
[[Կատեգորիա:Գրքեր]] |
[[Կատեգորիա:Գրքեր]] |
||
| Տող 13. | Տող 11. | ||
[[Կատեգորիա:Հայպետուսմանկհրատ]] |
[[Կատեգորիա:Հայպետուսմանկհրատ]] |
||
[[Կատեգորիա:Ոչ գեղարվեստական]] |
[[Կատեգորիա:Ոչ գեղարվեստական]] |
||
[[Պատկեր:Interesting_Algebra_Title_Page.png|500px|thumb|right|«Հետաքրքրաշարժ Հանրահաշիվ» գրքի 1962 թ․ հրատարակության տիտղոսաթերթը]] |
|||
== == |
== == |
||
| Տող 5643. | Տող 5643. | ||
Հարյուր հատ հացը բաժանել հինգ մարդկանց միջև այնպես, որ երկրորդը ստանա առաջինից այնքանով ավելի շատ որքան որ երրորդն է ստացել ավելի շատ երկրորդից, չորրորդը՝ ավելի շատ երրորդից և հինգերորդը՝ ավելի շատ չորրորդից։ Բացի այդ, առաջին երկուսը պետք է ստանան մնացած երեքից <math>7</math> անգամ քիչ։ |
Հարյուր հատ հացը բաժանել հինգ մարդկանց միջև այնպես, որ երկրորդը ստանա առաջինից այնքանով ավելի շատ որքան որ երրորդն է ստացել ավելի շատ երկրորդից, չորրորդը՝ ավելի շատ երրորդից և հինգերորդը՝ ավելի շատ չորրորդից։ Բացի այդ, առաջին երկուսը պետք է ստանան մնացած երեքից <math>7</math> անգամ քիչ։ |
||
Որքա՞ն պետք է ստանա |
Որքա՞ն պետք է ստանա յուրաքանչյուրը։ |
||
'''''Լուծում''''' |
'''''Լուծում''''' |
||
| Տող 5709. | Տող 5709. | ||
===ՀԱՆՐԱՀԱՇԻՎԸ ՎԱՆԴԱԿԱՎՈՐ ԹՂԹԻ ՎՐԱ=== |
===ՀԱՆՐԱՀԱՇԻՎԸ ՎԱՆԴԱԿԱՎՈՐ ԹՂԹԻ ՎՐԱ=== |
||
Չնայած պրոգրեսիաների վերաբերյալ այդ խնդրի հինգհազարամյա հնությանը, մեր դպրոցական կյանքում պրոգրեսիաները հայտնվել են համեմատաբար ավելի ուշ։ Մագնիցկու դասագրքում, որը հրատարակվել է երկու հարյուր տարի առաջ և որը ամբողջ կես դար հանդիսացել է դպրոցական ուսուցման համար հիմնական ձեռնարկ, թեև պրոգրեսիաներ կան, բայց դրանց մեջ մտնող մեծությունները կապակցող ընդհանուր բանաձևեր գոյություն չունեն։ Դրա համար էլ ինքը՝ դասագրքի կազմողը առանց դժվարությունների չէ, որ հաղթահարել է այդպիսի խնդիրները։ Մինչդեռ թվաբանական պրոգրեսիայի անդամների գումարի բանաձևը հեշտորեն արտածվում է վանդակավոր թղթի օգնությամբ՝ պարզ և դիտորդական եղանակով։ Այդպիսի թղթի վրա ցանկացած թվաբանական պրոգրեսիան պատկերվում է աստիճանաձև։ |
Չնայած պրոգրեսիաների վերաբերյալ այդ խնդրի հինգհազարամյա հնությանը, մեր դպրոցական կյանքում պրոգրեսիաները հայտնվել են համեմատաբար ավելի ուշ։ Մագնիցկու դասագրքում, որը հրատարակվել է երկու հարյուր տարի առաջ և որը ամբողջ կես դար հանդիսացել է դպրոցական ուսուցման համար հիմնական ձեռնարկ, թեև պրոգրեսիաներ կան, բայց դրանց մեջ մտնող մեծությունները կապակցող ընդհանուր բանաձևեր գոյություն չունեն։ Դրա համար էլ ինքը՝ դասագրքի կազմողը առանց դժվարությունների չէ, որ հաղթահարել է այդպիսի խնդիրները։ Մինչդեռ թվաբանական պրոգրեսիայի անդամների գումարի բանաձևը հեշտորեն արտածվում է վանդակավոր թղթի օգնությամբ՝ պարզ և դիտորդական եղանակով։ Այդպիսի թղթի վրա ցանկացած թվաբանական պրոգրեսիան պատկերվում է աստիճանաձև։ Օրինակ՝ 33-րդ նկարում <math>ABDC</math>-ն պատկերում է հետևյալ պրոգրեսիան՝ |
||
<math>2, \; 5, \; 8, \; 11, \; 14</math>։ |
<math>2, \; 5, \; 8, \; 11, \; 14</math>։ |
||
| Տող 5715. | Տող 5715. | ||
[[Պատկեր:Interesting_Algebra_Pic_33.png|400px|frameless|thumb|center]] |
[[Պատկեր:Interesting_Algebra_Pic_33.png|400px|frameless|thumb|center]] |
||
Նրա անդամների գումարը որոշելու համար գծագիրը լրացնենք մինչև <math>ABGE</math> ուղղանկյունը։ Կստանանք երկու հավասար պատկերներ <math>ABDC |
Նրա անդամների գումարը որոշելու համար գծագիրը լրացնենք մինչև <math>ABGE</math> ուղղանկյունը։ Կստանանք երկու հավասար պատկերներ <math>ABDC</math> և <math>DGEC</math>։ Նրանցից յուրաքանչյուրի մակերեսը պատկերում է մեր պրոգրեսիայի անդամների գումարը։ Նշանակում է՝ պրոգրեսիայի կրկնակի գումարը հավասար է <math>ABGE</math> ուղղանկյան մակերեսին, ալսինքն՝ |
||
<math>(AC+CE) \cdot AB</math>։ |
<math>(AC+CE) \cdot AB</math>։ |
||
| Տող 5731. | Տող 5731. | ||
'''''Խնդիր''''' |
'''''Խնդիր''''' |
||
Բանջարանոցն ունի <math>30</math> մարգ, յուրաքանչյուրը <math>16 \; մ</math> երկարությամբ և <math>2,5 \; մ</math> լայնությամբ։ Մարգերը ջրելիս բանջարանոցատերը ջրով լիքը դույլը բերում է ջրհորից, որը գտնվում է բանջարանոցից <math>14 \; մ</math> հեռավորության վրա (նկ․ 34), ընդ որում, անցնելով միջնակներով, մեկ անգամ բերված ջուրը բավականացնում է միայն մեկ մարգ ջրելու համար։ |
|||
Ի՞նչ երկարության ճանապարհ պետք է անցնի բանջարանոցատերը ամբողջ բանջարանոցը ջրելիս։ Ճանապարհը սկսվում և վերջանում է ջրհորի մոտ։ |
Ի՞նչ երկարության ճանապարհ պետք է անցնի բանջարանոցատերը ամբողջ բանջարանոցը ջրելիս։ Ճանապարհը սկսվում և վերջանում է ջրհորի մոտ։ |
||
| Տող 5737. | Տող 5737. | ||
'''''Լուծում''''' |
'''''Լուծում''''' |
||
Առաջին մարգը ջրելու համար բանջարանոցատերը պետք է անցնի հետևյալ |
Առաջին մարգը ջրելու համար բանջարանոցատերը պետք է անցնի հետևյալ ճանապարհը՝ |
||
<math>14+16+2,5+16+2,5+14=65 \; մ</math>։ |
<math>14+16+2,5+16+2,5+14=65 \; մ</math>։ |
||
| Տող 5773. | Տող 5773. | ||
<math>x \;=\; 31y</math>։ |
<math>x \;=\; 31y</math>։ |
||
Առաջին շաբաթում կծախսվեր <math>31 \; դլ</math>, երկրորդում՝ <math>30</math>, երրորդում՝ <math> |
Առաջին շաբաթում կծախսվեր <math>31 \; դլ</math>, երկրորդում՝ <math>30</math>, երրորդում՝ <math>29</math> և այլն, մինչև կրկնակի ժամանակի վերջին շաբաթը, երբ կծախսվեր |
||
<math>(31-2y+1) \; դլ</math>։<ref>Պարզաբանենք կերի ծախսը՝<br> |
<math>(31-2y+1) \; դլ</math>։<ref>Պարզաբանենք կերի ծախսը՝<br> |
||
| Տող 5813. | Տող 5813. | ||
Քանի որ <math>y</math>-ը զրոյի հավասար լինել չի կարող, ապա մենք կարող ենք հավասարության երկու մասերն էլ կրճատել այդ արտադրիչով։ Կստանանք՝ |
Քանի որ <math>y</math>-ը զրոյի հավասար լինել չի կարող, ապա մենք կարող ենք հավասարության երկու մասերն էլ կրճատել այդ արտադրիչով։ Կստանանք՝ |
||
<math>31 \;=\; 63-2y |
<math>31 \;=\; 63-2y</math> և <math>y=16</math>, |
||
որտեղից |
որտեղից |
||
| Տող 5845. | Տող 5845. | ||
<math>y</math> թիվը չի կարող հավասարվել զրոյի, ուստի այդ արտադրիչով հավասարումը կարելի է կրճատել, որից հետո կստանանք՝ |
<math>y</math> թիվը չի կարող հավասարվել զրոյի, ուստի այդ արտադրիչով հավասարումը կարելի է կրճատել, որից հետո կստանանք՝ |
||
<math>6x = 24 |
<math>6x = 24</math> և <math>x = 4</math>։ |
||
Այսպիսով, աշխատանքն սկսող վերջին հողափորը աշխատել է <math>4</math> ժամ։ |
Այսպիսով, աշխատանքն սկսող վերջին հողափորը աշխատել է <math>4</math> ժամ։ |
||
| Տող 5855. | Տող 5855. | ||
'''''Խնդիր''''' |
'''''Խնդիր''''' |
||
Այգեպանը առաջին գնորդին վաճառեց իր ունեցած խնձորների կեսը և էլի կես խնձոր, երկրորդ գնորդին՝ մնացածի կեսը և դարձյալ կես խնձոր, երրորդին՝ մնացածի կեսը և էլի կես խնձոր և այլն։ Յոթերորդ գնորդին նա վաճառեց մնացած խնձորների կեսը և դարձյալ կես խնձոր. դրանից հետո նրա մոտ խնձոր չմնաց։ Քանի՞ խնձոր |
Այգեպանը առաջին գնորդին վաճառեց իր ունեցած խնձորների կեսը և էլի կես խնձոր, երկրորդ գնորդին՝ մնացածի կեսը և դարձյալ կես խնձոր, երրորդին՝ մնացածի կեսը և էլի կես խնձոր և այլն։ Յոթերորդ գնորդին նա վաճառեց մնացած խնձորների կեսը և դարձյալ կես խնձոր. դրանից հետո նրա մոտ խնձոր չմնաց։ Քանի՞ խնձոր ուներ այգեպանը։ |
||
'''''Լուծում''''' |
'''''Լուծում''''' |
||
| Տող 5885. | Տող 5885. | ||
Հաշվելով փակագծերում եղած երկրաչափական պրոգրեսիայի անդամների գումարը, գտնում ենք՝ |
Հաշվելով փակագծերում եղած երկրաչափական պրոգրեսիայի անդամների գումարը, գտնում ենք՝ |
||
<math>\frac{x}{x+1} \;=\; 1-\frac{1}{2^7} |
<math>\frac{x}{x+1} \;=\; 1-\frac{1}{2^7}</math> և <math>x = 2^7-1 = 127</math>։ |
||
Խնձորների թիվը <math>127</math> էր։ |
Խնձորների թիվը <math>127</math> էր։ |
||
| Տող 5923. | Տող 5923. | ||
'''''Խնդիր''''' |
'''''Խնդիր''''' |
||
Մաթեմատիկայի ռուսական մի այլ հինավուրց դասագրքից, որ կրում է '''«Զուտ մաթեմատիկայի լրիվ դասնթաց, որը կազմվել է հրետանու |
Մաթեմատիկայի ռուսական մի այլ հինավուրց դասագրքից, որ կրում է '''«Զուտ մաթեմատիկայի լրիվ դասնթաց, որը կազմվել է հրետանու Շտիկ-Յունկեր և մաթեմատիկայի մսանավոր ուսուցիչ Եֆիմ Վոյտյախովսկու կողմից՝ ի օգուտ և գործածության պատանիների ու մաթեմատիկայի մեջ վարժվողների»''' (1795) ընդարձակ վերնագիրը, այստեղ բերենք հետևյալ խնդիրը. |
||
«Ռազմիկին տրվել է վարձատրություն՝ առաջին վերքի համար <math>1</math> կոպեկ, երկրորդի համար՝ <math>2</math> կոպեկ, երրորդի համար՝ <math>4</math> կոպեկ և այլն։ Հաշվարկումից պարզվեց, որ ռազմիկը ստացել է ընդամենը <math>655</math> ռուբ. <math>35</math> կոպ. վարձատրություն։ Պահանջվում է իմանալ նրա վերքերի թիվը»։ |
«Ռազմիկին տրվել է վարձատրություն՝ առաջին վերքի համար <math>1</math> կոպեկ, երկրորդի համար՝ <math>2</math> կոպեկ, երրորդի համար՝ <math>4</math> կոպեկ և այլն։ Հաշվարկումից պարզվեց, որ ռազմիկը ստացել է ընդամենը <math>655</math> ռուբ. <math>35</math> կոպ. վարձատրություն։ Պահանջվում է իմանալ նրա վերքերի թիվը»։ |
||
| Տող 5939. | Տող 5939. | ||
որտեղից կունենանք՝ |
որտեղից կունենանք՝ |
||
<math>65536 = |
<math>65536 = 2^x</math> և <math>x = 16</math> |
||
արդյունքը, որը հեշտությամբ գտնում ենք փորձելու ճանապարհով։ |
արդյունքը, որը հեշտությամբ գտնում ենք փորձելու ճանապարհով։ |
||
| Տող 5973. | Տող 5973. | ||
Վարժվելով լոգարիթմների գործածությանը և դրանց միջոցով հաշվումների հեշտացմանը՝ մեզ համար դժվար է պատկերացնել այն զարմանքը և հիացմունքը, որ առաջացրել են դրանք՝ իրենց հայտնվելու ժամանակ։ Նեպերի ժամանակակից Բրիգը, հետագայում փառաբանվելով տասնորդական լոգարիթմների գյուտով, Նեպերի երկերն ստանալիս գրել է. «Նեպերն իր նոր զարմանալի լոգարիթմներով ստիպեց ինձ ջերմեռանդորեն աշխատել և՛ գլխով, և՛ ոտքերով։ Ես հույս ունեմ ամռանը նրան տեսնել, քանի որ երբեք չեմ կարդացել այնպիսի գիրք, որը ինձ ավելի դուր գար և մեծ հիացմունք պատճառեր»։ Բրիգը իրագործեց իր ցանկությունը և ուղևորվեց Շոտլանդիա, որպեսզի այցելի լոգարիթմների գյուտարարին։ Նրան հանդիպելիս Բրիգն ասաց՝ |
Վարժվելով լոգարիթմների գործածությանը և դրանց միջոցով հաշվումների հեշտացմանը՝ մեզ համար դժվար է պատկերացնել այն զարմանքը և հիացմունքը, որ առաջացրել են դրանք՝ իրենց հայտնվելու ժամանակ։ Նեպերի ժամանակակից Բրիգը, հետագայում փառաբանվելով տասնորդական լոգարիթմների գյուտով, Նեպերի երկերն ստանալիս գրել է. «Նեպերն իր նոր զարմանալի լոգարիթմներով ստիպեց ինձ ջերմեռանդորեն աշխատել և՛ գլխով, և՛ ոտքերով։ Ես հույս ունեմ ամռանը նրան տեսնել, քանի որ երբեք չեմ կարդացել այնպիսի գիրք, որը ինձ ավելի դուր գար և մեծ հիացմունք պատճառեր»։ Բրիգը իրագործեց իր ցանկությունը և ուղևորվեց Շոտլանդիա, որպեսզի այցելի լոգարիթմների գյուտարարին։ Նրան հանդիպելիս Բրիգն ասաց՝ |
||
«Ես ձեռնարկեցի |
«Ես ձեռնարկեցի այս երկար ճանապարհորդությունը մի նպատակով՝ տեսնել ձեզ և իմանալ, թե ինչ արվեստի և սրամիտ զենքի օգնությամբ դուք եկաք այդ մտքին՝ աստղագիտության համար զարմանալի ձեռնարկին՝ լոգարիթմներին։ Սակայն այժմ ես ավելի եմ զարմանում, թե ինչո՞ւ ոչ մեկը առաջուց չի գտել, քանի որ դրանց հետ ծանոթանալուց հետո դրանք թվում են չափազանց պարզ»։ |
||
===ԼՈԳԱՐԻԹՄՆԵՐԻ ՄՐՑԱԿԻՑՆԵՐԸ=== |
===ԼՈԳԱՐԻԹՄՆԵՐԻ ՄՐՑԱԿԻՑՆԵՐԸ=== |
||
| Տող 6015. | Տող 6015. | ||
===ԼՈԳԱՐԻԹՄԱԿԱՆ ՏԱՐՕՐԻՆԱԿՈՒԹՅՈՒՆՆԵՐ=== |
===ԼՈԳԱՐԻԹՄԱԿԱՆ ՏԱՐՕՐԻՆԱԿՈՒԹՅՈՒՆՆԵՐ=== |
||
Եթե տեխնիկական առօրյայի և գործնական կյանքի հաշվողական պահանջները լրիվ ապահովվում են եռանիշ և քառանիշ աղյուսակներով, ապա, մյուս կողմից, տեսական հետազոտողի տրամադրության տակ կան և այնպիսի աղյուսակներ, որ ունեն ավելի շատ նիշեր, քան նույնիսկ Բրիգի 14-անիշ լոգարիթմները։ Ընդհանրապես ասած, լոգարիթմը մեծ մասամբ իռացիոնալ թիվ է և թվանշանների ոչ մի քանակով չի կարելի ճշտորեն արտահայտել։ Մեծ մասամբ թվերի լոգարիթմները, որքան էլ նիշեր վերցնելու լինենք, արտահայտվում են միայն մոտավոր կերպով և որքան դրանց մանտիսներում թվանշանները շատ են, այնքան դրանք ճիշտ են։ |
Եթե տեխնիկական առօրյայի և գործնական կյանքի հաշվողական պահանջները լրիվ ապահովվում են եռանիշ և քառանիշ աղյուսակներով, ապա, մյուս կողմից, տեսական հետազոտողի տրամադրության տակ կան և այնպիսի աղյուսակներ, որ ունեն ավելի շատ նիշեր, քան նույնիսկ Բրիգի <math>14</math>-անիշ լոգարիթմները։ Ընդհանրապես ասած, լոգարիթմը մեծ մասամբ իռացիոնալ թիվ է և թվանշանների ոչ մի քանակով չի կարելի ճշտորեն արտահայտել։ Մեծ մասամբ թվերի լոգարիթմները, որքան էլ նիշեր վերցնելու լինենք, արտահայտվում են միայն մոտավոր կերպով և որքան դրանց մանտիսներում թվանշանները շատ են, այնքան դրանք ճիշտ են։ |
||
Գիտական աշխատանքների համար <math>14</math>-անիշ լոգարիթմները<ref>Բրիգի <math>14</math>-անիշ լոգարիթմները կազմված են, ի միջի այլոց, միայն <math>1</math>-ից մինչև <math>20000 |
Գիտական աշխատանքների համար <math>14</math>-անիշ լոգարիթմները<ref>Բրիգի <math>14</math>-անիշ լոգարիթմները կազմված են, ի միջի այլոց, միայն <math>1</math>-ից մինչև <math>20000</math> և <math>90000</math>-ից մինչև <math>101000</math> թվերի համար։</ref> երբեմն ճիշտ չեն, բայց տարբեր տեսակի 300 լոգարիթմական աղյուսակներից, որոնք լույս են տեսել դրանց հայտնագործումից հետո, հետազոտողը միշտ կարող է գտնել այնպիսիները, որոնք կարող են նրան բավարարել։ Նշենք, օրինակ, <math>2</math>-ից մինչև <math>1200</math> թվերի <math>20</math>-անիշ լոգարիթմները, որ հրատարակվել է Ֆրանսիայի Կալլե (1795) քաղաքում։ Ավելի սահմանափակ թվերի խմբերի համար կան նաև վիթխարի թվով տասնորդական նիշերով լոգարիթմների աղյուսակներ՝ լոգարիթմական իսկական տարօրինակություններ, որոնց գոյության մասին, ինչպես ես համոզվել եմ, չեն կասկածում նաև բազմաթիվ մաթեմատիկոսներ։ |
||
Ահա այդ լոգարիթմ-հսկաները, դրանք բոլորը տասնորդական չեն, այլ բնական<ref>Բնական կոչվում են այն լոգարիթմները, որոնք ոչ թե <math>10</math> հիմքով են, այլ <math>2,718 \dots</math> հիմքով, որի մասին դեռ խոսելու ենք։</ref>։ |
Ահա այդ լոգարիթմ-հսկաները, դրանք բոլորը տասնորդական չեն, այլ բնական<ref>Բնական կոչվում են այն լոգարիթմները, որոնք ոչ թե <math>10</math> հիմքով են, այլ <math>2,718 \dots</math> հիմքով, որի մասին դեռ խոսելու ենք։</ref>։ |
||
| Տող 6029. | Տող 6029. | ||
Ադամսի <math>260</math>-անիշ լոգարիթմները։ |
Ադամսի <math>260</math>-անիշ լոգարիթմները։ |
||
Վերջին դեպքում մենք ունենք, ի միջի այլոց, ոչ թե աղյուսակ, այլ միայն այսպես կոչված հինգ թվերի բնական լոգարիթմներ՝ <math>2, \; 3, \; 5, \; 7 |
Վերջին դեպքում մենք ունենք, ի միջի այլոց, ոչ թե աղյուսակ, այլ միայն այսպես կոչված հինգ թվերի բնական լոգարիթմներ՝ <math>2, \; 3, \; 5, \; 7</math> և <math>10</math>, և փոխանցող (<math>260</math>-անիշ) արտադրիչ դրանք տասնորդականի վերածելու համար։ Սակայն, դժվար չէ հասկանալ, որ ունենալով այդ հինգ թվերի լոգարիթմները՝ պարզ գումարով կամ բազմապատկումով կարելի է ստանալ բարդ թվերի բազմության լոգարիթմները. օրինակ <math>12</math>-ի լոգարիթմը հավասար է <math>2, \; 2</math> և <math>3</math> թվերի լոգարիթմների գումարին և այլն։ |
||
Լրիվ կերպով կարելի է լոգարիթմական տարօրինակության շարքը դասել նաև հաշվեքանոնը, այդ «փայտե լոգարիթմները», եթե միայն շնորհիվ իր հարմարության այդ սրամիտ գործիքը չդառնար տեխնիկների համար այդքան սովորական հաշվող գործիք, ինչպես համրիչը գրասենյակային աշխատողների համար։ Սովորության հետևանքով մարում է հիացմունքի զգացումը լոգարիթմի սկզբունքով աշխատող սարքի առջև, մի սարք, որն իրենից օգտվողից չի պահանջում նույնիսկ գիտենալ, թե ինչ բան է լոգարիթմը։ |
Լրիվ կերպով կարելի է լոգարիթմական տարօրինակության շարքը դասել նաև հաշվեքանոնը, այդ «փայտե լոգարիթմները», եթե միայն շնորհիվ իր հարմարության այդ սրամիտ գործիքը չդառնար տեխնիկների համար այդքան սովորական հաշվող գործիք, ինչպես համրիչը գրասենյակային աշխատողների համար։ Սովորության հետևանքով մարում է հիացմունքի զգացումը լոգարիթմի սկզբունքով աշխատող սարքի առջև, մի սարք, որն իրենից օգտվողից չի պահանջում նույնիսկ գիտենալ, թե ինչ բան է լոգարիթմը։ |
||
| Տող 6120. | Տող 6120. | ||
Որոնելի լոգարիթմը կարող է գտնվել |
Որոնելի լոգարիթմը կարող է գտնվել |
||
<math>\frac{34}{31} |
<math>\frac{34}{31}</math> և <math>\frac{34,99}{31}</math> միջև կամ <math>1,09</math> և <math>1,13</math> միջև։ |
||
Այդ ինտերվալում կա միայն մեկ ամբողջ թվի լոգարիթմ, այն է՝ <math>13</math>-ի լոգարիթմը՝ <math>1,11</math>։ Այդ ճանապարհով էլ գտնված է ձեզ շշմեցնող արդյունքը։ Իհարկե, այդ բոլորը մտքով արագ կատարելու համար պետք է տիրապետել մասնագետի հնարամտությանը և հմտությանը, բայց ըստ էության, ինչպես տեսնում ենք, դա բավականին պարզ է։ Այժմ դուք ինքներդ էլ կարող եք կատարել նման ֆոկուսներ, եթե ոչ մտքով, գոնե թղթի վրա։ |
Այդ ինտերվալում կա միայն մեկ ամբողջ թվի լոգարիթմ, այն է՝ <math>13</math>-ի լոգարիթմը՝ <math>1,11</math>։ Այդ ճանապարհով էլ գտնված է ձեզ շշմեցնող արդյունքը։ Իհարկե, այդ բոլորը մտքով արագ կատարելու համար պետք է տիրապետել մասնագետի հնարամտությանը և հմտությանը, բայց ըստ էության, ինչպես տեսնում ենք, դա բավականին պարզ է։ Այժմ դուք ինքներդ էլ կարող եք կատարել նման ֆոկուսներ, եթե ոչ մտքով, գոնե թղթի վրա։ |
||
| Տող 6128. | Տող 6128. | ||
Չտեղեկանալով այն մասին, թե դա ինչ թիվ է, դուք կարող եք արմատ հանելու արդյունքը հայտարարել արմատը հավասար է <math>2</math>-ի։ |
Չտեղեկանալով այն մասին, թե դա ինչ թիվ է, դուք կարող եք արմատ հանելու արդյունքը հայտարարել արմատը հավասար է <math>2</math>-ի։ |
||
Իրոք, <math>lg \sqrt[64]{(20 \; թվանշան)} \;=\; \frac{19,\dots}{64}</math>, հետևաբար այն պետք է գտնվի <math>\frac{19}{64} |
Իրոք, <math>lg \sqrt[64]{(20 \; թվանշան)} \;=\; \frac{19,\dots}{64}</math>, հետևաբար այն պետք է գտնվի <math>\frac{19}{64}</math> և <math>\frac{19,99}{64}</math> միջև, այսինքն՝ <math>0,29</math> և <math>0,32</math> միջև։ Այդպիսի լոգարիթմը ամբողջ թվի համար միայն մեկն է՝ <math>0,30\dots</math> այսինքն՝ <math>2</math> թվի լոգարիթմը։ |
||
Դուք անգամ կարող եք վերջնականապես հաղթել հաշվողին, նրան հայտնելով, թե նա ինչպիսի թիվ էր ուզում ձեզ թելադրել. հռչակավոր շախմատային թիվը՝ |
Դուք անգամ կարող եք վերջնականապես հաղթել հաշվողին, նրան հայտնելով, թե նա ինչպիսի թիվ էր ուզում ձեզ թելադրել. հռչակավոր շախմատային թիվը՝ |
||
| Տող 6150. | Տող 6150. | ||
որտեղ <math>S_1</math>-ը <math>630 \; կգ</math> կշիռ ունեցող եզան մարմնի մակերևույթն է։ Երկրաչափությունից մենք գիտենք, որ նման մարմինների մակերևույթները (<math>S</math>) հարաբերում են, ինչպես նրանց գծային չափերի (<math>l</math>) քառակուսիները իսկ ծավալները՝ (և, հետևաբար, կշիռները), ինչպես գծային չափերի խորանարդները։ Ուստի՝ |
որտեղ <math>S_1</math>-ը <math>630 \; կգ</math> կշիռ ունեցող եզան մարմնի մակերևույթն է։ Երկրաչափությունից մենք գիտենք, որ նման մարմինների մակերևույթները (<math>S</math>) հարաբերում են, ինչպես նրանց գծային չափերի (<math>l</math>) քառակուսիները իսկ ծավալները՝ (և, հետևաբար, կշիռները), ինչպես գծային չափերի խորանարդները։ Ուստի՝ |
||
<math>\frac{S}{S_1} \;=\; \frac{l^2}{l_1^2}, \frac{420}{630} \;=\; \frac{l^3}{l_1^3} |
<math>\frac{S}{S_1} \;=\; \frac{l^2}{l_1^2}, \; \frac{420}{630} \;=\; \frac{l^3}{l_1^3}</math> և, նշանակում է՝ <math>\frac{l}{l_1} \;=\; \frac{\sqrt[3]{420}}{\sqrt[3]{630}}</math>, |
||
որտեղից |
որտեղից |
||
| Տող 6176. | Տող 6176. | ||
Երևակայեցեք, թե ինչպես իմ ընկերոջը տհաճ զարմանք պատճառեց այն, երբ ես նրան ապացուցեցի, որ նվագելով ժամանակակից դաշնամուրի ստեղների վրա, նա նվագում է, ճիշտն ասած, լոգարիթմների վրա... Եվ իրոք, այսպես կոչված տեմպերացված քրոմատիկ (ելևէջային) գամմաների աստիճանները դասավորված չեն հավասար հեռավորությամբ ''ո՛չ'' տատանումների թվերի նկատմամբ և ''ո՛չ'' էլ համապատասխան ձայնի ալիքների երկարության նկատմամբ, այլ իրենցից ներկայացնում են այդ մեծությունների ''լոգարիթմները''։ Միայն այդ լոգարիթմների հիմքը հավասար է <math>2</math>-ի, և ոչ թե <math>10</math>-ի, ինչպես ընդունված է մյուս դեպքում։ |
Երևակայեցեք, թե ինչպես իմ ընկերոջը տհաճ զարմանք պատճառեց այն, երբ ես նրան ապացուցեցի, որ նվագելով ժամանակակից դաշնամուրի ստեղների վրա, նա նվագում է, ճիշտն ասած, լոգարիթմների վրա... Եվ իրոք, այսպես կոչված տեմպերացված քրոմատիկ (ելևէջային) գամմաների աստիճանները դասավորված չեն հավասար հեռավորությամբ ''ո՛չ'' տատանումների թվերի նկատմամբ և ''ո՛չ'' էլ համապատասխան ձայնի ալիքների երկարության նկատմամբ, այլ իրենցից ներկայացնում են այդ մեծությունների ''լոգարիթմները''։ Միայն այդ լոգարիթմների հիմքը հավասար է <math>2</math>-ի, և ոչ թե <math>10</math>-ի, ինչպես ընդունված է մյուս դեպքում։ |
||
Ենթադրենք, որ ամենացածր օկտավայի do նոտան (նրան կանվանենք զրո օկտավա) սահմանված է վայրկյանում <math>n</math> տատանումներով։ Այդ ժամանակ առաջին օկտավայի do-ն վայրկյանում կանի <math> |
Ենթադրենք, որ ամենացածր օկտավայի do նոտան (նրան կանվանենք զրո օկտավա) սահմանված է վայրկյանում <math>n</math> տատանումներով։ Այդ ժամանակ առաջին օկտավայի do-ն վայրկյանում կանի <math>2n</math> տատանումներ, իսկ <math>m</math>-րդ օկտավան՝ <math>n \cdot 2^m</math> տատանումներ և այլն։ Դաշնամուրի խրոմատիկ գամմայի բոլոր նոտաները նշանակենք <math>p</math> համարներով, յուրաքանչյուր օկտավայի do տոնը ընդունելով որպես զրո. այդ ժամանակ, օրինակ, sol տոնը կլինի <math>7</math>-րդ, la-ն կլինի <math>9</math>-րդ և այլն. <math>12</math>-րդ տոնը նորից կլինի do միայն թե մի օկտավայով բարձր։ Քանի որ տեմպերացված քրոմատիկ գամմայի յուրաքանչյուր հետագա տոնը ունի <math>\sqrt[12]{2}</math> անգամ ավելի մեծ տատանումներ<ref>Գրքում վրիպակ է՝ <math>\sqrt[12]{2}</math>-ից ավելի մեծ տատանումներ— ''Մ.''։</ref>, քան նախորդը, ապա ցանկացած տոնի տատանումների թիվը կարելի է արտահայտել հետևյալ բանաձևով՝ |
||
<math>N_{pm} \;=\; n \cdot 2^m\left(\sqrt[12]{2}\right)^p</math>։ |
<math>N_{pm} \;=\; n \cdot 2^m\left(\sqrt[12]{2}\right)^p</math>։ |
||
| Տող 6182. | Տող 6182. | ||
Լոգարիթմելով այս բանաձևը, կստանանք՝ |
Լոգարիթմելով այս բանաձևը, կստանանք՝ |
||
<math>lgN_{pm} \;=\; |
<math>lgN_{pm} \;=\; lgn + mlg2+p\frac{lg2}{12}</math> |
||
կամ |
կամ |
||
| Տող 6188. | Տող 6188. | ||
<math>lgN_{pm} \;=\; lgn+\left(m+\frac{p}{12}\right)lg2</math>, |
<math>lgN_{pm} \;=\; lgn+\left(m+\frac{p}{12}\right)lg2</math>, |
||
իսկ do-ի ամենացածր տատանումների թիվն ընդունելով մեկ (<math> |
իսկ do-ի ամենացածր տատանումների թիվն ընդունելով մեկ (<math>n=1</math>) և բոլոր լոգարիթմները փոխադրելով <math>2</math> հիմքի (կամ պարզապես ընդունելով <math>lg2=1</math>), կունենանք՝ |
||
<math>lgN_{pm} = m+\frac{p}{12}</math>։ |
<math>lgN_{pm} = m+\frac{p}{12}</math>։ |
||
| Տող 6196. | Տող 6196. | ||
Մենք անգամ կարող ենք ասել, որ օկտավայի համարը իրենից ներկայացնում է այդ լոգարիթմի ''խարակտերիստիկան'', իսկ տվյալ օկտավայում<ref>Բաժանում <math>12</math>-ի վրա։</ref> ձայնի համարը՝ ''մանտիսան''։ |
Մենք անգամ կարող ենք ասել, որ օկտավայի համարը իրենից ներկայացնում է այդ լոգարիթմի ''խարակտերիստիկան'', իսկ տվյալ օկտավայում<ref>Բաժանում <math>12</math>-ի վրա։</ref> ձայնի համարը՝ ''մանտիսան''։ |
||
Օրինակ՝ պարզաբանում ենք, որ երրորդ օկտավի sol տոնում, այսինքն՝ <math>3+\frac{7}{12} (\approx 3,583)</math> թվի մեջ, <math>3</math> թիվը այդ տոնի տատանումների թվի լոգարիթմի խարակտերիստիկան է, իսկ <math>\frac{7}{12} (\approx 0,583)</math>-ը նույն լոգարիթմի մանտիսան <math>2</math> հիմքի դեպքում. տատանումների թիվը, հետևաբար |
Օրինակ՝ պարզաբանում ենք, որ երրորդ օկտավի sol տոնում, այսինքն՝ <math>3+\frac{7}{12} (\approx 3,583)</math> թվի մեջ, <math>3</math> թիվը այդ տոնի տատանումների թվի լոգարիթմի խարակտերիստիկան է, իսկ <math>\frac{7}{12} (\approx 0,583)</math>-ը նույն լոգարիթմի մանտիսան <math>2</math> հիմքի դեպքում. տատանումների թիվը, հետևաբար, <math>23,583</math>, այսինքն՝ <math>11,98</math> անգամ մեծ է առաջին օկտավայի do տոնի տատանումների թվից։ |
||
===ԱՍՏՂԵՐԸ, ԱՂՄՈՒԿԸ ԵՎ ԼՈԳԱՐԻԹՄՆԵՐԸ=== |
===ԱՍՏՂԵՐԸ, ԱՂՄՈՒԿԸ ԵՎ ԼՈԳԱՐԻԹՄՆԵՐԸ=== |
||
| Տող 6218. | Տող 6218. | ||
<math>10^{8,7-6,5} = 10^{2,2} = 158</math> անգամ։ |
<math>10^{8,7-6,5} = 10^{2,2} = 158</math> անգամ։ |
||
Այն աղմուկը, որի բարձրությունը մեծ է <math>8</math> բելից, մարդկային օրգանիզմի համար ճանաչվում է վնասակար։ Շատ գործարաններում օրենքով սահմանված նորման գերազանցվում է։ Այստեղ պատահում են <math>10</math> և ավելի բել աղմուկներ. մուրճի հարվածները, որ հասցվում են պողպատյա սալին, առաջացնում են <math>11</math> բել աղմուկ։ Այդ աղմուկները <math>100 |
Այն աղմուկը, որի բարձրությունը մեծ է <math>8</math> բելից, մարդկային օրգանիզմի համար ճանաչվում է վնասակար։ Շատ գործարաններում օրենքով սահմանված նորման գերազանցվում է։ Այստեղ պատահում են <math>10</math> և ավելի բել աղմուկներ. մուրճի հարվածները, որ հասցվում են պողպատյա սալին, առաջացնում են <math>11</math> բել աղմուկ։ Այդ աղմուկները <math>100</math> և </math>1000</math> անգամ ուժեղ են թույլատրելի նորմայից և <math>10—100</math> անգամ ավելի բարձր Նիագարայի ջրվեժի ամենաաղմկոտ տեղից (<math>9</math> բել)։ |
||
Պատահականությո՞ւն է արդյոք այն, որ լուսատուների տեսանելի պայծառությունը գնահատելիս և աղմուկի բարձրությունը չափելիս մենք գործ ունենք զգայության մեծության և այն առաջացնող գրգիռների միջև եղած լոգարիթմական կախվածության հետ։ Ոչ, և՛ մեկը, և՛ մյուսը հանդիսանում են ընդհանուր օրենքի հետևանք «Ֆեխների պսիխոֆիզիկական օրենք», որը պնդում է, թե զգայության մեծությունը համեմատական է գրգռման մեծության լոգարիթմին։ |
Պատահականությո՞ւն է արդյոք այն, որ լուսատուների տեսանելի պայծառությունը գնահատելիս և աղմուկի բարձրությունը չափելիս մենք գործ ունենք զգայության մեծության և այն առաջացնող գրգիռների միջև եղած լոգարիթմական կախվածության հետ։ Ոչ, և՛ մեկը, և՛ մյուսը հանդիսանում են ընդհանուր օրենքի հետևանք «Ֆեխների պսիխոֆիզիկական օրենք», որը պնդում է, թե զգայության մեծությունը համեմատական է գրգռման մեծության լոգարիթմին։ |
||
| Տող 6228. | Տող 6228. | ||
'''''Խնդիր''''' |
'''''Խնդիր''''' |
||
Այն բանի պատճառը, որ գազով լցված (հաճախ սխալմամբ անվանելով «կիսավատտային», լամպերն ավելի պայծառ լույս են տալիս, քան միևնույն նյութից պատրաստված մետաղյա լարով դատարկ լամպերը, թագնված է շիկացման լարի տարբեր ջերմաստիճանի մեջ։ Ֆիզիկայում սահմանված օրենքի համաձայն լույսի ընդհանուր քանակը, որ տարածվում է սպիտակ շիկացման դեպքում, աճում է բացարձակ ջերմաստիճանի <math>12</math>-րդ աստիճանին համեմատ։ Իմանալով այդ, կատարենք այսպիսի հաշվարկ. որոշենք, թե «կիսավատտային» լամպը, որի շիկացման լարի ջերմաստիճանը բացարձակ սանդղակում (այսինքն՝ հաշվելով -273°C-ից) 2500° է, քանի՞ անգամ ավելի շատ լույս է արտածում, քան դատարկ լամպը, որի լարի շիկացումը մինչև 2200° է։ |
Այն բանի պատճառը, որ գազով լցված (հաճախ սխալմամբ անվանելով «կիսավատտային», լամպերն ավելի պայծառ լույս են տալիս, քան միևնույն նյութից պատրաստված մետաղյա լարով դատարկ լամպերը, թագնված է շիկացման լարի տարբեր ջերմաստիճանի մեջ։ Ֆիզիկայում սահմանված օրենքի համաձայն լույսի ընդհանուր քանակը, որ տարածվում է սպիտակ շիկացման դեպքում, աճում է բացարձակ ջերմաստիճանի <math>12</math>-րդ աստիճանին համեմատ։ Իմանալով այդ, կատարենք այսպիսի հաշվարկ. որոշենք, թե «կիսավատտային» լամպը, որի շիկացման լարի ջերմաստիճանը բացարձակ սանդղակում (այսինքն՝ հաշվելով <math>-273°C</math>-ից) <math>2500°</math> է, քանի՞ անգամ ավելի շատ լույս է արտածում, քան դատարկ լամպը, որի լարի շիկացումը մինչև <math>2200°</math> է։ |
||
'''''Լուծում''''' |
'''''Լուծում''''' |
||
| Տող 6251. | Տող 6251. | ||
որտեղից՝ |
որտեղից՝ |
||
<math>lg \left(1+\frac{x}{100}\right) \;=\; \frac{lg2}{12} |
<math>lg \left(1+\frac{x}{100}\right) \;=\; \frac{lg2}{12}</math> և <math>x=6\%</math>։ |
||
Վերջապես, երրորդ հաշվարկը. որքանո՞վ է (տոկոսներով) աճում լամպի պայծառությունը, եթե նրա լարի ջերմաստիճանը (բացարձակ) բարձրացվում է 1%-ով։ |
Վերջապես, երրորդ հաշվարկը. որքանո՞վ է (տոկոսներով) աճում լամպի պայծառությունը, եթե նրա լարի ջերմաստիճանը (բացարձակ) բարձրացվում է 1%-ով։ |
||
| Տող 6273. | Տող 6273. | ||
===ԿՏԱԿ ՀԱՐՅՈՒՐ ՏԱՐՈՎ=== |
===ԿՏԱԿ ՀԱՐՅՈՒՐ ՏԱՐՈՎ=== |
||
Ո՞վ չի լսել ցորենի հատիկների այն առասպելական թվի մասին, որը, իբր թե, շախմատի խաղի գյուտարարը |
Ո՞վ չի լսել ցորենի հատիկների այն առասպելական թվի մասին, որը, իբր թե, շախմատի խաղի գյուտարարը պահանջել է որպես պարգև։ Այդ թիվը կազմվել է մեկը հաջորդաբար կրկնապատկելու ճանապարհով, շախմատային տախտակի առաջին դաշտի համար գյուտարարը պահանջել է <math>1</math> հատիկ, երկրորդի համար՝ <math>2</math> հատիկ և այլն, կրկնապատկելով բոլորը՝ մինչև, վերջին <math>64</math>-րդը։ |
||
Սակայն թվերն անսպասելի սրընթացությամբ աճում են ոչ միայն հաջորդական կրկնապատկման դեպքում, այլև՝ անհամեմատ ավելի չափավոր մեծացման դեպքում։ |
Սակայն թվերն անսպասելի սրընթացությամբ աճում են ոչ միայն հաջորդական կրկնապատկման դեպքում, այլև՝ անհամեմատ ավելի չափավոր մեծացման դեպքում։ |
||
| Տող 6311. | Տող 6311. | ||
Խնայդրամարկղներում տոկոսային փողերն ամեն տարի միացվում են հիմնական կապիտալին։ Եթե միացումը կատարվում է ավելի հաճախ, ապա կապիտալն աճում է ավելի արագ, քանի որ տոկոսների գոյացմանը մասնակցում է մեծ թվով գումար։ Վերցնենք միանգամայն տեսական, խիստ պարզեցված օրինակ։ Դիցուք, խնայդրամարկղում դրված է <math>100</math> ռուբլի՝ տարեկան 100%-ով։ Եթե տոկոսային փողերը հիմնական կապիտալին միացվեն միայն տարին լրանալուց հետո՝ ապա այդ ժամկետին <math>100</math> ռուբ. վերածվում է <math>200</math> ռուբլու։ Այժմ տեսնենք, թե <math>100</math> ռուբլին ինչքա՞ն է դառնում, եթե տոկոսային փողերը հիմնական կապիտալին միացնենք յուրաքանչյուր կես տարին մեկ։ Կես տարին անցնելուց հետո <math>100</math> ռուբլին կդառնա |
Խնայդրամարկղներում տոկոսային փողերն ամեն տարի միացվում են հիմնական կապիտալին։ Եթե միացումը կատարվում է ավելի հաճախ, ապա կապիտալն աճում է ավելի արագ, քանի որ տոկոսների գոյացմանը մասնակցում է մեծ թվով գումար։ Վերցնենք միանգամայն տեսական, խիստ պարզեցված օրինակ։ Դիցուք, խնայդրամարկղում դրված է <math>100</math> ռուբլի՝ տարեկան 100%-ով։ Եթե տոկոսային փողերը հիմնական կապիտալին միացվեն միայն տարին լրանալուց հետո՝ ապա այդ ժամկետին <math>100</math> ռուբ. վերածվում է <math>200</math> ռուբլու։ Այժմ տեսնենք, թե <math>100</math> ռուբլին ինչքա՞ն է դառնում, եթե տոկոսային փողերը հիմնական կապիտալին միացնենք յուրաքանչյուր կես տարին մեկ։ Կես տարին անցնելուց հետո <math>100</math> ռուբլին կդառնա |
||
<math>100 |
<math>100</math> ռուբ. <math>\cdot 1,5 = 150</math> ռուբ. |
||
և դարձյալ կես տարի հետո՝ |
և դարձյալ կես տարի հետո՝ |
||
<math>150 |
<math>150</math> ռուբ. <math>\cdot 1,5 = 225</math> ռուբ.։ |
||
Եթե միացումը կատարենք յուրաքանչյուր <math>\frac{1}{3}</math> տարին մեկ, ապա տարին անցնելուց հետո <math>100</math> |
Եթե միացումը կատարենք յուրաքանչյուր <math>\frac{1}{3}</math> տարին մեկ, ապա տարին անցնելուց հետո <math>100</math> ռուբ. կվերածվի |
||
<math>100 |
<math>100</math> ռուբ. <math>\cdot \left(1\frac{1}{3}\right)^3 \approx 237</math> ռուբ. <math>03</math> կոպ.-ի։ |
||
Ավելի հաճախակի դարձնենք տոկոսային փողերի միացման ժամկետները՝ մինչև <math>0,1, \; 0,01, \; 0,001</math> տարի և այլն։ Այդ ժամանակ մեկ տարի հետո 100 ռուբլուց կստացվի՝ |
Ավելի հաճախակի դարձնենք տոկոսային փողերի միացման ժամկետները՝ մինչև <math>0,1, \; 0,01, \; 0,001</math> տարի և այլն։ Այդ ժամանակ մեկ տարի հետո <math>100</math> ռուբլուց կստացվի՝ |
||
<TABLE border = 0> |
<TABLE border = 0> |
||
<TR> |
<TR> |
||
<TD><math>100 |
<TD><math>100</math> ռուբ. <math>\cdot 1,1^{10}</math></TD> |
||
<TD><math>\approx 259 |
<TD><math>\approx 259</math> ռուբ. <math>37</math> կոպ.</TD> |
||
</TR> |
</TR> |
||
<TR> |
<TR> |
||
<TD><math>100 |
<TD><math>100</math> ռուբ. <math>\cdot 1,01^{100}</math></TD> |
||
<TD><math>\approx 270 |
<TD><math>\approx 270</math> ռուբ. <math>48</math> կոպ.</TD> |
||
</TR> |
</TR> |
||
<TR> |
<TR> |
||
<TD><math>100 |
<TD><math>100</math> ռուբ. <math>\cdot 1,001^{1000}</math></TD> |
||
<TD><math>\approx 271 |
<TD><math>\approx 271</math> ռուբ. <math>69</math> կոպ.</TD> |
||
</TR> |
</TR> |
||
</TABLE> |
</TABLE> |
||
| Տող 6340. | Տող 6340. | ||
Բարձրագույն մաթեմատիկայի մեթոդներով ապացուցվում է, որ միացման ժամկետների անսահման կրճատման դեպքում աճող կապիտալը չի աճում անսահմանորեն, այլ մոտենում է որոշ սահմանի, որը մոտավորապես<ref>Կոպեկների կոտորակային մասն անտեսում ենք։</ref> հավասար է |
Բարձրագույն մաթեմատիկայի մեթոդներով ապացուցվում է, որ միացման ժամկետների անսահման կրճատման դեպքում աճող կապիտալը չի աճում անսահմանորեն, այլ մոտենում է որոշ սահմանի, որը մոտավորապես<ref>Կոպեկների կոտորակային մասն անտեսում ենք։</ref> հավասար է |
||
<math>271 |
<math>271</math> ռուբ. <math>83</math> կոպ.։ |
||
100%-ով դրված կապիտալը <math>2,7183</math>-ից ավել մեծանալ չի կարող, եթե անգամ աճող տոկոսները կապիտալին միացվեն յուրաքանչյուր վայրկյանում։ |
100%-ով դրված կապիտալը <math>2,7183</math>-ից ավել մեծանալ չի կարող, եթե անգամ աճող տոկոսները կապիտալին միացվեն յուրաքանչյուր վայրկյանում։ |
||
| Տող 6346. | Տող 6346. | ||
„<math>e</math>” ԹԻՎԸ |
„<math>e</math>” ԹԻՎԸ |
||
Ստացված <math>2,7183 \dots</math> թիվը, որը բարձրագույն մաթեմատիկայի մեջ վիթխարի դեր է խաղում, ոչ ավելի պակաս, քան հռչակավոր <math>\pi</math> թիվը, ունի հատուկ նշանակում՝ <math>e</math>։ Սա իռացիոնալ թիվ է. այն չի կարող թվանշանների<ref>Բացի այդ, այդ թիվը, ինչպես և <math>\pi</math> թիվը տրանսցենդենտ են, այսինքն՝ չեն կարող լինել ամբողջ գործակիցներով հանրահաշվական որևէ հավասարման լուծման արդյունք։</ref> |
Ստացված <math>2,7183 \dots</math> թիվը, որը բարձրագույն մաթեմատիկայի մեջ վիթխարի դեր է խաղում, ոչ ավելի պակաս, քան հռչակավոր <math>\pi</math> թիվը, ունի հատուկ նշանակում՝ <math>e</math>։ Սա իռացիոնալ թիվ է. այն չի կարող թվանշանների վերջավոր թվով ճշտորեն արտահայտվել<ref>Բացի այդ, այդ թիվը, ինչպես և <math>\pi</math> թիվը տրանսցենդենտ են, այսինքն՝ չեն կարող լինել ամբողջ գործակիցներով հանրահաշվական որևէ հավասարման լուծման արդյունք։</ref>, բայց հաշվվում է միայն մոտավորությամբ, ճշտության ցանկացած աստիճանով, հետևյալ շարքի միջոցով՝ |
||
<math>1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \frac{1}{1 \cdot 2 \cdot 3 \cdot 4} + \frac{1}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} + \dots</math> |
<math>1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \frac{1}{1 \cdot 2 \cdot 3 \cdot 4} + \frac{1}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} + \dots</math> |
||
| Տող 6356. | Տող 6356. | ||
արտահայտության սահմանն է <math>n</math>-ի անսահմանորեն աճելու դեպքում։ |
արտահայտության սահմանն է <math>n</math>-ի անսահմանորեն աճելու դեպքում։ |
||
Շատ պատճառներով, որոնք մենք այստեղ շարադրել չենք կարող, <math>e</math> թիվը նպատակահարմար է ընդունել որպես լոգարիթմների սիստեմի հիմք։ Այդպիսի աղյուսակները («բնական լոգարիթմների») գոյություն ունեն և լայն կիրառություն են գտնում գիտության և տեխնիկայի մեջ։ <math>48, 61, 102 և 260</math> թվանշաններով այն լոգարիթմ-հսկաները, որոնց մասին մենք խոսել ենք ավելի վաղ, հատկապես ունեն <math>e</math> հիմքը։ |
Շատ պատճառներով, որոնք մենք այստեղ շարադրել չենք կարող, <math>e</math> թիվը նպատակահարմար է ընդունել որպես լոգարիթմների սիստեմի հիմք։ Այդպիսի աղյուսակները («բնական լոգարիթմների») գոյություն ունեն և լայն կիրառություն են գտնում գիտության և տեխնիկայի մեջ։ <math>48, \; 61, \; 102</math> և <math>260</math> թվանշաններով այն լոգարիթմ-հսկաները, որոնց մասին մենք խոսել ենք ավելի վաղ, հատկապես ունեն <math>e</math> հիմքը։ |
||
<math>e</math> թիվը հաճախ հայտնվում է այնտեղ, որտեղ նրան ընդհանրապես չեն սպասում։ Դնենք, օրինակ, այսպիսի խնդիր։ |
<math>e</math> թիվը հաճախ հայտնվում է այնտեղ, որտեղ նրան ընդհանրապես չեն սպասում։ Դնենք, օրինակ, այսպիսի խնդիր։ |
||
Ի՞նչ մասերի պետք է բաժանել տրված a թիվը, որպեսզի բոլոր մասերի արտադրյալը լինի ամենամեծը։ |
Ի՞նչ մասերի պետք է բաժանել տրված <math>a</math> թիվը, որպեսզի բոլոր մասերի արտադրյալը լինի ամենամեծը։ |
||
Մենք արդեն դիտենք, որ հաստատուն գումարի դեպքում թվերն ամենամեծ արտադրյալը տալիս են այն դեպքում, երբ դրանք միմյանց հավասար են։ Պարզ է, որ <math>a</math> թիվը պետք է բաժանել հավասար մասերի։ Բայց |
Մենք արդեն դիտենք, որ հաստատուն գումարի դեպքում թվերն ամենամեծ արտադրյալը տալիս են այն դեպքում, երբ դրանք միմյանց հավասար են։ Պարզ է, որ <math>a</math> թիվը պետք է բաժանել հավասար մասերի։ Բայց քանի՞ հավասար մասի։ Երկուսի՞, երեքի՞, տասի՞։ Բարձրագույն մաթեմատիկայի եղանակներով կարելի է որոշել, որ ամենամեծ արտադրյալն ստացվում է, երբ մասերը ըստ հնարավորին մոտ են <math>e</math> թվին։ |
||
Օրինակ, <math>10</math>-ը պետք է բաժանել այնպիսի թվով հավասար մասերի, որպեսզի մասերն ըստ հնարավորին մոտ լինեն <math>2,718</math>-ին։ Դրա համար պետք է գտնել հետևյալ քանորդը՝ |
Օրինակ, <math>10</math>-ը պետք է բաժանել այնպիսի թվով հավասար մասերի, որպեսզի մասերն ըստ հնարավորին մոտ լինեն <math>2,718</math>-ին։ Դրա համար պետք է գտնել հետևյալ քանորդը՝ |
||
| Տող 6368. | Տող 6368. | ||
<math>\frac{10}{2,718} \;=\; 3,678 \dots</math> |
<math>\frac{10}{2,718} \;=\; 3,678 \dots</math> |
||
Քանի որ թիվը <math>3,678 \dots</math> հավասար մասերի վրա բաժանել չի կարելի |
Քանի որ թիվը <math>3,678 \dots</math> հավասար մասերի վրա բաժանել չի կարելի<ref>Գրքում վրիպակ է՝ Քանի որ <math>3,678 \dots</math> թիվը հավասար մասերի վրա բաժանել չի կարելի,— ''Մ.''։</ref>, ապա հարկ է լինում բաժանարարը վերցնել նրան ամենամոտ ամբողջ թիվը՝ <math>4</math>-ը։ Հետևաբար, <math>10</math>-ի մասերի ամենամեծ արտադրյալը, մենք կստանանք, եթե այդ մասերը հավասար են <math>\frac{10}{4}</math>, այսինքն՝ <math>2,5</math>։ |
||
Նշանակում է |
Նշանակում է |
||
| Տող 6374. | Տող 6374. | ||
<math>(2,5)^4 = 39,0625</math> |
<math>(2,5)^4 = 39,0625</math> |
||
ամենամեծ թիվն է, որը կարող է ստացվել <math>10</math>-ի միատեսակ մասերի բազմապատկումից։ Իրոք, <math>10</math>-ը բաժանելով <math>3 կամ 5</math> հավասար մասերի՝ մենք կստանանք փոքր արտադրյալ |
ամենամեծ թիվն է, որը կարող է ստացվել <math>10</math>-ի միատեսակ մասերի բազմապատկումից։ Իրոք, <math>10</math>-ը բաժանելով <math>3</math> կամ <math>5</math> հավասար մասերի՝ մենք կստանանք փոքր արտադրյալ |
||
<math>\left(\frac{10}{3}\right)^3 \;=\; 37, \left(\frac{10}{5}\right)^5 \;=\; 32</math>։ |
<math>\left(\frac{10}{3}\right)^3 \;=\; 37, \; \left(\frac{10}{5}\right)^5 \;=\; 32</math>։ |
||
<math>20</math> թվի մասերի ամենամեծ արտադրյալն ստանալու համար այն պետք է բաժանել <math>7</math> հավասար մասերի, քանի որ |
<math>20</math> թվի մասերի ամենամեծ արտադրյալն ստանալու համար այն պետք է բաժանել <math>7</math> հավասար մասերի, քանի որ |
||
<math>20 \;:\; 2,718 \dots \;=\; 7,36 \approx 7</math>։ |
<math>20 \;:\; 2,718 \dots \;=\; 7,36 \approx 7</math>։ |
||
| Տող 6384. | Տող 6384. | ||
<math>50</math> թիվը պետք է բաժանել <math>18</math> մասի, իսկ <math>100</math>-ը՝ <math>37</math>, քանի որ |
<math>50</math> թիվը պետք է բաժանել <math>18</math> մասի, իսկ <math>100</math>-ը՝ <math>37</math>, քանի որ |
||
<math>50 \;:\; 2,718 \dots = 18,4</math>, |
<math>50 \;:\; 2,718 \dots \;=\; 18,4</math>, |
||
<math>100 \;:\; 2,718 \dots = 36,8</math>։ |
<math>100 \;:\; 2,718 \dots \;=\; 36,8</math>։ |
||
<math>e</math> թիվը վիթխարի դեր է խաղում մաթեմատիկայի, ֆիզիկայի, աստղագիտության և մյուս գիտությունների մեջ։ Ահա մի քանի հարցեր, որոնք մաթեմատիկորեն դիտարկելու դեպքում հարկ է լինում օգտվել այդ թվից (ցանկը կարելի էր մեծացնել անսահմանափակ կերպով). |
<math>e</math> թիվը վիթխարի դեր է խաղում մաթեմատիկայի, ֆիզիկայի, աստղագիտության և մյուս գիտությունների մեջ։ Ահա մի քանի հարցեր, որոնք մաթեմատիկորեն դիտարկելու դեպքում հարկ է լինում օգտվել այդ թվից (ցանկը կարելի էր մեծացնել անսահմանափակ կերպով). |
||
| Տող 6426. | Տող 6426. | ||
'''''Լուծում''''' |
'''''Լուծում''''' |
||
Սխալը նրանումն է, որ <math>lg_{10}\left(\frac{1}{2}\right)</math>-ով կրճատելու դեպքում անհավասարության նշանը չփոխվեց (<math>></math>-ը <math><</math>-ով) այն ժամանակ անհրաժեշտ էր այդ անել, քանի որ <math>lg_{10}\left(\frac{1}{2} \right)</math> թիվը բացասական է։ [Իսկ եթե մենք լոգարիթմենք ոչ թե <math>10</math> հիմքով, այլ <math>\frac{1}{2}</math>-ից փոքր հիմքով, ապա <math>lg\left(\frac{1}{2}\right)</math>-ը կլիներ դրական թիվ, բայց մենք այն ժամանակ իրավացի չէինք լինի պնդելու, որ մեծ թվին համապատասխանում է մեծ |
Սխալը նրանումն է, որ <math>lg_{10}\left(\frac{1}{2}\right)</math>-ով կրճատելու դեպքում անհավասարության նշանը չփոխվեց (<math>></math>-ը <math><</math>-ով) այն ժամանակ անհրաժեշտ էր այդ անել, քանի որ <math>lg_{10}\left(\frac{1}{2} \right)</math> թիվը բացասական է։ [Իսկ եթե մենք լոգարիթմենք ոչ թե <math>10</math> հիմքով, այլ <math>\frac{1}{2}</math>-ից փոքր հիմքով, ապա <math>lg\left(\frac{1}{2}\right)</math>-ը կլիներ դրական թիվ, բայց մենք այն ժամանակ իրավացի չէինք լինի պնդելու, որ մեծ թվին համապատասխանում է մեծ լոգարիթմ]։ |
||
===ՑԱՆԿԱՑԱԾ ԹԻՎ՝ ԵՐԵՔ ԵՐԿՈՒՍՆԵՐՈՎ=== |
===ՑԱՆԿԱՑԱԾ ԹԻՎ՝ ԵՐԵՔ ԵՐԿՈՒՍՆԵՐՈՎ=== |
||
Ընթացիկ տարբերակը 13:02, 22 օգոստոսի 2017-ի դրությամբ
հեղինակ՝ Յա. Ի. Պերելման |


ԳԼՈՒԽ ԱՌԱՋԻՆ։ ՄԱԹԵՄԱՏԻԿԱԿԱՆ ՀԻՆԳԵՐՈՐԴ ԳՈՐԾՈՂՈՒԹՅՈՒՆ
ՀԻՆԳԵՐՈՐԴ ԳՈՐԾՈՂՈՒԹՅՈՒՆԸ
Հաճախ հանրահաշիվն անվանում են «Յոթ գործողությունների թվաբանություն», ցանկանալով ընդգծել, որ մաթեմատիկական հանրահայտ չորս գործողություններին այն միացնում է երեք նորը՝ աստիճան բարձրացնելը և դրան հակադարձ երկու գործողությունները։
Հանրահաշվական մեր զրույցները կսկսվեն «Հինգերորդ գործողություն»- ից՝ աստիճան բարձրացնելուց։
Այդ նոր գործողության կարիքն զգացվո՞ւմ է արդյոք պրակտիկ կյանքում։ Անպայման։ Մենք իրական կյանքում հաճախ ենք հանդիպում դրան։ Հիշենք մակերեսների և ծավալների հաշվման բազմաթիվ դեպքեր, որտեղ սովորաբար հարկ է լինում թվերը բարձրացնել երկրորդ և երրորդ աստիճան։ Այնուհետև՝ տիեզերական ձգողականության ուժը, էլեկտրաստատիկ և մագնիսական փոխազդեցությունները, լույսը, ձայնը թուլանում են հեռավորության քառակուսուն համեմատականորեն։ Մոլորակների պտույտի տևողությունը Արեգակի շուրջը (և արբանյակներինը՝ մոլորակների շուրջը) պտտման կենտրոնից նրանց ունեցած հեռավորությունների հետ նույնպես կապված է աստիճանային կախվածությամբ՝ պտտման ժամանակամիջոցների քառակուսիները միմյանց հարաբերում են այնպես, ինչպես հեռավորությունների խորանարդները։
Չպետք է մտածել, որ պրակտիկայում մենք հանդիպում ենք միայն երկրորդ և երրորդ աստիճանների, իսկ ավելի բարձր ցուցիչներ գոյության ունեն միայն հանրահաշվի խնդրագրքերի վարժություններում։ Ինժեները, կատարելով դիմացկունության վերաբերյալ հաշվարկներ, անընդհատ և միշտ գործ ունի չորրորդ աստիճանի հետ. իսկ այլ հաշվումների դեպքում, օրինակ շոգեմուղի խողովակների տրամագծի, անգամ վեցերորդ աստիճանի հետ։ Ուսումնասիրելով այն ուժը, որի դեպքում հոսուն ջուրը քշում է քարը, հիդրոտեխնիկը նույնպես առնչվում է վեցերորդ աստիճանի կախման հետ. եթե մի գետում հոսանքի արագությունը չորս անգամ մեծ է, քան մյուսում, ապա արագընթաց գետը ընդունակ է իր հունով գլորել այսինքն՝ [1] անգամ ավելի ծանր քարեր, քան դանդաղ գետը[2]։
Ավելի բարձր աստիճանների հետ մենք հանդիպում ենք՝ ուսումնասիրելով շիկացած մարմնի պայծառության կախումը ջերմաստիճանից, օրինակ՝ շիկացած լարինը էլեկտրական լամպում։ Ընդհանուր պայծառությունն աճում է բացարձակ ջերմաստիճանի տասներկուերորդ աստիճանով՝ սպիտակ շիկացման դեպքում և շերմաստիճանի երեսուներորդ աստիճանով՝ կարմրելիս։ Այս նշանակում է, մարմինը, որը տաքացած է, օրինակ, -ից մինչև Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 4000°} (բացարձակ), այսինքն՝ երկու անգամ ուժեղ, -ով պայծառ է դառնում, այլ կերպ ասած՝ ավելի քան անգամ։ Այն մասին, թե ինչպիսի նշանակություն ունի այդ յուրատեսակ կախումը էլեկտրական լամպերի պատրաստման տեխնիկայում, մենք դեռ կխոսենք այլ տեղ։
ԱՍՏՂԱԳԻՏԱԿԱՆ ԹՎԵՐ
Թերևս ոչ ոք այնպես լայնորեն չի օգտվում մաթեմատիկական հինգերորդ գործողությունից, ինչպես աստղագետները։ Տիեզերքն ուսումնասիրելիս, յուրաքանչյուր քայլափոխում հարկ է լինում հանդիպել հսկայական թվերի, որոնք կազմված են մեկից-երկու իմաստալից թվանշաններից և զրոների երկար շարքից։ Սովորական ձևով նման վիթխարի թվերի պատկերումը, իրավացիորեն անվանելով «աստղագիտական թվեր», անխուսափելիորեն կհանգեցներ մեծ անհարմարությունների, հատկապես հաշվումների ժամանակ։ Հեռավորությունը, օրինակ, մինչև Անդրոմեդի միգամածությունը, արտահայտված կիլոմետրերով սովորական կարգով, պատկերվում է այսպիսի թվով՝
Աստղագիտական հաշվումներ կատարելիս հաճախ անհրաժեշտ է լինում երկնային հեռավորություններն արտահայտել ոչ միայն կիլոմետրերով կամ ավելի խոշոր միավորներով, այլև սանտիմետրերով։ Այդ դեպքում դիտարկված հեռավորությունը պատկերվում է մի թվով, որը հինգ զրոներ ավելի ունի՝
Աստղերի զանգվածներն արտահայտվում են ավելի քան մեծ թվերով, հատկապես, եթե դրանք արտահայտել ենք գրամներով, ինչպես պահանջվում է շատ հաշվարկների համար։ Մեր արեգակի զանգվածը գրամներով հավասար է՝
Դժվար չէ պատկերացնել, թե ինչպիսի դժվարություններ կլինեին այդպիսի վիթխարի թվերով հաշվումներ կատարելիս և ինչպես հեշտությամբ այդ դեպքում կարելի էր սխալվել։ Իսկ չէ՞ որ այստեղ բերված են ամենևին էլ դեռ ոչ ամենամեծ աստղագիտական թվերը։
Մաթեմատիկական հինգերորդ գործողությանը հաշվողներին տալիս է այդ դժվարություններից դուրս գալու հասարակ ելք։ Մեկով և զրոներnվ պատկերվող թիվն իրենից ներկայացնում է տասի որոշակի աստիճան՝
և այլն։
Ուստի սկզբում բերված թվային հսկաները կարող են ներկայացվել այսպիսի տեսքով՝
| առաջինը | . . . . . . | , |
| երկրորդը | . . . . . . | ։ |
Այդ կատարվում է ոչ միայն տեղի խնայողության, այլև հաշվումների հեշտացման համար։ Իսկ եթե պահանջվեր, օրինակ, այդ երկու թվերն էլ բազմապատկել, ապա բավական կլիներ գտնել արտադրյալը և գրել այն արտադրիչից առաջ.
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 950\cdot10^{21}\cdot1983\cdot10^{36}\;=\;188\;385\cdot10^{52}։}
Այդ իհարկե, անհամեմատ հարմար է, քան թե նախ զրոյով, այնուհետև և, վերջապես, զրոյով թվեր գրելը. դա ոչ միայն հարմար է, այլև հուսալի, քանի որ տասնյակ զրոներ գրելիս հնարավոր է վրիպել մեկ-երկու զրո և ստանալ ոչ ճիշտ արդյունք։
ՈՐՔԱ՞Ն Է ԿՇՌՈՒՄ ՕԴԸ
Համոզվելու համար, թե որքան են հեշտանում գործնական հաշվումները մեծ թվերից աստիճանային պատկերմամբ օգտվելու դեպքում, կատարենք այսպիսի հաշվարկ՝ որոշենք, թե քանի անգամ երկրագնդի մասսան մեծ է նրան շրջապատող ամբողջ օդի մասսայից։
Մենք գիտենք, որ երկրի մակերևույթի յուրաքանչյուր քառ. սանտիմետրի վրա օդը ճնշում է մոտ մեկ կիլոգրամ ուժով։ Այդ նշանակում է, որ մթնոլորտի այն սյունի կշիռը, որը հենված է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1\;քառ.\;սմ} -ի վրա, հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1\;կգ} ։ Երկրի մթնոլորտային շերտը, կարծես թե, ամբողջությամբ կազմված է այդպիսի օդային սյուներից. դրանք այնքան են, որքան քառ. սանտիմետր պարունակում է մեր մոլորակի մակերևույթը. այդքան կիլոգրամ էլ կշռում է ամբողջ մթնոլորտը։ Նայելով տեղեկատուն, իմանում ենք, որ երկրագնդի մակերևույթի մեծությունը հավասար է միլիոն Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle քառ.\;կմ} , այսինքն՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 51\cdot10^7\;քառ.\;կմ} ։
Հաշվենք, թե մեկ քառակուսի կիլոմետրը քանի՛ քառակուսի սանտիմետր է։ Գծային կիլոմետրը պարունակում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1000\;մ} , յուրաքանչյուրում՝ -ական Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle սմ} , այսինքն հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10^5\;սմ} , իսկ քառ. կիլոմետրը պարունակում է քառ. սանտիմետր։ Ուստի՝ երկրագնդի ամբողջ մակերևույթը պարունակում է
քառ. սանտիմետր։ Երկրի մթնոլորտը այդքան կիլոգրամ էլ կշռում է։ Վերածելով տոննաների, կստանանք՝
։
Երկրագնդի մասսան արտահայտվում է հետևյալ թվով՝
տոննա։
Որպեսզի որոշենք, թե մեր մոլորակը որքան անգամ ծանր է իր օդային շերտից, կատարենք բաժանում՝
,
այսինքն՝ մթնոլորտի մասսան մոտավորապես կազմում է երկրագնդի մասսայի մեկ միլիոներորդական մասը։
ԱՅՐՈՒՄ՝ ԱՌԱՆՑ ԿՐԱԿԻ ԵՎ ՋԵՐՄՈՒԹՅԱՆ
Եթե դուք հարցնեք քիմիկոսին, թե ինչո՞ւ փայտը կամ ածուխն այրվում են միայն բարձր ջերմաստիճանում, նա ձեզ կպատասխանի, որ ածխածնի և թթվածնի միացումը կատարվում է, խիստ ասած, ամեն մի ջերմաստիճանի դեպքում, բայց ցածր ջերմաստիճանների դեպքում այդ պրոցեսն ընթանում է արտակարգ դանդաղ (այսինքն՝ ռեակցիայի մեջ են մտնում խիստ աննշան թվով մոլեկուլներ), այդ պատճառով էլ վրիպում է մեր տեսողությունից։ Քիմիական ռեակցիաների արագությունը որոշող օրենքն ասում է, որ ջերմաստիճանը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10°} -ով իջեցնելիս ռեակցիայի արագությունը (նրա մեջ մասնակցող մոլեկուլների թիվը) փոքրանում է երկու անգամ։
Ասվածը կիրառենք թթվածնի հետ բնափայտի միացման ռեակցիայի դեպքում, այսինքն՝ փայտի այրման պրոցեսի դեպքում։ Դիցուք, Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 600°} ջերմությամբ կրակի մեջ յուրաքանչյուր վայրկյանում այրվում է 1 գրամ բնափայտ։ Որքա՞ն ժամանակում կայրվի գրամ փայտը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20°} -ում։ Մենք արդեն գիտենք, որ երբ ջերմաստիճանը -ով իջնում է, ռեակցիայի արագությունը փոքրանում է անգամ, այսինքն՝ գրամ փայտն այրվում է վայրկյանում։
Քանի՞ տարվա է հավասար այդ ժամանակամիջոցը։ Մենք կարող ենք դա մոտավորապես հաշվել՝ չկատարելով կրկնվող բազմապատկումները երկուսով և շրջանցելով լոգարիթմական աղյուսակները։ Օգտվենք այն բանից, որ ։ Հետևաբար՝
,
այսինքն՝ մոտ քառորդ տրիլիոն վայրկյան։ Տարին ունի մոտ միլիոն, այսինքն՝ վայրկյան, ուստի՝
։
Տա՛սը միլիարդ տարի։ Ահա թե որքան ժամանակում կայրվեր մեկ գրամ փայտն առանց բոցի և ջերմության։
Այսպիսով, փայտը, ածուխը այրվում են և սովորական ջերմաստիճանում, ամենևին չվառվելով։ Կրակ ստանալու գործիքների գյուտը անխուսափելիորեն արագացրեց այդ չափազանց դանդաղ պրոցեսը միլիարդավոր անգամ։
ԵՂԱՆԱԿԻ ԲԱԶՄԱԶԱՆՈՒԹՅՈՒՆԸ
Խնդիր
Եղանակը մենք կբնութագրենք միայն մեկ հատկանիշով, այն է՝ երկինքը ամպամած է արդյոք, թե ոչ, այսինքն՝ կտարբերենք միայն պարզ և ամպամած օրերը։ Ի՞նչ եք կարծում, այդ դեպքում կլինե՞ն արդյոք շատ շաբաթներ՝ տարբեր եղանակի օրերի հաջորդումներով։
Թվում է թե քիչ. կանցնի մի երկու ամիս, և շաբաթվա պարզ ու ամպամած օրերի բոլոր կոմբինացիաները կսպառվեն, այդ ժամանակ անխուսափելիորեն կկրկնվի այն կոմբինացիաներից մեկը, որն արդեն դիտվել էր առաջ։
Փորձենք, սակայն, ճիշտ հաշվել, թե որքան տարբեր կոմբինացիաներ են հնարավոր այդ պայմաններում։ Դա այն խնդիրներից մեկն է, որն անսպասելիորեն հանգեցվում է մաթեմատիկական հինգերորդ գործողությանը։
Այսպիսով, մի շաբաթում պարզ և ամպամած օրերը քանի՞ տարբեր եղանակներով կարող են իրար հաջորդել։
Լուծում
Շաբաթվա աոաջին օրը կարող է լինել կամ պարզ, կամ ամպամած. նշանակում է, առայժմ ունենք երկու «կոմբինացիա»։
Երկու օրվա ընթացքում հնարավոր են պարզ և ամպամած օրերի հետևյալ հաջորդականությունը՝
պարզ և պարզ,
պարզ և ամպամած,
ամպամած և պարզ,
ամպամած և ամպամած։
Ընդամենը երկու օրվա ընթացքում կա տարբեր տեսակի հաջորդականություն։ Երեք օրվա ընթացքում առաջին երկու օրերի չորս կոմբինացիաներից յուրաքանչյուրը զուգակցվում է երրորդ օրվա, երկու կոմբինացիաների հետ. բոլոր տեսակի հաջորդականությունները կլինեն՝
։
Չորս օրերի ընթացքում հաջորդականությունների թիվը հասնում է՝
։
Հինգ օրերի համար հնարավոր է , վեց օրերի համար՝ և, վերջապես, շաբաթվա համար՝ տարբեր տեսակի հաջորդականություն։
Այստեղից հետևում է, որ շաբաթն ունի պարզ և ամպամած օրերի տարբեր հաջորդականություն։ օր հետո անհրաժեշտորեն պետք է կրկնվի նախկին միացություններից մեկը. կրկնությունը, իհարկե, կարող է տեղի ունենալ և շուտ, բայց օրը մի այնպիսի ժամանակ է, որն անցնելով՝ նման կրկնությունն անխուսափելի է։ Եվ հակառակը, կարող է անցնել ամբողջ երկու տարի, անգամ՝ ավելի ( տարի և օր), որոնց ընթացքում ոչ մի շաբաթ ըստ եղանակի նման չի լինի մյուսին։
ԳԱՂՏՆԻ ՓԱԿՈՎ ԿՈՂՊԵՔ
Խնդիր
Սովետական մի հիմնարկում հայտաբերվել էր մինչռևոլյուցիոն տարիներից մնացած չհրկիզվող պահարան։ Գտնվեց նաև նրա համար մի բանալի, սակայն նրանից օգտվելու համար պետք է իմանային կողպեքի գաղտնիքը. պահարանի դուռը կբացվեր միայն այն ժամանակ, երբ գռան շրջանակների օղերի վրա այբբենական կարգով դասավորված տառերից կազմեին որոշակի բառ։ Քանի որ ոչ ոք այդ բառը չգիտեր, ապա պահարանը չկոտրելու համար որոշվել էր փորձել շրջանակների մեջ եղած տառերի բոլոր կոմբինացիաները։ Մի կոմբինացիա կազմելու համար պահանջվում էր վայրկյան ժամանակ։
Կարելի՞ է արդյոք հուսալ, որ պահարանը կբացվի մոտակա աշխատանքային օրվա ընթացքում։
Լուծում
Հաշվենք, թե ընդամենը քանի՞ կոմբինացիա էր հարկավոր փորձել։
Առաջին շրջանակի տառերից յուրաքանչյուրը կարող է համադրվել երկրորդ շրջանակի տառերից յուրաքանչյուրի հետ։ Նշանակում է, հնարավոր է երկտառային
կոմբինացիա։
Այս կոմբինացիաներից յուրաքանչյուրին կարելի է միացնել երրորդ շրջանակի տառերից ցանկացածը։ Ուստի հնարավոր է եռատառային
կոմբինացիա։
Այս ձևով որոշում ենք, որ հնարավոր է չորստառային կոմբինացիաներ՝ , հինգառային՝ կամ ։ Ավելի քան միլիոն այս կոմբինացիաները կազմելու համար, եթե յուրաքանչյուրին հաշվենք վայրկյան, կպահանջվի
վայրկյան։
Այդ կազմում է մոտ ժամ կամ ութժամյա աշխատանքային օր՝ ավելի քան տարի։
Նշանակում է պահարանը մոտակա աշխատանքային օրում բացելու շանսը ունի -ը : -ի կամ -ը : -ի հավանականություն։ Դա շատ փոքր հավանականություն է։
ՍՆԱՀԱՎԱՏ ՀԵԾԱՆՎՈՐԴԸ
Խնդիր
Մեկը մի հեծանիվ գնեց, ցանկանալով քշել սովորել։ Պարզվեց, որ հեծանվի տերը բացառիկ սնահավատ մարդ է։ Իմանալով հեծանվի անվի «ութաձև» պտտվելու վնասվածքի գոյության մասին (восьмepка), նա գտավ, որ երբեք հաջողություն չի ունենա, եթե նրան ընկնի հեծանվի այնպիսի համար, որի մեջ թվանշաններից թեկուզ մեկը լինի։ Սակայն, համար ստանալու գնալիս նա իրեն մխիթարեց հետևյալ դատողությամբ։ Յուրաքանչյուր գրված թվի մեջ կարող է լինել թվանշան՝ ։ Դրանցից «անբախտը» հանդիսանում է միայն թվանշանը։ Ուստի տասից միայն մեկ համարը կարող է լինել «անբախտ»։
Ճիշտ է արդյո՞ք այդ դատողությունը։
Լուծում
Հեծանվային համարները վեցանիշ են լինում։ Ընդամենը կա համար՝ և այլն, մինչև ։ Հաշվենք, թե քանի «բախտավոր» համարներ գոյություն ունեն։ Առաջին տեղում կարող է լինել ինը «բախտավոր» թվանշաններից ցանկացածը ։ Երկրորդ տեղում՝ նույնպես այդ ինը թվանշաններից ցանկացածը։ Ուստի գոյություն կունենան «բախտավոր» երկանիշ կոմբինացիաներ։ Այդ կոմբինացիաներից յուրաքանչյուրին կարելի է կցագրել (երրորդ տեղում) ինը թվանշաններից ցանկացածը, այնպես որ հնարավոր է «բախտավոր» եռանիշ կոմբինացիաներ՝
։
Այսպիսով որոշում ենք, որ վեցանիշ «բախտավոր» կոմբինացիաների թիվը հավասար է ։ Սակայն անհրաժեշտ է հաշվի առնել, որ այդ թվի մեջ մտնում է կոմբինացիան, որը պիտանի չէ որպես հեծանվային համար։ Այսպիսով, հեծանվային համարների «բախտավոր» թիվը հավասար է , որը կազմում է բոլոր համարների -ից փոքր-ինչ ավելի, բայց ոչ -ը, ինչպես ենթադրում էր հեծանվորդը։
Թողնում ենք ընթերցողին ինքնուրույնաբար համոզվելու, որ ութանիշ համարների մեջ «անբախտ» համարներն ավելի շատ են, քան՝ «բախտավորները»։
ԿՐԿՆՎՈՂ ԿՐԿՆԱՊԱՏԿՄԱՆ ԱՐԴՅՈՒՆՔԸ
Կրկնվող կրկնապատկման դեպքում ամենափոքր մեծության չափազանց արագ աճման մասին զարմանալի օրինակ է տալիս շախմատ խաղի գյուտարարի պարգևատրման վերաբերյալ հանրածանոթ առասպելը[3]։ Կանգ չառնելով այդ կլասիկ օրինակի վրա՝ բերենք ուրիշ, ոչ այնքան հայտնի օրինակներ։
Խնդիր
Հողաթափիկ ինֆուզորիան (միաբջիջ միկրոսկոպիկ օրգանիզմ) յուրաքանչյուր ժամում, (միջին հաշվով) բաժանվում է երկու հավասար մասի։ Եթե այդպիսով ծնված բոլոր ինֆուզորիաները մնային կենդանի, ապա որքա՞ն ժամանակ հարկավոր կլիներ, որպեսզի մի հողաթափիկի սերնդի զբաղեցրած ծավալը հավասար լիներ Արեգակի ծավալին։
Հաշվելու տվյալներն են՝ հողաթափիկի -րդ սերունդը, որը բաժանվելուց հետո չի ոչնչացել, զբաղեցնում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1\;խոր.\;մ} ծավալ, Արեգակի ծավալն ընդունենք հավասար Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10^{27}\;խոր.\;մ} ։
Լուծում
Խնդիրը հանգում է այն բանին, թե քանի անգամ պետք կրկնապատկել Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1\;խոր.\;մ} -ը, որպեսզի ստացվի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10^{27}\;խոր.\;մ} ծավալ։ Կատարենք հետևյալ ձևափոխությունները՝
։
Քանի որ , ապա նշանակում է՝ Արեգակի ծավալին հասնելու համար քառասուներորդ սերունդը պետք է ենթարկվի դարձյալ բաժանման։ Սերունդների ընդհանուր թիվը, հաշվելով առաջինից, հավասար է ։ Հեշտ է հաշվել, որ այդ տեղի կունենա -րդ օրում։
Նկատենք, որ մի միկրոբիոլոգ (Մետալնիկովը) փաստորեն դիտել է հողաթափիկի բաժանումը։ Թողնում ենք ընթերցողին անձամբ հաշվելու, թե ինչպիսի հսկայական ծավալ կզբաղեցներ վերջին սերունդը, եթե ոչ մի ինֆուզորիա այդ քանակությունից չոչնչանար։
Այս խնդրում դիտարկված հարցը կարելի է շարադրել, այսպես ասած, հակադարձ տեսքով՝
Պատկերացնենք, որ մեր Արեգակը բաժանվել է երկու հավասար մասի, կեսը նույնպես բաժանվել է երկու հավասար մասի և այլն։ Քանի՞ այդպիսի բաժանումներ հարկավոր կլինի, որպեսզի ստացվեն ինֆուզորիայի մեծությամբ մասնիկներ։ Թեև պատասխանն արդեն հայտնի է ընթերցողներին (), այնուամենայնիվ, այն զարմացնում է իր անչափ համեստ լինելով։
Ինձ առաջարկել են նույն խնդիրը այսպիսի տեսքով։
Թղթի թերթը բաժանում են երկու հավասար մասի, ստացված մի կեսը նորից բաժանում են երկու հավասար մասի և այլն։ Որքա՞ն բաժանում հարկավոր կլինի, որպեսզի ստացվեն ատոմին հավասար մասնիկներ։
Ենթադրենք թղթի թերթը կշռում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; գ} և ընդունենք, որ ատոմի կշռի մեծությունը մոտ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \frac{1}{10^{24}}\;գ} է։ Քանի որ վերջին արտահայտության մեջ կարելի է -ը փոխարինել մոտավորապես նրան հավասար արտահայտությամբ, ապա պարզ է, որ թղթի երկու հավասար մասի բաժանելը կպահանջվեր կրկնել ընդամենը և ոչ թե միլիոն անգամ, ինչպես երբեմն լսվում է որպես այդ խնդրի հարցի պատասխան։
ԱՆԳԱՄ ԱՎԵԼԻ ԱՐԱԳ
Էլեկտրական գործիքը, որը կոչվում է տրիգեր, պարունակում է երկու, էլեկտրոնային լամպեր (այսինքն՝ մոտավորապես այնպիսի լամպեր, ինչպիսիք կիրառվում են ռադիոընդունիչների մեջ)։ Հոսանքը տրիգերում կարող է գնալ միայն մեկ լամպի միջով՝ կա՛մ «ձախի», կա՛մ «աջի»։ Տրիգերն ունի երկու կոնտակտ, որոնց կարելի է դրսից կարճատև էլեկտրական ազդանշան (իմպուլս) հաղորդել և երկու կոնտակտ, որոնցով տրիգերից ստացվում է պատասխան իմպուլսը։
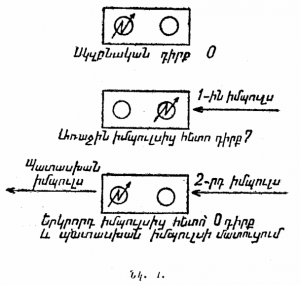
Դրսից էլեկտրական իմպուլսի մուտքի պահին տրիգերը հոսանքափոխվում է. այն լամպը, որի միջով հոսանքն անցել է, անջատվում է, և հոսանքն սկսում է գնալ արդեն մյուս լամպի միջով։ Պատասխան իմպուլսը տրիգերը տալիս է այն պահին, երբ անջատվում է աջ լամպը և միացվում ձախը։
Հետևենք, թե ինչպես կաշխատի տրիգերը, եթե մեկը մյուսի ետևից, նրան մոտեցնենք մի քանի էլեկտրական իմպուլսներ։
Տրիգերի վիճակը կբնութագրենք ըստ նրա աջ լամպի, եթե հոսանքն աջ լամպի միջով չի գնում, ապա կասենք, որ տրիգերը գտնվում է « դիրքում», իսկ եթե հոսանքն աջ լամպի միջով է գնում, ապա՝ « դիրքում»։
Դիցուք, տրիգերը սկզբում գտնվում է դիրքում, այսինքն՝ հոսանքն անցնում է ձախ լամպի միջով (նկ. 1)։ Առաջին իմպուլսից հետո հոսանքը կանցնի աջ լամպով, այսինքն՝ տրիգերը կփոխարկվի դիրքի։ Այդ դեպքում տրիգերից պատասխան իմպուլս չի ստացվի, քանի որ պատասխան ազդանշանը տրվում է աջ (այլ ոչ ձախ) լամպի անջատման պահին։
Երկրորդ իմպուլսից հետո հոսանքը կանցնի արդեն ձախ լամպով, այսինքն՝ տրիգերը նորից ընդունում է դիրքը։ Սակայն այդ դիրքում տրիգերը կտա պատասխան ազդանշան (իմպուլս)։
Վերջ ի վերջո (երկու իմպուլսներից հետո) տրիգերը կրկին կընդունի իր սկզբնական դրությունը։ Ուստի երրորդ իմպուլսից (ինչպես և առաջինից հետո) տրիգերը կընդունի , իսկ չորրորդից հետո (ինչպես և երկրորդից հետո) դիրքը՝ պատասխան ազդանշանի միաժամանակյա մատուցմամբ և այլն։ Յուրաքանչյուր երկու իմպուլսներից հետո տրիգերի դրությունը կրկնվում է։
Այժմ պատկերացնենք, որ կան մի քանի տրիգերներ և որ արտաքին իմպուլսները հաղորդվում են առաջին տրիգերին, առաջին տրիգերի պատասխան իմպուլսները հաղորդվում են երկրորդին, երկրորդի պատասխան իմպուլսները՝ երրորդին և այլն (նկ. 2-րդում տրիգերները դասավորված են մեկը մյուսից հետո՝ ձախից աջ)։ Հետևենք, թե ինչպես կաշխատի տրիգերների այդպիսի շղթան։
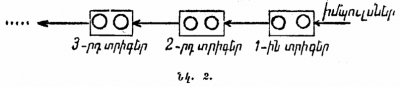
Դիցուք, սկզբից բոլոր տրիգերները գտնվում էին դիրքում։ Օրինակ, հինգ տրիգերներից կազմված շղթայի համար մենք ունեինք կոմբինացիան։ Առաջին իմպուլսից հետո առաջին տրիգերը (ամենաաջը) կընդունի դիրքը, իսկ քանի որ այդ դեպքում պատասխան իմպուլս չի լինի, ապա մնացած բոլոր տրիգերները կմնան դիրքերում, այսինքն՝ շղթան կբնութագրվի կոմբինացիայով։ Երկրորդ իմպուլսից հետո առաջին տրիգերը կանջատվի (կընդունի դիրքը), բայց այդ դեպքում ստացվում է պատասխան իմպուլս, որի շնորհիվ էլ միացվում է երկրորդ տրիգերը։ Մնացած տրիգերները կմնան դիրքերում, այսինքն՝ կստացվի կոմբինացիան։ Երրորդ իմպուլսից հետո միացվում է առաջին տրիգերը, իսկ մնացածները չեն փոխում իրենց դիրքերը։ Մենք կունենանք կոմբինացիան։ Չորրորդ իմպուլսից հետո անջատվում է առաջին տրիգերը՝ տալով պատասխան ազդանշան. այդ պատասխան իմպուլսից կանջատվի երկրորդ տրիգերը և նույնպես կտա պատասխան իմպուլս. վերջապես, այդ վերջին իմպուլսից միացվում է երրորդ տրիգերը։ Արդյունքում մենք կստանանք կոմբինացիան։
Համանման դատողությամբ կարելի է շարունակել և հետագայում։ Տեսնենք, թե այդ դեպքում ի՛նչ կստացվի.
| -ին | իմպուլս | կոմբինացիա | |
| -րդ | » | » | |
| -րդ | » | » | |
| -րդ | » | » | |
| -րդ | » | » | |
| -րդ | » | » | |
| -րդ | » | » | |
| -րդ | » | » |
Մենք նկատում ենք, որ տրիգերների շղթան «հաշվում է» դրսից տրված ազդանշանները և յուրատեսակ եղանակով՝ «գրում է» այդ ազդանշանների թիվը։ Դժվար չէ նկատել, որ տրված իմպուլսների թվի «գրելը» կատարվում է ոչ թե մեզ համար սովորական տասնորդական սիստեմով, այլ թվարկության երկուական սիստեմով։
Թվարկության երկուական սիստեմով ամեն մի թիվը գրվում է զրոներով և մեկերով։ Հաջորդ կարգի մեկը ոչ թե տասն անգամ (ինչպես սովորական տասնորդական գրառումը), այլ միայն երկու անգամ է մեծ նախորդ կարգի մեկից։ Երկուական գրառման մեջ վերջին տեղում (ամենաաջ) գրված մեկը, սովորական մեկ է։ Հաջորդ կարգի մեկը (աջից երկրորդ տեղում) նշանակում է երկու, հաջորդ մեկը նշանակում է չորս, այնուհետև ութ և այլն։
Օրինակ, թիվը երկուական սիստեմում գրվում է տեսքով։
Այսպիսով, տրիգերների շղթան «համրում է» տրված ազդանշանների թիվը և այն «գրում է» թվարկության երկուական սիստեմով։ Նշենք, որ տրիգերի հոսանքափոխումը, այսինքն՝ հաղորդվող մեկ իմպուլսի գրանցումը շարունակվում է ընդամենը... վայրկյանի մեկ տասմիլիոներորդի ընթացքում։ Ժամանակակից տրիգերային հաշվիչները կարող են մեկ վայրկյանում «համրել» մինչև իմպուլս և ավելին։ Դա մոտավորապես անգամ ավելի արագ է, քան այն հաշիվը, որը կարող է կատարել մարդը՝ առանց որևէ գործիքի. մարդու աչքը կարող է որոշակի տարբերել միմյանց հաջորդող ազդանշանները ոչ ավելի հաճախ, քան Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 0,1 \; վրկ} հետո։
Եթե շղթան կազմենք քսան տրիգերներից, այսինքն՝ տրված ազդանշանների թիվը գրենք երկուական վերլուծման ոչ ավելի քան քսան թվանշաններով, ապա կարելի է «հաշվել» մինչև . այս թիվը մեծ է միլիոնից։ Իսկ եթե շղթան կազմենք տրիգերներից, ապա դրանց միջոցով կարելի է գրել հայտնի «շախմատային թիվը»։
Վայրկյանում հարյուրավոր ազդանշանները համրելու հնարավորությունը շատ կարևոր է միջուկային ֆիզիկային վերաբերող էքսպերիմենտալ աշխատանքների համար։ Օրինակ, կարելի է համրել այս կամ այն տեսքի մասնիկների թիվը, որոնք թռչում են ատոմի տրոհման ժամանակ։
ՎԱՅՐԿՅԱՆՈՒՄ ԳՈՐԾՈՂՈՒԹՅՈՒՆ
Զարմանալի է, որ տրիգերային սխեմաները թույլ են տալիս նույնպես գործողություններ կատարել թվերի հետ։ Տեսնենք, օրինակ, թե ինչպես կարելի է իրագործել երկու թվերի գումարումը։
Դիցուք, տրիգերների երեք շղթաները միացած են այնպես, ինչպես ցույց է տրված 3-րդ նկարում։ Տրիգերների վերին շղթան ծառայում է առաջին գումարելին գրելու համար, երկրորդ շղթան՝ երկրորդ գումարելին գրելու համար, իսկ ներքևի շղթան՝ գումարը ստանալու համար։ Գործիքի միացման մոմենտին ներքևի շղթայի տրիգերին անցնում են իմպուլսներ վերին և միջին շղթաների այն տրիգերներից, որոնք գտնվում են դիրքում։
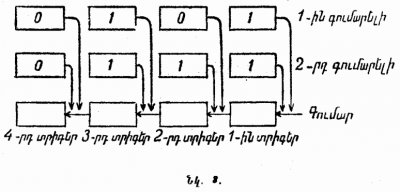
Դիսուք, օրինակ, ինչպես այդ ցույց է տրված 3-րդ նկարում,առաջին երկու շղթաներում գրված են և գումարելիները (թվարկության երկուական սիստեմով)։ Այդ ժամանակ ներքևի շղթայի առաջին (ամենաաջ) տրիգերի վրա գործիքի միացման պահին առաջանում են երկու իմպուլսներ՝ առաջին տրիգերների յուրաքանչյուր գումարելիներից։ Մենք արդեն գիտենք, որ երկու իմպուլսների ստացման հետևանքով առաջին տրիգերը կմնա դիրքում, բայց կտա պատասխան իմպուլս երկրորդ տրիգերին։ Բացի այդ, երկրորդ տրիգերին ազդանշան է գալիս երկրորդ գումարելիից։ Այսպիսով, երկրորդ տրիգերի վրա առաջանում են երկու իմպուլս, որի հետևանքով էլ երկրորդ տրիգերը կգտնվի դիրքում և կուղարկի պատասխան իմպուլս երրորդ տրիգերին։ Բացի այդ, երրորդ տրիգերին են գալիս դարձյալ երկու իմպուլսներ (գումարելիներից յուրաքանչյուրից)։ Ստացված երեք ազդանշանների հետևանքով երրորդ տրիգերը կանցնի դիրքին և կտա պատասխան իմպուլս։ Այդ պատասխան իմպուլսը չորրորդ տրիգերը կփոխադրի դիրքը (այլ ազդանշաններ չորրորդ տրիգերի վրա չեն ստացվում)։ Այսպիսով, 3-րդ նկարում պատկերված գործիքը կատարեց (թվարկության երկուական սիստեմով) երկու թվերի գումարում «սյունակով»։
կամ տասնորդական սիստեմով՝ ։ Տրիգերների ներքևի շղթայում պատասխան իմպուլսները համապատասխանում են նրան, որ գործիքը, կարծես թե, «հիշում է մտքում» մեկ միավոր և այն տեղափոխում հետևյալ կարգը, այսինքն՝ կատարում է նույնը, ինչ մենք կատարում ենք «սյունակով» գումարելիս։
Իսկ եթե յուրաքանչյուր շղթայում լիներ ոչ թե , այլ սսենք, տրիգեր, ապա կարելի էր կատարել թվերի գումարում միլիոնի սահմաններում, իսկ մեծ թվով տրիգերների դեպքում կարելի է գումարել է՛լ ավելի մեծ թվեր։
Նկատենք, որ իրականում գործիքը գումարումներ կատարելու համար պետք է ունենա զգալիորեն ավելի բարդ սխեմա, քան 3-րդ նկարում պատկերվածը։ Մասնավորապես գործիքին պետք է միացված լինի հատուկ հարմարանք, որը իրագործի ազդանշանների «ուշացումը»։ Ընդ որում ցույց տրված սխեմայում գործիքի ազդանշանները երկու գումարելիներից ներքևի շղթայի առաջին տրիգերն են անցնում միաժամանակ (գործիքի միացման պահին)։ Արդյունքում երկու ազդանշաններն էլ միաձուլվում են, և տրիգերը դրանց ընկալում է որպես մեկ ազդանշան, այլ ոչ թե՝ երկու։ Դրանից խուսափելու նպատակով պետք է, որ ազդանշանները գումարելիներից հաղորդվեին ոչ միաժամանակ, այլ մեկը մյուսից հետո, որոշ «ուշացումով»։ Այդպիսի «ուշացումների» առկայությունը հանգում է նրան, որ երկու թվերի գումարելի ավելի շատ ժամանակ է պահանջում, քան մեկ ազդանշանի գրանցումը տրիգերային հաշվիչում։
Փոխելով սխեման՝ կարելի է ստիպել, որ գործիքը կատարի ոչ թե գումարում, այլ հանում։ Կարելի է նույնպես իրագործել բազմապատկում (այն հանգում է գումարման հաջորդական կատարմանը, և դրա համար պահանջում է մի քանի անգամ ավելի շատ ժամանակ, քան գումարումը), բաժանումը և այլ օպերացիաներ։
Այն սարքավորումները, որոնց մասին խոսվեց վերևում, կիրառվում են ժամանակակից հաշվիչ մեքենաներում։ Այդ մեքենաները մեկ վայրկյանում թվերով կարող են կատարել մինչև և ավելի գործողություններ։ Թվում է, թե գործողություններ կատարելու այդպիսի գլխապտույտ արագությունը պետք չէ։ Օրինակ, ինչ տարբերություն այն բանում, թե որքան ժամանակում մեքենան 15-անիշ թիվը կբարձրացնի քառակուսի՝ վայրկյանի մեկ տասհազարերորդական մասո՞ւմ թե՞, ասենք, քառորդ վայրկյանում։ Ե՛վ այս, և՛ այն մեզ թվում է խնդրի «ակնթարթային լուծում»։
Սակայն մի շտապեք եզրակացություններ անելու։ Վերցնենք այսպիսի օրինակ։ Լավ շախմատիստը, նախքան խաղաքայլն անելը, վերլուծում է տասնյակ և անգամ հարյուրավոր հնարավոր տարբերակներ։ Եթե, ասենք, մի տարբերակի հետազոտումը պահանջում է մի քանի վայրկյան, ապա հարյուրավոր տարբերակների վերլուծման համար հարկավոր են րոպեներ և տասնյակ րոպեներ։
Շատ անգամ պատահում է, որ խաղացողները բարդ պարտիաներում ընկնում են «ցեյտնոտի» մեջ, այսինքն՝ հարկադրվում են խաղաքայլերն արագացնել, քանի որ նախորդ խաղաքայլերի մտածելու վրա նրանք ծախսել են գրեթե նրանց համար սահմանված ամբողջ ժամանակը։ Բայց ինչո՞ւ շախմատային պարտիաների տարբերակների հետազոտումը չհանձնարարել մեքենային։ Չէ՞ որ վայրկանում կատարելով հազար հաշվումներ՝ մեքենան հետազոտում է բոլոր տարբերակները «ակնթարթորեն» և երբեք չի ընկնում ցեյտնոտի մեջ...
Դուք, իհարկե, կառարկեք, որ այլ գործ է հաշվումները (թեկուզ և շատ բարդ)) և այլ շախմատ խաղալը։ Մեքենան չի կարող այդ անել։ Շախմատիստը տարբերակների հետազոտման ժամանակ չի հաշվում, այլ մտածում է։
Չվիճենք, մենք ստորև այդ հարցին դեռ կանդրադառնանք։
ՇԱԽՄԱՏԱՅԻՆ ՀՆԱՐԱՎՈՐ ՊԱՐՏԻԱՆԵՐԻ ԹԻՎԸ
Անդրադառնանք շախմատային տարբեր պարտիաների թվի մոտավոր հաշվարկմանը, այն է՝ ընդհանրապես քանի պարտիա կարող է խաղացվել շախմատային տախտակի վրա։ Տվյալ դեպքում ճիշտ հաշվարկը անհնարին է, բայց մենք ընթերցողին կծանոթացնենք շախմատային հնարավոր պարտիաների թվի մեծությունը մոտավորապես գնահատելու փորձի հետ։ Բելգիական մաթեմատիկոս Մ. Կրայչիկի „Математика игр и математические развлечения” գրքում գտնում ենք այսպիսի հաշվարկ.
«Առաջին քայլի ժամանակ սպիտակները կարող են ընտրել խաղաքայլերից մեկը ( խաղաքայլ ութ զինվորի համար, որոնցից յուրաքանչյուրը կարող է տեղաշարժվել մեկ կամ երկու դաշտի վրա, և 2-ական խաղաքայլ յուրաքանչյուր ձիու համար)։ Սպիտակների յուրաքանչյուր խաղաքայլին սևերը կարող են պատասխանել միևնույն խաղաքայլից մեկով։ Զուգադրելով սպիտակների յուրաքանչյուր խաղաքայլը սևերի յուրաքանչյուր խաղաքայլի հետ՝ կունենանք տարբեր պարտիաներ յուրաքանչյուր կողմի առաջին քայլից հետո։
Աոաջին քայլից հետո հնարավոր խաղաքայլերի թիվը մեծանում է։ Եթե, օրինակ, սպիտակներն արել են առաջին e2—e4 խաղաքայլը, նրանք երկրորդ քայլի համար կարող են ընտրել խաղաքայլից որևէ մեկը։ Հետագայում հնարավոր խաղաքայլերի թիվն ավելի մեծ է։ Միայն թագուհին, կանգնելով, օրինակ, d5 դաշտում՝ կարող է ընտրել խաղաքայլից մեկը (ենթադրելով, որ բոլոր դաշտերը, որտեղ նա կարող է կանգնել, ազատ են)։ Սակայն հաշվարկը պարզ դարձնելու համար նկատի կունենանք հետևյալ թվերի միջինը՝
առաջին հինգ խաղաքայլերում երկու կողմերի համար -ական հնարավոր խաղաքայլ։
հետագա խաղաքայլերի դեպքում երկու կողմերի համար էլ -ական հնարավոր խաղաքայլ։
Բացի դրանից։ ընդունենք, որ նորմալ պարտիայի խաղաքայլերի միջին թիվը հավասար է -ի։ Այն ժամանակ հնարավոր պարտիաների թվի համար կունենանք հետևյալ արտահայտությունը՝
։
Այս արտահայտության մոտավոր մեծությունը որոշելու համար օգտվենք հետևյալ ձևափոխություններից և պարզեցումներից՝
։
-ը փոխարինենք նրան մոտ թվով՝ -ով, այսինքն -ով։
արտահայտությունը ներկայացնենք հետևյալ տեսքով՝
։
Հետևաբար՝
։
Այս թվից շախմատի խաղի գյուտի համար պահանջված պարգևը՝ ցորենի հատիկների առասպելական բազմությունը չափազանց ետ է մնում։ Եթե երկրագնդի ամբողջ բնակչությունը օր ու գիշեր շախմատ խաղար, անելով ամեն վայրկյանում մեկական քայլ, ապա շախմատային բոլոր հնարավոր պարտիաները սպառելու համար այդպիսի ընդհանուր և անընդհատ խաղը պետք է շարունակվեր ոչ պակաս դար։
ՇԱԽՄԱՏԱՅԻՆ ԱՎՏՈՄԱՏԻ ԳԱՂՏՆԻՔԸ
Դուք, հավանաբար, շատ կզարմանաք՝ իմանալով, որ մի ժամանակ գոյություն են ունեցել շախմատային ավտոմատներ։ Իրոք, ինչպե՞ս այդ համատեղել այն բանի հետ, որ շախմատային տախտակի վրա ֆիգուրների կոմբինացիաները գործնականորեն անսահման են։
Դա պարզաբանվում է հեշտությամբ։ Գոյություն է ունեցել ոչ թե շախմատային ավտոմատ, այլ միայն հավատ նրա նկատմամբ։ Հատուկ ժողովրդականություն է ունեցել հունգարական մեխանիկ Վոլֆգանգ ֆոն Կեմպելենի (1734-1804) ավտոմատը, որն իր մեքենան ցույց տվեց ավստրիական և ռուսական պալատներում, իսկ այնուհետև հրապարակորեն ցուցադրեց Փարիզում և Լոնդոնում։
Նապոլեոն առաջինը խաղացել է այդ ավտոմատի հետ, վստահ լինելով, որ իր ուժը չափում է մեքենայի ուժի հետ։ Անցյալ դարի կեսերին հանրահայտ ավտոմատն ընկավ Ամերիկա, և այնտեղ էլ Ֆիլադելֆիայի հրդեհի ժամանակ վերջ տրվեց նրա գոյությանը։
Շախմատային խաղի մյուս ավտոմատները արդեն չեն ունեցել այդպիսի հռչակ։ Այնուամենայնիվ, հավատը նման ավտոմատորեն գործող մեքենաների գոյության նկատմամբ չսպառվեց նաև հետագայում։
Իրականում ոչ մի շախմատային մեքենա ավտոմատիկորեն չի գործել։ Ներսում թագնվում էր հմուտ, կենդանի շախմատիստ, որը և շարժում էր ֆիգուրները։ Այն կեղծ ավտոմատը, որի մասին մենք հիմա հիշատակեցինք, իրենից ներկայացրել է մեծածավալ արկղ բարդ մեխանիզմով։ Արկղի վրա կար շախմատային տախտակ՝ ֆիգուրներով, որոնք տեղաշարժվում էին մեծ տիկնիկի ձեռքով։ Նախքան խաղն սկսվելը հասարակությանը հնարավորություն էին տալիս համոզվելու, որ արկղի ներսում ոչինչ չկա, բացի մեխանիզմի դետալներից։ Սակայն նրա մեջ մնում էր բավականաչափ տեղ, որպեսզի թաքնվեր ոչ մեծ հասակի մարդ (այդ դերը խաղում էին հանրաճանաչ խաղացողներ Իոհան Ալգայերը և Վիլյամ Լյուիսը)։ Հավանական է, որ մինչև հասարակությանը հաջորդաբար ցույց էին տալիս արկղի տարբեր մասերը, թաքնված մարդը անաղմուկ տեղափոխվում էր հարևան բաժանմունքը։ Իսկ մեխանիզմը ապարատի աշխատանքին ոչ մի մասնակցություն չէր ունենում և միայն քողարկում էր կենդանի խաղացողի ներկայությունը։
Ամբողջ ասածից կարելի է անել հետևյալ եզրակացությունը՝ շախմատային պարտիաների թիվը գործնականորեն անսահման է, իսկ մեքենա, որը թույլատրում է ավտոմատիկորեն ընտրել ամենաճիշտ խաղաքայլը, գոյություն ունի միայն դյուրահավատ մարդկանց երևակայության մեջ։ Ուստի, շախմատային ճգնաժամի երկյուղ կրելու հարկ չկա։
Սակայն վերջին տարիներում տեղի են ունեցել դեպքեր, որոնք թույլ են տալիս կասկածելու այդ եզրակացության ճշտությունը։ Ներկայումս արդեն գոյություն ունեն շախմատ «խաղացող» մեքենաներ։ Դրանք բարդ հաշվիչ մեքենաներն են, որոնք հնարավորություն են տալիս վայրկյանում կատարել հազարավոր հաշվումներ։ Այդպիսի մեքենաների մասին մենք արդեն խոսել ենք։ Ինչպե՞ս կարող է մեքենան շախմատ «խաղալ»։
Իհարկե, հաշվիչ ոչ մի մեքենա ոչինչ անել չի կարող բացի թվերով գործողություններից։ Բայց մեքենայով հաշվումը կատարվում է գործողությունների որոշակի սխեմայով, նախապես կազմված որոշակի ծրագրով։
Շախմատային «ծրագիրը» կազմվում է մաթեմատիկոսների կողմից խաղի որոշակի տակտիկայի հիման վրա. ընդսմին, տակտիկա ասելով հասկացվում է կանոնների սիստեմը, որը թույլատրում է յուրաքանչյուր դիրքի համար ընտրել միակ («ամենալավագույն»-ը այդ տակտիկայի իմաստով) խաղաքայլը։ Ահա այդպիսի տակտիկայի օրինակներից մեկը։ Յուրաքանչյուր ֆիգուրին վերագրվում է միավորների որոշակի թիվ (արժեք)։
| Թագավոր | +200 միավոր | Զինվոր | +1 միավոր |
| Թագուհի | +9 միավոր | Ետ մնացած զինվոր | -0,5 միավոր |
| Նավակ | +5 միավոր | Մեկուսացված զինվոր | -0,5 միավոր |
| Փիղ | +3 միավոր | Կրկնակի զինվոր | -0,5 միավոր |
| Ձի | +3 միավոր |
Բացի այդ, որոշակի ձևով գնահատվում են դիրքային առավելությունները (ֆիգուրների շարժունակությունը, ֆիգուրների դասավորությունը կենտրոնին ավելի մոտ, քան ծայրերում և այլն), որոնք արտահայտվում են միավորի տասներորդ մասերով։ Սպիտակ ֆիգուրների համար միավորների ընդհանուր գումարից հանում ենք սև ֆիգուրների համար միավորների ընդհանուր գամարը։ Ստացված տարբերությունը որոշ չափով բնութագրվում է սպիտակների նյութական և դիրքային առավելությունը սևերի նկատմամբ։ Եթե այդ տարբերությունը դրական է, ապա սպիտակների մոտ ավելի հարմար դրություն է, քան սևերի մոտ, իսկ եթե այն բացասական է՝ ավելի քիչ հարմար դրություն։
Հաշվիչ մեքենան հաշվում է, թե ինչպես կարող է փոխվել մատնանշված տարբերությունը մոտակա երեք խաղաքայլերի ընթացքում, ընտրում է ամենալավագույն տարբերակը երեք խաղաքայլերի երեք հնարավոր կոմբինացիաներից և այն տպում է հատուկ քարտի վրա՝ «խաղաքայլն» արված է[4]։
Մեքենան մեկ խաղաքայլի վրա վատնում է շատ քիչ ժամանակ (նայած ծրագրի տեսակին և մեքենայի գործելու արագությանը), այնպես որ նա «ցեյտնոտից» չի վախենում։
Իհարկե, միայն երեք խաղաքայլ առաջ «մտածելը» մեքենային բնութագրում է որպես բավական թույլ «խաղացողի»[5], բայց կարելի է չկասկածել նրանում, որ ներկայումս հաշվիչ տեխնիկայի ավելի արագ կատարելագործմամբ մեքենաները շուտով «կսովորեն» անհամեմատ ավելի լավ «խաղալ» շախմատ։
Հաշվիչ մեքենաների համար շախմատային ծրագրեր կազմելու մասին ավելի մանրամասն պատմելը այս գրքում դժվար կլիներ։ Ծրագրերի մի քանի պարզագույն տեսակները մենք սխեմատիկ կերպով կդիտարկենք հաջորդ գլխում։
ԵՐԵՔ ԵՐԿՈՒՍՆԵՐՈՎ
Բոլորին հավանաբար հայտնի է, թե ինչպես պետք է գրել երեք թվանշան, որպեսզի նրանցով պատկերենք հնարավորին չափ մեծ թիվ։ Պետք է վերցնել երեք ինը և դրանց դասավորել այսպես՝
,
այսինքն՝ գրել երրորդ «գերաստիճան» -ից։
Այդ թիվն այնքան ահռելի մեծ է, որ ոչ մի բաղդատում չի օգնում պարզելու նրա վիթխարիությունը։ Տեսանելի տիեզերքի էլեկտրոնների թիվը չնչին է նրա հետ համեմատած։ Իմ «Հետաքրքրաշարժ թվաբանություն» գրքում (գլ. 10) արդեն ասվել է այդ մասին։ Անդրադառնում եմ այս խնդրին միայն նրա համար, որովհետև ուզում եմ այստեղ նրա ձևով առաջարկել մեկ ուրիշը։
Երեք երկուսներով գրել հնարավորին մեծ թիվ՝ չկիրառելով գործողությունների նշանները։
Լուծում
Ինների եռահարկ դասավորության թարմ տպավորության տակ դուք, հավանաբար, պատրաստ եք երկուսներին տալու այսպիսի դասավորություն՝
։
Սակայն այս անգամ սպասվելիք արդյունքը չի ստացվում։ Գրված թիվը մեծ չէ, անգամ փոքր է, քան -ը։ Իրոք, չէ՞ որ մենք ընդամենը գրել էինք միայն , այսինքն՝ ։
Իսկապես, երեք երկուսներից կազմված ամենամեծ թիվը ո՛չ է, և ո՛չ էլ (այսինքն՝ ), այլ՝
։
Օրինակը շատ ուսանելի է։ Այն ցույց է տալիս, որ մաթեմատիկայի մեջ վտանգավոր է վարվել համանմանությամբ. դա հեշտությամբ կարող է սխալ եզրակացությունների հասցնել։
ԵՐԵՔ ԵՐԵՔՆԵՐՈՎ
Խնդիր
Այժմ, հավանաբար, դուք զգուշորեն կմոտենաք հետևյալ խնդրի լուծմանը՝
Երեք երեքներով գրել հնարավորին մեծ թիվ՝ չկիրառելով գործողությունների նշանները։
Լուծում
Եռահարկ դասավորությունը ևս այստեղ չի բերում սպասելիք արդյունքին, քանի որ
-ը, այսինքն՝ -ը փոքր է, քան -ը։
Վերջին դասավորությունը տալիս է խնդրի հարցի պատասխանը։
ԵՐԵՔ ՉՈՐՍԵՐՈՎ
Խնդիր
Երեք չորսերով գրել հնարավորին մեծ թիվ՝ չկիրառելով գործողութսունների նշանները։
Լուծում
Եթե տվյալ դեպքում դուք վարվեք նախորդ երկու խնդիրների ձևով, այսինքն՝ տաք ալդպիսի պատասխան
,
ապա կսխալվեք, քանի որ այս անգամ եռահարկ դասավորությունը՝
հենց տալիս է ավելի մեծ թիվ։ Իրոք, , իսկ -ը մեծ է, քան -ը։
ԵՐԵՔ ՄԻԱՏԵՍԱԿ ԹՎԱՆՇԱՆՆԵՐՈՎ
Փորձենք խորանալ այդ կասկած առաջացնող երևույթի մեջ և պարզենք, թե ինչու որոշ թվանշաններ եռահարկ դասավորության դեպքում առաջացնում են թվային հսկաներ, իսկ մյուսները՝ ոչ։ Դիտարկենք ընդհանուր դեպքը։
Երեք հավասար թվանշաններով պատկերել հնարավորին մեծ թիվ չկիրառելով գործողությունների նշանները։
Թվանշանը նշանակենք տառով։
դասավորություններին համապատասխանում է հետևյալ արտահայտությունը՝
, այսինքն՝ ։
Իսկ եռահարկ դասավորությունն ընդհանուր տեսքով կպատկերվի այսպես`
Որոշենք` -ի ի՞նչ արժեքների դեպքում վերջին դասավորությունը կպատկերի ավելի մեծ թիվ, քան առաջին դասավորությունը։ Քանի որ երկու արտահայտություններն էլ հանդիսանում են հավասար ամբողջական հիմք ունեցող թվի աստիճաններ, ապա մեծ մեծությանը համապատասխանում է մեծ ցուցիչին։ Իսկ ե՞րբ կլինի՝
։[6]
Անհավասարության երկու մասն էլ բաժանենք -ի վրա, կստանանք՝
։
Հեշտ է նկատել, որ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a^{a—1}} -ն մեծ է -ից միայն այն պայմանի դեպքում, երբ -ն մեծ է -ից, քանի որ
,
մինչդեռ,
-ն և -ը
փոքր են -ից։
Այժմ հասկանալիի են այն անակնկալութլունները, որոնց մենք հանդիպեցինք նախորդ խնդիրները լուծելիս. երկուսների և երեքների համար հարկավոր էր վերցնել այլ դասավորություն, չորս և մեծ թվերի համար՝ այլ։
ՉՈՐՍ ՄԵԿԵՐՈՎ
Խնդիր
Չորս միավորներով գրել հնարավորին մեծ թիվ՝ չկիրառելով մաթեմատիկական գործողությունների և ոչ մի նշան։
Լուծում
Բնականորեն մտքով անցած թիվը չի պատասխանում խնդրի պահանջին, քանի որ՝
շատ անգամ մեծ է այդ թվից։ Հազիվ թե որևէ մեկը համբերություն ունենա այդ թիվը հաշվելու համար անգամ բազմապատկում կատարել -ով։ Բայց նրա մեծությունը անհամեմատ արագ կարելի է գնահատել լոգարիթմական աղյուսակների միջոցով։
Այդ թիվը գերազանցում է միլիարդը և, հետևաբար, թվից մեծ է ավելի քան միլիոն անգամ։
ՉՈՐՍ ԵՐԿՈՒՍՆԵՐՈՎ
Խնդիր
Դիտարկվող բնույթի խնդիրների զարգացման մեջ անենք հաջորդ քայլը և մեր հարցը դնենք չորս երկուսների համար։
Իչպիսի՞ դասավորության դեպքում են չորս երկուսները պատկերում ամենամեծ թիվ։
Լուծում
Հնարավոր են 8 կոմբինացիաներ՝
Այդ թվերից ո՞րն է ամենամեծը։
Նախ զբաղվենք վերին շարքով, այսինքն երկհարկ դասավորված թվերով։
Առաջինը՝ -ը, ակնհայտ է, փոքր է մնացած երեքից։ Հաջորդ երկուսը՝
և
բաղդատելու համար ձևափոխենք նրանցից երկրորդը՝
։
Վերջին թիվը մեծ է -ից, քանի որ աստիճանի թե՛ հիմքը, թե՛ ցուցիչը ավելի մեծ է։ քան -ը։
Այժմ -ը բաղդատենք առաջին տողի չորրորդ թվի՝ -ի հետ։ -ը փոխարինեք մեծ թվով և ցույց տանք, որ անգամ այդ մեծ թիվն իր մեծությամբ զիջում է թվին։
Իրոք՝
,
իսկ այս թիվը փոքր է քան թե -ը։
Այսպիսով, վերին տողի ամենամեծ թիվը -ն է։
Այժմ մեզ մնում է միմյանց հետ բաղդատել հինդ թվեր՝ հենց նոր ստացվածը և հետևյալ չորսը՝
։
Վերջին թիվն ընդամենը է և միանգամից դուրս է գալիս մրցությունից։
Այնուհետև, այդ շարքի առաջին թիվը հավասար է և փոքր է, քան -ը կամ -ը. փոքր է հաջորդ երկու թվերից յուրաքանչյուրից։ Բաղդատման ենթակա են, հետևաբար, երեք թվեր, որոնցից յուրաքանչյուրը -ի տարբեր աստիճաններն են։ Ակնհայտ է, որ մեծ է -ի այն աստիճանը, որի ցուցիչը մեծ է։ Բայց երեք ցուցիչներից՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 222,\:484\text{ և } 2^{20+2}\;(=\;2^{10\cdot2}\cdot2^2\approx10^6\cdot4)} [7]
վերջինը, բացահայտորեն ամենամեծն է։
Ուստի, ամենամեծ թիվը, որ կարելի է պատկերել չորս երկուսներով, այսպիսին է
։
Չդիմելով լոգարիթմական աղյուսակների, մենք կարող ենք մոտավոր պատկերացում կազմել այդ թվի մեծության մասին, օգտվելով հետևյալ մոտավոր հավասարությունից՝
։
Իրոք՝
։[8]
Այսպիսով, այդ թվի թվանշանների քանակը միլիոնից ավելի է։

ԳԼՈՒԽ ԵՐԿՐՈՐԴ։ ՀԱՆՐԱՀԱՇՎԻ ԼԵԶՈՒՆ
ՀԱՎԱՍԱՐՈՒՄՆԵՐ ԿԱԶՄԵԼՈՒ ԱՐՎԵՍՏԸ
Հանրահաշվի լեզուն հավասարումներն են։ «Թվերին կամ մեծությունների վերացական հարաբերություններին վերաբերող հարցը լուծելու համար։ Հարկավոր է միայն մայրենի լեզվից այն թարգմանել հանրահաշվական լեզվի»— գրել է մեծ Նյուտոնը հանրահաշվի իր դասագրքում, որը կոչվում է «Համընդհանուր թվաբանություն»։ Թե ինչպես է կատարվում այդպիսի թարգմանությունը մայրենի լեզվից հանրահաշվական լեզվի, Նյուտոնը ցույց է ավել օրինակներով։ Ահա դրանցից մեկը.
| Մայրենի լեզվով | Հանրահաշվի լեզվով |
| Վաճառականը ուներ մի որոշ գումար։ | |
| Առաջին տարում նա ծախսեց ֆունտ։ | |
| Մնացած գումարին նա ավելացրեց նրա երրորդ մասը։ | |
| Հաջորդ տարում նա նորից ծախսեց ֆունտ | |
| և մնացած գումարը մեծացրեց նրա երրորդ մասով։ | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \frac{4x—700}{3} + \frac{4x—700}{9} \;=\; \frac{16x-2800}{9}} |
| Երրորդ տարում նա դարձյալ ծախսեց ֆունտ։ | |
| Դրանից հետո, երբ նա մնացորդին ավելացրեց դրա երրորդ մասը, | |
| նրա դրամագլուխը դարձավ սկզբնականից երկու անգամ ավելի։ |
Վաճառականի սկզբնական դրամագլուխը որոշելու համար մնում է միայն լուծել վերջին հավասարումը։
Հավասարումների կազմելն ըստ խնդրի տվյալների ավելի դժվար է, քան դրանց լուծումը։ Դուք այժմ նկատեցիք, որ հավասարումներ կազմելու արվեստը իրոք հանգում է «մայրենի լեզվից հանրահաշվականի» հմտորեն թարգմանելուն։ Բայց հանրահաշվի լեզուն խիստ սակավաբառ է. դրա համար էլ մայրենի լեզվից հանրահաշվականի թարգմանելը այնքան էլ դյուրին գործ չէ։ Ըստ դժվարությունների թարգմանությունները լինում են տարբեր, դրանում կհամոզվի ընթերցողը առաջին աստիճանի հավասարումներ կազմելու վերաբերյալ բերված հետագա մի շարք օրինակներից։
ԴԻՈՖԱՆՏԻ ԿՅԱՆՔԸ
Խնդիր
Պատմությունը հնադարյան նշանավոր մաթեմատիկոս Դիոֆանտի կենսագրության վերաբերյալ մեզ քիչ բան է թողել։ Այն բոլորը, ինչ հայտնի է նրա մասին, վերցված է նրա գերեզմանաքարի վրայի արձանագրությունից, արձանագրություն, որը կազմված է մաթեմատիկական խնդրի տեսքով։ Բերենք այդ արձանագրությունը՝
| Մայրենի լեզվով | Հանրահաշվի լեզվով |
| Ճանապարհո՛րդ։ Այստեղ հանգչում է Դիոֆանտը, և թվերը կպատմեն քեզ, թե որքան է տևել նրա կյանքը։ | |
| Նրա կյանքի վեցերորդ մասը կազմել է սքանչելի մանկությունը։ | |
| Էլի կյանքի տասներկուերորդ մասն անցավ և դեմքը ծածկվեց աղվամազով։ | |
| Ամուսնությունից հետո կյանքի յոթերորդ մասն անզավակ ապրեց Դիոֆանտը։ | |
| Անցավ հինգ տարի և բախտավորվեց նա՝ ունենալով արու զավակ, | |
| որին ճակատագիրը հոր սքանչելի ու պայծառ կյանքի միայն կեսը պարգևեց։ | |
| Եվ խոր թախծի մեջ ծերուկը մահ ընդունեց, ապրելով միայն չորս տարի այն պահից ի վեր, երբ զրկվեց որդուց։ | |
| Ասա՛, քանի՞ տարեկան հասակում մահացավ Դիոֆանտը։ | |
Լուծում
Լուծելով հավասարումը և գտնելով, որ , իմանում ենք Դիոֆանտի կենսագրության հետևյալ գծերը. նա ամուսնացավ տարեկան հասակում, դարձավ հայր -րդ տարում, որդուն կորցրեց -րդ տարում և մեռավ տարեկան հասակում։
ՁԻՆ ԵՎ ՋՈՐԻՆ
Խնդիր
Ահա դարձյալ հինավուրց ոչ բարդ խնդիր, որը հեշտությամբ մայրենի լեզվից թարգմանվում է հանրահաշվական լեզվի։
«Ձին և ջորին գնում էին կողք-կողքի՝ ծանր բեռով բեռնված։ Ձին դժգոհեց իր անչափ ծանր բեռան համար։ Ինչո՞ւ ես դու դժգոհում,— պատասխանեց նրան ջորին,— չէ՞ որ եթե ես վերցնեմ քեզանից մեկ պարկ, իմ բեռը երկու անգամ ծանր կդառնա քոնից։ Իսկ եթե դու իմ մեջքից վերցնես մի պարկ, քո բեռը կդառնա իմին հավասար»։
Ասացե՛ք, իմաստուն մաթեմատիկոսներ, քանի՞ պարկ էր կրում ձին և քանի՞սը՝ ջորին։
Լուծում
| Եթե ես քեզանից վերցնեմ մի պարկ, | |
| իմ բեռը | |
| երկու անգամ ծանր կդառնա քոնից։ | |
| Իսկ եթե դու իմ բեռից վերցնես մի պարկ, | |
| քո բեռը | |
| իմին հավասար կդառնա։ |
Մենր խնդիրը բերեցինք երկու անհայտով հավասարումների սիստեմի.
կամ
Լուծելով այն, գտնում ենք ։ Ձին կրում էր պարկ, ջորին՝ ։
ՉՈՐՍ ԵՂԲԱՅՐՆԵՐ
Խնդիր
Չորս եղբայրներ ունեին ռուբլի։ Եթե առաջինի փողը ավելացնենք ռուբլով, երկրորդի փողը պակասեցնենք ռուբլով, երրորդի փողն ավելացնենք երկու անգամ, իսկ չորրորդի փողը պակասեցնենք երկու անգամ, ապա բոլորն էլ կունենան հավասարապես։ Որքա՞ն փող ուներ յուրաքանչյուրը։
Լուծում
| Չորս հղբայրներ ունեին ռուբլի, | |
| Եթե առաջինի փողը ավելացնենք ռուբլով, | |
| երկրորդի փողը պակասեցնենք ռուբլով, | |
| երրորդի փողը ավելացնենք երկու անգամ, | |
| չորրորդի փողը պակասեցնենք երկու անգամ, | |
| ապա բոլորն էլ կունենան հավասարապես։ |
Վերջին հավասարումը մասնատենք երեք մասերի՝
,
,
,
որտեղից՝
,
,
։
Այս արժեքները տեղադրելով առաջին հավասարման մեջ, կստանանք՝
,
որտեղից ։ Այնուհետև կգտնենք՝ ։ Այսպիսով, եղբայրներն ունեին՝ 8 ռ., 12 ռ., 5ռ., 20 ռ.։
ԹՌՉՈՒՆՆԵՐԸ ԳԵՏԻ ՄՈՏ
Խնդիր
11-րդ դարի արաբական մի մաթեմատիկոսի մոտ գտնում ենք հետևյալ խնդիրը։
Գետի երկու ափերին աճում են երկու արմավենիներ՝ մեկը մյուսի դիմաց։ Մեկի բարձրությունը կանգուն է, մյուսինը՝ ։ Դրանց հիմքերի միջև եղած հեռավորությունը կանգուն է։ Յուրաքանչյուր արմավենու կատարին նստած է մի թռչուն։ Երկու թռչունն էլ հանկարծ նկատեցին մի ձուկ, որը արմավենիների միջև ջրի մեջ լողում էր դեպի մակերևույթը։ Նրանք դեպի ձուկը նետվեցին միանգամից և նրան հասան միաժամանակ (նկ. 4)։

Բարձր արմավենու հիմքից ի՞նչ հեռավորության վրա երևաց ձուկը։
Լուծում
Սխեմատիկ գծագրից ելնելով (նկ. 5), օգտվելով Պյութագորի թեորեմայից, գտնում ենք՝
Բայց , քանի որ երկու թռչունն էլ այդ հեռավորությունները թռչել են միևնույն ժամանակում։ Ուստի՝
։
Բացելով փակագծերը և կատարելով պարզեցումները՝ կստանանք առաջին աստիճանի հավասարում.
,
որտեղից
։
Ձուկը երևաց կանգուն հեռու այն արմավենուց, որի բարձրությունը կանգուն է։
ԶԲՈՍԱՆՔ
Խնդիր
— Անցեք ինձ մոտ վաղը ցերեկով։— ասաց ծեր բժիշկն իր ծանոթին։
— Շնորհակալություն։ Ես դուրս կգամ ժամը երեքին։ Գուցե դուք ևս ցանկանաք զբոսնել, այդ դեպքում դուրս եկեք նույն ժամին, կհանդիպենք կիսաճանապարհին։
— Դուք մոռանում եք, որ ես ծեր եմ, ընդամենը ժամnւմ քայլում եմ միայն Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3 \; կմ} , իսկ դուք՝ երիտասարդ, ամենադանդաղ քայլելու դեպքում անցնում եք ժամում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 4 \; կմ} ։ Հանցանք չէր լինի ինձ մի փոքր արտոնություն տալ։
— Արդարացի է։ Քանի որ ես ձեզանից ժամում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; կմ} -ով ավելի եմ անցնում, ապա հավասարության համար այդ կիլոմետրը կտամ ձեզ, այսինքն՝ դուրս կգամ քառորդ ժամ առաջ։ Բավակա՞ն է։
— Ձեր կողմից դա մեծ սիրալիրություն է,— շտապեց համաձայնվել ծերունին։
Երիտասարդն այդպես էլ կատարեց. տնից դուրս եկավ երեքին քառորդ պակաս և անցավ ժամում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 4 \; կմ} արագությամբ։ Իսկ բժիշկը դուրս եկավ ուղիղ երեքին՝ ժամում անցնելով Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3 \; կմ} ։ Երբ նրանք հանդիպեցին, ծերունին ետ դարձավ և երիտասարդ բարեկամի հետ միասին ուղղվեց դեպի տուն։
Միայն տուն վերադառնալիս, երիտասարդը կշռադատեց, որ մի քառորդ ժամ արտոնության պատճառով, նա ընդհանրապես անցավ ոչ թե երկու, այլ չորս անգամ ավելի, քան բժիշկը։
Ի՞նչ հեռավորության վրա էր բժշկի տունը իր երիտասարդ ծանոթի տնից։
Լուծում
Տների միջև եղած հեռավորությունը նշանակենք -ով։
Երիտասարդն ընդամենը անցավ , իսկ բժիշկը չորս անգամ պակաս, այսինքն՝ ։ Մինչև հանդիպելը բժիշկն անցավ իր անցնելիք ճանապարհի կեսը, այսինքն , իսկ երիտասարդը մնացածը, այսինքն՝ ։ Բժիշկը ճանապարհի իր մասն անցավ ժամում, իսկ երիտասարդը ժամում, ընդ որում մենք գիտենք, որ նա ճանապարհին եղավ ¼ ժամով ավելի, քան բժիշկը։
Ունենք հետևյալ հավասարումը՝
,
որtեղից՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle x=2,4 \; կմ} ։
Երիտասարդի տնից մինչև բժշկի տունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2,4 \; կմ} է։
ՀՆՁՎՈՐՆԵՐԻ ԱՐՏԵԼԸ
Հայտնի ֆիզիկոս Ա. Վ. Ցինգերը Լ. Ն. Տոլստոյի մասին իր հիշողություններում պատմում է հետևյալ խնդրի մասին, որը մեծ գրողին շատ էր դուր եկել։
«Հնձվորների արտելը պետք է հնձեր երկու մարդագետին, մեկը մյուսից երկու անգամ մեծ։ Կես օր արտելը հունձ արեց մեծ մարգագետնում։ Դրանից հետո արտելը բաժանվեց երկու հավասար մասի՝ առաջին կեսը մնաց մեծ մարգագետնում և մինչև երեկո այն հնձեց ու վերջացրեց, իսկ երկրորդ կեսը հնձեց փոքր մարգագետինը, որի որոշ մասը երեկոյան մնաց չհնձված և որը հաջորդ օրվա ընթացքում հնձեց մի հնձվոր։ Քանի՞ հնձվոր կար արտելում։
Լուծում
Այս դեպքում, բացի գլխավոր անհայտից՝ հնձվորների թվից, որը մենք կնշանակվեք -ով, հարկ է լինում մտցնել օժանդակ անհայտ, այսինքն՝ այն հողամասի չափը, որը մի հնձվորը հնձում է մեկ օրում. այն նշանակենք -ով։ Թեպետ խնդիրը չի պահանջում նրա որոշելը, բայց այն հեշտացնում է գլխավոր անհայտի գտնելը։
Մեծ մարգագետնի մակերեսն արտահայտենք -ի և -ի միջոցով։ Այդ մարգագետինը հնձեցին հնձվորները կես օրում. նրանք հնձեցին՝
։

Օրվա երկրորդ կեսին այն հնձեց միայն արտելի կեսը, այսինքն՝ հնձվոր։ Նրանք հնձեցին
։
Քանի որ երեկոյան հնձվեց ամբողջ մարգագետինը, ապա նրա մակերեսը հավասար է՝
։
Այժմ փոքր մարգագետնի մակերեսն արտահայտենք -ի և -ի միջոցով։ Այն կես օրում հնձեցին հնձվորներ և հնձեցին մակերես։ Ավելացնենք չհնձված հողամասը, որ հավասար է -ի (մի հնձվորի մեկ աշխատանքային օրում հնձած մակերեսը), և կստանանք փոքր մարգագետնի մակերեսը՝
։
Մնում է հանրահաշվական լեզվի թարգմանել հետևյալ դարձվածքը. «Առաջին մարգագետինը երկու անգամ մեծ է երկրորդից» և հավասարումը կազմված է՝
կամ ։
Հավասարման ձախ մասի կոտորակը կրճատենք -ով։ Դրա շնորհիվ օժանդակ անհայտը արտաքսվում է, և հավասարումն ընդունում է հետևյալ տեսքը՝
կամ ,
որտեղից [9]։
Արտելում կար հնձվոր։
«Հետաքրքրաշարժ հանրահաշվի» առաջին հրատարակության լույս տեսնելուց հետո պրոֆ. Ա. Վ. Ցինգերը ինձ ուղարկեց այս խնդրի վերաբերյալ շատ հետաքրքիր և մանրամասն հաղորդում։ Խնդրի գլխավոր էֆեկտը, ըստ նրա կարծիքի, այն է, որ «այն բոլորովին էլ հանրահաշվական չէ, այլ թվաբանական է և այն էլ չափազանց հասարակ, միայն դժվարացնողը նրա ոչ շաբլոն ձևն է»։
«Այդ խնդրի պատմությունն այսպես է,— շարունակում է պրոֆ. Ա. Վ. Ցինգերը։— Մոսկվայի Համալսարանի մաթեմատիկական ֆակուլտետում այն ժամանակ, երբ այնտեղ սովորում էին իմ հայրը և իմ քեռին՝ Ի. Ի. Ռաևսկին (Լ. Տոլստոյի մոտիկ բարեկամը), այլ առարկաների հետ միասին դասավանդվում էր մանկավարժության նման ինչ-որ բան։ Այդ նպատակով ուսանողները պետք է հաճախեին համալսարանի համար հատկացված քաղաքային ժողովրդական դպրոցը և այնտեղ աշխատակցելով փորձված հմուտ ուսուցիչների հետ՝ վարժվեին դասավանդման մեջ։ Ցինգերի և Ռաևսկու ընկերների մեջ կար ոմն ուսանող՝ Պետրով, ըստ պատմածների — արտակարգ շնորհալի և յուրահատուկ մարդ։ Այդ Պետրովը (մահացել է շատ երիտասարդ հասակում, թվում է, թոքախտից) հաստատում էր, որ թվաբանության դասերին աշակերտներին փչացնում են՝ նրանց սովորեցնելով շաբլոն խնդիրներ և լուծման շաբլոն եղանակներ։ Իր միտքը հաստատելու համար Պետրովը հորինեց խնդիրներ, որոնք շաբլոն չլինելու հետևանքով շատ էին դժվարացնում «փորձված հմուտ ուսուցիչներին», բայց հեշտությամբ լուծվում էին ավելի ընդունակ աշակերտների կողմից» որոնք դեռ չէին փչացել այդ պարապմունքներում։ Այդպիսի խնդիրների (Պետրովը հնարել է նման մի քանի խնդիրներ) թվին է պատկանում նաև հնձվորների արտելի մասին խնդիրը։ Փորձված ուսուցիչները, անշուշտ, հեշտությամբ կարող էին լուծել այն՝ հավասարում կազմելու միջոցով, բայց թվաբանական պարզ լուծումը նրանց մտքով չէր անցնում։ Այնինչ խնդիրը այնքան պարզ է, որ նրա լուծման համար հանրահաշվական եղանակ մեջ բերել բոլորովին չարժե։
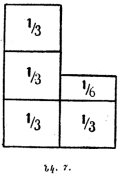
«Եթե մեծ մարգագետինը հնձել է մինչև օրվա կեսը ամբողջ արտելը և օրվա մյուս կեսը՝ արտելի կեսը, ապա պարզ է, որ կես օրում արտելի կեսը կարող է հնձել մարգագետնի մասը։
Հետևաբար, փոքր մարգագետնում մնում է չհնձված
հողամաս։ Եթե մեկ հնձվորը օրական հնձում է մարգագետնի -ը,
իսկ հնձվածը եղել է , ապա հնձվորները -ն էին։
Տոլստոյը, որ իր կյանքում սիրում էր ֆոկուսային և ոչ թե խիստ խորամանկ խնդիրներ, այդ խնդիրը սովորել էր իմ հորից դեռ երիտասարդ տարիներին։ Երբ այդ խնդրի մասին իմ և ծերունի Տոլստոյի միջև զրույց տեղի ունեցավ, նրան առանձնապես զմայլեց այն, որ խնդիրը դառնում է անհամեմատ պարզ և հստակ, եթե լուծելիս օգտվել միանգամայն պարզունակ գծագրից (նկ. 7)։
Ստորև մեզ կհանդիպեն ևս մի քանի խնդիրներ, որոնք որոշ ըմբռնողության դեպքում թվաբանորեն ավելի պարզ են լուծվում, քան հանրահաշվորեն։
ԿՈՎԵՐԸ ՄԱՐԳԱԳԵՏՆՈՒՄ
Խնդիր
«Գիտություններն ուսումնասիրելիս խնդիրներն ավելի օգտավետ են, քան կանոնները»— գրել է Նյուտոնը իր «Համընդհանուր թվաբանություն» աշխատության մեջ, և տեսական ցուցումներին նա կցում էր մի շարք օրինակներ։ Այդ վարժությունների թվում գտնում ենք մարգագետնում արածող կովերի մասին եղած խնդիրը, որը և հանդիսանում է հետևյալ խնդրի նման հատուկ տիպի յուրատեսակ խնդիրների նախամայրը։

«Ամբողջ մարգագետնում խոտն աճում է նույն խտությամբ և արագությամբ։ Հայտնի է, որ կովը այն կարածեին օրում, իսկ կովը՝ օրում։ Քանի՞ կով կարող էին արածել մարգագետնի ամբողջ խոտը օրում»։
Այս խնդիրը հումորիստական պատմվածքի համար սյուժետ դարձավ՝ հիշեցնելով չեխովյան „Penemumop”-ը։ Մի դպրոցականի հանձնարարել էին լուծելու այդ խնդիրը։ Նրա երկու չափահաս ազգականները ապարդյուն կերպով աշխատում էին նրա վրա և տարակուսում.
— Ստացվում է ինչ-որ տարօրինակ բան,— ասում է լուծողներից մեկը,— եթե օրում կովը արածում են մարգագետնի ամբողջ խոտը, ապա քանի՞ կով այն կարող է արածել օրում։ Իհարկե, -ի ¼-ը, այսինքն՝ ½ կով... Առաջին անհեթեթություն։ Եվ ահա երկրորդը՝ կով արածում են խոտը օրում, քանի՞ կով կարող է այն արածել օրում։ Ստացվում է ավելի վատ՝ ¾ կով։ Բացի այդ, եթե կովը խոտն արածում է օրում, ապա կովը այն կարածի օրում և ոչ թե օրում, ինչպես հաստատում է խնդիրը։
— Իսկ դուք հաշվի առնո՞ւմ եք, որ խոտն ամբողջ ժամանակ աճում է,— հարցնում է մյուսը։
Դիտողությունը խելացի է՝ խոտն անընդհատ աճում է, և եթե այդ հաշվի չառնվի, ապա ոչ միայն չի կարելի լուծել խնդիրը, այլև հենց նրա պայմանը կթվա հակասական։ Իսկ ինչպե՞ս է լուծվում խնդիրը։
Լուծում
Այստեղ ևս մտցնենք օժանդակ անհայտ, այսինքն՝ մարգագետնի խոտի օրվա աճը նրա պահեստի այն հողակտորներում, որ տվյալ օրը կովերը չեն արածում։ Մեկ օրում աճում է , օրում՝ . եթե ընդհանուր պաշարն ընդունենք , ապա օրվա ընթացքում կովերը կարածեն
։
Ամբողջ նախիրը ( կովից) մեկ օրում կարածի
,
իսկ մեկ կովը մեկ օրում՝
Նույն ձևով, քանի որ կովը միևնույն մարգագետնի խոտը կարածեր օրում, եզրակացնում ենք, որ մեկ կովը մեկ օրում արածում է
։
Բայց մի կովի մեկ օրում կերած խոտի քանակը երկու նախիրների համար հավասար է։ Ուստի՝
,
որտեղից՝
։
Գտնելով -ը (խոտի աճի մեծությունը), արդեն հեշտ է որոշել, թե մեկ կովը խոտի նախնական պաշարի ո՛ր մասը կուտի մեկ օրում.
։
Վերջապես, խնդրի վերջնական լուծման համար կազմենք հավասարում. եթե կովերի որոնելի թիվը է, ապա
,
որտեղից ։
կովը ամբողջ խոտը կարածեր օրում։
ՆՅՈՒՏՈՆԻ ԽՆԴԻՐԸ
Այժմ դիտարկենք եզների մասին նյուտոնյան խնդիրը, որի ձևով կազմված է ստորև դիտարկվող խնդիրը։
Խնդիրը, ի միջի այլոց, հորինված չէ հենց Նյուտոնի կողմից. այն ժողովրդի մաթեմատիկական ստեղծագործության արդյունքն է։
«Երեք մարգագետիններ, որոնք ծածկված են միատեսակ խտություն և աճման արագություն ունեցող խոտով, ունեն Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3^1/_3 \; հա} , Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10 \; հա} և Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 24 \; հա} մակերեսներ։ Առաջինում կերակրվում է եզ շաբաթվա ընթացքում. երկրորդում՝ եզ շաբաթվա ընթացքում։ Քանի՞ եզ կարող է կերակրել երրորդ մարգագետինը շաբաթվա ընթացքում»։
Լուծում
Մտցնենք օժանդակ անհայտ՝ , որը նշանակում է, թե խոտի նախնական պաշարի ո՞ր մասն է աճում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; հա} -ի վրա մեկ շաբաթվա ընթացքում։ Առաջին մարգագետնի վրա մեկ շաբաթվա ընթացքում աճում է նրա վրա եղած խոտի նախնական ամբողջ պաշարի , իսկ շաբաթվա ընթացքում` մասը։ Սա համարժեք է այն բանին, թե իբր մարգագետնի նախնական մակերեսը մեծացվել և հավասարվել է
հեկտարի։
Այլ խոսքով, եզները կերել են այնքան խոտ, որքան կծածկեր հեկտար մակերեսով մարգագետինը։ Մեկ շաբաթում եզը կուտեր այդ քանակի ¼-ը, իսկ մեկ եզը նույն քանակի, այսինքն՝
հեկտար մակերես ունեցող մարգագետնի խոտի պաշարի -ը։
Նույն ձևով, երկրորդ մարգագետնի տվյալներից գտնում ենք նրա այն մակերեսը, որ մեկ շաբաթում կերակրում է մեկ եզան։
| Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; հա} -ի | մեկ | շաբաթվա աճը = | , |
| Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; հա} -ի | շաբաթվա աճը = | , | |
| Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10 \; հա} -ի | շաբաթվա աճը = | ։ |
շաբաթ եզ կերակրելու համար խոտի պաշար ունեցող հողակտորի մակերեսը հավասար է
։
Մեկ շաբաթ եզանը կերակրելու համար անհրաժեշտ է
հեկտար։
Կերակրման երկու նորմաներն էլ պետք է լինեն հավասար՝
Լուծելով այդ հավասարումը կգտնենք ։ Այժմ որոշենք մարգագետնի այն մակերեսը, որի խոտի պաշարը բավականացնում է մեկ շաբաթվա ընթացքում մեկ եզ կերակրելու համար.
հեկտար։
Վերջապես մոտենում ենք խնդրի հարցին։ Նշանակելով եզների որոնելի թիվը -ով, կունենանք.
,
որտեղից ։ Երրորդ մարգագետինը շաբաթվա ընթացքում կարող է կերակրել եզ։
ԺԱՄԱՑՈՒՅՑԻ ՍԼԱՔՆԵՐԻ ՏԵՂԱՓՈԽՈՒԹՅՈՒՆԸ
Խնդիր
Հայտնի ֆիզիկոս Ա. Էյնշտեյնի կենսագիր և բարեկամ Ա. Մոշկովսկին, մեկ անգամ ցանկանալով զբաղեցնել իր մտերիմին նրա հիվանդության ժամանակ, նրան առաջարկեց հետևյալ խնդիրը (նկ. 9)։
«Վերցնենք սլաքների դիրքը ժամը -ին,— ասաց Մոշկովսկին։ Եթե այդ դիրքում մեծ և փոքր սլաքները փոխանակեին տեղերը, այնուամենայնիվ, նրանք ճիշտ ցույց կտային ժամանակը։ Բայց մյուս պահերին, օրինակ՝ ժամը -ին, սլաքների փոխադարձ տեղափոխումը կհանգեցներ անհեթեթության, մի դրության, որ կանոնավոր աշխատող ժամացույցների վրա տեղի չի ունենա, րոպե ցույց տվող սլաքը չի կարող կանգնել -ի վրա, երբ ժամ ցույց տվող սլաքը ցույց է տալիս -ը։ Հարց է առաջանում՝ ե՞րբ և քանի՞ ժամը մեկ ժամացույցի սլաքները գրավում են այնպիսի դիրք, որ մեկը մյուսով փոխարինելիս տալիս են այնպիսի նոր դիրք, որը նույնպես հնարավոր է ճիշտ աշխատող ժամացույցների համար։
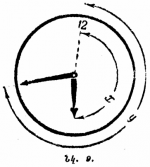
— Այո,— պատասխանեց Էյնշտեյնը, դա միանգամայն հարմար խնդիր է այն մարդու համար, որը որևէ հիվանդությունից հարկադրված՝ մնում է անկողնում. բավականաչափ հետաքրքիր է և շատ էլ հեշտ չէ։ Միայն վախենում եմ, որ զվարճությունը երկար չի տևի, ես արդեն նշմարեցի լուծման ճանապարհը։
Եվ մի փոքր բարձրանալով անկողնում, նա մի քանի գծանշումներով թղթի վրա գծեց խնդրի պայմանը պատկերող սխեման։ Լուծելու համար նրան հարկավոր եղավ ավելի քիչ ժամանակ, քան թե ինձ՝ խնդիրը ձևակերպելու համար...»
Ինչպե՞ս է լուծվում այս խնդիրը։
Լուծում
Շրջանագծի -երորդական մասերով կչափենք սլաքների հեռավորությունները թվացույցի շրջանով, այն կետից, որտեղ գրված է թվանշանը։
Դիցուք, սլաքների պահանջվող դիրքերից մեկը գիտվում է այն ժամանակ, երբ ժամ ցույց տվող սլաքը թվանշանից հեռացավ բաժանումով, իսկ րոպեներինը՝ բաժանումով։ Քանի որ ժամ ցույց տվող սլաքը ժամվա ընթացքում անցնում է բաժանում, այսինքն՝ ժամում բաժանում, ապա , բաժանումը նա կանցնի ժամում։ Այլ կերպ ասած, այն պահից հետո, երբ ժամացույցը ցույց էր տալիս -ը, անցավ ժամ։ Րոպե ցույց տվող սլաքը բաժանումն անցավ րոպեում, այսինքն՝ ժամում։ Այլ կերպ ասած, րոպե ցույց տվող սլաքը թվանշանն անցավ ժամ այն պահից առաջ, կամ ժամ այն պահից հետո, երբ երկու սլաքներն էլ գտնվում էին տասներկուսի վրա։ Այս թիվն ամբողջական է (զրոյից մինչև ), քանի որ նա ցույց է տալիս, թե քանի լրիվ ժամ անցավ տասներկուսից հետո։
Երբ սլաքները տեղերը փոխում են, մենք համանման ձևով գտնում ենք, որ ժամը -ից հետո անցած այն ժամանակը, որ ցույց են տալիս սլաքները, կազմում է
լրիվ ժամ։ Այդ թիվը նույնպես ամբողջական է (զրոյից մինչև )։
Ունենք հավասարումների հետևյալ սիստեմը՝
որտեղ -ը և -ը ամբողջ թվեր են, որոնք կարող են փոխվել -ից մինչև ։ Այդ սիստեմից գտնում ենք՝
։
-ին և -ին տալով -ից մինչև ամբողջ արժեքները, մենք որոշում ենք սլաքների բոլոր պահանջվող դիրքերը։ Քանի որ -ի արժեքներից յուրաքանչյուրը կարելի է համադրել -ի արժեքներից յուրաքանչյուրի հետ, ապա թվում է, թե բոլոր լուծումների թիվը հավասար է ։
Բայց իրականում այն հավասար է -ի, որովհետև երբ և երբ ստացվում է սլաքների միևնույն դիրքը։
-ի դեպքում ունենք՝
,
այսինքն՝ ժամացույցը ցույց է տալիս -ը այնպես, ինչպես դեպքում։
Բոլոր հնարավոր դիրքերը մենք չենք քննարկի, վերցնենք միայն երկու օրինակ։
Առաջին օրինակ.
.
,
այսինքն՝ ժամացույցը ցույց է տալիս ժամ րոպե. այդ պահին սլաքները համատեղվում են. դրանց տեղերը, իհարկե, կարելի է փոխել (ինչպես և սլաքների մյուս բոլոր համատեղումների դեպքերում)։
Երկրորդ օրինակ.
։
։
Համապատասխանող պահերն են` ժամ րոպե և ժամ րոպե։
Լուծումների թիվը մենք գիտենք՝ ։ Որպեսզի գտնենք թվացույցի ալն բոլոր կետերը, որոնք տալիս են սլաքների պահանջվող դիրքերը, պետք է թվացույցի շրջանագիծը բաժանենք հավասար մասի. կստանանք կետ, որոնք հանդիսանում են որոնելիներ։ Սլաքների պահանջվող դիրքերը այդ կետերի միջակայքներում հնարավոր չեն։
ԺԱՄԱՑՈՒՅՑԻ ՍԼԱՔՆԵՐԻ ՀԱՄԸՆԿՆՈՒՄԸ
Խնդիր
Կանոնավոր աշխատող ժամացույցի վրա քանի՞ դիրք կա, երբ ժամ և րոպե ցույց տվող սլաքները համատեղվում են։
Լուծում
Մենք կարող ենք օգտվել այն հավասարումներից, nրոնք ստացվել են նախորդ խնդիրը լուծելիս. չէ՞ որ, եթե ժամ և րոպե ցույց տվող սլաքները համատեղվել են, ապա կարելի է դրանց տեղերը փոխել. դրանից ոչինչ չի փոխվի։ Ընդ որում երկու սլաքներն էլ թվանշանից անցել են հավասար թվով բաժանումներ, այսինքն՝ ։ Այսպիսով, նախորդ խնդրի վերաբերյալ արած դատողություններից մենք արտածում ենք հետևյալ հավասարումը.
,
որտեղ -ը ամբողջ թիվ է՝ -ից մինչև ։ Այդ հավասարումից գտնում ենք՝
։
-ի համար տասներկու հնարավոր արժեքներից (-ից մինչև ) մենք կստանանք սլաքների ոչ թե , այլ միայն տարբեր դիրքեր, քանի որ դեպքում մենք գտնում ենք , այսինքն՝ երկու սլաքներն էլ անցել են բաժանում և գտնվում են թվանշանի վրա, այդ նույնը ստացվում է, երբ ։
ՅՈԹ ԽԱՂԱՑՈՂԵՐ
Խնդիր
Յոթ խաղացողներ պայմանավորվեցին, որ յուրաքանչյուր տարվող մնացած վեց խաղակիցներից յուրաքանչյուրին վճարի այնքան փող, որքան նա ունի, այլ խոսքով, կրկնապատկի նրա փողը։
Խաղացին պարտիա։ Բոլորն էլ տարվեցին՝ յուրաքանչյուրը մեկական անգամ։ Խաղն ավարտվելուց հետո հաշվեցին, թե յուրաքանչյուրը որքան փող ունի։ Պարզվեց, որ յուրաքանչյուրի մոտ կա ռուբ. կ.։
Յուրաքանչյուրը որքա՞ն փող ուներ խաղի սկզբին։
Լուծում
Չնայած թվացող բարդությանը, խնդիրը լուծվում է բավականին հեշտ, եթե ըմբռնենք, որ խաղի ժամանակ բոլոր խաղացողների մոտ փողի ընդհանուր գումարը եղել է անփոփոխ՝ միայն մեկի գրպանից այն անցել է մյուսը գրպանը։ Այստեղից հետևում է, որ խաղի սկզբին փողի ընդհանուր քանակը եղել է նույնը, ինչ որ վերջում, այսինքն՝ ռուբլի։
Հետևենք, թև առաջին տարվողի փողի քանակն ինչպես էր փոխվում խաղի ընթացքում։
Նրա մոտ խաղի սկզբին կար ռուբլի։
Առաջին պարտիայից հետո, տարվելով, նա վեց խաղակիցներին վճարեց այնքան, որքան նրանք բոլորն ունեին, այսինքն՝ ։ Առաջին պարտիայից հետո նրա մոտ մնաց՝
։
Երկրորդ պարտիայից հետո նրա փողը կրկնապատկվեց և, այդպիսով, հավասար եղավ՝
։
Երրորդ պարտիայից հետո նրա փողը նորից կրկնապատկվեց և կազմեց՝
։
Չորրորդ պարտիայից հետո նրա մոտ եղավ՝
։
Յոթերորդ պարտիայից հետո, այսինքն՝ խաղի ավարտից հետո, նա ուներ ռ., հետևաբար՝
։
Լուծենք այս հավասարումը՝
,
,
։
Այսպիսով, խաղի սկզբին առաջին խաղացողն ուներ ռ. կ.։ Նույն ձևով որոշենք երկրորդ տարվողի փողը։ Խաղի սկզբին նրա մոտ կար ։
Առաջին պարտիայից հետո նրա մոտ դարձավ ։
Երկրորդ պարտիան նա տարվեց և վճարեց
,
նրա մոտ մնաց
։
Երրորդ պարտիայից հետո նրա մոտ կար
։
Չորրորդից հետո`
։
Յոթերորդից հետո՝
։
Կունենանք հետևյալ հավասարումը
,
որտեղից՝
ռուբ. կ.։
Նման ձևով էլ կգտնենք երրորդ խաղացողի փողը՝ ռ. կ.։
Առաջարկում ենք ընթերցողին ինքնուրույնաբար որոշելու մնացած խաղացողների փողերը։ Լուծման ստուգումը կլինի այն, որ բոլոր խաղացողների փողերի ընդհանուր գումարը խաղից առաջ և հետո պետք է հավասար լինի։
ԿԵՂԾ ԱՆՀԵԹԵԹՈՒԹՅՈՒՆ
Խնդիր
Ահա մի խնդիր, որ կարող է միանգամայն անհեթեթ թվալ։
Ինչի՞ է հավասար -ը, եթե -ի։
Այս տարօրինակ հարցը իմաստից զուրկ չէ և խնդիրը հնարավոր է լուծել հավասարման միջոցով։
Փորձեցեք վերծանել այն։
Լուծում
Հավանաբար դուք գուշակեցիք, որ խնդրի մեջ մտնող թվերը գրված են ոչ տասնորդական սիստեմով, այլապես «ինչի է հավասար -ը» հարցը կլիներ անհեթեթ։ Դիցուք թվարկության անհայտ սիստեմի հիմքը է։ Այն ժամանակ «» թիվը նշանակում է երկրորդ կարգի միավոր և առաջինի՝ միավոր, այսինքն՝
„” ։
„” թիվը նշանակում է ։
Կունենանք հավասարումը, այսինքն՝ տասնորդական սիստեմում.
,
որտեղից ։ Թվերը գրված են տասներկուական սիստեմով, և „” ։ Նշանակում է՝ եթե „”, ապա „” ։
Նման ձևով էլ լուծվում է այդ տիպի այլ խնդիր։
Ինչի՞ է հավասար -ը, երբ ։
Պատասխան՝ (թվարկության իննական սիստեմ)։
ՀԱՎԱՍԱՐՈՒՄԸ ՄՏԱԾՈՒՄ Է ՄԵՐ ՓՈԽԱՐԵՆ
Եթե դուք կասկածում եք այն բանում, որ հավասարումը որոշ դեպքում մեզանից կանխատես է լինում, լուծեցեք հետևյալ խնդիրը.
Հայրը տարեկան է, տղան տարեկան։ Քանի՞ տարի հետո հայրը անգամ մեծ կլինի տղայից։
Որոնելի ժամանակը նշանակենք -ով։ տարի հետո հայրը կլինի տարեկան, տղան՝ ։ Եվ քանի որ հայրը այդ ժամանակ պետք է անգամ մեծ լինի տղայից, ապա կունենանք հետևյալ հավասարումը
։
Լուծելով այն, կստանանք ։
«Մինուս երկու տարի հետո» նշանակում է՝ «երկու տարի առաջ»։ Երբ մենք կազմեցինք հավասարումը, չմտածեցինք այն մասին, որ հոր տարիքը ապագայում երբեք անգամ չի կարող մեծ լինել տղայի տարիքից, այդպիսի հարաբերություն կարող էր տեղի ունենալ միմիայն անցյալում։ Հավասարումն ավելի խորհող հանդիսացավ, քան թե մենք և շտկեց սխալը։
ԿՈՒՐՅՈԶՆԵՐ ԵՎ ԱՆԱԿՆԿԱԼՈՒԹՅՈՒՆՆԵՐ
Հավասարումներ լուծելիս մենք երբեմն հանդիպում ենք այնպիսի պատասխանների, որոնք անփորձ մաթեմատիկոսին կարող են փակուղու, մեջ դնել։ Բերենք մի քանի օրինակներ։
I. Գտնել երկանիշ թիվ, որն ունենա հետևյալ հատկությունները։ Տասնավորների թվանշանը միավորների թվանշանից փոքր լինի -ով։ Եթե նույն թվանշաններով, բայց հակառակ կարգով գրված թվից հանենք որոնելի թիվը, ապա կստանանք ։
Նշանակելով տասնավորների թվանշանը -ով, իսկ միավորների թվանշանը՝ -ով, մենք այդ խնդրի համար հեշտությամբ կկազմենք հետևյալ հավասարումների սիստեմը՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} x \;=\; y-4,\\ (10y+x)-(10x+y) \;=\; 27։\\ \end{cases} }
Առաջին հավասարումից -ի արժեքը տեղադրելով երկրորդի մեջ՝ կգտնենք
,
իսկ ձևափոխությունից հետո՝
։
Մեզ մոտ չորոշվեցին անհայտների արժեքները, սակայն մենք իմացանք, որ ... Ի՞նչ է սա նշանակում։
Այս նշանակում է՝ որ տրված հավասարումներին բավարարող երկանիշ թվեր գոյություն չունեն և որ այդ հավասարումները հակասում են մեկը մյուսին։ Իսկապես առաջին հավասարման երկու մասերը բազմապատկելով -ով, մենք նրանից կգտնենք՝
։
իսկ երկրորդից (փակագծերը բացելուց և նման անդամների միացումից հետո)՝
։
Միևնույն մեծությունը՝ , համաձայն առաջին հավասարման, հավասար է -ի, իսկ համաձայն երկրորդի՝ -ի։ Դա անպայման անհնարին է, քանի որ ։
Նման թյուրիմացություն է սպասում նաև հետևյալ հավասարումների սիստեմը լուծողին՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} x^2y^2 = 8,\\ xy = 4։\\ \end{cases} }
Առաջին հավասարումը բաժանելով երկրորդի վրա, կստանանք
,
իսկ նոր ստացված հավասարումը համեմատելով երկրորդի հետ, նկատում ենք, որ
այսինքն՝ ։ Այդ սիստեմին բավարարող թվեր գոյություն չունեն։ (Այն հավասարումները, որոնց կազմած սիստեմը լուծումներ չունի, կոչվում են անհամատեղելի)։
II. Այլ տեսքի անսպասելիության կհանդիպենք մենք, եթե մասամբ փոխենք նախորդ խնդրի պայմանը։ Այն է՝ հաշվենք, որ տասնավորների թվանշանը ոչ թե -ով, այլ -ով է փոքր միավորների թվանշանից, իսկ խնդրի մնացած պայմանը նույնն է։ Ի՞նչ թիվ է դա։
Կազմում ենք հավասարում։ Եթե տասնավորների թվանշանը նշանակենք -ով, ապա միավորների թվանշանը կլինի ։ Խնդիրը թարգմանելով հանրահաշվի լեզվով, կստանանք՝
։
Կատարելով պարզումներ, կհանգենք հետևյալ հավասարությանը՝
։
Այս հավասարությունը անվիճելիորեն ճիշտ է, բայց նա մեզ ոչինչ չի ասի -ի արժեքի մասին։ Սա նշանակո՞ւմ է արդյոք, որ խնդրի պահանջին բավարարող թվեր գոյություն չունեն։
Ընդհակառակն, այդ նշանակում է, որ մեր կազմած հավասարումը նույնություն է, այսքիքն՝ այն ճիշտ է անհայտի ցանկացած արժեքի դեպքում։ Իսկապես, հեշտ է համոզվել նրանում, որ խնդրում նշված հատկությունն ունի յուրաքանչյուր երկանիշ թիվ, որի միավորների թվանշանը -ով մեծ է տասնավորների թվանշանից.
| , | , | |
| , | , | |
| , | ։ |
III. Գտնել եռանիշ թիվ, որն ունենա հետևյալ հատկությունները՝
1) տասնավորների թվանշանը է,
2) հարյուրավորների թվանշանը -ով փոքր է միավորների թվանշանից։
3) եթե այդ թվի թվանշանները դասավորենք հակառակ կարգով, ապա նոր թիվը -ով մեծ կլինի որոնելիից։
Կազմենք հավասարում, միավորների թվանշանը նշանակելով -ով.
։
Այս հավասարումը պարզեցնելուց հետո բերվում է հետևյալ հավասարությանը՝
։
Ընթերցողներն արդեն գիտեն, թե ինչպես պետք է մեկնաբանել նման արդյունքը։ Այն նշանակում է, որ յուրաքանչյուր եռանիշ թիվ, որի առաջին թվանշանը -ով փոքր է երրորդից[10], մեծանում է -ով, եթե թվանշանները գրենք հակառակ կարգով։
Մինչև այժմ մենք դիտարկել ենք խնդիրներ, որոնք քիչ թե շատ արհեստական, գրքային բնույթ ունեին։ Դրանք ուղղված էին հավասարումներ կազմելու և լուծելու համար հմտություն ձեռք բերելու նպատակին։ Այժմ տեսականորեն զինված զբաղվենք գործնական խնդիրների մի քանի օրինակներով՝ արտադրության, առօրյա կենցաղի, ռազմական գործի և սպորտի բնագավառներից։
ՎԱՐՍԱՎԻՐԱՆՈՑՈՒՄ
Խնդիր
Կարո՞ղ է արդյոք հանրահաշիվը պետք գալ վարսավիրանոցում։ Պարզվում է, որ այդպիսի դեպքեր պատահում են։ Ես դրանում համոզվեցի, երբ մի անգամ վարսավիրանոցում ինձ մոտեցավ վարպետը անսպասելի խնդրանքով՝
— Չէիք բարեհաճի մեզ օգնել լուծելու մի խնդիր, որից մենք ոչ մի կերպ գլուխ չենք հանում։
— Արդեն դրա պատճառով ինչքա՜ն լուծույթ է փչացել,— ավելացրեց մյուսը։
— Ինչո՞ւմն է խնդիրը,— հարց ու փորձ արի ես։
— Մենք ունենք ջրածնի պերօքսիդի երկու լուծույթ՝ տոկոսանոց և տոկոսանոց։ Հարկավոր է դրանք խառնել այնպես, որ ստացվի տոկոսանոց լուծույթ։ Չենք կարող գտնել ճիշտ հարաբերություն...
Ինձ տվեցին թուղթ, և պահանջված հարաբերությունը գտնվեց։
Պարզվեց, որ այն շատ պարզ է։ Իսկ ի՞նչու։
Լուծում
Խնդիրր կարելի է լուծել նաև թվաբանորեն, բայց այստեղ հանրահաշիվը նպատակին է հասցնում ավելի պարզ և ավելի արագ։ Դիցուք, տոկոսանոց խառնուրդ կազմելու համար պահանջվում է վերցնել գրամ տոկոսանոց և գրամ տոկոսանոց լուծույթներ։ Այդ ժամանակ առաջին բաժնում պարունակվում է գրամ մաքուր ջրածնի պերօքսիդ, երկրորդում՝ , իսկ ընդամենը՝
։
Արդյունքում ստացվում է գրամ լուծույթ, որի մեջ մաքուր պերօքսիդը պետք է լինի ։
Ունենք հետևյալ հավասարումը՝
։
Այս հավասարումից գտնում ենք , այսինքն՝ տոկոսանոց լուծույթից պետք է վերցնել երկու անգամ ավելի, քան տոկոսանոցից։
ՏՐԱՄՎԱՅԸ ԵՎ ՀԵՏԻՈՏՆԸ
Գնալով տրամվայի ճանապարհի երկարությամբ, ես նկատեցի, որ յուրաքանչյուր րոպեից հետո ինձ հասնում է տրամվայը, իսկ յուրաքանչյուր րոպեում ես ինքս եմ դիմավորում տրամվային։ Թե՛ ես, թե՛ տրամվայները շարժվում ենք հավասարաչափ։ Յուրաքանչյուր քանի՞ րոպեն մեկ տրամվայները մեկը մյուսի ետևից հեռանում են իրենց վերջին կետից։
Լուծում
Եթե վագոններն իրենց վերջին կետից հեռանում են յուրաքանչյուր րոպեն մեկ, ապա այդ նշանակում է, որ այն տեղով, որտեղ ես հանդիպել եմ տրամվայներից մեկին, յուրաքանչյուր րոպեն մեկ անցում է հաջորդ տրամվայը։ Եթե նա հասնում է իմ հետևից, ապա մնացած րոպեում նա պետք է անցնի այն ճանապարհը, որ ես կարողանում եմ անցնել րոպեում։ Նշանակում է, այն ճանապարհը, որը ես անցնում եմ րոպեում, տրամվայը կանցնի րոպեում։
Մինչդեռ, եթե տրամվայը գալիս է ինձ ընդառաջ, ապա նա ինձ կհանդիպի նախորդից րոպե հետո, իսկ մնացած րոպեում նա կանցնի այն ճանապարհը, որ ես կարողացա անցնել այդ րոպեում։ Հետևաբար, այն Ճանապարհը, որ ես անցնում եմ րոպեում, տրամվայը կանցներ րոպեում։
Կստանանք հետնյալ հավասարումը՝
։
Այստեղից ։ Վագոնները հեռանում են յուրաքանչյուր րոպեն մեկ։
Կարելի է նաև առաջարկել խնդրի հետևյալ (ըստ էության թվաբանորեն) լուծումը։ Մեկը մյուսին հաջորդող երկու տրամվայների միջև եղած հեռավորությունը նշանակենք -ով։ Այդ ժամանակ իմ և ինձ ընդառաջ շարժվող տրամվայի միջև եղած հեռավորությունը փոքրանում է րոպեում -ով (քանի որ հենց նոր անցնող տրամվայի և հաջորդի միջև եղած հեռավորությունը, որը հավասար է -ի, մենք միասին անցնում ենք րոպեում)։ Իսկ եթե տրամվայը հասնում է ինձ, ապա մեր միջև եղած հեռավորությունը ամեն րոպե փոքրանում է -ով։ Այժմ ենթադրենք, որ ես մի րոպե տևողությամբ շարժվեցի առաջ, իսկ այնուհետև շրջվեցի և գնացի էլի մի րոպե (այսինքն՝ վերադարձա նախկին տեղը)։ Այդ ժամանակ իմ և տրամվայի միջև որը սկզբում շարժվում էր ինձ ընդառաջ) եղած հեռավորությունը առաջին րոպեից հետո կփոքրանա -ով, իսկ երկրորդ րոպեում (երբ այդ տրամվայը արդեն հասել էր ինձ) կփոքրանա -ով։ Ընդամենը րոպեում մեր միջև եղած հեռավորությունը կփոքրանա -ով։ Նույնը տեղի կունենար, եթե ես ամբողջ ժամանակ կանգնած մնայի տեղում, քանի որ վերջին հաշվով ես վերադարձա ետ։ Այսպիսով, եթե ես շարժվեի, ապա մեկ րոպեում (և ոչ թե երկու) տրամվայը կմոտենար ինձ -ով, իսկ ամբողջ հեռավորությունը նա կանցներ րոպեում։ Այդ նշանակում է, որ անշարժ կանգնած դիտողի մոտով տրամվայներն անցնում են րոպե ընդմիջումներով։
ՇՈԳԵՆԱՎԸ ԵՎ ԼԱՍՏԱՆԱՎԵՐԸ
Խնդիր
քաղաքից դեպի քաղաքը շոգենավը գետի հոսանքով առանց կանգառումների անցավ ժամում։ Մինչդեռ հոսանքին հակառակ նա անցավ (շարժվելով սեփական նույն արագությամբ և առանց կանգառումների) ժամում։ Քանի՞ ժամում կանցնեն լաստանավերը -ից (լաստանավերը շարժվում են գետի հոսանքի արագությամբ)։
Լուծում
Այն ժամանակը, որը պետք է շոգենավին -ից մինչև հեռավորությունը կանգնած ջրում այսինքն՝ սեփական արագությամբ շարժվելիս, նշանակենք -ով, իսկ լաստանավերի շարժման ժամանակը՝ -ով։ Այդ ժամանակ շոգենավը մեկ ժամում կանցնի հեռավորության -ը, իսկ լաստանավերը (հոսանքը)՝ այդ հեռավորության -ը։ Ուստի՝ հոսանքի ուղղությամբ շոգենավը մեկ ժամում կանցնի հեռավորության -ը, իսկ հոսանքին հակառակ՝ -ը։ Բայց խնդրի պայմանից մենք գիտենք, որ հոսանքի ուղղությամբ շոգենավը մեկ ժամում անցնում է հեռավորության -ը, իսկ հոսանքին հակառակ՝ -ը։ Կստանանք հետևյալ սիստեմը՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} \frac{1}{x}+\frac{1}{y} \;=\; \frac{1}{5}, \\ \frac{1}{x}-\frac{1}{y} \;=\; \frac{1}{7}։ \end{cases} }
Նկատենք, որ այս սիստեմի լուծման համար պետք չէ ազատվել հայտարարներից, պետք է պարզապես առաջին հավասարումից հանել երկրորդը։ Արդյունքում մենք կստանանք՝
,
որտեղից՝ ։ Լաստանավերը -ից կգնան ժամում։
ԵՐԿՈՒ ԹԻԹԵՂԱՏՈՒՓ ՍՈՒՐՃ
Խնդիր
Սուրճով լփված երկու թիթեղատուփեր ունեն միատեսակ ձև և պատրաստված են միևնույն թիթեղից։ Առաջինը կշռում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2 \; կգ} և ունի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 12 \; սմ} բարձրություն. երկրորդը կշռում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; կգ} և ունի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 9,5 \; սմ} բարձրություն։
Որքա՞ն է սուրճի մաքուր կշիռը թիթեղատուփերում։
Լուծում
Մեծ թիթեղատուփի պարունակության կշիռը նշանակենք -ով, փոքրինը՝ -ով։ Թիթեղատուփերի կշիռը համապատասխանորեն նշանակենք -ով և -ով։ Կունենանք հետևյալ հավասարումները՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} x + z \;=\; 2, \\ y + t \;=\; 1։ \end{cases} }
Քանի որ լիքը թիթեղատուփերի պարունակության կշիռները հարաբերում են, ինչպես դրանց ծավալները, այսինքն՝ ինչպես դրանց բարձրությունների[11] խորանարդները, ապա
կամ ։
Իսկ դատարկ թիթեղատուփերի կշիռները հարաբերում են, ինչպես դրանց լրիվ մակերևույթները, այսինքն՝ ինչպես դրանց բարձրությունների քառակուսիները։ Ուստի՝
կամ ։
-ի և -ի արժեքները տեղադրելով առաջին հավասարման մեջ՝ կստանանք հետևյալ սեստեմը՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} 2,02y+1,60t \;=\; 2, \\ y+t \;=\; 1։ \end{cases} }
Լուծելով այն՝ գտնում ենք.
։
Եվ հետևաբար՝
։
Առանց տարայի սուրճի կշիռը մեծ թիթեղատուփի մեջ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1,92 \; կգ} է, փոքրում՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 0,95 \; կգ} [12]։
ԵՐԵԿՈՒՅԹ
Երեկույթին կային պարողներ։ Մարիան պարում էր յոթ պարողների հետ, Օլգան՝ ութի հետ, Վերան՝ իննի հետ և այդպես շարունակ մինչև Նինան, որը պարում էր բոլոր պարողների հետ։ Քանի՞ պարողներ (տղամարդ) կային երեկույթին։
Լուծում
Խնդիրր լուծվում է շատ պարզ, եթե անհայտը ընտրենք հաջողությամբ։ Կորոնենք ոչ թե պարողների թիվը, այլ պարողուհիների, որը կնշանակենք -ով։
| I-ը, | Մարիան | պարում էր | պարողների | հետ, | |
| II-ը, | Օլգան | » | » | » | |
| III-ը, | Վերան | » | » | » | |
| ............................................................................... | |||||
| -ը, | Նինան | » | » | » | |
Կունենանք հավասարումը՝
,
որտեղից
,
և, հետևաբար, պարող տղամարդկանց թիվը կլինի՝
։
ԾՈՎԱՅԻՆ ՀԵՏԱԽՈՒԶՈՒԹՅՈՒՆ
Խնդիր առաջին
Հետախույզին (հետախույզ նավին), որը շարժվում է նավախմբի հետ, տրված է առաջադրանք՝ նավախմբի շարժման ուղղությամբ հետազոտել ծովի շրջանը մղոնի վրա։ Նավախմբի արագությունը ժամում մղոն է, հետախույզի արագությունը ժամում մղոն։ Պահանջվում է որոշել որքա՞ն ժամանակից հետո հետախույզը կվերադառնա նավախումբը։
Լուծում
Ժամերի որոնելի թիվը նշանակենք -ով։ Այդ ժամանակամիջոցում նավախումբը կարող է անցնել մղոն, իսկ հետախուզող նավը՝ ։ Հետախույզն անցավ մղոն առաջ և դեպի ետ դարձավ այդ ճանապարհի մի մասը, իսկ նավախումբը անցավ այդ ճանապարհի մնացած մասը։ Նրանք միասին անցան ճանապարհ, որը հավասար է մղոն։ Ունենք հետևյալ հավասարումը՝
,
որտեղից՝
(ժամ)։
Հետախույզը նավախումբ է վերադառնում մոտավորապես ժամ րոպե հետո։
Խնդիր երկրորդ
Հետախույզը հրաման ստացավ հետախուզումը կատարել նավախմբի առջևից՝ նրա շարժման ուղղությամբ։ ժամ հետո այդ նավը պետք է վերադառնա նավախումբ։ Նավախումբը թողնելուց որքա՞ն ժամանակ անց հետախուզական նավը պետք է ետ դառնա, եթե նրա արագությունը հանգույց է, իսկ նավախմբի արագությանը՝ հանգույց։
Լուծում
Դիցուք հետախույզը պետք է ետ դառնա ժամ հետո. նշանակում է, նավախմբից նա հեռանում էր ժամ, իսկ գալիս է նրան ընդառաջ ժամ։ Քանի դեռ բոլոր նավերը գնում են մեկ ուղղությամբ, հետախույզը ժամում նավախմբից կհեռանա նրանց անցած ճանապարհների տարբերության չափով, այսինքն՝
։
Վերադարձին, մինչև նավախմբին հանդիպելը, հետախույզն անցավ ճանապարհ, իսկ նավախումբը՝ ։ Մեկը և մյուսը միասին անցան ։ Հետևաբար՝
,
որտեղից՝
։ Հետախույզը պետք է ետ դառնա նավախումբը թողնելուց ժամ րոպե հետո։
ՎԵԼՈԴՐՈՄՈՒՄ
Խնդիր
Վելոդրոմի շրջանաձև ճանապարհով գնում են երկու հեծանվորդներ անփոփոխ արագությամբ։ Երբ նրանք գնում են հակադիր ուղղություններով, ապա հանդիպում են յուրաքանչյուր վայրկյանը մեկ, իսկ երբ գնում են մի ուղղությամբ, ապա մեկը մյուսին հասնում է յուրաքանչյուր վայրկյանից հետո։ Որքա՞ն է յուրաքանչյուր հեծանվորդի արագությունը, եթե շրջանաձև ճանապարհի երկարությանը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 170 \; մ} է։
Լուծում
Եթե առաջին հեծանվորդի արագությունը է, ապա վայրկյանում նա անցնում է մետր, իսկ երկրորդը, շարժվելով նրան ընդառաջ, հանդիպումից մինչև մյուս հանդիպումն անցնում է շրջանի մնացած մասը, այսինքն՝ մետր։ Եթե երկրորդի արագությունը է, ապա դա կազմում է մետր. այսպիսով,
։
Իսկ եթե հեծանվորդները գնում են միևնույն ուղղությամբ, ապա վայրկյանում առաջինը անցնում է մետր, իսկ երկրորդը՝ մետր։ Եթե առաջինը երկրորդից արագ է գնում, ապա մի հանդիպումից մինչև մյուսը նա անցնում է երկրորդից մի շրջանով ավելի, այսինքն՝
։
Այդ հավասարումները պարզեցնելուց հետո կստանանք՝
,
որտեղից՝
(մետր վայրկյանում)։
ՄՈՏՈՑԻԿԼՆԵՐԻ ՄՐՑՈՒՄԸ
Խնդիր
Մոտոցիկլետային մրցումների դեպքում միաժամանակ ստարտ վերցնող երեք մեքենաներից մեկը, կատարելով ժամում առաջինից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 13 \; կմ} -ով պակաս և երրորդից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3 \; կմ} -ով ավել վազք, հասավ վերջին վայրը առաջինից րոպեով ավելի ուշ և երրորդից րոպեով շուտ։ Ճանապարհին կանգառումներ չեն եղել։
Պահանջվում է որոշել՝
ա) ի՞նչ մեծություն ունի ճանապարհի հատվածը.
բ) ի՞նչ մեծություն ունի յուրաքանչյուր մեքենայի արագությունը.
գ) որքա՞ն է յուրաքանչյուր մեքենայի վազքի տևողությունը։
Լուծում
Թեև պահանջվում է որոշել յոթ անհայտ մեծություններ, բայց խնդիրը լուծելիս մենք կբավարարվենք միայն երկուսով. կազմենք երկու անհայտով երկու հավասարումների սիստեմ։
Երկրորդ մեքենայի արագությունը նշանակենք -ով։ Այն ժամանակ առաջինի արագությունը կարտահայտվի -ով, իսկ երրորդինը -ով։
Ճանապարհի հատվածի երկարությունը նշանակենք տառով։ Այդ դեպքում վազքի տևողությունը կլինի՝
| առաջին | մեքենայի | համար | . . . | , |
| երկրորդ | » | » | . . . | , |
| երրորդ | » | » | . . . | ։ |
Մեն գիտենք, որ երկրորդ մեքենան ճանապարհին եղել է առաջինից րոպեով (այսինքն՝ ժամով) ավելի։ Ուստի՝
։
Երրորդ մեքենան ճանապարհին եղել է երկրորդից րոպեով (այսինքն, ժամով) ավելի։ Հետևաբար՝
։
Այդ հավասարումներից երկրորդը բազմապատկենք -ով և հանենք աոաջինից՝
։
Այս հավասարման բոլոր անդամները բաժանենք -ի վրա (այդ մեծությունը, ինչպես մենք գիտենք, զրոյի հավասար չէ) և դրանից հետո ազատվենք հայտարարներից։ Մենք կստանանք՝
կամ փակագծերը բացելուց և նման անդամների միացումից հետո՝
,
որտեղից՝
։
Գիտենալով -ը, առաջին հավասարումից գտնում ենք -ը՝
,
որտեղից՝
։
Այսպիսով, մեքենաների արագությունները որոշված են՝ ժամում և կիլոմետր։
Ամբողջ ճանապարհի երկարությունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle =90 \; կմ} ։
Ճանապարհի երկարությունը բաժանելով յուրաքանչյուր մեքենայի արագության վրա, գտնում ենք վազքերի տևողությունը՝
| առաջին մեքենայինը | . . . . | ժամ։ |
| երկրորդ մեքենայինը | . . . . | ժամ րոպե։ |
| երրորդ մեքենայինը | . . . . | ժամ րոպե։ |
Այսպիսով, բոլոր յոթ անհայտները որոշված են։
ԸՆԹԱՑՔԻ ՄԻՋԻՆ ԱՐԱԳՈՒԹՅՈՒՆԸ
Խնդիր
Ավտոմեքենան երկու քաղաքների միջև եղած հեռավորությունն անցավ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 60 \; կմ/ժամ} արագությամբ և վերադարձավ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 40 \; կմ/ժամ} արագությամբ։ Որքա՞ն է եղել նրա ընթացքի միջին արագությունը։
Լուծում
Խնդրի խաբուսիկ պարզությունը շատերին մոլորության մեջ է գցում։ Խորամուխ չլինելով հարցի պայմանի մեջ, հաշվում են -ի և -ի միջին թվաբանականը, այսինքն՝ գտնում են հետևյալ կիսագումարը՝
։
Այդ «պարզ» լուծումը ճիշտ կլիներ, եթե ընթացքը երկու ուղղությամբ էլ հավասար ժամանակ տևեր։ Բայց պարզ է, որ ետ վերադառնալը (փոքր արագությամբ) պետք է խլեր ավելի շատ ժամանակ, քան այնտեղ գնալը։ Նկատի ունենալով այս, մենք գտնում ենք, որ պատասխանը՝ -ը ճիշտ չէ։
Եվ իրոք, հավասարումը տալիս է այլ պատասխան։ Հավասարում կազմելը դժվար չէ, եթե մտցնենք օժանդակ անհայտ մեծությունը՝ քաղաքների միջև հղած հեռավորությունը։ Նշանակելով որոնելի միջին արագությունը -ով, կազմում ենք հավասարում՝
։
Քանի որ -ը զրոյի հավասար չէ, կարող ենք հավասարումը բաժանել -ի վրա. կստանանք՝
,
որտեղից՝
։
Այսպիսով, ճիշտ պատասխանը ոչ թե Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 50 \; կմ/ժամ} է, այլ՝ ։
Իսկ եթե մենք այդ խնդիրը լուծեինք տառային նշանակումներով (ավտոմեքենան գնում էր Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a \; կմ/ժամ} արագությամբ և ետ էր վերադառնում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle b \; կմ/ժամ} արագությամբ), ապա կստացվեր հետևյալ հավասարումը՝
,
որտեղից -ի համար կստանանք հետևյալ արժեքը՝
։
Այդ մեծությունը և մեծությունների համար կոչվում է միջին հարմոնիկ։
Այսպիսով, ընթացքի միջին արագությանը շարժման արագությունների համար արտահայտվում է ոչ թե միջին թվաբանականով, այլ միջին հարմոնիկով։ և դրական թվերի համար միջին հարմոնիկը միշտ փոքր է դրանք միջին թվաբանականից՝
-ից,
որը և մենք նկատեցինք թվային օրինակի վրա (-ը փոքր է -ից)։
ԱՐԱԳԱԳՈՐԾ ՀԱՇՎԻՉ ՄԵՔԵՆԱՆԵՐ
Հետաքրքրաշարժ հանրահաշվի» պլանում հավասարումների մասին եղած զրույցը չի կարող հաշվիչ մեքենաներով հավասարումների լուծման կողքով անցնել։ Մենք արդեն խոսել ենք այն մասին, որ հաշվիչ մեքենաները կարող են շախմատ (կամ շաշկի) «խաղալ»։ Մաթեմատիկական մեքենաները կարող են կատարել և այլ առաջադրանքներ, օրինակ, մի լեզվից մյուսին թարգմանելը, երաժշտական մելոդիաները նվագախմբի համար պատրաստելը և այլն։ Հարկավոր է միայն մշակել համապատասխան «ծրագիր», որով մեքենան գործելու է։
Իհարկե, մենք այստեղ չենք դիտարկի «ծրագրեր» մշակելու հարցը շախմատ խաղալու կամ մի լեզվից մյուսին թարգմանելու համար։ Այդ «ծրագրերը» ծայրահեղ բարդ են։ Մենք կվերլուծենք միայն երկու շատ հասարակ «ծրագրեր»։ Սակայն, սկզբում հարկավոր է մի քանի խոսք ասել հաշվիչ մեքենայի կառուցվածքի մասին։
Վերևում (գլ. I) մենք խոսել ենք այն հարմարանքների մասին, որոնք թույլատրում են վայրկյանում հազարավոր և տասը հազարավոր հաշվումներ կատարել։ Մեքենալի այն մասը, որը ծառայում է գործողությունները անմիջականորեն կատարելու համար (մեծ մասամբ թվարկության երկուական սիստեմով), կոչվում է արիֆմոմետր։ Բացի այդ, մեքենան կազմված է կառավարող հարմարանքից (որ կարգավորում է ամբողջ մեքենայի աշխատանքը) և այսպես կոչված հիշողությունից։ Հիշողությունը կամ, այլ կերպ, հիշող հարմարանքն իրենից ներկայացնում է թվերի և պայմանական ազդանշանների համար պահեստարան։ Վերջապես, մեքենան ունի հատուկ հարմարանքներ նիշավոր նոր տվյալներ մտցնելու և պատրաստի արդյունքներ ստանալու համար։ Այդ պատրաստի արդյունքները մեքենան տպում է (արդեն տասնորդական սիստեմով) հատուկ քարտերի վրա։
Բոլորին լավ հայտնի է, որ ձայնը կարելի է գրի առնել սկավառակի կամ ժապավենի վրա և այնուհետև վերարտադրել։ Բայց ձայնի գրառումը սկավառակի վրա հնարավոր է կատարել միայն մեկ անգամ. նոր գրանցման համար արդեն հարկավոր է նոր սկավառակ։ Փոքր ինչ այլ կերպ է իրականացվում մագնիտաֆոնով ձայնագրումը, որը տեղի է ունենում հատուկ ժապավենի մագնիսացման միջոցով։ Գրված ձայնը կարելի է վերարտադրել ուզածին չափ, իսկ եթե գրառումը հարկավոր չէ, ապա կարելի է ժապավենը «ապամագնիսացնել» և նրա վրա կատարել նոր գրանցում։ Միևնույն ժապավենի վրա կարելի է կատարել հաջորդաբար մի քանի գրանցումներ, ընդ որում յուրաքանչյուր նոր գրանցման դեպքում նախորդը «ջնջվում է»։
Նման սկզբունքի վրա էլ հիմնված է հիշող հարմարանքների գործողությունը։ Թվերը և պայմանական ազդանշանները գրանցվում են (էլեկտրական, մագնիսական կամ մեխանիկական ազդանշանների միջոցով) հատուկ թմբկագլանի, ժապավենի կամ այլ հարմարանքի վրա։ Անհրաժեշտ պահին գրված թիվը հնարավոր է «կարդալ», իսկ եթե այն այլևս հարկավոր չէ, ապա կարելի է ջնջել և նրա տեղը գրել նոր թիվ։ Թվերի կամ պայմանական ազդանշանների «հիշելը» և «կարդալը» ընդամենը տևում է վայրկյանի միլիոներորդ մասը։
«Հիշողությունը» կարող է պարունակել մի քանի հազար բջիջներ, յուրաքանչյուր բջիջ մի քանի տասնյակ էլեմենտներ, օրինակ՝ մագնիսական։ Թվերը երկուական սիստեմով գրելու համար պայմանավորվում ենք հաշվել, որ յուրաքանչյուր մագնիսացված էլեմենտ պատկերում է թվանշանը, իսկ չմագնիսացվածը՝ թվանշանը։ Դիցուք, հիշողության յուրաքանչյուր բջիջը պարունակում է էլեմենտ (կամ, ինչպես ասում են, «երկուական կարգեր»), ընդ որում բջիջի առանձին էլեմենտը ծառայում է թվի նշանը (+ կամ -) նշանակելու համար, հաջորդ կարգերը ծառայում են թվի ամբողջ մասը գրելու համար, իսկ վերջին կարգերը՝ կոտորակային մասը գրելու համար։ 11-րդ նկարում սխեմատիկորեն պատկերված են հիշողության երկու բջիջներ՝ յուրաքանչյուրը կարգով։ Մագնիսացված էլեմենտները նշանակված են + նշանով, չմագնիսացվածները՝ - նշանով։ Պատկերված բջիջներից դիտարկենք վերևինը (ստորակետը ցույց է տալիս, թե որտեղ է սկսվում թվի կոտորակային մասը, իսկ կետագիծը մնացածներից անջատում է առաջին կարգը, որը ծառայում է նշանը գրելու համար)։ Նրա մեջ գրված է (թվարկության երկուական սիստեմով) թիվը կամ մեզ համար սովորական թվարկության տասնորդական սիստեմով՝ թիվը։
Բացի թվերից, հիշողության բշիջներում գրվում են հրամաններ, որոնցից կազմված է ծրագիրը։ Դիտարկենք, թե ինչպիսի տեսք կունենան հրամանները այսպես կոչված երեքհասցեանի մեքենայի համար։ Այդ դեպքում հրամանը գրելիս հիշողության բջիջը բաժանվում է 4 մասի (կետագծերը ներքևի բջիջի վրա, նկ. 11)։ Առաջին մասը ծառայում է օպերացիան նշանակելու համար, ընդ որում օպերացիաները գրվում են թվերով (համարներով)։ Օրինակ,
| գումարում | — | օպերացիա | I | , | |
| հանում | — | օպերացիա | II | , | |
| բազմապատկում | — | օպերացիա | III | և այլն։ |
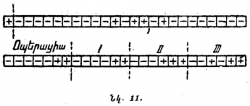
Հրամանները վերծանում են այսպես՝ բջիջի առաջին մասը օպերացիայի համարն է, երկրորդ և երրորդ մասերի բջիջների համարները (հասցեները), որոնցից պետք է վերցնել այդ օպերացիան կատարելու համար թվեր, չորրորդ մասը բջիջի համարն է (հասցեն), որտեղ պետք է ուղարկել ստացված արդյունքը։ Օրինակ, 11-րդ նկարի վրա ներքևի տողում) գրված են երկուական սիստեմով կամ տասնորդական սիստեմով՝ թվերը, որ նշանակում է հետևյալ հրամանը՝ կատարել III օպերացիան (այսինքն բազմապատկում) այն թվերի հետ, որոնք գտնվում են հիշողության երրորդ և յոթերորդ բջիջներում, իսկ ստացված արդյունքը «հիշել» (այսինքն՝ գրել) տասնմեկերորդ բջիջում։
Հետագայում մենք թվերը և հրւսմանները կգրենք ոչ թե պայմանական նշաններով, ինչպես 11-րդ նկարում է, այլ ուղղակի թվարկության տասնորդական սիստեմով։ Օրինակ, 11-րդ նկարի ներքևի տողում պատկերված հրամանը գրվում է այսպես՝
| բազմապատկում | ։ |
Այժմ դիտարկենք ծրագրերի երկու հասարակ օրինակներ։
| Ծրագիր 1 | ||||||
| 1) | գումարում | |||||
| 2) | բազմապատկում | |||||
| 3) | կ. փ. | |||||
| 4) | ||||||
| 5) | ||||||
Տեսնենք թե ինչպես կաշխատի մեքենան, որի առաջին հինգ բջիջներում գրված են այդ տվյալները։
1-ին հրաման՝ գումարել 4-րդ և 5-րդ բջիջներում գրված թվերը և արդյունքը նորից ուղարկել 4-րդ բջիջը (վաղօրոք այնտեղ գրվածի փոխարեն)։ Այսպիսով, մեքենան 4-րդ բջիջում գրում է թիվը։ Առաջին հրամանը կատարելուց հետո 4-րդ և 5-րդ բջիջներում կլինեն հետևյալ թվերը՝
| 4) | ||||
| 5) | ։ |
2-րդ հրամանը. չորրորդ բջիջում եղած թիվը բազմապատկել իրենով (այսինքն՝ այն բարձրացնել քառակուսի) և արդյունքը, այսինքն՝ , գրել քարտի վրա (սլաքը ցույց է տալիս պատրաստի արդյունքը)։
3-րդ հրաման՝ կառավարման փոխանցումը 1-ին բջիջին։ Այլ կերպ ասած, կ. փ. հրամանը նշանակում է, որ պետք է նորից կատարել բոլոր հրամանները ըստ կարգի, սկսած -ից։ Այսպիսով, նորից 1-ին հրաման։
1-ին հրաման. 4-րդ և 5-րդ բջիջներում եղած թվերը գումարել և արդյունքը նորից գրել 4-րդ բջիջում։ 4-րդ բջիջում արդյունքը կլինի թիվը
| 4) | ||||
| 5) | ։ |
2-րդ հրաման. 4-րդ բջիջում եղած թիվը բարձրացնել քառակուսի և ստացված արդյունքը, այսինքն , գրել քարտի վրա (սլաքը ցույց է տալիս արդյունքը)։
3-րդ հրաման. կատավարման փոխանցումը 1-ին բջիջին (այսինքն՝ դարձյալ անցում առաջին հրամանին)։
1-ին հրաման. թիվը ուղարկել 4-րդ բջիջին.
| 4) | ||||
| 5) | ։ |
2-րդ հրաման. քարտի վրա գրել թիվը։
3-րդ հրաման. կառավարման փոխանցումը 1-ին բջիջին և այլն։
Մենք տեսնում ենք, որ մեքենան մեկը մյուսի հետևից հաշվում է ամբողջ թվերի քառակուսիները և դրանք գրում է քարտի վրա։ Նկատեցեք, որ յուրաքանչյուր անգամ ձեռքով նոր թիվ հավաքելը պետք չէ, մեքենան ինքը իրար հետևից ընտրում է ամբողջ թվեր և դրանց բարձրացնում քառակուսի։ Գործելով այդ ծրագրով՝ մեքենան հաշվում է -ից մինչև -ը եղած բոլոր ամբողջ թվերի քառակուսիները մի քանի տասնյակ վայրկյանի ընթացքում։
Պետք է նշել, որ իրականում ամբողջ թվերի քառակուսիները հաշվելու համար ծրագիրը մասամբ ավելի բարդ կլինի, քան այն, որ բերված է վերևում։ Դա ամենից առաջ վերաբերում է 2-րդ հրամանին։ Բանն այն է, որ քարտի վրա պատրաստի արդյունքի գրելը պահանջում է ավելի շատ ժամանակ, քան մեքենայով մեկ օպերացիայի կատարելը։ Ուստի, սկզբից պատրաստի արդյունքները «հիշվում են» «հիշողության» ազատ բջիջներում, իսկ դրանից հետո «առանց շտապելու» արտադրվում են քարտի վրա։ Այսպիսով, առաջին վերջնական արդյունքը պետք է «հիշվի» «հիշողության» 1-ին ազատ բջիջում, երկրորդ արդյունքը՝ 2-րդ ազատ բջիջում, երրորդը՝ 3-րդում և այլն։ Վերը բերված պարզեցված ծրագրում դա ոչ մի կերպ հաշվի չէր առնված։
Բացի այդ, մեքենան չի կարող երկար ժամանակ զբաղվել քառակուսիների հաշվումներով, քանի որ «հիշողության» րջիջները չեն բավարարում, իսկ մենք չենք կարող «գուշակել», թե մեքենան արդեն հաշվե՞լ է մեզ անհրաժեշտ քառակուսիների թիվը, որպեսզի այդ պահին անջատենք այն. (չէ՞ որ մեքենան վայրկյանում կատարում է հազարավոր օպերացիաներ)։ Դրա համար էլ նախատեսված են հատուկ հրամաններ՝ պահանջված պահին մեքենաները կանգնեցնելու համար։ Օրինակ, ծրագիրը կարելի է կազմել այնպես, որ մեքենան հաշվի -ից մինչև բոլոր ամբողջ թվերի քառակուսիները և դրանից հետո ավտոմատորեն անջատվի։
Կան և հրամանների ուրիշ, ավելի բարդ տեսակները, որոնց մենք այստեղ չենք անդրադառնա պարզության համար։
Ահա թե ինչ տեսք կունենա -ից մինչն -ը բոլոր ամբողջ թվերի քառակուսիները հաշվելու ծրագիրը (ավելի լրիվ տեսքով)։
| Ծրագիր 1ա | ||||||
| 1) | գումարում | |||||
| 2) | բազմապատկում | |||||
| 3) | գումարում | |||||
| 4) | կ. պ. փ. (կառավարման պայմանական փոխանցում) |
|||||
| 5) | կանգնիր | |||||
| 6) | ||||||
| 7) | ||||||
| 8) | ||||||
| 9) | ||||||
| 10) | ||||||
| 11) | ||||||
| 12) | ||||||
| .................................. | ||||||
Առաջին երկու հրամանները քիչ են տարբերվում այն հրամաններից, որոնք կային նախորդ պարզեցված ծրագրում։ Այդ երկու հրամանների կատարումից հետո 8-րդ, 9-րդ և 10-րդ բջիջներում կլինեն հետևյալ թվերը՝
| 8) | ||||||
| 9) | ||||||
| 10) | ||||||
Երրորդ հրամանը շատ հետաքրքիր է. պետք է գումարել այն, ինչ կա 2-րդ և 6-րդ բջիջներում, և արդյունքները նորից գրել 2-րդ բջիջում, որից հետո 2-րդ բջիջը կունենա հետևյալ տեսքը՝
| 2) | բազմապատկում |
Ինչպես տեսնում եք, երրորդ հրամանը կատարելուց հետո փոխվում է երկրորդ հրամանը, ավելի ճիշտ՝ փոխվում է 2-րդ հրամանի հասցեներից մեկը։ Ստորև մենք կպարզաբանենք, թե ինչի համար է դա արվում։
Չորրորդ հրաման. կառավարման պայմանական փոխանցումը (ծրագրում վաղօրոք դիտարկված 3-րդ հրամանի փոխարեն)։ Այդ հրամանը կատարվում է այսպես. եթե 8-րդ բջիջում եղած թիվը փոքր է 7-րդ բջիջում եղած թվից, ապա կառավարումն հաղորդվում է 1-ին բջիջին. հակառակ դեպքում կատարվում է հաջորդ (այսինքն՝ 5-րդ) հրամանը։ Մեր դեպքում իրոք , այնպես որ տեղի կունենա կառավարման փոխանցում 1-ին բջիջին։ Այսպիսով, նորից 1-ին հրամանը։
1-ին հրամանը կատարելուց հետո, 8-րդ բջիջում կլինի թիվը.
Երկրորդ հրամանը, որն այժմ ունի հետևյալ տեսքը՝
| 2) | բազմապատկում |
կայանում է նրանում, որ թիվը ուղարկվում է 11-րդ բջիջին։ Այժմ պարզ է, թե ինչու ավելի շուտ կատարվեց 3-րդ հրամանը նոր թիվը, այսինքն , պետք է ընկնի ոչ թե 10-րդ բջիջում, որն արդեն զբաղված է, այլ հաջորդում։ 1-ին և 2-րդ հրամանները կատարվելուց հետո մենք կունենանք հետևյալ թվերը
| 8) | |
| 9) | |
| 10) | |
| 11) |
3-րդ հրամանը կատարվելուց հետո 2-րդ բջիջը կընդունի հետևյալ տեսքը՝
| 2) | բազմապատկում | ։ |
Քանի որ 8-րդ բջիջում դեռևս փոքր թիվ է գտնվում, քան 9-րդ բջիջում, ապա 4-րդ հրամանը նշանակում է կրկին կառավարման փոխանցում 1-ին բջիջին։
Այժմ 1-ին և 2-րդ հրամանները կատարվելուց հետո կստանանք՝
| 8) | |
| 9) | |
| 10) | |
| 11) | |
| 12) |
Մինչև ե՞րբ մեքենան այդ ծրագրով կհաշվի քառակուսիները։ Այնքան ժամանակ, մինչև որ 6-րդ բջիջում չի հայտնվել թիվը, այսինքն՝ քանի դեռ -ից մինչև թվերի քառակուսիները չեն հաշվարկվել։ Դրանից հետո 4-րդ հրամանը կառավարումն արդեն չի փոխանցի 1-ին բջիջին (քանի որ 8-րդ բջիջում եղած թիվը ոչ թե փոքր է, այլ հավասար է այն թվին, որը գտնում է 7-րդ բջիջում), այսինքն՝ 4-րդ հրամանից հետո մեքենան կատարում է 5-րդ հրամանը՝ կանգնում է (անջատվում է)։
Այժմ դիտարկենք ավելի բարդ ծրագրի օրինակ՝ հավասարումների սիստեմների լուծումը։ Այդ դեպքում մենք կդիտարկենք պարզեցված ծրագիրը։ Ցանկության դեպքում ընթերցողն ինքը կմտածի այն մասին, թե ինչպես կարտահայտվի այդպիսի ծրագիրը ավելի լրիվ տեսքով։
Դիցուք տրված է հավասարումների հետևյալ սիստեմը՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} ax+by=c, \\ dx+ey=f։ \end{cases} }
Այս սիստեմը դժվար չէ լուծել.
։
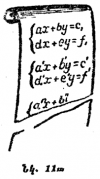
Այդպիսի սիստեմներ լուծելու համար ( գործակիցների տրված թվային արժեքներով) հավանաբար, ձեզ անհրաժեշտ է մի քանի տասնյակ վայրկյան։ Իսկ մեքենան կարող է լուծել վայրկյանում հարյուրավոր այդպիսի սիստեմներ։
Դիտարկենք համապատասխան ծրագիրը։ Ասենք թե միանգամից տրված են մի քանի սիստեմներ՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a, \; b, \; c, \; d, \; e, \; f, \; a՛, \; b՛, \dots} գործակիցների թվային արժեքներով։
Ահա համապատասխան ծրագիրը՝
| Ծրագիր 2 | |||||||||||||||||||||
| 1) | 14) | 27) | |||||||||||||||||||
| 2) | 15) | 28) | |||||||||||||||||||
| 3) | 16) | 29) | |||||||||||||||||||
| 4) | 17) | 30) | |||||||||||||||||||
| 5) | 18) | կ. փ. | 31) | ||||||||||||||||||
| 6) | 19) | 32) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a՛} | ||||||||||||||||||
| 7) | 20) | 33) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle b՛} | ||||||||||||||||||
| 8) | 21) | 34) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle c՛} | ||||||||||||||||||
| 9) | 22) | 35) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle d՛} | ||||||||||||||||||
| 10) | 23) | 36) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle e՛} | ||||||||||||||||||
| 11) | 24) | 37) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle f՛} | ||||||||||||||||||
| 12) | 25) | 38) | Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a՛՛} | ||||||||||||||||||
| 13) | 26) | ..... | |||||||||||||||||||
1-ին հրաման. կազմել 28-րդ և 30-րդ բջիջներում գտնվող թվերի արտադրյալը և արդյունքն ուղարկել 20-րդ բջիջին։ Այլ կերպ ասած, 20-րդ բջիջում կգրվի թիվը։
Համանման ձևով կատարվում են 2-րդից 6-րդ հրամանները։ Դրանց անջատումից հետո 20-րդից մինչև 25-րդ բջիջներում կգտնվեն հետևյալ թվերը՝
| 20) | |
| 21) | |
| 22) | |
| 23) | |
| 24) | |
| 25) |
7-րդ հրաման. 20-րդ բջիջում գտնվող թվերից հանել 21-րդ բջիջում գտնվող թիվը և արդյունքը (այսինքն՝ նորից գրել 20-րդ բջիջում։
Համանման ձևով կատարվում են 8-րդ և 9-րդ հրամանները։ 20-րդ, 21-րդ, 22-րդ բջիջներում կառաջանան հետևյալ թվերը
| 20) | |
| 21) | |
| 22) |
10-րդ և 11-րդ հրամաններ. կազմվում են
և
քանորդները և գրվում քարտի վրա (այսինքն՝ տրվում են՝ ինչպես պատրաստի արդյունքներ)։ Դա հենց հավասարումների առաջին սիստեմից ստացված անհայտների արժեքներն են։
Այսպիսով, առաջին սիստեմը լուծված է։ Ինչի՞ համար են հետագա հրամանները։ Ծրագրի հետագա մասը (12-րդից մինչև 19-րդ բջիջները) նշանակված է նրա համար, որպեսզի մեքենային ստիպեն «անցնելու» հավասարումների երկրորդ սիստեմին։ Տեսնենք, թե ինչպես է կատարվում այդ։
10-րդից մինչև 11-րդ հրամանները կայանում են նրանում, որ 1-ից 6-րդ բջիջների պարունակությանն ավելանում է այն գրանցումը, որն ունի 19-րդ բջիջը, իսկ արդյունքում նորից մնում են 1-ից 6-րդ բջիջները։ Այս ձևով 17-րդ հրամանը կատարելուց հետո առաջին վեց բջիջները կունենան հետևյալ տեսքը՝
| 1) | ||||||
| 2) | ||||||
| 3) | ||||||
| 4) | ||||||
| 5) | ||||||
| 6) |
18-րդ հրաման. կառավարման փոխանցումը առաջին բջիջին։
Առաջին վեց բջիջներում ինչո՞վ են տարբերվում նոր գրանցումները նախկին գրանցումներից։ Նրանով, որ այդ բջիջներում առաջին երկու հասցեներն ունեն ոչ թե 26-ից մինչև 31[13] համարները, ինչպես առաջ, այլ 32-ից մինչև 37 համարները։ Այլ կերպ ասած, մեքենան կրկին կկատարի նույն գործողությունները, բայց թվերը կվերցնի ոչ թե 20-րդ, 31-րդ բջիջներից, այլ 32-րդ, 37-րդ բջիջներից, որտեղ գտնվում են հավասարումների երկրորդ սիստեմի գործակիցները։ Այսպիսով, մեքենան լուծում է հավասարումների երկրորդ սիստեմը։ Երկրորդ սիստեմը լուծելուց հետո մեքենան անցնում է երրորդին և այլն։
Ասածից պարզ է դառնում, թե ինչքան կարևոր է ճիշտ «ծրագիր» կազմել կարողանալը։ Չէ՞ որ մեքենան «ինքը» ոչինչ անել չի «կարող»։ Նա կարող է կատարել միայն իրեն առաջադրված ծրագիրը։ Կան ծրագրեր, արմատներ, լոգարիթմներ, սինուսներ հաշվելու, բարձր աստիճանի հավասարումներ լուծելու համար և այլն։ Մենք արդեն վերևում խոսել ենք այն մասին, որ գոյություն ունեն ծրագրեր շախմատի խաղի, օտար լեզուներից թարգմանություն կատարելու համար,...։ Իհարկե, որքան բարդ է առաջադրանքը, այնքան էլ բարդ է նրան համապատասխանող ծրագիրը։
Վերջում նշենք, որ գոյություն ունեն այսպես կոչված ծրագրող ծրագրեր, այսինքն այնպիսիներ, որոնց օգնությամբ մեքենան ինքը կարող է կազմել խնդրի լուծման համար պահանջվող ծրագիրը։
Այդ զգալիորեն թեթևացնում է ծրագրի կազմելը, որը հաճախ շատ աշխատատար է լինում։

ԳԼՈՒԽ ԵՐՐՈՐԴ։ ՕԳՆՈՒԹՅՈՒՆ ԹՎԱԲԱՆՈՒԹՅԱՆԸ
Թվաբանությունը հաճախ ի վիճակի չէ սեփական միջոցներով խստորեն ապացուցել իր պնդումներից մի քանիսի ճշտությունը։ Այդպիսի դեպքերում ստիպված ենք լինում դիմել հանրահաշվի ընդհանրացնող եղանակներին։ Թվաբանության՝ հանրահաշվորեն հիմնավորված նման դրույթներին են պատկանում, օրինակ, գործողությունների կրճատ կատարման բազմաթիվ կանոնները, մի քանի թվերի հետաքրքիր առանձնահատկությունները, բաժանելիության հատկանիշները և այլն։ Այդպիսի հարցերի դիտարկմանն է նվիրված ներկա գլուխը։
ԱԿՆԹԱՐԹԱՅԻՆ ԲԱԶՄԱՊԱՏԿՈՒՄ
Վիրտուոզ հաշվողները բազմաթիվ դեպքերում իրենց հաշվողական աշխատանքը հեշտացնում են՝ դիմելով ոչ բարդ հանրահաշվական ձևափոխությունների։ Օրինակ հաշվումը կատարվում է այսպես՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 988 \times 988 \;=\; (988+12) \times (988-12)+12^2 \;=\; 1000 \times 976 + 144 \;=\; 976\;144։}
Հեշտ է հասկանալ, որ հաշվողն այդ դեպքում օգտվում է հետևյալ հանրահաշվական ձևափոխությունից՝
։
Բանավոր հաշվումների ժամանակ գործնականում մենք կարող ենք հաջողությամբ օգտվել այդ բանաձևից. օրինակ՝
,
,
,
,
,
։
Այնուհետև, բազմապատկումը կատարվում է այսպես՝
։
Ինչի՞ վրա է հիմնված այդ եղանակը։ Արտադրիչները ներկայացնենք հետևյալ տեսքով՝
և այդ երկանդամները բազմապատկենք հանրահաշվի կանոններով՝
։
Կատարենք ձևափոխությունները՝
։
Վերջին տողը պատկերում է հենց հաշվողի եղանակը։
Հետաքրքիր է երկու եռանիշ թվերի բազմապատկման եղանակը, որոնց տասնյակների թիվը նույնն է, իսկ միավորների թվանշանների գումարը հավասար է -ի։ Օրինակ,
։
Բազմապատկումը կատարում ենք այսպես՝
,
արդյունքը՝
։
Եղանակի հիմնավորումը պարզ է հետևյալ ձևափոխություններից՝
։
Նման բազմապատկումների կատարման համար հետևյալ եղանակն ավելի քան պարզ է՝
։
Այս օրինակում հարկ եղավ թիվը բարձրացնել քառակուսի։
-ով վերջացող թվերը արագ աստիճան բարձրացնելու համար շատ հարմար է հետևյալ եղանակը՝
։ Պատ. ,
։ Պատ. ,
։ Պատ. ։
Կանոնը կայանում է նրանում, որ տասնյակների թիվը բազմապատկում են նրանից մեկով մեծ թվով և արտադրյալին կցագրում ։
Եղանակը հիմնավորվում է հետևյալ կերպ։ Եթե տասնավորների թիվը է, ապա ամբողջ թիվը կարելի է պատկերել այսպես.
։
Այդ թվի քառակուսին, որպես երկանդամի քառակուսի, հավասար է՝
։
արտահայտությունը տասնյակների և նրան ամենամոտ մեծ թվի արտադրյալն է։ Թիվը -ով բազմապատկել և ստացածին ավելացնել, միևնույնն է, թե նրան կցագրել։
Նույն եղանակից հետևում է թիվը քառակուսի բարձրացնելու պարզ միջոցը, որը կազմված է ամբողջից և -ից։
Օրինակ՝
,
,
և այլն։
, ԵՎ ԹՎԱՆՇԱՆՆԵՐԸ
Հավանաբար բոլորը նկատել են, որ մեկով կամ հինգով վերջացող թվերի բազմապաակումից ստացվող թվերը վերջանում են միևնույն թվանշաններով։ Մինչդեռ, քչերը գիտեն, որ ասվածը վերաբերվում է նաև թվին։ Վեցով վերջացող թվի յուրաքանչյուր աստիճանը նույնպես վերջանում է վեցով։
Օրինակ՝
։
, և թվանշանների այդ հետաքրքիր առանձնահատկությունը կարելի է հիմնավորել հանրահաշվորեն։ Դիտարկենք այն -ի համար։
Վեցով վերջացող թվերը պատկերվում են այսպես՝
և այլն,
որտեղ -ն և -ն դրական ամբողջ թվեր են։
Երկու այդպիսի թվերի արտադրյալը հավասար է՝
։
Ինչպես տեսնում ենք, արտադրյալը կազմված է մի քանի տասնավորներից և թվանշանից, որն, անշուշտ, պետք է լինի վերջում։
Ապացուցման նույն եղանակը կարելի է կիրառել -ի և -ի համար։
| վերջանում է | -ով, | |
| » | -ով, | |
| » | -ով և այլն։ |
Ասվածը մեզ իրավունք է տալիս հաստատելու, որ , օրինակ,
ԵՎ ԹՎԵՐԸ
Կան երկանիշ թվեր, որոնք ունեն միևնույն հատկությունը, ինչ , և թվերը։ Այդ թիվը -ն է, և հավանական է, շատերի համար անսպասելի, թիվը։ Յուրաքանչյուր երկու թվեր, որոնք վերջանում են -ով, արտադրյալում տալիս են մի թիվ, որը վերջանում է -ով։
Ապացուցենք այդ։ Այդպիսի թվերի ընդհանուր արտահայտությունը այսպես է՝
և այլն։
Բազմապատկելով այդպիսի երկու թվեր՝ կստանանք.
։
Դրույթը ապացուցված է, արտադրյալը կվերջանա թվով։
Այստեղից հետևում է, որ -ով վերջացող թվի ամեն մի աստիճանը այնպիսի թիվ է, ինչպիսիք են՝
ԱՆՎԵՐՋ «ԹՎԵՐ»
Գոյություն ունեն ավելի մեծ խմբեր այնպիսի թվանշանների, որոնք գտնվելով թվերի վերջում, պահպանվում են նաև դրանց արտադրյալում։ Այդպիսի թվանշանների խմբերի թիվ, ինչպես մենք ցույց կտանք, անվերջ մեծ է։
Մենք գիտենք երկանիշ թվանշանների խմբեր, որոնք ունեն այդ հատկությունը՝ դա -ն է և -ը։ Որպեսզի գտնենք եռանիշ խմբեր, պետք է -ի կամ թվի առջևից կցագրել այնպիսի թվանշան, որ ստացված եռանիշ թվանշանների խումբը նույնպես ունենա պահանջված հատկությունը։
Ինչպիսի՞ թվանշան պետք է կցագրել թվին։ Նշանակենք այն -ով։ Այդ ժամանակ որոնելի եռանիշ թիվը կպատկերվի այսպես՝
։
Այդ թվանշանների խմբով վերջացող թվերի համար ընդհանուր արտահայտությունը այսպես է՝
և այլն։
Բազմապատկենք այս տեսքի երկու թվեր. կստանանք՝
։
Բոլոր գումարելիները, բացի վերջին երկուսից, վերջում ունեն երեք զրոյից ոչ պակաս։ Ուստի՝ արտադրյալը վերջանում է -ով, եթե
տարբերությունը բաժանվում է -ի։ Դա, ակնհայտ է, կլինի միայն այն դեպքում, երբ ։
Այսպիսով, որոնելի թվանշանների խումբն ունի տեսքը։ Ուստի և թվի ամեն մի աստիճանը վերջանում է -ով։ Օրինակ՝
։
Եթե մենք այժմ ցանկանանք գտնել թվանշանների քառանիշ խումբ, որն ունենա միևնույն հատկությունը, ապա -ի առջևից պետք է կցագրենք ես մեկ թվանշան։ Եթե այդ թվանշանը նշանակենք -ով, ապա կհանգենք հետևյալ խնդրին՝ -ի ի՞նչ արժեքի դեպքում
արտադրյալը վերջանում է -ով։ Եթե այս արտադրյալի մեջ բացենք փակագծերը և դեն գցենք այն բոլոր գումարելիները, որոնք վերջանում են և ավելի զրոներով, ապա կմնան հետևյալ անդամները՝
։
Արտադրյալը վերջանում է -ով, եթե
տարբերությունը բաժանվում է -ի վրա։ Դա, ակնհայտ է, կլինի միայն այն դեպքում, երբ ։
Որոնելի թվանշանների քառանիշ խումբն է ։
Ստացված թվանշանների քառանիշ խմբին կարելի է ավելացնել ես մեկ թվանշան, որի համար պետք է դատել ճիշտ այնպես, ինչպես և վերևում։ Մենք կստանանք ։ Կատարելով ես մի քայլ, գտնում ենք թվանշանների խումբը, այնուհետև և այլն։
Ձախից թվանշանների այդպիսի գրառումը կարելի է կատարել անսահմանափակորեն։ Արդյունքում մենք կստանանք մի «թիվ», որը կունենա անսահման շատ թվանշաններ՝
,
Նման «թվերը» կարելի է գումարել և բազմապատկել սովորական կանոնով, չէ՞ որ դրանք գրվում են աջից ձախ, իսկ գումարումը և բազմապատկումը («սյունակով») նույնպես կատարվում է աջից ձախ, այնպես որ այդպիսի երկու թվերի գումարում, արտադրյալում մեկը մյուսի հետևից կարելի է հաշվել թվանշաններ, որքան պետք է։
Հետաքրքիր է, որ վերը գրված անսահման «թիվը» բավարարում է
հավասարմանը, որքան էլ դա անհավանական չի թվում։
Իրոք, այդ «թվի» քառակուսին (այսինքն՝ բազմապատկումն ինքն իրենով) վերջանում է -ով, քանի որ արտադրիչներից յուրաքանչյուրը վերջում ունի . նույն պատճառով, գրված «թվի» քառակուսին վերջանում է -ով, վերջանում է -ով և այլն։ Այլ կերպ ասած, «թվի» թվանշանները, հաշվելով մեկը մյուսից հետո, որտեղ , մենք կստանանք այն թվանշանները, որոնք կան թվի մեջ, այնպես որ ։
Մենք դիտարկեցինք թվանշանների խմբեր, որոնք վերջանում են -ով[16]։ Եթե համանման դատողություններ անենք -ով վերջացող թվանշանների խմբերի համար, ապա մենք կստանանք թվանշանների այսպիսի խմբեր՝
և այլն։
Արդյունքում մենք կարող ենք գրել դարձյալ մի անսահման «թիվ».
,
որը նույնպես բավարարում է հավասարմանը։ Կարելի էր ցույց տալ, որ այդ անսահման «թիվը» «հավասար է»
Ստացված հետաքրքիր արդյունքն անսահման «թվերի» լեզվով ձևակերպվում է այսպես՝ հավասարումը, բացի սովորական և լուծումներից, ունի երկու «անսահման» լուծումներ՝
և ,
Իսկ այլ լուծումներ (թվարկության տասնորդական սիստեմում) գոյություն չունեն[17]։
ԼՐԱՑՈՒՑԻՉ ՎՃԱՐ
Հինավուրց ժողովրդական խնդիր
Հին ժամանակներում մի անգամ տեղի է ունեցել այսպիսի դեպք։ Երկու անասնավաճառներ վաճառեցին իրենց պատկանող եզների նախիրը, ընդ որում յուրաքանչյուր եզան համար ստացան այնքան ռուբլի, որքան եզներ կային նախիրում։ Ստացած դրամով գնեցին ոչխարների հոտ, յուրաքանչյուր ոչխարը ռուբլով և մեկ գառ։ Հավասարապես բաժանելու դեպքում մեկին մնաց մի ավելորդ ոչխար, իսկ մյուսը վերցրեց գառը և ընկերակցից ստացավ համապաmասխան լրացուցիչ վճար։ Ի՞նչքան էր եղել լրացուցիչ վճարը (ենթադրվում է, որ լրացուցիչ վճարը արտահայտվում է ամբողջ ռուբլիներով)։
Լուծում
Խնդիրը ուղղակիորեն, ենթակա չէ «հանրահաշվական լեզվի» թարգմանելուն, նրա համար հավասարումներ չի կարելի կազմել։ Հարկ է լինում այն լուծել հատուկ եղանակով, այսպես ասած մաթեմատիկական ազատ դատողություններով։ Բայց այստեղ ևս հանրահաշիվը թվաբանությանը ցույց է տալիս էական օգնություն։
Հոտի ամբողջ արժեքը ռուբլիներով ճիշտ քառակուսի է, քանի որ հոտը գնված է եզների վաճառքի դրամով, որոնցից յուրաքանչյուրը վաճառվել է -ական ռուբլի։ Ընկերակիցներից մեկին մնացել է ավելորդ ոչխար, հետևաբար՝ ոչխարների թիվը կենտ է. նշանակում է՝ թվի մեջ տասնավորների թիվը ևս կենտ է։ Ինչպիսի՞ն է միավորների թվանշանը։
Կարելի է ապացուցել, որ եթե ճիշտ քառակուսու մեջ տասնավորների թիվը կենտ է, ապա նրա միավորների թվանշանը կարող է լինել միայն -ը։
Իրոք, տասնավորների և միավորների յուրաքանչյուր թվի քառակուսին, այսինքն՝ -ն հավասար է
։
Այս թվի մեջ տասնյակների քանակն է , և էլի որոշ թվով տասնյակներ էլ պարունակում է -ին։ բաժանվում է -ի վրա, այս թիվը զույգ է։ Ուստի՝ տասնյակների թիվը, որ պարունակվում է մեջ, կլինի կենտ, եթե միայն թվի մեջ լինի կենտ թվով տասնյակներ։ Վերհիշենք, թե -ն ինչ է։ Այն միավորների թվանշանի քառակուսին է, այսինքն՝ հետևյալ թվերից մեկը
։
Դրանց միջև կենտ թվով տասնյակներ ունեն միայն -ը և -ը։ Երկուսն էլ վերջանում են -ով։ Նշանակում է ճիշտ քառակուսին՝
,
կարող է ունենալ կենտ թվով տասնյակներ միայն այն դեպքում, եթե վերջանում է -ով։
Այժմ հեշտ է գտնել խնդրի հարցի պատասխանը։ Պարզ է, որ գառը վաճառվել է ռուբլով։ Հետևաբար ընկերակիցը, որին մնացել է գառը, ստացավ մյուսից ռուբլով ավելի պակաս։ Մասերը հավասարեցնելու համար գառան տերն ընկերակցից պետք է ետ ստանար իր ռուբլին։
Լրացուցիչ վճարը հավասար է ռուբլու։
-Ի ԲԱԺԱՆԵԼԻՈՒԹՅՈՒՆԸ
Հանրահաշիվը խիստ հեշտացնում է այն հատկանիշների որոնումը, որոնցով կարելի է նախօրոք, չկատարելով բաժանում, որոշել, թե տվյալ թիվը բաժանվո՞ւմ է արդյոք այս կամ այն բաժանարարի վրա։ -ի բաժանելիության հատկանիշները հանրածանոթ են։ Արտածենք -ի բաժանելիության հատկանիշը. այն բավականին պարզ է և գործնական։
Դիցուք, բազմանիշ թիվն ունի միավորների թվանշանը, տասնավորների թվանշանը, հարյուրավորների թվանշանը, հազարավորների թվանշանը և այլն, այսինքն՝
.
որտեղ բազմակետը նշանակում է հետագա կարգերի գումարը։ -ից հանենք թիվը, տասնմեկի բազմապատիկը։ Այդ ժամանակ ստացված տարբերությունը, ինչպես հեշտ է նկատել, հավասար է՝
,
որը կունենա -ի վրա բաժանումից ստացված այն նույն մնացորդը, ինչ որ թիվը։ Այդ տարբերությանը ավելացնենք թիվը՝ տասնմեկի բազմապատիկը, մենք կստանանք՝
թիվը, որը նույնպես կունենա -ի վրա բաժանումից ստացված այն նույն մնացորդը, ինչ որ թիվը։ Նրանից հանենք թիվը, տասնմեկի բազմապատիկը և այլն։
Արդյունքում մենք կստանանք՝
թիվը, որն ունի է -ի վրա բաժանումից ստացված այն նույն մնացորդը, ինչ որ սկզբնական թիվը։
Այստեղից բխում է -ի բաժանելիության հետևյալ հատկանիշը՝ պետք է կենտ տեղերում գրված բոլոր թվանշանների գումարից հանել այն բոլոր թվանշանների գումարը, որոնք զբաղեցնում են զույգ տեղերը։ Եթե տարբերությունում ստացվում է -ի բազմապատիկ թիվ (դրական կամ բացասական), ապա և փորձարկվող թիվը -ի բազմապատիկն է, հակառակ դեպքում մեր թիվը առանց մնացորդի չի բաժանվի -ի վրա։
Փորձենք, օրինակ, թիվը՝
,
,
։
Նշանակում է, տրված թիվը բաժանվում է -ի վրա։ Գոյություն ունի -ի բաժանելիության և այլ հատկանիշ, որը հարմար է կարճ թվերի համար։ Այն կայանում է նրանում, որ փորձարկվող թիվը աջից ձախ բաժանում են խմբերի՝ յուրաքանչյուրում երկուական թվանշան և այդ խմբերը գումարում են։ Եթե ստացված գումարը առանց բաժանվի -ի վրա, ապա և փորձարկվող թիվը -ի բազմապատիկն է, հակառակ դեպքում՝ ոչ։ Դիցուք պահանջվում է փորձարկել թիվը։ Թիվը բաժանենք խմբերի և գումարենք երկու խմբերը՝
։
Քանի որ -ը բաժանվում է -ի վրա առանց մնացորդի, ապա թիվը -ի բազմապատիկն է՝
։
Ապացուցենք բաժանելիության այդ հատկանիշը։ բազմանիշ թիվը վերլուծենք խմբերի։ Այդ դեպքում մենք կստանանք երկանիշ (կամ միանիշ[18]) թվեր, որոնք նշանակենք (աջից ձախ) և այլն, այնպես որ թիվը կարելի է գրել հետևյալ տեսքով՝
։
թվից հանենք թիվը՝ տասնմեկի բազմապատիկը։ Ստացված թիվը՝
-ի վրա բաժանումից կունենա այն նույն մնացորդը, ինչ որ թիվը։ Այդ թվից հանենք թիվը՝ տասնմեկի բազմապատիկը և այլն։ Արդյունքում մենք կգտնենք, որ թիվը -ի վրա բաժանումից կունենա այն մնացորդը, ինչ որ
թիվը։
ԱՎՏՈՄԵՔԵՆԱՅԻ ՀԱՄԱՐԸ
Խնդիր
Քաղաքում շրջագայելիս երեք ուսանող-մաթեմատիկոսներ նկատեցին, որ ավտոմեքենայի վարորդը կոպիտ կերպով խախտեց փողոցի երթևեկության կանոնները։ Մեքենայի համարը (քառանիշ) ուսանողներից և ոչ մեկը չէր հիշում, բայց քանի որ նրանք մաթեմատիկոսներ էին, նրանցից յուրաքանչյուրը նկատել էր այդ քառանիշ թվի մի որևէ առանձնահատկություն։ Ուսանողներից մեկը վերհիշել է, որ թվի առաջին երկու թվանշանները միատեսակ էին։ Երկրորդը վերհիշել էլ որ վերջին երկու թվանշանները նույնպես համընկել են միմյանց։ Վերջապես, երրորդը հաստատել է, որ այդ ամբողջ քառանիշ թիվը ճիշտ քառակուսի է։ Հնարավո՞ր է արդյոք այդ տվյալներով իմանալ մեքենայի համարը։
Լուծում
Որոնելի թվի առաջին (և երկրորդ) թվանշանը նշանակենք -ով, իսկ երրորդը (և չորրորդը) -ով։ Այդ դեպքում ամբողջ թիվը հավասար կլինի՝
։
Այդ թիվը բաժանվում է -ի վրա, և այդ պատճառով (լինելով ճիշտ քառակուսի) նա բաժանվում է նաև -ու վրա։ Այլ կերպ ասած, թիվը բաժանվում է -ի վրա։ Կիրառելով -ի բաժանելիության վերը բերված երկու հատկանիշներից ցանկացածը, գտնում ենք, որ թիվը բաժանվում է -ի վրա։ Բայց այդ նշանակում է, որ
,
քանի որ թվանշաններից յուրաքանչյուրը փոքր է տասից։
թվի վերջին թվանշանը, որը ճիշտ քառակուսի է, կարող է ընդունել միայն հետևյալ արժեքները՝
։
Ուստի, թվանշանի համար, որը հավասար է , կգտնենք այսպիսի հնարավոր արժեքներ՝
։
Առաջին երկու արժեքները պիտանի չեն, մնում են հետևյալ հնարավորությունները՝
,
,
,
։
Մենք տեսնում ենք, որ ավտոմեքենայի համարը պետք է փնտրել հետևյալ չորս թվերի մեջ՝
։
Բայց այդ թվերից վերջին երեքը չեն հանդիսանում ճիշտ քառակուսիներ՝ թիվը բաժանվում է -ի վրա, բայց չի բաժանվում -ի. թիվը բաժանվում է -ի, բայց չի բաժանվում -ի. թիվը նույնպես չի հանդիսանում քառակուսի։ Մնում է միայն մեկ թիվ՝ , որը և տալիս է խնդրի լուծումը։
-Ի ԲԱԺԱՆԵԼԻՈՒԹՅՈՒՆԸ
Հիմնավորենք -ի բաժանելիության հետևյալ հատկանիշը։ Թիվը -ի վրա առանց մնացորդի բաժանվում է միայն այն ժամանակ, երբ նրա տասնավորների թիվը՝ գումարելով միավորների կրկնապատիկ թվի հետ տալիս է -ի բազմապատիկը։
Լուծում
Ամեն մի թիվ կարելի է ներկայացնել հետևյալ տեսքով՝
,
որտեղ -ը տասնավորների թիվն է (ոչ թե տասնավորների կարգի թվանշանը, այլ ամբողջ թվում ամբողջական տասնավորների ընդհանուր թիվը), -ը միավորների թվանշանն է։ Մեզ հարկավոր է ցույց տալ, որ -ը բազմապատիկ է -ին միայն այն ժամանակ, երբ
բազմապատիկ է -ին։ Դրա Տամար -ը բազմապատկենք -ով և այդ արտադրյալից հանենք -ը. կստանանք՝
։
Այստեղից երևում է, որ եթե -ը -ի բազմապատիկ է, ապա
ևս -ի վրա բաժանվում է առանց մնացորդի. և հակառակն, եթե -ը -ի վրա բաժանվում է առանց մնացորդի, ապա
-ի բազմապատիկ է, իսկ այդ դեպքում, ակնհայտ է, -ը ևս -ի վրա բաժանվում է առանց մնացորդի։
Դիցուք պահանջվում է որոշել, թե թիվը բաժանվո՞ւմ է արդյոք -ի վրա։
Հաջորդաբար կիրառենք բաժանելիության մեր հատկանիշը.
| / | ||||||||||||||
| / | ||||||||||||||
| / | ||||||||||||||
| / | ||||||||||||||
| / | ||||||||||||||
| / | ||||||||||||||
Քանի որ -ը բաժանվում է -ի վրա առանց մնացորդի, ապա -ի բազմապատիկներն են նաև թվերը։
Այսպիսով, մեր թիվը բաժանվում է -ի վրա։
ՍՈՖՅԱ ԺԵՐՄԵՆԻ ԹԵՈՐԵՄԱՆ
Ահա մի խնդիր, որն առաջարկել է ֆրանսիական հայտնի մաթեմատիկոս Սոֆյա Ժերմենը՝
Ապացուցել, որ տիպի յուրաքանչյուր թիվ բարդ թիվ է (եթե -ն հավասար չէ -ի)։
Լուծում
Ապացույցը բխում է հետևյալ ձևափոխությունից՝
։
Ինչպես մենք համոզվում ենք, թիվը կարող է պատկերվել երկու արտադրիչների արտադրյալի տեսքով, որոնցից մեկը հավասար չէ այդ թվին, իսկ մյուսը՝ մեկի[19], այլ խոսքով, այդ թիվը բարդ է։
ԲԱՐԴ ԹՎԵՐ
Պարզ թվերի քանակը անվերջ մեծ է։ (Պարզ թվերը մեկից մեծ այն ամբողջ թվերն են որոնք առանց մնացորդի ոչ մի ամբողջ թվի վրա չեն բաժանվում, բացի մեկից և իրենցից)։
Սկսվելով Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2, \; 3, \; 5, \; 7, \; 13, \; 17, \; 19, \; 23, \; 29, \; 31, \:...} թվերով, պարզ թվերի շարքը ձգվում է անվերջ։ Գտնվելով բարդ թվերի միջև, դրանք բնական թվերի շարքը տրոհում են բարդ թվերի քիչ թե շատ երկար մասերի։ Ինչպիսի՞ երկարություն են ունենում այդ մասերը։ Որևէ տեղ հաջորդո՞ւմ են արդյոք միմյանց, օրինակ, հազար բարդ թվեր, չընդհատվելով ոչ մի պարզ թվով։
Կարելի է ապացուցել (չնայած այդ կարող է թվալ անհավատալի), որ պարզ թվերի միջև եղած բարդ թվերի մասերը լինում են ցանկացած երկարությամբ։ Այդպիսի մասերի երկարության համար չկա սահման. դրանք կարող են բաղկացած լինել հազարավոր, միլիոնավոր, միլիարդավոր և այլն թվերից։
Հարմարության համար կօգտվենք պայմանական սիմվոլից, որը նշանակում է -ից մինչև ներառյալ բոլոր թվերի արտադրյալը։ Օրինակ ։ Մենք այժմ կապացուցենք, որ
շարքը կազմված է հաջորդական բարդ թվերից։
Բնական շարքում այդ թվերը անմիջականորեն ընթանում են մեկը մյուսի ետևից, քանի որ յուրաքանչյուր հաջորդը -ով մեծ է նախորդից։ Մնում է ապացուցել, որ այդ բոլոր թվերը բարդ են։
Առաջին թիվը՝
զույգ է, քանի որ նրա երկու գումարելիներն էլ պարունակում են արտադրիչը։ Իսկ -ից մեծ ամեն մի զույգ թիվ բարդ թիվ է։
Երկրորդ թիվը՝
կազմված է երկու գումարելիներից, որոնցից յուրաքանչյուրը -ի բազմապատիկն է։ Նշանակում է այդ թիվը ևս բարդ է։
Երրորդ թիվը՝
առանց մնացորդի բաժանվում է -ի, քանի որ կազմված է այնպիսի գումարելիներից, որոնք -ի բազմապատիկն են։
Նույն ձևով կհաստատենք, որ հետևյալ թիվը՝
-ը,
-ի բազմապատիկն է և այլն։ Այլ կերպ ասած, մեր շարքի յուրաքանչյուր թիվը պարունակում է մի արտադրիչ, որը տարբերվում է մեկից և ինքն իրենից, հետևաբար այն հանդիսանում է բարդ թիվ։
Եթե դուք ցանկանում եք գրել, օրինակ, հինգ հաջորդական բարդ թվեր, ձեզ բավական է վերը բերված շարքում
-ի փոխարեն տեղադրել թիվը։ Դուք կստանաք հետևյալ շարքը՝
։
Բայց դա հինգ հաջորդական բարդ թվերից միակ շարքը չէ։ Կան և ուրիշները, օրինակ՝
։
Կամ դարձյալ ավելի փոքր թվեր՝
։
Այժմ փորձենք լուծել հետևյալ խնդիրը.
Գրել տասը հաջորդական բարդ թվեր։
Լուծում
Քիչ առաջ ասվածի հիման վրա որոնելի տասը թվերից որպես առաջին թիվ կարելի է վերցնել
[20]։
Թվերի որոնելի սերիան, հետևաբար, կլինի այսպես՝
[21] և այլն։
Սակայն գոյություն ունեն անհամեմատ ավելի փոքր տասը հաջորդական բարդ թվերի սերիաներ։ Այսպես, կարելի է ցույց տալ ոչ միայն տասը, այլ նաև տասներեք հաջորդական բարդ թվերի սերիաներ արդեն երկրորդ հարյուրյակում՝
և այլն մինչև -ը ներառյալ։
ՊԱՐԶ ԹՎԵՐԻ ՔԱՆԱԿԸ
Միմյանց հաջորդող բարդ թվերի՝ ցանկացածին չափ երկար սերիաների գոյությունը կարող է կասկածանքի տեղիք տալ, թե արդյո՞ք պարզ թվերի շարքը վերջ չունի։ Դրա համար, ավելորդ չի լինի այստեղ բերել պարզ թվերի շարքի անսահմանության ապացույցը։
Այդ «սպացույցր պատկանում է հին հունական մաթեմատիկոս Էվկլիդին և շարադրված է նրա հռչակավոր «Սկզբունքներ» գրքի մեջ։ Այն վերաբերում է «հակասող ընդունելությամբ» ապացույցների կարգին։ Ենթադրենք, որ պարզ թվերի շարքը վերջավոր է և այդ շարքի վերջին պարզ թիվը նշանակենք տառով։ Կազմենք հետևյալ արտադրյալը
և նրան ավելացնենք ։ Կստանանք՝
։
Այս թիվը լինելով ամբողջ՝ կպարունակի գոնե մեկ պարզ արտադրիչ, այսինքն՝ կբաժանվի գոնե մեկ պարզ թվի վրա։ Բայց բոլոր պարզ թվերը, ըստ ենթադրության, չեն գերազանցում -ը, իսկ թիվը առանց մնացորդի չի բաժանվում -ից փոքր կամ նրան հավասար թվերից և ոչ մեկի վրա՝ ամեն անգամ ստացվում է մնացորդ։
Այսպիսով, չի կարելի ընդունել, որ պարզ թվերի շարքը վերջավոր է. այդ ենթադրությունը բերում է հակասության։ Նշանակում է՝ բնական թվերի շարքում հաջորդական բարդ թվերիին ինչպիսի երկար սերիալի էլ հանդիպենք, մենք համոզված կլինենք, որ նրանից հետո էլի կգտնվեն անվերջ բազմությամբ պարզ թվեր։
ՀԱՅՏՆԻ ԱՄԵՆԱՄԵԾ ՊԱՐԶ ԹԻՎԸ
Այլ բան է համոզված լինել, որ գոյություն ունեն որքան հնարավոր է մեծ պարզ թվեր, իսկ այլ բան է գիտենալ, թե որ թվերն են հանդիսանում պարզ թվեր։ Որքան մեծ է բնական թիվը, այնքան մեծ հաշվումներ պետք է կատարել, իմանալու համար՝ նա հանդիսանո՞ւմ է պարզ թիվ, թե ոչ։ Ահա մի մեծագույն թիվ, որի մասին ներկայումս հայտնի է, որ ալն պարզ է՝
[22]։
Այս թիվն ունի մոտ յոթ հարյուր տասնորդական նիշ։ Հաշվումները, որոնց օգնությամբ սահմանվել է, որ այդ թիվը հանդիսանում է պարզ թիվ, կատարվել են ժամանակակից հաշվիչ մեքենաներով (տե՛ս գլ. I, II)։
ՊԱՏԱՍԽԱՆԱՏՈՒ ՀԱՇՎԱՐԿ
Հաշվողական պրակտիկայում հանդիպում են այնպիսի զուտ թվաբանական հաշվումներ, որոնց կատարումը առանց հանրահաշվի հեշտացնող մեթոդների օգնության՝ արտակարգ դժվար է։ Դիցուք, պահանջվում է գտնել այսպիսի գործողությունների արդյունքը՝
(Այս հաշվարկն անհրաժեշտ է նրա համար, որպեսզի հաստատվի, թե իրավացի՞ է այն տեխնիկան, որը գործ ունի էլեկարամագնիսական ալիքների տարածման արագության համեմատ փոքր արագությամբ շարժվող մարմինների հետ, որպեսզի կարելի լինի օգտվել արագությունների գումարման նախկին օրենքից՝ հաշվի չառնելով այն փոփոխությունները, որոնք ներմուծված են մեխանիկայի մեջ հարաբերականության[23] տեսության կողմից։ Համաձայն հին մեխանիկայի, այն մարմինը, որը մասնակցում է վայրկյանում և կիլոմետր արագություններով միատեսակ ուղղված երկու շարժումների, վայրկյանում ունի կիլոմետր արագություն։ Մինչդեռ նոր գիտությունը մարմնի արագության համար տալիս է հետևյալ արտահայտությունը.
[24] կիլոմետր վայրկյանում,
որտեղ -ն լույսի տարածման արագությունն է դատարկության մեջ, որը վայրկյանում մոտավորապես հավասար է կիլոմետրի։ Մասնավորապես, մարմնի արագությունը, որը մասնակցում է միատեսակ ուղղված երկու շարժումների, որոնցից յուրաքանչյուրն ունի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; կմ/վրկ} արագություն, ըստ հին մեխանիկայի հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2 \; կմ/վրկ} , իսկ ըստ նորի՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \frac{2}{1+\frac{1}{90 \; 000 \; 000 \; 000}} \; կմ/վրկ}
Իսկ այդ արդյունքները որքանո՞վ են տարբերվում միմյանցից։ Որսո՞ւմ է արդյոք ամենանուրբ չափողական գործիքն այս տարբերությունը։ Այդ կարևոր հարցը պարզաբանելու համար էլ հենց հարկ է լինում կատարել վերոհիշյալ հաշվարկը)։
Այդ հաշվարկը կատար ենք երկու կերպ. նախ թվաբանական սովորական ճանապարհով, և ապա հանրահաշվի կիրառմամբ։ Սակայն բավական է մի հայացք գցենք ստորև բերված թվանշանների շարքի վրա և կհամոզվենք հանրահաշվական եղանակի առավելության անվիճելիության մեջ։
Նախ և առաջ ձևափոխենք մեր «բազմահարկ» կոտորակը
։
Այժմ կատարենք համարիչի բաժանումը հայտարարի վրա։
| [25] | |||||||||||||||||||||||
| [26] | |||||||||||||||||||||||
Հաշվարկը, ինչպես տեսնում ենք, հոգնեցուցիչ է, մանրակրկիտ, նրանում հեշտ է շփոթվել և սխալվել։ Մինչդեռ, խնդիրը լուծելու համար կարևոր է ճշտությամբ իմանալ որտեղ է հատկապես ընդհատվում ինների շարքը և սկսվում մյուս թվանշանների սերիան։
Այժմ համեմատեցեք, թե հանրահաշիվը որքան կարճ է կատարում այդ հաշվարկը։ Այն օգտվում է հետևյալ մոտավոր հավասարությունից՝ եթե -ն շատ փոքր կոտորակ է, ապա
,
որտեղ նշանը նշանակում է «մոտավորապես հավասար է»։ Այս պնդման իրավացիության մեջ համոզվելը շատ հեշտ է՝ բաժանելին բաղդատենք այն արտադրյալի հետ, որն ստացվում է բաժանարարը քանորդով բազմապատկելուց՝
,
այսինքն՝
,
Քանի որ -ն շատ փոքր կոտորակ է (օրինակ, ), ապա -ն ավելի քան փոքր կոտորակ է () և այն կարելի է անտեսել։
Ասվածը կիրառենք մեր հաշվարկի համար[27]
Մենք ստացանք միևնույն արդյունքը, ինչ որ առաջ, բայց անհամեմատ ավելի կարճ ճանապարհով։
(Հավանաբար ընթերցողին հետաքրքիր է իմանալ, թե մեխանիկայի բնագավառից բերված մեր խնդրում ստացված արդյունքն ի՛նչ արժեք ունի) Այդ արդյունքը ցույց է տալիս,որ լույսի արագության համեմատությամբ դիտարկվող արագությունները փոքր լինելու պատճառով արագությունների գումարման հին օրենքից շեղվելը պրակտիկորեն չի հայտնաբերվում՝ այն հայտնվում է որոշված թվի տասնմեկերորդ թվանշանի վրա, իսկ երկարության ամենաճշգրիտ չափումների ժամանակ էլ չեն վերցնում ինը թվանշանից ավելի. նույնիսկ սովորական տեխնիկայի մեջ սահմանափակվում են անգամ 3-4 թվանշաններով։ Դրա համար մենք, առանց որևէ վերապահության, իրավունք ունենք հաստատելու, որ էյնշտեյնյան նոր մեխանիկան գործնականորեն ոչինչ չի փոխում տեխնիկական հաշվումների մեջ, որը վերաբերում է (լույսի տարածման համեմատությամբ) «դանդաղ» շարժվող մարմիններին)։
ԵՐԲ ԱՌԱՆՑ ՀԱՆՐԱՀԱՇՎԻ ԱՎԵԼԻ ՊԱՐԶ Է
Այն դեպքերին զուգընթաց, երբ հանրահաշիվը թվաբանությանը ցnւյց է տալիս էական ծառայություններ, լինում են և այնպիսի դեպքեր, երբ հանրահաշվի միջամտությունը բերում է միայն անտեղի բարդացումներ։ Մաթեմատիկայի իրական արժեքը մաթեմատիկան միջոցներից հմտորեն օգտվելու մեջ է, որպեսզի ընտրենք միշտ ամենաուղիղ և հարմարավետ ճանապարհը՝ հաշվի առնելով այն, թե խնդրի լուծման մեթոդը վերաբերո՞ւմ է արդյոք թվաբանությանը, հանրահաշվին, երկրաչափությանը և այլն։ Այդ պատճառով օգտակար կլինի դիտարկել այն դեպքը, երբ հանրահաշվի ներմուծումը կարող է միայն շփոթեցնել լուծողին։ Ուսանելի օրինակ կարող է ծառայել հետևյալ խնդիրը։
Գտնել այն բոլոր թվերից ամենափոքրը, որոնք բաժանելիս
| -ի, | տալիս են | մնացորդ, | |
| -ի, | » | » | |
| -ի, | » | » | |
| -ի, | » | » | |
| -ի, | » | » | |
| -ի, | » | » | |
| -ի, | » | » | |
| -ի, | » | » |
Լուծում
Այս խնդիրն ինձ առաջարկել են հետևյալ բառերով՝ «Դուք ինչպե՞ս կլուծեիք այսպիսի խնդիրը։ Այստեղ չափազանց շատ հավասարումներ կան, դրանցից գլուխ հանել չի լինի»։
Գաղտնիքը հեշտ է բացվում. այս խնդրի լուծման համար ոչ մի հավասարում, ոչ մի հանրահաշիվ չի պահանջվում՝ այն լուծվում է պարզ թվաբանական դատողությամբ։
Որոնելի թվին ավելացնենք մեկ։ Այդ դեպքում ի՞նչ մնացորդ կտա այն -ի բաժանելիս։
Մնացորդը . այլ խոսքով, թիվը բաժանվում է -ի առանց մնացորդի։
Ճիշտ նույնպես այն բաժանվում է առանց մնացորդի և -ի, -ի, -ի, -ի, -ի, -ի, -ի։ Այդ թվերից ամենափոքրը , և որոնելի թիվը հավասար է , որը դժվար չէ ստուգել փորձելով։
ԳԼՈՒԽ ՉՈՐՐՈՐԴ։ ԴԻՈՖԱՆՏՅԱՆ ՀԱՎԱՍԱՐՈՒՄՆԵՐ
ՓՈՂԿԱՊ ԳՆԵԼԸ
Խնդիր
Խանութում գնված փողկապի համար դուք պետք է վճարեք ռուբ.։
Ձեր ունեցածը միայն երեք ռուբլիանոցներ են, գանձապահինը՝ միայն հինգ ռուբլիանոցներ։ Դուք կարո՞ղ եք արդյոք այդպիսի փողերի առկայության դեպքում գանձապահի հետ հաշիվները փակել և ինչպե՞ս։
Խնդրի հարցը պահանջում է իմանալ որքան երեք ռուբլիանոց պետք է դուք տաք գանձապահին, որպեսզի վճարելով ռուբլի, ստանաք հինգ ռուբլիանոցներով մանր դրամ։ Խնդրի անհայտները երկուսն են՝ երեք ռուբլիանոցների թիվը () և հինգ ռուբլիանոցների թիվը ()։ Բայց կարելի է կազմել մի այն մեկ հավասարում՝
։
Թեև երկու անհայտով մի հավասարումն ունի անթիվ բազմությամբ լուծումներ, բայց բնավ դեռ ակներև չէ, որ նրանց մեջ -ի և -ի համար գտնվի թեկուզ մեկ լուծում ամբողջ դրական թվերով (հիշենք, որ այն թղթադրամների թիվն է)։
Ահա թե ինչու հանրահաշիվը մշակել է նման «անորոշ» հավասարումների լուծման մեթոդ։ Դրանց հանրահաշվի մեջ ներմուծելու ծառայությունը պատկանում է այդ գիտության առաջին եվրոպական ներկայացուցչին, հեռավոր անցյալի հռչակավոր մաթեմատիկոս Դիոֆանտին, որի պատճառով այդպիսի հավասարումները հաճախ կոչվում են «դիոֆանտյան» հավասարումներ։
Լուծում
Բերված օրինակի վրա ցույց տանք, թե ինչպես պետք է լուծել նման հավասարումները։
հավասարման միջոցով պետք է գտնել -ի և -ի արժեքները, ընդ որում գիտենալով, որ -ը և -ը ամբողջ և դրական թվեր են։
Մեկուսացնենք այն անհայտը, որի գործակիցը փոքր է այսինքն՝ անդամը․ կստանանք՝
,
որտեղից՝
։
Քանի որ -ը, -ը և -ը ամբողջ թվեր են, ապա հավասարությունը կարող է ճիշտ լինել միայն այն պայմանի դեպքում, երբ -ը նույնպես ամբողջ թիվ է։ Նշանակենք այն տառով։ Այդ դեպքում
,
որտեղ
,
և, նշանակում է՝
։
Վերջին հավասարումից որոշենք -ը՝
։
Քանի որ -ը և -ն ամբողջ թվեր են, ապա և պետք է լինի մի որոշ ամբողջ թիվ։ Հետևաբար,
,
ընդ որում
,
որտեղից
և ։
արժեքը տեղադրենք նախորդ հավասարման մեջ՝
,
։
Այսպիսով, -ի և -ի համար մենք գտանք հետևյալ արտահայտությունները[28]
և թվերը, ինչպես գիտենք, ոչ միայն ամբողջ են, այլև դրական, այսինքն մեծ են -ից։ Հետևաբար,
,
։
Այս անհավասարությունից կստանանք՝
և ,
և ։
Դրանով էլ մեծությունը սահմանափակվում է. այն մեծ է, քան -ը[29] և, նշանակում է, առավել ևս մեծ է, քան ։ Բայց քանի որ -ը ամբողջ թիվ է, ապա եզրակացնում ենք, որ նրա համար հնարավոր են միայն հետևյալ արժեքները՝
-ի և -ի համար համապատասխան արժեքները կլինեն
Այժմ մենք որոշեցինք, թե ինչպես պետք է կատարել վճարումը։
Դուք կամ կվճարեք երեք ռուբլիանոցներ՝ ստանալով մի հինգ ռուբլիանոց մանր դրամ՝
,
կամ կվճարեք երեք ռուբլիանոցներ՝ ստանալով հինգ ռուբլիանոց մանր դրամ՝
և այլն։
Տեսականորեն խնդիրն ունի անթիվ բազմությամբ լուծումներ, իսկ գործնականում լուծումների թիվը սահմանափակ է, քանի որ ո՛չ գնորդի և ո՛չ էլ գանձապահի մոտ չկա անթիվ բազմությամբ թղթադրամ։ Եթե, օրինակ, յուրաքանչյուրի մոտ կա ընդամենը -ական թղթադրամ, ապա վճարումը հնարավոր է կատարել միայն մեկ եղանակով՝ երեք ռուբլիանոցներ վճարելով և ռուբլի մանր դրամ ստանալով։ Ինչպես տեսնում ենք, անորոշ հավասարումները գործնականում կարող են տալ միանգամայն որոշակի, զույգ լուծումներ։
Անդրադառնալով մեր խնդրին՝ առաջարկում ենք ընթերցողին որպես վարժություն ինքնուրույնաբար լուծել միայն այն վարիանտը, երբ գնորդն ունի միայն հինգ ռուբլիանոցներ, իսկ գանձապահը՝ միայն երեք ռուբլիանոցներ։ Արդյունքում ստացվում է լուծումների այսպիսի շարք՝
Իրոք,
,
,
,
..........................
Մենք այս արդյունքները կարող էինք ստանալ նաև հիմնական խնդրի արդեն պատրաստի լուծումներից՝ օգտվելով հանրահաշվական պարզ եղանակից։ Քանի որ տալ հինգ ռուբլիանոցներ և ստանալ երեք ռուբլիանոցներ միևնույնն է, թե «ստանալ բացասական հինգ ռուբլիանոցներ» և «տալ բացասական երեք ռուբլիանոցներ», ապա խնդրի նոր վարիանտը լուծվում է այն նույն հավասարմամբ, որը մենք կազմեցինք հիմնական խնդրի համար.
,
բայց այն պայմանով, որ -ը և -ը բացասական թվեր են։ Ուստի՝
հավասարություններից գիտենալով, որ , եզրակացնում ենք՝
,
և, հետևաբար,
։[30]
Ընդունելով և այլն, նախորդ բանաձևերից կստանանք -ի և -ի համար հետևյալ արժեքները։
Լուծումների առաջին զույգը՝ նշանակում է, որ գնորդը «վճարում է մինուս երեք ռուբլիանոցներ» և ստանում է մինուս հինգ ռուբլիանոցներ», այսինքն՝ սովորական լեզվով ասած, վճարում է հատ հինգ ռուբլիանոց և ստանում է հատ երեք ռուբլիանոց մանր դրամ։
Նման ձևով կմեկնաբանենք և մյուս լուծումները։
ՎԵՐՍՏՈՒԳՈՒՄ ԽԱՆՈՒԹՈՒՄ
Խնդիր
Խանութի առետրամատյանների ստուգման ժամանակ պարզվեց, որ գրանցումներից մեկը ծածկված է թանաքով, ունի այսպիսի տեսք՝

Հնարավոր չէր վերծանել վաճառված մետրերի թիվը, բայց կասկած չկար, որ այդ թիվը կոտորակային չէ. ստացված գումարում կարելի էր տարբերել միայն վերջին երեք թվանշանները, և դարձյալ հաստատել, որ դրանցից առաջ եղել են ինչ-որ երեք այլ թվանշաններ։
Կարո՞ղ է արդյոք վերստուգիչ հանձնաժողովը այդ հետքերով որոշել գրանցումը։
Լուծում
Մետրերի թիվը նշանակենք -ով։ Վաճառքից ստացված մուտքը արտահայտված կոպեկներով կլինի
։
Գրանցման դրամական գումարի երեք ծածկված թվանշաններով արտահայտված թիվը նշանակենք -ով։ Հավանորեն այդ թիվը հազար կոպեկների թիվ է, իսկ ամբողջ գումարը կոպեկներով կարտահայտվի այսպես՝
։
Կունենանք հետևյալ հավասարումը՝
,
կամ, -ով կրճատելուց հետո,
։
Այս հավասարման մեջ -ը և -ը ամբողջ թվեր են և ընդսմին -ը մեծ չէ -ից, քանի որ երեքից ավելի թվանշաններով այն կազմվել չի կարող։ Լուծենք այդ հավասարումը, ինչպես ցույց էր տրված առաջ՝
,
։
Այստեղ մենք ընդունեցինք , քանի որ մեզ ձեռնտու է ունենալ հնարավորին չափ ավելի փոքր մնացորդներ։
կոտորակը ամբողջ թիվ է, իսկ քանի որ -ը չի բաժանվում -ի, ապա կոտորակը պետք է լինի ամբողջ թիվ, որը և մենք նշանակել ենք -ով։
Այնուհետև
հավասարումից ունենք`
,
,
որտեղ
և, հետևաբար,
,
։[31]
Մենք գիտենք, որ
։
Հետևաբար,
,
որտեղից
և ։
Ակնհայտ է, որ -ի համար գոյություն ունի միայն մեկ ամբողջ արժեք՝
,
և այդ ժամանակ , այսինքն՝ վաճառված էր մետր կտոր ռ. կ. գումարով։ Գրանցումը վերականգնված է։
ՆԱՄԱԿԱՆԻՇԵՐԻ ԳՆՈՒՄ
Խնդիր
Պահանջվում է ռուբլով գնել հատ նամականիշ՝ -կոպեկանոց, -կոպեկանոց և կոպեկանոց։ Յուրաքանչյուր արժողության քանի՞ նամականիշ կարելի է գնել։
Լուծում
Այս դեպքում մենք ունենք երեք անհայտով երկու հավասարում՝
,
,
որտեղ -ը -կոպեկանոց նամականիշերի թիվն է, -ը՝ -կոպեկանոց, -ը՝ -կոպեկանոց։ Առաջին հավասարումը բաժանելով -ի և նրանից հանելով երկրորդը, կստանանք երկու անհայտով մեկ հավասարում՝
։
Գտնենք -ը՝
։
Հավանորեն, -ը ամբողջ թիվ է։ Այն նշանակենք -ով։ Կունենանք՝
։
-ի և -ի արտահայտությունները տեղադրենք սկզբնական հավասարումներից երկրորդի մեջ՝
,
կստանանք՝
։
Քանի որ , ապա դժվար չէ որոշել -ի սահմանները
,
որտեղից եզրակացնում ենք, որ -ի համար հնարավոր են միայն երկու ամբողջ արժեքներ՝
և ։
-ի, -ի և -ի համապատասխան արժեքները կլինեն այսպես՝
| Ստուգում | ||||
| , | ||||
| ։ | ||||
Այսպիսով, նամականիշերի, գնումը հնարավոր է կատարել միայն երկու եղանակով։
Հաջորդ խնդիրը միևնույն կարգի է։
ՄՐԳԵՐ ԳՆԵԼԸ
Խնդիր
ռուբլով գնված է հատ տարբեր տեսակի մրգեր, որոնց գները այսպիսին են՝
| ձմերուկ, | հատը | . . . . . | ռուբ.[32] | |
| խնձոր | » | . . . . . | » | |
| սալոր | » | . . . . . | կոպ.։ |
Որքա՞ն միրգ էր գնված յուրաքանչյուր տեսակից։
Լուծում
Ձմերուկների թիվը նշանակենք -ով խնձորներինը՝ -ով և սալորներինը՝ -ով. կազմենք երկու հավասարումներ՝
,
։
Առաջին հավասարումը բաժանելով -ի և նրանից հանելով երկրորդը, կստանանք երկու անհայտով մեկ հավասարում՝
։

Լուծման հետագա ընթացքը այսպիսին է՝
,
,
։
և
անհավասարություններից գտնում ենք, որ
և հետևաբար ։ Ուստի`
։
-ի և -ի այս արժեքները տեղադրելով երկրորդ հավասարման մեջ, կստանանք ։
Այսպիսով, գնված էր ձմերուկ, խնձոր և սալոր։
Այլ կոմբինացիաներ հնարավոր չեն։
ԾՆՆԴՅԱՆ ՕՐՎԱ ԳՈՒՇԱԿՈՒՄԸ
Խնդիր
Անորոշ հավասարումներ լուծել կարողանալը հնարավորություն է տալիս կատարելու մաթեմատիկական հետևյալ ֆոկուսը։
Դուք առաջարկում եք ձեր ընկերոջը իր ծննդյան ամսաթիվը բազմապատկել -ով, իսկ ամսվա համարը՝ -ով։ Նա հաղորդում է ձեզ երկու արտադրյալների գումարը, և դուք այդ թվով գտնում եք նրա ծննդյան ամիսը և ամսաթիվը։
Եթե, օրինակ, ձեր ընկերը ծնվել է փետրվարի -ին, ապա նա կատարում է հետևյալ հաշվումները՝
։
Այդ վերջին թիվը՝ -ը, նա հաղորդում է ձեզ, և դուք որոշում եք նրա մտածած ամսաթիվը։ Ինչպե՞ս։
Լուծում
Խնդիրը հանգում է ամբողջ և դրական թվերով՝
անորոշ հավասարման լուծմանը, ընդ որում ամսաթիվը մեծ չէ -ից, իսկ ամսվա համարը մեծ չէ -ից։
,
,
,
,
,
։
Գիտենալով, որ և , գտնում ենք -ի համար հետևյալ սահմանները՝
։
Հետևաբար՝
։
Ծննդյան ամսաթիվը երկրորդ ամսվա -րդ թիվն է, այսինքն՝ փետրվարի -ը։
Ապացուցենք, որ ֆոկուսը միշտ հաջողվում է, այսինքն՝ հավասարումը միշտ ունի դրական ամբողջ մեկ լուծում։ Այն թիվը, որ հաղորդեց ձեր ընկերը, նշանակենք -ով, այդ դեպքում նրա ծննդյան ամսաթվի գտնելը հանգում է
հավասարման լուծմանը։
Դատենք «հակառակը»։ Ենթադրենք, որ այդ հավասարումն ունի երկու տարբեր դրական ամբողջ լուծումներ, այն է՝ և , ընդ որում -ը և -ը չեն գերազանցում -ին, իսկ -ը և -ը չեն գերազանցում -ին։
Մենք ունենք՝
,
։
Առաջին հավասարությունից հանելով երկրորդը, կստանանք՝
։
Այս հավասարությունից հետևում է, որ թիվը բաժանվում է -ի։ Քանի որ թվերը դրական են և չեն գերազանցում -ին, ապա դրանց տարբերությունը փոքր է -ից։ Ուստի՝ թիվը կբաժանվի -ի միայն այն դեպքում, երբ , այսինքն՝ երբ առաջին լուծումը համընկնում է երկրորդի հետ։ Այսպիսով, երկու տարբեր լուծումների գոյության մասին ենթադրությունը բերում է հակասության։
ՃՏԵՐԻ ՎԱՃԱՌՔ
Հինավուրց խնդիր
Երեք քույրեր շուկա եկան ճտեր վաճառելու։ Վաճառքի համար մեկը բերեց ճուտ, մյուսը՝ , երրորդը՝ ։ Մինչև կեսօր նրանք իրենց Ճտերի մի մասը վաճառեցին միևնույն գնով։ Կեսօրից հետո, վախենալով, որ բոլոր ճտերը չեն վաճառվի, նրանք իջեցրին գինը և մնացած բոլոր ճտերը նորից վաճառեցին միևնույն գնով։ Երեքն էլ տուն վերադարձան հավասար դրամով՝ յուրաքանչյուր քույրը վաճառքից ստացավ ռուբլի։
Նրանք ի՞նչ գնով վաճառեցին ճտերը կեսօրից առաջ և հետո։
Լուծում
Մինչև կեսօր յուրաքանչյուր քրոջ վաճառած ճտերի թիվը նշանակենք ։ Օրվա երկրորդ կեսին նրանք վաճառեցին ճուտ։ Մինչև կեսօր գինը նշանակենք -ով, կեսօրից հետո՝ -ով։ Պարզության համար զուգադրենք այդ նշանակումները.
| Վաճառված ճտերի թիվը | Գինը | ||||
| Մինչև կեսօր | . . . | ||||
| Կեսօրից հետո | . . . | ||||
Առաջին քույրը վաճառքից ստացավ՝
, հետևաբար՝ ,
երկրորդը՝
, հետևաբար՝ ,
երրորդը՝
, հետևաբար՝ ։
Ձևափոխենք այս երեք հավասարումները.
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} (m-n)x+10n \;=\; 35, \\ (m-n)y+16n \;=\; 35, \\ (m-n)z+26n \;=\; 35։ \end{cases} }
Երրորդ հավասարումից հանելով առաջինը, այնուհետև երկրորդը, հաջորդաբար կստանանք՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} (m-n)(z-x)+16n \;=\; 0, \\ (m-n)(z-y)+10n \;=\; 0։ \end{cases} }
կամ
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} (m-n)(x-z) \;=\; 16n, \\ (m-n)(y-z) \;=\; 10n։ \end{cases} }
Այս հավասարումներից առաջինը բաժանենք երկրորդի վրա՝
կամ ։
Քանի որ -ը, -ը, -ը ամբողջ թվեր են, ապա և տարբերությունները նույնպես ամբողջ թվեր են։ Ոստի
հավասարման գոյության համար անհրաժեշտ է, որ -ը բաժանվի -ի, իսկ -ը՝ -ի։
Հետևաբար՝
,
որտեղից
,
։
Նկատենք, որ թիվը ոչ միայն ամբողջ է, այլև դրական, քանի որ (հակառակ դեպքում առաջին քույրը չէր կարող վաստակել այնքան, որ քան երրորդը)։
Քանի որ , ապա ։
Ամբողջ և դրական -ի ու -ի դեպքում վերջին անհավասարությունը բավարարվում է միայն մեկ դեպքում՝ երբ ։ Տեղադրելով այդ արժեքները
և
հավասարումների մեջ, գտնում ենք՝ ։
Այժմ անդրադառնանք հետևյալ հավասարումներին՝
,
,
և դրանց մեջ տեղադրենք -ի, -ի, -ի գտնված արժեքները. կիմանանք այն գները, որոնցով վաճառվեցին ճտերը՝
ռուբ., ռուբ.։
Այսպիսով, մինչև կեսօր վաճառվել են ռուբ. կոպ.-ով, կեսօրից հետո՝ ռուբ. կոպ.-ով։
ԵՐԿՈՒ ԹՎԵՐ ԵՎ ՉՈՐՍ ԳՈՐԾՈՂՈՒԹՅՈՒՆՆԵՐ
Խնդիր
Նախորդ խնդիրը, որը հանգեցրեց հինգ անհայտով երեք հավասարման, մենք լուծեցինք ոչ ընդհանուր ձևով, այլ մաթեմատիկական ազատ կշռադատությամբ։ Ճիշտ այդպես էլ կլուծենք երկրորդ աստիճանի անորոշ հավասարումների բերվող հետևյալ խնդիրները։
Ահա դրանցից առաջինը։
Երկու ամբողջ դրական թվերով կատարել են հետևյալ չորս գործողությունները՝
1) դրանք գումարել են.
2) մեծից հանել են փոքրը.
3) բազմապատկել են.
4) մեծը բաժանել են փոքրի վրա։
Ստացված արդյունքները գումարել են, որը կազմել է ։ Գտնել այդ թվերը։ Լուծում
Եթե մեծ թիվը է, փոքրը՝ , ապա
։
Եթե այս հավասարումը բազմապատկենք -ով, այնուհետև բացենք փակագծերը և կատարենք նման անդամների միացում, ապա կստանանք՝
։
Բայց
։
Ուստի՝
։
Որպեսզի -ը լինի ամբողջ թիվ, հայտարարը պետք է լինի -ի բաժանարարներից մեկը (որովհետև -ը -ի հետ չի կարող ունենալ ընդհանուր արտադրիչներ)։ Գիտենալով, որ –ի, եզրակացնում ենք, որ -ը բաժանվում է միայն հետևյալ թվերի վրա, որոնք հանդիսանում են ճիշտ քառակուսիներ՝ ։ Այսպիսով՝ -ն պետք է հավասար լինի կամ , որտեղից (հիշելով, որ -ը պետք է լինի դրական) գտնում ենք, որ -ը հավասար է կամ ։
Այդ դեպքում -ը հավասար է
կամ ։
Այսպիսով, որոնելի թվերն են՝ և կամ և ։
ԻՆՉՊԻՍԻ՞ ՈՒՂՂԱՆԿՅՈՒՆ Է
Խնդիր
Ուղղանկյան կողմերը արտահայտվում են ամբողջ թվերով։ Ի՞նչ երկարություններ պետք է ունենան դրանք, որպեսզի ուղղանկյան պարագիծը թվապես հավասարվի նրա մակերեսին։
Լուծում
Ուղղանկյան կողմերը նշանակելով -ով և -ով, կազմենք հետևյալ հավասարումը՝
,
որտեղից
։
Քանի որ -ը և -ը պետք է լինեն դրական, ապա դրական պետք է լինի նաև թիվը, այսինքն՝ -ը պետք է լինի -ից մեծ։
Նկատենք այժմ, որ
։
Քանի որ -ը պետք է լինի ամբողջ թիվ, ապա արտահայտությունը պետք է լինի ամբողջ թիվ։ Բայց դեպքում այդ հնարավոր է, եթե միայն հավասար է կամ ։ -ի համապատասխան արժեքները կլինեն ։
Այսպիսով, որոնելի պատկերը կա՛մ ուղղանկյուն է և կողմերով, կա՛մ քառակուսի՝ կողմով։
ԵՐԿՈՒ ԵՐԿԱՆԻՇ ԹՎԵՐ
Խնդիր
և թվերն ունեն հետաքրքիր առանձնահատկություն՝ դրանց արտադրյալը չի փոխվում, եթե տեղափոխենք այդ թվերի թվանշանները։
Իրոք,
։
Պահանջվում է որոշել՝ գոյություն ունե՞ն արդյոք երկանիշ թվերի այլ զույգեր՝ միևնույն հատկությամբ։ Ի՞նչպեսդրանց գտնել։
Լուծnւմ
Որոնելի թվերի թվանշանները նշանակելով և և , կազմենք հավասարում՝
։
Բացելով փակագծերը և պարզեցնելով, կստանանք՝
,
որտեղ -ը, -ը, -ը, -ն ամբողջ թվեր են և փոքր են -ից։ Լուծումները փնտրելու համար թվանշաններից կազմենք հավասար արտադրյալներով բոլոր զույգերը՝
Բոլոր հավասարությունները հատ են։ Յուրաքանչյուրից կարելի է կազմել թվերի մեկ կամ երկու որոնելի խումբ։ Օրինակ՝ հավասարությունից գտնում ենք մի լուծում՝
։
հավասարությունից գտնում ենք երկու լուծումներ՝
։
Այս ձևով որոնում ենք հետևյալ լուծումները՝
ՊՅՈՒԹԱԳՈՐՅԱՆ ԹՎԵՐ
Տեղանքում ուղղահայաց գծեր անցկացնելու համար հողաչափերի կողմից գործածվող շատ ճիշտ և հարմար միջոցը կայանում է հետևյալում։ Դիցուք, պահանջվում է. կետով ուղղին տանել ուղղահայաց (գծ. 13)։ կետից ուղղությամբ երեք անգամ տեղադրում են մի որևէ հեռավորություն։ Այնուհետև լարի վրա կապում են երեք հանգույց, որոնց միջև եղած հեռավորությունները հավասար են և . Ծայրերի հանգույցները կցելով և կետերին, լարը ձգում են միջին հանգույցի կողմը։ Լարը ստանում է եռանկյան ձև, որի մեջ անկյունը ուղիղ է։
Այդ հնադարյան եղանակը, որ կիրառում էին եգիպտական բուրգերի շինարարները դեռ հազարամյակներ սրանից առաջ, հիմնված էր այն բանի վրա, որ յուրաքանչյուր եռանկյան, եթե նրա կողմերը հարաբերում են՝ ինչպես , համաձայն Պյութագորի հանրածանոթ թեորեմայի, ուղղանկյուն է, քանի որ
։
Բացի թվերից, ինչպես հայտնի է, գոյություն անեն անթիվ բազմությամբ ամբողջ դրական թվեր, որոնք բավարարում են հետևյալ առնչությանը՝
։
Դրանք կոչվում են Պյութագորյան թվեր։ Պյութագորի թեորեմայի համաձայն այդպիսի թվերը կարող են ծառայել որպես որոշ ուղղանկյուն եռանկյան կողմերի երկարություններ. դրա համար էլ -ն և -ն կոչվում են «էջեր», իսկ -ն՝ «ներքնաձիգ»։
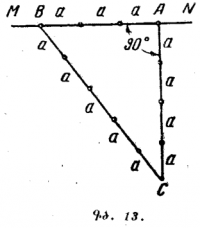
Պարզ է, որ եթե թվերը Պյութագորյան թվերի եռյակ են, ապա (որտեղ -ն ամբողջ արտադրիչ է) թվերը ևս պյութագորյան թվեր են։ Հակադարձաբար, եթե պյութագորյան թվերն ունեն ընդհանուր արտադրիչ, ապա այդ ընդհանուր արտադրիչով կարելի է դրանք բոլորը կրճատել, և նորից ստանալ պյութագորյան թվերի եռյակ։ Ուստի՝ սկզբում կհետազոտենք պյութադորյան թվերի միայն փոխադարձ պարզ եռյակները (մնացածները ստացվում են դրանցից՝ բազմապատկելով ամբողջ արտադրիչով)։
Ցույց տանք, որ տիպի եռյակներից յուրաքանչյուրի մեջ «էջեր»-ից մեկը պետք է լինի զույգ, իսկ մյուսը՝ կենտ։ Դատենք «հակառակը»։ Եթե և երկու «էջերն» էլ զույգ են, ապա զույգ կլինի թիվը. նշանակում է զույգ է նաև «ներքնաձիգը»։ Սակայն, այդ հակասում է այն բանին, որ թվերը չունեն ընդհանուր արտադրիչներ, քանի որ երեք զույգ թվերը ունեն ընդհանուր արտադրիչը։ Այսպիսով, և «էջեր»-ից թեկուզ մեկը կենտ է։
Մնում է դարձյալ մի հնարավորություն։ Երկու «էջերն» էլ կենտ են, իսկ «ներքնաձիգը» զույգ է։ Դժվար չէ ապացուցել, որ այդ հնարավոր չէ։ Իրոք, եթե «էջերն» ունեն հետևյալ տեսքը՝
և ,
ապա դրանց քառակուսիների գումարը հավասար է
,
այսինքն` իրենից ներկայացնում է մի թիվ, որը -ի բաժանելիս մնացորդում տալիս է ։ Այնինչ, ամեն մի զույգ թվի քառակուսին կբաժանվի -ի վրա առանց մնացորդի։ Նշանակում է՝ երկու կենտ թվերի քառակուսիների գումարը չի կարող լինել զույգ թվի քառակուսի. այլ կերպ ասած, մեր երեք թվերը պյութագորյան չեն։
Այսպիսով, «էջեր»-ից մեկը զույգ է, իսկ մյուսը՝ կենտ։ Ուստի՝ թիվը կենտ է, իսկ այս նշանակում է, որ կենտ է նաև «ներքնաձիգը»։
Պարզության համար, ենթադրենք, որ «էջը» հանդիսանում է կենտ, իսկ -ն՝ զույգ։
հավասարությունից մենք հեշտությամբ կստանանք՝
։
Աջ մասում գրված և արտադրիչները փոխադարձ պարզ են։ Իրոք, եթե այդ թվերն ոնենային մեկից տարբեր ընդհանուր պարզ արտադրիչ, ապա այդ արտադրիչի վրա կբաժանվեր և՛ գումարը՝
,
և՛ տարբերությունը՝
,
և՛ արտադրյալը
,
այսինքն` և թվերը կունենային ընղհանուր արտադրիչ։ Քանի որ -ն կենտ է, ապա այդ արտադրիչը երկուսից տարբեր է, և այս պատճառով էլ թվերն ունեն հենց այդ ընդհանուր արտադրիչը, որը, սակայն, հնարավոր չէ։
Ստացված հակասությունը ցույց է տալիս, որ և թվերը փոխադարձ պարզ են։
Բայց եթե փոխադարձ պարզ թվերի արտադրյալը ճիշտ քառակուսի է, ապա դրանցից յուրաքանչյուրը հանդիսանում է քառակուսի, այսինքն՝
Չհաջողվեց վերլուծել («\begin{cases}» անհայտ ֆունկցիա): {\displaystyle \begin{cases} c+b \;=\; m^2, \\ c-b \;=\; n^2։ \end{cases} }
Լուծելով այս սիստեմը, գտնում ենք՝
,
։
Այսպիսով, դիտարկված պյութագորյան թվերն ունեն հետևյալ տեսքը՝
,
որտեղ -ը և -ը որոշ փոխադարձ պարզ, կենտ թվեր են։ Ընթերցողը կարող է հեշտությամբ. համոզվել և հակադարձի մեջ՝ ցանկացած կենտ -ի և -ի դեպքում գրված բանաձևերը տալիս են պյութագորյան երեք թվեր։
Ահա պյութագորյան թվերի մի քանի եռյակներ, որոնք ստացվում են -ի և -ի տարբեր արժե քների դեպքում՝
։
(Պյութագորյան թվերի մնացած բոլոր եռյակները կա՛մ ունեն ընդհանուր արտադրիչներ, կա՛մ պարունակում են թվեր, որ մեծ են հարյուրից)։
Պյութագորյան թվերն ընդհանրապես մի շարք հետաքրքիր առանձնահատկություններ ունեն, որոնք մենք ստորև կթվարկենք առանց ապացուցումների։
1) «էջեր»-ից մեկը պետք է երեքի բազմապատիկը լինի։
2) «էջեր»-ից մեկը պետք է չորսի բազմապատիկը լինի։
3) Պյութագորյան թվերից մեկը պետք է հինգի բազմապատիկը լինի։
Ընթերցողը կարող է համոզվել այդ հատկությունների առկայության մեջ՝ նայելով պյութագորյան թվերի խմբերի վերը բերված օրինակները։
ԵՐՐՈՐԴ ԱՍՏԻՃԱՆԻ ԱՆՈՐՈՇ ՀԱՎԱՍԱՐՈՒՄ
Երեք ամբողջ թվերի խորանարդների գումարը կարող է լինել չորրորդ թվի խորանարդը։ Օրինակ՝
։
Այդ նշանակում է, ի միջի այլոց, որ խորանարդը, որի կողը հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 6 \; սմ} -ի, հավասարամեծ է երեք այնպիսի խորանարդների գումարին, որոնց կողերը հավասար են՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3 \; սմ, \; 4 \; սմ \text{ և } 5 \; սմ} (նկ. 14). այս առնչությունը, ըստ ավանդության, Պլատոնին չափազանց զբաղեցրել է։
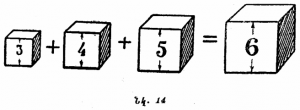
Փորձենք գտնել այդպիսի տեսքի այլ առնչություններ, այսինքն՝ մեր առջև դնենք այսպիսի խնդիր՝ գտնել հավասարման լուծուքմները։ Հարմար է, սակայն, անհայտը նշանակել -ով։ Այդ դեպքում հավասարումը կունենա ավելի պարզ տեսք
։
Դիտարկենք այն եղանակը, որը թույլ է տալիս գտնել այդ հավասարման անթիվ բազմությամբ ամբողջական լուծումները (դրական և բացասական)։ Դիցուք և Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle α, \; β, \; γ, \; δ} երկու քառյակ թվեր են, որոնք բավարարում են հավասարմանը։ Առաջին քառյակի թվերին ավելացնենք երկրորդ քառյակի թվերը՝ նախապես դրանք բազմապատկելռվ մի որոշ թվով, և աշխատենք թիվն ընտրել այնպես, որ ստացված
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a+kα, \; b+kβ, \; c+kγ, \; d+kδ}
թվերը նույնպես բավարարեն մեր հավասարմանը։ Այլ կերպ ասած, -ն ընտրենք այն ձևով, որպեսզի տեղի ունենա հետևյալ հավասարությունը՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle (a+kα)^3+(b+kβ)^3+(c+kγ)^3+(d+kδ)^3 \;=\; 0} ։
Բացելով փակագծերը և վերհիշելով, որ և Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle α, β, γ, δ} քառյակ թվերը բավարարում են մեր հավասարմանը, այսինքն՝ տեղի կունենան
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a^3+b^3+c^3+d^3 \;=\; 0, \; α^3+β^3+γ^3+δ^3 \;=\; 0} ,
հավասարությունները, մենք կստանանք՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3a^2kα+3ak^2α^2+3b^2kβ+3bk^2β^2+3c^2kγ+3ck^2γ^2+3d^2kδ+3dk^2δ^2 \;=\; 0}
կամ
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3k[(a^2α+b^2β+c^2γ+d^2δ)+k(aα^2+bβ^2+cγ^2+dδ^2)] \;=\; 0} ։[34]
Արտադրյալը կարող է դառնալ զրո միայն այն դեպքում, երբ նրա արտադրիչներից գոնե մեկը դառնում է զրո։ Արտադրիչներից յուրաքանչյուրը հավասարեցնելով զրոյի, -ի համար մենք կստանանք երկու արժեքներ։ Առաջին արժեքը , մեզ չի հետաքրքրում. այն նշանակում է, որ եթե թվերին ոչինչ չավելացնենք, ապա ստացված թվերը բավարարում են մեր հավասարմանը։ Ուստի՝ մենք -ի համար վերցնում ենք միայն երկրորդ արժեքը՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle k \;=\; -\frac{a^2α+b^2β+c^2γ+d^2δ} {aα^2+bβ^2+cγ^2+dδ^2}} ։
Այսպիսով, գիտենալով թվերի երկու քառյակներ, որոնք բավարարում են սկզբնական հավասարմանը, հնարավոր է գտնել նոր քառյակ. դրա համար պետք է առաջին քառյակի թվերին ավելացնել երկրորդ քառյակի թվերը՝ դրանք նախապես բազմապատկելով -ով, որտեղ -ն ունի վերը գրված արժեքը։
Այդ եղանակը կիրառելու համար պետք է գիտենալ թվերի երկու քառյակներ, որոնք բավարարում են սկզբնական հավասարմանը։ Այդպիսի մի քառյակ մենք արդեն գիտենք։ Որտեղի՞ց վերցնել ևս մեկ քառյակ։ Այդ դրությունից դուրս գալը շատ հեշտ է՝ որպես երկրորդ քառյակ կարելի է վերցնել թվերը, որոնք, ակնհայտորեն, բավարարում են սկզբնական հավասարմանը։ Այլ կերպ ասած, ընդունենք
,
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle α=r, \; β=-r, \; γ=s, \; δ=-s} ։
Այդ դեպքում, ինչպես հեշտ է նկատել, -ի համար մենք կստանանք հետևյալ արժեքը՝
,
իսկ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle a+kα, \; b+kβ, \; c+kγ, \; d+kδ} թվերը համապատասխանորեն հավասար կլինեն
։
Համաձայն վերը ասվածի, այդ չորս արտահայտությունները բավարարում են
սկզբնական հավասարմանը։
Քանի որ այդ բոլոր արտահայտություններն ունեն միատեսակ հայտարար, ապա այն կարելի է դեն գցել (այսինքն՝ այդ կոտորակների համարիչները նույնպես բավարարում են դիտարկվող հավասարմանը)։ Այսպիսով, գրված հավասարմանը բավարարում են (ցանկացած -ի և -ի դեպքում) հետևյալ թվերը՝
,
,
,
,
այդ բանում, իհարկե, կարելի է համոզվել և անմիջականորեն՝ այդ արտահայտությունները խորանարդ բարձրացնելով և գումարելով։ -ին և -ին տալով տարբեր, ամբողջ արժեքներ՝ մենք կարող ենք ստանալ մեր հավասարման ամբողջական լուծումների մի ամբողջ շարք։ Եթե այդ դեպքում ստացված թվերը կունենան ընդհանուր արտադրիչ, ապա նրա վրա կարելի է այդ թվերը բաժանել։ Օրինակ, երբ , -ի, -ի, -ի, -ի համար կստանանք հետևյալ արժեքները՝ կամ -ով կրճատելուց հետո՝ արժեքները։ Այսպիսով՝
։
Ահա ևս նույն տիպի հավասարությունների մի ամբողջ շարք (որոնք ստացվում են ընդհանուր արտադրիչով կրճատելուց հետո).
երբ ,
երբ ,
երբ ,
երբ ,
երբ ,
երբ ,
երբ ։
. . . . . . . . . . .
Նկատենք, որ եթե սկզբնական քառյակի մեջ կամ հենց նոր ստացված քառյակներից մեկի մեջ թվերի տեղերը փոխենք և կիրառենք նույն եղանակը, ապա կստանանք լուծումների նոր սերիա։ Օրինակ՝ վերցնելով քառյակը (այսինքն՝ ենթադրելով ), մենք -ի, -ի, -ի, -ի համար կստանանք հետևյալ արժեքները՝
,
,
,
։
Այստեղից -ի և -ի տարբեր արժեքների դեպքում կստանանք նոր առնչություններ՝
երբ ,
երբ ,
երբ ,
երբ ,
երբ ,
երբ
և այլն։
Այս ճանապարհով կարելի է ստանալ դիտարկվող հավասարման համար անթիվ բազմությամբ լուծումներ։
ՀԱՐՅՈՒՐ ՀԱԶԱՐ՝ ԹԵՈՐԵՄԱՅԻ ԱՊԱՑՈՒՑՄԱՆ ՀԱՄԱՐ
Անորոշ հավասարումներից մի խնդիր մեծ ճանաչում էր գտել, քանի որ այն ճիշտ լուծելու համար կտակված էր մի ամբողջ հարստություն՝ գերմանական մարկ։
Խնդիրը կայանում է նրանում, որպեսզի ապացուցվի Ֆերմայի թեորեմա կամ «մեծ առաջադրություն» կոչվող հետևյալ դրույթը։
Երկու ամբողջ թվերի միատեսակ աստիճանների գումարը չի կարող լինել որևէ երրորդ ամբողջ թվի նույն աստիճանը։ Բացառություն է կազմում միայն երկրորդ աստիճանը, որի համար այդ հնարավոր է։
Այլ կերպ ասած, պետք է ապացուցել, որ
հավասարումը լուծելի չէ ամբողջ թվերի համար։
Պարզաբանենք ասվածը։ Մենք տեսանք, որ
,
հավասարումները ունեն ցանկացածին չափ ամբողջական լուծումներ։ Բայց փորձեցեք գտնել երեք ամբողջ դրական թվեր, որոնց համար տեղի ունենա հավասարությունը. ձեր որոնումները կմնան ապարդյուն։
Նույն անհաջողությանը կմատնվեք դուք նաև չորրորդ, հինգերորդ, վեցերորդ և այլն աստիճանների համար օրինակներ փնտրելիս։ Հենց դա է հաստատում «Ֆերմայի մեծ առաջադրությունը»։
Իսկ ի՞նչ է պահանջվում նվիրատվություն փնտրողներից։ Նրանք պետք է ապացուցեն այդ դրույթը բոլոր այն աստիճանների համար, որոնց համար այն ճիշտ է։ Բանն այն է, որ Ֆերմայի թեորեման դեռ ապացուցված չէ և կախված է, այսպես ասած, օդում։[36]
Այն ժամանակից, երբ առաջարկվել է այդ թեորեման, անցել է երեք հարյուր տարի, սակայն մաթեմատիկոսներին չի հաջողվել մինչև այժմ էլ գտնել նրա ապացույցը։ Մեծագույն մաթեմատիկոսները ջանք են թափել այդ պրոբլեմի վրա, սակայն լավագույն դեպքում նրանց հաջողվել է ապացուցել թեորեման միայն այս կամ այն առանձին ցուցիչի համար կամ ցուցիչների խմբերի համար, անհրաժեշտ է գտնել ընդհանուր ապացույց ամեն մի ամբողջ ցուցիչի համար։
Զարմանալի է, որ Ֆերմայի թեորեմայի անըմբռնելի ապացույցը, ըստ երևույթին, մի անգամ արդեն գտնվել է, բայց այնուհետև նորից կորել է։ Թեորեմայի հեղինակը՝ 17-րդ դարի հանճարեղ մաթեմատիկոս Պիեռ Ֆերման[37] պնդում էր, որ նրա ապացույցը իրեն հայտնի է։ Իր «Մեծ առաջադրությունը» (ինչպես և մի շարք այլ թեորեմաներ թվերի տեսությունից) դիտողության տեսքով գրեց Դիոֆանտի երկերի լուսանցքներում, այն ուղեկցելով այսպիսի լրացումով՝
«Ես գտա այդ առադրության իսկապես զարմանալի ապացույցը, բայց այստեղ տեղը փոքր է, որպեսզի այն մեջ բերեմ»։
Մեծ մաթեմատիկոսի ո՛չ թղթերում, ո՛չ գրագրություններում և ընդհանրապես ոչ մի տեղ այդ ապացույցի հետքերը գտնել չհաջողվեց։
Ֆերմայի հետևորդները ստիպված էին գնալ ինքնուրույն ճանապարհով։ Ահա այդ ջանքերի արդյունքները. Էյլերը (1797) ապացուցեց Ֆերմայի թեորեման երրորդ և չորրորդ աստիճանների համար, հինգերորդ աստիճանի համար այն ապացուցեց Լեժանդրը (1823), յոթերորդի[38] համար՝ Լամեն և Լեբեգը (1840)։ 1849 թվականին Կումերը թեորեման ապացուցեց աստիճանների ընդհանուր խմբի համար և, ի միջի այլոց, հարյուրից փոքր բոլոր ցուցիչների համար։ Այդ վերջին աշխատանքները հեռանում են մաթեմատիկայի բնագավառի այն սահմաններից, որ ծանոթ էր Ֆերմային, և դառնում է հանելուկային, թե ինչպես վերջինս կարող էր իր «Մեծ առաջադրության» ընդհանուր ապացույց փնտրել։
Ֆերմայի խնդրի պատմությամբ և նրա ժամանակակից վիճակով հետաքրքրվողներին կարելի էր հանձնարարել Ա. Յա. Խինչինի «Ֆերմայի մեծ թեորեման» բրոշյուրը։ Մասնագետի կողմից գրված այս բրոշյուրը նախատեսված է մաթեմատիկայից տարրական գիտելիքներ ունեցող ընթերցողի համար։
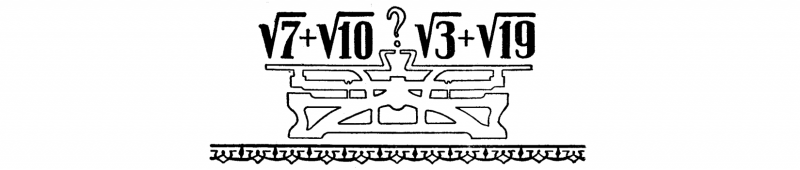
ԳԼՈՒԽ ՀԻՆԳԵՐՈՐԴ։ ՄԱԹԵՄԱՏԻԿԱԿԱՆ ՎԵՑԵՐՈՐԴ ԳՈՐԾՈՂՈՒԹՅՈՒՆԸ
ՎԵՑԵՐՈՐԴ ԳՈՐԾՈՂՈՒԹՅՈՒՆԸ
Գումարումը և բազմապատկումը ունեն մեկական հակադարձ գործողություն, որոնք կոչվում են հանում և բաժանում։ Մաթեմատիկական հինգերորդ գործողությունը՝ աստիճան բարձրացնելն ունի երկու հակադարձ գործողություն՝ հիմքի գտնելը և ցուցչի գտնելը։ Հիմքի գտնելը մաթեմատիկական վեցերորդ գործողությունն է և կոչվում է արմատ հանել։ Ցուցչի գտնելը՝ յոթերորդ գործողությունն է, որը կոչվում է լոգարիթմում։ Այն պատճառը, որ աստիճան բարձրացնելն ունի երկու հակադարձ գործողություն, իսկ գումարումը և բազմապատկումը միայն մեկական, հասկանալ դժվար չէ. երկու գումարելիներն էլ (առաջին և երկրորդ) իրավահավասար են, դրանց տեղերը կարելի է փոխել, նույնը ճիշտ է բազմապատկման վերաբերյալ։ Սակայն այն թվերը, որ մասնակցում են աստիճան բարձրացնելուն, այսինքն՝ հիմքը և աստիճանի ցուցիչը իրավահավասար չեն. դրանց տեղափոխել ընդհանրապես չի կարելի (օրինակ՝ )։
Ուստի, գումարման և բազմապատկման մեջ մասնակցող թվերից յուրաքանչյուրի գտնելը կատարվում է նույն ձևով, իսկ աստիճանի հիմքի և աստիճանի ցուցչի գտնելը՝ տարբեր ձևերով։
Վեցերորդ գործողությունը՝ արմատ հանելը, նշանակվում է նշանով։ Ոչ բոլորը գիտեն, որ դա լատինական «արմատ» բառի սկզբնատառի ձևափոխությունն է։ Եղել է ժամանակ (XVI դ.), երբ արմատի նշանը ծառայել է ոչ թե փոքրատառը, այլ գլխատառը, իսկ նրա կողքին գրվել է լատինական «քառակուսի» բառի առաջին տառը () կամ «խորանարդ» բառի առաջին տառը () որպեսզի ցույց տրվեր, թե ինչպիսի արմատ էր պահանջվում հանել[39]։ Օրինակ՝ այժմյան նշանակման փոխարեն գրում էին
։
Եթե դրան ավելացնենք, որ այն դարաշրջանում դեռ գործածական չէին պլյուսի, մինուսի համար ներկայիս նշանները, իսկ դրանց փոխարեն գրում էին և տառեր, և որ մեր փակագծերը փոխարինվում էին նշաններով, ապա պարզ է դառնում, թե ժամանակակից տեսանկյունով ինչպիսի անսովոր տեսք պետք է ունենար հանրահաշվական արտահայտությունները։
Ահա մի օրինակ հնագույն մաթեմատիկոս Բոմբելլիի գրքից (1572)։
։
Մենք կգրենք միևնույնը այլ նշաններով՝
։
Բացի նշանակումից, այժմ գործածվում է նույն գործողության համար դարձյալ մի ուրիշը՝ , որ ընդհանրացման իմաստով խիստ հարմար է. այն ակնհայտ ընդգծում էյ որ յուրաքանչյուր արմատ ոչ այլ ինչ է, քան աստիճան, որի ցուցիչը կոտորակային թիվ է։ Այն առաջադրվել է 16-րդ դարի հոլանդական նշանավոր մաթեմատիկոս Ստեվինի կողմից։
Ո՞ՐՆ Է ՄԵԾ
Խնդիր առաջին
Ո՞րն է մեծ՝ -ը, թե՞ -ը։
Այս և հետագա խնդիրները պահանջվում է լուծել, առանց արմատների արժեքները հաշվելու։
Լուծում
Երկու արտահայտություններն էլ բարձրացնելով -րդ աստիճան, կստանանք՝
։
Քանի որ , ապա
։
Խնդիր երկրորդ
Ո՞րն է մեծ՝ -ը թե՞ -ը։
Լուծում
Երկու արտահայտություններն էլ բարձրացնելով -րդ աստիճան, կստանանք՝
,
։
Քանի որ , ապա և
։
Խնդիր երրորդ
Ո՞րն է մեծ` -ը, թե՞ -ը։
Լուծում
Երկու արտահայտությունն էլ բարձրացնելով քառակուսի, կստանանք՝
,
։
Երկու արտահայտությունն էլ փոքրացնենք -ով, կստանանք
և ։
Այդ արտահայտությունները բարձրացնենք քառակուսի։ Կունենանք՝
և ։
Հանելով -ական, համեմատենք՝
և ։
Քանի որ մեծ է -ից, ապա ,
հետևաբար՝
։
ԼՈՒԾԵԼ ՄԵԿ ՀԱՅԱՑՔՈՎ
Խնդիր
Ուշադրությամբ նայեցեք
հավասարմանը և ասացեք` ինչի՞ է հավասար -ը։
Լուծում
Հանրահաշվական սիմվոլների հետ լավ վարժված յուրաքանչյուր ոք հասկանում է, որ
։
Իրոք. այդ դեպքում
,
և հետևաբար,
,
այն, ինչ պահանջվում էր։
Ում համար «մեկ հայացքով լուծումը» հանդիսանում է ուժից վեր, նա կարող է հեշտացնել անհայտի որոնելը հետևյալ ձևով.
Դիցուք
։
Այդ ժամանակ
,
և հավասարումը կընդունի հետևյալ տեսքը՝
,
կամ բարձրացնելով խորանարդ՝
։
Պարզ է, որ և, հետևաբար,
։
ՀԱՆՐԱՀԱՇՎԱԿԱՆ ԿՈՄԵԴԻԱՆԵՐ
Խնդիր առաջին
Մաթեմատիկական վեցերորդ գործողությունը հնարավորություն է տալիս իսկական հանրահաշվական կոմեդիաներ և ֆարսեր ցուցադրել այնպիսի սյուժեներով, ինչպես՝ և այլն։ Մաթեմատիկական նման ներկայացումների հումորը նրանում է, որ սխալը բավականին տարրական է, մասամբ քողարկվում և միանգամից աչքի չի ընկնում։
Այդ կոմիկական ռեպերտուարից ներկայացնենք երկու պիես հանրահաշվի վերաբերյալ։
Առաջին՝
։
Սկզբում գրատախտակին հայտնվում է հետևյալ անվիճելի հավասարությունը՝
։
Հաջորդ «էտապում» հավասարության երկու մասերին էլ ավելացվում եմ հավասար մեծություններ՝ ,
։
Կոմեդիայի հետագա քայլը կայանում է հետևյալ ձևափոխությունում,
,
։[40]
Հավասարության երկու մասից էլ քառակուսի արմատ հանելով, ստանում են՝
։
Երկու մասին էլ ավելացնելով , հանգում են անհեթեթ հավասարության՝
։
Որտե՞ղ է թաքնված սխալը։
Լուծում
Սխալը սպրդեց հետևյալ եզրակացության մեջ՝
։
հավասարությունից արվել է հետևություն, որ
։

Բայց քառակուսիների հավասարությունից երբեք չի հետևում, որ հավասար են նաև առաջին աստիճանները։ Չէ՞ որ , բայց -ը հավասար չէ -ի։ Քառակուսիները կարող են հավասար լինել և այն դեպքում, երբ առաջին աստիճանները տարբերվում են նշաններով։ Մեր օրինակում մենք ունենք հենց այդպիսի դեպք՝
,
բայց -ը հավասար չէ -ի։
Խնդիր երկրորդ
Մյուս հանրահաշվական ֆարսը (նկ. 15)
ներկայացվում է նախորդ ձևով և հիմնված է նույն տրյուկի վրա։ Գրատախտակի վրա հայտնվում է կասկած չհարուցող հետևյալ հավասարությունը՝
։
Ավելացնում են հավասար թվեր՝
և կատարում են հետևյալ ձևափոխությունները՝
,
։
Այնուհետև նույն ոչ օրինական եզրակացության միջոցով անցնում են ֆինալին՝
,
։
Այս կոմիկական դեպքերը սակավափորձ մաթեմատիկոսին պետք է նախազգուշացնեն արմատանշանի տակ անհայտ պարունակող հավասարումների հետ անզգույշ օպերացիաներ կատարելուց։

ԳԼՈՒԽ ՎԵՑԵՐՈՐԴ։ ԵՐԿՐՈՐԴ ԱՍՏԻՃԱՆԻ ՀԱՎԱՍԱՐՈՒՄՆԵՐ
ՁԵՌՔ ՍԵՂՄՈՒՄՆԵՐ
Խնդիր
Նիստի մասնակիցները միմյանց ձեռք սեղմեցին. մեկը հաշվեց, որ բոլոր ձեռքսեղմումները եղել են ։ Քանի՞ մարդ է ներկայացել նիստին։
Լուծում
Խնդիրը լուծվում է հանրահաշվորեն միանգամայն պարզ կերպով։ մասնակիցներից յուրաքանչյուրը սեղմեց ձեռք։ Նշանակում է բոլոր ձեռք սեղմողները պետք է լինեին . բայց պետք է ուշադրություն դարձնել, որ երբ Իվանովը սեղմում է Պետրովի ձեռքը, ապա և Պետրովը սեղմում է Իվանովի ձեռքը. այդ երկու ձեռքսեղմումները պետք է հաշվել որպես մեկ։ Ուստի հաշված ձեռքսեղմումների թիվը երկու անգամ փոքր է, քան թե ։ Ու նենք հետևյալ հավասարումը՝
կամ ձևափոխություններից հետո՝
,
որտեղից
։
Քանի որ բացասական լուծումը ( մարդ) տվյալ դեպքում ռեալ իմաստից զուրկ է, մենք այն անտեսում ենք և պահպանում ենք միայն առաջին արմատը. նիստին մասնակցել են մարդ։
ՄԵՂՎԱԽՈՒՄԲԸ
Խնդիր
Հնադարյան Հնդկաստանում տարածված էր սպորտի յուրատեսակ ձև, գլուխկոտրուկ խնդիրների լուծման հրապարակային մրցում։ Հնդկական մաթեմատիկական ուղեցույցները մասամբ նպատակ ունեին ծառայելու որպես ձեռնարկներ մտավոր սպորտի նման մրցումների առաջնության համար։ «Այստեղ շարադրված կանոնների համաձայն,— գրում է այդպիսի դասագրքերից մեկի կազմողը,— իմաստունը կարող էր մտածել հազար այլ խնդիրներ։ Ինչպես արևն է իր փայլով ստվերի մեջ թողնում աստղերին, այնպես էլ գիտնականը մթագնում է մյուսի փառքը ժողովրդական հավաքներում՝ առաջարկելով և լուծելով հանրահաշվական խնդիրներ»։ Բնագրում դա արտահայտված է բանաստեղծորեն, քանի որ ամբողջ գիրքը գրված է չափածո։ Խնդիրներին նույնպես տրված է չափածո տեսք։ Բերենք դրանցից մեկը՝ արձակի վերածած։
Մեղուները, որ թվով հավասար են նրանց ողջ խմբի կեսի քառակուսի արմատին, նստեցին հասմիկի թփին՝ իրենց ետևը թողնելով խմբի -ը։ Եվ նույն խմբից միայն մի մեղու, հրապուրված ընկերուհիների[41] բզզոցով՝ պտույտ է գալիս լոտոսի շուրջը, անզգուշորեն ընկնելով բուրումնավետ, ծաղկի ծուղակը։ Ընդամենը քանի՞ մեղու կար խմբում։
Լուծում
Եթե խմբի որոնելի թիվը նշանակենք -ով, ապա հավասարումը կունենա հետևյալ տեսքը՝
։
Մենք կարող ենք սրան տալ ավելի պարզ տեսք՝ մտցնելով օժանդակ անհայտ
։
Այդ ժամանակ , և հավասարումը կլինի՝
կամ ։
Լուծելով այն, -ի համար կստանանք երկու արժեքներ՝
։
-ի համապատասխան արժեքները կլինեն՝
։
Քանի որ մեղուների թիվը պետք է լինի ամբողջ և դրական, ապա խնդրին բավարարում է միայն առաջին արմատը, խումբը բաղկացած էր մեղուներից։ Ստուգենք՝
։
ԿԱՊԻԿՆԵՐԻ ԽՈՒՄԲԸ
Խնդիր
Հնդկական մյուս խնդիրը ես հնարավորություն ունեմ չափածոյի վերածած հաղորդել այնպես, ինչպես այն թարգմանել է «Ո՞վ է հայտնաագործել հանրահաշիվը» հիանալի գրքի հեղինակ Վ. Ի. Լեբեդևը.
Երկու խմբի բաժանվելով,
Զվարճանում են կապիկները։
Ութերորդի քառակուսին
Զվարթ խայտում է պուրակում,
Ուրախ ճիչով տասներկուսը
Թնդացնում են օդը մաքուր։
Ասա՛ դու ինձ, ընդամենը
Քանի՞ կապիկ կար պուրակում։
Լուծում
Եթե խմբի ընդհանուր թիվը է, ապա
,
որտեղից
։
Խնդիրն ունի երկու դրական լուծում` խմբում կարող էին լինել կապիկ կամ ։ Երկու պատասխաներն էլ լրիվ բավարարում են խնդրին։
ՀԱՎԱՍԱՐՈՒՄՆԵՐԻ ԿԱՆԽԱՏԵՍՈՒԹՅՈՒՆԸ
Դիտարկված դեպքերում հավասարումների ստացված երկու լուծումների հետ մենք վարվեցինք տարբեր ձևով՝ ելնելով խնդրի պայմաններից։ Առաջին դեպքում մենք դեն գցեցինք բացասական արմատը, որպես խնդրի բովանդակությանը չհամապատասխանող, երկրորդում՝ հրաժարվեցինք կոտորակային և բացասական արմատներից, երրորդ խնդրում, հակառակը, օգտվեցինք երկու արմատներից էլ։ Երկրորդ լուծման գոյությունը երբեմն անսպասելի է լինում ոչ միայն խնդիրը լուծողի համար, այլև այն հորինողի համար։ Բերենք օրինակ, երբ հավասարումն ավելի կանխատեսող է, քան նա ով կազմել է այն։
Գնդակը նետված է դեպի վեր Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 25 \; մ/վրկ} արագությամբ։ Քանի՞ վայրկյանից հետո այն կգտնվի երկրից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20 \; մ} բարձրության վրա։
Լուծում
Վեր նետված մարմնի համար, օդի դիմադրության բացակայության դեպքում, երկրի վրա մարմնի վերելքի բարձրության (), սկզբնական արագության (), ձգողականության արագացման () և ժամանակի () միջև մեխանիկան սահմանում է հետևյալ առնչությունը,
։
Օդի դիմադրությունը տվյալ դեպքում մենք կարող ենք արհամարհել, քանի որ աննշան արագության դեպքում նա այնքան մեծ չէ։ Հաշվումները պարզեցնելու համար ընդունենք -ն ոչ թե հավասար Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 9,8 \; մ/վրկ^2} , այլ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10 \; մ/վրկ^2} [42] (սխալը ընդամենը 2% է)։ Բերված բանաձևի մեջ տեղադրելով -ի, -ի և -ի արժեքները կստանանք հետևյալ հավասարումը՝
,
իսկ պարզեցնելուց հետո
։
Լուծելով հավասարումը, կունենանք՝
և ։
Գնդակը կլինի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20 \; մ} բարձրության վրա երկու անգամ՝ վայրկյան հետո և վայրկյան հետո։
Այդ կարող է, թերևս, թվալ անհավանական, և չմտածելով՝ մենք պատրաստ ենք երկրորդ լուծումն անտեսել։ Սակայն այդպես վարվելը սխալ կլիներ։ Երկրորդ լուծումը լրիվ իմաստ ունի. գնդակը պետք է իրոք երկու անգամ գտնվի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20 \; մ} բարձրության վրա՝ մեկ անգամ վերելքի դեպքում և երկրորդ անգամ հետադարձ անկման դեպքում։ Հեշտ է հաշվել, որ վայրկյանում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 25 \; մ} սկզբնական արագության դեպքում գնդակը կթռչեր դեպի վեր վայրկյան՝ հասնելով Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 31,25 \; մ} բարձրության։ վայրկյան հետո հասնելով Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20 \; մ} բարձրության, գնդակը կբարձրանա ևս վայրկյան, այնուհետև այդքան ժամանակ էլ ցած կիջնի մինչև Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20 \; մ} մակարդակը, և մի վայրկյան հետո կհասնի երկրին։
ԷՅԼԵՐԻ ԽՆԴԻՐԸ
Ստենդալը «Ինքնակենսագրության» մեջ իր ուսման տարիների մասին պատմում է հետևյալը.
«Ես նրա մոտ (մաթեմատիկայի ուսուցչի) գտա Էյլերին և նրա խնդիրը ձվերի թվի մասին, որոնք գեղչկուհին տանում էր շուկա... «Դա ինձ համար նորություն էր։ Ես հասկացա, թե ինչ է նշանակում օգտվել մի զենքից, որ կոչվում է հանրահաշիվ։ Բայց սատանան տանի, ոչ ոք ինձ այդ մասին ոչինչ չէր ասել»։
Ահա այդ խնդիրը Էյլերի «Հանրահաշվի ներածություն»-ից, որ երիտասարդ Ստենդալի վրա թողել էր այնքան ուժեղ տպավորություն։
Երկու գեղջկուհի միասին շուկա բերեցին ձու, մեկը ավելի շատ, քան մյուսը. երկուսն էլ վաստակեցին հավասար
գումարներ։ Այդ ժամանակ առաջինը երկրորդին ասաց՝ «Եթե քո ձվերը իմը լինեին, ես կվաստակեի կրեյցեր։Երկրորդը պատասխանում է՝ «Իսկ եթե քո ձվերը իմը լինեին, ես դրանց դիմաց կվաստակեի կրեյցեր։ Քանի՞ ձու ուներ յուրաքանչյուրը։
Լուծում
Դիցուք առաջին գեղջկուհին ուներ ձու. այդ ժամանակ երկրորդը կունենա՝ ։ Իսկ եթե առաջինը ունենար ձու, ապա նա կստանար, ինչպես գիտենք, կրեյցեր։ Նշանակում է, առաջին գեղջկուհին ձվերը կվաճառեր հատը
-ով։
Այս ձևով դանում ենք, որ երկրորդ գեղջկուհին ձվերը վաճառել է հատը
-ով։
Այժմ որոշենք յուրաքանչյուր գեղջկուհու իրականում ստացածը՝
առաջինը՝ ,
երկրորդը՝ ։
Քանի որ երկուսի մոտ էլ վաճառքից ստացած գումարները հավասար են, ապա
։
Ձևափոխությունից հետո կունենանք
,
որտեղից
։
Տվյալ դեպքում բացասական արմատը իմաստ չունի. խնդիրն ունի միայն մեկ լուծում. առաջին գեղջկուհին բերել էր ձու և ուրեմն երկրորդը՝ ։
Խնդիրը հնարավոր է լուծել այլ` ավելի կարճ ձևով։ Այդ ձևը անհամեմատ սրամիտ է, բայց դրա փոխարեն այն որոնելը զգալիորեն դժվար է։
Ենթադրենք, որ երկրորդ գեղջկուհին ուներ անգամ ավելի շատ ձու, քան առաջինը։ Նրանք ստացել են միահավասար գումարներ. այդ նշանակում է, որ առաջին գեղջկուհին իր ձվերը վաճառել է անգամ թանկ, քան երկրորդը։ Իսկ եթե նրանք վաճառելուց առաջ փոխանակեին ձվերը, ապա առաջին գեղջկուհին կունենար անգամ ավելի շատ ձու, քան երկրորդը, և դրանց կվաճառեր անգամ ավելի թանկ։ Այդ նշանակում է, որ նա կստանար -ով ավելի փող, քան երկրորդը։ Հետևաբար, կունենանք՝
,
այստեղից
։
Այժմ մնում է ձուն բաժանել հարաբերությամբ։ Հեշտությամբ կգտնենք, որ առաջին գեղջկուհին ուներ , իսկ երկրորդը՝ ձու։
ԲԱՐՁՐԱԽՈՍՆԵՐԸ
Խնդիր
Հրապարակում տեղակայված է բարձրախոս, որոնք բաժանված են երկու խմբի՝ մեկում , մյուսում ապարատ։ Խմբերի միջև հեռավորությունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 50 \; մ} է։ Որտե՞ղ պետք է կանգնել, որպեսզի երկու խմբերի ձայներն էլ հասնեն հավասար ուժով։
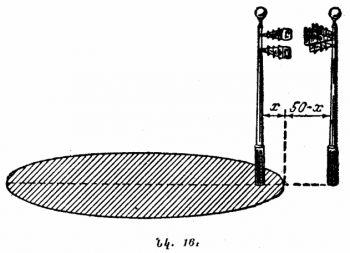
Լուծում
Եթե փոքր խմբից որոնելի կետի հեռավորությունը նշանակենք -ով, ապա մեծ խմբից այն կլինի (նկ. 16)։ Գիտենալով, որ ձայնի ուժը թուլանում է հեռավորության քառակուսուն համեմատական, կունենանք հետևյալ հավասարումը՝
,
որը պարզեցնելուց հետո բերվում է հետևյալ տեսքի՝
։
Լուծելով այն, կստանանք երկու արմատներ՝
,
։
Դրական արմատը հենց պատասխանում է խնդրի հարցին՝ հավասար լսելիության կետը երկու բարձրախոսների խմբից հեռացված է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 22,5 \; մ} -ով, իսկ երեք ապարատների խմբից՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 27,5 \; մ} -ով։
Բայց ի՞նչ է նշանակում հավասարման բացասական արմատը։ Ունի՞ նա որևէ իմաստ։
Անպայման։ Մինուս նշանը նշանակում է, որ հավասար լսելիության երկրորդ կետը ընկած է հակադիր այն ուղղությանը, որը ընդունված էր որպես դրական՝ հավասարումները կազմելիս։ Երկու ապարատների գտնվելու տեղից պահանջված ուղղությամբ անջատելով Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 222,5 \; մ} , գտնենք այն կետը, որտեղ երկու խմբերի բարձրախոսների ձայները հասնում են հավասար ուժով։ Երեք ապարատների խմբից այդ կետը հեռացած կլինի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 222,5 \; մ + 50 \; մ \;=\; 272 \; մ} ։
Այսպիսով, մենք գտանք հավասար լսելիության երկու կետերը, այն կետերը, որոնք ընկած են ձայնի աղբյուրները միացնող ուղիղի վրա։ Ուրիշ այդպիսի կետեր այդ գծի վրա չկան, բայց նրանք կան այդ գծից դուրս։ Կարելի է ապացուցել, որ այն կետերը երկրաչափական տեղը, որ բավարարում է մեր խնդրի պահանջներին, շրջանագիծ է, որը տարված է հենց նոր գտնված երկու կետերով որպես տրամագծի ծայրեր։ Այդ շրջանագիծը, ինչպես տեսնում ենք, սահմանափակում է բավականին ընդարձակ հատված (գծագրում ստվերագծված), որի ներսում երկու բարձրախոսների խմբի լսելիությանը հաղթահարում է երեք ապարատների խմբի լսելիությանը, իսկ այդ շրջանի սահմաններից դուրս նկատվում է հակառակ երևույթը։
ԼՈՒՍՆԱՅԻՆ ԹՌԻՉՔԻ ՀԱՆՐԱՀԱՇԻՎԸ
Բարձրախոսների մասին հենց նոր դիտարկված խնդիրը անսպասելիորեն զուգադիպում է հրթիռանավով Լուսնին թռչելու պրոբլեմին։ Շատերը կասկածանքով են արտահայտվում այն մասին, թե երկնքում այդ փոքրիկ թիրախի վրա դիպուկ ընկնելը չի՞ հանդիսանում արդյոք չափազանց դժվարին գործ։ Չէ՞ որ Լուսնի տրամագիծը մեզ երևում է ընդամենը կես աստիճանի անկյան տակ։ Հարցի մանրամասն քննարկումից պարզվում է, որ ձեռնարկման նպատակին կարելի է հասնել, եթե հրթիռին հաջողվի թռչելով անցնել Երկրի և Լուսնի հավասար ձգողականության կետից, այնուհետև՝ հրթիռանավն արդեն անխուսափելիորեն կշարժվի դեպի Լուսինը նրա ձգողականության ուժի ներգործությաբ։ Որոնենք հավասար ձգողականության այդ կետը։
Ըստ Նյուտոնի օրենքի, երկու մարմինների փոխադարձ ձգողականությունը ուղիղ համեմատական է ձգող մասսաների արտադրյալին և հակադարձ համեմատական նրանց միջև եղած հեռավորության քառակուսուն։ Եթե Երկրի մասսան է, իսկ հրթիռի հեռավորությունը նրանից՝ , ապա այն ուժը, որով երկիրը ձգում է հրթիռի մասսայի յուրաքանչյուր գրամը, արտահայտվում է
բանաձևով, որտեղ -ն Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1 \; սմ} հեռավորության վրա գտնվող երկու՝ մեկական գրամների փոխադարձ ձգողականության ուժն է։ Այն ուժը, որով Լուսինր ձգում է հրթիռի լուրաքանչյուր դրամը նուլն կետում, հավասար է
,
որտեղ -ը Լուսնի մասսան է, իսկ -ը՝ նրա հեռավորությունը Երկրից (ենթադրվում է, որ հրթիռը գտնվում է Երկրի և Լուսնի միջև՝ դրանց կենտրոնները միացնող ուղիղ գծի վրա)։ Խնդիրը պահանջում է, որ տեղի ունենա
կամ
։
հարաբերությունը, ինչպես հայտնի է աստղագիտությունից, մոտավորապես հավասար է . տեղադրելով, կունենաք՝
,
որտեղից
։
Լուծելով հավասարումը -ի նկատմամբ, կստանանք
։
Ինչպես բարձրախոսների մասին խնդրում, այնպես էլ այստեղ մենք գալիս ենք այն եզրակացության, որ Երկիր-Լուսին գծի վրա գոյություն ունեն երկու որոնելի կետեր. երկու այնպիսի կետեր, որոնցից հրթիռը պետք է միատեսակ ձգվի երկու լուսատուներից։ Մեկը նրանց հեռավորության -ից է, հաշված Երկրի կենտրոնից, մյուսը՝ նույն հեռավորության -ից։ Քանի որ Երկրի և Լուսնի կենտրոնների միջև հեռավորությունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \approx 384000 \; կմ} -ի, ապա որոնելի կետերից մեկը գտնվում է Երկրի կենտրոնից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 346000 \; կմ} -ի վրա, իսկ մյուսը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 430000 \; կմ} -ի վրա։
Բայց մենք գիտենք (տե՛ս նախորդ խնդիրը), որ շրջանագծի բոլոր կետերը միևնույն հատկությունն ունեն, և նրա բոլոր կետերն անցնում են գտնված երկու կետերով որպես տրամագծի ծայրեր։ Եթե այդ շրջանագիծն սկսենք պտտել Երկրի և Լուսնի կենտրոնները միացնող գծի շուրջը, ապա այն կգծի գնդային մակերևույթ, որի բոլոր կետերը կբավարարեն խնդրի պահանջներին։
Այդ գնդի տրամագիծը հավասար է
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 1,12l-0,9l=0,22l \approx 8400 \; կմ} ։
Եթե հրթիռը հայտնվի այդ գնդի ներսը (ունենալով ոչ չափազանց մեծ արագություն), նա անխուսափելիորեն կընկնի Լուսնի մակերևույթի վրա, քանի որ Լուսնի ձգողականության ուժը այդ շրջանում հաղթահարում է Երկրի ձգողականության ուժը (նկ. 17)։
Այն թիրախը, որի վրա ընկնում է հրթիռը մենք տեսնում ենք անհամեմատ մեծ, քան կարելի է պատկերացնել։ Նա երկնքում զբաղեցնում է ոչ թե կես աստիճան, այլ, ինչպես ցույց է տալիս երկրաչափական ոչ բարդ հաշվարկը, մոտ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 12°} ։ Դա զգալիորեն թեթևացնում է տիեզերագնացների[43] խնդիրը։
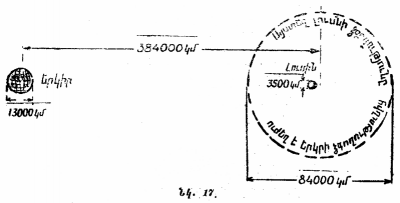
Այս անգամ հավասարումը ավելի կանխատեսող եղավ, քան նա, ով կազմել էր։ Ձեռնամուխ լինելով խնդրին, դուք մտածե՞լ եք արդյոք, որ երկրային ձգողականությունը ավելի մեծ է, քան Լուսնի ձգողականությունը ոչ միայն Լուսնի առջևից, այլև նրա ետևից։ Հանրահաշվական անալիզը անսպասելիորեն ձեր առջև բացեց այդ հանգամանքը և օգնեց ճշտությամբ սահմանազատել երկու լուսատուների ազդեցությունների սֆերաները։
ԴԺՎԱՐ ԽՆԴԻՐ
Բոգդանով-Բելսկու «Դժվար խնդիր» նկարը շատերին է հայտնի, բայց այդ նկարը դիտողներից քչերն են խորամուխ եղել այն «դժվար խնդրի» բովանդակության մեջ, որը պատկերված է նրա վրա։

Այն կայանում է նրանում, որպեսզի բանավոր հաշվով արագ գտնվի հետևյալ հաշվարկման արդյունքը՝
։
Իրոք խնդիրը հեշտ չէ։ Սակայն, նրանից լավ գլուխ հանեցին այն ուսուցչի աշակերտները, որը դեմքի նմանությամբ պատկերված է նկարում, դա հենց ինքը՝ բնական գիտությունների պրոֆեսոր Ս. Ա. Ռաչինսկին է, որը թողեց համալսարանի ամբիոնը գյուղական դպրոցի շարքային ուսուցիչ դառնալու համար։ Տաղանդավոր մանկավարժը իր դպրոցում մշակեց բանավոր հաշիվ, որ հիմնված էր թվերի հատկությունների վիրտուոզային օգտագործման վրա։ և թվերն ունեն հետաքրքիր առանձնահատկություն.
։
Բանի որ , ապա հեշտ է մտքում հաշվել, որ նկարում վերարտադրված արտահայտությունը հավասար է -ի։
Հանրահաշիվը մեզ հնարավորություն է տալիս թվերի այդ շարքի հետաքրքիր առանձնահատկության մասին հարցը ավելի լայն կերպով դնելու՝ միա՞կն է արդյոք հինգ հաջորդական թվերից կազմված այդ շարքը, որի առաջին երեք թվերի քառակուսիների գումարը հավասար է վերջին երկուսի քառակուսիների գումարին։
Լուծում
Նշանակելով որոնելի թվերից առաջինը -ով, կունենանք հետևյալ հավասարումը՝
։
Սակայն հարմար է նշանակել -ով ոչ թե առաջին, այլ որոնելի թվերից երկրորդը։ Այդ ժամանակ հավասարումը կունենա ավելի պարզ տեսք՝
։[44]
Բացելով փակագծերը և կատարելով պարզեցումներ, կստանանք`
,
որտեղից
։
Հետևաբար՝ գոյություն ունեն թվերի երկու շարք, որոնք ունեն պահանջվող հատկությունը՝
Ռաչինսկու շարքը՝
,
և հետևյալ շարքը՝
։
Իրոք՝
։
ԱՅԴ Ո՞Ր ԹՎԵՐՆ ԵՆ
Խնդիր
Գտնել երեք հաջորդական այնպիսի թվեր, որոնք տարբերվում են այն հատկությամբ, որ միջին թվի քառակուսին -ով մեծ է մնացած երկուսի արտադրյալից։
Լուծում
Եթե որոնելի թվերից առաջինը է, ապա հավասարումը կունենա հետևյալ տեսքը՝
։
Բացելով փակագծերը, կստանանք հավասարությունը՝
,
որից չի կարելի որոշել -ի մեծությունը։ Այդ ցույց է տալիս, որ մեր կազմած հավասարությունը նույնություն է. այն իրավացի է նրա մեջ մտնող տառի ցանկացած արժեքի դեպքում, այլ ոչ միայն որոշ արժեքների դեպքում ինչպես հավասարման ժամանակ։ Նշանակում է՝ ամեն մի երեք հաջորդական թվեր ունեն պահանջվող հատկությունը։ Իրոք, վերցնենք պատահական թվերը։
Մենք համոզվում ենք, որ
։
Այդպիսի առնչության անհրաժեշտությունը դառնում է ակնառու, եթե երկրորդ թիվը նշանակենք -ով։ Այն ժամանակ կստանանք հետևյալ հավասարությունը՝
,
այսինքն՝ հայտնի նույնությունը։

ԳԼՈՒԽ ՅՈԹԵՐՈՐԴ։ ԱՄԵՆԱՄԵԾ ԵՎ ԱՄԵՆԱՓՈՔՐ ԱՐԺԵՔՆԵՐ
Այս գլխում զետեղված խնդիրները պատկանում են որոշ մեծության ամենամեծ և ամենափոքր արժեքները որոնելու վերաբերյալ խնդիրների չափազանց հետաքրքիր տիպին։
Դրանք կարելի է լուծել տարբեր եղանակներով, որոնցից մեկն այժմ ցույց կտանք։
ԵՐԿՈՒ ԳՆԱՑՔ
Խնդիր
Երկաթուղային երկու ճանապարհներ խաչվում են ուղիղ անկյան տակ։ Այդ ճանապարհներով դեպի խաչմերուկ միաժամանակ սլանում են երկու գնացք. մեկը այն կայարանից, որը գտնվում է խաչմերուկից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 40 \; կմ} -ի վրա, իսկ մյուսը այն կայարանից, որը նույն խաչմերուկից գտնվում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 50 \; կմ} -ի վրա։ Առաջինն անցնում է րոպեում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 800 \; մ} , երկրորդը՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 600 \; մ} ։ Գնացքների մեկնման պահից հաշված քանի՞ րոպե հետո նրանք միմյանցից կլինեն ամենափոքր հեռավորության վրա։ Որքա՞ն է այդ հեռավորությունը։
Լուծում
Գծենք մեր խնդրի գնացքների շարժման սխեման։ Դիցուք -ն և -ն ճանապարհի խաչվող ուղիներն են (նկ. 19)։ կայարանը գտնվում է խաչման կետից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 40 \; կմ} -ի վրա։ կայարանը՝ նրանից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 30 \; կմ} -ի վրա։ Ենթադրենք, որ րոպե անց գնացքները կլինեն միմյանցից ամենակարճ հեռավորության վրա՝ ։ -ից դուրս եկող գնացքն այդ պահին կանցնի ճանապարհը, քանի որ մեկ րոպեի ընթացում նա անցնում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 800 \; մ = 0,8 \; կմ} ։ Հետևաբար՝ ։ Ճիշտ այդպես էլ գտնենք, որ ։ Ըստ Պլութագորի թեորեմայի
։
։
Հավասարման երկու մասն էլ բարձրացնելով քառակուսի և կատարելով պարզեցումներ, կստանանք՝
։
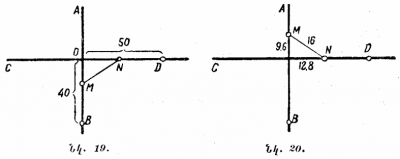
Լուծելով այս հավասարումը -ի նկատմամբ, կունենանք
։
Քանի որ -ը անցած րոպեների թիվն է, ուստի կեղծ լինել չի կարող, ապա պետք է լինի դրական մեծություն, կամ, ծայրահեղ դեպքում, հավասար զրոյի։ Վերջինը համապատասխանում է -ի ամենափոքր հնարավոր արժեքին, և այդ դեպքում
, այսինքն՝ ։
Ակնհայտ է, որ -ը -ից փոքր լինել չի կարող, այլապես -ը կդառնա կեղծ։ Իսկ եթե , ապա ։
Այսպիսով, գնացքները միմյանց ամենամոտ կլինեն րոպե հետո, և նրանց փոխադարձ հեռավորությունն այդ ժամանակ կլինի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 16 \; կմ} ։
Որոշենք, թե այդ պահին ինչպես են նրանք դասավորված։ Հաշվենք երկարությունը. այն հավասար է
[45]։
Մինուս նշանը նշանակում է, որ գնացքն անցնում է խաչմերուկից դուրս Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 9,6 \; կմ} -ով։ Իսկ հեռավորությունը հավասար է
,
այսինքն՝ երկրորդ գնացքը խաչմերուկին չի հասնի. նրանից հեռու կմնա Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 12,8 \; կմ} -ով։ Գնացքների դասավորությունը ցույց է տրված 20-րդ նկարում։ Ինչպես տեսնում ենք, ընդհանրապես նա այն չէ, ինչը մենք պատկերացնում էինք մինչև խնդրի լուծումը։ Պարզվեց, որ այս հավասարումը բավականին դիմացկուն է և, չնայած ոչ ճիշտ սխեմայի, ստացվեց ճիշտ լուծում։ Դժվար չէ հասկանալ, թե որտեղից է այդ դիմացկունությունը. այն պայմանավորված է հանրահաշվական նշանների կանոններով։
ՈՐՏԵ՞Ղ ԿԱՌՈՒՑԵԼ ԿԱՅԱՐԱՆԸ
Խնդիր
Երկաթուղու ուղղագիծ ճանապարհից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 20 \; կմ} հեռավորության վրա գտնվում է գյուղը (նկ. 21)։
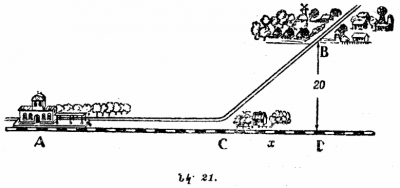
Որտե՞ղ պետք է կառուցել կիսակայարանը, որպեսզի երկաթուղով և խճուղով -ից մինչև գնալը խլի հնարավորին չափ քիչ ժամանակ։ Արագությունը երկաթուղով րոպեում կիլոմետր է, խճուղով՝ կիլոմետր։
Լուծում
հեռավորությունը (-ից մինչև -ին տարված ուղղահայացի հիմքը) նշանակենք -ով, -ն՝ -ով։ Այդ դեպքում , իսկ ։ Ժամանակը, որի ընթացքում գնացքն անցնում է ճանապարհը, հավասար է
։
ճանապարհը խճուղով անցնելու համար ժամանակը հավասար է
։
-ից գնալու ընդհանուր տևողությունը հավասար է
։
Այս գումարը, որ նշանակում ենք -ով, պետք է լինի ամենափոքրը։
հավասարումը ներկայացնենք հետևյալ տեսքով՝
։
Բազմապատկելով -ով, կունենանք՝
։
-ն նշանակելով -ով և հավասարումը ազատելով արմատից, կստանանք. քառակուսի հավասարում՝
,
որտեղից
։
Քանի որ , ապա -ի ամենափոքր արժեքի դեպքում -ն հասնում է ամենափոքր մեծության, և հակառակը[46]։ Բայց որպեսզի -ը լինի իրական, պետք է լինի -ից ոչ փոքր։ Նշանակում է՝ համար ամենափոքր մեծությունը -ն է։ Ուստի՝ -ը դառնում է ամենափոքր, երբ
,
որտեղից
,
և, հետևաբար,
։
Ինչպիսին էլ որ լինի երկարությունը, կիսակայարանը պետք է կառուցել կետից մոտավորապես Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 5 \; կմ} հեռավորության վրա։
Բայց, հասկանալի է, որ մեր լուծումն իմաստ ունի միայն այն դեպքում, երբ , քանի որ հավասարումը կազմելիս մենք արտահայտությունը հաշվեցինք դրական թիվ։
Եթե , ապա կիսակայարանի կառուցելը ընդհանրապես պետք չէ. խճուղին ուղղակի պետք է անցկացնել դեպի կայարան։ Այդպես պետք է վարվել և այն դեպքում, երբ հեռավորությունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 5,16 \; կմ} -ից ավելի կարճ է։
Այս անգամ մենք ավելի կանխատեսող եղանք, քան թե հավասարումը։ Իսկ եթե մենք կուրորեն հավատայինք հավասարմանը, մենք ստիպված կլինեինք ներկա դեպքում կիսակայարանը կառուցել կայարանի հետևում, որը բացահայտ անհեթեթություն կլիներ, այդ դեպքում , և այդ պատճառով
ժամանակը, որի ընթացքում հարկավոր է գնալ երկաթգծով, բացասական է։ Դեպքը ուսանելի է. այն ցույց է տալիս, որ մաթեմատիկական զենքից օգտվելիս պետք է պատշաճ շրջահայացությամբ վերաբերվել ստացված արդյունքներին՝ հիշելով, որ դրանք կարող են կորցնել իրենց իրական իմաստը, եթե չիրականացվեն այն նախադրյալները, որոնց վրա հիմնված է մեր մաթեմատիկական զենքի կիրառությունը։
ԻՆՉՊԵ՞Ս ԱՆՑԿԱՑՆԵԼ ԽՃՈՒՂԻՆ
Խնդիր
Գետամերձ քաղաքից պետք է բեռներ փոխադրել վայրը, որը տեղավորված է գետից կիլոմետր ներքև և ափից՝ կիլոմետր հեռու (նկ.22)։ -ից դեպի գետը ինչպե՞ս անցկացնել խճուղին, որպեսզի բեռների փոխադրումը -ից հնարավորին չափ էժան լինի, եթե տոննա-կիլոմետրի փոխադրավարձը գետով երկու անգամ էժան է, քան խճուղով։
Լուծում
հեռավորությունը նշանակենք -ով և խճուղու երկարությունը՝ -ով. ըստ ենթադրության երկարությունը հավասար է -ի, իսկ երկարությունը՝ -ի։
Քանի որ փոխադրումը խճուղով երկու անգամ թանկ է, քան գետով, ապա խնդրի պահանջի համաձայն
գումարը պետք է լինի ամենափոքրը։
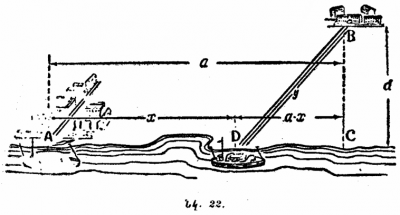
Այդ ամենափոքր արժեքը նշանակենք -ով։ Կունենանք հետևյալ հավասարումը
։
Բայց , իսկ , ուստի մեր հավասարումը կստանա հետևյալ տեսքը՝
,
կամ արմատից ազատվելուց հետո՝
։
Լուծենք այն.
։
Որպեսզի -ը լինի իրական, -ն պետք է -ուց փոքր չլինի։ -ու ամենափոքր արժեքը հավասար է , և այդ ժամանակ
։
, այսինքն՝
։
Բայց այն անկյունը, որի սինուսը հավասար է , հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 60°} ։ Նշանակում է ինչպիսին էլ որ լինի հեռավորությունը, խճուղին պետք է անցկացնել գետի նկատմամբ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 60°} -ի անկյան տակ։
Այստեղ նորից հանդիպում ենք այն նույն առանձնահատկությանը, որին մենք հանդիպեցինք նախորդ խնդրում։ Լուծումն իմաստ ունի միայն որոշակի պայմանի դեպքում։ Եթե վայրը տեղավորված է այնպես, որ խճուղին (որն անցկացվում է գետի նկատմամբ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 60°} -ի անկյան տակ) անցնում է քաղաքի այդ կողմով, ապա լուծումը կիրառելի չէ. այդ դեպքում պետք է վայրը քաղաքի հետ անմիջականորեն կապել խճուղով փոխադրումների համար ընդհանրապես չօգտվելով գետից։
ԱՐՏԱԴՐՅԱԼԸ ԵՐԲ Է ԼԻՆՈՒՄ ԱՄԵՆԱՄԵԾԸ
«Մաքսիմումի և մինիմումի» վերաբերյալ շատ խնդիրներ լուծելու համար, այսինքն՝ փոփոխական մեծության ամենամեծ և ամենափոքր արժեքները գտնելու համար կարելի է օգտվել հանրահաշվական մի թեորեմայից, որի հետ այժմ մենք կծանոթանանք։ Դիտարկենք հետևյալ խնդիրը՝
Ինչպիսի՞ երկու մասի պետք է բաժանել տրված թիվը, որպեսզի դրանց արտադրյալը լինի ամենամեծը։
Լուծում
Դիցուք -ն տրված թիվ է։ Այդ դեպքում մասերը, որոնցով բաժանված է թիվը, կարելի է նշանակել
և ,
որտեղ թիվը ցույց է տալիս, թե այդ մասերն ի՛նչ մեծությամբ են տարբերվում թվի կեսից։ Երկու մասերի արտադրյալը հավասար է
։
Պարզ է, որ վերցված մասերի արտադրյալը կմեծանա -ի փոքրանալու դեպքում, այսինքն՝ այդ մասերի տարբերության փոքրանալու դեպքում։ Ամենամեծ արտադրյալը կլինի, երբ , այսինքն՝ այն դեպքում, երբ երկու մասերն էլ հավասար են -ի։
Այսպիսով, թիվը պետք է բաժանել երկու հավասար մասի. երկու թվերի արտադրյալը (եթե դրանց գումարը հաստատուն է) կլինի ամենամեծ այն ժամանակ, երբ այդ թվերը միմյանց հավասար են։
Նույն հարցը քննարկենք երեք թվերի համար։
Ինչպիսի՞ երեք մասի պետք է բաժանել տրված թիվը, որպեսզի դրանց արտադրյալն ամենամեծը լինի։
Լուծում
Այս խնդիրը լուծելիս կհիմնվենք նախորդի վրա։
Դիցուք թիվը բաժանված է երեք մասի։ Սկզբից ենթադրենք, որ մասերից ոչ մեկը հավասար չէ -ի։ Այդ ժամանակ նրանց միջև կգտնվի մի մաս, որը մեծ է -ից (բոլոր երեքն էլ միաժամանակ չեն կարող փոքր լինել -ից). այն նշանակենք
-ով.
ճիշտ նույնպես էլ նրանց միջև կգտնվի մի մաս, որը փոքր է -ից. այն նշանակենք
-ով.
և թվերը դրական են։ Երրորդ մասը, ակնհայտ է, որ հավասար կլինի
։
և թվերն ունեն միևնույն գումարը, ինչ որ թվի առաջին երկու մասերը, իսկ դրանց միջև տարբերությունը, այսինքն՝ -ը փոքր է, քան առաջին երկու մասերի միջև եղած տարբերությունը, որ հավասար է ։ Ինչպես նախորդ խնդրի լուծումից մենք գիտենք, այստեղից հետևում է, որ
արտադրյալը մեծ է, քան թվի առաջին երկու մասերի արտադրյալը։
Այսպիսով, եթե թվի առաջին երկու մասերը փոխարինենք
և
թվերով, իսկ երրորդը թողենք անփոփոխ, ապա արտադրյալը կմեծանա։
Դիցուք այժմ մասերից մեկն արդեն է։ Այդ ժամանակ մյուս երկուսը կունենանք հետևյալ տեսքը՝
և ։
Եթե մենք այդ վերջին երկու մասերը հավասարեցնենք -ի (որից դրանց գումարը չի փոխվի), ապա արտադրյալը նորից կմեծանա և կդառնա հավասար
։
Այսպիսով, եթե թիվը բաժանված է մասի, որոնք միմյանց հավասար չեն, ապա այդ մասերի արտադրյալը փոքր է, քան -ը, այսինքն՝ քան երեք հավասար արտադրիչների արտադրյալը, որոնց գումարը կազմում է ։
Միանգամայն նույն ձևով կարելի է ապացուցել այդ թեորեման թե՛ չորս արտադրիչների համար և թե՛ հինգի համար և այլն։
Այժմ դիտարկենք ավելի ընդհանուր դեպք։
Գտնել -ի և -ի ո՛ր արժեքների դեպքում արտահայտությունը կլինի ամենամեծը, եթե ։
Լուծում
Պետք է գտնել՝ -ի ո՛ր արժեքի դեպքում
արտահայտությունը հասնում է ամենամեծ արժեքի։ Այդ արտահայտությունը բազմապատկենք թվով։ Կստանանք նոր արտահայտություն՝
,
որը, ակներևաբար, հասնում է ամենամեծ մեծության միայն այն դեպքում, որ դեպքում՝ նախասկզբնականը։
Նոր ստացված արտահայտությունը ներկայացնենք հետևյալ տեսքով՝
Այս արտահայտության բոլոր արտադրիչների գումարը հավասար է
,
այսինքն՝ հաստատուն մեծության։
Հիմնվելով նախորդում ապացուցվածի վրա, եզրակացնում ենք, որ
արտադրյալը հասնում է մաքսիմումի նրա բոլոր արտադրիչների հավասարության դեպքում, այսինքն, երբ
։
Գիտենալով, որ և տեղափոխելով անդամները, կստանանք հետևյալ համեմատությունը՝
։
Այսպիսով, գումարի հաստատուն լինելու դեպքում հասնում է ամենամեծ մեծության այն ժամանակ, երբ
։
Նույն ձևով կարելի է ապացուցել, որ
և այլն
արտադրյալնևրը և այլն գումարների հաստատուն լինելու դեպքում հասնում են ամենամեծ մեծության այն դեպքում, երբ
և այլն։
ԳՈՒՄԱՐԸ Ե՞ՐԲ Է ԼԻՆՈՒՄ ԱՄԵՆԱՓՈՔՐԸ
Ընթերցողը, եթե ցանկանում է իր ուժերը փորձել ապացուցելու հանրահաշվական օգտավետ թեորեմաներ, թող ինքնուրույն ապացուցի հետևյալ դրույթները՝
1. Երկու թվերի գումարը, որոնց արտադրյալն անփոփոխ է, դառնում է ամենափոքր, երբ այդ թվերը հավասար են։
Օրինակ՝ արտադրյալի համար՝ և, վերջապես, ։
2. Մի քանի թվերի գումարը, որոնց արտադրյալն անփոփոխ է, դառնում է ամենափոքր, երբ այդ թվերը հավասար են։
Օրինակ՝ արտադրյալի համար մինչդեռ ։
Մի շարք օրինակներով ցույց տանք, թե այդ թեորեմաները գործնականում ինչպես են կիրառվում։
ԱՄԵՆԱՄԵԾ ԾԱՎԱԼԻ ՉՈՐՍՈՒ
Խնդիր
Գլանաձև գերանից պետք է սղոցել ամենամեծ ծավալի ուղղանկյուն չորսու։ Ինչպիսի՞ ձև կունենա նրա հատվածքը (նկ. 23)։
Լուծում
Եթե -ը և -ը ուղղանկյան հատվածքի կողմերն են, ապա ըստ Պյութագորի թեորեմայի
,
որտեղ -ն գերանի տրամագիծն է։ Չորսուի ծավալը ամենամեծն է, երբ նրա հատվածքի մակերեսը ամենամեծն է, այսինքն՝ երբ -ը հասնում է առավելագույն մեծության։ Բայց եթե -ն ամենամեծն է, ապա ամենամեծը կլինի նաև արտադրյալը։ Քանի որ գումարը անփոփոխ է, ապա վաղօրոք ապացուցածի համաձայն արտադրյալն ամենամեծը կլինի, երբ կամ ։
Այսպիսով, չորսուի հատվածքը պետք է լինի քառակուսի։
ԵՐԿՈՒ ՀՈՂԱՄԱՍ
Խնդիրներ
1. Ի՞նչ ձև պետք է ունենա տրված ուղղանկյուն հողամասի մակերեսը, որպեսզի նրան սահմանափակող ցանկապատի երկարությունը լինի ամենափոքրը։
2. Ի՞նչ ձև պետք է ունենա ուղղանկյուն հողամասը, որպեսզի ցանկապատի տրված երկարության դեպքում նրա մակերեսը լինի ամենամեծը։
Լուծումներ
1. Ուղղանկյուն հողամասի ձևը որոշվում է նրա և կողմերի առնչությամբ։ և կողմեր ունեցող հողամաղի
մակերեսը հավասար է , իսկ ցանկապատի երկարությունը՝ ։ Ցանկապատի երկարությունը կլինի ամենափոքրը, եթե -ը հասնում է ամենափոքր մեծության։
արտադրյալի հաստատուն լինելու դեպքում գումարը ամենափոքր կլինի դեպքում։ Հետևաբար՝ որոնելի ուղղանկյունը քառակուսի է։
2. Եթե -ը և -ը ուղղանկյան կողմերն են, ապա -ը ցանկապատի երկարությունն է, իսկ -ը՝ մակերեսը։ Այդ արտադրյալը կլինի ամենամեծը այն դեպքում, որ դեպքում արտադրյալը, այսինքն՝ -ը․ վերջին արտադրյալը իր արտադրիչների գումարի հաստատուն լինելու դեպքում դառնում է ամենամեծ, երբ , այսինքն՝ երբ հողամասն ունի քառակուսու ձև։
Հետևաբար՝ երկրաչափությունից մեզ հայտնի քառակուսու հատկություններին մենք կարող ենք ավելացնել ևս հետևյալները՝ տրված մակերեսի դեպքում բոլոր ուղղանկյուններից միայն քառակուսին կունենա ամենափոքր պարագիծը և տրված պարագծի դեպքում՝ ամենամեծ մակերեսը։
ՕԴԱՊԱՐՈՒԿ
Խնդիր
Օդապարուկին, որն ունի շրջանի սեկտորի տեսք, ցանկանում են տալ այնպիսի ձև, որպեսզի այն տվյալ պարագծում տեղավորի ամենամեծ մակերես։ Ինչպիսի՞ն պետք է լինի սեկտորի ձևը։
Լուծում
Ճշտելով խնդրի պահանջը, մենք պետք է որոնենք՝ սեկտորի աղեղի երկարության և նրա շառավղի ինչպիսի հարաբերության դեպքում նրա մակերեսը կհասնի առավելագույն մեծության տվյալ պարագծի դեպքում։
Եթե -ը սեկտորի շառավիղն է, իսկ -ը աղեղը, ապա նրա պարագիծը և մակերեսը կարտահայտվեն այսպես (նկ. 24)։
։
մեծությունը կհասնի մաքսիմումի -ի այն արժեքի դեպքում, ինչ արժեքի դեպքում՝ արտադրյալը, այսինքն՝ քառապատկված մակերեսը։ Քանի որ արտադրիչների գումարը հաստատուն մեծություն է, ապա դրանց արտադրյալը ամենամեծը կլինի, երբ , որտեղից
։
Այսպիսով, տրված պարագծով սեկտորը շրջափակում է ամենամեծ մակերես այն դեպքում, երբ նրա շառավիղը կազմում է աղեղի կեսը (այսինքն՝ նրա աղեղի երկարությունը հավասար է շառավիղների գումարին կամ նրա պարագծի կոր մասի երկարությունը հավասար է բեկյալի երկարությանը)։ Սեկտորի անկյունը հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \approx 115°} (երկու ռադիանի)։ Թե ինչպիսին են այդպիսի լայն օդապարուկի թռչելու կարողությունները, այլ հարց է, որի դիտարկումը չի մտնում մեր խնդրի մեջ։
ՏԱՆ ԿԱՌՈՒՑՈՒՄԸ
Խնդիր
Ավերված տան տեղում, որից անվնաս է մնացել մի պատը, ցանկանամ են կառուցել նորը։ Անվնաս մնացած պատի երկարությունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 12 \; մ} է։ Նոր բնակարանի մակերեսը պետք է հավասար լինի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 112 \; քառ. \; մ} ։ Աշխատանքի արդյունավետ պայմանները այսպիսին են՝
1) պատի գծային մետրի վերանորոգումը նստում է նոր շարվածքի արժեքի 25%-ը.
2) հին պատի մեկ գծամետրի քանդելը և ստացված նյութից նոր պատի շարելը արժե նոր նյութից կառուցվող պատի մեկ գծամետրի արժեքի 50%-ը։
Այդպիսի պայմաններում ինչպե՞ս ամենաշահավետ ձևով օգտագործել անվնաս մնացած պատը։
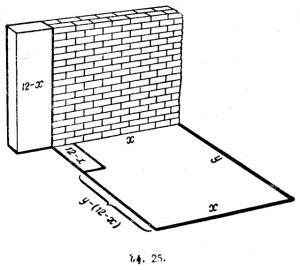
Լուծում
Դիցուք նախկին պատից պահպանվում է մետր, իսկ մնացած մետրը քանդում են, որպեսզի ստացված նյութից կրկին բարձրացնեն նոր տան պատի մասը (նկ. 25)։ Եթե նոր նյութից պատի շարվածքի մեկ գծամետրի արժեքը հավասար է , ապա հին պատի մետրի վերանորոգումը կարժենա երկարությամբ հատվածի բարձրացնելը՝ , այդ պատի մնացած մասինը՝ , այսինքն՝ . երրորդ պատինը՝ , չորրորդինը՝ ։ Ամբողջ աշխատանքը կարժենա
։
Վերջին արտահայտությունը հասնում է ամենափոքր մեծության այն դեպքում, որ դեպքում
գումարը։
Մենք գիտենք, որ տան մակերեսը հավասար է , հետևաբար՝
։
Հաստատուն արտադրյալի դեպքում գումարը հասնում է ամենափոքր մեծության այն ժամանակ, երբ
,
որտեղից՝
։
-ի փոխարեն տեղադրելով այս արտահայտությունը
հավասարման մեջ, կունենանք՝
։
Իսկ քանի որ հին պատի երկարությունը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 12 \; մ} է, ապա քանդման ենթակա է այդ պատի միայն մետրը։
ԱՄԱՌԱՆՈՑԱՅԻՆ ՏԵՂԱՄԱՍ
Խնդիր
Ամառանոց կառուցելիս հարկավոր էր ցանկապատել ամառանոցային տեղամասը։ Ցանկապատի համար կար գծամետր նյութ։ Բացի այդ, կարելի էր օգտվել ավելի վաղ կառուցված ցանկապատից (որպես տեղամասի կողմերից մեկը)։ Այդ պայմաններում ինչպե՞ս ցանկապատել ամենամեծ մակերեսի ուղղանկյուն տեղամասը։
Լուծում
Դիցուք տեղամասի երկարությունը (ցանկապատով) հավասար է -ի, իսկ լայնությունը (այսինքն՝ ցանկապատին ուղղահայաց ուղղությամբ տեղամասի չափսը) հավասար է -ի (նկ. 26)։ Այդ ժամանակ տվյալ տեղամասը ցանկապատելու համար հարկավոր է մետր ցանկապատ, այնպես որ
։
Տեղամասի մակերեսը հավասար է
։
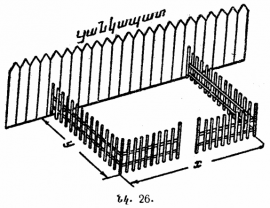
Սա ամենամեծ արժեք կընդունի
մեծության (մակերեսի կրկնապատիկի) հետ միաժամանակ, որն իրենից ներկայացնում է հաստատուն գումարով երկու արտադրիչների արտադրյալ։ Ուստի՝ ամենամեծ մակերեսի հասնելու համար պետք է տեղի ունենա
,
որտեղից
։
Այլ կերպ ասած, , այսինքն՝ տեղամասի երկարությունը պետք է նրա լայնությունից երկու անգամ մեծ լինի։
ԱՄԵՆԱՄԵԾ ՀԱՏՎԱԾՔԻ ՋՐՈՐԴԱՆ
Խնդիր
Մետաղյա ուղղանկյուն թերթը (նկ. 27) ջրորդանի համար պետք է ծռել հավասարակողմ սեղանի հատվածքի ձևով։ Ինչպես երևում է 28-րդ նկարից, այդ կարելի է անել տարբեր եղանակներով։ Ինչպիսի՞ լայնություններ պետք է ունենան կողմնային շերտերը և դրանք ի՞նչ անկյան տակ պետք է ծռված լինեն, որպեսզի ջրորդանի հատվածքն ամենամեծ մակերես ունենա (նկ. 29)։
Լուծում
Դիցուք թերթի լայնությունը է։ Կnղմնային շերտերի ծալաբացվածքների լայնությունը նշանակենք -ով, իսկ ջրորդանի հատակի լայնությունը՝ -ով։ Մտցնենք ևս մի անհայտ , որի նշանակությունը պարզ է 30-րդ նկարից։
Սեղանի մակերեսը, որ հանդիսանում է ջրորդանի հատվածքը, կլինի՝
։
Խնդիրը հանգեց -ի, -ի, -ի այն արժեքները որոշելուն, որոնց դեպքում -ը հասնում է առավելագույն մեծության. ընդ որում գումարը (այսինքն՝ թերթի լայնությունը) պահպանում է հաստատուն մեծությունը։ Կատարենք ձևափոխություններ՝
։
մեծությունը դառնում է ամենամեծ -ի, -ի, -ի այն արժեքների դեպքում, ինչ արժեքների դեպքում ամենամեծ է դառնում -ն, իսկ վերջինը կարելի է ներկայացնել հետևյալ արտադրյալի տեսքով՝
։
Այս չորս արտադրիչների գումարը հավասար է
,
այսինքն՝ անփոփոխ է։ Ուստի՝ մեր չորս արտադրիչների արտադրյալը ամենամեծն է, երբ դրանք միմյանց հավասար են, այսինքն՝
և ։
Առաջին հավասարումից կունենանք՝
,
իսկ քանի որ , ապա ։
Երկրորդ հավասարումից գտնում ենք
։
Այնուհետև, քանի որ էջը հավասար է ներքնաձիգի կեսին (նկ. 30), ապա այդ էջի դիմացի անկյունը հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 30°} , իսկ հիմքի նկատմամբ ջրորդանի կողմերի թեքության անկյունը հավասար է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 90°+30°= 120°} ։
Այսպիսով, ջրորդանը կունենա ամենամեծ հատվածք, երբ նրա նիստերը ծալված են կանոնավոր վեցանկյան երեք կից կողմերի ձևով։
ԱՄԵՆԱՄԵԾ ՏԱՐՈՂՈՒԹՅԱՆ ՁԱԳԱՐ
Խնդիր
Թիթեղյա շրջանից հարկավոր է պատրաստել ձագարի կոնական մասը։ Դրա համար շրջանից կտրում են սեկտոր և շրջանի մնացած մասը ծռում կոնաձև (նկ. 31)։ Քանի՞ աստիճան պետք է լինի կտրված սեկտորի աղեղը, որպեսզի կոնը ստացվի ամենամեծ տարողության։
Լուծում
Շրջանի այն մասի աղեղի երկարությունը, որը ծռվում է որպես կոն, նշանակենք -ով (գծային չափսերով)։ Հետևաբար՝ կոնի ծնորդը կլինի թիթեղյա շրջանի շառավիղը, իսկ հիմքի շրջանագիծը հավասար կլինի -ի։ Կոնի հիմքի շառավիղը որոշենք հետևյալ հավասարությունից՝
, որտեղից ։
Կոնի բարձրությունը (Պյութագորի թեորեմայով)
(նկ. 31)։ Այդ կոնի ծավալն ունի հետևյալ արժեքը՝
։
Այս արտահայտությունը հասնում է առավելագույն մեծության
արտահայտության և նրա քառակուսու՝
հետ միաժամանակ։ Քանի որ
մեծությունը հաստատուն է, ապա (նախօրոք ապացուցածի հիման վրա) վերջին արտադրյալը կունենա մաքսիմում -ի այն արժեքի դեպքում, երբ
,
որտեղից՝
,
[47]։
Աստիճաններով աղեղը հավասար կլինի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 295°} [48]. նշանակում է՝ կտրված սեկտորի աղեղը պետք է պարունակի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \approx 65°} ։
ԱՄԵՆԱՊԱՅԾԱՌ ԼՈՒՍԱՎՈՐՎԱԾՈՒԹՅՈՒՆԸ
Խնդիր
Սեղանից ի՞նչ բարձրության վրա պետք է գտնվի մոմի բոցը, որպեսզի սեղանի վրա եղած դրամը լուսավորվի ամենից պայծառ։
Լուծում
Թվում է, թե ամենալավ լուսավորվածության հասնելու համար բոցը պետք է ըստ հնարավորին ավելի ցածր տեղավորել։ Այդ սխալ է. ցածր դիրքում բոցի ճառագայթներն ընկնում են շատ թեք ձևով։ Մոմը բարձրացնել այնպես, որ ճառագայթներն ընկնեն շեշտակի՝ նշանակում է լույսի աղբյուրը հեռացնել։ Ակնհայտ է, որ լուսավորվածության տեսակետից ամենաձեռնտուն բոցի ինչ-որ միջին բարձրությունն է սեղանից։ Դա նշանակենք -ով (նկ. 32)։ բոցով անցնող ուղղահայացի հիմքից դրամի հեռավորությունը նշանակենք -ով։ Եթե -ն բոցի պայծառությունն է, ապա համաձայն օպտիկայի օրենքների, դրամի լուսավորվածությունը կարտահայտվի այսպես՝
,
որտեղ -ն ճառագայթների փնջի անկման անկյունն է։ Քանի որ
,
ապա լուսավորվածությունը հավասար է
։
Այս արտահայտությունը հասնում է մաքսիմումի -ի այն արժեքի դեպքում, որի դեպքում և նրա քառակուսին, այսինքն՝
։
Որպես հաստատուն մեծություն արտադրիչը բաց թողնենք, իսկ հետազոտվող արտահայտության մնացած մասը ձևափոխենք այսպես.
։
Ձևափոխված արտահայտությունը մաքսիմումի է հասնում
արտահայտության հետ միաժամանակ, քանի որ ներմուծված հաստատուն արտադրիչը չի ազդում -ի այն արժեքի վրա, որի դեպքում արտադրյալը հասնում է մաքսիմումի։ Նկատելով, որ այդ արտադրիչների առաջին աստիճանների գումարը հաստատուն մեծություն է՝
,
եզրակացնում ենք, որ դիտարկվող արտադրյալը դառնում է ամենամեծ, երբ
Կունենանք հետևյալ հավասարումը՝
։
Լուծելով այս հավասարումը, գտնում ենք`
։
Դրամը ամենից պայծառ կլուսավորվի, եթե լույսի աղբյուրը գտնվում է այնպիսի բարձրության վրա, որը հավասար է աղբյուրի պրոյեկցիայից մինչև դրամի հեռավորության մասին։ Այս հարաբերության գիտենալը օգնում է աշխատանքային տեղը ամենալավ ձևով լուսավորելու գործին։

ԳԼՈՒԽ ՈՒԹԵՐՈՐԴ։ ՊՐՈԳՐԵՍԻԱՆԵՐ
ՀՆԱԳՈՒՅՆ ՊՐՈԳՐԵՍԻԱ
Խնդիր
Պրոգրեսիայի վերաբերյալ հնագույն խնդիրը ոչ թե շախմատ հնարողի վարձատրության մասին եղած խնդիրն է, որն ունի երկու հազար տարվա հնություն, այլ հացը բաժանելու մասին խնդիրը, որը գրված է Ռինդի եգիպտական հռչակավոր մագաղաթում։ Այդ մագաղաթը, որ գտնված է Ռինդի կողմից անցյալ հարյուրամյակի վերջին, կազմված է մեր դարաշրջանից մոտ 200 տարի առաջ և հանդիսանում է մյուս՝ էլ ավելի հնագույն մաթեմատիկական աշխատության ձեռագիրը, որը հավանաբար վերաբերում է երրորդ հազարամյակին մինչ մեր դարաշրջանը։ Այդ փաստաթղթի թվաբանական, հանրահաշվական և երկրաչափական խնդիրների թվում կա այսպիսի խնդիր (բերենք այն ազատ թարգմանությամբ)։
Հարյուր հատ հացը բաժանել հինգ մարդկանց միջև այնպես, որ երկրորդը ստանա առաջինից այնքանով ավելի շատ որքան որ երրորդն է ստացել ավելի շատ երկրորդից, չորրորդը՝ ավելի շատ երրորդից և հինգերորդը՝ ավելի շատ չորրորդից։ Բացի այդ, առաջին երկուսը պետք է ստանան մնացած երեքից անգամ քիչ։
Որքա՞ն պետք է ստանա յուրաքանչյուրը։
Լուծում
Ակներևաբար, հացի քանակները, որ ստացել են մասնակիցները որպես բաժին, կազմում է աճող թվաբանական պրոգրեսիա։ Դիցուք նրա առաջին անդամը է, տարբերությունը ։ Այդ ժամանակ
| առաջինի | բաժինը | . . . . . . . . | |
| երկրորդի | » | . . . . . . . . | |
| երրորդի | » | . . . . . . . . | |
| չորրորդի | » | . . . . . . . . | |
| հինգերորդի | » | . . . . . . . . | ։ |
Խնդրի պայմանների հիման վրա կազմենք հետևյալ երկու հավասարումները՝
Պարզեցնելուց հետո առաջին հավասարումն ստանում է հետևյալ տեսքը՝
,
իսկ երկրորդը՝
։
Լուծելով այդ սիստեմը, կստանանք՝
։
Նշանակում է՝ հացը պետք է բաժանել հետևյալ մասերի՝
։
ՀԱՆՐԱՀԱՇԻՎԸ ՎԱՆԴԱԿԱՎՈՐ ԹՂԹԻ ՎՐԱ
Չնայած պրոգրեսիաների վերաբերյալ այդ խնդրի հինգհազարամյա հնությանը, մեր դպրոցական կյանքում պրոգրեսիաները հայտնվել են համեմատաբար ավելի ուշ։ Մագնիցկու դասագրքում, որը հրատարակվել է երկու հարյուր տարի առաջ և որը ամբողջ կես դար հանդիսացել է դպրոցական ուսուցման համար հիմնական ձեռնարկ, թեև պրոգրեսիաներ կան, բայց դրանց մեջ մտնող մեծությունները կապակցող ընդհանուր բանաձևեր գոյություն չունեն։ Դրա համար էլ ինքը՝ դասագրքի կազմողը առանց դժվարությունների չէ, որ հաղթահարել է այդպիսի խնդիրները։ Մինչդեռ թվաբանական պրոգրեսիայի անդամների գումարի բանաձևը հեշտորեն արտածվում է վանդակավոր թղթի օգնությամբ՝ պարզ և դիտորդական եղանակով։ Այդպիսի թղթի վրա ցանկացած թվաբանական պրոգրեսիան պատկերվում է աստիճանաձև։ Օրինակ՝ 33-րդ նկարում -ն պատկերում է հետևյալ պրոգրեսիան՝
։
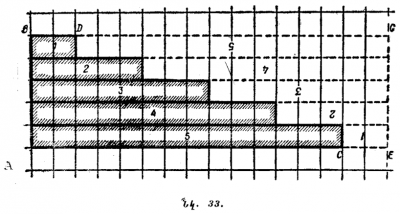
Նրա անդամների գումարը որոշելու համար գծագիրը լրացնենք մինչև ուղղանկյունը։ Կստանանք երկու հավասար պատկերներ և ։ Նրանցից յուրաքանչյուրի մակերեսը պատկերում է մեր պրոգրեսիայի անդամների գումարը։ Նշանակում է՝ պրոգրեսիայի կրկնակի գումարը հավասար է ուղղանկյան մակերեսին, ալսինքն՝
։
Բայց պատկերում է պրոգրեսիայի 1-ին և 5-րդ անդամների գումարը։ -ն պրոգրեսիայի անդամների թիվն է։ Ուստի՝ կրկնակի գումար
կամ
։
ԲԱՆՋԱՐԱՆՈՑԻ ՋՐԵԼԸ
Խնդիր
Բանջարանոցն ունի մարգ, յուրաքանչյուրը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 16 \; մ} երկարությամբ և Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2,5 \; մ} լայնությամբ։ Մարգերը ջրելիս բանջարանոցատերը ջրով լիքը դույլը բերում է ջրհորից, որը գտնվում է բանջարանոցից Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 14 \; մ} հեռավորության վրա (նկ․ 34), ընդ որում, անցնելով միջնակներով, մեկ անգամ բերված ջուրը բավականացնում է միայն մեկ մարգ ջրելու համար։
Ի՞նչ երկարության ճանապարհ պետք է անցնի բանջարանոցատերը ամբողջ բանջարանոցը ջրելիս։ Ճանապարհը սկսվում և վերջանում է ջրհորի մոտ։
Լուծում
Առաջին մարգը ջրելու համար բանջարանոցատերը պետք է անցնի հետևյալ ճանապարհը՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 14+16+2,5+16+2,5+14=65 \; մ} ։
Երկրորդը ջրելիս նա կանցնի՝
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 14+2,5+16+2,5+16+2,5+2,5+14=65+5=70 \; մ} ։
Յուրաքանչյուր հաջորդ մարգը նախորդից պահանջում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 5 \; մ} -ով երկար ճանապարհ։
Կունենանք հետևյալ պրոգրեսիան՝
։
Նրա անդամների գումարը հավասար է
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \frac{(65+65+5 \cdot 29)30}{2} \;=\; 4125 \; մ} ։
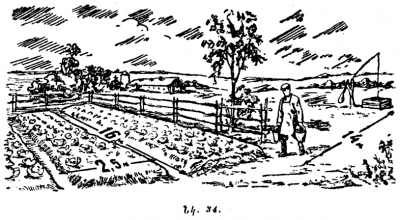
Ամբողջ բանջարանոցը ջրելիս բանջարանոցատերը կանցնի Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 4,125 \; կմ} ճանապարհ։
ՀԱՎԵՐԻՆ ԿԵՐԱԿՐԵԼԸ
Խնդիր
հավի համար պատրաստված էր որոշ քանակությամբ կեր՝ հաշվելով, որ յուրաքանչյուր հավին շաբաթական պետք է մեկական դեկալիտր։ Ընդ որում ենթադրվում էր, որ հավերի թիվը չի փոխվի։ Բայց քանի որ իրականում հավերի թիվը յուրաքանչյուր շաբաթում -ով պակասում էր, դրա համար էլ պատրաստված կերը բավարարեց կրկնակի ժամկետի։
Ինչքա՞ն էր կերի պաշարը և սկզբում որքա՞ն ժամանակի համար էր այն նախատեսված։
Լուծում
Դիցուք պատրաստված էր դեկալիտր կեր շաբաթվա համար։ Քանի որ կերը հաշված էր հավի համար՝ մեկ շաբաթում -ական դեկալիտր մեկ հավին, ապա
։
Առաջին շաբաթում կծախսվեր Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 31 \; դլ} , երկրորդում՝ , երրորդում՝ և այլն, մինչև կրկնակի ժամանակի վերջին շաբաթը, երբ կծախսվեր
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle (31-2y+1) \; դլ} ։[49]
Հետևաբար՝ ամբողջ պաշարը կազմել է
։
Պրոգրեսիայի անդամների գումարը, որի առաջին անդամը է, իսկ վերջինը՝ , հավասար է
։
Քանի որ -ը զրոյի հավասար լինել չի կարող, ապա մենք կարող ենք հավասարության երկու մասերն էլ կրճատել այդ արտադրիչով։ Կստանանք՝
և ,
որտեղից
։
Պատրաստված էր դեկալիտր կեր շաբաթվա համար։
ՀՈՂ ՓՈՐՈՂՆԵՐԻ ԱՐՏԵԼԸ
Խնդիր
Հող փորողների արտելը պարտավորվեց առու փորել։ Եթե նա աշխատեր լրիվ կազմով, առուն կփորվեր ժամում։
Բայց իրականում աշխատանքն սկզբից սկսեց միայն մեկ հողափոր։ Որոշ ժամանակ հետո միացավ երկրորդը. նույնքան ժամանակից հետո՝ դարձյալ երրորդը. այնուհետև միևնույն ժամանակամիջոցից հետո՝ չորրորդը և այդպես մինչև վերջինը։ Վերջում պարզվեց, որ առաջինը անգամ ավելի է աշխատել վերջինից։
Որքա՞ն ժամանակ աշխատեց վերջին հողափորը։

Լուծում
Դիցուք վերջին հողափորը աշխատել է ժամ, այդ ժամանակ առաջինը աշխատել է ժամ։ Այնուհետև, եթե արտելի անդամների թիվը է, ապա աշխատանքի ժամերի ընդհանուր թիվը որոշվում է որպես նվազող պրոգրեսիայի անդամների գումար, որի առաջին անդամը է, իսկ վերջինը՝ , այսինքն՝
։
Մյուս կողմից, հայտնի է, որ մարդուց բաղկացած արտելը, աշխատելով լրիվ կազմով, առուն կփորեր ժամում, այսինքն աշխատանքը կատարելու համար անհրաժեշտ է աշխատանքային ժամ։ Հետևաբար՝
։
թիվը չի կարող հավասարվել զրոյի, ուստի այդ արտադրիչով հավասարումը կարելի է կրճատել, որից հետո կստանանք՝
և ։
Այսպիսով, աշխատանքն սկսող վերջին հողափորը աշխատել է ժամ։
Մենք պատասխանեցինք խնդրի հարցին. բայց եթե մենք հետաքրքրվեինք իմանալ, թե քանի բանվոր կար արտելում, ապա չէինք կարող այդ որոշել, չնայած նրան, որ հավասարման մեջ այդ թիվը մասնակցել է ( տառով)։ Այդ հարցը լուծելու համար խնդրում անհրաժեշտ տվյալները բերված չեն։
ԽՆՁՈՐՆԵՐԸ
Խնդիր
Այգեպանը առաջին գնորդին վաճառեց իր ունեցած խնձորների կեսը և էլի կես խնձոր, երկրորդ գնորդին՝ մնացածի կեսը և դարձյալ կես խնձոր, երրորդին՝ մնացածի կեսը և էլի կես խնձոր և այլն։ Յոթերորդ գնորդին նա վաճառեց մնացած խնձորների կեսը և դարձյալ կես խնձոր. դրանից հետո նրա մոտ խնձոր չմնաց։ Քանի՞ խնձոր ուներ այգեպանը։
Լուծում
Եթե խնձորների սկզբնական թիվը է, ապա առաջին գնորդը ստացել է
,
երկրորդը՝
,
երրորդը՝
,
ութերորդ գնորդը՝
։
Կունենանք հետևյալ հավասարումը՝
կամ
Հաշվելով փակագծերում եղած երկրաչափական պրոգրեսիայի անդամների գումարը, գտնում ենք՝
և ։
Խնձորների թիվը էր։
ՁԻ ԳՆԵԼԸ
Խնդիր
Մագնիցկու հինավուրց թվաբանության մեջ մենք գտնում ենք հետևյալ զվարճալի խնդիրը, որը բերում ենք այստեղ չպահպանելով բնագրի լեզուն։

Մի մարդ ձին վաճառեց ռուբլով։ Բայց գնորդը միտքը փոխեց և ձին վերադարձրեց վաճառողին, ասելով՝
— Ինձ ձեռնտու չէ այդ գնով ձի գնելը, նա այդքան չարժե։
Այդ ժամանակ վաճառողը առաջարկեց այլ պայման՝
— Եթե ըստ քեզ ձիու գինը բարձր է, ապա գնիր միայն նրա պայտամեխերը, իսկ ձին այդ ժամանակ կստանաս անվճար՝ որպես վերադիր։ Յուրաքանչյուր պայտին խփված է մեխ։ Առաջին մեխի համար ինձ տուր ընդամենը կոպ., երկրորդի համար՝ կոպ., երրորդի համար՝ կոպ., և այլն։
Գնորդը, հրապուրվելով ցածր գնով և ցանկանալով ձին ստանալ ձրի՝ ընդունեց վաճառողի պայմանը, հաշվելով, որ մեխերի համար երևի կվճարի ոչ ավելի քան ռուբլի։ Որքանո՞վ սակարկեց գնորդը։
Լուծում
պայտամեխերի համար պետք է վճարել
կոպեկ։ Այդ գումարը հավասար է
կոպ.,
այսինքն՝ մոտ հազար ռուբլի։ Այդպիսի պայմանների դեպքում ցավ չէ, որ ձին տրվեր որպես վերադիր։
ՌԱԶՄԻԿԻ ՎԱՐՁԱՏՐՈՒՄԸ
Խնդիր
Մաթեմատիկայի ռուսական մի այլ հինավուրց դասագրքից, որ կրում է «Զուտ մաթեմատիկայի լրիվ դասնթաց, որը կազմվել է հրետանու Շտիկ-Յունկեր և մաթեմատիկայի մսանավոր ուսուցիչ Եֆիմ Վոյտյախովսկու կողմից՝ ի օգուտ և գործածության պատանիների ու մաթեմատիկայի մեջ վարժվողների» (1795) ընդարձակ վերնագիրը, այստեղ բերենք հետևյալ խնդիրը.
«Ռազմիկին տրվել է վարձատրություն՝ առաջին վերքի համար կոպեկ, երկրորդի համար՝ կոպեկ, երրորդի համար՝ կոպեկ և այլն։ Հաշվարկումից պարզվեց, որ ռազմիկը ստացել է ընդամենը ռուբ. կոպ. վարձատրություն։ Պահանջվում է իմանալ նրա վերքերի թիվը»։
Լուծում
Կազմենք հավասարում՝
կամ
,
որտեղից կունենանք՝
և
արդյունքը, որը հեշտությամբ գտնում ենք փորձելու ճանապարհով։
Վարձատրության այդպիսի մեծահոգի սիստեմի դեպքում ռազմիկը պետք է ստանար վերք և մնար կենդանի, որպեսզի արժանանար ռուբ. կոպ. պարգևի։

ԳԼՈՒԽ ԻՆՆԵՐՈՐԴ։ ՄԱԹԵՄԱՏԻԿԱԿԱՆ ՅՈԹԵՐՈՐԴ ԳՈՐԾՈՂՈՒԹՅՈՒՆ
ՅՈԹԵՐՈՐԴ ԳՈՐԾՈՂՈՒԹՅՈՒՆԸ
Մենք արդեն հիշատակեցինք, որ հինգերորդ գործողությունը՝ աստիճան բարձրացնելիս ունի երկու հակադարձ գործողություններ։ Եթե
,
ապա -ի գտնելը մի հակադարձ գործողություն է՝ արմատ հանել, իսկ -ի գտնելը մյուսը, լոգարիթմել։ Ենթադրում եմ, որ այս գրքի ընթերցողը ծանոթ է լոգարիթմների մասին ուսմունքի հիմունքներին դպրոցական դասընթացի ծավալով։ Հավանաբար, նրա համար դժվար չէ ըմբռնել, օրինակ, այսպիսի արտահայտությունը՝
։
Դվար չէ հասկանալ, որ եթե լոգարիթմի հիմքը բարձրացնենք թվի լոգարիթմի աստիճան, ապա կստացվի այդ թիվը։
Ինչի՞ համար են հնարված լոգարիթմները։ Իհարկե, հաշվումները արագացնելու և պարզեցնելու համար։ Առաջին լոգարիթմական աղյուսակների հնարող Նեպերը իր մտահղացումների մասին այսպես է ասում՝
«Որքան կարողացա ես աշխատեցի հրաժարվել հաշվումների դժվարություններից և ձանձրույթից, որոնց տաղտկալիությունը սովորաբար շատ շատերին վախեցնում է մաթեմատիկան ուսումնասիրելիս»։
Իրոք, լոգարիթմները արտակարգ հեշտացնում և արագացնում են հաշվումները, չխոսելով դեռ այն մասին, որ դրանք հնարավորություն են տալիս կատարել այնպիսի օպերացիաներ, որոնց կատարելն առանց նրանց օգնության՝ շատ դժվար է (ցանկացած աստիճանի արմատ հանելը)։
Անհիմն չէ, որ Լապլասը գրել է. «Լոգարիթմների գյուտը, հաշվումների մի քանի ամիսների աշխատանքը կրճատելով-հասցնելով մի քանի օրերի՝ գրեթե աստղագետների կյանքը կրկնապատկում է»։
Մեծ մաթեմատիկոսը խոսում է աստղագետների մասին, քանի որ հատկապես նրանց է հարկ լինում կատարել բարդ և հոգնեցուցիչ հաշվումներ։ Բայց նրա խոսքերը ամենայն իրավամբ կարելի է վերագրել ընդհանրապես բոլոր նրանց, ովքեր գործ ունեն թվային հաշվումների հետ։
Վարժվելով լոգարիթմների գործածությանը և դրանց միջոցով հաշվումների հեշտացմանը՝ մեզ համար դժվար է պատկերացնել այն զարմանքը և հիացմունքը, որ առաջացրել են դրանք՝ իրենց հայտնվելու ժամանակ։ Նեպերի ժամանակակից Բրիգը, հետագայում փառաբանվելով տասնորդական լոգարիթմների գյուտով, Նեպերի երկերն ստանալիս գրել է. «Նեպերն իր նոր զարմանալի լոգարիթմներով ստիպեց ինձ ջերմեռանդորեն աշխատել և՛ գլխով, և՛ ոտքերով։ Ես հույս ունեմ ամռանը նրան տեսնել, քանի որ երբեք չեմ կարդացել այնպիսի գիրք, որը ինձ ավելի դուր գար և մեծ հիացմունք պատճառեր»։ Բրիգը իրագործեց իր ցանկությունը և ուղևորվեց Շոտլանդիա, որպեսզի այցելի լոգարիթմների գյուտարարին։ Նրան հանդիպելիս Բրիգն ասաց՝
«Ես ձեռնարկեցի այս երկար ճանապարհորդությունը մի նպատակով՝ տեսնել ձեզ և իմանալ, թե ինչ արվեստի և սրամիտ զենքի օգնությամբ դուք եկաք այդ մտքին՝ աստղագիտության համար զարմանալի ձեռնարկին՝ լոգարիթմներին։ Սակայն այժմ ես ավելի եմ զարմանում, թե ինչո՞ւ ոչ մեկը առաջուց չի գտել, քանի որ դրանց հետ ծանոթանալուց հետո դրանք թվում են չափազանց պարզ»։
ԼՈԳԱՐԻԹՄՆԵՐԻ ՄՐՑԱԿԻՑՆԵՐԸ
Մինչ լոգարիթմների գյուտը, հաշվումների արագացման պահանջը ծնեց ուրույն տեսակի աղյուսակներ, որոնց օգնությամբ բազմապատկման գործողությունը փոխարինվում էր ոչ թե գումարումով, այլ հանումով։
Այդ աղյուսակների կառուցվածքը հիմնված է
նույնության վրա, որի ճշտության մեջ հեշտությամբ կարելի է համոզվել, եթե բացենք փակագծերը։
Ունենալով քառակուսիների պատրաստի քառորդները՝ կարելի է գտնել երկու թվերի արտադրյալը, չկատարելով բազմապատկումներ, այլ հանելով այդ թվերի գումարի քառակուսու քառորդից դրանց տարբերության քառակուսու քառորդը։ Այդ նույն աղյուսակները հեշտացնում են քառակուսի բարձրացնելը և քառակուսի արմատ հանելը, իսկ աղյուսակներին միացնելով հակադարձ թվերը՝ պարզեցնում են նաև բաժանման գործողությունը։ Լոգարիթմական աղյուսակների նկատմամբ դրանց առավելությունն այն է, որ դրանց օգնությամբ արդյունքներն ստացվում են ճիշտ, և ոչ թե մոտավոր։ Բայց դրանք զիջում են լոգարիթմականին գործնականորեն անհամեմատ ավելի կարևոր մի շարք կետերում։ Այն ժամանակ, երբ քառակուսիների քառորդների աղյուսակները թույլ են տալիս բազմապատկել միայն երկու թվեր, լոգարիթմները հնարավորություն են տալիս միանգամից գտնել ցանկացած թվով արտադրիչների արտադրյալը և, բացի այդ, բարձրացնել ցանկացած աստիճանը և ցանկացած ցուցիչով արմատ հանելը (ամբողջ կամ կոտորակային)։ Օրինակ՝ քառակուսիների քառորդների աղյուսակների օգնությամբ բարդ տոկոսներ գումարել չի կարելի։
Բայց և այնպես, քառակուսիների քառորդների աղյուսակները հրատարակվեցին և այն ժամանակ, երբ հայտնվեցին զանազան լոգարիթմական աղյուսակներ։
1856 թվականին Ֆրանսիայում լույս տեսան հետևյալ վերնագրով աղյուսակները՝
«Թվերի քառակուսիների աղյուսակ -ից մինչև միլիոն, որի օգնությամբ գտնվում են թվերի ճշգրիտ արտադրյալը շատ պարզ եղանակով, ավելի հարմար, քան լոգարիթմների օգնությամբ։ Կազմեց Ալեքսանդր Կոսսարը»։
Այս գաղափարն առաջանում է շատերի մոտ՝ չկասկածելով, որ այն վաղուց արդեն իրականացված է։
Նման աղյուսակների գյուտարարները մի երկու անգամ դիմել են ինձ և շատ են զարմացել իմանալով, որ այդ աղյուսակների գյուտը ավելի քան 300 տարվա պատմություն ունի։
Լոգարիթմների մյուս՝ ավելի երիտասարդ մրցակիցները հանդիսանում են հաշվիչ աղյուսակները, որոնք զետեղված են տեխնիկական բազմաթիվ տեղեկատուներում։ Դրանք տեղեկատու աղյուսակներ են, որոնք պարունակում են հետևյալ բաժինները՝ թվերի քառակուսիները, խորանարդները, քառակուսի արմատները, խորանարդ արմատները, հակադարձ թվերը շրջանագծի երկարությունները և շրջանների մակերեսները -ից մինչև թվերի համար։ Տեխնիկական բազմաթիվ հաշվարկների համար այդ աղյուսակները շատ հարմար են, սակայն դրանք ոչ միշտ են բավարար։ Լոգարիթմական աղյուսակներն անհամեմատ ավելի ընդարձակ կիրառություններ ունեն։
ԼՈԳԱՐԻԹՄԱԿԱՆ ԱՂՅՈՒՍԱԿՆԵՐԻ ԷՎՈԼՅՈՒՑԻԱՆ
Մեր դպրոցներում դեռ վերջերս գործածվում էին լոգարիթմական -անիշ աղյուսակները։ Այժմ դրանք վերածվել են քառանիշի, քանի որ լիովին բավարար են տեխնիկական հաշվարկների համար։ Բայց մեծ մասամբ գործնական պահանջների համար կարելի է հաջողությամբ ղեկավարվել անգամ եռանիշ մանտիսներով, չէ՞ որ առօրյա չափումները հազվադեպ է, որ կատարվում են երեքից ավելի նիշերով։
Ավելի կարճ մանտիսների բավարար լինելու միտքը համեմատաբար վերջերս է ըմբռնվել։ Դեռ հիշում եմ, երբ մեր դպրոցներում գործածվում էին -անիշ լոգարիթմների ծանր կշռով հատորները, որոնք իրենց տեղը զիջել են -անիշներին, միայն համառ պայքարից հետո։ Բայց -անիշ լոգարիթմներն էլ իրենց հայտնվելու դեպքում (1794) թվում էին անթույլատրելի նորամուծություն։
Առաջին տասնորդական լոգարիթմները, որ ստեղծվել են լոնդոնցի մաթեմատիկոս Հենրի Բրիգի աշխատանքով (1624), եղել են -անիշ։ Մի քանի տարի անց, դրանց փոխարինեցին հոլանդական մաթեմատիկոս Անդրիանա Վլակի -անիշ աղյուսակները։
Ինչպես տեսնում ենք, լոգարիթմական գործող աղյուսակների էվոլյուցիան բազմանիշ մանտիսներից ավելի կարճերին անցավ և այլևս չկատարելագործվեց մեր օրերում, քանի որ այժմ էլ շատերը չեն գիտակցել այն պարզ ճշմարտությունը, որ հաշվումների ճշտությունը չի կարող գերազանցել չափումների ճշտությանը։
Մանտիսների կարճացնելը ծնում է գործնական երկու կարևոր հետևանքներ՝ 1) աղյուսակների ծավալի նկատելի փոքրացումը և 2) դրա հետ կապված նրանցից օգտվելու պարզեցումը, իսկ դա նշանակում է դրանց օգնությամբ կատարվող հաշվումների արագացումը։ Թվերի յոթանիշ աղյուսակներն զբաղեցնում են մոտ 200 էջ մեծ չափսերով, -անիշները՝ երկու անգամ փոքր չափսերի 30 էջ, քառանիշներն զբաղեցնում են տասնապատիկ փոքր ծավալ, որը տեղավորվում է մեծ չափսերի երկու էջի վրա, իսկ եռանիշները կարող են տեղավորվել մեկ էջի վրա։
Ինչ վերաբերում է հաշվումների արագությանը, ապա հայտնի է, որ, օրինակ, հնգանիշ աղյուսակներով հաշվարկներ կատարելը պահանջում է երեք անգամ քիչ ժամանակ, քան յոթանիշով։
ԼՈԳԱՐԻԹՄԱԿԱՆ ՏԱՐՕՐԻՆԱԿՈՒԹՅՈՒՆՆԵՐ
Եթե տեխնիկական առօրյայի և գործնական կյանքի հաշվողական պահանջները լրիվ ապահովվում են եռանիշ և քառանիշ աղյուսակներով, ապա, մյուս կողմից, տեսական հետազոտողի տրամադրության տակ կան և այնպիսի աղյուսակներ, որ ունեն ավելի շատ նիշեր, քան նույնիսկ Բրիգի -անիշ լոգարիթմները։ Ընդհանրապես ասած, լոգարիթմը մեծ մասամբ իռացիոնալ թիվ է և թվանշանների ոչ մի քանակով չի կարելի ճշտորեն արտահայտել։ Մեծ մասամբ թվերի լոգարիթմները, որքան էլ նիշեր վերցնելու լինենք, արտահայտվում են միայն մոտավոր կերպով և որքան դրանց մանտիսներում թվանշանները շատ են, այնքան դրանք ճիշտ են։
Գիտական աշխատանքների համար -անիշ լոգարիթմները[50] երբեմն ճիշտ չեն, բայց տարբեր տեսակի 300 լոգարիթմական աղյուսակներից, որոնք լույս են տեսել դրանց հայտնագործումից հետո, հետազոտողը միշտ կարող է գտնել այնպիսիները, որոնք կարող են նրան բավարարել։ Նշենք, օրինակ, -ից մինչև թվերի -անիշ լոգարիթմները, որ հրատարակվել է Ֆրանսիայի Կալլե (1795) քաղաքում։ Ավելի սահմանափակ թվերի խմբերի համար կան նաև վիթխարի թվով տասնորդական նիշերով լոգարիթմների աղյուսակներ՝ լոգարիթմական իսկական տարօրինակություններ, որոնց գոյության մասին, ինչպես ես համոզվել եմ, չեն կասկածում նաև բազմաթիվ մաթեմատիկոսներ։
Ահա այդ լոգարիթմ-հսկաները, դրանք բոլորը տասնորդական չեն, այլ բնական[51]։
Վոլֆրամի -անիշ աղյուսակները մինչև թվերի համար։
Շարպի -անիշ աղյուսակները։
Պարկխերստի -անիշ աղյուսակները և, վերջապես, լոգարիթմական գերտարօրինակությունը՝
Ադամսի -անիշ լոգարիթմները։
Վերջին դեպքում մենք ունենք, ի միջի այլոց, ոչ թե աղյուսակ, այլ միայն այսպես կոչված հինգ թվերի բնական լոգարիթմներ՝ և , և փոխանցող (-անիշ) արտադրիչ դրանք տասնորդականի վերածելու համար։ Սակայն, դժվար չէ հասկանալ, որ ունենալով այդ հինգ թվերի լոգարիթմները՝ պարզ գումարով կամ բազմապատկումով կարելի է ստանալ բարդ թվերի բազմության լոգարիթմները. օրինակ -ի լոգարիթմը հավասար է և թվերի լոգարիթմների գումարին և այլն։
Լրիվ կերպով կարելի է լոգարիթմական տարօրինակության շարքը դասել նաև հաշվեքանոնը, այդ «փայտե լոգարիթմները», եթե միայն շնորհիվ իր հարմարության այդ սրամիտ գործիքը չդառնար տեխնիկների համար այդքան սովորական հաշվող գործիք, ինչպես համրիչը գրասենյակային աշխատողների համար։ Սովորության հետևանքով մարում է հիացմունքի զգացումը լոգարիթմի սկզբունքով աշխատող սարքի առջև, մի սարք, որն իրենից օգտվողից չի պահանջում նույնիսկ գիտենալ, թե ինչ բան է լոգարիթմը։
ԼՈԳԱՐԻԹՄՆԵՐԸ ԷՍՏՐԱԴԱՅՈՒՄ
Հասարակության առջև պրոֆեսիոնալ հաշվողների կողմից կատարված ամենաապշեցուցիչ համարներից են, անկասկած, հետևյալները. աֆիշայի միջոցով նախօրոք տեղեկանալով, որ վիրտուոզ հաշվողը բազմանիշ թվերից մտքով բարձր աստիճանի արմատ կհանի, դուք տանը համբերությամբ նախապատրաստում եք որևէ թվի -րդ աստիճանի հաշվարկը նպատակ ունենալով դիտավորյալ հարվածել հաշվողին -անիշ թվային լինկորով։ Պատշաճ պահին դուք դիմում եք հաշվողին՝ հետևյալ խոսքերով.
— Իսկ փորձեցեք -րդ աստիճանի արմատ հանել հետևյալ -անիշ թվից։ Գրեցե՛ք, ես թելադրում եմ։
Վիրտուոզ-հաշվողը վերցնում է կավիճը, բայց մինչև դուք բացում եք ձեր բերանը, որպեսզի արտասանեք առաջին թվանշանը, նա արդեն դրում է արդյունքը՝ ։
Չիմանալով թիվը, նա այդ թվից արմատ է հանում, նույնիսկ -րդ աստիճանի, անգամ մտքով, կայծակնայի՛ն արագությամբ։
Դուք զարմացած եք, ընկճված, մինչդեռ այդ բոլորի մեջ գերբնական ոչինչ չկա։ Գաղտնիքը ուղղակի նրանումն է, որ գոյություն ունի միայն մեկ թիվ, այն է՝ -ը, որը -րդ աստիճանում տալիս է -անիշ արդյունք։ -ից փոքր թվերը տալիս են թվանշանից փոքր, մեծերը մեծ։

Սակայն հաշվողը որտեղի՞ց իմացավ այդ։ Նա ինչպե՞ս գտավ թիվը։ Նրան օգնեցին լոգարիթմները, երկանիշ լոգարիթմները, որոնց նա հիշում է անգիր, առաջին թվերի համար։ Դրանց անգիր անելը այնքան էլ դժվար չէ, ինչպես թվում է, հատկապես, եթե գիտենանք, որ բարդ թվի լոգարիթմը հավասար է նրա պարզ արտադրիչների լոգարիթմների գումարին, հաստատորեն իմանալով -ի, -ի և [52]-ի լոգարիթմները, դուք արդեն գիտեք առաջին տասնյակի թվերի լոգարիթմները. երկրորդ տասնյակի համար պահանջվում է հիշել ևս չորս թվերի լոգարիթմները։
Ինչպես էլ որ լինի, էստրադային հաշվողը մտքով դասավորում է երկանիշ լոգարիթմների հետևյալ փոքրիկ աղյուսակը
| Թվեր | Լոգարիթմներ | Թվեր | Լոգարիթմներ |
Ձեզ զարմացնող մաթեմատիկական տրյուկը կայանում է հետևյալում.
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle lg \sqrt[31]{(35 \; թվանշան)} \;=\; \frac{34,\dots}{31}} ։
Որոնելի լոգարիթմը կարող է գտնվել
և միջև կամ և միջև։
Այդ ինտերվալում կա միայն մեկ ամբողջ թվի լոգարիթմ, այն է՝ -ի լոգարիթմը՝ ։ Այդ ճանապարհով էլ գտնված է ձեզ շշմեցնող արդյունքը։ Իհարկե, այդ բոլորը մտքով արագ կատարելու համար պետք է տիրապետել մասնագետի հնարամտությանը և հմտությանը, բայց ըստ էության, ինչպես տեսնում ենք, դա բավականին պարզ է։ Այժմ դուք ինքներդ էլ կարող եք կատարել նման ֆոկուսներ, եթե ոչ մտքով, գոնե թղթի վրա։
Դիցուք ձեզ առաջարկված է խնդիր՝ -րդ աստիճանի արմատ հանել -անիշ թվից։
Չտեղեկանալով այն մասին, թե դա ինչ թիվ է, դուք կարող եք արմատ հանելու արդյունքը հայտարարել արմատը հավասար է -ի։
Իրոք, Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle lg \sqrt[64]{(20 \; թվանշան)} \;=\; \frac{19,\dots}{64}} , հետևաբար այն պետք է գտնվի և միջև, այսինքն՝ և միջև։ Այդպիսի լոգարիթմը ամբողջ թվի համար միայն մեկն է՝ այսինքն՝ թվի լոգարիթմը։
Դուք անգամ կարող եք վերջնականապես հաղթել հաշվողին, նրան հայտնելով, թե նա ինչպիսի թիվ էր ուզում ձեզ թելադրել. հռչակավոր շախմատային թիվը՝
։
ԼՈԳԱՐԻԹՄՆԵՐԸ ԱՆԱՍՆԱՆՈՑՈՒՄ
Խնդիր
Այսպես կոչված «պահպանման» կերի քանակը (այսինքն կերի այն ամենափոքր քանակը, որը միայն լրացնում է օրգանիզմի ծախսերը ջերմության, ներքին օրգանների աշխատանքի, մեռնող բջիջների վերականգնման համար և այլն)[53] համեմատական է անասունի մարմնի արտաքին մակերևույթին։ Իմանալով այդ, որոշեցեք պահպանող կերի կալորիականությունը այն եզան համար, որո կշռում է Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 420 \; կգ} , եթե նույն պայմանների դեպքում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 630 \; կգ} կշռով եզը կարիք ունի կալորիայի։
Լուծում
Անասնապահության բնագավառից այդ գործնական խնդիրը լուծելու համար բացի հանրահաշվից հարկավոր է դիմել երկրաչափությանը։
Համաձայն խնդրի պայմանի որոնելի կալորիականությունը համեմատական է եզան մակերևույթին (), այսինքն՝
,
որտեղ -ը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 630 \; կգ} կշիռ ունեցող եզան մարմնի մակերևույթն է։ Երկրաչափությունից մենք գիտենք, որ նման մարմինների մակերևույթները () հարաբերում են, ինչպես նրանց գծային չափերի () քառակուսիները իսկ ծավալները՝ (և, հետևաբար, կշիռները), ինչպես գծային չափերի խորանարդները։ Ուստի՝
և, նշանակում է՝ ,
որտեղից
,
Լոգարիթմական աղյուսակների օգնությամբ գտնում ենք՝
։
Եզը կարիք ունի կալորիայի։
ԼՈԳԱՐԻԹՄՆԵՐԸ ԵՐԱԺՇՏՈՒԹՅԱՆ ՄԵՋ
Երաժիշտները հազվադեպ են հրապուրվում մաթեմատիկայով. նրանց մեծամասնությունը դեպի այդ գիտությունը հարգանք տածելով, գերադասում է նրանից շատ հեռու կանգնել։ Այնինչ երաժիշտները, նույնիսկ նրանք, ովքեր չեն ստուգում «հարմոնիան հանրահաշվով», ինչպես Պուշկինի մոտ Սալերին, մաթեմատիկայի հետ շփվում են ավելի հաճախ, քան ենթադրում են իրենք, ընդսմին այնպիսի ահեղ բաների հետ, ինչպիսին են լոգարիթմները։
Հարկ եմ համարում այդ առթիվ մեր հանգուցյալ ֆիզիկոս Ա. Էյխենվալդի[54] հոդվածից բերել մի հատված.
Իմ գիմնազիստ ընկերը սիրում էր դաշնամուր նվագել, բայց մաթեմատիկա չէր սիրում։ Նա նույնիսկ արհամարհանքով ասում էր, որ երաժշտությունը և մաթեմատիկան միմյանց հետ ընդհանուր ոչինչ չունեն։
«Ճիշտ է, Պյութագորը ձայնական տատանումների միջև գտավ ինչ-որ հարաբերություններ,— բայց չէ՞ որ հենց պյութագորյան գամման մեր երաժշտության համար ոչ կիրառելի եղավ»։
Երևակայեցեք, թե ինչպես իմ ընկերոջը տհաճ զարմանք պատճառեց այն, երբ ես նրան ապացուցեցի, որ նվագելով ժամանակակից դաշնամուրի ստեղների վրա, նա նվագում է, ճիշտն ասած, լոգարիթմների վրա... Եվ իրոք, այսպես կոչված տեմպերացված քրոմատիկ (ելևէջային) գամմաների աստիճանները դասավորված չեն հավասար հեռավորությամբ ո՛չ տատանումների թվերի նկատմամբ և ո՛չ էլ համապատասխան ձայնի ալիքների երկարության նկատմամբ, այլ իրենցից ներկայացնում են այդ մեծությունների լոգարիթմները։ Միայն այդ լոգարիթմների հիմքը հավասար է -ի, և ոչ թե -ի, ինչպես ընդունված է մյուս դեպքում։
Ենթադրենք, որ ամենացածր օկտավայի do նոտան (նրան կանվանենք զրո օկտավա) սահմանված է վայրկյանում տատանումներով։ Այդ ժամանակ առաջին օկտավայի do-ն վայրկյանում կանի տատանումներ, իսկ -րդ օկտավան՝ տատանումներ և այլն։ Դաշնամուրի խրոմատիկ գամմայի բոլոր նոտաները նշանակենք համարներով, յուրաքանչյուր օկտավայի do տոնը ընդունելով որպես զրո. այդ ժամանակ, օրինակ, sol տոնը կլինի -րդ, la-ն կլինի -րդ և այլն. -րդ տոնը նորից կլինի do միայն թե մի օկտավայով բարձր։ Քանի որ տեմպերացված քրոմատիկ գամմայի յուրաքանչյուր հետագա տոնը ունի անգամ ավելի մեծ տատանումներ[55], քան նախորդը, ապա ցանկացած տոնի տատանումների թիվը կարելի է արտահայտել հետևյալ բանաձևով՝
։
Լոգարիթմելով այս բանաձևը, կստանանք՝
կամ
,
իսկ do-ի ամենացածր տատանումների թիվն ընդունելով մեկ () և բոլոր լոգարիթմները փոխադրելով հիմքի (կամ պարզապես ընդունելով ), կունենանք՝
։
Այստեղից տեսնում ենք, որ դաշնամուրի ստեղների համարները իրենցից ներկայացնում են համապատասխան ձայների տատանումների թվի լոգարիթմներ[56]։
Մենք անգամ կարող ենք ասել, որ օկտավայի համարը իրենից ներկայացնում է այդ լոգարիթմի խարակտերիստիկան, իսկ տվյալ օկտավայում[57] ձայնի համարը՝ մանտիսան։
Օրինակ՝ պարզաբանում ենք, որ երրորդ օկտավի sol տոնում, այսինքն՝ թվի մեջ, թիվը այդ տոնի տատանումների թվի լոգարիթմի խարակտերիստիկան է, իսկ -ը նույն լոգարիթմի մանտիսան հիմքի դեպքում. տատանումների թիվը, հետևաբար, , այսինքն՝ անգամ մեծ է առաջին օկտավայի do տոնի տատանումների թվից։
ԱՍՏՂԵՐԸ, ԱՂՄՈՒԿԸ ԵՎ ԼՈԳԱՐԻԹՄՆԵՐԸ
Այս վերնագիրը, որ միացնում է այդքան, թվում է, միմյանց չմիացվոց առարկաներ, հավակնություն չունի լինել Կուզմա Պրուտկովի ստեղծագործության պարոդիան։ Իրականում խոսքը գնում է աստղերի և աղմուկի մասին՝ լոգարիթմների հետ սերտորեն կապված։
Աղմուկը և աստղերը այստեղ միացվում են նրա համար, որ թե՛ աղմուկի բարձր լինելը, և թե՛ աստղերի պայծառությունը գնահատվում են միատեսակ ձևով՝ ըստ լոգարիթմական սանդղակի։
Աստղագետները աստղերը բաժանում են ըստ նրանց տեսողության պայծառության աստիճանների՝ առաջին մեծության, երկրորդ մեծության, երրորդ մեծության լուսատուների և այլն։ Աստղերի հաջորդական մեծություններն աչքով ընկալվում են որպես թվաբանական պրոգրեսիայի անդամներ։ Բայց դրանց ֆիզիկական պայծառությունը փոփոխվում է այլ օրենքով՝ իրական պայծառությունները կազմում են քանորդով երկրաչափական պրոգրեսիա։ Հեշտ է հասկանալ, որ աստղի «մեծությունը» իրենից ներկայացնում է ոչ այլ ինչ, քան նրա ֆիզիկական պայծառության լոգարիթմը։ Օրինակ՝ երրորդ մեծության աստղը առաջին մեծության աստղից պայծառ է , այսինքն՝ անգամ։ Կարճ ասած, գնահատելով աստղերի տեսանելի պայծառությունը, աստղագետը հենվում է լոգարիթմների աղյուսակի վրա, որոնք կազմված են հիմքի համար։ Այստեղ մանրամասնորեն կանգ չենք առնի այդ հետաքրքրական առնչությունների վրա, քանի որ իմ մյուս՝ „Занимательная астрономия” գրքում դրանց հատկացվել է բավականին էջեր։
Համանման ձևով գնահատվում է նաև աղմուկի բարձրությունը։ Բանվորների առողջության և աշխատանքի արտադրողականության վրա արդյունաբերական աղմուկների վնասակար ազդեցությունը հարկադրել է մշակել աղմուկի բարձրության գնահատման թվային ճիշտ եղանակներ։ Բարձրության միավոր է հանդիսանում «բելը», գործնականում նրա տասներորդական մասը՝ «դեցիբելը»։ Բարձրության հաջորդական աստիճաններն են՝ բել, բել և այլն (գործնականում՝ դեցիբել, դեցիբել և այլն), որոնք մեր լսողության համար կազմում են թվաբանական պրոգրեսիա։ Այդ աղմուկների ֆիզիկական «ուժը» (ճշտորեն՝ էներգիան) կազմում է քանորդով երկրաչափական պրոգրեսիա։ Բարձրությունների բել տարբերությանը համապատասխանում է աղմուկների ուժերի -ի հարաբերությունը։ Նշանակում է՝ աղմուկի բարձրությունը (արտահայտած բելերով) հավասար է նրա ֆիզիկական ուժի տասնորդական լոգարիթմին։
Հարցը պարզ է դառնում, եթե դիտարկենք մի քանի օրինակներ։
Տերևների սոսափյունը գնահատվում է բել, բարձր խոսակցությունը՝ բել, առյուծի մռնչյունը՝ բել։ Այստեղից հետևում է, որ, ըստ ձայնի ուժի խոսակցությունը տերևների սոսափյունին գերազանցում է
անգամ.
առյուծի մռնչյունը բարձր խոսակցությունից ուժեղ է
անգամ։
Այն աղմուկը, որի բարձրությունը մեծ է բելից, մարդկային օրգանիզմի համար ճանաչվում է վնասակար։ Շատ գործարաններում օրենքով սահմանված նորման գերազանցվում է։ Այստեղ պատահում են և ավելի բել աղմուկներ. մուրճի հարվածները, որ հասցվում են պողպատյա սալին, առաջացնում են բել աղմուկ։ Այդ աղմուկները և </math>1000</math> անգամ ուժեղ են թույլատրելի նորմայից և Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10—100} անգամ ավելի բարձր Նիագարայի ջրվեժի ամենաաղմկոտ տեղից ( բել)։
Պատահականությո՞ւն է արդյոք այն, որ լուսատուների տեսանելի պայծառությունը գնահատելիս և աղմուկի բարձրությունը չափելիս մենք գործ ունենք զգայության մեծության և այն առաջացնող գրգիռների միջև եղած լոգարիթմական կախվածության հետ։ Ոչ, և՛ մեկը, և՛ մյուսը հանդիսանում են ընդհանուր օրենքի հետևանք «Ֆեխների պսիխոֆիզիկական օրենք», որը պնդում է, թե զգայության մեծությունը համեմատական է գրգռման մեծության լոգարիթմին։
Ինչպես տեսնում ենք, լոգարիթմները թափանցում են նաև հոգեբանության բնագավառը։
ԼՈԳԱՐԻԹՄՆԵՐԸ ԷԼԵԿՏՐԱԼՈՒՍԱՎՈՐՈՒԹՅԱՆ ՄԵՋ
Խնդիր
Այն բանի պատճառը, որ գազով լցված (հաճախ սխալմամբ անվանելով «կիսավատտային», լամպերն ավելի պայծառ լույս են տալիս, քան միևնույն նյութից պատրաստված մետաղյա լարով դատարկ լամպերը, թագնված է շիկացման լարի տարբեր ջերմաստիճանի մեջ։ Ֆիզիկայում սահմանված օրենքի համաձայն լույսի ընդհանուր քանակը, որ տարածվում է սպիտակ շիկացման դեպքում, աճում է բացարձակ ջերմաստիճանի -րդ աստիճանին համեմատ։ Իմանալով այդ, կատարենք այսպիսի հաշվարկ. որոշենք, թե «կիսավատտային» լամպը, որի շիկացման լարի ջերմաստիճանը բացարձակ սանդղակում (այսինքն՝ հաշվելով Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle -273°C} -ից) Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2500°} է, քանի՞ անգամ ավելի շատ լույս է արտածում, քան դատարկ լամպը, որի լարի շիկացումը մինչև Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2200°} է։
Լուծում
Նշանակելով որոնելի հարաբերությունը -ով, կունենանք հետևյալ հավասարումը՝
, որտեղից
։
Գազով լցված լամպի լույսը անգամ ավելի շատ է, քան թե դատարկինը։ Նշանակում է, եթե դատարկը տալիս է մոմի լույս, ապա նույն պայմանների դեպքում գազով լցվածը կտա մոմի լույս։
Կատարենք ևս մի հաշվարկ. բացարձակ ջերմաստիճանի ինչպիսի՞ բարձրացում է անհրաժեշտ (տոկոսներով) լամպի պայծառությունը կրկնապատկելու համար։
Լուծում
Կազմենք հավասարում՝
,
որտեղից՝
և ։
Վերջապես, երրորդ հաշվարկը. որքանո՞վ է (տոկոսներով) աճում լամպի պայծառությունը, եթե նրա լարի ջերմաստիճանը (բացարձակ) բարձրացվում է 1%-ով։
Լուծում
Լոգարիթմների օգնությամբ կատարելով
հաշվարկը, գտնում ենք՝
։
Պայծառությունը աճում է 13%-ով։
Կատարելով հաշվարկ ջերմաստիճանը 2%-ով բարձրացնելու համար, կգտնենք, որ պայծառությունը մեծանում է 27%-ով, իսկ ջերմաստիճանը 3%-ով բարձրացնելիս պայծառությունը մեծանում է 43%-ով։
Այստեղից պարզ է, թե ինչու տեխնիկայում էլեկտրալամպեր պատրաստելիս այդպես մտահոգվում են շիկացման լարի ջերմաստիճանը բարձրացնելու մասին, խնայելով յուրաքանչյուր ավելորդ աստիճան։
ԿՏԱԿ ՀԱՐՅՈՒՐ ՏԱՐՈՎ
Ո՞վ չի լսել ցորենի հատիկների այն առասպելական թվի մասին, որը, իբր թե, շախմատի խաղի գյուտարարը պահանջել է որպես պարգև։ Այդ թիվը կազմվել է մեկը հաջորդաբար կրկնապատկելու ճանապարհով, շախմատային տախտակի առաջին դաշտի համար գյուտարարը պահանջել է հատիկ, երկրորդի համար՝ հատիկ և այլն, կրկնապատկելով բոլորը՝ մինչև, վերջին -րդը։
Սակայն թվերն անսպասելի սրընթացությամբ աճում են ոչ միայն հաջորդական կրկնապատկման դեպքում, այլև՝ անհամեմատ ավելի չափավոր մեծացման դեպքում։
5% բերող կապիտալը տարեկան մեծանում է անգամ։ Կարծես թե այնքան շատ նկատելի չէ աճելը։ Մինչդեռ բավական ժամանակ անցնելուց հետո կապիտալը աճում և դառնում է վիթխարի գումար։ Դրանով էլ բացատրվում է կապիտալի ապշեցնող աճը, որը կտակված է շատ երկար ժամանակով։ Թվում է տարօրինակ, որ թողնելով բավականին համեստ գումար, կտակողը կարգադրություն է անում վիթխարի կապիտալի վճարման մասին։ Հայտնի է ամերիկյան պետական հռչակավոր գործիչ Վենյամին Ֆրանկլինի կտակը: Այն հրապարակվել է «Վենյամին Ֆրանկլինի տարբեր երկերի ժողովածուում»։ Ահա նրանից մի քաղվածք՝
«Հանձնում եմ հազար ֆունտ ստերլինգ Բոստոնի բնակիչներին։ Եթե նրանք ընդունեն այդ հազար ֆունտը, ապա այն պետք է հանձնել ամենաընտիր քաղաքացիներին, իսկ նրանք այդ փողը վարկով կտան երիտասարդ արհեստավորներին[58] տարին հարյուրին տոկոսով։ Այդ գումարը հարյուր տարի հետո կաճի մինչև ֆունտ ստերլինգի։ Ես ցանկանում եմ, որպեսզի այն ժամանակ ֆունտը ծախսվի հասարակական շենքերի կառույցի վրա, իսկ մնացած ֆունտը արվի տոկոսով՝ տարով։ Երկրորդ հարյուրամյակն անցնելուց հետո գումարը կաճի մինչև ֆունտ ստերլինգի, որից ֆունտը թողնում եմ Բոստոնի բնակիչների տնօրինությանը, իսկ -ը՝ Մասսաչուզետի համայնքի վարչությանը։ Այնուհետև չեմ համարձակվում տարածել իմ տեսակետը»։
Թողնելով ընդամենը ֆունտ, Ֆրանկլինը բաժանել է միլիոններ։ Այստեղ չկա, սակայն, ոչ մի թյուրիմացություն։ Մաթեմատիկական հաշվարկը հաստատում է, որ կտակողի խորհրդածումները լիովին ռեալ են։ ֆունտը յուրաքանչյուր տարի աճելով անգամ, տարուց հետո պետք է դառնա
ֆունտ։
Այս արտահայտությունը կարելի է հաշվել լոգարիթմների օգնությամբ՝
,
որտեղից
,
որ համապատասխանում է տեքստում եղած կտակին։ Այնուհետև, ֆունտը հաջորդ հարյուրամյակի ընթացքում դառնում է
,
որտեղից, հաշվելով լոգարիթմների օգնությամբ գտնում ենք՝
գումարը, որը էապես քիչ է տարբերվում կտակում ցույց տրվածից։
Ներկայացնում եմ ընթերցողին ինքնուրույնաբար լուծելու հետևյալ խնդիրը, որը վերցված է Սալտիկովի „Господа Головлевы”-ից.[59] «Պորֆիրի Վլադիմիրովիչը նստած էր իր կաբինետում և նիշեր գրելով՝ սպառում էր թղթի թերթերը։ Այս անգամ նրան զբաղեցնում էր մի հարց. այժմ նա ինչքա՞ն փող կունենար, եթե իր ռուբլին, որ նվիրել էր պապիկը նրան իր ծնված օրը «ատամների համար», մայրը չսեփականացներ, այլ դներ լոմբարդ փոքրիկ Պորֆիրիկի անունով։ Սակայն ստացվում էր ոչ շատ՝ ընդամենը ռուբլի»։
Ենթադրելով, որ հաշիվներ անելու ժամանակ Պորֆիրին տարեկան էր և ընդունելով, որ նա հաշվումները կատարել է ճիշտ (ենթադրությունը քիչ հավանական է, քանի որ դժվար թե Գոլովլյովը գիտեր լոգարիթմները և բարդ տոկոսները), պահանջվում է որոշել, թե այն ժամանակ լոմբարդը քանի տոկոս էր վճարում։
ԿԱՊԻՏԱԼԻ ԱՆԸՆԴՀԱՏ ԱՃԸ
Խնայդրամարկղներում տոկոսային փողերն ամեն տարի միացվում են հիմնական կապիտալին։ Եթե միացումը կատարվում է ավելի հաճախ, ապա կապիտալն աճում է ավելի արագ, քանի որ տոկոսների գոյացմանը մասնակցում է մեծ թվով գումար։ Վերցնենք միանգամայն տեսական, խիստ պարզեցված օրինակ։ Դիցուք, խնայդրամարկղում դրված է ռուբլի՝ տարեկան 100%-ով։ Եթե տոկոսային փողերը հիմնական կապիտալին միացվեն միայն տարին լրանալուց հետո՝ ապա այդ ժամկետին ռուբ. վերածվում է ռուբլու։ Այժմ տեսնենք, թե ռուբլին ինչքա՞ն է դառնում, եթե տոկոսային փողերը հիմնական կապիտալին միացնենք յուրաքանչյուր կես տարին մեկ։ Կես տարին անցնելուց հետո ռուբլին կդառնա
ռուբ. ռուբ.
և դարձյալ կես տարի հետո՝
ռուբ. ռուբ.։
Եթե միացումը կատարենք յուրաքանչյուր տարին մեկ, ապա տարին անցնելուց հետո ռուբ. կվերածվի
ռուբ. ռուբ. կոպ.-ի։
Ավելի հաճախակի դարձնենք տոկոսային փողերի միացման ժամկետները՝ մինչև տարի և այլն։ Այդ ժամանակ մեկ տարի հետո ռուբլուց կստացվի՝
| ռուբ. | ռուբ. կոպ. |
| ռուբ. | ռուբ. կոպ. |
| ռուբ. | ռուբ. կոպ. |
Բարձրագույն մաթեմատիկայի մեթոդներով ապացուցվում է, որ միացման ժամկետների անսահման կրճատման դեպքում աճող կապիտալը չի աճում անսահմանորեն, այլ մոտենում է որոշ սահմանի, որը մոտավորապես[60] հավասար է
ռուբ. կոպ.։
100%-ով դրված կապիտալը -ից ավել մեծանալ չի կարող, եթե անգամ աճող տոկոսները կապիտալին միացվեն յուրաքանչյուր վայրկյանում։
„” ԹԻՎԸ
Ստացված թիվը, որը բարձրագույն մաթեմատիկայի մեջ վիթխարի դեր է խաղում, ոչ ավելի պակաս, քան հռչակավոր թիվը, ունի հատուկ նշանակում՝ ։ Սա իռացիոնալ թիվ է. այն չի կարող թվանշանների վերջավոր թվով ճշտորեն արտահայտվել[61], բայց հաշվվում է միայն մոտավորությամբ, ճշտության ցանկացած աստիճանով, հետևյալ շարքի միջոցով՝
Բարդ տոկոսներով կապիտալի աճի վերը բերված օրինակից հեշտ է նկատել, որ թիվը
արտահայտության սահմանն է -ի անսահմանորեն աճելու դեպքում։
Շատ պատճառներով, որոնք մենք այստեղ շարադրել չենք կարող, թիվը նպատակահարմար է ընդունել որպես լոգարիթմների սիստեմի հիմք։ Այդպիսի աղյուսակները («բնական լոգարիթմների») գոյություն ունեն և լայն կիրառություն են գտնում գիտության և տեխնիկայի մեջ։ և թվանշաններով այն լոգարիթմ-հսկաները, որոնց մասին մենք խոսել ենք ավելի վաղ, հատկապես ունեն հիմքը։
թիվը հաճախ հայտնվում է այնտեղ, որտեղ նրան ընդհանրապես չեն սպասում։ Դնենք, օրինակ, այսպիսի խնդիր։
Ի՞նչ մասերի պետք է բաժանել տրված թիվը, որպեսզի բոլոր մասերի արտադրյալը լինի ամենամեծը։
Մենք արդեն դիտենք, որ հաստատուն գումարի դեպքում թվերն ամենամեծ արտադրյալը տալիս են այն դեպքում, երբ դրանք միմյանց հավասար են։ Պարզ է, որ թիվը պետք է բաժանել հավասար մասերի։ Բայց քանի՞ հավասար մասի։ Երկուսի՞, երեքի՞, տասի՞։ Բարձրագույն մաթեմատիկայի եղանակներով կարելի է որոշել, որ ամենամեծ արտադրյալն ստացվում է, երբ մասերը ըստ հնարավորին մոտ են թվին։
Օրինակ, -ը պետք է բաժանել այնպիսի թվով հավասար մասերի, որպեսզի մասերն ըստ հնարավորին մոտ լինեն -ին։ Դրա համար պետք է գտնել հետևյալ քանորդը՝
Քանի որ թիվը հավասար մասերի վրա բաժանել չի կարելի[62], ապա հարկ է լինում բաժանարարը վերցնել նրան ամենամոտ ամբողջ թիվը՝ -ը։ Հետևաբար, -ի մասերի ամենամեծ արտադրյալը, մենք կստանանք, եթե այդ մասերը հավասար են , այսինքն՝ ։
Նշանակում է
ամենամեծ թիվն է, որը կարող է ստացվել -ի միատեսակ մասերի բազմապատկումից։ Իրոք, -ը բաժանելով կամ հավասար մասերի՝ մենք կստանանք փոքր արտադրյալ
։
թվի մասերի ամենամեծ արտադրյալն ստանալու համար այն պետք է բաժանել հավասար մասերի, քանի որ
։
թիվը պետք է բաժանել մասի, իսկ -ը՝ , քանի որ
,
։
թիվը վիթխարի դեր է խաղում մաթեմատիկայի, ֆիզիկայի, աստղագիտության և մյուս գիտությունների մեջ։ Ահա մի քանի հարցեր, որոնք մաթեմատիկորեն դիտարկելու դեպքում հարկ է լինում օգտվել այդ թվից (ցանկը կարելի էր մեծացնել անսահմանափակ կերպով).
Բարոմետրական բանաձև (ճնշման փոքրանալը բարձրության հետ միասին),
Էյլերի բանաձևը[63],
Մարմինների սառելու օրենքը,
Ռադիոակտիվ տրոհումը և Երկրի տարիքը,
ճոճանակի տատանվելը օդում,
Ցիոլկովսկու բանաձևը հրթիռի արագության համար[64],
Տատանողական երևույթները ռադիոկոնտուրում,
Բջիջների աճելը։
ԼՈԳԱՐԻԹՄԱԿԱՆ ԿՈՄԵԴԻԱ
Խնդիր
Որպես լրացում մաթեմատիկական այն կոմեդիաների, որոնց ընթերցողը ծանոթացավ 5-րդ գլխում, բերենք նույն տեսքի ևս մի նմուշ, այն է՝ անհավասարության «ապացույցը»։ Այս անգամ ապացույցին մասնակցում է լոգարիթմումը։ «Կոմեդիան» սկսվում է
անհավասարությունով, որը անվիճելիորեն ճիշտ է։ Այնուհետև հետևում է ձևափոխությունը՝
,
որը նույնպես կասկած չի ներշնչում։ Մեծ թվին համապատասխանում է մեծ լոգարիթմ, նշանակում է՝
։
-ով կրճատելուց հետո կունենանք՝ ։ Ինչո՞մն է այդ ապացուցման սխալը։
Լուծում
Սխալը նրանումն է, որ -ով կրճատելու դեպքում անհավասարության նշանը չփոխվեց (-ը -ով) այն ժամանակ անհրաժեշտ էր այդ անել, քանի որ թիվը բացասական է։ [Իսկ եթե մենք լոգարիթմենք ոչ թե հիմքով, այլ -ից փոքր հիմքով, ապա -ը կլիներ դրական թիվ, բայց մենք այն ժամանակ իրավացի չէինք լինի պնդելու, որ մեծ թվին համապատասխանում է մեծ լոգարիթմ]։
ՑԱՆԿԱՑԱԾ ԹԻՎ՝ ԵՐԵՔ ԵՐԿՈՒՍՆԵՐՈՎ
Խնդիր
Գիրքն ավարտենք հանրահաշվական սրամիտ գլուխկոտրուկով, որով զվարճացել են ֆիզիկոսների մի համագումարի մասնակիցները Օդեսայում։ Առաջարկվում է հետևյալ խնդիրը՝ ցանկացած ամբողջ և դրական տրված թիվը պատկերել երեք երկուսներով և մաթեմատիկական սիմվոլներով։
Լուծում
Ցույց տանք, թե նախ ինչպես է խնդիրը լուծվում պատահական օրինակով։ Դիցուք -ը տրված թիվն է։ Այդ դեպքում խնդիրը լուծվում է այսպես՝
։
Այս հավասարության ճշտության մեջ հեշտ է համոզվել։
Իրոք՝
։
Իսկ եթե տված լիներ թիվը, մենք խնդիրը կլուծեինք նույն օրինակով՝
։
Ինչպես տեսնում ենք, մենք այստեղ օգտվում ենք այն բանից, որ քառակուսի արմատի դեպքում արմատի ցուցիչը չի գրվում։
Խնդրի ընդհանուր լուծումը այսպես է։ Եթե տրված թիվը է, ապա
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle N \;=\; -lg_2lg_2 \underbrace{\sqrt{\sqrt{ \dots \sqrt{\sqrt{2}}}}}_{N անգամ}} ,
ընդ որում արմատների թիվը հավասար է տրված թվի միավորների քանակին։
<references>
- ↑ Գրքում վրիպակ է՝ 4036։— Մ.։
- ↑ Այդ մասին մանրամասն տե՛ս իմ գրքում՝ „Занимательная механика”, գլուխ 9։
- ↑ Տե՛ս իմ գիրքը „Живая математика”, գլ. 7։
- ↑ Գոյություն ունեն շախմատային «տակտիկայի» և այլ տեսակներ։ Այսպես, օրինակ, հաշվումներում կարելի է դիտարկել հակառակորդի ոչ բոլոր հնարավոր պատասխան խաղաքայլերր, այլ միայն «ուժեղ» խաղաքայլերր (շախը, վերցնելը, հարձակումը, պաշտպանությունը և այլն)։ Այնուհետև, հակառակորդի հատուկ ուժեղ խաղաքայլերի դեպքում կարելի է անել հաշվումներ ոչ թե երեք, այլ վաղօրոք ավելի թվով խաղաքայլեր։ Կարելի է նույնպես օգտագործել ֆիգուրների արժեքի այլ սանդղակ։ Նայած այս կամ այն տակտիկայի ընտրության, փոխվում է մեքենայի «խաղի ոճը»։
- ↑ Շախմատային խաղի լավագույն վարպետների պարտիաներում հանդիպում են կոմբինացիաներ, որոնք հաշվարկված են 10 և ավելի խաղաքայլ առաջ։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Տասնավորների թվանշանը դեր չի խաղա։
- ↑ Այդ համեմատությունից թույլատրելի է օգտվել միայն այն դեպքում, երբ թիթեղատուփերի պատերը չափազանց հաստ չեն (քանի որ թիթեղատուփերի արտաքին և ներքին մակերևույթները, խիստ ասած, նման չեն և, բացի այդ, բանկայի ներքին խոռոչի բարձրությունը, խիստ ասած, տարբերվում է բանկայի բարձրությունից։
- ↑ Գրքում վրիպակ է՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 0,94 կգ} ։— Մ.։
- ↑ Գրքում վրիպակ է՝ 11։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Նկատենք, որ թվանշանների երկանիշ խումբը կարող է գտնվել վերևում արված դատողություններին համանման դատողությունների միջոցով. բավական է հարցը լուծենք այն մասին, թև ինչպիսի թվանշան պետք է կցագրել թվանշանի առջևից, որպեսզի ստացված թվանշանների երկանիշ խմբերն ունենան դիտարկվող հատկությունը։ Ուստի՝ «թիվը» կարելի է ստանալ՝ վեցի առջևից իրար հաջորդող թվանշաններ կցագրելու միջոցով։
- ↑ Անվերջ «թվեր» կարելի է դիտարկել ոչ միայն տասնորդական, այլև թվարկության ուրիշ սիստեմներում։ Այդպիսի թվերը, որոնք դիտարկվում են հիմքով թվարկության սիստեմում, կոչվում են -ական թվեր։ Այդ թվերի մասին որոշ բան կարելի է կարդալ Ե. Բ. Դինկինի և Վ. Ա. Ուսպենսկու, „Математические беседы” գրքում (Гостехиздат, 1952)։
- ↑ Եթե թիվը ունենար կենտ թվով թվանշաններ, ապա վերջին (ամենաձախ) խումբը կլիներ միանիշ, բացի այդ, տեսքի խումբը նույնպես պետք է դիտարկել որպես միանիշ թիվ՝ ։
- ↑ Վերջինս այն պատճառով, որ
։ - ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Ներկայումս (առ 2017 թ․ օգոստոսի 13-ը) ամենամեծ հայտնի պարզ թիվը Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 2^{74 \; 207 \; 281} − 1} է, որն ունի թվանշան։— Մ.։
- ↑ Գրքում վրիպակ է՝ հավանականության։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ — Մ.։
- ↑ Գրքում վրիպակ է՝ — Մ.։
- ↑ Այնուհետև մենք կօգտվենք հետևյալ մոտավոր հավասարությունից
։ - ↑ Խիստ ասած, մենք ապացուցեցինք միայն այն, որ հավասարման ամեն մի ամբողջ թվով լուծում ունի տեսքը, որտեղ -ը որևէ ամբողջ թիվ է։ Հակադարձը (այսինքն՝ այն, որ ցանկացած ամբողջի դեպքում մենք կստանանք մեզ տրված հավասարման մի քանի ամբողջ թվով լուծում) չի ապացուցվել։ Սակայն դրանում հեշտությամբ կարելի է համոզվել՝ տանելով հակադարձ կարգով դատողություններ կամ -ի և -ի գտնված արժեքները տեղադրելով սկզբնական հավասարման մեջ։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Ուշադրություն դարձրեք այն բանին, որ -ի դեպքում գործակիցները հավասար են սկզբնական հավասարման -ի և -ի գործակիցներին, ընդ որում -ի գործակիցներից մեկի մոտ նշանը հակառակ է։ Այդ պատահականություն չէ, կարելի է ապացուցել, որ միշտ այդպես կարող է լինել, եթե -ի և -ի գործակիցները փոխադարձ պարզ են։
- ↑ Գները թողնված են հին մասշտաբի՝ խնդիրների տվյալները պահպանելու համար։ Թարգմ. խմբ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 3k[(a^2α+b^3β+c^2γ+d^2δ)+ k(aα^2+bβ^2+cγ^2+dδ^2)] \;=\; 0} ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Ֆերմայի թեորեմն ապացուցել է Անդրյու Ուայլսը (Andrew Wiles) 1995 թ.։— Մ.։
- ↑ Ֆերման (1603—1660) մասնագետ-մաթեմատիկոս չէր։ Կրթությամբ իրավաբան, պառլամենտի խորհրդատու, նա զբաղվել է մաթեմատիկական հետազոտումներով միայն աշխատանքի ժամանակ։ Այդ նրան չխանգարեց անել արտակարգ կարևոր հայտնագործումներ, որոնք նա, այնուամենայնիվ, չհրապարակեց և ըստ իր դարաշրջանի սովորության, նամակներով իրազեկ դարձրեց իր գիտնական բարեկամներին՝ Պասկալին, Դեկարտին, Հյուգենսին, Ռոբերվալին և մյուսներին։
- ↑ Բարդ ցուցիչների համար (բացի -ից) հատուկ ապացույցներ չեն պահանջվում՝ այդ դեպքերը հանգում են պարզ ցուցիչներով դեպքերի։
- ↑ Մագնիցկու մաթեմատիկայի դասագրքում, որով մեզ մոտ սովորել են 18-րդ դարի ամբողջ առաջին կեսի ընթացքում, բոլորովին էլ չկա հատուկ նշան արմատ հանելու գործողության համար։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Հավասարումից երևում է, որ գրքում վրիպակ է։ Պետք է լինի՝ ընկերուհու։ Մ․։
- ↑ Գրքում վրիպակ է՝ -ն ոչ թե հավասար Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 9,8 \; մ} , այլ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 10 \; մ} ։— Մ.։
- ↑ Լուսնային թռիչքների նախագծերի մանրամասնությունների վրա մենք այստեղ, իհարկե, կանգ առնել չենք կարող։ Այդ պրոբլեմով հետաքրքրվողները կարող են նրա շարադրանքը և նրա հետ կապված մաթեմատիկական հարցերի վերլուծությունը գտնել իմ «Միջմոլորակային ճանապարհորդություններ» գրքում, 9-րդ հրատ., 1934 թ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Պետք է նկատի ունենալ, որ , քանի որ
։ - ↑ Գրքում վրիպակ է՝ ։— Մ.։
- ↑ Գրքում վրիպակ է՝ Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 235°} ։— Մ.։
- ↑ Պարզաբանենք կերի ծախսը՝
1-ին շաբաթում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 31 \; դլ} , 2-րդ » Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 31-1 \; դլ} , 3-րդ » Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 31-2 \; դլ} , . . . . . . . . . . . . . . . . . . . . . 2y-րդ » Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle 31-(2y-1) \; =\; 31-2y+1 \; դլ} ։ - ↑ Բրիգի -անիշ լոգարիթմները կազմված են, ի միջի այլոց, միայն -ից մինչև և -ից մինչև թվերի համար։
- ↑ Բնական կոչվում են այն լոգարիթմները, որոնք ոչ թե հիմքով են, այլ հիմքով, որի մասին դեռ խոսելու ենք։
- ↑ Հիշենք, որ ։
- ↑ Ի տարբերություն «մթերատու» կերից, այսինքն՝ կերի այն մասից, որը ծախսվում է անասնային մթերք ստանալու վրա։
- ↑ Այն տպվել է „Pyсский астрономический календарь”-ում 1919 թ. և վերնագրված է „О больших и малых расстояниях”.
- ↑ Գրքում վրիպակ է՝ -ից ավելի մեծ տատանումներ— Մ.։
- ↑ Բազմապատկում -ով։
- ↑ Բաժանում -ի վրա։
- ↑ Ամերիկայում այն ժամանակներում դեռ չկային վարկային հիմնարկներ։
- ↑ Գրքում վրիպակ է՝ Սալտիկովի „Господ Головлевых”։— Մ.։
- ↑ Կոպեկների կոտորակային մասն անտեսում ենք։
- ↑ Բացի այդ, այդ թիվը, ինչպես և թիվը տրանսցենդենտ են, այսինքն՝ չեն կարող լինել ամբողջ գործակիցներով հանրահաշվական որևէ հավասարման լուծման արդյունք։
- ↑ Գրքում վրիպակ է՝ Քանի որ թիվը հավասար մասերի վրա բաժանել չի կարելի,— Մ.։
- ↑ Այդ մասին տե՛ս „Жюль-Верновский силач и формула Эйлера” հոդվածը իմ «Հետաքրքրաշարժ ֆիզիկայի» 2-րդ գրքում։
- ↑ Տե՛ս իմ «Միջմոլորակային ճանապարհորդություններ» գիրքը։