«Ժամանակի համառոտ պատմություն»–ի խմբագրումների տարբերություն
(→2) |
(→Հավելված) |
||
| (13 intermediate revisions by the same user not shown) | |||
| Տող 62. | Տող 62. | ||
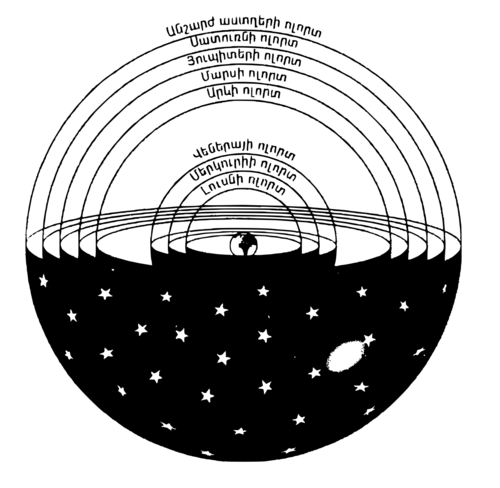
Ըստ Արիստոտելի, երկիրն անշարժ է, իսկ արևը, լուսինը, մոլորակները և աստղերը շրջանաձև պտտվում են նրա շուրջ։ Նա հավատում էր դրան, որովհետև կրոնական դրդապատճառներով համարում էր, որ երկիրը գտնվում է տիեզերքի կենտրոնում, իսկ շրջանաձև շարժումն ամենակատարյալն է։ Մ․թ․ II դարում Պտղոմեոսն այս գաղափարից բխեցրեց իր ամբողջական տիեզերագիտական մոդելը։ Ըստ այդ մոդելի՝ երկիրը գտնվում է տիեզերքի կենտրոնում՝ շրջապատված 8 ոլորտներով, որոնցում գտնվում են լուսինը, արևը, աստղերը և այն ժամանակ հայտնի հինգ մոլորակները՝ Մերկուրին, Վեներան, Մարսը, Յուպիտերը և Ստուռնը (նկ․ 1.1): Մոլորակներն իրենք պտտվում են ավելի փոքր ուղեծրերով, կապված մնալով իրենց համապատասխան ոլորտներին, սրանով էր բացատրվում մոլորակների՝ երկնքի դիտարկումներից բացահայտված բավականին բարդ ուղին։ Ամենահեռավոր ոլորտում գտնվում են, այսպես կոչված, սևեռված աստղերը, որոնք միմյանց նկատմամբ միշտ մնում են նույն դիրքում, բայց միասին պտտվում են երկնակամարում։ Թե ինչ կար վերջին ոլորտից այն կողմ, այնքան էլ հստակ չէր, բայց այն՝ իհարկե, մարդու համար դիտարկելի տիեզերքից դուրս էր։ | Ըստ Արիստոտելի, երկիրն անշարժ է, իսկ արևը, լուսինը, մոլորակները և աստղերը շրջանաձև պտտվում են նրա շուրջ։ Նա հավատում էր դրան, որովհետև կրոնական դրդապատճառներով համարում էր, որ երկիրը գտնվում է տիեզերքի կենտրոնում, իսկ շրջանաձև շարժումն ամենակատարյալն է։ Մ․թ․ II դարում Պտղոմեոսն այս գաղափարից բխեցրեց իր ամբողջական տիեզերագիտական մոդելը։ Ըստ այդ մոդելի՝ երկիրը գտնվում է տիեզերքի կենտրոնում՝ շրջապատված 8 ոլորտներով, որոնցում գտնվում են լուսինը, արևը, աստղերը և այն ժամանակ հայտնի հինգ մոլորակները՝ Մերկուրին, Վեներան, Մարսը, Յուպիտերը և Ստուռնը (նկ․ 1.1): Մոլորակներն իրենք պտտվում են ավելի փոքր ուղեծրերով, կապված մնալով իրենց համապատասխան ոլորտներին, սրանով էր բացատրվում մոլորակների՝ երկնքի դիտարկումներից բացահայտված բավականին բարդ ուղին։ Ամենահեռավոր ոլորտում գտնվում են, այսպես կոչված, սևեռված աստղերը, որոնք միմյանց նկատմամբ միշտ մնում են նույն դիրքում, բայց միասին պտտվում են երկնակամարում։ Թե ինչ կար վերջին ոլորտից այն կողմ, այնքան էլ հստակ չէր, բայց այն՝ իհարկե, մարդու համար դիտարկելի տիեզերքից դուրս էր։ | ||
| + | |||
| + | [[Պատկեր:H0.svg|right|500px]] | ||
Պտղոմեոսի մոդելն իրենից ներկայացնում էր բավականին ճշգրիտ մեթոդ, որով կարելի էր կանխագուշակել երկնային մարմինների դիրքը։ Սակայն այդ դիրքերը ճշգրիտ գուշակելու համար նա ստիպված էր ենթադրել, որ լուսնի հետագիծն այնպիսին է, որ երբեմն այն երկու անգամ ավելի մոտ է հայտնվում երկրին, քան սովորաբար։ Եվ դրանից հետևում է, որ լուսինը երբեմն երկու անգամ մեծ պիտի երևար սովորականից։ Պտղոմեոսը նկատեց այդ այդ թերությունը, որով հանդերձ, սակայն, մոդելը չնայած ոչ համընդհանուր, բայց լայն ընդունելություն գտավ։ Քրիստոնեական եկեղեցին նույնպես ընդունեց այն, քանի որ տիեզերքի այդ պատկերը համապատասխանում էր Աստվածաշնչին, ընդ որում, մեծ առավելություն ուներ, որ սևեռված աստղերի ոլորտից այն կողմ տեղ էր մնում նաև դժոխքի և դրախտի համար։1514֊ին ավելի պարզ մի մոդել առաջարկեց լեհ քահանա Նիկոլաս Կոպերնիկոսը։ (Սկզբում Կոպեռնիկոսն այն առաջարկեց անանուն, հավանաբար վախենալով, որ եկեղեցին հեղինակին հերետիկոս կհամարի)։ Նրա հիմնական գաղափարն այն էր, որ արևն անշարժ է և գտնվում է կենտրոնում, իսկ երկիրն ու մոլորակները պտտվում են նրա շուրջը՝ շրջանաձև ուղեծրերով։ Այս մոդելը լրջորեն ընդունվեց միայն շուրջ մեկ դար անց։ Թեև կոպեռնիկոսյան մոդելի կանխագուշակած ուղեծրերը ստույգ չէին համընկնում դիտարկումներին, երկու նշանավոր ասղագետներ՝ գերմանացի Յոհան Կեպլերն ու Իտալացի Գալիլեո Գալիլեյը հրապարակայնորեն պաշտպանեցին այն։ 1609֊ին արիստոտելյան֊պտղոմեոսյան տեսությունները կործանիչ հարված ստացան։ Այդ տարում նոր հայտնագործված հեռադիտակով Գալիլեոն սկսեց դիտարկել գիշերային երկնակամարը։ Նա, դիտելով Յուպիտերը, նկատեց, որ այն շրջապատված է մի քանի արբանյակներով կամ լուսիններով, որոնք պտտվում են նրա շուրջ։ Սա նշանակում էր, որ ոչ բոլոր մարմիններն են պտտվում երկրի շուրջ, ինչպես մտածում էին Արիստոտելն ու Պտղոմեոսը։ (Իհարկե, դեռ հնարավոր էր ենթադրել, որ երկիրը անշարժ է տիեզերքի կենտրոնում, իսկ Յուպիտերի լուսինները ծայրահեղ բարդ հետագծով պտտվում են երկրի շուրջ՝ տպավորություն ստեղծելով, թե դրանք պտտվում են Յուպիտերի շուրջ։ Սակայն Կոպեռնիկոսի տեսությունը շատ ավելի պարզ էր)։ Այդ նույն ժամանակ Յոհան Կեպլերը ձևափոխելով Կոպեռնիկոսի տեսությունը, առաջարկեց, որ մոլորակները պտտվում են ոչ թե շրջանաձև, այլ էլիպսաձև ուղեծրերով (էլիպսը ձգած շրջանագիծ է)։ Կանխագուշակված ուղեծրերն այդպիսով վերջնականապես համընկան դիտարկումներին։ | Պտղոմեոսի մոդելն իրենից ներկայացնում էր բավականին ճշգրիտ մեթոդ, որով կարելի էր կանխագուշակել երկնային մարմինների դիրքը։ Սակայն այդ դիրքերը ճշգրիտ գուշակելու համար նա ստիպված էր ենթադրել, որ լուսնի հետագիծն այնպիսին է, որ երբեմն այն երկու անգամ ավելի մոտ է հայտնվում երկրին, քան սովորաբար։ Եվ դրանից հետևում է, որ լուսինը երբեմն երկու անգամ մեծ պիտի երևար սովորականից։ Պտղոմեոսը նկատեց այդ այդ թերությունը, որով հանդերձ, սակայն, մոդելը չնայած ոչ համընդհանուր, բայց լայն ընդունելություն գտավ։ Քրիստոնեական եկեղեցին նույնպես ընդունեց այն, քանի որ տիեզերքի այդ պատկերը համապատասխանում էր Աստվածաշնչին, ընդ որում, մեծ առավելություն ուներ, որ սևեռված աստղերի ոլորտից այն կողմ տեղ էր մնում նաև դժոխքի և դրախտի համար։1514֊ին ավելի պարզ մի մոդել առաջարկեց լեհ քահանա Նիկոլաս Կոպերնիկոսը։ (Սկզբում Կոպեռնիկոսն այն առաջարկեց անանուն, հավանաբար վախենալով, որ եկեղեցին հեղինակին հերետիկոս կհամարի)։ Նրա հիմնական գաղափարն այն էր, որ արևն անշարժ է և գտնվում է կենտրոնում, իսկ երկիրն ու մոլորակները պտտվում են նրա շուրջը՝ շրջանաձև ուղեծրերով։ Այս մոդելը լրջորեն ընդունվեց միայն շուրջ մեկ դար անց։ Թեև կոպեռնիկոսյան մոդելի կանխագուշակած ուղեծրերը ստույգ չէին համընկնում դիտարկումներին, երկու նշանավոր ասղագետներ՝ գերմանացի Յոհան Կեպլերն ու Իտալացի Գալիլեո Գալիլեյը հրապարակայնորեն պաշտպանեցին այն։ 1609֊ին արիստոտելյան֊պտղոմեոսյան տեսությունները կործանիչ հարված ստացան։ Այդ տարում նոր հայտնագործված հեռադիտակով Գալիլեոն սկսեց դիտարկել գիշերային երկնակամարը։ Նա, դիտելով Յուպիտերը, նկատեց, որ այն շրջապատված է մի քանի արբանյակներով կամ լուսիններով, որոնք պտտվում են նրա շուրջ։ Սա նշանակում էր, որ ոչ բոլոր մարմիններն են պտտվում երկրի շուրջ, ինչպես մտածում էին Արիստոտելն ու Պտղոմեոսը։ (Իհարկե, դեռ հնարավոր էր ենթադրել, որ երկիրը անշարժ է տիեզերքի կենտրոնում, իսկ Յուպիտերի լուսինները ծայրահեղ բարդ հետագծով պտտվում են երկրի շուրջ՝ տպավորություն ստեղծելով, թե դրանք պտտվում են Յուպիտերի շուրջ։ Սակայն Կոպեռնիկոսի տեսությունը շատ ավելի պարզ էր)։ Այդ նույն ժամանակ Յոհան Կեպլերը ձևափոխելով Կոպեռնիկոսի տեսությունը, առաջարկեց, որ մոլորակները պտտվում են ոչ թե շրջանաձև, այլ էլիպսաձև ուղեծրերով (էլիպսը ձգած շրջանագիծ է)։ Կանխագուշակված ուղեծրերն այդպիսով վերջնականապես համընկան դիտարկումներին։ | ||
| Տող 151. | Տող 153. | ||
Յուրաքանչյուր դիտորդ կարող է ռադարի օգնությամբ իմանալ, թե որտեղ և երբ տեղի ունեցավ տվյալ պատահույթը՝ այնտեղ լույսի կամ ռադիոալիքների ազդանշան ուղարկելով։ Ազդանշանի մի մասը պատահույթի վայրից վերադառնում է, և դիտորդը չափում է արձագանքի ստացման ժամանակը։ Պատահույթի ժամանակ է կոչվում ազդանշանի հաղորդման և արձագանքի ստացման տևողությունների կիսագումարը, իսկ պատահույթի հեռավորությունն այդ շրջապտույտի կիսաժամանակի և լույսի արագության արտադրյալն է։ (Պատահույթ ասվածը, այս իմաստով, տարածության մի առանձին կետում և որոշակի ժամանակում տեղի ունեցածն է)։ Այս պատկերացումը ցույց է տրված նկ․21֊ում, որը տարածություն֊ժամանակ դիագրամի մի օրինակ է։ Այս ընթացակարգն օգտագործելով, դիտորդները, որոնք իրար նկատմամբ հարաբերական շարժման մեջ են, կարող են միևնույն երևույթին տարբեր դիրքեր և տարբեր ժամանակներ վերագրել։ Որևէ մեկի չափումն ավելի ճիշտ չի կարելի համարել մյուսի նկատմամբ, սակայն բոլոր չափումները կապված են միմյանց հետ։ Եթե դիտորդներից մեկին հայտնի է մյուսի շարժման հարաբերական արագությունը, ապա նա կարող է ճշգրտորեն իմանալ, թե այս վերջինը տվյալ դեպքի համար ինչ դիրք և ժամանակ է որոշել։ | Յուրաքանչյուր դիտորդ կարող է ռադարի օգնությամբ իմանալ, թե որտեղ և երբ տեղի ունեցավ տվյալ պատահույթը՝ այնտեղ լույսի կամ ռադիոալիքների ազդանշան ուղարկելով։ Ազդանշանի մի մասը պատահույթի վայրից վերադառնում է, և դիտորդը չափում է արձագանքի ստացման ժամանակը։ Պատահույթի ժամանակ է կոչվում ազդանշանի հաղորդման և արձագանքի ստացման տևողությունների կիսագումարը, իսկ պատահույթի հեռավորությունն այդ շրջապտույտի կիսաժամանակի և լույսի արագության արտադրյալն է։ (Պատահույթ ասվածը, այս իմաստով, տարածության մի առանձին կետում և որոշակի ժամանակում տեղի ունեցածն է)։ Այս պատկերացումը ցույց է տրված նկ․21֊ում, որը տարածություն֊ժամանակ դիագրամի մի օրինակ է։ Այս ընթացակարգն օգտագործելով, դիտորդները, որոնք իրար նկատմամբ հարաբերական շարժման մեջ են, կարող են միևնույն երևույթին տարբեր դիրքեր և տարբեր ժամանակներ վերագրել։ Որևէ մեկի չափումն ավելի ճիշտ չի կարելի համարել մյուսի նկատմամբ, սակայն բոլոր չափումները կապված են միմյանց հետ։ Եթե դիտորդներից մեկին հայտնի է մյուսի շարժման հարաբերական արագությունը, ապա նա կարող է ճշգրտորեն իմանալ, թե այս վերջինը տվյալ դեպքի համար ինչ դիրք և ժամանակ է որոշել։ | ||
| + | |||
| + | [[Պատկեր:H2 1.svg|thumb| Նկ․ 2․ 1 Ժամանակը տեղադրված է ուղղաձիգ, իսկ դիտորդից եղած հեռավորությունը՝ հորիզոնական առանցքնեիր վրա։ Դիտորդի ուղին տարածության և ժամանակի մեջ ներկայացված է ձախ մասում ցույց տրված ուղղաձիգ գծով։ Դեպի պատահույթը և նրանից անդրադարձած լույսի ճառագայթների ուղիները թեք գծերն են։]] | ||
Այժմ մենք հենց այս ռադարային եղանակն ենք օգտագործում հեռավորությունը ճշգրիտ չափելու համար, որովհետև կարող ենք ժամանակն ավելի մեծ ճշգրտությամբ չափել, քան հեռավորությունը։ Արդարև, մետրը սահմանված է որպես այնպիսի հեռավորություն, որը լույսն անցնում է 0,00000000 33356-40952 վայրկյանում՝ չափված ցեզիումային ժամացույցով։ (Այս հատուկ թվի ընտրությունը պայմանավորված է նրանով, որ դա համապատասխանում է մետրի պատմական սահմանը՝ որպես Փարիզում պահվող հատուկ պլատինե ձողի երկու նշանակետերով սահմանված երկարություն)։ Մենք հավասարապես կարող ենք օգտվել երկարության ավելի հարմար նոր միավորից՝ լուսավայրկյանից։ Դա ուղղակի այն հեռավորությունն է, որը լույսն անցնում է մեկ վայրկյանում։ Հարաբերականության տեսության մեջ մենք այժմ հեռավորությունը սահմանել ենք, ժամանակի և լույսի արագության միջոցով։ Հետևաբար յուրաքանչյուր դիտորդ լույսը չափելիս արագության համար պետք է օգտագործի միևնույն արժեքը (այսինքն՝ 1 մետր 0,000000003335640952 վայրկյանում)։ Որևէ կարիք չկա, որ ներմուծվի եթերի գաղափարը, ինչի գոյությունն ամենուր հնարավոր չէ հայտնաբերել, ինչպես ցույց է տալիս Մայքելսոն֊Մոռլիի փորձը։ Այսպիսով, հարաբերականության տեսությունը մեզ հիմք է տալիս հիմնավորապես փոխելու մեր պատկերացումները տարածության և ժամանակի մասին։ Մենք պետք է ընդունենք, որ ժամանակը լիովին անջատ և անկախ չէ տարածությունից, այլ նրանք միավորված են միմյանց հետ, որպես, այսպես կոչված, տարածություն֊ժամանակ։ | Այժմ մենք հենց այս ռադարային եղանակն ենք օգտագործում հեռավորությունը ճշգրիտ չափելու համար, որովհետև կարող ենք ժամանակն ավելի մեծ ճշգրտությամբ չափել, քան հեռավորությունը։ Արդարև, մետրը սահմանված է որպես այնպիսի հեռավորություն, որը լույսն անցնում է 0,00000000 33356-40952 վայրկյանում՝ չափված ցեզիումային ժամացույցով։ (Այս հատուկ թվի ընտրությունը պայմանավորված է նրանով, որ դա համապատասխանում է մետրի պատմական սահմանը՝ որպես Փարիզում պահվող հատուկ պլատինե ձողի երկու նշանակետերով սահմանված երկարություն)։ Մենք հավասարապես կարող ենք օգտվել երկարության ավելի հարմար նոր միավորից՝ լուսավայրկյանից։ Դա ուղղակի այն հեռավորությունն է, որը լույսն անցնում է մեկ վայրկյանում։ Հարաբերականության տեսության մեջ մենք այժմ հեռավորությունը սահմանել ենք, ժամանակի և լույսի արագության միջոցով։ Հետևաբար յուրաքանչյուր դիտորդ լույսը չափելիս արագության համար պետք է օգտագործի միևնույն արժեքը (այսինքն՝ 1 մետր 0,000000003335640952 վայրկյանում)։ Որևէ կարիք չկա, որ ներմուծվի եթերի գաղափարը, ինչի գոյությունն ամենուր հնարավոր չէ հայտնաբերել, ինչպես ցույց է տալիս Մայքելսոն֊Մոռլիի փորձը։ Այսպիսով, հարաբերականության տեսությունը մեզ հիմք է տալիս հիմնավորապես փոխելու մեր պատկերացումները տարածության և ժամանակի մասին։ Մենք պետք է ընդունենք, որ ժամանակը լիովին անջատ և անկախ չէ տարածությունից, այլ նրանք միավորված են միմյանց հետ, որպես, այսպես կոչված, տարածություն֊ժամանակ։ | ||
| Տող 161. | Տող 165. | ||
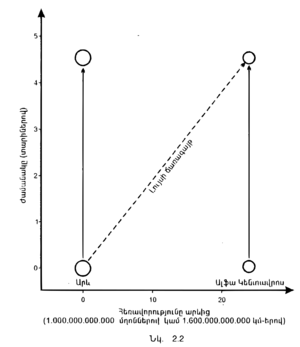
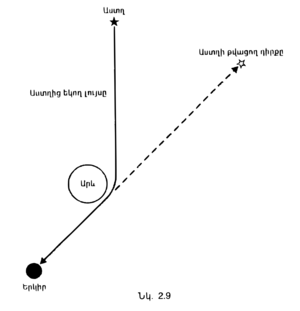
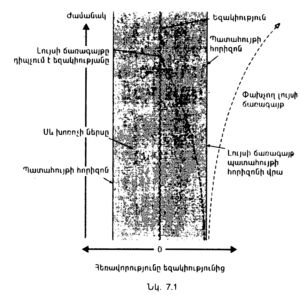
Հաճախ շատ օգտակար է մտածել, պատահույթի չորս կոորդինատների մասին՝ բնորոշելու նրա դիրքը քառաչափ տարածության մեջ, որը կոչվել է տարծություն֊ժամանակ։ Սակայն քառաչափ տարածությունն անհնար է պատկերացնել։ Ես ինքս դժվար եմ պատկերացնում նույնիսկ եռաչափ տարածությունը։ Այնուամենայնիվ, հեշտ է երկչափ տարածության դիագրամներ գծել, ինչպես, օրինակ, երկրագնդի մակերևույթը։ (Երկրագնդի մակերևույթը երկչափ է, որովհետև նրա վրա կետի դիրքը կարելի է որոշել երկու կոորդինատներով՝ լայնությամբ և երկարությամբ)։ Ես հիմնականում օգտագործելու եմ դիագրամներ, որոնցում ժամանակն աճման կարգով ցույց է տրվելու հեռանկարում։ (Դրանք կոչվում են տարածություն֊ժամանակ դիագրամներ, օրինակ, նկ․ 2.1֊ը)։ Դիցուկ, 2.2 նկարում ժամանակը տեղադրված է ուղղահայաց առանցքի վրա՝ տարիներով, իսկ հորիզոնական առանցքի վրա՝ արևի և Ալֆա Կենտավրոս աստղի միջև եղած հեռավորությունը՝ մղոններով։ Արևի և Ալֆա Կենտավրոսի հետագծերը տարածություն֊ժամանակ դիագրամում ցույց են տրված որպես ուղղաձիգ գծեր ձախ և աջ կողմերում։ Արևի լույսի ճառագայթը, անցնելով թեք անկյունագծով, չորս տարում արևից հասնում է Ալֆա Կենտավրոսին։ | Հաճախ շատ օգտակար է մտածել, պատահույթի չորս կոորդինատների մասին՝ բնորոշելու նրա դիրքը քառաչափ տարածության մեջ, որը կոչվել է տարծություն֊ժամանակ։ Սակայն քառաչափ տարածությունն անհնար է պատկերացնել։ Ես ինքս դժվար եմ պատկերացնում նույնիսկ եռաչափ տարածությունը։ Այնուամենայնիվ, հեշտ է երկչափ տարածության դիագրամներ գծել, ինչպես, օրինակ, երկրագնդի մակերևույթը։ (Երկրագնդի մակերևույթը երկչափ է, որովհետև նրա վրա կետի դիրքը կարելի է որոշել երկու կոորդինատներով՝ լայնությամբ և երկարությամբ)։ Ես հիմնականում օգտագործելու եմ դիագրամներ, որոնցում ժամանակն աճման կարգով ցույց է տրվելու հեռանկարում։ (Դրանք կոչվում են տարածություն֊ժամանակ դիագրամներ, օրինակ, նկ․ 2.1֊ը)։ Դիցուկ, 2.2 նկարում ժամանակը տեղադրված է ուղղահայաց առանցքի վրա՝ տարիներով, իսկ հորիզոնական առանցքի վրա՝ արևի և Ալֆա Կենտավրոս աստղի միջև եղած հեռավորությունը՝ մղոններով։ Արևի և Ալֆա Կենտավրոսի հետագծերը տարածություն֊ժամանակ դիագրամում ցույց են տրված որպես ուղղաձիգ գծեր ձախ և աջ կողմերում։ Արևի լույսի ճառագայթը, անցնելով թեք անկյունագծով, չորս տարում արևից հասնում է Ալֆա Կենտավրոսին։ | ||
| + | |||
| + | [[Պատկեր:H2 2.svg|thumb]] | ||
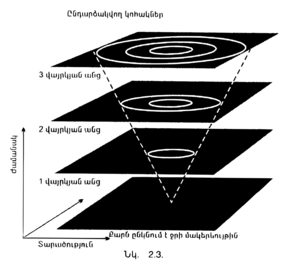
Ինչպես մենք արդեն գիտենք, Մաքսվելի հավասարումները կանխատեսում են, որ լույսի արագությունը նույնը պիտի լինի, անկախ աղբյուրի շարժման արագությունից, ինչը հաստատված է ճշգրիտ չափումներով։ Սրանից հետևում է, որ եթե որոշակի ժամանակում տարածության որոշակի կետից լուսային ազդանշան է արձակվել, ապա անցնող ժամանակի հետ լույսը պիտի տարածվի որպես լուսային գունդ, որի մեծությունն ու դիրքը կախված չեն աղբյուրի արագությունից։ Մեկ միլիոներորդ վայրկյան հետո լույսը պիտի տարածվի՝ առաջացնելով 300 մետր շառավիղ ունեցող գունդ, երկու միլիոներորդ վայրկյան հետո գնդի շառավիղը կլինի 600 մետր և այսպես շարունակ։ Սա նման կլինի լճակի մակերևույթին տարածվող ալիքներին, երբ լճակի մեջ քար է գցվում։ Ալիքները, տարածվելով շրջանաձև, ժամանակի հետ գնալով ավելի և ավելի են տարածվում։ Եթե այժմ պատկերացնենք եռաչափ տարածական մոդել՝ բաղկացած լճակի երկչափ մակերեսից և միաչափ ժամանակից, ապա տարածվող ալիքները ժամանակի ընթացքում կառաջացնեն մի կոն, որի գագաթը կհամապատասխանի այն տեղին և ժամանակին, երբ քարը խփվում է ջրին (նկ․2.3): | Ինչպես մենք արդեն գիտենք, Մաքսվելի հավասարումները կանխատեսում են, որ լույսի արագությունը նույնը պիտի լինի, անկախ աղբյուրի շարժման արագությունից, ինչը հաստատված է ճշգրիտ չափումներով։ Սրանից հետևում է, որ եթե որոշակի ժամանակում տարածության որոշակի կետից լուսային ազդանշան է արձակվել, ապա անցնող ժամանակի հետ լույսը պիտի տարածվի որպես լուսային գունդ, որի մեծությունն ու դիրքը կախված չեն աղբյուրի արագությունից։ Մեկ միլիոներորդ վայրկյան հետո լույսը պիտի տարածվի՝ առաջացնելով 300 մետր շառավիղ ունեցող գունդ, երկու միլիոներորդ վայրկյան հետո գնդի շառավիղը կլինի 600 մետր և այսպես շարունակ։ Սա նման կլինի լճակի մակերևույթին տարածվող ալիքներին, երբ լճակի մեջ քար է գցվում։ Ալիքները, տարածվելով շրջանաձև, ժամանակի հետ գնալով ավելի և ավելի են տարածվում։ Եթե այժմ պատկերացնենք եռաչափ տարածական մոդել՝ բաղկացած լճակի երկչափ մակերեսից և միաչափ ժամանակից, ապա տարածվող ալիքները ժամանակի ընթացքում կառաջացնեն մի կոն, որի գագաթը կհամապատասխանի այն տեղին և ժամանակին, երբ քարը խփվում է ջրին (նկ․2.3): | ||
| + | |||
| + | [[Պատկեր:H2 3.svg|thumb]] | ||
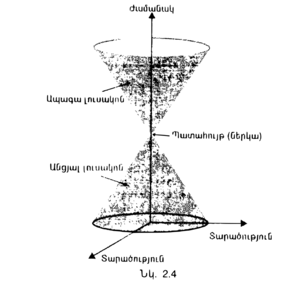
Նույն ձևով լույսը, մի պատահույթից տարածվելով, առաջացնում է եռաչափ մի կոն քառաչափ տարածություն֊ժամանակի մեջ։ Այս կոնը կոչվում է պատահույթի ապագայի լուսակոն։ Նույն ձևով մենք կարող ենք նկարել մեկ այլ կոն, որը կոչվում է անցյալի լուսակոն․ այն պատահույթի մի շարք է, որոնց լուսային ազդանշաններն ի վիճակի են հասնել տվյալ պատահույթին (նկ․2.4): | Նույն ձևով լույսը, մի պատահույթից տարածվելով, առաջացնում է եռաչափ մի կոն քառաչափ տարածություն֊ժամանակի մեջ։ Այս կոնը կոչվում է պատահույթի ապագայի լուսակոն։ Նույն ձևով մենք կարող ենք նկարել մեկ այլ կոն, որը կոչվում է անցյալի լուսակոն․ այն պատահույթի մի շարք է, որոնց լուսային ազդանշաններն ի վիճակի են հասնել տվյալ պատահույթին (նկ․2.4): | ||
| + | |||
| + | [[Պատկեր:H2 4.svg|thumb]] | ||
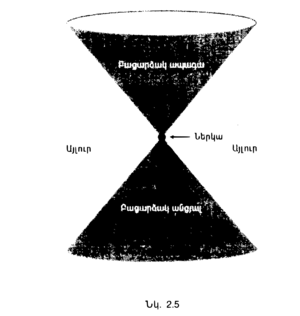
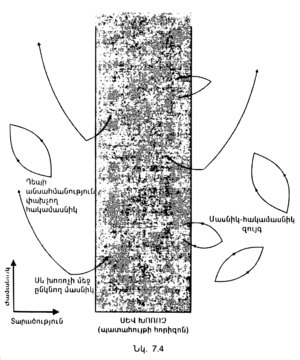
P ― պատահույթի անցյալի և ապագայի լուսակոները տարածություն֊ժամանակը բաժանում են երեք տիրույթի (նկ․ 2.5)։ Պատահույթի բացարձակ ապագան P֊ի ապագայի լուսակոնի ներսում պարփակված տիրույթն է։ Դա բոլոր այն պատահույթների շարքն է, որոնք կարող են ազդվել այն ամենից, ինչ տեղի է ունենում P֊ում։ P֊ի ազդանշանները չեն կարող հասնել P֊ի լուսակոնից դուրս տեղի ունեցող պատահույթներին, որովհետև լույսից արագ շարժվել հնարավոր չէ։ Հետևաբար, այդ պատահույթները չեն կարող ազդվել այն ամենից, ինչ տեղի է ունենում P֊ում։ P֊ի բացարձակ անցյալն անցյալի լուսակոնում պարփակված տիրույթն է։ Դա այն պատահույթների շարքն է, որոնցից ազդանշանները, շարժվելով լույսի արագությամբ կամ ավելի դանդաղ, կարող են հասնել P֊ին։ | P ― պատահույթի անցյալի և ապագայի լուսակոները տարածություն֊ժամանակը բաժանում են երեք տիրույթի (նկ․ 2.5)։ Պատահույթի բացարձակ ապագան P֊ի ապագայի լուսակոնի ներսում պարփակված տիրույթն է։ Դա բոլոր այն պատահույթների շարքն է, որոնք կարող են ազդվել այն ամենից, ինչ տեղի է ունենում P֊ում։ P֊ի ազդանշանները չեն կարող հասնել P֊ի լուսակոնից դուրս տեղի ունեցող պատահույթներին, որովհետև լույսից արագ շարժվել հնարավոր չէ։ Հետևաբար, այդ պատահույթները չեն կարող ազդվել այն ամենից, ինչ տեղի է ունենում P֊ում։ P֊ի բացարձակ անցյալն անցյալի լուսակոնում պարփակված տիրույթն է։ Դա այն պատահույթների շարքն է, որոնցից ազդանշանները, շարժվելով լույսի արագությամբ կամ ավելի դանդաղ, կարող են հասնել P֊ին։ | ||
| + | |||
| + | [[Պատկեր:H2 5.svg|thumb]] | ||
Դա, հետևաբար, բոլոր այն պատահույթների շարքն է, որոնք կարող են ազդել P֊ում կատարվող իրադարձությունների վրա։ Եթե մենք իմանանք, թե ինչ է տեղի ունեցել P֊ի անցյալի լուսակոնում պարփակված տարածության ցանկացած տիրույթում, ապա կարող ենք կանխագուշակել, թե ինչ պիտի տեղի ունենա P֊ում։ «Այլուրը» տարածություն֊ժամանակ դիագրամի այն տիրույթն է, որը դուրս է ապագայի և անցյալի լուսակոներից, այլուրում կատարվող պատահույթները չեն կարող ազդվել կամ ազդել P֊ի պատահույթների վրա։ Այսպես, եթե հենց այս պահին արևը դադարեր փայլելուց, դա Երկրի անցուդարձի վրա անմիջապես չէր կարող ազդել, քանի որ այն պահին, երբ արևը հանգի (նկ․ 2.6) երկիրը կգտնվի պատահույթի «այլուրում»։ Այդ մասին մենք կիմանանք 8 րոպե հետո միայն, այսինքն՝ այնքան ժամանակ անց, որը հարկավոր է, որպեսզի լույսը արևից հասնի մեզ։ Միայն այդ ժամանակ երկրի վրա պատահող պատահույթները կմտնեն արևի հանգման պատահույթի ապագայի լուսակոնի մեջ։ Նույն ձևով մենք չգիտենք, թե այս պահին ինչ է տեղի ունենում հեռավոր տիեզերքում։ Հեռավոր գալակտիկաների լույսը, որը մենք տեսնում ենք այսօր, արձակվել է միլիոնավոր տարիներ առաջ, իսկ ամենահեռավոր տեսանելի առարկաներից լույսը ճամփա է ընկել մի քանի ութ հազար միլիոն տարի առաջ։ | Դա, հետևաբար, բոլոր այն պատահույթների շարքն է, որոնք կարող են ազդել P֊ում կատարվող իրադարձությունների վրա։ Եթե մենք իմանանք, թե ինչ է տեղի ունեցել P֊ի անցյալի լուսակոնում պարփակված տարածության ցանկացած տիրույթում, ապա կարող ենք կանխագուշակել, թե ինչ պիտի տեղի ունենա P֊ում։ «Այլուրը» տարածություն֊ժամանակ դիագրամի այն տիրույթն է, որը դուրս է ապագայի և անցյալի լուսակոներից, այլուրում կատարվող պատահույթները չեն կարող ազդվել կամ ազդել P֊ի պատահույթների վրա։ Այսպես, եթե հենց այս պահին արևը դադարեր փայլելուց, դա Երկրի անցուդարձի վրա անմիջապես չէր կարող ազդել, քանի որ այն պահին, երբ արևը հանգի (նկ․ 2.6) երկիրը կգտնվի պատահույթի «այլուրում»։ Այդ մասին մենք կիմանանք 8 րոպե հետո միայն, այսինքն՝ այնքան ժամանակ անց, որը հարկավոր է, որպեսզի լույսը արևից հասնի մեզ։ Միայն այդ ժամանակ երկրի վրա պատահող պատահույթները կմտնեն արևի հանգման պատահույթի ապագայի լուսակոնի մեջ։ Նույն ձևով մենք չգիտենք, թե այս պահին ինչ է տեղի ունենում հեռավոր տիեզերքում։ Հեռավոր գալակտիկաների լույսը, որը մենք տեսնում ենք այսօր, արձակվել է միլիոնավոր տարիներ առաջ, իսկ ամենահեռավոր տեսանելի առարկաներից լույսը ճամփա է ընկել մի քանի ութ հազար միլիոն տարի առաջ։ | ||
| + | |||
| + | [[Պատկեր:H2 6.svg|thumb]] | ||
Այսպիսով, երբ մենք այսօր տիեզերքին ենք նայում, ապա տեսնում ենք այնպես, ինչպես նա եղել է անցյալում։ | Այսպիսով, երբ մենք այսօր տիեզերքին ենք նայում, ապա տեսնում ենք այնպես, ինչպես նա եղել է անցյալում։ | ||
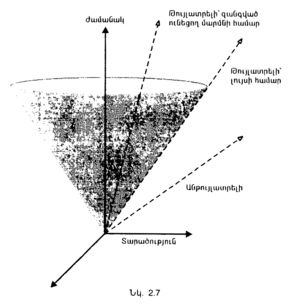
Եթե անտեսենք ձգողության ազդեցությունները, ինչպես այդ արեցին Էնշտեյնն ու Պուանկարեն 1905֊ին, ստացվում է, այսպես կոչված, հարաբերականության հատուկ տեսությունը։ Տարածություն֊ժամանակի մեջ տեղի ունեցող ցանկացած պատահույթի համար, մենք կարող ենք լուսակոն կառուցել (տարածություն֊ժամանակի մեջ տվյալ պատահույթի արձակած լույսի բոլոր հնարավոր հետագծերի շարքը), և որովհետև լույսի արագությունը նույնն է յուրաքանչյուր պատահույթի և ուղղության համար, բոլոր լուսակոները կլինեն նույնանման և կուղղվեն միևնույն ուղղությամբ։ Այս տեսությունը նույնպես ասում է, որ ոչինչ չի կարող լույսից ավելի արագ շարժվել։ Սա նշանակում է, որ որևէ առարկայի հետագիծը տարածության և ժամանակի մեջ պետք է ներկայացվի մի գծով, որը գտնվում է յուրաքանչյուր պատահույթի լուսակոնի ներսում (նկ․ 2.7)։ | Եթե անտեսենք ձգողության ազդեցությունները, ինչպես այդ արեցին Էնշտեյնն ու Պուանկարեն 1905֊ին, ստացվում է, այսպես կոչված, հարաբերականության հատուկ տեսությունը։ Տարածություն֊ժամանակի մեջ տեղի ունեցող ցանկացած պատահույթի համար, մենք կարող ենք լուսակոն կառուցել (տարածություն֊ժամանակի մեջ տվյալ պատահույթի արձակած լույսի բոլոր հնարավոր հետագծերի շարքը), և որովհետև լույսի արագությունը նույնն է յուրաքանչյուր պատահույթի և ուղղության համար, բոլոր լուսակոները կլինեն նույնանման և կուղղվեն միևնույն ուղղությամբ։ Այս տեսությունը նույնպես ասում է, որ ոչինչ չի կարող լույսից ավելի արագ շարժվել։ Սա նշանակում է, որ որևէ առարկայի հետագիծը տարածության և ժամանակի մեջ պետք է ներկայացվի մի գծով, որը գտնվում է յուրաքանչյուր պատահույթի լուսակոնի ներսում (նկ․ 2.7)։ | ||
| + | |||
| + | [[Պատկեր:H2 7.svg|thumb]] | ||
Հարաբերականության հատուկ տեսությունը մեծ հաջողությամբ բացատրեց, որ լույսի արագությունը նույնն է բոլոր դիտորդների համար (ինչպես ցույց էր տրվել Մայքելսոն֊Մոռլիի փորձով) և նկարագրեց, թե ինչ է պատահում, եթե առարկաները շարժվում են լույսի արագությանը մոտ արագությամբ։ Այն, սակայն, անհամատեղելի էր Նյուտոնի ձգողության տեսության հետ, որի համաձայն մարմինների՝ միմյանց ձգող ուժը կախված է նրանց միջև եղած հեռավորությունից։ Սա նշանակում է, որ երբ մարմիններից մեկը շարժվի, ապա մյուսի վրա ազդող ուժը պետք է ակնթարթորեն փոխվի։ Կամ, այլ կերպ ասած, ձգողական ազդեցությունները պետք է գործեն անսահման մեծ արագությամբ, այն դեպքում, երբ հարաբերականության հատուկ տեսությունը պահանջում է, որ այդ արագությունը լինի լույսի արագությանը հավասար կամ նրանից փոքր։ | Հարաբերականության հատուկ տեսությունը մեծ հաջողությամբ բացատրեց, որ լույսի արագությունը նույնն է բոլոր դիտորդների համար (ինչպես ցույց էր տրվել Մայքելսոն֊Մոռլիի փորձով) և նկարագրեց, թե ինչ է պատահում, եթե առարկաները շարժվում են լույսի արագությանը մոտ արագությամբ։ Այն, սակայն, անհամատեղելի էր Նյուտոնի ձգողության տեսության հետ, որի համաձայն մարմինների՝ միմյանց ձգող ուժը կախված է նրանց միջև եղած հեռավորությունից։ Սա նշանակում է, որ երբ մարմիններից մեկը շարժվի, ապա մյուսի վրա ազդող ուժը պետք է ակնթարթորեն փոխվի։ Կամ, այլ կերպ ասած, ձգողական ազդեցությունները պետք է գործեն անսահման մեծ արագությամբ, այն դեպքում, երբ հարաբերականության հատուկ տեսությունը պահանջում է, որ այդ արագությունը լինի լույսի արագությանը հավասար կամ նրանից փոքր։ | ||
Էնշտեյնը 1908֊ից մինչև 1914֊ը մի շարք անհաջող փորձեր կատարեց՝ ստեղծելու ձգողականության այնպիսի մի տեսություն, որը համատեղելի լիներ հարաբերականության հատուկ տեսության հետ։ Վերջապես1915 թվականին նա առաջարկեց այն, ինչն այսօր անվանում ենք հարաբերականության ընդհանուր տեսություն։ | Էնշտեյնը 1908֊ից մինչև 1914֊ը մի շարք անհաջող փորձեր կատարեց՝ ստեղծելու ձգողականության այնպիսի մի տեսություն, որը համատեղելի լիներ հարաբերականության հատուկ տեսության հետ։ Վերջապես1915 թվականին նա առաջարկեց այն, ինչն այսօր անվանում ենք հարաբերականության ընդհանուր տեսություն։ | ||
| + | |||
| + | [[Պատկեր:H2 8.svg|thumb]] | ||
Էնշտեյնը կատարեց հեղափոխական նշանակություն ունեցող մի առաջարկություն այն մասին, որ ձգողականությունը մյուս ուժերի նման ուժ չէ, այլ արդյունք է այն բանի, որ տարածություն֊ժամանակը հարթ չէ, ինչպես նախկինում ենթարվում էր, այլ կոր է կամ «կորացված»՝ իր մեջ առկա զանգվածի և էներգիայի բաշխման հետևանքով։ Մարմինները, ինչպիսին երկրագունդն է, ստեղծված չեն, որպեսզի շարժվեն կորաձև ուղեծրով ձգողություն կոչվող ուժի ազդեցության տակ, փոխարենը նրանք ուղղաձիգ են շարժվում կորաձև տարածության մեջ, որը կոչվում է գեոդեզիական տարածություն։ Գեոդեզիական է կոչվում երկու հարևան կետերի միջև ամենակարճ (կամ ամենաերկար) հեռավորությունը։ | Էնշտեյնը կատարեց հեղափոխական նշանակություն ունեցող մի առաջարկություն այն մասին, որ ձգողականությունը մյուս ուժերի նման ուժ չէ, այլ արդյունք է այն բանի, որ տարածություն֊ժամանակը հարթ չէ, ինչպես նախկինում ենթարվում էր, այլ կոր է կամ «կորացված»՝ իր մեջ առկա զանգվածի և էներգիայի բաշխման հետևանքով։ Մարմինները, ինչպիսին երկրագունդն է, ստեղծված չեն, որպեսզի շարժվեն կորաձև ուղեծրով ձգողություն կոչվող ուժի ազդեցության տակ, փոխարենը նրանք ուղղաձիգ են շարժվում կորաձև տարածության մեջ, որը կոչվում է գեոդեզիական տարածություն։ Գեոդեզիական է կոչվում երկու հարևան կետերի միջև ամենակարճ (կամ ամենաերկար) հեռավորությունը։ | ||
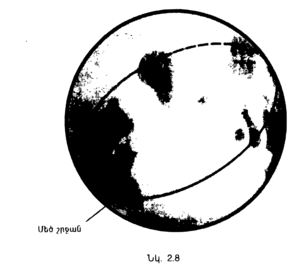
Օրինակ, երկրագնդի մակերևույթը երկչափանի կոր տարածություն է։ Երկրագնդի վրա գեոդեզիական է կոչվում մեծ շրջանագիծը, որը երկու կետերի միջև եղած ամենակարճ ճանապարհն է (նկ․ 2.8)։ Քանի որ գեոդեզիականն ամենակարճ ճանապարհն է ցանկացած երկու օդանավակայանների միջև, ապա շտուրմանը օդաչուին հրահանգում է թռիչքի համար ընտրել այդ ուղին։ Չնայած ընդհանուր հարաբերականության տեսության մեջ մարմինները միշտ շարժվում են ուղիղ գծով քառաչափ տարածություն֊ժամանակում, սակայն մեզ թվում է, թե նրանք մեր եռաչափ տարածության մեջ շարժվում են կորաձև։ (Սա շատ նման է այն բանին, որին մենք ականատես ենք լինում, երբ օդանավը թռչում է լեռնոտ տարածքի վրայով։ Թեև այն շարժվում է ուղղագծորեն՝ եռաչափ տարածության մեջ, բայց նրա ստվերը երկչափ գետնի վրա կորագիծ է։ | Օրինակ, երկրագնդի մակերևույթը երկչափանի կոր տարածություն է։ Երկրագնդի վրա գեոդեզիական է կոչվում մեծ շրջանագիծը, որը երկու կետերի միջև եղած ամենակարճ ճանապարհն է (նկ․ 2.8)։ Քանի որ գեոդեզիականն ամենակարճ ճանապարհն է ցանկացած երկու օդանավակայանների միջև, ապա շտուրմանը օդաչուին հրահանգում է թռիչքի համար ընտրել այդ ուղին։ Չնայած ընդհանուր հարաբերականության տեսության մեջ մարմինները միշտ շարժվում են ուղիղ գծով քառաչափ տարածություն֊ժամանակում, սակայն մեզ թվում է, թե նրանք մեր եռաչափ տարածության մեջ շարժվում են կորաձև։ (Սա շատ նման է այն բանին, որին մենք ականատես ենք լինում, երբ օդանավը թռչում է լեռնոտ տարածքի վրայով։ Թեև այն շարժվում է ուղղագծորեն՝ եռաչափ տարածության մեջ, բայց նրա ստվերը երկչափ գետնի վրա կորագիծ է։ | ||
| + | |||
| + | [[Պատկեր:H2 9.svg|thumb]] | ||
Արևի զանգվածն այնպես է կորացնում տարածություն֊ժամանակը, որ թեև երկրագունդը շարժվում է ուղղագծորեն քառաչափ տարածություն֊ժամանակի մեջ, բայց մեզ թվում է, թե այն եռաչափ տարածության մեջ շարժվում է շրջանաձև ուղեծրով։ Փաստորեն, մոլորակների ուղեծրի համար ընդհանուր հարաբերականության կանխագուշակությունը գրեթե ճշտորեն նույնն էր, ինչ կանխագուշակել էր Նյուտոնի ձգողականության տեսությունը։ Այնուամենայնիվ, Մերկուրիի դեպքում, որն արևին ամենամոտ մոլորակը լինելով, ենթարկվում է ձգողության ուժեղագույն ազդեցությանը և ունի բավականին երկարացված էլիպսաձև ուղեծիր, ընդհանուր հարաբերականության տեսությունը կանխատեսում է, որ էլիպսի երկար առանցքը պետք է պտտվի արևի նկատմամբ տասը հազար տարին մեկ աստիճան արագությամբ։ Այս շեղումը թեև փոքր, բայց դիտարկվել է 1915֊ից առաջ և Էյնշտեյնի ընդհանուր հարաբերականության տեսության հաստատմանը նպաստող առաջին փաստերից մեկն է։ Վերջին տարիներին ռադարային չափումների օգնությամբ դիտարկվել են այլ մոլորակների ավելի փոքր ուղեծրային շեղումներ նյուտոնյան կանխագուշակումներից և հաստատվել է ընդհանուր հարաբերականության տեսության կանխատեսումների հետ դրանց համապատասխանությունը։ | Արևի զանգվածն այնպես է կորացնում տարածություն֊ժամանակը, որ թեև երկրագունդը շարժվում է ուղղագծորեն քառաչափ տարածություն֊ժամանակի մեջ, բայց մեզ թվում է, թե այն եռաչափ տարածության մեջ շարժվում է շրջանաձև ուղեծրով։ Փաստորեն, մոլորակների ուղեծրի համար ընդհանուր հարաբերականության կանխագուշակությունը գրեթե ճշտորեն նույնն էր, ինչ կանխագուշակել էր Նյուտոնի ձգողականության տեսությունը։ Այնուամենայնիվ, Մերկուրիի դեպքում, որն արևին ամենամոտ մոլորակը լինելով, ենթարկվում է ձգողության ուժեղագույն ազդեցությանը և ունի բավականին երկարացված էլիպսաձև ուղեծիր, ընդհանուր հարաբերականության տեսությունը կանխատեսում է, որ էլիպսի երկար առանցքը պետք է պտտվի արևի նկատմամբ տասը հազար տարին մեկ աստիճան արագությամբ։ Այս շեղումը թեև փոքր, բայց դիտարկվել է 1915֊ից առաջ և Էյնշտեյնի ընդհանուր հարաբերականության տեսության հաստատմանը նպաստող առաջին փաստերից մեկն է։ Վերջին տարիներին ռադարային չափումների օգնությամբ դիտարկվել են այլ մոլորակների ավելի փոքր ուղեծրային շեղումներ նյուտոնյան կանխագուշակումներից և հաստատվել է ընդհանուր հարաբերականության տեսության կանխատեսումների հետ դրանց համապատասխանությունը։ | ||
| Տող 210. | Տող 230. | ||
Տիեզերքի ժամանակակից պատկերացման հիմքը դրվեց 1924֊ին, երբ ամերիկացի աստղագետ Էդվին Հաբլը ցույց տվեց որ տիեզերքում մեր գալակտիական միակը չէ։ Փաստորեն գոյություն ունեն շատ ուրիշ գալակտիկաներ, որոնք միմյանցից բաժանված են լայնատարած դատարկության գոտիներով։ Այդ բանը ապացուցելու համար Հաբլին հարկավոր էր որոշել գալակտիկաների հեռավորությունը, որոնք շատ հեռու լինելով մոտիկ գտնվող աստղերից, անշարժ են թվում։ Հաբլը ստիպված էր աննուղակի մի եղանակ օգտագործել այդ հեռավորությունները չափելու համար։ Աստղի թվացող պայծառությունը կախված է երկու գործոնից․ թե որքան լույս է արձակում այն (լուսատվություն) և ինչքան հեռու է գտնվում մեզանից։ Մենք կարող ենք չափել մոտիկ գտնվող աստղերի թվացող պայծառությունն ու հեռավորությունը, և դրանով որոշել աստղի լուսատվությունը։ Եվ հակառակը, եթե իմանանք աստղերի լուսատվություն այլ գալակտիկաներում, ապա նրանց թվացող պայծառությունը չափելով, կկարողանանք հաշվարկել նրանց հեռավորությունը։ Հաբլը նկատել էր, որ մեզ մոտիկ գտնվող որոշ տեսակի աստղեր մշտապես ունեն միևնույն լուսատվությունը և ենթադրել էր, որ եթե մենք նման աստղեր գտնենք այլ գալակտիկայում, ապա կարող ենք ընդունել, որ նրանց լուսատվությունը նույնն է և, այդպիսով հաշվել տվյալ գալակտիկայի հեռավորությունը։ Եթե մենք դա կարողանանք կատարել նույն գալակտիկային պատկանող մի քանի այդպիսի աստղերի համար և մեր հաշվումներով ստացված հեռավորությունները միշտ նույնը լինեն, ապա կարող ենք վստահ լինել մեր գնահատականի ճշտության մեջ։ | Տիեզերքի ժամանակակից պատկերացման հիմքը դրվեց 1924֊ին, երբ ամերիկացի աստղագետ Էդվին Հաբլը ցույց տվեց որ տիեզերքում մեր գալակտիական միակը չէ։ Փաստորեն գոյություն ունեն շատ ուրիշ գալակտիկաներ, որոնք միմյանցից բաժանված են լայնատարած դատարկության գոտիներով։ Այդ բանը ապացուցելու համար Հաբլին հարկավոր էր որոշել գալակտիկաների հեռավորությունը, որոնք շատ հեռու լինելով մոտիկ գտնվող աստղերից, անշարժ են թվում։ Հաբլը ստիպված էր աննուղակի մի եղանակ օգտագործել այդ հեռավորությունները չափելու համար։ Աստղի թվացող պայծառությունը կախված է երկու գործոնից․ թե որքան լույս է արձակում այն (լուսատվություն) և ինչքան հեռու է գտնվում մեզանից։ Մենք կարող ենք չափել մոտիկ գտնվող աստղերի թվացող պայծառությունն ու հեռավորությունը, և դրանով որոշել աստղի լուսատվությունը։ Եվ հակառակը, եթե իմանանք աստղերի լուսատվություն այլ գալակտիկաներում, ապա նրանց թվացող պայծառությունը չափելով, կկարողանանք հաշվարկել նրանց հեռավորությունը։ Հաբլը նկատել էր, որ մեզ մոտիկ գտնվող որոշ տեսակի աստղեր մշտապես ունեն միևնույն լուսատվությունը և ենթադրել էր, որ եթե մենք նման աստղեր գտնենք այլ գալակտիկայում, ապա կարող ենք ընդունել, որ նրանց լուսատվությունը նույնն է և, այդպիսով հաշվել տվյալ գալակտիկայի հեռավորությունը։ Եթե մենք դա կարողանանք կատարել նույն գալակտիկային պատկանող մի քանի այդպիսի աստղերի համար և մեր հաշվումներով ստացված հեռավորությունները միշտ նույնը լինեն, ապա կարող ենք վստահ լինել մեր գնահատականի ճշտության մեջ։ | ||
| + | |||
| + | [[Պատկեր:H3 1.jpg|thumb]] | ||
Այս եղանակով Էդվին Հաբլը որոշեց 9 տարբեր գալակտիկաների հեռավորությունները։ Այսօր մեզ հայտնի է, որ մեր գալակտիկան մի քանի հարյուր հազար միլիոն գալակտիկաներից մեկն է տիեզերքում, որոնք ժամանակակից աստղադիտակների օգնությամբ կարելի է տեսնել, իսկ գալակտիկաներից յուրաքանչյուրն իր հերթին պարունակում է մի քանի հարյուր հազար միլիոն աստղ։ | Այս եղանակով Էդվին Հաբլը որոշեց 9 տարբեր գալակտիկաների հեռավորությունները։ Այսօր մեզ հայտնի է, որ մեր գալակտիկան մի քանի հարյուր հազար միլիոն գալակտիկաներից մեկն է տիեզերքում, որոնք ժամանակակից աստղադիտակների օգնությամբ կարելի է տեսնել, իսկ գալակտիկաներից յուրաքանչյուրն իր հերթին պարունակում է մի քանի հարյուր հազար միլիոն աստղ։ | ||
| Տող 232. | Տող 254. | ||
Այն փաստը, որ ինչ ուղղությամբ էլ նայես, տիեզերքը նույնն է երևում, առաջին հայացքից կարող է մեզ ստիպել մտածել, թե երկիրը տիեզերքում առանձնահատուկ դիրք ունի։ Մասնավորապես այն փաստը, որ մեզ թվում է, թե բոլոր գալակտիկաները հեռանում են մեզանից, կարող է այն տպավորությունը թողնել, թե մենք պետք է տիեզերքի կենտրոնում գտնվենք։ Չմոռանանք, սակայն, որ գոյություն ունի այլընտրական մի բացատրություն ևս, երբ տիեզերքը դիտարկվում է այլ գալակտիկաներից, այն դարձյալ ամեն ուղղությամբ նույնատեսակ կարող է երևալ։ Ինչպես ասվեց, սա Ֆրիդմանի երկրորդ ենթադրությունն էր։ Մենք այս ենթադրության կողմ կամ դեմ որևէ գիտական փաստարկ չունենք։ Սակայն համեստությունը պահանջում է ընդունել այն, այլապես շատ ուշագրավ կլիներ, որ տիեզերքը բոլոր ուղղություններով նույնատեսակ լիներ լոկ մեր շրջապատում, բայց ոչ տիեզերքի այլ կետերի համար։ Ֆրիդմանի մոդելում բոլոր գալակտիկաները ուղղակի իրարից հեռանում են։ Վիճակը նման է օդապարիկի, որի վրա որոշ թվով կետեր են նկարված, իսկ օդապարիկը ընդարձակվում է։ Ընդարձակման հետ ցանկացած երկու կետերի միջև եղած հեռավորությունը մեծանում է, սակայն չի կարելի ասել, թե որևէ կետ ընդարձակման կենտրոնն է։ Ավելին, որքան կետերն իրարից հեռու են, նրանք այնքան արագ կհեռանան միմյանցից։ Նույն ձևով, Ֆրիդմանի մոդելում գալակտիկաների՝ միմյանցից հեռանալու արագությունը համեմատական է նրանց միջև եղած հեռավորությանը։ Այսպիսով, դա կանխագուշակում է, որ գալակտիկայի կարմիր շեղումը պետք է ուղիղ համեմատական լինի մեզանից նրա ունեցած հեռավորությանը, ճիշտ այնպես, ինչպես հաստատել էր Հաբլը։ Չնայած իր մոդելի հաջողությանն ու Հաբլի դիտարկումների կանխագուշակմանը, Ֆրիդմանի աշխատանքներն Արևմուտքին անհայտ մնացին, մինչև 1935 թվականին ամերիկացի ֆիզիկոս Հովարդ Ռոբերտսոնն ու անգլիացի մաթեմատիկոս Արթուր Ուոքերը նման մոդելներ առաջարկեցին՝ բացատրելու համար Հաբլի հայտնագործությունը՝ տիեզերքի համաչափ ընդարձակման մասին։ | Այն փաստը, որ ինչ ուղղությամբ էլ նայես, տիեզերքը նույնն է երևում, առաջին հայացքից կարող է մեզ ստիպել մտածել, թե երկիրը տիեզերքում առանձնահատուկ դիրք ունի։ Մասնավորապես այն փաստը, որ մեզ թվում է, թե բոլոր գալակտիկաները հեռանում են մեզանից, կարող է այն տպավորությունը թողնել, թե մենք պետք է տիեզերքի կենտրոնում գտնվենք։ Չմոռանանք, սակայն, որ գոյություն ունի այլընտրական մի բացատրություն ևս, երբ տիեզերքը դիտարկվում է այլ գալակտիկաներից, այն դարձյալ ամեն ուղղությամբ նույնատեսակ կարող է երևալ։ Ինչպես ասվեց, սա Ֆրիդմանի երկրորդ ենթադրությունն էր։ Մենք այս ենթադրության կողմ կամ դեմ որևէ գիտական փաստարկ չունենք։ Սակայն համեստությունը պահանջում է ընդունել այն, այլապես շատ ուշագրավ կլիներ, որ տիեզերքը բոլոր ուղղություններով նույնատեսակ լիներ լոկ մեր շրջապատում, բայց ոչ տիեզերքի այլ կետերի համար։ Ֆրիդմանի մոդելում բոլոր գալակտիկաները ուղղակի իրարից հեռանում են։ Վիճակը նման է օդապարիկի, որի վրա որոշ թվով կետեր են նկարված, իսկ օդապարիկը ընդարձակվում է։ Ընդարձակման հետ ցանկացած երկու կետերի միջև եղած հեռավորությունը մեծանում է, սակայն չի կարելի ասել, թե որևէ կետ ընդարձակման կենտրոնն է։ Ավելին, որքան կետերն իրարից հեռու են, նրանք այնքան արագ կհեռանան միմյանցից։ Նույն ձևով, Ֆրիդմանի մոդելում գալակտիկաների՝ միմյանցից հեռանալու արագությունը համեմատական է նրանց միջև եղած հեռավորությանը։ Այսպիսով, դա կանխագուշակում է, որ գալակտիկայի կարմիր շեղումը պետք է ուղիղ համեմատական լինի մեզանից նրա ունեցած հեռավորությանը, ճիշտ այնպես, ինչպես հաստատել էր Հաբլը։ Չնայած իր մոդելի հաջողությանն ու Հաբլի դիտարկումների կանխագուշակմանը, Ֆրիդմանի աշխատանքներն Արևմուտքին անհայտ մնացին, մինչև 1935 թվականին ամերիկացի ֆիզիկոս Հովարդ Ռոբերտսոնն ու անգլիացի մաթեմատիկոս Արթուր Ուոքերը նման մոդելներ առաջարկեցին՝ բացատրելու համար Հաբլի հայտնագործությունը՝ տիեզերքի համաչափ ընդարձակման մասին։ | ||
| + | |||
| + | [[Պատկեր:H3 2.svg|thumb]] | ||
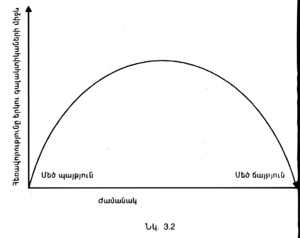
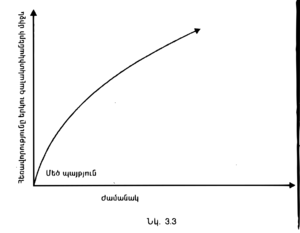
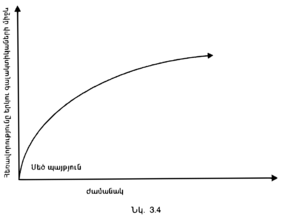
Այնուամենայնիվ, Ֆրիդմանն իր երկու հիմնական ենթադրությունների հիման վրա առաջարկել էր ընդարձակվող տիեզերքի միայն մեկ մոդել, թեև իրականում հնարավոր են երեքը։ Առաջին մոդելի դեպքում (որն առաջարկել էր Ֆրիդմանը) տիեզերքն ընդարձակվում է բավականին դանդաղ, ընդ որում տարբեր գալակտիկաների միջև գործող գրավիտացիոն ձգողությունն ստիպում է, որ ընդարձակումը դանդաղի և վերջապես կանգ առնի։ Այնուհետև գալակտիկաները սկսում են իրար մոտենալ, և տիեզերքը սեղմվում է։ Նկ․3.2֊ում ցույց է տրված, թե ինչպես է փոխվում երկու հարևան գալակտիկաների միջև եղած հեռավորությունը ժամանակի ընթացքում։ Այն սկսվում է զերոյից, աճում է մինչև առավելագույնը, ապա նվազում և նորից հասնում է զերոյի։ Երկրորդ մոդելը ցույց է տալիս, որ տիեզերքն այնքան արագ է ընդարձակվում, որ գրավիտացիոն ձգողականությունը երբեք չի կարողանում այն կասեցնել, թեև ինչ֊որ չափով դանդաղեցնում է։ Նկ․ 3.3֊ը ցույց է տալիս երկու հարևան գալակտիկաների միջհեռավորությունը այս մոդելում։ Այն սկսվում է զերոյից, աճում է արագ, իսկ ժամանակի ընթացքում երկու գալակտիկաները շարունակում են իրարից հեռանալ համաչափ արագությամբ։ Վերջապես, կա նաև լուծման 3-րդ մոդելը, որում տիեզերքը ընդարձակվում է հենց այնպիսի արագությամբ, որ նրա վերստին սեղմվելը (կոլապսվելը) հնարավոր չէ։ Նկ․ 3.4-ում ցույց է տրված, որ այդ դեպքում հեռավորությունը սկսում է զերոյից և աճում է մշտապես։ Սակայն այն արագությունը, որով գալակտիկաները հեռանում են իրարից, աստիճանաբար փոքրանում է, թեև զերոյի երբեք չի հասնում։ | Այնուամենայնիվ, Ֆրիդմանն իր երկու հիմնական ենթադրությունների հիման վրա առաջարկել էր ընդարձակվող տիեզերքի միայն մեկ մոդել, թեև իրականում հնարավոր են երեքը։ Առաջին մոդելի դեպքում (որն առաջարկել էր Ֆրիդմանը) տիեզերքն ընդարձակվում է բավականին դանդաղ, ընդ որում տարբեր գալակտիկաների միջև գործող գրավիտացիոն ձգողությունն ստիպում է, որ ընդարձակումը դանդաղի և վերջապես կանգ առնի։ Այնուհետև գալակտիկաները սկսում են իրար մոտենալ, և տիեզերքը սեղմվում է։ Նկ․3.2֊ում ցույց է տրված, թե ինչպես է փոխվում երկու հարևան գալակտիկաների միջև եղած հեռավորությունը ժամանակի ընթացքում։ Այն սկսվում է զերոյից, աճում է մինչև առավելագույնը, ապա նվազում և նորից հասնում է զերոյի։ Երկրորդ մոդելը ցույց է տալիս, որ տիեզերքն այնքան արագ է ընդարձակվում, որ գրավիտացիոն ձգողականությունը երբեք չի կարողանում այն կասեցնել, թեև ինչ֊որ չափով դանդաղեցնում է։ Նկ․ 3.3֊ը ցույց է տալիս երկու հարևան գալակտիկաների միջհեռավորությունը այս մոդելում։ Այն սկսվում է զերոյից, աճում է արագ, իսկ ժամանակի ընթացքում երկու գալակտիկաները շարունակում են իրարից հեռանալ համաչափ արագությամբ։ Վերջապես, կա նաև լուծման 3-րդ մոդելը, որում տիեզերքը ընդարձակվում է հենց այնպիսի արագությամբ, որ նրա վերստին սեղմվելը (կոլապսվելը) հնարավոր չէ։ Նկ․ 3.4-ում ցույց է տրված, որ այդ դեպքում հեռավորությունը սկսում է զերոյից և աճում է մշտապես։ Սակայն այն արագությունը, որով գալակտիկաները հեռանում են իրարից, աստիճանաբար փոքրանում է, թեև զերոյի երբեք չի հասնում։ | ||
| + | |||
| + | [[Պատկեր:H3 3.svg|thumb]] | ||
Ֆրիդմանի առաջին մոդելի ուշագրավ առանձնահատկությունն այն է, որ նրանում տիեզերքը տարածության մեջ անսահման չէ, բայց տարածությունն էլ որևէ սահմանագիծ չունի։ Ձգողության ուժն այնքան ուժեղ է, որ տարածությունն ինքն իր վրա կորացել է, ինչպես երկրի մակերևույթը։ Եթե մեկը ճամբորդի մի որոշակի ուղղությամբ երկրագնդի մակերևույթով, նա երբեք անանցանելի արգելքի չի հանդիպի և դուրս չի գլորվի այնտեղից, այլ ի վերջո կգա կհասնի այնտեղ, որտեղից դուրս էր եկել։ Ֆրիդմանի առաջին մոդելում տիեզերքը հենց այդպիսին է, սակայն եռաչափ է և ոչ թե երկչափ, ինչպես երկրագնդի մակերևույթը։ Չորրորդ չափը՝ ժամանակը, նույնպես վերջավոր է՝ նման երկու ծայր կամ սահմանագիծ՝ մի սկիզբ և մի վերջ ունեցող գծի։ Հետագայում կտեսնենք, որ երբ ընդհանուր հարաբերականույթունը միացվի քվանտային մեխանիկայի անորոշության սկզբունքի հետ, հնարավոր կդառնա, որ այդ երկուսն էլ՝ և՛ տարածությունը, և՛ ժամանակը, վերջավոր լինեն՝ առանց ծայրակետի սահմանագծի։ | Ֆրիդմանի առաջին մոդելի ուշագրավ առանձնահատկությունն այն է, որ նրանում տիեզերքը տարածության մեջ անսահման չէ, բայց տարածությունն էլ որևէ սահմանագիծ չունի։ Ձգողության ուժն այնքան ուժեղ է, որ տարածությունն ինքն իր վրա կորացել է, ինչպես երկրի մակերևույթը։ Եթե մեկը ճամբորդի մի որոշակի ուղղությամբ երկրագնդի մակերևույթով, նա երբեք անանցանելի արգելքի չի հանդիպի և դուրս չի գլորվի այնտեղից, այլ ի վերջո կգա կհասնի այնտեղ, որտեղից դուրս էր եկել։ Ֆրիդմանի առաջին մոդելում տիեզերքը հենց այդպիսին է, սակայն եռաչափ է և ոչ թե երկչափ, ինչպես երկրագնդի մակերևույթը։ Չորրորդ չափը՝ ժամանակը, նույնպես վերջավոր է՝ նման երկու ծայր կամ սահմանագիծ՝ մի սկիզբ և մի վերջ ունեցող գծի։ Հետագայում կտեսնենք, որ երբ ընդհանուր հարաբերականույթունը միացվի քվանտային մեխանիկայի անորոշության սկզբունքի հետ, հնարավոր կդառնա, որ այդ երկուսն էլ՝ և՛ տարածությունը, և՛ ժամանակը, վերջավոր լինեն՝ առանց ծայրակետի սահմանագծի։ | ||
| + | |||
| + | [[Պատկեր:H3 4.svg|thumb]] | ||
Այն միտքը, թե կարելի է տիեզերքի շուրջ պտտվել և վերադառնալ ելման կետ, լավ գիտական վիպագրության նյութ է, բայց դա գործնական մեծ նշանակություն ունենալ չի կարող, որովհետև կարելի է ցույց տալ, որ մինչև մարդ ավարտի իր ճամբորդությունը, տիեզերքը կսեղմվի (կկոլապսվի) իր զերոյական ծավալին։ Որպեսզի ճամփորդը վերադառնա ելման կետ տիեզերքի վախճանից առաջ, նա պետք լույսից ավելի արագ շարժվի, ինչը հնարավոր չէ։ | Այն միտքը, թե կարելի է տիեզերքի շուրջ պտտվել և վերադառնալ ելման կետ, լավ գիտական վիպագրության նյութ է, բայց դա գործնական մեծ նշանակություն ունենալ չի կարող, որովհետև կարելի է ցույց տալ, որ մինչև մարդ ավարտի իր ճամբորդությունը, տիեզերքը կսեղմվի (կկոլապսվի) իր զերոյական ծավալին։ Որպեսզի ճամփորդը վերադառնա ելման կետ տիեզերքի վախճանից առաջ, նա պետք լույսից ավելի արագ շարժվի, ինչը հնարավոր չէ։ | ||
| Տող 270. | Տող 298. | ||
Այս պատճառով, 1970֊ականների սկզբին ստիպված եղանք մեր ուշադրությունը շեղել արտակարգ ծավալունի տեսությունից դեպի արտակարգ փոքրի տեսությունը, ըմբռնելու համար տիեզերքի բուն էությունը։ Հաջորդ գլխում մենք կնկարագրենք քվանտային մեխանիկայի էությունը, որպեսզի պատրաստ լինենք հետագայում փորձել միավորելու այս երկու մասնակի հզոր տեսությունները մեկում՝ գրավիտացիոն քվանտային տեսության մեջ։ | Այս պատճառով, 1970֊ականների սկզբին ստիպված եղանք մեր ուշադրությունը շեղել արտակարգ ծավալունի տեսությունից դեպի արտակարգ փոքրի տեսությունը, ըմբռնելու համար տիեզերքի բուն էությունը։ Հաջորդ գլխում մենք կնկարագրենք քվանտային մեխանիկայի էությունը, որպեսզի պատրաստ լինենք հետագայում փորձել միավորելու այս երկու մասնակի հզոր տեսությունները մեկում՝ գրավիտացիոն քվանտային տեսության մեջ։ | ||
| + | |||
| + | |||
| + | ==4== | ||
| + | |||
| + | Անորոշության սկզբունքը | ||
| + | |||
| + | Գիտական մտքի հաջողությունները, մասնավորապես Նյուտոնի ձգողականության տեսությունը հիմք դարձան, որ տասնիներորդ դարի սկզբին ֆրանսիացի գիտնական մարկիզ դը Լապլասը պնդի, որ տիեզերքը լրիվ որոշադրական (դետերմինիստական) է, այսինքն՝ կամքի ազատություն չի կարող լինել։ Լապլասը գտնում էր, որ պետք է գոյություն ունենա գիտական օրենքների մի շարք, որով մենք ի վիճակի լինենք կանխատեսել տիեզերքում տեղի ունենալիք ամեն ինչ, եթե միայն մեզ հայտնի է տիեզերքի վիճակը որոշակի ժամանակում։ Օրինակ, եթե մեզ հայտնի են արևի և մոլորակների դիրքերն ու արագությունները ժամանակի որևէ պահի, ապա, օգտվելով Նյուտոնի օրենքներից, կարող ենք հաշվել Արեգակնային համակարգի վիճակը որևէ այլ ժամանակում։ Այստեղ ուշադրությունն ակնհայտ է, սակայն Լապլասն ավելի առաջ անցավ և ենթադրեց, որ նման օրենքներ կան ամենուրեք, ընդհուպ մինչև մարդկային վարքագիծը։ | ||
| + | |||
| + | Գիտական որոշադրության ուսմունքը շատերի կողմից դիմադրության հանդիպեց․ նրանք մտածում էին, որ դա սահմանափակում էր աշխարհի գործերին Աստծո ազատ միջամտությունը։ Այնուամենայնիվ, գիտության մեջ այն շարունակեց մնալ որպես սովորական մի ենթադրություն մինչև քսաներորդ դարի սկիզբը։ Այդ տեսակետից հրաժարվելու առաջին նշաններից մեկն ակնհայտ դարձավ, երբ անգլիացի գիտնականներ լորդ Ռելեն և պ֊ն Ջեյմս Ջինսը ցույց տվեցին, որ տաք առարկայի կամ մարմնի, ինչպիսին աստղն է, կողմից էներգիայի առաքումը կատարվում է անսահմանափակ քանակով։ Համաձայն այդ ժամանակ տարածված կարծիքի, տաք մարմինը էլեկտրամագնիսական ալիքներ է արձակում (ռադիոալիքներ, տեսանելի լույս կամ ռենտգենյան ճառագայթներ) բոլոր հաճախականություններով համաչափ։ Օրինակ, կարծում էին, որ տաք մարմինը նույնաքանակ էներգիա է ճառագայթում ինչպես մեկից մինչև երկու միլիոն միլիոն ալիք վայրկյանում, այնպես երկուսից մինչև երեք միլիոն միլիոն ալիք վայրյկանում տիրույթենրի հաճախականություններով։ Այսինքն, քանի որ ալիքների թիվը վայրկյանում սահմանափակված չէ, ապա ճառագայթված գումարային էներգիան նույնպես պետք է անսահմանափակ լինի։<ref>Ըստ Ռելե֊Ջինսի օրենքի, ճառագայթման էներգիան պետք է անսահման աճի ալիքի հաճախականության մեծությամբ, հասնելով արտասովոր մեծ արժեքների խորը ուլտրամանուշակագույն և ավելի կարճալիք տիրույթներում (հայտնի է է որպես, այսպես կոչված, «ուլտրամանուշակագույն աղետ»), բայց որի առավելագույն արժեքի, հաճախականության հետագա աճի հետ նվազում է։ Հաճախականությունների ամբողջ տիրույթում էներգիայի ճիշտ բաշխումը նկարագրվում է միայն քվանտային պատկերացումներով։</ref> | ||
| + | |||
| + | Այս ակնհայտ տարօրինակություններից խուսափելու համագերմանացի գիտնական Մաքս Պլանկը 1900֊ին մի միտք արտահայտեց․ այն է՝ ճառագայթող մարմինը չի կարող լուսային, ռենտգենյան կամ այլ ալիքային էներգիա առաքել կամայական քանակությամբ, այլ առաքում է որոշակի բաժիններով, որոնք նա անվանեց քվանտ։ Ավելին, յուրաքանչյուր քվանտ ունի որոշակի քանակի էներգիա, որն այնքան մեծ է, որքան բարձր է ալիքի հաճախականությունը, այնպես որ, բավականաչափ բարձր հաճախականության դեպքում մեկ քվանտի համար պահանջվում է ավելի էներգիա, քան հնարավոր է։ Այսպիսով բարձր հաճախականությունների տակ ճառագայթումը պետք է նվազի, և դրանով իսկ մարմնի էներգիա կորցնելու արագությունը պիտի լինի վերջավոր։ | ||
| + | |||
| + | Թեև քվանտային հիպոթեզը շատ լավ բացատրեց տաք մարմնի ճառագայթման բնույթը, բայց նրա նշանակությունը որոշադրական առումով չիրականացավ մինչև 1926 թ․, երբ մի այլ գերմանացի գիտնական՝ Վերներ Հայզենբերգը ձևակերպեց իր նշանավոր անորոշության սկզբունքը։ Մի մասնիկի ապագա դիրքն ու արագությունը կանխագուշակելու համար մարդ պետք է կարողանա մեծ ճշտությամբ որոշել նրա ներկա դիրքն ու արագությունը։ Դրա համար պետք է մասնիկը լուսավորել։ | ||
| + | |||
| + | Լույսի ալիքների մի մասը կցրվի մասնիկի կողմից, և դու ցույց կտա նրա դիրքը։ Սակայն հնարավոր չէ մասնիկի դիրքը որոշել ավելի մեծ ճշտությամբ, քան լույսի ալիքի գագաթների միջև եղած հեռավորությունը։ Հետևաբար մասնիկի դիրքը ճշգրիտ որոշելու համար անհրաժեշտ է օգտագործել կարճ ալիքի երկարություն ունեցող լույս։ Պլանկի քվանտային տեսության համաձայն, չի կարելի օգտագործել լույսի կամայական փոքր քանակություն, այլ առնվազն մեկ քվանտ։ Մասնիկի և այդ քվանտի բախման հետևանքով առաջինի արագությունը կմեծանա, որի չափը դժվար է կանխորոշել։ Ավելին, դիրքի որոշման բարձր ճշտության համար անհրաժեշտ է օգտագործել կարճալիք լույս, այսինքն՝ մեծ էներգիա ունեցող քվանտ։ Հետևաբար, մասնիկի արագության խոտորումը կլինի ավելի մեծ։ Այլ խոսքով ասած, որքան մեծ ճշտությամբ որոշվի մասնիկի դիրքը, այնքան փոքր կլինի նրա արագության որոշման ճշտությունը, և՝ հակառակը։ Հայզենբերգը ցույց տվեց, որ մասնիկի դիրքի և արագության որոշման անորոշությունների և զանգվածի արտադրյալը չի կարող ավելի փոքր լինել մի որոշակի մեծությունից, որը հայտնի է որպես Պլանկի հաստատուն։ Ավելին, այդ սահմանը կախված չէ այն բանից, թե ինչպիսի մասնիկ է դա, և ինչպես են որոշվում նրա դիրքն ու արագությունը։ Հայզենբերգի անորոշության սկզբունքը աշխարհի հիմնարար, անխուսափելի հատկանիշն է։ | ||
| + | |||
| + | Անորոշության սկզբունքը մեծ նշանակություն ունեցավ աշխարհընկալման առումով։ Այս բանը նույնիսկ ավելի քան հիսուն տարի անց դեռևս լրիվ չի գնահատվել փիլիսոփաների կողմից և բանավեճի առիթ է տալիս նաև այսօր։ Անորոշության սկզբունքը վերջ տվեց գիտության տեսության մասին լապլասյան երազանքին, այսինքն՝ տիեզերքի լրիվ որոշադրական պատկերացմանը։ Եթե հնարավոր չէ նույնիսկ տիեզերքի այժմյան վիճակը ճշգրտորեն որոշել, ապա, իհարկե, չի կարեի ճշգրտորեն կանխագուշակել նրա ապագա դեպքերը։ Թերևս կարելի է ենթադրել, որ մի գերբնական էակ կարող է դիտարկել տիեզերքի ներկա վիճակը առանց այն խախտելու, և նրա համար կա դեպքերի ընթացքը կատարելապես որոշող օրենքների մի շարք։ Այնուամենայնիվ, տիեզերքի այդպիսի մոդելները մեզ՝ սովորական մահկանացուներիս համար ոչ մի հետաքրքրություն չեն ներկայացնի։ | ||
| + | |||
| + | Թվում է, լավագույնը, Օկամի ածելի կոչված խնայողության սկզբուքն օգտագործելն ու տեսությունից կտրել, դեն նետելն է այն ամենը, ինչն ուղղակի դիտարկման ենթակա չէ։ Ահա այսպիսի մոտեցմամբ Հայզենբերգը, Էրվին Շրյոդինգերը և Պոլ Դիրակը 1920֊ական թվականներին մեխանիկան վերաձևակերպեցին մի նոր տեսության, որը կոչվում է քվանտային մեխանիկա և հիմնված է անորոշության սկզբունքի վրա։ Այս տեսության մեջ մասնիկները չեն առանձնանում ճշգրիտ որոշված դիրքերով և արագություններով, դրանք հնարավոր չէ դիտարկել։ Ընդհակառակը, դրանք գտնվում են քվանտային վիճակում, որը դիրքի ու արագության համակցություն է։ | ||
| + | |||
| + | Ընդհանուր առմամբ տվյալ դեպքի համար քվանտային մեխանիկան որոշակի արդյունք չի կանխագուշակում։ Փոխարենը կանխագուշակում է հնարավոր մի քանի տարբեր հետևանքներ և տալիս յուրաքանչյուրի հավանականությունը։ Այսպես, եթե նույնասկիզբ մեծ թվով համանման համակարգերի համար կատարվել են նույն չափումները, արդյունքը որոշակի թվով դեպքերի համար կլինի A, այլ թվով դեպքերի համար՝ B և այլն։ Կարելի է կանխագուշակել, թե արդյունքը մոտավորապես քանի անգամ կլինի A կամ B, բայց հնարավոր չէ կանխագուշակել յուրաքանչյուր չափման կոնկրետ արդյունքները։ Հետևաբար, քվանտային մեխանիկան գիտության մեջ մտցնում է պատահականության կամ անկանխագուշակելիության անխուսափելի մի տարր։ Էյնտշեյնը խիստ կերպով առարկեց դրան, հակառակ այն բանի, որ հենց ինքը շատ մեծ դեր խաղաց այդ գաղափարի զարգացման գործում։ Բավական է ասել, որ նրան Նոբելյան մրցանակ շնորհվեց հենց այն մեծ ավանդի համար, որ նա ներդրել էր քվանտային տեսության ստեղծման գործում։ Այնուամենայնիվ, Էյնշտեյնը երբեք չհաշտվեց այն մտքի հետ, որ տիեզերքը կառավարվում է պատահականությամբ։ Նրա տարակուսանքը ամփոփված է նրա իսկ հայտնի հայտարարության մեջ․ «Աստված զառ չի խաղում»։ Սակայն, համարյա բոլոր գիտնականները ընդունեցին քվանտային մեխանիկան, որովհետև այն կատարելապես համընկնում էր փորձնական տվյալների հետ։ Արդարև քվանտային մեխանիկան դարձավ արտակարգ հաջողված մի տեսություն և համարյա ժամանակակից գիտության ու տեխնոլոգիայի հիմքն է։ Այս տեսությունը կառավարում է տրանզիստորների և միասնական շղթաների աշխատանքը, որոնք հեռուսատացույցների, հաշվողական մեքենաների և նման էլեկտրոնային սարքերի հիմնական բաղադրամասերն են։ Քվանտային մեխանիկան նաև կենսաբանության և ժամանակակից քիմիայի հիմքն է։ Ֆիզիկական գիտությունների այն բնագավառները, որտեղ քվանտային մեխանիկան առ այսօր հիմնավոր կերպով մուտք չի գործել, տիեզերքի ձգողականության ու խոշորամասշտաբ կառուցվածքի հարցերն են։ | ||
| + | |||
| + | Չնայած լույսը կազմված է ալիքներից, շարժվում է ալիքաձև, սակայն Պլանկի քվանտային հիպոթեզը պնդում է, որ որոշ դեպքերում այն իրեն պահում է այնպես, կարծես մասնիկը կազմված լինի և կարող է առաքվել կամ կլանվել միայն մասերով՝ քվանտներով։ | ||
| + | |||
| + | [[Պատկեր:H4 1.svg|thumb]] | ||
| + | |||
| + | Մյուս կողմից՝ Հայզենբերգի անորոշության սկզբունքից բխում է, որ մասնիկները որոշ տեսակետից իրենց պահում են որպես ալիք, այսինքն՝ նրանք որոշակի տեղ չեն գրավում, այլ «ամպաձև», թեև որոշակի հավանականությամբ, բաշխված են տվյալ տարածքում։ Քվանտային մեխանիկայի տեսությունը հիմնված է բոլորովին նոր տեսակի մաթեմատիկայի վրա, որ իրական աշխարհն այլևս չի նկարագրում որպես մասնիկներ կամ ալիքներ, այլ որպես ալիքների ու մասնիկների մի երկվություն։ Որոշ նպատակներով հարմար է մասնիկները դիտարկել որպես ալիքներ, այլ նպատակների համար՝ ալիքները որպես մասնիկներ։ Դրա կարևոր հետևանքներից մեկը, որը կարելի է տեսնել, կոչվում է ինտերֆերենցիայի երևույթ՝ ալիքների և մասնիկների երկու շարքի միջև։ Ենթադրենք ալիքի մի շարքի գագաթները համընկել են մյուս շարքի փոսերի հետ։ Այդ դեպքում ալիքների երկու շարքը կոչնչացնեն միմյանց, արտաքուստ սպասվող՝ ալիքների ուժեղացման փոխարեն։ | ||
| + | |||
| + | Լույսի ալիքների ինտերֆերենցիայի գեղեցիկ մի օրինակ է օճառի պղպջակի վրա գուների առաջացման երևույթը։ Դրա պատճառը պղպջակը կազմող ջրի բարակ թաղանթի՝ երկու կողմերից լույսի անդրադարձումն է։ Սպիտակ լույսը կազմված է տարբեր ալիքի երկարություն ունեցող կամ տարբեր գույն ունեցող լույսի ալիքներից։ Պղպջակի մի կողմից որոշ ալիքի երկարություններ ունեցող լույսի անդրադարձող ալիքների գագաթները կարող են հանդիպել մյուս կողմից անդրադարձող համապատասխան ալիքների փոսերին։ Այդ երկարության ալիքների համապատասխանող գույները կբացակայեն անդրադարձող լույսի մեջ, որի հետևանքով այն կերևա գունավոր։ | ||
| + | |||
| + | [[Պատկեր:H4 2.svg|thumb]] | ||
| + | |||
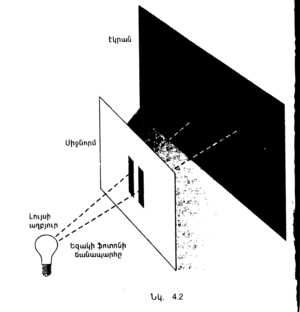
| + | Ինտերֆերենցիայի երևույթը դիտվում է նաև մասնիկների համար՝ քվանտային մեխանիկայի ներմուծած երկվության շնորհիվ։ Հանրահայտ օրինակ է, այսպես կոչված, երկու նեղ ճեղքերի փորձը (նկ․ 4.2): | ||
| + | |||
| + | Պատկերացնենք երկու զուգահեռ նեղ ճեղքեր ունեցող մի միջնապատ։ Այդ միջնապատի մի կողմում տեղադրենք որոշակի գույնի (այսինքն՝ որոշակի ալիքի երկարության) լուսաղբյուր։ Լույսի մեծ մասը կդիպչի միջնապատին, իսկ փոքր մասը կանցնի ճեղքերից։ Այժմ ենթադրենք միջնապատի մյուս կողմում տեղադրված է էկրան։ Էկրանի որոշ կետերի վրա կընկնեն ճեղքից անցած ալիքները։ Սակայն, սովորաբար, այն հեռավորությունը, որն անցնում լույսը աղբյուրից մինչև էկրան՝ երկու ճեղքերի միջով, տարբեր է։ Դա նշանակում է, որ ճեղքերից անցած ալիքները միևնույն փուլում չեն լինի էկրանին հասնելիս, ուստի էկրանի վրա որոշ տեղերում երկու ճեղքերից եկող ալիքները կոչնչացնեն միմյանց, այլ տեղերում՝ կուժեղացնեն։ Արդյունքում ստացվում է լուսավոր և խավար շերտերից կազմված լույսի ինտերֆերենցիայի նախշանկար։ | ||
| + | |||
| + | Ուշագրավ է այն փաստը, որ ճիշտ նման պատկեր է ստացվում, երբ լույսի աղբյուրի փոխարեն դրվում է մասնիկների աղբյուր, օրինակ, որոշակի արագությամբ շարժվող էլեկտրոններ (դա նշանակում է, որ համապատասխան ալիքներն ունեն որոշակի երկարություն)։ Խիստ հատկանշական է, որ երբ միջնապատի վրա մեկ ճեղք կա, էկրանին շերտեր չեն ստացվում, այլ ստացվում է էլեկտրոնների կանոնավոր բաշխում։ Կարելի է մտածել, որ երկրորդ ճեղքը բացելիս էկրանի վրա յուրաքանչյուր կետին հարվածող էլեկտրոնների թիվը կաճի, բայց քանի որ տեղի է ունենում ինտերֆերենցիա, նշանակում է որոշ տեղերում էլեկտրոնների թիվը իրականում նվազում է։ Թվում է, թե, եթե էլեկտրոնները մեկ առ մեկ շարժվեն դեպի ճեղքերը, ապա նրանցից յուրաքանչյուրը միաժամանակ կարող է անցնել ճեղքերից միայն մեկով, կարծես թե էլեկտրոնի համար ճեղքերից միայն մեկը գոյություն ունենա, որով անցնելով էլեկտրոնները պետք է հավասարաչափ բաշխվեն էկրանի վրա։ Իրականում, սակայն, էլեկտրոնների մեկ առ մեկ անցման դեպքում անգամ ստացվում է շերտավոր պատկեր։ Մնում է եզրակացնել, որ յուրաքանչյուր էլեկտրոն պետք է անցնի երկու ճեղքերով միաժամանակ։ | ||
| + | |||
| + | Մասնիկների ինտերֆերենցիայի երևույթի հայնտագործումը վճռական նշանակություն ունեցավ ատոմի կառուցվածքի էությունը իրապես ըմբռնելու համար։ Ատոմները քիմիայի և կենսաբանության հիմքը կազմող միավորներն են և այն շինարարական աղյուսները, որոնցով և՛ մենք, և՛ մեր շուրջ եղած ամեն ինչ կառուցված է։ Մեր դարաշրջանի սկզբներին մտածում էին, որ ատոմը կազմված է դրական լիցք ունեցող միջուկից, որի շուրջը շրջանաձև պտտվում են բացասական լիցք ունեցող էլեկտրոնները, ինչպես մոլորակները՝ արևի շուրջ։ Ենթադրվում էր, որ դրական և բացասական լիցքերի միջև ձգողությունը չեզոքացվում է, և էլեկտրոնները մնում են իրենց ուղեծրերում, ճիշտ այնպես, ինչպես արևի և մոլորակների միջև գրավիտացիոն ձգողությունն է մոլորակներին պահում իրենց ուղեծրերում։ Սակայն քվանտային մեխանիկայից առաջ եղած մեխանիկայի և էլեկտրականության օրենքներից հետևում էր, որ էլեկտրոնները աստիճանաբար էներգիա կորցնելով՝ պարուրաձև հետագծով պետք է ընկնեին միջուկի վրա։ Սա նշանակում էր, ատոմը և հետևապես նյութը ամբողջությամբ վերցրած, պիտի արագորեն կոլապսվեին մինչև անսահման խտություն ունեցող վիճակի։ Այս հարցն իր մասնակի լուծումը գտավ 1913 թվականին դանիացի գիտնական Նիլս Բորի կողմից։ Նա ենթադրեց, որ էլեկտրոնները չեն կարող պտտվել կենտրոնական միջուկից ցանկացած հեռավորության վրա, այլ շատ որոշակի, յուրահատուկ հեռավորությունների վրա են պտտվում։ Եթե ենթադրենք, որ միաժամանակ մեկ կամ երկու էլեկտրոն կարող են պտտվել այդ հեռավորություններից յուրաքանչյուրով, ապա դա կլուծի ատոմի կոլապսի խնդիրը, քանի որ էլեկտրոնները չեն կարող ամենափոքր հեռավորություն և էներգիա ունեցող ուղեծրից ավելի մոտիկ հեռավորության ուղեծիր անցնել։ | ||
| + | |||
| + | Այս մոդելը շատ գեղեցիկ կերպով բացատրեց ամենապարզ ատոմի՝ ջրածնի կառուցվածքը, որի միջուկի շուրջը պտտվում է միայն մեկ էլեկտրոն։ Բայց հստակ չէր, թե այն ինչպես կարելի է տարածել ավելի բարդ ատոմների վրա։ Ավելին, սահմանափակ թվով թույլատրելի ուղեծրերի հարցը շատ կամայական է թվում։ Քվանտային մեխանիկայի նոր տեսությունը հաջողությամբ լուծում տվեց այս դժվարին հարցին։ Բացահայտվեց, որ միջուկի շուրջ պտտվող էլեկտրոնը կարելի է պատկերացնել որպես ալիք, որի երկարությունը կախված է նրա արագությունից։ Համապատասխան ուղեծրերի համար երկարությունը հավասար է ամբողջական թվով (հակառակ կոտորակային թվի) ալիքի երկարության։ Այդ ուղեծրի համար ալիքի գագաթի փոսը յուրաքանչյուր պտույտի համար կլինի նույն դիրքում, հետևաբար, ալիքները կգումարվեն․ այդ ուղեծրերը համապատասխանում են Բորի թույլատրելի ուղեծրերին։ Իսկ այն ուղեծրերը, որոնց երկարությունը հավասար չէ ամբողջական թվով ալիքի երկարության, թույլատրելի չեն, որովհետև այդ դեպքում յուրաքանչյուր գագաթ հաջորդ շրջապտույտի ժամանակ կոչնչացվի համապատասխան փոսի կողմից։ | ||
| + | |||
| + | Ալիք֊մասնիկային երկվության մասին տեսանելի պատկերացում է տալիս ամերիկացի գիտնական Ռիչարդ Ֆեյնմանի առաջարկած, այսպես կոչված, պատմությունների գումարը։ Այս մոտեցման մեջ չի ենթադրվում, որ մասնիկը տարածություն ժամանակի մեջ ունի մի ուղի կամ մի պատմություն, ինչպես դասական կամ ոչ քվանտային տեսության մեջ։ Փոխարենը ենթադրվում է, որ մասնիկը A֊ից B գնում է ամեն հնարավոր ճանապարհով։ Յուրաքանչյուր ճանապարհ բնութագրվում է երկու թվով․ մեկը համապատասխանում է ալիքի չափին, մյուսը՝ դիրքին բոլորաշրջանի (ցիկլի) մեջ (այսինքն՝ որտեղ է գագաթին, որտեղ՝ փոսում)։ A֊ից B գնալու հավանականությունը կարեի է իմանալ բոլոր ուղիներով գնացող ալիքները գումարելով։ Ընդհանրապես, եթե մի խումբ հարևան ուղիներ համեմատենք, ապա դրանցում ալիքների դիրքերը կամ փուլերը իրարից շատ տարբեր կլինեն։ Սա նշանակում է, որ այդ ուղիներով շարժվող ալիքները գրեթե ճշգրտորեն իրար կմարեն։ Հետևաբար, այդ ուղիները թույլատրելի չեն լինի։ Սակայն որոշ հարևան ուղիների համար ալիքների փուլերը շատ չեն տարբերվի իրարից։ Այս ուղիների ալիքները իրար չեն մարի, այսինքն այս ուղիները համապատասխանում են Բորի թույլատրելի ուղեծրերին։ | ||
| + | |||
| + | Օգտագործելով այս գաղափարը՝ մշակվեց համապատասխան մաթեմատիկական բանաձև և հնարավոր դարձավ հաշվել բոլոր թույլատրված ուղեծրերը ավելի բարդ, բազմաէլեկտրոն ատոմների համար, նույնիսկ մոլեկուլների համար, որոնք կազմված են մեկից ավելի միջուկների շուրջ պտտվող էլեկտրոններով իրար հետ կապված ատոմներից։ Քանի որ մոլեկուլների կառուցվածքը և միմյանց հետ նրանց փոխազդեցություններն ընկած են քիմիայի և կենսաբանության հիմքում, ապա քվանտային մեխանիկան թույլ է տալիս սկզբունքորեն կանխորոշել գրեթե այն ամենը, ինչ կատարվում է մեր շրջապատում, իհարկե, անորոշության սկզբունքի սահմաններում։ (Գործնականում, սակայն, մեծ թվով էլեկտրոններ և միջուկներ պարունակող համակարգերի և դրանց փոխազդեցությունների համար հաշվումներն այն աստիճան բարդ են, որ համարյա անհնար է իրականացնել)։ | ||
| + | |||
| + | Թվում է, թե Էյնշտեյնի հարաբերականության ընդհանուր տեսությունը նկարագրում է տիեզերքի խոշորամասշտաբ կառուցվածքը։ Դա այն է, ինչը կոչվում է դասական տեսություն, որը հաշվի չի առնում քվանտային մեխանիկայի անորոշության սկզբունքը, ինչը հարկավոր է մյուս տեսությունների հետ ներդաշնակ լինելու համար։ Սակայն այս անտեսումը հարաբերականության ընդհանուր տեսության կանխատեսումների և դիտարկումների միջև հսկայական պատճառ չի դառնում, որովհետև գրավիտացիոն դաշտը, որի հետ մենք առնչվում ենք շատ թույլ է։ Բայց, ինչպես ցույց են տալիս վերը նշված եզակիության թեորեմները, ձգողական դաշտը խիստ ուժեղանում է առնվազն երկու պարագայում՝ սև խոռոչների և Մեծ պայթյունի համար։ Այսպիսի ուժեղ դաշտերում քվանտային մեխանիկայի դերը շատ կարևոր է։ Այլ կերպ ասած, դասական հարաբերականության ընդհանուր տեսությունը՝ կանխագուշակելով անսահման խիտ կետերի առաջացումը, նախանշեց իր սեփական անզորությունը ճիշտ այնպես, ինչպես դասական (այսինքն՝ ոչ քվանտային) մեխանիկան կանխագուշակեց իր կործանումը, կանխագուշակելով, որ ատոմները պիտի կոլապսվեն մինչև անսահման մեծ խտության։ Մենք դեռևս չունենք կատարյալ և հետևողական մի տեսություն, որը միավորեր ընդհանուր հարաբերականությունը և քվանտային մեխանիկան, բայց գիտենք, թե այդպիսի միացյալ տեսությունն ինչպիսի հատկանիշներ պիտի ունենա։ Թե այն ինչպիսի հետևանքներ կարող է ունենալ սև խոռոչների և Մեծ պայթյունի էությունները բացատրելու համար, կնգարագրվի հաջորդ գլուխներում։ Մի պահ, սակայն, անդրադառնանք ժամանակակից այն աշխատանքներին, որոնք փորձում են բնության մեջ գործող այլ ուժերի մասին մեր ունեցած պատկերացումներն ամփոփել մի եզակի, միացյալ քվանտային տեսության մեջ։ | ||
| + | |||
| + | |||
| + | ==5== | ||
| + | |||
| + | Տարրական մասնիկների և բնության ուժերը | ||
| + | |||
| + | Արիստոտելը հավատացած էր, որ տիեզերքում ամեն ինչ կազմված է չորս հիմնական տարրերից՝ հողից, օդից, կրակից և ջրից։ Այդ տարրերի վրա ազդում է երկու ուժ․ ծանրությունը, որի շնորհիվ հողն ու ջուրը ձգտում են ներքև իջնել, և թեթևությունը, որը օդի ու կրակի վեր բարձրանալու պատճառն է։ Տիեզերքի պարունակության այս բաժանումը նյութի և ուժերի՝ օգտագործվում է մինչև օրս։ | ||
| + | |||
| + | Արիստոտելը կարծում էր, որ նյութն անվերջ բաժանելի է, այն է՝ կարելի է նյութն անվերջ բաժանել մասերի և ոչ ոք չի գտնի նյութի այնպիսի հատիկ, որն այլևս բաժանել հնարավոր չլինի։ Սակայն Դեմոկրիտը և մի քանի հույներ պնդում էին, որ նյութն, ըստ էության, հատիկային բնույթ ունի և ամեն ինչ կառուցված է մեծ թվով տարբեր տեսակի ատոմներից (ատոմ բառը հունարեն նշանակում է «անբաժանելի»)։ Այդ վեճը շարունակվեց դարեր՝ առանց կողմերից որևէ մեկի ճշմարտացիությունը հաստատող իրական ապացույցների, մինչև 1803֊ին անգլիացի քիմիկոս և ֆիզիկոս Ջոն Դալտոնն ուշադրություն հրավիրեց այն փաստի վրա, որ քիմիական միացությունները, որ միշտ առաջանում են որոշակի հարաբերություններով, կարելի է ներկայացնել որպես միմյանց հետ ատոմների խմբավորում կազմած նոր միավորներ, որոնք կոչվում են մոլեկուլներ։ Սակայն այդ վեճը տեսակետների երկու դպրոցների միջև լուծվեց ի նպաստ ատոմիստների միայն մեր դարասկզբին։ Դրա ամենակարևոր ֆիզիկական ապացույցներից մեկը տվեց Էյնշտեյնը մի հոդվածում, հատուկ հարաբերականության մասին հայտնի հոդվածից մի քանի շաբաթ առաջ նշում էր, թե բրոունյան կոչված շարժումը՝ հեղուկում ընկղմված փոշու մասնիկների անկանոն, կամայական շարժումը կարող է բացատրվել նրանով, որ հեղուկի ատոմները բախվում են փոշու մասնիկների հետ։ | ||
| + | |||
| + | Այդ ժամանակ արդեն կասկածներ կային այն մասին, որ ատոմներն ի վերջո ևս բաժանելի պետք է լինեն։ Դրանից մի քանի տարի առաջ, Քեմբրիջի Թրինիթի քոլեջում, Ջ․ Ջ․ Թոմսոնը ցույց էր տվել նյութի էլեկտրոն կոչված մասնիկի գոյությունը, որի զանգվածը հազարից ավելի անգամ փոքր էր ամենաթեթև ատոմի՝ ջրածնի զանգվածից։ Թոմսոնի օգտագործած սարքը բավականին նման էր ժամանակակից հեռուստացույցի պատկերաստեղծ խողովակի․ կարմիր շիկացած մետաղական լարը էլեկտրոններ է արձակում և, որովհետև դրանք լիցքավորված են բացասական լիցքով, արագացվում են էլեկտրական դաշտով և ուղղվում դեպի ֆոսֆորապատ էկրանը։ Բախվելով էկրանին, էլեկտրոններն առաջացնում են լույսի փայլատակումներ։ Շուտով պարզվեց, որ այս էլեկտրոններն արձակվում են ատոմներից, և 1911֊ին անգլիացի ֆիզիկոս Էռնեստ Ռեզեֆորդը ցույց տվեց, որ ատոմն ունի ներքին կառուցվածք, այն կազմված է շատ փոքր, դրական լիցքավորված միջուկից, որի շուրջ պտտվում են որոշ թվով էլեկտրոններ։ Նա հանգեց այդ եզրակացությանը վերլուծելով ռադիոակտիվ տարրերի քայքայման արդյունքում առաջացող դրական լիցքավորված α֊մասնիկների՝ ատոմների հետ բախման հետևանքով, հետագծերի շեղումները։ | ||
| + | |||
| + | Սկզբնական շրջանում կարծում էին, թե միջուկը կազմված է էլեկտրոններից և տարբեր թվով դրական լիցքավորված մասնիկներից, որոնք անվանվեցին պրոտոններ՝ հունարեն «առաջին» բառից, քանի որ հավատացած էին, թե դա այն հիմնական միավորն է, որից կազմված է նյութը։ Սակայն 1932֊ին Քեմբրիջում Ռեզերֆորդի գործընկերներ Ջեյմս Չադվիկը հայտնաբերեց, որ միջուկում առկա է մի այլ մասնիկ ևս, որն անվանվեց նեյտրոն։ Այն համարյա նույն զանգվածն ունի, ինչ պրոտոնը, բայց էլեկտրաչեզոք է։ Այս հայտնագործության համար Չադվիկին շնորհվեց Նոբելյան մրցանակ, և նա ընտրվեց Քեմբրիջի Կայուս և Գոնվիլ քոլեջի ղեկավար (ես այժմ այդ քոլեջում խորհրդի անդամ եմ)։ Հետագայում Չադվիկը հրաժարվեց ղեկավար պաշտոնից՝ խորհրդի անդամների հետ անհամաձայնության պատճառով։ Քոլեջում խիստ լարված վիճակ էր ստեղծվել, այն բանից հետո, երբ պատերազմից վերադարձած շատ երիտասարդ գիտնականներ հեռացրել էին երկար տարիներ խորհրդում պաշտոն զբաղեցրած հին անդամներին։ Սա ինձնից առաջ էր, երբ ես 1965 թվականին դարձա քոլեջի խորհրդի անդամ, վեճի վերջին փուլն էր․ նմանօրինակ վեճերը պատճառ դարձան, որպեսզի մի այլ Նոբելյան մրցանակի դափնեկիր, մագիստրոս պրն Նեվիլ Մոտը նույնպես հրաժարական տար։ | ||
| + | |||
| + | Սրանից մոտավորապես քսան տարի առաջ տարածված էր այն տեսակետը, թե պրոտոնը և նեյտրոնը տարրական մասնիկներ են, սակայն, երբ ուսումնասիրվեցին մեծ արագությամբ շարժվող պրոտոնների բախումներն այլ պրոտոնների կամ էլեկտրոնների հետ, պարզվեց, որ դրանք կազմված են ավելի փոքր մասնիկնեից։ Երբ մասնիկներն անվանվեցին քվարկներ Կալիֆոռնիայի տեխնոլոգիական ինստիտուտի աշխատակից, ֆիզիկոս Մյուրել Գել֊Մանի կողմից, որը և 1969 թվականին այդ աշխատանքների համար արժանացավ Նոբելյան մրցանակի։ Քվարկ բառն ծագել է Ջեյմս Ջոյսի մի առեղծվածային մեջբերումից․ «երեք քվարկ Մուստեր Մարկի համար»։ Անգլերենում quark բառը պետք է արտասանվի guart֊ի նման, միայն թե k֊ով, բայց սովորաբար արտաբերվում է lark֊ հանգով։ | ||
| + | |||
| + | Կան քվարկների մի քանի տեսակներ․ ենթադրվում է, որ նրանք ունեն 6 «բույր», որոնք կոչվում են վեր, վար, տարօրինակություն, հմայք, հատակ և գագաթ։ Յուրաքանչյուր «բույր» ունի երեք «գույն»՝ կարմիր, կանաչ և կապույտ։ (Պետք է նշել, որ սրանք լոկ պիտակներ են՝ քվարկներն ավելի փոքր են, քան տեսանելի լույսի ալիքի երկարությունը և հետևաբար սովորական իմաստով գունավոր չեն։ Ժամանակակից ֆիզիկոսները, ինչպես երևում է, վառ երևակայություն ունեն և նոր մասնիկներն ու երևույթները անվանելիս այլևս չեն սահմանափակվում հունարեն լեզվով)։ Պրոտոնը կամ նեյտրոնը կազմված են երեք քվարկներից՝ յուրաքանչյուր գույնից մեկ հատ։ Պրոտոնը պարունակում է երկու վեր և մեկ վար քվարկ, իսկ նեյտրոնը՝ երկու վար և մեկ վեր քվարկ։ Հնարավոր է մասնիկներ ստեղծել, օգտագործելով մյուս քվարկները (տարօրինակություն, հմայք, հատակ և գագաթ), բայց այս քվարկների զանգվածները շատ մեծ են և արագ քայքայվելով՝ վերածվում են պրոտոնների և նեյտրոնների։ | ||
| + | |||
| + | Ինչպես արդեն տեսանք, ոչ միայն ատոմները, այլև նրանց կազմի մեջ մտնող պրոտոններն ու նեյտրոններն են բաժանելի։ Հարց է ծագում՝ որո՞նք են այն իրական տարրական մասնիկները՝ հիմնական շինաղյուսները, որոնցով շինված է ամեն ինչ։ Քանի որ լույսի ալիքի երկարությունն ավելի մեծ է, քան ատոմի չափը, հետևաբար մենք չենք կարող հուսալ, որ հնարավոր է «տեսնել» ատոմի մասերը սովորական ճանապարհով։ Այդ նպատակի համար պետք է օգտագործել ավելի փոքր ալիքի երկարություն ունեցող ինչ֊որ բան։ Քվանտային մեխանիկայի համաձայն, ինչպես տեսանք նախորդ գլխում, բոլոր մասնիկները փաստորեն միևնույն ժամանակ ալիքներ են, և որքան մեծ է մասնիկի էներգիան, այնքան փոքր է համապատասխան ալիքի երկարությունը։ Մեր հարցի պատասխանը կախված կլինի այն բանից, թե որքան բարձր էներգիայով օժտված մասնիկ կունենանք մեր տրամադրության տակ, որպեսզի համապատասխանաբար փոքր ալիքի երկարությամբ տեսանելի լինեն տարրական մասնիկները։ Մասնիկների էներգիան սովորաբար չափվում է Էլեկտրոն֊Վոլտ կոչվող միավորներով։ (Թոմսոնի էլեկտրոնների հետ կատարած փորձերից մենք տեսանք, որ նա էլեկտրոնների արագացման համար օգտագործել էր էլեկտրական դաշտը։ Այն էներգիան, որ էլեկտրոնը ձեռք է բերում մեկ Վոլտ լարվածություն ունեցող էլեկտրական դաշտում, կոչվում է Էլեկտրոն֊Վոլտ)։ XIX դարում, երբ մարդկությանը հայտնի էր մասնիկի համար միայն մի քանի Էլեկտրոն֊Վոլտ էներգիան, որն առաջանում էր այնպիսի քիմիական ռեակցիաներից, ինչպիսին այրումն է, տարածված էր այն կարծիքը, թե ատոմը փոքրագույն մասնիկն է։ Ռեզերֆորդի փորձերի ժամանակ α-մասնիկների էներգիան միլիոնավոր Էլեկտրոն֊Վոլտի էր հասնում։ Այժմ մենք գիտենք՝ ինչպես օգտագործել էլեկրտամագնիսական դաշտերի ուժը, որպեսզի մասնիկները ձեռք բերեն նախ միլիոնավոր, ապա հազար միլիոնավոր Էլեկտրոն֊Վոլտ էներգիա։ Այս առաջադիմության շնորհիվ այսօր գիտենք, որ այն մասնիկները, որոնք քսան տարի առաջ «տարրական» էին համարվում կազմված էին ավելի փոքր մասնիկներից։ Քանի որ այժմ հնարավոր է շատ ավելի մեծ էներգիա ունեցող մասնիկներ ունենալ, մեզ կհաջողվի՞ արդյոք տարրական համարվող մասնիկներում ավելի փոքր մասնիկներ գտնել։ Այս բանը, իհարկե, հնարավոր է, և՛ տեսական հիմքեր կան, և՛ կամ շատ ենք մոտեցել դրան, որպեսզի ընդունենք, որ բնության վերջակետային շինաղյուսները ճանաչելու համար բավարար գիտելիքներ կան։ | ||
| + | |||
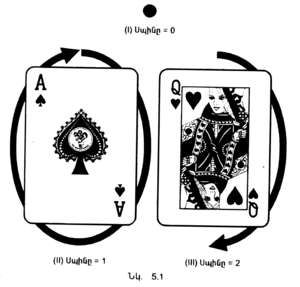
| + | Նախորդ գլխում քննարկված արլիք֊մասնիկային երկվվությունն օգտագործելով՝ մենք տիեզերքում ամեն ինչ, ներառյալ նաև լույսը և գրավիտացիան, կարող ենք նկարագրել մասնիկային տեսանկյունից։ Այս մասնիկները մի հատկություն ունեն, որը կոչվում է սպին։ Սպինը ըմբռնելու համար սովորաբար մասնիկը պատկերացնում են որպես փոքր հոլ, որը պտտվում է իր առանցքի շուրջ։ Այդպիսի պատկերացումը խաբուսիկ է, որովհետև քվանտային մեխանիկայի համաձայն, մասնիկները ճշգրիտ սահմանված պտտման առանցք չունեն։ Սպին ասելով պիտի հասկանալ, թե ինչպես է երևում մասնիկը, երբ այն դիտարկվում է տարբեր ուղղություններից։ Օրինակ, սպին չունեցող (0 սպին ունեցող) մասնիկը նման է կետի, որը բոլոր ուղղություններով միանման է երևում երևում (նկ․5.1 ― 1)։ Մյուս կողմից մեկ սպին ունեցող մասնիկը նման է կետի և տարբեր ուղղություններից տարբեր է երևում։ Միայն մեկ լրիվ շրջապտույտից հետո (360 աստիճան) գալիս է նույն տեսքին (նկ․ 5.1 ― 2)։ | ||
| + | |||
| + | [[Պատկեր:H5 1.svg|thumb]] | ||
| + | |||
| + | Իսկ 2 սպին ունեցող մասնիկը նման է երկկողմանի սլաքի (նկ․5.1 ― 3), այն նույն տեսքը կստանա կես (180 աստիճան) պտույտից հետո։ Նման ձևով ավելի մեծ սպին ունեցող մասնիկը նույնը կերևա, երբ պտտվի որոշակի անկյուններով։ Շատ տարօրինակ, բայց ուշադրության արժանի է այն, որ մասնիկներ կան, որոնք նույնը չեն երևում մի ամբողջ շրջան՝ 360 աստիճան, պտույտից հետո, որպեսզի դրանք նույնը երևան, պետք է երկու լրիվ շրջապտույտ կատարեն։ Այսպիսի մասնիկների սպինը պայմանականորեն ընդունված է 1/2: | ||
| + | |||
| + | Տիեզերքում մեզ հայտնի բոլոր մասնիկները կարելի է բաժանել երկու խմբի․ 1/2 սպին ունեցող մասնիկների, որոնք կազմում են տիեզերքի նյութը (նյութական մասնիկներ) և 0,1 ու 2 սպին ունեցող մասնիկների, որոնք, ինչպես հետո կտեսնենք, պայմանավորում են նյութական մասնիկների միջև գործող ուժերը։ Նյութական մասնիկները ենթարկվում են Պաուլիի արգելակման սկզբունքին։ Այս սկզբունքը 1925 թվականին հայտնագործել է ավստիացի ֆիզիկոս Վոլֆանգ Պաուլին, որի համար 1945 թվականին արժանացավ Նոբելյան մրցանակի։ Պաուլին տեսական ֆիզիկոսի նախատիպն էր․ նրա մասին ասում էին, թե բավական էր, որ նա գտնվեր տվյալ քաղաքում, որպեսզի ֆիզիկայի փորձերը ձախողվեն։ Պաուլիի սկզբունքի էությունն այն է, որ երկու միանման մասնիկներ չեն կարող նույն դիրքն ու նույն արագությունն ունենալ, անորոշության սկզբունքի սահմաններում։ Պաուլիի արգելակման սկզբունքը վճռական նշանակություն ունի, որովհետև բացատրում է, թե ինչու նյութական մասնիկները կոլապսի չեն ենթարկվում և չեն հասնում գերխիտ վիճակի՝ 0 և 2 ապին ունեցող մասնիկների առաջացրած ուժերի ազդեցության տակ։ Եթե նյութական մասնիկները մոտավորապես նույն դիրքն ունենան, պետք է տարբեր արագություններ ունենան և հետևաբար չեն կարող երկար ժամանակ միևնույն տեղում մնալ։ Ակնհայտ է, որ եթե աշխարհը ստեղծված լիներ առանց արգելակման սկզբունքի, ապա քվարկները չպիտի կարողնային ինքնուրույն որոշակի պրոտոններ և նեյտրոններ առաջացնել։ Իսկ վերջիններս իրենց հերթին չէին կարողանա էլեկտրոնների հետ ինքնուրույն որոշակի ատոմներ առաջացնել։ Տեղի կունենար մի մեծ կոլապս և կառաջանար քիչ թե շատ համասեռ, թանձր մի «ապուր»։ | ||
| + | |||
| + | Էլեկտրոնի և 1/2 սպին ունեցող այլ մասնիկների մասին ճշգրիտ գիտելիքներ ձեռք են բերվել սկսած միայն 1928 թ․, երբ Պոլ Դիրակը տվեց իր տեսությունը։ Դիրակը հետագայում ընտրվեց Քեմբրիջի համալսարանի մաթեմատիկայի լուկասյան պրոֆեսոր (պաշտոն, որը ժամանակին զբաղեցրել է Նյուտոնը, այսօր՝ ևս ես)։ Դիրակի տեսությունն առաջինն է իր տեսակի մեջ, որ համատեղելի էր և՛ քվանտային մեխանիկայի, և՛ հարաբերականության հատուկ տեսության հետ։ Այն մաթեմատիկորեն բացատրում էր, թե էլեկտրոնի սպինը ինչու է 1/2, այսինքն՝ էլեկտրոնն ինչո՞ւ ինքն իրեն չի նմանվում մեկ լրիվ շրջապտույտից հետո, այլ միայն՝ երկու շրջապտույտից հետո։ Կանխագուշակեց նաև, որ էլեկտրոնը պետք է մի զուգընկեր ունենա՝ հակաէլեկտրոն կամ պոզիտրոն։ Պոզիտրոնի հայտնագործումը 1932 թվականին հաստատեց Դիրակի տեսության ճշտությունը և 1933 թվականին նրան դարձրեց Նոբելյան մրցանակի դափնեկիր՝ ֆիզիկայի բնագավառում։<ref>Ավելի ուշ, 60 ― 70֊ական թվականներին, մի առիթով Դիրակը սրամտեց, որպեսզի իմանանք, թե ինչ բան է էլեկտրոնը, պետք է իմանալ՝ ինչ բան է էլեկտրականությունը, իսկ որպեսզի վերջինիս ինչ լինելը իմանանք, հարկավոր է իմանալ, թե ինչ բան է էլեկտրոնը։</ref> Մենք այժմ գիտենք, որ ամեն մասնիկ ունի իր հակամասնիկը, և երբ մասնիկն ու հակամասնիկը հանդիպեն միմյանց, տեղի կունենա դրանց ոչնչացում (աննիհիլացում)։ (Պետք է նշել, որ ուժակիր մասնիկների հակամասնիկները նրանցից ոչնչով չեն տարբերվում)։ Հնարավոր է, որ հակաաշխարհներ և նույնիսկ հակաժողովուրդներ գոյություն ունենան, որոնք կազմված են հակամասնիկներից։ Այնուամենայնիվ, եթե դուք հանդիպեք ձեր հակամարդուն, ձեռքը չսեղմեք, հակառակ դեպքում երկուսդ էլ կանէանաք՝ լույս արձակելով։ Թե ինչո՞ւ է թվում, որ մեր շրջապատում շատ ավելի մասնիկներ կան, քան հակամասնիկներ, չափազանց կարևոր հարց է, և ես դրան կանդրադառնամ այս գլխի վերջում։ | ||
| + | |||
| + | Ենթադրվում է, որ քվանտային մեխանիկայում նյութական մասնիկների միջև գործող բոլոր ուժերը կամ փոխազդեցությունները կրում են այն մասնիկները, որոնք ունեն ամբողջական սպիններ՝ 0,1 կամ 2։ Տեղի է ունենում հետևյալը․ նյութական մասնիկը, ինչպես, օրինակ, էլեկտրոնը կամ քվարկը, արձակում է ուժակիր մի մասնիկ։ Դրանով պայմանավորված հետհարվածը փոխում է նյութական մասնիկի արագությունը։ Արձակված ուժակիր մասնիկը բախվում է մի այլ նյութական մասնիկի հետ և կլանվում։ Հետևաբար, փոխվում է նաև երկրորդ նյութական մասնիկի արագությունը և ստացվում է այնպես, կարծես երկու նյութական մասնիկների միջև ուժ է գործում։ | ||
| + | |||
| + | Ուժակիր մասնիկների կարևոր հատկությունն այն է, որ նրանք չեն ենթարկվում արգելակման սկզբունքին։ Սա նշանակում է, որ կարող են կատարվել անսահման թվով փոխանակումներ և այսպիսով շատ հզոր փոխազդեցության ուժ առաջացնել։ Եթե ուժակիր մասնիկների զանգվածը մեծ լինի, ապա դրանց և՛ առաջացումը, և՛ փոխանակումը մեծ հեռավորությունների վրա դժվար կլինի։ | ||
| + | |||
| + | Այսպիսով, դրանցով պայմանավորված փոխազդեցության ուժերը կլինեն կարճազդեցության կարգի։ Մյուս կողմից, եթե ուժակիր մասնիկը սեփական զանգված չունենա, ապա փոխազդեցության ուժը կլինի հեռազդեցության կարգի։ Նյութական մասնիկների միջև փոխանակվող ուժակիր մասնիկները կոչվում են վիրտուալ մասնիկներ, որովհետև դրանք, ի տարբերություն «իրական» մասնիկների (նյութական մասնիկների), ուղղակիորեն չեն հայտնաբերվում մասնիկային դետեկտորով։ Սակայն մենք գիտենք, որ նրանք գոյություն ունեն, որովհետև թողնում են չափելի ազդեցություն՝ ուժեր են առաջացնում նյութական մասնիկների միջև։ 0,1 և 2 ապին ունեցող մասնիկները նույնպես որոշ պարագաներում գոյություն ունեն որպես իրական մասնիկներ և նրանց կարելի է ուղղակիորեն հայտնաբերել։ Այս դեպքում նրանք մեզ համար կներկայանան այն վիճակում, որը դասական ֆիզիկոսն անվանում է ալիք, ինչպես, օրինակ, լույսի կամ գրավիտացիոն ալիքները։ Դրանք որոշ դեպքերում կարող են արձակվել, երբ նյութական մասնիկները միմյանց հետ փոխազդելով փոխանակում են վիտուալ ուժակիր մասնիկներ։ (Օրինակ, երկու էլեկտրոնների միջև գործող վանողական ուժն արդյունք է վիրտուալ ֆոտոնների փախանակման, որոնք երբեք չեն կարող ուղղակիորեն հայտնաբերվել, սակայն, եթե մի էլեկտրոն մյուսի կողքով անցնի, կարող են իրական ֆոտոններ արձակվել, որոնք մենք կգրանցենք որպես լույսի ալիքներ)։ | ||
| + | |||
| + | Ուժակիր մասնիկները կարելի է բաժանել չորս դասի՝ կախված նրանց ուժի մեծությունից և այն բանից, թե ինչպիսի մասնիկների հետ են փոխազդում։ Պետք է նշել, որ այս բաժանումը պայմանական է, հարմար մասնակի տեսություններ մշակելու համար, սակայն խորը հիմնավորում չունի։ Վերջ ի վերջո ֆիզիկոսների մեծ մասը հույս ունի մի միացյալ տեսություն մշակել և այս չորս ուժերը բացատրել որպես նույն եզակի ուժի տարբեր արտահայտություններ։ | ||
| + | |||
| + | Կարելի է ասել, որ սա այսօր ֆիզիկոսների հիմնական նպատակն է։ Վերջերս հաջող փորձեր են արվել այս չորս դասից երեքը միավորելու, և ես այս գլխում կխոսեմ այդ մասին։ Մյուս դասի ուժի՝ գրավիտացիայի միավորման հարցը կքննարկենք հետագայում։ | ||
| + | |||
| + | Այդ չորս դասի ուժերից առաջինը գրավիտացիոն ուժն է։ Այն համոզիչ (ունիվերսալ) է, այսինքն՝ ամեն մասնիկ ենթարկվում է գրավիտացիոն ուժին՝ իր զանգվածի և էներգիայի համապատասխան։ Գրավիտացիան այդ չորս տեսակի ուժերից ամենաթույլն է, այնքան թույլ է, որ այն հնարավոր չէր լինի նկատել, եթե չունենար երկու առանձնահատկություն, այն է․ կարող է ազդել շատ մեծ հեռավորությունների վրա և իր բնույթով միշտ ձգողական է։ Դա նշանակում է, որ երկու մեծ մարմինների, ինչպիսիք են, օրինակ, արևը և երկիրը, առանձին մասնիկների միջև առկա բոլոր ձգողական թույլ ուժերը գումարվելով առաջացնում են զգալի մի ուժ։ Մյուս երեք ուժերը կամ գործում են շատ փոքր հեռավորությունների վրա, կամ ժամանակ առ ժամանակ ձգողական և վանողական դառնալով չեզոքացնում են միմյանց։ Գրավիտացիոն դաշտը քվանտային մեխանիկայի տեսանկյունից դիտելիս, երկու նյութական մասնիկների միջև գործող ուժը կրողը պատկերանում է որպես 2 սպին ունեցող մի մասնիկ, որը կոչվում է գրավիտոն։ Դա սեփական զանգված չունի, այդպիսով նրա կրած ուժը հեռազդող է։ Արևի և երկրի միջև առկա գրավիտացիոն ուժը վերագրվում է այս երկու մարմինները կազմող մասնիկների միջև գրավիտոնների փախանակմանը։ Թեև փախանակվող մասնիկները վիրտուալ են, սակայն նրանք տալիս են չափելի արդյունք, պայմանավորում են երկրի պտույտը արևի շուրջը։ Իրական գրավիտոնները, որոնք դասական ֆիզիկոսներն անվանում են գրավիտացիոն ալիքներ, շատ թույլ են և այնքան դժվար հայտնաբերելի, որ դեռ երբեք չեն դիտվել։ | ||
| + | |||
| + | Հաջորդ դասը էլեկտամագնիսական ուժն է, որը գործում է լիցքավորված մասնիկների միջև, ինչպիսիք են էլեկտրոնները և քվարկները, բայց ոչ երբեք գրավիտոնները, որոնք լիցքավորված չեն։ Էլեկտրամագնիսական ուժը շատ ավելի մեծ է, քան գրավիտացիոն ուժը․ երկու էլեկտրոնների միջև գործող էլեկտրամագնիսական ուժը գրավիտացիոն ուժի համեմատ մեծ է մոտավորապես միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն անգամ (1֊ից հետո 42 զերո)։ Ընդ որում, գոյություն ունի էլեկտրական լիցքերի երկու տեսակ՝ դրական և բացասական։ Երկու դրական լիցքերի միջև փոխազդեցության ուժը վանողական է, նույնը տեղի ունի նաև երկու բացասական լիցքերի միջև, բայց դրական և բացասական լիցքերի միջև ուժը ձգողական է։ Մեծ մարմինը, ինչպես օրինակ, արևը կամ երկիրը, պարունակում են մոտավորապես հավասար քանակով դրական և բացասական լիցքեր։ Հետևաբար նրանց առանձին մասնիկների միջև ձգողական և վանողական ուժերը իրար ոչնչացնում են, և էլեկտրամագնիսական ուժը շատ փոքր է։ Սակայն ատոմների և մոլեկուլների չափերի կարգի հեռավորություններում էլեկտամագնիսական ուժը տիրապետող է։ Բացասական էլեկտրոնների և միջուկի դրական պրոտոնների միջև էլեկտրամագնիսական ձգողությունը պայմանավորում է ատոմում էլեկտրոնների պտույտը միջուկի շուրջ այնպես, ինչպես գրավիտացիոն ձգողությունն է պատճառը, որ երկիրը պտտվի արևի շուրջ։ Էլեկտրամագնիսական ձգողությունը կարելի է պատկերել որպես մեծ թվով վիրտուալ, զանգված չունեցող, 1 սպինով մասնիկների՝ ֆոտոնների փոխանակման հետևանք։ Փոխանակվող ֆոտոնները նույնպես վիտուալ մասնիկներ են։ Ընդ որում, երբ ատոմի մեջ էլեկտրոնը մի թույլատրելի ուղեծրից անցնում է մյուսին՝ միջուկին ավելի մոտիկ ուղեծիր, ատոմից էներգիա է անջատվում և արձակվում է իրական ֆոտոն, որը կարող է դիտվել սովորական աչքով որպես տեսանելի լույս, եթե այն տեսանելիության տիրույթում է, կամ գրանցվել դետեկտորով՝ որպես լուսանկարչական ֆիլմ։ Հանգունորեն, եթե իրական ֆոտոնը բախվի ատոմի հետ, ապա այն կարող է էլեկտրոնը միջուկին մոտիկ ուղեծրից տեղափոխել ավելի հեռու գտնվող ուղեծիր։ Այս դեպքում տեղի է ունենում ֆոտոնի էներգիայի օգտագործում, այսինքն՝ ֆոտոնի կլանում։ | ||
| + | |||
| + | Ուժերի երրորդ դասը կոչվում է թույլ միջուկային ուժ, որը պատասխանատու է ռադիոակտիվության համար և ներգործում է 1/2 սպին ունեցող բոլոր նյութական մասնիկների վրա, բայց ոչ 0,1 կամ 2 սպին ունեցող մասնիկների, ինչպիսիք են ֆոտոնը և գրավիտոնը։ Թույլ միջուկային ուժի բնույթը հասկանալի չէր մինչև 1967 թիվը, երբ Լոնդոնի Կայսերական քոլեջից Աբդուս Սալամը և Հարվարդի համալսարանից Ստիվեն Ուայնբերգն առաջարկեցին իրենց տեսությունները․ սրանցում այդ փոխազդեցությունը միաձուլվել էր էլեկտրամագնիսական ուժի հետ, ինչպես դրանից հարյուր տարի առաջ Մաքսվելն էր միավորել էլեկտրամագնիսականությունը մագնիսականության հետ։ Նրանք այն միտքն արտահայտեցին, որ ֆոտոնից բացի կան 1 սպին ունեցող 3 այլ մասնիկներ ևս, որոնք թույլ ուժը կրողներ են և բոլորը միասին կոչվեցին զանգվածեղ վեկտոր բոզոններ։ Այդ բոզոնները կոչվում են W + (արտասանվում է դաբլյու պլյուս), W - (դաբլյու մինուս) և Z° (զեթ զերո) և յուրաքանչյուրի զանգվածը շուրջ 100 ԳԵՎ է (ԳԵՎ ― նշանակում է Գիգա Էլեկտրոն֊Վոլտ կամ հազար միլիոն Էլեկտրոն֊Վոլտ): Ուայնբերգ Սալամի տեսությունը բացահայտեց մի հատկություն, որ հայտնի է որպես ինքնակամ համաչափության խզում։ Այսինքն այն, որ թվում էր թե ցածր էներգիայի դեպքում մասնիկները բոլորովին տարբեր են, իրականում դրանք նույն տեսակի են, բայց գտնվում են տարբեր վիճակներում։ Բարձր էներգիայի պայմաններում բոլոր այս մասնիկների վարքը նույնն է։ Այս երևույթը նման է ռուլետի խաղանիվի գնդակի վարքին։ Բարձր էներգիաների դեպքում (երբ անիվը արագ է պտտվում) գնդակը միայն մի վարք ունի․ պտտվում է և պտտվում։ Բայց երբ անիվը դանդաղում է, գնդակի էներգիան նվազում է, և այն վերջապես ընկնում է անիվի երեսունյոթ անցքերից մեկի մեջ։ | ||
| + | |||
| + | Համաձայն Ուայնբերգ֊Սալամի տեսության, երբ էներգիան 100 ԳԵՎ֊ից բարձր է, ապա երեք նոր մասնիկները՝ W+, W- և Z°֊ն, ինչպես նաև ֆոտոնը կունենան նույնանման վարք։ Բայց քանի որ բնականոն պայմաններում մասնիկի էներգիան ցածր է լինում, մասնիկների համաչափությունը խզվում է։ W+ W- մասնիկների զանգվածները մեծանում են՝ նրանց կրած ուժերը դարձնելով շատ կարճազդեցության կարգի։ Երբ Ուայնբերգը և Սալամը առաջարկեցին այս տեսությունը, շատ քչերը հավատացին դրան, իսկ այն ժամանակ չկային բավարար հզորությամբ մասնիկների արագացուցիչներ, որոնք էներգիան հասցնեին 100 ԳԵՎ֊ի, ինչը պահանջում էր իրական W+, W- և Z° մասնիկներ առաջացնելու համար։ Այնուամենայնիվ, հաջորդ 10 տարիների ընթացքում այդ տեսության այլ կանխագուշակումները ցածր էներգիայի պայմաններում այնքան մեծ ճշգրտությամբ համընկան փորձնական տվյալների հետ, որ1979 թվականին Սալամն ու Ուայնբերգը և Հարվարդի համալսարանից Շելդոն Գլեշոուին, որը նույնանման միասնական մի տեսություն էր առաջարկել էլեկտրամագնիսական և թույլ միջուկային ուժերի համար, արժանացան Նոբելյան մրցանակի ֆիզիկայի բնագավառում։ Նոբելյան հանձնաժողովին սխալ գործած լինելու անհարմար վիճակից փրկեց Միջուկային հետազոտությունների եվրոպական կենտրոնը (ՑԵՌՆ ― CERN) երբ 1983 թվականին հայտնաբերվեցին ֆոտոնի զանգված ունեցող երեք զուգընկերները, որոնք ունեին ճշգրիտ կանխագուշակված զանգվածներ և այլ հատկությունները։ Կառլո Ռուբիան, որ ղեկավարում էր հայտնագործությունը կատարած հարյուրավոր ֆիզիկոսների աշխատանքը, և Սայմոն վան դեր Միըլրին, որ կառուցել էր հակամարմինների պահեստային համակարգ, 1984 թ․ արժանացան Նոբելյան մրցանակի։ (Այսօր փորձարարական ֆիզիկայի բնագավառում անհնարին է շոշափելի հաջողության հասնել, եթե արդեն իսկ բարձրունքների չես հասել)։ | ||
| + | |||
| + | Ուժերի չորրորդ դասը միջուկային փոխազդեցության հզոր ուժն է, որով քվարկներն իրար են կապվում պրոտոններում և նեյտրոններում, իսկ պրոտոնները և նեյտրոնները իրար են կապվում ատոմի միջուկում։ Կա այն կարծիքը, որ այս ուժը կրող մասնիկը 1 սպին ունի, այն կոչվում է գլյուոն և փոխազդում է ինքն իր և քվարկների հետ։ Հզոր միջուկային ուժը օժտված է շատ տարօրինակ հատկությամբ, որը կոչվում է կասեցում․ այն միշտ մասնիկներն իրար է կապում՝ առաջացնելով համակցություններ, որոնք գույն չունեն։ Քվարկը միայնակ չի կարող գոյություն ունենալ, որովհետև այն ունի գույն (կարմիր կանաչ և կապույտ)։ Որպեսզի այն գոյություն ունենա, պետք է կարմիր քվարկը միանա, ասենք, կանաչ և կապույտ քվարկների հետ գլյուոնների «լարանով» (կարմիր + կանաչ + կապույտ = սպիտակ)։ Այսպիսի եռյակ կազմություն է հենց պրոտոնը կամ նեյտրոնը։ Մեկ այլ հնարավորություն է քվարկ և հակաքվարկ զույգը (կարմիր+ հակակարմիր կամ կանաչ + հակականաչ կամ կապույտ = սպիտակ)։ Այսպիսի համակցություններն առաջացնում են, այսպես կոչված, մեզոններ, որոնք անկայուն են, քանի որ քվարկն ու հակաքվարկը կարող են իրար ոչնչացնել և առաջացնել էլեկտրոններ կամ այլ մասնիկներ։ Նման ձևով կասեցման հատկությունը թույլ չի տալիս նաև, որ գլյուոնը միայնակ գոյություն ունենա, քանի որ այն նույնպես գունավոր է։ Այս պատճառով կարող է գոյություն ունենալ գլյուոնների այնպիսի հավաքածու, որում գույների գումարը սպիտակ է։ Այդպիսի հավաքածուն առաջացնում է անկայուն մի մասնիկ, որը կոչվում է գլյուբոլ (անգլ․՝ սոսնձագունդ)։ | ||
| + | |||
| + | [[Պատկեր:H5 2.svg|thumb|Նկ․ 5․ 2 Պրոտոնը և հակապրոտոնը բախվում են բարձր էներգիայի տակ առաջացնելով գրեթե ազատ քվարկների զույգ։]] | ||
| + | |||
| + | Այն փաստը, որ կասեցման հատկությունը թույլ չի տալիս դիտարկել քվարկը և գլյուոնը մեկուսացած վիճակում, թերևս մտածել տա, որ քվարկ ու գլյուոն հասկացությունները, որպես մասնիկներ, ինչ֊որ չափով մետաֆիզիկական են։ Սակայն հզոր միջուկային ուժը մի այլ հատկություն ունի, որը կոչվում է սիմպտոմային ազատություն և որոշակիորեն իմաստավորում է քվարկներ և գլյուոններ հասկացությունները։ Սովորական էներգիայի պայմաններում հզոր միջուկային ուժը իսկապես այնքան ուժեղ է, որ մեծ ուժով իրար է կապում քվարկները։ Բայց մեծ մասնիկային արագացուցիչներով կատարված փորձերը ցույց են տալիս, որ բարձր էներգիաների պայմաններում միջուկային ուժը շատ է թուլանում, և քվարկներն ու գլյուոնները իրենց պահում են որպես ազատ մասնիկներ։ | ||
| + | |||
| + | Նկ․ 5.2֊ում ցույց է տրված բարձր էներգիայով պրոտոնի և հակապրոտոնի բախման լուսանկարը։ Առաջացել են մի քանի գրեթե ազատ, քվարկներ, և նկարում երևում են հետագծա «ցայտեր»։ | ||
| + | |||
| + | Էլեկտրամագնիսական և թույլ միջուկային ուժերի միասնականացման հաջողությունները պատճառ դարձան, որ սրանց միացվի հզոր միջուկային ուժը և ստեղծվի մի նոր միասնական տեսություն, որը կոչվում է մեծ միասնական տեսություն (ՄՄՏ ― GUT)։<ref>GUT անգլ․՝ grand unitied theory ― Մեծ միասնական տեսություն (ՄՄՏ):</ref> | ||
| + | |||
| + | Այստեղ անվանումն ավելի քան չափազանցված է, որովհետև ստացված տեսություններն այդքան էլ մեծ չեն և ոչ էլ լրիվ միասնական, քանի որ չեն ընգրկում գրավիտացիան։ | ||
| + | |||
| + | Կամ տեսությունները լրիվ չեն, քանի որ պարունակում են մի շարք պարամետրեր, որոնց արժեքները տեսականորեն կանխագուշակելի չեն, այլ ընտրված են փորձնական տվյալներին համապատասխան։ Այնուամենայնիվ, կատարվել է մի քայլ դեպի ամբողջական, կատարյալ միասնական տեսության ստեղծումը։ ՄՄՏ֊ի հիմնական գաղափարը հետևյալն է, ինչպես ասվեց վերևում, հզոր միջուկային ուժը թուլանում է բարձր էներգիաների պայմաններում։ Մյուս կողմից, էլեկտրամագնիսական և թույլ ուժերը, որոնք ասիմետրորեն ազատ չեն, հզորանում են բարձր էներգիաների պայմաններում, որը կոչվում է մեծ միասնական էներգիա, այս երեք դասի ուժերը կունենան նույն ուժգնությունը, և կլինեն մեկ ուժի տարբեր արտահայտություններ։ ՄՄՏ֊ի համաձայն, այս պայմաններում 1/2 սպին ունեցող տարբեր նյութական մասնիկները, ինչպես օրինակ, քվարկն ու էլեկտրոնը, հիմնականում կլինեն նույնը, այսինքն՝ այդպիսով իրագործվում է մեկ այլ միավորում։ | ||
| + | |||
| + | Մեծ միասնական էներգիայի արժեքը ճշգրիտ հայտնի չէ, բայց հավանաբար առնվազն հազար միլիոն միլիոն ԳԵՎ֊ի կարգի է։ Մասնիկային արագացուցիչների ժամանակակից սերունդը կարող է ապահովել մասնիկների բախումը մոտ հարյուր ԳԵՎ էներգիայի տակ, և ծրագրվում են այնպիսի արագացուցիչներ, որոնք կապահովեն մի քանի հազար ԳԵՎ էներգիա։ Բայց այն արագացուցիչը, որն ի վիճակի կլինի մասնիկներն արագացնել այնքան, որ նրանց էներգիան հասնի մեծ միասնության էներգիայի մակարդակին, պետք է այնքան մեծ լինի, որքան Արեգակնային համակարգն է, որն, իհարկե, ներկա տնտեսական պայմաններում անհնարին է։ Այսպիսով, մեծ միասնական տեսությունը հնարավոր չէ ուղղակիորեն ստուգել լաբորատոր պայմաններում։ Այնուամենայնիվ, ինչպես էլեկտրոմագնիսական և թույլ միջուկային ուժի միասնական տեսության դեպքում, այստեղ ևս կան ցածր էներգիական այնպիսի հետևանքներ, որոնք կարող են ստուգվել լաբորատոր պայմաններում։ | ||
| + | |||
| + | Մեծ միասնական տեսության համար ամենահետաքրքրականն այն է, որ կանխագուշակեց նյութի հիմնական զանգվածը կազմող պրոտոնների ինքնակամ քայքայումն ավելի թեթև մասնիկների, ինչպիսիք են հակաէլեկտրոնները։ Իսկ այդ քայքայումը հնարավոր է այն պատճառով, որ մեծ միասնության էներգիայի պայմաններում քվարկների և հակաէլեկտրոնների միջև մի էական տարբերություն չկա։ Պրոտոնի կազմում ներառված երեք քվարկները սովորաբար այնքան էներգիա չունեն, որպեսզի վերածավեն հակաէլեկտրոնների, սակայն անորոշության սկզբունքի համաձայն, պրոտոնի կազմում գտնվող քվարկի էներգիան չի կարող ճշգրտորեն սևեռված լինել և, հնարավոր է, որ մի քվարկի էներգիան այնքան բարձր լինի, որ տեղի ունենա նրա անցումը հակաէլեկտրոնի։ Այդ դեպքում պրոտոնը կքայքայվի։ Քվարկի բավարար էներգիա ձեռք բերելու հավանականությունն այնքան փոքր է, որ դրա համար հարկավոր է առնվազն միլիոն միլոն միլիոն միլիոն տարի (1֊ից հետո 30 զերո)։ Այս ժամանակը շատ ավելի մեծ է, քան Մեծ պայթյունից մինչև օրս անցած ժամանակը, որը մոտ տասը հազար միլիտարի է (1֊ից հետո 10 զերո)։ Հետևաբար, կարելի է եզրակացնել, որ պրոտոնի ինքնակամ քայքայումը լաբորատոր պայմաններում ստուգման ենթակա չէ։ Սակայն քայքայման հայտնաբերման հնարավորությունը կարելի է մեծացնել, եթե օգտագործենք մեծ քանակով այնպիսի նյութ, որը պարունակում է մեծ թվով պրոտոններ։ (Օրինակ, եթե հնարավոր լինի տասը միլիոն միլիոն միլիոն միլիոն միլիոն (1֊ից հետո 31 զերո) պրոտոն դիտարկել մեկ տարվա ընթացքում, ապա սպասելի է, որ ՄՄՏ֊ի համաձայն մեկից ավելի պրոտոն քայքայվի։ | ||
| + | |||
| + | Այդպիսի մի շարք փորձեր են դրվել, սակայն պրոտոնի կամ նեյտրոնի քայքայման որոշակի փաստ չի դիտվել։ Փորձերից մեկի համար օգտագործվեց ութը հազար տոննա ջուր Օհայո նահանգի Մորտոն աղահանքում (փորձը այնտեղ դրվեց տիեզերական ճառագայթման ազդեցության հետևանքներից խուսափելու համար)։ Քանի որ փորձի ընթացքում պրոտոնային ինքնակամ քայքայում չդիտվեց, ապա կարելի է եզրակացնել, որ պրոտոնի կյանքի տևողությունը տաս միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն (1֊ից հետո 31 զերո) տարուց մեծ է։ Դա ավելին է, քան կանխագուշակում է պարզագույն Մեծ միասնության տեսությունը, սակայն, կան բազմաթիվ առավել մշակված տեսական տարբերակներ, որոնք կանխագուշակում են պրոտոնի կյանքի ավելի երկար տևողություն։ Հետևաբար այդ նպատակի համար հարկավոր է օգտագործել ավելի մեծ քանակի նյութ և դնել ավելի ճշգրիտ փորձեր։ | ||
| + | |||
| + | Չնայած այսքան դժվար է պրոտոնի ինքնակամ քայքայում դիտելը, հնարավոր է, որ մեր իսկ գոյությունը պայմանավորված է հակադարձ գործընթացով՝ պրոտոնների կամ ավելի պարզ մասնիկների՝ քվարկների առաջացումով սկզբնական այնպիսի վիճակից, որում ավելի շատ հակաքվարկներ կային, քան քվարկներ, որը կարող է տիեզերքի սկզբնավորման ամենահավանական ճանապարհը լինել։ Երկրագնդի նյութը կազմված է հիմնականում պրոտոններից և նեյտրոններից, որոնք իրենց հերթին կազմված են քվարկներից։ Հակաքվարկներից առաջացած հակապրոտոններ և հականեյտրոններ չկան, բացառությամբ այն չնչին քանակի, որը հզոր արագացուցիչներում ստացել են ֆիզիկոսները։ Տիեզերական ճառագայթների հիման վրա ստացված արդյունքները ցույց են տալիս, որ վիճակը նույնն է մեր գալակտիկայում, ուր հակապրոտոններ և հականեյտրոններ չկան, բացի այն փոքր թվով մասնիկ֊հակամասնիկ զույգերից, որոնք առաջանում են բարձր էներգիա ունեցող մասնիկների բախման ընթացքում։ Եթե մեր գալակտիկայում լինեին հակամարմինների լայն տիրույթներ, ապա հակամարմին և մարմին պարունակող տիրույթների սահմանագծում շատ հզոր ճառագայթում կդիտվեր՝ շնորհիվ մասնիկ֊հակամասնիկ զույգերի փոխադարձ ոչնչացման։ | ||
| + | |||
| + | Մենք ուղղակի ապացույց չունենք այն մասին, որ այլ գալակտիկաներում նյութը կազմված է պրոտոններից ու նեյտրոններից կամ հակապրոտոններից ու հականեյտրոններից։ Բայց երկուսից մեկը պետք է լինի, քանի որ այն չի կարող մասնիկի և հակամասնիկի խառնուրդ լինել, այլապես նման դեպքում տեղի կունենար մասնիկների ոչնչացում և հզոր էներգիայի ճառագայթում։ Այդ պատճառով այսօր տարածված է այն կարծիքը, որ գալակտիկաները ավելի շուտ կազմված են քվարկներից, քան հակաքվարկներից։ Անհավանական է, որ որոշ գալակտիկաներ կազմված են նյութից, իսկ մյուսները՝ հականյութից։ | ||
| + | |||
| + | Իսկ ի՞նչն է պատճառը, որ ավելի շատ քվարկներ կան, քան հակաքվարկներ։ Ինչո՞ւ դրանք հավասար թվով չեն կարող լինել։ Սա ակնհայտ է, քանի որ այդ դեպքում քվարկներն ու հակաքվարկները կոչնչացնեին միմյանց, նախնական տիեզերքում նյութ գոյություն չէր ունենա, և տիեզերքը լցված կլիներ հզոր ճառագայթումով։ Գոյություն չէին ունենա գալակտիկաներ, աստղեր կամ մոլորակներ, որտեղ մարդկային կյանք կարող էր զարգանալ։ Բարեբախտաբար, մեծ միասնական տեսություններն ի վիճակի են բացատրել, թե ինչո՞ւ այժմ տիեզերքում ավելի շատ քվարկներ կան, քան հակաքվարկներ, նույնիսկ եթե սկզբնական շրջանում դրանց թիվը հավասար էր։ Ինչպես մենք տեսանք, ՄՄՏ֊ները թույլ են տալիս, որ բարձր էներգիայի պայմաններում քվարկները փոխարկվեն հակաէլեկտրոնների։ Դրանք թույլ են տալիս նաև հակառակ գործընթացը՝ հակաքվարկների փոխանակումը էլեկտրոնների և հակաէլեկտրոնների ու էլեկտրոնների փոխարկումը քվարկների ու հակաքվարկների։ Տիեզերքի շատ վաղ շրջանում, երբ այն չափազանց տաք էր, մասնիկների էներգիան այնքան բարձր էր, որ հնարավոր էին նման փոխարկումները։ Պատճառն այն է, որ ֆիզիկայի օրենքները ճիշտ նույնը չեն մասնիկների և հակամասնիկների համար։ | ||
| + | |||
| + | Մինչև 1956 թվականը տարածված էր այն կարծիքը, թե ֆիզիկայի օրենքները ենթարկվում են երեք առանձին համաչափություններից յուրաքանչյուրին․ դրանք կոչվում են C, P, T. համաչափություններ։ C֊համաչափություն նշանակում է, որ մասնիկի և հակամասնիկի համար ուժի մեջ է նույն օրենքը։ P֊համաչափությունը նշանակում է, որ օրենքները նույնն են որևէ դրության և նրա հայելային պատկերի համար (դեպի աջ պտտվող մասնիկի հայելապատկերը ձախ պտտվողն է)։ T֊համաչափությունը նշանակում է, որ եթե բոլոր մասնիկների ու հակամասնիկների շարժման ուղղությունը շրջվի, ապա համակարգը կվերադառնա իր նախնական վիճակին, այլ կերպ ասած, օրենքները նույնն են ժամանակի առաջընթաց և հետընթաց ուղղություններում։ | ||
| + | |||
| + | 1956֊ին երկու ամերիկացի ֆիզիկոսներ՝ Յունգ֊Դաո Լին և Չեն Նին Յանգը այն միտքն արտահայտեցին, թե թույլ ուժը համաչափությանը չի ենթարկվում։ Այլ կերպ ասած, թույլ ուժի ազդեցության տակ տիեզերքի զարգացումը բոլորովին այլ կլիներ, քան նրա հայելային պատկերի զարգացումը։ Նույն տարում նրանց պաշտոնակից Չյեն֊Շյունգ Վուն ապացուցեց, որ այդ կանխագուշակումը ճիշտ է։ Տիկին Վուն ռադիոակտիվ ատոմների միջուկները մագնիսական դաշտում այնպես էր դասավորել, որ բոլորը նույն ուղղությամբ էին պտտվում և գտել էր, որ էլեկտրոնների արձակումը ավելի մեծ է մի ուղղությամբ, քան մյուս ուղղությամբ։ Հաջորդ տարում Լին և Յանգը Նոբելյան մրցանակ ստացան իրենց գաղափարի համար։ Պարզվեց նաև, որ թույլ ուժը չի ենթարկվում նաև C֊համաչափությանը։ Այսինքն, այդ պատճառով հակամասնիկներից կազմված տիեզերքը պետք է տարբեր լիներ մեր տիեզերքից։ Այնուամենայնիվ թվում է, թե թույլ ուժը ենթարկվում է CP միացյալ համաչափությունը։ Այսինքն՝ տիեզերքն ու իր հայելային պատկերը նույն ձևով կզարգանային, եթե, որպես լրացում, ամեն մասնիկ փոխարինված լիներ իր հակամասնիկով։ Սակայն, 1964֊ին երկու ամերիկացի՝ Ջ․ Ու․ Կրոնինը և Վել Ֆիտչը հայտնաբերեցին, որ նույնիսկ CP համաչափությունը ուժի մեջ չէ K֊մեզոններ կոչվող որոշակի մասնիկների քայքայման համար։ Կրոնինը և Ֆիտչը իրենց աշխատանքի համար վերջապես 1980֊ին արժանացան Նոբելյան մրցանակի։ (Այսպիսով, բազմաթիվ Նոբելյան մրցանակներ են շնորհվել պարզապես այն բանի համար, որ ցույց է տրվել, որ տիեզերքը այնքան պարզ չէ, որքան կարծում ենք)։ | ||
| + | |||
| + | Կա մաթեմատիկական մի թեորեմ, որի համաձայն, ամեն տեսություն, որը ենթարկվում է քվանտային մեխանիկային և հարաբերականությանը, պետք է միշտ ենթարկվի CPT միացյալ համաչափությանը։ Այսինքն՝ տիեզերքի վարքագիծը չի փոխվի, եթե մասնիկները փոխարինվեն հակամասնիկներով, վերցվի տիեզերքի հայելային պատկերը և շրջվի ժամանակի ուղղությունը։ Բայց, ինչպես տեսանք, համաձայն Կրոնինի և Ֆիտչի, եթե մասնիկները փոխարինվեն իրենց հակամասնիկներով և վերցվի հայելային պատկերը, ապա տիեզերքը նույն վարքագիծը չի ունենա, քանի դեռ չի շրջվել ժամանակի ուղղությունը։ Այսինքն՝ եթե ժամանակը իր ուղղությունը փոխի, կփոխվեն նաև ֆիզիկայի օրենքները, հետևաբար դրանք չեն ենթարկվում T֊համաչափությանը։ | ||
| + | |||
| + | Իհարկե, նախնական տիեզերքը T֊համաչափությանը չի ենթարկվում․ այսպես՝ եթե ժամանակը շարժվում է առաջ, տիեզերքն ընդարձակվում է, իսկ եթե ժամանակը ետ շարժվի, տիեզերքը պետք է կծկվի։ Եվ քանի որ կան այնպիսի ուժեր, որոնք չեն ենթարկվում T֊համաչափությանը, հետևաբար այդ ուժերը կարող են պատճառ դառնալ, որ տիեզերքի ընդարձակման պայմաններում ավեի շատ հակաէլեկտրոններ վերածվեն քվարկների, քան էլեկտրոններ՝ հակաքվարկների։ Մինչ տիեզերքն ընդարձակվում և սառչում է, հակաքվարկները աստիճանաբար ոչնչանում են քվարկներով, սակայն, որովհետև վերջիններիս թիվը ավելի շատ է, քան հակաքվարկներինը, ապա ակնհայտ է, որ քվարկների փոքրիկ ավելցուկ կմնա տիեզերքում։ Հենց սա էլ կազմում է այն նյութական աշխարհը, որը մենք տեսնում ենք այսօր և, որից մենք ինքներս կազմված ենք։ Այսպիսով, հենց մեր գոյությունը հաստատում է մեծ միասնական տեսության ճշմարտացիությունը, թեև լոկ որակական առումով։ Անորոշությունն այն է, որ մենք չենք կարող հաշվել, թե ոչնչացումից հետո ինչ թվով քվարկներ կմնան կամ, դեռ ավելին, դրանք քվարկներ, թե հակաքվարկներ կլինեն։ (Այնուամենայնիվ, եթե մնացած մասնիկները հակաքվարկներ լինեին, մենք պարզապես դրանք կանվանեինք քվարկ, իսկ քվարկները՝ հակաքվարկներ, և դրանից ոչինչ չէր փոխվի)։ | ||
| + | |||
| + | Մեծ միասնական տեսությունները չեն ընդգրկում գրավիտացիոն ուժը։ Սա առանձնահատուկ նշանակություն չունի, որովհետև գրավիտացիոն ուժը այնքան թույլ է, որ կարելի է այն արհամարհել, երբ մենք գործ ունենք տարրական մասնիկների և ատոմների հետ։ Սակայն, այն փաստը, որ դրանք երկուսով հեռավոր ազդեցության ուժեր են և բնույթով՝ միշտ ձգողական, նշանակում է, որ նրանց ազդեցությունը գումարային է։ Այսինքն, եթե նյութական մասնիկների թիվը շատ մեծ է, ապա գրավիտացիոն ուժը կարող է գերազանցել մյուս բոլոր ուժերին։ Ահա թե ինչու է գրավիտացիոն ուժը<ref>Հարց է ծաում, գոյություն ունի՞ արդյոք փոխազդեցություն գրավիտացիոն ուժի և մյուս երեք քվանտային ուժերի միջև։ Բանն այն է, որ գրավիտացիոն ուժը տարածություն֊ժամանակի տիրույթում նյութի առկայության հետևանքն է։ Չնայած այդ ուժի էությունը մեզ հայտնի չէ դեռևս, բայց մենք գիտենք, որ նյութը որոշակի կառույց ունի, այն կազմված է որոշակի թվով պրոտոններից ու նեյտրոններից, նրանց կապի էներգիայից և վերջապես ատոմների ներքին փոխդասավորությունից։ Ըստ ոմանց, նյութի այդ կառուցվածքային առանձնահատկությունը պայմանավորում է մի հինգերորդ ուժ, որը հակազդում է գրավիտացիոն ուժին և գործում մինչև մի քանի հայրուր կիլոմետր հեռավորությունների վրա։ Սա վիճելի, բայց հետաքրքիր հարզ է, որի մասին մանրամասնորեն խոսվում է «National Geographic Magazine» ամսագրի 1989 թվականի մայիսի և սեպտեմբերի համարներում։</ref> որոշում տիեզերքի էվոլյուցիան։ Նույնիսկ այն չափի մարմինների համար, ինչպիսիք աստղերն են, գրավիտացիոն ձգողական ուժը կարող է գերազանցել մյուս բոլոր ուժերին և ստիպել, որ աստղը կոլապսվի։ 1970֊ի իմ ուսումնասիրությունները կենտրոնացած էին սև խոռոչներին, որոնք կարող են առաջանալ այդպիսի աստղային կոլապսի արդյունքում, և նրանց շուրջ առկա հզոր գրավիտացիոն դաշտերի վրա։ Այս էր պատճառը, որն ինձ հուշեց այն մասին, թե ինչպես կարող են ընդհանուր հարաբերականությունը և քվանտային մեխանիկան լրացնել միմյանց, և սա եղավ գրավիտացիոն քվանտային մեխանիկայի առաջին առկայծումը։ | ||
| + | |||
| + | |||
| + | ==6== | ||
| + | |||
| + | Սև խոռոչներ | ||
| + | |||
| + | Սև խոռոչ տերմինն առաջացել է ընդամենը վերջերս։ 1969֊ին այն ներմուծել է ամերիկացի գիտնական Ջոն Ուիլլերը, որպեսզի պատկերավոր ձևով նկարագրի մի գաղափար, որն առաջացել էր առնվազն երկու հարյուր տարի առաջ, երբ լույսի բնույթը բացատրող երկու տեսություն կար։ Մեկը Նյուտոնի առաջարկած լույսի մասնիկային տեսությունն էր, մյուսը՝ լույսի՝ ալիքներից կազմված լինելու տեսությունը։ Մենք այժմ գիտենք, որ այդ երկու տեսությունն էլ, իրապես ճիշտ են։ Համաձայն քվանտային մեխանիկայի, որի հիմքում ընկած է լույսի արլիք֊մասնիկային երկվությունը, լույսը կարելի է դիտել և՛ որպես մասնիկ, և՛ որպես ալիք։ Լույսի ալիքներից կազմված լինելու տեսությունը պարզ չէր սակայն, թե այն իրեն ինչպես կպահի գրավիտացիոն դաշտում։ Իսկ եթե լույսը կազմված է մասնիկներից, ապա սպասելի էր, որ գրավիտացիոն դաշտը լույսի վրա պետք է թողներ այնպիսի ազդեցություն, ինչպիսին թողնում է արկերի, հրթիռների և մոլորակների վրա։ Սկզբում մարդիկ մտածում էին, թե լույսի մասնիկները շարժվում են անսահման մեծ արագությամբ, ուստի գրավիտացիոն դաշտն ի վիճակի չէ դանդաղեցնել նրանց ընթացքը։ Բայց Ռոեմերի հայտնագործությունը, ըստ որի լույսն ունի վերջավոր արագություն, վկայում էր, որ գրավիտացիան կարող է էական ազդեցություն թողնել լույսի վրա։ | ||
| + | |||
| + | Այս ենթադրության հիման վրա Քեմբրիջի համալսարանի դասախոս Ջոն Միչելը 1783֊ին Լոնդոնի Թագավորական ընկերության փիլիսոփայական հաղորդակցություններում տպած մի հոդվածում ուշադրություն հրավիրեց այն հարցի վրա, որ, երբ աստղը բավականին զանգվածեղ և խիտ լինի, ապա այն պետք է այնպիսի գրավիտացիոն դաշտ ունենա, որ լույսը չկարողանա արձակվել, իսկ եթե, այնուամենայնիվ, որոշ լույս արձակվի աստղի մակերևույթից, ապա գրավիտացիոն դաշտը պետք է հետ քաշի այն և թույլ չտա իրենից հեռանալ։ Միչելը գտնում էր, որ այդպիսի աստղեր կարող են շատ լինել։ Չնայած մենք նրանց չենք կարող տեսնել, որովհետև նրանց լույսը մեզ չի հասնի, սակայն այդ աստղերի գրավիտացիոն ձգողականությունը կզգանք։ Հենց այսպիսի առարկաներն այն են, ինչ մենք անվանել ենք սև խոռոչներ, որովհետև դրանք, ըստ էության մթին դատարկություններ են տարածության մեջ։ Մի քանի տարի անց նմանօրինակ առաջարկություն արեց ֆրանսիացի գիտնական մարկիզ դը Լապլասը՝ ամենայն հավանականությամբ Միչելից անկախ։ Հետաքրքրական է բավականին, որ Լապլասը դա ներառել է իր՝ «Աշխարհի համակարգը» գրքի միայն առաջին և երկրորդ հրատարակություններում, սակայն ավելի ուշ հրատարակությունից հանել է, հավանաբար, ենթադրելով, որ անիմաստ է։ (Արդեն 19֊դարում լույսի մասնիկային տեսությունը մոռացվել էր և, կարծես ամեն ինչ կարելի էր բացատրել ալիքային տեսությամբ, որի համաձայն, ինչպես ասվեց, հստակ չէ գրավիտացիոն դաշտը կարո՞ղ էր արդյոք ներգործել ալիքային շարժման վրա ընդհանրապես)։ | ||
| + | |||
| + | Իրականում, բոլորովին անտեղի էր լույսի մասնիկը պատկերել որպես թնդանոթի արկ, ինչպես դա արվում է Նյուտոնի ձգողականության տեսության մեջ, այն պատճառով, որ լույսի արագությունը հաստատուն է։ (Որովհետև դեպի վեր կրակված արկը աստիճանաբար կդանդաղի ձգողական ուժի ազդեցության տակ և վերջապես վայր կընկնի):<ref>Եթե արագությունը մեծ է որոշ կրիտիկական (տիեզերական) արժեքից, ապա արկը կպոկվի երկրի ձգողական ուժից և դուրս կգա երկրաշուրջ ուղեծիր կամ միջմոլորակային տարածություն։</ref> | ||
| + | |||
| + | Ֆոտոնը, սակայն, հաստատուն արագությամբ կշարունակի բարձրանալ վեր։ Ինչպե՞ս կարող է այժմ նյուտոնյան ձգողականությունը ազդել լույսի վրա։ Լուսի վրա գրավիտացիոն դաշտի ազդեցության հետևողական տեսությունը տվեց շատ ավելի ուշ՝ 1915֊ին, երբ Էյնշտեյն առաջարկեց ընդհանուր հարաբերականությունը։ Սակայն նույնիսկ դրանից հետո երկար ժամանակ պահանջվեց, որպեսզի հասկացվեր մեծ զանգված ունեցող աստղերի տեսության նշանակությունը։ | ||
| + | |||
| + | Որպեսզի հասկանանք, թե ինչպես է առաջանում սև խոռոչը, առաջին հերթին հարկավոր է իմանալ, թե ի՞նչ բան է աստղի կյանքի շրջափուլը։ Աստղն առաջանում է, երբ մեծ քանակությամբ գազը (հիմնականում ջրածին) կոլապսվում է ինքն իր մեջ իր գրավիտացիոն ձգողության ազդեցությամբ։ Սեղմված գազի ատոմներն իրար ավելի հաճախ և աստիճանաբար ավելի մեծ արագությամբ են բախվում, և սեղմված գազը տաքանում է։ Վերջապես գազն այն աստիճան է տաքանում, որ իրար հետ բախվող ջրածնի ատոմները ոչ թե հետ են մղվում, այլ ընդհակառակը՝ իրար են միանում և առաջացնում հելիում։ Այս ռեակցիայի արդյունքում մեծ քանակի ջերմություն է անջատվում, ինչպես ջրածնային ռումբի պայթման ժամանակ, որից և աստղը փայլատակում է։ Այդ լրացուցիչ ջերմության շնորհիվ այնքան է բարձրանում գազի ճնշումը, մինչև որ բավարարի հավասարակշռելու գրավիտացիոն ձգողությունը, և գազի սեղմվելը դադարում է։ Այս վիճակը նման է օդապարիկի վիճակին, երբ գազի ներքին ճնշումը ձգտում է ընդարձակել օդապարիկը, իսկ ռետինե թաղանթի լարվածությունը՝ փոքրացնել ծավալը, և ստեղծվում է հավասարակշռություն։ Այդ նույն ձևով աստղերը կարող են այնքան ժամանակ կայուն մնալ, քանի դեռ միջուկային ռեակցիայի առաջացրած ջերմությունը հավասարակշռում է գրավիտացիոն ձգողականությանը։ Սակայն, ի վերջո, ջրածնի կամ այլ վառելանյութի պաշարները կսպառվեն։ Որքան էլ տարօրինակ է, ինչքան սկզբնական վառելանյութի պաշարը մեծ է, այնքան արագ է սպառվում այն։ Եվ որքան տաք է աստղը, այն այնքան արագ կսպառի իր պաշարը։ Մեր արեգակը հավանաբար բավական պաշար ունի՝ ավելի քան հինգ հազար միլիոն տարվա, բայց շատ ավելի զանգվածեղ աստղերն իրենց վառելայնությունը սպառած կլինեն ավելի փոքր՝ հարյուր միլիոն տարվա ընթացքում, որը շատ կարճ ժամանակամիջոց է տիեզերքի տարիքի համեմատ։ Երբ աստղերը սպառում են վառելանյութը, սկսում են սառչել և կծկվել։ Թե ինչպես է դա տեղի ունենում, պարզվեց միայն 1920֊ական թվականների վերջերին։ | ||
| + | |||
| + | 1928֊ին հնդիկ մի շրջանավարտ՝ Սուբրահամանիան Չանդրասեկհարը, Անգլիա ժամանեց Քեմբրիջի համալսարանում աստղագետ սըր Արթուր Էդինգտոնի մոտ ուսումնասիրություններ կատարելու համար, մի մարդու, որը հարաբերականության ընդհանուր տեսության խոշոր մասնագետ էր։ (Ըստ լայնորեն տարածված լուրերի, 1920֊ի սկզբներին մի լրագրող Էդինգտոնին իբր հարցրել է, թե ինքը լսել է, որ աշխարհում լոկ երեք գիտնական կարող են հասկանալ ընդհանուր հարաբերականությունը։ Էդինգտոնը մի պահ լսել և պատասխանել է․ «Փորձում եմ մտաբերել, թե ո՞վ է այդ երրորդը»)։ Չանդրասեկհարը Հնդկաստանից ճանապարհորդության ընթացքում լուծել է հետևյալ հարցը․ ի՞նչ չափսի պետք է լինի աստղը, որ իր ամբողջ վառելանյութը սպառելուց հետո կարողանա իր գոյությունը պահպանել սեփական գրավիտացիոն դաշտում։ Հարցի էությունը հետևյալն էր․ երբ աստղը կծկվում է, նյութական մասնիկները շատ են մոտենում իրար և, համաձայն Պաուլիի արգելակման սկզբունքների, պետք է շատ տարբեր արագություններ ունենան։ Դա ստիպում է նրանց հեռանալ միմյանցից և պատճառ դառնում, որ աստղը ընդարձակվի։ Ուստի աստղը կարող է հաստատուն շառավղով իր գոյությունը պահպանել, եթե գրավիտացիոն ձգողականությունը հավասարակշռվի այն վանողությամբ, որը առաջանում է արգելակման սկզբունքի շնորհիվ ճիշտ այնպես, ինչպես աստղի կյանքի սկզբնական շրջանում գրավիտացիոն ձգողականությունը հավասարակշռում էր անջատված ջերմությամբ։ | ||
| + | |||
| + | Ընդ որում Չանդրասեկհարը քաջատեղյակ էր, որ արգելակման սկզբունքով պայմանավորված վանողական ուժերը պետք է ինչ֊որ սահման ունենան։ Հարաբերականության տեսությունը աստղերում մասնիկների արագությունների միջև առավելագույն տարբերությունը սահմանափակում է լույսի արագությամբ։ Սա նշանակում է, որ երբ աստղը բավականաչափ խտացել է, անորոշության սկզբունքով պայմանավորված վանողականությունը գրավիտացիոն ձգողականությունից փոքր կլինի։ Չանդրասեկհարի հաշվումները ցույց տվեցին, որ, եթե սառը աստղի զանգվածը արեգակի զանգվածից մեծ է մոտ մեկուկես անգամ, ապա այն չի կարող դիմակայել իր գրավիտացիոն ձգողությանը։ (Այս զանգվածն այսօր հայտնի է որպես Չանդրասեկհարի սահման)։ | ||
| + | |||
| + | Գրեթե միևնույն ժամանակ նման հայտնագործություն էր կատարել նաև ռուս գիտնական Լև Դավիդովիչ Լանդաուն։ | ||
| + | |||
| + | Չանդրասեկհարի սահմանը կարևոր նշանակություն ունեցավ մեծ զանգվածով աստղերի ապագա վիճակի խնդրում։ Երբ աստղի զանգվածը փոքր է այդ սահմանային մեծությունից, ապա ի վերջո աստղը կդադարի կծկվել և կհասնի կայուն վիճակի, ինչպես «սպիտակ թզուկը», որի շառավիղը մի քանի հազար մղոն է, իսկ խտությունը՝ մի քանի տասնյակ տոննա խորանարդ դյույմում։ Սպիտակ թզուկն իր գոյությունը պահպանում է շնորհիվ էլեկտրոնների միջև առկա վանողական փոխազդեցության՝ համաձայն Պաուլիի արգելակման սկզբունքի։ Մենք մեծ թվով սպիտակ թզուկներ ենք հայտնաբերել։ Առաջիններից մեկը, որ հայտնաբերվել է, պտտվում է Սիրիուսի շուրջը, որը գիշերային երկնակամարի ամենափայլուն աստղն է։ | ||
| + | |||
| + | Լանդաուն նշել է, որ արեգակից մեկ կամ երկու անգամ մեծ սահմանային զանգված ունեցող աստղի համար հնարավոր է սպիտակ թզուկից շատ ավելի փոքր մի այլ վերջնական վիճակ։ Այս աստղերը պետք է կայուն լինեն արգելակման սկզբունքով պայմանավորված նեյտրոնների և պրոտոնների, քան էլեկտրոնների միջև վանողական փոխազդեցության շնորհիվ։ Այդ պատճառով էլ դրանք կոչվեցին նեյտրոնային աստղեր։ Սրանց շառավիղը կլինի մոտ տասը մղոն, իսկ խտությունը՝ տասնյակ միլիոն տոննա խորանարդ դյույումում։ Այն ժամանակ, երբ դրանք կանխագուշակվեցին, նեյտրոնային աստղերի դիտման միջոցներ դեռևս չկային։ Դրանք շատ ավելի ուշ հնարավոր եղավ հայտնաբերել։ | ||
| + | |||
| + | Չանդրասեկհարի սահմանից ավելի մեծ զանգված ունեցող աստղերի վիճակը, որոնք սպառում են իրենց վառելանյութը, խիստ հարցական է։ Որոշ դեպքերում կարող է պատահել, որ աստղը պայթի կամ կարողանա այնքան նյութ կորցնել, որ հասնի Չանդրասեկհարի սահմանին և խուսափի գրավիտացիոն կոլապսի աղետից։ Սակայն դժվար է հավատալ, որ այդպիսի բան միշտ կարող է պատահել, անկախ այն բանից, թե որքան մեծ է աստղը։ Այն ինչ իմանա, թե պետք է կշիռ կորցնել։ Եվ նույնիսկ, եթե ամեն աստղ կարողանա բավարար նյութ կորցնելով կոլապսից խուսափել, ապա ի՞նչ կպատահի, եթե թզուկին կամ նեյտրոնային աստղին հավելյալ նյութ ավելացվի, և նրանց զանգվածը անցնի սահմանից։ Այդ աստղերը, ուրեմն, կոլապսի՞ պիտի ենթարկվեն՝ հասնելով անվերջ խիտ վիճակի։ Էդինգտոնը ուղղակի ցնցված էր դրանից և հրաժարվեց ընդունել Չանդրասեկհարի եզրահնգումները։ Էդինգտոնը մտածում էր, որ պարզապես անհնար է, որ աստղը կարող է կոլապսվել և մի կետ դառնալ։ Այս նույն կարծիքին էր գիտնականների մեծամասնությունը․ Էյնշտեյնը հանդես եկավ մի հոդվածով, որում պնդում էր, թե աստղը չի կարող կծկվել մինչև զերո չափսը։ Գիտնականների և մանսավորապես իր նախկին ուսուցչի և աստղագիտության առաջնակարգ մասնագետ Էդինգտոնի անբայրացակամությունն այդ հարցում համոզեցին Չանդրասեկհարին հրաժարվել այդ ուղղությամբ իր ուսումնասիրություններից և նվիրվել աստղագիտության այլ հարցերի, ինչպես օրինակ, աստղային կույտերի շարժումներն են։ Այնուամենայնիվ, երբ 1983֊ին Չանդրասեկհարին շնորհվեց Նոբելյան մրցանակ, դա մասամբ սառը աստղերի սահմանային զանգվածի ուղղությամբ անցյալում նրա կատարած աշխատանքների համար էր։ | ||
| + | |||
| + | Չանդրասեկհարը ցույց էր տվել, որ արգելակման սկզբունքը բավարար չէ կանխելու այն աստղերի կոլապսումը, որոնց զանգվածը մեծ է Չանդրասեկհարի սահմանից։ Բայց թե ի՞նչ կպատահի այդպիսի աստղերի հետ ըստ հարաբերականության ընդհանուր տեսության, առաջինը պարզեց երիտասարդ ամերիկացի գիտնական Ռոբերտ Օպենհեյմերը 1939 թվականին։ Սակայն նրա եզրահանգումն այնպիսին էր, որ այդ ժամանակ օգտագործվող հեռադիտակներով հայտնաբերել և դիտել հնարավոր չէր։ Վրա հասավ Երկրորդ համաշխարհային պատերազմը, և Օպենհեյմերը մոտիկից ներգրավվեց ատոմական ռումբի ստեղծման աշխատանքներում։ Պատերազմի ավարտից հետո գրավիտացիոն կոլապսի հիմնահարցը հիմնովին մոռացության տրվեց, քանի որ գիտնականների մեծ մասն անցավ ատոմի միջուկի մասշտաբի հեռավորություններում տեղի ունեցող երևույթների ուսումնասիրությանը։ 1960֊ական թվականներին սակայն, շնորհիվ ժամանակակից տեխնիկական միջոցների կիրառման, հնարավոր եղավ աստղագիտական լայն մասշտաբի դիտարկումներ կատարել և հետքրքրությունը լայնամասշտաբ աստղագիտական և տիեզերագիտական ուսումնասիրությունների ուղղությամբ վերակենդանացավ։ Օպենհեյմերի աշխատանքները վերահայտնաբերվեցին, և շատերն այն ընդունեցին։ | ||
| + | |||
| + | Օպենհեյմերի աշխատանքներից ելնելով՝ հարցը կարելի է պատկերացնել այսպես․ աստղի գրավիտացիոն դաշտը փոխում է տարածություն֊ժամանակի մեջ տարածվող լույսի ճառագայթների ուղին, և աստղը երևում է այնտեղ, որտեղ իրականում չկա։ Լուսակոները, որոնք ցույց են տալիս նրանց գագաթի արձակված լույսի ճառագայթների ուղին տարածություն֊ժամանակի մեջ, աստղի մակերևույթի մոտ թեթևակի դեպի ներս թեքված կլինեն։ Դա կարելի է տեսնել հեռավոր աստղերից եկող լույսի թեքման միջոցով, ինչը դիտվում է արեգակի խավարման ժամանակ։ Երբ աստղը կծկվում է, գրավիտացիոն դաշտն ավելի է մեծանում, և լուսակոների՝ դեպի ներս թեքվածությունը խորանում է։ Այսպիսով, դա դժվարացնում է լույսի ձերբազատումը աստղից, և հեռվից դիտողին նրանցից եկող լույսը թուլացած կարմիր է երևում։ Վերջապես, երբ կծկման հետևանքով աստղի շառավիղը հասնում է որոշակի կրիտիկական մեծության, և գրավիտացիոն դաշտի ուժն այն աստիճան է աճում, և կոները այն աստիճան են կորանում, որ լույսը բոլորովին չի կարող արձակվել (նկ․ 6.1)։ Համաձայն հարաբերականության տեսության ոչինչ չի կարող շարժվել լույսից ավելի արագ։ Եվ քանի որ չի կարողանում պոկվել գրավիտացիոն դաշտից, ուստի ոչինչ չի կարողանա դա անել, ու ամեն ինչ գրավիրացիոն դաշտի կողմից ետ կձգվի։ Այսպիսով գոյություն ունի պատահարների մի շարք՝ մի տիրույթ տարածություն֊ժամանակի մեջ, որտեղից հնարավոր չէ ձերբազատվել և հասնել հեռավոր դիտողին։ Հենց այդ տիրույթն էլ կոչվում է սև խոռոչ։ Նրա սահմանագիծը կոչվում է պատահույթի հորիզոն և համընկնում է լուսային ճառագայթների այն ուղու հետ, որից դուրս չի կարող անցնել սև խոռոչից արձակված լույսը։ | ||
| + | |||
| + | Հասկանալու համար, թե մարդ ինչ կարող է տեսնել աստղի կոլապսի հետևանքով առաջացող սև խոռոչը դիտելիս, պետք է հիշել, որ համաձայն հարաբերականության տեսության, բացարձակ ժամանակ գոյություն չունի։ Յուրաքանչյուր դիտորդ ունի ժամանակի իր չափումը։ Աստղի գրավիտացիոն դաշտի պատճառով նրա վրա գտնվողի համար ժամանակն այլ է, քան նրանից որոշ հեռավորության վրա գտնվողի համար։ Ենթադրենք՝ մի անվեհեր տիեզերագնաց գտնվում է կոլապսի ենթարկվող աստղի մակերևույթին և աստղի հետ ինքն էլ է կոլապսվում և, իր ժամացույցով չափված, նա ամեն վայրկյան ազդանշան է ուղարկում դեպի աստղի շուրջ պտտվող տիեզերանավը։ Դիցուկ, նրա ժամացույցով ժամը 11.00֊ին աստղը կծկվելով փոքրացել է կրիտիկական շառավղից, և գրավիտացիոն դաշտը այնքան է ուժեղացել, որ որևէ ազդանշան այլևս չի կարող պոկվել նրանից և հասնել տիեզերանավին։ Մինչ ժամը մոտենում է 11.00֊ին, տիեզերանավի անձնակազմի համար ազդանշանների միջև ընկած ժամանակամիջոցները գնալով երկարում են, թեև այդ բանը ժամը 10 անց 59 րոպե 59 վայրկյանից առաջ շատ աննշան կլինի։ Այսպես, տիեզերագանացի10 անց 59 րոպե 58 վայրկյանին տրված ազդանշանից մինչև 10 անց 59 րոպե 59 վայրկյանի ազդանշանը մեկ վայրկյանից փոքր֊ինչ երկար կտևի, սակայն 11.00֊ի ազդանշանին նրանք կսպասեն անվերջ։ Տիեզերագնացի ժամացույցով ժամը 10 անց 59րոպե 59 վայրկանից մինչև 11.00֊ն աստղի մակերևույթից արձակված լույսի ալիքները ըստ տիեզերանավի անձնակազմի, կտարածվեն անսահման ժամանակամիջոցում։ Տիեզերանավին հասած՝ հաջորդական ալիքների միջև ընկած ժամանակամիջոցներն աստիճանաբար կերկարեն, ընդ որում աստղի ճառագայթումն աստիճանաբար ավելի կկարմրի և կթուլանա։ Ի վերջո աստղն այն աստիճան աղոտ կդառնա, որ տիեզերանավի համար կդառնա անտեսանելի, և այդ ամենի արդյունքում տիեզերքում կառաջանա մի սև խոռոչ։ Այնուամենայնիվ, աստղի գրավիտացիոն դաշտի ձգողության ուժը կգործի առաջվա նման, և տիեզերանավը կշարունակի պտտվել սև խոռոչի շուրջ։ | ||
| + | |||
| + | [[Պատկեր:H6 1.svg|thumb]] | ||
| + | |||
| + | Այս սցենարը, սակայն, լրիվ չի համապատասխանում իրականությանը հետևյալ պատճառով․ ձգողության ուժը թուլանում է աստղի մակերևույթից հեռանալիս, հետևաբար, այն միշտ ավելի ուժեղ կլինի մեր անվեհեր տիեզերագնացի ոտքերի մոտ, քան գլխի վրա։ Ուժերի այս տարբերությունը տիեզերագնացին կձգի մակարոնի նման և կամ բաժան֊բաժան կանի նրան՝ աստղը դեռ իր կրիտիկական շառաղվին չհասած, երբ ձևավորվում է պատահույթի հորիզոնը։ Սակայն մենք կարծում ենք, որ տիեզերքում կան ավելի զանգվածեղ մարմիններ, ինչպես գալակտիկաների կենտրոնական տիրույթները, որոնք կարող են գրավիտացիոն կոլապսի ենթարկվել և սև խոռոչ առաջացնել։ Այդ տեղերից մեկում գտնվող տիեզերագնացը մինչև սև խոռոչ առաջանալը կտոր֊կտոր չի լինի։ Կրիտիկական շառաղվին հասնելիս նա, փաստորեն, առանձնահատուկ ոչինչ չի զգում և անցում է կատարում դեպի անդարձություն՝ դա չնկատելով։ Այնուամենայնիվ, մինչ տիրույթը շարունակում է կոլապսվել, մի քանի ժամվա ընթացքում գրավիտացիոն ձգողական ուժերի տարբերությունը տիեզերագնացի ոտքերի և գլխի վրա այն աստիճան կմեծանա, որ նրան դարձյալ բաժան֊բաժան կանի։ | ||
| + | |||
| + | 1965֊ից մինչև 1970 թվականը Ռոջեր Պենրոուզի հետ իմ կատարած աշխատանքը ցույց տվեց, որ, ըստ հարաբերականության ընդհանուր տեսության, սև խոռոչում պետք է գոյություն ունենա անսահման խտություն և տարածություն֊ժամանակի կորության մի եզակիություն։ Սա բավականին նման է ժամանակի սկզբնավորման Մեծ պայթյունին, միայն այն տարբերությամբ, որ դա կոլապսվող մարմնի և տիեզերագնացի համար ժամանակի վերջն է։ Այս եզակիության համար գիտության օրենքներն ու մեր կանխագուշակման կարողությունը կորցնում են իրենց ուժը։ Բայց սև խոռոչից դուրս գտնվող ցանկացած դիտորդի համար կանխագուշակելու անկարողությունը որևէ նշանակություն չունի, որովհետև ո՛չ լույս, ո՛չ էլ որևէ այլ ազդանշան եզակիությայն կետից նրան չի կարող հասնել։ Այս ուշագրավ փաստը պատճառ դարձավ, որ Ռոջեր Պենրոուզը առաջարկեր տիեզերային գրաքննության վարկածը, որը կարելի է ձևակերպել հետևյալ կերպ․ «Աստված ատում է մերկ եզակիությունը»։ Այսինքն՝ գրավիտացիոն կոլապսի առաջացրած եզակիություններն առկա են միայն այնպիսի տեղերում, ինչպիսիք են սև խոռոչները, որոնք դրսից ղիտողներից պատշաճորեն թաքնվում են պատահութային հորիզոնով։ Խստորեն ասած, սա հայտնի է որպես թույլ տիեզերային գրաքննության վարկած․ դա սև խոռոչից դուրս գտնվող դիտորդներին պաշտպանում է եզակիության մեջ կանխատեսման անհնար լինելու հետևանքներից, սակայն ոչնչով չի օգնում խեղճ, դժբախտ տիեզերագնացին, որն ընկնում է խոռոչի մեջ։ | ||
| + | |||
| + | Ընդհանուր հարաբերականության հավասարումներն ունեն մի քանի լուծումներ, որոնք թույլ են տալիս տիեզերագնացին դիտել մերկ եզակիությունը․ նա կարող է ի վիճակի լինել խուսափելու եզակիության հետ բախումից և փոխարենն ընկնել «որդնածակի» մեջ ու դուրս գալ տիեզերքի մի այլ տիրույթ։ Կարծես լայն հնարավորություններ են ստեղծվում տարածության և ժամանակի մեջ ճամփորդելու համար, բայց, դժբախտաբար, ինչպես պարզվում է, այս լուծումները կարող են շատ անկայուն լինել՝ նվազագույն խանգարող հանգամանքն անգամ, ինչպես հենց տիեզերագնացի ներկայությունն այդ տիրույթում կարող է լուծումն այնպես փոխել, որ տիեզերագնացը չնշմարի եզակիությունը, մինչև չբախվի նրա հետ և չավարտվի նրա կյանքի ժամանակը։ Այլ խոսքով ասած, եզակիությունը միշտ կլինի նրա ապագայում, ոչ թե անցյալում։ Տիեզերային գրաքննության վարկածի խիստ տարբերակի համաձայն, երբ լուծումն իրական է, եզակիությունները կամ լրիվ ապագայում կլինեն (ինչպես գրավիտացիոն կոլապսի եզակիությունը), կամ՝ լրիվ անցյալում (ինչպես Մեծ պայթյունը)։ Պետք է հուսալ, նաև, որ կլինի գրաքննչական վարկածի ինչ֊որ մի տարբերակ, երբ տարածության֊ժամանակի մերկ եզակիություններին շատ մոտ հնարավոր կլինի գնալ դեպի անցյալը։ Այդպիսի ճամփորդությունը թերևս արկածային վեպերի հեղինակներին ոգևորի, բայց կնշանակի, որ մեզանից ոչ ոքի կյանքն ապահովագրված չի լինի՝ մեկը կարող է մուտք գործել անցյալի մեջ և սպանել հորդ կամ մորդ՝ քո ձևավորվելուց դեռևս առաջ։ | ||
| + | |||
| + | Պատահութային հորիզոնը, այսինքն՝ տարածության֊ժամանակի այն տիրույթի սահմանագիծը, որից դուրս ոչինչ չի կարող անցնել, կարելի է պատկերել որպես սև խոռոչը շրջափակող միակողմանի թաղանթ։ Ամեն ինչ, ինչպես անզգույշ տիեզերագնացը, կարող է պատահութային հորիզոնն անցնել և ընկնել սև խոռոչի մեջ, սակայն այնտեղից ոչինչ չի կարող դուրս գալ։ (Հիշեք, որ պատահությային հորիզոնը լույսի սահմանագիծն է և ոչինչ չի կարող լույսից ավելի արագ շարժվել)։ Պատահութային հորիզոնի մասին կարելի է կրկնել բանաստեղծ Դանթեի խոսքերը, արտասանված դժոխքի մուտքի առաջ․ «Ով մտնողներ, թողեք ձեր հույսը համայն» (թրգմ․ Ա․ Տայան)։ Ամեն ոք և ամեն ինչ, որ ներս է ընկնում պատահութային հորիզոնից, շուտով հասնում է անսահման մեծ խտության և ժամանակի վերջի տիրույթ։ | ||
| + | |||
| + | Ընդհանուր հարաբերականությունը կանխագուշակում է, որ ծանր առարկաները շարժվելիս, տարածության կորության մեջ առաջացնում են գրավիտացիոն ալիքներ (կոհակներ), որոնք տեղաշարժվում են լույսի արագությամբ։ Սրանք նման են լույսի ալիքների, որոնք էլեկտրամագնիսական դաշտի կոհակներ են, սակայն ավելի դժվար են հայտնաբերվում։ Լույսի նման, դրանք կրում են իրենց արձակած առարկայի (աղբյուրի) էներգիան։ Սպասելի է, որ մեծ զանգված ունեցող առարկաներն ի վերջո կհասնեն ստացիոնար վիճակի, որովհետև շարժման էներգիան կտարվի արձակվող գրավիտացիոն ալիքներով։ (Երևույթը նման է այն դեպքին, երբ խցանը նետում են ջրի մեջ․ սկզբում խցանը թափով վեր ու վար է շարժվում ջրի մեջ, սակայն երբ կոհակները ցրում են նրա էներգիան, այն աստիճանաբար հանդարտվում է և հասնում ստացիոնար վիճակի)։ Օրինակ, երկրի շրջապտույտն իր ուղեծրով արեգակի շուրջ առաջացնում է գրավիտացիոն ալիքներ։ Էներգիայի կորստի հետևանքով երկրի ուղեծիրը պիտի որ փոխվի, և երկիրն աստիճանաբար մոտենա արեգակին, բախվի նրա հետ և հասնի ստացիոնար վիճակի։ Այս դեպքում էներգիայի կորուստը շատ փոքր է՝ այն հազիվ կարող է բավարարել մի փոքրիկ էլեկտրական ջեռուցիչ աշխատեցնելու համար։ Դա նշանակում է, որ հազար միլիոն միլիոն միլիոն միլիոն տարի հետո միայն երկիրը կընկնի արեգակի վրա, այնպես որ, մտահոգվելու հարկ չկա։ Երկրի ուղեծրի փոփոխությունն այն աստիճան աննշան է, որ դիտարկելի չէ, բայց նման երևույթ վերջին տարիներին դիտվել է, այսպես կոչված, PSR 1913 + 16 համակարգում։ (PSR նշանակում է «պուլսար որը յուրահատուկ նեյտրոնային աստղ է և կանոնավոր կերպով ռադիոալիքներ է առաքում): Այս համակարգը պարունակում է երկու նեյտրոնային աստղեր, որոնք պտտվում են միմյանց շուրջ, և արձակված գրավիտացիոն ալիքներով նրանց կորցրած էներգիան ստիպում է, որ այդ երկու աստղերը պարուրաձև մոտենան իրար։ | ||
| + | |||
| + | Սև խոռոչ առաջացնելիս աստղի գրավիտացիոն կոլապսի ընթացքում շարժումները շատ արագ են տեղի ունենում և, հետևաբար, էներգիայի ցրման արագությունը ևս կլինի շատ բարձր։ Այդ պատճառով դա շուտով կհասնի ստացիոնար վիճակի։ Ի՞նչ տեսք կունենա այդ վերջնական վիճակը։ Կարելի է ենթադրել, որ դա կախված կլինի աստղի բոլոր բարդ առանձնահատկություններից, որոնցից այն կազմված է․ ոչ միայն նրա զանգվածից և պտույտի արագությունից, այլև տարբեր մասերի խտություններից և աստղի մեջ գտնվող գազերի խճճված շարժումներից։ Եթե առաջացած սև խոռոչներն այնպես տարբեր լինեն, ինչպես դրանք առաջացնող կոլապսվող մարմինները, ապա ընդհանրապես սև խոռոչների մասին կանխագուշակումներ անելը շատ դժվար կլինի։ | ||
| + | |||
| + | 1967֊ին, սակայն, սև խոռոչների ուսումնասիրության բնագավառում հեղաշրջում կատարեց կանադացի գիտնական Վերներ Իսրայելը (ծնվել է Բեռլինում, սովորել Հարավային Աֆրիկայում և դոկտորական աստիճան ստացել Իռլանդիայում)։ Իսրայելը ցույց տվեց, որ, համաձայն հարաբերականության ընդհանուր տեսության, պտտական շարժումից զրկված սև խոռոչները պետք է շատ պարզ լինեն, նրանք կատարյալ գնդաձև են, նրանց չափը կախված է միայն զանգվածից, և ցանկացած երկու սև խոռոչներ, որոնք նույն զանգվածն ունեն, նույնական են։ Դրանք փաստորեն, կարելի է նկարագրել Էյնշտեյնյան հավասարումների մասնակի լուծումներով, որոնք հայտնի են դեռևս 1917֊ից և հայտնագործվել են Կարլ Շվարցշիլդի կողմից՝ հարաբերականության ընդհանուր տեսության ստեղծումից անմիջապես հետո։ Սկզբնական շրջանում շատերը, այդ թվում նաև Իսրայելը գտնում էին՝ քանի որ սև խոռոչները կատարյալ գնդաձև են, ուստի պիտի առաջացած լինեն կատարյալ գնդաձև մարմինների կոլապսի հետևանքով։ Հետևաբար, որևէ իրական աստղ, որ երբեք կատարյալ գնդաձև չէ, կոլապսի հետևանքով կարող է առաջացնել միայն մի մերկ եզակիություն։ | ||
| + | |||
| + | Սակայն կար Իսրայելի տվյալների այլ մեկնաբանություն, ինչը արեցին մասնավորապես Ռոջեր Պենրոուզը և Ջոն Ուիլերը։ Նրանք պնդում էին, որ աստղի կոլապսի ընթացքում տեղի են ունենում արագ շարժումներ, ինչի հետևանքով արձակված գրավիտացիոն ալիքներն աստղն ավելի գնդաձև են դարձնում, ընդ որում, երբ այն հասնում է ստացիոնար վիճակի, արդեն ճշգրիտ գնդաձև է լինում։ Ըստ այս տեսակետի, յուրաքանչյուր աստղ, որ զրկված է պտտական շարժումից, որքան էլ բարդ ներքին կառուցվածք և ձև ունենա, գրավիտացիոն կոլապսից հետո կառաջացնի կատարելապես գնդաձև սև խոռոչ, որի շառավիղը կախված կլինի միայն նրա զանգվածից։ Հետագա հաշվումներն ապացուցեցին այս տեսակետի ճշտությունը, և այն շուտով ընդհանուր առմամբ ընդունվեց։ | ||
| + | |||
| + | Իսրայելի եզրահանգումները վերաբերում էին միայն այն սև խոռոչներին, որոնք առաջանում են պտտական շարժումից զրկված մարմիններից։ Նորզելանդացի գիտնական Ռոյ Քերն 1963֊ին հարաբերականության ընդհանուր տեսության հավասարումների այնպիսի լուծումների շարք գտավ, որոնք նկարագրում էին պտտվող սև խոռոչները։ Այսպես կոչված «Քեր» սև խոռոչները պտտվում են հաստատուն արագությամբ, նրանց չափն ու ձևը կախված են միայն պտտական արագությունից և զանգվածից։ Եթե պտույտը հավասար է զերոյի, ապա սև խոռոչը կատարյալ գնդաձև է, և լուծումը նույնական է Շվարցշիլդի առաջարկած լուծման հետ։ Եթե պտույտը զերոյական չէ, ապա սև խոռոչը հասարակածում ինչ֊որ չափով դուրս է ցցվում (ինչպես երկիրը կամ արեգակն են դուրս ցցվում պտույտի շնորհիվ), և դա մեծ է այնքան, որքան արագ է պտույտը։ Այսպիսով, Իսրայելի տեսությունը տարածելով նաև պտտվող մարմինների վրա ենթադրվեց, որ կոլապսի ենթարկվող ցանկացած պտտվող մարմին, որն առաջացնում է սև խոռոչ, ի վերջո կհասնի այնպիսի մի ստացիոնար վիճակի, որը նկարագրվում է Քերի լուծումով։ | ||
| + | |||
| + | 1970֊ին այս ենթադրությունն ապացուցելու գործին ձեռնամուխ եղավ իմ գործընկեր և ասպիրանտ Բրանդոն Քարտերը։ Նա ցույց տվեց, որ եթե պտտվող ստացիոնար սև խոռոչն ունենա համաչափության առանցք, ինչպես պտտվող հոլը, ապա խոռոչի չափն ու ձևը կախված կլինեն միայն նրա զանգվածից և պտտման արագությունից։ Իսկ 1971֊ին ես ապացուցեցի, որ որևէ պտտվող սև խոռոչ անպայման այդպիսի համաչափության առանցք պետք է ունենա։ Վերջապես, 1973֊ին Լոնդոնի Թագավորական քոլեջում Դեյվիդ Ռոբինսոնը, օգտագործելով Քարտերի և իմ տվյալները, ցույց տվեց, որ այդ ենթադրությունը ճիշտ է, և այդպիսի սև խոռոչն իրոք ունի Քերի լուծում։ Այսպիսով, գրավիտացիոն կոլապսից հետո առաջացած սև խոռոչը կհասնի մի վիճակի, որում այն կարող է պտտվել, բայց չի բաբախի։ Դեռ ավելին, նրա չափն ու ձևը կախված կլինեն լոկ նրա զանգվածից և պտտման արագությունից և ո՛չ սև խոռոչն առաջացնող կոլապսվող մարմնի բնույթից։ Այս արդյունքն արտահայտված է հետևյալ ասացվածքի մեջ․ «Սև խոռոչը գեսեր չունի»։ Այս «անգիսության» թեորեմը մեծ կիրառական կարևորություն ունի, որովհետև մեծ չափով սահմանափակում է սև խոռոչների հնարավոր տեսակների առկայությունը։ Այսպիսով, հնարավոր է սև խոռոչներ պարունակող առարկաների համար մանրամասն մոդելներ ստեղծել, կանխագուշակումներ անել և դրանք համեմատել դիտարկումների հետ։ Դա նշանակում է նաև, որ սև խոռոչ առաջացնող մարմնի կոլապսից հետո նրա մասին տեղեկությունների մեծ մասր կորչում է, որովհետև մենք ստացիոնար վիճակում կարող ենք չափել միայն նրա զանգվածն ու պտտման արագությունը։ Այս բանի նշանակությունը մենք կտեսնենք հաջորդ գլխում։ | ||
| + | |||
| + | Սև խոռոչը գիտության պատմության այն հազվադեպ երևույթներից մեկն է, որի տեսությունը մաթեմատիկական մեծ մանրամասնությամբ մշակվեց՝ դրա ակներևությունը դիտարկումներով ապացուցող որևէ փաստ ունենալուց առաջ։ Սև խոռոչների գոյության հակառակորդների գլխավոր փաստարկը հենց փորձնական տվյալների բացակայությունն էր․ ինչպե՞ս կարելի է հավատալ այն մարմինների գոյությանը, որոնց միակ ապացույցը հիմնված էր ընդհանուր հարաբերականության կասկածելի հաշվումների վրա։ Սակայն, ահա 1963֊ին Կալիֆոռնիայի Պալոմարի աստղադիտարանի աստղագետներից մեկը՝ Մարտեն Շմիդտը չափեց աղոտ աստղանման մի մարմնի կարմիր շեղումը՝ 3C273 կոչված ռադիոալիքների աղբյուրի ուղղությամբ (ռադիոաղբյուրների Քեմբրիջի 3֊րդ գրացուցակի 273 համարն է)։ Նա գտավ, որ դա շատ մեծ է գրավիտացիոն դաշտով պայմանավորված լինելու համար, եթե դա իրոք գրավիտացիոն կարմիր շեղումը լիներ, ապա այդ մարմինը այնքան զանգվածեղ և մեզ այնքան մոտ պետք է լիներ, որ պիտի խախտեր Արեգակնային համակարգի մոլորակների ուղեծրերը։ Սա նշանակում էր, որ կարմիր շեղումը տիեզերքի ընդարձակման արդյունք է, որն իր հերթին նշանակում է, որ թույլ լուսատու մարմինը շատ հեռու է գտնվում։ Հետևաբար, որպեսզի այդ մեծ հեռավորության վրա մարմինը տեսանելի լինի, պետք է այն շատ պայծառ լինի, կամ, այլ խոսքերով ասած, մեծ քանակի էներգիա արձակի։ Իսկ այդքան մեծաքանակ էներգիայի առաջացման միակ մեխանիզմը, որ մարդ կարող է ենթադրել, կարող է լինել ոչ թե մի աստղի, այլ գալակտիկայի ամբողջ կենտրոնական շրջանի գրավիտացիոն կոլապսը։ Մի շարք նման և «քվազիաստղային մարմիններ» կամ քվազարներ հայտնաբերվեցին՝ բոլորը մեծ կարմիր շեղումներով։ Սակայն, այս բոլորը չափազանց հեռավոր մարմիններ են, այդ պատճառով նրանց դիտարկումը դժվար է իրականացնել և ունենալ սև խոռոչների առկայության համոզիչ փաստարկներ։ | ||
| + | |||
| + | Սև խոռոչների գոյության մասին հուսադրող փաստեր տվեց Քեմբրիջի համալսարանի ասպիրանտ Ջոնսելին Բելը 1967֊ին երկնակամարում հայտնաբերելով կանոնավոր ռադիոալիքներ առաքող բաբախող մարմիններ։ Սկզբում Բելը և նրա ղեկավար Էնտոնի Հյուիշը մտածեցին, թե կարող է կապ են հաստատել գալակտիկայում արտերկրային քաղաքակրթության հոտ։ Արդարև, երբ սեմինարին նրանք զեկուցում էին այդ հայտնագործության մասին, հիշում եմ, իրենց գտած առաջին աղբյուրն անվանեցին ՓԿՄ 1―4, (անգլ․LGM՝ 1-4 «Little Gres Men», Փոքրիկ կանաչ մարդիկ)։ Հետագայում հեղինակները, ինչպես նաև մյուս գիտնականները, հանգեցին նվազ ռոմանտիկ այն եզրակացությանը, որ այդ երկնային մարմինները, որոնք կոչվեցին պուլսարներ, պտտվող նեյտրոնային աստղեր են, որոնք իրենց մագնիսական դաշտի և շրջակա նյութի մի բարդ փոխազդեցությունների շնորհիվ ռադիոալիքներ են արձակում՝ բաբախելով։ Իհարկե, տիեզերական արկածների հեղինակների համար սա վատ լուր էր, սակայն այդ ժամանակ սև խոռոչների գոյությանը հավատացող մեր փոքրաթիվ խմբին հույսեր էր ներշնչում․ սա նեյտրոնային աստղերի մասին առաջին դրական ապացույցն էր։ Նեյտրոնային աստղի շառավիղը մոտավորապես 10 մղոն է, միայն մի քանի անգամ է մեծ աստղի այն կրիտիկական շառավղից, որի դեպքում վերածվում է սև խոռոչի։ Ուրեմն, եթե մի աստղ կարող է կծկվել այդքան փոքր չափերի, ապա հակատրամաբանական չէ սպասել, որ այլ աստղեր կոլապսի հետևանքով կկծկվեն ավելի փոքր չափերի և կվերածվեն սև խոռոչների։ | ||
| + | |||
| + | Հարց է ծագում, քանի որ սև խոռոչից լույսի արձակումը հնարավոր չէ, ապա ի՞նչ հույս կա այն հայտնաբերելու։ Դա մի փոքր նման է ածխի պահեստում սև կատու փնտրելուն։ Բարեբախտաբար, դրա միջոցը կա։ Ջոն Միչելի՝ 1783֊ին հրատարած առաջին հաղորդագրության մեջ նշվում է, որ սև խոռոչը դեռևս ազդում է շրջապատի մարմինների վրա գրավիտացիոն ուժով։ Աստղագետները դիտարկել են շատ համակարգեր, որոնց երկու աստղեր պտտվում են իրար շուրջ և միմյանց ձգում գրավիտացիոն ուժով։ Դիտվել են նաև այնպիսի համակարգեր, որոնցում միայն մի տեսանելի աստղ պտտվում է ինչ֊որ անտեսանելի զուգընկերոջ շուրջ։ Ոչ ոք չի կարող, իհարկե, անմիջապես եզրակացնել, թե այդ անտեսանելի զուգընկերը սև խոռոչ է, որովհետև բացառված չէ, որ դա թույլ լուսատվություն ունեցող մի աստղ լինի։ Այնուամենայնիվ, այս համակարգերի մի մասը, ինչպես Սիգնուս X-1 կոչվողը (նկ․ 6.2), նաև ուժեղ ռենտգենյան ճառագայթման աղբյուրներ են։ Այս երևութի լավագույն բացատրությունն է նյութի ժայթքումը տեսանելի աստղի մակերևույթից։ Այդ նյութը անտեսանելի զուգընկերոջ վրա թափվելով, առաջացնում է պարուրաձև շարժում (ինչպես լողարանի ջուրը տաշտի անցքից դուրս հոսելիս), այն շատ է տաքանում և արձակում է ռենտգենյան ճառագայթներ (նկ․ 6.3)։ Որպեսզի այդպիսի բան պատահի, անհրաժեշտ է, որ անտեսանելի առարկան շատ փոքր լինի, ինչպես Սպիտակ թզուկը, նեյտրոնային աստղը կամ սև խոռոչը։ Տեսանելի աստղի ուղեծրի դիտարկումը թույլ է տալիս հաշվել անտեսանելի մարմնի հնարավոր նվազագույն զանգվածը։ Սիգնուս X-1֊ի դեպքում անտեսանելի մարմնի զանգվածը արեգակի զանգվածից մեծ է մոտ վեց անգամ, որը համաձայն Չանդրասեկհարի սահմանային օրենքի, շատ մեծ է Սպիտակ թզուկ լինելու համար։ Նեյտրոնային աստղ լինելու համար այս զանգվածը նույնպես շատ մեծ է։ Հետևաբար, թվում է, թե դա պետք է սև խոռոչ լինի։ | ||
| + | |||
| + | Կան այլ մոդելներ, որոնք Սիգնուս x-1 համակարգում բացառում են սև խոռոչի առկայությունը, սակայն դրանք շատ անբնական բնույթ ունեն։ Դիտարկվածի ամենահավանական բացատրությունը կարելի է համարել սև խոռոչի առկայությունը։ Հակառակ դրա ես գրազ եմ եկել Կալիֆոռնիայի տեխնոլոգիական ինստիտուտից Քիպ Թոռնի հետ, որ իրականում Սիգնուս X-1֊ի համակարգում սև խոռոչ գոյություն չունի։ Այս քայլին դիմելով, ես ինքս ինձ ապահովագրել եմ։ Ես մեծ աշխատանք եմ կատարել սև խոռոչների բնագավառում, և այն իզուր կանցնի, եթե սև խոռոչներ գոյություն չունենան։ Բայց այդ դեպքում գոնե գրազը կշահեմ և որպես մխիթարանք՝ Պրայվիթ Ս հանդեսի չորս տարվա բաժանորդագրություն կստանամ։ Իսկ եթե սև խոռոչներ գոյություն ունենան, Քիպը Պենթհաուզի տարեկան բաժանորդագրություն ձեռք կբերի։ 1975֊ին, երբ գրազ բռնվեցինք, մենք 80 տոկոսով վստահ էինք, որ Սիգնուսը սև խոռոչ է։ Այժմ կարող եմ ասել, որ վստահ ենք 95 տոկոսով, սակայն գրազը դեռ շարունակվում է։ | ||
| + | |||
| + | Մենք այժմ փաստեր ունենք մեր գալակտիկայում Սիգնա x―1֊ի նման համակարգերում և երկու հարևան գալակտիկաներում, որոնք կոչվում են Մագելանի ամպեր, մի քանի այլ խոռոչների գոյության մասին նույնպես։ Սակայն, տարակույս չկա, որ հավանաբար սև խոռոչների թիվն ավելի մեծ է․ տիեզերքի տևական պատմության ընթացքում բազմաթիվ աստղեր սպառած պիտի լինեին իրենց միջուկային վառելանյութը և կոլապսի ենթարկված։ Սև խոռոչների թիվը կարող է ավելի մեծ լինել, քան տեսանելի աստղերինը, ինչր միայն մեր գալակտիկայում հասնում է հարյուր հազար միլիոնի։ Ավելի մեծ թվով սև խոռոչների հավելյալ գրավիտացիոն ձգողական ուժը կարող է բացատրել մեր գալակտիկայի պտտական շարժման արագությունը․ տեսանելի աստղերի զանգվածը բավարար չէ դրա համար։ Որոշ փաստեր ունենք նաև այն մասին, որ մեր գալակտիկայի կենտրոնում մի մեծ սև խոռոչ կա, որի զանգվածը մոտ հարյուր հազար անգամ մեծ է արեգակի զանգվածից։ Գալակտիկայի այն աստղերը, որոնք մոտենում են այդ հսկա մեծ խոռոչին, դրան մոտ և հեռավոր կողմերի վրա ազդող գրավիտացիոն ուժերի տարբերության պատճառով, կտոր֊կտոր են լինում։ Դրանց մնացորդները և այդ աստղերից ժայթքող գազերն ընկնում են սև խոռոչի մեջ։ Ինչպես Սիգնուս x―1֊ի պարագայում գազերը պարուրաձև ներս են քաշվում և տաքանում, թեև ոչ այն աստիճան, ինչպես Սիգնուսի դեպքում։ Այստեղ ջերմությունը չի բավարարում ռենտգենյան ճառագայթների համար, սակայն բավարար է ռադիոալիքների և ինֆրակարմիր ճառագայթման շատ խիտ աղբյուր լինելու համար, որը և դիտվում է գալակտիկայի կենտրոնում։ | ||
| + | |||
| + | [[Պատկեր:H6 2.svg|thumb|Նկ․ 6․ 2 Լուսանկարի կենտրոնում կրկնակի աստղերից ավելի պայծառը Սիգնուս X֊1֊ն է, որն ըստ ենթադրության բաղկացած է սեւ խոռոչից և բնականոն աստղից, որոնք պտտվում են միմյանց շուրջ։]] | ||
| + | |||
| + | Այն կարծիքը կա, թե նման և նույնիսկ ավելի մեծ սև խոռոչներ կան քվազարների կենտրոններում, որոնց զանգվածն արեգակի զանգվածից մեծ է մոտ հարյուր միլիոն անգամ։ Միայն այդպիսի գերզանգված ունեցող սև խոռոչների մեջ նյութի մուտքը կարող է առաջացնել հզոր էներգիայի աղբյուր, որով և բացատրվում է դրանցից հսկայական էներգիայի արձակումը։ Երբ նյութը պարուրաձև մտնում է սև խոռոչի մեջ, վերջինիս ստիպում է պտտվել նույն ուղղությամբ և առաջացնել մագնիսական դաշտ՝ հար և նման երկրի մագնիսական դաշտին։ Ներս լցվող նյութը պատճառ է դառնում, որ սև խոռոչի մոտերքում առաջանան շատ բարձր էներգիա ունեցող մասնիկներ։ Մագնիսական դաշտն այնքան հզոր կլինի, որ նրա ազդեցության տակ մասնիկները կկիզակետվեն և դուրս կժայթքեն սև խոռոչի պտտման առանցքի ուղղությամբ, այսինքն՝ դրա հյուսիսային և հարավային բևեռների ուղղությամբ։ Այդպիսի ժայթքումներ իրոք դիտվել են մի շարք գալակտիկաներում և քվազարներում։ | ||
| + | |||
| + | Կարելի է նաև ենթադրել, որ արեգակից շատ փոքր զանգված ունեցող սև խոռոչներ նույնպես կան։ Այդպիսի սև խոռոչները չեն կարող առաջացած լինել գրավիտացիոն կոլապսից, քանի որ նրանց զանգվածները Չանդրասեկհարի սահմանային մեծությունից փոքր են․ այդքան փոքր զանգված ունեցող աստղերը կարող են դիմակայել գրավիտացիոն ուժերին, անգամ եթե սպառել են իրենց միջուկային վառելանյութը։ Փոքր զանգված ունեցող սև խոռոչները կարող են առաջանալ այն ժամանակ, երբ նյութը չափազանց խտանում է շատ բարձր արտաքին ճնշումների ազդեցությամբ։ Այսպիսի պայմաններ կարող են ստեղծվել շատ մեծ ջրածնային ռումբի մեջ։ Ֆիզիկոս Ջոն Ուիլերը հաշվել է, որ եթե աշխարհի բոլոր օվկիանոսներում եղած ամբողջ ծանր ջուրը<ref>Ծանր ջրի մոլեկուլներում ջրածնի բոլոր ատոմները փոխարինված են ծանր ջրածնի (դեյտերիումի) ատոմներով։ Սովորական ջուրը, այսպես ասած, «թեթև» և «ծանր» ջրերի խառնուրդ է, իսկ «ծանր» և «թեթև» ջրածինները իրարից տարբերվում են միջուկում եղած նեյտրոնների թվով (առաջինում մեկ, երկրորդում՝ զերո)։</ref> հավաքենք, ապա դրանից պատրաստված ջրածնային ռումբն այնպիսի մի ճնշում կառաջացնի, և նյութը կենտրոնում այն աստիճան կսեղմվի, որ կառաջանա մի սև խոռոչ։ (Իհարկե, մարդ չի մնա դա դիտելու համար)։ Գործնականում հնարավոր է, որ տիեզերքի սկզբնական շրջանում բարձր ճնշման և ջերմաստիճանի պայմաններում փոքր զանգված ունեցող սև խոռոչներ առաջացած լինեն։ Սև խոռոչներ կարող էին առաջանալ, եթե նախնական տիեզերքը կատարյալ հարթ և միօրինակ եղած չլիներ, որովհետև միայն միջինից ավելի խիտ մի տիրույթ կարող էր այն աստիճան սեղմվել, որ սև խոռոչ առաջանար։ Սակայն մենք գիտենք, որ ինչ֊որ խախտումներ պետք է եղած լինեն, հակառակ դեպքում նյութը մինչև օրս կատարյալ միօրինակ ձևով բաշխված կլիներ, աստղերով և գալակտիկաներով խմբավորված լինելու փոխարեն։ | ||
| + | |||
| + | [[Պատկեր:H6 3.svg|thumb| Նկ․ 6․3]] | ||
| + | |||
| + | Թե աստղերի և գալակտիկաների առաջացման համար անհրաժեշտ այդ խախտումները պատճառ եղե՞լ են արդյոք, որպեսզի որոշակի քանակությամբ «նախասկզբնական» սև խոռոչներ ևս ստեղծվեին՝ կախված է միայն նախնական տիեզերքի պայմանների մանրամասներից։ Հետևաբար, եթե կարողանանք որոշել, թե որքան նախասկզբնական սև խոռոչներ կան այսօր, մենք շատ բան կիմանանք տիեզերքի շատ վաղ անցյալի վիճակի մասին։ Նախասկզբնական այնպիսի սև խոռոչները, որոնց զանգվածը հազար միլիոն տոննայից մեծ է (մեծ լեռան զանգվածի չափ), կարելի է հայտնաբերել միայն, որոշելով նրանց գրավիտացիոն ազդեցությունը այլ տեսանելի նյութի կամ տիեզերքի ընդարձակման վրա։ Սակայն ինչպես հաջորդ գլխում կտեսնենք, սև խոռոչները իրականում այնքան էլ սև չեն, նրանք տաք մարմնի նման լուսարձակում են և որքան փոքր են, այնքան ուժեղ է լուսարձակումը։ Այսպիսով, որքան էլ պարադոքսային թվա, ստացվում է, որ փոքրիկ, սև խոռոչներն ավելի հեշտ է հայտնաբերել, քան մեծերը։ | ||
| + | |||
| + | |||
| + | ==7== | ||
| + | |||
| + | Սև խոռոչները այնքան էլ սև չեն | ||
| + | |||
| + | 1970֊ից առաջ ընդհանուր հարաբերականության ասպարեզում իմ կատարած ուսումնասիրությունների կենտրոնում գլխավորապես Մեծ պայթյունի եզակիության հարցն էր։ Այդ տարվա նոյեմբերի մի երեկո իմ աղջկա՝ Լյուսիի ծննդից քիչ հետո, քնելու պատրաստվելիս ես սկսեցի մտածել սև խոռոչների մասին։ Հաշմանդամությանս պատճառով դանդաղ եմ տեղաշարժվում, այդ պատճառով ես շատ ժամանակ ունեի մտածելու։ Այն ժամանակ չկար որոշակի սահմանում, թե տարածության֊ժամանակի որ կետերն են գտնվում սև խոռոչի ներսում, որոնք՝ նրանից դուրս։ Ես արդեն Ռոջեր Պենրոուզի հետ քննարկել էր այն գաղափարը, որ սև խոռոչը պիտի սահմանել որպես պատահույթների մի շարք, որից հնարավոր չէ ձերբազատվել և բավականին հեռանալ․ մի սահմանում, որն այսօր համընդհանուր ընդունելության է արժանացել։ Սա նշանակում է, որ սև խոռոչի սահմանագիծը՝ պատահութային հորիզոնը, տարածություն֊ժամանակի մեջ առաջանում է լույսի ճառագայթների այն ուղիներով, որոնք պարզապես չեն կարողանում ձերբազատվել սև խոռոչից և մշտապես սավառնում են եզրագծում (նկ․7.1): Սա փոքր֊ինչ նման է այն դեպքին, երբ մարդ փախչում է ոստիկանությունից և հազիվ է հասցնում մի քայլ առաջ ընկնել, բայց երբեք նրանից լրիվ ազատվել չի կարողանում։ | ||
| + | |||
| + | [[Պատկեր:H7 1.svg|thumb]] | ||
| + | |||
| + | Ես հանկարծ գլխի ընկա, որ լուսային ճառագայթների ուղիները երբեք իրար չեն կարող մոտենալ։ Եթե մոտենային, ապա նրանք ի վերջո պետք է խառնվեին իրար։ Վիճակը նման կլիներ այն դեպքին, երբ ոստիկանությունից փախչողը բախվեր հակառակ ուղղությամբ ընթացող և ոստիկանի կողմից հետապնդվող մի ուրիշի հետ՝ երկուսն էլ տեղն ու տեղը կբռնվեին (կամ, այս դեպքում, կընկնեին սև խոռոչի մեջ)։ Սակայն, եթե սև խոռոչը կլաներ այս լուսային ճառագայթները, ապա նրանք սահմանագծի վրա չէին կարող լինել։ Հետևաբար, պատահութային հորիզոնում լուսային ճառագայթների ուղիները կամ պետք է միշտ իրար զուգահեռ շարժվեն և կամ իրարից հեռանան։ Այլ կերպ ասած, պատահութային հորիզոնը՝ սև խոռոչի սահմանագիծը, նման է ստվերի՝ եզրի վերահաս կործանման ստվերի։ Եթե ուշադիր դիտենք հեռավոր լուսաղբյուրի, ինչպես օրինակ, արեգակի առաջացրած ստվերը, կտեսնենք, որ եզրում լույսի ճառագայթներն իրար չեն մոտենում։ | ||
| + | |||
| + | [[Պատկեր:H7 2.svg|thumb|Նկ․ 7․2 և 7․3]] | ||
| + | |||
| + | Հետևաբար, եթե պատահութային հորիզոնը՝ սև խոռոչի սահմանագիծը, կազմող լույսի ճառագայթները երբեք իրար չեն կարող մոտենալ, նշանակում է, որ պատահութային հորիզոնի մակերեսը կարող է ժամանակի ընթացքում նույնը մնալ կամ մեծանալ, բայց երբեք չի կարող փոքրանալ։ Քանի որ այս վերջին դեպքում սահմանի լույսի որոշ ճառագայթներ պետք է որ իրար մոտենային։ Իրականում մակերեսը կմեծանա՝ սև խոռոչի մեջ նյութ կամ ճառագայթում ընկնելիս (նկ․ 7.2)։ Կամ եթե երկու խոռոչներ բախվեն և միանան ու մի նոր սև խոռոչ առաջացնեն, ապա վերջինիս պատահութային հորիզոնի մակերեսը կարող է մեծ լինել կամ հավասար երկու սկզբնական սև խոռոչների պատահութային հորիզոնների մակերեսների գումարին ( նկ․ 7.3)։ Պատահութային հորիզոնի մակերեսի չփոքրանալու այդ հատկությունը սահմանափակում է սև խոռոչի հնարավոր վարքագիծը։ Այս հայտնագործությունն ինձ այն աստիճան ոգևորեց, որ ես չկարողացա քնել։ Հաջորդ օրը զանգահարեցի Ռոջեր Պենրոուզին։ Նա համաձայնեց իմ կարծիքին։ Կարծում եմ, որ նա, փաստորեն, իրազեկ էր սև խոռոչի մակերեսի այդ հատկությանը։ Թեև նա սև խոռոչի համար փոքր֊ինչ այլ սահմանում էր տալիս, բայց գլխի չէր ընկել, որ երկու սահմանումների պարագայում էլ սև խոռոչի սահմանները և նրանց մակերեսները նույնը կլինեն, եթե իհարկե, սև խոռոչը հասել է այնպիսի մի վիճակի, որը ժամանակի ընթացքում այլևս փոփոխության չի ենթարկվում։ | ||
| + | |||
| + | Սև խոռոչի չփոքրանալու հատկությունը ընդհանրություններ ունի էնտրոպիա կոչվող մի այլ ֆիզիկական մեծության վարքագծի հետ, այս մեծությունը չափում է անկանոնության աստիճանը։ Հայտնի է, որ առանց միջամտության առարկաները ժամանակի ընթացքում անկարգ վիճակում են հայտնվում (այս բանը ակնհայտ է դառնում, երբ տունը երկար ժամանակ չի վերանորոգվում)։ Իհարկե, կարելի է անկարգության վիճակից կարգավորվածության վիճակի անցնել, հնարավոր է կարգուկանոն մտցնել (օրինակ, կարելի է տունը ներկել), բայց դրա համար հարկավոր է աշխատել կամ էներգիա ծախսել, որի հետևանքով առկա կարգավորված էներգիայի քանակությունը կնվազի։ | ||
| + | |||
| + | Էնտրոպիայի մասին ավելի ճշգրիտ պատկերացում է տալիս թերմոդինամիկայի 2֊րդ օրենքը։ Համաձայն այս օրենքի, մեկուսացած համակարգի էնտրոպիան միշտ աճում է։<ref>Երբ տեղի են ունենում ինքնակամ պրոցեսներ։</ref> Երբ այդպիսի երկու համակարգ միացվում են<ref>Ավելի ճիշտ՝ խառնվում են</ref> միմյանց, ապա միացյալ համակարգի էնտրոպիան ավելի մեծ է լինում սկզբնական երկու առանձին համակարգերի էնտրոպիաների գումարից։ Դիցուկ, ունենք գազի մոլեկուլներով լեցուն մի տուփ։ Մոլեկուլները կարելի է պատկերել որպես բիլիարդի փոքրիկ գնդիկներ, որոնք շարունակաբար բախվում են իրար հետ և հետ հրվում տուփի պատերին բախվելիս։ Որքան բարձր լինի ջերմաստիճանը, այնքան արագ կշարժվեն մոլեկուլները, ավելի հաճախ և մեծ ուժով կհարվածեն տուփի պատերին, և, հետևաբար, պատերին ազդող ներքին ճնշումն ավելի բարձր կլինի։ Ենթադրենք, թե սկզբում բոլոր մոլեկուլները պարփակված են տուփի ձախ մասում, որն անջատված է մի միջնապատով։ Երբ միջնապատը հեռացվի, մոլեկուլները կձգտեն տարածվել և զբաղեցնել տուփի երկու բաժինները։ Հետագայում կարող է պատահել, որ բոլոր մոլեկուլները հավաքվեն տուփի միայն աջ կամ միայն ձախ մասում, սակայն շատ ավելի հավանական է, որ մոլեկուլները երկու մասում բաշխվեն հավասարապես։ Այս վիճակը նվազ կարգավորված է, կամ ավելի չկարգավորված, քան այն սկզբնական վիճակը, երբ մոլեկուլները գտնվում էին մի կեսում։ Հետևաբար, կարելի է ասել, որ գազի էնտրոպիան աճեց։<ref>Գազի ինքնակամ ընդարձակումը հաստատուն ջերմաստիճանում բերում է էնտրոպիայի աճի։</ref> | ||
| + | |||
| + | Դիցուկ, ունենք երկու տուփ, որոնցից մեկը լցված է թթվածնով, մյուսը՝ ազոտով։ | ||
| + | |||
| + | Երբ երկու տուփերը միացնենք իրար, ապա միջնորմը հեռացնելիս թթվածնի և ազոտի մոլեկուլները պիտի սկսեն խառնվել միմյանց։ Հետագայում առավել հավանական վիճակը կլինի այն, որ թթվածնի և ազոտի մոլեկուլները միօրինակ և հավասարապես բաշխված կլինեն երկու տուփերում։ Այս վիճակը նվազ կարգավորված է և ավելի մեծ էնտրոպիա կունենա, քան սկզբնական երկու առանձին տուփերի վիճակը։<ref>Խառնվելուց հետո երկու գազերի խառնուրդի էնտրոպիան ավելի մեծ է, քան առանձին վերցրած գազերի էնտրոպիաների գումարը՝ այն պատճառով, որ երկու տարբեր գազերն իրարից անջատելու համար հարկավոր է լրացուցիչ աշխատանք կատարել։ Դա կարելի է բացատրել նաև այն բանով, որ յուրաքանչյուր գազ ընդարձակվել է և մեծացրել էնտրոպիան։</ref> | ||
| + | |||
| + | Թերմոդինամիկայի երկրորդ օրենքը որոշ չափով այլ կարգավիճակ ունի, քան գիտական մյուս օրենքները, ինչպես, օրինակ, Նյուտոնի ձգողականության օրենքը, որովհետև այն ոչ միշտ է գործում՝ միայն դեպքերի ճնշող մեծամասնության պարագայում։ Հավանականությունն այն բանի, որ տուփի մեջ եղած բոլոր մոլեկուլները հետագայում առանձնանան նրա մի կեսում, մեկի մի քանի միլիոն միլիոներորդ մասից ավելի փոքր է, այդպիսի բան, սակայն, կարող է պատահել։ Այնուամենայնիվ, եթե ունենք մի սև խոռոչ, թվում է, երկրորդ օրենքը խախտելու մի հեշտ ճանապարհ կա։ Բավական է, որ մեծ էնտրոպիա ունեցող նյութ, ասենք մի տուփ գազ, նետվի սև խոռոչի մեջ։ Սև խոռոչից դուրս գտնվող նյութի ընդհանուր էնտրոպիան կնվազի։ Կարելի է, իհարկե, ասել, որ էնտրոպիայի ընդհանուր քանակությունը, ներառյալ սև խոռոչի էնտրոպիան, չի նվազել։ Բայց, քանի որ հնարավոր չէ սև խոռոչի ներսը տեսնել, չենք կարող ասել, թե այնտեղ գտնվող նյութն ինչքան էնտրոպիա ունի։ Հետևաբար ցանկալի կլիներ, որ սև խոռոչն օժտված լիներ այնպիսի մի հատկանիշով, որի օգնությամբ դրսից դիտողն իմանար նրա էնտրոպիայի մեծությունը, և վերջինս աճեր, երբ սև խոռոչի մեջ էնտրոպիա ունեցող նյութ ընկներ։ Ելնելով վերևում նկարագրված այն հայտնագործությունից, որ պատահութային հորիզոնի մակերեսը մեծանում է, երբ նյութ է ընկնում սև խոռոչի մեջ, Պրինստոնի համալսարանի ասպիրանտ Յակոբ Բեկենշտեյնն առաջարկեց, որ պատահութային հորիզոնի մակերեսը սև խոռոչի էնտրոպիայի չափանիշն է։ | ||
| + | |||
| + | Քանի որ պատահութային հորիզոնի մակերեսը մեծանում է, երբ սև խոռոչի մեջ էնտրոպիա ունեցող նյութ է ընկնում, ապա սև խոռոչի շրջապատի նյութի էնտրոպիայի և նրա հորիզոնի մակերեսի գումարը երբեք չի կարող նվազել։ | ||
| + | |||
| + | Բեկենշտեյնի այս առաջարկությունը, թվում է, ցույց էր տալիս, որ թերմոդինամիկայի երկրորդ օրենքը համարյա բոլոր իրավիճակներում ուժի մեջ է։ Սակայն այստեղ ճակատագրական մի սխալ կար։ Եթե սև խոռոչը էնտրոպիա ունի, ապա պետք է որ այն նաև ջերմաստիճան ունենա։ Իսկ որոշակի ջերմաստիճան ունեցող ամեն մարմին պետք է ինչ֊որ չափով ճառագայթի։ Հայտնի է, որ երբ շամփուրը տաքացվում է կրակի բոցի մեջ և կաս֊կարմիր է դառնում, այն ճառագայթ է արձակում, բայց ցածր ջերմաստիճանում գտնվող մարմինները ևս ճառագայթում են, թեև այնքան թույլ, որ սովորաբար նշմարելի չէ։ Այդպիսի ճառագայթումը պայմանավորված է թերմոդինամիկայի երկրորդ օրենքով։ Հետևաբար, սև խոռոչները պետք է որ ճառագայթներ արձակեն։ Սակայն, ըստ սահմանման, սև խոռոչներն այնպիսի մարմիններ են, որոնցից ոչինչ չի կարող հեռանալ։ Թվում է, հետևաբար, որ պատահութային հորիզոնի մակերեսը չի կարելի նույնացնել էնտրոպիայի հետ։ 1972֊ին Բրանդոն Քարտերի և իմ ամերիկացի կոլեգա Ջիմ Բարդինի հետ ես մի հոդվածով հանդես եկա, ուր մենք նշեցինք, որ թեև որոշ նմանություն կա էնտրոպիայի և պատահութային հորիզոնի մակերեսի միջև, սակայն գոյություն ունի այդ ակնհայտ ճակատագրական դժվարությունը։ Խոստովանում եմ, որ հոդվածը գրելուն ինձ մասամբ մղել էր իմ դժգոհությունն այն բանից, որ Բեկենշտեյնն ըստ իս, չարաշահել էր իմ հայտնագործությունը՝ պատահութային հորիզոնի մակերեսի մեծացման վերաբերյալ։ Հետագայում պարզվեց, սակայն, որ նա հիմնականում ճիշտ էր, թեև այն մի առումով, որն, իհարկե, ինքը չէր կարող ակնկալել։ | ||
| + | |||
| + | 1973֊ին, երբ ես այցելեցի Մոսկվա, սև խոռոչների մասին զրուցեցի երկու առաջնակարգ խորհրդային մասնագետներ Յակով Զելդովիչի և Ալեքսանդր Ստարոբինսկու հետ։ Նրանք ինձ համոզեցին, որ ըստ քվանտային մեխանիկայի անորոշության սկզբունքի, պտտվող սև խոռոչները պետք է առաջացնեն և արտազատեն մասնիկներ։ Ֆիզիկական առումով նրանց փաստերը համոզիչ էին, բայց ինձ դուր չեկավ այն մաթեմատիկական ապարատը, որով նրանք ճառագայթման հաշվարկումներ էին կատարել։ Հետևաբար, ես աշխատեցի ավելի կատարյալ մաթեմատիկական ապարատ ստեղծել, որի մասին զեկուցեցի 1973֊ի նոյեմբերի վերջին Օքսվորդում կայացած ոչ պաշտոնական սեմինարում։ Այդ ժամանակ ես դեռ ճառագայթման քանակական հաշվումներ դեռ չէի կատարել։ Սպասում էի, որ այդ քանակությունը կհամընկնի պտտվող սև խոռոչների համար Զելդովիչի և Ստարոբինսկու ճառագայթման կանխագուշակումներին։ Սակայն հաշվումների ավարտից հետո պատկերացրեք իմ զարմանքն ու դժգոհությունը, երբ պարզվեց, որ նույնիսկ չպպտվող սև խոռոչներն են մասնիկներ առաջացնում և արտազատում կայուն արագությամբ։ Սկզբում ես մտածեցի, որ այս առաքումը նշանակում է, թե իմ օգտագործած մոտավորություններից մեկն ընդունելի չէ։ Ես մտահոգված էի, որ եթե Բեկենշտեյնն իմանար այդ մասին, նա այդ փաստը ևս կօգտագործեր ի հաստատումն սև խոռոչների էնտրոպիայի գաղափարի, որին ես կողմնակից չէի։ Բայց ես որքան մտածում էի այդ մասին, այնքան համոզվում էի, որ մոտավորություններն իսկապես ընդունելի են։ Մասնիկների արձակման հավաստիությանը ես վերջնականապես հավատացի այն ժամանակ, երբ պարզվեց, որ արձակված մասնիկների սպեկտրը կատարելապես համընկնում է տաք մարմնի արձակած տվյալների հետ, և, որ սև խոռոչի արձակած մասնիկների քանակությունը ճշգրտորեն համընկնում է թերմիդինամիկայի 2-րդ օրենքին։ Դրանից հետո նույնանման հաշվումներ են կատարվել տարբեր ձևերով, տարբեր գիտնականների կողմից։ Բոլոր հաշվումները ցույց տվեցին, որ սև խոռոչը պետք է տաք մարմնի նման մասնիկներ և ճառագայթում արձակի տվյալ ջերմաստիճանում, որը կախված է սև խոռոչի զանգվածից։ Որքան զանգվածը մեծ է, այնքան ցածր է ջերմաստիճանը։ | ||
| + | |||
| + | Իսկ այդ ինչպե՞ս է պատահում, որ սև խոռոչը, պարզվում է, մասնիկներ է առաքում, երբ մենք գիտենք, որ նրա պատահութային հորիզոնից ոչինչ դուրս պոկվել չի կարող։ Դրա պատասխանը, համաձայն քվանտային մեխանիկայի, այն է, որ մասնիկները ոչ թե սև խոռոչի ներսից են գալիս, այլ այն «դատարկ» տարածությունից, որը գտնվում է պատահութային հորիզոնից փոքր֊ինչ դուրս։ Այս բանը կարելի է հասկանալ հետևյալ ձևով։ Այն ինչ մենք կոչում ենք «դատարկ» տարածություն, լրիվ դատարկ չի կարող լինել, քանի որ դա կնշանակեր, որ բոլոր տեսակի դաշտերը, ինչպես օրինակ, գրավիտացիոն կամ էլեկտրամագնիսական դաշտերը, պետք է լինեն զերո։ Սակայն դաշտի մեծությունը և նրա փոփոխման արագությունն ըստ ժամանակի նման են համապատասխանաբար մասնիկի դիրքին և արագությանը, որոնք որոշվում են ըստ անորոշության սկզբունքի՝ որքան ավելի ճշգրիտ իմանանք դրանցից մեկը, այնքան ավելի նվազ ճշգրիտ կիմանանք մյուսը։ Հետևաբար, դատարկ տարածության մեջ դաշտի մեծությունը չի կարելի ճշգրտորեն ընդունել զերոյին հավասար, որովհետև այդ դեպքում երկուսն էլ՝ և՛դաշտի մեծությունը, և՛ դրա փոփոխությունն ըստ ժամանակի ճշգրիտ (զերո) արժեք կունենան։ Պետք է, որ նվազագույն չափի անորոշություն լինի, կամ դաշտի մեծության մեջ լինեն քվանտային տատանումներ։ Այդ տատանումները կարելի է ընդունել որպես լույսի կամ գրավիտացիայի մասնիկների զույգեր, որոնք որոշ ժամանակ միասին են երևում, հեռանում են իրարից և ապա նորից միանում ու ոչնչացնում են իրար։ Այդ մասնիկները վիրտուալ մասնիկներ են, ինչպես այն մասնիկները, որոնք կրում են արեգակի գրավիտացիոն ուժը, և, ի տարբերություն իրական մասնիկների, դրանք ուղղակի դիտարկման ենթակա չեն մասնիկային դետեկտորով։ Սակայն վիրտուալ մասնիկների աննուղակի ազդեցությունը, ինչպես ատոմի և էլեկտրոնի ուղեծրերի էներգիայի փոքր փոփոխությունները, կարելի է չափել, ինչը մեծ ճշտությամբ համընկնում է տեսական հաշվումների հետ։ Անորոշության սկզբունքը նույնպես կանխագուշակում է, որ նյութական մասնիկների, ինչպիսիք են էլեկտրոնները կամ քվարկները, նմանատիպ վիրտուալ զույգեր պետք է լինեն։ Այս դեպքում, սակայն, զույգի մի անդամը կլինի մասնիկ, մյուսը՝ հակամասնիկ։ (Լույսի և գրավիտացիայի հակամասնիկները նույնն են, ինչ մասնիկներինը)։ | ||
| + | |||
| + | [[Պատկեր:H7 4.svg|thumb]] | ||
| + | |||
| + | Որովհետև ոչնչից էներգիա ստանալ հնարավոր չէ, ուստի մասնիկ֊հակամասնիկ զույգերից մեկը պետք է ունենա դրական էներգիա, մյուսը՝ բացասական։ Քանի որ իրական մասնիկները բնական պայմաններում ունեն դրական էներգիա, ապա բացասական էներգիան ստիպված պետք է վերագրել կարճատև կյանք ունեցող վիրտուալ մասնիկներին։ Հետևաբար, վիրտուալ մասնիկը փնտրելու է իր զուգընկերոջը և ոչնչանալու է նրա հետ։ Մեծ զանգված ունեցող մարմնից հեռու գտնվող իրական մասնիկի էներգիան մեծ կլինի մարմնի մեջ պարփակված վիճակում նրա էներգիայից, քանի որ նրան մարմնից հեռացնելիս հարկավոր է աշխատանք կատարել գրավիտացիոն ձգողության դեմ։ Բնական պայմաններում մասնիկի էներգիան դեռևս դրական է, բայց, քանի որ սև խոռոչի գրավիտացիոն դաշտը շատ հզոր է, այնտեղ ընկնելիս նույնիսկ իրական մասնիկը կունենա բացասական էներգիա։ Հնարավոր է նաև, որ բացասական էներգիա ունեցող վիրտուալ մասնիկն ընկնի սև խոռոչի մեջ և վերափոխվի իրական մասնիկի կամ հակամասնիկի։ Այս դեպքում վիրտուալ մասնիկն իր զուգընկերոջ հետ չի ոչնչանա։ Նրա լքյալ զուգընկերը նույնպես կարող է ընկնել սև խոռոչի մեջ, կամ, օժտված լինելով դրական էներգիայով, կարող է նաև հեռանալ սև խոռոչի մոտակայքից՝ որպես իրական մասնիկ կամ հակամասնիկ (նկ․ 7.4)։ Հեռվից դիտորդին կթվա, թե դա սև խոռոչից է արձակվել։ Եվ որքան փոքր է սև խոռոչը, այնքան ավելի կարճ ճանապարհ կանցնի բացասական էներգիա ունեցող մասնիկը մինչև իրական մասնիկ դառնալը, հետևաբար այնքան մեծ կլինի առաքման արագությունը և սև խոռոչի թվացող ջերմաստիճանը։ | ||
| + | |||
| + | Սև խոռոչից արձակվող ճառագայթման դրական էներգիան հավասարակշռվում է սև խոռոչ ներհոսող մասնիկների բացասական էներգիայով։ Համաձայն Էյնշտեյնի հավասարման՝ E=mc² (որտեղ E֊ն էներգիան է, m֊ը՝ զանգվածը, իսկ c֊ն՝ լույսի արագությունը), էներգիան համեմատական է զանգվածին։ Հետևաբար, բացասական էներգիայի ներհոսքը սև խոռոչ նվազեցնում է վերջինիս զանգվածը։ Իսկ սև խոռոչի զանգվածի նվազումը բերում է պատահութային հորիզոնի մակերեսի փոքրացման։ Այսինքն սև խոռոչի էնտրոպիան նվազում է։ Սակայն այս նվազումը առավել քան հակակշռվում է առաքված ճառագայթման էնտրոպիայով, և, հետևաբար, թերմոդինամիկայի երկրորդ օրենքը չի խախտվում։ | ||
| + | |||
| + | Դեռ ավելին, որքան փոքր է սև խոռոչի զանգվածը, այնքան բարձր է նրա ջերմաստիճանը։ Այսպիսով խոռոչի զանգվածի նվազմանը զուգընթաց նրա ջերմաստիճանը բարձրանում է, արձակման արագությունն աճում և, հետևաբար, այն ավելի արագ է զանգված կորցնում։ Թե ինչ կպատահի, երբ սև խոռոչի զանգվածն ի վերջո չափազանց փոքրանա, հնարավոր չէ որոշակիորեն ասել, բայց ամենատրամաբանական ենթադրությունն այն է, որ սև խոռոչը լրիվ կանհետանա վերջին արձակման ուժգին պայթյունից, որի հզորությունը կհամապատասխանի միլիոնավոր ջրածնային ռումբերի պայթման։ | ||
| + | |||
| + | Արեգակից մի քանի անգամ ավելի մեծ զանգված ունեցող սև խոռոչի ջերմաստիճանը բացարձակ զերոյից կարող է լոկ մեկի տաս միլիոներորդ աստիճանով բարձր լինել։ Սա անհամեմատ ավելի ցածր է, քան տիեզերքը լցնող միկրոալիքային ճառագայթման ջերմաստիճանը, որը բացարձակ զերոյից բարձր է մոտավորապես 2,7 աստիճանով։ Այսպիսով, մեծ զանված ունեցող սև խոռոչներն ավելի շատ էներգիա կկլանեն, քան կարձակեն։ Եթե տիեզերքը շարունակի հավերժ ընդլայնվել, ապա ի վերջո միկրոալիքային ճառագայթման ջերմաստիճանը պիտի նվազի և ավելի ցածր լինի այդպիսի սև խոռոչների ջերմաստիճանից, որոնք պիտի սկսեն ճառագայթել և զանգված կորցնել։ Սակայն մեծ զանգված ունեցող սև խոռոչների ջերմաստիճանը նույնիսկ այն ժամանակ այնքան ցածր կլիներ, որ միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն (մեկից հետո 66 զերո) տարի կպահանջվի, որ այդպիսի սև խոռոչները գոլորշիանան։ Այս ժամանակամիջոցն ավելի մեծ է, քան տիեզերքի տարիքը, որը տասից քսան հազար միլիոն տարի է (մեկ կամ երկուսից հետո 10 զերո)։ Մյուս կողմից, ինչպես 6֊րդ գլխում ասվեց, կարող են գոյություն ունենալ շատ ավելի փոքր զանգված ունեցող նախասկզբնական սև խոռոչներ, որոնք առաջացած լինեն տիեզերքի սկզբնավորման ժամանակ առկա անկանոնությունների կոլապսի հետևանքով։ | ||
| + | |||
| + | Այսպիսի սև խոռոչների ջերմաստիճանը շատ ավելի բարձր կլինի և, հետևաբար, ճառագայթման արագությունը՝ շատ մեծ։ Հազար միլիոն տոննա սկզբնական զանգված ունեցող նախասկզբնական սև խոռոչի կյանքի տևողությունը կլինի մոտավորապես տիեզերքի տարիքի չափ։ Այն սկզբնական սև խոռոչները, որոնց զանգվածներն ավելի փոքր են, այժմ լրիվ գոլորշիացած կլինեն, իսկ նրանք, որոնց զանգվածները փոքր֊ինչ ավելի մեծ են, դեռևս կշարունակեն ռենտգենյան կամ գամմա ճառագայթներ առաքել։ Այս ռենտգենյան և գամմա ճառագայթները նման են լույսի ալիքների, թեև նրանց երկարությունը շատ ավելի կարճ է։ Այսպիսի խոռոչները հազիվ թե սև համարվեն, իրականում սրանք սպիտակ և տաք են ու մեկ վայրկյանում մոտավորապես տասը հազար Մեգավատտ էներգիա են առաքում։ | ||
| + | |||
| + | Եթե հնարավոր լիներ օգտվել, այդպիսի սև խոռոչի առաքած էներգիայից, ապա կարելի էր էներգիայի 10 հզոր կայաններ աշխատեցնել։ Սակայն այս հարցի լուծումը շատ դժվար է։ Այդպիսի սև խոռոչի զանգվածը մոտավորապես հավասար կլինի մի մեծ լեռան զանգվածի, որը սեղմված է մոտ մեկի մեկուկես հարյուր հազար միլիոներորդ խորանարդ սանտիմետր ծավալում, այսինքն՝ ատոմի միջուկի ծավալի չափ ծավալում։ Եթե այդպիսի մի սև խոռոչ տեղադրվի երկրի մակերևույթին, ապա ոչ մի ուժ չի կարող խանգարել, որպեսզի այն չընկնի երկրի կենտրոն։ Սև խոռոչը կտատանվի կենտրոնից դեպի մակերևույթ և հակառակը, մինչև վերջնականապես նստի երկրի կենտրոնում։ Հետևաբար, եթե մենք ուզում ենք օգտագործել սև խոռոչի էներգիան, ապա այն պետք է երկրաշուրջ ուղեծիր դուրս բերել։ Իսկ որպեսզի սև խոռոչը պտտվի երկրի շուրջը, հարկավոր է բավական հզոր մի ձգող զանգված դնել նրա առջևում՝ նրան ուղեծիր դուրս բերելու համար, համառ ավանակի առաջ ստեպղին դնելու նման։ Սա գործնական առաջարկություն չի կարող լինել գոնե մոտավոր ապագայի համար։ | ||
| + | |||
| + | Եթե հնարավոր չէ օգտագործել նախասկզբնական սև խոռոչների ճառագայթումը, ապա դրանց դիտարկման ի՞նչ հնարավորություններ կան։ Մենք կարող ենք փնտրել այն գամմա ճառագայթները, որոնք առաքում են նախասկզբնական սև խոռոչներն իրենց գոյատեևման համարյա ամբողջ ընթացքում։ Թեև մեծ մասի ճառագայթումը կարող է թույլ լինել, որովհետև այն հեռվից է գալիս, սակայն բոլորինը միասին վերցրած հնարավոր է հայտնաբերել։ Գամմա ճառագայթման նման ֆոն մենք դիտարկել ենք։ Նկ․ 7.5֊ը ցույց է տալիս, որ դիտարկված ինտենսիվությունը<ref>Ֆոտոնների թիվը։</ref> տարբեր է տարբեր հաճախականություններում (վայրկյանում ալիքների թիվը)։<ref>Ֆոտոնի էներգիան համեմատական է հաճախականությանը։</ref> Այնուամենայնիվ, այս ֆոնի առաջացման պատճառը նախասկզբնական սև խոռոչներից բացի նաև այլ պրոցեսներ են, ինչը հավանաբար, իրոք այդպես է։ Նկ․ 7.6֊ում կետագծերով կորը ցույց է տալիս, թե ինչպես պետք է փոխվի նախասկզբնական սև խոռոչների առաքած գամմա ճառագայթման ինտենսիվությունն ըստ հաճախականության, եթե մեկ խորանարդ լուսատարի ծավալում միջին հաշվով լինեին 30 սև խոռոչներ։ Կարելի է ասել, որ գամմա ճառագայթման ֆոնի փորձնական տվյալները (դիտարկված կորը) նախասկզբնական սև խոռոչների առկայության դրական ապացույց չեն, բայց խոսում են այն մասին, որ միջին հաշվով մեկ խորանարդ լուսատարի ծավալում սև խոռոչների թիվը 300֊ից ավելի չի կարող լինել։ Այս սահմանափակումը նշանակում է, որ նախասկզբնական սև խոռոչների զանգվածը կարող է ամենաշատը լինել տիեզերքում գոյություն ունեցող նյութի մեկ միլիոներորդի չափ։ | ||
| + | |||
| + | Քանի որ նախասկզբնական սև խոռոչների թիվը շատ փոքր է, ապա անհավանական է, որ նրանցից մեկը գտնվեր մեր երկրին այնքան մոտիկ, որ կարողանայինք դիտարկել նրա գամմա ճառագայթումը։ Մյուս կողմից, որովհետև գրավիտացիոն նախասկզբնական սև խոռոչներին կձգի դեպի ցանկացած նյութ, ապա նրանց թիվը գալակտիկաներում կամ նրանց մոտակայքում ավելի մեծ կլինի։ Ճիշտ է, նրանց թիվը միջին հաշվով մեկ խորանարդ լուսատարում 300֊ից ավելի չի կարող լինել, սակայն մեր ունեցած տվյալներից հնարավոր չէ իմանալ, թե նրանց թիվը որքան է մեր սեփական գալակտիկայում։ | ||
| + | |||
| + | Եթե, ասենք, նրանց թիվը մեր գալակտիկայում այս թվից նույնիսկ մեկ միլիոն անգամ շատ լիներ, ապա ամենամոտիկ սև խոռոչը կգտնվեր երկրից հազար միլիոն կիլոմետր հեռավորության վրա, կամ այնքան, որքան հեռու է մեզանից ամենահեռավոր մոլորակը՝ Պլուտոնը։ Նույնիսկ այսքան մոտ հեռավորության վրա գտնվող սև խոռոչի արձակած կայուն ճառագայթումն անհնար կլիներ հայտնաբերել, եթե այն տասը հազար Մեգավատտ հզորություն ունենար։ Որպեսզի մարդ կարողանա նախասկզբնական սև խոռոչը դիտել, հարկավոր է, որ մի քանի քվանտ գամմա ճառագայթներ գան նույն ուղղությամբ, որոշակի ժամանակամիջոցում՝ ասենք մեկ շաբաթվա ընթացքում։ Այլապես ճառագայթումը ֆոնի պարզապես մի մասը կկազմի։ Սակայն, որովհետև գամմա ճառագայթները մեծ հաճախականություն ունեն, ապա համաձայն Պլանկի քվանտային սկզբունքի, գամմա ճառագայթի քվանտի էներգիան շատ մեծ կլինի, և, հետևբար, նույնիսկ տասը հազար Մեգավատտ ճառագայթման համար շատ քվանտներ պետք չեն։ Եվ որպեսզի դիտվի այս մի քանի քվանտի էներգիան, որը առաքվում է Պլուտոնի հեռավորությունից, հարկավոր է ունենալ ավելի խոշոր դետեկտոր, քան մինչև հիմա կառուցվածները։ Դեռ ավելին, դետեկտորը պետք է տեղավորել մթնոլորտից դուրս տարածության մեջ, քանի որ գամմա ճառագայթների համար երկրի մթնոլորտը անթափանցելի է։ | ||
| + | |||
| + | Իհարկե, եթե Պլուտոնի հեռավորության վրա գտնվող սև խոռոչը հասներ իր կյանքի վերջին և պայթեր, ապա հեշտ կլիներ հայտնաբերել վերջնական բռնկման ճառագայթումը։ Սակայն, եթե սև խոռոչն արդեն տասը կամ քսան հազար միլիոն տարի ճառագայթել է, հազիվ թե մի քանի տարվա ընթացքում հասնի իր վերջին։ Ավելի հավանական է, որ այն մի քանի միլիոն տարի առաջ է պայթել, կամ նույնքան ժամանակ հետո ապագայում պիտի պայթի։ Հետևաբար, եթե ցանկանում եք վերջնական մի պայթյուն դիտել ձեր ասպիրանտուրայի ժամկետը վերջանալուց առաջ, հարկավոր է մի այնպիսի եղանակ մշակել, որպեսզի կարողանաք մոտավորապես մեկ լուսատարի հեռավորության վրա տեղի ունեցող պայթյունը գրանցել։ Մի քանի գամմա ճառագայթային քվանտներ հայտնաբերելու համար դեռ հարկ կլինի լուծել խոշոր գամմա ճառագայթման դետեկտորի պրոբլեմը։ Այնուամենայնիվ, պայթման դեպքի համար պարտադիր չէ որոշել, թե բոլոր քվանտներն են արդյոք նույն ուղղությամբ գալիս։ Բավական է, որ բոլոր քվանտները կարճ ժամանակամիջոցում տեղ հասնեն, որպեսզի վստահ լինեք, որ դրանք գալիս են նույն պայթման աղբյուրից։ | ||
| + | |||
| + | Նախասկզբնական սև խոռոչների հայտնաբերման համար գամմա ճառագայթման լավագույն դետեկտորը երկրագնդի ամբողջ մթնոլորտն է։ (Համենայնդեպս, անհնարին է ավելի խոշոր դետեկտոր կառուցել)։ Երբ մեծ էներգիա կրող գամմա ճառագայթի քվանտը հարվածում մթնոլորտում գտնվող ատոմներին, առաջացնում է էլեկտրոնների և պոզիտրոնների (հակաէլեկտրոն) զույգեր։ Երբ սրանք են հարվածում ուրիշ ատոմներին, էլեկտրոնների և պոզիտրոնների նոր զույգեր են ծնվում, և արդյունքում առաջանում է այն, ինչը կոչվում է էլեկտրոնային տեղատարափ։ Արդյունքը մի տեսակ լուսավորություն է, որը կոչվում է չերենկովյան ճառագայթում։ Այսպիսով, կարելի է գամմա ճառագայթման բռնկումները հայտնաբերել գիշերային երկնակամարում՝ լույսի փայլատակումներ դիտելով։ Իհարկե, կան մի շարք այլ երևույթներ, ինչպես կայծակը, վայր ընկնող արբանյակների անդրադարձրած արևի լույսը և երկրի շուրջ պտտվող բեկորները, որոնք կարող են երկնակամարում փայլատակումներ առաջացնել։ Գամմա ճառագայթման բռնկումները կարելի է մյուս երևույթներից տարբերել, եթե միաժամանակ դիտարկումներ կատարվեն իրարից հեռու գտնվող երկու կամ ավելի տարբեր դիրքերից։ Դուբլինից երկու գիտնական՝ Նեյլ Պորտերը և Թրևըր Ուիքսը նման դիտարկումներ կատարեցին Արիզոնայում (ԱՄՆ) տեղադրված հեռադիտակներով։ Որոշ թվով փայլատակումներ դիտվեցին, սակայն, դրանցից ոչ մեկը չէր կարելի վերագրել սև խոռոչներից արձակված գամմա ճառագայթների բռնկումներին։ | ||
| + | |||
| + | Եթե նախասկզբնական սև խոռոչների փնտրտուքները բացասական արդյունք տան, ինչը երևի հնարավոր է, ապա միևնույն է, դրանով կարևոր տեղեկություններ կստանանք տիեզերքի սկզբնական վիճակների մասին։ Եթե վաղ տիեզերքը գտնվեր քաոսային և անկանոն վիճակում և կամ, եթե նյութի ճնշումը ցածր լիներ, կարելի էր սպասել, որ ավելի մեծ թվով նախասկզբնական սև խոռոչներ կառաջանային, քան այն, ինչ ցույց է տալիս մեր դիտարկումների հիման վրա ստացված գամմա ճառագայթման ֆոնը։ Եթե սկզբնական տիեզերքը շատ հարթ ու համաչափ լիներ, և ճնշումը՝ բարձր, ապա միայն այդ դեպքում կարելի կլիներ բացատրել դիտարկելի թվով նախասկզբնական սև խոռոչների բացակայությունը։ | ||
| + | |||
| + | * * * | ||
| + | Սև խոռոչներից ճառագայթման գաղափարը հիմնականում ընդհանուր հարաբերականության և քվանտային մեխանիկայի՝ դարիս երկու մեծ տեսությունների օգնությամբ կատարված կանխագուշակման առաջին օրինակն էր։ Այս գաղափարը սկզբում շատ մեծ դիմադրության հանդիպեց, որովհետև տակնուվրա արեց ընդունված տեսակետը՝ «սև խոռոչը ինչպե՞ս կարող է որևէ բան արձակել»։ Երբ Օքսվորդի մոտ գտնվող Ռեզերֆորդ֊ Ապելտոն լաբորատորիայում տեղի ունեցող մի գիտաժողովում ես առաջին անգամ հաղորդեցի իմ հաշվարկների արդյունքները, դա ընդունվեց ընդհանուր կասկածամտությամբ։ Իմ զեկուցման ավարտին նստաշրջանի նախագահը՝ Լոնդոնի Թագավորական քոլեջից Ջոն Գ․ Թեյլորը պնդեց, որ դա անմտություն է։ Նա նույնիսկ մի հոդված գրեց այդ մասին։ Այնուամենայնիվ, ի վերջո մեծամասնությունը, ներառյալ Ջոն Թեյլորը, եկան այն եզրակացության, որ սև խոռոչները տաք մարմինների նման պետք է ճառագայթեն, եթե մեր մյուս պատկերացումները ընդհանուր հարաբերականության և քվանտային մեխանիկայի մասին ճիշտ են։ Այսպիսով, թեև մեզ առայժմ չի հաջողվել նախասկզբնական սև խոռոչ հայտնաբերել, սակայն գրեթե բոլորը համաձայն են, որ եթե այդպիսին հայտնաբերվի, ապա բավական մեծ քանակությամբ գամմա և ռենտգենյան ճառագայթներ կառաքի։ | ||
| + | |||
| + | Սև խոռոչների ճառագայթման առկայությունը նշանակում է, որ գրավիտացիոն կոլապսն այնքան վերջնական և անդարձելի չէ, որքան սկզբում մտածում էինք։ Եթե տիեզերագնացն ընկնի սև խոռոչի մեջ, վերջինիս զանգվածը կաճի, բայց ի վերջո այդ հավելյալ զանգվածին համապատասխան էներգիա առաքվում է տիեզերք՝ որպես ճառագայթում։ Հետևաբար, տիեզերագնացը յուրահատուկ մի «շրջապտույտ» է կատարում։ Սա խեղճուկրակ անմահություն է, որովհետև տիեզերագնացի համար ամեն տեսակի անհատական ժամանակի հասկացություն վերջանում է, երբ նա սև խոռոչի մեջ կտոր֊կտոր է լինում։ Նույնիսկ, վերջին հաշվով, սև խոռոչից արձակվող մասնիկների տեսակները բոլորովին տարբեր կլինեն այն մասնիկներից, որոնցից կազմված էր տիեզերագնացը։ Այն, ինչ մնում է տիեզերագնացից, դա նրա զանգվածը կամ էներգիան է։ | ||
| + | |||
| + | Սև խոռոչից առաքված ճառագայթումը որոշելու համար կիրառած մոտավորություններն ուժի մեջ են, երբ սև խոռոչի զանգվածը գրամի մասից մեծ է։ Սակայն, երբ սև խոռոչի վերջը մոտենում է, նրա զանգվածը շատ է փոքրանում, իմ օգտագործած մոտավորություններն անիմաստ են դառնում։ Թվում է, թե ամենահավանական ելքը կլինի այն, որ սև խոռոչը կչքանա առնվազն տիեզերքի մի տիրույթում՝ իր հետ տանելով տիեզերագնացին, և իր մեջ ունեցած ամեն եզակիություն, եթե, իհարկե, այդպիսի գոնե մեկը կա։ Սա ընդհանուր հարաբերականության կանխագուշակված եզակիություններից ձերբազատվելու առաջին նշաններից մեկն էր, որն իրականացվում է՝ շնորհիվ քվանտային մեխանիկայի։ Այնուամենայնիվ, 1974֊ին և ուրիշների կողմից օգտագործված մեթոդներն ի վիճակի չեղան պատասխանելու այն հարցին, թե քվանտային գրավիտացիայի միացյալ տեսությունն արդո՞ք հնարավոր է համարում եզակիության առաջացումը:1975֊ից սկսած ես սկսեցի մշակել քվանտային գրավիտացիայի հարցերը լուծելու ավելի հզոր մի մոտեցում, որը հիմնված է Ռիչարդ Ֆեյնմանի պատմությունների գումարի գաղափարի վրա։ Հաջորդ երկու գլուխներում կնկարագրվի, թե այդ մոտեցումը ինչպիսի պատասխաններ է առաջարկում տիեզերքի սկզբնավորման, նրա ապագայի և պարունակության, ինչպես, օրինակ, տիեզերագնացների մասին։ | ||
| + | |||
| + | Մենք կտեսնենք, որ թեև անորոշության սկզբունքը սահմանափակում է կանխագուշակումների ճշգրտությունը, սակայն, միևնույն ժամանակ ազատում է մեզ այն հիմնական անկանխատեսելիությունից, որն ի հայտ է գալիս տարածություն֊ժամանակի եզակիության դեպքում։ | ||
| + | |||
| + | |||
| + | ==8== | ||
| + | |||
| + | Տիեզերքի սկզբնավորումն ու ապագան | ||
| + | |||
| + | Էյնշտեյնի հարաբերականության ընդհանուր տեսությունն ինքնուրույն կանխագուշակում էր, որ տարածություն֊ժամանակը սկիզբ է առել Մեծ պայթյունի եզակիությունից և վերջ կգտնի կամ Մեծ ճայթյունի եզակիությամբ (եթե տիեզերքն ամբողջապես նորից կոլապսի ենթարկվի) և կամ սև խոռոչային եզակիությամբ (եթե ինչ֊որ տեղայնացված մի տիրույթ, ինչպես աստղը, կոլապսի ենթարկվի)։ Խոռոչն ընկնող ամեն նյութ եզակիությունում ոչնչանալու է, և խոռոչից դուրս լոկ նրա զանգվածի գրավիտացիոն ազդեցությունը պիտի շարունակի գործել։ Մյուս կողմից, երբ սկսեցին հաշվի առնել քվանտային ազդեցությունները, թվաց, թե նյութի զանգվածը կամ էներգիան ի վերջո պետք է վերադառնա տիեզերքի մնացյալ մաս, և սև խոռոչն իր մեջ եղած եզակիության հետ միասին պետք է ցնդի ու անհետանա։ Քվանտային մեխանիկան արդյո՞ք նմանօրինակ ցնցող ազդեցություն կարող է ունենալ Մեծ պայթյունի և Մեծ ճայթյունի եզակիությունների վրա։ Իրականում ի՞նչ կպատահեր տիեզերքի ամենավաղ և ամենաուշ փուլերում, երբ գրավիտացիոն դաշտերն այն աստիճան հզոր լինեին, որ այլևս հնարավոր չլիներ անտեսել քվանտային ազդեցությունները։ Տիեզերքն իսկապես սկիզբ կամ վերջ ունի՞։ Եթե այո, ապա ի՞նչ տեսք ունեն դրանք։ | ||
| + | |||
| + | 1970֊ական թվականներին ես ուսումնասիրում էի հիմնականում սև խոռոչները, բայց 1981֊ին տիեզերքի սկզբնավորման և ապագայի հարցերի նկատմամբ իմ հետաքրքրությունը վերարթնացավ, երբ ներկա եղա Վատիկանում ճիզվիտների կազմակերպած տիեզերագիտական համաժողովին։ Կաթոլիկ եկեղեցին անցյալում կոպիտ սխալ էր գործել Գալիլեոյի նկատմամբ, երբ գիտական հարց լուծելիս փորձել էր պարտադրել իր եկեղեցական օրենքը՝ հայտարարելով, թե արեգակն է պտտվում երկրի շուրջ։ Այժմ, դարեր անց, որոշվել էր մի խումբ մասնագետներ հրավիրել, որպեսզի նրանք տիեզերագիտական հարցերի մասին խորհուրդներ տային եկեղեցուն։ Համաժողովի ավարտին պապն ընդունեց մասնակիցներին։ Նա մեզ ասաց, թե ընդունելի է տիեզերքի էվոլյուցիան Մեծ պայթյունից հետո ուսումնասիրելը, բայց չպետք է խորամուխ լինել Մեծ պայթյունի մեջ, որովհետև դա հենց արարման պահն է և, հետևաբար, Աստծո գործը։ Ես երջանիկ էի, որ պապն անտեղյակ էր իմ զեկուցման նյութին, որով հանդես գալով համաժողովում, ես խոսել էի այն մասին, թե հնարավոր է, որ տարածություն֊ժամանակը վերջավոր լինի, բայց և սահման չունենա։ Այս բանը նշանակում էր, որ տիեզերքը չի ունեցել սկիզբ և չի եղել Արարման պահ։ Ես ցանկություն չունեի արժանանալ Գալիլեոյի բախտին, որի հետ նույնանալու մեծ միտվածություն եմ միշտ ունեցել, մասամբ այն զուգադիպության պատճառով, որ ծնվել եմ նրա մահվանից ուղիղ 300 տարի հետո։ | ||
| + | |||
| + | Որպեսզի բացատրեմ իմ և ուրիշների գաղափարներն այն մասին, թե քվանտային մեխանիկան ինչպես կարող է ազդել տիեզերքի սկզբնավորման և ապագայի վրա, անհրաժեշտ է ամենից առաջ հասկանալ տիեզերքի համընդհանուր հավանության արժանացած պատմությունը, համաձայն այն պատկերացման, որը կոչվում է «տաք մեծ պայթյունի մոդել»։ Ենթադրվում է, որ տիեզերքը նկարագրվում է ըստ Ֆրիդմանյան մոդելի՝ Մեծ պայթյունից սկսած։ Համաձայն այս մոդելների, ընդարձակվելուն զուգընթաց նրա պարունակած նյութերն ու ճառագայթումը սառչում են։(Երբ տիեզերքը կրկնակի ընդարձակվի, ապա ջերմաստիճանը կիսով չափ կնվազի)։ Քանի որ ջերմաստիճանը պարզապես միջին էներգիայի կամ մասնիկների արագության չափանիշն է, ուստի տիեզերքի սառչելը մեծապես կազդի իր մեջ պարունակած նյութի վրա։ Բարձր ջերմաստիճանում մասնիկներն այնպիսի մեծ արագությամբ կշարժվեն, որ միջուկային ու էլեկտրոմագնիսական ուժերի շնորհիվ կհաղթահարեն ցանկացած ձգողություն, սակայն, քանի որ դրանք սառչում են, ապա սպասելի է, որ մասնիկների միջև գործող ձգողական ուժի շնորհիվ դրանք սկսեն խմբեր կազմել։ Դեռ ավելին, ջերմաստիճանից է կախված այն, թե ինչ տեսակի մասնիկներ կարող են գոյություն ունենալ տիեզերքում։ Բավականին բարձր ջերմաստիճաններում մասնիկների էներգիան այնքան մեծ է, որ իրար հետ բախվելիս կառաջանան բազմատեսակ մասնիկ֊հակամասնիկ զույգեր։ Եվ չնայած այդ մասնիկների մի մասն իրենց հակամասնիկների հետ բախվելով կոչնչանան (կանիհիլանան), սակայն ծնվածների թիվն ավելի մեծ կլինի, քան ոչնչացածներինը։ Ցածր ջերմաստիճաններում, սակայն, երբ իրար հետ բախվող մասնիկների էներգիան փոքր է, մասնիկ֊հակամասնիկ զույգերի առաջացումը դանդաղ է լինում, և ոչնչացումը տեղի է ունենում ավելի արագ, քան առաջացումը։ | ||
| + | |||
| + | Մեծ պայթյունի պահին, ենթադրվում է, որ տիեզերքի չափսը զերո էր, և, հետևաբար, այն անսահման տաք էր։ Բայց տիեզերքի ընդարձակմանը զուգընթաց՝ ճառագայթման ջերմաստիճանն ընկել է։ Մեծ պայթյունից մեկ վայրկյան անց ջերմաստիճանը պետք է մոտավորապես տասը հազար միլիոն աստիճանով ընկած լիներ։ Բավական է ասել, որ դա հազար անգամ բարձր է արեգակի կենտրոնի ջերմաստիճանից։ Այդպիսի բարձր ջերմաստիճաններ ստացվում են ջրածնային ռումբի պայթեցումների ժամաակ։ Տիեզերքն այդ ժամանակ առավելապես ֆոտոններ, էլեկտրոններ և նեյտրինոներ պետք է պարունակած լիներ (վերջիններս չափազանց թեթև մասնիկներ են, որոնց վրա միայն թույլ ուժերը և գրավիտացիան կարող են ներգործել), ինչպես նաև նրանց հակամասնիկները՝ որոշ թվով պրոտոնների և նեյտրոնների հետ միասին։ Մինչ տիեզերքը շարունակում էր ընդարձակվել, և ջերմաստիճանը՝ իջնել, բախումների հետևանքով էլեկտրոն֊հակաէլեկտրոն զույգերի առաջացման արագությունը պետք է որ նվազեր և իջներ դրանց անիհիլացմամբ ոչնչացման արագությունից։ Այսպիսով, էլեկտրոնների և հակաէլեկտրոնների (պոզիտրոն) մեծ մասն իրար արդեն ոչնչացրած և ֆոտոններ առաջացրած կլինեն, և շատ քիչ թվով էլեկտրոններ կլինեն մնացած։ Սակայն նեյտրինոներն ու հականեյտրինոներն անիհիլացված չեն լինի միմյանց, որովհետև այս մասնիկները միմյանց կամ այլ մասնիկների հետ շատ թույլ են փոխազդում։ Այսպիսով, նրանք մինչև օրս պետք է որ գոյություն ունենան։ Եթե մենք կարողանանք դիտել այդ մասնիկները, ապա դա կլինի տիեզերքի շատ տաք սկզբնավորումն ապացուցող լավագույն փաստը։ Սակայն, դժբախտաբար, նրանց էներգիան այսօր այնքան փոքր պետք է լինի, որ հնարավոր չլինի ուղղակի դիտել։ Բայց, եթե նեյտրինոները զանգվածից զուրկ չեն, այլ ունեն իրենց սեփական փոքր զանգվածը, ապա համաձայն 1981 թվականին ռուսների կողմից կատարված և դեռևս չհաստատված մի գիտափորձի, մենք կկարողանանք անուղղակիորեն հայտնաբերել դրանք։ Այդ մասնիկներն ի հայտ կգան «սև նյութի» մի այնպիսի ձևով, որի մասին վերևում նշվեց, և կունենան բավականին ուժեղ գրավիտացիոն ձգողական ուժ, որպեսզի արգելակեն տիեզերքի ընդարձակումը և պատճառ լինեն, որ այն դարձյալ կոլապսի ենթարկվի։ | ||
| + | |||
| + | Մեծ պայթյունից հարյուր վայրկյան անց ջերմաստիճանը պետք է որ իջներ մինչև հազար միլիոն աստիճան, ինչը համապատասխանում է ամենատաք աստղերի ներսում եղած ջերմաստիճանին։ Այս ջերմաստիճանում պրոտոնների ու նեյտրոնների էներգիան այլևս չէր բավարարի, որպեսզի նրանք ձերբազատվեին ուժեղ միջուկային ուժի ձգողությունից և կմիանային ու դեյտերիումի (ծանր ջրածնի) ատոմների միջուկներ կառաջացնեին, որոնք պարունակում են մեկ պրոտոն և մեկ նեյտրոն։<ref>Սովորական ջրածնի ատոմի միջուկը կազմված է մեկ պրոտոնից և դրա համար կոչվում է պրոտոն։ Դեյտերիումի (ծանր ջրածնի) ատոմի միջուկը պարունակում է մեկ պրոտոն ու մեկ նեյտրոն և կոչվում է դեյտրոն։</ref> Դեյտերիումի միջուկները կարող են միանալ պրոտոնների և նեյտրոնների հետ և առաջացնել հելիումի միջուկ, որը պարունակում է երկու պրոտոն և երկու նեյտրոն։ Կարող են առաջանալ նաև փոքր քանակությամբ ավելի ծանր երկու տարր․ լիթիում և բերիլիում։ Կարելի է հաշվարկներով պարզել, որ տաք մեծ պայթյունի մոդելում պրոտոնների և նեյտրոնների քառորդ մասը փոխարկված կլինեն հելիումի միջուկների, ինչպես նաև փոքր քանակությամբ ծանր ջրածնի և այլ տարրերի։ Ավելցուկ նեյտրոնները կքայքավեին և կառաջացնեին պրոտոններ, որոնք սովորական ջրածնի ատոմների միջուկներն են։ | ||
| + | |||
| + | Տիեզերքի վաղ ջերմ փուլի վերոհիշյալ պատկերացումն առաջին անգամ առաջարկել է Գեորգի Գամովը 1948֊ին, իր հայտնի աշխատությունում, որը գրել է իր աշակերտ Ռալֆ Ալֆերի հետ։ | ||
| + | |||
| + | Գամովը օժտված էր շատ նուրբ հումորով և համոզեց միջուկային գիտնական Հանս Բեթին, որպեսզի նա ևս իր անունը ավելացնի հողվածի հեղինակների անուններին և, այսպիսով հոդվածը գրված լինի «Ալֆեր, Բեթե, Գամով» հեղինակների կողմից, որը հիշեցնում է հունարեն այբուբենի առաջին երեք տառերի՝ «ալֆա, բետա, գամմա» հերթականությունը։ Դա շատ հարմար էր այնպիսի մի հոդվածի համար, որ վերաբերում էր տիեզերքի սկզբնավորմանը։ Այս աշխատությունում այն արժեքավոր կանխագուշակումն էր արվում, որ տիեզերքի շատ ջերմ հեռավոր փուլերում արձակված ճառագայթումը (ֆոտոնների ձևով) մինչև օրս իր գոյությունը պետք է պահած լինի, թեև շատ ցածր ջերմաստիճանում բացարձակ զերոյից (-273, 2°c) մի քանի աստիճան բարձր։<ref>Բացարձակ զերոն (որը կոչվում է նաև Կելվինի զերո աստիճան) սահմանային ամենացածր ջերմաստիճանն է։</ref> Ահա հենց այս ճառագայթումն էր, որ Պենզիասն ու Ուիլսոնը հայտնաբերել էին 1965֊ին։ Երբ Ալֆերը, Բեթեն և Գամովը հրատարակեցին իրենց աշխատությունը պրոտոնների և նեյտրոնների միջուկային ռեակցիայի մասին, շատ բան դեռ չգիտեինք։ Հետևաբար, տիեզերքի վաղ փուլերում տարբեր տարրերի հարաբերական քանակությունների կապակցությամբ արված կանխագուշակումները բավարար ճշգրիտ չէին, սակայն այս հաշվումները այժմ կրկնվել են նորագույն պատկերացումների հիման վրա և շատ լավ համընկնում են մեր ժամանակակից դիտարկումներին։ Դեռ ավելին, այլապես շատ դժվար կլիներ բացատրել, թե ինչո՞ւ պետք է այսքան մեծ քանակով հելիում գոյություն ունենար տիեզերքում։ Այդ պատճառով վստահությամբ կարող ենք ասել, որ մեր պատկերացումները տիեզերքի մասին, համենայն դեպս Մեծ պայթյունից մեկ վայրկյան անց, ճիշտ են։ | ||
| + | |||
| + | Մեծ պայթյունից մի քանի ժամ հետո հելիումի և մյուս տարրերի առաջացումը կդադարի։ Դրանից հետ, հետագա միլիոնավոր տարիների ընթացքում, տիեզերքը շարունակ կընդարձակվի առանց որևէ արտակարգ փոփոխությայն։ Վերջապես, երբ ջերմաստիճանն իջնի մինչև մի քանի հազար աստիճան, էլեկտրոնների ու միջուկների էներգիան այլևս բավարար չեն լինի, որպեսզի նրանց միջև էլեկտրոմագնիսական ձգողությունը հաղթահարվի, և նրանք կսկսեն միավորվել և ատոմներ առաջացնել։ Ամբողջությամբ վերցրած՝ տիեզերքը կշարունակի իր ընդարձակումը և սառչելը, բայց այն տիրույթներում, որտեղ նյութը համեմատաբար ավելի խիտ է, քան միջին խտությունը, ընդարձակումը կդանդաղի՝ հավելյալ գրավիտացիոն ձգողության պատճառով։ Մի քանի տիրույթներում ընդարձակումը վերջնականապես կանգ կառնի, և դրանք կսկսեն վերստին կոլապսի ենթարկվել։ Կոլապսի ընթացքում այդ տիրույթներից դուրս գտնվող նյութի գրավիտացիոն ձգողությունը պատճառ կլինի, որ կծկվող այդ տիրույթները դանդաղորեն պտտվեն։ Կոլապսի ենթարկվող տիրույթների փոքրացմանը զուգընթաց, նրանց պտտման արագությունը կաճի ճիշտ այնպես, ինչպես չմշկորդի պտտման արագությունը սառույցի վրա, երբ վերջինս ծալում է ձեռքերը։ Վերջապես, երբ տիրույթը բավական փոքրանա, նրանք այնպիսի արագությամբ կպտտվեն, որ հավասարակշռվի գրավիտացիոն ձգողությունը, և արդյունքում ծնունդ կառնեն սկավառակաձև պտտվող գալակտիկաներ։ Այլ տիրույթներ, զրկված լինելով պտտական շարժումից, կփոխակերպվեն ձվաձև մարմինների, որոնք այժմ կոչվում են էլիպսաձև գալակտիկաներ։ Այս դեպքում տիրույթը կոլապսի չի ենթարկվում, քանի որ գալակտիկայի առանձին մասեր իրենց կենտրոնի նկատմամբ կշարունակեն պտտվել կայուն կերպով, բայց գալակտիկան ամբողջությամբ վերցված զրկված կլինի պտտական շարժումից։ | ||
| + | |||
| + | Ժամանակի ընթացքում գալակտիկաներում ջրածին և հելիում գազերը կառաջացնեն փոքր ամպեր, որոնք իրենց գրավիտացիոն դաշտերի ազդեցության տակ կկոլապսվեն։ Կծկման ընթացքում նրանց մեջ գտնվող ատոմները կսկսեն բախվել միմյանց, գազի ջերմաստիճանը դրանով կբարձրանա, և, ի վերջո, այն այնքան կտաքանա, որ ջերմաստիճանը բավարար կլինի միջուկային սինթեզի ռեակցիաներ սկսելու համար։ Արդյունքում ջրածինը կփոխակերպվի հելիումի։ Առաջացած ջերմությունը պատճառ կդառնա, որ ճնշումը բարձրանա, և դրանով կանգ առնի ամպերի հետագա կծկումը։ Դրանք երկար ժամանակ կայուն վիճակում կշարունակեն իրենց գոյությունը՝ որպես աստղեր, ինչպես մեր արեգակը՝ ջրածնի այրումից հելիում առաջացնելով և ստացված էներգիան՝ որպես ջերմություն և լույս ճառագայթելով։ Ավելի մեծ զանգվածով աստղերը պետք է ավելի տաք լինեն, որպեսզի կարողանան հավասարակշռել իրենց ավելի ուժեղ գրավիտացիոն ձգողությունը։ Այսպիսով, դրանցում միջուկային սինթեզի ռեակցիաներն ավելի մեծ արագությամբ կընթանան, և իրենց ջրածինը կսպառեն հարյուր միլիոն տարուց ավելի շուտ։ Այնուհետև այդ մեծ զանգվածով աստղերը փոքր֊ինչ կսեղմվեն, և քանի որ դրանից տաքանում են, կսկսեն հելիումը փոխակերպել ծանր տարրերի, ինչպես, օրինակ, ածխածնի կամ թթվածնի։ Այս ռեակցիաները, սակայն, մեծ քանակության էներգիա չեն առաջացնի, և կստեղծվի ճգնաժամային մի վիճակ, ինչպես նկարագրվեց սև խոռոչների վերաբերյալ գլխում։ Թե հետագայում ի՞նչ է կատարվում՝ լրիվ պարզ չէ, բայց հավանական է, որ աստղի կենտրոնական տիրույթները կոլապսվեն և հասնեն ավելի խիտ վիճակի, ինչպիսիք են նեյտրոնային աստղը կամ սև խոռոչը։ Աստղի արտաքին տիրույթները կարող են երբեմն ժայթքել ահավոր մի պայթյունով․ դա կոչվում է գերաստղ և լուսավորությամբ գերազանցում է իր գալակտիակյի բոլոր աստղերին։ Աստղի կյանքի վերջին փուլերում առաջացած ծանր տարրերից մի քանիսը շպրտվում են հետ՝ գալակտիկայի գազի մեջ, և կարող են հիմք դառնալ աստղերի հաջորդ սերնդի համար։ Մեր արեգակը այդ ծանր տարրերից պարունակում է մոտ 2 տոկոս, քանի որ այն երկրորդ կամ երրորդ սերնդի աստղ է, որը ծնվել է մոտ հինգ հազար միլիոն տարի առաջ վաղեմի գերնոր աստղի մնացորդներ պարունակած պտտվող գազային ամպից։ Ամպի պարունակած գազի մեծ մասն օգտագործվել է արեգակի առաջացման համար կամ շպրտվել հեռուները, սակայն ծանր տարրերի փոքր քանակներն ի մի հավաքվելով, առաջացրել են մարմիններ, որոնք այժմ որպես մոլորակներ, ինչպես, օրինակ, մեր երկրագունդը, պտտվում են արեգակի շուրջը։ | ||
| + | |||
| + | Սկզբնական շրջանում երկիրը շատ տաք է եղել և առանց մթնոլորտի։ Ժամանակի ընթացքում այն սառել է, և ժայռերից արձակված գազերն առաջացրել են մթնոլորտ։ Վաղ շրջանի մթնոլորտը կյանքի համար պիտանի չէր։ Այն թթվածին չէր պարունակում, այլ պարունակում էր մարդու համար մի շարք թունավոր գազեր, ինչպես, օրինակ, ծծմբաջրածինը (նեխած ձվի հոտ արձակող մի գազ)։ Սակայն կյանքի պարզունակ որոշ ձևեր կան, որոնք այդպիսի պայմաններում կարող են պահպանել իրենց գոյությունը և զարգանալ։ Այն կարծիքը կա, որ կյանքի այդ ձևերը զարգացել են օվկիանոսներում, հավանաբար ատոմների պատահական միացումների ձևով, որոնք մեծ գոյացություններ՝ մակրոմոլեկուլներ են առաջացրել և ընդունակ եղել, օվկիանոսում գտնվող այլ ատոմների ի մի հավաքելով, իրենց նման գոյացություններ առաջացրել։ Այսպիսով, տեղի է ունենում վերարտադրություն և բազմացում։ Որոշ դեպքերում վերարտադրության ընթացքում պետք է խոտորումներ եղած լինեն։ Այդ խոտորումների մեծ մասը կարող էր այնպիսի բնույթի լինել, որ մակրոմոլեկուլը չվերարտադրեր իրեն և վերջ ի վերջո ոչնչանար։ Սակայն սխալների մի մասն էլ կբերի նոր տեսակի մակրոմոլեկուլների առաջացման, որոնք ինքնավերարտադրման առավել հաջող մեխանիզմ կունենան։ Հետևաբար, դրանք, օժտված լինելով առավելություններով, կձգտեն փոխարինել սկզբնական մակրոմոլեկուլներին։ Այսպիսով, սկիզբ է առել էվոլյուցիոն գործընթացը, ինչը բերել է ավելի և ավելի բարդ, ինքնավերարտադրող օրգանիզմների առաջացման։ Կյանքի առաջին պարզունակ ձևերը սնվել են տարբեր նյութերով, նաև ծծմբաջրածնով, և թթվածին անջատել։ Աստիճանաբար մթնոլորտի բաղադրությունը փոխվել է, և առաջացել այսօրվա մթնոլորտը, որը թույլ է տվել, որպեսզի ավելի բարդ ձևի կյանք զարգանար, ինչպես ձկները, սողունները, կաթնասուններն ու վերջապես մարդկային ցեղը։ | ||
| + | |||
| + | Այն պատկերացումը, թե տիեզերքը սկսում է շատ տաք վիճակից և սառչում է ընդարձակմանը զուգընթաց, համապատասխանում է մինչև օրս մեր դիտարկված բոլոր փաստերին։ Այնուամենայնիվ, մի շարք կարևոր հարցեր դեռևս մնում են առանց պատասխանի․ | ||
| + | |||
| + | 1) Ինչո՞ւ է վաղ տիեզերքը այդքան տաք եղել։ | ||
| + | |||
| + | 2) Ինչո՞ւ է տիեզերքն այս աստիճան հավասարաչափ՝ լայն մասշտաբով վերցրած։ Ինչո՞ւ է տիեզերքը նույնանման երևում տարածության բոլոր կետերից և բոլոր ուղղություններից։ Մասնավորապես, ինչո՞ւ է միկրոալիքային ճառագայթման ֆոնի ջերմաստիճանը մոտավորապես նույնը՝ տարբեր ուղղություններից չափելիս։ Սրանք կարծես ուսանողներին տրվող քննական հարցեր են։ Եվ եթե բոլորն այս հարցերին նույն պատասխանը տան, կարող եք վստահ լինել, որ նրանք նախապես պայմանավորվել են։ Այնուամենայնիվ, տվյալ մոդելում մեծ պայթյունից հետո ժամանակ չէր լինի, որպեսզի լույսը մի հեռավոր տիրույթից հասներ մի այլ տիրույթ, թեև այդ տիրույթները վաղ տիեզերքում իրար մոտիկ էին գտնվում։ Համաձայն հարաբերականության տեսության, եթե լույսը մի տիրույթից մի այլ տիրույթ չի կարող հասնել, ապա չի կարող հասնել նաև որևէ այլ ինֆորմացիա։ Հետևաբար, ոչ մի հնարավոր ճանապարհ չէր կարող գոյություն ունենալ, որով տարբեր տիրույթներ միմյանց հետ կապ հաստատեին վաղ տիեզերքում և ունենային նույն ջերմաստիճանը, մինչդեռ մի անբացատրելի պատճառով ամեն ինչ սկսվել է նույն ջերմաստիճանում։ | ||
| + | |||
| + | 3) Ինչո՞ւ է տիեզերքը սկիզբ առել մոտավորապես ընդարձակման այն կրիտիկական արագությամբ, որը վերակոլապսվող մոդելները զատում է ընդմիշտ ընդարձակվող մոդելներից այնպես, որ նույնիսկ այժմ՝ տասը հազար միլիոն տարի հետո այն դեռևս ընդարձակվում է նույն կրիտիկական արագությամբ։ Եթե ընդարձակման արագությունը Մեծ պայթյունից մեկ վայրկյան անց նույնիսկ մեկի հարյուր հազար միլիոն միլիոներորդ մասի չափով փոքր լիներ, ապա տիեզերքը վերակոլապսի ենթարկված կլիներ դեռ այսօրվա չափերին չհասած։ | ||
| + | |||
| + | 4) Չնայած այն բանին, որ տիեզերքը խոշոր մասշտաբով վերցրած այս աստիճան համաչափ է և համասեռ, այն տեղային անհամաչափություններ ունի, ինչպիսիք են աստղերը և գալակտիկաները։ Այն կարծիքը կա, որ սրանք առաջացել են, որովհետև վաղ տիեզերքի տարբեր տիրույթներում խտությունների փոքր տարբերություններ են եղել։ Խտության այդ տատանումների պատճառն ի՞նչն է եղել։ | ||
| + | |||
| + | Հարաբերականության ընդհանուր տեսությունը լոկ իր ուժերով չի կարող բացատրել այդ բնորոշ գծերի էությունը կամ պատասխանել տրված հարցերին, որովհետև այդ տեսությունը կանխագուշակում է, որ տիեզերքը սկիզբ է առել անսահման խիտ վիճակից Մեծ պայթյունի եզակիությամբ։ Ընդհանուր հարաբերականությունը և բոլոր մյուս ֆիզիկական տեսությունները եզակիությունում կորցնում են իրենց ուժը։ Անհնարին է կանխագուշակել, թե ի՞նչ փոխակերպում կարող է ստացվել եզակիությունից։ Ինչպես արդեն բացատրվել է, սա նշանակում է, որ կարելի է նաև հրաժարվել Մեծ պայթյունից և նրանից առաջ կատարված բոլոր պատահույթներից, որովհետև դրանք ոչ մի ազդեցություն չեն կարող ունենալ այն մեր դիտարկած երևույթների վրա։ Տարածություն֊ժամանակը պետք է սահման ունենար՝ մի սկիզբ Մեծ պայթյունի պահին։ | ||
| + | |||
| + | Թվում է, թե գիտությունը հայտնաբերել է օրենքների մի լրակազմ, որը անորոշության սկզբունքի պարտադրած սահմաններում մեզ ասում է, թե ինչպես պիտի զարգանա տիեզերքը ժամանակի ընթացքում, եթե մեզ հայտնի է վերջինիս վիճակը ժամանակի ցանկացած մեկ կետում։ Կարող է պատահել, որ այս օրենքներն Աստված է սահմանել, սակայն ինչպես երևում է, նա այնուհետև թույլ է տվել, որ տիեզերքը զարգանա համաձայն այդ օրենքների և այլևս չի միջամտում։ Բայց նա ինչպե՞ս ընտրեց տիեզերքի սկզբնական վիճակը կամ կոնֆիգուրացիան։ Որո՞նք էին ժամանակի սկզբնավորության «սահմանային պայմանները»։ | ||
| + | |||
| + | Այս հարցի հավանական պատասխաններից մեկն այն է, որ Աստված տիեզերքի սկզբնական կոնֆիգուրացիան ընտրել է այնպիսի նկատառումներով, որ մենք ի զորու չենք հասկանալ։ Իհարկե, այս բանն ամենազոր էակի իրավունքն է։ Բայց, եթե նրա Արարչության սկիզբն անըմբռնելի է, ապա ինչո՞ւ է որոշել թույլ տալ, որպեսզի տիեզերքը զարգանա մեր ըմբռնմանը հասու օրենքներով։ Գիտության ողջ պատմությունը աստիճանաբար բերել է այն եզրակացության, որ պատահույթները հանկարծադեպ իրադարձություններ չեն, այլ արտացոլում են տիեզերքին ներհատուկ կարգուկանոնը, ինչը կարող է լինել կամ չլինել աստվածային ներշնչման հետևանք։ Միանգամայն բնականաբար կարելի է ենթադրել, որ այս կարգուկանոնը պետք է վերաբերի ոչ միայն օրենքներին, այլ տարածություն֊ժամանակի սահմանային պայմաններին, որոնք բնորոշում են տիեզերքի սկզբնական վիճակը։ Կարող են լինել տիեզերքի մեծ թվով մոդելներ, բոլորովին տարբեր սկզբնական պայմաններով, որոնք բոլորն էլ կենթարկվեն այդ օրենքներին։ Պետք է ինչ֊որ սկզբունք լինի, որով ընտրվի որոշակի մի սկզբնական վիճակ, հետևաբար և մի մոդել, որը կներկայացնի մեր տիեզերքը։ | ||
| + | |||
| + | Հայտնի է մի այդպիսի հնարավորություն, որը կոչվում է քաոսային սահմանային պայմաններ։ Այդ քաոսային պայմաններն ինքնաբերաբար ենթադրում են, որ կամ տիեզերքը տարածականորեն անսահման է, և կամ գոյություն ունեն անսահման թվով տիեզերքներ։ Համաձայն քաոսային սահմանային պայմանների, Մեծ պայթյունից անմիջապես հետո, տվյալ կոնֆիգուրացիայում տարածության որոշակի տիրույթ գտնելու հավանականությունը որոշ իմաստով նույնն է, ինչ ցանկացած այլ կոնֆիգուրացիայում գտնելու հավանականությունը․ տիեզերքի սկզբնական վիճակի ընտրությունը զուտ պատահականություն է։ Սա նշանակում է, որ, հավանաբար, վաղ տիեզերքը շատ քաոսային և անկանոն պետք է եղած լինի, որովհետև տիեզերքի համար ավելի մեծ թվով քաոսային և անկանոն կոնֆիգուրացիաներ կան, քան հարթ ու կանոնավոր կոնֆիգուրացիաները։ (Եթե յուրաքանչյուր կոնֆիգուրացիա հավասարապես հավանական է, ճիշտ կլինի ասել, որ տիեզերքն սկիզբ է առել քաոսային և անկանոն վիճակից պարզապես այն պատճառով, որ դրանց թիվն ավելի շատ է)։ Դժվար է համաձայնել այն մտքին, թե այդպիսի սկզբնական քաոսային պայմաններն առաջացնեին ընդհանուր առմամբ այսպիսի հարթ ու կանոնավոր մի տիեզերք, ինչպիսին մերն է այսօր։ Սպասելի էր, որ այս մոդելի մեջ խտության տատանումները պատճառ կլինեն ավելի մեծ թվով նախասկզբնական սև խոռոչների առաջացման, քան տալիս է դիտարկված գամմա ճառագայթման ֆոնի վերին սահմանը։ | ||
| + | |||
| + | Եթե տիեզերքն իրոք տարածականորեն անսահման է և կամ գոյություն ունեն անսահման մեծ թվով տիեզերքներ, ապա, հավանաբար, ինչ֊որ տեղում կլինեն հարթ ու համաչափ ձևով առաջացած լայնատարած տիրույթներ։ Վիճակը նման է քաջածանոթ այն պատմությանը, երբ մի խումբ կապիկներ հարվածում են գրամեքենայի ստեղներին։ Նրանց մեքենագրությունների մեծ մասն աղբակույտ նետելու բան կլինի, բայց շատ պատահաբար, ուղղակի բախտի բերումով, նրանք կարող է և Շեքսպիրի սոնետներից մեկը մեքենագրեն։ Նույն ձևով մեր տիեզերքի պարագայում կարո՞ղ է արդյոք, որ մենք բախտի բերումով գտնվում ենք հարթ ու համաչափ մի տիրույթում։ Առաջին հայացքից կարող է թվալ, որ դա շատ անհավանական է, որովհետև այդպիսի հարթ տիրույթների համեմատությամբ քաոսային և անկանոն տիրույթների թիվն արտակարգ շատ է։ Այնուամենայնիվ, ենթադրենք, որ աստղեր և գալակտիկաներ առաջացել են միայն հարթ տիրույթներում, և պայմաններն այնպես են եղել, որ կարողացել են զարգանալ բարդ ինքնավերարտադրվող օրգանիզմներ, ինչպիսիք մենք ենք, որոնք ի վիճակի են հարցնել․ ինչո՞ւ է տիեզերքն այսքան հարթ։ Սա, այսպես կոչված մարդաբանական սկզբունքի կիրառման մի օրինակ է, որը կարելի է ձևակերպել այսպես․ «Մենք տիեզերքն այս ձևով ենք տեսնում, որովհետև մենք գոյություն ունենք»։ | ||
| + | |||
| + | Կա մարդաբանական սկզբունքի երկու տարբերակ՝ թույլ և ուժեղ։ Թույլ սկզբունքի համաձայն, տարածության և (կամ) ժամանակի մեջ լայնատարած և անսահման տիեզերքում բանական կյանքի զարգացման անհրաժեշտ պայմաններ կարող են լինել միայն տարածության և ժամանակի սահմանափակ որոշ տիրույթներում։ Այդ տիրույթներում գտնվող էակները, հետևաբար, չպիտի զարմանան, եթե տեսնեն, որ տիեզերքի այդ մասը բավարարում է իրենց գոյության համար հարկավոր պայմանների պահանջը։ Սա նման է հարուստի մտածելակերպին, որն, ապրելով մեծահարուստների հարևանությամբ, աղքատությունը չի տեսնում։ | ||
| + | |||
| + | Թույլ մարդաբանական սկզբունքի կիրառման մի օրինակ է հետևյալ «բացատրությունը»․ թե Մեծ պայթյունը տեղի ունեցավ սրանից մոտավորապես տասը հազար միլիոն տարի առաջ, որովհետև այդքան ժամանակ էր հարկավոր բանական էակների զարգացման համար։ Ինչպես վերևում բացատրվեց, դրանով նախ առաջացավ աստղերի հինավուրց մի սերունդ։ Այդ աստղերը սկզբնական ջրածնի և հելիումի մի մասը փոխակերպեցին ածխածնի և թթվածնի, որոնցից մենք ենք կազմված։ Ապա աստղերը պայթեցին որպես գերնոր աստղեր, դրանց մնացորդներից առաջացան այլ աստղեր և մոլորակներ, որոնցից են նաև մոտավորապես հինգ հազար միլիոն տարեկան մեր Արեգակնային համակարգի աստղերն ու մոլորակները։ Առաջին մեկ կամ երկու հազար միլիոն տարիներին երկիրը շատ տաք էր, որպեսզի բարդ նյութեր առաջանային։ Հաջորդ երեք հազար միլիոն տարիների ընթացքում տեղի ունեցավ կենսաբանական էվոլյուցիայի դանդաղ գործընթացը, որի հետևանքով առաջացան պարզագույն օրգանիզմներից մինչև այնպիսի էակներ, որոնք ի վիճակի են չափել Մեծ պայթյունից մինչև այսօր անցած ժամանակը։ | ||
| + | |||
| + | Քչերը պիտի առարկեն թույլ մարդաբանական սկզբունքի հավաստիության և օգտակարության դեմ։ Ոմանք, սակայն, շատ ավելի հեռու են գնում և սկզբունքի ուժեղ տարբերակ են առաջարկում։ Համաձայն այս տեսության, գոյություն ունեն բազմաթիվ տարբեր տիեզերքներ, կամ բազմաթիվ տարբեր տիրույթներ եզակի տիեզերքում, յուրաքանչյուրն իրեն հատուկ գիտական օրենքների շարքով։ Այդ տիեզերքներից շատերի պայմաններն այնպիսին չեն, որպեսզի բարդ օրգանիզմներ զարգանան, միայն մեր տիեզերքի նման մի քանի տիեզերքներում են զարգանում բանական էակներ և հարց տալիս, թե․ «Մենք ինչո՞ւ ենք տիեզերքն այսպես տեսնում»։ Պատասխանն այս դեպքում պարզ է, եթե տիեզերքն այլ լիներ, մենք այստեղ չէինք լինի։ | ||
| + | |||
| + | Գիտության օրենքները ներկայումս պարունակում են բազմաթիվ հիմնարար թվեր, ինչպես էլեկտրոնի էլեկտրական լիցքի մեծությունը և պրոտոնի ու էլեկտրոնի զանգվածների հարաբերությունը։ Հնարավոր չէ, գոնե այժմ, այս թվերի արժեքները տեսականորեն կանխագուշակել։ Դրանք որոշվում են փորձով։ Թերևս մի օր հնարավոր լինի կատարյալ միացյալ մի տեսություն մշակել և կանխագուշակել բոլոր թվերի արժեքները, բայց նաև հնարավոր է, որ այս թվերի մի մասը կամ բոլորի արժեքները տարբեր լինեն՝ տարբեր տիեզերքներում կամ մի տիեզերքի ներսում։ Ուշագրավ փաստ է, որ այս թվերի արժեքները կարծես նրբորեն այնպես են հարմարեցված, որ հնարավոր լինի կյանքի զարգացումը։ Օրինակ, եթե էլեկտրոնի էլեկտրական լիցքը փոքր֊ինչ տարբեր լիներ եղածից, աստղերը ջրածին և հելիում չէին կարող այրել և կամ չէին պայթի։ Իհարկե, հնարավոր են նաև բանական կյանքի այլ ձևեր ևս, որոնց մասին գիտական վեպերի հեղինակներն անգամ չեն երազել և, որոնց համար պարտադիր չեն արևի լույսը կամ այն ծանր տարրերը, որոնք առաջանում են աստղերում և, պայթման հետևանքով, տիեզերք շպրտվում։ Այնուամենայնիվ, պարզ է, որ թվերի արժեքների համեմատաբար սահմանափակ շարքեր կան, որոնք կապահովեն տարբեր ձևերի բնականոն կյանքի զարգացումը։ Արժեքների շարքերի մեծ մասը կարող է այնպիսի տիեզերքներ առաջացնել, որոնք թեև շատ գեղեցիկ կլինեն, բայց և զրկված՝ այդ գեղեցկությամբ հիացողներից։ Այս արդյունքը կարելի է համարել կամ Արարչագործության աստվածային նպատակի և գիտության օրենքների ընտրության վկայություն, կամ գնահատել, որպես ուժեղ մարդաբանական սկզբունքը հավաստող փաստարկ։ | ||
| + | |||
| + | Դիտարկվող տիեզերքի վիճակը բացատրելու կոչված ուժեղ մարդաբանական սկզբունքի դեմ կարելի է մի քանի առարկություններ անել։ Առաջինը․ ի՞նչ իմաստով է ասվում, թե այդ բոլոր տարբեր տիեզերքները կարող են գոյություն ունենալ։ Եթե դրանք իրոք անջատ են իրարից, ապա ինչ էլ որ պատահի այլ տիեզերքում, որևէ նկատելի հետևանք չի կարող ունենալ մեր տիեզերքում։ Հետևաբար, համաձայն խնայողության սկզբունքի, դրանք պետք է տեսությունից դուրս գցել։ Մյուս կողմից, եթե եզակի տիեզերքում առկա են տարբեր տիրույթներ, գիտության օրենքները պետք է նույնը լինեն յուրաքանչյուր տիրույթում, որովհետև հակառակ դեպքում հնարավոր չէր լինի շարունակաբար մի տիրույթից մյուսը տեղափոխվել։ Այս դեպքում տիրույթների միջև եղած միակ տարբերությունը կլինի նրանց սկզբնական կոնֆիգուրացիաները և, այսպիսով, ուժեղ մարդաբանական սկզբունքը կվերափոխվի թույլ մարդաբանական սկզբունքի։ | ||
| + | |||
| + | Ուժեղ մարդաբանական սկզբունքի դեմ երկրորդ առարկությունն այն է, որ դա դեմ է գնում ողջ գիտության պատմության հոսանքին։ Մենք զարգացել ենք Պտղոմեոսի և նրա նախորդների երկրակենտրոն տիեզերագիտությունից, անցել են Կոպեռնիկոսի և Գալիլոյի արևակենտրոն տիեզերագիտության միջով և հասել ենք ժամանակակից այն պատկերացմանը, ըստ որի երկիրը միջին չափի մի մոլորակ է, որը պտտվում է սովորական մի աստղի՝ արեգակի շուրջը, որն իր հերթին գտնվում է սովորական մի պարուրաձև գալակտիկայի ծայրամասում, իսկ այդ գալակտիկան տեսանելի տիեզերքի մոտավորապես միլիոն միլիոն գալակտիկաներից միայն մեկն է։ Ուժեղ մարդաբանական սկզբունքը պնդում է, թե այս լայնածավալ կառուցվածքը գոյություն ունի պարզապես մեզ համար։ Այսպիսի բաների դժվար է հավատալ։ Իհարկե, Արեգակնային համակարգը մեր գոյության նախապայմանն է, և կարելի է այս միտքը տարածել մեր գալակտիկայի վրա ամբողջությամբ, որպեսզի ընդգրկենք այն վաղեմի աստղերի սերունդը, որը ստեղծեծ ծանր տարրերը։ Սակայն մեր գոյության համար, թվում է, մյուս բոլոր գալակտիկաների, ինչպես նաև մեծ մասշտաբով վերցրած տիեզերքի՝ բոլոր ուղղություններով այսքան հավասարաչափ և միատեսակ լինելու կարիքը չկա։ | ||
| + | |||
| + | Մարդաբանական սկզբունքը, առնվազն իր թույլ տարբերակով, մեզ կարող էր բավարարել, եթե հնարավոր լիներ ցույց տալ, որ որոշ թվով տարբեր սկզբնական կոնֆիգուրացիաներ զարգացել են այնպես, որպեսզի առաջացնեն այնպիսի մի տիեզերք, ինչպիսին մենք տեսնում ենք։ Եթե այդպես է, ապա պատահական սկզբնական պայմաններից զարգացած տիեզերքը պիտի որ մի շարք տիրույթներ պարունակեր, որոնք հարթ ու համաչափ լինեին և բանական կյանքի էվոլյուցիայի համար՝ պիտանի։ | ||
| + | |||
| + | Մյուս կողմից, եթե տիեզերքի սկզբնական վիճակը ծայրաստիճան ուշադրությամբ ընտրվեր, որպեսզի ստացվեր այն, ինչ տեսնում ենք մեր շուրջը, հազիվ թե տիեզերքում գոյություն ունենար թեկուզ որևէ տիրույթ, որտեղ կյանք սկիզբ առներ։ Վերևում նկարագրված տաք Մեծ պայթյունի մոդելում բավարար ժամանակ չկար, որպեսզի վաղ տիեզերքում ջերմությունը մի տիրույթից մյուսը հոսեր։ Սա նշանակում է, որ տիեզերքի ջերմաստիճանը սկզբնական շրջանում ամենուրեք ճիշտ նույնը պետք է եղած լիներ, քանի որ միկրոալիքային ճառագայթման ֆոնի ջերմաստիճանը բոլոր ուղղություններով նույնն է այսօր։ Սկզբնական ընդարձակման արագությունը ևս պետք է շատ ճշգրիտ ընտրված լինի, որպեսզի ընդարձակման արագությունը դեռ մոտ լինի այն կրիտիկական արագությանը, որն անհրաժեշտ է վերստին կոլապսի ենթարկվելուց խուսափելու համար։ Այս ամենը նշանակում է, որ, իրոք, տիեզերքի սկզբնական վիճակը խնամքով է ընտրվել, եթե տաք Մեծ պայթյունի մոդելը ճիշտ է՝ ընդհուպ մինչև ժամանակի սկզբնավորությունը։ Շատ դժվար կլիներ բացատրել, թե տիեզերքն ինչո՞ւ պիտի այդպիսի սկզբնավորություն ունենար, բացի այն բացատրությունից, որ մեզ նման էակներ ստեղծելու մտադրություն ունեցող Աստծու գործն է եղել դա։ | ||
| + | |||
| + | Մասաչուսեթսի Տեխնոլոգիական ինստիտուտի գիտնական Ալան Գութը փորձեց տիեզերքի այնպիսի մի մոդել կառուցել, որում կարող էին զարգանալ բազմաթիվ տարբեր սկզբնական կոնֆիգուրաիցաներ և հասնել ժամանակակից տիեզերքին և առաջարկեց, որ սկզբնական տիեզերքը պետք է ունեցած լինի շատ արագ ընդարձակման մի փուլ։ Ըստ նրա, այդ ընդարձակումը տեղի է ունեցել «հարաճուն ընթացքով», այսինքն՝ որոշ ժամանակ տիեզերքն ընդարձակվել է աճող, քան նվազող արագությամբ, ինչպես տեղի է ունենում այժմ։ Համաձայն Գութի տիեզերքի շառավիղը միլիոն միլիոն միլիոն միլիոն միլիոն անգամ (1֊ից հետո 30 զերո) աճել է լոկ վայրկյանի մի փոքր մասի ընթացքում։ | ||
| + | |||
| + | Համաձայն Գութի, տիեզերքը սկիզբ է առել Մեծ պայթյունով, շատ տաք և բավականին քաոսային վիճակում։ Այդ բարձր ջերմաստիճանը նշանակում է, որ տիեզերքում մասնիկները պետք է շարժվեն մեծ արագությամբ և բարձր էներգիա ունենան։ Ինչպես մենք արդեն քննարկել ենք, սպասելի է, որ այդպիսի բարձր ջերմաստիճաններում ուժեղ և թույլ միջուկային ուժերն ու էլեկտրամագնիսական ուժը միավորվեն մի ընդհանուր ուժի մեջ։ Տիեզերքն ընդարձակմանը զուգընթաց սկսում է սառչել, և մասնիկների էներգիան նվազում է։ Վերջ ի վերջո տեղի է ունենում այն, ինչը կոչվում է ֆազային անցում, և խախտվում է ուժերի միջև առկա համաչափությունը, այսինքն՝ ուժեղ ուժը տարբերվում է թույլ և էլեկտրոմագնիսական ուժերից։ Ֆազային անցման լավագույն օրինակն է ջրի սառչելը։ Հեղուկ ջուրը համասեռ է, այսինքն՝ այն ամեն կետում և բոլոր ուղղություններով նույնական է։ Սակայն երբ առաջանում են սառույցի բյուրեղներ, դրանք որոշակի դիրքեր են գրավում և որոշակի ուղղությամբ շարք կազմում։ Այսպիսով, ջրի համասեռությունը խախտվում է։ | ||
| + | |||
| + | Ջրի դեպքում, եթե սառեցումը կատարվի զգուշությամբ, հնարավոր է «գերսառեցնել» այն, այսինքն՝ ջերմաստիճանը սառեցման կետից (0°C) ցածր իջեցնել, առանց սառույցի առաջացման։ Գութը ենթադրեց, որ տիեզերքը նույնպես կարող է նման հատկություն ունենալ․ ջերմաստիճանը կարող էր իջնել կրիտիկական արժեքից ցածր, առանց խախտելու ուժերի միջև առկա համաչափությունը։ Այս դեպքում տիեզերքը պետք է անկայուն վիճակում գտնվի՝ օժտված ավելի շատ էներգիայով, քան կունենար, եթե համաչափությունը խախտված լիներ։ Կարելի է ցույց տալ, որ այս հավելյալ էներգիան, հակագրավիտացիոն ազդեցություն կունենա․ կներգործի ճիշտ այնպես, ինչպես այն տիեզերաբանական հաստատունը, որն ընդհանուր հարաբերականության տեսությունն ներմուծեց Էյնշտեյնը, երբ փորձում էր տիեզերքի համար ստատիկ մի մոդել կառուցել։ Քանի որ տիեզերքը պետք է ընդարձակվի, ինչպես տաք Մեծ պայթյունի մոդելում, հետևաբար տիեզերաբանական հաստատունի վանողական գործոնը պատճառ կլինի, որ տիեզերքն ընդարձակվի հարաճուն արագությամբ։ Նույնիսկ այն տիրույթներում, որտեղ միջինից ավելի շատ նյութական մասնիկներ կան, տիեզերաբանական հաստատունի վանողական ներգործությունը կգերակշռի գրավիտացիոն ձգողությանը։ Հետևաբար այս տիրույթները նույնպես կընդարձակվեն հարաճուն արագությամբ։ Եթե ընդարձակումը շարունակվի, և նյութական մասնիկներն իրարից ավելի հեռանան, կառաջանա ընդարձակվող մի տիեզերք, որը հազիվ թե մասնիկներ պարունակի և դեռևս գտնվի գերսառեցրած վիճակում։ Տիեզերքում առկա անկանոնությունները ընդարձակման հետևանքով պարզապես պետք է հարթվեին ճիշտ այնպես, ինչպես փուչիկի ծալքերն են հարթվում՝ փչելիս։ Հետևաբար, տիեզերքի այժմյան հարթ և համաչափ վիճակը կարող է առաջացած լինել բազմաթիվ տարբեր, ոչ նույնանման սկզբնական վիճակներից։ | ||
| + | |||
| + | Նախնական տիեզերքում, որտեղ ընդարձակումը ոչ թե դանդաղում է նյութի գրավիտացիոն ձգողության ազդեցությամբ, այլ արագանում՝ շնորհիվ տիեզերաբանական հաստատունի, երկար ժամանակ չի պահանջվի, որպեսզի լույսը մի տիրույթից մյուսը տեղաշարժվի։ Այսպիսով, հնարավոր է լուծել ժամանակին արծածված այն հարցը, թե ինչո՞ւ են վաղ տիեզերքում երկու տարբեր տիրույթներ նույն հատկություններն ունեցել։ Դեռ ավելին, տիեզերքի ընդարձակման արագությունը պետք է ինքնաբերաբար մոտենա այն կրիտիկական արագությանը, որը որոշվում է տիեզերքի էներգիայի խտությամբ։ Դրանով է բացատրվում, թե ինչո՞ւ է ընդարձակման արագությունն այդքան մոտ կրիտիկական արագությանը, առանց ենթադրելու, որ տիեզերքի ընդարձակման արագությունն ընտրվել էր մեծ խնամքով։ | ||
| + | |||
| + | Հարաճուն արագացման պատկերացումը կարող է բացատրել նաև, թե ինչու այսքան շատ նյութ կա տիեզերքում։ Մեզ տեսանելի տիեզերքի տիրույթում կա տասը միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն մասնիկ (1֊ից հետո 85 զերո)։ Որտեղի՞ց են հայտնվել այդ մասնիկները։ Ըստ քվանտային տեսության, մասնիկներ կարելի է ստեղծել էներգիայից՝ որպես մասնիկ֊հակամասնիկ զույգեր։ Սակայն այստեղից ծագում է հաջորդ հարցը, որտեղի՞ց է գալիս այդ էներգիան։ Պատասխանն այն է, որ տիեզերքի էներգիան, ամբողջությամբ վերցրած, հավասար է զերոյի։ Տիեզերքում առկա նյութն առաջացել է դրական էներգիայից։ Սակայն, նյութը ենթակա է գրավիտացիոն ձգողության ազդեցությանը։ Իրար մոտիկ գտնվող երկու նյութական առարկաներ ավելի քիչ էներգիա ունեն, քան երբ նրանք իրարից հեռու են, որովհետև իրարից հեռացնելու համար պետք է էներգիա ծախսել, որպեսզի հաղթահարվի այդ առարկաներն իրար ձգող գրավիտացիոն ուժը։ Այսպիսով, որոշ իմաստով գրավիտացիոն դաշտի էներգիան բացասական է։ Տարածության մեջ մոտավորապես միակերպ տիեզերքի պարագայում կարելի է ցույց տալ, որ բացասական գրավիտացիոն էներգիան ճշգրտորեն հավասարակշռում է նյութի դրական էներգիան։ Այսպիսով, տիեզերքի լրիվ էներգիան հավասար է զերոյի։ Քանի որ երկու անգամ զերոն նույնպես զերո է, հետևաբար, եթե տիեզերքում կրկնապատկվեն ինչպես նյութի դրական էներգիան, այնպես էլ բացասական գրավիտացիոն էներգիան, ապա էներգիայի պահպանման օրենքը չի խախտվի։ Բնականոն ընդարձակման պայմաններում այդպիսի բան չի կարող պատահել, որովհետև նյութի էներգիայի խտությունը նվազում է, երբ տիեզերքը մեծանում է։ Սակայն սա հնարավոր է հարաճուն ընդարձակման դեպքում, որովհետև գերսառեցած վիճակում էներգիայի խտությունը մնում է հաստատուն, երբ տիեզերքն ընդարձակվում է։ Եթե տիեզերքը երկու անգամ մեծանա, ապա երկուսն էլ՝ դրական նյութական էներգիան և բացասական գրավիտացիոն էներգիան, կկրկնապատկվեն, և այսպիսով լրիվ էներգիան նորից հավասար կլինի զերոյի։ Հարաճուն ընդարձակման տիեզերքը չափազանց մեծանում է։ Այսպիսով, մասնիկների առաջացման համար հարկավոր ընդհանուր էներգիայի քանակը աճում է ինչպես Գութը նկատել է․ «Թեև ասում են, թե ձրի ճաշկերույթ չի լինում, բայց տիեզերքն ի վերջո ձրի ճաշկերույթ է»։<ref>Հարաճուն ընդլայման և գերսառեցման արդյունքում նաև պղպջակների առաջացման հարցերը բազմատեսակ են։ Այնուամենայնիվ, համաձայն պղպջակների տեսության կողմնակիցներից մեկի՝ Ռիչարդ Գոթի, ճառագայթումը թափանցելով պղպջակ, փոխակերպվում է նյութի, այսինքն զանգվածից զրկված քվարկները զանգված են ձեռք բերում։ Համաձայն Հոքինգի, «այս տեսությունները ավելի շատ հարցեր են արծարծում, քան լուծում (տես «Stephen Howkigs Unlvers» by Tohn Basbough, Avou Books, N4, էջ 101): Ինչպես երևում է, Ալան Գութը «ձրի ճաշկերույթ» ասելով, ակնարկում է ճառագայթման՝ նյութ առաջացնող աղբյուր լինելու գաղափարը։</ref> | ||
| + | |||
| + | Այսօր տիեզերքը հարաճուն ընդարձակման ենթակա չէ։ Հետևաբար, տիեզերաբանական հաստատունի ազդեցությունից ձերբազատվելու համար անհրաժեշտ է այնպիսի մի մեխանիզմ, որով ընդարձակումը տեղի ունենա ոչ թե արագացումով, այլ ինչպես այսօր է դիտվում, դանդաղի գրավիտացիոն ազդեցության տակ։ Սպասելի է, որ հարաճուն ընդարձակման դեպքում ուժերի միջև գոյություն ունեցող համաչափությունն ի վերջո կխախտվի ճիշտ այնպես, ինչպես գերսառած ջուրը վերջում միշտ բյուրեղանում է։ Անջատվում է համասեռ վիճակի հավելյալ էներգիան և տաքացնում տիեզերքը մինչև այն կրիտիկական ջերմաստիճանը, որը հատուկ է ուժերի միջև եղած համաչափությանը։ Տիեզերքը կշարունակի ընդարձակվել և աստիճանաբար սառել ճիշտ այնպես, ինչպես դա լինում է տաք Մեծ պայթյունի մոդելում։ Բայց մենք այժմ կարող ենք բացատրել, թե ինչո՞ւ է տիեզերքը ընդարձակվում ճիշտ կրիտիկական արագությամբ և ինչո՞ւ են տարբեր տիրույթների ջերմաստիճանները նույնը։ | ||
| + | |||
| + | Գութի սկզբնական առաջարկությունը ենթադրում էր, որ ֆազային անցումը տեղի է ունենում միանգամից, ինչպես շատ սառը ջրում սառույցի բյուրեղների առաջացումը։ Նկատի էր առնվում այն, որ խախտված համասեռությամբ այս նոր ֆազի «պղպջակները» պետք է առաջացած լինեն հին ֆազում, ինչպես լինում են եռացող ջրով շրջապատված պղպջակները։ Ենթադրվում էր, որ պղպջակները մեծանում և իրար են հանդիպում, երբ ողջ տիեզերքն անցում է կատարում նոր ֆազային վիճակի։ Դժբախտաբար, ինչպես ես, այնպես էլ շատերը, նշել ենք, որ տիեզերքն այնպիսի մեծ արագությամբ էր ընդարձակվում, որ եթե նույնիսկ պղպջակները մեծանային լույսի արագությամբ, ապա նրանք իրարից կհեռանային և, հետևաբար, չէին կարող իրար միանալ։ Տիեզերքը կունենար ոչ միաձև վիճակ, և որոշ տիրույթներում կպահպանվեր համաչափությունը տարբեր ուժերի միջև։ Այս մոդելը չէր կարող բնավ համապատասխանել մեր տեսածին։ | ||
| + | |||
| + | 1981֊ի հոկտեմբերին ես մեկնեցի Մոսկվա՝ մասնակցելու քվանտային գրավիտացիային նվիրված գիտաժողովին։ Գիտաժողովից հետո Ստեռնբերգի աստղագիտական ինստիտուտում զեկուցում կարդացի հարաճուն ընդարձակման մոդելի և դրան առնչվող հարցերին նվիրված սեմինարում։ Դրանից առաջ ես մեկ ուրիշի էի հանձնարարել կարդալ դասախոսություններս, որովհետև ունկնդիրներին իմ խոսքը հասկանալի չէր։ Բայց քանի որ սեմինարի նախապատրաստման համար ժամանակ չկար, ես ինքս խոսեցի, իսկ իմ ասպիրանտներից մեկը վերարտադրեց իմ ասածը։ Սեմինարը հաջող անցավ, և ես ուղղակի հաղորդակցության մեջ մտա իմ ունկնդիրների հետ։ Ներկաների մեջ էր Մոսկվայի Լեբեդևի անվան ինստիտուտի երիտասարդ ռուս գիտնական Անդրեյ Լինդեն։ Նա ասաց, թե պղպջակների միացման դժվարությունից կարելի է խուսափել, եթե պղպջակներն այնքան մեծ լինեն, որ տիեզերքի մեր տիրույթը պարփակվի մեկ ընդհանուր պղպջակի մեջ։ Որպեսզի այդպիսի բան տեղի ունենա, անհրաժեշտ է, որ պղպջակի մեջ համասեռ վիճակից անցումը խախտված համասեռությամբ վիճակի շատ դանդաղ տեղի ունեցած լինի, ինչը միանգամայն հնարավոր է՝ համաձայն մեծ միասնական տեսությունների։ Լինդեի գաղափարը համասեռության դանդաղ խախտման մասին լավն էր, բայց ես հետագայում հասկացա, որ նրա պղպջակները շատ ավելի մեծ պետք է եղած լինեին, քան այդ ժամանակվա տիեզերքը։ Ես ցույց տվեցի, որ փոխարենը՝ համասեռությունը պետք է միաժամանակ ամենուր խախտվեր, այլ ոչ թե միայն պղպջակների ներսում։ Դա կբերեր միակերտ տիեզերքի առաջացմանը, ինչը մենք այսօր տեսնում ենք։ Այս գաղափարն ինձ շատ ոգևորեց և ես այն քննարկեցի իմ ուսանողներից Իան Մոսի հետ։ Հետագայում, որպես Լինդեի բարեկամ, շատ անհարմար զգացի, երբ գիտական մի պարբերականից ինձ ուղարկեցին Լինդեի հոդվածն այս հարցի կապակցությամբ և ուզեցին իմ կարծիքը իմանալ դրա հրատարակության նպատակահարմարության մասին։ Ես պատասխանեցի, որ պղպջակների՝ տիեզերքից մեծ լինելու հարցը թերի է, սակայն այն հիմնական գաղափարը, թե համասեռությունն աստիճանաբար է խախտվում, շատ լավ է։ Ես երաշխավորեցի հոդվածը հրատարակել այնպես, ինչպես կա, որովհետև Լինդեի համար այն վերափոխելու գործն ամիսներ կպահանջեր զուտ այն պատճառով, որ Արևմուտք առաքվող ամեն հոդված ենթարկվում էր խորհրդային գրաքննության, որ գիտական հոդվածների հարցում հուսալիություն և արագություն չի ապահովում։ Փոխարենը Իան Մոսի հետ նույն պարբերականում մի կարճ աշխատություն տպեցինք, թե այն ինչպես կարելի է լուծել։ | ||
| + | |||
| + | Մոսկվայից վերադառնալուց հետո պետք է մեկնեի Ֆիլադելֆիա՝ Ֆրանկլինի ինստիտուտի պարգևատրած մեդալը ստանալու համար։ Քարտուղարուհիս՝ Ջուդի Ֆելան, իր արտակարգ հմայքն օգտագործելով, համոզել էր Բրիտանական ավիաուղիներ գործակալությանը (Բրիտիշ Էյրվեյզ), որպեսզի գովազդի դիմաց ինձ և իրեն Կոնկորդով ձրի փոխադրեն։ Դժբախտաբար, օդակայանի ճանապարհին ընկա հորդառատ անձրևի տակ և թռիչքից ուշացա։ Այնուամենայնիվ, մի կերպ հասա Ֆիլադելֆիա և ստացա մեդալը։ Ֆիլադելֆիայի Դրեքսել համալսարանի հրավերով հարաճուն ընդլայնվող տիեզերքի հարցին նվիրված սեմինար վարեցի և կրկնեցի Մոսկվայում իմ կարդացած զեկուցաշարը։ | ||
| + | |||
| + | Լինդեից անկախ՝ մի քանի ամիս անց նման գաղափար առաջ քաշեցին Փենսիլվանիայի համալսարանից Պոլ Ստեյնհարդը և Անդրեաս Ալբրեխտը։ Այժմ Լինդեին և նրանց է վերագրվում այսպես ասած, «հարաճուն ընդլայման նոր մոդելը», որը հիմնված է համասեռության խախտման գաղափարի վրա։ (Ալան Գութի՝ պղպջակների առաջացմամբ համասեռության արագ խախտման առաջարկությունը հարաճուն ընդլայման մոդելն էր)։ | ||
| + | |||
| + | Հարաճուն ընդլայման նոր մոդելը տիեզերքի որպիսությունը բացատրող, հաջող փորձ էր։ Սակայն ես և շատ ուրիշներ ցույց տվեցինք, որ առնվազն իր սկզբնական ձևով այդ մոդելը միկրոալիքային ճառագայթման ֆոնի համար կանխագուշակում էր ջերմաստիճանի շատ ավելի մեծ տատանումներ, քան դիտարկվել են։ Հետագա աշխատանքները կասկածելի դարձրին այն գաղափարը, թե այսպիսի ֆազային անցում երբևէ եղե՞լ է արդյոք շատ վաղ տիեզերքում։ Իմ անձնական կարծիքով, հարաճուն ընդլայման նոր մոդելը այժմ մեռած գիտական տեսություն է, թեև շատերը, թվում է, դեռ նրա վախճանի մասին չեն լսել և հոդվածներ են գրում, կարծես այն կենսունակ է։ 1983֊ին Լինդեն ավելի լավ մի մոդել առաջարկեց, որը կոչվում է քաոսային հարաճուն ընդլայման տեսություն։ Այստեղ ֆազային անցում և գերսառեցում չկան։ Փոխարենը առկա է 0 սպին ունեցող դաշտ, որը քվանտային տատանումների հետևանքով կարող է վաղ տիեզերքի որոշ տիրույթներում բարձր արժեքներ ունենալ։ Այս տիրույթներում դաշտի էներգիան գործում է տիեզերաբանական հաստատունի նման։ Տեղի է ունենում վանողական գրավիտացիոն ներգործություն, և այսպիսով՝ այս տիրույթները տարածվում են հարաճուն ընդլայման եղանակով։ Ընդարձակմանը զուգընթաց նրանցում դաշտի էներգիան աստիճանաբար նվազում է, և հարաճուն ընդարձակումը վերափոխվում է տաք Մեծ պայթյունի մոդելում առկա ընդարձակման, որը տեղի է ունենում։ Այդ տիրույթներից մեկն էլ դառնում է այն, ինչը մենք այսօր տեսնում ենք որպես տեսանելի տիեզերք։ Այս մոդելը օժտված է հարաճուն ընդլայման սկզբնական մոդելների բոլոր առավելություններով, հիմնված չէ կասկածելի ֆազային անցման վրա և ավելին, այն կարող է տալ միկրոալիքային ֆոնի ջերմաստիճանի տատանումների ընդունելի չափը, ինչը համընկնում է փորձնական տվյալների հետ։ | ||
| + | |||
| + | Հարաճուն ընդլայման մոդելների վրա կատարված ուսումնասիրությունները ցույց են տալիս, որ տիեզերքի այժմյան վիճակը կարող էր առաջանալ մեծ թվով սկզբնական կոնֆիգուրացիաներից։ Սա կարևոր է, որովհետև ցույց է տալիս, որ մեծ բծախնդրությամբ չէր կարող ընտրված լինել տիեզերքի այն մասը, որը մենք զբաղեցնում ենք այսօր։ Այսպիսով, ցանկության դեպքում, կարող ենք օգտագործել մարդաբանական սկզբունքը՝ բացատրելու, թե ինչո՞ւ է տիեզերքն այնպիսին, ինչպիսին երևում է այսօր։ Այնուամենայնիվ, սա չի նշանակում, թե ամեն սկզբնական կոնֆիգուրացիա կարող է վերաճել այնպիսի մի տիեզերքի, որն այսօր, մենք տեսնում ենք։ Այս բանը կարելի է ապացուցել այժմյան տիեզերքի համար բոլորովին տարբեր, ասենք, շատ ուռուցիկ և անկանոն մի վիճակ ընդունելով։ Գիտության օրենքների միջոցով կարելի է բացահայտել տիեզերքի զարգացման հետընթաց կարգը և որոշել, թե սկզբնական վիճակում ինչպիսի կոնֆիգուրացիա է ունեցել տիեզերքը։ Ընդհանուր հարաբերականության դասական տեսության եզակիության թեորեմներից դարձյալ Մեծ պայթյունի եզակիությունն է հետևում։ Այժմ, եթե այդ Մեծ պայթյունից հետո գիտության օրենքները կիրառելով շարժվենք տիեզերքի զարգացմանը զուգընթաց, կհասնենք ուռուցիկ և անկանոն այն վիճակին, որից սկսել էինք։ Հետևաբար, հնարավոր է, որ այնպիսի սկզբնական կոնֆիգուրացիաներ եղած լինեին, որոնք չհանգեցնեին այսօր մեր դիտարկած տիեզերքի վիճակին։ Այսպիսով, նույն մոդելը չի կարող ասել, թե տիեզերքի սկզբնական կոնֆիգուրացիան ինչո՞ւ այնպիսին չէ, որպեսզի այսօր մեր դիտարկածից շատ տարբեր մի բան առաջացներ։ Դա բացատրելու համար արդյո՞ք հարկ կա վերադառնալ մարդբանական սկզբունքին։ Արյդո՞ք այդ ամենը մի երջանիկ զուգադիպության արդյունք չէ։ Այսպիսի մոտեցումը հուսահատական մխիթարանք է, ըստ որի մենք ժխտած կլինեինք տիեզերքի ներքին կարգուկանոնը հասկանալու մեր բոլոր հույսերը։ | ||
| + | |||
| + | Որպեսզի մենք կարողանանք գուշակել, թե տիեզերքն ինչից է սկզբնավորվել, մեզ հարկավոր են այնպիսի օրենքներ, որոնք գործեն ժամանակի սկզբնավորման պահին։ Եթե ընդհանուր հարաբերականության դասական տեսությունը ճիշտ է, ապա ինչպես ցույց են ք տվել Ռոջեր Պենրոուզն ու ես, եզակիության թեորեմներից բխում է, որ ժամանակի սկիզբը պետք է անսահման խտություն ունեցած մի կետ եղած լինի և անսահման կորություն ունենա տարածություն֊ժամանակի մեջ։ Գիտության բոլոր հայտնի օրենքներն այդպիսի կետում ուժը կկորցնեն։ Կարելի է ենթադրել, որ կարող են այնպիսի օրենքներ լինել, որոնք գործեն եզակիության մեջ։ Բայց շատ դժվար է այդպիսի անկանոն հատկություններով օժտված կետերում գործող օրենքներ նույնիսկ ձևակերպել, և մենք լրիվ զրկված ենք դիտարկելու հնարավորությունից և չենք կարող ասել, թե այդ օրենքներն ի՞նչ տեսակ են։ Այնուամենայնիվ այն, ինչ իրապես ցույց են տալիս եզակիության թեորեմները, այն է, որ գրավիտացիոն դաշտն այդ կետում այնքան ուժեղ է լինում, որ քվանտային գրավիտացիոն ներգործությունը դառնում է շատ կարևոր․ դասական տեսությունն այլևս ի վիճակի չէ նկարագրել տիեզերքը։ Այսպիսով տիեզերքի շատ վաղ վիճակը քննարկելու համար պետք է օգտագործել գրավիտացիոն քվանտային տեսությունը։ Ինչպես կտեսնենք, հնարավոր է, որ քվանտային տեսության մեջ սովորական գիտության օրենքներն ի զորու լինեն ամենուրեք, ներառյալ ժամանակի սկզբնավորումը, հարկ չկա եզակիության նոր օրենքներ սահմանել, որովհետև քվանտային տեսության մեջ եզակիությունների անհրաժեշտություն չկա։ | ||
| + | |||
| + | Մենք դեռևս չունենք ամբողջական և հետևողական մի տեսություն, որը միավորեր քվանտային մեխանիկան և գրավիտացիան։ Այնուամենայնիվ, թե ինչպիսի որոշ առանձնահատկություններ պետք է ունենա այդ միասնական տեսությունը, մենք միանգամայն պատկերացնում ենք։ Դրանից մեկն այն է, որ այդ միասնական տեսությունն իր մեջ պիտի ներառի Ֆեյնմանի առաջարկությունը՝ քվանտային տեսությունը պատմությունների գումարի հիման վրա ձևակերպելու վերաբերյալ։ Այս մոտեցման համաձայն, մասնիկը գեթ մի եզակի պատմություն չունի, ինչպես դասական տեսություններում է լինում։ Դրա փոխարեն ենթադրվում է, որ տարածություն֊ժամանակի մեջ մասնիկը շարժվում է բոլոր հնարավոր ուղիներով, և այդ պատմություններից յուրաքանչյուրը բնութագրվում է երկու թվով, որոնցից մեկը վերաբերում է ալիքի չափին, իսկ մյուսը տալիս է նրա դիրքը պարբերաշրջանում (ցիկլում)՝ ֆազը։ Տվյալ որոշակի կետերով, ասենք մասնիկի անցման հավանականությունը գտնելու համար անհրաժեշտ է գումարել այդ կետով անցնող բոլոր հնարավոր պատմությունները բնութագրող ալիքները։ Սակայն այդ գումարելու գործողությունը կապված է մի շարք տեխնիկական պրոբլեմների հաղթահարման հետ։ Դրանք շրջանցելու համար առաջարկվում է հետևյալ տարօրինակ միջոցը․ պետք է գումարել մասնիկների պատմությունների այն ալիքները, որոնք գտնվում են ոչ թե մեզ հայտնի «իրական» ժամանակում, այլ, այսպես կոչված, «կեղծ» ժամանակում։ Կեղծ ժամանակը կարող է ոմանց վեպի նյութ թվալ, բայց իրականում այն որոշակիորեն սահմանված մաթեմատիկական հասկացություն է։ Եթե մենք վերցնենք մի սովորական թիվ («իրական» թիվ), բազմապատկենք նույն թվով, կստացվի դրական մի թիվ (այսպես օրինակ, 2 անգամ 2 հավասար է 4֊ի, նմանապես -2 անգամ -2 նորից հավասար է 4֊ի)։ Բայց ահա կան հատուկ թվեր (դրանք կոչվում են կեղծ), որոնք իրար բազմապատկելիս բացասական թվեր են տալիս։ (Այսպիսի մի թիվ է i֊ն, որն ինքն իր հետ բազմապատկելիս տալիս է -1, 2i֊ն ինքն իր հետ բազմապատկելիս տալիս է -4 և այլն)։ Այսպիսով, Ֆեյնմանի մեթոդով պատմությունների գումարը հաշվարկելիս տեխնիկական դժվարություններից խուսափելու համար հարկավոր է օգտվել կեղծ ժամանակից։ Այսինքն՝ հաշվումներ կատարելու համար ժամանակը պետք է չափել ոչ թե իրական թվերով, այլ կեղծ թվերով։ Սա հետաքրքրական փոփոխություն է մտցնում տարածություն֊ժամանակի հասկացության մեջ․ ժամանակի և տարածության միջև եղած տարբերությունը լրիվ անհետանում է։ Այն տարածություն֊ժամանակը, որում պատահույթներն ունեն ժամանակի կոորդինատի կեղծ արժեքներ, կոչվում է էվկլիդեսյան, հին հույն փիլիսոփա Էվկլիդեսի անվամբ, որը հիմնադրել է երկչափ մակերեսների երկրաչափությունը։ Այն, ինչ այսօր մենք անվանում ենք Էվկլիդեսյան տարածություն֊ժամանակ քառաչափ է, ոչ թե երկչափ։ Էվկլիդեսյան տարածություն֊ժամանակում ժամանակի ուղղության և տարածության մեջ ուղղությունների միջև տարբերություն չկա։ Մյուս կողմից, իրական տարածություն֊ժամանակի մեջ, որտեղ պատահույթները չափվում են սովորական ժամանակի կոորդինատի իրական արժեքներով, տարբերությունը ակնհայտ է՝ բոլոր կետերի ժամանակի ուղղությունը գտնվում է լուսակոնի սահմաններից ներս, իսկ տարածության ուղղությունները գտնվում են դրսում։ Այնուամենայնիվ, սովորական քվանտային մեխանիկա ներմուծված մեր օգտագործած կեղծ ժամանակը և էվկլիդեսյան տարածություն֊ժամանակը լոկ մաթեմատիկական հնարքներ են, որոնցով հեշտությամբ կարող ենք հաշվել իրական տարածություն֊ժամանակին վերաբերող պատասխանները։ | ||
| + | |||
| + | Երկրորդ առանձնահատկությունը, որը, մենք վստահ ենք պետք է վերջնական տեսության մաս կազմի, Էյնշտեյնի այն գաղափարն է, որ գրավիտացիոն դաշտը ներկայացված է կորաձև տարածություն֊ժամանակով։ Մասնիկները կորաձև տարածության մեջ ձգտում են շարժվել ուղղագիծ ճանապարհին ամենամոտ ուղղությամբ, բայց, որովհետև տարածություն֊ժամանակը հարթ չէ, նրանց ճանապարհները կոր են երևում, կարծես թե գտնվում են գրավիտացիոն դաշտում։ Երբ մենք Ֆեյնմանի պատմությունների մեթոդով հաշվարկված գումարը միավորենք Էյնշտեյնի գրավիտացիայի մասին գաղափարի հետ, մասնիկի պատմության նմանակն այժմ կլինի կատարյալ մի կորաձև տարածություն֊ժամանակ, որը ներկայացնում է ողջ տիեզերքի պատմությունը։ Պատմությունների գումարը հաշվարկելիս տեխնիկական դժվարություններից խուսափելու համար այն կորացած տարածություն֊ժամանակները պետք է համարել Էվկլիդեսյան։ Այսինքն՝ ժամանակը կեղծ է, և նրա ուղղությունը չի տարբերվում տարածության ուղղությունից։ Որոշակի հատկությամբ օժտված իրական տարածություն֊ժամանակի հավանականությունը հաշվելու համար, ասենք, օրինակի համար, ամեն կետում և ամեն ուղղությամբ նույնանման երևալու հավանականությունը, գումարվում են բոլոր այն ալիքները, որոնք հատկանշական են նույն հատկություններն ունեցող պատմություններին։ | ||
| + | |||
| + | Ընդհանուր հարաբերականության դասական տեսության մեջ կան բազմաթիվ տարբեր հնարավոր կորացած տարածություն֊ժամանակներ, որոնցից յուրաքանչյուրը համապատասխանում է տիեզերքի տարբեր սկզբնական վիճակի։ Եթե իմանայինք մեր տիեզերքի սկզբնական վիճակը, կիմանայինք նաև նրա լրիվ պատմությունը։ Նմանապես, գրավիտացիայի քվանտային տեսության մեջ հնարավոր են տիեզերքի բազմաթիվ տարբեր քվանտային վիճակներ։ Դարձյալ, եթե իմանայինք, թե պատմությունների գումարում էվկլիդեսյան կորացած տարածություն֊ժամանակն ինչ դրսևորումներ է ունեցել վաղ ժամանակներում, ապա մենք կիմանայինք տիեզերքի քվանտային վիճակը։ | ||
| + | |||
| + | Դասական գրավիտացիոն տեսության մեջ, որը հիմնված է իրական տարածություն֊ժամանակի վրա, կա տիեզերքի գոյության լոկ երկու հնարավոր եղանակ․ կամ այն գոյություն է ունեցել ի սկզբանե՝ անսահման ժամանակ ի վեր և կամ անցյալում սկզբնավորվել է վերջավոր ժամանակում եզակիության մեջ։ Քվանտային գրավիտացիոն տեսության մեջ, մյուս կողմից, առաջանում է մի երրորդ հավանականություն։ Քանի որ օգտագործվում է էվկլիդեսյան տարածություն֊ժամանակը, որում ժամանակի ուղղությունը նույնական է տարածության մեջ ուղղությունների հետ, հնարավոր է, որ տարածություն֊ժամանակը չափերով վերջավոր լինի, սակայն եզակիություններ և սահման ու եզր նույնպես չունենա։ Տարածություն֊ժամանակը կնմանվի երկրի մակերեսին, կունենա միայն երկու չափում։ Երկրի մակերեսը վերջավոր է իր չափերով, սակայն սահման կամ եզր չունի այն իմաստով, որ եթե նրանով դեպի արևմուտք ճամփորդես՝ եզրի չես հասնի և նրանից դուրս կամ եզակիության մեջ չես ընկնի։ (Այս բանը ես իմ անձնական փորձով գիտեմ, քանի որ ամբողջ աշխարհի շուրջը ճամփորդել եմ)։ | ||
| + | |||
| + | Եթե էվկլիդեսյան տարածություն֊ժամանակը հետադարձ երկարաձգվի մինչև անսահման կեղծ ժամանակը կամ, այլ կերպ ասած, սկիզբ առնի կեղծ ժամանակի եզակիությունից, հարցը ոչնչով չի տարբերվի դասական տեսությունից, որի նպատակը եղել է տիեզերքի սկզբնական վիճակի բնորոշումը։ Աստված գիտի, թե տիեզերքն ինչպես է սկիզբ առել, բայց մենք չենք կարող ասել, թե այն այսպես, կամ այնպես է տեղի ունեցել։ Մյուս կողմից, գրավիտացիոն քվանտային տեսությունը նոր հնարավորություն է տալիս, ըստ որի տարածություն֊ժամանակը ոչ մի սահման չի կարող ունենալ, և, հետևաբար, կարիք չկա, որ սահմանամերձ տիեզերքի վարքը բնորոշվի։ Ոչ մի եզակիություն չի կարող լինել, որպեսզի գիտության օրենքներն այնտեղ չգործեն, տարածություն֊ժամանակի ոչ մի եզր՝ որտեղ մարդ ապավինի Աստծուն կամ դիմի ինչ֊որ նոր օրենքի օգնությանը, որպեսզի որոշի տարածություն֊ժամանակի սահմանային պայմանները։ Կարելի է ասել․ «Տիեզերքի սահմանային պայմանն անսահմանությունն է»։ Տիեզերքը պետք է ինքնապարփակ լինի, և նրանից դուրս գտնվող ոչինչ չի կարող ազդել նրա վրա։ Տիեզերքը չի կարելի ո՛չ ստեղծել, ո՛չ էլ կործանել։ Այն պարզապես պետք է լինի։ | ||
| + | |||
| + | Վատիկանի՝ վերևում նշածս խորհրդակցության ժամանակ էր, երբ ես առաջին անգամ առաջարկեցի, որ թերևս ժամանակն ու տարածությունը միասին կազմում են վերջավոր մի մակերես, որը, սակայն, չունի ոչ մի սահման և եզր։ Իմ զեկուցումը, սակայն, բավական մաթեմատիկական բնույթի էր և, հետևաբար, շրջանցում էր տիեզերքի ստեղծման մեջ Աստծո դերի վերաբերյալ արված ենթադրությունն ընդհանրապես (ես ինքս անտեսել էի այդ հնարավորությունը)։ Վատիկանի խորհրդակցության ժամանակ ես չգիտեի, թե «սահման չունենալու» գաղափարն ինչպես պետք էր օգտագործել, որպեսզի հնարավոր լիներ տիեզերքի մասին կանխագուշակումներ կատարել։ Հաջորդ ամառը ես անցկացրի Կալիֆոռնիայի համալսարանում, Սանտա֊Բարբարայում։ Այնտեղ իմ գործընկեր և բարեկամ Ջիմ Հարտի հետ մենք մշակեցինք այն պայմանները, որոնց պետք է բավարարեր տիեզերքը, եթե տարածություն֊ժամանակը սահման չունենար։ Վերադառնալով Քեմբրիջ, ես իմ երկու ասպիրանտների՝ Ջուլիան Լաթրելի և Ջոնաթան Հոլիուելի հետ ես շարունակեցի այդ աշխատանքը։ | ||
| + | |||
| + | Ուզում եմ ընդգծել, որ այն պատկերացումը, թե ժամանակն ու տարածությունը վերջավոր են առանց սահմանափակման ուղղակի մի առաջարկություն է․ դա որևէ սկզբունքից չի բխում։ Ինչպես որևէ այլ գիտական տեսություն, սկզբում այն կարելի է գեղագիտական կամ մետաֆիզիկական նկատառումներով առաջարկել, բայց իրական չափանիշն այն է, թե այդ տեսության կանխագուշակումներն արդյոք համապատասխանո՞ւմ են մեր դիտարկումներին։ Դա դժվար է որոշել քվանտային գրավիտացիայի դեպքում՝ երկու պատճառով։ Առաջին, ինչպես դա կբացատրվի հաջորդ գլխում, մենք դեռևս վստահ չենք, թե ինչպիսին է այն տեսությունը, որը հաջողությամբ կմիավորի ընդհանուր հարաբերականությունը և քվանտային մեխանիկան, թեև բավական շատ բան գիտենք, թե այդ տեսությունը ինչ ձև է ունենալու։ Երկրորդ, տիեզերքը մանրամասնորեն նկարագրող ցանկացած մոդել մաթեմատիկորեն այն աստիճան բարդ կլինի, որ հնարավոր չի լինի ճշգրիտ կանխագուշակումներ կատարել։ Հետևաբար պետք է դիմել պարզեցնող ենթադրությունների և մոտավորությունների, նույնիսկ այն դեպքում, երբ կանխագուշակումներ կորզելու հարցը շատ դժվար լինի։ | ||
| + | |||
| + | Գումարային պատմությունների մեջ յուրաքանչյուր պատմություն ոչ միայն պիտի նկարագրի տարածություն֊ժամանակը, այլև նրա մեջ գտնվող ամեն ինչ, ներառյալ ցանկացած բարդ օրգանիզմ, ինչպես մարդկային էակներն են, որոնք ի վիճակի են դիտարկել տիեզերքի պատմությունը։ Այս բանը մեկ անգամ ևս արդարացնում է մարդաբանական սկզբունքի օգտագործումը, որովհետև, եթե բոլոր պատմությունները հնարավոր են, ապա այնքան ժամանակ, քանի դեռ մենք գոյություն ունենք պատմություններից մեկի մեջ, կարող ենք օգտագործել մարդաբանական սկզբունքը բացատրելու համար, թե ինչո՞ւ է տիեզերքն այնպիսին, ինչպիսին է։ Ճիշտն ասած, թե ինչ իմաստ կարող ենք տալ մյուս պատմություններին, որտեղ մենք գոյություն չունենք, հստակ չէ։ Գրավիտացիայի այս քվանտային տեսությունը շատ ավելի ընդունելի կլիներ, սակայն, եթե օգտագործելով պատմությունների գումարը, ցույց տրվեր, որ մեր տիեզերքը հնարավոր պատմություններից ոչ թե մեկը, այլ ամենահավանականն է։ Այս նպատակի համար, սահման չունեցող բոլոր հնարավոր էվկլիդեսյան տարածություն֊ժամանակների պատմությունները պետք է գումարել։ | ||
| + | |||
| + | Սահման չունենալու այս առաջարկությունը թույլ է տալիս պարզել, որ պատմությունների մեծ մասում տիեզերքի գտնվելու հնարավորությունը աննշան է։ Սակայն կան մի խումբ պատմություններ, որոնք շատ ավելի հավանական են, քան այլ պատմություններ։ Պատմությունները կարելի է նմանեցնել երկրագնդի մակերեսին, որի գնդի լայնական (հյուսիսային բևեռից հավասարահեռ) շրջանագիծը ներկայացնում է տիեզերքի տարածական չափը, իսկ հյուսիսային բևեռից ունեցած հեռավորությունը՝ կեղծ ժամանակը։ Տիեզերքը սկիզբ է առնում հյուսիսային բևեռից՝ որպես մի եզակի կետից։ Շարժվելով հարավ, հյուսիսային բևեռից հաստատուն հեռավորություն ունեցող շրջանագծերի լայնություններն աստիճանաբար մեծանում են, ինչը համապատասխանում է կեղծ ժամանակի ընթացքում ընդարձակմանը (նկ․ 8.1)։ Հասարակածում տիեզերքը կհասնի իր առավելագույն չափին և կեղծ ժամանակի հետագա աճի հետ կկծկվի մինչև հարավային բևեռի եզակի կետը։ Թեև տիեզերքի չափսը հավասար է զերոյի հյուսիսային և հարավային բևեռներում, այս կետերը եզակիություններ չեն, ինչպես երկրագնդի բևեռները եզակի չեն։ Հետևաբար, գիտության օրենքները կմնան ուժի մեջ ճիշտ այնպես, ինչպես երկրագնդի հյուսիսային և հարավային բևեռներում գործում են նույն օրենքները, ինչ հասարակածում։ | ||
| + | |||
| + | Սակայն իրական ժամանակում տիեզերքի պատմությունն այլ տեսք կունենա։ Մոտավորապես տասը կամ քսան հազար միլիոն տարի առաջ իր նվազագույն չափսն ուներ, որը հավասար էր կեղծ ժամանակում նրա պատմության առավելագույն շառավղին։ Հետագա իրական ժամանակներում տիեզերքը պետք է ընդարձակվեր Լինդեի առաջարկած քաոսային հարաճուն ընդարձակման մոդելի համաձայն (բայց պետք չէ ենթադրել, որ տիեզերքը ստեղծվել է ճշգրտված որոշակի վիճակում)։ Տիեզերքը պետք է ընդարձակվի, հասնի մեծ չափի և ի վերջո կոլապսվի ու վերածվի մի այնպիսի վիճակի, որը իրական ժամանակի մեջ նման կլինի եզակիության։ Այսպիսով, որոշ իմաստով մենք կործանման ենք դատապարտված, նույնիսկ եթե մեզ հաջողվի սև խոռոչներից հեռու մնալ։ Միայն այն դեպքում, երբ մենք տիեզերքը կարողանանք պատկերացնել կեղծ ժամանակում, եզակիություններ չեն լինի։ | ||
| + | |||
| + | [[Պատկեր:H8 1.svg|thumb|Նկ․ 8․1]] | ||
| + | |||
| + | Եթե տիեզերքը իրոք գտնվի այդպիսի մի քվանտային վիճակում, ապա կեղծ ժամանակում նրա պատմությունը եզակիություններ չի կարող ունենալ։ Հետևաբար կարող է թվալ, որ իմ վերջին աշխատանքը լրիվ արժեզրկում է եզակիությունների մասին ավելի վաղ կատարած իմ գործը։ Բայց, ինչպես ցույց տրվեց վերևում, եզակիության թեորեմների իրական կարևորությունն այն էր, որ նրանք ցույց տվեցին, որ գրավիտացիոն դաշտը կարող է այն աստիճան ուժեղանալ, որ քվանտային ձգողական ազդեցությունները չի կարելի անտեսել։ Այս բանը հանգեցրեց այն մտքին, որ տիեզերքը կեղծ ժամանակում կարող է վերջավոր լինել, բայց առանց սահմանների ու եզակիությունների։ Երբ վերադառնանք դեպի իրական ժամանակը, որում մենք ապրում ենք, այնուամենայնիվ, եզակիություններ միշտ կլինեն։ Սև խոռոչի մեջ ընկնելիս խեղճ տիեզերագնացի վերջը միշտ վատ կլինի․ եթե նա ապրեր կեղծ ժամանակում, ապա այդ պարագայում միայն չէր հանդիպի եզակիությունների։ | ||
| + | |||
| + | Սա կարող է մեզ հուշել, որ, այսպես կոչված, կեղծ ժամանակն իրականում իրական ժամանակն է, իսկ այն, ինչ մենք իրական ժամանակ ենք անվանում, մեր երևակայության խաբկանքն է։ Իրական ժամանակում տիեզերքը մի սկիզբ ունի և մի վերջ՝ եզակիությունում, որը տարածության֊ժամանակի սահմանն է, որտեղ գիտության օրենքները չեն գործում։ Իսկ կեղծ ժամանակում չկան ոչ եզակիություններ և ոչ էլ սահմաններ։ Հետևաբար, թերևս այն, ինչ մենք անվանում ենք կեղծ ժամանակ, ըստ էության, ավելի իրական է, իսկ այն, ինչ մենք կոչում ենք իրական՝ դա պարզապես հնարովի մի գաղափար է, որը մենք ներմուծել ենք, որպեսզի մեզ օգնի նկարագրելու տիեզերքի որպիսությունը։ Բայց ինչպես նկարագրել եմ 1֊ին գլխում, գիտական տեսությունը լոկ մաթեմատիկական մի մոդել է, որը մենք ստեղծում ենք նկարագրելու համար մեր դիտարկումները․ դա գոյություն ունի միայն մեր մտքում։ Հետևաբար անիմաստ է հարցնել, թե որ ժամանակն է «իրական» և որը՝ «կեղծ»։ Բանը պարզապես այն է, թե որն է առավել օգտակար։ | ||
| + | |||
| + | Մենք կարող ենք պատմությունների գումարն օգտագործել նաև որպես սահման չունենալու առաջարկություն, որպեսզի գտնենք, թե տիեզերքի որ հատկությունները կարող են միասին ի հայտ գալ։ Օրինակի համար, կարելի է հաշվել այն հավանականությունը, որով տիեզերքը բոլոր տարբեր ուղղություններով ընդարձակվում է համարյա նույն արագությամբ, երբ նրա խտությունն ունի այժմյան արժեքը։ Այս հավանականությունը շատ մեծ է ստացվում մինչև այժմ քննարկված պարզ մոդելների հիման վրա կատարված հաշվումների համաձայն։ Այսինքն, սահման չունենալու առաջարկությունը տանում է այն կանխագուշակման, ըստ որի չափազանց հավանական է, որ տիեզերքի այժմյան ընդարձակման արագությունը բոլոր ուղղություններով համարյա նույնն է։ Այս կանխագուշակումը համապատասխանում է միկրոալիքային ֆոնային ճառագայթմանը, որը բոլոր ուղղություններով բացարձակապես նույնն է։ Եթե տիեզերքը մի որևէ ուղղությամբ ավելի արագ ընդարձակվեր, քան այլ ուղղություններով, ապա ճառագայթման ինտենսիվությունն այն ուղղություններում պետք է նվազեր լրացուցիչ կարմիր շեղումով։ | ||
| + | |||
| + | Սահման չունենալու պայմաններում այլ կանխագուշակումների գծով աշխատանքներն այժմ շարունակվում են։ Առանձնապես շատ հետաքրքրական է այն պրոբլեմը, թե վաղ տիեզերքում համաչափ խտությունից փոքրիկ շեղումներն ինչ չափի են եղել, որոնք պատճառ են դարձել նախ գալակտիկաների, ապա աստղերի և վերջապես՝ մեր առաջացման։ Անորոշության սկզբունքից հետևում է, որ վաղ տիեզերքը լրիվ համաչափ չէր կարող լինել, որովհետև որոշ անորոշություններ և տատանումներ պետք է եղած լինեն մասնիկների դիրքերում և արագություններում։ Օգտագործելով սահման չունենալու պայմանը, մենք գտնում ենք, որ տիեզերքն իրոք սկսվել է այն նվազագույն անհամաչափությունից, որը թույլ է տրվում համաձայն անորոշության սկզբունքի։ Այսպիսով, տիեզերքն անցել է արագ ընդարձակման մի շրջան, ինչպես նկարագրվում է հարաճուն ընդարձակման մոդելներում։ Այդ շրջանում սկզբնական անհամաչափությունները պետք է ավելի շեշտված լինեն՝ այն աստիճան մեծ, որ հնարավոր լինի բացատրել մեր շուրջ գոյություն ունեցող կառուցվածքների առաջացումը։ Ընդարձակվող տիեզերքում, որտեղ նյութի խտությունն աննշան չափով է փոփոխվում մի տեղից մյուսը, գրավիտացիայի պատճառով խիտ տիրույթների ընդարձակումը դանդաղում է և ի վերջո սկսում է նրանց սեղմումը։ Սա հանգեցնում է գալակտիկաների, աստղերի և վերջապես նույնիսկ մեզ նման աննշան արարածների առաջացմանը։ Այսպիսով, տիեզերքում մեր տեսած բոլոր բարդ կառուցվածքների առաջացումը կարելի է բացատրել տիեզերքի սահման չունենալու պայմանի և քվանտային մեխանիկայի անորոշության սկզբունքի միացյալ հիմքի օգնությամբ։ | ||
| + | |||
| + | Այն գաղափարը, թե տարածությունը և ժամանակը կարող են մի փակ մակերես ստեղծել, որը սահման չունի, խոր նշանակություն ունի տիեզերական գործերում Աստծո խաղացած դերի հարցում։ Գիտական տեսությունների այն հաջողությունները, որոնք լավագույնս նկարագրեցին մեր շուրջ տեղի ունեցող դեպքերը, պատճառ եղան, որ շատերը հավատան, թե Աստված թույլ է տվել, որ տիեզերքը զարգանա մի շարք օրենքների համաձայն և այլևս չի միջամտում, որպեսզի այդ օրենքները չխախտվեն։ Սակայն այս օրենքները մեզ չեն ասում, թե ինչի նման պետք է եղած լիներ տիեզերքն իր սկզբնական շրջանում։ Աստված պետք է լարեր ժամացույցը և ընտրեր, թե ինչպես պետք է տիեզերքը սկիզբ առներ։ Քանի որ տիեզերքը սկիզբ է ունեցել, ապա մենք կարող ենք ենթադրել, որ այն ունեցել է իր արարիչը։ Սակայն, եթե տիեզերքն իրապես լրիվ ինքնապարփակ է, սահման և եզր չունի, չի կարող ոչ սկիզբ, ոչ էլ վերջ ունենալ, այլ այն պարզապես կա։ Ուստի այդ դեպքում արարչին այլևս անելիք չի մնում։ | ||
| + | |||
| + | |||
| + | ==9== | ||
| + | |||
| + | Ժամանակի նետը | ||
| + | |||
| + | Նախորդ գլուխներում մենք տեսանք, թե տարիների ընթացքում ինչպես են փոխվել ժամանակի մասին մեր ունեցած պատկերացումները։ Ընդհուպ մինչև մեր ունեցած պատկերացումները։ Ընդհուպ մինչև մեր դարասկիզբը մարդիկ համոզված էին, թե ժամանակը բացարձակ է։ Այսինքն՝ յուրաքանչյուր դեպք կարելի է համարակալել մի եզակի թվով, որը կոչվում է «Ժամանակ», և բոլոր ճշգրիտ ժամացույցները երկու հաջորդական դեպքերի միջև անցած ժամանակամիջոցի համար ցույց կտան նույն մեծությունը։ Սակայն այն հայտնագործությունը, թե լույսի արագությունը հաստատուն մեծություն է բոլոր դիտորդների համար՝ անկախ նրանց շարժման արագությունից, պատճառ եղավ հարաբերականության տեսության ստեղծման և եզակի, բացարձակ ժամանակի հասկացությունից հրաժարման։<ref>Ինչպես փորձն է ցույց տալիս, շարժվող լուսատու առարկան իրենից արձակված լույսի արագությանը չի կարող ավելացնել իր սեփական արագությունը։ Այսինքն՝ լույսի արագությունը միշտ հաստատուն է։ Իսկ քանի որ, համաձայն հարաբերականության տեսության, ամեն շարժում (բացի լույսի արագությունից) հարաբերական է (ինչպես ցույց է տալիս փորձը), հետևաբար գնացքով դեպի լույսի աղբյուրը շարժվող դիտորդին լույսն ավելի շուտ կհասնի, այսինքն նրա ժամացույցն ավելի կարճ ժամանակ ցույց կտա, քան կառամատույցում կանգնած մարդու ժամացույցը, որը նույն լույսն ավելի ուշ կտեսնի։ Դժբախտաբար, կառամատույցում կանգնած մարդը չի կարող գնացքի ուղևորի ժամացույցը տեսնել այդ բանը ստուգելու համար, սակայն հայտնի է, որ արագ շարժվող գնացքի պատուհանները նեղ են թվում։ Քանի որ տարածությունն ու ժամանակն իրար հետ կապված են, ապա ակնհայտ է, որ արագության աճի հետ տարածությունը կարճանում է, իսկ ժամանակը դանդաղում։ Իհարկե, փոքր արագությունների համար այս դանդաղումը հնարավոր չէ չափել, սակայն եթե գնացքը շարժվի լույսի արագության մոտ (300.000 կմ/վ) արագությամբ, ապա երկու տարի հետո ուղևորի տարիքը համարյա փոփոխության չի ենթարկվի։</ref> | ||
| + | |||
| + | Այսպիսով, ամեն դիտորդ ունի ժամանակի իր չափը, ինչը արձանագրում է դիտորդի ժամացույցը։ Պարտադիր չէ, որ տարբեր դիտորդների ժամացույցները նույն ժամանակը ցույց տան։ Մի խոսքով, ժամանակն առավել անհատական բնույթի հասկացություն է դարձել՝ կախված այն չափող դիտորդից։ | ||
| + | |||
| + | Երբ փորձ արվեց գրավիտացիան միավորել քվանտային մեխանիկայի հետ, ապա հարկ եղավ ներմուծել «կեղծ» ժամանակի գաղափարը։ Կեղծ ժամանակը կախված չէ տարածության մեջ ուղղություններից։ Եթե հնարավոր է դեպի հյուսիս ուղղությամբ շարժվել, ապա հնարավոր է նաև հետ շրջվել և շարժվել դեպի հարավ․ նմանապես, եթե հնարավոր է կեղծ ժամանակով առաջ ընթանալ, ապա հնարավոր պետք է լինի շրջվել և շարժվել կեղծ ժամանակի հետընթաց ուղղությամբ։ Սա նշանակում է, որ որևէ էական տարբերություն չի կարող լինել կեղծ ժամանակի առաջընթաց և հետընթաց ուղղությունների միջև։ Իսկ «իրական» ժամանակում այդ տարբերությունը շատ մեծ է, ինչպես բոլորս գիտենք։ Որտեղի՞ց է գալիս անցյալի և ապագայի միջև առկա այս տարբերությունը։ Մենք ինչո՞ւ ենք անցյալը հիշում, բայց ոչ ապագան։<ref>Հիշել ապագան, նշանակում է, որ մենք հետ ենք գնում դեպի անցյալը, այսինքն՝ իրական ժամանակը փոխում է իր ուղղությունը։</ref> | ||
| + | |||
| + | Գիտության օրենքները ոչ մի տարբերություն չեն դնում անցյալի և ապագայի միջև։ Ավելի հստակ ասած, ինչպես վերևում բացատրվեց, գիտության օրենքներն անփոփոխ են C, P, և T համար։ (C ― նշանակում է մասնիկը փոխել հակամասնիկի, P ― նշանակում է վերցնել հայելապատկերը, այնպես, որ ձախն ու աջը փոխեն իրենց տեղերը, և T ― նշանակում է շրջել բոլոր մասնիկների շարժման ուղղությունները, այսինքն՝ շարժմանը տալ հետադարձ ուղղություն)։ Բոլոր սովորական վիճակներում նյութի վարքագիծը կառավարող գիտության օրենքներն անփոփոխ են մնում C և P համակցության ազդեցության դեպքում։ Այլ խոսքերով ասած, կյանքը նույնը կլինի մի այլ մոլորակի բնակչության համար, ինչպես մերը, որտեղ մարդիկ մեր հայելապատկերներն են ու կազմված են ոչ թե մեր նյութից, այլ հականյութից։ | ||
| + | |||
| + | Եթե գիտության օրենքներն անփոփոխ են C և P գործողությունների համակցության, ինչպես նաև C, P և T համակցության ազդեցության դեպքում, պետք է որ անփոփոխ լինեն նաև T գործողության ազդեցության համար։ Այնուամենայնիվ, առօրյա կյանքում իրական ժամանակի առաջընթաց և հետընթաց ուղղությունների միջև շատ մեծ տարբերություն կա։ Պատկերացնենք սեղանին դրված մի բաժակ, որը սեղանից ընկնելով փշրվում է։ Եթե այդ բանը նկարահանենք ժապավենի վրա, ապա դիտման ժամանակ հեշտ է ասել՝ ֆիլմը առաջընթաց, թե հետընթաց ուղղությամբ է ցուցադրվում։ Եթե ցուցադրումը հետընթաց է, ապա կտեսնենք, թե ինչպես են ապակու կտորները հանկարծ ի մի հավաքվում, և հատակից ամբողջական բաժակը ցատկելով հայտնվում է սեղանի վրա։ Քանի որ իրական կյանքում այդպիսի բան տեղի չի ունենում, ուստի կասենք, որ ֆիլմը ցուցադրվում է հակառակ ուղղությամբ։ Արդարև, եթե այդպիսի բան տեղի ունենար, բաժակ արտադրողները կսնանկանային։ | ||
| + | |||
| + | Թե ջարդված բաժակները ինքնակամ կերպով հատակի վրա ինչո՞ւ ի մի չեն հավաքվում և չեն ցատկում սեղանին, սովորաբար բացատրվում է նրանով, որ դա արգելվում է ըստ թերմոդինամիկայի երկրորդ օրենքի։ Վերջինիս համաձայն, փակ համակարգում անկարգությունը կամ էնտրոպիան աճում է ժամանակին զուգընթաց։<ref>Այսինքն ժամանակի ընթացքում տեղի են ունենում ինքնակամ պրոցեսներ, որոնք բերում են կարգուկանոնի նվազման, որի չափանիշն է էնտրոպիայի աճը։</ref> Այլ կերպ ասած, սա Մերֆիի օրենքի մի տարատեսակ է, ըստ որի «ամեն ինչ աշխարհում միշտ թարս է գնում»։ Սեղանի վրա գտնվող ամբողջական բաժակը ներկայացնում է կատարյալ կարգուկանոնի վիճակը, իսկ հատակին փշրված բաժակը գտնվում է անկարգ վիճակում։ Դժվար չէ կազմակերպել անցումն անցյալում սեղանի վրա գտնվող բաժակի վիճակից դեպի ապագայում փշրված բաժակի վիճակի, բայց ոչ հակառակը։<ref>Կարևոր չէ, թե ինչպես բաժակը վայր ընկավ, այլ այն, որ ջարդված բաժակի վերականգնումը չի կարող ինքնակամ կերպով տեղի ունենալ։ Այդ անելու համար աշխատանք պետք է կատարել, որի հետևանքով կառաջանա մի այլ անկարգություն, կամ, որ նույն բանն է, համակարգի էնտրոպիան կաճի առավել մեծ չափով։</ref> | ||
| + | |||
| + | Ժամանակին զուգընթաց անկարգության կամ էնտրոպիայի աճը ժամանակի նետ կոչվող հասկացության օրինակներից է․ այս հասկացությունն է տարբերում անցյալն ապագայից՝ ժամանակին ուղղություն տալով։ Կան ժամանակի առնվազն երեք տարբեր նետեր։ Առաջինը ժամանակի թերմոդինամիկական նետն է, որը ցույց է տալիս ժամանակի այն ուղղությունը, որում անկարգությունը կամ էնտրոպիան աճում է։ Երկրորդը ժամանակի հոգեբանական նետն է։ Սա այն ուղղությունն է, որով, ըստ մեր զգացողության, անցնում է ժամանակը, ուղղություն, որով հիշում ենք անցյալը, սակայն ոչ ապագան։ Սա ժամանակի այն ուղղությունն է, որով տիեզերքը ավելի շատ ընդարձակվում է, քան սեղմվում։ | ||
| + | |||
| + | Այս գլխում ես կաշխատեմ հիմնավորել, թե ինչու տիեզերքի սահման չունենալու պայմանը, թույլ մարդաբանական սկզբունքի հետ միասին, կարող է բացատրել, թե ինչու են երեք նետերն էլ ուղղված միևնույն ուղղությամբ, ինչպես նաև այն, որ պետք է գոյություն ունենա հստակ սահմանված ժամանակի նետ հասկացությունն ընդհանրապես։ Կաշխատեմ հիմնավորել, որ հոգեբանական նետը պայմանավորված է թերմոդինամիկական նետով, և այս երկու նետերը պարտադիր կերպով միշտ նույն ուղղություն ունեն։ Եթե մենք ընդունենք տիեզերքի սահման չունենալու պայմանը, կտեսնենք, որ պետք է գոյություն ունենան հստակ որոշված թերմոդինամիկական և տիեզերաբանական ժամանակի նետեր, սակայն դրանք կարող են նույն ուղղությամբ ուղղված չլինել տիեզերքի ամբողջ պատմության ընթացքում։ Սակայն ես պիտի աշխատեմ հիմնավորել, որ միայն այն դեպքում, երբ այդ նետերն ունենան միևնույն ուղղությունը, կառաջանան բարենպաստ պայմաններ, որպեսզի զարգանան այնպիսի բանական էակներ, որոնք կարող են հարց տալ, թե ինչո՞ւ է անկարգությունը ժամանակի այն ուղղությամբ աճում, որով ընդարձակվում է տիեզերքը։ | ||
| + | |||
| + | Սկսենք թերմոդինամիկական ժամանակի նետի հարցի քննարկումից։ Թերմոդինամիկայի երկրորդ օրենքը հիմնված է այն փաստի վրա, որ գոյություն ունեն ավելի շատ անկարգ համակարգեր, քան կարգավորված համակարգեր։ Պատկերացրեք, օրինակ, որ մի նկար մասերի է բաժանված, և դրանք լցված են տուփի մեջ։ Մեկ և միայն մեկ դասավորություն կա, որով մասերը միանալով կառաջացնեն ամբողջական պատկերը։ Մյուս կողմից, գոյություն ունեն բազմաթիվ դասավորություններ, որոնցով ամբողջական պատկեր չի ստացվում։ | ||
| + | |||
| + | Ենթադրենք, ինչ֊որ համակարգ գտնվում է այդ փոքրաթիվ կանոնավոր վիճակներից մեկում։ Ժամանակի ընթացքում, գիտության օրենքներին համապատասխան, համակարգը պիտի զարգանա և իր վիճակը փոխի։ Քանի որ չկարգավորված վիճակներն ավելի շատ են, ապա հետագայում առավել հավանական է, որ համակարգը կարգավորված վիճակից անցնի չկարգավորված վիճակի։ Այսպիսով, եթե համակարգի սկզբնական վիճակը կարգավորված էր, ապա ժամանակի ընթացքում այն կձգտի անկանոն վիճակի։ | ||
| + | |||
| + | Այժմ ենթադրենք, որ նկարի մասերը այնպես են դասավորված տուփում, որ ստացվել է ամբողջական պատկեր։ Եթե տուփը թափահարենք, ապա մասերը ձեռք կբերեն մի նոր դասավորություն։ Ամենայն հավանականությամբ կստացվի մի անկանոն դասավորություն, որում մասերն ամբողջական պատկեր չեն կազմում․ դա պարզապես այն պատճառով, որ անհամեմատ մեծ թվով անկանոն դասավորություններ են հնարավոր։ Հնարավոր է, որ նկարի մասերի որոշ խմբեր կազմեն նկարի առանձին հատվածներ, բայց եթե շարունակենք տուփը թափահարել, ապա նկարի այդ հատվածները նույնպես կվերանան, և ստացված վիճակը կլինի խառնափնթոր մի դասավորություն, որը ոչ մի նկարի չի նմանվի։ Այսպիսով, եթե մենք սկսում ենք կարգավորված վիճակից, ապա ժամանակի ընթացքում մասերը ձգտում են ավելի բարձր անկանոն վիճակի։ | ||
| + | |||
| + | Ենթադրենք Աստված ցանկացել է, որ տիեզերքի զարգացումը պետք է ավարտվի բարձր աստիճանի կարգավորություն ունեցող մի վիճակով, անկախ այն բանից, թե ինչպիսի վիճակից է այն սկիզբ առել։ Տիեզերքը, ամենայն հավանականությամբ, վաղ ժամանակներում կարող էր գտնվել չկարգավորված վիճակում։ Բայց դա նշանակում է, որ անկանոնությունը ժամանակի ընթացքում նվազում է։ Այսինքն՝ ջարդված բաժակները պիտի ամբողջանան և ցատկեն սեղանի վրա։ Սակայն այս երևույթին ականատես մարդիկ կապրեին մի տիեզերքում, որտեղ անկանոնությունը նվազում է ժամանակի ընթացքում։ Կարելի է պնդել, որ այդպիսի էակների համար ժամանակի հոգեբանական նետը հակառակ ուղղություն պետք է ունենա։ Նրանք դեպքերը կհիշեն ապագայում, բայց՝ ոչ անցյալում։ Երբ տեսնեն փշրված բաժակը, նրանք կհիշեն սեղանին դրված լինելու պահը, իսկ երբ բաժակը տեսնեն սեղանին, նրանք չեն հիշի, որ այն գետին էր ընկած։<ref>Մարդիկ այդպիսի տիեզերքում կարող են հիշել լոկ բաժակի վերականգնումը, այսինքն անկանոն վիճակից ինքնակամ անցում կանոնավոր վիճակի։</ref> | ||
| + | |||
| + | Բավական դժվար է խոսել մարդկային հիշողության մասին, որովհետև մենք ուղեղի աշխատանքի մանրամասնություններին տեղյակ չենք։ Սակայն համակարգչի հիշողության աշխատանքի վերաբերյալ մենք ամեն ինչ գիտենք։ Հետևաբար, ես ուզում եմ քննարկել հաշվողական մեքենայի ժամանակի հոգեբանական նետը։ Կարծում եմ՝ կարելի է ենթադրել, որ համակարգիչների և մարդկանց նետերը (ժամանակի) նույնն են (նույն ուղղությունն ունեն)։ (Եթե այդպես չլիներ, ապա արժեթղթերի սակարանում մարդ մեծ հարստություն կդիզեր, օգտագործելով մի այնպիսի մեքենա, որը հիշեր արժեթղթերի վաղվա գները)։ | ||
| + | |||
| + | Հաշվողական մեքենայի հիշողությունը մի հարմարանք է, որը պարունակում է երկու տարբեր վիճակներից մեկում գտնվող տարրեր։ Սովորական հաշվապահական հաշվիչն այդպիսի հարմարանքի մի պարզ օրինակ է։ Դրա պարզագույն ձևը կազմված է մի քանի մետաղե ձողերից, որոնցից յուրաքանչյուրին հագցված է մի գնդիկ, որը կարելի է դնել երկու դիրքից մեկում։ Համակարգչի հիշողության մեջ ցանկացած տեղեկություն ներմուծելուց առաջ, նրա հիշողությունը գտնվում է անկանոն վիճակում՝ երկու հնարավոր վիճակներից յուրաքանչյուրին անցնելու հավասար հավանականությամբ։ (Հաշվիչի ձողերի վրա գնդիկները խառնիխուռն են բաշխված)։ Հիշողության մեջ արձանագրվելիք համակարի հետ փոխազդելուց հետո նրա հիշողությունն անպայման գալիս է որոշակի վիճակի՝ համակարգի վիճակին համապատասխան։ (Յուրաքանչյուր գնդիկ կգտնվի հաշվիչի ձողի կամ աջ, կամ ձախ կողմում)։ Այսպիսով, հիշողությունը անկանոն վիճակից անցել է կանոնավոր վիճակի։ Սակայն այս բանը անելու համար հարկավոր է աշխատանք կատարել (օրինակ, գնդիկը շարժել կամ համակարգիչը հոսանքով սնել)։ Այդ էներգիան ցրվում է որպես ջերմություն, և տիեզերքում աճում է անկանոնության աստիճանը։ Կարելի է ցույց տալ, որ այդպիսի անկանոնության աճն ավելի մեծ է, քան հիշողության մեջ կարգավորվածության աճը։<ref>Դրա պատճառն այն է, որ համաձայն թերմոդինամիկայի 2֊րդ օրենքի, ջերմությունը չի կարելի ամբողջությամբ փոխակերպել աշխատանքի, քանի որ դրա մի մասը անպայման շրջապատին է հաղորդվում՝ մնում է չօգտագործված։ Հակառակ դեպքում հնարավոր կլիներ ստեղծել II կարգի հավերժական մի շարժիչ․ ինչը հնարավոր չէ։</ref> | ||
| + | |||
| + | Այսպիսով, երբ համակարգիչը հիշողության գրանցում է կատարում, նրա հովհարիչի պտուտակի արտամղված ջերմությունը պատճառ է դառնում, որ տիեզերքում անկանոնության գումարային քանակությունն աճի։ Ժամանակի ուղղությունը, որով համակարգիչը հիշում է անցյալը, նույնն է, ինչ տիեզերքում անկանոնության աճի ուղղությունը։ | ||
| + | |||
| + | Ժամանակի ուղղության մեր ենթակայական զգացողությունը, ժամանակի հոգեբանական նետը, մեր ուղեղում որոշվում է ժամանակի թերմոդինամիկական նետի ուղղությամբ։ Համակարգչի նման մենք ևս անցյալը պիտի հիշենք այն կարգով, ինչ կարգով աճում է էնտրոպիան։ Այս տեսակետից թերմոդինամիկայի երկրորդ օրենքը կարծես պարզունակ է դառնում։ Անկանոնությունն աճում է ժամանակին զուգընթաց, որովհետև մենք ժամանակը չափում ենք այն ուղղությամբ, ինչ ուղղությամբ աճում է անկանոնությունը։ Դժվար թե հնարավոր լիներ կատարել ավելի պարզունակ պնդում։<ref>Էնտրոպիայի մասին խոսել լոկ անկարգավորվածության աճի տեսակետից, հավանաբար, բավարար չէ։ Բավական է ասել, որ եթե թերմոդինամիկայի առաջին օրենքը տալիս է էներգիայի փոխակերպման սկզբունքը, ապա երկրորդ օրենքը դրա ուղղությունը, որը կախված է լոկ ջերմություն֊էներգիա փոխակերպումից։</ref> | ||
| + | |||
| + | Բայց ինչո՞ւ պետք է ընդհանրապես գոյություն ունենա ժամանակի թերմոդինամիկական նետ։ Կամ, այլ կերպ ասած, ինչո՞ւ պետք է տիեզերքն ինչ֊որ ժամանակում, որը մենք անվանում ենք անցյալ, կանոնավոր եղած լինի։ Կամ ինչո՞ւ այն չպետք է անկանոն վիճակում լինի բոլոր ժամանակներում։ Վերջ ի վերջո այս վերջինն ավելի հավանական է թվում։ Եվ ինչո՞ւ է անկանոնությունը ժամանակի ընթացքում աճում այն ուղղությամբ, որով ընդարձակվում է տիեզերքը։ | ||
| + | |||
| + | Ընդհանուր հարաբերականության դասական տեսությունը մեզ թույլ չի տալիս կանխագուշակել, թե ինչպես է տիեզերքը ծագել, որովհետև գիտության բոլոր հայտնի օրենքները Մեծ պայթյունի եզակիությունում իրենց ուժը կորցնում են։ Հնարավոր է, որ տիեզերքը սկիզբ է առել մի համասեռ, խիստ կարգավորված վիճակում։ Սա կհանգեցներ ժամանակի հատուկ սահմանված թերմոդինամիկական և տիեզերաբանական նետերին, ինչը և դիտարկվում է։ Սակայն հավասարապես հնարավոր է, որ այն սկիզբ առներ խիստ անհամասեռ և անկանոն վիճակում։ Այս դեպքում տիեզերքն արդեն կատարյալ անկանոն վիճակում կլիներ, հետևաբար նրա անկանոնությունը չէր կարող աճել ժամանակին զուգընթաց։ Կամ անկանոնությունը անփոփոխ կմնար, որի դեպքում ժամանակի հստակ սահմանված թերմոդինամիկական նետ չէր կարող լինել, կամ անկանոնությունը կնվազեր, և այդ պարագայում թերմոդինամիկական նետն ուղղված կլիներ տիեզերաբանականի հակառակ ուղղությամբ։ Այս երկու հնարավորություններն էլ չեն համապատասխանում փորձնական դիտարկումներին։ Սակայն, ինչպես տեսանք, ընդհանուր հարաբերականության դասական տեսությունը կանխագուշակում է իր տապալումը։ Երբ տարածություն֊ժամանակի կորությունը շատ է մեծանում, քվանտային գրավիտացիոն ազդեցությունները դառնում են առաջնահերթ, և դասական տեսությունն ի վերջո կորցնում է տիեզերքը նկարագրելու կարողությունը։ Մենք ստիպված ենք դիմել գրավիտացիոն քվանտային տեսությանը, որպեսզի հասկանանք, թե ինչպես է սկիզբ առել տիեզերքը։ | ||
| + | |||
| + | Ինչպես նախորդ գլխում տեսանք, ըստ գրավիտացիոն քվանտային տեսության, տիեզերքի վիճակը բնորոշելու համար անհրաժեշտ է իմանալ, թե ինչպիսիք կարող էին լինել տիեզերքի հնարավոր պատմությունները անցյալում՝ տարածություն֊ժամանակի սահմանագծում։ Խուսափել այն բանը գիտենալու անհրաժեշտությունից, ինչը մենք չգիտենք և չենք կարող գիտենալ, կարելի է միայն այն դեպքում, եթե անցյալ պատմությունները բավարարում են սահման չունենալու պայմանին, այսինքն՝ դրանք վերջավոր են, բայց սահման, եզր կամ եզակիություն չունեն։ Այդ դեպքում ժամանակի սկիզբը կլիներ կանոնավոր, հարթ մի կետ տարածություն֊ժամանակի մեջ, և տիեզերքը, կսկսեր ընդարձակվել մի համասեռ ու կանոնավոր վիճակից։ Այն լրիվ միաձև չէր կարող լինել, որովհետև այդ դեպքում կխախտվեր քվանտային մեխանիկայի անորոշության սկզբունքը։ | ||
| + | |||
| + | Պետք է, որ լինեին մասնիկների խտության և արագությունների փոքր տատանումներ։ Սակայն անսահմանության պայմանի շնորհիվ այդ տատանումները պետք է հնարավորին չափ փոքր լինեն, որպեսզի չխախտվի անորոշության սկզբունքը։ | ||
| + | |||
| + | Ամենավաղ շրջանում տիեզերքը կարող էր ունենալ Էքսպոնենտային կամ «հարաճուն»<ref>բնագրում «ինֆլյացիոն»</ref> ընդարձակման մի ժամանակահատված, որի ընթացքում նրա մեծությունն աճեր մեծ գործակցով։ Այս ընդարձակման ժամանակ խտության տատանումները սկզբում փոքր կլինեին, իսկ հետագայում կսկսեին աճել։ Այն տիրույթներում, որտեղ խտությունը փոքր֊ինչ մեծ էր միջին արժեքից, ընդարձակումը կդանդաղեր հավելյալ զանգվածի գրավիտացիոն ձգողության շնորհիվ։ Վերջ ի վերջո այդպիսի տիրույթները կդադարեին ընդարձակվել, կոլապսի կենթարկվեին՝ առաջացնելով գալակտիկաներ, աստղեր և մեզ նման էակներ։ Այսպիսով տիեզերքը սկիզբ առած կլիներ համասեռ ու կանոնավոր վիճակից և ժամանակի ընթացքում կդառնար անհամասեռ ու անկանոն։ Այս կերպ կարելի է բացատրել ժամանակի թերմոդինամիկական նետի գոյությունը։ | ||
| + | |||
| + | Սակայն ի՞նչ կպատահեր, երբ տիեզերքը դադարեր ընդարձակվել և սկսեր սեղմվել։ Արդյո՞ք թերմոդինամիկական նետն այդ ընթացքում կփոխի իր ուղղությունը, և ժամանակին զուգընթաց կնվազի անկանոնությունը։ Սա ամեն տեսակի գիտաֆանտաստիկական հնարավորությունների առիթ է կստեղծեր բոլոր նրանց համար, որոնց բախտ կվիճակվեր ապրել ընդարձակումից սեղմանն անցման փուլից հետո։ Կտեսնե՞ն արդյոք նրանք, թե ինչպես են ամբողջանում ջարդուփշուր եղած բաժակներն ու գետնից ցատկում սեղանի վրա։ Գուցե նրանք ի վիճակի՞ կլինեն հիշել վաղվա գները և սակարանում հարստություն կդիզեն։ Անհանգստությունն այն բանի համար, սակայն, թե ինչ կկատարվի, եթե տիեզերքն սկսի կոլապսվել, լոկ գիտական հարց է, քանի որ սեղմում չի լինի դեռ առնվազն մի քանի տասնյակ միլիարդ տարի։ Բայց ավելի շուտ պարզելու համար, թե ինչ է պատահելու, բավական է նետվել սև խոռոչի մեջ։ Սև խոռոչ առաջացնող աստղի կոլապսը շատ նման է ամբողջ տիեզերքի կոլապսի վերջնական վիճակներին։ | ||
| + | |||
| + | Այսպիսով, եթե անկանոնությունը նվազելու է տիեզերքի կծկման փուլում, ապա կարելի է ակնկալել, որ այն կնվազի նաև սև խոռոչի ներսում։ Հետևաբար, սև խոռոչ ընկած տիեզերագնացը կարող է հարստանալ, ռուլետ խաղալով, քանի որ գրազ գալուց առաջ հիշելու է,<ref>Հավանաբար ճիշտ կլինի խոսել ոչ թե ապագան «հիշելու», այլ «տեսնելու» մասին։ Հեղինակը պատահական չի օգտագործում «հիշել» բառը, ցույց տալու համար այդպիսի հնարավորության վիճելի բնույթը։</ref> թե ուր է ընկել գնդակը։ (Դժբախտաբար, խաղը երկար չի տևի, նա խաղի հենց սկզբում սպագետիի նման կերկարի։ Նա ի վիճակի չի լինի մեզ տեղյակ պահել ո՛չ այն մասին, թե թերմոդինամիկական նետը շրջվեց հակառակ ուղղությամբ, ո՛չ էլ կկարողանա իր շահումը վերցնել, որովհետև նա, փաստորեն, դուրս գալու հնարավորություն չի ունենա սև խոռոչի պատահութային հորիզոնի հետևից)։ | ||
| + | |||
| + | Սկզբում ես հավատացած էի, որ կոլապսի հետևանքով տիեզերքի անկանոնությունը նվազելու է, որովհետև մտածում էի, թե երբ տիեզերքը դարձյալ փոքրանա, վերադառնալու է իր նախնական համեստ ու կանոնավոր վիճակին։ | ||
| + | |||
| + | Այսինքն՝ սեղմվելու փուլը նման է լինելու ժամանակի հետընթաց կարգով ընդարձակման փուլին։ Սեղման փուլում կյանքը պետք է ընթանար հակառակ ընթացքով․ մարդիկ ծնվելուց առաջ մեռնելու են, և քանի տիեզերքը փոքրանում է, նրանց տարիքը պիտի նվազի։<ref>Այսպիսի եզրակացությունը ոչ միայն անիմաստ է, այլ ցույց է տալիս, որ մաթեմատիկական եզրակացությունների հետ պետք է զգույշ վարվել։ Այսինքն՝ կարևորը մոդելն է, ոչ թե մաթեմատիկան։</ref> | ||
| + | |||
| + | Այս գաղափարը հրապուրիչ է այնքանով, որ ծնում է ընդարձակման և սեղմման փուլերի գեղեցիկ համաչափություն։ Սակայն դա հենց այնպես չի կարելի ընդունել՝ առանց հաշվի առնելու տիեզերքի մասին այլ պատկերացումները։ Հարց է առաջանում՝ այդ գաղափարը հետևում է տիեզերքի անսահմանության պայմանի՞ց, թե՞ ընդհակառակը, հակասում է դրան։ Ինչպես ասացի, սկզբում ես կարծում էի, թե անսահմանության պայմանն իսկապես նշանակում է, որ անկանոնությունը պիտի նվազի, երբ տիեզերքը սկսի սեղմվել։ Իսկ սխալը մասամբ բխում էր տիեզերքը երկրի մակերևույթի հետ նույնացնելուց։ Եթե ընդունենք, որ տիեզերքի սկիզբը համապատասխանում է հյուսիսային բևեռին, ապա տիեզերքի վերջը պետք է նման լինի իր սկզբին, քանի որ հարավային բևեռը նման է հյուսիսային բևեռին։ Սակայն հյուսիսային և հարավային բևեռները կեղծ ժամանակում համապատասխանում են տիեզերքի սկզբին և վերջին։ Իրական ժամանակում սկիզբն ու վերջը կարող են շատ տարբեր լինել միմյանցից։ Սխալս պայմանավորված էր նաև նրանով, որ աշխատանքիս համար օգտագործել էի մի պարզ մոդել, որում սեղմման փուլը նման էր ժամանակի հետընթաց կարգով ընդարձակմանը։ Պեննի պետական համալսարանի իմ գործընկեր Դոն Փեյջն իմ ուշադրությունը հրավիրեց այն բանի վրա, որ սահման չունենալու պայմանը բոլորովին էլ չի պահանջում, որ սեղմվող փուլը անպայման լինի ժամանակի հետընթաց կարգով ընդարձակման փուլ։ | ||
| + | |||
| + | Հետագայում իմ ուսանող Ռեյմոնդ Լաֆլեմը ցույց տվեց, որ եթե ավելի բարդ մոդել օգտագործվի, ապա տիեզերքի կոլապսը շատ տարբեր կլինի իր ընդարձակումից։ | ||
| + | |||
| + | Ակնհայտ էր, որ ես սխալվել էի․ անսահմանության պայմանը ենթադրում է, որ անկանոնությունը շարունակվելու է մեծանալ սեղմմանը զուգընթաց։ Ժամանակի թերմոդինամիկական և հոգեբանական նետերը չեն փոխում իրենց ուղղությունը՝ ոչ կծկվող տիեզերքում, ոչ էլ սև խոռոչում։ | ||
| + | |||
| + | Ի՞նչ կարելի է անել, երբ պարզվում է, որ այդպիսի սխալ է թույլ տրվել։ Ոմանք երբեք իրենց սխալը չեն ընդունում և շարունակում են փնտրել նոր բացատրությունները, հաճախ միմյանց հակասող, իրենց տեսակետները հաստատող փաստարկներ բերում, ինչպես, օրինակ, Էդինգտոնն արեց՝ հակադրվելով սև խոռոչների տեսությանը։ Ուրիշները հայտարարում են, թե իրենք երբեք սխալ տեսակետը չեն պաշտպանել և, եթե պաշտպանել են, ապա միայն այն պատճառով, որպեսզի ցույց տան նրա անհիմն լինելը։ Իմ կարծիքով, ավելի ճիշտ է, և նվազ շփոթ է առաջանում, եթե մարդ գրավոր կերպով ընդունում է իր սխալը։ Սրա լավագույն օրինակը տվել է Էյնշտեյնը, որն իր կյանքի մեծագույն սխալը համարեց տիեզերքի համար ստատիկ մոդել ստեղծելիս իր ներմուծած տիեզերաբանական հաստատունը։ | ||
| + | |||
| + | Վերադառնալով ժամանակի նետի հարցին՝ մնում է բացատրել, թե ինչո՞ւ են մեր դիտարկումները հաստատում, որ թերմոդինամիկական և տիեզերաբանական նետերը նույն ուղղությունն ունեն։ Կամ, այլ կերպ ասած, ինչո՞ւ է ժամանակին զուգընթաց անկանոնությունն աճում այն ուղղությամբ, որով ընդարձակվում է տիեզերքը։ Եթե ենթադրենք, որ տիեզերքն ընդարձակվելուց հետո կսկսի վերստին կծկվել, ապա, ինչպես հետևում է ամսահմանության պայմանից, թվում է, նետերի ուղղության խնդիրը հանգում է այն հարցին, թե մենք ինչո՞ւ պիտի գտնվենք տիեզերքի ընդարձակման և ոչ թե սեմման փուլում։ | ||
| + | |||
| + | Սրա պատասխանը կարելի է տալ՝ հենվելով թույլ մարդաբանական սկզբունքի վրա․ սեղմման փուլի պայմաններն անբարենպաստ են այնպիսի բանական էակների գոյության համար, որոնք հարցնեին, թե ինչո՞ւ է անկանոնությունն աճում ժամանակի նույն ուղղությամբ, ինչ ուղղությամբ ընդարձակվում է տիեզերքը։ Ամսահմանության պայմանը կանխագուշակում է տիեզերքի հարաճուն ընդարձակում նրա էվոլյուցիայի սկզբնական փուլերում։ Դա նշանակում է, որ տիեզերքը պետք է ընդարձակվի կրիտիկականին շատ մոտ արագությամբ, որպեսզի ընդհանրապես խուսափի կոլապսից կամ երկար ժամաակ կոլապսի չենթարկվի։ Մինչ այդ արդեն բոլոր աստղերը վառված և վերջացած կլինեն, իսկ նրանց առաջացրած պրոտոններն ու նեյտրոնները քայքայված և վերածված կլինեն լույսի մասնիկների ու ճառագայթման։ Ժամանակի հստակ որոշված թերմոդինամիկական նետ չէր լինի։ Այդ անկանոնությունն ավելի աճել չէր կարող, որովհետև տիեզերքն արդեն կգտնվեր համարյա լրիվ անկանոն վիճակում։ Սակայն հարկավոր է ուժեղ թերմոդինամիկական նետ, որպեսզի բանական կյանքը գոյություն ունենա։ Գոյատևելու համար մարդիկ պետք է սնունդ օգտագործեն, ինչն իրենից ներկայացնում է էներգիայի կարգավորված ձև, և այն փոխարկեն ջերմության, այսինքն՝ էներգիայի անկանոն ձևի։ Այսպիսով, տիեզերքի սեղմման փուլում որևէ բանական կյանք չի կարող գոյություն ունենալ։ Այսպես կարելի է բացատրել, թե ինչու են մեր դիտարկումները ցույց տալիս, որ թերմոդինամիկական և տիեզերաբանական նետերը նույն ուղղությունն ունեն։ Սխալ կլինի կարծել, թե, իբր, անկանոնությունն աճում է տիեզերքի ընդլայման պատճառով։ Ավելի ճիշտ կլինի ասել, որ այդ ամենի պատճառը անսահմանության պայմանն է։ Հենց դրա պատճառով է աճում անկանոնությունը, և միայն ընդարձակման փուլում են պայմաններ ստեղծվում բանական կյանքի գոյության համար։ | ||
| + | |||
| + | Այս ամենն ի մի բերելով կարելի է ասել, որ գիտության օրենքները տարբերություն չեն դնում ժամանակի առաջընթաց և հետընթաց ուղղությունների միջև։ Սակայն գոյություն ունեն ժամանակի առնվազն երեք նետեր, որոնք իրարից տարբերում են անցյալն ու ապագան։ Դրանք են․ թերմոդինամիկական նետը, որը ժամանակի այն ուղղությունն է, որով մենք հիշում ենք անցյալը, բայց ապագան՝ ոչ, և տիեզերաբանական նետը՝ ժամանակի այն ուղղությունն է, որում տիեզերքն ընդարձակվում է, ոչ թե սեղմվում։ Ես ցույց տվեցի, որ հոգեբանական նետը, ըստ էության, համարժեք է թերմոդինամիկական նետին, այնպես որ, երկու նետն էլ պետք է ունենան նույն ուղղությունը։ Տիեզերքի անսահմանության ենթադրությունից բխում է, որ պետք է գոյություն ունենա հատուկ սահմանված ժամանակի թերմոդինամիկական նետ, որովհետև տիեզերքը պետք է սկիզբ առներ համասեռ ու կանոնավոր վիճակում։ Իսկ թերմոդինամիկական և տիեզերաբանական նետերի ուղղությունների համընկնման պատճառն այն է, որ բանական էակները կարող են գոյություն ունենալ միայն ընդարձակման փուլում։ Սեղմման փուլը նրանց համար բարենպաստ չէ, որովհետև նրանում բացակայում է ժամանակի հատուկ արտահայտված թերմոդինամիկական նետը։ | ||
| + | |||
| + | Տիեզերքը հասկանալու գործում մարդկային առաջադիմության շնորհիվ կարգավորված մի փոքրիկ անկյուն է ստեղծվել տիեզերքի աճող քաոսում։ | ||
| + | |||
| + | Եթե դուք հիշեք այս գրքում եղած բոլոր բառերը, ապա ձեր հիշողությունը կարձանագրի մոտավորապես երկու միլիոն միավոր տարբեր տեղեկություններ, իսկ ձեր ուղեղում կարգուկանոնը կաճի մոտավորապես նույնքան։ Մյուս կողմից, այս գիրքը կարդալիս դուք սննդի ձևով ստացած առնվազն հազար կալորիա կարգավորված էներգիա կփոխանակեք անկանոն էներգիայի՝ ջերմության, որը շրջապատին կհաղորդեք կոնվեկցիայի կամ քրտինք գոլորշիացնելու ձևով։ Դա կբերի տիեզերքի անկանոնության մոտավորապես միլիոն միլիոն միլիոն միլիոն միավորով աճի, որը համապատասխանում է ձեր ուղեղում կարգավորվածության տաս միլիոն միլիոն միլիոն անգամ աճին, իսկ դա կկատարվի այն դեպքում, եթե դուք հիշեք իմ գրքում կարդացած ամեն ինչը։ Հաջորդ գլխում ես կաշխատեմ մինչև կոկորդը անորոշությունների մեջ խրված մեր մտածումներում ինչ֊որ չափով կարգավորվածություն մտցնել, բացատրելով, թե ինչպես են մարդիկ փորձում իրար հարմարեցնել նկարագրածս մասնակի տեսությունները, որոնք ես նկարագրել եմ, որպեսզի ստեղծվի տիեզերքի բացատրությունն ամփոփող մի կատարյալ միասնական տեսություն։<ref>Այնուամենայնիվ, երբեմն հարց է տրվում, թե ի՞նչ է ժամանակը, արդյո՞ք դա մի առեղծված չէ։ Այդ հարցին Ռ․ Ֆեյնմանը պատասխանել է․ «Մենք՝ ֆիզիկոսներս ամեն օր գործ ունենք ժամանակի հետ, բայց մեզ մի հարցրեք, թե ինչ բան է այն։ Շատ դժվար է խոսել այդ մասին»։ Ջ․ Բոսլոն պատմում է, որ ինքը Օստրեն քաղաքի մի սրճարանի պատի վրա կարդացել է հետևյալ մակագրությունը․ «Ժամանակը բնության կողմից ձեռք առնված մի միջոց է, որպեսզի ամեն ինչ միանգամից տեղի չունենա»։ Հոքինգն այստեղ ցույց է տալիս, որ առանց շարժման՝ ժամանակի հասկացությունն անիմաստ է։ Արդարև, ըստ Ջ․ Ուիլերի՝ «տիեզերքը նկարագրելու համար ժամանակը չի կարող եզրափակիչ հանգամանք լինել», քանի որ «այն լոկ մի չափականություն է, ինչպես տարածությունը, և բնության երկրորդական հատկանիշ է»։ Եվ վերջապես, ինչպես Հոքինգն է պնդում, բնության համար միայն մեկ բացարձակ մեծություն կա, դա ժամանակը չէ, այլ լույսի արագության հաստատունությունը։</ref> | ||
| + | |||
| + | |||
| + | ==10== | ||
| + | |||
| + | Ֆիզիկայի միասնականությունը | ||
| + | |||
| + | Ինչպես առաջին գլխում ցույց տրվեց, շատ դժվար է միանգամից կառուցել լրիվ միասնական մի տեսություն, որը ընդգրկի տիեզերքն ամբողջությամբ վերցրած։ Դրա փոխարեն, մենք հաջողությունների ենք հասել մասնակի տեսությունների մշակման մեջ, որոնք նկարագրում են մի շարք որոշակի երևույթներ՝ արհամարհելով այլ գործոններ կամ դրանք արտահայտելով մոտավորապես որոշակի թվերով։ (Քիմիան, օրինակ, թույլ է տալիս հաշվել ատոմների փոխազդեցություններն՝ առանց իմանալու ատոմի միջուկի ներքին կառուցվածքը)։ Այնուամենայնիվ, հույս կա, որ ի վերջո ստեղծվի ամբողջական հետևողական միասնական մի տեսություն, որում ընգրկված կլինեն բոլոր մասնակի տեսությունները որպես մոտավորություններ, և հարկ չի լինի որոշ պայմանական թվեր ներմուծել տեսությունը փաստերին ներդաշնակելու համար։ Այն որոնումները, որոնք տարվում են այդպիսի տեսության ստեղծման ուղղությամբ, հայտնի են որպես «ֆիզիկայի միասնականացում»։ Էյնշտեյնն իր կյանքի վերջին տարիների մեծ մասը նվիրեց այդպիսի միասնական տեսության ստեղծման գործին, բայց հաջողության չհասավ, որովհետև ժամանակները դրա համար չէին հասունացել․ կային գրավիտացիոն և էլեկտրամագնիսական ուժերի մասնակի տեսություններ, սակայն շատ քիչ բան էր հայտնի միջուկային ուժերի մասին։ Դեռ ավելին, Էյնշտեյնը հավատ չընծայեց քվանտային մեխանիկային, չնայած, որ նա ինքը կարևոր դեր է խաղացել դրա զարգացման մեջ։ Ակնհայտ է, որ անորոշության սկզբունքը մեր տիեզերքի հիմնարար առանձնահատկությունն է։ Հետևաբար, ցանկացած հաջող միասնական տեսություն անհրաժեշտորեն պետք է ներառի այդ սկզբունքը։ | ||
| + | |||
| + | Ինչպես հետագայում կտեսնենք, այդպիսի տեսություն գտնելու հեռանկարներն այժմ շատ ավելի մեծ են, որովհետև մենք այժմ ավելի շատ բան գիտենք տիեզերքի մասին։ Բայց պետք է զգուշանանք չափազանց ինքնավստահությունից․ անցյալում սխալ հայտնագործություններ շատ են եղել։ Օրինակ, այս դարասկզբին կարծում էին, թե ամեն ինչ կարելի է բացատրել շարունակական, հարափոփոխ նյութի հատկությունների օգնությամբ, ինչպիսիք են առաձգականությունն ու ջերմահաղորդականությունը։ Ատոմի կառույցի և անորոշության սկզբունքի հայտնագործությունը մեկընդմիշտ վերջ տվեցին դրան։ Հետո դարձյալ 1928֊ին ֆիզիկոս և նոբելյան մրցանակակիր Մաքս Բորնը Գյոթինգենի համալսարանում մի խումբ այցելուների ասաց, թե «ֆիզիկան այնպես, ինչպես մենք այն գիտենք, վեց ամիս հետո չի լինի այլևս»։ Ինքնավստահության հիմքն այն էր, որ Դիրակն այդ օրերին հայտնագործել էր մի հավասարում, որը նկարագրում էր էլեկտրոնի վարքը։ Այն կարծիքն էր տարածված, թե նմանօրինակ մի հավասարում էլ պիտի լինի պրոտոնի համար, որն այն ժամանակ հայտնի մյուս մասնիկն էր, և ահա տեսական ֆիզիկան կկործանվի։ Սակայն նեյտրոնի և միջուկային ուժերի հայտնագործությունը դրա գլխին էլ տվեց։ Այս բոլորն ասելով՝ ես դեռևս հավատում եմ, որ զգուշավոր լավատեսության հիմքեր կան հուսալու, որ մեր որոնումները մոտենում են վերջակետին՝ բնության վերջնական օրենքներին հասնելու գործում։ | ||
| + | |||
| + | Նախորդ գլուխներում ես նկարագրել եմ ընդհանուր հարաբերականությունը, գրավիտացիոն մասնակի տեսությունը և այն մասնակի տեսությունները, որոնք բնորոշում են թույլ, ուժեղ և էլեկտրամագնիսական ուժերը։ Վերջին երեք ուժերը կարելի է միավորել, այսպես ասած, մեծ միասնական տեսությունների՝ ՄՄՏ֊ի մեջ։ Պետք է ասել, որ այս միասնական տեսությունները թերի են, որովհետև գրավիտացիան չեն ընդգրկում և պարունակում են այնպիսի մեծություններ, ինչպիսիք են տարբեր մասնիկների հարաբերական զանգվածները, որոնք տեսությունից չեն բխում, այլ ընտրվում են դիտարկումներին համապատասխան։ Մյուս ուժերի հետ գրավիտացիայի միավորման տեսության ստեղծումը հիմնականում դժվարանում է այն պատճառով, որ ընդհանուր հարաբերականության տեսությունը «դասական» մի տեսություն է, այսինքն չի ընդգրկում քվանտային մեխանիկայի անորոշության սկզբունքը։ Մյուս կողմից, մնացած մասնակի տեսությունները հիմնականում կախված են քվանտային մեխանիկայից։ Հետևաբար առաջին անհրաժեշտ քայլն ընդհանուր հարաբերականության և քվանտային մեխանիկայի միավորումն է։ Ինչպես մենք արդեն տեսանք, այդպիսի միավորումը կարող է որոշ հատկանշական հետևանքներ առաջացնել, ինչպես այն, որ սև խոռոչներն այնքան էլ սև չեն, ճառագայթում են<ref>Դա այսօր հայտնի է որպես հոքինգյան ճառագայթում</ref> և այն, որ տիեզերքը եզակիություններ չունի, բայց լրիվ ինքնապարփակ է և անսահման։ Դժվարությունն այն է, ինչպես բացատրվել է 7֊րդ գլխում, որ անորոշության սկզբունքը նշանակում է, որ նույնիսկ «դատարկ» տարածությունը լցված է վիրտուալ մասնիկների և հակամասնիկների զույգերով։ Այս զույգերը պետք է անսահման քանակի էներգիա ունենան, հետևաբար, Էյնշտեյնի հայտնի E=mc² հավասարման համաձայն՝ անսահման քանակի զանգված։ Նրանց գրավիտացիոն ձգողությունը պետք է որ տիեզերքը կծկի և անսահման փոքրացնի։ | ||
| + | |||
| + | Համարյա համանման, անհեթեթ թվացող անսահմանություններ են առաջանում մյուս մասնակի տեսություններում, բայց այս բոլոր պարագաներում անսահմանությունները կարող են վերացվել վերանորմալացում կոչվող եղանակի օգնությամբ։ Դրա էությունն այն է, որ անսահմանությունները վերացվում են այլ անսահամնություններ ներմուծելով։ Թեև այս եղանակը մաթեմատիկորեն բավական կասկածելի է, բայց իրականում թվում է, թե գործում է և, այս տեսությունների հետ օգտագործվելով, թույլ է տալիս այնպիսի կանխագուշակումներ անել, որոնք արտակարգ ճշտությամբ համընկնում են դիտարկումների հետ։ Կատարյալ տեսության մշակման որոնման տեսանկյունից, սակայն, վերանորմալացումը մի լուրջ թերություն ունի, որովհետև նշանակում է, որ զանգվածների և ուժերի ուժգնությունների փաստական արժեքները չի կարելի տեսականորեն կանխագուշակել, այլ պետք է ընտրել դիտարկումներին համապատասխան։ | ||
| + | |||
| + | Անորոշության սկզբունքն ընդհանուր հարաբերականության տեսություն ներմուծելու համար պետք է հարմարեցնել միայն երկու մեծություն՝ գրավիտացիայի ուժգնությունը և տիեզերաբանական հաստատունի արժեքը։ | ||
| + | |||
| + | Սակայն սրանց հարմարեցումը բավարար չէ ազատվելու համար բոլոր անորոշություններից։ Հետևաբար, գործում է մի տեսություն, որի համաձայն, որոշակի մեծություններ, ինչպես, օրինակ, տարածություն֊ժամանակի կորությունը, իսկապես անսահման են, բայց և այնպես այդ մեծությունները<ref>գրավիտացիոն և տիեզերական հաստատունները</ref> կարող են դիտարկվել և չափվել որպես կատարելապես վերջավոր։ Ընդհանուր հարաբերականության տեսության և անորոշության սկզբունքի միավորման հիմնախնդիրը որոշ ժամանակ ի վեր ակնկալվում էր, բայց վերջնականապես հաստատվեց 1972֊ին մանրամասն հաշվարկներով։ Չորս տարի անց առաջարկվեց հնարավոր մի լուծում, որը կոչվում էր «գերգրավիտացիա»։ Դրա էությունը հետևյալն էր․ 2֊սպին ունեցող մասնիկը, որը կոչվում է գրավիտոն և գրավիտացիոն ուժի կրողն է, միավորել 3/2, 1, 1/2 և 0 սպին ունեցող նոր մասնիկների հետ։ Որոշ իմաստով բոլոր այս մասնիկները կարելի է համարել նույն «գերմասնիկի» տարբեր կերպարանքներ, և դրանով 1/2 և 3/2 սպինային նյութական մասնիկները միավորել 0, 1 և 2 սպինային ուժակիր մասնիկների հետ։ 1/2 և 3/2 սպինային վիրտուալ մասնիկ֊հակամասնիկ զույգերը բացասական էներգիա կունենան և այսպիսով կձգտեն ոչնչացնել 2, 1 և 0 սպինային վիրտուալ զույգերի դրական էներգիան։ Դա պետք է բերեր շատ հնարավոր անսահմանությունների վերացման, բայց ակնկալվում էր, որ որոշ թվով անսահմանություններ դեռևս կարող են մնալ։ Սակայն այդպիսի անսահմանությունների որոշման համար պահանջվող հաշվումներն այնքան երկար և դժվարին էին, որ ոչ ոք դրանք չձեռնարկեց։ Նույնիսկ հաշվողական մեքենայով դա կատարելու համար առնվազն չորս տարի կպահանջվեր և հնարավոր է, որ մեկ կամ ավելի սխալներ կատարվեին։ Հետևաբար, պատասխանի ճշտությանը մարդ կարող էր վստահ լինել միայն այն ժամանակ, եթե մեկ ուրիշը հաշվարկումները կրկներ և նույն պատասխանը ստանար, որն այնքան էլ հավանական չէր թվում։ | ||
| + | |||
| + | Հակառակ այս հիմնախնդիրներին և այն փաստին, որ գերգրավիտացիոն տեսությունների մեջ նկատի առնվող մասնիկները չեն համապատասխանում սովորաբար դիտարկված մասնիկներին, գիտնականների մեծամասնությունը այն կարծիքին էր, որ հավանաբար գերգրավիտացիան ֆիզիկայի միասնականացման ճիշտ պատասխանն է։ Մյուս ուժերի հետ գրավիտացիայի միավորման լավագույն ուղին պետք է լիներ դա։ Սակայն 1984֊ին տեղի ունեցավ կարծիքների նշանակալի փոփոխություն ի նպաստ, այսպես կոչված, լարային տեսությունների։ Այս տեսություններում հիմնական առարկաները ոչ թե մասնիկներն են, որոնք տարածության եզակի կետեր են գրավում, այլ բաներ, որոնք երկարություն ունեն, բայց այլ չափումներ չունեն, ինչպես լարի անսահման բարակ շերտ։ Այս լարերը կարող են ծայրեր ունենալ (այսպես ասած, բաց լարեր) կամ ծայրերը իրար միացած լինել փակ օղակի ձևով (փակ լարեր) (նկ․ 10.1 և 10.2)։ Մասնիկը ժամանակի յուրաքանչյուր պահի տարածության մեջ մի կետ է գրավում։ Այսպիսով նրա պատմությունը կարելի է ներկայացնել տարածության֊ժամանակի մեջ որպես գիծ («աշխարհագիծ»)։ Իսկ լարը յուրաքանչյուր պահի տարածության մեջ գիծ է։ Հետևաբար, տարածություն֊ժամանակի մեջ նրա պատմությունը առաջացնում է երկչափանի մակերես, որը կոչվում է աշխարհաթերթ։ (Աշխարհաթերթի վրա որևէ կետ նկարագրվում է երկու թվով․ մեկը բնորոշում է ժամանակը, մյուսը՝ կետի դիրքը լարի վրա)։ Բայց լարի աշխարհաթերթը մի ժապավեն է, որի եզրերը լարի երկու ծայրերի առաջացրած ուղիներն են (նկ․ 10.1)։ Փակ լարի աշխարհաթերթը մի գլան է կամ մի խողովակ (նկ․ 10.2)։ | ||
| + | |||
| + | Խողովակի լայնական կտրվածքը մի շրջան է, որը ցույց է տալիս փակ լարի դիրքը տվյալ որոշակի ժամանակում։ | ||
| + | |||
| + | [[Պատկեր:H10 1 2.svg|thumb]] | ||
| + | |||
| + | Երկու լար կարող են միանալ և առաջացնել մի լար, բաց լարերի դեպքում նրանք միանում են ծայրերով (նկ․10.3), այնինչ փակ լարերի միացումը նման է շալվարի երկու փողքերի միավորմանը (նկ․10.4): Նույն ձևով մի լարը կարող է բաժանվել երկու լարի։ Լարերի տեսության մեջ այն, ինչ նախապես ընդունվում էին որպես մասնիկներ, պատկերացվում են իբրև ալիքներ, որոնք տեղաշարժվում են լարն ի վար, ինչպես տատանվող օդապարիկի լարի ալիքները։ Մի մասնիկի առաքումը կամ կլանումը մեկ այլ մասնիկի կողմից համապատասխանում է լարերի բաժանմանը կամ միավորմանը։ Օրինակ, մասնիկային տեսություններում արևի գրավիտացիոն ուժը երկրի վրա պատկերվում է որպես արևի մեջ գտնվող մի մասնիկի կողմից գրավիտոնի արձակում և նրա կլանումը երկրի մեջ գտնվող մասնիկի կողմից (նկ․ 10.5): Լարային տեսությունում այս գործընթացը համապատասխանում է H֊ի ձև ունեցող մի խողովակի (նկ․ 10.6): Լարային տեսությունն ինչ֊որ չափով նման է խողովակաշինության։ H֊ի երկու ուղղահայաց կողմերը համապատասխանում են արևի և երկրի մեջ գտնվող մասնիկներին, իսկ հորիզոնական կապը համապատասխանում է նրանց միջև տեղափոխվող գրավիտոնին։ | ||
| + | |||
| + | [[Պատկեր:H10 3.svg|thumb]] | ||
| + | |||
| + | Լարային տեսության պատմությունը հետաքրքրական է։ Սկզբում այն ստեղծվեց 1960֊ին՝ ուժեղ ուժերը նկարագրող մի տեսություն գտնելու նպատակով։ Հիմնական գաղափարն այն էր, որ պրոտոնի ու նեյտրոնի նման մասնիկները կարելի է համարել լարի վրայի ալիքներ։ Մասնիկների միջև գործող ուժեղ ուժերը համապատասխանում են լարերի հատվածներին, որոնք իրար են կապում այլ լարի հատվածներ, ինչպես սարդոստյանն է։ Համաձայն այս տեսության, մասնիկների միջև դիտարկված մեծ ուժերը ստանալու համար անհրաժեշտ էր, որպեսզի այդ լարերը լինեն ռետինե կապերի նման՝ օժտված մոտավորապես տասը տոննա ձգման ամրությամբ։ | ||
| + | |||
| + | [[Պատկեր:H10 4.svg|thumb]] | ||
| + | |||
| + | 1974֊ին Ջոյլ Շերկը՝ Փարիզից և Ջոն Շվարցը՝ Կալիֆոռնիայի տեխնոլոգիական ինստիտուտից, մի հոդված հրատարակեցին այն մասին, որ լարային տեսությունը կարող է նկարագրել գրավիտացիոն ուժը, եթե միայն լարերում լարվածությունը շատ ավելի մեծ լինի, մոտավորապես հազար միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն տոննա (39 զերո մեկից հետո)։ Լարային տեսության կանխագուշակումները չեն տարբերվում ընդհանուր հարաբերականության տեսության կանխագուշակումներից սովորական հեռավորությունների համար, սակայն կտարբերվեն չափազանց փոքր տարածությունների՝ սանտիմետրի մեկ հազար միլիոն միլիոն միլիոն միլիոն միլիոներորդի համար (սանտիմետրը բաժանած 1֊ից հետո 30 զերոներով թվի)։ Նրանց աշխատությունը մեծ ուշադրության չարժանացավ, որովհետև հենց այդ ժամանակ շատերը հրաժարվեցին սկզբնական ուժեղ ուժի լարային տեսությունից՝ հօգուտ քվարկների ու գլյուոնների վրա հիմնված տեսության, որը թվում էր ավելի լավ է համընկնում փորձնական տվյալների հետ։ Շերկը մահացավ ողբերգական մահով (նա տառապում էր շաքարախտով, և կոմայի պահին նրա մոտ ոչ ոք չէր եղել, որպեսզի ինսուլին սրսկեր)։ Այսպիսով, Շվարցը մնաց միակ պաշտպանը լարային տեսության, որը, սակայն, լարի լարվածության համար շատ բարձր արժեք էր առաջարկում։ | ||
| + | |||
| + | [[Պատկեր:H10 6.svg|thumb]] | ||
| + | |||
| + | 1984֊ին լարերի նկատմամբ հետաքրքրությունը միանգամից աճեց հավանաբար երկու պատճառով։ Մեկն այն էր, որ գերգրավիտացիայի վերջավոր լինելու մասին տեսակետի առաջխաղացումը իրականում զգալի չէր և չէր բացատրում մեր դիտարկած մասնիկների որպիսությունը։ Մյուս պատճառն այն էր, որ Ջոն Շվարցը և Լոնդոնի Քուին Մերի քոլեջից Մայք Գրինը մի հոդվածում ցույց տվին, որ լարային տեսությունն ի վիճակի կլինի բացատրել ձախամետ ներքին կառուցվածք ունեցող մասնիկների գոյությունը՝ նման մեր դիտարկած մի քանի մասնիկների գոյությանը։ Ինչևէ, մեծ թվով գիտնականներ շուտով սկսեցին զբաղվել լարային տեսությամբ, և մի նոր տարբերակ առաջացավ, այսպես կոչված, տարատեսակ լար (heterotic), որը, թվում էր, ի վիճակի կլինի բացատրել մեր դիտարկած մասնիկների տեսակները։ | ||
| + | |||
| + | [[Պատկեր:H10 7.svg|thumb]] | ||
| + | |||
| + | Լարային տեսությունները նույնպես առաջացնում են անսահմանություններ, բայց այն կարծիքը կա, որ անսահմանությունները իրար կչեզոքացնեն տարատեսակ լարերի դեպքում (թեև այս բանը վերջնականապես ստույգ չէ)։ Սակայն լարային տեսություններն ավելի մեծ պրոբլեմ ունեն․ դրանք, թվում է, ամուր դիրքեր կունենան միայն այն դեպքում, եթե տարածություն֊ժամանակը լինի տասը կամ քսանվեց չափանի՝ սովորական չորսի փոխարեն։ Տարածություն֊ժամանակի բազմաչափություններն, իհարկե, գիտական վիպագրության մեջ սովորական բան են։ Արդարև, դրանք համարյա պարտադիր են, որովհետև, այլապես այն փաստը, թե հարաբերականությունը նշանակում է, որ մարդը լույսից արագ չի կարող շարժվել, նշանակում է, որ շատ երկար ժամանակ կպահանջվի, որպեսզի նա ճամփորդի աստղերի ու գալակտիկաների միջև։ Գիտական֊գեղարվեստական գաղափարն այն է, որ թերևս բարձր չափականության միջով մարդուն հաջողվի մի կարճ ճանապարհ գտնել։ Այս բանը կարելի է պատկերել հետևյալ կերպ։ Պատկերացնենք, թե մեր ապրած տարածությունը երկչափանի է և կորացած է ինչպես փրկողակը կամ տորը (նկ․ 10.7): Եթե դուք գտնվում եք օղակի ներսակողմի մի տեղում և ցանկանում եք գնալ մեկ այլ տեղ, ապա պետք է օղակի ներսակողմը շրջանցեք։ Սակայն եթե ձեզ տրվի եռաչափ ճամփորդության հնարավորություն, ապա դուք ուղիղ գծով կանցնեք այդ ճանապարհը։ | ||
| + | |||
| + | Այդ ինչպե՞ս է պատահում, որ մենք հավելյալ չափականությունները չենք տեսնում, եթե դրանք իրոք կան։ Մենք ինչո՞ւ ենք տարածության՝ երեք և ժամանակի մեկ չափականություն տեսնում։ Ենթադրվում է, որ մյուս չափականությունները կորացած են փոքր չափսերով մի տարածության մեջ՝ մոտավորապես մեկ սանտիմետրի չորս հարյուր հազար միլիոն միլիոն միլիոն միլիոներորդի մեծությամբ։ Դա այնքան փոքր է, որ մենք այն չենք նշմարում և տեսնում ենք ժամանակի լոկ մեկ և տարածության երեք չափականություններ, որում տարածություն֊ժամանակը բավականին հարթ է։ Այն նման է նարնջի մակերևույթի, որը եթե մոտիկից դիտեք՝ կորագծերով և խորշոմներով լեցուն է, բայց եթե հեռվից նայեք, ապա խորդուբորդությունները չեն երևա, ամեն ինչ թվում է հարթ։ Այսպիսին է նաև տարածություն֊ժամանակը․ փոքր մասշտաբով այն տասը չափանի է և շատ կորացած, բայց ավելի մեծ մասշտաբներով կորացումն ու լրացուցիչ չափումները չեն երևում։ Եթե այս պատկերացումը ճիշտ է, ապագա տիեզերական ճամփորդների համար դա վատ է․ հավելյալ չափականություններն այնքան փոքր կլինեն, որ թույլ չեն տա, որպեսզի տիեզերանավերը դրանցով անցնեն։ Սակայն մեկ այլ գլխավոր հիմնախնդիր է ծագում․ ինչո՞ւ պիտի չափումների որոշ մասը, այլ ոչ բոլորը ոլորված լինեն մի փոքրիկ գնդի մեջ։ Վաղ տիեզերքում հավանաբար բոլոր այդ չափումները պետք է որ ոլորված լինեն։ Ինչո՞ւ են ընդամենը ժամանակի մեկ չափում և տարածության երեք չափում հարթվել, երբ մյուս բոլոր չափումները մնացել են սեղմորեն ոլորված։ | ||
| + | |||
| + | [[Պատկեր:H10 8.svg|thumb]] | ||
| + | |||
| + | Դրա հնարավոր պատասխաններից մեկը մարդաբանական սկզբունքն է։ Ըստ դրա, երկու տարածական չափումները բավարար չեն, որպեսզի մեզ նման բարդ էակներ զարգանան։ Օրինակի համար, միաչափ երկրում ապրող երկչափ կենդանիները միմյանցից առաջ անցնելու համար պետք է իրար վրա մագլցեն։ Եթե երկչափանի արարածն ինչ֊որ բան ուտի, ապա լրիվ մարսել չի կարողանա, այն կուլ տվածի նման հետ կտա, որովհետև եթե նրա մարմնի միջով մի անընդմեջ ուղի անցնի, ապա դա կենդանուն կբաժանի երկու մասի, և երկչափանի կենդանին կտրոհվի (նկ․ 10.8): Նույն ձևով դժվար է պատկերացնել, թե ինչպես կարող է կատարվել երկչափանի արարածի արյան շրջանառությունը։ | ||
| + | |||
| + | Խնդիրներ են ծագում նաև երեքից ավելի չափումների դեպքում։ Երկու մարմինների միջև գործող գրավիտացիոն ուժը հեռավորության աճին զուգընթաց ավելի արագ կնվազի, քան դա տեղի կունենա եռաչափ պայմաններում (Եռաչափ տարածությունում գրավիտացիոն ուժը նվազում է 1/4֊ով, երբ հեռավորությունը կրկնապատկվում է։ Քառաչափում այն կնվազի 1/6֊ով, հնգաչափում՝ 1/16֊ով և այլն)։ Սա նշանակում է, որ երկրի նման մոլորակների ուղեծիրներն արևի շուրջ անկայուն կլինեն․ շրջանաձև ուղեծրից նվազագույն շեղումը (որը կառաջացնի այլ մոլորակների գրավիտացիոն ձգողությունը) կարող է բերել այն բանին, որ երկիրն ընկնի արևի վրա կամ արևից հեռանա պարուրաձև հետագծով։ Մենք կամ կսառչենք և կամ կվառվենք։ Փաստորեն, երեքից ավելի տարածական չափումների պայմաններում գրավիտացիայի այդպիսի փոփոխությունն ըստ հեռավորության նշանակում է, որ արևը ճնշման ու գրավիտացիայի հավասարակշռության պայմաններում կայուն վիճակում գոյություն ունենալ չի կարող։ Այն կամ պիտի կտոր֊կտոր լինի կամ կոլապսվի և վերածվի սև խոռոչի։ Երկու դեպքում էլ երկրի վրա կյանքի գոյության համար ջերմության և լույսի աղբյուր լինել չի կարող։ Նույնը տեղի կունենա նաև փոքր մասշտաբների վրա։ Էլեկտրական ուժերը, որոնք պայմանավորում են էլեկտրոնների պտույտը ատոմի միջուկի շուրջ, իրենց պահում են ինչպես գրավիտացիոն ուժերը։ Ուստի այդ պայմաններում էլեկտրոնները կամ ատոմից ընդհանրապես կհեռանան և կամ պարուրաձև կպտտվեն և կընկնեն միջուկի վրա։ Երկու դեպքում էլ ատոմները գոյություն չեն ունենա այն ձևով, ինչպես մենք գիտենք։ | ||
| + | |||
| + | Ուրեմն պարզ է, որ կյանքն առնվազն այնպես, ինչպես մենք այն ճանաչում ենք, կարող է գոյություն ունենալ տարածություն֊ժամանակի այնպիսի տիրույթներում, որտեղ ժամանակի մեկ չափումն ու տարածության երեք չափումը կծկված չեն լինի փոքրիկ կետում։ Սա նշանակում է, որ մարդ կարող է դիմել թույլ մարդաբանական սկզբունքին․ բավական է, որպեսզի ցույց տրվի, որ լարային տեսությունն առնվազն հնարավոր է համարում տիեզերքում այդպիսի տիրույթների գոյությունը։ Եվ իրոք, թվում է, թե լարային տեսությունը այդպիսի հնարավորություն ընձեռում է։ Բացառված չէ, որ տիեզերքում այլ տիրույթներ լինեն, կամ այլ տիեզերքներ գոյություն ունենան (ինչ էլ որ դրանք լինեն), որտեղ բոլոր չափումները կծկված լինեն փոքրիկ կետում, և կամ չորս չափումները համարյա հարթ լինեն, սակայն այդպիսի տիրույթներում բանական էակներ չեն կարող լինել, որպեսզի փաստացի չափումների տարբեր թվերը դիտարկեն։ | ||
| + | |||
| + | Բացի տարածություն ժամանակի չափականությունների թվի հարցից, պետք է լուծվեն դեռ բազմաթիվ այլ խնդիրներ, որպեսզի լարային տեսությունը հավանության արժանանա որպես ֆիզիկայի միասնական վերջնական տեսություն։ Մենք դեռևս չգիտենք, թե իրոք բոլոր անսահմանություններն են չեզոքացնում կեմը մյուսին, կամ թե լարի ալիքներն ինչպես են կապվում այն առանձին մասնիկների հետ, որոնք մենք դիտարկում ենք։ Այնուամենայնիվ, հնարավոր է, որ առաջիկա մի քանի տարվա ընթացքում այս հարցերի պատասխանները գտնվեն, և դարավերջին մենք իմանանք, որ իրոք լարային տեսությունը երկար որոնումների ակնկալած ֆիզիկայի միասնական տեսությունն է։ | ||
| + | |||
| + | Բայց մի՞թե այդպիսի միասնական տեսություն կարող է լինել։ Կամ, թերևս, դա մի պատրանք է։ Երեք հնարավոր տարբերակ կա․ | ||
| + | |||
| + | |||
| + | 1. Իսկապես կա կատարյալ մի միասնական տեսություն, որը մենք մի օր կհայտնաբերենք, եթե բավականաչափ խելացի ենք։ | ||
| + | |||
| + | 2. Տիեզերքի վերջնական տեսություն չկա, այլ կա տեսությունների մի անսահման շարք, և դրանք աստիճանաբար ավելի ճշգրիտ կնկարագրեն տիեզերքը։ | ||
| + | |||
| + | 3. Տիեզերքի տեսություն չկա․ դեպքերը չի կարելի կանխագուշակել, դրանք տեղի են ունենում որոշակի սահմանում պատահականորեն և ինքնակամորեն։ | ||
| + | |||
| + | |||
| + | Կարելի է փաստարկներ բերել հօգուտ երրորդ հնարավորության, պնդելով, որ եթե օրենքների համապարփակ մի շարք լիներ, ապա դա կսահմանափակեր Աստծո միտքը փոխելու և աշխարհի գործերին խառնվելու ազատությունը։ Դա նման է հինավուրց մի պարադոքսի․ Աստված ի վիճակի՞ է արդյոք, այնքան ծանր քար ստեղծել, որ ինքը չկարողանա բարձրացնել։ Բայց, ինչպես նշել է սբ․ Օգոստինոսը, այն գաղափարը, թե Աստված կուզենա իր միտքը փոխել, մոլորության (սոփեստության) մի օրինակ է և արդյունք է այն պատկերացման, թե Աստված ժամանակի ընթացքում գոյություն ունեցող մի էակ է։ Այնինչ ժամանակը Աստծու ստեղծած տիեզերքի մի հատկություն է։ Պետք է կարծել, որ Աստված գիտեր՝ ինչ է ուզում, երբ ստեղծեց տիեզերքը։ | ||
| + | |||
| + | Քվանտային մեխանիկայի ի հայտ գալուց հետո պարզվեց, որ դեպքերը կատարյալ ճշգրտությամբ կանխագուշակել չի կարելի, և միշտ ինչ֊որ չափով անորոշություն կա։ Եթե մարդ ցանկանա, ապա պատահականությունը կարող է համարել Աստծո միջամտություն, բայց դա կլինի միջամտության շատ տարօրինակ մի տեսակ․ ոչ մի փաստ չկա, որ դա որոշակի նպատակ է հետապնդում։ Արդարև, եթե այդպես լիներ, ապա դա պատահական չէր լինի։ Ներկայումս երրորդ հնարավորությունը ընդունել չի կարելի, որովհետև գիտության նպատակը այլ է․ ձևակերպել օրենքների մի այնպիսի շարք, որը թույլ տար կանխագուշակել դեպքերը գոնե անորոշության սկզբունքի սահմաններում։ | ||
| + | |||
| + | Երկրորդ հնարավորությունը, թե գոյություն ունի անսահման թվով առավել մշակված տեսությունների մի հաջորդականություն, շատ լավ համընկնում է մինչև այժմ կատարած մեր դիտարկումների հետ։ Շատ պարագաներում մեր չափումների ճշտության աստիճանը բարձրացրել ենք կամ նորանոր դիտարկումներ ենք կատարել՝ ընդամենը հայտնաբերելու նոր երևույթներ, որոնք գոյություն ունեցող տեսությունների կողմից չեն կանխագուշակվել, և որպեսզի հաշվի առնենք դրանք, ստիպված նոր, ավելի առաջավոր տեսություն ենք մշակել։ Հետևաբար, շատ զարմանալի չէր լինի, եթե ժամանակակից մեծ միասնական տեսությունների սերունդը սխալվեր և պնդեր, թե ըստ էության ոչինչ նոր չի կարող պատահել 100 ԳԵՎ թույլ էլեկտրական միասնական էներգիայի և մոտավորապես հազար միլիոն միլիոն ԳԵՎ միասնական էներգիայի միջակայքում։ Իրոք սպասելի է, որ հայտնաբերվեն բազմաթիվ նոր կառուցվածքային շերտեր, որոնք ավելի հիմնական լինեն, քան քվարկներն ու էլեկտրոնները, որոնց մենք ճանաչում ենք որպես «տարրական մասնիկներ»։ | ||
| + | |||
| + | Այնուամենայնիվ թվում է, թե գրավիտացիան կարող է վերջ դնել «տուփերի մեջ տուփերի» այս հաջորդականությունը։ Վերցնենք մի մասնիկ, որի էներգիան բարձր էր, այսպես կոչված, Պլանկի էներգիայից, այսինքն՝ տասը միլիոն միլիոն միլիոն (1֊ից հետո տասնինը զերո) ԳԵՎ է։ Նրա զանգվածն այն աստիճան խտացած կլինի, որ այդ մասնիկը կանջատվի ողջ տիեզերքից և փոքրիկ մի սև խոռոչ կառաջացնի։ Այստեղից հետևում է, որ մեկը մյուսից առավել կատարելագործված տեսությունների շարքը պետք է վերջ ունենա, երբ գնում ենք առավել բարձր էներգիաների։ Հետևաբար պետք է, որ տիեզերքի համար մի վերջնական տեսություն գոյություն ունենա։ Իհարկե, Պլանկի էներգիան չափազանց հեռու է հարյուրավոր ԳԷՎ֊ից, որն այն առավելագույնն է, ինչ այսօր մենք կարող ենք ստանալ լաբորատորիայում։ Մոտավոր ապագայում մասնիկային արագացուցիչների օգնությամբ այս անջրպետը չենք կարող հաղթահարել։ Սակայն տիեզերքի վաղ փուլերում կար մի վիճակ, երբ այդպիսի էներգիաներ եղել են։ Ես մտածում եմ, որ վաղ տիեզերքի ուսումնասիրությունը և մաթեմատիկական հետևողականությունը հնարավորություն կստեղծեն, որպեսզի մեզանից ոմանք կարողանան լրիվ միասնական մի տեսություն ստեղծել, պայմանով, որ մինչ այդ մենք մեզ չենք կործանի։ | ||
| + | |||
| + | Եթե մենք իրոք հայտնաբերենք տիեզերքի վերջնական տեսությունը, ապա ի՞նչ նշանակություն կունենա դա։ Ինչպես առաջին գլխում ենք բացատրել, մենք երբեք լիովին վստահ չենք կարող լինել, թե իսկապես գտել ենք ճիշտ տեսությունը, որովհետև դա հնարավոր չէ ապացուցել։ Սակայն եթե տեսությունը մաթեմատիկորեն հետևողական է և միշտ այնպիսի կանխագուշակումներ է անում, որոնք համապատասխանում են դիտարկումներին, ապա կարելի է վստահ լինել, որ դա ճիշտ է։ Այսպիսով, տիեզերքն ընբռնելու համար մարդկության մտավոր պայքարի պատմության երկար ու փառավոր գլուխը կավարտվի։ Միևնույն ժամանակ կհեղաշրջվի մեր իմացությունը տիեզերքը կառավարող օրենքների մասին։ Նյուտոնի ժամանակներում զարգացած մի մարդու համար բավարար էր, որ նա առնվազն ընդհանուր գծերով պատկերացում ունենար մարդկային ամբողջ մտավոր զարգացման մասին։ Բայց դրանից հետո գիտության զարգացումն այն դարձրեց անհնարին։ Սրա պատճառն այն է, որ տեսությունները միշտ փոխվում են, որպեսզի համապատասխանեն նոր դիտարկումներին, երբեք անհրաժեշտ չափով յուրացված կամ պարզեցված չեն լինում և անհասկանալի են մնում շատերի համար։ Պետք է, որ դուք մասնագիտանաք և միայն այդ ժամանակ կարող եք հուսալ ճշգրտորեն ըմբռնել գիտական տեսությունների փոքր մասը։ Դեռ ավելին, առաջընթացն այնպես արագ է տեղի ունենում, որ դպրոցում կամ համալսարանում մատուցվող գիտելիքները փոքր֊ինչ հնացած են։ Լոկ փոքր թվով մարդիկ կարող են արագորեն փոփոխվող գիտության առաջընթացին հետևել և հարկ կլինի իրենց ամբողջ ժամանակը նվիրել դրան ու մասնագիտանալ շատ նեղ բնագավառում։ Մարդկանց մյուս մասը քիչ բան գիտի գիտության առաջընթացի և դրա առաջացրած ոգևորության մասին։ Յոթանասուն տարի առաջ, եթե հավատանք Էդինգտոնի խոսքերին, լոկ երկու հոգի էին հասկանում հարաբերականության ընդհանուր տեսությունը։<ref>Դա, իհարկե ճիշտ չէ։ 1920֊ական թվականներին արդեն մեծ թվով գրքեր են հրատարակվել այդ և հարակից հարցերի մասին՝ դեռ չխոսելով առանձին աշխատանքների մասին։</ref> | ||
| + | |||
| + | Այսօր տասնյակ հազարավոր համալսարանականներ հասկանում են այն, և միլիոնավոր մարդիկ առնվազն ծանոթ են հիմնական գաղափարներին։ Եթե կատարյալ միասնական մի տեսություն հայտնագործվի, կպահանջվի որոշ ժամանակ, որպեսզի այն այնպես յուրացվի և պարզեցվի, որ գոնե ընդհանուր գծերով մտնի դպրոցական ծրագրի մեջ։ Այդ ժամանակ մենք բոլորս ի վիճակի կլինենք ինչ֊որ չափով ըմբռնել այն օրենքները, որոնք կառավարում են տիեզերքն ու պայմանավորում են մեր գոյությունը։ | ||
| + | |||
| + | Բայց եթե մենք նույնիսկ հայտնագործենք կատարելապես միասնական մի տեսություն, ապա դա չի կարող նշանակել, թե մեզ կհաջողվի ընդհանրապես դեպքերը կանխագուշակել հետևյալ երկու պատճառով։ Առաջինն այն է, որ քվանտային մեխանիկայի անորոշության սկզբունքը սահմանափակում է մեր կանխագուշակումները։ Մենք ոչինչ չենք կարող անել այդ հարցը շրջանցելու համար։ Իրականում, սակայն, այս առաջին սահմանափակումը նվազ արգելակող է, քան երկրորդը։ Դրա պատճառն այն է, որ տեսության հավասարումները մենք ճշգրտորեն չենք կարող լուծել, բացառությամբ շատ պարզ վիճակների հավասարումներից։ Մենք նույնիսկ երեք մարմինների շարժումը չենք կարող լուծել ճշգրտորեն՝ օգտվելով Նյուտոնի ձգողականության տեսությունից։ Սակայն դժվարություններն աճում են, երբ մարմինների թիվը մեծանում է, իսկ տեսությունն ավելի է բարդանում։ Մենք արդեն գիտենք նյութի վարքը նկարագրող այն օրենքները, որոնք ծայրահեղ դեպքերից բացի գործում են բոլոր պայմաններում։ Մասնավորապես, մենք գիտենք քիմիայի և կենսաբանության հիմնական օրենքները։ | ||
| + | |||
| + | Իհարկե, մենք չենք կարող այս բնագավառներին լուծված հարցի կարգավիճակ տալ․ մաթեմատիկական հավասարումների օգնությամբ մարդու կյանքը կանխագուշակելու փորձերը հաջողությամբ դեռ չեն պսակվել։ | ||
| + | |||
| + | Այսպիսով, նույնիսկ եթե մենք հիմնական օրենքների ամբողջական մի շարք գտնենք, ապա առաջիկա տարիների ընթացքում մարդկությունը կանգնած կլինի մտավոր կարևոր մի խնդրի առջև, այն է՝ լավագույն մոտավոր մեթոդներ մշակել, որպեսզի հնարավոր լինի բարդ ու իրական վիճակների հավանական ելքերի օգտակար կանխագուշակումներ կատարել։ Լրիվ հետևողական միասնական տեսությունը լոկ առաջին քայլն է․ մեր նպատակն է կատարելապես հասկանալ մեր շուրջ տեղի ունեցող դեպքերն ու հենց մեր սեփական գոյությունը։ | ||
| + | |||
| + | |||
| + | ==11== | ||
| + | |||
| + | Եզրակացություն | ||
| + | |||
| + | Մենք գտնվում ենք ապշեցնող աշխարհում։ Ցանկանում ենք շրջապատում տեսածն իմաստավորել և հարցնել․ ի՞նչն է տիեզերքի էությունը։ Ո՞րն է մեր տեղը նրանում, և որտեղի՞ց ենք նաև մենք գալիս։ Եվ ինչո՞ւ է այն այնպես, ինչպես որ է։ | ||
| + | |||
| + | Որպեսզի փորձենք պատասխանել այս հարցերին, ընդունում ենք «աշխարհի ինչ֊որ պատկեր»։ Հենց այդպիսի պատկեր է կրիաների անսահման աշտարակը, որն իր վրա է կրում հարթ երկիրը, այդպիսին է գերկապերի տեսությունը։ Երկուսն էլ տիեզերքի տեսություններ են, թեև վերջինը մաթեմատիկորեն ավելի ճշգրիտ է, քան առաջինը։ Երկու տեսություններն էլ չունեն բավականաչափ ապացույց, ոչ ոք երբեք չի տեսել հսկա կրիային՝ երկիրը մեջքին, ինչպես նաև ոչ ոք չի տեսել գերկապային երկիրը։ Այնուամենայնիվ, կրիաների տեսությունը չի բավարարում հիմնավորված գիտական տեսության պահանջներին, քանի որ այն կանխագուշակում էր, որ մարդիկ կարող էին դուրս ընկնել՝ աշխարհի եզրին հասնելով։ Սա չի համապատասխանում մարդկային փորձին, բացառությամբ, եթե միայն սրանով բացատրենք մարդկանց թվացյալ անհետացումը Բերմուդյան եռանկյունում։ | ||
| + | |||
| + | Տիեզերքը տեսականորեն նկարագրելու և բացատրելու ամենավաղ փորձերը հիմնված էին այն պատկերացման վրա, որ բնական երևույթներն ու դեպքերը ղեկավարվում էին ոգիներով, որոնք օժտված են մարդկային զգացումներով և որոնք գործում են շատ մարդանման ու անկանխատեսելի ձևով։ Այս ոգիներն ապրում էին բնության այնպիսի վայրերում, ինչպիսիք են գետերը, սարերը, ինչպես նաև երկնային մարմիններ արևն ու լուսինը։ Նրանց պետք էր սիրաշահել, որպեսզի ապահովվեր հողի բերիությունը և տարվա եղանակների հաջորդականությունը։ Այնուամենայնիվ, աստիճանաբար նկատվել էր որոշ երևույթների կանոնավոր կրկնությունը․ արևը միշտ ծագում է արևելքում և մայր մտնում արևմուտքում, անկախ այն բանից, թե արևի աստծուն զոհաբերություն եղել է, թե ոչ։ Դեռ ավելին, արևը, լուսինը և մոլորակները երկնքում շարժվում են որոշակի ուղեծրերով, որոնք հնարավոր էր բավականաչափ ճշգրտությամբ կանխագուշակել։ Արևն ու լուսինը դեռևս կարող էին համարվել աստվածներ, բայց դրանք խիստ օրենքների ենթարկվող աստվածներ էին, ըստ երևույթին, առանց որևէ բացառության, եթե հաշվի չառնենք Հեսուի կողմից արևի կանգնեցման պատմությունները։ | ||
| + | |||
| + | Սկզբում այս կանոններն ու օրենքները բացահայտ էին միայն աստղագիտության մեջ և մի քանի այլ դեպքերում։ Սակայն քաղաքակրթության զարգացման հետևանքով, հատկապես վերջին 300 տարվա ընթացքում, ավելի ու ավելի կանոններ և օրենքներ հայտնաբերվեցին։ Այս օրենքների հաջողությունը XIX դարի սկզբին Լապլասին ներշնչեց սահմանելու գիտական որոշադրության (դետերմինիզմի) հիմնադրույթը, այսինքն, նա առաջարկեց, որ պետք է լինի օրենքների մի խումբ, որով ճշգրտորեն որոշվի տիեզերքի էվոլյուցիան, երբ տրված է նրա կոնֆիգուրացիան որևէ ժամանակաշրջանի համար։ Լապլասի որոշադրությունը թերի էր երկու տեսակետից։ Այն չէր ասում, թե ինչպես պետք է ընտրվեն օրենքներ և չէր հատկորոշում տիեզերքի սկզբնական կոնֆիգուրացիան։ Սրանք թողնված էին Աստծուն։ Աստված պետք է ընտրեր, թե ինչպես է սկիզբ առել տիեզերքը և ինչ օրենքների պետք է այն ենթարկվեր, բայց նա չպետք է միջամտեր տիեզերքի գործերին, երբ այն արդեն սկիզբ էր առել։ Փաստորեն, Աստծո միջամտությունը վերապահվում էր միայն այն ոլորտների համար, որոնք XIX դարի գիտությունը չէր հասկանում։ | ||
| + | |||
| + | Մենք այժմ գիտենք, որ Լապլասի որոշադրության մասին հույսերն անիրականանալի էին, առնվազն այն ձևով, ինչպես ինքն էր մտածում։ Ըստ քվանտային մեխանիկայի անորոշության սկզբունքի, մեծությունների որոշ զույգերից, երկուսն էլ, ինչպես, օրինակ, մասնիկի դիրքն ու արագությունը, հնարավոր չէ լրիվ ճշգրտությամբ կանխագուշակել։ | ||
| + | |||
| + | Քվանտային մեխանիկան այս սահմանափակումից ձերբազատվում է իր մի խումբ քվանտային տեսություններով, որոնցում մասնիկները լավ սահմանված դիրք և արագություն չունեն, այլ ներկայացված են որպես ալիք։ Այդ քվանտային տեսությունները որոշադրական են այն իմաստով, որ նրանք սահմանում են ալիքի էվոլյուցիայի օրենքներ՝ ժամանակից կախված։ Այսպիսով, եթե մարդ գիտի ալիքը ժամանակի մի պահի, նա կարող է հաշվել այն ժամանակի ցանկացած այլ պահի համար։ Չկանխատեսված, պատահական տարր հայտնվում է միայն այն ժամանակ, երբ մենք փորձում ենք ալիքը մեկնաբանել մասնիկի դիրքով ու արագությամբ։ Բայց գուցե սա մեր սխալն է, գուցե գոյություն չունեն մասնիկի դիրքեր ու արագություններ, այլ կան միայն ալիքներ։ Գուցե մենք փորձում ենք ալիքները հարմարեցնել դիրքի և արագության մեջ կանխակալ պատկերացումների հետ։ Իսկ ստացված սխալ համադրությունն անկանխատեսելիության հավանական պատճառն է։ | ||
| + | |||
| + | Գործնականում մենք գիտության նպատակը վերասահմանել ենք որպես այնպիսի օրենքների հայտնաբերում, որոնք անորոշության սկզբունքի սահմաններում հնարավորություն կտան մեզ գուշակել իրադարձությունները։ Այնուամենայնիվ, հարցը մնում է այն, թե ինչպե՞ս կամ ինչո՞ւ էին ընտրվել տիեզերքի օրենքներն ու սկզբնական վիճակը։ | ||
| + | |||
| + | Այս գրքում ես հատուկ ուշադրություն եմ դարձրել այն օրենքներին, որոնք կառավարում են ձգողականությունը, որովհետև հենց ձգողականությամբ է պայմանավորված տիեզերքի մեծածավալ կառուցվածքի ձևավորումը, չնայած այն ամենաթույլն է ուժերի չորս տարատեսակների մեջ։ Ձգողականության օրենքներն անհամատեղելի են մինչև վերջերս գոյություն ունեցող այն տեսակների հետ, որը պնդում էր, որ տիեզերքը ժամանակի մեջ անփոփոխ է։ Այն փաստը, որ գրավիտացիան միշտ ձգողական է, նշանակում է, որ տիեզերքը կամ ընդարձակվում է, կամ կծկվում։ Համաձայն հարաբերականության ընդհանուր տեսության, անցյալում պետք է եղած լինի մի անսահման խիտ վիճակ՝ մեծ պայթյուն, որը պետք է ժամանակի իրական սկիզբը լիներ։ Նմանապես, եթե ամբողջ տիեզերքը կրկին կոլապսի ենթարկվի, ապա պետք է լինի մեկ այլ անսահման խիտ վիճակ ապագայում՝ մեծ ճայթում, որը ժամանակի վերջը կլինի։ Նույնիսկ եթե ամբողջ տիեզերքը վերստին կոլապսի չենթարկվի, որոշ տեղայնացված տիրույթներում կլինեն եզակիություններ, որոնց կոլապսով սև խոռոչներ կառաջանան։ Այս եզրակացությունները ժամանակի վերջը կլինեն սև խոռոչ ընկածների համար։ Մեծ պայթյունի ժամանակ և մյուս եզակիություններում բոլոր օրենքները կկորցնեն իրենց ուժը, այսպիսով Աստված դեռ լիակատար ազատություն ունեցած կլիներ ընտրելու, թե ի՞նչ պետք է կատարվեր, և ինչպե՞ս է տիեզերքը սկիզբ առել։ | ||
| + | |||
| + | Երբ մենք միավորում ենք քվանտային մեխանիկան ընդհանուր հարաբերականության տեսության հետ, թվում է, թե մի նոր հնարավորություն կա, որն առաջ ի հայտ գալ չէր կարող, այն է՝ տարածությունը և ժամանակը միասին կարող են առաջացնել վերջավոր, քառաչափ տիեզերք՝ առանց եզակիությունների և սահմանափակումների, օրինակ, երկրի մակերեսի նման, բայց ավելի մեծ թվով չափականություններով։ Թվում է, թե այս գաղափարը կարող էր բացատրել տիեզերքում դիտված շատ երևույթներ, ինչպես, օրինակ, նրա լայնամասշտաբ միակերպությունն ու փոքրամասշտաբ շեղումները համասեռությունից, ինչպիսիք են գալակտիկաները, աստղերը և նույնիսկ մարդկային էակները։ Սրանով կարելի է բացատրել նաև ժամանակի նետի գոյությունը, որը մենք արդեն ուսումնասիրել ենք։ Բայց եթե տիեզերքն ամբողջապես ինքնապարփակ է, առանց եզակիությունների կամ սահմանների և ամբողջապես նկարագրվում է միասնական տեսությամբ, ապա այս ամենը խոր նշանակություն ունի Աստծո՝ որպես արարչի դերի խնդրում։ | ||
| + | |||
| + | Էյնշտեյնը մեկ անգամ հարցրել է․ «Աստված որքա՞ն ընտրություն ուներ տիեզերքը ստեղծելիս»։ Եթե ամսահմանության տեսակետը ճիշտ էր, ապա նա սկզբնական պայմանները ընտրելու որևէ ազատություն չուներ։ Նա, անկասկած, դեռ ազատ էր ընտրելու այն օրենքները, որոնց ենթարկվում է տիեզերքը։ Սա, այնուամենայնիվ, լիիրավ ընտրություն չի նշանակում, այնտեղ կարող է եղած լիներ միայն մեկ, կամ շատ փոքր թվով ամբողջական միասնական տեսություններ, ինչպես, օրինակ, տարատեսակ լարի տեսությունը, որոնք ինքնաբավ են և թույլ են տալիս այնպիսի բարդ էակների գոյությունը, ինչպիսիք են մարդիկ, որոնք կարող են ուսումնասիրել տիեզերքի օրենքներն ու հարցնել Աստծո էության մասին։ | ||
| + | |||
| + | Նույնիսկ, եթե գոյություն ունի միայն մեկ միասնական տեսություն, ապա այն սոսկ կանոնների և հավասարումների մի խումբ է։ Ուստի հարց է առաջանում․ այն ի՞նչն է, որ իմաստ է տալիս հավասարումներին և տիեզերքը դարձնում է նկարագրելի։ Մաթեմատիկական մոդելներ ստեղծելու գիտության սովորական մոտեցումը չի կարող պատասխանել այն հարցին, թե ինչո՞ւ պետք է լինի տիեզերքի նկարագրելի մոդելը։ Ինչո՞ւ է տիեզերքն այդքան ջանքեր թափում իր գոյությունը պահպանելու համար։ Արդյո՞ք միասնական տեսությունն այդքան գրավիչ է, որ առաջարկում է իր իսկ գոյությունը։ Կամ արդյո՞ք այն Արարչի կարիք ունի, և եթե այդպես է, ապա արդյո՞ք նա ազդեցություն ունի տիեզերքի վրա։ Եվ ո՞վ է նրա Արարիչը։ | ||
| + | |||
| + | Մինչև օրս գիտնականների մեծ մասը շատ տարված է նոր տեսություններ զարգացնելով, որոնք նկարագրում են տիեզերքի որպիսությունը, որպեսզի հետագայում պարզվի ինչո՞ւ հարցը։ Մյուս կողմից մարդիկ, որոնց գործն է հարցնել՝ ինչո՞ւ, այսինքն՝ փիլիսոփաները, ի վիճակի չեն եղել համաքայլ ընթանալ գիտական տեսության առաջընթացի հետ։ XVIII դարում փիլիսոփաները հաշվի էին առել մարդկային գիտելիքներն ամբողջությամբ, ներառյալ նաև գիտությունը՝ որպես իրենց ասպարեզը, և քննարկում էին հարցեր, ինչպիսիք են, օրինակ, տիեզերքն արդյո՞ք սկիզբ ունեցել է։ Սակայն XIX և XX դարերում գիտությունը դարձավ չափազանց տեխնիկական ու մաթեմատիկական և փիլիսոփաների և էլի շատերի համար՝ անհասկանալի, մի քանի մասնագետներից բացի։ Փիլիսոփաներն այնքան սահմանափակեցին քննարկվող հարցերի հորիզոնը, որ դարիս ամենանշանավոր փիլիսոփա Վիտգենշտեյնն ասաց․ «Փիլիսոփայությանը մնացած միակ խնդիրը լեզուների վերլուծությունն է»։ Արիստոտելից մինչև Կանտ ընկած ժամանակաշրջանի փիլիսոփայության ավանդույթների ինչպիսի՜ անկում։ | ||
| + | |||
| + | Այնուամենայնիվ, եթե մենք իրոք հայտնագործենք մի ամբողջական տեսություն, այն ժամանակի ընթացքում պետք է ընդհանուր գծերով հասկանալի դառնա բոլորին և ո՛չ միայն փոքրաթիվ գիտնականների։ Այն ժամանակ մենք բոլորս՝ փիլիսոփաները, գիտնականները, նույնիսկ շարքային մարդիկ ի վիճակի կլինենք մասնակցելու այն հարցի քննարկմանը, թե ինչո՞ւ գոյություն ունենք մենք և տիեզերքը։ Եթե հաջողվի այս հարցի պատասխանը գտնել, ապա դա կլինի մարդկային մտածողության վերջնական հաղթանակը, քանի որ այդ ժամանակ մենք կհասկանանք Աստծո միտքը։ | ||
| + | |||
| + | |||
| + | ==Հավելված== | ||
| + | |||
| + | Ալբերտ Էյնշտեյն | ||
| + | |||
| + | Էյնշտեյնի առնչությունը միջուկային ռումբի ստեղծման քաղաքականության հետ լավ հայտնի է։ Նա ստորագրել է նախագահ Ֆրանկլին Ռուզվելտին ուղղված հայտնի նամակը, որով համոզում էր Միացյալ Նահանգներին լրջորեն մոտենալ այդ հարցին, իսկ ինքն անում էր կարելին՝ հետպատերազմյան շրջանում միջուկային պատերազմը կանխելու համար։ Բայց սրանք ստիպված քաղաքականությամբ զբաղվող գիտնականի սոսկ առանձին գործողություններ չէին։ Իր իսկ բառերով ասած՝ Էյնշտեյնի կյանքը, փաստորեն, բաժանված էր «քաղաքականության և հավասարումների միջև»։ | ||
| + | |||
| + | Էյնշտեյնի վաղ քաղաքական գործունեությունը սկսվել է դեռևս Առաջին համաշխարհային պատերազմի տարիներին, երբ նա պրոֆեսոր էր Բեռլինում։ Չափազանց հոգնած լինելով մարդկային բազմաթիվ կյանքերի կորուստներից և այն ամենից, ինչ ինքն էր տեսել, նա ընդգրկվեց հակապատերազմական ցույցերում։ Քաղաքական անհնազանդությունը պաշտպանելու և ընդհանուր զինապարտությունը մերժելու նրա հասարակական քաջալերանքը հանգեցրին աշխատակիցների և նրա միջև հարաբերությունների սրման։ Այնուհետև պատերազմից հետո Էյնշտեյն իր ջանքերն ուղղեց հաշտեցման և միջազգային հարաբերությունների բարելավման գործին։ Սա նույնպես չբարձրացրեց նրա հեղինակությունը, և շուտով նրա քաղաքական հայացքների պատճառով դժվարացավ Միացյալ Նահանգներ այցելեը նույնիսկ դասախոսություններ կարդալու համար։ | ||
| + | |||
| + | Էյնշտեյնի երկրորդ մեծ նպատակը սիոնիզմն էր։ Չնայած նա ծագումով հրեա էր, բայց մերժում էր Աստծո աստվածաշնչային գաղափարը։ Սակայն հակասեմիտիզմի աճող գիտակցությունը թե՛ Առաջին համաշխարհային պատերազմից առաջ, և թե՛ նրա ընթացքում նրան աստիճանաբար տարավ հրեական համայնքի հետ նույնացմանը և հետագայում սիոնիզմի բացահայտ պաշտպանությանը։ Ժողովդավարությունը կորցնելու վտանգն անգամ նրան հետ չպահեց իր մտքերն արտահայտելուց։ Նրա տեսությունները ենթարկվեցին հարձակման, և նույնիսկ հակաէյնշտեյնական կազմակերպություն հիմնվեց։ Մի մարդ, որը հրահրում էր ուրիշներին սպանել Էյնշտեյնին, դատապարտվեց և տուգանվեց ընդամենը վեց դոլարով։ Բայց Էյնշտեյն անդրդվելի էր։ Երբ մի գիրք հրատարակվեց, որը խորագրված էր «Հարյուր հեղինակներ ընդդեմ Էյնշտեյնի», նա պատասխանեց․ «Եթե ես իրոք սխալ էի, ապա մեկն էլ էր բավական»։ | ||
| + | |||
| + | 1933 թվականին Հիտլերը իշխանության գլուխ անցավ։ Էյնշտեյնը Ամերիկայում էր և հայտարարեց, որ ինքն այլևս չի վերադառնա Գերմանիա։ Այնուհետև, երբ նացիստական ոստիկանությունը ներխուժեց նրա բնակարանը և բռնագրավեց բանկային հաշիվը, Բեռլինի լրագրերից մեկում երևաց հետևյալ վերնագիրը՝ «Լավ լուրեր Էյնշտեյնից, նա հետ չի վերադառնալու»։ Նացիզմի սպառնալիքի տակ Էյնշտեյնը հրաժարվեց խաղաղասիրական գործունեությունից և վերջիվերջո վախենալով, որ գերմանացի գիտնականները կարող են միջուկային ռումբ ստեղծել, առաջարկեց, որպեսզի Միացյալ Նահանգներն ստեղծեն իրենց սեփականը։ Բայց առաջին ատոմական ռումբի պայթելուց դեռ շատ առաջ, Էյնշտեյնը հրապարակայնորեն զգուշացնում էր ատոմական պատերազմի սարսափների մասին և առաջարկում էր միջուկային զենքի վրա միջազգային հսկողություն սահմանել։ | ||
| + | |||
| + | Ամբողջ կյանքի ընթացքում Էյնշտեյնի խաղասիրական ջանքերը գրեթե շոշափելի արդյունք չտվեցին և, իհարկե, նա քիչ համախոհներ վաստակեց։ Սիոնիզմի նրա բացահայտ պաշտպանությունը, սակայն,1952 թվականին արդեն պատշաճ ճանաչում գտավ, երբ նրան առաջարկվեց դառնալ Իսրայելի նախագահ։ Նա մերժեց՝ ասելով, թե իր կարծիքով ինքը շատ միամիտ է քաղաքական ասպարեզում։ Բայց երևի դրա իրական պատճառն այլ էր, նրա իսկ խոսքերով ասած․ «Հավասարումներն ինձ համար շատ ավելի կարևոր են, որովհետև քաղաքականությունը միայն ներկա ժամանակաշրջանի համար է, իսկ հավասարումները վերաբերում են ապագային»։ | ||
| + | |||
| + | |||
| + | Գալիլեո Գալիլեյ | ||
| + | |||
| + | Գալիլեոյին թերևս ավելի, քան որևէ այլ անհատի ենք պարտական ժամանակակից գիտության ծննդի համար։ Նրա հայտնի ընդհարումը Կաթոլիկ եկեղեցու հետ նրա փիլիսոփայության առանցքն էր, քանի որ Գալիլեոն առաջինն էր, որ պնդում էր, թե մարդը կարող է հուսալ, որ մի օր կհասկանա, թե ինչպե՞ս է աշխարհը գործում և, դեռ ավելին, մենք այդ կարող ենք անել՝ ուսումնասիրելով իրական աշխարհը։ | ||
| + | |||
| + | Գալիլեոն վաղուց հավատացել էր Կոպեռնիկոսի տեսությանը (թե մոլորակնները պտտվում են արևի շուրջը), բայց նա հրապարակայնորեն սկսեց պաշտպանել այդ տեսակետը միայն այն ժամանակ, երբ բավականաչափ փաստեր ուներ այն ապացուցելու։ Նա Կոպեռնիկոսի տեսության մասին գրեց իտալերեն (ոչ սովորական ակադեմիական լատիներենով), և շուտով նրա տեսակետները լայնորեն պաշտպանեցին համալսարանական շրջանակներից դուրս։ Դա մտահոգեց արիստոտելական պրոֆեսորներին, որոնք էլ միավորվեցին և համոզեցին Կաթոլիկ եկեղեցուն, որպեսզի վերջինս արգելի Կոպեռնիկոսի տեսությունը (կոպեռնիկոսականությունը)։ | ||
| + | |||
| + | Դրանով մտահոգված Գալիլեոն մեկնեց Հռոմ, որպեսզի խոսի եկեղեցական հեղինակությունների հետ։ Նա պնդում էր, որ աստվածաշունչը նպատակ չունի մեզ որևէ տեղեկություն տալ գիտական տեսությունների մասին և եզրակացնում, որ երբ աստվածաշունչը հակասում է առողջ բանականությանը, պետք է ենթադրել, որ այն այլաբանական է։ Բայց եկեղեցին վախենում էր այն խայտառակությունից, որը կարող էր վատ ազդեցություն ունենալ բողոքականության դեմ իր պայքարում և այդ պատճառով դիմեց բռնի միջոցների։1616 թվականին այն Կոպեռնիկոսի տեսությունը հայտարարեց «կեղծ ու սխալ» և հրամայեց Գալիլեոին երբեք նորից «չպաշտպանել կամ չհետևել» այդ տեսությանը։ Գալիլեոն համաձայնեց։ | ||
| + | |||
| + | 1623֊ին Գալիլեոյի վաղեմի ընկերը դարձավ Հռոմի պապ։ Գալիլեոն անմիջապես փորձեց չեղյալ հայտարարել տալ 1616 թվականի հռչակագիրը։ Նրան այդ չհաջողվեց, բայց նա կարողացավ թույլտվություն ձեռք բերել գիրք գրելու և քննարկելու թե՛ Արիստոտելի և թե՛ Կոպեռնիկոսի տեսությունները։ Սակայն երկու պայմանով՝ նա որևէ մեկի կողմը չպետք է լիներ, և պետք է եզրակացներ, որ մարդ երբեք չի կարող որոշել, թե ինչպե՞ս է աշխարհը գործում, որովհետև Աստված կարող է մոտավորապես նույն ազդեցությունն առաջացնել մարդու համար աներևակայելի ձևերով, և մարդը չի կարող սահմանափակել Աստծու ամենազորությունը։ | ||
| + | |||
| + | «Երկխոսություն աշխարհի երկու գլխավոր համակարգերի մասին» գիրքը ավարտվեց և տպագրվեց 1632 թվականին գրաքննիչների լիակատար պաշտպանությամբ, և այն անմիջապես ընդունվեց ամբողջ Եվրոպայում, որպես գրական և փիլիսոփայական գլուխգործոց։ Շուտով, հասկանալով, որ ժողովուրդը գիրքը դիտում է որպես համոզիչ փաստարկ և նպաստ Կոպեռնիկոսի տեսության՝ Հռոմի պապը զղջաց, որ թույլ էր տվել այդ գրքի հրատարակությունը։ Պապը պնդում էր, որ չնայած գիրքը վայելում է գրաքննիչների պաշտոնական հավանությունը, այնուամենայնիվ, Գալիլեոն խախտել էր 1616 թվականի հռչակագիրը։ Նա Գալիլեոյին ինկվիզիցիայի ենթարկեց, նրան դատապարտեց ցմահ տնային բանտարկության և հրամայեց հրապարակայնորեն հրաժարվել Կոպեռնիկոսի տեսությունից։ Այսպիսով, Գալիլեոն ստիպված երկրորդ անգամ լուռ համաձայնեց։ | ||
| + | |||
| + | Գալիլեոն մնաց նվիրված կաթոլիկ, բայց նրա հավատը գիտության անկախության նկատմամբ չփշրվեց։ Մահից (1642 թվականին) չորս տարի առաջ, երբ նա դեռ գտնվում էր տնային բանտարկության մեջ, իր երկրորդ գլխավոր գրքի ձեռագիր օրինակը գաղտնի տարվեց Հոլանդիա՝ հրատարակչի մոտ։ Այն մեզ հասել է որպես «Երկու նոր գիտություն», որն ավելին էր, քան զուտ Կոպեռնիկոսի պաշտպանությունը և ժամանակակից ֆիզիկայի հիմքն էր։ | ||
| + | |||
| + | |||
| + | Իսահակ Նյուտոն | ||
| + | |||
| + | Իսահակ Նյուտոնը հաճելի անձնավորություն չէր։ Նրա հարաբերությունները մյուս ակադեմիկոսների հետ հայտնի էին իրենց անբարեհաճությամբ, և նա կյանքի մեծ մասն անցկացրել է բուռն վեճերի մեջ։ «Մաթեմատիկայի սկզբունքները» գրքի հրատարակությունից հետո, որն, անկասկած, ֆիզիկայի ոլորտում երբևէ գրված ամենալավ գիրքն է, Նյուտոնի համբավն արագ աճեց։ Նա առաջադրվեց Թագավորական ընկերության պրեզիդենտ և դարձավ առաջին գիտնականը, որն ստացավ ասպետի կոչում։ | ||
| + | |||
| + | Նյուտոնը շուտով բախվեց թագավորական աստղագետ Ջոն Ֆլամսթիդի հետ, որը նախկինում Սկզբունքների համար տվյալներ էր հայթայթել, բայց դրանք չէր տալիս Նյուտոնին։ Նյուտոնը «ոչը» չէր ընդունում որպես պատասխան և այդ իսկ պատճառով հասավ այն բանին, որ իրեն նշանակեցին Թագավորական աստղադիտարանի ղեկավար օրգանի անդամ և ճնշման ներքո հրատարակել տալ այդ տվյալները։ Վերջիվերջո, նրան հաջողվեց զավթել Ֆլամսիթի աշխատանքը և տպագրության պատրաստել նրա ոխերիմ թշնամի Էդմոնդ Հալլեի կողմից։ Բայց Ֆլամսիթն այդ դեպքի առիթով դիմեց դատարան և անմիջապես ստացավ դատարանի որոշումը, որը կանխում էր գողացված աշխատանքի տարածումը։ Նյուտոնը զայրացավ և իր վրեժը լուծեց՝ «Սկզբունքների» հաջորդ հրատարակությունում՝ բաց թողնելով Ֆլամսիթից կատարված բոլոր մեջբերումները։ | ||
| + | |||
| + | Ավելի լուրջ վեճ ծագեց գերմանացի փիլիսոփա Գոթֆրիդ Լայբնիցի հետ։ Երկուսն էլ՝ Լայբնիցն ու Նյուտոնը, միմյանցից անկախ զարգացրել էին մաթեմատիկայի մի ճյուղ, որը կոչվում էր հաշիվներ, որի վրա է հիմնված ժամանակակից ֆիզիկայի մեծ մասը։ Չնայած մենք այժմ գիտենք, որ Նյուտոնը Լայբնիցից տարիներ առաջ էր բացահայտել հաշիվները, բայց իր աշխատանքը հրատարակել է շատ ավելի ուշ։ Դրան հաջորդեց մի բուռն վիճաբանություն՝ ո՞վ է առաջինը։ Գիտնականները երկու մրցակցին էլ եռանդով պաշտպանում էին։ Այնուամենայնիվ, ուշագրավ փաստ է, որ Նյուտոնին պաշտպանող գրեթե բոլոր հոդվածները իրականում գրված էին նրա իսկ ձեռքով, բայց ստորագրված էին ընկերների ստորագրությամբ։ Երբ վեճը թեժացավ, Լայբնիցը սխալ քայլի դիմեց և բողոքեց Թագավորական ընկերությանը՝ խնդրին լուծում տալու համար։ Նյուտոնը, որպես պրեզիդենտ, այդ հարցը լուծելու համար ստեղծեց մի «չեզոք» հանձնաժողով, որն, ի դեպ, ամբողջապես կազմված էր իր ընկերներից։ Բայց դա դեռ բոլորը չէ․ նա այնուհետև ինքը գրեց հանձնաժողովի զեկույցը, պաշտոնապես Լայբնիցին մեղադրեց գրագողության մեջ և Թագավորական ընկերությանը ստիպեց տպագրել այն։ Դրանով չբավարարվելով, նա այնուհետև մի անստորագիր հոդված ևս գրեց այդ զեկույցի շուրջ, որը տպագրվեց Թագավորական ընկերության սեփական պարբերականում։ Լայբնիցի մահից հետո Նյուտոնը հայտարարել է, որ ինքը մեծագույն բավականություն է ստացել «Լայբնիցի սիրտը կոտրելով»։ | ||
| + | |||
| + | Այս երկու վիճաբանությունների ժամանակ Նյուտոնն արդեն թողել էր Քեմբրիջը և ակադեմիան։ Քեմբրիջում նա ակտիվ էր հակակաթոլիկական քաղաքականության մեջ, իսկ ավելի ուշ խորհրդարանում և ի վերջո պարգևատրվեց Թագավորական դրամահատարանի վարիչի շահավետ պաշտոնով։ Այստեղ նա օգտագործեց իր չարության և կծու հեգնանքի ամբողջ տաղանդը հասարակայնորեն ավելի ընդունելի ձևով, հաջողությամբ պայքարեց կեղծարարների դեմ, նույնիսկ կախաղան ուղարկեց մի շարք մարդկանց։ | ||
| + | |||
| + | |||
| + | ==Բառարան== | ||
| + | |||
| + | Ալիքի երկարություն ― Ալիքի երկու հաջորդական գագաթների կամ փոսերի միջև եղած հեռավորությունը։ | ||
| + | |||
| + | Ալիք֊մասնիկային երկվություն ― Քվանտամեխանիկական հասկացություն, ըստ որի մասնիկների և ալիքների միջև տարբերություն չկա։ Մասնիկն իրեն երբեմն պահում է որպես ալիք, իսկ ալիքը՝ որպես մասնիկ։ | ||
| + | |||
| + | Ատոմ ― Սովորական նյութի հիմնական միավոր, բաղկացած է շատ փոքր միջուկից, որը կազմված է պրոտոններից և նեյտրոններից և նրա շուրջ պտտվող էլեկտրոններից։ | ||
| + | |||
| + | Անորոշության սկզբունք ― Մասնիկի դիրքն ու արագությունը (էներգիան) նույնպիսի ճշգրտությամբ չի կարելի որոշել․ որքան մեծ ճշգրտությամբ իմանանք մեկը, նույնքան նվազ ճշտությամբ կիմանանք մյուսը։ | ||
| + | |||
| + | Արագացում ― Մարմնի արագության փոփոխությունը միավոր ժամանակում։ | ||
| + | |||
| + | Արգելակման սկզբունք ― Երկու նույնական ½ սպին ունեցող մասնիկները (ինչպես էլեկտրոնը) չեն կարող ունենալ նույն դիրքն ու նույն արագությունը (էներգիան) անորոշության սկզբունքի սահմաններում։ | ||
| + | |||
| + | Բացարձակ զերո ― Հնարավոր ամենացածր ջերմաստիճանը (-273,2°C), որում նյութը զրկված է ջերմային էներգիայից։ | ||
| + | |||
| + | Գամմա ճառագայթ ― Շատ կարճ ալիքի երկարություն ունեցող էլեկտրամագնիսական ճառագայթում, որն առաջանում է ռադիոակտիվ քայքայման կամ տարրական մասնիկների բախման հետևանքով։ | ||
| + | |||
| + | Գեոդեզիական ― Երկու կետերի միջև ամենակարճ (կամ ամենաերկար) հեռավորությունը երկրագնդի վրա։ | ||
| + | |||
| + | Դաշտ ― Այն, ինչ գոյություն ունի ամենուրեք տարածության և ժամանակի մեջ՝ ի տարբերություն մասնիկի, որը գոյություն ունի միայն մի կետում, որոշակի ժամանակում։ | ||
| + | |||
| + | Եզակիության թեորեմ ― Թեորեմ, որի համաձայն որոշակի պայմաններում պետք է գոյություն ունենա եզակիություն, մասնավորապես, տիեզերքը սկիզբ է առել եզակիությունից։ | ||
| + | |||
| + | Եզակիություն ― Տարածություն ժամանակի մեջ այնպիսի մի կետ, որում տարածություն ժամանակի կորությունը անսահման է։ | ||
| + | |||
| + | Զանգված ―Մարմնի մեջ եղած նյութի քանակը կամ այդ մարմնի իներցիան՝ արագացմանը դիմադրելու կարողությանը։ | ||
| + | |||
| + | Էլեկտրաթույլ միասնական էներգիա ― Էներգիայի այն մակարդակը (մոտավորապես 100 ԳԷՎ), որից վերև էլեկտրամագնիսական ուժի և թույլ ուժի միջև տարբերությունը վերանում է։ | ||
| + | |||
| + | Էլեկտրական լիցք ― Մասնիկի այն հատկությունը, որով նա վանում է (կամ ձգում) մեկ այլ մասնիկի, որն ունի նույն (կամ հակառակ) նշանը։ | ||
| + | |||
| + | Էլեկտրական ուժ ― Էլեկտրական լիցք ունեցող մասնիկների միջև առաջացող ուժը, ուժգնությամբ երկրորդը չորս հիմնական ուժերից։ | ||
| + | |||
| + | Էլեկտրոն ― Բացասական լիցքավորված տարրական մասնիկ, որը պտտվում է ատոմի միջուկի շուրջ։ | ||
| + | |||
| + | Էներգիայի պահպանման օրենք ― Բնության հիմնական օրենքը, ըստ որի էներգիան (կամ համարժեք զանգվածը) չի կարելի ոչ ստեղծել և ոչ ոչնչացնել։ | ||
| + | |||
| + | Էնտրոպիա ― Համակարգի կարգավորվածության աստիճանը ցույց տվող մեծություն։ Համաձայն տերմոդինամիկայի 2֊րդ օրենքի, բնության մեջ ինքնակամ պրոցեսները ընթանում են այնպես, որ համակարգը կանոնավոր վիճակից անցնում է անկանոն վիճակի, որի ընթացքում էնտրոպիան աճում է։ | ||
| + | |||
| + | Ընդհանուր հարաբերկանության տեսություն ― Էյնշտեյնի տեսությունը՝ հիմնված այն պատկերացման վրա, համաձայն որի գիտության օրենքները նույնն են բոլոր դիտորդների համար, անկախ այն բանից, թե ինչպես են նրանք շարժվում։ Գրավիտացիոն ուժը արտահայտվում է որպես քառաչափ տարածություն֊ժամանակի կորություն։ | ||
| + | |||
| + | Թույլ ուժ ― Չորս հիմնական ուժերից երկրորդ թույլ ուժը (գրավիտացիոն ուժից հետո), որը գործում է փոքր հեռավորությունների վրա։ Ազդում է բոլոր նյութական մասնիկների վրա, բացի ուժակիր մասնիկներից։ | ||
| + | |||
| + | Լուսավայրկյան (լուսատարի) ― Լույսի անցած ճանապարհը մեկ վայրկյանում (մեկ տարում): | ||
| + | |||
| + | Կեղծ ժամանակ ― Այն ժամանակը, որը չափվում է կեղծ թվերի օգնությամբ։ | ||
| + | |||
| + | Կշիռ ― Այն ուժը, որով գրավիտացիոն դաշտն ազդում է մարմնի վրա, համեմատական է մարմնի զանգվածին, բայց նրան հավասար չէ։ | ||
| + | |||
| + | Կոորդինատներ ― Այն թվերը, որոնցով որոշվում է կետի դիրքը տարածություն֊ժամանակի մեջ։ | ||
| + | |||
| + | Հակամասնիկ ― Յուրաքանչյուր տեսակի նյութական մասնիկ ունի իր համապատասխան հակամասնիկը (էլեկտրոն֊հակաէլեկտրոն֊պոզիտրոն)։ Երբ մի մասնիկ բախվում է իր հակամասնիկի հետ, երկուսն էլ անիհիլանում են՝ արձակելով միայն էներգիա։ | ||
| + | |||
| + | Հաճախականություն ― Ամբողջական ալիքների (ցիկլերի) թիվը մեկ վայրկյանում։ | ||
| + | |||
| + | Համեմատականություն ― «x֊ը համեմատական է y֊ին»՝ նշանակում է, որ x֊ը հավասար է y֊ի և որևէ թվի բազմապատկին։ «x֊ը հակադարձ համեմատական է y֊ին»՝ նշանակում է, որ երբ x֊ը բազմապատկվում է որևէ թվով, y֊ը բաժանվում է նույն թվին։ | ||
| + | |||
| + | Հարաբերականության հատուկ տեսություն ― Էյնշտեյնի տեսությունը, ըստ որի գիտության օրենքները նույնն են բոլոր ազատորեն շարժվող դիտորդների համար՝ անկախ նրանց շարժման արագությունից։ | ||
| + | |||
| + | Հզոր ուժ ― Չորս հիմնական ուժերից ամենաուժեղը, որը գործում է փոքր հեռավորությունների վրա։ Դրանք միմյանց են կապում քվարկները՝ պրոտոններում ու նեյտրոններում, և պրոտոններն ու նեյտրոնները՝ ատոմի միջուկում։ | ||
| + | |||
| + | Մագնիսական դաշտ ― Մագնիսական ուժերը պայմանավորող դաշտը, այժմ էլեկտրական դաշտի հետ միավորված է որպես էլեկտրամագնիսական դաշտ։ | ||
| + | |||
| + | Մասնիկ (իրական) ― Մասնիկային դետեկտորով ուղղակիորեն դիտարկվող (գրանցվող) նյութական մասնիկ, ինչպես պրոտոնը, էլեկտրոնը և այլն։ | ||
| + | |||
| + | Մասնիկ (վիրտուալ) ― Քվանտային մեխանիկայում այն մասնիկը, որը դետեկտորով հնարավոր չէ ուղղակիորեն գրանցել, ինչպես գրավիտոնը, բայց նրա գոյությունը թողնում է չափելի ազդեցություն։ | ||
| + | |||
| + | Մասնիկային արագացուցիչ ― Էլեկտրամասնիկների օգնությամբ լիցքավորված մասնիկներին մեծ արագություն (էներգիա) հաղորդող սարք։ | ||
| + | |||
| + | Մարդաբանական սկզբունք ― Մենք տիեզերքը տեսնում ենք այնպես, ինչպես կա, որովհետև, եթե տիեզերքն այլ լիներ, մենք այստեղ չէինք լինի այն տեսնելու համար։ | ||
| + | |||
| + | Մեծ միասնական էներգիա ― Էներգիայի այն մակարդակը, որից ավելի բարձր արժեքի համար, ըստ ամենայնի, էլեկտրամագնիսական ուժը, թույլ ուժը և ուժեղ ուժը դառնում են միմյանցից անզանազանելի։ | ||
| + | |||
| + | Մեծ միասնական տեսություն (ՄՄՏ) ― Այն տեսությունը, որը միավորում է էլեկտրամագնիսական, ուժեղ և թույլ ուժերը։ | ||
| + | |||
| + | Մեծ ճայթյուն ― Տիեզերքի վերջավորության եզակիությունը։ | ||
| + | |||
| + | Մեծ պայթյուն ― Տիեզերքի սկզբնավորման եզակիությունը։ | ||
| + | |||
| + | Մերկ եզակիություն ― Տարածության֊ժամանակի եզակիություն, որը շրջապատված չէ սև խոռոչով։ | ||
| + | |||
| + | Միկրոալիքային ճառագայթման ֆոն ― Սկզբնական տաք տիեզերքի հրաշեկ ճառագայթումն այժմ այն աստիճան է շեղված դեպի սպեկտրի կարմիր տիրույթը, որ երևում է ոչ որպես լույս, այլ որպես միկրոալիք (ռադիոլաիք՝ մի քանի սանտիմետր երկարությամբ)։ | ||
| + | |||
| + | Միջուկ ― Ատոմի կենտրոնական մասը, որը կազմված է պրոտոններից և նեյտրոններից, որոնք իրար միացած են ուժեղ ուժով։ | ||
| + | |||
| + | Միջուկային սինտեզ ― Այն պրոցեսը, որի արդյունքում երկու միջուկներ բախվելով միանում են իրար և առաջացնում մեկ, ավելի ծանր միջուկ։ | ||
| + | |||
| + | Նախասկզբնական սև խոռոչ ― Նախասկզբնական տիեզերքում առաջաց սև խոռոչ։ | ||
| + | |||
| + | Նեյտրինո ― Չափազանց թեթև (հավանաբար զանգված չունեցող) տարրական նյութական մասնիկ, որի վրա ազդում են լոկ թույլ ուժը և գրավիտացիան։ | ||
| + | |||
| + | Նեյտրոն ― Չեզոք (չլիցքավորված) մասնիկ, որը շատ նման է (բացի լիցքից) պրոտոնին և կազմում է ատոմի միջուկի մեջ մտնող մասնիկների մոտավորապես կեսը։ | ||
| + | |||
| + | Նեյտրոնային աստղ ― Սառը աստղ, որը գոյատևում է նեյտրոնների միջև արգելակման սկզբունքի համաձայն գործող վանողական փոխազդեցության շնորհիվ։ | ||
| + | |||
| + | Չանդրասեկհարի սահման ― Կայուն սառը աստղի հնարավոր առավելագույն զանգվածը (արևի զանգվածից մեկ և կես անգամ մեծ), որից ավելիի դեպքում աստղը կոլապսվում է սև խոռոչի։ | ||
| + | |||
| + | Չափականություն ― Քառաչափ տարածություն֊ժամանակի մեջ ժամանակի մեկ և տարածության երեք չափումներից մեկը։ | ||
| + | |||
| + | Պատահույթ (Դեպք) ― Տարածություն֊ժամանակի մեջ մի կետ, որը բնորոշվում է իր ժամանակով և տեղով։ | ||
| + | |||
| + | Պատահույթի հորիզոն ― Սև խոռոչի սահմանագիծը։ | ||
| + | |||
| + | Պլանկի քվանտային սկզբունք ― Այն պատկերացումը, թե լույսը (կամ որևէ դասական ալիք) առաքվում և կլանվում է որոշակի քվանտներով, որոնց էներգիան համեմատական է հաճախականությանը։ | ||
| + | |||
| + | Պոզիտրոն ― Դրական լիցքավորված տարրական մասնիկ, էլեկտրոնի հակամասնիկը։ | ||
| + | |||
| + | Պրոտոն ― Դրական լիցքավորված մասնիկ, որը կազմում է ատոմի միջուկի մասնիկների մոտ կեսը։ | ||
| + | |||
| + | Ռադար ― Ռադիոալիքային ազդանշաններ օգտագործող համակարգ, որը որոշում է առարկաների դիրքը՝ իր արձակած ազդանշանի՝ առարկային հասնելու և նրանից անդրադառնալու ժամանակամիջոցը չափելով։ | ||
| + | |||
| + | Ռադիոակտիվություն ― Մի տեսակի ատոմային միջուկի ինքնակամ քայքայումը մի այլ տեսակի։ | ||
| + | |||
| + | Սահման չունենալու պայման ― Այն տեսակետը, որ տիեզերքը վերջավոր է, բայց սահմանագիծ չունի (կեղծ ժամանակում)։ | ||
| + | |||
| + | Սև խոռոչ ― Տարածություն ժամանակի այն տիրույթը, որտեղից ոչինչ, նույնիսկ լույսը, չի կարողանում հեռանալ, որովհետև գրավիտացիան նրանում շատ ուժեղ է։ | ||
| + | |||
| + | Սպեկտր ― Էլեկտրամագնիսական ալիքների, օրինակ, տարբաղադրումը բաղադրիչ հաճախականությունների։ | ||
| + | |||
| + | Սպիտակ թզուկ ― Կայուն սառը աստղ, որը գոյատևում է անորոշության սկզբունքով պայմանավորված էլեկտրոնների միջև գործող վանողական փոխազդեցությամբ։ | ||
| + | |||
| + | Սպին ― Տարրական մասնիկի ներքին հատկություն, որը կապված է, սակայն չի նույնանում սովորական պտույտի հետ։ | ||
| + | |||
| + | Տարածություն֊ժամանակ ― Քառաչափ տարածություն, որի կետերը պատահույթ են։ | ||
| + | |||
| + | Տարրական մասնիկ ― Մասնիկ, որը, թվում է, չի կարող մասնատվել։ | ||
| + | |||
| + | Տիեզերաբանական հաստատուն ― Էյնշտեյնի օգտագործած մաթեմատիկական հնարք, որպեսզի տարածություն֊ժամանակը ինքնակամորեն ձգտի ընդարձակման։ | ||
| + | |||
| + | Տիեզերագիտություն ― Տիեզերքի ուսումնասիրությունն ամբողջությամբ վերցրած։ | ||
| + | |||
| + | Փուլ ― Ալիքի դիրքը ցիկլում որոշակի ժամանակամիջոցում, այսինքն՝ որտեղ է գտնվում՝ գագաթում, փոսում, թե որևէ այլ կետում։ | ||
| + | |||
| + | Քվանտ ― Էներգիայի միավոր, որով առաքվում կամ կլանվում են ալիքները։ | ||
| + | |||
| + | Քվանտային մեխանիկա ― Պլանկի քվանտային սկզբունքի և Հայզենբերգի անորոշության սկզբունքի հիման վրա մշակված տեսություն, որը նկարագրում է մասնիկի ալիքային շարժումը։ | ||
| + | |||
| + | Ֆոտոն ― Լույսի քվանտը։ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Ընթացիկ տարբերակը 23:07, 29 Հունվարի 2018-ի դրությամբ
հեղինակ՝ Ստեֆըն Հոքինգ |
Բովանդակություն
Ներածություն
1982֊ին Հարվարդի համալսարանում Լոբի դասախոսությունները կարդալուց հետո որոշեցի փորձել հանրամատչելի մի գիրք գրել ժամանակի և տարածության մասին։ Տիեզերքի սկզբնավորման և սև խոռոչների մասին շատ գրքեր են գրվել, սկսած ամենալավից՝ Ստիվեն Ուայնբերգի «Առաջին երեք րոպեն» գրքից, մինչև ամենավատը, որի անունը տալ չեմ ուզում։ Դրանցից և ոչ մեկը, իմ կարծիքով չի առնչվում այն հարցերին, որոնք ինձ մղել են գիտահետազոտական աշխատանքներ կատարելու տիեզերագիտության և քվանտային տեսության բնագավառներում։ Որտեղի՞ց է գալիս տիեզերքը։ Ինչպե՞ս և ինչո՞ւ։ Արդյո՞ք այն վերջ պիտի ունենա և, եթե այո, ինչպիսի՞ վերջ։ Սրանք հարցեր են, որոնք հետաքրքրում են մեզ բոլորիս։ Սակայն ժամանակակից գիտությունն այն աստիճան տեխնիկական է, որ միայն փոքրաթիվ մասնագետներ են ի վիճակի հասկանալ այս հարցերը նկարագրող մաթեմատիկական լեզուն։ Այնուամենայնիվ, տիեզերքի սկզբնավորմանը և ապագային վերաբերող հիմնական գաղափարները հնարավոր է արտահայտել բառերով, առանց մաթեմատիկայի օգնությանը դիմելու՝ այնպես, որ գիտական կրթություն չունեցող մարդիկ էլ ի վիճակի լինեն ըմբռնել դրանք։ Ահա ես հենց այդ եմ փորձել անել այս գրքում։ Իսկ թե որքանով է դա ինձ հաջողվել, թողնում եմ ընթերցողի դատին։
Մեկն ինձ ասաց, որ գրքում օգտագործված յուրաքանչյուր հավասարում կիսով չափ կնվազեցնի գրքի իրացումը։ Հետևաբար, ես որոշեցի ոչ մի հավասարում չօգտագործել։ Վերջում, սակայն, չկարողացա հրաժարվել Էյնշտեյնի հայտնի E=mc² հավասարումից։ Հուսով եմ, որ սա չի վախեցնի իմ հնարավոր ընթերցողների կեսին։
Ընդհանրապես կյանքում բախտավոր եմ եղել, բացի այն դժբախտությունից, որ հիվանդացա ԱԿՍ[1]֊ով կամ շարժիչ նեյրոնների ախտահարմամբ։
Այն հոգածու վերաբերմունքը, որով իմ կինը՝ Ջեյնը և իմ երեխաները՝ Ռոբերտը, Լյուսին ու Թիմմին, շրջապատում են ինձ, հնարավոր դարձրեց, որպեսզի ես բավական բնականոն մի կյանք վարեմ և հաջողակ կարիերա ունենամ։ Երջանիկ եմ նաև, որ մասնագիտացել եմ տեսական ֆիզիկայի բնագավառում, որովհետև այն զուտ մտավոր աշխատանք է։ Այսպիսով, իմ ֆիզիկական անկարողությունը լուրջ արգելք չի եղել։ Իսկ իմ գիտական գործընկերներն առանց բացառության շատ օգտակար են եղել ինձ։
Իմ կարիերայի առաջին՝ «դասական» փուլում առաջատար գործընկերներս ու աշխատակիցներս են եղել Ռոջեր Պենրոուզը, Ռոբերտ Գերոչը, Բրանտոն Քարտերը և Ջորջ Էլլիսը։ Ես երախտապարտ եմ նրանց՝ ցույց տված օգնության և համագործակցության համար։ Այդ շրջանի աշխատանքներն ամփոփված են «Տարածություն֊ժամանակի խորամասշտաբ կառուցվածքը» գրքում, որն Էլլիսն ու ես գրեցինք՝ 1973֊ին։ Իմ ընթերցողներին խորհուրդ չէի տա կարդալ այդ գիրքը՝ հավելյալ գիտելիքներ ձեռք բերելու համար, որովհետև այն հագեցած է տեխնիկական մանրամասներով և բավականին դժվարամարս է։ Կարծում եմ, ես այժմ սովորել եմ այնպես գրել, որ ընթերցողը հեշտությամբ հասկանա այն։
Իմ աշխատանքային երկրորդ՝ «քվանտային» փուլի, 1974֊ից սկսած, հիմնական գործընկերներն են եղել Գարի Գիբսոնը, Դոն Փեյջը և Ջիմ Հարթլը։ Ես նրանց շատ բանով եմ պարտական, ինչպես նաև իմ ասպիրանտներին, որոնք ինձ մեծ չափով օգնել են և՛ գործնական, և՛ տեսական ոլորտներում։ Ուսանողներից հետ չմնալու պահանջկոտությունը մեծ խթան է եղել և, կարծում եմ, թույլ չի տվել, որ ես լճանամ ու տեղում դոփեմ։
Այս գրքի աշխատանքներում ինձ շատ է օգնել իմ ուսանողներից Բրայեն Ուիտը։ Գրքի առաջին ուրվագիծը գրելուց հետո ես 1985֊ին հիվանդացա թոքերի բորբոքումով։ Շնչափողի վիրահատությունից կորցրի խոսելու ունակությունս և գրեթե անկարող էի հաղորդակցվել մարդկանց հետ։ Թվում էր, թե ես այլևս ի վիճակի չեմ լինի ավարտել գիրքը։ Սակայն Բրայենն ինձ օգնեց ոչ միայն վերանայել ձեռագիրը, այլև սովորեցրեց օգտագործել Կենդանի կենտրոն կոչվող հաղորդակցման մի ծրագիր, որն ինձ էր նվիրել Ուոլտ Ուոլտոզը՝ Կալիֆոռնիայի Սըննիվալի Ուորդս Պլուզ ընկերությունից։ Դրա շնորհիվ ես կարող եմ գրքեր գրել և նույնիսկ խոսել մարդկանց հետ, օգտագործելով խոսակցության սինթեզիչ մի սարք, որը ինձ նվիրել էր նույն Կալիֆոռնիայի Սըննիվալի Սպիչ Պլուզ ֆիրման։ Այս սինթեզիչը և մի փոքր անհատական համակարգիչն իմ անվակավոր բազկաթոռին ամրացրեց Դեյվիդ Մեյսոնը։ Այս համակարգն է, որ փոխել է աշխատանքիս ողջ ընթացքը։ Իրականում ես այժմ ավելի լավ եմ հաղորդակցվում մարդկանց հետ, քան ձայնս կորցնելուց առաջ։
Իրենց խորհուրդներով շատերն են ինձ օգնել բարելավելու այս գիրքը։ Մասնավորապես, Բանտամ Բուքսի իմ խմբագիր Պիտեր Գուզարդին էջերով մեկնաբանություններ և հարցեր էր ուղարկում ինձ տարբեր կետերի վերաբերյալ, որոնք, ըստ իրեն, ես չէի կարողացել հստակորեն բացատրել։ Ճիշտն ասած, ես սկզբում շատ սրտնեղեցի, երբ ստացա առաջարկվող փոփոխությունների նրա երկար ցուցակները, սակայն նա միանգամայն իրավացի էր։ Ես վստահ եմ, որ այդ պարտադիր աշխատանքի արդյունքում գիրքն ավելի բարելավվեց։ Ես երախտապարտ եմ իմ ասիստենտներ՝ Կոլին Ուիլյամսին, Դեյվիդ Թոմասին և Ռայմոնդ Լաֆլամին, իմ քարտուղարներ՝ Ջուդի Ֆելլային, Էնն Ռալֆին, Չերիլ Բիլինգթոնին, Սյու Մեյսիին և իմ հիվանդապահներին։ Այս գիրքը հնարավոր չէր լինի գրել, եթե չփակվեին իմ գիտահետազոտական և բուժման ծախսերը, որոնք հոգացին Գոնվիլ և Կայուս քոլեջը, գիտության և ճարտարագիտության գիտահետազոտական խորհուրդը և Լևերհուլմ, Մաք Արթուր, Նուֆիլդ և Ռալֆ Սմիթ հաստատությունները։ Բոլորին հայտնում եմ իմ խորին երախտագիտությունը։
- Ստեֆըն Հոգինգ
- 20 հոկտեմբերի1987
Նախաբան
Առօրյա կյանքում մենք համարյա անտեղյակ ենք աշխարհի կառուցվածքին։ Չենք մտածում կենարար արևի լույս արտադրող մեխանիզմի մասին, չենք մտածում, որ ձգողականության ուժը մեզ պահում է երկրի վրա, հակառակ դեպքում պետք է անկշիռ թափառեինք տարածության մեջ։ Մոռանում ենք, որ մենք կազմված ենք ատոմներից, որոնց կայունությամբ է պայմանավորված հիմնականում մեր գոյությունը։ Բացի երեխաներից (ովքեր բավականաչափ գիտելիք չունեն, որպեսզի կարևոր հարցեր չտան), փոքրաթիվ են այն այն մարդիկ, ովքեր շատ ժամանակ են տրամադրում խորհրդածելու, թե ինչո՞ւ է բնությունն այսպիսին, ինչպե՞ս է սկիզբ առել տիեզերքը, կամ մի՞շտ է գոյություն ունեցել այն, կարո՞ղ է արդյոք մի օր ժամանակը փոխի իր ուղղությունը հակառակի, այնպես, որ հետևանքը նախորդի պատճառին, և, վերջապես, արդյոք անհաղթահարելի սահման ունի՞ մարդկային իմացությունը։ Նույնիսկ երեխաներ կան, որոնցից ոմանց ես հանդիպել եմ, ովքեր ուզում են իմանալ, թե ինչի՞ է նման սև խոռոջը, ի՞նչ բան է նյութի ամենափոքրագույն մասնիկը, ինչո՞ւ ենք մենք անցյալը հիշում, բայց ապագան՝ ոչ, այդ ինչպե՞ս եղավ, որ, եթե սկզբում իրոք քաոս էր, առաջացավ այժմյան կարգուկանոնը և, վերջապես, ինչո՞ւ գոյություն ունի տիեզերքը։
Մեր հասարակության մեջ այսօր ընդունված է, որ ծնողներն ու ուսուցիչներն այս հարցերից շատերին պատասխանում են ուսերը թոթվելով, և կամ դիմում են մշուշապատ կրոնական պատմությունների։ Ոմանք անհարմար են զգում շոշափել այդ հարցերը, որովհետև անմիջապես ակնհայտ է դառնում մարդու գիտելիքների սահմանափակությունը։
Սակայն հենց այսպիսի հարցուփորձերն են խթանել փիլիսոփայության ու գիտություններից շատերի զարգացումը։ Աստիճանաբար աճում է այն մարդկանց թիվը, ովքեր նմանօրինակ հարցեր են տալիս և երբեմն լսում ապշեցուցիչ պատասխաններ։ Մարդն այսօր այնքան է ընդարձակել իր մտահորիզոնը, որ միաժամանակ կարող է հետազոտել ամենափոքր և ամենախոշոր օբյեկտները՝ ատոմից մինչև աստղերը։
1974֊ի գարնանը «Վիկինգ» տիեզերանավի՝ Մարսի վրա վայրեջք կատարելուց երկու տարի առաջ, Անգլիայում ես մասնակցում էի մի գիտաժողովի, որը կազմակերպել էր Լոնդոնի Թագավորական ընկերությունը և նվիրված էր արտերկրային քաղաքակրթության հայտնաբերման հարցերի հետազոտմանը։ Ընդմիջման ժամանակ նկատեցի, որ հարակից սրահում ավելի բազմամարդ մի հավաք կար և հետաքրքրությունից մղված ներս մտա։ Անմիջապես գլխի ընկա, որ այնտեղ տեղի էր ունենում հինավուրց մի արարողություն, ականատես էի դառնում մեր մոլորակի ամենահին գիտական կազմակերպություններից մեկի՝ Լոնդոնի Թագավորական ընկերության նոր անդամների ընդունման ծիսակատարությանը։ Առաջին շարքում իր անվակավոր բազկաթոռին նստած մի երիտասարդ դանդաղորեն իր անունն էր գրում այն գրքում, որի առաջին էջերից մեկում զետեղված էր Իսահակ Նյուտոնի ստորագրությունը։ Երբ ի վերջո նա ավարտեց ստորագրելը, սրահում թնդացին ծափահարությունները։ Այդ ժամանակ արդեն Ստեֆըն Հոքինգը լեգենդ էր։ Ներկայումս Հոքինգը Քեմբրիջի համալսարանի մաթեմատիկայի լուկասյան պրոֆեսոր է, ինչպես ժամանակին Նյուտոնն ու ապա Պ․ Ա․ Մ․ Դիրակն էին, երկու նշանավոր հետազոտողներ, որոնցից մեկն ուսումնասիրել է ամենախոշորը, մյուսը՝ ամենափոքրը։ Ստեֆըն Հոքինգը նրանց արժանավոր հաջորդն է։ Հոքինգի այս առաջին հանրամատչելի գրքով ընթերցողը բազմակողմանիորեն կվարձատրվի։ Այս գրքի բազմաբովանդակ պարունակության չափ հետաքրքիր է նաև ընթերցողին մատուցվող հեղինակի մտածելակերպը։ Այս գիրքը պարունակում է ֆիզիկային, աստղագիտությանը, տիեզերագիտությանը, ինչպես նաև մտքի խիզախության հետ առնչվող պարզ հայտնություններ։
Այս գիրքը նաև Աստծո մասին է․․․ կամ թերևս՝ Աստծո բացակայության մասին։ Գրքի էջերում հաճախ է հանդիպում «Աստված» բառը։ Հոքինգը ձգտում է պատասխանել Էնշտեյնի այն նշանավոր հարցին, թե տիեզերքն արարելիս Աստված ընտրության որևէ հնարավորություն ունե՞ր։ Իր իսկ միանշանակ պնդմամբ նա փորձում է հասկանալ Աստծո բանականությունը։ Ավելի անսպասելի է եզրակացությունը, թերևս ժամանակավոր, որին հանգեցրել են հետազոտությունները։ Տիեզերքը տարածության մեջ անեզր է, ժամանակի մեջ՝ անսկիզբ և անվերջ, իսկ Արարիչն այնտեղ անելիք չունի։
- Կարլ Սագան
- Կորնելի համալսարան, Իթակա, Նյու Յորք
1
Մեր պատկերացումները տիեզերքի մասին
Հանրահայտ մի գիտնական (ըստ ոմանց դա եղել է Բերտրան Ռասելը) հանրամատչելի դասախոսություն էր կարդում աստղագիտության մասին։ Նա նկարագրում էր, թե ինչպես է երկիրը պտտվում բազմաքանակ աստղերի կույտի՝ մեր գալակտիկայի կենտրոնի շուրջը։ Դասախոսության ավարտին վերջին շարքերից մի փոքրամարմին ծեր կին ոտքի կանգենց և հայտարարեց․ «Ինչ որ դուք ասացիք՝ անմտություն է։ Երկիրն իրականում մի հարթ ափսե է՝ հենված հսկա կրիայի մեջքին։ Գիտնականը ներողամտորեն ժպտաց և հարցրեց․ «Իսկ ինչի՞ վրա է դրված այդ հսկա կրիան»։ «Դուք շատ խորամանկն եք, երիտասարդ, շատ խորամանկը», ― ասաց ծեր կինը, ― բայց չէ՞ որ ամենուրեք իրար վրա դրված հսկա կրիաներ կան»։
Մարդկանց մեծամասնությունը ծիծաղելի կհամարի մեր տիեզերքի՝ որպես հսկա կրիաներից կազմված անսահմանափակ աշտարակի մասին պատկերացումը, սակայն ո՞վ ասաց, որ մենք ավելին գիտենք։
Մենք ի՞նչ գիտենք տիեզերքի մասին և որտեղի՞ց գիտենք։ Ինչպե՞ս է առաջացել տիեզերքը և ո՞ւր է գնում։ Տիեզերքն ունեցե՞լ է սկիզբ և, եթե այո, ապա դրանից առաջ ի՞նչ է եղել։ Ի՞նչ բան է ժամանակը։ Արդյոք երբևէ նա վերջ կունենա՞։ Ֆիզիկայի ժամանակակից նվաճումները, որոնք մասամբ իրականություն են դարձել արտակարգ նոր տեխնոլոգիաների օգնությամբ, այսօր հնարավոր են դարձնում առաջարկել այդ մշտական հարցերի մի մասի պատասխանները։ Մի օր այս պատասխանները կարող են նույնքան ակներև թվալ, որքան երկրի պտույտն արևի շուրջ, կամ գուցե նույնքան արտառոց, որքան հսկա կրիաների աշտարակը։ Դա լոկ ժամանակը ցույց կտա, ինչ էլ որ այն լինի։
Դեռևս մեր թվարկությունից առաջ՝ 340 թ֊վին հույն փիլիսոփա Արիստոտելն իր «Երկնքի մասին» գրքում երկու ծանրակշիռ փաստեր է բերել այն մասին, որ երկիրն ավելի շուտ գնդաձև է, քան հարթ ափսե։ Առաջին․ Արիստոտելը գտնում էր, որ լուսնի խավարումներն առաջանում են արևի և լուսնի միջև երկրի հայտնվելու հետևանքով։ Երկրի ստվերը լուսնի վրա միշտ կլոր էր, ինչը վկայում է երկրի գնդաձև լինելու մասին։ Եթե երկիրը լիներ հարթ սկավառակ, ապա նրա ստվերը կլիներ երկարացած ու էլիպսաձև, բացառությամբ եթե խավարումները մշտապես տեղի ունենային, երբ արևը լիներ սկավառակի ուղիղ կենտրոնի հետևում։ Երկրորդ․ ծովագնացությունից հույներին հայտնի էր, որ Հյուսիսային աստղը երկնքում ավելի ցածր է երևում հարավային և ավելի բարձր՝ հյուսիսային շրջաններից դիտելիս։ (Քանի որ Հյուսիսային աստղը գտնվում է հյուսիսային բևեռի վերևում, ապա այն հյուսիսային բևեռից դիտողին երևում է անմիջապես գլխավերևում, մինչդեռ հասարակածից դիտողի համար այն հայտնվում է ուղիղ հորիզոնում)։ Եգիպտոսում և Հունաստանում Հյուսիսային աստղի դիրքերի ակնհայտ տարբերությունից ելնելով, Արիստոտելը նույնիսկ գնահատեց գնդաձև երկրի շրջագծի երկարությունը՝ 400.000 ստադիա։ Թե որքան է ստադիան, ճշգրիտ չգիտենք, դա կարող էր լինել մոտավորապես 200 յարդ, որով երկրի արիստոտելյան շրջագիծը 2 անգամ մեծ է ստացվում այսօր ընդունված թվից։ Հույները երկրի գնդաձև լինելու մասին ունեին երրորդ ապացույցը ևս․ ինչո՞ւ մարդ ափին մոտեցող նավի նախ առագաստը տեսնում հորիզոնում, ապա միայն՝ իրանը։
Ըստ Արիստոտելի, երկիրն անշարժ է, իսկ արևը, լուսինը, մոլորակները և աստղերը շրջանաձև պտտվում են նրա շուրջ։ Նա հավատում էր դրան, որովհետև կրոնական դրդապատճառներով համարում էր, որ երկիրը գտնվում է տիեզերքի կենտրոնում, իսկ շրջանաձև շարժումն ամենակատարյալն է։ Մ․թ․ II դարում Պտղոմեոսն այս գաղափարից բխեցրեց իր ամբողջական տիեզերագիտական մոդելը։ Ըստ այդ մոդելի՝ երկիրը գտնվում է տիեզերքի կենտրոնում՝ շրջապատված 8 ոլորտներով, որոնցում գտնվում են լուսինը, արևը, աստղերը և այն ժամանակ հայտնի հինգ մոլորակները՝ Մերկուրին, Վեներան, Մարսը, Յուպիտերը և Ստուռնը (նկ․ 1.1): Մոլորակներն իրենք պտտվում են ավելի փոքր ուղեծրերով, կապված մնալով իրենց համապատասխան ոլորտներին, սրանով էր բացատրվում մոլորակների՝ երկնքի դիտարկումներից բացահայտված բավականին բարդ ուղին։ Ամենահեռավոր ոլորտում գտնվում են, այսպես կոչված, սևեռված աստղերը, որոնք միմյանց նկատմամբ միշտ մնում են նույն դիրքում, բայց միասին պտտվում են երկնակամարում։ Թե ինչ կար վերջին ոլորտից այն կողմ, այնքան էլ հստակ չէր, բայց այն՝ իհարկե, մարդու համար դիտարկելի տիեզերքից դուրս էր։
Պտղոմեոսի մոդելն իրենից ներկայացնում էր բավականին ճշգրիտ մեթոդ, որով կարելի էր կանխագուշակել երկնային մարմինների դիրքը։ Սակայն այդ դիրքերը ճշգրիտ գուշակելու համար նա ստիպված էր ենթադրել, որ լուսնի հետագիծն այնպիսին է, որ երբեմն այն երկու անգամ ավելի մոտ է հայտնվում երկրին, քան սովորաբար։ Եվ դրանից հետևում է, որ լուսինը երբեմն երկու անգամ մեծ պիտի երևար սովորականից։ Պտղոմեոսը նկատեց այդ այդ թերությունը, որով հանդերձ, սակայն, մոդելը չնայած ոչ համընդհանուր, բայց լայն ընդունելություն գտավ։ Քրիստոնեական եկեղեցին նույնպես ընդունեց այն, քանի որ տիեզերքի այդ պատկերը համապատասխանում էր Աստվածաշնչին, ընդ որում, մեծ առավելություն ուներ, որ սևեռված աստղերի ոլորտից այն կողմ տեղ էր մնում նաև դժոխքի և դրախտի համար։1514֊ին ավելի պարզ մի մոդել առաջարկեց լեհ քահանա Նիկոլաս Կոպերնիկոսը։ (Սկզբում Կոպեռնիկոսն այն առաջարկեց անանուն, հավանաբար վախենալով, որ եկեղեցին հեղինակին հերետիկոս կհամարի)։ Նրա հիմնական գաղափարն այն էր, որ արևն անշարժ է և գտնվում է կենտրոնում, իսկ երկիրն ու մոլորակները պտտվում են նրա շուրջը՝ շրջանաձև ուղեծրերով։ Այս մոդելը լրջորեն ընդունվեց միայն շուրջ մեկ դար անց։ Թեև կոպեռնիկոսյան մոդելի կանխագուշակած ուղեծրերը ստույգ չէին համընկնում դիտարկումներին, երկու նշանավոր ասղագետներ՝ գերմանացի Յոհան Կեպլերն ու Իտալացի Գալիլեո Գալիլեյը հրապարակայնորեն պաշտպանեցին այն։ 1609֊ին արիստոտելյան֊պտղոմեոսյան տեսությունները կործանիչ հարված ստացան։ Այդ տարում նոր հայտնագործված հեռադիտակով Գալիլեոն սկսեց դիտարկել գիշերային երկնակամարը։ Նա, դիտելով Յուպիտերը, նկատեց, որ այն շրջապատված է մի քանի արբանյակներով կամ լուսիններով, որոնք պտտվում են նրա շուրջ։ Սա նշանակում էր, որ ոչ բոլոր մարմիններն են պտտվում երկրի շուրջ, ինչպես մտածում էին Արիստոտելն ու Պտղոմեոսը։ (Իհարկե, դեռ հնարավոր էր ենթադրել, որ երկիրը անշարժ է տիեզերքի կենտրոնում, իսկ Յուպիտերի լուսինները ծայրահեղ բարդ հետագծով պտտվում են երկրի շուրջ՝ տպավորություն ստեղծելով, թե դրանք պտտվում են Յուպիտերի շուրջ։ Սակայն Կոպեռնիկոսի տեսությունը շատ ավելի պարզ էր)։ Այդ նույն ժամանակ Յոհան Կեպլերը ձևափոխելով Կոպեռնիկոսի տեսությունը, առաջարկեց, որ մոլորակները պտտվում են ոչ թե շրջանաձև, այլ էլիպսաձև ուղեծրերով (էլիպսը ձգած շրջանագիծ է)։ Կանխագուշակված ուղեծրերն այդպիսով վերջնականապես համընկան դիտարկումներին։
Ինչ վերաբերում է Կեպլերի էլիպսաձև ուղեծրին, ապա այն պարզապես պատահական հիպոթեզ էր և այդ իսկ պատճառով՝ անընդունելի, քանի որ էլիպսը նվազ կատարյալ էր, քան շրջանագիծը։ Բոլորովին պատահաբար հայտնագործելով, որ էլիպսաձև շարժումը լավ համընկնում է դիտարկումներին, նա չկարողացավ էլիպսաձև ուղեծրի պատկերացումը համաձայնեցնել իր այն տեսակետի հետ, համաձայն որի մոլորակներն արևի շուրջ պտտվում են մագնիսական ուժերի ազդեցության տակ։
Այս հարցն իր բացատրությունն ստացավ շատ ուշ՝ 1687֊ին, երբ Իսահակ Նյուտոնը հրատարակեց ֆիզիկական գիտությունների բնագավառում գրված թեևս իր ամենակարևոր, եզակի աշխատությունը՝ «Բնափիլիսափայության մաթեմատիկական հիմունքները»։ Այստեղ Նյուտոնը ոչ միայն առաջադրում էր տարածության և ժամանակի մեջ մարմինների շարժման տեսությունը, այլև զարգացնում էր այն բարդ մաթեմատիկական ապարատը, որը հարկավոր էր դրանց շարժման վերլուծության համար։ Ի լրումն դրա, Նյուտոնը սահմանեց տիեզերական ձգողության օրենքը, ըստ որի տիեզերքում յուրաքանչյուր մարմին իրեն է ձգում այլ մարմնի այնպիսի ուժով, որն այնքան մեծ է, որքան մեծ են մարմինների զանգվածները և փոքր՝ նրանց միջև հեռավորությունը։ Այդ նույն ուժն է նաև մարմինների՝ գետին ընկնելու պատճառը։ (Այն պատմությունը, թե իբր Նյուտոնը ներշնչվել է, երբ խնձորն ընկել է իր գլխին, իհարկե, մտացածին է։ Այն ինչ երբևէ Նյուտոնն ասել է այդ մասին, այն է, որ ձգողական ուժի գաղափարն իր մտքում ծագել է, երբ ինքը նստած էր «հայեցողական տրամադրությամբ» և «դրա առիթը խնձորի ընկնելն էր»)։ Նյուտոնը հետո ցույց տվեց, որ, իր օրենքի համաձայն, ձգողության ուժն է լուսնի՝ երկրի շուրջ էլիպսաձև ուղեծրով պտտվելու և երկրի ու մոլորակների՝ իրենց հերթին արևի շուրջ էլիպսաձև հետագծով պտտվելու պատճառը։
Կոպեռնիկոսյան մոդելը վերջ տվեց երկրի շուրջ պտտվող ոլորտների և միաժամանակ տիեզերքի որոշակի բնական սահմանների գոյության Պտղոմեոսի պատկերացումներին։ Քանի որ պարզվեց, որ «անշարժ աստղերը» իրենց դիրքը չեն փոխում միմյանց նկատմամբ, այլ միայն տարուբերվում են երկնքում, իսկ դրա պատճառը երկրի պտույտն է իր առանցքի շուրջ,[2] ապա բնական էր ենթադրել, որ անշարժ աստղերը ոչ այլ ինչ են, եթե ոչ մեր արևին նման մարմիններ, որոնք, սակայն, չափազանց հեռու են երկրից։
Նյուտոնը հասկացավ, որ, ձգողության իր տեսության համաձայն, աստղերը պետք է միմյանց ձգեն, հետևաբար չեն կարող անշարժ մնալ։ Հնարավո՞ր է արդյոք, որ աստղերը մի օր միասին ընկնեն։ 1691 թվականին իր ժամանակի առաջավոր մտածողներից մեկին՝ Ռիչարդ Բենտլիին ուղղած նամակում Նյուտոնը փաստարկում է, որ դա հնարավոր է միայն այն դեպքում, եթե տիեզերական որոշակի տարածության մեջ բաշխված լինեն միայն որոշակի թվով աստղեր։ Սակայն, մյուս կողմից, վիճարկում է նա, եթե աստղերի թիվն անսահման է և դրանք այս կամ այն կանոնավորությամբ բաշխված են անսահման տարածության մեջ, ապա նման բան տեղի ունենալ չի կարող, քանի որ չի կարող գոյություն ունենալ որևէ կենտրոն, որտեղ աստղերն ընկնեին։
Այս տեսակ փաստարկը որոգայթի մի օրինակ է, որին բախվում են անսահմանության մասին խոսելիս։
Սահման չունեցող տիեզերքում ամեն կետ կարող է դիտարկվել որպես կենտրոն, քանի որ նրանցից յուրաքանչյուրը բոլոր կողմերից շրջապատված է անսահման թվով աստղերով։ Ճիշտ կլինի, ինչպես շատ ավելի ուշ պարզվեց, ենթադրել մի որոշակի իրավիճակ, երբ բոլոր աստղերն ընկնում են միմյանց վրա և ապա հարց տալ, թե ի՞նչ կպատահի, եթե նոր աստղեր ավելացնենք, որոնք, մոտավորապես, կանոնավոր կերպով բաշխվեն այդ տարածքից դուրս։ Համաձայն Նյուտոնի ձգողականության օրենքի, հավելյալ աստղերը միջին հաշվով որևէ տարբերություն չեն առաջացնի սկզբնական աստղերի համար, և աստղերը կշարունակեն առաջվա արագությամբ ընկնել։ Մենք կարող ենք աստղերի կամայական քանակ ավելացնել, բայց նրանք միշտ կշարունակեն իրենք իրենց կոլապսվել։ Այժմ մենք արդեն գիտենք, որ անհնարին է ունենալ անսահման կայուն տիեզերքի մի մոդել, որում գրավիտացիոն ուժը մշտապես ձգողական լինի։
Չափազանց հետաքրքրական է այն փաստը, որ մինչև XX դարի սկիզբը մարդկային մտածողությունը հնարավոր չի համարել, որ տիեզերքը կարող է ընդարձակվել կամ սեղմվել։ Սովորաբար ընդունվել է, որ տիեզերքը կամ ընդմիշտ գոյություն է ունեցել այժմյան անփոփոխ վիճակով, կամ ստեղծվել է անցյալում, որոշակի ժամանակում, մոտավորապես այն նույն ձևով, ինչպես այսօր տեսնում ենք։ Այսպիսի մոտեցումը մասամբ արդյունք է այն բանի, որ ժողովուրդը ձգտում է հավիտենական ճշմարտություններին և, թերևս, մխիթարվում է, մտածելով, որ թեև մարդը ծերանում է և մահանում, սակայն տիեզերքն անփոփոխ է և հավիտենական։
Նույնիսկ նրանք, ովքեր գիտակցում էին, որ ըստ Նյուտոնի ձգողության տեսության տիեզերքը չի կարող կայուն լինել, չէին մտածում, որ այն կարող է ընդարձակվել։ Ընդհակառակը, փորձում էին տեսությունը բարեփոխել այնպես, որ շատ մեծ հեռավորությունների վրա գրավիտացիոն ուժը դառնար վանողական։ Այս մոտեցումը էականորեն չէր ազդում մոլորակների շարժումների վերաբերյալ եղած ենթադրությունների վրա, բայց թույլ էր տալիս, որպեսզի անորոշ թվով աստղերի բազմությունը մնար հավասարակշռության մեջ՝ իրար մոտ գտնվող աստղերի միջև գործող ձգողական ուժերի և իրարից շատ հեռու գտնվող աստղերի միջև գործող վանողական ուժերի համակշռման շնորհիվ։ Սակայն մենք այսօր համոզված ենք, որ այդպիսի հավասարակշռությունը կայուն պիտի լինի։ Եթե որևէ տիրույթում աստղերը միմյանց մի փոքր ավելի մոտենան, ապա նրանց միջև կմեծանան ձգողական ուժերը և կգերակշռեն վանողական ուժերին, և աստղերը կշարունակեն ընկնել միմյանց վրա։ Մյուս կողմից, եթե աստղերը միմյանցից մի փոքր հեռանան, ապա կգերակշռեն վանողական ուժերը և նրանց կմղեն ավելի հեռու։
Անսահման կայուն տիեզերքի պատկերացման դեմ հանդես եկավ գերմանացի փիլիսոփա Հայնրիխ Օլբերսը 1823֊ին։ Իրականում Նյուտոնի ժամանակակիցներից շատերը արծարծել էին այդ հարցը, և չի կարելի ասել, որ Օլբերսի հոդվածն առաջինն էր, որտեղ համոզիչ փաստեր էին բերվում անսահման կայուն տիեզերքի մոդելի դեմ։ Սակայն նրա հոդվածն առաջինը լայն ճանաչման արժանացավ։ Բանն այն է, որ անսահման կայուն տիեզերքում յուրաքանչյուր տեսանելի գիծ համարյա պիտի վերջանա աստղի մակերևույթի վրա։ Հետևաբար, կարելի էր ենթադրել, որ ամբողջ երկնակամարը նույնիսկ գիշերը պետք է փայլեր այնպես, ինչպես արևը։ Օլբերսի հակափաստարկն այն էր, որ հեռավոր աստղերից եկող լույսը պետք է թուլանա՝ կլանվելով միջաստղային տարածությունը լցնող նյութի կողմից։ Մինչդեռ, եթե դա տեղի ունենար, ապա այն կլանող նյութը պիտի այնքան տաքանար, որ շիկանար ու փայլեր աստղերի նման։ Գիշերային երկնակամարի՝ արևի պայծառությամբ լուսավորված լինելու եզրակացությունից խուսափելու համար մնում էր ենթադրել, որ ստղերը ոչ թե մշտապես են փայլում, այլ բռնկվել են լոկ անցյալի որոշակի ժամանակում։ Հետևաբար, կամ կլանող նյութը դեռևս չի տաքացել, կամ հեռավոր աստղերի լույսը դեռ մեզ չի հասել։ Այսպիսով, հարց առաջացավ, թե ի՞նչն է աստղերի բռնկման պատճառը։
Անշուշտ, սրանից շատ ավելի վաղ է քննարկվել տիեզերքի սկզբնավորման հարցը։ Համաձայն մի շարք վաղ անցյալի տիեզերագետների և ըստ հրեա/քրիստոնյա/մահմեդական ավանդության, տիեզերքը սկիզբ է առել ոչ շատ հեռավոր անցյալ ժամանակում։ Այդպիսի սկզբնավորման փաստարկներից մեկը տիեզերքի գոյությունը բացատրելու համար «Սկզբնական պատճառ» գտնելու մարդկային մղումն էր։ (Հայտնի բան է՝ մենք միշտ մի դեպքը բացատրում ենք որպես նախորդ դեպքի հետևանք, ուստի այդ եղանակով իր իսկ՝ տիեզերքի գոյությունը բացատրելի է դառնում, եթե այն միայն որոշակի սկիզբ ունենա)։ Մեկ այլ պատճառ է բերում սբ․ Օգոստինոսն իր «Աստծո քաղաքը» գրքում։ Նա նշում էր, որ քաղաքակրթությունն առաջադիմում է, և մենք միշտ հիշում ենք, թե ով է այս կամ այն գործի հեղինակը, կամ ով է մշակել տվյալ մեթոդը։ Հետևաբար, ինչպես մարդը, այնպես էլ հավանաբար տիեզերքը, կարող են գոյություն ունենալ շատ վաղուցվանից։ Աբ․ Օգոստինոսը գտնում է, որ տիեզերքը արարվել է մեր թվարկությունից առաջ5000 թվականին՝ ըստ Ծննդոց գրքի։ (Հետաքրքրական է, որ դա շատ հեռու չէ վերջին Սառցի դարաշրջանի ավարտից՝ մ․թ․ա․ 10.000 թվականից, երբ, համաձայն հնագետների, քաղաքակրթությունն իրապես սկսվել է)։
Մյուս կողմից սակայն, Արիստոտելը և հույն մյուս փիլիսոփաներից շատերը կողմնակից չէին արարչագործության գաղափարին, որովհետև դա շատ էր հիշեցնում ինչ֊որ աստվածային միջամտություն։ Նրանք հավատում էին, որ մարդկությունը և նրան շրջապատող աշխարհը միշտ գոյություն են ունեցել և գոյություն կունենան ընդմիշտ։ Իհարկե, հին հույները հաշվի էին առնում վերևում նկարագրված քաղաքակրթության և զարգացման փաստը և պատասխանում էին դրան, ասելով, որ պարբերաբար տեղի ունեցող ջրհեղեղներն ու այլ աղետները մարդկությանը շարունակաբար ետ են մղել դեպի քաղաքակրթության սկիզբը։
Հետագայում այն հարցին, թե տիեզերքն ունի՞ սկիզբ ժամանակի մեջ և սահմանափակվա՞ծ է արդյոք տարածության մեջ, անդրադարձել է փիլիսոփա Իմանուիլ Կանտն իր հիմնարար (և շատ խրթին) «Զուտ բանականության քննադատություն» գրքում,[3] որը լույս է տեսել 1781֊ին։
Կանտն այս հարցերն անվանում է մաքուր բանականության անտինոմիաներ (այսինքն՝ հակասություններ), որովհետև նա գտնում էր, որ կան հավասարապես ընդունելի փաստարկներ և՛ այն դրույթի օգտին, թե տիեզերքն ունեցել է սկիզբ, և դրա հակադրույթի օգտին, թե տիեզերքը գոյություն է ունեցել ընդմիշտ։ Դրույթի օգտին փաստարկը հետևյալն էր․ եթե տիեզերքը սկիզբ չունենար, ապա որևէ դեպքից առաջ պետք է եղած լիներ անվերջ մի ժամանակ, ինչը, նրա կարծիքով, անհեթեթ է։ Հակադրույթի օգտին փաստարկն այն է, որ եթե տիեզերքը սկիզբ ունենար, ապա դրանից առաջ նորից անվերջ մի ժամանակ պետք է լիներ, ուրեմն, ինչո՞ւ պիտի որևէ որոշակի ժամանակում առաջանար տիեզերքը։ Ըստ էության, երկուսի էլ՝ դրույթի և հակադրույթի փաստարկները նույնն են։ Երկուսն էլ հիմնված են այն լռին ենթադրության վրա, թե, անկախ այն բանից, տիեզերքը ընդմիշտ գոյություն ունեցել է, թե ոչ, ժամանակը մշտապես եղել է։ Հետագայում մենք կտեսնենք, որ ժամանակի հասկացությունը տիեզերքի սկզբնավորումից առաջ իմաստ չունի։ Այս խնդրին առաջին անգամ անդրադարձել է սբ․ Օգոստինոսը։ Այն հարցին, թե Աստված ի՞նչ էր անում տիեզերքն ստեղծելուց առաջ, սբ․ Օգոստինոսը չպատասխանեց․ նա դժոխք էր պատրաստում նման հարցեր տվողների համար։ Փախարենը նա ասել է, որ ժամանակն Աստծո արարած տիեզերքի հատկանիշն է, և տիեզերքի սկզբնավորումից առաջ ժամանակ գոյություն չի ունեցել։
Այն ժամանակ, երբ շատ մարդիկ հավատացած էին, թե տիեզերքը հիմնականում անշարժ է և անփոփոխ, դրա սկզբնավորման հարցը, ըստ էության, մետաֆիզիկայի և աստվածաբության խնդիրն էր։ Դիտարկումները նույն հաջողությամբ կարելի էր ճիշտ գնահատել և այն տեսության հիման վրա, թե տիեզերքն ընդմիշտ գոյություն է ունեցել, և կամ ենթադրելով, թե այն շարժման մեջ է դրվել որոշակի ժամանակահատվածում այնպես, որ թվա, թե ընդմիշտ եղել է։ Բայց ահա 1929 թվականին Էդվին Հաբլը կատարեց պատմական նշանակություն ունեցող, շրջադարձային մի դիտարկում բացահայտեց, որ ինչ ուղղությամբ էլ որ նայես, հեռավոր գալակտիկաներն արագորեն հեռանում են մեզանից։ Այլ կերպ ասած, տիեզերքն ընդարձակվում է։ Իսկ դա նշանակում է, որ վաղ անցյալում մարմիններն իրար շատ մոտ են եղել։ Փաստորեն, եղել է մի ժամանակ,՝ տասը կամ քսան միլիարդ տարի առաջ, երբ բոլոր մարմինները գտնվել են ճիշտ նույն տեղում, և, հետևաբար, տիեզերքի խտությունը անսահման մեծ է եղել։ Ահա այս հայտնագործությունը տիեզերքի սկզբնավորման հարցը վերջնականապես բերեց գիտության ասպարեզ։
Հաբլի դիտարկումներից հետևեց, որ եղել է ժամանակ, որը կոչվում է Մեծ պայթյուն, երբ տիեզերքն անվերջ փոքր էր և անսահման խիտ։ Միանգամայն պարզ է, որ այսպիսի պայմաններում մեր իմացած գիտության բոլոր օրենքները, հետևաբար ապագան գուշակելու մեր ողջ կարողությունը անզոր են։ Եթե մեծ սկզբին նախորդել են այլ դեպքեր, ապա դրանք, այնուամենայնիվ, չեն կարող ազդել ներկա ժամանակում կատարվող դեպքերի վրա։ Դրանց գոյությունն անցյալում կարելի է հաշվի չառնել, որովհետև դրանք նկատելի հետքեր չեն թողել։ Կարելի է ասել, թե ժամանակը սկիզբ է առել Մեծ պայթյունից այն առումով, որ ավելի վաղ ժամանակները պարզապես հնարավոր չէ սահմանել։ Պետք է ընդգծել, որ ժամանակի այդպիսի սկզբնավորման տեսությունը շատ տարբեր է նախկինում մեր քննարկված տեսություններից։ Անփոփոխ և կայուն տիեզերքում ժամանակային սկիզբը ենթադրում է տիեզերքից դուրս գտնվող մի կեցության միջամտություն, քանի որ տիեզերքի սկզբնավորման համար որևէ ֆիզիկական անհրաժեշտություն չկար։ Կարելի է երևակայել, որ Աստված տիեզերքն ստեղծեց անցյալի բառացիորեն ցանկացած պահի։ Մինչդեռ, եթե տիեզերքն ընդարձակվում է, ապա այդպիսի սկզբնավորման համար կարող են ֆիզիկական պատճառներ լինել։ Կարելի է ենթադրել, որ Աստված տիեզերքն ստեղծեց հենց Մեծ պայթյունի ժամանակ, կամ նույնիսկ դրանից հետո, այնպես, որ մեզ թվա, թե մեծ պայթյուն է եղել։ Բայց բոլորովին անիմաստ է ենթադրել, թե տիեզերքը ստեղծվել է Մեծ պայթյունից առաջ։ Այսպիսով, ընդարձակվող տիեզերքի պատկերացումը չի բացառում արարչագործության գաղափարը, այն լոկ սահմանափակում է դրա իրականացման ժամանակահատվածը։
Տիեզերքի բնույթի մասին խոսելիս և այնպիսի հարցեր քննարկելիս, ինչպիսիք են, օրինակ, տիեզերքն արդյոք սկիզբ ու վերջ ունի՞, անհրաժեշտ է հստակ պատկերացնել, թե ինչ է գիտական տեսությունը։ Դիցուկ, մի պարզունակ մոտեցմամբ ընդունենք, որ տեսությունը տիեզերքի կամ նրա սահմանափակ մի մասի մոդելն է՝ այն կանոններով հանդերձ, որոնցով այդ մոդելի պարամետրերը հարաբերվում են մեր դիտարկումներին։ Մոդելը գոյություն ունի մեր պատկերացումներում և այլ իրականության մեջ տեղ չունի (ինչ էլ որ սա նշանակի)։ Այնուամենայնիվ, առաջարկված տեսությունը լավն է, եթե բավարարում է երկու պահանջի․ պետք է ճշգրտորեն նկարագրի մեծ թվով դիտարկումների արդյունքները՝ հիմնված լինելով միայն քիչ թվով պայմանական տարրեր պարունակող մոդելի վրա, ինչպես նաև որոշակիորեն կանխատեսի ապագա դիտարկումների արդյունքները։ Օրինակ, Արիստոտելի տեսությունն այն մասին, թե ամեն ինչ կազմված է չորս տարրերից՝ հողից, օդից, կրակից և ջրից, բավականին պարզ է և ընդունելի, սակայն այն ոչինչ որոշակիորեն կանխատեսել չի կարող։ Մյուս կողմից, Նյուտոնի ձգողականության տեսությունը հիմնվում է անհամեմատ ավելի պարզ մի մոդելի վրա, ըստ որի մարմինները միմյանց ձգում են մի ուժով, որն ուղիղ համեմատական է նրանց մեծությանը, ինչն անվանում ենք զանգված, և հակադարձ համեմատական նրանց միջև եղած հեռավորության քառակուսուն։ Այս մոդելը թույլ է տալիս մեծ ճշգրտությամբ հաշվարկել արևի, լուսնի և մոլորակների շարժումները։
Ցանկացած ֆիզիկական տեսություն միշտ ժամանակավոր է այն իմաստով, որ կազմված է միայն հիպոթեզներից, որոնք երբեք ապացուցել չի լինի։ Անկախ այն բանից, թե փորձնական տվյալները քանի անգամ են համընկել տեսական կանխատեսումների հետ, դուք երբեք չեք կարող վստահ լինել, որ հաջորդ անգամ արդյունքը չի հակասի տեսությանը։ Մյուս կողմից, տեսության կանխատեսմանը հակասող մի դեպքն անգամ բավական է, որպեսզի դուք այն հերքեք։ Հետաքրքրական է փիլիսոփա Կարլ Պոպերի գնահատականը․ նա գտնում է, որ իրապես լավ տեսությունը բնութագրվում է նրանով, որ բազմաթիվ կանխատեսումներ է անում, որոնք սկզբունքորեն կարող են չհաստատվել կամ մերժվել՝ դիտարկումներով։ Երբ ամեն մի նոր փորձ համընկնում է տեսական կանխատեսմանը, ապա տեսությունը պահպանվում է, և նրա նկատմամբ մեր վստահությունն աճում է, բայց հենց մի նոր փաստ հակասի տեսությանը, մենք անհապաղ հրաժարվում կամ վերափոխում ենք տեսությունը։ Իհարկե, դա այդպես է, սակայն չպետք է մոռանալ, որ միշտ կարելի է կասկածի տակ դնել նաև փորձը կատարողի բանիմացությունը։
Գործնականում, ինչը հաճախ է պատահում, նոր տեսությունը սովորաբար նախորդի այս կամ այն չափով ընդլայնումն է։ Օրինակ, Մերկուրի մոլորակի համար ճշգրիտ չափումները ցույց տվեցին, որ մի փոքր տարբերություն կա Նյուտոնի ձգողականության տեսության հիման վրա արված կանխատեսումների և մոլորակի դիտարկված շարժման միջև։ Էնշտեյնի հարաբերականության ընդհանուր տեսությունը կանխատեսում էր շարժման այդպիսի փոքր շեղում՝ ի հակադրություն Նյուտոնի տեսության։ Հենց այն փաստը, որ Էնշտեյնի տեսությունը կանխատեսեց այն, ինչը դիտարկվեց, իսկ Նյուտոնի տեսությունը չկարողացավ դա անել, եղավ նոր տեսության հաջողության և ընդունման հիմնական պատճառներից մեկը։ Այնուամենայնիվ, մենք դեռես գործնականում լայնորեն օգտվում ենք Նյուտոնի տեսությունից, որովհետև սովորական պայմաններում, ինչի հետ մենք առնչվում ենք, երկու տեսությունների կանխատեսումների միջև քանակական տարբերությունները փոքր են։ (Նյուտոնի տեսությունը մի մեծ առավելություն ունի Էնշտեյնի տեսության նկատմամբ, այն անհամեմատ պարզ է)։
Ի վերջո, գիտության նպատակն է ստեղծել մի միասնական տեսություն, որն ի վիճակի լինի նկարագրել ամբողջ տիեզերքը։ Պետք է ասել, սակայն, որ գիտնականներից շատերն այդ խնդիրը բաժանում են երկու մասի։ Առաջինն այն օրենքներն են, որոնք նկարագրում են տիեզերքի փոփոխությունը ժամանակի ընթացքում։ (Ընդ որում, եթե մենք իմանանք, թե որևէ պահի ինչի է նման տիեզերքը, ապա ֆիզիկայի այդ օրենքները մեզ կհուշեն, թե ինչի կնմանվի այն որոշ ժամանակ անց)։ Երկրորդը տիեզերքի նախնական վիճակի խնդիրն է։ Ոմանց կարծիքով գիտությունը պետք է զբաղվի միայն առաջին մասին վերաբերող հարցերով, իսկ սկզբնական վիճակի խնդիրը վերաբերում է մետաֆիզիկայի կամ կրոնի ոլորտին։ Ասում են՝ ամենակարող Աստված կարող էր տիեզերքը շարժման մեջ դնել ըստ ցանկության։ Թող այդպես լինի, բայց չէ՞ որ այդ դեպքում կարող էր նաև ցանկացած ձևով նախանշել տիեզերքի զարգացման կամայական ուղի։ Բայց, ինչպես երևում է, ընտրությունն այնպես է կատարվել, որ տիեզերքը զարգանում է խիստ կանոնավոր ձևով, որոշ օրենքների համաձայն։ Ուստի, նույնքան տրամաբանական է ենթադրել, որ կան նաև սկզբնական վիճակը կառավարող օրենքներ։
Այնուամենայնիվ, պարզվում է, որ շատ դժվար է ստեղծել այնպիսի տեսություն, որը տիեզերքը նկարագրեր համապարփակ և միանշանակ ձևով։ Այն ստեղծելու փոխարեն մենք ստիպված հիմնախնդիրը բաժանում ենք մասերի և ստեղծում մի շարք մասնակի տեսություններ։ Մասնակի տեսություններից յուրաքանչյուրը նկարագրում և կանխատեսում է սահմանափակ դասի պատկանող որոշակի դիտարկումներ՝ անտեսելով այլ մեծությունների ազդեցությունները, կամ դրանք ներկայացնելով, որպես պարզ թվերի հավաքածու։ Այս մոտեցումը, թերևս, սխալ է ամբողջովին։ Եթե տիեզերքում ամեն ինչ սկզբունքորեն կախված է ամեն ինչից, ապա մասնակի և մեկուսացած ուսումնասիրությունների օգնությամբ հազիվ թե հնարավոր լինի նույնիսկ մոտենալ հիմնախնդրի ամբողջական լուծմանը։ Այնուամենայնիվ, հենց այդ եղանակով գիտությունը մեծ հաջողությունների է հասել անցյալում։ Դասական օրինակը դարձյալ Նյուտոնի ձգողականության տեսությունն է, համաձայն որի, երկու մարմինների միջև գործող ձգողական ուժը կախված է այդ մարմիններից յուրաքանչյուրին նկարագրող թվերից՝ նրանց զանգվածներից, բայց բոլորովին անկախ է այն բանից, թե այդ մարմիններն ինչ նյութից են կազմված։ Հետևաբար՝ արևի և մոլորակների ուղեծրերը հաշվելու համար մեզ հարկավոր չէ տեսություն ունենալ նրանց կառուցվածքի և կազմության մասին։
Այսօր գիտնականները տիեզերքը նկարագրում են հիմնականում երկու մասնակի տեսությունների՝ հարաբերականության ընդհանուր տեսության և քվանտային մեխանիկայի օգնությամբ։ Դրանք XX դարի առաջին կեսի մարդկային մտքի խոշոր նվաճումներն են։ Հարաբերականության ընդհանուր տեսությունը նկարագրում է տիեզերական ձգողության ուժն ու տիեզերքի լայնամասշտաբ կառուցվածքը․ մի քանի մղոնից մինչև միլիոն միլիոն միլիոն միլիոն մղոն (1 000000 000000 000000 000000) դիտարկելի տիեզերքի չափի սահմաններում։ Մյուս կողմից քվանտային մեխանիկան զբաղվում է այնպիսի երևույթներով, որոնք տեղի են ունենում չափազանց փոքր մասշտաբներում, ինչպիսին է, օրինակ, դյույմի միլիոն միլիոներորդ մասը (0.000000 000001): Դժբախտաբար, սակայն, այսօր հայտնի է, որ այս երկու տեսություններն անհամատեղելի են, այսինքն՝ երկուսով միաժամանակ ճիշտ լինել չեն կարող։ Ժամանակակից ֆիզիկայի ջանքերից գլխավորը և այս գրքի հիմնական խնդիրն է ստեղծել մի տեսություն, որը միավորի այդ երկու տեսությունները՝ քվանտային և ձգողականության։ Այսօր մենք այդպիսի տեսություն դեռ չունենք և երկար ճանապարհ պիտի անցնել այն ստեղծելու համար, սակայն մենք արդեն գիտենք այն բազմաթիվ հատկությունները, որոնք պետք է ունենա այդպիսի միասնական տեսությունը։ Հետագա գլուխներում մենք կտեսնենք, որ արդեն որոշ չափով գաղափար ունենք այն կանխատեսումների մասին, որ կարող է անել ձգողության քվանտային տեսությունը։
Այժմ, եթե դուք հավատում եք, որ տիեզերքը կամայական չէ և ղեկավարվում է որոշակի օրենքներով, ստիպված ենք ի վերջո մասնակի տեսությունները միաձուլել մի կատարյալ միասնական տեսության մեջ, որը կարողանա նկարագրել տիեզերքում տեղի ունեցող ամեն ինչը։ Սակայն կատարյալ միասնական տեսության մեր որոնումն իր մեջ պարունակում է մի հիմնարար պարադոքս։ Երբ մենք խոսում էինք գիտական տեսությունների մասին, լռելյայն ենթադրում էինք, որ մենք բանիմաց, խելացի էակներ ենք, և եթե ցանկանանք, կարող ենք ազատորեն դիտարկել տիեզերքն ու հանգել տրամաբանական եզրակացությունների։ Այսպիսի պայմանների առկայության դեպքում հնարավոր է ենթադրել, որ մենք աստիճանաբար կմոտենանք տիեզերքը կառավարող օրենքների ըմբռնմանը։ Եթե իրոք գոյություն ունի կատարյալ միասնական տեսություն, ապա այն ևս հավանաբար կարող է կողմնորոշել մեր գործողությունները։ Այսպիսով, հենց տեսությունն ինքը կորոշի մեր որոնումների ելքը։ Իսկ որտեղի՞ց իմանանք, թե տվյալ փաստերը մեզ ճիշտ եզրակացությունների կհանգեցնեն։ Մի՞թե նույնքան հնարավոր չէ, որ դրանք մեզ սխալ եզրահանգումների հանգեցնեն և կամ ոչ մի եզրահանգման չհանգեցնեն ընդհանրապես։
Միակ պատասխանը, որ ես կարող եմ տալ այս հարցին, հիմնված է Դարվինի՝ տեսակների բնական ընտրության սկզբունքի վրա։ Բանն այն է, որ կենդանի օրգանիզմների ինքնավերարտադրվող որևէ հանրույթի մեջ կարող են լինել գենետիկական նյութի փոփոխություններ և հանգեցնել նոր անհատականությունների առաջացման։ Այդ փոփոխությունների շնորհիվ որոշ անհատներ ավելի պիտանի կլինեն մյուսներից՝ շրջապատող աշխարհի մասին ճիշտ եզրահանգումներ անելու և համապատասխան կերպով գործելու առումով։ Այդպիսի անհատները լավագույնս կգոյատևեն, կվերարտադրվեն, և կտիրապետեն նրանց վարքագծին ու մտածողությանը։ Ճշմարիտ է, որ անցյալում բանականությունը և գիտական հայտնագործությունը եղել են գոյատևման բարենպաստ պայմանների երաշխիք։ Սակայն չի կարելի վստահորեն ասել, որ դա այդպես է նաև այսօր․ հնարավոր է, որ մեր գիտական հայտնագործությունները մեզ բոլորիս կործանեն, իսկ եթե դա չպատահի էլ, ապա կատարյալ միասնական տեսությունը թերևս որևէ դեր չխաղա մեր գոյատևման հարցում։ Այդուհանդերձ, եթե իրոք տիեզերքը զարգանում է կանոնավոր ձևով, ուրեմն կարելի է ակնկալել, որ բնական ընտրության շնորհիվ մեր մեջ զարգացող տրամաբանելու ընդունակությունը կօգնի միասնական տեսության մեր որոնումներում, որպեսզի սխալ եզրահանգումներ չանենք։
Քանի որ արդեն մեր ունեցած մասնակի տեսություններն այսօր բավարար են ճշգրիտ կանխատեսումներ անելու համար բոլոր իրավիճակների մասին, բացի ծայրահեղներից, ապա, թվում է, դժվար կլինի գործնականորեն արդարացնել այն որոնումները, որոնց նպատակն է տիեզերքի վերջնական մեկ տեսություն մշակելը։ (Պետք է նշել, որ նման փաստարկներ կարելի է բերել հարաբերականության ընդհանուր տեսության և քվանտային մեխանիկայի կապակցությամբ, այնինչ այդ տեսությունները մեզ տվին միջուկային էներգիա և միկրոէլեկտրոնիկա)։ Հնարավոր է, հետևաբար, որ կատարյալ միասնական տեսությունը չնպաստի մեր տեսակների գոյատևմանը։ Այն կարող է նաև ազդել մեր կենսակերպի վրա։ Սակայն քաղաքակրթության սկզբից ի վեր մարդը չի գոհացել չկապակցված և անբացատրելի դեպքերը դիտելով։ Նա միշտ ծարավի է եղել և ցանկացել է հասկանալ աշխարհի թաքնված կարգուկանոնի էությունը։ Այսօր, ինչպես միշտ, ձգտում ենք իմանալ, թե մենք ինչո՞ւ ենք այստեղ և որտեղի՞ց ենք գալիս։ Գիտելիքի հանդեպ մարդկության ցուցաբերած խորը հետաքրքրասիրութունը արդարացնում է մեր շարունակական որոնումները։ Եվ մեր նպատակն է առնվազն լրիվ և կատարյալ պատկերացում ունենալը տիեզերքի մասին, որտեղ մենք ապրում ենք։
2
Տարածություն և ժամանակ
Մարմինների շարժման մասին մեր արդի գիտելիքները գալիս են Գալիլեոյից և Նյուտոնից։ Ավելի վաղ իշխել է արիստոտելյան մտածողությունը, ըստ որի մարմնի բնական վիճակ համարվել է նրա դադարի վիճակը, իսկ մարմինը կարող է շարժվել միայն նրա վրա ուժի կամ ազդակի գործողության դեպքում։ Սրանից հետևում էր, որ ծանր մարմինն ավելի շուտ պիտի ընկնի գետին, քան թեթևը, որովհետև այն ավելի մեծ ուժով է ձգվում երկրի կողմից։
Արիստոտելյան ավանդության համաձայն, տիեզերքը կառավարող բոլոր օրենքները հնարավոր է ճանաչել զուտ բանականությամբ և պետք չէ դրանք փորձել ստուգել։ Գալիլեոյից առաջ ոչ ոքի մտքով չէր անցել ստուգել, թե իրո՞ք տարբեր կշիռ ունեցող մարմինները տարբեր արագություններով են ընկնում։ Ասում են, իբր, Գալիլեոն Արիստոտելի սխալը ցույց է տվել Պիզայի թեք աշտարակից տարբեր կշիռ ունեցող մարմիններ վայր գցելով։ Իհարկե, այս պատմությունը ճիշտ չէ, բայց Գալիլեոն համարժեք մի փորձ կատարել է․ տարբեր կշիռ ունեցող գնդիկներ է գլորել ողորկ մակերեսով թեքության վրայով։ Այստեղ իրավիճակը նույնն է, ինչ ուղղաաձիգ անկման դեպքում, սակայն դիտարկումն ավելի հեշտ է, որովհետև գնդիկները դանդաղ են շարժվում։ Գալիլեոյի չափումներից պարզվել է, որ գնդիկների արագության փոփոխությունն ըստ ժամանակի հաստատուն է բոլոր գնդիկների համար, անկախ նրանց կշռից։ Դիցուք, եթե թեքությունն այնպիսին է, որ յուրաքանչյուր տասը մետրի վրա այն նվազում է տասը մետրով, ապա, անկախ գնդիկի ծանրությունից, նրա արագությունը շարժման սկզբից մեկ վայրկյան հետո կլինի մեկ մետր վայրկյանում, երկու վայրկյան հետո՝ երկու մետր վայրկյանում, և այդպես շարունակ։ Այն փաստը, որ կապարե մարմինն ավելի արագ է ընկնում, քան փետուրը, բացատրվում է նրանով, որ փետուրի անկումը դանդաղում է օդի դիմադրության պատճառով։ Եթե ներքև գցվեն երկու մարմին, որոնց համար օդի դիմադրությունը մեծ չէ, ինչպես երկու տարբեր կապարե գնդերի դեպքում, նրանք կընկնեն միևնույն արագությամբ։
Գալիլեոյի տվյալները Նյուտոնն օգտագործեց որպես հիմք՝ շարժման իր օրենքները ձևակերպելու համար։ Գալիլեոյի կատարած փորձի ընթացքում մարմինը, թեքությունն ի վար գլորվեիս, ենթարկվում է միևնույն ուժի (իր ծանրության) ազդեցությանը, և հետևանքը լինում է նրա հաստատուն արագացումը։ Նախկինում կարծում էին, թե ուժի դերը լոկ մարմինը շարժման մեջ դնելն է։ Գալիլեոն ցույց տվեց, սակայն, որ ուժի իրական ազդեցությունն այն է, որ միշտ փոխի մարմնի արագությունը։ Նա ցույց տվեց նաև, որ մարմինը նույն արագությամբ կշարունակի շարժվել ուղիղ գծով, այնքան ժամանակ, քանի դեռ նրա վրա որևէ ուժ չի ազդում։ Այդ միտքը 1687 թվականին Նյուտոնը հստակորեն առաջ քաշեց իր «Մաթեմատիկայի սկզբունքները» գրքում, ինչը և հայտնի է որպես Նյուտոնի առաջին օրենք։ Իսկ թե ինչ է կատարվում մարմնի հետ, երբ նրա վրա ուժ է ազդում, տալիս է Նյուտոնի երկրորդ օրենքը։ Այդ օրենքի համաձայն, մարմնի արագությունը փոխվում է ազդող ուժին համեմատական կարգով՝ մարմինը ձեռք է բերում արագացում։ (Օրինակ, երբ ազդող ուժը մեծանա երկու անգամ, արագացումը ևս երկու անգամ կմեծանա)։ Մյուս կողմից, որքան մեծ է մարմնի զանգվածը (շատ է նյութի քանակը), այնքան փոքր է նրա արագացումը։ (Նույն ուժը երկու անգամ ավելի մեծ զանգված ունեցող մարմնի վրա ազդելիս կառաջացնի երկու անգամ փոքր արագացում): Բոլորին հայտնի է, որ որքան հզոր է ավտոմեքենայի շարժիչը, այնքան ավելի մեծ կլինի նրա արագացումը, իսկ որքան ծանր է մեքենան, այնքան փոքր է արագացումը՝ միևնույն շարժիչի դեպքում։
Ի լրումն շարժման օրենքի, Նյուտոնը հայտնագործեց նաև տիեզերական ձգողականության ուժի օրենքը, որի համաձայն յուրաքանչյուր մարմին ձգում է այլ մարմնի մի այնպիսի ուժով, որը համեմատական է մարմիններից յուրաքանչյուրի զանգվածին։ Այսպես, օրինակ, երկու մարմինների միջև ձգողության ուժը երկու անգամ մեծ կլինի, եթե նրանցից մեկի (ասենք A֊ի) զանգվածը երկու անգամ մեծացնենք։ Այս բանն ակնհայտ է, քանի որ նոր A֊ն կարելի է ընդունել որպես երկու նույն զանգվածն ունեցող մարմիններից կազմված, որոնցից յուրաքանչյուրը ձգում է B մարմինը սկզբնական ուժով։ Հետևաբար Նոր A-ի և B֊ի միջև ձգողական ուժը երկու անգամ մեծ կինի։ Այժմ ենթադրենք, թե մարմիններից մեկի զանգվածը մեծ է նախորդից 2 անգամ, իսկ մյուսինը՝ 3 անգամ, այդ դեպքում նրանց միջև ձգողական ուժը կմեծանա 6 անգամ։ Այստեղից ակնհայտ է, թե ինչու են բոլոր մարմինները վայր ընկնում միևնույն արագությամբ, եթե մի մարմնի կշիռը մյուսից երկու անգամ մեծ է, դեպի երկիր ձգող ուժը ևս երկու անգամ մեծ կլինի, սակայն այն երկու անգամ ավելի մեծ էլ զանգված ունի։ Համաձայն Նյուտոնի երկրորդ օրենքի, այս երկու ազդեցությունները միմյանց կչեզոքացնեն, և արագացումը բոլոր դեպքերում կլինի հաստատուն։
Նյուտոնի ձգողականության օրենքից բխում է նաև, որ որքան մարմինները իրարից հեռու են, այնքան փոքր է ձգողական ուժը։ Ըստ այդ օրենքի, մի աստղի ձգողության ուժն ուղիղ մեկ քառորդով փոքր կլինի նույն զանգվածով մեկ այլ աստղի ձգողությունից, որը երկու անգամ մոտ է գտնվում։ Այս օրենքը թույլ է տալիս մեծ ճշտությամբ կանխագուշակել երկրի, լուսնի և մոլորակների ուղեծրերը։ Եթե այնպես լիներ, որ աստղի ձգողական ուժը հեռավորությունից կախված նվազեր ավելի արագ, ապա երկրի, լուսնի և մոլորակների ուղեծրերը էլիպսաձև չէին լինի, կլինեին պարուրաձև և կուղղվեին դեպի արեգակը։ Իսկ եթե այն ավելի դանդաղ նվազեր, ապա աստղերի ձգողական ուժերը կգերազանցեին երկրի ձգողական ուժին։
Արիստոտելի և Գալիլելոյի ու Նյուտոնի մոտեցումների միջև ակնհայտ տարբերությունն այն է, որ Արիստոտելը հավատում էր, թե մարմինը ձգտում է դադարի նախընտրելի մի վիճակի, եթե նրա վրա ուժ կամ իմպուլս չի ազդում։ Մասնավորապես, նա մտածում էր, որ երկիրը գտնվում է դադարի վիճակում։ Նյուտոնի օրենքներից հետևում է, սակայն, որ դադարի եզակի ստանդարտ վիճակ չկա։ Կարելի է նույն հաջողությամբ ասել, որ A մարմինը դադարի վիճակում է, իսկ B֊ն շարժվում է հաստատուն արագությամբ A֊ի նկատմամբ և կամ հակառակը՝ B֊ն է դադարի վիճակում, իսկ A֊ն շարժվում է։ Եթե մի պահ մոռանանք, օրինակ, որ Երկիրը պտտվում է իր առանցքի և միաժամանակ արևի շուրջը, ապա կարող ենք ընդունել, որ երկիրը գտնվում է դադարի վիճակում և նրա վրա մի գնացք 90 մղոն (140 կմ/ժ) արագությամբ շարժվում է դեպի հյուսիս և կամ գնացքն է գտնվում դադարի վիճակում, իսկ երկիրը՝ նույն՝ 90 մղոն/ժ արագությամբ շարժվում է դեպի հարավ։ Եթե մենք գնացքի վրա շարժվող մարմինների հետ փորձեր կատարենք, ապա դրանք ճշգրտորեն կենթարկվեն Նյուտոնի շարժման օրենքներին։ Եվ եթե մենք սեղանի թենիս խաղանք գնացքում, ապա գնդակի շարժումները կենթարկվեն Նյուտոնի օրենքներին ճիշտ այնպես, ինչպես երկաթգծի վրա։ Հետևաբար չի կարելի միարժեքորեն ասել՝ գնա՞ցքն է շարժվում, թե՞ երկիրը։
Դադարի ստանդարտ վիճակի բացակայությունը նշանակում է, որ չի կարելի ասել, թե տարբեր ժամանակներում տեղի ունեցած երկու դեպքեր կատարվել են տարածության նույն դիրքում։ Ենթադրենք, օրինակ, մեր սեղանի թենիսի գնդակն ուղղահայաց ուղղությմաբ վեր ու վար է թռչում գնացքում գտնվող սեղանի վրա և նույն նշանակետին է հարվածում մեկ վայրկյան ընդմիջումով։ Երկաթգծի հարևանությամբ գտնվող դիտորդի համար երկու հարվածների միջև հեռավորությունը կթվա քառասուն մետր, որովհետև երկու հարվածների միջև ընկած ժամանակամիջոցում գնացքն այդքան ճանապարհ կանցնի։ Հետևաբար բացարձակ դադարի վիճակի բացակայությունը մեզ թույլ չի տալիս իմանալ դեպքի բացարձակ դիրքը տարածության մեջ, ինչպես Արիստոտելն էր ցանկանում։ Դեպքի դիրքերը և դրանց միջև հեռավորությունը տարբեր են գնացքում և երկաթգծի հարևանությամբ գտնվող դիտորդների համար, իսկ որևէ պատճառ չունենք մեկի դիրքը գերադասելու։
Նյուտոնն ինքը շատ էր մտահոգված, որ բացարձակ դիրք կամ ինչպես ընդունված էր ասել, բացարձակ տարածություն գոյություն չունի, որովհետև դա չէր համապատասխանում բացարձակ Աստծո իր տեսակետին։ Փաստորեն, նա հրաժարվեց ընդունել բացարձակ տարածության բացակայությունը, թեև դա բխում էր նրա օրենքներից։ Շատերը Նյուտոնին քննադատեցին նրա ոչ ռացիոնալ հավատի համար, մասնավորապես, Բերկլի Եպիսկոպոսը, մի փիլիսոփա, որը համոզված էր, թե բոլոր նյութական առարկաները և տարածությունն ու ժամանակը պատրանք են։ Երբ նշանավոր դոկտոր Ջոնսոնին հաղորդեցին Բերկլիի կարծիքը, նա բղավեց․ «Այսպիսով հերքում եմ այդ գաղափարը» և ոտքով հարվածեց մի մեծ քարի։
Ե՛վ Արիստոտելը, և՛ Նյուտոնը հավատում էին բացարձակ ժամանակի գոյությայնը։ Այսինքն՝ համոզված էին, որ երկու դեպքերի միջև ընկած ժամանակամիջոցը կարելի է ճշգրիտ որոշել, եթե լավ ժամացույց է օգտագործվում, անկախ այն բանից, թե այդ ժամանակն ով է չափում։ Համարում էին, թե ժամանակը լրիվ ինքնուրույն և անկախ է տարածությունից։ Սա շատերի համար տրամաբանական տեսակետ էր։ Սակայն, հարկ եղավ տարածության և ժամանակի մասին մեր պատկերացումը փոխել։ Թեև մեր հասարակ դատողությունը ճիշտ է համեմատաբար դանդաղ շարժվող խնձորների կամ մոլորակների համար, բայց այն ուժը կորցնում է, երբ առարկաները շարժվում են լույսի կամ նրան մոտ արագությամբ։
1676 թվականին դանիացի աստղագետ Օլե Քրիստենսեն Ռոեմերն առաջինը հայտնաբերեց, որ լույսը վերջավոր, բայց շատ մեծ արագություն ունի։ Նա բացահայտեց, որ այն ժամանակամիջոցները, որոնց ընթացքում Յուպիտերի լուսինները հայտնվում (ծագում) են, անցնելով մոլորակի հետևով, միմյանց հավասար չեն, ինչը սպասելի էր, եթե լուսինները Յուպիտերի շուրջ պտտվեին հաստատուն արագությամբ։ Արևի շուրջ պտտվելիս Յուպիտերի և երկրի միջև հեռավորությունը փոխվում է։ Ռոեմերը նկատեց, որ Յուպիտերի լուսինների խավարումներն այնքան ավելի ուշ են դիտվում, որքան երկիրը հեռու է գտնվում Յուպիտերից։ Նա եզրակացրեց, որ դա հետևանք է այն բանի, որ լույսը լուսիններից մեզ ուշ է հասնում, երբ մենք նրանից ավելի հեռու ենք։ Դժբախտաբար, Յուպիտերի և Երկրի միջև հեռավորության փոփոխությունների նրա չափումները շատ ճշգրիտ չէին, և դրա պատճառով, լույսի արագության մեծությունը ստացվեց 140.000 մղոն/վ (225.000 կմ/վ)՝ ներկայիս 186.000 մղոն/վ (298.000 կմ/վ) փոխարեն։ Այդուհանդերձ, Ռոեմերի հաջողությունը, որով ապացուցվեց ոչ միայն լույսի արագության վերջավոր լինելը, այլև չափվեց նրա մեծությունը, նշանակալից երևույթ էր, մանավանդ որ դա կատարվել էր Նյուտոնի «Մաթեմատիկայի սկզբունքները» գրքի լույսընծայումից տասնմեկ տարի առաջ։
Լույսի տարածման հարմար տեսություն գոյություն չուներ մինչև 1865 թ․, երբ անգլիացի ֆիզիկոս Ջեյմս Կլերկ Մաքսվելին հաջողվեց միավորել էլեկտական և մագնիսական ուժերը նկարագրող մինչ այդ հայտնի մասնակի տեսությունները։ Մաքսվելի հավասարումները կանխագուշակում էին, որ միացյալ էլեկտրամագնիսական դաշտում կարող են լինել ալիքանման գրգռումներ, որոնք պետք է որ տարածվեն հաստատուն արագությամբ, ճիշտ այնպես, ինչպես ջրավազանի ալիքները։ Եթե այս ալիքների երկարությունը (նրա մի գագաթից մինչև մյուսը եղած հեռավորությունը) մեկ մետր է կամ ավելի, մենք դրանց այժմ անվանում ենք ռադիոալիքներ։ Ավելի կարճ ալիքները հայտնի են որպես միկրոալիքներ (մի քանի սանտիմետր) և՝ ենթակարմիր ալիքներ (երբ ալիքի երկարությունը հասնում է սանտիմետրի հազարերորդ մասերի)։ Տեսանելի լույսի ալիքի երկարությունն ընկած է սանտիմետրի քառասունից մինչև ութսուն միլիոներորդ մասերի սահմաններում։ Ավելի կարճ ալիքի երկարություն ունեցողները կոչվում են ուլտրամանուշակագույն, ռենտգենյան և գամմա ճառագայթներ։
Ըստ Մաքսվելի տեսության, ռադիոալիքները կամ լույսի ալիքները պետք է շարժվեն որոշակի հաստատուն արագությամբ։ Բայց, քանի որ Նյուտոնի տեսությունը բացառել էր բացարձակ դադարի գաղափարը, և եթե ընդունենք, որ լույսը տարածվում է հաստատուն արագությամբ, ապա պետք է նշվի, որ այդ արագությունը չափված է ինչ֊որ բանի համեմատ։ Այսպիսով, ենթադրվեց, որ գոյություն ունի ինչ֊որ «եթեր» կոչված մի նյութ, որն առկա է ամենուր և լցնում է նույնիսկ «դատարկությունը»։ Այսինքն՝ լույսի ալիքները տարածվում են եթերի միջով այնպես, ինչպես ձայնի ալիքները՝ օդի միջով, հետևաբար լույսի արագությունը չափվելու է եթերի նկատմամբ։ Տարբեր դիտորդներ, շարժվելով եթերի նկատմամբ, ընդառաջ եկող լույսը տեսնելու են տարբեր արագություններով, բայց լույսի արագությունը եթերի նկատմամբ մնալու է հաստատուն։ Մասնավորապես, քանի որ երկիրը պտտվում է արևի շուրջը, շարժելով եթերի միջով, ապա լույսի արագությունը երկրի շարժման ուղղությամբ (երբ մենք շարժվում ենք դեպի լույսի աղբյուրը) ավելի մեծ կլինի, քան լույսի արագությունն այդ շարժմանն ուղղահայաց ուղղությամբ (երբ մենք չենք շարժվում դեպի լույսի աղբյուրը)։ 1887֊ին Ալբերտ Մայքելսոնը[4] (հետագայում Նոբելյան մրցանակակիր առաջին ամերիկացին ֆիզիկայի գծով) և Էդվարդ Մոռլին Քլիվլենդի Քեյզի կիրառական գիտությունների դպրոցում չափազանց ճշգրիտ փորձեր դրեցին։ Նրանք բաղդատեցին լույսի արագությունները երկրի շարժման և դրան ուղղահայաց ուղղություններով և, ի մեծ զարմանս իրենց, պարզեցին, որ դրանք ճշգրտորեն համընկնում են։
1887֊ից մինչև 1905 թվականները բազմաթիվ փորձեր են կատարվել, մասնավորապես, դանիացի ֆիզիկոս Հենրիկ Լորենցի կողմից, բացատրելու համար Մայքելսոն֊Մոռլիի ստացած արդյունքները՝ եթերի միջոցով շարժվող առարկաների սեղմանն և ժամացույցների դանդաղման վերաբերյալ։ Սակայն, ահա 1905 թվականին հրատարակվեց շատ նշանավոր մի հոդված, մինչ այդ անհայտ Ալբերտ Էնշտեյնի կողմից, որն աշխատում էր շվեյցարական արտոնագրման գրասենյակում։ Այդ հոդվածում նշվում էր, որ լույսի ալիքների շարժումը բացատրելու համար եթերի գաղափարի կարիքը չի լինի, եթե հրաժարվենք բացարձակ ժամանակի գաղափարից։ Դրանից մի քանի շաբաթ անց նման միտք էր արտահայտել նաև ֆրանսիացի առաջատար մաթեմատիկոս Հանրի Պուանկարեն։ Էյնշտեյնի փաստարկներն ավելի մոտ էին ֆիզիկային, քան Պուանկարեինը, որը խնդրին մոտենում էր զուտ մաթեմատիկորեն։ Այս նոր տեսությունը սովորաբար վերագրվում է Էնշեյնին, բայց Պուանկարեի անունը հիշատակվում է որպես տեսության կարևոր մի մասի ձևավորման մասնակցի։
Այդ այսպես կոչված, հարաբերականության տեսության առանցքային հիմնադրույթն այն է, որ գիտության օրենքները նույնը պիտի լինեն բոլոր ազատորեն շարժվող դիտորդների համար՝ անկախ նրանց շարժման ազատությունից։ Այդ բանը ճիշտ էր նաև Նյուտոնի շարժման օրենքների համար, սակայն գաղափարն այժմ ընդարձակվեց՝ ներառելով Մաքսվելի տեսությունը և լույսի արագությունը․ բոլոր դիտորդները, անկախ իրենց շարժման արագությունից, կչափեն լույսի միևնույն արագությունը։ Այս պարզ միտքը մի քանի արժեքավոր հետևանքներ ունեցավ։ Թերևս ամենահանրահայտը զանգվածի ու էներգիայի համարժեքության օրենքն է, որն արտահայտված է Էնշտեյնի նշանավոր E=mc² հավասարումով (որտեղ E-ն էներգիան է, m֊ը՝ զանգվածը, c֊ն՝ լույսի արագությունը) և այն օրենքը, ըստ որի ոչ մի մարմին չի կարող շարժվել լույսի արագությունից ավելի մեծ արագությամբ։ Էներգիայի և զանգվածի համարժեքությունից բխում է, որ շարժման ընթացքում մարմնի ձեռք բերած համապատասխան էներգիան գումարվելու է նրա զանգվածին։ Այսինքն՝ շարժման հետևանքով մարմնի զանգվածը մեծանալով, դժվարացնում է նրա արագության հետագա աճը։ Այս երևույթը իրականում նկատելի է դառնում, երբ մարմինը շարժվում է լույսի արագությանը մոտ արագությամբ։ Օրինակ, եթե մարմնի արագությունը հավասար է լույսի արագության 10 տոկոսին, մարմնի զանգվածը աճում է բնականի 0,5 տոկոսի չափով, իսկ երբ արագությունը լույսի արագության 90 տոկոսի չափ է, ապա մարմնի զանգվածը դառնում է բնականի ավելի քան կրկնակին։
Իսկ երբ մարմնի արագությունը մոտենում է լույսի արագությանը, ապա զանգվածն այնքան արագ է մեծանում, որ չափազանց մեծ էներգիա է պահանջում արագության հետագա փոփոխման համար։ Մարմնի արագությունը, փաստորեն, երբեք չի կարող հասնել լույսի արագությանը, քանի որ այդ դեպքում զանգվածն անսահման կմեծանա և, և զանգվածի և էներգիայի համարժեքության համաձայն, անսահման մեծ քանակի էներգիա կպահանջվի դրա համար։ Այդ իսկ պատճառով, ցանկացած բնական մարմին հարաբերականության տեսությամբ ընդմիշտ սահմանափակված է շարժվելու լույսի արագությունից ավելի փոքր արագությամբ։ Միայն լույսը կամ սեփական զանգված չունեցող այլ ալիքներ կարող են շարժվել լույսի արագությամբ։
Հարաբերականության տեսության հավասարարժեք հետևանքներից է նաև այն, որ հեղաշրջվեցին մեր պատկերացումները տարածության և ժամանակի մասին։ Նյուտոնի տեսության համաձայն, երբ մի տեղից դեպի մի այլ տեղ լուսային ազդանշան է հաղորդվում, տարբեր դիտորդներ համակարծիք կլինեն այդ տեղափոխման ժամանակի հարցում (քանի որ ժամանակը բացարձակ է), իսկ լույսի անցած ճանապարհի երկարության հարցում նրանք միշտ չէ, որ կհամաձայնեն միմյանց հետ (քանի որ տարածությունը բացարձակ չէ)։ Որովհետև լույսի արագությունը հաշվելու համար անհրաժեշտ է նրա անցած ճանապարհը բաժանել ժամանակի վրա, ուստի տարբեր դիտորդներ լույսի արագության տարբեր արժեքներ կչափեն։ Հարաբերականության տեսության մեջ, մյուս կողմից, բոլոր դիտորդները պետք է համակարծիք լինեն լույսի արագության մեծության հարցում։ Հետևաբար, եթե նրանք համակարծիք չեն լույսի անցած ճանապարհի հարցում, չպետք է համաձայն լինեն նաև ժամանակի հարցում։ (Ժամանակը լույսի անցած ճանապարհի, որի ճշգրտությունը դիտորդները չեն ընդունում, հարաբերությունն է լույսի արագությանը, որի հետ նրանք համաձայն են)։ Այլ կերպ ասած, հարաբերականության տեսությունը վերջ տվեց բացարձակ ժամանակի պատկերացմանը։ Թվում է, թե յուրաքանչյուր դիտորդ պետք է ունենա ժամանակի իր սեփական չափումը, որը կատարում է իր հետ վերցրած ժամացույցով, և տարբեր դիտորդների նույնանման ժամացույցներն անպայման չէ, որ կհամապատասխանեն միմյանց։
Յուրաքանչյուր դիտորդ կարող է ռադարի օգնությամբ իմանալ, թե որտեղ և երբ տեղի ունեցավ տվյալ պատահույթը՝ այնտեղ լույսի կամ ռադիոալիքների ազդանշան ուղարկելով։ Ազդանշանի մի մասը պատահույթի վայրից վերադառնում է, և դիտորդը չափում է արձագանքի ստացման ժամանակը։ Պատահույթի ժամանակ է կոչվում ազդանշանի հաղորդման և արձագանքի ստացման տևողությունների կիսագումարը, իսկ պատահույթի հեռավորությունն այդ շրջապտույտի կիսաժամանակի և լույսի արագության արտադրյալն է։ (Պատահույթ ասվածը, այս իմաստով, տարածության մի առանձին կետում և որոշակի ժամանակում տեղի ունեցածն է)։ Այս պատկերացումը ցույց է տրված նկ․21֊ում, որը տարածություն֊ժամանակ դիագրամի մի օրինակ է։ Այս ընթացակարգն օգտագործելով, դիտորդները, որոնք իրար նկատմամբ հարաբերական շարժման մեջ են, կարող են միևնույն երևույթին տարբեր դիրքեր և տարբեր ժամանակներ վերագրել։ Որևէ մեկի չափումն ավելի ճիշտ չի կարելի համարել մյուսի նկատմամբ, սակայն բոլոր չափումները կապված են միմյանց հետ։ Եթե դիտորդներից մեկին հայտնի է մյուսի շարժման հարաբերական արագությունը, ապա նա կարող է ճշգրտորեն իմանալ, թե այս վերջինը տվյալ դեպքի համար ինչ դիրք և ժամանակ է որոշել։
Այժմ մենք հենց այս ռադարային եղանակն ենք օգտագործում հեռավորությունը ճշգրիտ չափելու համար, որովհետև կարող ենք ժամանակն ավելի մեծ ճշգրտությամբ չափել, քան հեռավորությունը։ Արդարև, մետրը սահմանված է որպես այնպիսի հեռավորություն, որը լույսն անցնում է 0,00000000 33356-40952 վայրկյանում՝ չափված ցեզիումային ժամացույցով։ (Այս հատուկ թվի ընտրությունը պայմանավորված է նրանով, որ դա համապատասխանում է մետրի պատմական սահմանը՝ որպես Փարիզում պահվող հատուկ պլատինե ձողի երկու նշանակետերով սահմանված երկարություն)։ Մենք հավասարապես կարող ենք օգտվել երկարության ավելի հարմար նոր միավորից՝ լուսավայրկյանից։ Դա ուղղակի այն հեռավորությունն է, որը լույսն անցնում է մեկ վայրկյանում։ Հարաբերականության տեսության մեջ մենք այժմ հեռավորությունը սահմանել ենք, ժամանակի և լույսի արագության միջոցով։ Հետևաբար յուրաքանչյուր դիտորդ լույսը չափելիս արագության համար պետք է օգտագործի միևնույն արժեքը (այսինքն՝ 1 մետր 0,000000003335640952 վայրկյանում)։ Որևէ կարիք չկա, որ ներմուծվի եթերի գաղափարը, ինչի գոյությունն ամենուր հնարավոր չէ հայտնաբերել, ինչպես ցույց է տալիս Մայքելսոն֊Մոռլիի փորձը։ Այսպիսով, հարաբերականության տեսությունը մեզ հիմք է տալիս հիմնավորապես փոխելու մեր պատկերացումները տարածության և ժամանակի մասին։ Մենք պետք է ընդունենք, որ ժամանակը լիովին անջատ և անկախ չէ տարածությունից, այլ նրանք միավորված են միմյանց հետ, որպես, այսպես կոչված, տարածություն֊ժամանակ։
Սովորական փորձից հայտնի է, որ տարածության մեջ կետի դիրքը կարելի է որոշել նաև կետի ունեցած որոշակի լայնությամբ ու երկայնությամբ և որոշակի բարձրությամբ ծովի մակերևույթից։ Կարելի է օգտագործել նաև 3 հարմար կոորդինատներ, որոնք, սակայն, կարող են սահմանափակ օգտակար լինել։
Օրինակ, երկնակամարում լուսնի դիրքը հազիվ թե որևէ մեկը որոշի Պիլադիլի հրապարակից նրա՝ դեպի հյուսիս և արևելք ունեցած հեռավորությամբ՝ մղոններով, և ծովի մակերևույթից ունեցած բարձրությամբ՝ ոտնաչափով։ Ընդհակառակը, երկնային մարմնի դիրքը նպատակահարմար է ներկայացնել արևից, մոլորակների ուղեծրային հարթությունից ունեցած հեռավորություններով, լուսինը արևին միացնող և արևը Ալֆա Կենտավրոս աստղին միացնող գծերի կազմած անկյունով։ Նույնիսկ այսպիսի կոորդինատները չի կարելի մշտապես օգտագործել արևի դիրքը մեր գալակտիկայում և կամ մեր գալակտիկայի դիրքը գալակտիկաների կույտերի մեջ նկարագրելու համար։ Իրականում տիեզերքն ամբողջությամբ հնարավոր է նկարագրել իրար ծածկող կոորդինատային խմբերի հավաքածուի օգնությամբ։ Յուրաքանչյուր խմբում կարելի է օգտագործել 3 կոորդինատ՝ որևէ կետի դիրքը բնորոշելու համար։
Պատահույթն այն է, ինչ տեղի է ունենում տարածության որոշակի կետում և որոշակի ժամանակում։ Հետևաբար, պատահույթը կարելի է բնորոշել 4 թվով կամ կոորդինատով։ Այս պարագայում դարձյալ կոորդինատների ընտրությունը պայմանական է․ կարելի է ընտրել երեք հստակ սահմանված հատուկ կոորդինատներ և ժամանակի որևէ չափում։ Հարաբերականության տեսության մեջ իրական տարբերություն չկա տարածության և ժամանակի կոորդինատների միջև, ճիշտ այնպես, ինչպես իրական տարբերություն չկա տարածական կոորդինատներից որևէ երկուսի միջև։ Հնարավոր է ընտրել մի նոր կոորդինատային շարք, որում, ասենք, նորի առաջին տարածական կոորդինատը լինի նախկինի առաջին և երկրորդ տարածական կոորդինատների կոմբինացիան։ Օրինակ, կետի դիրքը երկրի վրա Պիկադիլից դեպի հյուսիս և արևմուտք եղած մղոններով որոշելու փոխարեն կարելի է օգտագործել Պիկադիլից հուսիս֊արևելք և հյուսիս֊արևմուտք ուղղություններով եղած մղոնները։ Նույն ձևով հարաբերականության տեսության մեջ կարելի է օգտագործել մի նոր ժամանակի կոորդինատ, որը լինի նախկին ժամանակի (վայրկյաններով) և Պիկադիլից դեպի հյուսիս անցած հեռավորության (լուսավայրկյաններով) գումարը։
Հաճախ շատ օգտակար է մտածել, պատահույթի չորս կոորդինատների մասին՝ բնորոշելու նրա դիրքը քառաչափ տարածության մեջ, որը կոչվել է տարծություն֊ժամանակ։ Սակայն քառաչափ տարածությունն անհնար է պատկերացնել։ Ես ինքս դժվար եմ պատկերացնում նույնիսկ եռաչափ տարածությունը։ Այնուամենայնիվ, հեշտ է երկչափ տարածության դիագրամներ գծել, ինչպես, օրինակ, երկրագնդի մակերևույթը։ (Երկրագնդի մակերևույթը երկչափ է, որովհետև նրա վրա կետի դիրքը կարելի է որոշել երկու կոորդինատներով՝ լայնությամբ և երկարությամբ)։ Ես հիմնականում օգտագործելու եմ դիագրամներ, որոնցում ժամանակն աճման կարգով ցույց է տրվելու հեռանկարում։ (Դրանք կոչվում են տարածություն֊ժամանակ դիագրամներ, օրինակ, նկ․ 2.1֊ը)։ Դիցուկ, 2.2 նկարում ժամանակը տեղադրված է ուղղահայաց առանցքի վրա՝ տարիներով, իսկ հորիզոնական առանցքի վրա՝ արևի և Ալֆա Կենտավրոս աստղի միջև եղած հեռավորությունը՝ մղոններով։ Արևի և Ալֆա Կենտավրոսի հետագծերը տարածություն֊ժամանակ դիագրամում ցույց են տրված որպես ուղղաձիգ գծեր ձախ և աջ կողմերում։ Արևի լույսի ճառագայթը, անցնելով թեք անկյունագծով, չորս տարում արևից հասնում է Ալֆա Կենտավրոսին։
Ինչպես մենք արդեն գիտենք, Մաքսվելի հավասարումները կանխատեսում են, որ լույսի արագությունը նույնը պիտի լինի, անկախ աղբյուրի շարժման արագությունից, ինչը հաստատված է ճշգրիտ չափումներով։ Սրանից հետևում է, որ եթե որոշակի ժամանակում տարածության որոշակի կետից լուսային ազդանշան է արձակվել, ապա անցնող ժամանակի հետ լույսը պիտի տարածվի որպես լուսային գունդ, որի մեծությունն ու դիրքը կախված չեն աղբյուրի արագությունից։ Մեկ միլիոներորդ վայրկյան հետո լույսը պիտի տարածվի՝ առաջացնելով 300 մետր շառավիղ ունեցող գունդ, երկու միլիոներորդ վայրկյան հետո գնդի շառավիղը կլինի 600 մետր և այսպես շարունակ։ Սա նման կլինի լճակի մակերևույթին տարածվող ալիքներին, երբ լճակի մեջ քար է գցվում։ Ալիքները, տարածվելով շրջանաձև, ժամանակի հետ գնալով ավելի և ավելի են տարածվում։ Եթե այժմ պատկերացնենք եռաչափ տարածական մոդել՝ բաղկացած լճակի երկչափ մակերեսից և միաչափ ժամանակից, ապա տարածվող ալիքները ժամանակի ընթացքում կառաջացնեն մի կոն, որի գագաթը կհամապատասխանի այն տեղին և ժամանակին, երբ քարը խփվում է ջրին (նկ․2.3):
Նույն ձևով լույսը, մի պատահույթից տարածվելով, առաջացնում է եռաչափ մի կոն քառաչափ տարածություն֊ժամանակի մեջ։ Այս կոնը կոչվում է պատահույթի ապագայի լուսակոն։ Նույն ձևով մենք կարող ենք նկարել մեկ այլ կոն, որը կոչվում է անցյալի լուսակոն․ այն պատահույթի մի շարք է, որոնց լուսային ազդանշաններն ի վիճակի են հասնել տվյալ պատահույթին (նկ․2.4):
P ― պատահույթի անցյալի և ապագայի լուսակոները տարածություն֊ժամանակը բաժանում են երեք տիրույթի (նկ․ 2.5)։ Պատահույթի բացարձակ ապագան P֊ի ապագայի լուսակոնի ներսում պարփակված տիրույթն է։ Դա բոլոր այն պատահույթների շարքն է, որոնք կարող են ազդվել այն ամենից, ինչ տեղի է ունենում P֊ում։ P֊ի ազդանշանները չեն կարող հասնել P֊ի լուսակոնից դուրս տեղի ունեցող պատահույթներին, որովհետև լույսից արագ շարժվել հնարավոր չէ։ Հետևաբար, այդ պատահույթները չեն կարող ազդվել այն ամենից, ինչ տեղի է ունենում P֊ում։ P֊ի բացարձակ անցյալն անցյալի լուսակոնում պարփակված տիրույթն է։ Դա այն պատահույթների շարքն է, որոնցից ազդանշանները, շարժվելով լույսի արագությամբ կամ ավելի դանդաղ, կարող են հասնել P֊ին։
Դա, հետևաբար, բոլոր այն պատահույթների շարքն է, որոնք կարող են ազդել P֊ում կատարվող իրադարձությունների վրա։ Եթե մենք իմանանք, թե ինչ է տեղի ունեցել P֊ի անցյալի լուսակոնում պարփակված տարածության ցանկացած տիրույթում, ապա կարող ենք կանխագուշակել, թե ինչ պիտի տեղի ունենա P֊ում։ «Այլուրը» տարածություն֊ժամանակ դիագրամի այն տիրույթն է, որը դուրս է ապագայի և անցյալի լուսակոներից, այլուրում կատարվող պատահույթները չեն կարող ազդվել կամ ազդել P֊ի պատահույթների վրա։ Այսպես, եթե հենց այս պահին արևը դադարեր փայլելուց, դա Երկրի անցուդարձի վրա անմիջապես չէր կարող ազդել, քանի որ այն պահին, երբ արևը հանգի (նկ․ 2.6) երկիրը կգտնվի պատահույթի «այլուրում»։ Այդ մասին մենք կիմանանք 8 րոպե հետո միայն, այսինքն՝ այնքան ժամանակ անց, որը հարկավոր է, որպեսզի լույսը արևից հասնի մեզ։ Միայն այդ ժամանակ երկրի վրա պատահող պատահույթները կմտնեն արևի հանգման պատահույթի ապագայի լուսակոնի մեջ։ Նույն ձևով մենք չգիտենք, թե այս պահին ինչ է տեղի ունենում հեռավոր տիեզերքում։ Հեռավոր գալակտիկաների լույսը, որը մենք տեսնում ենք այսօր, արձակվել է միլիոնավոր տարիներ առաջ, իսկ ամենահեռավոր տեսանելի առարկաներից լույսը ճամփա է ընկել մի քանի ութ հազար միլիոն տարի առաջ։
Այսպիսով, երբ մենք այսօր տիեզերքին ենք նայում, ապա տեսնում ենք այնպես, ինչպես նա եղել է անցյալում։
Եթե անտեսենք ձգողության ազդեցությունները, ինչպես այդ արեցին Էնշտեյնն ու Պուանկարեն 1905֊ին, ստացվում է, այսպես կոչված, հարաբերականության հատուկ տեսությունը։ Տարածություն֊ժամանակի մեջ տեղի ունեցող ցանկացած պատահույթի համար, մենք կարող ենք լուսակոն կառուցել (տարածություն֊ժամանակի մեջ տվյալ պատահույթի արձակած լույսի բոլոր հնարավոր հետագծերի շարքը), և որովհետև լույսի արագությունը նույնն է յուրաքանչյուր պատահույթի և ուղղության համար, բոլոր լուսակոները կլինեն նույնանման և կուղղվեն միևնույն ուղղությամբ։ Այս տեսությունը նույնպես ասում է, որ ոչինչ չի կարող լույսից ավելի արագ շարժվել։ Սա նշանակում է, որ որևէ առարկայի հետագիծը տարածության և ժամանակի մեջ պետք է ներկայացվի մի գծով, որը գտնվում է յուրաքանչյուր պատահույթի լուսակոնի ներսում (նկ․ 2.7)։
Հարաբերականության հատուկ տեսությունը մեծ հաջողությամբ բացատրեց, որ լույսի արագությունը նույնն է բոլոր դիտորդների համար (ինչպես ցույց էր տրվել Մայքելսոն֊Մոռլիի փորձով) և նկարագրեց, թե ինչ է պատահում, եթե առարկաները շարժվում են լույսի արագությանը մոտ արագությամբ։ Այն, սակայն, անհամատեղելի էր Նյուտոնի ձգողության տեսության հետ, որի համաձայն մարմինների՝ միմյանց ձգող ուժը կախված է նրանց միջև եղած հեռավորությունից։ Սա նշանակում է, որ երբ մարմիններից մեկը շարժվի, ապա մյուսի վրա ազդող ուժը պետք է ակնթարթորեն փոխվի։ Կամ, այլ կերպ ասած, ձգողական ազդեցությունները պետք է գործեն անսահման մեծ արագությամբ, այն դեպքում, երբ հարաբերականության հատուկ տեսությունը պահանջում է, որ այդ արագությունը լինի լույսի արագությանը հավասար կամ նրանից փոքր։
Էնշտեյնը 1908֊ից մինչև 1914֊ը մի շարք անհաջող փորձեր կատարեց՝ ստեղծելու ձգողականության այնպիսի մի տեսություն, որը համատեղելի լիներ հարաբերականության հատուկ տեսության հետ։ Վերջապես1915 թվականին նա առաջարկեց այն, ինչն այսօր անվանում ենք հարաբերականության ընդհանուր տեսություն։
Էնշտեյնը կատարեց հեղափոխական նշանակություն ունեցող մի առաջարկություն այն մասին, որ ձգողականությունը մյուս ուժերի նման ուժ չէ, այլ արդյունք է այն բանի, որ տարածություն֊ժամանակը հարթ չէ, ինչպես նախկինում ենթարվում էր, այլ կոր է կամ «կորացված»՝ իր մեջ առկա զանգվածի և էներգիայի բաշխման հետևանքով։ Մարմինները, ինչպիսին երկրագունդն է, ստեղծված չեն, որպեսզի շարժվեն կորաձև ուղեծրով ձգողություն կոչվող ուժի ազդեցության տակ, փոխարենը նրանք ուղղաձիգ են շարժվում կորաձև տարածության մեջ, որը կոչվում է գեոդեզիական տարածություն։ Գեոդեզիական է կոչվում երկու հարևան կետերի միջև ամենակարճ (կամ ամենաերկար) հեռավորությունը։
Օրինակ, երկրագնդի մակերևույթը երկչափանի կոր տարածություն է։ Երկրագնդի վրա գեոդեզիական է կոչվում մեծ շրջանագիծը, որը երկու կետերի միջև եղած ամենակարճ ճանապարհն է (նկ․ 2.8)։ Քանի որ գեոդեզիականն ամենակարճ ճանապարհն է ցանկացած երկու օդանավակայանների միջև, ապա շտուրմանը օդաչուին հրահանգում է թռիչքի համար ընտրել այդ ուղին։ Չնայած ընդհանուր հարաբերականության տեսության մեջ մարմինները միշտ շարժվում են ուղիղ գծով քառաչափ տարածություն֊ժամանակում, սակայն մեզ թվում է, թե նրանք մեր եռաչափ տարածության մեջ շարժվում են կորաձև։ (Սա շատ նման է այն բանին, որին մենք ականատես ենք լինում, երբ օդանավը թռչում է լեռնոտ տարածքի վրայով։ Թեև այն շարժվում է ուղղագծորեն՝ եռաչափ տարածության մեջ, բայց նրա ստվերը երկչափ գետնի վրա կորագիծ է։
Արևի զանգվածն այնպես է կորացնում տարածություն֊ժամանակը, որ թեև երկրագունդը շարժվում է ուղղագծորեն քառաչափ տարածություն֊ժամանակի մեջ, բայց մեզ թվում է, թե այն եռաչափ տարածության մեջ շարժվում է շրջանաձև ուղեծրով։ Փաստորեն, մոլորակների ուղեծրի համար ընդհանուր հարաբերականության կանխագուշակությունը գրեթե ճշտորեն նույնն էր, ինչ կանխագուշակել էր Նյուտոնի ձգողականության տեսությունը։ Այնուամենայնիվ, Մերկուրիի դեպքում, որն արևին ամենամոտ մոլորակը լինելով, ենթարկվում է ձգողության ուժեղագույն ազդեցությանը և ունի բավականին երկարացված էլիպսաձև ուղեծիր, ընդհանուր հարաբերականության տեսությունը կանխատեսում է, որ էլիպսի երկար առանցքը պետք է պտտվի արևի նկատմամբ տասը հազար տարին մեկ աստիճան արագությամբ։ Այս շեղումը թեև փոքր, բայց դիտարկվել է 1915֊ից առաջ և Էյնշտեյնի ընդհանուր հարաբերականության տեսության հաստատմանը նպաստող առաջին փաստերից մեկն է։ Վերջին տարիներին ռադարային չափումների օգնությամբ դիտարկվել են այլ մոլորակների ավելի փոքր ուղեծրային շեղումներ նյուտոնյան կանխագուշակումներից և հաստատվել է ընդհանուր հարաբերականության տեսության կանխատեսումների հետ դրանց համապատասխանությունը։
Լույսի ճառագայթները ևս տարածություն֊ժամանակի մեջ պետք է տարածվեն գեոդեզիական կանոններով։ Քանի որ տարածությունը կոր է, նշանակում է լույսը տարածության մեջ չի կարող ուղղագծորեն շարժվել։ Հարաբերականության ընդհանուր տեսությունը կանխագուշակում է, որ լույսը պետք է թեքվի ձգողականության դաշտի ազդեցության տակ։ Օրինակ, այդ տեսությունը կանխագուշակեց, որ արևին մոտիկ գտնվող կետերի լուսակոները պետք է փոքր֊ինչ դեպի ներս թեքված լինեն արևի զանգվածի ազդեցության տակ։ Սա նշանակում է, որ հեռավոր աստղից եկող լույսն արևի մոտով անցնելիս պետք է շեղվի փոքր անկյան տակ, որի հետևանքով երկրից դիտողի համար աստղը տարբեր դիրքերով պիտի երևա (նկ․ 2.9):
Իհարկե, եթե աստղից եկող լույսը միշտ արևի մոտով անցներ, մենք չէինք կարող ասել՝ արդյոք լո՞ւյսն է թեքվել, թե՞ աստղն է գտնվում հենց այնտեղ, որտեղ մենք նրան տեսնում ենք։ Սակայն, քանի որ երկիրը պտտվում է արևի շուրջը, ապա տարբեր աստղեր հայտնվում են արևի հետևում, և նրանց արձակած լույսը թեքվում է։ Հետևաբար նրանք իրենց թվացյալ դիրքը փոխում են մյուս աստղերի նկատմամբ։
Սովորաբար այս բանը դժվար է տեսնել, որովհետև արևից եկող լույսն անհնարին է դարձնում դիտարկել այն աստղերը, որոնք երկնքում արևի մոտ են երևում։ Բայց դա հնարավոր է դառնում արևի խավարման ժամանակ, երբ լուսինը ծածկում է արևից եկած լույսը։ Էնշտեյնի այս կանխագուշակությունը լույսի խոտորման մասին հնարավոր չեղավ անմիջապես ստուգել 1915֊ին։ Առաջին համաշխարհային պատերազմի ծավալման պատճառով։ Միայն 1919 թվականին անգլիական մի արշավախումբ Արևմտյան Աֆրիկայում արևի խավարում դիտարկելիս ցույց տվեց, որ լույսն իրոք խոտորվում է արևից ճիշտ այնպես, ինչպես կանխատեսել էր ընդհանուր հարաբերականության տեսությունը։ Անգլիացի գիտնականների կողմից գերմանական տեսության այս ապացույցը ժամանակին ողջունվեց բոլորի կողմից որպես պատերազմից հետո հաշտեցման կարևոր ակտ երկու երկրների միջև։ Սակայն գիտության հեգնանքը եղավ այն, որ արշավախմբի լուսանկարների հետագա ուսումնասիրությունը ցույց տվեց, որ փորձնական սխալներն ավելի մեծ էին, քան այն շեղումները, որոնք նրանք փորձել էին չափել։ Չափումները բախտի բերմամբ էին այդպես ստացվել, կամ գուցե, արդյունք էին այն բանի, որ մարդիկ գիտեին, թե ինչպիսի արդյունքն է ցանկալի, մի բան, որ հազվադեպ չէ գիտական աշխատանքներում։ Այնուամենայնիվ, լույսի խոտորումը հետագա բազմաթիվ դիտարկումներով ճշգրտորեն ապացուցվեց։
Ընդհանուր հարաբերականության տեսության մյուս կանխագուշակությունն այն էր, որ ժամանակը պետք է դանդաղեր երկրի նման մեծ զանգված ունեցող մարմնի մոտ։ Սրա պատճառն այն է, որ լույսի էներգիան և նրա հաճախականությունը (դա մեկ վայրկյանում տեղաշարժվող լույսի ալիքների թիվն է) իրար հետ կապված են՝ լույսի էներգիան այնքան մեծ է, որքան մեծ է նրա հաճախականությունը։ Երբ լույսն անցնում է երկրի ձգողականության դաշտով, այն էներգիա է կորցնում, հետևաբար նրա հաճախականությունը փոքրանում է։ Դա նշանակում է, որ ալիքի մի գագաթից հաջորդն անցնելու համար ավելի երկար ժամանակ է պահանջվում։ Վերևից նայողին կթվա, թե ներքևում ամեն ինչ ավելի դանդաղ է տեղի ունենում։ Այս կանխագուշակությունն ստուգվեց 1962֊ին․ մի ջրային աշտարակի գագաթին և ստորոտին տեղադրեցին երկու շատ ճշգրիտ ժամացույցներ։ Ստորոտին տեղադրված ժամացույցը, մոտիկ գտնվելով երկրին, ավելի դանդաղ էր աշխատել, ճիշտ հարաբերականության ընդհանուր տեսությանը համապատասխան։ Երկրի մակերևույթից տարբեր բարձրությունների վրա աշխատող ժամացույցների ցուցմունքների տարբերությունն այսօր կարևոր գործնական նշանակություն ունի արհեստական արբանյակներից ստացվող ազդանշանների հիման վրա նվազագույն ճշգրիտ համակարգի ներդրման համար։ Եթե հաշվի չառնվեն հարաբերականության ընդհանուր տեսության կանխագուշակումները, ապա հաշվարկված դիրքը սխալ կլինի մի քանի մղոնով։
Նյուտոնի շարժման օրենքները վերջ տվին տարածության մեջ բացարձակ դիրքի գաղափարին։ Հարաբերականության տեսությունն ազատվեց բացարձակ ժամանակից։ Դիցուկ ունենք երկվորյակների մեկ զույգ։ Ենթադրենք, այդ զույգից մեկն ապրում է լեռան գագաթին, իսկ մյուսը՝ ծովափին։ Առաջինն ավելի արագ կմեծանա, քան երկրորդը։ Երբ հետագայում նրանք նորից հանդիպեն, ապա մեկն ավելի ծեր կերևա մյուսից։ Իհարկե, այս դեպքում հասակների տարբերությունը շատ փոքր կլինի, բայց այդ տարբերությունը խիստ կմեծանա, եթե երկվորյակներից մեկը տիեզերանավով հեռավոր մի ճամբորդության մեկնի մոտավորապես լույսի արագությամբ։ Երբ նա վերադառնա հեռավոր ճամփորդությունից, շատ ավելի երիտասարդ կլինի երկրի վրա մնացողի համեմատ։ Սա կոչվում է երկվորյակների պարադոքս, որը, սակայն, պարադոքս է միայն այնքանով, որքանով մենք չենք ձերբազատվել բացարձակ ժամանակի գաղափարից։ Հարաբերականության տեսության մեջ չկա եզակիորեն բացարձակ ժամանակ, այլ ամեն անհատ ունի ժամանակի իր անձնական չափը, որը կախված է նրանից, թե նա որտեղ է գտնվում և ինչ արագությամբ է շարժվում։
1915֊ից առաջ տարածությունը և ժամանակը, պատկերացվում էին որպես անշարժ և կայուն մի հրապարակ, որտեղ պատահույթներ էին տեղի ունենում և որը, սակայն, իր մեջ տեղի ունեցածից չէր փոփոխվում։ Սա ճիշտ էր նաև հարաբերականության հատուկ տեսության համար։ Մարմինները շարժվում էին, ուժերը ձգում ու վանում էին, սակայն ժամանակն ու տարածությունը, բոլորովին անտարբեր, պարզապես շարունակվում էին։ Միանգամայն բնական էր մտածել, որ տարածությունն ու ժամանակն ընդմիշտ գոյություն կունենան։
Վիճակը, սակայն, բոլորովին այլ է հարաբերականության ընդհանուր տեսության մեջ։ Տարածությունն ու ժամանակն այստեղ դինամիկ մեծություններ են, երբ մարմինը շարժվում է, կամ ուժ է ազդում, դա ներգործում է ժամանակի և տարածության կորության վրա, իսկ տարածություն֊ժամանակ քառաչափ կառուցվածքն իր հերթին ներգործում է շարժվող մարմինների և ազդող ուժերի ընթացքի վրա։ Տարածությունը և ժամանակն այսպիսով ոչ միայն ազդում, այլև ազդվում են տիեզերքում տեղի ունեցող ամեն ինչից։ Ճիշտ այնպես, ինչպես մարդ չի կարող խոսել տիեզերքում տեղի ունեցող պատահույթների մասին՝ առանց պատկերացնելու տարածությունն ու ժամանակը, այդպես էլ ընդհանուր հարաբերականությայն մեջ անմիմաստ է խոսել ժամանակի և տարածության մասին տիեզերքի սահմաններից դուրս։
Հետագա տասնամյակներում տարածության և ժամանակի այս նոր հասկացությունը հեղափոխեց տիեզերքի մասին մեր պատկերացումը։ Հին պատկերացումը անփոփոխ տիեզերքի մասին, որը կարող էր գոյություն ունեցած լինել, կամ շարունակել գոյություն ունենալ, մեկընդմիշտ փոխարինվեց դինամիկ ընդարձակվող տիեզերքի հասկացությամբ։ Այս տիեզերքը՝ թվում է՝ սկիզբ է առել որոշակի ժամանակ առաջ և կարող է վերջ ունենալ ապագայում՝ որոշակի ժամանակ անց։ Հաջորդ գլուխը նվիրված է այդ հեղափոխությանը։
Եվ տարիներ անց դա դարձավ տեսական ֆիզիկայի իմ ուսումնասիրությունների սկիզբը։ Ռոջեր Պենրոուզն ու ես ցույց տվեցինք, որ Էնշտեյնի հարաբերականության ընդհանուր տեսությունից հետևում է, որ տիեզերքը պետք է սկիզբ և, հավանաբար, վերջ ունենա։
3
Ընդարձակվող տիեզերքը
Երբ անլուսին ու պարզկա գիշերը մեկը երկինք նայի, ապա երկնքում նրա տեսած ամենափայլուն երկնային մարմինները, հավանաբար, կլինեն Վեներա, Մարս, Յուպիտեր և Սատուռն մոլորակները։ Երկնակամարում կերևան նաև շատ մեծ թվով աստղեր, որոնք ճիշտ նման են մեր սեփական արևին, բայց մեզանից շատ հեռու են։ Այդ անշարժ աստղերի մի մասը թեև շատ աննշան, սակայն իրականում իրենց դիրքը փոխում են միմյանց նկատմամբ՝ արևի շուրջ երկրի պտույտի ընթացքում։ Հետևաբար, դրանք իրականում անշարժ չեն։ Դա այդպես է, որովհետև դրանք համեմատաբար մոտ են մեզ։ Քանի որ երկինքը պտտվում է արևի շուրջ, մենք մոտիկ գտնվող աստղերը տեսնում են տարբեր դիրքերից՝ ավելի հեռավոր աստղերի ֆոնի վրա։ Բարեբախտաբար դա հնարավորություն է տալիս անմիջականորեն չափել այդ աստղերի հեռավորությունը մեզանից․ որքան նրանք մոտ են մեզ, թվում է այնքան արագ են շարժվում։ Երկրին ամենամոտիկ աստղը, որը կոչվում է Կենտավրոսի Պրոկսիմա, երկրից հեռու է չորս լուսատարով (նրանից լույսը երկիր է հասնում չորս տարվա ընթացքում), կամ 23 միլիոն մղոնով։ Արդեն աչքով տեսանելի մյուս աստղերից շատերի հեռավորությունը մեզանից մինչև մի քանի հարյուր լուսատարի է։ Համեմատության համար ասենք, որ արևը երկրից հեռու է ութ լուսատարով։ Տեսանելի աստղերը գիշերային երկնակամարում ցրված են երևում, բայց իրականում կենտրոնացած են մի ծիրում, որը կոչվում է Ծիրկաթին։ Մի քանի աստղագետներ դեռևս 1750֊ին այն միտքն էին արտահայտել, թե Ծիրկաթինի տեսքը արդյունք է այն բանի, որ այն կազմող աստղերը սփռված են սկավառակաձև մի կոնֆիգուրացիայում, որի օրինակներից մեկն այսօր հայտնի պարուրաձև գալակտիկան է։ Աստղագետ սըր Ուիլյամ Հերշելը մի քանի տասնամյակ հետո միայն հաստատեց իր տեսակետի ճշտությունը՝ քրտնաջանորեն կազմելով մեծ թվով աստղերի հեռավորությունների և դիրքերի գրացուցակ։ Պետք է նշել սակայն, որ այդ պատկերացումը համընդհանուր ճանաչում գտավ լոկ մեր դարասկզբին։
Տիեզերքի ժամանակակից պատկերացման հիմքը դրվեց 1924֊ին, երբ ամերիկացի աստղագետ Էդվին Հաբլը ցույց տվեց որ տիեզերքում մեր գալակտիական միակը չէ։ Փաստորեն գոյություն ունեն շատ ուրիշ գալակտիկաներ, որոնք միմյանցից բաժանված են լայնատարած դատարկության գոտիներով։ Այդ բանը ապացուցելու համար Հաբլին հարկավոր էր որոշել գալակտիկաների հեռավորությունը, որոնք շատ հեռու լինելով մոտիկ գտնվող աստղերից, անշարժ են թվում։ Հաբլը ստիպված էր աննուղակի մի եղանակ օգտագործել այդ հեռավորությունները չափելու համար։ Աստղի թվացող պայծառությունը կախված է երկու գործոնից․ թե որքան լույս է արձակում այն (լուսատվություն) և ինչքան հեռու է գտնվում մեզանից։ Մենք կարող ենք չափել մոտիկ գտնվող աստղերի թվացող պայծառությունն ու հեռավորությունը, և դրանով որոշել աստղի լուսատվությունը։ Եվ հակառակը, եթե իմանանք աստղերի լուսատվություն այլ գալակտիկաներում, ապա նրանց թվացող պայծառությունը չափելով, կկարողանանք հաշվարկել նրանց հեռավորությունը։ Հաբլը նկատել էր, որ մեզ մոտիկ գտնվող որոշ տեսակի աստղեր մշտապես ունեն միևնույն լուսատվությունը և ենթադրել էր, որ եթե մենք նման աստղեր գտնենք այլ գալակտիկայում, ապա կարող ենք ընդունել, որ նրանց լուսատվությունը նույնն է և, այդպիսով հաշվել տվյալ գալակտիկայի հեռավորությունը։ Եթե մենք դա կարողանանք կատարել նույն գալակտիկային պատկանող մի քանի այդպիսի աստղերի համար և մեր հաշվումներով ստացված հեռավորությունները միշտ նույնը լինեն, ապա կարող ենք վստահ լինել մեր գնահատականի ճշտության մեջ։
Այս եղանակով Էդվին Հաբլը որոշեց 9 տարբեր գալակտիկաների հեռավորությունները։ Այսօր մեզ հայտնի է, որ մեր գալակտիկան մի քանի հարյուր հազար միլիոն գալակտիկաներից մեկն է տիեզերքում, որոնք ժամանակակից աստղադիտակների օգնությամբ կարելի է տեսնել, իսկ գալակտիկաներից յուրաքանչյուրն իր հերթին պարունակում է մի քանի հարյուր հազար միլիոն աստղ։
3.1 նկարում պատկերված է մի պարուրաձև գալակտիակյի լուսանկար, ինչը, մեր կարծիքով, նման է այն պատկերին, որը կերևար մեկ այլ գալակտիկայից մերին նայելիս։ Մենք ապրում ենք մի գալակտիկայում, որն ունի մոտ հարյուր հազար լուսատարի ձգվածություն և դանդաղ պտտվում է։ Աստղերը նրա պարուրաձև բազուկներում պտտվում են կենտրոնի շուրջ մի քանի միլիոն տարին մեկ անգամ։ Մեր արևը հենց սովորական, միջին մեծության մի դեղին աստղ է, որը գտնվում է պարուրաձև բազուկներից մեկի ներքին եզրում։ Ինչպես տեսնում ենք, մենք Արիստոտելի և Պտղոմեոսի պատկերացումներից շատ հեռուն ենք գնացել, երբ մտածում էինք, որ երկիրը անշարժ է և գտնվում է տիեզերքի կենտրոնում։
Աստղերն այնքան հեռու են, որ երկնակամարում երևում են որպես լուսավոր փոքրիկ կետեր։ Նրանց ոչ չափը, ոչ էլ ձևը չենք կարողանում տեսնել։ Հարց է ծագում, թե այդ դեպքում ինչպե՞ս են միմյանցից զանազանվում առանձին աստղերի տարբեր խմբերը։ Աստղերի ճնշող մեծամասնության համար կա դիտելի միայն մեկ հատկանշանական առանձնահատկություն, դա նրանց լույսի գույնն է։ Դեռևս Նյուտոնը հայտնագործել էր, որ երբ արևի լույսն անցնում է եռանկյունաձև ապակու կտորի միջով, որը կոչվում է պրիզմա, տրոհվում է բաղադրիչ գույների (լույսի սպեկտր), ինչպես, օրինակ, ծիածանը։ Աստղադիտակն ուղղելով մի առանձին աստղի կամ գալակտիկայի վրա, նման ձևով կարելի է դիտարկել աստղի կամ գալակտիկայի սպեկտրը։ Տարբեր աստղեր ունեն տարբեր սպեկտրներ, սակայն տարբեր գույների հարաբերական պայծառությունը ստացվում է ճիշտ այնպիսին, ինչ սպասելի էր, եթե լույս արձակող առարկան գտնվեր շիկակարմիր փայլող վիճակում։ (Փաստորեն շիկակարմիր, փայլող, անթափանց առարկայի արձակած լույսն ունի հատկանշական մի սպեկտր՝ ջերմային սպեկտր, որը կախված է միայն ջերմաստիճանից։ Դա նշանակում է, որ կարելի է որոշել աստղի ջերմաստիճանը նրա լույսի սպեկտրով)։ Ավելին, հայտնաբերվել է, որ որոշակի առանձնահատուկ գույներ բացակայում են աստղի սպեկտրում և այդ բացակա գույները տարբեր աստղերի համար կարող են տարբեր լինել։ Քանի որ հայտնի է, յուրաքանչյուր քիմիական տարր կլանում է որոշակի գույների հատկանշական մի շարք, ապա զուգադրելով աստղերի սպեկտրներում բացակա գույները մենք կարող ենք ճշգրտորեն որոշել, թե աստղի մթնոլորտում ինչպիսի քիմիական տարրեր կան։
1920֊ական թվականներին, երբ աստղագետներն սկսեցին ուսումնասիրել այլ գալակտիկաների աստղերի սպեկտրները շատ տարօրինակ մի փաստ արձանագրեցին։ Պարզվեց, որ մեր սեփական գալակտիկայի աստղերի նման, այլ գալակտիկաներում գտնվող աստղերի սպեկտրներում էլ են առակա բացակա գույների նույն բնորոշ շարքերը, բայց միևնույն հարաբերական չափով տեղաշարժված դեպի սպեկտրի կարմիր ծայրը։ Այս երևույթի նշանակությունը ըմբռնելու համար պետք է իմանալ թե ի՞նչ բան է Դոպլերի էֆեկտը։ Ինչպես արդեն գիտենք, տեսանելի լույսն իրենից ներկայացնում է էլեկտրամագնիսական դաշտի ֆլուկտուացիա կամ ալիք։ Լուսնի հաճախականությունը (մեկ վայրկյանում տեղաշարժվող ալիքների թիվը) շատ մեծ է և հասնում է վայրկյանում չորսից մինչև յոթը հարյուր միլիոն միլիոն ալիքի։ Մարդու աչքը լուսնի տարբեր հաճախականությունները տեսնում է որպես տարբեր գույներ, ընդ որում՝ ցածր հաճախականությունները լինում են սպեկտրի կարմիր տիրույթում, իսկ բարձր հաճախականությունները՝ կապույտ տիրույթում։ Այժմ պատկերացնենք, թե երկրից հաստատուն հեռավորության վրա գտնվող մի լուսատու աղբյուր, ասենք մի աստղ, հաստատուն հաճախականությամբ լույսի ալիքներ է արձակում։ Մեզ հասած լույսի հաճախականությունը (գալակտիկայի ձգողական դաշտը բավարար չափով հզոր չէ լույսի ալիքի վրա էականորեն ազդելու համար) կլինի ճիշտ նույնը, ինչպիսին եղել է արձակման պահին։ Այժմ ենթադրենք, թե լույսի աղբյուրն սկսում է շարժվել դեպի մեզ։ Այս դեպքում հաջորդ ալիքի արձակման պահին լույսի աղբյուրը մեզ ավելի մոտ կլինի, և, հետևաբար ալիքը մեզ ավելի կարճ ժամանակում կհասնի անշարժ աստղից եկածի համեմատ։ Դա նշանակում է, որ մեզ հասնող ալիքի երկու հաջորդական գագաթների միջև եղած ժամանակը կփոքրանա, և, հետևաբար մեկ վայրկյանում երկիր հասած ալիքների թիվը (այսինքն՝ լույսի հաճախականությունը) ավելի մեծ կլինի անշարժ լուսաղբյուրից եկած լույսի համեմատ։ Նույն ձևով, եթե լույսի աղբյուրը մեզանից հեռանում է, ապա մեզ հասնող ալիքի հաճախականությունը կփոքրանա։ Այսպիսով, երբ աստղը մոտենում է երկրին, նրա լույսի սպեկտրում կկատարվի տեղաշարժ դեպի սպեկտրի կապույտ տիրույթը (կապույտ շեղում), իսկ երբ աստղը հեռանում է երկրից՝ տեղաշարժը կլինի դեպի սպեկտրի կարմիր տիրույթը (կարմիր շեղում)։ Ալիքի հաճախականության և առարկայի շարժման արագության միջև եղած այս կապը կոչվում է Դոպլերի էֆեկտ, որը դիտվում է առօրյա կյանքում։ Օրինակ, ուշադիր լսիր ճանապարհով շարժվող ավտոմեքենաների ձայնը․ երբ մեքենան մոտենում է, նրա շարժիչի ձայնի տոնը բարձրանում է (համապատասխանում է ձայնի ալիքների հաճախականության մեծացմանը), իսկ երբ այն անցնում և հեռանում է, ձայնի տոնն իջնում է։ Լույսի և ռադիոալիքների վարքը նույնն է։ Հետևաբար ավտոտեսուչը, օգտվելով Դոպլերի էֆեկտից, չափելով մեքենայից անդրադարձած ռադիոալիքների բաբախման հաճախականությունը, կարող է որոշել մեքենայի շարժման արագությունը։
Այլ գալակտիակների գոյությունն ապացուցելուց տարիներ հետո Հաբլը ձեռնամուխ եղավ նրանց հեռավորությունների գրացուցակ կազմելու և սպեկտրերն ուսումնասիրելու գործին։ Այն ժամանակ շատերը կարծում էին, թե գալակտիկաների շարժումը բացարձակապես անկանոն է, և, հետևաբար պետք է լինեին բազմաթիվ կարմիր և կապույտ շեղումներ։ Ուստի ուղղակի զարմանալի էր 1929 թվականին Հաբլի այն հրապարակումը, թե գալակտիկաների կարմիր շեղման մեծությունը նույնպես անկանոն չէ, այլ ուղիղ համեմատական է գալակտիակյի հեռավորությանը երկրից։ Կամ, այլ կերպ ասած, որքան գալակտիկան հեռու է, այն այնքան ավելի արագ է հեռանում։ Այդ ամենը վկայում էր, որ տիեզերքն անշարժ լինել չի կարող, ինչպես նախապես ենթադրվում էր, այլ, փաստորեն, ընդարձակվում է, և գալակտիկաների միջև եղած հեռավորությունը շարունակ մեծանում է։
Տիեզերքի ընդարձակման փաստի հայտնագործումը XX դարում մարդկային մտքի խոշոր հեղաշրջումներից մեկն է։ Հետադարձ հայացք գցելիս կարելի է զարմանալ, թե ինչո՞ւ անցյալում ոչ ոք չէր մտածել այդ մասին։ Նյուտոնի և մյուսների համար դժվար չէր ըմբռնել, որ անշարժ տիեզերքն ի վերջո գձողական ուժի ազդեցության տակ պիտի սկսեր սեղմվել։ Պատկերացնենք, սակայն, որ տիեզերքն ընդարձակվող է։ Եթե այն ընդարձակվում է բավականին դանդաղ, ապա ձգողության ուժը ի վերջո կստիպի, որ ընդարձակումը դադարի, և սկսվի սեղմումը։ Սակայն եթե ընդարձակումն ընթանում է որոշակի կրիտիկականից ավելի մեծ արագությամբ, ապա ձգողությունը երբեք չի կարող այնքան ուժեղ լինել՝ այն դադարեցնելու, և տիեզերքն ընդմիշտ կշարունակի ընդարձակվել։ Դա մասամբ նման է այն բանին, երբ մենք երկրից հրթիռ ենք արձակում։ Եթե հրթիռի արագությունը բավականաչափ մեծ չէ, ապա ի վերջո երկրի ձգողությունը կդադարեցնի նրա շարժումը, և հրթիռը վայր կընկնի։ Մյուս կողմից, սակայն, եթե հրթիռի արագությունը մեծ է համապատասխան կրիտիկական արժեքից (վայրկյանում մոտ 7 մղոն․ 112 կմ/վ), ապա ձգողության ուժը բավարար չէ նրան վայր գցելու համար, ուստի հրթիռը կշարունակի իր ընթացքը անընդհատ և կհեռանա երկրից։ Տիեզերքի նման վարքը կարելի էր կանխագուշակել տասնիններորդ, տասնութերորդ դարերում, նույնիսկ՝ XVII դարի վերջին, ելնելով հենց Նյուտոնի ձգողականության օրենքից։ Սակայն անշարժ տիեզերքի մասին հավատն այնքան ուժեղ էր, որ այդ պատկերացումը գոյատևեց մինչև քսաներորդ դարի սկզբը։ Նույնիսկ Էնշտեյնը, երբ 1915 թվականին ձևակերպում էր հարաբերականության ընդհանուր տեսությունը, այն աստիճան վստահ էր տիեզերքի կայունության հարցում, որ այդ պատկերացումը պահպանելու համար իր տեսությունը վերափոխեց՝ իր հավասարումների մեջ ներմուծելով, այսպես կոչված «տիեզերաբանական» մի հաստատուն։ Էնշտեյնը ներմուծեց մի նոր ուժ՝ «հակաձգողություն», որն, ի տարբերություն այլ ուժերի չէր բխում որևէ առանձնահատուկ աղբյուրից, այլ շաղկապված էր հենց տարածություն֊ժամանակի կառուցվածքի հետ։ Նա պնդում էր, որ տարածություն֊ժամանակն ունի ընդարձակվելու ներքին մի մղում և հենց դրանով հավասարակշռում է տիեզերքում բոլոր մարմինների միջև առկա ձգողությունը, ինչի արդյունքը և լինում է կայուն տիեզերքը։ Միայն մի մարդ գտնվեց, որ ընդհանուր հարաբերականությունը հոժարակամ ընդունեց իր իսկական իմաստով, և մինչ Էյնշտեյնն ու ուրիշ ֆիզիկոսներ փորձում էին ամեն կերպ խուսափել անկայուն տիեզերքի մասին ընդհանուր հարաբերականության կանխագուշակումից, ռուս ֆիզիկոս և մաթեմատիկոս Ալեքսանդր Ֆրիդմանը ձեռնամուխ եղավ դա բացատրելուն։
Ֆրիդմանը երկու շատ պարզ ենթադրություններ արեց տիեզերքի մասին․ տիեզերքը նույնանման է երևում անկախ այն բանից, թե մենք ի՞նչ ուղղությամբ ենք դիտում, և տիեզերքը նույնանման կերևա, եթե մենք այն դիտարկենք որևէ այլ տեղից։ Այս երկու ենթադրության շնորհիվ միայն Ֆրիդմանին հաջողվեց ցույց տալ, որ տիեզերքը ստատիկ լինել չի կարող։ Փաստորեն 1922֊ին, Էդվին Հաբլի հայտնագործությունից մի քանի տարի առաջ, Ալեքսանդր Ֆրիդմանը կանխագուշակեց ճիշտ այն, ինչ հայտնաբերեց Հաբլը։
Ենթադրությունն այն մասին, թե տիեզերքը բոլոր ուղղություններով նույնանման է երևում, իրականում ճիշտ չէ։ Օրինակ, ինչպես տեսանք, մեր գալակտիկայի մյուս աստղերը գիշերային երկնքում կազմում են որոշակի մի լուսավոր ծիր՝ Ծիրկաթինը։ Մյուս կողմից, երբ նայենք հեռավոր գալակտիկաներին, ապա նրանց թիվը մոտավորապես նույնն է թվում։ Հետևաբար, տիեզերքը բոլոր ուղղություններով նույնանման կերևա, եթե այն դիտարկենք միայն միջգալակտիկական հեռավորությանը համաչափելի մասշտաբով և անտեսենք այն տարբերությունները, որոնք առկա են փոքր հեռավորությունների վրա։ Դա երկար ժամանակ բավարար համարվեց Ֆրիդմանի ենթադրությունների ճշտության համար, որպես իրական տիեզերքի պատկերի կոպիտ մոտավորություն։ Բայց բոլորովին վերջերս, մի երջանիկ պատահականություն բացահայտեց, որ Ֆրիդմանի ենթադրությունները, փաստորեն, արտակարգ ճշտությամբ նկարագրում էին մեր տիեզերքը։
1965֊ին երկու ամերիկացի ֆիզիկոսներ՝ Առնո Պենզիասն ու Ռոբերտ Վիլսոնը Նյու Ջերսիի Բել Տելեֆոն ընկերության լաբորատորիայում փորձարկում էին մի շատ զգայուն միկրոալիքային դետեկտոր։ (Միկրոալիքները ճիշտ նման են լույսի ալիքներին, բայց նրանց հաճախականությունը վայրկյանում միայն տասը հազար միլիոն ալիքի կարգի է)։ Պենզիասն ու Վիլսոնն անհանգստացան, երբ համոզվեցին, որ իրենց դետեկտորը շատ ավելի աղմուկ է որսում, քան սպասվում էր։ Աղմուկը որևէ որոշակի ուղղությունից չէր գալիս։ Սկզբում դետեկտորի մեջ թռչնածերտ հայտնաբերեցին, այնուհետև սկսեցին խանգարող այլ հավանական հանգամանքներ որոնել, սակայն շուտով հրաժարվեցին այդ փնտրտուքներից։ Նրանց հայտնի էր, որ մթնոլորտի միջով եկող աղմուկը ուժեղ է լինում, երբ դետեկտորը դեպի երկնակամար ուղղված չէ, որովհետև մոտ հորիզոնից եկող լույսը մթնոլորտի ավելի խիտ շերտի միջով է անցնում, քան ուղիղ գլխավերևից իջնողը։ Հավելյալ աղմուկը նույնն էր, անկախ այն բանից, թե ինչ ուղղությամբ էր դետեկտորն ուղղված, հետևաբար աղմուկը գալիս էր արտամթնոլորտային տարածությունից։ Աղմուկը նույնն էր նաև գիշեր ու ցերեկ և ամբողջ տարվա ընթացքում, հակառակ այն բանի, որը երկիրը պտտվում էր իր առանցքի ու նաև արևի շուրջը։ Դա ցույց էր տալիս, որ ճառագայթումը գալիս էր Արեգակնային համակարգից, նույնիսկ մեր գալակտիկայից դուրս գտնվող աղբյուրից, այլապես աղմուկի ուժգնությունը տարբեր կլիներ երկրագնդի շարժումով պայմանավորված ընդունիչի փոփոխվող դիրքից կախված։ Պարզ է, որ ճառագայթումը դեպի մեզ գալու ճանապարհին անցնում է տեսանելի տիեզերքի մեծ մասով, և քանի որ այն նույնն է բոլոր ուղղություններով, ապա տիեզերքը ևս նույնը պետք է լինի ցանկացած ուղղությամբ, գոնե լայն մասշտաբով վերցված։ Այժմ մենք գիտենք, որ այս աղմուկի ուժգնությունն ինչ ուղղությամբ էլ չափվի, չի փոխվում ավելի քան մեկ հազարերոդ մասով։ Այսպիսով, Պենզիասն ու Վիլսոնը ակամա և անսպասելի կերպով հաստատեցին Ֆրիդմանի առաջին ենթադրության ճշմարտությունը։
Համարյա նույն ժամանակ հարևան Պրինստոնի համալսարանում աշխատող երկու այլ ֆիզիկոսներ՝ Բոբ Դիքը և Ջիմ Փիբլզը ևս սկսեցին հետաքրքրվել միկրոալիքներով։ Նրանց աշխատանքի հիմքում ընկած էր Ալեքսանդր Ֆրիդմանի աշակերտներից մեկի՝ Գեորգի Գամովի այն միտքը, թե նախնական տիեզերքը պետք է որ շատ տաք և խիտ եղած լիներ, սպիտակ շիկացած և փայլուն։ Դիքը և Ֆիբլզը մտածում էին, որ մենք դեռևս տեսնում ենք փայլող նախնական տիեզերքը, որովհետև նրա շատ հեռավոր մասերի լույսը հազիվ մեր օրերում է մեզ հասնում։ Սակայն, քանի որ տիեզերքն ընդարձակվում է, ապա այդ լույսը պետք է այն աստիճան տեղաշարժված լիներ դեպի կարմիր ճառագայթման տիրույթը, որ մեզ հասներ որպես միկրոալիքային ճառագայթում։ Դիքը և Փիբլզը սկսեցին նախապատրաստվել այդ ճառագայթյումը դիտարկելու։ Երբ այդ մասին իմացան Պենզիասն ու Վիլսոնը, գլխի ընկան, որ իրենք արդեն որսացել են նախնական տիեզերքից եկող ճառագայթումը։ Այս հայտնագործության համար Պենզիասն ու Վիլսոնը 1978 թվականին արժանացան Նոբելյան մրցանակի (ինչն, իհարկե, ծանր էր Դիքի և Ֆիբլզի համար՝ մի կողմ թողնելով դեռ Գամովին։)
Այն փաստը, որ ինչ ուղղությամբ էլ նայես, տիեզերքը նույնն է երևում, առաջին հայացքից կարող է մեզ ստիպել մտածել, թե երկիրը տիեզերքում առանձնահատուկ դիրք ունի։ Մասնավորապես այն փաստը, որ մեզ թվում է, թե բոլոր գալակտիկաները հեռանում են մեզանից, կարող է այն տպավորությունը թողնել, թե մենք պետք է տիեզերքի կենտրոնում գտնվենք։ Չմոռանանք, սակայն, որ գոյություն ունի այլընտրական մի բացատրություն ևս, երբ տիեզերքը դիտարկվում է այլ գալակտիկաներից, այն դարձյալ ամեն ուղղությամբ նույնատեսակ կարող է երևալ։ Ինչպես ասվեց, սա Ֆրիդմանի երկրորդ ենթադրությունն էր։ Մենք այս ենթադրության կողմ կամ դեմ որևէ գիտական փաստարկ չունենք։ Սակայն համեստությունը պահանջում է ընդունել այն, այլապես շատ ուշագրավ կլիներ, որ տիեզերքը բոլոր ուղղություններով նույնատեսակ լիներ լոկ մեր շրջապատում, բայց ոչ տիեզերքի այլ կետերի համար։ Ֆրիդմանի մոդելում բոլոր գալակտիկաները ուղղակի իրարից հեռանում են։ Վիճակը նման է օդապարիկի, որի վրա որոշ թվով կետեր են նկարված, իսկ օդապարիկը ընդարձակվում է։ Ընդարձակման հետ ցանկացած երկու կետերի միջև եղած հեռավորությունը մեծանում է, սակայն չի կարելի ասել, թե որևէ կետ ընդարձակման կենտրոնն է։ Ավելին, որքան կետերն իրարից հեռու են, նրանք այնքան արագ կհեռանան միմյանցից։ Նույն ձևով, Ֆրիդմանի մոդելում գալակտիկաների՝ միմյանցից հեռանալու արագությունը համեմատական է նրանց միջև եղած հեռավորությանը։ Այսպիսով, դա կանխագուշակում է, որ գալակտիկայի կարմիր շեղումը պետք է ուղիղ համեմատական լինի մեզանից նրա ունեցած հեռավորությանը, ճիշտ այնպես, ինչպես հաստատել էր Հաբլը։ Չնայած իր մոդելի հաջողությանն ու Հաբլի դիտարկումների կանխագուշակմանը, Ֆրիդմանի աշխատանքներն Արևմուտքին անհայտ մնացին, մինչև 1935 թվականին ամերիկացի ֆիզիկոս Հովարդ Ռոբերտսոնն ու անգլիացի մաթեմատիկոս Արթուր Ուոքերը նման մոդելներ առաջարկեցին՝ բացատրելու համար Հաբլի հայտնագործությունը՝ տիեզերքի համաչափ ընդարձակման մասին։
Այնուամենայնիվ, Ֆրիդմանն իր երկու հիմնական ենթադրությունների հիման վրա առաջարկել էր ընդարձակվող տիեզերքի միայն մեկ մոդել, թեև իրականում հնարավոր են երեքը։ Առաջին մոդելի դեպքում (որն առաջարկել էր Ֆրիդմանը) տիեզերքն ընդարձակվում է բավականին դանդաղ, ընդ որում տարբեր գալակտիկաների միջև գործող գրավիտացիոն ձգողությունն ստիպում է, որ ընդարձակումը դանդաղի և վերջապես կանգ առնի։ Այնուհետև գալակտիկաները սկսում են իրար մոտենալ, և տիեզերքը սեղմվում է։ Նկ․3.2֊ում ցույց է տրված, թե ինչպես է փոխվում երկու հարևան գալակտիկաների միջև եղած հեռավորությունը ժամանակի ընթացքում։ Այն սկսվում է զերոյից, աճում է մինչև առավելագույնը, ապա նվազում և նորից հասնում է զերոյի։ Երկրորդ մոդելը ցույց է տալիս, որ տիեզերքն այնքան արագ է ընդարձակվում, որ գրավիտացիոն ձգողականությունը երբեք չի կարողանում այն կասեցնել, թեև ինչ֊որ չափով դանդաղեցնում է։ Նկ․ 3.3֊ը ցույց է տալիս երկու հարևան գալակտիկաների միջհեռավորությունը այս մոդելում։ Այն սկսվում է զերոյից, աճում է արագ, իսկ ժամանակի ընթացքում երկու գալակտիկաները շարունակում են իրարից հեռանալ համաչափ արագությամբ։ Վերջապես, կա նաև լուծման 3-րդ մոդելը, որում տիեզերքը ընդարձակվում է հենց այնպիսի արագությամբ, որ նրա վերստին սեղմվելը (կոլապսվելը) հնարավոր չէ։ Նկ․ 3.4-ում ցույց է տրված, որ այդ դեպքում հեռավորությունը սկսում է զերոյից և աճում է մշտապես։ Սակայն այն արագությունը, որով գալակտիկաները հեռանում են իրարից, աստիճանաբար փոքրանում է, թեև զերոյի երբեք չի հասնում։
Ֆրիդմանի առաջին մոդելի ուշագրավ առանձնահատկությունն այն է, որ նրանում տիեզերքը տարածության մեջ անսահման չէ, բայց տարածությունն էլ որևէ սահմանագիծ չունի։ Ձգողության ուժն այնքան ուժեղ է, որ տարածությունն ինքն իր վրա կորացել է, ինչպես երկրի մակերևույթը։ Եթե մեկը ճամբորդի մի որոշակի ուղղությամբ երկրագնդի մակերևույթով, նա երբեք անանցանելի արգելքի չի հանդիպի և դուրս չի գլորվի այնտեղից, այլ ի վերջո կգա կհասնի այնտեղ, որտեղից դուրս էր եկել։ Ֆրիդմանի առաջին մոդելում տիեզերքը հենց այդպիսին է, սակայն եռաչափ է և ոչ թե երկչափ, ինչպես երկրագնդի մակերևույթը։ Չորրորդ չափը՝ ժամանակը, նույնպես վերջավոր է՝ նման երկու ծայր կամ սահմանագիծ՝ մի սկիզբ և մի վերջ ունեցող գծի։ Հետագայում կտեսնենք, որ երբ ընդհանուր հարաբերականույթունը միացվի քվանտային մեխանիկայի անորոշության սկզբունքի հետ, հնարավոր կդառնա, որ այդ երկուսն էլ՝ և՛ տարածությունը, և՛ ժամանակը, վերջավոր լինեն՝ առանց ծայրակետի սահմանագծի։
Այն միտքը, թե կարելի է տիեզերքի շուրջ պտտվել և վերադառնալ ելման կետ, լավ գիտական վիպագրության նյութ է, բայց դա գործնական մեծ նշանակություն ունենալ չի կարող, որովհետև կարելի է ցույց տալ, որ մինչև մարդ ավարտի իր ճամբորդությունը, տիեզերքը կսեղմվի (կկոլապսվի) իր զերոյական ծավալին։ Որպեսզի ճամփորդը վերադառնա ելման կետ տիեզերքի վախճանից առաջ, նա պետք լույսից ավելի արագ շարժվի, ինչը հնարավոր չէ։
Ֆրիդմանի առաջին մոդելի պարագյում, երբ տիեզերքն ընդարձակվում և սեղմվում է, տարածությունն ինքն իր վրա կորանում է երկրագնդի մակերևույթի նման։ Հետևաբար տիեզերքը չափերով վերջավոր է։ Երկրորդ մոդելի դեպքում, երբ տիեզերքն ընդարձակվում է ընդմիշտ, տարածությունը կորացած է այլ կերպ՝ ինչպես թամբի մակերևույթն է։ Հետևաբար այս դեպքում տարածությունն անսահման է։ Վերջապես, Ֆրիդմանի երրորդ մոդելի պարագայում, երբ ընդարձակումը տեղի է ունենում ճիշտ կրիտիկական արագությամբ, տարածությունը հարթ է (հետևաբար նույնպես անսահման է)։
Բայց Ֆրիդմանի ո՞ր մոդելն է նկարագրում մեր տիեզերքը։ Արդյո՞ք տիեզերքը պիտի դադարի ընդարձակվել ու սկսի սեղմվել, թե՞ առհավետ պիտի ընդարձակվի։ Այս հարցին պատասխանելու համար մենք պետք է իմանանք տիեզերքի ընդարձակման ներկայիս արագությունը և միջին խտությունը։ Եթե խտությունը փոքր է որոշակի կրիտիկական արժեքից, որը որոշվում է ընդարձակման արագությամբ, ապա գրավիտացիոն ձգողականությունը նույնպես թույլ կլինի ընդարձակումը կանգնեցնելու համար։ Եթե խտությունը մեծ է այդ կրիտիկական արժեքից, ապա ձգողությունը կդադարեցնի ընդարձակումը որոշ ժամանակ անց և կստիպի, որ տիեզերքը սեղմվի։
Տիեզերքի ընդարձակման ներկայիս արագությունը կարելի է որոշել Դոպլերի էֆեկտի օգնությամբ, չափելով մյուս գալակտիկաների՝ մեզանից հեռանալու արագությունը։ Սա կարելի է իրականացնել մեծ ճշտությամբ։ Սակայն գալակտիկաների հեռավորությունները ճշգրիտ հայտնի չեն, որովհետև մենք դրանք կարող ենք չափել միայն անուղղակի եղանակով։ Մեր ողջ իմացածն այն է, որ տիեզերքը յուրաքանչյուր հազար միլիոն տարում ընդարձակվում է 5֊ից 10 տոկոսով։ Դժբախտաբար, տիեզերքի այժմյան խտության մասին մեր գիտելիքներն ավելի անորոշ են։ Եթե գումարենք մեր և մյուս գալակտիկաների տեսանելի աստղերի զանգվածները, ապա ստացված ամբողջ քանակությունը չի անցնում այն զանգվածի մեկ հարյուրերորդական մասից, որը հարկավոր էր, որպեսզի տիեզերքի ընդարձակումը կանգ առներ՝ նույնիսկ ընդարձակման արագության նվազագույն արժեքի դեպքում։ Սակայն ինչպես մեր, այնպես էլ այլ գալակտիկաներ պիտի պարունակեն մեծ քանակությամբ «սև նյութ», որն ուղղակի տեսնել չենք կարող, բայց գիտենք, որ այն առկա է, որովհետև գրավիտացիոն ձգողությամբ ազդում է գալակտիկաներում գտնվող աստղերի շարժման հետագծերի վրա։ Դեռ ավելին, գալակտիկաներից շատերը հավաքված են կույտերով, և մենք նույն ձևով գալակտիկաների շարժման վրա թողած ազդեցությունից կարող ենք եզրակացնել, որ գալակտիկաների միջև այդ կույտերում «սև նյութ» կա։ Եթե ավելացնենք նաև այդ սև նյութի զանգվածը, ապա կունենանք ընդարձակումը կանգնեցնելու համար հարկավոր քանակության մեկ տասներորդի չափ զանգված։ Այնուամենայնիվ բացառված չէ նաև, որ կարող են լինել նյութի այլ ձևեր՝ տիեզերքում համաչափորեն տարածված, որոնք մենք դեռևս չենք կարողացել հայտնաբերել, և այսպիսով, տիեզերքի միջին խտությունն ավելի բարձր կլինի այն կրիտիկական արժեքից, որը հարկավոր է տիեզերքի ընդարձակումը կանգնեցնելու համար։ Հետևաբար այսօր դեռևս կարելի է ասել, որ տիեզերքն ընդմիշտ ընդարձակվելու է։ Բայց, վստահորեն կարելի է ասել նաև, որ եթե տիեզերքը կոլապսվելու է, ապա դա ավելի շուտ, քան տաս հազար միլիոն տարի հետո չի կարող լինել, քանի որ այն արդեն այդքան ժամանակ ի վեր ընդարձակվում է։ Բայց մտահոգվելու կարիք չկա, որովհետև, եթե մարդկությանը մինչ այդ չհաջողվի մեր Արեգակնային համակարգից դուրս գաղթօջախ ստեղծել, ապա մենք, շատ ավելի շուտ, մեր արևի հետ արդեն ոչնչացած կլինենք։
Ֆրիդմանի բոլոր լուծումներին առանձնահատուկ է այն, որ ինչ֊որ ժամանակ հեռավոր անցյալում (տասից քսան հազար միլիոն տարի առաջ) հարևան գալակտիկաների միջև հեռավորությունը եղել է զերո։ Այն ժամանակ, որը մենք անվանում ենք Մեծ պայթյուն, տիեզերքի խտությունը ևս տարածություն֊ժամանակի կորությունը անսահման մեծ են եղել։ Քանի որ մաթեմատիկան անզոր է անսահմանության դեպքում, ուստի հարաբերականության ընդհանուր տեսությունը (որի վրա հիմնված են Ֆրիդմանի լուծումները) կանխագուշակում է, որ տիեզերքում կա մի կետ, որտեղ տեսությունն ինքը իր ուժը կորցնում է։ Այսպիսի կետը մաթեմատիկորեն կոչվում է եզակիություն (սինգուլյարություն)։ Մեր բոլորի գիտական տեսությունները փաստորեն ձևակերպված են՝ ելնելով այն ենթադրությունից, թե տարածություն֊ժամանակը ողորկ է և համարյա հարթ։ Հենց այդ պատճառով էլ Մեծ պայթյունի եզակիության կետում, որտեղ տարածություն֊ժամանակի կորությունը անսահման է, տեսությունն իր ուժը կորցնում է։ Սա նշանակում է, որ եթե նույնիսկ Մեծ պայթյունից առաջ որոշ դեպքեր տեղի ունեցել են, ապա դրանք կարելի է օգտագործել հետագայում կատարվելիքը որոշելու համար, որովհետև Մեծ պայթյունի կետում տեսությունը զրկվում է կանխագուշակելու կարողությունից։ Նույն ձևով, եթե մեզ հայտնի է հետևանքը, ապա մենք կարող ենք իմանալ, թե ինչ է եղել միայն Մեծ պայթյունից հետո, իսկ դրանից առաջ՝ ոչ։
Այսպիսով, մեզ համար նշանակություն չունի, թե ինչ դեպքեր են տեղի ունեցել Մեծ պայթյունից առաջ, քանի որ դրանք չեն կարող տեղ գտնել տիեզերքի գիտական մոդելում, դուրս են մնում մոդելից, և այդ պատճառով ասում ենք, որ ժամանակը սկիզբ է առել Մեծ պայթյունից։
Շատերը չէին պաշտպանում այն տեսակետը, թե ժամանակը սկիզբ է ունեցել, հավանաբար այն պատճառով, որ դա հակասում էր աստվածային ազատ միջամտությանը։ (Կաթոլիկ եկեղեցին, սակայն, համակրանքով ընդունեց Մեծ պայթյունի մոդելը և 1951 թվականին պաշտոնապես հայտարարեց, որ դա համապատասխանում է Աստվածաշնչին)։ Շատ փորձեր են եղել խուսափելու Մեծ պայթյունի գաղափարից։ Լայն տարածություն գտավ, այսպես կոչված, կայուն վիճակի տեսությունը։ Այս առաջարկությունն արեցին1948֊ին ֆաշիստների գրաված Ավստրիայից փախած Հերման Բոնդին և Թոմաս Գոլդը, անգլիացի Ֆրեդ Հոլլի հետ միասին, որը պատերազմի ժամանակ նրանց հետ աշխատել էր ռադարի կատարելագործման վրա։ Այս տեսության էությունն այն էր, որ միմյանցից հեռացող գալակտիկաների միջև առաջացած ճեղքվածքում շարունակաբար նոր գալակտիկաներ են ծնվում՝ անընդհատ առաջացող նոր նյութից։ Հետևաբար տիեզերքը նույնանման պետք է երևա բոլոր ժամանակներում և բոլոր կետերից։ Կայուն վիճակի տեսությունը պահանջում էր փոփոխություն մտցնել ընդհանուր հարաբերականության մեջ՝ հաշվի առնելու համար նյութի շարունակական առաջացումը։ Պետք է ասել, սակայն, որ նյութի առաջացման այդ արագությունը շատ փոքր էր (տարեկան մեկ մասնիկ մեկ խորանարդ կիլոմետրում) և փորձին չէր հակասում։ Համաձայն առաջին գլխում տրված բացատության, լավ է այն գիտական տեսությունը, որը պարզ է և ի վիճակի է այնպիսի կանխագուշակումներ անել, որոնք կարելի է փորձնականորեն ստուգել։ Այս կանխագուշակումներից մեկն այն էր, որ գալակտիկաների կամ նման առարկաների թիվը տարածության որևէ որոշակի ծավալում պետք է նույնը լինի, անկախ տեղից և դիտարկման ժամանակից։ 1950֊ի վերջերին և 1960֊ի սկզբներին Քեմբրիջում մի խումբ աստղագետներ, Մարտին Ռայլի ղեկավարությամբ (որը Բոնդի, Գոլդի և Հոլլի հետ պատերազմի ժամանակ նույնպես աշխատել էր ռադարի վրա) սկսեցին ուսումնասիրել հեռավոր տարածությունից առաքված ռադիոալիքների աղբյուրները։ Քեմբրիջյան խումբը ցույց տվեց, որ այս ռադիոաղբյուրների մեծ մասը մեր գալակտիկայից դուրս է գտնվում (իրոք շատ աղբյուրներ կարելի էր նույնացնել այլ գալակտիկաների հետ) և թույլ աղբյուրների թիվը ուժեղների համեմատ շատ ավելի մեծ է։
Նրանք եզրակացրին, որ ուժեղ աղբյուրները մեզ մոտիկ են, իսկ թույլերը՝ հեռու։ Հետագայում պարզվեց, որ մոտիկ գտնվող աղբյուրների թիվը միավոր ծավալում ավելի փոքր է, քան հեռու գտնվող աղբյուրների թիվը։ Սա նշանակում էր, որ մենք գտնվում ենք տիեզերքի մի մեծ հատվածի կենտրոնում, որում ճառագայթող աղբյուրների թիվն ավելի փոքր է, քան այլուր։ Դա կարող էր նշանակել նաև, որ անցյալում, երբ ռադիոալիքները սկսել են շարժվել դեպի մեզ, ճառագայթող աղբյուրների թիվը տիեզերքում ավելի մեծ է եղել, քան այսօր։ Երկու բացատրություններն էլ հակասում էին կայուն վիճակի տեսությանը։ Դեռ ավելին, 1965֊ին Պենզիասի և Վիլսոնի մեկրոալիքային ճառագայթման հայտնագործությունը նշանակում էր, որ անցյալում տիեզերքն ավելի խիտ է եղել, քան այժմ։ Այսպիսով հարկ եղավ հրաժարվել կայուն վիճակի տեսությունից։
1963֊ին երկու ռուս գիտնականներ՝ Եվգենի Լիֆշիցը և Իսահակ Խալատնիկովը փորձեցին հրաժարվել Մեծ պայթյունից և, հետևաբար, այն մտքից, թե ժամանակը սկիզբ է ունեցել։ Նրանց կարծիքով՝ Մեծ պայթյունը ֆրիդմանյան մոդելների առանձնահատկությունն է, որոնք տալիս են տիեզերքի միայն մոտավոր պատկերացում։ Տիեզերքի բոլոր մոտավոր մոդելներից միայն Ֆրիդմանի մոդելներն են, որ ունեն Մեծ պայթյունի եզակիություն։ Ֆրիդմանի մոդելների համաձայն, բոլոր գալակտիկաները հեռանում են միմյանցից, հետևաբար բնավ զարմանալի չէ, որ անցյալում ինչ֊որ ժամանակ բոլորը նույն տեղում եղած լինեն։ Իրականում, սակայն, գալակտիկաները ոչ միայն միմյանցից հեռանում են, այլ ունեն նաև կողմնային շարժման փոքր արագություններ։ Այսպիսով իրականում հազիվ թե նրանք բոլորը նույն տեղում գտնվեին, այլ կգտնվեին իրար շատ մոտ մի տիրույթում։ Թերևս, ուրեմն, ներկայիս ընդարձակվող տիեզերքը առաջացել է ոչ այնքան Մեծ պայթյունի եզակիությունից, որքան նախօրոք սեղմված մի փուլից։ Երբ տիեզերքը կոլապսվում է, ոչ բոլոր մասնիկներն են մերձենում իրար, այլ մեկը մյուսի կողքով է անցնում, իսկ այնուհետև հեռանալով իրարից, առաջացնում են այժմյան ընդարձակվող տիեզերքը։ Այսպիսով, ինչպե՞ս կարելի է ասել, թե իրական տիեզերքը կարող էր սկիզբ առնել Մեծ պայթյունից։ Փաստորեն Լիֆշիցը և Խալատնիկովը շարունակեցին ուսումնասիրել մոտավորապես այնպիսի մոդելներ, ինչպիսիք առաջարկել էր Ֆրիդմանը, միայն այն տարբերությամբ, որ այստեղ հաշվի էին առնվում գալակտիկաների շարժման որոշ անհարթությունները և անկանոն կողմնային արագությունները։ Նրանք ցույց տվեցին, որ թեև գալակտիկաները այլևս ուղղակիորեն իրարից չէին հեռանում, սակայն հնարավոր է, որ սկիզբ առած լինեն Մեծ պայթյունից։ Համենայն դեպս այս բանը տեղի կունենար բացառիկ մի քանի մոդելների համար, երբ բոլոր գալակտիկաները շարժվեցին ճիշտ պահանջված ուղղությամբ։ Նրանք փաստարկում էին նաև այն, թե, քանի որ շատ ավելի մեծ թվով ֆրիդմանատիպ մոդելներ կարող են լինել առանց Մեծ պայթյունի եզակիության, ուստի կարելի է եզրակացնել, որ իրականում Մեծ պայթյուն չի եղել։ Հետագայում նրանք գտան, որ գոյություն ունի ֆրիդմանյան մոդելների մի լայն դաս, որը եզակիություն ունի, և պարտադիր չէ, որ գալակտիկաները շարժվեն հատուկ ձևով։ Այսպիսով 1970 թվականին նրանք հրաժարվեցին իրենց պահանջից։
Լիֆշիցի և Խալատնիկովի աշխատությունն արժեքավոր է այն իմաստով, որ ցույց տվեց, որ տիեզերքը կարող է միայն մեկ եզակիություն ունենալ, մի Մեծ պայթյուն, եթե ճիշտ է հարաբերականության ընդհանուր տեսությունը։ Նրանց սակայն չհաջողվեց լուծել վճռական հարցը։ Արդյո՞ք ընդհանուր հարաբերականությունը կանխագուշակում է, որ մեր տիեզերքը պետք է ունեցած լինի Մեծ պայթյուն և ժամանակի կսիզբ։ Այս հարցի պատասխանը տրվեց 1965֊ին, երբ անգլիացի մաթեմատիկոս և ֆիզիկոս Ռոջեր Պենրոուզը ներմուծեց հարցի քննարկման բոլորովին այլ մի մոտեցում։ Օգտագործելով լուսակոների վարքագիծը ընդհանուր հարաբերականության մեջ և այն փաստը, որ ծանրության ուժը ձգողական բնույթ ունի, Պենրոուզը ցույց տվեց, որ իր ծանրության ուժի տակ կոլապսվող աստղը շրջափակվում է մի մարզում, որի մակերեսն ի վերջո նվազում է մինչև զերո։ Եվ որովհետև մակերեսը դառնում է զերո, ապա ծավալը նույնպես կդառնա զերո։ Աստղի ողջ զանգվածը կսեղմվի զերո ծավալով տիրույթում, որի հետևանքով նյութի խտությունը և տարածություն֊ժամանակի կորությունը կդառնան անսահման։ Այլ կերպ ասած, տարածություն֊ժամանակի որոշակի տիրույթում առաջանում է մի եզակիություն, ինչը հայտնի է որպես սև խոռոչ։
Առաջին հայացքից թվում էր, որ Պենրոուզի ստացած արդյունքը վերաբերում էր լոկ աստղերին։ Ոչինչ չէր ասված այն մասին, թե արդյո՞ք տիեզերքն ամբողջությամբ վերցրած անցյալում ունեցել է Մեծ պայթյունի եզակիություն։ Երբ Պենրոուզը ներկայացրեց իր թեորեմը, ես սովորում էի ասպիրանտուրայում և հուսահատորեն փնտրում էի այնպիսի մի հիմնահարց, որ հնարավոր դարձներ իմ դոկտորական ատենախոսության ավարտը։ Երկու տարի առաջ ախտորոշել էին, որ ես տառապում եմ ԱԿՍ֊ով, որը սովորաբար կոչվում է Լու Գեհրիգի, կամ շարժողական նեյրոնի հիվանդություն, և հասկացրել էին, որ ես ընդամենը մեկ կամ երկու տարվա կյանք ունեմ։ Իրերի այսպիսի վիճակում հազիվ թե իմաստ ունենար դոկտորական ատենախոսության վրա աշխատելը, քանի որ չէի մտածում, որ կապրեմ այդքան երկար։ Սակայն, երկու տարին արդեն անցել էր, և իմ վիճակը այնքան էլ վատ չէր։ Դեռ ավելին, առողջական վիճակս այնպիսին էր, որ նշանվել էի սքանչելի մի աղջկա՝ Ջեյն Ուայլդի հետ։ Բայց ամուսնանալու համար ինձ աշխատանք էր հարկավոր, իսկ աշխատանք գտնելու համար՝ դոկտորական աստիճան։
1965 թվականին ես ուշադիր կարդացի Պենրոուզի թեորեմը այն մասին, որ երբ որևէ մարմին ենթարկվում է գրավիտացիոն կոլապսի, վերջում պետք է մի եզակիություն առաջանա։ Անմիջապես գլխի ընկա, որ եթե Պենրոուզի թեորեմի մեջ ժամանակի ուղղությունը շրջենք, այսինքն մարմնի սեղմվելը փոխարինենք նրա ընդարձակումով, ապա թեորեմի պայմանները կմնան ուժի մեջ այն պայմանով, որ տիեզերքը մոտավորապես լինի այնպիսին, ինչպիսին լայն մասշտաբով վերցված Ֆրիդմանի մոդելն է։ Պենրոուզի թեորեմը ցույց տվեց, որ ցանկացած կոլապսվող աստղ պետք է վերջ գտնի եզակիության առաջացումով։ Միաժամանակ շրջված ժամանակի փաստարկը բացահայտեց, որ ցանկացած ֆրիդմանատիպ ընդարձակվող տիեզերք եզակիությամբ պիտի սկսվեր։ Զուտ տեխնիկական պատճառներով Պենրոուզի թեորեմը պահանջում էր, որ տիեզերքն անսահման լինի տարածության մեջ։ Այս բանը ես կարողացա փաստորեն օգտագործել ապացուցելու համար, որ եզակիություն կառաջանար լոկ այն դեպքում, երբ տիեզերքը ընդարձակվեր այնպիսի արագությամբ, որը բացառեր կոլապսի կրկնությունը։ (Քանի որ միայն այդպիսի ֆրիդմանյան մոդելներն են անսահման տարածության մեջ)։
Հաջորդ մի քանի տարիների ընթացքում ես մշակեցի մի նոր մաթեմատիկական ապարատ, որպեսզի այս և այլ տեխնիկական պայմաններից մաքրեմ եզակիությունների առաջացումն ապացուցող թեորեմները։
Վերջնական արդյունքն եղավ այն հաղորդագրությունը, որը Պենրոուզն ու ես հրատարակեցինք 1970֊ին, որտեղ վերջնականապես ապացուցվեց, որ մի Մեծ պայթյունի եզակիություն պետք է եղած լինի, պայմանով, որ ճիշտ է ընդհանուր հարաբերականությունը, և տիեզերքը պարունակում է այնքան նյութ, որքան մենք դիտարկել ենք։ Մեր աշխատանքը շատ մեծ ընդդիմության հանդիպեց, մասամբ խորհրդային գիտնականների կողմից, գիտական դետերմինիզմի նկատմամբ նրանց տածած մարքսիստական աշխարհայացքի պատճառով, մասամբ էլ նրանց կողմից, ում համար անհանդուրժելի էր հենց եզակիության միտքը և փչացնում էր Էնշտեյնի տեսության հմայքը։ Այնուամենայնիվ, ոչ ոք չէր կարող վիճարկել մաթեմատիկական թեորեմը։ Հետևաբար, մեր աշխատանքը վերջապես ընդհանուր ճանաչում գտավ և գրեթե ամեն ոք ընդունեց, որ տիեզերքն առաջացել է Մեծ պայթյունի եզակիությունից։ Թերևս գիտության հեգնանքն է այն, որ այսօր ես փոխել եմ իմ կարծիքը և աշխատում եմ համոզել ուրիշ ֆիզիկոսների, որ տիեզերքի սկզբնավորման ժամանակ փաստորեն ոչ մի եզակիություն չի եղել և, ինչպես հետագայում կտեսնեք, այդ եզակիությունը կանհետանա, հենց որ հաշվի առնվեն քվանտային ներգործությունները։
Այս գլխում տեսանք, թե ինչպես հազարամյակների ընթացքում տիեզերքի մասին մարդկային մտքի ստեղծած պատկերացումները մի հիսնամյակից ավելի կարճ ժամանակում հսկայական փոփոխության ենթարկվեցին։ Այս ամենի համար ելակետ եղան Հաբլի հայտնագործությունը ընդարձակվող տիեզերքի մասին և այն բանի գիտակցումը, որ անծայրածիր տիեզերքում մեր մոլորակը աննշմարելի է։ Մինչ կուտակվում էին փորձնական և տեսական փաստերը, գնալով պարզ դարձավ, որ տիեզերքը ժամանակի մեջ պետք է որ մի սկիզբ ունեցած լինի։ 1970֊ին Պենրոուզն ու ես վերջնականապես ապացուցեցինք այս բանը՝ Էյնշտեյնի հարաբերականության ընդհանուր տեսության հիման վրա։ Սակայն հենց մեր ապացույցը ցույց տվեց, որ Էյնշտեյնի ընդհանուր հարաբերականության տեսությունն անկատար է։ Այդ տեսությունը մեզ չի կարող ասել, թե ինչպես է սկիզբ առել տիեզերքը, քանի որ այն կանխագուշակում է, որ բոլոր ֆիզիկական տեսությունները, ներառյալ նաև ինքը, կորցնում են իրենց ուժը, երբ հարցը վերաբերում է տիեզերքի սկզբնավորմանը։
Հարաբերականության ընդհանուր տեսությունը մասնակի մի տեսություն լինելով հանդերձ, այնուամենայնիվ, ակնարկում է այն մասին, որ եզակիության թեորեմները նշանակում են, որ վաղ շրջանում եղել է մի ժամանակ, երբ տիեզերքն այնքան փոքր էր, որ չենք կարող այլևս անտեսել փոքր մասշտաբի այն երևույթները, որոնցով զբաղվում է քսաներորդ դարի մեկ այլ մասնակի հզոր տեսություն՝ քվանտային մեխանիկան։
Այս պատճառով, 1970֊ականների սկզբին ստիպված եղանք մեր ուշադրությունը շեղել արտակարգ ծավալունի տեսությունից դեպի արտակարգ փոքրի տեսությունը, ըմբռնելու համար տիեզերքի բուն էությունը։ Հաջորդ գլխում մենք կնկարագրենք քվանտային մեխանիկայի էությունը, որպեսզի պատրաստ լինենք հետագայում փորձել միավորելու այս երկու մասնակի հզոր տեսությունները մեկում՝ գրավիտացիոն քվանտային տեսության մեջ։
4
Անորոշության սկզբունքը
Գիտական մտքի հաջողությունները, մասնավորապես Նյուտոնի ձգողականության տեսությունը հիմք դարձան, որ տասնիներորդ դարի սկզբին ֆրանսիացի գիտնական մարկիզ դը Լապլասը պնդի, որ տիեզերքը լրիվ որոշադրական (դետերմինիստական) է, այսինքն՝ կամքի ազատություն չի կարող լինել։ Լապլասը գտնում էր, որ պետք է գոյություն ունենա գիտական օրենքների մի շարք, որով մենք ի վիճակի լինենք կանխատեսել տիեզերքում տեղի ունենալիք ամեն ինչ, եթե միայն մեզ հայտնի է տիեզերքի վիճակը որոշակի ժամանակում։ Օրինակ, եթե մեզ հայտնի են արևի և մոլորակների դիրքերն ու արագությունները ժամանակի որևէ պահի, ապա, օգտվելով Նյուտոնի օրենքներից, կարող ենք հաշվել Արեգակնային համակարգի վիճակը որևէ այլ ժամանակում։ Այստեղ ուշադրությունն ակնհայտ է, սակայն Լապլասն ավելի առաջ անցավ և ենթադրեց, որ նման օրենքներ կան ամենուրեք, ընդհուպ մինչև մարդկային վարքագիծը։
Գիտական որոշադրության ուսմունքը շատերի կողմից դիմադրության հանդիպեց․ նրանք մտածում էին, որ դա սահմանափակում էր աշխարհի գործերին Աստծո ազատ միջամտությունը։ Այնուամենայնիվ, գիտության մեջ այն շարունակեց մնալ որպես սովորական մի ենթադրություն մինչև քսաներորդ դարի սկիզբը։ Այդ տեսակետից հրաժարվելու առաջին նշաններից մեկն ակնհայտ դարձավ, երբ անգլիացի գիտնականներ լորդ Ռելեն և պ֊ն Ջեյմս Ջինսը ցույց տվեցին, որ տաք առարկայի կամ մարմնի, ինչպիսին աստղն է, կողմից էներգիայի առաքումը կատարվում է անսահմանափակ քանակով։ Համաձայն այդ ժամանակ տարածված կարծիքի, տաք մարմինը էլեկտրամագնիսական ալիքներ է արձակում (ռադիոալիքներ, տեսանելի լույս կամ ռենտգենյան ճառագայթներ) բոլոր հաճախականություններով համաչափ։ Օրինակ, կարծում էին, որ տաք մարմինը նույնաքանակ էներգիա է ճառագայթում ինչպես մեկից մինչև երկու միլիոն միլիոն ալիք վայրկյանում, այնպես երկուսից մինչև երեք միլիոն միլիոն ալիք վայրյկանում տիրույթենրի հաճախականություններով։ Այսինքն, քանի որ ալիքների թիվը վայրկյանում սահմանափակված չէ, ապա ճառագայթված գումարային էներգիան նույնպես պետք է անսահմանափակ լինի։[5]
Այս ակնհայտ տարօրինակություններից խուսափելու համագերմանացի գիտնական Մաքս Պլանկը 1900֊ին մի միտք արտահայտեց․ այն է՝ ճառագայթող մարմինը չի կարող լուսային, ռենտգենյան կամ այլ ալիքային էներգիա առաքել կամայական քանակությամբ, այլ առաքում է որոշակի բաժիններով, որոնք նա անվանեց քվանտ։ Ավելին, յուրաքանչյուր քվանտ ունի որոշակի քանակի էներգիա, որն այնքան մեծ է, որքան բարձր է ալիքի հաճախականությունը, այնպես որ, բավականաչափ բարձր հաճախականության դեպքում մեկ քվանտի համար պահանջվում է ավելի էներգիա, քան հնարավոր է։ Այսպիսով բարձր հաճախականությունների տակ ճառագայթումը պետք է նվազի, և դրանով իսկ մարմնի էներգիա կորցնելու արագությունը պիտի լինի վերջավոր։
Թեև քվանտային հիպոթեզը շատ լավ բացատրեց տաք մարմնի ճառագայթման բնույթը, բայց նրա նշանակությունը որոշադրական առումով չիրականացավ մինչև 1926 թ․, երբ մի այլ գերմանացի գիտնական՝ Վերներ Հայզենբերգը ձևակերպեց իր նշանավոր անորոշության սկզբունքը։ Մի մասնիկի ապագա դիրքն ու արագությունը կանխագուշակելու համար մարդ պետք է կարողանա մեծ ճշտությամբ որոշել նրա ներկա դիրքն ու արագությունը։ Դրա համար պետք է մասնիկը լուսավորել։
Լույսի ալիքների մի մասը կցրվի մասնիկի կողմից, և դու ցույց կտա նրա դիրքը։ Սակայն հնարավոր չէ մասնիկի դիրքը որոշել ավելի մեծ ճշտությամբ, քան լույսի ալիքի գագաթների միջև եղած հեռավորությունը։ Հետևաբար մասնիկի դիրքը ճշգրիտ որոշելու համար անհրաժեշտ է օգտագործել կարճ ալիքի երկարություն ունեցող լույս։ Պլանկի քվանտային տեսության համաձայն, չի կարելի օգտագործել լույսի կամայական փոքր քանակություն, այլ առնվազն մեկ քվանտ։ Մասնիկի և այդ քվանտի բախման հետևանքով առաջինի արագությունը կմեծանա, որի չափը դժվար է կանխորոշել։ Ավելին, դիրքի որոշման բարձր ճշտության համար անհրաժեշտ է օգտագործել կարճալիք լույս, այսինքն՝ մեծ էներգիա ունեցող քվանտ։ Հետևաբար, մասնիկի արագության խոտորումը կլինի ավելի մեծ։ Այլ խոսքով ասած, որքան մեծ ճշտությամբ որոշվի մասնիկի դիրքը, այնքան փոքր կլինի նրա արագության որոշման ճշտությունը, և՝ հակառակը։ Հայզենբերգը ցույց տվեց, որ մասնիկի դիրքի և արագության որոշման անորոշությունների և զանգվածի արտադրյալը չի կարող ավելի փոքր լինել մի որոշակի մեծությունից, որը հայտնի է որպես Պլանկի հաստատուն։ Ավելին, այդ սահմանը կախված չէ այն բանից, թե ինչպիսի մասնիկ է դա, և ինչպես են որոշվում նրա դիրքն ու արագությունը։ Հայզենբերգի անորոշության սկզբունքը աշխարհի հիմնարար, անխուսափելի հատկանիշն է։
Անորոշության սկզբունքը մեծ նշանակություն ունեցավ աշխարհընկալման առումով։ Այս բանը նույնիսկ ավելի քան հիսուն տարի անց դեռևս լրիվ չի գնահատվել փիլիսոփաների կողմից և բանավեճի առիթ է տալիս նաև այսօր։ Անորոշության սկզբունքը վերջ տվեց գիտության տեսության մասին լապլասյան երազանքին, այսինքն՝ տիեզերքի լրիվ որոշադրական պատկերացմանը։ Եթե հնարավոր չէ նույնիսկ տիեզերքի այժմյան վիճակը ճշգրտորեն որոշել, ապա, իհարկե, չի կարեի ճշգրտորեն կանխագուշակել նրա ապագա դեպքերը։ Թերևս կարելի է ենթադրել, որ մի գերբնական էակ կարող է դիտարկել տիեզերքի ներկա վիճակը առանց այն խախտելու, և նրա համար կա դեպքերի ընթացքը կատարելապես որոշող օրենքների մի շարք։ Այնուամենայնիվ, տիեզերքի այդպիսի մոդելները մեզ՝ սովորական մահկանացուներիս համար ոչ մի հետաքրքրություն չեն ներկայացնի։
Թվում է, լավագույնը, Օկամի ածելի կոչված խնայողության սկզբուքն օգտագործելն ու տեսությունից կտրել, դեն նետելն է այն ամենը, ինչն ուղղակի դիտարկման ենթակա չէ։ Ահա այսպիսի մոտեցմամբ Հայզենբերգը, Էրվին Շրյոդինգերը և Պոլ Դիրակը 1920֊ական թվականներին մեխանիկան վերաձևակերպեցին մի նոր տեսության, որը կոչվում է քվանտային մեխանիկա և հիմնված է անորոշության սկզբունքի վրա։ Այս տեսության մեջ մասնիկները չեն առանձնանում ճշգրիտ որոշված դիրքերով և արագություններով, դրանք հնարավոր չէ դիտարկել։ Ընդհակառակը, դրանք գտնվում են քվանտային վիճակում, որը դիրքի ու արագության համակցություն է։
Ընդհանուր առմամբ տվյալ դեպքի համար քվանտային մեխանիկան որոշակի արդյունք չի կանխագուշակում։ Փոխարենը կանխագուշակում է հնարավոր մի քանի տարբեր հետևանքներ և տալիս յուրաքանչյուրի հավանականությունը։ Այսպես, եթե նույնասկիզբ մեծ թվով համանման համակարգերի համար կատարվել են նույն չափումները, արդյունքը որոշակի թվով դեպքերի համար կլինի A, այլ թվով դեպքերի համար՝ B և այլն։ Կարելի է կանխագուշակել, թե արդյունքը մոտավորապես քանի անգամ կլինի A կամ B, բայց հնարավոր չէ կանխագուշակել յուրաքանչյուր չափման կոնկրետ արդյունքները։ Հետևաբար, քվանտային մեխանիկան գիտության մեջ մտցնում է պատահականության կամ անկանխագուշակելիության անխուսափելի մի տարր։ Էյնտշեյնը խիստ կերպով առարկեց դրան, հակառակ այն բանի, որ հենց ինքը շատ մեծ դեր խաղաց այդ գաղափարի զարգացման գործում։ Բավական է ասել, որ նրան Նոբելյան մրցանակ շնորհվեց հենց այն մեծ ավանդի համար, որ նա ներդրել էր քվանտային տեսության ստեղծման գործում։ Այնուամենայնիվ, Էյնշտեյնը երբեք չհաշտվեց այն մտքի հետ, որ տիեզերքը կառավարվում է պատահականությամբ։ Նրա տարակուսանքը ամփոփված է նրա իսկ հայտնի հայտարարության մեջ․ «Աստված զառ չի խաղում»։ Սակայն, համարյա բոլոր գիտնականները ընդունեցին քվանտային մեխանիկան, որովհետև այն կատարելապես համընկնում էր փորձնական տվյալների հետ։ Արդարև քվանտային մեխանիկան դարձավ արտակարգ հաջողված մի տեսություն և համարյա ժամանակակից գիտության ու տեխնոլոգիայի հիմքն է։ Այս տեսությունը կառավարում է տրանզիստորների և միասնական շղթաների աշխատանքը, որոնք հեռուսատացույցների, հաշվողական մեքենաների և նման էլեկտրոնային սարքերի հիմնական բաղադրամասերն են։ Քվանտային մեխանիկան նաև կենսաբանության և ժամանակակից քիմիայի հիմքն է։ Ֆիզիկական գիտությունների այն բնագավառները, որտեղ քվանտային մեխանիկան առ այսօր հիմնավոր կերպով մուտք չի գործել, տիեզերքի ձգողականության ու խոշորամասշտաբ կառուցվածքի հարցերն են։
Չնայած լույսը կազմված է ալիքներից, շարժվում է ալիքաձև, սակայն Պլանկի քվանտային հիպոթեզը պնդում է, որ որոշ դեպքերում այն իրեն պահում է այնպես, կարծես մասնիկը կազմված լինի և կարող է առաքվել կամ կլանվել միայն մասերով՝ քվանտներով։
Մյուս կողմից՝ Հայզենբերգի անորոշության սկզբունքից բխում է, որ մասնիկները որոշ տեսակետից իրենց պահում են որպես ալիք, այսինքն՝ նրանք որոշակի տեղ չեն գրավում, այլ «ամպաձև», թեև որոշակի հավանականությամբ, բաշխված են տվյալ տարածքում։ Քվանտային մեխանիկայի տեսությունը հիմնված է բոլորովին նոր տեսակի մաթեմատիկայի վրա, որ իրական աշխարհն այլևս չի նկարագրում որպես մասնիկներ կամ ալիքներ, այլ որպես ալիքների ու մասնիկների մի երկվություն։ Որոշ նպատակներով հարմար է մասնիկները դիտարկել որպես ալիքներ, այլ նպատակների համար՝ ալիքները որպես մասնիկներ։ Դրա կարևոր հետևանքներից մեկը, որը կարելի է տեսնել, կոչվում է ինտերֆերենցիայի երևույթ՝ ալիքների և մասնիկների երկու շարքի միջև։ Ենթադրենք ալիքի մի շարքի գագաթները համընկել են մյուս շարքի փոսերի հետ։ Այդ դեպքում ալիքների երկու շարքը կոչնչացնեն միմյանց, արտաքուստ սպասվող՝ ալիքների ուժեղացման փոխարեն։
Լույսի ալիքների ինտերֆերենցիայի գեղեցիկ մի օրինակ է օճառի պղպջակի վրա գուների առաջացման երևույթը։ Դրա պատճառը պղպջակը կազմող ջրի բարակ թաղանթի՝ երկու կողմերից լույսի անդրադարձումն է։ Սպիտակ լույսը կազմված է տարբեր ալիքի երկարություն ունեցող կամ տարբեր գույն ունեցող լույսի ալիքներից։ Պղպջակի մի կողմից որոշ ալիքի երկարություններ ունեցող լույսի անդրադարձող ալիքների գագաթները կարող են հանդիպել մյուս կողմից անդրադարձող համապատասխան ալիքների փոսերին։ Այդ երկարության ալիքների համապատասխանող գույները կբացակայեն անդրադարձող լույսի մեջ, որի հետևանքով այն կերևա գունավոր։
Ինտերֆերենցիայի երևույթը դիտվում է նաև մասնիկների համար՝ քվանտային մեխանիկայի ներմուծած երկվության շնորհիվ։ Հանրահայտ օրինակ է, այսպես կոչված, երկու նեղ ճեղքերի փորձը (նկ․ 4.2):
Պատկերացնենք երկու զուգահեռ նեղ ճեղքեր ունեցող մի միջնապատ։ Այդ միջնապատի մի կողմում տեղադրենք որոշակի գույնի (այսինքն՝ որոշակի ալիքի երկարության) լուսաղբյուր։ Լույսի մեծ մասը կդիպչի միջնապատին, իսկ փոքր մասը կանցնի ճեղքերից։ Այժմ ենթադրենք միջնապատի մյուս կողմում տեղադրված է էկրան։ Էկրանի որոշ կետերի վրա կընկնեն ճեղքից անցած ալիքները։ Սակայն, սովորաբար, այն հեռավորությունը, որն անցնում լույսը աղբյուրից մինչև էկրան՝ երկու ճեղքերի միջով, տարբեր է։ Դա նշանակում է, որ ճեղքերից անցած ալիքները միևնույն փուլում չեն լինի էկրանին հասնելիս, ուստի էկրանի վրա որոշ տեղերում երկու ճեղքերից եկող ալիքները կոչնչացնեն միմյանց, այլ տեղերում՝ կուժեղացնեն։ Արդյունքում ստացվում է լուսավոր և խավար շերտերից կազմված լույսի ինտերֆերենցիայի նախշանկար։
Ուշագրավ է այն փաստը, որ ճիշտ նման պատկեր է ստացվում, երբ լույսի աղբյուրի փոխարեն դրվում է մասնիկների աղբյուր, օրինակ, որոշակի արագությամբ շարժվող էլեկտրոններ (դա նշանակում է, որ համապատասխան ալիքներն ունեն որոշակի երկարություն)։ Խիստ հատկանշական է, որ երբ միջնապատի վրա մեկ ճեղք կա, էկրանին շերտեր չեն ստացվում, այլ ստացվում է էլեկտրոնների կանոնավոր բաշխում։ Կարելի է մտածել, որ երկրորդ ճեղքը բացելիս էկրանի վրա յուրաքանչյուր կետին հարվածող էլեկտրոնների թիվը կաճի, բայց քանի որ տեղի է ունենում ինտերֆերենցիա, նշանակում է որոշ տեղերում էլեկտրոնների թիվը իրականում նվազում է։ Թվում է, թե, եթե էլեկտրոնները մեկ առ մեկ շարժվեն դեպի ճեղքերը, ապա նրանցից յուրաքանչյուրը միաժամանակ կարող է անցնել ճեղքերից միայն մեկով, կարծես թե էլեկտրոնի համար ճեղքերից միայն մեկը գոյություն ունենա, որով անցնելով էլեկտրոնները պետք է հավասարաչափ բաշխվեն էկրանի վրա։ Իրականում, սակայն, էլեկտրոնների մեկ առ մեկ անցման դեպքում անգամ ստացվում է շերտավոր պատկեր։ Մնում է եզրակացնել, որ յուրաքանչյուր էլեկտրոն պետք է անցնի երկու ճեղքերով միաժամանակ։
Մասնիկների ինտերֆերենցիայի երևույթի հայնտագործումը վճռական նշանակություն ունեցավ ատոմի կառուցվածքի էությունը իրապես ըմբռնելու համար։ Ատոմները քիմիայի և կենսաբանության հիմքը կազմող միավորներն են և այն շինարարական աղյուսները, որոնցով և՛ մենք, և՛ մեր շուրջ եղած ամեն ինչ կառուցված է։ Մեր դարաշրջանի սկզբներին մտածում էին, որ ատոմը կազմված է դրական լիցք ունեցող միջուկից, որի շուրջը շրջանաձև պտտվում են բացասական լիցք ունեցող էլեկտրոնները, ինչպես մոլորակները՝ արևի շուրջ։ Ենթադրվում էր, որ դրական և բացասական լիցքերի միջև ձգողությունը չեզոքացվում է, և էլեկտրոնները մնում են իրենց ուղեծրերում, ճիշտ այնպես, ինչպես արևի և մոլորակների միջև գրավիտացիոն ձգողությունն է մոլորակներին պահում իրենց ուղեծրերում։ Սակայն քվանտային մեխանիկայից առաջ եղած մեխանիկայի և էլեկտրականության օրենքներից հետևում էր, որ էլեկտրոնները աստիճանաբար էներգիա կորցնելով՝ պարուրաձև հետագծով պետք է ընկնեին միջուկի վրա։ Սա նշանակում էր, ատոմը և հետևապես նյութը ամբողջությամբ վերցրած, պիտի արագորեն կոլապսվեին մինչև անսահման խտություն ունեցող վիճակի։ Այս հարցն իր մասնակի լուծումը գտավ 1913 թվականին դանիացի գիտնական Նիլս Բորի կողմից։ Նա ենթադրեց, որ էլեկտրոնները չեն կարող պտտվել կենտրոնական միջուկից ցանկացած հեռավորության վրա, այլ շատ որոշակի, յուրահատուկ հեռավորությունների վրա են պտտվում։ Եթե ենթադրենք, որ միաժամանակ մեկ կամ երկու էլեկտրոն կարող են պտտվել այդ հեռավորություններից յուրաքանչյուրով, ապա դա կլուծի ատոմի կոլապսի խնդիրը, քանի որ էլեկտրոնները չեն կարող ամենափոքր հեռավորություն և էներգիա ունեցող ուղեծրից ավելի մոտիկ հեռավորության ուղեծիր անցնել։
Այս մոդելը շատ գեղեցիկ կերպով բացատրեց ամենապարզ ատոմի՝ ջրածնի կառուցվածքը, որի միջուկի շուրջը պտտվում է միայն մեկ էլեկտրոն։ Բայց հստակ չէր, թե այն ինչպես կարելի է տարածել ավելի բարդ ատոմների վրա։ Ավելին, սահմանափակ թվով թույլատրելի ուղեծրերի հարցը շատ կամայական է թվում։ Քվանտային մեխանիկայի նոր տեսությունը հաջողությամբ լուծում տվեց այս դժվարին հարցին։ Բացահայտվեց, որ միջուկի շուրջ պտտվող էլեկտրոնը կարելի է պատկերացնել որպես ալիք, որի երկարությունը կախված է նրա արագությունից։ Համապատասխան ուղեծրերի համար երկարությունը հավասար է ամբողջական թվով (հակառակ կոտորակային թվի) ալիքի երկարության։ Այդ ուղեծրի համար ալիքի գագաթի փոսը յուրաքանչյուր պտույտի համար կլինի նույն դիրքում, հետևաբար, ալիքները կգումարվեն․ այդ ուղեծրերը համապատասխանում են Բորի թույլատրելի ուղեծրերին։ Իսկ այն ուղեծրերը, որոնց երկարությունը հավասար չէ ամբողջական թվով ալիքի երկարության, թույլատրելի չեն, որովհետև այդ դեպքում յուրաքանչյուր գագաթ հաջորդ շրջապտույտի ժամանակ կոչնչացվի համապատասխան փոսի կողմից։
Ալիք֊մասնիկային երկվության մասին տեսանելի պատկերացում է տալիս ամերիկացի գիտնական Ռիչարդ Ֆեյնմանի առաջարկած, այսպես կոչված, պատմությունների գումարը։ Այս մոտեցման մեջ չի ենթադրվում, որ մասնիկը տարածություն ժամանակի մեջ ունի մի ուղի կամ մի պատմություն, ինչպես դասական կամ ոչ քվանտային տեսության մեջ։ Փոխարենը ենթադրվում է, որ մասնիկը A֊ից B գնում է ամեն հնարավոր ճանապարհով։ Յուրաքանչյուր ճանապարհ բնութագրվում է երկու թվով․ մեկը համապատասխանում է ալիքի չափին, մյուսը՝ դիրքին բոլորաշրջանի (ցիկլի) մեջ (այսինքն՝ որտեղ է գագաթին, որտեղ՝ փոսում)։ A֊ից B գնալու հավանականությունը կարեի է իմանալ բոլոր ուղիներով գնացող ալիքները գումարելով։ Ընդհանրապես, եթե մի խումբ հարևան ուղիներ համեմատենք, ապա դրանցում ալիքների դիրքերը կամ փուլերը իրարից շատ տարբեր կլինեն։ Սա նշանակում է, որ այդ ուղիներով շարժվող ալիքները գրեթե ճշգրտորեն իրար կմարեն։ Հետևաբար, այդ ուղիները թույլատրելի չեն լինի։ Սակայն որոշ հարևան ուղիների համար ալիքների փուլերը շատ չեն տարբերվի իրարից։ Այս ուղիների ալիքները իրար չեն մարի, այսինքն այս ուղիները համապատասխանում են Բորի թույլատրելի ուղեծրերին։
Օգտագործելով այս գաղափարը՝ մշակվեց համապատասխան մաթեմատիկական բանաձև և հնարավոր դարձավ հաշվել բոլոր թույլատրված ուղեծրերը ավելի բարդ, բազմաէլեկտրոն ատոմների համար, նույնիսկ մոլեկուլների համար, որոնք կազմված են մեկից ավելի միջուկների շուրջ պտտվող էլեկտրոններով իրար հետ կապված ատոմներից։ Քանի որ մոլեկուլների կառուցվածքը և միմյանց հետ նրանց փոխազդեցություններն ընկած են քիմիայի և կենսաբանության հիմքում, ապա քվանտային մեխանիկան թույլ է տալիս սկզբունքորեն կանխորոշել գրեթե այն ամենը, ինչ կատարվում է մեր շրջապատում, իհարկե, անորոշության սկզբունքի սահմաններում։ (Գործնականում, սակայն, մեծ թվով էլեկտրոններ և միջուկներ պարունակող համակարգերի և դրանց փոխազդեցությունների համար հաշվումներն այն աստիճան բարդ են, որ համարյա անհնար է իրականացնել)։
Թվում է, թե Էյնշտեյնի հարաբերականության ընդհանուր տեսությունը նկարագրում է տիեզերքի խոշորամասշտաբ կառուցվածքը։ Դա այն է, ինչը կոչվում է դասական տեսություն, որը հաշվի չի առնում քվանտային մեխանիկայի անորոշության սկզբունքը, ինչը հարկավոր է մյուս տեսությունների հետ ներդաշնակ լինելու համար։ Սակայն այս անտեսումը հարաբերականության ընդհանուր տեսության կանխատեսումների և դիտարկումների միջև հսկայական պատճառ չի դառնում, որովհետև գրավիտացիոն դաշտը, որի հետ մենք առնչվում ենք շատ թույլ է։ Բայց, ինչպես ցույց են տալիս վերը նշված եզակիության թեորեմները, ձգողական դաշտը խիստ ուժեղանում է առնվազն երկու պարագայում՝ սև խոռոչների և Մեծ պայթյունի համար։ Այսպիսի ուժեղ դաշտերում քվանտային մեխանիկայի դերը շատ կարևոր է։ Այլ կերպ ասած, դասական հարաբերականության ընդհանուր տեսությունը՝ կանխագուշակելով անսահման խիտ կետերի առաջացումը, նախանշեց իր սեփական անզորությունը ճիշտ այնպես, ինչպես դասական (այսինքն՝ ոչ քվանտային) մեխանիկան կանխագուշակեց իր կործանումը, կանխագուշակելով, որ ատոմները պիտի կոլապսվեն մինչև անսահման մեծ խտության։ Մենք դեռևս չունենք կատարյալ և հետևողական մի տեսություն, որը միավորեր ընդհանուր հարաբերականությունը և քվանտային մեխանիկան, բայց գիտենք, թե այդպիսի միացյալ տեսությունն ինչպիսի հատկանիշներ պիտի ունենա։ Թե այն ինչպիսի հետևանքներ կարող է ունենալ սև խոռոչների և Մեծ պայթյունի էությունները բացատրելու համար, կնգարագրվի հաջորդ գլուխներում։ Մի պահ, սակայն, անդրադառնանք ժամանակակից այն աշխատանքներին, որոնք փորձում են բնության մեջ գործող այլ ուժերի մասին մեր ունեցած պատկերացումներն ամփոփել մի եզակի, միացյալ քվանտային տեսության մեջ։
5
Տարրական մասնիկների և բնության ուժերը
Արիստոտելը հավատացած էր, որ տիեզերքում ամեն ինչ կազմված է չորս հիմնական տարրերից՝ հողից, օդից, կրակից և ջրից։ Այդ տարրերի վրա ազդում է երկու ուժ․ ծանրությունը, որի շնորհիվ հողն ու ջուրը ձգտում են ներքև իջնել, և թեթևությունը, որը օդի ու կրակի վեր բարձրանալու պատճառն է։ Տիեզերքի պարունակության այս բաժանումը նյութի և ուժերի՝ օգտագործվում է մինչև օրս։
Արիստոտելը կարծում էր, որ նյութն անվերջ բաժանելի է, այն է՝ կարելի է նյութն անվերջ բաժանել մասերի և ոչ ոք չի գտնի նյութի այնպիսի հատիկ, որն այլևս բաժանել հնարավոր չլինի։ Սակայն Դեմոկրիտը և մի քանի հույներ պնդում էին, որ նյութն, ըստ էության, հատիկային բնույթ ունի և ամեն ինչ կառուցված է մեծ թվով տարբեր տեսակի ատոմներից (ատոմ բառը հունարեն նշանակում է «անբաժանելի»)։ Այդ վեճը շարունակվեց դարեր՝ առանց կողմերից որևէ մեկի ճշմարտացիությունը հաստատող իրական ապացույցների, մինչև 1803֊ին անգլիացի քիմիկոս և ֆիզիկոս Ջոն Դալտոնն ուշադրություն հրավիրեց այն փաստի վրա, որ քիմիական միացությունները, որ միշտ առաջանում են որոշակի հարաբերություններով, կարելի է ներկայացնել որպես միմյանց հետ ատոմների խմբավորում կազմած նոր միավորներ, որոնք կոչվում են մոլեկուլներ։ Սակայն այդ վեճը տեսակետների երկու դպրոցների միջև լուծվեց ի նպաստ ատոմիստների միայն մեր դարասկզբին։ Դրա ամենակարևոր ֆիզիկական ապացույցներից մեկը տվեց Էյնշտեյնը մի հոդվածում, հատուկ հարաբերականության մասին հայտնի հոդվածից մի քանի շաբաթ առաջ նշում էր, թե բրոունյան կոչված շարժումը՝ հեղուկում ընկղմված փոշու մասնիկների անկանոն, կամայական շարժումը կարող է բացատրվել նրանով, որ հեղուկի ատոմները բախվում են փոշու մասնիկների հետ։
Այդ ժամանակ արդեն կասկածներ կային այն մասին, որ ատոմներն ի վերջո ևս բաժանելի պետք է լինեն։ Դրանից մի քանի տարի առաջ, Քեմբրիջի Թրինիթի քոլեջում, Ջ․ Ջ․ Թոմսոնը ցույց էր տվել նյութի էլեկտրոն կոչված մասնիկի գոյությունը, որի զանգվածը հազարից ավելի անգամ փոքր էր ամենաթեթև ատոմի՝ ջրածնի զանգվածից։ Թոմսոնի օգտագործած սարքը բավականին նման էր ժամանակակից հեռուստացույցի պատկերաստեղծ խողովակի․ կարմիր շիկացած մետաղական լարը էլեկտրոններ է արձակում և, որովհետև դրանք լիցքավորված են բացասական լիցքով, արագացվում են էլեկտրական դաշտով և ուղղվում դեպի ֆոսֆորապատ էկրանը։ Բախվելով էկրանին, էլեկտրոններն առաջացնում են լույսի փայլատակումներ։ Շուտով պարզվեց, որ այս էլեկտրոններն արձակվում են ատոմներից, և 1911֊ին անգլիացի ֆիզիկոս Էռնեստ Ռեզեֆորդը ցույց տվեց, որ ատոմն ունի ներքին կառուցվածք, այն կազմված է շատ փոքր, դրական լիցքավորված միջուկից, որի շուրջ պտտվում են որոշ թվով էլեկտրոններ։ Նա հանգեց այդ եզրակացությանը վերլուծելով ռադիոակտիվ տարրերի քայքայման արդյունքում առաջացող դրական լիցքավորված α֊մասնիկների՝ ատոմների հետ բախման հետևանքով, հետագծերի շեղումները։
Սկզբնական շրջանում կարծում էին, թե միջուկը կազմված է էլեկտրոններից և տարբեր թվով դրական լիցքավորված մասնիկներից, որոնք անվանվեցին պրոտոններ՝ հունարեն «առաջին» բառից, քանի որ հավատացած էին, թե դա այն հիմնական միավորն է, որից կազմված է նյութը։ Սակայն 1932֊ին Քեմբրիջում Ռեզերֆորդի գործընկերներ Ջեյմս Չադվիկը հայտնաբերեց, որ միջուկում առկա է մի այլ մասնիկ ևս, որն անվանվեց նեյտրոն։ Այն համարյա նույն զանգվածն ունի, ինչ պրոտոնը, բայց էլեկտրաչեզոք է։ Այս հայտնագործության համար Չադվիկին շնորհվեց Նոբելյան մրցանակ, և նա ընտրվեց Քեմբրիջի Կայուս և Գոնվիլ քոլեջի ղեկավար (ես այժմ այդ քոլեջում խորհրդի անդամ եմ)։ Հետագայում Չադվիկը հրաժարվեց ղեկավար պաշտոնից՝ խորհրդի անդամների հետ անհամաձայնության պատճառով։ Քոլեջում խիստ լարված վիճակ էր ստեղծվել, այն բանից հետո, երբ պատերազմից վերադարձած շատ երիտասարդ գիտնականներ հեռացրել էին երկար տարիներ խորհրդում պաշտոն զբաղեցրած հին անդամներին։ Սա ինձնից առաջ էր, երբ ես 1965 թվականին դարձա քոլեջի խորհրդի անդամ, վեճի վերջին փուլն էր․ նմանօրինակ վեճերը պատճառ դարձան, որպեսզի մի այլ Նոբելյան մրցանակի դափնեկիր, մագիստրոս պրն Նեվիլ Մոտը նույնպես հրաժարական տար։
Սրանից մոտավորապես քսան տարի առաջ տարածված էր այն տեսակետը, թե պրոտոնը և նեյտրոնը տարրական մասնիկներ են, սակայն, երբ ուսումնասիրվեցին մեծ արագությամբ շարժվող պրոտոնների բախումներն այլ պրոտոնների կամ էլեկտրոնների հետ, պարզվեց, որ դրանք կազմված են ավելի փոքր մասնիկնեից։ Երբ մասնիկներն անվանվեցին քվարկներ Կալիֆոռնիայի տեխնոլոգիական ինստիտուտի աշխատակից, ֆիզիկոս Մյուրել Գել֊Մանի կողմից, որը և 1969 թվականին այդ աշխատանքների համար արժանացավ Նոբելյան մրցանակի։ Քվարկ բառն ծագել է Ջեյմս Ջոյսի մի առեղծվածային մեջբերումից․ «երեք քվարկ Մուստեր Մարկի համար»։ Անգլերենում quark բառը պետք է արտասանվի guart֊ի նման, միայն թե k֊ով, բայց սովորաբար արտաբերվում է lark֊ հանգով։
Կան քվարկների մի քանի տեսակներ․ ենթադրվում է, որ նրանք ունեն 6 «բույր», որոնք կոչվում են վեր, վար, տարօրինակություն, հմայք, հատակ և գագաթ։ Յուրաքանչյուր «բույր» ունի երեք «գույն»՝ կարմիր, կանաչ և կապույտ։ (Պետք է նշել, որ սրանք լոկ պիտակներ են՝ քվարկներն ավելի փոքր են, քան տեսանելի լույսի ալիքի երկարությունը և հետևաբար սովորական իմաստով գունավոր չեն։ Ժամանակակից ֆիզիկոսները, ինչպես երևում է, վառ երևակայություն ունեն և նոր մասնիկներն ու երևույթները անվանելիս այլևս չեն սահմանափակվում հունարեն լեզվով)։ Պրոտոնը կամ նեյտրոնը կազմված են երեք քվարկներից՝ յուրաքանչյուր գույնից մեկ հատ։ Պրոտոնը պարունակում է երկու վեր և մեկ վար քվարկ, իսկ նեյտրոնը՝ երկու վար և մեկ վեր քվարկ։ Հնարավոր է մասնիկներ ստեղծել, օգտագործելով մյուս քվարկները (տարօրինակություն, հմայք, հատակ և գագաթ), բայց այս քվարկների զանգվածները շատ մեծ են և արագ քայքայվելով՝ վերածվում են պրոտոնների և նեյտրոնների։
Ինչպես արդեն տեսանք, ոչ միայն ատոմները, այլև նրանց կազմի մեջ մտնող պրոտոններն ու նեյտրոններն են բաժանելի։ Հարց է ծագում՝ որո՞նք են այն իրական տարրական մասնիկները՝ հիմնական շինաղյուսները, որոնցով շինված է ամեն ինչ։ Քանի որ լույսի ալիքի երկարությունն ավելի մեծ է, քան ատոմի չափը, հետևաբար մենք չենք կարող հուսալ, որ հնարավոր է «տեսնել» ատոմի մասերը սովորական ճանապարհով։ Այդ նպատակի համար պետք է օգտագործել ավելի փոքր ալիքի երկարություն ունեցող ինչ֊որ բան։ Քվանտային մեխանիկայի համաձայն, ինչպես տեսանք նախորդ գլխում, բոլոր մասնիկները փաստորեն միևնույն ժամանակ ալիքներ են, և որքան մեծ է մասնիկի էներգիան, այնքան փոքր է համապատասխան ալիքի երկարությունը։ Մեր հարցի պատասխանը կախված կլինի այն բանից, թե որքան բարձր էներգիայով օժտված մասնիկ կունենանք մեր տրամադրության տակ, որպեսզի համապատասխանաբար փոքր ալիքի երկարությամբ տեսանելի լինեն տարրական մասնիկները։ Մասնիկների էներգիան սովորաբար չափվում է Էլեկտրոն֊Վոլտ կոչվող միավորներով։ (Թոմսոնի էլեկտրոնների հետ կատարած փորձերից մենք տեսանք, որ նա էլեկտրոնների արագացման համար օգտագործել էր էլեկտրական դաշտը։ Այն էներգիան, որ էլեկտրոնը ձեռք է բերում մեկ Վոլտ լարվածություն ունեցող էլեկտրական դաշտում, կոչվում է Էլեկտրոն֊Վոլտ)։ XIX դարում, երբ մարդկությանը հայտնի էր մասնիկի համար միայն մի քանի Էլեկտրոն֊Վոլտ էներգիան, որն առաջանում էր այնպիսի քիմիական ռեակցիաներից, ինչպիսին այրումն է, տարածված էր այն կարծիքը, թե ատոմը փոքրագույն մասնիկն է։ Ռեզերֆորդի փորձերի ժամանակ α-մասնիկների էներգիան միլիոնավոր Էլեկտրոն֊Վոլտի էր հասնում։ Այժմ մենք գիտենք՝ ինչպես օգտագործել էլեկրտամագնիսական դաշտերի ուժը, որպեսզի մասնիկները ձեռք բերեն նախ միլիոնավոր, ապա հազար միլիոնավոր Էլեկտրոն֊Վոլտ էներգիա։ Այս առաջադիմության շնորհիվ այսօր գիտենք, որ այն մասնիկները, որոնք քսան տարի առաջ «տարրական» էին համարվում կազմված էին ավելի փոքր մասնիկներից։ Քանի որ այժմ հնարավոր է շատ ավելի մեծ էներգիա ունեցող մասնիկներ ունենալ, մեզ կհաջողվի՞ արդյոք տարրական համարվող մասնիկներում ավելի փոքր մասնիկներ գտնել։ Այս բանը, իհարկե, հնարավոր է, և՛ տեսական հիմքեր կան, և՛ կամ շատ ենք մոտեցել դրան, որպեսզի ընդունենք, որ բնության վերջակետային շինաղյուսները ճանաչելու համար բավարար գիտելիքներ կան։
Նախորդ գլխում քննարկված արլիք֊մասնիկային երկվվությունն օգտագործելով՝ մենք տիեզերքում ամեն ինչ, ներառյալ նաև լույսը և գրավիտացիան, կարող ենք նկարագրել մասնիկային տեսանկյունից։ Այս մասնիկները մի հատկություն ունեն, որը կոչվում է սպին։ Սպինը ըմբռնելու համար սովորաբար մասնիկը պատկերացնում են որպես փոքր հոլ, որը պտտվում է իր առանցքի շուրջ։ Այդպիսի պատկերացումը խաբուսիկ է, որովհետև քվանտային մեխանիկայի համաձայն, մասնիկները ճշգրիտ սահմանված պտտման առանցք չունեն։ Սպին ասելով պիտի հասկանալ, թե ինչպես է երևում մասնիկը, երբ այն դիտարկվում է տարբեր ուղղություններից։ Օրինակ, սպին չունեցող (0 սպին ունեցող) մասնիկը նման է կետի, որը բոլոր ուղղություններով միանման է երևում երևում (նկ․5.1 ― 1)։ Մյուս կողմից մեկ սպին ունեցող մասնիկը նման է կետի և տարբեր ուղղություններից տարբեր է երևում։ Միայն մեկ լրիվ շրջապտույտից հետո (360 աստիճան) գալիս է նույն տեսքին (նկ․ 5.1 ― 2)։
Իսկ 2 սպին ունեցող մասնիկը նման է երկկողմանի սլաքի (նկ․5.1 ― 3), այն նույն տեսքը կստանա կես (180 աստիճան) պտույտից հետո։ Նման ձևով ավելի մեծ սպին ունեցող մասնիկը նույնը կերևա, երբ պտտվի որոշակի անկյուններով։ Շատ տարօրինակ, բայց ուշադրության արժանի է այն, որ մասնիկներ կան, որոնք նույնը չեն երևում մի ամբողջ շրջան՝ 360 աստիճան, պտույտից հետո, որպեսզի դրանք նույնը երևան, պետք է երկու լրիվ շրջապտույտ կատարեն։ Այսպիսի մասնիկների սպինը պայմանականորեն ընդունված է 1/2:
Տիեզերքում մեզ հայտնի բոլոր մասնիկները կարելի է բաժանել երկու խմբի․ 1/2 սպին ունեցող մասնիկների, որոնք կազմում են տիեզերքի նյութը (նյութական մասնիկներ) և 0,1 ու 2 սպին ունեցող մասնիկների, որոնք, ինչպես հետո կտեսնենք, պայմանավորում են նյութական մասնիկների միջև գործող ուժերը։ Նյութական մասնիկները ենթարկվում են Պաուլիի արգելակման սկզբունքին։ Այս սկզբունքը 1925 թվականին հայտնագործել է ավստիացի ֆիզիկոս Վոլֆանգ Պաուլին, որի համար 1945 թվականին արժանացավ Նոբելյան մրցանակի։ Պաուլին տեսական ֆիզիկոսի նախատիպն էր․ նրա մասին ասում էին, թե բավական էր, որ նա գտնվեր տվյալ քաղաքում, որպեսզի ֆիզիկայի փորձերը ձախողվեն։ Պաուլիի սկզբունքի էությունն այն է, որ երկու միանման մասնիկներ չեն կարող նույն դիրքն ու նույն արագությունն ունենալ, անորոշության սկզբունքի սահմաններում։ Պաուլիի արգելակման սկզբունքը վճռական նշանակություն ունի, որովհետև բացատրում է, թե ինչու նյութական մասնիկները կոլապսի չեն ենթարկվում և չեն հասնում գերխիտ վիճակի՝ 0 և 2 ապին ունեցող մասնիկների առաջացրած ուժերի ազդեցության տակ։ Եթե նյութական մասնիկները մոտավորապես նույն դիրքն ունենան, պետք է տարբեր արագություններ ունենան և հետևաբար չեն կարող երկար ժամանակ միևնույն տեղում մնալ։ Ակնհայտ է, որ եթե աշխարհը ստեղծված լիներ առանց արգելակման սկզբունքի, ապա քվարկները չպիտի կարողնային ինքնուրույն որոշակի պրոտոններ և նեյտրոններ առաջացնել։ Իսկ վերջիններս իրենց հերթին չէին կարողանա էլեկտրոնների հետ ինքնուրույն որոշակի ատոմներ առաջացնել։ Տեղի կունենար մի մեծ կոլապս և կառաջանար քիչ թե շատ համասեռ, թանձր մի «ապուր»։
Էլեկտրոնի և 1/2 սպին ունեցող այլ մասնիկների մասին ճշգրիտ գիտելիքներ ձեռք են բերվել սկսած միայն 1928 թ․, երբ Պոլ Դիրակը տվեց իր տեսությունը։ Դիրակը հետագայում ընտրվեց Քեմբրիջի համալսարանի մաթեմատիկայի լուկասյան պրոֆեսոր (պաշտոն, որը ժամանակին զբաղեցրել է Նյուտոնը, այսօր՝ ևս ես)։ Դիրակի տեսությունն առաջինն է իր տեսակի մեջ, որ համատեղելի էր և՛ քվանտային մեխանիկայի, և՛ հարաբերականության հատուկ տեսության հետ։ Այն մաթեմատիկորեն բացատրում էր, թե էլեկտրոնի սպինը ինչու է 1/2, այսինքն՝ էլեկտրոնն ինչո՞ւ ինքն իրեն չի նմանվում մեկ լրիվ շրջապտույտից հետո, այլ միայն՝ երկու շրջապտույտից հետո։ Կանխագուշակեց նաև, որ էլեկտրոնը պետք է մի զուգընկեր ունենա՝ հակաէլեկտրոն կամ պոզիտրոն։ Պոզիտրոնի հայտնագործումը 1932 թվականին հաստատեց Դիրակի տեսության ճշտությունը և 1933 թվականին նրան դարձրեց Նոբելյան մրցանակի դափնեկիր՝ ֆիզիկայի բնագավառում։[6] Մենք այժմ գիտենք, որ ամեն մասնիկ ունի իր հակամասնիկը, և երբ մասնիկն ու հակամասնիկը հանդիպեն միմյանց, տեղի կունենա դրանց ոչնչացում (աննիհիլացում)։ (Պետք է նշել, որ ուժակիր մասնիկների հակամասնիկները նրանցից ոչնչով չեն տարբերվում)։ Հնարավոր է, որ հակաաշխարհներ և նույնիսկ հակաժողովուրդներ գոյություն ունենան, որոնք կազմված են հակամասնիկներից։ Այնուամենայնիվ, եթե դուք հանդիպեք ձեր հակամարդուն, ձեռքը չսեղմեք, հակառակ դեպքում երկուսդ էլ կանէանաք՝ լույս արձակելով։ Թե ինչո՞ւ է թվում, որ մեր շրջապատում շատ ավելի մասնիկներ կան, քան հակամասնիկներ, չափազանց կարևոր հարց է, և ես դրան կանդրադառնամ այս գլխի վերջում։
Ենթադրվում է, որ քվանտային մեխանիկայում նյութական մասնիկների միջև գործող բոլոր ուժերը կամ փոխազդեցությունները կրում են այն մասնիկները, որոնք ունեն ամբողջական սպիններ՝ 0,1 կամ 2։ Տեղի է ունենում հետևյալը․ նյութական մասնիկը, ինչպես, օրինակ, էլեկտրոնը կամ քվարկը, արձակում է ուժակիր մի մասնիկ։ Դրանով պայմանավորված հետհարվածը փոխում է նյութական մասնիկի արագությունը։ Արձակված ուժակիր մասնիկը բախվում է մի այլ նյութական մասնիկի հետ և կլանվում։ Հետևաբար, փոխվում է նաև երկրորդ նյութական մասնիկի արագությունը և ստացվում է այնպես, կարծես երկու նյութական մասնիկների միջև ուժ է գործում։
Ուժակիր մասնիկների կարևոր հատկությունն այն է, որ նրանք չեն ենթարկվում արգելակման սկզբունքին։ Սա նշանակում է, որ կարող են կատարվել անսահման թվով փոխանակումներ և այսպիսով շատ հզոր փոխազդեցության ուժ առաջացնել։ Եթե ուժակիր մասնիկների զանգվածը մեծ լինի, ապա դրանց և՛ առաջացումը, և՛ փոխանակումը մեծ հեռավորությունների վրա դժվար կլինի։
Այսպիսով, դրանցով պայմանավորված փոխազդեցության ուժերը կլինեն կարճազդեցության կարգի։ Մյուս կողմից, եթե ուժակիր մասնիկը սեփական զանգված չունենա, ապա փոխազդեցության ուժը կլինի հեռազդեցության կարգի։ Նյութական մասնիկների միջև փոխանակվող ուժակիր մասնիկները կոչվում են վիրտուալ մասնիկներ, որովհետև դրանք, ի տարբերություն «իրական» մասնիկների (նյութական մասնիկների), ուղղակիորեն չեն հայտնաբերվում մասնիկային դետեկտորով։ Սակայն մենք գիտենք, որ նրանք գոյություն ունեն, որովհետև թողնում են չափելի ազդեցություն՝ ուժեր են առաջացնում նյութական մասնիկների միջև։ 0,1 և 2 ապին ունեցող մասնիկները նույնպես որոշ պարագաներում գոյություն ունեն որպես իրական մասնիկներ և նրանց կարելի է ուղղակիորեն հայտնաբերել։ Այս դեպքում նրանք մեզ համար կներկայանան այն վիճակում, որը դասական ֆիզիկոսն անվանում է ալիք, ինչպես, օրինակ, լույսի կամ գրավիտացիոն ալիքները։ Դրանք որոշ դեպքերում կարող են արձակվել, երբ նյութական մասնիկները միմյանց հետ փոխազդելով փոխանակում են վիտուալ ուժակիր մասնիկներ։ (Օրինակ, երկու էլեկտրոնների միջև գործող վանողական ուժն արդյունք է վիրտուալ ֆոտոնների փախանակման, որոնք երբեք չեն կարող ուղղակիորեն հայտնաբերվել, սակայն, եթե մի էլեկտրոն մյուսի կողքով անցնի, կարող են իրական ֆոտոններ արձակվել, որոնք մենք կգրանցենք որպես լույսի ալիքներ)։
Ուժակիր մասնիկները կարելի է բաժանել չորս դասի՝ կախված նրանց ուժի մեծությունից և այն բանից, թե ինչպիսի մասնիկների հետ են փոխազդում։ Պետք է նշել, որ այս բաժանումը պայմանական է, հարմար մասնակի տեսություններ մշակելու համար, սակայն խորը հիմնավորում չունի։ Վերջ ի վերջո ֆիզիկոսների մեծ մասը հույս ունի մի միացյալ տեսություն մշակել և այս չորս ուժերը բացատրել որպես նույն եզակի ուժի տարբեր արտահայտություններ։
Կարելի է ասել, որ սա այսօր ֆիզիկոսների հիմնական նպատակն է։ Վերջերս հաջող փորձեր են արվել այս չորս դասից երեքը միավորելու, և ես այս գլխում կխոսեմ այդ մասին։ Մյուս դասի ուժի՝ գրավիտացիայի միավորման հարցը կքննարկենք հետագայում։
Այդ չորս դասի ուժերից առաջինը գրավիտացիոն ուժն է։ Այն համոզիչ (ունիվերսալ) է, այսինքն՝ ամեն մասնիկ ենթարկվում է գրավիտացիոն ուժին՝ իր զանգվածի և էներգիայի համապատասխան։ Գրավիտացիան այդ չորս տեսակի ուժերից ամենաթույլն է, այնքան թույլ է, որ այն հնարավոր չէր լինի նկատել, եթե չունենար երկու առանձնահատկություն, այն է․ կարող է ազդել շատ մեծ հեռավորությունների վրա և իր բնույթով միշտ ձգողական է։ Դա նշանակում է, որ երկու մեծ մարմինների, ինչպիսիք են, օրինակ, արևը և երկիրը, առանձին մասնիկների միջև առկա բոլոր ձգողական թույլ ուժերը գումարվելով առաջացնում են զգալի մի ուժ։ Մյուս երեք ուժերը կամ գործում են շատ փոքր հեռավորությունների վրա, կամ ժամանակ առ ժամանակ ձգողական և վանողական դառնալով չեզոքացնում են միմյանց։ Գրավիտացիոն դաշտը քվանտային մեխանիկայի տեսանկյունից դիտելիս, երկու նյութական մասնիկների միջև գործող ուժը կրողը պատկերանում է որպես 2 սպին ունեցող մի մասնիկ, որը կոչվում է գրավիտոն։ Դա սեփական զանգված չունի, այդպիսով նրա կրած ուժը հեռազդող է։ Արևի և երկրի միջև առկա գրավիտացիոն ուժը վերագրվում է այս երկու մարմինները կազմող մասնիկների միջև գրավիտոնների փախանակմանը։ Թեև փախանակվող մասնիկները վիրտուալ են, սակայն նրանք տալիս են չափելի արդյունք, պայմանավորում են երկրի պտույտը արևի շուրջը։ Իրական գրավիտոնները, որոնք դասական ֆիզիկոսներն անվանում են գրավիտացիոն ալիքներ, շատ թույլ են և այնքան դժվար հայտնաբերելի, որ դեռ երբեք չեն դիտվել։
Հաջորդ դասը էլեկտամագնիսական ուժն է, որը գործում է լիցքավորված մասնիկների միջև, ինչպիսիք են էլեկտրոնները և քվարկները, բայց ոչ երբեք գրավիտոնները, որոնք լիցքավորված չեն։ Էլեկտրամագնիսական ուժը շատ ավելի մեծ է, քան գրավիտացիոն ուժը․ երկու էլեկտրոնների միջև գործող էլեկտրամագնիսական ուժը գրավիտացիոն ուժի համեմատ մեծ է մոտավորապես միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն անգամ (1֊ից հետո 42 զերո)։ Ընդ որում, գոյություն ունի էլեկտրական լիցքերի երկու տեսակ՝ դրական և բացասական։ Երկու դրական լիցքերի միջև փոխազդեցության ուժը վանողական է, նույնը տեղի ունի նաև երկու բացասական լիցքերի միջև, բայց դրական և բացասական լիցքերի միջև ուժը ձգողական է։ Մեծ մարմինը, ինչպես օրինակ, արևը կամ երկիրը, պարունակում են մոտավորապես հավասար քանակով դրական և բացասական լիցքեր։ Հետևաբար նրանց առանձին մասնիկների միջև ձգողական և վանողական ուժերը իրար ոչնչացնում են, և էլեկտրամագնիսական ուժը շատ փոքր է։ Սակայն ատոմների և մոլեկուլների չափերի կարգի հեռավորություններում էլեկտամագնիսական ուժը տիրապետող է։ Բացասական էլեկտրոնների և միջուկի դրական պրոտոնների միջև էլեկտրամագնիսական ձգողությունը պայմանավորում է ատոմում էլեկտրոնների պտույտը միջուկի շուրջ այնպես, ինչպես գրավիտացիոն ձգողությունն է պատճառը, որ երկիրը պտտվի արևի շուրջ։ Էլեկտրամագնիսական ձգողությունը կարելի է պատկերել որպես մեծ թվով վիրտուալ, զանգված չունեցող, 1 սպինով մասնիկների՝ ֆոտոնների փոխանակման հետևանք։ Փոխանակվող ֆոտոնները նույնպես վիտուալ մասնիկներ են։ Ընդ որում, երբ ատոմի մեջ էլեկտրոնը մի թույլատրելի ուղեծրից անցնում է մյուսին՝ միջուկին ավելի մոտիկ ուղեծիր, ատոմից էներգիա է անջատվում և արձակվում է իրական ֆոտոն, որը կարող է դիտվել սովորական աչքով որպես տեսանելի լույս, եթե այն տեսանելիության տիրույթում է, կամ գրանցվել դետեկտորով՝ որպես լուսանկարչական ֆիլմ։ Հանգունորեն, եթե իրական ֆոտոնը բախվի ատոմի հետ, ապա այն կարող է էլեկտրոնը միջուկին մոտիկ ուղեծրից տեղափոխել ավելի հեռու գտնվող ուղեծիր։ Այս դեպքում տեղի է ունենում ֆոտոնի էներգիայի օգտագործում, այսինքն՝ ֆոտոնի կլանում։
Ուժերի երրորդ դասը կոչվում է թույլ միջուկային ուժ, որը պատասխանատու է ռադիոակտիվության համար և ներգործում է 1/2 սպին ունեցող բոլոր նյութական մասնիկների վրա, բայց ոչ 0,1 կամ 2 սպին ունեցող մասնիկների, ինչպիսիք են ֆոտոնը և գրավիտոնը։ Թույլ միջուկային ուժի բնույթը հասկանալի չէր մինչև 1967 թիվը, երբ Լոնդոնի Կայսերական քոլեջից Աբդուս Սալամը և Հարվարդի համալսարանից Ստիվեն Ուայնբերգն առաջարկեցին իրենց տեսությունները․ սրանցում այդ փոխազդեցությունը միաձուլվել էր էլեկտրամագնիսական ուժի հետ, ինչպես դրանից հարյուր տարի առաջ Մաքսվելն էր միավորել էլեկտրամագնիսականությունը մագնիսականության հետ։ Նրանք այն միտքն արտահայտեցին, որ ֆոտոնից բացի կան 1 սպին ունեցող 3 այլ մասնիկներ ևս, որոնք թույլ ուժը կրողներ են և բոլորը միասին կոչվեցին զանգվածեղ վեկտոր բոզոններ։ Այդ բոզոնները կոչվում են W + (արտասանվում է դաբլյու պլյուս), W - (դաբլյու մինուս) և Z° (զեթ զերո) և յուրաքանչյուրի զանգվածը շուրջ 100 ԳԵՎ է (ԳԵՎ ― նշանակում է Գիգա Էլեկտրոն֊Վոլտ կամ հազար միլիոն Էլեկտրոն֊Վոլտ): Ուայնբերգ Սալամի տեսությունը բացահայտեց մի հատկություն, որ հայտնի է որպես ինքնակամ համաչափության խզում։ Այսինքն այն, որ թվում էր թե ցածր էներգիայի դեպքում մասնիկները բոլորովին տարբեր են, իրականում դրանք նույն տեսակի են, բայց գտնվում են տարբեր վիճակներում։ Բարձր էներգիայի պայմաններում բոլոր այս մասնիկների վարքը նույնն է։ Այս երևույթը նման է ռուլետի խաղանիվի գնդակի վարքին։ Բարձր էներգիաների դեպքում (երբ անիվը արագ է պտտվում) գնդակը միայն մի վարք ունի․ պտտվում է և պտտվում։ Բայց երբ անիվը դանդաղում է, գնդակի էներգիան նվազում է, և այն վերջապես ընկնում է անիվի երեսունյոթ անցքերից մեկի մեջ։
Համաձայն Ուայնբերգ֊Սալամի տեսության, երբ էներգիան 100 ԳԵՎ֊ից բարձր է, ապա երեք նոր մասնիկները՝ W+, W- և Z°֊ն, ինչպես նաև ֆոտոնը կունենան նույնանման վարք։ Բայց քանի որ բնականոն պայմաններում մասնիկի էներգիան ցածր է լինում, մասնիկների համաչափությունը խզվում է։ W+ W- մասնիկների զանգվածները մեծանում են՝ նրանց կրած ուժերը դարձնելով շատ կարճազդեցության կարգի։ Երբ Ուայնբերգը և Սալամը առաջարկեցին այս տեսությունը, շատ քչերը հավատացին դրան, իսկ այն ժամանակ չկային բավարար հզորությամբ մասնիկների արագացուցիչներ, որոնք էներգիան հասցնեին 100 ԳԵՎ֊ի, ինչը պահանջում էր իրական W+, W- և Z° մասնիկներ առաջացնելու համար։ Այնուամենայնիվ, հաջորդ 10 տարիների ընթացքում այդ տեսության այլ կանխագուշակումները ցածր էներգիայի պայմաններում այնքան մեծ ճշգրտությամբ համընկան փորձնական տվյալների հետ, որ1979 թվականին Սալամն ու Ուայնբերգը և Հարվարդի համալսարանից Շելդոն Գլեշոուին, որը նույնանման միասնական մի տեսություն էր առաջարկել էլեկտրամագնիսական և թույլ միջուկային ուժերի համար, արժանացան Նոբելյան մրցանակի ֆիզիկայի բնագավառում։ Նոբելյան հանձնաժողովին սխալ գործած լինելու անհարմար վիճակից փրկեց Միջուկային հետազոտությունների եվրոպական կենտրոնը (ՑԵՌՆ ― CERN) երբ 1983 թվականին հայտնաբերվեցին ֆոտոնի զանգված ունեցող երեք զուգընկերները, որոնք ունեին ճշգրիտ կանխագուշակված զանգվածներ և այլ հատկությունները։ Կառլո Ռուբիան, որ ղեկավարում էր հայտնագործությունը կատարած հարյուրավոր ֆիզիկոսների աշխատանքը, և Սայմոն վան դեր Միըլրին, որ կառուցել էր հակամարմինների պահեստային համակարգ, 1984 թ․ արժանացան Նոբելյան մրցանակի։ (Այսօր փորձարարական ֆիզիկայի բնագավառում անհնարին է շոշափելի հաջողության հասնել, եթե արդեն իսկ բարձրունքների չես հասել)։
Ուժերի չորրորդ դասը միջուկային փոխազդեցության հզոր ուժն է, որով քվարկներն իրար են կապվում պրոտոններում և նեյտրոններում, իսկ պրոտոնները և նեյտրոնները իրար են կապվում ատոմի միջուկում։ Կա այն կարծիքը, որ այս ուժը կրող մասնիկը 1 սպին ունի, այն կոչվում է գլյուոն և փոխազդում է ինքն իր և քվարկների հետ։ Հզոր միջուկային ուժը օժտված է շատ տարօրինակ հատկությամբ, որը կոչվում է կասեցում․ այն միշտ մասնիկներն իրար է կապում՝ առաջացնելով համակցություններ, որոնք գույն չունեն։ Քվարկը միայնակ չի կարող գոյություն ունենալ, որովհետև այն ունի գույն (կարմիր կանաչ և կապույտ)։ Որպեսզի այն գոյություն ունենա, պետք է կարմիր քվարկը միանա, ասենք, կանաչ և կապույտ քվարկների հետ գլյուոնների «լարանով» (կարմիր + կանաչ + կապույտ = սպիտակ)։ Այսպիսի եռյակ կազմություն է հենց պրոտոնը կամ նեյտրոնը։ Մեկ այլ հնարավորություն է քվարկ և հակաքվարկ զույգը (կարմիր+ հակակարմիր կամ կանաչ + հակականաչ կամ կապույտ = սպիտակ)։ Այսպիսի համակցություններն առաջացնում են, այսպես կոչված, մեզոններ, որոնք անկայուն են, քանի որ քվարկն ու հակաքվարկը կարող են իրար ոչնչացնել և առաջացնել էլեկտրոններ կամ այլ մասնիկներ։ Նման ձևով կասեցման հատկությունը թույլ չի տալիս նաև, որ գլյուոնը միայնակ գոյություն ունենա, քանի որ այն նույնպես գունավոր է։ Այս պատճառով կարող է գոյություն ունենալ գլյուոնների այնպիսի հավաքածու, որում գույների գումարը սպիտակ է։ Այդպիսի հավաքածուն առաջացնում է անկայուն մի մասնիկ, որը կոչվում է գլյուբոլ (անգլ․՝ սոսնձագունդ)։
Այն փաստը, որ կասեցման հատկությունը թույլ չի տալիս դիտարկել քվարկը և գլյուոնը մեկուսացած վիճակում, թերևս մտածել տա, որ քվարկ ու գլյուոն հասկացությունները, որպես մասնիկներ, ինչ֊որ չափով մետաֆիզիկական են։ Սակայն հզոր միջուկային ուժը մի այլ հատկություն ունի, որը կոչվում է սիմպտոմային ազատություն և որոշակիորեն իմաստավորում է քվարկներ և գլյուոններ հասկացությունները։ Սովորական էներգիայի պայմաններում հզոր միջուկային ուժը իսկապես այնքան ուժեղ է, որ մեծ ուժով իրար է կապում քվարկները։ Բայց մեծ մասնիկային արագացուցիչներով կատարված փորձերը ցույց են տալիս, որ բարձր էներգիաների պայմաններում միջուկային ուժը շատ է թուլանում, և քվարկներն ու գլյուոնները իրենց պահում են որպես ազատ մասնիկներ։
Նկ․ 5.2֊ում ցույց է տրված բարձր էներգիայով պրոտոնի և հակապրոտոնի բախման լուսանկարը։ Առաջացել են մի քանի գրեթե ազատ, քվարկներ, և նկարում երևում են հետագծա «ցայտեր»։
Էլեկտրամագնիսական և թույլ միջուկային ուժերի միասնականացման հաջողությունները պատճառ դարձան, որ սրանց միացվի հզոր միջուկային ուժը և ստեղծվի մի նոր միասնական տեսություն, որը կոչվում է մեծ միասնական տեսություն (ՄՄՏ ― GUT)։[7]
Այստեղ անվանումն ավելի քան չափազանցված է, որովհետև ստացված տեսություններն այդքան էլ մեծ չեն և ոչ էլ լրիվ միասնական, քանի որ չեն ընգրկում գրավիտացիան։
Կամ տեսությունները լրիվ չեն, քանի որ պարունակում են մի շարք պարամետրեր, որոնց արժեքները տեսականորեն կանխագուշակելի չեն, այլ ընտրված են փորձնական տվյալներին համապատասխան։ Այնուամենայնիվ, կատարվել է մի քայլ դեպի ամբողջական, կատարյալ միասնական տեսության ստեղծումը։ ՄՄՏ֊ի հիմնական գաղափարը հետևյալն է, ինչպես ասվեց վերևում, հզոր միջուկային ուժը թուլանում է բարձր էներգիաների պայմաններում։ Մյուս կողմից, էլեկտրամագնիսական և թույլ ուժերը, որոնք ասիմետրորեն ազատ չեն, հզորանում են բարձր էներգիաների պայմաններում, որը կոչվում է մեծ միասնական էներգիա, այս երեք դասի ուժերը կունենան նույն ուժգնությունը, և կլինեն մեկ ուժի տարբեր արտահայտություններ։ ՄՄՏ֊ի համաձայն, այս պայմաններում 1/2 սպին ունեցող տարբեր նյութական մասնիկները, ինչպես օրինակ, քվարկն ու էլեկտրոնը, հիմնականում կլինեն նույնը, այսինքն՝ այդպիսով իրագործվում է մեկ այլ միավորում։
Մեծ միասնական էներգիայի արժեքը ճշգրիտ հայտնի չէ, բայց հավանաբար առնվազն հազար միլիոն միլիոն ԳԵՎ֊ի կարգի է։ Մասնիկային արագացուցիչների ժամանակակից սերունդը կարող է ապահովել մասնիկների բախումը մոտ հարյուր ԳԵՎ էներգիայի տակ, և ծրագրվում են այնպիսի արագացուցիչներ, որոնք կապահովեն մի քանի հազար ԳԵՎ էներգիա։ Բայց այն արագացուցիչը, որն ի վիճակի կլինի մասնիկներն արագացնել այնքան, որ նրանց էներգիան հասնի մեծ միասնության էներգիայի մակարդակին, պետք է այնքան մեծ լինի, որքան Արեգակնային համակարգն է, որն, իհարկե, ներկա տնտեսական պայմաններում անհնարին է։ Այսպիսով, մեծ միասնական տեսությունը հնարավոր չէ ուղղակիորեն ստուգել լաբորատոր պայմաններում։ Այնուամենայնիվ, ինչպես էլեկտրոմագնիսական և թույլ միջուկային ուժի միասնական տեսության դեպքում, այստեղ ևս կան ցածր էներգիական այնպիսի հետևանքներ, որոնք կարող են ստուգվել լաբորատոր պայմաններում։
Մեծ միասնական տեսության համար ամենահետաքրքրականն այն է, որ կանխագուշակեց նյութի հիմնական զանգվածը կազմող պրոտոնների ինքնակամ քայքայումն ավելի թեթև մասնիկների, ինչպիսիք են հակաէլեկտրոնները։ Իսկ այդ քայքայումը հնարավոր է այն պատճառով, որ մեծ միասնության էներգիայի պայմաններում քվարկների և հակաէլեկտրոնների միջև մի էական տարբերություն չկա։ Պրոտոնի կազմում ներառված երեք քվարկները սովորաբար այնքան էներգիա չունեն, որպեսզի վերածավեն հակաէլեկտրոնների, սակայն անորոշության սկզբունքի համաձայն, պրոտոնի կազմում գտնվող քվարկի էներգիան չի կարող ճշգրտորեն սևեռված լինել և, հնարավոր է, որ մի քվարկի էներգիան այնքան բարձր լինի, որ տեղի ունենա նրա անցումը հակաէլեկտրոնի։ Այդ դեպքում պրոտոնը կքայքայվի։ Քվարկի բավարար էներգիա ձեռք բերելու հավանականությունն այնքան փոքր է, որ դրա համար հարկավոր է առնվազն միլիոն միլոն միլիոն միլիոն տարի (1֊ից հետո 30 զերո)։ Այս ժամանակը շատ ավելի մեծ է, քան Մեծ պայթյունից մինչև օրս անցած ժամանակը, որը մոտ տասը հազար միլիտարի է (1֊ից հետո 10 զերո)։ Հետևաբար, կարելի է եզրակացնել, որ պրոտոնի ինքնակամ քայքայումը լաբորատոր պայմաններում ստուգման ենթակա չէ։ Սակայն քայքայման հայտնաբերման հնարավորությունը կարելի է մեծացնել, եթե օգտագործենք մեծ քանակով այնպիսի նյութ, որը պարունակում է մեծ թվով պրոտոններ։ (Օրինակ, եթե հնարավոր լինի տասը միլիոն միլիոն միլիոն միլիոն միլիոն (1֊ից հետո 31 զերո) պրոտոն դիտարկել մեկ տարվա ընթացքում, ապա սպասելի է, որ ՄՄՏ֊ի համաձայն մեկից ավելի պրոտոն քայքայվի։
Այդպիսի մի շարք փորձեր են դրվել, սակայն պրոտոնի կամ նեյտրոնի քայքայման որոշակի փաստ չի դիտվել։ Փորձերից մեկի համար օգտագործվեց ութը հազար տոննա ջուր Օհայո նահանգի Մորտոն աղահանքում (փորձը այնտեղ դրվեց տիեզերական ճառագայթման ազդեցության հետևանքներից խուսափելու համար)։ Քանի որ փորձի ընթացքում պրոտոնային ինքնակամ քայքայում չդիտվեց, ապա կարելի է եզրակացնել, որ պրոտոնի կյանքի տևողությունը տաս միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն (1֊ից հետո 31 զերո) տարուց մեծ է։ Դա ավելին է, քան կանխագուշակում է պարզագույն Մեծ միասնության տեսությունը, սակայն, կան բազմաթիվ առավել մշակված տեսական տարբերակներ, որոնք կանխագուշակում են պրոտոնի կյանքի ավելի երկար տևողություն։ Հետևաբար այդ նպատակի համար հարկավոր է օգտագործել ավելի մեծ քանակի նյութ և դնել ավելի ճշգրիտ փորձեր։
Չնայած այսքան դժվար է պրոտոնի ինքնակամ քայքայում դիտելը, հնարավոր է, որ մեր իսկ գոյությունը պայմանավորված է հակադարձ գործընթացով՝ պրոտոնների կամ ավելի պարզ մասնիկների՝ քվարկների առաջացումով սկզբնական այնպիսի վիճակից, որում ավելի շատ հակաքվարկներ կային, քան քվարկներ, որը կարող է տիեզերքի սկզբնավորման ամենահավանական ճանապարհը լինել։ Երկրագնդի նյութը կազմված է հիմնականում պրոտոններից և նեյտրոններից, որոնք իրենց հերթին կազմված են քվարկներից։ Հակաքվարկներից առաջացած հակապրոտոններ և հականեյտրոններ չկան, բացառությամբ այն չնչին քանակի, որը հզոր արագացուցիչներում ստացել են ֆիզիկոսները։ Տիեզերական ճառագայթների հիման վրա ստացված արդյունքները ցույց են տալիս, որ վիճակը նույնն է մեր գալակտիկայում, ուր հակապրոտոններ և հականեյտրոններ չկան, բացի այն փոքր թվով մասնիկ֊հակամասնիկ զույգերից, որոնք առաջանում են բարձր էներգիա ունեցող մասնիկների բախման ընթացքում։ Եթե մեր գալակտիկայում լինեին հակամարմինների լայն տիրույթներ, ապա հակամարմին և մարմին պարունակող տիրույթների սահմանագծում շատ հզոր ճառագայթում կդիտվեր՝ շնորհիվ մասնիկ֊հակամասնիկ զույգերի փոխադարձ ոչնչացման։
Մենք ուղղակի ապացույց չունենք այն մասին, որ այլ գալակտիկաներում նյութը կազմված է պրոտոններից ու նեյտրոններից կամ հակապրոտոններից ու հականեյտրոններից։ Բայց երկուսից մեկը պետք է լինի, քանի որ այն չի կարող մասնիկի և հակամասնիկի խառնուրդ լինել, այլապես նման դեպքում տեղի կունենար մասնիկների ոչնչացում և հզոր էներգիայի ճառագայթում։ Այդ պատճառով այսօր տարածված է այն կարծիքը, որ գալակտիկաները ավելի շուտ կազմված են քվարկներից, քան հակաքվարկներից։ Անհավանական է, որ որոշ գալակտիկաներ կազմված են նյութից, իսկ մյուսները՝ հականյութից։
Իսկ ի՞նչն է պատճառը, որ ավելի շատ քվարկներ կան, քան հակաքվարկներ։ Ինչո՞ւ դրանք հավասար թվով չեն կարող լինել։ Սա ակնհայտ է, քանի որ այդ դեպքում քվարկներն ու հակաքվարկները կոչնչացնեին միմյանց, նախնական տիեզերքում նյութ գոյություն չէր ունենա, և տիեզերքը լցված կլիներ հզոր ճառագայթումով։ Գոյություն չէին ունենա գալակտիկաներ, աստղեր կամ մոլորակներ, որտեղ մարդկային կյանք կարող էր զարգանալ։ Բարեբախտաբար, մեծ միասնական տեսություններն ի վիճակի են բացատրել, թե ինչո՞ւ այժմ տիեզերքում ավելի շատ քվարկներ կան, քան հակաքվարկներ, նույնիսկ եթե սկզբնական շրջանում դրանց թիվը հավասար էր։ Ինչպես մենք տեսանք, ՄՄՏ֊ները թույլ են տալիս, որ բարձր էներգիայի պայմաններում քվարկները փոխարկվեն հակաէլեկտրոնների։ Դրանք թույլ են տալիս նաև հակառակ գործընթացը՝ հակաքվարկների փոխանակումը էլեկտրոնների և հակաէլեկտրոնների ու էլեկտրոնների փոխարկումը քվարկների ու հակաքվարկների։ Տիեզերքի շատ վաղ շրջանում, երբ այն չափազանց տաք էր, մասնիկների էներգիան այնքան բարձր էր, որ հնարավոր էին նման փոխարկումները։ Պատճառն այն է, որ ֆիզիկայի օրենքները ճիշտ նույնը չեն մասնիկների և հակամասնիկների համար։
Մինչև 1956 թվականը տարածված էր այն կարծիքը, թե ֆիզիկայի օրենքները ենթարկվում են երեք առանձին համաչափություններից յուրաքանչյուրին․ դրանք կոչվում են C, P, T. համաչափություններ։ C֊համաչափություն նշանակում է, որ մասնիկի և հակամասնիկի համար ուժի մեջ է նույն օրենքը։ P֊համաչափությունը նշանակում է, որ օրենքները նույնն են որևէ դրության և նրա հայելային պատկերի համար (դեպի աջ պտտվող մասնիկի հայելապատկերը ձախ պտտվողն է)։ T֊համաչափությունը նշանակում է, որ եթե բոլոր մասնիկների ու հակամասնիկների շարժման ուղղությունը շրջվի, ապա համակարգը կվերադառնա իր նախնական վիճակին, այլ կերպ ասած, օրենքները նույնն են ժամանակի առաջընթաց և հետընթաց ուղղություններում։
1956֊ին երկու ամերիկացի ֆիզիկոսներ՝ Յունգ֊Դաո Լին և Չեն Նին Յանգը այն միտքն արտահայտեցին, թե թույլ ուժը համաչափությանը չի ենթարկվում։ Այլ կերպ ասած, թույլ ուժի ազդեցության տակ տիեզերքի զարգացումը բոլորովին այլ կլիներ, քան նրա հայելային պատկերի զարգացումը։ Նույն տարում նրանց պաշտոնակից Չյեն֊Շյունգ Վուն ապացուցեց, որ այդ կանխագուշակումը ճիշտ է։ Տիկին Վուն ռադիոակտիվ ատոմների միջուկները մագնիսական դաշտում այնպես էր դասավորել, որ բոլորը նույն ուղղությամբ էին պտտվում և գտել էր, որ էլեկտրոնների արձակումը ավելի մեծ է մի ուղղությամբ, քան մյուս ուղղությամբ։ Հաջորդ տարում Լին և Յանգը Նոբելյան մրցանակ ստացան իրենց գաղափարի համար։ Պարզվեց նաև, որ թույլ ուժը չի ենթարկվում նաև C֊համաչափությանը։ Այսինքն, այդ պատճառով հակամասնիկներից կազմված տիեզերքը պետք է տարբեր լիներ մեր տիեզերքից։ Այնուամենայնիվ թվում է, թե թույլ ուժը ենթարկվում է CP միացյալ համաչափությունը։ Այսինքն՝ տիեզերքն ու իր հայելային պատկերը նույն ձևով կզարգանային, եթե, որպես լրացում, ամեն մասնիկ փոխարինված լիներ իր հակամասնիկով։ Սակայն, 1964֊ին երկու ամերիկացի՝ Ջ․ Ու․ Կրոնինը և Վել Ֆիտչը հայտնաբերեցին, որ նույնիսկ CP համաչափությունը ուժի մեջ չէ K֊մեզոններ կոչվող որոշակի մասնիկների քայքայման համար։ Կրոնինը և Ֆիտչը իրենց աշխատանքի համար վերջապես 1980֊ին արժանացան Նոբելյան մրցանակի։ (Այսպիսով, բազմաթիվ Նոբելյան մրցանակներ են շնորհվել պարզապես այն բանի համար, որ ցույց է տրվել, որ տիեզերքը այնքան պարզ չէ, որքան կարծում ենք)։
Կա մաթեմատիկական մի թեորեմ, որի համաձայն, ամեն տեսություն, որը ենթարկվում է քվանտային մեխանիկային և հարաբերականությանը, պետք է միշտ ենթարկվի CPT միացյալ համաչափությանը։ Այսինքն՝ տիեզերքի վարքագիծը չի փոխվի, եթե մասնիկները փոխարինվեն հակամասնիկներով, վերցվի տիեզերքի հայելային պատկերը և շրջվի ժամանակի ուղղությունը։ Բայց, ինչպես տեսանք, համաձայն Կրոնինի և Ֆիտչի, եթե մասնիկները փոխարինվեն իրենց հակամասնիկներով և վերցվի հայելային պատկերը, ապա տիեզերքը նույն վարքագիծը չի ունենա, քանի դեռ չի շրջվել ժամանակի ուղղությունը։ Այսինքն՝ եթե ժամանակը իր ուղղությունը փոխի, կփոխվեն նաև ֆիզիկայի օրենքները, հետևաբար դրանք չեն ենթարկվում T֊համաչափությանը։
Իհարկե, նախնական տիեզերքը T֊համաչափությանը չի ենթարկվում․ այսպես՝ եթե ժամանակը շարժվում է առաջ, տիեզերքն ընդարձակվում է, իսկ եթե ժամանակը ետ շարժվի, տիեզերքը պետք է կծկվի։ Եվ քանի որ կան այնպիսի ուժեր, որոնք չեն ենթարկվում T֊համաչափությանը, հետևաբար այդ ուժերը կարող են պատճառ դառնալ, որ տիեզերքի ընդարձակման պայմաններում ավեի շատ հակաէլեկտրոններ վերածվեն քվարկների, քան էլեկտրոններ՝ հակաքվարկների։ Մինչ տիեզերքն ընդարձակվում և սառչում է, հակաքվարկները աստիճանաբար ոչնչանում են քվարկներով, սակայն, որովհետև վերջիններիս թիվը ավելի շատ է, քան հակաքվարկներինը, ապա ակնհայտ է, որ քվարկների փոքրիկ ավելցուկ կմնա տիեզերքում։ Հենց սա էլ կազմում է այն նյութական աշխարհը, որը մենք տեսնում ենք այսօր և, որից մենք ինքներս կազմված ենք։ Այսպիսով, հենց մեր գոյությունը հաստատում է մեծ միասնական տեսության ճշմարտացիությունը, թեև լոկ որակական առումով։ Անորոշությունն այն է, որ մենք չենք կարող հաշվել, թե ոչնչացումից հետո ինչ թվով քվարկներ կմնան կամ, դեռ ավելին, դրանք քվարկներ, թե հակաքվարկներ կլինեն։ (Այնուամենայնիվ, եթե մնացած մասնիկները հակաքվարկներ լինեին, մենք պարզապես դրանք կանվանեինք քվարկ, իսկ քվարկները՝ հակաքվարկներ, և դրանից ոչինչ չէր փոխվի)։
Մեծ միասնական տեսությունները չեն ընդգրկում գրավիտացիոն ուժը։ Սա առանձնահատուկ նշանակություն չունի, որովհետև գրավիտացիոն ուժը այնքան թույլ է, որ կարելի է այն արհամարհել, երբ մենք գործ ունենք տարրական մասնիկների և ատոմների հետ։ Սակայն, այն փաստը, որ դրանք երկուսով հեռավոր ազդեցության ուժեր են և բնույթով՝ միշտ ձգողական, նշանակում է, որ նրանց ազդեցությունը գումարային է։ Այսինքն, եթե նյութական մասնիկների թիվը շատ մեծ է, ապա գրավիտացիոն ուժը կարող է գերազանցել մյուս բոլոր ուժերին։ Ահա թե ինչու է գրավիտացիոն ուժը[8] որոշում տիեզերքի էվոլյուցիան։ Նույնիսկ այն չափի մարմինների համար, ինչպիսիք աստղերն են, գրավիտացիոն ձգողական ուժը կարող է գերազանցել մյուս բոլոր ուժերին և ստիպել, որ աստղը կոլապսվի։ 1970֊ի իմ ուսումնասիրությունները կենտրոնացած էին սև խոռոչներին, որոնք կարող են առաջանալ այդպիսի աստղային կոլապսի արդյունքում, և նրանց շուրջ առկա հզոր գրավիտացիոն դաշտերի վրա։ Այս էր պատճառը, որն ինձ հուշեց այն մասին, թե ինչպես կարող են ընդհանուր հարաբերականությունը և քվանտային մեխանիկան լրացնել միմյանց, և սա եղավ գրավիտացիոն քվանտային մեխանիկայի առաջին առկայծումը։
6
Սև խոռոչներ
Սև խոռոչ տերմինն առաջացել է ընդամենը վերջերս։ 1969֊ին այն ներմուծել է ամերիկացի գիտնական Ջոն Ուիլլերը, որպեսզի պատկերավոր ձևով նկարագրի մի գաղափար, որն առաջացել էր առնվազն երկու հարյուր տարի առաջ, երբ լույսի բնույթը բացատրող երկու տեսություն կար։ Մեկը Նյուտոնի առաջարկած լույսի մասնիկային տեսությունն էր, մյուսը՝ լույսի՝ ալիքներից կազմված լինելու տեսությունը։ Մենք այժմ գիտենք, որ այդ երկու տեսությունն էլ, իրապես ճիշտ են։ Համաձայն քվանտային մեխանիկայի, որի հիմքում ընկած է լույսի արլիք֊մասնիկային երկվությունը, լույսը կարելի է դիտել և՛ որպես մասնիկ, և՛ որպես ալիք։ Լույսի ալիքներից կազմված լինելու տեսությունը պարզ չէր սակայն, թե այն իրեն ինչպես կպահի գրավիտացիոն դաշտում։ Իսկ եթե լույսը կազմված է մասնիկներից, ապա սպասելի էր, որ գրավիտացիոն դաշտը լույսի վրա պետք է թողներ այնպիսի ազդեցություն, ինչպիսին թողնում է արկերի, հրթիռների և մոլորակների վրա։ Սկզբում մարդիկ մտածում էին, թե լույսի մասնիկները շարժվում են անսահման մեծ արագությամբ, ուստի գրավիտացիոն դաշտն ի վիճակի չէ դանդաղեցնել նրանց ընթացքը։ Բայց Ռոեմերի հայտնագործությունը, ըստ որի լույսն ունի վերջավոր արագություն, վկայում էր, որ գրավիտացիան կարող է էական ազդեցություն թողնել լույսի վրա։
Այս ենթադրության հիման վրա Քեմբրիջի համալսարանի դասախոս Ջոն Միչելը 1783֊ին Լոնդոնի Թագավորական ընկերության փիլիսոփայական հաղորդակցություններում տպած մի հոդվածում ուշադրություն հրավիրեց այն հարցի վրա, որ, երբ աստղը բավականին զանգվածեղ և խիտ լինի, ապա այն պետք է այնպիսի գրավիտացիոն դաշտ ունենա, որ լույսը չկարողանա արձակվել, իսկ եթե, այնուամենայնիվ, որոշ լույս արձակվի աստղի մակերևույթից, ապա գրավիտացիոն դաշտը պետք է հետ քաշի այն և թույլ չտա իրենից հեռանալ։ Միչելը գտնում էր, որ այդպիսի աստղեր կարող են շատ լինել։ Չնայած մենք նրանց չենք կարող տեսնել, որովհետև նրանց լույսը մեզ չի հասնի, սակայն այդ աստղերի գրավիտացիոն ձգողականությունը կզգանք։ Հենց այսպիսի առարկաներն այն են, ինչ մենք անվանել ենք սև խոռոչներ, որովհետև դրանք, ըստ էության մթին դատարկություններ են տարածության մեջ։ Մի քանի տարի անց նմանօրինակ առաջարկություն արեց ֆրանսիացի գիտնական մարկիզ դը Լապլասը՝ ամենայն հավանականությամբ Միչելից անկախ։ Հետաքրքրական է բավականին, որ Լապլասը դա ներառել է իր՝ «Աշխարհի համակարգը» գրքի միայն առաջին և երկրորդ հրատարակություններում, սակայն ավելի ուշ հրատարակությունից հանել է, հավանաբար, ենթադրելով, որ անիմաստ է։ (Արդեն 19֊դարում լույսի մասնիկային տեսությունը մոռացվել էր և, կարծես ամեն ինչ կարելի էր բացատրել ալիքային տեսությամբ, որի համաձայն, ինչպես ասվեց, հստակ չէ գրավիտացիոն դաշտը կարո՞ղ էր արդյոք ներգործել ալիքային շարժման վրա ընդհանրապես)։
Իրականում, բոլորովին անտեղի էր լույսի մասնիկը պատկերել որպես թնդանոթի արկ, ինչպես դա արվում է Նյուտոնի ձգողականության տեսության մեջ, այն պատճառով, որ լույսի արագությունը հաստատուն է։ (Որովհետև դեպի վեր կրակված արկը աստիճանաբար կդանդաղի ձգողական ուժի ազդեցության տակ և վերջապես վայր կընկնի):[9]
Ֆոտոնը, սակայն, հաստատուն արագությամբ կշարունակի բարձրանալ վեր։ Ինչպե՞ս կարող է այժմ նյուտոնյան ձգողականությունը ազդել լույսի վրա։ Լուսի վրա գրավիտացիոն դաշտի ազդեցության հետևողական տեսությունը տվեց շատ ավելի ուշ՝ 1915֊ին, երբ Էյնշտեյն առաջարկեց ընդհանուր հարաբերականությունը։ Սակայն նույնիսկ դրանից հետո երկար ժամանակ պահանջվեց, որպեսզի հասկացվեր մեծ զանգված ունեցող աստղերի տեսության նշանակությունը։
Որպեսզի հասկանանք, թե ինչպես է առաջանում սև խոռոչը, առաջին հերթին հարկավոր է իմանալ, թե ի՞նչ բան է աստղի կյանքի շրջափուլը։ Աստղն առաջանում է, երբ մեծ քանակությամբ գազը (հիմնականում ջրածին) կոլապսվում է ինքն իր մեջ իր գրավիտացիոն ձգողության ազդեցությամբ։ Սեղմված գազի ատոմներն իրար ավելի հաճախ և աստիճանաբար ավելի մեծ արագությամբ են բախվում, և սեղմված գազը տաքանում է։ Վերջապես գազն այն աստիճան է տաքանում, որ իրար հետ բախվող ջրածնի ատոմները ոչ թե հետ են մղվում, այլ ընդհակառակը՝ իրար են միանում և առաջացնում հելիում։ Այս ռեակցիայի արդյունքում մեծ քանակի ջերմություն է անջատվում, ինչպես ջրածնային ռումբի պայթման ժամանակ, որից և աստղը փայլատակում է։ Այդ լրացուցիչ ջերմության շնորհիվ այնքան է բարձրանում գազի ճնշումը, մինչև որ բավարարի հավասարակշռելու գրավիտացիոն ձգողությունը, և գազի սեղմվելը դադարում է։ Այս վիճակը նման է օդապարիկի վիճակին, երբ գազի ներքին ճնշումը ձգտում է ընդարձակել օդապարիկը, իսկ ռետինե թաղանթի լարվածությունը՝ փոքրացնել ծավալը, և ստեղծվում է հավասարակշռություն։ Այդ նույն ձևով աստղերը կարող են այնքան ժամանակ կայուն մնալ, քանի դեռ միջուկային ռեակցիայի առաջացրած ջերմությունը հավասարակշռում է գրավիտացիոն ձգողականությանը։ Սակայն, ի վերջո, ջրածնի կամ այլ վառելանյութի պաշարները կսպառվեն։ Որքան էլ տարօրինակ է, ինչքան սկզբնական վառելանյութի պաշարը մեծ է, այնքան արագ է սպառվում այն։ Եվ որքան տաք է աստղը, այն այնքան արագ կսպառի իր պաշարը։ Մեր արեգակը հավանաբար բավական պաշար ունի՝ ավելի քան հինգ հազար միլիոն տարվա, բայց շատ ավելի զանգվածեղ աստղերն իրենց վառելայնությունը սպառած կլինեն ավելի փոքր՝ հարյուր միլիոն տարվա ընթացքում, որը շատ կարճ ժամանակամիջոց է տիեզերքի տարիքի համեմատ։ Երբ աստղերը սպառում են վառելանյութը, սկսում են սառչել և կծկվել։ Թե ինչպես է դա տեղի ունենում, պարզվեց միայն 1920֊ական թվականների վերջերին։
1928֊ին հնդիկ մի շրջանավարտ՝ Սուբրահամանիան Չանդրասեկհարը, Անգլիա ժամանեց Քեմբրիջի համալսարանում աստղագետ սըր Արթուր Էդինգտոնի մոտ ուսումնասիրություններ կատարելու համար, մի մարդու, որը հարաբերականության ընդհանուր տեսության խոշոր մասնագետ էր։ (Ըստ լայնորեն տարածված լուրերի, 1920֊ի սկզբներին մի լրագրող Էդինգտոնին իբր հարցրել է, թե ինքը լսել է, որ աշխարհում լոկ երեք գիտնական կարող են հասկանալ ընդհանուր հարաբերականությունը։ Էդինգտոնը մի պահ լսել և պատասխանել է․ «Փորձում եմ մտաբերել, թե ո՞վ է այդ երրորդը»)։ Չանդրասեկհարը Հնդկաստանից ճանապարհորդության ընթացքում լուծել է հետևյալ հարցը․ ի՞նչ չափսի պետք է լինի աստղը, որ իր ամբողջ վառելանյութը սպառելուց հետո կարողանա իր գոյությունը պահպանել սեփական գրավիտացիոն դաշտում։ Հարցի էությունը հետևյալն էր․ երբ աստղը կծկվում է, նյութական մասնիկները շատ են մոտենում իրար և, համաձայն Պաուլիի արգելակման սկզբունքների, պետք է շատ տարբեր արագություններ ունենան։ Դա ստիպում է նրանց հեռանալ միմյանցից և պատճառ դառնում, որ աստղը ընդարձակվի։ Ուստի աստղը կարող է հաստատուն շառավղով իր գոյությունը պահպանել, եթե գրավիտացիոն ձգողականությունը հավասարակշռվի այն վանողությամբ, որը առաջանում է արգելակման սկզբունքի շնորհիվ ճիշտ այնպես, ինչպես աստղի կյանքի սկզբնական շրջանում գրավիտացիոն ձգողականությունը հավասարակշռում էր անջատված ջերմությամբ։
Ընդ որում Չանդրասեկհարը քաջատեղյակ էր, որ արգելակման սկզբունքով պայմանավորված վանողական ուժերը պետք է ինչ֊որ սահման ունենան։ Հարաբերականության տեսությունը աստղերում մասնիկների արագությունների միջև առավելագույն տարբերությունը սահմանափակում է լույսի արագությամբ։ Սա նշանակում է, որ երբ աստղը բավականաչափ խտացել է, անորոշության սկզբունքով պայմանավորված վանողականությունը գրավիտացիոն ձգողականությունից փոքր կլինի։ Չանդրասեկհարի հաշվումները ցույց տվեցին, որ, եթե սառը աստղի զանգվածը արեգակի զանգվածից մեծ է մոտ մեկուկես անգամ, ապա այն չի կարող դիմակայել իր գրավիտացիոն ձգողությանը։ (Այս զանգվածն այսօր հայտնի է որպես Չանդրասեկհարի սահման)։
Գրեթե միևնույն ժամանակ նման հայտնագործություն էր կատարել նաև ռուս գիտնական Լև Դավիդովիչ Լանդաուն։
Չանդրասեկհարի սահմանը կարևոր նշանակություն ունեցավ մեծ զանգվածով աստղերի ապագա վիճակի խնդրում։ Երբ աստղի զանգվածը փոքր է այդ սահմանային մեծությունից, ապա ի վերջո աստղը կդադարի կծկվել և կհասնի կայուն վիճակի, ինչպես «սպիտակ թզուկը», որի շառավիղը մի քանի հազար մղոն է, իսկ խտությունը՝ մի քանի տասնյակ տոննա խորանարդ դյույմում։ Սպիտակ թզուկն իր գոյությունը պահպանում է շնորհիվ էլեկտրոնների միջև առկա վանողական փոխազդեցության՝ համաձայն Պաուլիի արգելակման սկզբունքի։ Մենք մեծ թվով սպիտակ թզուկներ ենք հայտնաբերել։ Առաջիններից մեկը, որ հայտնաբերվել է, պտտվում է Սիրիուսի շուրջը, որը գիշերային երկնակամարի ամենափայլուն աստղն է։
Լանդաուն նշել է, որ արեգակից մեկ կամ երկու անգամ մեծ սահմանային զանգված ունեցող աստղի համար հնարավոր է սպիտակ թզուկից շատ ավելի փոքր մի այլ վերջնական վիճակ։ Այս աստղերը պետք է կայուն լինեն արգելակման սկզբունքով պայմանավորված նեյտրոնների և պրոտոնների, քան էլեկտրոնների միջև վանողական փոխազդեցության շնորհիվ։ Այդ պատճառով էլ դրանք կոչվեցին նեյտրոնային աստղեր։ Սրանց շառավիղը կլինի մոտ տասը մղոն, իսկ խտությունը՝ տասնյակ միլիոն տոննա խորանարդ դյույումում։ Այն ժամանակ, երբ դրանք կանխագուշակվեցին, նեյտրոնային աստղերի դիտման միջոցներ դեռևս չկային։ Դրանք շատ ավելի ուշ հնարավոր եղավ հայտնաբերել։
Չանդրասեկհարի սահմանից ավելի մեծ զանգված ունեցող աստղերի վիճակը, որոնք սպառում են իրենց վառելանյութը, խիստ հարցական է։ Որոշ դեպքերում կարող է պատահել, որ աստղը պայթի կամ կարողանա այնքան նյութ կորցնել, որ հասնի Չանդրասեկհարի սահմանին և խուսափի գրավիտացիոն կոլապսի աղետից։ Սակայն դժվար է հավատալ, որ այդպիսի բան միշտ կարող է պատահել, անկախ այն բանից, թե որքան մեծ է աստղը։ Այն ինչ իմանա, թե պետք է կշիռ կորցնել։ Եվ նույնիսկ, եթե ամեն աստղ կարողանա բավարար նյութ կորցնելով կոլապսից խուսափել, ապա ի՞նչ կպատահի, եթե թզուկին կամ նեյտրոնային աստղին հավելյալ նյութ ավելացվի, և նրանց զանգվածը անցնի սահմանից։ Այդ աստղերը, ուրեմն, կոլապսի՞ պիտի ենթարկվեն՝ հասնելով անվերջ խիտ վիճակի։ Էդինգտոնը ուղղակի ցնցված էր դրանից և հրաժարվեց ընդունել Չանդրասեկհարի եզրահնգումները։ Էդինգտոնը մտածում էր, որ պարզապես անհնար է, որ աստղը կարող է կոլապսվել և մի կետ դառնալ։ Այս նույն կարծիքին էր գիտնականների մեծամասնությունը․ Էյնշտեյնը հանդես եկավ մի հոդվածով, որում պնդում էր, թե աստղը չի կարող կծկվել մինչև զերո չափսը։ Գիտնականների և մանսավորապես իր նախկին ուսուցչի և աստղագիտության առաջնակարգ մասնագետ Էդինգտոնի անբայրացակամությունն այդ հարցում համոզեցին Չանդրասեկհարին հրաժարվել այդ ուղղությամբ իր ուսումնասիրություններից և նվիրվել աստղագիտության այլ հարցերի, ինչպես օրինակ, աստղային կույտերի շարժումներն են։ Այնուամենայնիվ, երբ 1983֊ին Չանդրասեկհարին շնորհվեց Նոբելյան մրցանակ, դա մասամբ սառը աստղերի սահմանային զանգվածի ուղղությամբ անցյալում նրա կատարած աշխատանքների համար էր։
Չանդրասեկհարը ցույց էր տվել, որ արգելակման սկզբունքը բավարար չէ կանխելու այն աստղերի կոլապսումը, որոնց զանգվածը մեծ է Չանդրասեկհարի սահմանից։ Բայց թե ի՞նչ կպատահի այդպիսի աստղերի հետ ըստ հարաբերականության ընդհանուր տեսության, առաջինը պարզեց երիտասարդ ամերիկացի գիտնական Ռոբերտ Օպենհեյմերը 1939 թվականին։ Սակայն նրա եզրահանգումն այնպիսին էր, որ այդ ժամանակ օգտագործվող հեռադիտակներով հայտնաբերել և դիտել հնարավոր չէր։ Վրա հասավ Երկրորդ համաշխարհային պատերազմը, և Օպենհեյմերը մոտիկից ներգրավվեց ատոմական ռումբի ստեղծման աշխատանքներում։ Պատերազմի ավարտից հետո գրավիտացիոն կոլապսի հիմնահարցը հիմնովին մոռացության տրվեց, քանի որ գիտնականների մեծ մասն անցավ ատոմի միջուկի մասշտաբի հեռավորություններում տեղի ունեցող երևույթների ուսումնասիրությանը։ 1960֊ական թվականներին սակայն, շնորհիվ ժամանակակից տեխնիկական միջոցների կիրառման, հնարավոր եղավ աստղագիտական լայն մասշտաբի դիտարկումներ կատարել և հետքրքրությունը լայնամասշտաբ աստղագիտական և տիեզերագիտական ուսումնասիրությունների ուղղությամբ վերակենդանացավ։ Օպենհեյմերի աշխատանքները վերահայտնաբերվեցին, և շատերն այն ընդունեցին։
Օպենհեյմերի աշխատանքներից ելնելով՝ հարցը կարելի է պատկերացնել այսպես․ աստղի գրավիտացիոն դաշտը փոխում է տարածություն֊ժամանակի մեջ տարածվող լույսի ճառագայթների ուղին, և աստղը երևում է այնտեղ, որտեղ իրականում չկա։ Լուսակոները, որոնք ցույց են տալիս նրանց գագաթի արձակված լույսի ճառագայթների ուղին տարածություն֊ժամանակի մեջ, աստղի մակերևույթի մոտ թեթևակի դեպի ներս թեքված կլինեն։ Դա կարելի է տեսնել հեռավոր աստղերից եկող լույսի թեքման միջոցով, ինչը դիտվում է արեգակի խավարման ժամանակ։ Երբ աստղը կծկվում է, գրավիտացիոն դաշտն ավելի է մեծանում, և լուսակոների՝ դեպի ներս թեքվածությունը խորանում է։ Այսպիսով, դա դժվարացնում է լույսի ձերբազատումը աստղից, և հեռվից դիտողին նրանցից եկող լույսը թուլացած կարմիր է երևում։ Վերջապես, երբ կծկման հետևանքով աստղի շառավիղը հասնում է որոշակի կրիտիկական մեծության, և գրավիտացիոն դաշտի ուժն այն աստիճան է աճում, և կոները այն աստիճան են կորանում, որ լույսը բոլորովին չի կարող արձակվել (նկ․ 6.1)։ Համաձայն հարաբերականության տեսության ոչինչ չի կարող շարժվել լույսից ավելի արագ։ Եվ քանի որ չի կարողանում պոկվել գրավիտացիոն դաշտից, ուստի ոչինչ չի կարողանա դա անել, ու ամեն ինչ գրավիրացիոն դաշտի կողմից ետ կձգվի։ Այսպիսով գոյություն ունի պատահարների մի շարք՝ մի տիրույթ տարածություն֊ժամանակի մեջ, որտեղից հնարավոր չէ ձերբազատվել և հասնել հեռավոր դիտողին։ Հենց այդ տիրույթն էլ կոչվում է սև խոռոչ։ Նրա սահմանագիծը կոչվում է պատահույթի հորիզոն և համընկնում է լուսային ճառագայթների այն ուղու հետ, որից դուրս չի կարող անցնել սև խոռոչից արձակված լույսը։
Հասկանալու համար, թե մարդ ինչ կարող է տեսնել աստղի կոլապսի հետևանքով առաջացող սև խոռոչը դիտելիս, պետք է հիշել, որ համաձայն հարաբերականության տեսության, բացարձակ ժամանակ գոյություն չունի։ Յուրաքանչյուր դիտորդ ունի ժամանակի իր չափումը։ Աստղի գրավիտացիոն դաշտի պատճառով նրա վրա գտնվողի համար ժամանակն այլ է, քան նրանից որոշ հեռավորության վրա գտնվողի համար։ Ենթադրենք՝ մի անվեհեր տիեզերագնաց գտնվում է կոլապսի ենթարկվող աստղի մակերևույթին և աստղի հետ ինքն էլ է կոլապսվում և, իր ժամացույցով չափված, նա ամեն վայրկյան ազդանշան է ուղարկում դեպի աստղի շուրջ պտտվող տիեզերանավը։ Դիցուկ, նրա ժամացույցով ժամը 11.00֊ին աստղը կծկվելով փոքրացել է կրիտիկական շառավղից, և գրավիտացիոն դաշտը այնքան է ուժեղացել, որ որևէ ազդանշան այլևս չի կարող պոկվել նրանից և հասնել տիեզերանավին։ Մինչ ժամը մոտենում է 11.00֊ին, տիեզերանավի անձնակազմի համար ազդանշանների միջև ընկած ժամանակամիջոցները գնալով երկարում են, թեև այդ բանը ժամը 10 անց 59 րոպե 59 վայրկյանից առաջ շատ աննշան կլինի։ Այսպես, տիեզերագանացի10 անց 59 րոպե 58 վայրկյանին տրված ազդանշանից մինչև 10 անց 59 րոպե 59 վայրկյանի ազդանշանը մեկ վայրկյանից փոքր֊ինչ երկար կտևի, սակայն 11.00֊ի ազդանշանին նրանք կսպասեն անվերջ։ Տիեզերագնացի ժամացույցով ժամը 10 անց 59րոպե 59 վայրկանից մինչև 11.00֊ն աստղի մակերևույթից արձակված լույսի ալիքները ըստ տիեզերանավի անձնակազմի, կտարածվեն անսահման ժամանակամիջոցում։ Տիեզերանավին հասած՝ հաջորդական ալիքների միջև ընկած ժամանակամիջոցներն աստիճանաբար կերկարեն, ընդ որում աստղի ճառագայթումն աստիճանաբար ավելի կկարմրի և կթուլանա։ Ի վերջո աստղն այն աստիճան աղոտ կդառնա, որ տիեզերանավի համար կդառնա անտեսանելի, և այդ ամենի արդյունքում տիեզերքում կառաջանա մի սև խոռոչ։ Այնուամենայնիվ, աստղի գրավիտացիոն դաշտի ձգողության ուժը կգործի առաջվա նման, և տիեզերանավը կշարունակի պտտվել սև խոռոչի շուրջ։
Այս սցենարը, սակայն, լրիվ չի համապատասխանում իրականությանը հետևյալ պատճառով․ ձգողության ուժը թուլանում է աստղի մակերևույթից հեռանալիս, հետևաբար, այն միշտ ավելի ուժեղ կլինի մեր անվեհեր տիեզերագնացի ոտքերի մոտ, քան գլխի վրա։ Ուժերի այս տարբերությունը տիեզերագնացին կձգի մակարոնի նման և կամ բաժան֊բաժան կանի նրան՝ աստղը դեռ իր կրիտիկական շառաղվին չհասած, երբ ձևավորվում է պատահույթի հորիզոնը։ Սակայն մենք կարծում ենք, որ տիեզերքում կան ավելի զանգվածեղ մարմիններ, ինչպես գալակտիկաների կենտրոնական տիրույթները, որոնք կարող են գրավիտացիոն կոլապսի ենթարկվել և սև խոռոչ առաջացնել։ Այդ տեղերից մեկում գտնվող տիեզերագնացը մինչև սև խոռոչ առաջանալը կտոր֊կտոր չի լինի։ Կրիտիկական շառաղվին հասնելիս նա, փաստորեն, առանձնահատուկ ոչինչ չի զգում և անցում է կատարում դեպի անդարձություն՝ դա չնկատելով։ Այնուամենայնիվ, մինչ տիրույթը շարունակում է կոլապսվել, մի քանի ժամվա ընթացքում գրավիտացիոն ձգողական ուժերի տարբերությունը տիեզերագնացի ոտքերի և գլխի վրա այն աստիճան կմեծանա, որ նրան դարձյալ բաժան֊բաժան կանի։
1965֊ից մինչև 1970 թվականը Ռոջեր Պենրոուզի հետ իմ կատարած աշխատանքը ցույց տվեց, որ, ըստ հարաբերականության ընդհանուր տեսության, սև խոռոչում պետք է գոյություն ունենա անսահման խտություն և տարածություն֊ժամանակի կորության մի եզակիություն։ Սա բավականին նման է ժամանակի սկզբնավորման Մեծ պայթյունին, միայն այն տարբերությամբ, որ դա կոլապսվող մարմնի և տիեզերագնացի համար ժամանակի վերջն է։ Այս եզակիության համար գիտության օրենքներն ու մեր կանխագուշակման կարողությունը կորցնում են իրենց ուժը։ Բայց սև խոռոչից դուրս գտնվող ցանկացած դիտորդի համար կանխագուշակելու անկարողությունը որևէ նշանակություն չունի, որովհետև ո՛չ լույս, ո՛չ էլ որևէ այլ ազդանշան եզակիությայն կետից նրան չի կարող հասնել։ Այս ուշագրավ փաստը պատճառ դարձավ, որ Ռոջեր Պենրոուզը առաջարկեր տիեզերային գրաքննության վարկածը, որը կարելի է ձևակերպել հետևյալ կերպ․ «Աստված ատում է մերկ եզակիությունը»։ Այսինքն՝ գրավիտացիոն կոլապսի առաջացրած եզակիություններն առկա են միայն այնպիսի տեղերում, ինչպիսիք են սև խոռոչները, որոնք դրսից ղիտողներից պատշաճորեն թաքնվում են պատահութային հորիզոնով։ Խստորեն ասած, սա հայտնի է որպես թույլ տիեզերային գրաքննության վարկած․ դա սև խոռոչից դուրս գտնվող դիտորդներին պաշտպանում է եզակիության մեջ կանխատեսման անհնար լինելու հետևանքներից, սակայն ոչնչով չի օգնում խեղճ, դժբախտ տիեզերագնացին, որն ընկնում է խոռոչի մեջ։
Ընդհանուր հարաբերականության հավասարումներն ունեն մի քանի լուծումներ, որոնք թույլ են տալիս տիեզերագնացին դիտել մերկ եզակիությունը․ նա կարող է ի վիճակի լինել խուսափելու եզակիության հետ բախումից և փոխարենն ընկնել «որդնածակի» մեջ ու դուրս գալ տիեզերքի մի այլ տիրույթ։ Կարծես լայն հնարավորություններ են ստեղծվում տարածության և ժամանակի մեջ ճամփորդելու համար, բայց, դժբախտաբար, ինչպես պարզվում է, այս լուծումները կարող են շատ անկայուն լինել՝ նվազագույն խանգարող հանգամանքն անգամ, ինչպես հենց տիեզերագնացի ներկայությունն այդ տիրույթում կարող է լուծումն այնպես փոխել, որ տիեզերագնացը չնշմարի եզակիությունը, մինչև չբախվի նրա հետ և չավարտվի նրա կյանքի ժամանակը։ Այլ խոսքով ասած, եզակիությունը միշտ կլինի նրա ապագայում, ոչ թե անցյալում։ Տիեզերային գրաքննության վարկածի խիստ տարբերակի համաձայն, երբ լուծումն իրական է, եզակիությունները կամ լրիվ ապագայում կլինեն (ինչպես գրավիտացիոն կոլապսի եզակիությունը), կամ՝ լրիվ անցյալում (ինչպես Մեծ պայթյունը)։ Պետք է հուսալ, նաև, որ կլինի գրաքննչական վարկածի ինչ֊որ մի տարբերակ, երբ տարածության֊ժամանակի մերկ եզակիություններին շատ մոտ հնարավոր կլինի գնալ դեպի անցյալը։ Այդպիսի ճամփորդությունը թերևս արկածային վեպերի հեղինակներին ոգևորի, բայց կնշանակի, որ մեզանից ոչ ոքի կյանքն ապահովագրված չի լինի՝ մեկը կարող է մուտք գործել անցյալի մեջ և սպանել հորդ կամ մորդ՝ քո ձևավորվելուց դեռևս առաջ։
Պատահութային հորիզոնը, այսինքն՝ տարածության֊ժամանակի այն տիրույթի սահմանագիծը, որից դուրս ոչինչ չի կարող անցնել, կարելի է պատկերել որպես սև խոռոչը շրջափակող միակողմանի թաղանթ։ Ամեն ինչ, ինչպես անզգույշ տիեզերագնացը, կարող է պատահութային հորիզոնն անցնել և ընկնել սև խոռոչի մեջ, սակայն այնտեղից ոչինչ չի կարող դուրս գալ։ (Հիշեք, որ պատահությային հորիզոնը լույսի սահմանագիծն է և ոչինչ չի կարող լույսից ավելի արագ շարժվել)։ Պատահութային հորիզոնի մասին կարելի է կրկնել բանաստեղծ Դանթեի խոսքերը, արտասանված դժոխքի մուտքի առաջ․ «Ով մտնողներ, թողեք ձեր հույսը համայն» (թրգմ․ Ա․ Տայան)։ Ամեն ոք և ամեն ինչ, որ ներս է ընկնում պատահութային հորիզոնից, շուտով հասնում է անսահման մեծ խտության և ժամանակի վերջի տիրույթ։
Ընդհանուր հարաբերականությունը կանխագուշակում է, որ ծանր առարկաները շարժվելիս, տարածության կորության մեջ առաջացնում են գրավիտացիոն ալիքներ (կոհակներ), որոնք տեղաշարժվում են լույսի արագությամբ։ Սրանք նման են լույսի ալիքների, որոնք էլեկտրամագնիսական դաշտի կոհակներ են, սակայն ավելի դժվար են հայտնաբերվում։ Լույսի նման, դրանք կրում են իրենց արձակած առարկայի (աղբյուրի) էներգիան։ Սպասելի է, որ մեծ զանգված ունեցող առարկաներն ի վերջո կհասնեն ստացիոնար վիճակի, որովհետև շարժման էներգիան կտարվի արձակվող գրավիտացիոն ալիքներով։ (Երևույթը նման է այն դեպքին, երբ խցանը նետում են ջրի մեջ․ սկզբում խցանը թափով վեր ու վար է շարժվում ջրի մեջ, սակայն երբ կոհակները ցրում են նրա էներգիան, այն աստիճանաբար հանդարտվում է և հասնում ստացիոնար վիճակի)։ Օրինակ, երկրի շրջապտույտն իր ուղեծրով արեգակի շուրջ առաջացնում է գրավիտացիոն ալիքներ։ Էներգիայի կորստի հետևանքով երկրի ուղեծիրը պիտի որ փոխվի, և երկիրն աստիճանաբար մոտենա արեգակին, բախվի նրա հետ և հասնի ստացիոնար վիճակի։ Այս դեպքում էներգիայի կորուստը շատ փոքր է՝ այն հազիվ կարող է բավարարել մի փոքրիկ էլեկտրական ջեռուցիչ աշխատեցնելու համար։ Դա նշանակում է, որ հազար միլիոն միլիոն միլիոն միլիոն տարի հետո միայն երկիրը կընկնի արեգակի վրա, այնպես որ, մտահոգվելու հարկ չկա։ Երկրի ուղեծրի փոփոխությունն այն աստիճան աննշան է, որ դիտարկելի չէ, բայց նման երևույթ վերջին տարիներին դիտվել է, այսպես կոչված, PSR 1913 + 16 համակարգում։ (PSR նշանակում է «պուլսար որը յուրահատուկ նեյտրոնային աստղ է և կանոնավոր կերպով ռադիոալիքներ է առաքում): Այս համակարգը պարունակում է երկու նեյտրոնային աստղեր, որոնք պտտվում են միմյանց շուրջ, և արձակված գրավիտացիոն ալիքներով նրանց կորցրած էներգիան ստիպում է, որ այդ երկու աստղերը պարուրաձև մոտենան իրար։
Սև խոռոչ առաջացնելիս աստղի գրավիտացիոն կոլապսի ընթացքում շարժումները շատ արագ են տեղի ունենում և, հետևաբար, էներգիայի ցրման արագությունը ևս կլինի շատ բարձր։ Այդ պատճառով դա շուտով կհասնի ստացիոնար վիճակի։ Ի՞նչ տեսք կունենա այդ վերջնական վիճակը։ Կարելի է ենթադրել, որ դա կախված կլինի աստղի բոլոր բարդ առանձնահատկություններից, որոնցից այն կազմված է․ ոչ միայն նրա զանգվածից և պտույտի արագությունից, այլև տարբեր մասերի խտություններից և աստղի մեջ գտնվող գազերի խճճված շարժումներից։ Եթե առաջացած սև խոռոչներն այնպես տարբեր լինեն, ինչպես դրանք առաջացնող կոլապսվող մարմինները, ապա ընդհանրապես սև խոռոչների մասին կանխագուշակումներ անելը շատ դժվար կլինի։
1967֊ին, սակայն, սև խոռոչների ուսումնասիրության բնագավառում հեղաշրջում կատարեց կանադացի գիտնական Վերներ Իսրայելը (ծնվել է Բեռլինում, սովորել Հարավային Աֆրիկայում և դոկտորական աստիճան ստացել Իռլանդիայում)։ Իսրայելը ցույց տվեց, որ, համաձայն հարաբերականության ընդհանուր տեսության, պտտական շարժումից զրկված սև խոռոչները պետք է շատ պարզ լինեն, նրանք կատարյալ գնդաձև են, նրանց չափը կախված է միայն զանգվածից, և ցանկացած երկու սև խոռոչներ, որոնք նույն զանգվածն ունեն, նույնական են։ Դրանք փաստորեն, կարելի է նկարագրել Էյնշտեյնյան հավասարումների մասնակի լուծումներով, որոնք հայտնի են դեռևս 1917֊ից և հայտնագործվել են Կարլ Շվարցշիլդի կողմից՝ հարաբերականության ընդհանուր տեսության ստեղծումից անմիջապես հետո։ Սկզբնական շրջանում շատերը, այդ թվում նաև Իսրայելը գտնում էին՝ քանի որ սև խոռոչները կատարյալ գնդաձև են, ուստի պիտի առաջացած լինեն կատարյալ գնդաձև մարմինների կոլապսի հետևանքով։ Հետևաբար, որևէ իրական աստղ, որ երբեք կատարյալ գնդաձև չէ, կոլապսի հետևանքով կարող է առաջացնել միայն մի մերկ եզակիություն։
Սակայն կար Իսրայելի տվյալների այլ մեկնաբանություն, ինչը արեցին մասնավորապես Ռոջեր Պենրոուզը և Ջոն Ուիլերը։ Նրանք պնդում էին, որ աստղի կոլապսի ընթացքում տեղի են ունենում արագ շարժումներ, ինչի հետևանքով արձակված գրավիտացիոն ալիքներն աստղն ավելի գնդաձև են դարձնում, ընդ որում, երբ այն հասնում է ստացիոնար վիճակի, արդեն ճշգրիտ գնդաձև է լինում։ Ըստ այս տեսակետի, յուրաքանչյուր աստղ, որ զրկված է պտտական շարժումից, որքան էլ բարդ ներքին կառուցվածք և ձև ունենա, գրավիտացիոն կոլապսից հետո կառաջացնի կատարելապես գնդաձև սև խոռոչ, որի շառավիղը կախված կլինի միայն նրա զանգվածից։ Հետագա հաշվումներն ապացուցեցին այս տեսակետի ճշտությունը, և այն շուտով ընդհանուր առմամբ ընդունվեց։
Իսրայելի եզրահանգումները վերաբերում էին միայն այն սև խոռոչներին, որոնք առաջանում են պտտական շարժումից զրկված մարմիններից։ Նորզելանդացի գիտնական Ռոյ Քերն 1963֊ին հարաբերականության ընդհանուր տեսության հավասարումների այնպիսի լուծումների շարք գտավ, որոնք նկարագրում էին պտտվող սև խոռոչները։ Այսպես կոչված «Քեր» սև խոռոչները պտտվում են հաստատուն արագությամբ, նրանց չափն ու ձևը կախված են միայն պտտական արագությունից և զանգվածից։ Եթե պտույտը հավասար է զերոյի, ապա սև խոռոչը կատարյալ գնդաձև է, և լուծումը նույնական է Շվարցշիլդի առաջարկած լուծման հետ։ Եթե պտույտը զերոյական չէ, ապա սև խոռոչը հասարակածում ինչ֊որ չափով դուրս է ցցվում (ինչպես երկիրը կամ արեգակն են դուրս ցցվում պտույտի շնորհիվ), և դա մեծ է այնքան, որքան արագ է պտույտը։ Այսպիսով, Իսրայելի տեսությունը տարածելով նաև պտտվող մարմինների վրա ենթադրվեց, որ կոլապսի ենթարկվող ցանկացած պտտվող մարմին, որն առաջացնում է սև խոռոչ, ի վերջո կհասնի այնպիսի մի ստացիոնար վիճակի, որը նկարագրվում է Քերի լուծումով։
1970֊ին այս ենթադրությունն ապացուցելու գործին ձեռնամուխ եղավ իմ գործընկեր և ասպիրանտ Բրանդոն Քարտերը։ Նա ցույց տվեց, որ եթե պտտվող ստացիոնար սև խոռոչն ունենա համաչափության առանցք, ինչպես պտտվող հոլը, ապա խոռոչի չափն ու ձևը կախված կլինեն միայն նրա զանգվածից և պտտման արագությունից։ Իսկ 1971֊ին ես ապացուցեցի, որ որևէ պտտվող սև խոռոչ անպայման այդպիսի համաչափության առանցք պետք է ունենա։ Վերջապես, 1973֊ին Լոնդոնի Թագավորական քոլեջում Դեյվիդ Ռոբինսոնը, օգտագործելով Քարտերի և իմ տվյալները, ցույց տվեց, որ այդ ենթադրությունը ճիշտ է, և այդպիսի սև խոռոչն իրոք ունի Քերի լուծում։ Այսպիսով, գրավիտացիոն կոլապսից հետո առաջացած սև խոռոչը կհասնի մի վիճակի, որում այն կարող է պտտվել, բայց չի բաբախի։ Դեռ ավելին, նրա չափն ու ձևը կախված կլինեն լոկ նրա զանգվածից և պտտման արագությունից և ո՛չ սև խոռոչն առաջացնող կոլապսվող մարմնի բնույթից։ Այս արդյունքն արտահայտված է հետևյալ ասացվածքի մեջ․ «Սև խոռոչը գեսեր չունի»։ Այս «անգիսության» թեորեմը մեծ կիրառական կարևորություն ունի, որովհետև մեծ չափով սահմանափակում է սև խոռոչների հնարավոր տեսակների առկայությունը։ Այսպիսով, հնարավոր է սև խոռոչներ պարունակող առարկաների համար մանրամասն մոդելներ ստեղծել, կանխագուշակումներ անել և դրանք համեմատել դիտարկումների հետ։ Դա նշանակում է նաև, որ սև խոռոչ առաջացնող մարմնի կոլապսից հետո նրա մասին տեղեկությունների մեծ մասր կորչում է, որովհետև մենք ստացիոնար վիճակում կարող ենք չափել միայն նրա զանգվածն ու պտտման արագությունը։ Այս բանի նշանակությունը մենք կտեսնենք հաջորդ գլխում։
Սև խոռոչը գիտության պատմության այն հազվադեպ երևույթներից մեկն է, որի տեսությունը մաթեմատիկական մեծ մանրամասնությամբ մշակվեց՝ դրա ակներևությունը դիտարկումներով ապացուցող որևէ փաստ ունենալուց առաջ։ Սև խոռոչների գոյության հակառակորդների գլխավոր փաստարկը հենց փորձնական տվյալների բացակայությունն էր․ ինչպե՞ս կարելի է հավատալ այն մարմինների գոյությանը, որոնց միակ ապացույցը հիմնված էր ընդհանուր հարաբերականության կասկածելի հաշվումների վրա։ Սակայն, ահա 1963֊ին Կալիֆոռնիայի Պալոմարի աստղադիտարանի աստղագետներից մեկը՝ Մարտեն Շմիդտը չափեց աղոտ աստղանման մի մարմնի կարմիր շեղումը՝ 3C273 կոչված ռադիոալիքների աղբյուրի ուղղությամբ (ռադիոաղբյուրների Քեմբրիջի 3֊րդ գրացուցակի 273 համարն է)։ Նա գտավ, որ դա շատ մեծ է գրավիտացիոն դաշտով պայմանավորված լինելու համար, եթե դա իրոք գրավիտացիոն կարմիր շեղումը լիներ, ապա այդ մարմինը այնքան զանգվածեղ և մեզ այնքան մոտ պետք է լիներ, որ պիտի խախտեր Արեգակնային համակարգի մոլորակների ուղեծրերը։ Սա նշանակում էր, որ կարմիր շեղումը տիեզերքի ընդարձակման արդյունք է, որն իր հերթին նշանակում է, որ թույլ լուսատու մարմինը շատ հեռու է գտնվում։ Հետևաբար, որպեսզի այդ մեծ հեռավորության վրա մարմինը տեսանելի լինի, պետք է այն շատ պայծառ լինի, կամ, այլ խոսքերով ասած, մեծ քանակի էներգիա արձակի։ Իսկ այդքան մեծաքանակ էներգիայի առաջացման միակ մեխանիզմը, որ մարդ կարող է ենթադրել, կարող է լինել ոչ թե մի աստղի, այլ գալակտիկայի ամբողջ կենտրոնական շրջանի գրավիտացիոն կոլապսը։ Մի շարք նման և «քվազիաստղային մարմիններ» կամ քվազարներ հայտնաբերվեցին՝ բոլորը մեծ կարմիր շեղումներով։ Սակայն, այս բոլորը չափազանց հեռավոր մարմիններ են, այդ պատճառով նրանց դիտարկումը դժվար է իրականացնել և ունենալ սև խոռոչների առկայության համոզիչ փաստարկներ։
Սև խոռոչների գոյության մասին հուսադրող փաստեր տվեց Քեմբրիջի համալսարանի ասպիրանտ Ջոնսելին Բելը 1967֊ին երկնակամարում հայտնաբերելով կանոնավոր ռադիոալիքներ առաքող բաբախող մարմիններ։ Սկզբում Բելը և նրա ղեկավար Էնտոնի Հյուիշը մտածեցին, թե կարող է կապ են հաստատել գալակտիկայում արտերկրային քաղաքակրթության հոտ։ Արդարև, երբ սեմինարին նրանք զեկուցում էին այդ հայտնագործության մասին, հիշում եմ, իրենց գտած առաջին աղբյուրն անվանեցին ՓԿՄ 1―4, (անգլ․LGM՝ 1-4 «Little Gres Men», Փոքրիկ կանաչ մարդիկ)։ Հետագայում հեղինակները, ինչպես նաև մյուս գիտնականները, հանգեցին նվազ ռոմանտիկ այն եզրակացությանը, որ այդ երկնային մարմինները, որոնք կոչվեցին պուլսարներ, պտտվող նեյտրոնային աստղեր են, որոնք իրենց մագնիսական դաշտի և շրջակա նյութի մի բարդ փոխազդեցությունների շնորհիվ ռադիոալիքներ են արձակում՝ բաբախելով։ Իհարկե, տիեզերական արկածների հեղինակների համար սա վատ լուր էր, սակայն այդ ժամանակ սև խոռոչների գոյությանը հավատացող մեր փոքրաթիվ խմբին հույսեր էր ներշնչում․ սա նեյտրոնային աստղերի մասին առաջին դրական ապացույցն էր։ Նեյտրոնային աստղի շառավիղը մոտավորապես 10 մղոն է, միայն մի քանի անգամ է մեծ աստղի այն կրիտիկական շառավղից, որի դեպքում վերածվում է սև խոռոչի։ Ուրեմն, եթե մի աստղ կարող է կծկվել այդքան փոքր չափերի, ապա հակատրամաբանական չէ սպասել, որ այլ աստղեր կոլապսի հետևանքով կկծկվեն ավելի փոքր չափերի և կվերածվեն սև խոռոչների։
Հարց է ծագում, քանի որ սև խոռոչից լույսի արձակումը հնարավոր չէ, ապա ի՞նչ հույս կա այն հայտնաբերելու։ Դա մի փոքր նման է ածխի պահեստում սև կատու փնտրելուն։ Բարեբախտաբար, դրա միջոցը կա։ Ջոն Միչելի՝ 1783֊ին հրատարած առաջին հաղորդագրության մեջ նշվում է, որ սև խոռոչը դեռևս ազդում է շրջապատի մարմինների վրա գրավիտացիոն ուժով։ Աստղագետները դիտարկել են շատ համակարգեր, որոնց երկու աստղեր պտտվում են իրար շուրջ և միմյանց ձգում գրավիտացիոն ուժով։ Դիտվել են նաև այնպիսի համակարգեր, որոնցում միայն մի տեսանելի աստղ պտտվում է ինչ֊որ անտեսանելի զուգընկերոջ շուրջ։ Ոչ ոք չի կարող, իհարկե, անմիջապես եզրակացնել, թե այդ անտեսանելի զուգընկերը սև խոռոչ է, որովհետև բացառված չէ, որ դա թույլ լուսատվություն ունեցող մի աստղ լինի։ Այնուամենայնիվ, այս համակարգերի մի մասը, ինչպես Սիգնուս X-1 կոչվողը (նկ․ 6.2), նաև ուժեղ ռենտգենյան ճառագայթման աղբյուրներ են։ Այս երևութի լավագույն բացատրությունն է նյութի ժայթքումը տեսանելի աստղի մակերևույթից։ Այդ նյութը անտեսանելի զուգընկերոջ վրա թափվելով, առաջացնում է պարուրաձև շարժում (ինչպես լողարանի ջուրը տաշտի անցքից դուրս հոսելիս), այն շատ է տաքանում և արձակում է ռենտգենյան ճառագայթներ (նկ․ 6.3)։ Որպեսզի այդպիսի բան պատահի, անհրաժեշտ է, որ անտեսանելի առարկան շատ փոքր լինի, ինչպես Սպիտակ թզուկը, նեյտրոնային աստղը կամ սև խոռոչը։ Տեսանելի աստղի ուղեծրի դիտարկումը թույլ է տալիս հաշվել անտեսանելի մարմնի հնարավոր նվազագույն զանգվածը։ Սիգնուս X-1֊ի դեպքում անտեսանելի մարմնի զանգվածը արեգակի զանգվածից մեծ է մոտ վեց անգամ, որը համաձայն Չանդրասեկհարի սահմանային օրենքի, շատ մեծ է Սպիտակ թզուկ լինելու համար։ Նեյտրոնային աստղ լինելու համար այս զանգվածը նույնպես շատ մեծ է։ Հետևաբար, թվում է, թե դա պետք է սև խոռոչ լինի։
Կան այլ մոդելներ, որոնք Սիգնուս x-1 համակարգում բացառում են սև խոռոչի առկայությունը, սակայն դրանք շատ անբնական բնույթ ունեն։ Դիտարկվածի ամենահավանական բացատրությունը կարելի է համարել սև խոռոչի առկայությունը։ Հակառակ դրա ես գրազ եմ եկել Կալիֆոռնիայի տեխնոլոգիական ինստիտուտից Քիպ Թոռնի հետ, որ իրականում Սիգնուս X-1֊ի համակարգում սև խոռոչ գոյություն չունի։ Այս քայլին դիմելով, ես ինքս ինձ ապահովագրել եմ։ Ես մեծ աշխատանք եմ կատարել սև խոռոչների բնագավառում, և այն իզուր կանցնի, եթե սև խոռոչներ գոյություն չունենան։ Բայց այդ դեպքում գոնե գրազը կշահեմ և որպես մխիթարանք՝ Պրայվիթ Ս հանդեսի չորս տարվա բաժանորդագրություն կստանամ։ Իսկ եթե սև խոռոչներ գոյություն ունենան, Քիպը Պենթհաուզի տարեկան բաժանորդագրություն ձեռք կբերի։ 1975֊ին, երբ գրազ բռնվեցինք, մենք 80 տոկոսով վստահ էինք, որ Սիգնուսը սև խոռոչ է։ Այժմ կարող եմ ասել, որ վստահ ենք 95 տոկոսով, սակայն գրազը դեռ շարունակվում է։
Մենք այժմ փաստեր ունենք մեր գալակտիկայում Սիգնա x―1֊ի նման համակարգերում և երկու հարևան գալակտիկաներում, որոնք կոչվում են Մագելանի ամպեր, մի քանի այլ խոռոչների գոյության մասին նույնպես։ Սակայն, տարակույս չկա, որ հավանաբար սև խոռոչների թիվն ավելի մեծ է․ տիեզերքի տևական պատմության ընթացքում բազմաթիվ աստղեր սպառած պիտի լինեին իրենց միջուկային վառելանյութը և կոլապսի ենթարկված։ Սև խոռոչների թիվը կարող է ավելի մեծ լինել, քան տեսանելի աստղերինը, ինչր միայն մեր գալակտիկայում հասնում է հարյուր հազար միլիոնի։ Ավելի մեծ թվով սև խոռոչների հավելյալ գրավիտացիոն ձգողական ուժը կարող է բացատրել մեր գալակտիկայի պտտական շարժման արագությունը․ տեսանելի աստղերի զանգվածը բավարար չէ դրա համար։ Որոշ փաստեր ունենք նաև այն մասին, որ մեր գալակտիկայի կենտրոնում մի մեծ սև խոռոչ կա, որի զանգվածը մոտ հարյուր հազար անգամ մեծ է արեգակի զանգվածից։ Գալակտիկայի այն աստղերը, որոնք մոտենում են այդ հսկա մեծ խոռոչին, դրան մոտ և հեռավոր կողմերի վրա ազդող գրավիտացիոն ուժերի տարբերության պատճառով, կտոր֊կտոր են լինում։ Դրանց մնացորդները և այդ աստղերից ժայթքող գազերն ընկնում են սև խոռոչի մեջ։ Ինչպես Սիգնուս x―1֊ի պարագայում գազերը պարուրաձև ներս են քաշվում և տաքանում, թեև ոչ այն աստիճան, ինչպես Սիգնուսի դեպքում։ Այստեղ ջերմությունը չի բավարարում ռենտգենյան ճառագայթների համար, սակայն բավարար է ռադիոալիքների և ինֆրակարմիր ճառագայթման շատ խիտ աղբյուր լինելու համար, որը և դիտվում է գալակտիկայի կենտրոնում։
Այն կարծիքը կա, թե նման և նույնիսկ ավելի մեծ սև խոռոչներ կան քվազարների կենտրոններում, որոնց զանգվածն արեգակի զանգվածից մեծ է մոտ հարյուր միլիոն անգամ։ Միայն այդպիսի գերզանգված ունեցող սև խոռոչների մեջ նյութի մուտքը կարող է առաջացնել հզոր էներգիայի աղբյուր, որով և բացատրվում է դրանցից հսկայական էներգիայի արձակումը։ Երբ նյութը պարուրաձև մտնում է սև խոռոչի մեջ, վերջինիս ստիպում է պտտվել նույն ուղղությամբ և առաջացնել մագնիսական դաշտ՝ հար և նման երկրի մագնիսական դաշտին։ Ներս լցվող նյութը պատճառ է դառնում, որ սև խոռոչի մոտերքում առաջանան շատ բարձր էներգիա ունեցող մասնիկներ։ Մագնիսական դաշտն այնքան հզոր կլինի, որ նրա ազդեցության տակ մասնիկները կկիզակետվեն և դուրս կժայթքեն սև խոռոչի պտտման առանցքի ուղղությամբ, այսինքն՝ դրա հյուսիսային և հարավային բևեռների ուղղությամբ։ Այդպիսի ժայթքումներ իրոք դիտվել են մի շարք գալակտիկաներում և քվազարներում։
Կարելի է նաև ենթադրել, որ արեգակից շատ փոքր զանգված ունեցող սև խոռոչներ նույնպես կան։ Այդպիսի սև խոռոչները չեն կարող առաջացած լինել գրավիտացիոն կոլապսից, քանի որ նրանց զանգվածները Չանդրասեկհարի սահմանային մեծությունից փոքր են․ այդքան փոքր զանգված ունեցող աստղերը կարող են դիմակայել գրավիտացիոն ուժերին, անգամ եթե սպառել են իրենց միջուկային վառելանյութը։ Փոքր զանգված ունեցող սև խոռոչները կարող են առաջանալ այն ժամանակ, երբ նյութը չափազանց խտանում է շատ բարձր արտաքին ճնշումների ազդեցությամբ։ Այսպիսի պայմաններ կարող են ստեղծվել շատ մեծ ջրածնային ռումբի մեջ։ Ֆիզիկոս Ջոն Ուիլերը հաշվել է, որ եթե աշխարհի բոլոր օվկիանոսներում եղած ամբողջ ծանր ջուրը[10] հավաքենք, ապա դրանից պատրաստված ջրածնային ռումբն այնպիսի մի ճնշում կառաջացնի, և նյութը կենտրոնում այն աստիճան կսեղմվի, որ կառաջանա մի սև խոռոչ։ (Իհարկե, մարդ չի մնա դա դիտելու համար)։ Գործնականում հնարավոր է, որ տիեզերքի սկզբնական շրջանում բարձր ճնշման և ջերմաստիճանի պայմաններում փոքր զանգված ունեցող սև խոռոչներ առաջացած լինեն։ Սև խոռոչներ կարող էին առաջանալ, եթե նախնական տիեզերքը կատարյալ հարթ և միօրինակ եղած չլիներ, որովհետև միայն միջինից ավելի խիտ մի տիրույթ կարող էր այն աստիճան սեղմվել, որ սև խոռոչ առաջանար։ Սակայն մենք գիտենք, որ ինչ֊որ խախտումներ պետք է եղած լինեն, հակառակ դեպքում նյութը մինչև օրս կատարյալ միօրինակ ձևով բաշխված կլիներ, աստղերով և գալակտիկաներով խմբավորված լինելու փոխարեն։
Թե աստղերի և գալակտիկաների առաջացման համար անհրաժեշտ այդ խախտումները պատճառ եղե՞լ են արդյոք, որպեսզի որոշակի քանակությամբ «նախասկզբնական» սև խոռոչներ ևս ստեղծվեին՝ կախված է միայն նախնական տիեզերքի պայմանների մանրամասներից։ Հետևաբար, եթե կարողանանք որոշել, թե որքան նախասկզբնական սև խոռոչներ կան այսօր, մենք շատ բան կիմանանք տիեզերքի շատ վաղ անցյալի վիճակի մասին։ Նախասկզբնական այնպիսի սև խոռոչները, որոնց զանգվածը հազար միլիոն տոննայից մեծ է (մեծ լեռան զանգվածի չափ), կարելի է հայտնաբերել միայն, որոշելով նրանց գրավիտացիոն ազդեցությունը այլ տեսանելի նյութի կամ տիեզերքի ընդարձակման վրա։ Սակայն ինչպես հաջորդ գլխում կտեսնենք, սև խոռոչները իրականում այնքան էլ սև չեն, նրանք տաք մարմնի նման լուսարձակում են և որքան փոքր են, այնքան ուժեղ է լուսարձակումը։ Այսպիսով, որքան էլ պարադոքսային թվա, ստացվում է, որ փոքրիկ, սև խոռոչներն ավելի հեշտ է հայտնաբերել, քան մեծերը։
7
Սև խոռոչները այնքան էլ սև չեն
1970֊ից առաջ ընդհանուր հարաբերականության ասպարեզում իմ կատարած ուսումնասիրությունների կենտրոնում գլխավորապես Մեծ պայթյունի եզակիության հարցն էր։ Այդ տարվա նոյեմբերի մի երեկո իմ աղջկա՝ Լյուսիի ծննդից քիչ հետո, քնելու պատրաստվելիս ես սկսեցի մտածել սև խոռոչների մասին։ Հաշմանդամությանս պատճառով դանդաղ եմ տեղաշարժվում, այդ պատճառով ես շատ ժամանակ ունեի մտածելու։ Այն ժամանակ չկար որոշակի սահմանում, թե տարածության֊ժամանակի որ կետերն են գտնվում սև խոռոչի ներսում, որոնք՝ նրանից դուրս։ Ես արդեն Ռոջեր Պենրոուզի հետ քննարկել էր այն գաղափարը, որ սև խոռոչը պիտի սահմանել որպես պատահույթների մի շարք, որից հնարավոր չէ ձերբազատվել և բավականին հեռանալ․ մի սահմանում, որն այսօր համընդհանուր ընդունելության է արժանացել։ Սա նշանակում է, որ սև խոռոչի սահմանագիծը՝ պատահութային հորիզոնը, տարածություն֊ժամանակի մեջ առաջանում է լույսի ճառագայթների այն ուղիներով, որոնք պարզապես չեն կարողանում ձերբազատվել սև խոռոչից և մշտապես սավառնում են եզրագծում (նկ․7.1): Սա փոքր֊ինչ նման է այն դեպքին, երբ մարդ փախչում է ոստիկանությունից և հազիվ է հասցնում մի քայլ առաջ ընկնել, բայց երբեք նրանից լրիվ ազատվել չի կարողանում։
Ես հանկարծ գլխի ընկա, որ լուսային ճառագայթների ուղիները երբեք իրար չեն կարող մոտենալ։ Եթե մոտենային, ապա նրանք ի վերջո պետք է խառնվեին իրար։ Վիճակը նման կլիներ այն դեպքին, երբ ոստիկանությունից փախչողը բախվեր հակառակ ուղղությամբ ընթացող և ոստիկանի կողմից հետապնդվող մի ուրիշի հետ՝ երկուսն էլ տեղն ու տեղը կբռնվեին (կամ, այս դեպքում, կընկնեին սև խոռոչի մեջ)։ Սակայն, եթե սև խոռոչը կլաներ այս լուսային ճառագայթները, ապա նրանք սահմանագծի վրա չէին կարող լինել։ Հետևաբար, պատահութային հորիզոնում լուսային ճառագայթների ուղիները կամ պետք է միշտ իրար զուգահեռ շարժվեն և կամ իրարից հեռանան։ Այլ կերպ ասած, պատահութային հորիզոնը՝ սև խոռոչի սահմանագիծը, նման է ստվերի՝ եզրի վերահաս կործանման ստվերի։ Եթե ուշադիր դիտենք հեռավոր լուսաղբյուրի, ինչպես օրինակ, արեգակի առաջացրած ստվերը, կտեսնենք, որ եզրում լույսի ճառագայթներն իրար չեն մոտենում։
Հետևաբար, եթե պատահութային հորիզոնը՝ սև խոռոչի սահմանագիծը, կազմող լույսի ճառագայթները երբեք իրար չեն կարող մոտենալ, նշանակում է, որ պատահութային հորիզոնի մակերեսը կարող է ժամանակի ընթացքում նույնը մնալ կամ մեծանալ, բայց երբեք չի կարող փոքրանալ։ Քանի որ այս վերջին դեպքում սահմանի լույսի որոշ ճառագայթներ պետք է որ իրար մոտենային։ Իրականում մակերեսը կմեծանա՝ սև խոռոչի մեջ նյութ կամ ճառագայթում ընկնելիս (նկ․ 7.2)։ Կամ եթե երկու խոռոչներ բախվեն և միանան ու մի նոր սև խոռոչ առաջացնեն, ապա վերջինիս պատահութային հորիզոնի մակերեսը կարող է մեծ լինել կամ հավասար երկու սկզբնական սև խոռոչների պատահութային հորիզոնների մակերեսների գումարին ( նկ․ 7.3)։ Պատահութային հորիզոնի մակերեսի չփոքրանալու այդ հատկությունը սահմանափակում է սև խոռոչի հնարավոր վարքագիծը։ Այս հայտնագործությունն ինձ այն աստիճան ոգևորեց, որ ես չկարողացա քնել։ Հաջորդ օրը զանգահարեցի Ռոջեր Պենրոուզին։ Նա համաձայնեց իմ կարծիքին։ Կարծում եմ, որ նա, փաստորեն, իրազեկ էր սև խոռոչի մակերեսի այդ հատկությանը։ Թեև նա սև խոռոչի համար փոքր֊ինչ այլ սահմանում էր տալիս, բայց գլխի չէր ընկել, որ երկու սահմանումների պարագայում էլ սև խոռոչի սահմանները և նրանց մակերեսները նույնը կլինեն, եթե իհարկե, սև խոռոչը հասել է այնպիսի մի վիճակի, որը ժամանակի ընթացքում այլևս փոփոխության չի ենթարկվում։
Սև խոռոչի չփոքրանալու հատկությունը ընդհանրություններ ունի էնտրոպիա կոչվող մի այլ ֆիզիկական մեծության վարքագծի հետ, այս մեծությունը չափում է անկանոնության աստիճանը։ Հայտնի է, որ առանց միջամտության առարկաները ժամանակի ընթացքում անկարգ վիճակում են հայտնվում (այս բանը ակնհայտ է դառնում, երբ տունը երկար ժամանակ չի վերանորոգվում)։ Իհարկե, կարելի է անկարգության վիճակից կարգավորվածության վիճակի անցնել, հնարավոր է կարգուկանոն մտցնել (օրինակ, կարելի է տունը ներկել), բայց դրա համար հարկավոր է աշխատել կամ էներգիա ծախսել, որի հետևանքով առկա կարգավորված էներգիայի քանակությունը կնվազի։
Էնտրոպիայի մասին ավելի ճշգրիտ պատկերացում է տալիս թերմոդինամիկայի 2֊րդ օրենքը։ Համաձայն այս օրենքի, մեկուսացած համակարգի էնտրոպիան միշտ աճում է։[11] Երբ այդպիսի երկու համակարգ միացվում են[12] միմյանց, ապա միացյալ համակարգի էնտրոպիան ավելի մեծ է լինում սկզբնական երկու առանձին համակարգերի էնտրոպիաների գումարից։ Դիցուկ, ունենք գազի մոլեկուլներով լեցուն մի տուփ։ Մոլեկուլները կարելի է պատկերել որպես բիլիարդի փոքրիկ գնդիկներ, որոնք շարունակաբար բախվում են իրար հետ և հետ հրվում տուփի պատերին բախվելիս։ Որքան բարձր լինի ջերմաստիճանը, այնքան արագ կշարժվեն մոլեկուլները, ավելի հաճախ և մեծ ուժով կհարվածեն տուփի պատերին, և, հետևաբար, պատերին ազդող ներքին ճնշումն ավելի բարձր կլինի։ Ենթադրենք, թե սկզբում բոլոր մոլեկուլները պարփակված են տուփի ձախ մասում, որն անջատված է մի միջնապատով։ Երբ միջնապատը հեռացվի, մոլեկուլները կձգտեն տարածվել և զբաղեցնել տուփի երկու բաժինները։ Հետագայում կարող է պատահել, որ բոլոր մոլեկուլները հավաքվեն տուփի միայն աջ կամ միայն ձախ մասում, սակայն շատ ավելի հավանական է, որ մոլեկուլները երկու մասում բաշխվեն հավասարապես։ Այս վիճակը նվազ կարգավորված է, կամ ավելի չկարգավորված, քան այն սկզբնական վիճակը, երբ մոլեկուլները գտնվում էին մի կեսում։ Հետևաբար, կարելի է ասել, որ գազի էնտրոպիան աճեց։[13]
Դիցուկ, ունենք երկու տուփ, որոնցից մեկը լցված է թթվածնով, մյուսը՝ ազոտով։
Երբ երկու տուփերը միացնենք իրար, ապա միջնորմը հեռացնելիս թթվածնի և ազոտի մոլեկուլները պիտի սկսեն խառնվել միմյանց։ Հետագայում առավել հավանական վիճակը կլինի այն, որ թթվածնի և ազոտի մոլեկուլները միօրինակ և հավասարապես բաշխված կլինեն երկու տուփերում։ Այս վիճակը նվազ կարգավորված է և ավելի մեծ էնտրոպիա կունենա, քան սկզբնական երկու առանձին տուփերի վիճակը։[14]
Թերմոդինամիկայի երկրորդ օրենքը որոշ չափով այլ կարգավիճակ ունի, քան գիտական մյուս օրենքները, ինչպես, օրինակ, Նյուտոնի ձգողականության օրենքը, որովհետև այն ոչ միշտ է գործում՝ միայն դեպքերի ճնշող մեծամասնության պարագայում։ Հավանականությունն այն բանի, որ տուփի մեջ եղած բոլոր մոլեկուլները հետագայում առանձնանան նրա մի կեսում, մեկի մի քանի միլիոն միլիոներորդ մասից ավելի փոքր է, այդպիսի բան, սակայն, կարող է պատահել։ Այնուամենայնիվ, եթե ունենք մի սև խոռոչ, թվում է, երկրորդ օրենքը խախտելու մի հեշտ ճանապարհ կա։ Բավական է, որ մեծ էնտրոպիա ունեցող նյութ, ասենք մի տուփ գազ, նետվի սև խոռոչի մեջ։ Սև խոռոչից դուրս գտնվող նյութի ընդհանուր էնտրոպիան կնվազի։ Կարելի է, իհարկե, ասել, որ էնտրոպիայի ընդհանուր քանակությունը, ներառյալ սև խոռոչի էնտրոպիան, չի նվազել։ Բայց, քանի որ հնարավոր չէ սև խոռոչի ներսը տեսնել, չենք կարող ասել, թե այնտեղ գտնվող նյութն ինչքան էնտրոպիա ունի։ Հետևաբար ցանկալի կլիներ, որ սև խոռոչն օժտված լիներ այնպիսի մի հատկանիշով, որի օգնությամբ դրսից դիտողն իմանար նրա էնտրոպիայի մեծությունը, և վերջինս աճեր, երբ սև խոռոչի մեջ էնտրոպիա ունեցող նյութ ընկներ։ Ելնելով վերևում նկարագրված այն հայտնագործությունից, որ պատահութային հորիզոնի մակերեսը մեծանում է, երբ նյութ է ընկնում սև խոռոչի մեջ, Պրինստոնի համալսարանի ասպիրանտ Յակոբ Բեկենշտեյնն առաջարկեց, որ պատահութային հորիզոնի մակերեսը սև խոռոչի էնտրոպիայի չափանիշն է։
Քանի որ պատահութային հորիզոնի մակերեսը մեծանում է, երբ սև խոռոչի մեջ էնտրոպիա ունեցող նյութ է ընկնում, ապա սև խոռոչի շրջապատի նյութի էնտրոպիայի և նրա հորիզոնի մակերեսի գումարը երբեք չի կարող նվազել։
Բեկենշտեյնի այս առաջարկությունը, թվում է, ցույց էր տալիս, որ թերմոդինամիկայի երկրորդ օրենքը համարյա բոլոր իրավիճակներում ուժի մեջ է։ Սակայն այստեղ ճակատագրական մի սխալ կար։ Եթե սև խոռոչը էնտրոպիա ունի, ապա պետք է որ այն նաև ջերմաստիճան ունենա։ Իսկ որոշակի ջերմաստիճան ունեցող ամեն մարմին պետք է ինչ֊որ չափով ճառագայթի։ Հայտնի է, որ երբ շամփուրը տաքացվում է կրակի բոցի մեջ և կաս֊կարմիր է դառնում, այն ճառագայթ է արձակում, բայց ցածր ջերմաստիճանում գտնվող մարմինները ևս ճառագայթում են, թեև այնքան թույլ, որ սովորաբար նշմարելի չէ։ Այդպիսի ճառագայթումը պայմանավորված է թերմոդինամիկայի երկրորդ օրենքով։ Հետևաբար, սև խոռոչները պետք է որ ճառագայթներ արձակեն։ Սակայն, ըստ սահմանման, սև խոռոչներն այնպիսի մարմիններ են, որոնցից ոչինչ չի կարող հեռանալ։ Թվում է, հետևաբար, որ պատահութային հորիզոնի մակերեսը չի կարելի նույնացնել էնտրոպիայի հետ։ 1972֊ին Բրանդոն Քարտերի և իմ ամերիկացի կոլեգա Ջիմ Բարդինի հետ ես մի հոդվածով հանդես եկա, ուր մենք նշեցինք, որ թեև որոշ նմանություն կա էնտրոպիայի և պատահութային հորիզոնի մակերեսի միջև, սակայն գոյություն ունի այդ ակնհայտ ճակատագրական դժվարությունը։ Խոստովանում եմ, որ հոդվածը գրելուն ինձ մասամբ մղել էր իմ դժգոհությունն այն բանից, որ Բեկենշտեյնն ըստ իս, չարաշահել էր իմ հայտնագործությունը՝ պատահութային հորիզոնի մակերեսի մեծացման վերաբերյալ։ Հետագայում պարզվեց, սակայն, որ նա հիմնականում ճիշտ էր, թեև այն մի առումով, որն, իհարկե, ինքը չէր կարող ակնկալել։
1973֊ին, երբ ես այցելեցի Մոսկվա, սև խոռոչների մասին զրուցեցի երկու առաջնակարգ խորհրդային մասնագետներ Յակով Զելդովիչի և Ալեքսանդր Ստարոբինսկու հետ։ Նրանք ինձ համոզեցին, որ ըստ քվանտային մեխանիկայի անորոշության սկզբունքի, պտտվող սև խոռոչները պետք է առաջացնեն և արտազատեն մասնիկներ։ Ֆիզիկական առումով նրանց փաստերը համոզիչ էին, բայց ինձ դուր չեկավ այն մաթեմատիկական ապարատը, որով նրանք ճառագայթման հաշվարկումներ էին կատարել։ Հետևաբար, ես աշխատեցի ավելի կատարյալ մաթեմատիկական ապարատ ստեղծել, որի մասին զեկուցեցի 1973֊ի նոյեմբերի վերջին Օքսվորդում կայացած ոչ պաշտոնական սեմինարում։ Այդ ժամանակ ես դեռ ճառագայթման քանակական հաշվումներ դեռ չէի կատարել։ Սպասում էի, որ այդ քանակությունը կհամընկնի պտտվող սև խոռոչների համար Զելդովիչի և Ստարոբինսկու ճառագայթման կանխագուշակումներին։ Սակայն հաշվումների ավարտից հետո պատկերացրեք իմ զարմանքն ու դժգոհությունը, երբ պարզվեց, որ նույնիսկ չպպտվող սև խոռոչներն են մասնիկներ առաջացնում և արտազատում կայուն արագությամբ։ Սկզբում ես մտածեցի, որ այս առաքումը նշանակում է, թե իմ օգտագործած մոտավորություններից մեկն ընդունելի չէ։ Ես մտահոգված էի, որ եթե Բեկենշտեյնն իմանար այդ մասին, նա այդ փաստը ևս կօգտագործեր ի հաստատումն սև խոռոչների էնտրոպիայի գաղափարի, որին ես կողմնակից չէի։ Բայց ես որքան մտածում էի այդ մասին, այնքան համոզվում էի, որ մոտավորություններն իսկապես ընդունելի են։ Մասնիկների արձակման հավաստիությանը ես վերջնականապես հավատացի այն ժամանակ, երբ պարզվեց, որ արձակված մասնիկների սպեկտրը կատարելապես համընկնում է տաք մարմնի արձակած տվյալների հետ, և, որ սև խոռոչի արձակած մասնիկների քանակությունը ճշգրտորեն համընկնում է թերմիդինամիկայի 2-րդ օրենքին։ Դրանից հետո նույնանման հաշվումներ են կատարվել տարբեր ձևերով, տարբեր գիտնականների կողմից։ Բոլոր հաշվումները ցույց տվեցին, որ սև խոռոչը պետք է տաք մարմնի նման մասնիկներ և ճառագայթում արձակի տվյալ ջերմաստիճանում, որը կախված է սև խոռոչի զանգվածից։ Որքան զանգվածը մեծ է, այնքան ցածր է ջերմաստիճանը։
Իսկ այդ ինչպե՞ս է պատահում, որ սև խոռոչը, պարզվում է, մասնիկներ է առաքում, երբ մենք գիտենք, որ նրա պատահութային հորիզոնից ոչինչ դուրս պոկվել չի կարող։ Դրա պատասխանը, համաձայն քվանտային մեխանիկայի, այն է, որ մասնիկները ոչ թե սև խոռոչի ներսից են գալիս, այլ այն «դատարկ» տարածությունից, որը գտնվում է պատահութային հորիզոնից փոքր֊ինչ դուրս։ Այս բանը կարելի է հասկանալ հետևյալ ձևով։ Այն ինչ մենք կոչում ենք «դատարկ» տարածություն, լրիվ դատարկ չի կարող լինել, քանի որ դա կնշանակեր, որ բոլոր տեսակի դաշտերը, ինչպես օրինակ, գրավիտացիոն կամ էլեկտրամագնիսական դաշտերը, պետք է լինեն զերո։ Սակայն դաշտի մեծությունը և նրա փոփոխման արագությունն ըստ ժամանակի նման են համապատասխանաբար մասնիկի դիրքին և արագությանը, որոնք որոշվում են ըստ անորոշության սկզբունքի՝ որքան ավելի ճշգրիտ իմանանք դրանցից մեկը, այնքան ավելի նվազ ճշգրիտ կիմանանք մյուսը։ Հետևաբար, դատարկ տարածության մեջ դաշտի մեծությունը չի կարելի ճշգրտորեն ընդունել զերոյին հավասար, որովհետև այդ դեպքում երկուսն էլ՝ և՛դաշտի մեծությունը, և՛ դրա փոփոխությունն ըստ ժամանակի ճշգրիտ (զերո) արժեք կունենան։ Պետք է, որ նվազագույն չափի անորոշություն լինի, կամ դաշտի մեծության մեջ լինեն քվանտային տատանումներ։ Այդ տատանումները կարելի է ընդունել որպես լույսի կամ գրավիտացիայի մասնիկների զույգեր, որոնք որոշ ժամանակ միասին են երևում, հեռանում են իրարից և ապա նորից միանում ու ոչնչացնում են իրար։ Այդ մասնիկները վիրտուալ մասնիկներ են, ինչպես այն մասնիկները, որոնք կրում են արեգակի գրավիտացիոն ուժը, և, ի տարբերություն իրական մասնիկների, դրանք ուղղակի դիտարկման ենթակա չեն մասնիկային դետեկտորով։ Սակայն վիրտուալ մասնիկների աննուղակի ազդեցությունը, ինչպես ատոմի և էլեկտրոնի ուղեծրերի էներգիայի փոքր փոփոխությունները, կարելի է չափել, ինչը մեծ ճշտությամբ համընկնում է տեսական հաշվումների հետ։ Անորոշության սկզբունքը նույնպես կանխագուշակում է, որ նյութական մասնիկների, ինչպիսիք են էլեկտրոնները կամ քվարկները, նմանատիպ վիրտուալ զույգեր պետք է լինեն։ Այս դեպքում, սակայն, զույգի մի անդամը կլինի մասնիկ, մյուսը՝ հակամասնիկ։ (Լույսի և գրավիտացիայի հակամասնիկները նույնն են, ինչ մասնիկներինը)։
Որովհետև ոչնչից էներգիա ստանալ հնարավոր չէ, ուստի մասնիկ֊հակամասնիկ զույգերից մեկը պետք է ունենա դրական էներգիա, մյուսը՝ բացասական։ Քանի որ իրական մասնիկները բնական պայմաններում ունեն դրական էներգիա, ապա բացասական էներգիան ստիպված պետք է վերագրել կարճատև կյանք ունեցող վիրտուալ մասնիկներին։ Հետևաբար, վիրտուալ մասնիկը փնտրելու է իր զուգընկերոջը և ոչնչանալու է նրա հետ։ Մեծ զանգված ունեցող մարմնից հեռու գտնվող իրական մասնիկի էներգիան մեծ կլինի մարմնի մեջ պարփակված վիճակում նրա էներգիայից, քանի որ նրան մարմնից հեռացնելիս հարկավոր է աշխատանք կատարել գրավիտացիոն ձգողության դեմ։ Բնական պայմաններում մասնիկի էներգիան դեռևս դրական է, բայց, քանի որ սև խոռոչի գրավիտացիոն դաշտը շատ հզոր է, այնտեղ ընկնելիս նույնիսկ իրական մասնիկը կունենա բացասական էներգիա։ Հնարավոր է նաև, որ բացասական էներգիա ունեցող վիրտուալ մասնիկն ընկնի սև խոռոչի մեջ և վերափոխվի իրական մասնիկի կամ հակամասնիկի։ Այս դեպքում վիրտուալ մասնիկն իր զուգընկերոջ հետ չի ոչնչանա։ Նրա լքյալ զուգընկերը նույնպես կարող է ընկնել սև խոռոչի մեջ, կամ, օժտված լինելով դրական էներգիայով, կարող է նաև հեռանալ սև խոռոչի մոտակայքից՝ որպես իրական մասնիկ կամ հակամասնիկ (նկ․ 7.4)։ Հեռվից դիտորդին կթվա, թե դա սև խոռոչից է արձակվել։ Եվ որքան փոքր է սև խոռոչը, այնքան ավելի կարճ ճանապարհ կանցնի բացասական էներգիա ունեցող մասնիկը մինչև իրական մասնիկ դառնալը, հետևաբար այնքան մեծ կլինի առաքման արագությունը և սև խոռոչի թվացող ջերմաստիճանը։
Սև խոռոչից արձակվող ճառագայթման դրական էներգիան հավասարակշռվում է սև խոռոչ ներհոսող մասնիկների բացասական էներգիայով։ Համաձայն Էյնշտեյնի հավասարման՝ E=mc² (որտեղ E֊ն էներգիան է, m֊ը՝ զանգվածը, իսկ c֊ն՝ լույսի արագությունը), էներգիան համեմատական է զանգվածին։ Հետևաբար, բացասական էներգիայի ներհոսքը սև խոռոչ նվազեցնում է վերջինիս զանգվածը։ Իսկ սև խոռոչի զանգվածի նվազումը բերում է պատահութային հորիզոնի մակերեսի փոքրացման։ Այսինքն սև խոռոչի էնտրոպիան նվազում է։ Սակայն այս նվազումը առավել քան հակակշռվում է առաքված ճառագայթման էնտրոպիայով, և, հետևաբար, թերմոդինամիկայի երկրորդ օրենքը չի խախտվում։
Դեռ ավելին, որքան փոքր է սև խոռոչի զանգվածը, այնքան բարձր է նրա ջերմաստիճանը։ Այսպիսով խոռոչի զանգվածի նվազմանը զուգընթաց նրա ջերմաստիճանը բարձրանում է, արձակման արագությունն աճում և, հետևաբար, այն ավելի արագ է զանգված կորցնում։ Թե ինչ կպատահի, երբ սև խոռոչի զանգվածն ի վերջո չափազանց փոքրանա, հնարավոր չէ որոշակիորեն ասել, բայց ամենատրամաբանական ենթադրությունն այն է, որ սև խոռոչը լրիվ կանհետանա վերջին արձակման ուժգին պայթյունից, որի հզորությունը կհամապատասխանի միլիոնավոր ջրածնային ռումբերի պայթման։
Արեգակից մի քանի անգամ ավելի մեծ զանգված ունեցող սև խոռոչի ջերմաստիճանը բացարձակ զերոյից կարող է լոկ մեկի տաս միլիոներորդ աստիճանով բարձր լինել։ Սա անհամեմատ ավելի ցածր է, քան տիեզերքը լցնող միկրոալիքային ճառագայթման ջերմաստիճանը, որը բացարձակ զերոյից բարձր է մոտավորապես 2,7 աստիճանով։ Այսպիսով, մեծ զանված ունեցող սև խոռոչներն ավելի շատ էներգիա կկլանեն, քան կարձակեն։ Եթե տիեզերքը շարունակի հավերժ ընդլայնվել, ապա ի վերջո միկրոալիքային ճառագայթման ջերմաստիճանը պիտի նվազի և ավելի ցածր լինի այդպիսի սև խոռոչների ջերմաստիճանից, որոնք պիտի սկսեն ճառագայթել և զանգված կորցնել։ Սակայն մեծ զանգված ունեցող սև խոռոչների ջերմաստիճանը նույնիսկ այն ժամանակ այնքան ցածր կլիներ, որ միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն (մեկից հետո 66 զերո) տարի կպահանջվի, որ այդպիսի սև խոռոչները գոլորշիանան։ Այս ժամանակամիջոցն ավելի մեծ է, քան տիեզերքի տարիքը, որը տասից քսան հազար միլիոն տարի է (մեկ կամ երկուսից հետո 10 զերո)։ Մյուս կողմից, ինչպես 6֊րդ գլխում ասվեց, կարող են գոյություն ունենալ շատ ավելի փոքր զանգված ունեցող նախասկզբնական սև խոռոչներ, որոնք առաջացած լինեն տիեզերքի սկզբնավորման ժամանակ առկա անկանոնությունների կոլապսի հետևանքով։
Այսպիսի սև խոռոչների ջերմաստիճանը շատ ավելի բարձր կլինի և, հետևաբար, ճառագայթման արագությունը՝ շատ մեծ։ Հազար միլիոն տոննա սկզբնական զանգված ունեցող նախասկզբնական սև խոռոչի կյանքի տևողությունը կլինի մոտավորապես տիեզերքի տարիքի չափ։ Այն սկզբնական սև խոռոչները, որոնց զանգվածներն ավելի փոքր են, այժմ լրիվ գոլորշիացած կլինեն, իսկ նրանք, որոնց զանգվածները փոքր֊ինչ ավելի մեծ են, դեռևս կշարունակեն ռենտգենյան կամ գամմա ճառագայթներ առաքել։ Այս ռենտգենյան և գամմա ճառագայթները նման են լույսի ալիքների, թեև նրանց երկարությունը շատ ավելի կարճ է։ Այսպիսի խոռոչները հազիվ թե սև համարվեն, իրականում սրանք սպիտակ և տաք են ու մեկ վայրկյանում մոտավորապես տասը հազար Մեգավատտ էներգիա են առաքում։
Եթե հնարավոր լիներ օգտվել, այդպիսի սև խոռոչի առաքած էներգիայից, ապա կարելի էր էներգիայի 10 հզոր կայաններ աշխատեցնել։ Սակայն այս հարցի լուծումը շատ դժվար է։ Այդպիսի սև խոռոչի զանգվածը մոտավորապես հավասար կլինի մի մեծ լեռան զանգվածի, որը սեղմված է մոտ մեկի մեկուկես հարյուր հազար միլիոներորդ խորանարդ սանտիմետր ծավալում, այսինքն՝ ատոմի միջուկի ծավալի չափ ծավալում։ Եթե այդպիսի մի սև խոռոչ տեղադրվի երկրի մակերևույթին, ապա ոչ մի ուժ չի կարող խանգարել, որպեսզի այն չընկնի երկրի կենտրոն։ Սև խոռոչը կտատանվի կենտրոնից դեպի մակերևույթ և հակառակը, մինչև վերջնականապես նստի երկրի կենտրոնում։ Հետևաբար, եթե մենք ուզում ենք օգտագործել սև խոռոչի էներգիան, ապա այն պետք է երկրաշուրջ ուղեծիր դուրս բերել։ Իսկ որպեսզի սև խոռոչը պտտվի երկրի շուրջը, հարկավոր է բավական հզոր մի ձգող զանգված դնել նրա առջևում՝ նրան ուղեծիր դուրս բերելու համար, համառ ավանակի առաջ ստեպղին դնելու նման։ Սա գործնական առաջարկություն չի կարող լինել գոնե մոտավոր ապագայի համար։
Եթե հնարավոր չէ օգտագործել նախասկզբնական սև խոռոչների ճառագայթումը, ապա դրանց դիտարկման ի՞նչ հնարավորություններ կան։ Մենք կարող ենք փնտրել այն գամմա ճառագայթները, որոնք առաքում են նախասկզբնական սև խոռոչներն իրենց գոյատեևման համարյա ամբողջ ընթացքում։ Թեև մեծ մասի ճառագայթումը կարող է թույլ լինել, որովհետև այն հեռվից է գալիս, սակայն բոլորինը միասին վերցրած հնարավոր է հայտնաբերել։ Գամմա ճառագայթման նման ֆոն մենք դիտարկել ենք։ Նկ․ 7.5֊ը ցույց է տալիս, որ դիտարկված ինտենսիվությունը[15] տարբեր է տարբեր հաճախականություններում (վայրկյանում ալիքների թիվը)։[16] Այնուամենայնիվ, այս ֆոնի առաջացման պատճառը նախասկզբնական սև խոռոչներից բացի նաև այլ պրոցեսներ են, ինչը հավանաբար, իրոք այդպես է։ Նկ․ 7.6֊ում կետագծերով կորը ցույց է տալիս, թե ինչպես պետք է փոխվի նախասկզբնական սև խոռոչների առաքած գամմա ճառագայթման ինտենսիվությունն ըստ հաճախականության, եթե մեկ խորանարդ լուսատարի ծավալում միջին հաշվով լինեին 30 սև խոռոչներ։ Կարելի է ասել, որ գամմա ճառագայթման ֆոնի փորձնական տվյալները (դիտարկված կորը) նախասկզբնական սև խոռոչների առկայության դրական ապացույց չեն, բայց խոսում են այն մասին, որ միջին հաշվով մեկ խորանարդ լուսատարի ծավալում սև խոռոչների թիվը 300֊ից ավելի չի կարող լինել։ Այս սահմանափակումը նշանակում է, որ նախասկզբնական սև խոռոչների զանգվածը կարող է ամենաշատը լինել տիեզերքում գոյություն ունեցող նյութի մեկ միլիոներորդի չափ։
Քանի որ նախասկզբնական սև խոռոչների թիվը շատ փոքր է, ապա անհավանական է, որ նրանցից մեկը գտնվեր մեր երկրին այնքան մոտիկ, որ կարողանայինք դիտարկել նրա գամմա ճառագայթումը։ Մյուս կողմից, որովհետև գրավիտացիոն նախասկզբնական սև խոռոչներին կձգի դեպի ցանկացած նյութ, ապա նրանց թիվը գալակտիկաներում կամ նրանց մոտակայքում ավելի մեծ կլինի։ Ճիշտ է, նրանց թիվը միջին հաշվով մեկ խորանարդ լուսատարում 300֊ից ավելի չի կարող լինել, սակայն մեր ունեցած տվյալներից հնարավոր չէ իմանալ, թե նրանց թիվը որքան է մեր սեփական գալակտիկայում։
Եթե, ասենք, նրանց թիվը մեր գալակտիկայում այս թվից նույնիսկ մեկ միլիոն անգամ շատ լիներ, ապա ամենամոտիկ սև խոռոչը կգտնվեր երկրից հազար միլիոն կիլոմետր հեռավորության վրա, կամ այնքան, որքան հեռու է մեզանից ամենահեռավոր մոլորակը՝ Պլուտոնը։ Նույնիսկ այսքան մոտ հեռավորության վրա գտնվող սև խոռոչի արձակած կայուն ճառագայթումն անհնար կլիներ հայտնաբերել, եթե այն տասը հազար Մեգավատտ հզորություն ունենար։ Որպեսզի մարդ կարողանա նախասկզբնական սև խոռոչը դիտել, հարկավոր է, որ մի քանի քվանտ գամմա ճառագայթներ գան նույն ուղղությամբ, որոշակի ժամանակամիջոցում՝ ասենք մեկ շաբաթվա ընթացքում։ Այլապես ճառագայթումը ֆոնի պարզապես մի մասը կկազմի։ Սակայն, որովհետև գամմա ճառագայթները մեծ հաճախականություն ունեն, ապա համաձայն Պլանկի քվանտային սկզբունքի, գամմա ճառագայթի քվանտի էներգիան շատ մեծ կլինի, և, հետևբար, նույնիսկ տասը հազար Մեգավատտ ճառագայթման համար շատ քվանտներ պետք չեն։ Եվ որպեսզի դիտվի այս մի քանի քվանտի էներգիան, որը առաքվում է Պլուտոնի հեռավորությունից, հարկավոր է ունենալ ավելի խոշոր դետեկտոր, քան մինչև հիմա կառուցվածները։ Դեռ ավելին, դետեկտորը պետք է տեղավորել մթնոլորտից դուրս տարածության մեջ, քանի որ գամմա ճառագայթների համար երկրի մթնոլորտը անթափանցելի է։
Իհարկե, եթե Պլուտոնի հեռավորության վրա գտնվող սև խոռոչը հասներ իր կյանքի վերջին և պայթեր, ապա հեշտ կլիներ հայտնաբերել վերջնական բռնկման ճառագայթումը։ Սակայն, եթե սև խոռոչն արդեն տասը կամ քսան հազար միլիոն տարի ճառագայթել է, հազիվ թե մի քանի տարվա ընթացքում հասնի իր վերջին։ Ավելի հավանական է, որ այն մի քանի միլիոն տարի առաջ է պայթել, կամ նույնքան ժամանակ հետո ապագայում պիտի պայթի։ Հետևաբար, եթե ցանկանում եք վերջնական մի պայթյուն դիտել ձեր ասպիրանտուրայի ժամկետը վերջանալուց առաջ, հարկավոր է մի այնպիսի եղանակ մշակել, որպեսզի կարողանաք մոտավորապես մեկ լուսատարի հեռավորության վրա տեղի ունեցող պայթյունը գրանցել։ Մի քանի գամմա ճառագայթային քվանտներ հայտնաբերելու համար դեռ հարկ կլինի լուծել խոշոր գամմա ճառագայթման դետեկտորի պրոբլեմը։ Այնուամենայնիվ, պայթման դեպքի համար պարտադիր չէ որոշել, թե բոլոր քվանտներն են արդյոք նույն ուղղությամբ գալիս։ Բավական է, որ բոլոր քվանտները կարճ ժամանակամիջոցում տեղ հասնեն, որպեսզի վստահ լինեք, որ դրանք գալիս են նույն պայթման աղբյուրից։
Նախասկզբնական սև խոռոչների հայտնաբերման համար գամմա ճառագայթման լավագույն դետեկտորը երկրագնդի ամբողջ մթնոլորտն է։ (Համենայնդեպս, անհնարին է ավելի խոշոր դետեկտոր կառուցել)։ Երբ մեծ էներգիա կրող գամմա ճառագայթի քվանտը հարվածում մթնոլորտում գտնվող ատոմներին, առաջացնում է էլեկտրոնների և պոզիտրոնների (հակաէլեկտրոն) զույգեր։ Երբ սրանք են հարվածում ուրիշ ատոմներին, էլեկտրոնների և պոզիտրոնների նոր զույգեր են ծնվում, և արդյունքում առաջանում է այն, ինչը կոչվում է էլեկտրոնային տեղատարափ։ Արդյունքը մի տեսակ լուսավորություն է, որը կոչվում է չերենկովյան ճառագայթում։ Այսպիսով, կարելի է գամմա ճառագայթման բռնկումները հայտնաբերել գիշերային երկնակամարում՝ լույսի փայլատակումներ դիտելով։ Իհարկե, կան մի շարք այլ երևույթներ, ինչպես կայծակը, վայր ընկնող արբանյակների անդրադարձրած արևի լույսը և երկրի շուրջ պտտվող բեկորները, որոնք կարող են երկնակամարում փայլատակումներ առաջացնել։ Գամմա ճառագայթման բռնկումները կարելի է մյուս երևույթներից տարբերել, եթե միաժամանակ դիտարկումներ կատարվեն իրարից հեռու գտնվող երկու կամ ավելի տարբեր դիրքերից։ Դուբլինից երկու գիտնական՝ Նեյլ Պորտերը և Թրևըր Ուիքսը նման դիտարկումներ կատարեցին Արիզոնայում (ԱՄՆ) տեղադրված հեռադիտակներով։ Որոշ թվով փայլատակումներ դիտվեցին, սակայն, դրանցից ոչ մեկը չէր կարելի վերագրել սև խոռոչներից արձակված գամմա ճառագայթների բռնկումներին։
Եթե նախասկզբնական սև խոռոչների փնտրտուքները բացասական արդյունք տան, ինչը երևի հնարավոր է, ապա միևնույն է, դրանով կարևոր տեղեկություններ կստանանք տիեզերքի սկզբնական վիճակների մասին։ Եթե վաղ տիեզերքը գտնվեր քաոսային և անկանոն վիճակում և կամ, եթե նյութի ճնշումը ցածր լիներ, կարելի էր սպասել, որ ավելի մեծ թվով նախասկզբնական սև խոռոչներ կառաջանային, քան այն, ինչ ցույց է տալիս մեր դիտարկումների հիման վրա ստացված գամմա ճառագայթման ֆոնը։ Եթե սկզբնական տիեզերքը շատ հարթ ու համաչափ լիներ, և ճնշումը՝ բարձր, ապա միայն այդ դեպքում կարելի կլիներ բացատրել դիտարկելի թվով նախասկզբնական սև խոռոչների բացակայությունը։
- * *
Սև խոռոչներից ճառագայթման գաղափարը հիմնականում ընդհանուր հարաբերականության և քվանտային մեխանիկայի՝ դարիս երկու մեծ տեսությունների օգնությամբ կատարված կանխագուշակման առաջին օրինակն էր։ Այս գաղափարը սկզբում շատ մեծ դիմադրության հանդիպեց, որովհետև տակնուվրա արեց ընդունված տեսակետը՝ «սև խոռոչը ինչպե՞ս կարող է որևէ բան արձակել»։ Երբ Օքսվորդի մոտ գտնվող Ռեզերֆորդ֊ Ապելտոն լաբորատորիայում տեղի ունեցող մի գիտաժողովում ես առաջին անգամ հաղորդեցի իմ հաշվարկների արդյունքները, դա ընդունվեց ընդհանուր կասկածամտությամբ։ Իմ զեկուցման ավարտին նստաշրջանի նախագահը՝ Լոնդոնի Թագավորական քոլեջից Ջոն Գ․ Թեյլորը պնդեց, որ դա անմտություն է։ Նա նույնիսկ մի հոդված գրեց այդ մասին։ Այնուամենայնիվ, ի վերջո մեծամասնությունը, ներառյալ Ջոն Թեյլորը, եկան այն եզրակացության, որ սև խոռոչները տաք մարմինների նման պետք է ճառագայթեն, եթե մեր մյուս պատկերացումները ընդհանուր հարաբերականության և քվանտային մեխանիկայի մասին ճիշտ են։ Այսպիսով, թեև մեզ առայժմ չի հաջողվել նախասկզբնական սև խոռոչ հայտնաբերել, սակայն գրեթե բոլորը համաձայն են, որ եթե այդպիսին հայտնաբերվի, ապա բավական մեծ քանակությամբ գամմա և ռենտգենյան ճառագայթներ կառաքի։
Սև խոռոչների ճառագայթման առկայությունը նշանակում է, որ գրավիտացիոն կոլապսն այնքան վերջնական և անդարձելի չէ, որքան սկզբում մտածում էինք։ Եթե տիեզերագնացն ընկնի սև խոռոչի մեջ, վերջինիս զանգվածը կաճի, բայց ի վերջո այդ հավելյալ զանգվածին համապատասխան էներգիա առաքվում է տիեզերք՝ որպես ճառագայթում։ Հետևաբար, տիեզերագնացը յուրահատուկ մի «շրջապտույտ» է կատարում։ Սա խեղճուկրակ անմահություն է, որովհետև տիեզերագնացի համար ամեն տեսակի անհատական ժամանակի հասկացություն վերջանում է, երբ նա սև խոռոչի մեջ կտոր֊կտոր է լինում։ Նույնիսկ, վերջին հաշվով, սև խոռոչից արձակվող մասնիկների տեսակները բոլորովին տարբեր կլինեն այն մասնիկներից, որոնցից կազմված էր տիեզերագնացը։ Այն, ինչ մնում է տիեզերագնացից, դա նրա զանգվածը կամ էներգիան է։
Սև խոռոչից առաքված ճառագայթումը որոշելու համար կիրառած մոտավորություններն ուժի մեջ են, երբ սև խոռոչի զանգվածը գրամի մասից մեծ է։ Սակայն, երբ սև խոռոչի վերջը մոտենում է, նրա զանգվածը շատ է փոքրանում, իմ օգտագործած մոտավորություններն անիմաստ են դառնում։ Թվում է, թե ամենահավանական ելքը կլինի այն, որ սև խոռոչը կչքանա առնվազն տիեզերքի մի տիրույթում՝ իր հետ տանելով տիեզերագնացին, և իր մեջ ունեցած ամեն եզակիություն, եթե, իհարկե, այդպիսի գոնե մեկը կա։ Սա ընդհանուր հարաբերականության կանխագուշակված եզակիություններից ձերբազատվելու առաջին նշաններից մեկն էր, որն իրականացվում է՝ շնորհիվ քվանտային մեխանիկայի։ Այնուամենայնիվ, 1974֊ին և ուրիշների կողմից օգտագործված մեթոդներն ի վիճակի չեղան պատասխանելու այն հարցին, թե քվանտային գրավիտացիայի միացյալ տեսությունն արդո՞ք հնարավոր է համարում եզակիության առաջացումը:1975֊ից սկսած ես սկսեցի մշակել քվանտային գրավիտացիայի հարցերը լուծելու ավելի հզոր մի մոտեցում, որը հիմնված է Ռիչարդ Ֆեյնմանի պատմությունների գումարի գաղափարի վրա։ Հաջորդ երկու գլուխներում կնկարագրվի, թե այդ մոտեցումը ինչպիսի պատասխաններ է առաջարկում տիեզերքի սկզբնավորման, նրա ապագայի և պարունակության, ինչպես, օրինակ, տիեզերագնացների մասին։
Մենք կտեսնենք, որ թեև անորոշության սկզբունքը սահմանափակում է կանխագուշակումների ճշգրտությունը, սակայն, միևնույն ժամանակ ազատում է մեզ այն հիմնական անկանխատեսելիությունից, որն ի հայտ է գալիս տարածություն֊ժամանակի եզակիության դեպքում։
8
Տիեզերքի սկզբնավորումն ու ապագան
Էյնշտեյնի հարաբերականության ընդհանուր տեսությունն ինքնուրույն կանխագուշակում էր, որ տարածություն֊ժամանակը սկիզբ է առել Մեծ պայթյունի եզակիությունից և վերջ կգտնի կամ Մեծ ճայթյունի եզակիությամբ (եթե տիեզերքն ամբողջապես նորից կոլապսի ենթարկվի) և կամ սև խոռոչային եզակիությամբ (եթե ինչ֊որ տեղայնացված մի տիրույթ, ինչպես աստղը, կոլապսի ենթարկվի)։ Խոռոչն ընկնող ամեն նյութ եզակիությունում ոչնչանալու է, և խոռոչից դուրս լոկ նրա զանգվածի գրավիտացիոն ազդեցությունը պիտի շարունակի գործել։ Մյուս կողմից, երբ սկսեցին հաշվի առնել քվանտային ազդեցությունները, թվաց, թե նյութի զանգվածը կամ էներգիան ի վերջո պետք է վերադառնա տիեզերքի մնացյալ մաս, և սև խոռոչն իր մեջ եղած եզակիության հետ միասին պետք է ցնդի ու անհետանա։ Քվանտային մեխանիկան արդյո՞ք նմանօրինակ ցնցող ազդեցություն կարող է ունենալ Մեծ պայթյունի և Մեծ ճայթյունի եզակիությունների վրա։ Իրականում ի՞նչ կպատահեր տիեզերքի ամենավաղ և ամենաուշ փուլերում, երբ գրավիտացիոն դաշտերն այն աստիճան հզոր լինեին, որ այլևս հնարավոր չլիներ անտեսել քվանտային ազդեցությունները։ Տիեզերքն իսկապես սկիզբ կամ վերջ ունի՞։ Եթե այո, ապա ի՞նչ տեսք ունեն դրանք։
1970֊ական թվականներին ես ուսումնասիրում էի հիմնականում սև խոռոչները, բայց 1981֊ին տիեզերքի սկզբնավորման և ապագայի հարցերի նկատմամբ իմ հետաքրքրությունը վերարթնացավ, երբ ներկա եղա Վատիկանում ճիզվիտների կազմակերպած տիեզերագիտական համաժողովին։ Կաթոլիկ եկեղեցին անցյալում կոպիտ սխալ էր գործել Գալիլեոյի նկատմամբ, երբ գիտական հարց լուծելիս փորձել էր պարտադրել իր եկեղեցական օրենքը՝ հայտարարելով, թե արեգակն է պտտվում երկրի շուրջ։ Այժմ, դարեր անց, որոշվել էր մի խումբ մասնագետներ հրավիրել, որպեսզի նրանք տիեզերագիտական հարցերի մասին խորհուրդներ տային եկեղեցուն։ Համաժողովի ավարտին պապն ընդունեց մասնակիցներին։ Նա մեզ ասաց, թե ընդունելի է տիեզերքի էվոլյուցիան Մեծ պայթյունից հետո ուսումնասիրելը, բայց չպետք է խորամուխ լինել Մեծ պայթյունի մեջ, որովհետև դա հենց արարման պահն է և, հետևաբար, Աստծո գործը։ Ես երջանիկ էի, որ պապն անտեղյակ էր իմ զեկուցման նյութին, որով հանդես գալով համաժողովում, ես խոսել էի այն մասին, թե հնարավոր է, որ տարածություն֊ժամանակը վերջավոր լինի, բայց և սահման չունենա։ Այս բանը նշանակում էր, որ տիեզերքը չի ունեցել սկիզբ և չի եղել Արարման պահ։ Ես ցանկություն չունեի արժանանալ Գալիլեոյի բախտին, որի հետ նույնանալու մեծ միտվածություն եմ միշտ ունեցել, մասամբ այն զուգադիպության պատճառով, որ ծնվել եմ նրա մահվանից ուղիղ 300 տարի հետո։
Որպեսզի բացատրեմ իմ և ուրիշների գաղափարներն այն մասին, թե քվանտային մեխանիկան ինչպես կարող է ազդել տիեզերքի սկզբնավորման և ապագայի վրա, անհրաժեշտ է ամենից առաջ հասկանալ տիեզերքի համընդհանուր հավանության արժանացած պատմությունը, համաձայն այն պատկերացման, որը կոչվում է «տաք մեծ պայթյունի մոդել»։ Ենթադրվում է, որ տիեզերքը նկարագրվում է ըստ Ֆրիդմանյան մոդելի՝ Մեծ պայթյունից սկսած։ Համաձայն այս մոդելների, ընդարձակվելուն զուգընթաց նրա պարունակած նյութերն ու ճառագայթումը սառչում են։(Երբ տիեզերքը կրկնակի ընդարձակվի, ապա ջերմաստիճանը կիսով չափ կնվազի)։ Քանի որ ջերմաստիճանը պարզապես միջին էներգիայի կամ մասնիկների արագության չափանիշն է, ուստի տիեզերքի սառչելը մեծապես կազդի իր մեջ պարունակած նյութի վրա։ Բարձր ջերմաստիճանում մասնիկներն այնպիսի մեծ արագությամբ կշարժվեն, որ միջուկային ու էլեկտրոմագնիսական ուժերի շնորհիվ կհաղթահարեն ցանկացած ձգողություն, սակայն, քանի որ դրանք սառչում են, ապա սպասելի է, որ մասնիկների միջև գործող ձգողական ուժի շնորհիվ դրանք սկսեն խմբեր կազմել։ Դեռ ավելին, ջերմաստիճանից է կախված այն, թե ինչ տեսակի մասնիկներ կարող են գոյություն ունենալ տիեզերքում։ Բավականին բարձր ջերմաստիճաններում մասնիկների էներգիան այնքան մեծ է, որ իրար հետ բախվելիս կառաջանան բազմատեսակ մասնիկ֊հակամասնիկ զույգեր։ Եվ չնայած այդ մասնիկների մի մասն իրենց հակամասնիկների հետ բախվելով կոչնչանան (կանիհիլանան), սակայն ծնվածների թիվն ավելի մեծ կլինի, քան ոչնչացածներինը։ Ցածր ջերմաստիճաններում, սակայն, երբ իրար հետ բախվող մասնիկների էներգիան փոքր է, մասնիկ֊հակամասնիկ զույգերի առաջացումը դանդաղ է լինում, և ոչնչացումը տեղի է ունենում ավելի արագ, քան առաջացումը։
Մեծ պայթյունի պահին, ենթադրվում է, որ տիեզերքի չափսը զերո էր, և, հետևաբար, այն անսահման տաք էր։ Բայց տիեզերքի ընդարձակմանը զուգընթաց՝ ճառագայթման ջերմաստիճանն ընկել է։ Մեծ պայթյունից մեկ վայրկյան անց ջերմաստիճանը պետք է մոտավորապես տասը հազար միլիոն աստիճանով ընկած լիներ։ Բավական է ասել, որ դա հազար անգամ բարձր է արեգակի կենտրոնի ջերմաստիճանից։ Այդպիսի բարձր ջերմաստիճաններ ստացվում են ջրածնային ռումբի պայթեցումների ժամաակ։ Տիեզերքն այդ ժամանակ առավելապես ֆոտոններ, էլեկտրոններ և նեյտրինոներ պետք է պարունակած լիներ (վերջիններս չափազանց թեթև մասնիկներ են, որոնց վրա միայն թույլ ուժերը և գրավիտացիան կարող են ներգործել), ինչպես նաև նրանց հակամասնիկները՝ որոշ թվով պրոտոնների և նեյտրոնների հետ միասին։ Մինչ տիեզերքը շարունակում էր ընդարձակվել, և ջերմաստիճանը՝ իջնել, բախումների հետևանքով էլեկտրոն֊հակաէլեկտրոն զույգերի առաջացման արագությունը պետք է որ նվազեր և իջներ դրանց անիհիլացմամբ ոչնչացման արագությունից։ Այսպիսով, էլեկտրոնների և հակաէլեկտրոնների (պոզիտրոն) մեծ մասն իրար արդեն ոչնչացրած և ֆոտոններ առաջացրած կլինեն, և շատ քիչ թվով էլեկտրոններ կլինեն մնացած։ Սակայն նեյտրինոներն ու հականեյտրինոներն անիհիլացված չեն լինի միմյանց, որովհետև այս մասնիկները միմյանց կամ այլ մասնիկների հետ շատ թույլ են փոխազդում։ Այսպիսով, նրանք մինչև օրս պետք է որ գոյություն ունենան։ Եթե մենք կարողանանք դիտել այդ մասնիկները, ապա դա կլինի տիեզերքի շատ տաք սկզբնավորումն ապացուցող լավագույն փաստը։ Սակայն, դժբախտաբար, նրանց էներգիան այսօր այնքան փոքր պետք է լինի, որ հնարավոր չլինի ուղղակի դիտել։ Բայց, եթե նեյտրինոները զանգվածից զուրկ չեն, այլ ունեն իրենց սեփական փոքր զանգվածը, ապա համաձայն 1981 թվականին ռուսների կողմից կատարված և դեռևս չհաստատված մի գիտափորձի, մենք կկարողանանք անուղղակիորեն հայտնաբերել դրանք։ Այդ մասնիկներն ի հայտ կգան «սև նյութի» մի այնպիսի ձևով, որի մասին վերևում նշվեց, և կունենան բավականին ուժեղ գրավիտացիոն ձգողական ուժ, որպեսզի արգելակեն տիեզերքի ընդարձակումը և պատճառ լինեն, որ այն դարձյալ կոլապսի ենթարկվի։
Մեծ պայթյունից հարյուր վայրկյան անց ջերմաստիճանը պետք է որ իջներ մինչև հազար միլիոն աստիճան, ինչը համապատասխանում է ամենատաք աստղերի ներսում եղած ջերմաստիճանին։ Այս ջերմաստիճանում պրոտոնների ու նեյտրոնների էներգիան այլևս չէր բավարարի, որպեսզի նրանք ձերբազատվեին ուժեղ միջուկային ուժի ձգողությունից և կմիանային ու դեյտերիումի (ծանր ջրածնի) ատոմների միջուկներ կառաջացնեին, որոնք պարունակում են մեկ պրոտոն և մեկ նեյտրոն։[17] Դեյտերիումի միջուկները կարող են միանալ պրոտոնների և նեյտրոնների հետ և առաջացնել հելիումի միջուկ, որը պարունակում է երկու պրոտոն և երկու նեյտրոն։ Կարող են առաջանալ նաև փոքր քանակությամբ ավելի ծանր երկու տարր․ լիթիում և բերիլիում։ Կարելի է հաշվարկներով պարզել, որ տաք մեծ պայթյունի մոդելում պրոտոնների և նեյտրոնների քառորդ մասը փոխարկված կլինեն հելիումի միջուկների, ինչպես նաև փոքր քանակությամբ ծանր ջրածնի և այլ տարրերի։ Ավելցուկ նեյտրոնները կքայքավեին և կառաջացնեին պրոտոններ, որոնք սովորական ջրածնի ատոմների միջուկներն են։
Տիեզերքի վաղ ջերմ փուլի վերոհիշյալ պատկերացումն առաջին անգամ առաջարկել է Գեորգի Գամովը 1948֊ին, իր հայտնի աշխատությունում, որը գրել է իր աշակերտ Ռալֆ Ալֆերի հետ։
Գամովը օժտված էր շատ նուրբ հումորով և համոզեց միջուկային գիտնական Հանս Բեթին, որպեսզի նա ևս իր անունը ավելացնի հողվածի հեղինակների անուններին և, այսպիսով հոդվածը գրված լինի «Ալֆեր, Բեթե, Գամով» հեղինակների կողմից, որը հիշեցնում է հունարեն այբուբենի առաջին երեք տառերի՝ «ալֆա, բետա, գամմա» հերթականությունը։ Դա շատ հարմար էր այնպիսի մի հոդվածի համար, որ վերաբերում էր տիեզերքի սկզբնավորմանը։ Այս աշխատությունում այն արժեքավոր կանխագուշակումն էր արվում, որ տիեզերքի շատ ջերմ հեռավոր փուլերում արձակված ճառագայթումը (ֆոտոնների ձևով) մինչև օրս իր գոյությունը պետք է պահած լինի, թեև շատ ցածր ջերմաստիճանում բացարձակ զերոյից (-273, 2°c) մի քանի աստիճան բարձր։[18] Ահա հենց այս ճառագայթումն էր, որ Պենզիասն ու Ուիլսոնը հայտնաբերել էին 1965֊ին։ Երբ Ալֆերը, Բեթեն և Գամովը հրատարակեցին իրենց աշխատությունը պրոտոնների և նեյտրոնների միջուկային ռեակցիայի մասին, շատ բան դեռ չգիտեինք։ Հետևաբար, տիեզերքի վաղ փուլերում տարբեր տարրերի հարաբերական քանակությունների կապակցությամբ արված կանխագուշակումները բավարար ճշգրիտ չէին, սակայն այս հաշվումները այժմ կրկնվել են նորագույն պատկերացումների հիման վրա և շատ լավ համընկնում են մեր ժամանակակից դիտարկումներին։ Դեռ ավելին, այլապես շատ դժվար կլիներ բացատրել, թե ինչո՞ւ պետք է այսքան մեծ քանակով հելիում գոյություն ունենար տիեզերքում։ Այդ պատճառով վստահությամբ կարող ենք ասել, որ մեր պատկերացումները տիեզերքի մասին, համենայն դեպս Մեծ պայթյունից մեկ վայրկյան անց, ճիշտ են։
Մեծ պայթյունից մի քանի ժամ հետո հելիումի և մյուս տարրերի առաջացումը կդադարի։ Դրանից հետ, հետագա միլիոնավոր տարիների ընթացքում, տիեզերքը շարունակ կընդարձակվի առանց որևէ արտակարգ փոփոխությայն։ Վերջապես, երբ ջերմաստիճանն իջնի մինչև մի քանի հազար աստիճան, էլեկտրոնների ու միջուկների էներգիան այլևս բավարար չեն լինի, որպեսզի նրանց միջև էլեկտրոմագնիսական ձգողությունը հաղթահարվի, և նրանք կսկսեն միավորվել և ատոմներ առաջացնել։ Ամբողջությամբ վերցրած՝ տիեզերքը կշարունակի իր ընդարձակումը և սառչելը, բայց այն տիրույթներում, որտեղ նյութը համեմատաբար ավելի խիտ է, քան միջին խտությունը, ընդարձակումը կդանդաղի՝ հավելյալ գրավիտացիոն ձգողության պատճառով։ Մի քանի տիրույթներում ընդարձակումը վերջնականապես կանգ կառնի, և դրանք կսկսեն վերստին կոլապսի ենթարկվել։ Կոլապսի ընթացքում այդ տիրույթներից դուրս գտնվող նյութի գրավիտացիոն ձգողությունը պատճառ կլինի, որ կծկվող այդ տիրույթները դանդաղորեն պտտվեն։ Կոլապսի ենթարկվող տիրույթների փոքրացմանը զուգընթաց, նրանց պտտման արագությունը կաճի ճիշտ այնպես, ինչպես չմշկորդի պտտման արագությունը սառույցի վրա, երբ վերջինս ծալում է ձեռքերը։ Վերջապես, երբ տիրույթը բավական փոքրանա, նրանք այնպիսի արագությամբ կպտտվեն, որ հավասարակշռվի գրավիտացիոն ձգողությունը, և արդյունքում ծնունդ կառնեն սկավառակաձև պտտվող գալակտիկաներ։ Այլ տիրույթներ, զրկված լինելով պտտական շարժումից, կփոխակերպվեն ձվաձև մարմինների, որոնք այժմ կոչվում են էլիպսաձև գալակտիկաներ։ Այս դեպքում տիրույթը կոլապսի չի ենթարկվում, քանի որ գալակտիկայի առանձին մասեր իրենց կենտրոնի նկատմամբ կշարունակեն պտտվել կայուն կերպով, բայց գալակտիկան ամբողջությամբ վերցված զրկված կլինի պտտական շարժումից։
Ժամանակի ընթացքում գալակտիկաներում ջրածին և հելիում գազերը կառաջացնեն փոքր ամպեր, որոնք իրենց գրավիտացիոն դաշտերի ազդեցության տակ կկոլապսվեն։ Կծկման ընթացքում նրանց մեջ գտնվող ատոմները կսկսեն բախվել միմյանց, գազի ջերմաստիճանը դրանով կբարձրանա, և, ի վերջո, այն այնքան կտաքանա, որ ջերմաստիճանը բավարար կլինի միջուկային սինթեզի ռեակցիաներ սկսելու համար։ Արդյունքում ջրածինը կփոխակերպվի հելիումի։ Առաջացած ջերմությունը պատճառ կդառնա, որ ճնշումը բարձրանա, և դրանով կանգ առնի ամպերի հետագա կծկումը։ Դրանք երկար ժամանակ կայուն վիճակում կշարունակեն իրենց գոյությունը՝ որպես աստղեր, ինչպես մեր արեգակը՝ ջրածնի այրումից հելիում առաջացնելով և ստացված էներգիան՝ որպես ջերմություն և լույս ճառագայթելով։ Ավելի մեծ զանգվածով աստղերը պետք է ավելի տաք լինեն, որպեսզի կարողանան հավասարակշռել իրենց ավելի ուժեղ գրավիտացիոն ձգողությունը։ Այսպիսով, դրանցում միջուկային սինթեզի ռեակցիաներն ավելի մեծ արագությամբ կընթանան, և իրենց ջրածինը կսպառեն հարյուր միլիոն տարուց ավելի շուտ։ Այնուհետև այդ մեծ զանգվածով աստղերը փոքր֊ինչ կսեղմվեն, և քանի որ դրանից տաքանում են, կսկսեն հելիումը փոխակերպել ծանր տարրերի, ինչպես, օրինակ, ածխածնի կամ թթվածնի։ Այս ռեակցիաները, սակայն, մեծ քանակության էներգիա չեն առաջացնի, և կստեղծվի ճգնաժամային մի վիճակ, ինչպես նկարագրվեց սև խոռոչների վերաբերյալ գլխում։ Թե հետագայում ի՞նչ է կատարվում՝ լրիվ պարզ չէ, բայց հավանական է, որ աստղի կենտրոնական տիրույթները կոլապսվեն և հասնեն ավելի խիտ վիճակի, ինչպիսիք են նեյտրոնային աստղը կամ սև խոռոչը։ Աստղի արտաքին տիրույթները կարող են երբեմն ժայթքել ահավոր մի պայթյունով․ դա կոչվում է գերաստղ և լուսավորությամբ գերազանցում է իր գալակտիակյի բոլոր աստղերին։ Աստղի կյանքի վերջին փուլերում առաջացած ծանր տարրերից մի քանիսը շպրտվում են հետ՝ գալակտիկայի գազի մեջ, և կարող են հիմք դառնալ աստղերի հաջորդ սերնդի համար։ Մեր արեգակը այդ ծանր տարրերից պարունակում է մոտ 2 տոկոս, քանի որ այն երկրորդ կամ երրորդ սերնդի աստղ է, որը ծնվել է մոտ հինգ հազար միլիոն տարի առաջ վաղեմի գերնոր աստղի մնացորդներ պարունակած պտտվող գազային ամպից։ Ամպի պարունակած գազի մեծ մասն օգտագործվել է արեգակի առաջացման համար կամ շպրտվել հեռուները, սակայն ծանր տարրերի փոքր քանակներն ի մի հավաքվելով, առաջացրել են մարմիններ, որոնք այժմ որպես մոլորակներ, ինչպես, օրինակ, մեր երկրագունդը, պտտվում են արեգակի շուրջը։
Սկզբնական շրջանում երկիրը շատ տաք է եղել և առանց մթնոլորտի։ Ժամանակի ընթացքում այն սառել է, և ժայռերից արձակված գազերն առաջացրել են մթնոլորտ։ Վաղ շրջանի մթնոլորտը կյանքի համար պիտանի չէր։ Այն թթվածին չէր պարունակում, այլ պարունակում էր մարդու համար մի շարք թունավոր գազեր, ինչպես, օրինակ, ծծմբաջրածինը (նեխած ձվի հոտ արձակող մի գազ)։ Սակայն կյանքի պարզունակ որոշ ձևեր կան, որոնք այդպիսի պայմաններում կարող են պահպանել իրենց գոյությունը և զարգանալ։ Այն կարծիքը կա, որ կյանքի այդ ձևերը զարգացել են օվկիանոսներում, հավանաբար ատոմների պատահական միացումների ձևով, որոնք մեծ գոյացություններ՝ մակրոմոլեկուլներ են առաջացրել և ընդունակ եղել, օվկիանոսում գտնվող այլ ատոմների ի մի հավաքելով, իրենց նման գոյացություններ առաջացրել։ Այսպիսով, տեղի է ունենում վերարտադրություն և բազմացում։ Որոշ դեպքերում վերարտադրության ընթացքում պետք է խոտորումներ եղած լինեն։ Այդ խոտորումների մեծ մասը կարող էր այնպիսի բնույթի լինել, որ մակրոմոլեկուլը չվերարտադրեր իրեն և վերջ ի վերջո ոչնչանար։ Սակայն սխալների մի մասն էլ կբերի նոր տեսակի մակրոմոլեկուլների առաջացման, որոնք ինքնավերարտադրման առավել հաջող մեխանիզմ կունենան։ Հետևաբար, դրանք, օժտված լինելով առավելություններով, կձգտեն փոխարինել սկզբնական մակրոմոլեկուլներին։ Այսպիսով, սկիզբ է առել էվոլյուցիոն գործընթացը, ինչը բերել է ավելի և ավելի բարդ, ինքնավերարտադրող օրգանիզմների առաջացման։ Կյանքի առաջին պարզունակ ձևերը սնվել են տարբեր նյութերով, նաև ծծմբաջրածնով, և թթվածին անջատել։ Աստիճանաբար մթնոլորտի բաղադրությունը փոխվել է, և առաջացել այսօրվա մթնոլորտը, որը թույլ է տվել, որպեսզի ավելի բարդ ձևի կյանք զարգանար, ինչպես ձկները, սողունները, կաթնասուններն ու վերջապես մարդկային ցեղը։
Այն պատկերացումը, թե տիեզերքը սկսում է շատ տաք վիճակից և սառչում է ընդարձակմանը զուգընթաց, համապատասխանում է մինչև օրս մեր դիտարկված բոլոր փաստերին։ Այնուամենայնիվ, մի շարք կարևոր հարցեր դեռևս մնում են առանց պատասխանի․
1) Ինչո՞ւ է վաղ տիեզերքը այդքան տաք եղել։
2) Ինչո՞ւ է տիեզերքն այս աստիճան հավասարաչափ՝ լայն մասշտաբով վերցրած։ Ինչո՞ւ է տիեզերքը նույնանման երևում տարածության բոլոր կետերից և բոլոր ուղղություններից։ Մասնավորապես, ինչո՞ւ է միկրոալիքային ճառագայթման ֆոնի ջերմաստիճանը մոտավորապես նույնը՝ տարբեր ուղղություններից չափելիս։ Սրանք կարծես ուսանողներին տրվող քննական հարցեր են։ Եվ եթե բոլորն այս հարցերին նույն պատասխանը տան, կարող եք վստահ լինել, որ նրանք նախապես պայմանավորվել են։ Այնուամենայնիվ, տվյալ մոդելում մեծ պայթյունից հետո ժամանակ չէր լինի, որպեսզի լույսը մի հեռավոր տիրույթից հասներ մի այլ տիրույթ, թեև այդ տիրույթները վաղ տիեզերքում իրար մոտիկ էին գտնվում։ Համաձայն հարաբերականության տեսության, եթե լույսը մի տիրույթից մի այլ տիրույթ չի կարող հասնել, ապա չի կարող հասնել նաև որևէ այլ ինֆորմացիա։ Հետևաբար, ոչ մի հնարավոր ճանապարհ չէր կարող գոյություն ունենալ, որով տարբեր տիրույթներ միմյանց հետ կապ հաստատեին վաղ տիեզերքում և ունենային նույն ջերմաստիճանը, մինչդեռ մի անբացատրելի պատճառով ամեն ինչ սկսվել է նույն ջերմաստիճանում։
3) Ինչո՞ւ է տիեզերքը սկիզբ առել մոտավորապես ընդարձակման այն կրիտիկական արագությամբ, որը վերակոլապսվող մոդելները զատում է ընդմիշտ ընդարձակվող մոդելներից այնպես, որ նույնիսկ այժմ՝ տասը հազար միլիոն տարի հետո այն դեռևս ընդարձակվում է նույն կրիտիկական արագությամբ։ Եթե ընդարձակման արագությունը Մեծ պայթյունից մեկ վայրկյան անց նույնիսկ մեկի հարյուր հազար միլիոն միլիոներորդ մասի չափով փոքր լիներ, ապա տիեզերքը վերակոլապսի ենթարկված կլիներ դեռ այսօրվա չափերին չհասած։
4) Չնայած այն բանին, որ տիեզերքը խոշոր մասշտաբով վերցրած այս աստիճան համաչափ է և համասեռ, այն տեղային անհամաչափություններ ունի, ինչպիսիք են աստղերը և գալակտիկաները։ Այն կարծիքը կա, որ սրանք առաջացել են, որովհետև վաղ տիեզերքի տարբեր տիրույթներում խտությունների փոքր տարբերություններ են եղել։ Խտության այդ տատանումների պատճառն ի՞նչն է եղել։
Հարաբերականության ընդհանուր տեսությունը լոկ իր ուժերով չի կարող բացատրել այդ բնորոշ գծերի էությունը կամ պատասխանել տրված հարցերին, որովհետև այդ տեսությունը կանխագուշակում է, որ տիեզերքը սկիզբ է առել անսահման խիտ վիճակից Մեծ պայթյունի եզակիությամբ։ Ընդհանուր հարաբերականությունը և բոլոր մյուս ֆիզիկական տեսությունները եզակիությունում կորցնում են իրենց ուժը։ Անհնարին է կանխագուշակել, թե ի՞նչ փոխակերպում կարող է ստացվել եզակիությունից։ Ինչպես արդեն բացատրվել է, սա նշանակում է, որ կարելի է նաև հրաժարվել Մեծ պայթյունից և նրանից առաջ կատարված բոլոր պատահույթներից, որովհետև դրանք ոչ մի ազդեցություն չեն կարող ունենալ այն մեր դիտարկած երևույթների վրա։ Տարածություն֊ժամանակը պետք է սահման ունենար՝ մի սկիզբ Մեծ պայթյունի պահին։
Թվում է, թե գիտությունը հայտնաբերել է օրենքների մի լրակազմ, որը անորոշության սկզբունքի պարտադրած սահմաններում մեզ ասում է, թե ինչպես պիտի զարգանա տիեզերքը ժամանակի ընթացքում, եթե մեզ հայտնի է վերջինիս վիճակը ժամանակի ցանկացած մեկ կետում։ Կարող է պատահել, որ այս օրենքներն Աստված է սահմանել, սակայն ինչպես երևում է, նա այնուհետև թույլ է տվել, որ տիեզերքը զարգանա համաձայն այդ օրենքների և այլևս չի միջամտում։ Բայց նա ինչպե՞ս ընտրեց տիեզերքի սկզբնական վիճակը կամ կոնֆիգուրացիան։ Որո՞նք էին ժամանակի սկզբնավորության «սահմանային պայմանները»։
Այս հարցի հավանական պատասխաններից մեկն այն է, որ Աստված տիեզերքի սկզբնական կոնֆիգուրացիան ընտրել է այնպիսի նկատառումներով, որ մենք ի զորու չենք հասկանալ։ Իհարկե, այս բանն ամենազոր էակի իրավունքն է։ Բայց, եթե նրա Արարչության սկիզբն անըմբռնելի է, ապա ինչո՞ւ է որոշել թույլ տալ, որպեսզի տիեզերքը զարգանա մեր ըմբռնմանը հասու օրենքներով։ Գիտության ողջ պատմությունը աստիճանաբար բերել է այն եզրակացության, որ պատահույթները հանկարծադեպ իրադարձություններ չեն, այլ արտացոլում են տիեզերքին ներհատուկ կարգուկանոնը, ինչը կարող է լինել կամ չլինել աստվածային ներշնչման հետևանք։ Միանգամայն բնականաբար կարելի է ենթադրել, որ այս կարգուկանոնը պետք է վերաբերի ոչ միայն օրենքներին, այլ տարածություն֊ժամանակի սահմանային պայմաններին, որոնք բնորոշում են տիեզերքի սկզբնական վիճակը։ Կարող են լինել տիեզերքի մեծ թվով մոդելներ, բոլորովին տարբեր սկզբնական պայմաններով, որոնք բոլորն էլ կենթարկվեն այդ օրենքներին։ Պետք է ինչ֊որ սկզբունք լինի, որով ընտրվի որոշակի մի սկզբնական վիճակ, հետևաբար և մի մոդել, որը կներկայացնի մեր տիեզերքը։
Հայտնի է մի այդպիսի հնարավորություն, որը կոչվում է քաոսային սահմանային պայմաններ։ Այդ քաոսային պայմաններն ինքնաբերաբար ենթադրում են, որ կամ տիեզերքը տարածականորեն անսահման է, և կամ գոյություն ունեն անսահման թվով տիեզերքներ։ Համաձայն քաոսային սահմանային պայմանների, Մեծ պայթյունից անմիջապես հետո, տվյալ կոնֆիգուրացիայում տարածության որոշակի տիրույթ գտնելու հավանականությունը որոշ իմաստով նույնն է, ինչ ցանկացած այլ կոնֆիգուրացիայում գտնելու հավանականությունը․ տիեզերքի սկզբնական վիճակի ընտրությունը զուտ պատահականություն է։ Սա նշանակում է, որ, հավանաբար, վաղ տիեզերքը շատ քաոսային և անկանոն պետք է եղած լինի, որովհետև տիեզերքի համար ավելի մեծ թվով քաոսային և անկանոն կոնֆիգուրացիաներ կան, քան հարթ ու կանոնավոր կոնֆիգուրացիաները։ (Եթե յուրաքանչյուր կոնֆիգուրացիա հավասարապես հավանական է, ճիշտ կլինի ասել, որ տիեզերքն սկիզբ է առել քաոսային և անկանոն վիճակից պարզապես այն պատճառով, որ դրանց թիվն ավելի շատ է)։ Դժվար է համաձայնել այն մտքին, թե այդպիսի սկզբնական քաոսային պայմաններն առաջացնեին ընդհանուր առմամբ այսպիսի հարթ ու կանոնավոր մի տիեզերք, ինչպիսին մերն է այսօր։ Սպասելի էր, որ այս մոդելի մեջ խտության տատանումները պատճառ կլինեն ավելի մեծ թվով նախասկզբնական սև խոռոչների առաջացման, քան տալիս է դիտարկված գամմա ճառագայթման ֆոնի վերին սահմանը։
Եթե տիեզերքն իրոք տարածականորեն անսահման է և կամ գոյություն ունեն անսահման մեծ թվով տիեզերքներ, ապա, հավանաբար, ինչ֊որ տեղում կլինեն հարթ ու համաչափ ձևով առաջացած լայնատարած տիրույթներ։ Վիճակը նման է քաջածանոթ այն պատմությանը, երբ մի խումբ կապիկներ հարվածում են գրամեքենայի ստեղներին։ Նրանց մեքենագրությունների մեծ մասն աղբակույտ նետելու բան կլինի, բայց շատ պատահաբար, ուղղակի բախտի բերումով, նրանք կարող է և Շեքսպիրի սոնետներից մեկը մեքենագրեն։ Նույն ձևով մեր տիեզերքի պարագայում կարո՞ղ է արդյոք, որ մենք բախտի բերումով գտնվում ենք հարթ ու համաչափ մի տիրույթում։ Առաջին հայացքից կարող է թվալ, որ դա շատ անհավանական է, որովհետև այդպիսի հարթ տիրույթների համեմատությամբ քաոսային և անկանոն տիրույթների թիվն արտակարգ շատ է։ Այնուամենայնիվ, ենթադրենք, որ աստղեր և գալակտիկաներ առաջացել են միայն հարթ տիրույթներում, և պայմաններն այնպես են եղել, որ կարողացել են զարգանալ բարդ ինքնավերարտադրվող օրգանիզմներ, ինչպիսիք մենք ենք, որոնք ի վիճակի են հարցնել․ ինչո՞ւ է տիեզերքն այսքան հարթ։ Սա, այսպես կոչված մարդաբանական սկզբունքի կիրառման մի օրինակ է, որը կարելի է ձևակերպել այսպես․ «Մենք տիեզերքն այս ձևով ենք տեսնում, որովհետև մենք գոյություն ունենք»։
Կա մարդաբանական սկզբունքի երկու տարբերակ՝ թույլ և ուժեղ։ Թույլ սկզբունքի համաձայն, տարածության և (կամ) ժամանակի մեջ լայնատարած և անսահման տիեզերքում բանական կյանքի զարգացման անհրաժեշտ պայմաններ կարող են լինել միայն տարածության և ժամանակի սահմանափակ որոշ տիրույթներում։ Այդ տիրույթներում գտնվող էակները, հետևաբար, չպիտի զարմանան, եթե տեսնեն, որ տիեզերքի այդ մասը բավարարում է իրենց գոյության համար հարկավոր պայմանների պահանջը։ Սա նման է հարուստի մտածելակերպին, որն, ապրելով մեծահարուստների հարևանությամբ, աղքատությունը չի տեսնում։
Թույլ մարդաբանական սկզբունքի կիրառման մի օրինակ է հետևյալ «բացատրությունը»․ թե Մեծ պայթյունը տեղի ունեցավ սրանից մոտավորապես տասը հազար միլիոն տարի առաջ, որովհետև այդքան ժամանակ էր հարկավոր բանական էակների զարգացման համար։ Ինչպես վերևում բացատրվեց, դրանով նախ առաջացավ աստղերի հինավուրց մի սերունդ։ Այդ աստղերը սկզբնական ջրածնի և հելիումի մի մասը փոխակերպեցին ածխածնի և թթվածնի, որոնցից մենք ենք կազմված։ Ապա աստղերը պայթեցին որպես գերնոր աստղեր, դրանց մնացորդներից առաջացան այլ աստղեր և մոլորակներ, որոնցից են նաև մոտավորապես հինգ հազար միլիոն տարեկան մեր Արեգակնային համակարգի աստղերն ու մոլորակները։ Առաջին մեկ կամ երկու հազար միլիոն տարիներին երկիրը շատ տաք էր, որպեսզի բարդ նյութեր առաջանային։ Հաջորդ երեք հազար միլիոն տարիների ընթացքում տեղի ունեցավ կենսաբանական էվոլյուցիայի դանդաղ գործընթացը, որի հետևանքով առաջացան պարզագույն օրգանիզմներից մինչև այնպիսի էակներ, որոնք ի վիճակի են չափել Մեծ պայթյունից մինչև այսօր անցած ժամանակը։
Քչերը պիտի առարկեն թույլ մարդաբանական սկզբունքի հավաստիության և օգտակարության դեմ։ Ոմանք, սակայն, շատ ավելի հեռու են գնում և սկզբունքի ուժեղ տարբերակ են առաջարկում։ Համաձայն այս տեսության, գոյություն ունեն բազմաթիվ տարբեր տիեզերքներ, կամ բազմաթիվ տարբեր տիրույթներ եզակի տիեզերքում, յուրաքանչյուրն իրեն հատուկ գիտական օրենքների շարքով։ Այդ տիեզերքներից շատերի պայմաններն այնպիսին չեն, որպեսզի բարդ օրգանիզմներ զարգանան, միայն մեր տիեզերքի նման մի քանի տիեզերքներում են զարգանում բանական էակներ և հարց տալիս, թե․ «Մենք ինչո՞ւ ենք տիեզերքն այսպես տեսնում»։ Պատասխանն այս դեպքում պարզ է, եթե տիեզերքն այլ լիներ, մենք այստեղ չէինք լինի։
Գիտության օրենքները ներկայումս պարունակում են բազմաթիվ հիմնարար թվեր, ինչպես էլեկտրոնի էլեկտրական լիցքի մեծությունը և պրոտոնի ու էլեկտրոնի զանգվածների հարաբերությունը։ Հնարավոր չէ, գոնե այժմ, այս թվերի արժեքները տեսականորեն կանխագուշակել։ Դրանք որոշվում են փորձով։ Թերևս մի օր հնարավոր լինի կատարյալ միացյալ մի տեսություն մշակել և կանխագուշակել բոլոր թվերի արժեքները, բայց նաև հնարավոր է, որ այս թվերի մի մասը կամ բոլորի արժեքները տարբեր լինեն՝ տարբեր տիեզերքներում կամ մի տիեզերքի ներսում։ Ուշագրավ փաստ է, որ այս թվերի արժեքները կարծես նրբորեն այնպես են հարմարեցված, որ հնարավոր լինի կյանքի զարգացումը։ Օրինակ, եթե էլեկտրոնի էլեկտրական լիցքը փոքր֊ինչ տարբեր լիներ եղածից, աստղերը ջրածին և հելիում չէին կարող այրել և կամ չէին պայթի։ Իհարկե, հնարավոր են նաև բանական կյանքի այլ ձևեր ևս, որոնց մասին գիտական վեպերի հեղինակներն անգամ չեն երազել և, որոնց համար պարտադիր չեն արևի լույսը կամ այն ծանր տարրերը, որոնք առաջանում են աստղերում և, պայթման հետևանքով, տիեզերք շպրտվում։ Այնուամենայնիվ, պարզ է, որ թվերի արժեքների համեմատաբար սահմանափակ շարքեր կան, որոնք կապահովեն տարբեր ձևերի բնականոն կյանքի զարգացումը։ Արժեքների շարքերի մեծ մասը կարող է այնպիսի տիեզերքներ առաջացնել, որոնք թեև շատ գեղեցիկ կլինեն, բայց և զրկված՝ այդ գեղեցկությամբ հիացողներից։ Այս արդյունքը կարելի է համարել կամ Արարչագործության աստվածային նպատակի և գիտության օրենքների ընտրության վկայություն, կամ գնահատել, որպես ուժեղ մարդաբանական սկզբունքը հավաստող փաստարկ։
Դիտարկվող տիեզերքի վիճակը բացատրելու կոչված ուժեղ մարդաբանական սկզբունքի դեմ կարելի է մի քանի առարկություններ անել։ Առաջինը․ ի՞նչ իմաստով է ասվում, թե այդ բոլոր տարբեր տիեզերքները կարող են գոյություն ունենալ։ Եթե դրանք իրոք անջատ են իրարից, ապա ինչ էլ որ պատահի այլ տիեզերքում, որևէ նկատելի հետևանք չի կարող ունենալ մեր տիեզերքում։ Հետևաբար, համաձայն խնայողության սկզբունքի, դրանք պետք է տեսությունից դուրս գցել։ Մյուս կողմից, եթե եզակի տիեզերքում առկա են տարբեր տիրույթներ, գիտության օրենքները պետք է նույնը լինեն յուրաքանչյուր տիրույթում, որովհետև հակառակ դեպքում հնարավոր չէր լինի շարունակաբար մի տիրույթից մյուսը տեղափոխվել։ Այս դեպքում տիրույթների միջև եղած միակ տարբերությունը կլինի նրանց սկզբնական կոնֆիգուրացիաները և, այսպիսով, ուժեղ մարդաբանական սկզբունքը կվերափոխվի թույլ մարդաբանական սկզբունքի։
Ուժեղ մարդաբանական սկզբունքի դեմ երկրորդ առարկությունն այն է, որ դա դեմ է գնում ողջ գիտության պատմության հոսանքին։ Մենք զարգացել ենք Պտղոմեոսի և նրա նախորդների երկրակենտրոն տիեզերագիտությունից, անցել են Կոպեռնիկոսի և Գալիլոյի արևակենտրոն տիեզերագիտության միջով և հասել ենք ժամանակակից այն պատկերացմանը, ըստ որի երկիրը միջին չափի մի մոլորակ է, որը պտտվում է սովորական մի աստղի՝ արեգակի շուրջը, որն իր հերթին գտնվում է սովորական մի պարուրաձև գալակտիկայի ծայրամասում, իսկ այդ գալակտիկան տեսանելի տիեզերքի մոտավորապես միլիոն միլիոն գալակտիկաներից միայն մեկն է։ Ուժեղ մարդաբանական սկզբունքը պնդում է, թե այս լայնածավալ կառուցվածքը գոյություն ունի պարզապես մեզ համար։ Այսպիսի բաների դժվար է հավատալ։ Իհարկե, Արեգակնային համակարգը մեր գոյության նախապայմանն է, և կարելի է այս միտքը տարածել մեր գալակտիկայի վրա ամբողջությամբ, որպեսզի ընդգրկենք այն վաղեմի աստղերի սերունդը, որը ստեղծեծ ծանր տարրերը։ Սակայն մեր գոյության համար, թվում է, մյուս բոլոր գալակտիկաների, ինչպես նաև մեծ մասշտաբով վերցրած տիեզերքի՝ բոլոր ուղղություններով այսքան հավասարաչափ և միատեսակ լինելու կարիքը չկա։
Մարդաբանական սկզբունքը, առնվազն իր թույլ տարբերակով, մեզ կարող էր բավարարել, եթե հնարավոր լիներ ցույց տալ, որ որոշ թվով տարբեր սկզբնական կոնֆիգուրացիաներ զարգացել են այնպես, որպեսզի առաջացնեն այնպիսի մի տիեզերք, ինչպիսին մենք տեսնում ենք։ Եթե այդպես է, ապա պատահական սկզբնական պայմաններից զարգացած տիեզերքը պիտի որ մի շարք տիրույթներ պարունակեր, որոնք հարթ ու համաչափ լինեին և բանական կյանքի էվոլյուցիայի համար՝ պիտանի։
Մյուս կողմից, եթե տիեզերքի սկզբնական վիճակը ծայրաստիճան ուշադրությամբ ընտրվեր, որպեսզի ստացվեր այն, ինչ տեսնում ենք մեր շուրջը, հազիվ թե տիեզերքում գոյություն ունենար թեկուզ որևէ տիրույթ, որտեղ կյանք սկիզբ առներ։ Վերևում նկարագրված տաք Մեծ պայթյունի մոդելում բավարար ժամանակ չկար, որպեսզի վաղ տիեզերքում ջերմությունը մի տիրույթից մյուսը հոսեր։ Սա նշանակում է, որ տիեզերքի ջերմաստիճանը սկզբնական շրջանում ամենուրեք ճիշտ նույնը պետք է եղած լիներ, քանի որ միկրոալիքային ճառագայթման ֆոնի ջերմաստիճանը բոլոր ուղղություններով նույնն է այսօր։ Սկզբնական ընդարձակման արագությունը ևս պետք է շատ ճշգրիտ ընտրված լինի, որպեսզի ընդարձակման արագությունը դեռ մոտ լինի այն կրիտիկական արագությանը, որն անհրաժեշտ է վերստին կոլապսի ենթարկվելուց խուսափելու համար։ Այս ամենը նշանակում է, որ, իրոք, տիեզերքի սկզբնական վիճակը խնամքով է ընտրվել, եթե տաք Մեծ պայթյունի մոդելը ճիշտ է՝ ընդհուպ մինչև ժամանակի սկզբնավորությունը։ Շատ դժվար կլիներ բացատրել, թե տիեզերքն ինչո՞ւ պիտի այդպիսի սկզբնավորություն ունենար, բացի այն բացատրությունից, որ մեզ նման էակներ ստեղծելու մտադրություն ունեցող Աստծու գործն է եղել դա։
Մասաչուսեթսի Տեխնոլոգիական ինստիտուտի գիտնական Ալան Գութը փորձեց տիեզերքի այնպիսի մի մոդել կառուցել, որում կարող էին զարգանալ բազմաթիվ տարբեր սկզբնական կոնֆիգուրաիցաներ և հասնել ժամանակակից տիեզերքին և առաջարկեց, որ սկզբնական տիեզերքը պետք է ունեցած լինի շատ արագ ընդարձակման մի փուլ։ Ըստ նրա, այդ ընդարձակումը տեղի է ունեցել «հարաճուն ընթացքով», այսինքն՝ որոշ ժամանակ տիեզերքն ընդարձակվել է աճող, քան նվազող արագությամբ, ինչպես տեղի է ունենում այժմ։ Համաձայն Գութի տիեզերքի շառավիղը միլիոն միլիոն միլիոն միլիոն միլիոն անգամ (1֊ից հետո 30 զերո) աճել է լոկ վայրկյանի մի փոքր մասի ընթացքում։
Համաձայն Գութի, տիեզերքը սկիզբ է առել Մեծ պայթյունով, շատ տաք և բավականին քաոսային վիճակում։ Այդ բարձր ջերմաստիճանը նշանակում է, որ տիեզերքում մասնիկները պետք է շարժվեն մեծ արագությամբ և բարձր էներգիա ունենան։ Ինչպես մենք արդեն քննարկել ենք, սպասելի է, որ այդպիսի բարձր ջերմաստիճաններում ուժեղ և թույլ միջուկային ուժերն ու էլեկտրամագնիսական ուժը միավորվեն մի ընդհանուր ուժի մեջ։ Տիեզերքն ընդարձակմանը զուգընթաց սկսում է սառչել, և մասնիկների էներգիան նվազում է։ Վերջ ի վերջո տեղի է ունենում այն, ինչը կոչվում է ֆազային անցում, և խախտվում է ուժերի միջև առկա համաչափությունը, այսինքն՝ ուժեղ ուժը տարբերվում է թույլ և էլեկտրոմագնիսական ուժերից։ Ֆազային անցման լավագույն օրինակն է ջրի սառչելը։ Հեղուկ ջուրը համասեռ է, այսինքն՝ այն ամեն կետում և բոլոր ուղղություններով նույնական է։ Սակայն երբ առաջանում են սառույցի բյուրեղներ, դրանք որոշակի դիրքեր են գրավում և որոշակի ուղղությամբ շարք կազմում։ Այսպիսով, ջրի համասեռությունը խախտվում է։
Ջրի դեպքում, եթե սառեցումը կատարվի զգուշությամբ, հնարավոր է «գերսառեցնել» այն, այսինքն՝ ջերմաստիճանը սառեցման կետից (0°C) ցածր իջեցնել, առանց սառույցի առաջացման։ Գութը ենթադրեց, որ տիեզերքը նույնպես կարող է նման հատկություն ունենալ․ ջերմաստիճանը կարող էր իջնել կրիտիկական արժեքից ցածր, առանց խախտելու ուժերի միջև առկա համաչափությունը։ Այս դեպքում տիեզերքը պետք է անկայուն վիճակում գտնվի՝ օժտված ավելի շատ էներգիայով, քան կունենար, եթե համաչափությունը խախտված լիներ։ Կարելի է ցույց տալ, որ այս հավելյալ էներգիան, հակագրավիտացիոն ազդեցություն կունենա․ կներգործի ճիշտ այնպես, ինչպես այն տիեզերաբանական հաստատունը, որն ընդհանուր հարաբերականության տեսությունն ներմուծեց Էյնշտեյնը, երբ փորձում էր տիեզերքի համար ստատիկ մի մոդել կառուցել։ Քանի որ տիեզերքը պետք է ընդարձակվի, ինչպես տաք Մեծ պայթյունի մոդելում, հետևաբար տիեզերաբանական հաստատունի վանողական գործոնը պատճառ կլինի, որ տիեզերքն ընդարձակվի հարաճուն արագությամբ։ Նույնիսկ այն տիրույթներում, որտեղ միջինից ավելի շատ նյութական մասնիկներ կան, տիեզերաբանական հաստատունի վանողական ներգործությունը կգերակշռի գրավիտացիոն ձգողությանը։ Հետևաբար այս տիրույթները նույնպես կընդարձակվեն հարաճուն արագությամբ։ Եթե ընդարձակումը շարունակվի, և նյութական մասնիկներն իրարից ավելի հեռանան, կառաջանա ընդարձակվող մի տիեզերք, որը հազիվ թե մասնիկներ պարունակի և դեռևս գտնվի գերսառեցրած վիճակում։ Տիեզերքում առկա անկանոնությունները ընդարձակման հետևանքով պարզապես պետք է հարթվեին ճիշտ այնպես, ինչպես փուչիկի ծալքերն են հարթվում՝ փչելիս։ Հետևաբար, տիեզերքի այժմյան հարթ և համաչափ վիճակը կարող է առաջացած լինել բազմաթիվ տարբեր, ոչ նույնանման սկզբնական վիճակներից։
Նախնական տիեզերքում, որտեղ ընդարձակումը ոչ թե դանդաղում է նյութի գրավիտացիոն ձգողության ազդեցությամբ, այլ արագանում՝ շնորհիվ տիեզերաբանական հաստատունի, երկար ժամանակ չի պահանջվի, որպեսզի լույսը մի տիրույթից մյուսը տեղաշարժվի։ Այսպիսով, հնարավոր է լուծել ժամանակին արծածված այն հարցը, թե ինչո՞ւ են վաղ տիեզերքում երկու տարբեր տիրույթներ նույն հատկություններն ունեցել։ Դեռ ավելին, տիեզերքի ընդարձակման արագությունը պետք է ինքնաբերաբար մոտենա այն կրիտիկական արագությանը, որը որոշվում է տիեզերքի էներգիայի խտությամբ։ Դրանով է բացատրվում, թե ինչո՞ւ է ընդարձակման արագությունն այդքան մոտ կրիտիկական արագությանը, առանց ենթադրելու, որ տիեզերքի ընդարձակման արագությունն ընտրվել էր մեծ խնամքով։
Հարաճուն արագացման պատկերացումը կարող է բացատրել նաև, թե ինչու այսքան շատ նյութ կա տիեզերքում։ Մեզ տեսանելի տիեզերքի տիրույթում կա տասը միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն մասնիկ (1֊ից հետո 85 զերո)։ Որտեղի՞ց են հայտնվել այդ մասնիկները։ Ըստ քվանտային տեսության, մասնիկներ կարելի է ստեղծել էներգիայից՝ որպես մասնիկ֊հակամասնիկ զույգեր։ Սակայն այստեղից ծագում է հաջորդ հարցը, որտեղի՞ց է գալիս այդ էներգիան։ Պատասխանն այն է, որ տիեզերքի էներգիան, ամբողջությամբ վերցրած, հավասար է զերոյի։ Տիեզերքում առկա նյութն առաջացել է դրական էներգիայից։ Սակայն, նյութը ենթակա է գրավիտացիոն ձգողության ազդեցությանը։ Իրար մոտիկ գտնվող երկու նյութական առարկաներ ավելի քիչ էներգիա ունեն, քան երբ նրանք իրարից հեռու են, որովհետև իրարից հեռացնելու համար պետք է էներգիա ծախսել, որպեսզի հաղթահարվի այդ առարկաներն իրար ձգող գրավիտացիոն ուժը։ Այսպիսով, որոշ իմաստով գրավիտացիոն դաշտի էներգիան բացասական է։ Տարածության մեջ մոտավորապես միակերպ տիեզերքի պարագայում կարելի է ցույց տալ, որ բացասական գրավիտացիոն էներգիան ճշգրտորեն հավասարակշռում է նյութի դրական էներգիան։ Այսպիսով, տիեզերքի լրիվ էներգիան հավասար է զերոյի։ Քանի որ երկու անգամ զերոն նույնպես զերո է, հետևաբար, եթե տիեզերքում կրկնապատկվեն ինչպես նյութի դրական էներգիան, այնպես էլ բացասական գրավիտացիոն էներգիան, ապա էներգիայի պահպանման օրենքը չի խախտվի։ Բնականոն ընդարձակման պայմաններում այդպիսի բան չի կարող պատահել, որովհետև նյութի էներգիայի խտությունը նվազում է, երբ տիեզերքը մեծանում է։ Սակայն սա հնարավոր է հարաճուն ընդարձակման դեպքում, որովհետև գերսառեցած վիճակում էներգիայի խտությունը մնում է հաստատուն, երբ տիեզերքն ընդարձակվում է։ Եթե տիեզերքը երկու անգամ մեծանա, ապա երկուսն էլ՝ դրական նյութական էներգիան և բացասական գրավիտացիոն էներգիան, կկրկնապատկվեն, և այսպիսով լրիվ էներգիան նորից հավասար կլինի զերոյի։ Հարաճուն ընդարձակման տիեզերքը չափազանց մեծանում է։ Այսպիսով, մասնիկների առաջացման համար հարկավոր ընդհանուր էներգիայի քանակը աճում է ինչպես Գութը նկատել է․ «Թեև ասում են, թե ձրի ճաշկերույթ չի լինում, բայց տիեզերքն ի վերջո ձրի ճաշկերույթ է»։[19]
Այսօր տիեզերքը հարաճուն ընդարձակման ենթակա չէ։ Հետևաբար, տիեզերաբանական հաստատունի ազդեցությունից ձերբազատվելու համար անհրաժեշտ է այնպիսի մի մեխանիզմ, որով ընդարձակումը տեղի ունենա ոչ թե արագացումով, այլ ինչպես այսօր է դիտվում, դանդաղի գրավիտացիոն ազդեցության տակ։ Սպասելի է, որ հարաճուն ընդարձակման դեպքում ուժերի միջև գոյություն ունեցող համաչափությունն ի վերջո կխախտվի ճիշտ այնպես, ինչպես գերսառած ջուրը վերջում միշտ բյուրեղանում է։ Անջատվում է համասեռ վիճակի հավելյալ էներգիան և տաքացնում տիեզերքը մինչև այն կրիտիկական ջերմաստիճանը, որը հատուկ է ուժերի միջև եղած համաչափությանը։ Տիեզերքը կշարունակի ընդարձակվել և աստիճանաբար սառել ճիշտ այնպես, ինչպես դա լինում է տաք Մեծ պայթյունի մոդելում։ Բայց մենք այժմ կարող ենք բացատրել, թե ինչո՞ւ է տիեզերքը ընդարձակվում ճիշտ կրիտիկական արագությամբ և ինչո՞ւ են տարբեր տիրույթների ջերմաստիճանները նույնը։
Գութի սկզբնական առաջարկությունը ենթադրում էր, որ ֆազային անցումը տեղի է ունենում միանգամից, ինչպես շատ սառը ջրում սառույցի բյուրեղների առաջացումը։ Նկատի էր առնվում այն, որ խախտված համասեռությամբ այս նոր ֆազի «պղպջակները» պետք է առաջացած լինեն հին ֆազում, ինչպես լինում են եռացող ջրով շրջապատված պղպջակները։ Ենթադրվում էր, որ պղպջակները մեծանում և իրար են հանդիպում, երբ ողջ տիեզերքն անցում է կատարում նոր ֆազային վիճակի։ Դժբախտաբար, ինչպես ես, այնպես էլ շատերը, նշել ենք, որ տիեզերքն այնպիսի մեծ արագությամբ էր ընդարձակվում, որ եթե նույնիսկ պղպջակները մեծանային լույսի արագությամբ, ապա նրանք իրարից կհեռանային և, հետևաբար, չէին կարող իրար միանալ։ Տիեզերքը կունենար ոչ միաձև վիճակ, և որոշ տիրույթներում կպահպանվեր համաչափությունը տարբեր ուժերի միջև։ Այս մոդելը չէր կարող բնավ համապատասխանել մեր տեսածին։
1981֊ի հոկտեմբերին ես մեկնեցի Մոսկվա՝ մասնակցելու քվանտային գրավիտացիային նվիրված գիտաժողովին։ Գիտաժողովից հետո Ստեռնբերգի աստղագիտական ինստիտուտում զեկուցում կարդացի հարաճուն ընդարձակման մոդելի և դրան առնչվող հարցերին նվիրված սեմինարում։ Դրանից առաջ ես մեկ ուրիշի էի հանձնարարել կարդալ դասախոսություններս, որովհետև ունկնդիրներին իմ խոսքը հասկանալի չէր։ Բայց քանի որ սեմինարի նախապատրաստման համար ժամանակ չկար, ես ինքս խոսեցի, իսկ իմ ասպիրանտներից մեկը վերարտադրեց իմ ասածը։ Սեմինարը հաջող անցավ, և ես ուղղակի հաղորդակցության մեջ մտա իմ ունկնդիրների հետ։ Ներկաների մեջ էր Մոսկվայի Լեբեդևի անվան ինստիտուտի երիտասարդ ռուս գիտնական Անդրեյ Լինդեն։ Նա ասաց, թե պղպջակների միացման դժվարությունից կարելի է խուսափել, եթե պղպջակներն այնքան մեծ լինեն, որ տիեզերքի մեր տիրույթը պարփակվի մեկ ընդհանուր պղպջակի մեջ։ Որպեսզի այդպիսի բան տեղի ունենա, անհրաժեշտ է, որ պղպջակի մեջ համասեռ վիճակից անցումը խախտված համասեռությամբ վիճակի շատ դանդաղ տեղի ունեցած լինի, ինչը միանգամայն հնարավոր է՝ համաձայն մեծ միասնական տեսությունների։ Լինդեի գաղափարը համասեռության դանդաղ խախտման մասին լավն էր, բայց ես հետագայում հասկացա, որ նրա պղպջակները շատ ավելի մեծ պետք է եղած լինեին, քան այդ ժամանակվա տիեզերքը։ Ես ցույց տվեցի, որ փոխարենը՝ համասեռությունը պետք է միաժամանակ ամենուր խախտվեր, այլ ոչ թե միայն պղպջակների ներսում։ Դա կբերեր միակերտ տիեզերքի առաջացմանը, ինչը մենք այսօր տեսնում ենք։ Այս գաղափարն ինձ շատ ոգևորեց և ես այն քննարկեցի իմ ուսանողներից Իան Մոսի հետ։ Հետագայում, որպես Լինդեի բարեկամ, շատ անհարմար զգացի, երբ գիտական մի պարբերականից ինձ ուղարկեցին Լինդեի հոդվածն այս հարցի կապակցությամբ և ուզեցին իմ կարծիքը իմանալ դրա հրատարակության նպատակահարմարության մասին։ Ես պատասխանեցի, որ պղպջակների՝ տիեզերքից մեծ լինելու հարցը թերի է, սակայն այն հիմնական գաղափարը, թե համասեռությունն աստիճանաբար է խախտվում, շատ լավ է։ Ես երաշխավորեցի հոդվածը հրատարակել այնպես, ինչպես կա, որովհետև Լինդեի համար այն վերափոխելու գործն ամիսներ կպահանջեր զուտ այն պատճառով, որ Արևմուտք առաքվող ամեն հոդված ենթարկվում էր խորհրդային գրաքննության, որ գիտական հոդվածների հարցում հուսալիություն և արագություն չի ապահովում։ Փոխարենը Իան Մոսի հետ նույն պարբերականում մի կարճ աշխատություն տպեցինք, թե այն ինչպես կարելի է լուծել։
Մոսկվայից վերադառնալուց հետո պետք է մեկնեի Ֆիլադելֆիա՝ Ֆրանկլինի ինստիտուտի պարգևատրած մեդալը ստանալու համար։ Քարտուղարուհիս՝ Ջուդի Ֆելան, իր արտակարգ հմայքն օգտագործելով, համոզել էր Բրիտանական ավիաուղիներ գործակալությանը (Բրիտիշ Էյրվեյզ), որպեսզի գովազդի դիմաց ինձ և իրեն Կոնկորդով ձրի փոխադրեն։ Դժբախտաբար, օդակայանի ճանապարհին ընկա հորդառատ անձրևի տակ և թռիչքից ուշացա։ Այնուամենայնիվ, մի կերպ հասա Ֆիլադելֆիա և ստացա մեդալը։ Ֆիլադելֆիայի Դրեքսել համալսարանի հրավերով հարաճուն ընդլայնվող տիեզերքի հարցին նվիրված սեմինար վարեցի և կրկնեցի Մոսկվայում իմ կարդացած զեկուցաշարը։
Լինդեից անկախ՝ մի քանի ամիս անց նման գաղափար առաջ քաշեցին Փենսիլվանիայի համալսարանից Պոլ Ստեյնհարդը և Անդրեաս Ալբրեխտը։ Այժմ Լինդեին և նրանց է վերագրվում այսպես ասած, «հարաճուն ընդլայման նոր մոդելը», որը հիմնված է համասեռության խախտման գաղափարի վրա։ (Ալան Գութի՝ պղպջակների առաջացմամբ համասեռության արագ խախտման առաջարկությունը հարաճուն ընդլայման մոդելն էր)։
Հարաճուն ընդլայման նոր մոդելը տիեզերքի որպիսությունը բացատրող, հաջող փորձ էր։ Սակայն ես և շատ ուրիշներ ցույց տվեցինք, որ առնվազն իր սկզբնական ձևով այդ մոդելը միկրոալիքային ճառագայթման ֆոնի համար կանխագուշակում էր ջերմաստիճանի շատ ավելի մեծ տատանումներ, քան դիտարկվել են։ Հետագա աշխատանքները կասկածելի դարձրին այն գաղափարը, թե այսպիսի ֆազային անցում երբևէ եղե՞լ է արդյոք շատ վաղ տիեզերքում։ Իմ անձնական կարծիքով, հարաճուն ընդլայման նոր մոդելը այժմ մեռած գիտական տեսություն է, թեև շատերը, թվում է, դեռ նրա վախճանի մասին չեն լսել և հոդվածներ են գրում, կարծես այն կենսունակ է։ 1983֊ին Լինդեն ավելի լավ մի մոդել առաջարկեց, որը կոչվում է քաոսային հարաճուն ընդլայման տեսություն։ Այստեղ ֆազային անցում և գերսառեցում չկան։ Փոխարենը առկա է 0 սպին ունեցող դաշտ, որը քվանտային տատանումների հետևանքով կարող է վաղ տիեզերքի որոշ տիրույթներում բարձր արժեքներ ունենալ։ Այս տիրույթներում դաշտի էներգիան գործում է տիեզերաբանական հաստատունի նման։ Տեղի է ունենում վանողական գրավիտացիոն ներգործություն, և այսպիսով՝ այս տիրույթները տարածվում են հարաճուն ընդլայման եղանակով։ Ընդարձակմանը զուգընթաց նրանցում դաշտի էներգիան աստիճանաբար նվազում է, և հարաճուն ընդարձակումը վերափոխվում է տաք Մեծ պայթյունի մոդելում առկա ընդարձակման, որը տեղի է ունենում։ Այդ տիրույթներից մեկն էլ դառնում է այն, ինչը մենք այսօր տեսնում ենք որպես տեսանելի տիեզերք։ Այս մոդելը օժտված է հարաճուն ընդլայման սկզբնական մոդելների բոլոր առավելություններով, հիմնված չէ կասկածելի ֆազային անցման վրա և ավելին, այն կարող է տալ միկրոալիքային ֆոնի ջերմաստիճանի տատանումների ընդունելի չափը, ինչը համընկնում է փորձնական տվյալների հետ։
Հարաճուն ընդլայման մոդելների վրա կատարված ուսումնասիրությունները ցույց են տալիս, որ տիեզերքի այժմյան վիճակը կարող էր առաջանալ մեծ թվով սկզբնական կոնֆիգուրացիաներից։ Սա կարևոր է, որովհետև ցույց է տալիս, որ մեծ բծախնդրությամբ չէր կարող ընտրված լինել տիեզերքի այն մասը, որը մենք զբաղեցնում ենք այսօր։ Այսպիսով, ցանկության դեպքում, կարող ենք օգտագործել մարդաբանական սկզբունքը՝ բացատրելու, թե ինչո՞ւ է տիեզերքն այնպիսին, ինչպիսին երևում է այսօր։ Այնուամենայնիվ, սա չի նշանակում, թե ամեն սկզբնական կոնֆիգուրացիա կարող է վերաճել այնպիսի մի տիեզերքի, որն այսօր, մենք տեսնում ենք։ Այս բանը կարելի է ապացուցել այժմյան տիեզերքի համար բոլորովին տարբեր, ասենք, շատ ուռուցիկ և անկանոն մի վիճակ ընդունելով։ Գիտության օրենքների միջոցով կարելի է բացահայտել տիեզերքի զարգացման հետընթաց կարգը և որոշել, թե սկզբնական վիճակում ինչպիսի կոնֆիգուրացիա է ունեցել տիեզերքը։ Ընդհանուր հարաբերականության դասական տեսության եզակիության թեորեմներից դարձյալ Մեծ պայթյունի եզակիությունն է հետևում։ Այժմ, եթե այդ Մեծ պայթյունից հետո գիտության օրենքները կիրառելով շարժվենք տիեզերքի զարգացմանը զուգընթաց, կհասնենք ուռուցիկ և անկանոն այն վիճակին, որից սկսել էինք։ Հետևաբար, հնարավոր է, որ այնպիսի սկզբնական կոնֆիգուրացիաներ եղած լինեին, որոնք չհանգեցնեին այսօր մեր դիտարկած տիեզերքի վիճակին։ Այսպիսով, նույն մոդելը չի կարող ասել, թե տիեզերքի սկզբնական կոնֆիգուրացիան ինչո՞ւ այնպիսին չէ, որպեսզի այսօր մեր դիտարկածից շատ տարբեր մի բան առաջացներ։ Դա բացատրելու համար արդյո՞ք հարկ կա վերադառնալ մարդբանական սկզբունքին։ Արյդո՞ք այդ ամենը մի երջանիկ զուգադիպության արդյունք չէ։ Այսպիսի մոտեցումը հուսահատական մխիթարանք է, ըստ որի մենք ժխտած կլինեինք տիեզերքի ներքին կարգուկանոնը հասկանալու մեր բոլոր հույսերը։
Որպեսզի մենք կարողանանք գուշակել, թե տիեզերքն ինչից է սկզբնավորվել, մեզ հարկավոր են այնպիսի օրենքներ, որոնք գործեն ժամանակի սկզբնավորման պահին։ Եթե ընդհանուր հարաբերականության դասական տեսությունը ճիշտ է, ապա ինչպես ցույց են ք տվել Ռոջեր Պենրոուզն ու ես, եզակիության թեորեմներից բխում է, որ ժամանակի սկիզբը պետք է անսահման խտություն ունեցած մի կետ եղած լինի և անսահման կորություն ունենա տարածություն֊ժամանակի մեջ։ Գիտության բոլոր հայտնի օրենքներն այդպիսի կետում ուժը կկորցնեն։ Կարելի է ենթադրել, որ կարող են այնպիսի օրենքներ լինել, որոնք գործեն եզակիության մեջ։ Բայց շատ դժվար է այդպիսի անկանոն հատկություններով օժտված կետերում գործող օրենքներ նույնիսկ ձևակերպել, և մենք լրիվ զրկված ենք դիտարկելու հնարավորությունից և չենք կարող ասել, թե այդ օրենքներն ի՞նչ տեսակ են։ Այնուամենայնիվ այն, ինչ իրապես ցույց են տալիս եզակիության թեորեմները, այն է, որ գրավիտացիոն դաշտն այդ կետում այնքան ուժեղ է լինում, որ քվանտային գրավիտացիոն ներգործությունը դառնում է շատ կարևոր․ դասական տեսությունն այլևս ի վիճակի չէ նկարագրել տիեզերքը։ Այսպիսով տիեզերքի շատ վաղ վիճակը քննարկելու համար պետք է օգտագործել գրավիտացիոն քվանտային տեսությունը։ Ինչպես կտեսնենք, հնարավոր է, որ քվանտային տեսության մեջ սովորական գիտության օրենքներն ի զորու լինեն ամենուրեք, ներառյալ ժամանակի սկզբնավորումը, հարկ չկա եզակիության նոր օրենքներ սահմանել, որովհետև քվանտային տեսության մեջ եզակիությունների անհրաժեշտություն չկա։
Մենք դեռևս չունենք ամբողջական և հետևողական մի տեսություն, որը միավորեր քվանտային մեխանիկան և գրավիտացիան։ Այնուամենայնիվ, թե ինչպիսի որոշ առանձնահատկություններ պետք է ունենա այդ միասնական տեսությունը, մենք միանգամայն պատկերացնում ենք։ Դրանից մեկն այն է, որ այդ միասնական տեսությունն իր մեջ պիտի ներառի Ֆեյնմանի առաջարկությունը՝ քվանտային տեսությունը պատմությունների գումարի հիման վրա ձևակերպելու վերաբերյալ։ Այս մոտեցման համաձայն, մասնիկը գեթ մի եզակի պատմություն չունի, ինչպես դասական տեսություններում է լինում։ Դրա փոխարեն ենթադրվում է, որ տարածություն֊ժամանակի մեջ մասնիկը շարժվում է բոլոր հնարավոր ուղիներով, և այդ պատմություններից յուրաքանչյուրը բնութագրվում է երկու թվով, որոնցից մեկը վերաբերում է ալիքի չափին, իսկ մյուսը տալիս է նրա դիրքը պարբերաշրջանում (ցիկլում)՝ ֆազը։ Տվյալ որոշակի կետերով, ասենք մասնիկի անցման հավանականությունը գտնելու համար անհրաժեշտ է գումարել այդ կետով անցնող բոլոր հնարավոր պատմությունները բնութագրող ալիքները։ Սակայն այդ գումարելու գործողությունը կապված է մի շարք տեխնիկական պրոբլեմների հաղթահարման հետ։ Դրանք շրջանցելու համար առաջարկվում է հետևյալ տարօրինակ միջոցը․ պետք է գումարել մասնիկների պատմությունների այն ալիքները, որոնք գտնվում են ոչ թե մեզ հայտնի «իրական» ժամանակում, այլ, այսպես կոչված, «կեղծ» ժամանակում։ Կեղծ ժամանակը կարող է ոմանց վեպի նյութ թվալ, բայց իրականում այն որոշակիորեն սահմանված մաթեմատիկական հասկացություն է։ Եթե մենք վերցնենք մի սովորական թիվ («իրական» թիվ), բազմապատկենք նույն թվով, կստացվի դրական մի թիվ (այսպես օրինակ, 2 անգամ 2 հավասար է 4֊ի, նմանապես -2 անգամ -2 նորից հավասար է 4֊ի)։ Բայց ահա կան հատուկ թվեր (դրանք կոչվում են կեղծ), որոնք իրար բազմապատկելիս բացասական թվեր են տալիս։ (Այսպիսի մի թիվ է i֊ն, որն ինքն իր հետ բազմապատկելիս տալիս է -1, 2i֊ն ինքն իր հետ բազմապատկելիս տալիս է -4 և այլն)։ Այսպիսով, Ֆեյնմանի մեթոդով պատմությունների գումարը հաշվարկելիս տեխնիկական դժվարություններից խուսափելու համար հարկավոր է օգտվել կեղծ ժամանակից։ Այսինքն՝ հաշվումներ կատարելու համար ժամանակը պետք է չափել ոչ թե իրական թվերով, այլ կեղծ թվերով։ Սա հետաքրքրական փոփոխություն է մտցնում տարածություն֊ժամանակի հասկացության մեջ․ ժամանակի և տարածության միջև եղած տարբերությունը լրիվ անհետանում է։ Այն տարածություն֊ժամանակը, որում պատահույթներն ունեն ժամանակի կոորդինատի կեղծ արժեքներ, կոչվում է էվկլիդեսյան, հին հույն փիլիսոփա Էվկլիդեսի անվամբ, որը հիմնադրել է երկչափ մակերեսների երկրաչափությունը։ Այն, ինչ այսօր մենք անվանում ենք Էվկլիդեսյան տարածություն֊ժամանակ քառաչափ է, ոչ թե երկչափ։ Էվկլիդեսյան տարածություն֊ժամանակում ժամանակի ուղղության և տարածության մեջ ուղղությունների միջև տարբերություն չկա։ Մյուս կողմից, իրական տարածություն֊ժամանակի մեջ, որտեղ պատահույթները չափվում են սովորական ժամանակի կոորդինատի իրական արժեքներով, տարբերությունը ակնհայտ է՝ բոլոր կետերի ժամանակի ուղղությունը գտնվում է լուսակոնի սահմաններից ներս, իսկ տարածության ուղղությունները գտնվում են դրսում։ Այնուամենայնիվ, սովորական քվանտային մեխանիկա ներմուծված մեր օգտագործած կեղծ ժամանակը և էվկլիդեսյան տարածություն֊ժամանակը լոկ մաթեմատիկական հնարքներ են, որոնցով հեշտությամբ կարող ենք հաշվել իրական տարածություն֊ժամանակին վերաբերող պատասխանները։
Երկրորդ առանձնահատկությունը, որը, մենք վստահ ենք պետք է վերջնական տեսության մաս կազմի, Էյնշտեյնի այն գաղափարն է, որ գրավիտացիոն դաշտը ներկայացված է կորաձև տարածություն֊ժամանակով։ Մասնիկները կորաձև տարածության մեջ ձգտում են շարժվել ուղղագիծ ճանապարհին ամենամոտ ուղղությամբ, բայց, որովհետև տարածություն֊ժամանակը հարթ չէ, նրանց ճանապարհները կոր են երևում, կարծես թե գտնվում են գրավիտացիոն դաշտում։ Երբ մենք Ֆեյնմանի պատմությունների մեթոդով հաշվարկված գումարը միավորենք Էյնշտեյնի գրավիտացիայի մասին գաղափարի հետ, մասնիկի պատմության նմանակն այժմ կլինի կատարյալ մի կորաձև տարածություն֊ժամանակ, որը ներկայացնում է ողջ տիեզերքի պատմությունը։ Պատմությունների գումարը հաշվարկելիս տեխնիկական դժվարություններից խուսափելու համար այն կորացած տարածություն֊ժամանակները պետք է համարել Էվկլիդեսյան։ Այսինքն՝ ժամանակը կեղծ է, և նրա ուղղությունը չի տարբերվում տարածության ուղղությունից։ Որոշակի հատկությամբ օժտված իրական տարածություն֊ժամանակի հավանականությունը հաշվելու համար, ասենք, օրինակի համար, ամեն կետում և ամեն ուղղությամբ նույնանման երևալու հավանականությունը, գումարվում են բոլոր այն ալիքները, որոնք հատկանշական են նույն հատկություններն ունեցող պատմություններին։
Ընդհանուր հարաբերականության դասական տեսության մեջ կան բազմաթիվ տարբեր հնարավոր կորացած տարածություն֊ժամանակներ, որոնցից յուրաքանչյուրը համապատասխանում է տիեզերքի տարբեր սկզբնական վիճակի։ Եթե իմանայինք մեր տիեզերքի սկզբնական վիճակը, կիմանայինք նաև նրա լրիվ պատմությունը։ Նմանապես, գրավիտացիայի քվանտային տեսության մեջ հնարավոր են տիեզերքի բազմաթիվ տարբեր քվանտային վիճակներ։ Դարձյալ, եթե իմանայինք, թե պատմությունների գումարում էվկլիդեսյան կորացած տարածություն֊ժամանակն ինչ դրսևորումներ է ունեցել վաղ ժամանակներում, ապա մենք կիմանայինք տիեզերքի քվանտային վիճակը։
Դասական գրավիտացիոն տեսության մեջ, որը հիմնված է իրական տարածություն֊ժամանակի վրա, կա տիեզերքի գոյության լոկ երկու հնարավոր եղանակ․ կամ այն գոյություն է ունեցել ի սկզբանե՝ անսահման ժամանակ ի վեր և կամ անցյալում սկզբնավորվել է վերջավոր ժամանակում եզակիության մեջ։ Քվանտային գրավիտացիոն տեսության մեջ, մյուս կողմից, առաջանում է մի երրորդ հավանականություն։ Քանի որ օգտագործվում է էվկլիդեսյան տարածություն֊ժամանակը, որում ժամանակի ուղղությունը նույնական է տարածության մեջ ուղղությունների հետ, հնարավոր է, որ տարածություն֊ժամանակը չափերով վերջավոր լինի, սակայն եզակիություններ և սահման ու եզր նույնպես չունենա։ Տարածություն֊ժամանակը կնմանվի երկրի մակերեսին, կունենա միայն երկու չափում։ Երկրի մակերեսը վերջավոր է իր չափերով, սակայն սահման կամ եզր չունի այն իմաստով, որ եթե նրանով դեպի արևմուտք ճամփորդես՝ եզրի չես հասնի և նրանից դուրս կամ եզակիության մեջ չես ընկնի։ (Այս բանը ես իմ անձնական փորձով գիտեմ, քանի որ ամբողջ աշխարհի շուրջը ճամփորդել եմ)։
Եթե էվկլիդեսյան տարածություն֊ժամանակը հետադարձ երկարաձգվի մինչև անսահման կեղծ ժամանակը կամ, այլ կերպ ասած, սկիզբ առնի կեղծ ժամանակի եզակիությունից, հարցը ոչնչով չի տարբերվի դասական տեսությունից, որի նպատակը եղել է տիեզերքի սկզբնական վիճակի բնորոշումը։ Աստված գիտի, թե տիեզերքն ինչպես է սկիզբ առել, բայց մենք չենք կարող ասել, թե այն այսպես, կամ այնպես է տեղի ունեցել։ Մյուս կողմից, գրավիտացիոն քվանտային տեսությունը նոր հնարավորություն է տալիս, ըստ որի տարածություն֊ժամանակը ոչ մի սահման չի կարող ունենալ, և, հետևաբար, կարիք չկա, որ սահմանամերձ տիեզերքի վարքը բնորոշվի։ Ոչ մի եզակիություն չի կարող լինել, որպեսզի գիտության օրենքներն այնտեղ չգործեն, տարածություն֊ժամանակի ոչ մի եզր՝ որտեղ մարդ ապավինի Աստծուն կամ դիմի ինչ֊որ նոր օրենքի օգնությանը, որպեսզի որոշի տարածություն֊ժամանակի սահմանային պայմանները։ Կարելի է ասել․ «Տիեզերքի սահմանային պայմանն անսահմանությունն է»։ Տիեզերքը պետք է ինքնապարփակ լինի, և նրանից դուրս գտնվող ոչինչ չի կարող ազդել նրա վրա։ Տիեզերքը չի կարելի ո՛չ ստեղծել, ո՛չ էլ կործանել։ Այն պարզապես պետք է լինի։
Վատիկանի՝ վերևում նշածս խորհրդակցության ժամանակ էր, երբ ես առաջին անգամ առաջարկեցի, որ թերևս ժամանակն ու տարածությունը միասին կազմում են վերջավոր մի մակերես, որը, սակայն, չունի ոչ մի սահման և եզր։ Իմ զեկուցումը, սակայն, բավական մաթեմատիկական բնույթի էր և, հետևաբար, շրջանցում էր տիեզերքի ստեղծման մեջ Աստծո դերի վերաբերյալ արված ենթադրությունն ընդհանրապես (ես ինքս անտեսել էի այդ հնարավորությունը)։ Վատիկանի խորհրդակցության ժամանակ ես չգիտեի, թե «սահման չունենալու» գաղափարն ինչպես պետք էր օգտագործել, որպեսզի հնարավոր լիներ տիեզերքի մասին կանխագուշակումներ կատարել։ Հաջորդ ամառը ես անցկացրի Կալիֆոռնիայի համալսարանում, Սանտա֊Բարբարայում։ Այնտեղ իմ գործընկեր և բարեկամ Ջիմ Հարտի հետ մենք մշակեցինք այն պայմանները, որոնց պետք է բավարարեր տիեզերքը, եթե տարածություն֊ժամանակը սահման չունենար։ Վերադառնալով Քեմբրիջ, ես իմ երկու ասպիրանտների՝ Ջուլիան Լաթրելի և Ջոնաթան Հոլիուելի հետ ես շարունակեցի այդ աշխատանքը։
Ուզում եմ ընդգծել, որ այն պատկերացումը, թե ժամանակն ու տարածությունը վերջավոր են առանց սահմանափակման ուղղակի մի առաջարկություն է․ դա որևէ սկզբունքից չի բխում։ Ինչպես որևէ այլ գիտական տեսություն, սկզբում այն կարելի է գեղագիտական կամ մետաֆիզիկական նկատառումներով առաջարկել, բայց իրական չափանիշն այն է, թե այդ տեսության կանխագուշակումներն արդյոք համապատասխանո՞ւմ են մեր դիտարկումներին։ Դա դժվար է որոշել քվանտային գրավիտացիայի դեպքում՝ երկու պատճառով։ Առաջին, ինչպես դա կբացատրվի հաջորդ գլխում, մենք դեռևս վստահ չենք, թե ինչպիսին է այն տեսությունը, որը հաջողությամբ կմիավորի ընդհանուր հարաբերականությունը և քվանտային մեխանիկան, թեև բավական շատ բան գիտենք, թե այդ տեսությունը ինչ ձև է ունենալու։ Երկրորդ, տիեզերքը մանրամասնորեն նկարագրող ցանկացած մոդել մաթեմատիկորեն այն աստիճան բարդ կլինի, որ հնարավոր չի լինի ճշգրիտ կանխագուշակումներ կատարել։ Հետևաբար պետք է դիմել պարզեցնող ենթադրությունների և մոտավորությունների, նույնիսկ այն դեպքում, երբ կանխագուշակումներ կորզելու հարցը շատ դժվար լինի։
Գումարային պատմությունների մեջ յուրաքանչյուր պատմություն ոչ միայն պիտի նկարագրի տարածություն֊ժամանակը, այլև նրա մեջ գտնվող ամեն ինչ, ներառյալ ցանկացած բարդ օրգանիզմ, ինչպես մարդկային էակներն են, որոնք ի վիճակի են դիտարկել տիեզերքի պատմությունը։ Այս բանը մեկ անգամ ևս արդարացնում է մարդաբանական սկզբունքի օգտագործումը, որովհետև, եթե բոլոր պատմությունները հնարավոր են, ապա այնքան ժամանակ, քանի դեռ մենք գոյություն ունենք պատմություններից մեկի մեջ, կարող ենք օգտագործել մարդաբանական սկզբունքը բացատրելու համար, թե ինչո՞ւ է տիեզերքն այնպիսին, ինչպիսին է։ Ճիշտն ասած, թե ինչ իմաստ կարող ենք տալ մյուս պատմություններին, որտեղ մենք գոյություն չունենք, հստակ չէ։ Գրավիտացիայի այս քվանտային տեսությունը շատ ավելի ընդունելի կլիներ, սակայն, եթե օգտագործելով պատմությունների գումարը, ցույց տրվեր, որ մեր տիեզերքը հնարավոր պատմություններից ոչ թե մեկը, այլ ամենահավանականն է։ Այս նպատակի համար, սահման չունեցող բոլոր հնարավոր էվկլիդեսյան տարածություն֊ժամանակների պատմությունները պետք է գումարել։
Սահման չունենալու այս առաջարկությունը թույլ է տալիս պարզել, որ պատմությունների մեծ մասում տիեզերքի գտնվելու հնարավորությունը աննշան է։ Սակայն կան մի խումբ պատմություններ, որոնք շատ ավելի հավանական են, քան այլ պատմություններ։ Պատմությունները կարելի է նմանեցնել երկրագնդի մակերեսին, որի գնդի լայնական (հյուսիսային բևեռից հավասարահեռ) շրջանագիծը ներկայացնում է տիեզերքի տարածական չափը, իսկ հյուսիսային բևեռից ունեցած հեռավորությունը՝ կեղծ ժամանակը։ Տիեզերքը սկիզբ է առնում հյուսիսային բևեռից՝ որպես մի եզակի կետից։ Շարժվելով հարավ, հյուսիսային բևեռից հաստատուն հեռավորություն ունեցող շրջանագծերի լայնություններն աստիճանաբար մեծանում են, ինչը համապատասխանում է կեղծ ժամանակի ընթացքում ընդարձակմանը (նկ․ 8.1)։ Հասարակածում տիեզերքը կհասնի իր առավելագույն չափին և կեղծ ժամանակի հետագա աճի հետ կկծկվի մինչև հարավային բևեռի եզակի կետը։ Թեև տիեզերքի չափսը հավասար է զերոյի հյուսիսային և հարավային բևեռներում, այս կետերը եզակիություններ չեն, ինչպես երկրագնդի բևեռները եզակի չեն։ Հետևաբար, գիտության օրենքները կմնան ուժի մեջ ճիշտ այնպես, ինչպես երկրագնդի հյուսիսային և հարավային բևեռներում գործում են նույն օրենքները, ինչ հասարակածում։
Սակայն իրական ժամանակում տիեզերքի պատմությունն այլ տեսք կունենա։ Մոտավորապես տասը կամ քսան հազար միլիոն տարի առաջ իր նվազագույն չափսն ուներ, որը հավասար էր կեղծ ժամանակում նրա պատմության առավելագույն շառավղին։ Հետագա իրական ժամանակներում տիեզերքը պետք է ընդարձակվեր Լինդեի առաջարկած քաոսային հարաճուն ընդարձակման մոդելի համաձայն (բայց պետք չէ ենթադրել, որ տիեզերքը ստեղծվել է ճշգրտված որոշակի վիճակում)։ Տիեզերքը պետք է ընդարձակվի, հասնի մեծ չափի և ի վերջո կոլապսվի ու վերածվի մի այնպիսի վիճակի, որը իրական ժամանակի մեջ նման կլինի եզակիության։ Այսպիսով, որոշ իմաստով մենք կործանման ենք դատապարտված, նույնիսկ եթե մեզ հաջողվի սև խոռոչներից հեռու մնալ։ Միայն այն դեպքում, երբ մենք տիեզերքը կարողանանք պատկերացնել կեղծ ժամանակում, եզակիություններ չեն լինի։
Եթե տիեզերքը իրոք գտնվի այդպիսի մի քվանտային վիճակում, ապա կեղծ ժամանակում նրա պատմությունը եզակիություններ չի կարող ունենալ։ Հետևաբար կարող է թվալ, որ իմ վերջին աշխատանքը լրիվ արժեզրկում է եզակիությունների մասին ավելի վաղ կատարած իմ գործը։ Բայց, ինչպես ցույց տրվեց վերևում, եզակիության թեորեմների իրական կարևորությունն այն էր, որ նրանք ցույց տվեցին, որ գրավիտացիոն դաշտը կարող է այն աստիճան ուժեղանալ, որ քվանտային ձգողական ազդեցությունները չի կարելի անտեսել։ Այս բանը հանգեցրեց այն մտքին, որ տիեզերքը կեղծ ժամանակում կարող է վերջավոր լինել, բայց առանց սահմանների ու եզակիությունների։ Երբ վերադառնանք դեպի իրական ժամանակը, որում մենք ապրում ենք, այնուամենայնիվ, եզակիություններ միշտ կլինեն։ Սև խոռոչի մեջ ընկնելիս խեղճ տիեզերագնացի վերջը միշտ վատ կլինի․ եթե նա ապրեր կեղծ ժամանակում, ապա այդ պարագայում միայն չէր հանդիպի եզակիությունների։
Սա կարող է մեզ հուշել, որ, այսպես կոչված, կեղծ ժամանակն իրականում իրական ժամանակն է, իսկ այն, ինչ մենք իրական ժամանակ ենք անվանում, մեր երևակայության խաբկանքն է։ Իրական ժամանակում տիեզերքը մի սկիզբ ունի և մի վերջ՝ եզակիությունում, որը տարածության֊ժամանակի սահմանն է, որտեղ գիտության օրենքները չեն գործում։ Իսկ կեղծ ժամանակում չկան ոչ եզակիություններ և ոչ էլ սահմաններ։ Հետևաբար, թերևս այն, ինչ մենք անվանում ենք կեղծ ժամանակ, ըստ էության, ավելի իրական է, իսկ այն, ինչ մենք կոչում ենք իրական՝ դա պարզապես հնարովի մի գաղափար է, որը մենք ներմուծել ենք, որպեսզի մեզ օգնի նկարագրելու տիեզերքի որպիսությունը։ Բայց ինչպես նկարագրել եմ 1֊ին գլխում, գիտական տեսությունը լոկ մաթեմատիկական մի մոդել է, որը մենք ստեղծում ենք նկարագրելու համար մեր դիտարկումները․ դա գոյություն ունի միայն մեր մտքում։ Հետևաբար անիմաստ է հարցնել, թե որ ժամանակն է «իրական» և որը՝ «կեղծ»։ Բանը պարզապես այն է, թե որն է առավել օգտակար։
Մենք կարող ենք պատմությունների գումարն օգտագործել նաև որպես սահման չունենալու առաջարկություն, որպեսզի գտնենք, թե տիեզերքի որ հատկությունները կարող են միասին ի հայտ գալ։ Օրինակի համար, կարելի է հաշվել այն հավանականությունը, որով տիեզերքը բոլոր տարբեր ուղղություններով ընդարձակվում է համարյա նույն արագությամբ, երբ նրա խտությունն ունի այժմյան արժեքը։ Այս հավանականությունը շատ մեծ է ստացվում մինչև այժմ քննարկված պարզ մոդելների հիման վրա կատարված հաշվումների համաձայն։ Այսինքն, սահման չունենալու առաջարկությունը տանում է այն կանխագուշակման, ըստ որի չափազանց հավանական է, որ տիեզերքի այժմյան ընդարձակման արագությունը բոլոր ուղղություններով համարյա նույնն է։ Այս կանխագուշակումը համապատասխանում է միկրոալիքային ֆոնային ճառագայթմանը, որը բոլոր ուղղություններով բացարձակապես նույնն է։ Եթե տիեզերքը մի որևէ ուղղությամբ ավելի արագ ընդարձակվեր, քան այլ ուղղություններով, ապա ճառագայթման ինտենսիվությունն այն ուղղություններում պետք է նվազեր լրացուցիչ կարմիր շեղումով։
Սահման չունենալու պայմաններում այլ կանխագուշակումների գծով աշխատանքներն այժմ շարունակվում են։ Առանձնապես շատ հետաքրքրական է այն պրոբլեմը, թե վաղ տիեզերքում համաչափ խտությունից փոքրիկ շեղումներն ինչ չափի են եղել, որոնք պատճառ են դարձել նախ գալակտիկաների, ապա աստղերի և վերջապես՝ մեր առաջացման։ Անորոշության սկզբունքից հետևում է, որ վաղ տիեզերքը լրիվ համաչափ չէր կարող լինել, որովհետև որոշ անորոշություններ և տատանումներ պետք է եղած լինեն մասնիկների դիրքերում և արագություններում։ Օգտագործելով սահման չունենալու պայմանը, մենք գտնում ենք, որ տիեզերքն իրոք սկսվել է այն նվազագույն անհամաչափությունից, որը թույլ է տրվում համաձայն անորոշության սկզբունքի։ Այսպիսով, տիեզերքն անցել է արագ ընդարձակման մի շրջան, ինչպես նկարագրվում է հարաճուն ընդարձակման մոդելներում։ Այդ շրջանում սկզբնական անհամաչափությունները պետք է ավելի շեշտված լինեն՝ այն աստիճան մեծ, որ հնարավոր լինի բացատրել մեր շուրջ գոյություն ունեցող կառուցվածքների առաջացումը։ Ընդարձակվող տիեզերքում, որտեղ նյութի խտությունն աննշան չափով է փոփոխվում մի տեղից մյուսը, գրավիտացիայի պատճառով խիտ տիրույթների ընդարձակումը դանդաղում է և ի վերջո սկսում է նրանց սեղմումը։ Սա հանգեցնում է գալակտիկաների, աստղերի և վերջապես նույնիսկ մեզ նման աննշան արարածների առաջացմանը։ Այսպիսով, տիեզերքում մեր տեսած բոլոր բարդ կառուցվածքների առաջացումը կարելի է բացատրել տիեզերքի սահման չունենալու պայմանի և քվանտային մեխանիկայի անորոշության սկզբունքի միացյալ հիմքի օգնությամբ։
Այն գաղափարը, թե տարածությունը և ժամանակը կարող են մի փակ մակերես ստեղծել, որը սահման չունի, խոր նշանակություն ունի տիեզերական գործերում Աստծո խաղացած դերի հարցում։ Գիտական տեսությունների այն հաջողությունները, որոնք լավագույնս նկարագրեցին մեր շուրջ տեղի ունեցող դեպքերը, պատճառ եղան, որ շատերը հավատան, թե Աստված թույլ է տվել, որ տիեզերքը զարգանա մի շարք օրենքների համաձայն և այլևս չի միջամտում, որպեսզի այդ օրենքները չխախտվեն։ Սակայն այս օրենքները մեզ չեն ասում, թե ինչի նման պետք է եղած լիներ տիեզերքն իր սկզբնական շրջանում։ Աստված պետք է լարեր ժամացույցը և ընտրեր, թե ինչպես պետք է տիեզերքը սկիզբ առներ։ Քանի որ տիեզերքը սկիզբ է ունեցել, ապա մենք կարող ենք ենթադրել, որ այն ունեցել է իր արարիչը։ Սակայն, եթե տիեզերքն իրապես լրիվ ինքնապարփակ է, սահման և եզր չունի, չի կարող ոչ սկիզբ, ոչ էլ վերջ ունենալ, այլ այն պարզապես կա։ Ուստի այդ դեպքում արարչին այլևս անելիք չի մնում։
9
Ժամանակի նետը
Նախորդ գլուխներում մենք տեսանք, թե տարիների ընթացքում ինչպես են փոխվել ժամանակի մասին մեր ունեցած պատկերացումները։ Ընդհուպ մինչև մեր ունեցած պատկերացումները։ Ընդհուպ մինչև մեր դարասկիզբը մարդիկ համոզված էին, թե ժամանակը բացարձակ է։ Այսինքն՝ յուրաքանչյուր դեպք կարելի է համարակալել մի եզակի թվով, որը կոչվում է «Ժամանակ», և բոլոր ճշգրիտ ժամացույցները երկու հաջորդական դեպքերի միջև անցած ժամանակամիջոցի համար ցույց կտան նույն մեծությունը։ Սակայն այն հայտնագործությունը, թե լույսի արագությունը հաստատուն մեծություն է բոլոր դիտորդների համար՝ անկախ նրանց շարժման արագությունից, պատճառ եղավ հարաբերականության տեսության ստեղծման և եզակի, բացարձակ ժամանակի հասկացությունից հրաժարման։[20]
Այսպիսով, ամեն դիտորդ ունի ժամանակի իր չափը, ինչը արձանագրում է դիտորդի ժամացույցը։ Պարտադիր չէ, որ տարբեր դիտորդների ժամացույցները նույն ժամանակը ցույց տան։ Մի խոսքով, ժամանակն առավել անհատական բնույթի հասկացություն է դարձել՝ կախված այն չափող դիտորդից։
Երբ փորձ արվեց գրավիտացիան միավորել քվանտային մեխանիկայի հետ, ապա հարկ եղավ ներմուծել «կեղծ» ժամանակի գաղափարը։ Կեղծ ժամանակը կախված չէ տարածության մեջ ուղղություններից։ Եթե հնարավոր է դեպի հյուսիս ուղղությամբ շարժվել, ապա հնարավոր է նաև հետ շրջվել և շարժվել դեպի հարավ․ նմանապես, եթե հնարավոր է կեղծ ժամանակով առաջ ընթանալ, ապա հնարավոր պետք է լինի շրջվել և շարժվել կեղծ ժամանակի հետընթաց ուղղությամբ։ Սա նշանակում է, որ որևէ էական տարբերություն չի կարող լինել կեղծ ժամանակի առաջընթաց և հետընթաց ուղղությունների միջև։ Իսկ «իրական» ժամանակում այդ տարբերությունը շատ մեծ է, ինչպես բոլորս գիտենք։ Որտեղի՞ց է գալիս անցյալի և ապագայի միջև առկա այս տարբերությունը։ Մենք ինչո՞ւ ենք անցյալը հիշում, բայց ոչ ապագան։[21]
Գիտության օրենքները ոչ մի տարբերություն չեն դնում անցյալի և ապագայի միջև։ Ավելի հստակ ասած, ինչպես վերևում բացատրվեց, գիտության օրենքներն անփոփոխ են C, P, և T համար։ (C ― նշանակում է մասնիկը փոխել հակամասնիկի, P ― նշանակում է վերցնել հայելապատկերը, այնպես, որ ձախն ու աջը փոխեն իրենց տեղերը, և T ― նշանակում է շրջել բոլոր մասնիկների շարժման ուղղությունները, այսինքն՝ շարժմանը տալ հետադարձ ուղղություն)։ Բոլոր սովորական վիճակներում նյութի վարքագիծը կառավարող գիտության օրենքներն անփոփոխ են մնում C և P համակցության ազդեցության դեպքում։ Այլ խոսքերով ասած, կյանքը նույնը կլինի մի այլ մոլորակի բնակչության համար, ինչպես մերը, որտեղ մարդիկ մեր հայելապատկերներն են ու կազմված են ոչ թե մեր նյութից, այլ հականյութից։
Եթե գիտության օրենքներն անփոփոխ են C և P գործողությունների համակցության, ինչպես նաև C, P և T համակցության ազդեցության դեպքում, պետք է որ անփոփոխ լինեն նաև T գործողության ազդեցության համար։ Այնուամենայնիվ, առօրյա կյանքում իրական ժամանակի առաջընթաց և հետընթաց ուղղությունների միջև շատ մեծ տարբերություն կա։ Պատկերացնենք սեղանին դրված մի բաժակ, որը սեղանից ընկնելով փշրվում է։ Եթե այդ բանը նկարահանենք ժապավենի վրա, ապա դիտման ժամանակ հեշտ է ասել՝ ֆիլմը առաջընթաց, թե հետընթաց ուղղությամբ է ցուցադրվում։ Եթե ցուցադրումը հետընթաց է, ապա կտեսնենք, թե ինչպես են ապակու կտորները հանկարծ ի մի հավաքվում, և հատակից ամբողջական բաժակը ցատկելով հայտնվում է սեղանի վրա։ Քանի որ իրական կյանքում այդպիսի բան տեղի չի ունենում, ուստի կասենք, որ ֆիլմը ցուցադրվում է հակառակ ուղղությամբ։ Արդարև, եթե այդպիսի բան տեղի ունենար, բաժակ արտադրողները կսնանկանային։
Թե ջարդված բաժակները ինքնակամ կերպով հատակի վրա ինչո՞ւ ի մի չեն հավաքվում և չեն ցատկում սեղանին, սովորաբար բացատրվում է նրանով, որ դա արգելվում է ըստ թերմոդինամիկայի երկրորդ օրենքի։ Վերջինիս համաձայն, փակ համակարգում անկարգությունը կամ էնտրոպիան աճում է ժամանակին զուգընթաց։[22] Այլ կերպ ասած, սա Մերֆիի օրենքի մի տարատեսակ է, ըստ որի «ամեն ինչ աշխարհում միշտ թարս է գնում»։ Սեղանի վրա գտնվող ամբողջական բաժակը ներկայացնում է կատարյալ կարգուկանոնի վիճակը, իսկ հատակին փշրված բաժակը գտնվում է անկարգ վիճակում։ Դժվար չէ կազմակերպել անցումն անցյալում սեղանի վրա գտնվող բաժակի վիճակից դեպի ապագայում փշրված բաժակի վիճակի, բայց ոչ հակառակը։[23]
Ժամանակին զուգընթաց անկարգության կամ էնտրոպիայի աճը ժամանակի նետ կոչվող հասկացության օրինակներից է․ այս հասկացությունն է տարբերում անցյալն ապագայից՝ ժամանակին ուղղություն տալով։ Կան ժամանակի առնվազն երեք տարբեր նետեր։ Առաջինը ժամանակի թերմոդինամիկական նետն է, որը ցույց է տալիս ժամանակի այն ուղղությունը, որում անկարգությունը կամ էնտրոպիան աճում է։ Երկրորդը ժամանակի հոգեբանական նետն է։ Սա այն ուղղությունն է, որով, ըստ մեր զգացողության, անցնում է ժամանակը, ուղղություն, որով հիշում ենք անցյալը, սակայն ոչ ապագան։ Սա ժամանակի այն ուղղությունն է, որով տիեզերքը ավելի շատ ընդարձակվում է, քան սեղմվում։
Այս գլխում ես կաշխատեմ հիմնավորել, թե ինչու տիեզերքի սահման չունենալու պայմանը, թույլ մարդաբանական սկզբունքի հետ միասին, կարող է բացատրել, թե ինչու են երեք նետերն էլ ուղղված միևնույն ուղղությամբ, ինչպես նաև այն, որ պետք է գոյություն ունենա հստակ սահմանված ժամանակի նետ հասկացությունն ընդհանրապես։ Կաշխատեմ հիմնավորել, որ հոգեբանական նետը պայմանավորված է թերմոդինամիկական նետով, և այս երկու նետերը պարտադիր կերպով միշտ նույն ուղղություն ունեն։ Եթե մենք ընդունենք տիեզերքի սահման չունենալու պայմանը, կտեսնենք, որ պետք է գոյություն ունենան հստակ որոշված թերմոդինամիկական և տիեզերաբանական ժամանակի նետեր, սակայն դրանք կարող են նույն ուղղությամբ ուղղված չլինել տիեզերքի ամբողջ պատմության ընթացքում։ Սակայն ես պիտի աշխատեմ հիմնավորել, որ միայն այն դեպքում, երբ այդ նետերն ունենան միևնույն ուղղությունը, կառաջանան բարենպաստ պայմաններ, որպեսզի զարգանան այնպիսի բանական էակներ, որոնք կարող են հարց տալ, թե ինչո՞ւ է անկարգությունը ժամանակի այն ուղղությամբ աճում, որով ընդարձակվում է տիեզերքը։
Սկսենք թերմոդինամիկական ժամանակի նետի հարցի քննարկումից։ Թերմոդինամիկայի երկրորդ օրենքը հիմնված է այն փաստի վրա, որ գոյություն ունեն ավելի շատ անկարգ համակարգեր, քան կարգավորված համակարգեր։ Պատկերացրեք, օրինակ, որ մի նկար մասերի է բաժանված, և դրանք լցված են տուփի մեջ։ Մեկ և միայն մեկ դասավորություն կա, որով մասերը միանալով կառաջացնեն ամբողջական պատկերը։ Մյուս կողմից, գոյություն ունեն բազմաթիվ դասավորություններ, որոնցով ամբողջական պատկեր չի ստացվում։
Ենթադրենք, ինչ֊որ համակարգ գտնվում է այդ փոքրաթիվ կանոնավոր վիճակներից մեկում։ Ժամանակի ընթացքում, գիտության օրենքներին համապատասխան, համակարգը պիտի զարգանա և իր վիճակը փոխի։ Քանի որ չկարգավորված վիճակներն ավելի շատ են, ապա հետագայում առավել հավանական է, որ համակարգը կարգավորված վիճակից անցնի չկարգավորված վիճակի։ Այսպիսով, եթե համակարգի սկզբնական վիճակը կարգավորված էր, ապա ժամանակի ընթացքում այն կձգտի անկանոն վիճակի։
Այժմ ենթադրենք, որ նկարի մասերը այնպես են դասավորված տուփում, որ ստացվել է ամբողջական պատկեր։ Եթե տուփը թափահարենք, ապա մասերը ձեռք կբերեն մի նոր դասավորություն։ Ամենայն հավանականությամբ կստացվի մի անկանոն դասավորություն, որում մասերն ամբողջական պատկեր չեն կազմում․ դա պարզապես այն պատճառով, որ անհամեմատ մեծ թվով անկանոն դասավորություններ են հնարավոր։ Հնարավոր է, որ նկարի մասերի որոշ խմբեր կազմեն նկարի առանձին հատվածներ, բայց եթե շարունակենք տուփը թափահարել, ապա նկարի այդ հատվածները նույնպես կվերանան, և ստացված վիճակը կլինի խառնափնթոր մի դասավորություն, որը ոչ մի նկարի չի նմանվի։ Այսպիսով, եթե մենք սկսում ենք կարգավորված վիճակից, ապա ժամանակի ընթացքում մասերը ձգտում են ավելի բարձր անկանոն վիճակի։
Ենթադրենք Աստված ցանկացել է, որ տիեզերքի զարգացումը պետք է ավարտվի բարձր աստիճանի կարգավորություն ունեցող մի վիճակով, անկախ այն բանից, թե ինչպիսի վիճակից է այն սկիզբ առել։ Տիեզերքը, ամենայն հավանականությամբ, վաղ ժամանակներում կարող էր գտնվել չկարգավորված վիճակում։ Բայց դա նշանակում է, որ անկանոնությունը ժամանակի ընթացքում նվազում է։ Այսինքն՝ ջարդված բաժակները պիտի ամբողջանան և ցատկեն սեղանի վրա։ Սակայն այս երևույթին ականատես մարդիկ կապրեին մի տիեզերքում, որտեղ անկանոնությունը նվազում է ժամանակի ընթացքում։ Կարելի է պնդել, որ այդպիսի էակների համար ժամանակի հոգեբանական նետը հակառակ ուղղություն պետք է ունենա։ Նրանք դեպքերը կհիշեն ապագայում, բայց՝ ոչ անցյալում։ Երբ տեսնեն փշրված բաժակը, նրանք կհիշեն սեղանին դրված լինելու պահը, իսկ երբ բաժակը տեսնեն սեղանին, նրանք չեն հիշի, որ այն գետին էր ընկած։[24]
Բավական դժվար է խոսել մարդկային հիշողության մասին, որովհետև մենք ուղեղի աշխատանքի մանրամասնություններին տեղյակ չենք։ Սակայն համակարգչի հիշողության աշխատանքի վերաբերյալ մենք ամեն ինչ գիտենք։ Հետևաբար, ես ուզում եմ քննարկել հաշվողական մեքենայի ժամանակի հոգեբանական նետը։ Կարծում եմ՝ կարելի է ենթադրել, որ համակարգիչների և մարդկանց նետերը (ժամանակի) նույնն են (նույն ուղղությունն ունեն)։ (Եթե այդպես չլիներ, ապա արժեթղթերի սակարանում մարդ մեծ հարստություն կդիզեր, օգտագործելով մի այնպիսի մեքենա, որը հիշեր արժեթղթերի վաղվա գները)։
Հաշվողական մեքենայի հիշողությունը մի հարմարանք է, որը պարունակում է երկու տարբեր վիճակներից մեկում գտնվող տարրեր։ Սովորական հաշվապահական հաշվիչն այդպիսի հարմարանքի մի պարզ օրինակ է։ Դրա պարզագույն ձևը կազմված է մի քանի մետաղե ձողերից, որոնցից յուրաքանչյուրին հագցված է մի գնդիկ, որը կարելի է դնել երկու դիրքից մեկում։ Համակարգչի հիշողության մեջ ցանկացած տեղեկություն ներմուծելուց առաջ, նրա հիշողությունը գտնվում է անկանոն վիճակում՝ երկու հնարավոր վիճակներից յուրաքանչյուրին անցնելու հավասար հավանականությամբ։ (Հաշվիչի ձողերի վրա գնդիկները խառնիխուռն են բաշխված)։ Հիշողության մեջ արձանագրվելիք համակարի հետ փոխազդելուց հետո նրա հիշողությունն անպայման գալիս է որոշակի վիճակի՝ համակարգի վիճակին համապատասխան։ (Յուրաքանչյուր գնդիկ կգտնվի հաշվիչի ձողի կամ աջ, կամ ձախ կողմում)։ Այսպիսով, հիշողությունը անկանոն վիճակից անցել է կանոնավոր վիճակի։ Սակայն այս բանը անելու համար հարկավոր է աշխատանք կատարել (օրինակ, գնդիկը շարժել կամ համակարգիչը հոսանքով սնել)։ Այդ էներգիան ցրվում է որպես ջերմություն, և տիեզերքում աճում է անկանոնության աստիճանը։ Կարելի է ցույց տալ, որ այդպիսի անկանոնության աճն ավելի մեծ է, քան հիշողության մեջ կարգավորվածության աճը։[25]
Այսպիսով, երբ համակարգիչը հիշողության գրանցում է կատարում, նրա հովհարիչի պտուտակի արտամղված ջերմությունը պատճառ է դառնում, որ տիեզերքում անկանոնության գումարային քանակությունն աճի։ Ժամանակի ուղղությունը, որով համակարգիչը հիշում է անցյալը, նույնն է, ինչ տիեզերքում անկանոնության աճի ուղղությունը։
Ժամանակի ուղղության մեր ենթակայական զգացողությունը, ժամանակի հոգեբանական նետը, մեր ուղեղում որոշվում է ժամանակի թերմոդինամիկական նետի ուղղությամբ։ Համակարգչի նման մենք ևս անցյալը պիտի հիշենք այն կարգով, ինչ կարգով աճում է էնտրոպիան։ Այս տեսակետից թերմոդինամիկայի երկրորդ օրենքը կարծես պարզունակ է դառնում։ Անկանոնությունն աճում է ժամանակին զուգընթաց, որովհետև մենք ժամանակը չափում ենք այն ուղղությամբ, ինչ ուղղությամբ աճում է անկանոնությունը։ Դժվար թե հնարավոր լիներ կատարել ավելի պարզունակ պնդում։[26]
Բայց ինչո՞ւ պետք է ընդհանրապես գոյություն ունենա ժամանակի թերմոդինամիկական նետ։ Կամ, այլ կերպ ասած, ինչո՞ւ պետք է տիեզերքն ինչ֊որ ժամանակում, որը մենք անվանում ենք անցյալ, կանոնավոր եղած լինի։ Կամ ինչո՞ւ այն չպետք է անկանոն վիճակում լինի բոլոր ժամանակներում։ Վերջ ի վերջո այս վերջինն ավելի հավանական է թվում։ Եվ ինչո՞ւ է անկանոնությունը ժամանակի ընթացքում աճում այն ուղղությամբ, որով ընդարձակվում է տիեզերքը։
Ընդհանուր հարաբերականության դասական տեսությունը մեզ թույլ չի տալիս կանխագուշակել, թե ինչպես է տիեզերքը ծագել, որովհետև գիտության բոլոր հայտնի օրենքները Մեծ պայթյունի եզակիությունում իրենց ուժը կորցնում են։ Հնարավոր է, որ տիեզերքը սկիզբ է առել մի համասեռ, խիստ կարգավորված վիճակում։ Սա կհանգեցներ ժամանակի հատուկ սահմանված թերմոդինամիկական և տիեզերաբանական նետերին, ինչը և դիտարկվում է։ Սակայն հավասարապես հնարավոր է, որ այն սկիզբ առներ խիստ անհամասեռ և անկանոն վիճակում։ Այս դեպքում տիեզերքն արդեն կատարյալ անկանոն վիճակում կլիներ, հետևաբար նրա անկանոնությունը չէր կարող աճել ժամանակին զուգընթաց։ Կամ անկանոնությունը անփոփոխ կմնար, որի դեպքում ժամանակի հստակ սահմանված թերմոդինամիկական նետ չէր կարող լինել, կամ անկանոնությունը կնվազեր, և այդ պարագայում թերմոդինամիկական նետն ուղղված կլիներ տիեզերաբանականի հակառակ ուղղությամբ։ Այս երկու հնարավորություններն էլ չեն համապատասխանում փորձնական դիտարկումներին։ Սակայն, ինչպես տեսանք, ընդհանուր հարաբերականության դասական տեսությունը կանխագուշակում է իր տապալումը։ Երբ տարածություն֊ժամանակի կորությունը շատ է մեծանում, քվանտային գրավիտացիոն ազդեցությունները դառնում են առաջնահերթ, և դասական տեսությունն ի վերջո կորցնում է տիեզերքը նկարագրելու կարողությունը։ Մենք ստիպված ենք դիմել գրավիտացիոն քվանտային տեսությանը, որպեսզի հասկանանք, թե ինչպես է սկիզբ առել տիեզերքը։
Ինչպես նախորդ գլխում տեսանք, ըստ գրավիտացիոն քվանտային տեսության, տիեզերքի վիճակը բնորոշելու համար անհրաժեշտ է իմանալ, թե ինչպիսիք կարող էին լինել տիեզերքի հնարավոր պատմությունները անցյալում՝ տարածություն֊ժամանակի սահմանագծում։ Խուսափել այն բանը գիտենալու անհրաժեշտությունից, ինչը մենք չգիտենք և չենք կարող գիտենալ, կարելի է միայն այն դեպքում, եթե անցյալ պատմությունները բավարարում են սահման չունենալու պայմանին, այսինքն՝ դրանք վերջավոր են, բայց սահման, եզր կամ եզակիություն չունեն։ Այդ դեպքում ժամանակի սկիզբը կլիներ կանոնավոր, հարթ մի կետ տարածություն֊ժամանակի մեջ, և տիեզերքը, կսկսեր ընդարձակվել մի համասեռ ու կանոնավոր վիճակից։ Այն լրիվ միաձև չէր կարող լինել, որովհետև այդ դեպքում կխախտվեր քվանտային մեխանիկայի անորոշության սկզբունքը։
Պետք է, որ լինեին մասնիկների խտության և արագությունների փոքր տատանումներ։ Սակայն անսահմանության պայմանի շնորհիվ այդ տատանումները պետք է հնարավորին չափ փոքր լինեն, որպեսզի չխախտվի անորոշության սկզբունքը։
Ամենավաղ շրջանում տիեզերքը կարող էր ունենալ Էքսպոնենտային կամ «հարաճուն»[27] ընդարձակման մի ժամանակահատված, որի ընթացքում նրա մեծությունն աճեր մեծ գործակցով։ Այս ընդարձակման ժամանակ խտության տատանումները սկզբում փոքր կլինեին, իսկ հետագայում կսկսեին աճել։ Այն տիրույթներում, որտեղ խտությունը փոքր֊ինչ մեծ էր միջին արժեքից, ընդարձակումը կդանդաղեր հավելյալ զանգվածի գրավիտացիոն ձգողության շնորհիվ։ Վերջ ի վերջո այդպիսի տիրույթները կդադարեին ընդարձակվել, կոլապսի կենթարկվեին՝ առաջացնելով գալակտիկաներ, աստղեր և մեզ նման էակներ։ Այսպիսով տիեզերքը սկիզբ առած կլիներ համասեռ ու կանոնավոր վիճակից և ժամանակի ընթացքում կդառնար անհամասեռ ու անկանոն։ Այս կերպ կարելի է բացատրել ժամանակի թերմոդինամիկական նետի գոյությունը։
Սակայն ի՞նչ կպատահեր, երբ տիեզերքը դադարեր ընդարձակվել և սկսեր սեղմվել։ Արդյո՞ք թերմոդինամիկական նետն այդ ընթացքում կփոխի իր ուղղությունը, և ժամանակին զուգընթաց կնվազի անկանոնությունը։ Սա ամեն տեսակի գիտաֆանտաստիկական հնարավորությունների առիթ է կստեղծեր բոլոր նրանց համար, որոնց բախտ կվիճակվեր ապրել ընդարձակումից սեղմանն անցման փուլից հետո։ Կտեսնե՞ն արդյոք նրանք, թե ինչպես են ամբողջանում ջարդուփշուր եղած բաժակներն ու գետնից ցատկում սեղանի վրա։ Գուցե նրանք ի վիճակի՞ կլինեն հիշել վաղվա գները և սակարանում հարստություն կդիզեն։ Անհանգստությունն այն բանի համար, սակայն, թե ինչ կկատարվի, եթե տիեզերքն սկսի կոլապսվել, լոկ գիտական հարց է, քանի որ սեղմում չի լինի դեռ առնվազն մի քանի տասնյակ միլիարդ տարի։ Բայց ավելի շուտ պարզելու համար, թե ինչ է պատահելու, բավական է նետվել սև խոռոչի մեջ։ Սև խոռոչ առաջացնող աստղի կոլապսը շատ նման է ամբողջ տիեզերքի կոլապսի վերջնական վիճակներին։
Այսպիսով, եթե անկանոնությունը նվազելու է տիեզերքի կծկման փուլում, ապա կարելի է ակնկալել, որ այն կնվազի նաև սև խոռոչի ներսում։ Հետևաբար, սև խոռոչ ընկած տիեզերագնացը կարող է հարստանալ, ռուլետ խաղալով, քանի որ գրազ գալուց առաջ հիշելու է,[28] թե ուր է ընկել գնդակը։ (Դժբախտաբար, խաղը երկար չի տևի, նա խաղի հենց սկզբում սպագետիի նման կերկարի։ Նա ի վիճակի չի լինի մեզ տեղյակ պահել ո՛չ այն մասին, թե թերմոդինամիկական նետը շրջվեց հակառակ ուղղությամբ, ո՛չ էլ կկարողանա իր շահումը վերցնել, որովհետև նա, փաստորեն, դուրս գալու հնարավորություն չի ունենա սև խոռոչի պատահութային հորիզոնի հետևից)։
Սկզբում ես հավատացած էի, որ կոլապսի հետևանքով տիեզերքի անկանոնությունը նվազելու է, որովհետև մտածում էի, թե երբ տիեզերքը դարձյալ փոքրանա, վերադառնալու է իր նախնական համեստ ու կանոնավոր վիճակին։
Այսինքն՝ սեղմվելու փուլը նման է լինելու ժամանակի հետընթաց կարգով ընդարձակման փուլին։ Սեղման փուլում կյանքը պետք է ընթանար հակառակ ընթացքով․ մարդիկ ծնվելուց առաջ մեռնելու են, և քանի տիեզերքը փոքրանում է, նրանց տարիքը պիտի նվազի։[29]
Այս գաղափարը հրապուրիչ է այնքանով, որ ծնում է ընդարձակման և սեղմման փուլերի գեղեցիկ համաչափություն։ Սակայն դա հենց այնպես չի կարելի ընդունել՝ առանց հաշվի առնելու տիեզերքի մասին այլ պատկերացումները։ Հարց է առաջանում՝ այդ գաղափարը հետևում է տիեզերքի անսահմանության պայմանի՞ց, թե՞ ընդհակառակը, հակասում է դրան։ Ինչպես ասացի, սկզբում ես կարծում էի, թե անսահմանության պայմանն իսկապես նշանակում է, որ անկանոնությունը պիտի նվազի, երբ տիեզերքը սկսի սեղմվել։ Իսկ սխալը մասամբ բխում էր տիեզերքը երկրի մակերևույթի հետ նույնացնելուց։ Եթե ընդունենք, որ տիեզերքի սկիզբը համապատասխանում է հյուսիսային բևեռին, ապա տիեզերքի վերջը պետք է նման լինի իր սկզբին, քանի որ հարավային բևեռը նման է հյուսիսային բևեռին։ Սակայն հյուսիսային և հարավային բևեռները կեղծ ժամանակում համապատասխանում են տիեզերքի սկզբին և վերջին։ Իրական ժամանակում սկիզբն ու վերջը կարող են շատ տարբեր լինել միմյանցից։ Սխալս պայմանավորված էր նաև նրանով, որ աշխատանքիս համար օգտագործել էի մի պարզ մոդել, որում սեղմման փուլը նման էր ժամանակի հետընթաց կարգով ընդարձակմանը։ Պեննի պետական համալսարանի իմ գործընկեր Դոն Փեյջն իմ ուշադրությունը հրավիրեց այն բանի վրա, որ սահման չունենալու պայմանը բոլորովին էլ չի պահանջում, որ սեղմվող փուլը անպայման լինի ժամանակի հետընթաց կարգով ընդարձակման փուլ։
Հետագայում իմ ուսանող Ռեյմոնդ Լաֆլեմը ցույց տվեց, որ եթե ավելի բարդ մոդել օգտագործվի, ապա տիեզերքի կոլապսը շատ տարբեր կլինի իր ընդարձակումից։
Ակնհայտ էր, որ ես սխալվել էի․ անսահմանության պայմանը ենթադրում է, որ անկանոնությունը շարունակվելու է մեծանալ սեղմմանը զուգընթաց։ Ժամանակի թերմոդինամիկական և հոգեբանական նետերը չեն փոխում իրենց ուղղությունը՝ ոչ կծկվող տիեզերքում, ոչ էլ սև խոռոչում։
Ի՞նչ կարելի է անել, երբ պարզվում է, որ այդպիսի սխալ է թույլ տրվել։ Ոմանք երբեք իրենց սխալը չեն ընդունում և շարունակում են փնտրել նոր բացատրությունները, հաճախ միմյանց հակասող, իրենց տեսակետները հաստատող փաստարկներ բերում, ինչպես, օրինակ, Էդինգտոնն արեց՝ հակադրվելով սև խոռոչների տեսությանը։ Ուրիշները հայտարարում են, թե իրենք երբեք սխալ տեսակետը չեն պաշտպանել և, եթե պաշտպանել են, ապա միայն այն պատճառով, որպեսզի ցույց տան նրա անհիմն լինելը։ Իմ կարծիքով, ավելի ճիշտ է, և նվազ շփոթ է առաջանում, եթե մարդ գրավոր կերպով ընդունում է իր սխալը։ Սրա լավագույն օրինակը տվել է Էյնշտեյնը, որն իր կյանքի մեծագույն սխալը համարեց տիեզերքի համար ստատիկ մոդել ստեղծելիս իր ներմուծած տիեզերաբանական հաստատունը։
Վերադառնալով ժամանակի նետի հարցին՝ մնում է բացատրել, թե ինչո՞ւ են մեր դիտարկումները հաստատում, որ թերմոդինամիկական և տիեզերաբանական նետերը նույն ուղղությունն ունեն։ Կամ, այլ կերպ ասած, ինչո՞ւ է ժամանակին զուգընթաց անկանոնությունն աճում այն ուղղությամբ, որով ընդարձակվում է տիեզերքը։ Եթե ենթադրենք, որ տիեզերքն ընդարձակվելուց հետո կսկսի վերստին կծկվել, ապա, ինչպես հետևում է ամսահմանության պայմանից, թվում է, նետերի ուղղության խնդիրը հանգում է այն հարցին, թե մենք ինչո՞ւ պիտի գտնվենք տիեզերքի ընդարձակման և ոչ թե սեմման փուլում։
Սրա պատասխանը կարելի է տալ՝ հենվելով թույլ մարդաբանական սկզբունքի վրա․ սեղմման փուլի պայմաններն անբարենպաստ են այնպիսի բանական էակների գոյության համար, որոնք հարցնեին, թե ինչո՞ւ է անկանոնությունն աճում ժամանակի նույն ուղղությամբ, ինչ ուղղությամբ ընդարձակվում է տիեզերքը։ Ամսահմանության պայմանը կանխագուշակում է տիեզերքի հարաճուն ընդարձակում նրա էվոլյուցիայի սկզբնական փուլերում։ Դա նշանակում է, որ տիեզերքը պետք է ընդարձակվի կրիտիկականին շատ մոտ արագությամբ, որպեսզի ընդհանրապես խուսափի կոլապսից կամ երկար ժամաակ կոլապսի չենթարկվի։ Մինչ այդ արդեն բոլոր աստղերը վառված և վերջացած կլինեն, իսկ նրանց առաջացրած պրոտոններն ու նեյտրոնները քայքայված և վերածված կլինեն լույսի մասնիկների ու ճառագայթման։ Ժամանակի հստակ որոշված թերմոդինամիկական նետ չէր լինի։ Այդ անկանոնությունն ավելի աճել չէր կարող, որովհետև տիեզերքն արդեն կգտնվեր համարյա լրիվ անկանոն վիճակում։ Սակայն հարկավոր է ուժեղ թերմոդինամիկական նետ, որպեսզի բանական կյանքը գոյություն ունենա։ Գոյատևելու համար մարդիկ պետք է սնունդ օգտագործեն, ինչն իրենից ներկայացնում է էներգիայի կարգավորված ձև, և այն փոխարկեն ջերմության, այսինքն՝ էներգիայի անկանոն ձևի։ Այսպիսով, տիեզերքի սեղմման փուլում որևէ բանական կյանք չի կարող գոյություն ունենալ։ Այսպես կարելի է բացատրել, թե ինչու են մեր դիտարկումները ցույց տալիս, որ թերմոդինամիկական և տիեզերաբանական նետերը նույն ուղղությունն ունեն։ Սխալ կլինի կարծել, թե, իբր, անկանոնությունն աճում է տիեզերքի ընդլայման պատճառով։ Ավելի ճիշտ կլինի ասել, որ այդ ամենի պատճառը անսահմանության պայմանն է։ Հենց դրա պատճառով է աճում անկանոնությունը, և միայն ընդարձակման փուլում են պայմաններ ստեղծվում բանական կյանքի գոյության համար։
Այս ամենն ի մի բերելով կարելի է ասել, որ գիտության օրենքները տարբերություն չեն դնում ժամանակի առաջընթաց և հետընթաց ուղղությունների միջև։ Սակայն գոյություն ունեն ժամանակի առնվազն երեք նետեր, որոնք իրարից տարբերում են անցյալն ու ապագան։ Դրանք են․ թերմոդինամիկական նետը, որը ժամանակի այն ուղղությունն է, որով մենք հիշում ենք անցյալը, բայց ապագան՝ ոչ, և տիեզերաբանական նետը՝ ժամանակի այն ուղղությունն է, որում տիեզերքն ընդարձակվում է, ոչ թե սեղմվում։ Ես ցույց տվեցի, որ հոգեբանական նետը, ըստ էության, համարժեք է թերմոդինամիկական նետին, այնպես որ, երկու նետն էլ պետք է ունենան նույն ուղղությունը։ Տիեզերքի անսահմանության ենթադրությունից բխում է, որ պետք է գոյություն ունենա հատուկ սահմանված ժամանակի թերմոդինամիկական նետ, որովհետև տիեզերքը պետք է սկիզբ առներ համասեռ ու կանոնավոր վիճակում։ Իսկ թերմոդինամիկական և տիեզերաբանական նետերի ուղղությունների համընկնման պատճառն այն է, որ բանական էակները կարող են գոյություն ունենալ միայն ընդարձակման փուլում։ Սեղմման փուլը նրանց համար բարենպաստ չէ, որովհետև նրանում բացակայում է ժամանակի հատուկ արտահայտված թերմոդինամիկական նետը։
Տիեզերքը հասկանալու գործում մարդկային առաջադիմության շնորհիվ կարգավորված մի փոքրիկ անկյուն է ստեղծվել տիեզերքի աճող քաոսում։
Եթե դուք հիշեք այս գրքում եղած բոլոր բառերը, ապա ձեր հիշողությունը կարձանագրի մոտավորապես երկու միլիոն միավոր տարբեր տեղեկություններ, իսկ ձեր ուղեղում կարգուկանոնը կաճի մոտավորապես նույնքան։ Մյուս կողմից, այս գիրքը կարդալիս դուք սննդի ձևով ստացած առնվազն հազար կալորիա կարգավորված էներգիա կփոխանակեք անկանոն էներգիայի՝ ջերմության, որը շրջապատին կհաղորդեք կոնվեկցիայի կամ քրտինք գոլորշիացնելու ձևով։ Դա կբերի տիեզերքի անկանոնության մոտավորապես միլիոն միլիոն միլիոն միլիոն միավորով աճի, որը համապատասխանում է ձեր ուղեղում կարգավորվածության տաս միլիոն միլիոն միլիոն անգամ աճին, իսկ դա կկատարվի այն դեպքում, եթե դուք հիշեք իմ գրքում կարդացած ամեն ինչը։ Հաջորդ գլխում ես կաշխատեմ մինչև կոկորդը անորոշությունների մեջ խրված մեր մտածումներում ինչ֊որ չափով կարգավորվածություն մտցնել, բացատրելով, թե ինչպես են մարդիկ փորձում իրար հարմարեցնել նկարագրածս մասնակի տեսությունները, որոնք ես նկարագրել եմ, որպեսզի ստեղծվի տիեզերքի բացատրությունն ամփոփող մի կատարյալ միասնական տեսություն։[30]
10
Ֆիզիկայի միասնականությունը
Ինչպես առաջին գլխում ցույց տրվեց, շատ դժվար է միանգամից կառուցել լրիվ միասնական մի տեսություն, որը ընդգրկի տիեզերքն ամբողջությամբ վերցրած։ Դրա փոխարեն, մենք հաջողությունների ենք հասել մասնակի տեսությունների մշակման մեջ, որոնք նկարագրում են մի շարք որոշակի երևույթներ՝ արհամարհելով այլ գործոններ կամ դրանք արտահայտելով մոտավորապես որոշակի թվերով։ (Քիմիան, օրինակ, թույլ է տալիս հաշվել ատոմների փոխազդեցություններն՝ առանց իմանալու ատոմի միջուկի ներքին կառուցվածքը)։ Այնուամենայնիվ, հույս կա, որ ի վերջո ստեղծվի ամբողջական հետևողական միասնական մի տեսություն, որում ընգրկված կլինեն բոլոր մասնակի տեսությունները որպես մոտավորություններ, և հարկ չի լինի որոշ պայմանական թվեր ներմուծել տեսությունը փաստերին ներդաշնակելու համար։ Այն որոնումները, որոնք տարվում են այդպիսի տեսության ստեղծման ուղղությամբ, հայտնի են որպես «ֆիզիկայի միասնականացում»։ Էյնշտեյնն իր կյանքի վերջին տարիների մեծ մասը նվիրեց այդպիսի միասնական տեսության ստեղծման գործին, բայց հաջողության չհասավ, որովհետև ժամանակները դրա համար չէին հասունացել․ կային գրավիտացիոն և էլեկտրամագնիսական ուժերի մասնակի տեսություններ, սակայն շատ քիչ բան էր հայտնի միջուկային ուժերի մասին։ Դեռ ավելին, Էյնշտեյնը հավատ չընծայեց քվանտային մեխանիկային, չնայած, որ նա ինքը կարևոր դեր է խաղացել դրա զարգացման մեջ։ Ակնհայտ է, որ անորոշության սկզբունքը մեր տիեզերքի հիմնարար առանձնահատկությունն է։ Հետևաբար, ցանկացած հաջող միասնական տեսություն անհրաժեշտորեն պետք է ներառի այդ սկզբունքը։
Ինչպես հետագայում կտեսնենք, այդպիսի տեսություն գտնելու հեռանկարներն այժմ շատ ավելի մեծ են, որովհետև մենք այժմ ավելի շատ բան գիտենք տիեզերքի մասին։ Բայց պետք է զգուշանանք չափազանց ինքնավստահությունից․ անցյալում սխալ հայտնագործություններ շատ են եղել։ Օրինակ, այս դարասկզբին կարծում էին, թե ամեն ինչ կարելի է բացատրել շարունակական, հարափոփոխ նյութի հատկությունների օգնությամբ, ինչպիսիք են առաձգականությունն ու ջերմահաղորդականությունը։ Ատոմի կառույցի և անորոշության սկզբունքի հայտնագործությունը մեկընդմիշտ վերջ տվեցին դրան։ Հետո դարձյալ 1928֊ին ֆիզիկոս և նոբելյան մրցանակակիր Մաքս Բորնը Գյոթինգենի համալսարանում մի խումբ այցելուների ասաց, թե «ֆիզիկան այնպես, ինչպես մենք այն գիտենք, վեց ամիս հետո չի լինի այլևս»։ Ինքնավստահության հիմքն այն էր, որ Դիրակն այդ օրերին հայտնագործել էր մի հավասարում, որը նկարագրում էր էլեկտրոնի վարքը։ Այն կարծիքն էր տարածված, թե նմանօրինակ մի հավասարում էլ պիտի լինի պրոտոնի համար, որն այն ժամանակ հայտնի մյուս մասնիկն էր, և ահա տեսական ֆիզիկան կկործանվի։ Սակայն նեյտրոնի և միջուկային ուժերի հայտնագործությունը դրա գլխին էլ տվեց։ Այս բոլորն ասելով՝ ես դեռևս հավատում եմ, որ զգուշավոր լավատեսության հիմքեր կան հուսալու, որ մեր որոնումները մոտենում են վերջակետին՝ բնության վերջնական օրենքներին հասնելու գործում։
Նախորդ գլուխներում ես նկարագրել եմ ընդհանուր հարաբերականությունը, գրավիտացիոն մասնակի տեսությունը և այն մասնակի տեսությունները, որոնք բնորոշում են թույլ, ուժեղ և էլեկտրամագնիսական ուժերը։ Վերջին երեք ուժերը կարելի է միավորել, այսպես ասած, մեծ միասնական տեսությունների՝ ՄՄՏ֊ի մեջ։ Պետք է ասել, որ այս միասնական տեսությունները թերի են, որովհետև գրավիտացիան չեն ընդգրկում և պարունակում են այնպիսի մեծություններ, ինչպիսիք են տարբեր մասնիկների հարաբերական զանգվածները, որոնք տեսությունից չեն բխում, այլ ընտրվում են դիտարկումներին համապատասխան։ Մյուս ուժերի հետ գրավիտացիայի միավորման տեսության ստեղծումը հիմնականում դժվարանում է այն պատճառով, որ ընդհանուր հարաբերականության տեսությունը «դասական» մի տեսություն է, այսինքն չի ընդգրկում քվանտային մեխանիկայի անորոշության սկզբունքը։ Մյուս կողմից, մնացած մասնակի տեսությունները հիմնականում կախված են քվանտային մեխանիկայից։ Հետևաբար առաջին անհրաժեշտ քայլն ընդհանուր հարաբերականության և քվանտային մեխանիկայի միավորումն է։ Ինչպես մենք արդեն տեսանք, այդպիսի միավորումը կարող է որոշ հատկանշական հետևանքներ առաջացնել, ինչպես այն, որ սև խոռոչներն այնքան էլ սև չեն, ճառագայթում են[31] և այն, որ տիեզերքը եզակիություններ չունի, բայց լրիվ ինքնապարփակ է և անսահման։ Դժվարությունն այն է, ինչպես բացատրվել է 7֊րդ գլխում, որ անորոշության սկզբունքը նշանակում է, որ նույնիսկ «դատարկ» տարածությունը լցված է վիրտուալ մասնիկների և հակամասնիկների զույգերով։ Այս զույգերը պետք է անսահման քանակի էներգիա ունենան, հետևաբար, Էյնշտեյնի հայտնի E=mc² հավասարման համաձայն՝ անսահման քանակի զանգված։ Նրանց գրավիտացիոն ձգողությունը պետք է որ տիեզերքը կծկի և անսահման փոքրացնի։
Համարյա համանման, անհեթեթ թվացող անսահմանություններ են առաջանում մյուս մասնակի տեսություններում, բայց այս բոլոր պարագաներում անսահմանությունները կարող են վերացվել վերանորմալացում կոչվող եղանակի օգնությամբ։ Դրա էությունն այն է, որ անսահմանությունները վերացվում են այլ անսահամնություններ ներմուծելով։ Թեև այս եղանակը մաթեմատիկորեն բավական կասկածելի է, բայց իրականում թվում է, թե գործում է և, այս տեսությունների հետ օգտագործվելով, թույլ է տալիս այնպիսի կանխագուշակումներ անել, որոնք արտակարգ ճշտությամբ համընկնում են դիտարկումների հետ։ Կատարյալ տեսության մշակման որոնման տեսանկյունից, սակայն, վերանորմալացումը մի լուրջ թերություն ունի, որովհետև նշանակում է, որ զանգվածների և ուժերի ուժգնությունների փաստական արժեքները չի կարելի տեսականորեն կանխագուշակել, այլ պետք է ընտրել դիտարկումներին համապատասխան։
Անորոշության սկզբունքն ընդհանուր հարաբերականության տեսություն ներմուծելու համար պետք է հարմարեցնել միայն երկու մեծություն՝ գրավիտացիայի ուժգնությունը և տիեզերաբանական հաստատունի արժեքը։
Սակայն սրանց հարմարեցումը բավարար չէ ազատվելու համար բոլոր անորոշություններից։ Հետևաբար, գործում է մի տեսություն, որի համաձայն, որոշակի մեծություններ, ինչպես, օրինակ, տարածություն֊ժամանակի կորությունը, իսկապես անսահման են, բայց և այնպես այդ մեծությունները[32] կարող են դիտարկվել և չափվել որպես կատարելապես վերջավոր։ Ընդհանուր հարաբերականության տեսության և անորոշության սկզբունքի միավորման հիմնախնդիրը որոշ ժամանակ ի վեր ակնկալվում էր, բայց վերջնականապես հաստատվեց 1972֊ին մանրամասն հաշվարկներով։ Չորս տարի անց առաջարկվեց հնարավոր մի լուծում, որը կոչվում էր «գերգրավիտացիա»։ Դրա էությունը հետևյալն էր․ 2֊սպին ունեցող մասնիկը, որը կոչվում է գրավիտոն և գրավիտացիոն ուժի կրողն է, միավորել 3/2, 1, 1/2 և 0 սպին ունեցող նոր մասնիկների հետ։ Որոշ իմաստով բոլոր այս մասնիկները կարելի է համարել նույն «գերմասնիկի» տարբեր կերպարանքներ, և դրանով 1/2 և 3/2 սպինային նյութական մասնիկները միավորել 0, 1 և 2 սպինային ուժակիր մասնիկների հետ։ 1/2 և 3/2 սպինային վիրտուալ մասնիկ֊հակամասնիկ զույգերը բացասական էներգիա կունենան և այսպիսով կձգտեն ոչնչացնել 2, 1 և 0 սպինային վիրտուալ զույգերի դրական էներգիան։ Դա պետք է բերեր շատ հնարավոր անսահմանությունների վերացման, բայց ակնկալվում էր, որ որոշ թվով անսահմանություններ դեռևս կարող են մնալ։ Սակայն այդպիսի անսահմանությունների որոշման համար պահանջվող հաշվումներն այնքան երկար և դժվարին էին, որ ոչ ոք դրանք չձեռնարկեց։ Նույնիսկ հաշվողական մեքենայով դա կատարելու համար առնվազն չորս տարի կպահանջվեր և հնարավոր է, որ մեկ կամ ավելի սխալներ կատարվեին։ Հետևաբար, պատասխանի ճշտությանը մարդ կարող էր վստահ լինել միայն այն ժամանակ, եթե մեկ ուրիշը հաշվարկումները կրկներ և նույն պատասխանը ստանար, որն այնքան էլ հավանական չէր թվում։
Հակառակ այս հիմնախնդիրներին և այն փաստին, որ գերգրավիտացիոն տեսությունների մեջ նկատի առնվող մասնիկները չեն համապատասխանում սովորաբար դիտարկված մասնիկներին, գիտնականների մեծամասնությունը այն կարծիքին էր, որ հավանաբար գերգրավիտացիան ֆիզիկայի միասնականացման ճիշտ պատասխանն է։ Մյուս ուժերի հետ գրավիտացիայի միավորման լավագույն ուղին պետք է լիներ դա։ Սակայն 1984֊ին տեղի ունեցավ կարծիքների նշանակալի փոփոխություն ի նպաստ, այսպես կոչված, լարային տեսությունների։ Այս տեսություններում հիմնական առարկաները ոչ թե մասնիկներն են, որոնք տարածության եզակի կետեր են գրավում, այլ բաներ, որոնք երկարություն ունեն, բայց այլ չափումներ չունեն, ինչպես լարի անսահման բարակ շերտ։ Այս լարերը կարող են ծայրեր ունենալ (այսպես ասած, բաց լարեր) կամ ծայրերը իրար միացած լինել փակ օղակի ձևով (փակ լարեր) (նկ․ 10.1 և 10.2)։ Մասնիկը ժամանակի յուրաքանչյուր պահի տարածության մեջ մի կետ է գրավում։ Այսպիսով նրա պատմությունը կարելի է ներկայացնել տարածության֊ժամանակի մեջ որպես գիծ («աշխարհագիծ»)։ Իսկ լարը յուրաքանչյուր պահի տարածության մեջ գիծ է։ Հետևաբար, տարածություն֊ժամանակի մեջ նրա պատմությունը առաջացնում է երկչափանի մակերես, որը կոչվում է աշխարհաթերթ։ (Աշխարհաթերթի վրա որևէ կետ նկարագրվում է երկու թվով․ մեկը բնորոշում է ժամանակը, մյուսը՝ կետի դիրքը լարի վրա)։ Բայց լարի աշխարհաթերթը մի ժապավեն է, որի եզրերը լարի երկու ծայրերի առաջացրած ուղիներն են (նկ․ 10.1)։ Փակ լարի աշխարհաթերթը մի գլան է կամ մի խողովակ (նկ․ 10.2)։
Խողովակի լայնական կտրվածքը մի շրջան է, որը ցույց է տալիս փակ լարի դիրքը տվյալ որոշակի ժամանակում։
Երկու լար կարող են միանալ և առաջացնել մի լար, բաց լարերի դեպքում նրանք միանում են ծայրերով (նկ․10.3), այնինչ փակ լարերի միացումը նման է շալվարի երկու փողքերի միավորմանը (նկ․10.4): Նույն ձևով մի լարը կարող է բաժանվել երկու լարի։ Լարերի տեսության մեջ այն, ինչ նախապես ընդունվում էին որպես մասնիկներ, պատկերացվում են իբրև ալիքներ, որոնք տեղաշարժվում են լարն ի վար, ինչպես տատանվող օդապարիկի լարի ալիքները։ Մի մասնիկի առաքումը կամ կլանումը մեկ այլ մասնիկի կողմից համապատասխանում է լարերի բաժանմանը կամ միավորմանը։ Օրինակ, մասնիկային տեսություններում արևի գրավիտացիոն ուժը երկրի վրա պատկերվում է որպես արևի մեջ գտնվող մի մասնիկի կողմից գրավիտոնի արձակում և նրա կլանումը երկրի մեջ գտնվող մասնիկի կողմից (նկ․ 10.5): Լարային տեսությունում այս գործընթացը համապատասխանում է H֊ի ձև ունեցող մի խողովակի (նկ․ 10.6): Լարային տեսությունն ինչ֊որ չափով նման է խողովակաշինության։ H֊ի երկու ուղղահայաց կողմերը համապատասխանում են արևի և երկրի մեջ գտնվող մասնիկներին, իսկ հորիզոնական կապը համապատասխանում է նրանց միջև տեղափոխվող գրավիտոնին։
Լարային տեսության պատմությունը հետաքրքրական է։ Սկզբում այն ստեղծվեց 1960֊ին՝ ուժեղ ուժերը նկարագրող մի տեսություն գտնելու նպատակով։ Հիմնական գաղափարն այն էր, որ պրոտոնի ու նեյտրոնի նման մասնիկները կարելի է համարել լարի վրայի ալիքներ։ Մասնիկների միջև գործող ուժեղ ուժերը համապատասխանում են լարերի հատվածներին, որոնք իրար են կապում այլ լարի հատվածներ, ինչպես սարդոստյանն է։ Համաձայն այս տեսության, մասնիկների միջև դիտարկված մեծ ուժերը ստանալու համար անհրաժեշտ էր, որպեսզի այդ լարերը լինեն ռետինե կապերի նման՝ օժտված մոտավորապես տասը տոննա ձգման ամրությամբ։
1974֊ին Ջոյլ Շերկը՝ Փարիզից և Ջոն Շվարցը՝ Կալիֆոռնիայի տեխնոլոգիական ինստիտուտից, մի հոդված հրատարակեցին այն մասին, որ լարային տեսությունը կարող է նկարագրել գրավիտացիոն ուժը, եթե միայն լարերում լարվածությունը շատ ավելի մեծ լինի, մոտավորապես հազար միլիոն միլիոն միլիոն միլիոն միլիոն միլիոն տոննա (39 զերո մեկից հետո)։ Լարային տեսության կանխագուշակումները չեն տարբերվում ընդհանուր հարաբերականության տեսության կանխագուշակումներից սովորական հեռավորությունների համար, սակայն կտարբերվեն չափազանց փոքր տարածությունների՝ սանտիմետրի մեկ հազար միլիոն միլիոն միլիոն միլիոն միլիոներորդի համար (սանտիմետրը բաժանած 1֊ից հետո 30 զերոներով թվի)։ Նրանց աշխատությունը մեծ ուշադրության չարժանացավ, որովհետև հենց այդ ժամանակ շատերը հրաժարվեցին սկզբնական ուժեղ ուժի լարային տեսությունից՝ հօգուտ քվարկների ու գլյուոնների վրա հիմնված տեսության, որը թվում էր ավելի լավ է համընկնում փորձնական տվյալների հետ։ Շերկը մահացավ ողբերգական մահով (նա տառապում էր շաքարախտով, և կոմայի պահին նրա մոտ ոչ ոք չէր եղել, որպեսզի ինսուլին սրսկեր)։ Այսպիսով, Շվարցը մնաց միակ պաշտպանը լարային տեսության, որը, սակայն, լարի լարվածության համար շատ բարձր արժեք էր առաջարկում։
1984֊ին լարերի նկատմամբ հետաքրքրությունը միանգամից աճեց հավանաբար երկու պատճառով։ Մեկն այն էր, որ գերգրավիտացիայի վերջավոր լինելու մասին տեսակետի առաջխաղացումը իրականում զգալի չէր և չէր բացատրում մեր դիտարկած մասնիկների որպիսությունը։ Մյուս պատճառն այն էր, որ Ջոն Շվարցը և Լոնդոնի Քուին Մերի քոլեջից Մայք Գրինը մի հոդվածում ցույց տվին, որ լարային տեսությունն ի վիճակի կլինի բացատրել ձախամետ ներքին կառուցվածք ունեցող մասնիկների գոյությունը՝ նման մեր դիտարկած մի քանի մասնիկների գոյությանը։ Ինչևէ, մեծ թվով գիտնականներ շուտով սկսեցին զբաղվել լարային տեսությամբ, և մի նոր տարբերակ առաջացավ, այսպես կոչված, տարատեսակ լար (heterotic), որը, թվում էր, ի վիճակի կլինի բացատրել մեր դիտարկած մասնիկների տեսակները։
Լարային տեսությունները նույնպես առաջացնում են անսահմանություններ, բայց այն կարծիքը կա, որ անսահմանությունները իրար կչեզոքացնեն տարատեսակ լարերի դեպքում (թեև այս բանը վերջնականապես ստույգ չէ)։ Սակայն լարային տեսություններն ավելի մեծ պրոբլեմ ունեն․ դրանք, թվում է, ամուր դիրքեր կունենան միայն այն դեպքում, եթե տարածություն֊ժամանակը լինի տասը կամ քսանվեց չափանի՝ սովորական չորսի փոխարեն։ Տարածություն֊ժամանակի բազմաչափություններն, իհարկե, գիտական վիպագրության մեջ սովորական բան են։ Արդարև, դրանք համարյա պարտադիր են, որովհետև, այլապես այն փաստը, թե հարաբերականությունը նշանակում է, որ մարդը լույսից արագ չի կարող շարժվել, նշանակում է, որ շատ երկար ժամանակ կպահանջվի, որպեսզի նա ճամփորդի աստղերի ու գալակտիկաների միջև։ Գիտական֊գեղարվեստական գաղափարն այն է, որ թերևս բարձր չափականության միջով մարդուն հաջողվի մի կարճ ճանապարհ գտնել։ Այս բանը կարելի է պատկերել հետևյալ կերպ։ Պատկերացնենք, թե մեր ապրած տարածությունը երկչափանի է և կորացած է ինչպես փրկողակը կամ տորը (նկ․ 10.7): Եթե դուք գտնվում եք օղակի ներսակողմի մի տեղում և ցանկանում եք գնալ մեկ այլ տեղ, ապա պետք է օղակի ներսակողմը շրջանցեք։ Սակայն եթե ձեզ տրվի եռաչափ ճամփորդության հնարավորություն, ապա դուք ուղիղ գծով կանցնեք այդ ճանապարհը։
Այդ ինչպե՞ս է պատահում, որ մենք հավելյալ չափականությունները չենք տեսնում, եթե դրանք իրոք կան։ Մենք ինչո՞ւ ենք տարածության՝ երեք և ժամանակի մեկ չափականություն տեսնում։ Ենթադրվում է, որ մյուս չափականությունները կորացած են փոքր չափսերով մի տարածության մեջ՝ մոտավորապես մեկ սանտիմետրի չորս հարյուր հազար միլիոն միլիոն միլիոն միլիոներորդի մեծությամբ։ Դա այնքան փոքր է, որ մենք այն չենք նշմարում և տեսնում ենք ժամանակի լոկ մեկ և տարածության երեք չափականություններ, որում տարածություն֊ժամանակը բավականին հարթ է։ Այն նման է նարնջի մակերևույթի, որը եթե մոտիկից դիտեք՝ կորագծերով և խորշոմներով լեցուն է, բայց եթե հեռվից նայեք, ապա խորդուբորդությունները չեն երևա, ամեն ինչ թվում է հարթ։ Այսպիսին է նաև տարածություն֊ժամանակը․ փոքր մասշտաբով այն տասը չափանի է և շատ կորացած, բայց ավելի մեծ մասշտաբներով կորացումն ու լրացուցիչ չափումները չեն երևում։ Եթե այս պատկերացումը ճիշտ է, ապագա տիեզերական ճամփորդների համար դա վատ է․ հավելյալ չափականություններն այնքան փոքր կլինեն, որ թույլ չեն տա, որպեսզի տիեզերանավերը դրանցով անցնեն։ Սակայն մեկ այլ գլխավոր հիմնախնդիր է ծագում․ ինչո՞ւ պիտի չափումների որոշ մասը, այլ ոչ բոլորը ոլորված լինեն մի փոքրիկ գնդի մեջ։ Վաղ տիեզերքում հավանաբար բոլոր այդ չափումները պետք է որ ոլորված լինեն։ Ինչո՞ւ են ընդամենը ժամանակի մեկ չափում և տարածության երեք չափում հարթվել, երբ մյուս բոլոր չափումները մնացել են սեղմորեն ոլորված։
Դրա հնարավոր պատասխաններից մեկը մարդաբանական սկզբունքն է։ Ըստ դրա, երկու տարածական չափումները բավարար չեն, որպեսզի մեզ նման բարդ էակներ զարգանան։ Օրինակի համար, միաչափ երկրում ապրող երկչափ կենդանիները միմյանցից առաջ անցնելու համար պետք է իրար վրա մագլցեն։ Եթե երկչափանի արարածն ինչ֊որ բան ուտի, ապա լրիվ մարսել չի կարողանա, այն կուլ տվածի նման հետ կտա, որովհետև եթե նրա մարմնի միջով մի անընդմեջ ուղի անցնի, ապա դա կենդանուն կբաժանի երկու մասի, և երկչափանի կենդանին կտրոհվի (նկ․ 10.8): Նույն ձևով դժվար է պատկերացնել, թե ինչպես կարող է կատարվել երկչափանի արարածի արյան շրջանառությունը։
Խնդիրներ են ծագում նաև երեքից ավելի չափումների դեպքում։ Երկու մարմինների միջև գործող գրավիտացիոն ուժը հեռավորության աճին զուգընթաց ավելի արագ կնվազի, քան դա տեղի կունենա եռաչափ պայմաններում (Եռաչափ տարածությունում գրավիտացիոն ուժը նվազում է 1/4֊ով, երբ հեռավորությունը կրկնապատկվում է։ Քառաչափում այն կնվազի 1/6֊ով, հնգաչափում՝ 1/16֊ով և այլն)։ Սա նշանակում է, որ երկրի նման մոլորակների ուղեծիրներն արևի շուրջ անկայուն կլինեն․ շրջանաձև ուղեծրից նվազագույն շեղումը (որը կառաջացնի այլ մոլորակների գրավիտացիոն ձգողությունը) կարող է բերել այն բանին, որ երկիրն ընկնի արևի վրա կամ արևից հեռանա պարուրաձև հետագծով։ Մենք կամ կսառչենք և կամ կվառվենք։ Փաստորեն, երեքից ավելի տարածական չափումների պայմաններում գրավիտացիայի այդպիսի փոփոխությունն ըստ հեռավորության նշանակում է, որ արևը ճնշման ու գրավիտացիայի հավասարակշռության պայմաններում կայուն վիճակում գոյություն ունենալ չի կարող։ Այն կամ պիտի կտոր֊կտոր լինի կամ կոլապսվի և վերածվի սև խոռոչի։ Երկու դեպքում էլ երկրի վրա կյանքի գոյության համար ջերմության և լույսի աղբյուր լինել չի կարող։ Նույնը տեղի կունենա նաև փոքր մասշտաբների վրա։ Էլեկտրական ուժերը, որոնք պայմանավորում են էլեկտրոնների պտույտը ատոմի միջուկի շուրջ, իրենց պահում են ինչպես գրավիտացիոն ուժերը։ Ուստի այդ պայմաններում էլեկտրոնները կամ ատոմից ընդհանրապես կհեռանան և կամ պարուրաձև կպտտվեն և կընկնեն միջուկի վրա։ Երկու դեպքում էլ ատոմները գոյություն չեն ունենա այն ձևով, ինչպես մենք գիտենք։
Ուրեմն պարզ է, որ կյանքն առնվազն այնպես, ինչպես մենք այն ճանաչում ենք, կարող է գոյություն ունենալ տարածություն֊ժամանակի այնպիսի տիրույթներում, որտեղ ժամանակի մեկ չափումն ու տարածության երեք չափումը կծկված չեն լինի փոքրիկ կետում։ Սա նշանակում է, որ մարդ կարող է դիմել թույլ մարդաբանական սկզբունքին․ բավական է, որպեսզի ցույց տրվի, որ լարային տեսությունն առնվազն հնարավոր է համարում տիեզերքում այդպիսի տիրույթների գոյությունը։ Եվ իրոք, թվում է, թե լարային տեսությունը այդպիսի հնարավորություն ընձեռում է։ Բացառված չէ, որ տիեզերքում այլ տիրույթներ լինեն, կամ այլ տիեզերքներ գոյություն ունենան (ինչ էլ որ դրանք լինեն), որտեղ բոլոր չափումները կծկված լինեն փոքրիկ կետում, և կամ չորս չափումները համարյա հարթ լինեն, սակայն այդպիսի տիրույթներում բանական էակներ չեն կարող լինել, որպեսզի փաստացի չափումների տարբեր թվերը դիտարկեն։
Բացի տարածություն ժամանակի չափականությունների թվի հարցից, պետք է լուծվեն դեռ բազմաթիվ այլ խնդիրներ, որպեսզի լարային տեսությունը հավանության արժանանա որպես ֆիզիկայի միասնական վերջնական տեսություն։ Մենք դեռևս չգիտենք, թե իրոք բոլոր անսահմանություններն են չեզոքացնում կեմը մյուսին, կամ թե լարի ալիքներն ինչպես են կապվում այն առանձին մասնիկների հետ, որոնք մենք դիտարկում ենք։ Այնուամենայնիվ, հնարավոր է, որ առաջիկա մի քանի տարվա ընթացքում այս հարցերի պատասխանները գտնվեն, և դարավերջին մենք իմանանք, որ իրոք լարային տեսությունը երկար որոնումների ակնկալած ֆիզիկայի միասնական տեսությունն է։
Բայց մի՞թե այդպիսի միասնական տեսություն կարող է լինել։ Կամ, թերևս, դա մի պատրանք է։ Երեք հնարավոր տարբերակ կա․
1. Իսկապես կա կատարյալ մի միասնական տեսություն, որը մենք մի օր կհայտնաբերենք, եթե բավականաչափ խելացի ենք։
2. Տիեզերքի վերջնական տեսություն չկա, այլ կա տեսությունների մի անսահման շարք, և դրանք աստիճանաբար ավելի ճշգրիտ կնկարագրեն տիեզերքը։
3. Տիեզերքի տեսություն չկա․ դեպքերը չի կարելի կանխագուշակել, դրանք տեղի են ունենում որոշակի սահմանում պատահականորեն և ինքնակամորեն։
Կարելի է փաստարկներ բերել հօգուտ երրորդ հնարավորության, պնդելով, որ եթե օրենքների համապարփակ մի շարք լիներ, ապա դա կսահմանափակեր Աստծո միտքը փոխելու և աշխարհի գործերին խառնվելու ազատությունը։ Դա նման է հինավուրց մի պարադոքսի․ Աստված ի վիճակի՞ է արդյոք, այնքան ծանր քար ստեղծել, որ ինքը չկարողանա բարձրացնել։ Բայց, ինչպես նշել է սբ․ Օգոստինոսը, այն գաղափարը, թե Աստված կուզենա իր միտքը փոխել, մոլորության (սոփեստության) մի օրինակ է և արդյունք է այն պատկերացման, թե Աստված ժամանակի ընթացքում գոյություն ունեցող մի էակ է։ Այնինչ ժամանակը Աստծու ստեղծած տիեզերքի մի հատկություն է։ Պետք է կարծել, որ Աստված գիտեր՝ ինչ է ուզում, երբ ստեղծեց տիեզերքը։
Քվանտային մեխանիկայի ի հայտ գալուց հետո պարզվեց, որ դեպքերը կատարյալ ճշգրտությամբ կանխագուշակել չի կարելի, և միշտ ինչ֊որ չափով անորոշություն կա։ Եթե մարդ ցանկանա, ապա պատահականությունը կարող է համարել Աստծո միջամտություն, բայց դա կլինի միջամտության շատ տարօրինակ մի տեսակ․ ոչ մի փաստ չկա, որ դա որոշակի նպատակ է հետապնդում։ Արդարև, եթե այդպես լիներ, ապա դա պատահական չէր լինի։ Ներկայումս երրորդ հնարավորությունը ընդունել չի կարելի, որովհետև գիտության նպատակը այլ է․ ձևակերպել օրենքների մի այնպիսի շարք, որը թույլ տար կանխագուշակել դեպքերը գոնե անորոշության սկզբունքի սահմաններում։
Երկրորդ հնարավորությունը, թե գոյություն ունի անսահման թվով առավել մշակված տեսությունների մի հաջորդականություն, շատ լավ համընկնում է մինչև այժմ կատարած մեր դիտարկումների հետ։ Շատ պարագաներում մեր չափումների ճշտության աստիճանը բարձրացրել ենք կամ նորանոր դիտարկումներ ենք կատարել՝ ընդամենը հայտնաբերելու նոր երևույթներ, որոնք գոյություն ունեցող տեսությունների կողմից չեն կանխագուշակվել, և որպեսզի հաշվի առնենք դրանք, ստիպված նոր, ավելի առաջավոր տեսություն ենք մշակել։ Հետևաբար, շատ զարմանալի չէր լինի, եթե ժամանակակից մեծ միասնական տեսությունների սերունդը սխալվեր և պնդեր, թե ըստ էության ոչինչ նոր չի կարող պատահել 100 ԳԵՎ թույլ էլեկտրական միասնական էներգիայի և մոտավորապես հազար միլիոն միլիոն ԳԵՎ միասնական էներգիայի միջակայքում։ Իրոք սպասելի է, որ հայտնաբերվեն բազմաթիվ նոր կառուցվածքային շերտեր, որոնք ավելի հիմնական լինեն, քան քվարկներն ու էլեկտրոնները, որոնց մենք ճանաչում ենք որպես «տարրական մասնիկներ»։
Այնուամենայնիվ թվում է, թե գրավիտացիան կարող է վերջ դնել «տուփերի մեջ տուփերի» այս հաջորդականությունը։ Վերցնենք մի մասնիկ, որի էներգիան բարձր էր, այսպես կոչված, Պլանկի էներգիայից, այսինքն՝ տասը միլիոն միլիոն միլիոն (1֊ից հետո տասնինը զերո) ԳԵՎ է։ Նրա զանգվածն այն աստիճան խտացած կլինի, որ այդ մասնիկը կանջատվի ողջ տիեզերքից և փոքրիկ մի սև խոռոչ կառաջացնի։ Այստեղից հետևում է, որ մեկը մյուսից առավել կատարելագործված տեսությունների շարքը պետք է վերջ ունենա, երբ գնում ենք առավել բարձր էներգիաների։ Հետևաբար պետք է, որ տիեզերքի համար մի վերջնական տեսություն գոյություն ունենա։ Իհարկե, Պլանկի էներգիան չափազանց հեռու է հարյուրավոր ԳԷՎ֊ից, որն այն առավելագույնն է, ինչ այսօր մենք կարող ենք ստանալ լաբորատորիայում։ Մոտավոր ապագայում մասնիկային արագացուցիչների օգնությամբ այս անջրպետը չենք կարող հաղթահարել։ Սակայն տիեզերքի վաղ փուլերում կար մի վիճակ, երբ այդպիսի էներգիաներ եղել են։ Ես մտածում եմ, որ վաղ տիեզերքի ուսումնասիրությունը և մաթեմատիկական հետևողականությունը հնարավորություն կստեղծեն, որպեսզի մեզանից ոմանք կարողանան լրիվ միասնական մի տեսություն ստեղծել, պայմանով, որ մինչ այդ մենք մեզ չենք կործանի։
Եթե մենք իրոք հայտնաբերենք տիեզերքի վերջնական տեսությունը, ապա ի՞նչ նշանակություն կունենա դա։ Ինչպես առաջին գլխում ենք բացատրել, մենք երբեք լիովին վստահ չենք կարող լինել, թե իսկապես գտել ենք ճիշտ տեսությունը, որովհետև դա հնարավոր չէ ապացուցել։ Սակայն եթե տեսությունը մաթեմատիկորեն հետևողական է և միշտ այնպիսի կանխագուշակումներ է անում, որոնք համապատասխանում են դիտարկումներին, ապա կարելի է վստահ լինել, որ դա ճիշտ է։ Այսպիսով, տիեզերքն ընբռնելու համար մարդկության մտավոր պայքարի պատմության երկար ու փառավոր գլուխը կավարտվի։ Միևնույն ժամանակ կհեղաշրջվի մեր իմացությունը տիեզերքը կառավարող օրենքների մասին։ Նյուտոնի ժամանակներում զարգացած մի մարդու համար բավարար էր, որ նա առնվազն ընդհանուր գծերով պատկերացում ունենար մարդկային ամբողջ մտավոր զարգացման մասին։ Բայց դրանից հետո գիտության զարգացումն այն դարձրեց անհնարին։ Սրա պատճառն այն է, որ տեսությունները միշտ փոխվում են, որպեսզի համապատասխանեն նոր դիտարկումներին, երբեք անհրաժեշտ չափով յուրացված կամ պարզեցված չեն լինում և անհասկանալի են մնում շատերի համար։ Պետք է, որ դուք մասնագիտանաք և միայն այդ ժամանակ կարող եք հուսալ ճշգրտորեն ըմբռնել գիտական տեսությունների փոքր մասը։ Դեռ ավելին, առաջընթացն այնպես արագ է տեղի ունենում, որ դպրոցում կամ համալսարանում մատուցվող գիտելիքները փոքր֊ինչ հնացած են։ Լոկ փոքր թվով մարդիկ կարող են արագորեն փոփոխվող գիտության առաջընթացին հետևել և հարկ կլինի իրենց ամբողջ ժամանակը նվիրել դրան ու մասնագիտանալ շատ նեղ բնագավառում։ Մարդկանց մյուս մասը քիչ բան գիտի գիտության առաջընթացի և դրա առաջացրած ոգևորության մասին։ Յոթանասուն տարի առաջ, եթե հավատանք Էդինգտոնի խոսքերին, լոկ երկու հոգի էին հասկանում հարաբերականության ընդհանուր տեսությունը։[33]
Այսօր տասնյակ հազարավոր համալսարանականներ հասկանում են այն, և միլիոնավոր մարդիկ առնվազն ծանոթ են հիմնական գաղափարներին։ Եթե կատարյալ միասնական մի տեսություն հայտնագործվի, կպահանջվի որոշ ժամանակ, որպեսզի այն այնպես յուրացվի և պարզեցվի, որ գոնե ընդհանուր գծերով մտնի դպրոցական ծրագրի մեջ։ Այդ ժամանակ մենք բոլորս ի վիճակի կլինենք ինչ֊որ չափով ըմբռնել այն օրենքները, որոնք կառավարում են տիեզերքն ու պայմանավորում են մեր գոյությունը։
Բայց եթե մենք նույնիսկ հայտնագործենք կատարելապես միասնական մի տեսություն, ապա դա չի կարող նշանակել, թե մեզ կհաջողվի ընդհանրապես դեպքերը կանխագուշակել հետևյալ երկու պատճառով։ Առաջինն այն է, որ քվանտային մեխանիկայի անորոշության սկզբունքը սահմանափակում է մեր կանխագուշակումները։ Մենք ոչինչ չենք կարող անել այդ հարցը շրջանցելու համար։ Իրականում, սակայն, այս առաջին սահմանափակումը նվազ արգելակող է, քան երկրորդը։ Դրա պատճառն այն է, որ տեսության հավասարումները մենք ճշգրտորեն չենք կարող լուծել, բացառությամբ շատ պարզ վիճակների հավասարումներից։ Մենք նույնիսկ երեք մարմինների շարժումը չենք կարող լուծել ճշգրտորեն՝ օգտվելով Նյուտոնի ձգողականության տեսությունից։ Սակայն դժվարություններն աճում են, երբ մարմինների թիվը մեծանում է, իսկ տեսությունն ավելի է բարդանում։ Մենք արդեն գիտենք նյութի վարքը նկարագրող այն օրենքները, որոնք ծայրահեղ դեպքերից բացի գործում են բոլոր պայմաններում։ Մասնավորապես, մենք գիտենք քիմիայի և կենսաբանության հիմնական օրենքները։
Իհարկե, մենք չենք կարող այս բնագավառներին լուծված հարցի կարգավիճակ տալ․ մաթեմատիկական հավասարումների օգնությամբ մարդու կյանքը կանխագուշակելու փորձերը հաջողությամբ դեռ չեն պսակվել։
Այսպիսով, նույնիսկ եթե մենք հիմնական օրենքների ամբողջական մի շարք գտնենք, ապա առաջիկա տարիների ընթացքում մարդկությունը կանգնած կլինի մտավոր կարևոր մի խնդրի առջև, այն է՝ լավագույն մոտավոր մեթոդներ մշակել, որպեսզի հնարավոր լինի բարդ ու իրական վիճակների հավանական ելքերի օգտակար կանխագուշակումներ կատարել։ Լրիվ հետևողական միասնական տեսությունը լոկ առաջին քայլն է․ մեր նպատակն է կատարելապես հասկանալ մեր շուրջ տեղի ունեցող դեպքերն ու հենց մեր սեփական գոյությունը։
11
Եզրակացություն
Մենք գտնվում ենք ապշեցնող աշխարհում։ Ցանկանում ենք շրջապատում տեսածն իմաստավորել և հարցնել․ ի՞նչն է տիեզերքի էությունը։ Ո՞րն է մեր տեղը նրանում, և որտեղի՞ց ենք նաև մենք գալիս։ Եվ ինչո՞ւ է այն այնպես, ինչպես որ է։
Որպեսզի փորձենք պատասխանել այս հարցերին, ընդունում ենք «աշխարհի ինչ֊որ պատկեր»։ Հենց այդպիսի պատկեր է կրիաների անսահման աշտարակը, որն իր վրա է կրում հարթ երկիրը, այդպիսին է գերկապերի տեսությունը։ Երկուսն էլ տիեզերքի տեսություններ են, թեև վերջինը մաթեմատիկորեն ավելի ճշգրիտ է, քան առաջինը։ Երկու տեսություններն էլ չունեն բավականաչափ ապացույց, ոչ ոք երբեք չի տեսել հսկա կրիային՝ երկիրը մեջքին, ինչպես նաև ոչ ոք չի տեսել գերկապային երկիրը։ Այնուամենայնիվ, կրիաների տեսությունը չի բավարարում հիմնավորված գիտական տեսության պահանջներին, քանի որ այն կանխագուշակում էր, որ մարդիկ կարող էին դուրս ընկնել՝ աշխարհի եզրին հասնելով։ Սա չի համապատասխանում մարդկային փորձին, բացառությամբ, եթե միայն սրանով բացատրենք մարդկանց թվացյալ անհետացումը Բերմուդյան եռանկյունում։
Տիեզերքը տեսականորեն նկարագրելու և բացատրելու ամենավաղ փորձերը հիմնված էին այն պատկերացման վրա, որ բնական երևույթներն ու դեպքերը ղեկավարվում էին ոգիներով, որոնք օժտված են մարդկային զգացումներով և որոնք գործում են շատ մարդանման ու անկանխատեսելի ձևով։ Այս ոգիներն ապրում էին բնության այնպիսի վայրերում, ինչպիսիք են գետերը, սարերը, ինչպես նաև երկնային մարմիններ արևն ու լուսինը։ Նրանց պետք էր սիրաշահել, որպեսզի ապահովվեր հողի բերիությունը և տարվա եղանակների հաջորդականությունը։ Այնուամենայնիվ, աստիճանաբար նկատվել էր որոշ երևույթների կանոնավոր կրկնությունը․ արևը միշտ ծագում է արևելքում և մայր մտնում արևմուտքում, անկախ այն բանից, թե արևի աստծուն զոհաբերություն եղել է, թե ոչ։ Դեռ ավելին, արևը, լուսինը և մոլորակները երկնքում շարժվում են որոշակի ուղեծրերով, որոնք հնարավոր էր բավականաչափ ճշգրտությամբ կանխագուշակել։ Արևն ու լուսինը դեռևս կարող էին համարվել աստվածներ, բայց դրանք խիստ օրենքների ենթարկվող աստվածներ էին, ըստ երևույթին, առանց որևէ բացառության, եթե հաշվի չառնենք Հեսուի կողմից արևի կանգնեցման պատմությունները։
Սկզբում այս կանոններն ու օրենքները բացահայտ էին միայն աստղագիտության մեջ և մի քանի այլ դեպքերում։ Սակայն քաղաքակրթության զարգացման հետևանքով, հատկապես վերջին 300 տարվա ընթացքում, ավելի ու ավելի կանոններ և օրենքներ հայտնաբերվեցին։ Այս օրենքների հաջողությունը XIX դարի սկզբին Լապլասին ներշնչեց սահմանելու գիտական որոշադրության (դետերմինիզմի) հիմնադրույթը, այսինքն, նա առաջարկեց, որ պետք է լինի օրենքների մի խումբ, որով ճշգրտորեն որոշվի տիեզերքի էվոլյուցիան, երբ տրված է նրա կոնֆիգուրացիան որևէ ժամանակաշրջանի համար։ Լապլասի որոշադրությունը թերի էր երկու տեսակետից։ Այն չէր ասում, թե ինչպես պետք է ընտրվեն օրենքներ և չէր հատկորոշում տիեզերքի սկզբնական կոնֆիգուրացիան։ Սրանք թողնված էին Աստծուն։ Աստված պետք է ընտրեր, թե ինչպես է սկիզբ առել տիեզերքը և ինչ օրենքների պետք է այն ենթարկվեր, բայց նա չպետք է միջամտեր տիեզերքի գործերին, երբ այն արդեն սկիզբ էր առել։ Փաստորեն, Աստծո միջամտությունը վերապահվում էր միայն այն ոլորտների համար, որոնք XIX դարի գիտությունը չէր հասկանում։
Մենք այժմ գիտենք, որ Լապլասի որոշադրության մասին հույսերն անիրականանալի էին, առնվազն այն ձևով, ինչպես ինքն էր մտածում։ Ըստ քվանտային մեխանիկայի անորոշության սկզբունքի, մեծությունների որոշ զույգերից, երկուսն էլ, ինչպես, օրինակ, մասնիկի դիրքն ու արագությունը, հնարավոր չէ լրիվ ճշգրտությամբ կանխագուշակել։
Քվանտային մեխանիկան այս սահմանափակումից ձերբազատվում է իր մի խումբ քվանտային տեսություններով, որոնցում մասնիկները լավ սահմանված դիրք և արագություն չունեն, այլ ներկայացված են որպես ալիք։ Այդ քվանտային տեսությունները որոշադրական են այն իմաստով, որ նրանք սահմանում են ալիքի էվոլյուցիայի օրենքներ՝ ժամանակից կախված։ Այսպիսով, եթե մարդ գիտի ալիքը ժամանակի մի պահի, նա կարող է հաշվել այն ժամանակի ցանկացած այլ պահի համար։ Չկանխատեսված, պատահական տարր հայտնվում է միայն այն ժամանակ, երբ մենք փորձում ենք ալիքը մեկնաբանել մասնիկի դիրքով ու արագությամբ։ Բայց գուցե սա մեր սխալն է, գուցե գոյություն չունեն մասնիկի դիրքեր ու արագություններ, այլ կան միայն ալիքներ։ Գուցե մենք փորձում ենք ալիքները հարմարեցնել դիրքի և արագության մեջ կանխակալ պատկերացումների հետ։ Իսկ ստացված սխալ համադրությունն անկանխատեսելիության հավանական պատճառն է։
Գործնականում մենք գիտության նպատակը վերասահմանել ենք որպես այնպիսի օրենքների հայտնաբերում, որոնք անորոշության սկզբունքի սահմաններում հնարավորություն կտան մեզ գուշակել իրադարձությունները։ Այնուամենայնիվ, հարցը մնում է այն, թե ինչպե՞ս կամ ինչո՞ւ էին ընտրվել տիեզերքի օրենքներն ու սկզբնական վիճակը։
Այս գրքում ես հատուկ ուշադրություն եմ դարձրել այն օրենքներին, որոնք կառավարում են ձգողականությունը, որովհետև հենց ձգողականությամբ է պայմանավորված տիեզերքի մեծածավալ կառուցվածքի ձևավորումը, չնայած այն ամենաթույլն է ուժերի չորս տարատեսակների մեջ։ Ձգողականության օրենքներն անհամատեղելի են մինչև վերջերս գոյություն ունեցող այն տեսակների հետ, որը պնդում էր, որ տիեզերքը ժամանակի մեջ անփոփոխ է։ Այն փաստը, որ գրավիտացիան միշտ ձգողական է, նշանակում է, որ տիեզերքը կամ ընդարձակվում է, կամ կծկվում։ Համաձայն հարաբերականության ընդհանուր տեսության, անցյալում պետք է եղած լինի մի անսահման խիտ վիճակ՝ մեծ պայթյուն, որը պետք է ժամանակի իրական սկիզբը լիներ։ Նմանապես, եթե ամբողջ տիեզերքը կրկին կոլապսի ենթարկվի, ապա պետք է լինի մեկ այլ անսահման խիտ վիճակ ապագայում՝ մեծ ճայթում, որը ժամանակի վերջը կլինի։ Նույնիսկ եթե ամբողջ տիեզերքը վերստին կոլապսի չենթարկվի, որոշ տեղայնացված տիրույթներում կլինեն եզակիություններ, որոնց կոլապսով սև խոռոչներ կառաջանան։ Այս եզրակացությունները ժամանակի վերջը կլինեն սև խոռոչ ընկածների համար։ Մեծ պայթյունի ժամանակ և մյուս եզակիություններում բոլոր օրենքները կկորցնեն իրենց ուժը, այսպիսով Աստված դեռ լիակատար ազատություն ունեցած կլիներ ընտրելու, թե ի՞նչ պետք է կատարվեր, և ինչպե՞ս է տիեզերքը սկիզբ առել։
Երբ մենք միավորում ենք քվանտային մեխանիկան ընդհանուր հարաբերականության տեսության հետ, թվում է, թե մի նոր հնարավորություն կա, որն առաջ ի հայտ գալ չէր կարող, այն է՝ տարածությունը և ժամանակը միասին կարող են առաջացնել վերջավոր, քառաչափ տիեզերք՝ առանց եզակիությունների և սահմանափակումների, օրինակ, երկրի մակերեսի նման, բայց ավելի մեծ թվով չափականություններով։ Թվում է, թե այս գաղափարը կարող էր բացատրել տիեզերքում դիտված շատ երևույթներ, ինչպես, օրինակ, նրա լայնամասշտաբ միակերպությունն ու փոքրամասշտաբ շեղումները համասեռությունից, ինչպիսիք են գալակտիկաները, աստղերը և նույնիսկ մարդկային էակները։ Սրանով կարելի է բացատրել նաև ժամանակի նետի գոյությունը, որը մենք արդեն ուսումնասիրել ենք։ Բայց եթե տիեզերքն ամբողջապես ինքնապարփակ է, առանց եզակիությունների կամ սահմանների և ամբողջապես նկարագրվում է միասնական տեսությամբ, ապա այս ամենը խոր նշանակություն ունի Աստծո՝ որպես արարչի դերի խնդրում։
Էյնշտեյնը մեկ անգամ հարցրել է․ «Աստված որքա՞ն ընտրություն ուներ տիեզերքը ստեղծելիս»։ Եթե ամսահմանության տեսակետը ճիշտ էր, ապա նա սկզբնական պայմանները ընտրելու որևէ ազատություն չուներ։ Նա, անկասկած, դեռ ազատ էր ընտրելու այն օրենքները, որոնց ենթարկվում է տիեզերքը։ Սա, այնուամենայնիվ, լիիրավ ընտրություն չի նշանակում, այնտեղ կարող է եղած լիներ միայն մեկ, կամ շատ փոքր թվով ամբողջական միասնական տեսություններ, ինչպես, օրինակ, տարատեսակ լարի տեսությունը, որոնք ինքնաբավ են և թույլ են տալիս այնպիսի բարդ էակների գոյությունը, ինչպիսիք են մարդիկ, որոնք կարող են ուսումնասիրել տիեզերքի օրենքներն ու հարցնել Աստծո էության մասին։
Նույնիսկ, եթե գոյություն ունի միայն մեկ միասնական տեսություն, ապա այն սոսկ կանոնների և հավասարումների մի խումբ է։ Ուստի հարց է առաջանում․ այն ի՞նչն է, որ իմաստ է տալիս հավասարումներին և տիեզերքը դարձնում է նկարագրելի։ Մաթեմատիկական մոդելներ ստեղծելու գիտության սովորական մոտեցումը չի կարող պատասխանել այն հարցին, թե ինչո՞ւ պետք է լինի տիեզերքի նկարագրելի մոդելը։ Ինչո՞ւ է տիեզերքն այդքան ջանքեր թափում իր գոյությունը պահպանելու համար։ Արդյո՞ք միասնական տեսությունն այդքան գրավիչ է, որ առաջարկում է իր իսկ գոյությունը։ Կամ արդյո՞ք այն Արարչի կարիք ունի, և եթե այդպես է, ապա արդյո՞ք նա ազդեցություն ունի տիեզերքի վրա։ Եվ ո՞վ է նրա Արարիչը։
Մինչև օրս գիտնականների մեծ մասը շատ տարված է նոր տեսություններ զարգացնելով, որոնք նկարագրում են տիեզերքի որպիսությունը, որպեսզի հետագայում պարզվի ինչո՞ւ հարցը։ Մյուս կողմից մարդիկ, որոնց գործն է հարցնել՝ ինչո՞ւ, այսինքն՝ փիլիսոփաները, ի վիճակի չեն եղել համաքայլ ընթանալ գիտական տեսության առաջընթացի հետ։ XVIII դարում փիլիսոփաները հաշվի էին առել մարդկային գիտելիքներն ամբողջությամբ, ներառյալ նաև գիտությունը՝ որպես իրենց ասպարեզը, և քննարկում էին հարցեր, ինչպիսիք են, օրինակ, տիեզերքն արդյո՞ք սկիզբ ունեցել է։ Սակայն XIX և XX դարերում գիտությունը դարձավ չափազանց տեխնիկական ու մաթեմատիկական և փիլիսոփաների և էլի շատերի համար՝ անհասկանալի, մի քանի մասնագետներից բացի։ Փիլիսոփաներն այնքան սահմանափակեցին քննարկվող հարցերի հորիզոնը, որ դարիս ամենանշանավոր փիլիսոփա Վիտգենշտեյնն ասաց․ «Փիլիսոփայությանը մնացած միակ խնդիրը լեզուների վերլուծությունն է»։ Արիստոտելից մինչև Կանտ ընկած ժամանակաշրջանի փիլիսոփայության ավանդույթների ինչպիսի՜ անկում։
Այնուամենայնիվ, եթե մենք իրոք հայտնագործենք մի ամբողջական տեսություն, այն ժամանակի ընթացքում պետք է ընդհանուր գծերով հասկանալի դառնա բոլորին և ո՛չ միայն փոքրաթիվ գիտնականների։ Այն ժամանակ մենք բոլորս՝ փիլիսոփաները, գիտնականները, նույնիսկ շարքային մարդիկ ի վիճակի կլինենք մասնակցելու այն հարցի քննարկմանը, թե ինչո՞ւ գոյություն ունենք մենք և տիեզերքը։ Եթե հաջողվի այս հարցի պատասխանը գտնել, ապա դա կլինի մարդկային մտածողության վերջնական հաղթանակը, քանի որ այդ ժամանակ մենք կհասկանանք Աստծո միտքը։
Հավելված
Ալբերտ Էյնշտեյն
Էյնշտեյնի առնչությունը միջուկային ռումբի ստեղծման քաղաքականության հետ լավ հայտնի է։ Նա ստորագրել է նախագահ Ֆրանկլին Ռուզվելտին ուղղված հայտնի նամակը, որով համոզում էր Միացյալ Նահանգներին լրջորեն մոտենալ այդ հարցին, իսկ ինքն անում էր կարելին՝ հետպատերազմյան շրջանում միջուկային պատերազմը կանխելու համար։ Բայց սրանք ստիպված քաղաքականությամբ զբաղվող գիտնականի սոսկ առանձին գործողություններ չէին։ Իր իսկ բառերով ասած՝ Էյնշտեյնի կյանքը, փաստորեն, բաժանված էր «քաղաքականության և հավասարումների միջև»։
Էյնշտեյնի վաղ քաղաքական գործունեությունը սկսվել է դեռևս Առաջին համաշխարհային պատերազմի տարիներին, երբ նա պրոֆեսոր էր Բեռլինում։ Չափազանց հոգնած լինելով մարդկային բազմաթիվ կյանքերի կորուստներից և այն ամենից, ինչ ինքն էր տեսել, նա ընդգրկվեց հակապատերազմական ցույցերում։ Քաղաքական անհնազանդությունը պաշտպանելու և ընդհանուր զինապարտությունը մերժելու նրա հասարակական քաջալերանքը հանգեցրին աշխատակիցների և նրա միջև հարաբերությունների սրման։ Այնուհետև պատերազմից հետո Էյնշտեյն իր ջանքերն ուղղեց հաշտեցման և միջազգային հարաբերությունների բարելավման գործին։ Սա նույնպես չբարձրացրեց նրա հեղինակությունը, և շուտով նրա քաղաքական հայացքների պատճառով դժվարացավ Միացյալ Նահանգներ այցելեը նույնիսկ դասախոսություններ կարդալու համար։
Էյնշտեյնի երկրորդ մեծ նպատակը սիոնիզմն էր։ Չնայած նա ծագումով հրեա էր, բայց մերժում էր Աստծո աստվածաշնչային գաղափարը։ Սակայն հակասեմիտիզմի աճող գիտակցությունը թե՛ Առաջին համաշխարհային պատերազմից առաջ, և թե՛ նրա ընթացքում նրան աստիճանաբար տարավ հրեական համայնքի հետ նույնացմանը և հետագայում սիոնիզմի բացահայտ պաշտպանությանը։ Ժողովդավարությունը կորցնելու վտանգն անգամ նրան հետ չպահեց իր մտքերն արտահայտելուց։ Նրա տեսությունները ենթարկվեցին հարձակման, և նույնիսկ հակաէյնշտեյնական կազմակերպություն հիմնվեց։ Մի մարդ, որը հրահրում էր ուրիշներին սպանել Էյնշտեյնին, դատապարտվեց և տուգանվեց ընդամենը վեց դոլարով։ Բայց Էյնշտեյն անդրդվելի էր։ Երբ մի գիրք հրատարակվեց, որը խորագրված էր «Հարյուր հեղինակներ ընդդեմ Էյնշտեյնի», նա պատասխանեց․ «Եթե ես իրոք սխալ էի, ապա մեկն էլ էր բավական»։
1933 թվականին Հիտլերը իշխանության գլուխ անցավ։ Էյնշտեյնը Ամերիկայում էր և հայտարարեց, որ ինքն այլևս չի վերադառնա Գերմանիա։ Այնուհետև, երբ նացիստական ոստիկանությունը ներխուժեց նրա բնակարանը և բռնագրավեց բանկային հաշիվը, Բեռլինի լրագրերից մեկում երևաց հետևյալ վերնագիրը՝ «Լավ լուրեր Էյնշտեյնից, նա հետ չի վերադառնալու»։ Նացիզմի սպառնալիքի տակ Էյնշտեյնը հրաժարվեց խաղաղասիրական գործունեությունից և վերջիվերջո վախենալով, որ գերմանացի գիտնականները կարող են միջուկային ռումբ ստեղծել, առաջարկեց, որպեսզի Միացյալ Նահանգներն ստեղծեն իրենց սեփականը։ Բայց առաջին ատոմական ռումբի պայթելուց դեռ շատ առաջ, Էյնշտեյնը հրապարակայնորեն զգուշացնում էր ատոմական պատերազմի սարսափների մասին և առաջարկում էր միջուկային զենքի վրա միջազգային հսկողություն սահմանել։
Ամբողջ կյանքի ընթացքում Էյնշտեյնի խաղասիրական ջանքերը գրեթե շոշափելի արդյունք չտվեցին և, իհարկե, նա քիչ համախոհներ վաստակեց։ Սիոնիզմի նրա բացահայտ պաշտպանությունը, սակայն,1952 թվականին արդեն պատշաճ ճանաչում գտավ, երբ նրան առաջարկվեց դառնալ Իսրայելի նախագահ։ Նա մերժեց՝ ասելով, թե իր կարծիքով ինքը շատ միամիտ է քաղաքական ասպարեզում։ Բայց երևի դրա իրական պատճառն այլ էր, նրա իսկ խոսքերով ասած․ «Հավասարումներն ինձ համար շատ ավելի կարևոր են, որովհետև քաղաքականությունը միայն ներկա ժամանակաշրջանի համար է, իսկ հավասարումները վերաբերում են ապագային»։
Գալիլեո Գալիլեյ
Գալիլեոյին թերևս ավելի, քան որևէ այլ անհատի ենք պարտական ժամանակակից գիտության ծննդի համար։ Նրա հայտնի ընդհարումը Կաթոլիկ եկեղեցու հետ նրա փիլիսոփայության առանցքն էր, քանի որ Գալիլեոն առաջինն էր, որ պնդում էր, թե մարդը կարող է հուսալ, որ մի օր կհասկանա, թե ինչպե՞ս է աշխարհը գործում և, դեռ ավելին, մենք այդ կարող ենք անել՝ ուսումնասիրելով իրական աշխարհը։
Գալիլեոն վաղուց հավատացել էր Կոպեռնիկոսի տեսությանը (թե մոլորակնները պտտվում են արևի շուրջը), բայց նա հրապարակայնորեն սկսեց պաշտպանել այդ տեսակետը միայն այն ժամանակ, երբ բավականաչափ փաստեր ուներ այն ապացուցելու։ Նա Կոպեռնիկոսի տեսության մասին գրեց իտալերեն (ոչ սովորական ակադեմիական լատիներենով), և շուտով նրա տեսակետները լայնորեն պաշտպանեցին համալսարանական շրջանակներից դուրս։ Դա մտահոգեց արիստոտելական պրոֆեսորներին, որոնք էլ միավորվեցին և համոզեցին Կաթոլիկ եկեղեցուն, որպեսզի վերջինս արգելի Կոպեռնիկոսի տեսությունը (կոպեռնիկոսականությունը)։
Դրանով մտահոգված Գալիլեոն մեկնեց Հռոմ, որպեսզի խոսի եկեղեցական հեղինակությունների հետ։ Նա պնդում էր, որ աստվածաշունչը նպատակ չունի մեզ որևէ տեղեկություն տալ գիտական տեսությունների մասին և եզրակացնում, որ երբ աստվածաշունչը հակասում է առողջ բանականությանը, պետք է ենթադրել, որ այն այլաբանական է։ Բայց եկեղեցին վախենում էր այն խայտառակությունից, որը կարող էր վատ ազդեցություն ունենալ բողոքականության դեմ իր պայքարում և այդ պատճառով դիմեց բռնի միջոցների։1616 թվականին այն Կոպեռնիկոսի տեսությունը հայտարարեց «կեղծ ու սխալ» և հրամայեց Գալիլեոին երբեք նորից «չպաշտպանել կամ չհետևել» այդ տեսությանը։ Գալիլեոն համաձայնեց։
1623֊ին Գալիլեոյի վաղեմի ընկերը դարձավ Հռոմի պապ։ Գալիլեոն անմիջապես փորձեց չեղյալ հայտարարել տալ 1616 թվականի հռչակագիրը։ Նրան այդ չհաջողվեց, բայց նա կարողացավ թույլտվություն ձեռք բերել գիրք գրելու և քննարկելու թե՛ Արիստոտելի և թե՛ Կոպեռնիկոսի տեսությունները։ Սակայն երկու պայմանով՝ նա որևէ մեկի կողմը չպետք է լիներ, և պետք է եզրակացներ, որ մարդ երբեք չի կարող որոշել, թե ինչպե՞ս է աշխարհը գործում, որովհետև Աստված կարող է մոտավորապես նույն ազդեցությունն առաջացնել մարդու համար աներևակայելի ձևերով, և մարդը չի կարող սահմանափակել Աստծու ամենազորությունը։
«Երկխոսություն աշխարհի երկու գլխավոր համակարգերի մասին» գիրքը ավարտվեց և տպագրվեց 1632 թվականին գրաքննիչների լիակատար պաշտպանությամբ, և այն անմիջապես ընդունվեց ամբողջ Եվրոպայում, որպես գրական և փիլիսոփայական գլուխգործոց։ Շուտով, հասկանալով, որ ժողովուրդը գիրքը դիտում է որպես համոզիչ փաստարկ և նպաստ Կոպեռնիկոսի տեսության՝ Հռոմի պապը զղջաց, որ թույլ էր տվել այդ գրքի հրատարակությունը։ Պապը պնդում էր, որ չնայած գիրքը վայելում է գրաքննիչների պաշտոնական հավանությունը, այնուամենայնիվ, Գալիլեոն խախտել էր 1616 թվականի հռչակագիրը։ Նա Գալիլեոյին ինկվիզիցիայի ենթարկեց, նրան դատապարտեց ցմահ տնային բանտարկության և հրամայեց հրապարակայնորեն հրաժարվել Կոպեռնիկոսի տեսությունից։ Այսպիսով, Գալիլեոն ստիպված երկրորդ անգամ լուռ համաձայնեց։
Գալիլեոն մնաց նվիրված կաթոլիկ, բայց նրա հավատը գիտության անկախության նկատմամբ չփշրվեց։ Մահից (1642 թվականին) չորս տարի առաջ, երբ նա դեռ գտնվում էր տնային բանտարկության մեջ, իր երկրորդ գլխավոր գրքի ձեռագիր օրինակը գաղտնի տարվեց Հոլանդիա՝ հրատարակչի մոտ։ Այն մեզ հասել է որպես «Երկու նոր գիտություն», որն ավելին էր, քան զուտ Կոպեռնիկոսի պաշտպանությունը և ժամանակակից ֆիզիկայի հիմքն էր։
Իսահակ Նյուտոն
Իսահակ Նյուտոնը հաճելի անձնավորություն չէր։ Նրա հարաբերությունները մյուս ակադեմիկոսների հետ հայտնի էին իրենց անբարեհաճությամբ, և նա կյանքի մեծ մասն անցկացրել է բուռն վեճերի մեջ։ «Մաթեմատիկայի սկզբունքները» գրքի հրատարակությունից հետո, որն, անկասկած, ֆիզիկայի ոլորտում երբևէ գրված ամենալավ գիրքն է, Նյուտոնի համբավն արագ աճեց։ Նա առաջադրվեց Թագավորական ընկերության պրեզիդենտ և դարձավ առաջին գիտնականը, որն ստացավ ասպետի կոչում։
Նյուտոնը շուտով բախվեց թագավորական աստղագետ Ջոն Ֆլամսթիդի հետ, որը նախկինում Սկզբունքների համար տվյալներ էր հայթայթել, բայց դրանք չէր տալիս Նյուտոնին։ Նյուտոնը «ոչը» չէր ընդունում որպես պատասխան և այդ իսկ պատճառով հասավ այն բանին, որ իրեն նշանակեցին Թագավորական աստղադիտարանի ղեկավար օրգանի անդամ և ճնշման ներքո հրատարակել տալ այդ տվյալները։ Վերջիվերջո, նրան հաջողվեց զավթել Ֆլամսիթի աշխատանքը և տպագրության պատրաստել նրա ոխերիմ թշնամի Էդմոնդ Հալլեի կողմից։ Բայց Ֆլամսիթն այդ դեպքի առիթով դիմեց դատարան և անմիջապես ստացավ դատարանի որոշումը, որը կանխում էր գողացված աշխատանքի տարածումը։ Նյուտոնը զայրացավ և իր վրեժը լուծեց՝ «Սկզբունքների» հաջորդ հրատարակությունում՝ բաց թողնելով Ֆլամսիթից կատարված բոլոր մեջբերումները։
Ավելի լուրջ վեճ ծագեց գերմանացի փիլիսոփա Գոթֆրիդ Լայբնիցի հետ։ Երկուսն էլ՝ Լայբնիցն ու Նյուտոնը, միմյանցից անկախ զարգացրել էին մաթեմատիկայի մի ճյուղ, որը կոչվում էր հաշիվներ, որի վրա է հիմնված ժամանակակից ֆիզիկայի մեծ մասը։ Չնայած մենք այժմ գիտենք, որ Նյուտոնը Լայբնիցից տարիներ առաջ էր բացահայտել հաշիվները, բայց իր աշխատանքը հրատարակել է շատ ավելի ուշ։ Դրան հաջորդեց մի բուռն վիճաբանություն՝ ո՞վ է առաջինը։ Գիտնականները երկու մրցակցին էլ եռանդով պաշտպանում էին։ Այնուամենայնիվ, ուշագրավ փաստ է, որ Նյուտոնին պաշտպանող գրեթե բոլոր հոդվածները իրականում գրված էին նրա իսկ ձեռքով, բայց ստորագրված էին ընկերների ստորագրությամբ։ Երբ վեճը թեժացավ, Լայբնիցը սխալ քայլի դիմեց և բողոքեց Թագավորական ընկերությանը՝ խնդրին լուծում տալու համար։ Նյուտոնը, որպես պրեզիդենտ, այդ հարցը լուծելու համար ստեղծեց մի «չեզոք» հանձնաժողով, որն, ի դեպ, ամբողջապես կազմված էր իր ընկերներից։ Բայց դա դեռ բոլորը չէ․ նա այնուհետև ինքը գրեց հանձնաժողովի զեկույցը, պաշտոնապես Լայբնիցին մեղադրեց գրագողության մեջ և Թագավորական ընկերությանը ստիպեց տպագրել այն։ Դրանով չբավարարվելով, նա այնուհետև մի անստորագիր հոդված ևս գրեց այդ զեկույցի շուրջ, որը տպագրվեց Թագավորական ընկերության սեփական պարբերականում։ Լայբնիցի մահից հետո Նյուտոնը հայտարարել է, որ ինքը մեծագույն բավականություն է ստացել «Լայբնիցի սիրտը կոտրելով»։
Այս երկու վիճաբանությունների ժամանակ Նյուտոնն արդեն թողել էր Քեմբրիջը և ակադեմիան։ Քեմբրիջում նա ակտիվ էր հակակաթոլիկական քաղաքականության մեջ, իսկ ավելի ուշ խորհրդարանում և ի վերջո պարգևատրվեց Թագավորական դրամահատարանի վարիչի շահավետ պաշտոնով։ Այստեղ նա օգտագործեց իր չարության և կծու հեգնանքի ամբողջ տաղանդը հասարակայնորեն ավելի ընդունելի ձևով, հաջողությամբ պայքարեց կեղծարարների դեմ, նույնիսկ կախաղան ուղարկեց մի շարք մարդկանց։
Բառարան
Ալիքի երկարություն ― Ալիքի երկու հաջորդական գագաթների կամ փոսերի միջև եղած հեռավորությունը։
Ալիք֊մասնիկային երկվություն ― Քվանտամեխանիկական հասկացություն, ըստ որի մասնիկների և ալիքների միջև տարբերություն չկա։ Մասնիկն իրեն երբեմն պահում է որպես ալիք, իսկ ալիքը՝ որպես մասնիկ։
Ատոմ ― Սովորական նյութի հիմնական միավոր, բաղկացած է շատ փոքր միջուկից, որը կազմված է պրոտոններից և նեյտրոններից և նրա շուրջ պտտվող էլեկտրոններից։
Անորոշության սկզբունք ― Մասնիկի դիրքն ու արագությունը (էներգիան) նույնպիսի ճշգրտությամբ չի կարելի որոշել․ որքան մեծ ճշգրտությամբ իմանանք մեկը, նույնքան նվազ ճշտությամբ կիմանանք մյուսը։
Արագացում ― Մարմնի արագության փոփոխությունը միավոր ժամանակում։
Արգելակման սկզբունք ― Երկու նույնական ½ սպին ունեցող մասնիկները (ինչպես էլեկտրոնը) չեն կարող ունենալ նույն դիրքն ու նույն արագությունը (էներգիան) անորոշության սկզբունքի սահմաններում։
Բացարձակ զերո ― Հնարավոր ամենացածր ջերմաստիճանը (-273,2°C), որում նյութը զրկված է ջերմային էներգիայից։
Գամմա ճառագայթ ― Շատ կարճ ալիքի երկարություն ունեցող էլեկտրամագնիսական ճառագայթում, որն առաջանում է ռադիոակտիվ քայքայման կամ տարրական մասնիկների բախման հետևանքով։
Գեոդեզիական ― Երկու կետերի միջև ամենակարճ (կամ ամենաերկար) հեռավորությունը երկրագնդի վրա։
Դաշտ ― Այն, ինչ գոյություն ունի ամենուրեք տարածության և ժամանակի մեջ՝ ի տարբերություն մասնիկի, որը գոյություն ունի միայն մի կետում, որոշակի ժամանակում։
Եզակիության թեորեմ ― Թեորեմ, որի համաձայն որոշակի պայմաններում պետք է գոյություն ունենա եզակիություն, մասնավորապես, տիեզերքը սկիզբ է առել եզակիությունից։
Եզակիություն ― Տարածություն ժամանակի մեջ այնպիսի մի կետ, որում տարածություն ժամանակի կորությունը անսահման է։
Զանգված ―Մարմնի մեջ եղած նյութի քանակը կամ այդ մարմնի իներցիան՝ արագացմանը դիմադրելու կարողությանը։
Էլեկտրաթույլ միասնական էներգիա ― Էներգիայի այն մակարդակը (մոտավորապես 100 ԳԷՎ), որից վերև էլեկտրամագնիսական ուժի և թույլ ուժի միջև տարբերությունը վերանում է։
Էլեկտրական լիցք ― Մասնիկի այն հատկությունը, որով նա վանում է (կամ ձգում) մեկ այլ մասնիկի, որն ունի նույն (կամ հակառակ) նշանը։
Էլեկտրական ուժ ― Էլեկտրական լիցք ունեցող մասնիկների միջև առաջացող ուժը, ուժգնությամբ երկրորդը չորս հիմնական ուժերից։
Էլեկտրոն ― Բացասական լիցքավորված տարրական մասնիկ, որը պտտվում է ատոմի միջուկի շուրջ։
Էներգիայի պահպանման օրենք ― Բնության հիմնական օրենքը, ըստ որի էներգիան (կամ համարժեք զանգվածը) չի կարելի ոչ ստեղծել և ոչ ոչնչացնել։
Էնտրոպիա ― Համակարգի կարգավորվածության աստիճանը ցույց տվող մեծություն։ Համաձայն տերմոդինամիկայի 2֊րդ օրենքի, բնության մեջ ինքնակամ պրոցեսները ընթանում են այնպես, որ համակարգը կանոնավոր վիճակից անցնում է անկանոն վիճակի, որի ընթացքում էնտրոպիան աճում է։
Ընդհանուր հարաբերկանության տեսություն ― Էյնշտեյնի տեսությունը՝ հիմնված այն պատկերացման վրա, համաձայն որի գիտության օրենքները նույնն են բոլոր դիտորդների համար, անկախ այն բանից, թե ինչպես են նրանք շարժվում։ Գրավիտացիոն ուժը արտահայտվում է որպես քառաչափ տարածություն֊ժամանակի կորություն։
Թույլ ուժ ― Չորս հիմնական ուժերից երկրորդ թույլ ուժը (գրավիտացիոն ուժից հետո), որը գործում է փոքր հեռավորությունների վրա։ Ազդում է բոլոր նյութական մասնիկների վրա, բացի ուժակիր մասնիկներից։
Լուսավայրկյան (լուսատարի) ― Լույսի անցած ճանապարհը մեկ վայրկյանում (մեկ տարում):
Կեղծ ժամանակ ― Այն ժամանակը, որը չափվում է կեղծ թվերի օգնությամբ։
Կշիռ ― Այն ուժը, որով գրավիտացիոն դաշտն ազդում է մարմնի վրա, համեմատական է մարմնի զանգվածին, բայց նրան հավասար չէ։
Կոորդինատներ ― Այն թվերը, որոնցով որոշվում է կետի դիրքը տարածություն֊ժամանակի մեջ։
Հակամասնիկ ― Յուրաքանչյուր տեսակի նյութական մասնիկ ունի իր համապատասխան հակամասնիկը (էլեկտրոն֊հակաէլեկտրոն֊պոզիտրոն)։ Երբ մի մասնիկ բախվում է իր հակամասնիկի հետ, երկուսն էլ անիհիլանում են՝ արձակելով միայն էներգիա։
Հաճախականություն ― Ամբողջական ալիքների (ցիկլերի) թիվը մեկ վայրկյանում։
Համեմատականություն ― «x֊ը համեմատական է y֊ին»՝ նշանակում է, որ x֊ը հավասար է y֊ի և որևէ թվի բազմապատկին։ «x֊ը հակադարձ համեմատական է y֊ին»՝ նշանակում է, որ երբ x֊ը բազմապատկվում է որևէ թվով, y֊ը բաժանվում է նույն թվին։
Հարաբերականության հատուկ տեսություն ― Էյնշտեյնի տեսությունը, ըստ որի գիտության օրենքները նույնն են բոլոր ազատորեն շարժվող դիտորդների համար՝ անկախ նրանց շարժման արագությունից։
Հզոր ուժ ― Չորս հիմնական ուժերից ամենաուժեղը, որը գործում է փոքր հեռավորությունների վրա։ Դրանք միմյանց են կապում քվարկները՝ պրոտոններում ու նեյտրոններում, և պրոտոններն ու նեյտրոնները՝ ատոմի միջուկում։
Մագնիսական դաշտ ― Մագնիսական ուժերը պայմանավորող դաշտը, այժմ էլեկտրական դաշտի հետ միավորված է որպես էլեկտրամագնիսական դաշտ։
Մասնիկ (իրական) ― Մասնիկային դետեկտորով ուղղակիորեն դիտարկվող (գրանցվող) նյութական մասնիկ, ինչպես պրոտոնը, էլեկտրոնը և այլն։
Մասնիկ (վիրտուալ) ― Քվանտային մեխանիկայում այն մասնիկը, որը դետեկտորով հնարավոր չէ ուղղակիորեն գրանցել, ինչպես գրավիտոնը, բայց նրա գոյությունը թողնում է չափելի ազդեցություն։
Մասնիկային արագացուցիչ ― Էլեկտրամասնիկների օգնությամբ լիցքավորված մասնիկներին մեծ արագություն (էներգիա) հաղորդող սարք։
Մարդաբանական սկզբունք ― Մենք տիեզերքը տեսնում ենք այնպես, ինչպես կա, որովհետև, եթե տիեզերքն այլ լիներ, մենք այստեղ չէինք լինի այն տեսնելու համար։
Մեծ միասնական էներգիա ― Էներգիայի այն մակարդակը, որից ավելի բարձր արժեքի համար, ըստ ամենայնի, էլեկտրամագնիսական ուժը, թույլ ուժը և ուժեղ ուժը դառնում են միմյանցից անզանազանելի։
Մեծ միասնական տեսություն (ՄՄՏ) ― Այն տեսությունը, որը միավորում է էլեկտրամագնիսական, ուժեղ և թույլ ուժերը։
Մեծ ճայթյուն ― Տիեզերքի վերջավորության եզակիությունը։
Մեծ պայթյուն ― Տիեզերքի սկզբնավորման եզակիությունը։
Մերկ եզակիություն ― Տարածության֊ժամանակի եզակիություն, որը շրջապատված չէ սև խոռոչով։
Միկրոալիքային ճառագայթման ֆոն ― Սկզբնական տաք տիեզերքի հրաշեկ ճառագայթումն այժմ այն աստիճան է շեղված դեպի սպեկտրի կարմիր տիրույթը, որ երևում է ոչ որպես լույս, այլ որպես միկրոալիք (ռադիոլաիք՝ մի քանի սանտիմետր երկարությամբ)։
Միջուկ ― Ատոմի կենտրոնական մասը, որը կազմված է պրոտոններից և նեյտրոններից, որոնք իրար միացած են ուժեղ ուժով։
Միջուկային սինտեզ ― Այն պրոցեսը, որի արդյունքում երկու միջուկներ բախվելով միանում են իրար և առաջացնում մեկ, ավելի ծանր միջուկ։
Նախասկզբնական սև խոռոչ ― Նախասկզբնական տիեզերքում առաջաց սև խոռոչ։
Նեյտրինո ― Չափազանց թեթև (հավանաբար զանգված չունեցող) տարրական նյութական մասնիկ, որի վրա ազդում են լոկ թույլ ուժը և գրավիտացիան։
Նեյտրոն ― Չեզոք (չլիցքավորված) մասնիկ, որը շատ նման է (բացի լիցքից) պրոտոնին և կազմում է ատոմի միջուկի մեջ մտնող մասնիկների մոտավորապես կեսը։
Նեյտրոնային աստղ ― Սառը աստղ, որը գոյատևում է նեյտրոնների միջև արգելակման սկզբունքի համաձայն գործող վանողական փոխազդեցության շնորհիվ։
Չանդրասեկհարի սահման ― Կայուն սառը աստղի հնարավոր առավելագույն զանգվածը (արևի զանգվածից մեկ և կես անգամ մեծ), որից ավելիի դեպքում աստղը կոլապսվում է սև խոռոչի։
Չափականություն ― Քառաչափ տարածություն֊ժամանակի մեջ ժամանակի մեկ և տարածության երեք չափումներից մեկը։
Պատահույթ (Դեպք) ― Տարածություն֊ժամանակի մեջ մի կետ, որը բնորոշվում է իր ժամանակով և տեղով։
Պատահույթի հորիզոն ― Սև խոռոչի սահմանագիծը։
Պլանկի քվանտային սկզբունք ― Այն պատկերացումը, թե լույսը (կամ որևէ դասական ալիք) առաքվում և կլանվում է որոշակի քվանտներով, որոնց էներգիան համեմատական է հաճախականությանը։
Պոզիտրոն ― Դրական լիցքավորված տարրական մասնիկ, էլեկտրոնի հակամասնիկը։
Պրոտոն ― Դրական լիցքավորված մասնիկ, որը կազմում է ատոմի միջուկի մասնիկների մոտ կեսը։
Ռադար ― Ռադիոալիքային ազդանշաններ օգտագործող համակարգ, որը որոշում է առարկաների դիրքը՝ իր արձակած ազդանշանի՝ առարկային հասնելու և նրանից անդրադառնալու ժամանակամիջոցը չափելով։
Ռադիոակտիվություն ― Մի տեսակի ատոմային միջուկի ինքնակամ քայքայումը մի այլ տեսակի։
Սահման չունենալու պայման ― Այն տեսակետը, որ տիեզերքը վերջավոր է, բայց սահմանագիծ չունի (կեղծ ժամանակում)։
Սև խոռոչ ― Տարածություն ժամանակի այն տիրույթը, որտեղից ոչինչ, նույնիսկ լույսը, չի կարողանում հեռանալ, որովհետև գրավիտացիան նրանում շատ ուժեղ է։
Սպեկտր ― Էլեկտրամագնիսական ալիքների, օրինակ, տարբաղադրումը բաղադրիչ հաճախականությունների։
Սպիտակ թզուկ ― Կայուն սառը աստղ, որը գոյատևում է անորոշության սկզբունքով պայմանավորված էլեկտրոնների միջև գործող վանողական փոխազդեցությամբ։
Սպին ― Տարրական մասնիկի ներքին հատկություն, որը կապված է, սակայն չի նույնանում սովորական պտույտի հետ։
Տարածություն֊ժամանակ ― Քառաչափ տարածություն, որի կետերը պատահույթ են։
Տարրական մասնիկ ― Մասնիկ, որը, թվում է, չի կարող մասնատվել։
Տիեզերաբանական հաստատուն ― Էյնշտեյնի օգտագործած մաթեմատիկական հնարք, որպեսզի տարածություն֊ժամանակը ինքնակամորեն ձգտի ընդարձակման։
Տիեզերագիտություն ― Տիեզերքի ուսումնասիրությունն ամբողջությամբ վերցրած։
Փուլ ― Ալիքի դիրքը ցիկլում որոշակի ժամանակամիջոցում, այսինքն՝ որտեղ է գտնվում՝ գագաթում, փոսում, թե որևէ այլ կետում։
Քվանտ ― Էներգիայի միավոր, որով առաքվում կամ կլանվում են ալիքները։
Քվանտային մեխանիկա ― Պլանկի քվանտային սկզբունքի և Հայզենբերգի անորոշության սկզբունքի հիման վրա մշակված տեսություն, որը նկարագրում է մասնիկի ալիքային շարժումը։
Ֆոտոն ― Լույսի քվանտը։
- ↑ ԱԿՍ (լատ․ AZS) ― ամիոտրոֆիկ կողմնային սկլերոզ։ Այս և հետագա բոլոր բացատրությունները Տ․ Քրմոյանինն են։
- ↑ Աստղերն իհարկե, իրենց դիրքը փոխում են, սակայն դա տեսանելի կլինի միայն միլիոնավոր տարիների ընթացքում։
- ↑ Ի․ Կանտն առաջին անգամ արեգակնային համակարգի ծագման հարցերին անդրադարձել է «Համընդհանուր բնական պատմություն և երկնքի տեսություն» (1755) աշխատությունում և առաջարկել այժմ իր անվամբ հայտնի հիպոթեզը։
- ↑ Ա․ Մայքելսոնը լույսի արագության վրա երկրի շարժման ազդեցությունը չափելու առաջին փորձերը կատարել է 1881֊ին։
- ↑ Ըստ Ռելե֊Ջինսի օրենքի, ճառագայթման էներգիան պետք է անսահման աճի ալիքի հաճախականության մեծությամբ, հասնելով արտասովոր մեծ արժեքների խորը ուլտրամանուշակագույն և ավելի կարճալիք տիրույթներում (հայտնի է է որպես, այսպես կոչված, «ուլտրամանուշակագույն աղետ»), բայց որի առավելագույն արժեքի, հաճախականության հետագա աճի հետ նվազում է։ Հաճախականությունների ամբողջ տիրույթում էներգիայի ճիշտ բաշխումը նկարագրվում է միայն քվանտային պատկերացումներով։
- ↑ Ավելի ուշ, 60 ― 70֊ական թվականներին, մի առիթով Դիրակը սրամտեց, որպեսզի իմանանք, թե ինչ բան է էլեկտրոնը, պետք է իմանալ՝ ինչ բան է էլեկտրականությունը, իսկ որպեսզի վերջինիս ինչ լինելը իմանանք, հարկավոր է իմանալ, թե ինչ բան է էլեկտրոնը։
- ↑ GUT անգլ․՝ grand unitied theory ― Մեծ միասնական տեսություն (ՄՄՏ):
- ↑ Հարց է ծաում, գոյություն ունի՞ արդյոք փոխազդեցություն գրավիտացիոն ուժի և մյուս երեք քվանտային ուժերի միջև։ Բանն այն է, որ գրավիտացիոն ուժը տարածություն֊ժամանակի տիրույթում նյութի առկայության հետևանքն է։ Չնայած այդ ուժի էությունը մեզ հայտնի չէ դեռևս, բայց մենք գիտենք, որ նյութը որոշակի կառույց ունի, այն կազմված է որոշակի թվով պրոտոններից ու նեյտրոններից, նրանց կապի էներգիայից և վերջապես ատոմների ներքին փոխդասավորությունից։ Ըստ ոմանց, նյութի այդ կառուցվածքային առանձնահատկությունը պայմանավորում է մի հինգերորդ ուժ, որը հակազդում է գրավիտացիոն ուժին և գործում մինչև մի քանի հայրուր կիլոմետր հեռավորությունների վրա։ Սա վիճելի, բայց հետաքրքիր հարզ է, որի մասին մանրամասնորեն խոսվում է «National Geographic Magazine» ամսագրի 1989 թվականի մայիսի և սեպտեմբերի համարներում։
- ↑ Եթե արագությունը մեծ է որոշ կրիտիկական (տիեզերական) արժեքից, ապա արկը կպոկվի երկրի ձգողական ուժից և դուրս կգա երկրաշուրջ ուղեծիր կամ միջմոլորակային տարածություն։
- ↑ Ծանր ջրի մոլեկուլներում ջրածնի բոլոր ատոմները փոխարինված են ծանր ջրածնի (դեյտերիումի) ատոմներով։ Սովորական ջուրը, այսպես ասած, «թեթև» և «ծանր» ջրերի խառնուրդ է, իսկ «ծանր» և «թեթև» ջրածինները իրարից տարբերվում են միջուկում եղած նեյտրոնների թվով (առաջինում մեկ, երկրորդում՝ զերո)։
- ↑ Երբ տեղի են ունենում ինքնակամ պրոցեսներ։
- ↑ Ավելի ճիշտ՝ խառնվում են
- ↑ Գազի ինքնակամ ընդարձակումը հաստատուն ջերմաստիճանում բերում է էնտրոպիայի աճի։
- ↑ Խառնվելուց հետո երկու գազերի խառնուրդի էնտրոպիան ավելի մեծ է, քան առանձին վերցրած գազերի էնտրոպիաների գումարը՝ այն պատճառով, որ երկու տարբեր գազերն իրարից անջատելու համար հարկավոր է լրացուցիչ աշխատանք կատարել։ Դա կարելի է բացատրել նաև այն բանով, որ յուրաքանչյուր գազ ընդարձակվել է և մեծացրել էնտրոպիան։
- ↑ Ֆոտոնների թիվը։
- ↑ Ֆոտոնի էներգիան համեմատական է հաճախականությանը։
- ↑ Սովորական ջրածնի ատոմի միջուկը կազմված է մեկ պրոտոնից և դրա համար կոչվում է պրոտոն։ Դեյտերիումի (ծանր ջրածնի) ատոմի միջուկը պարունակում է մեկ պրոտոն ու մեկ նեյտրոն և կոչվում է դեյտրոն։
- ↑ Բացարձակ զերոն (որը կոչվում է նաև Կելվինի զերո աստիճան) սահմանային ամենացածր ջերմաստիճանն է։
- ↑ Հարաճուն ընդլայման և գերսառեցման արդյունքում նաև պղպջակների առաջացման հարցերը բազմատեսակ են։ Այնուամենայնիվ, համաձայն պղպջակների տեսության կողմնակիցներից մեկի՝ Ռիչարդ Գոթի, ճառագայթումը թափանցելով պղպջակ, փոխակերպվում է նյութի, այսինքն զանգվածից զրկված քվարկները զանգված են ձեռք բերում։ Համաձայն Հոքինգի, «այս տեսությունները ավելի շատ հարցեր են արծարծում, քան լուծում (տես «Stephen Howkigs Unlvers» by Tohn Basbough, Avou Books, N4, էջ 101): Ինչպես երևում է, Ալան Գութը «ձրի ճաշկերույթ» ասելով, ակնարկում է ճառագայթման՝ նյութ առաջացնող աղբյուր լինելու գաղափարը։
- ↑ Ինչպես փորձն է ցույց տալիս, շարժվող լուսատու առարկան իրենից արձակված լույսի արագությանը չի կարող ավելացնել իր սեփական արագությունը։ Այսինքն՝ լույսի արագությունը միշտ հաստատուն է։ Իսկ քանի որ, համաձայն հարաբերականության տեսության, ամեն շարժում (բացի լույսի արագությունից) հարաբերական է (ինչպես ցույց է տալիս փորձը), հետևաբար գնացքով դեպի լույսի աղբյուրը շարժվող դիտորդին լույսն ավելի շուտ կհասնի, այսինքն նրա ժամացույցն ավելի կարճ ժամանակ ցույց կտա, քան կառամատույցում կանգնած մարդու ժամացույցը, որը նույն լույսն ավելի ուշ կտեսնի։ Դժբախտաբար, կառամատույցում կանգնած մարդը չի կարող գնացքի ուղևորի ժամացույցը տեսնել այդ բանը ստուգելու համար, սակայն հայտնի է, որ արագ շարժվող գնացքի պատուհանները նեղ են թվում։ Քանի որ տարածությունն ու ժամանակն իրար հետ կապված են, ապա ակնհայտ է, որ արագության աճի հետ տարածությունը կարճանում է, իսկ ժամանակը դանդաղում։ Իհարկե, փոքր արագությունների համար այս դանդաղումը հնարավոր չէ չափել, սակայն եթե գնացքը շարժվի լույսի արագության մոտ (300.000 կմ/վ) արագությամբ, ապա երկու տարի հետո ուղևորի տարիքը համարյա փոփոխության չի ենթարկվի։
- ↑ Հիշել ապագան, նշանակում է, որ մենք հետ ենք գնում դեպի անցյալը, այսինքն՝ իրական ժամանակը փոխում է իր ուղղությունը։
- ↑ Այսինքն ժամանակի ընթացքում տեղի են ունենում ինքնակամ պրոցեսներ, որոնք բերում են կարգուկանոնի նվազման, որի չափանիշն է էնտրոպիայի աճը։
- ↑ Կարևոր չէ, թե ինչպես բաժակը վայր ընկավ, այլ այն, որ ջարդված բաժակի վերականգնումը չի կարող ինքնակամ կերպով տեղի ունենալ։ Այդ անելու համար աշխատանք պետք է կատարել, որի հետևանքով կառաջանա մի այլ անկարգություն, կամ, որ նույն բանն է, համակարգի էնտրոպիան կաճի առավել մեծ չափով։
- ↑ Մարդիկ այդպիսի տիեզերքում կարող են հիշել լոկ բաժակի վերականգնումը, այսինքն անկանոն վիճակից ինքնակամ անցում կանոնավոր վիճակի։
- ↑ Դրա պատճառն այն է, որ համաձայն թերմոդինամիկայի 2֊րդ օրենքի, ջերմությունը չի կարելի ամբողջությամբ փոխակերպել աշխատանքի, քանի որ դրա մի մասը անպայման շրջապատին է հաղորդվում՝ մնում է չօգտագործված։ Հակառակ դեպքում հնարավոր կլիներ ստեղծել II կարգի հավերժական մի շարժիչ․ ինչը հնարավոր չէ։
- ↑ Էնտրոպիայի մասին խոսել լոկ անկարգավորվածության աճի տեսակետից, հավանաբար, բավարար չէ։ Բավական է ասել, որ եթե թերմոդինամիկայի առաջին օրենքը տալիս է էներգիայի փոխակերպման սկզբունքը, ապա երկրորդ օրենքը դրա ուղղությունը, որը կախված է լոկ ջերմություն֊էներգիա փոխակերպումից։
- ↑ բնագրում «ինֆլյացիոն»
- ↑ Հավանաբար ճիշտ կլինի խոսել ոչ թե ապագան «հիշելու», այլ «տեսնելու» մասին։ Հեղինակը պատահական չի օգտագործում «հիշել» բառը, ցույց տալու համար այդպիսի հնարավորության վիճելի բնույթը։
- ↑ Այսպիսի եզրակացությունը ոչ միայն անիմաստ է, այլ ցույց է տալիս, որ մաթեմատիկական եզրակացությունների հետ պետք է զգույշ վարվել։ Այսինքն՝ կարևորը մոդելն է, ոչ թե մաթեմատիկան։
- ↑ Այնուամենայնիվ, երբեմն հարց է տրվում, թե ի՞նչ է ժամանակը, արդյո՞ք դա մի առեղծված չէ։ Այդ հարցին Ռ․ Ֆեյնմանը պատասխանել է․ «Մենք՝ ֆիզիկոսներս ամեն օր գործ ունենք ժամանակի հետ, բայց մեզ մի հարցրեք, թե ինչ բան է այն։ Շատ դժվար է խոսել այդ մասին»։ Ջ․ Բոսլոն պատմում է, որ ինքը Օստրեն քաղաքի մի սրճարանի պատի վրա կարդացել է հետևյալ մակագրությունը․ «Ժամանակը բնության կողմից ձեռք առնված մի միջոց է, որպեսզի ամեն ինչ միանգամից տեղի չունենա»։ Հոքինգն այստեղ ցույց է տալիս, որ առանց շարժման՝ ժամանակի հասկացությունն անիմաստ է։ Արդարև, ըստ Ջ․ Ուիլերի՝ «տիեզերքը նկարագրելու համար ժամանակը չի կարող եզրափակիչ հանգամանք լինել», քանի որ «այն լոկ մի չափականություն է, ինչպես տարածությունը, և բնության երկրորդական հատկանիշ է»։ Եվ վերջապես, ինչպես Հոքինգն է պնդում, բնության համար միայն մեկ բացարձակ մեծություն կա, դա ժամանակը չէ, այլ լույսի արագության հաստատունությունը։
- ↑ Դա այսօր հայտնի է որպես հոքինգյան ճառագայթում
- ↑ գրավիտացիոն և տիեզերական հաստատունները
- ↑ Դա, իհարկե ճիշտ չէ։ 1920֊ական թվականներին արդեն մեծ թվով գրքեր են հրատարակվել այդ և հարակից հարցերի մասին՝ դեռ չխոսելով առանձին աշխատանքների մասին։