«Տարերք/Գիրք 13»–ի խմբագրումների տարբերություն
(→Պնդում 1) |
|||
| (24 intermediate revisions by the same user not shown) | |||
| Տող 6. | Տող 6. | ||
}} | }} | ||
[[Կատեգորիա:Մաթեմատիկա]] | [[Կատեգորիա:Մաթեմատիկա]] | ||
| − | |||
| + | === '''Pages 506-530''' === | ||
| − | + | == Պնդում 1 == | |
| − | + | ||
| − | + | ||
Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն։ | Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն։ | ||
| − | [[Պատկեր:Nkar_1.png| | + | [[Պատկեր:Nkar_1.png|260px|thumb|left|Նկ․ 1]] |
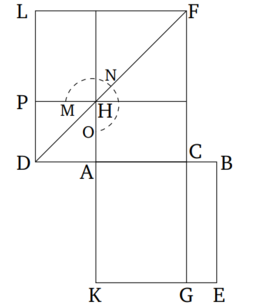
::::Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է ''(Նկ․ 1)''։ Շարունակենք AC հատվածը, և տեղադրենք <math>AD = \frac{AB}{2}</math>։ Ես պնդում եմ, որ <math>CD^2 = 5\cdot DA^2</math>: | ::::Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է ''(Նկ․ 1)''։ Շարունակենք AC հատվածը, և տեղադրենք <math>AD = \frac{AB}{2}</math>։ Ես պնդում եմ, որ <math>CD^2 = 5\cdot DA^2</math>: | ||
| Տող 24. | Տող 22. | ||
Այսպիսով, եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն, ինչը և պահանջվում էր ապացուցել։ | Այսպիսով, եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն, ինչը և պահանջվում էր ապացուցել։ | ||
| − | + | == Պնդում 2 == | |
| − | + | ||
Եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է։ | Եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է։ | ||
| − | [[Պատկեր:Nkar_2.png| | + | [[Պատկեր:Nkar_2.png|280px|thumb|left|Նկ․ 2]] |
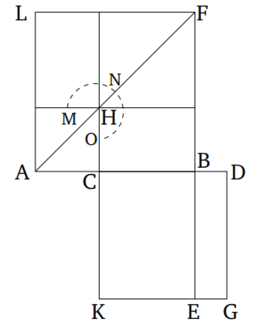
| − | ::::Դիցուք՝ եթե <math>AB^2 = 5\cdot AC^2</math> | + | ::::Դիցուք՝ եթե <math>AB^2 = 5\cdot AC^2</math> և СВ շարունակենք, այնպես, որ <math>CD = 2\cdot AC</math>, ապա CD-ն բաժանվում է արտաքին և միջին հարաբերությամբ, որտեղ մեծ հատվածը CB է ''(Նկ․ 2)''։ |
| − | ::::Դիտարկենք AB և CD կողմերով քառակուսիները՝ ALFB և СKGD ''(Նկ․ 2)'': Տանենք AF անկյունագիծը։ Շարունակենք FB հատվածը և հատենք KG-ի հետ E-ում: Քանի որ <math>AB^2 = 5\cdot AC^2< | + | ::::Դիտարկենք AB և CD կողմերով քառակուսիները՝ ALFB և СKGD ''(Նկ․ 2)'': Տանենք AF անկյունագիծը։ Շարունակենք FB հատվածը և հատենք KG-ի հետ E-ում: Քանի որ <math>AB^2 = 5\cdot AC^2</math>, հետևաբար AF անկյունագծով քառակուսու մակերեսը հավասար է 5 անգամ AH անկյունագծով քառակուսու մակերեսին։ Այսպիսով գնոմոն <math>MNO = 4\cdot AH</math>: Քանի որ <math>DC = 2\cdot CA</math>, հետևաբար <math>DC^2 = 4\cdot AC^2</math>, կամ նույնն է ինչ ասենք, որ СG անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ AH անկյունագծով քառակուսու մակերեսին։ Հետևաբար գնոմոն <math>MNO = CG</math> անկյունագծով քառակուսու մակերեսին (HB, HF, HL անկյունագծերով ուղղանկյունների մակերեսները հավասար են CDGK-ի մակերեսին): Եվ քանի որ <math>DC = 2\cdot CA</math>, <math>DC = CK</math>, <math>AC = CH</math> ապա <math>KC = 2\cdot CH</math> և KB անկյունագծով ուղղանկյան մակերեսը հավասար է 2 անգամ BH անկյունագծով ուղղանկյան մակերեսին ''(Պնդ․ 6․1)'' և քանի որ LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է երկու անգամ HB անկյունագծով ուղղանկյան մակերեսին ''(Պնդ․ 1.43)'', ապա KB անկյունագծով ուղղանկյան մակերեսը հավսար է LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց էր տրված վերևում գնոմոն MNO-ն հավասար է СG անկյունագծով քառակուսու մակերեսին։ Հետևում է, որ HF անկյունագծով ուղղանկյան մակերեսը հավասար է BDGE ուղղանկյան մակերեսին։ Իսկ վերջինս հավասար է СD և BD կողմերով կառուցված ուղղանկյան մակերեսին, <math>CD = DG</math>, HF անկյունագծով ուղղանկյան մակերեսը հավասար է <math>CB^2</math>։ Հետևաբար CD և BD կողմերով կառուցված ուղղանկյան մակերեսը հավասար է <math>CB^2</math> <math>(CB^2 = DC\cdot BD)</math>: Այսպիսով, ստանում ենք <math>\frac{DC}{CB} = \frac{CB}{BD}</math> ''(Պնդ․ 6․17)'': Եվ քանի որ DC ավելի մեծ է քան СB (տես Լեմմա, ներքևում), ապա СB-ն նույնպես ավելի մեծ է քան BD-ն։ Այսպիսով, եթե CD հատվածը բաժանված է արտաքին և միջին հարաբերությամբ, ապա СB-ն նրա մեծ հատվածն է։ |
Այսպիսով, եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է, ինչը և պահանջվում էր ապացուցել։ | Այսպիսով, եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է, ինչը և պահանջվում էր ապացուցել։ | ||
| + | |||
| + | == Լեմմա == | ||
| + | |||
| + | Ապացուցենք, որ <math>2\cdot AC (DC) > BC</math>։ | ||
| + | |||
| + | Ենթադրենք <math>2\cdot AC</math> ավելի մեծ չէ քան BC, և <math>BC = 2\cdot CA</math>։ Այսպիսով <math>BC^2 = 4\cdot CA^2</math>։ Հետևում է, որ <math>BC^2 + CA^2 = 5\cdot CA^2</math>։ Ենթադրվում էր, որ <math> BA^2 = 5\cdot CA^2</math>։ Հետևաբար, <math>BA^2 = BC^2 + CA^2</math>, որը և հակասում է պայմանին ''(Պնդ․ 2․4)''։ Այսպիսով <math>CB \neq 2\cdot AC</math>, նույն կերպ, կարող ենք ասել, որ CB-ից ավելի փոքր հատվածը հավասար չէ <math>2\cdot AC</math>: | ||
| + | Այսպիսով, <math>2\cdot AC > CB</math>, որն էլ պահանջվում էր ապացուցել։ | ||
| + | |||
| + | == Պնդում 3 == | ||
| + | |||
| + | Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա փոքր հատվածի և մեծ հատվածի կեսի գումարի քառակուսին հավասար է մեծ հատվածի կեսի քառակուսու հնգապատիկին։ | ||
| + | |||
| + | [[Պատկեր:Nkar_3.png|280px|thumb|left|Նկ․ 3]] | ||
| + | |||
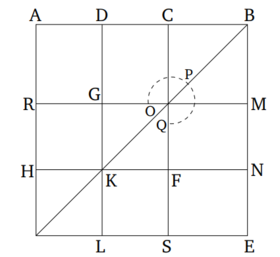
| + | ::::Դիցուք՝ եթե AB հատվածը բաժանենք արտաքին և միջին հարաբերությամբ C-ում, այնպես որ AC մեր մեծ հատվածն է, և AC-ն կիսենք D-ում, ապա <math>BD^2 = 5\cdot DC^2</math> ''(Նկ․ 3)'': | ||
| + | |||
| + | ::::Դիտարկենք AE անկյունագծով քառակուսին, ինչպես ցույց է տրված ''Նկ․ 3''-ում։ Քանի որ <math>DC = \frac{AC}{2}</math>, ապա <math>AC^2 = 4\cdot DC^2</math> (RS անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին)։ Եվ AB և BC կողմերով ուղղանկյան մակերեսը հավասար է AC կողմով քառակուսու մակերեսին ''(Սահմ․ 6․3, Պնդ․ 6․17)'', որն էլ հավասար է CBES ուղղանկյան մակերեսին, հետևաբար վերջինս հավասար է RS անկյունագծով քառակուսու մակերեսին։ Այսպիսով CBES ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին։ Ինչպես գիտենք <math>AD = DC</math>,և <math>HK = KF</math>, հետևաբար HL և GF անկյունագծերով քառակուսիների մակերեսները հավասար են։ Այսպիսով <math>GK = KL </math>, այնպես ինչպես <math>MN = NE</math>։ Քանի որ MF անկյունագծով ուղղանկյայն մակերեսը հավասար է FE և CG անկյունագծերով ուղանկյունների մակերեսներին, հետևաբար վերջիններս նույնպես հավասար են: Եթե СN անկյունագծով ուղղանկյունն ավելացնենք երկուսին էլ, ապա կարող ենք ասել, որ գնոմոն OPQ հավասար է CE անկյունագծով ուղղանկյան մակերեսին։ Եվ ինչպես ցույց էր տրվել վերևում, CE անկյունագծով ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին, հետևաբար գնոմոն OPQ-ն նույնպես հավասար է FG անկյունագծով քառակուսու մակերեսի քառապատիկին։ Հետևաբար գնոմոն OPQ հավասար է 5 անգամ FG-ի մակերեսին։ Բայց մենք գիտենք, որ գնոմոն OPQ-ի և FG անկյունագծով քառակուսու մակերեսի գումարը հավասար է DN անկյունագծով քառակուսու մակերեսին։ Իսկ վերջինիս մակերեսը հավասար է <math>DB^2</math>, իսկ GF անկյունագծով քառակուսու մակերեսը հավասար է <math>DC^2</math>: Այսպիսով <math>DB^2 = 5\cdot DC^2</math>, ինչը և պահանջվում էր ապացուցել։ | ||
| + | |||
| + | == Պնդում 4 == | ||
| + | |||
| + | Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա փոքր և մեծ հատվածների քառակուսիների գումարը հավասար է մեծ հատվածի քառակուսու եռապատիկին։ | ||
| + | |||
| + | [[Պատկեր:Nkar_4.png|280px|thumb|left|Նկ․ 4]] | ||
| + | |||
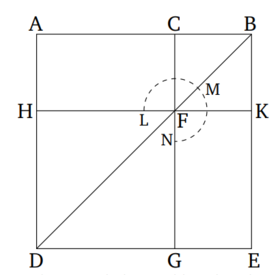
| + | ::::Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է ''(Նկ․ 4)''։ Ես պնդում եմ, որ <math>AB^2 + BC^2 = 3\cdot CA^2</math>: | ||
| + | |||
| + | Դիտարկենք քառակուսի ADEB ''(Նկ․ 4)'': Քանի որ AB մասնատված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է, ապա <math>AB \cdot BC = AC^2</math> AB և BC կողմերով ուղղանկյան մակերեսը AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17)։ AK անկյունագծով ուղղանկյունը հավասար է AB և BC կողմերով ուղղանկյանը, և HG անկյունագծով քառակուսին հավասար է AC կողմով քառակուսուն, հետևաբար AK և HG անկյունագծով ուղղանկյունների մակերեսները հավասար են։ Քանի որ AF և FE անկյունագծերով ուղղանկյունները հավասար են (Պնդ․ 1․43), և CBKF քառակուսին ընդհանուր է, հետևաբար ABKH և CBEG ուղանկյունները հավասար են։ Այսպիսով, AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին։ Քանի որ AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է գնոմոն LMN-ի և CK անկյունագծով քառակուսու մակերեսների գումարին, ապա գնոմոն LMN և CK-ն հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին: Եվ ինչպես ցույց էր տրվել վերևում, վերջինս հավասար է նաև HG անկյունագծով քառակուսուն, հետևաբար գնոմոն LMN-ը | ||
Ընթացիկ տարբերակը 11:09, 1 Դեկտեմբերի 2024-ի դրությամբ
հեղինակ՝ էվկլիդես |
Բովանդակություն
Pages 506-530
Պնդում 1
Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն։
- Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է (Նկ․ 1)։ Շարունակենք AC հատվածը, և տեղադրենք
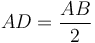 ։ Ես պնդում եմ, որ
։ Ես պնդում եմ, որ 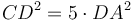 :
:
- Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է (Նկ․ 1)։ Շարունակենք AC հատվածը, և տեղադրենք
- Դիտարկենք AB և CD կողմերով քառակուսիները՝ ABEK և DLFC (Նկ․ 1)։ Տանենք DF անկյունագիծը և FC հատվածը շարունակելով հատենք KE-ի հետ G-ում։ Քանի որ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ C-ում, ապա AB և BC կողմերով ուղղանկյան մակերեսը հավասար է AC կողմով քառակուսու մակերեսին`
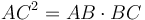 (Սահմ․ 6․3, Պնդ․ 6․17)։ Հետևաբար CBEG ուղղանկյան մակերեսը հավասար է FH անկյունագծով քառակուսու մակերեսին (Նկ․ 1): Եվ քանի որ
(Սահմ․ 6․3, Պնդ․ 6․17)։ Հետևաբար CBEG ուղղանկյան մակերեսը հավասար է FH անկյունագծով քառակուսու մակերեսին (Նկ․ 1): Եվ քանի որ 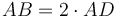 և
և 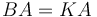 ,
, 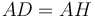 , հետևաբար
, հետևաբար 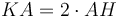 : Այսպիսով ստանում ենք հարաբերություն՝
: Այսպիսով ստանում ենք հարաբերություն՝ 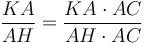 (Պնդ․ 6․1), հետևաբար՝ ACGK ուղղանկյան մակերեսը հավասար է երկու անգամ CH անկյունագծով ուղղանկյան մակերեսին: Եվ քանի որ LH անկյունագծով ուղղանկյունը հավասար է CH անկյունագծով ուղղանկյանը, ապա նրանց մակերեսների գումարը հավասար է երկու անգամ СH անկյունագծով ուղղանկյան մակերեսին (Պնդ․ 1․43): Այսպիսով ACKG ուղղանկյան մակերեսը հավասար է LH և HC անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց տրվեց վերևում, ուղղանկյուն СBEG-ի մակերեսը հավասար է FH անկյունագծով քառակուսու մակերեսին, հետևաբար ABEK-ի մակերեսը հավասար է գնոմոն MNO-ին (CH, FH, LH անկյունագծերով ուղղանկյունների մակերեսների գումարին): Քանի որ գնոմոն
(Պնդ․ 6․1), հետևաբար՝ ACGK ուղղանկյան մակերեսը հավասար է երկու անգամ CH անկյունագծով ուղղանկյան մակերեսին: Եվ քանի որ LH անկյունագծով ուղղանկյունը հավասար է CH անկյունագծով ուղղանկյանը, ապա նրանց մակերեսների գումարը հավասար է երկու անգամ СH անկյունագծով ուղղանկյան մակերեսին (Պնդ․ 1․43): Այսպիսով ACKG ուղղանկյան մակերեսը հավասար է LH և HC անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց տրվեց վերևում, ուղղանկյուն СBEG-ի մակերեսը հավասար է FH անկյունագծով քառակուսու մակերեսին, հետևաբար ABEK-ի մակերեսը հավասար է գնոմոն MNO-ին (CH, FH, LH անկյունագծերով ուղղանկյունների մակերեսների գումարին): Քանի որ գնոմոն 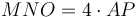 , հետևաբար DLFC քառակուսու մակերեսը հավասար է 5 անգամ AP անկյունագծով քառակուսու մակերեսին։ Այսպիսով
, հետևաբար DLFC քառակուսու մակերեսը հավասար է 5 անգամ AP անկյունագծով քառակուսու մակերեսին։ Այսպիսով 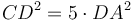 :
:
Այսպիսով, եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն, ինչը և պահանջվում էր ապացուցել։
Պնդում 2
Եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է։
- Դիցուք՝ եթե
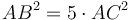 և СВ շարունակենք, այնպես, որ
և СВ շարունակենք, այնպես, որ 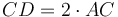 , ապա CD-ն բաժանվում է արտաքին և միջին հարաբերությամբ, որտեղ մեծ հատվածը CB է (Նկ․ 2)։
, ապա CD-ն բաժանվում է արտաքին և միջին հարաբերությամբ, որտեղ մեծ հատվածը CB է (Նկ․ 2)։
- Դիցուք՝ եթե
- Դիտարկենք AB և CD կողմերով քառակուսիները՝ ALFB և СKGD (Նկ․ 2): Տանենք AF անկյունագիծը։ Շարունակենք FB հատվածը և հատենք KG-ի հետ E-ում: Քանի որ
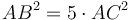 , հետևաբար AF անկյունագծով քառակուսու մակերեսը հավասար է 5 անգամ AH անկյունագծով քառակուսու մակերեսին։ Այսպիսով գնոմոն
, հետևաբար AF անկյունագծով քառակուսու մակերեսը հավասար է 5 անգամ AH անկյունագծով քառակուսու մակերեսին։ Այսպիսով գնոմոն 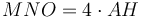 : Քանի որ
: Քանի որ 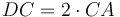 , հետևաբար
, հետևաբար 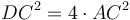 , կամ նույնն է ինչ ասենք, որ СG անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ AH անկյունագծով քառակուսու մակերեսին։ Հետևաբար գնոմոն
, կամ նույնն է ինչ ասենք, որ СG անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ AH անկյունագծով քառակուսու մակերեսին։ Հետևաբար գնոմոն 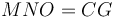 անկյունագծով քառակուսու մակերեսին (HB, HF, HL անկյունագծերով ուղղանկյունների մակերեսները հավասար են CDGK-ի մակերեսին): Եվ քանի որ
անկյունագծով քառակուսու մակերեսին (HB, HF, HL անկյունագծերով ուղղանկյունների մակերեսները հավասար են CDGK-ի մակերեսին): Եվ քանի որ 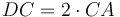 ,
, 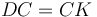 ,
, 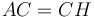 ապա
ապա 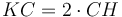 և KB անկյունագծով ուղղանկյան մակերեսը հավասար է 2 անգամ BH անկյունագծով ուղղանկյան մակերեսին (Պնդ․ 6․1) և քանի որ LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է երկու անգամ HB անկյունագծով ուղղանկյան մակերեսին (Պնդ․ 1.43), ապա KB անկյունագծով ուղղանկյան մակերեսը հավսար է LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց էր տրված վերևում գնոմոն MNO-ն հավասար է СG անկյունագծով քառակուսու մակերեսին։ Հետևում է, որ HF անկյունագծով ուղղանկյան մակերեսը հավասար է BDGE ուղղանկյան մակերեսին։ Իսկ վերջինս հավասար է СD և BD կողմերով կառուցված ուղղանկյան մակերեսին,
և KB անկյունագծով ուղղանկյան մակերեսը հավասար է 2 անգամ BH անկյունագծով ուղղանկյան մակերեսին (Պնդ․ 6․1) և քանի որ LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է երկու անգամ HB անկյունագծով ուղղանկյան մակերեսին (Պնդ․ 1.43), ապա KB անկյունագծով ուղղանկյան մակերեսը հավսար է LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց էր տրված վերևում գնոմոն MNO-ն հավասար է СG անկյունագծով քառակուսու մակերեսին։ Հետևում է, որ HF անկյունագծով ուղղանկյան մակերեսը հավասար է BDGE ուղղանկյան մակերեսին։ Իսկ վերջինս հավասար է СD և BD կողմերով կառուցված ուղղանկյան մակերեսին, 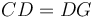 , HF անկյունագծով ուղղանկյան մակերեսը հավասար է
, HF անկյունագծով ուղղանկյան մակերեսը հավասար է 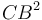 ։ Հետևաբար CD և BD կողմերով կառուցված ուղղանկյան մակերեսը հավասար է
։ Հետևաբար CD և BD կողմերով կառուցված ուղղանկյան մակերեսը հավասար է 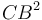
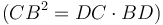 : Այսպիսով, ստանում ենք
: Այսպիսով, ստանում ենք 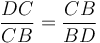 (Պնդ․ 6․17): Եվ քանի որ DC ավելի մեծ է քան СB (տես Լեմմա, ներքևում), ապա СB-ն նույնպես ավելի մեծ է քան BD-ն։ Այսպիսով, եթե CD հատվածը բաժանված է արտաքին և միջին հարաբերությամբ, ապա СB-ն նրա մեծ հատվածն է։
(Պնդ․ 6․17): Եվ քանի որ DC ավելի մեծ է քան СB (տես Լեմմա, ներքևում), ապա СB-ն նույնպես ավելի մեծ է քան BD-ն։ Այսպիսով, եթե CD հատվածը բաժանված է արտաքին և միջին հարաբերությամբ, ապա СB-ն նրա մեծ հատվածն է։
- Դիտարկենք AB և CD կողմերով քառակուսիները՝ ALFB և СKGD (Նկ․ 2): Տանենք AF անկյունագիծը։ Շարունակենք FB հատվածը և հատենք KG-ի հետ E-ում: Քանի որ
Այսպիսով, եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է, ինչը և պահանջվում էր ապացուցել։
Լեմմա
Ապացուցենք, որ 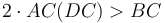 ։
։
Ենթադրենք 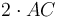 ավելի մեծ չէ քան BC, և
ավելի մեծ չէ քան BC, և 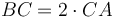 ։ Այսպիսով
։ Այսպիսով 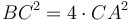 ։ Հետևում է, որ
։ Հետևում է, որ 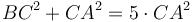 ։ Ենթադրվում էր, որ
։ Ենթադրվում էր, որ 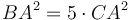 ։ Հետևաբար,
։ Հետևաբար, 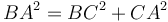 , որը և հակասում է պայմանին (Պնդ․ 2․4)։ Այսպիսով
, որը և հակասում է պայմանին (Պնդ․ 2․4)։ Այսպիսով 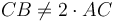 , նույն կերպ, կարող ենք ասել, որ CB-ից ավելի փոքր հատվածը հավասար չէ
, նույն կերպ, կարող ենք ասել, որ CB-ից ավելի փոքր հատվածը հավասար չէ 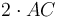 :
Այսպիսով,
:
Այսպիսով, 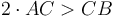 , որն էլ պահանջվում էր ապացուցել։
, որն էլ պահանջվում էր ապացուցել։
Պնդում 3
Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա փոքր հատվածի և մեծ հատվածի կեսի գումարի քառակուսին հավասար է մեծ հատվածի կեսի քառակուսու հնգապատիկին։
- Դիցուք՝ եթե AB հատվածը բաժանենք արտաքին և միջին հարաբերությամբ C-ում, այնպես որ AC մեր մեծ հատվածն է, և AC-ն կիսենք D-ում, ապա
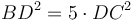 (Նկ․ 3):
(Նկ․ 3):
- Դիցուք՝ եթե AB հատվածը բաժանենք արտաքին և միջին հարաբերությամբ C-ում, այնպես որ AC մեր մեծ հատվածն է, և AC-ն կիսենք D-ում, ապա
- Դիտարկենք AE անկյունագծով քառակուսին, ինչպես ցույց է տրված Նկ․ 3-ում։ Քանի որ
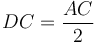 , ապա
, ապա 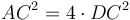 (RS անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին)։ Եվ AB և BC կողմերով ուղղանկյան մակերեսը հավասար է AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17), որն էլ հավասար է CBES ուղղանկյան մակերեսին, հետևաբար վերջինս հավասար է RS անկյունագծով քառակուսու մակերեսին։ Այսպիսով CBES ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին։ Ինչպես գիտենք
(RS անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին)։ Եվ AB և BC կողմերով ուղղանկյան մակերեսը հավասար է AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17), որն էլ հավասար է CBES ուղղանկյան մակերեսին, հետևաբար վերջինս հավասար է RS անկյունագծով քառակուսու մակերեսին։ Այսպիսով CBES ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին։ Ինչպես գիտենք 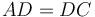 ,և
,և 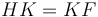 , հետևաբար HL և GF անկյունագծերով քառակուսիների մակերեսները հավասար են։ Այսպիսով
, հետևաբար HL և GF անկյունագծերով քառակուսիների մակերեսները հավասար են։ Այսպիսով 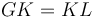 , այնպես ինչպես
, այնպես ինչպես 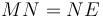 ։ Քանի որ MF անկյունագծով ուղղանկյայն մակերեսը հավասար է FE և CG անկյունագծերով ուղանկյունների մակերեսներին, հետևաբար վերջիններս նույնպես հավասար են: Եթե СN անկյունագծով ուղղանկյունն ավելացնենք երկուսին էլ, ապա կարող ենք ասել, որ գնոմոն OPQ հավասար է CE անկյունագծով ուղղանկյան մակերեսին։ Եվ ինչպես ցույց էր տրվել վերևում, CE անկյունագծով ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին, հետևաբար գնոմոն OPQ-ն նույնպես հավասար է FG անկյունագծով քառակուսու մակերեսի քառապատիկին։ Հետևաբար գնոմոն OPQ հավասար է 5 անգամ FG-ի մակերեսին։ Բայց մենք գիտենք, որ գնոմոն OPQ-ի և FG անկյունագծով քառակուսու մակերեսի գումարը հավասար է DN անկյունագծով քառակուսու մակերեսին։ Իսկ վերջինիս մակերեսը հավասար է
։ Քանի որ MF անկյունագծով ուղղանկյայն մակերեսը հավասար է FE և CG անկյունագծերով ուղանկյունների մակերեսներին, հետևաբար վերջիններս նույնպես հավասար են: Եթե СN անկյունագծով ուղղանկյունն ավելացնենք երկուսին էլ, ապա կարող ենք ասել, որ գնոմոն OPQ հավասար է CE անկյունագծով ուղղանկյան մակերեսին։ Եվ ինչպես ցույց էր տրվել վերևում, CE անկյունագծով ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին, հետևաբար գնոմոն OPQ-ն նույնպես հավասար է FG անկյունագծով քառակուսու մակերեսի քառապատիկին։ Հետևաբար գնոմոն OPQ հավասար է 5 անգամ FG-ի մակերեսին։ Բայց մենք գիտենք, որ գնոմոն OPQ-ի և FG անկյունագծով քառակուսու մակերեսի գումարը հավասար է DN անկյունագծով քառակուսու մակերեսին։ Իսկ վերջինիս մակերեսը հավասար է 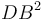 , իսկ GF անկյունագծով քառակուսու մակերեսը հավասար է
, իսկ GF անկյունագծով քառակուսու մակերեսը հավասար է 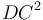 : Այսպիսով
: Այսպիսով 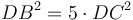 , ինչը և պահանջվում էր ապացուցել։
, ինչը և պահանջվում էր ապացուցել։
- Դիտարկենք AE անկյունագծով քառակուսին, ինչպես ցույց է տրված Նկ․ 3-ում։ Քանի որ
Պնդում 4
Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա փոքր և մեծ հատվածների քառակուսիների գումարը հավասար է մեծ հատվածի քառակուսու եռապատիկին։
- Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է (Նկ․ 4)։ Ես պնդում եմ, որ
 :
:
- Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է (Նկ․ 4)։ Ես պնդում եմ, որ
Դիտարկենք քառակուսի ADEB (Նկ․ 4): Քանի որ AB մասնատված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է, ապա 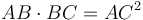 AB և BC կողմերով ուղղանկյան մակերեսը AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17)։ AK անկյունագծով ուղղանկյունը հավասար է AB և BC կողմերով ուղղանկյանը, և HG անկյունագծով քառակուսին հավասար է AC կողմով քառակուսուն, հետևաբար AK և HG անկյունագծով ուղղանկյունների մակերեսները հավասար են։ Քանի որ AF և FE անկյունագծերով ուղղանկյունները հավասար են (Պնդ․ 1․43), և CBKF քառակուսին ընդհանուր է, հետևաբար ABKH և CBEG ուղանկյունները հավասար են։ Այսպիսով, AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին։ Քանի որ AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է գնոմոն LMN-ի և CK անկյունագծով քառակուսու մակերեսների գումարին, ապա գնոմոն LMN և CK-ն հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին: Եվ ինչպես ցույց էր տրվել վերևում, վերջինս հավասար է նաև HG անկյունագծով քառակուսուն, հետևաբար գնոմոն LMN-ը
AB և BC կողմերով ուղղանկյան մակերեսը AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17)։ AK անկյունագծով ուղղանկյունը հավասար է AB և BC կողմերով ուղղանկյանը, և HG անկյունագծով քառակուսին հավասար է AC կողմով քառակուսուն, հետևաբար AK և HG անկյունագծով ուղղանկյունների մակերեսները հավասար են։ Քանի որ AF և FE անկյունագծերով ուղղանկյունները հավասար են (Պնդ․ 1․43), և CBKF քառակուսին ընդհանուր է, հետևաբար ABKH և CBEG ուղանկյունները հավասար են։ Այսպիսով, AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին։ Քանի որ AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է գնոմոն LMN-ի և CK անկյունագծով քառակուսու մակերեսների գումարին, ապա գնոմոն LMN և CK-ն հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին: Եվ ինչպես ցույց էր տրվել վերևում, վերջինս հավասար է նաև HG անկյունագծով քառակուսուն, հետևաբար գնոմոն LMN-ը