«Տարերք/Գիրք 11»–ի խմբագրումների տարբերություն

Գրապահարան-ից
Տող 2. Տող 2.
  
 
                          
 
                          
−
== '''Պնդում 7''' ==
+
== Պնդում 7 ==
  
  
Տող 9. Տող 9.
 
[[Պատկեր:Նկար-1.png]]
 
[[Պատկեր:Նկար-1.png]]
  
−
'''AB''' և '''CD''' երկու զուգահեռ ուղիղներ են, իսկ '''E''' և '''F''' կամայական կետեր են համապատասխանաբար AB և CD ուղիղներից։ Ուղիղը, որը միացնում է '''E''' և '''F''' կետերը, գտնվում է նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։
+
AB և CD երկու զուգահեռ ուղիղներ են, իսկ E և F կամայական կետեր են համապատասխանաբար AB և CD ուղիղներից։ Ուղիղը, որը միացնում է E և F կետերը, գտնվում է նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։
−
Եթե դա այդպես չէ, և հնարավոր է, որ ուղիղը անցնի ավելի բարձր հարթությամբ, թող դա լինի '''EGF''' հարթությունը։ Այսպիսով, այն կունենա ուղիղ հատված '''EF'''՝ հենակետային հարթության մեջ [Պնդ. 11.3]։ Հետևաբար, երկու ուղիղներ՝ '''EGF'''-ն և '''EF'''-ն (նույն '''E''' և '''F''' կետերով անցնող) կսահմանափակեն ինչ-որ տարածք, ինչը անհնար է։Հանգունորեն, '''E''' և '''F''' կետերով անցնող ուղիղը գտնվում է նույն հարթության մեջ, ինչ '''AB''' և '''CD''' զուգահեռ ուղիղները։
+
Եթե դա այդպես չէ, և հնարավոր է, որ ուղիղը անցնի ավելի բարձր հարթությամբ, թող դա լինի EGF հարթությունը։ Այսպիսով, այն կունենա ուղիղ հատված EF՝ հենակետային հարթության մեջ [Պնդ. 11.3]։ Հետևաբար, երկու ուղիղներ՝ EGF-ն և EF-ն (նույն E և F կետերով անցնող) կսահմանափակեն ինչ-որ տարածք, ինչը անհնար է։Հանգունորեն, E և F կետերով անցնող ուղիղը գտնվում է նույն հարթության մեջ, ինչ AB և CD զուգահեռ ուղիղները։
  
 
''Այսպիսով, եթե կա երկու զուգահեռ ուղիղ, և կամայական կետ նրանցից յուրաքանչյուրի վրա, ապա ուղիղը, որը կմիացնի այդ երկու կետերը, կլինի նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։ Որը վերջինիս պահանջվում էր ցույց տալ։''
 
''Այսպիսով, եթե կա երկու զուգահեռ ուղիղ, և կամայական կետ նրանցից յուրաքանչյուրի վրա, ապա ուղիղը, որը կմիացնի այդ երկու կետերը, կլինի նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։ Որը վերջինիս պահանջվում էր ցույց տալ։''
Տող 16. Տող 16.
  
  
−
== '''Պնդում 8''' ==
+
== Պնդում 8 ==
  
  
Տող 23. Տող 23.
 
[[Պատկեր:Նկար-2.png]]
 
[[Պատկեր:Նկար-2.png]]
  
−
'''AB''' և '''CD''' երկու զուգահեռ ուղիղներ են, և նրանցից մեկը՝ '''AB''', ուղղահայաց է դիտարկվող հարթությանը։ Մյուսը՝ '''CD''', նույնպես ուղղահայաց է նույն հարթությանը։
+
AB և CD երկու զուգահեռ ուղիղներ են, և նրանցից մեկը՝ AB, լինի ուղղահայաց դիտարկվող հարթությանը։ Ապա, մյուսը՝ CD, նույնպես կլինի ուղղահայաց նույն հարթությանը։
−
'''AB'''-ն և '''CD'''-ն հատվում են դիտարկվող հարթության հետ '''B''' և '''D'''կետերում  համապատասխանաբար, '''BD''' ուղիղը միացնում է այդ կետերը։ Հետևաբար, '''AB''', '''CD''' և '''BD''' գտնվում են նույն հարթության մեջ [Պնդում 11․7]։
+
AB-ն և CD-ն հատվում են դիտարկվող հարթության հետ կետերում B և D համապատասխանաբար, և BD ուղիղը միացնում է այդ կետերը։ Հետևաբար, AB, CD և BD գտնվում են նույն հարթության մեջ [Պնդում 11․7]։
−
'''DE''' ուղիղը ուղղահայաց է '''BD'''-ին դիտարկվող հարթություն մեջ և '''DE'''-ն հավասար է '''AB'''-ին։ Միացնենք '''BE''', '''AE''' և '''AD''' հատվածները։ 
+
DE ուղիղը ուղղահայաց է BD-ին դիտարկվող հարթություն մեջ և DE-ն հավասար է AB-ին։ Միացնենք BE, AE և AD գծերը։
−
Քանի որ '''AB''' ուղիղը ուղղահայաց է դիտարկվող հարթությանը, այն ուղղահայաց կլինի նաև բոլոր այն ուղիղներին, որոնք գտնվում են դիտարկվող հարթության մեջ [Սահմ 11․3]։ Հետևաբար, անկյուններ՝ '''ABD''' և '''ABE''', ուղիղ են։
+
Քանի որ AB ուղիղը ուղղահայաց է դիտարկվող հարթությանը, այն ուղղահայաց կլինի նաև բոլոր այն ուղիղներին, որոնք նրան են կցված և գտնվում են դիտարկվող հարթությունում [Սահմ 11․3]։ Հետևաբար, անկյուններ՝ ABD և ABE, ուղիղ են։
−
Եվ քանի որ '''BD''' ուղիղը հատում է '''AB''' և '''CD''' զուգահեռ ուղիղները, ապա '''ABD''' և '''CDB''' անկյունների գումարը հավասար է երկու ուղիղ անկյունների։ [Պնդում 1․29] Անկյուն '''ABD'''-ն ուղիղ է, հետևում է անկյուն '''CDB'''-ն նույնպես ուղիղ է։
+
Եվ քանի որ BD ուղիղը, հատում է AB և CD զուգահեռ ուղիղները, ապա ABD և CDB անկյունների գումարը հավասար է երկու ուղիղ անկյունների։[Պնդում 1․29] Անկյուն ABD-ն ուղիղ է, հետևում է անկյուն CDB-ն նույնպես ուղիղ է։
  
−
Եվ քանի որ '''AB'''-ն հավասար է '''DE'''-ին, իսկ '''BD'''-ն ընդհանուր է, ապա երկու ուղիղներ՝ '''AB''' և '''BE''', հավասար են '''ED''' և '''DA''' ուղիղներին, համապատասխանաբար։ Եվ '''ABD''' ուղիղ անկյունը հավասար է '''EDB''' անկյանը։ Հետևաբար '''AD''' հիմքը հավասար է '''BE''' հիմքին [Պնդում 1․4]։
+
Եվ քանի որ AB-ն հավասար է DE-ին, իսկ BD-ն ընդհանուր է, ապա երկու ուղիղներ՝ AB և BE, հավասար են ED և DA ուղիղներին , համապատասխանաբար։ Եվ ABD ուղիղ անկյունը հավասար է EDB անկյանը։ Հետևաբար AD հիմքը հավասար է BE հիմքին [Պնդում 1․4]։ Եվ քանի որ AB հատվածը հավասար է DE-ին, և BE-ն հավասար է AD հատվածին , և AB, BE հատվածները համապատասխանաբար հավասար են ED, DA հատվածներին։ Եվ նրանց հիմքը՝ AE-ն, ընդհանուր է։ Հետևաբար, անկյունը՝ ABE, հավասար է անկյանը՝ EDA ([Պնդում 1․8])։
−
Եվ քանի որ '''AB''' հատվածը հավասար է '''DE'''-ին, և '''BE'''-ն հավասար է '''AD''' հատվածին, և '''AB''', '''BE''' հատվածները համապատասխանաբար հավասար են '''ED''', '''DA''' հատվածներին։ Եվ նրանց հիմքը՝ '''AE'''-ն, ընդհանուր է։ Հետևաբար, անկյունը՝ '''ABE''', հավասար է '''EDA'''անկյանը ([Պնդում 1․8])։
+
Քանի որ անկյուն ABE-ն ուղիղ է, ապա անկյուն EDA-ն նույնպես ուղիղ է։ Հետևաբար, ED ուղիղը ուղղահայաց է AD-ին։ Եվ այն նաև ուղղահայաց է DB-ին։Այսպիսով, ED ուղիղը ուղիղ անկյուն է կազմում BD և DA ուղիղներով անցնող հարթության հետ ([Պնդում 11․4])։ Այդ պատճառով ED ուղիղ անկյուն կկազմի բոլոր այն ուղիղների հետ որոնք հատվում են իր հետ և ընկած են BDA հարթության մեջ։ DC ուղիղը գտնվում է BDA հարթությունում, քանի որ AB և BD ուղիղները նույնպես գտնվում են BDA հարթությունում ([Պնդում 11․2])։ Հետևաբար, ED ուղիղը ուղղահայաց է DC ուղիղին։Այսպիսով, CD ուղիղը նույնպես ուղղահայաց է DE-ին։ CD ուղիղը ուղղահայաց է նաև BD ուղիղին։
−
Քանի որ անկյուն '''ABE'''-ն ուղիղ է, ապա անկյուն '''EDA'''-ն նույնպես ուղիղ է։ Հետևաբար, '''ED''' ուղիղը ուղղահայաց է '''AD'''-ին։ Եվ այն նաև ուղղահայաց է '''DB'''-ին։ Այսպիսով, '''ED''' ուղիղը ուղիղ անկյուն է կազմում '''BD''' և '''DA''' ուղիղներով անցնող հարթության հետ ([Պնդում 11․4])։ Այդ պատճառով '''ED''' ուղիղ անկյուն կկազմի բոլոր այն ուղիղների հետ, որոնք հատվում են իր հետ և ընկած են '''BDA''' հարթության մեջ։ '''DC''' ուղիղը գտնվում է '''BDA''' հարթությունում, քանի որ '''AB''' և '''BD''' ուղիղները նույնպես գտնվում են '''BDA''' հարթությունում ([Պնդում 11․2])։
+
Հետևաբար, CD ուղիղը կանգնած է ուղղանկյուն երկու ուղիղների՝ DE և DB-ի հետ, որոնք հատվում են D կետում։ Այսպիսով, CD ուղիղը նաև ուղղահայաց է DE և DB ուղիղներով անցնող հարթությանը ([Պնդում 11․4])։
−
Հետևաբար, '''ED''' ուղիղը ուղղահայաց է '''DC''' ուղիղին։ Այսպիսով, '''CD''' ուղիղը նույնպես ուղղահայաց է '''DE'''-ին։ '''CD''' ուղիղը ուղղահայաց է նաև '''BD''' ուղիղին։
+
Եվ քանի որ DE և DB ուղիղներով անցնող հարթությունը դիտարկվող հարթությունն է, CD ուղիղը ուղղահայաց է նաև դիտարկվող հարթությանը։
−
Հետևաբար, '''CD''' ուղիղը կանգնած է ուղղանկյուն երկու ուղիղների՝ '''DE''' և '''DB'''-ի հետ, որոնք հատվում են '''D''' կետում։ Այսպիսով, '''CD''' ուղիղը նաև ուղղահայաց է '''DE''' և '''DB''' ուղիղներով անցնող հարթությանը ([Պնդում 11․4])։
+
−
Եվ քանի որ '''DE''' և '''DB''' ուղիղներով անցնող հարթությունը դիտարկվող հարթությունն է, '''CD''' ուղիղը ուղղահայաց է նաև դիտարկվող հարթությանը։  
+
 
   
 
   
 
''Հետևաբար, եթե երկու ուղիղներ զուգահեռ են, և դրանցից մեկը ուղղահայաց է որևէ հարթության, ապա մյուսը նույնպես կլինի ուղղահայաց նույն հարթությանը։ Որն էլ անհրաժեշտ էր ցույց տալ։''
 
''Հետևաբար, եթե երկու ուղիղներ զուգահեռ են, և դրանցից մեկը ուղղահայաց է որևէ հարթության, ապա մյուսը նույնպես կլինի ուղղահայաց նույն հարթությանը։ Որն էլ անհրաժեշտ էր ցույց տալ։''
Տող 41. Տող 39.
  
  
−
== '''Պնդում 9''' ==
+
== Պնդում 9 ==
  
  
Տող 48. Տող 46.
 
[[Պատկեր:Նկար-3.png]]
 
[[Պատկեր:Նկար-3.png]]
  
−
'''AB''' և '''CD''' ուղիղներից յուրաքանչյուրը զուգահեռ է '''EF''' ուղղին, որը նույն հարթության մեջ չէ։ Ցույց տանք, որ '''AB''' և '''CD''' ուղիղները զուգահեռ են։ Պատահականորեն վերցնենք մի '''G''' կետ '''EF''' ուղղի վրա։ '''GH''' ուղիղը '''EF''' ուղղի հետ կազմում է ուղիղ անկյուն '''EF''' և '''AB''' ուղիղներով անցնող հարթության մեջ։ Եվ  '''EF'''-ն ուղղահայաց է '''GK''' ուղղին՝ '''FE''' և '''CD''' ուղիղներով անցնող հարթության վրա։ 
+
AB և CD ուղիղներից յուրաքանչյուրը զուգահեռ է EF ուղղին, որը նույն հարթության մեջ չէ։ Ցույց տանք որ AB և CD ուղիղները զուգահեռ են։ Պատահականորեն վերցնենք մի G կետ EF ուղղի վրա։ GH ուղիղը EF ուղղի հետ կազմում է ուղիղ անկյուն EF և AB ուղիղներով անցնող հարթության մեջ։ Եվ  EF-ն ուղղահայաց է GK ուղղին՝ FE և CD ուղիղներով անցնող հարթության վրա:
  
−
Եվ քանի որ '''EF''' ուղիղը ուղղահայաց է '''GH'''-ին և '''GK'''-ին, ապա '''EF'''-ն ուղղաձիգ է նաև '''GH'''-ի և '''GK'''-ի միջով անցնող հարթությանը [Պնդ․ 11.4]: Եվ '''EF''' ուղիղը '''AB'''-ին զուգահեռ է։ Ուստի '''AB'''-ն նույնպես ուղղահայաց է '''HGK''' հարթությանը [Պնդ․ 11.8]: Հանգունորեն '''CD'''-ն նույնպես ուղղահայաց է '''HGK''' հարթությանը։ 
 
−
Արդյունքում՝ '''AB''' և '''CD''' ուղիղները ուղղահայաց են '''HGK''' հարթությանը։ Իսկ եթե երկու ուղիղներ նույն հարթությանն ուղղահայաց են, ապա այդ ուղիղները զուգահեռ են [Պնդ․ 11․6]: Ուստի '''AB'''-ն զուգահեռ է '''CD'''-ին։ Ինչ պետք էր ապացուցել։
 
  
 +
Եվ քանի որ EF ուղիղը ուղղահայաց է GH-ին և GK-ին, ապա EF-ն ուղղահայաց է նաև GH և GK ուղիղներով  անցնող հարթությանը [Պնդ․ 11.4]: Եվ EF ուղիղը AB-ին զուգահեռ է: Ուստի AB-ն նույնպես ուղղահայաց է HGK հարթությանը [Պնդ․ 11.8]: Հանգունորեն CD-ն նույնպես ուղղահայաց է HGK հարթությանը:
 +
''Արդյունքում՝ AB և CD ուղիղները ուղղահայաց են HGK հարթությանը: Իսկ եթե երկու ուղիղներ նույն հարթությանն ուղղահայաց են, ապա այդ ուղիղները զուգահեռ են [Պնդ․ 11․6]: Ուստի AB-ն զուգահեռ է CD-ին։ Ինչ պետք էր ապացուցել։''
  
  
−
== '''Պնդում 10''' ==
+
 
 +
 
 +
== Պնդում 10 ==
  
  
Տող 62. Տող 62.
 
[[Պատկեր:Նկար-4.png]]
 
[[Պատկեր:Նկար-4.png]]
  
−
Իրար միացած երկու ուղիղները՝ '''AB''' և '''BC''', զուգահեռ են (համապատասխանաբար) միմյանց միացած երկու ուղիղների՝ '''DE''' և '''EF''' որոնք վերջիններս ընկած չեն '''AB''' և '''BC''' ուղիղներով անցնող հարթությանը։ Ցույց տանք, որ '''ABC''' անկյունը հավասար է '''DEF''' անկյանին:
+
Իրար միացած երկու ուղիղները՝ AB և BC, զուգահեռ են (համապատասխանաբար) միմյանց միացած երկու ուղիղների՝ DE և EF որոնք վերջիններս ընկած չեն AB և BC ուղիղներով անցնող հարթությանը ։Ցույց տանք, որ ABC անկյունը հավասար է DEF անկյանը:
−
'''BA''', '''BC''', '''ED''' և '''EF''' ուղիղները կտրենք (այնպես, որ համապատասխանաբար հավասար լինեն միմյանց): Միացնենք '''AD''', '''CF''', '''BE''', '''AC''' և '''DF''' հատվածները: Եվ քանի որ '''BA''' ուղիղը հավասար և զուգահեռ է '''ED'''-ին, Հետևաբար '''AD''' ուղիղը, նույնպես հավասար և զուգահեռ է '''BE''' ուղղին [Պնդ. 1.33]: Հանգունորեն '''CF''' ուղիղը նույնպես հավասար և զուգահեռ է '''BE'''-ին: Այսպիսով, '''AD''' և '''CF''' հատվածներից յուրաքանչյուրը հավասար և զուգահեռ են '''BE'''-ին:
+
BA, BC, ED և EF ուղիղները կտրենք (այնպես, որ համապատասխանաբար հավասար լինեն միմյանց): Միացնենք AD, CF, BE, AC և DF հատվածները:Եվ քանի որ BA ուղիղը հավասար և զուգահեռ է ED-ին, Հետևաբար AD ուղիղը, նույնպես հավասար և զուգահեռ է BE ուղղին [Պնդ. 1.33]: Հանգունորեն CF ուղիղը նույնպես հավասար և զուգահեռ է BE-ին: Այսպիսով, AD և CF հատվածներից յուրաքանչյուրը հավասար և զուգահեռ են BE-ին: Նույն ուղղին զուգահեռ ուղիղները, որոնք նրա հետ նույն հարթության մեջ չեն, զուգահեռ են միմյանց [Պնդ. 11.9]։ Այսպիսով, AD հատվածը զուգահեռ է և հավասար է CF-ին: AC և DF միացնենք նրանց: Այսպիսով, AC-ը նույնպես հավասար է և զուգահեռ DF հատվածին  [Պնդ. 1.33]: Եվ քանի որ երկու հատվածներ AB-ն և BC-ն հավասար են երկու հատվածներին՝ DE-ին և EF-ին (համապատասխանաբար), իսկ AC հիմքը հավասար է DF հիմքին, այսպիսով ABC անկյունն  հավասար է DEF անկյանը [Պնդ. 1.8]:
−
Նույն ուղղին զուգահեռ ուղիղները, որոնք նրա հետ նույն հարթության մեջ չեն, զուգահեռ են միմյանց [Պնդ. 11.9]։ Այսպիսով, '''AD''' հատվածը զուգահեռ է և հավասար է '''CF'''-ին: '''AC''' և '''DF''' միացնենք նրանց: Այսպիսով, '''AC'''-ը նույնպես հավասար է և զուգահեռ '''DF''' հատվածին  [Պնդ. 1.33]:
+
−
Եվ քանի որ երկու հատվածներ '''AB'''-ն և '''BC'''-ն հավասար են երկու հատվածներին՝ '''DE'''-ին և '''EF'''-ին (համապատասխանաբար), իսկ '''AC''' հիմքը հավասար է '''DF''' հիմքին, այսպիսով '''ABC''' անկյունն  հավասար է '''DEF''' անկյանը [Պնդ. 1.8]:
+
  
 
''Հետևաբար, եթե միմյանց միացված երկու ուղիղները (համապատասխանաբար) զուգահեռ են միմյանց միացած երկու ուղիղներին, որոնք ընկած չեն նույն հարթության մեջ ինչ որ սկզբնական երկու ուղիղները, ապա դրանք կպարունակեն հավասար անկյուններ։ Որը անհրաժեշտ էր ցույց տալ։''
 
''Հետևաբար, եթե միմյանց միացված երկու ուղիղները (համապատասխանաբար) զուգահեռ են միմյանց միացած երկու ուղիղներին, որոնք ընկած չեն նույն հարթության մեջ ինչ որ սկզբնական երկու ուղիղները, ապա դրանք կպարունակեն հավասար անկյուններ։ Որը անհրաժեշտ էր ցույց տալ։''
 +
 +
 +
== Պնդում 11 ==
 +
 +
 +
Կետից հարթությանը ուղղահայաց ուղղի կառուցումը։
 +
 +
[[Պատկեր:Նկար-11.png]]
 +
 +
A կետը դիտարկվող կետն է: Այսպիսով, պահանջվում է ուղղահայաց ուղիղ գծել A կետից հարթությանը: Պատահական BC ուղիղ գծենք դիտարկվող հարթությունում, և AD ուղիղը գծենք BC-ին ուղղահայաց A կետից [Պնդ. 1.12]: Հետևաբար, եթե AD ուղիղը նույնպես ուղղահայաց է դիտարկվող հարթությանը, ապա տեղի կունենա այն, ինչ նախատեսված էր:Իսկ, եթե ոչ, D կետից՝ դիտարկվող հարթության մեջ BC ուղղին ուղահայաց DE ուղիղը գծենք [Պնդ. 1.11], և AF ուղիղը գծենք  A կետից  DE ուղղին ուղղահայաց վերջիններս կհատի DE ուղղին F կետում[Պնդ. 1.12], և F կետով անցնող GH ուղիղը գծենք, որը զուգահեռ է BC ուղղին [Պնդ. 1.31]:
 +
 +
Եվ քանի որ BC-ն ուղիղ անկյուն է կազմում DA և DE ուղիղներից յուրաքանչյուրիհետ,հետևաբար BC-ն, ուղղահայաց է EDA  հարթությանը [Պնդ. 11.4]: Իսկ GH ուղիղը զուգահեռ է BC-ին։ Եթե երկու ուղիղները զուգահեռ են, և դրանցից մեկը ուղղահայաց է ինչ-որ հարթությանը, ապա մյուսը նույնպես կլինի նույն հարթության ուղղահայաց[Պնդ. 11.8]:Այսպիսով, GH ուղիղը նույնպես ուղղահայաց է ED և DA ուղիղներով անցնող հարթությունը։
 +
Այսպիսով, GH ուղիղը ուղիղ անկյուն է կազմում իրեն միացած բոլոր ուղիղների հետ, որոնք նույնպես ED և AD ուղիղներով անցնող հարթության մեջ են [Սահմ. 11.3]: Եվ AF-ն, որը գտնվում է ED և AD ուղիղներով անցնող հարթության մեջ, միացված է դրան: Այսպիսով, GH  և AF ուղիղներըուղղահայաց են: Հետևաբար, AF-ն ուղղահայաց է HG ուղղին:  AF-ն նույնպես ուղղահայաց է DE ուղղին: Այսպիսով, AF-ն ուղղահայաց է GH և DE  ուղիղներից յուրաքանչյուրին: Եվ եթե ուղիղը կազմում են ուղիղ անկյուն դեպի երկու հատվող ուղիղների հետ, ապա այն ուղղահայաց կլինի այդ ուղիղներով անցնող հարթությանը [Պնդ. 11.4]: Այսպիսով, FA-ն ուղղահայաց է ED և GH ուղիղներով անցնող հարթությանը: Իսկ ED-ի և GH-ի ուղիղներով անցնող հարթությունը հենց դիտարկվող հարթությունն էր: Այսպիսով, AF ուղիղը ուղղահայաց է դիտարկվող հարթությանը:
 +
 +
''Այսպիսով, A կետով անցնող AF ուղիղը ուղղահայաց է դիտարկվող հարթությանը: Ինչը հենց պահանջվում էր կառուցել:''
 +
 +
 +
 +
== Պնդում 12 ==
 +
 +
 +
Տվյալ կետից, դիտարկվող հարթությանը տարված ուղղահայացի կառուցումը։
 +
 +
 +
[[Պատկեր:Նկար-12.png]]
 +
 +
 +
Տրված հարթությունը դիտարկվող հարթությունն է, իսկ A-ն այդ հարթությանը պատկանող կետ: Այսպիսով, պահանջվում է A կետով անցնող և դիտարկվող հարթությանը ուղղահայաց ուղիղ կառուցել:Կամայական B կետից տանենք ուղղահայաց դիտարկվող հարթությանը, որը կհատի հարթությունը C կետում [Պնդ. 11.11]: BC-ին զուգահեռ և A կետով անցնող ուղիղ գծենք AD-ն [Պնդ. 1.31]:Քանի որ AD-ն և CB-ն երկու զուգահեռ ուղիղներ են, և դրանցից մեկը՝ BC-ն, ուղղահայաց է դիտարկվող հարթությանը հետևաբար, AD ուղիղը նույնպես ուղղահայաց է դիտարկվող հարթությանը [Պնդ. 11.8]:
 +
''Հետևաբար AD ուղիղը A կետով անցնող և հարթությանը ուղղահայաց ուղիղ է։ Ինչը պահանջվում էր կառուցել։
 +
''
 +
 +
 +
== Պնդում 13 ==

14:20, 2 Դեկտեմբերի 2024-ի տարբերակ

Pages 431 - 455


Պնդում 7

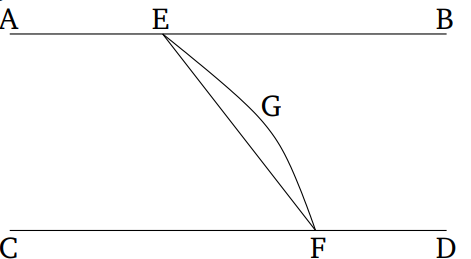
Եթե երկու զուգահեռ ուղիղների վրա վերցրած պատահական կետերից երկուսը միացնենք, ապա ստացված ուղիղը, որը անցնում է այդ կետերով, կլինի նույն հարթության մեջ, ինչ երկու զուգահեռ ուղիղները։ Նկար-1.png

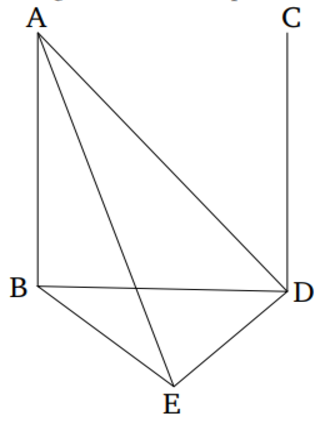
AB և CD երկու զուգահեռ ուղիղներ են, իսկ E և F կամայական կետեր են համապատասխանաբար AB և CD ուղիղներից։ Ուղիղը, որը միացնում է E և F կետերը, գտնվում է նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։ Եթե դա այդպես չէ, և հնարավոր է, որ ուղիղը անցնի ավելի բարձր հարթությամբ, թող դա լինի EGF հարթությունը։ Այսպիսով, այն կունենա ուղիղ հատված EF՝ հենակետային հարթության մեջ [Պնդ. 11.3]։ Հետևաբար, երկու ուղիղներ՝ EGF-ն և EF-ն (նույն E և F կետերով անցնող) կսահմանափակեն ինչ-որ տարածք, ինչը անհնար է։Հանգունորեն, E և F կետերով անցնող ուղիղը գտնվում է նույն հարթության մեջ, ինչ AB և CD զուգահեռ ուղիղները։

Այսպիսով, եթե կա երկու զուգահեռ ուղիղ, և կամայական կետ նրանցից յուրաքանչյուրի վրա, ապա ուղիղը, որը կմիացնի այդ երկու կետերը, կլինի նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։ Որը վերջինիս պահանջվում էր ցույց տալ։


Պնդում 8

Եթե երկու ուղիղներ զուգահեռ են, և նրանցից մեկը ուղիղ անկյուն է կազմում ինչ որ հարթության հետ, ապա մյուս ուղիղը նույնպես ուղղահայաց կլինի այդ հարթությանը։

Նկար-2.png

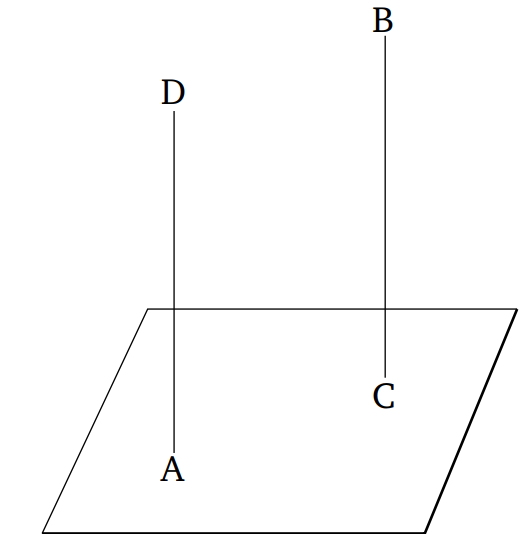
AB և CD երկու զուգահեռ ուղիղներ են, և նրանցից մեկը՝ AB, լինի ուղղահայաց դիտարկվող հարթությանը։ Ապա, մյուսը՝ CD, նույնպես կլինի ուղղահայաց նույն հարթությանը։ AB-ն և CD-ն հատվում են դիտարկվող հարթության հետ կետերում B և D համապատասխանաբար, և BD ուղիղը միացնում է այդ կետերը։ Հետևաբար, AB, CD և BD գտնվում են նույն հարթության մեջ [Պնդում 11․7]։ DE ուղիղը ուղղահայաց է BD-ին դիտարկվող հարթություն մեջ և DE-ն հավասար է AB-ին։ Միացնենք BE, AE և AD գծերը։ Քանի որ AB ուղիղը ուղղահայաց է դիտարկվող հարթությանը, այն ուղղահայաց կլինի նաև բոլոր այն ուղիղներին, որոնք նրան են կցված և գտնվում են դիտարկվող հարթությունում [Սահմ 11․3]։ Հետևաբար, անկյուններ՝ ABD և ABE, ուղիղ են։ Եվ քանի որ BD ուղիղը, հատում է AB և CD զուգահեռ ուղիղները, ապա ABD և CDB անկյունների գումարը հավասար է երկու ուղիղ անկյունների։[Պնդում 1․29] Անկյուն ABD-ն ուղիղ է, հետևում է անկյուն CDB-ն նույնպես ուղիղ է։

Եվ քանի որ AB-ն հավասար է DE-ին, իսկ BD-ն ընդհանուր է, ապա երկու ուղիղներ՝ AB և BE, հավասար են ED և DA ուղիղներին , համապատասխանաբար։ Եվ ABD ուղիղ անկյունը հավասար է EDB անկյանը։ Հետևաբար AD հիմքը հավասար է BE հիմքին [Պնդում 1․4]։ Եվ քանի որ AB հատվածը հավասար է DE-ին, և BE-ն հավասար է AD հատվածին , և AB, BE հատվածները համապատասխանաբար հավասար են ED, DA հատվածներին։ Եվ նրանց հիմքը՝ AE-ն, ընդհանուր է։ Հետևաբար, անկյունը՝ ABE, հավասար է անկյանը՝ EDA ([Պնդում 1․8])։ Քանի որ անկյուն ABE-ն ուղիղ է, ապա անկյուն EDA-ն նույնպես ուղիղ է։ Հետևաբար, ED ուղիղը ուղղահայաց է AD-ին։ Եվ այն նաև ուղղահայաց է DB-ին։Այսպիսով, ED ուղիղը ուղիղ անկյուն է կազմում BD և DA ուղիղներով անցնող հարթության հետ ([Պնդում 11․4])։ Այդ պատճառով ED ուղիղ անկյուն կկազմի բոլոր այն ուղիղների հետ որոնք հատվում են իր հետ և ընկած են BDA հարթության մեջ։ DC ուղիղը գտնվում է BDA հարթությունում, քանի որ AB և BD ուղիղները նույնպես գտնվում են BDA հարթությունում ([Պնդում 11․2])։ Հետևաբար, ED ուղիղը ուղղահայաց է DC ուղիղին։Այսպիսով, CD ուղիղը նույնպես ուղղահայաց է DE-ին։ CD ուղիղը ուղղահայաց է նաև BD ուղիղին։ Հետևաբար, CD ուղիղը կանգնած է ուղղանկյուն երկու ուղիղների՝ DE և DB-ի հետ, որոնք հատվում են D կետում։ Այսպիսով, CD ուղիղը նաև ուղղահայաց է DE և DB ուղիղներով անցնող հարթությանը ([Պնդում 11․4])։ Եվ քանի որ DE և DB ուղիղներով անցնող հարթությունը դիտարկվող հարթությունն է, CD ուղիղը ուղղահայաց է նաև դիտարկվող հարթությանը։

Հետևաբար, եթե երկու ուղիղներ զուգահեռ են, և դրանցից մեկը ուղղահայաց է որևէ հարթության, ապա մյուսը նույնպես կլինի ուղղահայաց նույն հարթությանը։ Որն էլ անհրաժեշտ էր ցույց տալ։



Պնդում 9

Երկու ուղիղներ զուգահեռ են երրորդ ուղղին որը նրանց հետ նույն հարթության մեջ չի գտնվում, ապա այդ ուղիղները միմյանց նկատմամբ նույնպես զուգահեռ են։

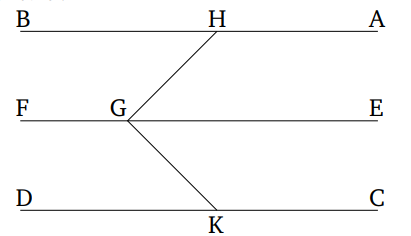
Նկար-3.png

AB և CD ուղիղներից յուրաքանչյուրը զուգահեռ է EF ուղղին, որը նույն հարթության մեջ չէ։ Ցույց տանք որ AB և CD ուղիղները զուգահեռ են։ Պատահականորեն վերցնենք մի G կետ EF ուղղի վրա։ GH ուղիղը EF ուղղի հետ կազմում է ուղիղ անկյուն EF և AB ուղիղներով անցնող հարթության մեջ։ Եվ EF-ն ուղղահայաց է GK ուղղին՝ FE և CD ուղիղներով անցնող հարթության վրա:


Եվ քանի որ EF ուղիղը ուղղահայաց է GH-ին և GK-ին, ապա EF-ն ուղղահայաց է նաև GH և GK ուղիղներով անցնող հարթությանը [Պնդ․ 11.4]: Եվ EF ուղիղը AB-ին զուգահեռ է: Ուստի AB-ն նույնպես ուղղահայաց է HGK հարթությանը [Պնդ․ 11.8]: Հանգունորեն CD-ն նույնպես ուղղահայաց է HGK հարթությանը: Արդյունքում՝ AB և CD ուղիղները ուղղահայաց են HGK հարթությանը: Իսկ եթե երկու ուղիղներ նույն հարթությանն ուղղահայաց են, ապա այդ ուղիղները զուգահեռ են [Պնդ․ 11․6]: Ուստի AB-ն զուգահեռ է CD-ին։ Ինչ պետք էր ապացուցել։



Պնդում 10

Եթե երկու հատվող ուղիղներ զուգահեռ են այլ հարթության մեջ գտնվող երկու հատվող ուղիղների, ապա հարթությունները պարունակում են հավասար անկյուններ։

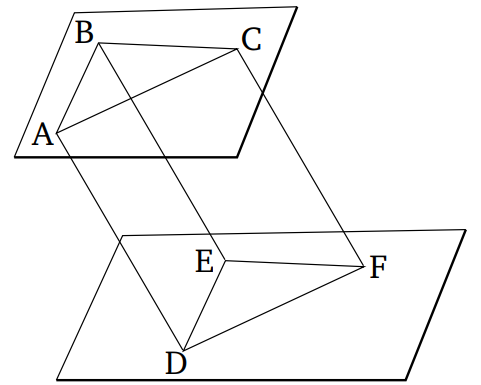
Նկար-4.png

Իրար միացած երկու ուղիղները՝ AB և BC, զուգահեռ են (համապատասխանաբար) միմյանց միացած երկու ուղիղների՝ DE և EF որոնք վերջիններս ընկած չեն AB և BC ուղիղներով անցնող հարթությանը ։Ցույց տանք, որ ABC անկյունը հավասար է DEF անկյանը: BA, BC, ED և EF ուղիղները կտրենք (այնպես, որ համապատասխանաբար հավասար լինեն միմյանց): Միացնենք AD, CF, BE, AC և DF հատվածները:Եվ քանի որ BA ուղիղը հավասար և զուգահեռ է ED-ին, Հետևաբար AD ուղիղը, նույնպես հավասար և զուգահեռ է BE ուղղին [Պնդ. 1.33]: Հանգունորեն CF ուղիղը նույնպես հավասար և զուգահեռ է BE-ին: Այսպիսով, AD և CF հատվածներից յուրաքանչյուրը հավասար և զուգահեռ են BE-ին: Նույն ուղղին զուգահեռ ուղիղները, որոնք նրա հետ նույն հարթության մեջ չեն, զուգահեռ են միմյանց [Պնդ. 11.9]։ Այսպիսով, AD հատվածը զուգահեռ է և հավասար է CF-ին: AC և DF միացնենք նրանց: Այսպիսով, AC-ը նույնպես հավասար է և զուգահեռ DF հատվածին [Պնդ. 1.33]: Եվ քանի որ երկու հատվածներ AB-ն և BC-ն հավասար են երկու հատվածներին՝ DE-ին և EF-ին (համապատասխանաբար), իսկ AC հիմքը հավասար է DF հիմքին, այսպիսով ABC անկյունն հավասար է DEF անկյանը [Պնդ. 1.8]:

Հետևաբար, եթե միմյանց միացված երկու ուղիղները (համապատասխանաբար) զուգահեռ են միմյանց միացած երկու ուղիղներին, որոնք ընկած չեն նույն հարթության մեջ ինչ որ սկզբնական երկու ուղիղները, ապա դրանք կպարունակեն հավասար անկյուններ։ Որը անհրաժեշտ էր ցույց տալ։


Պնդում 11

Կետից հարթությանը ուղղահայաց ուղղի կառուցումը։

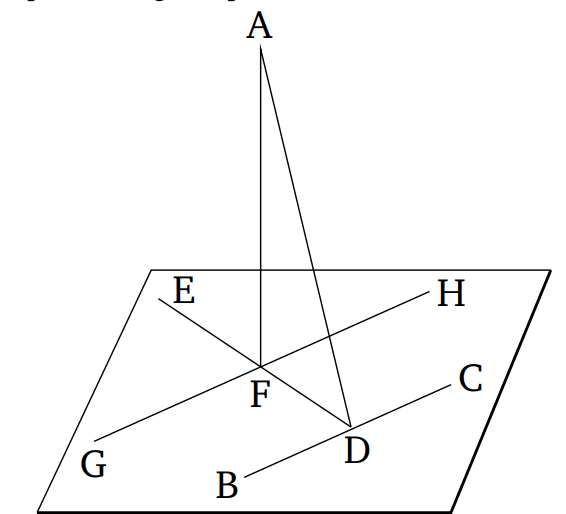
Նկար-11.png

A կետը դիտարկվող կետն է: Այսպիսով, պահանջվում է ուղղահայաց ուղիղ գծել A կետից հարթությանը: Պատահական BC ուղիղ գծենք դիտարկվող հարթությունում, և AD ուղիղը գծենք BC-ին ուղղահայաց A կետից [Պնդ. 1.12]: Հետևաբար, եթե AD ուղիղը նույնպես ուղղահայաց է դիտարկվող հարթությանը, ապա տեղի կունենա այն, ինչ նախատեսված էր:Իսկ, եթե ոչ, D կետից՝ դիտարկվող հարթության մեջ BC ուղղին ուղահայաց DE ուղիղը գծենք [Պնդ. 1.11], և AF ուղիղը գծենք A կետից DE ուղղին ուղղահայաց վերջիններս կհատի DE ուղղին F կետում[Պնդ. 1.12], և F կետով անցնող GH ուղիղը գծենք, որը զուգահեռ է BC ուղղին [Պնդ. 1.31]:

Եվ քանի որ BC-ն ուղիղ անկյուն է կազմում DA և DE ուղիղներից յուրաքանչյուրիհետ,հետևաբար BC-ն, ուղղահայաց է EDA հարթությանը [Պնդ. 11.4]: Իսկ GH ուղիղը զուգահեռ է BC-ին։ Եթե երկու ուղիղները զուգահեռ են, և դրանցից մեկը ուղղահայաց է ինչ-որ հարթությանը, ապա մյուսը նույնպես կլինի նույն հարթության ուղղահայաց[Պնդ. 11.8]:Այսպիսով, GH ուղիղը նույնպես ուղղահայաց է ED և DA ուղիղներով անցնող հարթությունը։ Այսպիսով, GH ուղիղը ուղիղ անկյուն է կազմում իրեն միացած բոլոր ուղիղների հետ, որոնք նույնպես ED և AD ուղիղներով անցնող հարթության մեջ են [Սահմ. 11.3]: Եվ AF-ն, որը գտնվում է ED և AD ուղիղներով անցնող հարթության մեջ, միացված է դրան: Այսպիսով, GH և AF ուղիղներըուղղահայաց են: Հետևաբար, AF-ն ուղղահայաց է HG ուղղին: AF-ն նույնպես ուղղահայաց է DE ուղղին: Այսպիսով, AF-ն ուղղահայաց է GH և DE ուղիղներից յուրաքանչյուրին: Եվ եթե ուղիղը կազմում են ուղիղ անկյուն դեպի երկու հատվող ուղիղների հետ, ապա այն ուղղահայաց կլինի այդ ուղիղներով անցնող հարթությանը [Պնդ. 11.4]: Այսպիսով, FA-ն ուղղահայաց է ED և GH ուղիղներով անցնող հարթությանը: Իսկ ED-ի և GH-ի ուղիղներով անցնող հարթությունը հենց դիտարկվող հարթությունն էր: Այսպիսով, AF ուղիղը ուղղահայաց է դիտարկվող հարթությանը:

Այսպիսով, A կետով անցնող AF ուղիղը ուղղահայաց է դիտարկվող հարթությանը: Ինչը հենց պահանջվում էր կառուցել:


Պնդում 12

Տվյալ կետից, դիտարկվող հարթությանը տարված ուղղահայացի կառուցումը։


Նկար-12.png


Տրված հարթությունը դիտարկվող հարթությունն է, իսկ A-ն այդ հարթությանը պատկանող կետ: Այսպիսով, պահանջվում է A կետով անցնող և դիտարկվող հարթությանը ուղղահայաց ուղիղ կառուցել:Կամայական B կետից տանենք ուղղահայաց դիտարկվող հարթությանը, որը կհատի հարթությունը C կետում [Պնդ. 11.11]: BC-ին զուգահեռ և A կետով անցնող ուղիղ գծենք AD-ն [Պնդ. 1.31]:Քանի որ AD-ն և CB-ն երկու զուգահեռ ուղիղներ են, և դրանցից մեկը՝ BC-ն, ուղղահայաց է դիտարկվող հարթությանը հետևաբար, AD ուղիղը նույնպես ուղղահայաց է դիտարկվող հարթությանը [Պնդ. 11.8]: Հետևաբար AD ուղիղը A կետով անցնող և հարթությանը ուղղահայաց ուղիղ է։ Ինչը պահանջվում էր կառուցել։


Պնդում 13

Ստացված է «https://grapaharan.org/index.php?title=Տարերք/Գիրք_11&oldid=14958» էջից