«Տարերք/Գիրք 13»–ի խմբագրումների տարբերություն

22:22, 11 Դեկտեմբերի 2024-ի տարբերակ

Տարերք, Գիրք 13

հեղինակ՝ էվկլիդես
աղբյուր՝ Euclid's Elements of Geometry, English translation by Richard Fitzpatrick

Տարերքի գրքեր

Գիրք 1 - Գիրք 2 - Գիրք 3 - Գիրք 4 - Գիրք 5 - Գիրք 6 - Գիրք 7 - Գիրք 8 - Գիրք 9 - Գիրք 10 - Գիրք 11 - Գիրք 12 - Գիրք 13

Pages 506-530

Պնդում 1

Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորի վրա քառակուսին, գումարած ամբողջի կեսը, հնգապատիկն է կեսի վրա քառակուսու։

Թող AB ուղիղ գիծը կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Թող AD ուղիղ գիծը երկարացվի՝ անցնելով CA։ Եվ թող AD-ն լինի AB-ի կեսը։ Ասում եմ, որ CD-ի վրա քառակուսին հնգապատիկն է DA-ի վրա քառակուսու։

Թող AB և DC վրա քառակուսիները՝ AE և DF, նկարագրվեն։ Եվ DF պատկերում գծվի։ Եվ թող գիծը FC գծվի՝ հասնելով G-ին։ Եվ քանի որ AB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ C կետում, ապա ABC բազմապատկիչը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ CE-ն ABC բազմապատկիչն է, իսկ FH-ն՝ AC-ի վրա քառակուսին։ Այսպիսով, CE-ն հավասար է FH-ին։ Եվ քանի որ BA-ն կրկնապատիկն է AD-ի, իսկ BA-ն հավասար է KA-ին, և AD-ն՝ AH-ին, ապա KA-ն նույնպես կրկնապատիկն է AH-ի։ Եվ քանի որ KA-ն AH-ի նկատմամբ հարաբերություն է, CK-ն նույնպես CH-ի կրկնապատիկն է [Պնդում 6.1]։ Այսպիսով, CK-ն կրկնապատիկն է CH-ի։ Եվ LH-ն գումարած HC կրկնապատիկն է CH-ի [Պնդում 1.43]։ Այսպիսով, KC-ն հավասար է LH-ի գումարած HC-ի։ Եվ CE-ն ցույց տրվեց, որ հավասար է HF-ին։ Այսպիսով, ամբողջ քառակուսի AE-ն հավասար է գնոմոն MNO-ին։

Եվ քանի որ BA-ն կրկնապատիկն է AD-ի, BA-ի վրա քառակուսին չորսապատիկն է AD-ի վրա քառակուսու՝ այսինքն, AE-ն չորսապատիկն է DH-ի։ Եվ AE-ն հավասար է գնոմոն MNO-ին։ Եվ, այսպիսով, գնոմոն MNO-ն նույնպես չորսապատիկն է AP-ի։ Այսպիսով, ամբողջ DF-ը հնգապատիկն է AP-ի։ Եվ DF-ը CD-ի վրա քառակուսին է, իսկ AP-ն՝ DA-ի վրա քառակուսին։ Այսպիսով, CD-ի վրա քառակուսին հնգապատիկն է DA-ի վրա քառակուսու։

Այսպիսով, եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորի վրա քառակուսին, գումարած ամբողջի կեսը, հնգապատիկն է կեսի վրա քառակուսու։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 2

Եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։

Թող AB ուղիղ գծի վրա քառակուսին հնգապատիկն է AC կտորի վրա քառակուսու։ Եվ թող CD-ն լինի կրկնապատիկ AC-ից։ Ասում եմ, որ եթե CD-ն կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի CB։

Թող AB և CD վրա քառակուսիները՝ AF և CG, նկարագրվեն։ Եվ թող AF պատկերում գծվի։ Եվ թող BE գիծը գծվի։ Եվ քանի որ BA-ի վրա քառակուսին հնգապատիկն է AC-ի վրա քառակուսու, ապա AF-ն հնգապատիկն է AH-ից։ Այսպիսով, գնոմոն MNO-ն է չորսապատիկ AH-ից։ Եվ քանի որ DC-ն կրկնապատիկն է CA-ից, ապա DC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու՝ այսինքն, CG-ն է չորսապատիկ AH-ից։ Եվ գնոմոն MNO-ն նույնպես ցույց տրվեց, որ չորսապատիկն է AH-ից։ Այսպիսով, գնոմոն MNO-ն հավասար է CG-ին։ Եվ քանի որ DC-ն կրկնապատիկն է CA-ից, և DC-ն հավասար է CK-ին, և AC-ն՝ CH-ին, [CK-ն կրկնապատիկն է CH-ից], իսկ KB-ն նույնպես կրկնապատիկն է BH-ից [Պնդում 6.1]։ Այսպիսով, KB-ն հավասար է LH-ի գումարած HB-ին։ Եվ ամբողջ գնոմոն MNO-ն նույնպես ցույց տրվեց, որ հավասար է ամբողջ CG-ին։ Այսպիսով, մնացորդ HF-ն նույնպես հավասար է մնացորդ BG-ին։ Եվ BG-ն այն բազմապատկիչն է, որը պարունակում է CDB։ Քանի որ CD-ն հավասար է DG-ին։ Եվ HF-ն CB-ի վրա քառակուսին է։ Այսպիսով, CDB բազմապատկիչը հավասար է CB-ի վրա քառակուսուն։

Այսպիսով, ինչպես DC-ն է CB-ի նկատմամբ, այնպես էլ CB-ն է BD-ի նկատմամբ [Պնդում 6.17]։ Եվ քանի որ DC-ն ավելի մեծ է, քան CB (տես լեմա), ապա CB-ն նույնպես ավելի մեծ է, քան BD [Պնդում 5.14]։ Այսպիսով, եթե CD ուղիղ գծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի CB։

Այսպիսով, եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Լեմմա

Եվ կարող է ցույց տրվել, որ կրկնապատիկ AC-ը (այսինքն՝ DC-ն) ավելի մեծ է, քան BC, ինչպես հետևյալը։

Եթե (կրկնապատիկ AC-ը) ոչ (մեծ է BC-ից), եթե հնարավոր է, թող BC-ն լինի կրկնապատիկ CA-ից։ Այսպիսով, BC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BC-ի և CA-ի վրա քառակուսիների (հավաքածուն) հնգապատիկն է CA-ի վրա քառակուսու։ Եվ BA-ի վրա քառակուսին համարվեց հնգապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BA-ի վրա քառակուսին հավասար է BC-ի և CA-ի վրա քառակուսիների (հավաքածուն)։ Սա՝ անխուսափելի է [Պնդում 2.4]։ Այսպիսով, CB-ն չի կարող լինել կրկնապատիկ AC-ից։ Ուստի, նմանապես, կարող ենք ցույց տալ, որ ուղիղ գիծը, որը փոքր է CB-ից, նույնպես չի կարող լինել կրկնապատիկ AC-ից։ Ասածը՝ ավելի մեծ հակասություն է։ Այսպիսով, կրկնապատիկ AC-ը ավելի մեծ է, քան CB։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 3

Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա փոքր հատվածի և մեծ հատվածի կեսի գումարի քառակուսին հավասար է մեծ հատվածի կեսի քառակուսու հնգապատիկին։

Նկ․ 3

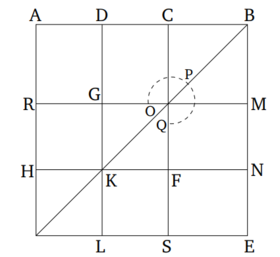
Դիցուք՝ եթե AB հատվածը բաժանենք արտաքին և միջին հարաբերությամբ C-ում, այնպես որ AC մեր մեծ հատվածն է, և AC-ն կիսենք D-ում, ապա 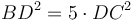$\text{[math]}$ (Նկ․ 3):

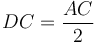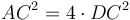Դիտարկենք AE անկյունագծով քառակուսին, ինչպես ցույց է տրված Նկ․ 3-ում։ Քանի որ $\text{[math]}$ , ապա $\text{[math]}$ (RS անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին)։ Եվ AB և BC կողմերով ուղղանկյան մակերեսը հավասար է AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17), որն էլ հավասար է CBES ուղղանկյան մակերեսին, հետևաբար վերջինս հավասար է RS անկյունագծով քառակուսու մակերեսին։ Այսպիսով CBES ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին։ Ինչպես գիտենք 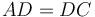$\text{[math]}$ ,և $\text{[math]}$ , 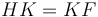հետևաբար HL և GF անկյունագծերով քառակուսիների մակերեսները հավասար են։ Այսպիսով 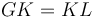$\text{[math]}$ , այնպես ինչպես 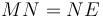$\text{[math]}$ ։ Քանի որ MF անկյունագծով ուղղանկյայն մակերեսը հավասար է FE և CG անկյունագծերով ուղանկյունների մակերեսներին, հետևաբար վերջիններս նույնպես հավասար են: Եթե СN անկյունագծով ուղղանկյունն ավելացնենք երկուսին էլ, ապա կարող ենք ասել, որ գնոմոն OPQ հավասար է CE անկյունագծով ուղղանկյան մակերեսին։ Եվ ինչպես ցույց էր տրվել վերևում, CE անկյունագծով ուղղանկյան մակերեսը հավասար է 4 անգամ FG անկյունագծով քառակուսու մակերեսին, հետևաբար գնոմոն OPQ-ն նույնպես հավասար է FG անկյունագծով քառակուսու մակերեսի քառապատիկին։ Հետևաբար գնոմոն OPQ հավասար է 5 անգամ FG-ի մակերեսին։ Բայց մենք գիտենք, որ գնոմոն OPQ-ի և FG անկյունագծով քառակուսու մակերեսի գումարը հավասար է DN անկյունագծով քառակուսու մակերեսին։ Իսկ վերջինիս մակերեսը հավասար է 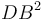$\text{[math]}$ , իսկ GF անկյունագծով քառակուսու մակերեսը հավասար է 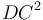$\text{[math]}$ : Այսպիսով 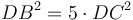$\text{[math]}$ , ինչը և պահանջվում էր ապացուցել։

Պնդում 4

Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա փոքր և մեծ հատվածների քառակուսիների գումարը հավասար է մեծ հատվածի քառակուսու եռապատիկին։

Նկ․ 4

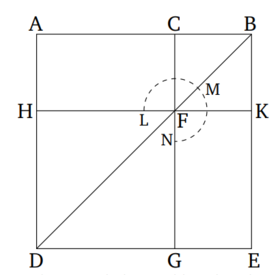
Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է (Նկ․ 4)։ Ես պնդում եմ, որ $\text{[math]}$ :

Դիտարկենք քառակուսի ADEB (Նկ․ 4): Քանի որ AB մասնատված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է, ապա 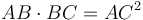$\text{[math]}$ AB և BC կողմերով ուղղանկյան մակերեսը AC կողմով քառակուսու մակերեսին (Սահմ․ 6․3, Պնդ․ 6․17)։ AK անկյունագծով ուղղանկյունը հավասար է AB և BC կողմերով ուղղանկյանը, և HG անկյունագծով քառակուսին հավասար է AC կողմով քառակուսուն, հետևաբար AK և HG անկյունագծով ուղղանկյունների մակերեսները հավասար են։ Քանի որ AF և FE անկյունագծերով ուղղանկյունները հավասար են (Պնդ․ 1․43), և CBKF քառակուսին ընդհանուր է, հետևաբար ABKH և CBEG ուղանկյունները հավասար են։ Այսպիսով, AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին։ Քանի որ AK և CE անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է գնոմոն LMN-ի և CK անկյունագծով քառակուսու մակերեսների գումարին, ապա գնոմոն LMN և CK-ն հավասար է AK անկյունագծով ուղղանկյան մակերեսի կրկնապատիկին: Եվ ինչպես ցույց էր տրվել վերևում, վերջինս հավասար է նաև HG անկյունագծով քառակուսուն, հետևաբար գնոմոն LMN-ը

@@ Տող 33. / Տող 33. @@
 Այսպիսով, եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
 == Լեմմա ==
-Ապացուցենք, որ <math>2\cdot AC (DC) > BC</math>։
+Եվ կարող է ցույց տրվել, որ կրկնապատիկ AC-ը (այսինքն՝ DC-ն) ավելի մեծ է, քան BC, ինչպես հետևյալը։
-Ենթադրենք <math>2\cdot AC</math> ավելի մեծ չէ քան BC, և <math>BC = 2\cdot CA</math>։ Այսպիսով <math>BC^2 = 4\cdot CA^2</math>։ Հետևում է, որ <math>BC^2 + CA^2 = 5\cdot CA^2</math>։ Ենթադրվում էր, որ  <math> BA^2 = 5\cdot CA^2</math>։ Հետևաբար, <math>BA^2  = BC^2 + CA^2</math>, որը և հակասում է պայմանին ''(Պնդ․ 2․4)''։ Այսպիսով <math>CB \neq 2\cdot AC</math>, նույն կերպ, կարող ենք ասել, որ CB-ից ավելի փոքր հատվածը հավասար չէ <math>2\cdot AC</math>:
+Եթե (կրկնապատիկ AC-ը) ոչ (մեծ է BC-ից), եթե հնարավոր է, թող BC-ն լինի կրկնապատիկ CA-ից։ Այսպիսով, BC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BC-ի և CA-ի վրա քառակուսիների (հավաքածուն) հնգապատիկն է CA-ի վրա քառակուսու։ Եվ BA-ի վրա քառակուսին համարվեց հնգապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BA-ի վրա քառակուսին հավասար է BC-ի և CA-ի վրա քառակուսիների (հավաքածուն)։ Սա՝ անխուսափելի է [Պնդում 2.4]։ Այսպիսով, CB-ն չի կարող լինել կրկնապատիկ AC-ից։ Ուստի, նմանապես, կարող ենք ցույց տալ, որ ուղիղ գիծը, որը փոքր է CB-ից, նույնպես չի կարող լինել կրկնապատիկ AC-ից։ Ասածը՝ ավելի մեծ հակասություն է։
-Այսպիսով, <math>2\cdot AC > CB</math>, որն էլ պահանջվում էր ապացուցել։
+Այսպիսով, կրկնապատիկ AC-ը ավելի մեծ է, քան CB։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
 == Պնդում 3 ==

«Տարերք/Գիրք 13»–ի խմբագրումների տարբերություն

22:22, 11 Դեկտեմբերի 2024-ի տարբերակ

Բովանդակություն

Pages 506-530

Պնդում 1

Պնդում 2

Լեմմա

Պնդում 3

Պնդում 4

Նավիգացիոն ցանկ

Անձնական գործիքներ

Անվանատարածքներ

Տարբերակներ

Դիտումները

Ավելին

Որոնում

Շրջել կայքում

Բաժիններ

Ժանրեր

ըստ երկրների

այլ էջեր

Գործիքներ