«Տարերք/Գիրք 6»–ի խմբագրումների տարբերություն
| (9 intermediate revisions by 3 users not shown) | |||
| Տող 7. | Տող 7. | ||
{{Տարերքի գրքեր}} | {{Տարերքի գրքեր}} | ||
[[Կատեգորիա:Մաթեմատիկա]] | [[Կատեգորիա:Մաթեմատիկա]] | ||
| − | |||
| − | |||
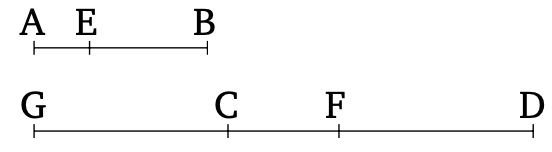
== Սահմանումներ == | == Սահմանումներ == | ||
| − | + | # Նման ուղղագծային պատկերներ կոչվում են այն պատկերները, որոնց համապատասխան անկյունները առանձին-առանձին հավասար են, իսկ (համապատասխանող) անկյունների կողմերը՝ համաչափ: | |
| + | # Ուղիղ գիծը , որը բաժանված է մեծ և միջին հարաբերությամբ, երբ ամբողջ գիծը մեծ հատվածի հետ նույն հարաբերության մեջ է, ինչ մեծ հատվածը՝ փոքր հատվածի հետ: | ||
| + | # Ցանկացած պատկերի բարձրությունը գագաթից հիմքին ուղղահայաց տարված ուղիղ գիծն է: | ||
| − | |||
| − | + | == Պնդում 1 == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Պնդում 1 | + | |
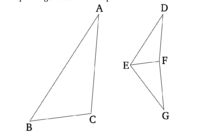
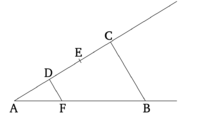
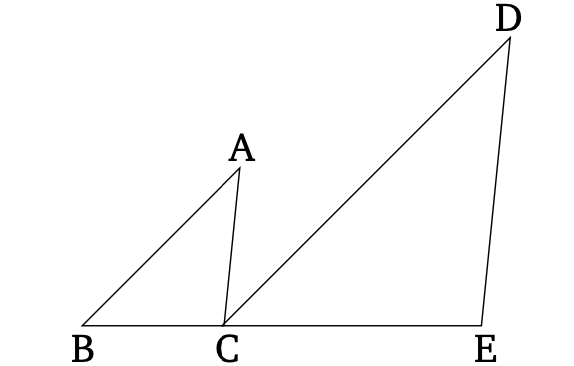
Այն եռանկյուններն ու զուգահեռագծերը, որոնք ունեն նույն բարձրությունը, ապա նրանց հիմքերը հարաբերվում են համապատասխանաբար: | Այն եռանկյուններն ու զուգահեռագծերը, որոնք ունեն նույն բարձրությունը, ապա նրանց հիմքերը հարաբերվում են համապատասխանաբար: | ||
| Տող 86. | Տող 28. | ||
** Սա պրոպ. 1.38-ի ուղղակի ընդհանրացումն է: | ** Սա պրոպ. 1.38-ի ուղղակի ընդհանրացումն է: | ||
| − | Պնդում 2 | + | |
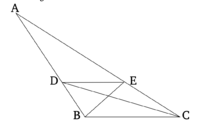
| + | == Պնդում 2 == | ||
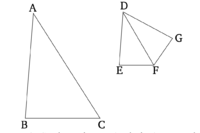
Երբ եռանկյան կողմերից մեկին զուգահեռ մի ուղիղ գիծ է գծվում, ապա այն կտրվածքով կտրում է եռանկյան (մյուս) կողմերը համաչափ։ Եվ եթե եռանկյան (երկու) կողմերը կտրում են համաչափ, ապա այդ կետերը միացնող ուղիղ գիծը կլինի զուգահեռ եռանկյան մնացած կողմին։ | Երբ եռանկյան կողմերից մեկին զուգահեռ մի ուղիղ գիծ է գծվում, ապա այն կտրվածքով կտրում է եռանկյան (մյուս) կողմերը համաչափ։ Եվ եթե եռանկյան (երկու) կողմերը կտրում են համաչափ, ապա այդ կետերը միացնող ուղիղ գիծը կլինի զուգահեռ եռանկյան մնացած կողմին։ | ||
| − | + | [[Պատկեր:Pndum2.png|center|200px]] | |
DE ուղիղ գիծը գծված է ABC եռանկյան BC կողմին զուգահեռ։ Ինչպես BD-ն DA-ին է հարաբերում է, այնպես էլ CE-ն EA-ին: | DE ուղիղ գիծը գծված է ABC եռանկյան BC կողմին զուգահեռ։ Ինչպես BD-ն DA-ին է հարաբերում է, այնպես էլ CE-ն EA-ին: | ||
Դիցուք, BE և CD գծերը միացված են։ | Դիցուք, BE և CD գծերը միացված են։ | ||
| Տող 97. | Տող 40. | ||
Այսպիսով, եթե եռանկյան կողմերից մեկին զուգահեռ ուղիղ գիծ գծենք, ապա այն համաչափ կբաժանի եռանկյան (մյուս) կողմերը։ Եվ եթե եռանկյան (երկու) կողմերը աժանվեն համաչափ, ապա այդ կետերը միացնող ուղիղ գիծը կլինի զուգահեռ եռանկյան մնացած կողմին։ (Այսինքն՝ այն, ինչ պետք էր ցույց տալ)։ | Այսպիսով, եթե եռանկյան կողմերից մեկին զուգահեռ ուղիղ գիծ գծենք, ապա այն համաչափ կբաժանի եռանկյան (մյուս) կողմերը։ Եվ եթե եռանկյան (երկու) կողմերը աժանվեն համաչափ, ապա այդ կետերը միացնող ուղիղ գիծը կլինի զուգահեռ եռանկյան մնացած կողմին։ (Այսինքն՝ այն, ինչ պետք էր ցույց տալ)։ | ||
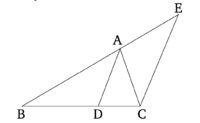
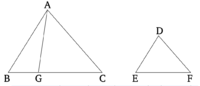
| − | + | == Պնդում 3 == | |
| − | Պնդում 3 | + | |
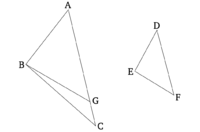
Եթե եռանկյան անկյունը կիսվում է, և այդ անկյունը կիսող ուղիղ գիծը կտրում է նաև հիմքը, ապա հիմքի հատվածները կունենան նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը։ Եվ եթե հիմքի հատվածները ունեն նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը, ապա գագաթը կետին միացնող ուղիղ գիծը կիսում է եռանկյան անկյունը։ | Եթե եռանկյան անկյունը կիսվում է, և այդ անկյունը կիսող ուղիղ գիծը կտրում է նաև հիմքը, ապա հիմքի հատվածները կունենան նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը։ Եվ եթե հիմքի հատվածները ունեն նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը, ապա գագաթը կետին միացնող ուղիղ գիծը կիսում է եռանկյան անկյունը։ | ||
Տրված է, ABC եռանկյունը։ Եվ թող BAC անկյունը կիսված լինի AD ուղիղ գծով։ Ինչպես BD-ն է հարավերվում DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ։ | Տրված է, ABC եռանկյունը։ Եվ թող BAC անկյունը կիսված լինի AD ուղիղ գծով։ Ինչպես BD-ն է հարավերվում DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ։ | ||
CE գիծը գծվի C կետից՝ զուգահեռ AD-ին։ Եվ BA գիծը (CE)-ին E կետում*։ | CE գիծը գծվի C կետից՝ զուգահեռ AD-ին։ Եվ BA գիծը (CE)-ին E կետում*։ | ||
| − | + | [[Պատկեր:Pndum3.png|center|200px]] | |
Քանի որ, AC ուղիղ գիծը անցնում է AD և EC զուգահեռ (ուղիղների) միջև, ապա ACE անկյունը հավասար է CAD-ին [Պնդ. 1.29]։ Ենթադրվում է, որ CAD անկյունը հավասար BAD-ին։ Հետևաբար, BAD անկյունը նույնպես հավասար է ACE-ին։ Քանի որ, BAE ուղիղ գիծը անցնում է AD և EC զուգահեռ (ուղիղների) միջև, ապա BAD արտաքին անկյունը հավասար է AEC ներքին (անկյանը) [Պնդ. 1.29]։ Իսկ ACE անկյունը նույնպես ցույց է տրվել, որ հավասար է BAD-ին։ Հետևաբար, ACE անկյունը նույնպես հավասար է AEC-ին։ Եվ, հետևաբար, AE կողմը հավասար է AC կողմին [Պնդ. 1.6]։ Այն պատճառով, որ AD գիծը գծված է BCE եռանկյանը և EC կողմին զուգահեռ, ապա համաչափորեն, ինչպես BD-ն է DC-ի նկատմամբ հարաբերվում, այնպես էլ BA-ն է AE-ի [Պնդ. 6.2]։ Իսկ AE-ն հավասար է AC-ին։ Հետևաբար, ինչպես BD-ն է DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ։ | Քանի որ, AC ուղիղ գիծը անցնում է AD և EC զուգահեռ (ուղիղների) միջև, ապա ACE անկյունը հավասար է CAD-ին [Պնդ. 1.29]։ Ենթադրվում է, որ CAD անկյունը հավասար BAD-ին։ Հետևաբար, BAD անկյունը նույնպես հավասար է ACE-ին։ Քանի որ, BAE ուղիղ գիծը անցնում է AD և EC զուգահեռ (ուղիղների) միջև, ապա BAD արտաքին անկյունը հավասար է AEC ներքին (անկյանը) [Պնդ. 1.29]։ Իսկ ACE անկյունը նույնպես ցույց է տրվել, որ հավասար է BAD-ին։ Հետևաբար, ACE անկյունը նույնպես հավասար է AEC-ին։ Եվ, հետևաբար, AE կողմը հավասար է AC կողմին [Պնդ. 1.6]։ Այն պատճառով, որ AD գիծը գծված է BCE եռանկյանը և EC կողմին զուգահեռ, ապա համաչափորեն, ինչպես BD-ն է DC-ի նկատմամբ հարաբերվում, այնպես էլ BA-ն է AE-ի [Պնդ. 6.2]։ Իսկ AE-ն հավասար է AC-ին։ Հետևաբար, ինչպես BD-ն է DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ։ | ||
Եվ այսպես, BD-ն հարաբերվի DC-ի նկատմամբ այնպես, ինչպես BA-ն AC-ի նկատմամբ, և AD գիծը միացվի։ Դիցուք, BAC անկյունը կիսված է AD ուղիղ գծով։ | Եվ այսպես, BD-ն հարաբերվի DC-ի նկատմամբ այնպես, ինչպես BA-ն AC-ի նկատմամբ, և AD գիծը միացվի։ Դիցուք, BAC անկյունը կիսված է AD ուղիղ գծով։ | ||
| Տող 112. | Տող 54. | ||
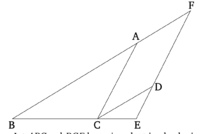
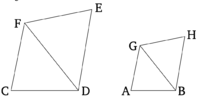
| − | Պնդում 4 | + | == Պնդում 4 == |
Նման (հավասարանկյուն) եռանկյուններում կողերն ունեն համեմատական հարաբերություն, և այն կողմերը, որոնք ունեն հավասար անկյուններ, համապատասխանում են միմյանց: | Նման (հավասարանկյուն) եռանկյուններում կողերն ունեն համեմատական հարաբերություն, և այն կողմերը, որոնք ունեն հավասար անկյուններ, համապատասխանում են միմյանց: | ||
| − | + | [[Պատկեր:Pndum4.png|center|200px]] | |
Դիցուք, ABC և DCE լինեն նման եռանկյուններ, որտեղ ABC անկյունը հավասար է DCE անկյանը, և BAC անկյունը՝ CDE անկյանը, և, ավելին, ACB անկյունը՝ CED-ին:Կարող ենք նշել, որ ABC և DCE եռանկյուններում համապատասխանաբար անկյունների կողմերն ունեն համեմատական հարաբերություն, և (կողմերը), որոնք համապատասխանաբար ունեն հավասար անկյուններ, համընկնում են: | Դիցուք, ABC և DCE լինեն նման եռանկյուններ, որտեղ ABC անկյունը հավասար է DCE անկյանը, և BAC անկյունը՝ CDE անկյանը, և, ավելին, ACB անկյունը՝ CED-ին:Կարող ենք նշել, որ ABC և DCE եռանկյուններում համապատասխանաբար անկյունների կողմերն ունեն համեմատական հարաբերություն, և (կողմերը), որոնք համապատասխանաբար ունեն հավասար անկյուններ, համընկնում են: | ||
Եկեք BC գիծը տեղադրենք CE-ի վրա։ Քանի որ, ABC և ACB անկյունները փոքր են երկու ուղիղ-անկյուններից[Պնդ.1.17], և ACB անկյունը հավասար է DEC անկյանը, հետևաբար, ABC և DEC անկյունները փոքր են երկու ուղիղ-անկյուններից։ Այսպիսով, BA և ED գծերը, որոնք երկարացվել են, կհանդիպեն [Հավ. 5]։ Դրանք երկարացվելով,ի վերջո հանդիպում են F կետում։ | Եկեք BC գիծը տեղադրենք CE-ի վրա։ Քանի որ, ABC և ACB անկյունները փոքր են երկու ուղիղ-անկյուններից[Պնդ.1.17], և ACB անկյունը հավասար է DEC անկյանը, հետևաբար, ABC և DEC անկյունները փոքր են երկու ուղիղ-անկյուններից։ Այսպիսով, BA և ED գծերը, որոնք երկարացվել են, կհանդիպեն [Հավ. 5]։ Դրանք երկարացվելով,ի վերջո հանդիպում են F կետում։ | ||
| Տող 122. | Տող 64. | ||
| − | Պնդում 5 | + | == Պնդում 5 == |
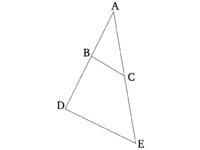
Եթե երկու եռանկյունները ունեն համաչափ կողմեր, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։ | Եթե երկու եռանկյունները ունեն համաչափ կողմեր, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։ | ||
| − | + | [[Պատկեր:Pndum5.png|center|200px]] | |
Դիցուք, ABC և DEF լինեն երկու եռանկյուններ, որոնց կողմերը համաչափ են, (այնպես որ) ինչպես AB հարաբերում է BC կողմին, այնպես էլ DE հարաբերում է EF կողմին, և ինչպես BC հարաբերում է CA-ին, այնպես էլ EF FD կողմին, և ավելին, ինչպես BA-ն է AC-ի նկատմամբ, այնպես էլ ED-ն է DF-ի նկատմամբ։ ABC եռանկյունը հավասարանկյուն է, որը հարաբերում է DEF եռանկյանը, և (այդ եռանկյունները) կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։ Այդպիսով, ABC (անկյունը) (հավասար է) DEF անկյանը, BCA՝ EFD-ին, և, ավելին, BAC՝ EDF-ին։ | Դիցուք, ABC և DEF լինեն երկու եռանկյուններ, որոնց կողմերը համաչափ են, (այնպես որ) ինչպես AB հարաբերում է BC կողմին, այնպես էլ DE հարաբերում է EF կողմին, և ինչպես BC հարաբերում է CA-ին, այնպես էլ EF FD կողմին, և ավելին, ինչպես BA-ն է AC-ի նկատմամբ, այնպես էլ ED-ն է DF-ի նկատմամբ։ ABC եռանկյունը հավասարանկյուն է, որը հարաբերում է DEF եռանկյանը, և (այդ եռանկյունները) կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։ Այդպիսով, ABC (անկյունը) (հավասար է) DEF անկյանը, BCA՝ EFD-ին, և, ավելին, BAC՝ EDF-ին։ | ||
Դիցուք, FEG անկյունը, որը հավասար է ABC անկյանը, և EFG, որը հավասար է ACB անկյանը, գտնվում են EF ուղիղ գծի վրա՝ համապատասխանաբար E և F կետերում [Պնդ. 1.23]։ Այսպիսով, A (անկյան) մյուս մասը հավասար է G անկյան մյուս մասին[Պնդ. 1.32]։ | Դիցուք, FEG անկյունը, որը հավասար է ABC անկյանը, և EFG, որը հավասար է ACB անկյանը, գտնվում են EF ուղիղ գծի վրա՝ համապատասխանաբար E և F կետերում [Պնդ. 1.23]։ Այսպիսով, A (անկյան) մյուս մասը հավասար է G անկյան մյուս մասին[Պնդ. 1.32]։ | ||
| Տող 132. | Տող 74. | ||
| − | Պնդում 6 | + | == Պնդում 6 == |
Եթե երկու եռանկյուններն ունեն համապատասխան անկյունը հավասար է, և այդ հավասար անկյունների կողմերը համաչափ են, ապա եռանկյունները կլինեն հավասարանկյուն և կունենան անկյուններ, որոնք համապատասխանում են այդ կողմերին: | Եթե երկու եռանկյուններն ունեն համապատասխան անկյունը հավասար է, և այդ հավասար անկյունների կողմերը համաչափ են, ապա եռանկյունները կլինեն հավասարանկյուն և կունենան անկյուններ, որոնք համապատասխանում են այդ կողմերին: | ||
| − | + | [[Պատկեր:Pndum6.png|center|200px]] | |
Դիցուք, ABC և DEF լինեն երկու եռանկյուններ, որոնցում BAC անկյունը հավասար է EDF անկյանը (համապատասխանաբար), և այդ անկյունների կողմերը համաչափ են ,այնպես որ,BA հարաբերվի AC կողմին այնպես, ինչպես ED կողմը DF-ին։ABC եռանկյունը հավասարանկյուն է DEF եռանկյանը, որտեղ ABC անկյունը հավասար է DEF անկյանը, իսկ ACB անկյունը DFE անկյանը: | Դիցուք, ABC և DEF լինեն երկու եռանկյուններ, որոնցում BAC անկյունը հավասար է EDF անկյանը (համապատասխանաբար), և այդ անկյունների կողմերը համաչափ են ,այնպես որ,BA հարաբերվի AC կողմին այնպես, ինչպես ED կողմը DF-ին։ABC եռանկյունը հավասարանկյուն է DEF եռանկյանը, որտեղ ABC անկյունը հավասար է DEF անկյանը, իսկ ACB անկյունը DFE անկյանը: | ||
FDG անկյունը, որը հավասար է BAC և EDF անկյուններին, և DFG անկյունը, որը հավասար է ACB անկյանը, կառուցվեն AF ուղիղ գծի վրա՝ համապատասխանաբար D և F կետերում [Պնդ. 1.23]։ Այսպիսով, B-ի առընթեր անկյունը հավասար է G-ի առընթեր անկյանը [Պնդ. 1.32]։ | FDG անկյունը, որը հավասար է BAC և EDF անկյուններին, և DFG անկյունը, որը հավասար է ACB անկյանը, կառուցվեն AF ուղիղ գծի վրա՝ համապատասխանաբար D և F կետերում [Պնդ. 1.23]։ Այսպիսով, B-ի առընթեր անկյունը հավասար է G-ի առընթեր անկյանը [Պնդ. 1.32]։ | ||
| Տող 142. | Տող 84. | ||
| − | Պնդում 7 | + | == Պնդում 7 == |
Եթե երկու եռանկյուններն ունեն մեկ անկյուն, որոնք հավասար են իրար ,և մյուս անկյունների կողմերն ունեն համապատասխանաբար նույն հարաբերությունը, իսկ մնացած անկյունները երկուսն էլ փոքր են կամ երկուսն էլ փոքր չեն ուղիղ անկյուններից, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան հավասար անկյուններ, որոնց համապատասխան կողմերը կունենան նույն հարաբերությունը։ | Եթե երկու եռանկյուններն ունեն մեկ անկյուն, որոնք հավասար են իրար ,և մյուս անկյունների կողմերն ունեն համապատասխանաբար նույն հարաբերությունը, իսկ մնացած անկյունները երկուսն էլ փոքր են կամ երկուսն էլ փոքր չեն ուղիղ անկյուններից, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան հավասար անկյուններ, որոնց համապատասխան կողմերը կունենան նույն հարաբերությունը։ | ||
| − | + | [[Պատկեր:Pndum7.png|center|200px]] | |
Դիցուք, ABC և DEF երկու եռանկյուններ են, որի BAC անկյունը հավասար է EDF անկյանը (համապատասխանաբար), և ABC և DEF անկյունների կողմերը հարաբերվում են (այնպես որ), AB և BC ունեն նույն հարաբերությունը, ինչպես DE և EF, իսկ մնացած անկյունները՝ C և F-ում, երկուսն էլ սկզբում փոքր են ուղիղ անկյունից։ ABC եռանկյունը նման է DEF եռանկյանը, և (այդ) ABC անկյունը հավասար կլինի DEF անկյանը, և (մնացած) անկյունը C անկյունը (պարզապես) հավասար կլինի F անկյանը։ | Դիցուք, ABC և DEF երկու եռանկյուններ են, որի BAC անկյունը հավասար է EDF անկյանը (համապատասխանաբար), և ABC և DEF անկյունների կողմերը հարաբերվում են (այնպես որ), AB և BC ունեն նույն հարաբերությունը, ինչպես DE և EF, իսկ մնացած անկյունները՝ C և F-ում, երկուսն էլ սկզբում փոքր են ուղիղ անկյունից։ ABC եռանկյունը նման է DEF եռանկյանը, և (այդ) ABC անկյունը հավասար կլինի DEF անկյանը, և (մնացած) անկյունը C անկյունը (պարզապես) հավասար կլինի F անկյանը։ | ||
Եթե ABC անկյունը հավասար չէ DEF (անկյանը), ապա դրանցից մեկը մեծ է մյուսից։ Դիցուք, ABC-ը մեծ լինի և թող ABG (անկյունը), որը հավասար է DEF անկյանը, կառուցված լինի AB ուղիղ գծի վրա՝ B կետում [Պնդ. 1.23]։ | Եթե ABC անկյունը հավասար չէ DEF (անկյանը), ապա դրանցից մեկը մեծ է մյուսից։ Դիցուք, ABC-ը մեծ լինի և թող ABG (անկյունը), որը հավասար է DEF անկյանը, կառուցված լինի AB ուղիղ գծի վրա՝ B կետում [Պնդ. 1.23]։ | ||
| Տող 154. | Տող 96. | ||
| − | Պնդում 8 | + | == Պնդում 8 == |
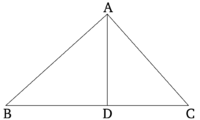
Եթե ուղղանկյուն եռանկյան ուղիղ անկյունից ուղիղ գիծ է գծվում ՝ ուղղահայաց հիմքի վրա, ապա ուղղահայաց գծի շուրջ գտնվող եռանկյունները նման են միմյանց և մեծ ուղանկյուն (եռանկյանը): | Եթե ուղղանկյուն եռանկյան ուղիղ անկյունից ուղիղ գիծ է գծվում ՝ ուղղահայաց հիմքի վրա, ապա ուղղահայաց գծի շուրջ գտնվող եռանկյունները նման են միմյանց և մեծ ուղանկյուն (եռանկյանը): | ||
Դիցուք, ABC ուղղանկյուն եռանկյուն է, որի BAC անկյունը ուղիղ անկյուն է, և թող AD ուղիղ գիծը գծված լինի A կետից՝ ուղղահայաց BC-ին [Պնդ. 1.12]։ ABD և ADC եռանկյունները յուրաքանչյուրն էլ նման են ABC-ին և միմյանց։ | Դիցուք, ABC ուղղանկյուն եռանկյուն է, որի BAC անկյունը ուղիղ անկյուն է, և թող AD ուղիղ գիծը գծված լինի A կետից՝ ուղղահայաց BC-ին [Պնդ. 1.12]։ ABD և ADC եռանկյունները յուրաքանչյուրն էլ նման են ABC-ին և միմյանց։ | ||
| − | + | [[Պատկեր:Pndum8.png|center|200px]] | |
Քանի որ BAC անկյունը հավասար է ADB անկյանը—երկուսն էլ ուղիղ անկյուններ են—իսկ B անկյունը ընդհանուր է ABC և ABD եռանկյունների համար, հետևաբար ACB անկյունը հավասար է BAD անկյանը[Պնդ. 1.32]։ Հետևաբար, ABC եռանկյունը նման է ABD եռանկյանը։ BC գտնվում է ABC եռանկյան ուղիղ անկյան դիմաց, BA ABD եռանկյան ուղիղ անկյան դիմաց, AB-ն, C անկյան դիմաց ABC- ում, (այդպես էլ) BD-ը, որը գտնվումէ BAD-ի դիմաց ABD եռանկյունում, AC և AD , (երկուսն էլ) B անկյանն են նայում, որը ընդհանուր է երկու եռանկյունների համար [Պնդ. 6.4]։ Հետևաբար, ABC եռանկյունը նման է ABD եռանկյանը և ունի հավասար անկյունների համապատասխան կողմերի նույն հարաբերությունը։ Հետևաբար, ABC եռանկյունւ նման է ABD եռանկյանը[Սահ. 6.1]։ Նույն կերպ, կարող ենք ցույց տալ, որ եռանկյուն ABC-ն նույնպես նման է ADC եռանկյանը։ Այսպիսով, ABD և ADC [եռանկյունները] նման են ABC եռանկյանը։ | Քանի որ BAC անկյունը հավասար է ADB անկյանը—երկուսն էլ ուղիղ անկյուններ են—իսկ B անկյունը ընդհանուր է ABC և ABD եռանկյունների համար, հետևաբար ACB անկյունը հավասար է BAD անկյանը[Պնդ. 1.32]։ Հետևաբար, ABC եռանկյունը նման է ABD եռանկյանը։ BC գտնվում է ABC եռանկյան ուղիղ անկյան դիմաց, BA ABD եռանկյան ուղիղ անկյան դիմաց, AB-ն, C անկյան դիմաց ABC- ում, (այդպես էլ) BD-ը, որը գտնվումէ BAD-ի դիմաց ABD եռանկյունում, AC և AD , (երկուսն էլ) B անկյանն են նայում, որը ընդհանուր է երկու եռանկյունների համար [Պնդ. 6.4]։ Հետևաբար, ABC եռանկյունը նման է ABD եռանկյանը և ունի հավասար անկյունների համապատասխան կողմերի նույն հարաբերությունը։ Հետևաբար, ABC եռանկյունւ նման է ABD եռանկյանը[Սահ. 6.1]։ Նույն կերպ, կարող ենք ցույց տալ, որ եռանկյուն ABC-ն նույնպես նման է ADC եռանկյանը։ Այսպիսով, ABD և ADC [եռանկյունները] նման են ABC եռանկյանը։ | ||
Այսպիսով, եռանկյունները ABD և ADC նույնպես նման են միմյանց։ | Այսպիսով, եռանկյունները ABD և ADC նույնպես նման են միմյանց։ | ||
| Տող 172. | Տող 114. | ||
*Այլ կերպ ասած, ուղղահայացը հիմքի հատվածների երկրաչափական միջինն է։ | *Այլ կերպ ասած, ուղղահայացը հիմքի հատվածների երկրաչափական միջինն է։ | ||
| − | Պնդում 9 | + | == Պնդում 9 == |
Տրված ուղիղ գծից հարկավոր է կտրել սահմանված մասը: | Տրված ուղիղ գծից հարկավոր է կտրել սահմանված մասը: | ||
| − | + | [[Պատկեր:Pndum9.png|center|200px]] | |
Դիցուք, AB լինի ուղիղ գիծ։ Այպիսով, AB-ից պահանջվում է կտրել սահմանված մասը։ | Դիցուք, AB լինի ուղիղ գիծ։ Այպիսով, AB-ից պահանջվում է կտրել սահմանված մասը։ | ||
Եկեք նշանակենք A կետից գծենք AC ուղիղ գիծը, որը կազմում է կամայական անկյուն AB-ի հետ։ AC գծի վրա նշանակենք D կետը ։ Թող DE և EC հատվածները լինեն հավասար AD հատվածին [Պնդ. 1.3] և միացնենք BC։ DF գիծը գծենք D կետի միջոցով՝ որը ուգահեռ կլինի BC գծին [Պնդ. 1.31]։ | Եկեք նշանակենք A կետից գծենք AC ուղիղ գիծը, որը կազմում է կամայական անկյուն AB-ի հետ։ AC գծի վրա նշանակենք D կետը ։ Թող DE և EC հատվածները լինեն հավասար AD հատվածին [Պնդ. 1.3] և միացնենք BC։ DF գիծը գծենք D կետի միջոցով՝ որը ուգահեռ կլինի BC գծին [Պնդ. 1.31]։ | ||
| Տող 182. | Տող 124. | ||
| − | Պնդում 10 | + | == Պնդում 10 == |
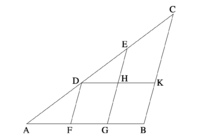
Տրված չկտրվող ուղիղ գիծը կտրել այնպես, ինչպես տվյալ կտրված ուղիղ գիծը: | Տրված չկտրվող ուղիղ գիծը կտրել այնպես, ինչպես տվյալ կտրված ուղիղ գիծը: | ||
| − | + | [[Պատկեր:Pnum10.png|center|200px]] | |
Դիցուք, AB տրված չկտրվող ուղիղ գիծն է, և AC ուղիղ գիծը, որը կտրված է D և E կետերում։ Թող AC գիծը տարվի այնպես, որ կազմի կամայական AB անկյան հետ։ Ապա, CB գիծը միացնենք։ DF և EG գծերը գծվեն D և E կետերով (համապատասխանաբար)՝ զուգահեռ BC գծին, և թող HK գիծը գծվի D կետի միջով՝ զուգահեռ AB գծին [Պնդ. 1.31]։ | Դիցուք, AB տրված չկտրվող ուղիղ գիծն է, և AC ուղիղ գիծը, որը կտրված է D և E կետերում։ Թող AC գիծը տարվի այնպես, որ կազմի կամայական AB անկյան հետ։ Ապա, CB գիծը միացնենք։ DF և EG գծերը գծվեն D և E կետերով (համապատասխանաբար)՝ զուգահեռ BC գծին, և թող HK գիծը գծվի D կետի միջով՝ զուգահեռ AB գծին [Պնդ. 1.31]։ | ||
Հետևաբար, FH և HB-ը զուգահեռագծեր են։ DH-ը հավասար է FG-ին, իսկ HK-ն՝ GB-ին [Պնդ. 1.34]։ Քանի որ, HE ուղիղ գիծը գծված է զուգահեռ DKC եռանկյան KC կողմին, ապա համապատասխանաբար, ինչպես CE հարաբերվում է ED-ին, այնպես էլ KH հարաբերում HD-իմ[Պնդ. 6.2]։KH-ն հավասար է BG-ին, իսկ HD-ն՝ GF-ին։ Հետևաբար, ինչպես CE և ED հատվածների հարաբերությունն է, այնպես էլ BG և GF հատվածներինը։ Քանի որ, FD գիծը գծված է զուգահեռ AGE եռանկյան GE կողմին, ապա համապատասխանաբար, ինչպես ED հարաբերում է DA-ին, այնպես էլ GF- ը FA-ի հատվածին [Պնդ. 6.2]։ Եվ ցույց է տրվել, CE և ED հարաբերակցությունը հավասար է BG և GF- ի հարաբերակցությանը ։ Հետևաբար, ինչպես CE հարաբերում ED-ին, այնպես էլ BG՝ GF-ին, և ինչպես ED՝DA-ին, այնպես էլ GF՝ FA հատվածին։ | Հետևաբար, FH և HB-ը զուգահեռագծեր են։ DH-ը հավասար է FG-ին, իսկ HK-ն՝ GB-ին [Պնդ. 1.34]։ Քանի որ, HE ուղիղ գիծը գծված է զուգահեռ DKC եռանկյան KC կողմին, ապա համապատասխանաբար, ինչպես CE հարաբերվում է ED-ին, այնպես էլ KH հարաբերում HD-իմ[Պնդ. 6.2]։KH-ն հավասար է BG-ին, իսկ HD-ն՝ GF-ին։ Հետևաբար, ինչպես CE և ED հատվածների հարաբերությունն է, այնպես էլ BG և GF հատվածներինը։ Քանի որ, FD գիծը գծված է զուգահեռ AGE եռանկյան GE կողմին, ապա համապատասխանաբար, ինչպես ED հարաբերում է DA-ին, այնպես էլ GF- ը FA-ի հատվածին [Պնդ. 6.2]։ Եվ ցույց է տրվել, CE և ED հարաբերակցությունը հավասար է BG և GF- ի հարաբերակցությանը ։ Հետևաբար, ինչպես CE հարաբերում ED-ին, այնպես էլ BG՝ GF-ին, և ինչպես ED՝DA-ին, այնպես էլ GF՝ FA հատվածին։ | ||
| Տող 191. | Տող 133. | ||
| − | Պնդում 11 | + | == Պնդում 11 == |
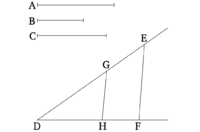
Հարկավոր է գտնել երրորդ ուղիղ գիծը, որը համաչափ է մյուս երկու ուղիղ գծերին: | Հարկավոր է գտնել երրորդ ուղիղ գիծը, որը համաչափ է մյուս երկու ուղիղ գծերին: | ||
Դիցուք, BA և AC տրված երկու ուղիղ գծերն են, և միասին կազմում են մի կամայական անկյուն։ Պահանջվում է գտնել երրորդ (ուղիղ գիծը), որը համաչափ է BA և AC ուղիղ գծերին։ BA և AC շարունակվեն դեպի D և E կետեր (համապատասխանաբար), և BD-ը հավասար լինի AC-ին [Պնդ. 1.3]։ Այնւհետև,BC գիծը միացվի։ DE գիծը գծեն D կետի միջով՝ զուգահեռ BC գծին [Պնդ. 1.31]։ | Դիցուք, BA և AC տրված երկու ուղիղ գծերն են, և միասին կազմում են մի կամայական անկյուն։ Պահանջվում է գտնել երրորդ (ուղիղ գիծը), որը համաչափ է BA և AC ուղիղ գծերին։ BA և AC շարունակվեն դեպի D և E կետեր (համապատասխանաբար), և BD-ը հավասար լինի AC-ին [Պնդ. 1.3]։ Այնւհետև,BC գիծը միացվի։ DE գիծը գծեն D կետի միջով՝ զուգահեռ BC գծին [Պնդ. 1.31]։ | ||
Քանի որ BC գիծը զուգահեռ է ADE եռանկյան DE կողմին, ապա համաչափորեն, ինչպես AB հարաբերում է BD-ին, այնպես էլ AC CE հատվածին [Պնդ. 6.2]։ Իսկ BD-ը հավասար է AC-ին։ Հետևաբար, ինչպես AB և AC հատվածների հարաբերությունն է, այնպես էլ AC և CE հատվածներինը: | Քանի որ BC գիծը զուգահեռ է ADE եռանկյան DE կողմին, ապա համաչափորեն, ինչպես AB հարաբերում է BD-ին, այնպես էլ AC CE հատվածին [Պնդ. 6.2]։ Իսկ BD-ը հավասար է AC-ին։ Հետևաբար, ինչպես AB և AC հատվածների հարաբերությունն է, այնպես էլ AC և CE հատվածներինը: | ||
| − | + | [[Պատկեր:Pndum11.png|center|200px]] | |
Այսպիսով, գտանք CE ուղիղ գիծը, որը համաչափ է տրված երկու ուղիղ գծերին՝ AB և AC։ Ապացուցվեց այն, ինչը պահանջվում էր: | Այսպիսով, գտանք CE ուղիղ գիծը, որը համաչափ է տրված երկու ուղիղ գծերին՝ AB և AC։ Ապացուցվեց այն, ինչը պահանջվում էր: | ||
| − | Պնդում 12 | + | == Պնդում 12 == |
Պահանջվում է գտնել չորրորդ ուղիղ գիծը , որը համաչափ կլինի տրված երեք ուղիղ գծերին: | Պահանջվում է գտնել չորրորդ ուղիղ գիծը , որը համաչափ կլինի տրված երեք ուղիղ գծերին: | ||
| − | + | [[Պատկեր:Pndum12.png|center|200px]] | |
Դիցուք A, B և C տրված երեք ուղիղ գծերն են։ Պահանջվում է գտնել չորրորդ (ուղիղ գիծը), որը համաչափ է A, B և C ուղիղ գծերին։ | Դիցուք A, B և C տրված երեք ուղիղ գծերն են։ Պահանջվում է գտնել չորրորդ (ուղիղ գիծը), որը համաչափ է A, B և C ուղիղ գծերին։ | ||
DE և DF երկու ուղիղ գծերը կազմում են (կամայական) EDF անկյունը։DG հատվածը հավասար է A հատվածին, GE-ը՝ B-ին, և DH-ը՝ C-ին [Պնդ. 1.3]։ E կետից տանենք ուղիղ, որը զուգահեռ GH գծին [Պնդ. 1.31]։ | DE և DF երկու ուղիղ գծերը կազմում են (կամայական) EDF անկյունը։DG հատվածը հավասար է A հատվածին, GE-ը՝ B-ին, և DH-ը՝ C-ին [Պնդ. 1.3]։ E կետից տանենք ուղիղ, որը զուգահեռ GH գծին [Պնդ. 1.31]։ | ||
| Տող 210. | Տող 152. | ||
| − | Պնդում 13 | + | == Պնդում 13 == |
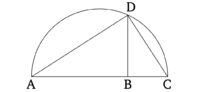
Գտնել ուղիղ գիծը, որը հավասար է երկու ուղիղ գծերի միջին համամասնությանը: | Գտնել ուղիղ գիծը, որը հավասար է երկու ուղիղ գծերի միջին համամասնությանը: | ||
| − | + | [[Պատկեր:Pndum13.png|center|200px]] | |
Դիցուք, AB և BC տրված երկու ուղիղ գծերն են։ Պահանջվում է գտնել AB և BC ուղիղ գծերի միջին համամասնությանը հավասար (ուղիղ գիծը)։ | Դիցուք, AB և BC տրված երկու ուղիղ գծերն են։ Պահանջվում է գտնել AB և BC ուղիղ գծերի միջին համամասնությանը հավասար (ուղիղ գիծը)։ | ||
AB և BC գտնվում են ուղիղ գծի վրա: Գծենք ADC կիսաշրջանագիծը, որի համար AC հատվածը հանդիսանում է տրամագիծը [Պնդ. 1.10]։ BD գիծը գծենք B կետից ուղիղ գիծ տանելով, որը ուղղահայաց կլինի AC հատվածին [Պնդ. 1.11]։ Այնուհետև, D կետից ուղիղներ տանելով, կազմենէ AD և DC գծերը։ | AB և BC գտնվում են ուղիղ գծի վրա: Գծենք ADC կիսաշրջանագիծը, որի համար AC հատվածը հանդիսանում է տրամագիծը [Պնդ. 1.10]։ BD գիծը գծենք B կետից ուղիղ գիծ տանելով, որը ուղղահայաց կլինի AC հատվածին [Պնդ. 1.11]։ Այնուհետև, D կետից ուղիղներ տանելով, կազմենէ AD և DC գծերը։ | ||
| Տող 220. | Տող 162. | ||
| − | Պնդում 14 | + | == Պնդում 14 == |
Հավասար և հավասարանկյուն զուգահեռագծերում հավասար անկյուններին համապատասխան կողմերը փոխադարձաբար համեմատական են։ Այդ հավասարանկյուն զուգահեռագծերը իրար հավասար են, քանի որ հավասար անկյունների կողմերը փոխադարձաբար համեմատական են են: | Հավասար և հավասարանկյուն զուգահեռագծերում հավասար անկյուններին համապատասխան կողմերը փոխադարձաբար համեմատական են։ Այդ հավասարանկյուն զուգահեռագծերը իրար հավասար են, քանի որ հավասար անկյունների կողմերը փոխադարձաբար համեմատական են են: | ||
Դիցուք, AB և BC հավասար և հավասարանկյուն զուգահեռագծեր են, որոնց B անկյունները հավասար են։ DB և BE գծերը դրված են մի ուղղի վրա։ Հետևաբար, FB և BG գծերը նույնպես մի ուղղու վրա են [Պնդ. 1.14]։ Հարկ է նշել, որ AB և BC զուգահեռագծերի հավասար անկյունների գտնվող կողմերը փոխադարձաբար համեմատական են, այսինքն՝ ինչպես DB հարաբերում է BE-ին, այնպես էլ GB-ն՝ BF-ին։ | Դիցուք, AB և BC հավասար և հավասարանկյուն զուգահեռագծեր են, որոնց B անկյունները հավասար են։ DB և BE գծերը դրված են մի ուղղի վրա։ Հետևաբար, FB և BG գծերը նույնպես մի ուղղու վրա են [Պնդ. 1.14]։ Հարկ է նշել, որ AB և BC զուգահեռագծերի հավասար անկյունների գտնվող կողմերը փոխադարձաբար համեմատական են, այսինքն՝ ինչպես DB հարաբերում է BE-ին, այնպես էլ GB-ն՝ BF-ին։ | ||
| − | + | [[Պատկեր:Pndum14.png|center|200px]] | |
Կազմենք նոր FE զուգահեռագիծը։ Քանի որ , AB զուգահեռագիծը հավասար է BC զուգահեռագծին, իսկ FE-ը այլ (զուգահեռագիծ) է, ապա ինչպես AB զուգահեռագիծը է հարաբերվում է FE զուգահեռագծին, այնպես էլ (զուգահեռագիծ) BC-ն՝ FE-ին [Պնդ. 5.7]։Ավելին, ինչպես AB զուգահեռագիծը FE զուգահեռագծին է հարաբերում, այնպես էլ DB հարաբերում է BE-ին, BC-ն FE-ին, այնպես էլ GB-ն՝ BF-ին[Պնդ. 6.1]։ Հետևաբար, DB և BE հարաբերությունը հավասար է, GB և BF զուգահեռագծերի հարաբերությունը։Արդյունքում, AB և BC զուգահեռագծերի համապատասխանաբար հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձաբար համեմատական են միմյանց։ | Կազմենք նոր FE զուգահեռագիծը։ Քանի որ , AB զուգահեռագիծը հավասար է BC զուգահեռագծին, իսկ FE-ը այլ (զուգահեռագիծ) է, ապա ինչպես AB զուգահեռագիծը է հարաբերվում է FE զուգահեռագծին, այնպես էլ (զուգահեռագիծ) BC-ն՝ FE-ին [Պնդ. 5.7]։Ավելին, ինչպես AB զուգահեռագիծը FE զուգահեռագծին է հարաբերում, այնպես էլ DB հարաբերում է BE-ին, BC-ն FE-ին, այնպես էլ GB-ն՝ BF-ին[Պնդ. 6.1]։ Հետևաբար, DB և BE հարաբերությունը հավասար է, GB և BF զուգահեռագծերի հարաբերությունը։Արդյունքում, AB և BC զուգահեռագծերի համապատասխանաբար հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձաբար համեմատական են միմյանց։ | ||
Ինչպես DB հարաբերում է BE զուգահեռագծին, այնպես էլ GB զուգահեռագիծը BF զուգահեռագծին։ Հետևաբար, AB զուգահեռագիծը հավասար է BC զուգահեռագծին։ | Ինչպես DB հարաբերում է BE զուգահեռագծին, այնպես էլ GB զուգահեռագիծը BF զուգահեռագծին։ Հետևաբար, AB զուգահեռագիծը հավասար է BC զուգահեռագծին։ | ||
| Տող 231. | Տող 173. | ||
| − | Պնդում 15 | + | == Պնդում 15 == |
Հավասար եռանկյուններում, որոնց համապատասխան մի անկյունը հավասար է, ապա այդ անկյունների կողմերը փոխադարձ համեմատական են։ Եվ այդ եռանկյունների հավասար անկյունների համապատասխան կողմերը փոխադարձ համեմատական են և հավասար: | Հավասար եռանկյուններում, որոնց համապատասխան մի անկյունը հավասար է, ապա այդ անկյունների կողմերը փոխադարձ համեմատական են։ Եվ այդ եռանկյունների հավասար անկյունների համապատասխան կողմերը փոխադարձ համեմատական են և հավասար: | ||
Դիցուք, ABC և ADE հավասար եռանկյուններ են, ուստի, մի անկյունը՝ BAC հավասար է համապատասխան DAE անկյանը։ABC և ADE եռանկյունների հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են, այսինքն՝ ինչպես CA-ն է AD-ին հարաբերվում, այնպես էլ EA-ն՝ AB-ին։ | Դիցուք, ABC և ADE հավասար եռանկյուններ են, ուստի, մի անկյունը՝ BAC հավասար է համապատասխան DAE անկյանը։ABC և ADE եռանկյունների հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են, այսինքն՝ ինչպես CA-ն է AD-ին հարաբերվում, այնպես էլ EA-ն՝ AB-ին։ | ||
| − | + | [[Պատկեր:Pndum15.png|center|200px]] | |
CA գիծը գծենք այնպես, որ լինի AD-ի ուղիղ շարունակությունը։ Հետևաբար, EA-ն նույնպես AB-ի ուղիղ շարունակությունն է [Պնդ. 1.14]։ B-ից ուղիղ գիծ իջեցնենք D-ին։ | CA գիծը գծենք այնպես, որ լինի AD-ի ուղիղ շարունակությունը։ Հետևաբար, EA-ն նույնպես AB-ի ուղիղ շարունակությունն է [Պնդ. 1.14]։ B-ից ուղիղ գիծ իջեցնենք D-ին։ | ||
Քանի որ, ABC եռանկյունը հավասար է ADE եռանկյանը, իսկ BAD այլ (եռանկյուն) է, ապա ինչպես CAB եռանկյունը հարաբերում է BAD եռանկյանը, այնպես էլ EAD՝BAD-ին[Պնդ. 5.7]։ Ավելին, ինչպես CAB և BAD եռանկյունների հարաբերությունը նունն է, ինչ CA և AD հարաբերությունը, և ինչպես EAD և BAD եռանկյուններինը, այնպես էլ EA և AB հարաբերությունն է[Պնդ. 6.1]։ Եվ հետևաբար, ինչպես CA-ն է AD-ին հարաբերվում, այնպես էլ EA-ն՝ AB-ին։ Հետևաբար, ABC և ADE եռանկյունների հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են։ | Քանի որ, ABC եռանկյունը հավասար է ADE եռանկյանը, իսկ BAD այլ (եռանկյուն) է, ապա ինչպես CAB եռանկյունը հարաբերում է BAD եռանկյանը, այնպես էլ EAD՝BAD-ին[Պնդ. 5.7]։ Ավելին, ինչպես CAB և BAD եռանկյունների հարաբերությունը նունն է, ինչ CA և AD հարաբերությունը, և ինչպես EAD և BAD եռանկյուններինը, այնպես էլ EA և AB հարաբերությունն է[Պնդ. 6.1]։ Եվ հետևաբար, ինչպես CA-ն է AD-ին հարաբերվում, այնպես էլ EA-ն՝ AB-ին։ Հետևաբար, ABC և ADE եռանկյունների հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են։ | ||
| Տող 243. | Տող 185. | ||
| − | Պնդում 16 | + | == Պնդում 16 == |
Եթե չորս ուղիղ գծեր համաչափ են, ապա (երկու) արտաքին կողմերով կազմված ուղղանկյունը հավասար է (երկու) միջին կողմերով կազմված ուղղանկյանը։ Եվ եթե այդ ուղղանկյունները իրար հավասար են, ապա, չորս ուղիղ գծերը կլինեն համաչափ։ | Եթե չորս ուղիղ գծեր համաչափ են, ապա (երկու) արտաքին կողմերով կազմված ուղղանկյունը հավասար է (երկու) միջին կողմերով կազմված ուղղանկյանը։ Եվ եթե այդ ուղղանկյունները իրար հավասար են, ապա, չորս ուղիղ գծերը կլինեն համաչափ։ | ||
| − | + | [[Պատկեր:Pndum16.png|center|200px]] | |
Դիցուք, AB, CD, E և F չորս համաչափ ուղիղ գծեր են (այնպես, որ ինչպես AB հարաբերում է CD հատվածին, այնպես էլ E հատվածի հարաբերությունը F հատվածին)։ AB և F ուղիղ գծերով կազմված ուղղանկյունը հավասար կլինի CD և E հատվածներով կազմված ուղղանկյանը։ | Դիցուք, AB, CD, E և F չորս համաչափ ուղիղ գծեր են (այնպես, որ ինչպես AB հարաբերում է CD հատվածին, այնպես էլ E հատվածի հարաբերությունը F հատվածին)։ AB և F ուղիղ գծերով կազմված ուղղանկյունը հավասար կլինի CD և E հատվածներով կազմված ուղղանկյանը։ | ||
A և C կետերից տանենք ուղիղ գիծ, արդյունքում ստանալով AG և CH գծերը, որոնք ուղղահայաց կլինեն AB և CD կողմերին(համապատասխանաբար) [Պնդ. 1.11]։ AG հատվածի երկարությունը հավասար է F հատվածի երկարությանը, իսկ CH՝ E հատվածի երկարությանը [Պնդ. 1.3]։ Այնուհետև կազմենք BG և DH ուղղանկյունները։ | A և C կետերից տանենք ուղիղ գիծ, արդյունքում ստանալով AG և CH գծերը, որոնք ուղղահայաց կլինեն AB և CD կողմերին(համապատասխանաբար) [Պնդ. 1.11]։ AG հատվածի երկարությունը հավասար է F հատվածի երկարությանը, իսկ CH՝ E հատվածի երկարությանը [Պնդ. 1.3]։ Այնուհետև կազմենք BG և DH ուղղանկյունները։ | ||
| Տող 255. | Տող 197. | ||
| − | Պնդում 17 | + | == Պնդում 17 == |
Եթե երեք ուղիղ գծեր համաչափ են միմյանց, ապա տրված (երկու) արտաքին հատվածներով կազմված ուղղանկյունը հավասար է միջին հատվածներով կազմված քառակուսուն։ Եվ եթե այդ ուղղանկյունը հավասար է քառակուսուն, ապա տվյալ երեք ուղիղ գծերը կլինեն համաչափ։ | Եթե երեք ուղիղ գծեր համաչափ են միմյանց, ապա տրված (երկու) արտաքին հատվածներով կազմված ուղղանկյունը հավասար է միջին հատվածներով կազմված քառակուսուն։ Եվ եթե այդ ուղղանկյունը հավասար է քառակուսուն, ապա տվյալ երեք ուղիղ գծերը կլինեն համաչափ։ | ||
| − | + | [[Պատկեր:Pndum17.png|center|200px]] | |
| − | + | ||
Դիցուք , A, B և C երեք համաչափ ուղիղ գծերեն (այնպես, որ ինչպես A հատվածն է հարաբերում B հատվածին, այնպես էլ B հատվածը C-ին)։ Ուստի, կարող եմ ասել ,որ A և C ուղիղ գծերով կառուցված ուղղանկյունը հավասար է B հատվածով կազմված քառակուսուն։ | Դիցուք , A, B և C երեք համաչափ ուղիղ գծերեն (այնպես, որ ինչպես A հատվածն է հարաբերում B հատվածին, այնպես էլ B հատվածը C-ին)։ Ուստի, կարող եմ ասել ,որ A և C ուղիղ գծերով կառուցված ուղղանկյունը հավասար է B հատվածով կազմված քառակուսուն։ | ||
Ուստի, D հատվածը հավասար են B հատվածին [Պնդ. 1.3]։ | Ուստի, D հատվածը հավասար են B հատվածին [Պնդ. 1.3]։ | ||
| Տող 268. | Տող 209. | ||
| − | Պնդում 18 | + | == Պնդում 18 == |
Նկարագրել ուղղագիծ պատկեր, որը նման է տրված ուղղագծային պատկերին: | Նկարագրել ուղղագիծ պատկեր, որը նման է տրված ուղղագծային պատկերին: | ||
| − | + | [[Պատկեր:Pndum18.png|center|200px]] | |
Դիցուք, AB տրված ուղիղ գիծն է,իսկ CE՝ տրված ուղղագծային պատկերը։ Անհրաժեշտ է նկարագրել ուղղագծային պատկեր, որը նման է CE ուղղագծային պատկերը ,որը կազմված կլինի AB ուղիղ գծի վրա: | Դիցուք, AB տրված ուղիղ գիծն է,իսկ CE՝ տրված ուղղագծային պատկերը։ Անհրաժեշտ է նկարագրել ուղղագծային պատկեր, որը նման է CE ուղղագծային պատկերը ,որը կազմված կլինի AB ուղիղ գծի վրա: | ||
D միացնենք F-ին, GAB անկյունը, որը հավասար է C անկյանը, և ABG անկյունը, որը հավասար է CDF անկյանը, այնուհետև A և B կետերով տարած ուղիղ գիծը՝ համապատասխանաբար [Պնդ. 1.23]։ Այսպիսով, CFD անկյունը հավասար է AGB անկյանը [Պնդ. 1.32]։ Հետևաբար, FCD եռանկյունը հավասարանկյուն է GAB եռանկյանը։ Այսպիսով, համապատասխանաբար, ինչպես FD հարաբերում է GB-ին, այնպես էլ FC ՝GA-ին, իսկ CD-ն՝ AB-ին [Պնդ. 6.4]։ Այսպիսով, BGH անկյունը, որը հավասար է DFE և GBH անկյանը, որը հավասար է FDE անկյանը, կկառուցվեն ուղիղ գծի՝ BG-ի G և B կետերում համապատասխանաբար [Պնդ. 1.23]։ Այսպիսով, E առընթեր անկյունը հավասար է H առընթեր անկյանը [Պնդ. 1.32]։ Հետևաբար, FDE եռանկյունը հավասարանկյուն է GHB եռանկյանը։ Այսպիսով, համապատասխանաբար, ինչպես FD և GB մհարաբերվում, այնպես էլ FE և GH-ն, իսկ ED-ն՝ HB-ին [Պնդ. 6.4]։ Ավելին, որ ինչպես FD և GB հարաբերությունն է, այնպես էլ FC և GA ունեն նույն հարաբերությունը, CD և AB նույնպես։ Հետևաբար, ինչպես FC-ն GA-ին է հարաբերում, այնպես էլ CD՝ AB-ին, և FE-ն՝ GH-ին, և, վերջապես, ED-ն՝ HB-ին։ Քանի որ, CFD անկյունը հավասար է AGB անկյանը, իսկ DFE անկյունը՝ BGH անկյանը, ապա ամբողջ CFE անկյունը հավասար կլինի ամբողջական AGH անկյանը։ Նույն կերպ, CDE անկյունը հավասար է ABH անկյանը։ C անկյունը նույնպես հավասար է A անկյանը, իսկ E անկյունը՝ H անկյանը։ Այսպիսով, AH պատկերը հավասարանկյուն է CE-ին։ Երկու պատկերների հավասար անկյուններին համապատասխան կողմերը համաչափ են։ Հետևաբար, AH ուղղագիծ պատկերը նման է CE ուղղագծային պատկերին [Սահմ. 6.1]։ | D միացնենք F-ին, GAB անկյունը, որը հավասար է C անկյանը, և ABG անկյունը, որը հավասար է CDF անկյանը, այնուհետև A և B կետերով տարած ուղիղ գիծը՝ համապատասխանաբար [Պնդ. 1.23]։ Այսպիսով, CFD անկյունը հավասար է AGB անկյանը [Պնդ. 1.32]։ Հետևաբար, FCD եռանկյունը հավասարանկյուն է GAB եռանկյանը։ Այսպիսով, համապատասխանաբար, ինչպես FD հարաբերում է GB-ին, այնպես էլ FC ՝GA-ին, իսկ CD-ն՝ AB-ին [Պնդ. 6.4]։ Այսպիսով, BGH անկյունը, որը հավասար է DFE և GBH անկյանը, որը հավասար է FDE անկյանը, կկառուցվեն ուղիղ գծի՝ BG-ի G և B կետերում համապատասխանաբար [Պնդ. 1.23]։ Այսպիսով, E առընթեր անկյունը հավասար է H առընթեր անկյանը [Պնդ. 1.32]։ Հետևաբար, FDE եռանկյունը հավասարանկյուն է GHB եռանկյանը։ Այսպիսով, համապատասխանաբար, ինչպես FD և GB մհարաբերվում, այնպես էլ FE և GH-ն, իսկ ED-ն՝ HB-ին [Պնդ. 6.4]։ Ավելին, որ ինչպես FD և GB հարաբերությունն է, այնպես էլ FC և GA ունեն նույն հարաբերությունը, CD և AB նույնպես։ Հետևաբար, ինչպես FC-ն GA-ին է հարաբերում, այնպես էլ CD՝ AB-ին, և FE-ն՝ GH-ին, և, վերջապես, ED-ն՝ HB-ին։ Քանի որ, CFD անկյունը հավասար է AGB անկյանը, իսկ DFE անկյունը՝ BGH անկյանը, ապա ամբողջ CFE անկյունը հավասար կլինի ամբողջական AGH անկյանը։ Նույն կերպ, CDE անկյունը հավասար է ABH անկյանը։ C անկյունը նույնպես հավասար է A անկյանը, իսկ E անկյունը՝ H անկյանը։ Այսպիսով, AH պատկերը հավասարանկյուն է CE-ին։ Երկու պատկերների հավասար անկյուններին համապատասխան կողմերը համաչափ են։ Հետևաբար, AH ուղղագիծ պատկերը նման է CE ուղղագծային պատկերին [Սահմ. 6.1]։ | ||
| Տող 277. | Տող 218. | ||
| − | Պնդում 19 | + | == Պնդում 19 == |
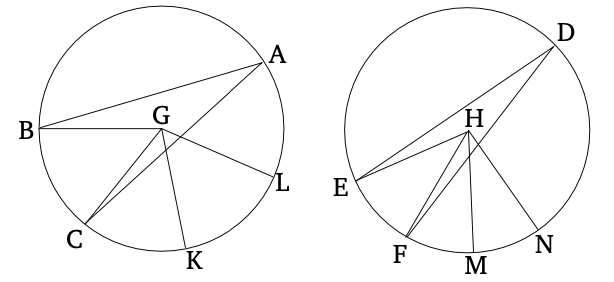
Նման եռանկյունները մեկմեկու ունեն համապատասխան կողմերի քառակուսի հարաբերություն: | Նման եռանկյունները մեկմեկու ունեն համապատասխան կողմերի քառակուսի հարաբերություն: | ||
| − | + | [[Պատկեր:Pndum19.png|center|200px]] | |
Դիցուք, ABC և DEF նման եռանկյուններ են, որտեղ B անկյունը հավասար է E անկյանը, իսկ AB հարաբերում է BC կողմին այնպես, ինչպես DE հարաբերում է EF կողմին, ընդ որում BC-ը համընկնում է EF-ի հետ։ Ուստի, ABC եռանկյունը ունի քառակուսի հարաբերություն DEF եռանկյան հետ՝ BC և EF կողմի քառակուսի հարաբերությամբ։ | Դիցուք, ABC և DEF նման եռանկյուններ են, որտեղ B անկյունը հավասար է E անկյանը, իսկ AB հարաբերում է BC կողմին այնպես, ինչպես DE հարաբերում է EF կողմին, ընդ որում BC-ը համընկնում է EF-ի հետ։ Ուստի, ABC եռանկյունը ունի քառակուսի հարաբերություն DEF եռանկյան հետ՝ BC և EF կողմի քառակուսի հարաբերությամբ։ | ||
BG ուղիղ գիծը գծենք այնպես, որ համեմատական լինի BC և EF-ի հետ, որպեսզի ինչպես BC և EF հարաբերությունը լինի, այնպես ինչպես EF՝ BG-ին [Պնդ. 6.11]։ Եվ թող A կետից հիմքին տանենք ուղիղ ։ | BG ուղիղ գիծը գծենք այնպես, որ համեմատական լինի BC և EF-ի հետ, որպեսզի ինչպես BC և EF հարաբերությունը լինի, այնպես ինչպես EF՝ BG-ին [Պնդ. 6.11]։ Եվ թող A կետից հիմքին տանենք ուղիղ ։ | ||
| Տող 292. | Տող 233. | ||
| − | Պնդում 20 | + | == Պնդում 20 == |
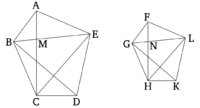
Նման բազմանկյունները կարող են բաժանվել նույն թվով նման եռանկյունների, որոնք համամասն են ամբողջական բազմանկյանը, և բազմանկյունը այլ բազմանկյան հետ քառակուսի հարաբերություն՝ համապատասխանաբար կողմով: | Նման բազմանկյունները կարող են բաժանվել նույն թվով նման եռանկյունների, որոնք համամասն են ամբողջական բազմանկյանը, և բազմանկյունը այլ բազմանկյան հետ քառակուսի հարաբերություն՝ համապատասխանաբար կողմով: | ||
| − | + | [[Պատկեր:Pndum20.png|center|200px]] | |
Դիցուք, ABCDE և FGHKL նման բազմանկյուններ են, որտեղ AB կողմը համապատասխանում է FG կողմին։ Նշենք, որ ABCDE և FGHKL բազմանկյունները կարելի է բաժանել նույն թվով նման եռանկյունների, որոնք համամասն են ամբողջական բազմանկյանը, ABCDE բազմանկյունը ունի քառակուսի հարաբերություն FGHKL բազմանկյան նկատմամբ՝ AB և FG կողմերի հարաբերությամբ։ | Դիցուք, ABCDE և FGHKL նման բազմանկյուններ են, որտեղ AB կողմը համապատասխանում է FG կողմին։ Նշենք, որ ABCDE և FGHKL բազմանկյունները կարելի է բաժանել նույն թվով նման եռանկյունների, որոնք համամասն են ամբողջական բազմանկյանը, ABCDE բազմանկյունը ունի քառակուսի հարաբերություն FGHKL բազմանկյան նկատմամբ՝ AB և FG կողմերի հարաբերությամբ։ | ||
BE, EC, GL և LH գծերը միացնենք իրար։ | BE, EC, GL և LH գծերը միացնենք իրար։ | ||
| Տող 309. | Տող 250. | ||
| − | Պնդում 21 | + | == Պնդում 21 == |
Ոււղղագիծ պատկերները, որոնք նման են միևնույն ուղղագծին, նույնպես միմյանց նման են: | Ոււղղագիծ պատկերները, որոնք նման են միևնույն ուղղագծին, նույնպես միմյանց նման են: | ||
| − | + | [[Պատկեր:Pndum21.png|center|200px]] | |
Դիցուք, A և B ուղղագիծ պատկերները նման լինեն C ուղղագիծ-ուղղանկյունաձև պատկերին։ Պետք է ցույց տալ, որ A-ն նույնպես նման է B-ին։ | Դիցուք, A և B ուղղագիծ պատկերները նման լինեն C ուղղագիծ-ուղղանկյունաձև պատկերին։ Պետք է ցույց տալ, որ A-ն նույնպես նման է B-ին։ | ||
Քանի որ A պատկերը նման է C-ին, ապա A համանկյուն է C-ին և ունի հավասար անկյունների կողմերին համաչափ (համապատասխանող) կողմեր [Սահմ. 6.1]։Նույն կերպ, ինչպես B-ն նման է C-ին, ապա B-ն նույնպես համանկյուն է C-ին և ունի հավասար անկյունների կողմերին համաչափ կողմեր [Սահմ. 6.1]։ | Քանի որ A պատկերը նման է C-ին, ապա A համանկյուն է C-ին և ունի հավասար անկյունների կողմերին համաչափ (համապատասխանող) կողմեր [Սահմ. 6.1]։Նույն կերպ, ինչպես B-ն նման է C-ին, ապա B-ն նույնպես համանկյուն է C-ին և ունի հավասար անկյունների կողմերին համաչափ կողմեր [Սահմ. 6.1]։ | ||
| Տող 318. | Տող 259. | ||
Այսպիսով, A ուղղագիծ պատկերը նման է B պատկերին[Սահմ. 6.1]։ Ապացուցվեց, ինչը որ պահանջվում էր: | Այսպիսով, A ուղղագիծ պատկերը նման է B պատկերին[Սահմ. 6.1]։ Ապացուցվեց, ինչը որ պահանջվում էր: | ||
| − | + | == Պնդում 22 == | |
| − | Պնդում 22 | + | |
Եթե չորս ուղիղ գծերը համաչափ են, համանման և նույն կերպ նկարագրված գծված, ապա իրենցով կազմված ուղղագիծ պատկերները նույնպես համաչափ կլինեն: Եվ եթե նմանատիպ և նույն կերպ նկարագրված ուղղագիծ պատկերները (գծված) համաչափ են, ապա ուղիղ գծերն իրենք նույնպես համաչափ կլինեն: | Եթե չորս ուղիղ գծերը համաչափ են, համանման և նույն կերպ նկարագրված գծված, ապա իրենցով կազմված ուղղագիծ պատկերները նույնպես համաչափ կլինեն: Եվ եթե նմանատիպ և նույն կերպ նկարագրված ուղղագիծ պատկերները (գծված) համաչափ են, ապա ուղիղ գծերն իրենք նույնպես համաչափ կլինեն: | ||
| − | + | [[Պատկեր:Pndum22.png|center|200px]] | |
Դիցուք, AB, CD, EF և GH չորս համեմատական ուղիղ գծեր են՝ այնպես, որ AB հարաբերում է CD-ին այնպես, ինչպես EF՝GH-ին: Եվ թող AB և CD գծերի վրա կառուցված լինեն KAB և LCD ուղղագծային պատկերները, որոնք նման են և դրված են նմանապես, իսկ EF և GH գծերի վրա կառուցված լինեն MF և NH ուղղագծային պատկերները, որոնք նույնպես նման են և դրված են նմանապես:Նշենք, որ KAB հարաբերի LCD-ին է, ինչպես MF՝ NH-ին: | Դիցուք, AB, CD, EF և GH չորս համեմատական ուղիղ գծեր են՝ այնպես, որ AB հարաբերում է CD-ին այնպես, ինչպես EF՝GH-ին: Եվ թող AB և CD գծերի վրա կառուցված լինեն KAB և LCD ուղղագծային պատկերները, որոնք նման են և դրված են նմանապես, իսկ EF և GH գծերի վրա կառուցված լինեն MF և NH ուղղագծային պատկերները, որոնք նույնպես նման են և դրված են նմանապես:Նշենք, որ KAB հարաբերի LCD-ին է, ինչպես MF՝ NH-ին: | ||
Դիցուք, O ուղիղ գիծը, որը համեմատական է AB և CD գծերին, և P՝ երրորդ ուղիղ գիծ, որը համեմատական է EF և GH գծերին [Պնդ. 6.11]: Եվ քանի որ AB հարաբերում է CD-ին այնպես, ինչպես EF՝GH-ին, և CD՝O-ին, GH՝P-ին, ապա հավասարության սկզբունքով՝ AB կհարաբերի O-ին, ինչպես EF՝P-ին [Պնդ. 5.22]:Ավելին, ինչպես AB հարաբերում O-ին, այնպես էլ KAB՝LCD-ին, ինպես EF՝ P-ին, այնպես էլ MF՝NH-իմ [Պ նդ. 5.19՝]: Եվ, հետևաբար, KAB կհարաբերի LCD-ին, ինչպես MF՝NH-ին: | Դիցուք, O ուղիղ գիծը, որը համեմատական է AB և CD գծերին, և P՝ երրորդ ուղիղ գիծ, որը համեմատական է EF և GH գծերին [Պնդ. 6.11]: Եվ քանի որ AB հարաբերում է CD-ին այնպես, ինչպես EF՝GH-ին, և CD՝O-ին, GH՝P-ին, ապա հավասարության սկզբունքով՝ AB կհարաբերի O-ին, ինչպես EF՝P-ին [Պնդ. 5.22]:Ավելին, ինչպես AB հարաբերում O-ին, այնպես էլ KAB՝LCD-ին, ինպես EF՝ P-ին, այնպես էլ MF՝NH-իմ [Պ նդ. 5.19՝]: Եվ, հետևաբար, KAB կհարաբերի LCD-ին, ինչպես MF՝NH-ին: | ||
| Տող 328. | Տող 268. | ||
Եվ քանի որ AB՝ CD-ին հարաբերում է, ինչպես EF՝QR-ին, ապա AB և CD գծերի վրա կառուցված KAB և LCD նման և նմանապես դրված ուղղագծային պատկերները համեմատական են , EF և QR գծերի վրա կառուցված MF և SR նման պատկերների հետ, հետևաբար KAB հարաբերվում է LCD-ին, ինչպես MF՝ SR-ին: Ենթադրվում է, որ KAB կհարաբերի LCD-ին, ինչպես MF՝NH-ին: Հետևաբար, MF հարաբերում է SR-իմ, ինչպես MF՝NH-ին [Պնդ. 5.11]: MF և NH հարաբերությունը հավասար է SR և NH հարաբերությանը: Հետևաբար, NH-ը հավասար է SR-ին [Պնդ. 5.9]: Եվ NH-ը նման է և նմանապես դրված է SR-ին: Հետևաբար, GH-ը հավասար է QR-ին: Եվ քանի որ AB հարաբերում է CD-ին, ինչպես EF՝QR-ին, իսկ QR-ը հավասար է GH-ին, հետևաբար AB հարաբերում է CD-ին, ինչպես EF՝GH-ին: | Եվ քանի որ AB՝ CD-ին հարաբերում է, ինչպես EF՝QR-ին, ապա AB և CD գծերի վրա կառուցված KAB և LCD նման և նմանապես դրված ուղղագծային պատկերները համեմատական են , EF և QR գծերի վրա կառուցված MF և SR նման պատկերների հետ, հետևաբար KAB հարաբերվում է LCD-ին, ինչպես MF՝ SR-ին: Ենթադրվում է, որ KAB կհարաբերի LCD-ին, ինչպես MF՝NH-ին: Հետևաբար, MF հարաբերում է SR-իմ, ինչպես MF՝NH-ին [Պնդ. 5.11]: MF և NH հարաբերությունը հավասար է SR և NH հարաբերությանը: Հետևաբար, NH-ը հավասար է SR-ին [Պնդ. 5.9]: Եվ NH-ը նման է և նմանապես դրված է SR-ին: Հետևաբար, GH-ը հավասար է QR-ին: Եվ քանի որ AB հարաբերում է CD-ին, ինչպես EF՝QR-ին, իսկ QR-ը հավասար է GH-ին, հետևաբար AB հարաբերում է CD-ին, ինչպես EF՝GH-ին: | ||
Այսպիսով, եթե չորս ուղիղ գծերը համաչափ են, համանման և նույն կերպ նկարագրված գծված, ապա իրենցով կազմված ուղղագիծ պատկերները նույնպես համաչափ կլինեն: Եվ եթե նմանատիպ և նույն կերպ նկարագրված ուղղագիծ պատկերները (գծված) համաչափ են, ապա ուղիղ գծերն իրենք նույնպես համաչափ կլինեն: Ապացուցվեց այն, ինչը հարկավոր էր ցույց տալ: | Այսպիսով, եթե չորս ուղիղ գծերը համաչափ են, համանման և նույն կերպ նկարագրված գծված, ապա իրենցով կազմված ուղղագիծ պատկերները նույնպես համաչափ կլինեն: Եվ եթե նմանատիպ և նույն կերպ նկարագրված ուղղագիծ պատկերները (գծված) համաչափ են, ապա ուղիղ գծերն իրենք նույնպես համաչափ կլինեն: Ապացուցվեց այն, ինչը հարկավոր էր ցույց տալ: | ||
| + | |||
| + | |||
| + | |||
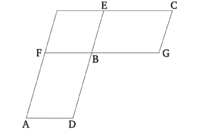
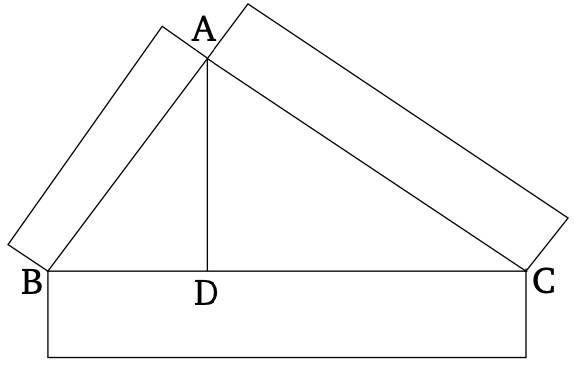
| + | == Առաջարկություն 24 == | ||
| + | |||
| + | Յուրաքանչյուր զուգահեռագծում, անկյունագծի շուրջ կառուցված զուգահեռագծերը նման են թե՛ ամբողջ զուգահեռագծին, թե՛ միմյանց: | ||
| + | Թող ABCD-ը լինի զուգահեռագիծ, իսկ AC-ը՝ նրա անկյունագիծը։ Եվ թող EG և HK լինեն զուգահեռագծեր, կառուցված AC անկյունագծի շուրջ։ Ասում եմ, որ EG և HK զուգահեռագծերը յուրաքանչյուրը նման են ամբողջ (ABCD) զուգահեռագծին և նաև միմյանց: | ||
| + | Քանի որ EF գիծը գծվել է ABC եռանկյան BC կողքին զուգահեռ, համեմատականորեն, ինչպես BE-ը EA-ի նկատմամբ է, այնպես էլ CF-ը FA-ի նկատմամբ [Բան. 6.2]: Նորից, քանի որ FG-ը գծվել է ACD եռանկյան CD կողքին զուգահեռ, նույն կերպ, ինչպես CF-ը FA-ի նկատմամբ է, այնպես էլ DG-ը GA-ի նկատմամբ [Բան. 6.2]: Բայց, ինչպես CF-ը FA-ի նկատմամբ է, նույն կերպ արդեն ցույց տրված է, որ BE-ը EA-ի նկատմամբ է։ Ուստի, ինչպես BE-ը EA-ի նկատմամբ է, այնպես էլ DG-ը GA-ի նկատմամբ։ Եվ, այսպես, համակցելով, ինչպես BA-ը AE-ի նկատմամբ է, այնպես էլ DA-ը AG-ի նկատմամբ [Բան. 5.18]: Եվ, այլընտրանքորեն, ինչպես BA-ը AD-ի նկատմամբ է, այնպես էլ EA-ը AG-ի նկատմամբ [Բան. 5.16]: Այսպիսով, ABCD և EG զուգահեռագծերում BAD ընդհանուր անկյան շուրջ կողմերը համաչափ են։ Եվ քանի որ GF-ը զուգահեռ է DC-ին, AFG անկյունը հավասար է DCA անկյանին [Բան. 1.29]: Եվ DAC անկյունը ընդհանուր է ADC և AGF եռանկյունների համար։ Ուստի ADC եռանկյունը հավանկյուն է AGF եռանկյանը [Բան. 1.32]: Նույն պատճառներով, ACB եռանկյունը հավանկյուն է AFE եռանկյանը, և ամբողջ ABCD զուգահեռագիծը հավանկյուն է EG զուգահեռագծին։ Այսպիսով, համաչափորեն, ինչպես AD-ը DC-ի նկատմամբ է, այնպես էլ AG-ը GF-ի նկատմամբ է, և ինչպես DC-ը CA-ի նկատմամբ է, այնպես էլ GF-ը FA-ի նկատմամբ է, և ինչպես AC-ը CB-ի նկատմամբ է, այնպես էլ AF-ը FE-ի նկատմամբ է, իսկ, հետագայում, ինչպես CB-ը BA-ի նկատմամբ է, այնպես էլ FE-ը EA-ի նկատմամբ [Բան. 6.4]: Եվ քանի որ ցույց տրված էր, որ ինչպես DC-ը CA-ի նկատմամբ է, այնպես էլ GF-ը FA-ի նկատմամբ է, և ինչպես AC-ը CB-ի նկատմամբ է, այնպես էլ AF-ը FE-ի նկատմամբ է, ապա, հավասարությամբ, ինչպես DC-ը CB-ի նկատմամբ է, այնպես էլ GF-ը FE-ի նկատմամբ է [Բան. 5.22]: Այսպիսով, ABCD և EG զուգահեռագծերում հավասար անկյունների շուրջ կողմերը համաչափ են։ Ուստի, ABCD զուգահեռագիծը նման է EG զուգահեռագծին [Սահմանում 6.1]: Նույն (պատճառներով), ABCD զուգահեռագիծը նման է նաև KH զուգահեռագծին։ Այսպիսով, EG և HK զուգահեռագծերը յուրաքանչյուրը նման են [ABCD] զուգահեռագծին։ Եվ (ուղղագծային) պատկերները, որոնք նման են նույն ուղղագծային պատկերին, նաև նման են միմյանց [Բան. 6.21]: Այսպիսով, EG զուգահեռագիծը նույնպես նման է HK զուգահեռագծին։ | ||
| + | [[Պատկեր:1.png]] | ||
| + | Այսպիսով, յուրաքանչյուր զուգահեռագծում անկյունագծի շուրջ գտնվող զուգահեռագծերը նման են թե՛ ամբողջին, թե՛ միմյանց։ | ||
| + | |||
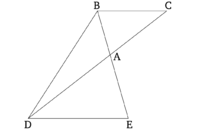
| + | == Առաջարկություն 25 == | ||
| + | Կառուցել մեկ (ուղղագծային պատկեր), որը նման է տրված ուղղագծային պատկերին և հավասար է մեկ այլ տրված ուղղագծային պատկերին։ | ||
| + | Թող ABC լինի տրված ուղղագծային պատկերը, որին պետք է կառուցել նման (ուղղագծային) պատկեր, իսկ D-ը լինի այն (ուղղագծային) պատկերը, որին պետք է հավասար լինի կառուցվող պատկերը։ Արդ, հարկավոր է կառուցել մեկ (ուղղագծային) պատկեր, որը նման է ABC-ին և հավասար է D-ին։ | ||
| + | Քանի որ զուգահեռագիծ BE-ն, հավասար ABC եռանկյունին, թող դրվի BC ուղղագծի վրա [Բան. 1.44], և զուգահեռագիծ CM-ը, հավասար D-ին, (դրվի) CE ուղղագծի վրա, FCE անկյան մեջ, որը հավասար է CBL անկյանին [Բան. 1.45]։ Այդպիսով, BC-ը ուղղագիծ է դեպի CF, իսկ LE-ն դեպի EM [Բան. 1.14]։ Եվ թող BC-ի և CF-ի միջին համեմատականը GH ընդունված լինի [Բան. 6.13]։ Եվ թող KGH պատկերը, նման և նույն կերպ դասավորված ABC-ին, գծված լինի GH-ի վրա [Բան. 6.18]։ | ||
| + | Եվ քանի որ ինչպես BC-ը GH-ի նկատմամբ է, այնպես էլ GH-ը CF-ի նկատմամբ է, իսկ եթե երեք ուղիղ գծեր համաչափ են, ապա ինչպես առաջինը երրորդի նկատմամբ է, այնպես էլ առաջինի վրա կառուցված պատկերն ընդհանրապես նման, նույն կերպ կառուցված երկրորդի վրա գտնվող պատկերին է [Բան. 6.19 ճշգրտում], ապա ինչպես BC-ը CF-ի նկատմամբ է, այնպես էլ ABC եռանկյունը KGH եռանկյան նկատմամբ է։ Բայց նաև, ինչպես BC-ը CF-ի նկատմամբ է, այնպես էլ BE զուգահեռագիծը EF զուգահեռագծի նկատմամբ է [Բան. 6.1]։ Ուստի, ինչպես ABC եռանկյունը KGH եռանկյան նկատմամբ է, նույնպես BE զուգահեռագիծը EF զուգահեռագծի նկատմամբ է։ Այսպես, այլընտրանքորեն, ինչպես ABC եռանկյունը BE զուգահեռագծի նկատմամբ է, այնպես էլ KGH եռանկյունը EF զուգահեռագծի նկատմամբ է [Բան. 5.16]։ Եվ քանի որ ABC եռանկյունը հավասար է BE զուգահեռագծին, հետևաբար KGH եռանկյունը նույնպես հավասար է EF զուգահեռագծին։ Բայց EF զուգահեռագիծը հավասար է D-ին։ Արդ, KGH-ն նույնպես հավասար է D-ին։ Եվ KGH-ն նաև նման է ABC-ին։ | ||
| + | Այսպիսով, մեկ (ուղղագծային) պատկեր KGH կառուցվեց, որը նման է տրված ուղղագծային պատկերին ABC և հավասար է այլ տրված (ուղղագծային) պատկերի D։ (Այս) հենց այն էր, ինչ պետք էր անել։ | ||
| + | |||
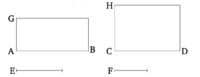
| + | ==Առաջարկություն 26== | ||
| + | |||
| + | Եթե զուգահեռագծից հանվի այլ զուգահեռագիծ, որը նման է և նույն կերպ դասավորված ամբողջին և ունի նրա հետ ընդհանուր անկյուն, ապա (հանված զուգահեռագիծը) կլինի նույն անկյունագծի շուրջ, ինչ ամբողջը։ | ||
| + | Քանզի զուգահեռագիծ ABCD-ից թող հանվի AF զուգահեռագիծը, որը նման և նույն կերպ դասավորված է ABCD-ին, ունենալով նրա հետ ընդհանուր DAB անկյունը։ Ասում եմ, որ ABCD-ը նույն անկյունագծի շուրջ է, ինչ AF-ը։ | ||
| + | [[Պատկեր:1.2.png]] | ||
| + | Եթե ոչ, ապա ենթադրենք հնարավոր է, որ AHC լինի [ABCD]-ի անկյունագիծը։ Եվ շարունակելով GF գիծը, թող այն անցնի H կետով։ Եվ թող HK-ը նույնպես գծվի H կետով, զուգահեռ AD-ին կամ BC-ին [Բան. 1.31]։ | ||
| + | Ուստի, քանի որ ABCD-ը նույն անկյունագծի շուրջ է, ինչ KG-ը, ապա ինչպես DA-ը AB-ի նկատմամբ է, այնպես էլ GA-ն AK-ի նկատմամբ [Բան. 6.24]։ Եվ ABCD և EG զուգահեռագծերի նմանության շնորհիվ, ինչպես DA-ը AB-ի նկատմամբ է, այնպես էլ GA-ը AE-ի նկատմամբ է։ Այսպիսով, ինչպես GA-ը AK-ի նկատմամբ է, այնպես էլ GA-ը AE-ի նկատմամբ է։ Ուրեմն GA-ն նույն հարաբերությունն ունի AK-ի և AE-ի նկատմամբ։ Հետևաբար AE-ը հավասար է AK-ին [Բան. 5.9], ավելի փոքրն ավելի մեծին։ Սա անհնար է։ Արդ, ABCD-ը չէ նույն անկյունագծի շուրջ, ինչ AF-ը։ Ուստի ABCD զուգահեռագիծը նույն անկյունագծի շուրջ է, ինչ AF զուգահեռագիծը։ | ||
| + | Այսպիսով, եթե զուգահեռագծից հանվի այլ զուգահեռագիծ, որը նման է և նույն կերպ դասավորված ամբողջին և ունի նրա հետ ընդհանուր անկյուն, ապա (հանված զուգահեռագիծը) նույն անկյունագծի շուրջ է, ինչ ամբողջը։ (Ահա թե ինչ էր կարիքը ցույց տալու)։ | ||
| + | |||
| + | == Առաջարկություն 27 == | ||
| + | |||
| + | Բոլոր այն զուգահեռագծերից, որոնք դրված են նույն ուղղագծի վրա և թերանում են հանման հետևանքով առաջացած զուգահեռագծային պատկերներով, որոնք նման են և նույն կերպ դասավորված այն (զուգահեռագծին), որ կառուցված է ուղղագծի կեսի վրա, ամենամեծը այն զուգահեռագիծն է, որը դրված է այդ կեսի վրա և նման է այն (զուգահեռագծին), որի միջոցով թերանում է։ | ||
| + | Թող AB լինի ուղղագիծ և թող այն բաժանված լինի կեսի վրա C կետով [Բան. 1.10]։ Եվ թող AD զուգահեռագիծը դրված լինի AB ուղղագծի վրա, թերանալով DB զուգահեռագծային պատկերով, որը կիրառված է AB-ի կեսին, այն է՝ CB-ին։ Ասում եմ, որ բոլոր այն զուգահեռագծերից, որոնք դրված են AB-ի վրա և թերանում են DB-ին նման և նույն կերպ դասավորված զուգահեռագծային պատկերներով, ամենամեծը AD-ն է։ Քանզի թող AF զուգահեռագիծը դրված լինի AB-ի վրա, թերանալով FB զուգահեռագծային պատկերով, որը նույնպես նման է և նույն կերպ դասավորված DB-ին։ Ասում եմ, որ AD-ն մեծ է AF-ից։ | ||
| + | [[Պատկեր:1.3.png]] | ||
| + | Քանի որ DB զուգահեռագիծը նման է FB զուգահեռագծին, ապա դրանք նույն անկյունագծի շուրջ են [Բան. 6.26]։ Թող նրանց (ընդհանուր) անկյունագիծը DB գծվի, և թող պատկերի մնացորդը լրացվի։ | ||
| + | Ուստի, քանի որ (լրացնող) CF-ը հավասար է (լրացնող) FE-ին [Բան. 1.43], և FB զուգահեռագիծը ընդհանուր է, ապա ամբողջ CH զուգահեռագիծը հավասար է ամբողջ KE զուգահեռագծին։ Բայց CH զուգահեռագիծը հավասար է CG-ին, քանի որ AC-ը նույնպես հավասար է CB-ին [Բան. 6.1]։ Ուստի GC զուգահեռագիծը նույնպես հավասար է EK-ին։ Թող CF զուգահեռագիծը ավելացվի երկուսին էլ։ Արդ, ամբողջ AF զուգահեռագիծը հավասար է LMN գномոնին։ Հետևաբար, DB զուգահեռագիծը, այսինքն AD-ը, մեծ է AF զուգահեռագծից։ | ||
| + | Այսպիսով, բոլոր այն զուգահեռագծերի համար, որոնք կիրառված են նույն ուղղագծի վրա և թերանում են (հանման հետևանքով առաջացած) զուգահեռագծային պատկերով, որը նման է և նույն կերպ դասավորված է այն զուգահեռագծին, որ կառուցված է ուղղագծի կեսի վրա, ամենամեծը այն է, որը դրված է հենց այդ կեսի վրա։ (Դա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | == Առաջարկություն 28 == | ||
| + | |||
| + | Որպեսզի ուղղագծին կիրառվի զուգահեռագիծ, հավասար տրված ուղղագծային պատկերին, այնպես, որ կիրառված զուգահեռագիծը թերանա մի զուգահեռագծային պատկերով, որը նման է տրված զուգահեռագծին, անհրաժեշտ է, որ տրված ուղղագծային պատկերը [որին հավասար զուգահեռագիծը պետք է կիրառվի] մեծ չլինի այն զուգահեռագծից, որը կառուցված է ուղղագծի կեսի վրա և նման է թերացման պատկերին։ | ||
| + | Թող AB-ն լինի տրված ուղղագիծը, իսկ C-ը տրված ուղղագծային պատկերը, որին AB-ի վրա կիրառվող զուգահեռագիծը պետք է հավասար լինի, ընդ որում C-ը մեծ չէ այն զուգահեռագծից, որը կառուցված է AB-ի կեսի վրա և նման է թերացման պատկերին։ D-ը այն զուգահեռագիծն է, որին պետք է նման լինի թերացումը։ Արդ, պետք է AB ուղղագծի վրա կիրառել զուգահեռագիծ, հավասար տրված C ուղղագծային պատկերին, թերանալով մի զուգահեռագծային պատկերով, որը նման է D-ին։ | ||
| + | [[Պատկեր:1.4.png]] | ||
| + | Թող AB-ը բաժանված լինի կետ E-ով երկու կեսի [Բան. 1.10], և թող (զուգահեռագիծ) EBFG, որը նման է ու նույն կերպ դասավորված D զուգահեռագծին, կառուցվի EB-ի վրա [Բան. 6.18]։ Եվ թող AG զուգահեռագիծը լրացվի։ | ||
| + | Եթե AG-ը հավասար է C-ին, ապա նախապես պահանջվածը կատարված է։ Որովհետև AG զուգահեռագիծը, հավասար տրված ուղղագծային պատկեր C-ին, կիրառված է AB ուղղագծի վրա, թերանալով GB զուգահեռագծային պատկերով, որը նման է D-ին։ Իսկ եթե ոչ, թող HE-ն մեծ լինի C-ից։ Եվ HE-ը հավասար է GB-ին [Բան. 6.1]։ Ուստի GB-ն նույնպես մեծ է C-ից։ Թող KLMN զուգահեռագիծը կառուցվի, որը թե՛ նման է և թե՛ նույն կերպ դասավորված D-ին, և հավասար GB-ի C-ից մեծ լինելու չափին [Բան. 6.25]։ Բայց GB-ն նման է D-ին։ Ուրեմն KM-ն նույնպես նման է GB-ին [Բան. 6.21]։ Ուստի թող KL-ը համապատասխանեցվի GE-ին, իսկ LM-ը GF-ին։ Եվ چونکہ GB զուգահեռագիծը հավասար է C պատկերին և KM զուգահեռագծին, GB-ն ավելի մեծ է KM-ից։ Հետևաբար GE-ն նույնպես մեծ է KL-ից, իսկ GF-ը LM-ից։ Թող GO-ը հավասարեցվի KL-ին, իսկ GP-ը LM-ին [Բան. 1.3]։ Եվ թող OGPQ զուգահեռագիծը լրացվի։ Այսպիսով [GQ]-ը հավասար է ու նման KM-ին (իսկ KM-ն նման է GB-ին), ուստի GQ-ն նույնպես նման է GB-ին [Բան. 6.21]։ Այսպիսով GQ և GB զուգահեռագծերը նույն անկյունագծի շուրջ են [Բան. 6.26]։ Թող GQB-ը լինի նրանց (ընդհանուր) անկյունագիծը, և թող պատկերի մնացորդը լրացվի։ | ||
| + | Քանի որ BG-ը հավասար է C-ին և KM-ին, որոնցից GQ-ը հավասար է KM-ին, մնացած գномոն VWU-ն նույնպես հավասար է C-ին։ Եվ քանի որ (լրացնող) PR-ը հավասար է (լրացնող) OS-ին [Բան. 1.43], թող QB զուգահեռագիծը ավելացվի երկուսին էլ։ Այդպիսով ամբողջ PB զուգահեռագիծը հավասար է ամբողջ OB զուգահեռագծին։ Իսկ OB-ն հավասար է TE-ին, քանի որ AE կողմը հավասար է EB կողմին [Բան. 6.1]։ Ուստի TE-ն նույնպես հավասար է PB-ին։ Թող (զուգահեռագիծ) OS-ը նույնպես ավելացվի երկուսին էլ։ Այդպիսով ամբողջ TS զուգահեռագիծը հավասար է VWU գномոնին։ Բայց VWU գномոնը ցույց տրվեց, որ հավասար է C-ին։ Ուստի TS զուգահեռագիծը նույնպես հավասար է C պատկերին։ | ||
| + | Այսպիսով, ST զուգահեռագիծը, հավասար տրված ուղղագծային պատկեր C-ին, կիրառվեց տրված AB ուղղագծի վրա, թերանալով QB զուգահեռագծային պատկերով, որը նման է D-ին [քանի որ QB-ն նման է GQ-ին [Բան. 6.24]]։ (Սա էլ հենց այն էր, ինչ պետք էր անել)։ | ||
| + | Ծանոթագրություն: Այս առաջարկությունը երկրաչափական լուծումն է x² – αx + β = 0 քառորդասնական հավասարման։ Այստեղ x-ը թերացման կողմի երկարության և D պատկերի համապատասխան կողմի հարաբերությունն է, α-ն AB ուղղագծի երկարության և D պատկերի այն կողմի երկարության հարաբերությունը, որը համապատասխանում է թերացման կողքին (AB-ի երկայնքով), իսկ β-ն C և D պատկերների մակերեսների հարաբերությունն է։ Պայմանադրությունը β < α²/4-ն է, որպեսզի հավասարումն ունենա իրական լուծումներ։ Այստեղ գտնվում է հավասարման միայն փոքր արմատը։ Մեծ արմատը կարելի է գտնել նմանատիպ մեթոդով։ | ||
| + | |||
| + | == Առաջարկություն 29 == | ||
| + | Ուղղագծին կիրառել մի զուգահեռագիծ, որը հավասար է տրված ուղղագծային պատկերին, այնպես, որ կիրառված զուգահեռագիծը անցնի սահմանվածից ավել (անցնի սահմանագիծը) մի զուգահեռագծային պատկերով, որը նման է տրված (զուգահեռագծին): | ||
| + | [[Պատկեր:1.5.png]] | ||
| + | Թող AB-ն լինի տրված ուղղագիծը, իսկ C-ը տրված ուղղագծային պատկերը, որին AB-ի վրա կիրառվող զուգահեռագիծը պետք է հավասար լինի։ D-ը այն զուգահեռագիծն է, которому նման պետք է լինի ավելացած մասը։ Արդ, անհրաժեշտ է AB ուղղագծի վրա կիրառել մի զուգահեռագիծ, հավասար C ուղղագծային պատկերին, բայց այնքան, որ այն անցնի սահմանվածից ավել, առաջացնելով մի զուգահեռագծային պատկեր, որը նման է D-ին։ | ||
| + | Թող AB-ը բաժանված լինի կեսի վրա E կետով [Բան. 1.10], և թող EB-ի վրա կառուցվի BF զուգահեռագիծը, որը նման և նույն կերպ դասավորված է D զուգահեռագծին [Բան. 6.18]։ Թող նաև կառուցվի GH զուգահեռագիծը, որը նույնպես նման է D-ին և հավասար BF-ի և C-ի գումարին [Բան. 6.25]։ Եվ թող KH-ը համապատասխանեցվի FL-ին, իսկ KG-ը FE-ին։ Քանի որ GH զուգահեռագիծը մեծ է FB զուգահեռագծից, հետևաբար KH-ը նույնպես մեծ է FL-ից, իսկ KG-ը մեծ է FE-ից։ Թող FL և FE գծերը երկարացվեն, և թող FLM երկարությունը հավասարեցվի KH-ին, իսկ FEN-ը հավասարեցվի KG-ին [Բան. 1.3]։ Եվ թող MN զուգահեռագիծը լրացվի։ Այսպիսով MN-ը հավասար և նման է GH-ին։ Բայց GH-ը նման է EL-ին։ Ուրեմն MN-ը նույնպես նման է EL-ին [Բան. 6.21]։ EL-ը, ուրեմն, նույն անկյունագծի շուրջ է, ինչ MN-ը [Բան. 6.26]։ Թող նրանց (ընդհանուր) անկյունագիծ FO գծվի, և թող պատկերի մնացած մասը լրացվի։ | ||
| + | Եվ քանի որ GH զուգահեռագիծը հավասար է EL զուգահեռագծին և (C) պատկերին, բայց GH-ը հավասար է նաև MN զուգահեռագծին, ուրեմն MN-ը նույնպես հավասար է EL-ին և C-ին։ Թող EL-ը հանվի երկուսից էլ։ Ուստի մնացող XWV գνομոնը հավասար է (C) պատկերին։ Եվ քանի որ AE-ը հավասար է EB-ին, AN զուգահեռագիծը նույնպես հավասար է NB զուգահեռագծին [Բան. 6.1], այսինքն LP զուգահեռագծին [Բան. 1.43]։ Թող EO զուգահեռագիծը ավելացվի երկուսին էլ։ Այդպիսով ամբողջ AO զուգահեռագիծը հավասար է VWX գνομոնին։ Բայց VWX գνομոնը հավասար է (C) պատկերին։ Ուստի AO զուգահեռագիծը նույնպես հավասար է C պատկերին։ | ||
| + | Այսպիսով AO զուգահեռագիծը, հավասար տրված ուղղագծային պատկեր C-ին, կիրառվել է տրված AB ուղղագծին, անցնելով ավել մի զուգահեռագծային պատկերով QP, որը նման է D-ին, քանի որ PQ-ն նույնպես նման է EL-ին [Բան. 6.24]։ (Սա էլ հենց այն էր, ինչ պետք էր անել)։ | ||
| + | Ծանոթագրություն: Այս առաջարկությունը քառակուսային հավասարման x² + αx – β = 0 երկրաչափական լուծումն է։ Այստեղ x-ը ավելցուկի կողմի և D պատկերի համապատասխան կողմի հարաբերությունն է, α-ն AB ուղղագծի երկարության և D պատկերի այն կողքի երկարության հարաբերությունը, որը համապատասխանում է ավելցուկի երկայնքով AB կողմին, իսկ β-ն C և D պատկերների մակերեսների հարաբերությունն է։ Այստեղ գտնվում է հավասարման միայն դրական արմատը։ | ||
| + | |||
| + | == Առաջարկություն 30 == | ||
| + | Տրված վերջավոր ուղղագծի հատվածումը ծայրագույն և միջին հարաբերությամբ։ | ||
| + | [[Պատկեր:1.5.png]] | ||
| + | Թող AB լինի տրված վերջավոր ուղղագիծը։ Ուրեմն անհրաժեշտ է AB ուղղագիծը բաժանել ծայրագույն և միջին հարաբերությամբ։ | ||
| + | Թող AB ուղղագծի վրա կառուցվի BC քառակուսին [Բան. 1.46], և թող BC-ին հավասար CD զուգահեռագիծը կիրառվի AC-ի վրա, անցնելով սահմանվածից ավելի AD պատկերով, որը նման է BC-ին [Բան. 6.29]։ | ||
| + | Քանի որ BC-ը քառակուսի է, ուրեմն AD-ն նույնպես քառակուսի է։ Եվ քանի որ BC-ը հավասար է CD-ին, թող CE ուղղանկյունը հանվի երկուսից էլ։ Այդպիսով, մնացած BF ուղղանկյունը հավասար է մնացած AD քառակուսուն։ Այն նաև հավանկյուն է նրա հետ։ Այսպիսով BF-ի և AD-ի կողմերը հավասար անկյունների շուրջ обратно (փոխադարձաբար) համաչափ են [Բան. 6.14]։ Ուստի, ինչպես FE-ն ED-ի նկատմամբ է, այնպես AE-ը EB-ի նկատմամբ է։ Եվ FE-ը հավասար է AB-ին, իսկ ED-ը AE-ին։ Հետևաբար, ինչպես BA-ը AE-ի նկատմամբ է, նույնպես AE-ը EB-ի նկատմամբ է։ Եվ քանի որ AB-ը մեծ է AE-ից, ուրեմն AE-ը նույնպես մեծ է EB-ից [Բան. 5.14]։ | ||
| + | Այսպիսով, AB ուղղագիծը բաժանվեց ծայրագույն և միջին հարաբերությամբ E կետում, և AE-ն նրա մեծ մասը դարձավ։ (Սա էլ հենց այն էր, ինչ պետք էր անել)։ | ||
| + | Ծանոթագրություն: Այս մեթոդը ուղղագծի բաժանման, որն ibland անվանվում է "ոսկե հատում", դիտեք Առաջարկություն 2.11: | ||
| + | |||
| + | == Առաջարկություն 31 == | ||
| + | Ուղղանկյուն եռանկյուններում, աջ անկյունը ծածկող կողմի վրա գծված պատկերն հավասար է աջ անկյունը շրջապատող կողմերի վրա կառուցված նման, և նույն կերպ նկարագրված պատկերների գումարին: | ||
| + | [[Պատկեր:1.7.png]] | ||
| + | |||
| + | Թող ABC-ն լինի ուղղանկյուն եռանկյուն, որտեղ BΑC անկյունը աջ անկյուն է։ Ասում եմ, որ BC կողմի վրա կառուցված պատկերը հավասար է BA և AC կողերին կառուցված նման, նույն կերպ նկարագրված պատկերների գումարին։ | ||
| + | Թող AD ուղղահայացը գծվի [Բան. 1.12]: | ||
| + | Ուստի, քանի որ ABC ուղղանկյուն եռանկյունում AD ուղիղը գծվեց A աջ անկյունից BC հիմքին ուղղահայաց, երեքանկյունները ABD և ADC ուղղահայացի շուրջ նման են թե՛ ամբողջ ABC եռանկյունին, թե՛ միմյանց [Բան. 6.8]: Եվ քանի որ ABC-ն նման է ABD-ին, ուրեմն ինչպես CB-ը BA-ի նկատմամբ է, այնպես էլ AB-ը BD-ի նկատմամբ է [Սահմ. 6.1]։ Եվ քանի որ երեք ուղղագծերը համաչափ են, ապա ինչպես առաջինը երրորդի նկատմամբ է, այնպես էլ առաջինի վրա կառուցված նման և նույն ձևով նկարագրված պատկերը երկրորդի վրա կառուցված պատկերի նկատմամբ է [Բան. 6.19 ուղղում]: Այսպիսով, ինչպես CB-ը BD-ի նկատմամբ է, այնպես էլ CB-ի վրա կառուցված պատկերը BA-ի վրա կառուցված նման, նույն կերպ նկարագրված պատկերի նկատմամբ է։ Նույն պատճառներով, ինչպես BC-ը CD-ի նկատմամբ է, այնպես էլ BC-ի վրա կառուցված պատկերը CA-ի վրա կառուցված պատկերի նկատմամբ է։ Հետևաբար, քանի որ BC-ը BD-ի և DC-ի նկատմամբ է, BC-ի վրա կառուցված պատկերը հավասար է BA և AC կողմերին կառուցված նման, նույն ձևով նկարագրված պատկերների գումարին [Բան. 5.24]: Եվ քանի որ BC-ը հավասար է BD-ին և DC-ին, BC-ի վրա կառուցված պատկերը նույնպես հավասար է BA-ի և AC-ի վրա կառուցված նման, նույն ձևով նկարագրված պատկերների գումարին [Բան. 5.9]։ | ||
| + | Արդ, ուղղանկյուն եռանկյուններում աջ անկյունը ծածկող կողի վրա կառուցված պատկերը հավասար է աջ անկյունը շրջապատող կողմերի վրա կառուցված նման, նույն կերպ նկարագրված պատկերների գումարին։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | == Առաջարկություն 32 == | ||
| + | Եթե երկու եռանկյուններ, որոնք ունեն երկու կողմեր համաչափ երկու այլ կողմերին, տեղադրված են մեկ ընդհանուր անկյան շուրջ այնպես, որ համապատասխանող կողմերը նույնպես զուգահեռ են, ապա եռանկյունների մնացած կողմերը կլինեն ուղղագծի վրա (միմյանց նկատմամբ): | ||
| + | [[Պատկեր:1.8.png]] | ||
| + | Թող ABC և DCE լինեն երկու եռանկյուններ, որոնց BA և AC երկու կողմերը համաչափ են DC և DE երկու կողմերին, այնպես որ ինչպես AB-ը AC-ի նկատմամբ է, նույն կերպ DC-ն DE-ի նկատմամբ է, և AB կողմը զուգահեռ է DC-ին, իսկ AC-ն DE-ին։ Ասում եմ, որ BC կողմը ուղիղ է CE-ի հետ։ | ||
| + | Քանզի AB-ը զուգահեռ է DC-ին, և AC ուղղագիծը անցնում է նրանց միջով, BAC և ACD փոխարինական անկյունները հավասար են միմյանց [Բան. 1.29]։ Նույն պատճառներով CDE-ն հավասար է ACD-ին։ Ուստի BAC-ը հավասար է CDE-ին։ Եվ քանի որ ABC և DCE են երկու եռանկյուններ, որոնք ունեն A անկյունը հավասար D անկյանը, իսկ հավասար անկյունների շուրջ գտնվող կողմերը համաչափ են (այնպես, որ ինչպես BA-ը AC-ի նկատմամբ է, այնպես էլ CD-ն DE-ի նկատմամբ է), ABC եռանկյունը հավանկյուն է DCE եռանկյունին [Բան. 6.6]։ Ուստի ABC անկյունը հավասար է DCE անկյանը։ Եվ (անկյուն) ACD-ն նույնպես ցույց տրվեց հավասար BAC անկյանը։ Դրա շնորհիվ (ամբողջ) ACE անկյունը հավասար է (ABC և BAC անկյունների) գումարին։ Թող ACB անկյունը նույնպես ավելացվի երկուսին։ Այդպիսով ACE և ACB անկյունները հավասար են BAC, ACB, և CBA անկյուններին։ Բայց BAC, ABC և ACB անկյունների գումարը հավասար է երկու ուղղանկյունների [Բան. 1.32]։ Ուստի ACE և ACB անկյունները նույնպես հավասար են երկու ուղղանկյունների։ Այսպիսով, BC և CE երկու ուղիղները, որոնք չեն գտնվում նույն կողմում, կազմում են ACE և ACB հարակից անկյուններ, որոնց գումարը հավասար է երկու ուղղանկյունների AC ուղղագծի վրա, C կետում։ Ուստի BC-ը ուղիղ է CE-ի հետ [Բան. 1.14]։ | ||
| + | Այսպիսով, եթե երկու եռանկյուններ, որոնք ունեն երկու կողմերը համաչափ երկու այլ կողմերին, տեղադրված են մեկ ընդհանուր անկյան շուրջ այնպես, որ համապատասխանող կողմերը նույնպես զուգահեռ են, ապա մնացած կողմերը կլինեն միևնույն ուղիղ գծի վրա (միմյանց նկատմամբ)։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | == Առաջարկություն 33 == | ||
| + | |||
| + | Հավասար շրջաններում անկյունները նույն հարաբերությունն ունեն այն շրջագծերի նկատմամբ, որոնց վրա կանգնած են, արդյոք նրանք գտնվում են շրջանների կենտրոններում, թե շրջագծերի վրա: | ||
| + | [[Պատկեր:1.9.png]] | ||
| + | Թող ABC և DEF լինեն հավասար շրջաններ, և թող BGC և EHF անկյունները լինեն դրանց կենտրոններում G և H կետերում համապատասխանաբար, իսկ BAC և EDF անկյունները լինեն դրանց շրջագծերի վրա։ Ասում եմ, որ ինչպես BC շրջագիծը EF շրջագծի նկատմամբ է, այնպես էլ BGC անկյունը EHF անկյան նկատմամբ է, և BAC անկյունը EDF անկյան նկատմամբ։ | ||
| + | Թող որևէ քանակի հաջորդական շրջագծաշղթաներ CK և KL լինեն հավասար BC շրջագծին, և որևէ քանակի FM և MN լինեն հավասար EF շրջագծին։ Թող GK, GL, HM, և HN գծերը ավելացվեն։ | ||
| + | Ուստի, քանի որ BC, CK և KL շրջագծերը հավասար են միմյանց, BGC, CGK և KGL անկյունները նույնպես հավասար են միմյանց [Բան. 3.27]։ Այսպիսով, քանի անգամ BL շրջագիծը բաժանվում է BC շրջագծի մեջ, նույնքան անգամ BGL անկյունը բաժանվում է BGC անկյան մեջ։ Եվ նույն պատճառներով, քանի անգամ NE շրջագիծը բաժանվում է EF-ի մեջ, նույնքան անգամ NHE անկյունը բաժանվում է EHF անկյան մեջ։ Արդ, եթե BL շրջագիծը հավասար է EN շրջագծին, ապա BGL անկյունը նույնպես հավասար է EHN անկյանին [Բան. 3.27]։ Եթե BL-ը մեծ է EN-ից, ապա BGL անկյունը նույնպես մեծ է EHN-ից, իսկ եթե BL-ը փոքր է EN-ից, ապա BGL անկյունը նույնպես փոքր է EHN-ից։ Արդ, ունենք չորս մեծություններ՝ երկու շրջագծեր BC և EF, և երկու անկյուններ BGC և EHF։ Եվ վերցվել են հավասար բազմապատիկներ BC շրջագծից և BGC անկյունից (մասնավորապես BL շրջագիծն ու BGL անկյունը) և EF շրջագծից ու EHF անկյունից (մասնավորապես EN շրջագիծն ու EHN անկյունը)։ Եվ ցույց տրվեց, որ եթե BL շրջագիծը գերազանցում է EN շրջագծին, ապա BGL անկյունը նույնպես գերազանցում է EHN անկյանը, եթե հավասար են, ապա հավասար են, իսկ եթե BL-ը փոքր է, ապա BGL անկյունը նույնպես փոքր է EHN-ից։ Այսպիսով, ինչպես BC շրջագիծը EF-ի նկատմամբ է, այնպես BGC անկյունը EHF-ի նկատմամբ է [Սահմանում 5.5]։ Բայց քանի որ BGC անկյունը EHF-ի նկատմամբ է, նույն կերպ BAC անկյունը EDF-ի նկատմամբ է [Բան. 5.15]։ Նախադրյալները կրկնապատկում են հետևությունները [Բան. 3.20]։ Ուստի, ինչպես BC շրջագիծը EF-ի նկատմամբ է, այնպես BGC անկյունը EHF-ի նկատմամբ է, և BAC անկյունը EDF-ի նկատմամբ է։ | ||
| + | Այսպիսով, հավասար շրջաններում անկյունները նույն հարաբերությունն ունեն այն շրջագծերի նկատմամբ, որոնց վրա կանգնած են, արդյոք նրանք գտնվում են շրջանների կենտրոններում, թե շրջագծերի վրա։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | Սահմանումներ | ||
| + | 1. Միավորը այն է, ըստ որի ամեն գոյող (բան) ասվում է «մեկ»։ | ||
| + | 2. Թիվը միավորներից կազմված բազմություն է։† | ||
| + | 3. Թիվը մաս է (ուրիշ) թիվի, փոքրագույնը մեծագույնի, երբ այն չափում է մեծագույնը։‡ | ||
| + | 4. Իսկ (եթե փոքրագույնը) մասեր է (մեծագույնի), երբ այն չի չափում այն։§ | ||
| + | 5. Եվ մեծագույն (թիվը) փոքրագույնի բազմապատիկն է, երբ մեծագույնը չափվում է փոքրագույնով։ | ||
| + | 6. Զույգ թիվը այն թիվն է, որ կարելի է բաժանել երկու հավասար մասերի։ | ||
| + | 7. Թեք (կամ կենտ) թիվը այն թիվն է, որը չի կարելի բաժանել երկու հավասար մասերի, կամ որը տարբերվում է զույգ թվից մեկ միավորով։ | ||
| + | 8. Զույգ-անգամ-զույգ թիվը այն է, որ չափվում է մի զույգ թվով, ըստ մի այլ զույգ թվի։¶ | ||
| + | 9. Իսկ զույգ-անգամ-թեք թիվը այն է, որ չափվում է մի զույգ թվով, ըստ մի թեք (կենտ) թվի։∗ | ||
| + | 10. Եվ թեք-անգամ-թեք թիվը այն է, որ չափվում է մի թեք (կենտ) թվով, ըստ մի այլ թեք (կենտ) թվի։$ | ||
| + | 11. Առաջնային∥ թիվը այն է, որ չափվում է միայն միավորով։ | ||
| + | 12. Թվերը, որոնք պարզ են (առաջնային) միմյանց նկատմամբ, այն թվերն են, որոնք չափվում են միայն միավորով որպես ընդհանուր չափ։ | ||
| + | 13. Բարդ թիվը այն է, որ չափվում է ինչ-որ թվով։ | ||
| + | 14. Եվ թվերը, որոնք բարդ են միմյանց նկատմամբ, այն թվերն են, որոնք չափվում են ինչ-որ թվով որպես ընդհանուր չափ։ | ||
| + | 15. Ասվում է, որ թիվը բազմապատկում է (ուրիշ) թիվը, երբ բազմապատկվող թիվը ինքն իրեն מוסարձակվում է այնքան անգամ, որքան միավորներ կան առաջին (բազմապատկող) թվում, և (այդ կերպ) առաջանում է մեկ այլ թիվ։ | ||
| + | 16. Եվ երբ երկու թվեր միմյանց բազմապատկելով առաջացնում են ինչ-որ (ուրիշ) թիվ, ապա (այդպիսով) առաջացած թիվը կոչվում է հարթ (ղեկավար տերմինը "plane" – "հարթ"), և նրա կողմերը այն թվերն են, որոնք բազմապատկում են միմյանց։ | ||
| + | 17. Եվ երբ երեք թվեր միմյանց բազմապատկելով առաջացնում են ինչ-որ (ուրիշ) թիվ, ապա (այդպիսով) առաջացած թիվը կոչվում է ծավալային (solid), և նրա կողմերը այն թվերն են, որոնք բազմապատկում են միմյանց։ | ||
| + | 18. Քառակուսի (square) թիվը հավասար բազմապատիկ է հավասարի, կամ (հարթ թիվ) է, պարփակված երկու հավասար թվերով։ | ||
| + | 19. Եվ խորանարդ (cube) թիվը հավասար-նշանակ բազմապատիկ է հավասարի, կրկին հավասարի, կամ (ծավալային թիվ) է, պարփակված երեք հավասար թվերով։ | ||
| + | 20. Թվերը համաչափ են, երբ առաջինը նույն բազմապատիկն է, կամ նույն մասը, կամ նույն մասերն են երկրորդի նկատմամբ, ինչ երրորդը չորրորդի նկատմամբ։ | ||
| + | 21. Նման հարթ և ծավալային թվերը այն թվերն են, որոնք ունեն համեմատական (համաչափ) կողմեր։ | ||
| + | 22. Կատարյալ թիվը այն է, որը հավասար է իր մասերի գումարին։†† | ||
| + | Ծանոթագրություններ: | ||
| + | † Այլ կերպ ասած, «թիվը» միավորից մեծ դրական ամբողջ թիվ է։ | ||
| + | ‡ Այլ կերպ ասած, թիվ a-ն մաս է թիվ b-ի, եթե գոյություն ունի թիվ n, այնպես, որ na = b։ | ||
| + | § Այլ կերպ ասած, a թիվը մասեր է b թիվի (որտեղ a < b), եթե գոյություն ունեն տարբեր թվեր m և n, այնպես որ na = m*b։ | ||
| + | ¶ Այլ կերպ ասած, զույգ-անգամ-զույգ թիվը երկու զույգ թվերի արտադրյալն է։ | ||
| + | ∗ Այլ կերպ ասած, զույգ-անգամ-թեք թիվը մեկ զույգ և մեկ թեք (կենտ) թվերի արտադրյալն է։ | ||
| + | $ Այլ կերպ ասած, թեք-անգամ-թեք թիվը երկու թեք (կենտ) թվերի արտադրյալն է։ | ||
| + | ∥ Բառացիորեն, «առաջին»։ | ||
| + | †† Այլ կերպ ասած, կատարյալ թիվը հավասար է իր բաժանարարների գումարին։ | ||
| + | |||
| + | == Առաջարկություն 1 == | ||
| + | Եթե տրվեն երկու անհավասար թվեր, և փոքրագույնը հերթով անընդհատ հանվի մեծագույնից, այնպես, որ մնացորդը երբեք չչափի իրեն նախորդող թիվը, մինչև չմնա մեկ միավոր, ապա սկզբնական թվերը կլինեն միմյանց նկատմամբ պարզ (արնչություն չունեն որևէ ընդհանուր բաժանարարից բացի մեկից): | ||
| + | [[Պատկեր:1.10.png]] | ||
| + | |||
| + | Երկու [անհավասար] թվերի, AB և CD-ի դեպքում, եթե փոքրագույնը հերթով անընդհատ հանվի մեծագույնից, թող մնացորդը երբեք չչափի իրեն նախորդող թիվը, մինչև չմնա մեկ միավոր։ Ասում եմ, որ AB և CD թվերը պարզ են միմյանց նկատմամբ, այսինքն՝ միայն միավորը չափում է (և) AB-ին, (և) CD-ին։ | ||
| + | Եթե AB և CD պարզ չլինեն միմյանց նկատմամբ, ապա որոշ թիվ նրանց կչափի։ Թող այդ թիվը լինի E։ Եվ թող CD-ն, չափելով BF-ը, թողնի FA մնացորդ, փոքր քան ինքն է, հետո AF-ը, չափելով DG-ն, թողնի GC մնացորդ, փոքր քան ինքն է, հետո GC-ն, չափելով FH-ը, թողնի HA միավորը։ | ||
| + | Փաստորեն, քանի որ E-ն չափում է CD-ն, և CD-ն չափում է BF-ը, E-ն նույնպես չափում է BF-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ BA-ն։ Ուստի (E-ն) նույնպես կչափի BA-ի մնացորդ AF-ը։ Եվ AF-ն չափում է DG-ն։ Այսպիսով, E-ն նույնպես չափում է DG-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ DC-ն։ Ուստի (E-ն) նույնպես կչափի CG մնացորդը։ Եվ CG-ն չափում է FH-ը։ Այսպիսով, E-ն նույնպես չափում է FH-ը։ Եվ (E-ն) նաև չափում է ամբողջ FA-ն։ Ուստի (E-ն) նույնպես կչափի HA մնացորդային միավորը, թեև դա ուղղակի միավոր է։ Սա բացարձակապես անհնար է։ | ||
| + | Հետևաբար գոյություն չունի թիվ, որը չափի (և) AB-ը, (և) CD-ը։ Այսպիսով, AB և CD թվերը պարզ են միմյանց նկատմամբ։ (Ահա թե ինչ էր անհրաժեշտ ցույց տալ): | ||
| + | Մեկնաբանություններ: | ||
| + | † Այստեղ օգտագործվում է չարտասանված ընդհանուր գաղափարը, որ եթե a-ն չափում է b-ին, և b-ն չափում է c-ին, ապա a-ն նույնպես չափում է c-ին, որտեղ բոլոր նշանները ներկայացնում են թվեր։ | ||
| + | ‡ Այստեղ օգտագործվում է չարտասանված ընդհանուր գաղափարը, որ եթե a-ն չափում է b-ին, և a-ն նաև չափում է b-ի մի մասը, ապա a-ն նույնպես չափում է b-ի մնացորդային մասը, որտեղ բոլոր նշանները ներկայացնում են թվեր։ | ||
| + | |||
| + | == Առաջարկություն 2 == | ||
| + | |||
| + | Գտնել երկու տրված թվերի (որոնք միմյանց նկատմամբ պարզ չեն) ամենամեծ ընդհանուր չափը: | ||
| + | [[Պատկեր:1.11.png]] | ||
| + | |||
| + | Թող AB և CD լինեն երկու տրված թվերը, որոնք միմյանց նկատմամբ պարզ չեն։ Արդ, անհրաժեշտ է գտնել AB և CD թվերի ամենամեծ ընդհանուր չափը։ | ||
| + | Իրոք, եթե CD-ը չափում է AB-ը, ապա CD-ը այդպիսով AB-ի և CD-ի ընդհանուր չափն է (քանի որ CD-ը նաև ինքն իրեն է չափում)։ Եվ ակնհայտ է, որ այն նաև ամենամեծ (ընդհանուր չափն) է։ Քանի որ ոչինչ, որ մեծ է CD-ից, չի կարող չափել CD-ին։ | ||
| + | Բայց եթե CD-ը չի չափում AB-ը, ապա AB-ից և CD-ից կմնա որոշ թիվ, երբ փոքրագույնը հերթով շարունակաբար հանենք մեծագույնից, որը կչափի իրեն նախորդող թիվը։ Որովհետև մեկ միավոր չի մնա։ Բայց եթե ոչ, ապա AB և CD թվերը պարզ կլինեն միմյանց նկատմամբ [Բան. 7.1]։ Սա հակասում է այն, ինչ ենթադրվել էր։ Ուստի կմնա մի թիվ, որը կչափի իրեն նախորդող թիվը։ ԵՎ թող CD-ը, չափելով BE-ն, թողնի EA մնացորդը, որը փոքր է իրենից, հետո EA-ն, չափելով DF-ը, թողնի FC մնացորդը, որը փոքր է իրենից, ապա CF-ը թող չափի AE-ը։ Ուստի, քանի որ CF-ը չափում է AE-ը, իսկ AE-ը չափում է DF-ը, CF-ը կհասկանանք, որ չափում է նաև DF-ը։ Եվ այն նաև ինքն իրեն է չափում։ Ուստի այն կչափի նաև ամբողջ CD-ը։ Իսկ CD-ը չափում է BE-ը։ Ուստի CF-ը նույնպես կչափի BE-ը։ Եվ այն նաև չափում է EA-ն։ Ուստի այն կչափի նաև ամբողջ BA-ն։ Այն նաև չափում է AE մնացորդը։ Եվ AE-ը չափում է DF-ը։ Ուստի CF-ը նույնպես կչափի DF-ը։ Եվ այն ինքն իրեն է չափում։ Ուստի այն կչափի նաև DC մնացորդը։ Այսպիսով, CF-ը չափում է և AB-ը, և CD-ը։ Ասում եմ, որ այն նաև ամենամեծ (ընդհանուր չափն) է։ Քանի որ եթե CF-ը AB և CD թվերի ամենամեծ ընդհանուր չափը չէ, ապա կգտնվի մի թիվ, որը մեծ է CF-ից և կչափի AB ու CD թվերը։ Թող այն չափի (AB և CD), և թող այդ թիվը լինի G։ Եվ քանի որ G-ն չափում է CD-ը, իսկ CD-ն չափում է BE-ը, G-ն նույնպես կչափի BE-ը։ Եվ այն նաև կչափի ամբողջ BA-ն։ Ուստի այն կչափի AE մնացորդը։ Իսկ AE-ը չափում է DF-ը։ Ուստի G-ն նույնպես կչափի DF-ը։ Այն նաև չափում է ամբողջ DC-ը։ Ուստի այն կչափի CF մնացորդը, մեծը չափելով փոքրին։ Սա անհնար է։ Ուստի ոչ մի թիվ, որը մեծ է CF-ից, չի կարող չափել AB և CD թվերը։ Այսպիսով, CF-ը AB և CD թվերի ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | Հաջորդակում (Corollary) | ||
| + | Այդպիսով ակնհայտ է, որ եթե մի թիվ չափում է երկու թիվ, ապա այն կչափի նաև նրանց ամենամեծ ընդհանուր չափը։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | == Առաջարկություն 3 == | ||
| + | Գտնել երեք տրված թվերի (որոնք միմյանց նկատմամբ պարզ չեն) ամենամեծ ընդհանուր չափը: | ||
| + | [[Պատկեր:1.12.png]] | ||
| + | |||
| + | Թող A, B և C լինեն երեք տրված թվերը, որոնք միմյանց նկատմամբ պարզ չեն։ Արդ, անհրաժեշտ է գտնել A, B և C թվերի ամենամեծ ընդհանուր չափը։ | ||
| + | Թող նախ վերցված լինի A և B երկու (թվերի) ամենամեծ ընդհանուր չափը D [Բան. 7.2]։ Ուրեմն D-ը կամ չափում է, կամ չի չափում C-ը։ Նախ ենթադրենք, որ այն չափում է (C-ը)։ Այն նաև չափում է A-ն և B-ը։ Ուստի D-ը չափում է A, B և C թվերը։ Այսպիսով, D-ը A, B և C թվերի ընդհանուր չափն է։ Ասում եմ, որ այն նաև ամենամեծ (ընդհանուր) չափն է։ Քանի որ եթե D-ը A, B և C ամենամեծ ընդհանուր չափը չլինի, ապա կգտնվի մի թիվ, ավելի մեծ քան D-ը, որը կչափի A, B և C թվերը։ Թող այն (այդպես) չափի (A, B, C) և կոչվի E։ Ուստի, քանի որ E-ը չափում է A, B և C, այն կչափի նաև A և B։ Այսպիսով, այն կչափի A և B ամենամեծ ընդհանուր չափը D-ը [Ընդհանր.` 7.2], իսկ D-ը ամենամեծ ընդհանուր չափն է A և B թվերի։ Այսպիսով, E-ը չափում է D-ը, մեծը չափում է փոքրին։ Սա բացարձակ անհնար է։ | ||
| + | Հետևաբար, ոչ մի թիվ, մեծ քան D-ը, չի կարող չափել A, B և C թվերը։ Ուստի D-ը A, B և C թվերի ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | Եթե D-ը չի չափում C-ը, ասում եմ նախ, որ C և D թվերը միմյանց նկատմամբ պարզ չեն։ Քանի որ A, B, C միմյանց նկատմամբ պարզ չեն, մի թիվ կգտնվի, որը կչափի դրանք։ Այսպիսով, A, B, C չափող թիվը կչափի նաև A և B, և կչափի A և B ամենամեծ ընդհանուր չափը D-ը [Ընդհանր. 7.2], և կչափի նաև C-ը։ Ուստի որոշ թիվ կչափի D և C թվերը։ Այսպիսով, D և C նույնպես պարզ չեն միմյանց նկատմամբ։ Թող D և C ամենամեծ ընդհանուր չափը, E-ը, վերցվի [Բան. 7.2]։ Եվ քանի որ E-ը չափում է D-ին, իսկ D-ը չափում է A և B, E-ը նույնպես չափում է A և B։ Այն նաև չափում է C-ը։ Ուստի E-ը A, B, C թվերի ընդհանուր չափն է։ Ասում եմ, որ այն նաև ամենամեծ ընդհանուր չափն է։ Քանի որ եթե E-ը A, B, C ամենամեծ ընդհանուր չափը չլինի, ապա կգտնվի թիվ, ավելի մեծ քան E-ը, որը կչափի A, B և C թվերը։ Թող այն (այդպես) չափի (A, B և C) և կոչվի F։ Եվ քանի որ F-ը չափում է A, B, C, այն կչափի նաև A և B։ Ուստի այն կչափի A և B ամենամեծ ընդհանուր չափը D-ը [Ընդհանր. 7.2], իսկ D-ը A և B ամենամեծ ընդհանուր չափն է։ Այսպիսով, F-ը չափում է D-ը։ Այն նաև չափում է C-ը։ Ուստի F-ը չափում է D և C թվերը, և կչափի D և C ամենամեծ ընդհանուր չափը [Ընդհանր.` 7.2]։ Իսկ E-ը D և C ամենամեծ ընդհանուր չափն է։ Այսպիսով, F-ը չափում է E-ին, մեծը չափում է փոքրին։ Սա անհնար է։ Ուստի ոչ մի թիվ, մեծ քան E-ը, չի չափում A, B, C թվերը։ Այսպիսով, E-ը A, B, C ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | |||
| + | == Առաջարկություն 4 == | ||
| + | Ցանկացած թիվ կամ մաս է, կամ մասեր են յուրաքանչյուր (ուրիշ) թվի, ավելի փոքրն ավելի մեծի։ | ||
| + | Թող A և BC լինեն երկու թվեր, և թող BC-ը լինի փոքրագույնը։ Ասում եմ, որ BC-ը կամ մաս է, կամ մասեր են A թվի։ | ||
| + | Քանի որ A և BC թվերը կամ պարզ են միմյանց նկատմամբ, կամ ոչ։ Նախ թող A և BC պարզ լինեն միմյանց նկատմամբ։ Այդ դեպքում, բաժանելով BC-ը նրա միավորներից կազմված բաղկացուցիչ մասերի, BC-ի յուրաքանչյուր միավոր կլինի A-ի ինչ-որ մասը։ Հետևաբար, BC-ը A-ի մասերից է։ | ||
| + | [[Պատկեր:1.13.png]] | ||
| + | |||
| + | Այսպիսով, թող A և BC պարզ չլինեն միմյանց նկատմամբ։ Ուրեմն BC-ը կամ չափում է A թիվը, կամ չի չափում։ Եթե BC-ը չափում է A-ը, ապա BC-ը A-ի մաս է։ Իսկ եթե ոչ, թող A և BC ամենամեծ ընդհանուր չափը, D-ը, վերցվի [Բան. 7.2], և թող BC-ը բաժանվի BE, EF, և FC մասերի, որոնք հավասար են D-ին։ Եվ քանի որ D-ը չափում է A-ը, D-ը A-ի մաս է։ Եվ D-ը հավասար է BE, EF և FC մասերին։ Հետևաբար, BE, EF, FC ամեն մեկը A-ի մաս է։ Ուրեմն BC-ը A-ի մասերից է։ | ||
| + | Այսպիսով, ցանկացած թիվ կամ մաս է, կամ մասեր են յուրաքանչյուր (ուրիշ) թվի, ավելի փոքրն ավելի մեծի։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | == Առաջարկություն 5 == | ||
| + | Եթե մի թիվ մաս է մեկ թվի, և մի այլ (թիվ) նույն մասը չէ մեկ ուրիշի, ապա (կատարյալ) առաջատար թվերի գումարը նույնպես կլինի նույն մասը հաջորդ թվերի գումարի, ինչ-որ մի թիվ մեկ այլ թվի։ | ||
| + | |||
| + | [[Պատկեր:1.14.png]] | ||
| + | |||
| + | Թող A թիվը լինի BC թվի մի մաս, իսկ D թիվը լինի նույն մասը EF թվի նկատմամբ, ինչ A-ն է BC-ի նկատմամբ: Ասում եմ, որ A և D թվերի գումարը նույնպես կլինի նույն մասը BC և EF գումարի նկատմամբ, ինչ A-ն է BC-ի նկատմամբ: | ||
| + | Քանի որ ինչ մաս էլ A-ն ունի BC-ի մեջ, D-ն նույն մասն ունի EF-ի մեջ, ուրեմն քանի A-ին հավասար թվեր կան BC-ում, նույնքան D-ին հավասար թվեր կան նաև EF-ում: Թող BC-ը բաժանվի BG-ի և GC-ի, որոնք հավասար են A-ին, իսկ EF-ը բաժանվի EH-ի և HF-ի, որոնք հավասար են D-ին: Այսպիսով BG, GC բաժանումների քանակը հավասար կլինի EH, HF բաժանումների քանակին: Եվ քանի որ BG-ը հավասար է A-ին, իսկ EH-ը D-ին, ապա BG, EH զույգը նույնպես հավասար է A, D զույգին: Նույն պատճառներով GC, HF զույգը նույնպես հավասար է A, D զույգին: Այսպիսով, քանի անգամ BC-ը բաժանվում է A-ով, նույնքան անգամ BC, EF գումարը բաժանվում է A, D գումարով: Հետևաբար, ինչ մաս A-ն BC-ի է, A, D գումարն էլ նույն մասն է BC, EF գումարի նկատմամբ: | ||
| + | (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | == Առաջարկություն 6 == | ||
| + | |||
| + | Եթե մի թիվ մասեր է մեկ թվի, իսկ մեկ այլ թիվ նույն մասերն ունի մեկ այլ թվի նկատմամբ, ապա առաջին երկուսի գումարն էլ նույն մասերը կլինի երկրորդ զույգի գումարի նկատմամբ, ինչպիսին առաջին թիվը երկրորդի նկատմամբ է: | ||
| + | [[Պատկեր:1.15.png]] | ||
| + | |||
| + | Թող AB թիվը մասեր լինի C թվի, իսկ DE թիվը նույն մասերը լինի F թվի նկատմամբ, ինչ մասեր AB-ն ունի C-ի մեջ։ Ասում եմ, որ AB և DE գումարը նույնպես նույն մասերն է կունենա C և F գումարի նկատմամբ, ինչ մասեր AB-ն ունի C-ի նկատմամբ։ | ||
| + | Քանի որ ինչ մասեր էլ AB-ն ունի C-ի մեջ, DE-ն նույն մասերը կունենա F-ի մեջ, ուրեմն քանի մասով AB-ն բաժանում է C-ն, նույնքան մասով DE-ն բաժանում է F-ը։ Թող AB թիվը բաժանվի AG և GB մասերի, որոնք C-ի մասեր են, իսկ DE թիվը բաժանվի DH և HE մասերի, որոնք F-ի մասեր են։ Այդպես AG, GB բաժանումների քանակը հավասար կլինի DH, HE բաժանումների քանակին։ Եվ քանի որ ինչ մաս AG-ը C-ի է, DH-ն նույն մասն է F-ի, ուրեմն ինչ մաս AG-ը C-ի է, AG և DH գումարը նույնպես նույն մասն է C և F գումարի նկատմամբ [Բան. 7.5]։ Նույն կերպ, ինչ մաս GB-ը C-ի է, GB և HE գումարը նույնպես նույն մասն է C և F գումարի նկատմամբ։ Ուստի, ինչ մասեր AB-ն ունի C-ի նկատմամբ, AB և DE գումարը նույնպես նույն մասերն է ունենալու C և F գումարի նկատմամբ։ | ||
| + | (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ | ||
| + | |||
| + | Ժամանակակից նշաններով: Այս առաջարկությունը ժամանակակից գրառմամբ ասում է, որ եթե a = (m/n)*c և d = (m/n)f, ապա (a+d) = (m/n)(c+f), որտեղ բոլոր նշանները թվեր են։ | ||
| + | |||
| + | |||
| + | == Առաջարկություն 7 == | ||
| + | |||
| + | Եթե մի թիվ այն նույն մասը լինի ինչ-որ թվի, ինչ (մասը) հանված AE-ն (է) հանված մասի CF-ից, ապա մնացորդը նույնպես կլինի նույն մասը մնացորդի, ինչ ամբողջ AB-ն է ամբողջ CD-ի նկատմամբ: | ||
| + | [[Պատկեր:1.16.png]] | ||
| + | |||
| + | |||
| + | Թող AB թիվը լինի այն մասը CD թվի, ինչ AE հանված մասը CF-ի նկատմամբ է: Ասում եմ, որ EB մնացորդը նույնպես կլինի նույն բաժինը FD մնացորդի նկատմամբ, ինչ AB-ն է CD-ի նկատմամբ: | ||
| + | Քանի որ (ինչ մաս AE-ն է CF-ի), թող EB-ն նույնպես լինի նույն մասը CG-ի: Եվ քանի որ (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասը կլինի CG-ի, ապա (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես նույն մասը կլինի GF-ի [Բան. 7.5]: Եվ (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես ընդունված է լինել նույն մասը CD-ի: Այսպիսով, (ինչ մաս AB-ն է GF-ի), (AB-ն) նույնպես նույն մասն է CD-ի: Ուրեմն GF-ը հավասար է CD-ին: Թող CF-ը հանվի երկուսից էլ: Ուստի GC մնացորդը հավասար է FD մնացորդին: Եվ քանի որ (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասը կլինի GC-ի, իսկ GC-ն հավասար է FD-ին, ապա (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասն է FD-ի: Բայց (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես նույն մասն է CD-ի: Ուրեմն EB մնացորդը նույն մասն է FD մնացորդի, ինչ AB-ն է CD-ի: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): | ||
| + | Նշում : Ժամանակակից նշանումներով, այս առաջարկությունը նշանակում է, որ եթե a = (m/n)*b և c = (m/n)d, ապա (a+c) = (m/n)(b+d), որտեղ բոլոր նշանները ներկայացնում են թվեր։ | ||
| + | |||
| + | == Առաջարկություն 8 == | ||
| + | Եթե մի թիվ այն նույն մասերն է մեկ թվի նկատմամբ, ինչ (հանված) AE մասը է (հանված) CF մասի նկատմամբ, ապա մնացորդը նույնպես կլինի նույն մասերի հարաբերությամբ մնացորդի նկատմամբ, ինչպիսին ամբողջը է ամբողջի նկատմամբ: | ||
| + | [[Պատկեր:1.17.png]] | ||
| + | |||
| + | Թող AB թիվը լինի այն նույն մասերն CD թվի նկատմամբ, ինչ AE հանված մասը CF-ի նկատմամբ է: Ասում եմ, որ EB մնացորդը նույնպես կլինի նույն մասերը FD մնացորդի նկատմամբ, ինչ AB-ն է CD-ի նկատմամբ: | ||
| + | Թող GH-ը դրվի հավասար AB-ին: Ուստի ինչ մասեր GH-ը ունի CD-ի նկատմամբ, AE-ն նույնպես նույն մասերն ունի CF-ի նկատմամբ: Թող GH-ը բաժանվի CD-ի մասերի՝ GK և KH, իսկ AE-ը՝ CF-ի մասերի՝ AL և LE: Այսպիսով, GK և KH բաժանումների քանակը հավասար կլինի AL և LE բաժանումների քանակին: Եվ քանի որ ինչ մաս GK-ը CD-ի նկատմամբ է, նույն մաս AL-ը CF-ի նկատմամբ է, և քանի որ CD-ն մեծ է CF-ից, GK-ն նույնպես մեծ է AL-ից: Թող GM-ը վերցվի հավասար AL-ին: Այսպիսով, ինչ մաս GK-ը CD-ի նկատմամբ է, GM-ը նույն մասն է CF-ի նկատմամբ: Ուստի MK մնացորդը նույնպես նույն մասն է FD մնացորդի նկատմամբ, ինչ GK ամբողջը CD ամբողջի նկատմամբ է [Բան. 7.5]: | ||
| + | Նույն կերպ, քանի որ ինչ մաս KH-ը CD-ի նկատմամբ է, EL-ը նույն մասն է CF-ի նկատմամբ, և CD-ն մեծ է CF-ից, HK-ն ավելի մեծ է EL-ից: Թող KN-ը հավասարեցվի EL-ին: Այսպիսով, ինչ մաս KH-ը CD-ի նկատմամբ է, KN-ը նույն մասն է CF-ի նկատմամբ: Ուստի NH մնացորդը նույնպես նույն մասն է FD մնացորդի նկատմամբ, ինչ KH ամբողջը CD ամբողջի նկատմամբ է [Բան. 7.5]: | ||
| + | Եվ MK մնացորդը նույնպես ցույց տրվեց, որ նույն մասն է FD մնացորդի նկատմամբ, ինչ GK ամբողջը CD ամբողջի նկատմամբ է: Ուստի MK և NH գումարը նույն մասերն են DF-ի նկատմամբ, ինչ HG ամբողջը CD ամբողջի նկատմամբ է: Եվ MK, NH գումարը հավասար է EB-ին, իսկ HG-ը՝ BA-ին: Ուստի EB մնացորդը նույնպես նույն մասերն է FD մնացորդի նկատմամբ, ինչ AB ամբողջը CD ամբողջի նկատմամբ է: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): | ||
| + | Նշում : Ժամանակակից նշանումներով, այս առաջարկությունը նշանակում է, որ եթե a = (m/n)*b և c = (m/n)d, ապա (a+c) = (m/n)(b+d), որտեղ բոլոր նշանները ներկայացնում են թվեր։ | ||
| + | |||
| + | == Առաջարկություն 9 == | ||
| + | Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասը (կամ նույն մասերն) է մեկ այլ թվի, ապա, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ առաջին (թիվը) լինի երրորդի նկատմամբ, երկրորդ (թիվը) նույնպես կլինի նույն մասը կամ մասերը մյուսի նկատմամբ կամ նույն մասերը, չորրորդ. | ||
| + | [[Պատկեր:1.18.png]] | ||
| + | |||
| + | Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասը (կամ նույն մասերն) է մեկ այլ թվի, ապա, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ առաջին (թիվը) լինի երրորդի նկատմամբ, երկրորդ (թիվը) նույնպես կլինի նույն մասը կամ մասերը մյուսի նկատմամբ: | ||
| + | Թող A թիվը լինի BC թվի մի մաս, և մեկ այլ (թիվ) D լինի նույն մասը մեկ այլ EF թվի, ինչ A-ն է BC-ի: Ասում եմ, որ նաև, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ A-ն ունենա D-ի նկատմամբ, BC-ն նույնպես կունենա նույն մասը, կամ նույն մասերը EF-ի նկատմամբ: | ||
| + | Քանի որ ինչ մաս A-ն ունի BC-ի նկատմամբ, D-ն նույն մասն ունի EF-ի նկատմամբ, ապա որքան թվեր կան BC-ի մեջ, որոնք հավասար են A-ին, նույնքան թվեր կլինեն EF-ի մեջ, որոնք հավասար են D-ին: Թող BC-ը բաժանված լինի BG և GC մասերի, հավասար A-ին, իսկ EF-ը բաժանված լինի EH և HF մասերի, հավասար D-ին: Այսպիսով, BG և GC բաժանումների քանակը հավասար կլինի EH և HF բաժանումների քանակին: | ||
| + | Եվ քանի որ BG և GC թվերը հավասար են միմյանց, իսկ EH և HF թվերը նույնպես հավասար են միմյանց, և BG, GC բաժանումների քանակը հավասար է EH, HF բաժանումների քանակին, ապա ինչ մասը, կամ մասերն էլ որ BG-ն ունենա EH-ի նկատմամբ, GC-ն նույնպես կունենա նույն մասը, կամ նույն մասերը HF-ի նկատմամբ: Եվ այդպիսով, ինչ մասը, կամ մասերն էլ BG-ն ունենա EH-ի նկատմամբ, BC-ի ամբողջությունն էլ նույն մասը կամ մասերը կունենա EF-ի ամբողջության նկատմամբ [Բան. 7.5, 7.6]: Եվ քանի որ BG-ը հավասար է A-ին, իսկ EH-ը հավասար է D-ին, ուրեմն ինչ մասը, կամ մասերն էլ A-ն ունենա D-ի նկատմամբ, BC-ն նույնպես կունենա նույն մասը կամ մասերը EF-ի նկատմամբ: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): | ||
| + | *(Ժամանակակից նշանմամբ, եթե a = (1/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)d, որտեղ բոլոր նշանները ներկայացնում են թվեր): | ||
| + | |||
| + | == Առաջարկություն 10† == | ||
| + | Եթե մի թիվ մասեր է ինչ-որ թվի, և մեկ այլ (թիվ) նույն մասերն է մեկ այլ թվի, ապա նաև, փոխարինաբար, թե որ մասերը կամ մասը առաջին թիվը ունենա երրորդի նկատմամբ, երկրորդ թիվը նույնպես կունենա նույն մասերը կամ նույն մասը չորրորդի նկատմամբ: | ||
| + | Թող AB թիվը լինի C թվի մասերը, իսկ DE թիվը լինի F թվի նույն մասերը: Ասում եմ, որ նաև, փոխարինաբար, թե որ մասերը, կամ որ մասը AB-ն ունի C-ի նկատմամբ, DE-ն նույնպես կունենա նույն մասերը կամ նույն մասը F-ի նկատմամբ: | ||
| + | [[Պատկեր:1.19.png]] | ||
| + | |||
| + | Քանի որ ինչ մասեր AB-ն ունի C-ի նկատմամբ, DE-ն նույնպես նույն մասերն ունի F-ի նկատմամբ, ապա որքան մասեր C-ի մեջ կան AB-ի չափ, նույնքան մասեր կլինեն F-ի մեջ DE-ի չափ: Թող AB-ը բաժանվի C-ի մասերի՝ AG և GB, իսկ DE-ը բաժանվի F-ի մասերի՝ DH և HE: Այսպիսով, AG և GB բաժանումների քանակը հավասար կլինի DH և HE բաժանումների քանակին: | ||
| + | Եվ քանի որ ինչ մասը, կամ մասեր AG-ն ունի C-ի նկատմամբ, DH-ն նույնպես ունի նույն մասը կամ մասերը F-ի նկատմամբ, նաև փոխարինաբար, ինչ մասը կամ մասերը AG-ն ունի DH-ի նկատմամբ, C-ն նույնպես նույն մասը կամ մասերը կունենա F-ի նկատմամբ [Բան. 7.9]: Նույն պատճառով, ինչ մասը կամ մասերը GB-ն ունի HE-ի նկատմամբ, C-ն նույնպես նույն մասը կամ մասերը կունենա F-ի նկատմամբ [Բան. 7.9]: Եվ ինչ մասը կամ մասերը AG-ն ունի DH-ի նկատմամբ, GB-ն նույն մասը կամ մասերը կունենա HE-ի նկատմամբ [Բան. 7.5, 7.6]: Բայց ինչ մասը կամ մասերը AG-ն ունի DH-ի նկատմամբ, նաև ցույց տրվեց, որ C-ն նույն մասը կամ մասերը ունի F-ի նկատմամբ: Ուստի, ինչ մասեր կամ ինչ մասը AB-ն ունի C-ի նկատմամբ, C-ն նույնպես նույն մասերը կամ samme մասը կունենա F-ի նկատմամբ: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): | ||
| + | *(Ժամանակակից նշանմամբ, եթե a = (m/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)d, որտեղ բոլոր նշանները թվեր են): | ||
| + | |||
| + | == Առաջարկություն 11 == | ||
| + | Եթե, ինչպես ամբողջ AB-ն ամբողջ CD-ի նկատմամբ է, նույն ձևով AE հանված մասը CF հանված մասի նկատմամբ է, ապա մնացորդը նույնպես կլինի մնացորդի նկատմամբ այն հարաբերությամբ, ինչ ամբողջը ամբողջի նկատմամբ է: | ||
| + | Թող ամբողջ AB-ն լինի ամբողջ CD-ի նկատմամբ այնպիսին, ինչպիսին AE հանված մասը CF հանված մասի նկատմամբ է: Ասում եմ, որ EB մնացորդը FD մնացորդի նկատմամբ նույն հարաբերությունն ունի, ինչ ամբողջ AB-ն ամբողջ CD-ի նկատմամբ: | ||
| + | [[Պատկեր:1.20.png]] | ||
| + | |||
| + | Քանի որ ինչպես AB-ը CD-ի նկատմամբ է, այնպես AE-ը CF-ի նկատմամբ է, ապա ինչ մասեր կամ մասը AB-ն ունի CD-ի նկատմամբ, AE-ն նույնպես նույն մասը կամ մասերն ունի CF-ի նկատմամբ [Սահմ. 7.20]: Ուստի EB մնացորդը նույնպես նույն մասը կամ մասերն ունի FD մնացորդի նկատմամբ, ինչ AB-ն ունի CD-ի նկատմամբ [Բան. 7.7, 7.8]: Այսպիսով, ինչպես EB-ն FD-ի նկատմամբ է, այնպես AB-ն CD-ի նկատմամբ է [Սահմ. 7.20]: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): | ||
| + | |||
| + | == Առաջարկություն 12† == | ||
| + | Եթե կամայական քանակի թվեր համաչափ են, ապա ինչպես առաջավոր (թվերից) մեկը (է) հետագային, այնպես էլ (արդյունքում) բոլոր առաջավոր (թվերի) գումարը (կլինի) բոլոր հետագա (թվերի) գումարի նկատմամբ: | ||
| + | |||
| + | [[Պատկեր:1.21.png]] | ||
| + | |||
| + | Թող կամայական քանակի թվեր A, B, C, D համաչափ լինեն (այնպես, որ ինչպես A-ն է B-ի նկատմամբ, այնպես C-ն D-ի նկատմամբ է): Ասում եմ, որ ինչպես A-ն է B-ի նկատմամբ, այնպես A և C (համատեղ) B և D (համատեղ) նկատմամբ են: | ||
| + | Քանի որ ինչպես A-ն է B-ի նկատմամբ, այնպես C-ն D-ի նկատմամբ է, ապա ինչ մասը, կամ մասերն էլ A-ն ունենա B-ի նկատմամբ, C-ն նույնպես նույն մասը կամ մասերն ունի D-ի նկատմամբ [Սահմ. 7.20]: Այդպիսով, A և C գումարը նույնպես նույն մասը, կամ նույն մասերն է B և D գումարի նկատմամբ, ինչ A-ն B-ի նկատմամբ [Բան. 7.5, 7.6]: Ուստի, ինչպես A-ն B-ի նկատմամբ է, այնպես A, C (համատեղ) B, D (համատեղ) նկատմամբ են [Սահմ. 7.20]: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): | ||
| + | |||
| + | Ժամանակակից մեկնություն (†) | ||
| + | Ժամանակակից նշանմամբ, այս առաջարկությունն ասում է, որ եթե a : b :: c : d, ապա a : b :: a + c : b + d, որտեղ բոլոր նշանները ներկայացնում են թվեր։ | ||
Ընթացիկ տարբերակը 23:27, 12 Դեկտեմբերի 2024-ի դրությամբ
հեղինակ՝ էվկլիդես |
Բովանդակություն
- 1 Սահմանումներ
- 2 Պնդում 1
- 3 Պնդում 2
- 4 Պնդում 3
- 5 Պնդում 4
- 6 Պնդում 5
- 7 Պնդում 6
- 8 Պնդում 7
- 9 Պնդում 8
- 10 Պնդում 9
- 11 Պնդում 10
- 12 Պնդում 11
- 13 Պնդում 12
- 14 Պնդում 13
- 15 Պնդում 14
- 16 Պնդում 15
- 17 Պնդում 16
- 18 Պնդում 17
- 19 Պնդում 18
- 20 Պնդում 19
- 21 Պնդում 20
- 22 Պնդում 21
- 23 Պնդում 22
- 24 Առաջարկություն 24
- 25 Առաջարկություն 25
- 26 Առաջարկություն 26
- 27 Առաջարկություն 27
- 28 Առաջարկություն 28
- 29 Առաջարկություն 29
- 30 Առաջարկություն 30
- 31 Առաջարկություն 31
- 32 Առաջարկություն 32
- 33 Առաջարկություն 33
- 34 Առաջարկություն 1
- 35 Առաջարկություն 2
- 36 Առաջարկություն 3
- 37 Առաջարկություն 4
- 38 Առաջարկություն 5
- 39 Առաջարկություն 6
- 40 Առաջարկություն 7
- 41 Առաջարկություն 9
- 42 Առաջարկություն 10†
- 43 Առաջարկություն 11
- 44 Առաջարկություն 12†
Սահմանումներ
- Նման ուղղագծային պատկերներ կոչվում են այն պատկերները, որոնց համապատասխան անկյունները առանձին-առանձին հավասար են, իսկ (համապատասխանող) անկյունների կողմերը՝ համաչափ:
- Ուղիղ գիծը , որը բաժանված է մեծ և միջին հարաբերությամբ, երբ ամբողջ գիծը մեծ հատվածի հետ նույն հարաբերության մեջ է, ինչ մեծ հատվածը՝ փոքր հատվածի հետ:
- Ցանկացած պատկերի բարձրությունը գագաթից հիմքին ուղղահայաց տարված ուղիղ գիծն է:
Պնդում 1
Այն եռանկյուններն ու զուգահեռագծերը, որոնք ունեն նույն բարձրությունը, ապա նրանց հիմքերը հարաբերվում են համապատասխանաբար:
Թող ABC-ն եւ ACD-ն լինեն եռանկյուններ, իսկ EC եւ CF զուգահեռագծեր՝ AC բարձրությանը հավասար:Ասում ենք, որ հիմք BC-ն հարաբերում է CD-ին, ուստի ABC եռանկյունը ACD եռանկյունին, իսկ զուգահեռագիծ EC-ը զուգահեռագծի CF-ին: Ենթադրենք, որ BD-ն տարված է յուրաքանչյուր ուղղությամբ մինչեւ H և L կետերը, և դիցուք (ուղիղ գծերի) [ցանկացած թիվ] BG-ն և GH-ը հավասարեցնեն BC հիմքին և (ուղիղ գծերի) ցանկացած թվի DK և KL՝ CD հիմքին: Եվ AG-ն, AH-ը, AK-ն և AL-ը միացնենք միմյանց: Եվ քանի որ CB-ն, BG-ն եւ GH-ը հավասար են միմյանց, AHG, AGB եւ ABC եռանկյունները նույնպես հավասար են միմյանց [Պնդ: 1.38]: Այսպիսով, քանի որ HC հիմքը մի քանի անգամ (բաժանվում է) BC հիմքով, այդքան անգամ էլ AHC եռանկյունը նույնպես (բաժանվում է) ABC եռանկյունու վրա: Այսպիսով, նույն տրամաբանությամբ LC հիմքը մի քանի անգամ (բաժանվում) է հիմք CD-ով, այդքան անգամ էլ ALC եռանկյունը նույնպես (բաժանվում է) ACD եռանկյունի: Եվ եթե HC հիմքը հավասար է CL հիմքին, ապա AHC եռանկյունը նույնպես հավասար է ACL եռանկյանը [Prop: 1.38]: Եվ եթե HC հիմքը գերազանցում է CL հիմքը, ապա AHC եռանկյունը նույնպես գերազանցում է ACL եռանկյանը:Եվ եթե (HC-ն) փոքր է (քան CL-ն, ապա AHC-ն նույնպես) փոքր է (քան ACL): Այսպիսով, դրանք լինելով չորս մեծություն, երկու հիմք՝ BC եւ CD, և երկու եռանկյուններ՝ ABC եւ ACD, հավասար բազմապատիկներ են վերցվել BC հիմքից և ABC—եռանկյունից (մասնավորապես), հիմք HC և եռանկյուն AHC—և CD հիմքի այլ ցանկացած բազմապատիկներ և եռանկյունի ADC— (մասնավորապես), հիմք LC եւ ALC եռանկյունին: Եվ ցույց է տրվել, որ եթե հիմք HC-ը գերազանցում է CL հիմքը, ապա AHC եռանկյունը նույնպես գերազանցում է ALC (և եթե (HC-ն) հավասար է (CL-ին, ապա AHC-ն նույնպես) հավասար է (ALC-ին), և եթե (HC-ն) փոքր է (քան CL-ն, ապա AHC-ն նույնպես) փոքր շէ (քան ALC): Այսպիսով, քանի որ BC հիմքը հարաբերում է CD-ի հիմքին, ուստի ABC եռանկյունը նույնպես հարաբում է (ACD եռանկյունին [Def: 5:5]: Եվ քանի որ EC զուգահեռագիծը կրկնակի ABC եռանկյունն է, իսկ FC ուգահեռագիծը կրկնակի ACD եռանկյունն է [Պնդ: 1:34], եւ մասերն ունեն նույն հարաբերակցությունը, ինչ նմանատիպ բազմապատիկները [Պնդ: 5:15], հետևաբար, որպես ABC եռանկյունի հարաբերում է ACD եռանկյանը, ուստի զուգահեռագիծ EC-ին հարաբերում է զուգահեռագիծ FC-ին: Իրականում, քանի որ BC հիմքը հարաբերում է CD-ին, այնպես որ ABC եռանկյունը հարաբերում է ACD եռանկյանը, և եռանկյունի ABC հարաբերում (է) ACD եռանկյանը, ուստի EC զուգահեռագիծը հարաբերում (է) CF զուգահեռագծին, հետեւաբար, նույնպես BC հիմքը CD-ին, ուստի EC-ին (է) զուգահեռագիծը FC [Պնդ: 5.11]: Այսպիսով, եռանկյունները և զուգահեռագծերը, որոնք ունեն նույն բարձրությունը, միմյանց նկատմամբ են, հարաբերում են այնպես, ինչպես իրենց հիմքերը: Հենց այն էր, ինչ պահանջվում էր ցույց տալ:
- Ինչպես կարելի է հեշտությամբ ցույց տալ, նույն գործում է նույնիսկ այն դեպքում, երբ եռանկյունները կամ զուգահեռականները չունեն ընդհանուր կողմ և/կամ ուղիղ անկյուն չեն:
- Սա պրոպ. 1.38-ի ուղղակի ընդհանրացումն է:
Պնդում 2
Երբ եռանկյան կողմերից մեկին զուգահեռ մի ուղիղ գիծ է գծվում, ապա այն կտրվածքով կտրում է եռանկյան (մյուս) կողմերը համաչափ։ Եվ եթե եռանկյան (երկու) կողմերը կտրում են համաչափ, ապա այդ կետերը միացնող ուղիղ գիծը կլինի զուգահեռ եռանկյան մնացած կողմին։
DE ուղիղ գիծը գծված է ABC եռանկյան BC կողմին զուգահեռ։ Ինչպես BD-ն DA-ին է հարաբերում է, այնպես էլ CE-ն EA-ին: Դիցուք, BE և CD գծերը միացված են։ Հետևաբար, եռանկյուն BDE-ն հավասար է CDE եռանկյանը։Նույն DE հիմքի վրա են և DE և BC զուգահեռների միջև [Պնդ. 1.38]։ Իսկ ADE-ն այլ եռանկյուն է։ Եվ հավասար (կողմերը) նույն (կողմի) հետ ունեն նույն հարաբերությունը [Պնդ. 5.7]։ Հետևաբար, ինչպես եռանկյուն BDE-ն հարաբերվում է [եռանկյունի] ADE-ին, այնպես էլ եռանկյունի CDE-ն (ADE) եռանկյանը։ Եվ, ինչպես եռանկյունի BDE-ն է եռանկյուն ADE-ի նկատմամբ, այնպես էլ BD-ն է DA-ի նկատմամբ։ Քանի որ ունեն նույն բարձրությունը՝ (մասնավորապես՝) E կետից գծված ուղղահայացը AB-ի վրա, նրանք իրար նկատմամբ ունեն նույն հարաբերությունը, ինչ իրենց հիմքերը [Պնդ. 6.1]։ Այդ իսկ պատճառով, ինչպես եռանկյուն CDE-ն հարաբերվում է ADE-ի նկատմամբ, այնպես էլ CE-ն է EA-ի նկատմամբ։ Եվ, հետևաբար ,ինչպես BD-ն է DA-ի նկատմամբ, այնպես էլ CE-ն է EA-ի նկատմամբ [Պնդ. 5.11]։ Դիցուք, ABC եռանկյան AB և AC կողմերը բաժանվեն համաչափորեն (այնպես որ) ինչպես BD հարաբերվի է DA-ի նկատմամբ, այնպես էլ CE-ն EA-ի նկատմամբ։ Եվ թող DE գիծը միացված լինի։ DE գիծը զուգահեռ է BC-ին։ Քանի որ, նույն եղանակով, ինչպես BD-ն է DA-ի նկատմամբ, այնպես էլ CE-ն է EA-ի նկատմամբ, սակայն ինչպես BD-ն է DA-ի նկատմամբ, այնպես էլ BDE եռանկյունն է ADE-ի նկատմամբ, և ինչպես CE-ն է EA-ի նկատմամբ, այնպես էլ եռանկյուն CDE-ն է ADE-ի նկատմամբ [Պնդ. 6.1], հետևաբար, եռանկյուն BDE-ն հարաբերվում ADE-ի նկատմամբ, այնպես էլ եռանկյուն CDE-ն է ADE-ի նկատմամբ [Պնդ. 5.11]։ Հետևաբար, BDE և CDE եռանկյունները յուրաքանչյուրն ունեն նույն հարաբերությունը ADE-ի նկատմամբ։ Արդյունքում, BDE եռանկյունը հավասար CDE եռանկյանը [Պնդ. 5.9]։ Եվ նրանք գտնվում են նույն DE հիմքի վրա։ Հավասար եռանկյունները, որոնք նույն հիմքի վրա են , գտնվում են նաև նույն զուգահեռների միջև [Պնդ. 1.39]։ Հետևաբար, DE գիծը զուգահեռ է BC-ին։ Այսպիսով, եթե եռանկյան կողմերից մեկին զուգահեռ ուղիղ գիծ գծենք, ապա այն համաչափ կբաժանի եռանկյան (մյուս) կողմերը։ Եվ եթե եռանկյան (երկու) կողմերը աժանվեն համաչափ, ապա այդ կետերը միացնող ուղիղ գիծը կլինի զուգահեռ եռանկյան մնացած կողմին։ (Այսինքն՝ այն, ինչ պետք էր ցույց տալ)։
Պնդում 3
Եթե եռանկյան անկյունը կիսվում է, և այդ անկյունը կիսող ուղիղ գիծը կտրում է նաև հիմքը, ապա հիմքի հատվածները կունենան նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը։ Եվ եթե հիմքի հատվածները ունեն նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը, ապա գագաթը կետին միացնող ուղիղ գիծը կիսում է եռանկյան անկյունը։ Տրված է, ABC եռանկյունը։ Եվ թող BAC անկյունը կիսված լինի AD ուղիղ գծով։ Ինչպես BD-ն է հարավերվում DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ։ CE գիծը գծվի C կետից՝ զուգահեռ AD-ին։ Եվ BA գիծը (CE)-ին E կետում*։
Քանի որ, AC ուղիղ գիծը անցնում է AD և EC զուգահեռ (ուղիղների) միջև, ապա ACE անկյունը հավասար է CAD-ին [Պնդ. 1.29]։ Ենթադրվում է, որ CAD անկյունը հավասար BAD-ին։ Հետևաբար, BAD անկյունը նույնպես հավասար է ACE-ին։ Քանի որ, BAE ուղիղ գիծը անցնում է AD և EC զուգահեռ (ուղիղների) միջև, ապա BAD արտաքին անկյունը հավասար է AEC ներքին (անկյանը) [Պնդ. 1.29]։ Իսկ ACE անկյունը նույնպես ցույց է տրվել, որ հավասար է BAD-ին։ Հետևաբար, ACE անկյունը նույնպես հավասար է AEC-ին։ Եվ, հետևաբար, AE կողմը հավասար է AC կողմին [Պնդ. 1.6]։ Այն պատճառով, որ AD գիծը գծված է BCE եռանկյանը և EC կողմին զուգահեռ, ապա համաչափորեն, ինչպես BD-ն է DC-ի նկատմամբ հարաբերվում, այնպես էլ BA-ն է AE-ի [Պնդ. 6.2]։ Իսկ AE-ն հավասար է AC-ին։ Հետևաբար, ինչպես BD-ն է DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ։ Եվ այսպես, BD-ն հարաբերվի DC-ի նկատմամբ այնպես, ինչպես BA-ն AC-ի նկատմամբ, և AD գիծը միացվի։ Դիցուք, BAC անկյունը կիսված է AD ուղիղ գծով։ Նույն եղանակով, ինչպես BD-ն է հարավերվում DC-ի նկատմամբ, այնպես էլ BA-ն է AC-ի նկատմամբ, ապա նաև, ինչպես BD հարաբերվում է DC-ի նկատմամբ, այնպես էլ BA-ն է AE-ի նկատմամբ։ Քանի որ, AD գիծը զուգահեռ է BCE եռանկյան EC կողմին [Պնդ. 6.2]։ Հետևաբար, ինչպես BA-ն է AC-ի նկատմամբ, այնպես էլ BA-ն է AE-ի նկատմամբ [Պնդ. 5.11]։ Արդյունքում AC-ն հավասար է AE-ին[Պնդ.5.9]։ Եվ, հետևաբար, AEC անկյունը հավասար է ACE անկյանը[Պնդ. 1.5]։ AEC անկյունը հավասար է BAD արտաքին (անկյանը), իսկ ACE անկյունը հավասար է CAD անկյանը[Պնդ. 1.29]։ Հետևաբար, BAD անկյունը նույնպես հավասար է CAD-ին։ Հետևաբար, BAC անկյունը կիսված է AD ուղիղ գծով։ Այսպիսով, եթե եռանկյան անկյունը կիսվում է, և այդ անկյունը կիսող ուղիղ գիծը բաժանում է նաև հիմքը, ապա հիմքի հատվածները կունենան նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը։ Եվ եթե հիմքի հատվածները ունեն նույն հարաբերությունը, ինչ եռանկյան մնացած կողմերը, ապա գագաթը կետին միացնող ուղիղ գիծը կիսում է եռանկյան անկյունը։ Ինչը հենց պահանջվում էր ապացուցել:
- Այն փաստը, որ երկու ուղիղ գծերը հանդիպում են, հետևում է այն բանից, որ ACE և CAE անկյունների գումարը փոքր է երկու ուղղանկյունից, ինչպես հեշտությամբ կարելի է ցույց տալ։
Պնդում 4
Նման (հավասարանկյուն) եռանկյուններում կողերն ունեն համեմատական հարաբերություն, և այն կողմերը, որոնք ունեն հավասար անկյուններ, համապատասխանում են միմյանց:
Դիցուք, ABC և DCE լինեն նման եռանկյուններ, որտեղ ABC անկյունը հավասար է DCE անկյանը, և BAC անկյունը՝ CDE անկյանը, և, ավելին, ACB անկյունը՝ CED-ին:Կարող ենք նշել, որ ABC և DCE եռանկյուններում համապատասխանաբար անկյունների կողմերն ունեն համեմատական հարաբերություն, և (կողմերը), որոնք համապատասխանաբար ունեն հավասար անկյուններ, համընկնում են: Եկեք BC գիծը տեղադրենք CE-ի վրա։ Քանի որ, ABC և ACB անկյունները փոքր են երկու ուղիղ-անկյուններից[Պնդ.1.17], և ACB անկյունը հավասար է DEC անկյանը, հետևաբար, ABC և DEC անկյունները փոքր են երկու ուղիղ-անկյուններից։ Այսպիսով, BA և ED գծերը, որոնք երկարացվել են, կհանդիպեն [Հավ. 5]։ Դրանք երկարացվելով,ի վերջո հանդիպում են F կետում։ Քանի որ,DCE անկյունը հավասար է ABC-ին, BF գիծը զուգահեռ է CD-ին [Պնդ. 1.28]։ Նույն տրամաբանությամբ, ACB անկյունը հավասար է DEC անկյանը, AC գիծը զուգահեռ է FE-ին [Պնդ. 1.28]։ Այսպիսով, FACD-ը զուգահեռագիծ է։ Հետևաբար, FA-ն հավասար է DC-ին, իսկ AC-ն՝ FD-ին [Պնդ. 1.34]։ Այնուհետև, AC գիծը գծված է FBE եռանկյանը և FE կողմին զուգահեռ, հետևաբար, ինչպես BA-ն է հարաբերվում AF-ի նկատմամբ, այնպես էլ BC-ն է CE-ի նկատմամբ [Պնդ. 6.2], և AF-ն հավասար է CD-ին։ Հետևաբար, ինչպես BA-ն է հարաբերվում CD-ի նկատմամբ, այնպես էլ BC-ն է CE-ին, և նույնաբար՝ ինչպես AB-ն է BC-ի նկատմամբ, այնպես էլ DC-ն է CE-ի նկատմամբ [Պնդ. 5.16]։ Նորից, քանի որ CD գիծը զուգահեռ է BF-ին, հետևաբար, ինչպես BC-ն է CE-ի նկատմամբ, այնպես էլ FD-ն է DE-ի նկատմամբ [Պնդ. 6.2]։ Եվ FD-ն հավասար է AC-ին։ Հետևաբար, ինչպես BC հարաբերում է CE-ին, այնպես էլ AC-ն DE-ին, և համապատասխանաբար՝ ինչպես BC-ն է CA-ի նկատմամբ, այնպես էլ CE-ն է ED-ի նկատմամբ [Պնդ. 6.2]։ Հետևաբար, ինչպես AB-ն է BC-ի նկատմամբ, այնպես էլ DC-ն է CE-ի, և ինչպես BC-ն է CA-ի նկատմամբ, այնպես էլ CE-ն է ED-ի նկատմամբ, այսպիսով՝ ըստ հավասարության՝ ինչպես BA-ն է AC-ի, այնպես էլ CD-ն է DE-ի նկատմամբ [Պնդ. 5.22]։ Այսպիսով, նման եռանկյուններում անկյունների կողերն ունեն համեմատական հարաբերություն, և (կողմերը), որոնք ենթարկվում են հավասար անկյուններին, համապատասխանում են։ Ինչը հենց պահանջվում էր ցույց տալ։
Պնդում 5
Եթե երկու եռանկյունները ունեն համաչափ կողմեր, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։
Դիցուք, ABC և DEF լինեն երկու եռանկյուններ, որոնց կողմերը համաչափ են, (այնպես որ) ինչպես AB հարաբերում է BC կողմին, այնպես էլ DE հարաբերում է EF կողմին, և ինչպես BC հարաբերում է CA-ին, այնպես էլ EF FD կողմին, և ավելին, ինչպես BA-ն է AC-ի նկատմամբ, այնպես էլ ED-ն է DF-ի նկատմամբ։ ABC եռանկյունը հավասարանկյուն է, որը հարաբերում է DEF եռանկյանը, և (այդ եռանկյունները) կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։ Այդպիսով, ABC (անկյունը) (հավասար է) DEF անկյանը, BCA՝ EFD-ին, և, ավելին, BAC՝ EDF-ին։ Դիցուք, FEG անկյունը, որը հավասար է ABC անկյանը, և EFG, որը հավասար է ACB անկյանը, գտնվում են EF ուղիղ գծի վրա՝ համապատասխանաբար E և F կետերում [Պնդ. 1.23]։ Այսպիսով, A (անկյան) մյուս մասը հավասար է G անկյան մյուս մասին[Պնդ. 1.32]։ Այսպիսով, ABC եռանկյունը հավասար է EGF եռանկյանը։ Այսպիսով, ABC և EGF եռանկյունների հավասար անկյունների համապատասխանաբար կողմերն ունեն նույն հարաբերությունը, և (այն) կողմերը, որոնք ենթարկվում են հավասար անկյուններին, համապատասխանաբար հավասար են [Պնդ. 6.4]։ Հետևաբար, ինչպես AB-ն հարաբերվում է BC-ին, այնպես էլ GE-ն EF-ին։ Բայց, ինչպես AB-ի հարաբերվածությունն է BC-ի նկատմամբ, այնպես էլ, ենթադրվում է, որ DE և EF ունեն նույն հարաբերվածությունը։ Հետևաբար, ինչպես DE-ն է EF-ի նկատմամբ, այնպես էլ GE-ն է EF-ի նկատմամբ [Պնդ. 5.11]։ Հետևաբար, DE-ն և GE-ն յուրաքանչյուրն ունեն նույն հարաբերությունը EF-ի նկատմամբ։ Հետևաբար, DE-ն հավասար է GE-ին[Պնդ. 5.9]։ Նույն պատճառներով, DF-ն նույնպես հավասար է GF-ին։ Հետևաբար, քանի որ DE-ն հավասար է EG-ին, և EF-ն ընդհանուր է, երկու (կողմերը) DE և EF հավասար են երկու (կողմերին) GE և EF (համապատասխանաբար)։ Իսկ DF հիմքը (հավասար է) հիմք FG հիմքին։ Հետևաբար, DEF անկյունը հավասար է GEF անկյանը [Պնդ. 1.8], և եռանկյուն DEF-ը (հավասար է) GEF եռանկյանը, և համապատասխանաբար կողմերի անկյունները նույնպես հավասար են[Պնդ. 1.4]։ Հետևաբար, DFE անկյունը նույնպես հավասար է GFE անկյանը, իսկ EDF-ն՝ EGF-ին։ Քանի որ, FED (անկյունը) հավասար է GEF-ին, և GEF-ը՝ ABC-ին, հետևաբար, ABC անկյունը նույնպես հավասար է DEF-ին։ Նույն պատճառներով, ACB (անկյունը) նույնպես հավասար է DFE-ին, և, ավելին, A անկյունը՝ D անկյանը։ Այսպիսով, եռանկյուն ABC-ն հավասար է DEF եռանկյանը: Այսպիսով, եթե երկու եռանկյունները ունեն համաչափ կողմեր, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան անկյուններ, որոնք համապատասխանում են համապատասխանաբար կողմերին։ Ապացուցվեց այն, ինչը պահանջվում էր:
Պնդում 6
Եթե երկու եռանկյուններն ունեն համապատասխան անկյունը հավասար է, և այդ հավասար անկյունների կողմերը համաչափ են, ապա եռանկյունները կլինեն հավասարանկյուն և կունենան անկյուններ, որոնք համապատասխանում են այդ կողմերին:
Դիցուք, ABC և DEF լինեն երկու եռանկյուններ, որոնցում BAC անկյունը հավասար է EDF անկյանը (համապատասխանաբար), և այդ անկյունների կողմերը համաչափ են ,այնպես որ,BA հարաբերվի AC կողմին այնպես, ինչպես ED կողմը DF-ին։ABC եռանկյունը հավասարանկյուն է DEF եռանկյանը, որտեղ ABC անկյունը հավասար է DEF անկյանը, իսկ ACB անկյունը DFE անկյանը: FDG անկյունը, որը հավասար է BAC և EDF անկյուններին, և DFG անկյունը, որը հավասար է ACB անկյանը, կառուցվեն AF ուղիղ գծի վրա՝ համապատասխանաբար D և F կետերում [Պնդ. 1.23]։ Այսպիսով, B-ի առընթեր անկյունը հավասար է G-ի առընթեր անկյանը [Պնդ. 1.32]։ Այսպիսով, ABC եռանկյունը DGF եռանկյունը ունեն հավասար անկյուն։ Հետևաբար, համապատասխանաբար, ինչպես BA և AC հարաբերությունը, այնպես էլ GD և DF ունեն նույն հարաբերությունը[Պնդ. 6.4]։ Եվ ենթադրվում է նաև, որ ինչպես BA կհարաբերվի AC-ին, այնպես էլ ED կողմը DF-ին։ Դրանից հետևում է, որ ինչպես ED հարաբերում է DF-ին ,այնպես էլ GD կողմը DF կողմին[Պնդ. 5.11]։ Ուստի, ED-ն հավասար է DG-ին [Պնդ. 5.9], իսկ DF-ն ընդհանուր է։ Այսպիսով, երկու (կողմերը)՝ ED և DF հավասար են երկու (կողմերին) ՝GD և DF (համապատասխանաբար)։ Իսկ անկյուն EDF-ը հավասար է GDF անկյանը։ EF հիմքը հավասար է GF հիմքին, և DEF եռանկյունը հավասար է GDF եռանկյանը, և մյուս անկյունները հավասար կլինեն եռանկյան անկյուններին, որոնք ենթարկվում են հավասար կողմերին [Պնդ. 1.4]։ Հետևաբար, DFG (անկյունը) հավասար է DFE-ին, DGF-ը՝ DEF-ին, իսկ DFG (անկյունը) հավասար կլինի ACB-ին։ Այդ ամենից կհետեևի , որ ACB անկյունը նույնպես հավասար է DFE անկյանը։ BAC անկյունը նույնպես ենթադրվում էր, որ հավասար պետք է լինի EDF-ին։ Հետևաբար, B անկյան առընթեր անկյունը հավասար է E առընթեր անկյանը[Պնդ. 1.32]։ Այսպիսով, եռանկյուն ABC-ն նման է DEF եռանկյանը: Այսպիսով, եթե երկու եռանկյունների ունեն անկյուն, որոնք հավասար են, և այդ անկյունների համապատասխանաբար կողմերը համապատասխանաբար համաչափ են, ապա եռանկյունները կլինեն նման(հավասարանկյուն) և կունենան անկյուններ, որոնք համապատասխանում են համաչափ կողմերին։ Ապացուցեցինք, այն ինչը պահանջվում էր:
Պնդում 7
Եթե երկու եռանկյուններն ունեն մեկ անկյուն, որոնք հավասար են իրար ,և մյուս անկյունների կողմերն ունեն համապատասխանաբար նույն հարաբերությունը, իսկ մնացած անկյունները երկուսն էլ փոքր են կամ երկուսն էլ փոքր չեն ուղիղ անկյուններից, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան հավասար անկյուններ, որոնց համապատասխան կողմերը կունենան նույն հարաբերությունը։
Դիցուք, ABC և DEF երկու եռանկյուններ են, որի BAC անկյունը հավասար է EDF անկյանը (համապատասխանաբար), և ABC և DEF անկյունների կողմերը հարաբերվում են (այնպես որ), AB և BC ունեն նույն հարաբերությունը, ինչպես DE և EF, իսկ մնացած անկյունները՝ C և F-ում, երկուսն էլ սկզբում փոքր են ուղիղ անկյունից։ ABC եռանկյունը նման է DEF եռանկյանը, և (այդ) ABC անկյունը հավասար կլինի DEF անկյանը, և (մնացած) անկյունը C անկյունը (պարզապես) հավասար կլինի F անկյանը։ Եթե ABC անկյունը հավասար չէ DEF (անկյանը), ապա դրանցից մեկը մեծ է մյուսից։ Դիցուք, ABC-ը մեծ լինի և թող ABG (անկյունը), որը հավասար է DEF անկյանը, կառուցված լինի AB ուղիղ գծի վրա՝ B կետում [Պնդ. 1.23]։ Քանի որ , A անկյունը հավասար է D անկյանը, և ABG անկյունը հավասար է DEF-ին, իսկ AGB առընթեր (անկյունը) հավասար է DFE առընթեր (անկյանը) [Պնդ. 1.32]։ Հետևաբար, ABG եռանկյունը նման է (հավասարանկյուն) DEF եռանկյանը։ Հետևաբար, ինչպես AB-ն է հարաբերվում BG-ին, այնպես էլ DE-ն է հարաբերվում EF-ին[Պնդ. 6.4]։ Եվ ինչպես DE-ն է EF-ի նկատմամբ, այնպես էլ ենթադրվում էր, որ AB-ն է BC-ի նկատմամբ։ Հետևաբար, AB և BC նույն հարաբերությունն ունեն BG-ի նկատմամբ [Պնդ. 5.11]։ Հետևաբար, BC-ն հավասար է BG-ին [Պնդ. 5.9]։ Այսպիսով, C անկյունը հավասար է BGC անկյանը [Պնդ. 1.5]։ Իսկ C անկյունը ենթադրվում է, որ փոքր է ուղիղ անկյունից, այսինքն սուր անկյուն է։ Հետևաբար, BGC անկյունը նույնպես սուր անկյուն է։ Հետևաբար, դրան հարակից անկյունը՝ AGB-ն, մեծ է ուղիղ անկյունից [Պնդ. 1.13]։ Ցույց տրվեց, որ AGB անկյունը հավասար է F անկյանը։ Հետևաբար, F անկյունն էլ մեծ է ուղիղ անկյունից։ Բայց ենթադրվում էր, որ փոքր է ուղիղ անկյունից։ Դա բացարձակ անհնար է։ Հետևաբար, անկյուն ABC-ը հավասար չէ DEF-ին։ Եվ A անկյունը նույնպես հավասար է D անկյանը։ ՈՒստի, C անկյանը կից անկյունը հավասար է F- ի կից անկյանը[Պնդ. 1.32]։ Հետևաբար, եռանկյուն ABC-ն նման է DEF եռանկյանը։ Ենթադրենք, C և F անկյունները փոքր չեն ուղիղ անկյունից։ Կրկին կնշեմ, որ եռանկյուն ABC-ն նման է DEF եռանկյանը այս դեպքում նույնպես։ Քանի որ նույն եղնակով կարող ենք ցույց տալ, որ BC-ը հավասար է BG-ին։ Հետևաբար, նաև C անկյունը հավասար է BGC-ին։ Իսկ C-ին (փոքր չէ) ուղիղ անկյունից։ Հետևաբար, BGC-ն (նույնպես) ուղիղ անկյունից փոքր չէ։ Այսպիսով, BGC եռանկյան երկու անկյունների գումարը ուղիղ անկյունից փոքր չէ։ Դա բացարձակ անհնար է [Պնդ. 1.17]։ Այս դեպքում էլ, ABC անկյունը հավասար չէ DEF-ին։ Հետևաբար, (այն) հավասար է։ A անկյունը նույնպես հավասար է D անկյանը։ Հետևաբար, C անկյան կից անկյունը հավասար է F-ի կից անկյանը[Պնդ.1.32]։ Հետևաբար, ABC եռանկյունը նման է DEF եռանկյանը։ Այսպիսով, եթե երկու եռանկյուններն ունեն մեկ անկյուն, որոնք հավասար են իրար,և մյուս անկյունների կողմերն ունեն համապատասխանաբար նույն հարաբերությունը, իսկ մնացած անկյունները երկուսն էլ փոքր են կամ երկուսն էլ փոքր չեն ուղիղ անկյուններից, ապա եռանկյունները կլինեն նման (հավասարանկյուն), և կունենան հավասար անկյուններ, որոնց համապատասխան կողմերը կունենան նույն հարաբերությունը: Ահա ապացուցվեց այն, ինչը հենց պահանջվում էր ցույց տալ։
Պնդում 8
Եթե ուղղանկյուն եռանկյան ուղիղ անկյունից ուղիղ գիծ է գծվում ՝ ուղղահայաց հիմքի վրա, ապա ուղղահայաց գծի շուրջ գտնվող եռանկյունները նման են միմյանց և մեծ ուղանկյուն (եռանկյանը): Դիցուք, ABC ուղղանկյուն եռանկյուն է, որի BAC անկյունը ուղիղ անկյուն է, և թող AD ուղիղ գիծը գծված լինի A կետից՝ ուղղահայաց BC-ին [Պնդ. 1.12]։ ABD և ADC եռանկյունները յուրաքանչյուրն էլ նման են ABC-ին և միմյանց։
Քանի որ BAC անկյունը հավասար է ADB անկյանը—երկուսն էլ ուղիղ անկյուններ են—իսկ B անկյունը ընդհանուր է ABC և ABD եռանկյունների համար, հետևաբար ACB անկյունը հավասար է BAD անկյանը[Պնդ. 1.32]։ Հետևաբար, ABC եռանկյունը նման է ABD եռանկյանը։ BC գտնվում է ABC եռանկյան ուղիղ անկյան դիմաց, BA ABD եռանկյան ուղիղ անկյան դիմաց, AB-ն, C անկյան դիմաց ABC- ում, (այդպես էլ) BD-ը, որը գտնվումէ BAD-ի դիմաց ABD եռանկյունում, AC և AD , (երկուսն էլ) B անկյանն են նայում, որը ընդհանուր է երկու եռանկյունների համար [Պնդ. 6.4]։ Հետևաբար, ABC եռանկյունը նման է ABD եռանկյանը և ունի հավասար անկյունների համապատասխան կողմերի նույն հարաբերությունը։ Հետևաբար, ABC եռանկյունւ նման է ABD եռանկյանը[Սահ. 6.1]։ Նույն կերպ, կարող ենք ցույց տալ, որ եռանկյուն ABC-ն նույնպես նման է ADC եռանկյանը։ Այսպիսով, ABD և ADC [եռանկյունները] նման են ABC եռանկյանը։ Այսպիսով, եռանկյունները ABD և ADC նույնպես նման են միմյանց։ Քանի որ BDA ուղիղ անկյունը հավասար է ADC ուղիղ անկյանը, և, BAD անկյունը նույնպես ցույց է տրվել, որ հավասար է C անկյանը, հետևաբար B անկյան առընթեր անկյունը նույնպես հավասար է DAC առընթեր անկյանը [Պնդ. 1.32]։ Հետևաբար, ABD եռանկյունը նման է ADC եռանկյանը։ Հետևաբար, ինչպես BD-ը, որը գտնվում է ABD եռանկյունում ՝BAD անկյան դիմաց, այնպես էլ DA-ն, C անկյան դիմաց ADC եռանկյունում, (որը) հավասար է BAD անկյանը, այդպես էլ նույն AD-ը, որը գնվում է B անկյան դիմաց ABD եռանկյունում, DC-ն, DAC անկյան դիմաց ADC եռանկյան մեջ, (որը) հավասար է B անկյանը, և, ավելին, ինչպես BA և AC, (երկուսն էլ) ուղիղ անկյան դիմաց են [Պնդ. 6.4]։ Հետևաբար, ABD եռանկյուն նման է ADC եռանկյանը[Սահ. 6.1]։ Այսպիսով, եթե ուղղանկյուն եռանկյան ուղիղ անկյունից ուղիղ գիծ է գծվում ՝ ուղղահայաց հիմքի վրա, ապա ուղղահայաց գծի շուրջ գտնվող եռանկյունները նման են միմյանց և մեծ ուղանկյուն եռանկյանը: Ապացուցեցինք, ինչ պահանջվում էր:
Հետևանք
Այսպիսով, ակնհայտ է, որ եթե ուղղանկյուն եռանկյան ուղիղ անկյունից ուղղահայաց գիծ տարվի հիմքին , ապա (այդպես) ուղիղ գծի հատվածները հարաբերվում էն հիմքի հատվածներին։ Այդ էր պահանջվում ցույց տալ:
- Այլ կերպ ասած, ուղղահայացը հիմքի հատվածների երկրաչափական միջինն է։
Պնդում 9
Տրված ուղիղ գծից հարկավոր է կտրել սահմանված մասը:
Դիցուք, AB լինի ուղիղ գիծ։ Այպիսով, AB-ից պահանջվում է կտրել սահմանված մասը։ Եկեք նշանակենք A կետից գծենք AC ուղիղ գիծը, որը կազմում է կամայական անկյուն AB-ի հետ։ AC գծի վրա նշանակենք D կետը ։ Թող DE և EC հատվածները լինեն հավասար AD հատվածին [Պնդ. 1.3] և միացնենք BC։ DF գիծը գծենք D կետի միջոցով՝ որը ուգահեռ կլինի BC գծին [Պնդ. 1.31]։ Հետևաբար, քանի որ FD գիծը զուգահեռ է ABC եռանկյան կողմերից մեկին՝ BC-ին, ապա համապատասխանաբար, ինչպես CD հատվածն է հարաբերում DA-ին, այնպես էլ BF հատվածը է FA հատվածին [Պնդ. 6.2]։ Եվ CD հատվածը հավասար է DA հատվածի կրկնակի արժեքինԼ Հետևաբար, BF-ն նույնպես կրկնակի է FA հատվածն է։ Հետևաբար, BA հավասար է եռակի FA։ Այսպիսով, սահմանված երրորդ մասը՝ AF, կտրել ենք տրված AB ուղիղ գծից։ Ապացուցվեց այն, ինչը պահանջվում էր:
Պնդում 10
Տրված չկտրվող ուղիղ գիծը կտրել այնպես, ինչպես տվյալ կտրված ուղիղ գիծը:
Դիցուք, AB տրված չկտրվող ուղիղ գիծն է, և AC ուղիղ գիծը, որը կտրված է D և E կետերում։ Թող AC գիծը տարվի այնպես, որ կազմի կամայական AB անկյան հետ։ Ապա, CB գիծը միացնենք։ DF և EG գծերը գծվեն D և E կետերով (համապատասխանաբար)՝ զուգահեռ BC գծին, և թող HK գիծը գծվի D կետի միջով՝ զուգահեռ AB գծին [Պնդ. 1.31]։ Հետևաբար, FH և HB-ը զուգահեռագծեր են։ DH-ը հավասար է FG-ին, իսկ HK-ն՝ GB-ին [Պնդ. 1.34]։ Քանի որ, HE ուղիղ գիծը գծված է զուգահեռ DKC եռանկյան KC կողմին, ապա համապատասխանաբար, ինչպես CE հարաբերվում է ED-ին, այնպես էլ KH հարաբերում HD-իմ[Պնդ. 6.2]։KH-ն հավասար է BG-ին, իսկ HD-ն՝ GF-ին։ Հետևաբար, ինչպես CE և ED հատվածների հարաբերությունն է, այնպես էլ BG և GF հատվածներինը։ Քանի որ, FD գիծը գծված է զուգահեռ AGE եռանկյան GE կողմին, ապա համապատասխանաբար, ինչպես ED հարաբերում է DA-ին, այնպես էլ GF- ը FA-ի հատվածին [Պնդ. 6.2]։ Եվ ցույց է տրվել, CE և ED հարաբերակցությունը հավասար է BG և GF- ի հարաբերակցությանը ։ Հետևաբար, ինչպես CE հարաբերում ED-ին, այնպես էլ BG՝ GF-ին, և ինչպես ED՝DA-ին, այնպես էլ GF՝ FA հատվածին։ Այսպիսով, տրված չկտրվող ուղիղ գիծը կտրել այնպես, ինչպես տվյալ կտրված ուղիղ գիծը: Ինչը հենց պահանջվում էր ապացուցել։
Պնդում 11
Հարկավոր է գտնել երրորդ ուղիղ գիծը, որը համաչափ է մյուս երկու ուղիղ գծերին: Դիցուք, BA և AC տրված երկու ուղիղ գծերն են, և միասին կազմում են մի կամայական անկյուն։ Պահանջվում է գտնել երրորդ (ուղիղ գիծը), որը համաչափ է BA և AC ուղիղ գծերին։ BA և AC շարունակվեն դեպի D և E կետեր (համապատասխանաբար), և BD-ը հավասար լինի AC-ին [Պնդ. 1.3]։ Այնւհետև,BC գիծը միացվի։ DE գիծը գծեն D կետի միջով՝ զուգահեռ BC գծին [Պնդ. 1.31]։ Քանի որ BC գիծը զուգահեռ է ADE եռանկյան DE կողմին, ապա համաչափորեն, ինչպես AB հարաբերում է BD-ին, այնպես էլ AC CE հատվածին [Պնդ. 6.2]։ Իսկ BD-ը հավասար է AC-ին։ Հետևաբար, ինչպես AB և AC հատվածների հարաբերությունն է, այնպես էլ AC և CE հատվածներինը:
Այսպիսով, գտանք CE ուղիղ գիծը, որը համաչափ է տրված երկու ուղիղ գծերին՝ AB և AC։ Ապացուցվեց այն, ինչը պահանջվում էր:
Պնդում 12
Պահանջվում է գտնել չորրորդ ուղիղ գիծը , որը համաչափ կլինի տրված երեք ուղիղ գծերին:
Դիցուք A, B և C տրված երեք ուղիղ գծերն են։ Պահանջվում է գտնել չորրորդ (ուղիղ գիծը), որը համաչափ է A, B և C ուղիղ գծերին։ DE և DF երկու ուղիղ գծերը կազմում են (կամայական) EDF անկյունը։DG հատվածը հավասար է A հատվածին, GE-ը՝ B-ին, և DH-ը՝ C-ին [Պնդ. 1.3]։ E կետից տանենք ուղիղ, որը զուգահեռ GH գծին [Պնդ. 1.31]։ Հետևաբար, քանի որ GH գիծը գծված է զուգահեռ DEF եռանկյան EF կողմին, ապա ինչպես DG հարաբերում GE-ի նկատմամբ, այնպես էլ DH և HF ունեն նույն հարաբերությունը[Պնդ. 6.2]։ DG հավասար է A-ին, GE-ը՝ B-ին, իսկ DH-ը՝ C-ին։ Հետևաբար, ինչպես A և B-ի հարաբերությունն է , այնպես էլ C և HF-ինը։ Այսպիսով, գտնվել է չորրորդ ուղիղ գիծը՝ HF, որը համաչափ է տրված երեք ուղիղ գծերին՝ A, B և C։ Ցույց տվեցինք ինչը պահանջվում էր։
Պնդում 13
Գտնել ուղիղ գիծը, որը հավասար է երկու ուղիղ գծերի միջին համամասնությանը:
Դիցուք, AB և BC տրված երկու ուղիղ գծերն են։ Պահանջվում է գտնել AB և BC ուղիղ գծերի միջին համամասնությանը հավասար (ուղիղ գիծը)։ AB և BC գտնվում են ուղիղ գծի վրա: Գծենք ADC կիսաշրջանագիծը, որի համար AC հատվածը հանդիսանում է տրամագիծը [Պնդ. 1.10]։ BD գիծը գծենք B կետից ուղիղ գիծ տանելով, որը ուղղահայաց կլինի AC հատվածին [Պնդ. 1.11]։ Այնուհետև, D կետից ուղիղներ տանելով, կազմենէ AD և DC գծերը։ Կիսաշրջանի ADC անկյունը՝ ուղիղ անկյուն է, քանի որ նայում է տրամագծին [Պնդ. 3.31]։ Եվ քանի որ, ADC ուղղանկյուն եռանկյուն է, և DB հատվածը ուղից անկյունից տարված ուղղահայացն է հիմքին, ապա DB-ն հավասար է հիմքի AB և BC հատվածների երկարության գումարի կեսին [Պնդ. 6.8 հետևություն]։ Այսպիսով, գտանք DB գիծը, որը հավասար է տրված երկու ուղիղ գծերի՝ AB և BC գումարի կեսին։ Ապացուցեցինք, ինչը պահանջվում էր:
Պնդում 14
Հավասար և հավասարանկյուն զուգահեռագծերում հավասար անկյուններին համապատասխան կողմերը փոխադարձաբար համեմատական են։ Այդ հավասարանկյուն զուգահեռագծերը իրար հավասար են, քանի որ հավասար անկյունների կողմերը փոխադարձաբար համեմատական են են: Դիցուք, AB և BC հավասար և հավասարանկյուն զուգահեռագծեր են, որոնց B անկյունները հավասար են։ DB և BE գծերը դրված են մի ուղղի վրա։ Հետևաբար, FB և BG գծերը նույնպես մի ուղղու վրա են [Պնդ. 1.14]։ Հարկ է նշել, որ AB և BC զուգահեռագծերի հավասար անկյունների գտնվող կողմերը փոխադարձաբար համեմատական են, այսինքն՝ ինչպես DB հարաբերում է BE-ին, այնպես էլ GB-ն՝ BF-ին։
Կազմենք նոր FE զուգահեռագիծը։ Քանի որ , AB զուգահեռագիծը հավասար է BC զուգահեռագծին, իսկ FE-ը այլ (զուգահեռագիծ) է, ապա ինչպես AB զուգահեռագիծը է հարաբերվում է FE զուգահեռագծին, այնպես էլ (զուգահեռագիծ) BC-ն՝ FE-ին [Պնդ. 5.7]։Ավելին, ինչպես AB զուգահեռագիծը FE զուգահեռագծին է հարաբերում, այնպես էլ DB հարաբերում է BE-ին, BC-ն FE-ին, այնպես էլ GB-ն՝ BF-ին[Պնդ. 6.1]։ Հետևաբար, DB և BE հարաբերությունը հավասար է, GB և BF զուգահեռագծերի հարաբերությունը։Արդյունքում, AB և BC զուգահեռագծերի համապատասխանաբար հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձաբար համեմատական են միմյանց։ Ինչպես DB հարաբերում է BE զուգահեռագծին, այնպես էլ GB զուգահեռագիծը BF զուգահեռագծին։ Հետևաբար, AB զուգահեռագիծը հավասար է BC զուգահեռագծին։ DB և BE հարաբերվում են այնպես, ինչպես GB և BF-ին, ավելին, ինչպես DB-ն է BE-ին, այնպես էլ AB զուգահեռագիծը՝ FE զուգահեռագծին, և ինչպես GB-ն՝ BF-ին, այնպես էլ BC զուգահեռագիծը՝ FE զուգահեռագծին[Պնդ. 6.1]: Հետևաբար, ինչպես AB և FE զուգահեռագծերի հարաբերությունն է, այնպես էլ BC և FE զուգահեռագծերինը [Պնդ. 5.11]։ Հետևաբար, AB զուգահեռագիծը հավասար է BC զուգահեռագծին [Պնդ. 5.9]։ Այսպիսով, հավասար և հավասարանկյուն զուգահեռագծերում հավասար անկյուններին համապատասխան կողմերը փոխադարձաբար համեմատական են։ Այդ հավասարանկյուն զուգահեռագծերը իրար հավասար են, քանի որ հավասար անկյունների կողմերը փոխադարձաբար համեմատական են են: Ինչը հենց պահանջվում էր ապացուցել։
Պնդում 15
Հավասար եռանկյուններում, որոնց համապատասխան մի անկյունը հավասար է, ապա այդ անկյունների կողմերը փոխադարձ համեմատական են։ Եվ այդ եռանկյունների հավասար անկյունների համապատասխան կողմերը փոխադարձ համեմատական են և հավասար: Դիցուք, ABC և ADE հավասար եռանկյուններ են, ուստի, մի անկյունը՝ BAC հավասար է համապատասխան DAE անկյանը։ABC և ADE եռանկյունների հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են, այսինքն՝ ինչպես CA-ն է AD-ին հարաբերվում, այնպես էլ EA-ն՝ AB-ին։
CA գիծը գծենք այնպես, որ լինի AD-ի ուղիղ շարունակությունը։ Հետևաբար, EA-ն նույնպես AB-ի ուղիղ շարունակությունն է [Պնդ. 1.14]։ B-ից ուղիղ գիծ իջեցնենք D-ին։ Քանի որ, ABC եռանկյունը հավասար է ADE եռանկյանը, իսկ BAD այլ (եռանկյուն) է, ապա ինչպես CAB եռանկյունը հարաբերում է BAD եռանկյանը, այնպես էլ EAD՝BAD-ին[Պնդ. 5.7]։ Ավելին, ինչպես CAB և BAD եռանկյունների հարաբերությունը նունն է, ինչ CA և AD հարաբերությունը, և ինչպես EAD և BAD եռանկյուններինը, այնպես էլ EA և AB հարաբերությունն է[Պնդ. 6.1]։ Եվ հետևաբար, ինչպես CA-ն է AD-ին հարաբերվում, այնպես էլ EA-ն՝ AB-ին։ Հետևաբար, ABC և ADE եռանկյունների հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են։ Եվ այսպես, թող ABC և ADE եռանկյունների կողմերը փոխադարձ համեմատական լինեն, և CA և AD հարաբերությունը լինի, ինչպես EA և AB- ի հարաբերակցությունը։ Ուստի, ABC եռանկյունը հավասար է ADE եռանկյանը։ Քանի որ BD միացնելով կազմել էինք նոր եռանկյուն, ապա CA և AD հարաբերությունը նույնն է, ինչ EA և AB-ինը: Ավելին ինչպես CA հարաբերում է AD-ին, այնպես էլ ABC եռանկյունը հարաբերում է BAD եռանկյանը, և ինչպես EA և AB հարաբերությունը, այնպես էլ EAD և BAD եռանկյուններինը [Պնդ. 6.1]: Այնուհոտև դիտարկենք ABC և BAD հարաբերությունը, որը նույն է ինչ EAD և BAD եռանկյունների հարաբերությունը։ Հետևաբար, ABC և EAD (եռանկյուններից) յուրաքանչյուրը նույն հարաբերությունը ունեն BAD եռանկյան հետ։ Հետևաբար, ABC և EAD եռանկյունները միմյանց հավասար են[Պնդ. 5.9]։ Այսպիսով, Հավասար եռանկյուններում, որոնց համապատասխան մի անկյունը հավասար է, ապա այդ անկյունների կողմերը փոխադարձ համեմատական են։ Եվ այդ եռանկյունների հավասար անկյունների համապատասխան կողմերը փոխադարձ համեմատական են և հավասար: Ապացուցեցինք, ինչ պահանջվում էր։
Պնդում 16
Եթե չորս ուղիղ գծեր համաչափ են, ապա (երկու) արտաքին կողմերով կազմված ուղղանկյունը հավասար է (երկու) միջին կողմերով կազմված ուղղանկյանը։ Եվ եթե այդ ուղղանկյունները իրար հավասար են, ապա, չորս ուղիղ գծերը կլինեն համաչափ։
Դիցուք, AB, CD, E և F չորս համաչափ ուղիղ գծեր են (այնպես, որ ինչպես AB հարաբերում է CD հատվածին, այնպես էլ E հատվածի հարաբերությունը F հատվածին)։ AB և F ուղիղ գծերով կազմված ուղղանկյունը հավասար կլինի CD և E հատվածներով կազմված ուղղանկյանը։ A և C կետերից տանենք ուղիղ գիծ, արդյունքում ստանալով AG և CH գծերը, որոնք ուղղահայաց կլինեն AB և CD կողմերին(համապատասխանաբար) [Պնդ. 1.11]։ AG հատվածի երկարությունը հավասար է F հատվածի երկարությանը, իսկ CH՝ E հատվածի երկարությանը [Պնդ. 1.3]։ Այնուհետև կազմենք BG և DH ուղղանկյունները։ Ինչպես նշվեց, AB և CD հարաբերակցությունը նույնն է, ինչ E և F հատվածներինը, իսկ E հատվածը հավասար է CH կողմին, իսկ F-ը՝ AG հատվածի երկարությանը, ապա ինչպես AB հարաբերվում CD կողմին, այնպես էլ CH՝ AG-ին։ Այսպիսով, BG և DH ուղղանկյունների հավասար անկյունների շուրջ գտնվող համապատասխանաբար կողմերը փոխադարձ համեմատական են։ Եվ այն հավասարանկյուն ուղղանկյունները, որոնց հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատ են, հավասար են [Պնդ. 6.14]։ Հետևաբար, BG ուղղանկյունը հավասար է DH ուղղանկյանը։ BG ուղղանկյունը AB և F ուղիղ գծերով կազմված ուղղանկյունն է, քանի որ AG կողմի երկարությունը հավասար է F հատվածի երկարությանը։ Եվ DH ուղղանկյունը CD և E հատվածներով (ուղիղ գծերով) կազմված ուղղանկյունն է, քանի որ E հատվածը հավասար CH կողմին։ Հետևաբար, AB և F ուղիղ գծերով կազմված ուղղանկյունը հավասար է CD և E ուղիղ գծերով կազմված ուղղանկյանը։ Եվ այսպես, AB և F հատվածներով կազմված ուղղանկյունը հավասար լինի CD և E հատվածներով կառուցված ուղղանկյանը։ Այսպիսով, այդ չորս ուղիղ գծերը կլինեն համաչափ (այնպես, որ ինչպես AB հարաբերի CD կողմին, այնպես էլ E՝ F-ին)։ Այսպիով, AB և F ուղիղներով կազմված ուղղանկյունը հավասար է CD և E ուղիղներով կազմված ուղղանկյանը։ Ինչպես նաև նշենք, որ BG ուղղանկյունը AB և F հատվածներով կազմված ուղղանկյունն է, քանի որ AG-ը հավասար է F-ին։ Եվ DH-ը CD և E ուղիղ գծերի պարունակած ուղղանկյունն է, քանի որ CH-ը հավասար է E-ին։ Հետևաբար, BG ուղղանկյունը հավասար է DH ուղղանկյանը և դրանք նաև հավասարանկյուն են։ Հավասար և հավասարանկյուն ուղղանկյուններում համապատասխան հավասար անկյունների շուրջ գտնվող կողմերը փոխադարձ համեմատական են [Պնդ. 6.14]։ Հետևաբար, ինչպես AB հարաբերում CD կողմին, այնպես էլ CH կողմը AG կողմին։ Եվ CH հավասար է E-ին, իսկ AG-ը՝ F-ին։ Հետևաբար, ինչպես AB և CD հարաբերությունը, այնպես էլ E և F հատվածների հարաբերությունն է։ Այսպիսով, եթե չորս ուղիղ գծեր համաչափ են միմյանց, ապա (երկու) արտաքին ուղիղ գծերով կազմված ուղղանկյունը հավասար է միջին ուղիներով կազմված ուղղանկյանը։ Եվ եթե այդ ուղղանկյունները միմյանց հավասար են, ապա չորս ուղիղ գծերը կլինեն համաչափ։ Ինչը հենց պահանջվում էր ցույց տալ։
Պնդում 17
Եթե երեք ուղիղ գծեր համաչափ են միմյանց, ապա տրված (երկու) արտաքին հատվածներով կազմված ուղղանկյունը հավասար է միջին հատվածներով կազմված քառակուսուն։ Եվ եթե այդ ուղղանկյունը հավասար է քառակուսուն, ապա տվյալ երեք ուղիղ գծերը կլինեն համաչափ։
Դիցուք , A, B և C երեք համաչափ ուղիղ գծերեն (այնպես, որ ինչպես A հատվածն է հարաբերում B հատվածին, այնպես էլ B հատվածը C-ին)։ Ուստի, կարող եմ ասել ,որ A և C ուղիղ գծերով կառուցված ուղղանկյունը հավասար է B հատվածով կազմված քառակուսուն։ Ուստի, D հատվածը հավասար են B հատվածին [Պնդ. 1.3]։ Ինչպես A հատվածը հարաբերում է B հատվածին, այնպես էլ B հատվածը C հատվածին , իսկ B հավասար է D-ին, ապա ինչպես A կհարաբերի B-ին, այնպես էլ D-ն C-ին։ Եթե չորս ուղիղ գծերը համաչափ են, ապա (երկու) արտաքին ուղիղ գծերով կազմված ուղղանկյունը հավասար է միջին ուղիղ գծով կառուցված ուղղանկյանը [Պնդ. 6.16]։ Հետևաբար, A և C ուղիղ գծերով կազմած ուղղանկյունը հավասար է B և D ուղիղ գծերի պարունակած ուղղանկյունին։ Բայց B և D ուղիղ գծերով կառուցված ուղղանկյանը, որը B հատվածով կազմված քառակուսին է, քանի որ B-ն հավասար է D-ին։ Հետևաբար, A և C ուղիղ գծերով կազմած ուղղանկյունը հավասար է B ուղիղ գծով կառուցված քառակուսուն։ Եվ այսպես, թող A և C ուղիղ գծերով կազմած ուղղանկյունը հավասար լինի B ուղիղ գծով կազմած քառակուսուն։ Նշեմ, որ ինչպես A հարաբերում B հատվածին, այնպես էլ B-ն է C-ին։ Ուստի, A և C ուղիղ գծերի կազմած ուղղանկյունը հավասար է B հատվածով կազմված քառակուսուն։ B հատվածով կազմված քառակուսին B և D ուղիղ գծերի կազմած ուղղանկյունն է, քանի որ B-ն հավասար է D-ին։ A և C ուղիղ գծերով կառուցված ուղղանկյունը հավասար է B և D ուղիղներով կազմած ուղղանկյանը։ Եվ եթե (երկու) արտաքին հատվածների կազմած ուղղանկյունը հավասար է միջին հատվածներով կազմած ուղղանկյանը, ապա չորս ուղիղ գծերը համաչափ են [ապնդ. 6.16]։ Հետևաբար, ինչպես A կհարաբերի B-ին, այնպես էլ D՝C-ին, իսկ B հատվածը հավասար է D հատվածին։ Հետևաբար, ինչպես A կհարաբերվի B-ին, այնպես էլ B ՝C-ին։ Այսպիսով, Եթե երեք ուղիղ գծեր համաչափ են միմյանց, ապա տրված (երկու) արտաքին հատվածներով կազմված ուղղանկյունը հավասար է միջին հատվածներով կազմված քառակուսուն։ Եվ եթե այդ ուղղանկյունը հավասար է քառակուսուն, ապա տվյալ երեք ուղիղ գծերը կլինեն համաչափ: Ապացուցեցինք, ինչըպահանջվում էր:
Պնդում 18
Նկարագրել ուղղագիծ պատկեր, որը նման է տրված ուղղագծային պատկերին:
Դիցուք, AB տրված ուղիղ գիծն է,իսկ CE՝ տրված ուղղագծային պատկերը։ Անհրաժեշտ է նկարագրել ուղղագծային պատկեր, որը նման է CE ուղղագծային պատկերը ,որը կազմված կլինի AB ուղիղ գծի վրա: D միացնենք F-ին, GAB անկյունը, որը հավասար է C անկյանը, և ABG անկյունը, որը հավասար է CDF անկյանը, այնուհետև A և B կետերով տարած ուղիղ գիծը՝ համապատասխանաբար [Պնդ. 1.23]։ Այսպիսով, CFD անկյունը հավասար է AGB անկյանը [Պնդ. 1.32]։ Հետևաբար, FCD եռանկյունը հավասարանկյուն է GAB եռանկյանը։ Այսպիսով, համապատասխանաբար, ինչպես FD հարաբերում է GB-ին, այնպես էլ FC ՝GA-ին, իսկ CD-ն՝ AB-ին [Պնդ. 6.4]։ Այսպիսով, BGH անկյունը, որը հավասար է DFE և GBH անկյանը, որը հավասար է FDE անկյանը, կկառուցվեն ուղիղ գծի՝ BG-ի G և B կետերում համապատասխանաբար [Պնդ. 1.23]։ Այսպիսով, E առընթեր անկյունը հավասար է H առընթեր անկյանը [Պնդ. 1.32]։ Հետևաբար, FDE եռանկյունը հավասարանկյուն է GHB եռանկյանը։ Այսպիսով, համապատասխանաբար, ինչպես FD և GB մհարաբերվում, այնպես էլ FE և GH-ն, իսկ ED-ն՝ HB-ին [Պնդ. 6.4]։ Ավելին, որ ինչպես FD և GB հարաբերությունն է, այնպես էլ FC և GA ունեն նույն հարաբերությունը, CD և AB նույնպես։ Հետևաբար, ինչպես FC-ն GA-ին է հարաբերում, այնպես էլ CD՝ AB-ին, և FE-ն՝ GH-ին, և, վերջապես, ED-ն՝ HB-ին։ Քանի որ, CFD անկյունը հավասար է AGB անկյանը, իսկ DFE անկյունը՝ BGH անկյանը, ապա ամբողջ CFE անկյունը հավասար կլինի ամբողջական AGH անկյանը։ Նույն կերպ, CDE անկյունը հավասար է ABH անկյանը։ C անկյունը նույնպես հավասար է A անկյանը, իսկ E անկյունը՝ H անկյանը։ Այսպիսով, AH պատկերը հավասարանկյուն է CE-ին։ Երկու պատկերների հավասար անկյուններին համապատասխան կողմերը համաչափ են։ Հետևաբար, AH ուղղագիծ պատկերը նման է CE ուղղագծային պատկերին [Սահմ. 6.1]։ Այսպիսով, AH ուղղագիծ պատկերը նման է CE ուղղագծային պատկերին, որը կառուցված է AB ուղիղ գծի վրա: Ապացուցեցինք, ինչը պահանջվում էր:
Պնդում 19
Նման եռանկյունները մեկմեկու ունեն համապատասխան կողմերի քառակուսի հարաբերություն:
Դիցուք, ABC և DEF նման եռանկյուններ են, որտեղ B անկյունը հավասար է E անկյանը, իսկ AB հարաբերում է BC կողմին այնպես, ինչպես DE հարաբերում է EF կողմին, ընդ որում BC-ը համընկնում է EF-ի հետ։ Ուստի, ABC եռանկյունը ունի քառակուսի հարաբերություն DEF եռանկյան հետ՝ BC և EF կողմի քառակուսի հարաբերությամբ։ BG ուղիղ գիծը գծենք այնպես, որ համեմատական լինի BC և EF-ի հետ, որպեսզի ինչպես BC և EF հարաբերությունը լինի, այնպես ինչպես EF՝ BG-ին [Պնդ. 6.11]։ Եվ թող A կետից հիմքին տանենք ուղիղ ։ Հետևաբար, ինչպես AB հարաբերում է BC-ին, այնպես էլ DE՝ EF-ին, հետևաբար՝ փոխադարձաբար, ինչպես AB հարաբերում է DE-ին, այնպես էլ BC-ը՝ EF-ին[Պնդ. 5.16]։ BC և EF հարաբերվում են այնպես, ինչպես EF-ը՝BG-ին։ AB և DE հարաբերվում են, ինչպես EF՝ BG կողմին։ Հետևաբար, ABG և DEF եռանկյունների համապատասխանաբար հավասար անկյունների կողմերը, հակադարձ համեմատություն ունեն։ Եվ այն եռանկյունները, որոնք ունեն հավասար անկյուն և այդ անկյունների շուրջ գտնվող կողմերը հակադարձ համամասնություն ունեն, ապա այդ եռանկյունները հավասար են [Պնդ. 6.15]։ Ուստի, ABG եռանկյունը հավասար է DEF եռանկյանը ։ Եվ քանի որ , BC հարաբերում է EF-ին , այնպես էլ EF-ը՝ BG-ին, և եթե երեք ուղիղ գծերը համաչափ են, ապա առաջինը ունի քառակուսի հարաբերություն երրորդի, երկրորդի հետ [Սահմ. 5.9], հետևաբար BC-ն ունի քառակուսի հարաբերություն BG-ի հետ՝ կապված CB-ի՝ EF-ի հե։տ Եվ ինչպես CB հարաբերում է BG-ին, այնպես էլ ABC եռանկյունը ABG եռանկյանը [Պնդ. 6.1]։ Հետևաբար, ABC եռանկյունը նույնպես ունի քառակուսի հարաբերություն ABG եռանկյան հետ, ինչը կապված BC և EF-ի հարաբերությամբ։ Ուստի, ABG եռանկյունը հավասար է DEF եռանկյանը: Հետևաբար, ABC եռանկյունը նույնպես ունի քառակուսի հարաբերություն DEF եռանկյան հետ, որը արտահայտվում է BC-ի և EF-ի հարաբերությամբ։ Այպիսով, նման եռանկյունները մեկմեկու ունեն համապատասխան կողմերի քառակուսի հարաբերություն։ Ապացուցվեց, ինչը հարկավոր էր:
Հետևանք
Այսպիսով, պարզ է, որ եթե երեք ուղիղ գծերը ունեն նույն համաչափությունը, ապա ինչպես առաջինը ունի հարաբերություն երրորդի հետ, այնպես էլ առաջին կողմի վրա կառուղված պատկերը համարժեք և նման է երկրորդ կողմի հիման վրա կառուցված պատկերին։ Ապացուցվեց:
Պնդում 20
Նման բազմանկյունները կարող են բաժանվել նույն թվով նման եռանկյունների, որոնք համամասն են ամբողջական բազմանկյանը, և բազմանկյունը այլ բազմանկյան հետ քառակուսի հարաբերություն՝ համապատասխանաբար կողմով:
Դիցուք, ABCDE և FGHKL նման բազմանկյուններ են, որտեղ AB կողմը համապատասխանում է FG կողմին։ Նշենք, որ ABCDE և FGHKL բազմանկյունները կարելի է բաժանել նույն թվով նման եռանկյունների, որոնք համամասն են ամբողջական բազմանկյանը, ABCDE բազմանկյունը ունի քառակուսի հարաբերություն FGHKL բազմանկյան նկատմամբ՝ AB և FG կողմերի հարաբերությամբ։ BE, EC, GL և LH գծերը միացնենք իրար։ Քանի որ, ABCDE բազմանկյունը նման է FGHKL բազմանկյանը, BAE անկյունը հավասար է GFL անկյուն, և ինչպես BA հարաբերում է AE-ին, այնպես էլ GF-ը՝ FL-ին [սահման. 6.1]։ Հետևաբար, քանի որ ABE և FGL երկու եռանկյուններն ունեն մի հավասար անկյուն, կողմեր, որոնք հավասար անկյունների շուրջ համաչափ են, հետևաբար ABE եռանկյունը նման է FGL եռանկյանը [Պնդ. 6.6]։ Այսպիսով՝ (նրանք) նույնպես նման են [Պնդ. 6.4, սահման. 6.1]։ Հետևաբար, անկյուն ABE-ն հավասար է FGL անկյանը։ Եվ ABC անկյունը հավասար է FGH անկյանը՝ հաշվի առնելով բազմանկյունների նմանությունը։ Ուստի, EBC անկյունը հավասար է LGH անկյանը։ Եվ քանի որ, ABE և FGL եռանկյունների նմանության հետևանքով, ինչպես EB-ն է BA-ի նկատմամբ, այնպես էլ LG-ը՝ GF-ի, նաև բազմանկյունների նմանության հետևանքով, ինչպես AB-ն է BC-ին հարաբերում, այնպես էլ FG-ը՝ GH-ին, հետևաբար, հավասարության սկզբունքով, ինչպես EB հարաբերում BC հատվածին, այնպես էլ LG-ը՝ GH-ին [Պնդ. 5.22], և հավասար անկյունների շուրջ կողմերը՝ EBC և LGH, համաչափ են։ Հետևաբար, EBC եռանկյունը հավասանկյուն է LGH եռանկյանը [Պնդ. 6.6]։ Ուստի, EBC եռանկյունը նույնպես նման է LGH եռանկյանը [Պնդ. 6.4, սահման. 6.1]։ Այսպիսով, նույպես, ECD եռանկյունը նույնպես նման է LHK եռանկյանը։ Ուստի, նման բազմանկյունները՝ ABCDE և FGHKL, բաժանված են հավասար թվով նման եռանկյունների։ Նաև նշենք, որ (եռանկյունները) համամասն են ամբողջական բազմանկյան հետ։ ABE, EBC և ECD եռանկյունները համաչափ են. եռանկյունները առաջատար մեծություններն են, և դրանց (համապատասխան) հաջորդող մեծությունները ՝ FGL, LGH և LHK (համապատասխանաբար)։ Նաև, ABCDE բազմանկյունը ունի քառակուսի հարաբերություն FGHKL բազմանկյան նկատմամբ՝ AB և FG համապատասխան կողմերի հարաբերությամբ ։ Միացնենք AC և FH գծերը։ ABC անկյունը հավասար է FGH անկյանը, և ինչպես AB հարաբերում է BC-ին, այնպես էլ FG-ը՝ GH-ին, բազմանկյունների նմանությունից օգտվելով, ABC եռանկյունը հավասանկյուն է FGH եռանկյանը [Պնդ. 6.6]։ Հետևաբար, անկյուն BAC-ն հավասար է GFH անկյանը, և BCA-ն՝ GHF-ին։ Եվ քանի որ, BAM անկյունը հավասար է GFN-ին, ABM՝ FGN-ին (տես նախորդը), հետևաբար, անկյուն AMB-ն նույնպես հավասար է FNG անկյանը[Պնդ. 1.32]։ Ուստի, ABM եռանկյունը նույնպես հավասանկյուն է FGN եռանկյանը։ Նմանապես կարող ենք ցույց տալ, որ եռանկյուն BMC-ն նույնպես հավասանկյուն է GNH եռանկյանը։ Ուստի համաչափորեն, ինչպես AM հարաբերում է MB-ին, այնպես էլ FN-ը՝ NG-ին, և ինչպես BM-ն է հարաբերվում MC-ին, այնպես էլ GN-ը՝ NH-ի [Պնդ. 6.4]։ Հետևաբար, հավասարության սկզբունքով, ինչպես AM-ն է MC-ի նկատմամբ հարաբերվում, այնպես էլ FN-ը՝ NH-ին [Պնդ. 5.22]։ Սակայն, ինչպես AM և MC հարաբերությունն է, այնպես էլ ABM և MBC, AME և EMC եռանկյուններինը։ Նրանց հիմքերը համեմատական համաչափ են մեկը մյուսի նկատմամբ [Պնդ. 6.1]։ Եվ ինչպես առաջնահերթ մեծություններն են հարաբեվում է երկրորդական մեծություններին, այնպես էլ բոլոր առաջնահերթ մեծությունների գումարը համեմատական է երկրորդականների գումարին[Պնդ. 5.12]։ Հետևաբար, ինչպես AMB և BMC եռանկյունների հարաբերությունն է, այնպես էլ ABE և CBE եռանկյուններինը։Ավելին, ինչպես եռանկյուն AMB հարաբերվում է BMC-ին, այնպես էլ AM՝MC-ին։ Հետևաբար, ինչպես AM՝ MC-ին, այնպես էլ եռանկյուն ABE՝EBC եռանկյանը։ Նմանապես, ինչպես FN կհարաբեվի NH-ին, այնպես էլ FGL եռանկյունը GLH եռանկյանը։ AM և MC հարաբերությունը այնպես է, ինչպես FN և NH։ Հետևաբար, ինչպես ABE եռանկյունն է BEC-ին հարաբերվում, այնպես էլ FGL եռանկյունը GLH-ին, և փոխադարձաբար, ինչպես ABE և FGL եռանկյունները, այնպես էլ եռանկյուն BEC՝ GLH-ին [Պնդ. 5.16]։ Նմանապես կարող ենք ցույց տալ՝ միացնելով BD և GK գծերը, այնուհետև կստացվի որ, ինչպես BEC եռանկյունն է հարաբերւմ LGH եռանկյանը, այնպես էլ եռանկյուն ECD-ն՝ LHK-ին։ ABE և FGL եռանկյունների հարաբերությունը հավասար է EBC և LGH, ECD և LHK եռանկյունների հարաբերությանը, և ինչպես առաջնահերթ մեծություններն են հարաբեվում է երկրորդական մեծություններին, այնպես էլ բոլոր առաջնահերթ մեծությունների գումարը համեմատական է երկրորդականների գումարին [Պնդ. 5.12]: Հետևաբար, ինչպես եռանկյուն ABE հարաբերում է FGL-ին, այնպես էլ ABCDE և FGHKL բազմանկյուննները միմյանց։ ABE և FGL եռանկյունները ունեն քառակուսի հարաբերություն ՝ համապատասխան AB և FG կողմերի հարաբերությամբ։ Նման եռանկյունները համապատասխան կողմերը ունեն քառակուսի հարաբերություն[Պնդ. 6.14]։ Հետևաբար, ABCDE բազմանկյունը նույնպես քառակուսի հարաբերություն ունի FGHKL բազմանկյան նկատմամբ՝ համապատասխան AB և FG կողմերի միջև։ Այսպիսով, նման բազմանկյունները կարելի է բաժանել հավասար թվով նման եռանկյունների, որոնք համաչափ են ամբողջականի հետ, և համապատասխան կողմերի շնորհիվ բազմանկյունները ունեն քառակուսի հարաբերություն։ Ապացուցեցինք այն, ինչը պահանջվում էր ցույց տալ։
Հետևանք
Եվ նույն կերպով կարելի է ցույց տալ նաև, որ նման քառանկյունները ունեն համապատասխան կողմերի միջև քառակուսի հարաբերություն։ Եվ սա արդեն ցույց է տրվել եռանկյունների համար։ Հետևաբար, ընդհանուր առմամբ, նման ուղիղանկյուն պատկերները նույնպես իրար նկատմամբ ունեն համապատասխան կողմերի միջև քառակուսի հարաբերություն։ Ապացուցվեց:
Պնդում 21
Ոււղղագիծ պատկերները, որոնք նման են միևնույն ուղղագծին, նույնպես միմյանց նման են:
Դիցուք, A և B ուղղագիծ պատկերները նման լինեն C ուղղագիծ-ուղղանկյունաձև պատկերին։ Պետք է ցույց տալ, որ A-ն նույնպես նման է B-ին։ Քանի որ A պատկերը նման է C-ին, ապա A համանկյուն է C-ին և ունի հավասար անկյունների կողմերին համաչափ (համապատասխանող) կողմեր [Սահմ. 6.1]։Նույն կերպ, ինչպես B-ն նման է C-ին, ապա B-ն նույնպես համանկյուն է C-ին և ունի հավասար անկյունների կողմերին համաչափ կողմեր [Սահմ. 6.1]։ Այսպիսով, A և B պատկերները երկուսն էլ համանկյուն են C-ին և ունեն հավասար անկյունների կողմերին համաչափ կողմեր [Ուստի, A-ն նույնպես համանկյուն է B-ին և ունի հավասար անկյունների կողմերին համաչափ կողմեր]։ Այսպիսով, A ուղղագիծ պատկերը նման է B պատկերին[Սահմ. 6.1]։ Ապացուցվեց, ինչը որ պահանջվում էր:
Պնդում 22
Եթե չորս ուղիղ գծերը համաչափ են, համանման և նույն կերպ նկարագրված գծված, ապա իրենցով կազմված ուղղագիծ պատկերները նույնպես համաչափ կլինեն: Եվ եթե նմանատիպ և նույն կերպ նկարագրված ուղղագիծ պատկերները (գծված) համաչափ են, ապա ուղիղ գծերն իրենք նույնպես համաչափ կլինեն:
Դիցուք, AB, CD, EF և GH չորս համեմատական ուղիղ գծեր են՝ այնպես, որ AB հարաբերում է CD-ին այնպես, ինչպես EF՝GH-ին: Եվ թող AB և CD գծերի վրա կառուցված լինեն KAB և LCD ուղղագծային պատկերները, որոնք նման են և դրված են նմանապես, իսկ EF և GH գծերի վրա կառուցված լինեն MF և NH ուղղագծային պատկերները, որոնք նույնպես նման են և դրված են նմանապես:Նշենք, որ KAB հարաբերի LCD-ին է, ինչպես MF՝ NH-ին: Դիցուք, O ուղիղ գիծը, որը համեմատական է AB և CD գծերին, և P՝ երրորդ ուղիղ գիծ, որը համեմատական է EF և GH գծերին [Պնդ. 6.11]: Եվ քանի որ AB հարաբերում է CD-ին այնպես, ինչպես EF՝GH-ին, և CD՝O-ին, GH՝P-ին, ապա հավասարության սկզբունքով՝ AB կհարաբերի O-ին, ինչպես EF՝P-ին [Պնդ. 5.22]:Ավելին, ինչպես AB հարաբերում O-ին, այնպես էլ KAB՝LCD-ին, ինպես EF՝ P-ին, այնպես էլ MF՝NH-իմ [Պ նդ. 5.19՝]: Եվ, հետևաբար, KAB կհարաբերի LCD-ին, ինչպես MF՝NH-ին: Դիցուք, KAB և LCD հարաբերությունը հավասար է MF և NH հարաբերությանը: Ասում եմ նաև, որ AB հարաբերում էCD-ին, ինչպես EF՝GH-ին: Եթե AB հարաբերում է CD-ին , իսկ EF՝GH-ին ոչ, ապա նշենք, որ AB և CD-ի հարաբերությունը հավասար կլինի EF և QR հարաբերությանը [Պնդ. 6.12]: Եվ թող QR գծի վրա կառուցված լինի SR ուղղագծային պատկերը, որը նման է և նմանապես դրված է MF-ի կամ NH-ինլատմամբ [Պնդ. 6.18, 6.21]: Եվ քանի որ AB՝ CD-ին հարաբերում է, ինչպես EF՝QR-ին, ապա AB և CD գծերի վրա կառուցված KAB և LCD նման և նմանապես դրված ուղղագծային պատկերները համեմատական են , EF և QR գծերի վրա կառուցված MF և SR նման պատկերների հետ, հետևաբար KAB հարաբերվում է LCD-ին, ինչպես MF՝ SR-ին: Ենթադրվում է, որ KAB կհարաբերի LCD-ին, ինչպես MF՝NH-ին: Հետևաբար, MF հարաբերում է SR-իմ, ինչպես MF՝NH-ին [Պնդ. 5.11]: MF և NH հարաբերությունը հավասար է SR և NH հարաբերությանը: Հետևաբար, NH-ը հավասար է SR-ին [Պնդ. 5.9]: Եվ NH-ը նման է և նմանապես դրված է SR-ին: Հետևաբար, GH-ը հավասար է QR-ին: Եվ քանի որ AB հարաբերում է CD-ին, ինչպես EF՝QR-ին, իսկ QR-ը հավասար է GH-ին, հետևաբար AB հարաբերում է CD-ին, ինչպես EF՝GH-ին: Այսպիսով, եթե չորս ուղիղ գծերը համաչափ են, համանման և նույն կերպ նկարագրված գծված, ապա իրենցով կազմված ուղղագիծ պատկերները նույնպես համաչափ կլինեն: Եվ եթե նմանատիպ և նույն կերպ նկարագրված ուղղագիծ պատկերները (գծված) համաչափ են, ապա ուղիղ գծերն իրենք նույնպես համաչափ կլինեն: Ապացուցվեց այն, ինչը հարկավոր էր ցույց տալ:
Առաջարկություն 24
Յուրաքանչյուր զուգահեռագծում, անկյունագծի շուրջ կառուցված զուգահեռագծերը նման են թե՛ ամբողջ զուգահեռագծին, թե՛ միմյանց:
Թող ABCD-ը լինի զուգահեռագիծ, իսկ AC-ը՝ նրա անկյունագիծը։ Եվ թող EG և HK լինեն զուգահեռագծեր, կառուցված AC անկյունագծի շուրջ։ Ասում եմ, որ EG և HK զուգահեռագծերը յուրաքանչյուրը նման են ամբողջ (ABCD) զուգահեռագծին և նաև միմյանց:
Քանի որ EF գիծը գծվել է ABC եռանկյան BC կողքին զուգահեռ, համեմատականորեն, ինչպես BE-ը EA-ի նկատմամբ է, այնպես էլ CF-ը FA-ի նկատմամբ [Բան. 6.2]: Նորից, քանի որ FG-ը գծվել է ACD եռանկյան CD կողքին զուգահեռ, նույն կերպ, ինչպես CF-ը FA-ի նկատմամբ է, այնպես էլ DG-ը GA-ի նկատմամբ [Բան. 6.2]: Բայց, ինչպես CF-ը FA-ի նկատմամբ է, նույն կերպ արդեն ցույց տրված է, որ BE-ը EA-ի նկատմամբ է։ Ուստի, ինչպես BE-ը EA-ի նկատմամբ է, այնպես էլ DG-ը GA-ի նկատմամբ։ Եվ, այսպես, համակցելով, ինչպես BA-ը AE-ի նկատմամբ է, այնպես էլ DA-ը AG-ի նկատմամբ [Բան. 5.18]: Եվ, այլընտրանքորեն, ինչպես BA-ը AD-ի նկատմամբ է, այնպես էլ EA-ը AG-ի նկատմամբ [Բան. 5.16]: Այսպիսով, ABCD և EG զուգահեռագծերում BAD ընդհանուր անկյան շուրջ կողմերը համաչափ են։ Եվ քանի որ GF-ը զուգահեռ է DC-ին, AFG անկյունը հավասար է DCA անկյանին [Բան. 1.29]: Եվ DAC անկյունը ընդհանուր է ADC և AGF եռանկյունների համար։ Ուստի ADC եռանկյունը հավանկյուն է AGF եռանկյանը [Բան. 1.32]: Նույն պատճառներով, ACB եռանկյունը հավանկյուն է AFE եռանկյանը, և ամբողջ ABCD զուգահեռագիծը հավանկյուն է EG զուգահեռագծին։ Այսպիսով, համաչափորեն, ինչպես AD-ը DC-ի նկատմամբ է, այնպես էլ AG-ը GF-ի նկատմամբ է, և ինչպես DC-ը CA-ի նկատմամբ է, այնպես էլ GF-ը FA-ի նկատմամբ է, և ինչպես AC-ը CB-ի նկատմամբ է, այնպես էլ AF-ը FE-ի նկատմամբ է, իսկ, հետագայում, ինչպես CB-ը BA-ի նկատմամբ է, այնպես էլ FE-ը EA-ի նկատմամբ [Բան. 6.4]: Եվ քանի որ ցույց տրված էր, որ ինչպես DC-ը CA-ի նկատմամբ է, այնպես էլ GF-ը FA-ի նկատմամբ է, և ինչպես AC-ը CB-ի նկատմամբ է, այնպես էլ AF-ը FE-ի նկատմամբ է, ապա, հավասարությամբ, ինչպես DC-ը CB-ի նկատմամբ է, այնպես էլ GF-ը FE-ի նկատմամբ է [Բան. 5.22]: Այսպիսով, ABCD և EG զուգահեռագծերում հավասար անկյունների շուրջ կողմերը համաչափ են։ Ուստի, ABCD զուգահեռագիծը նման է EG զուգահեռագծին [Սահմանում 6.1]: Նույն (պատճառներով), ABCD զուգահեռագիծը նման է նաև KH զուգահեռագծին։ Այսպիսով, EG և HK զուգահեռագծերը յուրաքանչյուրը նման են [ABCD] զուգահեռագծին։ Եվ (ուղղագծային) պատկերները, որոնք նման են նույն ուղղագծային պատկերին, նաև նման են միմյանց [Բան. 6.21]: Այսպիսով, EG զուգահեռագիծը նույնպես նման է HK զուգահեռագծին։
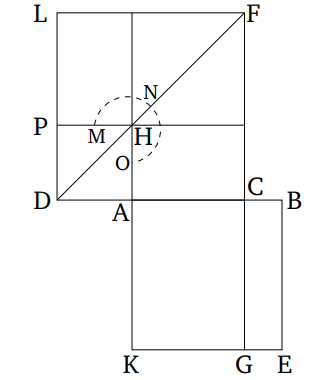Այսպիսով, յուրաքանչյուր զուգահեռագծում անկյունագծի շուրջ գտնվող զուգահեռագծերը նման են թե՛ ամբողջին, թե՛ միմյանց։
Առաջարկություն 25
Կառուցել մեկ (ուղղագծային պատկեր), որը նման է տրված ուղղագծային պատկերին և հավասար է մեկ այլ տրված ուղղագծային պատկերին։ Թող ABC լինի տրված ուղղագծային պատկերը, որին պետք է կառուցել նման (ուղղագծային) պատկեր, իսկ D-ը լինի այն (ուղղագծային) պատկերը, որին պետք է հավասար լինի կառուցվող պատկերը։ Արդ, հարկավոր է կառուցել մեկ (ուղղագծային) պատկեր, որը նման է ABC-ին և հավասար է D-ին։ Քանի որ զուգահեռագիծ BE-ն, հավասար ABC եռանկյունին, թող դրվի BC ուղղագծի վրա [Բան. 1.44], և զուգահեռագիծ CM-ը, հավասար D-ին, (դրվի) CE ուղղագծի վրա, FCE անկյան մեջ, որը հավասար է CBL անկյանին [Բան. 1.45]։ Այդպիսով, BC-ը ուղղագիծ է դեպի CF, իսկ LE-ն դեպի EM [Բան. 1.14]։ Եվ թող BC-ի և CF-ի միջին համեմատականը GH ընդունված լինի [Բան. 6.13]։ Եվ թող KGH պատկերը, նման և նույն կերպ դասավորված ABC-ին, գծված լինի GH-ի վրա [Բան. 6.18]։ Եվ քանի որ ինչպես BC-ը GH-ի նկատմամբ է, այնպես էլ GH-ը CF-ի նկատմամբ է, իսկ եթե երեք ուղիղ գծեր համաչափ են, ապա ինչպես առաջինը երրորդի նկատմամբ է, այնպես էլ առաջինի վրա կառուցված պատկերն ընդհանրապես նման, նույն կերպ կառուցված երկրորդի վրա գտնվող պատկերին է [Բան. 6.19 ճշգրտում], ապա ինչպես BC-ը CF-ի նկատմամբ է, այնպես էլ ABC եռանկյունը KGH եռանկյան նկատմամբ է։ Բայց նաև, ինչպես BC-ը CF-ի նկատմամբ է, այնպես էլ BE զուգահեռագիծը EF զուգահեռագծի նկատմամբ է [Բան. 6.1]։ Ուստի, ինչպես ABC եռանկյունը KGH եռանկյան նկատմամբ է, նույնպես BE զուգահեռագիծը EF զուգահեռագծի նկատմամբ է։ Այսպես, այլընտրանքորեն, ինչպես ABC եռանկյունը BE զուգահեռագծի նկատմամբ է, այնպես էլ KGH եռանկյունը EF զուգահեռագծի նկատմամբ է [Բան. 5.16]։ Եվ քանի որ ABC եռանկյունը հավասար է BE զուգահեռագծին, հետևաբար KGH եռանկյունը նույնպես հավասար է EF զուգահեռագծին։ Բայց EF զուգահեռագիծը հավասար է D-ին։ Արդ, KGH-ն նույնպես հավասար է D-ին։ Եվ KGH-ն նաև նման է ABC-ին։ Այսպիսով, մեկ (ուղղագծային) պատկեր KGH կառուցվեց, որը նման է տրված ուղղագծային պատկերին ABC և հավասար է այլ տրված (ուղղագծային) պատկերի D։ (Այս) հենց այն էր, ինչ պետք էր անել։
Առաջարկություն 26
Եթե զուգահեռագծից հանվի այլ զուգահեռագիծ, որը նման է և նույն կերպ դասավորված ամբողջին և ունի նրա հետ ընդհանուր անկյուն, ապա (հանված զուգահեռագիծը) կլինի նույն անկյունագծի շուրջ, ինչ ամբողջը։
Քանզի զուգահեռագիծ ABCD-ից թող հանվի AF զուգահեռագիծը, որը նման և նույն կերպ դասավորված է ABCD-ին, ունենալով նրա հետ ընդհանուր DAB անկյունը։ Ասում եմ, որ ABCD-ը նույն անկյունագծի շուրջ է, ինչ AF-ը։
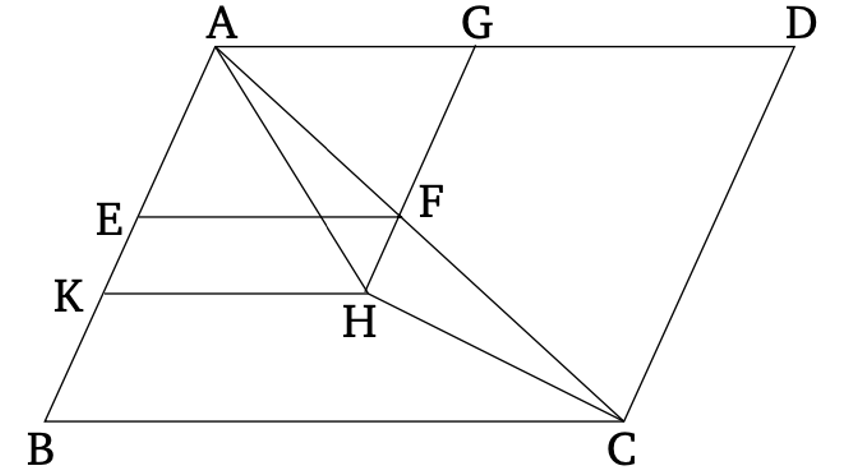Եթե ոչ, ապա ենթադրենք հնարավոր է, որ AHC լինի [ABCD]-ի անկյունագիծը։ Եվ շարունակելով GF գիծը, թող այն անցնի H կետով։ Եվ թող HK-ը նույնպես գծվի H կետով, զուգահեռ AD-ին կամ BC-ին [Բան. 1.31]։
Ուստի, քանի որ ABCD-ը նույն անկյունագծի շուրջ է, ինչ KG-ը, ապա ինչպես DA-ը AB-ի նկատմամբ է, այնպես էլ GA-ն AK-ի նկատմամբ [Բան. 6.24]։ Եվ ABCD և EG զուգահեռագծերի նմանության շնորհիվ, ինչպես DA-ը AB-ի նկատմամբ է, այնպես էլ GA-ը AE-ի նկատմամբ է։ Այսպիսով, ինչպես GA-ը AK-ի նկատմամբ է, այնպես էլ GA-ը AE-ի նկատմամբ է։ Ուրեմն GA-ն նույն հարաբերությունն ունի AK-ի և AE-ի նկատմամբ։ Հետևաբար AE-ը հավասար է AK-ին [Բան. 5.9], ավելի փոքրն ավելի մեծին։ Սա անհնար է։ Արդ, ABCD-ը չէ նույն անկյունագծի շուրջ, ինչ AF-ը։ Ուստի ABCD զուգահեռագիծը նույն անկյունագծի շուրջ է, ինչ AF զուգահեռագիծը։
Այսպիսով, եթե զուգահեռագծից հանվի այլ զուգահեռագիծ, որը նման է և նույն կերպ դասավորված ամբողջին և ունի նրա հետ ընդհանուր անկյուն, ապա (հանված զուգահեռագիծը) նույն անկյունագծի շուրջ է, ինչ ամբողջը։ (Ահա թե ինչ էր կարիքը ցույց տալու)։
Առաջարկություն 27
Բոլոր այն զուգահեռագծերից, որոնք դրված են նույն ուղղագծի վրա և թերանում են հանման հետևանքով առաջացած զուգահեռագծային պատկերներով, որոնք նման են և նույն կերպ դասավորված այն (զուգահեռագծին), որ կառուցված է ուղղագծի կեսի վրա, ամենամեծը այն զուգահեռագիծն է, որը դրված է այդ կեսի վրա և նման է այն (զուգահեռագծին), որի միջոցով թերանում է։
Թող AB լինի ուղղագիծ և թող այն բաժանված լինի կեսի վրա C կետով [Բան. 1.10]։ Եվ թող AD զուգահեռագիծը դրված լինի AB ուղղագծի վրա, թերանալով DB զուգահեռագծային պատկերով, որը կիրառված է AB-ի կեսին, այն է՝ CB-ին։ Ասում եմ, որ բոլոր այն զուգահեռագծերից, որոնք դրված են AB-ի վրա և թերանում են DB-ին նման և նույն կերպ դասավորված զուգահեռագծային պատկերներով, ամենամեծը AD-ն է։ Քանզի թող AF զուգահեռագիծը դրված լինի AB-ի վրա, թերանալով FB զուգահեռագծային պատկերով, որը նույնպես նման է և նույն կերպ դասավորված DB-ին։ Ասում եմ, որ AD-ն մեծ է AF-ից։
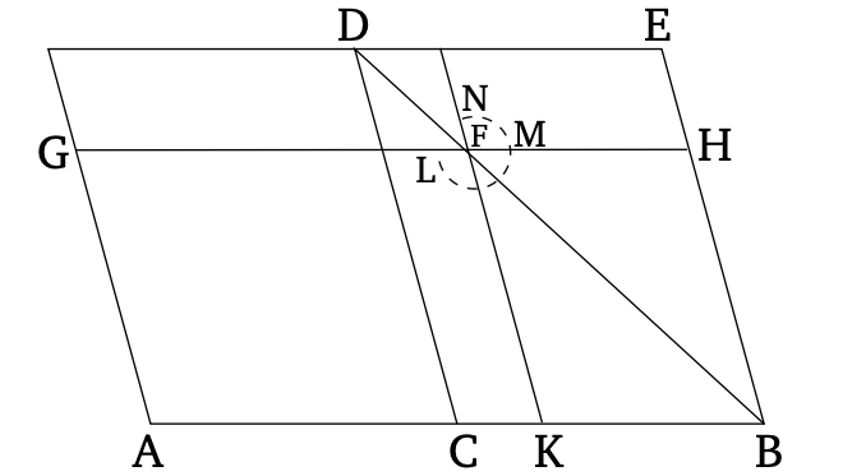Քանի որ DB զուգահեռագիծը նման է FB զուգահեռագծին, ապա դրանք նույն անկյունագծի շուրջ են [Բան. 6.26]։ Թող նրանց (ընդհանուր) անկյունագիծը DB գծվի, և թող պատկերի մնացորդը լրացվի։
Ուստի, քանի որ (լրացնող) CF-ը հավասար է (լրացնող) FE-ին [Բան. 1.43], և FB զուգահեռագիծը ընդհանուր է, ապա ամբողջ CH զուգահեռագիծը հավասար է ամբողջ KE զուգահեռագծին։ Բայց CH զուգահեռագիծը հավասար է CG-ին, քանի որ AC-ը նույնպես հավասար է CB-ին [Բան. 6.1]։ Ուստի GC զուգահեռագիծը նույնպես հավասար է EK-ին։ Թող CF զուգահեռագիծը ավելացվի երկուսին էլ։ Արդ, ամբողջ AF զուգահեռագիծը հավասար է LMN գномոնին։ Հետևաբար, DB զուգահեռագիծը, այսինքն AD-ը, մեծ է AF զուգահեռագծից։
Այսպիսով, բոլոր այն զուգահեռագծերի համար, որոնք կիրառված են նույն ուղղագծի վրա և թերանում են (հանման հետևանքով առաջացած) զուգահեռագծային պատկերով, որը նման է և նույն կերպ դասավորված է այն զուգահեռագծին, որ կառուցված է ուղղագծի կեսի վրա, ամենամեծը այն է, որը դրված է հենց այդ կեսի վրա։ (Դա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 28
Որպեսզի ուղղագծին կիրառվի զուգահեռագիծ, հավասար տրված ուղղագծային պատկերին, այնպես, որ կիրառված զուգահեռագիծը թերանա մի զուգահեռագծային պատկերով, որը նման է տրված զուգահեռագծին, անհրաժեշտ է, որ տրված ուղղագծային պատկերը [որին հավասար զուգահեռագիծը պետք է կիրառվի] մեծ չլինի այն զուգահեռագծից, որը կառուցված է ուղղագծի կեսի վրա և նման է թերացման պատկերին։ Թող AB-ն լինի տրված ուղղագիծը, իսկ C-ը տրված ուղղագծային պատկերը, որին AB-ի վրա կիրառվող զուգահեռագիծը պետք է հավասար լինի, ընդ որում C-ը մեծ չէ այն զուգահեռագծից, որը կառուցված է AB-ի կեսի վրա և նման է թերացման պատկերին։ D-ը այն զուգահեռագիծն է, որին պետք է նման լինի թերացումը։ Արդ, պետք է AB ուղղագծի վրա կիրառել զուգահեռագիծ, հավասար տրված C ուղղագծային պատկերին, թերանալով մի զուգահեռագծային պատկերով, որը նման է D-ին։
Թող AB-ը բաժանված լինի կետ E-ով երկու կեսի [Բան. 1.10], և թող (զուգահեռագիծ) EBFG, որը նման է ու նույն կերպ դասավորված D զուգահեռագծին, կառուցվի EB-ի վրա [Բան. 6.18]։ Եվ թող AG զուգահեռագիծը լրացվի։ Եթե AG-ը հավասար է C-ին, ապա նախապես պահանջվածը կատարված է։ Որովհետև AG զուգահեռագիծը, հավասար տրված ուղղագծային պատկեր C-ին, կիրառված է AB ուղղագծի վրա, թերանալով GB զուգահեռագծային պատկերով, որը նման է D-ին։ Իսկ եթե ոչ, թող HE-ն մեծ լինի C-ից։ Եվ HE-ը հավասար է GB-ին [Բան. 6.1]։ Ուստի GB-ն նույնպես մեծ է C-ից։ Թող KLMN զուգահեռագիծը կառուցվի, որը թե՛ նման է և թե՛ նույն կերպ դասավորված D-ին, և հավասար GB-ի C-ից մեծ լինելու չափին [Բան. 6.25]։ Բայց GB-ն նման է D-ին։ Ուրեմն KM-ն նույնպես նման է GB-ին [Բան. 6.21]։ Ուստի թող KL-ը համապատասխանեցվի GE-ին, իսկ LM-ը GF-ին։ Եվ چونکہ GB զուգահեռագիծը հավասար է C պատկերին և KM զուգահեռագծին, GB-ն ավելի մեծ է KM-ից։ Հետևաբար GE-ն նույնպես մեծ է KL-ից, իսկ GF-ը LM-ից։ Թող GO-ը հավասարեցվի KL-ին, իսկ GP-ը LM-ին [Բան. 1.3]։ Եվ թող OGPQ զուգահեռագիծը լրացվի։ Այսպիսով [GQ]-ը հավասար է ու նման KM-ին (իսկ KM-ն նման է GB-ին), ուստի GQ-ն նույնպես նման է GB-ին [Բան. 6.21]։ Այսպիսով GQ և GB զուգահեռագծերը նույն անկյունագծի շուրջ են [Բան. 6.26]։ Թող GQB-ը լինի նրանց (ընդհանուր) անկյունագիծը, և թող պատկերի մնացորդը լրացվի։ Քանի որ BG-ը հավասար է C-ին և KM-ին, որոնցից GQ-ը հավասար է KM-ին, մնացած գномոն VWU-ն նույնպես հավասար է C-ին։ Եվ քանի որ (լրացնող) PR-ը հավասար է (լրացնող) OS-ին [Բան. 1.43], թող QB զուգահեռագիծը ավելացվի երկուսին էլ։ Այդպիսով ամբողջ PB զուգահեռագիծը հավասար է ամբողջ OB զուգահեռագծին։ Իսկ OB-ն հավասար է TE-ին, քանի որ AE կողմը հավասար է EB կողմին [Բան. 6.1]։ Ուստի TE-ն նույնպես հավասար է PB-ին։ Թող (զուգահեռագիծ) OS-ը նույնպես ավելացվի երկուսին էլ։ Այդպիսով ամբողջ TS զուգահեռագիծը հավասար է VWU գномոնին։ Բայց VWU գномոնը ցույց տրվեց, որ հավասար է C-ին։ Ուստի TS զուգահեռագիծը նույնպես հավասար է C պատկերին։ Այսպիսով, ST զուգահեռագիծը, հավասար տրված ուղղագծային պատկեր C-ին, կիրառվեց տրված AB ուղղագծի վրա, թերանալով QB զուգահեռագծային պատկերով, որը նման է D-ին [քանի որ QB-ն նման է GQ-ին [Բան. 6.24]]։ (Սա էլ հենց այն էր, ինչ պետք էր անել)։ Ծանոթագրություն: Այս առաջարկությունը երկրաչափական լուծումն է x² – αx + β = 0 քառորդասնական հավասարման։ Այստեղ x-ը թերացման կողմի երկարության և D պատկերի համապատասխան կողմի հարաբերությունն է, α-ն AB ուղղագծի երկարության և D պատկերի այն կողմի երկարության հարաբերությունը, որը համապատասխանում է թերացման կողքին (AB-ի երկայնքով), իսկ β-ն C և D պատկերների մակերեսների հարաբերությունն է։ Պայմանադրությունը β < α²/4-ն է, որպեսզի հավասարումն ունենա իրական լուծումներ։ Այստեղ գտնվում է հավասարման միայն փոքր արմատը։ Մեծ արմատը կարելի է գտնել նմանատիպ մեթոդով։
Առաջարկություն 29
Ուղղագծին կիրառել մի զուգահեռագիծ, որը հավասար է տրված ուղղագծային պատկերին, այնպես, որ կիրառված զուգահեռագիծը անցնի սահմանվածից ավել (անցնի սահմանագիծը) մի զուգահեռագծային պատկերով, որը նման է տրված (զուգահեռագծին):
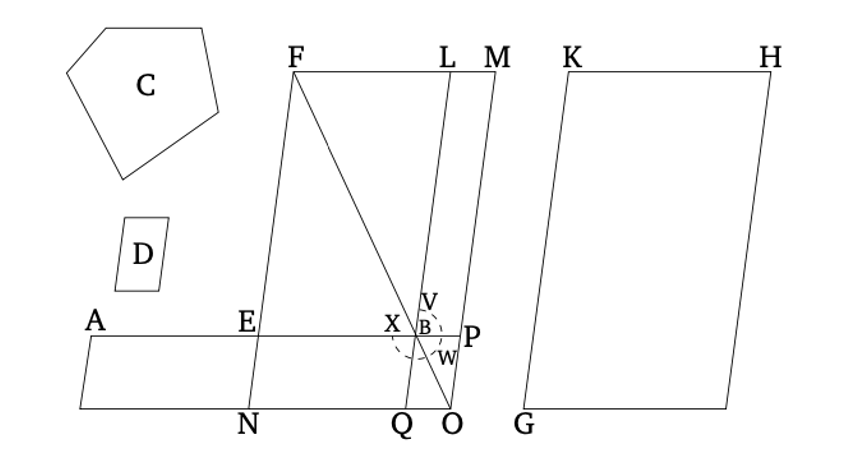Թող AB-ն լինի տրված ուղղագիծը, իսկ C-ը տրված ուղղագծային պատկերը, որին AB-ի վրա կիրառվող զուգահեռագիծը պետք է հավասար լինի։ D-ը այն զուգահեռագիծն է, которому նման պետք է լինի ավելացած մասը։ Արդ, անհրաժեշտ է AB ուղղագծի վրա կիրառել մի զուգահեռագիծ, հավասար C ուղղագծային պատկերին, բայց այնքան, որ այն անցնի սահմանվածից ավել, առաջացնելով մի զուգահեռագծային պատկեր, որը նման է D-ին։
Թող AB-ը բաժանված լինի կեսի վրա E կետով [Բան. 1.10], և թող EB-ի վրա կառուցվի BF զուգահեռագիծը, որը նման և նույն կերպ դասավորված է D զուգահեռագծին [Բան. 6.18]։ Թող նաև կառուցվի GH զուգահեռագիծը, որը նույնպես նման է D-ին և հավասար BF-ի և C-ի գումարին [Բան. 6.25]։ Եվ թող KH-ը համապատասխանեցվի FL-ին, իսկ KG-ը FE-ին։ Քանի որ GH զուգահեռագիծը մեծ է FB զուգահեռագծից, հետևաբար KH-ը նույնպես մեծ է FL-ից, իսկ KG-ը մեծ է FE-ից։ Թող FL և FE գծերը երկարացվեն, և թող FLM երկարությունը հավասարեցվի KH-ին, իսկ FEN-ը հավասարեցվի KG-ին [Բան. 1.3]։ Եվ թող MN զուգահեռագիծը լրացվի։ Այսպիսով MN-ը հավասար և նման է GH-ին։ Բայց GH-ը նման է EL-ին։ Ուրեմն MN-ը նույնպես նման է EL-ին [Բան. 6.21]։ EL-ը, ուրեմն, նույն անկյունագծի շուրջ է, ինչ MN-ը [Բան. 6.26]։ Թող նրանց (ընդհանուր) անկյունագիծ FO գծվի, և թող պատկերի մնացած մասը լրացվի։
Եվ քանի որ GH զուգահեռագիծը հավասար է EL զուգահեռագծին և (C) պատկերին, բայց GH-ը հավասար է նաև MN զուգահեռագծին, ուրեմն MN-ը նույնպես հավասար է EL-ին և C-ին։ Թող EL-ը հանվի երկուսից էլ։ Ուստի մնացող XWV գνομոնը հավասար է (C) պատկերին։ Եվ քանի որ AE-ը հավասար է EB-ին, AN զուգահեռագիծը նույնպես հավասար է NB զուգահեռագծին [Բան. 6.1], այսինքն LP զուգահեռագծին [Բան. 1.43]։ Թող EO զուգահեռագիծը ավելացվի երկուսին էլ։ Այդպիսով ամբողջ AO զուգահեռագիծը հավասար է VWX գνομոնին։ Բայց VWX գνομոնը հավասար է (C) պատկերին։ Ուստի AO զուգահեռագիծը նույնպես հավասար է C պատկերին։
Այսպիսով AO զուգահեռագիծը, հավասար տրված ուղղագծային պատկեր C-ին, կիրառվել է տրված AB ուղղագծին, անցնելով ավել մի զուգահեռագծային պատկերով QP, որը նման է D-ին, քանի որ PQ-ն նույնպես նման է EL-ին [Բան. 6.24]։ (Սա էլ հենց այն էր, ինչ պետք էր անել)։
Ծանոթագրություն: Այս առաջարկությունը քառակուսային հավասարման x² + αx – β = 0 երկրաչափական լուծումն է։ Այստեղ x-ը ավելցուկի կողմի և D պատկերի համապատասխան կողմի հարաբերությունն է, α-ն AB ուղղագծի երկարության և D պատկերի այն կողքի երկարության հարաբերությունը, որը համապատասխանում է ավելցուկի երկայնքով AB կողմին, իսկ β-ն C և D պատկերների մակերեսների հարաբերությունն է։ Այստեղ գտնվում է հավասարման միայն դրական արմատը։
Առաջարկություն 30
Տրված վերջավոր ուղղագծի հատվածումը ծայրագույն և միջին հարաբերությամբ։
Թող AB լինի տրված վերջավոր ուղղագիծը։ Ուրեմն անհրաժեշտ է AB ուղղագիծը բաժանել ծայրագույն և միջին հարաբերությամբ։ Թող AB ուղղագծի վրա կառուցվի BC քառակուսին [Բան. 1.46], և թող BC-ին հավասար CD զուգահեռագիծը կիրառվի AC-ի վրա, անցնելով սահմանվածից ավելի AD պատկերով, որը նման է BC-ին [Բան. 6.29]։ Քանի որ BC-ը քառակուսի է, ուրեմն AD-ն նույնպես քառակուսի է։ Եվ քանի որ BC-ը հավասար է CD-ին, թող CE ուղղանկյունը հանվի երկուսից էլ։ Այդպիսով, մնացած BF ուղղանկյունը հավասար է մնացած AD քառակուսուն։ Այն նաև հավանկյուն է նրա հետ։ Այսպիսով BF-ի և AD-ի կողմերը հավասար անկյունների շուրջ обратно (փոխադարձաբար) համաչափ են [Բան. 6.14]։ Ուստի, ինչպես FE-ն ED-ի նկատմամբ է, այնպես AE-ը EB-ի նկատմամբ է։ Եվ FE-ը հավասար է AB-ին, իսկ ED-ը AE-ին։ Հետևաբար, ինչպես BA-ը AE-ի նկատմամբ է, նույնպես AE-ը EB-ի նկատմամբ է։ Եվ քանի որ AB-ը մեծ է AE-ից, ուրեմն AE-ը նույնպես մեծ է EB-ից [Բան. 5.14]։ Այսպիսով, AB ուղղագիծը բաժանվեց ծայրագույն և միջին հարաբերությամբ E կետում, և AE-ն նրա մեծ մասը դարձավ։ (Սա էլ հենց այն էր, ինչ պետք էր անել)։ Ծանոթագրություն: Այս մեթոդը ուղղագծի բաժանման, որն ibland անվանվում է "ոսկե հատում", դիտեք Առաջարկություն 2.11:
Առաջարկություն 31
Ուղղանկյուն եռանկյուններում, աջ անկյունը ծածկող կողմի վրա գծված պատկերն հավասար է աջ անկյունը շրջապատող կողմերի վրա կառուցված նման, և նույն կերպ նկարագրված պատկերների գումարին:
Թող ABC-ն լինի ուղղանկյուն եռանկյուն, որտեղ BΑC անկյունը աջ անկյուն է։ Ասում եմ, որ BC կողմի վրա կառուցված պատկերը հավասար է BA և AC կողերին կառուցված նման, նույն կերպ նկարագրված պատկերների գումարին։ Թող AD ուղղահայացը գծվի [Բան. 1.12]: Ուստի, քանի որ ABC ուղղանկյուն եռանկյունում AD ուղիղը գծվեց A աջ անկյունից BC հիմքին ուղղահայաց, երեքանկյունները ABD և ADC ուղղահայացի շուրջ նման են թե՛ ամբողջ ABC եռանկյունին, թե՛ միմյանց [Բան. 6.8]: Եվ քանի որ ABC-ն նման է ABD-ին, ուրեմն ինչպես CB-ը BA-ի նկատմամբ է, այնպես էլ AB-ը BD-ի նկատմամբ է [Սահմ. 6.1]։ Եվ քանի որ երեք ուղղագծերը համաչափ են, ապա ինչպես առաջինը երրորդի նկատմամբ է, այնպես էլ առաջինի վրա կառուցված նման և նույն ձևով նկարագրված պատկերը երկրորդի վրա կառուցված պատկերի նկատմամբ է [Բան. 6.19 ուղղում]: Այսպիսով, ինչպես CB-ը BD-ի նկատմամբ է, այնպես էլ CB-ի վրա կառուցված պատկերը BA-ի վրա կառուցված նման, նույն կերպ նկարագրված պատկերի նկատմամբ է։ Նույն պատճառներով, ինչպես BC-ը CD-ի նկատմամբ է, այնպես էլ BC-ի վրա կառուցված պատկերը CA-ի վրա կառուցված պատկերի նկատմամբ է։ Հետևաբար, քանի որ BC-ը BD-ի և DC-ի նկատմամբ է, BC-ի վրա կառուցված պատկերը հավասար է BA և AC կողմերին կառուցված նման, նույն ձևով նկարագրված պատկերների գումարին [Բան. 5.24]: Եվ քանի որ BC-ը հավասար է BD-ին և DC-ին, BC-ի վրա կառուցված պատկերը նույնպես հավասար է BA-ի և AC-ի վրա կառուցված նման, նույն ձևով նկարագրված պատկերների գումարին [Բան. 5.9]։ Արդ, ուղղանկյուն եռանկյուններում աջ անկյունը ծածկող կողի վրա կառուցված պատկերը հավասար է աջ անկյունը շրջապատող կողմերի վրա կառուցված նման, նույն կերպ նկարագրված պատկերների գումարին։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 32
Եթե երկու եռանկյուններ, որոնք ունեն երկու կողմեր համաչափ երկու այլ կողմերին, տեղադրված են մեկ ընդհանուր անկյան շուրջ այնպես, որ համապատասխանող կողմերը նույնպես զուգահեռ են, ապա եռանկյունների մնացած կողմերը կլինեն ուղղագծի վրա (միմյանց նկատմամբ):
Թող ABC և DCE լինեն երկու եռանկյուններ, որոնց BA և AC երկու կողմերը համաչափ են DC և DE երկու կողմերին, այնպես որ ինչպես AB-ը AC-ի նկատմամբ է, նույն կերպ DC-ն DE-ի նկատմամբ է, և AB կողմը զուգահեռ է DC-ին, իսկ AC-ն DE-ին։ Ասում եմ, որ BC կողմը ուղիղ է CE-ի հետ։ Քանզի AB-ը զուգահեռ է DC-ին, և AC ուղղագիծը անցնում է նրանց միջով, BAC և ACD փոխարինական անկյունները հավասար են միմյանց [Բան. 1.29]։ Նույն պատճառներով CDE-ն հավասար է ACD-ին։ Ուստի BAC-ը հավասար է CDE-ին։ Եվ քանի որ ABC և DCE են երկու եռանկյուններ, որոնք ունեն A անկյունը հավասար D անկյանը, իսկ հավասար անկյունների շուրջ գտնվող կողմերը համաչափ են (այնպես, որ ինչպես BA-ը AC-ի նկատմամբ է, այնպես էլ CD-ն DE-ի նկատմամբ է), ABC եռանկյունը հավանկյուն է DCE եռանկյունին [Բան. 6.6]։ Ուստի ABC անկյունը հավասար է DCE անկյանը։ Եվ (անկյուն) ACD-ն նույնպես ցույց տրվեց հավասար BAC անկյանը։ Դրա շնորհիվ (ամբողջ) ACE անկյունը հավասար է (ABC և BAC անկյունների) գումարին։ Թող ACB անկյունը նույնպես ավելացվի երկուսին։ Այդպիսով ACE և ACB անկյունները հավասար են BAC, ACB, և CBA անկյուններին։ Բայց BAC, ABC և ACB անկյունների գումարը հավասար է երկու ուղղանկյունների [Բան. 1.32]։ Ուստի ACE և ACB անկյունները նույնպես հավասար են երկու ուղղանկյունների։ Այսպիսով, BC և CE երկու ուղիղները, որոնք չեն գտնվում նույն կողմում, կազմում են ACE և ACB հարակից անկյուններ, որոնց գումարը հավասար է երկու ուղղանկյունների AC ուղղագծի վրա, C կետում։ Ուստի BC-ը ուղիղ է CE-ի հետ [Բան. 1.14]։ Այսպիսով, եթե երկու եռանկյուններ, որոնք ունեն երկու կողմերը համաչափ երկու այլ կողմերին, տեղադրված են մեկ ընդհանուր անկյան շուրջ այնպես, որ համապատասխանող կողմերը նույնպես զուգահեռ են, ապա մնացած կողմերը կլինեն միևնույն ուղիղ գծի վրա (միմյանց նկատմամբ)։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 33
Հավասար շրջաններում անկյունները նույն հարաբերությունն ունեն այն շրջագծերի նկատմամբ, որոնց վրա կանգնած են, արդյոք նրանք գտնվում են շրջանների կենտրոններում, թե շրջագծերի վրա:
Թող ABC և DEF լինեն հավասար շրջաններ, և թող BGC և EHF անկյունները լինեն դրանց կենտրոններում G և H կետերում համապատասխանաբար, իսկ BAC և EDF անկյունները լինեն դրանց շրջագծերի վրա։ Ասում եմ, որ ինչպես BC շրջագիծը EF շրջագծի նկատմամբ է, այնպես էլ BGC անկյունը EHF անկյան նկատմամբ է, և BAC անկյունը EDF անկյան նկատմամբ։ Թող որևէ քանակի հաջորդական շրջագծաշղթաներ CK և KL լինեն հավասար BC շրջագծին, և որևէ քանակի FM և MN լինեն հավասար EF շրջագծին։ Թող GK, GL, HM, և HN գծերը ավելացվեն։ Ուստի, քանի որ BC, CK և KL շրջագծերը հավասար են միմյանց, BGC, CGK և KGL անկյունները նույնպես հավասար են միմյանց [Բան. 3.27]։ Այսպիսով, քանի անգամ BL շրջագիծը բաժանվում է BC շրջագծի մեջ, նույնքան անգամ BGL անկյունը բաժանվում է BGC անկյան մեջ։ Եվ նույն պատճառներով, քանի անգամ NE շրջագիծը բաժանվում է EF-ի մեջ, նույնքան անգամ NHE անկյունը բաժանվում է EHF անկյան մեջ։ Արդ, եթե BL շրջագիծը հավասար է EN շրջագծին, ապա BGL անկյունը նույնպես հավասար է EHN անկյանին [Բան. 3.27]։ Եթե BL-ը մեծ է EN-ից, ապա BGL անկյունը նույնպես մեծ է EHN-ից, իսկ եթե BL-ը փոքր է EN-ից, ապա BGL անկյունը նույնպես փոքր է EHN-ից։ Արդ, ունենք չորս մեծություններ՝ երկու շրջագծեր BC և EF, և երկու անկյուններ BGC և EHF։ Եվ վերցվել են հավասար բազմապատիկներ BC շրջագծից և BGC անկյունից (մասնավորապես BL շրջագիծն ու BGL անկյունը) և EF շրջագծից ու EHF անկյունից (մասնավորապես EN շրջագիծն ու EHN անկյունը)։ Եվ ցույց տրվեց, որ եթե BL շրջագիծը գերազանցում է EN շրջագծին, ապա BGL անկյունը նույնպես գերազանցում է EHN անկյանը, եթե հավասար են, ապա հավասար են, իսկ եթե BL-ը փոքր է, ապա BGL անկյունը նույնպես փոքր է EHN-ից։ Այսպիսով, ինչպես BC շրջագիծը EF-ի նկատմամբ է, այնպես BGC անկյունը EHF-ի նկատմամբ է [Սահմանում 5.5]։ Բայց քանի որ BGC անկյունը EHF-ի նկատմամբ է, նույն կերպ BAC անկյունը EDF-ի նկատմամբ է [Բան. 5.15]։ Նախադրյալները կրկնապատկում են հետևությունները [Բան. 3.20]։ Ուստի, ինչպես BC շրջագիծը EF-ի նկատմամբ է, այնպես BGC անկյունը EHF-ի նկատմամբ է, և BAC անկյունը EDF-ի նկատմամբ է։ Այսպիսով, հավասար շրջաններում անկյունները նույն հարաբերությունն ունեն այն շրջագծերի նկատմամբ, որոնց վրա կանգնած են, արդյոք նրանք գտնվում են շրջանների կենտրոններում, թե շրջագծերի վրա։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Սահմանումներ 1. Միավորը այն է, ըստ որի ամեն գոյող (բան) ասվում է «մեկ»։ 2. Թիվը միավորներից կազմված բազմություն է։† 3. Թիվը մաս է (ուրիշ) թիվի, փոքրագույնը մեծագույնի, երբ այն չափում է մեծագույնը։‡ 4. Իսկ (եթե փոքրագույնը) մասեր է (մեծագույնի), երբ այն չի չափում այն։§ 5. Եվ մեծագույն (թիվը) փոքրագույնի բազմապատիկն է, երբ մեծագույնը չափվում է փոքրագույնով։ 6. Զույգ թիվը այն թիվն է, որ կարելի է բաժանել երկու հավասար մասերի։ 7. Թեք (կամ կենտ) թիվը այն թիվն է, որը չի կարելի բաժանել երկու հավասար մասերի, կամ որը տարբերվում է զույգ թվից մեկ միավորով։ 8. Զույգ-անգամ-զույգ թիվը այն է, որ չափվում է մի զույգ թվով, ըստ մի այլ զույգ թվի։¶ 9. Իսկ զույգ-անգամ-թեք թիվը այն է, որ չափվում է մի զույգ թվով, ըստ մի թեք (կենտ) թվի։∗ 10. Եվ թեք-անգամ-թեք թիվը այն է, որ չափվում է մի թեք (կենտ) թվով, ըստ մի այլ թեք (կենտ) թվի։$ 11. Առաջնային∥ թիվը այն է, որ չափվում է միայն միավորով։ 12. Թվերը, որոնք պարզ են (առաջնային) միմյանց նկատմամբ, այն թվերն են, որոնք չափվում են միայն միավորով որպես ընդհանուր չափ։ 13. Բարդ թիվը այն է, որ չափվում է ինչ-որ թվով։ 14. Եվ թվերը, որոնք բարդ են միմյանց նկատմամբ, այն թվերն են, որոնք չափվում են ինչ-որ թվով որպես ընդհանուր չափ։ 15. Ասվում է, որ թիվը բազմապատկում է (ուրիշ) թիվը, երբ բազմապատկվող թիվը ինքն իրեն מוסարձակվում է այնքան անգամ, որքան միավորներ կան առաջին (բազմապատկող) թվում, և (այդ կերպ) առաջանում է մեկ այլ թիվ։ 16. Եվ երբ երկու թվեր միմյանց բազմապատկելով առաջացնում են ինչ-որ (ուրիշ) թիվ, ապա (այդպիսով) առաջացած թիվը կոչվում է հարթ (ղեկավար տերմինը "plane" – "հարթ"), և նրա կողմերը այն թվերն են, որոնք բազմապատկում են միմյանց։ 17. Եվ երբ երեք թվեր միմյանց բազմապատկելով առաջացնում են ինչ-որ (ուրիշ) թիվ, ապա (այդպիսով) առաջացած թիվը կոչվում է ծավալային (solid), և նրա կողմերը այն թվերն են, որոնք բազմապատկում են միմյանց։ 18. Քառակուսի (square) թիվը հավասար բազմապատիկ է հավասարի, կամ (հարթ թիվ) է, պարփակված երկու հավասար թվերով։ 19. Եվ խորանարդ (cube) թիվը հավասար-նշանակ բազմապատիկ է հավասարի, կրկին հավասարի, կամ (ծավալային թիվ) է, պարփակված երեք հավասար թվերով։ 20. Թվերը համաչափ են, երբ առաջինը նույն բազմապատիկն է, կամ նույն մասը, կամ նույն մասերն են երկրորդի նկատմամբ, ինչ երրորդը չորրորդի նկատմամբ։ 21. Նման հարթ և ծավալային թվերը այն թվերն են, որոնք ունեն համեմատական (համաչափ) կողմեր։ 22. Կատարյալ թիվը այն է, որը հավասար է իր մասերի գումարին։†† Ծանոթագրություններ: † Այլ կերպ ասած, «թիվը» միավորից մեծ դրական ամբողջ թիվ է։ ‡ Այլ կերպ ասած, թիվ a-ն մաս է թիվ b-ի, եթե գոյություն ունի թիվ n, այնպես, որ na = b։ § Այլ կերպ ասած, a թիվը մասեր է b թիվի (որտեղ a < b), եթե գոյություն ունեն տարբեր թվեր m և n, այնպես որ na = m*b։ ¶ Այլ կերպ ասած, զույգ-անգամ-զույգ թիվը երկու զույգ թվերի արտադրյալն է։ ∗ Այլ կերպ ասած, զույգ-անգամ-թեք թիվը մեկ զույգ և մեկ թեք (կենտ) թվերի արտադրյալն է։ $ Այլ կերպ ասած, թեք-անգամ-թեք թիվը երկու թեք (կենտ) թվերի արտադրյալն է։ ∥ Բառացիորեն, «առաջին»։ †† Այլ կերպ ասած, կատարյալ թիվը հավասար է իր բաժանարարների գումարին։
Առաջարկություն 1
Եթե տրվեն երկու անհավասար թվեր, և փոքրագույնը հերթով անընդհատ հանվի մեծագույնից, այնպես, որ մնացորդը երբեք չչափի իրեն նախորդող թիվը, մինչև չմնա մեկ միավոր, ապա սկզբնական թվերը կլինեն միմյանց նկատմամբ պարզ (արնչություն չունեն որևէ ընդհանուր բաժանարարից բացի մեկից):
Երկու [անհավասար] թվերի, AB և CD-ի դեպքում, եթե փոքրագույնը հերթով անընդհատ հանվի մեծագույնից, թող մնացորդը երբեք չչափի իրեն նախորդող թիվը, մինչև չմնա մեկ միավոր։ Ասում եմ, որ AB և CD թվերը պարզ են միմյանց նկատմամբ, այսինքն՝ միայն միավորը չափում է (և) AB-ին, (և) CD-ին։ Եթե AB և CD պարզ չլինեն միմյանց նկատմամբ, ապա որոշ թիվ նրանց կչափի։ Թող այդ թիվը լինի E։ Եվ թող CD-ն, չափելով BF-ը, թողնի FA մնացորդ, փոքր քան ինքն է, հետո AF-ը, չափելով DG-ն, թողնի GC մնացորդ, փոքր քան ինքն է, հետո GC-ն, չափելով FH-ը, թողնի HA միավորը։ Փաստորեն, քանի որ E-ն չափում է CD-ն, և CD-ն չափում է BF-ը, E-ն նույնպես չափում է BF-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ BA-ն։ Ուստի (E-ն) նույնպես կչափի BA-ի մնացորդ AF-ը։ Եվ AF-ն չափում է DG-ն։ Այսպիսով, E-ն նույնպես չափում է DG-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ DC-ն։ Ուստի (E-ն) նույնպես կչափի CG մնացորդը։ Եվ CG-ն չափում է FH-ը։ Այսպիսով, E-ն նույնպես չափում է FH-ը։ Եվ (E-ն) նաև չափում է ամբողջ FA-ն։ Ուստի (E-ն) նույնպես կչափի HA մնացորդային միավորը, թեև դա ուղղակի միավոր է։ Սա բացարձակապես անհնար է։ Հետևաբար գոյություն չունի թիվ, որը չափի (և) AB-ը, (և) CD-ը։ Այսպիսով, AB և CD թվերը պարզ են միմյանց նկատմամբ։ (Ահա թե ինչ էր անհրաժեշտ ցույց տալ): Մեկնաբանություններ: † Այստեղ օգտագործվում է չարտասանված ընդհանուր գաղափարը, որ եթե a-ն չափում է b-ին, և b-ն չափում է c-ին, ապա a-ն նույնպես չափում է c-ին, որտեղ բոլոր նշանները ներկայացնում են թվեր։ ‡ Այստեղ օգտագործվում է չարտասանված ընդհանուր գաղափարը, որ եթե a-ն չափում է b-ին, և a-ն նաև չափում է b-ի մի մասը, ապա a-ն նույնպես չափում է b-ի մնացորդային մասը, որտեղ բոլոր նշանները ներկայացնում են թվեր։
Առաջարկություն 2
Գտնել երկու տրված թվերի (որոնք միմյանց նկատմամբ պարզ չեն) ամենամեծ ընդհանուր չափը:
Թող AB և CD լինեն երկու տրված թվերը, որոնք միմյանց նկատմամբ պարզ չեն։ Արդ, անհրաժեշտ է գտնել AB և CD թվերի ամենամեծ ընդհանուր չափը։ Իրոք, եթե CD-ը չափում է AB-ը, ապա CD-ը այդպիսով AB-ի և CD-ի ընդհանուր չափն է (քանի որ CD-ը նաև ինքն իրեն է չափում)։ Եվ ակնհայտ է, որ այն նաև ամենամեծ (ընդհանուր չափն) է։ Քանի որ ոչինչ, որ մեծ է CD-ից, չի կարող չափել CD-ին։ Բայց եթե CD-ը չի չափում AB-ը, ապա AB-ից և CD-ից կմնա որոշ թիվ, երբ փոքրագույնը հերթով շարունակաբար հանենք մեծագույնից, որը կչափի իրեն նախորդող թիվը։ Որովհետև մեկ միավոր չի մնա։ Բայց եթե ոչ, ապա AB և CD թվերը պարզ կլինեն միմյանց նկատմամբ [Բան. 7.1]։ Սա հակասում է այն, ինչ ենթադրվել էր։ Ուստի կմնա մի թիվ, որը կչափի իրեն նախորդող թիվը։ ԵՎ թող CD-ը, չափելով BE-ն, թողնի EA մնացորդը, որը փոքր է իրենից, հետո EA-ն, չափելով DF-ը, թողնի FC մնացորդը, որը փոքր է իրենից, ապա CF-ը թող չափի AE-ը։ Ուստի, քանի որ CF-ը չափում է AE-ը, իսկ AE-ը չափում է DF-ը, CF-ը կհասկանանք, որ չափում է նաև DF-ը։ Եվ այն նաև ինքն իրեն է չափում։ Ուստի այն կչափի նաև ամբողջ CD-ը։ Իսկ CD-ը չափում է BE-ը։ Ուստի CF-ը նույնպես կչափի BE-ը։ Եվ այն նաև չափում է EA-ն։ Ուստի այն կչափի նաև ամբողջ BA-ն։ Այն նաև չափում է AE մնացորդը։ Եվ AE-ը չափում է DF-ը։ Ուստի CF-ը նույնպես կչափի DF-ը։ Եվ այն ինքն իրեն է չափում։ Ուստի այն կչափի նաև DC մնացորդը։ Այսպիսով, CF-ը չափում է և AB-ը, և CD-ը։ Ասում եմ, որ այն նաև ամենամեծ (ընդհանուր չափն) է։ Քանի որ եթե CF-ը AB և CD թվերի ամենամեծ ընդհանուր չափը չէ, ապա կգտնվի մի թիվ, որը մեծ է CF-ից և կչափի AB ու CD թվերը։ Թող այն չափի (AB և CD), և թող այդ թիվը լինի G։ Եվ քանի որ G-ն չափում է CD-ը, իսկ CD-ն չափում է BE-ը, G-ն նույնպես կչափի BE-ը։ Եվ այն նաև կչափի ամբողջ BA-ն։ Ուստի այն կչափի AE մնացորդը։ Իսկ AE-ը չափում է DF-ը։ Ուստի G-ն նույնպես կչափի DF-ը։ Այն նաև չափում է ամբողջ DC-ը։ Ուստի այն կչափի CF մնացորդը, մեծը չափելով փոքրին։ Սա անհնար է։ Ուստի ոչ մի թիվ, որը մեծ է CF-ից, չի կարող չափել AB և CD թվերը։ Այսպիսով, CF-ը AB և CD թվերի ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ Հաջորդակում (Corollary) Այդպիսով ակնհայտ է, որ եթե մի թիվ չափում է երկու թիվ, ապա այն կչափի նաև նրանց ամենամեծ ընդհանուր չափը։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 3
Գտնել երեք տրված թվերի (որոնք միմյանց նկատմամբ պարզ չեն) ամենամեծ ընդհանուր չափը:
Թող A, B և C լինեն երեք տրված թվերը, որոնք միմյանց նկատմամբ պարզ չեն։ Արդ, անհրաժեշտ է գտնել A, B և C թվերի ամենամեծ ընդհանուր չափը։ Թող նախ վերցված լինի A և B երկու (թվերի) ամենամեծ ընդհանուր չափը D [Բան. 7.2]։ Ուրեմն D-ը կամ չափում է, կամ չի չափում C-ը։ Նախ ենթադրենք, որ այն չափում է (C-ը)։ Այն նաև չափում է A-ն և B-ը։ Ուստի D-ը չափում է A, B և C թվերը։ Այսպիսով, D-ը A, B և C թվերի ընդհանուր չափն է։ Ասում եմ, որ այն նաև ամենամեծ (ընդհանուր) չափն է։ Քանի որ եթե D-ը A, B և C ամենամեծ ընդհանուր չափը չլինի, ապա կգտնվի մի թիվ, ավելի մեծ քան D-ը, որը կչափի A, B և C թվերը։ Թող այն (այդպես) չափի (A, B, C) և կոչվի E։ Ուստի, քանի որ E-ը չափում է A, B և C, այն կչափի նաև A և B։ Այսպիսով, այն կչափի A և B ամենամեծ ընդհանուր չափը D-ը [Ընդհանր.` 7.2], իսկ D-ը ամենամեծ ընդհանուր չափն է A և B թվերի։ Այսպիսով, E-ը չափում է D-ը, մեծը չափում է փոքրին։ Սա բացարձակ անհնար է։ Հետևաբար, ոչ մի թիվ, մեծ քան D-ը, չի կարող չափել A, B և C թվերը։ Ուստի D-ը A, B և C թվերի ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։ Եթե D-ը չի չափում C-ը, ասում եմ նախ, որ C և D թվերը միմյանց նկատմամբ պարզ չեն։ Քանի որ A, B, C միմյանց նկատմամբ պարզ չեն, մի թիվ կգտնվի, որը կչափի դրանք։ Այսպիսով, A, B, C չափող թիվը կչափի նաև A և B, և կչափի A և B ամենամեծ ընդհանուր չափը D-ը [Ընդհանր. 7.2], և կչափի նաև C-ը։ Ուստի որոշ թիվ կչափի D և C թվերը։ Այսպիսով, D և C նույնպես պարզ չեն միմյանց նկատմամբ։ Թող D և C ամենամեծ ընդհանուր չափը, E-ը, վերցվի [Բան. 7.2]։ Եվ քանի որ E-ը չափում է D-ին, իսկ D-ը չափում է A և B, E-ը նույնպես չափում է A և B։ Այն նաև չափում է C-ը։ Ուստի E-ը A, B, C թվերի ընդհանուր չափն է։ Ասում եմ, որ այն նաև ամենամեծ ընդհանուր չափն է։ Քանի որ եթե E-ը A, B, C ամենամեծ ընդհանուր չափը չլինի, ապա կգտնվի թիվ, ավելի մեծ քան E-ը, որը կչափի A, B և C թվերը։ Թող այն (այդպես) չափի (A, B և C) և կոչվի F։ Եվ քանի որ F-ը չափում է A, B, C, այն կչափի նաև A և B։ Ուստի այն կչափի A և B ամենամեծ ընդհանուր չափը D-ը [Ընդհանր. 7.2], իսկ D-ը A և B ամենամեծ ընդհանուր չափն է։ Այսպիսով, F-ը չափում է D-ը։ Այն նաև չափում է C-ը։ Ուստի F-ը չափում է D և C թվերը, և կչափի D և C ամենամեծ ընդհանուր չափը [Ընդհանր.` 7.2]։ Իսկ E-ը D և C ամենամեծ ընդհանուր չափն է։ Այսպիսով, F-ը չափում է E-ին, մեծը չափում է փոքրին։ Սա անհնար է։ Ուստի ոչ մի թիվ, մեծ քան E-ը, չի չափում A, B, C թվերը։ Այսպիսով, E-ը A, B, C ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 4
Ցանկացած թիվ կամ մաս է, կամ մասեր են յուրաքանչյուր (ուրիշ) թվի, ավելի փոքրն ավելի մեծի։ Թող A և BC լինեն երկու թվեր, և թող BC-ը լինի փոքրագույնը։ Ասում եմ, որ BC-ը կամ մաս է, կամ մասեր են A թվի։ Քանի որ A և BC թվերը կամ պարզ են միմյանց նկատմամբ, կամ ոչ։ Նախ թող A և BC պարզ լինեն միմյանց նկատմամբ։ Այդ դեպքում, բաժանելով BC-ը նրա միավորներից կազմված բաղկացուցիչ մասերի, BC-ի յուրաքանչյուր միավոր կլինի A-ի ինչ-որ մասը։ Հետևաբար, BC-ը A-ի մասերից է։
Այսպիսով, թող A և BC պարզ չլինեն միմյանց նկատմամբ։ Ուրեմն BC-ը կամ չափում է A թիվը, կամ չի չափում։ Եթե BC-ը չափում է A-ը, ապա BC-ը A-ի մաս է։ Իսկ եթե ոչ, թող A և BC ամենամեծ ընդհանուր չափը, D-ը, վերցվի [Բան. 7.2], և թող BC-ը բաժանվի BE, EF, և FC մասերի, որոնք հավասար են D-ին։ Եվ քանի որ D-ը չափում է A-ը, D-ը A-ի մաս է։ Եվ D-ը հավասար է BE, EF և FC մասերին։ Հետևաբար, BE, EF, FC ամեն մեկը A-ի մաս է։ Ուրեմն BC-ը A-ի մասերից է։ Այսպիսով, ցանկացած թիվ կամ մաս է, կամ մասեր են յուրաքանչյուր (ուրիշ) թվի, ավելի փոքրն ավելի մեծի։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 5
Եթե մի թիվ մաս է մեկ թվի, և մի այլ (թիվ) նույն մասը չէ մեկ ուրիշի, ապա (կատարյալ) առաջատար թվերի գումարը նույնպես կլինի նույն մասը հաջորդ թվերի գումարի, ինչ-որ մի թիվ մեկ այլ թվի։
Թող A թիվը լինի BC թվի մի մաս, իսկ D թիվը լինի նույն մասը EF թվի նկատմամբ, ինչ A-ն է BC-ի նկատմամբ: Ասում եմ, որ A և D թվերի գումարը նույնպես կլինի նույն մասը BC և EF գումարի նկատմամբ, ինչ A-ն է BC-ի նկատմամբ: Քանի որ ինչ մաս էլ A-ն ունի BC-ի մեջ, D-ն նույն մասն ունի EF-ի մեջ, ուրեմն քանի A-ին հավասար թվեր կան BC-ում, նույնքան D-ին հավասար թվեր կան նաև EF-ում: Թող BC-ը բաժանվի BG-ի և GC-ի, որոնք հավասար են A-ին, իսկ EF-ը բաժանվի EH-ի և HF-ի, որոնք հավասար են D-ին: Այսպիսով BG, GC բաժանումների քանակը հավասար կլինի EH, HF բաժանումների քանակին: Եվ քանի որ BG-ը հավասար է A-ին, իսկ EH-ը D-ին, ապա BG, EH զույգը նույնպես հավասար է A, D զույգին: Նույն պատճառներով GC, HF զույգը նույնպես հավասար է A, D զույգին: Այսպիսով, քանի անգամ BC-ը բաժանվում է A-ով, նույնքան անգամ BC, EF գումարը բաժանվում է A, D գումարով: Հետևաբար, ինչ մաս A-ն BC-ի է, A, D գումարն էլ նույն մասն է BC, EF գումարի նկատմամբ: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Առաջարկություն 6
Եթե մի թիվ մասեր է մեկ թվի, իսկ մեկ այլ թիվ նույն մասերն ունի մեկ այլ թվի նկատմամբ, ապա առաջին երկուսի գումարն էլ նույն մասերը կլինի երկրորդ զույգի գումարի նկատմամբ, ինչպիսին առաջին թիվը երկրորդի նկատմամբ է:
Թող AB թիվը մասեր լինի C թվի, իսկ DE թիվը նույն մասերը լինի F թվի նկատմամբ, ինչ մասեր AB-ն ունի C-ի մեջ։ Ասում եմ, որ AB և DE գումարը նույնպես նույն մասերն է կունենա C և F գումարի նկատմամբ, ինչ մասեր AB-ն ունի C-ի նկատմամբ։ Քանի որ ինչ մասեր էլ AB-ն ունի C-ի մեջ, DE-ն նույն մասերը կունենա F-ի մեջ, ուրեմն քանի մասով AB-ն բաժանում է C-ն, նույնքան մասով DE-ն բաժանում է F-ը։ Թող AB թիվը բաժանվի AG և GB մասերի, որոնք C-ի մասեր են, իսկ DE թիվը բաժանվի DH և HE մասերի, որոնք F-ի մասեր են։ Այդպես AG, GB բաժանումների քանակը հավասար կլինի DH, HE բաժանումների քանակին։ Եվ քանի որ ինչ մաս AG-ը C-ի է, DH-ն նույն մասն է F-ի, ուրեմն ինչ մաս AG-ը C-ի է, AG և DH գումարը նույնպես նույն մասն է C և F գումարի նկատմամբ [Բան. 7.5]։ Նույն կերպ, ինչ մաս GB-ը C-ի է, GB և HE գումարը նույնպես նույն մասն է C և F գումարի նկատմամբ։ Ուստի, ինչ մասեր AB-ն ունի C-ի նկատմամբ, AB և DE գումարը նույնպես նույն մասերն է ունենալու C և F գումարի նկատմամբ։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Ժամանակակից նշաններով: Այս առաջարկությունը ժամանակակից գրառմամբ ասում է, որ եթե a = (m/n)*c և d = (m/n)f, ապա (a+d) = (m/n)(c+f), որտեղ բոլոր նշանները թվեր են։
Առաջարկություն 7
Եթե մի թիվ այն նույն մասը լինի ինչ-որ թվի, ինչ (մասը) հանված AE-ն (է) հանված մասի CF-ից, ապա մնացորդը նույնպես կլինի նույն մասը մնացորդի, ինչ ամբողջ AB-ն է ամբողջ CD-ի նկատմամբ:
Թող AB թիվը լինի այն մասը CD թվի, ինչ AE հանված մասը CF-ի նկատմամբ է: Ասում եմ, որ EB մնացորդը նույնպես կլինի նույն բաժինը FD մնացորդի նկատմամբ, ինչ AB-ն է CD-ի նկատմամբ:
Քանի որ (ինչ մաս AE-ն է CF-ի), թող EB-ն նույնպես լինի նույն մասը CG-ի: Եվ քանի որ (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասը կլինի CG-ի, ապա (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես նույն մասը կլինի GF-ի [Բան. 7.5]: Եվ (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես ընդունված է լինել նույն մասը CD-ի: Այսպիսով, (ինչ մաս AB-ն է GF-ի), (AB-ն) նույնպես նույն մասն է CD-ի: Ուրեմն GF-ը հավասար է CD-ին: Թող CF-ը հանվի երկուսից էլ: Ուստի GC մնացորդը հավասար է FD մնացորդին: Եվ քանի որ (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասը կլինի GC-ի, իսկ GC-ն հավասար է FD-ին, ապա (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասն է FD-ի: Բայց (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես նույն մասն է CD-ի: Ուրեմն EB մնացորդը նույն մասն է FD մնացորդի, ինչ AB-ն է CD-ի: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ):
Նշում : Ժամանակակից նշանումներով, այս առաջարկությունը նշանակում է, որ եթե a = (m/n)*b և c = (m/n)d, ապա (a+c) = (m/n)(b+d), որտեղ բոլոր նշանները ներկայացնում են թվեր։
== Առաջարկություն 8 ==
Եթե մի թիվ այն նույն մասերն է մեկ թվի նկատմամբ, ինչ (հանված) AE մասը է (հանված) CF մասի նկատմամբ, ապա մնացորդը նույնպես կլինի նույն մասերի հարաբերությամբ մնացորդի նկատմամբ, ինչպիսին ամբողջը է ամբողջի նկատմամբ:
Թող AB թիվը լինի այն նույն մասերն CD թվի նկատմամբ, ինչ AE հանված մասը CF-ի նկատմամբ է: Ասում եմ, որ EB մնացորդը նույնպես կլինի նույն մասերը FD մնացորդի նկատմամբ, ինչ AB-ն է CD-ի նկատմամբ: Թող GH-ը դրվի հավասար AB-ին: Ուստի ինչ մասեր GH-ը ունի CD-ի նկատմամբ, AE-ն նույնպես նույն մասերն ունի CF-ի նկատմամբ: Թող GH-ը բաժանվի CD-ի մասերի՝ GK և KH, իսկ AE-ը՝ CF-ի մասերի՝ AL և LE: Այսպիսով, GK և KH բաժանումների քանակը հավասար կլինի AL և LE բաժանումների քանակին: Եվ քանի որ ինչ մաս GK-ը CD-ի նկատմամբ է, նույն մաս AL-ը CF-ի նկատմամբ է, և քանի որ CD-ն մեծ է CF-ից, GK-ն նույնպես մեծ է AL-ից: Թող GM-ը վերցվի հավասար AL-ին: Այսպիսով, ինչ մաս GK-ը CD-ի նկատմամբ է, GM-ը նույն մասն է CF-ի նկատմամբ: Ուստի MK մնացորդը նույնպես նույն մասն է FD մնացորդի նկատմամբ, ինչ GK ամբողջը CD ամբողջի նկատմամբ է [Բան. 7.5]: Նույն կերպ, քանի որ ինչ մաս KH-ը CD-ի նկատմամբ է, EL-ը նույն մասն է CF-ի նկատմամբ, և CD-ն մեծ է CF-ից, HK-ն ավելի մեծ է EL-ից: Թող KN-ը հավասարեցվի EL-ին: Այսպիսով, ինչ մաս KH-ը CD-ի նկատմամբ է, KN-ը նույն մասն է CF-ի նկատմամբ: Ուստի NH մնացորդը նույնպես նույն մասն է FD մնացորդի նկատմամբ, ինչ KH ամբողջը CD ամբողջի նկատմամբ է [Բան. 7.5]: Եվ MK մնացորդը նույնպես ցույց տրվեց, որ նույն մասն է FD մնացորդի նկատմամբ, ինչ GK ամբողջը CD ամբողջի նկատմամբ է: Ուստի MK և NH գումարը նույն մասերն են DF-ի նկատմամբ, ինչ HG ամբողջը CD ամբողջի նկատմամբ է: Եվ MK, NH գումարը հավասար է EB-ին, իսկ HG-ը՝ BA-ին: Ուստի EB մնացորդը նույնպես նույն մասերն է FD մնացորդի նկատմամբ, ինչ AB ամբողջը CD ամբողջի նկատմամբ է: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ): Նշում : Ժամանակակից նշանումներով, այս առաջարկությունը նշանակում է, որ եթե a = (m/n)*b և c = (m/n)d, ապա (a+c) = (m/n)(b+d), որտեղ բոլոր նշանները ներկայացնում են թվեր։
Առաջարկություն 9
Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասը (կամ նույն մասերն) է մեկ այլ թվի, ապա, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ առաջին (թիվը) լինի երրորդի նկատմամբ, երկրորդ (թիվը) նույնպես կլինի նույն մասը կամ մասերը մյուսի նկատմամբ կամ նույն մասերը, չորրորդ.
Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասը (կամ նույն մասերն) է մեկ այլ թվի, ապա, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ առաջին (թիվը) լինի երրորդի նկատմամբ, երկրորդ (թիվը) նույնպես կլինի նույն մասը կամ մասերը մյուսի նկատմամբ: Թող A թիվը լինի BC թվի մի մաս, և մեկ այլ (թիվ) D լինի նույն մասը մեկ այլ EF թվի, ինչ A-ն է BC-ի: Ասում եմ, որ նաև, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ A-ն ունենա D-ի նկատմամբ, BC-ն նույնպես կունենա նույն մասը, կամ նույն մասերը EF-ի նկատմամբ: Քանի որ ինչ մաս A-ն ունի BC-ի նկատմամբ, D-ն նույն մասն ունի EF-ի նկատմամբ, ապա որքան թվեր կան BC-ի մեջ, որոնք հավասար են A-ին, նույնքան թվեր կլինեն EF-ի մեջ, որոնք հավասար են D-ին: Թող BC-ը բաժանված լինի BG և GC մասերի, հավասար A-ին, իսկ EF-ը բաժանված լինի EH և HF մասերի, հավասար D-ին: Այսպիսով, BG և GC բաժանումների քանակը հավասար կլինի EH և HF բաժանումների քանակին: Եվ քանի որ BG և GC թվերը հավասար են միմյանց, իսկ EH և HF թվերը նույնպես հավասար են միմյանց, և BG, GC բաժանումների քանակը հավասար է EH, HF բաժանումների քանակին, ապա ինչ մասը, կամ մասերն էլ որ BG-ն ունենա EH-ի նկատմամբ, GC-ն նույնպես կունենա նույն մասը, կամ նույն մասերը HF-ի նկատմամբ: Եվ այդպիսով, ինչ մասը, կամ մասերն էլ BG-ն ունենա EH-ի նկատմամբ, BC-ի ամբողջությունն էլ նույն մասը կամ մասերը կունենա EF-ի ամբողջության նկատմամբ [Բան. 7.5, 7.6]: Եվ քանի որ BG-ը հավասար է A-ին, իսկ EH-ը հավասար է D-ին, ուրեմն ինչ մասը, կամ մասերն էլ A-ն ունենա D-ի նկատմամբ, BC-ն նույնպես կունենա նույն մասը կամ մասերը EF-ի նկատմամբ: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ):
- (Ժամանակակից նշանմամբ, եթե a = (1/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)d, որտեղ բոլոր նշանները ներկայացնում են թվեր):
Առաջարկություն 10†
Եթե մի թիվ մասեր է ինչ-որ թվի, և մեկ այլ (թիվ) նույն մասերն է մեկ այլ թվի, ապա նաև, փոխարինաբար, թե որ մասերը կամ մասը առաջին թիվը ունենա երրորդի նկատմամբ, երկրորդ թիվը նույնպես կունենա նույն մասերը կամ նույն մասը չորրորդի նկատմամբ: Թող AB թիվը լինի C թվի մասերը, իսկ DE թիվը լինի F թվի նույն մասերը: Ասում եմ, որ նաև, փոխարինաբար, թե որ մասերը, կամ որ մասը AB-ն ունի C-ի նկատմամբ, DE-ն նույնպես կունենա նույն մասերը կամ նույն մասը F-ի նկատմամբ:
Քանի որ ինչ մասեր AB-ն ունի C-ի նկատմամբ, DE-ն նույնպես նույն մասերն ունի F-ի նկատմամբ, ապա որքան մասեր C-ի մեջ կան AB-ի չափ, նույնքան մասեր կլինեն F-ի մեջ DE-ի չափ: Թող AB-ը բաժանվի C-ի մասերի՝ AG և GB, իսկ DE-ը բաժանվի F-ի մասերի՝ DH և HE: Այսպիսով, AG և GB բաժանումների քանակը հավասար կլինի DH և HE բաժանումների քանակին: Եվ քանի որ ինչ մասը, կամ մասեր AG-ն ունի C-ի նկատմամբ, DH-ն նույնպես ունի նույն մասը կամ մասերը F-ի նկատմամբ, նաև փոխարինաբար, ինչ մասը կամ մասերը AG-ն ունի DH-ի նկատմամբ, C-ն նույնպես նույն մասը կամ մասերը կունենա F-ի նկատմամբ [Բան. 7.9]: Նույն պատճառով, ինչ մասը կամ մասերը GB-ն ունի HE-ի նկատմամբ, C-ն նույնպես նույն մասը կամ մասերը կունենա F-ի նկատմամբ [Բան. 7.9]: Եվ ինչ մասը կամ մասերը AG-ն ունի DH-ի նկատմամբ, GB-ն նույն մասը կամ մասերը կունենա HE-ի նկատմամբ [Բան. 7.5, 7.6]: Բայց ինչ մասը կամ մասերը AG-ն ունի DH-ի նկատմամբ, նաև ցույց տրվեց, որ C-ն նույն մասը կամ մասերը ունի F-ի նկատմամբ: Ուստի, ինչ մասեր կամ ինչ մասը AB-ն ունի C-ի նկատմամբ, C-ն նույնպես նույն մասերը կամ samme մասը կունենա F-ի նկատմամբ: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ):
- (Ժամանակակից նշանմամբ, եթե a = (m/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)d, որտեղ բոլոր նշանները թվեր են):
Առաջարկություն 11
Եթե, ինչպես ամբողջ AB-ն ամբողջ CD-ի նկատմամբ է, նույն ձևով AE հանված մասը CF հանված մասի նկատմամբ է, ապա մնացորդը նույնպես կլինի մնացորդի նկատմամբ այն հարաբերությամբ, ինչ ամբողջը ամբողջի նկատմամբ է: Թող ամբողջ AB-ն լինի ամբողջ CD-ի նկատմամբ այնպիսին, ինչպիսին AE հանված մասը CF հանված մասի նկատմամբ է: Ասում եմ, որ EB մնացորդը FD մնացորդի նկատմամբ նույն հարաբերությունն ունի, ինչ ամբողջ AB-ն ամբողջ CD-ի նկատմամբ:
Քանի որ ինչպես AB-ը CD-ի նկատմամբ է, այնպես AE-ը CF-ի նկատմամբ է, ապա ինչ մասեր կամ մասը AB-ն ունի CD-ի նկատմամբ, AE-ն նույնպես նույն մասը կամ մասերն ունի CF-ի նկատմամբ [Սահմ. 7.20]: Ուստի EB մնացորդը նույնպես նույն մասը կամ մասերն ունի FD մնացորդի նկատմամբ, ինչ AB-ն ունի CD-ի նկատմամբ [Բան. 7.7, 7.8]: Այսպիսով, ինչպես EB-ն FD-ի նկատմամբ է, այնպես AB-ն CD-ի նկատմամբ է [Սահմ. 7.20]: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ):
Առաջարկություն 12†
Եթե կամայական քանակի թվեր համաչափ են, ապա ինչպես առաջավոր (թվերից) մեկը (է) հետագային, այնպես էլ (արդյունքում) բոլոր առաջավոր (թվերի) գումարը (կլինի) բոլոր հետագա (թվերի) գումարի նկատմամբ:
Թող կամայական քանակի թվեր A, B, C, D համաչափ լինեն (այնպես, որ ինչպես A-ն է B-ի նկատմամբ, այնպես C-ն D-ի նկատմամբ է): Ասում եմ, որ ինչպես A-ն է B-ի նկատմամբ, այնպես A և C (համատեղ) B և D (համատեղ) նկատմամբ են: Քանի որ ինչպես A-ն է B-ի նկատմամբ, այնպես C-ն D-ի նկատմամբ է, ապա ինչ մասը, կամ մասերն էլ A-ն ունենա B-ի նկատմամբ, C-ն նույնպես նույն մասը կամ մասերն ունի D-ի նկատմամբ [Սահմ. 7.20]: Այդպիսով, A և C գումարը նույնպես նույն մասը, կամ նույն մասերն է B և D գումարի նկատմամբ, ինչ A-ն B-ի նկատմամբ [Բան. 7.5, 7.6]: Ուստի, ինչպես A-ն B-ի նկատմամբ է, այնպես A, C (համատեղ) B, D (համատեղ) նկատմամբ են [Սահմ. 7.20]: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ):
Ժամանակակից մեկնություն (†) Ժամանակակից նշանմամբ, այս առաջարկությունն ասում է, որ եթե a : b :: c : d, ապա a : b :: a + c : b + d, որտեղ բոլոր նշանները ներկայացնում են թվեր։
