«Տարերք/Գիրք 12»–ի խմբագրումների տարբերություն
No edit summary |
No edit summary |
||
| (Միևնույն մասնակցի 3 միջանկյալ տարբերակներ թաքցված է) | |||
| Տող 20. | Տող 20. | ||
Դիտարկենք նույն բարձրության բուրգեր, որոնց հիմքերն են ABCDE և FGHKL բազմանկյունները, իսկ գագաթները՝ M և N կետերը (համապատասխանաբար): Ինչպես ABCDE հիմքը նման/հարաբերվում է է FGHKL-ին է, այնպես էլ ABCDEM բուրգը նման է FGHKLN բուրգին: |
Դիտարկենք նույն բարձրության բուրգեր, որոնց հիմքերն են ABCDE և FGHKL բազմանկյունները, իսկ գագաթները՝ M և N կետերը (համապատասխանաբար): Ինչպես ABCDE հիմքը նման/հարաբերվում է է FGHKL-ին է, այնպես էլ ABCDEM բուրգը նման է FGHKLN բուրգին: |
||
Թող AC, AD, FH և FK հատվածները միացված լինեն: Հետևաբար, քանի որ ABCM-ը և ACDM-ը երկու բուրգեր են, որոնք ունեն եռանկյունաձև հիմքեր և հավասար բարձրություն, դրանք միմյանց նկատմամբ համեմատելի են իրենց հիմքերի չափերով [Պնդ. 12.5]։ Այսպիսով, ինչպես ΑΒC հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCM-ն է հարաբերվում ACDM բուրգին: Եվ, կոմպոզիցիայի միջոցով, ինչպես ABCD հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCDM է հարաբերվում ACDM բուրգին [ |
Թող AC, AD, FH և FK հատվածները միացված լինեն: Հետևաբար, քանի որ ABCM-ը և ACDM-ը երկու բուրգեր են, որոնք ունեն եռանկյունաձև հիմքեր և հավասար բարձրություն, դրանք միմյանց նկատմամբ համեմատելի են իրենց հիմքերի չափերով [Պնդ. 12.5]։ Այսպիսով, ինչպես ΑΒC հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCM-ն է հարաբերվում ACDM բուրգին: Եվ, կոմպոզիցիայի միջոցով, ինչպես ABCD հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCDM է հարաբերվում ACDM բուրգին [Պնդ. 5.18]: Բայց, քանի որ ACD հիմքն է ահրաբերվում ADE հիմքին, այնպես էլ նաև ACDM բուրգն է հարաբերվում ADEM բուրգին [Պնդ. 12.5]։ Այսպիսով, հավասարության միջոցով, ABCD հիմքի հարաբերությաւոնը ADE հիմքին հավասար է ABCDM բուրգի հարաբորուտըանը ADEM բուրգին [Պնդ. 5.22]: Եվ, դարձյալ, կոմպոզիցիայի միջոցով, ինչպես ABCDE հիմքն է հարաբերվում ADE հիմքին, այնպես էլ ABCDEM բուրգն է հարաբերվում ADEM բուրգին [Պնդ. 5.18]: Այսպիսով, նման կերպով կարելի է նաև ցույց տալ, որ ինչպես FGHKL հիմքն է հարաբերվում FGH հիմքին, այնպես էլ FGHKLN բուրգն է հարաբերվում FGHN բուրգին: Եվ քանի որ ADEM-ը և FGHN-ը երկու բուրգեր են, որոնք ունեն եռանկյուն հիմքեր և հավասար բարձրություն, հետևաբար, ADE և FGH հիմքերի հարաբերությունը հավասար է ADEM և FGHN բուրգերի հարաբերությանը [Պնդ. 12.5]։ Բայց, ինչպես ADE հիմքն է հարաբերվում ABCDE հիմքին, այնպես էլ ADEM բուրգն է հարաբերվում ABCDEM բուրգին: Այսպիսով, հավասարության միջոցով, քանի որ ABCDE հիմքը հարաբերվում է FGH հիմքին, այնպես էլ ABCDEM բուրգը հարաբերվում է նաև FGHN բուրգին [Պնդ. 5.22]: Բայց, ավելին, ինչպես FGH հիմքն է հարաբերվում FGHKL հիմքինին, այնպես էլ FGHN բուրգն է նույնպես հարաբերվում FGHKLN բուրգին: Այսպիսով, հավասարության միջոցով, քանի որ ABCDE հիմքը հարաբերվում է FGHKL հիմքին, այնպես էլ ABCDEM բուրգը հարաբերվում է նաև FGHKLN բուրգին [Պնդ. 5.22]: Ինչը հենց այն է, ինչ պահանջվում էր ցույց տալ: |
||
== Պնդում 7 == |
== Պնդում 7 == |
||
| Տող 60. | Տող 60. | ||
Հավասար բուրգերի հիմքերը, որոնք նույնպես ունեն եռանկյունաձև հիմքեր, փոխադարձաբար համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյուն հիմքեր, որոնց հիմքերը փոխադարձաբար համեմատական են իրենց բարձրություններին, հավասար են։ |
Հավասար բուրգերի հիմքերը, որոնք նույնպես ունեն եռանկյունաձև հիմքեր, փոխադարձաբար համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյուն հիմքեր, որոնց հիմքերը փոխադարձաբար համեմատական են իրենց բարձրություններին, հավասար են։ |
||
[[Պատկեր:Պնդ9.png|200px|thumb|left|] |
[[Պատկեր:Պնդ9.png|200px|thumb|left|]] |
||
Որովհետև թող լինեն (երկու) հավասար բուրգեր, որոնք ունեն ABC և DEF եռանկյունաձև հիմքեր, իսկ գագաթներով G և H կետերը (համապատասխանաբար): Ես ասում եմ, որ ABCG և DEFH բուրգերի հիմքերը փոխադարձաբար համաչափ են իրենց բարձրություններին, և (այսպես) ինչպես ABC հիմքը հավասար է DEF-ին, այնպես էլ DEFH բուրգի բարձրությունը (է) ABCG բուրգի բարձրությանը: |
Որովհետև թող լինեն (երկու) հավասար բուրգեր, որոնք ունեն ABC և DEF եռանկյունաձև հիմքեր, իսկ գագաթներով G և H կետերը (համապատասխանաբար): Ես ասում եմ, որ ABCG և DEFH բուրգերի հիմքերը փոխադարձաբար համաչափ են իրենց բարձրություններին, և (այսպես) ինչպես ABC հիմքը հավասար է DEF-ին, այնպես էլ DEFH բուրգի բարձրությունը (է) ABCG բուրգի բարձրությանը: |
||
| Տող 71. | Տող 71. | ||
Ուստի, հավասար բուրգերի հիմքերը, որոնք նաև եռանկյունի հիմքեր ունեն, հակադարձ համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյունի հիմքեր և որոնց հիմքերը հակադարձ համեմատական են իրենց բարձրություններին, հավասար են: Այսինքն հենց այն բանը, որը պետք է ապացուցվեր: |
Ուստի, հավասար բուրգերի հիմքերը, որոնք նաև եռանկյունի հիմքեր ունեն, հակադարձ համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյունի հիմքեր և որոնց հիմքերը հակադարձ համեմատական են իրենց բարձրություններին, հավասար են: Այսինքն հենց այն բանը, որը պետք է ապացուցվեր: |
||
== Պնդում 10 == |
== Պնդում 10 == |
||
| Տող 78. | Տող 77. | ||
Թող լինի կոն նույն հիմքով ինչ գլանը, (մասնավորապես) շրջանագիծ ABCD-ն և հավասար բարձրություն: Ես ասում եմ, որ կոնը գլանի երրորդ մասն է, այսինքն՝ գլանը հավասար է երեք անգամ է կոնի ծավալին։ |
Թող լինի կոն նույն հիմքով ինչ գլանը, (մասնավորապես) շրջանագիծ ABCD-ն և հավասար բարձրություն: Ես ասում եմ, որ կոնը գլանի երրորդ մասն է, այսինքն՝ գլանը հավասար է երեք անգամ է կոնի ծավալին։ |
||
[[Պատկեր:Պնդ10.png|200px|thumb|left|]] |
|||
Քանի որ եթե գլանիկը կոնից երեք անգամ մեծ չլինի, ապա գլանիկը կլինի կամ երեք անգամից ավել մեծ, կամ երեք անգամից պակաս (կոնից): Թող նախ այն լինի երեք անգամից ավել մեծ (կոնից): Եվ թող ABCD քառակուսին ներգծված լինի ABCD շրջանի մեջ [Պնդ. 4.6]: Ուրեմն, ABCD քառակուսին ավելի քան կեսն է ABCD շրջանի [Պնդ. 12.2]: Եվ թող գլանիկի բարձրությանը հավասար բարձությամբ պրիզմա կառուցված լինի ABCD քառակուսու վրա: Ուրեմն, կառուցված պրիզման գլանիկից ավելի քան կեսն է, քանի որ եթե մենք նաև արտագծենք քառակուսի ABCD շրջանի շուրջ [Պնդ. 4.7], ապա ABCD շրջանի ներգծված քառակուսին կեսն է արտագծված քառակուսու: Եվ դրանց վրա կառուցված մարմինները զուգահեռանիստ պրիզմաներ են՝ հավասար բարձրություններով: Իսկ զուգահեռանիստ մարմինները, որոնք ունեն նույն բարձրությունը, միմյանց հետ հարաբերակցում են իրենց հիմքերի նմանությամբ [Պնդ. 11.32]: Ուստի ABCD քառակուսու վրա կառուցված պրիզման կեսն է արտագծված քառակուսու վրա կառուցված պրիզմայի: Իսկ գլանիկը պակաս է արտագծված քառակուսու վրա կառուցված պրիզմայից: Ուստի ABCD քառակուսու վրա կառուցված պրիզման, որը գլանիկի բարձրության հետ նույնն է, գլանիկից ավելի քան կեսն է: |
|||
Թող AB, BC, CD և DA շրջագծերը կեսից կտրած լինեն E, F, G և H կետերում: Եվ թող AE, EB, BF, FC, CG, GD, DH և HA հատվածները միացված լինեն: Ուստի AEB, BFC, CGD և DHA եռանկյուններից յուրաքանչյուրն ավելի քան կեսն է իր շուրջ գտնվող ABCD շրջանի հատվածից, ինչպես արդեն ցույց է տրվել [Պնդ. 12.2]: Թող պրիզմաներ՝ գլանիկի բարձրությանը հավասար, կառուցված լինեն AEB, BFC, CGD և DHA եռանկյունների վրա: Իսկ կառուցված պրիզմաներից յուրաքանչյուրը գլանիկի իրենց շուրջ գտնվող հատվածի կեսից ավելին է, քանի որ եթե գծենք AB, BC, CD և DA ուղղահայացներին զուգահեռ գծեր՝ անցնող E, F, G և H կետերով և լրացնենք զուգահեռագծերը AB, BC, CD և DA վրա, ապա AEB, BFC, CGD և DHA եռանկյունների վրա կառուցված պրիզմաները յուրաքանչյուրը կեսն են կառուցված զուգահեռանիստների: Իսկ գլանիկի հատվածները պակաս են կառուցված զուգահեռանիստներից: Ուստի AEB, BFC, CGD և DHA եռանկյունների վրա կառուցված պրիզմաները նույնպես գլանիկի իրենց շուրջ հատվածների կեսից ավելին են: |
|||
Ուստի, եթե մնացած շրջագծերը կեսից կտրվեն, և հատվածները միացվեն, և յուրաքանչյուր եռանկյունի վրա գլանիկի բարձրության պրիզմաներ կառուցվեն, և սա շարունակաբար կրկնվի, ապա ի վերջո կմնան գլանիկի որոշ հատվածներ, որոնց գումարը պակաս է այն ավելցուկից, որով գլանիկը գերազանցում է կոնից երեք անգամին [Պնդ. 10.1]: Թող դրանք մնացած լինեն և կոչվեն AE, EB, BF, FC, CG, GD, DH և HA: Ուստի մնացած պրիզման, որի հիմքը բազմանկյուն AEBFCGDH է, և բարձրությունը գլանիկի բարձրությանը հավասար է, երեք անգամից ավելի մեծ է կոնից: Բայց պրիզման, որի հիմքը բազմանկյուն AEBFCGDH է, և բարձրությունը գլանիկի բարձրության հավասար է, երեք անգամ մեծ է այն բուրգից, որի հիմքը բազմանկյուն AEBFCGDH է, իսկ գագաթը նույնն է, ինչ կոնինը [Պնդ. 12.7 հ.]: Ուստի բուրգը, որի հիմքը բազմանկյուն AEBFCGDH է, իսկ գագաթը նույնն է, ինչ կոնինը, ավելի մեծ է, քան հիմքը ABCD շրջան ունեցող կոնը: Բայց նաև ավելի փոքր է, քանի որ ներառված է նրա մեջ: Սա անհնար է: Ուստի գլանիկը չի գերազանցում կոնին երեք անգամ: |
|||
Այսպիսով, գլանն էլ չէ պակաս երեք անգամ կոնիից։ |
|||
Եվ այսպես, եթե հնարավոր է, թող գլանն ավելի քիչ լինի, քան երեք անգամ կոնիից։ Ուրեմն՝ հակադարձ, կոնն ավելի մեծ կլինի գլանի երրորդ մասից։ Թող ABCD քառակուսին ներգծված լինի ABCD շրջանին [Պնդ. 4.6]։ Այսպիսով, ABCD քառակուսին ավելի մեծ է ABCD շրջանի կեսից։ Թող կոնին նույն գագաթ ունեցող բուրգը կառուցված լինի ABCD քառակուսու վրա։ Այսպիսով, կառուցված բուրգն ավելի մեծ է կոնի կեսից, որովհետև նախորդիվ ցույց տվեցինք, որ եթե շրջանին արտագծենք քառակուսի [Պնդ. 4.7], ապա ABCD քառակուսին կլինի արտագծված քառակուսու կեսը [Պնդ. 12.2]։ Եվ եթե քառակուսիների վրա կառուցենք զուգահեռանիստներ, որոնք նաև կոչվում են պրիզմաներ, նույն բարձրությամբ, ինչ կոնը, ապա ABCD քառակուսու վրա կառուցված պրիզման կլինի արտագծված քառակուսու վրա կառուցված պրիզմայի կեսը։ Որովհետև դրանք համեմատական են իրենց հիմքերին [Պնդ. 11.32]։ Հետևաբար, նույնը ճիշտ է նաև երրորդ մասերի համար։ Այսպիսով, բուրգը, որի հիմքը ABCD քառակուսն է, կդառնա արտագծված քառակուսու վրա կառուցված բուրգի կեսը [Պնդ. 12.7 ճշտ.]։ Եվ արտագծված քառակուսու վրա կառուցված բուրգն ավելի մեծ է, քան կոնը, որովհետև այն ընդգրկում է այն։ Այսպիսով, բուրգը, որի հիմքը ABC'D քառակուսն է, և գագաթը նույնն է, ինչ կոնի գագաթը, ավելի մեծ է կոնի կեսից։ |
|||
Թող AB, BC, CD և DA շրջանագծերը կիսով չափ բաժանվեն EF, F, G և H կետերով։ Եվ թող միացված լինեն AEF, EB, BF, FC, CG, GD, DH և HA։ Եվ այսպիսով, յուրաքանչյուր եռանկյունի՝ AEB, BFC, CGD և DHA, ավելի մեծ է իրենց համապատասխան շրջանի հատվածների կեսից [Պնդ. 12.2]։ Եվ թող կոնի գագաթին համապատասխան բուրգեր կառուցված լինեն յուրաքանչյուր եռանկյունու վրա։ Այսպիսով, նույն ձևով, յուրաքանչյուր կառուցված բուրգ ավելի մեծ է համապատասխան կոնի հատվածի կեսից։ Հետևաբար, եթե մնացած շրջագծերը կրկին բաժանվեն կիսով չափ, և միացվեն ուղիղ գծերով, և կոնի գագաթին համապատասխան բուրգեր կառուցվեն յուրաքանչյուր եռանկյունու վրա, և սա արվի շարունակաբար, ապա մենք (վերջապես) կթողնենք կոնի որոշ հատվածներ, որոնց գումարը կպակասի գլանի երրորդ մասից գերազանցող չափից [Պնդ. 10.1]։ Թող դրանք թողնված լինեն, և թող լինեն հատվածներ՝ AE, EB, BF, FC, CG, GD, DH և HA-ի վրա։ Այսպիսով, մնացած բուրգը, որի հիմքը AEBFCGDH բազմանկյունն է, և գագաթը նույնն է, ինչ կոնի գագաթը, ավելի մեծ է գլանի երրորդ մասից։ Բայց բուրգը, որի հիմքը AEBFCGDH բազմանկյունն է, և գագաթը նույնն է, ինչ կոնի գագաթը, գլանի երրորդ մասն է, որի հիմքը նույն բազմանկյունն է և բարձրությունը նույնն է, ինչ գլանի բարձրությունը [Պնդ. 12.7 ճշտ.]։ |
|||
Այսպիսով, AEBFCGDH բազմանկյունի հիմքով և գլանի նույն բարձրությամբ պրիզման ավելի մեծ է, քան ABCD շրջանի հիմքով գլանը։ Բայց (այն) նաև փոքր է, որովհետև ընդգրկված է գլանի կողմից։ Սա անհնար է։ Այսպիսով, գլանն էլ չի կարող լինել պակաս երեք անգամ կոնիից։ Եվ արդեն ցույց է տրվել, որ այն չի կարող լինել ավելի մեծ, քան երեք անգամ կոնը։ Այսպիսով, գլանը (է) երեք անգամ կոնը։ Հետևաբար, կոնը գլանի երրորդ մասն է։ |
|||
Այսպիսով, յուրաքանչյուր կոն գլանի երրորդ մասն է, որն ունի նույն հիմքը, ինչ այն և հավասար բարձրություն: Սա հենց այն, ինչ պահանջվում էր ցույց տալ: |
|||
== Պնդում 11 == |
|||
Կոները և գլանները, որոնք ունեն նույն բարձրությունը, իրար հարաբերակցվում են իրենց հիմքերի հարաբերությամբ։ |
|||
Թող լինեն նույն բարձրությամբ կոներ և գլաններ, որոնց հիմքերը [են] ABCD և EFGH շրջանները, առանցքները՝ KL և MN, և հիմքերի տրամագծերը՝ AC և EG (համապատասխանաբար)։ Ասում եմ, որ ինչպես ABCD շրջանն է EFGH շրջանի հետ հարաբերակցվում, այնպես էլ AL կոնը՝ EN կոնին։ |
|||
[[Պատկեր:Պնդ11.png|200px|thumb|left|]] |
|||
Եթե հնարավոր է, թող ABCD շրջանը EFGH շրջանի հետ հարաբերակցվում է այնպես, ինչպես AL կոնը՝ որոշ մարմնի, որը կամ ավելի փոքր է, կամ ավելի մեծ, քան EN կոնը։ Նախ թող այդ հարաբերակցությունը լինի ավելի փոքր մարմնի, Օ-ի հետ։ Եվ թող X մարմինը հավասար լինի այն մեծությանը, որով Օ մարմինը պակաս է EN կոնից։ Այսպիսով, EN կոնը հավասար է Օ և X մարմինների գումարին։ Թող EFGH շրջանի մեջ գրառված լինի EF'GH քառակուսին [Պնդ. 4.6]։ Այսպիսով, քառակուսին ավելի մեծ է, քան շրջանի կեսը [Պնդ. 12.2]։ Թող նույն բարձրությամբ կոնից, որը հիմնված է EF'GH քառակուսու վրա, կազմված լինի բուրգ։ Այսպիսով, կազմված բուրգը ավելի մեծ է կոնից, քանի որ, եթե շրջանի շուրջ արտագծենք քառակուսի [Պնդ. 4.7], և նրա վրա նույն բարձրությամբ բուրգ կազմենք, ապա գրառված բուրգը կլինի արտագծված բուրգի կեսը։ Քանի որ դրանք իրար հետ հարաբերակցվում են իրենց հիմքերի նմանությամբ [Պնդ. 12.6], իսկ կոնը պակաս է արտագծված բուրգից։ |
|||
Թող EF, FG, GH և HE աղեղները բաժանված լինեն երկու մասի P, Q, R և S կետերում։ Եվ թող միացված լինեն HP, PE, EQ, QF, FR, RG, GS և SH։ Այսպիսով, HPE, EQF, FRG և GSH եռանկյուններից յուրաքանչյուրը մեծ է իրենց համապատասխան շրջանային հատվածների կեսից [Պնդ. 12.2]։ Թող նույն բարձրությամբ կոնից կազմված լինեն բուրգեր՝ հիմնված յուրաքանչյուր եռանկյան վրա։ Եվ այսպիսով, կազմված բուրգերից յուրաքանչյուրը մեծ է համապատասխան շրջանային հատվածի կեսից [Պնդ. 12.10]։ |
|||
Այսպիսով, եթե մնացած աղեղները կրկին բաժանվեն կեսերի, ուղիղ գծեր միացվեն, և բուրգեր կազմվեն, ապա վերջապես կմնան կոնից հատվածներ, որոնց գումարը պակաս է X մարմնի ավելցուկից [Պնդ. 10.1]։ Թող դրանք մնան՝ հիմնված HPE, EQF, FRG և GSH եռանկյունների վրա։ Այսպիսով, մնացած բուրգը, որի հիմքը HPEQFRGS բազմանկյունն է, իսկ բարձրությունը՝ կոնին հավասար, ավելի մեծ է Օ մարմնից [Պնդ. 6.18]։ |
|||
Հետևաբար, որպես հակասություն, պարզվեց, որ AL կոնը չի կարող հարաբերակցվել Օ մարմնի հետ։ Այսպիսով, հաստատվեց, որ կոները և գլանները, որոնք ունեն նույն բարձրությունը, իրար հետ հարաբերակցվում են իրենց հիմքերի հարաբերությամբ։ |
|||
Ուստի, ես ասում եմ, որ ոչ ոք չի կարող ասել, թե շրջան ABCD-ը շրջան EFGH-ին համեմատած, ինչպես կոն AL-ը համեմատած որևէ մարմնի, որը ավելի մեծ է քան կոնե EN-ը: |
|||
Որպեսզի, եթե հնարավոր է, թող այն (նման հարաբերությամբ) լինի (ինչ-որ) մեծ (մարմին), O: Այսպիսով, հակառակաբար, ինչպես ABCD շրջանագիծն է EFGH շրջանագծի նկատմամբ, այնպես էլ մարմին O-ն է կոն AL-ի նկատմամբ [Պնդ. 5.7 շտկում]: Բայց, ինչպես մարմին O-ն է կոն AL-ի նկատմամբ, այնպես էլ կոն EN-ն է (մի տեսակ) մարմնի նկատմամբ, որը փոքր է կոն AL-ից [Պնդ. 12.2 մոտ.]: Եվ այսպես, ինչպես EFGH շրջանագիծն է ABCD շրջանագծի նկատմամբ, այնպես էլ կոն EN-ն է (մի տեսակ) մարմնի նկատմամբ, որը փոքր է կոն AL-ից: Միևնույնն է, դա անհնար էր: Այսպիսով, ABCD շրջանագիծը չի համապատասխանում EFGH շրջանագծին, ինչպես կոն AL-ն է (մի տեսակ) մարմնի նկատմամբ, որը մեծ է կոն EN-ից: Եվ, ինչպես ցույց տրված էր, ոչ էլ (նման հարաբերությամբ) այն համապատասխանում է (ինչ-որ) փոքր մարմնի: Այսպիսով, ինչպես ABCD շրջանագիծն է EFGH շրջանագծի նկատմամբ, այնպես էլ կոն AL-ն է կոն EN-ի նկատմամբ: |
|||
Բայց, ինչպես կոնը (է) կոնին, այնպես էլ գլանը (է) գլանին: Մանրամասն, ամեն մեկը երեք անգամ է յուրաքանչյուրին [Պնդ. 12.10]: Այսպիսով, ABCD շրջանագիծը նույնպես համապատասխան է EFGH շրջանագծին, ինչպես (գլանների հարաբերությունը) նրանց վրա (որոնք ունեն) նույն բարձրությունը: |
|||
Այսպիսով, նույն բարձրություն ունեցող կոները և գլանները իրար նկատմամբ են ինչպես իրենց բազաները: Իրականում դա հենց այն բանն է, որը պետք է ապացուցվեր: |
|||
== Պնդում 12 == |
|||
Նման կոները և գլանները միմյանց հարաբերակցված են իրենց հիմքերի տրամագծերի խորացված հարաբերակցությամբ: |
|||
Թող լինեն համապատասխան կոներ և գլաններ, որոնց հիմքերը լինեն ABCD և EFGH շրջանները, հիմքերի տրամագծերը լինեն BD և FH, իսկ կոների և գլանների առանցքները լինեն KL և MN (համապատասխանաբար): Իմ հայտարարությունն է, որ այն կոնը, որի հիմքն է ABCD շրջանը, իսկ գագաթը՝ L կետը, կապված է այն կոնի հետ, որի հիմքն է EFGH շրջանը, իսկ գագաթը՝ N կետը, նրանց միջև կա BD-ի և FH-ի խորացված հարաբերակցությունը: |
|||
[[Պատկեր:Պնդ12.png|200px|thumb|left|]] |
|||
Եթե ABCDL կոնը չունի այնպիսի խորացված հարաբերակցություն, որը BD-ն ունի FH-ի հետ EFGHN կոնի նկատմամբ, ապա ABCDL կոնը կունենա նույն խորացված հարաբերակցությունը մի մարմնի հետ, որը կամ պակաս կլինի, կամ ավելին կլինի EFGHN կոնից: Նախ, թող այն ունենա (այդպիսի հարաբերակցություն) (ինչ-որ) պակաս (մարմնի), O-ի հետ: Եվ թող EFGH քառակուսին ներթղվել լինի EFGH շրջանի մեջ [Պնդ. 4.6]: Այսպես, EFGH քառակուսին մեծ է EFGH շրջանի կեսից [Պնդ. 12.2]: Եվ թող պիրամիդը, որը նույն խ顶ակն ունի, ինչ կոնը, տեղադրվի EFGH քառակուսի վրա: Այսպիսով, տեղադրված պիրամիդը մեծ է կոնի կեսից [Պնդ. 12.10]: Այդպես, թող EF’, FG, GH, և HE շրջանաձևությունները կտրեն կեսում P, Q, R, և S կետերում (համապատասխանաբար): Եվ թող EP, PF, FQ, QG, GR, RH, HS, և SE միանան: Եվ այսպես, յուրաքանչյուր EPF, FQG, GRH, և HSE եռանկյունիները մեծ են EFGH շրջանի հատվածի կեսից, որը նրանց շուրջն է [Պնդ. 12.2]: Եվ թող պիրամիդը, որը նույն խ顶ակն ունի, ինչ կոնը, տեղադրվի յուրաքանչյուր EPF, FQG, GRH, և HSE եռանկյան վրա: Եվ այսպես, յուրաքանչյուր տեղադրված պիրամիդը մեծ է կոնի հատվածի կեսից, որը դրա շուրջն է [Պնդ. 12.10]: Այսպես, (եթե) մնացած շրջանակաները կտրեն կեսում, և ուղղահայաց գծեր միանան, և պիրամիդներ, որոնք նույն խ顶ակն ունեն, ինչ կոնը, տեղադրվեն յուրաքանչյուր եռանկյան վրա, և սա անընդհատ շարունակվի, ապա մենք, վերջապես, կթողնենք կոնի մի քանի հատվածներ, որոնց (հավաքածուն) պակաս կլինի այն ավելցուկից, որով EFGHN կոնը գերազանցում է O մարմինը [Պնդ. 10.1]: Թող նրանք մնան, և թող դրանք լինեն (հավաքածուն) EP, PF, FQ, QG, GR, RH, HS, և SE վրա գտնվող հատվածները: Եվ այսպես, մնացած պիրամիդը, որի հիմքը բազմաբազմյուն EPFQGRHS է, և խ顶ակը՝ NV կետը, մեծ է O մարմնից: Եվ թող բազմաբազմյուն AT BUCV DW, որը նման է և նմանապես դասավորված է EPFQGRHS բազմաբազմյանը, լինի ABCD շրջանի մեջ տեղադրված [Պնդ. 6.18]: Եվ թող պիրամիդը, որի նույն խ顶ակն ունի, ինչ կոնը, տեղադրվի ATBUCV DW բազմաբազմյակի վրա: Եվ թող LBT լինի այն եռանկյունիներից մեկը, որը պարունակում է պիրամիդը, որի հիմքը AT BUCV DW բազմաբազմյակը, և խ顶ակը՝ L կետը: Եվ թող NFP լինի այն եռանկյունիներից մեկը, որը պարունակում է պիրամիդը, որի հիմքը EPFQGRHS եռանկյունին է, և խ顶ակը՝ NV կետը: Եվ թող KT և MP միացած լինեն: Եվ քանի որ ABCDL կոնը նման է EFGHN կոնին, ապա ինչպես BD-ն է FH-ի հետ, այնպես էլ առանցք KL-ը՝ առանցք MN-ին [Դեֆ. 11.24]: Եվ ինչպես BD-ն է FH-ի հետ, այնպես էլ BK-ն է FM-ի հետ: Եվ այդպես, ինչպես BK-ն է FM-ի հետ, այնպես էլ KL-ը՝ MN-ի հետ: Եվ այլ կերպ ասած, ինչպես BK-ն է KL-ի հետ, այնպես էլ FM-ը՝ MN-ի հետ [Պնդ. 5.16]: Եվ նույնական անկյուններով BK L և FMN-ի շուրջ գտնվող կողմերը համահունչ են: Այսպիսով, եռանկյունը BK L նման է եռանկյան FMN-ի [Պնդ. 6.6]: Այնպես որ, քանի որ ինչպես BK-ն է KT-ի հետ, այնպես էլ FM-ն է MP-ի հետ, և նրանք գտնվում են հավասար անկյուններով BKT և FMP, քանի որ ինչ-որ մասը BKT անկյունից, որը K կենտրոնում գտնվող չորս ուղղանկյուններից է, FMP անկյունը նույնպես նույն մասն է չորս ուղղանկյուններից՝ M կենտրոնում: Ուստի, քանի որ հավասար անկյուններով կողմերը համահունչ են, եռանկյունը BAT նման է եռանկյան FMP-ին [Պնդ. 6.6]: Դարձյալ, քանի որ ցույց տրվեց, որ ինչպես BK-ն է KL-ի հետ, այնպես էլ FM-ն է MN-ի հետ, և BK-ն հավասար է KT-ին, իսկ FM-ն՝ PM-ին, ապա ինչպես TK-ն է KL-ի հետ, այնպես էլ PM-ն՝ MN-ի հետ: Եվ հավասար անկյուններով TKL և PMN — քանի որ դրանք երկուսն էլ ուղղանկյուններ են — կողմերը համահունչ են: Այսպիսով, եռանկյունը LKT նման է եռանկյունի NMP-ին [Պնդ. 6.6]: Եվ քանի որ, համաձայն եռանկյունների LK B և NMF նմանության, ինչպես LB-ն է BK-ի հետ, այնպես էլ NF-ն է FM-ի հետ, և համաձայն եռանկյունների BKT և FMP նմանության, ինչպես KB-ն է BT-ի հետ, այնպես էլ MF-ն է FP-ի հետ [Դեֆ. 6.1], ուստի, հավասարությամբ, ինչպես LB-ն է BT-ի հետ, այնպես էլ NF-ն է FP-ի հետ [Պնդ. 5.22]: Դարձյալ, քանի որ, համաձայն եռանկյունների LT K և NPM նմանության, ինչպես LT-ն է TK-ի հետ, այնպես էլ NP-ն է PM-ի հետ, և համաձայն եռանկյունների TK B և PMF նմանության, ինչպես KT-ն է TB-ի հետ, այնպես էլ MP-ն է PF-ի հետ, ուստի, հավասարությամբ, ինչպես LT-ն է TB-ի հետ, այնպես էլ NP-ն է PF-ի հետ [Պնդ. 5.22]: Եվ ցույց է տրված, որ ինչպես TB-ն է BL-ի հետ, այնպես էլ PF-ն է FN-ի հետ: Ուստի, հավասարության միջոցով, ինչպես TL-ն է LB-ի հետ, այնպես էլ PN-ն է NF-ի հետ [Պնդ. 5.22]: Այսպիսով, LTB և NPF եռանկյունների կողմերը համահունչ են: Այսպիսով, LTB և NPF եռանկյունները հավասարանկյուն են [Պնդ. 6.5]: Եվ, հետևաբար, (նրանք) նման են [Դեֆ. 6.1]: Եվ, այսպես, այն պիրամիդը, որի հիմքը BKT եռանկյունն է, և գագաթը L կետն է, նման է այն պիրամիդին, որի հիմքը FMP եռանկյունն է, և գագաթը N կետն է: Չնայած որ նրանք պարունակում են նույն թիվն էլ նման թռուցիկներից [Դեֆ. 11.9]: Եվ նման պիրամիդները, որոնք նաև եռանկյունային հիմքեր ունեն, գտնվում են համապատասխան կողմերի խորացված հարաբերակցությունում [Պնդ. 12.8]: Այսպիսով, պիրամիդ BKTL-ն ունի պիրամիդ F'M PN-ին այն խորացված հարաբերակցությունը, որը ունի BK-ն՝ FM-ի հետ: Իսկ նմանապես, միացնելով ուղիղ գծեր (A, W, D, V, C և U կետերից) (կենտրոն) K-ի և (FE, S, H, R, G և Q կետերից) (կենտրոն) M-ի, և կանգնեցնելով պիրամիդներ, որոնց նույն գագաթները ունեն կոները յուրաքանչյուր եռանկյունում (որոնք ձևավորվում են), մենք նույնպես կարող ենք ցույց տալ, որ յուրաքանչյուր պիրամիդը (ABCԴ հիմքով) հերթով կունենա այն խորացված հարաբերակցությունը, որը կապված է համապարփակ կողմերի BK-ի հետ՝ համապատասխան կողմերի F4—այսինքն՝ BD-ի հետ՝ FH-ի նկատմամբ: Եվ (երկու sets համար համապարփակ չափերի) ինչպես մեկը առաջնորդող (չափը) է հաջորդներից մեկին, այնպես էլ (առաջնորդող չափերի) ամբողջությունը համամասն է (հաջորդ չափերի) ամբողջությանը [Պնդ. 5.12]: Եվ, այսպես, ինչպես պիրամիդը BKTL-ն է պիրամիդին F.MPN-ին, այնպես էլ ամբողջ պիրամիդը, որի հիմքն է բազմանկյուն AT BUCV DW, և գագաթը L կետն է, համամասն է ամբողջ պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը NV կետն է: Եվ, հետեւաբար, այն պիրամիդը, որի հիմքն է բազմանկյուն AT BUCV DW, և գագաթը L կետն է, համամասն է այն պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է, այն խորացված հարաբերակցությանը, որը BD-ն ունի FH-ի հետ: Եվ նաև ենթադրվել է, որ կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, համամասն է մարմնին O այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ: Այսպիսով, ինչպես կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, համամասն է մարմնին O, այնպես էլ այն պիրամիդը, որի հիմքն է [բազմանկյուն] AT BUCV DW, և գագաթը L կետն է, համամասն է այն պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է: Այդպես, փոխարենը, ինչպես կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, համամասն է նրա մեջ գտնվող պիրամիդին, որի հիմքն է բազմանկյուն ATBUCV DW, և գագաթը L կետն է, այնպես էլ [մարմին] O-ն համամասն է պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է [Պնդ. 5.16]: Եվ հիշատակված կոնը մեծ է նրանից պիրամիդին: Այն շրջապատում է այն: Այսպիսով, մարմինը O-ն նույնպես մեծ է այն պիրամիդից, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է: Բայց, այն նաև փոքր է: Հենց այսը անհնար է: Այսպիսով, կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, չի համամասնվում որևէ մարմնի, որը փոքր է կոնից, որի հիմքը EFGH շրջան է, և գագաթը N կետն է, այն խորացված հարաբերակցությամբ, որը BD-ն ունի EH-ի հետ: Այսպիսով, նույն ձևով, մենք կարող ենք ցույց տալ, որ EFGHN կոնը նույնպես չի համամասնվում որևէ մարմնի, որը փոքր է ABCDL կոնից, այն խորացված հարաբերակցությամբ, որը FH-ն ունի BD-ի հետ: |
|||
Այսպիսով, ես ասում եմ, որ ABC'DL կոնը չի համամասնվում որևէ մարմնի, որը մեծ է EFGHN կոնից, այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ: |
|||
Իրովի, եթե հնարավոր է, թող այն ունենա (համար) ավելի մեծ (մարմնի) O: Այսպիսով, հակառակը, մարմինը O-ն համամասն է ABCDL կոնին այն խորացված հարաբերակցությամբ, որը FH-ն ունի BD-ի հետ [Պնդ. 5.7 շտ.]: Եվ ինչպես մարմինը O-ն (է) ABCDL կոնին, այնպես էլ EFGHN կոնը (է) որևէ մարմնի համամասն, որը փոքր է ABCDL կոնից [12.2 քառ.]։ Այսպիսով, EFGHN կոնը նույնպես համամասն է որևէ մարմնի, որը փոքր է ABCDL կոնից, այն խորացված հարաբերակցությամբ, որը F'H-ն ունի BD-ի հետ: Նույնը ցույց տվեց, որ անհնար է: Այսպիսով, ABCDL կոնը չի համամասնվում որևէ մարմնի, որը մեծ է EFGHN կոնից, այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ: Եվ ցույց տրվեց, որ այն նաև չի ունենում (այդպիսի հարաբերակցություն) որևէ ավելի փոքր մարմնի հետ: Այսպիսով, ABCDL կոնը համամասն է EFGHN կոնին այն խորացված հարաբերակցությամբ, որը BD-ն ունի FG-ի հետ: |
|||
Եվ ինչպես կոնը կոնին, այնպես էլ գլանը գլանին: Քանզի գլանը երեք անգամ է կոնից նույն հիմքով և նույն բարձրությամբ [Պնդ. 12.10]: Այսպիսով, գլանը նույնպես ունի գլանին այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ: |
|||
Այսպիսով, նման կոներն ու գլանները գտնվում են իրենց հիմքերի տրամագծերի խորացված հարաբերակցությունում: Եվ սա է այն, ինչը պետք էր ապացուցել: |
|||
== Պնդում 13 == |
|||
Եթե գլանը կտրվի մի հարթությամբ, որը զուգահեռ է գլանի հակառակ մակերեսներին, ապա ինչպես գլանն է հարաբերվում գլանին, այնպես էլ առանցքը՝ առանցքին: |
|||
[[Պատկեր:Պնդ13.png|200px|thumb|left|]] |
|||
Թող գլանը AD կտրվի GH հարթությամբ, որը զուգահեռ է գլանի հակառակ մակերեսներին՝ AB և CD: Եվ թող GH հարթությունը հանդիպի առանցքին K’ կետում: Ասում եմ, որ ինչպես գլանն է BG-ին, այնպես էլ առանցքը EK-ն է՝ առանցքին KF: |
|||
Եվ թող առանցքը EF շարունակվի յուրաքանչյուր ուղղությամբ դեպի L և M կետերը։ Եվ թող որևէ թիվ, որ ուղղության վրա EN և NL, հավասար լինի առանցք EK-ին, նշված լինի առանցք EL-ի վրա, և որևէ թիվ, որ ուղղության վրա FO և OM, հավասար լինի առանցք FK-ին, նշված լինի առանցք KM-ի վրա։ Եվ թող գլան PW-ն, որի հիմքերը լինեն շրջանակները PQ և VW, կազմավորվի առանցք LM-ի վրա։ Եվ թող հարթություններ, որոնք զուգահեռ են AB-ին, CD-ին և գլան PW-ի հիմքերին, անցնեն N և O կետերից, և թող դրանք կազմեն շրջանակներ RS և TU, համապատասխանաբար, կենտրոններում N և O։ Եվ քանի որ առանցքները LN, NE և EK հավասար են միմյանց, գլանները QR, RB և BG միմյանց հետ կապված են իրենց հիմքերի հարաբերակցությամբ [Պնդ. 12.11]։ Բայց հիմքերը հավասար են։ Այսպես, գլանները QR, RB և BG նույնպես հավասար են միմյանց։ Այնպես որ, քանի որ առանցքները LN, NE և EK հավասար են միմյանց, և գլանները QR, RB և BG նույնպես հավասար են միմյանց, և նրանց թիվը հավասար է միմյանց, ապա ինչպես շատ բազմապատիկներ, որքան առանցք KL-ն է առանցք EK-ի, այնքան շատ բազմապատիկներ է գլան QG-ն նաև գլան GB-ի։ Եվ այդպես, նույն (պատճառներով), ինչպես շատ բազմապատիկներ, որքան առանցք MK-ն է առանցք KF-ի, այնքան շատ բազմապատիկներ է գլան WG-ն նույնպես գլան GD-ի։ Եվ եթե առանցք KL-ն հավասար է առանցք KM-ին, ապա գլան QG-ն նույնպես հավասար կլինի գլան GW-ի, և եթե առանցքը մեծ է քան առանցքը, ապա գլանը նույնպես մեծ կլինի քան գլանը, և եթե (առանցքը) փոքր է, ապա (գլանը) նույնպես փոքր կլինի։ Ուստի, կան չորս չափեր՝ առանցքներ EK և KF, և գլաններ BG և GD, և հավասար բազմապատիկներ են վերցվել առանցք EK-ից և գլան BG-ից՝ (պատրաստված) առանցք LK և գլան QG՝ և առանցք KF-ից և գլան GD-ից՝ (պատրաստված) առանցք KM և գլան GW։ Եվ ցույց է տրվել, որ եթե առանցք KL-ն մեծ է քան առանցք KM-ը, ապա գլան QG-ն նույնպես մեծ է քան գլան GW-ն, և եթե (առանցքները) հավասար են, ապա (գլանները) հավասար են, և եթե (KL-ն) փոքր է, ապա (QG-ն) փոքր է։ Ավելին, ինչպես առանցք EK-ն է՝ առանցք KF-ի, այնպես էլ գլան BG-ն է՝ գլան GD-ի [Անշ. 5.5]։ Այսինքն, սա հենց այն, ինչը պետք էր ցույց տալ։ |
|||
== Պնդում 14 == |
|||
Կոները և գլանները, որոնք ունեն հավասար հիմքեր, միմյանց նկատմամբ են, ինչպես իրենց բարձրությունները։ |
|||
[[Պատկեր:Պնդ14.png|200px|thumb|left|]] |
|||
Թող EB և FD լինեն գլաններ հավասար հիմքերով՝ namely՝ շրջաններ AB և CD (համապատասխանաբար): Ես ասում եմ, որ ինչպես գլանը FB է գլանին F'D, այնպես էլ առանցքը GH է առանցքին KL: |
|||
Թող առանցքը KL ձգվի դեպի N կետը: Եվ թող LN-ը հավասար լինի առանցք GH-ի: Եվ թող գլան CM գծվի LN առանցքի շուրջ: Դրա համար, քանի որ գլանները EB և C'M ունեն նույն բարձրությունը, նրանք միմյանց համապատասխան են որպես իրենց հիմքեր [Պնդ. 12.11]: Եվ հիմքերը հավասար են միմյանց: Ապա, գլաններ EB և CM նույնպես հավասար են միմյանց: Եվ քանի որ գլանը F'M կտրվել է C'D հարթությամբ, որը զուգահեռ է նրա հակառակ հարթություններին, ապա ինչպես գլանը CM է գլանին FD, այնպես էլ առանցքը LN է առանցքին KL [Պնդ. 12.13]: Եվ գլանը C'M հավասար է գլանին EB, և առանցքը LN հավասար է առանցք GH-ին: Դրա համար, ինչպես գլանը EB է գլանին F'D, այնպես էլ առանցքը GH է առանցքին KL: Եվ ինչպես գլանը FB է գլանին F'D, այնպես էլ կոնը ABG է կոնին CDK [Պնդ. 12.10]: Ապա, նաև, ինչպես առանցքը GH է առանցքին KL, այնպես էլ կոնը ABG է կոնին CDK, և գլանը EB գլանին FD: Սա այն ամենն է, ինչը պահանջվում էր ապացուցել: |
|||
== Պնդում 15 == |
|||
Հավասար կոների և գլանների հիմքերը փոխադարձաբար համամասն են իրենց բարձրություններին: Եվ նրանք, ում կոները և գլանները հիմքերը փոխադարձաբար համամասն են իրենց բարձրություններին, հավասար են: |
|||
[[Պատկեր:Պնդ15.png|200px|thumb|left|]] |
|||
Թող լինեն հավասար կոներ և գլաններ, որոնց հիմքերը ABCD և EFGH շրջաններն են, և դրանց հիմքերի տրամագծերը AC և EG, իսկ առանցքները KL և MN են, որոնք նույնպես են կոների և գլանների բարձրությունները (հարգերով): Եվ թող գլանները AO և EP կառուցվեն: Ես ասում եմ, որ գլանների AO և EP հիմքերը փոխադարձաբար համամասն են նրանց բարձրություններին, և այնպես, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN՝ բարձրությանը KL: |
|||
Թող բարձրությունը LK կամ հավասար լինի բարձրությանը MN, կամ ոչ: Առաջին հերթին թող այն հավասար լինի: Եվ գլան AO-ն նույնպես հավասար է գլան EP-ին: Եվ այն կոներն ու գլանները, որոնք ունեն նույն բարձրությունը, միմյանց համեմատվում են իրենց հիմքերին ըստ [Պնդ. 12.11]: Այդպես, հիմք ABCD-ն նույնպես հավասար է հիմք EFGH-ին: Եվ հետևաբար, փոխադարձաբար, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN՝ բարձրությանը KL: Եվ հիմա թող բարձրությունը LK չհավասարվի MN-ին, սակայն թող WN-ն ավելի մեծ լինի: Եվ թող QN, որը հավասար է KL-ին, կտրի բարձրությունից MN: Եվ թող գլան EP-ն կտրի, Q կետից, TUS հարթությամբ (որը) զուգահեռ է EFGH և RP շրջանների հարթությունների հետ: Եվ թող գլան ES-ն կառուցվի, որի հիմքը EFGH շրջանն է, և բարձրությունը NQ: Եվ քանի որ գլան AO-ն հավասար է գլան EP-ին, ապա ինչպես գլան AO-ն է գլան ES-ին, այնպես էլ գլան EP-ն է գլան E'S-ին [Պնդ. 5.7]: Իսկ քանի որ ինչպես գլան AO-ն է գլան E'S-ին, այնպես էլ հիմքը ABCD-ն է հիմքին EFGH: Որովհետև գլան AO-ն և ES-ն ունեն նույն բարձրությունը [Պնդ. 12.11]: Եվ ինչպես գլան EP-ն է գլան E'S-ին, այնպես էլ բարձրությունը MN-ն է բարձրությանը QN: Որովհետև գլան EP-ն կտրել է հարթությամբ, որը զուգահեռ է իր հակառակ հարթություններին [Պնդ. 12.13]: Եվ այսպես, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN-ն է բարձրությանը QN [Պնդ. 5.11]: Եվ բարձրությունը QN-ն հավասար է բարձրությանը KL: Այսպիսով, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN-ն է բարձրությանը KL: Այսպիսով, գլան AO-ի և EP-ի հիմքերը փոխադարձաբար համեմատելի են նրանց բարձրություններին: |
|||
Եվ այսպես, թող գլան AO-ի և EP-ի հիմքերը փոխադարձաբար համեմատելի լինեն նրանց բարձրություններին, և (այսպիսով) թող հիմքը ABCD լինի հիմքի EFGH-ի նկատմամբ, ինչպես բարձրությունը MN-ն է բարձրությանը AL: Ասում եմ, որ գլան AO-ն հավասար է գլան EP-ին: |
|||
Քանի որ նույն կառուցվածքով, քանի որ ինչպես հիմքը ABCD է հիմքին EFGH-ի, այնպես էլ բարձրությունը MN-ը՝ բարձրությանը KL, և բարձրությունը KL-ը հավասար է բարձրությանը QN, ապա ինչպես հիմքը ABCD է հիմքին EFGH-ի, այնպես էլ բարձրությունը MN-ը կլինի բարձրությանը QN: Բայց ինչպես հիմքը ABCD է հիմքին EFGH-ի, այնպես էլ գլան AO-ն է գլան E'S-ին: Քանի որ դրանք նույն բարձրությունն ունեն [Պնդ. 12.11]: Եվ ինչպես բարձրությունը MN-ը՝ [բարձրություն] QN-ին, այնպես էլ գլան EP-ն է գլան E'S-ին [Պնդ. 12.13]: Այսպիսով, ինչպես գլան AO-ն է գլան E'S-ին, այնպես էլ գլան EP-ն է (գլան) E'S-ին [Պնդ. 5.11]: Այսպիսով, գլան AO-ն հավասար է գլան EP-ին [Պնդ. 5.9]: Նույն կերպ, (առարկան) նույնպես (կարող է) ցույց տրվել կոների համար: Դա է այն, ինչ պահանջվում էր ցույց տալ: |
|||
== Պնդում 16 == |
|||
Իրավիճակում, որտեղ երկու շրջաններ կան նույն կենտրոնի շուրջ, ավելի մեծ շրջանում ներբեռնել հավասարաչափ և զույգ կողմերով բազմակողմանիություն, որը չի շոշափում փոքր շրջանը: |
|||
[[Պատկեր:Պնդ16.png|200px|thumb|left|]] |
|||
Թող ABCD և EFGH լինեն տրված երկու շրջաններ, որոնք ունեն նույն K կենտրոնը։ Ուրեմն, անհրաժեշտ է ներբեռնել հավասարաչափ և զույգ կողմերով բազմակողմանիություն ավելի մեծ ABCD շրջանում, որը չի շոշափում EFGH շրջանը։ |
|||
Թող ուղղաձիգ BD ուղղությամբ անցնի ուղիղ գիծ BK Դ, K կենտրոնով։ Եվ թող GA գիծը տրվել լինի, որը դրված է BD ուղղությանը զուգահեռ՝ G կետով, և թող այն գիծը լինի C կետին ուղղված։ Ուրեմն, AC-ն շոշափում է EFGH շրջան։ Եվ, եթե կտրենք BAD շրջանի շրջագիծը կեսով, իսկ հետո կեսը՝ նորից կեսի, և շարունակենք այսպես, մենք, վերջապես, կթողնենք մի շրջագիծ, որը պակաս է AD-ից [Պնդ. 10.1]։ Թող այսպիսով մնա, և թող այն լինի LD։ Եվ թող LM գիծը լինի, որը L-ից ուղղահայաց է BD-ին, և թող այն անցնի NV կետով։ Եվ թող LD և DN համախառնվեն։ Ուրեմն, LD-ը հավասար է DN-ին [Պնդ. 3.3, 1.4]։ Եվ քանի որ LN-ը զուգահեռ է AC-ին [Պնդ. 1.28], և AC-ն շոշափում է EFGH շրջան, ապա LN-ն նույնպես չի շոշափում EFGH շրջանը։ Ուրեմն, առավել ևս, LD-ն և DN-ը չեն շոշափում EFGH շրջան։ Եվ եթե շարունակաբար տեղադրենք LD-ի երկարությամբ ուղիղ գծեր ABCD շրջանում [Պնդ. 4.1], ապա հավասարաչափ և զույգ կողմերով բազմակողմանիություն, որը չի շոշափում փոքր EFGH շրջանը, կտեղադրվի ABCD շրջանի մեջ։ (Այսինքն) այն բանն է, որ պահանջվում էր անել։ |
|||
== Պնդում 17 == |
|||
Ուրեմն լինելով երկու գնդեր նույն կենտրոնով, որպեսզի մեծ գնդի մեջ տեղադրվի բազմանիստ պինդ մարմին, որը չի շոշափում փոքր գնդի մակերեսը։ |
|||
[[Պատկեր:Պնդ17.png|200px|thumb|left|]] |
|||
Թող, երկու գնդեր գծված լինեն նույն կենտրոն A-ով: Ուստի, անհրաժեշտ է ներգծել բազմանիստ մարմին մեծ գնդի մեջ, որը չի շոշափում փոքր գնդի մակերեսը: |
|||
Թող գնդերը կտրվեն ինչ-որ հարթությամբ, որը անցնում է կենտրոնից։ Ուստի, հատումները կլինեն շրջաններ, քանի որ գունդը ձևավորվում է մնացած տրամագծով, և կիսաշրջանը շրջվում է [Նիշ. 11.14]։ Եվ հետևաբար, որևիցե դիրք, որը կմտածենք կիսաշրջանի համար, հարթությունը, որը դրա վրայով անցկացվում է, կկազմի շրջան գնդի մակերեսի վրա։ Եվ ակնհայտ է, որ դա նույնպես մեծ (շրջան է), քանի որ գնդի տրամագիծը, որն ակնհայտորեն նաև կիսաշրջանի և շրջանի տրամագիծն է, ավելի մեծ է, քան բոլոր մյուս (ուղղահայացները), որոնք անցնում են շրջանում կամ գնդի մեջ [Պնդ. 3.15]։ Ուստի, թող BCDE լինի շրջան մեծ գնդում, իսկ FGH՝ շրջան փոքր գնդում։ Եվ թող նրանցից երկու տրամագիծներ քաղված լինեն իրարահակառակ ուղղությամբ, (հատկապես), BD և CE։ Եվ լինելով երկու շրջաններ նույն կենտրոնով՝ (այսինքն) BCDE և FGH՝ թող լինի հավասարաչափ և զույգ կողմերով պոլիգոն, որը գտնվել է մեծ շրջանի BCDE մեջ, առանց շփվելու փոքր շրջանի FGH-ի հետ [Պնդ. 12.16], որի կողմերը չորրորդանկյունում BE կլինեն BK, KL, LM և ME։ Եվ երբ KA միացվի, թող այն անցնի մինչև N։ Եվ թող AO-ն լիներ կանգնեցված A կետում, շրջանի BCDE-ի հարթության հետ ուղղահայաց։ Եվ թող այն հատեր (մեծ) գնդի մակերեսը O կետում։ Եվ թող հարթություններ լինեն անցկացված AO-ի և յուրաքանչյուր BD և KN-ի միջոցով։ Ուստի, ըստ վերոնշյալ քննարկման, դրանք կկազմեն մեծ շրջաններ (մեծ) գնդի մակերեսի վրա։ Թող նրանք կազմեն (մեծ շրջաններ), որոնցից BOD և KON կիսաշրջաններ կլինեն BD և KN տրամագծերի վրա (համապատասխանաբար)։ Եվ քանի որ OA-ն ուղղահայաց է BCDE շրջանի հարթությանը, բոլոր այն հարթությունները, որոնք անցնում են OA-ով, նույնպես կլինեն ուղղահայաց BCDE շրջանի հարթությանը [Պնդ. 11.18]։ Եվ այդպիսով, կիսաշրջանները BOD և KON նույնպես ուղղահայաց կլինեն BCDE շրջանի հարթությանը։ Եվ քանի որ կիսաշրջանները BED, BOD և KON հավասար են՝ քանի որ դրանք գտնվում են հավասար տրամագծերի BD և KN վրա [Պար. 3.1]՝ չորրորդանկյունները BE, BO և KO նույնպես հավասար են միմյանց։ Այդպիսով, որքան շատ կողմեր կան պոլիգոնում, որոնք գտնվում են BE չորրորդանկյունում, նույնքան էլ կան BO և KO չորրորդանկյուններում հավասար դեպի ուղիղ գծեր BK, KL, LM և ME։ Թող դրանք լինեն ներմուծված, և թող դրանք լինեն BP, PQ, QR, RO, KS, ST, TU և UO։ Եվ թող SP, TQ և UR միացվեն։ Եվ թող ուղղահայացներ լինեն անցկացված P և S կետերից դեպի BCDE շրջանի հարթություն [Պնդ. 11.11]։ Այնպես որ, նրանք կընկնեն BD և KN հարթությունների համատեղ հատվածների վրա (BCDE-ի հետ), քանի որ BOD և KON հարթությունները նույնպես ուղղահայաց են BCDE շրջանի հարթությանը [Պար. 11.4]։ Թող նրանք ընկնեն, և թող դրանք լինեն PV և SW։ Եվ թող WV-ը միացվի։ Եվ քանի որ BP և KS հավասար են (շրջաններ), որոնք կտրվել են հավասար կիսաշրջաններում BOD և KON [Պար. 3.28], և PV և SW-ը ուղղահայացներ են, որոնք անցկացվել են (նրանցից), PV-ն [այդպիսով] հավասար է SW-ին, և BV-ն՝ KW-ին [Պնդ. 3.27, 1.26]։ Եվ ամբողջ BA-ն նույնպես հավասար է ամբողջ KA-ին։ Եվ այդպիսով, ինչպես BV-ն է VA-ի նկատմամբ, այնպես էլ KW-ն՝ WA-ի նկատմամբ։ WV-ն այդպիսով զուգահեռ է KB-ին [Պնդ. 6.2]։ Եվ քանի որ PV և SW-ը յուրաքանչյուրն ուղղահայաց են BCDE շրջանի հարթությանը, PV-ն այդպիսով զուգահեռ է SW-ին [Պնդ. 11.6]։ Եվ նաև ցույց տրվել է (որ դրանք) հավասար են։ Եվ այդպիսով, WV և SP հավասար և զուգահեռ են [Պնդ. 1.33]։ Եվ քանի որ WV-ն զուգահեռ է SP-ին, բայց WV-ն զուգահեռ է KB-ին, SP-ն այդպիսով նաև զուգահեռ է KB-ին [Պնդ. 11.1]։ Եվ BP-ն և KS-ն միացնում են դրանք։ Այսպիսով, KBPS քառանկյունը գտնվում է մեկ հարթության մեջ, քանի որ եթե երկու զուգահեռ ուղղաձիգներ լինեն, և յուրաքանչյուրում վերցվի մի պատահական կետ, ապա այդ կետերը միացնող ուղղահայացը կլինի նույն հարթության մեջ, որտեղ գտնվում են զուգահեռ ուղղաձիգները [Պար. 11.7]։ Այդպես, նույն (պատճառներով), SPQT և TQRU քառանկյունները նույնպես գտնվում են մեկ հարթության մեջ։ Եվ URO եռանկյունը նույնպես գտնվում է մեկ հարթության մեջ [Պար. 11.2]։ Հետևաբար, եթե մենք պատկերացնենք ուղղահայացներ, որոնք միացնում են P, S, Q, T, R և U կետերը A կետին, ապա որոշ բազմանիստ մարմին կկառուցվի BO և KO շրջանների միջև, կազմված պիրամիդներից, որոնց հիմքերն են KBPS, SPQT, TQRU քառանկյունները և URO եռանկյունը, իսկ գագաթը՝ A կետը։ Եվ եթե մենք նույն կառուցվածքը անենք նաև KL, LM և ME կողմերի վրա, ինչպես BK-ի վրա, և ավելին, (կրկնենք կառուցվածքը) մնացած երեք քառորդներում, ապա մի բազմանիստ մարմին, որը պարփակված է esfera մեջ, կկառուցվի, կազմված պիրամիդներից, որոնց հիմքերն են նշված քառանկյունները և եռանկյունը, ինչպես նաև դրանց նման կազմակերպված քառանկյունները և եռանկյունները, և գագաթը՝ A կետը։ |
|||
Ուստի, ես ասում եմ, որ վերոնշյալ բազմանիստը չի շոշափում փոքր գնդիի մակերեսին, որտեղ գտնվում է FGH շրջանը։ |
|||
Թող ուղղանկյուն AX ուղիղ գիծը տրվի A կետից դեպի K BPS հարթություն, և թող այն հանդիպի հարթությանը X կետում [Պնդ. 11.11]: Եվ թող XB և XK գծերը միանան: Իսկ քանի որ AX-ն ուղղանկյուն է K BPS քառանկյունի հարթության նկատմամբ, այն նաև ուղղանկյուն է իր հետ միացված բոլոր ուղիղ գծերի նկատմամբ, որոնք նույնպես գտնվում են քառանկյունի հարթությունում [Թիմ. 11.3]: Ուստի, AX-ն ուղղանկյուն է նաև BX և XK ուղիղ գծերի նկատմամբ: Եվ քանի որ AB-ը հավասար է AK-ին, ապա AB-ի քառամեծությունը նույնպես հավասար է AK-ի քառամեծությանը: Եվ AX և XB-ի քառամեծությունների գումարը հավասար է AB-ի քառամեծությանը: Քանի որ X-ում անկյունը ուղղանկյուն է [Պնդ. 1.47]: Եվ AX և XK-ի քառամեծությունների գումարը հավասար է AK-ի քառամեծությանը [Պնդ. 1.47]: Ուստի, AX և XB-ի քառամեծությունների գումարը հավասար է AX և XK-ի քառամեծությունների գումարին: Թող AX-ի քառամեծությունը հանվի երկուսից: Ուստի, մնացած BX-ի քառամեծությունը հավասար է մնացած XK-ի քառամեծությանը: Ուստի, BX-ը հավասար է XK-ին: Այնպես որ, համապատասխանաբար, մենք կարող ենք ցույց տալ, որ X-ից դեպի P և S միացված ուղիղ գծերը հավասար են BX և XK-ի հետ: |
|||
Ուստի, քառանկյունի հարթության մեջ X կենտրոնով և XB կամ XK ճառագայթով նկարագրված շրջանը նույնպես կանցնի P և S կետերի միջով, և KBPS քառանկյունը կլինի շրջանի ներսում։ |
|||
Եվ քանի որ KB-ն մեծ է WV-ից, և WV-ը հավասար է SP-ին, ապա KB-ն մեծ է SP-ից։ Եվ քանի որ KB-ն հավասար է KS-ին և BP-ին, ապա KS-ը և BP-ն միմյանցից մեծ են SP-ից։ Եվ քանի որ KBPS քառանկյունը գտնվում է շրջանի մեջ, և KB-ն, BP-ն և KS-ը հավասար են միմյանց, իսկ PS-ը փոքր է նրանցից, և BX-ը շրջանի ճառագայթն է, ապա KB-ի քառակուսին մեծ է քան կրկնակի BX-ի քառակուսիի։ Թող KY ուղղահայացը գծվի K-ից դեպի BV։ Եվ քանի որ BD-ն փոքր է քան կրկնակի DY-ն, և քանի որ BD-ն հարաբերակցված է DY-ի, ապա DB և BY կողմից պարունակվող անկյունագիծը համեմատվում է DY և YB-ի կողմից պարունակվող անկյունագծին՝ BY վրա նկարագրված քառակուսիով, և YD-ի վրա կատարված զուգահեռանկյունային պարալելոգրամով՝ YB-ն հավասար է BY-ի կարճ կողմին։ Այսպիսով, DB և BY կողմից պարունակվող անկյունագիծը նույնպես փոքր է քան DY և YB-ի կողմից պարունակվող անկյունագիծը։ Եվ քանի որ KD-ը միացված է, DB և BY կողմից պարունակվող անկյունագիծը հավասար է BK-ի քառակուսուն, իսկ DY և YB կողմից պարունակվող անկյունագիծը հավասար է KY-ի քառակուսուն [Պնդ. 3.31, 6.8 ճշտ.]. Այսպիսով, KB-ի քառակուսին փոքր է քան կրկնակի KY-ի քառակուսին։ Բայց KB-ի քառակուսին մեծ է քան կրկնակի BX-ի քառակուսին։ Այսպիսով, KY-ի քառակուսին մեծ է քան BX-ի քառակուսին։ Եվ քանի որ BA-ն հավասար է KA-ին, BA-ի քառակուսին հավասար է AK-ի քառակուսուն։ Եվ BX և XA-ի քառակուսիների գումարը հավասար է BA-ի քառակուսուն, իսկ KY և YA-ի քառակուսիների գումարը հավասար է KA-ի քառակուսուն [Պնդ. 1.47]։ Այսպիսով, BX և XA-ի քառակուսիների գումարը հավասար է KY և YA-ի քառակուսիների գումարին, որոնցից KY-ի քառակուսին մեծ է քան BX-ի քառակուսին։ Այսպիսով, մնացած YA-ի քառակուսին փոքր է XA-ի քառակուսից։ Այսպիսով, AX-ը մեծ է քան AY։ Այսպիսով, AX-ը շատ ավելի մեծ է քան AG։ Եվ AX-ը ուղղահայաց է բազմանիստի հիմներից մեկի վրա, իսկ AG-ն ուղղահայաց է փոքր գնդի մակերեսի վրա։ Ուստի, բազմանիստը չի շոշափում փոքր գնդի մակերեսը։ |
|||
Այսպիսով, երկու գնդեր, որոնք գտնվում են նույն կենտրոնում, մեծ գնդի մեջ ներգծվել է բազմանիստ մարմին, որը չի շոշափում փոքր գնդի մակերեսը: (Այս է) այն, ինչ պահանջվում էր անել: |
|||
'' Եզրակացություն '' |
|||
''Եվ նաև, եթե BCDE գնդի մեջ այդպիսի բազմանիստ մարմինն ինքդեն ներգծվի մեկ այլ գնդի մեջ, ապա BCDE գնդի մեջ գտնվող բազմանիստ մարմինը պետք է ունենա մեկ այլ գնդի մեջ գտնվող բազմանիստ մարմնին այդ գնդի տրամագծի և BCDE գնդի տրամագծի խորացված հարաբերակցությունը։ Որովհետև եթե մարմինները բաժանվեն նմանապես թվարկված և նմանապես տեղադրված պիրամիդների մեջ, ապա պիրամիդները կլինեն նման։ Եվ նման պիրամիդները գտնվում են համապատասխան կողմերի խորացված հարաբերակցությունում [Պնդ. 12.8 կորէկցիա]։ Ուստի, այն պիրամիդը, որի հիմքը քառանկյուն KBPS է, և վերևում A կետն է, կունենա մեկ այլ գնդում համապատասխան տեղադրված պիրամիդին խորացված հարաբերակցություն, որը կապված է համապատասխան կողմի և համապատասխան կողմի հարաբերակցությանը։ Դա նշանակում է, որ A կենտրոնի շուրջ գտնվող գնդի AB ճառագայթը կապահովի այն ճառագայթին, որն ունի մեկ այլ գնդի համար։ Եվ նույն կերպ, A կենտրոնի շուրջ գտնվող յուրաքանչյուր պիրամիդը կապահովի մեկ այլ գնդում համապատասխան տեղադրված յուրաքանչյուր պիրամիդի համար խորացված հարաբերակցություն, որը կապված է AB-ի և մեկ այլ գնդի ճառագայթի միջև։ Եվ ինչպես մեկի հիմնական (մեծություն) համապատասխան է մեկի հետևյալից (երկու համեմատական մեծությունների շարքում), այնպես էլ (ամեն ինչի գումարը) հիմնականների բոլորի հետ կապված կլինի (հետևյալների գումարի հետ) [Պնդ. 5.12]։ Հետևաբար, ամբողջ բազմանիստ մարմինը A կենտրոնի շուրջ գտնվող գնդում պետք է լինի ամբողջ բազմանիստ մարմնին մեկ այլ գնդում խորացված հարաբերակցություն, որը կապված է AB ճառագայթի և մեկ այլ գնդի ճառագայթի հարաբերակցությանը։ Դա նշանակում է, որ BD տրամագիծը կապված է մեկ այլ գնդի տրամագծի հետ։ (Այս է) այն, ինչ պահանջվում էր ապացուցել։'' |
|||
== Պնդում 18 == |
|||
Գնդերը միմյանց գտնվում են իրենց համապատասխան տրամագծերի խորանարդ հարաբերակցությամբ։ |
|||
[[Պատկեր:Պնդ18.png|200px|thumb|left|]] |
|||
Թող, գնդերը ABC և DEF գծված լինեն, և նրանց տրամագծերը լինեն համապատասխանաբար BC և EF: Ես ասում եմ, որ գունդ ABC-ը ունի գունդ DEF-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ: |
|||
Իսկ եթե գունդ ABC-ը չունի գունդ DEF-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ, ապա գունդ ABC-ը կունենա որևէ այլ գնդի նկատմամբ, որը կամ փոքր է, կամ մեծ է գունդ DEF-ից, այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ: Թող, առաջին հերթին, այն ունենա այդպիսի հարաբերակցություն փոքր գնդի՝ GHK-ի նկատմամբ: Եվ թող DEF-ը գծված լինի նույն կենտրոնով, ինչ GHK-ն: Եվ թող բազմանիստ մարմին ներգծվի մեծ գնդի՝ DEF-ի մեջ, որը չի շոշափում փոքր գնդի՝ GHK-ի մակերեսը [Պնդ. 12.17]: Եվ թող բազմանիստ մարմին, որը նման է DEF-ի գնդում գտնվող բազմանիստին, նույնպես ներգծվի ABC գնդում: Ուստի, բազմանիստ մարմինը ABC գնդում ունի DEF գնդի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ [Պնդ. 12.17, համընթաց]: Եվ ABC գունդը նույնպես ունի GHK գնդի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ: Ուստի, ինչպես ABC գունդը է GHK գնդի նկատմամբ, այնպես էլ բազմանիստ մարմինը ABC գնդում է DEF գնդի բազմանիստ մարմնի նկատմամբ: Ուստի, փոխադարձաբար, ինչպես գունդ ABC-ն է բազմանիստի նկատմամբ, այնպես էլ գունդ GHK-ն է բազմանիստի նկատմամբ գունդ DEF-ում [Պնդ. 5.16]: Եվ գունդ ABC-ն ավելի մեծ է, քան դրա ներսում գտնվող բազմանիստը: Ուստի, գունդ GHK-ն նույնպես ավելի մեծ է, քան գունդ DEF-ի ներսում գտնվող բազմանիստը [Պնդ. 5.14]: Բայց այն նաև փոքր է, որովհետև այն շրջապատված է դրա կողմից: Ուստի, գունդ ABC-ը չի ունենում գնդի նկատմամբ, որը ավելի փոքր է, քան գունդ DEF, այն խորանարդ հարաբերակցությունը, որը BC-ի տրամագիծը ունի՝ EF-ի նկատմամբ: Հետևաբար, նմանապես, մենք կարող ենք ցույց տալ, որ գունդ DEF-ը նույնպես չի ունենում գնդի նկատմամբ, որը ավելի փոքր է, քան գունդ ABC, այն խորանարդ հարաբերակցությունը, որը EF-ն ունի՝ BC-ի նկատմամբ: |
|||
Ուստի, ես ասում եմ, որ գունդ ABC-ը չի ունենում գնդի նկատմամբ, որը ավելի մեծ է, քան գունդ DEF, այն խորանարդ հարաբերակցությունը, որը BC-ն ունի՝ EF-ի նկատմամբ: |
|||
Որպեսզի հնարավոր լինի, թող դա ունենա (խորանարդ հարաբերակցություն) ավելի մեծ (գնդի) հետ՝ LMN։ Ուստի, հակառակ ուղղությամբ, գունդ LMN-ը ունի գունդ ABC-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը տրամագիծը EF-ն ունի՝ տրամագիծ BC-ի նկատմամբ [Պնդ. 5.7 տես.։] Եվ ինչպես գունդ LMN-ը գտնվում է գունդ ABC-ի նկատմամբ, այնպես էլ գունդ DEF-ը գտնվում է այնպիսի (գնդի) նկատմամբ, որը փոքր է, քան գունդ ABC, քանի որ LMN-ը ավելի մեծ է, քան DEF-ը, ինչպես արդեն ցույց տրվեց [Պնդ. 12.2 լեմ.։] Եվ ուստի, գունդ DEF-ը ունի այնպիսի (գնդի) նկատմամբ, որը փոքր է, քան գունդ ABC, այն խորանարդ հարաբերակցությունը, որը EF-ն ունի՝ BC-ի նկատմամբ։ Վերոնշյալը անհնար է եղել։ Ուստի, գունդ ABC-ը չի ունենում այնպիսի (գնդի) նկատմամբ, որը ավելի մեծ է, քան գունդ DEF, այն խորանարդ հարաբերակցությունը, որը BC-ն ունի՝ EF-ի նկատմամբ։ Եվ ցույց տրվեց, որ դա չի լինի նաև փոքր (գնդի) նկատմամբ։ Ուստի, գունդ ABC-ը ունի գունդ DEF-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը BC-ն ունի՝ EF-ի նկատմամբ։ Դա հենց այն էր, ինչ պետք էր ցույց տալ։ |
|||
Ընթացիկ տարբերակը 02:43, 13 դեկտեմբերի 2024-ի դրությամբ
հեղինակ՝ էվկլիդես |
Pages 481 - 505
Պնդում 6
Բուրգերը, որոնք ունեն միևնույն բարձրություն և ունեն բազմանկյուն հիմքեր, միմյանց համար որպես հիմքեր են հանդիսանում:
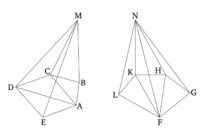
Դիտարկենք նույն բարձրության բուրգեր, որոնց հիմքերն են ABCDE և FGHKL բազմանկյունները, իսկ գագաթները՝ M և N կետերը (համապատասխանաբար): Ինչպես ABCDE հիմքը նման/հարաբերվում է է FGHKL-ին է, այնպես էլ ABCDEM բուրգը նման է FGHKLN բուրգին:
Թող AC, AD, FH և FK հատվածները միացված լինեն: Հետևաբար, քանի որ ABCM-ը և ACDM-ը երկու բուրգեր են, որոնք ունեն եռանկյունաձև հիմքեր և հավասար բարձրություն, դրանք միմյանց նկատմամբ համեմատելի են իրենց հիմքերի չափերով [Պնդ. 12.5]։ Այսպիսով, ինչպես ΑΒC հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCM-ն է հարաբերվում ACDM բուրգին: Եվ, կոմպոզիցիայի միջոցով, ինչպես ABCD հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCDM է հարաբերվում ACDM բուրգին [Պնդ. 5.18]: Բայց, քանի որ ACD հիմքն է ահրաբերվում ADE հիմքին, այնպես էլ նաև ACDM բուրգն է հարաբերվում ADEM բուրգին [Պնդ. 12.5]։ Այսպիսով, հավասարության միջոցով, ABCD հիմքի հարաբերությաւոնը ADE հիմքին հավասար է ABCDM բուրգի հարաբորուտըանը ADEM բուրգին [Պնդ. 5.22]: Եվ, դարձյալ, կոմպոզիցիայի միջոցով, ինչպես ABCDE հիմքն է հարաբերվում ADE հիմքին, այնպես էլ ABCDEM բուրգն է հարաբերվում ADEM բուրգին [Պնդ. 5.18]: Այսպիսով, նման կերպով կարելի է նաև ցույց տալ, որ ինչպես FGHKL հիմքն է հարաբերվում FGH հիմքին, այնպես էլ FGHKLN բուրգն է հարաբերվում FGHN բուրգին: Եվ քանի որ ADEM-ը և FGHN-ը երկու բուրգեր են, որոնք ունեն եռանկյուն հիմքեր և հավասար բարձրություն, հետևաբար, ADE և FGH հիմքերի հարաբերությունը հավասար է ADEM և FGHN բուրգերի հարաբերությանը [Պնդ. 12.5]։ Բայց, ինչպես ADE հիմքն է հարաբերվում ABCDE հիմքին, այնպես էլ ADEM բուրգն է հարաբերվում ABCDEM բուրգին: Այսպիսով, հավասարության միջոցով, քանի որ ABCDE հիմքը հարաբերվում է FGH հիմքին, այնպես էլ ABCDEM բուրգը հարաբերվում է նաև FGHN բուրգին [Պնդ. 5.22]: Բայց, ավելին, ինչպես FGH հիմքն է հարաբերվում FGHKL հիմքինին, այնպես էլ FGHN բուրգն է նույնպես հարաբերվում FGHKLN բուրգին: Այսպիսով, հավասարության միջոցով, քանի որ ABCDE հիմքը հարաբերվում է FGHKL հիմքին, այնպես էլ ABCDEM բուրգը հարաբերվում է նաև FGHKLN բուրգին [Պնդ. 5.22]: Ինչը հենց այն է, ինչ պահանջվում էր ցույց տալ:
Պնդում 7
Եռանկյուն հիմք ունեցող ցանկացած պրիզմա բաժանվում է երեք բուրգերի, որոնց եռանկյուն հիմքերը հավասար են միմյանց:
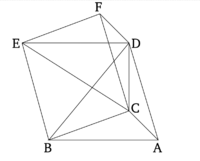
Դիտարկենք պրիզմա, որի հիմքը ABC եռանկյունին է, իսկ հակառակ հարթությունը DEF: Ենթադրենք, որ ABCDEF պրիզման բաժանված է երեք բուրգերի, որոնք ունեն միմյանց հավասար եռանկյուն հիմքեր:
Թող BD-ն, EC-ը և CD-ն միացված լինեն: Քանի որ ABED-ը զուգահեռագիծ է, իսկ BD-ն նրա անկյունագիծն է, հետևաբար ABD եռանկյունը հավասար է EBD եռանկյունին [Պնդ. 1.34]: Եվ այսպես, բուրգը, որի հիմքը ABD եռանկյունն է, իսկ գագաթը՝ C կետը, հավասար է բուրգին, որի հիմքը DEB եռանկյունն է, իսկ գագաթը՝ C կետը [Պնդ. 12.5]։ Բայց բուրգը, որի հիմքը DEB եռանկյունն է, իսկ գագաթը՝ C կետը, նույնն է, ինչ բուրգը, որի հիմքը EBC եռանկյունն է, իսկ գագաթը՝ D կետը։ Որովհետև դրանք սահմանափակված են նույն հարթություններում: Եվ այսպես, բուրգը, որի հիմքը ABD է, իսկ գագաթը՝ C կետը, հավասար է բուրգին, որի հիմքը EBC է, իսկ գագաթը՝ D կետը: Կրկին, քանի որ FCBE-ն զուգահեռագիծ է, իսկ CE-ն նրա անկյունագիծն է, CEF եռանկյունը հավասար է CBE եռանկյանը [Պնդ. 1.34]: Եվ այսպիսով, բուրգը, որի հիմքը BCE եռանկյունն է, և գագաթը D կետը, հավասար է բուրգին, որի հիմքը ECF եռանկյունն է, իսկ գագաթը D կետը [Պնդ. 12.5]։ Եվ բուրգը, որի հիմքը BCE եռանկյունն է, իսկ գագաթը D կետը, ցույց տրվեց, որ հավասար է այն բուրգին, որի հիմքը ABD եռանկյունն է, և գագաթը C կետն է: Այսպիսով, բուրգը, որի հիմքը CEF եռանկյունն է, իսկ գագաթը՝ D կետը, նույնպես հավասար է բուրգին, որի հիմքը ABD եռանկյունն է, իսկ գագաթնակետը C կետն է։ Այսպիսով, ABCDEF պրիզման բաժանվել է երեք բուրգերի, որոնք ունեն եռանկյուն հիմքեր, որոնք հավասար են միմյանց:
Եվ քանի որ բուրգը, որի հիմքը ABD եռանկյունն է, իսկ գագաթը՝ C կետը, նույնն է, ինչ բուրգը, որի հիմքը CAB եռանկյունն է, իսկ գագաթը՝ D կետը, դրանք սահմանափակված են նույն հարթություններում։ Իսկ բուրգը, որի հիմքը ABD եռանկյունին է, իսկ գագաթը՝ C կետը, ցույց տրվեց, որ այն պրիզմայի մեկ երրորդն է, որի հիմքը ABC եռանկյունն է, և հակառակ հարթությունը DEF, հետևաբար բուրգը, որի հիմքը ABC եռանկյունն է, և D կետի գագաթը, նույնպես բուրգի մեկ երրորդն է, որն ունի նույն հիմքը, ABC եռանկյունը և հակառակ հարթություն DEF:
Եզրակացություն
Եվ սրանից պարզ է դառնում, որ ցանկացած բուրգ պրիզմայի երրորդ մասն է, որն ունի իր նույն հիմքը և հավասար բարձրություն։ Իինչը հենց այն է, ինչ պահանջվում էր ցույց տալ:
Պնդում 8
Նման բուրգերը, որոնք նույնպես ունեն եռանկյուն հիմքեր, հարաբերվում են իրենց համապատասխան կողմերի խորանարդ հարաբերությամբ:
Թող լինեն նման և նույն ձևով դասավորված բուրգեր, որոնց հիմքերը ABC և DEF եռանկյուններն են, իսկ գագաթները՝ G և H կետերը (համապատասխանաբար): Ստուգենք արդյո՞ք ABCG բուրգի հարաբերությունը DEFH բուրգին հավասար է BC-ի հարաբեությանը EF-ին ըստ խորանարդ աստիճանի:
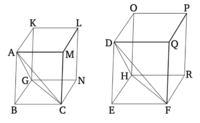
Թող զուգահեռանիստ պինդ մարմինները BGML և EHQP ամփոփ լինեն: Եվ քանի որ ABCG բուրգը նման է DEFH բուրգին, հետևաբար ABC անկյունը հավասար է DEF անկյանը, իսկ GBC-ն՝ HEF-ին և ABG-ն՝ DEH-ին: Եվ ինչպես AB-ն է հարաբերվում DE-ին, այնպես էլ BC է հարաբերվում EF-ին, իսկ BG-ն՝ EH-ին [Սահմանում. 11.9]։ Եվ քանի որ AB-ն DE-ին է հարաբերվում, ուստի BC հարաբերվում է EF-ին, և (այդպիսով) հավասար անկյունների շուրջ կողմերը համաչափ են, BM զուգահեռագիծն այսպիսով նման է EQ զուգահեռագծին: Այսպիսով, նույն (պատճառներով) BN-ն նույնպես նման է ER-ին, իսկ BK-ն՝ EO-ին: Այսպիսով, երեք զուգահեռագծերը MB, BK և BN նման են երեք զուգահեռագծերին EQ, EO, ER (համապատասխանաբար): Բայց երեք զուգահեռագծեր MB, BK և BN-ը և’ ) հավասար են, և’ նման են երեք հակադիր զուգահեռագծերին, իսկ երեք զուգահեռագծեր EQ, EO և ER և’ հավասար, և’ նման են երեք հակադիր զուգահեռագծերին [Պնդ. 11.24]: Այսպիսով, պինդ մարմիններ BGML և EHQP-ը սահմանափակված են հավասար թվով նման (և նմանապես դասավորված) հարթություններում: Այսպիսով, պինդ BGML-ը նման է պինդ EHQP-ին [Սահմ. 11.9]։ Իսկ նման զուգահեռանիստ պինդ մարմինները ունեն համապատասխան կողմերի խորանարդ հարաբերությունը [Պնդ. 11.33]:
Այսպիսով, պինդ մարմին BGML-ի հարաբերությունը պինդ մարմին EHQP-ին խորանարդային հարաբերակցությամբ, նույնն է, ինչ համապատասխան BC կողմի հարաբերությունը EF կողմին: Եվ ինչպես պինդ մարմին BGML-ն է հարաբերվում պինդ մարմին EHQP-ին, այնպես էլ ABCG բուրգն է հարաբերվում DEFH բուրգին, քանի որ բուրգը պինդ մարմնի վեցերորդ մասն է, պրիզմայի հաշվին, լինելով զուգահեռանիստ պինդ մարմնի կեսը [Պնդ. 11.28]՝ լինելով նաև բուրգի եռապատիկ [Պնդ. 12.7]: Այսպիսով, ABCG բուրգը նույնպես պետք է ունենա բուրգի DEFH խորանարդ հարաբերակցությունը, ինչպես BC -ի հարաբերությունը EF-ին: (Սա հենց այն է, ինչ պահանջվում էր ցույց տալ):
Եզրակացություն
Այսպիսով, սրանից պարզ է նաև, որ բազմանկյուն հիմքեր ունեցող նման բուրգերը միմյանց նկատմամբ ունեն իրենց համապատասխան կողմերի խորանարդային հարաբերակցությունը։ Որովհետև դրանք բաժանելով իրենց մեջ պարունակվող բուրգերի, որոնք ունեն եռանկյուն հիմքեր, ընդ որում հիմքերը նույնպես պաժանված նման եռանկյունների, որոնք և՛ թվով հավասար են, և՛ համընկնում են ամբողջին [Պնդ. 6.20]: Ինչպես առաջին բուրգում (ունեցող բազմանկյուն հիմք) եռանկյուն հիմք ունեցող առանձին բուրգը հարաբերակցվում է երկրորդ բուրգում (նաեւ ունենալով բազմանկյուն հիմք) եռանկյուն հիմք ունեցող առանձին բուրգին, այնպես էլ առաջին բուրգում բոլոր եռանկյուն հիմք ունեցող բուրգերի գումարը հարաբերակցվում է երկրորդ բուրգում բոլոր եռանկյուն հիմք ունեցող բուրգերի գումարին [Պնդ. 5.12]։ Սա նշանակում է, որ ամբողջ առաջին բուրգը՝ բազմանկյուն հիմքով, համաչափ է երկրորդ բուրգին՝ բազմանկյուն հիմքով։ Եվ եռանկյուն հիմք ունեցող բուրգը հարաբերակցվում է եռանկյուն հիմք ունեցող բուրգին կողմերի համապատասխան խորացված հարաբերությամբ [Պնդ. 12.8]։ Հետևաբար, բազմանկյուն հիմք ունեցող բուրգը նույնպես հարաբերակցվում է նման հիմք ունեցող բուրգին կողմի և համապատասխան կողմի խորացված հարաբերությամբ։
Պնդում 9
Հավասար բուրգերի հիմքերը, որոնք նույնպես ունեն եռանկյունաձև հիմքեր, փոխադարձաբար համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյուն հիմքեր, որոնց հիմքերը փոխադարձաբար համեմատական են իրենց բարձրություններին, հավասար են։
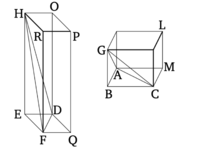
Որովհետև թող լինեն (երկու) հավասար բուրգեր, որոնք ունեն ABC և DEF եռանկյունաձև հիմքեր, իսկ գագաթներով G և H կետերը (համապատասխանաբար): Ես ասում եմ, որ ABCG և DEFH բուրգերի հիմքերը փոխադարձաբար համաչափ են իրենց բարձրություններին, և (այսպես) ինչպես ABC հիմքը հավասար է DEF-ին, այնպես էլ DEFH բուրգի բարձրությունը (է) ABCG բուրգի բարձրությանը:
Որովհետև զուգահեռանիստ մարմինները՝ BGML և EHQP, լրացված են: Եվ քանի որ ABCG բուրգը հավասար է DEFH բուրգին, և զուգահեռանիստ BGML մարմինը վեց անգամ մեծ է ABCG բուրգից (տե՛ս նախորդ պնդումը), և զուգահեռանիստ EHQP (է) վեց անգամ DEFH բուրգից, ապա զուգահեռանիստ BGML-ը հավասար է զուգահեռանիստ EHQP-ին: Իսկ հավասար զուգահեռանիստ մարմինների հիմքերը հակադարձորեն համեմատական են դրանց բարձրություններին [Պնդ. 11.34]: Հետևաբար, ինչպես BM հիմքն է EQ հիմքին, այնպես էլ զուգահեռանիստ EHQP-ի բարձրությունն է զուգահեռանիստ BGML-ի բարձրությանը: Բայց, ինչպես BM հիմքն է EQ հիմքին, այնպես էլ ABC եռանկյունին է DEF եռանկյունին [Պնդ. 1.34]: Եվ, հետևաբար, ինչպես ABC եռանկյունին է DEF եռանկյունին, այնպես էլ զուգահեռանիստ EHQP-ի բարձրությունն է զուգահեռանիստ BGML-ի բարձրությանը [Պնդ. 5.11]: Բայց զուգահեռանիստ EHQP-ի բարձրությունը նույնն է, ինչ DEFH բուրգի բարձրությունը, իսկ զուգահեռանիստ BGML-ի բարձրությունը նույնն է, ինչ ABCG բուրգի բարձրությունը: Հետևաբար, ինչպես ABC հիմքն է DEF հիմքին, այնպես էլ DEFH բուրգի բարձրությունն է ABCG բուրգի բարձրությանը: Հետևաբար, ABCG և DEFH բուրգերի հիմքերը հակադարձորեն համեմատական են դրանց բարձրություններին:
Ուստի, թող ABCG և DEFH բուրգերի հիմքերը լինեն հակադարձ համեմատական դրանց բարձրություններին, և թող ABC հիմքն լինի DEF հիմքին այնպես, ինչպես DEFH բուրգի բարձրությունն է ABCG բուրգի բարձրությանը: Ասում եմ, որ ABCG բուրգը հավասար է DEFH բուրգին:
Քանի որ նույն կառուցվածքով, քանի որ ABC հիմքն է DEF հիմքին, այնպես էլ DEFH բուրգի բարձրությունն է ABCG բուրգի բարձրությանը, բայց քանի որ ABC հիմքն է DEF հիմքին, այնպես էլ զուգահեռանիստ BM-ն է զուգահեռանիստ EQ-ին [Պնդ. 1.34], ուստի ինչպես զուգահեռանիստ BM-ն է զուգահեռանիստ EQ-ին, այնպես էլ DEFH բուրգի բարձրությունն է նաև ABCG բուրգի բարձրությանը [Պնդ. 5.11]: Բայց, DEFH բուրգի բարձրությունն նույնն է, ինչ զուգահեռանիստ EHQP-ի բարձրությունը, իսկ ABCG բուրգի բարձրությունն նույնն է, ինչ զուգահեռանիստ BGML-ի բարձրությունը: Ուստի, ինչպես BM հիմքն է EQ հիմքին, այնպես էլ EHQP զուգահեռանիստի բարձրությունն է BGML զուգահեռանիստի բարձրությանը: Իսկ այն զուգահեռանիստները, որոնց հիմքերը հակադարձ համեմատական են իրենց բարձրություններին, հավասար են [Պնդ. 11.34]: Ուստի, BGML զուգահեռանիստը հավասար է EHQP զուգահեռանիստին: Իսկ ABCG բուրգը BGML-ի վեցերորդ մասն է, իսկ DEFH բուրգը EHQP զուգահեռանիստի վեցերորդ մասն է: Ուստի, ABCG բուրգը հավասար է DEFH բուրգին:
Ուստի, հավասար բուրգերի հիմքերը, որոնք նաև եռանկյունի հիմքեր ունեն, հակադարձ համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյունի հիմքեր և որոնց հիմքերը հակադարձ համեմատական են իրենց բարձրություններին, հավասար են: Այսինքն հենց այն բանը, որը պետք է ապացուցվեր:
Պնդում 10
Յուրաքանչյուր կոն գլանի երրորդ մասն է, որն ունի դրա հիմքը և հավասար բարձրությունը:
Թող լինի կոն նույն հիմքով ինչ գլանը, (մասնավորապես) շրջանագիծ ABCD-ն և հավասար բարձրություն: Ես ասում եմ, որ կոնը գլանի երրորդ մասն է, այսինքն՝ գլանը հավասար է երեք անգամ է կոնի ծավալին։
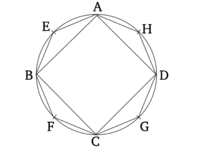
Քանի որ եթե գլանիկը կոնից երեք անգամ մեծ չլինի, ապա գլանիկը կլինի կամ երեք անգամից ավել մեծ, կամ երեք անգամից պակաս (կոնից): Թող նախ այն լինի երեք անգամից ավել մեծ (կոնից): Եվ թող ABCD քառակուսին ներգծված լինի ABCD շրջանի մեջ [Պնդ. 4.6]: Ուրեմն, ABCD քառակուսին ավելի քան կեսն է ABCD շրջանի [Պնդ. 12.2]: Եվ թող գլանիկի բարձրությանը հավասար բարձությամբ պրիզմա կառուցված լինի ABCD քառակուսու վրա: Ուրեմն, կառուցված պրիզման գլանիկից ավելի քան կեսն է, քանի որ եթե մենք նաև արտագծենք քառակուսի ABCD շրջանի շուրջ [Պնդ. 4.7], ապա ABCD շրջանի ներգծված քառակուսին կեսն է արտագծված քառակուսու: Եվ դրանց վրա կառուցված մարմինները զուգահեռանիստ պրիզմաներ են՝ հավասար բարձրություններով: Իսկ զուգահեռանիստ մարմինները, որոնք ունեն նույն բարձրությունը, միմյանց հետ հարաբերակցում են իրենց հիմքերի նմանությամբ [Պնդ. 11.32]: Ուստի ABCD քառակուսու վրա կառուցված պրիզման կեսն է արտագծված քառակուսու վրա կառուցված պրիզմայի: Իսկ գլանիկը պակաս է արտագծված քառակուսու վրա կառուցված պրիզմայից: Ուստի ABCD քառակուսու վրա կառուցված պրիզման, որը գլանիկի բարձրության հետ նույնն է, գլանիկից ավելի քան կեսն է:
Թող AB, BC, CD և DA շրջագծերը կեսից կտրած լինեն E, F, G և H կետերում: Եվ թող AE, EB, BF, FC, CG, GD, DH և HA հատվածները միացված լինեն: Ուստի AEB, BFC, CGD և DHA եռանկյուններից յուրաքանչյուրն ավելի քան կեսն է իր շուրջ գտնվող ABCD շրջանի հատվածից, ինչպես արդեն ցույց է տրվել [Պնդ. 12.2]: Թող պրիզմաներ՝ գլանիկի բարձրությանը հավասար, կառուցված լինեն AEB, BFC, CGD և DHA եռանկյունների վրա: Իսկ կառուցված պրիզմաներից յուրաքանչյուրը գլանիկի իրենց շուրջ գտնվող հատվածի կեսից ավելին է, քանի որ եթե գծենք AB, BC, CD և DA ուղղահայացներին զուգահեռ գծեր՝ անցնող E, F, G և H կետերով և լրացնենք զուգահեռագծերը AB, BC, CD և DA վրա, ապա AEB, BFC, CGD և DHA եռանկյունների վրա կառուցված պրիզմաները յուրաքանչյուրը կեսն են կառուցված զուգահեռանիստների: Իսկ գլանիկի հատվածները պակաս են կառուցված զուգահեռանիստներից: Ուստի AEB, BFC, CGD և DHA եռանկյունների վրա կառուցված պրիզմաները նույնպես գլանիկի իրենց շուրջ հատվածների կեսից ավելին են:
Ուստի, եթե մնացած շրջագծերը կեսից կտրվեն, և հատվածները միացվեն, և յուրաքանչյուր եռանկյունի վրա գլանիկի բարձրության պրիզմաներ կառուցվեն, և սա շարունակաբար կրկնվի, ապա ի վերջո կմնան գլանիկի որոշ հատվածներ, որոնց գումարը պակաս է այն ավելցուկից, որով գլանիկը գերազանցում է կոնից երեք անգամին [Պնդ. 10.1]: Թող դրանք մնացած լինեն և կոչվեն AE, EB, BF, FC, CG, GD, DH և HA: Ուստի մնացած պրիզման, որի հիմքը բազմանկյուն AEBFCGDH է, և բարձրությունը գլանիկի բարձրությանը հավասար է, երեք անգամից ավելի մեծ է կոնից: Բայց պրիզման, որի հիմքը բազմանկյուն AEBFCGDH է, և բարձրությունը գլանիկի բարձրության հավասար է, երեք անգամ մեծ է այն բուրգից, որի հիմքը բազմանկյուն AEBFCGDH է, իսկ գագաթը նույնն է, ինչ կոնինը [Պնդ. 12.7 հ.]: Ուստի բուրգը, որի հիմքը բազմանկյուն AEBFCGDH է, իսկ գագաթը նույնն է, ինչ կոնինը, ավելի մեծ է, քան հիմքը ABCD շրջան ունեցող կոնը: Բայց նաև ավելի փոքր է, քանի որ ներառված է նրա մեջ: Սա անհնար է: Ուստի գլանիկը չի գերազանցում կոնին երեք անգամ:
Այսպիսով, գլանն էլ չէ պակաս երեք անգամ կոնիից։
Եվ այսպես, եթե հնարավոր է, թող գլանն ավելի քիչ լինի, քան երեք անգամ կոնիից։ Ուրեմն՝ հակադարձ, կոնն ավելի մեծ կլինի գլանի երրորդ մասից։ Թող ABCD քառակուսին ներգծված լինի ABCD շրջանին [Պնդ. 4.6]։ Այսպիսով, ABCD քառակուսին ավելի մեծ է ABCD շրջանի կեսից։ Թող կոնին նույն գագաթ ունեցող բուրգը կառուցված լինի ABCD քառակուսու վրա։ Այսպիսով, կառուցված բուրգն ավելի մեծ է կոնի կեսից, որովհետև նախորդիվ ցույց տվեցինք, որ եթե շրջանին արտագծենք քառակուսի [Պնդ. 4.7], ապա ABCD քառակուսին կլինի արտագծված քառակուսու կեսը [Պնդ. 12.2]։ Եվ եթե քառակուսիների վրա կառուցենք զուգահեռանիստներ, որոնք նաև կոչվում են պրիզմաներ, նույն բարձրությամբ, ինչ կոնը, ապա ABCD քառակուսու վրա կառուցված պրիզման կլինի արտագծված քառակուսու վրա կառուցված պրիզմայի կեսը։ Որովհետև դրանք համեմատական են իրենց հիմքերին [Պնդ. 11.32]։ Հետևաբար, նույնը ճիշտ է նաև երրորդ մասերի համար։ Այսպիսով, բուրգը, որի հիմքը ABCD քառակուսն է, կդառնա արտագծված քառակուսու վրա կառուցված բուրգի կեսը [Պնդ. 12.7 ճշտ.]։ Եվ արտագծված քառակուսու վրա կառուցված բուրգն ավելի մեծ է, քան կոնը, որովհետև այն ընդգրկում է այն։ Այսպիսով, բուրգը, որի հիմքը ABC'D քառակուսն է, և գագաթը նույնն է, ինչ կոնի գագաթը, ավելի մեծ է կոնի կեսից։
Թող AB, BC, CD և DA շրջանագծերը կիսով չափ բաժանվեն EF, F, G և H կետերով։ Եվ թող միացված լինեն AEF, EB, BF, FC, CG, GD, DH և HA։ Եվ այսպիսով, յուրաքանչյուր եռանկյունի՝ AEB, BFC, CGD և DHA, ավելի մեծ է իրենց համապատասխան շրջանի հատվածների կեսից [Պնդ. 12.2]։ Եվ թող կոնի գագաթին համապատասխան բուրգեր կառուցված լինեն յուրաքանչյուր եռանկյունու վրա։ Այսպիսով, նույն ձևով, յուրաքանչյուր կառուցված բուրգ ավելի մեծ է համապատասխան կոնի հատվածի կեսից։ Հետևաբար, եթե մնացած շրջագծերը կրկին բաժանվեն կիսով չափ, և միացվեն ուղիղ գծերով, և կոնի գագաթին համապատասխան բուրգեր կառուցվեն յուրաքանչյուր եռանկյունու վրա, և սա արվի շարունակաբար, ապա մենք (վերջապես) կթողնենք կոնի որոշ հատվածներ, որոնց գումարը կպակասի գլանի երրորդ մասից գերազանցող չափից [Պնդ. 10.1]։ Թող դրանք թողնված լինեն, և թող լինեն հատվածներ՝ AE, EB, BF, FC, CG, GD, DH և HA-ի վրա։ Այսպիսով, մնացած բուրգը, որի հիմքը AEBFCGDH բազմանկյունն է, և գագաթը նույնն է, ինչ կոնի գագաթը, ավելի մեծ է գլանի երրորդ մասից։ Բայց բուրգը, որի հիմքը AEBFCGDH բազմանկյունն է, և գագաթը նույնն է, ինչ կոնի գագաթը, գլանի երրորդ մասն է, որի հիմքը նույն բազմանկյունն է և բարձրությունը նույնն է, ինչ գլանի բարձրությունը [Պնդ. 12.7 ճշտ.]։
Այսպիսով, AEBFCGDH բազմանկյունի հիմքով և գլանի նույն բարձրությամբ պրիզման ավելի մեծ է, քան ABCD շրջանի հիմքով գլանը։ Բայց (այն) նաև փոքր է, որովհետև ընդգրկված է գլանի կողմից։ Սա անհնար է։ Այսպիսով, գլանն էլ չի կարող լինել պակաս երեք անգամ կոնիից։ Եվ արդեն ցույց է տրվել, որ այն չի կարող լինել ավելի մեծ, քան երեք անգամ կոնը։ Այսպիսով, գլանը (է) երեք անգամ կոնը։ Հետևաբար, կոնը գլանի երրորդ մասն է։
Այսպիսով, յուրաքանչյուր կոն գլանի երրորդ մասն է, որն ունի նույն հիմքը, ինչ այն և հավասար բարձրություն: Սա հենց այն, ինչ պահանջվում էր ցույց տալ:
Պնդում 11
Կոները և գլանները, որոնք ունեն նույն բարձրությունը, իրար հարաբերակցվում են իրենց հիմքերի հարաբերությամբ։
Թող լինեն նույն բարձրությամբ կոներ և գլաններ, որոնց հիմքերը [են] ABCD և EFGH շրջանները, առանցքները՝ KL և MN, և հիմքերի տրամագծերը՝ AC և EG (համապատասխանաբար)։ Ասում եմ, որ ինչպես ABCD շրջանն է EFGH շրջանի հետ հարաբերակցվում, այնպես էլ AL կոնը՝ EN կոնին։
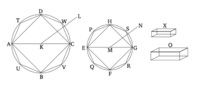
Եթե հնարավոր է, թող ABCD շրջանը EFGH շրջանի հետ հարաբերակցվում է այնպես, ինչպես AL կոնը՝ որոշ մարմնի, որը կամ ավելի փոքր է, կամ ավելի մեծ, քան EN կոնը։ Նախ թող այդ հարաբերակցությունը լինի ավելի փոքր մարմնի, Օ-ի հետ։ Եվ թող X մարմինը հավասար լինի այն մեծությանը, որով Օ մարմինը պակաս է EN կոնից։ Այսպիսով, EN կոնը հավասար է Օ և X մարմինների գումարին։ Թող EFGH շրջանի մեջ գրառված լինի EF'GH քառակուսին [Պնդ. 4.6]։ Այսպիսով, քառակուսին ավելի մեծ է, քան շրջանի կեսը [Պնդ. 12.2]։ Թող նույն բարձրությամբ կոնից, որը հիմնված է EF'GH քառակուսու վրա, կազմված լինի բուրգ։ Այսպիսով, կազմված բուրգը ավելի մեծ է կոնից, քանի որ, եթե շրջանի շուրջ արտագծենք քառակուսի [Պնդ. 4.7], և նրա վրա նույն բարձրությամբ բուրգ կազմենք, ապա գրառված բուրգը կլինի արտագծված բուրգի կեսը։ Քանի որ դրանք իրար հետ հարաբերակցվում են իրենց հիմքերի նմանությամբ [Պնդ. 12.6], իսկ կոնը պակաս է արտագծված բուրգից։
Թող EF, FG, GH և HE աղեղները բաժանված լինեն երկու մասի P, Q, R և S կետերում։ Եվ թող միացված լինեն HP, PE, EQ, QF, FR, RG, GS և SH։ Այսպիսով, HPE, EQF, FRG և GSH եռանկյուններից յուրաքանչյուրը մեծ է իրենց համապատասխան շրջանային հատվածների կեսից [Պնդ. 12.2]։ Թող նույն բարձրությամբ կոնից կազմված լինեն բուրգեր՝ հիմնված յուրաքանչյուր եռանկյան վրա։ Եվ այսպիսով, կազմված բուրգերից յուրաքանչյուրը մեծ է համապատասխան շրջանային հատվածի կեսից [Պնդ. 12.10]։
Այսպիսով, եթե մնացած աղեղները կրկին բաժանվեն կեսերի, ուղիղ գծեր միացվեն, և բուրգեր կազմվեն, ապա վերջապես կմնան կոնից հատվածներ, որոնց գումարը պակաս է X մարմնի ավելցուկից [Պնդ. 10.1]։ Թող դրանք մնան՝ հիմնված HPE, EQF, FRG և GSH եռանկյունների վրա։ Այսպիսով, մնացած բուրգը, որի հիմքը HPEQFRGS բազմանկյունն է, իսկ բարձրությունը՝ կոնին հավասար, ավելի մեծ է Օ մարմնից [Պնդ. 6.18]։
Հետևաբար, որպես հակասություն, պարզվեց, որ AL կոնը չի կարող հարաբերակցվել Օ մարմնի հետ։ Այսպիսով, հաստատվեց, որ կոները և գլանները, որոնք ունեն նույն բարձրությունը, իրար հետ հարաբերակցվում են իրենց հիմքերի հարաբերությամբ։
Ուստի, ես ասում եմ, որ ոչ ոք չի կարող ասել, թե շրջան ABCD-ը շրջան EFGH-ին համեմատած, ինչպես կոն AL-ը համեմատած որևէ մարմնի, որը ավելի մեծ է քան կոնե EN-ը:
Որպեսզի, եթե հնարավոր է, թող այն (նման հարաբերությամբ) լինի (ինչ-որ) մեծ (մարմին), O: Այսպիսով, հակառակաբար, ինչպես ABCD շրջանագիծն է EFGH շրջանագծի նկատմամբ, այնպես էլ մարմին O-ն է կոն AL-ի նկատմամբ [Պնդ. 5.7 շտկում]: Բայց, ինչպես մարմին O-ն է կոն AL-ի նկատմամբ, այնպես էլ կոն EN-ն է (մի տեսակ) մարմնի նկատմամբ, որը փոքր է կոն AL-ից [Պնդ. 12.2 մոտ.]: Եվ այսպես, ինչպես EFGH շրջանագիծն է ABCD շրջանագծի նկատմամբ, այնպես էլ կոն EN-ն է (մի տեսակ) մարմնի նկատմամբ, որը փոքր է կոն AL-ից: Միևնույնն է, դա անհնար էր: Այսպիսով, ABCD շրջանագիծը չի համապատասխանում EFGH շրջանագծին, ինչպես կոն AL-ն է (մի տեսակ) մարմնի նկատմամբ, որը մեծ է կոն EN-ից: Եվ, ինչպես ցույց տրված էր, ոչ էլ (նման հարաբերությամբ) այն համապատասխանում է (ինչ-որ) փոքր մարմնի: Այսպիսով, ինչպես ABCD շրջանագիծն է EFGH շրջանագծի նկատմամբ, այնպես էլ կոն AL-ն է կոն EN-ի նկատմամբ:
Բայց, ինչպես կոնը (է) կոնին, այնպես էլ գլանը (է) գլանին: Մանրամասն, ամեն մեկը երեք անգամ է յուրաքանչյուրին [Պնդ. 12.10]: Այսպիսով, ABCD շրջանագիծը նույնպես համապատասխան է EFGH շրջանագծին, ինչպես (գլանների հարաբերությունը) նրանց վրա (որոնք ունեն) նույն բարձրությունը:
Այսպիսով, նույն բարձրություն ունեցող կոները և գլանները իրար նկատմամբ են ինչպես իրենց բազաները: Իրականում դա հենց այն բանն է, որը պետք է ապացուցվեր:
Պնդում 12
Նման կոները և գլանները միմյանց հարաբերակցված են իրենց հիմքերի տրամագծերի խորացված հարաբերակցությամբ:
Թող լինեն համապատասխան կոներ և գլաններ, որոնց հիմքերը լինեն ABCD և EFGH շրջանները, հիմքերի տրամագծերը լինեն BD և FH, իսկ կոների և գլանների առանցքները լինեն KL և MN (համապատասխանաբար): Իմ հայտարարությունն է, որ այն կոնը, որի հիմքն է ABCD շրջանը, իսկ գագաթը՝ L կետը, կապված է այն կոնի հետ, որի հիմքն է EFGH շրջանը, իսկ գագաթը՝ N կետը, նրանց միջև կա BD-ի և FH-ի խորացված հարաբերակցությունը:
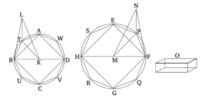
Եթե ABCDL կոնը չունի այնպիսի խորացված հարաբերակցություն, որը BD-ն ունի FH-ի հետ EFGHN կոնի նկատմամբ, ապա ABCDL կոնը կունենա նույն խորացված հարաբերակցությունը մի մարմնի հետ, որը կամ պակաս կլինի, կամ ավելին կլինի EFGHN կոնից: Նախ, թող այն ունենա (այդպիսի հարաբերակցություն) (ինչ-որ) պակաս (մարմնի), O-ի հետ: Եվ թող EFGH քառակուսին ներթղվել լինի EFGH շրջանի մեջ [Պնդ. 4.6]: Այսպես, EFGH քառակուսին մեծ է EFGH շրջանի կեսից [Պնդ. 12.2]: Եվ թող պիրամիդը, որը նույն խ顶ակն ունի, ինչ կոնը, տեղադրվի EFGH քառակուսի վրա: Այսպիսով, տեղադրված պիրամիդը մեծ է կոնի կեսից [Պնդ. 12.10]: Այդպես, թող EF’, FG, GH, և HE շրջանաձևությունները կտրեն կեսում P, Q, R, և S կետերում (համապատասխանաբար): Եվ թող EP, PF, FQ, QG, GR, RH, HS, և SE միանան: Եվ այսպես, յուրաքանչյուր EPF, FQG, GRH, և HSE եռանկյունիները մեծ են EFGH շրջանի հատվածի կեսից, որը նրանց շուրջն է [Պնդ. 12.2]: Եվ թող պիրամիդը, որը նույն խ顶ակն ունի, ինչ կոնը, տեղադրվի յուրաքանչյուր EPF, FQG, GRH, և HSE եռանկյան վրա: Եվ այսպես, յուրաքանչյուր տեղադրված պիրամիդը մեծ է կոնի հատվածի կեսից, որը դրա շուրջն է [Պնդ. 12.10]: Այսպես, (եթե) մնացած շրջանակաները կտրեն կեսում, և ուղղահայաց գծեր միանան, և պիրամիդներ, որոնք նույն խ顶ակն ունեն, ինչ կոնը, տեղադրվեն յուրաքանչյուր եռանկյան վրա, և սա անընդհատ շարունակվի, ապա մենք, վերջապես, կթողնենք կոնի մի քանի հատվածներ, որոնց (հավաքածուն) պակաս կլինի այն ավելցուկից, որով EFGHN կոնը գերազանցում է O մարմինը [Պնդ. 10.1]: Թող նրանք մնան, և թող դրանք լինեն (հավաքածուն) EP, PF, FQ, QG, GR, RH, HS, և SE վրա գտնվող հատվածները: Եվ այսպես, մնացած պիրամիդը, որի հիմքը բազմաբազմյուն EPFQGRHS է, և խ顶ակը՝ NV կետը, մեծ է O մարմնից: Եվ թող բազմաբազմյուն AT BUCV DW, որը նման է և նմանապես դասավորված է EPFQGRHS բազմաբազմյանը, լինի ABCD շրջանի մեջ տեղադրված [Պնդ. 6.18]: Եվ թող պիրամիդը, որի նույն խ顶ակն ունի, ինչ կոնը, տեղադրվի ATBUCV DW բազմաբազմյակի վրա: Եվ թող LBT լինի այն եռանկյունիներից մեկը, որը պարունակում է պիրամիդը, որի հիմքը AT BUCV DW բազմաբազմյակը, և խ顶ակը՝ L կետը: Եվ թող NFP լինի այն եռանկյունիներից մեկը, որը պարունակում է պիրամիդը, որի հիմքը EPFQGRHS եռանկյունին է, և խ顶ակը՝ NV կետը: Եվ թող KT և MP միացած լինեն: Եվ քանի որ ABCDL կոնը նման է EFGHN կոնին, ապա ինչպես BD-ն է FH-ի հետ, այնպես էլ առանցք KL-ը՝ առանցք MN-ին [Դեֆ. 11.24]: Եվ ինչպես BD-ն է FH-ի հետ, այնպես էլ BK-ն է FM-ի հետ: Եվ այդպես, ինչպես BK-ն է FM-ի հետ, այնպես էլ KL-ը՝ MN-ի հետ: Եվ այլ կերպ ասած, ինչպես BK-ն է KL-ի հետ, այնպես էլ FM-ը՝ MN-ի հետ [Պնդ. 5.16]: Եվ նույնական անկյուններով BK L և FMN-ի շուրջ գտնվող կողմերը համահունչ են: Այսպիսով, եռանկյունը BK L նման է եռանկյան FMN-ի [Պնդ. 6.6]: Այնպես որ, քանի որ ինչպես BK-ն է KT-ի հետ, այնպես էլ FM-ն է MP-ի հետ, և նրանք գտնվում են հավասար անկյուններով BKT և FMP, քանի որ ինչ-որ մասը BKT անկյունից, որը K կենտրոնում գտնվող չորս ուղղանկյուններից է, FMP անկյունը նույնպես նույն մասն է չորս ուղղանկյուններից՝ M կենտրոնում: Ուստի, քանի որ հավասար անկյուններով կողմերը համահունչ են, եռանկյունը BAT նման է եռանկյան FMP-ին [Պնդ. 6.6]: Դարձյալ, քանի որ ցույց տրվեց, որ ինչպես BK-ն է KL-ի հետ, այնպես էլ FM-ն է MN-ի հետ, և BK-ն հավասար է KT-ին, իսկ FM-ն՝ PM-ին, ապա ինչպես TK-ն է KL-ի հետ, այնպես էլ PM-ն՝ MN-ի հետ: Եվ հավասար անկյուններով TKL և PMN — քանի որ դրանք երկուսն էլ ուղղանկյուններ են — կողմերը համահունչ են: Այսպիսով, եռանկյունը LKT նման է եռանկյունի NMP-ին [Պնդ. 6.6]: Եվ քանի որ, համաձայն եռանկյունների LK B և NMF նմանության, ինչպես LB-ն է BK-ի հետ, այնպես էլ NF-ն է FM-ի հետ, և համաձայն եռանկյունների BKT և FMP նմանության, ինչպես KB-ն է BT-ի հետ, այնպես էլ MF-ն է FP-ի հետ [Դեֆ. 6.1], ուստի, հավասարությամբ, ինչպես LB-ն է BT-ի հետ, այնպես էլ NF-ն է FP-ի հետ [Պնդ. 5.22]: Դարձյալ, քանի որ, համաձայն եռանկյունների LT K և NPM նմանության, ինչպես LT-ն է TK-ի հետ, այնպես էլ NP-ն է PM-ի հետ, և համաձայն եռանկյունների TK B և PMF նմանության, ինչպես KT-ն է TB-ի հետ, այնպես էլ MP-ն է PF-ի հետ, ուստի, հավասարությամբ, ինչպես LT-ն է TB-ի հետ, այնպես էլ NP-ն է PF-ի հետ [Պնդ. 5.22]: Եվ ցույց է տրված, որ ինչպես TB-ն է BL-ի հետ, այնպես էլ PF-ն է FN-ի հետ: Ուստի, հավասարության միջոցով, ինչպես TL-ն է LB-ի հետ, այնպես էլ PN-ն է NF-ի հետ [Պնդ. 5.22]: Այսպիսով, LTB և NPF եռանկյունների կողմերը համահունչ են: Այսպիսով, LTB և NPF եռանկյունները հավասարանկյուն են [Պնդ. 6.5]: Եվ, հետևաբար, (նրանք) նման են [Դեֆ. 6.1]: Եվ, այսպես, այն պիրամիդը, որի հիմքը BKT եռանկյունն է, և գագաթը L կետն է, նման է այն պիրամիդին, որի հիմքը FMP եռանկյունն է, և գագաթը N կետն է: Չնայած որ նրանք պարունակում են նույն թիվն էլ նման թռուցիկներից [Դեֆ. 11.9]: Եվ նման պիրամիդները, որոնք նաև եռանկյունային հիմքեր ունեն, գտնվում են համապատասխան կողմերի խորացված հարաբերակցությունում [Պնդ. 12.8]: Այսպիսով, պիրամիդ BKTL-ն ունի պիրամիդ F'M PN-ին այն խորացված հարաբերակցությունը, որը ունի BK-ն՝ FM-ի հետ: Իսկ նմանապես, միացնելով ուղիղ գծեր (A, W, D, V, C և U կետերից) (կենտրոն) K-ի և (FE, S, H, R, G և Q կետերից) (կենտրոն) M-ի, և կանգնեցնելով պիրամիդներ, որոնց նույն գագաթները ունեն կոները յուրաքանչյուր եռանկյունում (որոնք ձևավորվում են), մենք նույնպես կարող ենք ցույց տալ, որ յուրաքանչյուր պիրամիդը (ABCԴ հիմքով) հերթով կունենա այն խորացված հարաբերակցությունը, որը կապված է համապարփակ կողմերի BK-ի հետ՝ համապատասխան կողմերի F4—այսինքն՝ BD-ի հետ՝ FH-ի նկատմամբ: Եվ (երկու sets համար համապարփակ չափերի) ինչպես մեկը առաջնորդող (չափը) է հաջորդներից մեկին, այնպես էլ (առաջնորդող չափերի) ամբողջությունը համամասն է (հաջորդ չափերի) ամբողջությանը [Պնդ. 5.12]: Եվ, այսպես, ինչպես պիրամիդը BKTL-ն է պիրամիդին F.MPN-ին, այնպես էլ ամբողջ պիրամիդը, որի հիմքն է բազմանկյուն AT BUCV DW, և գագաթը L կետն է, համամասն է ամբողջ պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը NV կետն է: Եվ, հետեւաբար, այն պիրամիդը, որի հիմքն է բազմանկյուն AT BUCV DW, և գագաթը L կետն է, համամասն է այն պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է, այն խորացված հարաբերակցությանը, որը BD-ն ունի FH-ի հետ: Եվ նաև ենթադրվել է, որ կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, համամասն է մարմնին O այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ: Այսպիսով, ինչպես կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, համամասն է մարմնին O, այնպես էլ այն պիրամիդը, որի հիմքն է [բազմանկյուն] AT BUCV DW, և գագաթը L կետն է, համամասն է այն պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է: Այդպես, փոխարենը, ինչպես կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, համամասն է նրա մեջ գտնվող պիրամիդին, որի հիմքն է բազմանկյուն ATBUCV DW, և գագաթը L կետն է, այնպես էլ [մարմին] O-ն համամասն է պիրամիդին, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է [Պնդ. 5.16]: Եվ հիշատակված կոնը մեծ է նրանից պիրամիդին: Այն շրջապատում է այն: Այսպիսով, մարմինը O-ն նույնպես մեծ է այն պիրամիդից, որի հիմքն է բազմանկյուն EPFQGRHS, և գագաթը N կետն է: Բայց, այն նաև փոքր է: Հենց այսը անհնար է: Այսպիսով, կոնը, որի հիմքը ABCD շրջան է, և գագաթը L կետն է, չի համամասնվում որևէ մարմնի, որը փոքր է կոնից, որի հիմքը EFGH շրջան է, և գագաթը N կետն է, այն խորացված հարաբերակցությամբ, որը BD-ն ունի EH-ի հետ: Այսպիսով, նույն ձևով, մենք կարող ենք ցույց տալ, որ EFGHN կոնը նույնպես չի համամասնվում որևէ մարմնի, որը փոքր է ABCDL կոնից, այն խորացված հարաբերակցությամբ, որը FH-ն ունի BD-ի հետ:
Այսպիսով, ես ասում եմ, որ ABC'DL կոնը չի համամասնվում որևէ մարմնի, որը մեծ է EFGHN կոնից, այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ:
Իրովի, եթե հնարավոր է, թող այն ունենա (համար) ավելի մեծ (մարմնի) O: Այսպիսով, հակառակը, մարմինը O-ն համամասն է ABCDL կոնին այն խորացված հարաբերակցությամբ, որը FH-ն ունի BD-ի հետ [Պնդ. 5.7 շտ.]: Եվ ինչպես մարմինը O-ն (է) ABCDL կոնին, այնպես էլ EFGHN կոնը (է) որևէ մարմնի համամասն, որը փոքր է ABCDL կոնից [12.2 քառ.]։ Այսպիսով, EFGHN կոնը նույնպես համամասն է որևէ մարմնի, որը փոքր է ABCDL կոնից, այն խորացված հարաբերակցությամբ, որը F'H-ն ունի BD-ի հետ: Նույնը ցույց տվեց, որ անհնար է: Այսպիսով, ABCDL կոնը չի համամասնվում որևէ մարմնի, որը մեծ է EFGHN կոնից, այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ: Եվ ցույց տրվեց, որ այն նաև չի ունենում (այդպիսի հարաբերակցություն) որևէ ավելի փոքր մարմնի հետ: Այսպիսով, ABCDL կոնը համամասն է EFGHN կոնին այն խորացված հարաբերակցությամբ, որը BD-ն ունի FG-ի հետ:
Եվ ինչպես կոնը կոնին, այնպես էլ գլանը գլանին: Քանզի գլանը երեք անգամ է կոնից նույն հիմքով և նույն բարձրությամբ [Պնդ. 12.10]: Այսպիսով, գլանը նույնպես ունի գլանին այն խորացված հարաբերակցությամբ, որը BD-ն ունի FH-ի հետ:
Այսպիսով, նման կոներն ու գլանները գտնվում են իրենց հիմքերի տրամագծերի խորացված հարաբերակցությունում: Եվ սա է այն, ինչը պետք էր ապացուցել:
Պնդում 13
Եթե գլանը կտրվի մի հարթությամբ, որը զուգահեռ է գլանի հակառակ մակերեսներին, ապա ինչպես գլանն է հարաբերվում գլանին, այնպես էլ առանցքը՝ առանցքին:
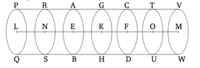
Թող գլանը AD կտրվի GH հարթությամբ, որը զուգահեռ է գլանի հակառակ մակերեսներին՝ AB և CD: Եվ թող GH հարթությունը հանդիպի առանցքին K’ կետում: Ասում եմ, որ ինչպես գլանն է BG-ին, այնպես էլ առանցքը EK-ն է՝ առանցքին KF:
Եվ թող առանցքը EF շարունակվի յուրաքանչյուր ուղղությամբ դեպի L և M կետերը։ Եվ թող որևէ թիվ, որ ուղղության վրա EN և NL, հավասար լինի առանցք EK-ին, նշված լինի առանցք EL-ի վրա, և որևէ թիվ, որ ուղղության վրա FO և OM, հավասար լինի առանցք FK-ին, նշված լինի առանցք KM-ի վրա։ Եվ թող գլան PW-ն, որի հիմքերը լինեն շրջանակները PQ և VW, կազմավորվի առանցք LM-ի վրա։ Եվ թող հարթություններ, որոնք զուգահեռ են AB-ին, CD-ին և գլան PW-ի հիմքերին, անցնեն N և O կետերից, և թող դրանք կազմեն շրջանակներ RS և TU, համապատասխանաբար, կենտրոններում N և O։ Եվ քանի որ առանցքները LN, NE և EK հավասար են միմյանց, գլանները QR, RB և BG միմյանց հետ կապված են իրենց հիմքերի հարաբերակցությամբ [Պնդ. 12.11]։ Բայց հիմքերը հավասար են։ Այսպես, գլանները QR, RB և BG նույնպես հավասար են միմյանց։ Այնպես որ, քանի որ առանցքները LN, NE և EK հավասար են միմյանց, և գլանները QR, RB և BG նույնպես հավասար են միմյանց, և նրանց թիվը հավասար է միմյանց, ապա ինչպես շատ բազմապատիկներ, որքան առանցք KL-ն է առանցք EK-ի, այնքան շատ բազմապատիկներ է գլան QG-ն նաև գլան GB-ի։ Եվ այդպես, նույն (պատճառներով), ինչպես շատ բազմապատիկներ, որքան առանցք MK-ն է առանցք KF-ի, այնքան շատ բազմապատիկներ է գլան WG-ն նույնպես գլան GD-ի։ Եվ եթե առանցք KL-ն հավասար է առանցք KM-ին, ապա գլան QG-ն նույնպես հավասար կլինի գլան GW-ի, և եթե առանցքը մեծ է քան առանցքը, ապա գլանը նույնպես մեծ կլինի քան գլանը, և եթե (առանցքը) փոքր է, ապա (գլանը) նույնպես փոքր կլինի։ Ուստի, կան չորս չափեր՝ առանցքներ EK և KF, և գլաններ BG և GD, և հավասար բազմապատիկներ են վերցվել առանցք EK-ից և գլան BG-ից՝ (պատրաստված) առանցք LK և գլան QG՝ և առանցք KF-ից և գլան GD-ից՝ (պատրաստված) առանցք KM և գլան GW։ Եվ ցույց է տրվել, որ եթե առանցք KL-ն մեծ է քան առանցք KM-ը, ապա գլան QG-ն նույնպես մեծ է քան գլան GW-ն, և եթե (առանցքները) հավասար են, ապա (գլանները) հավասար են, և եթե (KL-ն) փոքր է, ապա (QG-ն) փոքր է։ Ավելին, ինչպես առանցք EK-ն է՝ առանցք KF-ի, այնպես էլ գլան BG-ն է՝ գլան GD-ի [Անշ. 5.5]։ Այսինքն, սա հենց այն, ինչը պետք էր ցույց տալ։
Պնդում 14
Կոները և գլանները, որոնք ունեն հավասար հիմքեր, միմյանց նկատմամբ են, ինչպես իրենց բարձրությունները։
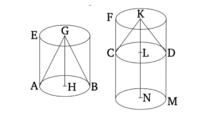
Թող EB և FD լինեն գլաններ հավասար հիմքերով՝ namely՝ շրջաններ AB և CD (համապատասխանաբար): Ես ասում եմ, որ ինչպես գլանը FB է գլանին F'D, այնպես էլ առանցքը GH է առանցքին KL:
Թող առանցքը KL ձգվի դեպի N կետը: Եվ թող LN-ը հավասար լինի առանցք GH-ի: Եվ թող գլան CM գծվի LN առանցքի շուրջ: Դրա համար, քանի որ գլանները EB և C'M ունեն նույն բարձրությունը, նրանք միմյանց համապատասխան են որպես իրենց հիմքեր [Պնդ. 12.11]: Եվ հիմքերը հավասար են միմյանց: Ապա, գլաններ EB և CM նույնպես հավասար են միմյանց: Եվ քանի որ գլանը F'M կտրվել է C'D հարթությամբ, որը զուգահեռ է նրա հակառակ հարթություններին, ապա ինչպես գլանը CM է գլանին FD, այնպես էլ առանցքը LN է առանցքին KL [Պնդ. 12.13]: Եվ գլանը C'M հավասար է գլանին EB, և առանցքը LN հավասար է առանցք GH-ին: Դրա համար, ինչպես գլանը EB է գլանին F'D, այնպես էլ առանցքը GH է առանցքին KL: Եվ ինչպես գլանը FB է գլանին F'D, այնպես էլ կոնը ABG է կոնին CDK [Պնդ. 12.10]: Ապա, նաև, ինչպես առանցքը GH է առանցքին KL, այնպես էլ կոնը ABG է կոնին CDK, և գլանը EB գլանին FD: Սա այն ամենն է, ինչը պահանջվում էր ապացուցել:
Պնդում 15
Հավասար կոների և գլանների հիմքերը փոխադարձաբար համամասն են իրենց բարձրություններին: Եվ նրանք, ում կոները և գլանները հիմքերը փոխադարձաբար համամասն են իրենց բարձրություններին, հավասար են:
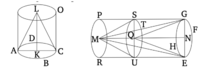
Թող լինեն հավասար կոներ և գլաններ, որոնց հիմքերը ABCD և EFGH շրջաններն են, և դրանց հիմքերի տրամագծերը AC և EG, իսկ առանցքները KL և MN են, որոնք նույնպես են կոների և գլանների բարձրությունները (հարգերով): Եվ թող գլանները AO և EP կառուցվեն: Ես ասում եմ, որ գլանների AO և EP հիմքերը փոխադարձաբար համամասն են նրանց բարձրություններին, և այնպես, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN՝ բարձրությանը KL:
Թող բարձրությունը LK կամ հավասար լինի բարձրությանը MN, կամ ոչ: Առաջին հերթին թող այն հավասար լինի: Եվ գլան AO-ն նույնպես հավասար է գլան EP-ին: Եվ այն կոներն ու գլանները, որոնք ունեն նույն բարձրությունը, միմյանց համեմատվում են իրենց հիմքերին ըստ [Պնդ. 12.11]: Այդպես, հիմք ABCD-ն նույնպես հավասար է հիմք EFGH-ին: Եվ հետևաբար, փոխադարձաբար, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN՝ բարձրությանը KL: Եվ հիմա թող բարձրությունը LK չհավասարվի MN-ին, սակայն թող WN-ն ավելի մեծ լինի: Եվ թող QN, որը հավասար է KL-ին, կտրի բարձրությունից MN: Եվ թող գլան EP-ն կտրի, Q կետից, TUS հարթությամբ (որը) զուգահեռ է EFGH և RP շրջանների հարթությունների հետ: Եվ թող գլան ES-ն կառուցվի, որի հիմքը EFGH շրջանն է, և բարձրությունը NQ: Եվ քանի որ գլան AO-ն հավասար է գլան EP-ին, ապա ինչպես գլան AO-ն է գլան ES-ին, այնպես էլ գլան EP-ն է գլան E'S-ին [Պնդ. 5.7]: Իսկ քանի որ ինչպես գլան AO-ն է գլան E'S-ին, այնպես էլ հիմքը ABCD-ն է հիմքին EFGH: Որովհետև գլան AO-ն և ES-ն ունեն նույն բարձրությունը [Պնդ. 12.11]: Եվ ինչպես գլան EP-ն է գլան E'S-ին, այնպես էլ բարձրությունը MN-ն է բարձրությանը QN: Որովհետև գլան EP-ն կտրել է հարթությամբ, որը զուգահեռ է իր հակառակ հարթություններին [Պնդ. 12.13]: Եվ այսպես, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN-ն է բարձրությանը QN [Պնդ. 5.11]: Եվ բարձրությունը QN-ն հավասար է բարձրությանը KL: Այսպիսով, ինչպես հիմքը ABCD է հիմքին EFGH, այնպես էլ բարձրությունը MN-ն է բարձրությանը KL: Այսպիսով, գլան AO-ի և EP-ի հիմքերը փոխադարձաբար համեմատելի են նրանց բարձրություններին:
Եվ այսպես, թող գլան AO-ի և EP-ի հիմքերը փոխադարձաբար համեմատելի լինեն նրանց բարձրություններին, և (այսպիսով) թող հիմքը ABCD լինի հիմքի EFGH-ի նկատմամբ, ինչպես բարձրությունը MN-ն է բարձրությանը AL: Ասում եմ, որ գլան AO-ն հավասար է գլան EP-ին:
Քանի որ նույն կառուցվածքով, քանի որ ինչպես հիմքը ABCD է հիմքին EFGH-ի, այնպես էլ բարձրությունը MN-ը՝ բարձրությանը KL, և բարձրությունը KL-ը հավասար է բարձրությանը QN, ապա ինչպես հիմքը ABCD է հիմքին EFGH-ի, այնպես էլ բարձրությունը MN-ը կլինի բարձրությանը QN: Բայց ինչպես հիմքը ABCD է հիմքին EFGH-ի, այնպես էլ գլան AO-ն է գլան E'S-ին: Քանի որ դրանք նույն բարձրությունն ունեն [Պնդ. 12.11]: Եվ ինչպես բարձրությունը MN-ը՝ [բարձրություն] QN-ին, այնպես էլ գլան EP-ն է գլան E'S-ին [Պնդ. 12.13]: Այսպիսով, ինչպես գլան AO-ն է գլան E'S-ին, այնպես էլ գլան EP-ն է (գլան) E'S-ին [Պնդ. 5.11]: Այսպիսով, գլան AO-ն հավասար է գլան EP-ին [Պնդ. 5.9]: Նույն կերպ, (առարկան) նույնպես (կարող է) ցույց տրվել կոների համար: Դա է այն, ինչ պահանջվում էր ցույց տալ:
Պնդում 16
Իրավիճակում, որտեղ երկու շրջաններ կան նույն կենտրոնի շուրջ, ավելի մեծ շրջանում ներբեռնել հավասարաչափ և զույգ կողմերով բազմակողմանիություն, որը չի շոշափում փոքր շրջանը:
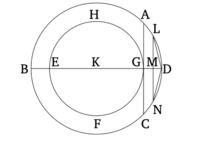
Թող ABCD և EFGH լինեն տրված երկու շրջաններ, որոնք ունեն նույն K կենտրոնը։ Ուրեմն, անհրաժեշտ է ներբեռնել հավասարաչափ և զույգ կողմերով բազմակողմանիություն ավելի մեծ ABCD շրջանում, որը չի շոշափում EFGH շրջանը։
Թող ուղղաձիգ BD ուղղությամբ անցնի ուղիղ գիծ BK Դ, K կենտրոնով։ Եվ թող GA գիծը տրվել լինի, որը դրված է BD ուղղությանը զուգահեռ՝ G կետով, և թող այն գիծը լինի C կետին ուղղված։ Ուրեմն, AC-ն շոշափում է EFGH շրջան։ Եվ, եթե կտրենք BAD շրջանի շրջագիծը կեսով, իսկ հետո կեսը՝ նորից կեսի, և շարունակենք այսպես, մենք, վերջապես, կթողնենք մի շրջագիծ, որը պակաս է AD-ից [Պնդ. 10.1]։ Թող այսպիսով մնա, և թող այն լինի LD։ Եվ թող LM գիծը լինի, որը L-ից ուղղահայաց է BD-ին, և թող այն անցնի NV կետով։ Եվ թող LD և DN համախառնվեն։ Ուրեմն, LD-ը հավասար է DN-ին [Պնդ. 3.3, 1.4]։ Եվ քանի որ LN-ը զուգահեռ է AC-ին [Պնդ. 1.28], և AC-ն շոշափում է EFGH շրջան, ապա LN-ն նույնպես չի շոշափում EFGH շրջանը։ Ուրեմն, առավել ևս, LD-ն և DN-ը չեն շոշափում EFGH շրջան։ Եվ եթե շարունակաբար տեղադրենք LD-ի երկարությամբ ուղիղ գծեր ABCD շրջանում [Պնդ. 4.1], ապա հավասարաչափ և զույգ կողմերով բազմակողմանիություն, որը չի շոշափում փոքր EFGH շրջանը, կտեղադրվի ABCD շրջանի մեջ։ (Այսինքն) այն բանն է, որ պահանջվում էր անել։
Պնդում 17
Ուրեմն լինելով երկու գնդեր նույն կենտրոնով, որպեսզի մեծ գնդի մեջ տեղադրվի բազմանիստ պինդ մարմին, որը չի շոշափում փոքր գնդի մակերեսը։
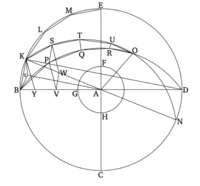
Թող, երկու գնդեր գծված լինեն նույն կենտրոն A-ով: Ուստի, անհրաժեշտ է ներգծել բազմանիստ մարմին մեծ գնդի մեջ, որը չի շոշափում փոքր գնդի մակերեսը:
Թող գնդերը կտրվեն ինչ-որ հարթությամբ, որը անցնում է կենտրոնից։ Ուստի, հատումները կլինեն շրջաններ, քանի որ գունդը ձևավորվում է մնացած տրամագծով, և կիսաշրջանը շրջվում է [Նիշ. 11.14]։ Եվ հետևաբար, որևիցե դիրք, որը կմտածենք կիսաշրջանի համար, հարթությունը, որը դրա վրայով անցկացվում է, կկազմի շրջան գնդի մակերեսի վրա։ Եվ ակնհայտ է, որ դա նույնպես մեծ (շրջան է), քանի որ գնդի տրամագիծը, որն ակնհայտորեն նաև կիսաշրջանի և շրջանի տրամագիծն է, ավելի մեծ է, քան բոլոր մյուս (ուղղահայացները), որոնք անցնում են շրջանում կամ գնդի մեջ [Պնդ. 3.15]։ Ուստի, թող BCDE լինի շրջան մեծ գնդում, իսկ FGH՝ շրջան փոքր գնդում։ Եվ թող նրանցից երկու տրամագիծներ քաղված լինեն իրարահակառակ ուղղությամբ, (հատկապես), BD և CE։ Եվ լինելով երկու շրջաններ նույն կենտրոնով՝ (այսինքն) BCDE և FGH՝ թող լինի հավասարաչափ և զույգ կողմերով պոլիգոն, որը գտնվել է մեծ շրջանի BCDE մեջ, առանց շփվելու փոքր շրջանի FGH-ի հետ [Պնդ. 12.16], որի կողմերը չորրորդանկյունում BE կլինեն BK, KL, LM և ME։ Եվ երբ KA միացվի, թող այն անցնի մինչև N։ Եվ թող AO-ն լիներ կանգնեցված A կետում, շրջանի BCDE-ի հարթության հետ ուղղահայաց։ Եվ թող այն հատեր (մեծ) գնդի մակերեսը O կետում։ Եվ թող հարթություններ լինեն անցկացված AO-ի և յուրաքանչյուր BD և KN-ի միջոցով։ Ուստի, ըստ վերոնշյալ քննարկման, դրանք կկազմեն մեծ շրջաններ (մեծ) գնդի մակերեսի վրա։ Թող նրանք կազմեն (մեծ շրջաններ), որոնցից BOD և KON կիսաշրջաններ կլինեն BD և KN տրամագծերի վրա (համապատասխանաբար)։ Եվ քանի որ OA-ն ուղղահայաց է BCDE շրջանի հարթությանը, բոլոր այն հարթությունները, որոնք անցնում են OA-ով, նույնպես կլինեն ուղղահայաց BCDE շրջանի հարթությանը [Պնդ. 11.18]։ Եվ այդպիսով, կիսաշրջանները BOD և KON նույնպես ուղղահայաց կլինեն BCDE շրջանի հարթությանը։ Եվ քանի որ կիսաշրջանները BED, BOD և KON հավասար են՝ քանի որ դրանք գտնվում են հավասար տրամագծերի BD և KN վրա [Պար. 3.1]՝ չորրորդանկյունները BE, BO և KO նույնպես հավասար են միմյանց։ Այդպիսով, որքան շատ կողմեր կան պոլիգոնում, որոնք գտնվում են BE չորրորդանկյունում, նույնքան էլ կան BO և KO չորրորդանկյուններում հավասար դեպի ուղիղ գծեր BK, KL, LM և ME։ Թող դրանք լինեն ներմուծված, և թող դրանք լինեն BP, PQ, QR, RO, KS, ST, TU և UO։ Եվ թող SP, TQ և UR միացվեն։ Եվ թող ուղղահայացներ լինեն անցկացված P և S կետերից դեպի BCDE շրջանի հարթություն [Պնդ. 11.11]։ Այնպես որ, նրանք կընկնեն BD և KN հարթությունների համատեղ հատվածների վրա (BCDE-ի հետ), քանի որ BOD և KON հարթությունները նույնպես ուղղահայաց են BCDE շրջանի հարթությանը [Պար. 11.4]։ Թող նրանք ընկնեն, և թող դրանք լինեն PV և SW։ Եվ թող WV-ը միացվի։ Եվ քանի որ BP և KS հավասար են (շրջաններ), որոնք կտրվել են հավասար կիսաշրջաններում BOD և KON [Պար. 3.28], և PV և SW-ը ուղղահայացներ են, որոնք անցկացվել են (նրանցից), PV-ն [այդպիսով] հավասար է SW-ին, և BV-ն՝ KW-ին [Պնդ. 3.27, 1.26]։ Եվ ամբողջ BA-ն նույնպես հավասար է ամբողջ KA-ին։ Եվ այդպիսով, ինչպես BV-ն է VA-ի նկատմամբ, այնպես էլ KW-ն՝ WA-ի նկատմամբ։ WV-ն այդպիսով զուգահեռ է KB-ին [Պնդ. 6.2]։ Եվ քանի որ PV և SW-ը յուրաքանչյուրն ուղղահայաց են BCDE շրջանի հարթությանը, PV-ն այդպիսով զուգահեռ է SW-ին [Պնդ. 11.6]։ Եվ նաև ցույց տրվել է (որ դրանք) հավասար են։ Եվ այդպիսով, WV և SP հավասար և զուգահեռ են [Պնդ. 1.33]։ Եվ քանի որ WV-ն զուգահեռ է SP-ին, բայց WV-ն զուգահեռ է KB-ին, SP-ն այդպիսով նաև զուգահեռ է KB-ին [Պնդ. 11.1]։ Եվ BP-ն և KS-ն միացնում են դրանք։ Այսպիսով, KBPS քառանկյունը գտնվում է մեկ հարթության մեջ, քանի որ եթե երկու զուգահեռ ուղղաձիգներ լինեն, և յուրաքանչյուրում վերցվի մի պատահական կետ, ապա այդ կետերը միացնող ուղղահայացը կլինի նույն հարթության մեջ, որտեղ գտնվում են զուգահեռ ուղղաձիգները [Պար. 11.7]։ Այդպես, նույն (պատճառներով), SPQT և TQRU քառանկյունները նույնպես գտնվում են մեկ հարթության մեջ։ Եվ URO եռանկյունը նույնպես գտնվում է մեկ հարթության մեջ [Պար. 11.2]։ Հետևաբար, եթե մենք պատկերացնենք ուղղահայացներ, որոնք միացնում են P, S, Q, T, R և U կետերը A կետին, ապա որոշ բազմանիստ մարմին կկառուցվի BO և KO շրջանների միջև, կազմված պիրամիդներից, որոնց հիմքերն են KBPS, SPQT, TQRU քառանկյունները և URO եռանկյունը, իսկ գագաթը՝ A կետը։ Եվ եթե մենք նույն կառուցվածքը անենք նաև KL, LM և ME կողմերի վրա, ինչպես BK-ի վրա, և ավելին, (կրկնենք կառուցվածքը) մնացած երեք քառորդներում, ապա մի բազմանիստ մարմին, որը պարփակված է esfera մեջ, կկառուցվի, կազմված պիրամիդներից, որոնց հիմքերն են նշված քառանկյունները և եռանկյունը, ինչպես նաև դրանց նման կազմակերպված քառանկյունները և եռանկյունները, և գագաթը՝ A կետը։
Ուստի, ես ասում եմ, որ վերոնշյալ բազմանիստը չի շոշափում փոքր գնդիի մակերեսին, որտեղ գտնվում է FGH շրջանը։
Թող ուղղանկյուն AX ուղիղ գիծը տրվի A կետից դեպի K BPS հարթություն, և թող այն հանդիպի հարթությանը X կետում [Պնդ. 11.11]: Եվ թող XB և XK գծերը միանան: Իսկ քանի որ AX-ն ուղղանկյուն է K BPS քառանկյունի հարթության նկատմամբ, այն նաև ուղղանկյուն է իր հետ միացված բոլոր ուղիղ գծերի նկատմամբ, որոնք նույնպես գտնվում են քառանկյունի հարթությունում [Թիմ. 11.3]: Ուստի, AX-ն ուղղանկյուն է նաև BX և XK ուղիղ գծերի նկատմամբ: Եվ քանի որ AB-ը հավասար է AK-ին, ապա AB-ի քառամեծությունը նույնպես հավասար է AK-ի քառամեծությանը: Եվ AX և XB-ի քառամեծությունների գումարը հավասար է AB-ի քառամեծությանը: Քանի որ X-ում անկյունը ուղղանկյուն է [Պնդ. 1.47]: Եվ AX և XK-ի քառամեծությունների գումարը հավասար է AK-ի քառամեծությանը [Պնդ. 1.47]: Ուստի, AX և XB-ի քառամեծությունների գումարը հավասար է AX և XK-ի քառամեծությունների գումարին: Թող AX-ի քառամեծությունը հանվի երկուսից: Ուստի, մնացած BX-ի քառամեծությունը հավասար է մնացած XK-ի քառամեծությանը: Ուստի, BX-ը հավասար է XK-ին: Այնպես որ, համապատասխանաբար, մենք կարող ենք ցույց տալ, որ X-ից դեպի P և S միացված ուղիղ գծերը հավասար են BX և XK-ի հետ:
Ուստի, քառանկյունի հարթության մեջ X կենտրոնով և XB կամ XK ճառագայթով նկարագրված շրջանը նույնպես կանցնի P և S կետերի միջով, և KBPS քառանկյունը կլինի շրջանի ներսում։
Եվ քանի որ KB-ն մեծ է WV-ից, և WV-ը հավասար է SP-ին, ապա KB-ն մեծ է SP-ից։ Եվ քանի որ KB-ն հավասար է KS-ին և BP-ին, ապա KS-ը և BP-ն միմյանցից մեծ են SP-ից։ Եվ քանի որ KBPS քառանկյունը գտնվում է շրջանի մեջ, և KB-ն, BP-ն և KS-ը հավասար են միմյանց, իսկ PS-ը փոքր է նրանցից, և BX-ը շրջանի ճառագայթն է, ապա KB-ի քառակուսին մեծ է քան կրկնակի BX-ի քառակուսիի։ Թող KY ուղղահայացը գծվի K-ից դեպի BV։ Եվ քանի որ BD-ն փոքր է քան կրկնակի DY-ն, և քանի որ BD-ն հարաբերակցված է DY-ի, ապա DB և BY կողմից պարունակվող անկյունագիծը համեմատվում է DY և YB-ի կողմից պարունակվող անկյունագծին՝ BY վրա նկարագրված քառակուսիով, և YD-ի վրա կատարված զուգահեռանկյունային պարալելոգրամով՝ YB-ն հավասար է BY-ի կարճ կողմին։ Այսպիսով, DB և BY կողմից պարունակվող անկյունագիծը նույնպես փոքր է քան DY և YB-ի կողմից պարունակվող անկյունագիծը։ Եվ քանի որ KD-ը միացված է, DB և BY կողմից պարունակվող անկյունագիծը հավասար է BK-ի քառակուսուն, իսկ DY և YB կողմից պարունակվող անկյունագիծը հավասար է KY-ի քառակուսուն [Պնդ. 3.31, 6.8 ճշտ.]. Այսպիսով, KB-ի քառակուսին փոքր է քան կրկնակի KY-ի քառակուսին։ Բայց KB-ի քառակուսին մեծ է քան կրկնակի BX-ի քառակուսին։ Այսպիսով, KY-ի քառակուսին մեծ է քան BX-ի քառակուսին։ Եվ քանի որ BA-ն հավասար է KA-ին, BA-ի քառակուսին հավասար է AK-ի քառակուսուն։ Եվ BX և XA-ի քառակուսիների գումարը հավասար է BA-ի քառակուսուն, իսկ KY և YA-ի քառակուսիների գումարը հավասար է KA-ի քառակուսուն [Պնդ. 1.47]։ Այսպիսով, BX և XA-ի քառակուսիների գումարը հավասար է KY և YA-ի քառակուսիների գումարին, որոնցից KY-ի քառակուսին մեծ է քան BX-ի քառակուսին։ Այսպիսով, մնացած YA-ի քառակուսին փոքր է XA-ի քառակուսից։ Այսպիսով, AX-ը մեծ է քան AY։ Այսպիսով, AX-ը շատ ավելի մեծ է քան AG։ Եվ AX-ը ուղղահայաց է բազմանիստի հիմներից մեկի վրա, իսկ AG-ն ուղղահայաց է փոքր գնդի մակերեսի վրա։ Ուստի, բազմանիստը չի շոշափում փոքր գնդի մակերեսը։
Այսպիսով, երկու գնդեր, որոնք գտնվում են նույն կենտրոնում, մեծ գնդի մեջ ներգծվել է բազմանիստ մարմին, որը չի շոշափում փոքր գնդի մակերեսը: (Այս է) այն, ինչ պահանջվում էր անել:
Եզրակացություն
Եվ նաև, եթե BCDE գնդի մեջ այդպիսի բազմանիստ մարմինն ինքդեն ներգծվի մեկ այլ գնդի մեջ, ապա BCDE գնդի մեջ գտնվող բազմանիստ մարմինը պետք է ունենա մեկ այլ գնդի մեջ գտնվող բազմանիստ մարմնին այդ գնդի տրամագծի և BCDE գնդի տրամագծի խորացված հարաբերակցությունը։ Որովհետև եթե մարմինները բաժանվեն նմանապես թվարկված և նմանապես տեղադրված պիրամիդների մեջ, ապա պիրամիդները կլինեն նման։ Եվ նման պիրամիդները գտնվում են համապատասխան կողմերի խորացված հարաբերակցությունում [Պնդ. 12.8 կորէկցիա]։ Ուստի, այն պիրամիդը, որի հիմքը քառանկյուն KBPS է, և վերևում A կետն է, կունենա մեկ այլ գնդում համապատասխան տեղադրված պիրամիդին խորացված հարաբերակցություն, որը կապված է համապատասխան կողմի և համապատասխան կողմի հարաբերակցությանը։ Դա նշանակում է, որ A կենտրոնի շուրջ գտնվող գնդի AB ճառագայթը կապահովի այն ճառագայթին, որն ունի մեկ այլ գնդի համար։ Եվ նույն կերպ, A կենտրոնի շուրջ գտնվող յուրաքանչյուր պիրամիդը կապահովի մեկ այլ գնդում համապատասխան տեղադրված յուրաքանչյուր պիրամիդի համար խորացված հարաբերակցություն, որը կապված է AB-ի և մեկ այլ գնդի ճառագայթի միջև։ Եվ ինչպես մեկի հիմնական (մեծություն) համապատասխան է մեկի հետևյալից (երկու համեմատական մեծությունների շարքում), այնպես էլ (ամեն ինչի գումարը) հիմնականների բոլորի հետ կապված կլինի (հետևյալների գումարի հետ) [Պնդ. 5.12]։ Հետևաբար, ամբողջ բազմանիստ մարմինը A կենտրոնի շուրջ գտնվող գնդում պետք է լինի ամբողջ բազմանիստ մարմնին մեկ այլ գնդում խորացված հարաբերակցություն, որը կապված է AB ճառագայթի և մեկ այլ գնդի ճառագայթի հարաբերակցությանը։ Դա նշանակում է, որ BD տրամագիծը կապված է մեկ այլ գնդի տրամագծի հետ։ (Այս է) այն, ինչ պահանջվում էր ապացուցել։
Պնդում 18
Գնդերը միմյանց գտնվում են իրենց համապատասխան տրամագծերի խորանարդ հարաբերակցությամբ։
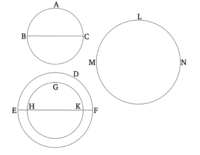
Թող, գնդերը ABC և DEF գծված լինեն, և նրանց տրամագծերը լինեն համապատասխանաբար BC և EF: Ես ասում եմ, որ գունդ ABC-ը ունի գունդ DEF-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ:
Իսկ եթե գունդ ABC-ը չունի գունդ DEF-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ, ապա գունդ ABC-ը կունենա որևէ այլ գնդի նկատմամբ, որը կամ փոքր է, կամ մեծ է գունդ DEF-ից, այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ: Թող, առաջին հերթին, այն ունենա այդպիսի հարաբերակցություն փոքր գնդի՝ GHK-ի նկատմամբ: Եվ թող DEF-ը գծված լինի նույն կենտրոնով, ինչ GHK-ն: Եվ թող բազմանիստ մարմին ներգծվի մեծ գնդի՝ DEF-ի մեջ, որը չի շոշափում փոքր գնդի՝ GHK-ի մակերեսը [Պնդ. 12.17]: Եվ թող բազմանիստ մարմին, որը նման է DEF-ի գնդում գտնվող բազմանիստին, նույնպես ներգծվի ABC գնդում: Ուստի, բազմանիստ մարմինը ABC գնդում ունի DEF գնդի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ [Պնդ. 12.17, համընթաց]: Եվ ABC գունդը նույնպես ունի GHK գնդի նկատմամբ այն խորանարդ հարաբերակցությունը, որը ունի BC-ն՝ EF-ի նկատմամբ: Ուստի, ինչպես ABC գունդը է GHK գնդի նկատմամբ, այնպես էլ բազմանիստ մարմինը ABC գնդում է DEF գնդի բազմանիստ մարմնի նկատմամբ: Ուստի, փոխադարձաբար, ինչպես գունդ ABC-ն է բազմանիստի նկատմամբ, այնպես էլ գունդ GHK-ն է բազմանիստի նկատմամբ գունդ DEF-ում [Պնդ. 5.16]: Եվ գունդ ABC-ն ավելի մեծ է, քան դրա ներսում գտնվող բազմանիստը: Ուստի, գունդ GHK-ն նույնպես ավելի մեծ է, քան գունդ DEF-ի ներսում գտնվող բազմանիստը [Պնդ. 5.14]: Բայց այն նաև փոքր է, որովհետև այն շրջապատված է դրա կողմից: Ուստի, գունդ ABC-ը չի ունենում գնդի նկատմամբ, որը ավելի փոքր է, քան գունդ DEF, այն խորանարդ հարաբերակցությունը, որը BC-ի տրամագիծը ունի՝ EF-ի նկատմամբ: Հետևաբար, նմանապես, մենք կարող ենք ցույց տալ, որ գունդ DEF-ը նույնպես չի ունենում գնդի նկատմամբ, որը ավելի փոքր է, քան գունդ ABC, այն խորանարդ հարաբերակցությունը, որը EF-ն ունի՝ BC-ի նկատմամբ:
Ուստի, ես ասում եմ, որ գունդ ABC-ը չի ունենում գնդի նկատմամբ, որը ավելի մեծ է, քան գունդ DEF, այն խորանարդ հարաբերակցությունը, որը BC-ն ունի՝ EF-ի նկատմամբ:
Որպեսզի հնարավոր լինի, թող դա ունենա (խորանարդ հարաբերակցություն) ավելի մեծ (գնդի) հետ՝ LMN։ Ուստի, հակառակ ուղղությամբ, գունդ LMN-ը ունի գունդ ABC-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը տրամագիծը EF-ն ունի՝ տրամագիծ BC-ի նկատմամբ [Պնդ. 5.7 տես.։] Եվ ինչպես գունդ LMN-ը գտնվում է գունդ ABC-ի նկատմամբ, այնպես էլ գունդ DEF-ը գտնվում է այնպիսի (գնդի) նկատմամբ, որը փոքր է, քան գունդ ABC, քանի որ LMN-ը ավելի մեծ է, քան DEF-ը, ինչպես արդեն ցույց տրվեց [Պնդ. 12.2 լեմ.։] Եվ ուստի, գունդ DEF-ը ունի այնպիսի (գնդի) նկատմամբ, որը փոքր է, քան գունդ ABC, այն խորանարդ հարաբերակցությունը, որը EF-ն ունի՝ BC-ի նկատմամբ։ Վերոնշյալը անհնար է եղել։ Ուստի, գունդ ABC-ը չի ունենում այնպիսի (գնդի) նկատմամբ, որը ավելի մեծ է, քան գունդ DEF, այն խորանարդ հարաբերակցությունը, որը BC-ն ունի՝ EF-ի նկատմամբ։ Եվ ցույց տրվեց, որ դա չի լինի նաև փոքր (գնդի) նկատմամբ։ Ուստի, գունդ ABC-ը ունի գունդ DEF-ի նկատմամբ այն խորանարդ հարաբերակցությունը, որը BC-ն ունի՝ EF-ի նկատմամբ։ Դա հենց այն էր, ինչ պետք էր ցույց տալ։