«Տարերք/Գիրք 7»–ի խմբագրումների տարբերություն
(→Պնդում 17) |
|||
| Տող 52. | Տող 52. | ||
== Պնդում 18 == | == Պնդում 18 == | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 18.png|center|250px]] | |
Եթե չորս թվեր համեմատական են միմյանց, ապա առաջին և չորրորդ թվերի բազմապատկումից ստացված թիվը կլինի հավասար երկրորդի և երրորդի բազմապատկումից ստացված թվին: Եվ եթե առաջինի և չորրորդի բազմապատկումից ստացված թիվը հավասար է երկրորդի և երրորդի բազմապատկումից ստացված թվին, ապա այդ չորս թվերը կլինեն համեմատական: | Եթե չորս թվեր համեմատական են միմյանց, ապա առաջին և չորրորդ թվերի բազմապատկումից ստացված թիվը կլինի հավասար երկրորդի և երրորդի բազմապատկումից ստացված թվին: Եվ եթե առաջինի և չորրորդի բազմապատկումից ստացված թիվը հավասար է երկրորդի և երրորդի բազմապատկումից ստացված թվին, ապա այդ չորս թվերը կլինեն համեմատական: | ||
Օրինակ, A, B, C և D համեմատական թվեր են: Ենթադրենք ինչպես A-ն է հարաբերում B-ին, այնպես էլ C-ն է D-ին: A-ն բազմապատկելով D-ն կստանք E թիվը, իսկ B-ն բազմապատկելով C- թվին կստանանք F թիվը: Կարելի է պնդել, որ E-ն հավասար է F-ին: | Օրինակ, A, B, C և D համեմատական թվեր են: Ենթադրենք ինչպես A-ն է հարաբերում B-ին, այնպես էլ C-ն է D-ին: A-ն բազմապատկելով D-ն կստանք E թիվը, իսկ B-ն բազմապատկելով C- թվին կստանանք F թիվը: Կարելի է պնդել, որ E-ն հավասար է F-ին: | ||
| Տող 63. | Տող 63. | ||
== Պնդում 20 == | == Պնդում 20 == | ||
Թող լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ ինչպես A-ն և B-ն: Ասում եմ, որ CD-ն չափում է A-ն այնքան անգամ, որքան և EF-ն չափում է B-ն՝ մեծը՝ մեծին, և փոքրն՝ փոքրին: Այնպես որ, թող CD և EF լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ A-ի և B-ի հետ համապատասխանաբար: Ես ասում եմ, որ CD-ն չափում է A-ն նույն քանակությամբ անգամ, որքան EF-ն չափում է B-ն։ | Թող լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ ինչպես A-ն և B-ն: Ասում եմ, որ CD-ն չափում է A-ն այնքան անգամ, որքան և EF-ն չափում է B-ն՝ մեծը՝ մեծին, և փոքրն՝ փոքրին: Այնպես որ, թող CD և EF լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ A-ի և B-ի հետ համապատասխանաբար: Ես ասում եմ, որ CD-ն չափում է A-ն նույն քանակությամբ անգամ, որքան EF-ն չափում է B-ն։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 20.png|center|250px]] | |
Եթե հնարավոր է, Դիցուք, CD-ն չլինի A-ի մաս: Եվ եթե EF-ն իսկապես այն նույն մասերն ունի B-ի, որոնք CD-ն ունի A-ի մասերից, ապա այն հնարավոր է։ Ինչքան որ մասեր կան CD-ում, նույնքան մասեր կան EF-ում՝ B-ի մասերից։ Let CD բաժանվի A-ի մասերի՝ CG և GD, իսկ EF բաժանվի B-ի մասերի՝ EH և HF։ Եվ այդ դեպքում, CG և GD բաժանումների թվաքանակը հավասար կլինի EH և HF բաժանումների թվաքանակին։ Եվ քանի որ CG և GD թվերը հավասար են միմյանց, նույնպես EH և HF թվերը հավասար են միմյանց, և հարաբերությունը CG-ի և EH-ի միջև նույնն է, ինչ հարաբերությունը GD-ի և HF-ի միջև։ Հետևաբար, ինչպես CG-ն է հարաբերակցվում EH-ի հետ, այնպես էլ GD-ն է հարաբերակցվում HF-ի հետ։ Դրանից հետո, որպես հետևանք, ինչպես յուրաքանչյուր առաջատար մաս՝ ΓΗ միանում է հետագային ΕΘ, այնպես էլ այն մագլցած մասերը ΓΔ և ΕΖ՝ նույն հարաբերությամբ՝ լինում են համարժեք։ | Եթե հնարավոր է, Դիցուք, CD-ն չլինի A-ի մաս: Եվ եթե EF-ն իսկապես այն նույն մասերն ունի B-ի, որոնք CD-ն ունի A-ի մասերից, ապա այն հնարավոր է։ Ինչքան որ մասեր կան CD-ում, նույնքան մասեր կան EF-ում՝ B-ի մասերից։ Let CD բաժանվի A-ի մասերի՝ CG և GD, իսկ EF բաժանվի B-ի մասերի՝ EH և HF։ Եվ այդ դեպքում, CG և GD բաժանումների թվաքանակը հավասար կլինի EH և HF բաժանումների թվաքանակին։ Եվ քանի որ CG և GD թվերը հավասար են միմյանց, նույնպես EH և HF թվերը հավասար են միմյանց, և հարաբերությունը CG-ի և EH-ի միջև նույնն է, ինչ հարաբերությունը GD-ի և HF-ի միջև։ Հետևաբար, ինչպես CG-ն է հարաբերակցվում EH-ի հետ, այնպես էլ GD-ն է հարաբերակցվում HF-ի հետ։ Դրանից հետո, որպես հետևանք, ինչպես յուրաքանչյուր առաջատար մաս՝ ΓΗ միանում է հետագային ΕΘ, այնպես էլ այն մագլցած մասերը ΓΔ և ΕΖ՝ նույն հարաբերությամբ՝ լինում են համարժեք։ | ||
| Տող 70. | Տող 70. | ||
Դիցուք, A եւ B թվերը պարզ թվեր ենէ : Կարելի է պնդել, , որ A եւ B թվերը, նրանց պես հարաբերություն ունեցող թվերից ամենափոքր թվերն են: Եթե դա այդպես չէ, ապա կլինեն ինչ-որ թվեր, որոնք A եւ B-ից փոքր կլինեն և նրանք կհարաբերեն նույնպես, ինչպես A եւ B-: Թող դրանք լինեն C եւ D: | Դիցուք, A եւ B թվերը պարզ թվեր ենէ : Կարելի է պնդել, , որ A եւ B թվերը, նրանց պես հարաբերություն ունեցող թվերից ամենափոքր թվերն են: Եթե դա այդպես չէ, ապա կլինեն ինչ-որ թվեր, որոնք A եւ B-ից փոքր կլինեն և նրանք կհարաբերեն նույնպես, ինչպես A եւ B-: Թող դրանք լինեն C եւ D: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 21.png|center|250px]] | |
Ասպիսով, քանի որ այս թվերը նվազագույններն են, որոնք նույն հարաբերությունն ունեն, և մեծ հարաբերությունը չափում է մեծին, և փոքրն այնքանն է, որքան փոքրին՝ այսինքն, ավելի մեծը հարաբերում է ավելի մեծին, իսկ ավելի փոքրը ՝ փոքրին։ Այսպիսով, որքան որ C հարաբերում է Aին, այնքան անգամեր թող լինեն E-ում։ Եվ D-ը, ամփոփելով B-ը, E-ում չափում է ըստ նույն միավորների։ Այսպես, քանի որ C-ը հարաբերում է Aին ըստ E-ում առկա միավորների, E-ն էլ, ըստ C-ի, հարաբերում է Aին նույնչափ ։ Հետևաբար E-ն և B-ը չափում են D-ում առկա միավորներով։ Այնպես որ, հնարավոր չէ, որպեսզի A-ի և B-ից ավելի փոքր թվեր լինեն, որոնք նույն հարաբերությունն ունեն A և B թվերի հետ։ Հետեւաբար, A և B-ն են այդ թվերը, որոնք նույն հարաբերությունն ունեն։ Սա հենց այն բանն է, որը պետք էր ապացուցել: | Ասպիսով, քանի որ այս թվերը նվազագույններն են, որոնք նույն հարաբերությունն ունեն, և մեծ հարաբերությունը չափում է մեծին, և փոքրն այնքանն է, որքան փոքրին՝ այսինքն, ավելի մեծը հարաբերում է ավելի մեծին, իսկ ավելի փոքրը ՝ փոքրին։ Այսպիսով, որքան որ C հարաբերում է Aին, այնքան անգամեր թող լինեն E-ում։ Եվ D-ը, ամփոփելով B-ը, E-ում չափում է ըստ նույն միավորների։ Այսպես, քանի որ C-ը հարաբերում է Aին ըստ E-ում առկա միավորների, E-ն էլ, ըստ C-ի, հարաբերում է Aին նույնչափ ։ Հետևաբար E-ն և B-ը չափում են D-ում առկա միավորներով։ Այնպես որ, հնարավոր չէ, որպեսզի A-ի և B-ից ավելի փոքր թվեր լինեն, որոնք նույն հարաբերությունն ունեն A և B թվերի հետ։ Հետեւաբար, A և B-ն են այդ թվերը, որոնք նույն հարաբերությունն ունեն։ Սա հենց այն բանն է, որը պետք էր ապացուցել: | ||
| Տող 77. | Տող 77. | ||
Այն նվազագույն թվերը, որոնք ունեն նույնպիսի հարաբերություն, միմյանց նկատմամբ | Այն նվազագույն թվերը, որոնք ունեն նույնպիսի հարաբերություն, միմյանց նկատմամբ | ||
ունեն ընդհանուր բազմապատիկ և նրանք պարզ թվեր են: | ունեն ընդհանուր բազմապատիկ և նրանք պարզ թվեր են: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 22.png|center|250px]] | |
Դիցուք A և B լինեն ամենափոքր թվերը նրանցից, որոնք ունեն նույն հարաբերակցությունը, ինչ նրանք։ Կարելի է պնդել, որ A-ն և B-ն փոխադարձաբար պարզ են։ | Դիցուք A և B լինեն ամենափոքր թվերը նրանցից, որոնք ունեն նույն հարաբերակցությունը, ինչ նրանք։ Կարելի է պնդել, որ A-ն և B-ն փոխադարձաբար պարզ են։ | ||
Քանի որ, եթե A-ն և B-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի նրանց։ Թող այդ թիվը լինի C : | Քանի որ, եթե A-ն և B-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի նրանց։ Թող այդ թիվը լինի C : | ||
| Տող 88. | Տող 88. | ||
== Պնդում 23 == | == Պնդում 23 == | ||
Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկը բաժանող թիվը կմնա փոխադարձաբար պարզ մյուս թվի հետ։ | Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկը բաժանող թիվը կմնա փոխադարձաբար պարզ մյուս թվի հետ։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 23.png|center|250px]] | |
Դիցուք A և B լինեն փոխադարձաբար պարզ թվեր, և թող մի թիվ C բաժանի A-ին։ Ասում եմ, որ C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ | Դիցուք A և B լինեն փոխադարձաբար պարզ թվեր, և թող մի թիվ C բաժանի A-ին։ Ասում եմ, որ C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ | ||
Եթե C-ն և B-ն փոխադարձաբար պարզ չեն, ապա մի թիվ կբաժանի C-ն և B-ն։ Թող այդ թիվը լինի D։ Քանի որ D-ն բաժանում է C-ն, իսկ C-ն բաժանում է A-ն, ապա D-ն նաև բաժանում է A-ն։ Եվ D-ն բաժանում է նաև B-ն։ | Եթե C-ն և B-ն փոխադարձաբար պարզ չեն, ապա մի թիվ կբաժանի C-ն և B-ն։ Թող այդ թիվը լինի D։ Քանի որ D-ն բաժանում է C-ն, իսկ C-ն բաժանում է A-ն, ապա D-ն նաև բաժանում է A-ն։ Եվ D-ն բաժանում է նաև B-ն։ | ||
| Տող 97. | Տող 97. | ||
== Պնդում 24 == | == Պնդում 24 == | ||
Եթե երկու թվեր փոխադարձաբար պարզ են որևէ թվի հետ, ապա դրանցից բազմապատկված, ստեղծված թիվը նույնպես փոխադարձաբար պարզ կլինի նույն թվի հետ։ | Եթե երկու թվեր փոխադարձաբար պարզ են որևէ թվի հետ, ապա դրանցից բազմապատկված, ստեղծված թիվը նույնպես փոխադարձաբար պարզ կլինի նույն թվի հետ։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 24.png|center|250px]] | |
Դիցուք, A և B լինեն երկու թվեր, որոնք երկուսն էլ փոխադարձաբար պարզ են C-ի հետ։ Թող A-ն B-ն բազմապատկելով ստեղծի D-ն։ Կարելի է պնդել, որ C-ն և D-ն նույնպես փոխադարձաբար պարզ են։ | Դիցուք, A և B լինեն երկու թվեր, որոնք երկուսն էլ փոխադարձաբար պարզ են C-ի հետ։ Թող A-ն B-ն բազմապատկելով ստեղծի D-ն։ Կարելի է պնդել, որ C-ն և D-ն նույնպես փոխադարձաբար պարզ են։ | ||
Եթե C-ն և D-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի C-ն և D-ն։ Թող այդ թիվը լինի E։ Եվ քանի որ C-ն և A-ն փոխադարձաբար պարզ են, իսկ E-ն բաժանում է C-ին, ապա A-ն և E-ն նույնպես փոխադարձաբար պարզ են։ | Եթե C-ն և D-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի C-ն և D-ն։ Թող այդ թիվը լինի E։ Եվ քանի որ C-ն և A-ն փոխադարձաբար պարզ են, իսկ E-ն բաժանում է C-ին, ապա A-ն և E-ն նույնպես փոխադարձաբար պարզ են։ | ||
| Տող 110. | Տող 110. | ||
Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկի քառակուսիով ստեղծված թիվը փոխադարձաբար պարզ կլինի մյուսի հետ։ | Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկի քառակուսիով ստեղծված թիվը փոխադարձաբար պարզ կլինի մյուսի հետ։ | ||
Դիցուք A և B երկու պարզ թվեր են, որոնք փոխադարձաբար պարզ են։ Թող A-ն ինքն իրեն բազմապատկելով ստեղծի C-ն։ Կարելի է պնդել , որ B-ն և C-ն փոխադարձաբար պարզ են։ | Դիցուք A և B երկու պարզ թվեր են, որոնք փոխադարձաբար պարզ են։ Թող A-ն ինքն իրեն բազմապատկելով ստեղծի C-ն։ Կարելի է պնդել , որ B-ն և C-ն փոխադարձաբար պարզ են։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 25.png|center|250px]] | |
Դիցուք D լինի հավասար A-ին։ Քանի որ A և B փոխադարձաբար պարզ են, իսկ A հավասար է D-ին, ապա D-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Այսպիսով, D-ն և A-ն երկուսն էլ փոխադարձաբար պարզ են B-ի հետ։ | Դիցուք D լինի հավասար A-ին։ Քանի որ A և B փոխադարձաբար պարզ են, իսկ A հավասար է D-ին, ապա D-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Այսպիսով, D-ն և A-ն երկուսն էլ փոխադարձաբար պարզ են B-ի հետ։ | ||
Այլ կերպ ասած, D-ից և A-ից ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի B-ի հետ։ Եվ C-ն է այն թիվը, որը ստացվում է D-ի և A-ի բազմապատկումով։ Այսպիսով, C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ցույց տալ։ | Այլ կերպ ասած, D-ից և A-ից ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի B-ի հետ։ Եվ C-ն է այն թիվը, որը ստացվում է D-ի և A-ի բազմապատկումով։ Այսպիսով, C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ցույց տալ։ | ||
| Տող 116. | Տող 116. | ||
== Պնդում 26 == | == Պնդում 26 == | ||
Եթե երկու թվերն էլ փոխադարձաբար պարզ են երկու թվերի հետ, ապա դրանցից բազմապատկված, ստացված թվերը նույնպես փոխադարձաբար պարզ կլինեն իրար հետ։ | Եթե երկու թվերն էլ փոխադարձաբար պարզ են երկու թվերի հետ, ապա դրանցից բազմապատկված, ստացված թվերը նույնպես փոխադարձաբար պարզ կլինեն իրար հետ։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 26.png|center|250px]] | |
Դիցուք A և B երկու թվեր լինեն, որոնք երկուսն էլ փոխադարձաբար պարզ են երկու այլ թվերի՝ C-ի և D-ի հետ։ Դիցուք, A-ն B-ի հետ բազմապատկելով ստանանք E-ն, և թող C-ն D-ի հետ բազմապատկելով ստանանք F-ն։ Ասում եմ, որ E և F փոխադարձաբար պարզ են։ | Դիցուք A և B երկու թվեր լինեն, որոնք երկուսն էլ փոխադարձաբար պարզ են երկու այլ թվերի՝ C-ի և D-ի հետ։ Դիցուք, A-ն B-ի հետ բազմապատկելով ստանանք E-ն, և թող C-ն D-ի հետ բազմապատկելով ստանանք F-ն։ Ասում եմ, որ E և F փոխադարձաբար պարզ են։ | ||
Քանի որ A-ն և B-ն երկուսն էլ փոխադարձաբար պարզ են C-ի հետ, ապա A-ի և B-ի բազմապատկմամբ ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի C-ի հետ։ Այսպիսով, E-ն և C-ն փոխադարձաբար պարզ են։ | Քանի որ A-ն և B-ն երկուսն էլ փոխադարձաբար պարզ են C-ի հետ, ապա A-ի և B-ի բազմապատկմամբ ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի C-ի հետ։ Այսպիսով, E-ն և C-ն փոխադարձաբար պարզ են։ | ||
| Տող 124. | Տող 124. | ||
== Պնդում 27 == | == Պնդում 27 == | ||
Եթե երկու թվեր փոխադարձաբար պարզ են իրարից, և յուրաքանչյուրը նրանցից որոշ թիվ է ստեղծում՝ ինքն իրեն բազմապատկելով, ապա դրանցից ստացված թվերը նույնպես կլինեն փոխադարձաբար պարզ։ Եվ եթե սկզբնական թվերը ստեղծեն որոշ թվեր՝ ստեղծված թվերը բազմապատկելով, ապա դրանք ևս կլինեն փոխադարձաբար պարզ։ Սա միշտ տեղի է ունենում ծայրամասերի վերաբերյալ։ | Եթե երկու թվեր փոխադարձաբար պարզ են իրարից, և յուրաքանչյուրը նրանցից որոշ թիվ է ստեղծում՝ ինքն իրեն բազմապատկելով, ապա դրանցից ստացված թվերը նույնպես կլինեն փոխադարձաբար պարզ։ Եվ եթե սկզբնական թվերը ստեղծեն որոշ թվեր՝ ստեղծված թվերը բազմապատկելով, ապա դրանք ևս կլինեն փոխադարձաբար պարզ։ Սա միշտ տեղի է ունենում ծայրամասերի վերաբերյալ։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 27.png|center|250px]] | |
Դիցուք A և B երկու թվեր են, որոնք փոխադարձապես պարզ են, և թող A ստեղծի C՝ ինքն իրեն բազմապատկելով, իսկ B՝ E՝ ինքն իրեն բազմապատկելով։ Եվ թող A բազմապատկի C՝ ստանալով D, իսկ B բազմապատկի E՝ ստանալով F։ Կարելի է պնդել, որ C և E, և D և F կլինեն փոխադարձաբար պարզ։ | Դիցուք A և B երկու թվեր են, որոնք փոխադարձապես պարզ են, և թող A ստեղծի C՝ ինքն իրեն բազմապատկելով, իսկ B՝ E՝ ինքն իրեն բազմապատկելով։ Եվ թող A բազմապատկի C՝ ստանալով D, իսկ B բազմապատկի E՝ ստանալով F։ Կարելի է պնդել, որ C և E, և D և F կլինեն փոխադարձաբար պարզ։ | ||
Որովհետև A և B փոխադարձապես պարզ են, և A ինքն իրեն բազմապատկելով ստեղծել է C, ապա C և B նույնպես կլինեն փոխադարձապես պարզ։ Այնպես որ, C և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ուստի C և E նույնպես փոխադարձապես պարզ են։ Նորից, քանի որ A և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ապա A և E նույնպես փոխադարձապես պարզ են։ Այնպես որ, քանի որ երկու թիվ՝ A և C, երկուսն էլ փոխադարձաբար պարզ են երկու թվերից՝ B և E, A և C բազմապատկելով ստացած թիվը (D) կլինի B և E բազմապատկելով ստացված թվից (F) փոխադարձապես պարզ։ | Որովհետև A և B փոխադարձապես պարզ են, և A ինքն իրեն բազմապատկելով ստեղծել է C, ապա C և B նույնպես կլինեն փոխադարձապես պարզ։ Այնպես որ, C և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ուստի C և E նույնպես փոխադարձապես պարզ են։ Նորից, քանի որ A և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ապա A և E նույնպես փոխադարձապես պարզ են։ Այնպես որ, քանի որ երկու թիվ՝ A և C, երկուսն էլ փոխադարձաբար պարզ են երկու թվերից՝ B և E, A և C բազմապատկելով ստացած թիվը (D) կլինի B և E բազմապատկելով ստացված թվից (F) փոխադարձապես պարզ։ | ||
| Տող 132. | Տող 132. | ||
Եթե երկու թիվեր պարզ են, ապա նրանց գումարը նույնպես կլինի պարզ յուրաքանչյուրին։ Եվ եթե այդ գումարը պարզ է ինչ-որ մեկի հետ, ապա սկզբնական թվերը նույնպես պարզ կլինեն | Եթե երկու թիվեր պարզ են, ապա նրանց գումարը նույնպես կլինի պարզ յուրաքանչյուրին։ Եվ եթե այդ գումարը պարզ է ինչ-որ մեկի հետ, ապա սկզբնական թվերը նույնպես պարզ կլինեն | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 28.png|center|250px]] | |
Դիցուք երկու թվերը՝ AB և BC, որոնք պարզ են, տրված են: Կարելի է պնդել, որ նրանց գումարը՝ AC, նույնպես պարզ կլինի յուրաքանչյուրի համար՝ AB և BC: | Դիցուք երկու թվերը՝ AB և BC, որոնք պարզ են, տրված են: Կարելի է պնդել, որ նրանց գումարը՝ AC, նույնպես պարզ կլինի յուրաքանչյուրի համար՝ AB և BC: | ||
Եթե քաղված AC և AB միմյանց պարզ չեն չեն, ապա կգտնվի ինչ-որ թիվ, որը չափում է AC և AB: Թող այդ թիվը լինի D: Ենթադրենք, որ D չափում է AC և AB, ապա այն նույնպես պետք է չափի BC: Բայց քանի որ AB և BC միմյանց պարզ են, դա անհնար է: Հետևաբար, AC և AB պետք է միմյանց պարզ լինեն: | Եթե քաղված AC և AB միմյանց պարզ չեն չեն, ապա կգտնվի ինչ-որ թիվ, որը չափում է AC և AB: Թող այդ թիվը լինի D: Ենթադրենք, որ D չափում է AC և AB, ապա այն նույնպես պետք է չափի BC: Բայց քանի որ AB և BC միմյանց պարզ են, դա անհնար է: Հետևաբար, AC և AB պետք է միմյանց պարզ լինեն: | ||
| Տող 141. | Տող 141. | ||
== Պնդում 29 == | == Պնդում 29 == | ||
Յուրաքանչյուր պարզ թիվ առաջին է բոլոր այն թվերի հետ, որոնք ինքը չի չափում | Յուրաքանչյուր պարզ թիվ առաջին է բոլոր այն թվերի հետ, որոնք ինքը չի չափում | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 29.png|center|250px]] | |
Դիցուք, A-ն պարզ թիվ է, և B-ն այնպիսի թիվ է, որ A-ն չի չափում։ Կարելի է, որ B-ն և A-ն միմյանց նկատմամբ պարզ են։ | Դիցուք, A-ն պարզ թիվ է, և B-ն այնպիսի թիվ է, որ A-ն չի չափում։ Կարելի է, որ B-ն և A-ն միմյանց նկատմամբ պարզ են։ | ||
Որպեսզի եթե B-ն և A-ն միմյանց նկատմամբ պարզ չեն, ապա մի թիվ կլինի, որը նրանց չափում է։ Թող C-ն չափի նրանց։ Քանի որ C-ն չափում է B-ն, իսկ A-ն չի չափում B-ն, ապա C-ն պետք է տարբեր լինի A-ից։ Եվ քանի որ C-ն չափում է B-ն և A-ն, ապա C-ն պետք է չափի նաև A-ն՝ չնայած նրան, որ չի համընկնում նրա հետ։ Բայց սա անհնար է։ Այնպես որ, չի կարող լինել որևէ թիվ, որը կչափի B-ն և A-ն։ Այդպիսով, A-ն և B-ն միմյանց նկատմամբ պետք է լինեն պարզ։ | Որպեսզի եթե B-ն և A-ն միմյանց նկատմամբ պարզ չեն, ապա մի թիվ կլինի, որը նրանց չափում է։ Թող C-ն չափի նրանց։ Քանի որ C-ն չափում է B-ն, իսկ A-ն չի չափում B-ն, ապա C-ն պետք է տարբեր լինի A-ից։ Եվ քանի որ C-ն չափում է B-ն և A-ն, ապա C-ն պետք է չափի նաև A-ն՝ չնայած նրան, որ չի համընկնում նրա հետ։ Բայց սա անհնար է։ Այնպես որ, չի կարող լինել որևէ թիվ, որը կչափի B-ն և A-ն։ Այդպիսով, A-ն և B-ն միմյանց նկատմամբ պետք է լինեն պարզ։ | ||
| Տող 147. | Տող 147. | ||
== Պնդում 30 == | == Պնդում 30 == | ||
Եթե երկու թիվը իրար բազմապատկելով ստանում են ինչ-որ թիվ, և այդ թվից մեկը չափվում է մի պարզ թվով, ապա սկզբնական թվերից մեկը նույնպես պետք է չափվի | Եթե երկու թիվը իրար բազմապատկելով ստանում են ինչ-որ թիվ, և այդ թվից մեկը չափվում է մի պարզ թվով, ապա սկզբնական թվերից մեկը նույնպես պետք է չափվի | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 30.png|center|250px]] | |
Թող երկու թիվ A և B ստեղծեն C՝ իրար բազմապատկելով, և թող ինչ-որ պարզ թիվ D հավասար լինի C-ին: Ես ասում եմ, որ D-ը պետք է հավասար լինի A կամ B: | Թող երկու թիվ A և B ստեղծեն C՝ իրար բազմապատկելով, և թող ինչ-որ պարզ թիվ D հավասար լինի C-ին: Ես ասում եմ, որ D-ը պետք է հավասար լինի A կամ B: | ||
Թող D-ն չհավասար է A, և քանի որ D-ը պարզ է, ապա A և D թվերը միմյանց նկատմամբ պարզ են: Եվ քանի որ D-ն հավասար է C-ին, ապա այն պետք է հավասար է E-ին այնքան անգամ, որքան D-ն հավասար է C-ին: Իսկ քանի որ D-ն հավասար է C-ին ըստ E-ի, ապա D-ն ստեղծում է C՝ բազմապատկելով E: Բայց իսկապես, նաև A-ն ստեղծում է C՝ B-ի հետ բազմապատկելով: Այսպիսով, ստեղծված թիվը D և E թվերից հավասար է A և B թվերի բազմապատկմանը: | Թող D-ն չհավասար է A, և քանի որ D-ը պարզ է, ապա A և D թվերը միմյանց նկատմամբ պարզ են: Եվ քանի որ D-ն հավասար է C-ին, ապա այն պետք է հավասար է E-ին այնքան անգամ, որքան D-ն հավասար է C-ին: Իսկ քանի որ D-ն հավասար է C-ին ըստ E-ի, ապա D-ն ստեղծում է C՝ բազմապատկելով E: Բայց իսկապես, նաև A-ն ստեղծում է C՝ B-ի հետ բազմապատկելով: Այսպիսով, ստեղծված թիվը D և E թվերից հավասար է A և B թվերի բազմապատկմանը: | ||
| Տող 155. | Տող 155. | ||
Ամեն բաղադրյալ թիվը չափվում է ինչ-որ պարզ թվով: | Ամեն բաղադրյալ թիվը չափվում է ինչ-որ պարզ թվով: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 31.png|center|250px]] | |
Դիցուք A-ն բաղադրյալ թիվ է։ Կարելի է պնդել, որ A-ն չափվում է ինչ-որ պարզ թվով։ | Դիցուք A-ն բաղադրյալ թիվ է։ Կարելի է պնդել, որ A-ն չափվում է ինչ-որ պարզ թվով։ | ||
| Տող 170. | Տող 170. | ||
Ամեն թիվ կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով։ | Ամեն թիվ կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով։ | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 32.png|center|250px]] | |
Դիցուք A թիվ է: Կարելի է պնդել, որ A-ն կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով: | Դիցուք A թիվ է: Կարելի է պնդել, որ A-ն կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով: | ||
Եթե A-ն պարզ է, ապա այն, ինչ նախատեսված էր, տեղի է ունենում: Իսկ եթե այն բաղադրյալ է, ապա ինչ-որ պարզ թիվ կչափի այն: | Եթե A-ն պարզ է, ապա այն, ինչ նախատեսված էր, տեղի է ունենում: Իսկ եթե այն բաղադրյալ է, ապա ինչ-որ պարզ թիվ կչափի այն: | ||
| Տող 179. | Տող 179. | ||
Թող A, B, և C լինեն ցանկացած տրված թվեր: Պետք է գտնենք նրանցից ամենափոքրին, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B, և C: | Թող A, B, և C լինեն ցանկացած տրված թվեր: Պետք է գտնենք նրանցից ամենափոքրին, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B, և C: | ||
Իրականում, եթե A, B և C իրար հետ պարզ են, ապա նրանք կլինեն ամենափոքրն այն թվերից, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես տրված թվերն են: | Իրականում, եթե A, B և C իրար հետ պարզ են, ապա նրանք կլինեն ամենափոքրն այն թվերից, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես տրված թվերն են: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 33.png|center|250px]] | |
Դիցուք ունենք A, B և C թվերի առավելագույն ընդհանուր չափը՝ D, և որքանով D չափում է A, B և C, այնքան ամեն մի թիվ՝ E, F և G, համապատասխանաբար չափում է A, B և C ըստ D-ի միավորների: | Դիցուք ունենք A, B և C թվերի առավելագույն ընդհանուր չափը՝ D, և որքանով D չափում է A, B և C, այնքան ամեն մի թիվ՝ E, F և G, համապատասխանաբար չափում է A, B և C ըստ D-ի միավորների: | ||
| Տող 193. | Տող 193. | ||
== Պնդում 34 == | == Պնդում 34 == | ||
Դիցուք A և B թվերը տրված են։ Պետք է գտնենք այն ամենափոքր թիվը, որը կչափեն երկու տրված թվերը: | Դիցուք A և B թվերը տրված են։ Պետք է գտնենք այն ամենափոքր թիվը, որը կչափեն երկու տրված թվերը: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 34.png|center|250px]] | |
Դիցուք, A և B լինի միմյանցից անկախ թվեր են:թող A C ստանա՝ բազմապատկելով B: Այսպիսով, B նույնպես C ստացրեց՝ բազմապատկելով A Այսպիսով, A և B երկուսն էլ չափում են C: | Դիցուք, A և B լինի միմյանցից անկախ թվեր են:թող A C ստանա՝ բազմապատկելով B: Այսպիսով, B նույնպես C ստացրեց՝ բազմապատկելով A Այսպիսով, A և B երկուսն էլ չափում են C: | ||
| Տող 206. | Տող 206. | ||
Այնպես որ, A-ի և E-ի բազմապատկմամբ ստացված թիվը հավասար է B-ի և F-ի բազմապատկմամբ ստացված թվին [Prop. 7.19]: Եվ թող A-ը ստանա C՝ բազմապատկելով E: Այսպիսով, B-ն նույնպես ստանում է C՝ բազմապատկելով F: Ուրեմն,, A և B երկուսն էլ հարաբերում են C: | Այնպես որ, A-ի և E-ի բազմապատկմամբ ստացված թիվը հավասար է B-ի և F-ի բազմապատկմամբ ստացված թվին [Prop. 7.19]: Եվ թող A-ը ստանա C՝ բազմապատկելով E: Այսպիսով, B-ն նույնպես ստանում է C՝ բազմապատկելով F: Ուրեմն,, A և B երկուսն էլ հարաբերում են C: | ||
Ես ասում եմ, որ C-ն նույնպես ամենափոքրն է (թիվը, որը նրանք երկուսն էլ հարաբերում են): Եթե ոչ, A և B երկուսն էլ կհարաբերեն մի թիվ, որը ավելի փոքր է, քան C: Թող նրանք երկուսն էլ հարաբերեն D (որը ավելի փոքր է, քան C): | Ես ասում եմ, որ C-ն նույնպես ամենափոքրն է (թիվը, որը նրանք երկուսն էլ հարաբերում են): Եթե ոչ, A և B երկուսն էլ կհարաբերեն մի թիվ, որը ավելի փոքր է, քան C: Թող նրանք երկուսն էլ հարաբերեն D (որը ավելի փոքր է, քան C): | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 34 part 2.png|center|250px]] | |
Եվ որքան անգամ A հարաբերում է D, նույնքան միավորներ թող լինեն G-ում: Եվ որքան անգամ B հարաբերում է D, նույնքան միավորներ թող լինեն H-ում: Այսպիսով, A ստացրեց D՝ բազմապատկելով G, իսկ B ստացրեց D՝ բազմապատկելով H: Այսպիսով, ինչպես A-ն է B-ին, այնպես էլ H-ն է G-ին [Prop. 7.19]: | Եվ որքան անգամ A հարաբերում է D, նույնքան միավորներ թող լինեն G-ում: Եվ որքան անգամ B հարաբերում է D, նույնքան միավորներ թող լինեն H-ում: Այսպիսով, A ստացրեց D՝ բազմապատկելով G, իսկ B ստացրեց D՝ բազմապատկելով H: Այսպիսով, ինչպես A-ն է B-ին, այնպես էլ H-ն է G-ին [Prop. 7.19]: | ||
Եվ քանի որ A-ը ստացավ C և D՝ բազմապատկելով E և G համապատասխանաբար, ապա ինչպես E-ն է G-ին, այնպես էլ C-ն է D-ին [Prop. 7.17]: Եվ E-ն հարաբերում է G: Այսպիսով, C-ն նույնպես հարաբերում է D՝ մեծը հարաբերում է փոքրին: Դա անհնար է: Այսպիսով, A և B չեն հարաբերում մի թիվ, որը ավելի փոքր է, քան C: Հետևաբար, C-ն այն ամենափոքր թիվն է, որը հարաբերում են A-ն և B-ն: Սա հենց այն է, ինչ պետք էր ցույց տալ: | Եվ քանի որ A-ը ստացավ C և D՝ բազմապատկելով E և G համապատասխանաբար, ապա ինչպես E-ն է G-ին, այնպես էլ C-ն է D-ին [Prop. 7.17]: Եվ E-ն հարաբերում է G: Այսպիսով, C-ն նույնպես հարաբերում է D՝ մեծը հարաբերում է փոքրին: Դա անհնար է: Այսպիսով, A և B չեն հարաբերում մի թիվ, որը ավելի փոքր է, քան C: Հետևաբար, C-ն այն ամենափոքր թիվն է, որը հարաբերում են A-ն և B-ն: Սա հենց այն է, ինչ պետք էր ցույց տալ: | ||
| Տող 212. | Տող 212. | ||
== Պնդում 35 == | == Պնդում 35 == | ||
Եթէ երկու թվերին հարաբերեն ինչ-որ թիվ, ապա դրանցից ամենափոքրը, որն իրենով հարաբերում է այդ թիվը, նույնպես կհարաբերի նույն թվին: | Եթէ երկու թվերին հարաբերեն ինչ-որ թիվ, ապա դրանցից ամենափոքրը, որն իրենով հարաբերում է այդ թիվը, նույնպես կհարաբերի նույն թվին: | ||
| − | + | ||
Եվ այո, Դիցուք, A և B, հարաբերում են ինչ-որ թիվ CD, և թող E լինի ամենափոքրը, որն հարաբերում է ինչպես A-ն, այնպես էլ B-ն: Ես ասում եմ, որ E նույնպես հարաբերում է CD: | Եվ այո, Դիցուք, A և B, հարաբերում են ինչ-որ թիվ CD, և թող E լինի ամենափոքրը, որն հարաբերում է ինչպես A-ն, այնպես էլ B-ն: Ես ասում եմ, որ E նույնպես հարաբերում է CD: | ||
Եթե E չի հարաբերում CD, թող E թողնի CF, որը փոքր է իրենից (հարաբերելով DF): Եվ քանի որ A-ն և B-ն հարաբերում են E-ին, իսկ E-ն հարաբերում է DF, ապա A-ն և B-ն նույնպես կհարաբերեն DF: Եվ (A-ն և B-ն) նույնպես հարաբերում են ամբողջ CD-ն: Այնպես որ, նրանք նույնպես կհարաբերեն մնացորդը՝ ΓΔ, որը փոքր է E-ից: Ինչպես տեսնում ենք, դա անհնար է: Այնպես որ, E չի կարող չհարաբերում CD-ին: Նշանակում է, որ (E) հարաբերում է CD: Այդ ամենը հենց այն է, ինչ պետք էր ապացուցել: | Եթե E չի հարաբերում CD, թող E թողնի CF, որը փոքր է իրենից (հարաբերելով DF): Եվ քանի որ A-ն և B-ն հարաբերում են E-ին, իսկ E-ն հարաբերում է DF, ապա A-ն և B-ն նույնպես կհարաբերեն DF: Եվ (A-ն և B-ն) նույնպես հարաբերում են ամբողջ CD-ն: Այնպես որ, նրանք նույնպես կհարաբերեն մնացորդը՝ ΓΔ, որը փոքր է E-ից: Ինչպես տեսնում ենք, դա անհնար է: Այնպես որ, E չի կարող չհարաբերում CD-ին: Նշանակում է, որ (E) հարաբերում է CD: Այդ ամենը հենց այն է, ինչ պետք էր ապացուցել: | ||
| Տող 219. | Տող 219. | ||
== Պնդում 36 == | == Պնդում 36 == | ||
Այսպես, A, B և C երեք տրված թվեր են։ Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է նրանց բոլորին: | Այսպես, A, B և C երեք տրված թվեր են։ Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է նրանց բոլորին: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 36.png|center|250px]] | |
Դիցուք A, B և C թվեր են, որոնցից յուրաքանչյուրն ունի որոշակի հարաբերություն։ | Դիցուք A, B և C թվեր են, որոնցից յուրաքանչյուրն ունի որոշակի հարաբերություն։ | ||
Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է բոլոր երեք թվերին։ | Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է բոլոր երեք թվերին։ | ||
| Տող 231. | Տող 231. | ||
== Պնդում 37 == | == Պնդում 37 == | ||
Եթե մի թիվ չափվում է մեկ այլ թվով, ապա այդ թիվը կունենա մաս, որն անվանվում է նույն անունով, ինչ մյուս թիվը: | Եթե մի թիվ չափվում է մեկ այլ թվով, ապա այդ թիվը կունենա մաս, որն անվանվում է նույն անունով, ինչ մյուս թիվը: | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 37.png|center|250px]] | |
Դիցուք A թիվը չափվում է B թվով։ Ես ասում եմ, որ A-ն ունի մաս, որը կոչվում է նույն անունով, ինչ B-ն։ Քանի անգամ B-ն հարաբերում է A-ին, այդքան շատ միավորներ լինեն C-ում։ Քանի որ B-ն չափում է A-ն ըստ C-ի միավորների, և D միավորը նույնպես չափում է C թիվը ըստ նրա մեջ եղած միավորների, ապա D միավորը այնքան անգամ կչափի C թիվը, որքան B-ն՝ A-ն։ Հետևաբար, D միավորը չափում է B թիվը, ինչպես C-ն՝ A-ն։ Եվ այսպես, ամեն մի մասնաբառ, որը D միավորը B թվի մաս է, նույն անունով մասն է նաև C-ի A թվի համար։ Հետևաբար, A-ն ունի C մասը, որը կոչվում է նույն անունով, ինչ B-ն։ Դա հենց այն է, ինչ պետք էր ապացուցել։ | Դիցուք A թիվը չափվում է B թվով։ Ես ասում եմ, որ A-ն ունի մաս, որը կոչվում է նույն անունով, ինչ B-ն։ Քանի անգամ B-ն հարաբերում է A-ին, այդքան շատ միավորներ լինեն C-ում։ Քանի որ B-ն չափում է A-ն ըստ C-ի միավորների, և D միավորը նույնպես չափում է C թիվը ըստ նրա մեջ եղած միավորների, ապա D միավորը այնքան անգամ կչափի C թիվը, որքան B-ն՝ A-ն։ Հետևաբար, D միավորը չափում է B թիվը, ինչպես C-ն՝ A-ն։ Եվ այսպես, ամեն մի մասնաբառ, որը D միավորը B թվի մաս է, նույն անունով մասն է նաև C-ի A թվի համար։ Հետևաբար, A-ն ունի C մասը, որը կոչվում է նույն անունով, ինչ B-ն։ Դա հենց այն է, ինչ պետք էր ապացուցել։ | ||
| Տող 237. | Տող 237. | ||
Եթե թիվը բաժանվում է որոշակի մասերի (մասնիկների), ապա այդ մասերից յուրաքանչյուրն ունի համապատասխան թվային նշանակություն, որը կոչվում է այդ մասի անվանումը | Եթե թիվը բաժանվում է որոշակի մասերի (մասնիկների), ապա այդ մասերից յուրաքանչյուրն ունի համապատասխան թվային նշանակություն, որը կոչվում է այդ մասի անվանումը | ||
| − | + | [[Պատկեր:Euclid Elements Book 7 Proposition 38.png|center|250px]] | |
Տրված լինի, որ թիվ A-ն ունի որևէ մաս, օրինակ՝ B։ Եվ թող C-ը լինի այն թիվը, որը կոչվում է նույն անունով, ինչ B (ինչպես՝ B-ն A-ի C-րդ մասը է): Ես ասում եմ, որ C-ն չափում է A-ն։ | Տրված լինի, որ թիվ A-ն ունի որևէ մաս, օրինակ՝ B։ Եվ թող C-ը լինի այն թիվը, որը կոչվում է նույն անունով, ինչ B (ինչպես՝ B-ն A-ի C-րդ մասը է): Ես ասում եմ, որ C-ն չափում է A-ն։ | ||
Քանի որ B-ն A-ի մի մասն է, որն ունի նույն անունը, ինչ C, ապա նաև D միավորը C-ի մաս է, որն ունի նույն անունը՝ այն է՝ D-ն C-ի C-րդ մասն է։ Եվ հետևաբար, ինչպես D-ն C-ն է չափում, այնպես էլ B-ն չափում է A-ն։ Այսպես, ի վերջո, D-ն B-ն է չափում նույնքան անգամ, ինչքան C-ն չափում է A-ն։ | Քանի որ B-ն A-ի մի մասն է, որն ունի նույն անունը, ինչ C, ապա նաև D միավորը C-ի մաս է, որն ունի նույն անունը՝ այն է՝ D-ն C-ի C-րդ մասն է։ Եվ հետևաբար, ինչպես D-ն C-ն է չափում, այնպես էլ B-ն չափում է A-ն։ Այսպես, ի վերջո, D-ն B-ն է չափում նույնքան անգամ, ինչքան C-ն չափում է A-ն։ | ||
| Տող 245. | Տող 245. | ||
Ենթադրենք, որ տրված մասերն են A, B և C։ Պետք է գտնվի նվազագույն թիվը, որը կունենա A, B և C մասերը։ | Ենթադրենք, որ տրված մասերն են A, B և C։ Պետք է գտնվի նվազագույն թիվը, որը կունենա A, B և C մասերը։ | ||
| + | [[Պատկեր:Euclid Elements Book 7 Proposition 39.png|center|250px]] | ||
Լավ, ենթադրենք, որ A, B և C մասերի համար գոյություն ունեն համանուն թվեր, որոնց անունները կհամապատասխանեն համապատասխան մասերին (A-ին՝ D, B-ին՝ E, C-ին՝ F)։ Այնպես որ, նվազագույն թիվը՝ G, որն ունի A, B և C մասերը, չափվում է D, E և F թվերով։ | Լավ, ենթադրենք, որ A, B և C մասերի համար գոյություն ունեն համանուն թվեր, որոնց անունները կհամապատասխանեն համապատասխան մասերին (A-ին՝ D, B-ին՝ E, C-ին՝ F)։ Այնպես որ, նվազագույն թիվը՝ G, որն ունի A, B և C մասերը, չափվում է D, E և F թվերով։ | ||
Եվ G-ն իր հերթին կունենա մասեր, որոնք համանուն են D, E և F թվերին։ Ուստի, G-ն կունենա նաև A, B և C մասերը։ Ապա ես ասում եմ, որ G-ն, լինելով նվազագույնը, եթե ոչ, ապա լինի մի թիվ՝ H, որը կլինի G-ից փոքր, բայց կունենա A, B և C մասերը։ Այս դեպքում, եթե H-ն ունի A, B և C մասերը, ապա այն կչափվի D, E և F թվերով։ Բայց քանի որ H-ն փոքր է G-ից, դա անհնար է։ | Եվ G-ն իր հերթին կունենա մասեր, որոնք համանուն են D, E և F թվերին։ Ուստի, G-ն կունենա նաև A, B և C մասերը։ Ապա ես ասում եմ, որ G-ն, լինելով նվազագույնը, եթե ոչ, ապա լինի մի թիվ՝ H, որը կլինի G-ից փոքր, բայց կունենա A, B և C մասերը։ Այս դեպքում, եթե H-ն ունի A, B և C մասերը, ապա այն կչափվի D, E և F թվերով։ Բայց քանի որ H-ն փոքր է G-ից, դա անհնար է։ | ||
00:27, 14 Դեկտեմբերի 2024-ի տարբերակ
հեղինակ՝ էվկլիդես |
Բովանդակություն
- 1 Պնդում 13
- 2 Պնդում 14[1]
- 3 Պնդում 15
- 4 Պնդում 16
- 5 Պնդում 17
- 6 Պնդում 18
- 7 Պնդում 20
- 8 Պնդում 21
- 9 Պնդում 22
- 10 Պնդում 23
- 11 Պնդում 24
- 12 Պնդում 25
- 13 Պնդում 26
- 14 Պնդում 27
- 15 Պնդում 28
- 16 Պնդում 29
- 17 Պնդում 30
- 18 Պնդում 31
- 19 Պնդում 32
- 20 Պնդում 33
- 21 Պնդում 34
- 22 Պնդում 35
- 23 Պնդում 36
- 24 Պնդում 37
- 25 Պնդում 38
- 26 Պնդում 39
- 27 Նշումներ
Պնդում 13
Եթե Չորս թվեր իրար հարաբերական են, ապա նրանք հարաբերական կլինեն նաև միմյանց.
Օրինակ վերցնենք A, B, C, D թվերը: Եթե A հարաբերում է B-ին ին ինչպես C-ն է հարաբերում D-ին, ապա կարող ենք պնդել, որ A-ն հարաբերում է C -ին, ինչպես B-ն հարաբերում է D-ին: Եթե A-ն կազմում է B-ի մի մասը, ապա C-ն նույնպես կազմում է D-ի նույն մասը: Այսպիսով, որերորդ մասը որ A-ն կազմում է C-ի մեջ, նույքան մաս B-ն կազմում է D-ի մեջ: Այսինքն ինչպես A-ն C-ին, այնպես էլ B-ն D-ին: Որը և մեզ անհրաժեշտ էր ցույց տալ:
Պնդում 14[1]
Եթե կա որևէ թվերի բազմություն, և մեկ այլ թվերի բազմություն նրանց հավասար,որոնք հարաբերում են միմյանց ինչպես նշվաց է Պնդում 13-ում,ապա նրանք նույնպես հավասար կհարաբերեն միմյանց:
Օրինակ, վերցնենք A,B,C թվերի բազմությունը և դրան համարժեք D,E,F թվերի բազմությունը: Եթե պնդում 13 գործում է, այսինքն A հարաբերում է B-ին ին ինչպես D -ն է հարաբերում E-ին, ապա նույն ձև B-ն հարաբերում է C-ին, ինչպես E-ն հարաբերում է F-ին: Ունենալով այս պնդումը, մենք կարող ենք պնդել նաև, որ A-ն հարաբերում է D-ին, ինչպես B-ն հարաբերում է E-ին, ինչպես C-ն հարաբերում է F-ին, որը և անհրաժեշտ էր ցույց տալ:
Պնդում 15
Եթե ունենք մեկ չափանիշ որը հավասար է որևէ թվի, և ունենք մեկ այլ թիվ որը մի քանի անգամ մեծ է և հավասար է մի քանի անգամ մեծ չափանիշի, ապա կարող ենք ասել որ, առաջինը թիվը հարաբերում է երկրորդ թվին այնպես, ինչպես առաջին չափանիշը երկրորդ չափանիշին:
Oրինակ, համարենք, որ A -ն համարժեք է BC չափին, և D-ն որը մի քանի անգամ մեծ է A-ից համարժեք լինի EF- ին, որը նույնքան անգամ մեծ է BC-ից:
Քանի որ A -ն համարժեք է BC չափին, և D-ն որը մի քանի անգամ մեծ է A-ից համարժեք է EF- ին, ապա կարող ենք ասել, որ որքան չափ կա BC-ում, նույնքան կա EF-ում, որը հավասար է D ին: Եթե BC-ն բաժանենք BG, GH և HC, իսկ EF-ը EK, KL, LF մասերի, ապա կարող ենք նկատել, որ նրանք միմյանց համարժեքորեն հարաբերում են: Այսինքն, BG հարաբերում է EKին, ինչպես GH KL-ին, ինչպես HC-ն LF-ին: Այսպիսով, կարող ենք եզրակացնել, որ այն թվերը որը համապատասխանորեն համարժեք են այդ թվերին նույնպես հարաբերում են: Այսպիսով, A-ն հարաբերում է D-ին, ինչպես BG-ն EK-ին, ինչպես GH-ն KL-ին, ինչպես HC-ն LF-ին, որը և պետք էր ապացուցել:
Պնդում 16
Եթե երկու թվեր բազմապատկենք միմյանցով և ստանանք մի քանի թվեր, ապա այդ մի քանի թվերը միմյանց հավասար կլինեն:
Թող A և B լինեն երկու թվեր: Ենթադրենք, A-ն ստեղծում է C-ն՝ բազմապատկելով B-ով, և B-ն ստեղծում է D-ն՝ բազմապատկելով A-ով: Կարող ենք պնդել,, որ C-ն հավասար է D-ին: Քանի որ A-ն ստեղծել է C-ն՝ բազմապատկելով B-ով, ուրեմն B-ն չափում է C-ն ըստ A-ի միավորների: Եվ E միավորը նույնպես չափում է A թիվը՝ ըստ նրա մեջ գտնվող միավորների: Ուրեմն E միավորը չափում է A թիվը նույնքան անգամ, որքան B-ն չափում է C-ն: Ուրեմն փոխադարձաբար, E միավորը չափում է B թիվը նույնքան անգամ, որքան A-ն չափում է C-ն: Քանի որ B-ն ստեղծել է D-ն՝ բազմապատկելով A-ով, ուրեմն A-ն չափում է D-ն՝ ըստ B-ի միավորների: Եվ E միավորը նույնպես չափում է B-ն՝ ըստ նրա մեջ գտնվող միավորների: Ուրեմն E միավորը չափում է B թիվը նույնքան անգամ, որքան A-ն չափում է D-ն: Եվ E միավորը չափում է B թիվը նույնքան անգամ, որքան A-ն չափում է C-ն: Ուրեմն A-ն նույնքան անգամ չափում է C-ն և D-ն: Հետևաբար, C-ն հավասար է D-ին, Ինչը և պետք էր ապացուցել:
Պնդում 17
Եթե մի թիվ բազմապատկելով երկու թվերով ստանանք այլ թվեր, ապա նրանցից առաջացած թվերը կունենան նույն հարաբերությունը, ինչ բազմապատկվող թվերը։
Քանի որ D և E թվերը ստացել ենք բազմապատկելով երկու թվերը՝ B և C (համապատասխանաբար), կարելի է պնդել, որ ինչպես B-ն է հարաբերում C-ին, այնպես էլ D-ն կհարաբերի E-ին: Քանի որ D թիվը ստացվել է A բազմապատկելով B-ն, ուրեմն B-ն չափում է D-ն՝ ըստ A-ի միավորների: Եվ F միավորը նույնպես չափում է A-ն՝ ըստ նրա մեջ գտնվող միավորների: Ուրեմն F միավորը չափում է A-ն նույնքան անգամ, որքան B-ն չափում է D-ն: Այսպիսով, ինչպես F ն է հարաբերում Aին, այնպես էլ B-ն է հարաբերում D-ին: Եվ նույն պատճառով, ինչպես Fն է A թվի հանդեպ, այնպես էլ C-ն է E-ի հանդեպ: Կարելի է պնդել, որ ինչպես B-ն է D-ի հանդեպ, այնպես էլ C-ն է E-ի հանդեպ: Ուրեմն փոխադարձաբար, ինչպես B-ն է C-ի հանդեպ, այնպես էլ D-ն է E-ի հանդեպ, Ինչը և պետք էր ապացուցել:
Պնդում 18
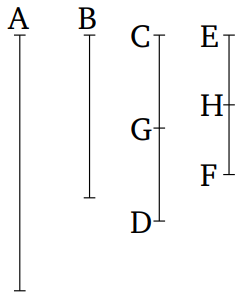
Եթե չորս թվեր համեմատական են միմյանց, ապա առաջին և չորրորդ թվերի բազմապատկումից ստացված թիվը կլինի հավասար երկրորդի և երրորդի բազմապատկումից ստացված թվին: Եվ եթե առաջինի և չորրորդի բազմապատկումից ստացված թիվը հավասար է երկրորդի և երրորդի բազմապատկումից ստացված թվին, ապա այդ չորս թվերը կլինեն համեմատական: Օրինակ, A, B, C և D համեմատական թվեր են: Ենթադրենք ինչպես A-ն է հարաբերում B-ին, այնպես էլ C-ն է D-ին: A-ն բազմապատկելով D-ն կստանք E թիվը, իսկ B-ն բազմապատկելով C- թվին կստանանք F թիվը: Կարելի է պնդել, որ E-ն հավասար է F-ին:
Դիցուք, A-ն C-ով բազմապատկելով ստացվում է G թիվը: Քանի որ A-ից ստացվել է G թիվը C-ով բազմապատկելո և E թիվը D-ով բազմապատկելո, ապա A-ից ստացվել են է G և E թվերը համապատասխանաբար բազմապատկվելով C և D թվերի հետ: Ուրեմն ինչպես C-ն է հարաբերում D ին այնպես էլ G-ն է հարաբերում E-ին: Ինչպես C-ն է հարաբերում D-ին , այնպես էլ A-ն է հարաբերում B-ին :Ինչպես A-ն է B-ի հետ հարաբերում, այնպես էլ G-ն է E-ի հետ հարաբերում: Պետք է նշել, որ ինչպես A-ն է B-ի հանդեպ, այնպես էլ G-ն է E-ի հանդեպ: Ուրեմն, ինչպես G-ն է E-ի հանդեպ, այնպես էլ G-ն է F-ի հանդեպ: Ուրեմն G-ն ունի նույն հարաբերությունը թե E-ի, թե F-ի հետ: Ուրեմն E-ն հավասար է F-ին: ՈՒնեքն այն փաստը, որ E-ն հավասար է F-ին: Կարելի է պնդել, որ ինչպես A-ն է B-ի հանդեպ, այնպես էլ C-ն է D-ի հանդեպ: Քանի որ նույն կառուցվածքով E-ն հավասար է F-ին, ուրեմն ինչպես G-ն է E-ի հետ համեմատում, այնպես էլ G-ն է F-ի հետ համեմատում: Ինչպես G-ն է հարաբերում E-ին, այնպես էլ C-ն է հարաբերում D-ին: Եվ ինչպես G-ն է F-ի հանդեպ, այնպես էլ A-ն է B-ի հանդեպ: Այսպիսով, ինչպես A-ն է B-ի հանդեպ, այնպես էլ C-ն է D-ի հանդեպ:
Պնդում 20
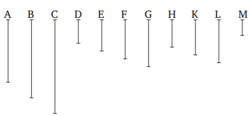
Թող լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ ինչպես A-ն և B-ն: Ասում եմ, որ CD-ն չափում է A-ն այնքան անգամ, որքան և EF-ն չափում է B-ն՝ մեծը՝ մեծին, և փոքրն՝ փոքրին: Այնպես որ, թող CD և EF լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ A-ի և B-ի հետ համապատասխանաբար: Ես ասում եմ, որ CD-ն չափում է A-ն նույն քանակությամբ անգամ, որքան EF-ն չափում է B-ն։
Եթե հնարավոր է, Դիցուք, CD-ն չլինի A-ի մաս: Եվ եթե EF-ն իսկապես այն նույն մասերն ունի B-ի, որոնք CD-ն ունի A-ի մասերից, ապա այն հնարավոր է։ Ինչքան որ մասեր կան CD-ում, նույնքան մասեր կան EF-ում՝ B-ի մասերից։ Let CD բաժանվի A-ի մասերի՝ CG և GD, իսկ EF բաժանվի B-ի մասերի՝ EH և HF։ Եվ այդ դեպքում, CG և GD բաժանումների թվաքանակը հավասար կլինի EH և HF բաժանումների թվաքանակին։ Եվ քանի որ CG և GD թվերը հավասար են միմյանց, նույնպես EH և HF թվերը հավասար են միմյանց, և հարաբերությունը CG-ի և EH-ի միջև նույնն է, ինչ հարաբերությունը GD-ի և HF-ի միջև։ Հետևաբար, ինչպես CG-ն է հարաբերակցվում EH-ի հետ, այնպես էլ GD-ն է հարաբերակցվում HF-ի հետ։ Դրանից հետո, որպես հետևանք, ինչպես յուրաքանչյուր առաջատար մաս՝ ΓΗ միանում է հետագային ΕΘ, այնպես էլ այն մագլցած մասերը ΓΔ և ΕΖ՝ նույն հարաբերությամբ՝ լինում են համարժեք։
Պնդում 21
Դիցուք, A եւ B թվերը պարզ թվեր ենէ : Կարելի է պնդել, , որ A եւ B թվերը, նրանց պես հարաբերություն ունեցող թվերից ամենափոքր թվերն են: Եթե դա այդպես չէ, ապա կլինեն ինչ-որ թվեր, որոնք A եւ B-ից փոքր կլինեն և նրանք կհարաբերեն նույնպես, ինչպես A եւ B-: Թող դրանք լինեն C եւ D:
Ասպիսով, քանի որ այս թվերը նվազագույններն են, որոնք նույն հարաբերությունն ունեն, և մեծ հարաբերությունը չափում է մեծին, և փոքրն այնքանն է, որքան փոքրին՝ այսինքն, ավելի մեծը հարաբերում է ավելի մեծին, իսկ ավելի փոքրը ՝ փոքրին։ Այսպիսով, որքան որ C հարաբերում է Aին, այնքան անգամեր թող լինեն E-ում։ Եվ D-ը, ամփոփելով B-ը, E-ում չափում է ըստ նույն միավորների։ Այսպես, քանի որ C-ը հարաբերում է Aին ըստ E-ում առկա միավորների, E-ն էլ, ըստ C-ի, հարաբերում է Aին նույնչափ ։ Հետևաբար E-ն և B-ը չափում են D-ում առկա միավորներով։ Այնպես որ, հնարավոր չէ, որպեսզի A-ի և B-ից ավելի փոքր թվեր լինեն, որոնք նույն հարաբերությունն ունեն A և B թվերի հետ։ Հետեւաբար, A և B-ն են այդ թվերը, որոնք նույն հարաբերությունն ունեն։ Սա հենց այն բանն է, որը պետք էր ապացուցել:
Պնդում 22
Այն նվազագույն թվերը, որոնք ունեն նույնպիսի հարաբերություն, միմյանց նկատմամբ ունեն ընդհանուր բազմապատիկ և նրանք պարզ թվեր են:
Դիցուք A և B լինեն ամենափոքր թվերը նրանցից, որոնք ունեն նույն հարաբերակցությունը, ինչ նրանք։ Կարելի է պնդել, որ A-ն և B-ն փոխադարձաբար պարզ են։ Քանի որ, եթե A-ն և B-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի նրանց։ Թող այդ թիվը լինի C : Եվ որքան անգամ C-ն բաժանի A-ին, այնքան միավոր թող լինի D-ում։ Եվ որքան անգամ C-ն բաժանի B-ին, այնքան միավոր թող լինի E-ում։ Քանի որ C-ն բաժանում է A-ն՝ համաձայն D-ի մեջ եղած միավորների, C-ն D-ն բազմապատկելով ստեղծել է A-ն։ Նույն պատճառներով C-ն E-ն բազմապատկելով ստացել ենք B-ն։ Այսպիսով, թիվ C-ն D-ն և E-ն բազմապատկելով ստացվել է է A-ն և B-ն։ Այսպիսով, ինչպես D-ն է վերաբերվում E-ին, այնպես էլ A-ն է վերաբերվում B-ին։ Այսպիսով, D-ն և E-ն ունեն նույն հարաբերակցությունը, ինչ A-ն և B-ն, բայց լինելով ավելի փոքր։ Սա անհնար է։ Ուստի, ոչ մի թիվ չի բաժանում A-ն և B-ն։ Այսպիսով, A-ն և B-ն փոխադարձաբար պարզ են։ Թեորեմն ապացուցված է:
Պնդում 23
Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկը բաժանող թիվը կմնա փոխադարձաբար պարզ մյուս թվի հետ։
Դիցուք A և B լինեն փոխադարձաբար պարզ թվեր, և թող մի թիվ C բաժանի A-ին։ Ասում եմ, որ C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Եթե C-ն և B-ն փոխադարձաբար պարզ չեն, ապա մի թիվ կբաժանի C-ն և B-ն։ Թող այդ թիվը լինի D։ Քանի որ D-ն բաժանում է C-ն, իսկ C-ն բաժանում է A-ն, ապա D-ն նաև բաժանում է A-ն։ Եվ D-ն բաժանում է նաև B-ն։ Այսպիսով, D-ն բաժանում է A-ն և B-ն, որոնք փոխադարձաբար պարզ են։ Սա անհնար է։ Ուստի, ոչ մի թիվ չի բաժանում C-ն և B-ն։ Այսպիսով, C-ն և B-ն փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ապացուցել:
Պնդում 24
Եթե երկու թվեր փոխադարձաբար պարզ են որևէ թվի հետ, ապա դրանցից բազմապատկված, ստեղծված թիվը նույնպես փոխադարձաբար պարզ կլինի նույն թվի հետ։
Դիցուք, A և B լինեն երկու թվեր, որոնք երկուսն էլ փոխադարձաբար պարզ են C-ի հետ։ Թող A-ն B-ն բազմապատկելով ստեղծի D-ն։ Կարելի է պնդել, որ C-ն և D-ն նույնպես փոխադարձաբար պարզ են։ Եթե C-ն և D-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի C-ն և D-ն։ Թող այդ թիվը լինի E։ Եվ քանի որ C-ն և A-ն փոխադարձաբար պարզ են, իսկ E-ն բաժանում է C-ին, ապա A-ն և E-ն նույնպես փոխադարձաբար պարզ են։ Քանի անգամ E-ն բաժանում է D-ն, այնքան միավոր թող լինի F-ում։ Ուստի, F-ն նույնպես բաժանում է D-ն՝ ըստ E-ի մեջ եղած միավորների։ E-ն F-ն բազմապատկելով ստեղծել է D-ն։ Սակայն A-ն նույնպես B-ն բազմապատկելով ստեղծել է D-ն։ Ուստի E-ի և F-ի բազմապատկումը հավասար է A-ի և B-ի բազմապատկմանը։ Եթե ծայրամասային թվերի (բազմապատկումը) հավասար է միջնամասային թվերի (բազմապատկմանը), ապա թվերը համեմատական են։ Ուստի, ինչպես EEE-ն է վերաբերվում A-ին, այնպես էլ B-ն է վերաբերվում F-ին։ A-ն և E-ն փոխադարձաբար պարզ են։ Եվ A-ն և E-ն լինելով փոխադարձաբար պարզ՝ նաև նվազագույն թվերն են։ Նվազագույն թվերը, որոնք ունեն նույն հարաբերակցությունը, կբաժանեն նույն հարաբերակցությամբ ունեցող թվերը՝ հավասար քանակով։ Առավել մեծը բաժանում է առավել մեծին, իսկ փոքրն՝ փոքրին։ Այսպիսով, E-ն բաժանում է B-ն։ Եվ E-ն նաև բաժանում է C-ն։ Ուստի E-ն բաժանում է B-ն և C-ն, որոնք փոխադարձաբար պարզ են։ Սա անհնար է։ Ուստի, ոչ մի թիվ չի կարող բաժանել C-ն և D-ն։ Այսպիսով, C-ն և D-ն փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ցույց տալ։
Պնդում 25
Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկի քառակուսիով ստեղծված թիվը փոխադարձաբար պարզ կլինի մյուսի հետ։ Դիցուք A և B երկու պարզ թվեր են, որոնք փոխադարձաբար պարզ են։ Թող A-ն ինքն իրեն բազմապատկելով ստեղծի C-ն։ Կարելի է պնդել , որ B-ն և C-ն փոխադարձաբար պարզ են։
Դիցուք D լինի հավասար A-ին։ Քանի որ A և B փոխադարձաբար պարզ են, իսկ A հավասար է D-ին, ապա D-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Այսպիսով, D-ն և A-ն երկուսն էլ փոխադարձաբար պարզ են B-ի հետ։ Այլ կերպ ասած, D-ից և A-ից ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի B-ի հետ։ Եվ C-ն է այն թիվը, որը ստացվում է D-ի և A-ի բազմապատկումով։ Այսպիսով, C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ցույց տալ։
Պնդում 26
Եթե երկու թվերն էլ փոխադարձաբար պարզ են երկու թվերի հետ, ապա դրանցից բազմապատկված, ստացված թվերը նույնպես փոխադարձաբար պարզ կլինեն իրար հետ։
Դիցուք A և B երկու թվեր լինեն, որոնք երկուսն էլ փոխադարձաբար պարզ են երկու այլ թվերի՝ C-ի և D-ի հետ։ Դիցուք, A-ն B-ի հետ բազմապատկելով ստանանք E-ն, և թող C-ն D-ի հետ բազմապատկելով ստանանք F-ն։ Ասում եմ, որ E և F փոխադարձաբար պարզ են։ Քանի որ A-ն և B-ն երկուսն էլ փոխադարձաբար պարզ են C-ի հետ, ապա A-ի և B-ի բազմապատկմամբ ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի C-ի հետ։ Այսպիսով, E-ն և C-ն փոխադարձաբար պարզ են։ Դրա համար նույն պատճառներով E-ն և D-ն նույնպես փոխադարձաբար պարզ են։ Այսպիսով, C-ն և D-ն երկուսն էլ փոխադարձաբար պարզ են E-ի հետ։ Եվ C-ի և D-ի բազմապատկմամբ ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի E-ի հետ։ Իսկ FFF-ն է այն թիվը, որը ստացվում է C-ի և D-ի բազմապատկումով։ Այսպիսով, E-ն և F-ն փոխադարձաբար պարզ են։
Պնդում 27
Եթե երկու թվեր փոխադարձաբար պարզ են իրարից, և յուրաքանչյուրը նրանցից որոշ թիվ է ստեղծում՝ ինքն իրեն բազմապատկելով, ապա դրանցից ստացված թվերը նույնպես կլինեն փոխադարձաբար պարզ։ Եվ եթե սկզբնական թվերը ստեղծեն որոշ թվեր՝ ստեղծված թվերը բազմապատկելով, ապա դրանք ևս կլինեն փոխադարձաբար պարզ։ Սա միշտ տեղի է ունենում ծայրամասերի վերաբերյալ։
Դիցուք A և B երկու թվեր են, որոնք փոխադարձապես պարզ են, և թող A ստեղծի C՝ ինքն իրեն բազմապատկելով, իսկ B՝ E՝ ինքն իրեն բազմապատկելով։ Եվ թող A բազմապատկի C՝ ստանալով D, իսկ B բազմապատկի E՝ ստանալով F։ Կարելի է պնդել, որ C և E, և D և F կլինեն փոխադարձաբար պարզ։ Որովհետև A և B փոխադարձապես պարզ են, և A ինքն իրեն բազմապատկելով ստեղծել է C, ապա C և B նույնպես կլինեն փոխադարձապես պարզ։ Այնպես որ, C և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ուստի C և E նույնպես փոխադարձապես պարզ են։ Նորից, քանի որ A և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ապա A և E նույնպես փոխադարձապես պարզ են։ Այնպես որ, քանի որ երկու թիվ՝ A և C, երկուսն էլ փոխադարձաբար պարզ են երկու թվերից՝ B և E, A և C բազմապատկելով ստացած թիվը (D) կլինի B և E բազմապատկելով ստացված թվից (F) փոխադարձապես պարզ։ Այնպես որ, D և F փոխադարձապես պարզ են։ Սա այն է, ինչ պետք էր ապացուցել։
Պնդում 28
Եթե երկու թիվեր պարզ են, ապա նրանց գումարը նույնպես կլինի պարզ յուրաքանչյուրին։ Եվ եթե այդ գումարը պարզ է ինչ-որ մեկի հետ, ապա սկզբնական թվերը նույնպես պարզ կլինեն
Դիցուք երկու թվերը՝ AB և BC, որոնք պարզ են, տրված են: Կարելի է պնդել, որ նրանց գումարը՝ AC, նույնպես պարզ կլինի յուրաքանչյուրի համար՝ AB և BC: Եթե քաղված AC և AB միմյանց պարզ չեն չեն, ապա կգտնվի ինչ-որ թիվ, որը չափում է AC և AB: Թող այդ թիվը լինի D: Ենթադրենք, որ D չափում է AC և AB, ապա այն նույնպես պետք է չափի BC: Բայց քանի որ AB և BC միմյանց պարզ են, դա անհնար է: Հետևաբար, AC և AB պետք է միմյանց պարզ լինեն: Անհրաժեշտության դեպքում, եթե AB և BC միմյանց պարզ չեն, ապա թիվ D կմատչի AB և BC, ինչը էլ ավելի անհավանական է, քանի որ D չափում է նաև AC ամբողջությամբ: Եվ քանի որ AB և BC միմյանց պարզ են, դա նույնպես անհնար է: Հետևաբար, AB և BC պետք է միմյանց պարզ լինեն: Այսպիսով, ապացուցվեց, որ երկու թիվ, որոնք միմյանց պարզ են, նրանց գումարը նույնպես պարզ կլինի միմյանց
Պնդում 29
Յուրաքանչյուր պարզ թիվ առաջին է բոլոր այն թվերի հետ, որոնք ինքը չի չափում
Դիցուք, A-ն պարզ թիվ է, և B-ն այնպիսի թիվ է, որ A-ն չի չափում։ Կարելի է, որ B-ն և A-ն միմյանց նկատմամբ պարզ են։ Որպեսզի եթե B-ն և A-ն միմյանց նկատմամբ պարզ չեն, ապա մի թիվ կլինի, որը նրանց չափում է։ Թող C-ն չափի նրանց։ Քանի որ C-ն չափում է B-ն, իսկ A-ն չի չափում B-ն, ապա C-ն պետք է տարբեր լինի A-ից։ Եվ քանի որ C-ն չափում է B-ն և A-ն, ապա C-ն պետք է չափի նաև A-ն՝ չնայած նրան, որ չի համընկնում նրա հետ։ Բայց սա անհնար է։ Այնպես որ, չի կարող լինել որևէ թիվ, որը կչափի B-ն և A-ն։ Այդպիսով, A-ն և B-ն միմյանց նկատմամբ պետք է լինեն պարզ։
Պնդում 30
Եթե երկու թիվը իրար բազմապատկելով ստանում են ինչ-որ թիվ, և այդ թվից մեկը չափվում է մի պարզ թվով, ապա սկզբնական թվերից մեկը նույնպես պետք է չափվի
Թող երկու թիվ A և B ստեղծեն C՝ իրար բազմապատկելով, և թող ինչ-որ պարզ թիվ D հավասար լինի C-ին: Ես ասում եմ, որ D-ը պետք է հավասար լինի A կամ B: Թող D-ն չհավասար է A, և քանի որ D-ը պարզ է, ապա A և D թվերը միմյանց նկատմամբ պարզ են: Եվ քանի որ D-ն հավասար է C-ին, ապա այն պետք է հավասար է E-ին այնքան անգամ, որքան D-ն հավասար է C-ին: Իսկ քանի որ D-ն հավասար է C-ին ըստ E-ի, ապա D-ն ստեղծում է C՝ բազմապատկելով E: Բայց իսկապես, նաև A-ն ստեղծում է C՝ B-ի հետ բազմապատկելով: Այսպիսով, ստեղծված թիվը D և E թվերից հավասար է A և B թվերի բազմապատկմանը: Դրանով, ինչպես D-ն A-ին հավասար է, այնպես էլ B-ն E-ին հավասար է: Եվ D-ն ու A թվերը պարզ են միմյանց հետ, ինչպես նաև B-ն ու E-ն:
Պնդում 31
Ամեն բաղադրյալ թիվը չափվում է ինչ-որ պարզ թվով:
Դիցուք A-ն բաղադրյալ թիվ է։ Կարելի է պնդել, որ A-ն չափվում է ինչ-որ պարզ թվով։
Քանի որ A-ն բաղադրյալ է, ինչ-որ թիվ այն կչափի։ Թող այդ թիվը լինի B։ Եվ եթե B-ն պարզ է, ապա այն, ինչ ուզում էինք, ապացուցված է։ Իսկ եթե B-ն բաղադրյալ է, ապա ինչ-որ թիվ կչափի այն։ Թող այդ թիվը լինի C։ Եվ քանի որ C-ն չափում է B-ն, իսկ B-ն չափում է A-ն, ապա C-ն նույնպես կչափի A-ն։
Եվ եթե C-ն պարզ է, ապա այն, ինչ նախատեսված էր, կատարվում է։ Իսկ եթե C-ն բաղադրյալ է, ապա ինչ-որ թիվ կչափի այն։ Այս շարունակական հետազոտությունների մեջ, որևէ պարզ թիվ կգտնվի, որը կչափի այն։ Եթե այդպիսի թիվ չի գտնվի, ապա մի քանի անսահման թվեր, որոնք մեկմեկից փոքր են, կչափեն A-ն։ Բայց դա անհնար է թվերի մեջ։ Ուստի, ինչ-որ պարզ թիվ կգտնվի, որը կչափի նախորդը, և որը նույնպես կչափի A-ն։
Ուստի, ամեն բաղադրյալ թիվը չափվում է ինչ-որ պարզ թվով։ Դա այն է, ինչ պետք էր ապացուցել:
Պնդում 32
Ամեն թիվ կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով։
Դիցուք A թիվ է: Կարելի է պնդել, որ A-ն կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով: Եթե A-ն պարզ է, ապա այն, ինչ նախատեսված էր, տեղի է ունենում: Իսկ եթե այն բաղադրյալ է, ապա ինչ-որ պարզ թիվ կչափի այն: Ուստի, ամեն թիվը կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով: Դա այն է, ինչ պետք էր ապացուցել:
Պնդում 33
Թող A, B, և C լինեն ցանկացած տրված թվեր: Պետք է գտնենք նրանցից ամենափոքրին, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B, և C: Իրականում, եթե A, B և C իրար հետ պարզ են, ապա նրանք կլինեն ամենափոքրն այն թվերից, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես տրված թվերն են:
Դիցուք ունենք A, B և C թվերի առավելագույն ընդհանուր չափը՝ D, և որքանով D չափում է A, B և C, այնքան ամեն մի թիվ՝ E, F և G, համապատասխանաբար չափում է A, B և C ըստ D-ի միավորների:
Այդպիսով, E, F և G չափում են A, B և C ըստ նույն հարաբերակցությամբ: Ուստի, E, F և G ունեն նույն հարաբերակցությունը՝ ինչպես A, B և C: Եթե E, F և G չեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B և C, ապա կլինեն այլ թվեր, որոնք փոքր կլինեն E, F և G և կկարողանան լինել նույն հարաբերակցությամբ՝ ինչպես A, B և C: Ներկայացնենք այդ թվերը՝ H, K, L:
Ուստի, H չափում է A, ինչպես K և L՝ B և C: Այնուհետև, քանի որ H չափում է A, M նույնպես կչափի A, ինչպես K և L՝ B և C: Եվ քանի որ H չափում է A, M նույնպես չափելու է B և C՝ ըստ նույն միավորների: Եվ քանի որ H չափում է A՝ ըստ M-ի միավորների, այնուհետև M նաև կչափի B և C՝ ըստ K և L-ի միավորների:
Այդպիսով, M չափում է A, B և C: Բայց այս հնարավորությունը անհնար է, քանի որ D՝ A, B և C թվերի առավելագույն ընդհանուր չափն է: Ուստի, հնարավոր չէ որևէ թիվ, որը փոքր է E, F և G և ունի նույն հարաբերակցությունը՝ ինչպես A, B և C: Այսպիսով, E, F և G կլինեն ամենափոքրը՝ այն թվերից, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B և C: Դա այն է, ինչ պետք էր ապացուցել:
Պնդում 34
Դիցուք A և B թվերը տրված են։ Պետք է գտնենք այն ամենափոքր թիվը, որը կչափեն երկու տրված թվերը:
Դիցուք, A և B լինի միմյանցից անկախ թվեր են:թող A C ստանա՝ բազմապատկելով B: Այսպիսով, B նույնպես C ստացրեց՝ բազմապատկելով A Այսպիսով, A և B երկուսն էլ չափում են C:
Ես ասում եմ, որ C-ն նույնպես ամենափոքրն է թիվ, որը նրանք երկուսն էլ չափում են: Եթե ոչ, A և B երկուսն էլ կչափեն մի այլ թիվ, որը ավելի փոքր է, քան C: Թող նրանք երկուսն էլ հավասար լինեն D (որը ավելի փոքր է քան C):
Եվ որքան անգամ A հարաբերում է D, նույնքան միավորներ թող լինեն E-ում: Եվ որքան անգամ B հարաբերում է D, նույնքան միավորներ թող լինեն F-ում: Այսպիսով, A ստացրեց D՝ բազմապատկելով E, իսկ B ստացրեց D՝ բազմապատկելով F: Այսպիսով, A և E-ից ստացված թիվը հավասար է B և F-ից ստացված թվին: Այսպիսով, ինչպես A-ն է B-ին, այնպես էլ F-ն է E-ին:
Եվ քանի որ A և B-ն անկախ են միմյանցից, իսկ անկախ թվերը ամենափոքրն են (այսինքն՝ այդ նույն հարաբերությունը ունեցող թվերը), ապա ավելի մեծը չափում է ավելի մեծը, իսկ փոքրն՝ ավելի փոքրին: Այսպիսով, B-ն չափում է E, ինչպես հետևյալ (համարների չափման) միջոցով: Եվ քանի որ A-ը ստացավ C և D՝ բազմապատկելով B և E համապատասխանաբար, ապա ինչպես B-ն է E-ին, այնպես էլ C-ն է D-ին : Եվ B-ն չափում է E: Այսպիսով, C-ն նույնպես չափում է D, ավելի մեծը՝ չափելով ավելի փոքրին: Հետևաբար, դա անհնար է: Այսպիսով, A և B-ն չեն չափում մի թիվ, որը ավելի փոքր է քան C: Հետևաբար, C-ն այն ամենափոքր թիվն է, որը չափում են A-ն և B-ն:
A և B անկախ թվեր չեն: Եվ թող նախ ի հայտ գան ամենափոքր թվերը՝ F և E, որոնք ունեն նույն հարաբերությունը A-ի և B-ի հետ (համապատասխանաբար Այնպես որ, A-ի և E-ի բազմապատկմամբ ստացված թիվը հավասար է B-ի և F-ի բազմապատկմամբ ստացված թվին [Prop. 7.19]: Եվ թող A-ը ստանա C՝ բազմապատկելով E: Այսպիսով, B-ն նույնպես ստանում է C՝ բազմապատկելով F: Ուրեմն,, A և B երկուսն էլ հարաբերում են C: Ես ասում եմ, որ C-ն նույնպես ամենափոքրն է (թիվը, որը նրանք երկուսն էլ հարաբերում են): Եթե ոչ, A և B երկուսն էլ կհարաբերեն մի թիվ, որը ավելի փոքր է, քան C: Թող նրանք երկուսն էլ հարաբերեն D (որը ավելի փոքր է, քան C):
Եվ որքան անգամ A հարաբերում է D, նույնքան միավորներ թող լինեն G-ում: Եվ որքան անգամ B հարաբերում է D, նույնքան միավորներ թող լինեն H-ում: Այսպիսով, A ստացրեց D՝ բազմապատկելով G, իսկ B ստացրեց D՝ բազմապատկելով H: Այսպիսով, ինչպես A-ն է B-ին, այնպես էլ H-ն է G-ին [Prop. 7.19]: Եվ քանի որ A-ը ստացավ C և D՝ բազմապատկելով E և G համապատասխանաբար, ապա ինչպես E-ն է G-ին, այնպես էլ C-ն է D-ին [Prop. 7.17]: Եվ E-ն հարաբերում է G: Այսպիսով, C-ն նույնպես հարաբերում է D՝ մեծը հարաբերում է փոքրին: Դա անհնար է: Այսպիսով, A և B չեն հարաբերում մի թիվ, որը ավելի փոքր է, քան C: Հետևաբար, C-ն այն ամենափոքր թիվն է, որը հարաբերում են A-ն և B-ն: Սա հենց այն է, ինչ պետք էր ցույց տալ:
Պնդում 35
Եթէ երկու թվերին հարաբերեն ինչ-որ թիվ, ապա դրանցից ամենափոքրը, որն իրենով հարաբերում է այդ թիվը, նույնպես կհարաբերի նույն թվին:
Եվ այո, Դիցուք, A և B, հարաբերում են ինչ-որ թիվ CD, և թող E լինի ամենափոքրը, որն հարաբերում է ինչպես A-ն, այնպես էլ B-ն: Ես ասում եմ, որ E նույնպես հարաբերում է CD: Եթե E չի հարաբերում CD, թող E թողնի CF, որը փոքր է իրենից (հարաբերելով DF): Եվ քանի որ A-ն և B-ն հարաբերում են E-ին, իսկ E-ն հարաբերում է DF, ապա A-ն և B-ն նույնպես կհարաբերեն DF: Եվ (A-ն և B-ն) նույնպես հարաբերում են ամբողջ CD-ն: Այնպես որ, նրանք նույնպես կհարաբերեն մնացորդը՝ ΓΔ, որը փոքր է E-ից: Ինչպես տեսնում ենք, դա անհնար է: Այնպես որ, E չի կարող չհարաբերում CD-ին: Նշանակում է, որ (E) հարաբերում է CD: Այդ ամենը հենց այն է, ինչ պետք էր ապացուցել:
Պնդում 36
Այսպես, A, B և C երեք տրված թվեր են։ Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է նրանց բոլորին:
Դիցուք A, B և C թվեր են, որոնցից յուրաքանչյուրն ունի որոշակի հարաբերություն։ Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է բոլոր երեք թվերին։
Եկեք ընդունենք, որ A և B ի համար այդ թիվը՝ Dն է ։ Եվ եթե C-ն հարաբերում է D-ին, ապա այն կլինի փաստը թր ուզում էինք ապացուցել։ Եթե ոչ, ապա A, B և C պետք է որոշեն E-ը, որը կլինի ամենափոքր թիվը, որը հարաբերում է D-ին։
Եթե E-ն ավելի փոքր է, քան D, ապա ստացվում է, որ E-ն չպետք է լինի ավելի փոքր։ Բայց այս փաստը հնարավոր չէ։ Այնպես որ, մենք պետք է հաստատենք, որ E-ն իսկապես ամենափոքր թիվն է, որը հարաբերում է A, B և C թվերին։
Այսպիսով, մենք ցույց տալիք խնդիրը, որ E-ն ամենափոքր թիվն է, որը հարաբերում է A, B և C թվերին։
Պնդում 37
Եթե մի թիվ չափվում է մեկ այլ թվով, ապա այդ թիվը կունենա մաս, որն անվանվում է նույն անունով, ինչ մյուս թիվը:
Դիցուք A թիվը չափվում է B թվով։ Ես ասում եմ, որ A-ն ունի մաս, որը կոչվում է նույն անունով, ինչ B-ն։ Քանի անգամ B-ն հարաբերում է A-ին, այդքան շատ միավորներ լինեն C-ում։ Քանի որ B-ն չափում է A-ն ըստ C-ի միավորների, և D միավորը նույնպես չափում է C թիվը ըստ նրա մեջ եղած միավորների, ապա D միավորը այնքան անգամ կչափի C թիվը, որքան B-ն՝ A-ն։ Հետևաբար, D միավորը չափում է B թիվը, ինչպես C-ն՝ A-ն։ Եվ այսպես, ամեն մի մասնաբառ, որը D միավորը B թվի մաս է, նույն անունով մասն է նաև C-ի A թվի համար։ Հետևաբար, A-ն ունի C մասը, որը կոչվում է նույն անունով, ինչ B-ն։ Դա հենց այն է, ինչ պետք էր ապացուցել։
Պնդում 38
Եթե թիվը բաժանվում է որոշակի մասերի (մասնիկների), ապա այդ մասերից յուրաքանչյուրն ունի համապատասխան թվային նշանակություն, որը կոչվում է այդ մասի անվանումը
Տրված լինի, որ թիվ A-ն ունի որևէ մաս, օրինակ՝ B։ Եվ թող C-ը լինի այն թիվը, որը կոչվում է նույն անունով, ինչ B (ինչպես՝ B-ն A-ի C-րդ մասը է): Ես ասում եմ, որ C-ն չափում է A-ն։ Քանի որ B-ն A-ի մի մասն է, որն ունի նույն անունը, ինչ C, ապա նաև D միավորը C-ի մաս է, որն ունի նույն անունը՝ այն է՝ D-ն C-ի C-րդ մասն է։ Եվ հետևաբար, ինչպես D-ն C-ն է չափում, այնպես էլ B-ն չափում է A-ն։ Այսպես, ի վերջո, D-ն B-ն է չափում նույնքան անգամ, ինչքան C-ն չափում է A-ն։ Ուստի, C-ն չափում է A-ն։ Եվ սա այն է, ինչ պետք է ապացուցվի
Պնդում 39
Ենթադրենք, որ տրված մասերն են A, B և C։ Պետք է գտնվի նվազագույն թիվը, որը կունենա A, B և C մասերը։
Լավ, ենթադրենք, որ A, B և C մասերի համար գոյություն ունեն համանուն թվեր, որոնց անունները կհամապատասխանեն համապատասխան մասերին (A-ին՝ D, B-ին՝ E, C-ին՝ F)։ Այնպես որ, նվազագույն թիվը՝ G, որն ունի A, B և C մասերը, չափվում է D, E և F թվերով։ Եվ G-ն իր հերթին կունենա մասեր, որոնք համանուն են D, E և F թվերին։ Ուստի, G-ն կունենա նաև A, B և C մասերը։ Ապա ես ասում եմ, որ G-ն, լինելով նվազագույնը, եթե ոչ, ապա լինի մի թիվ՝ H, որը կլինի G-ից փոքր, բայց կունենա A, B և C մասերը։ Այս դեպքում, եթե H-ն ունի A, B և C մասերը, ապա այն կչափվի D, E և F թվերով։ Բայց քանի որ H-ն փոքր է G-ից, դա անհնար է։ Այսպիսով, չի կարող լինել մի թիվ, որը փոքր լինի G-ից և ունենա A, B և C մասերը։ Սա հենց այն է, ինչը պետք էր ապացուցել։
Նշումներ
- ↑ Այս ժամանակակից նշանաբանությամբ, այս բացատրությունը ասում է, որ եթե a:b::d:e և b:c::e:f, ապա a:c::d:f, որտեղ բոլոր տառերը ներկայացնում են թվեր։