«Տարերք/Գիրք 13»–ի խմբագրումների տարբերություն

Գրապահարան-ից
(→‎Պնդում 2)
 
(38 intermediate revisions by 2 users not shown)
Տող 5. Տող 5.
 
|աղբյուր = [https://farside.ph.utexas.edu/Books/Euclid/Elements.pdf Euclid's Elements of Geometry, English translation by Richard Fitzpatrick]
 
|աղբյուր = [https://farside.ph.utexas.edu/Books/Euclid/Elements.pdf Euclid's Elements of Geometry, English translation by Richard Fitzpatrick]
 
}}
 
}}
 +
{{Տարերքի գրքեր}}
 
[[Կատեգորիա:Մաթեմատիկա]]
 
[[Կատեգորիա:Մաթեմատիկա]]
−
{{անավարտ}}
 
  
 +
== Պնդում 1 ==
  
−
==Pages 506-530==
+
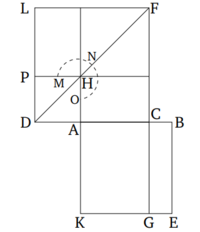
Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորի վրա քառակուսին, գումարած ամբողջի կեսը, հնգապատիկն է կեսի վրա քառակուսու։
  
−
===Պնդում 1===
+
[[Պատկեր:Նկար1.png|center|200px]]
  
−
Եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն։
+
Թող AB ուղիղ գիծը կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Թող AD ուղիղ գիծը երկարացվի՝ անցնելով CA։ Եվ թող AD-ն լինի AB-ի կեսը։ Ասում եմ, որ CD-ի վրա քառակուսին հնգապատիկն է DA-ի վրա քառակուսու։
  
−
[[Պատկեր:Nkar_1.png|200px|thumb|left|Նկ․ 1]]
+
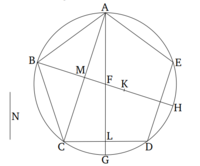
Թող AB և DC վրա քառակուսիները՝ AE և DF, նկարագրվեն։ Եվ DF պատկերում գծվի։ Եվ թող գիծը FC գծվի՝ հասնելով G-ին։ Եվ քանի որ AB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ C կետում, ապա ABC բազմապատկիչը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ CE-ն ABC բազմապատկիչն է, իսկ FH-ն՝ AC-ի վրա քառակուսին։ Այսպիսով, CE-ն հավասար է FH-ին։ Եվ քանի որ BA-ն կրկնապատիկն է AD-ի, իսկ BA-ն հավասար է KA-ին, և AD-ն՝ AH-ին, ապա KA-ն նույնպես կրկնապատիկն է AH-ի։ Եվ քանի որ KA-ն AH-ի նկատմամբ հարաբերություն է, CK-ն նույնպես CH-ի կրկնապատիկն է [Պնդում 6.1]։ Այսպիսով, CK-ն կրկնապատիկն է CH-ի։ Եվ LH-ն գումարած HC կրկնապատիկն է CH-ի [Պնդում 1.43]։ Այսպիսով, KC-ն հավասար է LH-ի գումարած HC-ի։ Եվ CE-ն ցույց տրվեց, որ հավասար է HF-ին։ Այսպիսով, ամբողջ քառակուսի AE-ն հավասար է գնոմոն MNO-ին։
  
−
::::Դիցուք՝ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ С-ում, որտեղ AC-ն մեծ հատվածն է ''(Նկ․ 1)''։ Շարունակենք AC հատվածը, և տեղադրենք <math>AD = \frac{AB}{2}</math>։ Ես պնդում եմ, որ <math>CD^2 = 5\cdot DA^2</math>:
+
Եվ քանի որ BA-ն կրկնապատիկն է AD-ի, BA-ի վրա քառակուսին չորսապատիկն է AD-ի վրա քառակուսու՝ այսինքն, AE-ն չորսապատիկն է DH-ի։ Եվ AE-ն հավասար է գնոմոն MNO-ին։ Եվ, այսպիսով, գնոմոն MNO-ն նույնպես չորսապատիկն է AP-ի։ Այսպիսով, ամբողջ DF-ը հնգապատիկն է AP-ի։ Եվ DF-ը CD-ի վրա քառակուսին է, իսկ AP-ն՝ DA-ի վրա քառակուսին։ Այսպիսով, CD-ի վրա քառակուսին հնգապատիկն է DA-ի վրա քառակուսու։
  
−
::::Դիտարկենք AB և CD կողմերով քառակուսիները՝ ABEK և DLFC ''(Նկ․ 1)''։ Տանենք DF անկյունագիծը և FC հատվածը շարունակելով հատենք KE-ի հետ G-ում։ Քանի որ AB հատվածը բաժանված է արտաքին և միջին հարաբերությամբ C-ում, ապա AB և BC կողմերով ուղղանկյան մակերեսը հավասար է AC կողմով քառակուսու մակերեսին`
+
Այսպիսով, եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորի վրա քառակուսին, գումարած ամբողջի կեսը, հնգապատիկն է կեսի վրա քառակուսու։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
−
<math>AC^2 = AB\cdot BC</math> ''(Սահմ․ 6․3, Պնդ․ 6․17)''։ Հետևաբար CBEG ուղղանկյան մակերեսը հավասար է FH անկյունագծով քառակուսու մակերեսին ''(Նկ․ 1)'': Եվ քանի որ <math>AB = 2\cdot AD</math> և <math>BA = KA</math>, <math>AD = AH</math>, հետևաբար <math>KA = 2\cdot AH</math>: Այսպիսով ստանում ենք հարաբերություն՝ <math>\frac{KA}{AH} = \frac{KA\cdot AC}{AH\cdot AC} </math> ''(Պնդ․ 6․1)'', հետևաբար՝ ACGK ուղղանկյան մակերեսը հավասար է երկու անգամ CH անկյունագծով ուղղանկյան մակերեսին: Եվ քանի որ LH անկյունագծով ուղղանկյունը հավասար է CH անկյունագծով ուղղանկյանը, ապա նրանց մակերեսների գումարը հավասար է երկու անգամ СH անկյունագծով ուղղանկյան մակերեսին ''(Պնդ․ 1․43)'': Այսպիսով ACKG ուղղանկյան մակերեսը հավասար է LH և HC անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց տրվեց վերևում, ուղղանկյուն СBEG-ի մակերեսը հավասար է FH անկյունագծով քառակուսու մակերեսին, հետևաբար ABEK-ի մակերեսը հավասար է գնոմոն MNO-ին (CH, FH, LH անկյունագծերով ուղղանկյունների մակերեսների գումարին): Քանի որ գնոմոն <math>MNO = 4\cdot AP</math>, հետևաբար DLFC քառակուսու մակերեսը հավասար է 5 անգամ AP անկյունագծով քառակուսու մակերեսին։ Այսպիսով <math>CD^2 = 5\cdot DA^2</math>:
+
  
−
Այսպիսով, եթե հատվածը մասնատենք արտաքին և միջին հարաբերությամբ, ապա մեծ հատվածի և ամբողջ հատվածի կեսի գումարի քառակուսին հավասար է 5 անգամ ամբողջ հատվածի կեսի քառակուսուն, ինչը և պահանջվում էր ապացուցել։
+
== Պնդում 2 ==
  
 +
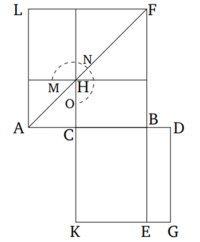
Եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։
  
−
===Պնդում 2===
+
[[Պատկեր:2.png|center|200px]]
  
−
Եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է։
+
Թող AB ուղիղ գծի վրա քառակուսին հնգապատիկն է AC կտորի վրա քառակուսու։ Եվ թող CD-ն լինի կրկնապատիկ AC-ից։ Ասում եմ, որ եթե CD-ն կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի CB։
  
−
[[Պատկեր:Nkar_2.png|200px|thumb|left|Նկ․ 2]]
+
Թող AB և CD վրա քառակուսիները՝ AF և CG, նկարագրվեն։ Եվ թող AF պատկերում գծվի։ Եվ թող BE գիծը գծվի։ Եվ քանի որ BA-ի վրա քառակուսին հնգապատիկն է AC-ի վրա քառակուսու, ապա AF-ն հնգապատիկն է AH-ից։ Այսպիսով, գնոմոն MNO-ն է չորսապատիկ AH-ից։ Եվ քանի որ DC-ն կրկնապատիկն է CA-ից, ապա DC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու՝ այսինքն, CG-ն է չորսապատիկ AH-ից։ Եվ գնոմոն MNO-ն նույնպես ցույց տրվեց, որ չորսապատիկն է AH-ից։ Այսպիսով, գնոմոն MNO-ն հավասար է CG-ին։ Եվ քանի որ DC-ն կրկնապատիկն է CA-ից, և DC-ն հավասար է CK-ին, և AC-ն՝ CH-ին, [CK-ն կրկնապատիկն է CH-ից], իսկ KB-ն նույնպես կրկնապատիկն է BH-ից [Պնդում 6.1]։ Այսպիսով, KB-ն հավասար է LH-ի գումարած HB-ին։ Եվ ամբողջ գնոմոն MNO-ն նույնպես ցույց տրվեց, որ հավասար է ամբողջ CG-ին։ Այսպիսով, մնացորդ HF-ն նույնպես հավասար է մնացորդ BG-ին։ Եվ BG-ն այն բազմապատկիչն է, որը պարունակում է CDB։ Քանի որ CD-ն հավասար է DG-ին։ Եվ HF-ն CB-ի վրա քառակուսին է։ Այսպիսով, CDB բազմապատկիչը հավասար է CB-ի վրա քառակուսուն։
  
−
::::Դիցուք՝ եթե <math>AB^2 = 5\cdot AC^2</math> ''(Նկ․ 2)'' և СВ շարունակենք, այնպես, որ <math>CD = 2\cdot AC</math>, ապա CD-ն բաժանվում է արտաքին և միջին հարաբերությամբ, որտեղ մեծ հատվածը CB է։
+
Այսպիսով, ինչպես DC-ն է CB-ի նկատմամբ, այնպես էլ CB-ն է BD-ի նկատմամբ [Պնդում 6.17]։ Եվ քանի որ DC-ն ավելի մեծ է, քան CB (տես լեմա), ապա CB-ն նույնպես ավելի մեծ է, քան BD [Պնդում 5.14]։ Այսպիսով, եթե CD ուղիղ գծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի CB։
  
−
::::Դիտարկենք AB և CD կողմերով քառակուսիները՝ ALFB և СKGD ''(Նկ․ 2)'': Տանենք AF անկյունագիծը։ Շարունակենք FB հատվածը և հատենք KG-ի հետ E-ում: Քանի որ <math>AB^2 = 5\cdot AC^2</math>, հետևաբար AF անկյունագծով քառակուսու մակերեսը հավասար է 5 անգամ AH անկյունագծով քառակուսու մակերեսին։ Այսպիսով գնոմոն <math>MNO = 4\cdot AH</math>: Քանի որ <math>DC = 2\cdot CA</math>, հետևաբար <math>DC^2 = 4\cdot AC^2</math>, կամ նույնն է ինչ ասենք, որ СG անկյունագծով քառակուսու մակերեսը հավասար է 4 անգամ AH անկյունագծով քառակուսու մակերեսին։ Հետևաբար գնոմոն <math>MNO = CG</math> անկյունագծով քառակուսու մակերեսին (HB, HF, HL անկյունագծերով ուղղանկյունների մակերեսները հավասար են CDGK-ի մակերեսին): Եվ քանի որ <math>DC = 2\cdot CA<\math>, <math>DC = CK<\math>, <math>AC = CH</math> ապա <math>KC = 2\cdot CH</math> և KB անկյունագծով ուղղանկյան մակերեսը հավասար է 2 անգամ BH անկյունագծով ուղղանկյան մակերեսին ''(Պնդ․ 6․1)'' և քանի որ LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարը հավասար է երկու անգամ HB անկյունագծով ուղղանկյան մակերեսին ''(Պնդ․ 1.43)'', ապա KB անկյունագծով ուղղանկյան մակերեսը հավսար է LH և HB անկյունագծերով ուղղանկյունների մակերեսների գումարին։ Ինչպես ցույց էր տրված վերևում գնոմոն MNO-ն հավասար է СG անկյունագծով քառակուսու մակերեսին։ Հետևում է, որ HF անկյունագծով ուղղանկյան մակերեսը հավասար է BDGE ուղղանկյան մակերեսին։ Իսկ վերջինս հավասար է СD և BD կողմերով կառուցված ուղղանկյան մակերեսին, <math>CD = DG</math>, HF անկյունագծով ուղղանկյան մակերեսը հավասար է <math>CB^2<\math>։ Հետևաբար CD և BD կողմերով կառուցված ուղղանկյան մակերեսը հավասար է <math>CB^2</math> <math>(CB^2 = DC\cdot BD)</math>: Այսպիսով, ստանում ենք <math>\frac{DC}{CB} = \frac{CB}{BD}</math> ''(Պնդ․ 6․17)'': Եվ քանի որ DC ավելի մեծ է քան СB (տես Լեմմա, ներքևում), ապա СB-ն նույնպես ավելի մեծ է քան BD-ն։ Այսպիսով, եթե CD հատվածը բաժանված է արտաքին և միջին հարաբերությամբ, ապա СB-ն նրա մեծ հատվածն է։
+
Այսպիսով, եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
  
−
Այսպիսով, եթե հատվածի քառակուսին հավասար է նրա հատվածներից մեկի քառակուսու հնգապատիկին, և երկու անգամ այդ փոքր հատվածը մասնատված է արտաքին և միջին հարաբերությամբ, ապա հարաբերության մեծ հատվածը սկզբնական հատվածի մյուս մնացորդ մասն է, ինչը և պահանջվում էր ապացուցել։
+
== Լեմմա ==
 +
 
 +
Եվ կարող է ցույց տրվել, որ կրկնապատիկ AC-ը (այսինքն՝ DC-ն) ավելի մեծ է, քան BC, ինչպես հետևյալը։ 
 +
 
 +
Եթե (կրկնապատիկ AC-ը) ոչ (մեծ է BC-ից), եթե հնարավոր է, թող BC-ն լինի կրկնապատիկ CA-ից։ Այսպիսով, BC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BC-ի և CA-ի վրա քառակուսիների (հավաքածուն) հնգապատիկն է CA-ի վրա քառակուսու։ Եվ BA-ի վրա քառակուսին համարվեց հնգապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BA-ի վրա քառակուսին հավասար է BC-ի և CA-ի վրա քառակուսիների (հավաքածուն)։ Սա՝ անխուսափելի է [Պնդում 2.4]։ Այսպիսով, CB-ն չի կարող լինել կրկնապատիկ AC-ից։ Ուստի, նմանապես, կարող ենք ցույց տալ, որ ուղիղ գիծը, որը փոքր է CB-ից, նույնպես չի կարող լինել կրկնապատիկ AC-ից։ Ասածը՝ ավելի մեծ հակասություն է։ 
 +
Այսպիսով, կրկնապատիկ AC-ը ավելի մեծ է, քան CB։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
 +
 
 +
== Պնդում 3 ==
 +
 +
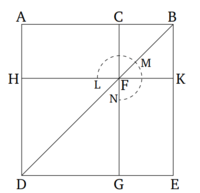
Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա փոքր կտորի վրա քառակուսին, ավելացված մեծ կտորի կեսին, հնգապատիկն է մեծ կտորի կեսի վրա քառակուսու։ 
 +
 
 +
[[Պատկեր:3.png|center|200px]]
 +
 
 +
Թող ինչ-որ ուղիղ գիծ AB կտրված լինի արտաքին և միջին հարաբերությամբ C կետում։ Եվ թող AC-ն լինի մեծ կտորը։ Եվ թող AC-ն կտրված լինի կեսում՝ D կետում։ Ասում եմ, որ BD-ի վրա քառակուսին հնգապատիկն է DC-ի վրա քառակուսու։ 
 +
Թող AE քառակուսին նկարագրված լինի AB-ի վրա։ Եվ թող պատկերն լիներ կրկնակի։ Քանի որ AC-ն կրկնապատիկ է DC-ից, ապա AC-ի վրա քառակուսին՝ դա չորսապատիկն է DC-ի վրա քառակուսու՝ այսինքն՝ RS-ն չորսապատիկն է FG-ից։ Եվ քանի որ ABC-ում պարունակվող ուղղանկյունը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17], և CE-ն ABC-ում պարունակվող ուղղանկյունն է, ապա CE-ն հավասար է RS-ին։ Եվ RS-ն չորսապատիկն է FG-ից։ Այսպիսով, CE-ն նույնպես չորսապատիկն է FG-ից։ Վերջապես, քանի որ AD-ն հավասար է DC-ին, ապա HK-ն նույնպես հավասար է KF-ին։ Ուստի, GF քառակուսին նույնպես հավասար է HL քառակուսուն։ Այսպիսով, GK-ն հավասար է KL-ին՝ այսինքն՝ MN-ն հավասար է NE-ին։ Ուստի, MF-ն նույնպես հավասար է FE-ին։ Բայց, MF-ն հավասար է CG-ին։ Այսպիսով, CG-ն նույնպես հավասար է FE-ին։ Թող CN-ը ավելացվի երկուսի վրա։ Այսպիսով, գնոմոնը OPQ հավասար է CE-ին։ Բայց, CE-ն ցույց տրված է, որ հավասար է չորսապատիկ GF-ին։ Այսպիսով, գնոմոնը OPQ նույնպես չորսապատիկն է GF քառակուսուց։ Այսպիսով, գնոմոնը OPQ գումարած GF քառակուսին հնգապատիկն է GF քառակուսուց։ Բայց, գնոմոնը OPQ գումարած GF քառակուսին դա DN քառակուսին է։ Եվ DN-ը DB-ի վրա քառակուսին է, իսկ GF-ն՝ DC-ի վրա քառակուսին։ Այսպիսով, DB-ի վրա քառակուսին հնգապատիկն է DC-ի վրա քառակուսու։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
 +
 
 +
== Պնդում 4 ==
 +
 
 +
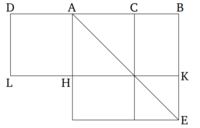
Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա ամբողջ գծի և փոքր կտորի վրա քառակուսիների գումարը երեքապատիկն է մեծ կտորի վրա քառակուսու։
 +
 
 +
[[Պատկեր:4.png|center|200px]]
 +
 
 +
Թող AB լինի ուղիղ գիծ, և թող այն կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Ասում եմ, որ AB և BC-ի վրա քառակուսիների գումարը երեքապատիկն է CA-ի վրա քառակուսուց։
 +
Թող ADEB քառակուսին նկարագրված լինի AB-ի վրա, և թող մնացած պատկերն ընդունի իր ձևը։ Քանի որ AB-ն կտրված է արտաքին և միջին հարաբերությամբ C կետում, և AC-ն մեծ կտոր է, ապա ABC-ում պարունակվող ուղղանկյունը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ AK-ն է ABC-ում պարունակվող ուղղանկյունը, և HG-ն՝ AC-ի վրա քառակուսին։ Այսպիսով, AK-ն հավասար է HG-ին։ Եվ քանի որ AF-ն հավասար է FE-ին [Պնդում 1.43], թող CK-ը ավելացվի երկուսի վրա։ Այսպիսով, ամբողջ AK-ն հավասար է ամբողջ CE-ին։ Այսպիսով, AK-ն և CE-ն միասին հավասար են երկու անգամ AK-ին։ Բայց, AK-ն և CE-ն միասին դա է գնոմոնը LMN, որը գումարած CK քառակուսին։ Այսպիսով, գնոմոն LMN գումարած CK քառակուսին հավասար է երկու անգամ AK-ին։ Բայց, իսկապես, AK-ն նաև ցույց տրված է, որ հավասար է HG-ին։ Այսպիսով, գնոմոն LMN գումարած CK քառակուսին հավասար է HG-ին։ Եվ այսպիսով, գնոմոն LMN գումարած CK և HG քառակուսիները երեքապատիկն են HG քառակուսուց։ Եվ գնոմոն LMN գումարած CK և HG քառակուսիները ամբողջ AE-ն են գումարած CK-ը՝ որոնք են AB և BC քառակուսիները (համապատասխանաբար), և GH-ը՝ AC-ի վրա քառակուսին։ Այսպիսով, AB և BC-ի վրա քառակուսիների գումարը երեքապատիկն է AC-ի վրա քառակուսուց։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
 +
 
 +
== Պնդում 5 ==
 +
 
 +
Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, և այդ մեծ կտորին հավասար ուղիղ գիծը ավելացվում է դրան, ապա ամբողջ ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, և սկզբնական ուղիղ գիծը մեծ կտորն է։ 
 +
 
 +
[[Պատկեր:5.png|center|200px]]
 +
 
 +
Թող AB լինի ուղիղ գիծ, և թող այն կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Եվ թող AD-ն [դառնա] հավասար AC-ին։ Ասում եմ, որ DB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ A կետում, և որ սկզբնական AB ուղիղ գիծը մեծ կտորն է։ 
 +
Թող AE քառակուսին նկարագրված լինի AB-ի վրա, և թող մնացած պատկերն ընդունի իր ձևը։ Քանի որ AB-ն կտրված է արտաքին և միջին հարաբերությամբ C կետում, ապա ABC-ում պարունակվող ուղղանկյունը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ CE-ն է ABC-ում պարունակվող ուղղանկյունը, և CH-ը՝ AC-ի վրա քառակուսին։ Բայց, HE-ն հավասար է CE-ին [Պնդում 1.43], և DH-ն հավասար է HC-ին։ Այսպիսով, DH-ն նաև հավասար է HE-ին։ [Թող HB-ն ավելացվի երկուսի վրա]։ Այսպիսով, ամբողջ DK-ն հավասար է ամբողջ AE-ին։ Եվ DK-ն է BD և DA-ում պարունակվող ուղղանկյունը։ Քանի որ AD-ն հավասար է DL-ին, և AE-ն է AB-ի վրա քառակուսին։ Այսպիսով, BD-ում պարունակվող ուղղանկյունը հավասար է AB-ի վրա քառակուսուն։ Այսպիսով, ինչպես DB-ն է BA-ի նկատմամբ, այնպես էլ BA-ն է AD-ի նկատմամբ [Պնդում 6.17]։ Եվ DB-ն ավելի մեծ է BA-ից։ Այսպիսով, BA-ն նույնպես ավելի մեծ է AD-ից [Պնդում 5.14]։ 
 +
Այսպիսով, DB-ն կտրված է արտաքին և միջին հարաբերությամբ A կետում, և մեծ կտորը AB-ն է։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։
 +
 
 +
== Պնդում 6 ==
 +
 +
Եթե մի ռացիոնալ ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա յուրաքանչյուր կտորը կլինի այն անպարբեր (ուղիղ գիծ), որ կոչվում է «ապոտոմ»։ 
 +
 
 +
[[Պատկեր:6.png|center|200px]]
 +
 
 +
Թող AB լինի ռացիոնալ ուղիղ գիծ, որը կտրված է արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Ասում եմ, որ AC և CB-ը, յուրաքանչյուրը, կլինեն այն անպարբեր (ուղիղ գիծ), որ կոչվում է «ապոտոմ»։ 
 +
 
 +
Թող BA-ն ընդարձակվի, և թող AD-ն արվի (հավասար) BA-ի կեսին։ Այսպիսով, քանի որ AB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ C կետում, և AD-ն, որը BA-ի կեսն է, ավելացվել է մեծ կտոր AC-ին, ապա CD-ի վրա քառակուսին կլինի հինգ անգամ DA-ի վրա քառակուսիին [Պնդում 13.1]։ Այսպիսով, CD-ի վրա քառակուսին և DA-ի վրա քառակուսին կունենան հարաբերություն, որը նման է մի թվի հարաբերությանը մյուս թվին։ CD-ի վրա քառակուսին, հետևաբար, համահունչ կլինի DA-ի վրա քառակուսուն [Պնդում 10.6]։ Իսկ DA-ի վրա քառակուսին կլինի ռացիոնալ, քանի որ DA-ն ռացիոնալ է, երբ որ AB-ն ռացիոնալ է։ Այսպիսով, CD-ի վրա քառակուսին նույնպես կլինի ռացիոնալ [Սահմանում 10.4]։ Այսպիսով, CD-ն նույնպես ռացիոնալ է։ Եվ քանի որ CD-ի վրա քառակուսին չի ունենում հարաբերություն DA-ի վրա քառակուսիին, որը նման է քառակուսի թվերի հարաբերությանը, ապա CD-ն չհամապատասխանում է DA-ի երկարության հետ [Պնդում 10.9]։ Այսպիսով, CD և DA-ը այն ռացիոնալ ուղիղ գծերն են, որոնք համահունչ են միայն քառակուսու տեսքով։ Այսպիսով, AC-ն կլինի ապոտոմ [Պնդում 10.73]։ 
 +
 
 +
Կրկին, քանի որ AB-ն կտրված է արտաքին և միջին հարաբերությամբ, և AC-ն մեծ կտորն է, ապա AB և BC-ի պարունակած ուղղանկյունը կլինի հավասար AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Այսպիսով, AC-ի վրա ապոտոմի քառակուսին, կիրառված ռացիոնալ ուղիղ գծի AB-ի վրա, կկազմի BC՝ որպես լայնություն։ Եվ ապոտոմի վրա քառակուսին, կիրառված ռացիոնալ ուղիղ գծի վրա, կկազմի առաջին ապոտոմը՝ որպես լայնություն [Պնդում 10.97]։ Այսպիսով, CB-ն կլինի առաջին ապոտոմ։ Եվ CA-ն նույնպես ցույց տրված է որպես ապոտոմ։ 
 +
 
 +
Այսպիսով, եթե մի ռացիոնալ ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա յուրաքանչյուր կտորը կլինի այն անպարբեր (ուղիղ գիծ), որ կոչվում է «ապոտոմ»։
 +
 
 +
Here are the corrected versions for the 7th and 8th propositions with the updated terminology for the shapes:
 +
 
 +
== Պնդում 7 ==
 +
 
 +
Թող երեք անկյունները, որոնք լինելու են կամ հաջորդական, կամ ոչ հաջորդական, հավասար կլինեն հավասարանկյուն հնգանկյունում, ապա հնգանկյունը կլինի հավասարանկյուն։
 +
 
 +
[[Պատկեր:7.png|center|200px]]
 +
 
 +
Դա ցույց տալու համար, թող հնգանկյունի ABCDE երեք անկյունները՝ առաջին հերթին A, B և C կետերում, հավասար լինեն իրար։ Ես ասում եմ, որ հնգանկյունը ABCDE հավասարանկյուն է։
 +
 
 +
Թող AC, BE և FD լինեն միացված։ Եվ քանի որ երկու (ուղղաձիգ գծերը) CB և BA հավասար են երկու (ուղղաձիգ գծերին) BA և AE համապատասխանաբար, և CBA անկյունը հավասար է BAE անկյունին, ապա AC հիմքը հավասար կլինի BE հիմքին, և ABC եռանկյունը հավասար կլինի ABE եռանկյունին, և մնացած անկյունները հավասար կլինեն մնացած անկյուններին, որոնք հավասար կողմերի տրված անկյուններին ենթադրում են [Պնդում. 1.4]։ Իսկ դա նշանակում է, որ BCA (հավասար է) BEA-ին, իսկ ABE-ը (հավասար է) CAB-ին։
 +
 
 +
Այսպիսով, AF կողմը նույնպես հավասար է BF կողմին [Պնդում. 1.6]։ Եվ ամբողջ AC-ն նույնպես ցույց է տրվել, որ հավասար է BE-ին։ Այսպիսով, մնացորդը FC նույնպես հավասար կլինի FE-ին։ Եվ CD-ն նույնպես հավասար է DE-ին։
 +
 
 +
Այսպիսով, երկու (ուղղաձիգ գծերը) FC և CD հավասար են երկու FE և ED համապատասխանաբար։ Իսկ FD-ը նրանց ընդհանուր հիմքն է։ Այսպիսով, FCD անկյունը հավասար է FED անկյունին [Պնդում. 1.8]։
 +
 
 +
Եվ BCA-ն նույնպես ցույց է տրվել, որ հավասար է AEB-ին։ Այսպիսով, ամբողջ BCD-ն հավասար է AED-ին։ Բայց, BCD անկյունը ենթադրվել էր, որ հավասար է A և B անկյուններին։ Այսպիսով, AED անկյունը նույնպես հավասար կլինի A և B անկյուններին։
 +
 
 +
Այսպիսով, նույն կերպ կարող ենք ցույց տալ, որ CDE անկյունը նույնպես հավասար է A, B, C անկյուններին։ Այսպիսով, հնգանկյունը ABCDE հավասարանկյուն է։
 +
 
 +
== Պնդում 8 ==
 +
 
 +
Եթե ուղղաձիգ գծերը կտրում են երկու հաջորդական անկյուններ հավասարանկյուն և հավասար կողմ ունեցող հնգանկյունում, ապա դրանք իրար կտրում են արտաքին և միջին հարաբերությամբ, և դրանց մեծ հատվածները հավասար են հնգանկյունի կողմերին։
 +
 
 +
[[Պատկեր:8.png|center|200px]]
 +
 
 +
Իսկ հիմա, եթե երկու ուղղաձիգ գծեր՝ AC և BE, հատում են իրար H կետում և դրանք ծածկում են հավասար անկյուններ՝ A և B համապատասխանաբար հավասարանկյուն հնգանկյունում ABCDE, ապա պետք է ապացուցենք, որ յուրաքանչյուր գիծ կտրված է արտաքին և միջին հարաբերությամբ H կետում և դրանց մեծ հատվածները հավասար են հնգանկյունի կողմերին։
 +
 
 +
Եկեք ընդունենք, որ ABCDE հնգանկյունի շուրջ է նկարագրված շրջան [Պնդում 4.14]: Եվ քանի որ երկու ուղղաձիգ գծերը՝ EA և AB հավասար են երկու ուղղաձիգ գծերին՝ AB և BC համապատասխանաբար, և նրանք պարունակում են հավասար անկյուններ, BE հիմքը հավասար կլինի AC հիմքին, և ABC և ABE եռանկյունները հավասար կլինեն, ուստի մնացած անկյունները նույնպես հավասար կլինեն [Պնդում 1.4]: Հետևաբար, անկյուն BAC հավասար կլինի անկյուն ABE-ին: Այսպիսով, անկյուն AHE-ն երկու անգամ մեծ է, քան անկյուն BAH [Պնդում 1.32]: Եվ EAC նույնպես երկու անգամ մեծ է BAC-ից, քանի որ շրջանագիծը EDC երկու անգամ մեծ է CB շրջանագծից [Առաջարկներ 3.28, 6.33]: Ուստի, անկյուն HAE-ն հավասար կլինի անկյուն AHE-ին: Հետևաբար, ուղղաձիգ HE-ը հավասար կլինի ուղղաձիգ EA-ին՝ այն է՝ AB [Պնդում 1.6]: Եվ քանի որ ուղղաձիգ BA-ն հավասար է AE-ին, ապա անկյուն ABE-ն նույնպես հավասար կլինի AEB-ին [Պնդում 1.5]: Բայց, ABE-ն արդեն ցույց տրված էր, որ հավասար է BAH-ին: Հետևաբար, BEA-ն նույնպես հավասար կլինի BAH-ին: Իսկ քանի որ անկյուն ABE-ն ընդհանուր է երկու եռանկյունների՝ ABE և ABH-ի համար, մնացած անկյունը՝ BAE, հավասար կլինի մնացած անկյունի՝ AHB [Պնդում 1.32]: Հետևաբար, եռանկյունը ABE հավասար է եռանկյունին ABH: Այսպիսով, համամասնորեն, ինչպես BE-ն հավասար է BA-ին, այնպես էլ AB-ն հավասար է BH-ին [Պնդում 6.4]: Եվ BA-ն հավասար է EH-ին: Այսպիսով, ինչպես BE-ն հավասար է EH-ին, այնպես էլ EH-ն հավասար է HB-ին: Եվ BE-ն ավելի մեծ է EH-ից: EH-ն ավելի մեծ է HB-ից [Պնդում 5.14]: Հետևաբար, BE-ն կտրված է արտաքին և միջին հարաբերությամբ H կետում, և մեծ հատվածը՝ EH, հավասար է հնգանկյունի կողմին: Ուստի նույն կերպ կարող ենք ցույց տալ, որ AC-ն նույնպես կտրված է արտաքին և միջին հարաբերությամբ H կետում, և դրա մեծ հատվածը՝ CH, հավասար է հնգանկյունի կողմին: Սա է այն, ինչ պետք էր ապացուցել:
 +
 
 +
== Պնդում 9 ==
 +
 
 +
Եթե նույն շրջանում ներգծված վեցանկյան և տասանկյան կողմերը միասին գումարվեն, ապա ամբողջ ուղղաձիգ գիծը կտրված է արտաքին և միջին հարաբերությամբ (հատման կետում), և նրա մեծ հատվածը տասանկյան կողմն է: <ref>"Եթե շրջանը միավոր շառավիղ ունի, ապա վեցանկյան կողմը հավասար է 1-ի, իսկ տասանկյան կողմը՝ (1/2)(√5 − 1):"</ref>
 +
 
 +
 
 +
[[Պատկեր:9.png|center|200px]]
 +
 
 +
Թող ABC լինի շրջան: Եվ ABC շրջանում նկարագրված պատկերներից, BC լինի տասանկյան կողմը, և CD (կողմը) վեցանկյան կողմը: Եվ թող դրանք դրված լինեն ուղղահայաց: Պետք է ապացուցվի, որ ամբողջ BD ուղղաձիգ գիծը կտրված է արտաքին և միջին հարաբերությամբ (C կետում), և որ CD-ն նրա մեծ հատվածն է:
 +
 
 +
Թող շրջանի կենտրոնը, E կետը, գտնվի [Պնդում 3.1], և թող EB, EC և ED կետերը միավորված լինեն, և թող BE-ը գծվի A կետին: Քանի որ BC-ն հավասարանկյուն տասանկյան կողմ է, ապա շրջանագիծ ACB-ն 5 անգամ մեծ է BC-ի երկարությունից: Այսպիսով, շրջանագիծ AC-ն 4 անգամ մեծ է CB-ից: Եվ քանի որ AC շրջանագիծը հավասար է CB-ին, այնպես էլ անկյուն AEC-ն հավասար է CEB-ին [Պնդում 6.33]: Այդպես, անկյուն AEC-ն 4 անգամ մեծ է CEB-ից: Եվ քանի որ անկյուն EBC-ն հավասար է ECB-ին [Պնդում 1.5], ապա անկյուն AEC-ն 2 անգամ մեծ է ECB-ից [Պնդում 1.32]: Եվ քանի որ ուղղաձիգ EC-ն հավասար է CD-ին, ապա անկյուն CED-ն հավասար է անկյուն CDE-ին [Պնդում 1.5]: Այդպես, անկյուն ECB-ն 2 անգամ մեծ է EDC-ից [Պնդում 1.32]: Սակայն AEC-ն արդեն ապացուցվել է, որ 4 անգամ մեծ է EDC-ից: Եվ AEC-ն նույնպես 4 անգամ մեծ է BEC-ից: Այսպիսով, EDC-ն հավասար է BEC-ին: Եվ անկյուն EBD-ն համատեղ է երկու եռանկյունում՝ BEC և BED: Այդպիսով, մնացած անկյուն BED-ն հավասար է անկյուն ECB-ին [Պնդում 1.32]: Այսպիսով, եռանկյունը EBD հավասար է եռանկյունին EBC: Այլ կերպ ասած, համեմատաբար, ինչպես BD-ն է BE-ին, այնպես էլ AB-ն է BH-ին [Պնդում 6.4]: Եվ BE-ն հավասար է CD-ին: Ուստի, ինչպես BD-ն է DC-ին, այնպես էլ DC-ն է CB-ին: Եվ BD-ն մեծ է DC-ից: Այսպիսով, DC-ն նույնպես մեծ է CB-ից [Պնդում 5.14]. Այսպիսով, BD ուղղաձիգ գիծը կտրված է արտաքին և միջին հարաբերությամբ (C կետում), և DC-ն նրա մեծ հատվածն է: (Այս է այն, ինչ անհրաժեշտ էր ապացուցել):
 +
 
 +
== Պնդում 10 ==
 +
 
 +
Եթե միևնույն շրջանում կանոնավոր հնգանկյուն է ներգծված, ապա հնգանկյան կողմի գծի քառակուսին հավասար է նույն շրջանում ներգծված վեցանկյանի և տասանկյանի կողմերի քառակուսիերի գումարին։ <ref>"Եթե շրջանը միավոր շառավիղ ունի, ապա հնգանկյան կողմը հավասար է (1/2)(√10 − 2√5):"</ref>
 +
 
 +
[[Պատկեր:10.png|center|200px]]
 +
 
 +
Թող ABCDE լինի շրջան։ Եվ թող ABCDE հավասարակողմ հնգանկյունը լինի դրված ABCDE շրջանում։ Պնդում եմ, որ հնգանկյան ABCDE կողմի քառակուսին հավասար է նույն շրջանում դրված վեցանկյանի և տասանկյանի կողմերի քառակուսիերի գումարին։
 +
 
 +
Թող կենտրոնի կետը լինի F, որը գտնվել է [Պնդում. 3.1]։ Եվ թող AF ուղղի միացված լինի, և թող այն անցնի G կետով։ Եվ թող F B միացված լինի։ Եվ թող FH ուղղը լինի F-ից ուղղահայաց AB-ին։ Եվ թող այն անցնի K կետով։ Եվ թող AK և K B միացված լինեն։ Եվ կրկին, թող F L ուղղը լինի F-ից ուղղահայաց AK-ին։ Եվ թող այն անցնի M կետով։ Եվ թող K N միացված լինի։
 +
 
 +
Քանի որ ABCG շրջանը հավասար է AEDG շրջանում, որի ABC-ն հավասար է AED-ին, մնացած շրջանը CG-ը այդպես էլ հավասար է մնացած GD շրջանին։ Եվ CD-ը (հնգանկյան կողմն է)։ CG-ը այդպես էլ (տասանկյանի կողմն է)։ Եվ քանի որ F A հավասար է F B-ին, և F H ուղղահայաց է (AB-ին), ապա անկյուն AFK-ը նույնպես հավասար է KFB-ին [Պնդում. 1.5, 1.26]։ Հետևաբար, AK շրջանը հավասար է KB-ի [Պնդում. 3.26]։ Այսպիսով, AB շրջանը կրկնակի է BK շրջանից։ Այսպիսով, ուղիղ գիծը AK տասանկյան կողմն է։ Այսպես, նույն պատճառներով, AK շրջանը կրկնակի է KM-ից։ Եվ քանի որ AB շրջանը կրկնակի է BK շրջանից, և CD շրջանը հավասար է AB շրջանին, ապա CD շրջանը նույնպես կրկնակի է BK շրջանից։ Եվ CD շրջանը նույնպես կրկնակի է CG-ից։ Այսպիսով, CG շրջանը հավասար է BK շրջանին։ Բայց, BK-ը կրկնակի է KM-ից, քանի որ KA-ը նույնպես (կրկնակի է KM-ից)։ Այսպես, CG շրջանը նույնպես կրկնակի է KM-ից։ Բայց, իսկապես, CB շրջանը նույնպես կրկնակի է BK-ից։ Քանի որ CB շրջանը հավասար է BA-ին։ Այսպիսով, ամբողջ GB շրջանը նույնպես կրկնակի է BM-ից։ Հետևաբար, անկյուն GFB [է] նույնպես կրկնակի անկյուն BF M [Պնդում. 6.33]։
 +
 
 +
==Պնդում 11==
 +
 +
Եթե հավասարակողմ հնգանկյունը ներգծված է շրջանի մեջ, որի տրամագիծը ռացիոնալ է, ապա հնգանկյան կողմը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր»։ 
 +
 
 +
[[Պատկեր:11.png|center|200px]]
 +
 
 +
Թող հավասարակողմ հնգանկյուն ABCDE-ն ներգծված լինի ABCDE շրջանի մեջ, որի տրամագիծը ռացիոնալ է։ Ասում եմ, որ հնգանկյան [ABCDE] կողմը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր»։ 
 +
 
 +
Թող գտնված լինի շրջանի կենտրոնը՝ F կետը [Պնդում 3.1]։ Եվ թող միացվեն AF-ն և FB-ն։ Եվ թող դրանք քաշվեն G և H կետերին (համապատասխանաբար)։ Եվ թող միացվի AC-ն։ Եվ թող FK-ն հավասար լինի AF-ի չորրորդ մասին։ AF-ն ռացիոնալ է։ Ուստի, FK-ն նույնպես ռացիոնալ է։ FB-ն նույնպես ռացիոնալ է։ Ուստի, ամբողջ BK-ն ռացիոնալ է։ Եվ քանի որ ACG աղեղն հավասար է ADG աղեղին, որոնցից ABC աղեղն հավասար է AED աղեղին, մնացորդային CG աղեղն, հետևաբար, հավասար է GD մնացորդային աղեղին։ 
 +
 
 +
Եվ եթե միացնենք AD-ն, ապա L կետում գտնվող անկյունները դառնում են ուղիղ անկյուններ, իսկ CD-ն հավասար է CL-ի կրկնակիին [Պնդում 1.4]։ Հետևաբար, նույն տրամաբանությամբ, M կետում անկյունները նույնպես ուղիղ են, իսկ AC-ն կրկնակի է CM-ի։ Ուստի, քանի որ ALC անկյունն հավասար է AMF անկյունին, և LAC անկյունն ընդհանուր է ACL և AMF եռանկյունների համար, ապա մնացորդային ACL անկյունն, հետևաբար, հավասար է MF A մնացորդային անկյունին [Պնդում 1.32]։ Ուստի, ACL եռանկյունն հավասանկյուն է AMF եռանկյան հետ։ Ուստի, համեմատաբար, ինչպես LC-ն է CA-ի նկատմամբ, այնպես էլ MF-ն է FA-ի նկատմամբ [Պնդում 6.4]։ 
 +
 
 +
Եվ (կարող ենք վերցնել) առաջատար մեծությունների կրկնակի արժեքները։ Ուստի, ինչպես LC-ի կրկնակին է CA-ի նկատմամբ, այնպես էլ MF-ն է FA-ի կեսի նկատմամբ։ Եվ, ուստի, ինչպես LC-ի կրկնակին է CA-ի կեսի նկատմամբ, այնպես էլ MF-ն է FA-ի չորրորդ մասի նկատմամբ։ Եվ DC-ն LC-ի կրկնակի է, իսկ CM-ն CA-ի կեսն է, իսկ FK-ն FA-ի չորրորդ մասը։ Ուստի, ինչպես DC-ն է CM-ի նկատմամբ, այնպես էլ MF-ն է FK-ի նկատմամբ։ 
 +
 
 +
Սկզբունքով, ինչպես DCM գումարը (այսինքն՝ DC և CM) CM-ի նկատմամբ, այնպես էլ MK-ն է KF-ի նկատմամբ [Պնդում 5.18]։ Եվ, ուստի, ինչպես DCM գումարի վրա կառուցված քառակուսին է CM-ի վրա կառուցված քառակուսու նկատմամբ, այնպես էլ MK-ի վրա կառուցված քառակուսին է KF-ի վրա կառուցված քառակուսու նկատմամբ։ 
 +
 
 +
Եվ քանի որ հնգանկյան երկու կողմերը սահմանող մեծ հատվածը, ինչպես AC-ն, որը բաժանված է ծայրագույն և միջին հարաբերությամբ, հավասար է հնգանկյան կողմին [Պնդում 13.8]՝ այսինքն DC-ին, և ամբողջի կեսին ավելացված մեծ հատվածի վրա կառուցված քառակուսին հնգապատիկ է ամբողջի կեսի վրա կառուցված քառակուսու, իսկ CM-ն AC-ի կեսն է։ Ուստի, DCM-ի վրա կառուցված քառակուսին, որպես ամբողջություն, հնգապատիկ է CM-ի վրա կառուցված քառակուսու։ 
 +
 
 +
Եվ DCM-ի վրա կառուցված քառակուսին, որպես ամբողջություն, CM-ի վրա կառուցված քառակուսու նկատմամբ այնպես է, ինչպես MK-ի վրա կառուցված քառակուսին KF-ի վրա կառուցված քառակուսու նկատմամբ։ Ուստի, MK-ի վրա կառուցված քառակուսին հնգապատիկ է KF-ի վրա կառուցված քառակուսու։ Եվ KF-ի վրա կառուցված քառակուսին ռացիոնալ է։ Քանի որ տրամագիծն ռացիոնալ է։ Ուստի, MK-ի վրա կառուցված քառակուսին նույնպես ռացիոնալ է։ 
 +
 
 +
Ուստի, MK-ն ռացիոնալ է [քառակուսու միայն]։ Եվ քանի որ BF-ն FK-ի չորս անգամն է, BK-ն, ուստի, FK-ի հինգ անգամն է։ Ուստի, BK-ի վրա կառուցված քառակուսին FK-ի վրա կառուցված քառակուսու քսանհինգ անգամն է։ Եվ MK-ի վրա կառուցված քառակուսին FK-ի վրա կառուցված քառակուսու հնգապատիկն է։ Ուստի, BK-ի վրա կառուցված քառակուսին MK-ի վրա կառուցված քառակուսու նկատմամբ չունի այն հարաբերությունը, որ քառակուսի թվերը ունեն քառակուսի թվերի նկատմամբ։ Ուստի, BK-ն անհամաչափ է երկարությամբ MK-ի հետ [Պնդում 10.9]։ 
 +
 
 +
Եվ երկուսն էլ ռացիոնալ (ուղիղ գծեր) են։ Ուստի, BK-ն և MK-ն ռացիոնալ (ուղիղ գծեր են), որոնք համաչափ են քառակուսու միայն։ Եվ եթե ռացիոնալ (ուղիղ գծից) հանենք ռացիոնալ (ուղիղ գիծ), որը քառակուսու միայն համաչափ է առաջինի հետ, ապա ստացվում է անհամաչափ (ուղիղ գիծ)։ 
 +
 
 +
Եվ քանի որ KF-ն համաչափ է երկարությամբ BF-ի հետ, ապա, ըստ կազմի, BK-ն նույնպես համաչափ է երկարությամբ BF-ի հետ [Պնդում 10.15]։ Բայց BF-ն համաչափ է երկարությամբ BH-ի հետ։ Հետևաբար, BK-ն նույնպես համաչափ է երկարությամբ BH-ի հետ [Պնդում 10.12]։ Եվ քանի որ BK-ի վրա կառուցված քառակուսին հնգապատիկ է MK-ի վրա կառուցված քառակուսուն, ապա BK-ի վրա կառուցված քառակուսին, հետևաբար, ունի MK-ի վրա կառուցված քառակուսու նկատմամբ այն հարաբերությունը, որը 5-ն ունի 1-ի նկատմամբ։ 
 +
 
 +
Հետևաբար, հակադարձմամբ՝ BK-ի վրա կառուցված քառակուսին ունի \( N \)-ի վրա կառուցված քառակուսու նկատմամբ այն հարաբերությունը, որը 5-ն ունի 4-ի նկատմամբ [Պնդում 5.19՝ ուղղում], ինչը չի համապատասխանում քառակուսի թվի և քառակուսի թվի հարաբերությանը։ 
 +
 
 +
BK-ն, հետևաբար, անհամաչափ է երկարությամբ \( N \)-ի հետ [Պնդում 10.9]։ Հետևաբար, քանի որ BK-ի վրա կառուցված քառակուսին մեծ է MK-ի վրա կառուցված քառակուսուց \( N \)-ի վրա կառուցված անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, և ամբողջը՝ BK-ն, համաչափ է նախկինում տրված ռացիոնալ (ուղիղ գծի)՝ BH-ի հետ, MB-ն, հետևաբար, չորրորդ ափոտոմ է [Սահմանում 10.14]։ 
 +
 
 +
Եվ ռացիոնալ (ուղիղ գծի) և չորրորդ ափոտոմի միջև պարունակվող ուղղանկյունը անհամաչափ է, և դրա քառակուսի արմատը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր» [Պնդում 10.94]։ Եվ AB-ի վրա կառուցված քառակուսին ուղղանկյունն է, որը պարունակում է HBM-ը, հաշվի առնելով, որ AH-ի միացման դեպքում եռանկյուն ABH-ը դառնում է հավասանկյուն եռանկյուն ABM-ի հետ [Պնդում 6.8], և (համեմատաբար) ինչպես HB-ն է BA-ի նկատմամբ, այնպես էլ AB-ն է BM-ի նկատմամբ։ 
 +
 
 +
Հետևաբար, հնգանկյան կողմ AB-ն այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր»։ <ref>"Եթե շրջանը միավոր շառավիղ ունի, ապա հնգանկյան կողմը հավասար է (1/2)(√10 − 2√5): Այնուամենայնիվ, այս երկարությունը կարող է գրվել «փոքր» ձևով (տես Առ. 10.94)՝ (ρ/√2)(1 + k/√1 + k²) − (ρ/√2)(1 − k/√1 + k²), որտեղ ρ = √5/2 և k = 2:"</ref> 
 +
 
 +
Սա այն էր, ինչը պահանջվում էր ապացուցել։
 +
 
 +
==Պնդում 12==
 +
 +
Եթե հավասարակողմ եռանկյունը ներգծված է շրջանի մեջ, ապա եռանկյան կողմի վրա կառուցված քառակուսին երեք անգամ մեծ է շրջանի շառավղի վրա կառուցված քառակուսուց։ 
 +
 
 +
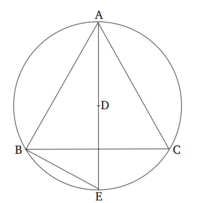
Թող լինի ABC շրջան, և թող հավասարակողմ եռանկյուն ABC-ն ներգծված լինի դրանում [Պնդում 4.2]։ Ասում եմ, որ եռանկյուն ABC-ի որևէ կողմի վրա կառուցված քառակուսին երեք անգամ մեծ է ABC շրջանի շառավղի վրա կառուցված քառակուսուց։ 
 +
 
 +
[[Պատկեր:12.png|center|200px]]
 +
 
 +
Թող գտնված լինի ABC շրջանի կենտրոնը՝ D կետը [Պնդում 3.1]։ Եվ AD (լինելով) միացված, թող անցկացվի E կետի միջով։ Եվ թող BE-ն միացվի։ 
 +
 
 +
Եվ քանի որ եռանկյուն ABC-ն հավասարակողմ է, ուստի BEC կամարը, հետևաբար, ABC շրջանի կամարի երրորդ մասն է։ Ուստի, BE կամարը շրջանի կամարի վեցերորդ մասն է։ Ուստի, ուղիղ գիծ BE-ն վեցանկյան կողմն է։ Ուստի, այն հավասար է շառավղի՝ DE-ի [Պնդում 4.15, ուղղում]։ Եվ քանի որ AE-ն կրկնակի է DE-ի, ապա AE-ի վրա կառուցված քառակուսին չորս անգամ մեծ է DE-ի վրա կառուցված քառակուսուց՝ այսինքն՝ BE-ի վրա կառուցված քառակուսուց։ 
 +
 
 +
Եվ AE-ի վրա կառուցված քառակուսին հավասար է AB-ի և BE-ի վրա կառուցված քառակուսիների գումարին [Պնդումներ 3.31, 1.47]։ Ուստի, AB-ի և BE-ի վրա կառուցված քառակուսիների գումարը չորս անգամ մեծ է BE-ի վրա կառուցված քառակուսուց։ Ուստի, ըստ բաժանման, AB-ի վրա կառուցված քառակուսին երեք անգամ մեծ է BE-ի վրա կառուցված քառակուսուց։ Եվ BE-ն հավասար է DE-ին։ Ուստի, AB-ի վրա կառուցված քառակուսին երեք անգամ մեծ է DE-ի վրա կառուցված քառակուսուց։ 
 +
 
 +
Ուստի, եռանկյան կողմի վրա կառուցված քառակուսին երեք անգամ մեծ է շրջանի շառավղի վրա կառուցված քառակուսուց։ <ref>"Եթե գնդի շառավիղը միավոր է, ապա բուրգի (այսինքն՝ տետրահեդրոնի) կողմը հավասար է √8/3:"</ref> 
 +
 
 +
Սա այն էր, ինչը պահանջվում էր ապացուցել։
 +
 
 +
==Պնդում 13==
 +
 +
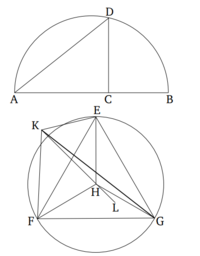
Կառուցել (կանոնավոր) բուրգ (այսինքն՝ տետրահեդրոն), այն ներգծել տրված գնդի մեջ և ցույց տալ, որ գնդի տրամագծի վրա կառուցված քառակուսին մեկ ու կես անգամ մեծ է բուրգի կողմի վրա կառուցված քառակուսուց։ 
 +
 
 +
[[Պատկեր:13.png|center|200px]]
 +
 
 +
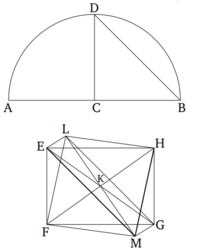
Թող տրված գնդի տրամագիծը լինի AB, և այն կետ C-ում բաժանվի այնպես, որ AC-ն կրկնակի լինի CB-ին [Պնդում 6.10]։ Եվ թող AB-ի վրա կառուցվի կեսաշրջագիծ ADB։ Եվ թող C կետից ուղղանկյուն լինի գծված CD ուղիղը AB-ի նկատմամբ։ Եվ թող միացվի DA։ Եվ թող DC շառավղով գծվի շրջան EFG, որի մեջ ներգծված կլինի հավասարակողմ եռանկյուն EFG [Պնդում 4.2]։ Թող գտնվի շրջանի կենտրոնը՝ H կետը [Պնդում 3.1]։ Թող միացվեն EH, HF, և HG։ Թող H կետում ուղղանկյուն լինի գծված HK ուղիղը EFG շրջանի հարթության նկատմամբ [Պնդում 11.12]։ Եվ թող HK ուղիղի վրա կտրվի հատված, որը հավասար կլինի AC ուղիղին։ Թող KE, KF, և KG գծերը միացվեն։ 
 +
 
 +
Քանի որ KH ուղիղը ուղղանկյուն է EFG շրջանի հարթության նկատմամբ, այն ուղղանկյուն կլինի նաև իր հետ միացող բոլոր ուղիղների նկատմամբ, որոնք գտնվում են EFG շրջանի հարթությունում [սահմանում 11.3]։ HE, HF, և HG ուղղերը միանում են դրան։ Ուստի, HK-ն ուղղանկյուն է HE-ի, HF-ի և HG-ի նկատմամբ։ 
 +
 
 +
Քանի որ AC-ն հավասար է HK-ին, և CD-ն՝ HE-ին, իսկ նրանք պարունակում են ուղղանկյուններ, ապա հիմքը՝ DA-ն, հավասար է հիմքին՝ KE [Պնդում 1.4]։ Նույն պատճառներով KF-ն և KG-ն նույնպես հավասար են DA-ին։ Ուստի, KE, KF և KG երեք ուղիղները հավասար են միմյանց։ 
 +
 
 +
Քանի որ AC-ն կրկնակի է CB-ի, ուստի AB-ն եռակի է CB-ին։ Եվ ինչպես AB-ն CB-ի նկատմամբ, այնպես էլ AD-ի վրա կառուցված քառակուսին DC-ի վրա կառուցված քառակուսու նկատմամբ, ինչպես ցույց կտրվի ստորև [տես լեմմա]։ Ուստի, AD-ի վրա կառուցված քառակուսին երեք անգամ մեծ է DC-ի վրա կառուցված քառակուսուց։ Եվ FE-ի վրա կառուցված քառակուսին նույնպես երեք անգամ մեծ է EH-ի վրա կառուցված քառակուսուց [Պնդում 13.12], և DC-ն հավասար է EH-ին։ Ուստի, DA-ն հավասար է EF-ին։ 
 +
 
 +
Բայց DA-ն ցույց տրվեց, որ հավասար է KE, KF և KG յուրաքանչյուրին։ Ուստի EF, FG, և GE-ն հավասար են KE, KF, և KG-ին համապատասխանաբար։ Ուստի, EFG, KEF, KFG, և KEG չորս եռանկյունները հավասարակողմ են։ 
 +
 
 +
Ուստի, կառուցվել է բուրգ, որի հիմքը եռանկյուն EFG-ն է, իսկ գագաթը՝ K կետը։ 
 +
 
 +
Այժմ անհրաժեշտ է այն ներգծել տրված գնդի մեջ և ցույց տալ, որ գնդի տրամագծի վրա կառուցված քառակուսին մեկ ու կես անգամ մեծ է բուրգի կողմի վրա կառուցված քառակուսուց։ 
 +
 
 +
Թող HL ուղիղը երկարացվի K H ուղղի շարունակությամբ, և HL-ը հավասար լինի CB-ին։ Եվ քանի որ ինչպես AC-ն CD-ի նկատմամբ, այնպես էլ CD-ն CB-ի նկատմամբ [Պնդում 6.8, ուղղում], իսկ AC-ն հավասար է KH-ին, CD-ն՝ HE-ին, և CB-ն՝ HL-ին, ուստի ինչպես KH-ն HE-ի նկատմամբ, այնպես էլ EH-ն HL-ի նկատմամբ։ Ուստի, K H և HL ուղղագծերի պարունակած ուղղանկյունը հավասար է EH-ի վրա կառուցված քառակուսուն [Պնդում 6.17]։ 
 +
 
 +
Եվ քանի որ AC-ն կրկնակի է CB-ի, ապա AB-ն եռակի է CB-ի։ Ուստի, AB-ն մեկ ու կես անգամ մեծ է AC-ից։ Եվ ինչպես AB-ն AC-ի նկատմամբ, այնպես էլ AB-ի վրա կառուցված քառակուսին AC-ի վրա կառուցված քառակուսու նկատմամբ։ Եվ քանի որ AB-ն գնդի տրամագիծն է, իսկ AD-ն՝ բուրգի կողմը, ապա AB-ի վրա կառուցված քառակուսին մեկ ու կես անգամ մեծ է AD-ի վրա կառուցված քառակուսուց։ 
 +
 
 +
Սա էր պահանջվում ցույց տալ։
 +
 
 +
[[Պատկեր:14.png|center|200px]]
 +
 
 +
==Լեմմա==
 +
 
 +
Ապացուցել, որ ինչպես AB գիծը BC գծի նկատմամբ, այնպես էլ AD գծի վրա կառուցված քառակուսին DC գծի վրա կառուցված քառակուսու նկատմամբ են հավասար: 
 +
 
 +
Թող կեսաշրջագծի պատկերը կազմվի, և DB գիծը միացվի։ Թող AC-ի վրա կառուցվի EC քառակուսին։ Եվ թող FB զուգահեռագիծը լրացվի։ 
 +
 
 +
Քանի որ եռանկյուն DAB-ը համաչափ է եռանկյուն DAC -ին [Պնդումներ 6.8, 6.4], հետևում է, որ ինչպես BA գիծը AD գծի նկատմամբ, այնպես էլ AD գիծը AC գծի նկատմամբ են հավասար։ Ուստի, BA և AC գծերի պարունակած ուղղանկյունը հավասար է AD-ի վրա կառուցված քառակուսուն [Պնդում 6.17]։ 
 +
 
 +
Քանի որ ինչպես AB գիծը BC գծի նկատմամբ, այնպես էլ EB ուղղանկյունը BF ուղղանկյունի նկատմամբ են հավասար [Պնդում 6.1], EB-ը հավասար է BA և AC գծերի պարունակած ուղղանկյանին (քանի որ EA = AC), իսկ BF-ը հավասար է AC և CB գծերի պարունակած ուղղանկյանին։ 
 +
 
 +
Այսպիսով, ինչպես AB գիծը BC գծի նկատմամբ, այնպես էլ AD գծի վրա կառուցված քառակուսին DC գծի վրա կառուցված քառակուսու նկատմամբ են հավասար։
 +
 
 +
==Պնդում 14==
 +
 +
Կառուցել ութանկյուն և փակել այն տրված գնդի մեջ՝ ինչպես նախորդ պնդումներում, և ցույց տալ, որ գնդի տրամագծի քառակուսին կրկնապատիկ է ութանկյոնի կողի քառակուսուց։ 
 +
 
 +
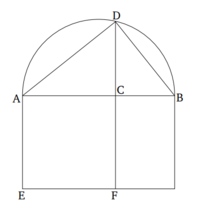
Թող տրված գնդի տրամագիծը լինի AB, և այն կիսվի C կետում։ Նկարել ADB կիսամորթը AB վրա։ Նկարել CD ուղղահայաց AB-ին C-ից։ Միացնել DB։ 
 +
 
 +
Կառուցել EFGH քառակուսին, որի յուրաքանչյուր կողմը հավասար է DB-ին։ Միացնել HF-ը և EG-ը։ Սահմանել ուղիղ գիծ KL K-ում, ուղղահայաց դեպի EFGH քառակուսիի պլանը (Պնդում 11.12), և նկարել մեկ այլ գիծ՝ KM, որը գտնվում է պլանի մյուս կողմում։ 
 +
 
 +
Կտրել KL-ը և KM-ը՝ հավասարեցնելով մեկին EK-ի, FK-ի, GK-ի և HK-ի։ Միացնել LE-ը, LF-ը, LG-ը, LH-ը, ME-ը, MF-ը, MG-ը և MH-ը։ 
 +
 
 +
[[Պատկեր:15.png|center|200px]]
 +
 
 +
Քանի որ KE = KH և անկյունը EKH ուղիղ անկյուն է, ապա HE-ի քառակուսին կրկնապատիկ է EK-ի քառակուսուց (Պնդում 1.47)։ Նույն կերպ, քանի որ LK = KE և անկյունը LKE ուղիղ անկյուն է, ապա EL-ի քառակուսին կրկնապատիկ է EK-ի քառակուսուց (Պնդում 1.47)։ Եվ քանի որ HE-ի քառակուսին նույնպես կրկնապատիկ է EK-ի քառակուսուց, ապա LE-ի քառակուսին հավասար է EH-ի քառակուսուն։ 
 +
 
 +
Ուստի, LE = EH։ Նույն պատճառներով, LH = HE։ LEH եռանկյունը հավասարակողմ է։ Այսպիսով, մենք կարող ենք նույն կերպ ցույց տալ, որ մնացած բոլոր եռանկյունիները, որոնց հիմքերը EFGH քառակուսիի կողմերն են, և գագաթները L-ն ու M-ն են, հավասարակողմ են։ Այսպես, ութանկյուն, որը բաղկացած է ութ հավասարակողմ եռանկյունիներից, կառուցվել է։ 
 +
 
 +
Այժմ պետք է ցույց տրվի, որ այն փակվում է տրված գնդի մեջ, և որ գնդի տրամագծի քառակուսին կրկնապատիկ է ութանկյոնի կողի քառակուսուց։ 
 +
 
 +
Քանի որ LK = KM և KE ընդհանուր է, և նրանք պարունակում են ուղիղ անկյուններ, ապա LE-ի հիմքը հավասար է EM-ին (Պնդում 1.4)։ Եվ քանի որ անկյունը LEM ուղիղ անկյուն է՝ ըստ կիսամորթի (Պնդում 3.31), ապա LM-ի քառակուսին կրկնապատիկ է LE-ի քառակուսուն (Պնդում 1.47)։ 
 +
 
 +
Այնուհետև, քանի որ AC = CB, AB-ն կրկնապատիկ է BC-ի։ Եվ ինչպես AB-ը BC-ին է, այնպես էլ AB-ի քառակուսին հավասար է BD-ի քառակուսուն (Պնդում 6.8, սահման. 5.9)։ Այսպիսով, AB-ի քառակուսին կրկնապատիկ է BD-ի քառակուսուց։ 
 +
 
 +
Եվ LM-ի քառակուսին նույնպես ցույց տրված է, որ կրկնապատիկ է LE-ի քառակուսուց։ Եվ DB-ի քառակուսին հավասար է LE-ի քառակուսուն։ Քանի որ EH-ը հավասար է DB-ին։ 
 +
 
 +
Այսպիսով, AB-ի քառակուսին նույնպես հավասար է LM-ի քառակուսուն։ Այսպիսով, AB = LM։ Եվ AB-ն տրված գնդի տրամագծն է։ Ուստի, LM-ը հավասար է տրված գնդի տրամագծին։ 
 +
 
 +
Այսպիսով, ութանկյունը ներգծված է տրված գնդի մեջ, և միաժամանակ ցույց տրված է, որ գնդի տրամագծի քառակուսին կրկնապատիկ է ութանկյոնի կողի քառակուսուց։<ref>"Եթե գնդի շառավիղը միավոր է, ապա ութանիստի կողմը հավասար է √2:"</ref>
 +
 +
(Այսինքն) հենց այն, ինչ պետք էր ցույց տալ։
 +
 
 +
==Պնդում 15==
 +
 
 +
Կառուցել խորանարդ և փակել այն տրված գնդի մեջ, ինչպես պիրամիդի դեպքում, և ցույց տալ, որ գնդի տրամագծի քառակուսին երեք անգամ գերազանցում է խորանարդի կողմի քառակուսուն։ 
 +
 
 +
Թող տրված գնդի տրամագիծը լինի AB, և այն կիսվի C կետում այնպես, որ AC-ն երկու անգամ մեծ է քան CB-ն։ Նկարել ADB կիսամորթը AB վրա։ Նկարել CD ուղղահայաց AB-ին C-ից։ Միացնել DB։ 
 +
 
 +
Կառուցել EFGH քառակուսին, որի յուրաքանչյուր կողմը հավասար է DB-ին։ Նկարել EK-ը, FL-ը, GM-ը և HN-ը՝ E, F, G և H կետերից համապատասխանաբար, ուղղահայաց դեպի EFGH քառակուսիի պլանը։ Նկարել EK-ը, FL-ը, GM-ը և HN-ը՝ հավասարեցնելով EF, FG, GH և HE կողմերին, և կտրել դրանք համապատասխանաբար EK-ից, FL-ից, GM-ից և HN-ից։ Միացնել KL-ը, LM-ը, MN-ը և NK-ը։ Այսպիսով, խորանարդը, որը բաղկացած է վեց հավասար քառակուսիներից, կառուցվել է։ 
 +
 
 +
Այժմ պետք է այն փակվի տրված գնդի մեջ, և ցույց տրվի, որ գնդի տրամագծի քառակուսին երեք անգամ գերազանցում է խորանարդի կողմի քառակուսուն։ 
 +
 
 +
[[Պատկեր:16.png|center|200px]]
 +
 
 +
Թող KG և EG միացվեն։ Քանի որ անկյուն KEG-ն ճիշտ անկյուն է՝ հաշվի առնելով, որ KE-ն նաև ուղղահայաց է EG-ի պլանին և ակնհայտորեն նաև ուղղահայաց է EG ուղիղ գծին (Սահման. 11.3), ապա KG-ի վրա նկարած կիսամորթը նույնպես կանցնի E կետով։ Նույն կերպ, քանի որ GF-ն ուղղահայաց է FL և FE-ի ամեն մի մասի, GF-ն նույնպես ուղղահայաց է FK-ի պլանին (Պնդում 11.4)։ Հետևաբար, եթե մենք միացնենք FK-ը, GF-ն նույնպես կլինի ուղղահայաց FK-ի հետ։ Եվ քանի որ դա այդպես է, GK-ի վրա նկարած կիսամորթը նույնպես կանցնի F կետով։ Նույն կերպ, այն կհասնի խորանարդի մնացած անկյուններին։ 
 +
 
 +
Այսպիսով, եթե KG-ը մնա (ապացուցված) և կիսամորթը տեղափոխվի, ապա այն կվերադառնա սկզբնական դիրքին, և խորանարդը փակվել է տրված գնդի մեջ։ Դրանից մենք տեսնում ենք, որ այն փակված է տրված գնդի մեջ։ Քանի որ GF-ը հավասար է FE-ին, և անկյունը F-ում ճիշտ անկյուն է, ապա EG-ի քառակուսին կրկնապատիկ է EF-ի քառակուսուց (Պնդում 1.47)։ Եվ FE-ը հավասար է EK-ին։ Այսպիսով, EG-ի քառակուսին կրկնապատիկ է EK-ի քառակուսուց։ 
 +
 
 +
Ուստի, GE և EK քառակուսիների գումարը՝ այսինքն՝ GK-ի քառակուսին (Պնդում 1.47), երեք անգամ գերազանցում է EK-ի քառակուսուն։ Եվ քանի որ AB-ը երեք անգամ գերազանցում է BC-ին, և ինչպես AB-ը BC-ին, այնպես էլ AB-ի քառակուսին հավասար է BD-ի քառակուսուն (Պնդում 6.8, սահման. 5.9), ապա AB-ի քառակուսին երեք անգամ գերազանցում է BD-ի քառակուսին։ 
 +
 
 +
Եվ GK-ի քառակուսին նույնպես ցույց տրված է, որ երեք անգամ գերազանցում է KE-ի քառակուսին։ Եվ KE-ն հավասարեցված էր DB-ի հետ։ Այսպիսով, KG-ն հավասար է AB-ին։ Իսկ AB-ն տրված գնդի տրամագիծն է։ Ուստի, KG-ն հավասար է տրված գնդի տրամագծին։ 
 +
 
 +
Այսպիսով, խորանարդը ներգծված է տրված գնդի մեջ։ Եվ միաժամանակ ցույց տրվել է, որ գնդի տրամագծի քառակուսին երեք անգամ գերազանցում է խորանարդի կողմի քառակուսուն։<ref>"Եթե գնդի շառավիղը միավոր է, ապա խորանարդի կողմը հավասար է √4/3:"</ref>
 +
(Այսինքն) հենց այն, ինչ պետք էր ցույց տալ։ 
 +
 
 +
==Պնդում 16==
 +
 +
Կառուցել իկոսահեդրոն <ref>"տասնութ նիստերով բազմանիստ է, որն ունի 20 ճիշտ եռանկյունիներ, ունի 12 գագաթներ և 30 եզրեր"</ref> և այն փակել շրջանակով, ինչպես նշված վերոնշյալ պատկերներում, և ցույց տալ, որ իկոսահեդրոնի կողմը այն իռացիոնալ ուղիղ գիծն է, որը կոչվում է փոքր:
 +
 
 +
[[Պատկեր:17.png|center|200px]]
 +
 
 +
Թող գնդի տրամագիծը AB լինի, և թող այն լինի կտրված C կետում, այնպես, որ AC լինի վեց անգամ ավելի մեծ, քան CB [Պրո. 6.10]։ Եվ թող գծի ADB ծածկվել լինի AB-ի վրա։ Եվ թող ուղղաձիգ CD գիծը նշվի C-ից AB-ի նկատմամբ։ Եվ թող DB-ն միախառնվի։ Եվ թող շրջան EFGHK լինի տեղադրված, և թող դրա շառավիղը հավասար լինի DB-ի։ Եվ թող հավասարազանգված և հավասարանկյուն հնգանկյան EFGHK ներառված լինի EFGHK շրջանի մեջ [Պրո. 4.11]։ Եվ թող շրջանների EF, FG, GH, HK և KE կեսը հատվի L, M, N, O և P կետերում համապատասխանաբար։ Եվ թող LM, MN, NO, OP, PL և EP միախառնվեն։ Այսպիսով, LMNOP հնգանկյանը նույնպես հավասարազանգված է, և EP-ն (կողմն է) տասանկյան (համապատասխան շրջանագծում):
 +
 
 +
Եվ թող գծերը EQ, FR, GS, HT, KU, որոնք հավասար են EFGHK շրջանի շառավիղին, տեղադրված լինեն ուղղանկյուն ձևով շրջանի մակարդակում, E, F, G, H, և K կետերում համապատասխանաբար։ Եվ թող QR, RS, ST, TU, UQ, QL, LR, RM, MS, SN, NT, TO, OU, UP և PQ միախառնվեն։
 +
Եվ քանի որ EQ և KU-ն ուղղանկյուն են նույն ինքնուրույն շրջանագծին, EQ-ն այսպիսով զուգահեռ է KU-ին [Պրո. 11.6]։ Եվ դրանք հավասար են։ Եվ համարժեք ուղղաձիգները միևնույն կողմում հավասար և զուգահեռ են [Պրո. 1.33]։ Այսպիսով, QU-ն հավասար և զուգահեռ է EK-ին: Եվ EK-ն (կողմն է) հավասարազանգված հնգանկյան (inscribed in the circle EFGHK): Այսպիսով, QU-ն (կողմն է) նույնպես հավասարազանգված հնգանկյան (EFGHK շրջանի մեջ):
 +
 
 +
Այսպիսով, նույն (պատճառներով), QR, RS, ST, և TU-ն նույնպես հավասարազանգված կողմեր են, EFGHK շրջանի մեջ: Հնգանկյուն QRSTU (կողմն է) հետևաբար հավասարազանգված:
 +
Ուղղանկյուն QE-ն (կողմն է) վեցանկյան (EFGHK շրջանում), և EP (կողմն է) տասանկյան, իսկ QEP անկյունը ուղղանկյուն է, այսպիսով QP-ն (կողմն է) հնգանկյան (նույն շրջանի մեջ):
 +
Քանի որ վեցանկյան կողմի քառորդը հավասար է այն կողմերի քառորդներին, որոնք տեղադրված են մեկ ընդհանուր գծով շրջանագծում [Պրո. 13.10]: Այսպիսով, նույն (պատճառներով), PU-ն նույնպես հնգանկյան կողմն է:
 +
Այսպիսով, QU-ն նույնպես (կողմն է) հնգանկյան։ Այսպիսով, QPU եռանկյունը հավասար է։
 +
Այսպիսով, նույն (պատճառներով), QLR, RMS, SNT և TOU եռանկյունները հավասար են։ Եվ քանի որ QL-ն և QP-ն (կողմն են) հնգանկյան, և LP-ն նույնպես (կողմն է) հնգանկյան, triangle QLP-ն հավասարազանգված է։
 +
 
 +
Այսպիսով, նույն (պատճառներով) LRM, MSN, NTO և OUP եռանկյունները հավասար են։
 +
 
 +
Թող կենտրոնը, V կետը, լինի նշված [Պրո. 3.1]։ Եվ թող VZ-ն տեղադրվի, V կետում, ուղղանկյունորեն շրջանի մակարդակին։ Եվ թող այն լինի արտաշարժված մյուս կողմում (շրջանի), ինչպես VX։ Եվ թող VW-ն կտրվի XZ-ից այնպես, որ հավասար լինի վեցանկյան կողմին, իսկ յուրաքանչյուր VX և WZ (հավասար լինի) տասանկյանի կողմին։ Եվ թող QZ, QW, UZ, EV, LV, LX և XM միախառնվեն։
 +
 
 +
Եվ քանի որ VW-ն և QE-ն ուղղանկյուն են շրջանի մակարդակին, VW-ն զուգահեռ է QE-ին [Պնդում 11.6]։ Եվ նրանք հավասար են։ EV-ն և QW-ն հավասար և զուգահեռ են [Պնդում 1.33]։ Եվ EV-ն (կողմն է) վեցանկյան։ Այսպիսով, QW-ն (կողմն է) նույնպես վեցանկյան։ Եվ քանի որ QW-ն (կողմն է) վեցանկյան, և WZ-ն (կողմն է) տասանկյանի, և QWZ անկյունը ուղղանկյուն է [Սահմանում 11.3, Պնդում 1.29], ապա QZ-ն (կողմն է) հնգանկյան [Պնդում 13.10]։ Այդպես, նույն (պատճառներով), UZ-ն նույնպես (կողմն է) հնգանկյան, քանի որ եթե մենք միացնենք VK և WU, ապա դրանք կլինեն հավասար և հակադարձ։ Եվ VK-ն, որը հավասար է գնդի շառավիղին, (կողմն է) վեցանկյան [Պնդում 4.15 շտկված]։ Այսպիսով, WU-ն նույնպես (կողմն է) վեցանկյան։ Եվ WZ-ն (կողմն է) տասանկյան, և UWZ անկյունը ուղղանկյուն է։ Այսպիսով, UZ-ն (կողմն է) հնգանկյան [Պրո. 13.10]։ Եվ QU-ն (կողմն է) հնգանկյան։ Triangle QUZ-ն հավասար է։ Այսպիսով, նույն (պատճառներով), մնացած բոլոր եռանկյունները, որոնց հիմքերը են QR, RS, ST, և TU գծերը, և բարձունքները Z կետում, նույնպես հավասար են։ Եվ քանի որ VL-ն (կողմն է) վեցանկյան, և VX-ն (կողմն է) տասանկյան, և LVX անկյունը ուղղանկյուն է, ապա LX-ն (կողմն է) հնգանկյան [Պնդում 13.10]։ Այդպես, նույն (պատճառներով), եթե մենք միացնենք MV, որը (կողմն է) վեցանկյան, ապա MX-ն նույնպես կլինի (կողմն է) հնգանկյան։ Եվ LM-ն (կողմն է) հնգանկյան։ Այսպիսով, triangle LMX-ը հավասար է։ Այսպես, նմանապես, կարող է ցուցադրվել, որ մնացած բոլոր եռանկյունները, որոնց հիմքերը են MN, NO, OP, և PL գծերը, և բարձունքները X կետում, նույնպես հավասար են։ Այսպիսով, իկոսիադրոնը, որը բաղկացած է քսան հավասարազանգված եռանկյուններից, կառուցվել է։ Այսպիսով, պետք է նաև տեղադրել այն տրամադրված գնդի մեջ և ցույց տանք, որ իկոսիադրոնի կողմը այն անկյունագիծն է, որը կոչվում է միկրո։ Ուրեմն, քանի որ VW-ն (կողմն է) վեցանկյան, և WZ-ն (կողմն է) տասանկյան, VZ-ն այստեղ կտրված է էքստրեմալ և միջին հարաբերությամբ W-ում, և VW-ն նրա մեծ մասը է [Պնդում 13.9]։ Այդպես, երբ ZV-ն VW-ին համեմատվում է, VW-ն համեմատվում է WZ-ի։ Եվ VW-ն հավասար է VE-ին, WZ-ն՝ VX-ին։ Այդպես, ZV-ն համեմատվում է VE-ի հետ, իսկ EV-ն՝ VX-ի հետ։ Եվ անկյունները ZVE և EVX են ուղղանկյուն։
 +
 
 +
Ուրեմն, նույն (պատճառներով), քանի որ ZV-ն նման է VW-ին, այնպես որ VW-ն նման է WZ-ին, և ZV-ն հավասար է XW-ին, իսկ VW-ը նման է WQ-ին, ապա ինչպես XW-ն նման է WQ-ին, այնպես էլ QW-ն նման է WZ-ին: Եվ կրկին, այս պատճառով, եթե մենք միացնենք QX-ը, ապա Q-ում գտնվող անկյունը կլինի ուղղանկյուն [Պնդում 6.8]: Ուրեմն, XZ-ի վրա նկարագրված կես շրջանը նույնպես կանցնի Q-ի միջով [Պնդում 3.31]: Եվ եթե XZ-ը մնա անշարժ, և կես շրջանը տեղաշարժվի, ապա այն նորից կտեղադրվի նույն (հայեցողական) դիրքում, որտեղից այն սկսել է շարժվել, ապա այն նույնպես կանցնի (Q) կետի միջով, և (կանցնի) իկոսահեդրոնի մնացած անկյունային կետերի միջով: Եվ իկոսահեդրոնը կշրջապատվի գնդի կողմից: Ուրեմն, ես ասում եմ, որ այն նույնպես շրջապատված է տրված (գնդով): Թող ՎW-ն կիսվել է a-ի վրա: Եվ քանի որ ուղիղ գիծը VZ կիսվել է ծայրահեղ և միջին հարաբերությամբ W-ին, և ZW-ն դրա փոքր մասը է, ապա ZW-ի վրա նկարված քառորդը և ավելի մեծ մասի կեսը՝ W a-ն, հավասար է հինգ անգամ (այդ) մասի քառորդին [Պնդում 13.3]: Ուրեմն, Za-ի վրա նկարված քառորդը հինգ անգամ մեծ է (aW)-ի վրա նկարված քառորդից: Եվ ZX-ը երկակի է Za-ից, և VW-ն երկակի է aW-ից: Ուրեմն, ZX-ի վրա նկարված քառորդը հինգ անգամ մեծ է VW-ի վրա նկարված քառորդից: Եվ քանի որ AC-ն չորս անգամ մեծ է CB-ից, ապա AB-ն հինգ անգամ մեծ է BC-ից: Եվ ինչպես AB-ն է BC-ին, այնպես էլ AB-ի վրա նկարված քառորդը է BD-ի վրա նկարված քառորդից [Պնդում 6.8, Սահմանում 5.9]: Ուրեմն, AB-ի վրա նկարված քառորդը հինգ անգամ մեծ է BD-ի վրա նկարված քառորդից: Եվ ZX-ի վրա նկարված քառորդը նույնպես ցույց է տվել, որ հինգ անգամ մեծ է VW-ի վրա նկարված քառորդից: Եվ DB-ն հավասար է VW-ին: Քանզի երկուսը նույնպես հավասար են EFGHK շրջանակի ռադիուսին: Ուրեմն, AB-ն նույնպես հավասար է XZ-ին: Եվ AB-ն տրված գնդի տրամագիծն է: Ուրեմն, XZ-ն հավասար է տրված գնդի տրամագծին: Ուրեմն, իկոսահեդրոնը շրջապատված է տրված գնդով:
 +
 
 +
Ուրեմն, ես ասում եմ, որ իկոսահեդրոնի կողմը այն անհամաչափ (ուղղահայաց) ուղիղ գիծն է, որը կոչվում է փոքր: Քանզի գնդի տրամագիծը համաչափ է, և դրա քառորդը հինգ անգամ մեծ է EFGHK շրջանակի ռադիուսի վրա նկարված քառորդից, ապա EFGHK շրջանակի ռադիուսը նույնպես համաչափ է: Ուրեմն, դրա տրամագիծը նույնպես համաչափ է: Եվ եթե հավասարակողմ պենտագոն ներկառուցվի շրջանի մեջ, որը ունի համաչափ տրամագիծ, ապա պենտագոնի կողմը այն անհամաչափ (ուղղահայաց) ուղիղ գիծն է, որը կոչվում է փոքր [Պնդում 13.11]: Եվ EFGHK պենտագոնի կողմը այն կողմն է, որը համընկնում է իկոսահեդրոնի կողմի հետ: Ուրեմն, իկոսահեդրոնի կողմը այն անհամաչափ (ուղղահայաց) ուղիղ գիծն է, որը կոչվում է փոքր:
 +
 
 +
Հետևանք
 +
 
 +
Ուրեմն, ակնհայտ է, որ գնդի տրամագծի քառորդը հինգ անգամ մեծ է այն շրջանակի ռադիուսի քառորդից, որի միջոցով նկարագրված է իկոսահեդրոնը, և որ գնդի տրամագիծը հավասար է նույն շրջանակի մեջ ներկառուցված վեցանկու եզրը և երկու տասանկու եզրերի գումարին:
 +
 
 +
==Նշումներ==
 +
<references />

Ընթացիկ տարբերակը 03:15, 17 Դեկտեմբերի 2024-ի դրությամբ

Տարերք, Գիրք 13

հեղինակ՝ էվկլիդես
աղբյուր՝ Euclid's Elements of Geometry, English translation by Richard Fitzpatrick
Տարերքի գրքեր

Գիրք 1 - Գիրք 2 - Գիրք 3 - Գիրք 4 - Գիրք 5 - Գիրք 6 - Գիրք 7 - Գիրք 8 - Գիրք 9 - Գիրք 10 - Գիրք 11 - Գիրք 12 - Գիրք 13

Պնդում 1

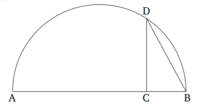
Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորի վրա քառակուսին, գումարած ամբողջի կեսը, հնգապատիկն է կեսի վրա քառակուսու։

Նկար1.png

Թող AB ուղիղ գիծը կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Թող AD ուղիղ գիծը երկարացվի՝ անցնելով CA։ Եվ թող AD-ն լինի AB-ի կեսը։ Ասում եմ, որ CD-ի վրա քառակուսին հնգապատիկն է DA-ի վրա քառակուսու։

Թող AB և DC վրա քառակուսիները՝ AE և DF, նկարագրվեն։ Եվ DF պատկերում գծվի։ Եվ թող գիծը FC գծվի՝ հասնելով G-ին։ Եվ քանի որ AB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ C կետում, ապա ABC բազմապատկիչը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ CE-ն ABC բազմապատկիչն է, իսկ FH-ն՝ AC-ի վրա քառակուսին։ Այսպիսով, CE-ն հավասար է FH-ին։ Եվ քանի որ BA-ն կրկնապատիկն է AD-ի, իսկ BA-ն հավասար է KA-ին, և AD-ն՝ AH-ին, ապա KA-ն նույնպես կրկնապատիկն է AH-ի։ Եվ քանի որ KA-ն AH-ի նկատմամբ հարաբերություն է, CK-ն նույնպես CH-ի կրկնապատիկն է [Պնդում 6.1]։ Այսպիսով, CK-ն կրկնապատիկն է CH-ի։ Եվ LH-ն գումարած HC կրկնապատիկն է CH-ի [Պնդում 1.43]։ Այսպիսով, KC-ն հավասար է LH-ի գումարած HC-ի։ Եվ CE-ն ցույց տրվեց, որ հավասար է HF-ին։ Այսպիսով, ամբողջ քառակուսի AE-ն հավասար է գնոմոն MNO-ին։

Եվ քանի որ BA-ն կրկնապատիկն է AD-ի, BA-ի վրա քառակուսին չորսապատիկն է AD-ի վրա քառակուսու՝ այսինքն, AE-ն չորսապատիկն է DH-ի։ Եվ AE-ն հավասար է գնոմոն MNO-ին։ Եվ, այսպիսով, գնոմոն MNO-ն նույնպես չորսապատիկն է AP-ի։ Այսպիսով, ամբողջ DF-ը հնգապատիկն է AP-ի։ Եվ DF-ը CD-ի վրա քառակուսին է, իսկ AP-ն՝ DA-ի վրա քառակուսին։ Այսպիսով, CD-ի վրա քառակուսին հնգապատիկն է DA-ի վրա քառակուսու։

Այսպիսով, եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորի վրա քառակուսին, գումարած ամբողջի կեսը, հնգապատիկն է կեսի վրա քառակուսու։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 2

Եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։

2.png

Թող AB ուղիղ գծի վրա քառակուսին հնգապատիկն է AC կտորի վրա քառակուսու։ Եվ թող CD-ն լինի կրկնապատիկ AC-ից։ Ասում եմ, որ եթե CD-ն կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի CB։

Թող AB և CD վրա քառակուսիները՝ AF և CG, նկարագրվեն։ Եվ թող AF պատկերում գծվի։ Եվ թող BE գիծը գծվի։ Եվ քանի որ BA-ի վրա քառակուսին հնգապատիկն է AC-ի վրա քառակուսու, ապա AF-ն հնգապատիկն է AH-ից։ Այսպիսով, գնոմոն MNO-ն է չորսապատիկ AH-ից։ Եվ քանի որ DC-ն կրկնապատիկն է CA-ից, ապա DC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու՝ այսինքն, CG-ն է չորսապատիկ AH-ից։ Եվ գնոմոն MNO-ն նույնպես ցույց տրվեց, որ չորսապատիկն է AH-ից։ Այսպիսով, գնոմոն MNO-ն հավասար է CG-ին։ Եվ քանի որ DC-ն կրկնապատիկն է CA-ից, և DC-ն հավասար է CK-ին, և AC-ն՝ CH-ին, [CK-ն կրկնապատիկն է CH-ից], իսկ KB-ն նույնպես կրկնապատիկն է BH-ից [Պնդում 6.1]։ Այսպիսով, KB-ն հավասար է LH-ի գումարած HB-ին։ Եվ ամբողջ գնոմոն MNO-ն նույնպես ցույց տրվեց, որ հավասար է ամբողջ CG-ին։ Այսպիսով, մնացորդ HF-ն նույնպես հավասար է մնացորդ BG-ին։ Եվ BG-ն այն բազմապատկիչն է, որը պարունակում է CDB։ Քանի որ CD-ն հավասար է DG-ին։ Եվ HF-ն CB-ի վրա քառակուսին է։ Այսպիսով, CDB բազմապատկիչը հավասար է CB-ի վրա քառակուսուն։

Այսպիսով, ինչպես DC-ն է CB-ի նկատմամբ, այնպես էլ CB-ն է BD-ի նկատմամբ [Պնդում 6.17]։ Եվ քանի որ DC-ն ավելի մեծ է, քան CB (տես լեմա), ապա CB-ն նույնպես ավելի մեծ է, քան BD [Պնդում 5.14]։ Այսպիսով, եթե CD ուղիղ գծը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի CB։

Այսպիսով, եթե ուղիղ գծի վրա քառակուսին հնգապատիկն է դրա մի կտորի վրա քառակուսու, և կրկնապատիկ այդ կտորը կտրված է արտաքին և միջին հարաբերությամբ, ապա մեծ կտորը կլինի սկզբնական ուղիղ գծի մնացած մասը։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Լեմմա

Եվ կարող է ցույց տրվել, որ կրկնապատիկ AC-ը (այսինքն՝ DC-ն) ավելի մեծ է, քան BC, ինչպես հետևյալը։

Եթե (կրկնապատիկ AC-ը) ոչ (մեծ է BC-ից), եթե հնարավոր է, թող BC-ն լինի կրկնապատիկ CA-ից։ Այսպիսով, BC-ի վրա քառակուսին չորսապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BC-ի և CA-ի վրա քառակուսիների (հավաքածուն) հնգապատիկն է CA-ի վրա քառակուսու։ Եվ BA-ի վրա քառակուսին համարվեց հնգապատիկն է CA-ի վրա քառակուսու։ Այսպիսով, BA-ի վրա քառակուսին հավասար է BC-ի և CA-ի վրա քառակուսիների (հավաքածուն)։ Սա՝ անխուսափելի է [Պնդում 2.4]։ Այսպիսով, CB-ն չի կարող լինել կրկնապատիկ AC-ից։ Ուստի, նմանապես, կարող ենք ցույց տալ, որ ուղիղ գիծը, որը փոքր է CB-ից, նույնպես չի կարող լինել կրկնապատիկ AC-ից։ Ասածը՝ ավելի մեծ հակասություն է։ Այսպիսով, կրկնապատիկ AC-ը ավելի մեծ է, քան CB։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 3

Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա փոքր կտորի վրա քառակուսին, ավելացված մեծ կտորի կեսին, հնգապատիկն է մեծ կտորի կեսի վրա քառակուսու։

3.png

Թող ինչ-որ ուղիղ գիծ AB կտրված լինի արտաքին և միջին հարաբերությամբ C կետում։ Եվ թող AC-ն լինի մեծ կտորը։ Եվ թող AC-ն կտրված լինի կեսում՝ D կետում։ Ասում եմ, որ BD-ի վրա քառակուսին հնգապատիկն է DC-ի վրա քառակուսու։ Թող AE քառակուսին նկարագրված լինի AB-ի վրա։ Եվ թող պատկերն լիներ կրկնակի։ Քանի որ AC-ն կրկնապատիկ է DC-ից, ապա AC-ի վրա քառակուսին՝ դա չորսապատիկն է DC-ի վրա քառակուսու՝ այսինքն՝ RS-ն չորսապատիկն է FG-ից։ Եվ քանի որ ABC-ում պարունակվող ուղղանկյունը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17], և CE-ն ABC-ում պարունակվող ուղղանկյունն է, ապա CE-ն հավասար է RS-ին։ Եվ RS-ն չորսապատիկն է FG-ից։ Այսպիսով, CE-ն նույնպես չորսապատիկն է FG-ից։ Վերջապես, քանի որ AD-ն հավասար է DC-ին, ապա HK-ն նույնպես հավասար է KF-ին։ Ուստի, GF քառակուսին նույնպես հավասար է HL քառակուսուն։ Այսպիսով, GK-ն հավասար է KL-ին՝ այսինքն՝ MN-ն հավասար է NE-ին։ Ուստի, MF-ն նույնպես հավասար է FE-ին։ Բայց, MF-ն հավասար է CG-ին։ Այսպիսով, CG-ն նույնպես հավասար է FE-ին։ Թող CN-ը ավելացվի երկուսի վրա։ Այսպիսով, գնոմոնը OPQ հավասար է CE-ին։ Բայց, CE-ն ցույց տրված է, որ հավասար է չորսապատիկ GF-ին։ Այսպիսով, գնոմոնը OPQ նույնպես չորսապատիկն է GF քառակուսուց։ Այսպիսով, գնոմոնը OPQ գումարած GF քառակուսին հնգապատիկն է GF քառակուսուց։ Բայց, գնոմոնը OPQ գումարած GF քառակուսին դա DN քառակուսին է։ Եվ DN-ը DB-ի վրա քառակուսին է, իսկ GF-ն՝ DC-ի վրա քառակուսին։ Այսպիսով, DB-ի վրա քառակուսին հնգապատիկն է DC-ի վրա քառակուսու։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 4

Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա ամբողջ գծի և փոքր կտորի վրա քառակուսիների գումարը երեքապատիկն է մեծ կտորի վրա քառակուսու։

4.png

Թող AB լինի ուղիղ գիծ, և թող այն կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Ասում եմ, որ AB և BC-ի վրա քառակուսիների գումարը երեքապատիկն է CA-ի վրա քառակուսուց։ Թող ADEB քառակուսին նկարագրված լինի AB-ի վրա, և թող մնացած պատկերն ընդունի իր ձևը։ Քանի որ AB-ն կտրված է արտաքին և միջին հարաբերությամբ C կետում, և AC-ն մեծ կտոր է, ապա ABC-ում պարունակվող ուղղանկյունը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ AK-ն է ABC-ում պարունակվող ուղղանկյունը, և HG-ն՝ AC-ի վրա քառակուսին։ Այսպիսով, AK-ն հավասար է HG-ին։ Եվ քանի որ AF-ն հավասար է FE-ին [Պնդում 1.43], թող CK-ը ավելացվի երկուսի վրա։ Այսպիսով, ամբողջ AK-ն հավասար է ամբողջ CE-ին։ Այսպիսով, AK-ն և CE-ն միասին հավասար են երկու անգամ AK-ին։ Բայց, AK-ն և CE-ն միասին դա է գնոմոնը LMN, որը գումարած CK քառակուսին։ Այսպիսով, գնոմոն LMN գումարած CK քառակուսին հավասար է երկու անգամ AK-ին։ Բայց, իսկապես, AK-ն նաև ցույց տրված է, որ հավասար է HG-ին։ Այսպիսով, գնոմոն LMN գումարած CK քառակուսին հավասար է HG-ին։ Եվ այսպիսով, գնոմոն LMN գումարած CK և HG քառակուսիները երեքապատիկն են HG քառակուսուց։ Եվ գնոմոն LMN գումարած CK և HG քառակուսիները ամբողջ AE-ն են գումարած CK-ը՝ որոնք են AB և BC քառակուսիները (համապատասխանաբար), և GH-ը՝ AC-ի վրա քառակուսին։ Այսպիսով, AB և BC-ի վրա քառակուսիների գումարը երեքապատիկն է AC-ի վրա քառակուսուց։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 5

Եթե ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, և այդ մեծ կտորին հավասար ուղիղ գիծը ավելացվում է դրան, ապա ամբողջ ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, և սկզբնական ուղիղ գիծը մեծ կտորն է։

5.png

Թող AB լինի ուղիղ գիծ, և թող այն կտրված լինի արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Եվ թող AD-ն [դառնա] հավասար AC-ին։ Ասում եմ, որ DB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ A կետում, և որ սկզբնական AB ուղիղ գիծը մեծ կտորն է։ Թող AE քառակուսին նկարագրված լինի AB-ի վրա, և թող մնացած պատկերն ընդունի իր ձևը։ Քանի որ AB-ն կտրված է արտաքին և միջին հարաբերությամբ C կետում, ապա ABC-ում պարունակվող ուղղանկյունը հավասար է AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Եվ CE-ն է ABC-ում պարունակվող ուղղանկյունը, և CH-ը՝ AC-ի վրա քառակուսին։ Բայց, HE-ն հավասար է CE-ին [Պնդում 1.43], և DH-ն հավասար է HC-ին։ Այսպիսով, DH-ն նաև հավասար է HE-ին։ [Թող HB-ն ավելացվի երկուսի վրա]։ Այսպիսով, ամբողջ DK-ն հավասար է ամբողջ AE-ին։ Եվ DK-ն է BD և DA-ում պարունակվող ուղղանկյունը։ Քանի որ AD-ն հավասար է DL-ին, և AE-ն է AB-ի վրա քառակուսին։ Այսպիսով, BD-ում պարունակվող ուղղանկյունը հավասար է AB-ի վրա քառակուսուն։ Այսպիսով, ինչպես DB-ն է BA-ի նկատմամբ, այնպես էլ BA-ն է AD-ի նկատմամբ [Պնդում 6.17]։ Եվ DB-ն ավելի մեծ է BA-ից։ Այսպիսով, BA-ն նույնպես ավելի մեծ է AD-ից [Պնդում 5.14]։ Այսպիսով, DB-ն կտրված է արտաքին և միջին հարաբերությամբ A կետում, և մեծ կտորը AB-ն է։ (Իսկ դա էր, ինչ պետք էր ցույց տալ)։

Պնդում 6

Եթե մի ռացիոնալ ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա յուրաքանչյուր կտորը կլինի այն անպարբեր (ուղիղ գիծ), որ կոչվում է «ապոտոմ»։

6.png

Թող AB լինի ռացիոնալ ուղիղ գիծ, որը կտրված է արտաքին և միջին հարաբերությամբ C կետում, և թող AC-ն լինի մեծ կտորը։ Ասում եմ, որ AC և CB-ը, յուրաքանչյուրը, կլինեն այն անպարբեր (ուղիղ գիծ), որ կոչվում է «ապոտոմ»։

Թող BA-ն ընդարձակվի, և թող AD-ն արվի (հավասար) BA-ի կեսին։ Այսպիսով, քանի որ AB ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ C կետում, և AD-ն, որը BA-ի կեսն է, ավելացվել է մեծ կտոր AC-ին, ապա CD-ի վրա քառակուսին կլինի հինգ անգամ DA-ի վրա քառակուսիին [Պնդում 13.1]։ Այսպիսով, CD-ի վրա քառակուսին և DA-ի վրա քառակուսին կունենան հարաբերություն, որը նման է մի թվի հարաբերությանը մյուս թվին։ CD-ի վրա քառակուսին, հետևաբար, համահունչ կլինի DA-ի վրա քառակուսուն [Պնդում 10.6]։ Իսկ DA-ի վրա քառակուսին կլինի ռացիոնալ, քանի որ DA-ն ռացիոնալ է, երբ որ AB-ն ռացիոնալ է։ Այսպիսով, CD-ի վրա քառակուսին նույնպես կլինի ռացիոնալ [Սահմանում 10.4]։ Այսպիսով, CD-ն նույնպես ռացիոնալ է։ Եվ քանի որ CD-ի վրա քառակուսին չի ունենում հարաբերություն DA-ի վրա քառակուսիին, որը նման է քառակուսի թվերի հարաբերությանը, ապա CD-ն չհամապատասխանում է DA-ի երկարության հետ [Պնդում 10.9]։ Այսպիսով, CD և DA-ը այն ռացիոնալ ուղիղ գծերն են, որոնք համահունչ են միայն քառակուսու տեսքով։ Այսպիսով, AC-ն կլինի ապոտոմ [Պնդում 10.73]։

Կրկին, քանի որ AB-ն կտրված է արտաքին և միջին հարաբերությամբ, և AC-ն մեծ կտորն է, ապա AB և BC-ի պարունակած ուղղանկյունը կլինի հավասար AC-ի վրա քառակուսուն [Սահմանում 6.3, Պնդում 6.17]։ Այսպիսով, AC-ի վրա ապոտոմի քառակուսին, կիրառված ռացիոնալ ուղիղ գծի AB-ի վրա, կկազմի BC՝ որպես լայնություն։ Եվ ապոտոմի վրա քառակուսին, կիրառված ռացիոնալ ուղիղ գծի վրա, կկազմի առաջին ապոտոմը՝ որպես լայնություն [Պնդում 10.97]։ Այսպիսով, CB-ն կլինի առաջին ապոտոմ։ Եվ CA-ն նույնպես ցույց տրված է որպես ապոտոմ։

Այսպիսով, եթե մի ռացիոնալ ուղիղ գիծը կտրված է արտաքին և միջին հարաբերությամբ, ապա յուրաքանչյուր կտորը կլինի այն անպարբեր (ուղիղ գիծ), որ կոչվում է «ապոտոմ»։

Here are the corrected versions for the 7th and 8th propositions with the updated terminology for the shapes:

Պնդում 7

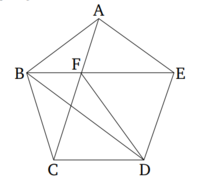
Թող երեք անկյունները, որոնք լինելու են կամ հաջորդական, կամ ոչ հաջորդական, հավասար կլինեն հավասարանկյուն հնգանկյունում, ապա հնգանկյունը կլինի հավասարանկյուն։

7.png

Դա ցույց տալու համար, թող հնգանկյունի ABCDE երեք անկյունները՝ առաջին հերթին A, B և C կետերում, հավասար լինեն իրար։ Ես ասում եմ, որ հնգանկյունը ABCDE հավասարանկյուն է։

Թող AC, BE և FD լինեն միացված։ Եվ քանի որ երկու (ուղղաձիգ գծերը) CB և BA հավասար են երկու (ուղղաձիգ գծերին) BA և AE համապատասխանաբար, և CBA անկյունը հավասար է BAE անկյունին, ապա AC հիմքը հավասար կլինի BE հիմքին, և ABC եռանկյունը հավասար կլինի ABE եռանկյունին, և մնացած անկյունները հավասար կլինեն մնացած անկյուններին, որոնք հավասար կողմերի տրված անկյուններին ենթադրում են [Պնդում. 1.4]։ Իսկ դա նշանակում է, որ BCA (հավասար է) BEA-ին, իսկ ABE-ը (հավասար է) CAB-ին։

Այսպիսով, AF կողմը նույնպես հավասար է BF կողմին [Պնդում. 1.6]։ Եվ ամբողջ AC-ն նույնպես ցույց է տրվել, որ հավասար է BE-ին։ Այսպիսով, մնացորդը FC նույնպես հավասար կլինի FE-ին։ Եվ CD-ն նույնպես հավասար է DE-ին։

Այսպիսով, երկու (ուղղաձիգ գծերը) FC և CD հավասար են երկու FE և ED համապատասխանաբար։ Իսկ FD-ը նրանց ընդհանուր հիմքն է։ Այսպիսով, FCD անկյունը հավասար է FED անկյունին [Պնդում. 1.8]։

Եվ BCA-ն նույնպես ցույց է տրվել, որ հավասար է AEB-ին։ Այսպիսով, ամբողջ BCD-ն հավասար է AED-ին։ Բայց, BCD անկյունը ենթադրվել էր, որ հավասար է A և B անկյուններին։ Այսպիսով, AED անկյունը նույնպես հավասար կլինի A և B անկյուններին։

Այսպիսով, նույն կերպ կարող ենք ցույց տալ, որ CDE անկյունը նույնպես հավասար է A, B, C անկյուններին։ Այսպիսով, հնգանկյունը ABCDE հավասարանկյուն է։

Պնդում 8

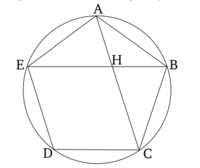
Եթե ուղղաձիգ գծերը կտրում են երկու հաջորդական անկյուններ հավասարանկյուն և հավասար կողմ ունեցող հնգանկյունում, ապա դրանք իրար կտրում են արտաքին և միջին հարաբերությամբ, և դրանց մեծ հատվածները հավասար են հնգանկյունի կողմերին։

8.png

Իսկ հիմա, եթե երկու ուղղաձիգ գծեր՝ AC և BE, հատում են իրար H կետում և դրանք ծածկում են հավասար անկյուններ՝ A և B համապատասխանաբար հավասարանկյուն հնգանկյունում ABCDE, ապա պետք է ապացուցենք, որ յուրաքանչյուր գիծ կտրված է արտաքին և միջին հարաբերությամբ H կետում և դրանց մեծ հատվածները հավասար են հնգանկյունի կողմերին։

Եկեք ընդունենք, որ ABCDE հնգանկյունի շուրջ է նկարագրված շրջան [Պնդում 4.14]: Եվ քանի որ երկու ուղղաձիգ գծերը՝ EA և AB հավասար են երկու ուղղաձիգ գծերին՝ AB և BC համապատասխանաբար, և նրանք պարունակում են հավասար անկյուններ, BE հիմքը հավասար կլինի AC հիմքին, և ABC և ABE եռանկյունները հավասար կլինեն, ուստի մնացած անկյունները նույնպես հավասար կլինեն [Պնդում 1.4]: Հետևաբար, անկյուն BAC հավասար կլինի անկյուն ABE-ին: Այսպիսով, անկյուն AHE-ն երկու անգամ մեծ է, քան անկյուն BAH [Պնդում 1.32]: Եվ EAC նույնպես երկու անգամ մեծ է BAC-ից, քանի որ շրջանագիծը EDC երկու անգամ մեծ է CB շրջանագծից [Առաջարկներ 3.28, 6.33]: Ուստի, անկյուն HAE-ն հավասար կլինի անկյուն AHE-ին: Հետևաբար, ուղղաձիգ HE-ը հավասար կլինի ուղղաձիգ EA-ին՝ այն է՝ AB [Պնդում 1.6]: Եվ քանի որ ուղղաձիգ BA-ն հավասար է AE-ին, ապա անկյուն ABE-ն նույնպես հավասար կլինի AEB-ին [Պնդում 1.5]: Բայց, ABE-ն արդեն ցույց տրված էր, որ հավասար է BAH-ին: Հետևաբար, BEA-ն նույնպես հավասար կլինի BAH-ին: Իսկ քանի որ անկյուն ABE-ն ընդհանուր է երկու եռանկյունների՝ ABE և ABH-ի համար, մնացած անկյունը՝ BAE, հավասար կլինի մնացած անկյունի՝ AHB [Պնդում 1.32]: Հետևաբար, եռանկյունը ABE հավասար է եռանկյունին ABH: Այսպիսով, համամասնորեն, ինչպես BE-ն հավասար է BA-ին, այնպես էլ AB-ն հավասար է BH-ին [Պնդում 6.4]: Եվ BA-ն հավասար է EH-ին: Այսպիսով, ինչպես BE-ն հավասար է EH-ին, այնպես էլ EH-ն հավասար է HB-ին: Եվ BE-ն ավելի մեծ է EH-ից: EH-ն ավելի մեծ է HB-ից [Պնդում 5.14]: Հետևաբար, BE-ն կտրված է արտաքին և միջին հարաբերությամբ H կետում, և մեծ հատվածը՝ EH, հավասար է հնգանկյունի կողմին: Ուստի նույն կերպ կարող ենք ցույց տալ, որ AC-ն նույնպես կտրված է արտաքին և միջին հարաբերությամբ H կետում, և դրա մեծ հատվածը՝ CH, հավասար է հնգանկյունի կողմին: Սա է այն, ինչ պետք էր ապացուցել:

Պնդում 9

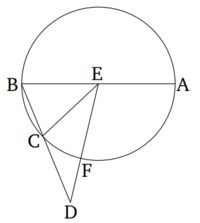
Եթե նույն շրջանում ներգծված վեցանկյան և տասանկյան կողմերը միասին գումարվեն, ապա ամբողջ ուղղաձիգ գիծը կտրված է արտաքին և միջին հարաբերությամբ (հատման կետում), և նրա մեծ հատվածը տասանկյան կողմն է: [1]


9.png

Թող ABC լինի շրջան: Եվ ABC շրջանում նկարագրված պատկերներից, BC լինի տասանկյան կողմը, և CD (կողմը) վեցանկյան կողմը: Եվ թող դրանք դրված լինեն ուղղահայաց: Պետք է ապացուցվի, որ ամբողջ BD ուղղաձիգ գիծը կտրված է արտաքին և միջին հարաբերությամբ (C կետում), և որ CD-ն նրա մեծ հատվածն է:

Թող շրջանի կենտրոնը, E կետը, գտնվի [Պնդում 3.1], և թող EB, EC և ED կետերը միավորված լինեն, և թող BE-ը գծվի A կետին: Քանի որ BC-ն հավասարանկյուն տասանկյան կողմ է, ապա շրջանագիծ ACB-ն 5 անգամ մեծ է BC-ի երկարությունից: Այսպիսով, շրջանագիծ AC-ն 4 անգամ մեծ է CB-ից: Եվ քանի որ AC շրջանագիծը հավասար է CB-ին, այնպես էլ անկյուն AEC-ն հավասար է CEB-ին [Պնդում 6.33]: Այդպես, անկյուն AEC-ն 4 անգամ մեծ է CEB-ից: Եվ քանի որ անկյուն EBC-ն հավասար է ECB-ին [Պնդում 1.5], ապա անկյուն AEC-ն 2 անգամ մեծ է ECB-ից [Պնդում 1.32]: Եվ քանի որ ուղղաձիգ EC-ն հավասար է CD-ին, ապա անկյուն CED-ն հավասար է անկյուն CDE-ին [Պնդում 1.5]: Այդպես, անկյուն ECB-ն 2 անգամ մեծ է EDC-ից [Պնդում 1.32]: Սակայն AEC-ն արդեն ապացուցվել է, որ 4 անգամ մեծ է EDC-ից: Եվ AEC-ն նույնպես 4 անգամ մեծ է BEC-ից: Այսպիսով, EDC-ն հավասար է BEC-ին: Եվ անկյուն EBD-ն համատեղ է երկու եռանկյունում՝ BEC և BED: Այդպիսով, մնացած անկյուն BED-ն հավասար է անկյուն ECB-ին [Պնդում 1.32]: Այսպիսով, եռանկյունը EBD հավասար է եռանկյունին EBC: Այլ կերպ ասած, համեմատաբար, ինչպես BD-ն է BE-ին, այնպես էլ AB-ն է BH-ին [Պնդում 6.4]: Եվ BE-ն հավասար է CD-ին: Ուստի, ինչպես BD-ն է DC-ին, այնպես էլ DC-ն է CB-ին: Եվ BD-ն մեծ է DC-ից: Այսպիսով, DC-ն նույնպես մեծ է CB-ից [Պնդում 5.14]. Այսպիսով, BD ուղղաձիգ գիծը կտրված է արտաքին և միջին հարաբերությամբ (C կետում), և DC-ն նրա մեծ հատվածն է: (Այս է այն, ինչ անհրաժեշտ էր ապացուցել):

Պնդում 10

Եթե միևնույն շրջանում կանոնավոր հնգանկյուն է ներգծված, ապա հնգանկյան կողմի գծի քառակուսին հավասար է նույն շրջանում ներգծված վեցանկյանի և տասանկյանի կողմերի քառակուսիերի գումարին։ [2]

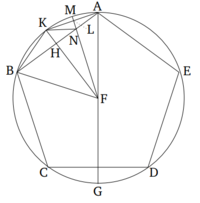
10.png

Թող ABCDE լինի շրջան։ Եվ թող ABCDE հավասարակողմ հնգանկյունը լինի դրված ABCDE շրջանում։ Պնդում եմ, որ հնգանկյան ABCDE կողմի քառակուսին հավասար է նույն շրջանում դրված վեցանկյանի և տասանկյանի կողմերի քառակուսիերի գումարին։

Թող կենտրոնի կետը լինի F, որը գտնվել է [Պնդում. 3.1]։ Եվ թող AF ուղղի միացված լինի, և թող այն անցնի G կետով։ Եվ թող F B միացված լինի։ Եվ թող FH ուղղը լինի F-ից ուղղահայաց AB-ին։ Եվ թող այն անցնի K կետով։ Եվ թող AK և K B միացված լինեն։ Եվ կրկին, թող F L ուղղը լինի F-ից ուղղահայաց AK-ին։ Եվ թող այն անցնի M կետով։ Եվ թող K N միացված լինի։

Քանի որ ABCG շրջանը հավասար է AEDG շրջանում, որի ABC-ն հավասար է AED-ին, մնացած շրջանը CG-ը այդպես էլ հավասար է մնացած GD շրջանին։ Եվ CD-ը (հնգանկյան կողմն է)։ CG-ը այդպես էլ (տասանկյանի կողմն է)։ Եվ քանի որ F A հավասար է F B-ին, և F H ուղղահայաց է (AB-ին), ապա անկյուն AFK-ը նույնպես հավասար է KFB-ին [Պնդում. 1.5, 1.26]։ Հետևաբար, AK շրջանը հավասար է KB-ի [Պնդում. 3.26]։ Այսպիսով, AB շրջանը կրկնակի է BK շրջանից։ Այսպիսով, ուղիղ գիծը AK տասանկյան կողմն է։ Այսպես, նույն պատճառներով, AK շրջանը կրկնակի է KM-ից։ Եվ քանի որ AB շրջանը կրկնակի է BK շրջանից, և CD շրջանը հավասար է AB շրջանին, ապա CD շրջանը նույնպես կրկնակի է BK շրջանից։ Եվ CD շրջանը նույնպես կրկնակի է CG-ից։ Այսպիսով, CG շրջանը հավասար է BK շրջանին։ Բայց, BK-ը կրկնակի է KM-ից, քանի որ KA-ը նույնպես (կրկնակի է KM-ից)։ Այսպես, CG շրջանը նույնպես կրկնակի է KM-ից։ Բայց, իսկապես, CB շրջանը նույնպես կրկնակի է BK-ից։ Քանի որ CB շրջանը հավասար է BA-ին։ Այսպիսով, ամբողջ GB շրջանը նույնպես կրկնակի է BM-ից։ Հետևաբար, անկյուն GFB [է] նույնպես կրկնակի անկյուն BF M [Պնդում. 6.33]։

Պնդում 11

Եթե հավասարակողմ հնգանկյունը ներգծված է շրջանի մեջ, որի տրամագիծը ռացիոնալ է, ապա հնգանկյան կողմը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր»։

11.png

Թող հավասարակողմ հնգանկյուն ABCDE-ն ներգծված լինի ABCDE շրջանի մեջ, որի տրամագիծը ռացիոնալ է։ Ասում եմ, որ հնգանկյան [ABCDE] կողմը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր»։

Թող գտնված լինի շրջանի կենտրոնը՝ F կետը [Պնդում 3.1]։ Եվ թող միացվեն AF-ն և FB-ն։ Եվ թող դրանք քաշվեն G և H կետերին (համապատասխանաբար)։ Եվ թող միացվի AC-ն։ Եվ թող FK-ն հավասար լինի AF-ի չորրորդ մասին։ AF-ն ռացիոնալ է։ Ուստի, FK-ն նույնպես ռացիոնալ է։ FB-ն նույնպես ռացիոնալ է։ Ուստի, ամբողջ BK-ն ռացիոնալ է։ Եվ քանի որ ACG աղեղն հավասար է ADG աղեղին, որոնցից ABC աղեղն հավասար է AED աղեղին, մնացորդային CG աղեղն, հետևաբար, հավասար է GD մնացորդային աղեղին։

Եվ եթե միացնենք AD-ն, ապա L կետում գտնվող անկյունները դառնում են ուղիղ անկյուններ, իսկ CD-ն հավասար է CL-ի կրկնակիին [Պնդում 1.4]։ Հետևաբար, նույն տրամաբանությամբ, M կետում անկյունները նույնպես ուղիղ են, իսկ AC-ն կրկնակի է CM-ի։ Ուստի, քանի որ ALC անկյունն հավասար է AMF անկյունին, և LAC անկյունն ընդհանուր է ACL և AMF եռանկյունների համար, ապա մնացորդային ACL անկյունն, հետևաբար, հավասար է MF A մնացորդային անկյունին [Պնդում 1.32]։ Ուստի, ACL եռանկյունն հավասանկյուն է AMF եռանկյան հետ։ Ուստի, համեմատաբար, ինչպես LC-ն է CA-ի նկատմամբ, այնպես էլ MF-ն է FA-ի նկատմամբ [Պնդում 6.4]։

Եվ (կարող ենք վերցնել) առաջատար մեծությունների կրկնակի արժեքները։ Ուստի, ինչպես LC-ի կրկնակին է CA-ի նկատմամբ, այնպես էլ MF-ն է FA-ի կեսի նկատմամբ։ Եվ, ուստի, ինչպես LC-ի կրկնակին է CA-ի կեսի նկատմամբ, այնպես էլ MF-ն է FA-ի չորրորդ մասի նկատմամբ։ Եվ DC-ն LC-ի կրկնակի է, իսկ CM-ն CA-ի կեսն է, իսկ FK-ն FA-ի չորրորդ մասը։ Ուստի, ինչպես DC-ն է CM-ի նկատմամբ, այնպես էլ MF-ն է FK-ի նկատմամբ։

Սկզբունքով, ինչպես DCM գումարը (այսինքն՝ DC և CM) CM-ի նկատմամբ, այնպես էլ MK-ն է KF-ի նկատմամբ [Պնդում 5.18]։ Եվ, ուստի, ինչպես DCM գումարի վրա կառուցված քառակուսին է CM-ի վրա կառուցված քառակուսու նկատմամբ, այնպես էլ MK-ի վրա կառուցված քառակուսին է KF-ի վրա կառուցված քառակուսու նկատմամբ։

Եվ քանի որ հնգանկյան երկու կողմերը սահմանող մեծ հատվածը, ինչպես AC-ն, որը բաժանված է ծայրագույն և միջին հարաբերությամբ, հավասար է հնգանկյան կողմին [Պնդում 13.8]՝ այսինքն DC-ին, և ամբողջի կեսին ավելացված մեծ հատվածի վրա կառուցված քառակուսին հնգապատիկ է ամբողջի կեսի վրա կառուցված քառակուսու, իսկ CM-ն AC-ի կեսն է։ Ուստի, DCM-ի վրա կառուցված քառակուսին, որպես ամբողջություն, հնգապատիկ է CM-ի վրա կառուցված քառակուսու։

Եվ DCM-ի վրա կառուցված քառակուսին, որպես ամբողջություն, CM-ի վրա կառուցված քառակուսու նկատմամբ այնպես է, ինչպես MK-ի վրա կառուցված քառակուսին KF-ի վրա կառուցված քառակուսու նկատմամբ։ Ուստի, MK-ի վրա կառուցված քառակուսին հնգապատիկ է KF-ի վրա կառուցված քառակուսու։ Եվ KF-ի վրա կառուցված քառակուսին ռացիոնալ է։ Քանի որ տրամագիծն ռացիոնալ է։ Ուստի, MK-ի վրա կառուցված քառակուսին նույնպես ռացիոնալ է։

Ուստի, MK-ն ռացիոնալ է [քառակուսու միայն]։ Եվ քանի որ BF-ն FK-ի չորս անգամն է, BK-ն, ուստի, FK-ի հինգ անգամն է։ Ուստի, BK-ի վրա կառուցված քառակուսին FK-ի վրա կառուցված քառակուսու քսանհինգ անգամն է։ Եվ MK-ի վրա կառուցված քառակուսին FK-ի վրա կառուցված քառակուսու հնգապատիկն է։ Ուստի, BK-ի վրա կառուցված քառակուսին MK-ի վրա կառուցված քառակուսու նկատմամբ չունի այն հարաբերությունը, որ քառակուսի թվերը ունեն քառակուսի թվերի նկատմամբ։ Ուստի, BK-ն անհամաչափ է երկարությամբ MK-ի հետ [Պնդում 10.9]։

Եվ երկուսն էլ ռացիոնալ (ուղիղ գծեր) են։ Ուստի, BK-ն և MK-ն ռացիոնալ (ուղիղ գծեր են), որոնք համաչափ են քառակուսու միայն։ Եվ եթե ռացիոնալ (ուղիղ գծից) հանենք ռացիոնալ (ուղիղ գիծ), որը քառակուսու միայն համաչափ է առաջինի հետ, ապա ստացվում է անհամաչափ (ուղիղ գիծ)։

Եվ քանի որ KF-ն համաչափ է երկարությամբ BF-ի հետ, ապա, ըստ կազմի, BK-ն նույնպես համաչափ է երկարությամբ BF-ի հետ [Պնդում 10.15]։ Բայց BF-ն համաչափ է երկարությամբ BH-ի հետ։ Հետևաբար, BK-ն նույնպես համաչափ է երկարությամբ BH-ի հետ [Պնդում 10.12]։ Եվ քանի որ BK-ի վրա կառուցված քառակուսին հնգապատիկ է MK-ի վրա կառուցված քառակուսուն, ապա BK-ի վրա կառուցված քառակուսին, հետևաբար, ունի MK-ի վրա կառուցված քառակուսու նկատմամբ այն հարաբերությունը, որը 5-ն ունի 1-ի նկատմամբ։

Հետևաբար, հակադարձմամբ՝ BK-ի վրա կառուցված քառակուսին ունի \( N \)-ի վրա կառուցված քառակուսու նկատմամբ այն հարաբերությունը, որը 5-ն ունի 4-ի նկատմամբ [Պնդում 5.19՝ ուղղում], ինչը չի համապատասխանում քառակուսի թվի և քառակուսի թվի հարաբերությանը։

BK-ն, հետևաբար, անհամաչափ է երկարությամբ \( N \)-ի հետ [Պնդում 10.9]։ Հետևաբար, քանի որ BK-ի վրա կառուցված քառակուսին մեծ է MK-ի վրա կառուցված քառակուսուց \( N \)-ի վրա կառուցված անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, և ամբողջը՝ BK-ն, համաչափ է նախկինում տրված ռացիոնալ (ուղիղ գծի)՝ BH-ի հետ, MB-ն, հետևաբար, չորրորդ ափոտոմ է [Սահմանում 10.14]։

Եվ ռացիոնալ (ուղիղ գծի) և չորրորդ ափոտոմի միջև պարունակվող ուղղանկյունը անհամաչափ է, և դրա քառակուսի արմատը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր» [Պնդում 10.94]։ Եվ AB-ի վրա կառուցված քառակուսին ուղղանկյունն է, որը պարունակում է HBM-ը, հաշվի առնելով, որ AH-ի միացման դեպքում եռանկյուն ABH-ը դառնում է հավասանկյուն եռանկյուն ABM-ի հետ [Պնդում 6.8], և (համեմատաբար) ինչպես HB-ն է BA-ի նկատմամբ, այնպես էլ AB-ն է BM-ի նկատմամբ։

Հետևաբար, հնգանկյան կողմ AB-ն այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է «փոքր»։ [3]

Սա այն էր, ինչը պահանջվում էր ապացուցել։

Պնդում 12

Եթե հավասարակողմ եռանկյունը ներգծված է շրջանի մեջ, ապա եռանկյան կողմի վրա կառուցված քառակուսին երեք անգամ մեծ է շրջանի շառավղի վրա կառուցված քառակուսուց։

Թող լինի ABC շրջան, և թող հավասարակողմ եռանկյուն ABC-ն ներգծված լինի դրանում [Պնդում 4.2]։ Ասում եմ, որ եռանկյուն ABC-ի որևէ կողմի վրա կառուցված քառակուսին երեք անգամ մեծ է ABC շրջանի շառավղի վրա կառուցված քառակուսուց։

12.png

Թող գտնված լինի ABC շրջանի կենտրոնը՝ D կետը [Պնդում 3.1]։ Եվ AD (լինելով) միացված, թող անցկացվի E կետի միջով։ Եվ թող BE-ն միացվի։

Եվ քանի որ եռանկյուն ABC-ն հավասարակողմ է, ուստի BEC կամարը, հետևաբար, ABC շրջանի կամարի երրորդ մասն է։ Ուստի, BE կամարը շրջանի կամարի վեցերորդ մասն է։ Ուստի, ուղիղ գիծ BE-ն վեցանկյան կողմն է։ Ուստի, այն հավասար է շառավղի՝ DE-ի [Պնդում 4.15, ուղղում]։ Եվ քանի որ AE-ն կրկնակի է DE-ի, ապա AE-ի վրա կառուցված քառակուսին չորս անգամ մեծ է DE-ի վրա կառուցված քառակուսուց՝ այսինքն՝ BE-ի վրա կառուցված քառակուսուց։

Եվ AE-ի վրա կառուցված քառակուսին հավասար է AB-ի և BE-ի վրա կառուցված քառակուսիների գումարին [Պնդումներ 3.31, 1.47]։ Ուստի, AB-ի և BE-ի վրա կառուցված քառակուսիների գումարը չորս անգամ մեծ է BE-ի վրա կառուցված քառակուսուց։ Ուստի, ըստ բաժանման, AB-ի վրա կառուցված քառակուսին երեք անգամ մեծ է BE-ի վրա կառուցված քառակուսուց։ Եվ BE-ն հավասար է DE-ին։ Ուստի, AB-ի վրա կառուցված քառակուսին երեք անգամ մեծ է DE-ի վրա կառուցված քառակուսուց։

Ուստի, եռանկյան կողմի վրա կառուցված քառակուսին երեք անգամ մեծ է շրջանի շառավղի վրա կառուցված քառակուսուց։ [4]

Սա այն էր, ինչը պահանջվում էր ապացուցել։

Պնդում 13

Կառուցել (կանոնավոր) բուրգ (այսինքն՝ տետրահեդրոն), այն ներգծել տրված գնդի մեջ և ցույց տալ, որ գնդի տրամագծի վրա կառուցված քառակուսին մեկ ու կես անգամ մեծ է բուրգի կողմի վրա կառուցված քառակուսուց։

13.png

Թող տրված գնդի տրամագիծը լինի AB, և այն կետ C-ում բաժանվի այնպես, որ AC-ն կրկնակի լինի CB-ին [Պնդում 6.10]։ Եվ թող AB-ի վրա կառուցվի կեսաշրջագիծ ADB։ Եվ թող C կետից ուղղանկյուն լինի գծված CD ուղիղը AB-ի նկատմամբ։ Եվ թող միացվի DA։ Եվ թող DC շառավղով գծվի շրջան EFG, որի մեջ ներգծված կլինի հավասարակողմ եռանկյուն EFG [Պնդում 4.2]։ Թող գտնվի շրջանի կենտրոնը՝ H կետը [Պնդում 3.1]։ Թող միացվեն EH, HF, և HG։ Թող H կետում ուղղանկյուն լինի գծված HK ուղիղը EFG շրջանի հարթության նկատմամբ [Պնդում 11.12]։ Եվ թող HK ուղիղի վրա կտրվի հատված, որը հավասար կլինի AC ուղիղին։ Թող KE, KF, և KG գծերը միացվեն։

Քանի որ KH ուղիղը ուղղանկյուն է EFG շրջանի հարթության նկատմամբ, այն ուղղանկյուն կլինի նաև իր հետ միացող բոլոր ուղիղների նկատմամբ, որոնք գտնվում են EFG շրջանի հարթությունում [սահմանում 11.3]։ HE, HF, և HG ուղղերը միանում են դրան։ Ուստի, HK-ն ուղղանկյուն է HE-ի, HF-ի և HG-ի նկատմամբ։

Քանի որ AC-ն հավասար է HK-ին, և CD-ն՝ HE-ին, իսկ նրանք պարունակում են ուղղանկյուններ, ապա հիմքը՝ DA-ն, հավասար է հիմքին՝ KE [Պնդում 1.4]։ Նույն պատճառներով KF-ն և KG-ն նույնպես հավասար են DA-ին։ Ուստի, KE, KF և KG երեք ուղիղները հավասար են միմյանց։

Քանի որ AC-ն կրկնակի է CB-ի, ուստի AB-ն եռակի է CB-ին։ Եվ ինչպես AB-ն CB-ի նկատմամբ, այնպես էլ AD-ի վրա կառուցված քառակուսին DC-ի վրա կառուցված քառակուսու նկատմամբ, ինչպես ցույց կտրվի ստորև [տես լեմմա]։ Ուստի, AD-ի վրա կառուցված քառակուսին երեք անգամ մեծ է DC-ի վրա կառուցված քառակուսուց։ Եվ FE-ի վրա կառուցված քառակուսին նույնպես երեք անգամ մեծ է EH-ի վրա կառուցված քառակուսուց [Պնդում 13.12], և DC-ն հավասար է EH-ին։ Ուստի, DA-ն հավասար է EF-ին։

Բայց DA-ն ցույց տրվեց, որ հավասար է KE, KF և KG յուրաքանչյուրին։ Ուստի EF, FG, և GE-ն հավասար են KE, KF, և KG-ին համապատասխանաբար։ Ուստի, EFG, KEF, KFG, և KEG չորս եռանկյունները հավասարակողմ են։

Ուստի, կառուցվել է բուրգ, որի հիմքը եռանկյուն EFG-ն է, իսկ գագաթը՝ K կետը։

Այժմ անհրաժեշտ է այն ներգծել տրված գնդի մեջ և ցույց տալ, որ գնդի տրամագծի վրա կառուցված քառակուսին մեկ ու կես անգամ մեծ է բուրգի կողմի վրա կառուցված քառակուսուց։

Թող HL ուղիղը երկարացվի K H ուղղի շարունակությամբ, և HL-ը հավասար լինի CB-ին։ Եվ քանի որ ինչպես AC-ն CD-ի նկատմամբ, այնպես էլ CD-ն CB-ի նկատմամբ [Պնդում 6.8, ուղղում], իսկ AC-ն հավասար է KH-ին, CD-ն՝ HE-ին, և CB-ն՝ HL-ին, ուստի ինչպես KH-ն HE-ի նկատմամբ, այնպես էլ EH-ն HL-ի նկատմամբ։ Ուստի, K H և HL ուղղագծերի պարունակած ուղղանկյունը հավասար է EH-ի վրա կառուցված քառակուսուն [Պնդում 6.17]։

Եվ քանի որ AC-ն կրկնակի է CB-ի, ապա AB-ն եռակի է CB-ի։ Ուստի, AB-ն մեկ ու կես անգամ մեծ է AC-ից։ Եվ ինչպես AB-ն AC-ի նկատմամբ, այնպես էլ AB-ի վրա կառուցված քառակուսին AC-ի վրա կառուցված քառակուսու նկատմամբ։ Եվ քանի որ AB-ն գնդի տրամագիծն է, իսկ AD-ն՝ բուրգի կողմը, ապա AB-ի վրա կառուցված քառակուսին մեկ ու կես անգամ մեծ է AD-ի վրա կառուցված քառակուսուց։

Սա էր պահանջվում ցույց տալ։

14.png

Լեմմա

Ապացուցել, որ ինչպես AB գիծը BC գծի նկատմամբ, այնպես էլ AD գծի վրա կառուցված քառակուսին DC գծի վրա կառուցված քառակուսու նկատմամբ են հավասար:

Թող կեսաշրջագծի պատկերը կազմվի, և DB գիծը միացվի։ Թող AC-ի վրա կառուցվի EC քառակուսին։ Եվ թող FB զուգահեռագիծը լրացվի։

Քանի որ եռանկյուն DAB-ը համաչափ է եռանկյուն DAC -ին [Պնդումներ 6.8, 6.4], հետևում է, որ ինչպես BA գիծը AD գծի նկատմամբ, այնպես էլ AD գիծը AC գծի նկատմամբ են հավասար։ Ուստի, BA և AC գծերի պարունակած ուղղանկյունը հավասար է AD-ի վրա կառուցված քառակուսուն [Պնդում 6.17]։

Քանի որ ինչպես AB գիծը BC գծի նկատմամբ, այնպես էլ EB ուղղանկյունը BF ուղղանկյունի նկատմամբ են հավասար [Պնդում 6.1], EB-ը հավասար է BA և AC գծերի պարունակած ուղղանկյանին (քանի որ EA = AC), իսկ BF-ը հավասար է AC և CB գծերի պարունակած ուղղանկյանին։

Այսպիսով, ինչպես AB գիծը BC գծի նկատմամբ, այնպես էլ AD գծի վրա կառուցված քառակուսին DC գծի վրա կառուցված քառակուսու նկատմամբ են հավասար։

Պնդում 14

Կառուցել ութանկյուն և փակել այն տրված գնդի մեջ՝ ինչպես նախորդ պնդումներում, և ցույց տալ, որ գնդի տրամագծի քառակուսին կրկնապատիկ է ութանկյոնի կողի քառակուսուց։

Թող տրված գնդի տրամագիծը լինի AB, և այն կիսվի C կետում։ Նկարել ADB կիսամորթը AB վրա։ Նկարել CD ուղղահայաց AB-ին C-ից։ Միացնել DB։

Կառուցել EFGH քառակուսին, որի յուրաքանչյուր կողմը հավասար է DB-ին։ Միացնել HF-ը և EG-ը։ Սահմանել ուղիղ գիծ KL K-ում, ուղղահայաց դեպի EFGH քառակուսիի պլանը (Պնդում 11.12), և նկարել մեկ այլ գիծ՝ KM, որը գտնվում է պլանի մյուս կողմում։

Կտրել KL-ը և KM-ը՝ հավասարեցնելով մեկին EK-ի, FK-ի, GK-ի և HK-ի։ Միացնել LE-ը, LF-ը, LG-ը, LH-ը, ME-ը, MF-ը, MG-ը և MH-ը։

15.png

Քանի որ KE = KH և անկյունը EKH ուղիղ անկյուն է, ապա HE-ի քառակուսին կրկնապատիկ է EK-ի քառակուսուց (Պնդում 1.47)։ Նույն կերպ, քանի որ LK = KE և անկյունը LKE ուղիղ անկյուն է, ապա EL-ի քառակուսին կրկնապատիկ է EK-ի քառակուսուց (Պնդում 1.47)։ Եվ քանի որ HE-ի քառակուսին նույնպես կրկնապատիկ է EK-ի քառակուսուց, ապա LE-ի քառակուսին հավասար է EH-ի քառակուսուն։

Ուստի, LE = EH։ Նույն պատճառներով, LH = HE։ LEH եռանկյունը հավասարակողմ է։ Այսպիսով, մենք կարող ենք նույն կերպ ցույց տալ, որ մնացած բոլոր եռանկյունիները, որոնց հիմքերը EFGH քառակուսիի կողմերն են, և գագաթները L-ն ու M-ն են, հավասարակողմ են։ Այսպես, ութանկյուն, որը բաղկացած է ութ հավասարակողմ եռանկյունիներից, կառուցվել է։

Այժմ պետք է ցույց տրվի, որ այն փակվում է տրված գնդի մեջ, և որ գնդի տրամագծի քառակուսին կրկնապատիկ է ութանկյոնի կողի քառակուսուց։

Քանի որ LK = KM և KE ընդհանուր է, և նրանք պարունակում են ուղիղ անկյուններ, ապա LE-ի հիմքը հավասար է EM-ին (Պնդում 1.4)։ Եվ քանի որ անկյունը LEM ուղիղ անկյուն է՝ ըստ կիսամորթի (Պնդում 3.31), ապա LM-ի քառակուսին կրկնապատիկ է LE-ի քառակուսուն (Պնդում 1.47)։

Այնուհետև, քանի որ AC = CB, AB-ն կրկնապատիկ է BC-ի։ Եվ ինչպես AB-ը BC-ին է, այնպես էլ AB-ի քառակուսին հավասար է BD-ի քառակուսուն (Պնդում 6.8, սահման. 5.9)։ Այսպիսով, AB-ի քառակուսին կրկնապատիկ է BD-ի քառակուսուց։

Եվ LM-ի քառակուսին նույնպես ցույց տրված է, որ կրկնապատիկ է LE-ի քառակուսուց։ Եվ DB-ի քառակուսին հավասար է LE-ի քառակուսուն։ Քանի որ EH-ը հավասար է DB-ին։

Այսպիսով, AB-ի քառակուսին նույնպես հավասար է LM-ի քառակուսուն։ Այսպիսով, AB = LM։ Եվ AB-ն տրված գնդի տրամագծն է։ Ուստի, LM-ը հավասար է տրված գնդի տրամագծին։

Այսպիսով, ութանկյունը ներգծված է տրված գնդի մեջ, և միաժամանակ ցույց տրված է, որ գնդի տրամագծի քառակուսին կրկնապատիկ է ութանկյոնի կողի քառակուսուց։[5]

(Այսինքն) հենց այն, ինչ պետք էր ցույց տալ։

Պնդում 15

Կառուցել խորանարդ և փակել այն տրված գնդի մեջ, ինչպես պիրամիդի դեպքում, և ցույց տալ, որ գնդի տրամագծի քառակուսին երեք անգամ գերազանցում է խորանարդի կողմի քառակուսուն։

Թող տրված գնդի տրամագիծը լինի AB, և այն կիսվի C կետում այնպես, որ AC-ն երկու անգամ մեծ է քան CB-ն։ Նկարել ADB կիսամորթը AB վրա։ Նկարել CD ուղղահայաց AB-ին C-ից։ Միացնել DB։

Կառուցել EFGH քառակուսին, որի յուրաքանչյուր կողմը հավասար է DB-ին։ Նկարել EK-ը, FL-ը, GM-ը և HN-ը՝ E, F, G և H կետերից համապատասխանաբար, ուղղահայաց դեպի EFGH քառակուսիի պլանը։ Նկարել EK-ը, FL-ը, GM-ը և HN-ը՝ հավասարեցնելով EF, FG, GH և HE կողմերին, և կտրել դրանք համապատասխանաբար EK-ից, FL-ից, GM-ից և HN-ից։ Միացնել KL-ը, LM-ը, MN-ը և NK-ը։ Այսպիսով, խորանարդը, որը բաղկացած է վեց հավասար քառակուսիներից, կառուցվել է։

Այժմ պետք է այն փակվի տրված գնդի մեջ, և ցույց տրվի, որ գնդի տրամագծի քառակուսին երեք անգամ գերազանցում է խորանարդի կողմի քառակուսուն։

16.png

Թող KG և EG միացվեն։ Քանի որ անկյուն KEG-ն ճիշտ անկյուն է՝ հաշվի առնելով, որ KE-ն նաև ուղղահայաց է EG-ի պլանին և ակնհայտորեն նաև ուղղահայաց է EG ուղիղ գծին (Սահման. 11.3), ապա KG-ի վրա նկարած կիսամորթը նույնպես կանցնի E կետով։ Նույն կերպ, քանի որ GF-ն ուղղահայաց է FL և FE-ի ամեն մի մասի, GF-ն նույնպես ուղղահայաց է FK-ի պլանին (Պնդում 11.4)։ Հետևաբար, եթե մենք միացնենք FK-ը, GF-ն նույնպես կլինի ուղղահայաց FK-ի հետ։ Եվ քանի որ դա այդպես է, GK-ի վրա նկարած կիսամորթը նույնպես կանցնի F կետով։ Նույն կերպ, այն կհասնի խորանարդի մնացած անկյուններին։

Այսպիսով, եթե KG-ը մնա (ապացուցված) և կիսամորթը տեղափոխվի, ապա այն կվերադառնա սկզբնական դիրքին, և խորանարդը փակվել է տրված գնդի մեջ։ Դրանից մենք տեսնում ենք, որ այն փակված է տրված գնդի մեջ։ Քանի որ GF-ը հավասար է FE-ին, և անկյունը F-ում ճիշտ անկյուն է, ապա EG-ի քառակուսին կրկնապատիկ է EF-ի քառակուսուց (Պնդում 1.47)։ Եվ FE-ը հավասար է EK-ին։ Այսպիսով, EG-ի քառակուսին կրկնապատիկ է EK-ի քառակուսուց։

Ուստի, GE և EK քառակուսիների գումարը՝ այսինքն՝ GK-ի քառակուսին (Պնդում 1.47), երեք անգամ գերազանցում է EK-ի քառակուսուն։ Եվ քանի որ AB-ը երեք անգամ գերազանցում է BC-ին, և ինչպես AB-ը BC-ին, այնպես էլ AB-ի քառակուսին հավասար է BD-ի քառակուսուն (Պնդում 6.8, սահման. 5.9), ապա AB-ի քառակուսին երեք անգամ գերազանցում է BD-ի քառակուսին։

Եվ GK-ի քառակուսին նույնպես ցույց տրված է, որ երեք անգամ գերազանցում է KE-ի քառակուսին։ Եվ KE-ն հավասարեցված էր DB-ի հետ։ Այսպիսով, KG-ն հավասար է AB-ին։ Իսկ AB-ն տրված գնդի տրամագիծն է։ Ուստի, KG-ն հավասար է տրված գնդի տրամագծին։

Այսպիսով, խորանարդը ներգծված է տրված գնդի մեջ։ Եվ միաժամանակ ցույց տրվել է, որ գնդի տրամագծի քառակուսին երեք անգամ գերազանցում է խորանարդի կողմի քառակուսուն։[6] (Այսինքն) հենց այն, ինչ պետք էր ցույց տալ։

Պնդում 16

Կառուցել իկոսահեդրոն [7] և այն փակել շրջանակով, ինչպես նշված վերոնշյալ պատկերներում, և ցույց տալ, որ իկոսահեդրոնի կողմը այն իռացիոնալ ուղիղ գիծն է, որը կոչվում է փոքր:

17.png

Թող գնդի տրամագիծը AB լինի, և թող այն լինի կտրված C կետում, այնպես, որ AC լինի վեց անգամ ավելի մեծ, քան CB [Պրո. 6.10]։ Եվ թող գծի ADB ծածկվել լինի AB-ի վրա։ Եվ թող ուղղաձիգ CD գիծը նշվի C-ից AB-ի նկատմամբ։ Եվ թող DB-ն միախառնվի։ Եվ թող շրջան EFGHK լինի տեղադրված, և թող դրա շառավիղը հավասար լինի DB-ի։ Եվ թող հավասարազանգված և հավասարանկյուն հնգանկյան EFGHK ներառված լինի EFGHK շրջանի մեջ [Պրո. 4.11]։ Եվ թող շրջանների EF, FG, GH, HK և KE կեսը հատվի L, M, N, O և P կետերում համապատասխանաբար։ Եվ թող LM, MN, NO, OP, PL և EP միախառնվեն։ Այսպիսով, LMNOP հնգանկյանը նույնպես հավասարազանգված է, և EP-ն (կողմն է) տասանկյան (համապատասխան շրջանագծում):

Եվ թող գծերը EQ, FR, GS, HT, KU, որոնք հավասար են EFGHK շրջանի շառավիղին, տեղադրված լինեն ուղղանկյուն ձևով շրջանի մակարդակում, E, F, G, H, և K կետերում համապատասխանաբար։ Եվ թող QR, RS, ST, TU, UQ, QL, LR, RM, MS, SN, NT, TO, OU, UP և PQ միախառնվեն։ Եվ քանի որ EQ և KU-ն ուղղանկյուն են նույն ինքնուրույն շրջանագծին, EQ-ն այսպիսով զուգահեռ է KU-ին [Պրո. 11.6]։ Եվ դրանք հավասար են։ Եվ համարժեք ուղղաձիգները միևնույն կողմում հավասար և զուգահեռ են [Պրո. 1.33]։ Այսպիսով, QU-ն հավասար և զուգահեռ է EK-ին: Եվ EK-ն (կողմն է) հավասարազանգված հնգանկյան (inscribed in the circle EFGHK): Այսպիսով, QU-ն (կողմն է) նույնպես հավասարազանգված հնգանկյան (EFGHK շրջանի մեջ):

Այսպիսով, նույն (պատճառներով), QR, RS, ST, և TU-ն նույնպես հավասարազանգված կողմեր են, EFGHK շրջանի մեջ: Հնգանկյուն QRSTU (կողմն է) հետևաբար հավասարազանգված: Ուղղանկյուն QE-ն (կողմն է) վեցանկյան (EFGHK շրջանում), և EP (կողմն է) տասանկյան, իսկ QEP անկյունը ուղղանկյուն է, այսպիսով QP-ն (կողմն է) հնգանկյան (նույն շրջանի մեջ): Քանի որ վեցանկյան կողմի քառորդը հավասար է այն կողմերի քառորդներին, որոնք տեղադրված են մեկ ընդհանուր գծով շրջանագծում [Պրո. 13.10]: Այսպիսով, նույն (պատճառներով), PU-ն նույնպես հնգանկյան կողմն է: Այսպիսով, QU-ն նույնպես (կողմն է) հնգանկյան։ Այսպիսով, QPU եռանկյունը հավասար է։ Այսպիսով, նույն (պատճառներով), QLR, RMS, SNT և TOU եռանկյունները հավասար են։ Եվ քանի որ QL-ն և QP-ն (կողմն են) հնգանկյան, և LP-ն նույնպես (կողմն է) հնգանկյան, triangle QLP-ն հավասարազանգված է։

Այսպիսով, նույն (պատճառներով) LRM, MSN, NTO և OUP եռանկյունները հավասար են։

Թող կենտրոնը, V կետը, լինի նշված [Պրո. 3.1]։ Եվ թող VZ-ն տեղադրվի, V կետում, ուղղանկյունորեն շրջանի մակարդակին։ Եվ թող այն լինի արտաշարժված մյուս կողմում (շրջանի), ինչպես VX։ Եվ թող VW-ն կտրվի XZ-ից այնպես, որ հավասար լինի վեցանկյան կողմին, իսկ յուրաքանչյուր VX և WZ (հավասար լինի) տասանկյանի կողմին։ Եվ թող QZ, QW, UZ, EV, LV, LX և XM միախառնվեն։

Եվ քանի որ VW-ն և QE-ն ուղղանկյուն են շրջանի մակարդակին, VW-ն զուգահեռ է QE-ին [Պնդում 11.6]։ Եվ նրանք հավասար են։ EV-ն և QW-ն հավասար և զուգահեռ են [Պնդում 1.33]։ Եվ EV-ն (կողմն է) վեցանկյան։ Այսպիսով, QW-ն (կողմն է) նույնպես վեցանկյան։ Եվ քանի որ QW-ն (կողմն է) վեցանկյան, և WZ-ն (կողմն է) տասանկյանի, և QWZ անկյունը ուղղանկյուն է [Սահմանում 11.3, Պնդում 1.29], ապա QZ-ն (կողմն է) հնգանկյան [Պնդում 13.10]։ Այդպես, նույն (պատճառներով), UZ-ն նույնպես (կողմն է) հնգանկյան, քանի որ եթե մենք միացնենք VK և WU, ապա դրանք կլինեն հավասար և հակադարձ։ Եվ VK-ն, որը հավասար է գնդի շառավիղին, (կողմն է) վեցանկյան [Պնդում 4.15 շտկված]։ Այսպիսով, WU-ն նույնպես (կողմն է) վեցանկյան։ Եվ WZ-ն (կողմն է) տասանկյան, և UWZ անկյունը ուղղանկյուն է։ Այսպիսով, UZ-ն (կողմն է) հնգանկյան [Պրո. 13.10]։ Եվ QU-ն (կողմն է) հնգանկյան։ Triangle QUZ-ն հավասար է։ Այսպիսով, նույն (պատճառներով), մնացած բոլոր եռանկյունները, որոնց հիմքերը են QR, RS, ST, և TU գծերը, և բարձունքները Z կետում, նույնպես հավասար են։ Եվ քանի որ VL-ն (կողմն է) վեցանկյան, և VX-ն (կողմն է) տասանկյան, և LVX անկյունը ուղղանկյուն է, ապա LX-ն (կողմն է) հնգանկյան [Պնդում 13.10]։ Այդպես, նույն (պատճառներով), եթե մենք միացնենք MV, որը (կողմն է) վեցանկյան, ապա MX-ն նույնպես կլինի (կողմն է) հնգանկյան։ Եվ LM-ն (կողմն է) հնգանկյան։ Այսպիսով, triangle LMX-ը հավասար է։ Այսպես, նմանապես, կարող է ցուցադրվել, որ մնացած բոլոր եռանկյունները, որոնց հիմքերը են MN, NO, OP, և PL գծերը, և բարձունքները X կետում, նույնպես հավասար են։ Այսպիսով, իկոսիադրոնը, որը բաղկացած է քսան հավասարազանգված եռանկյուններից, կառուցվել է։ Այսպիսով, պետք է նաև տեղադրել այն տրամադրված գնդի մեջ և ցույց տանք, որ իկոսիադրոնի կողմը այն անկյունագիծն է, որը կոչվում է միկրո։ Ուրեմն, քանի որ VW-ն (կողմն է) վեցանկյան, և WZ-ն (կողմն է) տասանկյան, VZ-ն այստեղ կտրված է էքստրեմալ և միջին հարաբերությամբ W-ում, և VW-ն նրա մեծ մասը է [Պնդում 13.9]։ Այդպես, երբ ZV-ն VW-ին համեմատվում է, VW-ն համեմատվում է WZ-ի։ Եվ VW-ն հավասար է VE-ին, WZ-ն՝ VX-ին։ Այդպես, ZV-ն համեմատվում է VE-ի հետ, իսկ EV-ն՝ VX-ի հետ։ Եվ անկյունները ZVE և EVX են ուղղանկյուն։

Ուրեմն, նույն (պատճառներով), քանի որ ZV-ն նման է VW-ին, այնպես որ VW-ն նման է WZ-ին, և ZV-ն հավասար է XW-ին, իսկ VW-ը նման է WQ-ին, ապա ինչպես XW-ն նման է WQ-ին, այնպես էլ QW-ն նման է WZ-ին: Եվ կրկին, այս պատճառով, եթե մենք միացնենք QX-ը, ապա Q-ում գտնվող անկյունը կլինի ուղղանկյուն [Պնդում 6.8]: Ուրեմն, XZ-ի վրա նկարագրված կես շրջանը նույնպես կանցնի Q-ի միջով [Պնդում 3.31]: Եվ եթե XZ-ը մնա անշարժ, և կես շրջանը տեղաշարժվի, ապա այն նորից կտեղադրվի նույն (հայեցողական) դիրքում, որտեղից այն սկսել է շարժվել, ապա այն նույնպես կանցնի (Q) կետի միջով, և (կանցնի) իկոսահեդրոնի մնացած անկյունային կետերի միջով: Եվ իկոսահեդրոնը կշրջապատվի գնդի կողմից: Ուրեմն, ես ասում եմ, որ այն նույնպես շրջապատված է տրված (գնդով): Թող ՎW-ն կիսվել է a-ի վրա: Եվ քանի որ ուղիղ գիծը VZ կիսվել է ծայրահեղ և միջին հարաբերությամբ W-ին, և ZW-ն դրա փոքր մասը է, ապա ZW-ի վրա նկարված քառորդը և ավելի մեծ մասի կեսը՝ W a-ն, հավասար է հինգ անգամ (այդ) մասի քառորդին [Պնդում 13.3]: Ուրեմն, Za-ի վրա նկարված քառորդը հինգ անգամ մեծ է (aW)-ի վրա նկարված քառորդից: Եվ ZX-ը երկակի է Za-ից, և VW-ն երկակի է aW-ից: Ուրեմն, ZX-ի վրա նկարված քառորդը հինգ անգամ մեծ է VW-ի վրա նկարված քառորդից: Եվ քանի որ AC-ն չորս անգամ մեծ է CB-ից, ապա AB-ն հինգ անգամ մեծ է BC-ից: Եվ ինչպես AB-ն է BC-ին, այնպես էլ AB-ի վրա նկարված քառորդը է BD-ի վրա նկարված քառորդից [Պնդում 6.8, Սահմանում 5.9]: Ուրեմն, AB-ի վրա նկարված քառորդը հինգ անգամ մեծ է BD-ի վրա նկարված քառորդից: Եվ ZX-ի վրա նկարված քառորդը նույնպես ցույց է տվել, որ հինգ անգամ մեծ է VW-ի վրա նկարված քառորդից: Եվ DB-ն հավասար է VW-ին: Քանզի երկուսը նույնպես հավասար են EFGHK շրջանակի ռադիուսին: Ուրեմն, AB-ն նույնպես հավասար է XZ-ին: Եվ AB-ն տրված գնդի տրամագիծն է: Ուրեմն, XZ-ն հավասար է տրված գնդի տրամագծին: Ուրեմն, իկոսահեդրոնը շրջապատված է տրված գնդով:

Ուրեմն, ես ասում եմ, որ իկոսահեդրոնի կողմը այն անհամաչափ (ուղղահայաց) ուղիղ գիծն է, որը կոչվում է փոքր: Քանզի գնդի տրամագիծը համաչափ է, և դրա քառորդը հինգ անգամ մեծ է EFGHK շրջանակի ռադիուսի վրա նկարված քառորդից, ապա EFGHK շրջանակի ռադիուսը նույնպես համաչափ է: Ուրեմն, դրա տրամագիծը նույնպես համաչափ է: Եվ եթե հավասարակողմ պենտագոն ներկառուցվի շրջանի մեջ, որը ունի համաչափ տրամագիծ, ապա պենտագոնի կողմը այն անհամաչափ (ուղղահայաց) ուղիղ գիծն է, որը կոչվում է փոքր [Պնդում 13.11]: Եվ EFGHK պենտագոնի կողմը այն կողմն է, որը համընկնում է իկոսահեդրոնի կողմի հետ: Ուրեմն, իկոսահեդրոնի կողմը այն անհամաչափ (ուղղահայաց) ուղիղ գիծն է, որը կոչվում է փոքր:

Հետևանք

Ուրեմն, ակնհայտ է, որ գնդի տրամագծի քառորդը հինգ անգամ մեծ է այն շրջանակի ռադիուսի քառորդից, որի միջոցով նկարագրված է իկոսահեդրոնը, և որ գնդի տրամագիծը հավասար է նույն շրջանակի մեջ ներկառուցված վեցանկու եզրը և երկու տասանկու եզրերի գումարին:

Նշումներ

  1. ↑ "Եթե շրջանը միավոր շառավիղ ունի, ապա վեցանկյան կողմը հավասար է 1-ի, իսկ տասանկյան կողմը՝ (1/2)(√5 − 1):"
  2. ↑ "Եթե շրջանը միավոր շառավիղ ունի, ապա հնգանկյան կողմը հավասար է (1/2)(√10 − 2√5):"
  3. ↑ "Եթե շրջանը միավոր շառավիղ ունի, ապա հնգանկյան կողմը հավասար է (1/2)(√10 − 2√5): Այնուամենայնիվ, այս երկարությունը կարող է գրվել «փոքր» ձևով (տես Առ. 10.94)՝ (ρ/√2)(1 + k/√1 + k²) − (ρ/√2)(1 − k/√1 + k²), որտեղ ρ = √5/2 և k = 2:"
  4. ↑ "Եթե գնդի շառավիղը միավոր է, ապա բուրգի (այսինքն՝ տետրահեդրոնի) կողմը հավասար է √8/3:"
  5. ↑ "Եթե գնդի շառավիղը միավոր է, ապա ութանիստի կողմը հավասար է √2:"
  6. ↑ "Եթե գնդի շառավիղը միավոր է, ապա խորանարդի կողմը հավասար է √4/3:"
  7. ↑ "տասնութ նիստերով բազմանիստ է, որն ունի 20 ճիշտ եռանկյունիներ, ունի 12 գագաթներ և 30 եզրեր"
Ստացված է «https://grapaharan.org/index.php?title=Տարերք/Գիրք_13&oldid=15826» էջից