«Տարերք/Գիրք 5»–ի խմբագրումների տարբերություն
No edit summary |
|||
| (32 intermediate revisions by 2 users not shown) | |||
| Տող 8. | Տող 8. | ||
[[Կատեգորիա:Մաթեմատիկա]] |
[[Կատեգորիա:Մաթեմատիկա]] |
||
| ⚫ | |||
== pages 129-130 == |
|||
| ⚫ | |||
1. Մեծությունը համարվում է մեկ այլ մեծության |
1. Մեծությունը համարվում է մեկ այլ մեծության |
||
մաս՝ փոքրը մեծի, երբ այն չափում է մեծը։ |
մաս՝ փոքրը մեծի, երբ այն չափում է մեծը։ |
||
| Տող 83. | Տող 81. | ||
# Բաժանման հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես առաջինի և հաջորդողի տարբերություն, իսկ հաջորդողը մնում է նույնը։ |
# Բաժանման հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես առաջինի և հաջորդողի տարբերություն, իսկ հաջորդողը մնում է նույնը։ |
||
# Փոխարկման հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես առաջին իսկ հաջորդող, որպես առաջինի և հաջորդողի տարբերություն։ |
# Փոխարկման հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես առաջին իսկ հաջորդող, որպես առաջինի և հաջորդողի տարբերություն։ |
||
# Կան մի քանի մեծություններ և դրանց հավասար թվով այլ մեծություններ, որոնք ունեն նույն հարաբերությունը զույգ առ զույգ վերցված, հարաբերությունը հավասարության միջոցով տեղի է ունենում, երբ առաջինը մինչև վերջինն է առաջինում մեծությունների բազմությունում, ուստի առաջինը (է) մինչև վերջինը երկրորդ |
# Կան մի քանի մեծություններ և դրանց հավասար թվով այլ մեծություններ, որոնք ունեն նույն հարաբերությունը զույգ առ զույգ վերցված, հարաբերությունը հավասարության միջոցով տեղի է ունենում, երբ առաջինը մինչև վերջինն է առաջինում մեծությունների բազմությունում, ուստի առաջինը (է) մինչև վերջինը երկրորդ արտաքին (մեծությունների) (հարաբերակցությունը) հեռացնելով ներքինը (մեծությունները). |
||
արտաքին (մեծությունների) (հարաբերակցությունը) հեռացնելով ներքինը (մեծությունները). |
|||
== Պնդում 1 == |
== Պնդում 1 == |
||
| Տող 90. | Տող 87. | ||
Եթե որևէ քանակի մեծություններ համապատասխանաբար բազմապատիկ են հավասար թվով ուրիշ մեծությունների, ապա քանի անգամ մեծություններից մեկը մեծ է իրեն համապատասխան մեծությունից, այնքան անգամ մնացած բոլոր մեծությունները մեծ են իրենց համապատասխան մեծություններից։ |
Եթե որևէ քանակի մեծություններ համապատասխանաբար բազմապատիկ են հավասար թվով ուրիշ մեծությունների, ապա քանի անգամ մեծություններից մեկը մեծ է իրեն համապատասխան մեծությունից, այնքան անգամ մնացած բոլոր մեծությունները մեծ են իրենց համապատասխան մեծություններից։ |
||
[[Պատկեր:Պնդում1.png|center|400px]] |
|||
Stex screenshot piti dnem |
|||
Թող լինի ցանկացած քանակի քանակության, AB, CD մեծություններ որոնք հավասար բազմապատիկ են, համապատասխանաբար, որոշ այլ հավասար թվով մեծությունների՛ E, F։ քանի անգամ AB-ն բաժանվում է E-ի, այնքան անգամ AB-ն, CD-ն նույնպես կբաժանվի E, F-ի: Քանի որ AB-ն, CD-ն հավասար է E, F-ի բազմապատիկին, ապա AB-ում այնքան մեծություններ հավասար են E-ին, ինչքան CD-ում հավասար են F-ի: Թող AB-ն բաժանվի AG, GB, հավասար E-ի և CD-ն CH, HD, հավասար F: Այսպիսով, AG, GB-ի թիվը հավասար կլինի CH, HD-ի թվին:Եվ քանի որ AG-ը հավասար է E-ի, իսկ CH-ն F-ն է, ապա AG (հավասար), հետևաբար, հավասար է E-ի, իսկ AG, CH - E, F: Այսպիսով, նույն (պատճառներով) GB-ն հավասար է E-ի, և GB, HD - E, F. |
Թող լինի ցանկացած քանակի քանակության, AB, CD մեծություններ որոնք հավասար բազմապատիկ են, համապատասխանաբար, որոշ այլ հավասար թվով մեծությունների՛ E, F։ քանի անգամ AB-ն բաժանվում է E-ի, այնքան անգամ AB-ն, CD-ն նույնպես կբաժանվի E, F-ի: Քանի որ AB-ն, CD-ն հավասար է E, F-ի բազմապատիկին, ապա AB-ում այնքան մեծություններ հավասար են E-ին, ինչքան CD-ում հավասար են F-ի: Թող AB-ն բաժանվի AG, GB, հավասար E-ի և CD-ն CH, HD, հավասար F: Այսպիսով, AG, GB-ի թիվը հավասար կլինի CH, HD-ի թվին:Եվ քանի որ AG-ը հավասար է E-ի, իսկ CH-ն F-ն է, ապա AG (հավասար), հետևաբար, հավասար է E-ի, իսկ AG, CH - E, F: Այսպիսով, նույն (պատճառներով) GB-ն հավասար է E-ի, և GB, HD - E, F. |
||
| Տող 108. | Տող 105. | ||
համապատասխանաբար C-ի և F-ի հավասար բազմապատիկներ: |
համապատասխանաբար C-ի և F-ի հավասար բազմապատիկներ: |
||
[[Պատկեր:պնդում2.png|center|400px]] |
|||
STEX PITI SCREENSHOT LINI #2 |
|||
Քանի որ AB-ն և DE-ն են C-ի և F-ի հավասար բազմապատիկներ են, ապա այնքան մեծություն որքան AB-ում հավասար են C-ին, այնքան էլ մեծություն DE-ում հավասար են F-ին: Եվ նույն պատճառներով, նույնքան մեծություններ BG-ում հավասար են C-ի, այնքան էլ EH-ում հավասար են F-ին: |
Քանի որ AB-ն և DE-ն են C-ի և F-ի հավասար բազմապատիկներ են, ապա այնքան մեծություն որքան AB-ում հավասար են C-ին, այնքան էլ մեծություն DE-ում հավասար են F-ին: Եվ նույն պատճառներով, նույնքան մեծություններ BG-ում հավասար են C-ի, այնքան էլ EH-ում հավասար են F-ին: |
||
| Տող 133. | Տող 130. | ||
Այսպիսով, նույն պատճառներով KF-ն և LH-ն հավասար են B-ի և D-ի բազմապատիկներին (համապատասխանաբար): Հետևաբար, առաջին մեծություն EK-ն և երրորդ GL-ը հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար), իսկ հինգերորդ մեծությունը KF-ը և վեցերորդ LH-ը նույնպես հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար), ապա առաջին մեծությունն ու հինգերորդը, գումարվելով միասին (այնպես, որ տալիս են EF), և երրորդն ու վեցերորդը գումարվելով միասին (GH ստանալու համար), հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար): |
Այսպիսով, նույն պատճառներով KF-ն և LH-ն հավասար են B-ի և D-ի բազմապատիկներին (համապատասխանաբար): Հետևաբար, առաջին մեծություն EK-ն և երրորդ GL-ը հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար), իսկ հինգերորդ մեծությունը KF-ը և վեցերորդ LH-ը նույնպես հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար), ապա առաջին մեծությունն ու հինգերորդը, գումարվելով միասին (այնպես, որ տալիս են EF), և երրորդն ու վեցերորդը գումարվելով միասին (GH ստանալու համար), հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար): |
||
[[Պատկեր:պնդում3.png|center|400px]] |
|||
Stex screenshot petqa lini #3 |
|||
Այսպիսով, եթե առաջինը (մեծությունը) և երրորդը հավասար են երկրորդի և չորրորդի համապատասխան բազմապատիկներին, և վերցված են առաջինի և երրորդի հավասար բազմապատիկները, ապա (հավասարության միջոցով) վերցված արժեքները նույնպես հավասար կլինեն երկրորդի և չորրորդը, համապատասխան բազմապատիկներին: Ինչը պետք էր ցույց տալ: |
Այսպիսով, եթե առաջինը (մեծությունը) և երրորդը հավասար են երկրորդի և չորրորդի համապատասխան բազմապատիկներին, և վերցված են առաջինի և երրորդի հավասար բազմապատիկները, ապա (հավասարության միջոցով) վերցված արժեքները նույնպես հավասար կլինեն երկրորդի և չորրորդը, համապատասխան բազմապատիկներին: Ինչը պետք էր ցույց տալ: |
||
| Տող 143. | Տող 140. | ||
թող առաջին մեծությունը` A-ն ունենա նույն հարաբերությունը երկրորդ B-ի հետ, ինչ երրորդ C-ն ունի չորրորդ D-ի հետ: Եվ թող E-ն և F-ը լինեն A-ի և C-ի համապատասխանաբար հավասար բազմապատիկները, իսկ B-ից և D-ից համապատասխանաբար այլ պատահական հավասար բազմապատիկներ՝ G-ն և H-ը: Ապա E-ն հարաբերում է G-ին ինչպես F-ը D-ին։ |
թող առաջին մեծությունը` A-ն ունենա նույն հարաբերությունը երկրորդ B-ի հետ, ինչ երրորդ C-ն ունի չորրորդ D-ի հետ: Եվ թող E-ն և F-ը լինեն A-ի և C-ի համապատասխանաբար հավասար բազմապատիկները, իսկ B-ից և D-ից համապատասխանաբար այլ պատահական հավասար բազմապատիկներ՝ G-ն և H-ը: Ապա E-ն հարաբերում է G-ին ինչպես F-ը D-ին։ |
||
[[Պատկեր:պնդում4.png|center|400px]] |
|||
Stex piti screenshot lini #4 |
|||
Թող հավասար բազմապատիկներ K-ն ու L-ը վերցված լինեն համապատասխանաբար E-ից և F-ից և ուրիշ պատահական հավասար բազմապատիկներ M-ն ու N-ը համապատասախանաբար G-ից ու H-ից։ |
Թող հավասար բազմապատիկներ K-ն ու L-ը վերցված լինեն համապատասխանաբար E-ից և F-ից և ուրիշ պատահական հավասար բազմապատիկներ M-ն ու N-ը համապատասախանաբար G-ից ու H-ից։ |
||
| Տող 156. | Տող 153. | ||
Եթե մեծությունը նույն մեծության բազմապատիկն է, ինչ վերցված մասը (է) վերցված մասի, ապա մնացորդը նույնպես կլինի մնացորդի նույն բազմապատիկը, ինչ ամբողջը ամբողջից (համապատասխանաբար): |
Եթե մեծությունը նույն մեծության բազմապատիկն է, ինչ վերցված մասը (է) վերցված մասի, ապա մնացորդը նույնպես կլինի մնացորդի նույն բազմապատիկը, ինչ ամբողջը ամբողջից (համապատասխանաբար): |
||
[[Պատկեր:պնդում5.png|center|400px]] |
|||
Stex piti screenshot lini #5 |
|||
Թող AB մեծությունը լինի CD մեծության նույն բազմապատիկը, ինչ վերցված AE մասը վերցված CF մասից է: Ես ասում եմ, որ մնացորդ EB-ն նույնպես կլինի մնացորդի FD-ի նույն բազմապատիկը, ինչ որ ամբողջ AB-ն ամբողջ CD-ի է: |
Թող AB մեծությունը լինի CD մեծության նույն բազմապատիկը, ինչ վերցված AE մասը վերցված CF մասից է: Ես ասում եմ, որ մնացորդ EB-ն նույնպես կլինի մնացորդի FD-ի նույն բազմապատիկը, ինչ որ ամբողջ AB-ն ամբողջ CD-ի է: |
||
| Տող 170. | Տող 167. | ||
Թող AB և CD մեծությունները լինեն E-ի, և F-ի համապատասխանաբար հավասար բազմապատիկներ: Եվ թող առաջինից վերցված մասերը՝ AG-ն և CH-ը լինեն համապատասխաբար E-ի և F-ի հավասար բազմապատիկներ: Ես ասում եմ որ GB և HD մնացորդները կամ նույնպես հավար են E-ի և F-ի կամ նրանց հավասար բազմապատիկներ են: |
Թող AB և CD մեծությունները լինեն E-ի, և F-ի համապատասխանաբար հավասար բազմապատիկներ: Եվ թող առաջինից վերցված մասերը՝ AG-ն և CH-ը լինեն համապատասխաբար E-ի և F-ի հավասար բազմապատիկներ: Ես ասում եմ որ GB և HD մնացորդները կամ նույնպես հավար են E-ի և F-ի կամ նրանց հավասար բազմապատիկներ են: |
||
[[Պատկեր:պնդում6.png|center|400px]] |
|||
Stex piti screenshot lini #6 |
|||
Թող GB-ն լինի հավասար E-ին: Ես ասում եմ որ HD-ն նույնպես հավասար է F-ին: |
Թող GB-ն լինի հավասար E-ին: Ես ասում եմ որ HD-ն նույնպես հավասար է F-ին: |
||
| Տող 184. | Տող 181. | ||
Թող A և B-ն լինեն հավասար մեծություններ, և C-ն պատահական մեծություն։ Ես ասում եմ որ A և B-ն ունեն նույն հարաբերությունը C-ին և C-ն ունի նույն հարաբերությունը A և B-ին։ |
Թող A և B-ն լինեն հավասար մեծություններ, և C-ն պատահական մեծություն։ Ես ասում եմ որ A և B-ն ունեն նույն հարաբերությունը C-ին և C-ն ունի նույն հարաբերությունը A և B-ին։ |
||
[[Պատկեր:պնդում7.png|center|400px]] |
|||
Stex piti screenshot lini #7 |
|||
Թող D և E հավասար բազմապատիկները համապատասխանաբար վերցված լինեն A-ից և B-ից, և ինչ-որ ուրիշ պատահական F-ը C-ից։ |
Թող D և E հավասար բազմապատիկները համապատասխանաբար վերցված լինեն A-ից և B-ից, և ինչ-որ ուրիշ պատահական F-ը C-ից։ |
||
Հետևաբար, քանի որ D և E-ն A-ի և B-ի հավասար բազմապատիկներ են և A-ն հավասար է B-ին, հետևաբար D-ն հավասար է E-ին։ Եվ F-ը ուրիշ պատահական է։ Հետևաբար, եթե D-ն գերազանցում է |
Հետևաբար, քանի որ D և E-ն A-ի և B-ի հավասար բազմապատիկներ են և A-ն հավասար է B-ին, հետևաբար D-ն հավասար է E-ին։ Եվ F-ը ուրիշ պատահական է։ Հետևաբար, եթե D-ն գերազանցում է |
||
| Տող 193. | Տող 191. | ||
Այսպիսով՝ հավասար մեծությունները ունեն հավասար հարաբերություն նույն մեծությանը, և վերջին մեծությունը ունի հավասար հարաբերություն հավասար մեծություններին։ |
Այսպիսով՝ հավասար մեծությունները ունեն հավասար հարաբերություն նույն մեծությանը, և վերջին մեծությունը ունի հավասար հարաբերություն հավասար մեծություններին։ |
||
== Հետևանք == |
== Հետևանք == |
||
Այսպիսով այստեղից պարզ է որ երե որոշ մեծություններ պրոպորցիոնալ են, ապա նրանք նույնպես կլինեն հակադարձորեն պրոպորցիոնալ։ Ինչը պետք էր ցույց տալ: |
Այսպիսով այստեղից պարզ է որ երե որոշ մեծություններ պրոպորցիոնալ են, ապա նրանք նույնպես կլինեն հակադարձորեն պրոպորցիոնալ։ Ինչը պետք էր ցույց տալ: |
||
| Տող 202. | Տող 200. | ||
Թող AB-ն ու C-ն լինեն անհավասար մեծություններ, և թող AB-ն լինի նրանցից մեծը, և D-ն ուրիշ պատահական մեծություն է։ Ես ասում եմ որ, AB-ն ունի ունի ավելի մեծ հարաբերություն D-ին քան C-ն D-ին և որ D-ն ունի ավելի մեծ հարաբերություն C-ին քան AB-ին։ |
Թող AB-ն ու C-ն լինեն անհավասար մեծություններ, և թող AB-ն լինի նրանցից մեծը, և D-ն ուրիշ պատահական մեծություն է։ Ես ասում եմ որ, AB-ն ունի ունի ավելի մեծ հարաբերություն D-ին քան C-ն D-ին և որ D-ն ունի ավելի մեծ հարաբերություն C-ին քան AB-ին։ |
||
[[Պատկեր:պնդում8.png|center|400px]] |
|||
mekel screenshot #8 |
|||
Քանի որ AB-ն մեծ է C-ից, թող BE-ն լինի հավասար C-ին։ Այսպիսով AE-ի և EB-ից փոքրը, բազմապատկելով երբեմն մեծ կլինի D-ից [Սահմանում 5.4]: Առաջինը, թող AE-ն փոքր կլինի քան |
Քանի որ AB-ն մեծ է C-ից, թող BE-ն լինի հավասար C-ին։ Այսպիսով AE-ի և EB-ից փոքրը, բազմապատկելով երբեմն մեծ կլինի D-ից [Սահմանում 5.4]: Առաջինը, թող AE-ն փոքր կլինի քան |
||
| Տող 215. | Տող 213. | ||
D-ին։ Թող դա լինի բազմապատկված, եվ թող GH-ը լինի EB—ի բազմապատիկ, որը մեծ է D-ից։ Եվ այնքան անգամ որքան GH-ը բաժանվում է EB-ի այնքան ագամ էլ թող FG-ն նույնպես բաժանվի AE-ին, իսկ K-ն C-ին։ Հանգունորեն մենք կարող ենք ցույց տալ որ որ FH-ը ու K-ն AB-ի և C-ի հավասար բազմապատիկեր են։ Եվ վերոնշյալին հանգունորեն մենք կարող ենք ցույց տալ որ FH-ն ու K-ն AB-ի և C-ի հավասար բազմապատիկեր են։ Եվ վերոնշյալին հանգունորեն թող N-ն ու D-ն (որը առաջին բազմապատիկն է մեծ քան FG—ն) վերցված են։ Այսպես FG-ն կրկին փոքր չէ քան M-ը։ Եվ GH-ը մեծ է D-ից։ Այդ իսկ պատճառով ամբողջ FH-ը գերազանցում է D-ին և M-ին, որը N-ն է։ Եվ K-ն չի գերազանցում N-ին, աjնքանով որքան FG-ն, որը մեծ է GH-ից։ այսինքն՝ K—ն նույնպես չի գերազանցում է N-ին: Եվ շարունակելով նույն պնդումներով մենք կարող ենք ավարտել ապացույցը։ |
D-ին։ Թող դա լինի բազմապատկված, եվ թող GH-ը լինի EB—ի բազմապատիկ, որը մեծ է D-ից։ Եվ այնքան անգամ որքան GH-ը բաժանվում է EB-ի այնքան ագամ էլ թող FG-ն նույնպես բաժանվի AE-ին, իսկ K-ն C-ին։ Հանգունորեն մենք կարող ենք ցույց տալ որ որ FH-ը ու K-ն AB-ի և C-ի հավասար բազմապատիկեր են։ Եվ վերոնշյալին հանգունորեն մենք կարող ենք ցույց տալ որ FH-ն ու K-ն AB-ի և C-ի հավասար բազմապատիկեր են։ Եվ վերոնշյալին հանգունորեն թող N-ն ու D-ն (որը առաջին բազմապատիկն է մեծ քան FG—ն) վերցված են։ Այսպես FG-ն կրկին փոքր չէ քան M-ը։ Եվ GH-ը մեծ է D-ից։ Այդ իսկ պատճառով ամբողջ FH-ը գերազանցում է D-ին և M-ին, որը N-ն է։ Եվ K-ն չի գերազանցում N-ին, աjնքանով որքան FG-ն, որը մեծ է GH-ից։ այսինքն՝ K—ն նույնպես չի գերազանցում է N-ին: Եվ շարունակելով նույն պնդումներով մենք կարող ենք ավարտել ապացույցը։ |
||
Այսպիսով՝ Անհավասար մեծությունների համար, ավելի մեծ մեծությունը ունի ավելի մեծ հարաբերություն քան փոքրը նույն հարաբերությանը։ |
Այսպիսով՝ Անհավասար մեծությունների համար, ավելի մեծ մեծությունը ունի ավելի մեծ հարաբերություն քան փոքրը նույն հարաբերությանը։ |
||
== Պնդում 9 == |
== Պնդում 9 == |
||
| Տող 221. | Տող 218. | ||
Մեծություններ, որոնք ունեն նույն հարաբերությունը նույն մեծությանը հավասար են մեկը մյուսին։ Եվ այն մեծությունները, որին նույն մեծությունը ունի նույն հարաբերությունը հավասար են։ |
Մեծություններ, որոնք ունեն նույն հարաբերությունը նույն մեծությանը հավասար են մեկը մյուսին։ Եվ այն մեծությունները, որին նույն մեծությունը ունի նույն հարաբերությունը հավասար են։ |
||
[[Պատկեր:պնդում9.png|center|400px]] |
|||
screenshot #9 |
|||
Թող A-ից և B-ից յուրաքանչյուրը ունենա նույն հարաբերությունը C-ին։ Ես ասում եմ որ A-ն հավասար է B-ին։ |
Թող A-ից և B-ից յուրաքանչյուրը ունենա նույն հարաբերությունը C-ին։ Ես ասում եմ որ A-ն հավասար է B-ին։ |
||
| Տող 231. | Տող 228. | ||
== Պնդում 10 == |
== Պնդում 10 == |
||
Երկու մեծություններ ունեն հարաբերություններ նույն մեծությանը։ Այն մեծությունը որը ունի մեծ հարաբերություն այդ երկուսից մեծն է։ Եվ այն մեծությունը, որին վերջին մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է։ |
|||
[[Պատկեր:պնդում10.png|center|400px]] |
|||
screenshot #10 |
|||
Թող A-ն ունենա ավելի մեծ հարաբերություն C-ին քան B-ն C-ին։ Ես ասում եմ որ A-ն մեծ է B-ից։ |
|||
Եթե ոչ A-ն հաստատ հավասար է կամ մեծ է B-ից: A-ն հավասար չէ B-ին, Քանի որ հակառակ դեպքում A-ն և B-ն կունենային նույն հարաբերությունը C-ին |
|||
[Պնդում 5.7]: Բայց նրանք չունեն հավասար հարաբերություններ։ Հետևաբար, A-ն հավասար չի B-ին։ Նույնպես, իրոք A-ն փոքր չէ B-ից: Հակառակ դեպքում A-ն կունենա ավելի փոքր հարաբերություն C-ին քան B-ն C-ին [Պնդում 5.8]: Բայց դա այդպես չէ։ Հետևաբար, A-ն փոքր չէ B-ից: Եվ մենք ցույց էինք տվել որ նրանք հավասար չեն։ Հետևաբար A-ն մեծ է B-ից: |
[Պնդում 5.7]: Բայց նրանք չունեն հավասար հարաբերություններ։ Հետևաբար, A-ն հավասար չի B-ին։ Նույնպես, իրոք A-ն փոքր չէ B-ից: Հակառակ դեպքում A-ն կունենա ավելի փոքր հարաբերություն C-ին քան B-ն C-ին [Պնդում 5.8]: Բայց դա այդպես չէ։ Հետևաբար, A-ն փոքր չէ B-ից: Եվ մենք ցույց էինք տվել որ նրանք հավասար չեն։ Հետևաբար A-ն մեծ է B-ից: |
||
Կրկին, Թող C-ն ունենա ավելի մեծ հարաբերություն B-ին քան C-ն A-ին։ Ես ասում եմ որ B-ն փոքր է A-ից: |
|||
Եթե ոչ հաստատ հավասար կամ մեծ է: A-ն հավասար չէ B-ին, Քանի որ հակառակ դեպքում C-ն կունենար նույն հարաբերությունը A-ին և B-ին [Պնդում 5.7]: Բայց դա այդպես չէ։ Նույնպես, իրոք B-ն մեծ չէ A-ից: Հակառակ դեպքում C-ն կունենա ավելի փոքր հարաբերություն B-ին քան A-ին [Պնդում 5.8]: Բայց դա այդպես չէ։ Հետևաբար, B-ն մեծ չէ A-ից: Եվ մենք ցույց էինք տվել որ նրանք հավասար չեն։ Հետևաբար B-ն փոք է A-ից: |
|||
Այսպիսով, եթե երկու մեծություններ ունեն հարաբերություններ նույն մեծությանը։ ՀԵտևաբար, այն մեծությունը որը ունի մեծ հարաբերություն այդ երկուսից մեծն է։ Եվ այն մեծությունը, որին վերջին մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է։ |
|||
== Պնդում 11 == |
== Պնդում 11 == |
||
| Տող 246. | Տող 243. | ||
Հարաբերությունները որոնք նույն են նույն հարաբերության հետ նույնպես նույնն են իրար հետ։ |
Հարաբերությունները որոնք նույն են նույն հարաբերության հետ նույնպես նույնն են իրար հետ։ |
||
[[Պատկեր:պնդում11.png|center|400px]] |
|||
screenshot #11 |
|||
Թող A-ն հարաբերի B-ին ինչպես C-ն D-ին և C-ն հարաբերում է D-ին ինչպես E-ն F-ին։ Ես ասում եմ որ A-ն հարաբերում է B-ին ինչպես E-ն F-ին։ |
Թող A-ն հարաբերի B-ին ինչպես C-ն D-ին և C-ն հարաբերում է D-ին ինչպես E-ն F-ին։ Ես ասում եմ որ A-ն հարաբերում է B-ին ինչպես E-ն F-ին։ |
||
| Տող 264. | Տող 261. | ||
Եթե կան կամայական քանակի համաչափ մեծություններ, ապա ինչպես առաջնային մեծություններից մեկը հարաբերում է իր հետևողին, այդպես էլ կհարաբերեն բոլոր մնացած առաջնային մեծությունները իրենց հետևողներին։ |
Եթե կան կամայական քանակի համաչափ մեծություններ, ապա ինչպես առաջնային մեծություններից մեկը հարաբերում է իր հետևողին, այդպես էլ կհարաբերեն բոլոր մնացած առաջնային մեծությունները իրենց հետևողներին։ |
||
[[Պատկեր:պնդում12.png|center|400px]] |
|||
screenshot #12 |
|||
Թող վերցված լինեն կամայական քանակի համաչափ մեծություններ: Oրինակ ` A, B, C, D, E, F Այնպես որ A-ն հարաբերում է B-ին ինչպես C-ն D-ին և E-ն F-ին։ |
Թող վերցված լինեն կամայական քանակի համաչափ մեծություններ: Oրինակ ` A, B, C, D, E, F Այնպես որ A-ն հարաբերում է B-ին ինչպես C-ն D-ին և E-ն F-ին։ |
||
| Տող 282. | Տող 279. | ||
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչպիսին ունի երրորդը չորրորդին և երրորդ մեծությունը ունի ավելի մեծ հարաբերություն չորրորդին քան հինգերորրդը վեցերորդին, ապա առաջին մեծությունը կունենա ավելի մեծ հարաբերություն երկրորդին քան հինգերորդը վեցերորդին։ |
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչպիսին ունի երրորդը չորրորդին և երրորդ մեծությունը ունի ավելի մեծ հարաբերություն չորրորդին քան հինգերորրդը վեցերորդին, ապա առաջին մեծությունը կունենա ավելի մեծ հարաբերություն երկրորդին քան հինգերորդը վեցերորդին։ |
||
[[Պատկեր:պնդում13.png|center|400px]] |
|||
screenshot # 13 |
|||
Թող առաջին մեծությունը A-ն ունենեա նույն հարաբերությունը երկրորդ B-ին ինչպիսին ունի երրորդ C-ն չորրորդ D-ին և թող երրորդ մեծություն C-ն ունենա ավելի մեծ հարաբերություն չորրորդ D-ին քան հինգերորրդ E-ն ունի վեցերորդ |
Թող առաջին մեծությունը A-ն ունենեա նույն հարաբերությունը երկրորդ B-ին ինչպիսին ունի երրորդ C-ն չորրորդ D-ին և թող երրորդ մեծություն C-ն ունենա ավելի մեծ հարաբերություն չորրորդ D-ին քան հինգերորրդ E-ն ունի վեցերորդ |
||
| Տող 288. | Տող 285. | ||
Քանի որ կան C-ի և E-ի հավասար բազմապատիկներ, և ուրիշ պատահական D-ի և F-ի հավասար բազմապատիկներ, որոնց համար C-ի բազմապատիկը չի գերազանցում D-ի բազմապատիկը և E-ի բազմապատիկը չի գերազանցում F-ինը [Պնդում 5.7], թող նրանք վերցված լինեն։ Եվ թող G, H-ը լինեն համապատասխանաբար |
Քանի որ կան C-ի և E-ի հավասար բազմապատիկներ, և ուրիշ պատահական D-ի և F-ի հավասար բազմապատիկներ, որոնց համար C-ի բազմապատիկը չի գերազանցում D-ի բազմապատիկը և E-ի բազմապատիկը չի գերազանցում F-ինը [Պնդում 5.7], թող նրանք վերցված լինեն։ Եվ թող G, H-ը լինեն համապատասխանաբար |
||
C, E-ի հավասար բազմապատիկներ և K, L-ը համապատասխանաբար D և F-ի ուրիշ պատահական հավասար բազմապատիկներ են, այնպես որ G-ն գերազանցում K-ին, բայց H-ը չի գերազանցում Լ-ին։ Եվ այնքան անգամ ինչքան G-ն բաժանվում է C-ին այնքան անգամ էլ M-ը բաժանվում է A-ին։ Եվ այնքան անգամ ինչքան K-ն բաժանվում է D-ին այնքան անգամ էլ թող N-ը բաժանվի է B-ին։ |
C, E-ի հավասար բազմապատիկներ և K, L-ը համապատասխանաբար D և F-ի ուրիշ պատահական հավասար բազմապատիկներ են, այնպես որ G-ն գերազանցում K-ին, բայց H-ը չի գերազանցում Լ-ին։ Եվ այնքան անգամ ինչքան G-ն բաժանվում է C-ին այնքան անգամ էլ M-ը բաժանվում է A-ին։ Եվ այնքան անգամ ինչքան K-ն բաժանվում է D-ին այնքան անգամ էլ թող N-ը բաժանվի է B-ին։ |
||
Քանի որ A-ն հարաբերում է B-ին այնքան ինչքան C-ն Դ-ին և M, G հավասար բազմապատիկները վերցված են եղել համապատասխանաբար A-ից և C-ից և ուրիշ հավասար բազմապատիկները N և K-ն համապատասխանաբար B-ից և D-ից, հետևաբար եթե M-ը գերազանցում է N-ին, ապա G-ն նույնպես գերազանցում է K-ին, և եթե |
|||
M-ը հավասար է N-ին, ապա G-ն նույնպես հավասար է K-ին, և եթե M-ը փոքր է |
M-ը հավասար է N-ին, ապա G-ն նույնպես հավասար է K-ին, և եթե M-ը փոքր է |
||
N-ից, ապա G-ն նույնպես փոքր է K-ից [Սահմանում 5.5]: Եվ G-ն գերազանցում է |
N-ից, ապա G-ն նույնպես փոքր է K-ից [Սահմանում 5.5]: Եվ G-ն գերազանցում է |
||
| Տող 298. | Տող 295. | ||
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչ երրորդը չորրորդին և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից։ |
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչ երրորդը չորրորդին և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից։ |
||
[[Պատկեր:պնդում14.png|center|400px]] |
|||
screenshot # 14 |
|||
Թող առաջին մեծություն A-ն ունենա նույն հարաբերությունը երկրորդ B-ին ինչ երրորդ C-ն ունի չորրորդ D-ին և A-ն մեծ է C-ից։ Ես ասում եմ որ B-ն նույնպես մեծ է D-ից։ |
Թող առաջին մեծություն A-ն ունենա նույն հարաբերությունը երկրորդ B-ին ինչ երրորդ C-ն ունի չորրորդ D-ին և A-ն մեծ է C-ից։ Ես ասում եմ որ B-ն նույնպես մեծ է D-ից։ |
||
Քանի որ A-ն մեծ է C-ից և B-ն ուրիշ պատահական մեծություն է, A-ն հետևաբար ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին [Պնդում 5.8]։ Եվ ինչպես A-ն հարաբերում է B-ին, այնպես էլ C-ն հարաբերում է D-ին։ Հետևաբար, C-ն ունի ավելի մեծ հարաբերություն D-ին քան C-ն B-ին։ Եվ այն մեծությունը, որին նույն մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է [Պնդում 5.10]։ Հետևաբար D-ն փոքր է B-ից։ Հետևաբար, B-ն մեծ է D-ից։ |
Քանի որ A-ն մեծ է C-ից և B-ն ուրիշ պատահական մեծություն է, A-ն հետևաբար ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին [Պնդում 5.8]։ Եվ ինչպես A-ն հարաբերում է B-ին, այնպես էլ C-ն հարաբերում է D-ին։ Հետևաբար, C-ն ունի ավելի մեծ հարաբերություն D-ին քան C-ն B-ին։ Եվ այն մեծությունը, որին նույն մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է [Պնդում 5.10]։ Հետևաբար D-ն փոքր է B-ից։ Հետևաբար, B-ն մեծ է D-ից։ |
||
| Տող 308. | Տող 306. | ||
Մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ։ |
Մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ։ |
||
[[Պատկեր:պնդում15.png|center|400px]] |
|||
screenshot #15 |
|||
Թող AB-ն և DE-ն լինեն C-ի և F-ի համապատասխանաբար հավասար բազմապատիկներ։ Ես ասում եմ որ C-ն հարաբերում է F-ին ինչպես AB-ն DE—ին։ |
Թող AB-ն և DE-ն լինեն C-ի և F-ի համապատասխանաբար հավասար բազմապատիկներ։ Ես ասում եմ որ C-ն հարաբերում է F-ին ինչպես AB-ն DE—ին։ |
||
| Տող 319. | Տող 317. | ||
Թող հավասար բազմապատիկներ E-ն ու F-ը վերցված լինեն համապատասխաբար A-ից և B-ից, և ուրիշ պատահական G, H հավասար բազմապատիկներ համապատասխանաբար C-ից և D-ից։ |
Թող հավասար բազմապատիկներ E-ն ու F-ը վերցված լինեն համապատասխաբար A-ից և B-ից, և ուրիշ պատահական G, H հավասար բազմապատիկներ համապատասխանաբար C-ից և D-ից։ |
||
[[Պատկեր:պնդում16.png|center|400px]] |
|||
screenshot #16 |
|||
Եվ քանի որ E-ն ու F-ը համապատասխաբար A-ի և B-ի հավասար բազմապատիկներ են, և մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ [Պնդում 5.15]։ Հետևաբար A-ն հարաբերում է B-ին ինչպես E-ն F-ին, բայց A-ն հարաբերում է B-ին ինչպես C-ն D-ին և հետևաբար C-ն հարաբերում է D-ին ինչպես E-ն F-ին [Պնդում 5.11]։ Կրկին Եվ քանի որ G-ն ու H-ը համապատասխաբար C-ի և D-ի հավասար բազմապատիկներ են, հետևաբար C-ն հարաբերում է D-ին ինչպես G-ն H-ին [Պնդում 5.15], բայց C-ն հարաբերում է D-ին ինչպես E-ն F-ին և հետևաբար E-ն հարաբերում է F-ին ինչպես G-ն H-ին [Պնդում 5.11]։ Եվ Եթե չորս մեծություններ համաչափ են և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից |
Եվ քանի որ E-ն ու F-ը համապատասխաբար A-ի և B-ի հավասար բազմապատիկներ են, և մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ [Պնդում 5.15]։ Հետևաբար A-ն հարաբերում է B-ին ինչպես E-ն F-ին, բայց A-ն հարաբերում է B-ին ինչպես C-ն D-ին և հետևաբար C-ն հարաբերում է D-ին ինչպես E-ն F-ին [Պնդում 5.11]։ Կրկին Եվ քանի որ G-ն ու H-ը համապատասխաբար C-ի և D-ի հավասար բազմապատիկներ են, հետևաբար C-ն հարաբերում է D-ին ինչպես G-ն H-ին [Պնդում 5.15], բայց C-ն հարաբերում է D-ին ինչպես E-ն F-ին և հետևաբար E-ն հարաբերում է F-ին ինչպես G-ն H-ին [Պնդում 5.11]։ Եվ Եթե չորս մեծություններ համաչափ են և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից |
||
| Տող 330. | Տող 328. | ||
Եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված։ |
Եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված։ |
||
[[Պատկեր:պնդում17.png|center|400px]] |
|||
screenshot #17 |
|||
Թող AB-ն BE-ն CD-ն և DF-ը լինեն համադրված մեծություններ, որոնք համաչափ են, այնպես որ AB-ն հարաբերում է BE-ին, այնպես ինչպես CD-ին DF-ին։ Ես ասում եմ որ նրանք նույնպես համաչափ կլինեն բաժանված, այնպես որ AE-ն կհարաբերի EB-ին ինչպես CF-ը DF-ին։ |
Թող AB-ն BE-ն CD-ն և DF-ը լինեն համադրված մեծություններ, որոնք համաչափ են, այնպես որ AB-ն հարաբերում է BE-ին, այնպես ինչպես CD-ին DF-ին։ Ես ասում եմ որ նրանք նույնպես համաչափ կլինեն բաժանված, այնպես որ AE-ն կհարաբերի EB-ին ինչպես CF-ը DF-ին։ |
||
| Տող 341. | Տող 339. | ||
MP-ին, և եթե GK-ն հավասար է HO-ին, ապա LN-ը նույնպես հավասար է MP-ին, և եթե GK-ն փոքր է HO-ից, ապա LN-ը նույնպես փոքր է MP-ից [Սահմանում 5.5]։ Թող GK-ն գերազանցի HO-ին հետևաբար հանելով HK-ն երկուսից էլ GH-ն կգերազանցի |
MP-ին, և եթե GK-ն հավասար է HO-ին, ապա LN-ը նույնպես հավասար է MP-ին, և եթե GK-ն փոքր է HO-ից, ապա LN-ը նույնպես փոքր է MP-ից [Սահմանում 5.5]։ Թող GK-ն գերազանցի HO-ին հետևաբար հանելով HK-ն երկուսից էլ GH-ն կգերազանցի |
||
KO-ին։ Բայց մենք տեսել ենք որ եթե GK-ն գերազանցում է HO-ին , ապա LN-ը նույնպես գերազանցում է MP-ին։ Հետևաբար LN-ը նույնպես գերազանցում է MP-ին և MN-ը երկուսից էլ հանենք LM-ը նույնպես կգերազանցի NP-ին։ ՀԵտևաբար եթե GH-ը գերազանցում է KO-ին, ապա LM-ը նույնպես կգերազանցի NP-ին։ Հանգունորեն մենք կարեղ ենք ցույց տալ որ եթե GH-ը հավասար է KO-ին ապա LM-ը նույնպես հավասար է NP-ին և եթե GH-ը փոքր է KO-ից, ապա LM-ը նույնպես փոքր է NP-ից։ Եվ GH-ն ու LM-ը AE-ի և CF-ի հավասար բազմապատիկներ են և KO-ն ու NP—ն ուրիշ պատահական EB-ի և FD-ի հավասար բազմապատիկներ են։ ՀԵտևաբար, AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին [Սահմանում 5.5]։ |
KO-ին։ Բայց մենք տեսել ենք որ եթե GK-ն գերազանցում է HO-ին , ապա LN-ը նույնպես գերազանցում է MP-ին։ Հետևաբար LN-ը նույնպես գերազանցում է MP-ին և MN-ը երկուսից էլ հանենք LM-ը նույնպես կգերազանցի NP-ին։ ՀԵտևաբար եթե GH-ը գերազանցում է KO-ին, ապա LM-ը նույնպես կգերազանցի NP-ին։ Հանգունորեն մենք կարեղ ենք ցույց տալ որ եթե GH-ը հավասար է KO-ին ապա LM-ը նույնպես հավասար է NP-ին և եթե GH-ը փոքր է KO-ից, ապա LM-ը նույնպես փոքր է NP-ից։ Եվ GH-ն ու LM-ը AE-ի և CF-ի հավասար բազմապատիկներ են և KO-ն ու NP—ն ուրիշ պատահական EB-ի և FD-ի հավասար բազմապատիկներ են։ ՀԵտևաբար, AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին [Սահմանում 5.5]։ |
||
Այսպիսով Եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված։ Ինչը պետք էր ցույց տալ: |
Այսպիսով Եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված։ Ինչը պետք էր ցույց տալ: |
||
== Պնդում 18 == |
== Պնդում 18 == |
||
| Տող 347. | Տող 345. | ||
Եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված։ |
Եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված։ |
||
[[Պատկեր:պնդում18.png|center|400px]] |
|||
screenshot #18 |
|||
Թող AE-ն, EB-ն, CF-ը և FD-ն լինեն բաժանված մեծություններ որոնք համաչափ են, այնպես որ AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին։ Ես ասում եմ որ նրանք նույնպես համաչափ կլինեն համադրված, այսինքն AB-ն կհարաբերի BE-ին ինչպես |
Թող AE-ն, EB-ն, CF-ը և FD-ն լինեն բաժանված մեծություններ որոնք համաչափ են, այնպես որ AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին։ Ես ասում եմ որ նրանք նույնպես համաչափ կլինեն համադրված, այսինքն AB-ն կհարաբերի BE-ին ինչպես |
||
| Տող 356. | Տող 354. | ||
Հետևաբար, երկրորդ մեծություն GD-ն նույնպես մեծ է չորրորդ FD-ից |
Հետևաբար, երկրորդ մեծություն GD-ն նույնպես մեծ է չորրորդ FD-ից |
||
[Պնդում 5.14]։ Բայց նա նույնպես փոքր է, ինչը անհնար է։ Հետևաբար սա այն դեպքը չէ, երբ AB-ն հարաբերում է BE-ին ինչպես CD-ն FD-ից փոքրին։ Հանգունորեն մենք կարող ենք ցույց տալ նաև որ սա FD-ից մեծ դեպքը չէ։ Հետևաբար, սա հավասար FD-ին դեպքն է։ |
[Պնդում 5.14]։ Բայց նա նույնպես փոքր է, ինչը անհնար է։ Հետևաբար սա այն դեպքը չէ, երբ AB-ն հարաբերում է BE-ին ինչպես CD-ն FD-ից փոքրին։ Հանգունորեն մենք կարող ենք ցույց տալ նաև որ սա FD-ից մեծ դեպքը չէ։ Հետևաբար, սա հավասար FD-ին դեպքն է։ |
||
Հետևաբար, եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված։ Ինչը պետք էր ցույց տալ: |
|||
== Պնդում 19 == |
== Պնդում 19 == |
||
| Տող 362. | Տող 360. | ||
Եթե ամբողջ մասը հարաբերում է ամբողջ մասին ինչպես վերցված մասը վերցված մասին, ապա մնացորդը կհարաբերի մնացորդին ինչպես ամբողջ մասը ամբողջին։ |
Եթե ամբողջ մասը հարաբերում է ամբողջ մասին ինչպես վերցված մասը վերցված մասին, ապա մնացորդը կհարաբերի մնացորդին ինչպես ամբողջ մասը ամբողջին։ |
||
[[Պատկեր:պնդում19.png|center|400px]] |
|||
screenshot #19 |
|||
Թող ամբողջ մաս AB-ն հարաբերի ամբողջ մաս CD ինչպես վերցված մաս AE-ն CF վերցված մասին։ Ես ասում եմ որ, EB մնացորդը կհարաբերի CD մնացորդին ինչպես ամբողջ մաս AB-ն CD ամբողջին։ |
Թող ամբողջ մաս AB-ն հարաբերի ամբողջ մաս CD ինչպես վերցված մաս AE-ն CF վերցված մասին։ Ես ասում եմ որ, EB մնացորդը կհարաբերի CD մնացորդին ինչպես ամբողջ մաս AB-ն CD ամբողջին։ |
||
| Տող 370. | Տող 368. | ||
Հետևաբար, EB մնացորդը հարաբերում է FD մնացորդին, ինչպես ամբողջ AB-ն կհարաբերի ամբողջ CD-ին։ |
Հետևաբար, EB մնացորդը հարաբերում է FD մնացորդին, ինչպես ամբողջ AB-ն կհարաբերի ամբողջ CD-ին։ |
||
Այսպիսով՝ եթե ամբողջ մասը հարաբերում է ամբողջ մասին ինչպես վերցված մասը վերցված մասին, ապա մնացորդը կհարաբերի մնացորդին ինչպես ամբողջ մասը ամբողջին։ Ինչը պետք էր ցույց տալ: |
Այսպիսով՝ եթե ամբողջ մասը հարաբերում է ամբողջ մասին ինչպես վերցված մասը վերցված մասին, ապա մնացորդը կհարաբերի մնացորդին ինչպես ամբողջ մասը ամբողջին։ Ինչը պետք էր ցույց տալ: |
||
Եվ քանի որ ցույց տրված եղել էր որ AB-ն հարաբերում է CD-ին ինչպես EB-ն |
|||
FD-ին, Սա նույնպես այն դեպքն է հակադարձ, որ AB-ն հարաբերում է BE-ին ինչպես CD-ն FD-ին։ Հետևաբար համադրված մեծությունները համաչափ են։ Եվ ցույց տրված եղել է որ BA-ն հարաբերում է AE-ին ինչպես DC-ն CF-ին։ Եվ վերջինս ստացվել է առաջինից։ |
FD-ին, Սա նույնպես այն դեպքն է հակադարձ, որ AB-ն հարաբերում է BE-ին ինչպես CD-ն FD-ին։ Հետևաբար համադրված մեծությունները համաչափ են։ Եվ ցույց տրված եղել է որ BA-ն հարաբերում է AE-ին ինչպես DC-ն CF-ին։ Եվ վերջինս ստացվել է առաջինից։ |
||
| Տող 381. | Տող 379. | ||
Եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ |
Եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ |
||
[[Պատկեր:պնդում20.png|center|400px]] |
|||
Screenshot #20 |
|||
Թող A, B, C-ն լինեն երեք մեծություններ և D, E, F-ը ուրիշ մեծություններ նրանց թվով հավասար և նույնպես զույգ առ զույգ վերցված հավասար հարաբերություններով, այնպես որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին, և |
Թող A, B, C-ն լինեն երեք մեծություններ և D, E, F-ը ուրիշ մեծություններ նրանց թվով հավասար և նույնպես զույգ առ զույգ վերցված հավասար հարաբերություններով, այնպես որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին, և |
||
| Տող 393. | Տող 391. | ||
Եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե նրանց հարաբերությունը խանգառված է, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ |
Եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե նրանց հարաբերությունը խանգառված է, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ |
||
[[Պատկեր:պնդում21.png|center|400px]] |
|||
screenshot #21 |
|||
ող A, B, C-ն լինեն երեք մեծություններ և D, E, F-ը ուրիշ մեծություններ նրանց թվով հավասար և նույնպես զույգ առ զույգ վերցված հավասար հարաբերություններով, և խանգառված հարաբերությամբ, այնպես որ A-ն հարաբերում է B-ին ինչպես Ե-ն Ֆ-ին, և |
ող A, B, C-ն լինեն երեք մեծություններ և D, E, F-ը ուրիշ մեծություններ նրանց թվով հավասար և նույնպես զույգ առ զույգ վերցված հավասար հարաբերություններով, և խանգառված հարաբերությամբ, այնպես որ A-ն հարաբերում է B-ին ինչպես Ե-ն Ֆ-ին, և |
||
B-ն C-ին, ինչպես Դ-ն Ե-ին։ Եվ թող A-ն մեծ լինի C-ից ըստ հավասարության։ Ես ասում եմ որ D-ն նույնպես մեծ կլինի F-ից, և եթե A-ն հավասար է C-ին, ապա D-ն նույնպես հավասար կլինի F-ին։ Եվ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի F-ից։ |
B-ն C-ին, ինչպես Դ-ն Ե-ին։ Եվ թող A-ն մեծ լինի C-ից ըստ հավասարության։ Ես ասում եմ որ D-ն նույնպես մեծ կլինի F-ից, և եթե A-ն հավասար է C-ին, ապա D-ն նույնպես հավասար կլինի F-ին։ Եվ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի F-ից։ |
||
Քանի որ A-ն մեծ է C-ից և B-ն մեկ ուրիշ մեծություն է, հետևաբար A-ն ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին [Պնդում 5.8]։ Բայց A-ն հարաբերում է B-ին, ինչպես Ե-ն Ֆ-ին։ Եվ հակադարձորեն C-ն հարաբերում է B-ին այնպես ինչպես Ե-ը Դ-ին [Պնդում 5.7-ի հետևանք]։ Հետևաբար Ե-ն նույնպես ունի ավելի մեծ հարաբերություն Ֆ-ին քան Ե-ը Դ-ին [Պնդում 5.13]։ Եվ մեծությունները ունեն հարաբերություն նույն մեծությանը, այն մեծությունը որը ունի մեծ հարաբերություն մեծն է [Պնդում 5.10]։ Հետևաբար Ֆ-ը փոքր է Դ-ից։ Հետևաբար Դ-ն մեծ է Ֆ-ից։ Հանգունորեն մենք կարոզ ենք ցույց տալ, որ եթե նույնիսկ A-ն հավասար է C-ին ապա D-ն նույնպես հավասար կլինի F-ին և նույնիսկ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի քան F-ը։ |
Քանի որ A-ն մեծ է C-ից և B-ն մեկ ուրիշ մեծություն է, հետևաբար A-ն ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին [Պնդում 5.8]։ Բայց A-ն հարաբերում է B-ին, ինչպես Ե-ն Ֆ-ին։ Եվ հակադարձորեն C-ն հարաբերում է B-ին այնպես ինչպես Ե-ը Դ-ին [Պնդում 5.7-ի հետևանք]։ Հետևաբար Ե-ն նույնպես ունի ավելի մեծ հարաբերություն Ֆ-ին քան Ե-ը Դ-ին [Պնդում 5.13]։ Եվ մեծությունները ունեն հարաբերություն նույն մեծությանը, այն մեծությունը որը ունի մեծ հարաբերություն մեծն է [Պնդում 5.10]։ Հետևաբար Ֆ-ը փոքր է Դ-ից։ Հետևաբար Դ-ն մեծ է Ֆ-ից։ Հանգունորեն մենք կարոզ ենք ցույց տալ, որ եթե նույնիսկ A-ն հավասար է C-ին ապա D-ն նույնպես հավասար կլինի F-ին և նույնիսկ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի քան F-ը։ |
||
Այսպիսով՝ եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե նրանց հարաբերությունը խանգառված է, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե հավասարման միջոցով առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ Ինչը պետք էր ցույց տալ: |
|||
== Պնդում 22 == |
== Պնդում 22 == |
||
| Տող 404. | Տող 402. | ||
Եթե կան որևէ քանակի մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։ |
Եթե կան որևէ քանակի մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։ |
||
[[Պատկեր:պնդում22.png|center|600px]] |
|||
screenshot #22 |
|||
Թող լինեն կամայական քանակի մեծություններ A, B, C և ուրիծ մեծություններ D, E, F նրանց քանակով հավասար, որոնք զույգ առ զույգ վերցված նույն հարաբերությունը ունեն այնպես որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին և |
Թող լինեն կամայական քանակի մեծություններ A, B, C և ուրիծ մեծություններ D, E, F նրանց քանակով հավասար, որոնք զույգ առ զույգ վերցված նույն հարաբերությունը ունեն այնպես որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին և |
||
| Տող 419. | Տող 417. | ||
Եթե կան երեք մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, և եթե նրանց հարաբերությունը խանգառված է, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։ |
Եթե կան երեք մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, և եթե նրանց հարաբերությունը խանգառված է, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։ |
||
[[Պատկեր:պնդում23.png|center|400px]] |
|||
screenshot #23 |
|||
Թող A, B, C մեծությունները և D, E, F ուրիշ մեծությունները նրանց քանակով հավասար, որոնք զույգ առ զույգ վերցված նույն հարաբերությունը ունեն։ Եվ թող նրանց հարաբերությունը խանգառված լինի, այնպես որ A-ն հարաբերում է B-ին ինչպես E-ն F-ին և B-ն C-ին ինչպես D-ն F-ին։ Ես ասում եմ որ A-ն կհարաբերի C-ին ինչպես D-ն F-ին։ |
Թող A, B, C մեծությունները և D, E, F ուրիշ մեծությունները նրանց քանակով հավասար, որոնք զույգ առ զույգ վերցված նույն հարաբերությունը ունեն։ Եվ թող նրանց հարաբերությունը խանգառված լինի, այնպես որ A-ն հարաբերում է B-ին ինչպես E-ն F-ին և B-ն C-ին ինչպես D-ն F-ին։ Ես ասում եմ որ A-ն կհարաբերի C-ին ինչպես D-ն F-ին։ |
||
| Տող 432. | Տող 430. | ||
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին, ինչն ունի երրորդը չորրորդին և հինգերորդը նույնպես ունի նույն հարաբերություն երկրորդին ինչպիսին վեցերորդը ունի չորրորդին, ապա առաջին և հինգերորդ մեծությունները գումարված կունենան նույն հարաբերությունը երկրորդին ինչ երրորդն ու վեցերորդը գումարված չորրորդին։ |
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին, ինչն ունի երրորդը չորրորդին և հինգերորդը նույնպես ունի նույն հարաբերություն երկրորդին ինչպիսին վեցերորդը ունի չորրորդին, ապա առաջին և հինգերորդ մեծությունները գումարված կունենան նույն հարաբերությունը երկրորդին ինչ երրորդն ու վեցերորդը գումարված չորրորդին։ |
||
[[Պատկեր:պնդում24.png|center|400px]] |
|||
screenshot #24 |
|||
Թող առաջին մեծություն ԱԲ-ն ունենա նույն հարաբերությունը երկրորդ C-ին, ինչն երրորդ DE-ն ունի չորրորդ F-ին։ Եվ թող հինգերորդ BG-ն նույնպես ունենա նույն հարաբերությունը երկրորդ C-ին ինչպիսին վեցերորդ EH-ը ունի չորրորդ |
Թող առաջին մեծություն ԱԲ-ն ունենա նույն հարաբերությունը երկրորդ C-ին, ինչն երրորդ DE-ն ունի չորրորդ F-ին։ Եվ թող հինգերորդ BG-ն նույնպես ունենա նույն հարաբերությունը երկրորդ C-ին ինչպիսին վեցերորդ EH-ը ունի չորրորդ |
||
F-ին։ Ես ասում եմ որ առաջին և հինգերորդ մեծությունները գումարված՝ AG-ն կունենա նույն հարաբերությունը երկրորդ C-ին ինչ կունենան երրորդն ու վեցերորդը գումարված՝ DH-ը չորրորդ F-ին։ |
F-ին։ Ես ասում եմ որ առաջին և հինգերորդ մեծությունները գումարված՝ AG-ն կունենա նույն հարաբերությունը երկրորդ C-ին ինչ կունենան երրորդն ու վեցերորդը գումարված՝ DH-ը չորրորդ F-ին։ |
||
Քանի որ BG-ն հարաբերում է C-ին այնպես ինչպես EH-ը F-ին հետևաբար հակադարձորեն C-ն հարաբերում է BG-ին այնպես ինչպես F-ը EH-ին |
Քանի որ BG-ն հարաբերում է C-ին այնպես ինչպես EH-ը F-ին հետևաբար հակադարձորեն C-ն հարաբերում է BG-ին այնպես ինչպես F-ը EH-ին |
||
[Պնդում 5.7-ի հետևանք]։ ՀԵտևաբար քանի որ AB-ն հարաբերում է C-ին այնպես ինչպես DE-ն F-ին և C-ն հարաբերում է BG—ին այնպես ինչպես F-ը EH-ին, հետևաբար ըստ հավասարման AB-ն հարաբերում է BG-ին, ինչպես DE-ն EH-ին |
([[#Պնդում 7|Պնդում 5.7-ի հետևանք]])։ ՀԵտևաբար քանի որ AB-ն հարաբերում է C-ին այնպես ինչպես DE-ն F-ին և C-ն հարաբերում է BG—ին այնպես ինչպես F-ը EH-ին, հետևաբար ըստ հավասարման AB-ն հարաբերում է BG-ին, ինչպես DE-ն EH-ին |
||
[Պնդում 5.22]: Եվ Եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված [Պնդում 5.18]։ Այդ իսկ պատճառով AG-ն հարաբերում է GB-ին այնպես ինչպես DH-ը HE-ին։ Եվ նաև BG-ն հարաբերում է |
[Պնդում 5.22]: Եվ Եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված [Պնդում 5.18]։ Այդ իսկ պատճառով AG-ն հարաբերում է GB-ին այնպես ինչպես DH-ը HE-ին։ Եվ նաև BG-ն հարաբերում է |
||
C-ին այնպես ինչպես EH-ը F-ին։ ՀԵտևաբար ըստ հավասարման AG-ն հարաբրերում |
C-ին այնպես ինչպես EH-ը F-ին։ ՀԵտևաբար ըստ հավասարման AG-ն հարաբրերում |
||
| Տող 448. | Տող 446. | ||
Եթե չորս մեծություններ համաչափ են, ապա նրանցից մեծագույնի և փոքրագույնի գումարը մեծ կլինի մնացած երկուսի գումարից։ |
Եթե չորս մեծություններ համաչափ են, ապա նրանցից մեծագույնի և փոքրագույնի գումարը մեծ կլինի մնացած երկուսի գումարից։ |
||
[[Պատկեր:պնդում25.png|center|400px]] |
|||
screenshot #25 |
|||
Թող AB-ն, CD-ն, E-ն F-ը լինեն չորս համաչափ մեծություններ, այնպես որ AB-ն հարաբերում է CD-ին այնպես ինչպես E-ն F-ին։ Եվ թող AB-ն լինի նրանցից մեծագույնը, իսկ F-ը փոքրագույնը։ Ես ասում եմ որ, AB-ն և F-ը մեծ են քան CD-ն և E-ն։ |
Թող AB-ն, CD-ն, E-ն F-ը լինեն չորս համաչափ մեծություններ, այնպես որ AB-ն հարաբերում է CD-ին այնպես ինչպես E-ն F-ին։ Եվ թող AB-ն լինի նրանցից մեծագույնը, իսկ F-ը փոքրագույնը։ Ես ասում եմ որ, AB-ն և F-ը մեծ են քան CD-ն և E-ն։ |
||
Ընթացիկ տարբերակը 00:51, 21 դեկտեմբերի 2024-ի դրությամբ
հեղինակ՝ էվկլիդես |
Սահմանումներ
1. Մեծությունը համարվում է մեկ այլ մեծության մաս՝ փոքրը մեծի, երբ այն չափում է մեծը։ 2. Եվ մեծը համարվում է փոքրի բազմապատիկ, երբ այն չափվում է փոքրով։ 3. Հարաբերությունը որոշակի պայման է, որը վերաբերում է երկու նույն տեսակի մեծությունների մեծության։ 4. (Այն) մեծություններն ունեն հարաբերություն միմյանց նկատմամբ, որոնք, բազմապատկվելով, կարող են գերազանցել մեկը մյուսին։ 5. Մեծությունները համարվում են նույն հարաբերության մեջ՝ առաջինը երկրորդի հետ, և երրորդը՝ չորրորդի, երբ առաջինի և երրորդի հավասար բազմապատիկները կամ երկուսն էլ գերազանցում են, կամ հավասար են, կամ փոքր են երկրորդի և չորրորդի հավասար բազմապատիկներից՝ վերցված համապատասխան կարգով և ցանկացած բազմապատկման եղանակով։ 6. Եվ թող այն մեծությունները, որոնք ունեն նույն հարաբերությունը, կոչվեն համաչափ։ 7. Եվ երբ հավասար բազմապատիկների դեպքում (ինչպես Սահման․ 5-ում), առաջինի բազմապատիկը գերազանցում է երկրորդի բազմապատիկին, իսկ երրորդի բազմապատիկը չի գերազանցում չորրորդի բազմապատիկին, ապա առաջինն ունի մեծ հարաբերություն երկրորդի նկատմամբ, քան երրորդը՝ չորրորդի։ 8. Եվ երեք անդամներում հարաբերությունը նվազագույնն է։ 9. Եվ երբ երեք մեծությունները համաչափ են, առաջինը հարաբերում է երրորդին այն հարաբերության քառակուսով, որն (այն ունի) երկրորդի նկատմամբ։ 10. Եվ երբ չորս մեծություններ (հաջորդաբար) համաչափ են, առաջինը հարաբերում է չորրորդին այն հարաբերության խորանարդով, որն (այն ունի) երկրորդի նկատմամբ և այսպես շարունակ։ 11. Այս մեծությունները համարվում են համապատասխան՝ առաջնայինը՝ առաջնայինին, իսկ հետևողը՝ հետևողին։ 12. Փոխադարձ հարաբերությունը (առաջնայինի հարաբերության) ընդունումն է դեպի առաջնային (երկու հավասար հարաբերություններից) և (այն հավասարեցնելը) հետևողի (հարաբերությանը) դեպի հետևող։ 13. Հակադարձ հարաբերությունը (հետևողի հարաբերության) ընդունումն է որպես առաջնային, իսկ առաջնայինի՝ որպես հետևող։ 14. Հարաբերության համադրումը (առաջնայինի և հետևողի հարաբերության) ընդունումն է՝ առաջնայինին գումարած հետևողը՝ որպես մեկը, դեպի միայն հետևողը։
Սահմանումներ
- Մեծությունը ուրիշ մեծության մաս է (փոքրը մեծի), երբ նա չափում է մեծը։
- Եվ մեծ մեծությունը բազմապատիկ է փոքրին, երբ նա չափվում է փոքրով։
- Հարաբերությունը պայմանի որոշակի տեսակ է երկու նույն մեծությունների չափերի նկատմամբ:
- Այդ մեծություններն ունեն հարաբերություն միմյանց նկատմամբ, որոնք, բազմապատկելով կարող են գերազանցել մեկը մյուսին:
- Մեծությունների հարաբերությունները հավասար են, համապատասխանաբար առաջինը երկրորդին, երրորդը՝ չորրորդին, երբ հավասար առաջինի և երրորդի բազմապատիկներից երկուսն էլ գերազանցում են, երկուսն էլ հավասար են, կամ երկուսն էլ փոքր են, համապատասխանաբար երկրորդի և չորրորդի հավասար բազմապատիկներից՝ վերցված համապատասխան հերթականությամբ՝ ցանկացած տեսակի բազմապատկման համաձայն։
- Նույն հարաբերություն ունեցող մեծությունները կոչվում են պրոպորցիոնալ:
- Երբ հավասար բազմապատիկների համար (ինչպես սահմանում 5-ում),առաջին բազմապատիկի մեծությունը գերազանցում է երկրորդի բազմապատիկինը, իսկ երրորդ բազմապատիկի մեծությունը չի գերազանցում չորրորդ բազմապատիկինը, ապա առաջին մեծությունը երկրորդի նկատմամբ ավելի մեծ հարաբերություն ունի, քան երրորդը մեծությունը չորրորդի նկատմամբ:
- Եվ երեք անդամով հարաբերությունը ամենափոքրն է (հնարավոր):
- Եվ երբ երեք մեծություն պրոպորցիոնալ են, առաջինը երրորդին ունի նույն հարաբերությունը ինչ առաջինը երկրորդին բարձրացրած քառակուսի
- Եվ երբ չորս մեծություն (շարունակաբար) պրոպորցիոնալ են, առաջինը չորրորդին ունի նույն հարաբերությունը ինչ առաջինը երկրորդին բարձրացրած խորանարդ։ Եվ այսպես շարունակ, նմանապես, հաջորդական հերթականությամբ, ինչպիսին էլ որ կարող է լինել (շարունակական) հարաբերությունը:
- երկու հարաբերությունների առաջին անդամները, և հաջորդող անդամները կոչվում են համապատասխան մեծություններ։
- Այլընտրանքային հարաբերությունը ստացվում է երկու հարաբերությունների առաջինների հարաբերությունը հավասարեցնելով երկու հարաբերությունների հաջորդողների հարաբերությանը։
- Հակադարձ հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես հաջորդող և հաջորդողը առաջին:
- Բաղադրյալ հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես հաջորդողի և առաջինի գումար, իսկ հաջորդողը մնում է նույնը։
- Բաժանման հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես առաջինի և հաջորդողի տարբերություն, իսկ հաջորդողը մնում է նույնը։
- Փոխարկման հարաբերություն է ստացվում վերցնելով հարաբերության առաջին, որպես առաջին իսկ հաջորդող, որպես առաջինի և հաջորդողի տարբերություն։
- Կան մի քանի մեծություններ և դրանց հավասար թվով այլ մեծություններ, որոնք ունեն նույն հարաբերությունը զույգ առ զույգ վերցված, հարաբերությունը հավասարության միջոցով տեղի է ունենում, երբ առաջինը մինչև վերջինն է առաջինում մեծությունների բազմությունում, ուստի առաջինը (է) մինչև վերջինը երկրորդ արտաքին (մեծությունների) (հարաբերակցությունը) հեռացնելով ներքինը (մեծությունները).
Պնդում 1
Եթե որևէ քանակի մեծություններ համապատասխանաբար բազմապատիկ են հավասար թվով ուրիշ մեծությունների, ապա քանի անգամ մեծություններից մեկը մեծ է իրեն համապատասխան մեծությունից, այնքան անգամ մնացած բոլոր մեծությունները մեծ են իրենց համապատասխան մեծություններից։
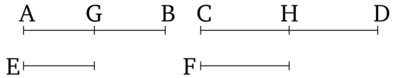
Թող լինի ցանկացած քանակի քանակության, AB, CD մեծություններ որոնք հավասար բազմապատիկ են, համապատասխանաբար, որոշ այլ հավասար թվով մեծությունների՛ E, F։ քանի անգամ AB-ն բաժանվում է E-ի, այնքան անգամ AB-ն, CD-ն նույնպես կբաժանվի E, F-ի: Քանի որ AB-ն, CD-ն հավասար է E, F-ի բազմապատիկին, ապա AB-ում այնքան մեծություններ հավասար են E-ին, ինչքան CD-ում հավասար են F-ի: Թող AB-ն բաժանվի AG, GB, հավասար E-ի և CD-ն CH, HD, հավասար F: Այսպիսով, AG, GB-ի թիվը հավասար կլինի CH, HD-ի թվին:Եվ քանի որ AG-ը հավասար է E-ի, իսկ CH-ն F-ն է, ապա AG (հավասար), հետևաբար, հավասար է E-ի, իսկ AG, CH - E, F: Այսպիսով, նույն (պատճառներով) GB-ն հավասար է E-ի, և GB, HD - E, F.
Այսպիսով, որքան շատ արժեքներ AB-ում հավասար են E-ին, այնքան շատ կան AB, CD-ն հավասար է E-ի, F-ին: Այսպիսով, քանի անգամ AB-ն (բաժանում է) E-ի վրա, այդքան անգամ AB-ն, CD-ն նույնպես ( բաժանել) E-ով, F:
Այսպիսով, եթե կա որևէ քանակի մեծություն (որոնք) հավասար են, համապատասխանաբար, որոշ (այլ) թվով (նրանց) հավասար քանակություններ, ապա այդքան շատ քանի անգամ (առաջին) մեծություններից մեկը կբաժանվի մեկին (երկրորդին), այդքան անգամ բոլորը (առաջին մեծությունները) նույնպես կբաժանվեն մեկով (երկրորդից):
առաջին մեծությունները) նաև (բաժանել) բոլորի (երկրորդ): (ինչը պետք էր ցույց տալ):
Պնդում 2
Եթե առաջին մեծությունը և երրորդը հավասար են երկրորդ և չորրորդ մեծությունների համապատասխան բազմապատիկներին, իսկ հինգերորդը մեծությունը և վեցերորդը նույնպես հավասար են երկրորդի և չորրորդի համապատասխան բազմապատիկներին, ապա առաջին մեծությունը և հինգերորդը՝ գումարվելով միասին, իսկ երրորդն ու վեցերորդը ՝ գումարվելով միասին, նույնպես կլինեն երկրորդ և չորրորդ մեծությունների համապատասխան բազմապատիկները:
Թող առաջին մեծություն AB-ն և երրորդը DE-ն հավասար լինեն երկրորդ C-ի և չորրորդ F-ի համապատասխան բազմապատիկներին: Եվ թող հինգերորդ մեծությունը BG-ն և վեցերորդ EH-ը նույնպես աբար հավասար լինեն երկրորդ C-ի և չորրորդ F-ի համապատասխան բազմապատիկներին: Ապա առաջին մեծությունը և հինգերորդը, գումարվելով միասին, կտա AG, իսկ երրորդը մեծությունը և վեցերորդը, գումարվելով միասին, կտա DH, որոնք նույնպես կլինեն համապատասխանաբար C-ի և F-ի հավասար բազմապատիկներ:
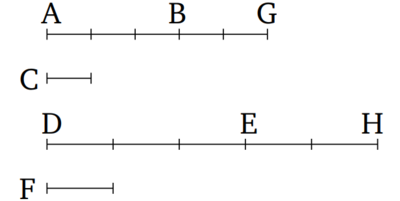
Քանի որ AB-ն և DE-ն են C-ի և F-ի հավասար բազմապատիկներ են, ապա այնքան մեծություն որքան AB-ում հավասար են C-ին, այնքան էլ մեծություն DE-ում հավասար են F-ին: Եվ նույն պատճառներով, նույնքան մեծություններ BG-ում հավասար են C-ի, այնքան էլ EH-ում հավասար են F-ին:
Այսպիսով, որքան արժեքներ կան ամբողջ AG-ում, որոնք հավասար են C-ին, այնքան էլ կա ամբողջ DH-ում, որը հավասար է F-ին: Այսպիսով, որքան անգամ AG-ն բաժանվի C-ի, այնքան էլ DH-ն նույնպես կբաժանվի F-ի։ Այսպիսով, առաջինը (մեծությունը) և հինգերորդը, գումարվելով միասին կտան AG, իսկ երրորդը (մեծությունը) և վեցերորդը գումարվելով միասին (DH ստանալու համար), կլինեն երկրորդ C-ի և չորրորդ F-ի համապատասխան հավասար բազմապատիկեր:
Այսպիսով, եթե առաջինը (մեծությունը) և երրորդը հավասար են երկրորդի և չորրորդի (համապատասխանաբար) բազմապատիկներին, իսկ հինգերորդը (մեծությունը) և վեցերորդը նույնպես հավասար են երկրորդի և չորրորդի (համապատասխանաբար) բազմապատիկներին, ապա առաջինը և հինգերորդը մեծությունները, գումարվելով միասին, իսկ երրորդն ու վեցերորդը, գումարվելով միասին, նույնպես կլինեն երկրորդի և չորրորդի (համապատասխանաբար) բազմապատիկները:
(ինչը որ պետք էր ցույց տալ):
Պնդում 3
Եթե առաջինը (մեծությունը) և երրորդը հավասար են երկրորդի և չորրորդի համապատասխան բազմապատիկներին, և հավասար բազմապատիկ վերցված են առաջինից և երրորդից, ապա հավասարության միջոցով վերցված (մեծությունները) նույնպես կլինեն երկրորդի (մեծությունը) և չորրորդի համապատասխան հավասար բազմապատիկ։ Թող առաջին (մեծություն) A-ն և երրորդ C-ն լինեն հավասար բազմապատիկներ երկրորդ B-ի և չորրորդ D-ի (համապատասխանաբար), իսկ EF-ը և GH-ը համապատասխանաբար A-ի և C-ի հավասար բազմապատիկները: Ապա EF-ը և GH-ը B-ի և D-ի հավասար բազմապատիկ են (համապատասխանաբար):
Քանի որ EF-ը և GH-ը հավասար են A-ի և C-ի բազմապատիկներին (համապատասխանաբար), ապա այնքան (արժեքներ) EF-ում հավասար են A-ին, նույնքան GH-ում հավասար են C-ի:
Թող EF-ը բաժանվի EK, KF արժեքների հավասար A-ին, իսկ GH-ն՝ GL-ի, LH-ն հավասար C-իn: Այսպիսով EK, KF արժեքների թիվը հավասար կլինի GL, LH մեծությունների թվին:
Եվ քանի որ A-ն և C-ն հավասար են B-ի և D-ի բազմապատիկներին (համապատասխանաբար), իսկ EK-ն հավասար է A-ի, իսկ GL-ը հավասար է C-ին, ուրեմն EK-ն և GL-ն, հավասար են B-ի և D-ի (համապատասխանաբար) բազմապատիկներին:
Այսպիսով, նույն պատճառներով KF-ն և LH-ն հավասար են B-ի և D-ի բազմապատիկներին (համապատասխանաբար): Հետևաբար, առաջին մեծություն EK-ն և երրորդ GL-ը հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար), իսկ հինգերորդ մեծությունը KF-ը և վեցերորդ LH-ը նույնպես հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար), ապա առաջին մեծությունն ու հինգերորդը, գումարվելով միասին (այնպես, որ տալիս են EF), և երրորդն ու վեցերորդը գումարվելով միասին (GH ստանալու համար), հավասար են երկրորդ B-ի և չորրորդ D-ի բազմապատիկներին (համապատասխանաբար):
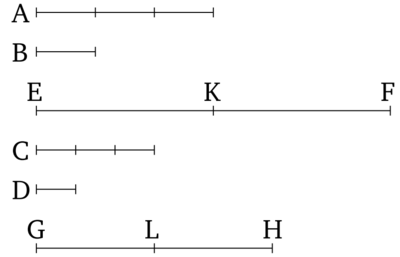
Այսպիսով, եթե առաջինը (մեծությունը) և երրորդը հավասար են երկրորդի և չորրորդի համապատասխան բազմապատիկներին, և վերցված են առաջինի և երրորդի հավասար բազմապատիկները, ապա (հավասարության միջոցով) վերցված արժեքները նույնպես հավասար կլինեն երկրորդի և չորրորդը, համապատասխան բազմապատիկներին: Ինչը պետք էր ցույց տալ:
Պնդում 4
Եթե առաջինը (մեծությունը) ունի նույն հարաբերությունը երկրորդի հետ, ինչ երրորդը (ունի) չորրորդի, ապա առաջին (մեծության) և երրորդի հավասար բազմապատիկները նույնպես կունենան նույն հարաբերությունը երկրորդի և չորրորդի հավասար բազմապատիկներին՝ վերցված համապատասխան հերթականությամբ՝ ըստ ցանկացած բազմապատկման ձևի։
թող առաջին մեծությունը` A-ն ունենա նույն հարաբերությունը երկրորդ B-ի հետ, ինչ երրորդ C-ն ունի չորրորդ D-ի հետ: Եվ թող E-ն և F-ը լինեն A-ի և C-ի համապատասխանաբար հավասար բազմապատիկները, իսկ B-ից և D-ից համապատասխանաբար այլ պատահական հավասար բազմապատիկներ՝ G-ն և H-ը: Ապա E-ն հարաբերում է G-ին ինչպես F-ը D-ին։
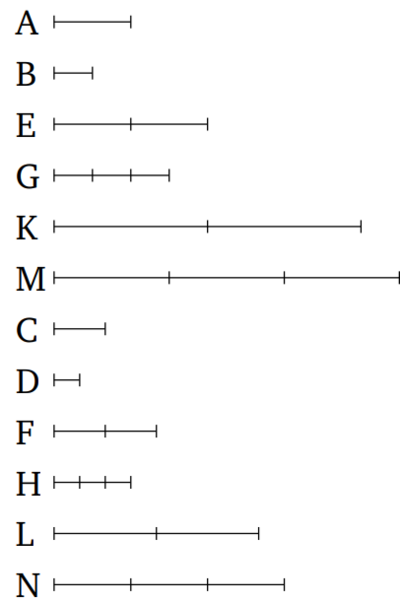
Թող հավասար բազմապատիկներ K-ն ու L-ը վերցված լինեն համապատասխանաբար E-ից և F-ից և ուրիշ պատահական հավասար բազմապատիկներ M-ն ու N-ը համապատասախանաբար G-ից ու H-ից։ Եվ քանի որ E-ն ու F-ը համապատասխաբար A-ի ու C-ի հավասար բազմապատիկներ են, և հավասար բազմապատիկներ K-ն ու L-ը վերցված են եղել համապատասխանաբար E-ից ու F-ից, K-ն ու L-ը հետևաբար A-ի և C-ի հավասար բազմապատիկներ են [Պնդում 5.3]: Այսպիսով, նույն պատճառներով M-ն ու N-ը համապատասխանաբար B-ի և D-ի հավասար բազմապատիկներ են։ Եվ քանի որ A-ն հարաբերում է B-ին այնպես ինչպես C-ն D-ին և հավասար բազմապատիկներ K-ն ու L-ը վերցված են եղել համապատասխանաբար A-ից ու C-ից, և ուրիշ պատահական հավասար բազմապատիկներ M N-ը համապատասխանաբար B-ից և D-ից, ապա եթե K-ն գերազանցում է M-ին ապա L-ը նույնպես գերազանցում է N-ին, և եթե K-ն հավասար է M-ին, ապա L-ը նույնպես հավասար է N-ին, և եթե K-ն փոքր է M-ից, ապա L-ը նույնպես փոքր է N-ից [Սահմանում 5.5]: Եվ K-ն ու L-ը համապատասխանաբար E-ի և F-ի հավասար բազմապատիկներ են և M-ն ու N-ը ուրիշ պատահական G-ի և H-ի հավասար բազմապատիկներ։ ՀԵտևաբար E-ն հարաբերում է G-ին ինչպես F-ը H-ին [Սահմանում 5.5]։ Այսպիսով՝ Եթե առաջինը (մեծությունը) ունի նույն հարաբերությունը երկրորդի հետ, ինչ երրորդը (ունի) չորրորդի, ապա առաջին (մեծության) և երրորդի հավասար բազմապատիկները նույնպես կունենան նույն հարաբերությունը երկրորդի և չորրորդի հավասար բազմապատիկներին՝ վերցված համապատասխան հերթականությամբ՝ ըստ ցանկացած բազմապատկման ձևի։
Պնդում 5
Եթե մեծությունը նույն մեծության բազմապատիկն է, ինչ վերցված մասը (է) վերցված մասի, ապա մնացորդը նույնպես կլինի մնացորդի նույն բազմապատիկը, ինչ ամբողջը ամբողջից (համապատասխանաբար):
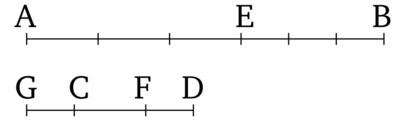
Թող AB մեծությունը լինի CD մեծության նույն բազմապատիկը, ինչ վերցված AE մասը վերցված CF մասից է: Ես ասում եմ, որ մնացորդ EB-ն նույնպես կլինի մնացորդի FD-ի նույն բազմապատիկը, ինչ որ ամբողջ AB-ն ամբողջ CD-ի է: Քանի անգամ AE-ն բաժանվում է CF-ին, այնքան անգամ էլ թող EB-ն բաժանվի CG-ին։ Եվ քանի որ AE EB համապատասխանաբար CF GF հավասար բազմապատիկներ են, հետևաբար AE AB համապատասխանաբար CF CD հավասար բազմապատիկներ են (Պնդում 1)։ Եվ AE-ն ու AB-ն ենթադրվում է որ լինեն CF-ի և CD-ի համապատասխանաբար հավասար բազմապատիկներ: Հետևաբար AB-ն GF-ի և CD-ի հավասար բազմապատիկ է. Հետևաբար GF-ը հավասար է CD. Թող երկուսից էլ հանենք CF-ը: Հետևաբար GC մնացորդը հավասար է FD մնացորդին: Եվ քանի որ AE-ն ու EB-ն CF-ի և GC-ի համապատասխանաբար հավասար բազմապատիկներ են և GC-ն հավասար է DF-ին, ապա AE-ն և EB-ն համապատասխանաբար CF-ի ու FD-ի համապատասխանաբար հավասար բազմապատիկներ են։ Եվ AE-ն ու AB-ն ենթադրվում է որ լինեն CF-ի և CD-ի համապատասխանաբար հավասար բազմապատիկներ: Հետևաբար, EB-ն ու AB-ն FD-ի և CD-ի համապատասխանաբար հավասար բազմապատիկներ են: Հետևաբար, EB մնացորդը նույնպես կլինի FD մնացորդի հավասար բազմապատիկ ինչ համապատասխանաբար ողջ AB-ն CD-ին: Հետևաբար, մեծությունը նույն մեծության բազմապատիկն է, ինչ վերցված մասը վերցված մասի, և մնացորդը նույնպես մնացորդի նույն բազմապատիկն է, ինչ ամբողջը ամբողջի (համապատասխանաբար): Ինչը պետք էր ցույց տալ:
Պնդում 6
Եթե երկու մեծություններ երկու այլ մեծությունների հավասար բազմապատիկներ են, իսկ առաջին և վերջին մեծություններից որոշ վերցված մասեր համապատասխանաբար հավասար բազմապատիկներ են, ապա մնացորդները նույնպես կամ հավասար են վերջին մեծություններին, կամ համապատասխանաբար դրանց հավասար բազմապատիկ են։ Թող AB և CD մեծությունները լինեն E-ի, և F-ի համապատասխանաբար հավասար բազմապատիկներ: Եվ թող առաջինից վերցված մասերը՝ AG-ն և CH-ը լինեն համապատասխաբար E-ի և F-ի հավասար բազմապատիկներ: Ես ասում եմ որ GB և HD մնացորդները կամ նույնպես հավար են E-ի և F-ի կամ նրանց հավասար բազմապատիկներ են:
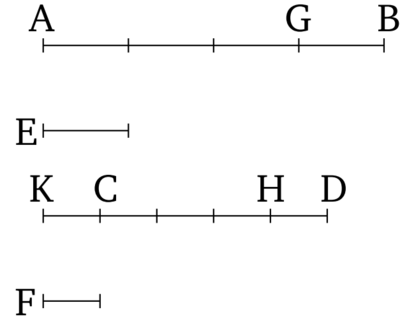
Թող GB-ն լինի հավասար E-ին: Ես ասում եմ որ HD-ն նույնպես հավասար է F-ին: Թող CK-ն լինի հավասար F-ին: Քանի որ AG-ն և CH-ը համապատասխանաբար E-ի և F-ի հավասար բազմապատիկներ են, և GB-ն հավասար է E-ին և KC-ն F-ին։ AB-ն և KH-ը հետևաբար E-ի և F-ի հավասար բազմապատիկներ են (2)։ Եվ AB-ն ու CD-ն ենթադրվում է որ լինեն E-ի և F-ի համապատասխանաբար հավասար բազմապատիկներ: Հետևաբար KH-ը և CD-ն համապաստասխանաբար F-ի և F-ի հավասար բազմապատիկներ են: Հետևաբար KH-ը և CD-ն յուրաքանչյուրը F-ի հավասար բազմապատիկներ են: ՀԵտրևաբար KH-ը հավասար է CD-ին: Թող CH-ը հանենք երկուսից էլ: Հետևաբար KC մնացորդը հավասար է HD մնացորդին: Բայց F-ը հավասար է KC-ին։ Հետևաբար HD-ն նույնպես հավասար է F-ին։ Հետաևբար եթե GB-ն հավասար է E-ին, ապա HD-ն նույնպես հավասար կլինի F-ին։ Հանգունորեն մենք կարող ենք ցույց տալ, որ եթե GB-ն E-ի բազմապատիկ է, ապա HD-ն նույնպես F-ի նույն բազմապատիկը կլինի: Հետևաբար, Եթե երկու մեծություններ երկու այլ մեծությունների հավասար բազմապատիկներ են, իսկ առաջին և վերջին մեծություններից որոշ վերցված մասերի համապատասխանաբար հավասար բազմապատիկներ են, ապա մնացորդները նույնպես կամ հավասար են վերջին մեծություններին, կամ համապատասխանաբար դրանց հավասար բազմապատիկ են։ Ինչը պետք էր ցույց տալ:
Պնդում 7
Հավասար մեծությունները ունեն նույն հարաբերությունը նույն մեծությանը, և վերջինս ունի նույն հարաբերությունը հավասար մեծություններին։ Թող A և B-ն լինեն հավասար մեծություններ, և C-ն պատահական մեծություն։ Ես ասում եմ որ A և B-ն ունեն նույն հարաբերությունը C-ին և C-ն ունի նույն հարաբերությունը A և B-ին։
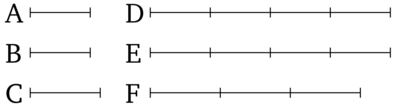
Թող D և E հավասար բազմապատիկները համապատասխանաբար վերցված լինեն A-ից և B-ից, և ինչ-որ ուրիշ պատահական F-ը C-ից։ Հետևաբար, քանի որ D և E-ն A-ի և B-ի հավասար բազմապատիկներ են և A-ն հավասար է B-ին, հետևաբար D-ն հավասար է E-ին։ Եվ F-ը ուրիշ պատահական է։ Հետևաբար, եթե D-ն գերազանցում է F-ին, ապա E-ն նույնպես գերազանցում է F-ին, և եթե D-ն հավասար է F-ին, ապա E-ն հավասար է F-ին, և եթե եթե D-ն չի գերազանցում է F-ին, ապա E-ն նույնպես չի գերազանցում է F-ին։ Եվ D-ն ու E-ն համապատասխանաբար A ու B-ի հավասար բազմապատիկներ են և F-ը ուրիշ պատահական C-ի։ Հետրաբար A-ն հարաբերում է C-ին ինչպես B-ն C-ին (Սահմանում 5.5)։ Այսպիսով ես ասում եմ, որ C-ն նույնպես ունի նույն հարաբերությունը A-ին և B-ին։ Հանգունորեն մենք կարող ենք ցույց տալ, որ D-ն հավասար է E-ին։ Եվ F-ը ունի մեկ այլ արժեք։ Հետևաբար, եթե F-ն գերազանցում է D-ին, նա նույնպես գերազանցում է E-ին, և եթե F-ը հավասար է D-ին, ապա նա նույնպես հավասար է E-ին, և եթե F-ը չի գերազանցում է D-ին, ապա նա նույնպես չի գերազանցում է E-ին։ Եվ F-ը C-ի բազմապատիկն է ու D-ն և E-ն ուրիշ պատահական A-ի և B-ի բազմապատիկ։ Հետևաբար, C-ն հարաբերում է A-ին ինչպես C-ն B-ին [Սահմանում 5.5]: Այսպիսով՝ հավասար մեծությունները ունեն հավասար հարաբերություն նույն մեծությանը, և վերջին մեծությունը ունի հավասար հարաբերություն հավասար մեծություններին։
Հետևանք
Այսպիսով այստեղից պարզ է որ երե որոշ մեծություններ պրոպորցիոնալ են, ապա նրանք նույնպես կլինեն հակադարձորեն պրոպորցիոնալ։ Ինչը պետք էր ցույց տալ:
Պնդում 8
Անհավասար մեծությունների համար, ավելի մեծ մեծությունը ունի ավելի մեծ հարաբերություն քան փոքրը նույն հարաբերությանը։ Թող AB-ն ու C-ն լինեն անհավասար մեծություններ, և թող AB-ն լինի նրանցից մեծը, և D-ն ուրիշ պատահական մեծություն է։ Ես ասում եմ որ, AB-ն ունի ունի ավելի մեծ հարաբերություն D-ին քան C-ն D-ին և որ D-ն ունի ավելի մեծ հարաբերություն C-ին քան AB-ին։
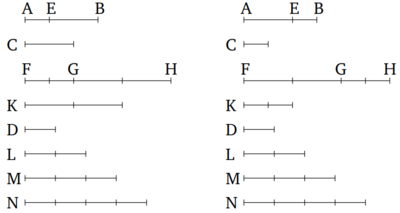
Քանի որ AB-ն մեծ է C-ից, թող BE-ն լինի հավասար C-ին։ Այսպիսով AE-ի և EB-ից փոքրը, բազմապատկելով երբեմն մեծ կլինի D-ից [Սահմանում 5.4]: Առաջինը, թող AE-ն փոքր կլինի քան EB-ն և թող AE-ն լինի բազմապատկված, և թող FG-ն լինի դրա բազմապատիկը, որը ավելի մեծ է քան D-ն։ Եվ քանի անգամ FG-ն բաժանվում է AE-ի այդքան անգամ էլ թող GH-ն բաժանվի EB-ին և K-ն C-ին։ Եվ թող D-ի կրկնապատիկ L-ը վերցված լինի և եռակի բազմապատիկ M-ը և ուրիշները՝ յուրաքանչյուրը մեծանալով մեկով ըստ հերթականության, մինչև որ վերցված բազմապատիկը լինում է D-ի առաջին բազմապատիկը, որը մեծ է K-ից։ Թող դա վերցված լինի և թող դա նույնպես լինի D-ի քառակի բազմապատիկ N-ը՝ առաջին բազմապտիկը K-ից մեծ։ Հետևաբար քանի որ K-ն փոքր է N-ից, ապա K-ն փոքր չէ M-ից։ Եվ քանի որ FG-ն ու GH-ը համապատասխանաբար AE-ի և EB-ի հավասար բազմապատիկներ են, հետևաբար FG-ն ու FH-ը AE-ի և AB—ի համապատասխանաբար հավասար բազմապատիկներ են [Պնդում 5.1]։ Եվ FG-ն ու K-ն AE-ի և C—ի համապատասխանաբար հավասար բազմապատիկներ են։ Այդ իսկ պատճառով FH-ն ու K-ն AB-ի և C-ի համապատասխանաբար հավասար բազմապատիկներ են։ Կրկին, քանի որ GH-ն ու K-ն EB-ի և C-ի հավասար բազմապատիկներ են և EB-ն հավասար է C-ին, ապա GH-ը նույնպես հավասար է K-ին։ Եվ K-ն փոքր չէ M-ից։ Հետևաբար, GH-ը նույնպես փոքր չէ M-ից նույնպես։ Եվ FG-ն մեծ է D-ից։ Հետևաբար ամբողջ FH-ը քան D-ն և M-ը գումարված իրար։ Բայց D-ն ու M-ը գումարված հավասար են N-ին, այնքանով որ M-ը D-ի եռապատիկն է և M-ն ու D-ն գումարված հավասար է չորս անգամ D-ի և N-ը նույնպես չորս անգամ D-ն է։ Այսպիսով M-ն ու D-ը գումարված հավասար է N-ի։ Բայց FH-ը մեծ է M-ից ու D-ից։ ՀԵտևաբար FH-ը գերազանցում է N-ին։ Եվ K-ն չի գերազանցում N-ին։ Եվ FH-ն ու K-ն AB—ի և AC-ի հավասար բազմապատիկներ են ու N-ը ուրիշ պատահական D-ի բազմապատիկ է։ Հետևաբար AB-ն ունի ավելի մեծ հաևաբերություն քան D—ին քան C-ն D-ին [Սահմանում 5.7]: Այսպիսով՝ ես ասում եմ որ D-ն ունի ավելի մեծ հարաբերություն C-ին քան D-ն ունի AB-ին։ Հանգունորեն մենք կարող ենք ցույց տալ, որ N-ը գերազանցում է K-ին ու N-ը չի գերազանցում FH-ին։ Եվ N-ը D-ի բազմապատիկ է ու FH, K-ն համապատասխանաբար AB-ի C—ի ուրիշ պատահական հավասար բազմապատիկներ են։ Այդ իսկ պատճառով D-ն ունի ավելի մեծ հարաբերություն C-ին քան D-ն AB-ին [Սահմանում 5.5]։ Եվ թող AB-ն մեծ լինի EB-ից։ Այսպիսով փոքր EB-ն լինելով բազմապատկված երբեմն կգերազանցի D-ին։ Թող դա լինի բազմապատկված, եվ թող GH-ը լինի EB—ի բազմապատիկ, որը մեծ է D-ից։ Եվ այնքան անգամ որքան GH-ը բաժանվում է EB-ի այնքան ագամ էլ թող FG-ն նույնպես բաժանվի AE-ին, իսկ K-ն C-ին։ Հանգունորեն մենք կարող ենք ցույց տալ որ որ FH-ը ու K-ն AB-ի և C-ի հավասար բազմապատիկեր են։ Եվ վերոնշյալին հանգունորեն մենք կարող ենք ցույց տալ որ FH-ն ու K-ն AB-ի և C-ի հավասար բազմապատիկեր են։ Եվ վերոնշյալին հանգունորեն թող N-ն ու D-ն (որը առաջին բազմապատիկն է մեծ քան FG—ն) վերցված են։ Այսպես FG-ն կրկին փոքր չէ քան M-ը։ Եվ GH-ը մեծ է D-ից։ Այդ իսկ պատճառով ամբողջ FH-ը գերազանցում է D-ին և M-ին, որը N-ն է։ Եվ K-ն չի գերազանցում N-ին, աjնքանով որքան FG-ն, որը մեծ է GH-ից։ այսինքն՝ K—ն նույնպես չի գերազանցում է N-ին: Եվ շարունակելով նույն պնդումներով մենք կարող ենք ավարտել ապացույցը։ Այսպիսով՝ Անհավասար մեծությունների համար, ավելի մեծ մեծությունը ունի ավելի մեծ հարաբերություն քան փոքրը նույն հարաբերությանը։
Պնդում 9
Մեծություններ, որոնք ունեն նույն հարաբերությունը նույն մեծությանը հավասար են մեկը մյուսին։ Եվ այն մեծությունները, որին նույն մեծությունը ունի նույն հարաբերությունը հավասար են։
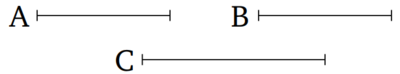
Թող A-ից և B-ից յուրաքանչյուրը ունենա նույն հարաբերությունը C-ին։ Ես ասում եմ որ A-ն հավասար է B-ին։ Եթե ոչ A-ն և B-ն չեն ունենա նույն հարաբերությունը C-ին [պնդում 5.8]։ Բայց նրանք ունեն։ Հետևաբար A-ն հավասար է B-ին։ Կրկին թող C-ն ունենա նույն հարաբերությունը A-ին և B-ին։ Ես ասում եմ որ A-ն հավասար է B-ին։ Եթե ոչ C-ն չի ունենա նույն հարաբերությունը A-ին և B-ին [պնդում 5.8]։ Բայց նա ունի։ Հետևաբար A-ն հավասար է B-ին։ Այսպիսով՝ մեծությունները, որոնք ունեն նույն հարաբերությունը նույն մեծությանը հավասար են մեկը մյուսին։ Եվ այն մեծությունները, որին նույն մեծությունը ունի նույն հարաբերությունը հավասար են։ Ինչը պետք էր ցույց տալ:
Պնդում 10
Երկու մեծություններ ունեն հարաբերություններ նույն մեծությանը։ Այն մեծությունը որը ունի մեծ հարաբերություն այդ երկուսից մեծն է։ Եվ այն մեծությունը, որին վերջին մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է։

Թող A-ն ունենա ավելի մեծ հարաբերություն C-ին քան B-ն C-ին։ Ես ասում եմ որ A-ն մեծ է B-ից։ Եթե ոչ A-ն հաստատ հավասար է կամ մեծ է B-ից: A-ն հավասար չէ B-ին, Քանի որ հակառակ դեպքում A-ն և B-ն կունենային նույն հարաբերությունը C-ին [Պնդում 5.7]: Բայց նրանք չունեն հավասար հարաբերություններ։ Հետևաբար, A-ն հավասար չի B-ին։ Նույնպես, իրոք A-ն փոքր չէ B-ից: Հակառակ դեպքում A-ն կունենա ավելի փոքր հարաբերություն C-ին քան B-ն C-ին [Պնդում 5.8]: Բայց դա այդպես չէ։ Հետևաբար, A-ն փոքր չէ B-ից: Եվ մենք ցույց էինք տվել որ նրանք հավասար չեն։ Հետևաբար A-ն մեծ է B-ից: Կրկին, Թող C-ն ունենա ավելի մեծ հարաբերություն B-ին քան C-ն A-ին։ Ես ասում եմ որ B-ն փոքր է A-ից: Եթե ոչ հաստատ հավասար կամ մեծ է: A-ն հավասար չէ B-ին, Քանի որ հակառակ դեպքում C-ն կունենար նույն հարաբերությունը A-ին և B-ին [Պնդում 5.7]: Բայց դա այդպես չէ։ Նույնպես, իրոք B-ն մեծ չէ A-ից: Հակառակ դեպքում C-ն կունենա ավելի փոքր հարաբերություն B-ին քան A-ին [Պնդում 5.8]: Բայց դա այդպես չէ։ Հետևաբար, B-ն մեծ չէ A-ից: Եվ մենք ցույց էինք տվել որ նրանք հավասար չեն։ Հետևաբար B-ն փոք է A-ից: Այսպիսով, եթե երկու մեծություններ ունեն հարաբերություններ նույն մեծությանը։ ՀԵտևաբար, այն մեծությունը որը ունի մեծ հարաբերություն այդ երկուսից մեծն է։ Եվ այն մեծությունը, որին վերջին մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է։
Պնդում 11
Հարաբերությունները որոնք նույն են նույն հարաբերության հետ նույնպես նույնն են իրար հետ։
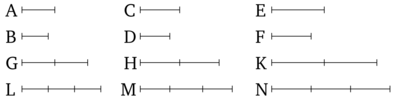
Թող A-ն հարաբերի B-ին ինչպես C-ն D-ին և C-ն հարաբերում է D-ին ինչպես E-ն F-ին։ Ես ասում եմ որ A-ն հարաբերում է B-ին ինչպես E-ն F-ին։ Թող հավասար բազմապատիկներ G, H, K-ն համապատասխանաբար վերցված լինեն A, C, E-ից և ուրիշ պատահական հավասար բազմապատիկներ L, M, N-ը համապատասխանաբար B, D, F-ից։ Քանի որ A-ն հարաբերում է B-ին ինչպես C-ն D-ին և հավասար բազմապատիկներ G-ն և H-ը վերցված են եղել համապատասխանաբար A-ից և C-ից և ուրիշ պատահական հավասար բազմապատինկեր L և M-ը համապապատասխանաբար B-ից և D-ից, հետևաբար եթե G-ն գերազանցում է L-ին, ապա H-ը նույնպես գերազանցում է M-ին, և եթե G-ն հավասար է L-ին, ապա H-ը նույնպես հավասար է M-ին, և եթե G-ն փոքր է L-ից, ապա H-ը նույնպես փոքր է M-ից [Պնդում 5.5]: Կրկին, Քանի որ C-ն հարաբերում է D-ին ինչպես E-ն F-ին և հավասար բազմապատիկներ H և K-ն վերցված են եղել համապատասխանաբար C-ից և E-ից և ուրիշ պատահական հավասար բազմապատինկեր M և N-ը համապապատասխանաբար D-ից և F-ից, հետևաբար եթե H-ն գերազանցում է M-ին, ապա K-ը նույնպես գերազանցում է N-ին, և եթե H-ն հավասար է M-ին, ապա K-ը նույնպես հավասար է N-ին, և եթե H-ն փոքր է M-ից, ապա K-ը նույնպես փոքր է N-ից [Սահմանում 5.5]: Բայց մենք նկատել էինք, որ եթե H-ը գերազանցում է M-ին, ապա G-ն նույնպես գերազանցում է L-ին, և եթե H-ը հավասար է M-ին, ապա G-ն նույնպես հավասար է L-ին, և եթե H-ը փոքր է M-ից, ապա G-ն նույնպես փոքր է L-ից: Եվ քանի որ եթե G-ն գերազանցում է L-ին, ապա K-ը նույնպես գերազանցում է N-ին, և եթե G-ն հավասար է L-ին, ապա K-ը նույնպես հավասար է N-ին, և եթե G-ն փոքր է L-ից, ապա K-ը նույնպես փոքր է N-ից [Սահմանում 5.5]: Եվ G, K-ն համապատասխանաբար A-ի և E-ի հավասար բազմապատիկներ են և L, N-ը համապատասխանաբար B, F-ի ուրիշ պատահական հավասար բազմապատիկներ են։ Հետևաբար, A-ն հարաբերում է B-ին ինչպես E-ն F-ին [Սահմանում 5.5]։ Հետևաբար, հարաբերությունները որոնք նույն են նույն հարաբերության հետ նույնպես նույնն են իրար հետ։
Պնդում 12
Եթե կան կամայական քանակի համաչափ մեծություններ, ապա ինչպես առաջնային մեծություններից մեկը հարաբերում է իր հետևողին, այդպես էլ կհարաբերեն բոլոր մնացած առաջնային մեծությունները իրենց հետևողներին։
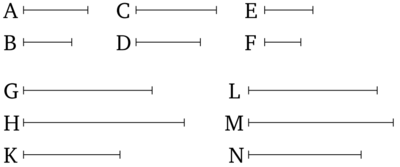
Թող վերցված լինեն կամայական քանակի համաչափ մեծություններ: Oրինակ ` A, B, C, D, E, F Այնպես որ A-ն հարաբերում է B-ին ինչպես C-ն D-ին և E-ն F-ին։ Ես ասում եմ որ A-ն հարաբերում է B-ին ինչպես A, C, E-ն B, D, F-ին։ Թող հավասար բազմապատիկներ G, H, K-ն համապատասխանաբար վերցված լինեն A, C, E-ից և ուրիշ պատահական հավասար բազմապատիկներ L, M, N-ը համապատասխանաբար B, D, F-ից։ Եվ քանի որ A-ն հարաբերում է B-ին ինչպես C-ն D-ին և E-ն F-ին, և հավասար բազմապատիկներ G, H, K-ն համապատասխանաբար վերցված են եղել A, C, E-ից և ուրիշ պատահական հավասար բազմապատիկներ L, M, N-ը համապատասխանաբար B, D, F-ից, ապա եթե G-ն գերազանցում է L-ին, ապա H-ը նույնպես գերազանցում է M-ին և K-ն գերազանցում է N-ին, և եթե G-ն հավասար է L-ին, ապա H-ը նույնպես հավասար է M-ին, և K-ն հավասար է N-ին, և եթե G-ն փոքր է L-ից, ապա H-ը նույնպես փոքր է M-ից և K-ն փոքր է N-ից [Սահմանում 5.5]: Հետևաբար, եթե G-ն գերազանցում է L-ին, ապա G, H, K-ն նույնպես գերազանցում են L, M, N-ին, և եթե G-ն հավասար է L-ին, ապա G, H, K-ն նույնպես հավասար են L, M, N-ին, և եթե G-ն փոքր է L-ից, ապա G, H, K-ն նույնպես փոքր են L, M, N-ից: Եվ G-ն ու G, H, K-ն համապատասխանաբար A-ի և A, C, E-ի հավասար բազմապատիկներ են, այնքանով որ եթե կամայական քանակով մեծություններ, որոնք համապատասխանաբար հավասար բազմապատինկեր են ուրիշ մեծությունների, իրենց քանակով հավասար, ապա այնքան անգամ ինչքան առաջին մեծություններից մեկը մեծ է իրեն հետևողից այնքան անգամ էլ մնացած բոլոր առաջին մեծությունները մեծ են իրենց հետևողներից [Պնդում 5.1]: Այսպիսով նույն պատճառով L-ն ու L, M, N-ը համապատասխանաբար B-ի և B, D, F-ի հավասար բազմապատիկներ են: Այսպիսով եթե կան կամայական քանակի համաչափ մեծություններ, ապա ինչպես առաջնային մեծություններից մեկը հարաբերում է իր հետևողին, այդպես էլ կհարաբերեն բոլոր մնացած առաջնային մեծությունները իրենց հետևողներին։ Ինչը պետք էր ցույց տալ:
Պնդում 13
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչպիսին ունի երրորդը չորրորդին և երրորդ մեծությունը ունի ավելի մեծ հարաբերություն չորրորդին քան հինգերորրդը վեցերորդին, ապա առաջին մեծությունը կունենա ավելի մեծ հարաբերություն երկրորդին քան հինգերորդը վեցերորդին։
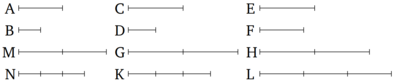
Թող առաջին մեծությունը A-ն ունենեա նույն հարաբերությունը երկրորդ B-ին ինչպիսին ունի երրորդ C-ն չորրորդ D-ին և թող երրորդ մեծություն C-ն ունենա ավելի մեծ հարաբերություն չորրորդ D-ին քան հինգերորրդ E-ն ունի վեցերորդ F-ին։ Ես ասում եմ որ, առաջին մեծություն A-ն կունենա ավելի մեծ հարաբերություն երկրորդ B-ին քան հինգերորդ E-ն վեցերորդ F-ին։ Քանի որ կան C-ի և E-ի հավասար բազմապատիկներ, և ուրիշ պատահական D-ի և F-ի հավասար բազմապատիկներ, որոնց համար C-ի բազմապատիկը չի գերազանցում D-ի բազմապատիկը և E-ի բազմապատիկը չի գերազանցում F-ինը [Պնդում 5.7], թող նրանք վերցված լինեն։ Եվ թող G, H-ը լինեն համապատասխանաբար C, E-ի հավասար բազմապատիկներ և K, L-ը համապատասխանաբար D և F-ի ուրիշ պատահական հավասար բազմապատիկներ են, այնպես որ G-ն գերազանցում K-ին, բայց H-ը չի գերազանցում Լ-ին։ Եվ այնքան անգամ ինչքան G-ն բաժանվում է C-ին այնքան անգամ էլ M-ը բաժանվում է A-ին։ Եվ այնքան անգամ ինչքան K-ն բաժանվում է D-ին այնքան անգամ էլ թող N-ը բաժանվի է B-ին։ Քանի որ A-ն հարաբերում է B-ին այնքան ինչքան C-ն Դ-ին և M, G հավասար բազմապատիկները վերցված են եղել համապատասխանաբար A-ից և C-ից և ուրիշ հավասար բազմապատիկները N և K-ն համապատասխանաբար B-ից և D-ից, հետևաբար եթե M-ը գերազանցում է N-ին, ապա G-ն նույնպես գերազանցում է K-ին, և եթե M-ը հավասար է N-ին, ապա G-ն նույնպես հավասար է K-ին, և եթե M-ը փոքր է N-ից, ապա G-ն նույնպես փոքր է K-ից [Սահմանում 5.5]: Եվ G-ն գերազանցում է K-ին։ Հետևաբար M-ը նույպես գերազանցում է N-ին։ Եվ M-ն ու H-ը համապատասխանաբար A-ի և E-ի հավասար բազմապատիկներ են ու N-ը ու L-ը համապատասխանաբար B-ի և F-ի ուրիշ հավասար բազմապատիկներ են։ Հետևաբար, A-ն ունի ավելի մեծ հարաբերություն B-ին քան E-ն F-ին [Սահմանում 5.7] ։ Այսպիսով եթե առաջին մեծությունն ունի նույն հարաբերությունը երկրորդին ինչպիսին ունի երրորդը չորրորդին և երրորդ մեծությունը ունի ավելի մեծ հարաբերություն չորրորդին քան հինգերորրդը վեցերորդին, ապա առաջին մեծությունը կունենա ավելի մեծ հարաբերություն երկրորդին քան հինգերորդը վեցերորդին։ Ինչը պետք էր ցույց տալ:
Պնդում 14
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչ երրորդը չորրորդին և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից։
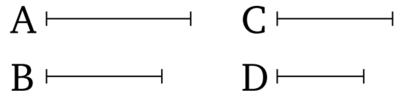
Թող առաջին մեծություն A-ն ունենա նույն հարաբերությունը երկրորդ B-ին ինչ երրորդ C-ն ունի չորրորդ D-ին և A-ն մեծ է C-ից։ Ես ասում եմ որ B-ն նույնպես մեծ է D-ից։ Քանի որ A-ն մեծ է C-ից և B-ն ուրիշ պատահական մեծություն է, A-ն հետևաբար ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին [Պնդում 5.8]։ Եվ ինչպես A-ն հարաբերում է B-ին, այնպես էլ C-ն հարաբերում է D-ին։ Հետևաբար, C-ն ունի ավելի մեծ հարաբերություն D-ին քան C-ն B-ին։ Եվ այն մեծությունը, որին նույն մեծությունը ունի ավելի մեծ հարաբերություն փոքրն է [Պնդում 5.10]։ Հետևաբար D-ն փոքր է B-ից։ Հետևաբար, B-ն մեծ է D-ից։ Հանգունորեն մենք կարող ենք ցույց տալ, որ նույնիսկ եթե A-ն հավասար է C-ին, ապա B-ն նույնպես հավասար կլինի D-ին և նույնիսկ եթե A-ն փոքր է C-ից, ապա B-ն նույնպես փոքր կլինի D-ից։ Այսպիսով եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին ինչ երրորդը չորրորդին և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից։
Պնդում 15
Մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ։
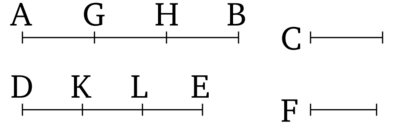
Թող AB-ն և DE-ն լինեն C-ի և F-ի համապատասխանաբար հավասար բազմապատիկներ։ Ես ասում եմ որ C-ն հարաբերում է F-ին ինչպես AB-ն DE—ին։ Քանի որ AB-ն և DE-ն C-ի և F-ի համապատասխանաբար հավասար բազմապատիկներ, հետևաբար այնքան մեծություններ որքան AB-ում հավասար են C-ին, այնքան էլ կան DE-ում հավասար F-ին։ Թող AB-ն բաժանված լինի մեծությունների ՝ AG, GH, HB հավասար C-ին և DE-ն, DK, KL, LE-ին հավասար F-ի։ Այսպիսով AG, GH, HB մեծությունների քանակը հավասար կլինի DK, KL, LE մեծությունների քանակին։ Եվ քանի որ AG, GH, HB-ն հավասար են իրար և DK, KL, LE-ն հավասար նույնպես հավասար են իրար։ Հետևաբար AG-ն հարաբերում է DK-ին ինչպես GH-ը KL-ին և HB-ն LE-ին [Պնդում]։ Եվ համաչափ մեծությունների համար, ինչպես առաջնային մեծություններից մեկը հարաբերում է իր հետևողին, այդպես էլ կհարաբերեն բոլոր մնացած առաջնային մեծությունները իրենց հետևողներին [Պնդում]։ ՀԵտևաբար AG-ն հարաբերում է DK-ին ինչպես AB—ն DE-ին։ Եվ AG-ն հավասար է C-ին և DK-ն F-ին։ Հետևաբար C-ն հարաբերում է F-ին ինչպես AB-ն DE-ին։ Այսպիսով մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ։ Ինչը պետք էր ցույց տալ:
Պնդում 16
Եթե չորս մեծություններ համաչափ են, ապա նրանք նույնպես փոխադարձ կլինեն։ Թող A, B, C, D-ն լինեն չորս համաչափ մեծություններ, այնպես որ A-ն հարաբերում է B-ին ինչպես C-ն D-ին։ Ես ասում եմ որ նրանք նույնպես փոխադարձ համաչափ կլինեն, այնպես որ A-ն հարաբերում է C-ին ինչպես B-ն D-ին։ Թող հավասար բազմապատիկներ E-ն ու F-ը վերցված լինեն համապատասխաբար A-ից և B-ից, և ուրիշ պատահական G, H հավասար բազմապատիկներ համապատասխանաբար C-ից և D-ից։
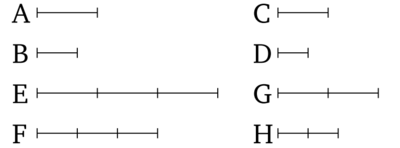
Եվ քանի որ E-ն ու F-ը համապատասխաբար A-ի և B-ի հավասար բազմապատիկներ են, և մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները, վերցված համապատասխանաբար հերթականությամբ [Պնդում 5.15]։ Հետևաբար A-ն հարաբերում է B-ին ինչպես E-ն F-ին, բայց A-ն հարաբերում է B-ին ինչպես C-ն D-ին և հետևաբար C-ն հարաբերում է D-ին ինչպես E-ն F-ին [Պնդում 5.11]։ Կրկին Եվ քանի որ G-ն ու H-ը համապատասխաբար C-ի և D-ի հավասար բազմապատիկներ են, հետևաբար C-ն հարաբերում է D-ին ինչպես G-ն H-ին [Պնդում 5.15], բայց C-ն հարաբերում է D-ին ինչպես E-ն F-ին և հետևաբար E-ն հարաբերում է F-ին ինչպես G-ն H-ին [Պնդում 5.11]։ Եվ Եթե չորս մեծություններ համաչափ են և առաջին մեծությունը մեծ է երրորդից, ապա երկրորդ մեծությունը նույնպես մեծ կլինի չորրորդից։ Եվ եթե առաջին մեծությունը հավասար է երրորդին, ապա երկրորդ մեծությունը նույնպես հավասար կլինի չորրորդին։ Եվ եթե առաջին մեծությունը փոքր է երրորդից, ապա երկրորդ մեծությունը նույնպես փոքր կլինի չորրորդից [Պնդում 5.14]։ Հետևաբար, եթե E-ն գերազանցում է G-ին, ապա F-ը նույնպես գերազանցում է H-ին, և եթե E-ն հավասար է G-ին, ապա F-ը նույնպես հավասար է H-ին, և եթե E-ն փոքր է G-ից, ապա F-ը նույնպես փոքր է H-ից: Եվ E-ն ու F-ը համապատասխանաբար A-ի և B-ի հավասար բազմապատիկներ են, և G-ն և H-ը C-ի և D-ի համապատասխաբար ուրիշ պատահական հավասար բազմապատիկներ են։ Հետևաբար A-ն հարաբերում է C-ին ինչպես B-ն D-ին [Սահմանում 5.5]: Այսպիսով եթե չորս մեծություններ համաչափ են, ապա նրանք նույնպես փոխադարձ կլինեն։ Ինչը պետք էր ցույց տալ:
Պնդում 17
Եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված։
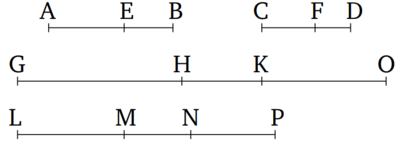
Թող AB-ն BE-ն CD-ն և DF-ը լինեն համադրված մեծություններ, որոնք համաչափ են, այնպես որ AB-ն հարաբերում է BE-ին, այնպես ինչպես CD-ին DF-ին։ Ես ասում եմ որ նրանք նույնպես համաչափ կլինեն բաժանված, այնպես որ AE-ն կհարաբերի EB-ին ինչպես CF-ը DF-ին։ Թող հավասար բազմապատիկներ GH, HK, LM և MN-ը վերցված լինեն համապատասխանաբար AE, EB, CF և FD—ից։ Եվ ուրիշ պատահական հավասար բազմապատիկներ KO և NP-ն համապատասխանաբար EB-ից և FD-ից։ Եվ քանի որ GH-ն ու HK-ն AE-ի և EB-ի համապատասխանաբար հավասար բազմապատիկներ են, հետևաբար GH-ն ու GK-ն AE-ի և AB-ի համապատասխանաբար հավասար բազմապատիկներ են [Պնդում 5.1]: Սակայն GH-ն և LM-ը AE-ի և CF-ի համապատասխանաբար հավասար բազմապատիկներ են, հետևաբար GK-ն ու LM-ը AB-ի և CF-ի համապատասխանաբար հավասար բազմապատիկներ են։ Կրկին, քանի որ LM-ը և MN-ը CF-ի և FD-ի համապատասխանաբար հավասար բազմապատիկներ են, ապա LM-ը և LM-ը CF-ի և CD-ի համապատասխանաբար հավասար բազմապատիկներ են [Պնդում 5.1]։ Եվ LM-ն ու GK-ն CF—ի և AB-ի համապատասխանաբար հավասար բազմապատիկներ են, հետևաբար GK-ն ու LN-ը AB-ի CD—ի համապատասխանաբար հավասար բազմապատիկներ են։ Դրա պատճառով GK-ն և LN-ը AB-ի և CD-ի հավասար բազմապատիկներ են։ Կրկին, քանի որ HK-ն և MN-ը EB-ի և FD-ի համապատասխանաբար հավասար բազմապատիկներ են և KO-ն ու NP-ն EB-ի և FD-ի համապատասխանաբար հավասար բազմապատիկներ են, ապա գումարված իրար, HO-ն ու MP-ն նույնպես EB-ի և FD-ի համապատասխանաբար հավասար բազմապատիկներ են [Պնդում 5.2]։ Եվ քանի որ AB-ն հարաբերում է BE-ին այնպես ինչպես CD-ն DF-ին և հավասար բազմապատիկներ GK-ն ու LN-ը վերցված են եղել AB-ից ու CD-ից և հավասար բազմապատիկներ HO-ն ու MP-ն EB-ից և FD-ից, հետևաբար եթե GK-ն գերազանցում է HO-ին, ապա LN-ը նույնպես գերազանցում է MP-ին, և եթե GK-ն հավասար է HO-ին, ապա LN-ը նույնպես հավասար է MP-ին, և եթե GK-ն փոքր է HO-ից, ապա LN-ը նույնպես փոքր է MP-ից [Սահմանում 5.5]։ Թող GK-ն գերազանցի HO-ին հետևաբար հանելով HK-ն երկուսից էլ GH-ն կգերազանցի KO-ին։ Բայց մենք տեսել ենք որ եթե GK-ն գերազանցում է HO-ին , ապա LN-ը նույնպես գերազանցում է MP-ին։ Հետևաբար LN-ը նույնպես գերազանցում է MP-ին և MN-ը երկուսից էլ հանենք LM-ը նույնպես կգերազանցի NP-ին։ ՀԵտևաբար եթե GH-ը գերազանցում է KO-ին, ապա LM-ը նույնպես կգերազանցի NP-ին։ Հանգունորեն մենք կարեղ ենք ցույց տալ որ եթե GH-ը հավասար է KO-ին ապա LM-ը նույնպես հավասար է NP-ին և եթե GH-ը փոքր է KO-ից, ապա LM-ը նույնպես փոքր է NP-ից։ Եվ GH-ն ու LM-ը AE-ի և CF-ի հավասար բազմապատիկներ են և KO-ն ու NP—ն ուրիշ պատահական EB-ի և FD-ի հավասար բազմապատիկներ են։ ՀԵտևաբար, AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին [Սահմանում 5.5]։ Այսպիսով Եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված։ Ինչը պետք էր ցույց տալ:
Պնդում 18
Եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված։
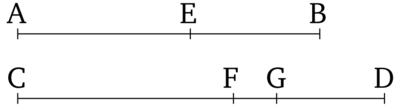
Թող AE-ն, EB-ն, CF-ը և FD-ն լինեն բաժանված մեծություններ որոնք համաչափ են, այնպես որ AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին։ Ես ասում եմ որ նրանք նույնպես համաչափ կլինեն համադրված, այսինքն AB-ն կհարաբերի BE-ին ինչպես CD-ն FD-ին։ Հակառակ դեպքւմ եթե AB-ն չի հարաբերում BE-ին ինչպես CD-ն FD-ին, ապա այդ դեպքում AB-ն կհարաբերի BE-ին, այնպես ինչպես որ CD-ն որևէ մեծ կամ փոքր մեծության քան DF-ը։ Թող առաջինը այդ մեծությունը լինի փոքր քան DF-ը և կոչվի DG։ Եվ քանի որ համադրված մեծությունները համաչափ են, այնպես որ AB-ն հարաբերում է BE-ին ինչպես CD-ն DG-ին, ապա նրանք նույնպես կլինեն համաչափ բաժանված [Պնդում 5.17]: ՀԵտևաբար AE-ն հարաբերում է EB-ին CG-ն GD-ին, բայց մենք նույնպես ենթադրել էինք որ AE-ն հարաբերում է EB-ին ինչպես CF-ը FD-ին [Պնդում 5.11]։ Եվ առաջին մեծություն CG-ն մեծ է քան երրորդ CF-ը։ Հետևաբար, երկրորդ մեծություն GD-ն նույնպես մեծ է չորրորդ FD-ից [Պնդում 5.14]։ Բայց նա նույնպես փոքր է, ինչը անհնար է։ Հետևաբար սա այն դեպքը չէ, երբ AB-ն հարաբերում է BE-ին ինչպես CD-ն FD-ից փոքրին։ Հանգունորեն մենք կարող ենք ցույց տալ նաև որ սա FD-ից մեծ դեպքը չէ։ Հետևաբար, սա հավասար FD-ին դեպքն է։ Հետևաբար, եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված։ Ինչը պետք էր ցույց տալ:
Պնդում 19
Եթե ամբողջ մասը հարաբերում է ամբողջ մասին ինչպես վերցված մասը վերցված մասին, ապա մնացորդը կհարաբերի մնացորդին ինչպես ամբողջ մասը ամբողջին։

Թող ամբողջ մաս AB-ն հարաբերի ամբողջ մաս CD ինչպես վերցված մաս AE-ն CF վերցված մասին։ Ես ասում եմ որ, EB մնացորդը կհարաբերի CD մնացորդին ինչպես ամբողջ մաս AB-ն CD ամբողջին։ Քանի որ AB-ն հարաբերում է CD-ին ինչպես AE-ն CF-ին, նույնպես փոխադարձ BA-ն հարաբերում Է AE-ին ինչպես DC-ն CF-ին [Պնդում 5.16]։ Եվ քանի որ եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն բաժանված, ապա BE-ն հարաբերում է EA—ին ինչպես DF-ը CF-ին [Պնդում 5.17]։ Նույնպես հակադարձ BE-ն հարաբերում է DF-ին ինչպես EA-ն FC-ին [Պնդում 5.16]։ Եվ ենթադրվում էր, որ AE-ն հարաբերում էր CF-ին ինչպես ամբողջ AB-ն CD-ին։ Հետևաբար, EB մնացորդը հարաբերում է FD մնացորդին, ինչպես ամբողջ AB-ն կհարաբերի ամբողջ CD-ին։ Այսպիսով՝ եթե ամբողջ մասը հարաբերում է ամբողջ մասին ինչպես վերցված մասը վերցված մասին, ապա մնացորդը կհարաբերի մնացորդին ինչպես ամբողջ մասը ամբողջին։ Ինչը պետք էր ցույց տալ: Եվ քանի որ ցույց տրված եղել էր որ AB-ն հարաբերում է CD-ին ինչպես EB-ն FD-ին, Սա նույնպես այն դեպքն է հակադարձ, որ AB-ն հարաբերում է BE-ին ինչպես CD-ն FD-ին։ Հետևաբար համադրված մեծությունները համաչափ են։ Եվ ցույց տրված եղել է որ BA-ն հարաբերում է AE-ին ինչպես DC-ն CF-ին։ Եվ վերջինս ստացվել է առաջինից։
Հետևանք
Այսպիսով այստեղից պարզ է, որ եթե համադրված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն ձևափոխված։ Ինչը պետք էր ցույց տալ:
Պնդում 20
Եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։
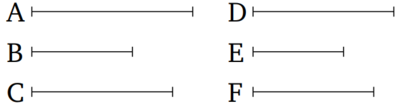
Թող A, B, C-ն լինեն երեք մեծություններ և D, E, F-ը ուրիշ մեծություններ նրանց թվով հավասար և նույնպես զույգ առ զույգ վերցված հավասար հարաբերություններով, այնպես որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին, և B-ն C-ին, ինչպես E-ն F-ին։ Եվ թող A-ն մեծ լինի C-ից ըստ հավասարության։ Ես ասում եմ որ D-ն նույնպես մեծ կլինի F-ից, և եթե A-ն հավասար է C-ին, ապա D-ն նույնպես հավասար կլինի F-ին։ Եվ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի F-ից։ Քանի որ A-ն մեծ է C-ից և B-ն մեկ ուրիշ մեծություն է, և մեծ մեծությունը ունի ավելի մեծ հարաբերություն քան փոքրը նույն հարաբերությանը [Պնդում 5.8], հետևաբար A-ն ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին։ Բայց A-ն հարաբերում է B-ին, ինչպես D-ն E-ին։ Եվ հակադարձորեն C-ն հարաբերում է B-ին այնպես ինչպես F-ը E-ին [Պնդում 5.7-ի հետևանք]։ Հետևաբար D-ն նույնպես ունի ավելի մեծ հարաբերություն E-ին քան F-ը E-ին [Պնդում 5.13]։ Եվ մեծությունները ունեն հարաբերություն նույն մեծությանը, այն մեծությունը որը ունի մեծ հարաբերություն մեծն է [Պնդում 5.10]։ Հետևաբար D-ն մեծ է F-ից։ Հանգունորեն մենք կարոզ ենք ցույց տալ, որ եթե նույնիսկ A-ն հավասար է C-ին ապա D-ն նույնպես հավասար կլինի F-ին և նույնիսկ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի քան F-ը։ Այսպիսով՝ եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե հավասարման միջոցով առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ Ինչը պետք էր ցույց տալ:
Պնդում 21
Եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե նրանց հարաբերությունը խանգառված է, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։
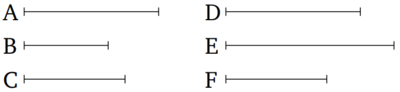
ող A, B, C-ն լինեն երեք մեծություններ և D, E, F-ը ուրիշ մեծություններ նրանց թվով հավասար և նույնպես զույգ առ զույգ վերցված հավասար հարաբերություններով, և խանգառված հարաբերությամբ, այնպես որ A-ն հարաբերում է B-ին ինչպես Ե-ն Ֆ-ին, և B-ն C-ին, ինչպես Դ-ն Ե-ին։ Եվ թող A-ն մեծ լինի C-ից ըստ հավասարության։ Ես ասում եմ որ D-ն նույնպես մեծ կլինի F-ից, և եթե A-ն հավասար է C-ին, ապա D-ն նույնպես հավասար կլինի F-ին։ Եվ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի F-ից։ Քանի որ A-ն մեծ է C-ից և B-ն մեկ ուրիշ մեծություն է, հետևաբար A-ն ունի ավելի մեծ հարաբերություն B-ին քան C-ն B-ին [Պնդում 5.8]։ Բայց A-ն հարաբերում է B-ին, ինչպես Ե-ն Ֆ-ին։ Եվ հակադարձորեն C-ն հարաբերում է B-ին այնպես ինչպես Ե-ը Դ-ին [Պնդում 5.7-ի հետևանք]։ Հետևաբար Ե-ն նույնպես ունի ավելի մեծ հարաբերություն Ֆ-ին քան Ե-ը Դ-ին [Պնդում 5.13]։ Եվ մեծությունները ունեն հարաբերություն նույն մեծությանը, այն մեծությունը որը ունի մեծ հարաբերություն մեծն է [Պնդում 5.10]։ Հետևաբար Ֆ-ը փոքր է Դ-ից։ Հետևաբար Դ-ն մեծ է Ֆ-ից։ Հանգունորեն մենք կարոզ ենք ցույց տալ, որ եթե նույնիսկ A-ն հավասար է C-ին ապա D-ն նույնպես հավասար կլինի F-ին և նույնիսկ եթե A-ն փոքր է C-ից, ապա D-ն նույնպես փոքր կլինի քան F-ը։ Այսպիսով՝ եթե կան երեք մեծություններ և ուրիշ մեծություններ նրանց հավասար թվով, նաև նրանց հարաբաերությունները զույգ առ զույգ վերցված հավասար են, և եթե նրանց հարաբերությունը խանգառված է, և եթե հավասարման միջոցով առաջինը մեծ է երրորդից, ապա չորրորդը նույնպես մեծ կլինի վեցերորդից, և եթե հավասարման միջոցով առաջինը հավասար է երրորդին, ապա չորրորդը նույնպես հավասար կլինի վեցերորդին, և եթե առաջինը փոքր է երրորդից, ապա չորրորդը նույնպես փոքր կլինի վեցերորդից։ Ինչը պետք էր ցույց տալ:
Պնդում 22
Եթե կան որևէ քանակի մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։

Թող լինեն կամայական քանակի մեծություններ A, B, C և ուրիծ մեծություններ D, E, F նրանց քանակով հավասար, որոնք զույգ առ զույգ վերցված նույն հարաբերությունը ունեն այնպես որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին և B-ն C-ին ինչպես E-ն F-ին։ Ես ասում եմ որ նրանք նույն հարաբերության կլինեն հավսարման միջոցով։ Այսինքն A-ն կհարաբերի C-ին ինչպես D-ն F-ին։ Թող հավասար բազմապատիկներ G-ն և H-ը համապատասխանաբար վերցված լինեն A-ից և D-ից, և ուրիշ պատահական հավասար բազմապատիկներ K-ն ու L-ը համապատասխանաբար B-ից և E-ից, և դեռ ուրիշ պատահական հավասար բազմապատիկներ M-ն ու N-ը համապատասխանաբար C-ից և F-ից։ Եվ քանի որ A-ն հարաբերում է B-ին ինչպես D-ն E-ին և հավասար բազմապատիկներ G-ն և H-ը համապատասխանաբար վերցված են A-ից և D-ից և ուրիշ պատահական հավասար բազմապատիկներ K-ն ու L-ը համապատասխանաբար B-ից և E-ից, ապա G-ն հարաբերում է K-ին ինչպես H-ը L-ին [Պնդում 5.4]։ Եվ քանի որ նույն պատճառով K-ն հարաբերում է M-ին ինչպես L-ը N-ին։ Հետևաբար, քանի որ G, K, M-ը երեք մեծություն են և H, L, N-ը ուրիշ մեծություններ նրանց քանակով հավասար, որոնք նույնպես նույն հարաբերությունը ունեն զույգ առ զույգ վերցված, հետևաբար հավասարման միջոցով եթե G-ն գերազանցում է M-ին, ապա H-ը նույնպես գերազանցում է N-ին, և եթե G-ն հավասար է M-ին, ապա H-ը նույնպես հավասար է N-ին, և եթե G-ն փոքր է M-ից, ապա H-ը նույնպես փոքր է N-ից [Պնդում 5.20]։ Եվ G-ն ու H-ը համապատասխանաբար A-ի և D-ի հավասար բազմապատիկներ են, M-ն ու N-ը համապատասխանաբար C-ի և F-ի ուրիշ հավասար բազմապատիկներ են։ Հետևաբար, A-ն հարաբերում է C-ին ինչպես D-ն F-ին [Սահմանում 5.5]։ Այսպիսով՝ եթե կան որևէ քանակի մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։ Ինչը պետք էր ցույց տալ:
Պնդում 23
Եթե կան երեք մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, և եթե նրանց հարաբերությունը խանգառված է, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։
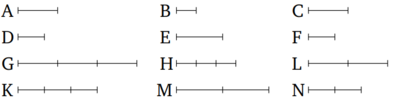
Թող A, B, C մեծությունները և D, E, F ուրիշ մեծությունները նրանց քանակով հավասար, որոնք զույգ առ զույգ վերցված նույն հարաբերությունը ունեն։ Եվ թող նրանց հարաբերությունը խանգառված լինի, այնպես որ A-ն հարաբերում է B-ին ինչպես E-ն F-ին և B-ն C-ին ինչպես D-ն F-ին։ Ես ասում եմ որ A-ն կհարաբերի C-ին ինչպես D-ն F-ին։ Թող հավասար բազմապատիկներ G-ն, H-ը և K-ն համապատասխանաբար վերցված լինեն A-ից, Բ-ից և D-ից, և ուրիշ պատահական հավասար բազմապատիկներ L-ը M-ը ու N-ը համապատասխանաբար C-ից, E-ից և F-ից։ Եվ քանի որ հավասար բազմապատիկները G-ն և H-ը վերցված են համապատասխանաբար A-ից և B-ից և մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները [Պնդում 5.15], հետևաբար A-ն հարաբերում է B-ին ինչպես G-ն H-ին։ Եվ նույն պատճառներով E-ն հարաբերում է M-ը N-ին։ Եվ A-ն հարաբերում է B-ին այնպես ինչպես E-ն F-ին։ Հետևաբար G-ն հարաբերում է H-ին M-ը N-ին [Պնդում 5.11]։ Եվ քանի որ B-ն հարաբերում է C-ին ինչպես D-ն E-ին, նաև փոխադարձորոն B-ն հարաբերում է D-ին ինչպես C-ն E-ին [Պնդում 5.16]։ Եվ քանի որ H-ն ու K-ն համապատասխանաբար B-ի և D-ի հավասար բազմապատիկներ են և մասերը ունեն նույն հարաբերությունը ինչպես նման բազմապատիկները [Պնդում 5.15] հետևաբար B-ն հարաբերում է D-ին ինչպես H-ը K-ին։ Բայց B-ն հարաբերում է D-ին ինչպես C-ն E-ին։ Եվ հետևաբար H-ը հարաբերում K-ին ինչպես C-ն E-ին [Պնդում 5.11]։ Կրկին, քանի որ L-ն ու M-ը C—ի և E-ի համապատասխանաբար հավասար բազմապատիկներ են, հետևաբար C-ն հարաբերում է E-ին այնպես ինչպես L-ը M-ին [Պնդում 5.15]։ Նաև փոխադարձորեն H-ը հարաբերում է L-ին այնպես ինչպես K-ն M-ին [Պնդում 5.16]։ Եվ մենք նույնպես ցույց էինք տվել որ G-ն հարաբերում է H-ին այնպես ինչպես M-ը N-ին։ Հետևաբար քանի որ A, B, C երեք մեծություններ են և K, M, N-ը ուրիշ մեծությունները նրանց քանակով հավասար, զույգ առ զույգ վերցված նույն հարաբերությամբ և խանգառված հարաբերություն ունեն, ապա ըստ հավասարման, եթե G-ն գերազանցում է L-ին, ապա K-ն նույնպես գերազանցում է N-ին, և եթե G-ն հավասար է L-ին, ապա K-ն նույնպես հավասար է N-ին, և եթե G-ն փոքր է L-ից, ապա K-ն նույնպես փոքր է N-ից [Պնդում 5.21]։ Եվ G-ն ու K-ն համապատասխանաբար A-ի և D-ի հավասար բազմապատիկներ են, և L-ն ու N-ը համապատասխանաբար C-ի և F-ի։ Հետևաբար, A-ն հարաբերում է C-ին այնպես ինչպես D-ն F-ին [Սահմանում 5.5]։ Այսպիսով՝ Եթե կան երեք մեծություններ և ուրիշ նրանց քանակով հավասար մեծություններ, որոնք զույգ առ զույգ վերցված ունեն նույն հարաբերությունը, և եթե նրանց հարաբերությունը խանգառված է, ապա նրանք նույնպես կլինեն նույն հարաբերության ըստ հավասարման։ Ինչը պետք էր ցույց տալ:
Պնդում 24
Եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին, ինչն ունի երրորդը չորրորդին և հինգերորդը նույնպես ունի նույն հարաբերություն երկրորդին ինչպիսին վեցերորդը ունի չորրորդին, ապա առաջին և հինգերորդ մեծությունները գումարված կունենան նույն հարաբերությունը երկրորդին ինչ երրորդն ու վեցերորդը գումարված չորրորդին։
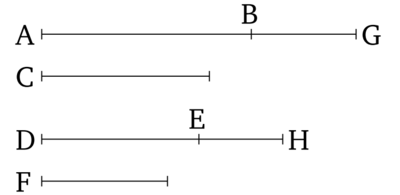
Թող առաջին մեծություն ԱԲ-ն ունենա նույն հարաբերությունը երկրորդ C-ին, ինչն երրորդ DE-ն ունի չորրորդ F-ին։ Եվ թող հինգերորդ BG-ն նույնպես ունենա նույն հարաբերությունը երկրորդ C-ին ինչպիսին վեցերորդ EH-ը ունի չորրորդ F-ին։ Ես ասում եմ որ առաջին և հինգերորդ մեծությունները գումարված՝ AG-ն կունենա նույն հարաբերությունը երկրորդ C-ին ինչ կունենան երրորդն ու վեցերորդը գումարված՝ DH-ը չորրորդ F-ին։
Քանի որ BG-ն հարաբերում է C-ին այնպես ինչպես EH-ը F-ին հետևաբար հակադարձորեն C-ն հարաբերում է BG-ին այնպես ինչպես F-ը EH-ին (Պնդում 5.7-ի հետևանք)։ ՀԵտևաբար քանի որ AB-ն հարաբերում է C-ին այնպես ինչպես DE-ն F-ին և C-ն հարաբերում է BG—ին այնպես ինչպես F-ը EH-ին, հետևաբար ըստ հավասարման AB-ն հարաբերում է BG-ին, ինչպես DE-ն EH-ին [Պնդում 5.22]: Եվ Եթե բաժանված մեծությունները համաչափ են, ապա նրանք նույնպես համաչափ կլինեն համադրված [Պնդում 5.18]։ Այդ իսկ պատճառով AG-ն հարաբերում է GB-ին այնպես ինչպես DH-ը HE-ին։ Եվ նաև BG-ն հարաբերում է C-ին այնպես ինչպես EH-ը F-ին։ ՀԵտևաբար ըստ հավասարման AG-ն հարաբրերում C-ին ինչպես DH-ը F-ին [Պնդում 5.22]։ Հետևաբար եթե առաջին մեծությունը ունի նույն հարաբերությունը երկրորդին, ինչն ունի երրորդը չորրորդին և հինգերորդը նույնպես ունի նույն հարաբերություն երկրորդին ինչպիսին վեցերորդը ունի չորրորդին, ապա առաջին և հինգերորդ մեծությունները գումարված կունենան նույն հարաբերությունը երկրորդին ինչ երրորդն ու վեցերորդը գումարված չորրորդին։ Ինչը պետք էր ցույց տալ:
Պնդում 25
Եթե չորս մեծություններ համաչափ են, ապա նրանցից մեծագույնի և փոքրագույնի գումարը մեծ կլինի մնացած երկուսի գումարից։
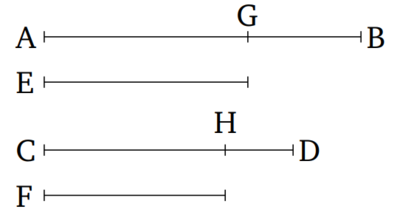
Թող AB-ն, CD-ն, E-ն F-ը լինեն չորս համաչափ մեծություններ, այնպես որ AB-ն հարաբերում է CD-ին այնպես ինչպես E-ն F-ին։ Եվ թող AB-ն լինի նրանցից մեծագույնը, իսկ F-ը փոքրագույնը։ Ես ասում եմ որ, AB-ն և F-ը մեծ են քան CD-ն և E-ն։ Թող AG-ն լինի հավասար E-ին, իսկ CH-ը F-ին։ Քանի որ AB-ն հարաբերում է CD—ին ինչպես E-ն F-ին ու E-ն հավասար է հավասար է AG-ին և F-ը CH-ին, հետևաբար AB-ն հարաբերում է CD-ին ինչպես AG-ն CH-ին։ Եվ քանի որ ամբողջ AB-ն հարաբերում է ամբողջ CD-ին այնպես ինչպես վերցված մաց AG-ն վերցված մաս CH-ին, ապա մնացորդ GB-ն նույնպես կհարաբերի մնացորդ HD—ին ինչպես ամբողջ AB-ն ամբողջ CD-ին [Պնդում 5.19]: Եվ AB-ն մեծ է CD-ից։ Հետևաբար GB-ն նույնպես մեծ է քան HD-ն։ Եվ քանի որ AG-Ն հավասար է E-ին ու CH-ը F-ին, ապա AG-ն և F-ը հավասար են CH-ին ու E-ին։ Եվ քանի որ հավասար մեծությունները գումարված են անհավասար մեծություններին, ապա ամբողջ մասերը անհավասար են, հետևաբար եթե AG-ն ու F-ը գումարված են GB-ին և CH-ը ու E-ն HD-ին և GB-ն ու HD-ն անհավասար են և GB-ն մեծագույնն է կարող ենք հետևեցնել որ AB-ն ու F-ը մեծ են CD և F-ից։ Այսպիսով՝ եթե չորս մեծություններ համաչափ են, ապա նրանցից մեծագույնի և փոքրագույնի գումարը մեծ կլինի մնացած երկուսի գումարից։ Ինչը պետք էր ցույց տալ: