«Մասնակից:NaneMambreyan»–ի խմբագրումների տարբերություն
No edit summary |
No edit summary |
||
| (Միևնույն մասնակցի 2 միջանկյալ տարբերակներ թաքցված է) | |||
| Տող 10. | Տող 10. | ||
† Այլ կերպ ասած` s |
† Այլ կերպ ասած`<math> s \cdot \frac{q \left[\sqrt{1 + k^2} + k\right]}{2(1 + k^2)} + \frac{q \left[\sqrt{1 + k^2} - k\right]}{2(1 + k^2)} = \frac{q \left[\sqrt{1 + k'^2} + k'\right]}{2(1 + k'^2)} + \frac{q \left[\sqrt{1 + k'^2} - k'\right]}{2(1 + k'^2)} </math> ունի միայն մեկ արմատ, այն է: k′ = k. |
||
| Տող 25. | Տող 25. | ||
† Այլ կերպ ասած, <math> k'^{1/4} \cdot \frac{q \left[1 + \frac{k}{\sqrt{1 + k^2}}\right]}{2} + k'^{1/4} \cdot \frac{q \left[1 - \frac{k}{\sqrt{1 + k^2}}\right]}{2} = k'''^{1/4} \cdot \frac{q \left[1 + \frac{k''}{\sqrt{1 + k''^2}}\right]}{2} + k'''^{1/4} \cdot \frac{q \left[1 - \frac{k''}{\sqrt{1 + k''^2}}\right]}{2}. </math> ունի միայն մեկ արմատ, այն է, k′′ = k և k′′′ = k′. |
|||
† Այլ կերպ ասած, k′1/4q[1 + k/(1 + k2)1/2]/2 + k′1/4q[1 − k/(1 + k2)1/2]/2 = k′′′1/4q[1 + k′′/(1 + k′′2)1/2]/2 |
|||
+k′′′1/4q[1 − k′′/(1 + k′′2)1/2]/2 ունի միայն մեկ արմատ, այն է, k′′ = k և k′′′ = k′. |
|||
| Տող 44. | Տող 43. | ||
Առաջին երկբաղադրիչ ուղիղ գիծը գտնելու համար: |
Առաջին երկբաղադրիչ ուղիղ գիծը գտնելու համար: |
||
Տանենք ԱՑ և ՑԲ երկարություններով հատվածներն այնպես, որ դրանց ԱԲ գումարը ԲՑ-ի նկատմամբ ունենա այնպիսի հարաբերություն ինչպիսին (որևէ) քառակուսի թիվ ունի (մեկ այլ) քառակուսի թվի նկատմամբ, բայց չունենա |
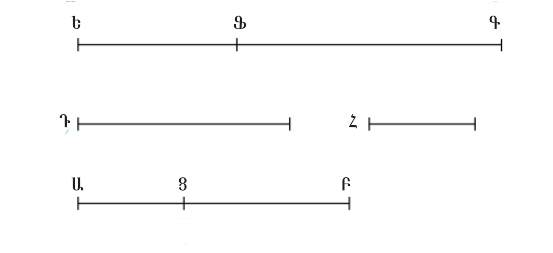
Տանենք ԱՑ և ՑԲ երկարություններով հատվածներն այնպես, որ դրանց ԱԲ գումարը ԲՑ-ի նկատմամբ ունենա այնպիսի հարաբերություն ինչպիսին (որևէ) քառակուսի թիվ ունի (մեկ այլ) քառակուսի թվի նկատմամբ, բայց չունենա ՑԱ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին (որևէ) քառակուսի թիվ ունի (մեկ այլ) քառակուսի թվի նկատմամբ [[Պնդում 10.28, լեմմա I | Պնդում 10.28, լեմմա I]]: Նաև տանենք ռացիոնալ երկարությամբ Դ ուղիղ գիծը: Բացի այդ, ԵՖ-ն երկարոթյամբ համաչափելի է Դ-ին: Ուստի ԵՖ-ը նույնպես ռացիոնալ է [[Սահմանում 10.3 | Սահմանում 10.3]]։ Եվ թող սահմանվի, որ այնպես ինչպես ԲԱ-ն է հարաբերվում ԱՑ-ին, նույն կերպ էլ ԵՖ-ի քառակուսին ՖԳ-ի քառակուսուն [[Պնդում 10.6 հետևանք | Պնդում 10.6 հետևանք ]]: ԵՎ ԱԲ-ն ԱՑ-ի հետ ունի այն նույն հարաբերությունը, ինչը ինչ-որ թիվ ունի մեկ այլ թվի հետ: Այսպիսով, ԵՖ քառակուսին ՖԳ քառակուսու նկատմամբ ունի այն նույն հարաբերությունը ինչ մի թիվ ունի մյուսի նկատմամբ: Հետևաբար ԵՖ-ով կազմված թառակուսին համաչափելի է ՖԳ-ով կառուցված քառակուսուն [[Պնդում 10.6 | Պնդում 10.6]]։ Նաև ԵՖ-ն ռացիոնալ է: հետևաբար ՖԳ-ն ևս ռացիոնալ է: Եվ քանի որ ԲԱ-ն ԱՑ-ի նկատմամբ չունի այն նույն հարաբերությունը ինչ մի քառակուսի ունի մյուսի նկատմամբ, հետևաբար ԵՖ քառակուսին չունի ՖԳ-ի նկատմամբ այնպիսի հարաբերություն ինչպես մի քառակուսին մյուսի նկատմամբ ունի ևս: Հետևաբար ԵՖ-ն երկարությամբ անհամաչափելի է ՖԳ-ին [[Պնդում 10.9 | Պնդում 10.9]]։ Ստացվում է, որ ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով: Հետևաբար ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է [[Պնդում 10.36 | Պնդում 10.36]]։ Այն է, դա նաև առաջին երկբաղադրիչ ուղիղ գիծ է: |
||
[[Պատկեր:48.png]] |
[[Պատկեր:48.png]] |
||
| Տող 53. | Տող 52. | ||
†Եթե ռացիոնաI ուղիղն ունի միավոր երկարություն, ապա առաջին երկբաղադրիչ ուղիղ գծի երկարությունը կլինի k + |
†Եթե ռացիոնաI ուղիղն ունի միավոր երկարություն, ապա առաջին երկբաղադրիչ ուղիղ գծի երկարությունը կլինի <math> k + k\sqrt{1 - k'^2} </math> դա առաջին ապոտոմենն է, որի երկարությունն է՝ <math> k - k\sqrt{1 - k'^2}. </math> [[Պնդում 10.85 | Պնդում 10.85]], հետևյալ <math> x^2 - 2kx + k^2k'^2 = 0. </math> հավասարման արմատներն են։ |
||
| Տող 64. | Տող 63. | ||
Տանենք ԱՑ և ՑԲ երկարություններով հատվածներն այնպես, որ դրանց գումար ԱԲ-ն ԲՑ-ի հետ ունենա հարաբերություն, որը հավասար է ինչ-որ քառակուսու հարաբերությանը մեկ այլ քառակուսուն, և ԱՑ-ի հետ չունենա հաարաբերություն, որը հավասար է ինչ-որ քառակուսու հարաբերությանը մեկ այլ քառակուսուն [[Պնդում 10.28, լեմմա I | Պնդում 10.28, լեմմա I |
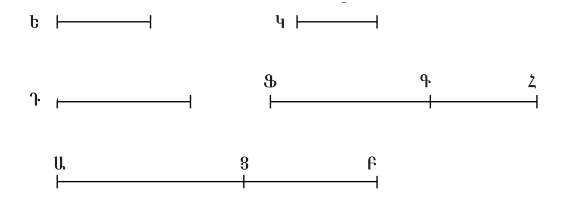
Տանենք ԱՑ և ՑԲ երկարություններով հատվածներն այնպես, որ դրանց գումար ԱԲ-ն ԲՑ-ի հետ ունենա հարաբերություն, որը հավասար է ինչ-որ քառակուսու հարաբերությանը մեկ այլ քառակուսուն, և ԱՑ-ի հետ չունենա հաարաբերություն, որը հավասար է ինչ-որ քառակուսու հարաբերությանը մեկ այլ քառակուսուն [[Պնդում 10.28, լեմմա I | Պնդում 10.28, լեմմա I]]: Տանենք ռացիոնալ Դ երկարությամբ ուղիղը: ԵՖ-ը Դ-ի հետ երկարությամբ համաչափելի է: Հետևաբար ԵՖ-ն ռացիոնալ ուղիղ գիծ է: Եվ թող սահմանվի, որ այնպես, ինչպես CA-ն ունի հարաբերություն AB-ի նկատմամբ, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին ունի հարաբերություն FG-ի վրա կառուցված քառակուսու նկատմամբ [[Պնդում 10.6, հետևանք | Պնդում 10.6, հետևանք]]։ Այսպիսով, ԵՖ-ի քառակուսին համաչափելի է ՖԳ-ի քառակուսուն [[Պնդում 10.6 | Պնդում 10.6 ]]: Ստացվուն է, որ ՖԳ-ն ևս ռացիոնալ ուղի գիծ է: Եվ քանի որ ՑԱ-ն ԱԲ-ի նկատմամբ չունի նույն հարաբերությունը ինչ մի քառակուսի մյուսի նկատմամբ, ԵՖ քառակուսինՖԳ-ի նկատմամբ չունի նույն հարաբերությունը, ինչ մի քառակուսի մյուսի նկատմամբ ևս: Հետևաբար ԵՖ-ն երկարությամբ անհամաչափելի է ՖԳ-ին [[Պնդում 10.9 | Պնդում 10.9]]: Հետևաբար ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր, որոնք միայն քառակուսով են համաչափելի: Այսպիսով, ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է [[Պնդում 10.9 | Պնդում 10.9]]: Ստացվում է, որ ԵՖ-ն ու ՖԳ-ն ռացիոնալ ուղիղ միայն քառակուսով համաչափելի ուղիղ գծեր են:Ուրեմն ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է [[Պնդում 10.36 | Պնդում 10.36]]: Այսպիսով մենք պետք է ցույց տանք, որ այն նաև երկրորդ երկբաղադրիչ ուղիղ գիծ է: Քանի որ, հակադարձ հարաբերությամբ, ինչպես ԲԱ-ն ունի ԱՑ-ի նկատմամբ, այնպես էլ ԳՖ-ի վրա կառուցված քառակուսին ՖԵ-ի վրա կառուցված քառակուսու նկատմամբ [[Պնդում 5.7, հետևանք | Պնդում 5.7, հետևանք]], և ԲԱ-ն ավելի մեծ է, քան ԱՑ-ն, ապա ԳՖ-ի վրա կառուցված քառակուսին նույնպես ավելի մեծ է, քան ՖԵ-ի վրա կառուցված քառակուսին [[Պնդում 5.14 | Պնդում 5.14 ]]։ Թող ԵՖ-ի և Հ-ի վրա կառուցված քառակուսիների գումարը հավասար լինի ԳՖ-ի վրա կառուցված քառակուսուն։ Ուստի, ինչպես ԱԲ-ն ունի հարաբերություն ԲՑ-ի նկատմամբ, այնպես էլ ՖԳ-ի վրա կառուցված քառակուսին ունի հարաբերություն Հ-ի վրա կառուցված քառակուսու նկատմամբ [[Պնդում 5.14 | Պնդում 5.14]]: Բայց ԱԲ-ն ունի ԲՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվ ունի մեկ այլ քառակուսի թվի նկատմամբ։ Ուստի, ՖԳ-ի վրա կառուցված քառակուսին նույնպես ունի Հ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվ ունի մեկ այլ քառակուսի թվի նկատմամբ։ Ուստի, ՖԳ-ն երկարությամբ համաչափելի է Հ-ի հետ [[Պնդում 10.9 | Պնդում 10.9]]։ Ուստի, ՖԳ-ի վրա կառուցված քառակուսին ավելի մեծ է ՖԵ-ի վրա կառուցված քառակուսուց այն քառակուսի չափով, որը ուղիղ գծի վրա է, համաչափելի երկարությամբ ՖԳ-ի հետ։ Եվ ՖԳ-ն և ՖԵ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ Իսկ փոքր հատվածը՝ ՖԵ-ն, երկարությամբ համաչափելի է նախապես տրված ռացիոնալ ուղիղ գծի՝ Դ-ի հետ։ |
||
Ուստի, ԵԳ-ն երկրորդ երկբաղադրիչ ուղիղ գիծն է [[Սահմանում 10.6 | Սահմանում 10.6]]։† Որն էլ հենց պահանջվում էր ցույց տալ: |
Ուստի, ԵԳ-ն երկրորդ երկբաղադրիչ ուղիղ գիծն է [[Սահմանում 10.6 | Սահմանում 10.6]]։† Որն էլ հենց պահանջվում էր ցույց տալ: |
||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երկրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի k |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երկրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի <math> \frac{k}{\sqrt{1 - k'^2}} + k. </math> Սա և երկրորդ ապոտոմեն, որի երկարությունը <math> \frac{k}{\sqrt{1 - k'^2}} - k. </math> է [[Պնդում 10.86 | Պնդում 10.86]], <math> x^2 - \left(\frac{2k}{\sqrt{1 - k'^2}}\right)x + k^2\left[\frac{k'^2}{1 - k'^2}\right] = 0. </math> հավասարման արմատներն են։ |
||
| Տող 86. | Տող 85. | ||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի <math> k^{1/2} \left(1 + \sqrt{1 - k'^2}\right). </math>. Սա և երրորդ ապոտոմեն, որի երկարությունը <math> k^{1/2} \left(1 - \sqrt{1 - k'^2}\right). </math> [[Պնդում 10.87 | Պնդում 10.87]], <math> f x^2 - 2k^{1/2} x + k k'^2 = 0. </math> հավասարման արմատներն են: |
||
| Տող 103. | Տող 102. | ||
Քանի որ ինչպես ԲԱ-ն է ԱՑ-ին հարաբերվում, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսուն ՖԳ-ի վրա կառուցված քառակուսուն, ավելին, ԲԱ-ն մեծ է ԱՑ-ից, ուրեմն քառակուսին ԵՖ-ի վրա մեծ է քառակուսուց ՖԳ-ի վրա։ Հետևաբար, թող ՖԳ-ի և Հ-ի վրա գտնվող քառակուսիների գումարը հավասար լինի ԵՖ-ի վրա գտնվող քառակուսուն։ Ուստի, ինչպես ԱԲ-ն է հարաբերում ԲՑ-ին, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին է հարաբերում Հ-ի վրա գտնվող քառակուսուն։ Եվ ԱԲ-ն ԲՑ-ի հետ չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե այլ քառակուսի թվի հետ։ Ուստի ԵՖ քառակուսին չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե քառակուսի թվի հետ։ Ուստի ԵՖ-ն համաչափելի չէ Հ-ի հետ երկարությամբ։ Ուստի քառակուսին ԵՖ-ի վրա մեծ է ՖԳ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը գտնվում է մի ուղիղ գծի վրա, որը համաչափելի չէ ԵՖ-ի հետ երկարությամբ։ Եվ ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով։ Եվ ԵՖ-ն համաչափելի է Դ-ի հետ երկարությամբ։ Հետևաբար, ԵԳ-ն չորրորդ երկբաղադրիչ ուղիղ գիծ է [[Սահմանում 10.8 | Սահմանում 10.8]]:†։ Ինչն էլ հենց պահանջվում էր ցույց տալ: |
Քանի որ ինչպես ԲԱ-ն է ԱՑ-ին հարաբերվում, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսուն ՖԳ-ի վրա կառուցված քառակուսուն, ավելին, ԲԱ-ն մեծ է ԱՑ-ից, ուրեմն քառակուսին ԵՖ-ի վրա մեծ է քառակուսուց ՖԳ-ի վրա։ Հետևաբար, թող ՖԳ-ի և Հ-ի վրա գտնվող քառակուսիների գումարը հավասար լինի ԵՖ-ի վրա գտնվող քառակուսուն։ Ուստի, ինչպես ԱԲ-ն է հարաբերում ԲՑ-ին, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին է հարաբերում Հ-ի վրա գտնվող քառակուսուն։ Եվ ԱԲ-ն ԲՑ-ի հետ չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե այլ քառակուսի թվի հետ։ Ուստի ԵՖ քառակուսին չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե քառակուսի թվի հետ։ Ուստի ԵՖ-ն համաչափելի չէ Հ-ի հետ երկարությամբ։ Ուստի քառակուսին ԵՖ-ի վրա մեծ է ՖԳ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը գտնվում է մի ուղիղ գծի վրա, որը համաչափելի չէ ԵՖ-ի հետ երկարությամբ։ Եվ ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով։ Եվ ԵՖ-ն համաչափելի է Դ-ի հետ երկարությամբ։ Հետևաբար, ԵԳ-ն չորրորդ երկբաղադրիչ ուղիղ գիծ է [[Սահմանում 10.8 | Սահմանում 10.8]]:†։ Ինչն էլ հենց պահանջվում էր ցույց տալ: |
||
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի k (1+1 |
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի <math> k \left(1 + \frac{1}{\sqrt{1 + k'}}\right). </math> Սա և չորրորդ ապոտոմեն, որի երկարությունը <math> k \left(1 - \frac{1}{\sqrt{1 + k'}}\right). </math> [[Պնդում 10.8 | Պնդում 10.8]], <math> x^2 - 2kx + \frac{k^2 k'}{1 + k'} = 0. </math> հավասարման արմատներն են: |
||
| Տող 118. | Տող 117. | ||
Ուստի ՖԳ-ն համաչափելի չէ Հ-ի հետ երկարությամբ [[Պնդում. 10.9 | Պնդում. 10.9]]։ Ուստի ՖԳ-ի վրա գտնվող քառակուսին մեծ է ԵՖ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը մի ուղիղ գծի վրա է, որը համաչափելի չէ ՖԳ-ի հետ երկարությամբ։ Եվ ԳՖ-ն և ԵՖ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ Եվ ավելի փոքր կողմը` ԵՖ-ն համաչափելի է երկարությամբ այն ռացիոնալ ուղիղ գծի հետ, որը նախկինում տարվել էր Դ-ով†: Ուստի ԵԳ-ն հինգերորդ երկբաղադրիչ ուղիղ գիծ է։ Ինչն էլ հենց պահանջվում էր ցույց տալ: |
Ուստի ՖԳ-ն համաչափելի չէ Հ-ի հետ երկարությամբ [[Պնդում. 10.9 | Պնդում. 10.9]]։ Ուստի ՖԳ-ի վրա գտնվող քառակուսին մեծ է ԵՖ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը մի ուղիղ գծի վրա է, որը համաչափելի չէ ՖԳ-ի հետ երկարությամբ։ Եվ ԳՖ-ն և ԵՖ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ Եվ ավելի փոքր կողմը` ԵՖ-ն համաչափելի է երկարությամբ այն ռացիոնալ ուղիղ գծի հետ, որը նախկինում տարվել էր Դ-ով†: Ուստի ԵԳ-ն հինգերորդ երկբաղադրիչ ուղիղ գիծ է։ Ինչն էլ հենց պահանջվում էր ցույց տալ: |
||
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա հինգերորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի k ( |
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա հինգերորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի <math> k \left(\sqrt{1 + k'} + 1\right). </math> Սա և հինգերորդ ապոտոմեն, որի երկարությունը <math> k \left(\sqrt{1 + k'} - 1\right). </math> [[Պնդում 10.89 | Պնդում 10.89]], <math> x^2 - 2k\sqrt{1 + k'}x + k^2 k' = 0. </math> հավասարման արմատներն են: |
||
| Տող 136. | Տող 135. | ||
Ուրեմն, ՖՀ-ն վեցերորդ երկբաղադրիչ ուղիղ գիծն է [[Սահմանում 10.10 | Սահմանում 10.10]]։† Ինչն էլ պահանջբում էր ցույց տալ: |
Ուրեմն, ՖՀ-ն վեցերորդ երկբաղադրիչ ուղիղ գիծն է [[Սահմանում 10.10 | Սահմանում 10.10]]։† Ինչն էլ պահանջբում էր ցույց տալ: |
||
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա վեցերորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի √k + √k′: Սա և վեցերորդ ապոտոմեն, որի երկարությունը √k −√k′ է [[Պնդում 10.90 | Պնդում 10.90]], |
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա վեցերորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի √k + √k′: Սա և վեցերորդ ապոտոմեն, որի երկարությունը √k −√k′ է [[Պնդում 10.90 | Պնդում 10.90]], <math> x^2 - 2\sqrt{k}x + (k - k') = 0. </math>. հավասարման արմատներն են: |
||
| Տող 169. | Տող 168. | ||
Այսպիսով, ՄՕ-ն և՛ երկբաղադրիչ ուղիղ գիծ է [[Պնդում 10.36 | Պնդում 10.36]], և՛ ԱՑ-ի քառակուսի արմատը: Ինչն էլ հենց պահանջվում էր ապացուցել: |
Այսպիսով, ՄՕ-ն և՛ երկբաղադրիչ ուղիղ գիծ է [[Պնդում 10.36 | Պնդում 10.36]], և՛ ԱՑ-ի քառակուսի արմատը: Ինչն էլ հենց պահանջվում էր ապացուցել: |
||
† Եթե ռացիոնալ ուղիղ գիծը ունի միավոր երկարություն, ապա այս տեսության համաձայն, առաջին երկբաղադրիչ ուղիղ գծի քառակուսի արմատը ևս երկբաղաադրիչ ուղիղ գիծ է: Այն է, առաջին երկբաղադրիչ ուղիղ գիծը ունի k + |
† Եթե ռացիոնալ ուղիղ գիծը ունի միավոր երկարություն, ապա այս տեսության համաձայն, առաջին երկբաղադրիչ ուղիղ գծի քառակուսի արմատը ևս երկբաղաադրիչ ուղիղ գիծ է: Այն է, առաջին երկբաղադրիչ ուղիղ գիծը ունի <math> k + k\sqrt{1 - k'^2}. </math> երկարությունը, որի քառակուսի արմատը <math> \rho \left(1 + \sqrt{k''}\right). </math>-ն է, որտեղ <math> \rho = \frac{pk(1 + k')}{2}. </math> և <math> k'' = \frac{1 - k'}{1 + k'}. </math>. Սա երկբաղադրիչ ուղիղ գծի երկարությունն է (Տես Պնդում 10.36), քանի որ ρ-ն ռացիոնալ է: |
||
| Տող 190. | Տող 189. | ||
Այսպիսով, ՄՕ-ն առաջին երկմիջային ուղիղ գիծ է , ինչն էլ պահանջվում էր ցույց տալ: |
Այսպիսով, ՄՕ-ն առաջին երկմիջային ուղիղ գիծ է , ինչն էլ պահանջվում էր ցույց տալ: |
||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` երկրորդ երկբաղադրիչ ուղիղ գծի քառակուսի արմատը հավասար է k |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` երկրորդ երկբաղադրիչ ուղիղ գծի քառակուսի արմատը հավասար է <math> \frac{k}{\sqrt{1 - k'^2}} + k. </math>, որի քառակուսի արմատը կլինի <math> \rho \left(k''^{1/4} + k''^{3/4}\right). </math>, որտեղ <math> \rho = p \left( \frac{k}{2} \right) \frac{(1 + k')}{(1 - k')}, </math> <math> k'' = \frac{1 - k'}{1 + k'}. </math>: Սա առաջին երկբաղադրիչ ուղիղ գծի երկարությունն է (Տես Պնդում 10.3), քանի որ ρ-ն ռացիոնալ է: |
||
| Տող 208. | Տող 207. | ||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` երրորդ երկբաղադրիչ ուղիղ գծի քառակուսի արմատը երկրորդ երկմիջնորդ ուղիղ գիծ է. այն է` երրորդ երկբաղադրիչ ուղիղ գիծը ունի |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` երրորդ երկբաղադրիչ ուղիղ գծի քառակուսի արմատը երկրորդ երկմիջնորդ ուղիղ գիծ է. այն է` երրորդ երկբաղադրիչ ուղիղ գիծը ունի <math> k^{1/2} \left(1 + \sqrt{1 - k'^2}\right). </math> երկարություն, որի քառակուսի արմատն է` <math> \rho \left(k^{1/4} + \frac{k''^{1/2}}{k^{1/4}}\right). </math>, որտեղ <math> \rho = p \left( \frac{1 + k'}{2} \right). </math> և <math> k'' = \frac{k(1 - k')}{1 + k'}. </math>. Սա երկրորդ երկմիջնորդի երկարությունն է (Տես Պնդում 10.38), քանի որ ρ-ն ռացիոնալ է: |
||
| Տող 227. | Տող 226. | ||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` չորրորդ երկբաղադրիչ ուղիղ գիծն ունի k (1 + 1 |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` չորրորդ երկբաղադրիչ ուղիղ գիծն ունի <math> k \left(1 + \frac{1}{\sqrt{1 + k'}}\right). </math> երկարությունը, որի արմատը <math> \rho q \left[ \frac{1 + \frac{k''}{\sqrt{1 + k''^2}}}{2} \right] + \rho q \left[ \frac{1 - \frac{k''}{\sqrt{1 + k''^2}}}{2} \right]. </math>-ն է, որտեղ ρ = √k և k′′ 2 = k′, սա առանցքային ուղիղ գծի երկարությունն է (Տես Պնդում. 10.39), քանի որ ρ-ն ռացիոնալ է: |
||
| Տող 249. | Տող 248. | ||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` հինգերորդ երկբաղադրիչ ուղիղ գծի արմատը հավասար է ռացիոնալ թվի արմատի և միջնականի գումարին, այն է, հինգերորդ երկբաղադրիչ ուղիղ գծի երկարությունը k ( |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` հինգերորդ երկբաղադրիչ ուղիղ գծի արմատը հավասար է ռացիոնալ թվի արմատի և միջնականի գումարին, այն է, հինգերորդ երկբաղադրիչ ուղիղ գծի երկարությունը <math> k \left(\sqrt{1 + k'} + 1\right). </math> է, որի արմատը <math> \rho q \left[ \frac{\sqrt{1 + k''^2} + k''}{2(1 + k''^2)} \right] + \rho q \left[ \frac{\sqrt{1 + k''^2} - k''}{2(1 + k''^2)} \right]. </math>-ն է, որտեղ ρ = pk (1 + k′′ 2) և k′′ 2 = k, սա ռացիոնալ թվի արմատի և միջնականի գումարն է (Տես Պնդում. 10.40), քանի որ ρ-ն ռացիոնալ է: |
||
| Տող 267. | Տող 266. | ||
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` վեցերորս երկբաղադրիչ ուղիղ գիծը երկու միջնականների գումարի արմատն է, այն է, վեցերորդ ուղիղ գիծն ունի √k + √k′ երկարություն, որի քառակուսի արմատն է |
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` վեցերորս երկբաղադրիչ ուղիղ գիծը երկու միջնականների գումարի արմատն է, այն է, վեցերորդ ուղիղ գիծն ունի √k + √k′ երկարություն, որի քառակուսի արմատն է |
||
<math> k^{1/4} \left[ q \left( \frac{1 + \frac{k''}{\sqrt{1 + k''^2}}}{2} \right) + q \left( \frac{1 - \frac{k''}{\sqrt{1 + k''^2}}}{2} \right) \right]. </math>, որտեղ k′′ 2 = (k −k′)/k′ . Սա երկու միջնականների գումարի քառակուսի արմատն է (Տես Պնդում 10.41): |
|||
Ընթացիկ տարբերակը 02:29, 21 դեկտեմբերի 2024-ի դրությամբ
Պնդում 46
Ռացիոնալ թվի քառակուսային արմատի և միջնականի գումարը կարելի է բաժանել դրան պատկանող հատվածների) միայն մեկ կետում։†
Ենթադրենք ԱԲ-ն ռացիոնալ թվի քառակուսային արմատի և միջնականի գումարն է, որը բաժանվել է Ց կետում, այնպես, որ ԱՑ և ՑԲ հատվածների մակերեսները քառակուսիները) անհամաչափելի են, այնպես, որ ԱՑ և ՑԲ հատվածների քառակուսիների գումարը միջնական է և հավասար է ԱՑ և ՑԲ ռացիոնալ երկարություններով հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկին: Այն է, ԱԲ հատվածը այս կերպ հնարավոր չէ բաժանել այլ կետով: Ենթադրենք, ԱԲ-ն հնարավոր է Դ կետով ևս բաժանել այնպես, որ ԱԴ և ԴԲ-ի քառակուսիները ևս անհամաչափելի են, այսպիսով, ԱԴ և ԴԲ հատվածների երկարությունների քառակուսիների գումարը հավասար է միջնականին և ԱԴ և ԴԲ ռացիոնալ հատվածներով կազմված ուղղանկյան կրկնապատկին: Այսպիսով, քանի որ ինչ որ քանակության և ԱՑ, ՑԲ հատվածները պարունակող ուղղանկյան կրկնակի մակերեսի արտադրյալը հավասար չէ ԴԲ, ԱԴ հատվածնեով կազմված ուղղանկյան մակերեսին, հետևաբար ԱԴ և ԴԲ հատվածների քառակեւսիների գումարը ևս հավասար չէ ԱՑ և ՑԲ հատվածների թառակուսիների գումարին: Եվ ԱՑ, ՑԲ հատվածներով կազմված ուղղանկյան մակերեսի կրկնապատիկը ինչ-որ ռացիոնալ թվով մեծ է ԱՑ, ՑԲ հատվածներով կազմված ուղղանկյան մակերեսի կրկնապատկից: Հետևաբար, ԱԴ և ԴԲ քառակուսիների գումարը ևս ինչ-որ ռացիոնալ թվով արտահայտվող մակերեսով մեծ է ԱՑ և ՑԲ քառակուսիների գումարից, չնայած որ երկուսն էլ միջնականներ են: Այսպիսի բան անհնարին է: Այսպիսով, ռացիոնալ թվի քառակուսային արմատի և միջնականի գումարը չի կարող բաժանվել բաղկացուցիչ մասերի մեկ այլ կետում: Այն կարող է այդպես բաժանվել միայն մեկ կետում, որն էլ և պահանջվում էր ցույց տալ:
† Այլ կերպ ասած` ունի միայն մեկ արմատ, այն է: k′ = k.
Պնդում 47
Երկու միջնական մակերեսների գումարի քառակուսային արմատը կարող է բաժանվել մասերի միայն մեկ կետով:†
Ենթադրենք ԱԲ-ն երկու միջնական մակերեսների գումարի քառակուսային արմատն է, որը բաժանվել է Ց կետով այնպես, որ ԱՑ և ՑԲ հատվածներով կազմված քառակուսիները անհամաչափելի են, այսպիսով, ԱՑ և ՑԲ քառակուսիների գումարը միջնական է, ԱՑ և ՑԲ կողմերով կազմված ուղղանկյան մակերեսը միջննական է, ավելի, անհամաչափելի է ԱՑ և ՑԲ քառակուսիների գումարի հետ: Այն է, ԱԲ-ն չի կարող որևէ այլ կետով բաժանվել այնպես, որ բավարարի վերոնշյալ պայմաններին:
Ենթադրենք այն Դ կետով բաժանվել է հատվածների այնպես, որ ԱՑ-ն կրկին ակնհայտորեն հավասար չէ ԴԲ-ին, բայց ԱՑ-ն ըստ հիպոթեզի ավելի մեծ է: Տանենք ԵՖ ռացիոնալ երկարությամբ ուղիղ գիծը: Ենթադրենք, ԵԳ-ն, (որը հավասր է ԱՑ, ՑԲ հատվածներով կառուցված քառակուսիների գումարին), և ՀԿ-ն, (որը հավասար է ԱՑ, ՑԲ կողմերով ուղղանկյան մակերեսի կրկնապատիկին), օգտագործվել են որպես ԵՖ-ի հետ կազմված ուղղանկյունների բարձրություններ: Այսպիսով, ԵԿ-ն հավասար է ԱԲ քառակուսուն: Նաև ենթադրենք, որ ԵԼ-ը, որը հավասար է ԱԴ և ԴԲ քառակուսիների գումարին, օգտագործվել է որպես ԵՖ-ով կազմված ուղղանկյան կողմ: Այսպիսով մնացածը` ԱԴ և ԴԲ հատվածներով կազմված ուղղանկյան մակերեսի կրկնապատիկը, հավասար է ՄԿ-ին: Եվ քանի որ ԱՑ, ՑԲ քառակուսիների գումարը ենթադրաբար միջնական էր, ԵԳ-ն ևս միջնական է և ռացիոնալ ԵՖ երկարությամբ հատվածի հետ կազմում է ուղղանկյուն: Հետևաբար ՀԵ-ն ռացիոնալ է ևերկարությամբ անհամաչափելի է ԵՖ-ի հետ: Նույն պատճառով, ՀՆ-ն ևս ռացիոնալ է և ԵՖ-ի հետ անհամաչափելի: Եվ քանի որ ԱՑ, ՑԲ քառակուսիների գումարը անհամաչափելի է ԱՑ, ՑԲ հատվածներով կազմված ուղղանկյան կրկնակի մակերեսի հետ, ԵԳ-ն ևս անհամաչափելի է ԳՆ-ի հետ: Հետևաբար, ԵՀ-ն նաև անհամաչափելի է ՀՆ-ին: Եվ, դրանք երկուսն էլ ռացիոնալ ուղիղ գծեր են: Այսպիսով, ԵՀ-ն և ՀՆ-ն ռացիոնալ ուղիղ գծեր են, և միայն դրանցով կազմված քառակուսինեն են անհամաչափելի: Այսպիսով, ԵՆ-ն երկբաղադրիչ ուղիղ գիծ է, որը Հ կետով բաժանված է դրան պատկանող կետերի: Նման կերպով կարող ենք նաև ցույց տալ, որ այն բաժանված է Մ կետով: Ավելին, ԵՀ-ն հավասար չէ ՄՆ-ին: Այն է, երկբաղադրիչ ուղիղ գիծը բաժանվում է դրան պատկանող հատվածների տարբեր կետերով: Սա անհեթեթություն է: Հետևաբար, երկու միջնական մակերեսների գումարի քառակուսի արմատը հնարավոր չէ տարբեր կետերով բաժանել դրան պատկանող հատվածների: Այսպիսով, այն կարող է այդպես բաժանվել միայն մեկ կետով:
† Այլ կերպ ասած, ունի միայն մեկ արմատ, այն է, k′′ = k և k′′′ = k′.
Սահմանում II
5. Եթե տրված է ռացիոնալ ուղիղ գիծ և երկբաղադրիչ ուղիղ գիծ, որը բաժանված է իրեն պատկանող մասերի, որոնցից ավելի մեծ մասի վրա կառուցված քառակուսին ավելի մեծ է փոքր մասի վրա կառուցված քառակուսուց, այնպիսի քառակուսու չափով, որը կառուցված է մեծ կողմին համաչափելի է երկարությամբ գծի վրա, ապա եթե մեծ կողմը երկարությամբ համաչափելի է նախապես տարված ուղիղ գծին, ամբողջական ուղիղ գիծը կարող է կոչվել առաջնային երկբաղադրիչ ուղիղ գիծ: 6. Եվ եթե դրանցից փոքրը երկարությամբ համաչափելի նախապես գծված ռացիոնալ երկարությամբ ուղիղ գծին, ապա այդ ամբողջ ուղիղը կարող ենք անվանել երկրորդ երկբաղադրիչ ուղիղ գիծ: 7. Եվ եթե դրանցից ոչ մեկը երկարությամբ համաչափելի չէ նախապես տարված ռացիոնալ երկարությամբ ուղիղ գծին, ապա այդ ամբողջ ուղիղը կարող ենք անվանել երրորդ երկբաղադրիչ ուղիղ գիծ: 8. Այսպիսով, եթե մեծ կողմի քառակուսին փոքր կողմի քառակուսուց մեծ է ինչ-ոչ ուղիղ գծի վրա կառուցված քառակուսով, որը երկարությամբ անհամաչափելի է մեծ կողմին, ապա եթե մեծ կողմը համաչափելի է նախկինում տարված ռացիոնալ ուղիղ գծին, ուրեմն ամբողջ այդ ուղիղը կանվանենք չորրորդ երկբաղադրիչ ուղիղ գիծ: 9. Եթե փոքր կողմն է համաչափելի` հինգերորդ երկբաղադրիչ ուղիղ գիծ: 10. Եթե դրանցից և ոչ մեկը համաչափելի չեն` վեցերորդ երկբաղադրիչ ուղիղ գիծ:
Պնդում 48
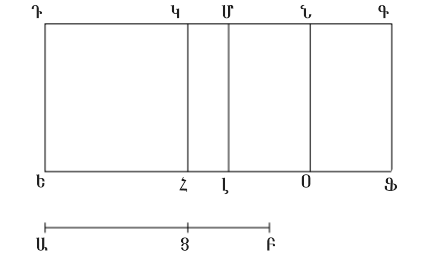
Առաջին երկբաղադրիչ ուղիղ գիծը գտնելու համար: Տանենք ԱՑ և ՑԲ երկարություններով հատվածներն այնպես, որ դրանց ԱԲ գումարը ԲՑ-ի նկատմամբ ունենա այնպիսի հարաբերություն ինչպիսին (որևէ) քառակուսի թիվ ունի (մեկ այլ) քառակուսի թվի նկատմամբ, բայց չունենա ՑԱ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին (որևէ) քառակուսի թիվ ունի (մեկ այլ) քառակուսի թվի նկատմամբ Պնդում 10.28, լեմմա I: Նաև տանենք ռացիոնալ երկարությամբ Դ ուղիղ գիծը: Բացի այդ, ԵՖ-ն երկարոթյամբ համաչափելի է Դ-ին: Ուստի ԵՖ-ը նույնպես ռացիոնալ է Սահմանում 10.3։ Եվ թող սահմանվի, որ այնպես ինչպես ԲԱ-ն է հարաբերվում ԱՑ-ին, նույն կերպ էլ ԵՖ-ի քառակուսին ՖԳ-ի քառակուսուն Պնդում 10.6 հետևանք : ԵՎ ԱԲ-ն ԱՑ-ի հետ ունի այն նույն հարաբերությունը, ինչը ինչ-որ թիվ ունի մեկ այլ թվի հետ: Այսպիսով, ԵՖ քառակուսին ՖԳ քառակուսու նկատմամբ ունի այն նույն հարաբերությունը ինչ մի թիվ ունի մյուսի նկատմամբ: Հետևաբար ԵՖ-ով կազմված թառակուսին համաչափելի է ՖԳ-ով կառուցված քառակուսուն Պնդում 10.6։ Նաև ԵՖ-ն ռացիոնալ է: հետևաբար ՖԳ-ն ևս ռացիոնալ է: Եվ քանի որ ԲԱ-ն ԱՑ-ի նկատմամբ չունի այն նույն հարաբերությունը ինչ մի քառակուսի ունի մյուսի նկատմամբ, հետևաբար ԵՖ քառակուսին չունի ՖԳ-ի նկատմամբ այնպիսի հարաբերություն ինչպես մի քառակուսին մյուսի նկատմամբ ունի ևս: Հետևաբար ԵՖ-ն երկարությամբ անհամաչափելի է ՖԳ-ին Պնդում 10.9։ Ստացվում է, որ ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով: Հետևաբար ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է Պնդում 10.36։ Այն է, դա նաև առաջին երկբաղադրիչ ուղիղ գիծ է:
Քանի որ ինչպես ԲԱ-ն ԱՑ-ին է հարաբերվում, այնպես էլ ԵՖ քառակուսին ՖԳ քառակուսուն և ԲԱ-ն մեծ է ԱՑ-ից, հետևաբար ԵՖ քառակուսոին ևս մեծ է ՖԳ-ից Պնդում 5.14։ Այդ իսկ պատճառով ՖԳ քառակուսու և Հ-ի գումարը թող լինի ԵՖ քառակուսուն: Եվ քանի որ ինչպես ԲԱ-ն ԱՑ-ին, այնպես էլ ԵՖ քառակուսին ՖԳ-ին, ապա ենթադրաբար, ինչպես AB-ն ունի հարաբերություն BC-ի նկատմամբ, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին ունի հարաբերություն H-ի վրա կառուցված քառակուսու նկատմամբ Պնդում 5.19։ ԵՎ ԱԲ-ն ԲՑ-ի նկատմամբ ունի այն հարաբերությունը, որը ինչ-որ քառակուսի ունի մեկ այլ քառակուսու նկատմամբ: Այսպիսով, ԵՖ քառակուսին Հ ով կազմված քառակուսու նկատմամբ ևս ունի նույն հարաբերությունը ինչ ինչ-որ քառակուսի ունի մեկ այլ քառակուսու նկատմամբ: Հետևաբար ԵՖ-ն երկարությամբ համաչափելի է Հ-ին Պնդում 10.9։ Այսպիսով, ԵՖ քառակուսին Ֆգ քառակուսուց մեծ է մի քառակուսիով որը կառուցված է մի ուղիղ գծից, որը երկարությամբ համաչափելի է ԵՖ-ին: Եվ ԵՖ-ն ու ՖԳ-ն ռացիոնալ ուղիղ գծեր են: Եվ ԵՖ-ն երոկարությամբ համաչափելի է Դ-ին:
Այսպիսով, ԵԳ-ն առաջին երկբաղադրիչ ուղիղ գիծ է Պնդում 10.5։ † Որն էլ և պահանջվուն էր ցույց տալ:
†Եթե ռացիոնաI ուղիղն ունի միավոր երկարություն, ապա առաջին երկբաղադրիչ ուղիղ գծի երկարությունը կլինի դա առաջին ապոտոմենն է, որի երկարությունն է՝ Պնդում 10.85, հետևյալ հավասարման արմատներն են։
Պնդում 49
Երկրորդ երկբաղադրիչ ուղիղ գիծը գտնելու համար:
Տանենք ԱՑ և ՑԲ երկարություններով հատվածներն այնպես, որ դրանց գումար ԱԲ-ն ԲՑ-ի հետ ունենա հարաբերություն, որը հավասար է ինչ-որ քառակուսու հարաբերությանը մեկ այլ քառակուսուն, և ԱՑ-ի հետ չունենա հաարաբերություն, որը հավասար է ինչ-որ քառակուսու հարաբերությանը մեկ այլ քառակուսուն Պնդում 10.28, լեմմա I: Տանենք ռացիոնալ Դ երկարությամբ ուղիղը: ԵՖ-ը Դ-ի հետ երկարությամբ համաչափելի է: Հետևաբար ԵՖ-ն ռացիոնալ ուղիղ գիծ է: Եվ թող սահմանվի, որ այնպես, ինչպես CA-ն ունի հարաբերություն AB-ի նկատմամբ, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին ունի հարաբերություն FG-ի վրա կառուցված քառակուսու նկատմամբ Պնդում 10.6, հետևանք։ Այսպիսով, ԵՖ-ի քառակուսին համաչափելի է ՖԳ-ի քառակուսուն Պնդում 10.6 : Ստացվուն է, որ ՖԳ-ն ևս ռացիոնալ ուղի գիծ է: Եվ քանի որ ՑԱ-ն ԱԲ-ի նկատմամբ չունի նույն հարաբերությունը ինչ մի քառակուսի մյուսի նկատմամբ, ԵՖ քառակուսինՖԳ-ի նկատմամբ չունի նույն հարաբերությունը, ինչ մի քառակուսի մյուսի նկատմամբ ևս: Հետևաբար ԵՖ-ն երկարությամբ անհամաչափելի է ՖԳ-ին Պնդում 10.9: Հետևաբար ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր, որոնք միայն քառակուսով են համաչափելի: Այսպիսով, ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է Պնդում 10.9: Ստացվում է, որ ԵՖ-ն ու ՖԳ-ն ռացիոնալ ուղիղ միայն քառակուսով համաչափելի ուղիղ գծեր են:Ուրեմն ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է Պնդում 10.36: Այսպիսով մենք պետք է ցույց տանք, որ այն նաև երկրորդ երկբաղադրիչ ուղիղ գիծ է: Քանի որ, հակադարձ հարաբերությամբ, ինչպես ԲԱ-ն ունի ԱՑ-ի նկատմամբ, այնպես էլ ԳՖ-ի վրա կառուցված քառակուսին ՖԵ-ի վրա կառուցված քառակուսու նկատմամբ Պնդում 5.7, հետևանք, և ԲԱ-ն ավելի մեծ է, քան ԱՑ-ն, ապա ԳՖ-ի վրա կառուցված քառակուսին նույնպես ավելի մեծ է, քան ՖԵ-ի վրա կառուցված քառակուսին Պնդում 5.14 ։ Թող ԵՖ-ի և Հ-ի վրա կառուցված քառակուսիների գումարը հավասար լինի ԳՖ-ի վրա կառուցված քառակուսուն։ Ուստի, ինչպես ԱԲ-ն ունի հարաբերություն ԲՑ-ի նկատմամբ, այնպես էլ ՖԳ-ի վրա կառուցված քառակուսին ունի հարաբերություն Հ-ի վրա կառուցված քառակուսու նկատմամբ Պնդում 5.14: Բայց ԱԲ-ն ունի ԲՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվ ունի մեկ այլ քառակուսի թվի նկատմամբ։ Ուստի, ՖԳ-ի վրա կառուցված քառակուսին նույնպես ունի Հ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվ ունի մեկ այլ քառակուսի թվի նկատմամբ։ Ուստի, ՖԳ-ն երկարությամբ համաչափելի է Հ-ի հետ Պնդում 10.9։ Ուստի, ՖԳ-ի վրա կառուցված քառակուսին ավելի մեծ է ՖԵ-ի վրա կառուցված քառակուսուց այն քառակուսի չափով, որը ուղիղ գծի վրա է, համաչափելի երկարությամբ ՖԳ-ի հետ։ Եվ ՖԳ-ն և ՖԵ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ Իսկ փոքր հատվածը՝ ՖԵ-ն, երկարությամբ համաչափելի է նախապես տրված ռացիոնալ ուղիղ գծի՝ Դ-ի հետ։
Ուստի, ԵԳ-ն երկրորդ երկբաղադրիչ ուղիղ գիծն է Սահմանում 10.6։† Որն էլ հենց պահանջվում էր ցույց տալ:
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երկրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի Սա և երկրորդ ապոտոմեն, որի երկարությունը է Պնդում 10.86, հավասարման արմատներն են։
Պնդում 50
Երրորդ երկբաղադրիչ ուղիղ գիծը գտնելու համար:
Թող երկու թվեր՝ ԱՑ և ՑԲ, տրվեն այնպես, որ դրանց գումարը՝ ԱԲ-ն, ունենա ԲՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ, բայց չունենա ԱՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ։ Եվ թող տրվի ևս մեկ ոչ քառակուսի թիվ՝ Դ, և թող Դ-ն չունենա ԲԱ-ի կամ ԱՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ։ Եվ թող ինչ-որ ռացիոնալ ուղիղ գիծ՝ Ե, տրվի, և թող սահմանվի, որ ինչպես Դ-ն ունի ԱԲ-ի նկատմամբ, այնպես էլ Ե-ի վրա կառուցված քառակուսին ունի ՖԳ-ի վրա կառուցված քառակուսու նկատմամբ հարաբերություն Պնդում 10.6, հետևանք։ Ուստի Ե-ի վրա կառուցված քառակուսին համաչափելի է ՖԳ-ի վրա կառուցված քառակուսու հետ Պնդում 10.6։ Ե-ն ռացիոնալ ուղիղ գիծ է։ Ուստի ՖԳ-ն նույնպես ռացիոնալ ուղիղ գիծ է։ Եվ քանի որ Դ-ն չունի ԱԲ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ, ապա Ե-ի վրա կառուցված քառակուսին չի կարող ունենալ ՖԳ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ։ Ուստի Ե-ն երկարությամբ անհամաչափ է ՖԳ-ի հետ Պնդում 10.9։
Նույն ձևով, թող սահմանվի, որ ինչպես ԲԱ-ն ունի ԱՑ-ի նկատմամբ, այնպես էլ ՖԳ-ի վրա կառուցված քառակուսին ունի ԳՀ-ի վրա կառուցված քառակուսու նկատմամբ հարաբերություն [[Պնդում 10.6, հետևանք]։ Ուստի ՖԳ-ի վրա կառուցված քառակուսին համաչափելի է ԳՀ-ի վրա կառուցված քառակուսու հետ։ Եվ ՖԳ-ն ռացիոնալ ուղիղ գիծ է։ Ուստի ԳՀ-ն նույնպես ռացիոնալ ուղիղ գիծ է։ Եվ քանի որ ԲԱ-ն չունի ԱՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ, ապա ՖԳ-ի վրա կառուցված քառակուսին չի կարող ունենալ ԳՀ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի մեկ այլ քառակուսի թվի նկատմամբ։ Ուստի ՖԳ-ն երկարությամբ անհամաչափ է ԳՀ-ի հետ։
ՖԳ-ն և ԳՀ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ Ուստի ՖՀ-ն երկբաղադրիչ ուղիղ գիծ է [[Պնդում 10.36]։ Ուստի սա նույնպես երրորդ երկբաղադրիչ ուղիղ գիծ է։ Քանի որ ինչպես Դ-ն ունի ԱԲ-ի նկատմամբ հարաբերություն, այնպես էլ Ե-ի վրա կառուցված քառակուսին ունի ՖԳ-ի վրա կառուցված քառակուսու նկատմամբ, և ինչպես ԲԱ-ն ունի ԱՑ-ի նկատմամբ հարաբերություն, այնպես էլ ՖԳ-ի վրա կառուցված քառակուսին ունի ԳՀ-ի վրա կառուցված քառակուսու նկատմամբ, ուստի, ըստ հավասարության, ինչպես Դ-ն ունի ԱՑ-ի նկատմամբ հարաբերություն, այնպես էլ Ե-ի վրա կառուցված քառակուսին ունի ԳՀ-ի վրա կառուցված քառակուսու նկատմամբ [[Պնդում 5.22] | Պնդում 5.22]]։ Եվ Դ-ն չունի ԱՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ: Ուստի Ե-ն չունի ԳՀ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ։ Ուստի Ե-ն անհամաչափելի է երկարությամբ ԳՀ-ի հետ Պնդում 10.9։ Եվ քանի որ ԲԱ-ն հարաբերվում է ԱՑ-ին, ՖԳ-ի վրա կառուցված քառակուսին ունի ԳՀ-ի վրա կառուցված քառակուսու նկատմամբ նույն հարաբերությունը։ Ուստի ՖԳ-ի վրա կառուցված քառակուսին ավելի մեծ է, քան ԳՀ-ի վրա կառուցված քառակուսին։ Հետևաբար, թող ԳՀ-ի և Կ-ի վրա կառուցված քառակուսիների գումարը հավասար լինի ՖԳ-ի վրա կառուցված քառակուսուն։ Ուստի, ըստ փոխարկման, ինչպես ԱԲ-ն ունի ԲՑ-ի նկատմամբ, այնպես էլ ՖԳ-ի վրա կառուցված քառակուսին ունի Կ-ի վրա կառուցված քառակուսու նկատմամբ հարաբերություն Պնդում 5.19 հետևանք։ Եվ ԱԲ-ն ունի ԲՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ։ Ուստի ՖԳ-ի վրա կառուցված քառակուսին նույնպես ունի Կ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ։ Ուստի ՖԳ-ն համաչափելի է երկարությամբ Կ-ի հետ Պնդում 10.9։ Հետևաբար ՖԳ-ի վրա կառուցված քառակուսին ավելի մեծ է, քան ԳՀ-ի վրա կառուցված քառակուսին Կ-ի հետ երկարությամբ համաչափելի ուղիղ գծի վրա կառուցված քառակուսով։ Եվ ՖԳ-ն և ԳՀ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով, և նրանցից ոչ մեկը համաչափելի չէ Ե-ի հետ։
Ուստի ՖՀ-ն երրորդ երկբաղադրիչ ուղիղ գիծ է։ Ինչն էլ հենց պահանջվում էր ցույց տալ Սահմանում 10.7:†
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի . Սա և երրորդ ապոտոմեն, որի երկարությունը Պնդում 10.87, հավասարման արմատներն են:
Պնդում 51
Չորրորդ երկբաղադրիչ ուղիղ գիծը գտնելու համար:
Թող ԱՑ և ՑԲ թվերը տարված լինեն այնպես, որ ԱԲ-ն չունենա ՑԲ-ի կամ ԱՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ։ Տանենք ռացիոնալ ուղիղ գիծ Դ երկարությամբ։ Եվ թող ԵՖ ուղիղ գիծը լինի համաչափելի երկարությամբ Դ-ի հետ։ Ուստի ԵՖ-ն նույնպես ռացիոնալ ուղիղ գիծ է։ Ենթադրենք, որ ինչպես թիվ ԲԱ-ն ունի ԱՑ-ի նկատմամբ հարաբերություն, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին ունի ՖԳ-ի վրա կառուցված քառակուսու նկատմամբ։ Ուստի ԵՖ-ի վրա կառուցված քառակուսին համաչափելի է ՖԳ-ի վրա կառուցված քառակուսու հետ։ Ուստի ՖԳ-ն նույնպես ռացիոնալ ուղիղ գիծ է։ Եվ քանի որ ԲԱ-ն չունի ԱՑ-ի նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ, ապա ԵՖ-ի վրա կառուցված քառակուսին նույնպես չունի ՖԳ-ի վրա կառուցված քառակուսու նկատմամբ այնպիսի հարաբերություն, ինչպիսին որևէ քառակուսի թիվն ունի որևէ քառակուսի թվի նկատմամբ։ Ուստի ԵՖ-ն համաչափելի չէ ՖԳ-ի հետ երկարությամբ։ Ուստի ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով։ Հետևաբար, ԵԳ-ն բինոմիալ ուղիղ գիծ է։ Ուստի ասում եմ, որ այն նաև չորրորդ բինոմիալ ուղիղ գիծ է։
Քանի որ ինչպես ԲԱ-ն է ԱՑ-ին հարաբերվում, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսուն ՖԳ-ի վրա կառուցված քառակուսուն, ավելին, ԲԱ-ն մեծ է ԱՑ-ից, ուրեմն քառակուսին ԵՖ-ի վրա մեծ է քառակուսուց ՖԳ-ի վրա։ Հետևաբար, թող ՖԳ-ի և Հ-ի վրա գտնվող քառակուսիների գումարը հավասար լինի ԵՖ-ի վրա գտնվող քառակուսուն։ Ուստի, ինչպես ԱԲ-ն է հարաբերում ԲՑ-ին, այնպես էլ ԵՖ-ի վրա կառուցված քառակուսին է հարաբերում Հ-ի վրա գտնվող քառակուսուն։ Եվ ԱԲ-ն ԲՑ-ի հետ չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե այլ քառակուսի թվի հետ։ Ուստի ԵՖ քառակուսին չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե քառակուսի թվի հետ։ Ուստի ԵՖ-ն համաչափելի չէ Հ-ի հետ երկարությամբ։ Ուստի քառակուսին ԵՖ-ի վրա մեծ է ՖԳ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը գտնվում է մի ուղիղ գծի վրա, որը համաչափելի չէ ԵՖ-ի հետ երկարությամբ։ Եվ ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով։ Եվ ԵՖ-ն համաչափելի է Դ-ի հետ երկարությամբ։ Հետևաբար, ԵԳ-ն չորրորդ երկբաղադրիչ ուղիղ գիծ է Սահմանում 10.8:†։ Ինչն էլ հենց պահանջվում էր ցույց տալ:
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա երրորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի Սա և չորրորդ ապոտոմեն, որի երկարությունը Պնդում 10.8, հավասարման արմատներն են:
Պնդում 52
Հինգերորդ երկբաղադրիչ ուղիղ գիծը գտնելու համար:
Թող ԱՑ և ՑԲ հատվածները տարվեն այնպես, որ ԱԲ-ն նրանցից որևէ մեկի հետ չունենա այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե քառակուսի թվի հետ [[Պնդում 10.38 լեմմա].։ Տանենք նաև Դ ռացիոնալ երկարությամբ ուղիղ։ Թող ԵՖ-ն երկարությամբ համաչափելի լինի Դ-ի հետ: Ուստի ԵՖ-ն ռացիոնալ ուղիղ գիծ է։ Ենթադրենք ինչպես ԱՑ-ն է ԱԲ-ին հարաբերում, այնպես էլ ԵՖ-ի վրա գտնվող քառակուսին է ՖԳ-ի վրա գտնվող քառակուսուն հարաբերում [[Պնդում 10.6 հետևանք]։ Եվ ԱՑ-նմ ԱԲ-ի հետ չունի այն հարաբերությունը, որը որևիցե քառակուսի թիվ ունի որևիցե քառակուսի թվի հետ։ Ուստի ԵՖ-ի վրա գտնվող քառակուսին ՖԳ-ի վրա գտնվող քառակուսու հետ նույնպես չունի այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուստի ԵՖ-ն և ՖԳ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով Պնդում 10.9։ Ուստի ԵԳ-ն երկբաղադրիչ ուղիղ գիծ է Պնդում. 10.36։ Ուրեմն, կարող ենք պնդել, որ այն նաև հինգերորդ բինոմիական ուղիղ գիծ է։
Քանի որ ինչպես ԱՑ-ն հարաբերում է ԱԲ-ին, այնպես էլ ԵՖ-ի վրա գտնվող քառակուսին է հարաբերում ՖԳ-ի վրա գտնվող քառակուսուն, համապատասխանաբար, ինչպես ԲԱ-ն ԱՑ-ին, այնպես էլ ՖԳ-ի վրա գտնվող քառակուսին ԵՖ-ի վրա գտնվող քառակուսուն Պնդում 5.7։ Ուստի ԳՖ-ի վրա գտնվող քառակուսին մեծ է ԵՖ-ի վրա գտնվող քառակուսուց Պնդում 5.14։ Հետևաբար, թող ԵՖ-ի և Հ-ի վրա գտնվող քառակուսիների գումարը հավասար լինի ԳՖ-ի վրա գտնվող քառակուսուն։ Ուստի փոխակերպման միջոցով, ինչպես ԱԲ թիվը ՑԲ-ին, այնպես էլ ԳՖ-ի վրա գտնվող քառակուսին Հ-ի վրա գտնվող քառակուսուն է հարաբերում Պնդում 5.19։ Եվ ԱԲ-ն ՑԲ-ի հետ չունի այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուստի ՖԳ-ի վրա գտնվող քառակուսին Հ-ի վրա գտնվող քառակուսու հետ նույնպես չունի այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։
Ուստի ՖԳ-ն համաչափելի չէ Հ-ի հետ երկարությամբ Պնդում. 10.9։ Ուստի ՖԳ-ի վրա գտնվող քառակուսին մեծ է ԵՖ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը մի ուղիղ գծի վրա է, որը համաչափելի չէ ՖԳ-ի հետ երկարությամբ։ Եվ ԳՖ-ն և ԵՖ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ Եվ ավելի փոքր կողմը` ԵՖ-ն համաչափելի է երկարությամբ այն ռացիոնալ ուղիղ գծի հետ, որը նախկինում տարվել էր Դ-ով†: Ուստի ԵԳ-ն հինգերորդ երկբաղադրիչ ուղիղ գիծ է։ Ինչն էլ հենց պահանջվում էր ցույց տալ:
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա հինգերորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի Սա և հինգերորդ ապոտոմեն, որի երկարությունը Պնդում 10.89, հավասարման արմատներն են:
Պնդում 53
Հինգերորդ երկբաղադրիչ ուղիղ գիծը գտնելու համար:
Ահա ձեր տրամադրած տեքստի հայերեն թարգմանությունը.
Թող ԱՑ և ՑԲ թվերը դրվեն այնպես, որ ԱԲ-ը նրանցից յուրաքանչյուրի հետ չունենա այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Եվ թող Դ-ն նույնպես լինի ուրիշ թիվ, որը քառակուսի չէ և չունի ԲԱ-ի և ԱՑ-ի հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ Պնդում. 10.28, լեմմաI։ Նաև տանենք Ե ռացիոնալ երկարությամբ ուղիղ գիծ։ Ինչպես Դ-ն է ԱԲ-ի հարաբերում, այնպես էլ Ե-ի վրա գտնվող քառակուսին ՖԳ-ի վրա գտնվող քառակուսուն է հարաբերում Պնդում. 10.6, հետևանք։ Ուրեմն, Ե-ի վրա գտնվող քառակուսին համաչափելի է ՖԳ-ի վրա գտնվող քառակուսու հետ Պնդում 10.6։ Եվ Ե-ն ռացիոնալ է։ Ուրեմն, ՖԳ-ն նույնպես ռացիոնալ է։ Եվ քանի որ Դ-ն ԱԲ-ի հետ չունի այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ, Ե-ի վրա գտնվող քառակուսին նույնպես չունի ՖԳ-ի վրա գտնվող քառակուսու հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուրեմն, Ե-ն համաչափելի չէ երկարությամբ ՖԳ-ի հետ Պնդում 10.9։
Կրկին ենթադրենք, որ ինչպես ԲԱ-ն է ԱՑ-ին հարաբերում, այնպես էլ ՖԳ-ի վրա գտնվող քառակուսին ԳՀ-ի վրա գտնվող քառակուսուն Պնդում. 10.6, հետևանք։ Ուրեմն, ՖԳ-ի վրա գտնվող քառակուսին համաչափելի է ԳՀ-ի վրա գտնվող քառակուսու հետ Պնդում 10.6։ ԳՀ-ի վրա գտնվող քառակուսին ռացիոնալ է։ Ուրեմն, ԳՀ-ն ռացիոնալ է։ Եվ քանի որ ԲԱ-ն ԱՑ-ի հետ չունի այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ, ՖԳ-ի վրա գտնվող քառակուսին նույնպես չունի ԳՀ-ի վրա գտնվող քառակուսու հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուրեմն, ՖԳ-ն համաչափելի չէ երկարությամբ ԳՀ-ի հետ Պնդում 10.9։
Ուրեմն, ՖԳ-ն և ԳՀ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով։ Ուրեմն, ՖՀ-ն երկբաղոդրիչ ուղիղ գիծ է Պնդում 10.36։ Հետևաբար, մենք պետք է ցույց տանք, որ դա նաև վեցերորդ երկբաղադրիչ ուղիղ գիծն է։
Քանի որ ինչպես Դ-ն է ԱԲ-ին հարաբերում, այնպես էլ Ե-ի վրա գտնվող քառակուսին ՖԳ-ի վրա գտնվող քառակուսուն, և ինչպես ԲԱ-ն է ԱՑ-ին, այնպես էլ ՖԳ-ի վրա գտնվող քառակուսին ԳՀ-ի վրա գտնվող քառակուսուն, ուստի, ըստ հավասարության, ինչպես Դ-ն է ԱՑ-ին հարաբերում, այնպես էլ Ե-ի վրա գտնվող քառակուսին ԳՀ-ի վրա գտնվող քառակուսուն Պնդում 5.22։ Եվ Դ-ն չունի ԱՑ-ի հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուրեմն, Ե-ի վրա գտնվող քառակուսին նույնպես չունի ԳՀ-ի վրա գտնվող քառակուսու հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուրեմն, Ե-ն համաչափելի չէ երկարությամբ ԳՀ-ի հետ Պնդում. 10.9։ Եվ ցույց էր տրված, որ Ե-ն նույնպես համաչափելի չէ ՖԳ-ի հետ։ Ուրեմն, ՖԳ-ն և ԳՀ-ն երկուսն էլ երկարությամբ համաչափելի չեն Ե-ի հետ:
Եվ քանի որ ինչպես ԲԱ-ն է ԱՑ-ին է հարաբերում, այնպես էլ ՖԳ-ի վրա գտնվող քառակուսին ԳՀ-ի վրա գտնվող քառակուսուն, ուրեմն, ՖԳ-ի վրա գտնվող քառակուսին մեծ է ԳՀ-ի վրա գտնվող քառակուսուց Պնդում 5.14։ Հետևաբար, թող ԳՀ-ի և Կ-ի վրա գտնվող քառակուսիների գումարը հավասար լինի ՖԳ-ի վրա գտնվող քառակուսուն։ Ուստի, ինչպես ԱԲ-ն է ԲՑ-ին հարաբերում, այնպես էլ ՖԳ-ի վրա գտնվող քառակուսին Կ-ի վրա գտնվող քառակուսուն Պնդում 5.19 հետևանք։ Եվ ԱԲ-ն չունի ԲՑ-ի հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուրեմն, ՖԳ-ի վրա գտնվող քառակուսին նույնպես չունի Կ-ի վրա գտնվող քառակուսու հետ այն հարաբերությունը, որը որևէ քառակուսի թիվ ունի որևէ քառակուսի թվի հետ։ Ուրեմն, ՖԳ-ն երկարությամբ համաչափելի չէ Կ-ի հետ Պնդում 10.9։ ՖԳ-ի վրա գտնվող քառակուսին մեծ է ԳՀ-ի վրա գտնվող քառակուսուց այն քառակուսու չափով, որը որևէ ուղիղ գծի վրա է և համաչափելի չէ ՖԳ-ի հետ երկարությամբ։ Եվ ՖԳ-ն և ԳՀ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով, և ոչ մեկը երկարությամբ համաչափելի չէ նախկինում տարված ռացիոնալ երկարությամբ ուղիղ գծին՝ Ե-ին։
Ուրեմն, ՖՀ-ն վեցերորդ երկբաղադրիչ ուղիղ գիծն է Սահմանում 10.10։† Ինչն էլ պահանջբում էր ցույց տալ:
†Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա վեցերորդ երկբաղադրիչ ուղիղ գծի երկարությունը կլինի √k + √k′: Սա և վեցերորդ ապոտոմեն, որի երկարությունը √k −√k′ է Պնդում 10.90, . հավասարման արմատներն են:
Լեմմա
Ահա ձեր տրամադրած տեքստի հայերեն թարգմանությունը․ Թող ԱԲ և ԲՑ ն երկու քառակուսիներն այնպիսին լինեն, որ որ ԴԲ-ն շարունակի ԲԵ-ին։ Ուրեմն, ՖԲ-ն նույնպես շարունակում է ԲԳ-ին։ Եվ թող ԱՑ զուգահեռագիծը լրացված լինի: ԱՑ-ն քառակուսի է, ԴԳ-ն միջին համեմատականն է ԱԲ-ի և ԲՑ-ի, և, ավելիին, ԴՑ-ն միջին համեմատականն է ԱՑ-ի և ԲՑ-ի:
Քանի որ ԴԲ-ն հավասար է ՖԲ-ին, և ԲԵ-ն հավասար է ԲԳ-ին, ուրեմն ամբողջ ԴԵ-ն հավասար է ամբողջ ՖԳ-ին։ Բայց ԴԵ-ն հավասար է թե՛ ԱՀ-ին, թե՛ ԿՑ-ին, իսկ ՖԳ-ն հավասար է թե՛ ԱԿ-ին, թե՛ ՀՑ-ին Պնդում 1.34։ Ուրեմն, ԱՀ-ն և ԿՑ-ն նույնպես համապատասխանաբար հավասար են ԱԿ-ին և ՀՑ-ին։ Ուստի զուգահեռագիծ ԱՑ-ն հավասարակողմ է։ Եվ (այն) նաև ուղղանկյուն է։ Ուրեմն, ԱՑ-ն քառակուսի է։
Այսպիսով, ինչպես ՖԲ-ն է ԲԳ-ի հետ, այնպես էլ ԴԲ-ն է ԲԵ-ի հետ հարաբերում, ինչպես ՖԲ-ն է ԲԳ-ի հետ, այնպես էլ ԱԲ-ն է ԴԳ-ի հետ հարաբերում, և ինչպես ԴԲ-ն է ԲԵ-ի հետ, այնպես էլ ԴԳ-ն է ԲՑ-ի հետ հարաբերում Պնդում 6.1, ուստի նույնպես ինչպես ԱԲ-ն է ԴԳ-ի հետ, այնպես էլ ԴԳ-ն է ԲՑ-ի հետ հարաբերում Պնդում 6.1։ Ուրեմն, ԴԳ-ն միջին համեմատականն է ԱԲ-ի և ԲՑ-ի:
Կարող ենք պնդել, որ ԴՑ-ն միջին համեմատականն է ԱՑ-ի և ԲՑ-ի:
Այսպիսով, ինչպես ԱԴ-ն է ԴԿ-ի հետ, այնպես էլ ԿԳ-ն է ԳՑ-ի հետ հարաբերում։ Քանի որ նրանք համապատասխանաբար հավասար են։ Ավելին, ինչպես ԱԿ-ն է ԿԴ-ի հետ, այնպես էլ ԿՑ-ն է ԳՑ-ի հետ հարաբերում Պնդում 5.18։ Ինչպես ԱԿ-ն է ԿԴ-ի հետ, այնպես էլ ԱՑ-ն է ԴՑ-ի հետ հարաբերում, և ինչպես ԿՑ-ն է ԳՑ-ի հետ, այնպես էլ ԴՑ-ն է ԲՑ-ի հետ հարաբերում Պնդում 6.1։ Ուրեմն նույնպես ինչպես ԱՑ-ն է ԴՑ-ի հետ, այնպես էլ ԴՑ-ն է ԲՑ-ի հետ հարաբերում Պնդում 5.11։ Ուրեմն, ԴՑ-ն միջին համեմատականն է ԱՑ-ի և ԲՑ-ի: Որն էլ հենց պահանջվում էր ցույց տալ:
Պնդում 54
Եթե մի մակերես կազմված է ռացիոնալ ուղիղ գծով և առաջին երկբաղադրիչ/երկանդամ ուղիղ գծով, ապա այդ մակերեսի քառակուսի արմատը իռացիոնալ ուղիղ գիծ է, որը կոչվում է երկանդամ։
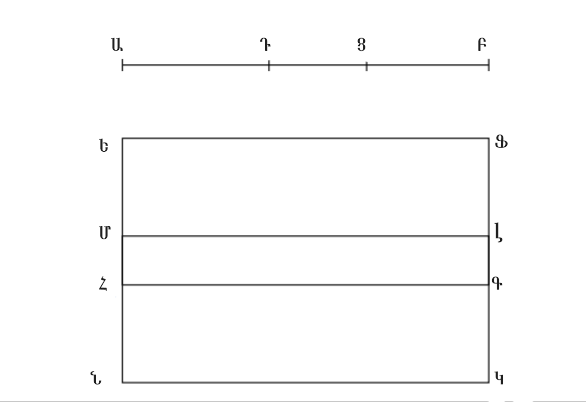
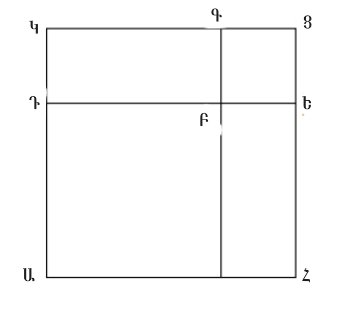
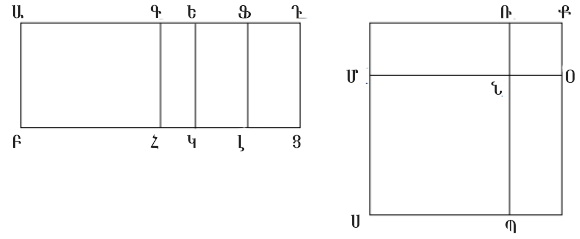
Թող ԱՑ տարածությունը պարունակի ԱԲ ռացիոնալ ուղիղ գիծը և ԱԴ առաջին երկանդամ ուղիղ գիծը: ԱՑ տարածության քառակուսու արմատը իռացիոնալ ուղիղ գիծ է, որը կոչվում է երկանդամ: Քանի որ ԱԴ-ն առաջին երկանդամ ուղիղ գիծ է, թող այն բաժանվի իր բաղադրիչ մասերի Ե կետում, և թող ԱԵ-ն լինի մեծ մասը: Պարզ է դառնում որ, ԱԵ-ն և ԵԴ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով, և որ ԱԵ-ի քառակուսին ավելի մեծ է, քան ԵԴ-ի քառակուսին, ինչ-որ ուղիղ գծի վրա կառուցված քառակուսով, որը համաչափելի է ԱԵ երկարության հետ, և որ ԱԵ-ն երկարությամբ համաչափելի է ԱԲ ռացիոնալ ուղիղ գծի հետ, որը նախապես տարվել էր Սահմանում 10.5: Այժմ թող ԵԴ-ն կիսվի F կետում: Եվ քանի որ ԱԵ-ի քառակուսին ավելի մեծ է, քան ԵԴ-ի քառակուսին, ինչ-որ ուղիղ գծի վրա կառուցված քառակուսով, որը համաչափելի է ԱԵ երկարության հետ, ապա եթե ուղղանկյունը հավասար է փոքր մասի քառորդին՝ այսինքն՝ ԵՖ-ին, (որը փոքր է ինչ-որ քառակուսով), դրված է մեծ մասի՝ ԱԵ-ի վրա, ապա այն բաժանում է այն համաչափելի մասերի Պնդում 10.17: Ուստի, թող ԱԳ և ԳԵ-ն պարունակող ուղղանկյունը, որը հավասար է ԵՖ քառակուսիին, դրվի ԱԵ-ի վրա: ԱԳ-ն ուստի երկարությամբ համաչափելի է ԳԵ-ի հետ: Եվ թող ԳՀ, ԵԿ, և ՖԼ գծերը դուրս գան Գ, Ե, Ֆ կետերից համապատասխանաբար, և լինեն ԱԲ կամ ՑԴ-ին զուգահեռ: Կառուցենք ՍՆ քառակուսին, որը հավասար է ԱՀ զուգահեռագծին, և ՆՔ քառակուսին, որը հավասար է ԳԿ զուգահեռագծին Պնդում 2.14: Եվ թող ՄՆ-ն տարվի այնպես, որ շարունակի ՆՕ-ին: ՌՆ-ն ուստի նույնպես շարունակում է ՆՊ-ին: Եվ թող ՍՔ զուգահեռագիծը լինի փակ: ՍՔ-ն ուստի քառակուսի է Պնդում 10.53 լեմմա: Եվ քանի որ ԱԳ և ԳԵ-ն պարունակող ուղղանկյունը հավասար է ԵՖ քառակուսուն, ապա ինչպես ԱԳ-ն՝ ԵՖ-ին, այնպես էլ ՖԵ-ն՝ ԵԳ-ին Պնդում 6.17: Եվ այդ դեպքերում, ինչպես ԱՀ-ն՝ ԵԼ-ին, այնպես էլ ԵԼ-ն՝ ԿԳ-ին Պնդում 6.1: Ուստի, ԵԼ-ն ԱՀ-ի և ԳԿ-ի միջին համեմատականն է: Բայց ԱՀ-ն հավասար է ՍՆ-ին, իսկ ԳԿ-ն՝ ՆՔ-ին: ԵԼ-ն, ուրեմն, ՍՆ-ի և ՆՔ-ի միջին համեմատականն է: Եվ ՄՌ-ն նույնպես դրանց միջին համեմատականն է, այսինքն ՍՆ-ի և ՆՔ-ի Պնդում. 10.53 լեմմա: ԵԼ-ն, ուրեմն, հավասար է ՄՌ-ին: Հետևաբար, այն նաև հավասար է ՊՕ-ին Պնդում. 1.43: Եվ ԱՀ գումարած ԳԿ հավասար է ՍՆ-ին գումարած ՆՔ-ն: Ուստի, ԱՑ-ի ամբողջը հավասար է ՍՔ-ի ամբողջին՝ այսինքն ՄՕ-ի քառակուսու մակերեսին: Ուստի, ՄՕ-ն ԱՑ մակերեսի քառակուսի արմատն է: Կարող ենք պնդել, որ ՄՕ-ն երկբաղադրիչ ուղիղ գիծ է։ Քանի որ ԱԳ-ն երկարությամբ համաչափ է ԳԵ-ի հետ, ԱԵ-ն նույնպես երկարությամբ համաչափ է ԱԳ-ի և ԳԵ-ի հետ Պնդում 10.15: Եվ ԱԵ-ն ենթադրվել է, որ համաչափ է ԱԲ-ի հետ: Ուստի ԱԳ-ն և ԳԵ-ն նույնպես երկարությամբ համաչափ են ԱԲ-ի հետ Պնդում. 10.12: Իսկ ԱԲ-ն ռացիոնալ է: Ուստի ԱԳ-ն և ԳԵ-ն նույնպես ռացիոնալ են: Հետևաբար, ԱՀ-ն և ԳԿ-ն նույնպես ռացիոնալ մակերեսներ են, և ԱՀ-ն համաչափ է ԳԿ-ի հետ Պնդում. 10.19: Բայց ԱՀ-ն հավասար է ՍՆ-ին, իսկ ԳԿ-ն՝ ՆՔ-ին: Ուստի ՍՆ-ն ու ՆՔ-ն, այսինքն՝ ՄՆ-ի և ՆՕ-ի (համապատասխանաբար) քառակուսիները, նույնպես ռացիոնալ են և համաչափ: Եվ քանի որ ԱԵ-ն երկարությամբ անհամաչափելի է ԵԴ-ի հետ, սակայն ԱԵ-ն երկարությամբ համաչափելի է ԱԳ-ի հետ, իսկ ԴԵ-ն համաչափելի է ԵՖ-ի հետ, ապա ԱԳ-ն նույնպես երկարությամբ անհամաչափելի է ԵՖ-ի հետ Պնդում 10.13: Հետևաբար, ԱՀ-ն նույնպես անհամաչափելի է ԵԼ-ի հետ Պնդում 6.1, 10.11: Բայց ԱՀ-ն հավասար է ՍՆ-ին, իսկ ԵԼ-ն՝ ՄՌ-ին: Ուստի ՍՆ-ն նույնպես անհամաչափելի է ՄՌ-ի հետ: Բայց ինչպես ՍՆ-ն ՄՌ-ին, այնպես էլ ՊՆ-ն ՆՌ-ին Պնդում 6.1: Ուստի ՊՆ-ն երկարությամբ անհամաչափելի է ՆՌ-ի հետ Պնդում 10.11: Եվ ՊՆ-ն հավասար է ՄՆ-ին, իսկ ՆՌ-ն՝ ՆՕ-ին: Ուստի ՄՆ-ն երկարությամբ անհամաչափելի է ՆՕ-ի հետ: Իսկ ՄՆ-ի վրա գտնվող քառակուսին համաչափելի է ՆՕ-ի վրա գտնվող քառակուսու հետ, և երկուսն էլ ռացիոնալ են: Հետևաբար, ՄՆ-ն և ՆՕ-ն ռացիոնալ ուղիղ գծեր են, որոնք միայն քառակուսիներով են համաչափ: Այսպիսով, ՄՕ-ն և՛ երկբաղադրիչ ուղիղ գիծ է Պնդում 10.36, և՛ ԱՑ-ի քառակուսի արմատը: Ինչն էլ հենց պահանջվում էր ապացուցել:
† Եթե ռացիոնալ ուղիղ գիծը ունի միավոր երկարություն, ապա այս տեսության համաձայն, առաջին երկբաղադրիչ ուղիղ գծի քառակուսի արմատը ևս երկբաղաադրիչ ուղիղ գիծ է: Այն է, առաջին երկբաղադրիչ ուղիղ գիծը ունի երկարությունը, որի քառակուսի արմատը -ն է, որտեղ և . Սա երկբաղադրիչ ուղիղ գծի երկարությունն է (Տես Պնդում 10.36), քանի որ ρ-ն ռացիոնալ է:
Պնդում 55
Եթե որևէ մակերես կազմված է ռացիոնալ ուղիղ գծով և երկրորդ երկբաղադրիչ ուղիղ գծով, ապա այդ մակերեսի քառակուսի արմատը իռացիոնալ ուղիղ գիծ է, որը կոչվում է առաջին երկմիջային։
Ենթադրենք ԱԲՑԴ մակերեսը կազմված է ռացիոնալ ուղիղ գծով` ԱԲ-ով և երկրորդ երկբաղադրիչ ուղիղ գծով` ԱԴ-ով։ Կարող ենք պնդել, որ ԱՑ-ի քառակուսի արմատը առաջին երկմիջային ուղիղ գիծ է։ Քանի որ ԱԴ-ն երկրորդ երկբաղադրիչ ուղիղ գիծ է, թող այն բաժանված լինի դրան պատկանող մասերին Ե-ով, այնպես, որ ԱԵ-ն մեծ մասն է։ Այսպիսով, ԱԵ-ն և ԵԴ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսով, և ԱԵ-ի վրա կառուցված քառակուսին մեծ է ԵԴ-ի վրա կառուցված քառակուսուց ինչ-որ ուղիղ գծի վրա կառուցված քառակուսու չափով, որն ԱԵ-ի հետ համաչափելի է, իսկ փոքր մասը՝ ԵԴ-ն, երկարությամբ համաչափելի է ԱԲ-ին Սահմանում 10.6։ Կիսենք ԵԴ-ն Ֆ կետում։ Եվ թող ԱԳԵ-ով պարփակված ուղղանկյունը, որը հավասար է ԵՖ-ի վրա կառուցված քառակուսուն, վերադրված լինի ԱԵ-ին և փոքր լինի դրանից ինչ-որ քառակուսի չափով: ԱԳ-ն, հետևաբար, երկարությամբ համաչափելի է ԳԵ-ի հետ Պնդում 10.17։ Եվ թող ԳՀ-ն, ԵԿ-ն և ՖԼ-ը գծված լինեն Գ-ից, Ե-ից և Ֆ-ից սկզբնակետերից համապատասխանաբար՝ զուգահեռ լինելով ԱԲ-ին և ՑԴ-ին։ Եվ թող կառուցված լինի ՍՆ քառակուսին, որը հավասար է ԱՀ զուգահեռագծին, և ՆՔ քառակուսին, որը հավասար է ԳԿ-ին։ Եվ թող ՄՆ-ն շարունակի ՆՕ-ին։ Հետևաբար, ՌՆ-ն նույնպես ծարունակում է ՆՊ-ին։ Եվ թող ՍՔ քառակուսին լինի փակ։ Այսպիսով, նախապես ապացուցված Պնդումից պարզ է դառնում Պնդում 10.53 լեմմա որ ՄՌ-ն միջին համեմատականն է ՍՆ-ի և ՆՔ-ի, և հավասար է ԵԼ-ին, իսկ ՄՕ-ն ԱՑ-ի քառակուսի արմատն է։ Այսպիսով, մենք պետք է ապացուցենք, որ ՄՕ-ն առաջին երկմիջային ուղիղ գիծ է։
Քանի որ ԱԵ-ն երկարությամբ անհամաչափելի է ԵԴ-ի հետ, իսկ ԵԴ-ն համաչափելի է երկարությամբ ԱԲ-ի հետ, հետևաբար ԱԵ-ն նույնպես անհամաչափելի է ԱԲ-ի հետ Պնդում 10.13։ Եվ քանի որ ԱԳ-ն երկարությամբ համաչափելի է ԳԵ-ի հետ, ԱԵ-ն նույնպես երկարությամբ համաչափելի է ԱԳ-ի և ԳԵ-ի հետ Պնդում 10.15։ Բայց ԱԵ-ն երկարությամբ անհամաչափելի է ԱԲ-ի հետ։ Ուստի, ԱԳ-ն և ԳԵ-ն նույնպես երկարությամբ անհամաչափելի են ԱԲ-ի հետ Պնդում 10.13։ Այսպիսով, ԲԱ-ն, ԱԳ-ն, և ԳԵ-ն զույգերով ռացիոնալ ուղիղ գծեր են, որոնք միայն քառակուսով են համաչափելի: Եվ, հետևաբար, ԱՀ-ն և ԳԿ-ն միջնականներ են Պնդում 10.21։ Հետևաբար, ՍՆ-ն և ՆՔ-ն նույնպես միջնականներ են։ Ուստի, ՄՆ-ն և ՆՕ-ն միջնական ուղիղ գծեր են։ Եվ քանի որ ԱԳ-ն երկարությամբ համաչափելի է ԳԵ-ի հետ, ԱՀ-ն նույնպես համաչափելի է ԳԿ-ի հետ, այն է` ՍՆ-ն ՆՔ-ի հետ, այն է ` ՄՆ-ի վրա կառուցված քառակուսուն ՆՕ-ի վրա կառուցված քառակուսու հետ [այդ իսկ պատճառով, ՄՆ-ն և ՆՕ-ն քառակուսով համաչափելի են] Պնդում 6.1, 10.11։ Եվ քանի որ ԱԵ-ն երկարությամբ անհամաչափելի է ԵԴ-ի հետ, բայց ԱԵ-ն համաչափելի է ԱԳ-ի հետ, իսկ ԵԴ-ն համաչափելի է ԵՖ-ի հետ, ԱԳ-ն, այսպիսով, անհամաչափելի է ԵՖ-ի հետ Պնդում 10.13։ Հետևաբար, ԱՀ-ն նույնպես անհամաչափելի է ԵԼ-ի հետ, այսինքն՝ ՍՆ-ն ՄՌ-ի հետ, այսինքն՝ ՊՆ-ն ՆՌ-ի հետ, այսինքն՝ ՄՆ-ն ՆՕ-ի հետ Պնդում 6.1, 10.11։ Բայց ՄՆ-ն և ՆՕ-ն արդեն ցույց է տրվել, որ միջնականներ են, որոնք քառակուսով համաչափելի են։ Ուստի, ՄՆ-ն և ՆՕ-ն միջնականներ են, որոնք քառակուսով են միայն համաչափելի: Ուստի դրանք ունեն ռացիոնալ մակերես։ Քանի որ արդեն ենթադրել էինք, որ ԴԵ-ն համաչափելի է ԱԲ-ի և ԵՖ-ի հետ, ապա ԵՖ-ը նույնպես համաչափելի է ԵԿ-ի հետ Պնդում 10.12։ Եվ նրանք երկուսն էլ ռացիոնալ են։ Ուստի, ԵԼ-ն, այսինքն՝ ՄՌ-ն ևս, ռացիոնալ են Պնդում 10.19։ Եվ ՄՌ-ն ՄՆՕ-ով արտագծված ուղղանկյունն է։ Եվ եթե երկու միջնականները, որոնք քառակուսով են միայն համաչափելի և ունեն ռացիոնալ մակերես, գումարվեն իրար, ապա ամբողջը կլինի այն իռացիոնալ ուղիղ գիծը, որը կոչվում է առաջին երկմիջային ուղիղ գիծ է Պնդում 10.37։
Այսպիսով, ՄՕ-ն առաջին երկմիջային ուղիղ գիծ է , ինչն էլ պահանջվում էր ցույց տալ:
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` երկրորդ երկբաղադրիչ ուղիղ գծի քառակուսի արմատը հավասար է , որի քառակուսի արմատը կլինի , որտեղ : Սա առաջին երկբաղադրիչ ուղիղ գծի երկարությունն է (Տես Պնդում 10.3), քանի որ ρ-ն ռացիոնալ է:
Պնդում 56
Եթե մակերեսը ռացիոնալ ուղիղ գծով և երրորդ երկբաղադրիչ ուղիղ գծով է ստեղծված, ապա այդ մակերեսի քառակուսի արմատը այն իռացիոնալ ուղիղ գիծն է, որը կոչվում է երկրորդ երկմիջին։†
Թող ԱԲՑԴ մակերեսը կառուցված լինի ռացիոնալ ուղիղ գծով` ԱԲ-ով և երրորդ երկբաղադրիչ ուղիղ գծով ԱԴ-ով, որը բաժանված է հատվածների Ե-ով, որոնցից ԱԵ-ն մեծն է։ Ապա կարող ենք պնդել, որ ԱՑ մակերեսի քառակուսի արմատը այն իռացիոնալ ուղիղ գիծն է, որը կոչվում է երկրորդ երկմիջնորդ։
Ստանանք նույն երկրաչափական պատկերը, ինչպես նախորդ դեպքում։ Եվ քանի որ ԱԴ-ն երրորդ երկբաղադրիչ ուղիղ գիծ է, ԱԵ-ն և ԵԴ-ն ռացիոնալ ուղիղ գծեր են, որոնք միայն քառակուսով են համաչափելի, և ԱԵ-ի վրա կառուցված քառակուսին մեծ է ԵԴ-ի վրա կառուցված քառակուսուց ինչ-որ ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափելի է երկարությամբ ԱԵ-ի հետ, և ոչ ԱԵ, ոչ էլ ԵԴ-ն համաչափելի չեն ԱԲ-ի հետ երկարությամբ Սահմանում 10.7։ Հետևաբար, ինչպես արդեն ապացուցել ենք, կարելի է ցույց տալ, որ ՄՕ-ն ԱՑ մակերեսի քառակուսի արմատն է, իսկ ՄՆ-ն և ՆՕ-ն միջինական ուղիղ գծեր են, որոնք միայն քառակուսով են համաչափելի։ Հետևաբար, ՄՕ-ն երկմիջնորդ է։ Ապացուցենք, որ այն նաև երկրորդ երկմիջնորդ է։
Եվ քանի որ ԴԵ-ն ԱԲ-ի հետ համաչափելի չէ երկարությամբ՝ այսինքն նաև ԵԿ-ի հետ, բայց ԴԵ-ն համաչափելի է ԵՖ-ի հետ, ապա ԵՖ-ն ԵԿ-ի հետ համաչափելի չէ երկարությամբ Պնդում 10.13։ Եվ երկուսն էլ ռացիոնալ ուղիղ գծեր են։ Ուստի, ՖԵ-ն և ԵԿ-ն ռացիոնալ ուղիղ գծեր են, որոնք միայն քառակուսով են համաչափելի։ Այսպիսով, ԵԼ-ն, այսինքն՝ ՄՌ-ն ևս, միջինական է Պնդում 10.21։ Այն արտագծված է ՄՆՕ-ով։ Ուստի, ՄՆՕ-ով արտագծված ուղղանկյունը միջինական է։ Հետըաբար, ՄՕ-ն երկրորդ երկմիջնորդ ուղիղ գիծ է Պնդում 10.38։ Ինչն էլ պահանջվում էր ցույց տալ:
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` երրորդ երկբաղադրիչ ուղիղ գծի քառակուսի արմատը երկրորդ երկմիջնորդ ուղիղ գիծ է. այն է` երրորդ երկբաղադրիչ ուղիղ գիծը ունի երկարություն, որի քառակուսի արմատն է` , որտեղ և . Սա երկրորդ երկմիջնորդի երկարությունն է (Տես Պնդում 10.38), քանի որ ρ-ն ռացիոնալ է:
Պնդում 57
Եթե որևէ մակերես կառուցված է ռացիոնալ ուղիղ գծով և չորրորդ երկբաղադրիչ ուղիղ գծով, ապա այդ մակերեսի քառակուսի արմատը ուղիղ գիծ է, որը կոչվում է առանցքային։†
Թող ԱՑ մակերեսը կառուցված լինի ԱԲ ռացիոնալ ուղիղ գծով և ԱԴ չորրորդ երկբաղադրիչ ուղիղ գծով, որը բաժանված է իր հատվածների Ե կետում, որոնցից ԱԵ-ն թող լինի մեծը։ Կարող ենք պնդել, որ ԱՑ-ի քառակուսի արմատը իռացիոնալ ուղիղ գիծ է, որը կոչվում է առանցքային։ Քանի որ ԱԴ ուղիղ գիծը չորրորդ երկբաղադրիչ է, ԱԵ-ն և ԵԴ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն իրենց քառակուսիներով, ԱԵ-ի վրա կառուցված քառակուսին մեծ է ԵԴ-ի վրա կառուցված քառակուսուց՝ ԱԵ-ի հետ անհամաչափելի ուղիղ գծի վրա կառուցված քառակուսու չափով, և ԱԵ-ն համաչափելի է ԱԲ-ի հետ երկարությամբ Սահմանում 10.8։ Թող ԴԵ-ն բաժանված լինի երկու հավասար մասի Ֆ-ով։ Եվ թող ԱԵ-ին կից ԱԳ-ով և ԳԵ-ով կառուցված զուգահեռագիծը, որը հավասար է ԵՖ-ի վրա կառուցված քառակուսուն (և փոթր է դրանից ինչ-որ քառակուսով)։ ԱԳ-ն, հետևաբար, անհամաչափելի է ԳԵ-ի հետ երկարությամբ Պնդում 10.18։ Թող ԳՀ, ԵԿև ՖԼ-ն տարված լինեն զուգահեռ ԱՆ-ին։ Եվ թող մնացած կառուցումը կատարվի նույն ձևով, ինչպես նախորդ առաջադրանքում։ Հետևաբար, պարզ է, որ ՄՕ-ն ԱՑ մակերեսի քառակուսի արմատն է։ Հետևաբար, պետք է ցույց տալ, որ ՄՕ-ն այն իռացիոնալ ուղիղ գիծն է, որը կոչվում է առանցքային։
Քանի որ ԱԳ-ն անհամաչափելի է ԵԳ-ի հետ երկարությամբ, ապա ԱՀ-ն նույնպես անհամաչափելի է ԳԿ-ի հետ, այսինքն՝ ՍՆ-ն անհամաչափելի է ՆՔ-ի հետ Պնդում 6.1, 10.11։ Ուստի, ՄՆ-ն ու ՆՕ-ն անհամաչափելի են քառակուսիներով։ Եվ քանի որ ԱԵ-ն համաչափելի է ԱԲ-ի հետ երկարությամբ, ապա ԱԿ-ն ռացիոնալ է Պնդում 10.19։ Եվ այն հավասար է ՄՆ և ՆՕ-ի վրա կառուցված քառակուսիների գումարին։ Ուստի, ՄՆ և ՆՕ-ի վրա կառուցված քառակուսիների գումարը նույնպես ռացիոնալ է։ Եվ քանի որ ԴԵ-ն անհամաչափ է ԱԲ-ի հետ երկարությամբ Պնդում 10.13՝ այսինքն՝ ԵԿ-ի հետ, բայց ԴԵ-ն համաչափ է ԵՖ-ի հետ, ապա ԵՖ-ն անհամաչափ է եԿ-ի հետ երկարությամբ Պնդում 10.13։ Ուստի, ԵԿ և ԵՖ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափ են միայն քառակուսիներով։ ԼԵ-ն՝ այսինքն՝ ՄՌ-ն ևս, միջնական է Պնդում 10.21։ Եվ այն կառուցված է ՄՆ և ՆՕ-ի մեջ։ ՄՆ-ի և ՆՕ-ի վրա կառուցված ուղղանկյունը միջնական է։ Եվ ՄՆ-ի և ՆՕ-ի վրա կառուցված քառակուսիների գումարը ռացիոնալ է, իսկ ՄՆ և ՆՕ-ն անհամաչափ են քառակուսիներով։ Եվ եթե երկու ուղղիղ գծեր որոնք անհամաչափ են քառակուսիներով, և դրանց քառակուսիների գումարը ռացիոնալ է, իսկ դրանցով պարունակվող ուղղանկյունը միջնական է, ապա նրանց գումարը իռացիոնալ ուղիղ գիծ է, որը կոչվում է առանցքային Պնդում 10.39։ Ուստի, ՄՕ-ն այն իռացիոնալ ուղիղ գիծն է, որը կոչվում է առանցքային։ Եվ այն ԱՑ մակերեսի քառակուսի արմատն է։ Ինչն էլ հենց պահանջվում էր ապացուցել:
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` չորրորդ երկբաղադրիչ ուղիղ գիծն ունի երկարությունը, որի արմատը -ն է, որտեղ ρ = √k և k′′ 2 = k′, սա առանցքային ուղիղ գծի երկարությունն է (Տես Պնդում. 10.39), քանի որ ρ-ն ռացիոնալ է:
Պնդում 58
Եթե մի մակերես կառուցված է ռացիոնալ ուղղիղ գիծով և հինգերորդ երկբաղադրիչ ուղղիղ գծով, ապա մակերեսի քառակուսի արմատը այն իռացիոնալ ուղղիղ գիծն է, որը հավասար է ռացիոնալ թվի արմատի միջականի գումարին:†
Թող ԱՑ մակերեսը կառուցված լինի ԱԲ ռացիոնալ ուղիղ գծով և հինգերորդ երկբաղադրիչ ուղիղ գծով` ԱԴ-ով, որը բաժանվել է հատվածների Ե կետում, այնպես որ ԱԵ-ն մեծ հատվածն է: Ուստի, կարող ենք պնդել, որ ԱՑ մակերեսի քառակուսի արմատը իռացիոնալ ուղիղ գիծ է, որը հավասար է ռացիոնալ թվի արմատի և միջնականի գումարին:
Ունենք արդեն իսկ նկարագրված երկրաչափական պատկերը։ Այսպիսով, ակնհայտ է, որ ՄՕ-ն ԱՑ տարածության քառակուսի արմատն է։ Ուստի, պետք է ցույց տրվի, որ ՄՕ-ն ռացիոնալ թվի արմատւ և միջնականի գումարն է։ Որպեսզի դա ցույց տրվի, հաշվի առնենք, որ քանի որ ԱԳ-ն անհամաչափելի է ԳԵ-ին երկարությամբ Պնդում 10.18, ԱՀ-ն նույնպես անհամաչափելի է ՀԵ-ի հետ։ Այսինքն՝ ՄՆ-ի քառակուսին անհամաչափելի է ՆՕ-ի քառակուսու հետ Պնդում 6.1, 10.11։ Այսպիսով, ՄՆ-ն և ՆՕ-ն քառակուսիներով անհամաչափելի են։ Եվ քանի որ ԱԴ-ն հինգերորդ երկբաղադրիչ ուղիղ գիծ է, իսկ ԵԴ-ն դրա փոքր հատվածն է, ԵԴ-ն երկարությամբ համաչափելի է ԱԲ-ի հետ Սահմանում 10.9։ Բայց քանի որ ԱԵ-ն անհամաչափելի է ԵԴ-ի հետ, ԱԲ-ն նույնպես անհամաչափելի է ԱԵ-ի հետ [ԲԱ-ն ու ԱԵ-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով] Պնդում 10.13։ Այսպիսով, ԱԿ-ն՝ այնսինքն նաև ՄՆ-ն և ՆՕ-ի քառակուսիների գումարը, միջնական է Պնդում 10.21։ Եվ քանի որ ԴԵ-ն համաչափելի է ԱԲ-ի հետ՝ այսինքն նաև՝ ԵԿ-ի հետ, բայց ԴԵ-ն համաչափելի է ԵՖ-ի հետ, ԵՖ-ն նույնպես համաչափելի է ԵԿ-ի հետ Պնդում 10.12։ Եվ ԵԿ-ն ռացիոնալ է։ Այսպիսով, ԵԼ-ն՝ այսինքն նաև՝ ՄՌ-ն՝ այսինքն՝ ՄՆՕ -ից դուրս եկող ճառագայթը, նույնպես ռացիոնալ է Պնդում 10.19։ ՄՆ-ն և ՆՕ-ն այսպիսով քառակուսիներով անհամաչափելի են, որի արդյունքում դրանցով կառուցված քառակուսիների գումարը միջնական է դառնում, իսկ նրանցով կազմված փակ ուղղանկյունը` ռացիոնալ։ Այսպիսով, MO-ն ռացիոնալ թվի քառակուսի արմատի և միջնականի գումար է Պնդում 10.40։ Եվ ԱՑ մակերեսի քառակուսի արմատն է։ Ինչն էլ հենց պահանջվում էր ապացուցել:
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` հինգերորդ երկբաղադրիչ ուղիղ գծի արմատը հավասար է ռացիոնալ թվի արմատի և միջնականի գումարին, այն է, հինգերորդ երկբաղադրիչ ուղիղ գծի երկարությունը է, որի արմատը -ն է, որտեղ ρ = pk (1 + k′′ 2) և k′′ 2 = k, սա ռացիոնալ թվի արմատի և միջնականի գումարն է (Տես Պնդում. 10.40), քանի որ ρ-ն ռացիոնալ է:
Պնդում 59
Եթե որևէ մակերես սահմանափակված է ռացիոնալ ուղիղ գծով և վեցերորդ երկբաղադրիչ ուղիղ գծով, ապա մակերեսի քառակուսի արմատը անվանում են այն իռացիոնալ ուղիղ գիծը, որը հավասար է երկու միջնականների գումարի քառակուսի արմատին:
Թող ԱԲՑԴ մակերեսը սահմանափակված լինի ռացիոնալ ԱԲ ուղիղ գծով և վեցերորդ երկբաղադրիչ ԱԴ ուղիղ գծով, որը բաժանված է իր բաղադրիչ մասերի Ե-ում՝ ԱԵ-ն մեծ հատվածն է: Կարող ենք պնդել, որ ԱՑ-ի քառակուսի արմատը երկու միջնականների գումարի քառակուսի արմատն է:
Տանենք արդեն ցույց տրված երկրաչափական պատկերը: Այսպիսով, ակնհայտ է, որ ՄՕ-ն ԱՑ-ի քառակուսի արմատն է, իսկ ՄՆ-ն քառակուսով անհամաչափելի է ՆՕ-ի հետ: Եվ քանի որ ԵԱ-ն անհամաչափելի է երկարությամբ ԱԲ-ի հետ Սահմանում 10.10, ԵՍ-ն և ԱԲ-ն ռացիոնալ ուղիղ գծեր են, որոնք քառակուսիներով համաչափելի են: Այսպիսով, ԱԿ-ն, այսինքն ՄՆ-ի և ՆՕ-ի քառակուսիների գումարը, միջնական է Պնդում 10.21: Կրկին, քանի որ ԵԴ-ն անհամաչափելի է երկարությամբ ԱԲ-ի հետ Սահմանում 10.10, ՖԵ-ն նույնպես անհամաչափելի է ԵԿ-ի հետ Պնդում 10.13: Այսպիսով, ՖԵ-ն և ԵԿ-ն ռացիոնալ ուղիղ գծեր են, որոնք քառակուսիներով համաչափելի են: Այսպիսով, ԵԼ-ն, այսինքն ՄՌ-ն, այսինքն ՄՆՕ-ով կառուցված ուղղանկյունը միջնական է Պնդում 10.21: Եվ քանի որ ԱԵ-ն անհամաչափելի է երկարությամբ ԵՖ-ի հետ, ԱԿ-ն նույնպես անհամաչափելի է ԵԼ-ի հետ Պնդում 6.1, 10.11: Բայց ԱԿ-ն ՄՆ-ի և ՆՕ-ի քառակուսիների գումարն է, իսկ ԵԼ-ն ՄՆՕ-ի պարունակած ուղղանկյունն է: Այսպիսով, ՄՆՕ-ի քառակուսիների գումարը անհամաչափելի է ՄՆՕ-ի պարունակած ուղղանկյան հետ: Եվ դրանցից յուրաքանչյուրը միջնական է: Իսկ ՄՆ-ն և ՆՕ-ն քառակուսիներով անհամաչափելի են:
Այսպիսով, ՄՕ-ն երկու միջնականների գումարի քառակուսի արմատն է Պնդում 10.41: Եվ այն ԱՑ-ի քառակուսի արմատն է: Ինչն էլ հենց պահանջվում էր ապացուցել:
† Եթե ռացիոնալ ուղիղ գիծն ունի միավոր երկարություն, ապա, այս տեսության համաձայն` վեցերորս երկբաղադրիչ ուղիղ գիծը երկու միջնականների գումարի արմատն է, այն է, վեցերորդ ուղիղ գիծն ունի √k + √k′ երկարություն, որի քառակուսի արմատն է , որտեղ k′′ 2 = (k −k′)/k′ . Սա երկու միջնականների գումարի քառակուսի արմատն է (Տես Պնդում 10.41):
Լեմմա
Եթե ուղիղ գիծը բաժանվի անհավասար մասերի, ապա այդ անհավասար մասերի վրա կառուցված քառակուսիների գումարը մեծ կլինի այդ մասերով կառուցված ուղղանկյան կրկնապատիկիից։
Թող ԱԲ-ն լինի ուղիղ գիծ, որը բաժանված է անհավասար մասերի Ց կետում, և թող ԱՑ-ն լինի ավելի մեծ, քան ՑԲ-ն: Կարող ենք պնդել, որ ԱՑ-ի և ՑԲ-ի վրա կառուցված քառակուսիների գումարը մեծ է ԱՑ-ի և ՑԲ-ի վրա կառուցված ուղղանկյան կրկնապատիկից։ Թող ԱԲ գիծը բաժանված լինի երկու հավասար մասերի Դ կետում։ Ուստի, քանի որ ուղիղ գիծը Դ կետում բաժանված է հավասար մասերի, իսկ Ց կետում՝ անհավասար մասերի, ապա ԱՑ-ի և ՑԲ-ի վրա կառուցված ուղղանկյան գումարը ՑԴ-ի վրա կառուցված քառակուսու հետ հավասար է ԱԴ-ի վրա կառուցված քառակուսուն Պնդում 2.5։ Ուստի, ԱՑ-ի և ՑԲ-ի վրա կառուցված ուղղանկյունը փոքր է ԱԴ-ի վրա կառուցված քառակուսուց։ Ուստի, ԱՑ-ի և ՑԲ-ի վրա կառուցված ուղղանկյան կրկնապատիկը փոքր է ԱԴ-ի վրա կառուցված քառակուսու կրկնապատիկից։ Բայց ԱՑ-ի և ՑԲ-ի վրա կառուցված քառակուսիների գումարը հավասար է ԱԴ-ի և ԴՑ-ի վրա կառուցված քառակուսիների գումարի կրկնապատիկից Պնդում, 2.9։ Ուստի, ԱՑ-ի և ՑԲ-ի վրա կառուցված քառակուսիների գումարը մեծ է ԱՑ-ի և ՑԲ-ի վրա կառուցված ուղղանկյան կրկնապատիկից։ Ինչն էլ հենց պահանջվում էր ցույց տալ:
Պնդում 60
Երկբաղադրիչ ուղիղ գծի վրա կառուցված քառակուսին, որը տեղադրված է ռացիոնալ ուղիղ գծի վրա, որպես լայնություն առաջացնում է առաջին երկբաղադրիչ ուղիղ գիծ։†
Թող ԱԲ-ն լինի երկբաղադրիչ ուղիղ գիծ, որը բաժանված է իր բաղադրիչ մասերի Ց-ում, այնպես, որ ԱՑ-ն լինի մեծը: Տանենք ԴԵ-ն այնպես, որ լինի ռացիոնալ ուղիղ գիծ: Եվ թող ԴԵՖԳ ուղղանկոյւնը, որը հավասար է ԱԲ-ի քառակուսուն, տեղադրվի ԴԵ-ի վրա, և դրա լայնությունը լինի ԴԳ-ն: Կարող ենք պնդել, որ ԴԳ-ն առաջին երկբաղադրիչ ուղիղ գիծ է: Դրա համար, թող ԴՀ-ն, որը հավասար է ԱՑ-ի քառակուսուն, և ԿԼ-ն, որը հավասար է ԲՑ-ի քառակուսուն, տեղադրվեն ԴԵ-ի վրա: Ուստի մնացածը` ԱՑ և ՑԲ-ով կառուցված ուղղանկյան կրկնապատիկը, հավասար է ՄՖ-ին Պնդում 2.4: Կիսենք ՄԳ-ն Ն կետով, և թող ՆՕ-ն լինի ՄԼ-ին և ԳՖ-ին զուգահեռ։ ՄՕ-ն և ՆՖ-ն, հետևաբար, յուրաքանչյուրը հավասար է ԱՑԲ-ով կազմված ուղղանկյանը: Եվ քանի որ ԱԲ-ն երկբաղադրիչ ուղիղ գիծ է, որը բաժանվել է իր բաղադրիչ անդամներին Ց-ում, ԱՑ-ն և ՑԲ-ն, հետևաբար, ռացիոնալ ուղիղ գծեր են, որոնք միայն քառակուսիներով են համաչափելի Պնդում 10.36: Ուստի, ԱՑ և ՑԲ-ի քառակուսիները ռացիոնալ են և իրար հետ համաչափելի են: Եվ հետևաբար, ԱՑ և ՑԲ-ի քառակուսիների գումարը ռացիոնալ է Պնդում 10.15, և հավասար է ԴԼ-ին: Ուստի ԴԼ-ն ռացիոնալ է: Եվ այն վերադրված է ռացիոնալ ուղիղ գծի` ԴԵ-ի վրա: ԴՄ-ն հետևաբար ռացիոնալ է, և երկարությամբ համաչափելի է ԴԵ-ի հետ Պնդում 10.20: Եվ կրկին, քանի որ ԱՑ և ՑԲ-ն ռացիոնալ են (ուղիղ գծեր, որոնք միայն քառակուսիներով են համաչափելի), ԱՑ և ՑԲ-ով կառուցված ուղղանկյան կրկնապատիկը, այսինքն՝ ՄՖ-ն, հետևաբար, միջնական է Պնդում 10.21: Եվ այն տեղադրված է ռացիոնալ ուղիղ գծի` ՄԼ-ի վրա: ՄԳ-ն, հետևաբար, նույնպես ռացիոնալ է, և երկարությամբ անհամաչափելի է ՄԼ-ի հետ՝ այսինքն՝ ԴԵ-ի հետ նույնպես Պնդում 10.22: Իսկ ՄԴ-ն նույնպես ռացիոնալ է, և երկարությամբ համաչափելի է ԴԵ-ի հետ: Ուստի, ԴՄ-ն երկարությամբ անհամաչափելի է ՄԳ-ի հետ Պնդում 10.13: Եվ դրանք ռացիոնալ են: ԴՄ և ՄԳ ուղիղ գծերը, հետևաբար, ռացիոնալ են, որոնք միայն քառակուսիներով են համաչափելի: Ուստի, ԴԳ-ն երկբաղադրիչ ուղիղ գիծ է Պնդում 10.36: Ինչն էլ հենց պահանջվում էր ցույց տալ:
Քանի որ ԱՑԲ-ով կազմված ուղղանկյունը միջին հարաբերակցությունն է ԱՑ-ի և ՑԲ-ի քառակուսիների միջև Պնդում 10.53 լեմմա, ապա ՄՕ-ն նույնպես միջին հարաբերակցությունն է ԴՀ-ի և ԿԼ-ի միջև: Ուստի, ինչպես ԴՀ-ն է ՄՕ-ին համեմատական, այնպես էլ ՄՕ-ն է ԿԼ-ին համեմատական, այսինքն՝ ինչպես ԴԿ-ն է ՄՆ-ին համեմատական, այնպես էլ ՄՆ-ն է ՄԿ-ին համեմատական Պնդում 6.1: Ուստի, ԴԿ և ՄԿ-ով կազմված ուղղանկյունը հավասար է ՄՆ-ի քառակուսուն Պնդում 6.17: Եվ քանի որ ԱՑ-ի քառակուսին համաչափելի է ՑԲ-ի քառակուսու հետ, ԴՀ-ն նույնպես համաչափելի է ԿԼ-ի հետ: Հետևաբար, ԴԿ-ն նույնպես համաչափելի է ՄԿ-ի հետ Պնդումներ 6.1, 10.11: Եվ քանի որ ԱՑ-ի և ՑԲ-ի քառակուսիների գումարը մեծ է, քան ԱՑ և ՑԲ-ով կազմված ուղղանկյան կրկնապատիկը Պնդում 10.59 լեմմա, ԴԼ-ն, հետևաբար, նույնպես մեծ է ՄՖ-ից: Հետևաբար, ԴՄ-ն նույնպես մեծ է ՄԳ-ից Պնդումներ 6.1, 5.14: Եվ ԴԿ և ՄԿ-ով կազմված ուղղանկյունը հավասար է ՄՆ-ի քառակուսուն, այսինքն՝ ՄԳ-ի քառակուսու քառորդին: Եվ ԴԿ-ն համաչափելի է ՄԿ-ի հետ: Եվ եթե երկու անհավասար ուղիղ գծեր կան, և դրանցից փոքրագույնի վրա տեղադրված է ուղղանկյուն, որը հավասար է քառակուսու չորրորդ մասին, որն ընկնում է փոքրագույնի վրա և քառակուսով անհամաչափելի է, ապա ավելի մեծի վրա տեղադրված այս ուղղանկյունը բաժանում է այպիսի մասերի որոնց երկարությունները համաչափելի են, ապա ավելի մեծի քառակուսին մեծ է, փոքրի քառակուսուց՝ փոքր մասի վրա տեղադրված ուղղանկյան քառակուսի չափով, որը համաչափելի է ավելի մեծի հետ Պնդում 10.17: Ուստի, ԴՄ-ի քառակուսին մեծ է ՄԳ-ի քառակուսուց՝ ինչ-որ ուղիղ գծի քառակուսով, որը համաչափելի է ԴՄ-ի հետ: ԴՄ-ն և ՄԳ-ն ռացիոնալ են: Եվ ԴՄ-ն, որն ավելի մեծ է, երկարությամբ համաչափելի է նախկինում տարված ռացիոնալ ուղիղ գծի՝ ԴԵ-ի հետ:
Հետևաբար ԴԳ-ն առաջին երկբաղադրիչ ուղիղ գիծ է Սահմանում 10.5. Ինչն էլ հենց պահանջվում էր ցույց տալ:
† Այլ կերպ ասած` երկբաղադրիչի քառակուսի արմատը առաջին երկբաղադրիչ է; Տես Պնդում 10.54:
Պնդում 61
Առաջին երկմիջին ուղիղ գծի արմատը ռացիոնալ ուղիղ գծի վրա վերադրելիա, , որպես երկարություն ատացվում է երկրորդ երկբաղադրիչ ուղիղ գիծ:†
Թող ԱԲ-ն լինի առաջին երկմիջին ուղիղ գիծ, որը բաժանված է իր բաղադրիչ միջնական ուղիղ գծերի Ց-ում, որոնցից ԱՑ-ն մեծ է: Տանենք ռացիոնալ ուղիղ գիծ ԴԵ-ն: Թող ԴՖ-ն, որը հավասար է ԱԲ-ի քառակուսուն, տեղադրվի ԴԵ-ի վրա, այնպես, որ ԴԳ-ն դառնա լայնություն: Կարող ենք պնդել, որ ԴԳ-ն երկրորդ երկբաղադրիչ ուղիղ գիծ է:
Ստանանք նույն երկրաչափական պատկերը, ինչպես նախորդ դեպքում: Եվ քանի որ ԱԲ-ն առաջին երկմիջին ուղիղ գիծ է, որը բաժանված է Ց-ում, ԱՑ-ն և ՑԲ-ն, հետևաբար, միջնական ուղիղ գծեր են, որոնք միայն քառակուսիներով են համաչափելի, և ստեղծում են ռացիոնալ մակերես Պնդում 10.37: Ուստի, ԱՑ և ՑԲ-ի քառակուսիները նույնպես միջնական են Պնդում 10.21: Եվ ԴԼ-ն միջնական է Պնդումներ 10.15, 10.23 հետևանք: Եվ այն վերադրված է ռացիոնալ ուղիղ գծի` ԴԵ-ի վրա: ԴՄ-ն, հետևաբար, ռացիոնալ է և երկարությամբ անհամաչափելի է ԴԵ-ի հետ Պնդում 10.22: Եվ կրկին, քանի որ ԱՑ և ՑԲ-ով կազմված ուղղանկյան կրկնապատիկը ռացիոնալ է, ՄՖ-ն նույնպես ռացիոնալ է: Եվ այն վերադրված է ռացիոնալ ուղիղ գծի` ՄԼ-ի վրա: Ուստի, ՄԳ-ն նույնպես ռացիոնալ է և երկարությամբ համաչափելի է ՄԼ-ի հետ՝ այսինքն՝ ԴԵ-ի հետ ևս Պնդում 10.20: ԴՄ-ն, հետևաբար, երկարությամբ անհամաչափելի է ՄԳ-ի հետ Պնդում 10.13: Եվ դրանք ռացիոնալ են: ԴՄ և ՄԳ ուղիղ գծերը, հետևաբար, ռացիոնալ են, որոնք միայն քառակուսիներով են համաչափելի: ԴԳ-ն, հետևաբար, երկբաղադրիչ ուղիղ գիծ է Պնդում 10.36: Ուստի, պետք է ցույց տրվի, որ այն նաև երկրորդ երկբաղադրիչ ուղիղ գիծ է:
Քանի որ ԱՑ և ՑԲ-ի քառակուսիների գումարը մեծ է ԱՑ և ՑԲ-ով կազմված ուղղանկյան կրկնապատիկից Պնդում 10.59, ԴԼ-ն, հետևաբար, նույնպես մեծ է ՄՖ-ից: Ուստի, ԴՄ-ն նույնպես մեծ է ՄԳ-ից Պնդում 6.1: Եվ քանի որ ԱՑ-ի քառակուսին համաչափելի է ՑԲ-ի քառակուսու հետ, ԴՀ-ն նույնպես համաչափելի է ԿԼ-ի հետ: Ուստի, ԴԿ-ն երկարությամբ համաչափելի է ԿՄ-ի հետ Պնդումներ 6.1, 10.11: Եվ ԴԿՄ-ով կազմված ուղղանկյունը հավասար է ՄՆ-ի քառակուսուն: Ուստի, ԴՄ-ի քառակուսին մեծ է ՄԳ-ի քառակուսուց այնքանով, որքանով մի ուղիղ գիծը, որը երկարությամբ համաչափ է ԴՄ-ի հետ Պնդում 10.17: Եվ ՄԳ-ն երկարությամբ համաչափ է ԴԵ-ի հետ: Ուստի, ԴԳ-ն երկրորդ երկբաղադրիչ ուղիղ գիծ է Սահմանում 10.6:
† Այլ կերպ ասած` առաջին երկբաղադրիչի քառակուսի արմատը երկրորդ երկբաղադրիչ է; Տես Պնդում 10.55:
Պնդում 62
Երկրորդ երկմիջին ուղիղ գծի քառակուսին, որը վերադրվում է ռացիոնալ ուղիղ գծի վրա, ստեղծում է որպես լայնություն երրորդ երկբաղադրիչ ուղիղ գիծ:†
Թող ԱԲ-ն լինի երկրորդ երկմիջին ուղիղ գիծ, որը բաժանված է իր բաղադրիչ միջնական ուղիղ գծերի Ց-ում, այնպես, որ ԱՑ-ն լինի մեծ հատվածը: Տանենք ԴԵ ռացիոնալ ուղիղ գիծը: Եվ թող ԴՖ-ն, որը հավասար է ԱԲ-ի քառակուսուն, տեղադրվի ԴԵ-ի վրա, այնպես, որ ԴԳ-ն դառնա լայնություն: Կարող ենք պնդել, որ ԴԳ-ն երրորդ երկբաղադրիչ ուղիղ գիծ է:
Ստանանք նույն երկրաչափական պատկերը, ինչպես նախորդ դեպքում: Քանի որ ԱԲ-ն երկրորդ երկմիջին ուղիղ գիծ է, որը բաժանված է Ց-ում, ԱՑ-ն և ՑԲ-ն, հետևաբար, միջնական ուղիղ գծեր են, որոնք միայն քառակուսիներով են համաչափելի և ստեղծում են միջնական մակերես Պնդում 10.38: Ուստի, ԱՑ և ՑԲ-ի քառակուսիների գումարը նույնպես միջական է Պնդում 10.15, 10.23 հետևանք: Եվ այն հավասար է ԴԼ-ին: Ուստի, ԴԼ-ն նույնպես միջական է: Եվ այն տեղադրված է ռացիոնալ ուղիղ գծի ԴԵ-ի վրա: ԴՄ-ն, հետևաբար, նույնպես ռացիոնալ է, և երկարությամբ անհամաչափելի է ԴԵ-ի հետ Պնդում 10.22: Այսպես, նույն պատճառով, ՄԳ-ն նույնպես ռացիոնալ է և երկարությամբ անհամաչափելի է ՄԼ-ի հետ՝ այսինքն՝ ԴԵ-ի հետ նույնպես: Ուստի, ԴՄ-ն և ՄԳ-ն ռացիոնալ են, և երկարությամբ անհամաչափելի են ԴԵ-ի հետ: Եվ քանի որ ԱՑ-ն երկարությամբ անհամաչափելի է ՑԲ-ի հետ, և ինչպես ԱՑ-ն է ՑԲ-ի հետ, այնպես էլ ԱՑ-ի քառակուսին՝ ԱՑԲ-ով կառուցված ուղղանկյան կրկնապատիկի հետ Պնդում 10.21 հետևանք, ԱՑ-ի քառակուսին նույնպես անհամաչափելի է ԱՑԲ-ով կառուցված ուղղանկյան կրկնապատիկի հետ Պնդում 10.11: Ուստի, ԱՑ և ՑԲ-ի քառակուսիների գումարը անհամաչափելի է ԱՑԲ-ով կառուցված ուղղանկյանի կրկնապատիկի հետ, այսինքն՝ ԴԼ-ն ՄՖ-ի հետ ևս Պնդում 10.12, 10.13: Ուստի, ԴՄ-ն նույնպես անհամաչափելի է ՄԳ-ի հետ Պնդում 6.1, 10.11: Եվ դրանք ռացիոնալ են: ԴԳ-ն, հետևաբար, երկբաղադրիչ ուղիղ գիծ) է Պնդում 10.36: Ուրեմն] մենք պետք է ցույց տանք, որ այն նաև երրորդ երկբաղադրիչ ուղիղ գիծ է:
Ինչպես նախորդ Պնդումներում, այստեղ ևս կարող ենք եզրակացնել, որ ԴՄ-ն մեծ է ՄԳ-ից, և ԴԿ-ն համաչափելի է երկարությամբ ԿՄ-ի հետ: Իսկ ԴԿՄ-ով կառուցված ուղղանկյունը հավասար է ՄՆ-ի քառակուսուն: Ուստի, ԴՄ-ի քառակուսին մեծ է ՄԳ-ի քառակուսուց՝ ինչ-որ ուղիղ գծի քառակուսով, որը համաչափելի է երկարությամբ ԴՄ-ի հետ Պնդում 10.17: Եվ ոչ ԴՄ-ն, ոչ էլ ՄԳ-ն համաչափելի չեն երկարությամբ ԴԵ-ի հետ: Ուստի, ԴԳ-ն երրորդ երկբաղադրիչ ուղիղ գիծ է Պնդում10.7: Ինչն էլ հենց պահանջվում էր ցույց տալ:
† Այլ կերպ ասած` երկրորդ երկբաղադրիչի քառակուսի արմատը երրորդ երկբաղադրիչ է; Տես Պնդում 10.56:
Պնդում 63
Առանցքային գծի վրա կառուցված քառակուսին ռացիոնալ երկարությամբ ուղիղ գծի վրա վերադրելիս ստացած երկարությունը չորրորդ երկմիջին է:†
Թող ԱԲ-ն լինի առանցքային ուղիղ գիծ, որը բաժանված է Ց-ում, այնպես, որ ԱՑ-ն մեծ է: ԴԵ-ն ռացիոնալ ուղիղ գիծ է: Եվ թող ԴՖ-ն, որը հավասար է ԱԲ-ի քառակուսուն, տեղադրվի ԴԵ-ի վրա, այնպես, որ ԴԳ-ն դառնա լայնություն: Կարող ենք պնդել, որ ԴԳ-ն չորրորդ երկբաղադրիչ ուղիղ գիծ է:
Ստանանք նույն երկրաչափական պատկերը, ինչպես նախորդ դեպքում: Եվ քանի որ ԱԲ-ն առանցքային ուղիղ գիծ է, որը բաժանվել է Ց-ում, ԱՑ և ՑԲ ուղիղ գծերը անհամաչափելի են քառակուսիներով, ինչը նշանակում է, որ դրանց քառակուսիների գումարը ռացիոնալ է, և դրանցով կազմված ուղղանկյունը միջնական է Պնդում 10.39: Ուստի, քանի որ ԱՑ և ՑԲ-ի քառակուսիների գումարը ռացիոնալ է, ԴԼ-ն ևս ռացիոնալ է: Ուստի, ԴՄ-ն նույնպես ռացիոնալ է և երկարությամբ համաչափելի է ԴԵ-ի հետ Պնդում 10.20: Կրկին, քանի որ ԱՑ և ՑԲ-ով կազմված ուղղանկյանի կրկնապատիկը, այսինքն՝ ՄՖ-ն, միջնական է և այն կիրառվում է ռացիոնալ ուղիղ գծի` ՄԼ-ի վրա, ՄԳ-ն նույնպես ռացիոնալ է, և երկարությամբ անհամաչափելի է ԴԵ-ի հետ Պնդում 10.22: Ուստի, ԴՄ-ն նույնպես երկարությամբ անհամաչափելի է ՄԳ-ի հետ Պնդում 10.13: ԴՄ-ն և ՄԳ-ն, հետևաբար, ռացիոնալ են, և միայն քառակուսիներով են համաչափելի: Ուստի, ԴԳ-ն երկբաղադրիչ ուղիղ գիծ է Պնդում 10.36. Ուրեմն պետք է ցույց տանք, որ այն նաև չորրորդ երկբաղադրիչ ուղիղ գիծ է:
Ուստի, նախորդ Պնդումների նման, մենք կարող ենք ցույց տալ, որ ԴՄ-ն մեծ է ՄԳ-ից, և որ ԴԿՄ-ով կազմված ուղղանկյունը հավասար է ՄՆ-ի քառակուսուն: Հետևաբար, քանի որ ԱՑ-ի քառակուսին անհամաչափելի է ՑԲ-ի քառակուսու հետ, ԴՀ-ն նույնպես անհամաչափելի է ԿԼ-ի հետ: Այդպիսով, ԴԿ-ն նույնպես անհամաչափելի է ՔՄ-ի հետ Պնդում 6.1, 10.11: Եվ եթե կան երկու անհավասար ուղիղ գծեր, և ուղղանկյուն, որը հավասար է փոքրագույնի քառակուսու չորրորդ մասին, որը պակասում է քառակուսի պատկերով, վերադրվում է մեծագույնի վրա և բաժանում այն անհամաչափելի մասերի, ապա մեծագույնի քառակուսին կլինի փոքրագույնի քառակուսուց մեծ ավելի քան ինչ-որ ուղիղ գծի քառակուսով, որը երկարությամբ անհամաչափելի է մեծագույնի հետ Պնդում 10.18: Ուստի, ԴՄ-ի քառակուսին ավելի մեծ է ՄԳ-ի քառակուսուց, ինչ-որ ուղիղ գծի չափով, որը երկարությամբ անհամաչափելի է ԴՄ-ի հետ: Եվ ԴՄ-ն և ՄԳ-ն ռացիոնալ են (ուղիղ գծեր, որոնք միայն քառակուսիներով են համաչափելի): ԴՄ-ն երկարությամբ համաչափելի է ռացիոնալ ուղիղ գծի` ԴԵ-ի հետ: Ուստի, ԴԳ-ն չորրորդ երկբաղադրիչ ուղիղ գիծ է Պնդում. 10.8: Ինչն էլ հենց պահանջվում էր ցույց տալ:
† Այլ կերպ ասած`, առանցքային գծի վրա կառուցված քառակուսին չորրորդ երկմիջին է; Տես Պնդում 10.57.