|վերնագիր = Մեխանիկայից ստացված երկրաչափական լուծումներ (կամ Մեխանիկական թեորեմների մեթոդը)
|հեղինակ = [[Արքիմեդ]]
|թարգմանիչ = [[Մասնակից:GasparyanMeri|GasparyanMeri]], [[Մասնակից:Annna|Annna]]
|աղբյուր = [http://euclid.trentu.ca/math/sb/3810H/Winter-2022/Method-Archimedes.pdf Geometrical Solutions Derived from Mechanics English translation by Dr. J. L. Heiberg]
}}
[[Պատկեր:Example.jpg]]
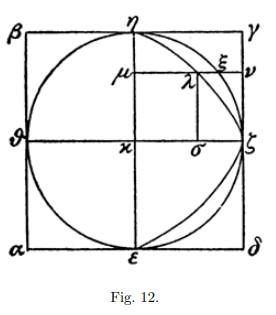
Թող քառակուսի <math>\alpha \beta \gamma \delta</math> [նկ. 12] լինի ուղղահայաց պրիզմայի հիմքը, որն ունի քառակուսի հիմքեր, և թող պրիզմայի մեջ լինի տեղադրված գլան, որի հիմքը <math>\epsilon \zeta \eta \theta</math> շրջանագիծն է, որն առնչվում է αβγδ զուգահեռագծի կողմերին՝ ∈<math>\epsilon, ζ\zeta, η և θ \eta, \theta</math> կետերում։ Անցկացնելով հարթություն նրա կենտրոնով և քառակուսու հակառակ կողմով (համապատասխանող γδ կողմին), այն կառանձնանա ամբողջ պրիզմայից՝ ձևավորելով երկրորդ պրիզմա, որն ամբողջ պրիզմայի 1/4 մասն է, և որը, սահմանափակվում է երեք զուգահեռագծերով և երկու հակառակ եռանկյուններով։
∈ζη կիսաշրջանագծի մեջ նկարենք պարաբոլ, որի սկզբնակետը η∈ է, իսկ առանցքը՝ ζκ, իսկ δη զուգահեռագծի մեջ գծենք µνkκζ-ը։ Այն կանցնի կիսաշրջանագծի շրջանագծով ξ կետում, պարաբոլով՝ λ կետում, և µν × νλ = νζ²
(քանի որ սա ակնհայտ է [Ապոլոնիոս, Կոն. I, 11]): Հետևաբար µν : νλ = κη² : λσ²։
Բայց զուգահեռագիծ δη = 3/2 պարաբոլի և ուղիղ ∈η-ի միջև գտնվող հատվածին (ինչպես ցույց է տրվել ավելի վաղ հրապարակված աշխատանքում), հետևաբար նաև պրիզման հավասար է գլանի հատվածի մեկուկես անգամին։
Հետևաբար, երբ գլանի հատվածը = 2, պրիզման = 3, և ամբողջ պրիզման, որը պարունակում է գլանը, հավասար է 12, որովհետև այն 4 անգամ մեծ է մյուս պրիզմայից. հետևաբար գլանի հատվածը հավասար է պրիզմայի 1/6-ին, Q. E. D.
'''== Պնդում XIV =='''
[Գծեք գլան] ուղղանկյուն պրիզմայի ներսում, որը ունի քառակուսի հիմքեր [և թող այն հատի հարթությամբ, որը անցնում է գլանի հիմքի կենտրոնով և հակառակ քառակուսու մի կողmով:] Այնուհետև այս հարթությունը կհատի պրիզմայից մեկ հատված և մեկ հատված գլանից։ Կարելի է ապացուցել, որ գլանից կտրված հատվածը կազմում է ամբողջ պրիզմայի մեկ վեցերորդ մասը։ Սակայն նախ մենք կապացուցենք, որ հնարավոր է գլանի հատվածում ներգծել մի մարմին և դուրս գրել մեկ այլ մարմին, որը կազմված է հավասար բարձրության պրիզմաներից, որոնց հիմքերը նման եռանկյունիներ են, այնպես, որ դուրս գրված մարմինը գերազանցի ներգծվածին ցանկացած տրված մեծությունից պակաս չափով։
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
Սակայն արդեն ցույց է տրված, որ թեք հարթությամբ կտրված պրիզման < 3/2 գլանի հատվածում ներգծված մարմնի։ Այժմ թեք հարթությամբ կտրված պրիզման : գլանի հատվածում ներգծված մարմինը = զուգահեռագիծ δη: Զուգահեռագծերը, որոնք ներգծված են պարաբոլով և ուղիղ գծով սահմանափակված հատվածում։ Ուստի զուգահեռագիծ δη < 3/2 պարաբոլով և ուղիղ գծով սահմանափակված հատվածի զուգահեռագծերի ուղիղով ∈η։ Բայց սա անհնար է, որովհետև այլուր ցույց է տրված, որ զուգահեռագիծ δη-ն մեկ ու կես անգամ մեծ է պարաբոլով և ուղիղ գծով սահմանափակված հատվածից, հետևաբար . . չի կարող ավելի մեծ լինել ․․․
Բոլոր պրիզմաները թեք հարթությամբ հատված պրիզմայում : բոլոր պրիզմաները գլանի հատվածի շուրջ նկարագրված մարմնում = բոլոր զուգահեռագծերը զուգահեռագծում
δη: բոլոր զուգահեռագծերը պարաբոլով և ուղիղ գծով սահմանափակված հատվածի շուրջ նկարագրված մարմնում, այսինքն՝ թեք հարթությամբ կտրված պրիզման : գլանի հատվածի շուրջ նկարագրված մարմինը = զուգահեռագիծ δη: պարաբոլով և ուղիղ գծով սահմանափակված հատվածի մարմինը։ Սակայն թեք հարթությամբ կտրված պրիզման մեկ ու կես անգամ գերազանցում է գլանի հատվածի շուրջ նկարագրված մարմնին . . .
== Պնդում XIV ==
[Ուղղահայաց պրիզմայի մեջ քառակուսի հիմքերով տեղադրեք գլան և կտրեք այն հարթությամբ, որը անցնում է գլանի հիմքի կենտրոնով և հակառակ քառակուսու մեկ կողմով:] Այդ հարթությունը կկտրի պրիզմայից պրիզմայի մի մաս և գլանից գլանի մի մաս։ Կարելի է ապացուցել, որ գլանից հարթությամբ կտրված մասը հավասար է ամբողջ պրիզմայի 1/6-ին։ Բայց նախ մենք կպարզենք, որ հնարավոր է գլանի հատվածի մեջ տեղադրել մարմին և շրջապատել մեկ այլ մարմնով, որոնք կազմված են հավասար բարձրությամբ պրիզմաներից և ունեն նման եռանկյուններ հիմքում այնպես, որ շրջապատող մարմինը գերազանցի ներսում տեղադրվածին ավելի փոքր չափով, քան ցանկացած տրված մեծություն։
[Ներծեք գլան] ուղղանկյուն պրիզմայի ներսում, որը ունի քառակուսի հիմքեր [և թող այն հատի հարթությամբ, որը անցնում է գլանի հիմքի կենտրոնով և հակառակ քառակուսու մի կողmով:] Այնուհետև այս հարթությունը կհատի պրիզմայից մեկ հատված և մեկ հատված գլանից։ Կարելի է ապացուցել, որ գլանից կտրված հատվածը կազմում է ամբողջ պրիզմայի մեկ վեցերորդ մասը։ Սակայն նախ մենք կապացուցենք, որ հնարավոր է գլանի հատվածում ներգծել մի մարմին և դուրս գրել մեկ այլ մարմին, որը կազմված է հավասար բարձրության պրիզմաներից, որոնց հիմքերը նման եռանկյունիներ են, այնպես, որ դուրս գրված մարմինը գերազանցի ներգծվածին ցանկացած տրված մեծությունից պակաս չափով։ ...Բայց . . . . . . . . . . . . . . . . . . . . . . . . . Սակայն արդեն ցույց է տրվելտրված, որ թեք հարթությամբ կտրված պրիզման < 3/2 գլանի հատվածում ներսում տեղադրված մարմնից։ Իսկ ներգծված մարմնի։ Այժմ թեք հարթությամբ կտրված պրիզման : գլանի հատվածում ներսում տեղադրված ներգծված մարմինը = δη զուգահեռագիծ δη: Զուգահեռագծերը, որոնք ներգծված են պարաբոլով և ուղիղ �η-ով գծով սահմանափակված հատված։ Հետևաբար հատվածում։ Ուստի զուգահեռագիծ δη զուգահեռագիծը < 3/2 պարաբոլով և ուղիղ �ηգծով սահմանափակված հատվածի զուգահեռագծերի ուղիղով ∈η։ Բայց սա անհնար է, որովհետև այլուր ցույց է տրված, որ զուգահեռագիծ δη-ով ն մեկ ու կես անգամ մեծ է պարաբոլով և ուղիղ գծով սահմանափակված հատվածի։հատվածից, հետևաբար . . չի կարող ավելի մեծ լինել ․․․
Բայց սա անհնար է, որովհետև այլ տեղ ցույց է տրվել, որ Բոլոր պրիզմաները թեք հարթությամբ հատված պրիզմայում՝ բոլոր պրիզմաները գլանի հատվածի շուրջ նկարագրված մարմնում = բոլոր զուգահեռագծերը զուգահեռագծում δη զուգահեռագիծը մեկուկես անգամ մեծ է : բոլոր զուգահեռագծերը պարաբոլով և ուղիղ �η-ով գծով սահմանափակված հատվածիցհատվածի շուրջ նկարագրված մարմնում, հետևաբար..այսինքն՝ թեք հարթությամբ կտրված պրիզման : գլանի հատվածի շուրջ նկարագրված մարմինը = զուգահեռագիծ δη: պարաբոլով և ուղիղ գծով սահմանափակված հատվածի մարմինը։ Սակայն թեք հարթությամբ կտրված պրիզման մեկ ու կես անգամ գերազանցում է գլանի հատվածի շուրջ նկարագրված մարմնին .