«Տարերք/Գիրք 2»–ի խմբագրումների տարբերություն
չNo edit summary |
չNo edit summary |
||
| (29 intermediate revisions by 2 users not shown) | |||
| Տող 2. | Տող 2. | ||
|վերնագիր = [[Տարերք]], Գիրք 2 |
|վերնագիր = [[Տարերք]], Գիրք 2 |
||
|հեղինակ = [[էվկլիդես]] |
|հեղինակ = [[էվկլիդես]] |
||
|թարգմանիչ = [[Մասնակից:Արարատ Ղազարյան|Արարատ Ղազարյան]], [[Մասնակից:Ani Mikayelyan|Ani Mikayelyan]] |
|||
|թարգմանիչ = |
|||
|աղբյուր = [https://farside.ph.utexas.edu/Books/Euclid/Elements.pdf Euclid's Elements of Geometry, English translation by Richard Fitzpatrick] |
|աղբյուր = [https://farside.ph.utexas.edu/Books/Euclid/Elements.pdf Euclid's Elements of Geometry, English translation by Richard Fitzpatrick] |
||
}} |
}} |
||
{{Տարերքի գրքեր}} |
{{Տարերքի գրքեր}} |
||
[[Կատեգորիա:Մաթեմատիկա]] |
[[Կատեգորիա:Մաթեմատիկա]] |
||
== Pages 49-55 == |
|||
== Սահմանումներ == |
== Սահմանումներ == |
||
# Ցանկացած ուղղանկյուն զուգահեռագիծ |
# Ցանկացած ուղղանկյուն զուգահեռագիծ սահմանափակված է ուղիղ անկյուն կազմող երկու ուղիղ գծերով։ |
||
# Ցանկացած զուգահեռագիծ պատկերում նրա անկյունագծի շուրջ (վերցված) ցանկացած զուգահեռագիծ իր երկու լրացումների հետ միասին կոչվում է գնոմոն։ |
# Ցանկացած զուգահեռագիծ պատկերում նրա անկյունագծի շուրջ (վերցված) ցանկացած զուգահեռագիծ իր երկու լրացումների հետ միասին կոչվում է գնոմոն։ |
||
== Պնդում 1 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>a (b + c + d + ... ) = a b + a c + a d + ...</math></ref>== |
== Պնդում 1 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>a (b + c + d + ... ) = a b + a c + a d + ...</math></ref>== |
||
| ⚫ | |||
| ⚫ | |||
[[Պատկեր:ElementsBook2-Propostion1.png|center|200px]] |
[[Պատկեր:ElementsBook2-Propostion1.png|center|200px]] |
||
A-ն և BC-ն երկու |
A-ն և BC-ն երկու ուղիղներ են և BC-ն կամայականորեն բաժանված է D և E կետերում: Պնդումն այն է, որ A-ի և BC-ի կազմած ուղղանկյունը հավասար է A-ի և BD-ի, A-ի և DE-ի, A-ի և EC-ի կազմած ուղղանկյունների գումարին. |
||
В կետից գծված է BF ուղիղը, որը ուղղահայաց է BC ուղղին [Պնդում 1.11], իսկ BG ուղիղը հավասար է A ուղղին [Պնդում 1.3]։ G կետով գծված է GH ուղիղը, որը զուգահեռ է BC ուղղին [Պնդում 1.31]: D, E և C կետերով դծված են համապատասխան DK, EL, CH ուղիղները, որոնք զուգահեռ են BG ուղղին [Պնդում 1.31]: |
В կետից գծված է BF ուղիղը, որը ուղղահայաց է BC ուղղին [ [[Տարերք/Գիրք 1#Պնդում 11|Պնդում 1.11]] ], իսկ BG ուղիղը հավասար է A ուղղին [ [[Տարերք/Գիրք 1#Պնդում 3|Պնդում 1.3]] ]։ G կետով գծված է GH ուղիղը, որը զուգահեռ է BC ուղղին [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]: D, E և C կետերով դծված են համապատասխան DK, EL, CH ուղիղները, որոնք զուգահեռ են BG ուղղին [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]: |
||
Այսպիսով, BH ուղղանկյունը հավասար է BK, DL և EH ուղղանկյունների գումարին: Ավելին, BH-ն ուղղանկյուն է, որը ձևավորված է A և BC ուղիղներով, քանի որ այն պարփակված է GB և BC ուղիղների միջև միջև, իսկ BG ուղիղը հավասար է A ուղղին: BK ուղղանկյունը ձևավորված է A և BD ուղիղներով, քանի որ այն պարփակված է GB և BD ուղիների միջև, իսկ BG ուղիղը հավասար է A ուղղին: Նմանապես, DL ուղղանկյունը ձևավորվում է A և DE ուղիղներով, քանի որ DK ուղիղը (հավասար է BG-ին) հավասար է A-ին: Վերջապես, EH ուղղանկյունը ձևավորված է A և EC ուղիղներով: Այսպիսով, A և BC ուղիներով կազմած ուղղանկյունը հավասար է A և BD, A և DE, A և EC ուղիղներվ կազմած ուղղանկյունների գումարին: |
Այսպիսով, BH ուղղանկյունը հավասար է BK, DL և EH ուղղանկյունների գումարին: Ավելին, BH-ն ուղղանկյուն է, որը ձևավորված է A և BC ուղիղներով, քանի որ այն պարփակված է GB և BC ուղիղների միջև միջև, իսկ BG ուղիղը հավասար է A ուղղին: BK ուղղանկյունը ձևավորված է A և BD ուղիղներով, քանի որ այն պարփակված է GB և BD ուղիների միջև, իսկ BG ուղիղը հավասար է A ուղղին: Նմանապես, DL ուղղանկյունը ձևավորվում է A և DE ուղիղներով, քանի որ DK ուղիղը (հավասար է BG-ին) հավասար է A-ին: Վերջապես, EH ուղղանկյունը ձևավորված է A և EC ուղիղներով: Այսպիսով, A և BC ուղիներով կազմած ուղղանկյունը հավասար է A և BD, A և DE, A և EC ուղիղներվ կազմած ուղղանկյունների գումարին: |
||
Այսպիսով, եթե կան երկու ուղիղներ, և դրանցից մեկը բաժանված է կամայական թվով մասերի, ապա այս երկու ուղիղ գծերով կազմված ուղղանկյունը հավասար է չկտրված գծի և մասերից յուրաքանչյուրի կազմած ուղղանկյունների գումարին։ Ահա այն ինչ պահանջվում էր ապացուցել։ |
Այսպիսով, եթե կան երկու ուղիղներ, և դրանցից մեկը բաժանված է կամայական թվով մասերի, ապա այս երկու ուղիղ գծերով կազմված ուղղանկյունը հավասար է չկտրված գծի և մասերից յուրաքանչյուրի կազմած ուղղանկյունների գումարին։ Ահա այն ինչ պահանջվում էր ապացուցել։ |
||
== Պնդում 2 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>a b + a c = a^2</math> եթե <math>a = b + c</math></ref>== |
|||
== Պնդում 2 == |
|||
Եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա յուրաքանչյուր մասով կազմված ուղղանկյունների գումարը հավասար է ամբողջ ուղղով կազմված քառակուսուն: |
|||
== Պնդում 3 == |
|||
[[Պատկեր:ElementsBook2-Propostion2.png|center|200px]] |
|||
== Պնդում 4 == |
|||
AB ուղիղը կամայականորեն բաժանված է C կետում: Պնդումն այն է, որ AB և BC ուղիղներով կազմված ուղղանկյան և BA և AC ուղիղներով կազմված ուղղանկյան գումարը հավասար է AB ուղղով կազմված քառակուսուն: AB ուղղով կառուցված է ADEB քառակուսին [ [[Տարերք/Գիրք 1#Պնդում 46|Պնդում 1.46]] ], իսկ C կետով գծված է AD կամ BE կողմերից մեկին զուգահեռ CF ուղիղը [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]: |
|||
== Պնդում 5 == |
|||
Այսպիսով, AE-ն AB կողմով քառակուսի է և հավասար է AF և CE ուղղանկյուններին: AF-ը ուղղանկյուն է, որը կազմված է BA և AC կողմերով: Ի վերջո, այն կազմված է DA և AC կողմերով, իսկ AD-ն հավասար է AB-ին: CE-ն ուղղանկյուն է, որը կազմված է AB և BC կողմերով, իսկ BE-ն հավասար է AB-ին: Այսպիսով, BA և AC ուղիղներով կազմված ուղղանկյան և AB և BC ուղիղներով կազմված ուղղանկյան գումարը հավասար է AB-ի քառակուսուն: |
|||
Հետևաբար, եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա յուրաքանչյուր մասով կազմված ուղղանկյունների գումարը հավասար է ամբողջ ուղղով կազմված քառակուսուն: Սա այն էր, ինչ պետք էր ապացուցել։ |
|||
== Պնդում 3 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>(a + b) a = ab + a^2</math></ref>== |
|||
== Pages 56-68 == |
|||
Եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա մասերից մեկով կազմված ուղղանկյունը հավասար է այդ մասով կազմված քառակուսու և ուղղի երկու մասերով կազմված ուղղանկյան գումարին։ |
|||
== Պնդում 6† == |
|||
[[Պատկեր:ElementsBook2-Propostion3.png|center|200px]] |
|||
| ⚫ | Հետևաբար, քանի որ AC-Ն և CB-Ն հավասար են, AL և CH անկյունագծերով ուղղանկյունները նույնպես հավասար են [Պնդում 1.36]։ CH անկյունագծով ուղղանկյունն էլ հավասար է HF անկյունագծովին [Պնդում 1.43], որից հետևում է, որ AL անկյունագծով ուղղանկյունը հավասար է HF անկյունագծովին։ Երկու կողմերին էլ ավելացնենք CM անկյունագծով ուղղանկյունը։ Կստացվի, որ AM անկյունագծով ուղղանկյունը և NOP գնոմոնը հավասար են։ Իսկ AM անկյունածով ուղղանկյունը կարող ենք կառուցել AD և DB կողմերով։ DM-ն ու DB-ն նույնպես հավասար են, հետևաբար NOP գնոմոնը հավասար է AD-ով և DB-ով կառուցված ուղղանկյանը։ Երկու կողմին էլ ավելացնենք LG անկյունագծով քառակուսին, որը հավասար է BC հիմքով քառակուսուն։ Այսպիսով՝ AD և DB կողմերով ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է NOP գնոմոնի և LG անկյունագծով քառակուսու գումարին։ Սակայն NOP գնոմոնն ու LG անկյունագծով քառակուսին համարժեք են ողջ CEFD-ին, որը ընկած է CD-ի վրա։ Հետևում է, որ AD-ով և DB-ով կառուցված ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է CD հիմքով քառակուսուն։ |
||
B ուղիղը կամայականորեն բաժանված C կետում: Պնդումն այն է, որ AB և BC ուղիղներով կազմված ուղղանկյունը հավասար է AC և CB ուղիղներով կազմված ուղղանկյան և BC ուղղով կազմված քառակուսու գումարին: |
|||
| ⚫ | |||
CB ուղղով կառուցված է CDEB քառակուսին [ [[Տարերք/Գիրք 1#Պնդում 46|Պնդում 1.46]] ], F կետով գծված է ED ուղիղը , իսկ A կետով գծված է AF ուղիղը՝ զուգահեռ CD կամ BE ուղիղներից մեկին [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]: Այսպիսով, AE ուղղանկյունը հավասար է AD ուղղանկյան և CE քառակուսու գումարին և այն կազմված է AB և BC ուղիղներով։ Ի վերջո, այն կազմված է AB և BE ուղիղներով, իսկ BE-ն հավասար է BC-ի: AD-ն ուղղանկյուն է, որը կազմված է AC և CB ուղիղներով:, իսկ DC-ն հավասար է CB-ին: DB-ն քառակուսի է` կազմված CB կողմեվ: Այսպիսով, AB և BC ուղիղներով կազմված ուղղանկյունը հավասար է AC և CB կողմերով կազմված ուղղանկյան և BC կողմով կազմված քառակուսու գումարին: |
|||
Հետևաբար, ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա մասերից մեկով կազմված ուղղանկյունը հավասար է այդ մասով կազմված քառակուսու և ուղղի երկու մասերով կազմված ուղղանկյան գումարին։ Սա այն էր, ինչ պետք էր ապացուցել։ |
|||
== Պնդում 4 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>(a + b)^2 = a^2 + b^2 + 2ab.</math></ref>== |
|||
Եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով կազմված քառակուսին հավասար է նրա մասերի քառակուսիների գումարին և այդ մասերի արտադրյալի կրկնապատիկին: |
|||
[[Պատկեր:ElementsBook2-Propostion4.png|center|200px]] |
|||
AB ուղիղը կամայականորեն բաժանված է C կետում: Պնդումն այն է, որ AB-ի քառակուսին հավասար է AC և CB ուղիղների քառակուսիների և AC և CB ուղիղների արտադրյալի քառակուսու գումարին: |
|||
AB ուղիղը կամայականորեն բաժանված է C կետում: Պնդումն այն է, որ AB-ի քառակուսին հավասար է AC և CB ուղիղների քառակուսիների և AC և CB ուղիղների արտադրյալի քառակուսու գումարին:ADEB քառակուսին կազմված է AB կողմեվ [ [[Տարերք/Գիրք 1#Պնդում 46|Պնդում 1.46]] ] և գծված է BD անկյունագիծը։ C կետով գծված է CF ուղիղը, որը զուգահեռ է AD կամ BE կողմին, իսկ G կետվ գծված է HK ուղիղը, որը զուգահեռ է AB կամ DE կողմին [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]: Քանի որ CF-ը զուգահեռ է AD-ին և BD-ն հատում է դրանք, CGB արտաքին անկյունը հավասար է ADB ներքին անկյանը [ [[Տարերք/Գիրք 1#Պնդում 29|Պնդում 1.29]] ]: ADB անկյունը հավասար է ABD անկյանը, քանի որ BA և AD կողմերը հավասար են [ [[Տարերք/Գիրք 1#Պնդում 5|Պնդում 1.5]] ]: Հետևաբար, CGB անկյունը հավասար է GBC անկյանը, իսկ BC կողմը հավասար է CG կողմին [ [[Տարերք/Գիրք 1#Պնդում 6|Պնդում 1.6]] ]: Նաև CB-ն հավասար է GK կողմին, իսկ CG-ն հավասար է KB կողմին [ [[Տարերք/Գիրք 1#Պնդում 34|Պնդում 1.34]] ]: Այսպիսով, GK-ն հավասար է KB կողմին, իսկ CGKB պատկերը հավասարակողմ է։ Այն նաև ուղղանկյուն է, քանի որ CG և BK կողմերը զուգահեռ են և CB-ն հատում է դրանք, KBC և GCB անկյունները հավասար են և ուղիղ [ [[Տարերք/Գիրք 1#Պնդում 29|Պնդում 1.29]] ]։ KBC-ն ուղիղ անկյուն է։ BCG-ն նույնպես ուղիղ անկյուն է, ինչպես նաև CGK և GKB անկյունները [ [[Տարերք/Գիրք 1#Պնդում 34|Պնդում 1.34]] ]: Հետևաբար, CGKB ուղղանկյուն է։ Քանի որ CGKB-ն նաև հավասարակողմ, հետևաբար այն քառակուսի է։ Նույն կերպով, HF-ը նույնպես քառակուսի է [ [[Տարերք/Գիրք 1#Պնդում 34|Պնդում 1.34]] ]։ Հետևաբար HF-ը և KC-ն համապատասխանաբար AC և CB կողմերով կառուցված քառակուսիներ են և AG ուղղանկյունը հավասար է GE ուղղանկյանը [ [[Տարերք/Գիրք 1#Պնդում 43|Պնդում 1.43]] ]։ AG-ն ուղղանկյուն է՝ կազմված AC և CB կողմերով, և GC կողմը հավասար է CB կողմին։ GE ուղղանկյունը հավասար է AC և CB կողմերով կազմված ուղղանկյանը։ Հետևաբար AG և GE ուղղանկյունները հավասար են AC և CB կողմերով կազմված ուղղանկյան կրկնապատիկին։ HF-ը և CK-ը AC և CB կողմերով կազմված քառակուսիներ են։ Այսպիսով, չորս պատկերները՝ HF, CK, AG և GE, հավասար են AC և BC կողմերի քառակուսիների գումարին և AC և CB կողմերով կազմված ուղղանկյան կրկնապատիկին։ Բայց այս չորս պատկերները հավասար են ամբողջ ADEB պատկերին, որը AB կողմով կազմված քառակուսի է։ Հետևաբար, AB քառակուսին հավասար է AC և CB քառակուսիների և AC և CB կողմերով կազմված ուղղանկյան կրկնապատիկին։ |
|||
Այսպիսով, եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով կազմված քառակուսին հավասար է նրա մասերի քառակուսիների գումարին և այդ մասերի արտադրյալի կրկնապատիկին։ Սա այն էր, ինչ պետք էր ապացուցել։ |
|||
== Պնդում 5 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>ab+(\frac{a + b}{2}-b)^2=(\frac{a+b}{2})^2</math>.</ref>== |
|||
Եթե ուղիղը բաժանված է հավասար և անհավասար մասերի, ապա ամբողջ ուղղի անհավասար մասերից կազմված ուղղանկյան և հավասար և անհավասար մասերի տարբերության քառակուսու գումարը հավասար է գծի կեսի քառակուսուն։ |
|||
[[Պատկեր:ElementsBook2-Propostion5.png|center|200px]] |
|||
AB ուղիղը հավասարաչափ բաժանված է C կետում և անհավասարաչափ՝ D կետում։ Պնդումն այն է, որ AD և DB ուղիղներով կազմված ուղղանկյան և CD քառակուսու գումարը հավասար է CB քառակուսուն։ |
|||
CEFB քառակուսին կառուցված է CB կողմով [ [[Տարերք/Գիրք 1#Պնդում 46|Պնդում 1.46]] ]։ Գծված է BE անկյունագիծը և D կետով գծված է DG ուղիղը, որը զուգահեռ է CE կամ BF կողմին [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]։ H կետով գծված է KM ուղիղը, որը զուգահեռ է Ab կամ EF կողմին [ [[Տարերք/Գիրք 1#Պնդում 31|Պնդում 1.31]] ]։ Քանի որ CH և HF ուղղանկյունները հավասար են [ [[Տարերք/Գիրք 1#Պնդում 43|Պնդում 1.43]] ], երկու ուղղանկյուններին գումարենք DM քառակուսին գումարենք։ Հետևաբար, CM ուղղանկյունը հավասար է DF ուղղանկյանը: Բայց, CM ուղղանկյունը նաև հավասար է AL ուղղանկյանը, քանի որ AC կեղմը հավասար է CB կողմին [ [[Տարերք/Գիրք 1#Պնդում 36|Պնդում 1.36]] ]։ Հետևաբար, AL ուղղանկյունը հավասար է DF ուղղանկյանը։ Այդ երկու ուղղանկյուններին գումարենք CH ուղղանկյունը։ Կստանանք, որ ամբողջ AH ուղղանկյունը հավասար է NOP գնոմոնին։ Բայց AH ուղղանկյունը կազմված է AD և DB կողմերով ը DH-ը հավասար է DB-ին։ Հետևաբար, NOP գնոմոնը հավասար է AD և DB կողմերով կազմված ուղղանկյանը։ LG-ն, որը հավասար է CD-ին, ավելացված է այդ երկու կողմերին։ Հետևաբար, NOP գնոմոնը և LG քառակուսին հավասար են AD և DB կողմերով կազմված ուղղանկյանը և CD քառակուսուն։ Բայց, NOP գնոմոնը և LG քառակուսին հավասար են ամբողջ CEFB քառակուսուն, որը կազմված է CB կողմով։ Հետևաբար, AD և DB կողմերով կազմված ուղղանկյան և CD քառակուսու գումարը հավասար է CB քառակուսուն։ |
|||
Հետևաբար, եթե ուղիղը բաժանված է հավասար և անհավասար մասերի, ապա ամբողջ ուղղի անհավասար մասերից կազմված ուղղանկյան և հավասար և անհավասար մասերի տարբերության քառակուսու գումարը հավասար է գծի կեսի քառակուսուն։ Սա այն էր, ինչ պետք էր ապացուցել։ |
|||
== Պնդում 6 <ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math>(2a+b)\cdot b + a^2 = (a+b)^2 </math></ref>== |
|||
Հատվածը կիսելու և դրան ուղիղ գծով այլ հատված կցելու արդյունքում՝ ստացված ողջ հատվածով և ավելացված մասով կառուցված ուղղանկյան և հատվածի կեսով կառուցված քառակուսու գումարը հավասար է նախնական հատվածի կեսի և կցված հատվածի գումարով ստացված նոր հատվածով կառուցված քառակուսուն։ |
|||
[[Պատկեր:ElementsBook2-Propostion6.png|center|200px]] |
|||
AB ուղղիղը բաժանված է հավասար մասերի C կետում և BD հատվածը ավելացված է AB ուղղին։ Պնդումն այն է, որ AD և DB կողմերով կազմված ուղղանկյան և CB քառակուսու գումարը հավասար է CD կողմով կազմված քառակուսուն։ |
|||
| ⚫ | CD կողմով կազմված է CEFD քառակուսին [Պնդում 1.46 և գծված է DE անկյունագիծ։ B կետով գծված է BG ուղիղը՝ զուգահեռ EC կամ DF կողմին [Պնդում 1.31] և H կետով դծված է KM ուղիղը՝ զուգահեռ AB կամ EF կողմին [Պնդում 1.31]։ Վերջապես, A կետով գծված է AK ուղիղը՝ զուգահեռ CL կամ DM կողմին [Պնդում 1.31]։ Հետևաբար, քանի որ AC-Ն և CB-Ն հավասար են, AL և CH անկյունագծերով ուղղանկյունները նույնպես հավասար են [Պնդում 1.36]։ CH անկյունագծով ուղղանկյունն էլ հավասար է HF անկյունագծովին [Պնդում 1.43], որից հետևում է, որ AL անկյունագծով ուղղանկյունը հավասար է HF անկյունագծովին։ Երկու կողմերին էլ ավելացնենք CM անկյունագծով ուղղանկյունը։ Կստացվի, որ AM անկյունագծով ուղղանկյունը և NOP գնոմոնը հավասար են։ Իսկ AM անկյունածով ուղղանկյունը կարող ենք կառուցել AD և DB կողմերով։ DM-ն ու DB-ն նույնպես հավասար են, հետևաբար NOP գնոմոնը հավասար է AD-ով և DB-ով կառուցված ուղղանկյանը։ Երկու կողմին էլ ավելացնենք LG անկյունագծով քառակուսին, որը հավասար է BC հիմքով քառակուսուն։ Այսպիսով՝ AD և DB կողմերով ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է NOP գնոմոնի և LG անկյունագծով քառակուսու գումարին։ Սակայն NOP գնոմոնն ու LG անկյունագծով քառակուսին համարժեք են ողջ CEFD-ին, որը ընկած է CD-ի վրա։ Հետևում է, որ AD-ով և DB-ով կառուցված ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է CD հիմքով քառակուսուն։ |
||
| ⚫ | |||
== Պնդում 7<ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math> (a+b)^2 + a^2 = 2\cdot (a+b) \cdot a + b^2 </math>։</ref> == |
== Պնդում 7<ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math> (a+b)^2 + a^2 = 2\cdot (a+b) \cdot a + b^2 </math>։</ref> == |
||
| Տող 58. | Տող 93. | ||
AG և GE անկյունագծերով ուղղանկյունները հավասար են, երկուսին էլ կցենք CF անկյունագծով քառակուսին։ Արդյունքում AF և CE անկյունագծերով ուղղանկյունները հավասար կլինեն։ Հետևաբար, AF և CE անկյունագծերով ուղղանկյունների գումարը հավասար է AF անկյունագծով ուղղանկյան կրկնապատիկին։ Սակայն AF և CE անկյունագծերով ուղղանկյունների գումարը KLM գնոմոնն է և CF անկյունագծով քառակուսին։ Հետևաբար, KLM գնոմոնը և CF անկյունագծով քառակուսին AF անկյունագծով ուղղանկյան կրկնապատիկն են կազմում։ Մինչդեռ AF անկյունագծով ուղղանկյան կրկնապատիկը նաև AB և BC կողմերով կառուցված ուղղանկյան կրկնապատիկին է հավասար։ BF-ն ու BC-ն հավասար են։ Հետևում է, որ KLM գնոմոնն ու CF քառակուսին հավասար են AB և BC կողմորով կառուված ուղղանկյան կրկնապատիկին։ Երկու կողմերին էլ ավելացնենք DG անկյունագծով քառակուսին։ Արդյունքում՝ KLM գնոմոնն ու BG և GD անկյունագծերով քառակուսիները հավասար են AB և BC կողմերով կառուցաված ուղղանկյանն ու AC անկյունագծովո քառակուսուն։ Բայց KLM գնոմոնն ու BG և GD քառակուսիները հավասարարժեք են ողջ ADEB-ին և CF-ին, որոնք AB և BC քառակուսիներն են։ Հետևաբար, AB և BC քառակուսիների գումարը հավասար է AB և BC կողմերով կազմված քառակուսու կրկնապատիկին և AC քառակուսուն։ |
AG և GE անկյունագծերով ուղղանկյունները հավասար են, երկուսին էլ կցենք CF անկյունագծով քառակուսին։ Արդյունքում AF և CE անկյունագծերով ուղղանկյունները հավասար կլինեն։ Հետևաբար, AF և CE անկյունագծերով ուղղանկյունների գումարը հավասար է AF անկյունագծով ուղղանկյան կրկնապատիկին։ Սակայն AF և CE անկյունագծերով ուղղանկյունների գումարը KLM գնոմոնն է և CF անկյունագծով քառակուսին։ Հետևաբար, KLM գնոմոնը և CF անկյունագծով քառակուսին AF անկյունագծով ուղղանկյան կրկնապատիկն են կազմում։ Մինչդեռ AF անկյունագծով ուղղանկյան կրկնապատիկը նաև AB և BC կողմերով կառուցված ուղղանկյան կրկնապատիկին է հավասար։ BF-ն ու BC-ն հավասար են։ Հետևում է, որ KLM գնոմոնն ու CF քառակուսին հավասար են AB և BC կողմորով կառուված ուղղանկյան կրկնապատիկին։ Երկու կողմերին էլ ավելացնենք DG անկյունագծով քառակուսին։ Արդյունքում՝ KLM գնոմոնն ու BG և GD անկյունագծերով քառակուսիները հավասար են AB և BC կողմերով կառուցաված ուղղանկյանն ու AC անկյունագծովո քառակուսուն։ Բայց KLM գնոմոնն ու BG և GD քառակուսիները հավասարարժեք են ողջ ADEB-ին և CF-ին, որոնք AB և BC քառակուսիներն են։ Հետևաբար, AB և BC քառակուսիների գումարը հավասար է AB և BC կողմերով կազմված քառակուսու կրկնապատիկին և AC քառակուսուն։ |
||
Այսպիսով՝ հատվածը կամայական կետում հատելիս՝ ստացված հատվածներից պատահականորեն ընտրված մեկի և ողջ հատվածի քառակուսիների գումարը հավասար է ողջ և նախապես ընտրված հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկի և հատման արդյունքում առաջացած մյուս հատվածի երկարության քառակուսու գումարին։ |
Այսպիսով՝ հատվածը կամայական կետում հատելիս՝ ստացված հատվածներից պատահականորեն ընտրված մեկի և ողջ հատվածի քառակուսիների գումարը հավասար է ողջ և նախապես ընտրված հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկի և հատման արդյունքում առաջացած մյուս հատվածի երկարության քառակուսու գումարին։ |
||
| Տող 84. | Տող 120. | ||
C կետով՝ AB-ին ուղղահայաց կառուցենք CE հատվածը [Պնդում 1․11], այնպես, որ հավասար լինի AC-ին և CB-ին [Պնդում 1․3]։ Միացնենք EA-ն և EB-ն։ EC-ին զուգահեռ՝ D կետով կառուցենք DF-ը [Պնդում 1․31], իսկ AB-ին զուգահեռ՝ FG-ը F կետով [Պնդում 1․31]։ Միացնենք AF-ը։ Քանի որ AC-ն ու CE-ն հավասար են, անկյուն EAC-ն հավասար է AEC-ին [Պնդում 1․5]։ Եվ քանի որ C անկյունը ուղիղ անկյեւն է, EAC և AEC անկյունների գումարը նույնպես ուղիղ անկյուն է կազմում [Պնդում 1․32]։ Հետևում է, որ CEA CAE անկյուններից յուրաքանչյուրը ուղիղ անկյան կեսն է։ Նույն պատճառով՝ CEB և EBC անկյունները նույնպես հավասար են ուղիղ անկյան կեսին։ Հետևում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ GEF-ն ուղիղ անկյան կես է, իսկ EGF՝ ուղիղ անկյուն (որը հավասար է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ EFG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Հետևաբար, GEF անկյունը հավասար է EFG-ին, իսկ EG կողմը՝ GF-ին [Պնդում 1․6]։ Քանի որ անկյուն B-ն ուղիղ անկյան կես է, իսկ FDB-ն՝ ուղիղ անկյուն (որը հավասր է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ BFD անկյունը նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Այսպիսով՝ B և DFB անկյունները, FD և DB կողմերը նույնպես հավասար են [Պնդում 1․6]։ Քանի որ AC-ն և CE-ն հավասար են, այդ կողմերով կառուցված համապատասխան քառակուսիները ևս հավասար են։ Հետևաբար, AC-ի և CE-ի վրա կառուցված քառակուսիների գումարը հավասար է AC-ի վրա կառուցված քառակուսու կրկնապատիկին։ EA հիմքով քառակուսին հավասար է AC և CE հիմքերով քառակուսիների գումարին։ ACE անկյունն էլ ուղիղ է [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Քանի որ EG-ն և GF-ը հավասար են, համապատասխան հիմքերով քառակուսիները նույնպես հավասար են, և դրանց գումարը GF հիմքով քառակուսու կրկնապատիկն է։ EF-ի վրա կառուցված քառակուսին էլ հավասար է EG-ի և GF-ի վրա կառուցած քառակուսիների գումարին [Պնդում 1․47]։ Այսպիսով՝ EF հիմքով քառակուսին GF հիմքովի կրկնապատիկն է։ GF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ Հետևաբար, EF հիմքով քառակուսին CD հիմքովի կրկնապատիկն է, EA հիմքովն էլ՝ AC-ի։ Հետևում է, որ AE և EF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AF հիմով քառակուսին AE և EF հիմքերովների գումարին է հավասար։ AEF-ն ուղիղ անկյուն է [Պնդում 1․47]։ Հետևաբար, AF հիմքով քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DF հիմքերով քառակուսիների գումարը հավասար է AF հիմքով քառակուսուն։ D-ն ուղիղ անկյուն է [Պնդում 1․47], հետևաբար AD և DF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների կրկնապատիկն է։ DF-ն էլ հավասար է DB-ին։ Արդյունքում՝ AD-ի և DB-ի վրա ընկած քառակուսիների գումարը AC-ի և CD-ի վրա ընկած քառակուսիների գումարի կրկնապատիկն է։ |
C կետով՝ AB-ին ուղղահայաց կառուցենք CE հատվածը [Պնդում 1․11], այնպես, որ հավասար լինի AC-ին և CB-ին [Պնդում 1․3]։ Միացնենք EA-ն և EB-ն։ EC-ին զուգահեռ՝ D կետով կառուցենք DF-ը [Պնդում 1․31], իսկ AB-ին զուգահեռ՝ FG-ը F կետով [Պնդում 1․31]։ Միացնենք AF-ը։ Քանի որ AC-ն ու CE-ն հավասար են, անկյուն EAC-ն հավասար է AEC-ին [Պնդում 1․5]։ Եվ քանի որ C անկյունը ուղիղ անկյեւն է, EAC և AEC անկյունների գումարը նույնպես ուղիղ անկյուն է կազմում [Պնդում 1․32]։ Հետևում է, որ CEA CAE անկյուններից յուրաքանչյուրը ուղիղ անկյան կեսն է։ Նույն պատճառով՝ CEB և EBC անկյունները նույնպես հավասար են ուղիղ անկյան կեսին։ Հետևում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ GEF-ն ուղիղ անկյան կես է, իսկ EGF՝ ուղիղ անկյուն (որը հավասար է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ EFG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Հետևաբար, GEF անկյունը հավասար է EFG-ին, իսկ EG կողմը՝ GF-ին [Պնդում 1․6]։ Քանի որ անկյուն B-ն ուղիղ անկյան կես է, իսկ FDB-ն՝ ուղիղ անկյուն (որը հավասր է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ BFD անկյունը նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Այսպիսով՝ B և DFB անկյունները, FD և DB կողմերը նույնպես հավասար են [Պնդում 1․6]։ Քանի որ AC-ն և CE-ն հավասար են, այդ կողմերով կառուցված համապատասխան քառակուսիները ևս հավասար են։ Հետևաբար, AC-ի և CE-ի վրա կառուցված քառակուսիների գումարը հավասար է AC-ի վրա կառուցված քառակուսու կրկնապատիկին։ EA հիմքով քառակուսին հավասար է AC և CE հիմքերով քառակուսիների գումարին։ ACE անկյունն էլ ուղիղ է [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Քանի որ EG-ն և GF-ը հավասար են, համապատասխան հիմքերով քառակուսիները նույնպես հավասար են, և դրանց գումարը GF հիմքով քառակուսու կրկնապատիկն է։ EF-ի վրա կառուցված քառակուսին էլ հավասար է EG-ի և GF-ի վրա կառուցած քառակուսիների գումարին [Պնդում 1․47]։ Այսպիսով՝ EF հիմքով քառակուսին GF հիմքովի կրկնապատիկն է։ GF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ Հետևաբար, EF հիմքով քառակուսին CD հիմքովի կրկնապատիկն է, EA հիմքովն էլ՝ AC-ի։ Հետևում է, որ AE և EF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AF հիմով քառակուսին AE և EF հիմքերովների գումարին է հավասար։ AEF-ն ուղիղ անկյուն է [Պնդում 1․47]։ Հետևաբար, AF հիմքով քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DF հիմքերով քառակուսիների գումարը հավասար է AF հիմքով քառակուսուն։ D-ն ուղիղ անկյուն է [Պնդում 1․47], հետևաբար AD և DF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների կրկնապատիկն է։ DF-ն էլ հավասար է DB-ին։ Արդյունքում՝ AD-ի և DB-ի վրա ընկած քառակուսիների գումարը AC-ի և CD-ի վրա ընկած քառակուսիների գումարի կրկնապատիկն է։ |
||
Ստաղվում է, որ հատվածը հավասար և անհավասար մասերի բաժանելիս՝ անհավասար մասերի վրա կառուցված քառակուսիների գումարը հավասար է հատվածի կեսի և հավասար ու անհավասար մասերի տարբերության վրա կառուված քառակուսիների գումարի կրկնապատիկին։ |
Ստաղվում է, որ հատվածը հավասար և անհավասար մասերի բաժանելիս՝ անհավասար մասերի վրա կառուցված քառակուսիների գումարը հավասար է հատվածի կեսի և հավասար ու անհավասար մասերի տարբերության վրա կառուված քառակուսիների գումարի կրկնապատիկին։ |
||
| Տող 95. | Տող 132. | ||
C կետով կառուցենք CE հատվածը, որը կլինի AB-ին ուղղահայաց [Պնդում 1․11] և AC-ին ու CB-ին հավասար [Պնդում 1․3]։ Կառուցենք նաև EA և EB հատվածները։ AD-ին զուգահեռ՝ E կետով տանենք EF հատվածը [Պնդում 1․31]։ CE-ին զուգահեռ՝ FD-ն՝ D կետով [Պնդում 1․3]։ Եվ քանի որ EF-ն հատվում է EC և FD զուգահեռ հատվածների հետ, CEF և EFD ներքին անկյունները հավասար են ուղիղ անկյունների [Պնդում 1․29]։ Հետևաբար, FEB և EFD անկյուննեը փոքր են երկու ուղիղ անկյուններից։ Եվ երկու ներքին անկյուններից (որոնց գումարը ավելի փոքր է քան երկու ուղիղ անկյունների գումար) առաջացած հատվածները հատվում էն [Կանխադրույթ 1.5]։ Հետևաբար, B-ի և D-ի ուղղություններով կառուցված EB և FD հատվածները կհատվեն։ Կռուցենք դրանք, որպես հատման կետ նշանակնեք G-ն և միացնենք AG-ն։ Քանի որ AC-ն և CE-ն հավասար են, EAC և AEC անկյունները նույնպես հավասար են [Կանխադրույթ 1.5]։ Անկյուն C-ն ուղիղ անկյուն է։ Հետևում է, որ EAC-ն ու AEC-ը ուղիղ անկյան կեսեր են [Պնդում 1․32]։ Նույն պատճառներով՝ CEB-ն ու EBC-ն նույնպես ուղիղ անկյան կեսեր են։ Ստացվում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ EBC-ն ուղիղ անկյան կես է, DBG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․15]։ BDG-ն նունպես ուղիղ անկյուն է, որը հավասար է DCE-ին։ Այսինքն դրանք համարժեք/այլընտրանքային անկյուններ են [Պնդում 1․29]։ Հետևաբար, մնացյալ DGB-ն ուղիղ անկյան կես է։ DGB-ն ու DGB-ն հավասար են։ BD-ն էլ հավասար է GD-ին [Պնդում 1․6]։ Կրկին, քանի որ EGF-ն ուղիղ անկյան կես է, իսկ F-ը՝ ուղիղ անկյուն, այն հավասար է հակառակ C անկյանը[Պնդում 1․34], մնացյալ FEG անկյունն էլ կրկին ուղիղ անկյան կես է։ Հետևում է, որ EGF և FEG անկյունները հավասար են։ GF կողմն էլ հավասար է EF-ին [Պնդում 1․6]։ Եվ քանի որ EC-ն ու CA-ն հավասար են, EC և CA հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ EC և CA հիմքերով քառակուսիների գումարը CA հիմքով քառակուսու կրկնապատիկն է։ EA հիմքով քառակուսին էլ հավասար է EC և CA հիմքերով քառակուսինորի գումարին [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Կրկին, քանի որ FG-ն ու EF-ն հավասար են, FG և FE հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ GF-ի և FE-ի վրա կառուցված քառակուսիները EF հիքով քառակուսու կրկնապատիկն են։ EG հիմքով քառակուսին էլ GF և FE հիմքերով քառակուսիների գումարի կրկնապատիկն է [Պնդում 1․47]։ Հետևաբար, EG հիմքով քառակուսին EF հիմքովի կրկնապատիկն է։ EF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ EG հիմքով քառակուսին CD հիմքովի կրկնապատիկն է։ Սակայն ցույց էր տրվել նաև, որ EA-ի վրա կառուցված քառակուսին AC-ի վրա կառուցվածի կրկնապատիկն է։ Արդյունքում՝ AE և EC հիմքերով քառակուսիների գումարը AC և DC հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AG, AE և EG հիմքերով քառակուսիներն էլ հավասար են [Պնդում 1․47]։ AG-ի վրա կառուցված քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DG հիմքերով քառակուսիների գումարն էլ հավասար է AG հիմքով քառակուսուն [Պնդում 1․47]։ Հետևաբար, AD և DG հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարին հավասար։ DG- հավասար է DB-ին։ Հետրաբար, AD և DB հիմքերով քառակուսիների գումարը AC և CD հմքերով քառակուսիների գումարի կրկնապատիկն է։ |
C կետով կառուցենք CE հատվածը, որը կլինի AB-ին ուղղահայաց [Պնդում 1․11] և AC-ին ու CB-ին հավասար [Պնդում 1․3]։ Կառուցենք նաև EA և EB հատվածները։ AD-ին զուգահեռ՝ E կետով տանենք EF հատվածը [Պնդում 1․31]։ CE-ին զուգահեռ՝ FD-ն՝ D կետով [Պնդում 1․3]։ Եվ քանի որ EF-ն հատվում է EC և FD զուգահեռ հատվածների հետ, CEF և EFD ներքին անկյունները հավասար են ուղիղ անկյունների [Պնդում 1․29]։ Հետևաբար, FEB և EFD անկյուննեը փոքր են երկու ուղիղ անկյուններից։ Եվ երկու ներքին անկյուններից (որոնց գումարը ավելի փոքր է քան երկու ուղիղ անկյունների գումար) առաջացած հատվածները հատվում էն [Կանխադրույթ 1.5]։ Հետևաբար, B-ի և D-ի ուղղություններով կառուցված EB և FD հատվածները կհատվեն։ Կռուցենք դրանք, որպես հատման կետ նշանակնեք G-ն և միացնենք AG-ն։ Քանի որ AC-ն և CE-ն հավասար են, EAC և AEC անկյունները նույնպես հավասար են [Կանխադրույթ 1.5]։ Անկյուն C-ն ուղիղ անկյուն է։ Հետևում է, որ EAC-ն ու AEC-ը ուղիղ անկյան կեսեր են [Պնդում 1․32]։ Նույն պատճառներով՝ CEB-ն ու EBC-ն նույնպես ուղիղ անկյան կեսեր են։ Ստացվում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ EBC-ն ուղիղ անկյան կես է, DBG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․15]։ BDG-ն նունպես ուղիղ անկյուն է, որը հավասար է DCE-ին։ Այսինքն դրանք համարժեք/այլընտրանքային անկյուններ են [Պնդում 1․29]։ Հետևաբար, մնացյալ DGB-ն ուղիղ անկյան կես է։ DGB-ն ու DGB-ն հավասար են։ BD-ն էլ հավասար է GD-ին [Պնդում 1․6]։ Կրկին, քանի որ EGF-ն ուղիղ անկյան կես է, իսկ F-ը՝ ուղիղ անկյուն, այն հավասար է հակառակ C անկյանը[Պնդում 1․34], մնացյալ FEG անկյունն էլ կրկին ուղիղ անկյան կես է։ Հետևում է, որ EGF և FEG անկյունները հավասար են։ GF կողմն էլ հավասար է EF-ին [Պնդում 1․6]։ Եվ քանի որ EC-ն ու CA-ն հավասար են, EC և CA հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ EC և CA հիմքերով քառակուսիների գումարը CA հիմքով քառակուսու կրկնապատիկն է։ EA հիմքով քառակուսին էլ հավասար է EC և CA հիմքերով քառակուսինորի գումարին [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Կրկին, քանի որ FG-ն ու EF-ն հավասար են, FG և FE հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ GF-ի և FE-ի վրա կառուցված քառակուսիները EF հիքով քառակուսու կրկնապատիկն են։ EG հիմքով քառակուսին էլ GF և FE հիմքերով քառակուսիների գումարի կրկնապատիկն է [Պնդում 1․47]։ Հետևաբար, EG հիմքով քառակուսին EF հիմքովի կրկնապատիկն է։ EF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ EG հիմքով քառակուսին CD հիմքովի կրկնապատիկն է։ Սակայն ցույց էր տրվել նաև, որ EA-ի վրա կառուցված քառակուսին AC-ի վրա կառուցվածի կրկնապատիկն է։ Արդյունքում՝ AE և EC հիմքերով քառակուսիների գումարը AC և DC հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AG, AE և EG հիմքերով քառակուսիներն էլ հավասար են [Պնդում 1․47]։ AG-ի վրա կառուցված քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DG հիմքերով քառակուսիների գումարն էլ հավասար է AG հիմքով քառակուսուն [Պնդում 1․47]։ Հետևաբար, AD և DG հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարին հավասար։ DG- հավասար է DB-ին։ Հետրաբար, AD և DB հիմքերով քառակուսիների գումարը AC և CD հմքերով քառակուսիների գումարի կրկնապատիկն է։ |
||
Ստացվում է, եթե հատվածը հավասար կիսենք և որպես հատվածի շարունակություն նրան կցենք նոր հատված, ապա ստացված ողջ և ավելացված հատվածի վրա կառուցված քառակուսիների գումարը հավասար կլինի նախնական հատվածի կեսի և այդ կեսի ու կցված հատվածի վրա կառուցված քառակուսիների գումարին։ |
Ստացվում է, եթե հատվածը հավասար կիսենք և որպես հատվածի շարունակություն նրան կցենք նոր հատված, ապա ստացված ողջ և ավելացված հատվածի վրա կառուցված քառակուսիների գումարը հավասար կլինի նախնական հատվածի կեսի և այդ կեսի ու կցված հատվածի վրա կառուցված քառակուսիների գումարին։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։ |
||
== Պնդում 11<ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math> (2\cdot a + b)^2 + b^2 = 2 \cdot [a^2 + (a+b)^2] </math>:</ref> == |
== Պնդում 11<ref>Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ <math> (2\cdot a + b)^2 + b^2 = 2 \cdot [a^2 + (a+b)^2] </math>:</ref> == |
||
Ընթացիկ տարբերակը 14:11, 23 դեկտեմբերի 2024-ի դրությամբ
հեղինակ՝ էվկլիդես |
Սահմանումներ
- Ցանկացած ուղղանկյուն զուգահեռագիծ սահմանափակված է ուղիղ անկյուն կազմող երկու ուղիղ գծերով։
- Ցանկացած զուգահեռագիծ պատկերում նրա անկյունագծի շուրջ (վերցված) ցանկացած զուգահեռագիծ իր երկու լրացումների հետ միասին կոչվում է գնոմոն։
Պնդում 1 [1]
Եթե կան երկու ուղիղներ, և դրանցից մեկը բաժանված է ցանկացած թվով մասերի, ապա այս երկու ուղիղներով կազմված ուղղանկյունը հավասար է չբաժանված ուղղի և բաժանված ուղղի յուրաքանչյուր մասի կազմած ուղղանկյունների գումարին։
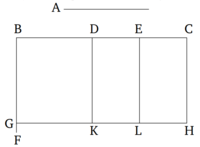
A-ն և BC-ն երկու ուղիղներ են և BC-ն կամայականորեն բաժանված է D և E կետերում: Պնդումն այն է, որ A-ի և BC-ի կազմած ուղղանկյունը հավասար է A-ի և BD-ի, A-ի և DE-ի, A-ի և EC-ի կազմած ուղղանկյունների գումարին.
В կետից գծված է BF ուղիղը, որը ուղղահայաց է BC ուղղին [ Պնդում 1.11 ], իսկ BG ուղիղը հավասար է A ուղղին [ Պնդում 1.3 ]։ G կետով գծված է GH ուղիղը, որը զուգահեռ է BC ուղղին [ Պնդում 1.31 ]: D, E և C կետերով դծված են համապատասխան DK, EL, CH ուղիղները, որոնք զուգահեռ են BG ուղղին [ Պնդում 1.31 ]: Այսպիսով, BH ուղղանկյունը հավասար է BK, DL և EH ուղղանկյունների գումարին: Ավելին, BH-ն ուղղանկյուն է, որը ձևավորված է A և BC ուղիղներով, քանի որ այն պարփակված է GB և BC ուղիղների միջև միջև, իսկ BG ուղիղը հավասար է A ուղղին: BK ուղղանկյունը ձևավորված է A և BD ուղիղներով, քանի որ այն պարփակված է GB և BD ուղիների միջև, իսկ BG ուղիղը հավասար է A ուղղին: Նմանապես, DL ուղղանկյունը ձևավորվում է A և DE ուղիղներով, քանի որ DK ուղիղը (հավասար է BG-ին) հավասար է A-ին: Վերջապես, EH ուղղանկյունը ձևավորված է A և EC ուղիղներով: Այսպիսով, A և BC ուղիներով կազմած ուղղանկյունը հավասար է A և BD, A և DE, A և EC ուղիղներվ կազմած ուղղանկյունների գումարին:
Այսպիսով, եթե կան երկու ուղիղներ, և դրանցից մեկը բաժանված է կամայական թվով մասերի, ապա այս երկու ուղիղ գծերով կազմված ուղղանկյունը հավասար է չկտրված գծի և մասերից յուրաքանչյուրի կազմած ուղղանկյունների գումարին։ Ահա այն ինչ պահանջվում էր ապացուցել։
Պնդում 2 [2]
Եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա յուրաքանչյուր մասով կազմված ուղղանկյունների գումարը հավասար է ամբողջ ուղղով կազմված քառակուսուն:
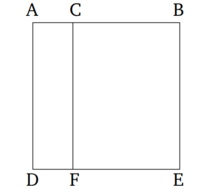
AB ուղիղը կամայականորեն բաժանված է C կետում: Պնդումն այն է, որ AB և BC ուղիղներով կազմված ուղղանկյան և BA և AC ուղիղներով կազմված ուղղանկյան գումարը հավասար է AB ուղղով կազմված քառակուսուն: AB ուղղով կառուցված է ADEB քառակուսին [ Պնդում 1.46 ], իսկ C կետով գծված է AD կամ BE կողմերից մեկին զուգահեռ CF ուղիղը [ Պնդում 1.31 ]: Այսպիսով, AE-ն AB կողմով քառակուսի է և հավասար է AF և CE ուղղանկյուններին: AF-ը ուղղանկյուն է, որը կազմված է BA և AC կողմերով: Ի վերջո, այն կազմված է DA և AC կողմերով, իսկ AD-ն հավասար է AB-ին: CE-ն ուղղանկյուն է, որը կազմված է AB և BC կողմերով, իսկ BE-ն հավասար է AB-ին: Այսպիսով, BA և AC ուղիղներով կազմված ուղղանկյան և AB և BC ուղիղներով կազմված ուղղանկյան գումարը հավասար է AB-ի քառակուսուն: Հետևաբար, եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա յուրաքանչյուր մասով կազմված ուղղանկյունների գումարը հավասար է ամբողջ ուղղով կազմված քառակուսուն: Սա այն էր, ինչ պետք էր ապացուցել։
Պնդում 3 [3]
Եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա մասերից մեկով կազմված ուղղանկյունը հավասար է այդ մասով կազմված քառակուսու և ուղղի երկու մասերով կազմված ուղղանկյան գումարին։
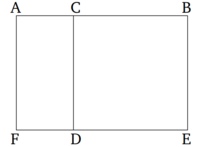
B ուղիղը կամայականորեն բաժանված C կետում: Պնդումն այն է, որ AB և BC ուղիղներով կազմված ուղղանկյունը հավասար է AC և CB ուղիղներով կազմված ուղղանկյան և BC ուղղով կազմված քառակուսու գումարին: CB ուղղով կառուցված է CDEB քառակուսին [ Պնդում 1.46 ], F կետով գծված է ED ուղիղը , իսկ A կետով գծված է AF ուղիղը՝ զուգահեռ CD կամ BE ուղիղներից մեկին [ Պնդում 1.31 ]: Այսպիսով, AE ուղղանկյունը հավասար է AD ուղղանկյան և CE քառակուսու գումարին և այն կազմված է AB և BC ուղիղներով։ Ի վերջո, այն կազմված է AB և BE ուղիղներով, իսկ BE-ն հավասար է BC-ի: AD-ն ուղղանկյուն է, որը կազմված է AC և CB ուղիղներով:, իսկ DC-ն հավասար է CB-ին: DB-ն քառակուսի է` կազմված CB կողմեվ: Այսպիսով, AB և BC ուղիղներով կազմված ուղղանկյունը հավասար է AC և CB կողմերով կազմված ուղղանկյան և BC կողմով կազմված քառակուսու գումարին: Հետևաբար, ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով և նրա մասերից մեկով կազմված ուղղանկյունը հավասար է այդ մասով կազմված քառակուսու և ուղղի երկու մասերով կազմված ուղղանկյան գումարին։ Սա այն էր, ինչ պետք էր ապացուցել։
Պնդում 4 [4]
Եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով կազմված քառակուսին հավասար է նրա մասերի քառակուսիների գումարին և այդ մասերի արտադրյալի կրկնապատիկին:
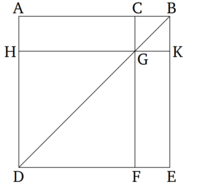
AB ուղիղը կամայականորեն բաժանված է C կետում: Պնդումն այն է, որ AB-ի քառակուսին հավասար է AC և CB ուղիղների քառակուսիների և AC և CB ուղիղների արտադրյալի քառակուսու գումարին:
AB ուղիղը կամայականորեն բաժանված է C կետում: Պնդումն այն է, որ AB-ի քառակուսին հավասար է AC և CB ուղիղների քառակուսիների և AC և CB ուղիղների արտադրյալի քառակուսու գումարին:ADEB քառակուսին կազմված է AB կողմեվ [ Պնդում 1.46 ] և գծված է BD անկյունագիծը։ C կետով գծված է CF ուղիղը, որը զուգահեռ է AD կամ BE կողմին, իսկ G կետվ գծված է HK ուղիղը, որը զուգահեռ է AB կամ DE կողմին [ Պնդում 1.31 ]: Քանի որ CF-ը զուգահեռ է AD-ին և BD-ն հատում է դրանք, CGB արտաքին անկյունը հավասար է ADB ներքին անկյանը [ Պնդում 1.29 ]: ADB անկյունը հավասար է ABD անկյանը, քանի որ BA և AD կողմերը հավասար են [ Պնդում 1.5 ]: Հետևաբար, CGB անկյունը հավասար է GBC անկյանը, իսկ BC կողմը հավասար է CG կողմին [ Պնդում 1.6 ]: Նաև CB-ն հավասար է GK կողմին, իսկ CG-ն հավասար է KB կողմին [ Պնդում 1.34 ]: Այսպիսով, GK-ն հավասար է KB կողմին, իսկ CGKB պատկերը հավասարակողմ է։ Այն նաև ուղղանկյուն է, քանի որ CG և BK կողմերը զուգահեռ են և CB-ն հատում է դրանք, KBC և GCB անկյունները հավասար են և ուղիղ [ Պնդում 1.29 ]։ KBC-ն ուղիղ անկյուն է։ BCG-ն նույնպես ուղիղ անկյուն է, ինչպես նաև CGK և GKB անկյունները [ Պնդում 1.34 ]: Հետևաբար, CGKB ուղղանկյուն է։ Քանի որ CGKB-ն նաև հավասարակողմ, հետևաբար այն քառակուսի է։ Նույն կերպով, HF-ը նույնպես քառակուսի է [ Պնդում 1.34 ]։ Հետևաբար HF-ը և KC-ն համապատասխանաբար AC և CB կողմերով կառուցված քառակուսիներ են և AG ուղղանկյունը հավասար է GE ուղղանկյանը [ Պնդում 1.43 ]։ AG-ն ուղղանկյուն է՝ կազմված AC և CB կողմերով, և GC կողմը հավասար է CB կողմին։ GE ուղղանկյունը հավասար է AC և CB կողմերով կազմված ուղղանկյանը։ Հետևաբար AG և GE ուղղանկյունները հավասար են AC և CB կողմերով կազմված ուղղանկյան կրկնապատիկին։ HF-ը և CK-ը AC և CB կողմերով կազմված քառակուսիներ են։ Այսպիսով, չորս պատկերները՝ HF, CK, AG և GE, հավասար են AC և BC կողմերի քառակուսիների գումարին և AC և CB կողմերով կազմված ուղղանկյան կրկնապատիկին։ Բայց այս չորս պատկերները հավասար են ամբողջ ADEB պատկերին, որը AB կողմով կազմված քառակուսի է։ Հետևաբար, AB քառակուսին հավասար է AC և CB քառակուսիների և AC և CB կողմերով կազմված ուղղանկյան կրկնապատիկին։
Այսպիսով, եթե ուղիղը կամայականորեն բաժանված է մասերի, ապա ամբողջ ուղղով կազմված քառակուսին հավասար է նրա մասերի քառակուսիների գումարին և այդ մասերի արտադրյալի կրկնապատիկին։ Սա այն էր, ինչ պետք էր ապացուցել։
Պնդում 5 [5]
Եթե ուղիղը բաժանված է հավասար և անհավասար մասերի, ապա ամբողջ ուղղի անհավասար մասերից կազմված ուղղանկյան և հավասար և անհավասար մասերի տարբերության քառակուսու գումարը հավասար է գծի կեսի քառակուսուն։
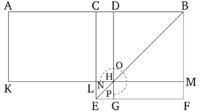
AB ուղիղը հավասարաչափ բաժանված է C կետում և անհավասարաչափ՝ D կետում։ Պնդումն այն է, որ AD և DB ուղիղներով կազմված ուղղանկյան և CD քառակուսու գումարը հավասար է CB քառակուսուն։
CEFB քառակուսին կառուցված է CB կողմով [ Պնդում 1.46 ]։ Գծված է BE անկյունագիծը և D կետով գծված է DG ուղիղը, որը զուգահեռ է CE կամ BF կողմին [ Պնդում 1.31 ]։ H կետով գծված է KM ուղիղը, որը զուգահեռ է Ab կամ EF կողմին [ Պնդում 1.31 ]։ Քանի որ CH և HF ուղղանկյունները հավասար են [ Պնդում 1.43 ], երկու ուղղանկյուններին գումարենք DM քառակուսին գումարենք։ Հետևաբար, CM ուղղանկյունը հավասար է DF ուղղանկյանը: Բայց, CM ուղղանկյունը նաև հավասար է AL ուղղանկյանը, քանի որ AC կեղմը հավասար է CB կողմին [ Պնդում 1.36 ]։ Հետևաբար, AL ուղղանկյունը հավասար է DF ուղղանկյանը։ Այդ երկու ուղղանկյուններին գումարենք CH ուղղանկյունը։ Կստանանք, որ ամբողջ AH ուղղանկյունը հավասար է NOP գնոմոնին։ Բայց AH ուղղանկյունը կազմված է AD և DB կողմերով ը DH-ը հավասար է DB-ին։ Հետևաբար, NOP գնոմոնը հավասար է AD և DB կողմերով կազմված ուղղանկյանը։ LG-ն, որը հավասար է CD-ին, ավելացված է այդ երկու կողմերին։ Հետևաբար, NOP գնոմոնը և LG քառակուսին հավասար են AD և DB կողմերով կազմված ուղղանկյանը և CD քառակուսուն։ Բայց, NOP գնոմոնը և LG քառակուսին հավասար են ամբողջ CEFB քառակուսուն, որը կազմված է CB կողմով։ Հետևաբար, AD և DB կողմերով կազմված ուղղանկյան և CD քառակուսու գումարը հավասար է CB քառակուսուն։
Հետևաբար, եթե ուղիղը բաժանված է հավասար և անհավասար մասերի, ապա ամբողջ ուղղի անհավասար մասերից կազմված ուղղանկյան և հավասար և անհավասար մասերի տարբերության քառակուսու գումարը հավասար է գծի կեսի քառակուսուն։ Սա այն էր, ինչ պետք էր ապացուցել։
Պնդում 6 [6]
Հատվածը կիսելու և դրան ուղիղ գծով այլ հատված կցելու արդյունքում՝ ստացված ողջ հատվածով և ավելացված մասով կառուցված ուղղանկյան և հատվածի կեսով կառուցված քառակուսու գումարը հավասար է նախնական հատվածի կեսի և կցված հատվածի գումարով ստացված նոր հատվածով կառուցված քառակուսուն։
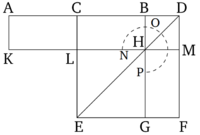
AB ուղղիղը բաժանված է հավասար մասերի C կետում և BD հատվածը ավելացված է AB ուղղին։ Պնդումն այն է, որ AD և DB կողմերով կազմված ուղղանկյան և CB քառակուսու գումարը հավասար է CD կողմով կազմված քառակուսուն։
CD կողմով կազմված է CEFD քառակուսին [Պնդում 1.46 և գծված է DE անկյունագիծ։ B կետով գծված է BG ուղիղը՝ զուգահեռ EC կամ DF կողմին [Պնդում 1.31] և H կետով դծված է KM ուղիղը՝ զուգահեռ AB կամ EF կողմին [Պնդում 1.31]։ Վերջապես, A կետով գծված է AK ուղիղը՝ զուգահեռ CL կամ DM կողմին [Պնդում 1.31]։ Հետևաբար, քանի որ AC-Ն և CB-Ն հավասար են, AL և CH անկյունագծերով ուղղանկյունները նույնպես հավասար են [Պնդում 1.36]։ CH անկյունագծով ուղղանկյունն էլ հավասար է HF անկյունագծովին [Պնդում 1.43], որից հետևում է, որ AL անկյունագծով ուղղանկյունը հավասար է HF անկյունագծովին։ Երկու կողմերին էլ ավելացնենք CM անկյունագծով ուղղանկյունը։ Կստացվի, որ AM անկյունագծով ուղղանկյունը և NOP գնոմոնը հավասար են։ Իսկ AM անկյունածով ուղղանկյունը կարող ենք կառուցել AD և DB կողմերով։ DM-ն ու DB-ն նույնպես հավասար են, հետևաբար NOP գնոմոնը հավասար է AD-ով և DB-ով կառուցված ուղղանկյանը։ Երկու կողմին էլ ավելացնենք LG անկյունագծով քառակուսին, որը հավասար է BC հիմքով քառակուսուն։ Այսպիսով՝ AD և DB կողմերով ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է NOP գնոմոնի և LG անկյունագծով քառակուսու գումարին։ Սակայն NOP գնոմոնն ու LG անկյունագծով քառակուսին համարժեք են ողջ CEFD-ին, որը ընկած է CD-ի վրա։ Հետևում է, որ AD-ով և DB-ով կառուցված ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է CD հիմքով քառակուսուն։
Հետևաբար, հատվածը կիսելու և դրան ուղիղ գծով այլ հատված կցելու արդյունքում՝ ստացված ողջ հատվածով և ավելացված մասով կառուցված ուղղանկյան և հատվածի կեսով կառուցված քառակուսու գումարը հավասար է նախնական հատվածի կեսի և կցված հատվածի գումարով ստացված նոր հատվածով կառուցված քառակուսուն։
Պնդում 7[7]
Հատվածը կամայական կետում հատելիս՝ ստացված հատվածներից պատահականորեն ընտրված մեկի և ողջ հատվածի քառակուսիների գումարը հավասար է ողջ և նախապես ընտրված հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկի և հատման արդյունքում առաջացած մյուս հատվածի երկարության քառակուսու գումարին։

Տրված AB հատվածը հատենք C կետում: AB և BC հատվածների քառակուսիների գումարը հավասար է AB և BC հատվածներով որոշված ուղղանկյան մակերեսի կրկնապատիկի և CA կողմով քառակուսու մակերեսի գումարին։
Կառուցենք ADEB քառակուսին՝ AB կողմով սահմանված։ Կառուցենք նաև գծագրի մնացած մասը։
AG և GE անկյունագծերով ուղղանկյունները հավասար են, երկուսին էլ կցենք CF անկյունագծով քառակուսին։ Արդյունքում AF և CE անկյունագծերով ուղղանկյունները հավասար կլինեն։ Հետևաբար, AF և CE անկյունագծերով ուղղանկյունների գումարը հավասար է AF անկյունագծով ուղղանկյան կրկնապատիկին։ Սակայն AF և CE անկյունագծերով ուղղանկյունների գումարը KLM գնոմոնն է և CF անկյունագծով քառակուսին։ Հետևաբար, KLM գնոմոնը և CF անկյունագծով քառակուսին AF անկյունագծով ուղղանկյան կրկնապատիկն են կազմում։ Մինչդեռ AF անկյունագծով ուղղանկյան կրկնապատիկը նաև AB և BC կողմերով կառուցված ուղղանկյան կրկնապատիկին է հավասար։ BF-ն ու BC-ն հավասար են։ Հետևում է, որ KLM գնոմոնն ու CF քառակուսին հավասար են AB և BC կողմորով կառուված ուղղանկյան կրկնապատիկին։ Երկու կողմերին էլ ավելացնենք DG անկյունագծով քառակուսին։ Արդյունքում՝ KLM գնոմոնն ու BG և GD անկյունագծերով քառակուսիները հավասար են AB և BC կողմերով կառուցաված ուղղանկյանն ու AC անկյունագծովո քառակուսուն։ Բայց KLM գնոմոնն ու BG և GD քառակուսիները հավասարարժեք են ողջ ADEB-ին և CF-ին, որոնք AB և BC քառակուսիներն են։ Հետևաբար, AB և BC քառակուսիների գումարը հավասար է AB և BC կողմերով կազմված քառակուսու կրկնապատիկին և AC քառակուսուն։
Այսպիսով՝ հատվածը կամայական կետում հատելիս՝ ստացված հատվածներից պատահականորեն ընտրված մեկի և ողջ հատվածի քառակուսիների գումարը հավասար է ողջ և նախապես ընտրված հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկի և հատման արդյունքում առաջացած մյուս հատվածի երկարության քառակուսու գումարին։
Պնդում 8[8]
Հատվածը կամայական կետում հատելիս՝ այդ հատվածով և հատման արդյունքում առաջացած կտորներից մեկով սահմանված ուղղանկյան մակերեսի քառապատիկի և հատման արդյունքում առաջացած մյուս հատվածով կառուցված քառակուսու մակերեսի գումարը հավասար է վերոնշյալ և ողջ հատվածների գումարով սահմանված քառակուսու մակերեսին։

Տրված AB հատվածը հատենք C կետում: AB և BC կողմերով ուղղանկյան մակերեսի քառապատիկի և AC կողմով քառակուսու մակերեսի գումարը հավասար է AB և BC կողմերի գումարով սահմանված քառակուսու մակերեսին։
Շարունակելով AB հատվածը՝ կառուցենք BD-ն այնպես, որ հավասար այն հավասար լինի CB-ին։ Ապա, Կառուցենք AEFD քառակուսին՝ AD կողմով։ Կառուցենք նաև գծագրի մնացած մասը։
Հետևաբար, քանի որ CB-ն և BD-ն, CB-ն և GK-ը, BD-ն և KN-ը հավասար են, GK-ը և KN-ը նույնպես հավասար են։ Նույն պատճառով հավասար են նաև QR-ը և RP-ն։ Եվ քանի որ BC-ն ու BD-ն, GK-ն ու KN-ը հավասար են՝ CK և KD, GR և RN անկյունագծերով քառակուսիները նույնպես հավասար են։ Հավասար են նաև CK և RN անկյունգծերով քառակուսիները, որոնք CP անկյունագծով զուգահեռագծի մաս են կազմում։ Հետևաբար, KD և GR անկյունագծով քառակուսիները նույնպես հավասար են։ Հավասար են նաև DK, CK, GR և RN անկյունագծերով քառակուսիները, հետևաբար, այդ 4-ը միասին CK անկյունագծով քառակուսու քառակին են։ Հաջորդիվ դիտարկենք հետևյալ հավասարությունները՝ CB=BD=BK, CG=CB=GK, GQ=CG=GQ։
CG=CQ, QR=RP, այս հավասարություննեից էլ հետևում է որ AG և MQ, QL և RF, MQ և QL անկյունագծերով ուղղանկյունները հավասար են և ML անկյունագծով զուգահեռագծի մաս են կազմում։ AG և RF ուղղանկյունները ևս հավասար են։ Հետևաբար, AG, MQ, QL և RF ուղղանկյունները միմյանց հավասար են, և այդ չորսը իրար հետ վերցված AG ուղղանկյան քառապատիկն են։ Ցույց էր տրված նաև, որ CK, KD, GR և RN քառակուսիները միասին CK-ի քառապատիկն են։ Հետևում է, որ STU գնոմոնը կազմեղ վերոնշյալ 8 պատկերները AK ուղղանկյան քառապատիկն են։ BK=BD հավասարությունից ելնելով AK ուղղանկյունը ստացվել է AB և BD կողմերից։ Այդ ուղղանկյան քառապատիկը AK-ի քառապատիկն է։ Սակայն STU գնոմոնը նույնպես AK-ի քառապատիկն էր։ Հետևաբար, AB և BD կողմերով ուղղանկյունը հավասար է STU գնոմոնին։ Դիցուք, վերոնշյալ երկուսին էլ գումարենք OH-ը, որը հավասար է AC կողմով քառակուս։ Կստացվի, որ AB և BD կողմերով ուղղանկյանը AC-ի հետ միասին հավասար է STU գնոմոնին և OH քառակուսուն։ Սակայն STU գնոմոնն ու OH քառակուսին համարժեք են ոնջ AEFD քառակուսուն, որը կառուցված է AD կողմով։ Հետևում է, որ AB և BD կողերով հազմված ուղղանկյան քառապատիկը AC քառակուսու հետ միասին հավասար է AD քառակուսուն։ BD-ն էլ հավասար է BC-ին։ Հետևում է, որ AB և BC կողմերով ուղղանկյան քառապատիկը AC քառակուսու հետ միասին հավասար է AD քառակուսուն, որը սահմանված է AB և BC հատվածների գումարը որպես կողմ վերցնելով։ Հետէաբար, հատվածը կամայական կետում հատելիս՝ այդ հատվածով և հատման արդյունքում առաջացած կտորներից մեկով սահմանված ուղղանկյան մակերեսի քառապատիկի և հատման արդյունքում առաջացած մյուս հատվածով կառուցված քառակուսու մակերեսի գումարը հավասար է վերոնշյալ և ողջ հատվածների գումարով սահմանված քառակուսու մակերեսին։ Ահա այն ինչ պահանջվում էր ապացուցել։
Պնդում 9[9]
Հատվածը հավասար և անհավասար մասերի բաժանելիս՝ անհավասար մասերի վրա կառուցված քառակուսիների գումարը հավասար է հատվածի կեսի և հավասար ու անհավասար մասերի տարբերության վրա կառուված քառակուսիների գումարի կրկնապատիկին։

Տրված AB հատվածը հավասար կիսենք C կետով, անհավասար՝ D-ով։ AD և DB հավտածների վրա կառուցված քառակուսիների գումարը հավասար է AC և CD կողմերով քառակուսիների գումարի կրկնապատիկին։
C կետով՝ AB-ին ուղղահայաց կառուցենք CE հատվածը [Պնդում 1․11], այնպես, որ հավասար լինի AC-ին և CB-ին [Պնդում 1․3]։ Միացնենք EA-ն և EB-ն։ EC-ին զուգահեռ՝ D կետով կառուցենք DF-ը [Պնդում 1․31], իսկ AB-ին զուգահեռ՝ FG-ը F կետով [Պնդում 1․31]։ Միացնենք AF-ը։ Քանի որ AC-ն ու CE-ն հավասար են, անկյուն EAC-ն հավասար է AEC-ին [Պնդում 1․5]։ Եվ քանի որ C անկյունը ուղիղ անկյեւն է, EAC և AEC անկյունների գումարը նույնպես ուղիղ անկյուն է կազմում [Պնդում 1․32]։ Հետևում է, որ CEA CAE անկյուններից յուրաքանչյուրը ուղիղ անկյան կեսն է։ Նույն պատճառով՝ CEB և EBC անկյունները նույնպես հավասար են ուղիղ անկյան կեսին։ Հետևում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ GEF-ն ուղիղ անկյան կես է, իսկ EGF՝ ուղիղ անկյուն (որը հավասար է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ EFG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Հետևաբար, GEF անկյունը հավասար է EFG-ին, իսկ EG կողմը՝ GF-ին [Պնդում 1․6]։ Քանի որ անկյուն B-ն ուղիղ անկյան կես է, իսկ FDB-ն՝ ուղիղ անկյուն (որը հավասր է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ BFD անկյունը նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Այսպիսով՝ B և DFB անկյունները, FD և DB կողմերը նույնպես հավասար են [Պնդում 1․6]։ Քանի որ AC-ն և CE-ն հավասար են, այդ կողմերով կառուցված համապատասխան քառակուսիները ևս հավասար են։ Հետևաբար, AC-ի և CE-ի վրա կառուցված քառակուսիների գումարը հավասար է AC-ի վրա կառուցված քառակուսու կրկնապատիկին։ EA հիմքով քառակուսին հավասար է AC և CE հիմքերով քառակուսիների գումարին։ ACE անկյունն էլ ուղիղ է [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Քանի որ EG-ն և GF-ը հավասար են, համապատասխան հիմքերով քառակուսիները նույնպես հավասար են, և դրանց գումարը GF հիմքով քառակուսու կրկնապատիկն է։ EF-ի վրա կառուցված քառակուսին էլ հավասար է EG-ի և GF-ի վրա կառուցած քառակուսիների գումարին [Պնդում 1․47]։ Այսպիսով՝ EF հիմքով քառակուսին GF հիմքովի կրկնապատիկն է։ GF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ Հետևաբար, EF հիմքով քառակուսին CD հիմքովի կրկնապատիկն է, EA հիմքովն էլ՝ AC-ի։ Հետևում է, որ AE և EF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AF հիմով քառակուսին AE և EF հիմքերովների գումարին է հավասար։ AEF-ն ուղիղ անկյուն է [Պնդում 1․47]։ Հետևաբար, AF հիմքով քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DF հիմքերով քառակուսիների գումարը հավասար է AF հիմքով քառակուսուն։ D-ն ուղիղ անկյուն է [Պնդում 1․47], հետևաբար AD և DF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների կրկնապատիկն է։ DF-ն էլ հավասար է DB-ին։ Արդյունքում՝ AD-ի և DB-ի վրա ընկած քառակուսիների գումարը AC-ի և CD-ի վրա ընկած քառակուսիների գումարի կրկնապատիկն է։
Ստաղվում է, որ հատվածը հավասար և անհավասար մասերի բաժանելիս՝ անհավասար մասերի վրա կառուցված քառակուսիների գումարը հավասար է հատվածի կեսի և հավասար ու անհավասար մասերի տարբերության վրա կառուված քառակուսիների գումարի կրկնապատիկին։
Պնդում 10[10]
Եթե հատվածը հավասար կիսենք և որպես հատվածի շարունակություն նրան կցենք նոր հատված, ապա ստացված ողջ և ավելացված հատվածի վրա կառուցված քառակուսիների գումարը հավասար կլինի նախնական հատվածի կեսի և այդ կեսի ու կցված հատվածի վրա կառուցված քառակուսիների գումարին։

Տրված է AB հատվածը, հավասար կիսենք այն C կետում և որպես AB-ի շարունակություն կցենք BD հատվածը։ Պետք է ցույց տալ, որ AD և DB հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների կրկնապատիկն է։
C կետով կառուցենք CE հատվածը, որը կլինի AB-ին ուղղահայաց [Պնդում 1․11] և AC-ին ու CB-ին հավասար [Պնդում 1․3]։ Կառուցենք նաև EA և EB հատվածները։ AD-ին զուգահեռ՝ E կետով տանենք EF հատվածը [Պնդում 1․31]։ CE-ին զուգահեռ՝ FD-ն՝ D կետով [Պնդում 1․3]։ Եվ քանի որ EF-ն հատվում է EC և FD զուգահեռ հատվածների հետ, CEF և EFD ներքին անկյունները հավասար են ուղիղ անկյունների [Պնդում 1․29]։ Հետևաբար, FEB և EFD անկյուննեը փոքր են երկու ուղիղ անկյուններից։ Եվ երկու ներքին անկյուններից (որոնց գումարը ավելի փոքր է քան երկու ուղիղ անկյունների գումար) առաջացած հատվածները հատվում էն [Կանխադրույթ 1.5]։ Հետևաբար, B-ի և D-ի ուղղություններով կառուցված EB և FD հատվածները կհատվեն։ Կռուցենք դրանք, որպես հատման կետ նշանակնեք G-ն և միացնենք AG-ն։ Քանի որ AC-ն և CE-ն հավասար են, EAC և AEC անկյունները նույնպես հավասար են [Կանխադրույթ 1.5]։ Անկյուն C-ն ուղիղ անկյուն է։ Հետևում է, որ EAC-ն ու AEC-ը ուղիղ անկյան կեսեր են [Պնդում 1․32]։ Նույն պատճառներով՝ CEB-ն ու EBC-ն նույնպես ուղիղ անկյան կեսեր են։ Ստացվում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ EBC-ն ուղիղ անկյան կես է, DBG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․15]։ BDG-ն նունպես ուղիղ անկյուն է, որը հավասար է DCE-ին։ Այսինքն դրանք համարժեք/այլընտրանքային անկյուններ են [Պնդում 1․29]։ Հետևաբար, մնացյալ DGB-ն ուղիղ անկյան կես է։ DGB-ն ու DGB-ն հավասար են։ BD-ն էլ հավասար է GD-ին [Պնդում 1․6]։ Կրկին, քանի որ EGF-ն ուղիղ անկյան կես է, իսկ F-ը՝ ուղիղ անկյուն, այն հավասար է հակառակ C անկյանը[Պնդում 1․34], մնացյալ FEG անկյունն էլ կրկին ուղիղ անկյան կես է։ Հետևում է, որ EGF և FEG անկյունները հավասար են։ GF կողմն էլ հավասար է EF-ին [Պնդում 1․6]։ Եվ քանի որ EC-ն ու CA-ն հավասար են, EC և CA հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ EC և CA հիմքերով քառակուսիների գումարը CA հիմքով քառակուսու կրկնապատիկն է։ EA հիմքով քառակուսին էլ հավասար է EC և CA հիմքերով քառակուսինորի գումարին [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Կրկին, քանի որ FG-ն ու EF-ն հավասար են, FG և FE հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ GF-ի և FE-ի վրա կառուցված քառակուսիները EF հիքով քառակուսու կրկնապատիկն են։ EG հիմքով քառակուսին էլ GF և FE հիմքերով քառակուսիների գումարի կրկնապատիկն է [Պնդում 1․47]։ Հետևաբար, EG հիմքով քառակուսին EF հիմքովի կրկնապատիկն է։ EF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ EG հիմքով քառակուսին CD հիմքովի կրկնապատիկն է։ Սակայն ցույց էր տրվել նաև, որ EA-ի վրա կառուցված քառակուսին AC-ի վրա կառուցվածի կրկնապատիկն է։ Արդյունքում՝ AE և EC հիմքերով քառակուսիների գումարը AC և DC հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AG, AE և EG հիմքերով քառակուսիներն էլ հավասար են [Պնդում 1․47]։ AG-ի վրա կառուցված քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DG հիմքերով քառակուսիների գումարն էլ հավասար է AG հիմքով քառակուսուն [Պնդում 1․47]։ Հետևաբար, AD և DG հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարին հավասար։ DG- հավասար է DB-ին։ Հետրաբար, AD և DB հիմքերով քառակուսիների գումարը AC և CD հմքերով քառակուսիների գումարի կրկնապատիկն է։
Ստացվում է, եթե հատվածը հավասար կիսենք և որպես հատվածի շարունակություն նրան կցենք նոր հատված, ապա ստացված ողջ և ավելացված հատվածի վրա կառուցված քառակուսիների գումարը հավասար կլինի նախնական հատվածի կեսի և այդ կեսի ու կցված հատվածի վրա կառուցված քառակուսիների գումարին։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։
Պնդում 11[11]
Հատվածը հատել այնպես, որ ողջ հատվածով և հատման արդյունքում առաջացած հատվածներիից մեկով կառուցված ուղղանկյունը հավասար լինի հատման արդյունքում առաջացած հատվածներիից մյուսի վրա սահմանված քառակուսուն։

Տրված է AB հատվածը։ Այն պետք է բաժանել այնպես, որ AB-ով և հատման արդյունքում առաջացած մասերից մեկով կառուցաված քառակուսին հավասար լինի հատման արդյունքում առաջացած մյուս մասով կառուցված քառակուսուն։
AB-ով կառուցենք ABDC քառակուսին [Պնդում 1․4], AC-ն էլ կիսենք E կետում [Պնդում 1․10] և միացնենք B-ն ու E-ն՝ BE հատվածով։ Շարունակենք CA-ն և շարունակության վրա նշանակենք F կետն այնպես, որ EF-ն ու BE-ը հավասար լինեն [Պնդում 1․3]։ AF կողմով հառուցենք FH անկյունագծով քառակուսին [Պնդում 1․46], և GH-ը շարունակելով՝ հատենք այն CD-ի հետ՝ K կետում։ Կարելի է ասել, որ AB-ն H կետում հատելիս՝ AB և BH կողմերով քառակուսին հավասարվում է AH կողմով քառակուսուն։ Քանի որ AC-ն E կետով բաժանված է հավասար մասերի և նրան ավելացված է FA-ը, CF և FA կողմերով ուղղանկյան և AE կողմով քառակուսու գումարը հավասար է EF հիմքով քառակուսուն [Պնդում 2․6]։ EF-ն ու EB-ն հավասար են։ Հետևաբար, CF և FA կողմերով կառուցված ուղղանկյան և AE հիմքով քառակուսու գումարը հավասար է EB հիմքով քառակուսուն։ Սակայն BA և AE հիմքերով քառակուսիների գումարը հավասար է EB հիմքով քառակուսուն։ Անկյուն A-ն ուղիղ անկյուն է [Պնդում 1․47]։ Այդ պատճառով էլ, CF և FA կողմերով ուղղանկյան և AE կողմով քառակուսու գումարը հավասար է BA և AE հիմքերով քառակուսիների գումարին։ Երկու կողմից էլ հանենք AE հիմքով քառակուսին։ CF և FA կողմերով մնացյալ ուղղանկյունը հավասար է AB կողով քառակուսուն։ FK անկյունագծով ուղղանկյունն էլ կառուցված է CF-ով և FA-ով։ AF-ը հավասար է FG-ին։ Իսկ AD անկյունագծով քառակուսին AB հիմքով կառուցված քառակուսին է։ Հետևաբար, FK նակյունագծով ուղղանկյունը հավասար է AD անկյունագծով քառակուսուն։ Երկու կողմերից էլ հանենք AK անկյունագծով ուղղանկյունը։ FH անկյունագծով մնացյալ քառակուսին հավասար է HD անկյունագծով ուղղանկյանը։ Իսկ HD անկյունագծով ուղղանկյունը AB և BH կողմերով է կառուցված։ AB-ն հավասար է BD-ին։ FH անկյունագծով քառակուսին AH հիմքով է սահմանված։ Այսպիսով՝ AB և BH կողերով ուղղանկյունը հավասար է HA հիմքով քառակուսուն։
Հետևում է, որ AB հատվածը հատվեց H կետում այնպես, որ AB և BH կողերով ուղղանկյունը հավասար եղավ HA կողով քառակուսուն։ Սա հենց այն էր, ինչ պետք էր ստանալ։
† Հատվածի այսպիսի հատման ձևը, երբ ողջ հատվածի և հատման արդյունքում առաջացած ավելի մեծ մասի հարաբերությունը հավասար է հատման արդյունքում առաջացած մեծ և փոքր մասեր հարաբերությանը, երբեմն անվանվում է «Ոսկե հարաբերակցություն»։
Պնդում 12[12]
Բութանկյուն եռանկյուններում բութ անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին բութ անկյանը կից կողմերով կառուցված քառակուսիների գումարից մեծ է բութ անկյանը կից կողմով, որի վրա ընած է ուղղահայացը և դրսի կողմից բութ անկյանը միացող հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։

Դիցուք՝ ABC-ն բութանկյուն եռանկյուն է, որում BAC-ն բութ անկյունն է։ B կետով՝ CA-ին ուղղահայաց կառուցենք BD ուղիղը [Պնդում 1․12]։ Արդյունքում՝ BC-ի վրա կառուցված քառակուսին BA և AC կողմերի վրա կառուցված քառակուսիների գումարից մեծ է CA և AD կողմերով կառուցված ուղղանկյան կրկնապատիկի չափով։ Քանի որ CD-ն հատված է կամայական A կետում, DC-ի վրա կառուցված քառակուսին հավասար է CA-ի և AD-ի վրա կառուցված քառակուսիների գումարին և CA և AD կողմերով կառուցած ուղղանկյան կրկնապատիկին [Պնդում 2․4]։ Երկու կողմին էլ ավելացնենք DB կողով կառուցվածքառակուսին։ Հետևաբար, CD և DB հիմքերով քառակուսիների գումարը հավասար է CA, AD և DB հիմքերով քառակուսինեի գումարին և CA ու AD կողմերով կառուցված ուղղանկյան կրկնապատիկին։ Սակայն CB-ի վրա ընկած քառակուսին էլ հավասար է CD և DB հիմքերով քառակուսիների գումարին։ Անկյուն D-ն ուղիղ անկյուն է [Պնդում 1․47]։ AB-ի վրա կառուցված քառակուսին էլ հավասար է AD և DB կողմերով քառակուսիների գումարին [Պնդում1․47]։ Հետևում է, որ CB-ի վրա ընկած քառակուսին հավասար է CA-ի և AB-ի վրա ըհնկած քառակուսիների գումարին և CA ու AD կողմերով ուղղանկյան կրկնապատիկին։ Այսպիսով՝ CB-ի վրա ընկած քառակուսին CA և AB հիմքերով քառակուսինեի գումարից մեծ է CA և AD կողմերով ուղղանկյան կրկնապատիկի չափով։
Հետևաբար, բութանկյուն եռանկյուններում բութ անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին բութ անկյանը կից կողմերով կառուցված քառակուսիների գումարից մեծ է բութ անկյանը կից կողմով, որի վրա ընած է ուղղահայացը և դրսի կողմից բութ անկյանը միացող հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։
Պնդում 13[13]
Սուրանկյուն եռանկյուններում սուր անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին սուր անկյանը կից կողմերի վրա կառուցված քառակուսիների գումարից փոքր է սուր անկյանը այն կից կողմով, որի վրա ընկնում է ուղղահայացը և ներսի կողմից եռանկյան սուր անկյանը միացող այն հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։

Դիցուք՝ ABC-ն սուրանկյուն եռանկյուն է, որում B-ն սուր անկյունն է։ A կետով՝ BC-ին ուղղահայաց կառուցենք AD-ն [Պնդում 1․12]։ Արդյունքում՝ AC հիմքով քառակուսին CB և BA հիմքերով քառակուսիներից փոքր է CB և BD կողմերով կառուցված ուղղանկյան կրկնապատիկի չափով։
Քանի որ CB հատվածը հատած է կամայական D կետում, CB և BD կողերով քառակուսինեի գումարը հավսաքար է CB և BD կողերով ուղղանկյան կրկնապատիկին և DC հիմքով քառակուսուն [Պնդում 2․7]։ Երկու կողմին էլ ավելացնենք DA հիմքով քառակուսին։ Արդյունքում՝ CB, BD և DA հիմքերով քառակուսիների գումարը հավասար է CB և BD կողերով ուղղանկյան կրկնապատիկին և AD ու DC հիմքերով քառակուսիների գւմարին։ Սակայն AB հիմքով քառակուսին էլ հավասար է BD և DA հիմքերով քառակուսիների գումարին։ Անկյուն D-ն ուղիղ անկյուն է [Պնդում 1․47]։ AC-ի վրա կառուցված քառակուսին էլ հավասար է AD և DC հիմքերով քառակուսիների գումարին [Պնդում 1․47]։ Այդ պատճառով էլ CB և BA հիմքերով քառակուսիների գումարը հավասար է AC հիմքով քառակուսուն և CB ու BD կողմերով կառուցված ուղղանկյան կրկնապատիկին։ Հետևաբար, AC հիմքով քառակուսին առանձին վերցված CB և BA հիմքերով քառակուսիներից ավելի փոքր է CB-ով և BD-ով կառուցված ուղղանկյան կրկնապատիկի չափով։
Այսպիսով՝ ոուրանկյուն եռանկյուններում սուր անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին սուր անկյանը կից կողմերի վրա կառուցված քառակուսիների գումարից փոքր է սուր անկյանը այն կից կողմով, որի վրա ընկնում է ուղղահայացը և ներսի կողմից եռանկյան սուր անկյանը միացող այն հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։
Պնդում 14
Կառուցել տրված ուղղագիծ պատկերին հավասար քառակուսի։

Դիցուք՝ տրված է A ուղղագիծ պատկերը։ Պահանջվում է կառուցել A-ին հավասար քառակուսի։ Կառուցենք BD անկյունագծով զուգահեռագիծն այնպես, որ հավասար լինի A-ին [Պնդում 1․45]։ Հետևաբար, եթե BE-ն հավասար լինի ED-ին, ապա տեղի կունան այն, ինչ պետք է ցույղ տալ։ Կառուցենք A-ին հավասար BD անկյունագծով քառակուսին։ Եթե այպես չստացվի, կնշանակի, որ BE-ից կամ ED-ից մեկը մյուսից մեծ է։ Դիցուք՝ BE-ն ավելի մեծ է, շարունակենք այն մինչ F կետն այնպես, որ EF-ն ու ED-ն հավասար լինեն [Պնդում 1․3]։ G կետով հավասար լիսենք BF հատվածը [Պնդում 1․10]։ G կենտրոնով և GB կամ GF շառավղով կառուցենք BHF կիսաշրջանը։ Շարունակենք DE-ն մինչ H կետը և միացնենք GH հատվածը։
Հետևաբար, քանզի BF-ը G կետով բաժանված է հավասար մասերի և E-ով՝ անհավասար, BE և EF կողմերով ուղղանկյան և EG հիմքով քառակուսու գումարը հավասար է GF հիմքով քառակուսուն [Պնդում 2․5]։ GF-ն էլ հավասար է GH-ին։ Հետևաբար, BE և EF կողմերով ուղղանկյան և GE հիմքով քառակուսու գումարը հավասար է GH հիմքով քառակուսուն։ HE և EG հիմքերով քառակուսիների գումարն էլ հավասար է GH հիմքով քառակուսուն [Պնդում 1․47]։ Այսպիսով՝ BE և EF կողմորով ուղղանկյոան և GE կողով քառակուսու գումարը հավասար է HE և EG հիմքերով քառակուսիների գումարին։ Երկոը կողմերին էլ ավելացնենք GE հիմքով քառակուսին։ Հետևում է, որ BE և EF կողերով մնացյալ ուղղանկյունը հավասար է EH կողով քառակուսուն։ Սակայն BD անկյունագծով ուղղանկյունը BE և EF կողերով է կառուցված։ EF-ը հավասար է ED-ին։ Այս ամենի արդյունքում էլ BD անկյունագծով զուգահեռագիծը հավասար է HE հիմքով քառակուսուն։ BD անկյունագծով ուղղանկյունն էլ հավասար է ուղղագիծ A պատկերին։ Հետևաբար, ուղղագիծ A պատկերը ևս հավասար է քառակուսուն, որը կարելի է կառուցել EH հատվածով։
Այսպիսով՝ կառուցվեց A ուղղագիծ պատկերին հավասար քառակուսին, որը կարելի է սահմանել EH հատվածի վրա: Սա հենց այն էր, ինչ պետք էր ցույց տալ:
Նշումներ
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ եթե
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ .
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ ։
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ ։
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ ։
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ :
- ↑ Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ :
- ↑ Այս պնդումը համարժեք է բոլորիս հայտնի կոսինուսնորի բանաձևին՝ , քանի որ ։
- ↑ Այս պնդումը համարժեք է բոլորիս հայտնի կոսինուսնորի բանաձևին՝ , քանի որ :