«Աստղագիտություն»–ի խմբագրումների տարբերություն
No edit summary |
No edit summary |
||
| Տող 117. | Տող 117. | ||
Դատողություններ անելով լուսատուների ծագելու, մայր մտնելու և ուրիշ նման երևույթն երի մասին, մենք նկատի ենք ունենում միայն այն '''ուղղությունը''', որով երևում են աստղերը (օրինակ, հորիզոնի մոտ, մեր գլխավերևը և այլն), ուստի միևնույն է, թե ինչպիսի շառավիղ մենք կերևակայենք երկնային սֆերայի համար։ Նկ. 7-ը, օրինակ, ցույց է տալիս, որ դիտողին որևէ ուղղությամբ երևացող ամեն մի աստղ հենց այդ ուղղությամբ էլ կերևա, թեկուզ ի՛նչպիսի սֆերայի վրա էլ նրան պատկերացնելու լինենք՝ R<sub>1</sub> շառավիղ ունեցող սֆերայի, թե R<sub>2</sub> շառավիղ ունեցող սֆերայի վրա։ Այդ պատճառով էլ ասում են, որ երկնային սֆերան անորոշ կամ կամայական շառավիղ ունի։ |
Դատողություններ անելով լուսատուների ծագելու, մայր մտնելու և ուրիշ նման երևույթն երի մասին, մենք նկատի ենք ունենում միայն այն '''ուղղությունը''', որով երևում են աստղերը (օրինակ, հորիզոնի մոտ, մեր գլխավերևը և այլն), ուստի միևնույն է, թե ինչպիսի շառավիղ մենք կերևակայենք երկնային սֆերայի համար։ Նկ. 7-ը, օրինակ, ցույց է տալիս, որ դիտողին որևէ ուղղությամբ երևացող ամեն մի աստղ հենց այդ ուղղությամբ էլ կերևա, թեկուզ ի՛նչպիսի սֆերայի վրա էլ նրան պատկերացնելու լինենք՝ R<sub>1</sub> շառավիղ ունեցող սֆերայի, թե R<sub>2</sub> շառավիղ ունեցող սֆերայի վրա։ Այդ պատճառով էլ ասում են, որ երկնային սֆերան անորոշ կամ կամայական շառավիղ ունի։ |
||
[[Պատկեր:Astronomy_pic_007.png|400px|frameless|thumb|center]] |
|||
'''Անցնելով դիտողի աչքով, ուղղաձիգ գիծը երկնային սֆերան հատում է զենիթի կետում։ Զենիթը դիտողի գլխավերևի ամենաբարձր կետն է'''։ Ուղղաձիգ գծի ուղղությունը ցույց է տալիս ուղղալարը՝ թելից կախած փոքրիկ ծանրությունը։ Ուղղաձիգ գծին ուղղահայաց հարթությունը կոչվում է հորիզոնական հարթություն։ |
'''Անցնելով դիտողի աչքով, ուղղաձիգ գիծը երկնային սֆերան հատում է զենիթի կետում։ Զենիթը դիտողի գլխավերևի ամենաբարձր կետն է'''։ Ուղղաձիգ գծի ուղղությունը ցույց է տալիս ուղղալարը՝ թելից կախած փոքրիկ ծանրությունը։ Ուղղաձիգ գծին ուղղահայաց հարթությունը կոչվում է հորիզոնական հարթություն։ |
||
| Տող 156. | Տող 158. | ||
Նույնպիսի դիտում կատարելով երկնքի արևմտյան մասում գտնվող աստղերից մեկի նկատմամբ, մենք կհամոզվենք, որ աստղերը Արեգակի և Լուսնի նման բարձրանում են հորիզոնի արևելյան կողմից, հասնում են իրենց ամենաբարձր դիրքին՝ երկնքի հարավային մասում և այնուհետև մայր են մտնում հորիզոնի արևմտյան կողմում։ Հաջորդ օրը նրանք կկատարեն նույն շարժումը, ըստ երևույթին, այդպիսով օրվա ընթացքում մի լրիվ շրջան կատարելով երկնքում։ |
Նույնպիսի դիտում կատարելով երկնքի արևմտյան մասում գտնվող աստղերից մեկի նկատմամբ, մենք կհամոզվենք, որ աստղերը Արեգակի և Լուսնի նման բարձրանում են հորիզոնի արևելյան կողմից, հասնում են իրենց ամենաբարձր դիրքին՝ երկնքի հարավային մասում և այնուհետև մայր են մտնում հորիզոնի արևմտյան կողմում։ Հաջորդ օրը նրանք կկատարեն նույն շարժումը, ըստ երևույթին, այդպիսով օրվա ընթացքում մի լրիվ շրջան կատարելով երկնքում։ |
||
[[Պատկեր:Astronomy_pic_008.png|500px|frameless|thumb|center]] |
|||
Այդ օրական պտույտի ժամանակ բոլոր աստղերը տեղաշարժվում են առանց իրենց փոխադարձ դասավորությունը փոխելու։ Թվում է, թե աստղային երկինքը պտտվում է ինչպես մի ամբողջություն ժամացույցի սլաքի շարժման ուղղությամբ՝ օրական մի լրիվ պտույտի արագությամբ։ |
Այդ օրական պտույտի ժամանակ բոլոր աստղերը տեղաշարժվում են առանց իրենց փոխադարձ դասավորությունը փոխելու։ Թվում է, թե աստղային երկինքը պտտվում է ինչպես մի ամբողջություն ժամացույցի սլաքի շարժման ուղղությամբ՝ օրական մի լրիվ պտույտի արագությամբ։ |
||
| Տող 169. | Տող 174. | ||
Քանի որ Երկիրը մի լրիվ պտույտ (360°) կատարում է 24 ժամում, ուստի երկայնության յուրաքանչյուր 15° հավասար է երկայնության 1 ժամին և այդպիսով՝ 1° = 4 րոպեի, 1 րոպեն = 15՛ և 1 վայրկյանը =15՛՛։ Մոսկվայի և Գրինվիչի միջօրեականների հարթությունների միջև կազմած անկյունը հավասար է 37°34՛։ Մոսկվայի երկայնությունը Գրինվիչից հենց այդ 37°34՛ կամ 2 ժամ 30,3 րոպեին է հավասար. այդ երկայնությունն արևելյան է։ |
Քանի որ Երկիրը մի լրիվ պտույտ (360°) կատարում է 24 ժամում, ուստի երկայնության յուրաքանչյուր 15° հավասար է երկայնության 1 ժամին և այդպիսով՝ 1° = 4 րոպեի, 1 րոպեն = 15՛ և 1 վայրկյանը =15՛՛։ Մոսկվայի և Գրինվիչի միջօրեականների հարթությունների միջև կազմած անկյունը հավասար է 37°34՛։ Մոսկվայի երկայնությունը Գրինվիչից հենց այդ 37°34՛ կամ 2 ժամ 30,3 րոպեին է հավասար. այդ երկայնությունն արևելյան է։ |
||
[[Պատկեր:Astronomy_pic_009.png|240px|frameless|thumb|left]] |
|||
'''Աշխարհագրական լայնությունը չափվում է այն անկյան մեծությամբ, որ հասարակածի հարթության հետ կազմում է երկրի տվյալ վայրով անցնող ուղղաձիգ գիծը'''։ Եթե Երկիրն իսկական գունդ համարենք, ապա ուղղաձիգ գիծն ամենուր անցնում է ուղիղ Երկրի կենտրոնով և համընկնում է տվյալ վայրում Երկրի շառավղի հետ։ |
'''Աշխարհագրական լայնությունը չափվում է այն անկյան մեծությամբ, որ հասարակածի հարթության հետ կազմում է երկրի տվյալ վայրով անցնող ուղղաձիգ գիծը'''։ Եթե Երկիրն իսկական գունդ համարենք, ապա ուղղաձիգ գիծն ամենուր անցնում է ուղիղ Երկրի կենտրոնով և համընկնում է տվյալ վայրում Երկրի շառավղի հետ։ |
||
| Տող 181. | Տող 188. | ||
Ներքոհիշյալ հետաքրքիր փորձը, որ մատչելի է լուսանկարչությանը ծանոթ ամեն մի դպրոցականի, ակնառու կերպով ցույց է տալիս երկնային սֆերայի օրական պտույտի ընթացքը։ Անլուսին պարզ գիշերը լուսանկարչական ապարատը տեղակայելով «անսահմանության վրա», ուղղում են դեպի Բևեռային աստղը՝ ցածից ամրացնելով որևէ հենարանի վրա։ Ապարատն այդպես ամրացված վիճակում մի քանի ժամով թողնում են բաց փականակով, այնուհետև թիթեղը հայտածում են։ Լուսանկարչական թիթեղի (նեգատիվի) վրա հայտնվում են աստղերի սև հետքերը (պոզիտիվի վրա՝ սպիտակ հետքերը, նկ. 10)։ Այդ բոլոր գծերը համակենտրոն աղեղների տեսք ունեն։ Այդ աղեղների գծային երկարությունները տարբեր են, բայց աստիճանային չափերով նրանք հավասար են։ Նրանց կենտրոնում ընկած Է պտտման կենտրոնը։ |
Ներքոհիշյալ հետաքրքիր փորձը, որ մատչելի է լուսանկարչությանը ծանոթ ամեն մի դպրոցականի, ակնառու կերպով ցույց է տալիս երկնային սֆերայի օրական պտույտի ընթացքը։ Անլուսին պարզ գիշերը լուսանկարչական ապարատը տեղակայելով «անսահմանության վրա», ուղղում են դեպի Բևեռային աստղը՝ ցածից ամրացնելով որևէ հենարանի վրա։ Ապարատն այդպես ամրացված վիճակում մի քանի ժամով թողնում են բաց փականակով, այնուհետև թիթեղը հայտածում են։ Լուսանկարչական թիթեղի (նեգատիվի) վրա հայտնվում են աստղերի սև հետքերը (պոզիտիվի վրա՝ սպիտակ հետքերը, նկ. 10)։ Այդ բոլոր գծերը համակենտրոն աղեղների տեսք ունեն։ Այդ աղեղների գծային երկարությունները տարբեր են, բայց աստիճանային չափերով նրանք հավասար են։ Նրանց կենտրոնում ընկած Է պտտման կենտրոնը։ |
||
[[Պատկեր:Astronomy_pic_010.png|360px|frameless|thumb|center]] |
|||
Պտտման ճիշտ նույնպիսի կենտրոն կարելի Է գտնել երկնքի նաև հարավային կիսագնդում։ Նա գտնվում Է երկնային սֆերայի մի կետում, որն ուղիղ հակադիր է աշխարհի հյուսիսային կիսագնդի հենց այն կետին, որի մասին քիչ առաջ խոսեցինք։ Բայց չէ՞ որ երկնային սֆերայի կենտրոնում գտնվում է մեր աչքը։ Հետևաբար, դիտելով երկինքը, մենք համոզվում ենք, որ երկն աչին սֆերան որպես մի ամբողջություն պտտվում է մի ինչ-որ առանցքի շուրջը, որն անցնում է մեր աչքով։ '''Երկնային սֆերայի օրական պտույտի առանցքը կոչվում է աշխարհի առանցք'''։ Այդ առանցքի ուղղությունը մենք կգտնենք, եթե մեր աչքով մտքով ուղիղ գիծ տանենք դեպի երկնքի՝ վերը նկարագրած ձևով գտած կետը, որը չի մասնակցում երկնային սֆերայի օրական պտույտին։ |
Պտտման ճիշտ նույնպիսի կենտրոն կարելի Է գտնել երկնքի նաև հարավային կիսագնդում։ Նա գտնվում Է երկնային սֆերայի մի կետում, որն ուղիղ հակադիր է աշխարհի հյուսիսային կիսագնդի հենց այն կետին, որի մասին քիչ առաջ խոսեցինք։ Բայց չէ՞ որ երկնային սֆերայի կենտրոնում գտնվում է մեր աչքը։ Հետևաբար, դիտելով երկինքը, մենք համոզվում ենք, որ երկն աչին սֆերան որպես մի ամբողջություն պտտվում է մի ինչ-որ առանցքի շուրջը, որն անցնում է մեր աչքով։ '''Երկնային սֆերայի օրական պտույտի առանցքը կոչվում է աշխարհի առանցք'''։ Այդ առանցքի ուղղությունը մենք կգտնենք, եթե մեր աչքով մտքով ուղիղ գիծ տանենք դեպի երկնքի՝ վերը նկարագրած ձևով գտած կետը, որը չի մասնակցում երկնային սֆերայի օրական պտույտին։ |
||
| Տող 197. | Տող 206. | ||
''Հորիզոնի կետերը։'' Հորիզոնը հատվում է երկնային միջօրեականի հետ՝ հյուսիսի (N) և հարավի (S) կետերում, իսկ երկնային հասարակածի հետ՝ արևելքի (E) և արևմուտքի (W) կետերում։ Եթե մենք կանգնենք երեսներս դեպի աշխարհի բևեռը (Բևեռային աստղը), ապա ուղիղ նրա տակ՝ հորիզոնի վրա կունենանք հյուսիսի կետը, մեր թիկունքի կողմը՝ հարավի կետը, աջ կողմում՝ արևելքի կետը և ձախ կողմում՝ արևմուտքի կետը։ Հիշելով այդ, մենք միշտ էլ կարող ենք կողմն որոշվել տեղանքում։ |
''Հորիզոնի կետերը։'' Հորիզոնը հատվում է երկնային միջօրեականի հետ՝ հյուսիսի (N) և հարավի (S) կետերում, իսկ երկնային հասարակածի հետ՝ արևելքի (E) և արևմուտքի (W) կետերում։ Եթե մենք կանգնենք երեսներս դեպի աշխարհի բևեռը (Բևեռային աստղը), ապա ուղիղ նրա տակ՝ հորիզոնի վրա կունենանք հյուսիսի կետը, մեր թիկունքի կողմը՝ հարավի կետը, աջ կողմում՝ արևելքի կետը և ձախ կողմում՝ արևմուտքի կետը։ Հիշելով այդ, մենք միշտ էլ կարող ենք կողմն որոշվել տեղանքում։ |
||
[[Պատկեր:Astronomy_pic_011.png|270px|frameless|thumb|left]] |
|||
Այս պարագրաֆում բերված սահմանումները պետք է հիմնավորապես ըմբռնել և լավ հիշել, որովհետև առանց նրանց թե՛ երկնային ամենապարզ երևույթները և թե՛ աստղագիտության գործնական կիրառումները անհասկանալի կմնան։ Որպեսզի ավելի լավ պատկերացնենք այն բոլորը, ինչ որ վերն ասված է, երկնային սֆերան պատկերացնեն գծագրի վրա (նկ. 11)։ Այդ գծագրի վրա C երկնային սֆերայի կենտրոնն է, որտեղ գտնվում է դիտողի աչքը Z՛CZ ուղղաձիգ գիծն է, ընդ որում՝ Z — զենիթն է, Z՛ — նադիրը (զենիթի հակադիր կետը երկնային սֆերայում)։ P՛P աշխարհի առանցքն է, P — աշխարհի հյուսիսային բևեռն է, P՛ — աշխարհի հարավային բևեռը, EAWQ — երկնային հասարակածն է, որի հարթությունն ուղղահայաց է աշխարհի առանցքին, EAWN — հորիզոնն է, S — հարավի կետն է, N — հյուսիսի կետը, E — արևելքի կետը և W — արևմուտքի կետը։ Դժվար չէ հասկանալ, որ հորիզոնից վերև երևում են երկնային սֆերայի ուղիղ կեսը և երկնային հասարակածի նույնպես ուղիղ կեսը, նաև այն, որ E և W կետերում (որոնք N և S կետերից գտնվում են 90° հեռավորության վրա) և՛ հորիզոնը, և՛ հասարակածը կիսվում են։ |
Այս պարագրաֆում բերված սահմանումները պետք է հիմնավորապես ըմբռնել և լավ հիշել, որովհետև առանց նրանց թե՛ երկնային ամենապարզ երևույթները և թե՛ աստղագիտության գործնական կիրառումները անհասկանալի կմնան։ Որպեսզի ավելի լավ պատկերացնենք այն բոլորը, ինչ որ վերն ասված է, երկնային սֆերան պատկերացնեն գծագրի վրա (նկ. 11)։ Այդ գծագրի վրա C երկնային սֆերայի կենտրոնն է, որտեղ գտնվում է դիտողի աչքը Z՛CZ ուղղաձիգ գիծն է, ընդ որում՝ Z — զենիթն է, Z՛ — նադիրը (զենիթի հակադիր կետը երկնային սֆերայում)։ P՛P աշխարհի առանցքն է, P — աշխարհի հյուսիսային բևեռն է, P՛ — աշխարհի հարավային բևեռը, EAWQ — երկնային հասարակածն է, որի հարթությունն ուղղահայաց է աշխարհի առանցքին, EAWN — հորիզոնն է, S — հարավի կետն է, N — հյուսիսի կետը, E — արևելքի կետը և W — արևմուտքի կետը։ Դժվար չէ հասկանալ, որ հորիզոնից վերև երևում են երկնային սֆերայի ուղիղ կեսը և երկնային հասարակածի նույնպես ուղիղ կեսը, նաև այն, որ E և W կետերում (որոնք N և S կետերից գտնվում են 90° հեռավորության վրա) և՛ հորիզոնը, և՛ հասարակածը կիսվում են։ |
||
| Տող 209. | Տող 220. | ||
Քանի որ Բևեռային աստղը աշխարհի բևեռում չի գտնվում, ուստի միջօրեի գիծն այդ ձևով որոշելու ժամանակ մենք կարող ենք սխալվել մի անկյունով, որը Լենինգրադի լայնության վրա հասնում է մոտ 2°-ի, իսկ ավելի հյուսիս ընկած վայրերում՝ դրանից էլ ավելի։ |
Քանի որ Բևեռային աստղը աշխարհի բևեռում չի գտնվում, ուստի միջօրեի գիծն այդ ձևով որոշելու ժամանակ մենք կարող ենք սխալվել մի անկյունով, որը Լենինգրադի լայնության վրա հասնում է մոտ 2°-ի, իսկ ավելի հյուսիս ընկած վայրերում՝ դրանից էլ ավելի։ |
||
[[Պատկեր:Astronomy_pic_012.png|120px|frameless|thumb|left]] |
|||
բ) ''Ցերեկը՝ ըստ Արեգակի։'' Հարթ մակերևույթի վրա ամրացնենք մի ուղղահայաց (ուղղալարի միջոցով) ձող (նկ. 12)։ Կեսօրից 2 ժամ առաջ այդ հարթության վրա ձողի ստվերի ծայրը նշանակենք A-ով և ձողի S հիմքից, որպես կենտրոնից, մի շրջանագիծ գծենք՝ ստվերի AS երկարությանը հավասար շառավղով։ Ձողի ստվերը կսկսի աստիճանաբար կարճանալ և թեքվել դեպի հյուսիս։ Կեսօրից հետո նա կսկսի երկարանալ, շարունակելով թեքվել նույն ուղղությամբ։ Երեկոյան կողմը ստվերի ծայրը նորից կհասնի մեր շրջանագծին և կշոշափի մի կետում, նշանակենք B տառով։ A և B կետերը միացնենք ուղիղ գծով, որի N մեջտեղը միացնելով ձողի S հիմքի հետ, կստանանք միջօրեի գծի ուղղությունը։ |
բ) ''Ցերեկը՝ ըստ Արեգակի։'' Հարթ մակերևույթի վրա ամրացնենք մի ուղղահայաց (ուղղալարի միջոցով) ձող (նկ. 12)։ Կեսօրից 2 ժամ առաջ այդ հարթության վրա ձողի ստվերի ծայրը նշանակենք A-ով և ձողի S հիմքից, որպես կենտրոնից, մի շրջանագիծ գծենք՝ ստվերի AS երկարությանը հավասար շառավղով։ Ձողի ստվերը կսկսի աստիճանաբար կարճանալ և թեքվել դեպի հյուսիս։ Կեսօրից հետո նա կսկսի երկարանալ, շարունակելով թեքվել նույն ուղղությամբ։ Երեկոյան կողմը ստվերի ծայրը նորից կհասնի մեր շրջանագծին և կշոշափի մի կետում, նշանակենք B տառով։ A և B կետերը միացնենք ուղիղ գծով, որի N մեջտեղը միացնելով ձողի S հիմքի հետ, կստանանք միջօրեի գծի ուղղությունը։ |
||
| Տող 241. | Տող 254. | ||
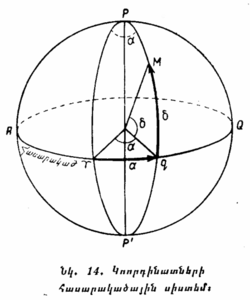
§ 15. ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՀՈՐԻԶՈՆԱԿԱՆ ՍԻՍՏԵՄ։ Նկ. 13-ում պատկերված է երկնային սֆերայի այն կեսը, որ երևում է հորիզոնից վերև։ NQS շրջանագիծը հորիզոնն է, Z — զենիթն է, S — հարավի կետն է։ Երկնային սֆերայում եղած M կետի դիրքը որոշելու համար զենիթից այդ կետի վրայով անցկացնենք մեծ ուղղաձիգ շրջանի ZQ աղեղը։ M կետի հորիզոնական կոորդինատները կլինեն՝ QM '''աղեղով չափվող բարձրությունը''' (h), '''որն արտահայտում է''' M '''կետի անկյունային հեռավորությունը հորիզոնից, և''' SQ '''աղեղով չափվող ազիմուտը''' (A), '''որը հարավի''' S '''կետից հաշվվում է դեպի արևմուտք և արտահայտում է երկնային միջօրեականով և''' M '''կետով անցնող ուղղաձիգ շրջանագծով կազմած անկյունը։''' |
§ 15. ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՀՈՐԻԶՈՆԱԿԱՆ ՍԻՍՏԵՄ։ Նկ. 13-ում պատկերված է երկնային սֆերայի այն կեսը, որ երևում է հորիզոնից վերև։ NQS շրջանագիծը հորիզոնն է, Z — զենիթն է, S — հարավի կետն է։ Երկնային սֆերայում եղած M կետի դիրքը որոշելու համար զենիթից այդ կետի վրայով անցկացնենք մեծ ուղղաձիգ շրջանի ZQ աղեղը։ M կետի հորիզոնական կոորդինատները կլինեն՝ QM '''աղեղով չափվող բարձրությունը''' (h), '''որն արտահայտում է''' M '''կետի անկյունային հեռավորությունը հորիզոնից, և''' SQ '''աղեղով չափվող ազիմուտը''' (A), '''որը հարավի''' S '''կետից հաշվվում է դեպի արևմուտք և արտահայտում է երկնային միջօրեականով և''' M '''կետով անցնող ուղղաձիգ շրջանագծով կազմած անկյունը։''' |
||
[[Պատկեր:Astronomy_pic_013.png|250px|frameless|thumb|left]] |
|||
[[Պատկեր:Astronomy_pic_014.png|250px|frameless|thumb|right]] |
|||
'''Հաճախ''' h '''բարձրության փոխարեն գործ են ածում զենիթային հեռավորությունը՝''' z, '''որը հավասար է''' 90°—h '''և իրենից ներկայացնում է''' M '''կետի անկյունային հեռավորությունը զենիթից։''' Բարձրությունը, զենիթային հեռավորությունը և ազիմուտը արտահայտում են աստիճաններով։ |
'''Հաճախ''' h '''բարձրության փոխարեն գործ են ածում զենիթային հեռավորությունը՝''' z, '''որը հավասար է''' 90°—h '''և իրենից ներկայացնում է''' M '''կետի անկյունային հեռավորությունը զենիթից։''' Բարձրությունը, զենիթային հեռավորությունը և ազիմուտը արտահայտում են աստիճաններով։ |
||
| Տող 249. | Տող 265. | ||
Այսպիսով, լուսատուների հակումը նման է աշխարհագրական լայնությանը, իսկ ուղղակի ծագումը՝ աշխարհագրական երկայնությանը։ Աստղային քարտեզների վրա (տե՛ս, օրինակ, կցված դասագրքին ) գծվում է այդ կոորդինատների ցանցը, իսկ ինքը՝ երկնային սֆերան պատկերվում է հարթության վրա այնպես, ինչպես պատկերվում է երկրագունդը։ |
Այսպիսով, լուսատուների հակումը նման է աշխարհագրական լայնությանը, իսկ ուղղակի ծագումը՝ աշխարհագրական երկայնությանը։ Աստղային քարտեզների վրա (տե՛ս, օրինակ, կցված դասագրքին ) գծվում է այդ կոորդինատների ցանցը, իսկ ինքը՝ երկնային սֆերան պատկերվում է հարթության վրա այնպես, ինչպես պատկերվում է երկրագունդը։ |
||
[[Պատկեր:Astronomy_pic_015.png|200px|frameless|thumb|right]] |
|||
§ 17*. ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՈՐԴԻՆԱՏՆԵՐԸ ՈՐՈՇԵԼՈՒ ԳՈՐԾՆԱԿԱՆ ԵՂԱՆԱԿՆԵՐԸ։ Եթե իմանայինք լուսատուների հասարակածային կոորդինատները, որոնք կախում չունեն ո՛չ դիտողի՝ Երկրի վրա ունեցած դիրքից , և ոչ էլ օրվա ժամից, ապա այդ կոորդինատները կարելի կլիներ գրանցել կատալոգների մեջ և այդ լուսատուների դիրքերը պատկերել աստղային քարտեզի վրա։ Բայց ինչպե՞ս գործնականորեն որոշել այդ կոորդինատները, ինչպե՞ս չափել նրանց՝ դիտումների միջոցով։ |
§ 17*. ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՈՐԴԻՆԱՏՆԵՐԸ ՈՐՈՇԵԼՈՒ ԳՈՐԾՆԱԿԱՆ ԵՂԱՆԱԿՆԵՐԸ։ Եթե իմանայինք լուսատուների հասարակածային կոորդինատները, որոնք կախում չունեն ո՛չ դիտողի՝ Երկրի վրա ունեցած դիրքից , և ոչ էլ օրվա ժամից, ապա այդ կոորդինատները կարելի կլիներ գրանցել կատալոգների մեջ և այդ լուսատուների դիրքերը պատկերել աստղային քարտեզի վրա։ Բայց ինչպե՞ս գործնականորեն որոշել այդ կոորդինատները, ինչպե՞ս չափել նրանց՝ դիտումների միջոցով։ |
||
| Տող 259. | Տող 277. | ||
§ 18*. ՄԹՆՈԼՈՐՏԱՅԻՆ ՌԵՖՐԱԿՑԻԱՆ ԼՈՒՅՍԻ ԲԵԿՈՒՄՆ է ԵՐԿՐԻ ՄԹՆՈԼՈՐՏՈՒՄ, ՈՐՆ ԱՂԱՎԱՂՈՒՄ է ԼՈՒՍԱՏՈՒՆԵՐԻ ՏԵՍԱՆԵԼԻ ԴԻՐՔԸ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՎՐԱ։ Երկնային լուսատուների լույսը անօդ տարածությունից մտնելով Երկրի մթնոլորտը, նրա մեջ բեկվում է։ Լույսի ճառագայթը որքան ավելի է մոտենում Երկրի մակերևույթին, այնքան նա օդի ավելի ու ավելի խիտ շերտերի է հանդիպում և հետզհետե ավելի ուժեղ բեկվելով այդ շերտերում՝ մոտենում է ուղղաձիգ ուղղության։ Հետևանքը լինում է այն, որ լույսի ճառագայթը Երկրի մթնոլորտում կորանում Է, ինչպես այդ ցույց է տրված նկ. 16-ում։ M կետում գտնվող դիտողը լուսատուն տեսնում է ոչ թե MA ուղղությամբ, այլ մի ուղղությամբ, որը բնորոշվում Է AM կորագծի շոշափողով, որի ուղղությամբ, ռեֆրակցիայի հետևանքով գալիս են ճառագայթները։ Եվ իսկապես, այն ուղղությունը, որով գիտողը տեսնում է լուսատուն, դա լուսատուից դեպի դիտողի աչքը եկող ճառագայթների ուղղությունն է, իսկ M կետում կորացված ճառագայթի ուղղությունը այդ կորագծի M կետում շոշափողի ուղղությունն է (մեր նկարում ճառագայթի ուղու կորացումը ցույց է տրված միայն մեկ ճառագայթի համար և այն էլ ակնառության համար չափազանցրած)։ |
§ 18*. ՄԹՆՈԼՈՐՏԱՅԻՆ ՌԵՖՐԱԿՑԻԱՆ ԼՈՒՅՍԻ ԲԵԿՈՒՄՆ է ԵՐԿՐԻ ՄԹՆՈԼՈՐՏՈՒՄ, ՈՐՆ ԱՂԱՎԱՂՈՒՄ է ԼՈՒՍԱՏՈՒՆԵՐԻ ՏԵՍԱՆԵԼԻ ԴԻՐՔԸ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՎՐԱ։ Երկնային լուսատուների լույսը անօդ տարածությունից մտնելով Երկրի մթնոլորտը, նրա մեջ բեկվում է։ Լույսի ճառագայթը որքան ավելի է մոտենում Երկրի մակերևույթին, այնքան նա օդի ավելի ու ավելի խիտ շերտերի է հանդիպում և հետզհետե ավելի ուժեղ բեկվելով այդ շերտերում՝ մոտենում է ուղղաձիգ ուղղության։ Հետևանքը լինում է այն, որ լույսի ճառագայթը Երկրի մթնոլորտում կորանում Է, ինչպես այդ ցույց է տրված նկ. 16-ում։ M կետում գտնվող դիտողը լուսատուն տեսնում է ոչ թե MA ուղղությամբ, այլ մի ուղղությամբ, որը բնորոշվում Է AM կորագծի շոշափողով, որի ուղղությամբ, ռեֆրակցիայի հետևանքով գալիս են ճառագայթները։ Եվ իսկապես, այն ուղղությունը, որով գիտողը տեսնում է լուսատուն, դա լուսատուից դեպի դիտողի աչքը եկող ճառագայթների ուղղությունն է, իսկ M կետում կորացված ճառագայթի ուղղությունը այդ կորագծի M կետում շոշափողի ուղղությունն է (մեր նկարում ճառագայթի ուղու կորացումը ցույց է տրված միայն մեկ ճառագայթի համար և այն էլ ակնառության համար չափազանցրած)։ |
||
[[Պատկեր:Astronomy_pic_016.png|350px|frameless|thumb|center]] |
|||
Այսպիսով, '''ռեֆրակցիայի հետևանքով լուսատուներն ավելի մոտ են երևում զենիթին, քան նրանք իրականում կան'''։ Հորիզոնի մոտ ռեֆրակցիան բարձրացնում է լուսատուն 35՛-ով և ավելի քիչ՝ երբ նա բարձր է գտնվում։ |
Այսպիսով, '''ռեֆրակցիայի հետևանքով լուսատուներն ավելի մոտ են երևում զենիթին, քան նրանք իրականում կան'''։ Հորիզոնի մոտ ռեֆրակցիան բարձրացնում է լուսատուն 35՛-ով և ավելի քիչ՝ երբ նա բարձր է գտնվում։ |
||
| Տող 306. | Տող 326. | ||
տարածությունը երկնային սֆերայի ձևով պտտվում է մի այնպիսի առանցքի շուրջը, որը զուգահեռ, է Երկրի պտտման առանցքին։ Երկնային սֆերայի պտտման CP առանցքը մենք անվանեցինք աշխարհի առանցք և այժմ տեսնում ենք, որ նա ամեն մի դիտողի համար զուգահեռ է Երկրի պտտման առանցքին։ |
տարածությունը երկնային սֆերայի ձևով պտտվում է մի այնպիսի առանցքի շուրջը, որը զուգահեռ, է Երկրի պտտման առանցքին։ Երկնային սֆերայի պտտման CP առանցքը մենք անվանեցինք աշխարհի առանցք և այժմ տեսնում ենք, որ նա ամեն մի դիտողի համար զուգահեռ է Երկրի պտտման առանցքին։ |
||
[[Պատկեր:Astronomy_pic_017.png|250px|frameless|thumb|right]] |
|||
Քանի որ Բևեռային աստղը մեզնից չափազանց հեռու է գտնվում, ուստի CP գիծը և Երկրի պտտման առանցքը, որը զուգահեռ է նրան, ուղղված են դեպի Բևեռային աստղը։ Այն դիտողի համար, որ կարողանար տեղավորվել Երկրի կենտրոնում կամ նրա բևեռներում, Երկրի պտտման առանցքը և աշխարհի առանցքը միմյանց կհամընկնեին։ |
Քանի որ Բևեռային աստղը մեզնից չափազանց հեռու է գտնվում, ուստի CP գիծը և Երկրի պտտման առանցքը, որը զուգահեռ է նրան, ուղղված են դեպի Բևեռային աստղը։ Այն դիտողի համար, որ կարողանար տեղավորվել Երկրի կենտրոնում կամ նրա բևեռներում, Երկրի պտտման առանցքը և աշխարհի առանցքը միմյանց կհամընկնեին։ |
||
| Տող 316. | Տող 338. | ||
§ 21. ԲԵՎԵՌԻ ԲԱՐՁՐՈՒԹՅՈՒՆԸ ՀՈՐԻԶՈՆԻՑ ԵՎ ՏԵՂԻ ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԼԱՅՆՈՒԹՈՒՆԸ։ '''Աշխարհի բևեռի անկյունային բարձրությունը հորիզոնից կամ, ավելի կարճ ասած, բևեռի բարձրությունը հավասար է դիտման վայրի աշխարհագրական լայնությանը։''' Դրանում կարելի է համոզվել, եթե նկ. 17-ի վրա հետևենք, թե ի՛նչպես կփոփոխվի PCN անկյունը (իսկ դրա հետ միասին՝ նաև PN աղեղը, այսինքն՝ բևեռի բարձրությունը), եթե C կետի դիտողը Երկրի հասարակածից սկսի շարժվել դեպի Երկրի բևեռը։ Այդպիսի շարժման դեպքում աշխարհի CP առանցքը կմնա ինքն իրեն զուգահեռ, իսկ հորիզոնի հարթության վրա ընկած CN գիծը PC գծի հետ ավելի ու ավելի մեծ անկյուն կկազմի։ |
§ 21. ԲԵՎԵՌԻ ԲԱՐՁՐՈՒԹՅՈՒՆԸ ՀՈՐԻԶՈՆԻՑ ԵՎ ՏԵՂԻ ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԼԱՅՆՈՒԹՈՒՆԸ։ '''Աշխարհի բևեռի անկյունային բարձրությունը հորիզոնից կամ, ավելի կարճ ասած, բևեռի բարձրությունը հավասար է դիտման վայրի աշխարհագրական լայնությանը։''' Դրանում կարելի է համոզվել, եթե նկ. 17-ի վրա հետևենք, թե ի՛նչպես կփոփոխվի PCN անկյունը (իսկ դրա հետ միասին՝ նաև PN աղեղը, այսինքն՝ բևեռի բարձրությունը), եթե C կետի դիտողը Երկրի հասարակածից սկսի շարժվել դեպի Երկրի բևեռը։ Այդպիսի շարժման դեպքում աշխարհի CP առանցքը կմնա ինքն իրեն զուգահեռ, իսկ հորիզոնի հարթության վրա ընկած CN գիծը PC գծի հետ ավելի ու ավելի մեծ անկյուն կկազմի։ |
||
[[Պատկեր:Astronomy_pic_018.png|250px|frameless|thumb|left]] |
|||
Դա ավելի պարզ կարելի է յուրացնել նկ. 18-ի օգնությամբ, որտեղ երկրագունդը պատկերված է տեղի միջօրեականի հարթության հատվածով։ M կետում գտնվող դիտողը աշխարհի P բևեռը կտեսնի աշխարհի առանցքի MP՛ ուղղությամբ, որը զուգահեռ է Երկրի TP առանցքին։ Երկրագունդը շոշափող հորիզոնի հարթությունը մեր գծագրի վրա կպատկերվի SMN ուղիղ գծով, որը M կետում շոշափում է երկրագունդը պատկերող շրջանը։ AQ Երկրի հասարակածն է, TZ ուղղաձիգ գիծն է կետում, ուստի և AMT անկյունը, ըստ § 9-ի, հանդիսանում է կետի աշխարհագրական φ լայնությունը։ |
Դա ավելի պարզ կարելի է յուրացնել նկ. 18-ի օգնությամբ, որտեղ երկրագունդը պատկերված է տեղի միջօրեականի հարթության հատվածով։ M կետում գտնվող դիտողը աշխարհի P բևեռը կտեսնի աշխարհի առանցքի MP՛ ուղղությամբ, որը զուգահեռ է Երկրի TP առանցքին։ Երկրագունդը շոշափող հորիզոնի հարթությունը մեր գծագրի վրա կպատկերվի SMN ուղիղ գծով, որը M կետում շոշափում է երկրագունդը պատկերող շրջանը։ AQ Երկրի հասարակածն է, TZ ուղղաձիգ գիծն է կետում, ուստի և AMT անկյունը, ըստ § 9-ի, հանդիսանում է կետի աշխարհագրական φ լայնությունը։ |
||
| Տող 332. | Տող 356. | ||
''Միջին լայնություններում,'' օրինակ, ՍՍՌՄ-ում, աշխարհի առանցքը և երկնային հասարակածը թեքված են դեպի հորիզոնը, ուստի և աստղերի օրական ուղիները նույնպես թեքված են հորիզոնի նկատմամբ (նկ. 19 ա)։ Այն աստղերը, որոնք աշխարհի բևեռից հեռու են գտնվում ոչ ավելի, քան φ աստիճանով (այստեղ φ աշխարհագրական լայնությունն է), մայր չմտնող աստղեր են։ Իսկ այն աստղերը, որոնք բևեռից հեռու են գտնվում ավելի քան φ աստիճանով, ծագող և մայր մտնող աստղեր են։ Հարավային կիսագնդի աստղերի մի մասը, որոնք երկնային սֆերայում ընկած են ավելի հարավ (ցած), քան այն փոքր զուգահեռականը, որը զուգահեռ է հասարակածին և անցնում է S կետով (տե՛ս նկ. 19 ա), երբեք չեն ծագում՝ նրանք անտեսանելի են։ |
''Միջին լայնություններում,'' օրինակ, ՍՍՌՄ-ում, աշխարհի առանցքը և երկնային հասարակածը թեքված են դեպի հորիզոնը, ուստի և աստղերի օրական ուղիները նույնպես թեքված են հորիզոնի նկատմամբ (նկ. 19 ա)։ Այն աստղերը, որոնք աշխարհի բևեռից հեռու են գտնվում ոչ ավելի, քան φ աստիճանով (այստեղ φ աշխարհագրական լայնությունն է), մայր չմտնող աստղեր են։ Իսկ այն աստղերը, որոնք բևեռից հեռու են գտնվում ավելի քան φ աստիճանով, ծագող և մայր մտնող աստղեր են։ Հարավային կիսագնդի աստղերի մի մասը, որոնք երկնային սֆերայում ընկած են ավելի հարավ (ցած), քան այն փոքր զուգահեռականը, որը զուգահեռ է հասարակածին և անցնում է S կետով (տե՛ս նկ. 19 ա), երբեք չեն ծագում՝ նրանք անտեսանելի են։ |
||
[[Պատկեր:Astronomy_pic_019.png|500px|frameless|thumb|center]] |
|||
''Երկրի հասարակածում'' աշխարհի առանցքը պառկած է հորիզոնի հարթության վրա և համընկնում է միջօրեի գծին, իսկ աշխարհի բևեռները՝ հյուսիսի և հարավի կետերին (նկ. 19 բ)։ Հասարակածը դառնում է հորիզոնին, ուղղահայաց և անցնում է Z, զենիթով։ Բոլոր աստղերի օրական ուղիներն ուղղահայաց են հորիզոնին և նրանցից յուրաքանչյուրը օրվա կեսի ընթացքում լինում է հորիզոնից վեր և մյուս կեսի ընթացքում՝ հորիզոնից ցած։ Լրիվ օրվա ընթացքում, եթե ցերեկն Արեգակը չխանգարեր, կարելի կլիներ տեսնել երկնքի երկու կիսագնդերի բոլոր աստղերը։ Այնտեղ չծագող աստղեր չկան, ինչպես չկան նաև մայր չմտնող աստղեր։ Մասնավորապես, մեզ ծանոթ Մեծ Արջը այնտեղ մայր մտնող համաստեղությունների թվին է պատկանում։ |
''Երկրի հասարակածում'' աշխարհի առանցքը պառկած է հորիզոնի հարթության վրա և համընկնում է միջօրեի գծին, իսկ աշխարհի բևեռները՝ հյուսիսի և հարավի կետերին (նկ. 19 բ)։ Հասարակածը դառնում է հորիզոնին, ուղղահայաց և անցնում է Z, զենիթով։ Բոլոր աստղերի օրական ուղիներն ուղղահայաց են հորիզոնին և նրանցից յուրաքանչյուրը օրվա կեսի ընթացքում լինում է հորիզոնից վեր և մյուս կեսի ընթացքում՝ հորիզոնից ցած։ Լրիվ օրվա ընթացքում, եթե ցերեկն Արեգակը չխանգարեր, կարելի կլիներ տեսնել երկնքի երկու կիսագնդերի բոլոր աստղերը։ Այնտեղ չծագող աստղեր չկան, ինչպես չկան նաև մայր չմտնող աստղեր։ Մասնավորապես, մեզ ծանոթ Մեծ Արջը այնտեղ մայր մտնող համաստեղությունների թվին է պատկանում։ |
||
| Տող 376. | Տող 402. | ||
2) Լուսնի խավարումների ժամանակ Երկրի ստվերը, որ ընկնում է լուսնի վրա, միշտ կլորաձև ուրվանկար ունի։ Բոլոր մարմիններիդ միայն գունդն է, որ իր բոլոր դիրքերում կլոր ստվեր է գցում։ |
2) Լուսնի խավարումների ժամանակ Երկրի ստվերը, որ ընկնում է լուսնի վրա, միշտ կլորաձև ուրվանկար ունի։ Բոլոր մարմիններիդ միայն գունդն է, որ իր բոլոր դիրքերում կլոր ստվեր է գցում։ |
||
[[Պատկեր:Astronomy_pic_020.png|400px|frameless|thumb|center]] |
|||
[[Պատկեր:Astronomy_pic_021.png|500px|frameless|thumb|center]] |
|||
§ 24. ԵՐԿՐԻ ՉԱՓԵՐԸ ՈՐՈՇԵԼԸ։ '''Երկրի չափերի որոշումը կայանում է նրանում, որ մենք չափում ենք միջօրեականի աղեղը գծային միավորներով և աստիճաններով։''' Երկրագնդի միևնույն միջօրեականի վրա գտնվող երկու կետերի միջև որոշում են գծային հեռավորությունը, որը, ասենք, հավասար է n կիլոմետրի։ Աստղագիտական եղանակով որոշում են նաև այդ կետերի աշխարհագրական լայնությունների տարբերությունը (օրինակ, այդ կետերում Բևեռային աստղի բարձրության տարբերության միջոցով), որը, ենթադրենք, հավասար է m աստիճանի։ Այդ դեպքում <math>\frac{m}{360°}</math> քանորդը ցույց կտա, թե շրջանագծի ո՛ր մասն է իրենից ներկայացնում նրա այն աղեղը, որ գտնվում է մեր վերցրած երկու կետերի միջև։ Դրա հիման վրա գտնում են ամբողջ շրջանագծի երկարությունը կիլոմետրերով հետևյալ պարզ հարաբերության միջոցով. |
§ 24. ԵՐԿՐԻ ՉԱՓԵՐԸ ՈՐՈՇԵԼԸ։ '''Երկրի չափերի որոշումը կայանում է նրանում, որ մենք չափում ենք միջօրեականի աղեղը գծային միավորներով և աստիճաններով։''' Երկրագնդի միևնույն միջօրեականի վրա գտնվող երկու կետերի միջև որոշում են գծային հեռավորությունը, որը, ասենք, հավասար է n կիլոմետրի։ Աստղագիտական եղանակով որոշում են նաև այդ կետերի աշխարհագրական լայնությունների տարբերությունը (օրինակ, այդ կետերում Բևեռային աստղի բարձրության տարբերության միջոցով), որը, ենթադրենք, հավասար է m աստիճանի։ Այդ դեպքում <math>\frac{m}{360°}</math> քանորդը ցույց կտա, թե շրջանագծի ո՛ր մասն է իրենից ներկայացնում նրա այն աղեղը, որ գտնվում է մեր վերցրած երկու կետերի միջև։ Դրա հիման վրա գտնում են ամբողջ շրջանագծի երկարությունը կիլոմետրերով հետևյալ պարզ հարաբերության միջոցով. |
||
| Տող 384. | Տող 413. | ||
§ 25. ԵՐԿՐԻ ՍԵՂՄՎԱԾՈՒԹՅՈՒՆԸ։ Երկրի տարբեր վայրերում կատարած չափումների միջոցով համոզվել են, որ Երկրի կորությունը հասարակածի մոտ ավելի մեծ է, քան բևեռներում (նկ. 22)։ Դա նշանակում է, որ '''Երկիրը գնդաձև չէ. նա բևեռների մոտ մի քիչ սեղմված է'''։ Երկրի բևեռային շառավիղը հասարակածային շառավղից կարճ է համարյա 21 կիլոմետրով, այսինքն՝ մոտավորապես հասարակածային շառավղի 1/300 չափով։ Երկրի ձևը ճշտվել է սովետական գիտնականների կողմից։ |
§ 25. ԵՐԿՐԻ ՍԵՂՄՎԱԾՈՒԹՅՈՒՆԸ։ Երկրի տարբեր վայրերում կատարած չափումների միջոցով համոզվել են, որ Երկրի կորությունը հասարակածի մոտ ավելի մեծ է, քան բևեռներում (նկ. 22)։ Դա նշանակում է, որ '''Երկիրը գնդաձև չէ. նա բևեռների մոտ մի քիչ սեղմված է'''։ Երկրի բևեռային շառավիղը հասարակածային շառավղից կարճ է համարյա 21 կիլոմետրով, այսինքն՝ մոտավորապես հասարակածային շառավղի 1/300 չափով։ Երկրի ձևը ճշտվել է սովետական գիտնականների կողմից։ |
||
[[Պատկեր:Astronomy_pic_022.png|300px|frameless|thumb|right]] |
|||
Երկրի սեղմվածությունը հետևանք է այն կենտրոնախույս ուժի ազդեցության, որ զարգացնում է Երկիրն իր առանցքի շուրջը պտտվելու ժամանակ։ Դա կարելի է ցուցադրել դպրոցական կենտրոնախույս մեքենայի առանցքի վրա պտտեցնելով պողպատյա բարակ օղակապը։ Երկնային մարմնի սեղմվելն իր պտտվելու հետևանքով ընդհանուր կանոն է։ Օրինակ, Յուպիտեր և Սատուրն մոլորակները, որոնք իրենց առանցքի շուրջն ավելի արագ են պտտվում քան Երկիրը, ավելի շատ են սեղմված (Յուպիտերի սեղմվածությունը շատ լավ նկատվում է հեռադիտակով)։ Սեղմվածության հետևանքով Երկիրը գնդաձև չէ, այլ պտտման էլիպսոիդ։ |
Երկրի սեղմվածությունը հետևանք է այն կենտրոնախույս ուժի ազդեցության, որ զարգացնում է Երկիրն իր առանցքի շուրջը պտտվելու ժամանակ։ Դա կարելի է ցուցադրել դպրոցական կենտրոնախույս մեքենայի առանցքի վրա պտտեցնելով պողպատյա բարակ օղակապը։ Երկնային մարմնի սեղմվելն իր պտտվելու հետևանքով ընդհանուր կանոն է։ Օրինակ, Յուպիտեր և Սատուրն մոլորակները, որոնք իրենց առանցքի շուրջն ավելի արագ են պտտվում քան Երկիրը, ավելի շատ են սեղմված (Յուպիտերի սեղմվածությունը շատ լավ նկատվում է հեռադիտակով)։ Սեղմվածության հետևանքով Երկիրը գնդաձև չէ, այլ պտտման էլիպսոիդ։ |
||
| Տող 390. | Տող 421. | ||
Բայց միջօրեականի աղեղի գծային երկարությունը չափելու ժամանակ, մանավանդ եթե Երկրի չափերը ավելի մեծ ճշտությամբ որոշելու համար բավական երկար աղեղ վերցնելու լինենք, մենք մի շարք գործնական դժվարությունների կհանդիպենք. այդ աղեղի սկզբից մինչև նրա վերջավորությունը ճանապարհին կարող են ձորեր, լեռներ, ճահիճներ և այլ խոչընդոտներ հանդիպել։ Ուստի, միջօրեականի աղեղի երկարությունը և առհասարակ Երկրի մակերևույթի վրա մեծ տարածություններ չափելու համար (որոնք, մասնավորապես, հարկավոր են լինում աշխարհագրական քարտեզներ կազմելու համար) օգտվում են '''տրիանգուլյացիայի''' եղանակից։ |
Բայց միջօրեականի աղեղի գծային երկարությունը չափելու ժամանակ, մանավանդ եթե Երկրի չափերը ավելի մեծ ճշտությամբ որոշելու համար բավական երկար աղեղ վերցնելու լինենք, մենք մի շարք գործնական դժվարությունների կհանդիպենք. այդ աղեղի սկզբից մինչև նրա վերջավորությունը ճանապարհին կարող են ձորեր, լեռներ, ճահիճներ և այլ խոչընդոտներ հանդիպել։ Ուստի, միջօրեականի աղեղի երկարությունը և առհասարակ Երկրի մակերևույթի վրա մեծ տարածություններ չափելու համար (որոնք, մասնավորապես, հարկավոր են լինում աշխարհագրական քարտեզներ կազմելու համար) օգտվում են '''տրիանգուլյացիայի''' եղանակից։ |
||
[[Պատկեր:Astronomy_pic_023.png|180px|frameless|thumb|left]] |
|||
Տրիանգուլյացիան կայանում է հետևյալում։ Եթե հարկավոր է չափել միջօրեականի AA՛ աղեղը (նկ. 23), ընտրում են հարթ տարածության վրա ընկած AB գիծը և չափում նրա երկարությունը ամենայն հնարավոր ճշտությամբ։ Այդպիսի գիծը կոչվում է բազիս (հիմք)։ Բացի այդ, ընտրում են C կետը, որը երևում է և՛ A կետից, և՛ B կետից։ Այնուհետև անկյունաչափ գործիքի օգնությամբ չափում են A, B կետերի մոտ ընկած անկյունները և, բացի այդ, բազիսի և միջօրեականի AA՛ ուղղության միջև ընկած K անկյունը։ Ապա արդեն հաշվարկումների միջոցով գտնում են AC, BC կողմերի երկարությունը և C անկյան մեծությունը։ Դրանից հետո ընտրում են D կետը, որը երևում է և՛ C, և՛ B կետերից, և տեղավորվելով այդ կետերում, անկյունաչափ գործիքով չափում են BCD և CBD անկյունները։ Քանի որ CB գծի երկարությունն արդեն հաշված էր, ուստի այժմ նախորդի օրինակով կարելի է հաշվել CD և BD կողմերի երկարությունը, և բացի այդ, AB և AA՛ գծերով կազմված անկյունը։ |
Տրիանգուլյացիան կայանում է հետևյալում։ Եթե հարկավոր է չափել միջօրեականի AA՛ աղեղը (նկ. 23), ընտրում են հարթ տարածության վրա ընկած AB գիծը և չափում նրա երկարությունը ամենայն հնարավոր ճշտությամբ։ Այդպիսի գիծը կոչվում է բազիս (հիմք)։ Բացի այդ, ընտրում են C կետը, որը երևում է և՛ A կետից, և՛ B կետից։ Այնուհետև անկյունաչափ գործիքի օգնությամբ չափում են A, B կետերի մոտ ընկած անկյունները և, բացի այդ, բազիսի և միջօրեականի AA՛ ուղղության միջև ընկած K անկյունը։ Ապա արդեն հաշվարկումների միջոցով գտնում են AC, BC կողմերի երկարությունը և C անկյան մեծությունը։ Դրանից հետո ընտրում են D կետը, որը երևում է և՛ C, և՛ B կետերից, և տեղավորվելով այդ կետերում, անկյունաչափ գործիքով չափում են BCD և CBD անկյունները։ Քանի որ CB գծի երկարությունն արդեն հաշված էր, ուստի այժմ նախորդի օրինակով կարելի է հաշվել CD և BD կողմերի երկարությունը, և բացի այդ, AB և AA՛ գծերով կազմված անկյունը։ |
||
| Տող 398. | Տող 431. | ||
Այսպիսով, '''տրիանգուլյացիան կայանում է նրանում, որ մեծ հեռավորությունները որոշվում են եռանկյունների օգնությամբ, որտեղ չափվում են միայն անկյունները և բազիսը, իսկ կողմերը որոշվում են հաշվարկումներով'''։ Այդ եղանակի անվանումը ծագել է լատիներեն «տրիանգուլյում» — եռանկյուն բառից։ |
Այսպիսով, '''տրիանգուլյացիան կայանում է նրանում, որ մեծ հեռավորությունները որոշվում են եռանկյունների օգնությամբ, որտեղ չափվում են միայն անկյունները և բազիսը, իսկ կողմերը որոշվում են հաշվարկումներով'''։ Այդ եղանակի անվանումը ծագել է լատիներեն «տրիանգուլյում» — եռանկյուն բառից։ |
||
[[Պատկեր:Astronomy_pic_024.png|240px|frameless|thumb|right]] |
|||
Տրիանգուլյացիայից օգտվում են ոչ միայն Երկրի չափերը որոշելու համար, այլև աշխարհագրական քարտեզներ կազմելիս, երբ պահանջվում է չափել մեծ հեռավորություններ։ |
Տրիանգուլյացիայից օգտվում են ոչ միայն Երկրի չափերը որոշելու համար, այլև աշխարհագրական քարտեզներ կազմելիս, երբ պահանջվում է չափել մեծ հեռավորություններ։ |
||
| Տող 410. | Տող 445. | ||
Բերենք դրանցից երկու առավել ակնհայտ ապացույցներ. |
Բերենք դրանցից երկու առավել ակնհայտ ապացույցներ. |
||
[[Պատկեր:Astronomy_pic_025.png|180px|frameless|thumb|left]] |
|||
ա) ''Վայր ընկնող մարմինների խոտորումը դեպի արևելք։'' Պատկերացնենք մի խոր ուղղաձիգ AB հանքահոր, որը պտտվում է Երկրի հետ միասին (նկ. 25)։ Նրա մուտքր (A) պտտման ժամանակ գծային ավելի մեծ արագություն ունի, քան հիմքը (B), որովհետև նա ավելի հեռու է գտնվում պտտման կենտրոնից, տվյալ դեպքում երկրի օրական պտույտի առանցքից։ Հանքահորի մուտքի մոտ ընկած քարն այս դեպքում նույն արագությունը կունենա, ինչ և այդ մուտքը։ Հանքահորի մեջ ընկնելու դեպքում նա, իներցիայի շնորհիվ, կպահպանի այդ արագությունը։ Ընկնելով ցած և միաժամանակ պահպանելով իր դեպի արևելք շարժման (որովհետև Երկիրը պտտվում է արևմուտքից դեպի արևելք) ավելի մեծ արագությունը, քան հանքահորի հիմքի շարժման արագությունն է, քարն իր դեպի արևելք շարժման մեջ ավելի առաջ կանցնի հանքահորի հիմքից։ Քարը կընկնի ոչ թե Ճիշտ Երկրի կենտրոնի ուղղությամբ, այլ կշեղվի դեպի արևելք, որը չէր պատահի, եթե Երկիրը պտտվելիս չլիներ։ Երկրի հասարակածի վրա այդ խոտորումը ամենից մեծ է, իսկ բևեռներում հավասար է զրոյի։ |
ա) ''Վայր ընկնող մարմինների խոտորումը դեպի արևելք։'' Պատկերացնենք մի խոր ուղղաձիգ AB հանքահոր, որը պտտվում է Երկրի հետ միասին (նկ. 25)։ Նրա մուտքր (A) պտտման ժամանակ գծային ավելի մեծ արագություն ունի, քան հիմքը (B), որովհետև նա ավելի հեռու է գտնվում պտտման կենտրոնից, տվյալ դեպքում երկրի օրական պտույտի առանցքից։ Հանքահորի մուտքի մոտ ընկած քարն այս դեպքում նույն արագությունը կունենա, ինչ և այդ մուտքը։ Հանքահորի մեջ ընկնելու դեպքում նա, իներցիայի շնորհիվ, կպահպանի այդ արագությունը։ Ընկնելով ցած և միաժամանակ պահպանելով իր դեպի արևելք շարժման (որովհետև Երկիրը պտտվում է արևմուտքից դեպի արևելք) ավելի մեծ արագությունը, քան հանքահորի հիմքի շարժման արագությունն է, քարն իր դեպի արևելք շարժման մեջ ավելի առաջ կանցնի հանքահորի հիմքից։ Քարը կընկնի ոչ թե Ճիշտ Երկրի կենտրոնի ուղղությամբ, այլ կշեղվի դեպի արևելք, որը չէր պատահի, եթե Երկիրը պտտվելիս չլիներ։ Երկրի հասարակածի վրա այդ խոտորումը ամենից մեծ է, իսկ բևեռներում հավասար է զրոյի։ |
||
Այս ձևի բազմաթիվ փորձերը ցույց են տալիս, որ դիտումները միանգամայն համապատասխանում են կատարած հաշվարկումներին. օրինակ, միջին լայնություններում 85 մ բարձրությունից վայր ընկնող քարը շեղվում է դեպի արևելք 10,5 մմ։ |
Այս ձևի բազմաթիվ փորձերը ցույց են տալիս, որ դիտումները միանգամայն համապատասխանում են կատարած հաշվարկումներին. օրինակ, միջին լայնություններում 85 մ բարձրությունից վայր ընկնող քարը շեղվում է դեպի արևելք 10,5 մմ։ |
||
[[Պատկեր:Astronomy_pic_026.png|270px|frameless|thumb|right]] |
|||
բ) ''Ֆուկոյի ճոճանակը։'' Առաջին անդամ 1851 թ. ֆրանսիացի գիտնական Ֆուկոյի դրած փորձում կիրառվել է մի ճոճանակ, որը իրենից ներկայացնում էր մի շատ երկար ու բարակ լար, որի ծայրից կախված էր ծանր գունդ։ Հայտնի է, և այդ կարելի է ստուգել կենտրոնախույս մեքենայի վրա կատարած փորձով, որ ամեն մի այդպիսի ճոճանակ իր տատանումների հարթությունը պահպանում է առանց փոփոխության, թեկուզ ինչպես էլ պտտելու լինենք այն հենարանը, որից նա կախված է։ (ճոճանակի լարը երկար է վերցվում այն նկատառումով, որպեսզի փորձն ավելի ակնառու լինի, և ճոճանակը բավական երկար ժամանակ տատանելու անհրաժեշտությունից։) |
բ) ''Ֆուկոյի ճոճանակը։'' Առաջին անդամ 1851 թ. ֆրանսիացի գիտնական Ֆուկոյի դրած փորձում կիրառվել է մի ճոճանակ, որը իրենից ներկայացնում էր մի շատ երկար ու բարակ լար, որի ծայրից կախված էր ծանր գունդ։ Հայտնի է, և այդ կարելի է ստուգել կենտրոնախույս մեքենայի վրա կատարած փորձով, որ ամեն մի այդպիսի ճոճանակ իր տատանումների հարթությունը պահպանում է առանց փոփոխության, թեկուզ ինչպես էլ պտտելու լինենք այն հենարանը, որից նա կախված է։ (ճոճանակի լարը երկար է վերցվում այն նկատառումով, որպեսզի փորձն ավելի ակնառու լինի, և ճոճանակը բավական երկար ժամանակ տատանելու անհրաժեշտությունից։) |
||
20:36, 2 սեպտեմբերի 2018-ի տարբերակ
հեղինակ՝ Բ. Ա. Վորոնցով-Վելյամինով |
|
Այս ստեղծագործությունը դեռ ամբողջովին տեղադրված չէ Գրապահարանում |
ՆԵՐԱԾՈՒԹՅՈՒՆ
§ 1. ԱՍՏՂԱԳԻՏՈՒԹՅԱՆ ԱՌԱՐԿԱՆ։ Աստղագիտությունն ուսումնասիրում է երկնային մարմինների և նրանց համակարգությունների շարժումը, կառուցվածքն ու զարգացումը։ Նա բոլոր գիտություններից ամենահնագույնն է. նրա սաղմերը մենք հանդիպում ենք դեռևս Աֆրիկայի և Ասիայի կուլտուրական այն ժողովուրդների մոտ, որոնք ապրելիս են եղել մեզանից մի քանի հազար տարի առաջ։
Երկինքն առաջին անգամ դիտողներն արդեն նկատել էին, որ Արեգակի և աստղերի դիրքով կարելի է որոշել ժամանակը։ Օրինակ, օրվա կեսին՝ կեսօրին, Արեգակը երկնքում գրավում է, տվյալ օրվա ընթացքում, ամենաբարձր դիրքը։ Լուսնի տեսքի փոփոխությամբ (եղջյուր, լրիվ սկավառակ և այլն) և երկնքի մյուս լուսատուների դիրքով կարելի է չափել մեծ ժամանակահատվածներ, այսինքն կազմել օրացույց։ Քոչվոր ժողովուրդները և ծովագնացները սովորել էին աստղերի օգնությամբ որոշել իրենց պետք եղած ուղղությունը։
Աստղագիտությունն այդ նպատակին ծառայում է նաև մեր ժամանակներում։ Աստղերի օգնությամբ որոշվում է ծովում նավերի, իսկ օդում՝ ինքնաթիռների ուղղությունն ու դիրքը։ Ճիշտ ժամանակը, որը հաղորդվում է ռադիոյով, որոշվում է աստղագետների կողմից՝ երկնային լուսատուները դիտելու միջոցով։ Առանց երկնային լուսատուների դիտումների հնարավոր չէր լինի նաև աշխարհագրական ճիշտ քարտեզներ կազմել։ Այսպիսով, աստղագիտությունն առաջ է եկել մարդու գործնական պահանջների հիման վրա և զարգացել է նրանց հետ միասին։
Դիտելով ամենօրյա արևածագն ու արևամուտը և աստղերի տեսանելի շարժումը հորիզոնի նկատմամբ, մարդիկ կարծում էին, թե բոլոր երկնային լուսատուները իսկապես շարժվում են անշարժ Երկրի շուրջը։ Երկնայինն ու երկրայինը խիստ կերպով սահմանազատվում էին միմյանցից։ Այդ սխալ պատկերացումը, որ հովանավորվում էր կրոնի կողմից, ժխտվել է մատերիալիստական գիտության կողմից։
Հաստատվել է, որ Երկիրը նույնպիսի մի երկնային մարմին է, ինչպես և երկնային մյուս լուսատուները, որ նա նրանցից ոչ մի բանով չի տարբերվում, որ Երկիրը և նրան նմանվող երկնային մարմինները, որոնք մոլորակներ են կոչվում, բոլորվում են Արեգակի շուրջը, որ աստղերը այնպիսի լուսատուներ են, որոնք նման են մեր Արեգակին, այսինքն՝ բաղկացած են շիկացած գազից և անհամեմատ ավելի մեծ չափեր ունեն, քան Երկիրը և նույնիսկ (շատ դեպքերում) իրենց չափերով բավականաչափ գերազանցում են մեր հսկայական Արեգակին։
Տիեզերքի մասին եղած նախկին միամիտ պատկերացումները, որոնք հիմնվում էին հեռավոր անցյալի մարդկանց մոլորությունների վրա, արտացոլված են կրոնական ուսմունքներում։ Այդ ուսմունքների համաձայն աշխարհն ստեղծվել է աստծու կամ աստվածների կողմից և իբր գոյություն ունի անփոփոխ։ Տիեզերքի իսկական կառուցվածքի հայտնագործումը մարդկանց ցույց տվեց, որ աշխարհն իրականում բնավ այնպիսին չէ, ինչպես նա նկարագրվում է այսպես կոչված «սրբազան» գրքերում։
Իմանալով բնության օրենքները, մարդիկ հնարավորություն ստացան այն նվաճելու, նրան ստիպեցին ծառայել իրենց։ Իմանալով երկնային այնպիսի երևույթների պատճառները, ինչպիսիք են՝ Արեգակի խավարումը, գիսավորների հայտնվելը և այլն, մարդիկ դադարեցին սնահավատորեն սարսափել նրանցից։ Տիեզերքի իսկական կառուցվածքը չիմանալուց առաջացող սնահավատությունը կարող է պահպանվել միայն հետամնաց մարդկանց մեջ, որոնք չգիտեն աշխարհի կառուցվածքը։ Ուստի՝ առանց աստղագիտության հիմունքներն իմանալու, չի կարելի գիտական առաջավոր աշխարհայացք ունենալ։
Երկնային լուսատուներին վերաբերող գիտությունը պատմում է մեզ, որ կան երկնային այնպիսի մարմիններ, որոնք բոլորովին նման չեն մեր երկրագնդին, որ միմիայն Երկիրը չէ, որ կարող է բնակեցված լինել կենդանի էակներով, որ աշխարհում ամեն ինչ փոփոխվում է հենց իրեն՝ բնության օրենքների համաձայն, որ տիեզերքը հավիտենական է՝ երբեք չի ստեղծվել և երբեք չի դադարի գոյություն ունենալուց։
Ուսումնասիրելով աստղագիտությունը, մենք տեղեկանում ենք մոլորակներէ մյուս երկրների մասին, որոնք շրջապատված են շատ լուսիններով, տեղեկանում ենք հեռավոր աստղերի ու աստղային կուտակումների մասին, որոնք այնքան հեռու են գտնվում մեզանից, որ նրանց լույսը, տարածվելով մոտ 300000 կմ/վրկ արագությամբ, հասնում է մեզ տարիների և, նույնիսկ, միլիոնավոր տարիների ընթացքում։
Աստղագիտության տվյալներն օգտակար են մյուս գիտությունների զարգացման համար, օրինակ, ֆիզիկայի։ Օժանդակելով մյուս գիտություններին, աստղագիտությունն իր հերթին օգտվում է այդ գիտությունների ծառայություններից։ Ֆիզիկոսներն օգնում են աստղագետներին երկնային լուսատուների ուսումնասիրության նոր միջոցներ գտնելու գործում, մաթեմատիկոսները տալիս են զանազան հաշվարկումների համար նոր, ավելի լավ եղանակներ, առանց որի՝ աստղագիտությունը չի կարող զարգանալ, և այլն։
Աստղագետները հաճախ օգնում են պատմաբաններին՝ որոշելու թե ե՛րբ են տեղի ունեցել որոշ իրադարձություններ, օրինակ, Հունաստանում ճակատամարտերից մեկի ժամանակ (միդիացիների և լիդիացիների միջև) տեղի է ունեցել մի հազվադեպ երևույթ` Արեգակի լրիվ խավարում։ Աստղագետները կարողացել են հաշվել, թե ե՛րբ տվյալ խավարումը կարող էր երևալ այդ վայրում։ Այդպիսով, որոշվել է այդ պատմական ճակատամարտի տարեթիվը։
Աստղագիտությունը հիմնված է երկնային երևույթների դիտումների վրա։ Առանց այդ դիտումների՝ աստղագիտությունը, ինչպես հարկն է, յուրացնել հնարավոր չէ։ Ուստի ամեն մի սովորող պետք է ծանոթանա երկնքում տեղի ունեցող հիմնական երևույթների հետ և հաճախակի ուշադիր կերպով դիտի աստղային երկինքը և աշխատի ինքն իր աչքով տեսնել այն, ինչի մասին խոսվում է դասագրքում։ Այդ երևույթներից շատերը մեկ անգամից չի կարելի նկատել։ Նրանք պարզվում են միայն տարբեր ժամանակ կատարված դիտումները միմյանց հետ համեմատելուց հետո։ Աստղագիտությունը ուսումնասիրում է բնությունը նրա մեծասքանչ արտահայտություններում, և բնությանը անձնական փորձի միջոցով ծանոթ չլինելու դեպքում նրա ուսումնասիրությունը մնում է գրքային ու մեռյալ, պատկերացումները՝ անորոշ և անկայուն։
Ուրեմն հաճախ կարդացեք բնության այդ մեծ գիրքը՝ աստղային երկինքը, որը մշտապես տարածված է ձեր գլխավերևը։
ԳԼՈՒԽ I։ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱ ԵՎ ԵՐԿԻՐ
ԵՐԿՆԱՅԻՆ ՍՖԵՐԱ
§ 2. ԵՐԿՆԱԿԱՄԱՐ ԵՎ ՀԱՄԱՍՏԵՂՈՒԹՅՈՒՆՆԵՐ. Բաց և ընդարձակ վայրում, թեկուզ ո՛րտեղ էլ մենք գտնվելիս լինենք (բաց դաշտում, տափաստանում կամ ծովի վրա), երկինքը՝ ամպամած լինի նա թե պարզ, երևում է մեզ ինչպես մի գմբեթ, որ շրջված է մեր գլխավերևը։ Այդ երկնային գմբեթը կամ երկնակամարը ցերեկը պարզ եղանակին կապույտ է, ամպամած եղանակին՝ մոխրագույն, իսկ պարզ գիշերները ծածկված է լինում աստղերով։
Այդ ժամանակ Երկիրը մեզ թվում է որպես մի շրջան, որի կենտրոնում կանգնած ենք մենք և որի եզրերը կարծես թե միանում են երկնակամարի հետ հորիզոնով։ Մենք գիտենք, որ իրականում երկինքը չի միանում Երկրին և որ հորիզոնի գիծը Երկրի մակերևույթի տեսանելի մասի երևակայական սահմանն է։ Ճիշտ այդպես էլ երկնակամարը, որպես երկնային գմբեթ, իրականում գոյություն չունի։ Երկնային լուսատուները, այսինքն՝ Արեգակը, Լուսինը և աստղերը, միայն թվում է, թե կպած են երկնակամարին և կարծես բոլորը միևնույն հեռավորության վրա են գտնվում մեզանից։ Իսկ իրականում բոլոր այդ լուսատուները գտնվում են մեզանից չափազանց տարբեր և շատ մեծ հեռավորությունների վրա։
Ցերեկային երկնքի կա պույտ գույնը առաջանում է նրանից, որ Երկրի մթնոլորտը, որը շրջապատում է ողջ երկրագունդը, ցրում է ամեն կողմի վրա իր միջով անցնող արեգակնային լույսը։ Բայց սպիտակ արեգակնային լույսը, ինչպես հայտնի է, բաղկացած է ծիածանի բոլոր գույների խառնուրդից, իսկ օդը կապույտ ճառագայթներն ավելի ուժեղ է ցրում, քան մյուս գույնի ճառագայթները։ Ուստի օդը կարծես «ներկվում է» կապույտ գույնով։
Որքան ավելի վեր բարձրանանք Երկրի մակերևույթից, այնքան քիչ մթնոլորտ կմնա մեր գլխավերևը և այնքան նրա կողմից թույլ կլինի արեգակնային լույսի ցրումը։ Այնտեղ (օրինակ, շատ բարձր լեռան գագաթից կամ ինքնաթիռից ու ստրատոստատից) երկինքն ավելի խավար է թվում, և նրա վրա նույնիսկ ցերեկը նկատելի են լինում առավել պայծառ աստղերը։ Ցերեկային երկինքը հեռադիտակով նայելիս նույնպես ավելի խավար է թվում, քան չզինված աչքի համար։ Հեռադիտակով պայծառ աստղերը կարելի է տեսնել նաև ցերեկը։ Հետևաբար, եթե ցերեկը երկնակամարի վրա մենք աստղեր չենք տեսնում, ապա միայն այն պատճառով, որ Երկրի մթնոլորտի կողմից ցրվող արեգակնային լույսը խանգարում է տեսնել նրանց։ Արեգակի լրիվ խավարման ժամանակ երկինքը մթնում է, և աստղերը չզինված աչքով տեսանելի են դառնում։
Մեզ թվում է, թե գիշերային երկնակամարի վրա ցրված աստղերն անթիվ են և որ նրանցից ոչ մի կերպ հնարավոր չէ մի բան հասկանալ։ Սակայն, եթե ուշադրությամբ նայենք երկնքին, կտեսնենք, որ աստղերի թիվն այնքան էլ մեծ չէ, և նրանց ճանաչելն էլ առանձնապես դժվար չէ։ Հորիզոնից վեր չզինված աչքով միաժամանակ, ամենաբարենպաստ պայմանների դեպքում, կարելի է տեսնել ոչ ավելի, քան 3000 աստղ։
Ամբողջ աստղային երկինքը բաժանված է մասերի։ Աստղային երկնքի այդ մասերը կոչվում են համաստեղություններ։
Դեռևս երկնքի հնադարյան դիտողներն են հազարավոր տարիներ առաջ աստղային երկինքը բաժանել մասերի, որտեղ աստղերը միանգամայն կամայականորեն խմբավորել են զանազան կերպարանքների՝ համաստեղությունների մեջ։ Նրանք այդ խմբերին (համաստեղություններին) տվել են երևակայական անուններ, որոնք պահպանվել են մինչև մեր օրերը։ Այդ անուններից շատերը այժմ մեղ համար տարօրինակ են հնչում, որովհետև համաստեղությունները կրում են այնպիսի առարկաների և էակների անուններ, որոնց հետ աստղերի դասավորությունը հաճախ ոչ մի նմանություն չունի։ Մի շարք դեպքերում այդ անունները կապվել են հին դարերի զանազան առասպելների հետ։
Երկնքում զատված է ընդամենը 88 համաստեղություն։ Նրանցից բավական է ճանաչել և կարողանալ երկնքում գանել մի քանիսը, որոնք պայծառ աստղեր ունեն։ Համաստեղությունները գտնելը հեշտացնելու համար նրանց առավել պայծառ աստղերը մտովի միացնում են ուղիղ գծերով այնպես, որ ստացվեն երկրաչափական պարզ ֆիգուրաներ կամ սխեմատիկ նկարներ։
Համաստեղությունների աստղերը չեն փոխում իրենց փոխադարձ դասավորությունը։ Նրանցից տարբերվում են մոլորակները, այն լուսատուները, որոնք փոխում են իրենց տեսանելի տեղը համաստեղությունների միջև, տեղաշարժվելով բարդ գծերով, որոնք հիշեցնում են մերուկներ։
Չզինված աչքով երևում են 5 մոլորակներ, որոնք իրենց տեսքով նման են պայծառ աստղերին։ Դրանք են՝ Մերկուրին, Վեներան, Մարսը, Յուպիտերը և Սատուրնը։
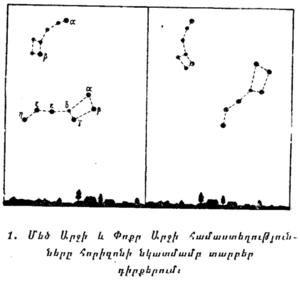
§ 3. ՀԱՄԱՍՏԵՂՈՒԹՅՈՒՆՆԵՐԸ ԳՏՆԵԼԸ ԵՐԿՆՔՈՒՄ։ Ամենից առաջ, յուրաքանչյուրը պետք է կարողանա երկնքում գտնել Մեծ Արջի համաստեղությունը։ Նա բնորոշ է իր յոթ պայծառ աստղերով։ Նրանց կարելի է մտովի միացնել ուղիղ գծերով այնպես, որ ստացվի շերեփի կամ կոթավոր կաթսայի պատկեր (նկ. 1)։ Միայն հարկավոր է նկատի ունենալ, որ երբեմն «շերեփի» կոթը ուղղված է լինում դեպի ձախ, երբեմն դեպի վեր կամ դեպի ցած, իսկ երբեմն էլ այդ «շերեփը», երբ նա գտնվելիս է լինում ուղիղ մեր գլխավերևը, շրջվում է «երեսնիվայր»։
Նկ. 2-ում պատկերված է աստղային երկնքի ժամանակակից քարտեզի մի մասը, որտեղ գտնվում է Մեծ Արջի համաստեղությունը։
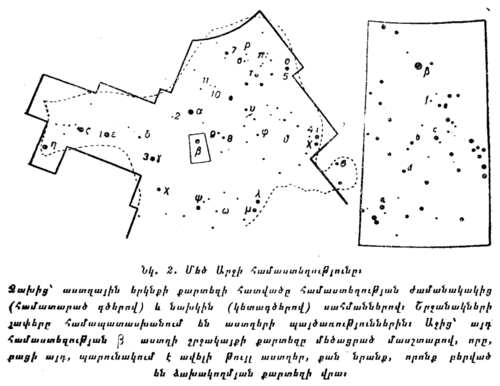
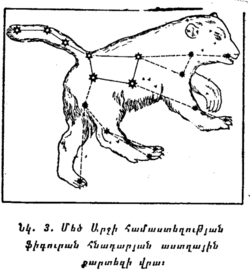
Նկ. 3-ում վերարտադրված է աստղային մի հինավուրց քարտեզ, որտեղ բացի աստղերից պատկերացվել է նաև այն գազանի պատկերը, որի անունով կոչվում է համաստեղությունը։
Ելնելով Մեծ Արջի համաստեղությունից, գտեք. Փոքր Արջի համաստեղությունը։ Եթե նրա 7 գլխավոր աստղերը (որոնք ավելի թույլ պայծառություն ունեն, քան Մեծ Արջի աստղերը) մտովի միացնենք ուղիղ գծերով, ինչպես այդ ցույց է տրված նկ. 1-ում, նույնպես կստացվի փոքր չափի շերեփ։ Այդ համաստեղության մեջ ամենապայծառ աստղը («շերեփի» կոթի ծայրինը) կրում է Բևեռային անունը։
Բևեռային աստղից այն կողմը, եթե շարժվելու լինենք Մեծ Արջից, մոտավորապես նույն հեռավորության վրա, փռված է Կասիոպեի համաստեղությունը։ Նա բնորոշ է իր հինգ բավականաչափ պայծառ աստղերով, որոնք դասավորված են W տառի կամ շրջված ու հիմքի մոտ ձգված M տառի ձևով։
Կասիոպեից ցած գտնվում են Անդրոմեդայի և Պեգասի համաստեղությունները։ Մ. Արջը Կասիոպեի հետ միացնող գծի երկու կողմերում դասավորված են Կարապի, Քնարի և Արծվի (մեկ կողմում) համաստեղությունները և Կառավարի, Երկվորյակների, Ցուլի, Օրիոնի, Մեծ Շան ու Փոքր Շան (մյուս կողմում) համաստեղությունները։
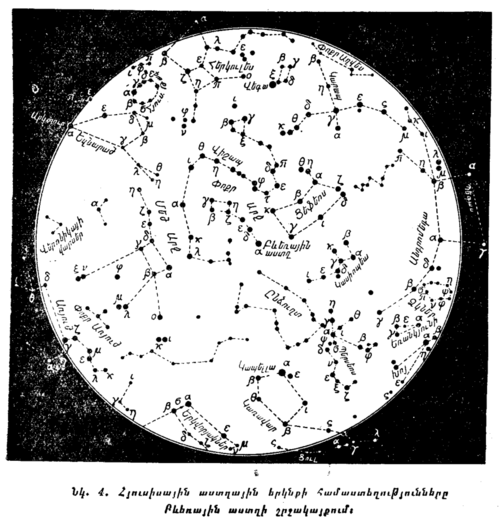
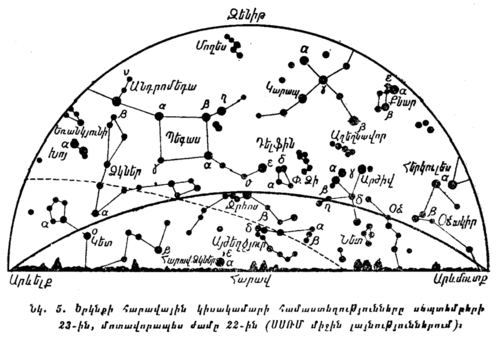
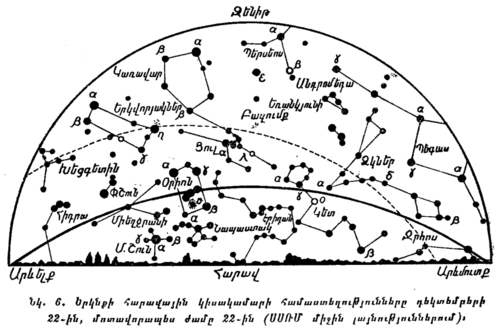
Յուրաքանչյուր սովորող պետք է կարողանա երկնքում գտնել նշված համաստեղությունները, հիշելով նրանց պայծառ աստղերի բնորոշ դասավորությունը։ Այդ համաստեղությունները ցույց են արված նկ. 4-ում, 5-ում և 6-ում։
Երկնքում համաստեղություններն ավելի հեշտ կարելի է գտնել այնպիսի գիշերը, երբ Լուսնի պայծառ լույսը դրան չի խանգարում։ Հարկավոր է նկատի ունենալ, որ որոշ համաստեղություններ (թվածներից երկու Արջերը և Կասիոպեն) միշտ երևում են երկնքում։ Մյուս համաստեղությունները երբեմն երևում են, երբեմն գտնվում են հորիզոնից ցած։ Բացի այդ, յուրաքանչյուր համաստեղություն օրվա տարբեր ժամերին և տարվա տարբեր ժամանակներին հորիզոնի նկատմամբ տարբեր դիրք է գրավում։ Համաստեղություններն ավելի հեշտ գտնելու համար առանձնապես հարմար է օգտվել երկնքի շարժական քարտեզից, որովհետև նա ցույց է տալիս հորիզոնի նկատմամբ համաստեղությունների ունեցած դասավորությունը՝ տարվա ամեն մի օրվա ու ժամվա համար (տե՛ս հավելված VI)։
Համաստեղությունները գտնելը հեշտացնելու համար հարկավոր է մեկ՝ արդեն ծանոթ, համաստեղությունից աստիճանաբար անցնել մյուսին՝ դեռևս չգտնվածին։ Ըստ որում պետք է նկատել, թե մեզ ծանոթ համաստեղությունից դեպի ո՞ր կողմն է գտնվում այն համաստեղությունը, որ մենք փնտրում ենք։ Հարկավոր է ուշադրություն դարձնել աստղերի համեմատական պայծառության վրա, որը քարտեզի վրա ցույց է տրված տարբեր մեծության շրջանակներով։ Քարտեզի վրա ցույց է տրված, թե ի՛նչ գծերով է հարմար միացնել աստղերը, թեև դա սոսկ պայմանական մի ձև է։
Վերոհիշյալ համաստեղություններից ամեն երեկո Քնարը (Վեգա կոչված պայծառ աստղով), Կարապն ու Արծիվը (Ալտաիր կոչված աստղով) երևում են ամբողջ գիշերը՝ գարնանն ու աշնանը, Եզնարածը (Արկտուր կոչված պայծառ աստղով)՝ գարնանն ու ամռանը, Կառավարը, Ցուլը և Մեծ Շունը (երկնքի ամենապայծառ աստղի՝ Սիրիուսի հետ միասին)՝ միայն ձմռանը, Պերսեոսը, Անդրոմեդան և Պեգասը՝ սրանք ամառային և աշնանային համաստեղություններ են։
§ 4. ԱՍՏՂԱՅԻՆ ՄԵԾՈՒԹՅՈՒՆՆԵՐ։ Աստղերն ըստ իրենց տեսանելի պայծառության տարբեր են լինում։ Հին ժամանակներից ի վեր ամենապայծառ աստղերն անվանել են առաջին մեծության աստղեր։ Այն աստղերը, որոնք նրանցից թույլ են 2½ անգամ, անվանվում են երկրորդ մեծության աստղեր, և այլն։ Ամենաթույլ աստղերը, որոնք երևում են անլուսին գիշերը սրատես աչքով, վեցերորդ մեծության աստղեր են։ Նրանք իրենց փայլով 100 անգամ թույլ են առաջին մեծության աստղերից։
«Աստղային մեծություն» հնուց ի վեր արմատացած անունը ոչ մի առնչություն չունի աստղի չափերի և աստղի իրակ ան մեծության հետ։ «Աստղային մեծություն» հասկացողությունը բնորոշում է աստղերի պայծառությունը։ Որքան աստղը թույլ է, այնքան նրա աստղային մեծությունը մեծ է։ Սա նման է այն բանին, ինչպես, օրինակ, ավելի խոշոր պտուղները համարում են առաջին տեսակի, մանրերը՝ երկրորդ տեսակի և այլն։
Մեծ Արջի գլխավոր յոթ աստղերից վեցը և Բևեռшյին աստղը երկրորդ մեծության աստղերի օրինակ են հանդիսանում։ Առաջին մեծության աստղերի օրինակ են ծառայում Արկտուրը և Ալտաիրը։
Աստղերի փայլի ճշգրիտ չափումները պահանջ են առաջացրել կիրառելու աստղային մեծության միջակա կոտորակային նշանակումներ, օրինակ, 1,2 կամ 5,9։ Որպես 1,0 մեծության նմուշ ընդունված աստղերից ավելի պայծառ լուսատուների համար մտցրել են 0 աստղային մեծություն, -1, -2 մեծություններ (բացասական նշանով) և այլն։ Օրինակ, Սիրիուսի աստղային մեծությունը հավասար է -1,6։
Հեռադիտակով կարելի է տեսնել ավելի թույլ աստղեր, քան վեցերորդ մեծության աստղերն են՝ յոթերորդ, ութերորդ և ավելի բարձր մեծության աստղեր։ Որքան աստղերը թույլ են, այնքան նրանց թիվը մեծ է։ Առաջին մեծության և ավելի պայծառ աստղերի թիվը հասնում է մոտավորապես 20-ի։ Վեցերորդ մեծության և ավելի պայծառ աստղերը մոտավորապես վեց հազար հատ են։
§ 5. ԱՍՏՂԵՐԻ ԱՆՎԱՆՈՒՄՆԵՐՆ ՈՒ ՆՇԱՆԱԿՈՒՄՆԵՐԸ։ Առաջին մեծության աստղերը դեռևս հնում ստացել են հատուկ անվանումներ, ինչպես, օրինակ, Սիրիուս, Վեգա, Ալտաիր։ Բացի այդ պայծառ աստղերից, յուրաքանչյուր համաստեղության մեջ առանձին կերպով, նշանակում են հունական այբուբենի տառերով՝ α, β, γ, ... և այլն՝ մասնավորապես նրանց պայծառության նվազման կարգով։ Այսպես, օրինակ, Սիրիուսը միևնույն ժամանակ Մեծ Շան α-ն է, Բևեռային աստղը՝ Փոքր Արջի α-ն է, Ռիգելը՝ Օրիոնի β-ն է և այլն։
Ավելի թույլ աստղերից շատերը նշանակվում են լատինական այբուբենի տառերով։ Վերջապես բոլոր աստղերի, նույն թվում նաև ամենաթույլ աստղերի համար, որոնց այբուբենի բոլոր տառերը բնականաբար չեն բավականացել, կարելի է ցույց տալ նրանց աստղային մեծությունը և այն տեղը, որ նրանք զբաղեցնում են երկնքում, կամ այն համարը, որի տակ նրանք գրանցված են այս կամ այն մասնագիտական աստղային կատալոգում։
Հունական այբուբենը և բոլոր առաջին մեծության այն աստղերի հատուկ անունները, որոնք երևում են ՍՍՌՄ տերիտորիայից, տրված են II և III հավելվածներում։
§ 6. ԵՐԿՆԱՅԻՆ ՍՖԵՐԱ, ԶԵՆԻԹ ԵՎ ՀՈՐԻԶՈՆ։ Բոլոր աստղերը մեզանից միևնույն հեռավորության վրա են թվում։ Ուստի՝ հարմար է պայմանական կերպով ընդունել, որ բոլոր աստղերն էլ իբր թե գտնվում են կամայական շառավիղ ունեցող մի գնդի ներքին մակերևույթի վրա, որ կոչվում է երկնային սֆերա և որի կենտրոնում գտնվում է դիտողի աչքը։
Չափազանց տարբեր են աստղերի իսկական հեռավորությունները մեզանից, և այդ հեռավորությունները մենք կարող ենք որոշել միայն շատ ճշգրիտ չափումների և հաշվարկումների միջոցով։ Մինչդեռ աչքի համար հեռավորությունների մեջ եղած այդ տարբերությունը բոլորովին աննկատելի է, և այնպիսի երևույթները, ինչպիսիք են աստղերի ծագելն ու մայր մտնելը, տեղի են ունենում անկախ մեզնից ունեցած նրանց հեռավորությունից։ Երկնային սֆերայի հասկացողությունից մենք օգտվում ենք երկնային տեսանելու ամենապարզ երևույթների քննարկումը հարմար դարձնելու համար, օրինակ, այնպիսի երևույթների, ինչպես լուսատուների ծագելն ու մայր մտնելն է։ Մենք գիտենք, որ մեր գլխավերևը իրականում գոյություն չունի ոչ կարծր գմբեթի ձև ունեցող երկնակամար և ոչ էլ որևէ ռեալ երկնային սֆերա։ Իսկ հին ժամանակներում երկնային այդ սֆերան համարում էին ոչ թե որպես մաթեմատիկական մի հասկացողություն, ինչպես մենք նրան համարում ենք, այլ որպես իսկապես գոյություն ունեցող բյուրեղապակյա մի գունդ։
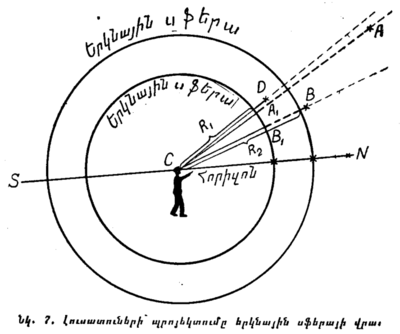
Դատողություններ անելով լուսատուների ծագելու, մայր մտնելու և ուրիշ նման երևույթն երի մասին, մենք նկատի ենք ունենում միայն այն ուղղությունը, որով երևում են աստղերը (օրինակ, հորիզոնի մոտ, մեր գլխավերևը և այլն), ուստի միևնույն է, թե ինչպիսի շառավիղ մենք կերևակայենք երկնային սֆերայի համար։ Նկ. 7-ը, օրինակ, ցույց է տալիս, որ դիտողին որևէ ուղղությամբ երևացող ամեն մի աստղ հենց այդ ուղղությամբ էլ կերևա, թեկուզ ի՛նչպիսի սֆերայի վրա էլ նրան պատկերացնելու լինենք՝ R1 շառավիղ ունեցող սֆերայի, թե R2 շառավիղ ունեցող սֆերայի վրա։ Այդ պատճառով էլ ասում են, որ երկնային սֆերան անորոշ կամ կամայական շառավիղ ունի։
Անցնելով դիտողի աչքով, ուղղաձիգ գիծը երկնային սֆերան հատում է զենիթի կետում։ Զենիթը դիտողի գլխավերևի ամենաբարձր կետն է։ Ուղղաձիգ գծի ուղղությունը ցույց է տալիս ուղղալարը՝ թելից կախած փոքրիկ ծանրությունը։ Ուղղաձիգ գծին ուղղահայաց հարթությունը կոչվում է հորիզոնական հարթություն։
Մաթեմատիկական հորիզոն է կոչվում երկնային սֆերայի և այն հորիզոնական հարթության հատման գիծը, որ անցնում է երկնային սֆերայի կենտրոնով։ Այս հորիզոնից այսպես կոչված՝ տեսանելի հորիզոնը տարբերվում է նրանով, որ վերջինս սահմանափակված է մի գծով, որով, ինչպես մեզ թվում է, երկինքը «միանում» է Երկրին։ Հորիզոնի հարթությունը կարելի է որոշել հարթաչափի միջոցով։
§ 7. ԱՆԿՅՈՒՆԱՅԻՆ ՉԱՓՈՒՄՆԵՐ։ Պայմանականորեն ընդունելով, որ բոլոր լուսատուները դասավորված են երկնային սֆերայի վրա, (ավելի Ճիշտ՝ պրոյեկտված են նրա վրա), մենք կարող ենք չափել միայն այն ուղղությունների միջև ընկած անկյունները, որով մենք տեսնում ենք այդ լուսատուները։ Երկնային սֆերայի վրա այդ անկյուններին համապատասխանում են մեծ շրջանների աղեղներ։ Օրինակ (տե՛ս նկ. 7), մենք ասում ենք, որ երկնային սֆերայի վրա A և B աստղերը միմյանցից գտնվում են 23° հեռավորության վրա, եթե այդ աստղերի CA և CB ուղղությունների միջև ընկած անկյունը (<ACB) կազմում է 23°։ Երկնային սֆերայի վրա այդ անկյանը համապատասխանում է A1B1 աղեղը, որը հավասար է 23°։ A աստղը կարող է մեզանից շատ ավելի հեռու լինել, քան D աստղը, բայց եթե նրանք երկուսն էլ մեզ երևում են գրեթե միևնույն ուղղությամբ, մենք կասենք, որ երկնային սֆերայի վրա D աստղը շատ ավելի մոտ է A աստղին, քան B աստղին, թեև տարածության մեջ A-ի գծային հեռավորությունը (օրինակ, կիլոմետրերով) D-ից կարող է շատ ավելի մեծ լինել։
Ճիշտ այդպես էլ Արեգակի և Լուսնի տեսանելի անկյունային տրամագծերը գրեթե հավասար են՝ կազմելով մոտավորապես կես աստիճան, թեև իրականում Լուսնի տրամագիծը համարյա 400 անգամ փոքր է Արեգակի տրամագծից։ Բայց դրա փոխարեն նա նույնքան անգամ ավելի մոտ է մեզ, քան Արեգակը, այդ պատճառով էլ թվում է, թե նրանց անկյունային չափերը հավասար են։ Լուսնի տեսանելի անկյունային տրամագիծը կոպեկանոցի կամ ափսեի հետ համեմատելն անիմաստ կլինի, եթե վերջիններին որևէ հեռավորություն չի վերագրվում։ Եվ իսկապես, պարզած ձեռքի հեռավորության վրա կոպեկանոցը կծածկի միայն Լուսինը, իսկ եթե կոպեկանոցը մոտեցնենք աչքին, նրանով կարելի է ծածկել ամբողջ աշխարհը։ Լուսինը կարելի է համեմատել կոպեկանոցի հետ, եթե ավելացնելու լինենք, թե ինչ հեռավորության վրա պետք է պահենք կոպեկանոցը։ Անմտություն են նույնպես հետևյալ տիպի արտահայտությունները. «Լուսինը հորիզոնից բարձրացել է կես մետրի չափ» կամ «երկու աստղերի միջև եղած հեռավորությունը երկնքում կազմում է 2 մետր»։
Այսպիսով, երկնային սֆերայի վրա կարելի է կատարել միայն անկյունային չափումներ։
Լուսատուի բարձրություն անվանում են նրա անկյունային հեռավորությունը հորիզոնից։ Օրինակ, B լուսատուի բարձրությունը (նկ. 7) չափվում է BCN անկյունով։
Մարդ եթե առաջ պարզի իր ձեռքը, հեռացնելով իրարից բթամատը և ցուցամատը, մատների ծայրերի միջև ընկած հեռավորությունը նա կտեսնի 16°-ի տակ։ Այդպիսի «անկյունային քառորդով» կարելի է, իհարկե շատ կոպիտ կերպով, անկյունային չափումներ կատարել երկնքում։ Լավ կլինի նաև հիշել, որ Մ. Արջի α և β աստղերի միջև անկյունային հեռավորությունը հավասար է 5°-ի, իսկ Մ. Արջի α աստղի և Բևեռային աստղի միջև գրեթե 30°-ի (ավելի ճիշտ 28°-ի)։
Աստղագիտական հատուկ գործիքների օգնությամբ անկյունային հեռավորությունները կարելի է չափել մինչև 0՛՛,01 ճշտությամբ։ Չափման ճշտությունը պատկերացնելու համար նշենք, որ 0՛՛,01 անկյան տակ է երևում լուցկու հաստությունը 20 կմ հեռավորության վրայից, իսկ մարդու մազը առաջ պարզած ձեռքի հեռավորությունից երևում է 20՛՛ անկյան տակ։
ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ
- Ի՞նչ է ուսումնասիրում աստղագիտությունը։
- Ի՞նչ նշանակություն ունի աստղագիտությունը աշխարհայացքի համար։
- Ինչպիսի՞ նշանակություն ունեն դիտումները աստղագիտությունն ուսումնասիրելու համար։
- Ի՞նչ են համաստեղությունները և ինչպե՞ս են նրանց գտնում երկնքում։ Ինչպիսի՞ համաստեղություններ գիտեք։
- Ինչպե՞ս են «աստղային մեծությամբ» բնութագրում աստղերի փայլը։
- Ինչպե՞ս են նշանակվում աստղերը համաստեղություններում։
- Նշեցեք առաջին մեծության մի քանի աստղեր։
- Ի՞նչ է երկնային սֆերան և ինչի՞ համար է պետք այդ հասկացողոլթյունը։
- Ի՞նչ է հորիզոնը և ի՞նչ է զենիթը։
- Ինչո՞ւ երկնային սֆերայի վրա հնարավոր են միայն անկյունային չափումները։
- *Ի՞նչն է կոչվում լուսատուի բարձրություն։
ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ
- Ինչպիսի՞ հեռավորության վրա պետք է պահել 15 կոպեկանոցը (նրա տրամագիծը 2 սմ է), որպեսզի նա երևա այնպիսի անկյան տակ, ինչպես Լուսինն է երևում (հաշվարկման համար հիշենք, որ միավոր շառավիղ ունեցող շրջանի 1° աղեղի երկարությունը հավասար 1/57, իսկ 1՛՛ աղեղի երկարությունը հավասար է 1/206265)։
- Գծեցեք իրարից 1 մմ հեռավորության վրա 1 մմ հաստություն ունեցող երկու զուգահեռ ուղիներ։ Որոշեցեք, թե ինչպիսի հեռավորության վրա նրանք ձեզ համար կմիաձուլվեն և նախորդի նման հաշվեցեք, թե տեսականորեն ինչպիսի անկյան տակ է երևում ձեզ նրանց միջև եղած միլիմետրական արանքը։ Դա կբնորոշի, ինչպես ասում են, ձեր աչքի բաժանող ուժը։
§ 8. ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՕՐԱԿԱՆ ՊՏՈՒՅՏԸ։ Դուրս գալով երեկոյան մի բաց տեղ, հորիզոնին մոտիկ՝ նրա արևելյան կողմում նշմարենք մի որևէ պայծառ աստղի դիրքը։ Մեկ ժամից հետո դարձյալ նայենք այդ աստղին։ Մենք կհամոզվենք, որ աստղը բարձրացել է հորիզոնից և որոշ չափով շեղվել դեպի աջ (նկ. 8)։
Նույնպիսի դիտում կատարելով երկնքի արևմտյան մասում գտնվող աստղերից մեկի նկատմամբ, մենք կհամոզվենք, որ աստղերը Արեգակի և Լուսնի նման բարձրանում են հորիզոնի արևելյան կողմից, հասնում են իրենց ամենաբարձր դիրքին՝ երկնքի հարավային մասում և այնուհետև մայր են մտնում հորիզոնի արևմտյան կողմում։ Հաջորդ օրը նրանք կկատարեն նույն շարժումը, ըստ երևույթին, այդպիսով օրվա ընթացքում մի լրիվ շրջան կատարելով երկնքում։

Այդ օրական պտույտի ժամանակ բոլոր աստղերը տեղաշարժվում են առանց իրենց փոխադարձ դասավորությունը փոխելու։ Թվում է, թե աստղային երկինքը պտտվում է ինչպես մի ամբողջություն ժամացույցի սլաքի շարժման ուղղությամբ՝ օրական մի լրիվ պտույտի արագությամբ։
Ուշադրությամբ դիտելով, մենք կնկատենք, որ տարբեր համաստեղությունների աստղերը տարբեր չափերի շրջաններ են գծում։ Որոշ համաստեղություններ օրվա ընթացքում գծում են մեծ չտփի շրջաններ, որոնց մի մասը գտնվում է հորիզոնի տակ։ Այդպիսի համաստեղություններն օրվա ընթացքում ծագում ու մայր են մտնում, ինչպես, օրինակ, Պեգասը, Պերսեոսը, Օրիոնը, Ցուլը։ Մյուս համաստեղությունները, ինչպես, օրինակ, Մեծ Արջը, գծում են փոքր չափի շրջաններ։ Նրանց շարժման ամբողջ շրջանը մնում է հորիզոնից վեր,— սրանք մայր չմտնող համաստեղություններ են։
Իրականում պտտվում է երկրագունդը։ Նա պտտվում է ժամացույցի սլաքի շարժման հակառակ ուղղությամբ՝ եթե նրան դիտենք հյուսիսային բևեռից։ Երկրի պտույտը մենք չենք զգում և. մեզ թվում է, որ, ընդհակառակը, երկինքն է պտտվում հակառակ կողմի վրա՝ ժամացույցի սլաքի շարժման ուղղությամբ։
§ 9. ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԿՈՈՐԴԻՆԱՏՆԵՐ։ Աշխարհագրության դասընթացից հայտնի է, որ երկրագնդի վրա որևէ կետի դիրքը կարելի է որոշել աշխարհագրական երկու կոորդինատներով՝ աշխարհագրական լայնությամբ (նշանակվում է φ-ով) և աշխարհագրական երկայնությամբ (նշանակվում է λ-ով)։
Այդ նպատակով Երկրի բևեռների վրայով անց են կացնում մեծ շրջանի աղեղներ, որոնք կոչվում են միջօրեականներ։ Դրանցից մեկը, որը անցնում է Գրինվիչի աստղադիտարանով (Լոնդոնի մոտ), ընդունում են որպես սկզբնական միջօրեական։ Բացի այդ, Երկրի վրա, հասարակածին զուգահեռ, անց են կացնում փոքր շրջանագծեր, որոնք կոչվում են աշխարհագրական զուգահեռականներ։ (Հասարակածը մեծ շրջանագիծ է, որի հարթությունն անցնում է Երկրի կենտրոնով և ուղղահայաց է նրա առանցքին)։
Աշխարհագրական երկայնությունը չափվում է հասարակածի կամ զուգահեռականի այն աղեղով, որը պարփակված է սկզբնական միջօրեականի և տվյալ կետով անցնող միջօրեականի միջև։ Երկայնությունն սկզբնական միջօրեականից դեպի արևելք չափվում է այն ժամանակով, որ հարկավոր է, որպեսզի Երկիրը պտտվի իր առանցքի շուրջը՝ երկայնությունը չափող աղեղի համապատասխան անկյան չափով։ Երկայնությունը կարելի է չափել թե՛ դեպի արևմուտք և թե՛ դեպի արևելք, և այն ժամանակ, համապատասխանաբար ասում են արևմտյան կամ արևելյան երկայնություն։
Քանի որ Երկիրը մի լրիվ պտույտ (360°) կատարում է 24 ժամում, ուստի երկայնության յուրաքանչյուր 15° հավասար է երկայնության 1 ժամին և այդպիսով՝ 1° = 4 րոպեի, 1 րոպեն = 15՛ և 1 վայրկյանը =15՛՛։ Մոսկվայի և Գրինվիչի միջօրեականների հարթությունների միջև կազմած անկյունը հավասար է 37°34՛։ Մոսկվայի երկայնությունը Գրինվիչից հենց այդ 37°34՛ կամ 2 ժամ 30,3 րոպեին է հավասար. այդ երկայնությունն արևելյան է։
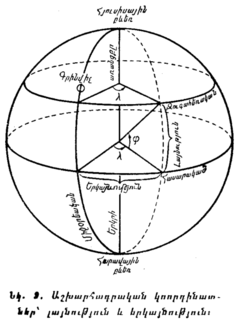
Աշխարհագրական լայնությունը չափվում է այն անկյան մեծությամբ, որ հասարակածի հարթության հետ կազմում է երկրի տվյալ վայրով անցնող ուղղաձիգ գիծը։ Եթե Երկիրն իսկական գունդ համարենք, ապա ուղղաձիգ գիծն ամենուր անցնում է ուղիղ Երկրի կենտրոնով և համընկնում է տվյալ վայրում Երկրի շառավղի հետ։
Աշխարհագրական քարտեզի կամ գլոբուսի վրա աշխարհագրական լայնությունը հաշվվում է միջօրեականի ուղղությամբ՝ հասարակածից մինչև այն աշխարհագրական զուգահեռականը, որը անցնում է տվյալ կետով։ Նա արտահայտվում է աստիճաններով։ Հասարակածից դեպի հյուսիս հաշվվող լայնությունը կոչվում է հյուսիսային լայնություն (նշանը՝ +), իսկ դեպի հարավ՝ հարավային լայնություն (նշանը՝ -), [օրինակ, Աշխաբադի լայնությունը՝ +37°57՛ է, իսկ Մելբուռնի լայնությունը կազմում է -37°50՛]։
§ 10. ԱՇԽԱՐՀԻ ԲԵՎԵՌՆԵՐԸ ԵՎ ԱՌԱՆՑՔԸ։ Ուշադրությամբ նայելով դեպի երկինք, մենք կնկատենք, որ օրվա ընթացքում Մեծ Արջի համաստեղությունը երկնքում բավական մեծ շրջան է գծում, Փոքր Արջի շերեփը՝ ավելի փոքր շրջան, իսկ այդ շերեփի կոթի ծայրին գտնվող պայծառ աստղը գրեթե անշարժ է թվում։ Հենց այդ աստղն էլ անվանում են Բևեռային աստղ։ Օրվա ընթացքում նա համարյա աննկատելի շրջանիկ է գծում և միշտ երևում է հորիզոնից, գրեթե միևնույն բարձրության վրա երկնքի հյուսիսային կողմում։ Փոքր Արջի համաստեղության մյուս աստղերն օրվա ընթացքում այնքան ավելի մեծ շրջաններ են գծում, որքան հեռու են գտնվում Բևեռային աստղից։
Բևեռային աստղը (Փոքր Արջի α) գտնում են հետևյալ կերպ. Մեծ Արջի «շերեփի» երկու ծայրամասայինդ աստղերով (Մեծ Արջի α-ից դեպի β-ն) պետք է մտքով ուղիղ գիծ տանել և շարունակել այդ երկու աստղերի միջև եղած հեռավորության հնգապատիկի չափով։ Հենց այդ գծի ծայրին կտեսնենք Բևեռային աստղը։
Նկ. 1-ում ցույց է տրված Մեծ Արջի համաստեղության դիրքի փոփոխությունը հորիզոնի նկատմամբ օրվա ընթացքում և Բևեռային աստղի դիրքի անփոփոխությունը։ Այնուամենայնիվ, անհրաժեշտ է, որպեսզի դիտումներ կատարելով՝ ինքներդ համոզվեք, որ դա իրոք հենց այդպես էլ լինում է։
Ներքոհիշյալ հետաքրքիր փորձը, որ մատչելի է լուսանկարչությանը ծանոթ ամեն մի դպրոցականի, ակնառու կերպով ցույց է տալիս երկնային սֆերայի օրական պտույտի ընթացքը։ Անլուսին պարզ գիշերը լուսանկարչական ապարատը տեղակայելով «անսահմանության վրա», ուղղում են դեպի Բևեռային աստղը՝ ցածից ամրացնելով որևէ հենարանի վրա։ Ապարատն այդպես ամրացված վիճակում մի քանի ժամով թողնում են բաց փականակով, այնուհետև թիթեղը հայտածում են։ Լուսանկարչական թիթեղի (նեգատիվի) վրա հայտնվում են աստղերի սև հետքերը (պոզիտիվի վրա՝ սպիտակ հետքերը, նկ. 10)։ Այդ բոլոր գծերը համակենտրոն աղեղների տեսք ունեն։ Այդ աղեղների գծային երկարությունները տարբեր են, բայց աստիճանային չափերով նրանք հավասար են։ Նրանց կենտրոնում ընկած Է պտտման կենտրոնը։

Պտտման ճիշտ նույնպիսի կենտրոն կարելի Է գտնել երկնքի նաև հարավային կիսագնդում։ Նա գտնվում Է երկնային սֆերայի մի կետում, որն ուղիղ հակադիր է աշխարհի հյուսիսային կիսագնդի հենց այն կետին, որի մասին քիչ առաջ խոսեցինք։ Բայց չէ՞ որ երկնային սֆերայի կենտրոնում գտնվում է մեր աչքը։ Հետևաբար, դիտելով երկինքը, մենք համոզվում ենք, որ երկն աչին սֆերան որպես մի ամբողջություն պտտվում է մի ինչ-որ առանցքի շուրջը, որն անցնում է մեր աչքով։ Երկնային սֆերայի օրական պտույտի առանցքը կոչվում է աշխարհի առանցք։ Այդ առանցքի ուղղությունը մենք կգտնենք, եթե մեր աչքով մտքով ուղիղ գիծ տանենք դեպի երկնքի՝ վերը նկարագրած ձևով գտած կետը, որը չի մասնակցում երկնային սֆերայի օրական պտույտին։
Այն կետերը, որտեղ երկնային սֆերան հատվում է աշխարհի առանցքի հետ, կոչվում են աշխարհի բևեռներ։ Բևեռային աստղը գտնվում է աշխարհի հյուսիսային բևեռի մոտ (մոտ 1° հեռավորության վրա)։ Աշխարհի հարավային բևեռը երևում է Երկրի միայն հարավային կիսագնդից, և նրա մոտերքը ոչ մի պայծառ աստղ չկա։
Այն հարթությունը, որ ուղղահայաց է աշխարհի առանցքին և անցնում է երկնային սֆերայի կենտրոնով, կոչվում է երկնային հասարակածի հարթություն, իսկ նրա հատման գիծը երկնային սֆերայի հետ կոչվում է երկնային հասարակած։ Այսպիսով, երկնային հասարակածը երկնային սֆերայի այն մեծ շրջանն է, որն ուղղահայաց է աշխարհի առանցքին։
Հասարակածը երկնային սֆերան բաժանում է երկու կիսագնդերի՝ հյուսիսային և հարավային։ Մենք տեսնում ենք, որ աշխարհի առանցքը, աշխարհի բևեռները և երկնային հասարակածը համանման են Երկրի առանցքին, բևեռներին և հասարակածին։ Բայց այդ բնական է, որովհետև վերոհիշյալ անունները կապված են երկնային սֆերայի թվացող պտույտի հետ, իսկ դա ինքը երկրագնդի իրական պտույտի հետևանք է։
§ 11. ԵՐԿՆԱՅԻՆ ՄԻՋՕՐԵԱԿԱՆ ԵՎ ՄԻՋՕՐԵԻ ԳԻԾ։ Երկնային միջօրեական։ Միջօրեականի հարթություն կոչվում է այն հարթությունը, որն անցնում է ուղղաձիգ գծով և աշխարհի առանցքով։ Այդ հարթությունը, հատվելով երկնային սֆերայի հետ, առաջացնում է երկնային միջօրեականի գիծը։ Միջօրեականի հարթությունը մոտավորապես կլինի այն ուղղաձիգ հարթությունը, որ անցնում է բևեռային աստղով և դիտողով։
Միջօրեի գիծ կոչվում է միջօրեականի և հորիզոնի հարթությունների հատման գիծը։ Դա մի հորիզոնական գիծ է։
Երկրի ցանկացած վայրում երկնային միջօրեականի հարթությունը համընկնում է տվյալ վայրի աշխարհագրական միջօրեականի հարթության հետ։
Հորիզոնի կետերը։ Հորիզոնը հատվում է երկնային միջօրեականի հետ՝ հյուսիսի (N) և հարավի (S) կետերում, իսկ երկնային հասարակածի հետ՝ արևելքի (E) և արևմուտքի (W) կետերում։ Եթե մենք կանգնենք երեսներս դեպի աշխարհի բևեռը (Բևեռային աստղը), ապա ուղիղ նրա տակ՝ հորիզոնի վրա կունենանք հյուսիսի կետը, մեր թիկունքի կողմը՝ հարավի կետը, աջ կողմում՝ արևելքի կետը և ձախ կողմում՝ արևմուտքի կետը։ Հիշելով այդ, մենք միշտ էլ կարող ենք կողմն որոշվել տեղանքում։
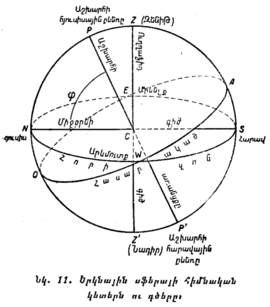
Այս պարագրաֆում բերված սահմանումները պետք է հիմնավորապես ըմբռնել և լավ հիշել, որովհետև առանց նրանց թե՛ երկնային ամենապարզ երևույթները և թե՛ աստղագիտության գործնական կիրառումները անհասկանալի կմնան։ Որպեսզի ավելի լավ պատկերացնենք այն բոլորը, ինչ որ վերն ասված է, երկնային սֆերան պատկերացնեն գծագրի վրա (նկ. 11)։ Այդ գծագրի վրա C երկնային սֆերայի կենտրոնն է, որտեղ գտնվում է դիտողի աչքը Z՛CZ ուղղաձիգ գիծն է, ընդ որում՝ Z — զենիթն է, Z՛ — նադիրը (զենիթի հակադիր կետը երկնային սֆերայում)։ P՛P աշխարհի առանցքն է, P — աշխարհի հյուսիսային բևեռն է, P՛ — աշխարհի հարավային բևեռը, EAWQ — երկնային հասարակածն է, որի հարթությունն ուղղահայաց է աշխարհի առանցքին, EAWN — հորիզոնն է, S — հարավի կետն է, N — հյուսիսի կետը, E — արևելքի կետը և W — արևմուտքի կետը։ Դժվար չէ հասկանալ, որ հորիզոնից վերև երևում են երկնային սֆերայի ուղիղ կեսը և երկնային հասարակածի նույնպես ուղիղ կեսը, նաև այն, որ E և W կետերում (որոնք N և S կետերից գտնվում են 90° հեռավորության վրա) և՛ հորիզոնը, և՛ հասարակածը կիսվում են։
SN գիծը միջօրեի գիծն է, որը կոչվում է այդպես, որովհետև կեսօրին առարկաների ստվերները ճիշտ այդ ուղղությամբ են ընկնում. իսկ NZAS աղեղը աշխարհի միջօրեականն է։
Անհրաժեշտ է սովորել երկնային սֆերա գծագրելը գրատախտակի կամ թղթի վրա։ Վարժությունների ժամանակ աշխարհի առանցքի և հորիզոնի հարթության միջև ընկած PCN անկյունը կարելի է վերցնել ցանկացած մեծության։ Ինչպես մենք հետո կտեսնենք, այդ անկյան մեծությունը կախված է երկրագնդի վրա դիտողի գտնված վայրից։
§ 12*. ՄԻՋՕՐԵԻ ԳԾԻ ՈՒՂՂՈՒԹՅԱՆ ՈՐՈՇՈՒՄԸ ԳՈՐԾՆԱԿԱՆՈՒՄ։ Միջօրեի գծի դիրքը, իսկ նրա օգնությամբ նաև երկնային միջօրեականի դիրքը տեղում որոշելու համար գոյություն ունեն շատ միջոցներ։ Դրանցից ամենապարզը, բայց ոչ այնքան ճշգրիտ միջոցները հետևյալներն են.
ա) Գիշերը՝ ըստ Բևեռային աստղի։ Ուղղալարը (թելից կախված ծանրոցը) որևէ ձևով կախում ենք անշարժ կերպով և նշանակում այն տեղը, որտեղ ցածում նա դիպչում է գետնին։ Այնուհետև ձեռքում բռնելով երկրորդ ուղղալարը պահում ենք մեր աչքի առաջ այնպես, որ Բևեռային աստղը և երկու ուղղալարերը համընկնեն, այսինքն՝ որպեսզի մեկ ուղղալարը լիովին ծածկի մյուսին, և երկուսը միասին ծածկեն աստղը։ Նշանակում ենք նաև այն տեղը, որին դիպչում Է երկրորդ ուղղալարը։ Պարզ է, որ երկու ուղղալարերով անցնող հարթությունը կլինի միջօրեականի հարթությունը, իսկ գետնի վրա մեր նշանակած երկու կետերը իրար միացնող ուղիղը կլինի միջօրեի գիծը։
Քանի որ Բևեռային աստղը աշխարհի բևեռում չի գտնվում, ուստի միջօրեի գիծն այդ ձևով որոշելու ժամանակ մենք կարող ենք սխալվել մի անկյունով, որը Լենինգրադի լայնության վրա հասնում է մոտ 2°-ի, իսկ ավելի հյուսիս ընկած վայրերում՝ դրանից էլ ավելի։
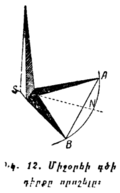
բ) Ցերեկը՝ ըստ Արեգակի։ Հարթ մակերևույթի վրա ամրացնենք մի ուղղահայաց (ուղղալարի միջոցով) ձող (նկ. 12)։ Կեսօրից 2 ժամ առաջ այդ հարթության վրա ձողի ստվերի ծայրը նշանակենք A-ով և ձողի S հիմքից, որպես կենտրոնից, մի շրջանագիծ գծենք՝ ստվերի AS երկարությանը հավասար շառավղով։ Ձողի ստվերը կսկսի աստիճանաբար կարճանալ և թեքվել դեպի հյուսիս։ Կեսօրից հետո նա կսկսի երկարանալ, շարունակելով թեքվել նույն ուղղությամբ։ Երեկոյան կողմը ստվերի ծայրը նորից կհասնի մեր շրջանագծին և կշոշափի մի կետում, նշանակենք B տառով։ A և B կետերը միացնենք ուղիղ գծով, որի N մեջտեղը միացնելով ձողի S հիմքի հետ, կստանանք միջօրեի գծի ուղղությունը։
Տեսականորեն միջօրեի գծի դիրքը կարելի է որոշել՝ պարզապես նշելով ստվերի ուղղությունը այն մոմենտին, երբ նա ամենակարճն է լինում։ Սակայն, գործնականում այդ եղանակը չափազանց անճշգրիտ է, որովհետև կեսօրի մոտ, երբ ստվերն ամենակարճն է, նրա երկարությունը չափազանց դանդաղ, գրեթե աննկատելի կերպով է փոփոխվում, մինչդեռ ստվերի ուղղությունն արագ է փոփոխվում։
§ 13. ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՒԼՄԻՆԱՑԻԱՆ։ Միջօրեականի դիրքը որոշելուց հետո հետևենք աստղային երկնքի կատարած պտույտին։ Մենք կհամոզվենք, որ աշխարհի առանցքի շուրջը ամեն մի լուսատու իր կատարած օրական պտույտի ժամանակ երկու անգամ հատում-անցնում է միջօրեականով։ Միջօրեականով լուսատուի անցնելու երևույթը կոչվում է կուլմինացիա։ Ընդ որում նա հորիզոնի նկատմամբ մեկ անգամ գրավում է ամենաբարձր դիրք, դա վերին կուլմինացիան է, իսկ մյուս անգամ՝ ամենացածր դիրք, գա էլ ստորին կուլմինացիան է։ Վերին և ստորին կուլմինացիաների միջև ընկած ժամանակամիջոցը կազմում է կեսօր։
Այդ կուլմինացիաներից մեկը (ծագող և մայր մանող լուսատուների համար) կամ երկուսն էլ (չծագող լուսատուների համար) կարող են տեղի ունենալ հորիզոնից ցած և անտեսանելի մնալ։
Արեգակի վերին կուլմինացիայի մոմենտը կոչվում է իրական կեսօր։ Արեգակի ստորին կուլմինացիայի մոմենտը կոչվում է իրական կեսգիշեր։
Առաջին կուլմինացիայի ժամանակ Արեգակը երևում է, երկրորդի ժամանակ՝ չի երևում։ Սակայն շուրջբևեռային երկրներում երբեմն Արեգակի երկու կուլմինացիաներն էլ տեղի են ունենում հորիզոնից վերև (այսինքն՝ գիշեր չի լինում)։ Իսկ երբեմն էլ նրանք տեղի են ունենում հորիզոնից ցած (այսինքն՝ Արեգակը չի ծագում)։ Մյուս լուսատուների կուլմինացիաների մոմենտը կախված է երկնային սֆերայում ունեցած նրանց դիրքից և տարվա եղանակներից։
Ամեն գիշեր դիտելով մի որևէ աստղ, մենք կհամոզվենք, որ տվյալ վայրում յուրաքանչյուր աստղի կուլմինացիան տեղի է ունենում հորիզոնից միևնույն բարձրության վրա. թե հատկապես ի՞նչ բարձրության վրա՝ դա կախված է երկնային սֆերայում նրա գրաված դիրքից և դիտավայրի աշխարհագրական լայնությունից։
Արեգակի վերին կուլմինացիայի մոմենտին նրա բարձրությունը հորիզոնից տարբեր է լինում՝ ոչ միայն տարբեր վայրերի համար (օրինակ, Լենինդրադում և Սևաստոպոլում), այլև տարվա տարբեր եղանակներին (ձմեռը նա փոքր է, ամառը՝ մեծ)։ Լուսնի և մոլորակների համար այդ բարձրությունը փոփոխվում է ավելի բարդ ձևով։
§ 14. ԵՐԿՆԱՅԻՆ ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՈՐԴԻՆԱՏՆԵՐԸ։ Երկնային լուսատուներից յուրաքանչյուրի դիրքը երկնային սֆերայում որոշվում է երկու սֆերիկ կոորդինատներով, որոնք արտահայտվում են երկու թվով, ճիշտ այնպես, ինչպես երկրագնդի վրա յուրաքանչյուր տեղի դիրքը որոշվում է նրա աշխարհագրական կոորդինատներով։
Երկնային լուսատուների կոորդինատները տարբեր են լինում՝ նայած թե ո՛ր գծերի նկատմամբ ենք մենք այդ կոորդինատները չափում։ Երկրի վրա կոորդինատները չափում են երկրային հասարակածի և Գրինվիչի միջօրեականի նկատմամբ։
Երկնային սֆերայում կոորդինատները կարելի է չափել երկնային հասարակածի (ինչպես աշխարհագրական լայնությունը) և հակման սկզբնական շրջանի (ինչպես աշխարհագրական երկայնությունը որոշելիս վերցնում են սկզբնական միջօրեականը) նկատմամբ։ Դա կլինի կոորդինատների հասարակածային սիստեմը։
Իսկ եթե լուսատուների կոորդինատները չափելու լինենք հորիզոնի և երկնային միջօրեականի նկատմամբ, ապա կստանանք կոորդինատների հորիզոնական սիստեմը։
Լուսատուի բարձրությունը (հորիզոնի նկատմամբ), որի մասին մենք խոսել ենք § 7-ում, հանդիսանում է հորիզոնական սիստեմի կոորդինատներից մեկը։
Երկնային հասարակածի դիրքը երկնային սֆերայում կախում չունի ո՛չ Երկրի վրա դիտողի ունեցած դիրքից, ո՛չ օրվա ժամից և ո՛չ էլ տարվա եղանակից։ Ուստի աստղերի հասարակածային կոորդինատները չեն փոփոխվում։ Իսկ լուսատուների հորիզոնական կոորդինատները ժամանակի ընթացքում անընդհատ փոփոխվում են և, բացի դրանից, կախված են Երկրի վրա դիտողի ունեցած դիրքից, որովհետև Երկրի տվյալ կետում հորիզոնի հարթությունը Երկրի հետ միասին պտտվում է տիեզերական տարածության նկատմամբ։ Ժամանակի և երկրագնդի վրա դիտողի դիրքի (կողմնորոշում) որոշելը պահանջում են լուսատուների հորիզոնական կոորդինատների չափում՝ դիտումների միջոցով։ Իսկ երկնքի քարտեզը կազմելու և երկնային լուսատուները կատալոգների մեջ մտցնելու համար հարկավոր է օգտվել կոորդինատների հասարակածային սիստեմից։
Միևնույն լուսատուի հասարակածային և հորիզոնական կոորդինատները կապված են մեկը մյուսի հետ և կոորդինատների մեկ սիստեմից կարելի է անցնել մյուսին վերահաշվարկման միջոցով (բայց երկրագնդի վրա դիտողի որոշ մոմենտում ունեցած որոշ դիրքի համար այն)։ Գործնականում լուսատուների կոորդինատները չափվում են հատուկ անկյունաչափական գործ ի քների օգնությամբ։
§ 15. ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՀՈՐԻԶՈՆԱԿԱՆ ՍԻՍՏԵՄ։ Նկ. 13-ում պատկերված է երկնային սֆերայի այն կեսը, որ երևում է հորիզոնից վերև։ NQS շրջանագիծը հորիզոնն է, Z — զենիթն է, S — հարավի կետն է։ Երկնային սֆերայում եղած M կետի դիրքը որոշելու համար զենիթից այդ կետի վրայով անցկացնենք մեծ ուղղաձիգ շրջանի ZQ աղեղը։ M կետի հորիզոնական կոորդինատները կլինեն՝ QM աղեղով չափվող բարձրությունը (h), որն արտահայտում է M կետի անկյունային հեռավորությունը հորիզոնից, և SQ աղեղով չափվող ազիմուտը (A), որը հարավի S կետից հաշվվում է դեպի արևմուտք և արտահայտում է երկնային միջօրեականով և M կետով անցնող ուղղաձիգ շրջանագծով կազմած անկյունը։
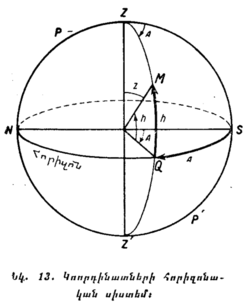
Հաճախ h բարձրության փոխարեն գործ են ածում զենիթային հեռավորությունը՝ z, որը հավասար է 90°—h և իրենից ներկայացնում է M կետի անկյունային հեռավորությունը զենիթից։ Բարձրությունը, զենիթային հեռավորությունը և ազիմուտը արտահայտում են աստիճաններով։
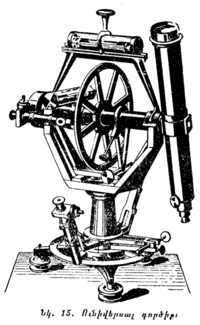
§ 16. ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՀԱՍԱՐԱԿԱԾԱՅԻՆ ՍԻՍՏԵՄ։ Նկ. 14-ում պատկերված է երկնային սֆերան իր հասարակածով։ Երկնային սֆերայի այն մեծ շրջանը, որի հարթությունն ուղղահայաց է երկնային հասարակածի հարթությանը և անցնում է նրա այն կետով, որ կոչվում է գարնանային գիշերահավասարի կետ և նշվում է ♈ հատուկ նշանով, հանդիսանում է հակման սկզբնական շրջան։ M կետի դիրքը որոշելու համար աշխարհի P բևեռից նրա վրայով անցկացնենք հակման PQq շրջանր։ M կետի հասարակածային կոորդինատները կլինեն՝ qM աղեղով չափվող հակումը (δ), որն արտահայտում է M կետի անկյունային հեռավորությունը երկնային հասարակածից և ♈q աղեղով չափվող ուղղակի ծագումը (α), որը հաշվվում է ♈ կետից ժամացույցի սլաքի շարժմանը հակառակ ուղղությամբ (եթե նայելու լինենք աշխարհի հյուսիսային բևեռից) և արտահայտում է հակման սկզբնական շրջանով և M կետով անցնող հակման շրջանով կազմած անկյանը։
Հակումը (δ) արտահայտվում է աստիճաններով և հասարակածից դեպի հյուսիս համարվում է դրական (+), իսկ դեպի հարավի բացասական (-). ուղղակի ծագումը (α) չափվում է ոչ թե աստիճաններով, այլ ժամանակով, այնպես, ինչպես աշխարհագրական երկայնությունը։
Այսպիսով, լուսատուների հակումը նման է աշխարհագրական լայնությանը, իսկ ուղղակի ծագումը՝ աշխարհագրական երկայնությանը։ Աստղային քարտեզների վրա (տե՛ս, օրինակ, կցված դասագրքին ) գծվում է այդ կոորդինատների ցանցը, իսկ ինքը՝ երկնային սֆերան պատկերվում է հարթության վրա այնպես, ինչպես պատկերվում է երկրագունդը։
§ 17*. ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՈՐԴԻՆԱՏՆԵՐԸ ՈՐՈՇԵԼՈՒ ԳՈՐԾՆԱԿԱՆ ԵՂԱՆԱԿՆԵՐԸ։ Եթե իմանայինք լուսատուների հասարակածային կոորդինատները, որոնք կախում չունեն ո՛չ դիտողի՝ Երկրի վրա ունեցած դիրքից , և ոչ էլ օրվա ժամից, ապա այդ կոորդինատները կարելի կլիներ գրանցել կատալոգների մեջ և այդ լուսատուների դիրքերը պատկերել աստղային քարտեզի վրա։ Բայց ինչպե՞ս գործնականորեն որոշել այդ կոորդինատները, ինչպե՞ս չափել նրանց՝ դիտումների միջոցով։
Երկնային մարմինների հորիզոնական կոորդինատները շափում են ունիվերսալ գործիքի օգնությամբ, որը կոչվում է նաև թեոդոլիտ (նկ. 15)։ Թեոդոլիտ է կոչվում փոքրիկ դիտակը, որին հարմարեցված են բաժանմունքների բաժանված շրջաններ՝ լուսատուների բարձրությունը և ազիմուտները հաշվելու համար։ Հաշվումները դյուրացնելու նպատակով ցուցիչները դիտակը հորիզոնական դիրքում եղած ժամանակ ուղղաձիգ շրջանի վրա ցույց են տալիս 0° (որը ստուգվում է հարթաչափի օգնությամբ), և հորիզոնական շրջանի վրա 0°, դիտակը միջօրեականի հարթությամբ դեպի հարավ ուղղված լինելու դեպքում, այսինքն այն հարթությամբ, որ անցնում է զենիթով, աշխարհի բևեռով և հարավի կետով։
Լուսատուների հորիզոնական կոորդինատները չափում են միայն Երկրի վրա զանազան կետերի ժամանակը կամ աշխարհագրական կոորդինատները որոշելու համար, որը պահանջում է գործիքը տեղից տեղ փոխադրել։ Այդ պատճառով թեոդոլիտները դյուրակիր ձևով են կառուցվում։
Հասարակածային կոորդինատների որոշելը բարդ է և կատարվում է ուրիշ գործիքով՝ միջօրեականային շրջանով։
§ 18*. ՄԹՆՈԼՈՐՏԱՅԻՆ ՌԵՖՐԱԿՑԻԱՆ ԼՈՒՅՍԻ ԲԵԿՈՒՄՆ է ԵՐԿՐԻ ՄԹՆՈԼՈՐՏՈՒՄ, ՈՐՆ ԱՂԱՎԱՂՈՒՄ է ԼՈՒՍԱՏՈՒՆԵՐԻ ՏԵՍԱՆԵԼԻ ԴԻՐՔԸ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՎՐԱ։ Երկնային լուսատուների լույսը անօդ տարածությունից մտնելով Երկրի մթնոլորտը, նրա մեջ բեկվում է։ Լույսի ճառագայթը որքան ավելի է մոտենում Երկրի մակերևույթին, այնքան նա օդի ավելի ու ավելի խիտ շերտերի է հանդիպում և հետզհետե ավելի ուժեղ բեկվելով այդ շերտերում՝ մոտենում է ուղղաձիգ ուղղության։ Հետևանքը լինում է այն, որ լույսի ճառագայթը Երկրի մթնոլորտում կորանում Է, ինչպես այդ ցույց է տրված նկ. 16-ում։ M կետում գտնվող դիտողը լուսատուն տեսնում է ոչ թե MA ուղղությամբ, այլ մի ուղղությամբ, որը բնորոշվում Է AM կորագծի շոշափողով, որի ուղղությամբ, ռեֆրակցիայի հետևանքով գալիս են ճառագայթները։ Եվ իսկապես, այն ուղղությունը, որով գիտողը տեսնում է լուսատուն, դա լուսատուից դեպի դիտողի աչքը եկող ճառագայթների ուղղությունն է, իսկ M կետում կորացված ճառագայթի ուղղությունը այդ կորագծի M կետում շոշափողի ուղղությունն է (մեր նկարում ճառագայթի ուղու կորացումը ցույց է տրված միայն մեկ ճառագայթի համար և այն էլ ակնառության համար չափազանցրած)։
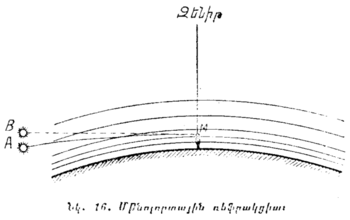
Այսպիսով, ռեֆրակցիայի հետևանքով լուսատուներն ավելի մոտ են երևում զենիթին, քան նրանք իրականում կան։ Հորիզոնի մոտ ռեֆրակցիան բարձրացնում է լուսատուն 35՛-ով և ավելի քիչ՝ երբ նա բարձր է գտնվում։
Դիտումների ժամանակ լուսատուների չափված զենիթային հեռավորությունները հարկավոր է ուղղել ռեֆրակցիայի ազդեցության չափով։
Ռեֆրակցիայի հետևանքով երկնային լուսատուները, նույն թվում և Արեգակը, ավելի շուտ են ծագում և ավելի ուշ են մայր մտնում, քան այդ ստացվում է երկրաչափական նկատառումներից։ Լուսնի և Արեգակի սկավառակների վերին և ստորին եզրերի համար ռեֆրակցիայի մեծության զգալի տարբերության հետևանքով, երբ նրանք մոտ են հորիզոնին, սկավառակները թվում են տափակացած։
§ 19. ՄԹՆՇԱՂ ԵՎ ԱՍՏՂԵՐԻ ՇՈՂՇՈՂՈՒՄ։ Ինչպես առավոտյան, նույնպես և երեկոյան՝ մթնշաղը հետևանք է այն բանի, որ երբ Արեգակը մեզնից ծածկված է հորիզոնի տակ (ոչ այնքան խոր), այնուամենայնիվ նա լուսավորում է մեր գլխավերևի օդը, իսկ օդը, ինչպես մենք արդեն գիտենք, Արեգակի լույսը ցրում է։ Հենց Արեգակի լույսն է, որ ցրվելով օդում, առաջացնում է մթնշաղի երևույթ։
Հյուսիսային վայրերում, ինչպես՝ Կարելիայում, Արխանգելսկի և Կիրովի մարզերում և նույնիսկ Լենինգրադում ամռան գիշերները Արեգակն այնքան էլ շատ չի սուզվում հորիզոնի տակ, ուստի և արշալույսն ավելի շուտ է վրա հասնում, քան վերջանում է երեկոյան աղջամուղջը։ Այդպիսի գիշերներին այնտեղ կատարյալ մթություն բոլորովին չի լինում, այդ պատճառով էլ նրանց «սպիտակ գիշերներ» են անվանում։ Այս դեպքում ասում են, որ «արշալույսը դիմավորում է վեր ջալույսին»։
Գիշերները գրեթե միշտ կարելի է նկատել աստղերի շողշողում, ամենից ուժեղ՝ հորիզոնի մոտ։ Շողշողումը կայանում է նրանում, որ աստղերը կարծես դողդողում են, մերթ փայլում են պայծառ, մերթ սկսում են խավարել, իսկ հորիզոնի մոտ գտնվող պայծառ աստղերը նույնիսկ փայլփլում են ծիածանի բոլոր գույներով։
Այդ երևույթի պատճառն այն է, որ աստղի լույսը հասնում է մեզ օդի միջով։ Նրա ճանապարհին հանդիպող օդի զանազան հոսանքների անընդհատ փոփոխումը փոփոխում է ճառագայթների բեկման չափը։ Բացի այդ, աստղից եկող լույսն օդում բեկվելու դեպքում, ինչպես Արեգակի ճառագայթը ապակյա պրիզմայում, տարրալուծվում է իր բաղադրիչ մասերին՝ ծիածանի գույների։
ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ
- Ի՞նչ են աշխարհագրական լայնությունը և երկայնությունը և ինչպե՞ս են արտահայտում ժամանակով։
- Ի՞նչ են աշխարհի բևեռները և աշխարհի առանցքը։
- Ինչպե՞ս գտնել երկնքում Բևեռային աստղը։
- Ի՞նչ է երկնային հասարակածը և ինչպե՞ս է նա բաժանում երկնային սֆերան։
- *Ինչո՞ւմն է կայանում հորիզոնական և հասարակածային կոորդինատների միջև եղած տարբերությունը։
- Ի՞նչ է երկնային միջօրեականը և միջօրեի գիծը։
- *Գծեցեք երկնային սֆերան որևէ աստղի հորիզոնական կոորդինատներով։
- Գծեցեք երկնային սֆերան որևէ աստղի հասարակածային կոորդինատներով։
- Ինչպիսի՞ ցանց է գծվում աստղային քարտեզների վրա։
- *Ինչի՞ համար է ծառայում ունիվերսալ գործիքը կամ թեոդոլիտը։ Ի՞նչ առանցքների շուրջն է դառնում նրա դիտախողովակը։
- *Ինչո՞ւմն է կայանում մթնոլորտային ռեֆրակցիան։ Ինչպե՞ս է նա ազգում լուսատուի բարձրության վրա, ծագման ու մայրամուտի վրա։
- *Ի՞նչն է առաջ բերում աղջամուղջի երևույթ։
- *Ինչո՞ւ են առկայծում աստղերը։
- Ինչպե՞ս որոշել տեսականորեն և ինչպե՞ս գտնել գործնականում (դաշտում) հորիզոնի չորս հիմնական կետերը։
- Գծեցե՛ք երկնային սֆերան՝ հասարակածով, միջօրեականով և միջօրեի գծով։ Նշեցե՛ք նրա վրա հորիզոնի հիմնական կետերը։
- *Ինչպե՞ս ցերեկը և գիշերը գործնականում կարելի է որոշել միջօրեի գծի ուղղությունը։
- Ի՞նչն է կոչվում կուլմինացիա։ Կուլմինացիաներից ո՞րն է կոչվում վերին և ո՞րը ստորին։
- Ինչքա՞ն ժամանակից հետո են կուլմինացիաները հաջորդում իրար և ինչպե՞ս են կոչվում Արեգակի կուլմինացիայի մոմենտները։
ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ
- Արտահայտել 131°15՛54՛՛ երկայնությունը ժամանակի միավորներով։
- Վերածել 7 ժ. 30 ր. 18 վ. երկայնությունը աստիճանային միավորների։
- Գծագրեցեք երկնային սֆերայի վրա, միաժամանակ միևնույն աստղի հորիզոնական և հասարակածային կոորդինատները։
- Երկնքի շարժական քարտեզի վրա (տրված է գրքի հավելվածում) կոորդինատական ցանցի օգնությամբ հաշվեցեք մի քանի աստղերի մոտավոր հասարակածային կոորդինատները։
- Օգտվելով պայծառ աստղերի հասարակածային կոորդինատների ցուցակից (տե՛ս IV հավելվածը) ըստ այդ կոորդինատների, վերոհիշյալ քարտեզի վրա գտեք որոշ աստղեր։
§ 20. ԵՐԿՐԻ ԵՎ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՄԻՋԵՎ ԵՂԱԾ ՀԱՐԱԲԵՐԱԿՑՈՒԹՅՈԻՆԸ։ Երկրի պտտման առանցքը տարածության մեջ ուղղված է դեպի Բևեռային աստղը։ Երկրի որևէ C կետում (նկ. 17) գտնվող և Երկրի պտտվելը չզգացող դիտողին թվում է, թե ամբողջ տիեզերական
տարածությունը երկնային սֆերայի ձևով պտտվում է մի այնպիսի առանցքի շուրջը, որը զուգահեռ, է Երկրի պտտման առանցքին։ Երկնային սֆերայի պտտման CP առանցքը մենք անվանեցինք աշխարհի առանցք և այժմ տեսնում ենք, որ նա ամեն մի դիտողի համար զուգահեռ է Երկրի պտտման առանցքին։
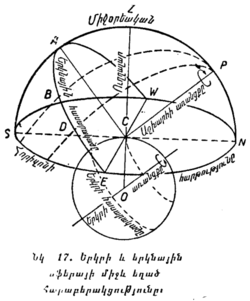
Քանի որ Բևեռային աստղը մեզնից չափազանց հեռու է գտնվում, ուստի CP գիծը և Երկրի պտտման առանցքը, որը զուգահեռ է նրան, ուղղված են դեպի Բևեռային աստղը։ Այն դիտողի համար, որ կարողանար տեղավորվել Երկրի կենտրոնում կամ նրա բևեռներում, Երկրի պտտման առանցքը և աշխարհի առանցքը միմյանց կհամընկնեին։
Ուստի երկնային հասարակածի CEAW հարթությունը, որպես աշխարհի առանցքին ուղղահայաց մի հարթություն, զուգահեռ է Երկրի հասարակածի հարթությանը։ Երկրի կենտրոնում գտնվող դիտողի համար այդ երկու հարթությունները միմյանց կհամընկնեին։
Եթե ընդունենք, որ Երկիրը գնդաձև է, ապա CZ ուղղաձիգ գիծը հանդիսանում է Երկրի OC շառավղի շարունակությունը, որը Երկրի կենտրոնից անց է կացված դեպի այն կետը, որտեղ գտնվում է դիտողը։ Ուստի հորիզոնի հարթությունը,— որն անցնում է երկնային սֆերայի կենտրոնով (C կետով, եթե այդ կետումն է գտնվում դիտողը) և ուղղահայաց է ուղղաձիգ գծին,— մի հարթություն է, որը շոշափում է երկրագունդը C կետում։ Վերջապես, երկնային միջօրեականի SAZPN հարթությունը համընկնում է աշխարհագրական միջօրեականի հարթության հետ։
Այսպիսով, Երկիրը պտտվելու ժամանակ պտտվում է նաև դիտողը, իսկ նրա հետ միասին միջօրեականի ու հորիզոնի հարթությունները և ուղղաձիգ գիծը։ Ուստի օրվա տարբեր ժամերին պտտվող հորիզոնը, որը դիտողի համար տեսանելի տարածությունը սահմանափակում է ոչ-տեսանելի (Երկրի մարմնով ծածկված) տարածությունից, անցնում է երկնային սֆերայի տարբեր մասերով։ Տարբեր լուսատուներին է ուղղվում նաև Z զենիթը։ Մինչդեռ երկնային հասարակածը սահում է իր սեփական հարթության մեջ, իսկ աշխարհի առանցքը մնում է զուգահեռ ինքն իրեն։ Այդ պատճառով էլ նրանք աստղերի միջև շարունակ միևնույն դիրքն են գրավում։
§ 21. ԲԵՎԵՌԻ ԲԱՐՁՐՈՒԹՅՈՒՆԸ ՀՈՐԻԶՈՆԻՑ ԵՎ ՏԵՂԻ ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԼԱՅՆՈՒԹՈՒՆԸ։ Աշխարհի բևեռի անկյունային բարձրությունը հորիզոնից կամ, ավելի կարճ ասած, բևեռի բարձրությունը հավասար է դիտման վայրի աշխարհագրական լայնությանը։ Դրանում կարելի է համոզվել, եթե նկ. 17-ի վրա հետևենք, թե ի՛նչպես կփոփոխվի PCN անկյունը (իսկ դրա հետ միասին՝ նաև PN աղեղը, այսինքն՝ բևեռի բարձրությունը), եթե C կետի դիտողը Երկրի հասարակածից սկսի շարժվել դեպի Երկրի բևեռը։ Այդպիսի շարժման դեպքում աշխարհի CP առանցքը կմնա ինքն իրեն զուգահեռ, իսկ հորիզոնի հարթության վրա ընկած CN գիծը PC գծի հետ ավելի ու ավելի մեծ անկյուն կկազմի։
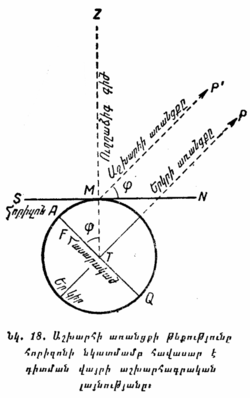
Դա ավելի պարզ կարելի է յուրացնել նկ. 18-ի օգնությամբ, որտեղ երկրագունդը պատկերված է տեղի միջօրեականի հարթության հատվածով։ M կետում գտնվող դիտողը աշխարհի P բևեռը կտեսնի աշխարհի առանցքի MP՛ ուղղությամբ, որը զուգահեռ է Երկրի TP առանցքին։ Երկրագունդը շոշափող հորիզոնի հարթությունը մեր գծագրի վրա կպատկերվի SMN ուղիղ գծով, որը M կետում շոշափում է երկրագունդը պատկերող շրջանը։ AQ Երկրի հասարակածն է, TZ ուղղաձիգ գիծն է կետում, ուստի և AMT անկյունը, ըստ § 9-ի, հանդիսանում է կետի աշխարհագրական φ լայնությունը։
Աշխարհի առանցքի և հորիզոնի հարթության միջև ընկած P՛MN անկյունը բևեռի բարձրությունն է ներկայացնում։
P՛MN և ATM (այսինքն՝ աշխարհագրական լայնությունը) անկյունները հավասար են, որպես փոխադարձ ուղղահայաց կողմեր ունեցող անկյուններ։ Եվ իսկապես, MN որպես հորիզոնական գիծ, ուղղահայաց է MT ուղղաձիգ գծին, իսկ MP՛, որպես աշխարհի առանցք, ուղղահայաց է AQ հասարակածին։
Մենք տեսնում ենք, որ տեղի աշխարհագրական լայնությունդ գործնականորեն կարելի է որոշել, շափելով բևեռի բարձրությունը դիտումների միջոցով։
§ 22. ԱՍՏՂԱՅԻՆ ԵՐԿՆՔԻ ՏԵՍՔԸ՝ ԿԱԽՎԱԾ ԴԻՏՈՂԻ ԴԻՐՔԻՑ ԵՐԿՐԱԳՆԴԻ ՎՐԱ։ Ինչպես հենց նոր տեսանք, աշխարհի առանցքի թեքությունը հորիզոնի նկատմամբ (բևեռի բարձրությունը) հավասար տեղի աշխարհագրական լայնությանը։ Այդ հանգամանքը պետք է նկատի ունենալ տվյալ վայրի համար նկ. 11-ը արտագծելու ժամանակ։
Այսպիսով, երկնային սֆերայի կետերի և գծերի դասավորությունը հորիզոնի նկատմամբ կախված կլինի տեղի լայնությունից։
Վերոհիշյալի հիման վրա, հեշտ է սահմանել հետևյալը։
Միջին լայնություններում, օրինակ, ՍՍՌՄ-ում, աշխարհի առանցքը և երկնային հասարակածը թեքված են դեպի հորիզոնը, ուստի և աստղերի օրական ուղիները նույնպես թեքված են հորիզոնի նկատմամբ (նկ. 19 ա)։ Այն աստղերը, որոնք աշխարհի բևեռից հեռու են գտնվում ոչ ավելի, քան φ աստիճանով (այստեղ φ աշխարհագրական լայնությունն է), մայր չմտնող աստղեր են։ Իսկ այն աստղերը, որոնք բևեռից հեռու են գտնվում ավելի քան φ աստիճանով, ծագող և մայր մտնող աստղեր են։ Հարավային կիսագնդի աստղերի մի մասը, որոնք երկնային սֆերայում ընկած են ավելի հարավ (ցած), քան այն փոքր զուգահեռականը, որը զուգահեռ է հասարակածին և անցնում է S կետով (տե՛ս նկ. 19 ա), երբեք չեն ծագում՝ նրանք անտեսանելի են։
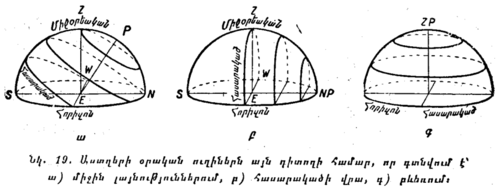
Երկրի հասարակածում աշխարհի առանցքը պառկած է հորիզոնի հարթության վրա և համընկնում է միջօրեի գծին, իսկ աշխարհի բևեռները՝ հյուսիսի և հարավի կետերին (նկ. 19 բ)։ Հասարակածը դառնում է հորիզոնին, ուղղահայաց և անցնում է Z, զենիթով։ Բոլոր աստղերի օրական ուղիներն ուղղահայաց են հորիզոնին և նրանցից յուրաքանչյուրը օրվա կեսի ընթացքում լինում է հորիզոնից վեր և մյուս կեսի ընթացքում՝ հորիզոնից ցած։ Լրիվ օրվա ընթացքում, եթե ցերեկն Արեգակը չխանգարեր, կարելի կլիներ տեսնել երկնքի երկու կիսագնդերի բոլոր աստղերը։ Այնտեղ չծագող աստղեր չկան, ինչպես չկան նաև մայր չմտնող աստղեր։ Մասնավորապես, մեզ ծանոթ Մեծ Արջը այնտեղ մայր մտնող համաստեղությունների թվին է պատկանում։
Երկրի բևեռում երկնային հասարակածը համընկնում է հորիզոնին, իսկ աշխարհի առանցքը համընկնում է ուղղաձիգ գծին (նկ. 19 գ)։ Այնտեղ Բևեռային աստղը փայլում է զենիթի մոտ։ Արևելքի և արևմուտքի կետերը, ինչպես հասարակածի և հորիզոնի հատման կետեր, դառնում են անորոշ։ Միջօրեականը, որ անցնում է աշխարհի բևեռներով ու զենիթով, նույնպես անորոշ է դառնում, իսկ դրա հետ միասին կորցնում են իրենց իմաստը նաև հարավ, հյուսիս, արևելք և արևմուտք հասկացողությունները։ Երկրի հյուսիսային բևեռից բոլոր ուղղությունները տանում են դեպի հարավ։ Այնտեղ աստղերի օրական ուղիները զուգահեռ են հորիզոնին. ոչ մի աստղ չի ծագում և ոչ մի աստղ մայր չի մտնում։ Որպես մայր չմտնող երևում են երկնքի հյուսիսային կիսագնդի բոլոր աստղերը, բայց հարավային կիսագնդի աստղերից և ոչ մեկը երբեք չի երևում։
ՀԱՐՑԵՐ ԻՆՔՆԱՏՈՒԳՄԱՆ ՀԱՄԱՐ
- Ինչպե՞ս է աշխարհի առանցքը դասավորված Երկրի առանցքի նկատմամբ։ Ինչպիսի՞ պայմաններում են նրանք համընկնում։
- Ինչպե՞ս է երկնային հասարակածը դասավորված Երկրի հասարակածի նկատմամբ։ Որտե՞ղ են նրանք համընկնում։
- Ինչո՞ւ բոլոր տեղերից էլ Բևեռային աստղը երևում է աշխարհի բևեռի մոտ։
- Երկրագնդի նկատմամբ ինչպիսի՞ հարթություն է հանդիսանում ցանկացած հորիզոնի հարթությունը։
- Ինչո՞ւ որոշ աստղեր ծագում և մայր են մտնում։
- Ինչպե՞ս է Բևեռի բարձրությունը հորիզոնից կապված տեղանքի աշխարհագրական լայնության հետ։ Ապացուցեցե՛ք այդ։
- Ինչպե՞ս է տեղի ունենում աստղերի օրական պտույտը հորիզոնի նկատմամբ միջին լայնություններում։ Բացատրեցե՛ք այդ գծագրով։
- Ինչպե՞ս է տեղի ունենում լուսատուների օրական պտույտը հասարակածում գտնվող դիտողի համար։ Բացատրեցե՛ք այդ գծագրով։
- Ինչպե՞ս են շարժվում լուսատուներն օրվա ընթացքում այն դիտողի համար, որ գտնվում է Երկրի բևեռում։ Բացատրեցե՛ք այդ գծագրով։
ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ
- Քանի՞ աստիճան է զենիթից մինչև արևելքի և հարավի կետերը եղած հեռավորությունը։
- Մի աստղի ուղղակի ծագումը 3 ժամ է, մյուսինը՝ 5 ժամ 18 րոպե։ Նրանցից ո՞րը ավելի շուտ կուլմինացիա կկատարի և ինչքա՞ն ժամանակով։
- Տեղանքի լայնությունը 35° է։ Այդ վայրի համար բևեռը քանի՞ աստիճան է հեռու զենիթից։
- Տեղանքի լայնությունը 57° է։ Այն տեղ զենիթից ինչպիսի հեռավորության վրա է միջօրեականը հատվում հասարակածի հետ։
- Իսկ ինչպիսի՞ն է այնտեղ հասարակածի ամենաբարձր կետի բարձրությունը հորիզոնի նկատմամբ։
- Մուրմանսկի լայնությունը 68°58՛ է։ Կարելի՞ է արդյոք այնտեղ հորիզոնից վեր տեսնել Սիրիուս աստղը (երկնքի ամենապայծառ աստղը), եթե նրա հակումը՝ δ = +16°։
- Լենինգրադի լայնությունը 59°56՛ է։ Հնարավո՞ր է արդյոք այնտեղ տեսնեք Վեգա աստղի երկու կուլմինացիան էլ, եթե նրա հակումը՝ δ = +39°։
ԵՐԿԻՐ
§ 23. ԵՐԿՐԻ ԳՆԴԱՁԵՎՈՒԹՅՈՒնԸ։ Հաճախ Երկրի գնդաձև լինելն ապացուցելու համար վկայակոչում են այնպիսի երևույթներ, որոնք իրականում միայն նրա մակերևույթի ուռուցիկությունը կամ կորությունն են ապացուցում։ Երկրի մակերևույթի կորությունը ապացուցող այդպիսի երևույթներն են՝
1) Նավը ծովափին մոտենալիս հորիզոնի տակից առաջ նրա կայմերի գագաթներն են երևում, իսկ այնուհետև հետզհետե նաև ամբողջ իրանը (նկ. 20 և 21)։
2) Դեպի վեր բարձրանալու դեպքում տեսադաշտը լայնանում է և հորիզոնի վրա երևացող առարկաների հեռավորությունը մեծանում։
3) Արեգակի մայր մտնելոց հետո նրա ճառագայթները շարունակում են լուսավորել բարձր շենքերի տանիքները, լեռների գագաթներն ու ամպերը, ավելի ուշ՝ միայն բարձր լեռների գագաթներն ու ամպերը, էլ ավելի ուշ՝ միայն ամպերը։
Շուրջերկրյա ճանապարհորդությունները միայն ապացուցում են, որ Երկրի ձևն ինքնապարփակ է, որ նա տարածության մեջ մեկուսացած է, որ նա որևէ տեղ երկնքի հետ միաձուլվող եզրեր չունի։
Երկրի գնդաձև լինելը ապացուցող փաստ կարելի է համարել հետևյալ երկու երևույթը.
1) Երկրի ամեն մի վայրում հորիզոնը շրջագծի ձևով է երևում և հորիզոնի հեռավորությունն ամենուրեք համահավասար է։
2) Լուսնի խավարումների ժամանակ Երկրի ստվերը, որ ընկնում է լուսնի վրա, միշտ կլորաձև ուրվանկար ունի։ Բոլոր մարմիններիդ միայն գունդն է, որ իր բոլոր դիրքերում կլոր ստվեր է գցում։

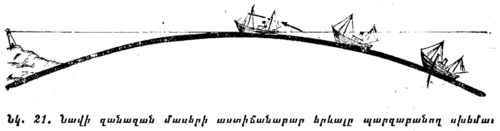
§ 24. ԵՐԿՐԻ ՉԱՓԵՐԸ ՈՐՈՇԵԼԸ։ Երկրի չափերի որոշումը կայանում է նրանում, որ մենք չափում ենք միջօրեականի աղեղը գծային միավորներով և աստիճաններով։ Երկրագնդի միևնույն միջօրեականի վրա գտնվող երկու կետերի միջև որոշում են գծային հեռավորությունը, որը, ասենք, հավասար է n կիլոմետրի։ Աստղագիտական եղանակով որոշում են նաև այդ կետերի աշխարհագրական լայնությունների տարբերությունը (օրինակ, այդ կետերում Բևեռային աստղի բարձրության տարբերության միջոցով), որը, ենթադրենք, հավասար է m աստիճանի։ Այդ դեպքում Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle \frac{m}{360°}} քանորդը ցույց կտա, թե շրջանագծի ո՛ր մասն է իրենից ներկայացնում նրա այն աղեղը, որ գտնվում է մեր վերցրած երկու կետերի միջև։ Դրա հիման վրա գտնում են ամբողջ շրջանագծի երկարությունը կիլոմետրերով հետևյալ պարզ հարաբերության միջոցով.
Չհաջողվեց վերլուծել (շարահյուսության սխալ): {\displaystyle S = n\left(\frac{360°}{m}\right)}
Նկարագրած եղանակը կոչվում է աստիճանային չափում։ Իմանալով Երկրի շրջանագծի երկարությունը, և այն բաժանելով 2π-ի, կստանանք Երկրի շառավղի երկարությունը։ Այսպիսով որոշվել է, որ Երկրի շառավիղը, եթե այն գնդաձև համարենք, հավասար է 6371 կմ, իսկ շրջանագիծը՝ գրեթե ուղիղ 40 000 կմ է։
§ 25. ԵՐԿՐԻ ՍԵՂՄՎԱԾՈՒԹՅՈՒՆԸ։ Երկրի տարբեր վայրերում կատարած չափումների միջոցով համոզվել են, որ Երկրի կորությունը հասարակածի մոտ ավելի մեծ է, քան բևեռներում (նկ. 22)։ Դա նշանակում է, որ Երկիրը գնդաձև չէ. նա բևեռների մոտ մի քիչ սեղմված է։ Երկրի բևեռային շառավիղը հասարակածային շառավղից կարճ է համարյա 21 կիլոմետրով, այսինքն՝ մոտավորապես հասարակածային շառավղի 1/300 չափով։ Երկրի ձևը ճշտվել է սովետական գիտնականների կողմից։
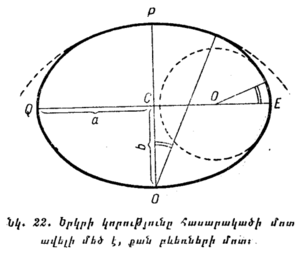
Երկրի սեղմվածությունը հետևանք է այն կենտրոնախույս ուժի ազդեցության, որ զարգացնում է Երկիրն իր առանցքի շուրջը պտտվելու ժամանակ։ Դա կարելի է ցուցադրել դպրոցական կենտրոնախույս մեքենայի առանցքի վրա պտտեցնելով պողպատյա բարակ օղակապը։ Երկնային մարմնի սեղմվելն իր պտտվելու հետևանքով ընդհանուր կանոն է։ Օրինակ, Յուպիտեր և Սատուրն մոլորակները, որոնք իրենց առանցքի շուրջն ավելի արագ են պտտվում քան Երկիրը, ավելի շատ են սեղմված (Յուպիտերի սեղմվածությունը շատ լավ նկատվում է հեռադիտակով)։ Սեղմվածության հետևանքով Երկիրը գնդաձև չէ, այլ պտտման էլիպսոիդ։
§ 26 ՏՐԻԱՆԳՈՒԼՅԱՏԻԱ (Եռանկյունաչափական ընդօրինակություն)։ Երկրի չափերը որոշելու ժամանակ հարկավոր է միջօրեականի աղեղի երկարությունը չափել աստիճաններով և գծային չափերով։ Առաջինը, ակներևորեն, որոշվում է որպես միջօրեականի այդ աղեղի սկզբի և վերջին ծայրերի աշխարհագրական լայնությունների տարբերություն։ Իսկ աշխարհագրական լայնությունը կարելի է որոշել չափելով աշխարհի բևեռի բարձրությունը։
Բայց միջօրեականի աղեղի գծային երկարությունը չափելու ժամանակ, մանավանդ եթե Երկրի չափերը ավելի մեծ ճշտությամբ որոշելու համար բավական երկար աղեղ վերցնելու լինենք, մենք մի շարք գործնական դժվարությունների կհանդիպենք. այդ աղեղի սկզբից մինչև նրա վերջավորությունը ճանապարհին կարող են ձորեր, լեռներ, ճահիճներ և այլ խոչընդոտներ հանդիպել։ Ուստի, միջօրեականի աղեղի երկարությունը և առհասարակ Երկրի մակերևույթի վրա մեծ տարածություններ չափելու համար (որոնք, մասնավորապես, հարկավոր են լինում աշխարհագրական քարտեզներ կազմելու համար) օգտվում են տրիանգուլյացիայի եղանակից։
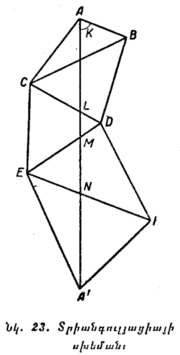
Տրիանգուլյացիան կայանում է հետևյալում։ Եթե հարկավոր է չափել միջօրեականի AA՛ աղեղը (նկ. 23), ընտրում են հարթ տարածության վրա ընկած AB գիծը և չափում նրա երկարությունը ամենայն հնարավոր ճշտությամբ։ Այդպիսի գիծը կոչվում է բազիս (հիմք)։ Բացի այդ, ընտրում են C կետը, որը երևում է և՛ A կետից, և՛ B կետից։ Այնուհետև անկյունաչափ գործիքի օգնությամբ չափում են A, B կետերի մոտ ընկած անկյունները և, բացի այդ, բազիսի և միջօրեականի AA՛ ուղղության միջև ընկած K անկյունը։ Ապա արդեն հաշվարկումների միջոցով գտնում են AC, BC կողմերի երկարությունը և C անկյան մեծությունը։ Դրանից հետո ընտրում են D կետը, որը երևում է և՛ C, և՛ B կետերից, և տեղավորվելով այդ կետերում, անկյունաչափ գործիքով չափում են BCD և CBD անկյունները։ Քանի որ CB գծի երկարությունն արդեն հաշված էր, ուստի այժմ նախորդի օրինակով կարելի է հաշվել CD և BD կողմերի երկարությունը, և բացի այդ, AB և AA՛ գծերով կազմված անկյունը։
Շարունակելով չափումները նկարագրած ձևով, մենք A-ից մինչև տարածությունը կծածկենք մի շարք եռանկյուններով, որտեղ բոլոր անկյունները չափված են, իսկ բոլոր կողմերը՝ որոշված հաշվարկումների միջոցով։ Այն ժամանակ AA՛ երկարությունը կարելի է գտնել որպես ACEA՛ (կամ ABDFA՛) բեկյալ գծի պրոյեկցիան այդ ուղղի վրա։ Այդ երկարությունը գտնում են հաշվարկումների միջոցով։
Ըստ որում, բնականաբար, հաշվի է առնվում նաև այն հանգամանքը, որ այդ չափումները կատարվել են ոչ թե հարթության վրա, այլ Երկրի կոր մակերևույթի վրա։
Այսպիսով, տրիանգուլյացիան կայանում է նրանում, որ մեծ հեռավորությունները որոշվում են եռանկյունների օգնությամբ, որտեղ չափվում են միայն անկյունները և բազիսը, իսկ կողմերը որոշվում են հաշվարկումներով։ Այդ եղանակի անվանումը ծագել է լատիներեն «տրիանգուլյում» — եռանկյուն բառից։

Տրիանգուլյացիայից օգտվում են ոչ միայն Երկրի չափերը որոշելու համար, այլև աշխարհագրական քարտեզներ կազմելիս, երբ պահանջվում է չափել մեծ հեռավորություններ։
1816—1855 թթ. ռուսական գիտնականների կողմից, ակադեմիկոս Վ. Յա. Ստրուվեի ղեկավարությամբ, կատարվել է միջօրեականի 25°20՛ հսկայական աղեղի չափումը։
Քարտեզագրական աշխատանքների համար մեծ մասշտաբի տրիանգուլյացիոն աշխատանքներ են կատարում և ներկայումս։
24-րդ նկարում ցույց է տրված փայտե աշտարակ, որը կոչվում է գեոդեզիական նշանակետ և կանգնեցվում է տրիանգուլյացիայի համար ընտրված եռանկյունների գագաթներում։
§ 27. ԵՐԿՐԻ ՕՐԱԿԱՆ ՊՏՈՒՅՏԻ ԱՊԱՑՈՒՅՑՆԵՐԸ, Երկրի գնդաձևության մասին գիտեին դեռևս հնում, սակայն, Երկրի օրական պտույտի գոյությունը առաջին անգամ ամենայն որոշակիությամբ հաստատեց միայն Կոպեռնիկոսը (XVI դ. կեսերին), իսկ դրա անհերքելի ապացույցները գտնվել են է՛լ ավելի ուշ։
Բերենք դրանցից երկու առավել ակնհայտ ապացույցներ.
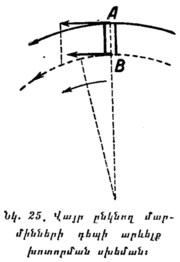
ա) Վայր ընկնող մարմինների խոտորումը դեպի արևելք։ Պատկերացնենք մի խոր ուղղաձիգ AB հանքահոր, որը պտտվում է Երկրի հետ միասին (նկ. 25)։ Նրա մուտքր (A) պտտման ժամանակ գծային ավելի մեծ արագություն ունի, քան հիմքը (B), որովհետև նա ավելի հեռու է գտնվում պտտման կենտրոնից, տվյալ դեպքում երկրի օրական պտույտի առանցքից։ Հանքահորի մուտքի մոտ ընկած քարն այս դեպքում նույն արագությունը կունենա, ինչ և այդ մուտքը։ Հանքահորի մեջ ընկնելու դեպքում նա, իներցիայի շնորհիվ, կպահպանի այդ արագությունը։ Ընկնելով ցած և միաժամանակ պահպանելով իր դեպի արևելք շարժման (որովհետև Երկիրը պտտվում է արևմուտքից դեպի արևելք) ավելի մեծ արագությունը, քան հանքահորի հիմքի շարժման արագությունն է, քարն իր դեպի արևելք շարժման մեջ ավելի առաջ կանցնի հանքահորի հիմքից։ Քարը կընկնի ոչ թե Ճիշտ Երկրի կենտրոնի ուղղությամբ, այլ կշեղվի դեպի արևելք, որը չէր պատահի, եթե Երկիրը պտտվելիս չլիներ։ Երկրի հասարակածի վրա այդ խոտորումը ամենից մեծ է, իսկ բևեռներում հավասար է զրոյի։
Այս ձևի բազմաթիվ փորձերը ցույց են տալիս, որ դիտումները միանգամայն համապատասխանում են կատարած հաշվարկումներին. օրինակ, միջին լայնություններում 85 մ բարձրությունից վայր ընկնող քարը շեղվում է դեպի արևելք 10,5 մմ։

բ) Ֆուկոյի ճոճանակը։ Առաջին անդամ 1851 թ. ֆրանսիացի գիտնական Ֆուկոյի դրած փորձում կիրառվել է մի ճոճանակ, որը իրենից ներկայացնում էր մի շատ երկար ու բարակ լար, որի ծայրից կախված էր ծանր գունդ։ Հայտնի է, և այդ կարելի է ստուգել կենտրոնախույս մեքենայի վրա կատարած փորձով, որ ամեն մի այդպիսի ճոճանակ իր տատանումների հարթությունը պահպանում է առանց փոփոխության, թեկուզ ինչպես էլ պտտելու լինենք այն հենարանը, որից նա կախված է։ (ճոճանակի լարը երկար է վերցվում այն նկատառումով, որպեսզի փորձն ավելի ակնառու լինի, և ճոճանակը բավական երկար ժամանակ տատանելու անհրաժեշտությունից։)
Եթե մի այդպիսի ճոճանակ ճոճվելիս լիներ Երկրի բևեռի վրա, ապա Երկիրը, պտտվելով նրա տակ, կդառնար մեկ ժամում 15° արագությամբ (360° : 24 ժամ)։ Դրա հետևանքով մենք կնկատեինք, որ ճոճանակի տատանման հարթությունը Երկրի մակերևույթի նկատմամբ դառնում է այդ նույն 15° մեկ ժամում արագությամբ և Երկրի պտույտին հակառակ ուղղությամբ։
Երկրի հասարակածի վրա ճոճանակի ճոճումների ուղղությունը ոչ մի փոփոխություն չէր կրի, իսկ միջակա լայնություններում ճոճանակի տատանումների հարթությունը, ինչպես տեսությունն է ցույց տալիս, պետք է դառնա մեկ ժամում 15° sinφ, որտեղ φ աշխարհագրական լայնությունն է։
Իրականում հենց այդպես էլ դիտվում է։ Պարզ է, որ եթե Երկիրը չպտտվեր, ճոճանակի ճոճումների ուղղությունն ամեն տեղ կմնար անփոփոխ։
Լենինգրադում, նախկին Իսաակիևսկի տաճարի շենքում, ցուցադրվում է մի ճոճանակ՝ 98 մ երկարությամբ։ Նրա ճոճումների ուղղությունը փոխվում է ժամում 13° արագությամբ՝ Ճիշտ այնպես, ինչպես պահանջվում է Երկրի պտույտի տեսությամբ։
ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ
- Ինչպիսի՞ երևույթներն են խոսում ոչ միայն Երկրի կորության, այլև նրա գնդաձևության մասին։
- Ինչպիսի՞ն է այն եղանակը, որով որոշում են Երկրի չափերը։
- Ինչի՞ են հավասար Երկրի շառավիղն ու շրջագիծը։
- Ի՞նչ բան է Երկրի սեղմվածությունը։ Սեղմվածության մեծությունը։
- *Ի՞նչ է տրիանգոլլյացիան։ Ինչի՞ համար և ինչպե՞ս են այն կիրառում։
- Ինչպիսի՞ փորձեր են ապացուցում Երկրի օրական պտույտը։ Ինչո՞ւմն կայանում այդ փորձերի էությունը։
ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ
- XIX դ. առաջին կեսում ռուս գիտնականների կողմից որոշվել է, որ Ֆուգլենեսսի (φ = 70°50՛) և Ստարո-Նեկրասովսկայի (φ = 45°20՛) միջև եղած հեռավորությունը միջօրեականով հավասար է 2822 կմ։ Այստեղից որոշեցեք Երկրի միջօրեականի քառորդը և շառավիղը։
- Եթե Երկիրը պատկերացնենք 30 սմ տրամագիծ ունեցող գլոբուսով, այդ դեպքում ի՞նչ մեծությամբ կպատկերացվի Երկրի բևեռային և հասարակածային շառավիղների տարբերությունը։
- Ինչի՞ է հավասար հասարակածային կետերի արագությունը մետրերով՝ Երկրի օրական պտույտի ժամանակ։
- *Իսկ ինչպիսի՞ն է հիշյալ արագությունը ձեր բնակավայրի համար (վերջինիս աշխարհագրական լայնությունը վերցնել քարտեզից), այն հաշվելու համար կառուցելով գծագիր օգտվեցեք եռանկյունաչափությունից։
<references>