«Տարերք/Գիրք 1»–ի խմբագրումների տարբերություն

11:43, 12 Դեկտեմբերի 2024-ի տարբերակ (դիտել վիքիկոդը) Արարատ Ղազարյան (Քննարկում | ներդրում) (→‎Պնդում 29) ← Նախորդ խմբագրում		11:44, 12 Դեկտեմբերի 2024-ի տարբերակ (դիտել վիքիկոդը) Hovhannes003 (Քննարկում | ներդրում) Հաջորդ խմբագրում →
Տող 52.		Տող 52.
−	1․ Եթե մի քանի բան հավասար են մեկ այլ բանի, ապա այդ մի քանի բաներն իրար էլ են հավասար։	+	# Եթե մի քանի բան հավասար են մեկ այլ բանի, ապա այդ մի քանի բաներն իրար էլ են հավասար։
−	2․ Եթե հավասար բաներին ավելացնենք հավասար բաներ, ապա ամբողջները հավասար կլինեն:	+	# Եթե հավասար բաներին ավելացնենք հավասար բաներ, ապա ամբողջները հավասար կլինեն:
−	3․ Եթե հավասար բաներից հանենք հավասար բաներ, ապա մնացորդները հավասար կլինեն:	+	# Եթե հավասար բաներից հանենք հավասար բաներ, ապա մնացորդները հավասար կլինեն:
−	4․ Իրար համընկող բաներն իրար հավասար են:	+	<ref>As an obvious extension of C.N.s 2 & 3—if equal things are added or subtracted from the two sides of an inequality then the inequality remains  an inequality of the same type.</ref>
−	5․ Ամբողջը ավելի մեծ է, քան դրա մի մասը:	+	# Իրար համընկող բաներն իրար հավասար են:
		+	# Ամբողջը ավելի մեծ է, քան դրա մի մասը:
Տող 233.		Տող 234.
	== Պնդում 47 ==		== Պնդում 47 ==
	== Պնդում 48 ==		== Պնդում 48 ==
		+
		+	== Նշումներ ==
		+	<references/>

---

11:44, 12 Դեկտեմբերի 2024-ի տարբերակ

Տարերք, Գիրք 1 հեղինակ՝ էվկլիդես աղբյուր՝ Euclid's Elements of Geometry, English translation by Richard Fitzpatrick

Տարերքի գրքեր

Գիրք 1 - Գիրք 2 - Գիրք 3 - Գիրք 4 - Գիրք 5 - Գիրք 6 - Գիրք 7 - Գիրք 8 - Գիրք 9 - Գիրք 10 - Գիրք 11 - Գիրք 12 - Գիրք 13

Pages 6-30

Սահմանումներ

1. Կետը այն է, որում չկան մասեր։

Գիծը երկարությունն է առանց լայնությաան։

3․ Գծի եզրերը կետեր են։ 4․ Ուղիղ գիծը դա այն գիծն է, որն ուղիղ անցնում է այդ կետերով։ 5․ Հարթոոթյուն է երկարություն և լայնություն ունեցող պատկերը։ 6․ Հարթության եզրերը գծերն են։ 7․ Հարթ մակերեսը այդ գծերի միջև համաչափ բաշխված է։ 8․ Հարթության անկյունը գծերի փոխադարձ հակվածությունն է, երբ հարթությունում երկու գիծ հանդիպում են միմյանց և չեն գտնվում միևնույն ուղիղ գծի վրա: 9․ Երբ անկյուն պարունակող գծերը ուղղահայաց են, այդ անկյունը կոչվում է ուղղանկյուն: 10․ Երբ մի ուղիղ գծերը հատում են իրար, և առաջացնում է հարակից անկյուններ, որոնք հավասար են միմյանց, այդ հավասար անկյուններից յուրաքանչյուրը կոչվում է ուղիղ անկյուն, իսկ առաջին ուղիղ գիծը կոչվում է ուղղահայաց այն գծին, որին հատում է: 11․ Բութ անկյունն ավելի մեծ է, քան ուղիղ անկյունը։ 12․ Սուր անկյունն ավելի փոքր է, քան ուղիղ անկյունը։ 13․ Սահմանը դա ինչ-որ բանի եզրերն են։ 14․ Պատկերը պարունակում է որոշակի սահմաններ։ 15․ Շրջանագիծը հարթության մի պատկեր է, որը պարփակված է մի գծով (որը կոչվում է շրջագիծ), այնպես, որ բոլոր ուղիղ գծերը, որոնք ուղղվում են դեպի շրջագիծը, ելնելով այդ պատկերի ներսում գտնվող մի կետից, հավասար են միմյանց: 16․ Այդ կետը կենտրոնն է։ 17․ Շրջանի տրամագիծը ցանկացած ուղիղ գիծ է, որը անցնում է կենտրոնով և ավարտվում է երկու ուղղություններով շրջագծի սահմաններում: Այդպիսի ցանկացած գիծ նաև կիսում է շրջանը երկու հավասար մասերի: 18․ Կիսաշրջանը այն պատկերն է, որը պարփակված է տրամագծով և շրջագծով, որն այդ տրամագիծն առանձնացնում է: Եվ կիսաշրջանի կենտրոնը նույն կետն է, ինչ շրջանի կենտրոնը: 19․ Ուղղագծային պատկերները (ֆիգուրները) այն պատկերներն են, որոնք պարփակված են ուղիղ գծերով. եռակողմ պատկերները պարփակված են երեք ուղիղ գծերով, քառակողմերը՝ չորս, և բազմակողմերը՝ ավելի քան չորս: 20․ Եռակողմ պատկերներից՝ հավասարակողմ եռանկյունը այն է, որն ունի երեք հավասար կողմ, հավասարասրուն եռանկյունը՝ այն, որն ունի միայն երկու հավասար կողմ, իսկ անհավասարասրուն եռանկյունը՝ այն, որն ունի երեք անհավասար կողմ: 21․ Եռակողմ պատկերների շարքում՝ ուղղանկյուն եռանկյունը այն է, որն ունի ուղիղ անկյուն, բութանկյուն եռանկյունը՝ այն, որն ունի բութ անկյուն, իսկ սուրանկյուն եռանկյունը՝ այն, որն ունի երեք սուր անկյուն: 22․ Քառակողմ պատկերների շարքում՝ քառակուսին այն պատկերն է, որը ուղիղանկյուն է և հավասարակողմ, ուղղանկյունը՝ այն, որը ուղիղանկյուն է, բայց ոչ հավասարակողմ, հնգանկյունը՝ այն, որը հավասարակողմ է, բայց ոչ ուղիղանկյուն, իսկ շեղանկյունը՝ այն, որի հակադիր կողմերն ու անկյունները հավասար են միմյանց, բայց այն ոչ ուղիղանկյուն է և ոչ էլ հավասարակողմ: Եվ թող քառակողմ պատկերները, որոնք այս դասերին չեն պատկանում, կոչվեն թրապեզիաներ: 23․ Զուգահեռ գծերը ուղիղ գծեր են, որոնք գտնվում են նույն հարթության մեջ և, անվերջ շարունակվելով երկու ուղղությամբ, չեն հատվում միմյանց ոչ մի ուղղությամբ:

Աքսիոմաներ

1. Կարելի է գծել ուղիղ գիծ ցանկացած կետից դեպի ցանկացած կետ:
2. Կարելի է շարունակել սահմանափակ ուղիղ գիծը անվերջ միևնույն ուղիղ գծի վրա:
3. Կարելի է գծել շրջան ցանկացած կենտրոնով և շառավղով:
4. Բոլոր ուղիղ անկյուններն հավասար են իրար։
5. Եթե ուղիղ գիծը հատում է երկու (այլ) ուղիղ գծերը և ստեղծում ներքին անկյուններ նույն կողմում (որոնց գումարը) փոքր է երկու ուղիղ անկյուններից, ապա այդ երկու (այլ) ուղիղ գծերը, շարունակվելով անվերջ, հանդիպում են այն կողմում (որն ունի փոքր անկյունների գումար), և չեն հանդիպում մյուս կողմում:

Ընդհանուր հասկացություններ

1. Եթե մի քանի բան հավասար են մեկ այլ բանի, ապա այդ մի քանի բաներն իրար էլ են հավասար։
2. Եթե հավասար բաներին ավելացնենք հավասար բաներ, ապա ամբողջները հավասար կլինեն:
3. Եթե հավասար բաներից հանենք հավասար բաներ, ապա մնացորդները հավասար կլինեն:

^[1]

1. Իրար համընկող բաներն իրար հավասար են:
2. Ամբողջը ավելի մեծ է, քան դրա մի մասը:

Հատկություն 1

Կառուցենք հավասարակողմ եռանկյուն, տրված վերջավոր ուղիղ գծի վրա։

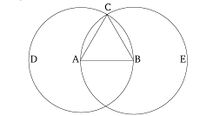
Թող AB-ն լինի տրված սահմանափակ ուղիղ գիծը:

Անհրաժեշտ է կառուցել հավասարակողմ եռանկյուն այդ AB ուղիղ գծի վրա:

Թող գծվի BCD շրջանը՝ կենտրոն A-ով և AB շառավղով [Հոդված 3], և կրկին թող գծվի ACE շրջանը՝ կենտրոն B-ով և BA շառավղով [Հոդված 3]: Եվ թող գծվեն CA և CB ուղիղ գծերը, որտեղ շրջանակները հատվում են միմյանց, դեպի A և B կետերը (համապատասխանաբար) [Հոդված 1]:

Քանի որ A կետը CDB շրջանի կենտրոնն է, AC հավասար է AB-ին [Սահմանում 1.15]: Կրկին, քանի որ B կետը CAE շրջանի կենտրոնն է, BC հավասար է BA-ին [Սահմանում 1.15]: Սակայն, նաև ցույց է տրվել, որ CA հավասար է AB-ին: Այսպիսով, CA-ն և CB-ն երկուսն էլ հավասար են AB-ին: Իսկ այն բաները, որոնք հավասար են նույն բանին, նույնպես հավասար են միմյանց [Համընդհանուր սկզբունք 1]: Այսպիսով, CA-ն հավասար է նաև CB-ին: Այսպիսով, երեք (ուղիղ գծերը) CA, AB և BC հավասար են միմյանց:

Այսպիսով, ABC եռանկյունը հավասարակողմ է և կառուցված է տրված AB սահմանափակ ուղիղ գծի վրա: Դա հենց այն էր, ինչ անհրաժեշտ էր անել:

Հատկություն 2

---

Հատկություն 3

---

Հատկություն 4

---

Հատկություն 5

---

Հատկություն 6

---

Հատկություն 7

---

Հատկություն 8

---

Հատկություն 9

---

Հատկություն 10

---

Հատկություն 11

---

Հատկություն 12

---

Հատկություն 13

---

Հատկություն 14

---

Հատկություն 15

---

Հատկություն 16

---

Հատկություն 17

---

Հատկություն 18

---

Հատկություն 19

---

Հատկություն 20

---

Հատկություն 21

---

Հատկություն 22

---

Հատկություն 23

---

Հատկություն 24

---

Հատկություն 25

---

Հատկություն 26

---

Հատկություն 27

---

Պնդում 27

Դա անհնար է [Պնդում 1.16]: Հետևաբար AB և CD ուղիղները՝ գծվելով, չեն հատվի B և D ուղղությամբ։ Նմանապես, կարող ենք ցույց տալ, որ դրանք չեն հատվի A և C ուղղություններվ։ Բայց ուղիղները, որոնք չեն հատվում ոչ մի ուղղությամբ, զուգահեռ են [Սահմանում 1.23]: Հետևաբար, AB և CD ուղիղները զուգահեռ են։ Հետևաբար, եթե երկու ուղիղներ հատող ուղիղը ստեղծում է հավասար խաչադիր անկյուններ, ապա այդ երկու ուղիղները զուգահեռ են։ Սա այն էր, ինչ պետք էր ապացուցել։

Pages 31-48

Պնդում 28

Եթե երկու ուղիղները հատող ուղիղը կազմում է արտաքին անկյուն, որը հավասար է ներքին և հակադիր անկյանը նույն կողմի վրա կամ նույն կողմի վրա գտնվող անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների, ապա այդ երկու ուղիղները զուգահեռ են։

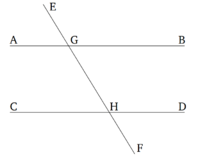
EF ուղիղը, որը հատում է AB և CD ուղիղները, կազմում է EGB արտաքին անկյուն, որը հավասար է ներքին և հակադիր GHD անկյանը, կամ նույն կողմի վրա գտնվող BGH և GHD անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների։ Պնդումն այն է, որ AB և CD ուղիղները զուգահեռ են։

Առաջին դեպքում EGB անկյունը հավասար է GHD անկյանը, բայց EGB անկյունը նաև հավասար է AGH անկյանը [Պնդում 1.15], հետևաբար, AGH անկյունը հավասար է GHD անկյանը։ Դրանք նաև խաչադիր անկյուններ են։ Հետևաբար, AB և CD ուղիղները զուգահեռ են [Պնդում. 1.27]։

Երկրորդ դեպքում, կրկին, BGH և GHD անկյունների գումարը հավասար է երկու ուղիղ անկյունների, ինչպես նաև AGH և BGH անկյունների գումարն է հավասար երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, AGH և BGH անկյունների գումարը հավասար է BGH և GHD անկյունների գումարին։ Երկուսից էլ հանենք BGH անկյունը։ Հետևաբար, մնացորդ AGH անկյունը հավասար է մնացորդ GHD անկյանը և դրանք խաչադիր անկյուններ են։ Հետևաբար, AB և CD ուղիղները զուգահեռ են [Պնդում 1.27]։

Հետևաբար, եթե երկու ուղիղները հատող ուղիղը կազմում է արտաքին անկյուն, որը հավասար է ներքին և հակադիր անկյանը նույն կողմի վրա կամ նույն կողմի վրա գտնվող անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների, ապա այդ երկու ուղիղները զուգահեռ են։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 29

Զուգահեռ ուղիղները հատող ուղղիղը ստեղծում է հավասար խաչադիր անկյուններ, արտաքին անկյուն՝ հավասար ներքին և հակադիր անկյանը, և նույն կողմի վրա գտնվող ներքին անկյունների գումարը հավասարվում է երկու ուղիղ անկյունների։

EF ուղիղը հատում է զուգահեռ AB և CD ուղիղները։ Պնդումն այն է, որ այն դարձնում է AGH և GHD անկյունները հավասար, EGB արտաքին անկյունը՝ հավասար ներքին և հակադիր GHD անկյանը, և նույն կողմի վրա գտնվող BGH և GHD ներքին անկյունների գումարը՝ հավասար երկու ուղիղ անկյունների։

Եթե AGH անկյունը հավասար չէ GHD անկյանը, ապա նրանցից մեկը մեծ է։ Ենթադրենք AGH անկյունը մեծ է։ Երկու անկյուններին ավելացնենք BGH անկյունը։ Հետևաբար, AGH և BGH անկյունների գումարը մեծ է BGH և GHD անկյունների գումարից։ Բայց, AGH և BGH անկյունների գումարը հավասար է երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, BGH և GHD անկյունների գումարը փոքր է երկու ուղիղ անկյուններից։ Բայց, ուղիղները գծված են անվերջ ներքին անկյուններից, որոնց գումարը փոքր է հատվող երկու ուղիղ անկյուններից [Կանխադրույթ 5]: Հետևաբար, անվերջ գծված AB և CD ուղիղները կհատվեն։ Բայց, նրանք չեն հատվում, եթե հաշվի առնենք, որ իսկզբանե դրանք զուգահեռ էին [Սահմանում 1.23]։ Հետևաբար, AGH և GHD անկյունները չեն կարող հավասար չլինել՝ հավասար են։ Բայց, AGH և EGB անկյունները նույնպես հավասար են [Պնդում 1.15]։ EGB անկյունը, հետևաբար, հավասար է GHD անկյանը։ Երկուսին էլ ավելացնենք BGH անկյունը։ Հետևաբար, EGB և BGH անկյունների գումարը հավասար է BGH և GHD անկյունների գումարին։ Բայց, EGB և BGH անկյունների գումարը հավասար է երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, BGH և GHD անկյունների գումարը նույնպես հավասար է երկու ուղիղ անկյունների։

Հետևաբար, զուգահեռ ուղիղները հատող ուղղիղը ստեղծում է հավասար հակադիր անկյուններ, արտաքին անկյուն՝ հավասար ներքին և հակադիր անկյանը, և նույն կողմի վրա գտնվող ներքին անկյունների գումարը հավասարվում է երկու ուղիղ անկյունների։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 30

Պնդում 31

Պնդում 32

Պնդում 33

Պնդում 34

Պնդում 35

Պնդում 36

Պնդում 37

Պնդում 38

Պնդում 39

Պնդում 40

Պնդում 41

Պնդում 42

Պնդում 43

Պնդում 44

Պնդում 45

Պնդում 46

Պնդում 47

Պնդում 48

Նշումներ

1. ↑ As an obvious extension of C.N.s 2 & 3—if equal things are added or subtracted from the two sides of an inequality then the inequality remains an inequality of the same type.