«Տարերք/Գիրք 1»–ի խմբագրումների տարբերություն

16:22, 16 Դեկտեմբերի 2024-ի տարբերակ

Pages 6-30

Սահմանումներ

1. Կետը այն է, որում չկան մասեր։
2. Գիծը երկարությունն է առանց լայնությաան։
3. Գծի եզրերը կետեր են։
4. Ուղիղ գիծը դա այն գիծն է, որն ուղիղ անցնում է այդ կետերով։
5. Հարթոոթյուն է երկարություն և լայնություն ունեցող պատկերը։
6. Հարթության եզրերը գծերն են։
7. Հարթ մակերեսը այդ գծերի միջև համաչափ բաշխված է։
8. Հարթության անկյունը գծերի փոխադարձ հակվածությունն է, երբ հարթությունում երկու գիծ հանդիպում են միմյանց և չեն գտնվում միևնույն ուղիղ գծի վրա:
9. Երբ անկյուն պարունակող գծերը ուղղահայաց են, այդ անկյունը կոչվում է ուղղանկյուն:
10. Երբ մի ուղիղ գծերը հատում են իրար, և առաջացնում է հարակից անկյուններ, որոնք հավասար են միմյանց, այդ հավասար անկյուններից յուրաքանչյուրը կոչվում է ուղիղ անկյուն, իսկ առաջին ուղիղ գիծը կոչվում է ուղղահայաց այն գծին, որին հատում է:
11. Բութ անկյունն ավելի մեծ է, քան ուղիղ անկյունը։
12. Սուր անկյունն ավելի փոքր է, քան ուղիղ անկյունը։
13. Սահմանը դա ինչ-որ բանի եզրերն են։
14. Պատկերը պարունակում է որոշակի սահմաններ։
15. Շրջանագիծը հարթության մի պատկեր է, որը պարփակված է մի գծով (որը կոչվում է շրջագիծ), այնպես, որ բոլոր ուղիղ գծերը, որոնք ուղղվում են դեպի շրջագիծը, ելնելով այդ պատկերի ներսում գտնվող մի կետից, հավասար են միմյանց:
16. Այդ կետը կենտրոնն է։
17. Շրջանի տրամագիծը ցանկացած ուղիղ գիծ է, որը անցնում է կենտրոնով և ավարտվում է երկու ուղղություններով շրջագծի սահմաններում: Այդպիսի ցանկացած գիծ նաև կիսում է շրջանը երկու հավասար մասերի:
18. Կիսաշրջանը այն պատկերն է, որը պարփակված է տրամագծով և շրջագծով, որն այդ տրամագիծն առանձնացնում է: Եվ կիսաշրջանի կենտրոնը նույն կետն է, ինչ շրջանի կենտրոնը:
19. Ուղղագծային պատկերները (ֆիգուրները) այն պատկերներն են, որոնք պարփակված են ուղիղ գծերով. եռակողմ պատկերները պարփակված են երեք ուղիղ գծերով, քառակողմերը՝ չորս, և բազմակողմերը՝ ավելի քան չորս:
20. Եռակողմ պատկերներից՝ հավասարակողմ եռանկյունը այն է, որն ունի երեք հավասար կողմ, հավասարասրուն եռանկյունը՝ այն, որն ունի միայն երկու հավասար կողմ, իսկ անհավասարասրուն եռանկյունը՝ այն, որն ունի երեք անհավասար կողմ:
21. Եռակողմ պատկերների շարքում՝ ուղղանկյուն եռանկյունը այն է, որն ունի ուղիղ անկյուն, բութանկյուն եռանկյունը՝ այն, որն ունի բութ անկյուն, իսկ սուրանկյուն եռանկյունը՝ այն, որն ունի երեք սուր անկյուն:
22. Քառակողմ պատկերների շարքում՝ քառակուսին այն պատկերն է, որը ուղիղանկյուն է և հավասարակողմ, ուղղանկյունը՝ այն, որը ուղիղանկյուն է, բայց ոչ հավասարակողմ, հնգանկյունը՝ այն, որը հավասարակողմ է, բայց ոչ ուղիղանկյուն, իսկ շեղանկյունը՝ այն, որի հակադիր կողմերն ու անկյունները հավասար են միմյանց, բայց այն ոչ ուղիղանկյուն է և ոչ էլ հավասարակողմ: Եվ թող քառակողմ պատկերները, որոնք այս դասերին չեն պատկանում, կոչվեն թրապեզիաներ:
23. Զուգահեռ գծերը ուղիղ գծեր են, որոնք գտնվում են նույն հարթության մեջ և, անվերջ շարունակվելով երկու ուղղությամբ, չեն հատվում միմյանց ոչ մի ուղղությամբ:

Աքսիոմաներ

1. Կարելի է գծել ուղիղ գիծ ցանկացած կետից դեպի ցանկացած կետ:
2. Կարելի է շարունակել սահմանափակ ուղիղ գիծը անվերջ միևնույն ուղիղ գծի վրա:
3. Կարելի է գծել շրջան ցանկացած կենտրոնով և շառավղով:
4. Բոլոր ուղիղ անկյուններն հավասար են իրար։
5. Եթե ուղիղ գիծը հատում է երկու (այլ) ուղիղ գծերը և ստեղծում ներքին անկյուններ նույն կողմում (որոնց գումարը) փոքր է երկու ուղիղ անկյուններից, ապա այդ երկու (այլ) ուղիղ գծերը, շարունակվելով անվերջ, հանդիպում են այն կողմում (որն ունի փոքր անկյունների գումար), և չեն հանդիպում մյուս կողմում:

Ընդհանուր հասկացություններ

1. Եթե մի քանի բան հավասար են մեկ այլ բանի, ապա այդ մի քանի բաներն իրար էլ են հավասար։
2. Եթե հավասար բաներին ավելացնենք հավասար բաներ, ապա ամբողջները հավասար կլինեն:
3. Եթե հավասար բաներից հանենք հավասար բաներ, ապա մնացորդները հավասար կլինեն:^[1]
4. Իրար համընկող բաներն իրար հավասար են:
5. Ամբողջը ավելի մեծ է, քան դրա մի մասը:

Պնդում 1

Կառուցենք հավասարակողմ եռանկյուն, տրված վերջավոր ուղիղ գծի վրա։

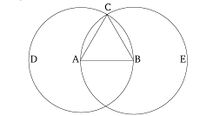
Թող AB-ն լինի տրված սահմանափակ ուղիղ գիծը:

Անհրաժեշտ է կառուցել հավասարակողմ եռանկյուն այդ AB ուղիղ գծի վրա:

Թող գծվի BCD շրջանը՝ կենտրոն A-ով և AB շառավղով [Աքսիոմա 3], և կրկին թող գծվի ACE շրջանը՝ կենտրոն B-ով և BA շառավղով [Աքսիոմա 3]: Եվ թող գծվեն CA և CB ուղիղ գծերը, որտեղ շրջանակները հատվում են միմյանց, դեպի A և B կետերը (համապատասխանաբար) [Աքսիոմա 1]:

Քանի որ A կետը CDB շրջանի կենտրոնն է, AC հավասար է AB-ին [Սահմանում 1.15]: Կրկին, քանի որ B կետը CAE շրջանի կենտրոնն է, BC հավասար է BA-ին [Սահմանում 1.15]: Սակայն, նաև ցույց է տրվել, որ CA հավասար է AB-ին: Այսպիսով, CA-ն և CB-ն երկուսն էլ հավասար են AB-ին: Իսկ այն բաները, որոնք հավասար են նույն բանին, նույնպես հավասար են միմյանց [ընհանուր հասկացություն 1]: Այսպիսով, CA-ն հավասար է նաև CB-ին: Այսպիսով, երեք (ուղիղ գծերը) CA, AB և BC հավասար են միմյանց:

Այսպիսով, ABC եռանկյունը հավասարակողմ է և կառուցված է տրված AB սահմանափակ ուղիղ գծի վրա: Դա հենց այն էր, ինչ անհրաժեշտ էր անել:

Պնդում 2

Ուղիղ գիծը մի կետում (որպես եզրագիծ) տրված ուղիղ գծի հետ հավասար դիրքավորելու համար:

Թող A կետը տրված կետ լինի, իսկ BC՝ տրված ուղիղ գիծ: Այսպիսով, անհրաժեշտ է A կետում դիրքավորել ուղիղ գիծ, որը հավասար է BC գծին:

Եթե վերցնենք ուղիղ գիծ AB-ն կառուցված A կետից մինչև B կետ [աքսիոմա 1], և թող հավասարակողմ եռանկյուն DAB-ն կառուցված լինի դրա վրա [պնդում 1.1]:

Եվ թող ուղիղ գծերը AE և BF երկարացված լինեն որպես ուղիղ գիծ համապատասխանաբար DA-ի և DB-ի հետ [աքսիոմա 2]: Եվ թող շրջանակ CGH-ն B կենտրոնով և BC շառավղով գծված լինի [աքսիոմա 3]: Եվ նորից թող շրջանակ GKL-ը D կենտրոնով և DG շառավղով գծված լինի [աքսիոմա 3]:

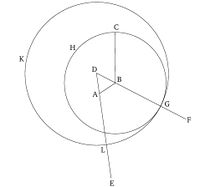
Հետևաբար, քանի որ B կետը CGH շրջանակի կենտրոնն է, BC հավասար է BG-ին [սահմանում 1.15]: Նույն կերպ, քանի որ D կետը GKL շրջանակի կենտրոնն է, DL հավասար է DG-ին [սահմանում 1.15]: Եվ այս դեպքերում DA հավասար է DB-ին: Հետևաբար, մնացորդը AL հավասար է մնացորդին BG-ին [ընդհանուր հասկացություն 3]: Սակայն BC-ն նույնպես ցույց տրվեց, որ հավասար է BG-ին: Հետևաբար, AL և BC-ն երկուսն էլ հավասար են BG-ին: Սակայն բաները, որոնք հավասար են նույնին, նույնպես հավասար են միմյանց [ընդհանուր հասկացություն 1]: Հետևաբար, AL նույնպես հավասար է BC-ին:

Հետևաբար, AL ուղիղ գիծը, որը հավասար է տրված BC ուղիղ գծին, դիրքավորված է տրված A կետում: (Սա հենց այն է, ինչ անհրաժեշտ էր անել):

Պնդում 3

Երկու տրված անհավասար ուղիղ գծերի համար կտրել մեծից ուղիղ գիծ, որը հավասար է փոքրին:

Թող AB և C լինեն երկու տրված անհավասար ուղիղ գծեր, որոնցից AB-ն մեծ է: Այսպիսով, անհրաժեշտ է կտրել ուղիղ գիծ, որը հավասար է C-ին, մեծ AB-ից:

Թող AD գիծը, որը հավասար է C ուղիղ գծին, դիրքավորված լինի A կետում [պնդում 1.2]: Եվ թող DEF շրջանակը գծված լինի A կենտրոնով և AD շառավղով [աքսիոմա 3]:

Եվ քանի որ A կետը DEF շրջանակի կենտրոնն է, AE-ն հավասար է AD-ին [սահմանում 1.15]: Սակայն C-ն նույնպես հավասար է AD-ին: Հետևաբար, AE-ն և C-ն երկուսն էլ հավասար են AD-ին: Այսպիսով, AE-ն նույնպես հավասար է C-ին [ընդհանուր հասկացություն 1]:

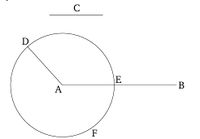
Այսպիսով, երկու տրված անհավասար ուղիղ գծերի AB-ի և 𝐶-ի համար, AE ուղիղ գիծը, որը հավասար է փոքր C-ին, կտրած է մեծ AB-ից: (Սա հենց այն է, ինչ պահանջվում էր անել):

Պնդում 4

Եթե երկու եռանկյուններն ունեն երկու կողմեր, որոնք հավասար են երկու կողմերին (համապատասխանաբար), և ունեն անկյուն(ներ), որոնք ընդգրկված են հավասար ուղիղ գծերով, ապա դրանք նույնպես կունենան հիմքը հավասար հիմքին, և եռանկյունը կլինի հավասար եռանկյունին, իսկ հավասար կողմերով ստեղծված մնացած անկյունները կլինեն հավասար համապատասխան մնացած անկյուններին:

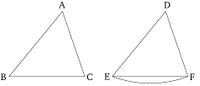
Թող ABC-ն և DEF-ը լինեն երկու եռանկյուններ, որոնց երկու կողմերը AB-ն և AC-ն հավասար են DE և DF կողմերին համապատասխանաբար։ (Այսինքն՝ AB-ն հավասար է DE-ին, իսկ AC հավասար է DF-ին): Եվ թող անկյուն BAC-ն հավասար լինի անկյուն EDF-ին։ Ես ասում եմ, որ հիմքը BC-ն նույնպես հավասար է հիմքին EF-ին, իսկ եռանկյուն ABC-ն հավասար կլինի եռանկյուն DEF-ին, իսկ հավասար կողմերով ստեղծված մնացած անկյունները կլինեն հավասար համապատասխան մնացած անկյուններին։ (Այսինքն՝ ABC=DEF և ACB=DFE):

Քանի որ, եթե եռանկյուն ABC-ն կիրառվում է եռանկյուն DEF-ի վրա՝ A կետը տեղադրվում է D կետում, իսկ ուղիղ գիծ AB-ն DE-ի վրա, ապա B կետը նույնպես կհամընկնի E-ի հետ, AB-ի և DE-ի հավասար լինելու հաշվին։ Ուստի, AB-ի և DE-ի համընկնելու պատճառով, ուղիղ գիծ AC-ն նույնպես կհամընկնի DF-ի հետ՝ BAC անկյան EDF-ի հետ հավասարության պատճառով: C կետը նույնպես կհամընկնի F կետի հետ՝ AC-ի և DF-ի հավասարության պատճառով: Սակայն B կետը հաստատապես կհամընկնի E կետի հետ այնպես, որ հիմքը BC կհամընկնի հիմքի EF-ի հետ: Եթե B-ն համընկնում է E-ի հետ և C-ն համընկնում է F-ի հետ, իսկ հիմքը BC չի համընկնում EF-ի հետ, ապա երկու ուղիղ գծերը կգրեն տարածք: Սա շատ բան է, որ հնարավոր չէ [աքսիոմա 1]:

Հետևաբար, հիմքը BC-ն կհամընկնի EF-ի հետ և կլինի հավասար EF-ին [ընդհանուր հասկացություն 4]: Այսպիսով, ամբողջ եռանկյուն ABC-ն կհամընկնի ամբողջ եռանկյուն DEF-ի հետ և կլինի հավասար [ընդհանուր հասկացություն 4]: Եվ մնացած անկյունները կհամընկնեն մնացած անկյուններին և կլինեն հավասար [ընդհանուր հասկացություն 4]: (Այսինքն՝ ABC=DEF, և ACB=DFE [ընդհանուր հասկացություն 4]):

Այսպիսով, եթե երկու եռանկյուններ ունեն երկու կողմեր, որոնք հավասար են երկու կողմերին (համապատասխանաբար), և ունեն անկյուն(ներ), որոնք ընդգրկված են հավասար ուղիղ գծերով, ապա հիմքը ևս հավասար կլինի հիմքին, եռանկյունը կլինի հավասար եռանկյանը, իսկ հավասար կողմերով ստեղծված մնացած անկյունները կլինեն հավասար համապատասխան մնացած անկյուններին։ Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ։

Պնդում 5

Հավասարակողմ եռանկյունների համար հիմքի անկյունները հավասար են միմյանց, և եթե հավասար կողմերը երկարացվեն, ապա հիմքի տակ գտնվող անկյունները նույնպես կլինեն հավասար միմյանց:

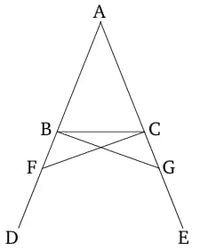
Թող ABC լինի հավասարակողմ եռանկյուն, որի կողմը AB-ն հավասար է կողմ AC-ին, և թող ուղիղ գծերը BD և CE երկարացված լինեն AB-ի և AC-ի ուղղությամբ համապատասխանաբար [աքսիոմա 2]: Ես ասում եմ, որ անկյուն ABC-ն հավասար է անկյուն ACB-ին, և CBD-ն հավասար է BCE-ին:

Քանի որ, F կետը վերցված է պատահականորեն BD-ի վրա, և AG-ն կտրված է մեծ AE-ից, հավասար AF-ին [պնդում 1.3]: Բացի այդ, թող FC և GB ուղիղ գծերը միացված լինեն [աքսիոմա 1]:

Փաստորեն, քանի որ AF հավասար է AG-ին, և AB հավասար է AC-ին, ուղիղ գծերը FA, AC հավասար են GA, AB ուղիղ գծերին համապատասխանաբար։ Դրանք ներառում են նաև ընդհանուր անկյուն FAG: Հետևաբար, հիմքը FC-ն հավասար է հիմք GB-ին GB, և եռանկյուն AFC-ն հավասար կլինի եռանկյուն AGB-ին, իսկ հավասար կողմերով ստեղծված մնացած անկյունները կլինեն հավասար համապատասխան մնացած անկյուններին [պնդում 1.4]: (Այսինքն՝ ACF=ABG-ի և AFC=AGB):

Քանի որ AF-ն ամբողջությամբ հավասար է AG-ին, որի մեջ AB-ն հավասար է AC-ին, մնացորդը BF-ն հավասար կլինի մնացորդ CG-ին [ընդհանուր հասկացություն 3]: Սակայն FC-ն նույնպես ցույց տրվեց, որ հավասար է GB-ին: Հետևաբար, ուղիղ գծերը BF-ն ու FC-ն հավասար են CG ու GB ուղիղ գծերին համապատասխանաբար, և անկյուն BFC-ն հավասար է անկյուն CGB-ին, և հիմքը BC-ն ընդհանուր է դրանց համար։ Այսպիսով, եռանկյուն BFC-ն հավասար կլինի եռանկյուն CGB-ին, իսկ հավասար կողմերով ստեղծված մնացած անկյունները կլինեն հավասար համապատասխան մնացած անկյուններին [պնդում 1.4]:

Հետևաբար, FBC-ն հավասար է GCB-ին, և BCF-ն հավասար է CBG-ին։ Հետևաբար, քանի որ ամբողջ անկյուն ABG-ն ցույց տրվեց, որ հավասար է ամբողջ անկյան ACF-ին, որի մեջ CBG-ն հավասար է BCF-ին, մնացորդը ABC-ն նույնպես հավասար է մնացորդին ACB [ընդհանուր հասկացություն 3]: Եվ դրանք գտնվում են եռանկյուն ABC-ի հիմքում։ FBC-ն նույնպես ցույց տրվեց, որ հավասար է GCB-ին։ Եվ դրանք գտնվում են հիմքի տակ։

Այսպիսով, հավասարակողմ եռանկյունների համար հիմքի անկյունները հավասար են միմյանց, և եթե հավասար կողմերը երկարացվեն, ապա հիմքի տակ գտնվող անկյունները նույնպես կլինեն հավասար միմյանց։ Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ։

Պնդում 6

Եթե եռանկյունն ունի երկու անկյուն, որոնք հավասար են միմյանց, ապա հավասար անկյուններին դիմաց գտնվող կողմերը նույնպես կլինեն հավասար միմյանց:

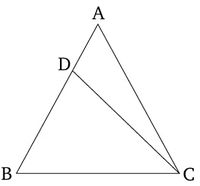
Թող ABC լինի եռանկյուն, որի ABC անկյունը հավասար է ACB անկյանը: Ես ասում եմ, որ կողմ AB-ն նույնպես հավասար է կողմ AC-ին:

Եթե AB-ն հավասար չէ AC-ին, ապա դրանցից մեկը մեծ է: Թող AB-ն լինի մեծը: Եվ թող DB-ն, որը հավասար է փոքր AC-ին, կտրված լինի մեծ AB-ից [պնդում 1.3]: Եվ թող DC-ն միացված լինի [աքսիոմա 1]:

Հետևաբար, քանի որ DB-ն հավասար է AC-ին, և BC-ն ընդհանուր է, երկու կողմերը DB, BC հավասար են երկու կողմերին AC, CB համապատասխանաբար, իսկ անկյուն DBC-ն հավասար է անկյուն ACB-ին: Այսպիսով, հիմքը DC-ն հավասար է հիմքին AB, իսկ եռանկյուն DBC-ն հավասար կլինի եռանկյուն ACB-ին [պնդում 1.4], փոքրից մեծին: Ինքը գաղափարը (հակասում է) աբսուրդ է [ընդհանուր հասկացություն 5]: Այսպիսով, AB-ն հավասար չէ AC-ին: Հետևաբար, AB-ն հավասար է AC-ին:

Այսպիսով, եթե եռանկյունն ունի երկու անկյուն, որոնք հավասար են միմյանց, ապա հավասար անկյունների դիմաց գտնվող կողմերը նույնպես կլինեն հավասար միմյանց: Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ:

Պնդում 7

Նույն ուղիղ գծի վրա, երկու այլ ուղիղ գծեր, որոնք հավասար են համապատասխանաբար տրված (երկու) ուղիղ գծերին (որոնք հատվում են), չեն կարող կառուցվել (հատվելով) նույն կողմում գտնվող այլ կետում՝ ունենալով նույն ծայրակետերը, ինչ տրված ուղիղ գծերը:

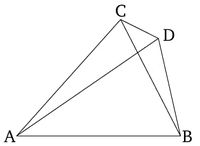
Եթե հնարավոր է, թող AC, CB ուղիղ գծերը, որոնք հավասար են երկու այլ ուղիղ գծերին AD, DB համապատասխանաբար, կառուցված լինեն նույն AB ուղիղ գծի վրա՝ հատվելով տարբեր կետերում C և 𝐷, AB-ի նույն կողմում և ունենալով նույն ծայրակետերը AB-ի վրա։ Ուստի CA=DA ունենալով նույն A ծայրակետը, իսկ CB-ն հավասար է DB-ին՝ ունենալով նույն B ծայրակետը։ Եվ թող CD-ն միացված լինի [աքսիոմա 1]:

Հետևաբար, քանի որ AC-ն հավասար է AD-ին, անկյուն ACD-ն նույնպես հավասար է անկյուն ADC-ին[պնդում 1.5]: Այսպիսով, ADC-ն (անկյուն) մեծ է DCB-ից [ընդհանուր հասկացություն 5]: Այսպիսով, CDB-ն շատ ավելի մեծ է DCB-ից [ընդհանուր հասկացություն 5]: Նորից, քանի որ CB-ն հավասար է DB-ին, անկյուն CDB-ն նույնպես հավասար է անկյուն DCB-ին[պնդում 1.5]: Բայց ցույց տրվեց, որ առաջինը (անկյունը) նույնպես շատ ավելի մեծ է (երկրորդից), ինչը պարզապես անհնար է:

Այսպիսով, նույն ուղիղ գծի վրա, երկու այլ ուղիղ գծեր, որոնք հավասար են համապատասխանաբար տրված (երկու) ուղիղ գծերին (որոնք հատվում են), չեն կարող կառուցվել (հատվելով) նույն ուղիղ գծի նույն կողմում գտնվող այլ կետում՝ ունենալով նույն ծայրակետերը, ինչ տրված ուղիղ գծերը: (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 8

Եթե երկու եռանկյուններն ունեն երկու կողմեր, որոնք հավասար են երկու կողմերին (համապատասխանաբար), և հիմքը նույնպես հավասար է հիմքին, ապա դրանք նաև կունենան հավասար անկյուններ, որոնք ընդգրկված են հավասար ուղիղ գծերով:

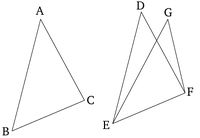
Թող ABC և DEF լինեն երկու եռանկյուններ, որոնց երկու կողմերը՝ AB և AC, հավասար են համապատասխանաբար DE և DF կողմերին։ (Այսինքն՝ AB-ն հավասար է DE-ին, և AC-ն հավասար է DF-ին): Թող նաև հիմքը BC հավասար լինի հիմքին EF: Անկյուն BAC-ն նույնպես հավասար է անկյուն EDF-ին:

Եթե եռանկյուն ABC-ն կիրառվում է DEF-ի վրա, B կետը տեղադրվում է E կետի վրա, և BC ուղիղ գիծը EF-ի վրա, ապա C կետը նույնպես կհամընկնի F կետի հետ՝ BC-ի հավասարության պատճառով EF-ին: Ուստի, BC-ի համընկնելու պատճառով EF-ի հետ, BA և CA կողմերը նույնպես կհամընկնեն ED և DF-ի հետ համապատասխանաբար:

Եթե հիմքը BC-ն համընկնում է հիմքին EF-ին, բայց AB և AC կողմերը չեն համընկնում ED և DF-ի հետ համապատասխանաբար, այլ չեն համապատասխանում, օրինակ, EG և GF ուղիղ գծերի հետ (նկարում ցույց տրված է), ապա մենք կունենանք նույն ուղիղ գծի վրա կառուցված երկու այլ ուղիղ գծեր, որոնք հավասար են երկու տրված ուղիղ գծերին և հատվում են նույն կողմում գտնվող տարբեր կետում՝ ունենալով նույն ծայրակետերը: Բայց (այդպիսի ուղիղ գծեր) չեն կարող կառուցվել [Պնդում 1.7]:

Ուստի, BC հիմքը կիրառվելով EF-ի վրա, BA և AC կողմերը չեն կարող համընկնել ED և DF-ի հետ համապատասխանաբար: Հետևաբար, դրանք կհամընկնեն: Այսպիսով, անկյուն BAC-ն նույնպես կհամընկնի անկյան EDF-ի հետ և հավասար կլինի նրան [Ընդհանուր հասկացություն 4]:

Այսպիսով, եթե երկու եռանկյուններ ունեն երկու կողմեր, որոնք հավասար են երկու կողմերին (համապատասխանաբար), և հիմքը նույնպես հավասար է հիմքին, ապա դրանք նույնպես կունենան հավասար անկյուններ, որոնք ընդգրկված են հավասար ուղիղ գծերով: (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 9

Տրված ուղիղ անկյունը կիսելու համար:

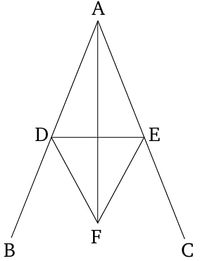
Թող BAC-ն լինի տրված ուղիղ անկյունը։ Այսպիսով, անհրաժեշտ է այն կիսել։

Թող D կետը պատահականորեն վերցված լինի AB-ի վրա, և թող AE-ն, որը հավասար է AD-ին, կտրված լինի AC-ից [Պնդում 1.3], և թող DE-ն միացված լինի: Թող հավասարակողմ եռանկյուն DEF-ն կառուցված լինի DE-ի վրա [Պնդում 1.1], և թող AF-ն միացված լինի: Ես ասում եմ, որ անկյուն BAC-ն կիսված է ուղիղ գծով AF-ով:

Քանի որ AD-ն հավասար է AE-ին, և AF-ը ընդհանուր է, երկու DA, AF ուղիղ գծերը հավասար են EA, AF ուղիղ գծերին համապատասխանաբար։ Եվ հիմքը DF-ն հավասար է հիմքին EF-ին: Այսպիսով, անկյուն DAF-ն հավասար է անկյուն EAF-ին[Պնդում 1.8]:

Այսպիսով, տրված ուղիղ անկյուն BAC-ն կիսված է ուղիղ գծով AF-ով։ (Սա հենց այն է, ինչ անհրաժեշտ էր անել):

Պնդում 10

Տրված վերջավոր ուղիղ գիծը կիսելու համար:

Թող AB-ն լինի տրված վերջավոր ուղիղ գիծը։ Այսպիսով, անհրաժեշտ է կիսել վերջավոր ուղիղ գիծը AB-ն։

Թող հավասարակողմ եռանկյուն ABC-ն կառուցված լինի AB-ի վրա [Պնդում 1.1], և թող անկյուն ACB-ն կիսված լինի ուղիղ գծով CD-ով [Պնդում 1.9]: Ես ասում եմ, որ ուղիղ գիծ AB-ն կիսված է D կետում:

Քանի որ AC-ն հավասար է CB-ին, և CD-ն ընդհանուր է, երկու ուղիղ գծերը AC, CD հավասար են BC, CD ուղիղ գծերին համապատասխանաբար։ Եվ անկյուն ACD-ն հավասար է անկյուն BCD-ին: Այսպիսով, հիմքը AD-ն հավասար է BD հիմքին [Պնդում 1.4]:

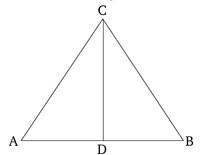
Այսպիսով, տրված վերջավոր ուղիղ գիծը AB կիսված է D կետում։ (Սա հենց այն է, ինչ անհրաժեշտ էր անել):

Պնդում 11

տրված ուղիղ գծին, տրված կետից, որը գտնվում է այդ գծի վրա:

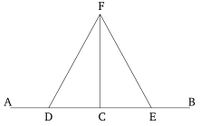
Թող AB լինի տրված ուղիղ գիծը, և C տրված կետը դրա վրա։ Այսպիսով, անհրաժեշտ է գծել ուղիղ գիծ C կետից, որը ուղղանկյուն է կազմում AB ուղիղ գծին։

Թող D կետը պատահականորեն վերցված լինի AC հատվածի վրա, և CE-ն հավասար լինի CD-ին [Պնդում 1.3], և թող FDE հավասարակողմ եռանկյունը կառուցված լինի DE-ի վրա [Պնդում 1.1], և թող FC-ն միացված լինի։ Ես ասում եմ, որ FC ուղիղ գիծը նկարած է ուղղանկյուն տրված AB ուղիղ գծին C կետից:

Քանի որ DC-ն հավասար է CE-ին, և CF-ը ընդհանուր է, երկու ուղիղ գծերը DC, CF հավասար են EC, CF ուղիղ գծերին համապատասխանաբար։ Եվ հիմքը DF-ը հավասար է հիմքին FE: Այսպիսով, անկյուն DCF-ն հավասար է անկյունին ECF [Պնդում 1.8], և դրանք հարակից են։

Երբ ուղիղ գիծ ընկած է (մեկ այլ) ուղիղ գծի վրա և հարակից անկյունները հավասար են միմյանց, յուրաքանչյուր հավասար անկյուն ուղղանկյուն է [Սահմանում 1.10]: Այսպիսով, յուրաքանչյուր անկյուն DCF և FCE ուղղանկյուն է:

Այսպիսով, CF ուղիղ գիծը նկարած է ուղղանկյուն տրված AB ուղիղ գծին C կետից: (Սա հենց այն է, ինչ անհրաժեշտ էր անել):

Պնդում 12

Նկարչել ուղիղ գիծ՝ ուղղահայաց տրված անսահման ուղիղ գծին, տրված կետից, որը չի գտնվում այդ գծի վրա:

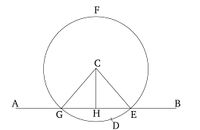
Թող AB-ն լինի տրված անսահման ուղիղ գիծը, իսկ C-ն՝ տրված կետը, որը չի գտնվում AB-ի վրա։ Այսպիսով, անհրաժեշտ է նկարել ուղիղ գիծ՝ ուղղահայաց տրված անսահման AB ուղիղ գծին C կետից, որը չի գտնվում AB-ի վրա։

Թող D կետը պատահականորեն վերցված լինի AB-ի մյուս կողմում (C-ի նկատմամբ), և թող EFG շրջանը գծված լինի C կենտրոնով և CD շառավղով [Աքսիոմա 3], և թող EG ուղիղ գիծը կիսված լինի H կետում [Պնդում 1.10], և թող CG, CH, CE ուղիղ գծերը միացված լինեն։ Ես ասում եմ, որ CH ուղիղ գիծը նկարած է ուղղահայաց տրված անսահման AB ուղիղ գծին C կետից, որը չի գտնվում AB-ի վրա։

Քանի որ GH-ն հավասար է HE-ին, և HC-ն ընդհանուր է, երկու ուղիղ գծերը GH, HC հավասար են EH, HC ուղիղ գծերին համապատասխանաբար, իսկ հիմքը CG-ն հավասար է հիմքին CE։ Այսպիսով, անկյուն CHG-ն հավասար է անկյուն EHC-ին[Պնդում 1.8], և դրանք հարակից են։ Սակայն, երբ ուղիղ գիծը ընկած է (մեկ այլ) ուղիղ գծի վրա և հարակից անկյունները հավասար են միմյանց, յուրաքանչյուր հավասար անկյուն ուղղանկյուն է, իսկ առաջին ուղիղ գիծը կոչվում է ուղղահայաց այն գծին, որի վրա այն կանգնած է [Սահմանում 1.10]։

Այսպիսով, CH ուղիղ գիծը նկարած է ուղղահայաց տրված անսահման AB ուղիղ գծին C կետից, որը չի գտնվում AB-ի վրա։ (Սա հենց այն է, ինչ անհրաժեշտ էր անել):

Պնդում 13

Եթե ուղիղ գիծը ընկած է (մեկ այլ) ուղիղ գծի վրա և ստեղծում է անկյուններ, ապա այն անպայման կամ կստեղծի երկու ուղղանկյուն, կամ (անկյուններ, որոնց գումարը) հավասար կլինի երկու ուղղանկյան։

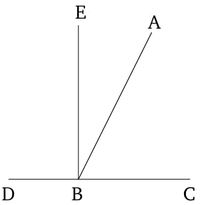
Թող AB ուղիղ գիծը ընկած լինի CD ուղիղ գծի վրա և կազմի CBA և ABD անկյունները։ Ես ասում եմ, որ անկյունները CBA և ABD հաստատ կամ երկու ուղղանկյուն են, կամ գումարը հավասար է երկու ուղղանկյան։

Փաստորեն, եթե CBA-ն հավասար է ABD-ին, ապա դրանք երկու ուղղանկյուն են [Սահմանում 1.10]։ Բայց, եթե ոչ, թող BE-ն գծվի B կետից՝ CD ուղիղ գծին ուղղանկյուն [Պնդում 1.11]։ Այսպիսով, CBE և EBD անկյունները երկու ուղղանկյուն են։ Քանի որ CBE-ն հավասար է երկու անկյունների՝ CBA և ABE-ի, թող EBD-ն ավելացվի երկուսին։ Այսպիսով, անկյունների CBE և EBD գումարը հավասար է CBA, ABE և EBD երեք անկյունների գումարին [Ընդհանուր հասկացություն 2]։

Նույն կերպ, քանի որ DBA-ն հավասար է երկու անկյունների՝ DBE և EBA-ի, թող ABC-ն ավելացվի երկուսին։ Այսպիսով, անկյունների DBA-ի և ABC-ի գումարը հավասար է DBE-ի, EBA-ի, և ABC-ի գումարին [Ընդհանուր հասկացություն 2]։ Բայց անկյունների CBE և EBD գումարը նույնպես ցույց տրվեց, որ հավասար է նույն երեք անկյունների գումարին։ Իսկ բաները, որոնք հավասար են նույնին, նույնպես հավասար են միմյանց [Ընդհանուր հասկացություն 1]։

Հետևաբար, անկյունների CBE և EBD գումարը հավասար է անկյունների DBA և ABC գումարին։ Բայց CBE և EBD-ի գումարը երկու ուղղանկյուն է։ Այսպիսով, ABD և ABC-ի գումարը նույնպես հավասար է երկու ուղղանկյան։

Այսպիսով, եթե ուղիղ գիծը ընկած է (մեկ այլ) ուղիղ գծի վրա և ստեղծում է անկյուններ, ապա այն հաստատ կամ կստեղծի երկու ուղղանկյուն, կամ (անկյուններ, որոնց գումարը) հավասար կլինի երկու ուղղանկյան։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 14

Եթե երկու ուղիղ գծեր, որոնք չեն գտնվում նույն կողմում, հարակից անկյուններ են ստեղծում (որոնց գումարը) հավասար է երկու ուղղանկյան ինչ-որ ուղիղ գծի հետ, դրա վրա գտնվող մի կետում, ապա այդ երկու ուղիղ գծերը կհանդիսանան ուղղահայց (միմյանց նկատմամբ):

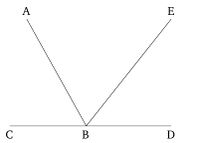
Թող BC և BD ուղիղ գծերը, որոնք չեն գտնվում նույն կողմում, կազմեն հարակից անկյուններ ABC և ABD, որոնց գումարը հավասար է երկու ուղղանկյան AB ուղիղ գծի հետ B կետում։ Ես ասում եմ, որ BD-ն ուղղահայաց է CB-ի նկատմամբ։

Եթե BD-ն ուղիղ չէ BC-ի նկատմամբ, ապա թող BE-ն լինի ուղիղ CB-ի նկատմամբ։ Հետևաբար, քանի որ AB ուղիղ գիծը ընկած է CBE ուղիղ գծի վրա, անկյունների ABC և ABE գումարը հավասար է երկու ուղղանկյան [Պնդում 1.13]։ Բայց անկյունների ABC և ABD գումարը նույնպես հավասար է երկու ուղղանկյան։ Այսպիսով, CBA և ABE անկյունների գումարը հավասար է CBA և ABD անկյունների գումարին [Ընդհանուր հասկացություն 1]։ Թող անկյուն CBA-ն հանվի երկուսից։ Հետևաբար, մնացորդ ABE-ն հավասար է մնացորդ ABD-ին [Ընդհանուր հասկացություն 3], փոքրից մեծին։ Սա անհնար է։ Ուստի, BE-ն ուղղահայաց չէ CB-ի նկատմամբ։ Նույն կերպ, կարող ենք ցույց տալ, որ BD-ից բացի որևէ այլ ուղղահայաց գիծ չկա։ Այսպիսով, CB-ն ուղղահայաց է BD-ի նկատմամբ։

Այսպիսով, եթե երկու ուղիղ գծեր, որոնք չեն գտնվում նույն կողմում, կազմեն հարակից անկյուններ (որոնց գումարը) հավասար է երկու ուղղանկյան ինչ-որ ուղիղ գծի հետ, դրա վրա գտնվող մի կետում, ապա այդ երկու ուղիղ գծերը կլինեն ուղիղ միմյանց նկատմամբ։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 15

Եթե երկու ուղիղ գծեր հատում են միմյանց, ապա նրանք ստեղծում են ուղղահայաց հակադարձ անկյուններ, որոնք հավասար են միմյանց։ Թող AB և CD ուղիղ գծերը հատեն միմյանց E կետում։ Ես ասում եմ, որ անկյուն AEC-ն հավասար է անկյունին DEB, իսկ անկյուն CEB-ն՝ անկյունին AED:

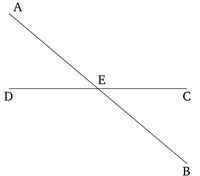
Քանի որ AE ուղիղ գիծը ընկած է CD ուղիղ գծի վրա՝ կազմելով CEA և AED անկյունները, ապա CEA և AED անկյունների գումարը հավասար է երկու ուղղանկյան [Պնդում 1.13]։ Նույն կերպ, քանի որ DE ուղիղ գիծը ընկած է AB ուղիղ գծի վրա՝ կազմելով AED և DEB անկյունները, ապա AED և DEB անկյունների գումարը նույնպես հավասար է երկու ուղղանկյան [Պնդում 1.13]։ Բայց CEA և AED անկյունների գումարը նույնպես ցույց տրվեց, որ հավասար է երկու ուղղանկյան։ Այսպիսով, CEA և AED անկյունների գումարը հավասար է AED և DEB անկյունների գումարին [Ընդհանուր հասկացություն 1]։ Թող AED-ն հանվի երկուսից։ Այսպիսով, CEA-ի մնացորդը հավասար է BED-ի մնացորդին [Ընդհանուր հասկացություն 3]։ Նույն կերպ կարելի է ցույց տալ, որ CEB և DEA անկյունները նույնպես հավասար են։

Այսպիսով, եթե երկու ուղիղ գծեր հատում են միմյանց, ապա նրանք ստեղծում են ուղղահայաց հակառակ անկյուններ, որոնք հավասար են միմյանց։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 16

Ամեն եռանկյունի համար, երբ կողմերից մեկը երկարացվում է, արտաքին անկյունը մեծ է ներքին և հակադիր անկյուններից յուրաքանչյուրից։

Թող ABC լինի եռանկյուն, և թող դրա կողմերից մեկը՝ BC-ն, երկարացվի D։ Ես ասում եմ, որ արտաքին անկյուն ACD-ն մեծ է ներքին և հակադիր անկյուններից յուրաքանչյուրից՝ CBA և BAC-ից։ Թող AC ուղիղ գիծը կիսվի E կետում [Պնդում 1.10]։ BE-ն միացնելով՝ թող այն երկարացվի մինչև F կետ ուղիղ գծով։ EF-ը հավասար լինի BE-ին [Պնդում 1.3], և FC-ն միացվի, և AC-ն անցկացվի G կետով։

Հետևաբար, քանի որ AE-ն հավասար է EC-ին, և BE-ն հավասար է EF-ին, ապա երկու ուղիղ գծերը՝ AE, EB, հավասար են երկու ուղիղ գծերին՝ CE, EF համապատասխանաբար։

Բացի այդ, անկյուն AEB-ն հավասար է անկյունին FEC, քանի որ դրանք ուղղահայաց հակառակ անկյուններ են [Պնդում 1.15]։ Այսպիսով, հիմքը AB-ն հավասար է հիմքին FC, և եռանկյուն ABE-ն հավասար է եռանկյուն FEC-ին, իսկ հավասար կողմերով ստեղծված մնացած անկյունները հավասար են համապատասխան մնացած անկյուններին [Պնդում 1.4]։

Այսպիսով, BAE-ն հավասար է ECF-ին։ Բայց ECD-ն մեծ է ECF-ից։ Հետևաբար, ACD-ն մեծ է BAE-ից։ Նմանապես, BC-ն կիսելով, կարելի է ցույց տալ, որ BCG—այսինքն ACD—ն նույնպես մեծ է ABC-ից։

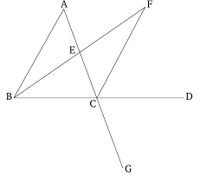
Այսպիսով, ցանկացած եռանկյունի համար, երբ կողմերից մեկը երկարացվում է, արտաքին անկյունը մեծ է ներքին և հակադիր անկյուններից յուրաքանչյուրից։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 17

Ցանկացած եռանկյունի համար, ցանկացած երկու անկյունների (գումարը) միասին վերցված փոքր է երկու ուղղանկյունից։

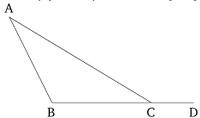
Թող ABC լինի եռանկյուն։ Ես ասում եմ, որ եռանկյուն ABC-ի ցանկացած երկու անկյունների (գումարը) միասին վերցված փոքր է երկու ուղղանկյունից։

Թող BC կողմը երկարացվի մինչև D։ Քանի որ ACD անկյունը եռանկյուն ABC-ի արտաքին անկյունն է, այն մեծ է ներքին և հակադիր ABC անկյունից [Պնդում 1.16]։ Թող ACB անկյունը ավելացվի երկուսին։ Այսպիսով, ACD և ACB անկյունների գումարը մեծ է ABC և BCA անկյունների գումարից։ Բայց ACD և ACB անկյունների գումարը հավասար է երկու ուղղանկյան [Պնդում 1.13]։

Այսպիսով, ABC և BCA անկյունների գումարը փոքր է երկու ուղղանկյունից։ Նմանապես, կարելի է ցույց տալ, որ BAC և ACB անկյունների գումարն էլ փոքր է երկու ուղղանկյունից։ Եվ վերջապես, CAB և ABC անկյունների գումարն էլ փոքր է երկու ուղղանկյունից։

Այսպիսով, ցանկացած եռանկյունի համար, ցանկացած երկու անկյունների (գումարը) միասին վերցված փոքր է երկու ուղղանկյունից։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 18

Ցանկացած եռանկյունում ավելի մեծ կողմը դիմաց է գտնվում ավելի մեծ անկյունին։

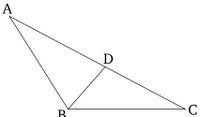
Թող ABC լինի եռանկյուն, որի AC կողմը մեծ է AB-ից։ Ես ասում եմ, որ ABC անկյունը նույնպես մեծ է BCA-ից։ Քանի որ AC-ն մեծ է AB-ից, թող AD-ն լինի հավասար AB-ին [Պնդում 1.3], և թող BD-ն միացվի։ Քանի որ ADB անկյունը եռանկյուն BCD-ի արտաքին անկյունն է, այն մեծ է ներքին և հակադիր DCB անկյունից [Պնդում 1.16]։ Բայց ADB-ն հավասար է ABD-ին, քանի որ AB-ն հավասար է AD-ին [Պնդում 1.5]։ Այսպիսով, ABD-ն նույնպես մեծ է ACB-ից։ Հետևաբար, ABC-ն շատ ավելի մեծ է ACB-ից։ Այսպիսով, ցանկացած եռանկյունում ավելի մեծ կողմը դիմաց է գտնվում ավելի մեծ անկյունին։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 19

Ցանկացած եռանկյունում ավելի մեծ անկյունը դիմաց է գտնվում ավելի մեծ կողմին։

Թող ABC լինի եռանկյուն, որի ABC անկյունը մեծ է BCA-ից։ Ես ասում եմ, որ AC կողմը նույնպես մեծ է AB-ից։ Եթե ոչ, ապա AC-ն կամ հավասար է, կամ փոքր է AB-ից։ Փաստորեն, AC-ն հավասար չէ AB-ին, քանի որ այդ դեպքում ABC անկյունը նույնպես հավասար կլիներ ACB անկյանը [Պնդում 1.5]։ Բայց դա այդպես չէ։ Հետևաբար, AC-ն հավասար չէ AB-ին։ Նույն կերպ, AC-ն փոքր չէ AB-ից, քանի որ այդ դեպքում ABC անկյունը փոքր կլիներ ACB-ից [Պնդում 1.18]։ Բայց դա այդպես չէ։ Հետևաբար, AC-ն ոչ հավասար է, ոչ էլ փոքր AB-ից։ Այսպիսով, AC-ն մեծ է AB-ից։

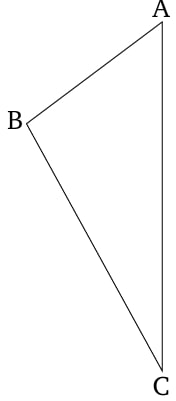
Այսպիսով, ցանկացած եռանկյունում ավելի մեծ անկյունը դիմաց է գտնվում ավելի մեծ կողմին։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 20

Ցանկացած եռանկյունում, ցանկացած երկու կողմերի (գումարը) միասին վերցված մեծ է մնացած (կողմից)։

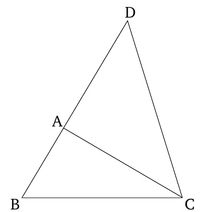
Թող ABC լինի եռանկյուն։ Ես ասում եմ, որ ABC եռանկյունում ցանկացած երկու կողմերի (գումարը) միասին վերցված մեծ է մնացած (կողմից)։ (Այսինքն, BA և AC կողմերի գումարը մեծ է BC-ից, AB և BC կողմերի գումարը մեծ է AC-ից, իսկ BC և CA կողմերի գումարը մեծ է AB-ից)։ Թող BA-ն երկարացվի D կետով, և թող AD-ն հավասար լինի CA-ին [Պնդում 1.3], և թող DC-ն միացվի։

Քանի որ DA-ն հավասար է AC-ին, ապա անկյուն ADC-ն նույնպես հավասար է ACD-ին [Պնդում 1.5]։ Այսպիսով, BCD-ն մեծ է ADC-ից։ Իսկ DCB եռանկյունում, BCD անկյունն ավելի մեծ է BDC-ից, և ավելի մեծ անկյունը դիմաց է գտնվում ավելի մեծ կողմին [Պնդում 1.19], DB-ն մեծ է BC-ից։ Բայց DA-ն հավասար է AC-ին։ Հետևաբար, BA և AC կողմերի գումարը մեծ է BC-ից։ Նմանապես, կարելի է ցույց տալ, որ AB և BC կողմերի գումարը նույնպես մեծ է CA-ից, և BC և CA կողմերի գումարը մեծ է AB-ից։

Այսպիսով, ցանկացած եռանկյունում ցանկացած երկու կողմերի (գումարը) միասին վերցված մեծ է մնացած (կողմից)։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 21

Եթե եռանկյունի կողմերից մեկի վրա նրա ծայրակետերից ներս կառուցվեն երկու ուղիղ գծեր, ապա կառուցված ուղիղ գծերը փոքր կլինեն եռանկյունի մյուս երկու կողմերից, սակայն կկազմեն ավելի մեծ անկյուն։

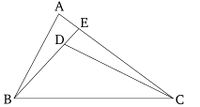
Թող BD և DC երկու ներքին ուղիղ գծեր կառուցված լինեն եռանկյուն ABC-ի BC կողմի վրա՝ իր B և C ծայրերից։ Ես ասում եմ, որ BD և DC-ն փոքր են եռանկյունի մյուս երկու կողմերից՝ BA-ից և AC-ից, սակայն ընդգրկում են անկյուն BDC, որը մեծ է BAC-ից։ Թող BD-ն երկարացվի E կետով։ Եվ քանի որ ցանկացած եռանկյունում (ցանկացած) երկու կողմերի գումարը մեծ է մնացած (կողմից) [Պնդում 1.20], ապա եռանկյուն ABE-ում AB և AE կողմերի գումարը մեծ է BE-ից։ Թող EC-ն ավելացվի երկուսին։ Այսպիսով, BA և AC կողմերի գումարը մեծ է BE և EC գումարից։ Նույն կերպ, եռանկյուն CED-ում CE և ED կողմերի գումարը մեծ է CD-ից։ Թող DB-ն ավելացվի երկուսին։ Այսպիսով, CE և EB կողմերի գումարը մեծ է CD և DB գումարից։ Սակայն ցույց տրվեց, որ BA և AC կողմերի գումարը մեծ է BE և EC գումարից։ Հետևաբար, BA և AC կողմերի գումարը շատ ավելի մեծ է BD և DC գումարից։

Կրկին, քանի որ ցանկացած եռանկյունում արտաքին անկյունը մեծ է ներքին և հակադիր անկյուններից [Պնդում 1.16], ապա եռանկյուն CDE-ում արտաքին անկյուն BDC-ն մեծ է CED-ից։ Հետևաբար, նույն պատճառով, եռանկյուն ABE-ում արտաքին անկյուն CEB-ն նույնպես մեծ է BAC-ից։ Բայց BDC-ն ցույց տրվեց, որ մեծ է CEB-ից։ Հետևաբար, BDC-ն շատ ավելի մեծ է BAC-ից։

Այսպիսով, եթե երկու ներքին ուղիղ գծեր կառուցված են եռանկյունի կողմերից մեկի վրա՝ նրա ծայրերից, ապա կառուցված ուղիղ գծերը փոքր կլինեն եռանկյունի մյուս երկու կողմերից, սակայն ընդգրկում են ավելի մեծ անկյուն։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 22

Եռանկյուն կառուցելու համար երեք ուղիղ գծերից, որոնք հավասար են երեք տրված ուղիղ գծերին, անհրաժեշտ է, որ ցանկացած երկու ուղիղ գծերի (գումարը) միասին վերցված մեծ լինի մնացածից։ Սա հիմնված է այն փաստի վրա, որ ցանկացած եռանկյունում ցանկացած երկու կողմերի (գումարը) միասին վերցված մեծ է մնացած (կողմից) [Պնդում 1.20]։

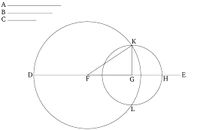
Թող A, B և C-ն լինեն երեք տրված ուղիղ գծեր, որոնցից ցանկացած երկու ուղիղ գծերի (գումարը) միասին վերցված մեծ է մնացածից։ (Այսինքն, A և B գումարը մեծ է C-ից, A և C գումարը մեծ է B-ից, և B և C գումարը մեծ է A-ից): Պետք է կառուցել եռանկյուն, որի կողմերը հավասար են A, B և C ուղիղ գծերին։

Թող կամայական ուղիղ գիծ DE տեղադրվի, ավարտվի D-ում և լինի անսահման դեպի E-ն։ Թող DF-ը հավասար լինի A-ին, FG-ն հավասար լինի B-ին, և GH-ն հավասար լինի C-ին [Պնդում 1.3]։ Թող շրջան DKL կառուցվի կենտրոնով F-ում և շառավղով FD։ Նույն կերպ, թող շրջան KLH կառուցվի կենտրոնով G-ում և շառավղով GH։ Թող KF և KG գծերը միացվեն։ Ես ասում եմ, որ եռանկյուն KFG-ն կառուցված է A, B, և C ուղիղ գծերից։

Քանի որ F կետը շրջանի DKL կենտրոնն է, FD-ն հավասար է FK-ին։ Բայց FD-ն հավասար է A-ին։ Հետևաբար, KF-ն նույնպես հավասար է A-ին։ Նույն կերպ, G կետը շրջանի KLH կենտրոնն է, GH-ն հավասար է GK-ին։ Բայց GH-ն հավասար է C-ին։ Հետևաբար, KG-ն նույնպես հավասար է C-ին։ FG-ն նույնպես հավասար է B-ին։ Այսպիսով, KF, FG, և GK ուղիղ գծերը հավասար են A, B, և C ուղիղ գծերին (համապատասխանաբար):

Այսպիսով, եռանկյուն KFG-ն կառուցված է KF, FG, և GK ուղիղ գծերից, որոնք հավասար են տրված A, B, և C ուղիղ գծերին (համապատասխանաբար): (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ):

Պնդում 23

Կառուցել ուղիղ անկյուն, որը հավասար է տրված ուղիղ անկյանը՝ տրված ուղիղ գծի վրա տրված կետում։

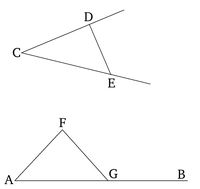
Թող AB լինի տրված ուղիղ գիծը, A՝ նրա վրա գտնվող տրված կետը, և DCE՝ տրված ուղիղ անկյունը։ Ուրեմն անհրաժեշտ է կառուցել DCE ուղիղ անկյանին հավասար անկյուն FAG AB տրված ուղիղ գծի վրա A կետում։

Թող D և E կետերը վերցվեն պատահականորեն ուղիղ գծերի CD և CE վրա (համապատասխանաբար), և թող DE-ն միացվի։ Թող եռանկյուն AFG կառուցվի երեք ուղիղ գծերից, որոնք հավասար են CD, DE, և CE ուղիղ գծերին, այնպես, որ CD-ն հավասար լինի AF-ին, CE-ն հավասար լինի AG-ին, և DE-ն հավասար լինի FG-ին [Պնդում 1.22]։

Հետևաբար, քանի որ երկու ուղիղ գծերը՝ DC և CE, հավասար են երկու ուղիղ գծերին՝ FA և AG, իսկ DE հիմքը հավասար է FG-ին, ապա անկյուն DCE-ն հավասար է անկյուն FAG-ին [Պնդում 1.8]։

Այսպիսով, FAG ուղիղ անկյունը, որը հավասար է տրված DCE ուղիղ անկյանը, կառուցված է AB տրված ուղիղ գծի վրա A տրված կետում։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ)։

Պնդում 24

Եթե երկու եռանկյուններ ունեն երկու կողմեր, որոնք հավասար են միմյանց համապատասխանաբար, բայց դրանցից մեկը ունի հավասար ուղիղ գծերով պարփակված անկյուն, որը մեծ է մյուսի համապատասխան անկյունից, ապա առաջին եռանկյունը նույնպես կունենա հիմք, որը մեծ է երկրորդի հիմքից։

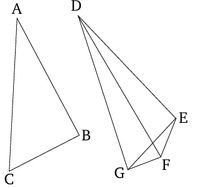
Թող ABC և DEF լինեն երկու եռանկյուններ, որոնց AB և AC կողմերը հավասար են DE և DF կողմերին, համապատասխանաբար։ (Այսինքն, AB հավասար է DE-ին, իսկ AC հավասար է DF-ին)։ Թող դրանք նաև ունենան միևնույն անկյունը A կետում և D կետում։ Ես ասում եմ, որ հիմքը BC-ն նույնպես մեծ է հիմքից EF։

Քանի որ անկյուն BAC-ը մեծ է EDF անկյունից, թող EDG անկյունը, որը հավասար է BAC-ին, կառուցվի D կետում DE ուղիղ գծի վրա [Պնդում 1.23]։ Թող DG-ն հավասար լինի AC-ին կամ DF-ին [Պնդում 1.3], և թող EG և FG միացվեն։

Քանի որ AB-ն հավասար է DE-ին և AC-ն հավասար է DG-ին, BA և AC ուղիղ գծերը հավասար են ED և DG ուղիղ գծերին, համապատասխանաբար։ BAC անկյունը նույնպես հավասար է EDG անկյանը։ Հետևաբար, BC հիմքը հավասար է EG հիմքին [Պնդում 1.4]։ Նույնպես, քանի որ DF-ն հավասար է DG-ին, DGF անկյունը նույնպես հավասար է DFG անկյանը [Պնդում 1.5]։ Այսպիսով, DFG-ն մեծ է EGF-ից։ Եվ քանի որ եռանկյուն EFG-ն ունի անկյուն EFG, որը մեծ է EGF-ից, իսկ մեծ անկյունը դիմաց է գտնվում ավելի մեծ կողմին [Պնդում 1.19], EG կողմը մեծ է EF-ից։ Բայց EG-ն հավասար է BC-ին։ Այսպիսով, BC-ն նույնպես մեծ է EF-ից։

Այսպիսով, եթե երկու եռանկյուններ ունեն երկու կողմեր, որոնք հավասար են միմյանց համապատասխանաբար, բայց դրանցից մեկը ունի հավասար ուղիղ գծերով պարփակված անկյուն, որը մեծ է մյուսի համապատասխան անկյունից, ապա առաջին եռանկյունը նույնպես կունենա հիմք, որը մեծ է երկրորդի հիմքից։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ)։

Պնդում 25

Եթե երկու եռանկյուններ ունեն երկու կողմեր, որոնք հավասար են միմյանց համապատասխանաբար, բայց դրանցից մեկի հիմքը մեծ է մյուսի հիմքից, ապա առաջին եռանկյունն ունի նաև հավասար ուղիղ գծերով պարփակված անկյուն, որը մեծ է մյուսի համապատասխան անկյունից։

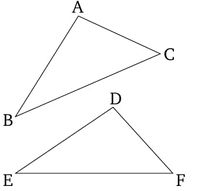
Թող ABC և DEF լինեն երկու եռանկյուններ, որոնց AB և AC կողմերը հավասար են DE և DF կողմերին, համապատասխանաբար։ (Այսինքն՝ AB հավասար է DE-ին, AC հավասար է DF-ին): Թող նաև BC հիմքը մեծ լինի EF հիմքից։ Ես ասում եմ, որ BAC անկյունը նույնպես մեծ է EDF անկյունից։

Եթե ոչ, BAC անկյունը կամ հավասար է, կամ փոքր է EDF անկյունից։ Սակայն BAC անկյունը հավասար չէ EDF անկյունին, քանի որ այդ դեպքում BC հիմքը նույնպես հավասար կլիներ EF հիմքին [Պնդում 1.4]։ Բայց դա այդպես չէ։ Նույնպես, BAC անկյունը փոքր չէ EDF անկյունից, քանի որ այդ դեպքում BC հիմքը նույնպես փոքր կլիներ EF հիմքից [Պնդում 1.24]։ Բայց դա նույնպես այդպես չէ։ Հետևաբար, BAC անկյունը ոչ հավասար է, ոչ էլ փոքր EDF անկյունից։ Այսպիսով, BAC անկյունը մեծ է EDF անկյունից։

Այսպիսով, եթե երկու եռանկյուններ ունեն երկու կողմեր, որոնք հավասար են միմյանց համապատասխանաբար, բայց դրանցից մեկի հիմքը մեծ է մյուսի հիմքից, ապա առաջին եռանկյունն ունի նաև հավասար ուղիղ գծերով պարփակված անկյուն, որը մեծ է մյուսի համապատասխան անկյունից։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ)։

Պնդում 26

Եթե երկու եռանկյուններ ունեն երկու անկյուններ, որոնք հավասար են միմյանց համապատասխանաբար, և մեկ կողմ, որը հավասար է մեկ այլ կողմի՝ կամ հավասար անկյունների կողքին գտնվող, կամ դրանցից մեկի դիմաց գտնվող կողմը, ապա այդ եռանկյունները նույնպես կունենան մնացած կողմերը հավասար իրենց համապատասխան մնացած կողմերին, և մնացած անկյունը՝ հավասար մնացած անկյունին։

Թող ABC և DEF լինեն երկու եռանկյուններ, որոնց երկու անկյունները՝ ABC և BCA, հավասար են DEF և EFD անկյուններին, համապատասխանաբար։ (Այսինքն՝ ABC հավասար է DEF-ին, իսկ BCA հավասար է EFD-ին)։ Թող նրանք ունենան նաև մեկ կողմ, որը հավասար է մեկ այլ կողմի։ Նախ, թող դա լինի հավասար անկյունների կողքին գտնվող կողմը։ (Այսինքն՝ BC հավասար է EF-ին): Ես ասում եմ, որ նրանք կունենան մնացած կողմերը հավասար իրենց համապատասխան մնացած կողմերին։ (Այսինքն՝ AB հավասար է DE-ին, իսկ AC հավասար է DF-ին)։ Եվ նրանք կունենան մնացած անկյունը՝ հավասար մնացած անկյունին։ (Այսինքն՝ BAC հավասար է EDF-ին)։

Եթե AB հավասար չէ DE-ին, ապա դրանցից մեկը մեծ է։ Թող AB-ն լինի մեծը, և BG-ն թող հավասար լինի DE-ին [Պնդում 1.3], և թող GC-ն միացվի։

Քանի որ BG-ն հավասար է DE-ին, իսկ BC-ն հավասար է EF-ին, ապա GB, BC ուղիղ գծերը հավասար են DE, EF ուղիղ գծերին, համապատասխանաբար։ Եվ GBC անկյունը հավասար է DEF անկյունին։ Այսպիսով, GC հիմքը հավասար է DF հիմքին, և GBC եռանկյունը հավասար է DEF եռանկյունին։ Եվ հավասար կողմերի դիմաց ընկած մնացած անկյունները նույնպես հավասար են համապատասխան մնացած անկյուններին [Պնդում 1.4]։ Այսպիսով, GCB հավասար է DFE-ին։ Բայց DFE-ն ընդունվում էր հավասար BCA-ին։ Այսպիսով, BCG-ն նույնպես հավասար է BCA-ին, ինչը անհնար է։ Հետևաբար, AB-ն հավասար չէ DE-ին։ Այսպիսով, դրանք հավասար են։ Եվ BC-ն նույնպես հավասար է EF-ին։ Այսպիսով, AB, BC ուղիղ գծերը հավասար են DE, EF ուղիղ գծերին, համապատասխանաբար։ Եվ ABC անկյունը հավասար է DEF անկյունին։ Այսպիսով, AC հիմքը հավասար է DF հիմքին, և մնացած անկյունը BAC հավասար է EDF անկյունին [Պնդում 1.4]։

Բայց, կրկին, թող հավասար անկյունների դիմաց ընկած կողմերը հավասար լինեն։ Օրինակ, AB-ն հավասար է DE-ին։ Ես ասում եմ, որ մնացած կողմերը նույնպես հավասար կլինեն։ (Այսինքն՝ AC-ն հավասար է DF-ին, և BC-ն հավասար է EF-ին): Հետևաբար, մնացած անկյունը BAC հավասար է մնացած անկյունին EDF-ին։

Այսպիսով, եթե երկու եռանկյուններ ունեն երկու անկյուններ, որոնք հավասար են միմյանց համապատասխանաբար, և մեկ կողմ, որը հավասար է մեկ այլ կողմի՝ կամ հավասար անկյունների կողքին գտնվող, կամ դրանցից մեկի դիմաց գտնվող կողմը, ապա այդ եռանկյունները նույնպես կունենան մնացած կողմերը հավասար իրենց համապատասխան մնացած կողմերին, և մնացած անկյունը՝ հավասար մնացած անկյունին։ (Սա հենց այն է, ինչ անհրաժեշտ էր ցույց տալ)։

Պնդում 27

Եթե երկու ուղիղներ հատող ուղիղը ստեղծում է հավասար խաչադիր անկյուններ, ապա այդ երկու ուղիղները զուգահեռ են։

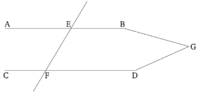
AB և CD ուղիղները հատող EF ուղիղը ստեղծում է AEF և EFD խաչադիր անկյուններ, որոնք հավասար են միմյանց։ Պնդումն այն է, որ AB և CD ուղիղները զուգահեռ են։

Հակառակ դեպքում, AB-ն և CD-ն անպայման կհատվեին՝ կամ B և D ուղղություններով, կամ A և C ուղղություններով [Պնդում 1.23]: Ենթադրենք դրանք հատվում են B և D ուղղություններով G կետում։ Այսպիսով, GEF եռանկյան արտաքին AEF անկյունը հավասար է ներքին և հակադիր EFG անկյանը։ Դա անհնար է [Պնդում 1.16]: Հետևաբար AB և CD ուղիղները՝ գծվելով, չեն հատվի B և D ուղղությամբ։ Նմանապես, կարող ենք ցույց տալ, որ դրանք չեն հատվի A և C ուղղություններվ։ Բայց ուղիղները, որոնք չեն հատվում ոչ մի ուղղությամբ, զուգահեռ են [Սահմանում 1.23]: Հետևաբար, AB և CD ուղիղները զուգահեռ են։

Հետևաբար, եթե երկու ուղիղներ հատող ուղիղը ստեղծում է հավասար խաչադիր անկյուններ, ապա այդ երկու ուղիղները զուգահեռ են։ Սա այն էր, ինչ պետք էր ապացուցել։

Pages 31-48

Պնդում 28

Եթե երկու ուղիղները հատող ուղիղը կազմում է արտաքին անկյուն, որը հավասար է ներքին և հակադիր անկյանը նույն կողմի վրա կամ նույն կողմի վրա գտնվող անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների, ապա այդ երկու ուղիղները զուգահեռ են։

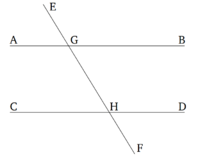
EF ուղիղը, որը հատում է AB և CD ուղիղները, կազմում է EGB արտաքին անկյուն, որը հավասար է ներքին և հակադիր GHD անկյանը, կամ նույն կողմի վրա գտնվող BGH և GHD անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների։ Պնդումն այն է, որ AB և CD ուղիղները զուգահեռ են։

Առաջին դեպքում EGB անկյունը հավասար է GHD անկյանը, բայց EGB անկյունը նաև հավասար է AGH անկյանը [Պնդում 1.15], հետևաբար, AGH անկյունը հավասար է GHD անկյանը։ Դրանք նաև խաչադիր անկյուններ են։ Հետևաբար, AB և CD ուղիղները զուգահեռ են [Պնդում. 1.27]։

Երկրորդ դեպքում, կրկին, BGH և GHD անկյունների գումարը հավասար է երկու ուղիղ անկյունների, ինչպես նաև AGH և BGH անկյունների գումարն է հավասար երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, AGH և BGH անկյունների գումարը հավասար է BGH և GHD անկյունների գումարին։ Երկուսից էլ հանենք BGH անկյունը։ Հետևաբար, մնացորդ AGH անկյունը հավասար է մնացորդ GHD անկյանը և դրանք խաչադիր անկյուններ են։ Հետևաբար, AB և CD ուղիղները զուգահեռ են [Պնդում 1.27]։

Հետևաբար, եթե երկու ուղիղները հատող ուղիղը կազմում է արտաքին անկյուն, որը հավասար է ներքին և հակադիր անկյանը նույն կողմի վրա կամ նույն կողմի վրա գտնվող անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների, ապա այդ երկու ուղիղները զուգահեռ են։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 29

Զուգահեռ ուղիղները հատող ուղղիղը ստեղծում է հավասար խաչադիր անկյուններ, արտաքին անկյուն՝ հավասար ներքին և հակադիր անկյանը, և նույն կողմի վրա գտնվող ներքին անկյունների գումարը հավասարվում է երկու ուղիղ անկյունների։

EF ուղիղը հատում է զուգահեռ AB և CD ուղիղները։ Պնդումն այն է, որ այն դարձնում է AGH և GHD անկյունները հավասար, EGB արտաքին անկյունը՝ հավասար ներքին և հակադիր GHD անկյանը, և նույն կողմի վրա գտնվող BGH և GHD ներքին անկյունների գումարը՝ հավասար երկու ուղիղ անկյունների։

Եթե AGH անկյունը հավասար չէ GHD անկյանը, ապա նրանցից մեկը մեծ է։ Ենթադրենք AGH անկյունը մեծ է։ Երկու անկյուններին ավելացնենք BGH անկյունը։ Հետևաբար, AGH և BGH անկյունների գումարը մեծ է BGH և GHD անկյունների գումարից։ Բայց, AGH և BGH անկյունների գումարը հավասար է երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, BGH և GHD անկյունների գումարը փոքր է երկու ուղիղ անկյուններից։ Բայց, ուղիղները գծված են անվերջ ներքին անկյուններից, որոնց գումարը փոքր է հատվող երկու ուղիղ անկյուններից [Կանխադրույթ 5]: Հետևաբար, անվերջ գծված AB և CD ուղիղները կհատվեն։ Բայց, նրանք չեն հատվում, եթե հաշվի առնենք, որ իսկզբանե դրանք զուգահեռ էին [Սահմանում 1.23]։ Հետևաբար, AGH և GHD անկյունները չեն կարող հավասար չլինել՝ հավասար են։ Բայց, AGH և EGB անկյունները նույնպես հավասար են [Պնդում 1.15]։ EGB անկյունը, հետևաբար, հավասար է GHD անկյանը։ Երկուսին էլ ավելացնենք BGH անկյունը։ Հետևաբար, EGB և BGH անկյունների գումարը հավասար է BGH և GHD անկյունների գումարին։ Բայց, EGB և BGH անկյունների գումարը հավասար է երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, BGH և GHD անկյունների գումարը նույնպես հավասար է երկու ուղիղ անկյունների։

Հետևաբար, զուգահեռ ուղիղները հատող ուղղիղը ստեղծում է հավասար հակադիր անկյուններ, արտաքին անկյուն՝ հավասար ներքին և հակադիր անկյանը, և նույն կողմի վրա գտնվող ներքին անկյունների գումարը հավասարվում է երկու ուղիղ անկյունների։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 30

Նույն ուղղին զուգահեռ ուղիղները նաև զուգահեռ են միմյանց։

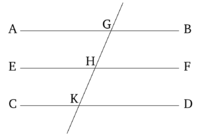
AB և CD ուղիղներից յուրաքանչյուրը զուգահեռ է EF ուղղին։

Պնդումն այն է, որ AB և CD ուղիղները նույնպես զուգահեռ են։ GK ուղիղը հատում է AB, CD և EF ուղիղները։

Քանի որ GK ուղիղը հատում է EB և EF զուգահեռ ուղիղները, AGK անկյունը, հետևաբար, հավասար է GHF անկյանը [Պնդում 1.29]։ Կրկին, քնաի որ GK ուղիղը հատում է EF և CD զուգահեռ ուղիղները, GHF անկյունը հավասար է GKD անկյանը [Պնդում 1.29]։ Բայց ցույց տրվեց, որ AGK անկյունը հավասար է GHF անկյանը։ Հետևաբար, AGK անկյունը հավասար է GKD անկյանը և դրանք խաչադիր անկյուններ են։ Հետևաբար, AB ուղիղը զուգահեռ է CD ուղղին [Պնդում 1.27]։

Հետևաբար, նույն ուղղին զուգահեռ ուղիղները նաև զուգահեռ են միմյանց։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 31

Գծել ուղիղ, զուգահեռ տրված ուղղին, որը կանցնի տրված կետով։

A-ն տրված կետն է և BC-ն տրված ուղիղը։ Պահանջվում է գծել ուղիղ, որը զուգահեռ կլինի BC ուղղին և կանցնի A կետով։

BC ուղղի վրա վերցնենք պատահական D կետ և գծենք AD հատավծը։

ADC անկյանը հավասար DAE անկյունը կառուցված է DA ուղղի վրա՝ A կետում [Պնդում 1.23]։ AF ուղիղը կառուցված է EA ուղղի վրա։

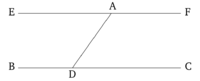
Քանի որ AD ուղիղը՝ հատելով BC և EF ուղիղները, ստեղծում է խաչադիր EAD և ADC անկյունները, EAF ուղիղը հավասար է BC ուղղին [Պնդում 1.27]:

Հետևաբար, EAF ուղիղը գծված է զուգահեռ տրված BC ուղղին և անցնում է տրված A կետով։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 32

Եթե ցանկացած եռանկյան կողմերից մեկը ընդարձակենք, ապա արտաքին անկյունը հավասար կլինի երկու ներքին և հակադիր անկյունների գումարին, իսկ երեք ներքին անկյունների գումարը հավասար կլինի երկու ուղիղ անկյունների։

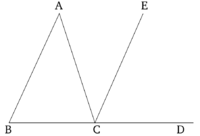
ABC-ն եռանկյուն է և նրա կողմերից մեկին՝ BC-ին, ավելացված է D հատվածը։ Պնդումն այն է, որ ACD արտաքին անկյունը հավասար է երկու ներքին և հակադիր անկյուններ CAB-ի և ABC-ի գումարին և եռանկյան երեք ներքին անկյունների՝ ABC, BCA, և CAB, գումարը հավասար է երկու ուղիղ անկյան։

AB ուղղին զուգահեռ գծված է CE ուղիղը, որն անցնում է C կետով [Պնդում 1.31]։

Քանի որ AB և CE հատվածները զուգահեռ են, BAC և ACE խաչադիր անկյունները իրար հավասար են [Պնդում 1.29]։ Կրկին, քանի որ AB և CE ուղիղները զուգահեռ են և BD ուղիղը հատում է դրանք ECD արտաքին անկյունը հավասար է ABC ներքին և հակադիր անկյանը [Պնդում 1.29]։ Բայց, ցույց է տրված, որ ACE անկյունը հավասար է BAC անկյանը։ Հետևաբար, ACD անկյունը ամբողջությամբ հավասար է երկու ներքին և հակադիր անկյունների՝ BAC-ի և ABC-ի, գումրին։

Երկու անկյուններին ավելացնենք ACB անկյունը։ Հետևաբար, ACD և ACB անկյուննեի գումարը հավասար է երեք անկյուններ ABC, BCA, և CAB-ի գումարին։ Բայց, ACD և ACB անկյունների գումարը հավասար է երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, ACB, CBA և CAB անկյունների գումարը նույնպես հավասար է երկու ուղիղ անկյան։

Հետևաբար, եթե ցանկացած եռանկյան կողմերից մեկը ընդարձակենք, ապա արտաքին անկյունը հավասար կլինի երկու ներքին և հակադիր անկյունների գումարին, իսկ երեք ներքին անկյունների գումարը հավասար կլինի երկու ուղիղ անկյունների։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 33

Ուղիղները, որոնք միացնում են հավասար և զուգահեռ ուղիղներ նույն կողմի վրա, նույնպես հավասար են և զուգահեռ։

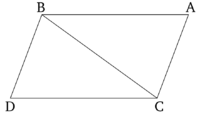
AB և CD ուղիղները հավասար են և զուգահեռ, իսկ AC և BD ուղիղները միացնում են դրանք նույն կողմի վրա։ Պնդումն այն է, որ AC և BD ուղիղները նույնպես հավասար են և զուգահեռ։

Գծված է BC անկյունագիծը։ Քանի որ AB-ն զուդահեռ է CD-ին և BC-ն հատում է դրանք, ABC և BCD խաչադիր անկյունները հավասար են միմյանց [Պնդում 1.29]։ Քանի որ AB-ն հավասար է CD-ին և BC-ն ընդհանուր է, AB և BC ուղիղները հացվասար են DC և CB ուղիղներին։ Նաև ABC անկյունը հավասար է BCD անկյանը։ Հետևաբար, AC հիմքը հավասար է BD հիմքին և ABC եռանկյունը հավասար է BCD եռանկյանը։ Մյուս անկյունները նույնպես հավասար կլինեն համապատասխան անկյուններին, որոնք հենվում են հավասար կեղմերի վրա [Պնդում 1.4]։ Հետևաբար, ACB անկյունը հավասար է CBD անկյանը։ Նաև, քանի որ BC ուղիղը, որը հատում է AC և BD ուղիղները, կազմում է խաչադիր և հավասար ACB և CBD անկյունները, AC ուղիղը, հետևաբար, հավասար է BD ուղղին [Պնդում 1.27]։ Նաև ցույց է տրված, որ AC ուղիղը հավասար է BD ուղղին:

Հետևաբար, ուղիղները, որոնք միացնում են հավասար և զուգահեռ ուղիղներ նույն կողմի վրա, նույնպես հավասար են և զուգահեռ։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 34

Զուգահեռագիծ պատկերներում հակառակ կողմերն ու անկյունները հավասար են միմյանց, իսկ անկյունագիծը կիսում է դրանք հավասար մասերի:

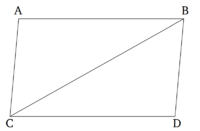
ACDB-ն զուգահեռագիծ պատկեր է և BC-ն դրա անկյունագիծն է։ Պնդումն այն է, որ ACDB զուգահեռագծում հակադիր կողմերը և անկյունները հավասար են միմյանց և BC անկյունագիծը կիսում է այն հավասար մասերի։

Քանի որ AB ուղիղը զուգահեռ է CD ուղղին և BC ուղիղը հատում է դրանք, խաչադիր ABC և BCD անկյունները հավասար են միմյանց [Պնդում 1.29]։ Կրկին, քանի որ AC և BD ուղիղները զուգահեռ են և BC ուղիղը հատում է դրանք, խաչադիր ACB և CBD անկյունները հավասար են միմյանց [Պնդում 1.29]։

Այսպիսով, ABC-ն և BCD-ն երկու եռանկյուններ են, որոնց համապատասխան ABC և BCA ու BCD և CBD անկյունները համապատասխանաբար հավասար են միմյանց և նրանց մի կողմը՝ հավասար անկյուններով, ընդհանուր է։ Դա BC կողմն է։ Հետևաբար, դրանց համապատասխան կողմերը նունյպես հավասար են և երրորդ անկյունը նույնպես համապատասխանաբար հավասար է [Պնդում 1.26]։ Հետևաբար, AB կողմը հավասար է CD կողմին և AC կողմը հավասար է BD կողմին։ Ավելին, BAC անկյունը հավասար է CDB անկյանը։ Քանի որ ABC անկյունը հավասար է BCD անկյանը և CBD անկյունը հավասար է ACB անկյանը, ամբողջ ABD անկյունը, հետևաբար, հավասար է ամբողջ ACD անկյանը։ Ցույց է տրված նաև, որ BAC-ն հավասար է CDB-ին։

Հետևաբար, զուգահեռագիծ պատկերում հակադիր կողմերը և անկյունները հավասար են միմյանց։

Նաև պնդումն այն է, որ անկյունագիծը կիսում է այն երկու հավասար մասի։ Քանի որ AB կողմը հավասար է CD կողմին և BC-ն ընդհանուր է AB և BC ուղիղները, համապատասխանաբար, հավասար են DC և CB ուղիղներին։ Նաև ABC անկյունը հավասար է BCD անկյանը։ Հետևաբար, AC հիմքը նույնպես հավասար է DB-ին և ABC եռանկյունը հավասար է BCD եռանկյանը [Պնդում 1.4]։

Հետևաբար, BC անկյունագիծը կիսում է ACDB զուգահեռագիծը երկու հավասար մասի։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 35

Նույն հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված զուգահեռագծերը հավասար ^[2] են միմյանց։

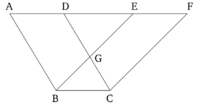
Նույն BC հիմքով ABCD և EBCF զուգահեռագծերը կառուցված են AF և BC զուգահեռ ուղիղների միջև։ Պնդումն այն է, որ ABCD և EBCF զուգահեռագծերը հավասար են։

Քանի որ ABCD-ն զուգահեռագիծ է AD-ն հավասար է BC-ին [Պնդում 1.34]։ Նույն պատճառով EF-ը հավասար է BC-ին։ Հետևաբար, ամբողջ AE ուղիղը հավասար է ամբողջ DF ուղղին։ AB-ն նույնպես հավասար է DC-ին։ Այսպիսով EA և AB ուղիղները համապատասխանաբար հավասար են FDև DC ուղիղներին։ Իսկ FDC անկյունը հավասար է EAB անկյանը՝ արտաքինը ներքինին [Պնդում 1.29]: Հետևաբար EB հիմքը հավասար է FC հիմքին և EAB եռանկյունին հավասար է DFC եռանկյունուն [Պնդում 1.4]: Երկուսից էլ հանենք DGE-ն։ Հետևաբար, հավելյալ ABGD սեղանը հավասար է հավելյալ EGCF սեղանին։ Երկուսին էլ ավելացնենք GBC եռանկյունը։ Հետևաբար, ամբողջ ABCD զուգահեռագիծը հավասար է ամբողջ EBCF զուգահեռագծին։

Հետևաբար, նույն հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված զուգահեռագծերը հավասար։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 36

Հավասար հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված զուգահեռագծերը հավասար են միմյանց։

ABCD-ն և EFGH-ն զուգահեռագծեր են, որոնք կառուցված են հավասար BC և FG հիմքերով և AH և BG նույն զուգահեռ ուղիղների միջև։ Պնդումն այն է, որ ABCD և EFGH զուգահեռագծերը հավասար են։

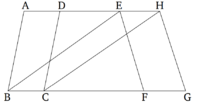
Գծված են BE և CH ուղիղները։ Քանի որ BC-n հավասար է FG-ին և FG-ն էլ հավասար է EH-ին [Պնդում 1.34], հետևաբար, BC-ն հավասար է EH-ին։ Նրանք նաև զուգահեռ են և EB ու HC ուղիղները միացնում են դրանք։ Բայց ուղիղները, որոնք միացնում են հավասար և զուգահեռ ուղիղներ նույն կողմի վրա, իրենք էլ հավասար են և զուգահեռ [Պնդում 1.33] (հետևաբար EB-ն և HC-ն նույնպես հավասար են և զուգահեռ)։ Հետևաբար, EBCH-ը զուգահեռագիծ է [Պնդում 1.34] և հավասար է ABCD-ին: Այն ունի նույն BC հիմքը, այնպես ինչպես ABCD-ն և գտնվում է նույն BC և AH զուգահեռների միջև, այնպես ինչպես ABCD-ն [Պնդում 1.35]։ Նույն պատճառով EFGH-ն հավասար է նույն EBCH զուգահեռագծին [Պնդում 1.34]։ Այսպիսով, ABCD զուգահեռագիծը հավասար է EFGH զուգահեռագծին։

Հետևաբար, հավասար հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված զուգահեռագծերը հավասար են միմյանց։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 37

Նույն հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված եռանկյունները հավասար են միմյանց։

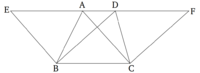
ABC և DBC եռանկյունները կառուցված են նույն BC հիմքով և նույն AD և BC զուգահեռ ուղիղների միջև։ Պնդումն այն է, որ ABC եռանկյունը հավասար է DBC եռանկյանը։

AD-ն ձգված է E և F ուղղություններով և B կետով գծված է BE ուղիղը, զուգահեռ CA-ին [Պնդում 1.31]։ Նաև C կետով գծված է CF ուղիղը, զուգահեռ BD-ին [Պնդում 1.31]։ Հետևաբար, EBCA-ն և DBCF-ն զուգահեռագծեր են և հավասար են։ Դրանք նույն BC հիմքի վրա են և գտնվում են նույն BC և EF զուգահեռ ուղիղների միջև [Պնդում 1.35]։ ABC եռանկյունը EBCA զուգահեռագծի կեսն է։ AB անկյունագիծը կիսում է վերջինս երկու մասի [Պնդում 1.34]։ DBC եռանկյունը DBCF զուգահեռագծի կեսն է։ DC անկյունագիծը կիսում է վերջինս երկու մասի [Պնդում 1.34] (հավասար պատկերների կեսերը հավասար են միմյանց)։ Հետևաբար, ABC եռանկյունը հավասար է DBC եռանկյանը։

Հետևաբար, նույն հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված եռանկյունները հավասար են միմյանց։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 38

Հավասար հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված եռանկյունները հավասար են միմյանց։

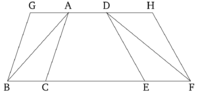
ABC և DEF եռանկյունները կառուցված են հավասար BC և EF հիմքերով և նույն BF և AD զուգահեռ ուղիղների միջև։ Պնդումն այն է, որ ABC եռանկյունը հավասար է DEF եռանկյանը։

AD-ն ձգված է G և H ուղղություններով և B կետով գծված է BG ուղիղը, զուգահեռ CA-ին [Պնդում 1.31]: Նաև F կետով գծված է FH ուղիղը, զուգահեռ DE-ին [Պնդում 1.31]։ Հետևաբար, GBCA-ն և DEFH-ն զուգահեռագծեր են և հավասար են։ Դրանք հավասար BC և EF հիմքերի վրա են և գտնվում են նույն BF և GH զուգահեռ ուղիղների միջև [Պնդում 1.36]։ ABC եռանկյունը GBCA զուգահեռագծի կեսն է։ AB անկյունագիծը կիսում է վերջինս երկու մասի [Պնդում 1.34]։ FED եռանկյունը DEFH զուգահեռագծի կեսն է։ DF անկյունագիծը կիսում է վերջինս երկու մասի (հավասար պատկերների կեսերը հավասար են միմյանց)։ Հետևաբար, ABC եռանկյունը հավասար է DEF եռանկյանը։

Հետևաբար, հավասար հիմքով և նույն զուգահեռ ուղիղների միջև կառուցված եռանկյունները հավասար են միմյանց։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 39

Հավասար եռանկյունները, որոնք նույն հիմքի և նույն կողմի վրա են կառուցված, նաև գտնվում են նույն զուգահեռների միջև։

ABC-ն և DBC-ն նույն BC հիմքի նույն կողմում կառուցված եռանկյուններ են։ Պնդումն այն է, որ դրանք նաև նույն զուգահեռների միջև են։

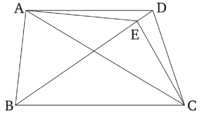
Գծված է AD կողմը։ Պնդումն այն է, որ AD-ն և BC-ն զուգահեռ են։

Հակառակ դեպքում, A կետով գծված է AE ուղիղը, որը զուգահեռ է BC ուղղին [Պնդում 1.31] և գծված է EC կողմը։ Հետևաբար, ABC եռանկյունը հավասար է EBC եռանկյանը։ Վերջինս նույն BC հիմքի վրա է և նույն զուգահեռների միջև է [Պնդում 1.37]։ Բայց ABC-ն հավասար է DBC-ին։ Հետևաբար, DBC-ն նաև հավասար է EBC-ին, մեծը՝ փոքրին, ինչը անհնար է։ Հետևաբար AE-ն զուգահեռ չէ BC-ին։ Նմանապես, կարող ենք ցույց տալ, որ BC-ն, ոչ մի այլ ուղղի քան AD-ն, զուգահեռ չէ։ Հետևաբար, AD-ն զուգահեռ է BC-ին։

Հետևաբար, հավասար եռանկյունները, որոնք նույն հիմքի և նույն կողմի վրա են կառուցված, նաև գտնվում են նույն զուգահեռների միջև։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 40 ^[3]

Հավասար հիմքի նույն կողմում կառուցված հավասար եռանկյունները նաև նույն զուգահեռների միջև են։

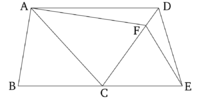
ABC-ն և CDE-ն համապատասխանաբար BC և CE հավասար հիմքերի նույն կողմում կառուցված հավասար եռանկյուններ են։ Պնդումն այն է, որ դրանք նաև նույն զուգահեռների միջև են։

Գծված է AD կողմը։ Պնդում այն է, որ AD-ն զուգահեռ է BE-ին։

Հակառակ դեպքում, A կետով գծված է AF ուղիղը, որը զուգահեռ է BE-ին [Պնդում 1.31] և գծված է FE կողմը։ Հետևաբար, ABC եռանկյունը հավասար է FCE եռանկյանը։ Դրանք հավասար BC և CE հիմքերի վրա են կառուցված և նույն BE և AF զուգահեռների միջև են [Պնդում 1.38]։ Բայց, ABC եռանկյունը հավասար է DCE եռանկյանը։ Հետևաբար, DCE-ն նաև հավասար է FCE-ին, մեծը՝ փոքրին, ինչը անհնար է։ Հետևաբար AF-ը զուգահեռ չէ BE-ին։ Նմանապես, կարող ենք ցույց տալ, որ BE-ն, ոչ մի այլ ուղղի քան AD-ն, զուգահեռ չէ։ Հետևաբար, AD-ն զուգահեռ է BE-ին։

Հետևաբար, հավասար հիմքի նույն կողմում կառուցված հավասար եռանկյունները նաև նույն զուգահեռների միջև են։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 41

Եթե զուգահեռագիծը և եռանկյունը ունեն նույն հիմքը և նույն զուգահեռների միջև են, ապա զուգահեռագծի մակերեսը եռանկյան մակերեսի կրկնապատիկն է։

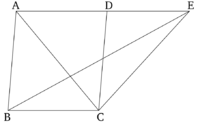
ABCD զուգահեռագիծը և EBC եռանկյունը ունեն նույն BC հիմքը և գտնվում են նույն BC և AE զուգահեռների միջև։ Պնդումն այն է, որ ABCD-ի մակերեսը BEC-ի մակերեսի կրկնապատիկն է։

Միացված է AC հատվածը։ Այսպիսով, ABC եռանկյունը հավասար է EBC եռանկյանը։ Այն նույն BC հիմքի վրա է (EBC) և գտնվում է նույն BC և AE զուգահեռների միջև [Պնդում 1.37]։ Բայց, ABCD զուգահեռագծի մակերեսը ABC եռանկյան մակերեսի կրկնապատիկն է։ AC անկյունագիծը կիսում է վերջինս երկու մասի [Պնդում 1.34]։ Այսպիսով, ABCD զուգահեռագծի մակերեսը EBC եռանկյան մակերեսի կրկնապատիկն է։

Հետևաբար, եթե զուգահեռագիծը և եռանկյունը ունեն նույն հիմքը և նույն զուգահեռների միջև են, ապա զուգահեռագծի մակերեսը եռանկյան մակերեսի կրկնապատիկն է։ Սա այն էր, ինչ պետք էր ապացուցել։

Պնդում 42

Տրված ուղղագիծ անկյունով կառուցել տրված եռանկյանը հավասար զուգահեռագիծ.

ABC-ն տրված եռանկյունն է, իսկ D-ն՝ տրված ուղղագիծ անկյունը: Այսպիսով, անհրաժեշտ է կառուցել D անկյունով զուգահեռագիծ, որը հավասար է ABC եռանկյանը:

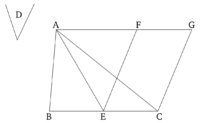
BC-ն E կետում կիսված է երկու հավասար մասի [Պնդում 1.10] և միացված է AE ուղիղը։ D անկյանը հավասար CEF անկյունը կառուցված է E կետում՝ EC կողմի վրա [Պնդում 1.23]։ A կետով գծված է AG ուղիղը, որը զուգահեռ է EC-ին [Պնդում 1.31] և C կետով գծված է CG ուղիղը, որը զուգահեռ է EF-ին [Պնդում 1.31]։ Հետևաբար, FECG-ն զուգահեռագիծ է։ Քանի որ BE-ն հավասար է EC-ին, ABE եռանկյունը հավասար է AEC եռանկյանը։ Դրանք հավասար BE և EC հիմքերի վրա են և նույն BC և AG զուգահեռների միջև [Պնդում 1.38]։ Հետևաբար, ABC եռանկյան մակերեսը AEC եռանկյան մակերեսի կրկնապատիկն է։ FECG զուգահեռագծի մակերեսը նույնպես AEC եռանկյան մակերեսի կրկնապատիկն է։ Այն ունի նույն հիմքը (AEC) և նույն զուգահեռների միջև է (AEC)[Պնդում 1.41]։ Հետևաբար, FECG զուգահեռագիծը հավասար է ABC եռանկյանը։ Իսկ FECG-ի CEF անկյունը հավասար է D անկյանը։

Հետևաբար, ABC եռանկյանը հավասար FECG զուգահեռագիծը կառուցված է CEF անկյունով, որը հավասար է D անկյանը։ Սա այն էր, ինչ պետք էր անել։

Պնդում 43

Ցանկացած զուգահեռագծի համար անկյունագծի շուրջ զուգահեռագծերի լրացումները հավասար են միմյանց:

ABCD-ն զուգահեռագիծ է, իսկ AC-ն՝ նրա անկյունագիծը: EH-ը և FG-ն զուգահեռագծեր են AC-ի շուրջ, իսկ BK-ն և KD-ն՝ այսպես կոչված լրացումները (AC-ի շուրջ): Պնդումն այն է, որ BK լրացումը հավասար է KD լրացմանը:

Քանի որ ABCD-ն զուգահեռագիծ է և AC-ն նրա անկյունագիծն է, ABC եռանկյունը հավասար է ACD եռանկյանը [Պնդում 1.34]։ Կրկին, քանի որ EH-ը զուգահեռագիծ է և AK-ը նրա անկյունագիծը, AEK եռանկյունը հավասար է AHK եռանկյանը [Պնդում 1.34]։ Այսպիսով, նույն պատճառով, KFC եռանկյունը հավասար է KGC եռանկյանը։ հետևաբար, քնաի որ AEK եռանկյունը հավասար է AHK եռանկյանը և KFC-ն KGC-ին, AEK և KGC եռանկյունների գումարը հավասար է AHK և KFC եռանկյունների գումարին։ Իսկ ամբողջ ABC եռանկյունը հավասար է ամբողջ ADC եռանկյանը։ Հետևաբար, հավելյալ BK լրացումը հավասար է հավելյալ KD լրացմանը։

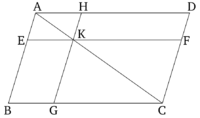
Հետևաբար, ցանկացած զուգահեռագծի համար անկյունագծի շուրջ զուգահեռագծերի լրացումները հավասար են միմյանց: Սա այն էր, ինչ պետք էր ցույց տալ։

Պնդում 44

Տրված ուղղագիծ անկյանով տրված ուղիղ գծի վրա կառուցել տրված եռանկյանը հավասար զուգահեռագիծ:

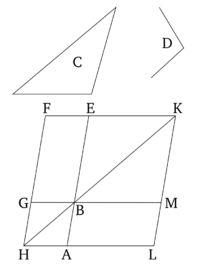
AB-ն տրված ուղիղն է, C-ն՝ տրված եռանկյունը, D-ն՝ տրված ուղղագիծ անկյունը։ Այսպիսով, պահանջվում է տրված C եռանկյանը հավասար զուգահեռագիծ կառուցել տրված AB ուղղի վրա՝ D-ին հավասար անկյան տակ։

BEFG զուգահեռագիծը՝ հավասար C եռանկյանը, կառուցված է EBG անկյունով, որը հավասար է D անկյանը [Պնդում 1.42]։ Այն տեղադրված է այնպես, որ BE-ն ընկնում է ուղիղ AB-ի վրա^[4]։ H կետով գծված է FG-ն և A կետով գծված է AH-ը, զուգահեռ BG-ին կամ EF-ին [Պնդում 1.31] և միացված է HB հատվածը։ Քանի որ HF ուղիղը հատում է AH և EF զուգահեռները, AHF և HFE անկյունները, հետևաբար, հավասար են երկու ուղիղ անկյունների [Պնդում 1.29]։ Հետևաբար, BHG-ի և GFE-ի գումարը փոքր է երկու ուղիղ անկյունից և ներքին անկյուններից (որոնց գումարը փոքր է երկու ուղիղ անկյուններից) ձգվող և անվերձության ձգտող ուղիղները հատվում են [Կանխադրույթ 5]: Հետևաբար, HB-ն և FE-ն, եթե գծվեն, կհատվեն։ Ենթադրենք դրանք գծված են և հատվում են K կետում։ K կետով գծված է KL-ը, որը զուգահեռ է EA-ին կմա FH-ին [Պնդում 1.31]։ Ենթադրենք, նաև, որ գծված են HA-ն և GB-ն համապատասխանաբար L և M կետերից։ Հետևաբար, HLKF-ն զուգահեռագիծ է և HK-ն դրա անկյունագիծն է։ AG-ն և ME-ն նույնպես զուգահեռագծեր են և LB-ն ու BF-ը այսպես կոչված լրացումներ են HK-ին։ Հետևաբար, LB-ն հավասար է BF-ին [Պնդում 1.43]։ Բայց, BF-ը հավասար է C եռանկյանը։ Հետևաբար, LB-ն հավասար է C-ին։ Նաև, քանի որ GBE-ն հավասար է ABM-ին [Պնդում 1.15], բայց GBE-ն նաև հավասար է D-ին, հետևաբար, ABM-ը հավասար է D-ին։

Հետևաբար, LB զուգահեռագիծը, որը հավասար է C եռանկյանը, կառուցված է տրված AB ուղղի վրա՝ ABM անկյունով, որը հավասար է D անկյանը։ Սա այն էր, ինչ պետք էր անել։

Պնդում 45

Կառուցել զուգահեռագիծ՝ տրված ուղղագիծ անկյանով տրված ուղղագիծ պատկերին հավասար:

ABCD-ն տրված ուղղագիծ պատկերն է^[5] , իսկ E-ն տրված ուղղագիծ անկյունը։

Գծված է DB կողմը։ E անկյանը հավասար HKF անկյունով կառուցված է ABD եռանկյանը հավասար FH զուգահեռագիծը [Պնդում 1.42]։ E անկյանը հավասար GHM անկյունով GH ուղղի վրա կառուցված է DBC եռանկյանը հավասար GM զուգահեռագիծը [Պնդում 1.44]։ Քանի որ E անկյունը հավասար է HKF և GHM անկյուններին, հետևաբար․ HKF անկյունը հավասար է GHM անկյանը։ Երկուսին էլ ավելացնենք KHG-ն։ Հետևաբար, FKH և KHG անկյունների գումարը հավասար է KHG և GHM անկյունների գումարին։ Բայց FKH և KHG անկյունների գումարը հավասար է երկու ուղիղ անկյան [Պնդում 1.29]։ Հետևաբար, KHG և GHM անկյունների գումարը նույնպես հավասար է երկու ուղիղ անկյան։ Այսպիսով, նույն կողմի վրա չնկնող KH և HM ուղիղները ստեղծում են կից անկյուններ GH ուղղի վրա H կետում, որի գումարը հավասար է երկու ուղիղ անկյան։ Հետևաբար KH-ը ընկնում է ուղիղ HM-ի վրա [Պնդում 1.14]։ Քանի որ HG ուղիղը հատում է KM և FG ուղիղները, խաչադիր MHG և HGF անկյունները հավասար են [Պնդում 1.29]։ Երկուսին էլ ավելացնենք HGL-ն։ Հետևաբար, MHG և HGL անկյունների գումարը հավասար է HGF և HGL անկյունների գումարին։ Բայց MHG և HGL անկյունների գումարը հավասար է երկու ուղիղ անկյան [Պնդում 1.29]։ Հետևաբար HGF և HGL անկյունների գումարը նույնպես հավասար է երկու ուղիղ անկյան։ Հետևաբար, FG-ն ընկնում է ուղիղ Gl-ի վրա [Պնդում 1.14]։ Քանի որ FK-ն հավասար է և զուգահեռ HG-ին [Պնդում 1.34], բայց նաև HG-n հավասար է և զուգահեռ ML-ին [Պնդում 1.34], հետևաբար, KF-ը նույնպես հավասար է և զուգահեռ ML-ին [Պնդում 1.30]: KM և FL ուղիղները միացնում են դրանք։ Հետևաբար, KM և FL նույնպես հավասար են և զուգահեռ [Պնդում1.33]։ Հետևաբար, KFLM-ը զուգահեռագիծ է։ Քանի որ ABD եռանկյունը հավասար է FH զուգահեռագծին և DBC-ն հավասար է GM, ամբողծ ABCD ուղղագիծ պատկերը, հետևաբար, հավասար է ամբողջ KFLM զուգահեռագծին։

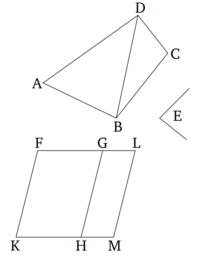
Հետևաբար, տրված ABCD ուղղագիծ պատկերին հավասար KFLM զուգահեռագիծը կառուցված է տրված E անկյանը հավասար FKM անկյունով։ Սա այն էր, ինչ պետք էր անել։

Պնդում 46

Տրված ուղղով կառուցել քառակուսի։

Տրված է AB ուղիղը։ Պահանջվում է կառուցել քառակուսի AB կողմի վրա։

AC-ն գծված է ուղղահայաց AB ուղղին A կետում [Պնդում 1.11] և AD-ն հավասար է AB-ին [Պնդում 1.4]: D կետով գծված է DE ուղիղը՝ զուգահեռ AB-ին [Պնդում 1.31] և B կետով գծված է BE ուղիղը՝ զուգահեռ AD-ին [Պնդում 1.31]։ Հետևաբար, ADEB-ն զուգահեռագիծ է։ AB-ն հավասար է DE-ին, իսկ DE-ն՝ BE-ին։ Բայց AB-ն նաև հավասար է AD-ին։ Հետևաբար, չորս կողմերը՝ BA, AD, DE և EB, հավասար են միմյանց։ Հետևաբար, ADEB զուգահեռագիծը հավասարակողմ է։ Այն ուղղանկյուն է։ Քանի որ AD ուղիղը հատում է AB և DE զուգահեռները BAD և ADE անկյունների գումարը հավասար է երկու ուղիղ անկյան [Պնդում 1.29]։ Բայց BAD-ը ուղիղ անկյուն է։ Հետևաբար, ADE-ն նույնպես ուղիղ անկյուն է։ Զուգահեռագիծ պատկերներում հակադիր կողմերը և անկյունները հավասար են միմյանց [Պնդում 1.34]։ Հետևաբար, ABE և BED հակադիր անկյուններից յուրաքանչյուրը նույնպես ուղիղ անկյուն է։ Հետևաբար, ADEB-ն ուղղանկյուն է։ Ցույց է տրված նաև, որ այն հավասարակողմ է։

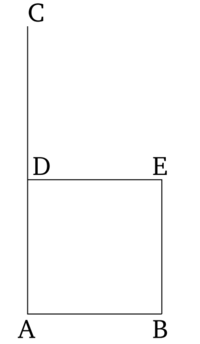
Հետևաբար, ADEB-ն քառակուսի է [Սահմանում 1.22] և այն կառուցված է AB ուղղով։ Սա այն էր, ինչ պետք էր անել։

Պնդում 47

Ուղղանկյուն եռանկյան ուղիղ անկյանի դիմացի կողմի քառակուսին հավասար է մյուս կողմերի քառակուսիների գումարին։

ABC-ն ուղղանկյուն եռանկյուն է՝ BAC ուղիղ անկյունով։ Պնդումն այն է, որ BC-ի քառակուսին հավասար է BA-ի և AC-ի քառակուսիների գումարին գումարին։

BC-ի վրակառուցված է BDEC քառակուսին և GB ու HC քառակուսիները՝ AB-ի ու AC-ի վրա համապատասխանաբար [Պնդում 1.46]։ A կետից գծված է AL-ը, որը զուգահեռ է BD-ին կամ CE-ին [Պնդում 1.31]։ AD-ն և FC-ն միացված են։ Քանի որ BAC և BAG անկյուններից յուրաքանչյուրը ուղիղ անկյուն է, ապա նույն կողմի վրա չնկնող AC և AG երկու ուղիղները ստեղծում են կից անկյուններ BA ուղղով՝ A կետում, որի գումարը հավասար է երկու ուղիղ անկյունների։ Հետևաբար CA-ն ընկնում է AB-ի վրա [Պնդում 1.14]։ Նույն պատճառով BA-ն ընկնում է AH-ի վրա։ Քանի որ DBC անկյունը հավասար է FBA անկյանը, կամ երկուսն էլ ուղիղ անկյուն են, երկուսին էլ ավելացնենք ABC-ն։ Հետևաբար, ամբողջ DBA անկյունը հավասար է FBC ամբողջ անկյանը։ Քանի որ DB-ն հավասար է BC-ին և FB-ն BA-ին, երկու ուղիղները՝ DB-ն և BA-ն,համապատասխանաբար հավասար են CB և BF ուղիղներին։ Իսկ DBA անկյունը հավասար է FBC անկյանը։։ Հետևաբար, AD հիմքը հավասար է FC հիմքին և ABD անկյունը հավասար է FBC անկյանը [Պնդում 1.4]: Իսկ BL զուգահեռագծի մակերեսը ABD եռանկյան մակերեսի կրկնապատիկն է։ Դրանք ունեն նույն BD հիմքը և ընկած են նույն BD և AL զուգահեռների միջև [Պնդում 1.41]: GB քառակուսու մակերեսը FBC եռանկյան մակերեսի կրկնապատիկն է։ Կրկին, դրանք ունեն նույն FB հիմքը և ընկած են նույն FB և GC զուգահեռների միջև [Պնդում 1.41] (հավասար պատկերների կեսերը հավասար են միմյանց)^[6]: Հետևաբար, BL զուգահեռագիծը հավասար է GB քառակուսուն։ Նույն կերպ, AE-ն և BK-ը միացված են և կարող ենք ցույց տալ, որ CL զուգահեռագիծը հավասար է HC քառակուսուն։ Հետևաբար, ամբողջ BDEC քառակուսին հավասար է GB և HC քառակուսիների գումարին։ BDEC քառակուսին կառուցված է BC- վրա․ իսկ GB և HC քառակուսիները՝ BA-ի և AC-ի վրա համապատասխանաբար։ Հետևաբար, BC կողմի քառակուսին հավասար է BA և AC կողմերի քառակուսիների գումարին։

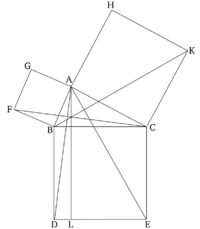
Հետևաբար, ուղղանկյուն եռանկյան ուղիղ անկյանի դիմացի կողմի քառակուսին հավասար է մյուս կողմերի քառակուսիների գումարին։ Սա այն էր, ինչ պետք էր ցույց տալ։

Պնդում 48

Եթե ​​եռանկյան մի կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին, ապա մնացած երկու կողմերի մեջ պարունակվող անկյունն ուղղանկյուն է։

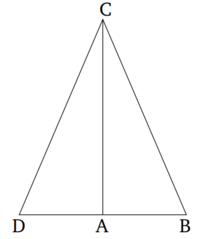
Ենթադրենք ABC երանկյան կողմերից մեկի՝ BC-ի քառակուսին հավասար է BA և AC կողմերի քառակուսիների գումարին։ Պնդումն այն է, որ BAC-ն ուղիղ անկյուն է։

A կետով գծված է AD ուղիղը, որը ուղղահայաց է AC կողմին [Պնդում 1.11], AD-ն հավասար է BA-ին [Պնդում 1.3] և DC-ն միացված է։ Քանի որ DA-ն հավասար է AB-ին, ապա DA քառակուսին նույնպես հավասար է AB քառակուսուն ^[7]։ AC քառակուսին ավելացված է երկուսին էլ։ Հետևաբար, DA և AC քառակուսիների գումարը հավասար է BA և AC քառակուսիների գումարին։ Բայց DC քառակուսին հավասար է DA և AC քառակուսիների գումարին։ Իսկ DAC-ն ուղիղ անկյուն է [Պնդում 1.47]։ Բայց, BC քառակուսին հավասար է BA և AC քառակուսիների գումարին։ Դա ենթադրվում է։ Հետևաբար, DC քառակուսին հավասար է BC քառակուսուն։ Այսպիսով, DC-ն նույնպես հավասար է BC-ին։ Քանի որ DA-ն հավասար է AB-ին և AC-ն ընդհանուր է, DA և AC երկու ուղիղները հավասար են BA և AC երկու ուղիղներին։ Իսկ DC հիմքը հավասար է BC հիմքին։ Հետևաբար, DAC անկյունը հավասար է BAC անկյանը [Պնդում 1.8]։ Բայց DAC-ն ուղիղ անկյուն է։ Հետևաբար, BAC-ն նույնպես ուղիղ անկյուն է։

Հետևաբար, եթե ​​եռանկյան մի կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին, ապա մնացած երկու կողմերի մեջ պարունակվող անկյունն ուղղանկյուն է։ Սա այն էր, ինչ պետք էր ցույց տալ։

Նշումներ

1. ↑ Որպես ակնհայտ ընդարձակում As an obvious extension of C.N.s 2 & 3—if equal things are added or subtracted from the two sides of an inequality then the inequality remains an inequality of the same type.
2. ↑ Այստեղ առաջին անգամ «հավասար» նշանակում է «մակերեսով հավասար», այլ ոչ թե «համապատասխան»։
3. ↑ Այս ամբողջ պնդումը Հայբերգի կողմից դիտվում է որպես սկզբնական տեքստի համեմատաբար վաղ ինտերպոլացիա:
4. ↑ Սրան կարելի է հասնել օգտագործելով 1.3, 1.23, և 1.31 պնդումները։
5. ↑ Ապացույցը տրվում է միայն քառակողմ պատկերի համար: Այնուամենայնիվ, բազմակողմ պատկերի դեպքում կիրառումը պարզ է:
6. ↑ Սա լրացուցիչ ընդհանուր հասկացություն է:
7. ↑ Այստեղ օգտագործվում է լրացուցիչ ընդհանուր հասկացություն, որ հավասար իրերի քառակուսիներն իրենք էլ հավասար են: Հետագայում օգտագործվում է հակադարձ հասկացությունը։