Տարերք/Գիրք 10

հեղինակ՝ էվկլիդես աղբյուր՝ Euclid's Elements of Geometry, English translation by Richard Fitzpatrick

Տարերքի գրքեր

Պնդում 102

Այն (ուղիղ գիծը), որի վրա կառուցված քառակուսին միջինական մակերեսի հետ միասին կազմում է միջինական ամբողջություն, ռացիոնալ (ուղիղ գծի) վրա դրված` ստանում է վեցերորդ կտրվածք (ապոտոմե) որպես լայնություն։

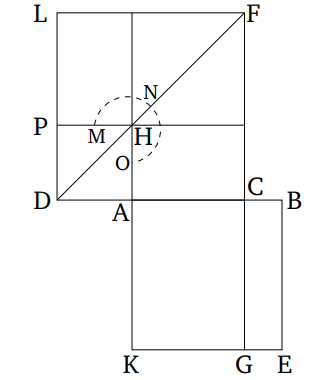
Թող AB-ն լինի այն ուղիղ գիծը, որը միջինական մակերեսի հետ կազմում է միջինական ամբողջություն, և CD-ն լինի ռացիոնալ (ուղիղ գիծ): Եվ թող CE-ն, որը հավասար է AB-ի վրա կառուցված քառակուսուն, դրված լինի CD-ի վրա, պարփակված AG-ով և GB-ով, որոնք միջինական են, և AG-ի և GB-ի վրա կառուցված քառակուսիների գումարը անհամաչափ է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյունին [Տե՛ս "Տարրեր" 10.78]:

Ուստի, թող CH-ն, որը հավասար է AG-ի վրա կառուցված քառակուսուն, դրված լինի CD-ի վրա, արտադրելով CK որպես լայնություն, և KL-ը, որը հավասար է GB-ի վրա կառուցված քառակուսուն։ Այսպիսով, CL-ի ամբողջությունը հավասար է AG-ի և GB-ի վրա կառուցված քառակուսիների գումարին։ CL-ը, հետևաբար, միջինական է։ Եվ այն դրված է ռացիոնալ CD-ի վրա, արտադրելով CM որպես լայնություն։ Ուստի, CM-ը ռացիոնալ է և անհամաչափ է երկարությամբ CD-ի հետ [Տե՛ս "Տարրեր" 10.22]:

Հետևաբար, քանի որ CL-ը հավասար է AG-ի և GB-ի վրա կառուցված քառակուսիների գումարին, որոնցից CE-ն հավասար է AB-ի վրա կառուցված քառակուսուն, մնացորդ FL-ը, հետևաբար, հավասար է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյունին [Տե՛ս "Տարրեր" 2.7]: Եվ քանի որ AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյունը միջինական է, FL-ը նույնպես միջինական է։ Եվ այն դրված է ռացիոնալ FE-ի վրա, արտադրելով FM որպես լայնություն։ Ուստի, FM-ը ռացիոնալ է և անհամաչափ է երկարությամբ CD-ի հետ [Տե՛ս "Տարրեր" 10.22]:

Քանի որ AG-ի և GB-ի վրա կառուցված քառակուսիների գումարը անհամաչափ է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյան հետ, CL-ը հավասար է AG-ի և GB-ի վրա կառուցված քառակուսիների գումարին, իսկ FL-ը հավասար է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյան, CL-ը, հետևաբար, անհամաչափ է FL-ի հետ։ Եվ ինչպես CL-ն է FL-ի նկատմամբ, այնպես էլ CM-ը MF-ի նկատմամբ է [Տե՛ս "Տարրեր" 6.1]:

Ուստի, CM-ը երկարությամբ անհամաչափ է MF-ի հետ [Տե՛ս "Տարրեր" 10.11]: Եվ երկուսն էլ ռացիոնալ են։ Ուստի, CM-ն և MF-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ CF-ը, հետևաբար, ապոտոմե է [Տե՛ս "Տարրեր" 10.73]: Ուրեմն, ես ասում եմ, որ այն նաև վեցերորդ (կտրվածքն) է։

Քանի որ FL-ը հավասար է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյանին, թող FM-ը բաժանված լինի կեսի վրա N-ում, և թող NO-ն քաշված լինի N-ի միջով, զուգահեռ CD-ին։ Այսպիսով, FO-ն և NL-ը յուրաքանչյուրն հավասար են AG-ով և GB-ով պարփակված ուղղանկյան։ Եվ քանի որ AG-ն և GB-ն անհամաչափ են քառակուսով, AG-ի վրա կառուցված քառակուսին, հետևաբար, անհամաչափ է GB-ի վրա կառուցված քառակուսու հետ։ Սակայն, CH-ը հավասար է AG-ի վրա կառուցված քառակուսուն, իսկ KL-ը հավասար է GB-ի վրա կառուցված քառակուսուն։

Ուստի, CH-ը անհամաչափ է KL-ի հետ։ Եվ ինչպես CH-ն է KL-ի նկատմամբ, այնպես էլ CK-ն KM-ի նկատմամբ է [Տե՛ս "Տարրեր" 6.1]: Ուստի, CK-ն երկարությամբ անհամաչափ է KM-ի հետ [Տե՛ս "Տարրեր" 10.11]: Եվ քանի որ AG-ով և GB-ով պարփակված ուղղանկյունը միջին չափաբաժին է AG-ի և GB-ի վրա կառուցված քառակուսիների միջև [Տե՛ս "Տարրեր" 10.21-ի լեմմա], իսկ CH-ը հավասար է AG-ի վրա կառուցված քառակուսուն, KL-ը՝ GB-ի վրա կառուցված քառակուսուն, NL-ը՝ AG-ով և GB-ով պարփակված ուղղանկյունին, NL-ը, հետևաբար, նույնպես միջին չափաբաժին է CH-ի և KL-ի միջև։

Ուստի, ինչպես CH-ն է NL-ի նկատմամբ, այնպես էլ NL-ը KL-ի։ Եվ նույն տրամաբանությամբ, CM-ի վրա կառուցված քառակուսին մեծ է MF-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը լայնությամբ արտադրում է CF։ Ես ասում եմ, որ CF-ը վեցերորդ ապոտոմեն է։

Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 103

Ուղիղ գիծը, որը երկարությամբ համաչափ է ապոտոմեի հետ, ինքն էլ ապոտոմե է և նույն կարգի է։

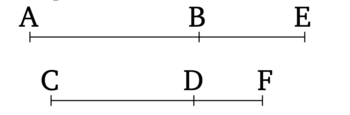
Թող AB-ն լինի ապոտոմե, և թող CD-ն լինի երկարությամբ համաչափ AB-ի հետ։ Ասում եմ, որ CD-ն նույնպես ապոտոմե է և նույն կարգի է, ինչ AB-ն։

Քանի որ AB-ն ապոտոմե է, թող BE-ն լինի կցորդ դրան։ Այսպիսով, AE-ն և EB-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.73]։ Եվ թող այնպես լինի, որ BE-ի և DF-ի հարաբերությունը նույնն է, ինչ AB-ի և CD-ի հարաբերությունը [Տե՛ս "Տարրեր" 6.12]։ Այսպիսով, ինչպես մեկ է մեկի նկատմամբ, այնպես էլ ամեն ինչ՝ ամեն ինչի [Տե՛ս "Տարրեր" 5.12]։ Եվ ինչպես ամբողջ AE-ն է ամբողջ CF-ի նկատմամբ, այնպես էլ AB-ն է CD-ի նկատմամբ։ Եվ AB-ն համաչափ է երկարությամբ CD-ի հետ։ AE-ն, հետևաբար, նույնպես համաչափ է CF-ի հետ, և BE-ն՝ DF-ի հետ [Տե՛ս "Տարրեր" 10.11]։

Եվ AE-ն և BE-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ Այսպիսով, CF-ն և FD-ն նույնպես ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.13]։ Ուստի, CD-ն ապոտոմե է։ Ասում եմ, որ այն նույնպես նույն կարգի է, ինչ AB-ն։

Ուստի, քանի որ ինչպես AE-ն է CF-ի նկատմամբ, այնպես էլ BE-ն է DF-ի նկատմամբ, ապա, այլընտրանքով, ինչպես AE-ն է EB-ի նկատմամբ, այնպես էլ CF-ն է FD-ի նկատմամբ [Տե՛ս "Տարրեր" 5.16]։ Այսպիսով, AE-ի վրա կառուցված քառակուսին մեծ է EB-ի վրա կառուցված քառակուսուց կամ որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափ է կամ անհամաչափ AE-ի հետ։

Ուստի, եթե AE-ի վրա կառուցված քառակուսին մեծ է EB-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափ է AE-ի հետ, ապա CF-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի FD-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափ է CF-ի հետ [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե AE-ն երկարությամբ համաչափ է նախապես տրված ռացիոնալ ուղիղ գծի հետ, ապա նույնը նաև CF-ն է [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե BE-ն համաչափ է, ապա նաև DF-ը։ Եվ եթե ոչ AE-ն և ոչ էլ EB-ն համաչափ չեն, ապա նույնը նաև CF-ն և FD-ն [Տե՛ս "Տարրեր" 10.13]։

Եվ եթե AE-ի վրա կառուցված քառակուսին մեծ է EB-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը անհամաչափ է AE-ի հետ, ապա CF-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի FD-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը անհամաչափ է CF-ի հետ [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե AE-ն երկարությամբ համաչափ է նախապես տրված ռացիոնալ ուղիղ գծի հետ, ապա նույնը նաև CF-ն է [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե BE-ն համաչափ է, ապա նաև DF-ը։ Եվ եթե ոչ AE-ն և ոչ էլ EB-ն համաչափ չեն, ապա նույնը նաև CF-ն և FD-ն [Տե՛ս "Տարրեր" 10.13]։

Ուստի, CD-ն ապոտոմե է և նույն կարգի է, ինչ AB-ն [Տե՛ս "Տարրեր" 10.11-10.16]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 104

Ուղիղ գիծը, որը երկարությամբ համաչափ է միջինական ապոտոմեի հետ, ինքն էլ միջինական ապոտոմե է և նույն կարգի է։

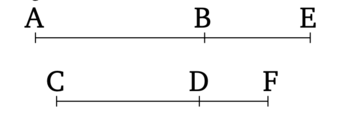
Թող AB-ն լինի միջինական ապոտոմե, և թող CD-ն լինի երկարությամբ համաչափ AB-ի հետ։ Ասում եմ, որ CD-ն նույնպես միջինական ապոտոմե է և նույն կարգի է, ինչ AB-ն։

Քանի որ AB-ն միջինական ապոտոմե է, թող EB-ն լինի կցորդ դրան։ Այսպիսով, AE-ն և EB-ն միջինական (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.74, 10.75]։ Եվ թող այնպես լինի, որ ինչպես AB-ն է CD-ի նկատմամբ, այնպես էլ BE-ն լինի DF-ի նկատմամբ [Տե՛ս "Տարրեր" 6.12]։ Այսպիսով, AE-ն նույնպես համաչափ է CF-ի հետ, և BE-ն՝ DF-ի հետ [Տե՛ս "Տարրեր" 5.12, 10.11]։

Եվ AE-ն և EB-ն միջինական (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ CF-ն և FD-ն նույնպես միջինական (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.23, 10.13]։ Ուստի, CD-ն միջինական ապոտոմե է [Տե՛ս "Տարրեր" 10.74, 10.75]։ Ասում եմ, որ այն նույնպես նույն կարգի է, ինչ AB-ն։

Քանի որ ինչպես AE-ն է EB-ի նկատմամբ, այնպես էլ CF-ն է FD-ի նկատմամբ [Տե՛ս "Տարրեր" 5.12, 5.16], և ինչպես AE-ն է EB-ի նկատմամբ, այնպես էլ AE-ի վրա կառուցված քառակուսին է AE-ի և EB-ի ուղղանկյան նկատմամբ, և ինչպես CF-ն է FD-ի նկատմամբ, այնպես էլ CF-ի վրա կառուցված քառակուսին է CF-ի և FD-ի ուղղանկյան նկատմամբ, ապա ինչպես AE-ի վրա կառուցված քառակուսին է AE-ի և EB-ի ուղղանկյան նկատմամբ, այնպես էլ CF-ի վրա կառուցված քառակուսին է CF-ի և FD-ի ուղղանկյան նկատմամբ [Տե՛ս "Տարրեր" 10.21-ի լեմմա]։

Եվ, այլընտրանքով, ինչպես AE-ի վրա կառուցված քառակուսին է CF-ի վրա կառուցված քառակուսու նկատմամբ, այնպես էլ AE-ի և EB-ի ուղղանկյունը է CF-ի և FD-ի ուղղանկյան նկատմամբ։ Եվ AE-ի վրա կառուցված քառակուսին համաչափ է CF-ի վրա կառուցված քառակուսու հետ։ Ուստի, AE-ի և EB-ի ուղղանկյունը նույնպես համաչափ է CF-ի և FD-ի ուղղանկյան հետ [Տե՛ս "Տարրեր" 5.16, 10.11]։

Ուստի, կամ AE-ի և EB-ի ուղղանկյունը ռացիոնալ է, և CF-ի և FD-ի ուղղանկյունը նույնպես ռացիոնալ կլինի [Տե՛ս "Տարրեր" 10.4-ի սահմանում], կամ AE-ի և EB-ի ուղղանկյունը միջինական է, և CF-ի և FD-ի ուղղանկյունը նույնպես միջինական կլինի [Տե՛ս "Տարրեր" 10.23-ի եզրակացություն]։

Ուստի, CD-ն միջինական ապոտոմե է և նույն կարգի է, ինչ AB-ն [Տե՛ս "Տարրեր" 10.74, 10.75]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 105

Ուղիղ գիծը, որը երկարությամբ համաչափ է փոքր (ուղիղ գծի) հետ, ինքն էլ փոքր (ուղիղ գիծ) է։

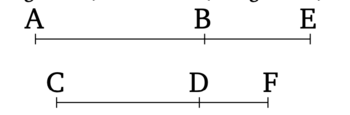
Թող AB-ն լինի փոքր (ուղիղ գիծ), և թող CD-ն լինի երկարությամբ համաչափ AB-ի հետ։ Ասում եմ, որ CD-ն նույնպես փոքր (ուղիղ գիծ) է։

Թող նույն պայմանները ստեղծված լինեն (ինչպես նախորդ պնդման մեջ)։ Եվ քանի որ AE-ն և EB-ն (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով [Տե՛ս "Տարրեր" 10.76], CF-ն և FD-ն նույնպես (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով [Տե՛ս "Տարրեր" 10.13]։ Ուստի, քանի որ ինչպես AE-ն է EB-ի նկատմամբ, այնպես էլ CF-ն է FD-ի նկատմամբ [Տե՛ս "Տարրեր" 5.12, 5.16], ապա նաև ինչպես AE-ի վրա կառուցված քառակուսին է EB-ի վրա կառուցված քառակուսու նկատմամբ, այնպես էլ CF-ի վրա կառուցված քառակուսին է FD-ի վրա կառուցված քառակուսու նկատմամբ [Տե՛ս "Տարրեր" 6.22]։

Այսպիսով, համալրումով, ինչպես AE-ի և EB-ի վրա կառուցված քառակուսիների գումարն է EB-ի վրա կառուցված քառակուսու նկատմամբ, այնպես էլ CF-ի և FD-ի վրա կառուցված քառակուսիների գումարն է FD-ի վրա կառուցված քառակուսու նկատմամբ [Տե՛ս "Տարրեր" 5.18], [նաև այլընտրանքով]։ Եվ BE-ի վրա կառուցված քառակուսին համաչափ է DF-ի վրա կառուցված քառակուսու հետ [Տե՛ս "Տարրեր" 10.104]։ AE-ի և EB-ի վրա կառուցված քառակուսիների գումարը, հետևաբար, նույնպես համաչափ է CF-ի և FD-ի վրա կառուցված քառակուսիների գումարի հետ [Տե՛ս "Տարրեր" 5.16, 10.11]։

Եվ AE-ի և EB-ի վրա կառուցված քառակուսիների գումարը ռացիոնալ է [Տե՛ս "Տարրեր" 10.76]։ Ուստի, CF-ի և FD-ի վրա կառուցված քառակուսիների գումարը նույնպես ռացիոնալ է [Տե՛ս "Տարրեր" 10.4-ի սահմանում]։ Կրկին, քանի որ ինչպես AE-ի վրա կառուցված քառակուսին է AE-ի և EB-ի ուղղանկյան նկատմամբ, այնպես էլ CF-ի վրա կառուցված քառակուսին է CF-ի և FD-ի ուղղանկյան նկատմամբ [Տե՛ս "Տարրեր" 10.21-ի լեմմա], և AE-ի վրա կառուցված քառակուսին համաչափ է CF-ի վրա կառուցված քառակուսու հետ, AE-ի և EB-ի ուղղանկյունը նույնպես համաչափ է CF-ի և FD-ի ուղղանկյան հետ։

Եվ AE-ի և EB-ի ուղղանկյունը միջինական է [Տե՛ս "Տարրեր" 10.76]։ Ուստի, CF-ի և FD-ի ուղղանկյունը նույնպես միջինական է [Տե՛ս "Տարրեր" 10.23-ի եզրակացություն]։ CF-ն և FD-ն, հետևաբար, (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով, որոնց վրա կառուցված քառակուսիների գումարը ռացիոնալ է, իսկ նրանց վրա կառուցված ուղղանկյունը միջինական։

Ուստի, CD-ն փոքր (ուղիղ գիծ) է [Տե՛ս "Տարրեր" 10.76]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 106

Ուղիղ գիծը, որը երկարությամբ համաչափ է (ուղիղ գծի) հետ, որը ռացիոնալ (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն, ինքն էլ (ուղիղ գիծ) է, որը ռացիոնալ (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն։

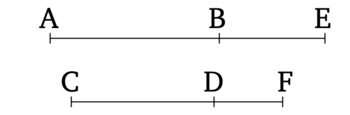
Թող AB-ն լինի (ուղիղ գիծ), որը ռացիոնալ (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն, և թող CD-ն լինի երկարությամբ համաչափ AB-ի հետ։ Ասում եմ, որ CD-ն նույնպես (ուղիղ գիծ) է, որը ռացիոնալ (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն։

Թող BE-ն լինի կցորդ AB-ին։ Այսպիսով, AE-ն և EB-ն (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով, որոնց վրա կառուցված քառակուսիների գումարը միջինական է, իսկ նրանց ուղղանկյունը ռացիոնալ է [Տե՛ս "Տարրեր" 10.77]։ Եվ թող նույն կառուցումը կատարված լինի (ինչպես նախորդ պնդումներում)։ Նմանապես նախորդ (պնդումների) հետ, մենք կարող ենք ցույց տալ, որ CF-ն և FD-ն նույն հարաբերությունն ունեն, ինչ AE-ն և EB-ն, և AE-ի և EB-ի վրա կառուցված քառակուսիների գումարը համաչափ է CF-ի և FD-ի վրա կառուցված քառակուսիների գումարի հետ, և AE-ի և EB-ի ուղղանկյունը համաչափ է CF-ի և FD-ի ուղղանկյան հետ։

Ուստի, CF-ն և FD-ն նույնպես (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով, որոնց վրա կառուցված քառակուսիների գումարը միջինական է, իսկ նրանց ուղղանկյունը ռացիոնալ։

CD-ն, հետևաբար, (ուղիղ գիծ) է, որը ռացիոնալ (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն [Տե՛ս "Տարրեր" 10.77]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 107

Ուղիղ գիծը, որը երկարությամբ համաչափ է (ուղիղ գծի) հետ, որը միջինական (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն, ինքն էլ (ուղիղ գիծ) է, որը միջինական (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն։

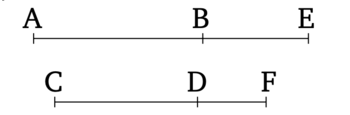
Թող AB-ն լինի (ուղիղ գիծ), որը միջինական (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն, և թող CD-ն լինի երկարությամբ համաչափ AB-ի հետ։ Ասում եմ, որ CD-ն նույնպես (ուղիղ գիծ) է, որը միջինական (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն։

Թող BE-ն լինի կցորդ AB-ին։ Եվ թող նույն կառուցումը կատարված լինի (ինչպես նախորդ պնդումներում)։ Այսպիսով, AE-ն և EB-ն (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով, որոնց վրա կառուցված քառակուսիների գումարը միջինական է, իսկ նրանց ուղղանկյունը միջինական է, և, ավելին, նրանց վրա կառուցված քառակուսիների գումարը անհամաչափ է նրանց ուղղանկյան հետ [Տե՛ս "Տարրեր" 10.78]։ Եվ ինչպես արդեն ցույց է տրվել, AE-ն և EB-ն երկարությամբ համաչափ են համապատասխանաբար CF-ի և FD-ի հետ, ինչպես նաև AE-ի և EB-ի վրա կառուցված քառակուսիների գումարը համաչափ է CF-ի և FD-ի վրա կառուցված քառակուսիների գումարի հետ, իսկ AE-ի և EB-ի ուղղանկյունը համաչափ է CF-ի և FD-ի ուղղանկյան հետ։

Ուստի, CF-ն և FD-ն նույնպես (ուղիղ գծեր են, որոնք) անհամաչափ են քառակուսով, որոնց վրա կառուցված քառակուսիների գումարը միջինական է, իսկ նրանց ուղղանկյունը միջինական է, և, ավելին, նրանց վրա կառուցված քառակուսիների գումարը անհամաչափ է նրանց ուղղանկյան հետ։

CD-ն, հետևաբար, (ուղիղ գիծ) է, որը միջինական (մակերեսի) հետ միասին կազմում է միջինական ամբողջություն [Տե՛ս "Տարրեր" 10.78]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 108

Եթե միջինական (մակերես) հանվում է ռացիոնալ (մակերեսից), ստացվում է երկու անհամաչափ (ուղիղ գծերից) մեկը որպես մնացորդի մակերեսի քառակուսի արմատ՝ կամ ապոտոմե, կամ փոքր (ուղիղ գիծ)։

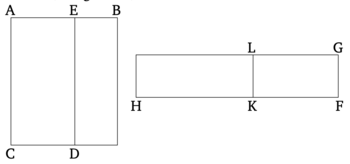
Թող միջինական (մակերեսը) BD հանված լինի ռացիոնալ (մակերեսից) BC։ Ասում եմ, որ մնացորդ (մակերեսի) EC քառակուսի արմատով ստացվում է երկու անհամաչափ (ուղիղ գծերից) մեկը՝ կամ ապոտոմե, կամ փոքր (ուղիղ գիծ)։

Թող ռացիոնալ (ուղիղ գիծը) FG դրված լինի, և թող ուղիղանկյուն զուգահեռագիծը GH, որը հավասար է BC-ին, դրված լինի FG-ի վրա, և թող GK, որը հավասար է BD-ին, հանված լինի (GH-ից)։ Այսպիսով, մնացորդը EC հավասար է LH-ին։

Ուստի, քանի որ BC-ն ռացիոնալ (մակերես) է, և BD-ն միջինական (մակերես), և BC-ն հավասար է GH-ին, իսկ BD-ն՝ GK-ին, ապա GH-ը ռացիոնալ (մակերես) է, իսկ GK-ը՝ միջինական (մակերես)։ Եվ դրանք դրված են ռացիոնալ (ուղիղ գծի) FG-ի վրա։ Ուստի, FH-ն ռացիոնալ է և երկարությամբ համաչափ FG-ի հետ [Տե՛ս "Տարրեր" 10.20], և FK-ն նույնպես ռացիոնալ է, բայց երկարությամբ անհամաչափ FG-ի հետ [Տե՛ս "Տարրեր" 10.22]։ Ուստի, FH-ն երկարությամբ անհամաչափ է FK-ի հետ [Տե՛ս "Տարրեր" 10.13]։

FH-ն և FK-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ Ուստի, KH-ը ապոտոմե է [Տե՛ս "Տարրեր" 10.73], իսկ KF-ը՝ դրա կցորդ։ Այսպիսով, HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց որոշակի (ուղիղ գծի) վրա կառուցված քառակուսու չափով, որը կամ համաչափ է HF-ի հետ, կամ անհամաչափ։

Նախ, թող քառակուսին (մեծ լինի) HF-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով։ Եվ ամբողջ HF-ն համաչափ է երկարությամբ նախապես տրված ռացիոնալ (ուղիղ գծի) FG-ի հետ։ Ուստի, KH-ը առաջին ապոտոմե է [Տե՛ս "Տարրեր" 10.1-ի սահմանում]։ Եվ ռացիոնալ (ուղիղ գծի) և առաջին ապոտոմեի վրա պարփակված (մակերեսի) քառակուսի արմատը ապոտոմե է [Տե՛ս "Տարրեր" 10.91]։ Ուստի, LH-ի քառակուսի արմատը՝ այսինքն՝ EC-ն, ապոտոմե է։

Եվ եթե HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց HF-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, և (քանի որ) ամբողջ HF-ն համաչափ է երկարությամբ նախապես տրված ռացիոնալ (ուղիղ գծի) FG-ի հետ, ապա KH-ը չորրորդ ապոտոմե է [Տե՛ս "Տարրեր" 10.14]։ Եվ ռացիոնալ (ուղիղ գծի) և չորրորդ ապոտոմեի վրա պարփակված (մակերեսի) քառակուսի արմատը փոքր (ուղիղ գիծ) է [Տե՛ս "Տարրեր" 10.94]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 109

Ռացիոնալ (մակերես) հանվելով միջինական (մակերեսից), ստացվում են երկու այլ անհամաչափ (ուղիղ գծեր) որպես մնացորդի մակերեսի քառակուսի արմատ՝ կամ միջինական (ուղիղ գծի) առաջին ապոտոմե, կամ (ուղիղ գիծ), որը ռացիոնալ (մակերեսի) հետ կազմում է միջինական ամբողջություն։

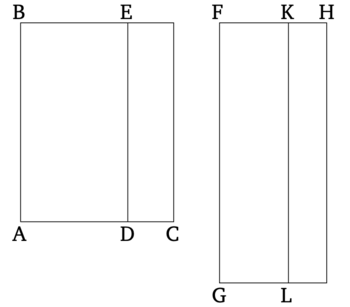
Թող ռացիոնալ (մակերեսը) BD հանված լինի միջինական (մակերեսից) BC։ Ասում եմ, որ մնացորդի (մակերեսի) EC քառակուսի արմատով ստացվում է երկու անհամաչափ (ուղիղ գծերից) մեկը՝ կամ միջինական (ուղիղ գծի) առաջին ապոտոմե, կամ (ուղիղ գիծ), որը ռացիոնալ (մակերեսի) հետ կազմում է միջինական ամբողջություն։

Թող ռացիոնալ (ուղիղ գիծը) FG դրված լինի, և թող նախորդ պնդման նման կառուցումներ կիրառված լինեն։ Ուստի, համաձայնաբար, FH-ը ռացիոնալ է և երկարությամբ անհամաչափ FG-ի հետ, իսկ KF-ը նույնպես ռացիոնալ է և երկարությամբ համաչափ FG-ի հետ։ Ուստի, FH-ը և FK-ը ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.13]։ KH-ը, հետևաբար, ապոտոմե է [Տե՛ս "Տարրեր" 10.73], իսկ FK-ը դրա կցորդ։ Այսպիսով, HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց կամ HF-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, կամ HF-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով։

Ուստի, եթե HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց HF-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, և (քանի որ) կցորդ FK-ը համաչափ է երկարությամբ նախապես տրված ռացիոնալ (ուղիղ գծի) FG-ի հետ, KH-ը երկրորդ ապոտոմե է [Տե՛ս "Տարրեր" 10.12-ի սահմանում]։ Եվ FG-ն ռացիոնալ է։ Ուստի, LH-ի քառակուսի արմատը՝ այսինքն՝ EC-ն, միջինական (ուղիղ գծի) առաջին ապոտոմե է [Տե՛ս "Տարրեր" 10.92]։

Եվ եթե HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց HF-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, և (քանի որ) կցորդ FK-ը համաչափ է երկարությամբ նախապես տրված ռացիոնալ (ուղիղ գծի) FG-ի հետ, KH-ը հինգերորդ ապոտոմե է [Տե՛ս "Տարրեր" 10.15-ի սահմանում]։ Ուստի, EC-ի քառակուսի արմատը (ուղիղ գիծ) է, որը ռացիոնալ (մակերեսի) հետ կազմում է միջինական ամբողջություն [Տե՛ս "Տարրեր" 10.95]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 110

Միջինական (մակերես), որը անհամաչափ է ամբողջության հետ, հանվելով միջինական (մակերեսից), ստացվում են երկու մնացորդային անհամաչափ (ուղիղ գծեր) որպես մնացորդի մակերեսի քառակուսի արմատ՝ կամ միջինական (ուղիղ գծի) երկրորդ ապոտոմե, կամ (ուղիղ գիծ), որը միջինական (մակերեսի) հետ կազմում է միջինական ամբողջություն։

Ինչպես նախորդ նկարներում, թող միջինական (մակերեսը) BD, որը անհամաչափ է ամբողջության հետ, հանված լինի միջինական (մակերեսից) BC։ Ասում եմ, որ EC-ի քառակուսի արմատը երկու անհամաչափ (ուղիղ գծերից) մեկն է՝ կամ միջինական (ուղիղ գծի) երկրորդ ապոտոմե, կամ (ուղիղ գիծ), որը միջինական (մակերեսի) հետ կազմում է միջինական ամբողջություն։

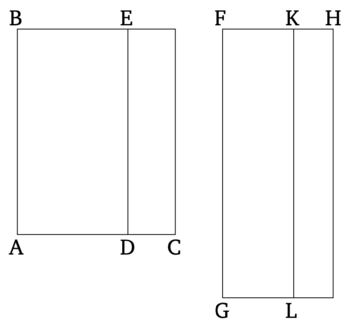
Քանի որ BC-ն և BD-ն երկուսն էլ միջինական (մակերեսներ) են, և BC-ն անհամաչափ է BD-ի հետ, ապա, ըստ այդմ, FH-ն և FK-ն կլինեն ռացիոնալ (ուղիղ գծեր), և երկարությամբ անհամաչափ FG-ի հետ [Տե՛ս "Տարրեր" 10.22]։ Եվ քանի որ BC-ն անհամաչափ է BD-ի հետ, այսինքն՝ GH-ը GK-ի հետ, ապա HF-ն նույնպես անհամաչափ է FK-ի հետ [Տե՛ս "Տարրեր" 6.1, 10.11]։ Ուստի, FH-ն և FK-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ KH-ը, հետևաբար, ապոտոմե է [Տե՛ս "Տարրեր" 10.73], իսկ FK-ը դրա կցորդ։

Այսպիսով, HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց կամ HF-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, կամ HF-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով։

Եթե HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց HF-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, և (քանի որ) ոչ HF-ն, ոչ FK-ը համաչափ չեն նախապես տրված ռացիոնալ (ուղիղ գծի) FG-ի հետ, ապա KH-ը երրորդ ապոտոմե է [Տե՛ս "Տարրեր" 10.3-ի սահմանում]։ Եվ KL-ը ռացիոնալ է։ Եվ ռացիոնալ (ուղիղ գծի) և երրորդ ապոտոմեի վրա պարփակված ուղղանկյունը անհամաչափ է, և դրա քառակուսի արմատը այն անհամաչափ (ուղիղ գիծն) է, որը կոչվում է միջինական (ուղիղ գծի) երկրորդ ապոտոմե [Տե՛ս "Տարրեր" 10.93]։ Ուստի, LH-ի քառակուսի արմատը՝ այսինքն՝ EC-ն, միջինական (ուղիղ գծի) երկրորդ ապոտոմե է։

Եվ եթե HF-ի վրա կառուցված քառակուսին մեծ է FK-ի վրա կառուցված քառակուսուց HF-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսի չափով, և (քանի որ) ոչ HF-ն, ոչ FK-ը համաչափ չեն FG-ի հետ, ապա KH-ը վեցերորդ ապոտոմե է [Տե՛ս "Տարրեր" 10.16-ի սահմանում]։ Եվ ռացիոնալ (ուղիղ գծի) և վեցերորդ ապոտոմեի վրա պարփակված (մակերեսի) քառակուսի արմատը (ուղիղ գիծ) է, որը միջինական (մակերեսի) հետ կազմում է միջինական ամբողջություն [Տե՛ս "Տարրեր" 10.96]։ Ուստի, LH-ի քառակուսի արմատը՝ այսինքն՝ EC-ն, (ուղիղ գիծ) է, որը միջինական (մակերեսի) հետ կազմում է միջինական ամբողջություն։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 111

Ապոտոմեն նույնը չէ, ինչ բինոմը։

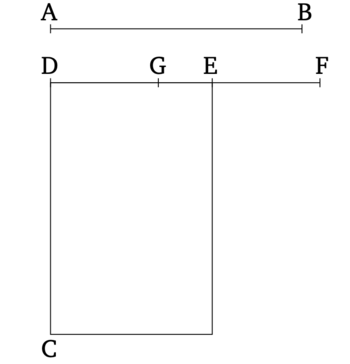
Թող AB-ն լինի ապոտոմե։ Ասում եմ, որ AB-ն նույնը չէ, ինչ բինոմ։

Եթե հնարավոր է, թող այն նույնը լինի։ Եվ թող ռացիոնալ (ուղիղ գիծը) DC դրված լինի։ Եվ թող ուղղանկյունը CE, որը հավասար է AB-ի վրա կառուցված քառակուսուն, դրված լինի CD-ի վրա՝ արտադրելով DE որպես լայնություն։ Ուստի, քանի որ AB-ն ապոտոմե է, DE-ն առաջին ապոտոմե է [Տե՛ս "Տարրեր" 10.97]։ Թող EF-ը լինի դրա կցորդ։ Այսպիսով, DF-ն և FE-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով, և DF-ի վրա կառուցված քառակուսին մեծ է FE-ի վրա կառուցված քառակուսուց որոշակի (ուղիղ գծի) վրա կառուցված քառակուսու չափով, որը համաչափ է DF-ի հետ, և DF-ն համաչափ է նախապես տրված ռացիոնալ (ուղիղ գծի) DC-ի հետ [Տե՛ս "Տարրեր" 10.10-ի սահմանում]։

Կրկին, քանի որ AB-ն բինոմ է, DE-ն, հետևաբար, առաջին բինոմ է [Տե՛ս "Տարրեր" 10.60]։ Թող (DE-ն) բաժանված լինի իր (կազմող) տերմիններով G կետում, և թող DG-ն լինի մեծ տերմինը։ Այսպիսով, DG-ն և GE-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով, և DG-ի վրա կառուցված քառակուսին մեծ է GE-ի վրա կառուցված քառակուսուց որոշակի (ուղիղ գծի) վրա կառուցված քառակուսու չափով, որը համաչափ է DG-ի հետ, և մեծ (տերմին) DG-ն համաչափ է նախապես տրված ռացիոնալ (ուղիղ գծի) DC-ի հետ [Տե՛ս "Տարրեր" 10.5-ի սահմանում]։

Ուստի, DF-ն նույնպես համաչափ է DG-ի հետ [Տե՛ս "Տարրեր" 10.12]։ Մնացորդ GF-ն, հետևաբար, համաչափ է DF-ի հետ [Տե՛ս "Տարրեր" 10.15]։ Ուստի, քանի որ DF-ն համաչափ է GF-ի հետ, և DF-ն ռացիոնալ է, GF-ն նույնպես ռացիոնալ է։ Ուստի, քանի որ DF-ն համաչափ է GF-ի հետ, DF-ն երկարությամբ անհամաչափ է EF-ի հետ։ Ուստի, FG-ն նույնպես երկարությամբ անհամաչափ է EF-ի հետ [Տե՛ս "Տարրեր" 10.13]։ GF-ն և FE-ն, հետևաբար, ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ Ուստի, EG-ն ապոտոմե է [Տե՛ս "Տարրեր" 10.73]։ Բայց, (այն) նաև ռացիոնալ է։ Սա անհնար է։

Ուստի, ապոտոմեն նույնը չէ, ինչ բինոմ։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Հետևանք

Ապոտոմեն և դրան հաջորդող անհամաչափ (ուղիղ գծերը) ոչ նույնն են, ինչ միջինական (ուղիղ գիծը), և ոչ էլ նույնն են մեկը մյուսի հետ։

Քանի որ միջինական (ուղիղ գծի) վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն ռացիոնալ (ուղիղ գիծ), որը երկարությամբ անհամաչափ է այն (ուղիղ գծի) հետ, որի վրա դրված է (մակերեսը) [Տե՛ս "Տարրեր" 10.22]։ Եվ ապոտոմեի վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն առաջին ապոտոմե [Տե՛ս "Տարրեր" 10.97]։ Եվ միջինական (ուղիղ գծի) առաջին ապոտոմեի վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն երկրորդ ապոտոմե [Տե՛ս "Տարրեր" 10.98]։ Եվ միջինական (ուղիղ գծի) երկրորդ ապոտոմեի վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն երրորդ ապոտոմե [Տե՛ս "Տարրեր" 10.99]։ Եվ փոքր (ուղիղ գծի) վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն չորրորդ ապոտոմե [Տե՛ս "Տարրեր" 10.100]։ Եվ (ուղիղ գծի) վրա կառուցված քառակուսին, որը ռացիոնալ (մակերեսի) հետ արտադրում է միջինական ամբողջություն, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն հինգերորդ ապոտոմե [Տե՛ս "Տարրեր" 10.101]։ Եվ (ուղիղ գծի) վրա կառուցված քառակուսին, որը միջինական (մակերեսի) հետ արտադրում է միջինական ամբողջություն, դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն վեցերորդ ապոտոմե [Տե՛ս "Տարրեր" 10.102]։

Ուստի, քանի որ վերը նշված լայնությունները տարբեր են առաջինից և մեկը մյուսից՝ առաջինից, քանի որ այն ռացիոնալ է, և մեկը մյուսից, քանի որ դրանք նույն կարգի չեն, պարզ է, որ անհամաչափ (ուղիղ գծերն) իրենք էլ տարբեր են մեկը մյուսից։ Եվ քանի որ ցույց է տրվել, որ ապոտոմեն նույնը չէ, ինչ բինոմը [Տե՛ս "Տարրեր" 10.111], և (որ) ապոտոմեին հաջորդող (անհամաչափ ուղիղ գծերը), դրված ռացիոնալ (ուղիղ գծի) վրա, արտադրում են որպես լայնություն, յուրաքանչյուրը ըստ իր կարգի, ապոտոմեներ, և (որ) բինոմին հաջորդող (անհամաչափ ուղիղ գծերը) նույնպես (արտադրում են որպես լայնություն) ըստ իրենց կարգի բինոմներ, ապոտոմեին հաջորդող (անհամաչափ ուղիղ գծերը) հետևաբար տարբեր են, և բինոմին հաջորդող (անհամաչափ ուղիղ գծերը) նույնպես տարբեր են, այնպես որ ընդհանուր առմամբ կա կարգով 13 անհամաչափ (ուղիղ գիծ)։

1. Միջինական 2. Բինոմ 3. Առաջին երկմիջինական 4. Երկրորդ երկմիջինական 5. Մեծ 6. Ռացիոնալ գումարած միջինական (մակերեսի) քառակուսի արմատ, 7. Երկու միջինական (մակերեսների) գումարի քառակուսի արմատ, 8. Ապոտոմե, 9. Միջինական առաջին ապոտոմե, 10. Միջինական երկրորդ ապոտոմե, 11. Փոքր, 12. Այն, որը ռացիոնալ (մակերեսի) հետ արտադրում է միջինական ամբողջություն, 13. Այն, որը միջինական (մակերեսի) հետ արտադրում է միջինական ամբողջություն։

Պնդում 112

Ռացիոնալ (ուղիղ գծի) վրա կառուցված քառակուսին, դրված բինոմ (ուղիղ գծի) վրա, արտադրում է որպես լայնություն ապոտոմե, որի տերմինները համաչափ են բինոմի տերմինների հետ երկարությամբ և, ավելին, նույն հարաբերությամբ։ Բացի այդ, ստեղծված ապոտոմեն կունենա նույն կարգը, ինչ բինոմը։

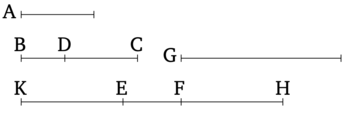
Թող A-ն լինի ռացիոնալ (ուղիղ գիծ), և BC-ն՝ բինոմ (ուղիղ գիծ), որի DC-ն լինի մեծ տերմինը։ Եվ թող BC-ի և EF-ի վրա պարփակված ուղղանկյունը հավասար լինի A-ի վրա կառուցված քառակուսուն։ Ասում եմ, որ EF-ն ապոտոմե է, որի տերմինները համաչափ են CD-ի և DB-ի հետ երկարությամբ և նույն հարաբերությամբ, և, ավելին, EF-ն կունենա նույն կարգը, ինչ BC-ն։

Թող կրկին BD-ի և G-ի վրա պարփակված ուղղանկյունը հավասար լինի A-ի վրա կառուցված քառակուսուն։ Ուստի, քանի որ BC-ի և EF-ի վրա պարփակված ուղղանկյունը հավասար է BD-ի և G-ի վրա պարփակված ուղղանկյունին, ապա ինչպես CB-ն է BD-ի նկատմամբ, այնպես էլ G-ն է EF-ի նկատմամբ [Տե՛ս "Տարրեր" 6.16]։ Եվ CB-ն մեծ է BD-ից։ Ուստի, G-ն նույնպես մեծ է EF-ից [Տե՛ս "Տարրեր" 5.16, 5.14]։ Թող EH-ը հավասար լինի G-ին։ Ուստի, ինչպես CB-ն է BD-ի նկատմամբ, այնպես էլ HE-ն է EF-ի նկատմամբ։ Ուստի, տարանջատմամբ, ինչպես CD-ն է BD-ի նկատմամբ, այնպես էլ HF-ը FE-ի նկատմամբ [Տե՛ս "Տարրեր" 5.17]։

Թող այն կազմակերպված լինի, որ ինչպես HF-ն է FE-ի նկատմամբ, այնպես էլ FK-ն KE-ի նկատմամբ։ Եվ, հետևաբար, ամբողջ HK-ն KF-ի նկատմամբ այնպես է, ինչպես FK-ն KE-ի նկատմամբ։ Քանի որ, ինչպես առաջատար (համամասնությունները) հաջորդողներից մեկի նկատմամբ են, այնպես էլ բոլորը՝ բոլորի նկատմամբ [Տե՛ս "Տարրեր" 5.12]։ Եվ ինչպես FK-ն KE-ի նկատմամբ է, այնպես էլ CD-ն DB-ի նկատմամբ է [Տե՛ս "Տարրեր" 5.11]։ Եվ, հետևաբար, ինչպես HK-ն է KF-ի նկատմամբ, այնպես էլ CD-ն DB-ի նկատմամբ է [Տե՛ս "Տարրեր" 5.11]։

Եվ CD-ի վրա կառուցված քառակուսին համաչափ է DB-ի վրա կառուցված քառակուսու հետ [Տե՛ս "Տարրեր" 10.36]։ Ուստի, HK-ի վրա կառուցված քառակուսին նույնպես համաչափ է KF-ի վրա կառուցված քառակուսու հետ [Տե՛ս "Տարրեր" 6.22, 10.11]։ Եվ ինչպես HK-ի վրա կառուցված քառակուսին է KF-ի վրա կառուցված քառակուսու նկատմամբ, այնպես էլ HK-ն է KE-ի նկատմամբ, քանի որ HK, KF, և KE ուղիղ գծերը համամասնություններ են [Տե՛ս "Տարրեր" 5.9-ի սահմանում]։ Ուստի, HK-ն երկարությամբ համաչափ է KE-ի հետ [Տե՛ս "Տարրեր" 10.11]։ Հետևաբար, HE-ն նույնպես երկարությամբ համաչափ է EK-ի հետ [Տե՛ս "Տարրեր" 10.15]։

Եվ քանի որ A-ի վրա կառուցված քառակուսին հավասար է EH-ի և BD-ի վրա պարփակված ուղղանկյան, և A-ի վրա կառուցված քառակուսին ռացիոնալ է, EH-ի և BD-ի վրա պարփակված ուղղանկյունը նույնպես ռացիոնալ է։ Եվ այն դրված է ռացիոնալ (ուղիղ գծի) BD-ի վրա։ Ուստի, EH-ն ռացիոնալ է և երկարությամբ համաչափ BD-ի հետ [Տե՛ս "Տարրեր" 10.20]։ Եվ, հետևաբար, դրան համաչափ (ուղիղ գիծը) EK-ն նույնպես ռացիոնալ է [Տե՛ս "Տարրեր" 10.3-ի սահմանում] և երկարությամբ համաչափ BD-ի հետ [Տե՛ս "Տարրեր" 10.12]։ Ուստի, քանի որ ինչպես CD-ն է DB-ի նկատմամբ, այնպես էլ FK-ն KE-ի նկատմամբ, և CD-ն և DB-ն (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով, FK-ն և KE-ն նույնպես համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.11]։ Եվ KE-ն ռացիոնալ է։ Ուստի, FK-ն նույնպես ռացիոնալ է։ FK-ն և KE-ն, հետևաբար, ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ Ուստի, EF-ն ապոտոմե է [Տե՛ս "Տարրեր" 10.73]։

Եվ CD-ի վրա կառուցված քառակուսին մեծ է DB-ի վրա կառուցված քառակուսուց կամ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, որը համաչափ է CD-ի հետ, կամ անհամաչափ։

Ուստի, եթե CD-ի վրա կառուցված քառակուսին մեծ է DB-ի վրա կառուցված քառակուսուց CD-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, ապա FK-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի KE-ի վրա կառուցված քառակուսուց FK-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե CD-ն համաչափ է նախապես տրված ռացիոնալ (ուղիղ գծի) հետ, ապա FK-ն նույնպես [Տե՛ս "Տարրեր" 10.11, 10.12]։ Եվ եթե BD-ն համաչափ է, ապա KE-ն նույնպես [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե ոչ CD-ն, ոչ DB-ն համաչափ չեն, ապա ոչ FK-ն, ոչ KE-ն չեն լինի։

Եվ եթե CD-ի վրա կառուցված քառակուսին մեծ է DB-ի վրա կառուցված քառակուսուց CD-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, ապա FK-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի KE-ի վրա կառուցված քառակուսուց FK-ի հետ անհամաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե CD-ն համաչափ է նախապես տրված ռացիոնալ (ուղիղ գծի) հետ, ապա FK-ն նույնպես [Տե՛ս "Տարրեր" 10.11, 10.12]։ Եվ եթե BD-ն համաչափ է, ապա KE-ն նույնպես [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե ոչ CD-ն, ոչ DB-ն համաչափ չեն, ապա ոչ FK-ն, ոչ KE-ն չեն լինի։ Ուստի, FE-ն ապոտոմե է, որի տերմինները՝ FK-ն և KE-ն, համաչափ են բինոմի տերմինների՝ CD-ի և DB-ի հետ երկարությամբ և նույն հարաբերությամբ։ Եվ (FE-ն) ունի նույն կարգը, ինչ BC-ն [Տե՛ս "Տարրեր" 10.5-10.10-ի սահմանումները]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 113

Ռացիոնալ (ուղիղ գծի) վրա կառուցված քառակուսին, դրված ապոտոմեի վրա, արտադրում է որպես լայնություն բինոմ, որի տերմինները համաչափ են ապոտոմեի տերմինների հետ երկարությամբ և նույն հարաբերությամբ։ Բացի այդ, ստեղծված բինոմը կունենա նույն կարգը, ինչ ապոտոմեն։

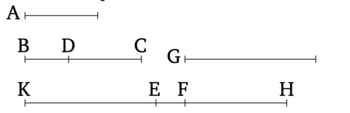
Թող A-ն լինի ռացիոնալ (ուղիղ գիծ), և BD-ն՝ ապոտոմե։ Եվ թող BD-ի և KH-ի վրա պարփակված ուղղանկյունը հավասար լինի A-ի վրա կառուցված քառակուսուն՝ այնպես, որ ռացիոնալ (ուղիղ գծի) A-ի վրա կառուցված քառակուսին, դրված ապոտոմե BD-ի վրա, արտադրի KH-ը որպես լայնություն։ Ասում եմ, որ KH-ը բինոմ է, որի տերմինները համաչափ են BD-ի տերմինների հետ և նույն հարաբերությամբ, և, ավելին, KH-ն ունի նույն կարգը, ինչ BD-ն։

Թող DC-ն լինի BD-ի կցորդ։ Ուստի, BC-ն և CD-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.73]։ Եվ թող BC-ի և G-ի վրա պարփակված ուղղանկյունը նույնպես հավասար լինի A-ի վրա կառուցված քառակուսուն։ Եվ A-ի վրա կառուցված քառակուսին ռացիոնալ է։ Ուստի, BC-ի և G-ի վրա պարփակված ուղղանկյունը նույնպես ռացիոնալ է։ Եվ այն դրված է ռացիոնալ (ուղիղ գծի) BC-ի վրա։ Ուստի, G-ն ռացիոնալ է և երկարությամբ համաչափ BC-ի հետ [Տե՛ս "Տարրեր" 10.20]։

Ուստի, քանի որ BC-ի և G-ի վրա պարփակված ուղղանկյունը հավասար է BD-ի և KH-ի վրա պարփակված ուղղանկյան, ապա համամասնորեն, ինչպես CB-ն է BD-ի նկատմամբ, այնպես էլ KH-ն է G-ի նկատմամբ [Տե՛ս "Տարրեր" 6.16]։ Եվ BC-ն մեծ է BD-ից։ Ուստի, KH-ն նույնպես մեծ է G-ից [Տե՛ս "Տարրեր" 5.16, 5.14]։ Թող KE-ն լինի հավասար G-ին։ Ուստի, KE-ն երկարությամբ համաչափ է BC-ի հետ։ Եվ քանի որ ինչպես CB-ն է BD-ի նկատմամբ, այնպես էլ HK-ն է KE-ի նկատմամբ, ապա տարանջատմամբ, ինչպես BC-ն է CD-ի նկատմամբ, այնպես էլ KH-ն է HE-ի նկատմամբ [Տե՛ս "Տարրեր" 5.19]։

Թող այն կազմակերպված լինի, որ ինչպես KH-ն է HE-ի նկատմամբ, այնպես էլ HF-ն է FE-ի նկատմամբ։ Եվ, հետևաբար, մնացորդ KF-ը FH-ի նկատմամբ այնպես է, ինչպես KH-ն է HE-ի նկատմամբ, այսինքն՝ ինչպես BC-ն է CD-ի նկատմամբ [Տե՛ս "Տարրեր" 5.19]։ Եվ BC-ն և CD-ն համաչափ են միայն քառակուսիներով։ Ուստի, KF-ն և FH-ն նույնպես համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.11]։

Քանի որ ինչպես KH-ն է HE-ի նկատմամբ, այնպես էլ KF-ն է FH-ի նկատմամբ, բայց ինչպես KH-ն է HE-ի նկատմամբ, այնպես էլ HF-ն է FE-ի նկատմամբ, ուստի, նույնպես ինչպես KF-ն է FH-ի նկատմամբ, այնպես էլ HF-ն է FE-ի նկատմամբ [Տե՛ս "Տարրեր" 5.11]։ Եվ հետևաբար, ինչպես առաջինն է երրորդի նկատմամբ, այնպես էլ առաջինի վրա կառուցված քառակուսին է երկրորդի վրա կառուցված քառակուսու նկատմամբ [Տե՛ս "Տարրեր" 5.9-ի սահմանում]։

Ուստի, ինչպես KF-ն է FE-ի նկատմամբ, այնպես էլ KF-ի վրա կառուցված քառակուսին է FH-ի վրա կառուցված քառակուսու նկատմամբ։ Եվ KF-ի վրա կառուցված քառակուսին համաչափ է FH-ի վրա կառուցված քառակուսու հետ։ Քանի որ KF-ն և FH-ն համաչափ են քառակուսիներով։ Ուստի, KF-ն նույնպես համաչափ է FE-ի հետ [Տե՛ս "Տարրեր" 10.11]։ Ուստի, KF-ն նույնպես համաչափ է KE-ի հետ [Տե՛ս "Տարրեր" 10.15]։

Եվ KE-ն ռացիոնալ է և երկարությամբ համաչափ BC-ի հետ։ Ուստի, KF-ն նույնպես ռացիոնալ է և երկարությամբ համաչափ BC-ի հետ [Տե՛ս "Տարրեր" 10.12]։ Եվ քանի որ ինչպես BC-ն է CD-ի նկատմամբ, այնպես էլ KF-ն է FH-ի նկատմամբ, ապա հակադարձաբար, ինչպես BC-ն է KF-ի նկատմամբ, այնպես էլ DC-ն է FH-ի նկատմամբ [Տե՛ս "Տարրեր" 5.16]։ Եվ BC-ն համաչափ է KF-ի հետ։ Ուստի, FH-ն նույնպես համաչափ է CD-ի հետ [Տե՛ս "Տարրեր" 10.11]։

Եվ BC-ն և CD-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ Ուստի, KF-ն և FH-ն նույնպես ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.3-ի սահմանումը, 10.13]։ Ուստի, KH-ն բինոմ է [Տե՛ս "Տարրեր" 10.36]։

Ուստի, եթե BC-ի վրա կառուցված քառակուսին մեծ է CD-ի վրա կառուցված քառակուսուց BC-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով, ապա KF-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի FH-ի վրա կառուցված քառակուսուց KF-ի հետ համաչափ (ուղիղ գծի) վրա կառուցված քառակուսու չափով [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե BC-ն համաչափ է նախապես տրված ռացիոնալ (ուղիղ գծի) հետ, ապա KF-ն նույնպես [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե CD-ն համաչափ է նախապես տրված ռացիոնալ (ուղիղ գծի) հետ, ապա FH-ն նույնպես [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե ոչ BC-ն, ոչ CD-ն համաչափ չեն, ապա ոչ KF-ն, ոչ FH-ն չեն լինի [Տե՛ս "Տարրեր" 10.13]։

KH-ն, հետևաբար, բինոմ է, որի տերմինները՝ KF-ն և FH-ն, համաչափ են ապոտոմեի տերմինների՝ BC-ի և CD-ի հետ երկարությամբ և նույն հարաբերությամբ։ Եվ KH-ն ունի նույն կարգը, ինչ BC-ն [Տե՛ս "Տարրեր" 10.5-10.10-ի սահմանումները]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 114

Եթե մակերեսը պարփակված է ապոտոմեի և բինոմի կողմից, որոնց տերմինները համաչափ են ապոտոմեի տերմիններին և նույն հարաբերությամբ, ապա մակերեսի քառակուսի արմատը ռացիոնալ (ուղիղ գիծ) է։

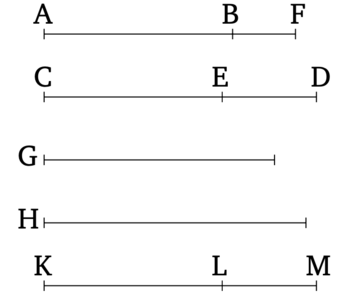
Թող մակերեսը՝ ուղղանկյունը, որը պարփակված է AB և CD կողմից, պարփակված լինի ապոտոմե AB-ի և բինոմ CD-ի կողմից, որոնց մեծ տերմինը CE-ն է։ Եվ թող բինոմի տերմինները՝ CE-ն և ED-ն, համաչափ լինեն ապոտոմեի տերմիններին՝ AF և FB (համապատասխանաբար), և նույն հարաբերությամբ։ Եվ թող մակերեսի՝ AB և CD-ի կողմից պարփակված ուղղանկյան քառակուսի արմատը լինի G։ Ասում եմ, որ G-ն ռացիոնալ (ուղիղ գիծ) է։

Թող ռացիոնալ (ուղիղ գիծը) H դրված լինի։ Եվ թող ուղղանկյունը, որը հավասար է H-ի վրա կառուցված քառակուսուն, դրված լինի CD-ի վրա՝ արտադրելով KL որպես լայնություն։ Ուստի, KL-ը ապոտոմե է, որի տերմինները՝ KM-ն և ML-ը, համաչափ են բինոմի տերմինների՝ CE-ի և ED-ի հետ (համապատասխանաբար), և նույն հարաբերությամբ [Տե՛ս "Տարրեր" 10.112]։ Բայց CE-ն և ED-ն նույնպես համաչափ են AF-ի և FB-ի հետ (համապատասխանաբար), և նույն հարաբերությամբ։ Ուստի, ինչպես AF-ն է FB-ի նկատմամբ, այնպես էլ KM-ն է ML-ի նկատմամբ։ Հետևաբար, ինչպես AF-ն է KM-ի նկատմամբ, այնպես էլ BF-ն է LM-ի նկատմամբ [Տե՛ս "Տարրեր" 5.16]։ Ուստի, մնացորդ AB-ն նույնպես KL-ի նկատմամբ այնպես է, ինչպես AF-ն է KM-ի նկատմամբ [Տե՛ս "Տարրեր" 5.19]։ Եվ AF-ն համաչափ է KM-ի հետ [Տե՛ս "Տարրեր" 10.12]։ Ուստի, AB-ն նույնպես համաչափ է KL-ի հետ [Տե՛ս "Տարրեր" 10.11]։

Եվ ինչպես AB-ն է KL-ի նկատմամբ, այնպես էլ CD-ի և AB-ի վրա պարփակված ուղղանկյունը CD-ի և KL-ի վրա պարփակված ուղղանկյան նկատմամբ է [Տե՛ս "Տարրեր" 6.1]։ Ուստի, CD-ի և AB-ի վրա պարփակված ուղղանկյունը նույնպես համաչափ է CD-ի և KL-ի վրա պարփակված ուղղանկյան հետ [Տե՛ս "Տարրեր" 10.11]։ Եվ CD-ի և KL-ի վրա պարփակված ուղղանկյունը հավասար է H-ի վրա կառուցված քառակուսուն։ Ուստի, CD-ի և AB-ի վրա պարփակված ուղղանկյունը համաչափ է H-ի վրա կառուցված քառակուսու հետ։ Եվ G-ի վրա կառուցված քառակուսին հավասար է CD-ի և AB-ի վրա պարփակված ուղղանկյան։ Ուստի, G-ի վրա կառուցված քառակուսին համաչափ է H-ի վրա կառուցված քառակուսու հետ։ Եվ H-ի վրա կառուցված քառակուսին ռացիոնալ է։ Ուստի, G-ի վրա կառուցված քառակուսին նույնպես ռացիոնալ է։ G-ն, հետևաբար, ռացիոնալ է։ Եվ դա CD-ի և AB-ի կողմից պարփակված ուղղանկյան քառակուսի արմատն է։

Ուստի, եթե մակերեսը պարփակված է ապոտոմեի և բինոմի կողմից, որոնց տերմինները համաչափ են ապոտոմեի տերմիններին և նույն հարաբերությամբ, ապա մակերեսի քառակուսի արմատը ռացիոնալ (ուղիղ գիծ) է։

Հետևանք

Եվ սա մեզ ցույց է տալիս, որ հնարավոր է ռացիոնալ մակերեսը պարփակված լինի անհամաչափ ուղիղ գծերով։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 115

Հնարավոր է ստեղծել անհաշվելի (շարք) անհամաչափ (ուղիղ գծեր) միջինական (ուղիղ գծից), և դրանցից ոչ մեկը չի կրկնվում նախորդ (ուղիղ գծերից)։

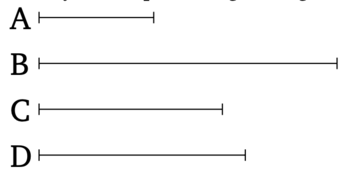
Թող A-ն լինի միջինական (ուղիղ գիծ)։ Ասում եմ, որ հնարավոր է ստեղծել անհաշվելի (շարք) անհամաչափ (ուղիղ գծեր) A-ից, և դրանցից ոչ մեկը չի կրկնվում նախորդ (ուղիղ գծերից)։

Թող ռացիոնալ (ուղիղ գիծը) B դրված լինի։ Եվ թող C-ի վրա կառուցված քառակուսին հավասար լինի B-ի և A-ի վրա պարփակված ուղղանկյանը։ Ուստի, C-ն անհամաչափ է [Տե՛ս "Տարրեր" 10.4-ի սահմանումը]։ Քանի որ անհամաչափ և ռացիոնալ (ուղիղ գծերի) վրա պարփակված մակերեսը անհամաչափ է [Տե՛ս "Տարրեր" 10.20]։ Եվ (C-ն) չի կրկնվում նախորդ (ուղիղ գծերից) որևէ մեկին։ Քանի որ նախորդ (ուղիղ գծերից) որևէ մեկի վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, չի արտադրում միջինական (ուղիղ գիծ) որպես լայնություն։

Ուստի, կրկին, թող D-ի վրա կառուցված քառակուսին հավասար լինի B-ի և C-ի վրա պարփակված ուղղանկյանը։ Ուստի, D-ի վրա կառուցված քառակուսին անհամաչափ է [Տե՛ս "Տարրեր" 10.20]։ D-ն, հետևաբար, անհամաչափ է [Տե՛ս "Տարրեր" 10.4-ի սահմանումը]։ Եվ (D-ն) չի կրկնվում նախորդ (ուղիղ գծերից) որևէ մեկին։ Քանի որ նախորդ (ուղիղ գծերից) որևէ մեկի վրա կառուցված քառակուսին, դրված ռացիոնալ (ուղիղ գծի) վրա, չի արտադրում C որպես լայնություն։

Ուստի, այսպիսի կառուցվածքի շարունակական զարգացմամբ դեպի անսահմանություն, պարզ է, որ հնարավոր է ստեղծել անհաշվելի (շարք) անհամաչափ (ուղիղ գծեր) միջինական (ուղիղ գծից), և դրանցից ոչ մեկը չի կրկնվում նախորդ (ուղիղ գծերից)։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

հեղինակ՝ էվկլիդես աղբյուր՝ Euclid's Elements of Geometry, English translation by Richard Fitzpatrick

Տարերքի գրքեր

Սահմանումներ

1. Մարմինը (ֆիգուր) է, որն ունի երկարություն, լայնություն և խորություն։

2. Մարմնի եզրը (ֆիգուր) մակերևույթն է։

3. Ուղիղ գիծը ուղղահայաց է հարթությանը, երբ այն կազմում է ուղիղ անկյուններ իր հետ միացված բոլոր ուղիղ գծերի հետ, որոնք նույնպես գտնվում են հարթության մեջ։

4. Հարթությունը ուղղահայաց է մեկ այլ հարթության, երբ մեկ հարթության մեջ ուղղված բոլոր ուղիղ գծերը, որոնք ուղղահայաց են հարթությունների ընդհանուր հատվածին, ուղղահայաց են մնում մյուս հարթության նկատմամբ։

5. Ուղիղ գծի և հարթության միջև անկումը այն անկյունն է, որը պարփակվում է գծված և կանգնած (ուղիղ գծերով), երբ կանգնած ուղիղ գծի ծայրից ուղղահայաց է տարվում դեպի հարթություն, և գծվում է մի ուղիղ գիծ կանգնած ուղիղ գծի ծայրից դեպի ստացված կետ։

6. Հարթության և մեկ այլ հարթության միջև անկումը սուր անկյունն է, որը պարփակվում է (ուղիղ գծերով), որոնք գծվում են յուրաքանչյուր հարթությունում և ուղղահայաց են ընդհանուր հատվածին։

7. Ասում են, որ հարթությունը հարթությանը նման անկումով է, երբ նշված անկումները հավասար են։

8. Զուգահեռ հարթություններն են նրանք, որոնք չեն հատվում։

9. Նման մարմնական ֆիգուրներն են նրանք, որոնք պարփակված են հավասար թվով նման հարթություններով (որոնք նման ձևով են դասավորված)։

10. Հավասար և նման մարմնական ֆիգուրներն են նրանք, որոնք պարփակված են նման հարթություններով, հավասար թվով և մեծությամբ (նման ձևով դասավորված)։

11. Մարմնային անկյունը կազմված է երկուից ավելի գծերի միացումից, որոնք չեն գտնվում նույն մակերեսի վրա։ Կամ՝ մարմնային անկյունը այն է, որը պարփակվում է երկուից ավելի հարթ անկյուններով, որոնք կառուցված են միևնույն կետում, բայց չեն գտնվում նույն հարթությունում։

12. Պիրամիդը մարմնական ֆիգուր է, որը պարփակված է հարթություններով և կառուցված է մեկ հարթությունից դեպի մեկ կետ։

13. Պրիզման մարմնական ֆիգուր է, որը պարփակված է հարթություններով, որոնց երկու հակառակ (հարթությունները) հավասար են, նման և զուգահեռ, իսկ մնացածները ուղղանկյուններ են։

14. Գունդը այն ֆիգուրն է, որը ստացվում է, երբ կիսաշրջանագծի տրամագիծը մնում է ֆիքսված, և կիսաշրջանը պտտվում է։

15. Գնդի առանցքը այն ֆիքսված ուղիղ գիծն է, որի շուրջ պտտվում է կիսաշրջանը։

16. Գնդի կենտրոնը նույնն է, ինչ կիսաշրջանի կենտրոնը։

17. Գնդի տրամագիծը ցանկացած ուղիղ գիծ է, որը անցնում է կենտրոնով և ավարտվում գնդի մակերևույթում։

18. Կոնն այն ֆիգուրն է, որը ստացվում է, երբ ուղղանկյուն եռանկյան կողմերից մեկը մնում է ֆիքսված, և եռանկյունը պտտվում է։ Եթե ֆիքսված ուղիղ գիծը հավասար է եռանկյունի մյուս կողմին, կոնը կլինի ուղղանկյուն։

19. Կոնի առանցքը այն ֆիքսված ուղիղ գիծն է, որի շուրջ պտտվում է եռանկյունը։

20. Կոնի հիմքը այն շրջանն է, որը գծվում է պտտվող կողմի միջոցով։

21. Գլանիկն այն ֆիգուրն է, որը ստացվում է, երբ ուղղանկյուն զուգահեռագծի կողմերից մեկը մնում է ֆիքսված, և զուգահեռագիծը պտտվում է։

22. Գլանիկի առանցքը այն ֆիքսված ուղիղ գիծն է, որի շուրջ պտտվում է զուգահեռագիծը։

23. Գլանիկի հիմքերը այն շրջաններն են, որոնք գծվում են երկու հակառակ կողմերով։

24. Նման կոններն ու գլանիկներն են նրանք, որոնց առանցքները և հիմքերի տրամագծերը համեմատական են։

25. Խորանարդը մարմնական ֆիգուր է, որը պարփակված է վեց հավասար քառակուսիներով։

26. Ութանիստը մարմնական ֆիգուր է, որը պարփակված է ութ հավասար և հավասարակողմ եռանկյուններով։

27. Իկոսանիստը մարմնական ֆիգուր է, որը պարփակված է քսան հավասար և հավասարակողմ եռանկյուններով։

28. Դոդեկանիստը մարմնական ֆիգուր է, որը պարփակված է տասներկու հավասար, հավասարակողմ և հավասարանկյուն հնգանկյուններով։

Պնդում 1

Ուղիղ գծի մի մասը չի կարող գտնվել հարթության մեջ, իսկ մի մասը՝ ավելի բարձր հարթությունում։

Եթե հնարավոր է, թող ուղիղ գծի AB մասը գտնվի հարթության մեջ, իսկ BC մասը՝ ավելի բարձր հարթությունում։

Հարթության մեջ կլինի մի ուղիղ գիծ, որը շարունակական է AB-ի հետ։ Թող դա լինի BD։ Ուստի, AB-ն ընդհանուր հատված կլինի երկու (տարբեր) ուղիղ գծերի՝ ABC-ի և ABD-ի։ Սա անհնար է, քանի որ եթե գծենք շրջան B կենտրոնով և AB շառավղով, ապա շրջանագծի անիվները, որոնք կտրվեն ABC և ABD տրամագծերով, կլինեն անհավասար։

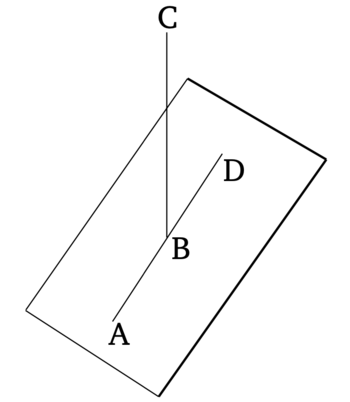
Ուստի, ուղիղ գծի մի մասը չի կարող գտնվել հարթության մեջ, իսկ մի մասը՝ ավելի բարձր հարթությունում։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 2

Եթե երկու ուղիղ գծեր հատում են իրար, ապա դրանք գտնվում են մեկ հարթության մեջ, և այդ գծերով կազմված ցանկացած եռանկյուն գտնվում է մեկ հարթության մեջ։

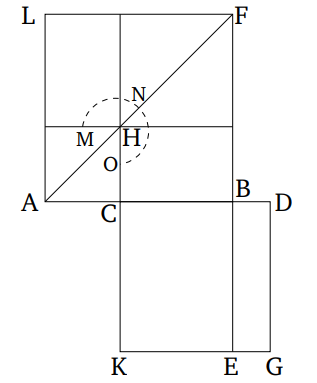
Թող երկու ուղիղ գծերը AB-ն և CD-ն հատեն իրար E կետում։ Ասում եմ, որ AB-ն և CD-ն գտնվում են մեկ հարթության մեջ, և այդ գծերով կազմված ցանկացած եռանկյուն գտնվում է մեկ հարթության մեջ։

Թող պատահական F և G կետերը վերցված լինեն EC և EB գծերի վրա (համապատասխանաբար)։ Թող CB-ն և FG-ն միացված լինեն, և թող FH-ն և GK-ն գծվեն։ Ասում եմ, նախ և առաջ, որ եռանկյուն ECB-ն գտնվում է մեկ (հիմնական) հարթության մեջ։ Քանի որ եթե եռանկյուն ECB-ի մի մասը, օրինակ՝ FHC կամ GBK, գտնվում է հիմնական հարթության մեջ, իսկ մնացած մասը՝ այլ հարթությունում, ապա EC կամ EB ուղիղ գծերից մեկի մի մասը նույնպես կլինի հիմնական հարթության մեջ, իսկ մի մասը՝ այլ հարթությունում։ Եվ եթե եռանկյուն ECB-ի FCBG մասը գտնվում է հիմնական հարթության մեջ, իսկ մնացած մասը՝ այլ հարթությունում, ապա EC և EB ուղիղ գծերից երկուսն էլ կունենան մասեր, որոնք կլինեն հիմնական հարթության մեջ, իսկ մասեր՝ այլ հարթությունում։ Սա արդեն ցույց է տրվել որպես անհնարին [Տե՛ս "Տարրեր" 11.1]։ Ուստի, եռանկյուն ECB-ն գտնվում է մեկ հարթության մեջ։ Եվ այն հարթությունում, որտեղ գտնվում է եռանկյուն ECB-ն, այնտեղ կլինեն EC և EB գծերը։ Եվ այն հարթությունում, որտեղ գտնվում են EC և EB գծերը, այնտեղ կլինեն AB և CD ուղիղ գծերը նույնպես [Տե՛ս "Տարրեր" 11.1]։ Ուստի, AB և CD ուղիղ գծերը գտնվում են մեկ հարթության մեջ, և այդ գծերով կազմված ցանկացած եռանկյուն գտնվում է մեկ հարթության մեջ։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 3

Եթե երկու հարթություններ հատում են իրար, ապա դրանց ընդհանուր հատվածը ուղիղ գիծ է։

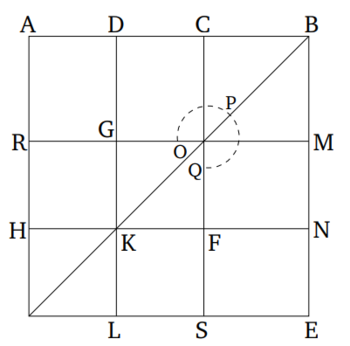
Թող երկու հարթությունները՝ AB-ն և BC-ն, հատեն իրար, և թող դրանց ընդհանուր հատվածը լինի DB գիծը։ Ասում եմ, որ DB գիծը ուղիղ է։

Եթե ոչ, թող DEB ուղիղ գիծը միացվի D կետից B կետին AB հարթության մեջ, և DF B ուղիղ գիծը՝ BC հարթության մեջ։ Ուստի, DEB և DFB ուղիղ գծերը կունենան նույն ծայրերը և ակնհայտորեն կփակեն տարածք։ Սա անհնար է։ Ուստի, DEB և DFB գծերը չեն կարող լինել ուղիղ գծեր։ Նույն կերպ կարելի է ցույց տալ, որ D կետից B կետին հնարավոր չէ միացնել որևէ այլ ուղիղ գիծ, բացի DB-ից, որը AB և BC հարթությունների ընդհանուր հատվածն է։

Ուստի, եթե երկու հարթություններ հատում են իրար, ապա դրանց ընդհանուր հատվածը ուղիղ գիծ է։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 4

Եթե ուղիղ գիծը տեղադրված է ուղղահայաց երկու ուղիղ գծերին, որոնք հատում են իրար ընդհանուր հատման կետում, ապա այն կլինի նաև ուղղահայաց այդ գծերով անցնող հարթությանը։

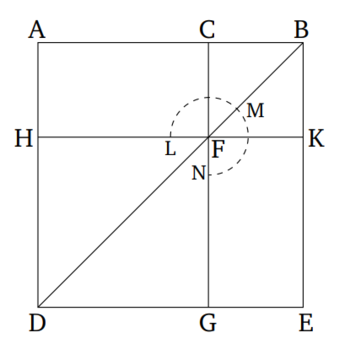
Թող ուղիղ գիծը՝ EF-ը, տեղադրված լինի ուղղահայաց AB և CD գծերին, որոնք հատում են իրար E կետում։ Ասում եմ, որ EF-ը կլինի նաև ուղղահայաց AB և CD գծերով անցնող հարթությանը։

Թող AE, EB, CE և ED հատվածները կտրված լինեն (այդ երկու գծերից այնպես, որ լինեն) հավասար։ Թող GEH գիծը գծվի պատահականորեն E կետով (AB և CD գծերով անցնող հարթության մեջ)։ Եվ թող AD-ն և CB-ն միացվեն։ Ավելին, թող FA, FG, FD, FC, FH և FB գծերը միացվեն EF գծի պատահական F կետից։

Քանի որ AE և ED հատվածները հավասար են CE և EB հատվածներին, և դրանք պարփակում են հավասար անկյուններ [Տե՛ս "Տարրեր" 1.15], AD հիմքը հավասար է CB հիմքին, և AED եռանկյունը հավասար է CEB եռանկյունին [Տե՛ս "Տարրեր" 1.4]։ Ուստի, DAE անկյունը հավասար է EBC անկյունին։ Եվ AEG անկյունը նույնպես հավասար է BEH անկյունին [Տե՛ս "Տարրեր" 1.15]։ Այսպիսով, AGE և BEH եռանկյունները ունեն երկու անկյուններ, որոնք հավասար են երկու անկյուններին (համապատասխանաբար), և մեկ կողմ, որը հավասար է մեկ կողմին՝ այդ անկյուններով, (այսինքն՝) AE և EB։ Ուստի, դրանք կունենան նաև մնացած կողմերը հավասար [Տե՛ս "Տարրեր" 1.26]։ Ուստի, GE-ն հավասար է EH-ին, իսկ AG-ն՝ BH-ին։ Եվ քանի որ AE-ն հավասար է EB-ին, իսկ FE-ն ընդհանուր է և ուղղահայաց, FA հիմքը նույնպես հավասար է FB հիմքին [Տե՛ս "Տարրեր" 1.4]։ Նույն պատճառներով, FC-ն նույնպես հավասար է FD-ին։ Եվ քանի որ AD-ն հավասար է CB-ին, իսկ FA-ն նույնպես հավասար է FB-ին, FA և AD երկու գծերը հավասար են FB և BC երկու գծերին համապատասխանաբար։ Իսկ FD հիմքը ցույց է տրվել, որ հավասար է FC հիմքին։ Ուստի, FAD անկյունը նույնպես հավասար է FBC անկյունին [Տե՛ս "Տարրեր" 1.8]։ Եվ կրկին, քանի որ AG-ն ցույց է տրվել, որ հավասար է BH-ին, իսկ FA-ն նույնպես հավասար է FB-ին, FA և AG երկու գծերը հավասար են FB և BH երկու գծերին (համապատասխանաբար)։ Եվ FAG անկյունը ցույց է տրվել, որ հավասար է FBH անկյունին։ Ուստի, FG հիմքը հավասար է FH հիմքին [Տե՛ս "Տարրեր" 1.4]։ Եվ կրկին, քանի որ GE-ն ցույց է տրվել, որ հավասար է EH-ին, իսկ EF-ը ընդհանուր է, GE և EF երկու գծերը հավասար են HE և EF երկու գծերին (համապատասխանաբար)։ Եվ FG հիմքը հավասար է FH հիմքին։ Ուստի, GEF անկյունը հավասար է HEF անկյունին [Տե՛ս "Տարրեր" 1.8]։ GEF և HEF անկյուններից յուրաքանչյուրը, հետևաբար, ուղղանկյուններ են [Տե՛ս "Տարրեր" 1.10]։ Ուստի, FE-ն ուղղահայաց է GH գծին, որը պատահականորեն գծվել է E կետով (AB և AC գծերով անցնող հարթության մեջ)։ Նույն կերպ կարելի է ցույց տալ, որ FE-ն ուղղանկյուններ կկազմի բոլոր գծերի հետ, որոնք միացված են դրան և գտնվում են հարթության մեջ։ Եվ գիծը ուղղահայաց է հարթությանը, երբ այն ուղղանկյուններ է կազմում բոլոր գծերի հետ, որոնք միացված են դրան և գտնվում են հարթությունում [Տե՛ս "Տարրեր" 11.3 սահմանում]։ Ուստի, FE-ն ուղղահայաց է հիմնական հարթությանը։ Իսկ հիմնական հարթությունը այն հարթությունն է, որը անցնում է AB և CD ուղիղ գծերով։ Ուստի, FE-ն ուղղահայաց է AB և CD գծերով անցնող հարթությանը։

Ուստի, եթե ուղիղ գիծը տեղադրված է ուղղահայաց երկու ուղիղ գծերին, որոնք հատում են իրար ընդհանուր հատման կետում, ապա այն կլինի նաև ուղղահայաց այդ գծերով անցնող հարթությանը։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 5

Եթե ուղիղ գիծը կանգնեցված է ուղղանկյուն երեք ուղիղ գծերին, որոնք հատում են մեկը մյուսին ընդհանուր հատման կետում, ապա երեք ուղիղ գծերը գտնվում են նույն հարթության մեջ։

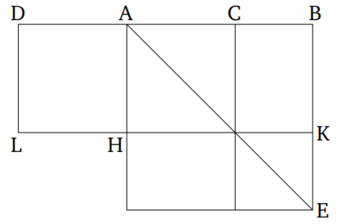
Թող AB ուղիղ գիծը կանգնեցված լինի ուղղանկյուն BC, BD և BE երեք ուղիղ գծերին ընդհանուր հատման կետում՝ B։ Ասում եմ, որ BC, BD և BE ուղիղ գծերը գտնվում են նույն հարթության մեջ։

Եթե ոչ, և հնարավոր է, թող BD-ն և BE-ն գտնվեն հենքային հարթության մեջ, իսկ BC-ն՝ ավելի բարձր (հարթության մեջ)։ Եվ թող AB և BC ուղիղ գծերով անցնող հարթությունը շարունակված լինի։ Այսպիսով, այն հենքային հարթության հետ կունենա ուղիղ գիծ որպես ընդհանուր հատում [Տե՛ս "Տարրեր" 11.3-ի սահմանումը]։ Թող այն լինի BF։ Ուստի, AB, BC և BF երեք ուղիղ գծերը գտնվում են նույն հարթության մեջ՝ (այսինքն) AB և BC ուղիղ գծերով անցնող հարթության մեջ։ Եվ քանի որ AB-ն ուղղանկյուն է ինչպես BD-ին, այնպես էլ BE-ին, AB-ն հետևաբար ուղղանկյուն է նաև BD և BE ուղիղ գծերով անցնող հարթությանը [Տե՛ս "Տարրեր" 11.4]։ Եվ BD և BE ուղիղ գծերով անցնող հարթությունը հենքային հարթությունն է։ Ուստի, AB-ն ուղղանկյուն է հենքային հարթությանը։ Հետևաբար, AB-ն ուղղանկյուն կլինի նաև բոլոր այն ուղիղ գծերին, որոնք միացված են դրան և գտնվում են հենքային հարթությունում [Տե՛ս "Տարրեր" 11.3-ի սահմանումը]։ Եվ BF, որը գտնվում է հենքային հարթությունում, միացված է դրան։ Ուստի, ABF անկյունը ուղղանկյուն է։ Իսկ ABC-ն նույնպես ուղղանկյուն է ենթադրվել։ Ուստի, ABF անկյունը հավասար է ABC անկյանը։ Իսկ դրանք գտնվում են նույն հարթության մեջ։ Սա անհնար է։ Ուստի, BC-ն ավելի բարձր հարթությունում չէ։ Ուստի, BC, BD և BE երեք ուղիղ գծերը գտնվում են նույն հարթության մեջ։

Այսպիսով, եթե ուղիղ գիծը կանգնեցված է ուղղանկյուն երեք ուղիղ գծերին, որոնք հատում են մեկը մյուսին ընդհանուր հատման կետում, ապա երեք ուղիղ գծերը գտնվում են նույն հարթության մեջ։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։

Պնդում 6

Եթե երկու ուղիղ գիծ ուղղանկյուն են նույն հարթությանը, ապա ուղիղ գծերը կլինեն զուգահեռ։

Թող AB և CD ուղիղ գծերը ուղղանկյուն լինեն հենքային հարթությանը։ Ասում եմ, որ AB-ն զուգահեռ է CD-ին։

Թող նրանք հատեն հենքային հարթությունը համապատասխանաբար B և D կետերում։ Եվ թող BD ուղիղ գիծը միացված լինի։ Եվ թող DE-ն կառուցված լինի ուղղանկյուն BD-ին հենքային հարթությունում։ Եվ թող DE-ն հավասար լինի AB-ին։ Եվ թող BE, AE և AD ուղիղ գծերը միացված լինեն։

Եվ քանի որ AB-ն ուղղանկյուն է հենքային հարթությանը, այն [հետևաբար] ուղղանկյուն կլինի նաև բոլոր այն ուղիղ գծերին, որոնք միացված են դրան և գտնվում են հենքային հարթությունում [Տե՛ս "Տարրեր" 11.3-ի սահմանումը]։

Եվ BD և BE, որոնք գտնվում են հենքային հարթությունում, յուրաքանչյուրը միացված են AB-ին։ Ուստի, ABD և ABE անկյուններից յուրաքանչյուրը ուղղանկյուն է։ Ուստի, նույն պատճառներով, CDB և CDE անկյուններից յուրաքանչյուրը նույնպես ուղղանկյուն է։ Եվ քանի որ AB-ն հավասար է DE-ին, իսկ BD-ն ընդհանուր է, AB և BD երկու ուղիղ գծերը հավասար են ED և DB երկու ուղիղ գծերին (համապատասխանաբար)։ Եվ դրանք ընդգրկում են ուղղանկյուններ։ Ուստի, AD հիմքը հավասար է BE հիմքին [Տե՛ս "Տարրեր" 1.4]։ Եվ քանի որ AB-ն հավասար է DE-ին, իսկ AD-ն նույնպես հավասար է BE-ին, AB և BE երկու ուղիղ գծերը, հետևաբար, հավասար են ED և DA երկու ուղիղ գծերին (համապատասխանաբար)։ Եվ նրանց հիմքը AE-ն ընդհանուր է։ Ուստի, ABE անկյունը հավասար է EDA անկյանը [Տե՛ս "Տարրեր" 1.8]։ Եվ ABE-ն ուղղանկյուն է։ Ուստի, EDA-ն նույնպես ուղղանկյուն է։ ED-ն, հետևաբար, ուղղանկյուն է DA-ին։ Եվ այն նաև ուղղանկյուն է ինչպես BD-ին, այնպես էլ DC-ին։ Ուստի, ED-ն ուղղանկյուն է BD, DA և DC երեք ուղիղ գծերին ընդհանուր հատման կետում։ Ուստի, BD, DA և DC երեք ուղիղ գծերը գտնվում են նույն հարթության մեջ [Տե՛ս "Տարրեր" 11.5]։ Եվ որի (հարթության) մեջ BD և DA (գտնվում են), նույն հարթության մեջ AB-ն նույնպես (կգտնվի)։ Քանի որ ցանկացած եռանկյուն գտնվում է մեկ հարթության մեջ [Տե՛ս "Տարրեր" 11.2]։ Եվ ABD և BDC անկյուններից յուրաքանչյուրը ուղղանկյուն է։ Ուստի, AB-ն զուգահեռ է CD-ին [Տե՛ս "Տարրեր" 1.28]։

Այսպիսով, եթե երկու ուղիղ գիծ ուղղանկյուն են նույն հարթությանը, ապա ուղիղ գծերը կլինեն զուգահեռ։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։