Տարերք/Գիրք 7
հեղինակ՝ էվկլիդես |
Սահմանումներ
- Միավորը այն է, ըստ որի ամեն գոյող (բան) ասվում է «մեկ»։
- Թիվը միավորներից կազմված բազմություն է։†
- Թիվը մաս է (ուրիշ) թիվի, փոքրագույնը մեծագույնի, երբ այն չափում է մեծագույնը։‡
- Իսկ (եթե փոքրագույնը) մասեր է (մեծագույնի), երբ այն չի չափում այն։§
- Եվ մեծագույն (թիվը) փոքրագույնի բազմապատիկն է, երբ մեծագույնը չափվում է փոքրագույնով։
- Զույգ թիվը այն թիվն է, որ կարելի է բաժանել երկու հավասար մասերի։
- Թեք (կամ կենտ) թիվը այն թիվն է, որը չի կարելի բաժանել երկու հավասար մասերի, կամ որը տարբերվում է զույգ թվից մեկ միավորով։
- Զույգ-անգամ-զույգ թիվը այն է, որ չափվում է մի զույգ թվով, ըստ մի այլ զույգ թվի։¶
- Իսկ զույգ-անգամ-թեք թիվը այն է, որ չափվում է մի զույգ թվով, ըստ մի թեք (կենտ) թվի։∗
- Եվ թեք-անգամ-թեք թիվը այն է, որ չափվում է մի թեք (կենտ) թվով, ըստ մի այլ թեք (կենտ) թվի։$
- Առաջնային∥ թիվը այն է, որ չափվում է միայն միավորով։
- Թվերը, որոնք պարզ են (առաջնային) միմյանց նկատմամբ, այն թվերն են, որոնք չափվում են միայն միավորով որպես ընդհանուր չափ։
- Բարդ թիվը այն է, որ չափվում է ինչ-որ թվով։
- Եվ թվերը, որոնք բարդ են միմյանց նկատմամբ, այն թվերն են, որոնք չափվում են ինչ-որ թվով որպես ընդհանուր չափ։
- Ասվում է, որ թիվը բազմապատկում է (ուրիշ) թիվը, երբ բազմապատկվող թիվը ինքն իրեն բազմապատկվում է այնքան անգամ, որքան միավորներ կան առաջին (բազմապատկող) թվի, և (այդպես) առաջանում է մեկ այլ թիվ։
- Եվ երբ երկու թվեր միմյանց բազմապատկելով առաջացնում են ինչ-որ (ուրիշ) թիվ, ապա (այդպիսով) առաջացած թիվը կոչվում է հարթ (ղեկավար տերմինը "plane" – "հարթ"), և նրա կողմերը այն թվերն են, որոնք բազմապատկում են միմյանց։
- Եվ երբ երեք թվեր միմյանց բազմապատկելով առաջացնում են ինչ-որ (ուրիշ) թիվ, ապա (այդպիսով) առաջացած թիվը կոչվում է ծավալային (solid), և նրա կողմերը այն թվերն են, որոնք բազմապատկում են միմյանց։
- Քառակուսի (square) թիվը հավասար բազմապատիկ է հավասարի, կամ (հարթ թիվ) է, պարփակված երկու հավասար թվերով։
- Եվ խորանարդ (cube) թիվը հավասար-նշանակ բազմապատիկ է հավասարի, կրկին հավասարի, կամ (ծավալային թիվ) է, պարփակված երեք հավասար թվերով։
- Թվերը համաչափ են, երբ առաջինը նույն բազմապատիկն է, կամ նույն մասը, կամ նույն մասերն են երկրորդի նկատմամբ, ինչ երրորդը չորրորդի նկատմամբ։
- Նման հարթ և ծավալային թվերը այն թվերն են, որոնք ունեն համեմատական (համաչափ) կողմեր։
- Կատարյալ թիվը այն է, որը հավասար է իր մասերի գումարին։††
Ծանոթագրություններ: † Այլ կերպ ասելով, «թիվը» միավորից մեծ դրական ամբողջ թիվ է։ ‡ Այլ կերպ ասելով, թիվ a-ն մաս է թիվ b-ի, եթե գոյություն ունի թիվ n, այնպես որ na = b։ § Այլ կերպ ասելով, a թիվը մասեր է b թիվի, (որտեղ a < b), եթե գոյություն ունեն տարբեր թվեր m և n, այնպես որ na = m*b։ ¶ Այլ կերպ ասելով, զույգ-անգամ-զույգ թիվը երկու զույգ թվերի արտադրյալն է։ ∗ Այլ կերպ ասելով, զույգ-անգամ-թեք թիվը մեկ զույգ և մեկ թեք (կենտ) թվերի արտադրյալն է։ $ Այլ կերպ ասելով, թեք-անգամ-թեք թիվը երկու թեք (կենտ) թվերի արտադրյալն է։ ∥ Բառացիորեն, «առաջին»։ †† Այլ կերպ ասելով, կատարյալ թիվը հավասար է իր բաժանարարների գումարին։
Պնդում 1
Եթե տրվեն երկու անհավասար թվեր, և փոքրագույնը հերթով անընդհատ հանվի մեծագույնից, այնպես, որ մնացորդը երբեք չչափի իրեն նախորդող թիվը, մինչև չմնա մեկ միավոր, ապա սկզբնական թվերը կլինեն միմյանց նկատմամբ պարզ (արնչություն չունեն որևէ ընդհանուր բաժանարարից բացի մեկից):
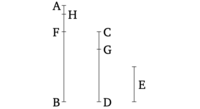
Երկու [անհավասար] թվերի, AB և CD-ի դեպքում, եթե փոքրագույնը հերթով անընդհատ հանվի մեծագույնից, թող մնացորդը երբեք չչափի իրեն նախորդող թիվը, մինչև չմնա մեկ միավոր։ Բանաձև եմ, որ AB և CD թվերը պարզ են միմյանց նկատմամբ, այսինքն՝ միայն միավորը չափում է (և) AB-ին, (և) CD-ին։
Եթե AB և CD պարզ չլինեն միմյանց նկատմամբ, ապա որոշ թիվ նրանց կչափի։ Թող այդ թիվը լինի E։ Եվ թող CD-ն, չափելով BF-ը, թողնի FA մնացորդ, փոքր քան ինքն է, հետո AF-ը, չափելով DG-ն, թողնի GC մնացորդ, փոքր քան ինքն է, հետո GC-ն, չափելով FH-ը, թողնի HA միավորը։
Փաստորեն, քանի որ E-ն չափում է CD-ն, և CD-ն չափում է BF-ը, E-ն նույնպես չափում է BF-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ BA-ն։ Ուստի (E-ն) նույնպես կչափի BA-ի մնացորդ AF-ը։ Եվ AF-ն չափում է DG-ն։ Այսպիսով, E-ն նույնպես չափում է DG-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ DC-ն։ Ուստի (E-ն) նույնպես կչափի CG մնացորդը։ Եվ CG-ն չափում է FH-ը։ Այսպիսով, E-ն նույնպես չափում է FH-ը։ Եվ (E-ն) նաև չափում է ամբողջ FA-ն։ Ուստի (E-ն) նույնպես կչափի HA մնացորդային միավորը, թեև դա ուղղակի միավոր է։ Սա բացարձակապես անհնար է։
Հետևաբար գոյություն չունի թիվ, որը չափի (և) AB-ը, (և) CD-ը։ Այսպիսով, AB և CD թվերը պարզ են միմյանց նկատմամբ։ (Ահա թե ինչ էր անհրաժեշտ ցույց տալ):
Մեկնաբանություններ: † Այստեղ օգտագործվում է չարտասանված ընդհանուր գաղափարը, որ եթե a-ն չափում է b-ին, և b-ն չափում է c-ին, ապա a-ն նույնպես չափում է c-ին, որտեղ բոլոր նշանները ներկայացնում են թվեր։ ‡ Այստեղ օգտագործվում է չարտասանված ընդհանուր գաղափարը, որ եթե a-ն չափում է b-ին, և a-ն նաև չափում է b-ի մի մասը, ապա a-ն նույնպես չափում է b-ի մնացորդային մասը, որտեղ բոլոր նշանները ներկայացնում են թվեր։
Պնդում 2
Գտնել երկու տրված թվերի (որոնք միմյանց նկատմամբ պարզ չեն) ամենամեծ ընդհանուր չափը:
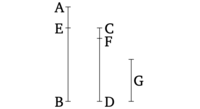
Թող AB և CD լինեն երկու տրված թվերը, որոնք միմյանց նկատմամբ պարզ չեն։ Արդ, անհրաժեշտ է գտնել AB և CD թվերի ամենամեծ ընդհանուր չափը։
Իրոք, եթե CD-ը չափում է AB-ը, ապա CD-ը այդպիսով AB-ի և CD-ի ընդհանուր չափն է (քանի որ CD-ը նաև ինքն իրեն է չափում)։ Եվ ակնհայտ է, որ այն նաև ամենամեծ (ընդհանուր չափն) է։ Քանի որ ոչինչ, որ մեծ է CD-ից, չի կարող չափել CD-ին։
Բայց եթե CD-ը չի չափում AB-ը, ապա AB-ից և CD-ից կմնա որոշ թիվ, երբ փոքրագույնը հերթով շարունակաբար հանենք մեծագույնից, որը կչափի իրեն նախորդող թիվը։ Որովհետև մեկ միավոր չի մնա։ Բայց եթե ոչ, ապա AB և CD թվերը պարզ կլինեն միմյանց նկատմամբ [Բանաձև 7.1]։ Սա հակասում է այն, ինչ ենթադրվել էր։ Ուստի կմնա մի թիվ, որը կչափի իրեն նախորդող թիվը։ ԵՎ թող CD-ը, չափելով BE-ն, թողնի EA մնացորդը, որը փոքր է իրենից, հետո EA-ն, չափելով DF-ը, թողնի FC մնացորդը, որը փոքր է իրենից, ապա CF-ը թող չափի AE-ը։ Ուստի, քանի որ CF-ը չափում է AE-ը, իսկ AE-ը չափում է DF-ը, CF-ը կհասկանանք, որ չափում է նաև DF-ը։ Եվ այն նաև ինքն իրեն է չափում։ Ուստի այն կչափի նաև ամբողջ CD-ը։ Իսկ CD-ը չափում է BE-ը։ Ուստի CF-ը նույնպես կչափի BE-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ BA-ն։ Ուստի (E-ն) նույնպես կչափի AE մնացորդ AF-ը։ Եվ AF-ն չափում է DG-ը։ Այսպիսով, E-ն նույնպես չափում է DG-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ DC-ը։ Ուստի (E-ն) նույնպես կչափի CG մնացորդը։ Եվ CG-ն չափում է FH-ը։ Այսպիսով, E-ն նույնպես չափում է FH-ը։ Եվ (E-ն) նաև չափում է ամբողջ FA-ն։ Ուստի (E-ն) նույնպես կչափի HA մնացորդային միավորը, թեև դա ուղղակի միավոր է։ Սա բացարձակապես անհնար է։
Հետևաբար գոյություն չունի թիվ, որը չափի (և) AB-ը, (և) CD-ը։ Այսպիսով, AB և CD թվերը պարզ են միմյանց նկատմամբ։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Հաջորդակում (Corollary)
Այդպիսով ակնհայտ է, որ եթե մի թիվ չափում է երկու թիվ, ապա այն կչափի նաև նրանց ամենամեծ ընդհանուր չափը։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Պնդում 3
Գտնել երեք տրված թվերի (որոնք միմյանց նկատմամբ պարզ չեն) ամենամեծ ընդհանուր չափը:
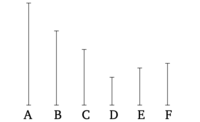
Թող A, B և C լինեն երեք տրված թվերը, որոնք միմյանց նկատմամբ պարզ չեն։ Արդ, անհրաժեշտ է գտնել A, B և C թվերի ամենամեծ ընդհանուր չափը։
Թող նախ վերցված լինի A և B երկու (թվերի) ամենամեծ ընդհանուր չափը D [Բանաձև 7.2]։ Ուրեմն D-ը կամ չափում է, կամ չի չափում C-ը։ Նախ ենթադրենք, որ այն չափում է (C-ը)։ Այն նաև չափում է A-ն և B-ը։ Ուստի D-ը չափում է A, B և C թվերը։ Այսպիսով, D-ը A, B և C թվերի ընդհանուր չափն է։ Բանաձև եմ, որ այն նաև ամենամեծ (ընդհանուր) չափն է։ Քանի որ եթե D-ը A, B և C ամենամեծ ընդհանուր չափը չլինի, ապա կգտնվի մի թիվ, որը ավելի մեծ քան D-ը, որը կչափի A, B և C թվերը։ Թող այն լինի E։ Եվ քանի որ E-ն չափում է CD-ը, իսկ CD-ն չափում է BE-ը, E-ն նույնպես չափում է BE-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ BA-ն։ Ուստի (E-ն) նույնպես կչափի BA-ի մնացորդ AF-ը։ Եվ AF-ն չափում է DG-ն։ Այսպիսով, E-ն նույնպես չափում է DG-ը։ Եվ (E-ն) նույնպես չափում է ամբողջ DC-ն։ Ուստի (E-ն) նույնպես կչափի CG մնացորդը։ Եվ CG-ն չափում է FH-ը։ Այսպիսով, E-ն նույնպես չափում է FH-ը։ Եվ (E-ն) նաև չափում է ամբողջ FA-ն։ Ուստի (E-ն) նույնպես կչափի HA մնացորդային միավորը, թեև դա ուղղակի միավոր է։ Սա բացարձակապես անհնար է։
Հետևաբար, ոչ մի թիվ, որը մեծ է CF-ից, չի կարող չափել AB և CD թվերը։ Այսպիսով, CF-ը AB և CD թվերի ամենամեծ ընդհանուր չափն է։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Հաջորդակում (Corollary)
Այդպիսով ակնհայտ է, որ եթե մի թիվ չափում է երկու թիվ, ապա այն կչափի նաև նրանց ամենամեծ ընդհանուր չափը։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Պնդում 4
Ցանկացած թիվ կամ մաս է, կամ մասեր են յուրաքանչյուր (ուրիշ) թվի, ավելի փոքրն ավելի մեծի։
Թող A և BC լինեն երկու թվեր, և թող BC-ը լինի փոքրագույնը։ Բանաձև եմ, որ BC-ը կամ մաս է, կամ մասեր են A թվի։
Քանի որ A և BC թվերը կամ պարզ են միմյանց նկատմամբ, կամ ոչ։ Նախ թող A և BC պարզ լինեն միմյանց նկատմամբ։ Այդ դեպքում, բաժանելով BC-ը նրա միավորներից բաղկացուցիչ մասերի, BC-ի յուրաքանչյուր միավոր կլինի A-ի ինչ-որ մասը։ Հետևաբար, BC-ը A-ի մասերից է։
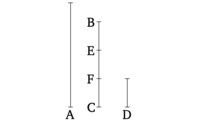
Այսպիսով, թող A և BC պարզ չլինեն միմյանց նկատմամբ։ Ուրեմն BC-ը կամ չափում է A թիվը, կամ չի չափում։ Եթե BC-ը չափում է A-ը, ապա BC-ը A-ի մաս է։ Իսկ եթե ոչ, թող A և BC ամենամեծ ընդհանուր չափը, D-ը, վերցվի [Բանաձև 7.2]։ Եվ թող BC-ը բաժանվի BE, EF, և FC մասերի, որոնք հավասար են D-ին։ Եվ, քանի որ D-ը չափում է A-ը, D-ը A-ի մաս է։ Եվ D-ը հավասար է BE, EF և FC մասերին։ Հետևաբար, BE, EF, FC ամեն մեկը A-ի մաս է։ Ուրեմն BC-ը A-ի մասերից է։
Այսպիսով, ցանկացած թիվ կամ մաս է, կամ մասեր են յուրաքանչյուր (ուրիշ) թվի, ավելի փոքրն ավելի մեծի։ (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ)։
Պնդում 5
Եթե մի թիվ մաս է մեկ թվի, և մի այլ (թիվ) նույն մասը չէ մեկ ուրիշի, ապա (կատարյալ) առաջատար թվերի գումարը նույնպես կլինի նույն մասը հաջորդ թվերի գումարի, ինչ-որ մի թիվ մեկ այլ թվի։
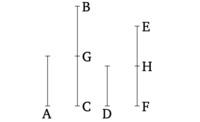
Թող A թիվը լինի BC թվի մի մաս, իսկ D թիվը լինի նույն մասը EF թվի նկատմամբ, ինչ A-ն է BC-ի նկատմամբ։ Բանաձև եմ, որ A և D թվերի գումարը նույնպես կլինի նույն մասը BC և EF գումարի նկատմամբ, ինչ A-ն է BC-ի նկատմամբ։
Քանի որ ինչ մաս էլ A-ն ունի BC-ի մեջ, D-ն նույն մաս ունի EF-ի մեջ, ուրեմն քանի մասով A-ն բաժանում է BC-ը, նույնքան մասով D-ն բաժանում է EF-ը։ Թող BC-ը բաժանվի BG-ի և GC-ի, որոնք հավասար են A-ին, իսկ EF-ը բաժանվի EH-ի և HF-ի, որոնք հավասար են D-ին։ Այսպես, BG, GC բաժանումների քանակը հավասար կլինի EH, HF բաժանումների քանակին։ Եվ, քանի որ BG-ը հավասար է A-ին, իսկ EH-ը D-ին, ապա BG, EH զույգը նույնպես հավասար է A, D զույգին։ Նույն պատճառներով GC, HF զույգը նույնպես հավասար է A, D զույգին։ Այսպիսով, քանի անգամ BC-ը բաժանվում է A-ով, նույնքան անգամ BC, EF գումարը բաժանվում է A, D գումարով։ Հետևաբար, ինչ մաս A-ն BC-ի է, A, D գումարը էլ նույն մաս է BC, EF գումարի նկատմամբ։
(Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
Պնդում 6
Եթե մի թիվ մասեր է մեկ թվի, իսկ մեկ այլ (թիվ) նույն մասերը ունի մեկ այլ թվի, ապա առաջին երկուսի գումարն էլ նույն մասերը կլինի երկրորդ զույգի գումարի նկատմամբ, ինչպիսին առաջին թիվը երկրորդի նկատմամբ է։
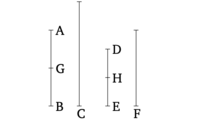
Թող AB թիվը մասեր լինի C թվի, իսկ DE թիվը նույն մասերը լինի F թվի նկատմամբ, ինչ մասեր AB-ն ունի C-ի մեջ։ Բանաձև եմ, որ AB և DE գումարը նույնպես նույն մասերն է կունենա C և F գումարի նկատմամբ, ինչ մասեր AB-ն ունի C-ի նկատմամբ։
Քանի որ ինչ մասեր էլ AB-ն ունի C-ի մեջ, DE-ն նույն մասերը կունենա F-ի մեջ, ուրեմն քանի մասով AB-ն բաժանում է C-ն, նույնքան մասով DE-ն բաժանում է F-ը։ Թող AB թիվը բաժանվի AG և GB մասերի, որոնք C-ի մասեր են, իսկ DE թիվը բաժանվի DH և HE մասերի, որոնք F-ի մասեր են։ Այսպիսով, AG և GB բաժանումների քանակը հավասար կլինի DH և HE բաժանումների քանակին։ Եվ, քանի որ ինչ մաս AG-ը C-ի նկատմամբ է, DH-ն նույն մասն է F-ի նկատմամբ է, և, փոխարինաբար, ինչ մաս կամ մասեր AG-ն DH-ի նկատմամբ է, C-ն նույնպես նույն մասերը կամ նույն մասը կունենա F-ի նկատմամբ [Բանաձև 7.9]։ Նույն պատճառով, ինչ մաս կամ մասերը GB-ն HE-ի նկատմամբ է, C-ն նույնպես նույն մասերը կամ մասերը կունենա F-ի նկատմամբ [Բանաձև 7.9]։ Եվ ինչ մաս կամ մասերը AG-ն DH-ի նկատմամբ է, GB-ն նույն մասերը կամ մասերը կունենա HE-ի նկատմամբ [Բանաձև 7.5, 7.6]։ Բայց ինչ մաս կամ մասերը AG-ն DH-ի նկատմամբ է, նաև ցույց տրվեց, որ C-ն նույն մասը կամ մասերը ունի F-ի նկատմամբ։ Ուստի, ինչ մասեր կամ որ մասը AB-ն ունի C-ի նկատմամբ, C-ն նույնպես նույն մասերը կամ samu մասերը կունենա F-ի նկատմամբ։ (Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
- (Ժամանակակից նշանմամբ, եթե a = (m/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)*d, որտեղ բոլոր նշանները թվեր են):
Պնդում 7
Եթե մի թիվ այն նույն մասը լինի ինչ-որ թվի, ինչ (մասը) հանված AE-ն (է) հանված մասի CF-ից, ապա մնացորդը նույնպես կլինի նույն մասը մնացորդի, ինչ հարաբերությամբ, ինչ ամբողջ AB-ն է ամբողջ CD-ի նկատմամբ։
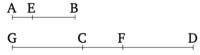
Թող AB թիվը լինի այն համեմատաբար CD թվի, ինչ AE հանված մասը CF-ի նկատմամբ է։ Բանաձև եմ, որ EB մնացորդը նույնպես կլինի նույն բաժինը FD մնացորդի նկատմամբ, ինչ AB-ն է CD-ի նկատմամբ։
Քանի որ (ինչ մաս AE-ն է CF-ի), թող EB-ն նույնպես նույն մաս լինի CG-ի։ Եվ, քանի որ (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մաս կլինի CG-ի, ապա (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես նույն մասը կլինի GF-ի [Բանաձև 7.5]։ Եվ (ինչ մաս AE-ն է CF-ի), AB-ն նաև ընդունված է լինել նույն մասը CD-ի [Բանաձև 7.7, 7.8]։ Այսպիսով, (ինչ մաս AB-ն է GF-ի), (AB-ն) նույնպես նույն մասը է CD-ի [Բանաձև 7.7, 7.8]։ Ուրեմն GF-ը հավասար է CD-ին։ Թող CF-ը հանվի երկուսից էլ։ Ուստի GC մնացորդը հավասար է FD մնացորդին։ Եվ, քանի որ (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասը կլինի GC-ի, իսկ GC-ն հավասար է FD-ին, ապա (ինչ մաս AE-ն է CF-ի), EB-ն նույնպես նույն մասը է FD-ի։ Բայց (ինչ մաս AE-ն է CF-ի), AB-ն նույնպես նույն մաս է CD-ի։ Ուրեմն EB մնացորդը նույն մասը է FD մնացորդի, ինչ AB-ն է CD-ի։ (Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
Նշում: Ժամանակակից նշանմամբ, եթե a = (m/n)*b և c = (m/n)*d, ապա (a+c) = (m/n)(b+d), որտեղ բոլոր նշանները ներկայացնում են թվեր։
Պնդում 8
Եթե մի թիվ այն նույն մասերն է մեկ թվի նկատմամբ, ինչ (հանված) AE մասը է (հանված) CF մասի նկատմամբ, ապա մնացորդը նույնպես կլինի նույն մասերի հարաբերությամբ մնացորդի նկատմամբ, ինչպիսին ամբողջը է ամբողջի նկատմամբ։
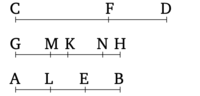
Թող AB թիվը լինի այն նույն մասերն CD թվի նկատմամբ, ինչ AE հանված մասը CF-ի նկատմամբ է։ Բանաձև եմ, որ EB մնացորդը նույնպես կլինի նույն մասերը FD մնացորդի նկատմամբ, ինչ AB-ն է CD-ի նկատմամբ։
Թող GH-ը դրվի հավասար AB-ին։ Ուստի ինչ մասեր GH-ը ունի CD-ի նկատմամբ, AE-ն նույնպես նույն մասերն ունի CF-ի նկատմամբ։ Թող GH-ը բաժանվի CD-ի մասերի՝ GK և KH, իսկ AE-ը՝ CF-ի մասերի՝ AL և LE։ Այսպիսով, GK և KH բաժանումների քանակը հավասար կլինի AL և LE բաժանումների քանակին։ Եվ, քանի որ ինչ մաս GK-ը CD-ի նկատմամբ է, նույն մասը AL-ը CF-ի նկատմամբ է, և, քանի որ CD-ն մեծ է CF-ից, GK-ը նույնպես մեծ է AL-ից։ Թող GM-ը վերցվի հավասար AL-ին։ Այսպիսով, ինչ մաս GK-ը CD-ի նկատմամբ է, GM-ը նույն մասը է CF-ի նկատմամբ։ Ուստի MK մնացորդը նույնպես նույն մաս է FD մնացորդի նկատմամբ, ինչ GK ամբողջը CD ամբողջի նկատմամբ է [Բանաձև 7.5]։
Նույն կերպ, քանի որ ինչ մաս KH-ը CD-ի նկատմամբ է, EL-ը նույն մաս է CF-ի նկատմամբ, և CD-ն մեծ է CF-ից, HK-ն ավելի մեծ է EL-ից։ Թող KN-ը հավասարեցվի EL-ին։ Այսպիսով, ինչ մաս KH-ը CD-ի նկատմամբ է, KN-ը նույն մաս է CF-ի նկատմամբ։ Ուստի NH մնացորդը նույնպես նույն մաս է FD մնացորդի նկատմամբ, ինչ KH ամբողջը CD ամբողջի նկատմամբ է [Բանաձև 7.5]։
Ուստի MK մնացորդը նույնպես ցույց տրվեց, որ նույն մաս է FD մնացորդի նկատմամբ, ինչ GK ամբողջը CD ամբողջի նկատմամբ է։ Ուստի MK և NH գումարը նույն մասերն են DF-ի նկատմամբ, ինչ HG ամբողջը CD ամբողջի նկատմամբ է։ Եվ MK, NH գումարը հավասար է EB-ին, իսկ HG-ը՝ BA-ին։ Ուստի EB-ն մնացորդը նույնպես նույն մասերն է FD մնացորդի նկատմամբ, ինչ AB ամբողջը CD ամբողջի նկատմամբ է։ (Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
Նշում: Ժամանակակից նշանմամբ, եթե a = (m/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)*d, որտեղ բոլոր նշանները թվեր են։
Պնդում 9
Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասը (կամ նույն մասերն) է մեկ այլ թվի, ապա, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ առաջին (թիվը) լինի երրորդի նկատմամբ, երկրորդ (թիվը) նույնպես կլինի նույն մասը կամ մասերը մյուսի նկատմամբ կամ նույն մասերը, չորրորդ։
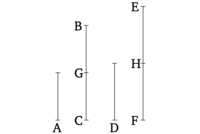
Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասը (կամ նույն մասերն) է մեկ այլ թվի, ապա, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ առաջին (թիվը) լինի երրորդի նկատմամբ, երկրորդ (թիվը) նույնպես կլինի նույն մասը կամ մասերը մյուսի նկատմամբ։
Թող A թիվը լինի BC թվի մի մաս, և D թիվը լինի նույն մասը մեկ այլ EF թվի, ինչ A-ն է BC-ի։ Բանաձև եմ, որ նաև, փոխարինաբար, թե որ մասը, կամ մասերն էլ որ A-ն ունենա D-ի նկատմամբ, BC-ն նույնպես կունենա նույն մասը, կամ մասերը EF-ի նկատմամբ։
Քանի որ ինչ մաս A-ն ունի BC-ի նկատմամբ, D-ն նույն մաս ունի EF-ի նկատմամբ, ապա քանի թվեր կան BC-ի մեջ, որոնք հավասար են A-ին, նույնքան թվեր կլինեն EF-ի մեջ, որոնք հավասար են D-ին։ Թող BC-ը բաժանված լինի BG և GC մասերի, հավասար A-ին, իսկ EF-ը բաժանված լինի EH և HF մասերի, հավասար D-ին։ Այսպիսով, BG և GC բաժանումների քանակը հավասար կլինի EH և HF բաժանումների քանակին։
Ուստի, քանի որ BG և GC թվերը հավասար են միմյանց, իսկ EH և HF թվերը նույնպես հավասար են միմյանց, և BG, GC բաժանումների քանակը հավասար է EH, HF բաժանումների քանակին, ապա ինչ մասը, կամ մասերը եւ որ BG-ն ունենա EH-ի նկատմամբ, նույնքան մաս է GB-ն ունենալու HE-ի նկատմամբ։ Եվ այդպիսով, ինչ մասը, կամ մասերը հետագա բաժանումներում համապատասխանում են, իսկ ինքը համաչափաբար համապատասխանում են։ Եվ, հետևաբար, ինչ մասը, կամ մասերը AB-ն ունի C-ի նկատմամբ, C-ն նույնպես նույն մասերը կամ նույն մասը կունենա F-ի նկատմամբ։ (Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
- (Ժամանակակից նշանմամբ, եթե a = (1/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)*d, որտեղ բոլոր նշանները ներկայացնում են թվեր):
Պնդում 10†
Եթե մի թիվ մաս է մեկ թվի, և մեկ այլ (թիվ) նույն մասերն է մեկ այլ թվի, ապա նաև, փոխարինաբար, թե որ մասերը կամ մասերը էլ որ առաջին թիվը ունենա երրորդի նկատմամբ, երկրորդ թիվը նույնպես կունենա նույն մասերը կամ նույն մասերը, չորրորդի նկատմամբ։
Թող AB թիվը լինի C թվի մասերը, իսկ DE թիվը լինի F թվի նույն մասերը։ Բանաձև եմ, որ նաև, փոխարինաբար, թե որ մասը, կամ մասերը AB-ն ունի C-ի նկատմամբ, DE-ն նույնպես կունենա նույն մասերը կամ նույն մասը F-ի նկատմամբ։
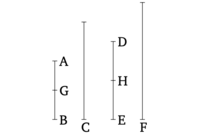
Քանի որ ինչ մասեր AB-ն ունի C-ի նկատմամբ, DE-ն նույն մասերը կունենա F-ի մեջ, ուրեմն քանի մասով AB-ն բաժանում է C-ը, նույնքան մասով DE-ն բաժանում է F-ը։ Թող AB-ը բաժանվի C-ի մասերի՝ AG և GB, իսկ DE-ը բաժանվի F-ի մասերի՝ DH և HE։ Այսպիսով, AG և GB բաժանումների քանակը հավասար կլինի DH և HE բաժանումների քանակին։ Եվ, քանի որ ինչ մաս կամ մասեր AG-ն ունի C-ի նկատմամբ, DH-ն նույնպես ունի նույն մասերը կամ մասերը F-ի նկատմամբ, նաև փոխարինաբար, ինչ մաս կամ մասերը AG-ն ունի DH-ի նկատմամբ, C-ն նույնպես նույն մասերը կամ նույն մասը կունենա F-ի նկատմամբ [Բանաձև 7.9]։ Նույն պատճառով, ինչ մաս կամ մասերը GB-ն HE-ի նկատմամբ է, C-ն նույնպես նույն մասերը կամ մասերը կունենա F-ի նկատմամբ [Բանաձև 7.9]։ Եվ ինչ մաս կամ մասերը AG-ն DH-ի նկատմամբ է, GB-ն նույն մասերը կամ մասերը կունենա HE-ի նկատմամբ [Բանաձև 7.5, 7.6]։ Բայց ինչ մաս կամ մասերը AG-ն DH-ի նկատմամբ է, նաև ցույց տրվեց, որ C-ն նույն մասը կամ մասերը ունի F-ի նկատմամբ։ Ուստի, ինչ մասեր կամ որ մասը AB-ն ունի C-ի նկատմամբ, C-ն նույնպես նույն մասերը կամ samu մասերը կունենա F-ի նկատմամբ։ (Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
- (Ժամանակակից նշանմամբ, եթե a = (m/n)*d, ապա եթե a = (k/l)*c, ապա b = (k/l)*d, որտեղ բոլոր նշանները թվեր են):
Պնդում 11
Եթե, ինչպես ամբողջ AB-ն ամբողջ CD-ի նկատմամբ է, նույն ձևով AE հանված մասը CF հանված մասի նկատմամբ է, ապա մնացորդը նույնպես կլինի նույն մասը մնացորդի, ինչ հարաբերությամբ, ինչ ամբողջը է ամբողջի նկատմամբ։
Թող ամբողջ AB-ն լինի ամբողջ CD-ի նկատմամբ այնպիսին, ինչ AE հանված մասը CF հանված մասի նկատմամբ է։ Բանաձև եմ, որ EB մնացորդը նույնպես կլինի նույն բաժինը FD մնացորդի նկատմամբ, ինչ ամբողջ AB-ն է ամբողջ CD-ի նկատմամբ։
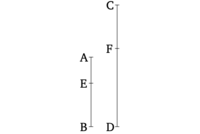
Քանի որ ինչպես AB-ը CD-ի նկատմամբ է, այնպես AE-ը CF-ի նկատմամբ է, ապա ինչ մասեր կամ մասը AB-ն ունի CD-ի նկատմամբ, AE-ն նույնպես նույն մասը կամ մասերն ունի CF-ի նկատմամբ [Սահմ. 7.20]։ Ուստի EB մնացորդը նույնպես նույն մասը կամ մասերն ունի FD մնացորդի նկատմամբ, ինչ AB-ն ունի CD-ի նկատմամբ [Բանաձև 7.7, 7.8]։ Այսպիսով, ինչպես EB-ն FD-ի նկատմամբ է, այնպես AB-ն CD-ի նկատմամբ է [Սահմ. 7.20]։ (Սա էլ հենց այն էր, ինչ պետք էր, ինչ)։
Պնդում 12†
Եթե կամայական քանակի թվեր համաչափ են, ապա ինչպես առաջավոր (թվերից) մեկը (է) հետագային, այնպես էլ (արդյունքում) բոլոր առաջավոր (թվերի) գումարը (կլինի) բոլոր հետագա (թվերի) գումարի նկատմամբ:
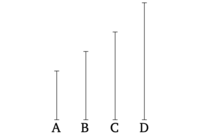
Թող կամայական քանակի թվեր A, B, C, D համաչափ լինեն (այնպես, որ ինչպես A-ն է B-ի նկատմամբ, այնպես C-ն D-ի նկատմամբ է): Ասում եմ, որ ինչպես A-ն է B-ի նկատմամբ, այնպես էլ A և C (համատեղ) B և D (համատեղ) նկատմամբ են: Քանի որ ինչպես A-ն է B-ի նկատմամբ, այնպես էլ C-ն D-ի նկատմամբ է, ապա ինչ մաս կամ մասերն էլ A-ն ունենա B-ի նկատմամբ, C-ն նույնպես նույն մաս կամ մասերն ունի D-ի նկատմամբ [Սահմ. 7.20]: Այդպիսով, A և C գումարը նույնպես նույն մաս կամ նույն մասերն են B և D գումարի նկատմամբ, ինչ A-ն B-ի նկատմամբ [Բանաձև 7.5, 7.6]: Ուստի, ինչպես A-ն B-ի նկատմամբ է, այնպես էլ A, C (համատեղ) B, D (համատեղ) նկատմամբ են [Սահմ. 7.20]: (Սա էլ հենց այն էր, ինչ պետք էր ցույց տալ):
Ժամանակակից մեկնություն (†) Ժամանակակից նշանմամբ, այս առաջարկությունն ասում է, որ եթե a : b :: c : d, ապա a : b :: a + c : b + d, որտեղ բոլոր նշանները ներկայացնում են թվեր։
Պնդում 13[1]
Եթե Չորս թվեր իրար հարաբերական են, ապա նրանք հարաբերական կլինեն նաև միմյանց.

Օրինակ վերցնենք A, B, C, D թվերը: Եթե A հարաբերում է B-ին ին ինչպես C-ն է հարաբերում D-ին, ապա կարող ենք պնդել, որ A-ն հարաբերում է C -ին, ինչպես B-ն հարաբերում է D-ին: Եթե A-ն կազմում է B-ի մի մասը, ապա C-ն նույնպես կազմում է D-ի նույն մասը: Այսպիսով, որերորդ մասը որ A-ն կազմում է C-ի մեջ, նույքան մաս B-ն կազմում է D-ի մեջ: Այսինքն ինչպես A-ն C-ին, այնպես էլ B-ն D-ին: Որը և մեզ անհրաժեշտ էր ցույց տալ:
Պնդում 14[2]
Եթե կա որևէ թվերի բազմություն, և մեկ այլ թվերի բազմություն նրանց հավասար,որոնք հարաբերում են միմյանց ինչպես նշվաց է Պնդում 13-ում,ապա նրանք նույնպես հավասար կհարաբերեն միմյանց:

Օրինակ, վերցնենք A,B,C թվերի բազմությունը և դրան համարժեք D,E,F թվերի բազմությունը: Եթե պնդում 13 գործում է, այսինքն A հարաբերում է B-ին ին ինչպես D -ն է հարաբերում E-ին, ապա նույն ձև B-ն հարաբերում է C-ին, ինչպես E-ն հարաբերում է F-ին: Ունենալով այս պնդումը, մենք կարող ենք պնդել նաև, որ A-ն հարաբերում է D-ին, ինչպես B-ն հարաբերում է E-ին, ինչպես C-ն հարաբերում է F-ին, որը և անհրաժեշտ էր ցույց տալ:
Պնդում 15
Եթե ունենք մեկ չափանիշ որը հավասար է որևէ թվի, և ունենք մեկ այլ թիվ որը մի քանի անգամ մեծ է և հավասար է մի քանի անգամ մեծ չափանիշի, ապա կարող ենք ասել որ, առաջինը թիվը հարաբերում է երկրորդ թվին այնպես, ինչպես առաջին չափանիշը երկրորդ չափանիշին:

Oրինակ, համարենք, որ A -ն համարժեք է BC չափին, և D-ն որը մի քանի անգամ մեծ է A-ից համարժեք լինի EF- ին, որը նույնքան անգամ մեծ է BC-ից:
Քանի որ A -ն համարժեք է BC չափին, և D-ն որը մի քանի անգամ մեծ է A-ից համարժեք է EF- ին, ապա կարող ենք ասել, որ որքան չափ կա BC-ում, նույնքան կա EF-ում, որը հավասար է D ին: Եթե BC-ն բաժանենք BG, GH և HC, իսկ EF-ը EK, KL, LF մասերի, ապա կարող ենք նկատել, որ նրանք միմյանց համարժեքորեն հարաբերում են:[3] Այսինքն, BG հարաբերում է EKին, ինչպես GH KL-ին, ինչպես HC-ն LF-ին: Այսպիսով, կարող ենք եզրակացնել, որ այն թվերը որը համապատասխանորեն համարժեք են այդ թվերին նույնպես հարաբերում են: Այսպիսով, A-ն հարաբերում է D-ին, ինչպես BG-ն EK-ին, ինչպես GH-ն KL-ին, ինչպես HC-ն LF-ին, որը և պետք էր ապացուցել:
Պնդում 16 [4]
Եթե երկու թվեր բազմապատկենք միմյանցով և ստանանք մի քանի թվեր, ապա այդ մի քանի թվերը միմյանց հավասար կլինեն:

Թող A և B լինեն երկու թվեր: Ենթադրենք, A-ն ստեղծում է C-ն՝ բազմապատկելով B-ով, և B-ն ստեղծում է D-ն՝ բազմապատկելով A-ով: Կարող ենք պնդել,, որ C-ն հավասար է D-ին: Քանի որ A-ն ստեղծել է C-ն՝ բազմապատկելով B-ով, ուրեմն B-ն չափում է C-ն ըստ A-ի միավորների: Եվ E միավորը նույնպես չափում է A թիվը՝ ըստ նրա մեջ գտնվող միավորների: Ուրեմն E միավորը չափում է A թիվը նույնքան անգամ, որքան B-ն չափում է C-ն: Ուրեմն փոխադարձաբար, E միավորը չափում է B թիվը նույնքան անգամ, որքան A-ն չափում է C-ն: Քանի որ B-ն ստեղծել է D-ն՝ բազմապատկելով A-ով, ուրեմն A-ն չափում է D-ն՝ ըստ B-ի միավորների: Եվ E միավորը նույնպես չափում է B-ն՝ ըստ նրա մեջ գտնվող միավորների: Ուրեմն E միավորը չափում է B թիվը նույնքան անգամ, որքան A-ն չափում է D-ն: Եվ E միավորը չափում է B թիվը նույնքան անգամ, որքան A-ն չափում է C-ն: Ուրեմն A-ն նույնքան անգամ չափում է C-ն և D-ն: Հետևաբար, C-ն հավասար է D-ին, Ինչը և պետք էր ապացուցել:
Պնդում 17 [5]
Եթե մի թիվ բազմապատկելով երկու թվերով ստանանք այլ թվեր, ապա նրանցից առաջացած թվերը կունենան նույն հարաբերությունը, ինչ բազմապատկվող թվերը։

Քանի որ D և E թվերը ստացել ենք բազմապատկելով երկու թվերը՝ B և C (համապատասխանաբար), կարելի է պնդել, որ ինչպես B-ն է հարաբերում C-ին, այնպես էլ D-ն կհարաբերի E-ին: Քանի որ D թիվը ստացվել է A բազմապատկելով B-ն, ուրեմն B-ն չափում է D-ն՝ ըստ A-ի միավորների: Եվ F միավորը նույնպես չափում է A-ն՝ ըստ նրա մեջ գտնվող միավորների: Ուրեմն F միավորը չափում է A-ն նույնքան անգամ, որքան B-ն չափում է D-ն: Այսպիսով, ինչպես F ն է հարաբերում Aին, այնպես էլ B-ն է հարաբերում D-ին: Եվ նույն պատճառով, ինչպես Fն է A թվի հանդեպ, այնպես էլ C-ն է E-ի հանդեպ: Կարելի է պնդել, որ ինչպես B-ն է D-ի հանդեպ, այնպես էլ C-ն է E-ի հանդեպ: Ուրեմն փոխադարձաբար, ինչպես B-ն է C-ի հանդեպ, այնպես էլ D-ն է E-ի հանդեպ, Ինչը և պետք էր ապացուցել:
Պնդում 18 [6]

Եթե չորս թվեր համեմատական են միմյանց, ապա առաջին և չորրորդ թվերի բազմապատկումից ստացված թիվը կլինի հավասար երկրորդի և երրորդի բազմապատկումից ստացված թվին: Եվ եթե առաջինի և չորրորդի բազմապատկումից ստացված թիվը հավասար է երկրորդի և երրորդի բազմապատկումից ստացված թվին, ապա այդ չորս թվերը կլինեն համեմատական: Օրինակ, A, B, C և D համեմատական թվեր են: Ենթադրենք ինչպես A-ն է հարաբերում B-ին, այնպես էլ C-ն է D-ին: A-ն բազմապատկելով D-ն կստանք E թիվը, իսկ B-ն բազմապատկելով C- թվին կստանանք F թիվը: Կարելի է պնդել, որ E-ն հավասար է F-ին:
Դիցուք, A-ն C-ով բազմապատկելով ստացվում է G թիվը: Քանի որ A-ից ստացվել է G թիվը C-ով բազմապատկելո և E թիվը D-ով բազմապատկելո, ապա A-ից ստացվել են է G և E թվերը համապատասխանաբար բազմապատկվելով C և D թվերի հետ: Ուրեմն ինչպես C-ն է հարաբերում D ին այնպես էլ G-ն է հարաբերում E-ին: Ինչպես C-ն է հարաբերում D-ին , այնպես էլ A-ն է հարաբերում B-ին :Ինչպես A-ն է B-ի հետ հարաբերում, այնպես էլ G-ն է E-ի հետ հարաբերում: Պետք է նշել, որ ինչպես A-ն է B-ի հանդեպ, այնպես էլ G-ն է E-ի հանդեպ: Ուրեմն, ինչպես G-ն է E-ի հանդեպ, այնպես էլ G-ն է F-ի հանդեպ: Ուրեմն G-ն ունի նույն հարաբերությունը թե E-ի, թե F-ի հետ: Ուրեմն E-ն հավասար է F-ին: ՈՒնեքն այն փաստը, որ E-ն հավասար է F-ին: Կարելի է պնդել, որ ինչպես A-ն է B-ի հանդեպ, այնպես էլ C-ն է D-ի հանդեպ: Քանի որ նույն կառուցվածքով E-ն հավասար է F-ին, ուրեմն ինչպես G-ն է E-ի հետ համեմատում, այնպես էլ G-ն է F-ի հետ համեմատում: Ինչպես G-ն է հարաբերում E-ին, այնպես էլ C-ն է հարաբերում D-ին: Եվ ինչպես G-ն է F-ի հանդեպ, այնպես էլ A-ն է B-ի հանդեպ: Այսպիսով, ինչպես A-ն է B-ի հանդեպ, այնպես էլ C-ն է D-ի հանդեպ:
Պնդում 19 [7]
Եթե չորս թվերը համեմատական են, ապա թվերը, որոնք առաջանում են առաջինի և չորրորդի բազմապատկման արդյունքում, հավասար կլինեն այն թվի հետ, որը առաջանում է երկրորդի և երրորդի բազմապատկման արդյունքում։ Եվ եթե թվերը, որոնք առաջանում են առաջինի և չորրորդի բազմապատկման արդյունքում, հավասար են երկրորդի և երրորդի բազմապատկման արդյունքին, ապա այդ չորս թվերը համեմատական կլինեն։
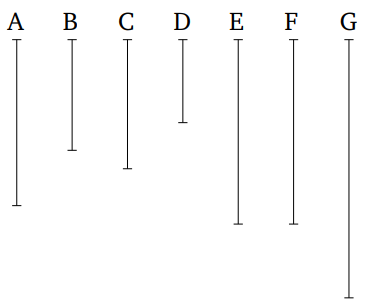
Թող A, B, C, D լինեն չորս համեմատական թվեր։ Այնպես, ինչպես A-ն կապված է B-ի հետ, այնպես էլ C-ն կապված է D-ի հետ։A բազմապատկելով D-ով, կստացվի ստանա E, իսկ B բազմապատկելով C-ով, կստանանք F։ Եվ ես ասում եմ, որ E-ն հավասար է F-ի:
A բազմապատկի C-ով՝ ստեղծելով G։ Այնպես, որ A ստեղծեց G, բազմապատկելով C-ով, և նույնպես ստեղծեց E, բազմապատկելով D-ով։ Հետևաբար, քանի որ A-ն ստեղծեց G և E՝ բազմապատկելով համապատասխանաբար C և D թվերով,ուրեմն ինչպես C-ն կապված է D-ի հետ, այնպես էլ G-ն կապված է E-ի հետ։
Այսպիսով, ինչպես C-ն կապված է D-ի հետ, այնպես էլ A-ն կապված է B-ի հետ։ Եվ այսպես, ինչպես A-ն կապված է B-ի հետ, այնպես էլ G-ն կապված է E-ի հետ։Քանի որ A-ն ստեղծեց G՝ բազմապատկելով C-ով, իսկ B-ն նույնպես ստեղծեց F՝ բազմապատկելով C-ով, ապա A-ն և B-ն ստեղծեցին համապատասխանաբար G և F՝ բազմապատկելով C։ Հետևաբար, ինչպես A-ն կապված է B-ի հետ, այնպես էլ G-ն կապված է F-ի հետ։
Այլ կերպ ասած, ինչպես G-ն կապված է E-ի հետ, այնպես էլ G-ն կապված է F-ի հետ։ Այնպես որ, G-ն ունի նույն հարաբերությունը թե E-ի, թե F-ի հետ։ Հետևաբար, E-ն հավասար է F-ին։
Այժմ, թող E-ն հավասար լինի F-ին։ Ես ասում եմ, որ ինչպես A-ն կապված է B-ի հետ, այնպես էլ C-ն կապված է D-ի հետ։ Վերջապես, նույն կառուցվածքով, քանի որ E-ն հավասար է F-ին, ինչպես G-ն կապված է E-ի հետ, այնպես էլ G-ն կապված է F-ի հետ։ Բայց ինչպես G-ն կապված է F-ի հետ, այնպես էլ ինչպես A-ն կապված է B-ի հետ։ Եվ այսպես, ինչպես A-ն է կապված B-ի հետ, այնպես էլ C-ն է կապված D-ի հետ: Թեորեմն ապացուցված է:
Պնդում 20
Թող լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ ինչպես A-ն և B-ն: Ասում եմ, որ CD-ն չափում է A-ն այնքան անգամ, որքան և EF-ն չափում է B-ն՝ մեծը՝ մեծին, և փոքրն՝ փոքրին: Այնպես որ, թող CD և EF լինեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերությունը՝ A-ի և B-ի հետ համապատասխանաբար: Ես ասում եմ, որ CD-ն չափում է A-ն նույն քանակությամբ անգամ, որքան EF-ն չափում է B-ն։
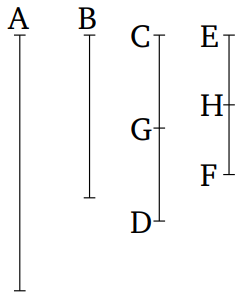
Եթե հնարավոր է, Դիցուք, CD-ն չլինի A-ի մաս: Եվ եթե EF-ն իսկապես այն նույն մասերն ունի B-ի, որոնք CD-ն ունի A-ի մասերից, ապա այն հնարավոր է։ Ինչքան որ մասեր կան CD-ում, նույնքան մասեր կան EF-ում՝ B-ի մասերից։ Let CD բաժանվի A-ի մասերի՝ CG և GD, իսկ EF բաժանվի B-ի մասերի՝ EH և HF։ Եվ այդ դեպքում, CG և GD բաժանումների թվաքանակը հավասար կլինի EH և HF բաժանումների թվաքանակին։ Եվ քանի որ CG և GD թվերը հավասար են միմյանց, նույնպես EH և HF թվերը հավասար են միմյանց, և հարաբերությունը CG-ի և EH-ի միջև նույնն է, ինչ հարաբերությունը GD-ի և HF-ի միջև։ Հետևաբար, ինչպես CG-ն է հարաբերակցվում EH-ի հետ, այնպես էլ GD-ն է հարաբերակցվում HF-ի հետ։ Դրանից հետո, որպես հետևանք, ինչպես յուրաքանչյուր առաջատար մաս՝ ΓΗ միանում է հետագային ΕΘ, այնպես էլ այն մագլցած մասերը ΓΔ և ΕΖ՝ նույն հարաբերությամբ՝ լինում են համարժեք։
Պնդում 21
Դիցուք, A եւ B թվերը պարզ թվեր ենէ : Կարելի է պնդել, , որ A եւ B թվերը, նրանց պես հարաբերություն ունեցող թվերից ամենափոքր թվերն են: Եթե դա այդպես չէ, ապա կլինեն ինչ-որ թվեր, որոնք A եւ B-ից փոքր կլինեն և նրանք կհարաբերեն նույնպես, ինչպես A եւ B-: Թող դրանք լինեն C եւ D:

Ասպիսով, քանի որ այս թվերը նվազագույններն են, որոնք նույն հարաբերությունն ունեն, և մեծ հարաբերությունը չափում է մեծին, և փոքրն այնքանն է, որքան փոքրին՝ այսինքն, ավելի մեծը հարաբերում է ավելի մեծին, իսկ ավելի փոքրը ՝ փոքրին։ Այսպիսով, որքան որ C հարաբերում է Aին, այնքան անգամեր թող լինեն E-ում։ Եվ D-ը, ամփոփելով B-ը, E-ում չափում է ըստ նույն միավորների։ Այսպես, քանի որ C-ը հարաբերում է Aին ըստ E-ում առկա միավորների, E-ն էլ, ըստ C-ի, հարաբերում է Aին նույնչափ ։ Հետևաբար E-ն և B-ը չափում են D-ում առկա միավորներով։ Այնպես որ, հնարավոր չէ, որպեսզի A-ի և B-ից ավելի փոքր թվեր լինեն, որոնք նույն հարաբերությունն ունեն A և B թվերի հետ։ Հետեւաբար, A և B-ն են այդ թվերը, որոնք նույն հարաբերությունն ունեն։ Սա հենց այն բանն է, որը պետք էր ապացուցել:
Պնդում 22
Այն նվազագույն թվերը, որոնք ունեն նույնպիսի հարաբերություն, միմյանց նկատմամբ ունեն ընդհանուր բազմապատիկ և նրանք պարզ թվեր են:

Դիցուք A և B լինեն ամենափոքր թվերը նրանցից, որոնք ունեն նույն հարաբերակցությունը, ինչ նրանք։ Կարելի է պնդել, որ A-ն և B-ն փոխադարձաբար պարզ են։ Քանի որ, եթե A-ն և B-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի նրանց։ Թող այդ թիվը լինի C : Եվ որքան անգամ C-ն բաժանի A-ին, այնքան միավոր թող լինի D-ում։ Եվ որքան անգամ C-ն բաժանի B-ին, այնքան միավոր թող լինի E-ում։ Քանի որ C-ն բաժանում է A-ն՝ համաձայն D-ի մեջ եղած միավորների, C-ն D-ն բազմապատկելով ստեղծել է A-ն։ Նույն պատճառներով C-ն E-ն բազմապատկելով ստացել ենք B-ն։ Այսպիսով, թիվ C-ն D-ն և E-ն բազմապատկելով ստացվել է է A-ն և B-ն։ Այսպիսով, ինչպես D-ն է վերաբերվում E-ին, այնպես էլ A-ն է վերաբերվում B-ին։ Այսպիսով, D-ն և E-ն ունեն նույն հարաբերակցությունը, ինչ A-ն և B-ն, բայց լինելով ավելի փոքր։ Սա անհնար է։ Ուստի, ոչ մի թիվ չի բաժանում A-ն և B-ն։ Այսպիսով, A-ն և B-ն փոխադարձաբար պարզ են։ Թեորեմն ապացուցված է:
Պնդում 23
Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկը բաժանող թիվը կմնա փոխադարձաբար պարզ մյուս թվի հետ։

Դիցուք A և B լինեն փոխադարձաբար պարզ թվեր, և թող մի թիվ C բաժանի A-ին։ Ասում եմ, որ C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Եթե C-ն և B-ն փոխադարձաբար պարզ չեն, ապա մի թիվ կբաժանի C-ն և B-ն։ Թող այդ թիվը լինի D։ Քանի որ D-ն բաժանում է C-ն, իսկ C-ն բաժանում է A-ն, ապա D-ն նաև բաժանում է A-ն։ Եվ D-ն բաժանում է նաև B-ն։ Այսպիսով, D-ն բաժանում է A-ն և B-ն, որոնք փոխադարձաբար պարզ են։ Սա անհնար է։ Ուստի, ոչ մի թիվ չի բաժանում C-ն և B-ն։ Այսպիսով, C-ն և B-ն փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ապացուցել:
Պնդում 24
Եթե երկու թվեր փոխադարձաբար պարզ են որևէ թվի հետ, ապա դրանցից բազմապատկված, ստեղծված թիվը նույնպես փոխադարձաբար պարզ կլինի նույն թվի հետ։

Դիցուք, A և B լինեն երկու թվեր, որոնք երկուսն էլ փոխադարձաբար պարզ են C-ի հետ։ Թող A-ն B-ն բազմապատկելով ստեղծի D-ն։ Կարելի է պնդել, որ C-ն և D-ն նույնպես փոխադարձաբար պարզ են։ Եթե C-ն և D-ն փոխադարձաբար պարզ չեն, ապա ինչ-որ թիվ կբաժանի C-ն և D-ն։ Թող այդ թիվը լինի E։ Եվ քանի որ C-ն և A-ն փոխադարձաբար պարզ են, իսկ E-ն բաժանում է C-ին, ապա A-ն և E-ն նույնպես փոխադարձաբար պարզ են։ Քանի անգամ E-ն բաժանում է D-ն, այնքան միավոր թող լինի F-ում։ Ուստի, F-ն նույնպես բաժանում է D-ն՝ ըստ E-ի մեջ եղած միավորների։ E-ն F-ն բազմապատկելով ստեղծել է D-ն։ Սակայն A-ն նույնպես B-ն բազմապատկելով ստեղծել է D-ն։ Ուստի E-ի և F-ի բազմապատկումը հավասար է A-ի և B-ի բազմապատկմանը։ Եթե ծայրամասային թվերի (բազմապատկումը) հավասար է միջնամասային թվերի (բազմապատկմանը), ապա թվերը համեմատական են։ Ուստի, ինչպես EEE-ն է վերաբերվում A-ին, այնպես էլ B-ն է վերաբերվում F-ին։ A-ն և E-ն փոխադարձաբար պարզ են։ Եվ A-ն և E-ն լինելով փոխադարձաբար պարզ՝ նաև նվազագույն թվերն են։ Նվազագույն թվերը, որոնք ունեն նույն հարաբերակցությունը, կբաժանեն նույն հարաբերակցությամբ ունեցող թվերը՝ հավասար քանակով։ Առավել մեծը բաժանում է առավել մեծին, իսկ փոքրն՝ փոքրին։ Այսպիսով, E-ն բաժանում է B-ն։ Եվ E-ն նաև բաժանում է C-ն։ Ուստի E-ն բաժանում է B-ն և C-ն, որոնք փոխադարձաբար պարզ են։ Սա անհնար է։ Ուստի, ոչ մի թիվ չի կարող բաժանել C-ն և D-ն։ Այսպիսով, C-ն և D-ն փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ցույց տալ։
Պնդում 25
Եթե երկու թվեր փոխադարձաբար պարզ են, ապա դրանցից մեկի քառակուսիով ստեղծված թիվը փոխադարձաբար պարզ կլինի մյուսի հետ։ Դիցուք A և B երկու պարզ թվեր են, որոնք փոխադարձաբար պարզ են։ Թող A-ն ինքն իրեն բազմապատկելով ստեղծի C-ն։ Կարելի է պնդել , որ B-ն և C-ն փոխադարձաբար պարզ են։

Դիցուք D լինի հավասար A-ին։ Քանի որ A և B փոխադարձաբար պարզ են, իսկ A հավասար է D-ին, ապա D-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Այսպիսով, D-ն և A-ն երկուսն էլ փոխադարձաբար պարզ են B-ի հետ։ Այլ կերպ ասած, D-ից և A-ից ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի B-ի հետ։ Եվ C-ն է այն թիվը, որը ստացվում է D-ի և A-ի բազմապատկումով։ Այսպիսով, C-ն և B-ն նույնպես փոխադարձաբար պարզ են։ Սա է այն, ինչ պետք էր ցույց տալ։
Պնդում 26
Եթե երկու թվերն էլ փոխադարձաբար պարզ են երկու թվերի հետ, ապա դրանցից բազմապատկված, ստացված թվերը նույնպես փոխադարձաբար պարզ կլինեն իրար հետ։

Դիցուք A և B երկու թվեր լինեն, որոնք երկուսն էլ փոխադարձաբար պարզ են երկու այլ թվերի՝ C-ի և D-ի հետ։ Դիցուք, A-ն B-ի հետ բազմապատկելով ստանանք E-ն, և թող C-ն D-ի հետ բազմապատկելով ստանանք F-ն։ Ասում եմ, որ E և F փոխադարձաբար պարզ են։ Քանի որ A-ն և B-ն երկուսն էլ փոխադարձաբար պարզ են C-ի հետ, ապա A-ի և B-ի բազմապատկմամբ ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի C-ի հետ։ Այսպիսով, E-ն և C-ն փոխադարձաբար պարզ են։ Դրա համար նույն պատճառներով E-ն և D-ն նույնպես փոխադարձաբար պարզ են։ Այսպիսով, C-ն և D-ն երկուսն էլ փոխադարձաբար պարզ են E-ի հետ։ Եվ C-ի և D-ի բազմապատկմամբ ստացված թիվը նույնպես փոխադարձաբար պարզ կլինի E-ի հետ։ Իսկ FFF-ն է այն թիվը, որը ստացվում է C-ի և D-ի բազմապատկումով։ Այսպիսով, E-ն և F-ն փոխադարձաբար պարզ են։
Պնդում 27 [8]
Եթե երկու թվեր փոխադարձաբար պարզ են իրարից, և յուրաքանչյուրը նրանցից որոշ թիվ է ստեղծում՝ ինքն իրեն բազմապատկելով, ապա դրանցից ստացված թվերը նույնպես կլինեն փոխադարձաբար պարզ։ Եվ եթե սկզբնական թվերը ստեղծեն որոշ թվեր՝ ստեղծված թվերը բազմապատկելով, ապա դրանք ևս կլինեն փոխադարձաբար պարզ։ Սա միշտ տեղի է ունենում ծայրամասերի վերաբերյալ։

Դիցուք A և B երկու թվեր են, որոնք փոխադարձապես պարզ են, և թող A ստեղծի C՝ ինքն իրեն բազմապատկելով, իսկ B՝ E՝ ինքն իրեն բազմապատկելով։ Եվ թող A բազմապատկի C՝ ստանալով D, իսկ B բազմապատկի E՝ ստանալով F։ Կարելի է պնդել, որ C և E, և D և F կլինեն փոխադարձաբար պարզ։ Որովհետև A և B փոխադարձապես պարզ են, և A ինքն իրեն բազմապատկելով ստեղծել է C, ապա C և B նույնպես կլինեն փոխադարձապես պարզ։ Այնպես որ, C և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ուստի C և E նույնպես փոխադարձապես պարզ են։ Նորից, քանի որ A և B փոխադարձապես պարզ են, և B ինքն իրեն բազմապատկելով ստեղծել է E, ապա A և E նույնպես փոխադարձապես պարզ են։ Այնպես որ, քանի որ երկու թիվ՝ A և C, երկուսն էլ փոխադարձաբար պարզ են երկու թվերից՝ B և E, A և C բազմապատկելով ստացած թիվը (D) կլինի B և E բազմապատկելով ստացված թվից (F) փոխադարձապես պարզ։ Այնպես որ, D և F փոխադարձապես պարզ են։ Սա այն է, ինչ պետք էր ապացուցել։
Պնդում 28
Եթե երկու թիվեր պարզ են, ապա նրանց գումարը նույնպես կլինի պարզ յուրաքանչյուրին։ Եվ եթե այդ գումարը պարզ է ինչ-որ մեկի հետ, ապա սկզբնական թվերը նույնպես պարզ կլինեն

Դիցուք երկու թվերը՝ AB և BC, որոնք պարզ են, տրված են: Կարելի է պնդել, որ նրանց գումարը՝ AC, նույնպես պարզ կլինի յուրաքանչյուրի համար՝ AB և BC: Եթե քաղված AC և AB միմյանց պարզ չեն չեն, ապա կգտնվի ինչ-որ թիվ, որը չափում է AC և AB: Թող այդ թիվը լինի D: Ենթադրենք, որ D չափում է AC և AB, ապա այն նույնպես պետք է չափի BC: Բայց քանի որ AB և BC միմյանց պարզ են, դա անհնար է: Հետևաբար, AC և AB պետք է միմյանց պարզ լինեն: Անհրաժեշտության դեպքում, եթե AB և BC միմյանց պարզ չեն, ապա թիվ D կմատչի AB և BC, ինչը էլ ավելի անհավանական է, քանի որ D չափում է նաև AC ամբողջությամբ: Եվ քանի որ AB և BC միմյանց պարզ են, դա նույնպես անհնար է: Հետևաբար, AB և BC պետք է միմյանց պարզ լինեն: Այսպիսով, ապացուցվեց, որ երկու թիվ, որոնք միմյանց պարզ են, նրանց գումարը նույնպես պարզ կլինի միմյանց
Պնդում 29
Յուրաքանչյուր պարզ թիվ առաջին է բոլոր այն թվերի հետ, որոնք ինքը չի չափում

Դիցուք, A-ն պարզ թիվ է, և B-ն այնպիսի թիվ է, որ A-ն չի չափում։ Կարելի է, որ B-ն և A-ն միմյանց նկատմամբ պարզ են։ Որպեսզի եթե B-ն և A-ն միմյանց նկատմամբ պարզ չեն, ապա մի թիվ կլինի, որը նրանց չափում է։ Թող C-ն չափի նրանց։ Քանի որ C-ն չափում է B-ն, իսկ A-ն չի չափում B-ն, ապա C-ն պետք է տարբեր լինի A-ից։ Եվ քանի որ C-ն չափում է B-ն և A-ն, ապա C-ն պետք է չափի նաև A-ն՝ չնայած նրան, որ չի համընկնում նրա հետ։ Բայց սա անհնար է։ Այնպես որ, չի կարող լինել որևէ թիվ, որը կչափի B-ն և A-ն։ Այդպիսով, A-ն և B-ն միմյանց նկատմամբ պետք է լինեն պարզ։
Պնդում 30
Եթե երկու թիվը իրար բազմապատկելով ստանում են ինչ-որ թիվ, և այդ թվից մեկը չափվում է մի պարզ թվով, ապա սկզբնական թվերից մեկը նույնպես պետք է չափվի

Թող երկու թիվ A և B ստեղծեն C՝ իրար բազմապատկելով, և թող ինչ-որ պարզ թիվ D հավասար լինի C-ին: Ես ասում եմ, որ D-ը պետք է հավասար լինի A կամ B: Թող D-ն չհավասար է A, և քանի որ D-ը պարզ է, ապա A և D թվերը միմյանց նկատմամբ պարզ են: Եվ քանի որ D-ն հավասար է C-ին, ապա այն պետք է հավասար է E-ին այնքան անգամ, որքան D-ն հավասար է C-ին: Իսկ քանի որ D-ն հավասար է C-ին ըստ E-ի, ապա D-ն ստեղծում է C՝ բազմապատկելով E: Բայց իսկապես, նաև A-ն ստեղծում է C՝ B-ի հետ բազմապատկելով: Այսպիսով, ստեղծված թիվը D և E թվերից հավասար է A և B թվերի բազմապատկմանը: Դրանով, ինչպես D-ն A-ին հավասար է, այնպես էլ B-ն E-ին հավասար է: Եվ D-ն ու A թվերը պարզ են միմյանց հետ, ինչպես նաև B-ն ու E-ն:
Պնդում 31
Ամեն բաղադրյալ թիվը չափվում է ինչ-որ պարզ թվով:

Դիցուք A-ն բաղադրյալ թիվ է։ Կարելի է պնդել, որ A-ն չափվում է ինչ-որ պարզ թվով։
Քանի որ A-ն բաղադրյալ է, ինչ-որ թիվ այն կչափի։ Թող այդ թիվը լինի B։ Եվ եթե B-ն պարզ է, ապա այն, ինչ ուզում էինք, ապացուցված է։ Իսկ եթե B-ն բաղադրյալ է, ապա ինչ-որ թիվ կչափի այն։ Թող այդ թիվը լինի C։ Եվ քանի որ C-ն չափում է B-ն, իսկ B-ն չափում է A-ն, ապա C-ն նույնպես կչափի A-ն։
Եվ եթե C-ն պարզ է, ապա այն, ինչ նախատեսված էր, կատարվում է։ Իսկ եթե C-ն բաղադրյալ է, ապա ինչ-որ թիվ կչափի այն։ Այս շարունակական հետազոտությունների մեջ, որևէ պարզ թիվ կգտնվի, որը կչափի այն։ Եթե այդպիսի թիվ չի գտնվի, ապա մի քանի անսահման թվեր, որոնք մեկմեկից փոքր են, կչափեն A-ն։ Բայց դա անհնար է թվերի մեջ։ Ուստի, ինչ-որ պարզ թիվ կգտնվի, որը կչափի նախորդը, և որը նույնպես կչափի A-ն։
Ուստի, ամեն բաղադրյալ թիվը չափվում է ինչ-որ պարզ թվով։ Դա այն է, ինչ պետք էր ապացուցել:
Պնդում 32
Ամեն թիվ կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով։

Դիցուք A թիվ է: Կարելի է պնդել, որ A-ն կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով: Եթե A-ն պարզ է, ապա այն, ինչ նախատեսված էր, տեղի է ունենում: Իսկ եթե այն բաղադրյալ է, ապա ինչ-որ պարզ թիվ կչափի այն: Ուստի, ամեն թիվը կամ պարզ է, կամ չափվում է ինչ-որ պարզ թվով: Դա այն է, ինչ պետք էր ապացուցել:
Պնդում 33
Թող A, B, և C լինեն ցանկացած տրված թվեր: Պետք է գտնենք նրանցից ամենափոքրին, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B, և C: Իրականում, եթե A, B և C իրար հետ պարզ են, ապա նրանք կլինեն ամենափոքրն այն թվերից, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես տրված թվերն են:
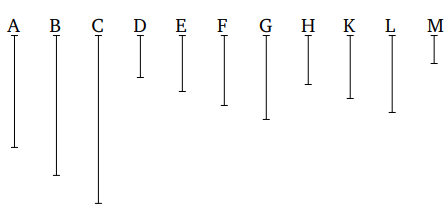
Դիցուք ունենք A, B և C թվերի առավելագույն ընդհանուր չափը՝ D, և որքանով D չափում է A, B և C, այնքան ամեն մի թիվ՝ E, F և G, համապատասխանաբար չափում է A, B և C ըստ D-ի միավորների:
Այդպիսով, E, F և G չափում են A, B և C ըստ նույն հարաբերակցությամբ: Ուստի, E, F և G ունեն նույն հարաբերակցությունը՝ ինչպես A, B և C: Եթե E, F և G չեն ամենափոքր թվերը, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B և C, ապա կլինեն այլ թվեր, որոնք փոքր կլինեն E, F և G և կկարողանան լինել նույն հարաբերակցությամբ՝ ինչպես A, B և C: Ներկայացնենք այդ թվերը՝ H, K, L:
Ուստի, H չափում է A, ինչպես K և L՝ B և C: Այնուհետև, քանի որ H չափում է A, M նույնպես կչափի A, ինչպես K և L՝ B և C: Եվ քանի որ H չափում է A, M նույնպես չափելու է B և C՝ ըստ նույն միավորների: Եվ քանի որ H չափում է A՝ ըստ M-ի միավորների, այնուհետև M նաև կչափի B և C՝ ըստ K և L-ի միավորների:
Այդպիսով, M չափում է A, B և C: Բայց այս հնարավորությունը անհնար է, քանի որ D՝ A, B և C թվերի առավելագույն ընդհանուր չափն է: Ուստի, հնարավոր չէ որևէ թիվ, որը փոքր է E, F և G և ունի նույն հարաբերակցությունը՝ ինչպես A, B և C: Այսպիսով, E, F և G կլինեն ամենափոքրը՝ այն թվերից, որոնք ունեն նույն հարաբերակցությունը՝ ինչպես A, B և C: Դա այն է, ինչ պետք էր ապացուցել:
Պնդում 34
Դիցուք A և B թվերը տրված են։ Պետք է գտնենք այն ամենափոքր թիվը, որը կչափեն երկու տրված թվերը:
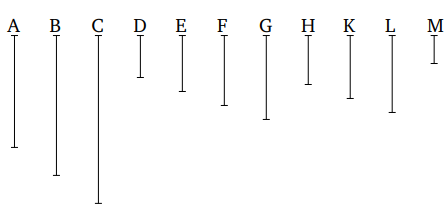
Դիցուք, A և B լինի միմյանցից անկախ թվեր են:թող A C ստանա՝ բազմապատկելով B: Այսպիսով, B նույնպես C ստացրեց՝ բազմապատկելով A Այսպիսով, A և B երկուսն էլ չափում են C:
Ես ասում եմ, որ C-ն նույնպես ամենափոքրն է թիվ, որը նրանք երկուսն էլ չափում են: Եթե ոչ, A և B երկուսն էլ կչափեն մի այլ թիվ, որը ավելի փոքր է, քան C: Թող նրանք երկուսն էլ հավասար լինեն D (որը ավելի փոքր է քան C):
Եվ որքան անգամ A հարաբերում է D, նույնքան միավորներ թող լինեն E-ում: Եվ որքան անգամ B հարաբերում է D, նույնքան միավորներ թող լինեն F-ում: Այսպիսով, A ստացրեց D՝ բազմապատկելով E, իսկ B ստացրեց D՝ բազմապատկելով F: Այսպիսով, A և E-ից ստացված թիվը հավասար է B և F-ից ստացված թվին: Այսպիսով, ինչպես A-ն է B-ին, այնպես էլ F-ն է E-ին:
Եվ քանի որ A և B-ն անկախ են միմյանցից, իսկ անկախ թվերը ամենափոքրն են (այսինքն՝ այդ նույն հարաբերությունը ունեցող թվերը), ապա ավելի մեծը չափում է ավելի մեծը, իսկ փոքրն՝ ավելի փոքրին: Այսպիսով, B-ն չափում է E, ինչպես հետևյալ (համարների չափման) միջոցով: Եվ քանի որ A-ը ստացավ C և D՝ բազմապատկելով B և E համապատասխանաբար, ապա ինչպես B-ն է E-ին, այնպես էլ C-ն է D-ին : Եվ B-ն չափում է E: Այսպիսով, C-ն նույնպես չափում է D, ավելի մեծը՝ չափելով ավելի փոքրին: Հետևաբար, դա անհնար է: Այսպիսով, A և B-ն չեն չափում մի թիվ, որը ավելի փոքր է քան C: Հետևաբար, C-ն այն ամենափոքր թիվն է, որը չափում են A-ն և B-ն:
A և B անկախ թվեր չեն: Եվ թող նախ ի հայտ գան ամենափոքր թվերը՝ F և E, որոնք ունեն նույն հարաբերությունը A-ի և B-ի հետ (համապատասխանաբար Այնպես որ, A-ի և E-ի բազմապատկմամբ ստացված թիվը հավասար է B-ի և F-ի բազմապատկմամբ ստացված թվին [Prop. 7.19]: Եվ թող A-ը ստանա C՝ բազմապատկելով E: Այսպիսով, B-ն նույնպես ստանում է C՝ բազմապատկելով F: Ուրեմն,, A և B երկուսն էլ հարաբերում են C: Ես ասում եմ, որ C-ն նույնպես ամենափոքրն է (թիվը, որը նրանք երկուսն էլ հարաբերում են): Եթե ոչ, A և B երկուսն էլ կհարաբերեն մի թիվ, որը ավելի փոքր է, քան C: Թող նրանք երկուսն էլ հարաբերեն D (որը ավելի փոքր է, քան C):

Եվ որքան անգամ A հարաբերում է D, նույնքան միավորներ թող լինեն G-ում: Եվ որքան անգամ B հարաբերում է D, նույնքան միավորներ թող լինեն H-ում: Այսպիսով, A ստացրեց D՝ բազմապատկելով G, իսկ B ստացրեց D՝ բազմապատկելով H: Այսպիսով, ինչպես A-ն է B-ին, այնպես էլ H-ն է G-ին [Prop. 7.19]: Եվ քանի որ A-ը ստացավ C և D՝ բազմապատկելով E և G համապատասխանաբար, ապա ինչպես E-ն է G-ին, այնպես էլ C-ն է D-ին [Prop. 7.17]: Եվ E-ն հարաբերում է G: Այսպիսով, C-ն նույնպես հարաբերում է D՝ մեծը հարաբերում է փոքրին: Դա անհնար է: Այսպիսով, A և B չեն հարաբերում մի թիվ, որը ավելի փոքր է, քան C: Հետևաբար, C-ն այն ամենափոքր թիվն է, որը հարաբերում են A-ն և B-ն: Սա հենց այն է, ինչ պետք էր ցույց տալ:
Պնդում 35
Եթէ երկու թվերին հարաբերեն ինչ-որ թիվ, ապա դրանցից ամենափոքրը, որն իրենով հարաբերում է այդ թիվը, նույնպես կհարաբերի նույն թվին:
Եվ այո, Դիցուք, A և B, հարաբերում են ինչ-որ թիվ CD, և թող E լինի ամենափոքրը, որն հարաբերում է ինչպես A-ն, այնպես էլ B-ն: Ես ասում եմ, որ E նույնպես հարաբերում է CD: Եթե E չի հարաբերում CD, թող E թողնի CF, որը փոքր է իրենից (հարաբերելով DF): Եվ քանի որ A-ն և B-ն հարաբերում են E-ին, իսկ E-ն հարաբերում է DF, ապա A-ն և B-ն նույնպես կհարաբերեն DF: Եվ (A-ն և B-ն) նույնպես հարաբերում են ամբողջ CD-ն: Այնպես որ, նրանք նույնպես կհարաբերեն մնացորդը՝ ΓΔ, որը փոքր է E-ից: Ինչպես տեսնում ենք, դա անհնար է: Այնպես որ, E չի կարող չհարաբերում CD-ին: Նշանակում է, որ (E) հարաբերում է CD: Այդ ամենը հենց այն է, ինչ պետք էր ապացուցել:
Պնդում 36
Այսպես, A, B և C երեք տրված թվեր են։ Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է նրանց բոլորին:

Դիցուք A, B և C թվեր են, որոնցից յուրաքանչյուրն ունի որոշակի հարաբերություն։ Պետք է գտնել այն ամենափոքր թիվը, որը հարաբերում է բոլոր երեք թվերին։
Եկեք ընդունենք, որ A և B ի համար այդ թիվը՝ Dն է ։ Եվ եթե C-ն հարաբերում է D-ին, ապա այն կլինի փաստը թր ուզում էինք ապացուցել։ Եթե ոչ, ապա A, B և C պետք է որոշեն E-ը, որը կլինի ամենափոքր թիվը, որը հարաբերում է D-ին։
Եթե E-ն ավելի փոքր է, քան D, ապա ստացվում է, որ E-ն չպետք է լինի ավելի փոքր։ Բայց այս փաստը հնարավոր չէ։ Այնպես որ, մենք պետք է հաստատենք, որ E-ն իսկապես ամենափոքր թիվն է, որը հարաբերում է A, B և C թվերին։
Այսպիսով, մենք ցույց տալիք խնդիրը, որ E-ն ամենափոքր թիվն է, որը հարաբերում է A, B և C թվերին։
Պնդում 37
Եթե մի թիվ չափվում է մեկ այլ թվով, ապա այդ թիվը կունենա մաս, որն անվանվում է նույն անունով, ինչ մյուս թիվը:

Դիցուք A թիվը չափվում է B թվով։ Ես ասում եմ, որ A-ն ունի մաս, որը կոչվում է նույն անունով, ինչ B-ն։ Քանի անգամ B-ն հարաբերում է A-ին, այդքան շատ միավորներ լինեն C-ում։ Քանի որ B-ն չափում է A-ն ըստ C-ի միավորների, և D միավորը նույնպես չափում է C թիվը ըստ նրա մեջ եղած միավորների, ապա D միավորը այնքան անգամ կչափի C թիվը, որքան B-ն՝ A-ն։ Հետևաբար, D միավորը չափում է B թիվը, ինչպես C-ն՝ A-ն։ Եվ այսպես, ամեն մի մասնաբառ, որը D միավորը B թվի մաս է, նույն անունով մասն է նաև C-ի A թվի համար։ Հետևաբար, A-ն ունի C մասը, որը կոչվում է նույն անունով, ինչ B-ն։ Դա հենց այն է, ինչ պետք էր ապացուցել։
Պնդում 38
Եթե թիվը բաժանվում է որոշակի մասերի (մասնիկների), ապա այդ մասերից յուրաքանչյուրն ունի համապատասխան թվային նշանակություն, որը կոչվում է այդ մասի անվանումը

Տրված լինի, որ թիվ A-ն ունի որևէ մաս, օրինակ՝ B։ Եվ թող C-ը լինի այն թիվը, որը կոչվում է նույն անունով, ինչ B (ինչպես՝ B-ն A-ի C-րդ մասը է): Ես ասում եմ, որ C-ն չափում է A-ն։ Քանի որ B-ն A-ի մի մասն է, որն ունի նույն անունը, ինչ C, ապա նաև D միավորը C-ի մաս է, որն ունի նույն անունը՝ այն է՝ D-ն C-ի C-րդ մասն է։ Եվ հետևաբար, ինչպես D-ն C-ն է չափում, այնպես էլ B-ն չափում է A-ն։ Այսպես, ի վերջո, D-ն B-ն է չափում նույնքան անգամ, ինչքան C-ն չափում է A-ն։ Ուստի, C-ն չափում է A-ն։ Եվ սա այն է, ինչ պետք է ապացուցվի
Պնդում 39
Ենթադրենք, որ տրված մասերն են A, B և C։ Պետք է գտնվի նվազագույն թիվը, որը կունենա A, B և C մասերը։

Լավ, ենթադրենք, որ A, B և C մասերի համար գոյություն ունեն համանուն թվեր, որոնց անունները կհամապատասխանեն համապատասխան մասերին (A-ին՝ D, B-ին՝ E, C-ին՝ F)։ Այնպես որ, նվազագույն թիվը՝ G, որն ունի A, B և C մասերը, չափվում է D, E և F թվերով։ Եվ G-ն իր հերթին կունենա մասեր, որոնք համանուն են D, E և F թվերին։ Ուստի, G-ն կունենա նաև A, B և C մասերը։ Ապա ես ասում եմ, որ G-ն, լինելով նվազագույնը, եթե ոչ, ապա լինի մի թիվ՝ H, որը կլինի G-ից փոքր, բայց կունենա A, B և C մասերը։ Այս դեպքում, եթե H-ն ունի A, B և C մասերը, ապա այն կչափվի D, E և F թվերով։ Բայց քանի որ H-ն փոքր է G-ից, դա անհնար է։ Այսպիսով, չի կարող լինել մի թիվ, որը փոքր լինի G-ից և ունենա A, B և C մասերը։ Սա հենց այն է, ինչը պետք էր ապացուցել։
Նշումներ
- ↑ Սա պնդում է,որ եթե a:b:c:d, ապա a:b::a+c:b+d, որտեղ բոլոր տառերը թվեր են։
- ↑ Այս ժամանակակից նշանաբանությամբ, այս բացատրությունը ասում է, որ եթե a:b::d:e և b:c::e:f, ապա a:c::d:f, որտեղ բոլոր տառերը ներկայացնում են թվեր։
- ↑ Այս պնդումը պնդում 7.9-ի հատուկ դեպքն է
- ↑ Այս պնդումը ասում է,որ ab=ba, որտեղ բոլոր տառեը թվեր են:
- ↑ Այս պնդումը ասում է, որ եթե d=ab, e=ac, ապա d:e::b:c,որտեղ բոլոր տառեըրը թվեր են
- ↑ Այս մոդեռը պնդում է,որ եթե ac=d, bc= e, a:b::d:e որտեղ բոլոր տառերը թվեր են
- ↑ Այս մոդեռը պնդում է,որ եթե a:b:c ապա ad=bc, որտեղ բոլոր տառերը թվեր են
- ↑ Այս մոդեռը պնդում է,որ եթե a պարզ է b-ի նկատմամբ, ապա a քառակուսին նույնպես պարզ կլինի b քառակուսու նկատմամբ, որտեղ բոլոր տառերը թվեր են