Տարերք/Գիրք 1
հեղինակ՝ էվկլիդես |
Բովանդակություն
- 1 Pages 6-30
- 2 Պնդում 27
- 3 Pages 31-48
- 4 Պնդում 28
- 5 Պնդում 29
- 6 Պնդում 30
- 7 Պնդում 31
- 8 Պնդում 32
- 9 Պնդում 33
- 10 Պնդում 34
- 11 Պնդում 35
- 12 Պնդում 36
- 13 Պնդում 37
- 14 Պնդում 38
- 15 Պնդում 39
- 16 Պնդում 40
- 17 Պնդում 41
- 18 Պնդում 42
- 19 Պնդում 43
- 20 Պնդում 44
- 21 Պնդում 45
- 22 Պնդում 46
- 23 Պնդում 47
- 24 Պնդում 48
Pages 6-30
Պնդում 27
Դա անհնար է [Պնդում 1.16]: Հետևաբար AB և CD ուղիղները՝ գծվելով, չեն հատվի B և D ուղղությամբ։ Նմանապես, կարող ենք ցույց տալ, որ դրանք չեն հատվի A և C ուղղություններվ։ Բայց ուղիղները, որոնք չեն հատվում ոչ մի ուղղությամբ, զուգահեռ են [Սահմանում 1.23]: Հետևաբար, AB և CD ուղիղները զուգահեռ են։ Հետևաբար, եթե երկու ուղիղներ հատող ուղիղը ստեղծում է հավասար խաչադիր անկյուններ, ապա այդ երկու ուղիղները զուգահեռ են։ Սա այն էր, ինչ պետք էր ապացուցել։
Pages 31-48
Պնդում 28
Եթե երկու ուղիղները հատող ուղիղը կազմում է արտաքին անկյուն, որը հավասար է ներքին և հակադիր անկյանը նույն կողմի վրա կամ նույն կողմի վրա գտնվող անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների, ապա այդ երկու ուղիղները զուգահեռ են։
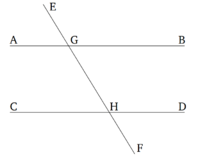
EF ուղիղը, որը հատում է AB և CD ուղիղները, կազմում է EGB արտաքին անկյուն, որը հավասար է ներքին և հակադիր GHD անկյանը, կամ նույն կողմի վրա գտնվող BGH և GHD անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների։ Պնդումն այն է, որ AB և CD ուղիղները զուգահեռ են։ Առաջին դեպքում EGB անկյունը հավասար է GHD անկյանը, բայց EGB անկյունը նաև հավասար է AGH անկյանը [Պնդում 1.15], հետևաբար, AGH անկյունը հավասար է GHD անկյանը։ Դրանք նաև խաչադիր անկյուններ են։ Հետևաբար, AB և CD ուղիղները զուգահեռ են [Պնդում. 1.27]։ Երկրորդ դեպքում, կրկին, BGH և GHD անկյունների գումարը հավասար է երկու ուղիղ անկյունների, ինչպես նաև AGH և BGH անկյունների գումարն է հավասար երկու ուղիղ անկյունների [Պնդում 1.13]։ Հետևաբար, AGH և BGH անկյունների գումարը հավասար է BGH և GHD անկյունների գումարին։ Երկուսից էլ հանենք BGH անկյունը։ Հետևաբար, մնացորդ AGH անկյունը հավասար է մնացորդ GHD անկյանը և դրանք խաչադիր անկյուններ են։ Հետևաբար, AB և CD ուղիղները զուգահեռ են [Պնդում 1.27]։ Հետևաբար, եթե երկու ուղիղները հատող ուղիղը կազմում է արտաքին անկյուն, որը հավասար է ներքին և հակադիր անկյանը նույն կողմի վրա կամ նույն կողմի վրա գտնվող անկյունների գումարը հավասարեցնում է երկու ուղիղ անկյունների, ապա այդ երկու ուղիղները զուգահեռ են։ Սա այն էր, ինչ պետք էր ապացուցել։
