Տարերք/Գիրք 10
հեղինակ՝ էվկլիդես |
Պնդում 102
Այն (ուղիղ գիծը), որի վրա կառուցված քառակուսին միջինական մակերեսի հետ միասին կազմում է միջինական ամբողջություն, ռացիոնալ (ուղիղ գծի) վրա դրված` ստանում է վեցերորդ կտրվածք (ապոտոմե) որպես լայնություն։
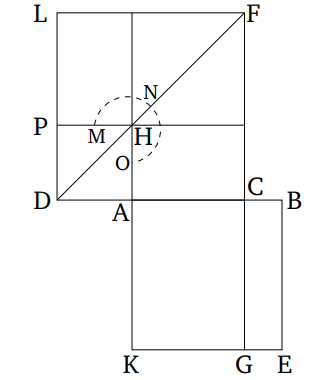
Թող AB-ն լինի այն ուղիղ գիծը, որը միջինական մակերեսի հետ կազմում է միջինական ամբողջություն, և CD-ն լինի ռացիոնալ (ուղիղ գիծ): Եվ թող CE-ն, որը հավասար է AB-ի վրա կառուցված քառակուսուն, դրված լինի CD-ի վրա, պարփակված AG-ով և GB-ով, որոնք միջինական են, և AG-ի և GB-ի վրա կառուցված քառակուսիների գումարը անհամաչափ է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյունին [Տե՛ս "Տարրեր" 10.78]:
Ուստի, թող CH-ն, որը հավասար է AG-ի վրա կառուցված քառակուսուն, դրված լինի CD-ի վրա, արտադրելով CK որպես լայնություն, և KL-ը, որը հավասար է GB-ի վրա կառուցված քառակուսուն։ Այսպիսով, CL-ի ամբողջությունը հավասար է AG-ի և GB-ի վրա կառուցված քառակուսիների գումարին։ CL-ը, հետևաբար, միջինական է։ Եվ այն դրված է ռացիոնալ CD-ի վրա, արտադրելով CM որպես լայնություն։ Ուստի, CM-ը ռացիոնալ է և անհամաչափ է երկարությամբ CD-ի հետ [Տե՛ս "Տարրեր" 10.22]:
Հետևաբար, քանի որ CL-ը հավասար է AG-ի և GB-ի վրա կառուցված քառակուսիների գումարին, որոնցից CE-ն հավասար է AB-ի վրա կառուցված քառակուսուն, մնացորդ FL-ը, հետևաբար, հավասար է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյունին [Տե՛ս "Տարրեր" 2.7]: Եվ քանի որ AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյունը միջինական է, FL-ը նույնպես միջինական է։ Եվ այն դրված է ռացիոնալ FE-ի վրա, արտադրելով FM որպես լայնություն։ Ուստի, FM-ը ռացիոնալ է և անհամաչափ է երկարությամբ CD-ի հետ [Տե՛ս "Տարրեր" 10.22]:
Քանի որ AG-ի և GB-ի վրա կառուցված քառակուսիների գումարը անհամաչափ է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյան հետ, CL-ը հավասար է AG-ի և GB-ի վրա կառուցված քառակուսիների գումարին, իսկ FL-ը հավասար է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյան, CL-ը, հետևաբար, անհամաչափ է FL-ի հետ։ Եվ ինչպես CL-ն է FL-ի նկատմամբ, այնպես էլ CM-ը MF-ի նկատմամբ է [Տե՛ս "Տարրեր" 6.1]:
Ուստի, CM-ը երկարությամբ անհամաչափ է MF-ի հետ [Տե՛ս "Տարրեր" 10.11]: Եվ երկուսն էլ ռացիոնալ են։ Ուստի, CM-ն և MF-ն ռացիոնալ ուղիղ գծեր են, որոնք համաչափելի են միայն քառակուսիներով։ CF-ը, հետևաբար, ապոտոմե է [Տե՛ս "Տարրեր" 10.73]: Ուրեմն, ես ասում եմ, որ այն նաև վեցերորդ (կտրվածքն) է։
Քանի որ FL-ը հավասար է AG-ով և GB-ով պարփակված կրկնապատիկ ուղղանկյանին, թող FM-ը բաժանված լինի կեսի վրա N-ում, և թող NO-ն քաշված լինի N-ի միջով, զուգահեռ CD-ին։ Այսպիսով, FO-ն և NL-ը յուրաքանչյուրն հավասար են AG-ով և GB-ով պարփակված ուղղանկյան։ Եվ քանի որ AG-ն և GB-ն անհամաչափ են քառակուսով, AG-ի վրա կառուցված քառակուսին, հետևաբար, անհամաչափ է GB-ի վրա կառուցված քառակուսու հետ։ Սակայն, CH-ը հավասար է AG-ի վրա կառուցված քառակուսուն, իսկ KL-ը հավասար է GB-ի վրա կառուցված քառակուսուն։
Ուստի, CH-ը անհամաչափ է KL-ի հետ։ Եվ ինչպես CH-ն է KL-ի նկատմամբ, այնպես էլ CK-ն KM-ի նկատմամբ է [Տե՛ս "Տարրեր" 6.1]: Ուստի, CK-ն երկարությամբ անհամաչափ է KM-ի հետ [Տե՛ս "Տարրեր" 10.11]: Եվ քանի որ AG-ով և GB-ով պարփակված ուղղանկյունը միջին չափաբաժին է AG-ի և GB-ի վրա կառուցված քառակուսիների միջև [Տե՛ս "Տարրեր" 10.21-ի լեմմա], իսկ CH-ը հավասար է AG-ի վրա կառուցված քառակուսուն, KL-ը՝ GB-ի վրա կառուցված քառակուսուն, NL-ը՝ AG-ով և GB-ով պարփակված ուղղանկյունին, NL-ը, հետևաբար, նույնպես միջին չափաբաժին է CH-ի և KL-ի միջև։
Ուստի, ինչպես CH-ն է NL-ի նկատմամբ, այնպես էլ NL-ը KL-ի։ Եվ նույն տրամաբանությամբ, CM-ի վրա կառուցված քառակուսին մեծ է MF-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը լայնությամբ արտադրում է CF։ Ես ասում եմ, որ CF-ը վեցերորդ ապոտոմեն է։
Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։
Պնդում 103
Ուղիղ գիծը, որը երկարությամբ համաչափ է ապոտոմեի հետ, ինքն էլ ապոտոմե է և նույն կարգի է։
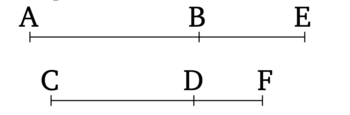
Թող AB-ն լինի ապոտոմե, և թող CD-ն լինի երկարությամբ համաչափ AB-ի հետ։ Ասում եմ, որ CD-ն նույնպես ապոտոմե է և նույն կարգի է, ինչ AB-ն։
Քանի որ AB-ն ապոտոմե է, թող BE-ն լինի կցորդ դրան։ Այսպիսով, AE-ն և EB-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.73]։ Եվ թող այնպես լինի, որ BE-ի և DF-ի հարաբերությունը նույնն է, ինչ AB-ի և CD-ի հարաբերությունը [Տե՛ս "Տարրեր" 6.12]։ Այսպիսով, ինչպես մեկ է մեկի նկատմամբ, այնպես էլ ամեն ինչ՝ ամեն ինչի [Տե՛ս "Տարրեր" 5.12]։ Եվ ինչպես ամբողջ AE-ն է ամբողջ CF-ի նկատմամբ, այնպես էլ AB-ն է CD-ի նկատմամբ։ Եվ AB-ն համաչափ է երկարությամբ CD-ի հետ։ AE-ն, հետևաբար, նույնպես համաչափ է CF-ի հետ, և BE-ն՝ DF-ի հետ [Տե՛ս "Տարրեր" 10.11]։
Եվ AE-ն և BE-ն ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով։ Այսպիսով, CF-ն և FD-ն նույնպես ռացիոնալ (ուղիղ գծեր են, որոնք) համաչափ են միայն քառակուսիներով [Տե՛ս "Տարրեր" 10.13]։ Ուստի, CD-ն ապոտոմե է։ Ասում եմ, որ այն նույնպես նույն կարգի է, ինչ AB-ն։
Ուստի, քանի որ ինչպես AE-ն է CF-ի նկատմամբ, այնպես էլ BE-ն է DF-ի նկատմամբ, ապա, այլընտրանքով, ինչպես AE-ն է EB-ի նկատմամբ, այնպես էլ CF-ն է FD-ի նկատմամբ [Տե՛ս "Տարրեր" 5.16]։ Այսպիսով, AE-ի վրա կառուցված քառակուսին մեծ է EB-ի վրա կառուցված քառակուսուց կամ որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափ է կամ անհամաչափ AE-ի հետ։
Ուստի, եթե AE-ի վրա կառուցված քառակուսին մեծ է EB-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափ է AE-ի հետ, ապա CF-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի FD-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը համաչափ է CF-ի հետ [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե AE-ն երկարությամբ համաչափ է նախապես տրված ռացիոնալ ուղիղ գծի հետ, ապա նույնը նաև CF-ն է [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե BE-ն համաչափ է, ապա նաև DF-ը։ Եվ եթե ոչ AE-ն և ոչ էլ EB-ն համաչափ չեն, ապա նույնը նաև CF-ն և FD-ն [Տե՛ս "Տարրեր" 10.13]։
Եվ եթե AE-ի վրա կառուցված քառակուսին մեծ է EB-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը անհամաչափ է AE-ի հետ, ապա CF-ի վրա կառուցված քառակուսին նույնպես մեծ կլինի FD-ի վրա կառուցված քառակուսուց որոշակի ուղիղ գծի վրա կառուցված քառակուսու չափով, որը անհամաչափ է CF-ի հետ [Տե՛ս "Տարրեր" 10.14]։ Եվ եթե AE-ն երկարությամբ համաչափ է նախապես տրված ռացիոնալ ուղիղ գծի հետ, ապա նույնը նաև CF-ն է [Տե՛ս "Տարրեր" 10.12]։ Եվ եթե BE-ն համաչափ է, ապա նաև DF-ը։ Եվ եթե ոչ AE-ն և ոչ էլ EB-ն համաչափ չեն, ապա նույնը նաև CF-ն և FD-ն [Տե՛ս "Տարրեր" 10.13]։
Ուստի, CD-ն ապոտոմե է և նույն կարգի է, ինչ AB-ն [Տե՛ս "Տարրեր" 10.11-10.16]։ Սա այն էր, ինչ անհրաժեշտ էր ապացուցել։