Աստղագիտություն — Գրապահարան

Աստղագիտություն

հեղինակ՝ Բ. Ա. Վորոնցով-Վելյամինով
թարգմանիչ՝ անհայտ
աղբյուր՝ «Աստղագիտություն»

Անավարտ
Այս ստեղծագործությունը դեռ ամբողջովին տեղադրված չէ Գրապահարանում

ՆԵՐԱԾՈՒԹՅՈՒՆ

§ 1. ԱՍՏՂԱԳԻՏՈՒԹՅԱՆ ԱՌԱՐԿԱՆ։ Աստղագիտությունն ուսումնասիրում է երկնային մարմինների և նրանց համակարգությունների շարժումը, կառուցվածքն ու զարգացումը։ Նա բոլոր գիտություններից ամենահնագույնն է. նրա սաղմերը մենք հանդիպում ենք դեռևս Աֆրիկայի և Ասիայի կուլտուրական այն ժողովուրդների մոտ, որոնք ապրելիս են եղել մեզանից մի քանի հազար տարի առաջ։

Երկինքն առաջին անգամ դիտողներն արդեն նկատել էին, որ Արեգակի և աստղերի դիրքով կարելի է որոշել ժամանակը։ Օրինակ, օրվա կեսին՝ կեսօրին, Արեգակը երկնքում գրավում է, տվյալ օրվա ընթացքում, ամենաբարձր դիրքը։ Լուսնի տեսքի փոփոխությամբ (եղջյուր, լրիվ սկավառակ և այլն) և երկնքի մյուս լուսատուների դիրքով կարելի է չափել մեծ ժամանակահատվածներ, այսինքն կազմել օրացույց։ Քոչվոր ժողովուրդները և ծովագնացները սովորել էին աստղերի օգնությամբ որոշել իրենց պետք եղած ուղղությունը։

Աստղագիտությունն այդ նպատակին ծառայում է նաև մեր ժամանակներում։ Աստղերի օգնությամբ որոշվում է ծովում նավերի, իսկ օդում՝ ինքնաթիռների ուղղությունն ու դիրքը։ Ճիշտ ժամանակը, որը հաղորդվում է ռադիոյով, որոշվում է աստղագետների կողմից՝ երկնային լուսատուները դիտելու միջոցով։ Առանց երկնային լուսատուների դիտումների հնարավոր չէր լինի նաև աշխարհագրական ճիշտ քարտեզներ կազմել։ Այսպիսով, աստղագիտությունն առաջ է եկել մարդու գործնական պահանջների հիման վրա և զարգացել է նրանց հետ միասին։

Դիտելով ամենօրյա արևածագն ու արևամուտը և աստղերի տեսանելի շարժումը հորիզոնի նկատմամբ, մարդիկ կարծում էին, թե բոլոր երկնային լուսատուները իսկապես շարժվում են անշարժ Երկրի շուրջը։ Երկնայինն ու երկրայինը խիստ կերպով սահմանազատվում էին միմյանցից։ Այդ սխալ պատկերացումը, որ հովանավորվում էր կրոնի կողմից, ժխտվել է մատերիալիստական գիտության կողմից։

Հաստատվել է, որ Երկիրը նույնպիսի մի երկնային մարմին է, ինչպես և երկնային մյուս լուսատուները, որ նա նրանցից ոչ մի բանով չի տարբերվում, որ Երկիրը և նրան նմանվող երկնային մարմինները, որոնք մոլորակներ են կոչվում, բոլորվում են Արեգակի շուրջը, որ աստղերը այնպիսի լուսատուներ են, որոնք նման են մեր Արեգակին, այսինքն՝ բաղկացած են շիկացած գազից և անհամեմատ ավելի մեծ չափեր ունեն, քան Երկիրը և նույնիսկ (շատ դեպքերում) իրենց չափերով բավականաչափ գերազանցում են մեր հսկայական Արեգակին։

Տիեզերքի մասին եղած նախկին միամիտ պատկերացումները, որոնք հիմնվում էին հեռավոր անցյալի մարդկանց մոլորությունների վրա, արտացոլված են կրոնական ուսմունքներում։ Այդ ուսմունքների համաձայն աշխարհն ստեղծվել է աստծու կամ աստվածների կողմից և իբր գոյություն ունի անփոփոխ։ Տիեզերքի իսկական կառուցվածքի հայտնագործումը մարդկանց ցույց տվեց, որ աշխարհն իրականում բնավ այնպիսին չէ, ինչպես նա նկարագրվում է այսպես կոչված «սրբազան» գրքերում։

Իմանալով բնության օրենքները, մարդիկ հնարավորություն ստացան այն նվաճելու, նրան ստիպեցին ծառայել իրենց։ Իմանալով երկնային այնպիսի երևույթների պատճառները, ինչպիսիք են՝ Արեգակի խավարումը, գիսավորների հայտնվելը և այլն, մարդիկ դադարեցին սնահավատորեն սարսափել նրանցից։ Տիեզերքի իսկական կառուցվածքը չիմանալուց առաջացող սնահավատությունը կարող է պահպանվել միայն հետամնաց մարդկանց մեջ, որոնք չգիտեն աշխարհի կառուցվածքը։ Ուստի՝ առանց աստղագիտության հիմունքներն իմանալու, չի կարելի գիտական առաջավոր աշխարհայացք ունենալ։

Երկնային լուսատուներին վերաբերող գիտությունը պատմում է մեզ, որ կան երկնային այնպիսի մարմիններ, որոնք բոլորովին նման չեն մեր երկրագնդին, որ միմիայն Երկիրը չէ, որ կարող է բնակեցված լինել կենդանի էակներով, որ աշխարհում ամեն ինչ փոփոխվում է հենց իրեն՝ բնության օրենքների համաձայն, որ տիեզերքը հավիտենական է՝ երբեք չի ստեղծվել և երբեք չի դադարի գոյություն ունենալուց։

Ուսումնասիրելով աստղագիտությունը, մենք տեղեկանում ենք մոլորակներէ մյուս երկրների մասին, որոնք շրջապատված են շատ լուսիններով, տեղեկանում ենք հեռավոր աստղերի ու աստղային կուտակումների մասին, որոնք այնքան հեռու են գտնվում մեզանից, որ նրանց լույսը, տարածվելով մոտ 300000 կմ/վրկ արագությամբ, հասնում է մեզ տարիների և, նույնիսկ, միլիոնավոր տարիների ընթացքում։

Աստղագիտության տվյալներն օգտակար են մյուս գիտությունների զարգացման համար, օրինակ, ֆիզիկայի։ Օժանդակելով մյուս գիտություններին, աստղագիտությունն իր հերթին օգտվում է այդ գիտությունների ծառայություններից։ Ֆիզիկոսներն օգնում են աստղագետներին երկնային լուսատուների ուսումնասիրության նոր միջոցներ գտնելու գործում, մաթեմատիկոսները տալիս են զանազան հաշվարկումների համար նոր, ավելի լավ եղանակներ, առանց որի՝ աստղագիտությունը չի կարող զարգանալ, և այլն։

Աստղագետները հաճախ օգնում են պատմաբաններին՝ որոշելու թե ե՛րբ են տեղի ունեցել որոշ իրադարձություններ, օրինակ, Հունաստանում ճակատամարտերից մեկի ժամանակ (միդիացիների և լիդիացիների միջև) տեղի է ունեցել մի հազվադեպ երևույթ` Արեգակի լրիվ խավարում։ Աստղագետները կարողացել են հաշվել, թե ե՛րբ տվյալ խավարումը կարող էր երևալ այդ վայրում։ Այդպիսով, որոշվել է այդ պատմական ճակատամարտի տարեթիվը։

Աստղագիտությունը հիմնված է երկնային երևույթների դիտումների վրա։ Առանց այդ դիտումների՝ աստղագիտությունը, ինչպես հարկն է, յուրացնել հնարավոր չէ։ Ուստի ամեն մի սովորող պետք է ծանոթանա երկնքում տեղի ունեցող հիմնական երևույթների հետ և հաճախակի ուշադիր կերպով դիտի աստղային երկինքը և աշխատի ինքն իր աչքով տեսնել այն, ինչի մասին խոսվում է դասագրքում։ Այդ երևույթներից շատերը մեկ անգամից չի կարելի նկատել։ Նրանք պարզվում են միայն տարբեր ժամանակ կատարված դիտումները միմյանց հետ համեմատելուց հետո։ Աստղագիտությունը ուսումնասիրում է բնությունը նրա մեծասքանչ արտահայտություններում, և բնությանը անձնական փորձի միջոցով ծանոթ չլինելու դեպքում նրա ուսումնասիրությունը մնում է գրքային ու մեռյալ, պատկերացումները՝ անորոշ և անկայուն։

Ուրեմն հաճախ կարդացեք բնության այդ մեծ գիրքը՝ աստղային երկինքը, որը մշտապես տարածված է ձեր գլխավերևը։

ԳԼՈՒԽ I։ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱ ԵՎ ԵՐԿԻՐ

ԵՐԿՆԱՅԻՆ ՍՖԵՐԱ

§ 2. ԵՐԿՆԱԿԱՄԱՐ ԵՎ ՀԱՄԱՍՏԵՂՈՒԹՅՈՒՆՆԵՐ. Բաց և ընդարձակ վայրում, թեկուզ ո՛րտեղ էլ մենք գտնվելիս լինենք (բաց դաշտում, տափաստանում կամ ծովի վրա), երկինքը՝ ամպամած լինի նա թե պարզ, երևում է մեզ ինչպես մի գմբեթ, որ շրջված է մեր գլխավերևը։ Այդ երկնային գմբեթը կամ երկնակամարը ցերեկը պարզ եղանակին կապույտ է, ամպամած եղանակին՝ մոխրագույն, իսկ պարզ գիշերները ծածկված է լինում աստղերով։

Այդ ժամանակ Երկիրը մեզ թվում է որպես մի շրջան, որի կենտրոնում կանգնած ենք մենք և որի եզրերը կարծես թե միանում են երկնակամարի հետ հորիզոնով։ Մենք գիտենք, որ իրականում երկինքը չի միանում Երկրին և որ հորիզոնի գիծը Երկրի մակերևույթի տեսանելի մասի երևակայական սահմանն է։ Ճիշտ այդպես էլ երկնակամարը, որպես երկնային գմբեթ, իրականում գոյություն չունի։ Երկնային լուսատուները, այսինքն՝ Արեգակը, Լուսինը և աստղերը, միայն թվում է, թե կպած են երկնակամարին և կարծես բոլորը միևնույն հեռավորության վրա են գտնվում մեզանից։ Իսկ իրականում բոլոր այդ լուսատուները գտնվում են մեզանից չափազանց տարբեր և շատ մեծ հեռավորությունների վրա։

Ցերեկային երկնքի կա պույտ գույնը առաջանում է նրանից, որ Երկրի մթնոլորտը, որը շրջապատում է ողջ երկրագունդը, ցրում է ամեն կողմի վրա իր միջով անցնող արեգակնային լույսը։ Բայց սպիտակ արեգակնային լույսը, ինչպես հայտնի է, բաղկացած է ծիածանի բոլոր գույների խառնուրդից, իսկ օդը կապույտ ճառագայթներն ավելի ուժեղ է ցրում, քան մյուս գույնի ճառագայթները։ Ուստի օդը կարծես «ներկվում է» կապույտ գույնով։

Որքան ավելի վեր բարձրանանք Երկրի մակերևույթից, այնքան քիչ մթնոլորտ կմնա մեր գլխավերևը և այնքան նրա կողմից թույլ կլինի արեգակնային լույսի ցրումը։ Այնտեղ (օրինակ, շատ բարձր լեռան գագաթից կամ ինքնաթիռից ու ստրատոստատից) երկինքն ավելի խավար է թվում, և նրա վրա նույնիսկ ցերեկը նկատելի են լինում առավել պայծառ աստղերը։ Ցերեկային երկինքը հեռադիտակով նայելիս նույնպես ավելի խավար է թվում, քան չզինված աչքի համար։ Հեռադիտակով պայծառ աստղերը կարելի է տեսնել նաև ցերեկը։ Հետևաբար, եթե ցերեկը երկնակամարի վրա մենք աստղեր չենք տեսնում, ապա միայն այն պատճառով, որ Երկրի մթնոլորտի կողմից ցրվող արեգակնային լույսը խանգարում է տեսնել նրանց։ Արեգակի լրիվ խավարման ժամանակ երկինքը մթնում է, և աստղերը չզինված աչքով տեսանելի են դառնում։

Մեզ թվում է, թե գիշերային երկնակամարի վրա ցրված աստղերն անթիվ են և որ նրանցից ոչ մի կերպ հնարավոր չէ մի բան հասկանալ։ Սակայն, եթե ուշադրությամբ նայենք երկնքին, կտեսնենք, որ աստղերի թիվն այնքան էլ մեծ չէ, և նրանց ճանաչելն էլ առանձնապես դժվար չէ։ Հորիզոնից վեր չզինված աչքով միաժամանակ, ամենաբարենպաստ պայմանների դեպքում, կարելի է տեսնել ոչ ավելի, քան 3000 աստղ։

Ամբողջ աստղային երկինքը բաժանված է մասերի։ Աստղային երկնքի այդ մասերը կոչվում են համաստեղություններ։

Դեռևս երկնքի հնադարյան դիտողներն են հազարավոր տարիներ առաջ աստղային երկինքը բաժանել մասերի, որտեղ աստղերը միանգամայն կամայականորեն խմբավորել են զանազան կերպարանքների՝ համաստեղությունների մեջ։ Նրանք այդ խմբերին (համաստեղություններին) տվել են երևակայական անուններ, որոնք պահպանվել են մինչև մեր օրերը։ Այդ անուններից շատերը այժմ մեղ համար տարօրինակ են հնչում, որովհետև համաստեղությունները կրում են այնպիսի առարկաների և էակների անուններ, որոնց հետ աստղերի դասավորությունը հաճախ ոչ մի նմանություն չունի։ Մի շարք դեպքերում այդ անունները կապվել են հին դարերի զանազան առասպելների հետ։

Երկնքում զատված է ընդամենը 88 համաստեղություն։ Նրանցից բավական է ճանաչել և կարողանալ երկնքում գանել մի քանիսը, որոնք պայծառ աստղեր ունեն։ Համաստեղությունները գտնելը հեշտացնելու համար նրանց առավել պայծառ աստղերը մտովի միացնում են ուղիղ գծերով այնպես, որ ստացվեն երկրաչափական պարզ ֆիգուրաներ կամ սխեմատիկ նկարներ։

Համաստեղությունների աստղերը չեն փոխում իրենց փոխադարձ դասավորությունը։ Նրանցից տարբերվում են մոլորակները, այն լուսատուները, որոնք փոխում են իրենց տեսանելի տեղը համաստեղությունների միջև, տեղաշարժվելով բարդ գծերով, որոնք հիշեցնում են մերուկներ։

Չզինված աչքով երևում են 5 մոլորակներ, որոնք իրենց տեսքով նման են պայծառ աստղերին։ Դրանք են՝ Մերկուրին, Վեներան, Մարսը, Յուպիտերը և Սատուրնը։

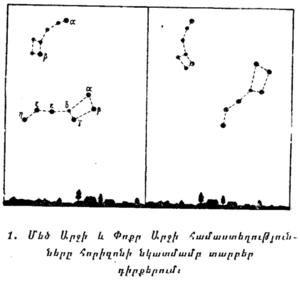
§ 3. ՀԱՄԱՍՏԵՂՈՒԹՅՈՒՆՆԵՐԸ ԳՏՆԵԼԸ ԵՐԿՆՔՈՒՄ։ Ամենից առաջ, յուրաքանչյուրը պետք է կարողանա երկնքում գտնել Մեծ Արջի համաստեղությունը։ Նա բնորոշ է իր յոթ պայծառ աստղերով։ Նրանց կարելի է մտովի միացնել ուղիղ գծերով այնպես, որ ստացվի շերեփի կամ կոթավոր կաթսայի պատկեր (նկ. 1)։ Միայն հարկավոր է նկատի ունենալ, որ երբեմն «շերեփի» կոթը ուղղված է լինում դեպի ձախ, երբեմն դեպի վեր կամ դեպի ցած, իսկ երբեմն էլ այդ «շերեփը», երբ նա գտնվելիս է լինում ուղիղ մեր գլխավերևը, շրջվում է «երեսնիվայր»։

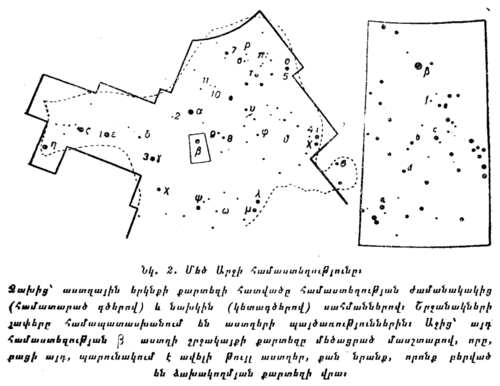
Նկ. 2-ում պատկերված է աստղային երկնքի ժամանակակից քարտեզի մի մասը, որտեղ գտնվում է Մեծ Արջի համաստեղությունը։

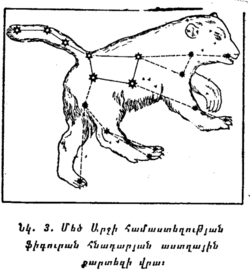
Նկ. 3-ում վերարտադրված է աստղային մի հինավուրց քարտեզ, որտեղ բացի աստղերից պատկերացվել է նաև այն գազանի պատկերը, որի անունով կոչվում է համաստեղությունը։

Ելնելով Մեծ Արջի համաստեղությունից, գտեք. Փոքր Արջի համաստեղությունը։ Եթե նրա 7 գլխավոր աստղերը (որոնք ավելի թույլ պայծառություն ունեն, քան Մեծ Արջի աստղերը) մտովի միացնենք ուղիղ գծերով, ինչպես այդ ցույց է տրված նկ. 1-ում, նույնպես կստացվի փոքր չափի շերեփ։ Այդ համաստեղության մեջ ամենապայծառ աստղը («շերեփի» կոթի ծայրինը) կրում է Բևեռային անունը։

Բևեռային աստղից այն կողմը, եթե շարժվելու լինենք Մեծ Արջից, մոտավորապես նույն հեռավորության վրա, փռված է Կասիոպեի համաստեղությունը։ Նա բնորոշ է իր հինգ բավականաչափ պայծառ աստղերով, որոնք դասավորված են W տառի կամ շրջված ու հիմքի մոտ ձգված M տառի ձևով։

Կասիոպեից ցած գտնվում են Անդրոմեդայի և Պեգասի համաստեղությունները։ Մ. Արջը Կասիոպեի հետ միացնող գծի երկու կողմերում դասավորված են Կարապի, Քնարի և Արծվի (մեկ կողմում) համաստեղությունները և Կառավարի, Երկվորյակների, Ցուլի, Օրիոնի, Մեծ Շան ու Փոքր Շան (մյուս կողմում) համաստեղությունները։

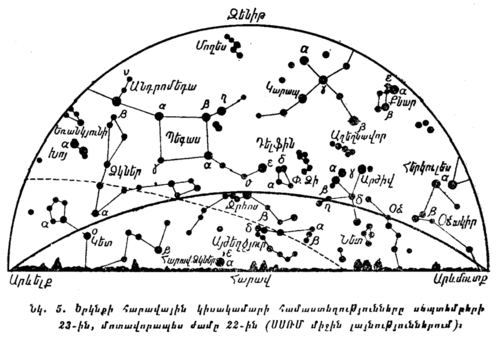
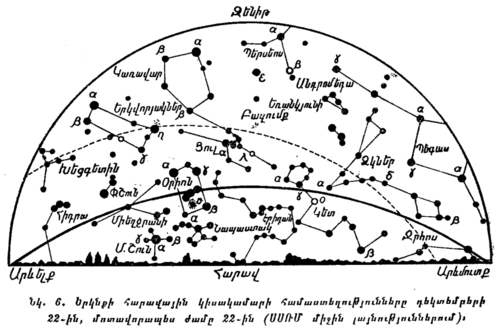
Յուրաքանչյուր սովորող պետք է կարողանա երկնքում գտնել նշված համաստեղությունները, հիշելով նրանց պայծառ աստղերի բնորոշ դասավորությունը։ Այդ համաստեղությունները ցույց են արված նկ. 4-ում, 5-ում և 6-ում։

Երկնքում համաստեղություններն ավելի հեշտ կարելի է գտնել այնպիսի գիշերը, երբ Լուսնի պայծառ լույսը դրան չի խանգարում։ Հարկավոր է նկատի ունենալ, որ որոշ համաստեղություններ (թվածներից երկու Արջերը և Կասիոպեն) միշտ երևում են երկնքում։ Մյուս համաստեղությունները երբեմն երևում են, երբեմն գտնվում են հորիզոնից ցած։ Բացի այդ, յուրաքանչյուր համաստեղություն օրվա տարբեր ժամերին և տարվա տարբեր ժամանակներին հորիզոնի նկատմամբ տարբեր դիրք է գրավում։ Համաստեղություններն ավելի հեշտ գտնելու համար առանձնապես հարմար է օգտվել երկնքի շարժական քարտեզից, որովհետև նա ցույց է տալիս հորիզոնի նկատմամբ համաստեղությունների ունեցած դասավորությունը՝ տարվա ամեն մի օրվա ու ժամվա համար (տե՛ս հավելված VI)։

Համաստեղությունները գտնելը հեշտացնելու համար հարկավոր է մեկ՝ արդեն ծանոթ, համաստեղությունից աստիճանաբար անցնել մյուսին՝ դեռևս չգտնվածին։ Ըստ որում պետք է նկատել, թե մեզ ծանոթ համաստեղությունից դեպի ո՞ր կողմն է գտնվում այն համաստեղությունը, որ մենք փնտրում ենք։ Հարկավոր է ուշադրություն դարձնել աստղերի համեմատական պայծառության վրա, որը քարտեզի վրա ցույց է տրված տարբեր մեծության շրջանակներով։ Քարտեզի վրա ցույց է տրված, թե ի՛նչ գծերով է հարմար միացնել աստղերը, թեև դա սոսկ պայմանական մի ձև է։

Վերոհիշյալ համաստեղություններից ամեն երեկո Քնարը (Վեգա կոչված պայծառ աստղով), Կարապն ու Արծիվը (Ալտաիր կոչված աստղով) երևում են ամբողջ գիշերը՝ գարնանն ու աշնանը, Եզնարածը (Արկտուր կոչված պայծառ աստղով)՝ գարնանն ու ամռանը, Կառավարը, Ցուլը և Մեծ Շունը (երկնքի ամենապայծառ աստղի՝ Սիրիուսի հետ միասին)՝ միայն ձմռանը, Պերսեոսը, Անդրոմեդան և Պեգասը՝ սրանք ամառային և աշնանային համաստեղություններ են։

§ 4. ԱՍՏՂԱՅԻՆ ՄԵԾՈՒԹՅՈՒՆՆԵՐ։ Աստղերն ըստ իրենց տեսանելի պայծառության տարբեր են լինում։ Հին ժամանակներից ի վեր ամենապայծառ աստղերն անվանել են առաջին մեծության աստղեր։ Այն աստղերը, որոնք նրանցից թույլ են 2½ անգամ, անվանվում են երկրորդ մեծության աստղեր, և այլն։ Ամենաթույլ աստղերը, որոնք երևում են անլուսին գիշերը սրատես աչքով, վեցերորդ մեծության աստղեր են։ Նրանք իրենց փայլով 100 անգամ թույլ են առաջին մեծության աստղերից։

«Աստղային մեծություն» հնուց ի վեր արմատացած անունը ոչ մի առնչություն չունի աստղի չափերի և աստղի իրակ ան մեծության հետ։ «Աստղային մեծություն» հասկացողությունը բնորոշում է աստղերի պայծառությունը։ Որքան աստղը թույլ է, այնքան նրա աստղային մեծությունը մեծ է։ Սա նման է այն բանին, ինչպես, օրինակ, ավելի խոշոր պտուղները համարում են առաջին տեսակի, մանրերը՝ երկրորդ տեսակի և այլն։

Մեծ Արջի գլխավոր յոթ աստղերից վեցը և Բևեռшյին աստղը երկրորդ մեծության աստղերի օրինակ են հանդիսանում։ Առաջին մեծության աստղերի օրինակ են ծառայում Արկտուրը և Ալտաիրը։

Աստղերի փայլի ճշգրիտ չափումները պահանջ են առաջացրել կիրառելու աստղային մեծության միջակա կոտորակային նշանակումներ, օրինակ, 1,2 կամ 5,9։ Որպես 1,0 մեծության նմուշ ընդունված աստղերից ավելի պայծառ լուսատուների համար մտցրել են 0 աստղային մեծություն, -1, -2 մեծություններ (բացասական նշանով) և այլն։ Օրինակ, Սիրիուսի աստղային մեծությունը հավասար է -1,6։

Հեռադիտակով կարելի է տեսնել ավելի թույլ աստղեր, քան վեցերորդ մեծության աստղերն են՝ յոթերորդ, ութերորդ և ավելի բարձր մեծության աստղեր։ Որքան աստղերը թույլ են, այնքան նրանց թիվը մեծ է։ Առաջին մեծության և ավելի պայծառ աստղերի թիվը հասնում է մոտավորապես 20-ի։ Վեցերորդ մեծության և ավելի պայծառ աստղերը մոտավորապես վեց հազար հատ են։

§ 5. ԱՍՏՂԵՐԻ ԱՆՎԱՆՈՒՄՆԵՐՆ ՈՒ ՆՇԱՆԱԿՈՒՄՆԵՐԸ։ Առաջին մեծության աստղերը դեռևս հնում ստացել են հատուկ անվանումներ, ինչպես, օրինակ, Սիրիուս, Վեգա, Ալտաիր։ Բացի այդ պայծառ աստղերից, յուրաքանչյուր համաստեղության մեջ առանձին կերպով, նշանակում են հունական այբուբենի տառերով՝ α, β, γ, ... և այլն՝ մասնավորապես նրանց պայծառության նվազման կարգով։ Այսպես, օրինակ, Սիրիուսը միևնույն ժամանակ Մեծ Շան α-ն է, Բևեռային աստղը՝ Փոքր Արջի α-ն է, Ռիգելը՝ Օրիոնի β-ն է և այլն։

Ավելի թույլ աստղերից շատերը նշանակվում են լատինական այբուբենի տառերով։ Վերջապես բոլոր աստղերի, նույն թվում նաև ամենաթույլ աստղերի համար, որոնց այբուբենի բոլոր տառերը բնականաբար չեն բավականացել, կարելի է ցույց տալ նրանց աստղային մեծությունը և այն տեղը, որ նրանք զբաղեցնում են երկնքում, կամ այն համարը, որի տակ նրանք գրանցված են այս կամ այն մասնագիտական աստղային կատալոգում։

Հունական այբուբենը և բոլոր առաջին մեծության այն աստղերի հատուկ անունները, որոնք երևում են ՍՍՌՄ տերիտորիայից, տրված են II և III հավելվածներում։

§ 6. ԵՐԿՆԱՅԻՆ ՍՖԵՐԱ, ԶԵՆԻԹ ԵՎ ՀՈՐԻԶՈՆ։ Բոլոր աստղերը մեզանից միևնույն հեռավորության վրա են թվում։ Ուստի՝ հարմար է պայմանական կերպով ընդունել, որ բոլոր աստղերն էլ իբր թե գտնվում են կամայական շառավիղ ունեցող մի գնդի ներքին մակերևույթի վրա, որ կոչվում է երկնային սֆերա և որի կենտրոնում գտնվում է դիտողի աչքը։

Չափազանց տարբեր են աստղերի իսկական հեռավորությունները մեզանից, և այդ հեռավորությունները մենք կարող ենք որոշել միայն շատ ճշգրիտ չափումների և հաշվարկումների միջոցով։ Մինչդեռ աչքի համար հեռավորությունների մեջ եղած այդ տարբերությունը բոլորովին աննկատելի է, և այնպիսի երևույթները, ինչպիսիք են աստղերի ծագելն ու մայր մտնելը, տեղի են ունենում անկախ մեզնից ունեցած նրանց հեռավորությունից։ Երկնային սֆերայի հասկացողությունից մենք օգտվում ենք երկնային տեսանելու ամենապարզ երևույթների քննարկումը հարմար դարձնելու համար, օրինակ, այնպիսի երևույթների, ինչպես լուսատուների ծագելն ու մայր մտնելն է։ Մենք գիտենք, որ մեր գլխավերևը իրականում գոյություն չունի ոչ կարծր գմբեթի ձև ունեցող երկնակամար և ոչ էլ որևէ ռեալ երկնային սֆերա։ Իսկ հին ժամանակներում երկնային այդ սֆերան համարում էին ոչ թե որպես մաթեմատիկական մի հասկացողություն, ինչպես մենք նրան համարում ենք, այլ որպես իսկապես գոյություն ունեցող բյուրեղապակյա մի գունդ։

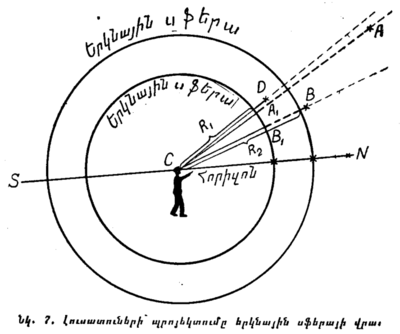
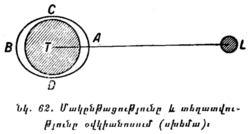
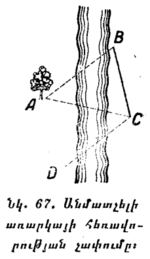
Դատողություններ անելով լուսատուների ծագելու, մայր մտնելու և ուրիշ նման երևույթն երի մասին, մենք նկատի ենք ունենում միայն այն ուղղությունը, որով երևում են աստղերը (օրինակ, հորիզոնի մոտ, մեր գլխավերևը և այլն), ուստի միևնույն է, թե ինչպիսի շառավիղ մենք կերևակայենք երկնային սֆերայի համար։ Նկ. 7-ը, օրինակ, ցույց է տալիս, որ դիտողին որևէ ուղղությամբ երևացող ամեն մի աստղ հենց այդ ուղղությամբ էլ կերևա, թեկուզ ի՛նչպիսի սֆերայի վրա էլ նրան պատկերացնելու լինենք՝ R₁ շառավիղ ունեցող սֆերայի, թե R₂ շառավիղ ունեցող սֆերայի վրա։ Այդ պատճառով էլ ասում են, որ երկնային սֆերան անորոշ կամ կամայական շառավիղ ունի։

Անցնելով դիտողի աչքով, ուղղաձիգ գիծը երկնային սֆերան հատում է զենիթի կետում։ Զենիթը դիտողի գլխավերևի ամենաբարձր կետն է։ Ուղղաձիգ գծի ուղղությունը ցույց է տալիս ուղղալարը՝ թելից կախած փոքրիկ ծանրությունը։ Ուղղաձիգ գծին ուղղահայաց հարթությունը կոչվում է հորիզոնական հարթություն։

Մաթեմատիկական հորիզոն է կոչվում երկնային սֆերայի և այն հորիզոնական հարթության հատման գիծը, որ անցնում է երկնային սֆերայի կենտրոնով։ Այս հորիզոնից այսպես կոչված՝ տեսանելի հորիզոնը տարբերվում է նրանով, որ վերջինս սահմանափակված է մի գծով, որով, ինչպես մեզ թվում է, երկինքը «միանում» է Երկրին։ Հորիզոնի հարթությունը կարելի է որոշել հարթաչափի միջոցով։

§ 7. ԱՆԿՅՈՒՆԱՅԻՆ ՉԱՓՈՒՄՆԵՐ։ Պայմանականորեն ընդունելով, որ բոլոր լուսատուները դասավորված են երկնային սֆերայի վրա, (ավելի Ճիշտ՝ պրոյեկտված են նրա վրա), մենք կարող ենք չափել միայն այն ուղղությունների միջև ընկած անկյունները, որով մենք տեսնում ենք այդ լուսատուները։ Երկնային սֆերայի վրա այդ անկյուններին համապատասխանում են մեծ շրջանների աղեղներ։ Օրինակ (տե՛ս նկ. 7), մենք ասում ենք, որ երկնային սֆերայի վրա A և B աստղերը միմյանցից գտնվում են 23° հեռավորության վրա, եթե այդ աստղերի CA և CB ուղղությունների միջև ընկած անկյունը (<ACB) կազմում է 23°։ Երկնային սֆերայի վրա այդ անկյանը համապատասխանում է A1B1 աղեղը, որը հավասար է 23°։ A աստղը կարող է մեզանից շատ ավելի հեռու լինել, քան D աստղը, բայց եթե նրանք երկուսն էլ մեզ երևում են գրեթե միևնույն ուղղությամբ, մենք կասենք, որ երկնային սֆերայի վրա D աստղը շատ ավելի մոտ է A աստղին, քան B աստղին, թեև տարածության մեջ A-ի գծային հեռավորությունը (օրինակ, կիլոմետրերով) D-ից կարող է շատ ավելի մեծ լինել։

Ճիշտ այդպես էլ Արեգակի և Լուսնի տեսանելի անկյունային տրամագծերը գրեթե հավասար են՝ կազմելով մոտավորապես կես աստիճան, թեև իրականում Լուսնի տրամագիծը համարյա 400 անգամ փոքր է Արեգակի տրամագծից։ Բայց դրա փոխարեն նա նույնքան անգամ ավելի մոտ է մեզ, քան Արեգակը, այդ պատճառով էլ թվում է, թե նրանց անկյունային չափերը հավասար են։ Լուսնի տեսանելի անկյունային տրամագիծը կոպեկանոցի կամ ափսեի հետ համեմատելն անիմաստ կլինի, եթե վերջիններին որևէ հեռավորություն չի վերագրվում։ Եվ իսկապես, պարզած ձեռքի հեռավորության վրա կոպեկանոցը կծածկի միայն Լուսինը, իսկ եթե կոպեկանոցը մոտեցնենք աչքին, նրանով կարելի է ծածկել ամբողջ աշխարհը։ Լուսինը կարելի է համեմատել կոպեկանոցի հետ, եթե ավելացնելու լինենք, թե ինչ հեռավորության վրա պետք է պահենք կոպեկանոցը։ Անմտություն են նույնպես հետևյալ տիպի արտահայտությունները. «Լուսինը հորիզոնից բարձրացել է կես մետրի չափ» կամ «երկու աստղերի միջև եղած հեռավորությունը երկնքում կազմում է 2 մետր»։

Այսպիսով, երկնային սֆերայի վրա կարելի է կատարել միայն անկյունային չափումներ։

Լուսատուի բարձրություն անվանում են նրա անկյունային հեռավորությունը հորիզոնից։ Օրինակ, B լուսատուի բարձրությունը (նկ. 7) չափվում է BCN անկյունով։

Մարդ եթե առաջ պարզի իր ձեռքը, հեռացնելով իրարից բթամատը և ցուցամատը, մատների ծայրերի միջև ընկած հեռավորությունը նա կտեսնի 16°-ի տակ։ Այդպիսի «անկյունային քառորդով» կարելի է, իհարկե շատ կոպիտ կերպով, անկյունային չափումներ կատարել երկնքում։ Լավ կլինի նաև հիշել, որ Մ. Արջի α և β աստղերի միջև անկյունային հեռավորությունը հավասար է 5°-ի, իսկ Մ. Արջի α աստղի և Բևեռային աստղի միջև գրեթե 30°-ի (ավելի ճիշտ 28°-ի)։

Աստղագիտական հատուկ գործիքների օգնությամբ անկյունային հեռավորությունները կարելի է չափել մինչև 0՛՛,01 ճշտությամբ։ Չափման ճշտությունը պատկերացնելու համար նշենք, որ 0՛՛,01 անկյան տակ է երևում լուցկու հաստությունը 20 կմ հեռավորության վրայից, իսկ մարդու մազը առաջ պարզած ձեռքի հեռավորությունից երևում է 20՛՛ անկյան տակ։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ

Ի՞նչ է ուսումնասիրում աստղագիտությունը։
Ի՞նչ նշանակություն ունի աստղագիտությունը աշխարհայացքի համար։
Ինչպիսի՞ նշանակություն ունեն դիտումները աստղագիտությունն ուսումնասիրելու համար։
Ի՞նչ են համաստեղությունները և ինչպե՞ս են նրանց գտնում երկնքում։ Ինչպիսի՞ համաստեղություններ գիտեք։
Ինչպե՞ս են «աստղային մեծությամբ» բնութագրում աստղերի փայլը։
Ինչպե՞ս են նշանակվում աստղերը համաստեղություններում։
Նշեցեք առաջին մեծության մի քանի աստղեր։
Ի՞նչ է երկնային սֆերան և ինչի՞ համար է պետք այդ հասկացողոլթյունը։
Ի՞նչ է հորիզոնը և ի՞նչ է զենիթը։
Ինչո՞ւ երկնային սֆերայի վրա հնարավոր են միայն անկյունային չափումները։
*Ի՞նչն է կոչվում լուսատուի բարձրություն։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

Ինչպիսի՞ հեռավորության վրա պետք է պահել 15 կոպեկանոցը (նրա տրամագիծը 2 սմ է), որպեսզի նա երևա այնպիսի անկյան տակ, ինչպես Լուսինն է երևում (հաշվարկման համար հիշենք, որ միավոր շառավիղ ունեցող շրջանի 1° աղեղի երկարությունը հավասար 1/57, իսկ 1՛՛ աղեղի երկարությունը հավասար է 1/206265)։
Գծեցեք իրարից 1 մմ հեռավորության վրա 1 մմ հաստություն ունեցող երկու զուգահեռ ուղիներ։ Որոշեցեք, թե ինչպիսի հեռավորության վրա նրանք ձեզ համար կմիաձուլվեն և նախորդի նման հաշվեցեք, թե տեսականորեն ինչպիսի անկյան տակ է երևում ձեզ նրանց միջև եղած միլիմետրական արանքը։ Դա կբնորոշի, ինչպես ասում են, ձեր աչքի բաժանող ուժը։

§ 8. ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՕՐԱԿԱՆ ՊՏՈՒՅՏԸ։ Դուրս գալով երեկոյան մի բաց տեղ, հորիզոնին մոտիկ՝ նրա արևելյան կողմում նշմարենք մի որևէ պայծառ աստղի դիրքը։ Մեկ ժամից հետո դարձյալ նայենք այդ աստղին։ Մենք կհամոզվենք, որ աստղը բարձրացել է հորիզոնից և որոշ չափով շեղվել դեպի աջ (նկ. 8)։

Նույնպիսի դիտում կատարելով երկնքի արևմտյան մասում գտնվող աստղերից մեկի նկատմամբ, մենք կհամոզվենք, որ աստղերը Արեգակի և Լուսնի նման բարձրանում են հորիզոնի արևելյան կողմից, հասնում են իրենց ամենաբարձր դիրքին՝ երկնքի հարավային մասում և այնուհետև մայր են մտնում հորիզոնի արևմտյան կողմում։ Հաջորդ օրը նրանք կկատարեն նույն շարժումը, ըստ երևույթին, այդպիսով օրվա ընթացքում մի լրիվ շրջան կատարելով երկնքում։

Այդ օրական պտույտի ժամանակ բոլոր աստղերը տեղաշարժվում են առանց իրենց փոխադարձ դասավորությունը փոխելու։ Թվում է, թե աստղային երկինքը պտտվում է ինչպես մի ամբողջություն ժամացույցի սլաքի շարժման ուղղությամբ՝ օրական մի լրիվ պտույտի արագությամբ։

Ուշադրությամբ դիտելով, մենք կնկատենք, որ տարբեր համաստեղությունների աստղերը տարբեր չափերի շրջաններ են գծում։ Որոշ համաստեղություններ օրվա ընթացքում գծում են մեծ չտփի շրջաններ, որոնց մի մասը գտնվում է հորիզոնի տակ։ Այդպիսի համաստեղություններն օրվա ընթացքում ծագում ու մայր են մտնում, ինչպես, օրինակ, Պեգասը, Պերսեոսը, Օրիոնը, Ցուլը։ Մյուս համաստեղությունները, ինչպես, օրինակ, Մեծ Արջը, գծում են փոքր չափի շրջաններ։ Նրանց շարժման ամբողջ շրջանը մնում է հորիզոնից վեր,— սրանք մայր չմտնող համաստեղություններ են։

Իրականում պտտվում է երկրագունդը։ Նա պտտվում է ժամացույցի սլաքի շարժման հակառակ ուղղությամբ՝ եթե նրան դիտենք հյուսիսային բևեռից։ Երկրի պտույտը մենք չենք զգում և. մեզ թվում է, որ, ընդհակառակը, երկինքն է պտտվում հակառակ կողմի վրա՝ ժամացույցի սլաքի շարժման ուղղությամբ։

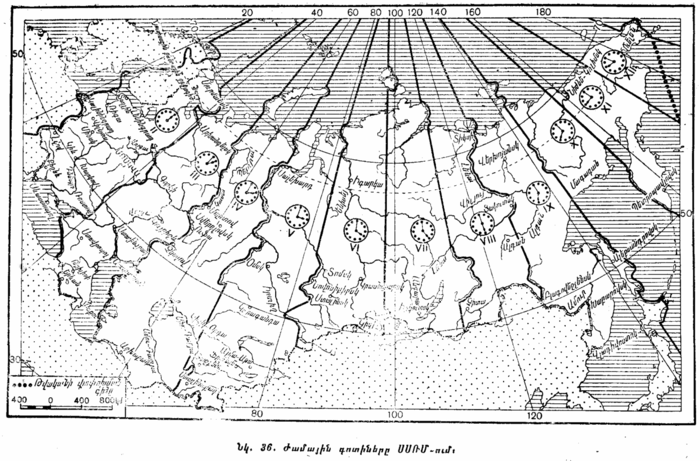
§ 9. ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԿՈՈՐԴԻՆԱՏՆԵՐ։ Աշխարհագրության դասընթացից հայտնի է, որ երկրագնդի վրա որևէ կետի դիրքը կարելի է որոշել աշխարհագրական երկու կոորդինատներով՝ աշխարհագրական լայնությամբ (նշանակվում է φ-ով) և աշխարհագրական երկայնությամբ (նշանակվում է λ-ով)։

Այդ նպատակով Երկրի բևեռների վրայով անց են կացնում մեծ շրջանի աղեղներ, որոնք կոչվում են միջօրեականներ։ Դրանցից մեկը, որը անցնում է Գրինվիչի աստղադիտարանով (Լոնդոնի մոտ), ընդունում են որպես սկզբնական միջօրեական։ Բացի այդ, Երկրի վրա, հասարակածին զուգահեռ, անց են կացնում փոքր շրջանագծեր, որոնք կոչվում են աշխարհագրական զուգահեռականներ։ (Հասարակածը մեծ շրջանագիծ է, որի հարթությունն անցնում է Երկրի կենտրոնով և ուղղահայաց է նրա առանցքին)։

Աշխարհագրական երկայնությունը չափվում է հասարակածի կամ զուգահեռականի այն աղեղով, որը պարփակված է սկզբնական միջօրեականի և տվյալ կետով անցնող միջօրեականի միջև։ Երկայնությունն սկզբնական միջօրեականից դեպի արևելք չափվում է այն ժամանակով, որ հարկավոր է, որպեսզի Երկիրը պտտվի իր առանցքի շուրջը՝ երկայնությունը չափող աղեղի համապատասխան անկյան չափով։ Երկայնությունը կարելի է չափել թե՛ դեպի արևմուտք և թե՛ դեպի արևելք, և այն ժամանակ, համապատասխանաբար ասում են արևմտյան կամ արևելյան երկայնություն։

Քանի որ Երկիրը մի լրիվ պտույտ (360°) կատարում է 24 ժամում, ուստի երկայնության յուրաքանչյուր 15° հավասար է երկայնության 1 ժամին և այդպիսով՝ 1° = 4 րոպեի, 1 րոպեն = 15՛ և 1 վայրկյանը =15՛՛։ Մոսկվայի և Գրինվիչի միջօրեականների հարթությունների միջև կազմած անկյունը հավասար է 37°34՛։ Մոսկվայի երկայնությունը Գրինվիչից հենց այդ 37°34՛ կամ 2 ժամ 30,3 րոպեին է հավասար. այդ երկայնությունն արևելյան է։

Աշխարհագրական լայնությունը չափվում է այն անկյան մեծությամբ, որ հասարակածի հարթության հետ կազմում է երկրի տվյալ վայրով անցնող ուղղաձիգ գիծը։ Եթե Երկիրն իսկական գունդ համարենք, ապա ուղղաձիգ գիծն ամենուր անցնում է ուղիղ Երկրի կենտրոնով և համընկնում է տվյալ վայրում Երկրի շառավղի հետ։

Աշխարհագրական քարտեզի կամ գլոբուսի վրա աշխարհագրական լայնությունը հաշվվում է միջօրեականի ուղղությամբ՝ հասարակածից մինչև այն աշխարհագրական զուգահեռականը, որը անցնում է տվյալ կետով։ Նա արտահայտվում է աստիճաններով։ Հասարակածից դեպի հյուսիս հաշվվող լայնությունը կոչվում է հյուսիսային լայնություն (նշանը՝ +), իսկ դեպի հարավ՝ հարավային լայնություն (նշանը՝ -), [օրինակ, Աշխաբադի լայնությունը՝ +37°57՛ է, իսկ Մելբուռնի լայնությունը կազմում է -37°50՛]։

§ 10. ԱՇԽԱՐՀԻ ԲԵՎԵՌՆԵՐԸ ԵՎ ԱՌԱՆՑՔԸ։ Ուշադրությամբ նայելով դեպի երկինք, մենք կնկատենք, որ օրվա ընթացքում Մեծ Արջի համաստեղությունը երկնքում բավական մեծ շրջան է գծում, Փոքր Արջի շերեփը՝ ավելի փոքր շրջան, իսկ այդ շերեփի կոթի ծայրին գտնվող պայծառ աստղը գրեթե անշարժ է թվում։ Հենց այդ աստղն էլ անվանում են Բևեռային աստղ։ Օրվա ընթացքում նա համարյա աննկատելի շրջանիկ է գծում և միշտ երևում է հորիզոնից, գրեթե միևնույն բարձրության վրա երկնքի հյուսիսային կողմում։ Փոքր Արջի համաստեղության մյուս աստղերն օրվա ընթացքում այնքան ավելի մեծ շրջաններ են գծում, որքան հեռու են գտնվում Բևեռային աստղից։

Բևեռային աստղը (Փոքր Արջի α) գտնում են հետևյալ կերպ. Մեծ Արջի «շերեփի» երկու ծայրամասայինդ աստղերով (Մեծ Արջի α-ից դեպի β-ն) պետք է մտքով ուղիղ գիծ տանել և շարունակել այդ երկու աստղերի միջև եղած հեռավորության հնգապատիկի չափով։ Հենց այդ գծի ծայրին կտեսնենք Բևեռային աստղը։

Նկ. 1-ում ցույց է տրված Մեծ Արջի համաստեղության դիրքի փոփոխությունը հորիզոնի նկատմամբ օրվա ընթացքում և Բևեռային աստղի դիրքի անփոփոխությունը։ Այնուամենայնիվ, անհրաժեշտ է, որպեսզի դիտումներ կատարելով՝ ինքներդ համոզվեք, որ դա իրոք հենց այդպես էլ լինում է։

Ներքոհիշյալ հետաքրքիր փորձը, որ մատչելի է լուսանկարչությանը ծանոթ ամեն մի դպրոցականի, ակնառու կերպով ցույց է տալիս երկնային սֆերայի օրական պտույտի ընթացքը։ Անլուսին պարզ գիշերը լուսանկարչական ապարատը տեղակայելով «անսահմանության վրա», ուղղում են դեպի Բևեռային աստղը՝ ցածից ամրացնելով որևէ հենարանի վրա։ Ապարատն այդպես ամրացված վիճակում մի քանի ժամով թողնում են բաց փականակով, այնուհետև թիթեղը հայտածում են։ Լուսանկարչական թիթեղի (նեգատիվի) վրա հայտնվում են աստղերի սև հետքերը (պոզիտիվի վրա՝ սպիտակ հետքերը, նկ. 10)։ Այդ բոլոր գծերը համակենտրոն աղեղների տեսք ունեն։ Այդ աղեղների գծային երկարությունները տարբեր են, բայց աստիճանային չափերով նրանք հավասար են։ Նրանց կենտրոնում ընկած Է պտտման կենտրոնը։

Պտտման ճիշտ նույնպիսի կենտրոն կարելի Է գտնել երկնքի նաև հարավային կիսագնդում։ Նա գտնվում Է երկնային սֆերայի մի կետում, որն ուղիղ հակադիր է աշխարհի հյուսիսային կիսագնդի հենց այն կետին, որի մասին քիչ առաջ խոսեցինք։ Բայց չէ՞ որ երկնային սֆերայի կենտրոնում գտնվում է մեր աչքը։ Հետևաբար, դիտելով երկինքը, մենք համոզվում ենք, որ երկն աչին սֆերան որպես մի ամբողջություն պտտվում է մի ինչ-որ առանցքի շուրջը, որն անցնում է մեր աչքով։ Երկնային սֆերայի օրական պտույտի առանցքը կոչվում է աշխարհի առանցք։ Այդ առանցքի ուղղությունը մենք կգտնենք, եթե մեր աչքով մտքով ուղիղ գիծ տանենք դեպի երկնքի՝ վերը նկարագրած ձևով գտած կետը, որը չի մասնակցում երկնային սֆերայի օրական պտույտին։

Այն կետերը, որտեղ երկնային սֆերան հատվում է աշխարհի առանցքի հետ, կոչվում են աշխարհի բևեռներ։ Բևեռային աստղը գտնվում է աշխարհի հյուսիսային բևեռի մոտ (մոտ 1° հեռավորության վրա)։ Աշխարհի հարավային բևեռը երևում է Երկրի միայն հարավային կիսագնդից, և նրա մոտերքը ոչ մի պայծառ աստղ չկա։

Այն հարթությունը, որ ուղղահայաց է աշխարհի առանցքին և անցնում է երկնային սֆերայի կենտրոնով, կոչվում է երկնային հասարակածի հարթություն, իսկ նրա հատման գիծը երկնային սֆերայի հետ կոչվում է երկնային հասարակած։ Այսպիսով, երկնային հասարակածը երկնային սֆերայի այն մեծ շրջանն է, որն ուղղահայաց է աշխարհի առանցքին։

Հասարակածը երկնային սֆերան բաժանում է երկու կիսագնդերի՝ հյուսիսային և հարավային։ Մենք տեսնում ենք, որ աշխարհի առանցքը, աշխարհի բևեռները և երկնային հասարակածը համանման են Երկրի առանցքին, բևեռներին և հասարակածին։ Բայց այդ բնական է, որովհետև վերոհիշյալ անունները կապված են երկնային սֆերայի թվացող պտույտի հետ, իսկ դա ինքը երկրագնդի իրական պտույտի հետևանք է։

§ 11. ԵՐԿՆԱՅԻՆ ՄԻՋՕՐԵԱԿԱՆ ԵՎ ՄԻՋՕՐԵԻ ԳԻԾ։ Երկնային միջօրեական։ Միջօրեականի հարթություն կոչվում է այն հարթությունը, որն անցնում է ուղղաձիգ գծով և աշխարհի առանցքով։ Այդ հարթությունը, հատվելով երկնային սֆերայի հետ, առաջացնում է երկնային միջօրեականի գիծը։ Միջօրեականի հարթությունը մոտավորապես կլինի այն ուղղաձիգ հարթությունը, որ անցնում է բևեռային աստղով և դիտողով։

Միջօրեի գիծ կոչվում է միջօրեականի և հորիզոնի հարթությունների հատման գիծը։ Դա մի հորիզոնական գիծ է։

Երկրի ցանկացած վայրում երկնային միջօրեականի հարթությունը համընկնում է տվյալ վայրի աշխարհագրական միջօրեականի հարթության հետ։

Հորիզոնի կետերը։ Հորիզոնը հատվում է երկնային միջօրեականի հետ՝ հյուսիսի (N) և հարավի (S) կետերում, իսկ երկնային հասարակածի հետ՝ արևելքի (E) և արևմուտքի (W) կետերում։ Եթե մենք կանգնենք երեսներս դեպի աշխարհի բևեռը (Բևեռային աստղը), ապա ուղիղ նրա տակ՝ հորիզոնի վրա կունենանք հյուսիսի կետը, մեր թիկունքի կողմը՝ հարավի կետը, աջ կողմում՝ արևելքի կետը և ձախ կողմում՝ արևմուտքի կետը։ Հիշելով այդ, մենք միշտ էլ կարող ենք կողմն որոշվել տեղանքում։

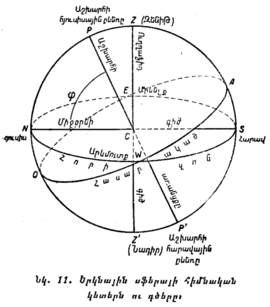
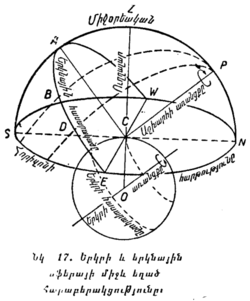
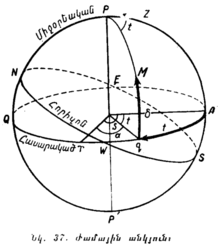
Այս պարագրաֆում բերված սահմանումները պետք է հիմնավորապես ըմբռնել և լավ հիշել, որովհետև առանց նրանց թե՛ երկնային ամենապարզ երևույթները և թե՛ աստղագիտության գործնական կիրառումները անհասկանալի կմնան։ Որպեսզի ավելի լավ պատկերացնենք այն բոլորը, ինչ որ վերն ասված է, երկնային սֆերան պատկերացնեն գծագրի վրա (նկ. 11)։ Այդ գծագրի վրա C երկնային սֆերայի կենտրոնն է, որտեղ գտնվում է դիտողի աչքը Z՛CZ ուղղաձիգ գիծն է, ընդ որում՝ Z — զենիթն է, Z՛ — նադիրը (զենիթի հակադիր կետը երկնային սֆերայում)։ P՛P աշխարհի առանցքն է, P — աշխարհի հյուսիսային բևեռն է, P՛ — աշխարհի հարավային բևեռը, EAWQ — երկնային հասարակածն է, որի հարթությունն ուղղահայաց է աշխարհի առանցքին, EAWN — հորիզոնն է, S — հարավի կետն է, N — հյուսիսի կետը, E — արևելքի կետը և W — արևմուտքի կետը։ Դժվար չէ հասկանալ, որ հորիզոնից վերև երևում են երկնային սֆերայի ուղիղ կեսը և երկնային հասարակածի նույնպես ուղիղ կեսը, նաև այն, որ E և W կետերում (որոնք N և S կետերից գտնվում են 90° հեռավորության վրա) և՛ հորիզոնը, և՛ հասարակածը կիսվում են։

SN գիծը միջօրեի գիծն է, որը կոչվում է այդպես, որովհետև կեսօրին առարկաների ստվերները ճիշտ այդ ուղղությամբ են ընկնում. իսկ NZAS աղեղը աշխարհի միջօրեականն է։

Անհրաժեշտ է սովորել երկնային սֆերա գծագրելը գրատախտակի կամ թղթի վրա։ Վարժությունների ժամանակ աշխարհի առանցքի և հորիզոնի հարթության միջև ընկած PCN անկյունը կարելի է վերցնել ցանկացած մեծության։ Ինչպես մենք հետո կտեսնենք, այդ անկյան մեծությունը կախված է երկրագնդի վրա դիտողի գտնված վայրից։

§ 12*. ՄԻՋՕՐԵԻ ԳԾԻ ՈՒՂՂՈՒԹՅԱՆ ՈՐՈՇՈՒՄԸ ԳՈՐԾՆԱԿԱՆՈՒՄ։ Միջօրեի գծի դիրքը, իսկ նրա օգնությամբ նաև երկնային միջօրեականի դիրքը տեղում որոշելու համար գոյություն ունեն շատ միջոցներ։ Դրանցից ամենապարզը, բայց ոչ այնքան ճշգրիտ միջոցները հետևյալներն են.

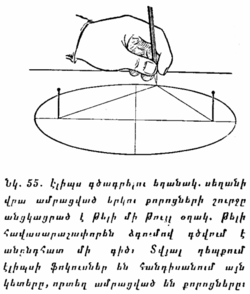
ա) Գիշերը՝ ըստ Բևեռային աստղի։ Ուղղալարը (թելից կախված ծանրոցը) որևէ ձևով կախում ենք անշարժ կերպով և նշանակում այն տեղը, որտեղ ցածում նա դիպչում է գետնին։ Այնուհետև ձեռքում բռնելով երկրորդ ուղղալարը պահում ենք մեր աչքի առաջ այնպես, որ Բևեռային աստղը և երկու ուղղալարերը համընկնեն, այսինքն՝ որպեսզի մեկ ուղղալարը լիովին ծածկի մյուսին, և երկուսը միասին ծածկեն աստղը։ Նշանակում ենք նաև այն տեղը, որին դիպչում Է երկրորդ ուղղալարը։ Պարզ է, որ երկու ուղղալարերով անցնող հարթությունը կլինի միջօրեականի հարթությունը, իսկ գետնի վրա մեր նշանակած երկու կետերը իրար միացնող ուղիղը կլինի միջօրեի գիծը։

Քանի որ Բևեռային աստղը աշխարհի բևեռում չի գտնվում, ուստի միջօրեի գիծն այդ ձևով որոշելու ժամանակ մենք կարող ենք սխալվել մի անկյունով, որը Լենինգրադի լայնության վրա հասնում է մոտ 2°-ի, իսկ ավելի հյուսիս ընկած վայրերում՝ դրանից էլ ավելի։

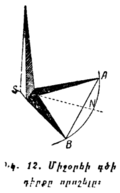
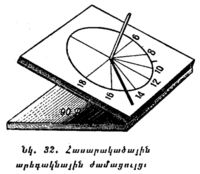
բ) Ցերեկը՝ ըստ Արեգակի։ Հարթ մակերևույթի վրա ամրացնենք մի ուղղահայաց (ուղղալարի միջոցով) ձող (նկ. 12)։ Կեսօրից 2 ժամ առաջ այդ հարթության վրա ձողի ստվերի ծայրը նշանակենք A-ով և ձողի S հիմքից, որպես կենտրոնից, մի շրջանագիծ գծենք՝ ստվերի AS երկարությանը հավասար շառավղով։ Ձողի ստվերը կսկսի աստիճանաբար կարճանալ և թեքվել դեպի հյուսիս։ Կեսօրից հետո նա կսկսի երկարանալ, շարունակելով թեքվել նույն ուղղությամբ։ Երեկոյան կողմը ստվերի ծայրը նորից կհասնի մեր շրջանագծին և կշոշափի մի կետում, նշանակենք B տառով։ A և B կետերը միացնենք ուղիղ գծով, որի N մեջտեղը միացնելով ձողի S հիմքի հետ, կստանանք միջօրեի գծի ուղղությունը։

Տեսականորեն միջօրեի գծի դիրքը կարելի է որոշել՝ պարզապես նշելով ստվերի ուղղությունը այն մոմենտին, երբ նա ամենակարճն է լինում։ Սակայն, գործնականում այդ եղանակը չափազանց անճշգրիտ է, որովհետև կեսօրի մոտ, երբ ստվերն ամենակարճն է, նրա երկարությունը չափազանց դանդաղ, գրեթե աննկատելի կերպով է փոփոխվում, մինչդեռ ստվերի ուղղությունն արագ է փոփոխվում։

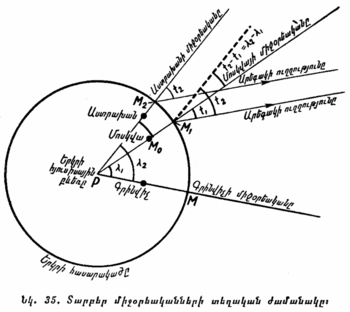
§ 13. ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՒԼՄԻՆԱՑԻԱՆ։ Միջօրեականի դիրքը որոշելուց հետո հետևենք աստղային երկնքի կատարած պտույտին։ Մենք կհամոզվենք, որ աշխարհի առանցքի շուրջը ամեն մի լուսատու իր կատարած օրական պտույտի ժամանակ երկու անգամ հատում-անցնում է միջօրեականով։ Միջօրեականով լուսատուի անցնելու երևույթը կոչվում է կուլմինացիա։ Ընդ որում նա հորիզոնի նկատմամբ մեկ անգամ գրավում է ամենաբարձր դիրք, դա վերին կուլմինացիան է, իսկ մյուս անգամ՝ ամենացածր դիրք, գա էլ ստորին կուլմինացիան է։ Վերին և ստորին կուլմինացիաների միջև ընկած ժամանակամիջոցը կազմում է կեսօր։

Այդ կուլմինացիաներից մեկը (ծագող և մայր մանող լուսատուների համար) կամ երկուսն էլ (չծագող լուսատուների համար) կարող են տեղի ունենալ հորիզոնից ցած և անտեսանելի մնալ։

Արեգակի վերին կուլմինացիայի մոմենտը կոչվում է իրական կեսօր։ Արեգակի ստորին կուլմինացիայի մոմենտը կոչվում է իրական կեսգիշեր։

Առաջին կուլմինացիայի ժամանակ Արեգակը երևում է, երկրորդի ժամանակ՝ չի երևում։ Սակայն շուրջբևեռային երկրներում երբեմն Արեգակի երկու կուլմինացիաներն էլ տեղի են ունենում հորիզոնից վերև (այսինքն՝ գիշեր չի լինում)։ Իսկ երբեմն էլ նրանք տեղի են ունենում հորիզոնից ցած (այսինքն՝ Արեգակը չի ծագում)։ Մյուս լուսատուների կուլմինացիաների մոմենտը կախված է երկնային սֆերայում ունեցած նրանց դիրքից և տարվա եղանակներից։

Ամեն գիշեր դիտելով մի որևէ աստղ, մենք կհամոզվենք, որ տվյալ վայրում յուրաքանչյուր աստղի կուլմինացիան տեղի է ունենում հորիզոնից միևնույն բարձրության վրա. թե հատկապես ի՞նչ բարձրության վրա՝ դա կախված է երկնային սֆերայում նրա գրաված դիրքից և դիտավայրի աշխարհագրական լայնությունից։

Արեգակի վերին կուլմինացիայի մոմենտին նրա բարձրությունը հորիզոնից տարբեր է լինում՝ ոչ միայն տարբեր վայրերի համար (օրինակ, Լենինդրադում և Սևաստոպոլում), այլև տարվա տարբեր եղանակներին (ձմեռը նա փոքր է, ամառը՝ մեծ)։ Լուսնի և մոլորակների համար այդ բարձրությունը փոփոխվում է ավելի բարդ ձևով։

§ 14. ԵՐԿՆԱՅԻՆ ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՈՐԴԻՆԱՏՆԵՐԸ։ Երկնային լուսատուներից յուրաքանչյուրի դիրքը երկնային սֆերայում որոշվում է երկու սֆերիկ կոորդինատներով, որոնք արտահայտվում են երկու թվով, ճիշտ այնպես, ինչպես երկրագնդի վրա յուրաքանչյուր տեղի դիրքը որոշվում է նրա աշխարհագրական կոորդինատներով։

Երկնային լուսատուների կոորդինատները տարբեր են լինում՝ նայած թե ո՛ր գծերի նկատմամբ ենք մենք այդ կոորդինատները չափում։ Երկրի վրա կոորդինատները չափում են երկրային հասարակածի և Գրինվիչի միջօրեականի նկատմամբ։

Երկնային սֆերայում կոորդինատները կարելի է չափել երկնային հասարակածի (ինչպես աշխարհագրական լայնությունը) և հակման սկզբնական շրջանի (ինչպես աշխարհագրական երկայնությունը որոշելիս վերցնում են սկզբնական միջօրեականը) նկատմամբ։ Դա կլինի կոորդինատների հասարակածային սիստեմը։

Իսկ եթե լուսատուների կոորդինատները չափելու լինենք հորիզոնի և երկնային միջօրեականի նկատմամբ, ապա կստանանք կոորդինատների հորիզոնական սիստեմը։

Լուսատուի բարձրությունը (հորիզոնի նկատմամբ), որի մասին մենք խոսել ենք § 7-ում, հանդիսանում է հորիզոնական սիստեմի կոորդինատներից մեկը։

Երկնային հասարակածի դիրքը երկնային սֆերայում կախում չունի ո՛չ Երկրի վրա դիտողի ունեցած դիրքից, ո՛չ օրվա ժամից և ո՛չ էլ տարվա եղանակից։ Ուստի աստղերի հասարակածային կոորդինատները չեն փոփոխվում։ Իսկ լուսատուների հորիզոնական կոորդինատները ժամանակի ընթացքում անընդհատ փոփոխվում են և, բացի դրանից, կախված են Երկրի վրա դիտողի ունեցած դիրքից, որովհետև Երկրի տվյալ կետում հորիզոնի հարթությունը Երկրի հետ միասին պտտվում է տիեզերական տարածության նկատմամբ։ Ժամանակի և երկրագնդի վրա դիտողի դիրքի (կողմնորոշում) որոշելը պահանջում են լուսատուների հորիզոնական կոորդինատների չափում՝ դիտումների միջոցով։ Իսկ երկնքի քարտեզը կազմելու և երկնային լուսատուները կատալոգների մեջ մտցնելու համար հարկավոր է օգտվել կոորդինատների հասարակածային սիստեմից։

Միևնույն լուսատուի հասարակածային և հորիզոնական կոորդինատները կապված են մեկը մյուսի հետ և կոորդինատների մեկ սիստեմից կարելի է անցնել մյուսին վերահաշվարկման միջոցով (բայց երկրագնդի վրա դիտողի որոշ մոմենտում ունեցած որոշ դիրքի համար այն)։ Գործնականում լուսատուների կոորդինատները չափվում են հատուկ անկյունաչափական գործ ի քների օգնությամբ։

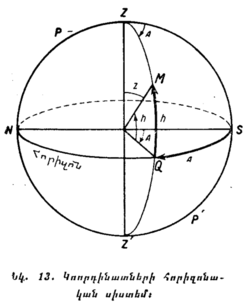
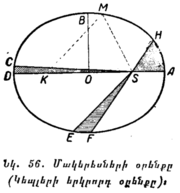
§ 15. ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՀՈՐԻԶՈՆԱԿԱՆ ՍԻՍՏԵՄ։ Նկ. 13-ում պատկերված է երկնային սֆերայի այն կեսը, որ երևում է հորիզոնից վերև։ NQS շրջանագիծը հորիզոնն է, Z — զենիթն է, S — հարավի կետն է։ Երկնային սֆերայում եղած M կետի դիրքը որոշելու համար զենիթից այդ կետի վրայով անցկացնենք մեծ ուղղաձիգ շրջանի ZQ աղեղը։ M կետի հորիզոնական կոորդինատները կլինեն՝ QM աղեղով չափվող բարձրությունը (h), որն արտահայտում է M կետի անկյունային հեռավորությունը հորիզոնից, և SQ աղեղով չափվող ազիմուտը (A), որը հարավի S կետից հաշվվում է դեպի արևմուտք և արտահայտում է երկնային միջօրեականով և M կետով անցնող ուղղաձիգ շրջանագծով կազմած անկյունը։

Հաճախ h բարձրության փոխարեն գործ են ածում զենիթային հեռավորությունը՝ z, որը հավասար է 90°—h և իրենից ներկայացնում է M կետի անկյունային հեռավորությունը զենիթից։ Բարձրությունը, զենիթային հեռավորությունը և ազիմուտը արտահայտում են աստիճաններով։

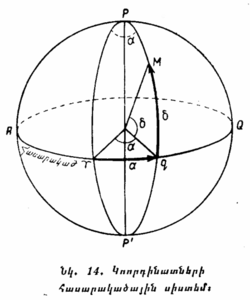
§ 16. ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՀԱՍԱՐԱԿԱԾԱՅԻՆ ՍԻՍՏԵՄ։ Նկ. 14-ում պատկերված է երկնային սֆերան իր հասարակածով։ Երկնային սֆերայի այն մեծ շրջանը, որի հարթությունն ուղղահայաց է երկնային հասարակածի հարթությանը և անցնում է նրա այն կետով, որ կոչվում է գարնանային գիշերահավասարի կետ և նշվում է ♈ հատուկ նշանով, հանդիսանում է հակման սկզբնական շրջան։ M կետի դիրքը որոշելու համար աշխարհի P բևեռից նրա վրայով անցկացնենք հակման PQq շրջանր։ M կետի հասարակածային կոորդինատները կլինեն՝ qM աղեղով չափվող հակումը (δ), որն արտահայտում է M կետի անկյունային հեռավորությունը երկնային հասարակածից և ♈q աղեղով չափվող ուղղակի ծագումը (α), որը հաշվվում է ♈ կետից ժամացույցի սլաքի շարժմանը հակառակ ուղղությամբ (եթե նայելու լինենք աշխարհի հյուսիսային բևեռից) և արտահայտում է հակման սկզբնական շրջանով և M կետով անցնող հակման շրջանով կազմած անկյանը։

Հակումը (δ) արտահայտվում է աստիճաններով և հասարակածից դեպի հյուսիս համարվում է դրական (+), իսկ դեպի հարավի բացասական (-). ուղղակի ծագումը (α) չափվում է ոչ թե աստիճաններով, այլ ժամանակով, այնպես, ինչպես աշխարհագրական երկայնությունը։

Այսպիսով, լուսատուների հակումը նման է աշխարհագրական լայնությանը, իսկ ուղղակի ծագումը՝ աշխարհագրական երկայնությանը։ Աստղային քարտեզների վրա (տե՛ս, օրինակ, կցված դասագրքին ) գծվում է այդ կոորդինատների ցանցը, իսկ ինքը՝ երկնային սֆերան պատկերվում է հարթության վրա այնպես, ինչպես պատկերվում է երկրագունդը։

§ 17*. ԼՈՒՍԱՏՈՒՆԵՐԻ ԿՈՈՐԴԻՆԱՏՆԵՐԸ ՈՐՈՇԵԼՈՒ ԳՈՐԾՆԱԿԱՆ ԵՂԱՆԱԿՆԵՐԸ։ Եթե իմանայինք լուսատուների հասարակածային կոորդինատները, որոնք կախում չունեն ո՛չ դիտողի՝ Երկրի վրա ունեցած դիրքից , և ոչ էլ օրվա ժամից, ապա այդ կոորդինատները կարելի կլիներ գրանցել կատալոգների մեջ և այդ լուսատուների դիրքերը պատկերել աստղային քարտեզի վրա։ Բայց ինչպե՞ս գործնականորեն որոշել այդ կոորդինատները, ինչպե՞ս չափել նրանց՝ դիտումների միջոցով։

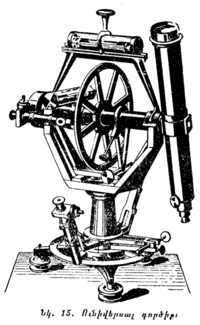
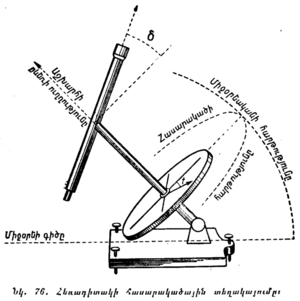
Երկնային մարմինների հորիզոնական կոորդինատները շափում են ունիվերսալ գործիքի օգնությամբ, որը կոչվում է նաև թեոդոլիտ (նկ. 15)։ Թեոդոլիտ է կոչվում փոքրիկ դիտակը, որին հարմարեցված են բաժանմունքների բաժանված շրջաններ՝ լուսատուների բարձրությունը և ազիմուտները հաշվելու համար։ Հաշվումները դյուրացնելու նպատակով ցուցիչները դիտակը հորիզոնական դիրքում եղած ժամանակ ուղղաձիգ շրջանի վրա ցույց են տալիս 0° (որը ստուգվում է հարթաչափի օգնությամբ), և հորիզոնական շրջանի վրա 0°, դիտակը միջօրեականի հարթությամբ դեպի հարավ ուղղված լինելու դեպքում, այսինքն այն հարթությամբ, որ անցնում է զենիթով, աշխարհի բևեռով և հարավի կետով։

Լուսատուների հորիզոնական կոորդինատները չափում են միայն Երկրի վրա զանազան կետերի ժամանակը կամ աշխարհագրական կոորդինատները որոշելու համար, որը պահանջում է գործիքը տեղից տեղ փոխադրել։ Այդ պատճառով թեոդոլիտները դյուրակիր ձևով են կառուցվում։

Հասարակածային կոորդինատների որոշելը բարդ է և կատարվում է ուրիշ գործիքով՝ միջօրեականային շրջանով։

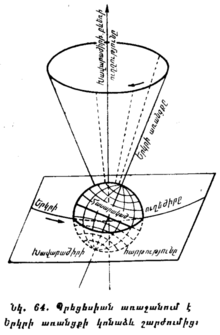
§ 18*. ՄԹՆՈԼՈՐՏԱՅԻՆ ՌԵՖՐԱԿՑԻԱՆ ԼՈՒՅՍԻ ԲԵԿՈՒՄՆ է ԵՐԿՐԻ ՄԹՆՈԼՈՐՏՈՒՄ, ՈՐՆ ԱՂԱՎԱՂՈՒՄ է ԼՈՒՍԱՏՈՒՆԵՐԻ ՏԵՍԱՆԵԼԻ ԴԻՐՔԸ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՎՐԱ։ Երկնային լուսատուների լույսը անօդ տարածությունից մտնելով Երկրի մթնոլորտը, նրա մեջ բեկվում է։ Լույսի ճառագայթը որքան ավելի է մոտենում Երկրի մակերևույթին, այնքան նա օդի ավելի ու ավելի խիտ շերտերի է հանդիպում և հետզհետե ավելի ուժեղ բեկվելով այդ շերտերում՝ մոտենում է ուղղաձիգ ուղղության։ Հետևանքը լինում է այն, որ լույսի ճառագայթը Երկրի մթնոլորտում կորանում Է, ինչպես այդ ցույց է տրված նկ. 16-ում։ M կետում գտնվող դիտողը լուսատուն տեսնում է ոչ թե MA ուղղությամբ, այլ մի ուղղությամբ, որը բնորոշվում Է AM կորագծի շոշափողով, որի ուղղությամբ, ռեֆրակցիայի հետևանքով գալիս են ճառագայթները։ Եվ իսկապես, այն ուղղությունը, որով գիտողը տեսնում է լուսատուն, դա լուսատուից դեպի դիտողի աչքը եկող ճառագայթների ուղղությունն է, իսկ M կետում կորացված ճառագայթի ուղղությունը այդ կորագծի M կետում շոշափողի ուղղությունն է (մեր նկարում ճառագայթի ուղու կորացումը ցույց է տրված միայն մեկ ճառագայթի համար և այն էլ ակնառության համար չափազանցրած)։

Այսպիսով, ռեֆրակցիայի հետևանքով լուսատուներն ավելի մոտ են երևում զենիթին, քան նրանք իրականում կան։ Հորիզոնի մոտ ռեֆրակցիան բարձրացնում է լուսատուն 35՛-ով և ավելի քիչ՝ երբ նա բարձր է գտնվում։

Դիտումների ժամանակ լուսատուների չափված զենիթային հեռավորությունները հարկավոր է ուղղել ռեֆրակցիայի ազդեցության չափով։

Ռեֆրակցիայի հետևանքով երկնային լուսատուները, նույն թվում և Արեգակը, ավելի շուտ են ծագում և ավելի ուշ են մայր մտնում, քան այդ ստացվում է երկրաչափական նկատառումներից։ Լուսնի և Արեգակի սկավառակների վերին և ստորին եզրերի համար ռեֆրակցիայի մեծության զգալի տարբերության հետևանքով, երբ նրանք մոտ են հորիզոնին, սկավառակները թվում են տափակացած։

§ 19. ՄԹՆՇԱՂ ԵՎ ԱՍՏՂԵՐԻ ՇՈՂՇՈՂՈՒՄ։ Ինչպես առավոտյան, նույնպես և երեկոյան՝ մթնշաղը հետևանք է այն բանի, որ երբ Արեգակը մեզնից ծածկված է հորիզոնի տակ (ոչ այնքան խոր), այնուամենայնիվ նա լուսավորում է մեր գլխավերևի օդը, իսկ օդը, ինչպես մենք արդեն գիտենք, Արեգակի լույսը ցրում է։ Հենց Արեգակի լույսն է, որ ցրվելով օդում, առաջացնում է մթնշաղի երևույթ։

Հյուսիսային վայրերում, ինչպես՝ Կարելիայում, Արխանգելսկի և Կիրովի մարզերում և նույնիսկ Լենինգրադում ամռան գիշերները Արեգակն այնքան էլ շատ չի սուզվում հորիզոնի տակ, ուստի և արշալույսն ավելի շուտ է վրա հասնում, քան վերջանում է երեկոյան աղջամուղջը։ Այդպիսի գիշերներին այնտեղ կատարյալ մթություն բոլորովին չի լինում, այդ պատճառով էլ նրանց «սպիտակ գիշերներ» են անվանում։ Այս դեպքում ասում են, որ «արշալույսը դիմավորում է վեր ջալույսին»։

Գիշերները գրեթե միշտ կարելի է նկատել աստղերի շողշողում, ամենից ուժեղ՝ հորիզոնի մոտ։ Շողշողումը կայանում է նրանում, որ աստղերը կարծես դողդողում են, մերթ փայլում են պայծառ, մերթ սկսում են խավարել, իսկ հորիզոնի մոտ գտնվող պայծառ աստղերը նույնիսկ փայլփլում են ծիածանի բոլոր գույներով։

Այդ երևույթի պատճառն այն է, որ աստղի լույսը հասնում է մեզ օդի միջով։ Նրա ճանապարհին հանդիպող օդի զանազան հոսանքների անընդհատ փոփոխումը փոփոխում է ճառագայթների բեկման չափը։ Բացի այդ, աստղից եկող լույսն օդում բեկվելու դեպքում, ինչպես Արեգակի ճառագայթը ապակյա պրիզմայում, տարրալուծվում է իր բաղադրիչ մասերին՝ ծիածանի գույների։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ

Ի՞նչ են աշխարհագրական լայնությունը և երկայնությունը և ինչպե՞ս են արտահայտում ժամանակով։
Ի՞նչ են աշխարհի բևեռները և աշխարհի առանցքը։
Ինչպե՞ս գտնել երկնքում Բևեռային աստղը։
Ի՞նչ է երկնային հասարակածը և ինչպե՞ս է նա բաժանում երկնային սֆերան։
*Ինչո՞ւմն է կայանում հորիզոնական և հասարակածային կոորդինատների միջև եղած տարբերությունը։
Ի՞նչ է երկնային միջօրեականը և միջօրեի գիծը։
*Գծեցեք երկնային սֆերան որևէ աստղի հորիզոնական կոորդինատներով։
Գծեցեք երկնային սֆերան որևէ աստղի հասարակածային կոորդինատներով։
Ինչպիսի՞ ցանց է գծվում աստղային քարտեզների վրա։
*Ինչի՞ համար է ծառայում ունիվերսալ գործիքը կամ թեոդոլիտը։ Ի՞նչ առանցքների շուրջն է դառնում նրա դիտախողովակը։
*Ինչո՞ւմն է կայանում մթնոլորտային ռեֆրակցիան։ Ինչպե՞ս է նա ազգում լուսատուի բարձրության վրա, ծագման ու մայրամուտի վրա։
*Ի՞նչն է առաջ բերում աղջամուղջի երևույթ։
*Ինչո՞ւ են առկայծում աստղերը։
Ինչպե՞ս որոշել տեսականորեն և ինչպե՞ս գտնել գործնականում (դաշտում) հորիզոնի չորս հիմնական կետերը։
Գծեցե՛ք երկնային սֆերան՝ հասարակածով, միջօրեականով և միջօրեի գծով։ Նշեցե՛ք նրա վրա հորիզոնի հիմնական կետերը։
*Ինչպե՞ս ցերեկը և գիշերը գործնականում կարելի է որոշել միջօրեի գծի ուղղությունը։
Ի՞նչն է կոչվում կուլմինացիա։ Կուլմինացիաներից ո՞րն է կոչվում վերին և ո՞րը ստորին։
Ինչքա՞ն ժամանակից հետո են կուլմինացիաները հաջորդում իրար և ինչպե՞ս են կոչվում Արեգակի կուլմինացիայի մոմենտները։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

Արտահայտել 131°15՛54՛՛ երկայնությունը ժամանակի միավորներով։
Վերածել 7 ժ. 30 ր. 18 վ. երկայնությունը աստիճանային միավորների։
Գծագրեցեք երկնային սֆերայի վրա, միաժամանակ միևնույն աստղի հորիզոնական և հասարակածային կոորդինատները։
Երկնքի շարժական քարտեզի վրա (տրված է գրքի հավելվածում) կոորդինատական ցանցի օգնությամբ հաշվեցեք մի քանի աստղերի մոտավոր հասարակածային կոորդինատները։
Օգտվելով պայծառ աստղերի հասարակածային կոորդինատների ցուցակից (տե՛ս IV հավելվածը) ըստ այդ կոորդինատների, վերոհիշյալ քարտեզի վրա գտեք որոշ աստղեր։

§ 20. ԵՐԿՐԻ ԵՎ ԵՐԿՆԱՅԻՆ ՍՖԵՐԱՅԻ ՄԻՋԵՎ ԵՂԱԾ ՀԱՐԱԲԵՐԱԿՑՈՒԹՅՈԻՆԸ։ Երկրի պտտման առանցքը տարածության մեջ ուղղված է դեպի Բևեռային աստղը։ Երկրի որևէ C կետում (նկ. 17) գտնվող և Երկրի պտտվելը չզգացող դիտողին թվում է, թե ամբողջ տիեզերական

տարածությունը երկնային սֆերայի ձևով պտտվում է մի այնպիսի առանցքի շուրջը, որը զուգահեռ, է Երկրի պտտման առանցքին։ Երկնային սֆերայի պտտման CP առանցքը մենք անվանեցինք աշխարհի առանցք և այժմ տեսնում ենք, որ նա ամեն մի դիտողի համար զուգահեռ է Երկրի պտտման առանցքին։

Քանի որ Բևեռային աստղը մեզնից չափազանց հեռու է գտնվում, ուստի CP գիծը և Երկրի պտտման առանցքը, որը զուգահեռ է նրան, ուղղված են դեպի Բևեռային աստղը։ Այն դիտողի համար, որ կարողանար տեղավորվել Երկրի կենտրոնում կամ նրա բևեռներում, Երկրի պտտման առանցքը և աշխարհի առանցքը միմյանց կհամընկնեին։

Ուստի երկնային հասարակածի CEAW հարթությունը, որպես աշխարհի առանցքին ուղղահայաց մի հարթություն, զուգահեռ է Երկրի հասարակածի հարթությանը։ Երկրի կենտրոնում գտնվող դիտողի համար այդ երկու հարթությունները միմյանց կհամընկնեին։

Եթե ընդունենք, որ Երկիրը գնդաձև է, ապա CZ ուղղաձիգ գիծը հանդիսանում է Երկրի OC շառավղի շարունակությունը, որը Երկրի կենտրոնից անց է կացված դեպի այն կետը, որտեղ գտնվում է դիտողը։ Ուստի հորիզոնի հարթությունը,— որն անցնում է երկնային սֆերայի կենտրոնով (C կետով, եթե այդ կետումն է գտնվում դիտողը) և ուղղահայաց է ուղղաձիգ գծին,— մի հարթություն է, որը շոշափում է երկրագունդը C կետում։ Վերջապես, երկնային միջօրեականի SAZPN հարթությունը համընկնում է աշխարհագրական միջօրեականի հարթության հետ։

Այսպիսով, Երկիրը պտտվելու ժամանակ պտտվում է նաև դիտողը, իսկ նրա հետ միասին միջօրեականի ու հորիզոնի հարթությունները և ուղղաձիգ գիծը։ Ուստի օրվա տարբեր ժամերին պտտվող հորիզոնը, որը դիտողի համար տեսանելի տարածությունը սահմանափակում է ոչ-տեսանելի (Երկրի մարմնով ծածկված) տարածությունից, անցնում է երկնային սֆերայի տարբեր մասերով։ Տարբեր լուսատուներին է ուղղվում նաև Z զենիթը։ Մինչդեռ երկնային հասարակածը սահում է իր սեփական հարթության մեջ, իսկ աշխարհի առանցքը մնում է զուգահեռ ինքն իրեն։ Այդ պատճառով էլ նրանք աստղերի միջև շարունակ միևնույն դիրքն են գրավում։

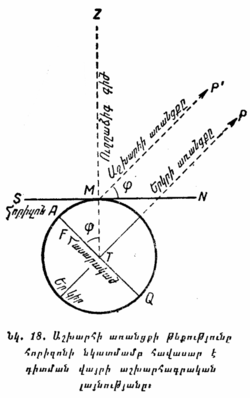
§ 21. ԲԵՎԵՌԻ ԲԱՐՁՐՈՒԹՅՈՒՆԸ ՀՈՐԻԶՈՆԻՑ ԵՎ ՏԵՂԻ ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԼԱՅՆՈՒԹՈՒՆԸ։ Աշխարհի բևեռի անկյունային բարձրությունը հորիզոնից կամ, ավելի կարճ ասած, բևեռի բարձրությունը հավասար է դիտման վայրի աշխարհագրական լայնությանը։ Դրանում կարելի է համոզվել, եթե նկ. 17-ի վրա հետևենք, թե ի՛նչպես կփոփոխվի PCN անկյունը (իսկ դրա հետ միասին՝ նաև PN աղեղը, այսինքն՝ բևեռի բարձրությունը), եթե C կետի դիտողը Երկրի հասարակածից սկսի շարժվել դեպի Երկրի բևեռը։ Այդպիսի շարժման դեպքում աշխարհի CP առանցքը կմնա ինքն իրեն զուգահեռ, իսկ հորիզոնի հարթության վրա ընկած CN գիծը PC գծի հետ ավելի ու ավելի մեծ անկյուն կկազմի։

Դա ավելի պարզ կարելի է յուրացնել նկ. 18-ի օգնությամբ, որտեղ երկրագունդը պատկերված է տեղի միջօրեականի հարթության հատվածով։ M կետում գտնվող դիտողը աշխարհի P բևեռը կտեսնի աշխարհի առանցքի MP՛ ուղղությամբ, որը զուգահեռ է Երկրի TP առանցքին։ Երկրագունդը շոշափող հորիզոնի հարթությունը մեր գծագրի վրա կպատկերվի SMN ուղիղ գծով, որը M կետում շոշափում է երկրագունդը պատկերող շրջանը։ AQ Երկրի հասարակածն է, TZ ուղղաձիգ գիծն է կետում, ուստի և AMT անկյունը, ըստ § 9-ի, հանդիսանում է կետի աշխարհագրական φ լայնությունը։

Աշխարհի առանցքի և հորիզոնի հարթության միջև ընկած P՛MN անկյունը բևեռի բարձրությունն է ներկայացնում։

P՛MN և ATM (այսինքն՝ աշխարհագրական լայնությունը) անկյունները հավասար են, որպես փոխադարձ ուղղահայաց կողմեր ունեցող անկյուններ։ Եվ իսկապես, MN որպես հորիզոնական գիծ, ուղղահայաց է MT ուղղաձիգ գծին, իսկ MP՛, որպես աշխարհի առանցք, ուղղահայաց է AQ հասարակածին։

Մենք տեսնում ենք, որ տեղի աշխարհագրական լայնությունդ գործնականորեն կարելի է որոշել, շափելով բևեռի բարձրությունը դիտումների միջոցով։

§ 22. ԱՍՏՂԱՅԻՆ ԵՐԿՆՔԻ ՏԵՍՔԸ՝ ԿԱԽՎԱԾ ԴԻՏՈՂԻ ԴԻՐՔԻՑ ԵՐԿՐԱԳՆԴԻ ՎՐԱ։ Ինչպես հենց նոր տեսանք, աշխարհի առանցքի թեքությունը հորիզոնի նկատմամբ (բևեռի բարձրությունը) հավասար տեղի աշխարհագրական լայնությանը։ Այդ հանգամանքը պետք է նկատի ունենալ տվյալ վայրի համար նկ. 11-ը արտագծելու ժամանակ։

Այսպիսով, երկնային սֆերայի կետերի և գծերի դասավորությունը հորիզոնի նկատմամբ կախված կլինի տեղի լայնությունից։

Վերոհիշյալի հիման վրա, հեշտ է սահմանել հետևյալը։

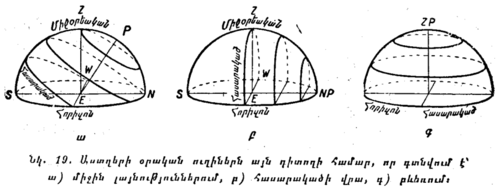
Միջին լայնություններում, օրինակ, ՍՍՌՄ-ում, աշխարհի առանցքը և երկնային հասարակածը թեքված են դեպի հորիզոնը, ուստի և աստղերի օրական ուղիները նույնպես թեքված են հորիզոնի նկատմամբ (նկ. 19 ա)։ Այն աստղերը, որոնք աշխարհի բևեռից հեռու են գտնվում ոչ ավելի, քան φ աստիճանով (այստեղ φ աշխարհագրական լայնությունն է), մայր չմտնող աստղեր են։ Իսկ այն աստղերը, որոնք բևեռից հեռու են գտնվում ավելի քան φ աստիճանով, ծագող և մայր մտնող աստղեր են։ Հարավային կիսագնդի աստղերի մի մասը, որոնք երկնային սֆերայում ընկած են ավելի հարավ (ցած), քան այն փոքր զուգահեռականը, որը զուգահեռ է հասարակածին և անցնում է S կետով (տե՛ս նկ. 19 ա), երբեք չեն ծագում՝ նրանք անտեսանելի են։

Երկրի հասարակածում աշխարհի առանցքը պառկած է հորիզոնի հարթության վրա և համընկնում է միջօրեի գծին, իսկ աշխարհի բևեռները՝ հյուսիսի և հարավի կետերին (նկ. 19 բ)։ Հասարակածը դառնում է հորիզոնին, ուղղահայաց և անցնում է Z, զենիթով։ Բոլոր աստղերի օրական ուղիներն ուղղահայաց են հորիզոնին և նրանցից յուրաքանչյուրը օրվա կեսի ընթացքում լինում է հորիզոնից վեր և մյուս կեսի ընթացքում՝ հորիզոնից ցած։ Լրիվ օրվա ընթացքում, եթե ցերեկն Արեգակը չխանգարեր, կարելի կլիներ տեսնել երկնքի երկու կիսագնդերի բոլոր աստղերը։ Այնտեղ չծագող աստղեր չկան, ինչպես չկան նաև մայր չմտնող աստղեր։ Մասնավորապես, մեզ ծանոթ Մեծ Արջը այնտեղ մայր մտնող համաստեղությունների թվին է պատկանում։

Երկրի բևեռում երկնային հասարակածը համընկնում է հորիզոնին, իսկ աշխարհի առանցքը համընկնում է ուղղաձիգ գծին (նկ. 19 գ)։ Այնտեղ Բևեռային աստղը փայլում է զենիթի մոտ։ Արևելքի և արևմուտքի կետերը, ինչպես հասարակածի և հորիզոնի հատման կետեր, դառնում են անորոշ։ Միջօրեականը, որ անցնում է աշխարհի բևեռներով ու զենիթով, նույնպես անորոշ է դառնում, իսկ դրա հետ միասին կորցնում են իրենց իմաստը նաև հարավ, հյուսիս, արևելք և արևմուտք հասկացողությունները։ Երկրի հյուսիսային բևեռից բոլոր ուղղությունները տանում են դեպի հարավ։ Այնտեղ աստղերի օրական ուղիները զուգահեռ են հորիզոնին. ոչ մի աստղ չի ծագում և ոչ մի աստղ մայր չի մտնում։ Որպես մայր չմտնող երևում են երկնքի հյուսիսային կիսագնդի բոլոր աստղերը, բայց հարավային կիսագնդի աստղերից և ոչ մեկը երբեք չի երևում։

ՀԱՐՑԵՐ ԻՆՔՆԱՏՈՒԳՄԱՆ ՀԱՄԱՐ

Ինչպե՞ս է աշխարհի առանցքը դասավորված Երկրի առանցքի նկատմամբ։ Ինչպիսի՞ պայմաններում են նրանք համընկնում։
Ինչպե՞ս է երկնային հասարակածը դասավորված Երկրի հասարակածի նկատմամբ։ Որտե՞ղ են նրանք համընկնում։
Ինչո՞ւ բոլոր տեղերից էլ Բևեռային աստղը երևում է աշխարհի բևեռի մոտ։
Երկրագնդի նկատմամբ ինչպիսի՞ հարթություն է հանդիսանում ցանկացած հորիզոնի հարթությունը։
Ինչո՞ւ որոշ աստղեր ծագում և մայր են մտնում։
Ինչպե՞ս է Բևեռի բարձրությունը հորիզոնից կապված տեղանքի աշխարհագրական լայնության հետ։ Ապացուցեցե՛ք այդ։
Ինչպե՞ս է տեղի ունենում աստղերի օրական պտույտը հորիզոնի նկատմամբ միջին լայնություններում։ Բացատրեցե՛ք այդ գծագրով։
Ինչպե՞ս է տեղի ունենում լուսատուների օրական պտույտը հասարակածում գտնվող դիտողի համար։ Բացատրեցե՛ք այդ գծագրով։
Ինչպե՞ս են շարժվում լուսատուներն օրվա ընթացքում այն դիտողի համար, որ գտնվում է Երկրի բևեռում։ Բացատրեցե՛ք այդ գծագրով։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

Քանի՞ աստիճան է զենիթից մինչև արևելքի և հարավի կետերը եղած հեռավորությունը։
Մի աստղի ուղղակի ծագումը 3 ժամ է, մյուսինը՝ 5 ժամ 18 րոպե։ Նրանցից ո՞րը ավելի շուտ կուլմինացիա կկատարի և ինչքա՞ն ժամանակով։
Տեղանքի լայնությունը 35° է։ Այդ վայրի համար բևեռը քանի՞ աստիճան է հեռու զենիթից։
Տեղանքի լայնությունը 57° է։ Այն տեղ զենիթից ինչպիսի հեռավորության վրա է միջօրեականը հատվում հասարակածի հետ։
Իսկ ինչպիսի՞ն է այնտեղ հասարակածի ամենաբարձր կետի բարձրությունը հորիզոնի նկատմամբ։
Մուրմանսկի լայնությունը 68°58՛ է։ Կարելի՞ է արդյոք այնտեղ հորիզոնից վեր տեսնել Սիրիուս աստղը (երկնքի ամենապայծառ աստղը), եթե նրա հակումը՝ δ = +16°։
Լենինգրադի լայնությունը 59°56՛ է։ Հնարավո՞ր է արդյոք այնտեղ տեսնեք Վեգա աստղի երկու կուլմինացիան էլ, եթե նրա հակումը՝ δ = +39°։

ԵՐԿԻՐ

§ 23. ԵՐԿՐԻ ԳՆԴԱՁԵՎՈՒԹՅՈՒնԸ։ Հաճախ Երկրի գնդաձև լինելն ապացուցելու համար վկայակոչում են այնպիսի երևույթներ, որոնք իրականում միայն նրա մակերևույթի ուռուցիկությունը կամ կորությունն են ապացուցում։ Երկրի մակերևույթի կորությունը ապացուցող այդպիսի երևույթներն են՝

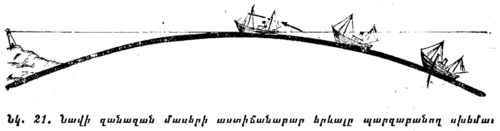
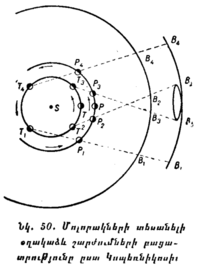
1) Նավը ծովափին մոտենալիս հորիզոնի տակից առաջ նրա կայմերի գագաթներն են երևում, իսկ այնուհետև հետզհետե նաև ամբողջ իրանը (նկ. 20 և 21)։

2) Դեպի վեր բարձրանալու դեպքում տեսադաշտը լայնանում է և հորիզոնի վրա երևացող առարկաների հեռավորությունը մեծանում։

3) Արեգակի մայր մտնելոց հետո նրա ճառագայթները շարունակում են լուսավորել բարձր շենքերի տանիքները, լեռների գագաթներն ու ամպերը, ավելի ուշ՝ միայն բարձր լեռների գագաթներն ու ամպերը, էլ ավելի ուշ՝ միայն ամպերը։

Շուրջերկրյա ճանապարհորդությունները միայն ապացուցում են, որ Երկրի ձևն ինքնապարփակ է, որ նա տարածության մեջ մեկուսացած է, որ նա որևէ տեղ երկնքի հետ միաձուլվող եզրեր չունի։

Երկրի գնդաձև լինելը ապացուցող փաստ կարելի է համարել հետևյալ երկու երևույթը.

1) Երկրի ամեն մի վայրում հորիզոնը շրջագծի ձևով է երևում և հորիզոնի հեռավորությունն ամենուրեք համահավասար է։

2) Լուսնի խավարումների ժամանակ Երկրի ստվերը, որ ընկնում է լուսնի վրա, միշտ կլորաձև ուրվանկար ունի։ Բոլոր մարմիններիդ միայն գունդն է, որ իր բոլոր դիրքերում կլոր ստվեր է գցում։

§ 24. ԵՐԿՐԻ ՉԱՓԵՐԸ ՈՐՈՇԵԼԸ։ Երկրի չափերի որոշումը կայանում է նրանում, որ մենք չափում ենք միջօրեականի աղեղը գծային միավորներով և աստիճաններով։ Երկրագնդի միևնույն միջօրեականի վրա գտնվող երկու կետերի միջև որոշում են գծային հեռավորությունը, որը, ասենք, հավասար է n կիլոմետրի։ Աստղագիտական եղանակով որոշում են նաև այդ կետերի աշխարհագրական լայնությունների տարբերությունը (օրինակ, այդ կետերում Բևեռային աստղի բարձրության տարբերության միջոցով), որը, ենթադրենք, հավասար է m աստիճանի։ Այդ դեպքում Չհաջողվեց վերլուծել (բառական սխալ):

քանորդը ցույց կտա, թե շրջանագծի ո՛ր մասն է իրենից ներկայացնում նրա այն աղեղը, որ գտնվում է մեր վերցրած երկու կետերի միջև։ Դրա հիման վրա գտնում են ամբողջ շրջանագծի երկարությունը կիլոմետրերով հետևյալ պարզ հարաբերության միջոցով.

Չհաջողվեց վերլուծել (բառական սխալ):

Նկարագրած եղանակը կոչվում է աստիճանային չափում։ Իմանալով Երկրի շրջանագծի երկարությունը, և այն բաժանելով 2π-ի, կստանանք Երկրի շառավղի երկարությունը։ Այսպիսով որոշվել է, որ Երկրի շառավիղը, եթե այն գնդաձև համարենք, հավասար է 6371 կմ, իսկ շրջանագիծը՝ գրեթե ուղիղ 40 000 կմ է։

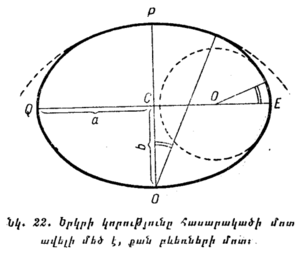
§ 25. ԵՐԿՐԻ ՍԵՂՄՎԱԾՈՒԹՅՈՒՆԸ։ Երկրի տարբեր վայրերում կատարած չափումների միջոցով համոզվել են, որ Երկրի կորությունը հասարակածի մոտ ավելի մեծ է, քան բևեռներում (նկ. 22)։ Դա նշանակում է, որ Երկիրը գնդաձև չէ. նա բևեռների մոտ մի քիչ սեղմված է։ Երկրի բևեռային շառավիղը հասարակածային շառավղից կարճ է համարյա 21 կիլոմետրով, այսինքն՝ մոտավորապես հասարակածային շառավղի 1/300 չափով։ Երկրի ձևը ճշտվել է սովետական գիտնականների կողմից։

Երկրի սեղմվածությունը հետևանք է այն կենտրոնախույս ուժի ազդեցության, որ զարգացնում է Երկիրն իր առանցքի շուրջը պտտվելու ժամանակ։ Դա կարելի է ցուցադրել դպրոցական կենտրոնախույս մեքենայի առանցքի վրա պտտեցնելով պողպատյա բարակ օղակապը։ Երկնային մարմնի սեղմվելն իր պտտվելու հետևանքով ընդհանուր կանոն է։ Օրինակ, Յուպիտեր և Սատուրն մոլորակները, որոնք իրենց առանցքի շուրջն ավելի արագ են պտտվում քան Երկիրը, ավելի շատ են սեղմված (Յուպիտերի սեղմվածությունը շատ լավ նկատվում է հեռադիտակով)։ Սեղմվածության հետևանքով Երկիրը գնդաձև չէ, այլ պտտման էլիպսոիդ։

§ 26 ՏՐԻԱՆԳՈՒԼՅԱՏԻԱ (Եռանկյունաչափական ընդօրինակություն)։ Երկրի չափերը որոշելու ժամանակ հարկավոր է միջօրեականի աղեղի երկարությունը չափել աստիճաններով և գծային չափերով։ Առաջինը, ակներևորեն, որոշվում է որպես միջօրեականի այդ աղեղի սկզբի և վերջին ծայրերի աշխարհագրական լայնությունների տարբերություն։ Իսկ աշխարհագրական լայնությունը կարելի է որոշել չափելով աշխարհի բևեռի բարձրությունը։

Բայց միջօրեականի աղեղի գծային երկարությունը չափելու ժամանակ, մանավանդ եթե Երկրի չափերը ավելի մեծ ճշտությամբ որոշելու համար բավական երկար աղեղ վերցնելու լինենք, մենք մի շարք գործնական դժվարությունների կհանդիպենք. այդ աղեղի սկզբից մինչև նրա վերջավորությունը ճանապարհին կարող են ձորեր, լեռներ, ճահիճներ և այլ խոչընդոտներ հանդիպել։ Ուստի, միջօրեականի աղեղի երկարությունը և առհասարակ Երկրի մակերևույթի վրա մեծ տարածություններ չափելու համար (որոնք, մասնավորապես, հարկավոր են լինում աշխարհագրական քարտեզներ կազմելու համար) օգտվում են տրիանգուլյացիայի եղանակից։

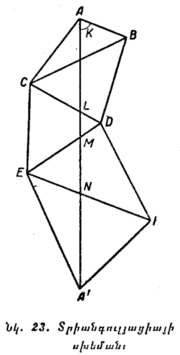
Տրիանգուլյացիան կայանում է հետևյալում։ Եթե հարկավոր է չափել միջօրեականի AA՛ աղեղը (նկ. 23), ընտրում են հարթ տարածության վրա ընկած AB գիծը և չափում նրա երկարությունը ամենայն հնարավոր ճշտությամբ։ Այդպիսի գիծը կոչվում է բազիս (հիմք)։ Բացի այդ, ընտրում են C կետը, որը երևում է և՛ A կետից, և՛ B կետից։ Այնուհետև անկյունաչափ գործիքի օգնությամբ չափում են A, B կետերի մոտ ընկած անկյունները և, բացի այդ, բազիսի և միջօրեականի AA՛ ուղղության միջև ընկած K անկյունը։ Ապա արդեն հաշվարկումների միջոցով գտնում են AC, BC կողմերի երկարությունը և C անկյան մեծությունը։ Դրանից հետո ընտրում են D կետը, որը երևում է և՛ C, և՛ B կետերից, և տեղավորվելով այդ կետերում, անկյունաչափ գործիքով չափում են BCD և CBD անկյունները։ Քանի որ CB գծի երկարությունն արդեն հաշված էր, ուստի այժմ նախորդի օրինակով կարելի է հաշվել CD և BD կողմերի երկարությունը, և բացի այդ, AB և AA՛ գծերով կազմված անկյունը։

Շարունակելով չափումները նկարագրած ձևով, մենք A-ից մինչև տարածությունը կծածկենք մի շարք եռանկյուններով, որտեղ բոլոր անկյունները չափված են, իսկ բոլոր կողմերը՝ որոշված հաշվարկումների միջոցով։ Այն ժամանակ AA՛ երկարությունը կարելի է գտնել որպես ACEA՛ (կամ ABDFA՛) բեկյալ գծի պրոյեկցիան այդ ուղղի վրա։ Այդ երկարությունը գտնում են հաշվարկումների միջոցով։

Ըստ որում, բնականաբար, հաշվի է առնվում նաև այն հանգամանքը, որ այդ չափումները կատարվել են ոչ թե հարթության վրա, այլ Երկրի կոր մակերևույթի վրա։

Այսպիսով, տրիանգուլյացիան կայանում է նրանում, որ մեծ հեռավորությունները որոշվում են եռանկյունների օգնությամբ, որտեղ չափվում են միայն անկյունները և բազիսը, իսկ կողմերը որոշվում են հաշվարկումներով։ Այդ եղանակի անվանումը ծագել է լատիներեն «տրիանգուլյում» — եռանկյուն բառից։

Տրիանգուլյացիայից օգտվում են ոչ միայն Երկրի չափերը որոշելու համար, այլև աշխարհագրական քարտեզներ կազմելիս, երբ պահանջվում է չափել մեծ հեռավորություններ։

1816—1855 թթ. ռուսական գիտնականների կողմից, ակադեմիկոս Վ. Յա. Ստրուվեի ղեկավարությամբ, կատարվել է միջօրեականի 25°20՛ հսկայական աղեղի չափումը։

Քարտեզագրական աշխատանքների համար մեծ մասշտաբի տրիանգուլյացիոն աշխատանքներ են կատարում և ներկայումս։

24-րդ նկարում ցույց է տրված փայտե աշտարակ, որը կոչվում է գեոդեզիական նշանակետ և կանգնեցվում է տրիանգուլյացիայի համար ընտրված եռանկյունների գագաթներում։

§ 27. ԵՐԿՐԻ ՕՐԱԿԱՆ ՊՏՈՒՅՏԻ ԱՊԱՑՈՒՅՑՆԵՐԸ, Երկրի գնդաձևության մասին գիտեին դեռևս հնում, սակայն, Երկրի օրական պտույտի գոյությունը առաջին անգամ ամենայն որոշակիությամբ հաստատեց միայն Կոպեռնիկոսը (XVI դ. կեսերին), իսկ դրա անհերքելի ապացույցները գտնվել են է՛լ ավելի ուշ։

Բերենք դրանցից երկու առավել ակնհայտ ապացույցներ.

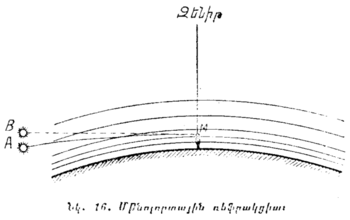
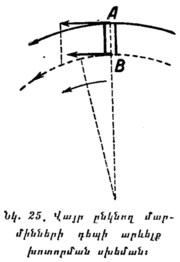
ա) Վայր ընկնող մարմինների խոտորումը դեպի արևելք։ Պատկերացնենք մի խոր ուղղաձիգ AB հանքահոր, որը պտտվում է Երկրի հետ միասին (նկ. 25)։ Նրա մուտքր (A) պտտման ժամանակ գծային ավելի մեծ արագություն ունի, քան հիմքը (B), որովհետև նա ավելի հեռու է գտնվում պտտման կենտրոնից, տվյալ դեպքում երկրի օրական պտույտի առանցքից։ Հանքահորի մուտքի մոտ ընկած քարն այս դեպքում նույն արագությունը կունենա, ինչ և այդ մուտքը։ Հանքահորի մեջ ընկնելու դեպքում նա, իներցիայի շնորհիվ, կպահպանի այդ արագությունը։ Ընկնելով ցած և միաժամանակ պահպանելով իր դեպի արևելք շարժման (որովհետև Երկիրը պտտվում է արևմուտքից դեպի արևելք) ավելի մեծ արագությունը, քան հանքահորի հիմքի շարժման արագությունն է, քարն իր դեպի արևելք շարժման մեջ ավելի առաջ կանցնի հանքահորի հիմքից։ Քարը կընկնի ոչ թե Ճիշտ Երկրի կենտրոնի ուղղությամբ, այլ կշեղվի դեպի արևելք, որը չէր պատահի, եթե Երկիրը պտտվելիս չլիներ։ Երկրի հասարակածի վրա այդ խոտորումը ամենից մեծ է, իսկ բևեռներում հավասար է զրոյի։

Այս ձևի բազմաթիվ փորձերը ցույց են տալիս, որ դիտումները միանգամայն համապատասխանում են կատարած հաշվարկումներին. օրինակ, միջին լայնություններում 85 մ բարձրությունից վայր ընկնող քարը շեղվում է դեպի արևելք 10,5 մմ։

բ) Ֆուկոյի ճոճանակը։ Առաջին անդամ 1851 թ. ֆրանսիացի գիտնական Ֆուկոյի դրած փորձում կիրառվել է մի ճոճանակ, որը իրենից ներկայացնում էր մի շատ երկար ու բարակ լար, որի ծայրից կախված էր ծանր գունդ։ Հայտնի է, և այդ կարելի է ստուգել կենտրոնախույս մեքենայի վրա կատարած փորձով, որ ամեն մի այդպիսի ճոճանակ իր տատանումների հարթությունը պահպանում է առանց փոփոխության, թեկուզ ինչպես էլ պտտելու լինենք այն հենարանը, որից նա կախված է։ (ճոճանակի լարը երկար է վերցվում այն նկատառումով, որպեսզի փորձն ավելի ակնառու լինի, և ճոճանակը բավական երկար ժամանակ տատանելու անհրաժեշտությունից։)

Եթե մի այդպիսի ճոճանակ ճոճվելիս լիներ Երկրի բևեռի վրա, ապա Երկիրը, պտտվելով նրա տակ, կդառնար մեկ ժամում 15° արագությամբ (360° : 24 ժամ)։ Դրա հետևանքով մենք կնկատեինք, որ ճոճանակի տատանման հարթությունը Երկրի մակերևույթի նկատմամբ դառնում է այդ նույն 15° մեկ ժամում արագությամբ և Երկրի պտույտին հակառակ ուղղությամբ։

Երկրի հասարակածի վրա ճոճանակի ճոճումների ուղղությունը ոչ մի փոփոխություն չէր կրի, իսկ միջակա լայնություններում ճոճանակի տատանումների հարթությունը, ինչպես տեսությունն է ցույց տալիս, պետք է դառնա մեկ ժամում 15° sinφ, որտեղ φ աշխարհագրական լայնությունն է։

Իրականում հենց այդպես էլ դիտվում է։ Պարզ է, որ եթե Երկիրը չպտտվեր, ճոճանակի ճոճումների ուղղությունն ամեն տեղ կմնար անփոփոխ։

Լենինգրադում, նախկին Իսաակիևսկի տաճարի շենքում, ցուցադրվում է մի ճոճանակ՝ 98 մ երկարությամբ։ Նրա ճոճումների ուղղությունը փոխվում է ժամում 13° արագությամբ՝ Ճիշտ այնպես, ինչպես պահանջվում է Երկրի պտույտի տեսությամբ։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ

Ինչպիսի՞ երևույթներն են խոսում ոչ միայն Երկրի կորության, այլև նրա գնդաձևության մասին։
Ինչպիսի՞ն է այն եղանակը, որով որոշում են Երկրի չափերը։
Ինչի՞ են հավասար Երկրի շառավիղն ու շրջագիծը։
Ի՞նչ բան է Երկրի սեղմվածությունը։ Սեղմվածության մեծությունը։
*Ի՞նչ է տրիանգոլլյացիան։ Ինչի՞ համար և ինչպե՞ս են այն կիրառում։
Ինչպիսի՞ փորձեր են ապացուցում Երկրի օրական պտույտը։ Ինչո՞ւմն կայանում այդ փորձերի էությունը։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

XIX դ. առաջին կեսում ռուս գիտնականների կողմից որոշվել է, որ Ֆուգլենեսսի (φ = 70°50՛) և Ստարո-Նեկրասովսկայի (φ = 45°20՛) միջև եղած հեռավորությունը միջօրեականով հավասար է 2822 կմ։ Այստեղից որոշեցեք Երկրի միջօրեականի քառորդը և շառավիղը։
Եթե Երկիրը պատկերացնենք 30 սմ տրամագիծ ունեցող գլոբուսով, այդ դեպքում ի՞նչ մեծությամբ կպատկերացվի Երկրի բևեռային և հասարակածային շառավիղների տարբերությունը։
Ինչի՞ է հավասար հասարակածային կետերի արագությունը մետրերով՝ Երկրի օրական պտույտի ժամանակ։
*Իսկ ինչպիսի՞ն է հիշյալ արագությունը ձեր բնակավայրի համար (վերջինիս աշխարհագրական լայնությունը վերցնել քարտեզից), այն հաշվելու համար կառուցելով գծագիր օգտվեցեք եռանկյունաչափությունից։

ԳԼՈՒԽ II։ ԱՐԵԳԱԿԻ ՏԱՐԵԿԱՆ ՇՐՋԱՊՏՈՒՅՏԸ ԵՎ ԵՐԿՐԻ ՇԱՐԺՈՒՄԸ ԺԱՄԱՆԱԿԻ ԵՎ ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՈՐՈՇԵԼԸ

ԱՐԵԳԱԿԻ ՏԱՐԵԿԱՆ ՇՐՋԱՊՏՈՒՅՏԸ

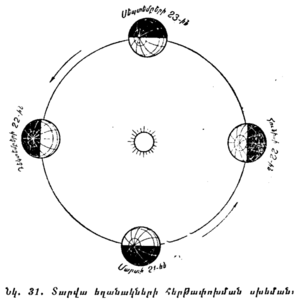
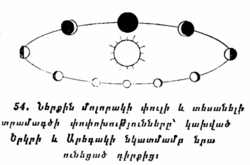
§ 28. ԱՐԵԳԱԿԻ ԿԵՍՕՐՅԱ ԲԱՐՁՐՈՒԹՅԱՆ ԵՎ ԱՍՏՂԱՅԻՆ ԵՐԿՆՔԻ ՏԵՍՔԻ ՏԱՐԵԿԱՆ ՓՈՓՈԽՈՒԹՅՈՒՆՆԵՐԸ։ Յուրաքանչյուրին լավ հայտնի է, որ կեսօրին Արեգակի բարձրությունը հորիզոնից, այսինքն՝ նրա բարձրությունը վերին կուլմինացիայում, տարվա ընթացքում փոփոխության է ենթարկվում։ Ամռանը կեսօրին Արեգակը բարձրանում է շատ բարձր, ամենաբարձր դիրքում նա լինում է հունիսի 22-ին։ Այդ օրն անվանում են ամառային արևադարձի օր։ Հաջորդ օրերում Արեգակի կուլմինացիոն կետը հետզհետե իջնում է, և նրա ամենացածր կուլմինացիան տեղի է ունենում դեկտեմբերի 22-ին. դա ձմեռային արևադարձի օրն է։ Դրան համապատասխան, դեկտեմբերի 22-ին ցերեկն ամենակարճն է լինում, որովհետև այդ օրը Արեգակն ամենից քիչ է մնում հորիզոնից վերևանա ուշ է ծագում ևշուտ մայր մտնում։

Մարտի 21-ին և սեպտեմբերի 23-ին մոտ Արեգակի բարձրությունը վերին կուլմինացիայում լինում է նրա ամառային և ձմեռային արևադարձի օրերին վերին կուլմինացիայում ունեցած բարձրությունների միջինը, իսկ ցերեկը հավասարվում է գիշերվան, ուստի մարտի 21-ը անվանում են գարնանային գիշերահավասարի օր, իսկ սեպտեմբերի 23-ը աշնանային գիշերահավասարի օր։

Եթե Արեգակի բարձրությունը կուլմինացիայում փոփոխվում է, ուրեմն երկնային սֆերայում փոփոխվում է նաև նրա դիրքն աշխարհի բևեռի և երկնային հասարակածի նկատմամբ։ Եվ իսկապես, այն աստղերը, որոնք աշխարհի բևեռի և երկնային հասարակածի նկատմամբ անփոփոխ դիրք են գրավում, կուլմինացիայի կետով անցնում են յուրաքանչյուրը մի որոշակի՝ հորիզոնից միշտ միևնույն բարձրության վրա։ Հենց այդ պատճառով էլ յուրաքանչյուր աստղ ծագում և մայր է մտնում մի որոշ՝ հորիզոնի միշտ միևնույն կետում։ Մինչդեռ Արեգակը, օրինակ, ամռանը մայր է մտնում հյուսիս-արևմուտքում, ձմռանը՝ հարավ-արևմուտքում, իսկ գիշերահավասարի օրերին՝ արևմուտքի կետում։ Չափումների միջոցով դժվար չէ համոզվել այն բանում, որ գիշերահավասարի օրերին Արեգակը կեսօրին հորիզոնից վեր է գտնվում 90°-φ անկյան չափով։ Բայց հենց ճիշտ այդ բարձրության վրա էլ երկնային հասարակածը հատվում է միջօրեականի հետ (տե՛ս նկ․ 11)։ (Դա հեշտ է ստուգել, հիշելով, որ աշխարհի բևեռից հասարակածի հեռավորությունը հավասար է 90°-ի, և որ հորիզոնից աշխարհի բևեռի հեռավորությունը հավասար է φ աստիճանի)։

Հետևաբար, գիշերահավասարի օրերին Արեգակը գտնվում է երկնային հասարակածի վրա։ Դա երևում է և նրանից, որ այդ օրերին Արեգակը ծագում է արևելքի կետում և մայր է մտնում արևմուտքի կետում, իսկ այդ կետերում հորիզոնի հետ հատվում է երկնային հասարակածը։

Եթե ամառվա կեսօրին Արեգակի բարձրությունն ավելի է լինում, քան 90°-φ, այսինքն՝ գերազանցում է երկնային հասարակածի բարձրությանը հորիզոնից, նշանակում է՝ Արեգակն այդ ժամանակ գտնվում է հասարակածից ավելի վերև (երկնքի հյուսիսային կիսագնդում)։ Ճիշտ նույն կերպով էլ կարելի է համոզվել, որ ձմռանն Արեգակը գտնվում է երկնքի հարավային կիսագնդում՝ հասարակածից ցած։ Չափելով Արեգակի բարձրությունները կեսօրին անկյունաչափ գործիքով, մենք կհամոզվենք, որ Արեգակի առավելագույն հեռավորությունը հասարակածից դեպի հյուսիս կազմում է 23°27՛ (հունիսի 22-ին) և ճիշտ նույն չափի է նաև նրա առավելագույն հեռավորությունը հասարակածից դեպի հարավ (դեկտեմբերի 22-ին)։

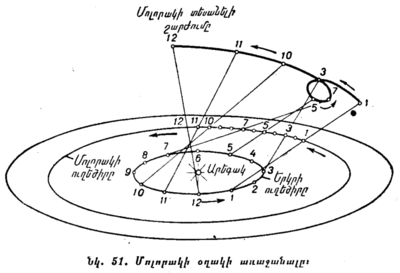
Սակայն տարվա ընթացքում Արեգակը երկնային սֆերայում տեղաշարժվում է ոչ միայն երկնային հասարակածի նկատմամբ, այլև երկնային սֆերայի օրական պտույտին հակառակ ուղղությամբ։ նրա այդ տարեկան շարժումը, որը շատ դանդաղ է կատարվում, չպետք է շփոթել նրա օրական, համեմատաբար արագ շարժման հետ, որը կատարվում է ժամացույցի սլաքի շարժման ուղղությամբ։ Արեգակի այդ տարեկան շարժումը տեղի է ունենում նրա օրական շարժման հակառակ ուղղությամբ։

Այս բանում կարելի է համոզվել, նկատելով, թե կես-գիշերին ո՛ր աստղերն են լինում վերին կուլմինացիայում, այսինքն՝ երկնային սֆերայում, որ համաստեղություններն են գտնվում Արեգակի հակադիր կողմում։ Տարվա ընթացքում այդ համաստեղությունները շարունակ փոփոխվում են։ Ձմռան կես-գիշերին կուլմինացիա են կատարում մի որոշ համաստեղությունների աստղեր, ամռանը՝ այլ համաստեղությունների աստղեր։

Բացի այդ, կարելի է նկատել, որ եթե Արեգակի մայր մտնելուց անմիջապես հետո որևէ համաստեղություն մայր է մտնում, ասենք, 4 ժամ ուշացումով, ապա մեկ ամիս անց՝ նա մայր կմտնի արդեն երկու ժամ ուշացումով, իսկ ավելի ևս ուշ՝ նա, թաղվելով Արեգակի ճառագայթների մեջ, բոլորովին չի երևա։ Նշանակում է՝ այդ ժամանակամիջոցում Արեգակը երկնային սֆերայում տեղաշարժվել է այդ համաստեղությանն ընդառաջ արևմուտքից դեպի արևելք։ Որոշ ժամանակ ևս անցնելուց հետո հիշյալ համաստեղությունը կերևա հորիզոնի տակից, նախորդելով արևածաղին ավելի ու ավելի շուտ։

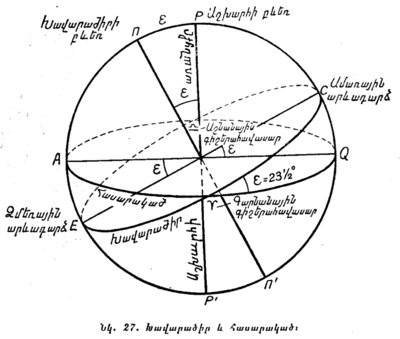
§ 29. ԱՐԵԳԱԿԻ ԹՎԱՑՈՂ ՇԱՐԺՈՒՄԸ ԽԱՎԱՐԱԾՐՈՎ (ԷԿԼԻՊՏԻԿԱ)։ Վերը նկարագրված բոլոր դիտումները համեմատելով միմյանց հետ, մենք գալիս ենք այն եզրակացության, որ Արեգակը տարվա ընթացքում երկնային սֆերայում տեղաշարժվում է մի մեծ շրջանով, որը կոչվում է խավարածիր (էկլիպտիկա), որի հարթությունը թեքված է երկնային հասարակածի նկատմամը 23°27՛-ով: Այլ կերպ ասած, խավարածիրը երկնային հասարակածի հետ հատվում է 23°27՛ անկյան տակ (նկ. 27)։ Տարվա ընթացքում Արեգակը խավարածրով մի լթիվ շրջան է կատարում՝ շարժվելով ժամացույցի սլաքի շարժման հակառակ ուղղությամբ։ Իսկ օրվա ընթացքում Արեգակը խավարածրով շարժվում է դեպի արևելք 360°։365 չափով կամ մոտավորապես 1 աստիճան։

Խավարածրի և երկնային հասարակածի հատման կետերը կոչվում են գարնանային և աշնանային գիշերահավասարի կետեր, նայած, թե Արեգակը ե՛րբ է լինում այդ կետում:

Գարնանային գիշերահավասարի կետը նշանակվում է ՞՞՞ նշանով, իսկ աշնանային գիշերահավասարի կետը՝ ՞՞՞ նշանով։ Խավարածրի վրա արևադարձի կետերը գիշերահավասարի կետերից գտնվում են 90° հեռավորության վրա և բոլորից շատ են հեռացած հասարակածից։

Արեգակի շարժումը խավարածրով, ինչպես և Արեգակի օրական շարժումը հորիզոնի նկատմամբ, թվացող շարժումներ են։ Վերջինը առաջանում է Երկրի՝ իր առանցքի շուրջը օրական պտույտի հետևանքով, իսկ առաջինը՝ Արեգակի շուրջը Երկրի կատարած տարեկան բոլորման հետևանքով։

Երկնային սֆերայի պտտման հետևանքով խավարածրի դիրքը հորիզոնի նկատմամբ շարունակ փոփոխվում է, ուստի երկնային սֆերայի գծագրում հորիզոնի և միջօրեականի հետ խավարածիրը չեն պատկերում։

Ներկայումս գարնանային գիշերահավասարի կետը գտնվում է Ձկների համաստեղության մեջ, աշնանային գիշերահավասարինը՝ Կույսի համաստեղության մեջ, ամառային արևաղարձինը՝ Երկվորյակների համաստեղության մեջ, իսկ ձմեռային արևադարձինը՝ Աղեղնավորի համաստեղության մեջ։

Այն տասներկու համաստեղությունները, որոնցով անցնում է խավարածիրը, կոչվում են կենդանակերպային (զոդիակային) համաստեղություններ: Դուք կարող եք նրանց գտնել 28-րդ նկարի վրա:

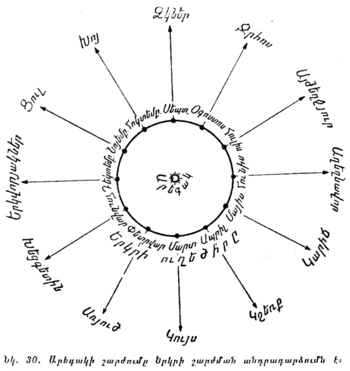
§ 30. ԿԵՆԳԱՆԱԿԵՐՊԻ (ԶՈԴԻԱԿԱՅԻՆ) ՀԱՄԱՍՏԵՂՈՒԹՅՈՒՆՆԵՐԸ։ Այն 12 համաստեղությունները, որոնք կոչվում են Կենդանակերպի Հզոդիակային) համաստեղություններ, երկնքում դասավորված են մեծ շրջանի երկարությամբ։ Կենդանակերպ կոչվում է այդ 12 համաստեղությունների համակցությունը։ Կենդանակերպ հունարեն զոդիակ բառից է, որը բառացի նշանակում է «կենդանիների շրջան», քանի որ այդ համաստեղությունների անուններից շատերը կենդանիների անուններ են։ Ահա այդ անունները. Խոյ, Ցուլ, Երկվորյակներ, Խեցգետին, Առյուծ, Կույս, Կշեռք, Կարիճ, Աղեղնավոր, Այծեղջյուր, Ջրհոս, Ձկներ։

Կենդանակերպի համաստեղությունները կամ Կենդանակերպի նշանները՝ ինչպես նրանց անվանում են, ունեն այսպիսի սիմվոլիկ նշանակումներ.

Ջկներ ՞՞՞ երկվորյակներ ՞՞՞ Կույս ՞՞՞ Աղեղնավոր ՞՞՞ Խոյ ՞՞՞ Խեցպետին ՞՞՞ Կշեոք ՞՞՞ Այծեղջյուր Ցուլ ՞՞՞ Աոյուծ ՞՞՞ Կարիճ ՞՞՞ ՋրՀոս

Կենդանակերպի գեղարվեստորեն ձևավորված նշանները հաճախ գործ են ածվում զարդարանքի համար՝ ինչպես ճարտարապետական օռնամենտներ կամ ինչպես տարվա ամիսներիդ սիմվոլներ, որովհետև Արեգակն այդ համաստեղություններից յուրաքանչյուրում գտնվում է տարվա մեկ տասներկուերորդական մասի ընթացքում, այսինքն՝ մեկ ամիս։ Կենդանակերպի նշանները բարձրաքանդակ ոսկեզօծ ֆիգուրաների ձևով կարելի է տեսնել, օրինակ, Մոսկվայում՝ Կազանի կայարանի ժամացույցի թվատախտակի վրա։

Մոտավորապես կես-գիշերին երկնքի հարավային կողմում միշտ գտնվում է Կենդանակերպի այն համաստեղությունը, որ տվյալ ամսում ուղիղ հակադիր է Արեգակին։ Օրինակ, նոյեմբերին Արեգակը գտնվում է Կարիճի համաստեղությունում, իսկ նոյեմբեր ամսում մոտ կես-գիշերին կուլմինացիա են կատարում նրան հակադիր Ցուլի համաստեղության աստղերը։ Կեսօրվա մոտ կուլմինացիա է կատարում (բայց նա երևում է միայն Արեգակի լրիվ խավարման ժամանակ) Կենդանակերպի այն համաստեղությունը, որտեղ այդ ժամանակ գտնվում է Արեգակը։

§ 31. ԱՐԵԳԱԿԻ ՕՐԱԿԱՆ ՃԱՆԱՊԱՐՀԻ ՓՈՓՈԽՈՒԹՅՈՒՆՆԵՐԸ ՏԱՐԲԵՐ ԼԱՅՆՈՒԹՅՈՒՆՆԵՐՈՒՄ։ § 22-ում մենք տեսանք, որ աշխարհագրական տարբեր լայնություններում երկնային լուսատուների օրվա ընթացքում անցած ուղիները հորիզոնի նկատմամբ տարբեր են լինում։ Դա վերաբերում է, անշուշտ, նաև Արեգակին։ Տարվա ընթացքում Արեգակն ինքը փոխում է իր դիրքը երկնային հասարակածի նկատմամբ։ Ուստի տարվա տարբեր եղանակներին այլ է լինում նաև նրա ուղին Երկրի միևնույն վայրի հորիզոնի նկատմամբ։ Թե ի՛նչպես է գարնանից ամռանն անցնելուց և այնուհետև ձմռանն անցնելուց մեր լայնություններում փոխվում Արեգակի օրական ուղին հորիզոնի նկատմամբ՝ խոսվել է § 28-ում։

Ինչ վերաբերում է տարբեր լայնություններում Արեգակի օրական ուղու փոփոխություններին, ապա նրանք ընդհանուր առմամբ հետևյալն են․

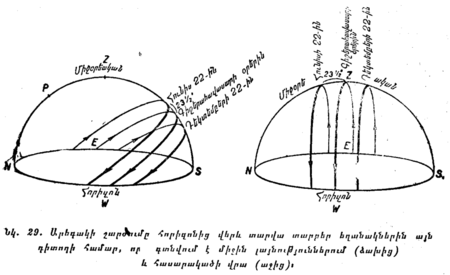
Կաղապար:Լայն Արեգակը, ինչպես և երկնային մյուս բոլոր լուսատուները միշտ հորիզոնի նկատմամբ ծագում և մայր են մտնում ուղղաձգորեն։ Ուստի այնտեղ կլոր տարին ցերեկն ու գիշերը հավասար են (այնտեղ Արեգակի օրական ուղին հորիզոնով կիսվում է երկու հավասար մասերի), իսկ աղջամուղջները շատ կարճ են լինում։ Արեգակն արագորեն իջնում է հորիզոնից ցած։ Այնտեղ կեսօրին Արեգակը զենիթում լինում է տարեկան երկու անգամ, այն է՝ գիշերահավասարի օրերին։

Երկրի վրա կան տեղեր, որտեղ Արեգակը տարեկան միայն մեկ անգամ է կեսօրին լինում զենիթում։ Դա տեղի է ունենում հունիսի 22-ին աշխարհագրական +23°27' լայնության վրա։ Այդ աշխարհագրական զուգահեռականը կոչվում է Խեցգետնի արևադարձ: Դեկտեմբերի 22-ին Արեգակը լինում է այն տեղերի զենիթում, որոնք գտնվում են հարավային -23°27՚ զուգահեռականի վրա։ Այդ զուգահեռականը կոչվում է Այծեղջյուրի արևադարձ:

Այդ աշխարհագրական զուգահեռականներն իրենց անվանումներն ստացել են հին ժամանակներում՝ այն կապակցությամբ, որ Արեգակի կուլմինացիան զենիթում տեղի էր ունենում արևադարձներում այն ժամանակ, երբ Արեգակը գտնվում էր Խեցգետնի և Այծեղջյուրի համաստեղություններում։ Այն ժամանակներում հենց այդ համաստեղություններումն էին գտնվում ամառվա և ձմեռվա արևադարձի կետերը, որոնք այն ժամանակվանից ի վեր անցած մի քանի հազարամյակների ընթացքում մինչև մեր օրերը փոխադրվել են հարևան Երկվորյակների և Աղեղնավորի համաստեղությունները։ «Արևադարձ» (տրոպիկ) անվանումը ծագում է հունարեն «տրոպոս» բառից, որ նշանակում է «դարձ»։ Այդ անվանումը կապված է Արեգակի դարձի հետ՝ երկնային հասարակածի նկատմամբ։

Երկրի բևեռներում, քանի դեռ Արեգակը գտնվում է հորիզոնից վեր, գծում է շրջանագծեր համարյա զուգահեռ հորիզոնին, որն այստեղ համընկնում է երկնային հասարակածի հետ։ Ինչպես արդեն մենք գիտենք, դա տևում է ոլղիղ կես տարի՝ հյուսիսային բևեռում մարտի 21-ից մինչև սեպտեմբերի 23-ը։ Քանի որ սկսած մարտի 21-ից մինչև հունիսի 22-ը Արեգակն անընդհատ բարձրանում է երկնային հասարակածից վեր՝ դեպի հյուսիս, ուստի մենք գալիս ենք հետևյալ եզրակացության․

Երկրի Կաղապար:Լայն Արեգակը ծագում է տարեկան մեկ անգամ՝ մոտավորապես մարտի 21-ին և, մայր չմտնելով, կես տարի շարունակ ամեն օր լրիվ շրջան է գծում հորիզոնից վեր, միաժամանակ մինչև հունիսի 22-ը հետզհետե քիչ-քիչ բարձրանում է հորիզոնից։ Պտտվելով հորիզոնի վրա, Արեգակը պարույրի փաթույթներ է գծում՝ բարձրանալով հետզհետե վեր։ Հունիսի 22-ից մինչև սեպտեմբերի 23-ը Արեգակը, նույնպես պարուրաձև պտույտներով, հետզհետե իջնում է դեպի հորիզոնը և սեպտեմբերի 23-ին մայր է մտնում ամբողջ կես տարով։ Բևեռում կես տարի տևում է գիշերը և կես տարի՝ ցերեկը։

Հյուսիսային բևեռից որքան հեռանանք դեպի հարավ, այնքան տարվա մեջ ավելի ու ավելի շատ այնպիսի օրեր կլինեն, երբ Արեգակը ծագում և մայր է մտնում, բայց այնուամենայնիվ ամռանը լինում է մի շրջան, երբ շատ օրեր շարունակ նա մայր չի մտնում, և ձմռանը լինում են օրեր, երբ նա բոլորովին չի ծագում։ Այդպիսի երևույթներ, մասնավորապես Արեգակի ստորին կուլմինացիան կես-գիշերին, ՍՍՌՄ-ում կարելի է դիտել Մուրմանսկում և մի շարք այլ բնակետերում, որոնք գտնվում են բևեռային շրջանից դեպի հյուսիս։

Դժվար չէ համոզվել այն բանում, որ Երկրի վրա կան այնպիսի տեղեր, որտեղ Արեգակը տարվա մեջ միայն մեկ անգամ, այն է՝ հունիսի 22-ին, մայր չի մտնում, այլ միայն շոշափում է հորիզոնը (հյուսիսի կետում) իր ստորին կուլմինացիայի մոմենտին (կես-գիշերին): Դեկտեմբերի 22-ին և միայն այդ օրը այդ վայրերում Արեգակը չի ծագում, այլ կեսօրին նա միայն շոշափում է հարավի կետը՝ մնալով հորիզոնից ցած։ Երկրագնդի վրա այդ վայրերը գտնվում են աշխարհագրական 66°33' զուգահեռականի վրա, որը կոչվում է հյուսիսային բևեռային շրջան։

Երկրի Կաղապար:Լայն նկատվում են ճիշտ նույն երևույթները, ինչ և հյուսիսային բևեռում, միայն այնտեղ բևեռային ցերեկը տևում է սեպտեմբերի 33-ից մինչև մարտի 21-ը, իսկ բևեռային գիշերը՝ մարտի 21-ից մինչև սեպտեմբերի 23-ը։ Հարավային բևեռային շրջանում (հարավային 66°33' լայնության վրա) առանց արևածագի օրը լինում է հունիսի 22-ին, իսկ առանց արևը մայր մտնելու օրը՝ դեկտեմբերի 22-ին։

Հյուսիսային բևեռային շրջանից փոքր-ինչ հարավ ընկած վայրերում, ինչպես, օրինակ, Լենինգրագում, հունիսի 22-ի մոտերքը գիշերները Արեգակն իջնում է հորիզոնից ցած, բայց ոչ այնքան երկար ժամանակով և ոչ այնքան խոր։ Ուստի նրա ճառագայթներն ուժեղ կերպով լուսավորում են երկինքը հորիզոնի մոտ («սպիտակ գիշերներ»)։

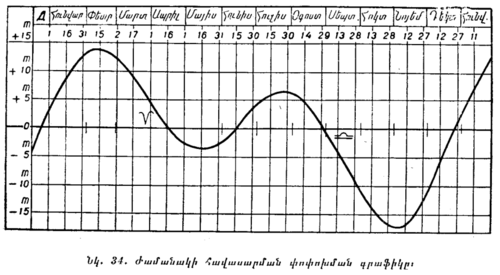
Բոլոր այստեղ ասածներից պարզ է, և դա պետք է լավ հիշել, որ արևածագի և արևամուտի ժամանակը կախված է ոչ միայն տարվա տվյալ օրից, այլև աշխարհագրական այն լայնությունից, որտեղ գտնվում է դիտողը: Ուստի սովորական օրացույցներում ցույց տրվող արևածագի և արևամուտի ժամանակը կարող է ճիշտ լինել միայն մի որևէ լայնության, այլ ոչ թե ամբողջ ՍՍՌՄ-ի համար։

ԵՐԿՐԻ ՇԱՐԺՈՒՄԸ

§ 32. ԵՐԿՐԻ ՊՏՈՒՅՏՆ ԱՐԵԳԱԿԻ ՇՈՒՐՋԸ. Արեգակի թվացող տարեկան շարժումը խավարածրով և դրա հետ կապված բոլոր այն երևույթները, որոնք նկարագրված են սույն գլխի նախորդ պարագրաֆներում, հետևանք են այն բանի, որ իրականում Երկիրը շարժվում է Արեգակի շուրջը:

Արեգակի շուրջը Երկրի գծած ուղին կոչվում է նրա ուղեծիրը (օրբիտ):

Արեգակի շուրջը Երկիրը մի լրիվ շրջան կատարում է 365¼ օրում (այդ ժամանակամիջոցը մենք անվանում ենք տարի)։ Ընդ որում Երկրի օրական պտույտի աոանցքը մնում է ինքն իրեն զուկահեո և Երկրի ոսլեծրի հարթության նկատմամբ չի փոխում իր թեքությունը:

Երկրի ուղեծրի (օրբիտի) հարթությունը երկնային սֆերայի հետ հատվում է մի գծով, որը և հենց խավարածիրն է հանդիսանում։ Այլ կերպ ասած՝ խավարածիրն այն գիծն է, որով Երկրի ուղեծրի հարթությունը հատում է երկնային սֆերային: Այդ հարթությունն անվանում են խավարածրի հարթություն։

Երկրի օրական պտույտի առանցքը խավարածրի հարթության նկատմամբ թեքված է 66½°-ով, իսկ հասարակածը խավարածրի նկատմամբ թեքված է 90° - 66½° = 23½°, ավելի ճիշտ` 23°27՛ անկյունով։

Քանի որ մենք Երկրի հետ միասին կատարած մեր շարժումը չենք զգում, ուստի մեզ թվում է, որ մենք անշարժ ենք, և որ Արեգակն է շարժվում խավարածրով։ Այսպիսով, Արեգակի շարժումը խավարածրով՝ Երկրի շարժման անդրադարձումն է։ Այդ մեզ համար ավելի պարզ կլինի, եթե դիտենք նկ. 30-ը, որտեղ գծագրի ձևով պատկերված է Երկրի շարժումը։ Եթե մենք գծագրի հարթության վրա մտքով Երկրի հետ միասին շարժվելու լինենք Արեգակի շուրջը, ապա մենք Արեգակը կտեսնենք միշտ նորանոր ուղղությամբ՝ տարբեր համաստեղությունների ուղղությամբ (համ․ § 30)։ Լրիվ շրջապտույտից հետո մեզ կթվա, որ իբր այդ ժամանակամիջոցում Արեգակը մի լրիվ շրջան կատարեց հենց նույն հարթության վրա, որով մենք ինքներս շարժվեցինք։ Եթե, օրինակ, Արեգակը գտնվում է Երկվորյակների համաստեղության ուղղության վրա, ապա Արեգակից նայելու դեպքում մենք Երկիրը ճիշտ հակադիր համաստեղության մեջ կտեսնեինք, մեր օրինակում՝ Աղեղնավորի համաստեղության մեջ։ Երկրից իր հերթին նայելիս այդ ժամանակ Աղեղնավորի համաստեղությունը կես-գիշերին կերևա հարավային կողմում։

§ 33. ԵՐԿՈՒ ՇԱՐԺՄԱՆ ԺԱՄԱՆԱԿ ՑԵՐԵԿՎԱ ՈԻ ԳԻՇԵՐՎԱ ԵՎ ՏԱՐՎԱ ԵՂԱՆԱԿՆԵՐԻ ՀԵՐԹԱՓՈԽՈՒԹՅՈՒՆԸ։ Հայտնի է, որ տվյալ մակերեսի վրա ընկնող ջերմության քանակը կախված է Արեգակի բարձրությունից. որքան Արեգակը հորիզոնից ավելի վեր է բարձրանում, այնքան նա ավելի ուժեղ է տաքացնում։ Երկրի վրա գոյություն ունեցող ջերմային տարբեր (տաք, բարեխառն և ցուրտ) գոտիները բացատրվում են նրանով, որ երկրագնդի տարբեր վայրերում Արեգակը տարբեր չափով է բարձրանում։ Հայտնի է նաև այն, որ մեզ մոտ ամառն Արեգակը ավելի վեր է բարձրանում և երկար է մնում հորիզոնի վրա, այսինքն՝ ցերեկը երկարատև է լինում (Մոսկվայում մոտ տասնյոթ ժամ, իսկ Երևանում 15 ժամից ավելի)։ Ձմեռը պատկերն այլ է․ Արեգակը հորիզոնից շատ չի բարձրանում, նրա ցերեկային տեսանելի ուղին մեծ չէ՝ ցերեկներր կարճ են։

Դրա հետ կապված ամեն տարի ցուրտ և տաք ժամանակներ են լինում, որոնք աստիճանաբար փոխարինում են մեկը մյուսին։ Բնության այդ երևույթը կոչվում է տարվա եղանակների հերթափոխություն:

Այդ փոփոխությունների պատճառն այն է, որ Երկրի առանցքը որոշ չափով թեքված է Երկրի ուղեծրի նկատմամբ և չի փոխում իր ուղղությանը Արեգակի շուրշը Երկրի կատարած պտույտի ժամանակ:

Դիմենք նկ․ 31-ին։

Նկարի աջ կողմում Երկրի առանցքի հյուսիսային ծայրը նայում է դեպի Արեգակը։ Երկրագնդի այս դիրքը համապատասխանում է ամռանը Երկրի հյուսիսային կիսագնդում և ձմռանը հարավային կիսագնդում։ Արեգակի ճառագայթները հյուսիսային կիսագնդի վրա ընկնում են ավելի փոքր թեքությամբ, ուստի և ավելի ուժեղ են տաքացնում Երկիրը, ճիշտ այնպես, ինչպես կեսօրին նրանք ավելի ուժեղ են տաքացնում գետինը, քան առավոտյան, երբ Արեգակի ճառագայթներն ավելի մեծ թեքությամբ են ընկնում։

Այս դիրքում հյուսիսային բևեռային շրջաններն օրեր շարունակ լուսավորվում են մայր չմտնող Արեգակի կողմից։ Ճիշտ նույնպես՝ օրեր շարունակ, այսինքն Երկրի՝ իր առանցքի շուրջը կատարած բազմաթիվ պտույտների ընթացքում, հարավային բևեռային շարջաններր զուրկ են մնում Արեգակի լույսից։ Այնտեղ երկարատև բևեռային գիշեր է։

Հյուսիսային միջին լայնություններում Երկրի օրական պտույտի ժամանակ նրա մակերևույթի յուրաքանչյուր կետն Արեգակի ճառագայթների տակ ավելի երկար ուղի է անցնում, այսինքն՝ ցերեկը երկար է լինում, քան գիշերը։ Իսկ Երկրի հարավային կիսագնդում հակառակ պատկերն է լինում, այնտեղ Արեգակի ճառագայթներն ընկնում են շեղակի՝ մեծ թեքությամբ, ցերեկները կարճ են լինում, գիշերները՝ երկար (ձմեռ է)։

Ինչպես § 28-ում մենք այդ արդեն նկարագրեցինք, ամառը Արեգակի ուղղության և Երկրի հասարակածի հարթության միջև ընկած անկյունը հասնում է առավելագույն չափին (23½°), այդ պատճառով ամառվա ամենաեռուն շրջանում Արեգակի կեսօրյա բարձրությունը Մոսկվայում հասնում ի համարյա 58°–ի (23½°+34½°)։

Հյուսիսային կիսագնդի համար Երկրի դիրքը ձմեռային արևադարձի ժամանակ պատկերված է նկարի ձախ կողմում։ Այս դիրքում Երկրի հյուսիսային կիսագնդի մասին ճիշտ նույնը կարելի է ասել, ինչ որ հենց նոր ասվեց Երկրի հարավային կիսագնդի մասին, և հակառակը։

Երկրի դիրքը գարնանային գիշերահավասարի մոմենտում պատկերված է նկ․ 31-ի ցածի մասում։ Մենք տեսնում ենք, որ Երկրի այս դիրքի ժամանակ Արեգակի ճառագայթները հասարակածի վրա ընկնում են ուղղաձիգ կերպով. Արեգակը գտնվում է երկնային հասարակածի լիրա։ Երկրի երկու կիսագնդերի միջին լայնություններում Արեգակի ճառագայթների անկման անկյունն իր մեծությամբ ամառվա և ձմեռվա շրջաններում ճառագայթների անկման անկյունների միջինն է կազմում։ Երկրի երկու բևեռներումն էլ Արեգակը երևում է հորիզոնի հարթության վրա, որովհետև այդ հարթությունը շոշափում է երկրագունդը նրա բևեռներում, ուստի և զուգահեռ է հասարակածի հարթությանը։

Արեգակն այնքան էլ մոտ չէ Երկրին, ինչպես այդ ցույց է տրված նկարում, այլ չափազանց հեռու է գտնվում։ Ուստի նրա ճառադա քթները Երկրի մակերևույթի վրա ընկնում են գրեթե միմյանց զուգահեռ։ Հետևաբար, Արեգակը գիշերահավասարի օրը գտնվելով երկնային հասարակածի վրա, միաժամանակ բևեռներում եղած՝ դիտողների համար գտնվում է նաև հորիզոնի հարթության վրա։ Երկիրը ճիշտ նույն դիրքն ունի Արեգակի ճառագայթների նկատմամբ նաև աշնանային գիշերահավասարի օրը։

Գիշերահավասարի օրերին գիշերվա և ցերեկվա սահմանն անցնում է Երկրի երկու բևեռներով և Երկիրն իր առանցքի շուրջը պտտվելու ժամանակ Երկրի ամեն մի կետը նրա թե՞ լուսավոր և թե՞ խավար կողմում միահավասար ուղի է անցնում, այսինքն՝ ամբողջ Երկրի վրա ցերեկը պետք է հավասար լինի գիշերվան։

ՀԱՐՑԵՐ ԻՆՔՆԱՏՈԻԳՄԱՆ ՀԱՄԱՐ

Նշեցեք արևադարձների և գիշերահավասարների ժամանակը և բնութագրեցե՛ք այդ ժամանակներին համապատասխանող ցերեկներն ու գիշերները։
Եթե տեղանքն ունի φ լայնություն, ապա ինչպիսի՞ն է այնտեղ Արեգակի կեսօրյա բարձրությունը հունիսի 22-ին, դեկտեմբերի 22-ին և գիշերահավասարի օրերին։
Ի՞նչ է խավարածիրը։
Ինչպիսի՞ անկյան տակ է խավարածիրը հատվում հասարակածի հետ։
*Ի՞նչ ուղղությամբ է տեղի ունենում Արեգակի թվացող շարժումը խավարածրով։
Ինչքա՞ն է, մոտավորապես, Արեգակը մեկ օրում տեղաշարժվում խավարածրով։
Գծագրեցե՛ք երկնային սֆերան հասարակածով և խավարածրով։ Նշեցե՛ք գծագրի վրա խավարածրի 4 հիմնական կետերը և ասացեք, թե ինչպե՞ս են նրանք կոչվում։
Ի՞նչ է Կենդանակերպը և կենդանակերպային համաստեղությունները։ Թվեցե՛ք այն։
Ինչպե՞ս է փոփոխվում տարվա ընթացքում Արեգակի օրական ճանապարհը երկնակամարում, ա) միջին լայնություններում, բ) երկրի հասարակածում և գ) Երկրի բևեռում գտնվող դիտողների համար։
Ի՞նչ են արևադարձները, ինչպե՞ս են նրանք կոչվում և ինչո՞ւ։
Ինչո՞վ է բնորոշվում հյուսիսային բևեռային շրջանի դիրքո Երկրի վրա։
Ի՞նչ հանգամանքներից է կախված Արեգակի ծագման ու մայրամուտի ժամանակը։
Ինչպե՞ս է կոչվում Երկրի ուղին Արեգակի շուրջը։
Ի՞նչ առնչություն կա նրա և խավարածրի միջև։
Ինչպիսի՞ անկյան տակ է թեքված Երկրի առանցքը նրա ուղեծրի հարթության նկատմամբ։ Փոխվո՞ւմ է արդյոք նա տարվա ընթացքում։
Ինչո՞վ են բացատրվում տարվա եղանակների հերթափոխությունները և նրանց ուղեկցող, տարբեր աշխարհագրական լայնություններում ցերեկվա ու գիշերվա տևողության փոփոխությունները։

ՎԱՐԺՈԻԹՅՈԻՆՆԵՐ

Ինչի՞ է հավասար Արեգակի կեսօրյա բարձրությունը ձեր բնակավայրում սեպտեմբերի 23-ին։
Լենինգրադի լայնությունը 60° է, Երևանինը՝ 40°։ Որոշեցե՛ք Արեգակի կեսօրյա բարձրությունը այդ քաղաքներում ամառային և ձմեռային արևադարձների ժամանակ և համեմատեցեք այն։
Ո՞րտեղ և ե՞րբ տան չորս պատերն էլ դարձած են դեպի հարավ, բայց պարզ երկնքի ժամանակ Արեգակը շատ օրերի ընթացքում նրանցից և ոչ մեկը չի լուսավորում։
Երկրի վրա ո՞րտեղ և ե՞րբ տներն ստվեր չեն գցում։
Օգոստոսի 5-ին Արեգակը Մոսկվայում մայր է մտնում մի որևէ ժամի։ Մայր կմտնի՞ արդյոք նա այդ նույն ժամին Թբիլիսիում և Արխանգելսկում։
Մարտի 21-ին Լենինգրադում Արեգակը մայր է մտել մի որևէ ժամի։ Մայր կմտնի՞ արդյոք նա այդ նույն ժամին Մինսկում, Ալմա-Աթայում և Նովոսիբիրսկում։
Արեգակի մայրամուտը օգոստոսի 5-ին ո՞րտեղ ավելի շատ կտարբերվի Մոսկվայի ժամանակից, Վլադիվոստոկում թե՞ Սիմֆերոպոլում։
Ինչպե՞ս կազդեր տարվա եղանակների վրա ձեր քաղաքում Երկրի առանցքի 45°–ի թեքությունը, այժմյան 66°½-ի փոխարեն։
Ինչպե՞ս կփոփոխվեր կլիման, եթե Երկրի առանցքը պառկած յիներ նրա ուղեծրի հարթության վրա։

ԺԱՄԱՆԱԿԻ ՉԱՓՈՒՄԸ

§ 34. ԻՐԱԿԱՆ ԱՐԵԳԱԿՆԱՅԻՆ ՕՐ։ Մարդկանց աշխատանքային ժամանակի բաշխումը կապված է ցերեկվա ու գիշերվա հերթափոխման հետ, ուստի և առօրյա կենցաղում ժամանակը որոշում են երկնքում Արեգակի ունեցած դիրքով։

Արեգակի սկավառակի կենտրոնի վերին կուլմինացիայի մոմենտոը կոչվում է իրական կեսօր։ Արեգակի տեսանելի սկավառակի կենտրոնի երկու հաջորդական վերին կուլմինացիաների միջև ընկած ժամանակամիջոցը կոչվում է իրական արեգակնային օր։ Իրական արեգակնային օրվա սկիզբ է ընդունվում կեսօրը։

Իրական արեգակնային օրվա տևողությունը տարվա ընթացքում ենթարկվում է փոփոխության՝ Երկիրն իր ուղեծրով անհավասարաչափ շարժվելու և երկրային հասարակածն այդ ուղեծրի նկատմամբ թեքված լինելու հետևանքով։

Հիշյալ երկու պատճառների շնորհիվ իրական արեգակնային օրվա տևողությունը տարվա ընթացքում փոփոխվում է չափազանց բարդ ձևով։ Աչ մի մեխանիկական ժամացույց չի կարող ճիշտ Արեգակի շարժման համապատասխան աշխատել։

Իրական արեգակնային ժամանակը կարող են ցույց տալ միմիայն արեգակնային ժամացույցները։ Նրանք իրենցից ներկայացնում են մի ձող կամ եռանկյունի, որի ստվերը ժամացույցի սլաքի դեր է կատարում, շարժվում է թվատախտակի դեր կատարող հարթ տախտակի մակերևույթով։ Տախտակի վրա տարված են գծեր, որոնց ուղղությամբ օրվա որոշ ժամերին ընկնում է ձողի ստվերը։ Այդ գծերի ծայրերին գրվում են օրվա ժամերի թվանշանները։

Արեգակնային ժամացույցները կարող են տարբեր տիպի լինել, բայց նրանց ձողը միշտ պետք է ուղղված լինի դեպի աշխարհի բևեռը։

§ 35*. ԱՐԵԳԱԿՆԱՅԻՆ ԺԱՄԱՑՈՒՅՑՆԵՐԻ ԿԱՌՈՒՑՎԱԾՔԸ։ Հասարակածային արեգակնային ժամացույց (նկ. 32) պատրաստելն ամենից հեշտ է։ Դրա համար վերցնում ենք մի տախտակ և նրա կենտրոնից տախտակի բոԼոբ կողմերի վրա տանում ենք հավասարապես տարածվող գծեր այնպես, որ երկու հարևան գծերի միջև րնկած անկյունը կազմի ուղիղ 15°, և գծերի ծայրերին նշանակում ենք 12 ժամ, 1 ժամ, 2 ժամ և այլն, քանի որ հասարակածային հարթության վրա ստվերը շարունակ շարժվում է հավասարաչափորեն։ Այդ գծերի հատման կետում տախտակին ուղղահայաց դիրքով ամրացնում ենք մի ձող։

Թեքելով տախտակն իր ձողի հետ միասին հորիզոնի նկատմամբ 45°-φ անկյան չափ, որտեղ (φ-ն դիտման վայրի աշխարհագրական լայնությունն է, տախտակն ամրացնում ենք այնպես, որ 12 թվանշանն ունեցող գիծը համընկնի ուղիղ միջօրեի գծի հետ։ Վերջինս արեգակնային ժամացույցի տեղակայմ ան վայրում որոշում և գծում ենք այնպես, ինչպես այդ նկարագրված է § 12-ում։

Այդպիսի ժամացույցի անհարմարությունն այն Է, որ սեպտեմբերի 23-ից մինչև մարաի 21-ը ձողի ստվերը թվատախտակի վրա ցածից է ընկնում։

Հորիզոնական արեգակնային ժամացույցը (նկ․ 33) այդ տեսակետից ավելի հարմար է։ Վերցնում ենք մի տախտակ և նրա վրա ուղղահայաց դիրքով ամրացնում սուրանկյուն եռանկյունի, որի սուր անկյունը հավասար է տեղավայրի φ լայնությանը։ Որպես եռանկյան հիմքի շարունակություն տանում ենք մի գիծ և այդ գծի ծայրին գրում ժամը 12-ը։ Մյուս ժամերին համապատասխանող գծերը տանում ենք այդ գծից x անկյան տակ՝ նայած աշխարհագրական լայնությանը, հաշվելով երանգ հետևյալ ֆորմուլայով,

tgx = sinφ tgt.

որտեղ t-ի փոխարեն, որ հավասար է 1 ժամի, 2 ժամի, 3 ժամի և այլն, գրում ենք 25°, 30°, 45° և այլն։ Հաջորդական Ժամերի միջև ընկած x անկյունը հավասար չէ 15°-ի, ինչպես այդ հասարակածային ժամացույցումն էր, որովհետև Արեգակի t ժամային անկյունը համաչափ փոփոխվելու պայմաններում ձողի ստվերը հորիզոնական հարթության վրա անհամաչափորեն է տեղափոխվում։

Հորիզոնական արեգակնային ժամացույցների թվատախտակի միջօրեի գիծը նույնպես պետք է տանել հյուսիսից–հարավ ուղղությամբ։

§ 36. ՄԻՋԻՆ ԱՐԵԳԱԿՆԱՅԻՆ ԺԱՄԱՆԱԿ ԵՎ ԺԱՄԱՆԱԿԻ ՀԱՎԱՍԱՐՈՒՄ․ Իրական արեգակնային օրերը տարվա տարբեր Ժամանակներում իրար հավասար չլինելու հանգամանքը խանգարում է իրական արեգակնային ժամանակից օգտվելուն։ Ուստի գործնականում օգտվում են այսպես կոչված միջին արեգակնային ժամանակով, որը միանգամայն համաչափ է ընթանում և համապատասխանում է միջին օրերի Ժամին, իսկ միջին օրը՝ դա իրական օրերի միջին տևողությանն է։

Տարբերություն․ միջին ժամանակից հանած իրական ժամանակը կոչվում է ժամանակի հավասարում։ Այլ կերպ ասած՝ ժամանակի հավասարումն այն հանրահաշվական մեծությունն է, որ պետք է գումարել (իր պլյուս կամ մինուս նշանով) իրական ժամանակին, որպեսզի ստացվի միջին ժամանակը։

Տարվա ընթացքում ժամանակի հավասարումը փոփոխվում է բարդ ձևով, ինչպես այդ ցույց է տրված կորագծով) նկ․ 34-ում։ ժամանակի հավասարման առավելագույն մեծությունը կազմում է 16½ րոպե (մինուս նշանով, նոյեմբերի մոտ 3-ին)։

Ուրեմն, միջին ժամանակն ստանալու համար հարկավոր է արեգակնային ժամացույցի ցուցմունքին՝ որը ցույց է տալիս իրական արեգակնային ժամանակը, ավելացնել տարվա տվյալ օրվան համապատասխանող ժամանակի հավասարումը։ Այդ հավասարման մեծությունը տարվա ցանկացած օրվա համար հեշտությամբ կարելի է հաշվել, օգտվելով նկ. 34-ի կորագծից։ Աստղագիտական, բոլոր օրացուցային տեղեկատուներում զետեղվում են ժամանակի հավասարման աղյուսակներ։

§ 37. ՏԵՂԱԿԱՆ ժԱՄԱՆԱԿ ԵՎ ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԵՐԿԱՅՆՈՒԹՅՈՒՆ։ Արեգակնային ժամանակը, որը որոշվում է երկնքում Արեգակի ունեցած դիրքով, տարբեր կլինի Երկրի տարբեր միջօրեականների վրա գտնվող վայրերի համար, ուստի այդպիսի ժամանակը կոչվում է տեղական ժամանակ։

Նկ. 35-ում պատկերված է երկրագունդը, որին նայում ենք Երկրի առանցքի ուղղությամբ՝ հյուսիսային բևեռից։

Ենթադրենք, որ Աստրախանում կեսօր է։ Ինչքա՞ն ժամանակից հետո Մոսկվայում վրա կհասնի կեսօրը, եթե Մոսկվայի երկայնությունը՝ λ = 2 ժ. 30 ր., իսկ Աստրախանինը՝ λ_A = 3 ժ. 12 ր.։ Ակնհայտ կեսօրը Մոսկվայում վրա կհասնի այն ժամանակ, երբ Երկիրը կպտտվի այնպիսի անկյունով, ինչպիսին կա զմում են Աստրախանի և Մոսկվայի միջօրեականների հարթությունները, այսինքն՝λ_A - λ = 0 ժ 42 ր. անկյունով։ Ըտյց երբ Մոսկվայում վրա հասնի կեսօրը, ապա Աստրախանում արդեն կլինի ցերեկվա ժամը 12 անց 42 րոպե։ Հետևաբար, Երկրի երկու տարբեր կետերում տեղական ժամանակները տարբերվում են ճիշտ այնքանով, որքանով տարբերվում են այդ կետերի երկայնությունները։

§ 38. ԺԱՄԱՆԱԿԻ ՏԵՂԱԿԱՆ, ԳՈՏԻԱԿԱՆ ԵՎ ԴԵԿՐԵՏԱՅԻՆ ՀԱՇԻՎԸ։ Ներկայումս օրվա հաշիվը, որպես կանոն, տարվում է սկսած կես-գիշերից։

Եթե օգտվելու լինենք վերը նկարագրված ժամանակի տեղական հաշվով, ապա այն վայրերում, որոնք ըստ իրենց երկայնության թեկուզ չեչին չափով զանազանվում են միմլանցից, կարիք է լինում ժամանակն արդեն մի քիչ այլ կերպ հաշվել։ Դա մեծ անհարմարություններ է ստեղծում։

Համարյա թե բոլոր երկրներում ընդունված է այսպես կոչված ժամանակի գոտիական հաշիվը, որի էությունը հետևյալն է.

Երկրագնդի ամբողջ մակերևույթը միջօրեականներով բաժանված է 24 գոտիների (նկ. 36), այնպես որ, միջօրեականները՝ յուրաքանչյուր գոտու սահմանները մեկը մյուսից գտնվում են 15°, այսինքն՝ 1 ժամ հեռավորության վրա։ Հետևաբար, գոտու ծայրամասերում տեղական ժամանակը գոտու կենտրոնի տեղական ժամանակից տարբերվում է կես ժամով։ Սկզբնական գոտու միջին միջօրեականը, որ կրում է զրո համարը, Ղրէնվիչի միջօրեականն է։ Հաջորդ գոտին արևելյան ուղղությամբ կոչվում է առաջին (I) գոտի և այլն։

Պայմանավորվել են յուրաքանչյուր գոտու ներսում ժամանակը հաշվել այդ գոտու միջին միջօրեականի տեղական ժամանակով, և ոչ թե ամեն մի վայրի՝ իրեն տեղական ժամանակով։ Օրինակ, Ուֆայում և Սամարղանդում ժամը 12-ը համարում են այն ժամանակ, երբ Սվերդլովսկում, որն ընկած է IV գոտու գրեթե մեջտեղում, տեղական ժամանակով ժամը 12-ն է։ Քանի որ Ուֆայի երկայնությունը հավասար է 3 ժամ 44 րոպեի, իսկ Սամարղանդի երկայնությունը՝ 4 ժամ 28 րոպեի, ուստի Ուֆայում գոտիական ժամանակը տեղականից առաջ է 4 ժամ — 3 ժամ 44 րոպե, այսինքն՝ 16 րոպեով, իսկ Սամարղանդի գոտիական ժամանակը տեղականից ետ է մնում 4 ժամ 28 րոպե — 4 ժամ = 28 րոպեով։ Իմանալով վայրի երկայնությունը և այն գոտու համարը (տե՛ս V աղյուսակը՝ հավելված), որտեղ նա գտնվում է, հեշտությամբ կարելի է հաշվել տեղական ժամանակի և գոտիական ժամանակի միջև եղած տարբերությունը։

Արևելյան կողմի հարևան գոտում նույն մոմենտում ամենուրեք ընդունում են մեկ ժամով ավելի։ Ժամային գոտու սահմանն անցնելուց ժամացույցը պետք է ոլդիղ մեկ ժամով առաջ կամ ետ գցել։ Գոտիական ժամանակով ապրող բոլոր երկրներում րոպեները ցույց տվող սլաքների դիրքը միևնույն մոմենտում համընկնում է. տարբերվում է միայն ժամասլաքների դիրքը՝ գոտիներին համապատասխան։

Զանազան պատճառներով՝ ժամային դոտիների սահմանները պայմանավորվել են երբեմն անցկացնել ոչ թե ուղիղ միջօրեականով, այլ գետերի, երկաթուղիների, մարզերի և այլ տեսակի բնագծերով։ Օրինակ, II և III ժամագոտիների միջնասահմանը, եթե այն անցկացնելու լինենք 2 ժամ 30 րոպե երկայնություն ունեցող միջօրեականի ուղղությամբ, կանցներ ուղիղ Մոսկվայի վրայով։ Ուստի այդ սահմանը տեղափոխված է մի քիչ դեպի արևելք, ներգրավելով Մոսկվայի մարզի արևելյան շրջանները։ Երկաթուղային տրանսպորտում գնացքների չվացուցակներն ամբողջ ՍՍՌՄ-ում կազմվում են այն ժամանակով, որը ընդունված է Մոսկվայում։

Էլեկտրոէներգիան և էներգիա արտադրելու ու լուսավորության նպատակներով գործածվող վառելանյութերն ավելի ռացիոնալ կերպով ծախսելու համար, ըստ որում այնպես, որ մարդիկ ստիպված չլինեն փոխելու իրենց աշխատանքային օրվա սովորական կարգն ու կանոնը, ՍՍՌՄ ԺԿՍ 1930 թ. հունիսի 16-ի դեկրետով ամբողջ երկրում ժամային սլաքները մեկ ժամով առաջ են ցցված։ Այս ձևով ստացված ժամանակի հաշիվը կոչվում է դեկրետային հաշիվ։

Այսպիսով, դեկրետային ժամանակը հավասար է գոտիական ժամանակին գումարած մեկ ժամ։

Երբեմն կարիք է լինում հաշվել, թե ե՞րբ կլինի իրական կեսօրը մեր ժամացույցով, որն աշխատում է դեկրետային ժամանակով։ Այստեղ ցույց կտանք, թե ի նչպես պետք է անել այդ՝ կոնկրետ օրինակի վրա։

Դիցուք հարկավոր է որոշել նոյեմբերի 6-ի իրական կեսօրի մոմենտը մի ժամացույցով, որն աշխատում է Սարատովում ընդունված սովորական ժամանակով և որն ունի 4 րոպեի ուղղում այդ ժամանակի համար։ Պարտեզի միջոցով պարզում ենք, որ Սարատովը գտնվում է III ժամագոտում։ Հետևաբար, Սարատովում ընդունված դեկրետային ժամանակը 3 ժամ + 1 ժամ, այսինքն՝ 4 ժամ 0 րոպեով առաջ է Գրինվիչի ժամանակից։ Մինչդեռ Սարատովփ երկայնությունը հավասար է 3 ժամ 4 րոպեի, ուստի և Սարատովի տեղական միջին ժամանակը պետք է որ 3 ժամ 4 րոպեով առաջ լինի Գրինվիչի ժամանակից։

Պարզ է, որ Սարատովում տեղական միջին ժամանակը 4 ժամ 0 րոպեից — 3 ժամ 4 րոպեով, այսինքն՝ 56 րոպեով ետ է մնում դեկրետային ժամանակից։ Օրացույցից կամ 34-րդ նկարից իմանում ենք, որ նոյեմբերի 6-ի ժամանակի հավասարումը կազմում է 16 րոպե, այսինքն՝ այդքան րոպե պետք է ավելացնել (հանրահաշվորեն) իրական ժամանակին, որպես ստացվի միջին ժամանակը։

իրական արեգակնային ժամանակով իրական կեսօրը 13 ժամ 0 րոպեին է, իսկ տեղական միջին ժամանակով այս դեպքում կեսօրը լինում է 12 ժամ 0 րոպեից — 16 րոպե = 11 ժամ 44 րոպեին։ Դեկրետային ժամանակը Սարատովում տեղական միջին ժամանակից առաջ է անցնում 56 րոպեով (տե՛ս վերը), և հետևաբար, իրական կեսօրի մոմենտին դեկրետային ժամանակով աշխատող ժամացույցները ցույց կտան 11 ժամ 44 րոպե + 56 րոպե = 12 ժամ 40 րոպե։ Սակայն մեր ժամացույցը Սարատովում 4 րոպեով առաջ է անցնում դեկրետային ժամանակից (տե՛ս վերը)։ Նշանակում է, վերջին հաշվով, այդ ժամացույցը իրական կեսօրին պետք է ցույց տա 12 ժամ 44 րոպե։

§ 39. ՏԱՐԵԹՎԻ (ԱՄՍԱԹՎԻ) ՓՈՓՈԽՄԱՆ ԳԻԾԸ։ Անհրաժեշտ է պայմանավորվել, թե Երկրի միջօրեականներից որի՞ վրա է առաջինը սկսվում նոր ամսաթիվ, օրինակ, Երկրի վրա որտե՞ղ է առաջինը սկսվում հունվարի 1-ը։ Եթե մի այդպիսի գիծ չսահմանվի, ապա բազմաթիվ թյուրիմացություններ տեղի կունենան։

Պայմանավորվել են, որ յուրաքանչյուր նոր թվական, ամսվա ամեն մի նոր օրը սկսվում է այն գծի վրա, որն անցնում Գրինվիչից 180°-ի միջօրեականի մոտերքով՝ Ասիայի և Ամերիկայի միջև։ Այսպիսով, տարվա ամեն մի նոր օրը սկսվում է Կամչատկայի վրա, այնուհետև՝ Սիբիրում, հետո՝ Եվրոպայում և ամենից ուշ՝ Ալյասկայում։

Արևելյան ուղղությամբ ամսաթվի փոփոխման գիծը հատող նավի վրա միևնույն ամսաթիվը վերա դրվում է երկու հաջորդական օրերին։ Օրինակ, այդ գիծը ապրիլի 13-ին՝ հինգշաբթի օրը հատելու դեպքում նավի վրա հաջորդ օրը դարձյալ անվանում են հինգշաբթի՝ ապրլի 13֊ը։ Այդ գիծն արևմտյան ուղղությամբ հատելու դեպքում՝ նավի վրա մեկ օրը բաց է թողնվում։ Օրինակ, ապրիլի 15-ի շաբաթ օրվան հաջորդող օրն անվանում են ապրիլի 17-ը՝ երկուշաբթի։ Երբ այդպիսի նավերը հասնում են նավահանգիստ, նրանց ամսաթիվը համընկնում է նավահանգստի բնակիչների ամսաթվին։

§ 40. ԺԱՄԱՅԻՆ ԱՆԿՅՈՒՆ ԵՎ ԺԱՄԱՆԱԿԻ ՉԱՓՈՒՄ, Նկ. 37-ում միաժամանակ արտահայտված են հասարակածային կոորդինատները և ժամային անկյունը։ Որևէ M կետի հակման շրջանի և դիտողի MPZS միջօրեականի կազմած անկյունը ի հակադրություն α անկյան, երկնային սֆերայի պտտվելու հետևանքով, ժամանակի ընթացքում փոփոխվում է միևնույն անկյունային արագությամբ։

Aq աղեղը, որը հաշվվում է երկնային հասարակածով ժամացույցի սլաքի շարժման ուղղությամբ՝ դիտողի միջօրեականի հարավային մասից մինչև M կետով անցնող հակման շրջանը, կոչվում է տվյալ կետի t ժամային անկյուն, նա արտահայտվում է ժամանակի միավորներով։

Ժամային անկյան հասկացողությունը հնարավորություն է տալիս ավելի ճիշտ կերպով սահմտնել ժամանակի չափման եղանակը. Իրական արեգակնային ժամանակը հաշված կեսօրից, չափվում է Արեգակի ժամային անկյունով։

§ 41. ԱՍՏՂԱՅԻՆ ԺԱՄԱՆԱԿ ԵՎ ԱՐԵԳԱԿՆԱՅԻՆ ԺԱՄԱՆԱԿ։ Գարնանային գիշերահավասարի կետը, ինչպես և երկնային սֆերայի ամեն մի կետ, տվյալ դիտողի համար ունի ժամային անկյուն, որը ժամանակի ընթացքում փոփոխվում է համաչափորեն։

Գարնանային գիշերահավասարի կետի ժամային անկյունը կոչվում է աստղային ժամանակ (նշանակվում է s տառով)։ Նկ. 37-ում նա պատկերված է Aqγ աղեղով։

Ակներև է, որ գարնանային գիշերահավասարի կետի վերին կուլմինացիայի մոմենտին աստղային ժամանակը՝ s = 0։

Աստղադիտարաններում կան այնպիսի ժամացույցներ, որոնք աշխատում են ըստ աստղային ժամանակի և գարնանային գիշերահավասարի կետի վերին կուլմինացիայի մոմենտին ցույց են տալիս 0 ժամ 0 րոպե 0 վայրկյան։

Քանի որ լուսատուի վերին կուլմինացիայի մոմենտում նրա ժամային անկյունը՝ t = 0, ուստի այդ լուսատուի համար՝

s = α,

այսինքն՝ աստղային ժամանակը հավասար է այդ մոմենտին վերին կուլմինացիայում ղտնվող լուսատուների ուղղակի ծագմանը։ Այդ կարևոր կանոնը անհրաժեշտ է հիշել նաև այս ձևակերպմամբ. յուրաքանչյուր լուսատու վերին կուլմինացիայումն է գտնվում աստղային ժամանակի այն մոմենտին, որը հավասար է այղ լուսատուի ուղղակի ծագմանը։

Աստղային օր կոչվում է այն ժամանակամիջոցը, որն անցնում է գարնանային գիշերահավասարի կետի երկու հաջորդական վերին կուլմինացիաների միջև։ Դժվար չէ կռահել, որ դա այն ժամանակամիջոցն է, որի ընթացքում Երկիրը մի լրիվ պտույտ է կատարում իր առանցքի շուրջը։

Աստղային օրը արեգակնային օրից կարճ է մոտավորապես 4 րոպեով։ Աստղային ժամանակը արեգակնային ժամանակի համեմատությամբ անընդհատ առաջ է անցնում, որը տարվա ընթացքում կազմում է մեկ օր։

§ 42. ԱՐԵԳԱԿՆԱՅԻՆ ԺԱՄԱՆԱԿԻ ԿԱՊՆ ԱՍՏՂԱՅԻՆ ԺԱՄԱՆԱԿԻ ՀԵՏ, ԼՈԻՍԱՏՈՒՆԵՐԻ ԿՈՒԼՄԻՆԱՅԻԱՅԻ ՄՈՄԵՆՏՆ ԸՍՏ ԱՐԵԳԱԿՆԱՅԻՆ ԺԱՄԱՆԱԿԻ։ Գարնանային դիշերահավա սարի կետի վերին կուլմինացիայի մոմենտին աստղային ժամանակը հավասար է 0 ժամ 0 րոպե 0 վայրկյանի։ Մարտի 21-ին Արեգակը գտնվում է այդ կետի մոտերքում։ Ուստի այդ զբր տեղական արեգակնային և աստղային ժամանակները գրեթե համընկնում են, քանի որ աստղային ժամանակը արեգակնայինից առաջ է անցնում գրեթե 4 րոպեով (ավելի ճիշտ՝ 3 րոպե 56 վրկ.), ուստի նա 30-օրյա ամսվա ընթացքում արեգակնային ժամանակից առաջ կանցնի մոտավորապես 2 ժամով, իսկ տարվա ընթացքում՝ ուղիղ մեկ օրով։

Դժվար չէ հաշվել, որ կեսօրին աստղային ժամանակը մոտավորապես հավասար է․

մարտի 21-ին հավասար է 0 ժամ 0 րոպեի

մարտի 22-ին հավասար է 0 ժամ 4 րոպեի

մարտի 23-ին հավասար է 0 ժամ 8 րոպեի և այլն։

Որպեսզի տեղական կեսօրից հետո տվյալ ժամի համար ստանանք մոտավոր աստղային ժամանակը, հարկավոր է աստղային ժամանակը հաշվարկեց տարվա տվյալ օրվա կեսօրի համար և դրան ավելացնել կեսօրից մինչև տվյալ մոմենտն անցած ժամանակամիջոցը։

Օրինակի համար, հաշվարկենք մայիսի 1-ի երեկոյան ժամը 10-ի (տեղական արեգակնային ժամանակով) աստղային ժամանակը։ Մարտի 21-ից մինչև մայիսի 1-ը անցել է 41 օր, հետևաբար, մայիսի 1-ի կեսօրին աստղային ժամանակը հավասար կլինի 4 րոպե ՞՞՞x 41 = 164 րոպե = 2 ժամ 44 րոպեի։ Կեսօրից մինչև երեկոյան ժամը 10-ն անցել է ես 10 Ժամ, հետևաբար, մայիսի 1-ի երեկոյան ժամը 10-ին աստղային ժամանակը հավասար է 2 ժամ 44 րոպե + 10 ժամ = 12 ժամ 44 րոպեի։

Տարվա տվյալ օրվա համար աստղային տվյալ ժամանակին համապատասխանող իրական արեգակնային ժամանակը ստանալու համար, հարկավոր է աստղային ժամանակի այդ մոմենտից հանել տարվա տվյալ օրվա կեսօրին համապատասխանող աստղային ժամանակը։

Օրինակի համար, հաշվարկենք հուլիսի 3-ի աստղային ժամանակով ժամը 20-ին համապատասխանող իրական արեգակնային ժամանակը։ Մարտի 21-ից մինչև հուլիսի 3-ն անցել է 104 օր, հետևաբար, հուլիսի 3-ի կեսօրին աստղային ժամանակը կլինի 4 րոպե ՞՞՞ 104 = 416 րոպե = 6 ժամ 56 րոպեի։ Հուլիսի 3-ին աստղային ժամանակով ժամը 20-ին արեգակնային ժամանակով կլինի 20 ժամից — 6 ժամ 56 րոպե = 13 ժամ 4 րոպեի կեսօրից հետո, այսինքն՝ գիշերվա ժամը 1-ն անց 4 րոպեի։

Աստղային ժամանակը միջին տեղական արեգակնային կամ դեկրետային ժամանակի վերածելու համար և ընդհակառակն, հարկավոր է հաշվի առնել նրանց զանազանությունը իրական արեգակնային ժամանակից։

Այս բոլոր ասածներից հետևում է, որ երբ լուսատուի ուղղակի ծագումը հայտնի է, նրա կուլմինացիայի մոմենտը կարելի է հաշվարկել հետևյալ կերպ.

Աստղային ժամանակով լուսատուի կուլմինացիայի մոմենտը հավասար է նրա ուղղակի ծագմանը։ Որպեսզի լուսատուի տվյալ օրվա կուլմինացիա փ մոմենտն ստանանք արեգակնային ժամանակով, հարկավոր է աստղափքւ ժամանակի այղ մոմենտը վերածել արեգակնային ժամանակի մոմենտի, ղեկավարվելով այս պարագրաֆում նկարագրված կանոնով։

Մեզ հետաքրքրող լուսատուի ուղղակի ծագումը կարող ենք իմանալ որևէ տեղեկագրքից, կամ որոշել այն ըստ աստղային քարտեզի կամ աստղային գլոբուսի, օգտվելով նրանց վրա գծագրված կոորդինատացանցից։

Օգտվելով նախորդ օրինակի թվական տվյալներից, կարելի էր, օրինակ, հաշվել, որ այն աստղը, որի ուղղակի ծագումը՝ ՞՞՞ = 20 ժամի, հուլիսի 3-ին կոլյմինացիա կկատարի գիշերվա 1 ժամ 06 րոպեին։ Ավելի ճշգրիտ հաշվարկումները պահանջում են տարբերել աստղային ժամանակը իրական և միջին կեսօրին և հաշվի առնել, որ աստղային ժամանակը հոսում է արեգակնայինից արագ, օրինակ, կեսօրից անցած 6 արեգակնային ժամի փոխարեն անցնում է աստղային ժամանակի 6 Ժամ 1 րոպե։

§ 43. ՍՏՈՒՅԳ ԺԱՄԱՆԱԿԻ ԾԱՌԱՅՈՒԹՅՈՒՆ։ Ճիշտ ժամանակն իմանալու կարիքն զգում են հիմնարկությունները, գործարանները, հեռագրատունը, տրանսպորտային կազմակերպություններն ու առանձին քաղաքացիներ։ Երկաթուղային տարբեր կայարաններում ժամացույցները սխալ և միմյանց հետ չհամաձայնեցված կերպով աշխատելու հետևանքով կարող են գնացքների ընդհարումներ տեղի ունենալ։ Հիշյալ «ստույգ ժամանակի օգտագործողները» պետք է ժամանակն իմանան մինչև մեկ րոպեի ճշտությամբ և հենց այդ ճշտությամբ էլ նրանք ստուգում են իրենց ժամացույցները։

Արտագրության և տրանսպորտի մի քանի տեսակներ կարիք են ունենում ժամանակն իմանալու մինչև մեկ վայրկյանի, իսկ հաճախ նույնիսկ մինչև վայրկյանի հարյուրերորդական մասի ճշտությամբ։ 0րինակ, Երկըի տարրեր վայրերում ծանրության ուժը չափելու միջոցով օգտակար հանածոների հետախուզությունը, աշխարհագրական քարտեզներ կազմելը, բաց ծովում նավավարումը պահանջում են Ժամացույցի առավել ճիշտ ստուգում և այն էլ օրական մի քանի անգամ, որովհետև ամեն մի ժամացույց, թեկուզ և շատ չնչին չափով, կարող է առաջ անցնել կամ ետ մնալ։

Այդ նպատակի համար և՛ ՍՍՌՄ-ում, և՛ ուրիշ երկրներում կազմակերպված է «ստույգ ժամանակի ծառայություն»։ Նրա խնդիրն է որոշել, պահպանել և հադորդել ստույգ ժամանակը։

Ստույգ աստղային ժամանակը որոշվում է աստղադիտարաններում՝ աստղերը գիտելու միջոցով։

Աստղային ժամանակը հեշտությամբ կարելի է վերածել արեգակնային ժամանակի։ (Ժամանակը որոշելն անմիջապես Արեգակը գիտելու միջոցով նվազ ճշտություն է տալիս, իսկ արեգակնային ժամացույցների անբավարար ճշտության մասին խոսելն անգամ ավելորդ է)։

Ստույգ ժամանակի պահ պան ումը կայանում է նրանում, որ հնարավորին չափ հաճախակի որոշում են աստղադիտարանի միևնույն (գլխավոր) ժամացույցների ուղղումները և ուսումնասիրում այդ ժամացույցների աշխատանքի ընթացքը՝ թե օրվա ընթացքում որքանով է նա առաջ անցնում կամ ետ մնում։

Ստույգ ժամանակի հաղորդումը կատարում են ռադիոկայաններն ավտոմատիկորեն՝ աստղադիտարանի ժամացույցի ճոճանակի օգնությամբ ձա յն ահ աղո րղիչում էլեկտրական հոսանքի միացումով։ Ժամանակի այդ ռադիոհաղորդումը տրվում է ՍՍՌՄ-ի և երկրագնդի տարբեր ռադիոկայանների կողմից, որոշակի ժամերի։ ՍՍՌՄ-ի լայն հաղորդիչ ռադիոկայանները մոտավորապես 0,1 վայրկյանի ճշտությամբ ժամանակը հաղորդում են երկու նախազգուշական երկարատև հնչյունի և մեկ կարճ հնչյունի ձևով, որը նշում է ժամանակի որոշ մոմենտը։ Ռադիոհեռագրակայաններր ժամանակի ազդանշանները հաղորդում են մեծ ճշտությամբ՝ ավելի բարդ կանոններով։

§ 44. ԱՍՏՂԱԳԻՏՈՒԹՅԱՆ ԳԼԽԱՎՈՐ ԳՈՐԾՆԱԿԱՆ ԿԻՐԱՌՈՒԹՅՈԻՆՆԵՐԸ։ Աստղագիտության գլխավոր գործնական կիրառությունները կատանում են ժամանակը ճիշտ չափելու և կողմնոաշման զանազան եղանակների մեջ։

Ճիշտ ժամանակն իմանալու կարիքն ունեն առանձին քաղաքացիները, հիմնարկությունները (առանձնապես երկաթուղիներն ոլ կապի հիմնարկները), արտադրություններից շատերը, օգտակար հանածոներ փնտրողները, Սովետական Բանակն ու ն ավատ որմը, նույնպես և բոլոր նրանք, ովքեր զգում են աստղագիտական կողմնորոշման կարիքը, այսինքն՝ գեոդեզիստ–քարտեզագիրները, ծովագնացները, օդաչուները, ճանապարհորդները, նոր երկրներ ու վայրեր հետազոտոդներր և այլն։

Աստղագիտական կողմնորոշումը կայանում է հարկավոր ուղղությունը (հյուսիսը, հարավը և այլն) որոշելու մեջ, նույնպես և երկրագնդի վրա դիտողի տեղը, այսինքն՝ աշխարհագրական լայնությունն ու երկաթյությունը որոշելու մեջ։ Լայնությունն ու երկայնությունը կարելի է որոշել միայն աստղագիտական դիտումների նիման վրա։

ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԿՈՈՐԴԻՆԱՏՆԵՐԻ ՈՐՈՇԵԼԸ

§ 45. ԱՇԽԱՐՀԱԳՐԱԿԱՆ ԵՐԿԱՅՆՈՒԹՅԱՆ ԵՎ ԼԱՅՆՈՒԹՅԱՆ ՈՐՈՇԵԼԸ։ Աշխարհագրական երկայնությունը որոշվում է տվյալ մոմենտում տվյալ կետի տեղական ժամանակը սկզբնական միջօրեականի (կամ այն կետի, որի երկայնությանն արդեն հայտնի է) տեղական ժամանակի հետ համեմատելու միջոցով, քանի որ երկու կետերի աշխարհագրական երկայնությունների տարբերությունը հավասար է նրանց միևնույն մոմենտին համապատասխանող տեղական ժամանակների տարբերությանը (տե՛ս § 37)։

Այսպիսով՝ աշխարհագրական երկայնությունը որոշելու խնդիրը վեր է ածվում երկու խնդրի, որոշել տվյալ կետի տեղական ժամանակը և իմանա, մի որևէ կետի տեղական ժամանակը, որի աշխարհագրական երկայնությունն արդեն հայտնի է։

Նախապես հայտնի աշխարհագրական երկայնության ունեցող բնակավայրի տեղական ժամանակը կարելի է իմանալ, ընդունելով այդ կետից ոադիոյով հաղորդվող հիշտ ժամանակի ազդանշանները։ Ռադիոազդանշանների ընդունման մոմենտին պետք է նշեք սեփական ժամացույցի ցուցումը, որն աշխատում է ըստ տեղական ժամանակի։

Օրինակ, հայտնի է, որ Մոսկվայի ռադիոկայանը դեկրետային ստույգ ժամանակի ազդանշանը հաղորդում է ճիշտ 19 ժամ 00 րոպեին։ Այդ ազդանշանը կլինի 11 գոտու +1 ժամ ժամանակով, այսինքն՝ այն միջօրեականի ժամանակով, որի երկայնությունը հավասար է 3 ժամ 00 րոպե 00 վայրկյան։

Օգտվելով աստղագիտական դիտումներից՝ աստղագետը իր ժամացույցը դրել է ըստ տեղական ժամանակի։ Մոսկվայի ոագիոագգանշանը նա ընդունել է, երբ նրա ժամացույցը ցույց է տվել 23 ժամ 49 րոպե։ Դրանից նա եզրակացնում է, որ իր բնակավայրի երկայնությունը հավասար է՝ 23 ժամ 49 րոպե — 19 ժամ 00 րոպե = 4 ժամ 49 րոպեի, այսինքն՝ այղքանով նա դեպի արևելք է գտնվում այն միջօրեականից, որը Գրինվիչի նկատմամբ ունի 3 ժամ 00 րոպե 00 վայրկյան երկայնություն։ Հետևապես, տվյալ կետի երկայնությունը Գրինվիչի նկատմամբ հավասար է 4 ժամ 49 վայրկյան + 3 ժամ = 7 Ժամ 49 րոպեի։

Աշխարհագրական յայնության որոշումը կատարվում է վերին կամ ստորին կուլմինացիայի ժամանակ Րևեռային աստղի՝ հորիզոնի նկատմամբ ունեցած բարձրությանը որոշելու միջոցով, հաշվի առնելով նաև նրա հեռավորությունը աշխարհի բևեռից։ Գոյություն ունեն նաև այլ, ավելի բարդ եղանակներ՝ լայնությունը որոշելու համար։ Աշխարհագրական լայնության և երկայնության որոշելը հանդիսանում է մեր հայրենիքի, այլ երկրների և ամբողջ երկրագնդի քարտեզագրության հիմքը։

§ 46. ԱՍՏՂԱԳԻՏԱԿԱՆ ԴԻՏՈՒՄՆԵՐԸ ԾՈՎԱՅԻՆ ԵՎ ՕԴԱՅԻՆ ՆԱՎԱՏՈՐՄՆԵՐՈՒՄ։ Ծովային նավերի և ինքնաթիռների համար, որոնք անընդհատ գտնվում են շարժման մեջ, աշխարհագրական կոորդինատների որոշելը հանդիսանում է առօրյա կենսական խնդիրներից մեկը, որը շատ հաճախ լուծվում է օրական մի քանի անգամ։ Շոգենավերի ե ինքնաթիռների օրորվելը թույլ չի տալիս օգտվելու այնպիսի գործիքից, որը տեղակայվում Լ ըստ հարթաչափի։ Լուսատուների բարձրությունը չափելիս, որն անհրաժեշտ է աշխարհագրական լայնությունը և երկայնությունը որոշելու համար, այդ պայմաններում օգտվում են սեքստանից։

Սեքստան կոչվում է այն գործիքր, որով չափում են լուսատուների անկյունային հեռավորությունը հորիզոնից՝ դիտումների ժամանակ Ա|ահելով այն ճեոքին բռնած (նկ. 38)։ Նա րաղկացած է շրջանագծի 60° սեկտորից և բռնակի օգնությամբ պահվում է ուղղաձիգ դիրքում։

Հորիզոնական դիտակով դիտողը տեսնում է հորիզոնը։ Պտտելով քանոնը հայելու հետ միասին, հարկավոր է նրան այնպիսի դիրք տալ, որ լուսատուի ճառագայթը, անդրադառնալով պտտվող հայելուց, ընկնի մյուս հայելու վրա, իսկ այնտեղից անդրադառնալով դիտողի աչքը։ Այն ժամանակ դիտողը լուսատուի պատկերը կտեսնի հորիզոնի գծի վրա։ Քանոնի ցուցիչը սեկտորի աղեղի վրա ցույց կտա այն թիվը, որը համապատասխանում է լուսատուի բարձրությանը հորիզոնից՝ դիտման մոմենտին։

Բացի սեքստանից, օդային նավատորմում ինքնաթիռների ուղղությունները որոշելու համար կիրառվում են նաև աստղադիտական այլ գործիքներ։

Շոգենավեր և ինքնաթիռներ վարողների (շտուրմանների) կարիքների համար ՍՍՌՄ-ում հաշվարկվում և հրատարակվում են հատուկ «Ծովային աստղադիտական տարեգիրք» և «Ավիացիոն աստղագիտական տարեգիրք», որոնք իրենց մեջ պարունակում են երկնային լուսատուների մասին տվյալ տարվան վերաբերող զանազան կարևոր տեղեկություններ և հաշվարկումներ կատարելու համար հատուկ աղյուսակներ։

Կողմնորոշման աստղագիտական եղանակների շնորհիվ հնարավոր դարձան մեր օդաչուների անզուգական թռիչքները դեպի Հյուսիսային բևեռ, Արկտիկայի վրայով ՍՍՌՄ-ից դեպի Ամերիկա, մեր ռմբակոծիչների հերոսական հարձակումները թշնամու հեռավոր օբյեկտների վրա և այլն։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ

*I՞նչ է իրական կեսօրը, և ինչպե՞ս է որոշվում իրական արեգակնալին օրվա տևողաթյունը։
Ինչո՞ւ է իրական օրերի տևողությունը փոփոխվում։
Ինչպե՞ս են կաո ուցված արեգակնային ժամացույցները և ինչպիսի՞ ժամանակն են նրանք ցույց տալիս։
Քանի տեսակի արեգակնային ժամացույցներ կան և ինչո՞վ են նրանք իրարից տարբերվում։
Ի՞նչ է միջին արեգակնային ժամանակը։
Ի՞նչ է «ժամանակի հավասարումը» և ի՞նչ սահմաններումն է նա փոփոխվում։
Ինչպիսի՞ ժամանակն է կոչվում տեղական։
Ինչպե՞ս է տարբերվում տեղական ժամանակը երկու քաղաքներում, որոնք ունեն տարբեր երկայնություններ։
Ինչո՞ւմն է կայանում ժամանակի գոտիական հաշիվը։
Ի՞նչ է դեկրետային ժամանակը։
*Ի՞նչ է ամսաթվի փոփոխման գիծը և որտեղո՞վ է նա անցնում։
*Ի՞նչ է ժամային անկյունը։
*Ինչպիսի՞ կապ գոյություն ունի Արեգակի ժամային անկյան և իրական արեգակնային ժամանակի միջև։
*Ի՞նչ է աստղային ժամանակը։
*Աստղային ժամանակով ե՞րբ կուլմինացիա կկատարի այն աստղը, որի ուղղակի ծագումն է α։
*Ի՞նչ է աստղային օրը։
*Ո՞րն է կարճ, արեգակնայի՞ն օրը թե աստղային օրը, և ինչքանո՞վ։
*Ինչպե՞ս հաշվել տվյալ օրվա կեսօրին համապատասխան աստղային ժամանակը։
*Ինչպե՞ս հաշվել տարվա տվյալ օրվա ցանկացած ժամի համար աստղային ժամանակը։
*Ո՞վ և ինչո՞ւ կարիք ոձւի իմանալ ճշգրիտ ժամանակը։
Ինչո՞ւմն են արտահայտվում աստղագիտության գլխավոր գործնական կիրառությունները։
Ինչի՞ վրա է հիմնված աշխարհագրական երկայնության որոշելը։
Ինչպիսի՞ երկու խնդրի է բաժանվում այդ խնդիրը։
Ինչպե՞ս են իմանում տեղական ժամանակը մի այլ քաղաքում։
*Ի՞նչ է սեքստանը, որտե՞ղ և ինչի՞ համար է նա հարկավոր։
Ինչպե՞ս կարելի է որոշել տեղանքի աշխարհագրական լայնությունը։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

Արեգակնային ժամացույցը ցույց է տալիս առավոտյան 8 ժամ 10 րոպե։ Օգտվելով 34-րդ նկարից՝ որոշեցեք համապատասխան միջին ժամանակը փետրվարի 15-ին, հունիսի 15-ին և նոյեմբերի 3-ին։
Ինչպիսի՞ ժամանակ կլինի այդ․ տեղական, թե՞ գոտիական։
Ո՞ր տեղական ժամանակն է առաջ և ինչքանո՞վ․ Կույբիշևի՞նը, թե՞ Սվերդլովսկինը (տես V հավելվածը), Տոմսկի՞նը, թե՞ Իրկուտսկինը, Մուրմանսկի՞նը, թե՞ Տաշքենտինը։
Օգտվելով V հավելվածից, որոշեցեք, թե այդ քաղաքներից յուրաքանչյուրում ինչպիսի՞ ժամանակն է առաջ, տեղակա՞նը, թե՞ գոտիականը, և ինչքանո՞վ, դեկրետայի՞նը, թե՞ տեղականը, և ինչքանո՞վ։
Որոշեցե՛ք Ռիգայի տեղական ժամանակը, երբ Չիտայում դեկրետային ժամանակով կեսօր է։
Խարկովում արեգակնային ժամացույցները ցույց են տալիս առավոտյան 7 ժամ 19 րոպե։ Գտնել այդ պահին համապատասխան դեկրետային ժամանակը Խարկովում, Լվովում, Գորկիում և Կրասնոյարսկում։
Սյունի ստվերը դեկրետային կեսօրին անցնո՞ւմ է արդյոք միջօրեի գծով։
Դեկրետային ժամանակով Տուլայում և Ռիգայում միաժամանակ երեկոյան ժամը 6-ն է։ Միատեսա՞կ են արդյոք այդ քաղաքների նաև տեղական ժամանակները (տե՛ս V հավելվածը)։
*Կհամընկնե՞ն արդյոք երկու ճանապարհորդների ժամանակի հաշիվները (ամսաթվերը), որոնք միաժամանակ մայիսի 1-ին դուրս են եկել Մոսկվայից, ըստ որում նրանցից մեկը շարժվում է դեպի արևմուտք, իսկ մյուսը՝ դեպի արևելք, և անցնում են օրական միահավասար 15° ըստ երկայնության։ Նրանք ի՞նչ կկատարեն, երբ հատեն ամսաթվի փոփոխման գիծը։
*Երկու աստղերի ուղղակի ծագումներն են՝ 3 ժամ և 7 ժամ։ Աստղային ժամանակով ե՞րբ այդ աստղերը կուլմինացիա կկատարեն։
*Հաշվեցե՛ք աստղային ժամանակը կեսօրին և երեկոյան ժամը 6-ին մայիսի 1-ի, օգոստոսի 1-ի և մարտի 1-ի համար։
*Մայիսի 1–ին, օգոստոսի 1-ին և մարտի 1-ին տեղական արեգակնային ժամանակով ժամը քանիսի ն կուլմինացիա կկատարեն այն աստղերը, որոնց ուղղակի ծագումն է՝ 3 ժամ, 7 ժամ, 23 ժամ։ Փաստորեն այդ կուլմինացիաներից բոլո՞րը հնարավոր կլինի տեսնել թե ոչ։
Տեղական ժամանակով աշխատող ժամացույցը ցույց էր տալիս երեկոյան 9 ժամ 13 րոպե, երբ լսվեցին Գրինվիչի կեսօրի ռադիոազդանշանները։ Ինչի՞ է հավասար բնակավայրի երկայնությունը։
Մոսկվայից ռադիոազդանշան լսվեց, որ այնտեղ երեկոյան ժամը 7-ն է (դեկրետային ժամանակով)։ Այդ պահին տեղական ժամանակով աշխատող ժամացույցը ցույց էր տալիս 13 ժամ 43 րոպե։ Ինչպիսի՞ն է բնակավայրի երկայնությունը Գրինվիչի նկատմամբ։
Կարելի՞ է արդյոք, ունենալով արեգակնային ժամացույց և ռադիոընդունիչ, կոպիտ մոտավորությամբ որոշել բնակավայրի երկայնությունը։
Կարելի՞ է արդյոք որոշել բնակավաւրի երկայնությունը համեմատելով քաղաքային ժամացույցների ցուցումները ռադիոազդանշանների հետ։
Բևեռային աստղը հեռու է բևեռից 1°։ Ե՞րբ պետք է չափել նրա բարձրությունը հորիզոնից և ինչպիսի՞ ուղղում պետք է մտցնել ստացած արդյունքի մեջ, որպեսզի ճշտորեն որոշվի տեղանքի լայնությունը։

ԼՈՒՍՆԻ ՇԱՐԺՈՒՄԸ ԵՎ ՕՐԱՑՈՒՅՑ

§ 47. ԼՈՒՍՆԻ ՇԱՐԺՈՒՄԸ ԵՎ ԱՄԻՍ։ Լուսինը այն միակ երկնային մարմինն է, որ պտտվում է Երկրի շուրջը։

Այն ժամանակամիջոցը, որի ընթացքում Լուսինը մի լրիվ շրջան է կատարում Երկրի շուրջը, կոչվում է աստղային (կամ սիդերիկ) ամիս, նա կազմում է 2⅓ օր։

Հետևենք, թե ի՛նչպես Լուսինը մի որևէ աստղի նկատմամբ արդեն հաջորդ օրը նկատելի տեղաշարժվել է ձախ կողմի վրա՝ դեպի արևելք (մեկ օրում մոտավորապես 13°)։

Դժվար չէ նկատել, որ աստղային երկնքում Լուսինը տեղաշարժվում է անընդհատ և 27⅓ օրից հետո վերադառնում է նույն աստղերի մոտ, երկնային սֆերա յում գծելով լրիվ շրջանագիծ։ Հենց այդ պատճառով էլ Լուսնի պտտման ժամանակաշրջանը (աստղերի նկատմամբ) կոչվում է աստղային (սիդերիկ)։ Մեկ ժամվա ընթացքում Լուսինը երկնային սֆերայում հասցնում է տեղաշարժվել (դեպի արևելք)

Չհաջողվեց վերլուծել (բառական սխալ):

չափով, այսինքն՝

½°, մոտավորապես իր տեսանելի տրամագծի մեծության չափ։

Լուսինը երկնա յին սֆերայում շարժվելիս հաճախ առժամանակ մեզանից ծածկում է աստղերն ու մոլորակները։ Դա ցույց է տալիս, որ Լուսինը մեզ ավելի մոտ է գտնվում, քան աստղերն ու մոլորակները։

Լուսնի տեսանելի շարժումը երկնային սֆերայում կատարվում է խավարածրի մոտերքը, բայց Լուսնի աղեծրի հարթությանը թեքված է Երկրի ուղեծրի հարթության (խավարածրի հարթության) նկատմամբ 5°–ով։ Լուսնի աղեծրի հատման կետերը խավարածրի հետ կոչվում են Լուսնի աղեծրի հանգույցներ։

Լուսնի միջին հեռավորությանը Երկրից կազմում է 384000 կմ կամ մոտավորապես 30 երկրային տրամագիծ։ Քանի որ Լուսինը Երկրի շուրջը շարժվում է էլիպսով, ուստի նրա հեռավորությունը երկու կողմերի վրա փոփոխվում է մոտ 20 000 կմ սահմաններում։ Լուսնի աղեծրի Երկրին ամևնամերձավոր կետը կոչվում է պերիգեյ (մերձակետ), ամենահեռավոր կետը՝ ապոգեյ (հեռակետ)։

§ 48. ԼՈՒՍՆԻ ՓՈՒԼԵՐԸ ԵՎ ՄՈԽՐԱԳՈՒՅՆ ԼՈՒՅՍԸ։ Լուսնի տեսքի փոփոխությունը և նրա փուլերի կրկնումներն աոաջանում են այն բանի շնորհիվ, որ Լուսինը Երկրի և իրեն լուսավորող Արեգակի նկատմամբ գրավում է տարբեր դիրքեր։

Լուսինը գնդաձև, խավար մարմին է։ Երբ Լուսինը գտնվում է Երկրի և Արեգակի միջև, նրա դեպի մեզ դարձած կիսագունդն Արեգակի կողմից չի լուսավորվում, և մենք նրան չենք տեսնում։ Լուսնի այդ փուլը կոչվում է նորալուսին։ Երբ Լուսինը գտնվում է ուղիղ Արեգակի դիմաց, այսինքն՝ Երկիրը լինում է Արեգակի և Լուսնի միջև, Լուսնի դեպի մեզ դարձած ամբողջ կիսագունդը պայծառ կերպով լուսավորված է լինում Արեգակի ճառագայթներով։ Այդ փուլը կոչվում է լիալուսին։ Միջակա դիրքերում մենք նրա լուսավորված կիսադնդի այս կամ այն մասը տեսնում ենք կողքից» Հ-թանից էլ Լուսինը ունենում է կիսասկավառակի (առաջին քառորդ և վերջին քառորդ), ավելի կամ պակաս Լափով նեղ եղջյուրի և այլ տեսքեր։ 40-րդ նկարը պարզաբանում է Լուսնի փուլերի կապը նրա՝ իր ուղեծրում ունեցած այս կամ այն դիրքի հետ. Արեգակի ճառագայթներն ընկնում են վերևից՝ գծագրի հարթության ուղղությամբ։

Հասկանալի է, որ Լուսնի վերին կուլմինացիան նորալուսնի ժամանակ տեղի է ունենում կեսօրին, լիալուսնի ժամանակ՝ կես-գիշերին , առաջին քանորդի ժամանակ՝ մոտավորապես ժամը 18-ին և վերջին քառորդի ժամանակ՝ մոտավորապես ժամը 6-ին (արեգակնային ժամանակով)։

Լուսնի իրար հաջորդող երկու միատեսակ փալերի միջև ընկած ժամանակամիջոցը կոչվում է սինոդիկ ամիս, այն հավասար է 29½ օրվա։

Լուսնի փուլերի պարբերաշրջանը կամ սինոդիկ ամիսը ավելի երկարատև է սիդերիկ ամսից։ Դրա պատճառն այն է, որ Լուսնի միատեսակ փուլերը թևակոխում են այն մամանակ, երբ Լուսինը նույն դիրքն է ընդունում Արեգակի նկատմամբ։ Նկ․ 41-ում Լուսինը L կետում պատկերված է T Երկրի և S Արեգակի միջև՝ նորալուսնի դիրքում։ Այն ժամանակամիջոցում, երբ Լուսինը Երկրի շուրջը մի լրիվ պտույտ է կատարում, Երկիրը Լուսնի հետ միասին Արեգակի նկատմամբ արդեն անցած է լինում իր ուղեծրի ¹/₁₃-րդ մասը և գտնվում է T₁ կետում։ Լուսինը, շարժվելով սլաքի ուղղությամբ, կընդունի L1 դիրքը, որը, ինչպես մենք տեսնում ենք, դեռևս չի կարող նորալուսնին համապատասխանել։ Նորալուսնի L'₁ դիրքին հասնելու համար Լուսինը պետք է դառնա ST₁L₁ անկյան չափով, որը տևում է մոտավորապես երկու օր։

Լուսնի վրա գտնվող դիտողի համար Երկիրը նույնպես տարբեր դիրքեր է գրավում Արեգակի նկատմամբ։ Ուստի Լուսնի վրայից դիտելու դեպքում՝ Արեգակի ճառագայթներով լուսավորված Երկիրը նույնպես պետք է փոփոխի իր փուլերը և այն էլ ճիշտ նույն պարբերությամբ, միայն այն տարբերությամբ, որ երբ Երկրի վրա դիտվում է, օրինակ, լիալուսին , Լուսնի վրա պետք է դիտվի «նորաերկիր», և ընդհակառակն։ Դա դժվար չէ հասկանալ, ելնելով նույն 40-րդ նկարից։ Միայն պետք է պատկերացնել, որ դիտողը շարժվում է Լուսնի հետ միասին և այնտեղից նայում Երկրին։

Երկրի մակերևույթը 14 անգամ մեծ է Լուսնի մակերևույթից։ Ուստի «լիաերկրի» ժամանակ Լուսինը անհամեմատ ավելի ուժեղ է լուսավորվում Երկրի կողմից, քան լիալուսնի ժամանակ Երկիրը Լուսնից։ Բացի այդ, Երկրի մակերևույթը յոթ անգամ ավելի ուժեղ է անդրադարձնում Արեգակի ճառագայթները, քան Լուսինը, որովհետև Երկրի վրա կան շատ լուսավոր շրջաններ (ձյուն, ամպեր, ավազոտ անապատներ)։ Այդ պատճառով «լիաերկրի» ժամանակ Լուսինը լուսավորվում է Երկրից շատ ավելի ուժեղ, քան թե լիալուսնի ժամանակ Երկիրը լուսավորվում է Լուսնից։ Դրանով է բացատրվում «մոխրագույն լույսի» երևույթը, այսպես է կոչվում այն մեղմ կապտականաչավուն լուսարձակումը, որը նկատվում է Լուսնի սկավառակի՝ Արեգակի ճառագայթներով չլուսավորված մասում՝ նորալուսնից փոքր-ինչ առաջ և նրանից անմիջապես հետո, երբ Լուսնի պայծառ մասը երևում է նեղ եղջյուրի ձևով։ Այդ ժամանակ Երկիրը պայծառ լույս է սփռում Լուսնի մակերևույթի վրա։

§ 49. ԱՐԵՎԱԴԱՐՏԱՅԻՆ ԵՎ ՕՐԱՏՈԻՏԱՅԻՆ ՏԱՐԻՆԵՐ։ Մեծ ժամանակամիջոցների հաշվարկման սիստեմը կոչվում է օրացույց։ Ներկայումս գրեթե բոլոր երկրներն օգտվում են արեգակնային օրացույցից, այսինքն՝ մի օրացույցով, որը հիմնված է Արեգակի խավարածրով կատարած տարեկան շրջապտույտի վրա, ուստի և կապված է տարվա եղանակների պարբերաբար փոփոխվելու հետ։

Ամեն մի արեգակնային օրացույցում որպես հիմք ընդունվում է արևադարձային տարին։ Արևադարձային տարի է կոչվում Արեգակի կենտրոնի՝ գարնանային գիշերահավասարի կետով երկու հաջորդական անցումների միջև ընկած ժամանակամիջոցը։

Արևադարձային տարին հավասար է 365 օրվա 5 ժամվա 48 րոպեի ու 46,1 վայրկյանի։ Հենց այդ հանգամանքն է, որ օրացույց կազմելու գործում դժվարություններ է հարուցում, որովհետև յուրաքանչյուր օրացուցային տարին հարմարության տեսակետից պետք է իր մեջ ամբողջ թվով օրեր պարունակի։ Կապված այն բանի հետ, թե ինչպես է օրացույցը հարմարվում արևադարձային տարվա հետ և ինչպես է նա իրականացնում այդ հարմարեցումը, կարող էն տարբեր օրացույցներ լինել։

§ 50. ՀԻՆ ԵՎ ՆՈՐ ՏՈՄԱՐՆԵՐ։ Մինչև Հոկտեմբերյան Սոցիալիստական Մեծ ռևոլյուցիան Ռուսաստանում ընդունված օրացույցը կոչվում էր հին տոմար։

Հին տոմարում հաշվի պարզության համար ընդունված է, որ արևադարձային տարին կազմում է հիշտ 365 օր 6 ժամ, այսինքն՝ 365¼ օր։ Որպեսզի օրացուցային տարին միշտ ամբողջ թվով օրեր պարունակի, ընղունվել էր 3 տարի իրար հետևից հաշվել 365-ական օր, իսկ հաջորդ (չորրորդ) տարին՝ 366 օր, որից հետո դարձյալ երեք տարի հաշվել 365-ական օր և այլն։ Այն ժամանակ տարվա միջին տևողությունը հավասար կլինի (365 +365 + 365 + 366):4 = 365¼ օրվա, այսինքն՝ հավասար է արևադարձային տարվա ընդունված տևողությանը։

Տարվա ավելորդ օրը ավելացվում է փետրվարի վերջում (փետրվարի 29), և այդպիսի տարին կոչվում է նահանջ տարի։ Ընդունված է նահանջ (366 օրից կազմված) համարել այն տարիները, որոնց համարներն աոանց մնացորդի թաժանվում են 4-ի, օրինակ 1944, 1948, 1952 թվականները։

Հին տոմարը ժամանակի իրական ընթացքից ետ է մնում, որովհետև տարվա միջին, տևողությունը նա ընդունում է ավելի երկար, քան նա իսկապես կա (11 րոպե 14 վայրկյանով)։ Յուրաքանչյուր 400 տարում (ավելի ճիշտ՝ 384 տարում) հին տոմարը ետ է մնում 3 օրով։

ՍՍՌՄ-ում և շատ երկրներում ընդունված նոր տոմարը, որը մի շարք երկրներում մտցվել է դեռևս 1582 թ., գրեթե ազատ է վերոհիշյալ թերությունից։

XVI դարում հին տոմարը բնությունից արդեն 10 օրով ետ էր մնացել (այդ օրացույցը քրիստոնեական կրոնն ընդունած երկրների կենցաղի մեջ մտցվել էր 325 թ․)։ Օրացույցի ետ ընկնելը վերացնելու նպատակով 1582 թ․ հոկտեմբերի 5-ի փոխարեն միանգամից հաշվեցին հոկտեմբերի 15֊ը։ Իսկ որպեսզի սխալը նորից չկուտակվի, յուրաքանչյուր 400 տարվա ընթացքում հին օրացույցում կուտակվող երեք ավելորդ օրերը վերացվում են նրանով, որ ամեն մի այդպիսի 400–ամյա ժամանակաշրջանի երեք նահանջ տարիները համարվում են հասարակ տարիներ։ Պայմանավորվել են, որ հասարակ կհամարվեն հին օրացույցի այն հարյուրամյա նահանջ տարիները, որոնց հարյուրյակների թիվն առանց մնացորդի չի բաժանվում 4-ի։ Այսպիսով, 1600 թվականը երկու օրացույցներումն էլ նահանջ էր և XVII դարում հին և նոր տոմարների միջև եղած տարբերությունը մնաց 10 օր։ Նոր տոմարով 1700 թվականը ոչ թե նահանջ էր, այլ հասարակ, ուստի և այդ օրացույցների տարբերությունը դարձավ 11 օր։ 1800 թվականից հետո տարբերությունը դարձավ 12 օր, 1900 թվականից հետո՝ 13 օր, իսկ 2000 թ, հետո այդ տարբերությունը դեռևս կմնա 13 օր։

Նոր տոմարը նույնպես կատարելապես ճիշտ չէ, բայց րնոլթյունիէք նրա տարբերվելը միայն 3000 տարվա ընթացքումն է կուտակվում մեկ օրվա չափ։ Այդպիսի սխալը, բնականաբար, գործնական նշանակու֊ թյուն չունի։

§ 51․ *ԱՄՍՎԱ ԵՎ ՇԱԲԱԹՎԱ ԾԱԳՈՒՄԸ։ Օրացուցային թվականությունն Նախնադարյան շրջանում այն երկրներում, որոնք ավելի որսորդության և անասնապահության, քան հողագործության հետ կին կապված, ընդունված էր այնպիսի օրացույց, որը կառուցված կր Լուսնի փուլերի հերթափոխման, այսինքն՝ սինոդիկ ամսվա (29½ օրվա) վրա։ Օրացուցային ամիսները հաղորդում կին միմյանց, ունենալով մերթ 29, մերթ 30 օր։ Մեր արեգակնային օրացույցում տարվա մեկ, տասներկուերորդ մասը կոչվում է ամիս, բայց նա Լուսնի հետ ոչ մի առնչություն չունի, օրացուցային ամիսները, որոնք ունեն 28-ից մինչև 31-օրյա տարբեր տևողություն, Լուսնի փուլերի հերթափոխության հետ ոչ մի կերպ կապված չեն։

Յոթօրյա շաբաթը սկիզբ է առել հազարավոր տարիներ առաջ այն հավատմունքի կապակցությամբ, որ ուներ աստղագուշակությունը մոլորակների ազդեցության նկատմամբ։ Այն ժամանակ հայտնի հինգ մոլորակներից յուրաքանչյուրին, նույնպես և Արեգակին ու Լուսնին կին նվիրված առանձին օրերը՝ որոշ կարզով, շաբաթը — Սատուրնին (Սատուրնի օր), կիրակին — Արեգակին, երկուշաբթին — Լուսնին և այլն։ Գերմաներեն մինչև այժմ էլ, օրինակ, կիրակին կոչվում է Sonntag (Sonnen tag — Արեգակի օր), երկուշաբթին — Montag (Լուսնի օր), անգլերեն շաբաթը կոչվում է Saturday (Սատուրնի օր), կիրակին — Sunday (Արեգակի օր), ֆրանսերեն երեքշաբթին կոչվում է Mardi (Martis dies — Մարսի օր), չորեքշաբթին - Mercredi(Մերկուրի օր) և այլն։

Տարիների թվարկության սկիզթթ կոչվում է օրացուցային թվականություն (էրա)։ Հռոմեացիները տարիների թվարկումը երկար ժամանակ տանում կին իրենց, մայրաքաղաքի Հռոմի հիմնադրման տարվանից։ Նման տարբեր տեսակի թվականությունների միմյանց հետ համեմատելն ու մեկից մյուսին անցնելը բավականին անհարմար է։

Հազար հինգ հարյուր տարի առաջ առաջարկվել է տարիների թվարկումը հաշվել այսպես կոչված «քրիստոսի ծննդյան» տարեթվից։ Այդ առասպելական իրադարձության տարեթիվը, իհարկե, չի կարելի սահմանել, և այն «հաշվել են» կամավոր կերպով։ Սակայն «քրիստոսի ծննդից սկսած այդ թվականությունը» աստիճանաբար տարածվել կ շատ երկրներում և ներկայումս գրեթե ընդունված է բոլորի կողմից, հաճախ մենք նրան անվանում ենք «մեր թվականություն» (մ․ թ․)։ Մենք այն պահպանել ենք, քանի որ հարմար է, որպեսզի բոլոր ժողովուրդներն էլ հազարամյակների ընթացքում ունենան միևնույն թվականությունը։

ՀԱՐՑԵՐ ԻՆՔՆԱՏՈԻԴՄԱՆ ՀԱՄԱՐ

Ի՞նչ է աստղային (սիդերիկ) ամիսը և ինչի՞ է նա հավասար։
Աստղային երկնքի ֆոնի վրա ի՞նչ չափով է տեղաշարժվում Լուսինը. ա) մեկ ժամում և բ) մեկ օրում։
Համընկնո՞ւմ է արդյոք Լուսնի ուղեծիրը խավարածրի հետ։
Ինչի՞ է հավասար Լուսնի միջին հեռավորությունը Երկրից։
Ինչպե՞ս են կոչվում Լուսնի ուղեծրի՝ Երկրին ամենամոտ և ամենահեռու կետերը։
Պատրաստեցեք գծագիր և նրանով բացատրեցեք, թե ինչո՞ւ և ինչպե՞ս է կատարվում Լուսնի փուլերի հերթափոխությունը։
Ո՞ր ժամին է կատարվում Լուսնի կուլմինացիան, երբ նա գտնվում է ա) առաջին քառորդում, բ) լիալուսին է և գ) վերջին քառորդում։
Ի՞նչ է Լուսնի մոխրագույն լույսը։
Ինչպե՞ս է կոչվում Լուսնի փուլերի լրիվ հերթափոխության պարբերաշրջանը և ինչի՞ է նա հավասար։
Ի՞նչն է կոչվում օրացույց։
Ի՞նչն է կոչվում արևադարձային տարի և ինչի՞ է նա հավասար։
Ինչպե՞ս են իրար հաջորդում հասարակ և նահանջ տարիները օրացույցի հին տոմարում։
Ինչի՞ է հավասար տարվա միջին տևողությանը հին տոմարում։ Ինչո՞ւմն է կայանում նրա անճշգրտությունը։
Ինչպե՞ս են իրար հաջորդում հասարակ և նահանջ տարիները օրացույցի նոր տոմարում։ Ե՞րբ է նա մտցվել ՍՍՌՄ-ում։
Ինչպե՞ս են տարբեր դարերում ամսաթվերը հին տոմարով վերածվում նոր տոմարի, և ընդհակառակն։
*Մեր օրացույցում որտեղի՞ց են հանդես եկել ամիսները։
*Ե՞րբ և ինչո՞ւ է առաջացել յոթօրյա շաբաթը։
Ի՞նչ է օրացուցային դարագլուխը։

ՎԱՐԺՈԻԹՅՈԻՆնԵԻ

Լուսինը առաջին քառորդի փուլում հորիզոնին մոտ է։ ժամը քանի՞սն է (մոտավորապես)։ Հորիզոնի ո՞ր կողմն է նա գտնվում։
Այսօր Լուսինը մայր է մտել կես-գիշերին։ Մոտավորապես ե՞րբ նա մայր կմտնի վաղը։
Լուսինը մոտ է լրման։ Այդ ժամանակ ինչպե՞ս կերևա Երկիրը Լուսնից դիտողի համար։
Լուսնեղջյուրն իր ուռուցիկությամբ դարձած է դեպի աջ և գտնվում է հորիզոնին մոտ։ Հորիզոնի ո՞ր կողմն եք դուք նայում։
*Ինչո՞ւ արևադարձային երկրներում «մաշվող» Լուսնի նոր ծագող եղջյուրը ծովի վրա այնպես է երևում, կարծես թե նավակ է լողում ջրի վրա։
Ինչո՞ւ Հոկտեմբերյան Սոցիալիստական Մեծ ռևոլյուցիայի տարեդարձը տոնվում է նոյեմբերին։
Ե՞րբ է տեղի ունեցել դեկաբրիստների 1825 թ, ապստամբությունը նոր տոմարով։
Մ․ Վ․ Լոմոնոսովը հին տոմարով ծնվել է 1711 թ, նոյեմբերի 8-ին։ Այժմ ե՞րբ պետք է նշենք նրա ծնունդը։
*Ինչպե՞ս և ե՞րբ պետք է երթևեկի նավը Ասիայի և Ալյասկայի միջև, որպեսզի նրա անձնակազմի համար փետրվարի ընթացքում լինի 10 կիրակի։

ԽԱՎԱՐՈՒՄՆԵՐ

§ 52. ԽԱՎԱՐՈՒՄՆԵՐ։ Եթե Լուսնի ուղեծրի հարթությունը համընկներ խավարածրի հարթությանը, ապա ամեն ամիս խավարում տեղի կունենար։ Ամեն անգամ նորալուսինի ժամանակ Լուսինը լինելով Երկրի և Արեգակի միջև՝ նրանց հետ միասին կգտնվեր մի ուղիղ գծի վրա և իր ոչ-թափանցիկ մարմնով կփակեր Արեգակի առաջը։ Դրա հետևանքով ամեն անգամ կնկատվեր մի երևույթ, որ մենք անվանում ենք Արեգակի խավարում։ Ճիշտ նույն ձևով ամեն անգամ լիալուսնի Ժամանակ Լուսինը կմտներ Երկրի՝ Արեգակի նկատմամբ հակառակ կողմը նետած ստվերի մեջ, որի հետևանքով տեղի կունենար Լուսնի խավարում։ Շնորհիվ այն բանի, որ Լուսնի ուղեծիրը որոշ չափով թեքված է խավարածրի նկատմամբ. Լուսինը նորալուսնի և լիալուսնի ժամանակ մեծ մասամբ անցնում է խավարածրից վեր կամ նրանից ցած, և խավարում չի լինում։

Խավարումներ կարող են տեղի ունենալ միայն այն ժամանակ, երբ Լուսնի նորումը կամ լրումը տեղի է ունենում Լուսնի ուղեծրի երկու հանգույցներից որևէ մեկի մոտ, այսինքն, խավարածրի հարթության հետ Լուսնի ուղեծրի հատման կետերի մոտ (§ 47)։ Այլ կերպ ասած՝ Արեգակն ու Լուսինը պետք է միաժամանակ Լուսնի ուղեծրի հանգույցներին մոտ լինեն։

Քանի որ այդ հանգույցները երկուսն են, իսկ Արեգակը խավարածրով լրիվ շրջան է կատարում մեկ տարում, ուստի տարեկան լինում է երկու շրջան (մեկը մյուսից կես տարի անց), երբ կարող են խավարումներ տեղի ունենար Լուսնի հանգույցների գիրքը անընդհատ փոփոխվում է, որի հետևանքով խավարումների տեղի ունենալու պարբերությաններր ամեն տարի փոփոխվում են։ Ավելի ճիշտ հաշվումները ցույց են տալիս, որ տարեկան պետք է տեղի ունենան Արեգակի առնվազն երկու, բայց ոչ ավելի, քան հինգ խավարումներ և Լուսնի՝ ոչ ավելի, քան երեք խավարումներ, բայց Լուսնի խավարումներ կարող են բոլորովին չլինել։ Ամենից հաճախ տարեկան լինում է Արեգակի և Լուսնի երկուական խավարում։

§ 53. ԼՈՒՍՆԻ ԽԱՎԱՐՈՒՄՆԵՐԸ։ Երկիրը Արեգակի նկատմամբ հակաղիր կողմի վրա նետում է կոնաձև ստվեր։ Երբ Լուսնի լրումր տեղի է ունենում իր ուղեծրի հանգույցի մոտերքևը, ապա Լուսինը իր այդ փուլում մասամբ կամ ամբողջապես ընկղմվում է Երկրի ստվերի մեջ, ուստի և տեղի է ունենում Լուսնի մասնակի կամ լրիվ խավարում։

Լուսնի խավարումը տեսանելի է լինում Երկթի այն կիսագնդում (ամբողջ կիսագնդում միաժամանակ), որը խավարման ժամանակ դարձած է դեպի Լուսինը։

Լուսնի հեռավորության վրա Երկրի ստվերի տրամագիծը 2½ անգամ մեծ է Լուսնի տրամագծից։ Ընդ որում, եթե Լուսինը անցնի ստվերի կենտրոնով, Լուսնի լրիվ խավարումը կտևի մոտ 1 ժամ 40 րոպե, չհաշված այն ժամանակը, որի ընթացքում Լուսինը հետզհետե ընկղմվում է Երկրի ստվերի մեջ և հետզհետե դուրս գալիս այդ ստվերից, որը տևում է դարձյալ երկու ժամ։

Խավարման ժամանակ սովորաբար Լուսինը բոլորովին չի անհետանում, այլ շարունակում է երևալ, թեև շատ աղոտ կերպով։ Ընդ Որում նա ընդունում է քիչ թե շատ խավար կամ լուսավոր նրբերանգի գորշ-կարմիր գույն։ Դրա պատճառն այն է, որ Արեգակի ճառագայթները, բեկվելով Երկիրը շրջապատող մթնոլորտում, թափանցում են Երկրի նետած կոնաձև ստվերի ներսը։ Սակայն, ծիածանի բոլոր գույներից, որոնք կազմում են Արեգակի սպիտակ լույսը, մթնոլորտը ուժեղ կերպով կլանում է կապտավուն և նրա հարևան ճառագայթները, իսկ այդ կոնաձև ստվերի մեջ է բաց թողնում գերազանցապես կարմիր ճառագայթները, որոնց նա համեմատաբար թույլ է կլանում։ Հենց այդ ճառագայթներն են, որ խավարման ժամանակ լուսավորում են Լուսինը։

Մթնոլորտի կողմից կապտագույն ճառագայթների ուժեղ կլանում է տեղի ունենում նաև արևածագի և արևամուտի ժամանակ։ Առավոտյան և երեկոյան, երբ ճառագայթներր թեք ուղղությամբ են անցնում մթնոլորտի միջով, Արեգակի լույսն այդ ժամանակ օդի ավելի ստվար շերտերով է անցնում, քան ցերեկվա կեսերին, և կապույտ ու բաց-կապույտ ճառագայթներն ավելի ուժեղ կերպով են կլանվում։ Ուստի օդը կապտավուն գույն է ստանում, իսկ Արեգակը արևածագի և արևամուտի ժամանակ կարմիր է թվում։

§ 54. ԱՐԵԳԱԿԻ ԽԱՎԱՐՈՒՄՆԵՐԸ։ Լուսինը փոքր է Երկրից, ուստի Լուսնի նետած կոնաձև ստվերի տրամագիծը փոքր է Երկրի տրամագծից։ Լուսնի ստվերը չի կարող միաժամանակ ծածկել ոչ միայն ամբողջ Երկիրը, այլև նույնիսկ նրա զգալի մասը։ Արեգակի լրիվ խավարում գիտվում է միայն այն համեմատաբար փոքր բծի ներսում, որ Երկրի մակերևույթի վրա առաջացնում է Լուսնի ստվերը։ Այդ ստվերային բիծը, որ էլիպսի ձև ունի, իր տրամագծով երբեք չի հասնում նույնիսկ 300 կմ և սովորաբար շատ ավելի փոքր է լինում։ Այդ բծից դուրս, որտեղ Լուսնի կիսաստվերն է ընկնում, մոտ 4 000 կմ շառավղով տարածության վրա նկատվում է մասնակի խավարում, այսինքն՝ Լուսինը ծածկում է Արեգակի սկավառակի միայն մի մասը (նկ. 43)։ Երկրի մյուս մասերում, ստվերից և կիսաստվերից դուրս, Արեգակի խավարում չի լինում։

Այն պատճառով, որ Երկիրը պտտվում է իր առանցքի շուրջը, իսկ Լուս ինը՝ Երկրի շուրջը, ուստի լուսնի ստվերը տեղաշարժվում է Երկրի մակերևույթի վրայով, և Արեգակի խավարումը հաջորդաբար (տարբեր մոմենտներում) դիտվում է Երկրի մակերևույթի տարբեր վայրերում։ Գա տեղի է ունենում՝ այսպես կոչված՝ լրիվ խավարման գոտում, որը ձգվում է Երկրի մակերևույթով։ Այդ դոտու երկու կողմերից միայն մասնակի խավարում է դիտվում, և որքան վայրը հեռու է գտնվում լրիվ խավարման գոտուց, այնքան մասնակի խավարումը ավելի քիչ (փոքր փուլով) է նկատվում։

Խավարման փուլ կոչվում է Արեգակի տրամագծի՝ Լուսնի կողմից առավել չափով ծածկված հատվածի հարաթերոՆթյունջ Արեգակի ամթողջ տրամագծին։ Նա արտահայտվում է Արեգակի տրամագծի մասերով։

Ինչպես Լուսնի, այնպես էլ Երկրի ուղեծրերն էլիպսաձև լինելու հետևանքով, Լուսնի տեսանելի (անկյունային) տրամագիծը Արեգակի տրամագծից մերթ մեծ է լինում, մերթ հավասար և մերթ փոքր։ Առաջին դեպքում լրիվ Արեգակի խավարումը տևում է որոշ ժամանակ (ոչ ավելի, քան 7 րոպե 40 վայրկյան), երկրորդ դեպքում՝ միայն մի ակնթարթ, իսկ վերջին դեպքում Լուսինն առհասարակ Արեգակի սկավառակն ամբողջապես չի ծածկում․ նրա եզրերը Լուսնի խավար սկավառակի շրջապատից երևում են, տեղի է ունենում օղակաձև խավարում (նկ․ 44)։

Արեգակի խավարման պատկերն այսպես է ընթանում։ Սկզբում Արեգակի սկավառակի արևմտյան (աջակողմյան) եզրին առաջանում է մի փոքրիկ սև փորվածք։ Այդ փորվածքը հետզհետե մեծանում է, և Արեգակը ավելի ու ավելի է ծածկվում Լուսնի կողմից։ Այսպես անցնում է մոտավորապես մեկ ժամ։ Մինչև լրիվ խավարում սկսվելը Արեգակի լույսը նվազում է աստիճանաբար, բայց ոչ այնքան նկատելի կերպով։ Լրիվ խավարումն սկսվելուց հետո պատկերը միանգամից փոխվում է․ մթնում է, և երկնքի վրա սկսում են երևալ առավել պայծառ աստղերն ու մոլորակները, Արեգակի շուրջը հեռադիտակով երևում են պայծառ հրավառ ցայտեր (պրոտուբերանցներ)՝ Արեգակից դուրս ձգվող վարդագույն փոքր լեզվակների ձևով։ Խավարած Արեգակի շուրջը բոցավառվում է արևապսակը, որն իրենից ներկայացնում է Արեգակի մթնոլորտի արտաքին մասերը։ Լրիվ խավարումը վերջանալուց հետո Լուսնի աջ եզրի հետևից հայտնվում է Արեգակի պայծառ լույս սփռող նեղ եղջյուրիկը, և պսակը, հրվիժակներն ու աստղերը միանդամից անհետանում են։ Եղջյուրիկը հետզհետե մեծանում է, և Լուսինն էլի մոտավորապես մեկ ժամվա ընթացքում հեռանում է Արեգակի սկավառակի վրայից։

Թեև Արեգակի խավարումներ ավելի հաճախակի են գինում, քան Լուսնի խավարումներ, բայց Երկրի վրա միևնույն տեղում Արեգակի խավարումները, մանավանգ քրիվ խավարումները, անհամեմատ սակավ են նկատվում, քան Լուսնի խավարումները։ Երկրագնդի որևէ վայրում Արեգակի լրիվ խավարում դիտվում է միջին հաշվով մոտավորապես 300 տարին մեկ անգամ, իհարկե, հնարավոր շեղումներով։ ՍՍՌՄ-ի սահմաններում Արեգակի լրիվ խավարումներ դիտվել են 1914 թ., 1936 թ., 1941 թ., 1945 թ., 1952 թ. և 1954 թ.։ Մոտակա, հաջորդ Արեգակի լրիվ խավարում, որ կերևա ՍՍՌՄ-ում, տեղի է ունենալու 1961 թ. փետրվարի 15-ին։ Նրա շերտը կանցնի Ղրիմի, Ստալինգրադի և Արևմտյան Սիբիրի վրայով։

Լրիվ խավարումների ժամանակ հաջողվում է դիտել այնպիսի երևույթներ, որոնք ուրիշ ժամանակ տեսնելն անհնարին է։ Ուստի այդ երևույթները դիտելու համար լրիվ խավարման գոտին հատուկ արշավախմբեր են ուղարկվում։

Երկայնակի գծերով միացված են այն կետերը, որտեղ խավարման փուլերը միատեսակ են (իզոֆազեր)։ Լայնակի գծերով միացված են այն կետերը, որտեղ խավարումը տեղի է ունեցել միաժամանակ (ցույց է տրված միջազգային ժամանակը)։ Մեջտեղի ստվերագծված գոտիով նշանակված են այն տեղերը, որտեղ խավարումը լրիվ է եղել։

Արեգակի 1936 թ․ խավարումը տեսանելի էր ՍՍՌՄ-ի համարյա ամբողջ տերիտորիայի վրա (տե՛ս նկ․ 45) և որպես լրիվ խավարում՝ մի երկար գոտում, որը ձգվում էր Սև ծովից մինչև Խաղաղ օվկիանոսը։ Դա հնարավորություն է տվել կազմակերպել մի շարք արշավախմբեր աստղագիտական և ֆիզիկական հատուկ հարցեր լուծելու նպատակով։ Սովետական արշավախմբերից շատերը արժեքավոր արդյունքներ ստացան։ 1941 և 1945 թվականներին ևս, չնայած պատերազմական իրադրությանը, ՍՍՌՄ-ում Արեգակի խավարումների լայն դիտումներ են կատարվել։

Կար ժամանակ, երբ մարդիկ շատ էին վախենում խավարումներից, համարելով այն վատ նախագուշակություն կամ աստծո բարկության արտահայտություն։ Հաճախ այդպիսի սնոտիապաշտությունները պաշտպանվում էին պաշտամունքի սպասավորների կողմից՝ աշխատավոր մասսաներին վախեցնելու համար։ Այժմ գիտնականները, ծանոթ լինելով Լուսնի շարժման տեսությանը, նախապես հաշվում են յուրաքանչյուր խավարման ճիշտ ժամանակը՝ նույնիսկ վայրկյանի տասներորդական մասի ճշտությամբ (դիտումների և կատարած հաշվարկումների միջև նկատվող ոչ այնքան մեծ շեղումները առիթ են տալիս ավելի ևս ճշգրտելու Լուսնի շարժման տեսությունը)։

Արեգակի խավարումների համար սովորաբար կաղմվում է քարտեզ, որտեղ գծագրվում է Լուսնի՝ Երկրի վրայով անցնող ստվերի ուղին և տարվում են գծեր — իզոքրոններ (խավարման սկսման, միջին և վերջանալու միատեսակ մոմենտների գծերը) և իզոֆազեր (մասնակի խավարման միանման ամենամեծ փուլերի գծերը)։ Առավելապես ճշգրիտ այդպիսի քարտեզներ հաշվարկվում են ՍՍՌՄ-ում պրոֆ․ Ա․ Ա․ Միխայլովի ղեկավարությամբ։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈԻԳՄԱՆ ՀԱՄԱՐ

Ինչի՞ց են առաջանում Արեգակի և Լուսնի խավարումները։
Ինչպիսի՞ պայմաններումն է Լուսինը մտնում Երկրի ստվրի մեջ և Լուսնի ստվերն ընկնում Երկրի վրա։
Ինչո՞ւ ամեն ամիս խավարում չի լինում։
Ի՞նչ են Լուսնի հանգույցները, և հաստատո՞ւն է արդյոք նրանց դիրքը։
Ինչո՞ւ խավարումները շարունակ տարվա միևնույն ժամանակ չեն տեղի ունենում։
Քանի՞ և ինչպիսի՞ խավարումներ կարող են լինել տարվա ընթացքում։
Ինչպե՞ս է առաջանում Լուսնի խավարումը։ Ինչո՞ւ Լուսինը խավարման ժամանակ կարմիր է լինում։
Արեգակի քանի՞ տեսակ խավարումներ են լինում։
Արեգակի խավարումը դիտվո՞ւմ է ամենուր միաժամանակ ու միատեսակ։
Ինչո՞ւ Արեգակի և Լոէսնի խավարումների տեսքը լինում է տարբեր։
Ի՞նչ է խավարման փուլը։
Ի՞նչ արտասովոր բան է երևում Արեգակի լրիվ խավարումների Ժամանակ։

ՎԱՐԺՈԻԹՅՈԻՆՆԵՐ

Երեկ եղել է լիալուսին։ Կարո՞ղ է պատահել, որ մեկ շաբաթից հետո լինի արէգակի խավարում։
Վաղը չէ մյուս օրը լինելու է Արեգակի խավարում։ Այսօր կարո՞ղ է լինել «լուսնյակ գիշեր»։
Կարո՞ղ է լինել Լուսնի օղակաձև խավարում։
Ինչո՞ւ Լուսնի խավարումները երբեմն տեսանելի չեն լինում տվյալ վայրում։
Կարելի՞ է արդյոք Երկրի հյուսիսային բևեռից նոյեմբերի 15-ին դիտել Արեգակի խավարում։
Կարելի՞ է արդյոք Երկրի հյուսիսային բևեռից դիտել հունիսին և նոյեմբերին տեղի ունեցող խավարումները։
Ինչպե՞ս տարբերել Լուսնի սովորական «մաշը» նրա խավարման փուլից։

ԳԼՈՒԽ III։ ԳԻՏԱԿԱՆ ԱՇԽԱՐՀԱՅԱՅՔԻ ԶԱՐԳԱՑՈՒՄԸ

ԱՍՏՂԱԳԻՏՈՒԹՅՈՒՆԸ ՀԻՆ ԴԱՐԵՐՈՒՄ

§ 55. ԵՐԿՆԱՅԻՆ ԼՈՒՍԱՏՈՒՆԵՐԻ ՊԱՇՏԱՄՈՒՆՔԸ ԵՎ ԱՍՏՂԱԳՈՒՇԱԿՈՒԹՅՈՒՆԸ։ Երբ մարդը դեռևս չգիտեր բնության օրենքները, նա ամեն քայլափոխում զգում էր իր անզորությունը և շրջապատի աշխարհից ունեցած կախումը։ Նա կուրորեն խոնարհվում էր բնության ուժերի առաջ, աստվածացնում էր այդ ուժերը։ Աստվածացվում էին կայծակը , որոտը, քամին և երկնային լուսատուները, առաջին հերթին՝ Արեգակն ու Լուսինը։ Ամենից շատ զարգացած էր Արեգակին երկրպագելը (արևապաշտությունը)։ Տեսնելով Արեգակի ճառագայթների կենդանարար ազդեցությունը ամբողջ բնության վրա, բայց չկարողանալով իմանալ, թե ո՞րն է նրանց աղբյուրը և ինչպե՞ս են նրանք ներգործում, մարդիկ Արեգակը մի բարի և հզոր աստված էին պատկերացնում։ Այսպես, բնության օրենքները չիմանալու հետևանքով ծնունդ է առել հավատը դեպի գերբնական ուժերը և զարգացել նրանց երկրպագությունը, գոյություն են առել կրոնական հավատալիքներն ու պատկերացումները։

Արեգակին և նրա պատկերներին երկրպագելր գոյություն է ունեցել հնադարյան շատ ժողովուրդների մոտ։ Սլավոնների մոտ Արեգակի աստվածը կոչվում էր Յարիլո։ Լույս֊աստծո այլաբանական ձևով նկարագրված արկածները, այսինքն՝ Արեգակի կատարած ճանապարհորդությունը խավաըածրով, շատ ժողովուրդների մոտ կազմում են արեգակնային առասպելների բովանդակությունը։

Արեգակնային առասպելներն իրենց արտացոլումն են գտել կրոններում և մասնավորապես քրիստոնեական կրոնում։ Օրինակ, «Քրիստոսի ծննդյան» տոնը, որը հարմարեցված է ձմեռային արևադարձի ժամանակին, հնադարյան մնացուկներից մեկն է՝ Արեգակի աստծո ծննդյան տոնն է հանդիսանում։

Սուրբ Հովհաննես Մկրտչի քրիստոնեական-կռապաջտական տոնը (հունիսի 24-ը), երբ ն ախառևոլյուցիոն Ռուսաստանի գյուղերում ցատկում էին վառվող խարույկների վրայով, կապված է հին ժամանակներում Արեգակի հուրը երկրպագելու հետ (որը նշանավորվում էր խարույկով)։ Դա կապված է ամառային արևադարձի հետ։

Լուսնի երկրպագումն իր հետքերը պահպանել է մուսուլմանական (այլ կերպ՝ մահմեդական) կրոնում, որտեղ լուսն եղջյուրը («կիսալուսինը») կրոնական սիմվոլ է հանդիսանում։ Նրա պատկերը դնում են մզկիթների վրա, նկարում են դրոշակն երի վրա, օգտագործում են հագուստները և զենքերը զարդարելու համար։

Կրոնական մոլորությունների, երկնային լուսատուները պաշտելու և սոցիալական երևույթների պատճառները չիմանալու հիման վրա առաջ են եկել ֆանտաստիկ պատկերացումներ այն մասին, որ իբր երկնային լուսատուներն ազդում են երկրային իրադարձությունների վրա։ Այդ ազդեցության և ըստ երկնային լուսատուների դիրքի՝ իրադարձությունները նախագուշակելու հնարավորության մասին եղած ուսմունքը ստացել է աստղագուշակություն անունը;

Նման գուշակություններով զբաղվող մարդիկ կոչվում էին աստղագուշակներ։

Հին ժամանակներում և միջին դարերում թագավորները, իշխանները, կառավարիչներն ու զորավարները ունեին իրենց մշտական պալատական աստղագուշակները, որոնց գուշակություններին էլ դիմում էին նրանք՝ պետությունը կառավարելու և պատերազմ վարելու ժամանակ, ինչպես և անձնական գործերում։

Մոլորակների բարդ օղակապտույտ շարժումների պատճառները չհասկանալն աստղագուշակության զարգացման համար բարենպաստ հող էր ստեղծում։ Հավատը դեպի երկնաբնակ էակները, որոնք իբր թե կառավարում են ողջ աշխարհը, առաջ բերեց այդ լուսատուների աստվածացում։ Այդ պատճառով էլ նրանց տրվել են աստվածների անուններ, որոնց համբավաբերներն էին համարվում մոլորակները։ Մարդիկ չիմանալով, որ բնության ամեն մի երևույթ և հասարակական ամեն մի իրադարձություն որոշվում է բնական՝ միանգամայն օրինաչափ պատճառներով, որ նրանք կախում չունեն զանազան ոգիների և աստվածների կամքից, հավատում էին աստղագուշակներին: Այդ հողի վրա էլ առաջացել է «բախտավոր աստղին» և «անբախտ մոլորակին» հավատալը։

Գիտական ճիշտ պատկերացումների զարգացումը ավելի ու ավելի սահմանափակել է սնահավատության բնագավառը։ Բայց և այնպես մինչև հիմա էլ հետամնաց մարդկանց մեջ նման անմիտ նախապաշարմունքներր դեռ շարունակում են մնալ (խաղաթղթով գուշակություն, հավատը դեպի ճակատագիրը , դեպի նշանակները և այլն)։

Ժողովրդական մասսաներին խոնարհ պահելու և աշխատավորներին անպատիժ կերպով շահագործելու համար շահագործող դասակարգերը ամեն կերպ սերմանում են խավարամտություն և զանազան սնահավատություններ։ Նրանք քաջալերում են նաև աստղագուշակությունը, որպես անիմաց մարդկանց անխուսափելի, խորհրդավոր ճակատագրի մասին առասպելներով թմրեցնելու միջոցներից մեկը։ Այդ բանը հատկապես վառ կերպով դրսևորվում է ԱՄՆ-ում, որտեղ այսպես կոչված «դեմոկրատական ազատությունների» անվան տակ տեղի են ունենում ամենավայրենի սնահավատությունների ու սնոտիապաշտությունների սանձարձակություններ։

§ 56. ԱՍՏՂԱԳԻՏՈՒԹՅՈՒՆԸ ՀՆԱԴԱՐՅԱՆ ԺՈՂՈՎՈՒՐԴՆԵՐԸ ՄՈՏ։ Հնադարյան քոչվոր ժողովուրդների աստղագիտական իմացությունները առաջ են եկել օրվա ժամանակը որոշելու և գիշերը տափաստանում կամ անապատում ճիշտ ուղղությունր գտնելու կարիքի հետևանքով։

Մարդու՝ հողագործության անցնելու հետ միասին աստղագիտության հանդեպ ունեցած կարիքը մեծացավ։ Հողագործին անհրաժեշտ էր օրացույց ունենալ, որպեսզի տարվա եղանակների համեմատ կարողանար գյուղատնտեսական աշխատանքները նախապես կարգավորել։

Ծովագնացները շարունակ կարիք էին ունենում կողմն որոշվելու աստղերի միջոցով։

Հնադարյան եգիպտացիներն ու բաբելացիները կարողանում էին ջոկել թափառող լուսատուները՝ մոլորակները և հասկանալ նրանց տեսանելի օղակապտույտ շարժումները։

Թե՛ բաբելացիների և թե՛ եգիպտացիների մոտ գիտությունը օգտագործվում էր քրմերի՝ կրոնի սպասավորների կողմից, իրենց սեփական կաստային նպատակների համար։ Քրմերն իրենց գիտելիքները խիստ գաղտնի էին պահում, որպեսզի կարողանան պահպանել իրենց հեղինակությունն ու իշխանությունը։ Ամսաթվերի, նույն թվում երկնային լուսատուների պաշտամունքի հետ կապված կրոնական տոների սահմանումը ամրապնդել է աստղագիտական գիտելիքներին տիրապետող քրմերի իշխանությունը։ Քրմերր երկնային երևույթների վերաբերյալ մեծ քանակությամբ փաստական տվյալներ էին կուտակել, բայց անկարող էին նրանց ճիշտ բացատրել։ Երկնային մարմինների բնությունն ուսումնասիրելու փոխարեն քրմերը զարգացնում էին աստղագուշակությունը և այդպիսով սարսափի մեջ էին պահում ոչ միայն ժողովրդին, այլ հաճախ նաև նրա կառավարիչներին։

Ըստ հին բաբելական առասպելի, որը փոխ են առել հրեաները իրենց ստրկացնողներից՝ բաբելացիներից, և որը մտել է «սուրբ» Աստվածաշնչի մեջ, երկինքն իրենից մի կարծր գմբեթ է ներկայացնում («երկնային հաստատություն»), որը հենվում է տափարակ Երկրի եզրերի վրա։ Երկինքը աշխարհն ստեղծող «երկնաբնակների» ապրելու վայրն է։ Այդ տեսակետների հիման վրա է աճել այն խոր տարբերության պատկերացումը, որ դրվում էր երկրայինի և երկնայինի, «այս աշխարհի» և «հանդերձյալ աշխարհի», բնականի և գերբնականի, նյութականի և հոգեկանի, իմանալիի և իբր թե անիմանալիի միջև։ Այստեղից էլ մինչև օրս պահպանվել է այս դարձվածքը՝ «տարբերվում է ինչպես երկինքը Երկրից»։

Այն բանից հետո, երբ քաղաքական և կուլտուրական կենտրոնը Րաբելոնից և Եգիպտոսից փոխադրվեց Հունաստան, աստղագիտության բնագավառում կուտակված տեղեկությունները հույն մտածողների սեփականությունը դարձան։ Աստղագիտությունը նրանց մոտ ստացավ իր հետագա զարգացումը, որովհետև հույները, որպես խիզախ ծովագնացներ, առանձնապես զգում էին այդ գիտության կարիքը և այդ բնագավառում հաջողությամբ կիրառեցին իրենց մաթեմատիկական գիտելիքները։

§ 57․ ՄՈԼՈՐԱԿՆԵՐԸ ԵՎ ՆՐԱՆՑ ՏԵՍԱՆԵԼԻ ՇԱՐԺՈՒՄԸ։ Չզինված աչքով երևում է հինգ մոլորակ՝ Մերկուրին, Վեներան, Մարսը, Յուպիտերը և Սատուրնը։ Նրանք փայլում են այնպես, ինչպես ամենապայծառ աստղերն են փայլում։ Ուստի կարելի է հայտնաբերել մոլորակը, որպես մի «ավելորդ» պայծառ աստղ որևէ համաստեղության մեջ (նկ. 46)։ Մոլորակների հայտնաբերելուն կարող է օժանդակել նաև երկնքի համեմատությունն աստղային քարտեզի հետ, որտեղ մոլորակների դիրքը, իհարկե, ցույց չի տրված, որովհետև այդ լուսատուները երկնքում անընդհատ փոփոխում են իրենց դիրքը։

Դիտումները ցույց են տալիս, որ յուրաքանչյուր մոլորակ տարվա որոշ մասն անց է կացնում Արեգակին շատ մոտ, և այդ ժամանակ նա անհետանում է Արեգակի ճառագայթների մեջ։ Հետևաբար, չի կարելի հուսալ, որ ամեն երեկո կարելի է տեսնել բոլոր մոլորակները միասին։ Բացի այդ, լինում է այնպես, որ որևէ մոլորակ ծագում է միայն առավոտյան դեմ կամ երեկոն դեռ չհասած արդեն մայր է մտնում։ Այնպես որ, կարող է պատահել, որ տվյալ մոմենտում երկնակամարի վրա ոչ մի մոլորակ չերևա։

Դիտելով լուսատուները՝ մարդիկ համոզվել են, որ այն ժամանակ, երբ Մարսը, Յուպիտերը և Սատուրնը, առհասարակ, կարելի է տեսնել գիշերվա ցանկացած ժամին, Վեներա և մանավանդ Մերկուրի մոլորակները Արեգակից երբեք շատ չեն հեռանում։ Մերկարին և Վեներան կարող են դիտվել միայն երկու դեպքերում — կա՛մ երեկոյան՝ Արեգակը մայր մտնելուց անմիջապես հետո՝ արևմուտքում, կամ առավոտյան՝ Արեգակը ծագելուց քիչ առաջ՝ արևելքում։ Ըստ որում Մերկուրին նույնիսկ Արեգակից իր տեսանելի, այսինքն անկյունային, առավելագույն չափով հեռացման շրջանում, դժվարությամբ է երևում արշալույսի ճառագայթների մեջ և հորիզոնին մոտ է։ Այսպիսով, և՛ Մերկուրին, և՛ Վեներան գիտվում են կա՛մ որպես «լուսաստղ)), կա՛մ որպես «երեկոյան» աստղեր և նրանք գիշերը երբեք չեն երևում։ Նրանք երևում են երկնքի միայն արևմտյան կամ արևելյան կողմում։

Վեներան անհամեմատ ավելի պայծառ է փայլում, քան մյուս մոլորակներն ոլ աստղերը և սպիտակ գույն ունի։ Յուպիտերը ավելի թույլ է, քան Վեներան, բայց շատ ավելի պայծառ է առաջին մեծության աստղերից և մյուս մոլորակներից» նա դեղնավուն գույնի է։ Մարսը կարմրանարնջագույն է և երբեմն նույնքան պայծառ է լինում, ինչպես Յուպիտերը, բայց հաճախ փայլում է ինչպես առաջին մեծության աստղ։ Սատուրնր քիչ է տարբվերվում առաջին մեծության աստղերից և դեղնավուն է։

Շատ հետաքրքիր և օգտակար է հետևել աստղերի նկատմամբ մո լորակների կատարած տեղաշարժումներին, աստղային քարտեզի վյրա ժամանակ առ ժամանակ նշելով նրանց դիրքը։ Չզինված աչքով ավելի շուտ կարելի է նկատել Մարսի կատարած շարժումը։ Սակայն բոլոր մոլորակների համար էլ միայն մի քանի ամիս շարունակ կատարած դիտումներից հետո է պարզվում նրանց տեսանելի տեղաշարժումների գլխավոր առանձնահատկությունը։ Յուրաքանչյուր մոլորակի շարժման առանձնահատկությունն այն է, որ նա մերթ արագ է շարժվում, մերթ դանղաղ, մերթ երկնային սֆերայի օրական շարժման ուղղությամբ, մերթ հակառակ ուղղությամբ, և տարեկան մեկ անգամ աստղային երկնքի ֆոնի վրա կարծես մի օղակ է գծում։

Նկ. 47-ում ցույց են տրված աստղային քարտեզի մի մասը և այն օղակաձև ուղին, որը 1939 թ.ընթացքում անցել է Մարսը։ Այդ նկարի վրա նշված է, թե տարվա որոշ օրերին Մարսը իր անցած ուղու ո՛ր կետերումն է գտնվելիս եղել։

Ամենաարագ շարժվողը և ավելի մեծ օղակ գծողը (աստիճաններով հաշված ) Մարսն է, նրանից պակասը՝ 3ուպիտերը , է՛լ ավելի պակասը՝ Սատուրնը։ Օղակներ գծելով, յուրաքանչյուր մոլորակ միևնույն Ժամանակ շարունակում է տեղափոխվել աստղային երկնքի ֆոնի վրա, նրա օրական պտույտի հակառակ ուղղությամբ։

Մերկուրիի և Վեներայի շարժումների մասին ավելի մանրամասն չենք խոսում, որովհետև արշալույսի պայծառ ֆոնի վրա, որտեղ աստղերի աղոտ լույսն անհետանում է, նրանց հետևելը դժվար է, բայց նրանք ևս այդ ձևի օղակներ են գծում։

§ 58․ ԱՐԻՍՏՈՏԵԼԻ ԵՎ ՊՏՂՈՄԵՈՍԻ՝ ԱՇԽԱՐՀԻ ՍԻՍՏԵՄՆԵՐԸ։ Հին հունական գիտության բոլոր նվաճումների ընդհանրացումը տվել է հին աշխարհի մեծագույն գիտնականներից մեկը՝ Արիստոտելը (384—322 մ. թ. ա, ) IV դարում մեր թվականությունից առաջ։ Այնուամենայնիվ, հունական գիտնականների մեծ մասի պատկերացումը աշխարհի կառուցվածքի մասին եղել է դեռևս շատ հեռու իրականուփյունից։

Ըստ Արիստոտելի, մոլորակները, Արեգակը և Լուսինը ամրացված են երկնային կարծր և թափանցիկ սֆերաների վրա, ըստ որում յուրաքանչյուր լուսատուն՝ իր սեփական սֆերայի վրա։ Այդպիսի սֆերաներից ամենահեռավորի վրա դասավորված են աստղերը։ Այդ սֆերաները համակենտրոն կերպով տեղավորված են մեկը մյուսի մեջ և նրանց կենտրոնում գտնվում է անշարժ երկրագունդը։ Երկնային սֆերաները տարբեր արագությամբ պտտվում են Երկրի շուրջը՝ մասամբ ձգելով ու տանելով մեկը մյուսին, որից էլ, ինչպես Արիստոտելն էր ասում, տեղի են ունենում երկնային լուսատուների տեսանելի շարժումները։

Աշխարհի այդ ամբողջ սիստեմը, որի կենտրոնում տեղավորված է Երկիրը, կոչվում է գեոցենտրիկ սիստեմ։

Հին հունական աստղագիտության նվաճումների գագաթնակետը հանդիսացավ մեր թվականության II դ. ալեքսանդրիացի գիտնական կլավդիոս Պտղոմեոսի մշակած աշխարհի սիստեմը։ Նա նույնպես գեոցենտրիկ պատկերացումներից էր ելնում։ Մոլորակների օղակաձև շարժումները բացատրելու համար Պտղոմեոսը ենթադրեց, որ յուրաքանչյուր մոլորակ շարժվում է համաչափորեն մի փոքր շրջան ագծով (որն անվանեց էպիցիկլ), մինչդեռ այդ շրջանագծի կենտրոնն իր հերթին մի մեծ շրջանագծով շարժվում է Երկրի ջուրջը։ Զանազան հարթությունների վրա տեղփ ունեցող հենց այդ երկու շարժումների զուգակցությունն է, որ Երկրից նայելու դեպքում ստեղծում է մոլորակներիօղակաձև շարժում մերթ դեպի առաջ, մերթ դեպի ետ։

§ 59*. ՄԻՋՆԱԴԱՐՅԱՆ ՊԱՏԿԵՐԱՑՈՒՄՆԵՐԸ ԱՇԽԱՐՀԻ ԿԱՌՈՒՑՎԱԾՔԻ ՄԱՍԻՆ։ Հունական պետությունների և նրանց կուլտուրայի անկումից հետո սկսվեց Արևմտյան Եվրոպայի պետությունների զարգացումը։ Սակայն միջին դարերում այնտեղ գոյություն ուներ պրիմիտիվ տնտեսություն, որը գիտությունների զարգացման համար դեռ քիչ էր շահագրգռված։ Ծովագնացությունը թույլ էր զարգացած, իսկ քրիստոնեական եկեղեցին, որն իշխում էր մարդկանց մտքի վրա և օժտված էր նույնպիսի իշխանությամբ, ինչպես որ անցյալի քրմերը, արգելում էր բնության ուսումնասիրությունը՝ համարելով այն մեղսական զբաղմունք։

Այն ժամանակ տիեզերքի մասին է՛լ ավելի միամիտ ու կոպիտ պատկերացումներ կային, քան եգիպտացիների և հույների մոտ։ Երկրի գնդաձևությունն իսկ հերքվում էր․ կրոնական պատկերացումների համաձայն՝ Երկիրը պատկերվում էր որպես տափարակ շրջան կամ նույնիսկ քառանկյունի։ Իսկ աստղերը համարվում էին երկնակամարին խփված ոսկե մեխեր կամ կանթեղներ, որ վառում են հրեշտակները։

Աշխարհագրական մեծագույն հայտնագործությունների դարաշրջանում, երբ եվրոպացիները նոր հարստություններ զավթելու նպատակով խիզախում էին լողալ ծովերում և նույնիսկ օվկիանոսներում, կամա-ակամա հարկ եղավ դիմել աստղագիտությանը։ Լույս աշխարհ հանվեցին Արիստոտելի և Պտղոմեոսի տեսությունները՝ հույների ժառանգությունը։ Այն շրջանում, երբ քրիստոնեական եկեղեցին ֆանատիկորեն հալածում էր այն ամենը, ինչ հակառակ էր կրոնին, հին հունական գրողների երկերն անխուսափելի կորստից կարողացել էին փրկել միջնադարյան արաբները։ Աստղագիտական շատ անուններ և տերմիններ մնացել են արաբներից, որոնք, զարգացնելով ծովագնացությունը, գնահատում էին աստղագիտությունը և զբաղվում այդ գիտությամբ։

Եկեղեցական պարագլուխները ևս շահագրգռված լինելով անդրծովյան ճանապարհորդություններից ստացվող շահույթներով, որոշեցին թույլատրել Պտղոմեոսի տեսության ուսումնասիրությունը՝ անելով որոշ վերապահումներ ու լրացումներ իրենց կրոնական ուսմունքների ոգով։

ՌԵՎՈԼՅՈՒՑԻԱ ԱՇԽԱՐՀԱՅԱՑՔՈՒՄ

§ 60. ԿՈՊԵՌՆԻԿՈՍԻ ՌԵՎՈԼՅՈՒՑԻՈՆ ՀԱՅՏՆԱԳՈՐԾՈՒԹՅՈՒՆԸ։ Ծովային կապերի զարգացումն աստղագիտական հաշիվների ավելի մեծ ճշտություն էր պահանջում։ Պտղոմեոսի տեսությունն այդ չէր կարողանում տալ, չնայած մեծ ճշտությամբ կատարվող դիտումների հետ համաձայնեցնելու համար հարկ եղավ Պտղոմեոսի տեսությունը խիստ կերպով բարդացնել։ Պտղոմեոսի տեսությունը հաշվարկումների համար դարձավ անհարմար և մեծածավալ, և դրա հետ միասին սկսեց նաև անարժանահավատ թվալ։

Տիեզերքի իսկական կաոուցվածքը բացահայտելը և դրանով իսկ մարդկանց բնության մեջ իրենց գրաված իսկական տեղը ցույց տալը վիճակվեց հանճարեղ սլավոնացի Նիկոլայ Կոպեոնիկոսին (1473—1543)։

Կոպեռնիկոսը եկավ այն համոզմունքին, որ Երկիրը շարժվում է, և այն հետևության, որ երկնային լուսատուների նկատելի շարժումները կարելի է պարզ ու հասկանալի կերպով բացատրել եթե ելնենք Երկրի շարժումից։

Կանգնելով այդ տեսակետի վրա, Կոպեռնիկոսը լուսատուների ծագելն ու մայր մտնելը բացատրեց Երկրի օրական պտույտով, իսկ Արեգակի տեսանելի շարժումը խավարածրով՝ Արեգակի շուրջը Երկրի կատարած տարեկան պտույտով։ Ըստ Կոպեռնիկոսի, մյուս մոլորակները նույնպես պատվում են Արեգակի և ոչ թե Երկրի շուրջը։

Մոլորակները սեփական լույս չունեն․ նրանց․ ինչպես և Երկրին լուսավորում է Արեգակը։ Միայն դրա շնորհիվ է, որ մենք կարողանում ենք նրանց տեսնել։

Այսպիսով, Կոպեռնիկոսի տեսության համաձայն, երկիրը դարձավ մոլորակներից մեկը, որն Արեգակից ունեցած հեռավորության տեսակետից երրորդ տեղն է գրավում։ Մոլորակները դասավորված են հետևյալ կարգով. Մերկուրի, Վեներա, Երկիր, Մարս, Յուպիտեր և Սատուրն։

Կոպեռնիկոսը մոլորակների տեսանելի օղակաձև շարժումները բացատրեց նրանով, որ երկրի շարժումը գուգակցվում է յուրաքանչյուր մոլորակի շարժման հետ։ Որովհետև տարբեր մոլորակներ Արեգակի շուրջը մի լրիվ պտույտ կատարում են ոչ-հավասար ժամանակամիջոցում, ուստի պատահում է այնպես, որ, օրինակ, Երկիրը կարծես հասնում ու անցնում է մոլորակից, և այն ժամանակ թվում է, թե մոլորակն աստղերի նկատմամբ դեպի արևմուտը է տեղաշարժվում։ Իսկ երբ Երկիրն սկսում է շարժվել մոլորակի շարժմանը կարծես թե հակառակ ուղղությամբ (պտտվելով Արեգակի շուրջը), ապա մոլորակը տեսանելիորեն դեպի արևելք է տեղաշարժվում։

Կոպեռնիկոսը որոշեց մոլորակների պտտման պարբերությունները (կամ ժամանակը) և նրանց համեմատական հեռավորություններն Արեգակից՝ որպես միավոր ընդունելով Երկրի հեռավորությունն Արեգակից։

Կոպեռնիկոսը քիչ տագնապ չի ապրել հանդեպ իր հայտնագործության և սիրտ է արել այն հրատարակել երկար, տանջալի կասկածանքներից հետո միայն։ Նա գիտակցում էր, որ իր հայտնագործությունը, հակասելով այն ժամանակաշրջանի ողջ աշխարհայացքի ամենաէական սկզբունքներին, հսկայական հետևանքներ կունենա։ Նրա գիտական խիզախության մեջ հանդես է գալիս իսկական գիտության ամենաէական հիմքը, գիտության, որը չգիտի ոչ մի զիջում, ոչ մի կոմպրոմիս, և համարձակորեն փշրում է հնացած նորմաներն ու սկզբունքները՝ թեկուզ և նրանք լինեն հանրաճանաչ։

Կոպեռնիկոսը իր ուսմունքով սկիզբ դրեց աստղագիտության զարգացմանը միանգամայն նոր հիմունքների վրա և մարդկությանը դրդեց անցնել բնության ուսումնասիրությանն՝ առանց ետ նայելու դեպի անցյալի տգիտության վրա հիմնված եկեղեցական հնացած ուսմունքները։ Կոպեռնիկոսից առաջ եկեղեցական ուսմունքները կամ այն ուսմունքները, որոնց պաշտպանում էր եկեղեցին, ինչպես, օրինակ, Պտղոմեոսի ուսմունքը, որոնք չէին հակասում Աստվածաշնչին, կաշկանդում էին ոչ միայն աստղագիտության, այլև մյուս գիտությունների զարգացումը։ Կոպեռնիկոսի հայտնագործությունը ռևոլյուցիա առաջացրեց մարդկանց աշխարհայացքի մեջ, նրանց կողմից բնությունն ըմբռնելու և այն ճանաչելու միջոցների մեջ։ Ուստի այն ժամանակվանից ի վեր մյուս գիտությունները ևս սկսեցին ավելի արագ և ճիշտ կերպով զարգանալ։

Այդ մասին Ֆ․ Էնգելսը այսպես է ասում, «Ինչ որ կրոնական բնագավառում պապի կոնդակի այրումն էր Լյութերի կողմից, այն էլ բնագիտության մեջ եղավ Կոպեռնիկոսի մեծ աշխատությունը, որի մեջ նա,— թեև երկչոտությամբ, 36-ամյա տատանումներից հետո և, այսպես ասած, մահվան մահճում,— մրցահրավեր ուղղեց եկեղեցական սնահավատությանը։ Այդ ժամանակվանից բնության ուսումնասիրությունը ըստ էության ազատվեց կրոնից, թեև բոլոր մանրամասնությունների վերջնական պարզաբանումը մինչև այժմ է է ձգձգվում է․․․ Բայց այդ ժամանակից ի վեր գիտության զարգացումը առաջ գնաց հսկայական քայլերով...»։ («Բնության դիալեկտիկա», էջ 214, Հայպետհրատ, 1950 թ․)։

Պետք է նշել, որ ներկայումս ևս, երբ մեզ մոտ՝ Սովետական Միության մեջ, զարգանում է առաջավոր գիտությունը, ուր զարգանում են մատերիալիստական տեսությունները, ինչպես, օրինակ, Միչուրինի ուսմունքը բնագիտության բնագավառում, արտասահմանյան երկրներում գոյություն ունեն և պաշտպանվում են հօգուտ ունևոր դասակարգերի, զանազան ռեակցիոն տեսություններ։ Այսպես, օրինակ, այնտեղ հանդիպում են փորձեր Կոպեռնիկոսի հայտնագործության էության ժխտման և քողարկված ձևով վերադառնալու միջնադարյան հակագիտական պատկերացումներին, վերականգնելու կրոնի հեղինակությունը բնության նկատմամբ ունեցած աշխարհայացքի տեսակետից։

Այսպիսով, պայքարը ընդդեմ կրոնական իդեոլոգիայի հարկավոր է և այժմ, քանի որ նեխվող կապիտալիզմի աշխարհայացքը ամեն կերպ պաշտպանում է նման սնահավատությունները։

§ 61*. ՄՈԼՈՐԱԿՆԵՐԻ ՏԵՍԱՆԵԼԻ ՇԱՐԺՄԱՆ ԲԱՑԱՏՐՈՒԹՅՈՒՆՆ ԸՍՏ ԿՈՊԵՌՆԻԿՈՍԻ ՏԵՍՈՒԹՅԱՆ։ Որպեսզի ավելի պարզ պատկերացնենք երկնային սֆերայում (աստղերի ֆոնի վրա) մոլորակների կատարած տեսանելի օղակաձև շարժումները է քննության առնենք նկ. 50-ը։ Նկարում S-ը պատկերում է Արեգակը, T₁, T₂, T₃, T₄ շրջանագիծը՝ Երկրի տարեկան ուղին, իսկ P₁, P₂, P₃, P₄ շրջանագիծը՝ այն ուղին, որով որևէ մոլորակ, ասենք՝ Մարսը, պտտվում է Արեգակի շուրջը։ Որքան մոլորակն Արեգակից հեռու է գտնվում, այնքան փոքր է նրա շարժման և՛ անկյունային, և՛ գծային արագությունը։ Միատեսակ նշաններ ունեցող T և P տառերով նշանակված են Երկրի և Մարսի միևնույն ժամանակում ունեցած դիրքերը։ Շրջանագծի B₁B₂B₃B₄ հատվածը իրենից պատկերում է երկնային սֆերայի մի մասը, որի վրա, դիտելով Երկրից, պրոյեկտում ենք մոլորակը։

Երբ Երկիրը գտնվում է T₁ կետում, Մարսը գտնվում է P₁ կետում, և մենք նրան տեսնում ենք T₁P₁ ուղղությամբ՝ երկնային սֆերայի B₁ կետում։ Որոշ ժամանակից հետո Երկիրը կփոխադրվի T₂ կետը, Մարսը՝ P₂ կետը, իսկ նրա պրոյեկցիան երկնային սֆերայի վրա՝ B₂ կետը։ Շարունակելով նման ձևով կառուցումները և հետևելով, թե ինչպե՛ս է գրա հետ կապված շարժվում Մարսի պրոյեկցիան երկնային սֆերայի վրա, մենք կհամոզվենք, որ Մարսը աստղային երկնքի ֆոնի վրա սկզբում շարժվում էր ձախ՝ դեպի արևելք (այսպես կոչված «ուղիղ շարժում» B₁ կետից մինչև B₂ կետը), հետո նա կարծես կանգ է առնում, իսկ B₂ կետից նա շարժվում է B₃ կետի ուղղությամբ, այսինքն աջ՝ դեպի արևմուտք (այսպես կոչված «հետընթաց շարժում»)։ Սա մի տեսանելի, թվացող շարժում է, որն առաջ է գալիս տարածության մեջ դիտողի՝ Երկրի հետ միասին կատարած շարժման և Արեգակի շուրջը մոլորակի կատարած իսկական շարժման զուգակցությունից։

Մոլորակը փոխանակ երկնային սֆերայում ուղիղ գծով տատանումներ կատարելու, քիչ թե շատ չափով բացված օղակ է գծում, որովհետև Երկրի և մոլորակի շարժման հարթությունները չեն համընկնում։

Մոլորակի օղակի ձևով ստացվող տեսանելի շարժումը ցույց է տրված նկ. 50-ում։ Այդ նկարը Երկրի և մոլորակի անցած ուղին պատկերում է պլանում։ Նկ. 51-ը նույնը պատկերում է տարածության մեջ։ Նման գծագրեր կարելի է կառուցել նաև այնպիսի մոլորակի համար, որն ավելի մոտ է գտնվում Արեգակին, քան Երկիրը։

§ 62*. ՄՈԼՈՐԱԿՆԵՐԻ ԿՈՆՖԻԳՈՒՐԱՑԻԱՆ։ Մոլորակի՝ տիեզերական տարածության մեջ գծած ուղին կոչվում է նրա ուղեծիրը (օրբիտը)։ Այն մոլորակները, որոնց ուղեծրերը գտնվում են Երկրի ուղեծրի ներսում, կոչվում են ներքին մոլորակներ։ Իսկ այն մոլորակները, որոնք ավելի հեռու են գտնվում Արեգակից, քան Երկիրը, կոչվում են արտաքին մոլորակներ։

Ամեն մի մոլորակ ժամանակի յուրաքանչյուր մոմենտում որոշակի տեղ է գրավում իր ուղեծրի վրա։ Երկրի և Արեգակի նկատմամբ մոլորակի գրաված գիրքը կոչվում է նրա կոնֆիգուրացիան։

Ներքին և արտաքին մոլորակների կոնֆիգուրացիաները տարբեր են լինում և ցույց են տրված նկ․ 53-ում։

Ներքին մոլորակների համար (այսինքն՝ Մերկուրիի և Վեներայի համար) բնորոշ են հետևյալ կոնֆիգուրացիաները․ վերին և ստորին միացումներ, էլոնգացիաներ։ Միացումներում մոլորակը Արեգակի հետ գտնվում է մի ուղիղ գծի վրա (Երկրի վրայից դիտելիս)։

Մոլորակը վերին միացման մոտերքում չի երևում, որովհետև գտնվելով Արեգակից այն կողմը, նա թաղվում է Արեգակի պայծառ ճառագայթների մեջ։ Մոլորակը ստորին միացման մեջ գտնվելու ժամանակ Երկրից ամենամոտ դիրքն է ունենում, բայց այս դեպքում ևս նա թաղված է լինում արևի ճառագայթների մեջ։ Հեռադիտակով Երկրից նայելիս՝ ստորին միացման մոտերքում մոլորակը բարակ եղջյուրի տեսք է ունենում։

Երբեմն ներքին մոլորակները, գտնվելով ստորին միացման մեջ, փոքր սև շրջանիկների ձևով պրոյեկտվում են ուղիղ Արեգակի սկավառակի վրա։ Մի աժամանակ նրանք տեղաշարժվում են սկավառակի վրայով, ուստի և այդ երևույթր կոչվում է անցումներ Արեգակի սկավառակով։ Մերկուրին այդ անցումները հաճախ է կատարում (սովորաբար 13 տարին մեկ անգամ), իսկ Վեներան՝ շատ հազվադեպ (նրա վերջին անցումը եղել է 1882 թ․, իսկ հաջորդը տեղի կունենա միայն 2004 թ.)։

Արեգակից առավելագույն չափի տեսանելի անկյունային հեռացումների ժամանակ, որոնք էլոնգացիաներ են կոչվում, ներքին մոլորակները լուսավոր կիսասկավառակների տեսք ունեն։ նայած, թե Արեգակի ո՛ր կողմումն է երևում մոլորակը, ըստ այնմ էլ ասում են՝ արևմտյան կամ արևելյան էլոնգացիա։ Մերկուրիի առավելագույն էլոնգացիան կազմում է 28°, իսկ Վեներայինը՝ 48°։

Ներքին մոլորակի տեսանելի անկյունային տրամագծի և տեսանելի ձևի փոփոխությունները (փուլերի հաջորդումը) պատկերված են նկ. 54-ում։ Ներքին մոլորակները ամենից լավ դիտվում են իրենց էլոնգացիաների շրջանում, երբ նրանք երևում են արևածագից առաջ և արևամուտից հետո և հորիզոնից բավականաչափ բարձր են գտնվում։

Արտաքին մոլորակի համար (Մարս, Յուպիտեր և այլն) հատկանշական են միացումն Արեգակի հետ և դիմակայությունը։ Առաջին դեպքում մոլորակը չի երևում (նա գտնվում է Արեգակից այն կողմը), երկրորդ դեպքում նա ուղղակի հակադիր է Արեգակին՝ եթե նայենք Երկրից։ Դիմակայությունը ամենալավ ժամանակն է արտաքին մոլորակը դիտելու համար, որովհետև այս դեպքում նա մեզնից ամենամոտ դիրքն ունի և կուլմինացիայի կետից անցնում է կես-գիշերին, այսինքն՝ երևում է ամբողջ գիշերը կամ նրա մեծ մասի ընթացքում։

Այն կոնֆիգուրացիան, որի ժամանակ Երկրից դեպի մոլորակ ընթացող ուղղությունն Արեգակի ուղղության հետ ուղիղ անկյուն է կազմում, կոչվում է քաոակուսացում (կվադրատուրա): Մոլորակը քառակուսացման մեջ երևում է միայն գիշերվա կեսի ընթացքում (երեկոյից կամ կես-գիշերից հետո)։

Մոլորակի տեսանելիության պայմանների վրա ազդում է նաև այն, թե նա կենդանակերպային ո՞ր համաստեղությունումն է գտնվում։ Օրինակ, մեր լայնություններում Կարիճի և Աղեղնավորի համաստեղությունները հորիզոնից շատ չեն բարձրանում և հորիզոնի վրա երկար չեն մնում, որը զգալի չափով վատացնում է այդ համաստեղություններում գտնվող մոլորակները դիտելու պայմանները։

§ 63․ ՄՈԼՈՐԱԿՆԵՐԻ ՊՏՏՄԱՆ ՍԻԴԵՐԻԿ ԵՎ ՍԻՆՈԴԻԿ ՊԱՐԲԵՐՈՒԹՅՈՒՆՆԵՐԸ։ Մոլորակի պատման սիդերիկ (կամ աստղային) պարբերություն կոչվում է այն ժամանակամիջոցը, որի ընթացքում նա Արեգակի շուրջը մի լրիվ շրջան է կատարում։ Որքան մոլորակը հեռու է գտնվում Արեգակից, այնքան նրա սիդերիկ պարբերությունը երկար է լինում։ Այդ պարբերությունը դիտումներով անմիջականորեն չի կարելի որոշել։ Այն կարելի է հաշվել նախապես դիտումներով որոշելով մոլորակի սինոդիկ պարբերությունը։ Առաջին անգամ Կոպեռնիկոսն էր, որ այդպես վարվեց։

Մոլորակի սինոդիկ պարբերություն է կոչվում այն ժամանակամիջոցը, որ անցնում է մոլորակի երկու միատեսակ կոնֆիգուրացիաների միջև, օրինակ, երկու հաջորդական դիմակայությունների միջև։

Դիմակայության ժամանակ մոլորակը կուլմինացիա է կատարում կես-գիշերին։ Այդ հատկանիշով դժվար չէ որոշել մոլորակի սինոդիկ պարբերությունը, իսկ նրա միջոցութ նաև սիդերիկ պարբերությունը։

Որևէ մոլորակի S սիղերիկ պարբերության երկարության և P սինոդիկ պարբերության երկարության միջև եղած կապը որոշվում է հետևյալ կերպ, Երկրի սիդերիկ պարբերության երկարությունը, այսինքն՝ մեկ տարին, նշանակենք T տառով։ Այն ժամանակ Երկիրը մեկ օրում իր ուղիով անցնում է մի աղեղ, որ հավասար է 360°:T, իսկ մոլորակը՝ 360°:S: Եթե վերցնելու լինենք արտաքին մոլորակ, որն Արեգակի շուրջն ավելի դանդաղ է պտտվում, քան Երկիրը, ապա ամեն օր Երկիրը մոլորակից առաջ կանցնի (360°:T)—(360°:S) մեծության չափով։ Եթե մոլորակը մի որևէ մոմենտում եղել է դիմակայության մեջ, ապա P օր անցնելուց հետո մոլորակը դարձյալ դիմակայության մեջ կգտնվի, որովհետև P-ն մոլորակի սինոդիկ պարբերությունն է։ Այդ ժամանակամիջոցում Երկիրն առաջ անցած կլինի մոլորակից 360°-ով։ Հետևաբար,

Չհաջողվեց վերլուծել (բառական սխալ):

Կրճատելով 360°-ով և փոխադրելով (P-ն հավասարման աջ կողմը, կստանանք՝

$\text{[math]}$ ։

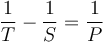Այս ֆորմուլան թույլ է տալիս որոշել մոլորակի S սիդերիկ պարբերությունը, եթե դիտումներից մեզ հայտնի են T և P մեծություններր։ճիշտ նույն ձևով ներքին մոլորակի համար կարելի է ստանալ այս ֆորմուլան.

$\text{[math]}$ ։

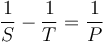Որտեղից՝

$\text{[math]}$ ։

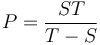Բոլոր մոլորակների համար S և P մեծությունները բերված են դասագրքի վերջում՝ VI աղյուսակում։

§ 64. ԿԵՊԼԵՐԻ ՕՐԵՆՐՆԵՐԸ։ Կոպեռնիկոսը հաստատեց, որ Երկրի և մոլորակների շարժման կենտրոնը հանդիսանում է Արեգակը, բայց մոլորակների ուղեծրեոի իրական ձևերը նա չկարողացավ ստույգ կերպով որոշել։ Կոպեռնիկոսը, նման հնադարի բոլոր գիտնականներին ու փիլիսոփաներին, համոզված էր, որ երկնքում բոլոր շարժումները պետք է լինեն համաչափ և պետք է կատարվեն շրջանաձև։ Ուստի Կոպեռնիկոսի տեսությունը հազիվ թե ավելի լավ էր համապատասխանում մոլորակների շարժումների ճշգրիտ դիտումներին, քան Պտղոմեոսի տեսությունը։

Այդ անհամապատասխանության պատճառները XVII դարի սկզբներին բացահայտեց Իոհան Կեպլերը (1571—1630)։

Կեպլերը սահմանեց մոլորակային շարժումների երեք օրենք, որոնք միանգամայն համընկնում էին երկնային սֆերայում մոլորակների շարժումների դիտումների հետ։

Առաջին օրենքը։ Յուրաքանչյուր մոյորակ շարժվում է էլիպսով, որի ֆոկուսներից մեկում գտնվում է Արեգակը։

Էլիպս կոչվում է հարթ պարփակված կորը) որը օժտված է այն հատկությամբ, որ նրա յուրաքանչյուր կետի՝ ֆոկուսներ կոչված երկու կետերից ունեցած հեռավրրությունների գումարը մնում է հաստատուն։ Նկ․ 56-ում O էլիպսի կենտրոնն է, DA նրա մեծ առանցքն է, K և S էլիպսի ֆոկուսներն են, այնպես որ KM + SM = DA = էլիպսի մեծ առանցքին, էլիպսի մեծ առանցքի տվյալ մեծության դեպքում՝ որքան մեծ է նրա ֆոկուսների միջև եղած հեռավորությունը, այնքան նա ավելի ձգված է լինում։ Էլիպսի ձգվածության աստիճանդ նրա էքսցենտրիսիտետի մեծությամբ է բնորոշվում։ Էքսցենտրիսիտետ կոփվում է էլիպսի կենտրոնի՝ որևէ ֆոկուսից ունեցած հեռավորության և մեծ կիսառանցքի երկարության հարաբերությունը։

Էքսցենտրիսիտետ

$\text{[math]}$ ։

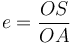Մոլորակների էլիպսաձև ուղեծրերը քիչ են տարբերվում շրջանագծից, և նրանց էքսցենտրիսիտետները զրոյից մի փոքր մեծ են (տե՛ս աղյուսակ VI, 5)։

Կեպլերի առաջին օրենքից հետևում է, որ մոլորակների հեռավորությունն Արեգակից փոփոխվում է'։ Ուղեծրի՝ Արեգակին ամենամոտիկ կետը կոչվում է պերիհելիում (արևամոտ), իսկ ամենահեռավորը՝ աֆելիում (արևահեռ)։

Երկրի ուղեծիրը նույնպես էլիպսաձև է։ Պերիհելիումում Երկիրը ջինում է մոտավորապես հունվարի 1-ին, իսկ աֆելիումում՝ մոտավորապես հուլիսի 1-ին։ Թեև, այսպիսով, Երկրի հյուսիսային կիսագնդում ձմեռը Արեգակից ամենակարճ հեռավորության վրա է լինում, այնուամենայնիվ, արևի ճառագայթների անկման անկյան և ցերեկվա տևողության տարբերությունները ավելի ուժեղ են ազդում, քան շրջանագծից շատ քիչ տարբերվող ուղեծրով շարժվող Երկրի՝ Արեգակից ունեցած հեռավորության չնչփն փոփոխությունները։

Երկրորդ օրենքը կամ մակերեսների օրենքը։ Մոլորակի շառավիղ-վեկտորը հավասար ժամանակներում հավասար մակերեսներ է գծում։

Մոլորակի շառավիղ-վեկտոր է կոչվում ուղիղ գծի այն հատվածը, որով մոլորակը միացվում է Արեգակի հետ։ Մոլորակի արագությունն իր շարժման ընթացքում փոփոխվում է այնպես, որ մոլորակն իր ուղեծրի թեկուզ ո՛ր մասումն էլ գտնվելիս լինի, որևէ ժամանակի, ասենք՝ մեկ շաբաթվա ընթացքում նրա շառավիղ-վեկտորի գծած մակերեսի մեծությունը մնում է միևնույնը։ Նկ. 56-ում SDC, ESF ASH մակերեսները հավասար են, եթե մոլորակը DC, EF և AH աղեղները հավասար ժամանակամիջոցներումն է գծել։ Այսպիսով, պերիհելիումի մոտերքում մոլորակը ամենամեծ արագությունն է ունենում, իսկ աֆելիումի մոտերքում՝ ամենափոքրը։

Երրորդ օրենքը։ Մոլորակների պտտման սիդերիկ պարբերությունների քառակուսիները հարաբերում են միմյանց այնպես, ինչպես նրանց ողեծրերի մեծ կիսառանցքների խորանարդները։

Եթե մոլորակներից մեկի սիդերիկ պարբերությունը և ուղեծրի մեծ կիսառանցքը նշանակենք T₁ և a₁ տառերով, իսկ մյուս մոլորակինը՝ T₂ և a₂ տառերով, ապա Կեպլերի երրորդ օրենքը կարտահայտվի հետևյալ ֆորմուլայով.

$\text{[math]}$

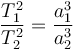
Որոշելով մոլորակների սիդերիկ պարբերությունները մեզ արդեն ծանոթ եղանակով, այս օրենքի ֆորմուլայով կարելի է որոշել մոլորակների ուղեծրերի մեծ կիսառանցքները Երկրի ուղեծրի մեծ կիսառանցքի համեմատությամբ՝ ընդունելով վերջինս որպես միավոր։ Նշենք, որ մոլորակի ուղեծրի մեծ կիսառանցքը նրա միջին հեռավորությունն է Արեգակից։ (Արեգակից մոլորակի աֆելիումում և պերիհելիումում ունեցած հեռավորությունների կիսագումարը հավասար է մոլորակի մեծ կիսառանցքին, նկ. 56-ում 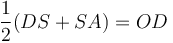$\text{[math]}$ ):

Քանի որ արեգակնային համակարգության մեջ եղած բոլոր հեռավորությունները Կեպլերի երրորդ օրենքի օգնությամբ կարելի է արտահայտել Արեգակից Երկրի ունեցած միջին հեռավորության միջոցով, ուստի Երկրի ուղեծրի մեծ կիսաոանցքի երկարությունը աստղագիտության մեջ համարում են հեռավորությունների միավոր և այն անվանում են աստղագիտական միավոր․ նա կազմում է 149 500 000 կմ։

§ 65. ՀԵՌԱԴԻՏԱԿԻ ԳՅՈՒՏԸ ԵՎ ԳԱԼԻԼԵՅԻ ՀԱՅՏՆԱԳՈՐԾՈՒԹՅՈՒՆՆԵՐԸ։ Լսելով, որ Հոլանդիայում դիտախողովակ կամ հեռադիտակ են հնարել, իտալացի գիտնական Գալիլեյը (1564—1642) 1609 թվականին ինքն էլ մի այդպիսի հեռադիտակ պատրաստեց և սկսեց այն օգտագործել երկնային լուսատուները դիտելու համար։ Հեռադիտակի օգնությամբ Գալիլեյը բազմաթիվ նշանավոր հայտնագործություններ կատարեց։ Նրա ճիշտ մեկնաբանությունների շնորհիվ այդ հայտնագործությունն երբ փայլուն կերպով հաստատեցին Կոպեռնիկոսի տեսության ճշմարտությունը։

Ամենից առաջ Գալիլեյը հայտնաբերեց լեռների գոյությունը Լուսնի վրա։ Դա հաստատում էր, որ երկնային մարմինները նման են Երկրին, և որ սխալ է այն ենթադրությունը, որ իբր երկրայինի ու երկնայինի միջև գոյություն ունի մեծ տարբերություն։

Այնուհետև Գալիլեյը հայտնաբերեց, որ Յուպիտեր մոլորակի շուրջը պտտվում են չորս արբանյակ, ճիշտ այնպես, ինչպես Լուսինն է պտտվում Երկրի շուրջը։ Սա ակներևորեն ապացուցում էր այն ժամանակվա պատկերացումների սխալ լինելը, որ իբր միայն Երկիրն է երկնային մարմինների շարժման կենտրոն հանդիսանում։ Սա հեշտացնում էր ապացուցել նաև այն ենթադրությունը , որ մոլորակները պտտվում են Արեգակի և ոչ թե Երկրի շուրջը։

Այնուհետև Գալիլեյը հայտնաբերեց Վեներայի փուլերը, այսինքն՝ հաստատեց, որ նա Լուսնի նման փոփոխում է իր տեսքը։ Դա ապացուցում էր, որ Վեներան լուսավոր է երևում Արեգակի լույսի արտացոլումով և պտտվում է Արեգակի և ոչ թե Երկրի շուրջը։

Արեգակի վրա, որը կրոնական պատկերացումներով երկնային անբիծ մաքրության սիմվոլ էր հանդիսանում, Գալիլեյը իր հեռադիտակով խավար բծեր դիտեց։ Արեգակի սկավառակի վրա այդ բծերի կատարած տեսանելի տեղաշարժներից Գալիլեյը եզրակացրեց, որ Արեգակը պտտվում է իր առանցքի շուրջը։ Համոզվելով այն բանում, որ երկնային մարմինը պտտվում է իր առանցքի շուրջը, հեշտ էր ընդունել նաև այն, որ Երկիրը ևս պտտվում է նույն ձևով։

Վերջապես, Գալիլեյը հեռադիտակով հայտնաբերեց, որ Ծիր Կաթինը՝ աստղային երկնքի տյդ լուսավոր շերտը թույլ աստղերի մի խառնախումբ է հանդիսանում։ Դա ապացուցում էր, որ տիեզերքը շատ ավելի վիթխարի է, քան այդ համարում էին առաջ։ Այս բոլորից հետո այլևս դժվար էր ենթադրել, որ այդ հսկայական տիեզերքը մեկ օրվա ընթացքում կարող է պտտվել Երկրի շուրջը։

Գալիլեյը իր այդ հայտնագործություններով և մի շարք ուրիշ սրամիտ փաստարկումներով հաստատեց Կոպեռնիկոսի տեսության ճշմարտությունը։

Նա ընթերցողների լայն շրջաններին մատչելի ձևով պրոպագանդում էր Կոպեռնիկոսի ուսմունքը։ Մինչդեռ Գալիլեյից առաջ Կոպեռնիկոսի աշխատությունը, որ գրված էր լատիներեն մաթեմատիկական բարդ լեզվով, շատ քչերին էր մատչելի ու հայտնի։ Գալիլեյի գործունեությունը նպաստեց Կոպեռնիկտսի ուսմունքի տարածմանը։

§ 66. ԵԿԵՂԵՑՈՒ ՊԱՅՔԱՐԸ ԳԻՏՈՒԹՅԱՆ ԴԵՄ։ Կոպեռնիկոսի գաղափարների տարածմանը,— որոնք հակասում էին «սուրբ գրքին», որտեղ ասված է, որ Երկիրն անշարժ է,— օժանդակեց մի այլ կրակոտ կոպեռնիկոսական՝ Գալիլեյի հայրենակից և ժամանակակից, գրող և փիլիսոփա Ջորդանո Բրունոն (նրա ծննդյան թիվը ճիշտ հայտնի չէ)։ Նա, բացի այդ, պնդում էր, որ աստղերը մեզանից շատ հեռու գտնվող Արեգակներ են, որ տիեզերքն անսահման է, որ այնտեղ աշխարհների՝ աստղերի ու մոլորակների թիվն անսահման մեծ է, և որ մյուս մոլորակների վրա, մյուս աշխարհների վրա նույնպես պետք է գոյություն ունենա կյանք, ինչպես նա գոյություն ունի Երկրի վրա, որը մոլորակ է հանդիսանում։ Սա նույնպես հակասում էր «սուրբ գրքին» և վնասում եկեղեցու հեղինակությանը։ Եկեղեցու գազազած ներկայացուցիչները Բրունոյին ենթարկեցին ինկվիզիցիայի դատին, որը հաստատված էր այլախոհների դեմ պայքարելու համար։ Բրունոյից պահանջում էին հրաժարվել իր համոզմունքներից։ Որովհետև Բրունոն հրաժարվեց այդ անելուց, նրան ենթարկերին տանջալի մահապատժի՝ կենդանի-կենդանի այրեցին խարույկի վրա 1600 թ․ Հռոմում։

Գալիլեյը 1616 թ․ կանչվում է Հռոմի պապի մոտ և զգուշացվում, որ Կոպեռնիկոսի ուսմունքը պաշտպանելն ու տարածելն արգելված է, բայց գիտական ճշմարտություններին հավատարիմ Գալիլեյը արիաբար շարունակում էր պայքարել հանուն Կոպեռնիկոսի ուսմունքի։ 1633 թվականին Գալիլեյը ինկվիզիցիոն տրիբունալի կողմից դատապարտվեց ցմահ բանտարկության, որը փոխարինվեց արգելումով՝ իր սեփական տնից ուրիշ տեղ գնալ, Գալիլեյի կողմից տրված «զղջման» ցուցմունքների կապակցությամբ։

Կոպեռնիկոսի, Բրունոյի և Գալիլեյի գործունեությունը կատարյալ ռևոլյուցիա առաջացրեց աշխարհայացքում և ցույց տվեց կրոնական ուսմունքի հակագիտականությունը, ըստ որի Երկիրը և մարդկությունը հատուկ տեղ են գրավում տիեզերքում։ Մատերիալիստական գիտությունը հաստատել է այդ գիտնականների հայացքների ճշմարտությունը։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈԻԳՄԱՆ ՀԱՄԱՐ

Ինչպե՞ս է առաջացել երկնային Լուսատուների աստվածացումը։
Ի՞նչ է աստղագուշակությունը և ինչպե՞ս է նա առաջացել։
Տեսանելիության ինչպիսի՞ առանձնահատկություններ ունեն Մերկուրին և Վեներան։
Ինչո՞վ է աստղային երկնքի ֆոնի վրա մոլորակների տեղաշարժը տարբերվում Լուսնի և Արեգակի տեղաշարժից։
Ինչպե՞ս է պատկերացրել տիեզերքը Արիստոտելը։
*Ինչպե՞ս է նկարագրել տիեզերքի կառուցվածքը Պտղոմեոսը և ինչպե՞ս է նա բացատրել մոլորակների օղակաձև շարժումները։
*Ինչպե՞ս են պատկերացրել տիեզերքը միջին դարերում։
Ինչո՞ւ Պտղոմեոսի սիստեմը XVI դ․ առաջ է բերել տարակուսանք։
Ինչո՞ւմն է կայանում Կոպեռնիկոսի հայտնագործությունը և ե՞րբ է նատեղի ունեցել։
Ինչպե՞ս է Նոպեռնիկոսը բացատրել մոլորակների օղակաձև թվացող շարժումները։
*Ո՞ր մոլորակներն են կոչվում ներքին և որո՞նք՝ արտաքին։
*Ի՞նչ բան է Մերկուրիի և Վեներայի անցումն Արեգակի սկավառակով։
*Ի՞նչն է կոչվում մոլորակների էլոնգացիա, և ո՞ր մոլորակներն են ունենում։
*Ի՞նչ է ներքին միացումը, և ո՞ր մոլորակներն են ունենում այն։
*Ի՞նչ է վերին միացումը։
*Ի՞նչ է մոլորակների դիմակայությունը և ինչո՞վ է նա բնորոշ։
*Ի՞նչ է մոլորակների քառակուսացումը (կվադրատուրա)։
*Ինչպե՞ս տարբերել արևելյան քառակուսացումները և էլոնգացիան արևմտյանից։
*Ինչպիսի՞ կոնֆիգուրացիաներն են նպաստավոր մոլորակների դիտումների համար և որո՞նք՝ անբարենպաստ։
*Ի՞նչն է կոչվում մոլորակի աստղային կամ սիդերիկ պարբերություն։
*Ի՞նչն է կոչվում մոլորակի սինոդիկ պարբերություն։
*Ինչպե՞ս են այդ երկու պարբերությունները կապված իրար հետ։ Ապացուցեցեք այդ։
Ձևակերպեցեք Կեպլերի III օրենքը։
Ի՞նչ է ուղեծրի մեծ կիսառանցք։
Ինչպե՞ս են կոչվում ուղեծրի՝ Արեգակին ամենամոտ և ամենահեռու կետերը։
Ուղեծրի ո՞ր մասումն է մոլորակի շարժումն ամենաարագը։
Ո՞վ և ե՞րբ է առաջին անգամ հեռադիտակը օգտագործել լուսատուները դիտելու համար։
Ինչպիսի՞ հեռադիտակային հայտնագործությունները և ինչպե՞ս հաստատեցին Կոպեռնիկոսի հայտնագործությունները։
Ինչո՞ւ եկեղեցին չկարողացավ հաշտվել Կոպեռնիկոսի ու Գալիլեյի հայտնագործությունների և Բրունոյի ուսմունքի հետ։

ՎԱՐԺՈԻՒՅՈԻՆՆԵՐ

*Յուպիտերի աստղային պարբերությունը հավասար է 12 տ․։ Ինչքա՞ն ժամանակից հետո կկրկնվի նրա դիմակայությունը։
*Նկատվել է, որ մոլորակներից մեկի դիմակայությունը կրկնվում է 2 տարուց հետո։ Ինչպիսի՞ն է նրա պտտման պարբերությունը Արեգակի շուրջը։ Ինչի՞ հավասար նրա ուղեծրի մեծ կիսաոանցքը։
Մարսը Արեգակից 1½ անգամ ավելի հեռու է, քան Երկիրը։ Ինչի՞ է հավասար Մարսի «տարին»։
*Պլուտոնի պտտման պարբերությունը հավասար է 250 տարվա։ Ինչի՞ է հավասար նրա ուղեծրի մեծ կիսառանցքը։

ՏԻԵԶԵՐԱԿԱՆ ՁԳՈՂԱԿԱՆՈՒԹՅՈՒՆ

§ 67. ՏԻԵԶԵՐԱԿԱՆ ՁԳՈՂԱԿԱՆՈՒԹՅԱՆ ՕՐԵՆՔԸ։ Կոպեռնիկոսը սահմանեց, որ մոլորակների շարժման կենտրոնն Արեգակն է, իսկ Կեպլերը հայտնագործեց մոլորակների շարժման օրենքները։ Բայց այդ շարժումների պատճառը մնում էր անհայտ, մինչև որ XVII դարի վերջերին անգլիացի գիտնական Նյուտոնը (1643—1727) գտավ տիեզերական ձգողական ութ յան օրենքը։ Այդ օրենքի էությունն այն է, որ տիեզերքում գտնվող բոլոր մարմինները (ինչպես և առհասարակ մատերիայի բոլոր մասնիկները) փոխադարձաբար ձգում են միմյանց այնպիսի ուժով, որը համեմատական է նրանց մասսաների արտադրյալին և հակադարձ համեմատական նրանց միջև եղած հեռավորության քառակուսուն։ Դա ֆորմուլայի ձևով կարելի է այսպես գրել.

$\text{[math]}$ ,

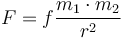որտեղ m₂₁ և m₂ քննարկվող երկու մարմինների մասսաներն են, r նրանց միջև եղած հեռավորությունն է, իսկ f մի գործակից է, որի թվական մեծությունը կախված է այն միավորներից, որոնցով արտահայտված են՝ մասսաներն ու հեռավորությունը։ Փորձից հայտնի է, որ մեկական գրամ կշիռ ունեցող երկու մասսա 1 սմ հեռավորության վրա միմյանց փոխադարձաբար ձգում են 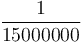$\text{[math]}$ դին ուժով։ Ուստի, արտահայտելով մասսաները գրամներով, իսկ r սանտիմետրերով, մենք պետք է (որպեսզի F ստանանք դիներով) ընդունենք $\text{[math]}$ ։

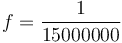Նյուտոնը ապացուցեց, որ Երկրի ձգողականությունը, որի ազդեցության տակ բոլոր մարմիններն ընկնում են նրա վրա, տարածվում է շատ ավելի հեռուն, հասնելով մինչև Լուսինը և թուլանալով Երկրի կենտրոնից հաշված հեռավորության քառակուսուն համեմատական։ Դա նշանակում է, որ ձգողության ազդեցությունը կամ Երկրի ծանրության ուժի ազդեցությունը տարածվում է մինչև անսահմանություն։ Երկրի ծանրության ուժն է, որ Լուսնին պահում է իր ուղեծրի վրա, այլապես Լուսինը կբաժանվեր Երկրից և կսլանար իր ուղեծրի շոշափողի ուղղությամբ։

Դեպի Երկիրը Լուսնի հենց այդ ձգումն էլ հանդիսանում է այն կենտրոնաձիգ ուժը, որը բնութագրվում է Լուսնի շարժման մեջ դիտվող կենտրոնաձիգ արագացումով։ Եվ իսկապես, առանց դեպի կենտրոն (այսինքն՝ դեպի Երկիրը) ուղղված ուժի ներգործության, Լուսնի շարժումը կենտրոնաձիգ արագացում չէր ունենա, այսինքն՝ նրա ուղին անընդհատ չէր կորանա, այլ իրենից մի ուղիղ գիծ կներկալացներ։ Ինչպես մենք գիտենք, առանց գործաղրվող ուժի ազդեցության, ամեն մի մարմին շարժվում է ըստ իներցիայի՝ ուղղագիծ և հավասարաչափ։

Մյուս կողմից, եթե Լուսինը չունենար շարժման այն արագությունը, որ նա ստացել է իր գոյանալու պահին, ապա, Երկրի ձգողականության շնորհիվ, Լուսինը կընկներ Երկրի վրա ճիշտ այնպես, ինչպես վայր է ընկնում, օրինակ, քարը։

Արեգակի մասսան ոչ միայն անհամեմատ մեծ է յուրաքանչյուր մոլորակի մասսայից, այլև 750 անգամ մեծ է բոլոր մոլորակների մասսաներից՝ միասին վերցրած։ Հենց այդ պատճառով էլ բոլոր մոլորակները պտտվում են Արեգակի շուրջը՝ դրսևորելով կենտրոնաձիգ արագացում դեպի նա։ Արեգակի ձգողության ազդեցությանը միշտ կորացնում է Երկրի և մոլորակների ուղիները։ Ավելի կոնկրետ, բոլոր մոլորակները և Արեգակը պտտվում են իրենց ընդհանուր ծանրության կենտրոնի շուրջը։

Մոլորակների արբանյակները պտտվում են իրենց մոլորակների շուրջը նրանց ձգողության ազդեցության տակ, ճիշտ այնպես, ինչպես Լուսինն է պտտվում Երկրի ձգողության ազդեցությամբ։

Արեգակնային համակարգության սահմաններից դուրս կան շատ կրկնակի աստղերի սիստեմներ, որտեղ տվյալ զույգի աստղերից յուրաքանչյուրը, նույնպես ձգողության ազդեցությամբ, պտտվում է սիստեմի ընդհանուր ծանրության կենտրոնի շուրջը․ Այդ պատճառով էլ Նյուտոնի հայտնագործած օրենքը կոչվում է տիեզերական ձգողականության օրենք։

Նյուտոնը ապացուցեց, որ տիեզերական ձգողականության գոյության շնորհիվ մոլորակները պետք է շարժվեն ճիշտ Կեպլերի օրենքների համաձայն. այդ օրենքներն ավելի մեծ ճշտությամբ սահմանվեցին Նյուտոնի կողմից։ Նյուտոնը ապացուցեց, որ որոշ պայմաններում մարմիններից մեկը մյուսի ձգողության ազդեցությամբ կարող է շարժվել ոչ միայն էլիպսով, այլև շրջանագծով, պարաբոլով և հիպերբոլով։

Պարաբոլը մի բացված կոր է, որի ճյուղերը քանի հեռանում, այնքան ավելի են ձգտում միմյանց զուգահեռ ընթանալ։ Հիպերբոլը ավելի ևս բացված կոր է (նկ. 60)։

Այնուհետև Նյուտոնը ապացուցեց, որ Կեպլերի երրորդ օրենքն այնքան էլ ճիշտ չէ և պետք է փոխարինվի հետևյալ օրենքով․

$\text{[math]}$ ։

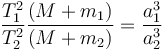որտեղ M Արեգակի մասսան է, իսկ m₁ և m₂ երկու մոլորակների մասսաները։ Քանի որ մոլորակների մասսաները Արեգակի մասսայի համեմատությամբ չափազանց փոքր են, ուստի (M+m₁)։(M+m₂) հարաբերությունը շատ քիչ է տարբերվում մեկից։ Եթե այդ հարաբերությունը փոխարինենք մեկով, ապա կստանանք Կեպլերի երրորդ օրենքը հենց այն ձևով, ինչ ձևով գտել էր այն Կեպլերն ինքը։ Այս օրենքը չափազանց կարևոր է, քանի որ նա հնարավորություն է տալիս որոշել երկնային մարմինների մասսաները։ Իրոք, վերևում բերված ֆորմուլայից երևում է, որ

$\text{[math]}$

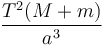
արտահայտությունը հաստատուն մեծություն է ցանկացած սիստեմի համար, որը բաղկացած է մասսայից և նրա շուրջը պտտվող m մասսայից, որն ունի T պարբերություն և գտնվում է a հեռավորության վրա։ Իմանալով այդպիսի սիստեմների համար T և a, օրինակ, Յուպիտերի և նրա արբանյակի համար, կարելի է գտնել նրանց մասսաների գումարը՝ Երկրի և Լուսնի մասսաների գումարի համեմատությամբ։

Տիեզերական ձգողականության օրենքով Նյուտոնը կարողացավ բացատրել ոչ միայն մոլորակների ու նրանց արբանյակների շարժումը, այլև բնության շատ ուրիշ երևույթներ, որ մինչև այդ անհնար էր ճիշտ բացատրել։

§ 68*. ՁԳՈՂԱԿԱՆՈՒԹՅԱՆ ԵՎ ԾԱՆՐՈՒԹՅԱՆ ՈՒԺԻ ՆՈՒՅՆՈՒԹՅՈՒՆԸ։ Նյուտոնի մեծագույն ծառայությունը հանդիսացավ նաև այն, որ նա ապացուցեց իր հայտնագործած՝ տիեզերական մարմինների միջև եղած ձգողական ուժի և մարդկանց փորձից վաղուց հայտնի՝ Երկրի ծանրության ուժի նույնությունը։ Նյուտոնը ապացուցեց, որ այդ՝ թե՛ մեկ և թե՛ մյուս ուժերը փոխվում են հակադարձ համեմատական հեռավորության քառակուսուն և որ, մասնավորապես, դեպի Երկիրը Լուսնի անկման արագացումը ճշտորեն հավասար է այն արագացման, որով վայր կընկներ քարը, եթե այն տեղավորեինք Երկրից Լուսնի ունեցած հեռավորության վրա։

Հեշտ է հաշվել, որ արագացումներից առաջինը ( որը, ինչպես արդեն ասացինք, միաժամանակ կենտրոնաձիգ արագացումն է), հավասար է 0,27 սմ/վրկ²։ Սա հաշվարկվում է հետևյալ հայտնի ֆորմուլայով․

$\text{[math]}$ ,

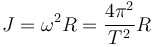որտեղ R Լուսնի հեռավորությունն է Երկրի կենտրոնից (380 000 կմ), իսկ T Լուսնի պտտման պարբերությունն է, որը կազմում է 27,3 օր։

Ծանրության ուժի արագացումը Երկրի մակերևույթի վրա կազմում է 981 սմ/վրկ²։ Լուսնի հեռավորության վրա նա պետք է (60)² = 3600 անգամ պակաս լինի, որովհետև Լուսնի հեռավորությունը 60 անգամ մեծ է Երկրի շառավղիր։ 981։3600 = 0,27 սմ/վրկ², այսինքն՝ իրոք որ Երկրի ծանրության ուժի հաշվարկած արագացումը այնտեղ, որտեղ գտնվում Լ Լուսինը, հավասար է Լուսնի շարժման մեջ մեր գիտած կենտրոնաձիգ արագացմանը։

§ 69*. ԵՐԿՆԱՅԻՆ ՄԱՐՄԻՆՆԵՐԻ ՄԱՍՍԱՆԵՐԻ ՈՐՈՇԵԼԸ։ Այն երկնային մարմնի մասսան, որի շուրջն արբանյակ է պտտվում, կարելի է որոշել, օգտվելով Կեպլերի երրորդ օրենքի ֆորմուլայից՝ նրա ճշգրտված ձևով.

$\text{[math]}$

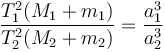
Օրինակ, Արեգակի մասսան որոշելու համար, ₂ նշանները մենք կվերագրենք Երկրի շուրջը Լուսնի կատարած շարժմանը, ընդ որում M₂ տակ պետք է հասկանալ Երկրի մասսան, իսկ m₂ տակ՝ Լուսնի մասսան։ Արեգակի շուրջը Երկրի կատարած շարժմանը վերագրելով ₁ նշանը, այդ ժամանակ M₁ տակ պետք է հասկանալ Արեգակի մասսան, իսկ m₁ տակ այս դեպքում՝ Երկրի մասսան։ Քանի որ Լուսնի մասսան անհամեմատ (81 անգամ) փոքր է Երկրի մասսայից, իսկ Երկրի մասսան Արեգակի մասսայի համեմատությամբ աննշան է, ուստի ֆորմուլայի համարիչում, առանց մեծ սխալ կատարած լինելու, կարելի է հաշվի չառնել m₁ իսկ հայտարարում հաշվի չառնել m₂: Այդ դեպքում կստանանք՝

$\text{[math]}$

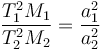
որտեղից հետևում է, որ

$\text{[math]}$

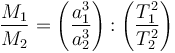
Հենց դա էլ Արեգակի որոնելի մասսան է՝ արտահայտված Երկրի մասսայի միավորներով։ Նույն միավորներով կարելի է որոշել նաև մոլորակների մասսաները։ Այս դեպքում սկզբնական ֆորմուլա յում ₁ նշանները պետք է վերագրել արբանյակի շարժմանն իր մոլորակի շուրջը, ընդ որում M₁ տակ պետք է հասկանալ մոլորակի որոնելի մասսան, իսկ m₁ տակ՝ նրա արբանյակի մասսան, որը մենք դարձյալ կանտեսենք, որպես աննշան մեծություն M₁ համեմատությամբ։ Այդ ժամանակ մենք կստանանք մոլորակի մասսայի հարաբերությունը Երկրի մասսային։

Արբանյակ չունեցող մոլորակի մասսան կարելի է որոշել այն խոտորումների հիման վրա, որը նա իր ձգողականությամբ առաջ է բերում մյուս մոլորակների շարժումներում։ Մոլորակների և Արեգակի մասսաները բերված են դասագրքի վերջում՝ VI աղյուսակում։

Մոլորակների և Արեգակի մասսաները բացարձակ միավորներով, օրինակ, գրամներով իմանալու համար, հարկավոր է որևէ կերպ որոշել Երկրի մասսան։

§ 70. ԵՐԿՐԻ ՄԱՍՍԱՅԻ ՈՐՈՇԵԼԸ։ Երկրի մասսան որոշելու առավել ակնառու եղանակն այն է, որ դիտում են ուղղալարի խոտորումը ուղղաձիգ գծից, որն առաջ է գալիս մոտակայքում գտնվող լեռան մասսայի ձգումից։ Լեռան հեռավորությունը կարելի է չափել, իսկ նրա մասսան կարելի է որոշել՝ բազմապատկելով նրա ծավալը այն հանքատեսակների միջին խտությամբ, որից կազմված է լեռը։ Ուղղալարի խոտորման անկյունը կախված է Երկրի մասսայի և լեռան մեզ արդեն հայտնի մասսայի հարաբերությունից։

Կան անհամեմատ ավելի ճշգրիտ, բայց ոչ այնքան ակնառու, ուրիշ եղանակներ ևս։ Դրանցից մեկն այն է, որ ձգողականության այս ֆորմուլայից՝

$\text{[math]}$

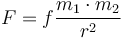
հետևում է, որ ծանրության ուժի արագացումը Երկրի վրա

981 սմ/վրկ² = 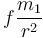$\text{[math]}$ ,

եթե m₁ տակ հասկանանք Երկրի մասսան, քանի որ արագացումը, ինչպես մենք գիտենք, հավասար է մարմնի վրա ազդող ուժին՝ բաժանած այդ մարմնի մասսայի վրա։ Այս ֆորմուլայի մեջ r՝ Երկրի շառավիղը հայտնի է, հայտնի է նաև f գործակիցը, որը որոշված է լաբորատորական փորձերով, նա հավասար է՝

$\text{[math]}$ ։

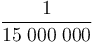Հետևաբար, Երկրի մասսան՝

Չհաջողվեց վերլուծել (բառական սխալ):

գրամի։

Ահա թե ի՛նչպես լաբորատորիայում որոշելով f մեծությունը, դրանով իսկ հաջողվել է «կշռել» երկրագունդը։

§ 71. ԽԱՆԳԱՐՈՒՄՆԵՐԸ ՄՈԼՈՐԱԿՆԵՐԻ ՇԱՐԺՈՒՄՆԵՐՈՒՄ։ Եթե Արեգակի շուրջը միայն մեկ մոլորակ պտտվեր, ապա նա կշարժվեր ճիշտ Կեպլերի օրենքների համաձայն։ Բայց իրականում գոյություն ունեն նաև ուրիշ մոլորակներ, որոնք փոխադարձաբար ձգում են միմյանց։ Այդ պատճառով էլ մոլորակների շարժումները շեղվում են Կեպլերի օրենքներով սահմանված շարժումներից։ Մոլորակների շարժումների այդ, առհասարակ, շատ չնչին շեղումները Կեպլերի օրենքներին համապատասխանող շարժումներից՝ կոչվում են խանգարումներ։

Խանգարումների հետևանքով մոլորակները Կեպլերի երկրորդ օրենքին համապատասխանող արագությունից մերթ արադ են շարժվում, մերթ դանդաղ, նրանց ուղեծրերր նույնպես կանոնավոր էլիպսի ձև չունեն և աստիճանաբար փոփոխվում են։ Ժամանակակից գիտությունը՝ իմանալով Արեգակի ու մոլորակների մասսաները, ինչպես և նրանց միջև եղած հեռավորությունը, տիեզերական ձգողականության տեսության հիման վրա մեծ ճշտությամբ հաշվի է առնում այդ խանգարումները։

§ 72. ՆԵՊՏՈՒՆ ԵՎ ՊԼՈՒՏՈՆ ՄՈԼՈՐԱԿՆԵՐԻ ՀԱՅՏՆԱԴՈՐԾՈՒՄԸ։ XVIII դարի վերջերին (1781 թ.) անգլիացի աստղագետ Վիլյամ Հերշելը (1738 —1822), որն այն ժամանակ դեռևս աստղագիտության մի անհայտ սիրող էր, իր ձեռքով պատրաստած հեռադիտակով հայտնագործեց մինչ այդ բոլորին անհայտ մի մոլորակ, որն Արեգակից իր հեռավորությամբ յոթերորդ տեղն է գրավում։ Մոլորակն ստացավ Ուրան անունը։

XIX դարի սկզբներին պարզվեց, որ Ուրան մոլորակի շարժումը մի քիչ չի համապատասխանում նրա այն շարժմանը, որը նախապես հաշվված էր՝ նկատի ունենալով նրա ձգվելը ինչպես Արեգակի, այնպես էլ բոլոր, այն ժամանակ հայտնի, մոլորակների կողմից։ Որքան էլ փոքր էին դիտումների շեղումները տեսությունից, այնուամենայնիվ աստղագետները չէին կարող հաշտվել այդ երևույթի հետ։ Ենթադրվում էր, որ Ուրանի շարժման այդ նկատվող շեղումներն առաջանում են մի ինչ-որ անհայտ մոլորակի ձգողության ազդեցությամբ, և որ այդ մոլորակը ավելի հեռու է գտնվում Արեգակից, քան Ուրանը։ Ֆրանսիացի գիտնական Լեվերյեն (1811—1877) հաշվարկեց այդ մոլորակի դիրքը երկնքում, և նրա ցուցումների համաձայն, 1846 թ․ այդ դեռևս անհայտ մոլորակն իսկապես հայտնաբերվեց։ Այդ մոլորակը անվանեցին Նեպտուն։

Մոլորակի հայտնաբերումը, որ արվել էր կաբինետում, ինչպես ասում են՝ «գրչի ծայրով», հանդիսանում է մարդկային մտքի մեծագույն նվաճումներից մեկը, և դա փայլուն կերպով ապացուցում է, որ գիտության հզոր մեթոդներով հնարավոր է ճանաչել բնությունը։

Նեպտունի ուղեծրից այն կողմը, 1930 թ. դարձյալ մի մեծ մոլորակ է հայտնաբերվել, որը անվանվել է Պլուտոն։ Այդ մոլորակի գոյությանը ևս նախատեսվել է Ուրանի շարժումների այն չափազանց աննշան անկանոնությունների ուսումնասիրության հիման վրա, որոնք Նեպտունի հայտնաբերումից հետո իսկ մնացել էին չբացատրված, բայց Պլուտոնի փ աստ ական, հ ա յտնա բեր ումը կատարվել է աստղային երկնքի լուսանկարների վրա, այդ մոլորակի երկարատև որոնումներից հետո։

§ 73. ՄԱԿԸՆԹԱՑՈՒԹՅՈՒՆՆԵՐ ԵՎ ՏԵՂԱՏՎՈՒԹՅՈՒՆՆԵՐ։ Բաց ծովերի և օվկիանոսների ափին ամեն օր ջրի մակարդակի տատանումներ են նկատվում։ Օրական երկու անգամ ջրի մակարդակը բարձրանում է, և ջուրը ծածկում է առափնյա ավազուտները — դա մակընթացությունն է («առատ ջուր»)։ Օրական երկու անգամ էլ ջուրը ետ է քաշվում ափերից, նրա մակարդակն իջնում է. դա տեղատվությունն է («սակավ ջուր»)։ Տեղատվությունը («սակավ ջուրը») սկսվում է մակընթացությունից («առատ ջրից») մոտավորապես 6 ժամ հետո, իսկ դարձյալ 6 ժամից հետո նորից սկսվում է մակընթացությունը, այնպես որ մեկ մակընթացությունից մինչև մյուսը տևում է 12 ժամ (ավելի ճիշտ՝ 12 ժամ 25 րոպե)։ Այսպիսով, միջին հաշվով 24 ժամ 50 րոպեում երկու մակընթացություն և երկու տեղատվություն է լինում։ Բայց, ընդհանրապես, հենց նույնքան ժամանակ էլ ընկած է Լուսնի երկու հարևան, համանուն կուլմինացիաների միջև։ Նյուտոնը ապացուցեց, որ մակընթացություններն ու տեղատվություններն իրոք կապված են Լուսնի հետ, նրա ձգողության հետ։

Պարզության համար պատկերացնենք, որ ամբողջ երկրագունդը հավասարաչափորեն ծածկված է ջրային շերտով։ Լուսինը Երկրի մակերևույթի դեպի իր կողմը դարձած մասի ջրային մասնիկներն ավելի ուժեղ կերպով է ձգում, քան Երկրի կենտրոնին, որովհետև նրանք ավելի մոտ են գտնվում Լուսնին, քան Երկրի կենտրոնը։ Ձգողական ուժի այդպիսի տարբերության հետևանքով այդ ջրային մասնիկները Երկրի կենտրոնի նկատմամբ կտեղաշարժվեն Լուսնի ուղղությամբ։ Լուսինը Երկրի մյուս՝ իրեն հակադիր կողմի ջրային մասնիկներն ավելի թույլ կերպով է ձգում, քան Երկրի կենտրոնին։ Այդ մասնիկները կարծես ետ են մնում Երկրի կենտրոնից։ Հետևանքը լինում է այն, որ Երկրի ջրային շերտը ձգվում է Երկիրը Լուսնին միացնող գծի ուղղությամբ։ Երկրի օվկիանոսներում երկու ջրային սապատ կամ երկու մակընթացային ալիք է առաջանում (նկ․ 62)։ Օվկիանոսների այդ տեղերը եզրապատող վայրերի և կղզիների ափերին ջրի մակարդակը կլինի ամենաբարձրը («առատ ջուր»)։ Երկրի մակընթացությունների շրջաններից 90° հեռու գտնվող շրջաններում ջրի (որն այստեղից հոսում է դեպի մակընթացության շրջանները) մակերևույթը կիջնի։ Այնտեղ կդիտվի տեղատվություն («սակավ ջուր»)։ Բայց Երկիրը պտտվում է իր առանցքի շուրջը (նկ. 62-ում՝ գծագրի հարթության վրա)։ Քանի որ օվկիանոսի շարժունակ ջրի մակընթացային ելունը միշտ ուղղված է լինում դեպի Լուսինը, ուստի 6 ժամից հետո ցամաքի այն մասը, որ գտնվում է մակընթացության շերտում, կընկնի տեղատվության շերտը։ Դարձյալ 6 ժամից հետո երկրային ցամաքի նույն մասերը կընկնեն երկրորդ մակընթացության շերտը, որը տեղ)։ կունենա Երկրի՝ Լ ուսնին հակառակ ուղղված կողմում։ Ահա թե ինչու մակընթացություններն ու տեղատվությունները 6 ժամը մեկ անգամ հաջորդում են միմյանց։

Սակայն Լուսինը Երկրի նկատմամբ անշարժ չի մնում, այլ պտտվում է նրա շուրջն այն ուղղությամբ, ո՛ր ուղղությամբ Երկիրն է պտտվում իր առանցքի շուրջը։ Ուստի 24 ժամ հետո Երկրի որևէ վայրը, որը մինչ այդ եղել էր «առատ ջրի» շերտում, այդ շրջանին դեռ չի հասնի, որովհետև այդ ժամանակամիջոցում մակընթացային ելունը Լուսնի հետևից առաջ կանցնի։ Կպահանջվի ևս 50 րոպե ժամանակ, որպեսզի Երկրի տվյալ վայրը, նրա պտտվելու շնորհիվ, հասնի ջրի առավելագույն վերելքի շրջանին։ Ահա թե ինչու մակընթացությունները կրկնվում են ոչ թե ճիշտ 12 ժամից, այլ 12 ժամ 25 րոպեից հետո։

Արեգակը, Լուսնի նման, օվկիանոսներում մակընթացություններ և տեղատվություններ է առաջացնում, բայց սրանք իրենց մեծությամբ երկու անգամ փոքր են Լուսնի առաջացրած մակընթացություններից ու տեղատվություններից։ Երբ Արեգակն ու Լուսինը Երկրի ջրային թաղանթը ձգում են միևնույն ուղղությամբ (նորալուսնի և լիալուսնի ժամանակ), ապա երկու մակընթացությունները (Արեգակինը և Լուսնինը) գումարվում են։ Այդ ժամանակ մակընթացությունն առանձնապես բարձր է լինում։ Մակընթացությունների և տեղատվությունների պատկերը բարդանում է, նրանով, որ Երկրի վրա կան մայր ցամաքներ ու կղզիներ, ծովերի մեծ ու փոքր խորություններ՝ ծովային հատակի փոփոխական ռելեֆով։

Ծովագնացների համար չափազանց կարևոր է նախապես իմանալ մակընթացության տեղի ունենալու ժամանակը և նրա բարձրությունը, որովհետև օվկիանսսային նավերը միայն մակընթացության ժամանակ են կարողանում մտնել որոշ գետերի գետաբերաններն ու ծանծաղուտ նավահանգիստները։ Մակընթացության էներգիան կարելի է օգտագործել հիդրոէլեկտրակայաններում։ Ներկայումս արդեն փորձեր են կատարվում օգտագործելու այն վիթխարի էներգիան, որ բերում է իր հետ մակընթացություն առաջացնող ջրի մասսան։ Կառուցելով, օրինակ, ամբարտակ Ջիբրալտարի նեղուցում, կարելի է մակընթացություններից ստանալ հսկայական քանակությամբ էներգիա, բայց քանի դեռ գոյություն ունեն կապիտալիստական երկրներ իրենց մրցավազքով ու պատերազմներով, այդպիսի գաղափարների իրականացումը անհնար է։

ՍՍՌՄ-ում մակընթացություններ դիտվում են հյուսիսային ծովափում, օրինակ, Մուրմանսկում և Հեռավոր Արևելքում։ Երկրի մի քանի վայրերում մակընթացության բարձրությունը հասնում է մեկ ու կես — երկու տասնյակ մետրի։

§ 74. ՊՐԵՑԵՍԻԱ ԿԱՄ ԳԻՇԵՐԱՀԱՎԱՍԱՐՆԵՐԻ ԿԱՆԽԱԴԻՊՈՒՄ։ Դեռևս երկու հազար տարի առաջ հույն գիտնական Հիպպարխը հայտնաբերել է, որ գարնանային գիշերահավասարի կետն աստղերի միջև դանդաղ կերպով շարժվում է արևելքից դեպի արևմուտք։ Մի լրիվ պտույտ երկնքում նա պետք է կատարի 26 000 տարվա ընթացքում։ Մոտ երկու հազար տարի առաջ նա գտնվել է ոչ թե Ձկների համաստեղությունում՝ ինչպես հիմա, այլ Խոյի համաստեղությունում։ Այն ժամանակ ամառվա և ձմեռվա արևադարձի կետերը գտնվել են Խեցգետնի և Այծեղջյուրի համաստեղություններում։

Գիշերահավասարի և արևադարձի կետերի դիրքը որոշող երկնային հասարակածի տեղաշարժման հետ միասին աստղերի միջև տեղաշարժվում է նաև աշխարհի բևեռը։ Մի լրիվ շրջան երկնքում նա կատարում է 26 000 տարվա ընթացքում, այնպես, ինչպես ցույց է տրված նկ. 63-ում։ Այժմ աշխարհի բևեռը գտնվում է Փոքր Արջի α աստղի մոտ, բայց 6000 տարի հետո բևեռային աստղ կդառնա Ցեֆեոսի α աստղը, իսկ 13 000 տարի հետո բևեռային աստղ կդառնա առաջին մեծության Վեգա աստղը՝ քնարի համաստեղությունում։ Այդ փոփոխությունների հետ մեկտեղ, որոշ համաստեղություններ, օրինակ, Օրիոնը, Եվրոպայում այլևս չեն երևա և մեր հորիզոնի վրա կհայտնվեն երկնքի հարավային կիսագնդի այլ համաստեղություններ, օրինակ, Հարավային Խաչը։

Արդեն Կոպեռնիկոսի համար էլ պարզ էր, որ աստղերի միջև աշխարհի բևեռի կատարած տեղաշարժն առաջանում է այն բանից, որ Երկրի առանցքը դանդաղ կերպով փոխում է իր ուղղությունը տիեզերական տարածության մեջ։ Երկրի առանցքը, չփոխելով իր թեքությունը խավարածրի հարթության նկատմամբ, 26 000 տարվա ընթացքում մի լրիվ կոն է գծում։

Վերը նկարագրված երևույթները կոչվում են պրեցեսիա կամ գիշերահավասարների կանխադիպում, որովհետև, շնորհիվ այն բանի, որ գարնանային գիշերահավասարի կետը տեղաշարժվում է Արեգակի՝ խավարածրով կատարած տարեկան շարժմանն ընդառաջ, Արեգակը ավելի շուտ է վերադառնում այդ կետը, քան նա հասցնում է աստղերի նկատմամբ մի լրիվ շրջան կատարել երկնքում։ Այդպիսով, գիշերահավասարները կանխադիպում են, ավելի շուտ են թևակոխում, քան Երկիրը հասցնում է կատարել իր լրիվ շրջանն Արեգակի շուրջը։

Արեգակի շուրջը Երկրի պատման սիդերիկ պարբերությունը, կամ, որ միևնույն է, աստղերի նկատմամբ Արեգակի տեսանելի պտտման պարբերությանը կոչվում է աստղային տարի և կազմում է 365 օր 6 ժամ 9 րոպե 10 վայրկյան։

Գարնանային գիշերահավասարի կետով Արեգակի երկու հաջորդական անցումների միջև եղած պարբերությունը պրեցեսիայի հետևանքով 20 րոպե 23 վայրկյանով կարճ է աստղային տարուց և կոչվում է արևադարձային տարի։ Արևադարձային տարին հավասար է 385 օր 5 ժամ 48 րոպե 46 վայրկյանի։ Տարվա եղանակների հաջորդումները որոշվում են արևադարձային տարվա տևողությամբ, ուստի և օրացույցը հիմնված է նրա վրա։

Նյուտոնը պրեցեսիայի երևույթը բացատրեց այն բանով, որ Արեգակի և Լուսնի ձգողությունը ազդելով Երկրի այն ուռուցիկ մասի վրա, որ նրա բևեռներից սեղմվելու հետևանքով առաջ է եկել հասարակածի ուղղությամբ, ձգտում է թեքել Երկրի առանցքը։ (Եթե Երկիրը կանոնավոր գունդ լիներ՝ այդ ձգտումը չէր լինի, չէր լինի նաև պրեցեսիայի երևույթը)։ Երկրի պտտման իներցիան խանգարում է դրան, և այդ երկու պտտողական շարժումների զուգակցման հետևանքով Երկրի առանցքը տարածության մեջ կոն է գծում։ Ճիշտ նույն երևույթն է ներկայացնում պտտվող հոլը։ Եթե մենք փորձենք պտտվելու ժամանակ մի կողմ թեքել նրա առանցքը, նա կսկսի կոն գծել։

§ 75. ՈԻՂԵԾՐԻ ՁԵՎԻ ԿԱԽՈՒՄՆ ՍԿԶԲՆԱԿԱՆ ԱՐԱԳՈՒԹՅՈՒՆԻՑ։ Ձգողականության տեսությունը ցույց է տալիս, որ այն ուղեծիրը, որ մարմիններից մեկը կգծի ենթարկվելով մյուս մարմնի ձգողության ազդեցությանը, կախված է նրանց մասսաներից և տվյալ հեռավորության վրա նրա ունեցած արագությունից։ Օրինակ, պարզված է, որ Երկրի՝ իր ուղեծրով կատարած շարժման արագությունը մոտ է այն արագությանը, որի դեպքում մարմինն Արեգակի ջուրջը պետք է որ շրջանագիծ գծի։ Արեգակից նույն հեռավորության վրա գտնվող մարմինն ավելի արագ շարժվելու դեպքում ձգված էլիպս կգծեր, իսկ 42 կմ/վրկ արագության դեպքում նա պարաբոլ կգծեր և, շրջանցելով Արեգակի շուրջը, այլևս դեպի նա չէր վերադառնա։ Ավելի ևս մեծ արագության դեպքում նա հիպերբոլ կգծեր և նույնպես երբեք դեպի Արեգակը չէր վերադառնա։

ճիշտ այդպես էլ Երկրի վրա թնդանոթից հորիզոնական ուղղությամբ արձակած արկը փոքր արագություն ունենալու դեպքում կընկնի երկրի վրա։ Մարմինը 8 կմ/վրկ արագություն ունենալու դեպքում (որ մի քանի անդամ գերազանցում է հրետանային արկի արագությանը) այլևս Երկրի մակերևույթին չի ընկնի, այլ փոքր արբանյակի նման կպտտվի նրա շուրջը, գծելով կլոր ուղեծիր։ Ավելի մեծ արագության դեպքում մարմինն էլիպս կգծի, իսկ 11 կմ/վրկ արագությունից ավելին ունենալու դեպքում նա պարաբոլ կգծի և Երկրից ընդմիշտ կհեռանա դեպի անսահմանություն։ Օդի դիմադրությունը բոլոր նկարագրած դեպքերումն էլ կստիպեր հաղորդել մարմնին մի քիչ ավելի մեծ արագություն, քան հիշվեց այստեղ։

§ 76. ՄԻՋՄՈԼՈՐԱԿԱՅԻՆ ՃԱՆԱՊԱՐՀՈՐԴՈՒԹՅՈՒՆՆԵՐ։ Միջմոլորակային ճանապարհորդությունների, այսինքն՝ դեպի մյուս մոլորակները և Լուսինը թռչելու գաղափարի իրագործումը պահանջում է հաղթահարել Երկրի ձգողականությունը։ Միջմոլորակային ճանապարհորդությունների համար կիրառվող՝ արկի ձև ունեցող թռչող ապարատին հարկավոր է հաղորդել ոչ պակաս, քան 11 կմ/վրկ արագություն, որպեսզի նա, հաղթահարելով Երկրի ձգողությունը, կարողանա շարժվել ցանկացած ուղղությամբ։ Մշակվել են արկին այդպիսի մեծ արագություն հաղորդելու եղանակներ, ընդ որում նրանցից ամենալավն այն արկի կառուցվածքն է, որ հրթիռի նման շարժվում է ետահարման հարվածի օգնությամբ։

Միջմոլորակային ճանապարհորդությունների հարցի և ռեակտիվ շարժիչների բնագավառում մեծ աշխատանք է կատարել ռուս նշանավոր գյուտարար Կ․ Է․ Ցիալկովսկին (1857—1935)։

Միջմոլորակային ճանապարհորդությունների խնդրի լիակատար լուծումն ամենամոտ տասնամյակների, գուցե և միայն մի քանի տարվա հարց է։ Միջմոլորակային ճանապարհորդությունների համար ատոմային էներգիայի օգտագործումը շատ գյուտարարների այդ բաղձալի երազանքը դարձնում է ռեալ և իրականացման մոտ։ Բայց հարկավոր է հիշել, որ մոլորակների միջև եղած հեռավորությունը շատ մեծ է՝ (տես VI աղյուսակը գրքի վերջում) և որ միջմոլորակային թռիչքները կտևեն տարիներ։

ՀԱՐՑԵՐ ԻՆՔՆՍՏՈՒԳՄԱՆ ՀԱՄԱՐ

Ո՞ւմ կողմից և ե՞րբ է հայտնաբերվել տիեզերական ձգողության օրենքը։
Ձևակերպեցեք այդ օրենքը։
Ի՞նչ ուժով են փոխադարձորեն ձգվում 1 գրամ մասսա ունեցող մարմինները, որոնք բաժանվում են իրարից 1 սանտիմետր տարածությամբ։
Ինչո՞ւ Լուսինը չի շարժվում ուղիղ գծով։
Ինչպիսի՞ ուղեծրեր կարող է գծել մարմինը ըստ ձգողականության օրենքի։
Գրեցեք Կեպլերի երրորդ օրենքը ավելի ճիշտ ձևով։
*Ինչպե՞ս կարելի է կիրառել այդ օրենքը արբանյակ ունեցող մոլորակների մասսան որոշելու համար։
*Ինչպե՞ս է ապացուցվել ձգողականության և ծանրության ուժի նույնությունը։
Ի՞նչ են խանգարումները մոլորակների շարժումներում։
Ինչպե՞ս և ե՞րբ է հայտնաբերվել Նեպտունը։
Ինչպե՞ս է տեղի ունենում մակընթացության և տեղատվության երևույթը։ Ինչպե՞ս են նրանք իրար հաջորդում։
Ինչո՞վ է բացատրվում մակընթացությունների գոյությունը։ Ինչո՞ւ նրանք իրար հաջորդում են 12 ժ․ 23 ր․ հետո։
*Անշա՞րժ է արդյոք աստղերի նկատմամբ գարնանային գիշերահավասարի կետը։
*Ինչպե՞ս է տեղաշարժվում երկնքում աշխարհի բևեռը և ինչպիսի՞ պարբերությունով։
*Ինչի՞ց է դա առաջանում, այսինքն՝ ի՞նչ է իրականում տեղի ունենում Երկրի հետ։
*Ի՞նչ է պրեցեսիան։ Այլ կերպ՝ էլ ինչպե՞ս է նա կոչվում և ինչո՞ւ է այդպես կոչվում։
*Ինչո՞ւմն է տարբերությունը արևադարձային և աստղային տարիների միջև։
*Ինչպե՞ս է մարմնի ուղեծրի ձևը կախված ձգողության կենտրոնից՝ տվյալ հեռավորության վրա նրա ունեցած արագությունից։
*Ինչո՞ւմն է կայանում միջմոլորակային ճանապարհորդությունների իրականացման հիմնական պահանջը։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

*Որոշեցեք Յուպիտերի մասսան Երկիր—Լուսին սիստեմի համեմատությամբ, եթե 3ապիտերի առաջին արբանյակը հեռու է նրանից 422 000 կմ և ունի 1,77–օրյա պտտման պարբերություն։ Լուսնի վերաբերյալ տվյալները պետք է որ ձեզ հայտնի լինեն։
*Նկատի ունենալով պրեցեսիայի գոյությունը։ Ինչպե՞ս բացատրել այն, որ գարնանային գիշերահավասարի կետը, որն այժմ գտնվում է Ձկների համաստեղության մեջ, նշանակվում է այն պայմանական նշանով, ինչով նշանակվում է Խոյի համաստեղությունը։
*Ինչո՞ւ երկրագնդի վրա հյուսիսային և հարավային արևադարձները կոչվել են Խեցգետնի և Այծեղջյուրի արևադարձներ։
Հաշվել, թե Երկրից ի՞նչ հեռավորության վրա Երկրի և Լուսնի ձգողական ուժերը կլինեն իրար հավասար, իմանալով, որ Լուսնի հեռավորռւթյունը Երկրից հավասար է 60 երկրային շառավղի և Երկրի ու Լուսնի զանգվածները հարաբերում են ինչպես 81:1։

ԳԼՈՒԽ IV։ ՏԻԵԶԵՐՔԻ ՈՒՍՈՒՄՆԱՍԻՐՈՒԹՅԱՆ ՀԻՄՆԱԿԱՆ ՄեԹՈԴՆԵՐԸ

ԼՈՒՍԱՏՈՒՆԵՐԻ ՀԵՌԱՎՈՐՈՒԹՅԱՆ ԵՎ ՉԱՓԵՐԻ ՈՐՈՇԵԼԸ

§ 77. ՊԱՐԱԼԱՔՍԱՅԻՆ ՇԵՂՈՒՄ։ Երկնային լուսատուների հեռավորությունը որոշելու համար օգտվում են պարալաքսային շեղման երևույթից։ Պարալաքսային շեղումն առարկաների թվացող շեղումն է, որ առաջ է գալիս դիտողի տեղաշարժվելուց։ Այլ կերպ ասած, պարալաքսային շեղումը այն ուղղության փոփոխությունն է, որով երևում է առարկան՝ կապված գիտողի տեղաշարժման հետ։

Բացատրենք այդ հետևյալ օրինակով։ Եթե դուք նայեք առաստաղից կախված լամպին, ապա առաստաղի ֆոնի վրա այն կտեսնեք մի որոշ ուղղությամբ։ Եթե այժմ հեռանաք մի կողմի վրա և դարձյալ նայեք լամպին, ապա այն կտեսնեք մեկ ուրիշ ուղղությամբ՝ նա առաստաղի ֆոնի վրա կերևա մի այլ տեղում։

Այն երկու կետերի միշև ուղիղ գծով եղած հեռավորությունը, որոնցից գիտողը որոշում է առարկայի ուղղությունը, կոչվում է բազիս։

Բազիսի մեծանալուց և դիտվող առարկայի հեռավորությունը փոքրանալուց պարալաքսային շեղումը մեծանում է։ Դրանում հեշտությամբ կարելի է համոզվել, եթե սենյակում ավելի շատ հեռանանք դիտման առաջին դիրքից։ Այո դեպքում լամպն առաստաղի ֆոնի վրա ավելի շատ կտեղաշարժվի։ Մյուս կողմից, ձեզանից մոտ տարածության վրա գտնվող հեռագրասյան կամ ծառի պարալաքսային շեղումը հեռավոր անտառի ֆոնի վրա, երբ դուք անցնում եք նրա մոտով, ավելի մեծ կլինի, քան այն հեռագրասյան կամ ծառի շեղումը, որ ձեզանից ավելի հեռու է գտնվում։

Գիտենալով բազիսի երկարությունը և չափելով ըազիսի և նրա ծայրերից գեւղի առարկան տանող ուղղությունների միշև ընկած անկյունները, կարելի է հաշվելով որոշել առարկայի հեռավորությունը, առանց անմիջականորեն չափելու այդ հեռավորությունը։ Այդ հնարավորությունից մեծ չափով օգտվում են հողաչափական աշխատանքների ժամանակ, պատերազմում՝ երբ կարիք է լինում որոշելու նշանակետի հեռավորությունը, և աստղագիտության մեջ՝ երկնային մարմինների հեռավորությունը որոշելու համար։

Դիցուք հարկավոր է որոշել, օրինակ, A ծառ ի AB հեռավորությունը (նկ․ 67), որը գտնվում է գետի մյուս ափին։ Այդ նպատակով մեր ափին կընտրենք C կետը, այնպես որ BC գիծը ծառայի որպես բազիս, որի երկարությունը կարելի լինի հարմար ձևով և ճիշտ չափել։ Այնուհետև անկյունաչափ գործիքի օգնությամբ, տեղավորվելով B կետում, կչափենք ABC անկյունը, դրա համար գործիքն առաջ կուղղենք դեպի առարկան, իսկ հետո դեպի C կետը (որտեղ սովորաբար փոքր ցցիկ են խփում)։

Այնուհետև մեր գործիքը տեղափոխում ենք C կետը և ճիշտ նույն ձևով չափում ACB անկյունը։ Մենք ստանում ենք մի եռանկյուն, որտեղ հայտնի են մեկ կողմը (BC բազիսի երկարությունը) և նրան հարակից երկու անկյունները։ Այս դեպքում, ըստ եռանկյունաչափության կանոնների, կարելի է հաշվել մյուս երկու կողմերի՝ BA-ի և CA–ի, երկարությունը, այսինքն՝ առարկայի հեռավորությունը։

Որ եռանկյան երկու կողմերի երկարությունը հնարավոր է որոշել երրորդ կողմը և նրան հարակից երկու անկյունները հայտնի լինելու դեպքում, ապա դրանում կարելի է համոզվել նույնիսկ չդիմելով եռանկյունաչափությանը, այլ կառուցման միջոցով։

Հեռավորություններն «աչքաչափով» գնահատելը հիմնված է հենց նույն պարալաքսային շեղման երևույթի վրա զուգորդված փորձի հետ։ Հեռավոր առարկան դիտվում է աջ և ձախ աչքով, իսկ որպես բազիս ծառայում է աչքերի հեռավորությունը միմյանցից։ Մեկ աչքից կոպր մարդիկ առարկաների հեռավորությունը դժվարությամբ են որոշում։ Ռազմական գործում նշանակետի հեռավորությունը որոշելու համար գործածվող հեոաչափները նույնպես նկարագրված երևույթի վրա են հիմնված։ Հեռաչափի երկու օբյեկտիվների միջև եղած հեռավորությունն ավելի մեծ է, քան աչքերի հեռավորությունը միմյանցից, ուստի և հեռաչափով պարալաքսային շեղումն ավելի լավ է նկատվում։

Նշենք նաև այն, որ նկ․ 67-ում պարալաքսային շեղումը ներկայացվում է ACD անկյունով, որը հավասար է CA–ի (A առարկայի ուղղությունը C կետից) և CD–ի (B կետից առարկայի ուղղությանը զուգահեռ ուղղությունը) միջև ընկած անկյանը։

Այն անկյունը, որի տակ առարկայից երևում է դիտողի բազիսը, կոչվում է պարալաքս։ Նկ. 67-ում պարալաքսը կլիՆի BAC անկյունը։ Պարալաքսը և պարալաքսային շեղումը հավասար են։ Որքան մոտ լինի օբյեկտը բազիսից և որքան երկար լինի բազիսը, այնքան մեծ կլինի նրա պարալաքսը։ Տվյալ հեռավորության վրա բազիսը մեծացնելու դեպքում մեծանում է պարալաքսի չափման ճշտությունը, և հետևաբար, մեծանում է այդ հեռավորությունը որոշելու ճշտությունը։

§ 78. ԵՐԿՆԱՅԻՆ ԼՈՒՍԱՏՈՒՆԵՐԻ ՀԵՌԱՎՈՐՈՒԹՅԱՆ ՈՐՈՇԵԼԸ։ Երկնային լուսատուների հեռավորությունը որոշելու հիմնական եղանակը նրանց պարալաքսների որոշելն է։ Սակայն այս դեպքում հարկ է լինում արեգակնային համակարգության մարմինների և նրա սահմաններից շատ ավելի հեռու գտնվող մարմինների համար վերցնել տարբեր բազիսներ։

Արեգակնային համակարգության մարմինների համար, որոնք համեմատաբար մոտ են գտնվում մեզանից, օրինակ, Արեգակի, Լուսնի և մոլորակների համար, Երկրի շառավիղը բավարար մեծության բազիս է հանդիսանում։

Երկու դիտող, որոնցից մեկի համար լուսատուն գտնվում է հորիզոնի վրա, իսկ մյուսի համար՝ զենիթում, միաժամանակ դիտում են այդ լուսատուն։ Այդ երկու ուղղություններով կազմված անկյունը (կամ որ միևնույն է՝ լուսատուի պարալաքսային շեղումը) հենց տվյալ լուսատուի հորիզոնական պարալաքսն է։

Հորիզոնական պարալաքս կոչվում է այն անկյունը, որի տակ լուսատուից երևում է Երկրի՝ տեսողական ճառագայթին ուղղահայաց շառավիղը (նկ. 68-ում ASB անկյունը)։

Արեգակի, Լուսնի կամ մոլորակների պարալաքսը որոշելու դեպքում անհրաժեշտ է, որպեսզի լուսատուն միաժամանակ դիտեն երկու դիտող։ Օրինակ, նկ․ 68-ում դիտողներից մեկը կարող է տեղավորվել A կետում, իսկ մյուսը՝ B կետում։ Բայց իրականում դիտողներն ստիպված են լինում այլ կերպ դասավորվել, և այս դեպքում պարալաքսի հաշվարկումը, ելնելով դիտումներից, մի քիչ ավելի բարդ եղանակով է կատարվում։

Արեգակնային համակարգության սահմաններից շատ ավելի հեռու գտնվող լուսատուների, այսինքն՝ աստղերի համար, Երկրի շառավիղը և տրամագիծը որպես բազիս չափազանց փոքր են։ Աստղերի համար որպես բազիս վերցնում են Երկրի ուղեծրի շառավիղը, բայց աստղերից շատերի, մանավանդ հեռավոր աստղերի համար այդ բազիսը ևս շատ փոքր է։

Տարեկան պարալաքս կոչվում է այն անկյունը, որի տակ լուսատուից երևում է Երկրի ուղեծրի մեծ կիսառանցքը, որը ենթադրվում է տեսողական ճառագայթին ուղղահայաց։

Եթե ճշգրիտ և խնամքով կատարված չափումների միջոցով լուսատուի պարալաքսն արդեն չափված է, ապա նրա D հեռավորությունը որոշվում է հասարակ հաշվարկումների միջոցով։ Նկ. 68-ից երևում է, 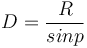$\text{[math]}$ , որտեղ R-ն ընդունված բազիսն է (AC), իսկ p-ն հորիզոնական պարալաքսը (<ASC)։ Ընդունելով R Երկրի շառավիղը որպես միավոր, մենք կստանանք լուսատուի D հեռավորությունը՝ արտահայտված Երկրի շառավղով։

Վերջին ժամանակներս Լուսնի հեռավորությունը Երկրից որոշելու համար կիրառվել է սովետական գիտնական Ն. Դ. Պապալեկիի մեթոդը։ Այդ մեթոդի էությունն այն է, որ որոշվում է այն ժամանակը, որի ընթացքում դեպի Լուսին ուղարկված ռադիոալիքը հասնում է նրան ու անդրադառնալով՝ ետ վերադառնում։ Լուսնի հեռավորությունը ստացվել է այնպիսին, ինչպիսին ստացվում է աստղագիտական եղանակներով։

Ահա կարևորագույն պարալաքսները և նրանց համապատասխան հեռավորությունները։ Լուսնի հորիզոնական պարալաքսը հավասար է 57՛, հեռավորությունը Երկրից՝ 384.000 կմ (կլոր թվով՝ 400.000 կմ)։ Արեգակի հորիզոնական պարալաքսը հավասար է 8՛՛,8, հեռավորությունը Երկրից՝ 149.500.000 կմ (կլոր թվով՝ 150 միլիոն կմ)։

Երկրի հեռավորությունը Արեգակից կոչվում է հեռավորության աստղագիտական միավոր։

§ 79. ԵՐԿՆԱՅԻՆ ՄԱՐՄԻՆՆԵՐԻ ՉԱՓԵՐԻ ՈՐՈՇԵԼԸ։ Երկնային լուսատուների գծային չափերը որոշելու համար հարկավոր է չափել այն անկյունը, որի տակ մենք տեսնում ենք նրա շառավիղը, և իմանալ նրա հեռավորությունը։

Նկ. 69-ում դիտողը Երկրի O կենտրոնից լուսատուի գծային R շառավփղը կտեսնի p անկյան տակ։

Երկրի կենտրոնի հեռավորությունը լուսատուի կենտրոնից նշանակենք D տառով, այդ դեպքում

R = Dsinp

R-ը նույն միավորներով է արտահայտվում, ինչ միավորներով որ արտահայտվում է D-ն։ Եթե D արտահայտենք Երկրի շառավղով, ապա R նույնպես կգտնենք Երկրի շառավղով արտահայտված։ Եթե D արտահայտենք կիլոմետրերով, ապա R ևս կիլոմետրերով կստացվի։

Օրինակ, Լուսնի հեռավորությունը՝ D = 60 երկրային շառավղի, իսկ Լուսնի շառավիղը մենք 16՛ անկյան տակ ենք տեսնում։ Լուսնի համար

R = 60 . sin16՛ = 0,27 Երկրի շառավղի։

§ 80. ՏԱՐԵԿԱՆ ՊԱՐԱԼԱՔՍԸ ՈՐՊԵՍ ԵՐԿԻՐԸ ԱՐԵԳԱԿԻ ՇՈՒՐՋԸ ՊՏՏՎԵԼՈՒ ԱՊԱ8ՈՒՅՑ։ Որ Երկիրն իսկապես շարժվում է Արեգակի շուրջը, Կոպեռնիկոսը չկարողացավ միանգամայն խիստ կերպով ապացուցել։ Ներկայումս այդպիսի ապացույցներ շատ կան։

Մենք կբերենք Երկիրն Արեգակի շուրջը պտտվելու ապացույցներից միայն մեկը, այն է՝ աստղերի տարեկան պարալաքսի գոյությունը։ Եթե Երկիրն անշարժ լիներ, ապա Երկրից դիտողը յուրաքանչյուր աստղ կտեսներ միշտ միևնույն ուղղությամբ, միշտ երկնային սֆերայի միևնույն կետում։ Սակայն Երկիրը շարժվում է, և նրա հետ միասին փոփոխվում է նաև դիտողի դիրքը տիեզերական տարածության մեջ։ Քանի որ դիտողը տեղաշարժվում է, ուստի աստղերը պետք է որ պարալաքսային շեղման ենթարկվեն։ Եթե դիտողը Երկրի հետ միասին տեղաշարժվեր ուղիղ գծով, ապա պարալաքսային շեղումը անընդհատ միևնույն ուղղությամբ տեղի կունենար, և որևէ աստղ ամսե ամիս և տարեցտարի երկնքում միշտ միևնույն կողմի վրա կշարժվեր։

Քանի որ դիտողը Երկրի հետ միասին մեկ տարվա ընթացքում պտույտ է գործում Արեգակի շուրջը գրեթե շրջանագծով և մեկ տարուց հետո դարձյալ կրկնում է այդ ուղին, ուստի աստղերի պարալաքսային շեղումը պետք է կատարվի նույնպես մեկ տարի ժամանակամիջոցում։ Ամեն տարի աստղերի այդ թվացող տեղաշարժը պետք է նորից կրկնվի, նա պետք է պարբերական լինի։ Բացի այդ, պարալաքսային շեղումը, ինչպես մենք արդեն գիտենք, կախված է հեռավորությունից։ Ուստի մեզ ավելի մոտ գտնվող աստղերը պետք է ավելի մեծ պարալաքսային շեղման ենթարկվեն, իսկ հեռու գտնվող աստղերը՝ ավելի փոքր շեղման։

Աստղերի տարեկան պարալաքսային շեղումները հեշտությամբ կարելի է պատկերացնել հետևյալ փորձի օգնությամբ։

Հետևենք, թե ինչպիսի տեղեր է գրավում լամպն առաստաղի ֆոնի վրա այն դեպքում, երբ դիտողն սկսում է պտտվել լամպի տակ գտնվող սեղանի շուրջը։ Առաստաղի ֆոնի վրա լամպը, ինչպես մեզ կերևա, մի որոշ պարփակված ուղի կգծի։

Նկ. 70-ում սխեմատիկ կերպով ցույց է տրված աստղերի պարալաքսային շեղումը՝ Երկիրն Արեգակի շուրջը պտտվելու ժամանակ, երբ այդ աստղերը տարբեր հեռավորության վրա են գտնվում, և նրանց տեսանելի ուղղությունները տարբեր են։

Տարեկան պարալաքսի երևույթը կայանում է նրանում, որ տարվա ընթացքում յուրաքանչյուր աստղ երկնքում գծում է ինքնապարփակ մի կոր, որի ձևը կախված է աստղի ուղղությունից, իսկ անկյունային չափերը՝ նրա հեռավորությունից։

Կոպեռնիկոսը ճիշտ էր ենթադրում, որ պետք է գոյություն ունենա աստղերհ տարեկան պարալաքս։ Սակայն աստղերի հեռավորությունը Երկրից այնքան մեծ է, որ նրանց պարալաքսային շեղումներն աննշան են։ Ուստի, ո՛չ Կոպեռնիկոսը և ո՛չ XVII և XVIII դարերի աստղգետները աստղերի պարալաքսային շեղումները չէին կարող նկատել, որովհետև պետք եղածի չափ ճշգրիտ գործիքներ չունեին։

Միայն մեգնից հարյուր տարի առաջ ռուս գիտնական Վ․ Յա․ Ստրուվեին հաջողվել է առաջինն ի հայտ բերել և ճշգրիտ գործիքների օգնությամբ չափել ամենամոտ աստղերից մեկի պարալաքսը։

Ամենամեծ պարալաքսն ունի մեզ ամենամոտ աստղը, որ կոչվում է «Կենտավրոսի Պրոքսիմա» (լատիներեն «պրոքսիմա» նշանակում է «մերձավորագույն»։ ՍՍՌՄ-ում Կենտավրոսի համաստեղությունը չի երևում)։ Երկնային սֆերայում նրա ծայրային, առավելագույն շեղումների միջև եղած տարբերությունը (ժամանակի՝ կես տարով տարբերվող մոմենտներում) ընդամենը 0՛՛,762 է կազմում։ Այդ անկյան տակ է երևում լուցկու հաստությունը՝ 130 մ հեռավորության վրա։ Որքա՜ն մեծ ճշտությամբ պետք է կառուցված լինի հեռադիտակը և որքա՜ն մեծ պետք է լինի գիտողների հմտությունը, որպեսզի կարելի լինի չափել աստղերի այդչափ չնչին տեղաշարժը։

Կենտավրոսի Պրոքսիման չզինված աչքի համար անտեսանելի է, ուստի երբեմն ամենամոտ աստղ են անվանում նըան հարևան՝ Կենտավրոսի աստղը, որը քիչ ավելի հեռու է մեզնից, քան թե Պրոքսիման։

Նկատենք, որ Երկրի նման Արեգակի շուրջը պտտվող լուսատուների, օրինակ, մոլորակների և գիսավորների համար տարեկան պարալաքսի հասկացողությունը կիրառելի չէ։

ՀԱՐՑԵՐ ԻՆՐՆՍՏՈԻԳՄԱՆ ՀԱՄԱՐ

Ի՞նչ է պարալաքսային շեղումը։
Ի՞նչ է բազիսը։
Ի՞նչ է պարալաքսը։
Ի՞նչ է հորիզոնական պարալաքսը։ Բացատրեցե՛ք գծագրով։
Ինչպե՞ս որոշել լուսատուի հեռավորությունը, եթե նրա հորիզոնական պարայաքսր հայտնի է։
Ո՞ր լուսատուների հորիզոնական պարալաքսն է հնարավոր որոշել։
Ի՞նչ է «աստղագիտական միավորը» և քանի կիլոմետրի է հավասար։
Ինչի՞ է հավասար Լուսնի և Արեգակի հորիզոնական պարալաքսը։
Ինչի՞ է հավասար Լուսնի միջին հեոավորությունւ։
*Ինչպե՞ս են որոշում մոլորակների գծային չափերը։
Ինչպիսի՞ երևույթն է ապացուցում Երկրի պտույտը Արեգակի շուրջը։
*Ինչո՞ւմն է արտահայտվում աստղերի տարեկան պարալաքսի երևույթը։
*Ո՞վ և ե՞րբ է առաջին անգամ հայտնաբերել աստղերի պարալաքսը։

ՎԱՐԺՈՒԹՅՈՒՆՆԵՐ

Արեգակի պարալաքսը հավասար է 8՛՛,80, իսկ նրա տեսանելի անկյունային շառավիղը՝ 16՛1՛՛։ Քանի՞ անգամ է Արեգակը մեծ Երկրից ըստ տրամազծի։
Լուսնի հորիզոնական պարալաքսը կազմում է 57՛։ Ինշպիսի՞ անկյան տակ է Լուսնից երևում Երկրի տրամագիծը։
Ինչքանո՞վ կփոփոխվի համաստեղությունների գծագրվածքը, եթե նրանք դիտվեն ոչ թե Երկրից, այլ Պլուտոնից։
*Ինշպիսի՞ ամենամեծ անկյունային հեռավորության վրա, եթե նայենք Երկրից, կերևա այն մոլորակը, որը, ենթադրենք՝ պտտվում է Կենտավրոսի α աստղի շուրջը՝ 150 000 000 կմ հեռավորության վրա։

ՀԵՌԱԴԻՏԱԿՆԵՐ ԵՎ ՍՊԵԿՏՐԱՅԻՆ ԱՆԱԼԻԶ

§ 81. ՀԵՌԱԴԻՏԱԿՆԵՐԻ ԿԱՌՈՒՑՎԱԾՔԸ։ Հեռադիտակները նախատեսված են այն բանի համար, որպեսզի տան երկնային լուսատուների լուսապատկերը, որ հնարավոր լինի դիտել խոշորացված տեսքով, լուսանկարել կամ ուսումնասիրել այլ կերպ։ Երկնային լուսատուներից եկող լույսը հեռադիտակ-ռեֆրակտորում հավաքվում է ուռուցիկ, կլոր ապակիով (օբյեկտիվով), իսկ հեռաղիտակ-ռեֆլեկտորում՝ գոգավոր հայելիով (նկ. 71)։

Ինչքան մեծ է օբյեկտիվի կամ հայելու տրամագիծը, այնքան ավելի շատ լույս է հավաքում հեռադիտակը և այնքան ավելի թույլ աստղեր են նրանով երևում։ Ինչպես հայտնի է ֆիզիկայից, հեռադիտակի խոշորացնելու, ունակությունը այնքան մեծ է, որքան մեծ է նրա ֆոկուսային հեռավորությունը՝ F, այսինքն՝ հեռավորությունը օբյեկտիվից կամ հայելուց մինչև այն կետը, որտեղ նրանք տալիս են լուսատուի լուսապատկերը։ Այդ լուսապատկերը դիտվում է օկուլյարի (կատարելագործված խոշորացնող ապակի) միջոցով, որն ունի իր սեփական ֆոկուսային հեռավորությունը՝ f։

Հեռադիտակի խոշորացումը՝ W = F : f, այնպես որ, ունենալով մի քանի տարբեր օկուլյարներ, կարելի կլինի նրանցով ստանալ տարբեր չափի խոշորացումներ։

Սովետական գիտնական Դ. Դ. Մակսուտովը 1941 թ․ հնարել է հեռադիտակի նոր տեսակ, որ միացնում է ռեֆրակտորի և ռեֆլեկտորի առավելությունները։ Նրա սիստեմով են կառուցված ժամանակակից դպրոցական հեռադիտակները։

Երկնային լուսատուների ֆիզիկական բնությունն ուսումնասիրելու համար կիրառվում են զանազան տեսակի հեռադիտակներ։ Որոշ հեռադիտակներով լուսատուներն անմիջականորեն դիտվում են աչքով, մյուսների օգնությամբ լուսատուները նկարահանվում են։ Աստղերը լուսանկարելու համար կիրառվող հեռադիտակները կոչվում են աստրոգրաֆներ։ Նրանք, ինչպես և մյուս բոլոր խոշոր հեռադիտակները, ընտրած աստղի ուղղությամբ տեղակայելուց հետո, ժամացույցի մեխանիզմի օգնությամբ շարժման մեջ են դրվում դեպի աշխարհի բևեռն ուղղած առանցքի շուրջը։ Դրա շնորհիվ դիտողը, չնայած երկնքի կատարած օրական պտույտին, իր հեռադիտակի տեսողության դաշտում անընդհատ տեսնում է լուսատուն, իսկ աստղերի պատկերներն ընկնում են լուսանկարչական ապակու միշտ միևնույն տեղը։

Ներկայումս լուսանկարչությունը շնորհիվ իր բազմաթիվ առավելությունների՝ դուրս է վանում անմիջականորեն աչքով դիտումը։ Երկնքի և երկնային լուսատուների ստացվող պատկերներն արձանագրում են նրանց նկարահանման մոմենտում ունեցած փաստական վիճակը։ Լուսանկարները, որոնք անընդհդատ համալրում են պահարաններր՝ այնուհետև հարմար պայմաններում ուսումնասիրվում են լաբորատորիաներում, որտեղ լուսանկարչությամբ կատարված բոլոր չափումները կարելի է ստուգել և ցանկացած ժամանակ կրկնել։ Լուսանկարչության միջոցով կատարվող չափումները, նրանց հետ կապված հաշվարկումները, ստացվող արդյունքների ուսումնասիրությունն ավելի շատ ժամանակ են խլում աստղագետներից, քան հենց այդ դիտումների կատարումը։

Հեռաղիտակներից շատերը օժտված են օժանդակ գործիքներով, որոնք ծառայում են երկնային լուսատուների լույսի ուժն ու հատկությանները ուսումնասիրելու համար։

Չպետք է կարծել, որ խոշոր հեռադիտակներ կառուցելու ձգտումը առաջ է գալիս բացառապես երկնային մարմիններն ավելի խոշորացրած տեսնելու ցանկությունից։ Օդի բոլոր հոսանքները հեռադիտակի մեջ ավելի ևս նկատելի են դառնում, այնպես որ օդում շարունակ գոյություն ունեցող ալեկոծումները գործնականորեն կիրառելի խոշորացումը սահմանափակում են։ Հեռադիտակով դիտումներ կատարելիս հազվագյուտ դեպքում 500 անգամից ավելի խոշորացում են օգտագործում, թեև մեծ դիտակները ինքնըստինքյան կարող են մի քանի հազար անգամով խոշորացում տալ։ Այդպիսի մեծ խոշորացումների դեպքում լուսատուների վրա եղած մանրամասնությունները, օդի ավելի նկատելի ալեկոծությունների պատճառով, ավելի վատ, ավելի աղոտ են երևում, քան փոքր խոշորացումների դեպքում։

Դրա փոխարեն խոշոր հեռադիտակները թույլ են տալիս տեսնելու ավելի թույլ, և հետևաբար, մեզանից ավելի հեռու գտնվող լուսատուները, թույլ են տալիս ավելի խորը թափանցելու տիեզերական անհուն տարածության մեջ։ Այդպիսի հեռադիտակների օդնությամբ լուսատուների լուսանկարները ավելի արադ և շատ մանրամասն կերպով են ստացվում։

ՍՍՌՄ-ում առավել խոշոր աստղադիտարաններ կան Մոսկվայում, Տաշքենտում, Կազանում, Աբասթումանում, Ղրիմում։ Գերմանական ֆաշիստները պատերազմի ժամանակ կործանել են Պուլկովփ և Սիմեիզի աստղադիտարանները, որտեղ գտնվում էին ՍՍՌՄ-ի ամենախոշոր հեռադիտակները։ Այդ աստղադիտարանների վերականգնումը Համարյա ավարտված է, և նույնպես կառուցվում են նորերը, Պուլկովի աստղադիտարանը, որ հիմնադրել է Վ. Յա․ Ստրուվեն 1839 թ., արտասահմանում ճանաչվել է որպես «աշխարհի աստղագիտական մայրաքաղաք», քանի որ նա եղել է լավագույն կերպով կահավորված և մեծ փառքի է արժանացել իր դիտական աշխատանքների բացառիկ ճշտությամբ ու մտածվածությամբ։ Պուլկովի աստղադիտարանը կատարելագործվելու են եկել տարբեր երկրների գիտնականներ։

§ 82. ՀԵՌԱԴԻՏԱԿՆԵՐԻ ՏԵՂԱԿԱՅՄԱՆ ԵՐԿՈՒ ԵՂԱՆԱԿ ԵՎ ՆՐԱՆ8 ՀԵՏ ՎԱՐՎԵԼԸ։ Գոյություն ունի հեռադիտակը հաստատոցի (շտատիվի) վրա տեղակւսյելոլ երկու եղանակ։

Ազիմուտային տեղակայում ունեցող հաստատոցը (նկ․ 75) թույլ է տալիս դիտակը հոդակապի (շառնիր) վրա դարձնել դեպի վեր և դեպի վար, այսինքն՝ ըստ բարձրության (ուղղաձիգ հարթությամբ և ուղղաձիգ առանցքի շուրջը՝ աջ և ձախ, այսինքն՝ ըստ ազիմուտի։ Ուստի և այդպիսի տեղակայումը կոչվում է ազիմուտային։

Քանի որ երկնային լուսատուները հորիզոնի նկատմամբ թեք ուղղությամբ են շարժվում և միաժամանակ անընդհատ փոփոխվում է և՛ նրանց բարձրությունը և՛ նրանց ազիմուտը, ուստի որևէ աստղ դիտելու ժամանակ ազիմուտային տեղակայում ունեցող հեռադիտակը հարկ է լինում գրեթե անընդհատ շարժել թե՛ ըստ բարձրության և թե՛ ըստ ազիմուտի, այսինքն՝ նրանով գրեթե միաժամանակ կատարել երկու շարժում, որպեսզի լուսատուն անընդհատ մնա հեռադիտակի տեսադաշտում։ Դա շատ անհարմար է, մանավանդ, երբ հեռադիտակով ցանկանում են նայել հերթով մի քանի մարդիկ։

Ուստի երկնային լուսատուները դիտելու համար ամենից հարմար է օգտվել հասարակածային տեղակայում ունեցող դիտակով, իսկ լուսատուները լուսանկարելու համար այդ տեղակայումը ուղղակի անհրաժեշտ է։

Հասարակածային տեղակայում ունեցող հաստատոցը թույլ է տալիս հեռադիտակը դարձնելու աշխարհի առանցքի ուղղությանը համընկնող առանցքի շուրջը (որ կոչվում է ժամային առանցք) և նրան ուղղահայաց առանցքի շուրջը (որ կոչվում է հակման առանցք)։ Մի այդպիսի տեղակայում պատկերված է նկ. 76-ում և սկզբունքորեն այդ տեղակայումը կարելի է ստանալ ազիմուտային տեղակայումից, եթե վերջինիս առանցքը հորիզոնի նկատմամբ թեքենք այնպես, որ նա ուղղվի դեպի աշխարհի բևեռը։ Այն ժամանակ եթե հեռադիտակը պտտելու լինենք ժամային առանցքի շուրջը (այդպես թեքելու դեպքում ուղղաձիգ առանցքը կընդունի ժամային առանցքի դիրք), նա կսկսի շարժվել հասարակածին զուգահեռ հարթությամբ, այսինքն՝ կգծի լուսատուի օրական զուգահեռականը։

Եթե այսպիսի տեղակայում ունեցող հեռադիտակը ուղղելու լինենք որևէ լուսատուի վրա, ապա այլևս կարիք չի լինի նրան դարձնելու հակման ա ռան ցքի շուրջը, այլ կմնա միմիայն դարձնել այն ժամային առանցքի շուրջը, և այն էլ համաչափ արագությամբ։ Այդ պտտեցումը հարմար և ավելի սահուն դարձնելու նպատակով օգտվում են մի հատուկ պտուտակից, որ կոչվում է մի կրոմետրիկ պտուտակ։

Խոշոր հեռադիտակները պտտեցվում են ժամացույցի մեխանիզմի օգնությամբ։ Ժամացույցի մեխանիզմը հեռադիտակը պտտեցնում է օրական մի լրիվ շրջանի (ժամում 15°) արագությամբ, այնպես որ լուսատուն շարունակ մնում է ակնապակու (օկուլյարի) տեսողության դաշտում։ Դիտողը կարիք է ունենում միայն երբեմն կարգավորելու ժամացույցի մեխանիզմի ընթացքը կամ Կաղապար:Լայն պտուտակի օգնությամբ ուղղելու նրա աշխատանքի անհարթությունները։

Սովորաբար հեռադիտակը մի քանի ակնապակի է ունենում։ Ամրացնելով նրանցից որևէ մեկը հեռադիտակի վրա, կարելի է փոքր կամ մեծ խոշորացում ստանալ։ Լավ հեռադիտակը, ամենաուժեղ ակնապակու առկայության դեպքում (որի ֆոկուսային հեռավորությունը մոտ 5 մմ է կազմում), թույլ է տալիս ստանալու առավելագույն խոշորացում, որը հավասար է լինում օբյեկտիվի կրկնակի կամ եռակի տրամագծին՝ արտահայտված միլիմետրերով։

Օրինակ, 50 միլիմետրանոց օբյեկտիվ ունեցող հեռադիտակը կարող է առավելագույն խոշորացումը հասցնել 100-ից մինչև 150 անգամի։

Հեշտ է նկատել, որ որքան ուժեղ լինի ակնապակին և որքան մեծ լինի նրա տված խոշորացումը, այնքան փոքր կլինի նրանով երևացող տեսողության դաշտը։ Լուսինը 30—50 անգամ մեծացվելու դեպքում տեսողության դաշտում երևում է ամբողջությամբ։ 150 անգամ մեծացվելու դեպքում տեսողության դաշտում տեղավորվում է Լուսնի միայն մի փոքրիկ մասը, բայց արդեն շատ մանրամասնություններ են երևում։ Որքան խոշորացումն ավելի մեծ է լինում, այնքան ավելի նկատելի են դառնում օբյեկտիվի շինվածքի անկատարելագործվածությունը և մթնոլորտում եղած օդային հոսանքները։ Հետևանքը լինում է այն, որ երկնային լուսատուների վրա մանրամասնություններն ավելի վատ են երևում, քան փոքր խոշորացման դեպքում, ուստի և հեռադիտակի ուժեղ խոշորացման չպետք է հետապնդել։

Որպեսզի համոզվենք, որ հեռադիտակն իրոք որ խոշորացնում է, խորհուրդ է տրվում միաժամանակ երկու աչքով նայել Լուսնին մեկով անմիջականորեն, իսկ մյուսով՝ հեռադիտակով։

Միգամածություններ և աստղակույտեր դիտելու ժամանակ պետք է գործածել նվազ խոշորացում և տեսողության մեծ դաշտ ունեցող ակնապակի։ Արեգակը, Լուսինը, մոլորակները և աստղերը դիտելու դեպքում պետք է վերցնել այնպիսի ակնապակի, որը տվյալ պայմաններում հնարավոր խոշորացումներից տալիս է ոչ թե ամենամեծ, այլ ամենապարզ խոշորացումը։ Հարկավոր է լավ հիշել, որ երբեմն երկրային օդի վիճակը թույլ չի տալիս պարզ տեսնելու երկնային լուսատուներր նույնիսկ չափավոր խոշորացման դեպքում։

Գիսավորները, միգամածությունները և նույնիսկ թույլ աստղերը Լուսնի լույսի տակ վատ են երևում կամ բոլորովին չեն երևում։

§ 83. ՍՊԵԿՏՐԱՅԻՆ ԱՆԱԼԻԶ։ Անցյալ դարի կեսերին հայտնագործվեց լույսի ուսումնասիրման մի առանձին եղանակ, որը սպեկտրային, անալիլյ է կոչվում։ Նա հիմնված է այն բանի վրա, որ տարբեր գույնի ճառագայթները, որոնք ի մի խառնվելով սպիտակ լույս են տալիս, մի միջավայրից մյուս միջավայրը, օրինակ, օդից ապակու մեջ անցնել ու ժամանակ, բեկվում են տարբեր չափով։

Անցած ժամանակաշրջանում լույսի ուսումնասիրման այդ եղանակը կատարելագործվել է և գտել բազմազան կիրառություններ։ Նրան ենք մենք պարտական մեր այն տեղեկությունների մեծամասնությամբ, որ ունենք Երկնային մարմինների ֆիզիկական բնույթի և քիմիական բաղադրության վերաբերյալ։

Սպեկտրային անալիզը կատարվում է մի գործիքի միջոցով, որը կոչվում է սպեկտրոսկոպ (նկ. 77)։ Սպեկտրոսկոպը բաղկացած է մեկ կամ մի քանի ապակյա պրիզմաներից և երկու խողովակից։ Նրանցից մեկը (նկարում՝ ձախակողմյանը), որ կոչվում է կոլլիմատոր, առջևի ծայրին ունի մի նեղ ճեղք, որի միջով անցնում է ուսումնասիրվող լուսատուի լույսը։ Մյուս ծայրում դրված է օբյեկտիվը, որի հենց ֆոկուսումն էլ տեղավորված է ճեղքը։ Ուստի լույսի ճառագայթները մտնելով ճեղքից, որը սպեկտրոսկոպի համար կարծես լույսի աղբյուր է ծառայում, դուրս են գալիս ճեղքից զուգահեռ փնջով և բոլորը միևնույն անկյուն տակ ընկնում են պրիզմայի վրա։ Հենց այս է կոլլիմատորի դերը։

Տարբեր գույնի ճառագայթներից բաղկացած բարդ լույսը պրիզմայում տարաբաժանվում է իր բաղադրիչ մասերին։ Տարբեր գույնի ճառագայթները բաժանվում են միմյանցից, որովհետև պրիզմայում նրանք տարբեր ձևով են բեկվում։ Լույսն այդ վիճակում մտնում է դիտախողովակը։ Եթե դիտախողովակի ծայրին օկուլյարի փոխարեն լուսանկարչական ապակի դնելու լինենք, ապա մենք կստանանք ուսումնասիրվող լույսի բաղադրիչ մասերի լուսանկարը, որ կոչվում է սպեկտրագրամմա։ Այս դեպքում գործիքը կոչվում է սպեկտրոգրաֆ։

Պարզված է, որ շիկացած կարծր և հեղուկ մարմինները, նույնպես և շիկացած ոչ այնքան թափանցիկ էլեկտրականացած կամ ուժեղ կերպով սեղմված գազերը տալիս են այսպես կոչված անընդհատ սպեկտր, որը ծիածանային շերտի տեսք ունի (նկ.78, 1)։ Այդպիսի սպեկտրում հաջորդաբար մեկից մյուսին են անցնում կարմիր, նարնջի, դեղին, կանաչ, երկնագույն, կապույտ և մանուշակագույն գույները։ Արեգակի սպիտակ լույսը բաղկացած է ծիածանի բոլոր գույներից։ Ինչպես հայտնի է, լույսը տարածվում է ալիքների ձևով, և սպեկտրի յուրաքանչյուր գույն ունի իր ալիքի երկարությունը։ Ավելի ճիշտ՝ սպեկտրի յուրաքանչյուր կետին համապատասխանում է ալիքի որոշ երկարություն։ Այդ երկարությունը միատեսակ է միայն մեկ՝ սպեկտրի երկարությանն ուղղահայաց գծի վրա եղած կետերի համար, այսինքն՝ սպեկտրի վրա լայնակի ընկած գծի համար։ Օրինակ, սպեկտրի վրա երկու հարևան դեղին շերտերը, որոնց գույների տարբերությունն աչքով չի կարելի նշմարել, տարբեր երկարության ալիքներ ունեն։

Թափանցիկ գազերն ու գոլորշիները, երբ նրանք նոսր վիճակումն են գտնվում և շիկացած լինելու պատճառով կամ էլեկտրական պարպումի ազդեցության տակ (ինչպես, օրինակ, էլեկտրական կայծում) լույս են արձակում, տալիս են մի սպեկտր, որը կազմված է լինում մուգ ֆոնի վրա երևացող գունավոր պայծառ գծերից (նկ. 78, 3 և 79՝ ներքևում)։ Այդպիսի սպեկտրում գծերի դասավորությունն ըստ ալիքների երկարության կախված է տվյալ գազի քիմիական բաղադրությունից։ Միևնույն գազը, որ գտնվում է լուսարձակման քիչ թե շատ միատեսակ պայմաններում, սպեկտրում տալիս է միևնույն գծերը։ Այսպիսով, սպեկտրի վրա եղած գծերի օգնությամբ կարելի է որոշել լույս արձակող գազի քիմիական բաղադրությանը։

Եթե անընդհատ սպեկտր տվող լույսի աղբյուրի առջև ավելի ցածր ջերմաստիճան ունեցող գազեր կամ գոլորշիներ տեղավորենք, նրանք այդ Լույսի մի մասը կկլանեն։ Այդ դեպքում սպեկտրոսկոպում կերևա մի անընդհատ սպեկտր, որը կտրտված կլինի մութ գծերով (նկ, 78, 2 և 79 վերևի)։ Մութ գծերը կգտնվեն սպեկտրի ճիշտ այն տեղերում (նրանք ունեն ալիքի ճիշտ նույն երկարությունը), որտեղ հենց գոլորշիները կամ գազերն իրենք սպեկտրի պայծառ գծեր են տալիս, երբ նրանք պայծառ լուսարձակման վիճակումն են գտնվում։

(Դա սա գրքին կցված է սպեկտրների գունավոր աղյուսակը)։

§ 84. ԵՐԿՆԱՅԻՆ ՄԱՐՄԻՆՆԵՐԻ ՔԻՄԻԱԿԱՆ ԲԱՎԱԴՐՈՒԹՅԱՆ, ԱՐԱԳՈՒԹՅՈՒՆՆԵՐԻ ԵՎ ՋԵՐՄԱՍՏԻՃԱՆՆԵՐԻ ՈՐՈՇԵԼԸ։ Սպեկտրային անալիզի միջոցով գազերի քիմիական բաղադրությունը կարելի է որոշել միայն այն դեպքերում, երբ այդ գազերը կա՛մ իրենք են լույս արձակում, կա՛մ կլանում են անընդհատ սպեկտր տվող լուսաղբյուրի լույսը և դրանով իսկ անընդհատ սպեկտրում մութ գծեր են առաջացնում։ Վերջին դեպքը վերաբերում է այն մթնոլորտներին, որոնք շրջապատում են այնպիսի երկնային մարմիններ, ինչպես, օրինակ, Արեգակը և աստղերը։ Աստղերի և Արեգակի սպեկտրներն անընդհատ են և կտրտված մութ գծերով։ Համեմատելով այդ գծերը մեզ հայտնի քիմիական էլեմենտների սպեկտրներում եղած գծերի հետ, մենք կարողանում ենք իմանալ Արեգակի և աստղերի արտաքին՝ ոչ այնքան տաք՝ շերտերի քիմիական բաղադրությունը։ Այդ լուսատուների վրա հայտնաբերված են միայն այնպիսի քիմիական էլեմենտներ, որոնք կան նաև Երկրի վրա, իսկ դա հաստատում է տիեզերքի նյութական միասնությունը և ժխտում բնության անճանաչելիության մասին եղած կեղծ գիտությունը։

Լուսինը և մոլորակները լուսավորվում են Արեգակի անդրադարձ լույսով, ուստի և սպեկտրային անալիզի միջոցով նրանց քիմիական բաղադրությունը չի կարելի որոշել։ Բայց Արեգակի լույսը, նախ քան մոլորակի մակերևույթից անդրադառնալը, անցնում է մոլորակի մթնոլորտով, իսկ անդրադառնալուց հետո՝ դեպի մեզ ուղղվելիս կրկին անգամ անցնում է նրա մթնոլորտով։ Արեգակի լույսը մոլորակի մթնոլորտով անցնելուլ ժամանակ կլանվում է նրա կողմից, ուստի և մոլորակների սպեկտորներում առաջանում են լրացուցիչ մութ գծեր (Արեգակի սպեկտրի համեմատությամբ)։ Այդ երևույթը թույլ է տալիս որոշելու մոլորակների մթնոլորտների բաղադրությունը։

Երկնային մարմինների՝ Երկրի նկատմամբ տեսողական ճառագայթի ուղղությամբ (մեզնից կամ դեպի մեզ) կատարած շարժման արագությունները որոշվում են սպեկտրային անալիզի միջոցով՝ այսպես կոչված Դոպլեր-Ֆիզոյի սկզբունքի հիման վրա։ Դոպլեր-Ֆիզոյի սկզբունքը կայանում է նրանում, որ երբ լույսի աղբյուրը և դիտողը մոտենում են միմյանց, սպեկտրի բոլոր զծերը տեղաշարժվում են դեպի նրա մանուշակագույն ծայրը, իսկ երբ դիտողը և լույսի աղբյարը հեռանում են իրարից՝ նրա սպեկտրում բոլոր զծերը տեղաշարժվում են դեպի կարմիր ծայրը։ (Դա նման է այն երևույթին, որ նկատվում է ձայնի աղրյուրր մոտենալու կամ հեռանալու մամանակ. ձայնական ալիքի հաճախացումը կամ նոսրացումը կարճացնում կամ երկարացնում է այդ ալիքը, որն ազդում է ձայնի տոնի վրա։ Լույսի ալիքները ենթարկվում են նույն կանոններին)։ Գծերի տեղաշարժման մեծությունը կախված է շարժման արագությունից, և այն կարելի է չափել։ Այդ ամենի ճշմարտացիությունը փորձով առաջինը ապացուցել է ակադեմիկոս Աէ Ա. Բելապոլսկին (1854—1934) Պուլկովի աստղադիտարանում (նկ. 91)։

Լուսատուների՝ տեսողական ճառագայթեն ուղղահայաց ուղղությամբ կատարած շարժման իսկական արագությունը կարելի է որոշել, իմանալով լուսատուի երկնային սֆերայում կատարած շարժման տեսանելի անկյունային արագությունը և նրա մեզանից ունեցած հեռավորությունը։

Երկնայինինք նալուսատու մարմինների, ինչպես՝ Արեգակի և աստղերի, ջերմաստիճանները որոշվում են նրանց սպեկտրի տարբեր մասերում պայծառության բաշխվածության ուսումնասիրությամբ։ Ցածր ջերմաստիճան ունեցող ինքնալուսատու մարմինը կարմիր գույնի է լինում, որովհետև նրա սպեկտրում ամենապայծառ տեղը հանդիսանում է հատկապես կարմիր գույնը։ Ավելի տաք մարմինը դեղին լույս է արձակում, որովհետև նրա սպեկտրում ամենապայծաո տեղերը գրավում են դեղին և կարմիր գույները։ Ավելի ևս շիկացած մարմինը սպիտակ գույն է ունենում, որովհետև նրա սպեկտրում գույների պայծառությունն այնպիսին է, որ միախառնվելու դեպքում նրանք սպիտակ գույն են տալիս։ Է՛լ ավելի տաք մարմնի սպեկտրում առավել պայծառը երկնագույն մասն է, այդ պատճառով էլ նրա գույնը երկնագույն է թվում։ Լույսի ուսումնասիրության տեսությունը, որ ստուգված է նաև փորձով, ցույց է տալիս, թե ինչպես պայծառության բաշխվածությունը ըստ սպեկտրի զանազան գույների՝ կախված է մարմնի ջերմաստիճանից։ Ուսումնասիրելով պայծառության բաշխվածությունը Արեգակի և աստղերի սպեկտրներում, մենք կարող ենք որոշել, թե այդ բաշխվածությունը ո՛ր ջերմաստիճանին է համապատասխանում։

Մոլորակների և Լուսնի ջերմաստիճանները, որոնք լուսավորվում են արևի լույսով, որոշվում են տարբեր մետաղներից շինված երկու շատ բարակ յարերի զոդվածքի օգնությամբ․ դա այսպես կոչված ջերմաէլեմենտն' է (տերմոէլեմենտ)։ Այդպիսի զոդվածքը տաքացնելու դեպքում նրա մեջ էլեկտրական հոսանք է առաջանում։ Աստղագիտության մեջ կիրառվում են հեռադիտակներին միացրած այնպիսի զգայուն ջերմաէլեմենտներ, որոնք կարողանում են որսալ մի քանի կիլոմետր հեռավորության վրա վառվող մոմի ջերմությունը։ Այդ ջերմաէլեմենտները տեղավորվում են հեռադիտակի օբյեկտիվի ֆոկուսում՝ ճիշտ այնտեղ, որտեղ ստացվում է մոլորակի պատկերը։ Մոլորակի առհասարակ շատ աննշան ճառագայթումը տաքացնում է ջերմաէլեմենտը, և նրա մեջ էլեկտրական թույլ հոսանք է առաջանում, որը և չափվում է զգայուն գալվանոմետրով։ Իմանալով հոսանքի ուժը, կարելի է որոշել այն ջերմության քանակը, որ այդ մոլորակից հասնում է Երկիր, իսկ իմանալով մոլորակի հեռավորությունը Երկրից, կարելի է այդ տվյալների հիման վրա հաշվել մոլորակի ջերմաստիճանը։

Մենք տեսնում ենք, որ ժամանակակից գիտությունը տիեզերքն ուսումնասիրելու համար ունի մի շարք հզոր միջոցներ։ Այդ միջոցները թույլ են տալիս միանգամայն վստահ կերպով ուսումնասիրել երկնային մարմինների բնույթը, նրանց դարժումները, քիմիական բաղադրությունը և ջերմաստիճանը։ Այսպիսով, երկնային մարմինների վերաբերյալ եղած ժամանակակից տվյալները ոչ թե սոսկ ենթադրական են, այլ կատարված չափումների և բազմաթիվ անգամ փորձով ստուգված օրենքների կիրառման արժանահավատ արդյունքներ են։

ՀԱՐՑԵՐ ԻՆՐՆՍՏՈԻԳՄԱՆ ՀԱՄԱՐ

Ինչի՞ համար են հարկավոր հեռադիտակները։
Ինչո՞ւմն է կայանամ ռեֆրակտորի և ռեֆլեկտորի տարբերությունը։ Գծագրեցե՛ք նրանց սխեմաները։
Ինչո՞վ և ինչպե՞ս է պայմանավորված հեռադիտակի տված մեծարումը։
Ի՞նչ է աստրոգրաֆը։
Կարելի՞ է արդյոք գործնականում դիտել հազար անգամ մեծացված լուսատուները։
*Հեռադիտակների տեղակայման ինչպիսի՞ երկու գլխավոր եղանակներ գոյություն ունեն։
*Ինչպիսի՞ շահում և անհարմարություն է բերում մեծ խոշորացումից օգտվելը։
Գծագրեցեք սպեկտրոսկոպի կառուցվածքի սխեման և բացատրեցեք այն։
Ի՞նչ է սպեկտրոգրամման։
Սպեկտրների ի՞նչ տեսակներ գիտեք։
Ի՞նչ տեսք ունեն Արեգակի ու աստղերի սպեկտրները։
Ինչո՞ւ այդ սպեկտրներում երևում են մութ գծեր։
Ինչպե՞ս են որոշում լուսատու գազերի և Արեգակի ու աստղերի քիմիական բաղադրությունը։
Կարելի՞ է արդյոք սպեկտրային անալիզի օգնությամբ որոշել մոլորակների մակերևույթի ու նրանց մթնոլորտների քիմիական բաղադրությունը։
Ինչո՞ւմն է կայանում Դոպլեր—Ֆիզոյի սկզբունքը։ Ինչպե՞ս են որոշում երկնային մարմինների արագությունն ու շարժման ուղղությունը։
Ի՞նչ եղանակներով ու գործիքներով են որոշում երկնային մաոմինների ջերմաստիճանը։