Pages 49-55
Սահմանումներ
1. Ցանկացած ուղղանկյուն զուգահեռագիծ համարվում է սահմանափակված ուղիղ անկյուն կազմող երկու ուղիղ գծերով։
2. Ցանկացած զուգահեռագիծ պատկերում նրա անկյունագծի շուրջ (վերցված) ցանկացած զուգահեռագիծ իր երկու լրացումների հետ միասին կոչվում է գնոմոն։
Պնդում 1
Պնդում 2
Պնդում 3
Պնդում 4
Պնդում 5
Pages 56-68
Պնդում 6†
Հետևաբար, քանի որ AC-Ն և CB-Ն հավասար են, AL և CH անկյունագծերով ուղղանկյունները նույնպես հավասար են [Պնդում 1.36]։ CH անկյունագծով ուղղանկյունն էլ հավասար է HF անկյունագծովին [Պնդում 1.43], որից հետևում է, որ AL անկյունագծով ուղղանկյունը հավասար է HF անկյունագծովին։ Երկու կողմերին էլ ավելացնենք CM անկյունագծով ուղղանկյունը։ Կստացվի, որ AM անկյունագծով ուղղանկյունը և NOP գնոմոնը հավասար են։ Իսկ AM անկյունածով ուղղանկյունը կարող ենք կառուցել AD և DB կողմերով։ DM-ն ու DB-ն նույնպես հավասար են, հետևաբար NOP գնոմոնը հավասար է AD-ով և DB-ով կառուցված ուղղանկյանը։ Երկու կողմին էլ ավելացնենք LG անկյունագծով քառակուսին, որը հավասար է BC հիմքով քառակուսուն։ Այսպիսով՝ AD և DB կողմերով ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է NOP գնոմոնի և LG անկյունագծով քառակուսու գումարին։ Սակայն NOP գնոմոնն ու LG անկյունագծով քառակուսին համարժեք են ողջ CEFD-ին, որը ընկած է CD-ի վրա։ Հետևում է, որ AD-ով և DB-ով կառուցված ուղղանկյան և CB հիմքով քառակուսու գումարը հավասար է CD հիմքով քառակուսուն։ Հետևաբար, հատվածը կիսելու և դրան ուղիղ գծով այլ հատված կցելու արդյունքում՝ ստացված ողջ հատվածով և ավելացված մասով կառուցված ուղղանկյան և հատվածի կեսով կառուցված քառակուսու գումարը հավասար է նախնական հատվածի կեսի և կցված հատվածի գումարով ստացված նոր հատվածով կառուցված քառակուսուն։
† Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ 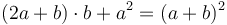 ։
։
Պնդում 7†
Հատվածը կամայական կետում հատելիս՝ ստացված հատվածներից պատահականորեն ընտրված մեկի և ողջ հատվածի քառակուսիների գումարը հավասար է ողջ և նախապես ընտրված հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկի և հատման արդյունքում առաջացած մյուս հատվածի երկարության քառակուսու գումարին։
Տրված AB հատվածը հատենք C կետում: AB և BC հատվածների քառակուսիների գումարը հավասար է AB և BC հատվածներով որոշված ուղղանկյան մակերեսի կրկնապատիկի և CA կողմով քառակուսու մակերեսի գումարին։ Կառուցենք ADEB քառակուսին՝ AB կողմով սահմանված։ Կառուցենք նաև գծագրի մնացած մասը։ AG և GE անկյունագծերով ուղղանկյունները հավասար են, երկուսին էլ կցենք CF անկյունագծով քառակուսին։ Արդյունքում AF և CE անկյունագծերով ուղղանկյունները հավասար կլինեն։ Հետևաբար, AF և CE անկյունագծերով ուղղանկյունների գումարը հավասար է AF անկյունագծով ուղղանկյան կրկնապատիկին։ Սակայն AF և CE անկյունագծերով ուղղանկյունների գումարը KLM գնոմոնն է և CF անկյունագծով քառակուսին։ Հետևաբար, KLM գնոմոնը և CF անկյունագծով քառակուսին AF անկյունագծով ուղղանկյան կրկնապատիկն են կազմում։ Մինչդեռ AF անկյունագծով ուղղանկյան կրկնապատիկը նաև AB և BC կողմերով կառուցված ուղղանկյան կրկնապատիկին է հավասար։ BF-ն ու BC-ն հավասար են։ Հետևում է, որ KLM գնոմոնն ու CF քառակուսին հավասար են AB և BC կողմորով կառուված ուղղանկյան կրկնապատիկին։ Երկու կողմերին էլ ավելացնենք DG անկյունագծով քառակուսին։ Արդյունքում՝ KLM գնոմոնն ու BG և GD անկյունագծերով քառակուսիները հավասար են AB և BC կողմերով կառուցաված ուղղանկյանն ու AC անկյունագծովո քառակուսուն։ Բայց KLM գնոմոնն ու BG և GD քառակուսիները հավասարարժեք են ողջ ADEB-ին և CF-ին, որոնք AB և BC քառակուսիներն են։ Հետևաբար, AB և BC քառակուսիների գումարը հավասար է AB և BC կողմերով կազմված քառակուսու կրկնապատիկին և AC քառակուսուն։ Այսպիսով՝ հատվածը կամայական կետում հատելիս՝ ստացված հատվածներից պատահականորեն ընտրված մեկի և ողջ հատվածի քառակուսիների գումարը հավասար է ողջ և նախապես ընտրված հատվածներով կառուցված ուղղանկյան մակերեսի կրկնապատիկի և հատման արդյունքում առաջացած մյուս հատվածի երկարության քառակուսու գումարին։
† Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ 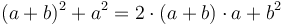 ։
։
Պնդում 8†
Հատվածը կամայական կետում հատելիս՝ այդ հատվածով և հատման արդյունքում առաջացած կտորներից մեկով սահմանված ուղղանկյան մակերեսի քառապատիկի և հատման արդյունքում առաջացած մյուս հատվածով կառուցված քառակուսու մակերեսի գումարը հավասար է վերոնշյալ և ողջ հատվածների գումարով սահմանված քառակուսու մակերեսին։
Տրված AB հատվածը հատենք C կետում: AB և BC կողմերով ուղղանկյան մակերեսի քառապատիկի և AC կողմով քառակուսու մակերեսի գումարը հավասար է AB և BC կողմերի գումարով սահմանված քառակուսու մակերեսին։ Շարունակելով AB հատվածը՝ կառուցենք BD-ն այնպես, որ հավասար այն հավասար լինի CB-ին։ Ապա, Կառուցենք AEFD քառակուսին՝ AD կողմով։ Կառուցենք նաև գծագրի մնացած մասը։ Հետևաբար, քանի որ CB-ն և BD-ն, CB-ն և GK-ը, BD-ն և KN-ը հավասար են, GK-ը և KN-ը նույնպես հավասար են։ Նույն պատճառով հավասար են նաև QR-ը և RP-ն։ Եվ քանի որ BC-ն ու BD-ն, GK-ն ու KN-ը հավասար են՝ CK և KD, GR և RN անկյունագծերով քառակուսիները նույնպես հավասար են։ Հավասար են նաև CK և RN անկյունգծերով քառակուսիները, որոնք CP անկյունագծով զուգահեռագծի մաս են կազմում։ Հետևաբար, KD և GR անկյունագծով քառակուսիները նույնպես հավասար են։ Հավասար են նաև DK, CK, GR և RN անկյունագծերով քառակուսիները, հետևաբար, այդ 4-ը միասին CK անկյունագծով քառակուսու քառակին են։ Հաջորդիվ դիտարկենք հետևյալ հավասարությունները՝ CB=BD=BK, CG=CB=GK, GQ=CG=GQ։ CG=CQ, QR=RP, այս հավասարություննեից էլ հետևում է որ AG և MQ, QL և RF, MQ և QL անկյունագծերով ուղղանկյունները հավասար են և ML անկյունագծով զուգահեռագծի մաս են կազմում։ AG և RF ուղղանկյունները ևս հավասար են։ Հետևաբար, AG, MQ, QL և RF ուղղանկյունները միմյանց հավասար են, և այդ չորսը իրար հետ վերցված AG ուղղանկյան քառապատիկն են։ Ցույց էր տրված նաև, որ CK, KD, GR և RN քառակուսիները միասին CK-ի քառապատիկն են։ Հետևում է, որ STU գնոմոնը կազմեղ վերոնշյալ 8 պատկերները AK ուղղանկյան քառապատիկն են։ BK=BD հավասարությունից ելնելով AK ուղղանկյունը ստացվել է AB և BD կողմերից։ Այդ ուղղանկյան քառապատիկը AK-ի քառապատիկն է։ Սակայն STU գնոմոնը նույնպես AK-ի քառապատիկն էր։ Հետևաբար, AB և BD կողմերով ուղղանկյունը հավասար է STU գնոմոնին։ Դիցուք, վերոնշյալ երկուսին էլ գումարենք OH-ը, որը հավասար է AC կողմով քառակուս։ Կստացվի, որ AB և BD կողմերով ուղղանկյանը AC-ի հետ միասին հավասար է STU գնոմոնին և OH քառակուսուն։ Սակայն STU գնոմոնն ու OH քառակուսին համարժեք են ոնջ AEFD քառակուսուն, որը կառուցված է AD կողմով։ Հետևում է, որ AB և BD կողերով հազմված ուղղանկյան քառապատիկը AC քառակուսու հետ միասին հավասար է AD քառակուսուն։ BD-ն էլ հավասար է BC-ին։ Հետևում է, որ AB և BC կողմերով ուղղանկյան քառապատիկը AC քառակուսու հետ միասին հավասար է AD քառակուսուն, որը սահմանված է AB և BC հատվածների գումարը որպես կողմ վերցնելով։ Հետէաբար, հատվածը կամայական կետում հատելիս՝ այդ հատվածով և հատման արդյունքում առաջացած կտորներից մեկով սահմանված ուղղանկյան մակերեսի քառապատիկի և հատման արդյունքում առաջացած մյուս հատվածով կառուցված քառակուսու մակերեսի գումարը հավասար է վերոնշյալ և ողջ հատվածների գումարով սահմանված քառակուսու մակերեսին։ Ահա այն ինչ պահանջվում էր ապացուցել։
† Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ 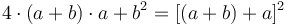 ։
։
Պնդում 9[1]
Հատվածը հավասար և անհավասար մասերի բաժանելիս՝ անհավասար մասերի վրա կառուցված քառակուսիների գումարը հավասար է հատվածի կեսի և հավասար ու անհավասար մասերի տարբերության վրա կառուված քառակուսիների գումարի կրկնապատիկին։
Տրված AB հատվածը հավասար կիսենք C կետով, անհավասար՝ D-ով։ AD և DB հավտածների վրա կառուցված քառակուսիների գումարը հավասար է AC և CD կողմերով քառակուսիների գումարի կրկնապատիկին։ C կետով՝ AB-ին ուղղահայաց կառուցենք CE հատվածը [Պնդում 1․11], այնպես, որ հավասար լինի AC-ին և CB-ին [Պնդում 1․3]։ Միացնենք EA-ն և EB-ն։ EC-ին զուգահեռ՝ D կետով կառուցենք DF-ը [Պնդում 1․31], իսկ AB-ին զուգահեռ՝ FG-ը F կետով [Պնդում 1․31]։ Միացնենք AF-ը։ Քանի որ AC-ն ու CE-ն հավասար են, անկյուն EAC-ն հավասար է AEC-ին [Պնդում 1․5]։ Եվ քանի որ C անկյունը ուղիղ անկյեւն է, EAC և AEC անկյունների գումարը նույնպես ուղիղ անկյուն է կազմում [Պնդում 1․32]։ Հետևում է, որ CEA CAE անկյուններից յուրաքանչյուրը ուղիղ անկյան կեսն է։ Նույն պատճառով՝ CEB և EBC անկյունները նույնպես հավասար են ուղիղ անկյան կեսին։ Հետևում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ GEF-ն ուղիղ անկյան կես է, իսկ EGF՝ ուղիղ անկյուն (որը հավասար է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ EFG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Հետևաբար, GEF անկյունը հավասար է EFG-ին, իսկ EG կողմը՝ GF-ին [Պնդում 1․6]։ Քանի որ անկյուն B-ն ուղիղ անկյան կես է, իսկ FDB-ն՝ ուղիղ անկյուն (որը հավասր է ներքին ECB անկյանը [Պնդում 1․29]), մնացյալ BFD անկյունը նույնպես ուղիղ անկյան կես է [Պնդում 1․32]։ Այսպիսով՝ B և DFB անկյունները, FD և DB կողմերը նույնպես հավասար են [Պնդում 1․6]։ Քանի որ AC-ն և CE-ն հավասար են, այդ կողմերով կառուցված համապատասխան քառակուսիները ևս հավասար են։ Հետևաբար, AC-ի և CE-ի վրա կառուցված քառակուսիների գումարը հավասար է AC-ի վրա կառուցված քառակուսու կրկնապատիկին։ EA հիմքով քառակուսին հավասար է AC և CE հիմքերով քառակուսիների գումարին։ ACE անկյունն էլ ուղիղ է [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Քանի որ EG-ն և GF-ը հավասար են, համապատասխան հիմքերով քառակուսիները նույնպես հավասար են, և դրանց գումարը GF հիմքով քառակուսու կրկնապատիկն է։ EF-ի վրա կառուցված քառակուսին էլ հավասար է EG-ի և GF-ի վրա կառուցած քառակուսիների գումարին [Պնդում 1․47]։ Այսպիսով՝ EF հիմքով քառակուսին GF հիմքովի կրկնապատիկն է։ GF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ Հետևաբար, EF հիմքով քառակուսին CD հիմքովի կրկնապատիկն է, EA հիմքովն էլ՝ AC-ի։ Հետևում է, որ AE և EF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AF հիմով քառակուսին AE և EF հիմքերովների գումարին է հավասար։ AEF-ն ուղիղ անկյուն է [Պնդում 1․47]։ Հետևաբար, AF հիմքով քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DF հիմքերով քառակուսիների գումարը հավասար է AF հիմքով քառակուսուն։ D-ն ուղիղ անկյուն է [Պնդում 1․47], հետևաբար AD և DF հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների կրկնապատիկն է։ DF-ն էլ հավասար է DB-ին։ Արդյունքում՝ AD-ի և DB-ի վրա ընկած քառակուսիների գումարը AC-ի և CD-ի վրա ընկած քառակուսիների գումարի կրկնապատիկն է։ Ստաղվում է, որ հատվածը հավասար և անհավասար մասերի բաժանելիս՝ անհավասար մասերի վրա կառուցված քառակուսիների գումարը հավասար է հատվածի կեսի և հավասար ու անհավասար մասերի տարբերության վրա կառուված քառակուսիների գումարի կրկնապատիկին։
Պնդում 10†
Եթե հատվածը հավասար կիսենք և որպես հատվածի շարունակություն նրան կցենք նոր հատված, ապա ստացված ողջ և ավելացված հատվածի վրա կառուցված քառակուսիների գումարը հավասար կլինի նախնական հատվածի կեսի և այդ կեսի ու կցված հատվածի վրա կառուցված քառակուսիների գումարին։
Տրված է AB հատվածը, հավասար կիսենք այն C կետում և որպես AB-ի շարունակություն կցենք BD հատվածը։ Պետք է ցույց տալ, որ AD և DB հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների կրկնապատիկն է։ C կետով կառուցենք CE հատվածը, որը կլինի AB-ին ուղղահայաց [Պնդում 1․11] և AC-ին ու CB-ին հավասար [Պնդում 1․3]։ Կառուցենք նաև EA և EB հատվածները։ AD-ին զուգահեռ՝ E կետով տանենք EF հատվածը [Պնդում 1․31]։ CE-ին զուգահեռ՝ FD-ն՝ D կետով [Պնդում 1․3]։ Եվ քանի որ EF-ն հատվում է EC և FD զուգահեռ հատվածների հետ, CEF և EFD ներքին անկյունները հավասար են ուղիղ անկյունների [Պնդում 1․29]։ Հետևաբար, FEB և EFD անկյուննեը փոքր են երկու ուղիղ անկյուններից։ Եվ երկու ներքին անկյուններից (որոնց գումարը ավելի փոքր է քան երկու ուղիղ անկյունների գումար) առաջացած հատվածները հատվում էն [Կանխադրույթ 1.5]։ Հետևաբար, B-ի և D-ի ուղղություններով կառուցված EB և FD հատվածները կհատվեն։ Կռուցենք դրանք, որպես հատման կետ նշանակնեք G-ն և միացնենք AG-ն։ Քանի որ AC-ն և CE-ն հավասար են, EAC և AEC անկյունները նույնպես հավասար են [Կանխադրույթ 1.5]։ Անկյուն C-ն ուղիղ անկյուն է։ Հետևում է, որ EAC-ն ու AEC-ը ուղիղ անկյան կեսեր են [Պնդում 1․32]։ Նույն պատճառներով՝ CEB-ն ու EBC-ն նույնպես ուղիղ անկյան կեսեր են։ Ստացվում է, որ AEB-ն ուղիղ անկյուն է։ Եվ քանի որ EBC-ն ուղիղ անկյան կես է, DBG-ն նույնպես ուղիղ անկյան կես է [Պնդում 1․15]։ BDG-ն նունպես ուղիղ անկյուն է, որը հավասար է DCE-ին։ Այսինքն դրանք համարժեք/այլընտրանքային անկյուններ են [Պնդում 1․29]։ Հետևաբար, մնացյալ DGB-ն ուղիղ անկյան կես է։ DGB-ն ու DGB-ն հավասար են։ BD-ն էլ հավասար է GD-ին [Պնդում 1․6]։ Կրկին, քանի որ EGF-ն ուղիղ անկյան կես է, իսկ F-ը՝ ուղիղ անկյուն, այն հավասար է հակառակ C անկյանը[Պնդում 1․34], մնացյալ FEG անկյունն էլ կրկին ուղիղ անկյան կես է։ Հետևում է, որ EGF և FEG անկյունները հավասար են։ GF կողմն էլ հավասար է EF-ին [Պնդում 1․6]։ Եվ քանի որ EC-ն ու CA-ն հավասար են, EC և CA հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ EC և CA հիմքերով քառակուսիների գումարը CA հիմքով քառակուսու կրկնապատիկն է։ EA հիմքով քառակուսին էլ հավասար է EC և CA հիմքերով քառակուսինորի գումարին [Պնդում 1․47]։ Հետևաբար, EA հիմքով քառակուսին AC հիմքովի կրկնապատիկն է։ Կրկին, քանի որ FG-ն ու EF-ն հավասար են, FG և FE հիմքերով քառակուսիները նույնպես հավասար են։ Ստացվում է, որ GF-ի և FE-ի վրա կառուցված քառակուսիները EF հիքով քառակուսու կրկնապատիկն են։ EG հիմքով քառակուսին էլ GF և FE հիմքերով քառակուսիների գումարի կրկնապատիկն է [Պնդում 1․47]։ Հետևաբար, EG հիմքով քառակուսին EF հիմքովի կրկնապատիկն է։ EF-ն էլ հավասար է CD-ին [Պնդում 1․34]։ EG հիմքով քառակուսին CD հիմքովի կրկնապատիկն է։ Սակայն ցույց էր տրվել նաև, որ EA-ի վրա կառուցված քառակուսին AC-ի վրա կառուցվածի կրկնապատիկն է։ Արդյունքում՝ AE և EC հիմքերով քառակուսիների գումարը AC և DC հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AG, AE և EG հիմքերով քառակուսիներն էլ հավասար են [Պնդում 1․47]։ AG-ի վրա կառուցված քառակուսին AC և CD հիմքերով քառակուսիների գումարի կրկնապատիկն է։ AD և DG հիմքերով քառակուսիների գումարն էլ հավասար է AG հիմքով քառակուսուն [Պնդում 1․47]։ Հետևաբար, AD և DG հիմքերով քառակուսիների գումարը AC և CD հիմքերով քառակուսիների գումարին հավասար։ DG- հավասար է DB-ին։ Հետրաբար, AD և DB հիմքերով քառակուսիների գումարը AC և CD հմքերով քառակուսիների գումարի կրկնապատիկն է։ Ստացվում է, եթե հատվածը հավասար կիսենք և որպես հատվածի շարունակություն նրան կցենք նոր հատված, ապա ստացված ողջ և ավելացված հատվածի վրա կառուցված քառակուսիների գումարը հավասար կլինի նախնական հատվածի կեսի և այդ կեսի ու կցված հատվածի վրա կառուցված քառակուսիների գումարին։ ։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։
† Այս պնդումը հետևյալ հանրահաշվական նույնության երկրաչափական տարբերակն է՝ 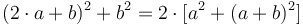 :
:
Պնդում 11†
Հատվածը հատել այնպես, որ ողջ հատվածով և հատման արդյունքում առաջացած հատվածներիից մեկով կառուցված ուղղանկյունը հավասար լինի հատման արդյունքում առաջացած հատվածներիից մյուսի վրա սահմանված քառակուսուն։
Տրված է AB հատվածը։ Այն պետք է բաժանել այնպես, որ AB-ով և հատման արդյունքում առաջացած մասերից մեկով կառուցաված քառակուսին հավասար լինի հատման արդյունքում առաջացած մյուս մասով կառուցված քառակուսուն։ AB-ով կառուցենք ABDC քառակուսին [Պնդում 1․4], AC-ն էլ կիսենք E կետում [Պնդում 1․10] և միացնենք B-ն ու E-ն՝ BE հատվածով։ Շարունակենք CA-ն և շարունակության վրա նշանակենք F կետն այնպես, որ EF-ն ու BE-ը հավասար լինեն [Պնդում 1․3]։ AF կողմով հառուցենք FH անկյունագծով քառակուսին [Պնդում 1․46], և GH-ը շարունակելով՝ հատենք այն CD-ի հետ՝ K կետում։ Կարելի է ասել, որ AB-ն H կետում հատելիս՝ AB և BH կողմերով քառակուսին հավասարվում է AH կողմով քառակուսուն։ Քանի որ AC-ն E կետով բաժանված է հավասար մասերի և նրան ավելացված է FA-ը, CF և FA կողմերով ուղղանկյան և AE կողմով քառակուսու գումարը հավասար է EF հիմքով քառակուսուն [Պնդում 2․6]։ EF-ն ու EB-ն հավասար են։ Հետևաբար, CF և FA կողմերով կառուցված ուղղանկյան և AE հիմքով քառակուսու գումարը հավասար է EB հիմքով քառակուսուն։ Սակայն BA և AE հիմքերով քառակուսիների գումարը հավասար է EB հիմքով քառակուսուն։ Անկյուն A-ն ուղիղ անկյուն է [Պնդում 1․47]։ Այդ պատճառով էլ, CF և FA կողմերով ուղղանկյան և AE կողմով քառակուսու գումարը հավասար է BA և AE հիմքերով քառակուսիների գումարին։ Երկու կողմից էլ հանենք AE հիմքով քառակուսին։ CF և FA կողմերով մնացյալ ուղղանկյունը հավասար է AB կողով քառակուսուն։ FK անկյունագծով ուղղանկյունն էլ կառուցված է CF-ով և FA-ով։ AF-ը հավասար է FG-ին։ Իսկ AD անկյունագծով քառակուսին AB հիմքով կառուցված քառակուսին է։ Հետևաբար, FK նակյունագծով ուղղանկյունը հավասար է AD անկյունագծով քառակուսուն։ Երկու կողմերից էլ հանենք AK անկյունագծով ուղղանկյունը։ FH անկյունագծով մնացյալ քառակուսին հավասար է HD անկյունագծով ուղղանկյանը։ Իսկ HD անկյունագծով ուղղանկյունը AB և BH կողմերով է կառուցված։ AB-ն հավասար է BD-ին։ FH անկյունագծով քառակուսին AH հիմքով է սահմանված։ Այսպիսով՝ AB և BH կողերով ուղղանկյունը հավասար է HA հիմքով քառակուսուն։ Հետևում է, որ AB հատվածը հատվեց H կետում այնպես, որ AB և BH կողերով ուղղանկյունը հավասար եղավ HA կողով քառակուսուն։ Սա հենց այն էր, ինչ պետք էր ստանալ։
† Հատվածի այսպիսի հատման ձևը, երբ ողջ հատվածի և հատման արդյունքում առաջացած ավելի մեծ մասի հարաբերությունը հավասար է հատման արդյունքում առաջացած մեծ և փոքր մասեր հարաբերությանը, երբեմն անվանվում է «Ոսկե հարաբերակցություն»։
Պնդում 12[2]
Բութանկյուն եռանկյուններում բութ անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին բութ անկյանը կից կողմերով կառուցված քառակուսիների գումարից մեծ է բութ անկյանը կից կողմով, որի վրա ընած է ուղղահայացը և դրսի կողմից բութ անկյանը միացող հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։
Դիցուք՝ ABC-ն բութանկյուն եռանկյուն է, որում BAC-ն բութ անկյունն է։ B կետով՝ CA-ին ուղղահայաց կառուցենք BD ուղիղը [Պնդում 1․12]։ Արդյունքում՝ BC-ի վրա կառուցված քառակուսին BA և AC կողմերի վրա կառուցված քառակուսիների գումարից մեծ է CA և AD կողմերով կառուցված ուղղանկյան կրկնապատիկի չափով։ Քանի որ CD-ն հատված է կամայական A կետում, DC-ի վրա կառուցված քառակուսին հավասար է CA-ի և AD-ի վրա կառուցված քառակուսիների գումարին և CA և AD կողմերով կառուցած ուղղանկյան կրկնապատիկին [Պնդում 2․4]։ Երկու կողմին էլ ավելացնենք DB կողով կառուցվածքառակուսին։ Հետևաբար, CD և DB հիմքերով քառակուսիների գումարը հավասար է CA, AD և DB հիմքերով քառակուսինեի գումարին և CA ու AD կողմերով կառուցված ուղղանկյան կրկնապատիկին։ Սակայն CB-ի վրա ընկած քառակուսին էլ հավասար է CD և DB հիմքերով քառակուսիների գումարին։ Անկյուն D-ն ուղիղ անկյուն է [Պնդում 1․47]։ AB-ի վրա կառուցված քառակուսին էլ հավասար է AD և DB կողմերով քառակուսիների գումարին [Պնդում1․47]։ Հետևում է, որ CB-ի վրա ընկած քառակուսին հավասար է CA-ի և AB-ի վրա ըհնկած քառակուսիների գումարին և CA ու AD կողմերով ուղղանկյան կրկնապատիկին։ Այսպիսով՝ CB-ի վրա ընկած քառակուսին CA և AB հիմքերով քառակուսինեի գումարից մեծ է CA և AD կողմերով ուղղանկյան կրկնապատիկի չափով։ Հետևաբար, բութանկյուն եռանկյուններում բութ անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին բութ անկյանը կից կողմերով կառուցված քառակուսիների գումարից մեծ է բութ անկյանը կից կողմով, որի վրա ընած է ուղղահայացը և դրսի կողմից բութ անկյանը միացող հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։
Պնդում 13†
Սուրանկյուն եռանկյուններում սուր անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին սուր անկյանը կից կողմերի վրա կառուցված քառակուսիների գումարից փոքր է սուր անկյանը այն կից կողմով, որի վրա ընկնում է ուղղահայացը և ներսի կողմից եռանկյան սուր անկյանը միացող այն հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։
Դիցուք՝ ABC-ն սուրանկյուն եռանկյուն է, որում B-ն սուր անկյունն է։ A կետով՝ BC-ին ուղղահայաց կառուցենք AD-ն [Պնդում 1․12]։ Արդյունքում՝ AC հիմքով քառակուսին CB և BA հիմքերով քառակուսիներից փոքր է CB և BD կողմերով կառուցված ուղղանկյան կրկնապատիկի չափով։ Քանի որ CB հատվածը հատած է կամայական D կետում, CB և BD կողերով քառակուսինեի գումարը հավսաքար է CB և BD կողերով ուղղանկյան կրկնապատիկին և DC հիմքով քառակուսուն [Պնդում 2․7]։ Երկու կողմին էլ ավելացնենք DA հիմքով քառակուսին։ Արդյունքում՝ CB, BD և DA հիմքերով քառակուսիների գումարը հավասար է CB և BD կողերով ուղղանկյան կրկնապատիկին և AD ու DC հիմքերով քառակուսիների գւմարին։ Սակայն AB հիմքով քառակուսին էլ հավասար է BD և DA հիմքերով քառակուսիների գումարին։ Անկյուն D-ն ուղիղ անկյուն է [Պնդում 1․47]։ AC-ի վրա կառուցված քառակուսին էլ հավասար է AD և DC հիմքերով քառակուսիների գումարին [Պնդում 1․47]։ Այդ պատճառով էլ CB և BA հիմքերով քառակուսիների գումարը հավասար է AC հիմքով քառակուսուն և CB ու BD կողմերով կառուցված ուղղանկյան կրկնապատիկին։ Հետևաբար, AC հիմքով քառակուսին առանձին վերցված CB և BA հիմքերով քառակուսիներից ավելի փոքր է CB-ով և BD-ով կառուցված ուղղանկյան կրկնապատիկի չափով։ Այսպիսով՝ ոուրանկյուն եռանկյուններում սուր անկյանը հանդիպակաց կողմի վրա կառուցված քառակուսին սուր անկյանը կից կողմերի վրա կառուցված քառակուսիների գումարից փոքր է սուր անկյանը այն կից կողմով, որի վրա ընկնում է ուղղահայացը և ներսի կողմից եռանկյան սուր անկյանը միացող այն հատվածով, որը հատած է ուղղահայացով, կառուցված ուղղանկյան կրկնապատիկի չափով։
† Այս պնդումը համարժեք է բոլորիս հայտնի կոսինուսնորի բանաձևին՝ 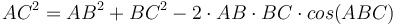 , քանի որ
, քանի որ 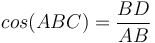 :
:
Պնդում 14
Կառուցել տրված ուղղագիծ պատկերին հավասար քառակուսի։
Դիցուք՝ տրված է A ուղղագիծ պատկերը։ Պահանջվում է կառուցել A-ին հավասար քառակուսի։ Կառուցենք BD անկյունագծով զուգահեռագիծն այնպես, որ հավասար լինի A-ին [Պնդում 1․45]։ Հետևաբար, եթե BE-ն հավասար լինի ED-ին, ապա տեղի կունան այն, ինչ պետք է ցույղ տալ։ Կառուցենք A-ին հավասար BD անկյունագծով քառակուսին։ Եթե այպես չստացվի, կնշանակի, որ BE-ից կամ ED-ից մեկը մյուսից մեծ է։ Դիցուք՝ BE-ն ավելի մեծ է, շարունակենք այն մինչ F կետն այնպես, որ EF-ն ու ED-ն հավասար լինեն [Պնդում 1․3]։ G կետով հավասար լիսենք BF հատվածը [Պնդում 1․10]։ G կենտրոնով և GB կամ GF շառավղով կառուցենք BHF կիսաշրջանը։ Շարունակենք DE-ն մինչ H կետը և միացնենք GH հատվածը։ Հետևաբար, քանզի BF-ը G կետով բաժանված է հավասար մասերի և E-ով՝ անհավասար, BE և EF կողմերով ուղղանկյան և EG հիմքով քառակուսու գումարը հավասար է GF հիմքով քառակուսուն [Պնդում 2․5]։ GF-ն էլ հավասար է GH-ին։ Հետևաբար, BE և EF կողմերով ուղղանկյան և GE հիմքով քառակուսու գումարը հավասար է GH հիմքով քառակուսուն։ HE և EG հիմքերով քառակուսիների գումարն էլ հավասար է GH հիմքով քառակուսուն [Պնդում 1․47]։ Այսպիսով՝ BE և EF կողմորով ուղղանկյոան և GE կողով քառակուսու գումարը հավասար է HE և EG հիմքերով քառակուսիների գումարին։ Երկոը կողմերին էլ ավելացնենք GE հիմքով քառակուսին։ Հետևում է, որ BE և EF կողերով մնացյալ ուղղանկյունը հավասար է EH կողով քառակուսուն։ Սակայն BD անկյունագծով ուղղանկյունը BE և EF կողերով է կառուցված։ EF-ը հավասար է ED-ին։ Այս ամենի արդյունքում էլ BD անկյունագծով զուգահեռագիծը հավասար է HE հիմքով քառակուսուն։ BD անկյունագծով ուղղանկյունն էլ հավասար է ուղղագիծ A պատկերին։ Հետևաբար, ուղղագիծ A պատկերը ևս հավասար է քառակուսուն, որը կարելի է կառուցել EH հատվածով։
Այսպիսով՝ կառուցվեց A ուղղագիծ պատկերին հավասար քառակուսին, որը կարելի է սահմանել EH հատվածի վրա: Սա հենց այն էր, ինչ պետք էր ցույց տալ:







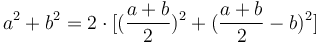 ։
։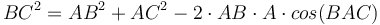 , քանի որ
, քանի որ 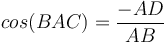 ։
։