Տարերք/Գիրք 12

Բուրգերը, որոնք ունեն միևնույն բարձրություն և ունեն բազմանկյուն հիմքեր, միմյանց համար որպես հիմքեր են հանդիսանում:

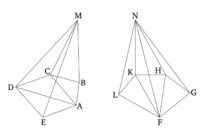
Դիտարկենք նույն բարձրության բուրգեր, որոնց հիմքերն են ABCDE և FGHKL բազմանկյունները, իսկ գագաթները՝ M և N կետերը (համապատասխանաբար): Ինչպես ABCDE հիմքը նման/հարաբերվում է է FGHKL-ին է, այնպես էլ ABCDEM բուրգը նման է FGHKLN բուրգին:

Թող AC, AD, FH և FK հատվածները միացված լինեն: Հետևաբար, քանի որ ABCM-ը և ACDM-ը երկու բուրգեր են, որոնք ունեն եռանկյունաձև հիմքեր և հավասար բարձրություն, դրանք միմյանց նկատմամբ համեմատելի են իրենց հիմքերի չափերով [Պնդ. 12.5]։ Այսպիսով, ինչպես ΑΒC հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCM-ն է հարաբերվում ACDM բուրգին: Եվ, կոմպոզիցիայի միջոցով, ինչպես ABCD հիմքն է հարաբերվում ACD հիմքին, այնպես էլ բուրգը ABCDM է հարաբերվում ACDM բուրգին [Prop. 5.18]: Բայց, քանի որ ACD հիմքն է ահրաբերվում ADE հիմքին, այնպես էլ նաև ACDM բուրգն է հարաբերվում ADEM բուրգին [Պնդ. 12.5]։ Այսպիսով, հավասարության միջոցով, ABCD հիմքի հարաբերությաւոնը ADE հիմքին հավասար է ABCDM բուրգի հարաբորուտըանը ADEM բուրգին [Պնդ. 5.22]: Եվ, դարձյալ, կոմպոզիցիայի միջոցով, ինչպես ABCDE հիմքն է հարաբերվում ADE հիմքին, այնպես էլ ABCDEM բուրգն է հարաբերվում ADEM բուրգին [Պնդ. 5.18]: Այսպիսով, նման կերպով կարելի է նաև ցույց տալ, որ ինչպես FGHKL հիմքն է հարաբերվում FGH հիմքին, այնպես էլ FGHKLN բուրգն է հարաբերվում FGHN բուրգին: Եվ քանի որ ADEM-ը և FGHN-ը երկու բուրգեր են, որոնք ունեն եռանկյուն հիմքեր և հավասար բարձրություն, հետևաբար, ADE և FGH հիմքերի հարաբերությունը հավասար է ADEM և FGHN բուրգերի հարաբերությանը [Պնդ. 12.5]։ Բայց, ինչպես ADE հիմքն է հարաբերվում ABCDE հիմքին, այնպես էլ ADEM բուրգն է հարաբերվում ABCDEM բուրգին: Այսպիսով, հավասարության միջոցով, քանի որ ABCDE հիմքը հարաբերվում է FGH հիմքին, այնպես էլ ABCDEM բուրգը հարաբերվում է նաև FGHN բուրգին [Պնդ. 5.22]: Բայց, ավելին, ինչպես FGH հիմքն է հարաբերվում FGHKL հիմքինին, այնպես էլ FGHN բուրգն է նույնպես հարաբերվում FGHKLN բուրգին: Այսպիսով, հավասարության միջոցով, քանի որ ABCDE հիմքը հարաբերվում է FGHKL հիմքին, այնպես էլ ABCDEM բուրգը հարաբերվում է նաև FGHKLN բուրգին [Պնդ. 5.22]: Ինչը հենց այն է, ինչ պահանջվում էր ցույց տալ:

Եռանկյուն հիմք ունեցող ցանկացած պրիզմա բաժանվում է երեք բուրգերի, որոնց եռանկյուն հիմքերը հավասար են միմյանց:

Դիտարկենք պրիզմա, որի հիմքը ABC եռանկյունին է, իսկ հակառակ հարթությունը DEF: Ենթադրենք, որ ABCDEF պրիզման բաժանված է երեք բուրգերի, որոնք ունեն միմյանց հավասար եռանկյուն հիմքեր:

Թող BD-ն, EC-ը և CD-ն միացված լինեն: Քանի որ ABED-ը զուգահեռագիծ է, իսկ BD-ն նրա անկյունագիծն է, հետևաբար ABD եռանկյունը հավասար է EBD եռանկյունին [Պնդ. 1.34]: Եվ այսպես, բուրգը, որի հիմքը ABD եռանկյունն է, իսկ գագաթը՝ C կետը, հավասար է բուրգին, որի հիմքը DEB եռանկյունն է, իսկ գագաթը՝ C կետը [Պնդ. 12.5]։ Բայց բուրգը, որի հիմքը DEB եռանկյունն է, իսկ գագաթը՝ C կետը, նույնն է, ինչ բուրգը, որի հիմքը EBC եռանկյունն է, իսկ գագաթը՝ D կետը։ Որովհետև դրանք սահմանափակված են նույն հարթություններում: Եվ այսպես, բուրգը, որի հիմքը ABD է, իսկ գագաթը՝ C կետը, հավասար է բուրգին, որի հիմքը EBC է, իսկ գագաթը՝ D կետը: Կրկին, քանի որ FCBE-ն զուգահեռագիծ է, իսկ CE-ն նրա անկյունագիծն է, CEF եռանկյունը հավասար է CBE եռանկյանը [Պնդ. 1.34]: Եվ այսպիսով, բուրգը, որի հիմքը BCE եռանկյունն է, և գագաթը D կետը, հավասար է բուրգին, որի հիմքը ECF եռանկյունն է, իսկ գագաթը D կետը [Պնդ. 12.5]։ Եվ բուրգը, որի հիմքը BCE եռանկյունն է, իսկ գագաթը D կետը, ցույց տրվեց, որ հավասար է այն բուրգին, որի հիմքը ABD եռանկյունն է, և գագաթը C կետն է: Այսպիսով, բուրգը, որի հիմքը CEF եռանկյունն է, իսկ գագաթը՝ D կետը, նույնպես հավասար է բուրգին, որի հիմքը ABD եռանկյունն է, իսկ գագաթնակետը C կետն է։ Այսպիսով, ABCDEF պրիզման բաժանվել է երեք բուրգերի, որոնք ունեն եռանկյուն հիմքեր, որոնք հավասար են միմյանց:

Եվ քանի որ բուրգը, որի հիմքը ABD եռանկյունն է, իսկ գագաթը՝ C կետը, նույնն է, ինչ բուրգը, որի հիմքը CAB եռանկյունն է, իսկ գագաթը՝ D կետը, դրանք սահմանափակված են նույն հարթություններում։ Իսկ բուրգը, որի հիմքը ABD եռանկյունին է, իսկ գագաթը՝ C կետը, ցույց տրվեց, որ այն պրիզմայի մեկ երրորդն է, որի հիմքը ABC եռանկյունն է, և հակառակ հարթությունը DEF, հետևաբար բուրգը, որի հիմքը ABC եռանկյունն է, և D կետի գագաթը, նույնպես բուրգի մեկ երրորդն է, որն ունի նույն հիմքը, ABC եռանկյունը և հակառակ հարթություն DEF:

Եզրակացություն

Եվ սրանից պարզ է դառնում, որ ցանկացած բուրգ պրիզմայի երրորդ մասն է, որն ունի իր նույն հիմքը և հավասար բարձրություն։ Իինչը հենց այն է, ինչ պահանջվում էր ցույց տալ:

Նման բուրգերը, որոնք նույնպես ունեն եռանկյուն հիմքեր, հարաբերվում են իրենց համապատասխան կողմերի խորանարդ հարաբերությամբ:

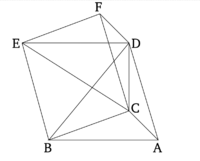
Թող լինեն նման և նույն ձևով դասավորված բուրգեր, որոնց հիմքերը ABC և DEF եռանկյուններն են, իսկ գագաթները՝ G և H կետերը (համապատասխանաբար): Ստուգենք արդյո՞ք ABCG բուրգի հարաբերությունը DEFH բուրգին հավասար է BC-ի հարաբեությանը EF-ին ըստ խորանարդ աստիճանի:

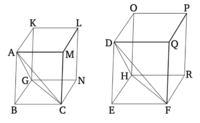
Թող զուգահեռանիստ պինդ մարմինները BGML և EHQP ամփոփ լինեն: Եվ քանի որ ABCG բուրգը նման է DEFH բուրգին, հետևաբար ABC անկյունը հավասար է DEF անկյանը, իսկ GBC-ն՝ HEF-ին և ABG-ն՝ DEH-ին: Եվ ինչպես AB-ն է հարաբերվում DE-ին, այնպես էլ BC է հարաբերվում EF-ին, իսկ BG-ն՝ EH-ին [Սահմանում. 11.9]։ Եվ քանի որ AB-ն DE-ին է հարաբերվում, ուստի BC հարաբերվում է EF-ին, և (այդպիսով) հավասար անկյունների շուրջ կողմերը համաչափ են, BM զուգահեռագիծն այսպիսով նման է EQ զուգահեռագծին: Այսպիսով, նույն (պատճառներով) BN-ն նույնպես նման է ER-ին, իսկ BK-ն՝ EO-ին: Այսպիսով, երեք զուգահեռագծերը MB, BK և BN նման են երեք զուգահեռագծերին EQ, EO, ER (համապատասխանաբար): Բայց երեք զուգահեռագծեր MB, BK և BN-ը և’ ) հավասար են, և’ նման են երեք հակադիր զուգահեռագծերին, իսկ երեք զուգահեռագծեր EQ, EO և ER և’ հավասար, և’ նման են երեք հակադիր զուգահեռագծերին [Պնդ. 11.24]: Այսպիսով, պինդ մարմիններ BGML և EHQP-ը սահմանափակված են հավասար թվով նման (և նմանապես դասավորված) հարթություններում: Այսպիսով, պինդ BGML-ը նման է պինդ EHQP-ին [Սահմ. 11.9]։ Իսկ նման զուգահեռանիստ պինդ մարմինները ունեն համապատասխան կողմերի խորանարդ հարաբերությունը [Պնդ. 11.33]: Այսպիսով, պինդ մարմին BGML-ի հարաբերությունը պինդ մարմին EHQP-ին խորանարդային հարաբերակցությամբ, նույնն է, ինչ համապատասխան BC կողմի հարաբերությունը EF կողմին: Եվ ինչպես պինդ մարմին BGML-ն է հարաբերվում պինդ մարմին EHQP-ին, այնպես էլ ABCG բուրգն է հարաբերվում DEFH բուրգին, քանի որ բուրգը պինդ մարմնի վեցերորդ մասն է, պրիզմայի հաշվին, լինելով զուգահեռանիստ պինդ մարմնի կեսը [Պնդ. 11.28]՝ լինելով նաև բուրգի եռապատիկ [Պնդ. 12.7]: Այսպիսով, ABCG բուրգը նույնպես պետք է ունենա բուրգի DEFH խորանարդ հարաբերակցությունը, ինչպես BC -ի հարաբերությունը EF-ին: (Սա հենց այն է, ինչ պահանջվում էր ցույց տալ):

Եզրակացություն

Այսպիսով, սրանից պարզ է նաև, որ բազմանկյուն հիմքեր ունեցող նման բուրգերը միմյանց նկատմամբ ունեն իրենց համապատասխան կողմերի խորանարդային հարաբերակցությունը։ Որովհետև դրանք բաժանելով իրենց մեջ պարունակվող բուրգերի, որոնք ունեն եռանկյուն հիմքեր, ընդ որում հիմքերը նույնպես պաժանված նման եռանկյունների, որոնք և՛ թվով հավասար են, և՛ համընկնում են ամբողջին [Պնդ. 6.20]: Ինչպես առաջին բուրգում (ունեցող բազմանկյուն հիմք) եռանկյուն հիմք ունեցող առանձին բուրգը հարաբերակցվում է երկրորդ բուրգում (նաեւ ունենալով բազմանկյուն հիմք) եռանկյուն հիմք ունեցող առանձին բուրգին, այնպես էլ առաջին բուրգում բոլոր եռանկյուն հիմք ունեցող բուրգերի գումարը հարաբերակցվում է երկրորդ բուրգում բոլոր եռանկյուն հիմք ունեցող բուրգերի գումարին [Պնդ. 5.12]։ Սա նշանակում է, որ ամբողջ առաջին բուրգը՝ բազմանկյուն հիմքով, համաչափ է երկրորդ բուրգին՝ բազմանկյուն հիմքով։ Եվ եռանկյուն հիմք ունեցող բուրգը հարաբերակցվում է եռանկյուն հիմք ունեցող բուրգին կողմերի համապատասխան խորացված հարաբերությամբ [Պնդ. 12.8]։ Հետևաբար, բազմանկյուն հիմք ունեցող բուրգը նույնպես հարաբերակցվում է նման հիմք ունեցող բուրգին կողմի և համապատասխան կողմի խորացված հարաբերությամբ։

Հավասար բուրգերի հիմքերը, որոնք նույնպես ունեն եռանկյունաձև հիմքեր, փոխադարձաբար համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյուն հիմքեր, որոնց հիմքերը փոխադարձաբար համեմատական ​​են իրենց բարձրություններին, հավասար են։

[[Պատկեր:Պնդ9.png|200px|thumb|left|]

Որովհետև թող լինեն (երկու) հավասար բուրգեր, որոնք ունեն ABC և DEF եռանկյունաձև հիմքեր, իսկ գագաթներով G և H կետերը (համապատասխանաբար): Ես ասում եմ, որ ABCG և DEFH բուրգերի հիմքերը փոխադարձաբար համաչափ են իրենց բարձրություններին, և (այսպես) ինչպես ABC հիմքը հավասար է DEF-ին, այնպես էլ DEFH բուրգի բարձրությունը (է) ABCG բուրգի բարձրությանը:

Որովհետև զուգահեռանիստ մարմինները՝ BGML և EHQP, լրացված են: Եվ քանի որ ABCG բուրգը հավասար է DEFH բուրգին, և զուգահեռանիստ BGML մարմինը վեց անգամ մեծ է ABCG բուրգից (տե՛ս նախորդ պնդումը), և զուգահեռանիստ EHQP (է) վեց անգամ DEFH բուրգից, ապա զուգահեռանիստ BGML-ը հավասար է զուգահեռանիստ EHQP-ին: Իսկ հավասար զուգահեռանիստ մարմինների հիմքերը հակադարձորեն համեմատական են դրանց բարձրություններին [Պնդ. 11.34]: Հետևաբար, ինչպես BM հիմքն է EQ հիմքին, այնպես էլ զուգահեռանիստ EHQP-ի բարձրությունն է զուգահեռանիստ BGML-ի բարձրությանը: Բայց, ինչպես BM հիմքն է EQ հիմքին, այնպես էլ ABC եռանկյունին է DEF եռանկյունին [Պնդ. 1.34]: Եվ, հետևաբար, ինչպես ABC եռանկյունին է DEF եռանկյունին, այնպես էլ զուգահեռանիստ EHQP-ի բարձրությունն է զուգահեռանիստ BGML-ի բարձրությանը [Պնդ. 5.11]: Բայց զուգահեռանիստ EHQP-ի բարձրությունը նույնն է, ինչ DEFH բուրգի բարձրությունը, իսկ զուգահեռանիստ BGML-ի բարձրությունը նույնն է, ինչ ABCG բուրգի բարձրությունը: Հետևաբար, ինչպես ABC հիմքն է DEF հիմքին, այնպես էլ DEFH բուրգի բարձրությունն է ABCG բուրգի բարձրությանը: Հետևաբար, ABCG և DEFH բուրգերի հիմքերը հակադարձորեն համեմատական են դրանց բարձրություններին:

Ուստի, թող ABCG և DEFH բուրգերի հիմքերը լինեն հակադարձ համեմատական դրանց բարձրություններին, և թող ABC հիմքն լինի DEF հիմքին այնպես, ինչպես DEFH բուրգի բարձրությունն է ABCG բուրգի բարձրությանը: Ասում եմ, որ ABCG բուրգը հավասար է DEFH բուրգին:

Քանի որ նույն կառուցվածքով, քանի որ ABC հիմքն է DEF հիմքին, այնպես էլ DEFH բուրգի բարձրությունն է ABCG բուրգի բարձրությանը, բայց քանի որ ABC հիմքն է DEF հիմքին, այնպես էլ զուգահեռանիստ BM-ն է զուգահեռանիստ EQ-ին [Պնդ. 1.34], ուստի ինչպես զուգահեռանիստ BM-ն է զուգահեռանիստ EQ-ին, այնպես էլ DEFH բուրգի բարձրությունն է նաև ABCG բուրգի բարձրությանը [Պնդ. 5.11]: Բայց, DEFH բուրգի բարձրությունն նույնն է, ինչ զուգահեռանիստ EHQP-ի բարձրությունը, իսկ ABCG բուրգի բարձրությունն նույնն է, ինչ զուգահեռանիստ BGML-ի բարձրությունը: Ուստի, ինչպես BM հիմքն է EQ հիմքին, այնպես էլ EHQP զուգահեռանիստի բարձրությունն է BGML զուգահեռանիստի բարձրությանը: Իսկ այն զուգահեռանիստները, որոնց հիմքերը հակադարձ համեմատական են իրենց բարձրություններին, հավասար են [Պնդ. 11.34]: Ուստի, BGML զուգահեռանիստը հավասար է EHQP զուգահեռանիստին: Իսկ ABCG բուրգը BGML-ի վեցերորդ մասն է, իսկ DEFH բուրգը EHQP զուգահեռանիստի վեցերորդ մասն է: Ուստի, ABCG բուրգը հավասար է DEFH բուրգին:

Ուստի, հավասար բուրգերի հիմքերը, որոնք նաև եռանկյունի հիմքեր ունեն, հակադարձ համեմատական են իրենց բարձրություններին: Իսկ այն բուրգերը, որոնք ունեն եռանկյունի հիմքեր և որոնց հիմքերը հակադարձ համեմատական են իրենց բարձրություններին, հավասար են: Այսինքն հենց այն բանը, որը պետք է ապացուցվեր:

Յուրաքանչյուր կոն գլանի երրորդ մասն է, որն ունի դրա հիմքը և հավասար բարձրությունը:

Թող լինի կոն նույն հիմքով ինչ գլանը, (մասնավորապես) շրջանագիծ ABCD-ն և հավասար բարձրություն: Ես ասում եմ, որ կոնը գլանի երրորդ մասն է, այսինքն՝ գլանը հավասար է երեք անգամ է կոնի ծավալին։