Տարերք/Գիրք 11

Pages 431 - 455

Պնդում 7

Եթե երկու զուգահեռ ուղիղների վրա վերցրած պատահական կետերից երկուսը միացնենք, ապա ստացված ուղիղը, որը անցնում է այդ կետերով, կլինի նույն հարթության մեջ, ինչ երկու զուգահեռ ուղիղները։

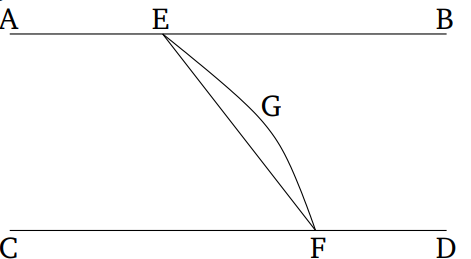
AB և CD երկու զուգահեռ ուղիղներ են, իսկ E և F կամայական կետեր են համապատասխանաբար AB և CD ուղիղներից։ Ուղիղը, որը միացնում է E և F կետերը, գտնվում է նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։ Եթե դա այդպես չէ, և հնարավոր է, որ ուղիղը անցնի ավելի բարձր հարթությամբ, թող դա լինի EGF հարթությունը։ Այսպիսով, այն կունենա ուղիղ հատված EF՝ հենակետային հարթության մեջ [Պնդ. 11.3]։ Հետևաբար, երկու ուղիղներ՝ EGF-ն և EF-ն (նույն E և F կետերով անցնող) կսահմանափակեն ինչ-որ տարածք, ինչը անհնար է։Հանգունորեն, E և F կետերով անցնող ուղիղը գտնվում է նույն հարթության մեջ, ինչ AB և CD զուգահեռ ուղիղները։

Այսպիսով, եթե կա երկու զուգահեռ ուղիղ, և կամայական կետ նրանցից յուրաքանչյուրի վրա, ապա ուղիղը, որը կմիացնի այդ երկու կետերը, կլինի նույն հարթության մեջ, ինչ զուգահեռ ուղիղները։ Որը վերջինիս պահանջվում էր ցույց տալ։

Պնդում 8

Եթե երկու ուղիղներ զուգահեռ են, և նրանցից մեկը ուղիղ անկյուն է կազմում ինչ որ հարթության հետ, ապա մյուս ուղիղը նույնպես ուղղահայաց կլինի այդ հարթությանը։

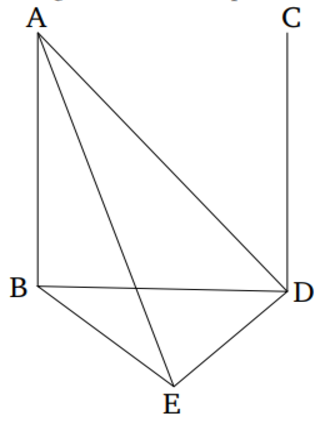
AB և CD երկու զուգահեռ ուղիղներ են, և նրանցից մեկը՝ AB, ուղղահայաց է դիտարկվող հարթությանը։ Մյուսը՝ CD, նույնպես ուղղահայաց է նույն հարթությանը։ AB-ն և CD-ն հատվում են դիտարկվող հարթության հետ B և Dկետերում համապատասխանաբար, BD ուղիղը միացնում է այդ կետերը։ Հետևաբար, AB, CD և BD գտնվում են նույն հարթության մեջ [Պնդում 11․7]։ DE ուղիղը ուղղահայաց է BD-ին դիտարկվող հարթություն մեջ և DE-ն հավասար է AB-ին։ Միացնենք BE, AE և AD հատվածները։ Քանի որ AB ուղիղը ուղղահայաց է դիտարկվող հարթությանը, այն ուղղահայաց կլինի նաև բոլոր այն ուղիղներին, որոնք գտնվում են դիտարկվող հարթության մեջ [Սահմ 11․3]։ Հետևաբար, անկյուններ՝ ABD և ABE, ուղիղ են։ Եվ քանի որ BD ուղիղը հատում է AB և CD զուգահեռ ուղիղները, ապա ABD և CDB անկյունների գումարը հավասար է երկու ուղիղ անկյունների։ [Պնդում 1․29] Անկյուն ABD-ն ուղիղ է, հետևում է անկյուն CDB-ն նույնպես ուղիղ է։

Եվ քանի որ AB-ն հավասար է DE-ին, իսկ BD-ն ընդհանուր է, ապա երկու ուղիղներ՝ AB և BE, հավասար են ED և DA ուղիղներին, համապատասխանաբար։ Եվ ABD ուղիղ անկյունը հավասար է EDB անկյանը։ Հետևաբար AD հիմքը հավասար է BE հիմքին [Պնդում 1․4]։ Եվ քանի որ AB հատվածը հավասար է DE-ին, և BE-ն հավասար է AD հատվածին, և AB, BE հատվածները համապատասխանաբար հավասար են ED, DA հատվածներին։ Եվ նրանց հիմքը՝ AE-ն, ընդհանուր է։ Հետևաբար, անկյունը՝ ABE, հավասար է EDAանկյանը ([Պնդում 1․8])։ Քանի որ անկյուն ABE-ն ուղիղ է, ապա անկյուն EDA-ն նույնպես ուղիղ է։ Հետևաբար, ED ուղիղը ուղղահայաց է AD-ին։ Եվ այն նաև ուղղահայաց է DB-ին։ Այսպիսով, ED ուղիղը ուղիղ անկյուն է կազմում BD և DA ուղիղներով անցնող հարթության հետ ([Պնդում 11․4])։ Այդ պատճառով ED ուղիղ անկյուն կկազմի բոլոր այն ուղիղների հետ, որոնք հատվում են իր հետ և ընկած են BDA հարթության մեջ։ DC ուղիղը գտնվում է BDA հարթությունում, քանի որ AB և BD ուղիղները նույնպես գտնվում են BDA հարթությունում ([Պնդում 11․2])։ Հետևաբար, ED ուղիղը ուղղահայաց է DC ուղիղին։ Այսպիսով, CD ուղիղը նույնպես ուղղահայաց է DE-ին։ CD ուղիղը ուղղահայաց է նաև BD ուղիղին։ Հետևաբար, CD ուղիղը կանգնած է ուղղանկյուն երկու ուղիղների՝ DE և DB-ի հետ, որոնք հատվում են D կետում։ Այսպիսով, CD ուղիղը նաև ուղղահայաց է DE և DB ուղիղներով անցնող հարթությանը ([Պնդում 11․4])։ Եվ քանի որ DE և DB ուղիղներով անցնող հարթությունը դիտարկվող հարթությունն է, CD ուղիղը ուղղահայաց է նաև դիտարկվող հարթությանը։

Հետևաբար, եթե երկու ուղիղներ զուգահեռ են, և դրանցից մեկը ուղղահայաց է որևէ հարթության, ապա մյուսը նույնպես կլինի ուղղահայաց նույն հարթությանը։ Որն էլ անհրաժեշտ էր ցույց տալ։