Տարերք/Գիրք 3

Սահմանումներ

1. Հավասար են համարվում այն շրջանները, որոնց տրամագծերը կամ կենտրոնից շրջանագիծ ընկած հեռավորությունները հավասար են (շառավղերը հավասար են)։

2. Հատվածը համարվում է շրջանագծի շոշափող, եթե այն շրջանագծին հասնելիս և շարունակվելիս՝ չի հատում այն։

3. Իրար շոշափող են համարվում այն շրջանները, որոնք միմյանց հասնելիս՝ մեկը մյուսին չեն հատում։

4. Շրջանագծում հատվածները կենտրոնից նույն հեռավորությունը կունենան, եթե կենտրոնից նրանց տարված ուղղահայացները հավասար լինեն։

5. Շրջանագծում հատվածներից կենտրոնից ավելի հեռու է համարվում այն մեկը, որին կենտրոնից տարված ուղղահայացը ավելի երկար է։

6. Շրջանի սեգմենտը այն պատկերն է, որը պարունակում են հատվածն ու շրջանագիծը։

7. Սեգմենտի անկյունը այն այնկյունն է, որը պարունակում են հատվածն ու շրջանագիծը։

8. Սեգմենտի միջի անկյունը այն այնկյունն է, որը պարունակում են շրջանագծի վրա վերցված կետից տարված երկու հատվածները, որոնք միանում են այն հատվածի գագաթներին որը սեգմենտի հիմքն է։

9. Աղեղի վրա ընկած անկյունը այն անկյունն է, որին կից հատվածները հատում են շրջանագիծը՝ իրենց մեջ առնելով դրա որոշ հատված։

10. Շրջանի սեկտորը այն պատկերն է, որն ընկած է շրջանի կոնտրոնում կառուցված անկյանը կից հատվածների և դրանցով կտրված շրջանագծի ներսում։

11. Շրջանի սեգմենտները համարվում են նման, երբ կա՛մ ընկած են հավասար անկյունների վրա, կա՛մ պարունակում են հավասար անկյուններ։

Պնդում 1

Գտնել տրված շրջանի կենտրոնը։

Դիցուք՝ տրված է ABC շրջանը։ Պահանջվում է գտնել ABC շրջանի կենտրոնը։ ABC շրջանով կառուցենք կամայական AB հատված և հավասար կիսենք այն D կետում [Պնդում 1․9]։ AB-ին ուղղահայաց՝D կետով կառուցենք DC-ն [Պնդում 1․11]։ E կետով էլ կառուցենք CD-ն։ CE-ն հավասար կիսենք F կետով [Պնդում 1․9]։ Ես պնդում էմ, որ F-ը ABC շրջանի կենտրոնն է։ Եթե այդպես չէ, ապա ենթադրենք, որ կենտրոնը G-ն է և կառուցենք GA, GD և GB հատվածները։ Եվ քանի որ AD-ն ու DB-ն հավասար են, DG էլ՝ ընդհանուր, AD և DG, BD և DG համապատասխանաբար հավասար են։ Հավասար են նաև GA և GB հիմքերը, քանի որ երկուսն էլ շառավիղներ են։ Հետևաբար, ADG անկյունը հավասար է GDB անկյանը [Պնդում 1․8]։ Երբ միմյանց ուղղահայաց հատվածները իրար հավասար կից անկյուններ են կազմում, նշանակում է, որ այդ անկյունները ուղիղ անկյուններ են [Սահմանում 1․10]։ Հետևում է, որ GDB-ն և FDB-ն ուղիղ անկյուններ են և հետևաբար, հավասար են միմյանց։ Սակայն անկյուններից մոկը մյուսից մեծ է, ինչը հնարավոր չէ։ Ստացվում է, որ G-ն շրջանի կենտրոնը չէ։ Նույն կերպ կարող ենք ցույց տալ նաև, որ ցանկացաց կետ բացի F-ից, ABC շրջանի կենտրոնը չէ։

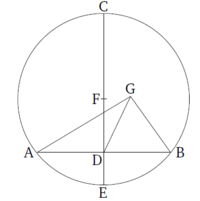
Հետևաբար, F-ը ABC շրջանի կենտրոնն է։

Հետևանք

Եթե շրջանում հատվածը այլ հատվածի ուղիղ անկյան տակ հավասար կիսում է, ապա շրջանի կենտրոնը գտնվում է նախնական հատվածի վրա։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։

Պնդում 2

Շրջանագծի վրա վերցված կամայական կետերը միացնելիս ստացված հատվածը ընկած է շրջանի ներսում։

Դիցուք՝ տրված է ABC շրջանը։ Շրջանագծի վրա ընտրենք կամայական A և B կետեր։ Ես պնդում եմ, որ A և B կետերը միացնող հատվածը ընկած է շրջանի ներսում։ Ենթադրենք, որ դա ճիշտ չէ, և այն ընկած է շրջանից դուրս՝ ինչպես AEB պատկերում։ Գտնենք ABC շրջանի կենտրոնը [Պնդում 3․1], և ենթադրենք, որ այն D-ն է։ Կառուցենք DA-ն, DB-ն և DFE-ն։ Հետևաբար, քանի որ DA-ն ու DB-ն հավասար են, DAE և DBE անկյունները նույնպես հավասար են [Պնդում 1․5]։ Քանի որ կառուցել ենք DAE եռանկյան AEB կողմը, DEB անկյունը DAE-ից մեծ է [Պնդում 1․16]։ DAE-ն էլ հավասար է DEB-ին [Պնդում 1․5]։ Հետևաբար, DEB-ն DBE-ից մեծ է։ Ավելի մեծ անկյունն ընկած է ավելի մեծ կողմի վրա [Պնդում 1․19]։ Ստացվում է, որ DB-ն DE-ից մեծ է։ DB-ն ու DF-ն էլ հավասար են։ Հետևում է, որ DF-ը DE-ից մեծ է, ինչը հնարավոր չէ։ Այսպիսով՝ A և B կետերը միացնող հատվածը չի ընկնի շրջանի մեջ։ Նույն կերպ կարող ենք ցույց տալ նաև, որ այն շրջանագծի վրա նույնպես չի ընկնի։ Հետևաբար, կընկնի շրջանի ներսում։

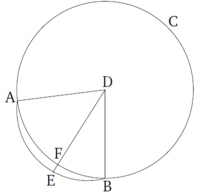
Այսպիսով՝ շրջանագծի վրա վերցված կամայական կետերը միացնելիս ստացված հատվածը ընկած է շրջանի ներսում։ Սա հենց այն էր, ինչ պետք էր ցույց տալ։

Պնդում 3

Եթե շրջանի կենտրոնով անցնող հատվածը հավասար է կիսում է այլ հատվածի, որը կենտրոնով չի անցնում, ապա հատումը տեղի է ունենում ուղիղ անկյան տակ։ Եվ ընդհակառակը, եթե հատումը տեղի է ունենում ուղիղ անկյան տակ, ապա կենտրոնով անցնող հատվածը մյուսիս հավասար կիսում է։ Դիցուք՝ տրված է ABC շրջանը, որում կենտրոնով անցնող CD հատվածը F կետով մեջտեղից կիսում է կենտրոնով չանցնող AB հատվածը։ Ես պնդում եմ, որ CD-ն հատում է AB-ն ուղիղ անկյան տակ։ Գտնենք ABC շրջանի կենտրոնը [Պնդում 3.1], նշանակենք այն E-ով և կառուցեք EA-ն ու EB-ն։ Քանի որ AF-ը հավասար է FB-ին, FE-ն էլ ընդհանուր է, AFE ուղղանկյան 2 կողմերը հավասար են BFE եռանկյան երկու կողմերին։ EA և EB հիմքերը հավասար են։ Հետևաբար, AFE անկյունը հավասար է BFE-ին [Պնդում 1․8]։ Եվ երբ մեկ հատվածի վրա կառուցված այլ հատված ստեղծում է հավասար կիս անկյուններ, նշանակում է, որ այդ անկյուններից յուրաքանչյունը ուղիղ անկյուն է [Պնդում 1․10]։ Ստացվում է, որ AFE և BFE անկյունները ուղիղ են։ Հետևաբար, կենտրոնով անցնող և AB-ն հավասար կիսող CD հատվածը հատում է AB-ն ուղիղ անկյան տակ։

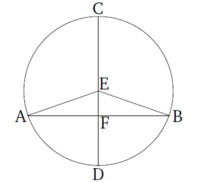
Ստացվենց, որ CD-ն հատում է AB-ն ուղիղ անկյան տակ։ Ես պնդում եմ նաև, որ այն AB-ն մեջտեղից կիսում է։ Նույնն է ասել, որ AF-ն ու FB-ն հավասար են։ Օգտվենք նույն գծագրից։ Քանի որ EA-ն ու EB-ն հավասար են, EAF և EBF անկյունները նույնպես հավասար են [Պնդում 1․5]։ Ուղիղ անկյուն AFE-ն էլ հավասար է BFE ուղիղ անկյանը։ Հետևաբար, EAF-ն ու EFB-ը երկու եռանկյուններ են, որոնց երկու անկյուններն ու մեկ կողմը հավասար են, այդ կողմը EF-ն է, որը ընդհանուր է։ Հետևում է, որ մնացյալ կողմերը նույնպես համապատասխանաբար հավասար կլինեն [Պնդում 1․26]։ Ստացվում է, որ AF-ն ու FB-ն հավասար են։ Այսպիսով՝ եթե շրջանի կենտրոնով անցնող հատվածը հավասար է կիսում է այլ հատվածի, որը կենտրոնով չի անցնում, ապա հատումը տեղի է ունենում ուղիղ անկյան տակ։ Եվ ընդհակառակը, եթե հատումը տեղի է ունենում ուղիղ անկյան տակ, ապա կենտրոնով անցնող հատվածը մյուսիս հավասար կիսում է։ Սա այն էր, ինչ պահանջվում էի ցույց տալ։