Մեխանիկական թեորեմների մեթոդը

հեղինակ՝ Արքիմեդ թարգմանիչ՝ Annna աղբյուր՝ [Geometrical Solutions Derived from Mechanics English translation by Dr. J. L. Heiberg]

Անավարտ Այս ստեղծագործությունը դեռ ամբողջովին տեղադրված չէ Գրապահարանում

== Պնդում XIII ==

Թող քառակուսի αβγδ [նկ. 1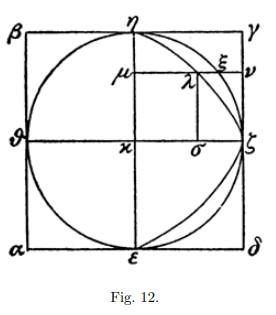2] լինի ուղղահայաց պրիզմայի հիմքը, որն ունի քառակուսի հիմքեր, և թող պրիզմայի մեջ լինի տեղադրված գլան, որի հիմքը ∈ζηθ շրջանագիծն է, որն առնչվում է αβγδ զուգահեռագծի կողմերին՝ ∈, ζ, η և θ կետերում։ Անցկացնելով հարթություն նրա կենտրոնով և քառակուսու հակառակ կողմով (համապատասխանող γδ կողմին), այն կառանձնանա ամբողջ պրիզմայից՝ ձևավորելով երկրորդ պրիզմա, որն ամբողջ պրիզմայի 1/4 մասն է, և որը, սահմանափակվում է երեք զուգահեռագծերով և երկու հակառակ եռանկյուններով։ ∈ζη կիսաշրջանագծի մեջ նկարենք պարաբոլ, որի սկզբնակետը η∈ է, իսկ առանցքը՝ ζκ, իսկ δη զուգահեռագծի մեջ գծենք µνkκζ-ը։ Այն կանցնի կիսաշրջանագծի շրջանագծով ξ կետում, պարաբոլով՝ λ կետում, և µν × νλ = νζ² (քանի որ սա ակնհայտ է [Ապոլոնիոս, Կոն. I, 11]): Հետևաբար µν : νλ = κη² : λσ²։

µν-ի վրա կառուցենք հարթություն, որը զուգահեռ է ∈η-ին։ Այն կկտրվի ամբողջ պրիզմայից կտրած պրիզմայի մեջ ուղիղանկյուն եռանկյունով, որի մի կողմը µν-ն է, իսկ մյուսը՝ γδ հարթության վրա գտնվող ուղիղ գիծը, որն ուղղահայաց է γδ-ին՝ ν կետում և հավասար է գլանի առանցքին։ Հիպոթենուզը կլինի կտրված հարթության մեջ։ Այն կկտրվի գլանից կտրված մասից (մասն, որը կտրել է ∈η հարթությունը և քառակուսու հակառակ կողմը γδ-ի նկատմամբ) ուղիղանկյուն եռանկյունով, որի մի կողմը µξ-ն է, իսկ մյուսը՝ գլանի մակերեսին գտնվող գիծը, որը ուղղահայաց է κν հարթությանը:․․․․․Եվ բոլոր եռանկյուններին պրիզմայում

: բոլոր եռանկյունները գլանի հատվածում = բոլոր ուղիղ գծերին δη զուգահեռագծում : բոլոր ուղիղ գծերը պարաբոլի և ∈η ուղիղի միջև։ Եվ պրիզման կազմված է պրիզմայում գտնվող եռանկյուններից, գլանի հատվածը՝ գլանի հատվածում գտնվող եռանկյուններից, δη զուգահեռագիծը՝ զուգահեռագծում գտնվող ուղիղ գծերից, իսկ պարաբոլի հատվածը՝ պարաբոլի և ուղիղ ∈η-ի միջև կտրված գծերից։ Հետևաբար, պրիզմա : գլանի հատված = δη զուգահեռագիծ : ∈ζη հատված, որը սահմանափակված է պարաբոլով և ուղիղ ∈η-ով։

Բայց զուգահեռագիծ δη = 3/2 պարաբոլի և ուղիղ ∈η-ի միջև գտնվող հատվածին (ինչպես ցույց է տրվել ավելի վաղ հրապարակված աշխատանքում), հետևաբար նաև պրիզման հավասար է գլանի հատվածի մեկուկես անգամին։ Հետևաբար, երբ գլանի հատվածը = 2, պրիզման = 3, և ամբողջ պրիզման, որը պարունակում է գլանը, հավասար է 12, որովհետև այն 4 անգամ մեծ է մյուս պրիզմայից. հետևաբար գլանի հատվածը հավասար է պրիզմայի 1/6-ին, Q. E. D.

== Պնդում XIV ==

[Գծեք գլան] ուղղանկյուն պրիզմայի ներսում, որը ունի քառակուսի հիմքեր [և թող այն հատի հարթությամբ, որը անցնում է գլանի հիմքի կենտրոնով և հակառակ քառակուսու մի կողmով:] Այնուհետև այս հարթությունը կհատի պրիզմայից մեկ հատված և մեկ հատված գլանից։ Կարելի է ապացուցել, որ գլանից կտրված հատվածը կազմում է ամբողջ պրիզմայի մեկ վեցերորդ մասը։ Սակայն նախ մենք կապացուցենք, որ հնարավոր է գլանի հատվածում ներգծել մի մարմին և դուրս գրել մեկ այլ մարմին, որը կազմված է հավասար բարձրության պրիզմաներից, որոնց հիմքերը նման եռանկյունիներ են, այնպես, որ դուրս գրված մարմինը գերազանցի ներգծվածին ցանկացած տրված մեծությունից պակաս չափով։ . . . . . . . . . . . . . . . . . . . . . . . . . . . . Սակայն արդեն ցույց է տրված, որ թեք հարթությամբ կտրված պրիզման < 3/2 գլանի հատվածում ներգծված մարմնի։ Այժմ թեք հարթությամբ կտրված պրիզման : գլանի հատվածում ներգծված մարմինը = զուգահեռագիծ δη: Զուգահեռագծերը, որոնք ներգծված են պարաբոլով և ուղիղ գծով սահմանափակված հատվածում։ Ուստի զուգահեռագիծ δη < 3/2 պարաբոլով և ուղիղ գծով սահմանափակված հատվածի զուգահեռագծերի ուղիղով ∈η։ Բայց սա անհնար է, որովհետև այլուր ցույց է տրված, որ զուգահեռագիծ δη-ն մեկ ու կես անգամ մեծ է պարաբոլով և ուղիղ գծով սահմանափակված հատվածից, հետևաբար . . չի կարող ավելի մեծ լինել ․․․

Բոլոր պրիզմաները թեք հարթությամբ հատված պրիզմայում : բոլոր պրիզմաները գլանի հատվածի շուրջ նկարագրված մարմնում = բոլոր զուգահեռագծերը զուգահեռագծում δη: բոլոր զուգահեռագծերը պարաբոլով և ուղիղ գծով սահմանափակված հատվածի շուրջ նկարագրված մարմնում, այսինքն՝ թեք հարթությամբ կտրված պրիզման : գլանի հատվածի շուրջ նկարագրված մարմինը = զուգահեռագիծ δη: պարաբոլով և ուղիղ գծով սահմանափակված հատվածի մարմինը։ Սակայն թեք հարթությամբ կտրված պրիզման մեկ ու կես անգամ գերազանցում է գլանի հատվածի շուրջ նկարագրված մարմնին . . .

Պնդում XIV

[Ուղղահայաց պրիզմայի մեջ քառակուսի հիմքերով տեղադրեք գլան և կտրեք այն հարթությամբ, որը անցնում է գլանի հիմքի կենտրոնով և հակառակ քառակուսու մեկ կողմով:] Այդ հարթությունը կկտրի պրիզմայից պրիզմայի մի մաս և գլանից գլանի մի մաս։ Կարելի է ապացուցել, որ գլանից հարթությամբ կտրված մասը հավասար է ամբողջ պրիզմայի 1/6-ին։ Բայց նախ մենք կպարզենք, որ հնարավոր է գլանի հատվածի մեջ տեղադրել մարմին և շրջապատել մեկ այլ մարմնով, որոնք կազմված են հավասար բարձրությամբ պրիզմաներից և ունեն նման եռանկյուններ հիմքում այնպես, որ շրջապատող մարմինը գերազանցի ներսում տեղադրվածին ավելի փոքր չափով, քան ցանկացած տրված մեծություն։

... Բայց ցույց է տրվել, որ թեք հարթությամբ կտրված պրիզման < 3/2 գլանի հատվածում ներսում տեղադրված մարմնից։ Իսկ թեք հարթությամբ կտրված պրիզման : գլանի հատվածում ներսում տեղադրված մարմինը = δη զուգահեռագիծ : պարաբոլով և ուղիղ �η-ով սահմանափակված հատված։ Հետևաբար δη զուգահեռագիծը < 3/2 պարաբոլով և ուղիղ �η-ով սահմանափակված հատվածի։

Բայց սա անհնար է, որովհետև այլ տեղ ցույց է տրվել, որ δη զուգահեռագիծը մեկուկես անգամ մեծ է պարաբոլով և ուղիղ �η-ով սահմանափակված հատվածից, հետևաբար...